The Project Gutenberg EBook of Encyclopaedia Britannica, 11th Edition,
Volume 8, Slice 9, by Various
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
Title: Encyclopaedia Britannica, 11th Edition, Volume 8, Slice 9
"Dyer" to "Echidna"
Author: Various
Release Date: January 8, 2011 [EBook #34878]
Language: English
Character set encoding: ISO-8859-1
*** START OF THIS PROJECT GUTENBERG EBOOK ENCYCLOPAEDIA BRITANNICA ***
Produced by Marius Masi, Don Kretz and the Online
Distributed Proofreading Team at http://www.pgdp.net
| Transcriber’s note: |
A few typographical errors have been corrected. They
appear in the text like this, and the
explanation will appear when the mouse pointer is moved over the marked
passage. Sections in Greek will yield a transliteration
when the pointer is moved over them, and words using diacritic characters in the
Latin Extended Additional block, which may not display in some fonts or browsers, will
display an unaccented version. Links to other EB articles: Links to articles residing in other EB volumes will be made available when the respective volumes are introduced online. |
Articles in This Slice
DYER, SIR EDWARD (d. 1607), English courtier and poet, son of Sir Thomas Dyer, Kt., was born at Sharpham Park, Somersetshire. He was educated, according to Anthony à Wood, either at Balliol College or at Broadgates Hall, Oxford. He left the university without taking a degree, and after some time spent abroad appeared at Queen Elizabeth’s court. His first patron was the earl of Leicester, who seems to have thought of putting him forward as a rival to Sir Christopher Hatton in the queen’s favour. He is mentioned by Gabriel Harvey with Sidney as one of the ornaments of the court. Sidney in his will desired that his books should be divided between Fulke Greville (Lord Brooke) and Dyer. He was employed by Elizabeth on a mission (1584) to the Low Countries, and in 1589 was sent to Denmark. In a commission to inquire into manors unjustly alienated from the crown in the west country he did not altogether please the queen, but he received a grant of some forfeited lands in Somerset in 1588. He was knighted and made chancellor of the order of the Garter in 1596. William Oldys says of him that he “would not stoop to fawn,” and some of his verses seem to show that the exigencies of life at court oppressed him. He was buried at St Saviour’s, Southwark, on the 11th of May 1607. Wood says that many esteemed him to be a Rosicrucian, and that he was a firm believer in alchemy. He had a great reputation as a poet among his contemporaries, but very little of his work has survived. Puttenham in the Arte of English Poesie speaks of “Maister Edward Dyar, for Elegie most sweete, solempne, and of high conceit.” One of the poems universally accepted as his is “My Mynde to me a kingdome is.” Among the poems in England’s Helicon (1600), signed S.E.D., and included in Dr A.B. Grosart’s collection of Dyer’s works (Miscellanies of the Fuller Worthies Library, vol. iv., 1876) is the charming pastoral “My Phillis hath the morninge sunne,” but this comes from the Phillis of Thomas Lodge. Grosart also prints a prose tract entitled The Prayse of Nothing (1585). The Sixe Idillia from Theocritus, reckoned by J.P. Collier among Dyer’s works, were dedicated to, not written by, him.
DYER, JOHN (c. 1700-1758), British poet, the son of a solicitor, was born in 1699 or 1700 at Aberglasney, in Carmarthenshire. He was sent to Westminster school and was destined for the law, but on his father’s death he began to study painting. He wandered about South Wales, sketching and occasionally painting portraits. In 1726 his first poem, Grongar Hill, appeared in a miscellany published by Richard Savage, the poet. It was an irregular ode in the so-called Pindaric style, but Dyer entirely rewrote it into a loose measure of four cadences, and printed it separately in 1727. It had an immediate and brilliant success. Grongar Hill, as it now stands, is a short poem of only 150 lines, describing in language of much freshness and picturesque charm the view from a hill overlooking the poet’s native vale of Towy. A visit to Italy bore fruit in The Ruins of Rome (1740), a descriptive piece in about 600 lines of Miltonic blank verse. He was ordained priest in 1741, and held successively the livings of Calthorp in Leicestershire, Belchford (1751), Coningsby (1752), and Kirby-on-Bane (1756), the last three being Lincolnshire parishes. He married, in 1741, a Miss Ensor, said to be descended from the brother of Shakespeare. In 1757 he published his longest work, the didactic blank-verse epic of The Fleece, in four books, discoursing of the tending of sheep, of the shearing and preparation of the wool, of weaving, and of trade in woollen manufactures. The town took no interest in it, and Dodsley facetiously prophesied that “Mr Dyer would be buried in woollen.” He died at Coningsby of consumption, on the 15th of December 1758.
His poems were collected by Dodsley in 1770, and by Mr Edward Thomas in 1903 for the Welsh Library, vol. iv.
DYER, THOMAS HENRY (1804-1888), English historical and antiquarian writer, was born in London on the 4th of May 1804. He was originally intended for a business career, and for some time acted as clerk in a West India house; but finding his services no longer required after the passing of the Negro Emancipation Act, he decided to devote himself to literature. In 1850 he published the Life of Calvin, a conscientious and on the whole impartial work, though the character of Calvin is somewhat harshly drawn, and his influence in the religious world generally is insufficiently appreciated. Dyer’s first historical work was the History of Modern Europe (1861-1864; 3rd ed. revised and continued to the end of the 19th century, by A. Hassall, 1901), a meritorious compilation and storehouse of facts, but not very readable. The History of the City of Rome (1865) down to the end of the middle ages was followed by the History of the Kings of Rome (1868), which, upholding against the German school the general credibility of the account of early Roman history, given in Livy and other classical authors, was violently attacked by J.R. Seeley and the Saturday Review, as showing ignorance of the comparative method. More favourable opinions of the work were expressed by others, but it is generally agreed that the author’s scholarship is defective and that his views are far too conservative. Roma Regalis (1872) and A Plea for Livy (1873) were written in reply to his critics. Dyer frequently visited Greece and Italy, and his topographical works are probably his best; amongst these mention may be made of Pompeii, its History, Buildings and Antiquities (1867, new ed. in Bohn’s Illustrated Library), and Ancient Athens, its History, Topography and Remains (1873). His last publication was On Imitative Art (1882). He died at Bath on the 30th of January 1888.
DYMOKE, the name of an English family holding the office of king’s champion. The functions of the champion were to ride into Westminster Hall at the coronation banquet, and challenge all comers to impugn the king’s title (see Champion). The earliest record of the ceremony at the coronation of an English king dates from the accession of Richard II. On this occasion the champion was Sir John Dymoke (d. 1381), who held the manor of Scrivelsby, Lincolnshire, in right of his wife Margaret, granddaughter of Joan Ludlow, who was the daughter and co-heiress of Philip Marmion, last Baron Marmion. The Marmions claimed descent from the lords of Fontenay, hereditary champions of the dukes of Normandy, and held the castle of Tamworth, Leicestershire, and the manor of Scrivelsby, Lincolnshire. The right to the championship was disputed with the Dymoke family by Sir Baldwin de Freville, lord of Tamworth, who was descended from an elder daughter of Philip Marmion. The court of claims eventually decided in favour of the owners of Scrivelsby on the ground that Scrivelsby was held in grand serjeanty, that is, that its tenure was dependent on rendering a special service, in this case the championship.
Sir Thomas Dymoke (1428?-1471) joined a Lancastrian rising in 1469, and, with his brother-in-law Richard, Lord Willoughby and Welles, was beheaded in 1471 by order of Edward IV. after he had been induced to leave sanctuary on a promise of personal safety. The estates were restored to his son Sir Robert Dymoke (d. 1546), champion at the coronations of Richard III., Henry VII. and Henry VIII., who distinguished himself at the siege of Tournai and became treasurer of the kingdom. His descendants acted as champions at successive coronations. Lewis Dymoke (d. 1820) put in an unsuccessful claim before the House of Lords for the barony of Marmion. His nephew Henry (1801-1865) was champion at the coronation of George IV. He was accompanied on that occasion by the duke of Wellington and Lord Howard of Effingham. Henry Dymoke was created a baronet; he was succeeded by his brother John, rector of Scrivelsby (1804-1873), whose son Henry Lionel died without 756 issue in 1875, when the baronetcy became extinct, the estate passing to a collateral branch of the family. After the coronation of George IV. the ceremony was allowed to lapse, but at the coronation of King Edward VII. H.S. Dymoke bore the standard of England in Westminster Abbey.
DYNAMICS (from Gr. δύναμις, strength), the name of a branch of the science of Mechanics (q.v.). The term was at one time restricted to the treatment of motion as affected by force, being thus opposed to Statics, which investigated equilibrium or conditions of rest. In more recent times the word has been applied comprehensively to the action of force on bodies either at rest or in motion, thus including “dynamics” (now termed kinetics) in the restricted sense and “statics.”
Analytical Dynamics.—The fundamental principles of dynamics, and their application to special problems, are explained in the articles Mechanics and Motion, Laws of, where brief indications are also given of the more general methods of investigating the properties of a dynamical system, independently of the accidents of its particular constitution, which were inaugurated by J.L. Lagrange. These methods, in addition to the unity and breadth which they have introduced into the treatment of pure dynamics, have a peculiar interest in relation to modern physical speculation, which finds itself confronted in various directions with the problem of explaining on dynamical principles the properties of systems whose ultimate mechanism can at present only be vaguely conjectured. In determining the properties of such systems the methods of analytical geometry and of the infinitesimal calculus (or, more generally, of mathematical analysis) are necessarily employed; for this reason the subject has been named Analytical Dynamics. The following article is devoted to an outline of such portions of general dynamical theory as seem to be most important from the physical point of view.
1. General Equations of Impulsive Motion.
The systems contemplated by Lagrange are composed of discrete particles, or of rigid bodies, in finite number, connected (it may be) in various ways by invariable geometrical relations, the fundamental postulate being that the position of every particle of the system at any time can be completely specified by means of the instantaneous values of a finite number of independent variables q1, q2, ... qn, each of which admits of continuous variation over a certain range, so that if x, y, z be the Cartesian co-ordinates of any one particle, we have for example
x = ƒ(q1, q2, ... qn), y = &c., z = &c.,
where the functions ƒ differ (of course) from particle to particle. In modern language, the variables q1, q2, ... qn are generalized co-ordinates serving to specify the configuration of the system; their derivatives with respect to the time are denoted by q˙1, q˙2, ... q˙n, and are called the generalized components of velocity. The continuous sequence of configurations assumed by the system in any actual or imagined motion (subject to the given connexions) is called the path.
For the purposes of a connected outline of the whole subject it is convenient to deviate somewhat from the historical order of development, and to begin with the consideration of Impulsive motion. impulsive motion. Whatever the actual motion of the system at any instant, we may conceive it to be generated instantaneously from rest by the application of proper impulses. On this view we have, if x, y, z be the rectangular co-ordinates of any particle m,
mẋ = X′, mẏ = Y′, mz˙ = Z′,
where X′, Y′, Z′ are the components of the impulse on m. Now let δx, δy, δz be any infinitesimal variations of x, y, z which are consistent with the connexions of the system, and let us form the equation
Σm(ẋδx + ẏδy + z˙δz) = Σ(X′δx + Y′δy + Z′δz),
where the sign Σ indicates (as throughout this article) a summation extending over all the particles of the system. To transform (3) into an equation involving the variations δq1, δq2, ... of the generalized co-ordinates, we have
| ẋ = | ∂x | q˙1 + | ∂x | q˙2 + ..., &c., &c. |
| ∂q1 | ∂q2 |
| δx = | ∂x | δq1 + | ∂x | δq2 + ..., &c., &c. |
| ∂q1 | ∂q2 |
and therefore
Σm(ẋδx + ẏδy + z˙δz) = A11q˙1 + A12q˙2 + ...)δq1 + (A21q˙1 + A22q˙2 + ...)δq2 + ...,
where
| Arr = Σm { ( | ∂x | ) | ² | + ( | ∂y | ) | ² | + ( | ∂z | ) | ² | }, |
| ∂qr | ∂qr | ∂qr |
| Ars = Σm { | ∂x | ∂x | + | ∂y | ∂y | + | ∂z | ∂z | } = Asr. |
| ∂qr | ∂qs | ∂qr | ∂qs | ∂qr | ∂qs |
If we form the expression for the kinetic energy Τ of the system, we find
2Τ = Σm(ẋ² + ẏ² + z˙²) = A11q˙1² + A22q˙2² ... 2A12q˙1q˙2 + ...
The coefficients A11, A22, ... A12, ... are by an obvious analogy called the coefficients of inertia of the system; they are in general functions of the co-ordinates q1, q2,.... The equation (6) may now be written
| Σm(ẋδx + ẏδy + z˙δz) = | ∂Τ | δq1 + | ∂Τ | δq2 + ... |
| ∂q˙1 | ∂q˙2 |
This maybe regarded as the cardinal formula in Lagrange’s method. For the right-hand side of (3) we may write
Σ(X′δx + Y′δy + Z′δz) = Q′1δq1 + Q′2δq2 + ... ,
where
| Q′r = Σ(X′ | ∂x | + Y′ | ∂y | + Z′ | ∂z | ). |
| ∂qr | ∂qr | ∂qr |
The quantities Q1, Q2, ... are called the generalized components of impulse. Comparing (9) and (10), we have, since the variations δq1, δq2,... are independent,
| ∂Τ | = Q′1, | ∂Τ | = Q′2, ... |
| ∂q˙1 | ∂q˙2 |
These are the general equations of impulsive motion.
It is now usual to write
| pr = | ∂Τ | . |
| ∂q˙r |
The quantities p1, p2, ... represent the effects of the several component impulses on the system, and are therefore called the generalized components of momentum. In terms of them we have
Σm(ẋδx + ẏδy + z˙δz) = p1δq1 + p2δq2 + ...
Also, since Τ is a homogeneous quadratic function of the velocities q˙1, q˙2 ...,
2Τ = p1q˙1 + p2q˙2 + ...
This follows independently from (14), assuming the special variations δx = ẋdt, &c., and therefore δq1 = q˙1dt, δq2 = q˙2dt, ...
Again, if the values of the velocities and the momenta Reciprocal theorems. in any other motion of the system through the same configuration be distinguished by accents, we have the identity
p1q˙′1 + p2q˙′2 + ... = p′1q˙1 + p′2q˙2 + ...,
each side being equal to the symmetrical expression
A11q˙1q˙′1 + A22q˙2q˙′2 + ... + A12(q˙1q˙′2 + q˙′1q˙2) + ...
The theorem (16) leads to some important reciprocal relations. Thus, let us suppose that the momenta p1, p2, ... all vanish with the exception of p1, and similarly that the momenta p′1, p′2, ... all vanish except p′2. We have then p1q˙′1 = p′2q˙2, or
q˙2 : p1 = q˙′1 : p′2
The interpretation is simplest when the co-ordinates q1, q2 are both of the same kind, e.g. both lines or both angles. We may then conveniently put p1 = p′2, and assert that the velocity of the first type due to an impulse of the second type is equal to the velocity of the second type due to an equal impulse of the first type. As an example, suppose we have a chain of straight links hinged each to the next, extended in a straight line, and free to move. A blow at right angles to the chain, at any point P, will produce a certain velocity at any other point Q; the theorem asserts that an equal velocity will be produced at P by an equal blow at Q. Again, an impulsive couple acting on any link A will produce a certain angular velocity in any other link B; an equal couple applied to B will produce an equal angular velocity in A. Also if an impulse F applied at P produce an angular velocity ω in a link A, a couple Fa applied to A will produce a linear velocity ωa at P. Historically, we may note that reciprocal relations in dynamics were first recognized by H.L.F. Helmholtz in the domain of acoustics; their use has been greatly extended by Lord Rayleigh.
The equations (13) determine the momenta p1, p2,... as linear functions of the velocities q˙1, q˙2,... Solving these, we can express q˙1, q˙2 ... as linear functions of p1, p2,... The resulting equations give us the velocities produced by any given Velocities in terms of momenta. system of impulses. Further, by substitution in (8), we can express the kinetic energy as a homogeneous quadratic function of the momenta p1, p2,... The kinetic energy, as so expressed, will be denoted by Τ`; thus
2Τ` = A`11p1² + A`22p2² + ... + 2A`12p-p2 + ...
where A`11, A`22,... A`12,... are certain coefficients depending on the configuration. They have been called by Maxwell the coefficients of mobility of the system. When the form (19) is given, the values 757 of the velocities in terms of the momenta can be expressed in a remarkable form due to Sir W.R. Hamilton. The formula (15) may be written
p1q˙1 + p2q˙2 + ... = Τ + Τ`,
where Τ is supposed expressed as in (8), and Τ` as in (19). Hence if, for the moment, we denote by δ a variation affecting the velocities, and therefore the momenta, but not the configuration, we have
p1δq˙1 + q˙1δp + p2δq˙2 + q˙2δp2 + ... = δΤ + δΤ`
| = | ∂Τ | δq˙1 + | ∂Τ | δq˙2 + ... + | ∂Τ` | δp1 + | ∂Τ` | δp2 + ... |
| ∂q˙1 | ∂q˙2 | ∂p1 | ∂p2 |
In virtue of (13) this reduces to
| q˙1δp1 + q˙2δp2 + ... = | ∂Τ` | δp1 + | ∂Τ` | δp2 + ... |
| ∂p1 | ∂p2 |
Since δp1, δp2, ... may be taken to be independent, we infer that
| q˙1 = | ∂Τ` | , q˙2 = | ∂Τ` | , ... |
| ∂p1 | ∂p2 |
In the very remarkable exposition of the matter given by James Clerk Maxwell in his Electricity and Magnetism, the Hamiltonian expressions (23) for the velocities in terms of the impulses are obtained directly from first principles, and the formulae (13) are then deduced by an inversion of the above argument.
An important modification of the above process was introduced by E.J. Routh and Lord Kelvin and P.G. Tait. Instead of expressing the kinetic energy in terms of the velocities alone, or in terms of the momenta alone, we may express it in Routh’s modification. terms of the velocities corresponding to some of the co-ordinates, say q1, q2, ... qm, and of the momenta corresponding to the remaining co-ordinates, which (for the sake of distinction) we may denote by χ, χ′, χ″, .... Thus, Τ being expressed as a homogeneous quadratic function of q˙1, q˙2, ... q˙m, χ˙, χ˙′, χ˙″, ..., the momenta corresponding to the co-ordinates χ, χ′, χ″, ... may be written
| κ = | ∂Τ | , κ′ = | ∂Τ | , κ″ = | ∂Τ | , ... |
| ∂χ˙ | ∂χ˙′ | ∂χ˙″ |
These equations, when written out in full, determine χ˙, χ˙′, χ˙″, ... as linear functions of q˙1, q˙2, ... q˙m, κ, κ′, κ″,... We now consider the function
R = Τ − κχ˙ − κ′χ˙′ − κ″χ˙″ − ... ,
supposed expressed, by means of the above relations in terms of q˙1, q˙2, ... q˙m, κ, κ′, κ″, ... Performing the operation δ on both sides of (25), we have
| ∂R | δq˙1 + ... + | ∂R | δκ + ... = | ∂Τ | δq˙1 + ... + | ∂Τ | δχ˙ + ... − κ∂χ˙ − χ˙δκ − ... , |
| ∂q˙1 | ∂κ | ∂q˙1 | ∂χ˙ |
where, for brevity, only one term of each type has been exhibited. Omitting the terms which cancel in virtue of (24), we have
| ∂R | δq˙1 + ... + | ∂R | δκ + ... = | ∂Τ | δq˙1 + ... − χ˙δκ − ... |
| ∂q˙1 | ∂κ | ∂q˙1 |
Since the variations δq1, δq2, ... δqm, δκ, δκ′, δκ″, ... may be taken to be independent, we have
| p1 = | ∂Τ | = | ∂R | , p2 = | ∂Τ | = | ∂R | , ... |
| ∂q˙1 | ∂q˙1 | ∂q˙2 | ∂q˙2 |
and
| χ˙ = − | ∂R | , χ˙′ = − | ∂R | , χ˙″ = − | ∂R | , ... |
| ∂κ | ∂κ′ | ∂κ″ |
An important property of the present transformation is that, when expressed in terms of the new variables, the kinetic energy is the sum of two homogeneous quadratic functions, thus
Τ = ⅋ + K,
where ⅋ involves the velocities q˙1, q˙2, ... q˙m alone, and K the momenta κ, κ′, κ″, ... alone. For in virtue of (29) we have, from (25),
| Τ = R − (κ | ∂R | + κ′ | ∂R | + κ″ | ∂R | + ... ), |
| ∂κ | ∂κ′ | ∂κ″ |
and it is evident that the terms in R which are bilinear in respect of the two sets of variables q˙1, q˙2, ... q˙m and κ, κ′, κ″, ... will disappear from the right-hand side.
It may be noted that the formula (30) gives immediate proof of two important theorems due to Bertrand and to Lord Kelvin respectively. Let us suppose, in the first place, that the system is started by given impulses of certain types, Maximum and minimum energy. but is otherwise free. J.L.F. Bertrand’s theorem is to the effect that the kinetic energy is greater than if by impulses of the remaining types the system were constrained to take any other course. We may suppose the co-ordinates to be so chosen that the constraint is expressed by the vanishing of the velocities q˙1, q˙2, ... q˙m, whilst the given impulses are κ, κ′, κ″,... Hence the energy in the actual motion is greater than in the constrained motion by the amount ⅋.
Again, suppose that the system is started with prescribed velocity components q˙1, q˙2, ... q˙m, by means of proper impulses of the corresponding types, but is otherwise free, so that in the motion actually generated we have κ = 0, κ′ = 0, κ″ = 0, ... and therefore K = 0. The kinetic energy is therefore less than in any other motion consistent with the prescribed velocity-conditions by the value which K assumes when κ, κ′, κ″, ... represent the impulses due to the constraints.
Simple illustrations of these theorems are afforded by the chain of straight links already employed. Thus if a point of the chain be held fixed, or if one or more of the joints be made rigid, the energy generated by any given impulses is less than if the chain had possessed its former freedom.
2. Continuous Motion of a System.
We may proceed to the continuous motion of a system. The Lagrange’s equations. equations of motion of any particle of the system are of the form
mẍ = X, mÿ = Y, mz¨ = Z
Now let x + δx, y + δy, z + δz be the co-ordinates of m in any arbitrary motion of the system differing infinitely little from the actual motion, and let us form the equation
Σm (ẍδx + ÿδy + z¨δz) = Σ (Xδx + Yδy + Zδz)
Lagrange’s investigation consists in the transformation of (2) into an equation involving the independent variations δq1, δq2, ... δqn.
It is important to notice that the symbols δ and d/dt are commutative, since
| δẋ = | d | (x + δx) − | dx | = | d | δx, &c. |
| dt | dt | dt |
Hence
| Σm(ẍδx + ÿδy + z¨δz) = | d | Σm (ẋδx + ẏδy + z˙δz) − Σm (ẋδẋ + ẏδẏ + z˙δz˙) |
| dt |
| = | d | (p1δq1 + p2δq2 + ...) − δΤ, |
| dt |
by § 1 (14). The last member may be written
| ṗ1δq1 + p1δq˙1 + ṗ2δq2 + p2δq˙2 + ... − | ∂Τ | δq˙1 − | ∂Τ | δq1 − | ∂Τ | δq˙2 − | ∂Τ | δq2 − ... |
| ∂q˙1 | ∂q1 | ∂q˙2 | ∂q2 |
Hence, omitting the terms which cancel in virtue of § 1 (13), we find
| Σm(ẍδx + ÿδy + z¨δz) = (ṗ1 − | ∂Τ | ) δq1 + (ṗ2 − | ∂Τ | ) δq2 + ... |
| ∂q1 | ∂q2 |
For the right-hand side of (2) we have
Σ(Xδx + Yδy + Zδz) = Q1δq1 + Q2δq2 + ... ,
where
| Qr = Σ (X | ∂x | + Y | ∂y | + Z | ∂z | ). |
| ∂qr | ∂qr | ∂qr |
The quantities Q1, Q2, ... are called the generalized components of force acting on the system.
Comparing (6) and (7) we find
| ṗ1 − | ∂Τ | = Q1, ṗ2 − | ∂Τ | = Q2, ... , |
| ∂q˙1 | ∂q˙2 |
or, restoring the values of p1, p2, ...,
| d | ( | ∂Τ | ) − | ∂Τ | = Q1, | d | ( | ∂Τ | ) − | ∂Τ | = Q2, ... |
| dt | ∂q˙1 | ∂q1 | dt | ∂q˙2 | ∂q2 |
These are Lagrange’s general equations of motion. Their number is of course equal to that of the co-ordinates q1, q2, ... to be determined.
Analytically, the above proof is that given by Lagrange, but the terminology employed is of much more recent date, having been first introduced by Lord Kelvin and P.G. Tait; it has greatly promoted the physical application of the subject. Another proof of the equations (10), by direct transformation of co-ordinates, has been given by Hamilton and independently by other writers (see Mechanics), but the variational method of Lagrange is that which stands in closest relation to the subsequent developments of the subject. The chapter of Maxwell, already referred to, is a most instructive commentary on the subject from the physical point of view, although the proof there attempted of the equations (10) is fallacious.
In a “conservative system” the work which would have to be done by extraneous forces to bring the system from rest in some standard configuration to rest in the configuration (q1, q2, ... qn) is independent of the path, and may therefore be regarded as a definite function of q1, q2, ... qn. Denoting this function (the potential energy) by V, we have, if there be no extraneous force on the system,
Σ (Xδx + Yδy + Zδz) = − δV,
and therefore
| Q1 = − | ∂V | , Q2 = − | ∂V | , .... |
| ∂q1 | ∂q2 |
Hence the typical Lagrange’s equation may be now written in the form
| d | ( | ∂Τ | ) − | ∂Τ | = − | ∂V | , |
| dt | ∂q˙r | ∂qr | ∂qr |
or, again,
| ṗr = − | ∂ | (V − Τ). |
| ∂qr |
It has been proposed by Helmholtz to give the name kinetic potential to the combination V − Τ.
As shown under Mechanics, § 22, we derive from (10)
| dΤ | = Q1q˙1 + Q2q˙2 + ... , |
| dt |
and therefore in the case of a conservative system free from extraneous force,
| d | (Τ + V) = 0 or Τ + V = const., |
| dt |
which is the equation of energy. For examples of the application of the formula (13) see Mechanics, § 22.
3. Constrained Systems.
It has so far been assumed that the geometrical relations, if any, which exist between the various parts of the system Case of varying relations. are of the type § 1 (1), and so do not contain t explicitly. The extension of Lagrange’s equations to the case of “varying relations” of the type
x = ƒ(t, q1, q2, ... qn), y = &c., z = &c.,
was made by J.M.L. Vieille. We now have
| ẋ = | ∂x | + | ∂x | q˙1 + | ∂x | q˙2 + ..., &c., &c., |
| ∂t | ∂q1 | ∂q2 |
| ∂x = | ∂x | δq1 + | ∂x | δq2 + ..., &c., &c., |
| ∂q1 | ∂q2 |
so that the expression § 1 (8) for the kinetic energy is to be replaced by
2Τ = α0 + 2α1q˙1 + 2α2q˙2 + ... + A11q˙1² + A22q˙2² + ... + A12q˙1q˙2 + ...,
where
| α0 = Σm { ( | ∂x | ) | ² | + ( | ∂y | ) | ² | + ( | ∂z | ) | ² | }, |
| ∂t | ∂t | ∂t |
| αr = Σm { | ∂x | ∂x | + | ∂y | ∂y | + | ∂z | ∂z | }, | |||
| ∂t | ∂qr | ∂t | ∂qr | ∂t | ∂qr |
and the forms of Arr, Ars are as given by § 1 (7). It is to be remembered that the coefficients α0, α1, α2, ... A11, A22, ... A12 ... will in general involve t explicitly as well as implicitly through the co-ordinates q1, q2,.... Again, we find
Σm (ẋδx + ẏδy + z˙δz) = (α1 + A11q˙1 + A12q˙2 + ...) δq1 + (α2 + A21q˙1 + A22q˙2 + ...) ∂q2 + ...
| = | ∂Τ | δq1 + | ∂Τ | δq2 + ... = p1δq1 + p2δq2 + ..., |
| ∂q˙1 | ∂q˙2 |
where pr is defined as in § 1 (13). The derivation of Lagrange’s equations then follows exactly as before. It is to be noted that the equation § 2 (15) does not as a rule now hold. The proof involved the assumption that Τ is a homogeneous quadratic function of the velocities q˙1, q˙2....
It has been pointed out by R.B. Hayward that Vieille’s case can be brought under Lagrange’s by introducing a new co-ordinate (χ) in place of t, so far as it appears explicitly in the relations (1). We have then
2Τ = α0χ˙² + 2(α1q˙1 + α2q˙2 + ...) χ˙ + A11q˙1² + A22q˙2² + ... + 2A12q˙1q˙2 + ....
The equations of motion will be as in § 2 (10), with the additional equation
| d | ∂Τ | − | ∂Τ | = X, | |
| dt | ∂χ˙ | ∂χ |
where X is the force corresponding to the co-ordinate χ. We may suppose X to be adjusted so as to make χ¨ = 0, and in the remaining equations nothing is altered if we write t for χ before, instead of after, the differentiations. The reason why the equation § 2 (15) no longer holds is that we should require to add a term Xχ˙ on the right-hand side; this represents the rate at which work is being done by the constraining forces required to keep χ˙ constant.
As an example, let x, y, z be the co-ordinates of a particle relative to axes fixed in a solid which is free to rotate about the axis of z. If φ be the angular co-ordinate of the solid, we find without difficulty
2Τ = m (ẋ² + ẏ² +z˙²) + 2φ˙m (xẏ − yẋ) + {I + m (x² + y²)} φ˙²,
where I is the moment of inertia of the solid. The equations of motion, viz.
| d | ∂Τ | − | ∂Τ | = X, | d | ∂Τ | − | ∂Τ | = Y, | d | ∂Τ | − | ∂Τ | = Z, | |||
| dt | ∂ẋ | ∂x | dt | ∂ẏ | ∂y | dt | ∂z˙ | ∂z |
and
| d | ∂Τ | − | ∂Τ | = Φ, | |
| dt | ∂φ˙ | ∂φ |
become
m (ẍ − 2φ˙ẏ − xφ˙² − yφ¨) = X, m (ÿ + 2φ˙ẋ − yφ˙² + xφ¨) = Y, mz¨ = Z,
and
| d | [{I + m (x² + y²)} φ˙ + m (xẏ − yẋ)] = Φ. |
| dt |
If we suppose Φ adjusted so as to maintain φ¨ = 0, or (again) if we suppose the moment of inertia I to be infinitely great, we obtain the familiar equations of motion relative to moving axes, viz.
m (ẍ − 2ωẏ − ω²x) = X, m (ÿ + 2ωẋ − ω²y) = Y, mz¨ = Z,
where ω has been written for φ. These are the equations which we should have obtained by applying Lagrange’s rule at once to the formula
2Τ = m (ẋ² + ẏ² + z˙²) + 2mω (xẏ − yẋ) + mω² (x² + y²),
which gives the kinetic energy of the particle referred to axes rotating with the constant angular velocity ω. (See Mechanics, § 13.)
More generally, let us suppose that we have a certain group of co-ordinates χ, χ′, χ″, ... whose absolute values do not affect the expression for the kinetic energy, and that by suitable forces of the corresponding types the velocity-components χ˙, χ˙′, χ˙″, ... are maintained constant. The remaining co-ordinates being denoted by q1, q2, ... qn, we may write
2T = ⅋ + T0 + 2(α1q˙1 + α2q˙2 + ...) χ˙ + 2(α′1q˙1 + α′2q˙2 + ...) χ˙′ + ...,
where ⅋ is a homogeneous quadratic function of the velocities q˙1, q˙2, ... q˙n of the type § 1 (8), whilst Τ0 is a homogeneous quadratic function of the velocities χ˙, χ˙′, χ˙″, ... alone. The remaining terms, which are bilinear in respect of the two sets of velocities, are indicated more fully. The formulae (10) of § 2 give n equations of the type
| d | ( | ∂⅋ | ) − | ∂⅋ | + (r, 1) q˙1 + (r, 2) q˙2 + ... − | ∂T0 | = Qr |
| dt | ∂qr | ∂qr | ∂qr |
where
| (r, s) = ( | ∂αr | − | ∂αs | )χ˙ + ( | ∂α′r | − | ∂α′s | )χ˙′ + .... |
| ∂qs | ∂qr | ∂qs | ∂qr |
These quantities (r, s) are subject to the relations
(r, s) = −(s, r), (r, r) = 0
The remaining dynamical equations, equal in number to the co-ordinates χ, χ′, χ″, ..., yield expressions for the forces which must be applied in order to maintain the velocities χ˙, χ˙′, χ˙″, ... constant; they need not be written down. If we follow the method by which the equation of energy was established in § 2, the equations (17) lead, on taking account of the relations (19), to
| d | (⅋ − T0) = Q1q˙1 + Q2q˙2 + ... + Qnq˙n, |
| dt |
or, in case the forces Qr depend only on the co-ordinates q1, q2, ... qn and are conservative,
⅋ + V − T0 = const.
The conditions that the equations (17) should be satisfied by zero values of the velocities q˙1, q˙2, ... q˙n are
| Qr = − | ∂T0 | , |
| ∂qr |
or in the case of conservative forces
| ∂ | (V − T0) = 0, |
| ∂qr |
i.e. the value of V − Τ0 must be stationary.
We may apply this to the case of a system whose configuration relative to axes rotating with constant angular velocity (ω) is defined by means of the n co-ordinates q1, q2, ... qn. Rotating axes. This is important on account of its bearing on the kinetic theory of the tides. Since the Cartesian co-ordinates x, y, z of any particle m of the system relative to the moving axes are functions of q1, q2, ... qn, of the form § 1 (1), we have, by (15)
2⅋ = Σm (ẋ² + ẏ² + z˙²), 2Τ0 = ω²Σm (x² + y²),
| αr = Σm (x | ∂y | − y | ∂x | ), |
| ∂qr | ∂qr |
whence
| (r, s) = 2ω·Σm | ∂(x, y) | . |
| ∂(qs, qr) |
The conditions of relative equilibrium are given by (23).
It will be noticed that this expression V − T0, which is to be stationary, differs from the true potential energy by a term which represents the potential energy of the system in relation to fictitious “centrifugal forces.” The question of stability of relative equilibrium will be noticed later (§ 6).
It should be observed that the remarkable formula (20) may in the present case be obtained directly as follows. From (15) and (14) we find
| dT | = | d | (⅋ + T0) + ω·Σm (xÿ − yẍ) = | d | (⅋ − T0) + ω·Σ (xY − yX). |
| dt | dt | dt |
This must be equal to the rate at which the forces acting on the system do work, viz. to
ωΣ (xY − yX) + Q1q˙1 + Q2q˙2 + ... + Qnq˙n,
where the first term represents the work done in virtue of the rotation.
We have still to notice the modifications which Lagrange’s equations undergo when the co-ordinates q1, q2, ... qn Constrained systems. are not all independently variable. In the first place, we may suppose them connected by a number m (< n) of relations of the type
A (t, q1, q2, ... qn) = 0, B (t, q1, q2, ... qn) = 0, &c.
These may be interpreted as introducing partial constraints into a previously free system. The variations δq1, δq2, ... δqn in the expressions (6) and (7) of § 2 which are to be equated are no longer independent, but are subject to the relations
| ∂A | δq1 + | ∂A | δq2 + ... = 0, | ∂B | δq1 + | ∂B | δq2 + ... = 0, &c. |
| ∂q1 | ∂q2 | ∂q1 | ∂q2 |
Introducing indeterminate multipliers λ, μ, ..., one for each of these equations, we obtain in the usual manner n equations of the type
| d | ∂T | − | ∂T | = Qr + λ | ∂A | + μ | ∂B | + ..., | |
| dt | ∂q˙r | ∂qr | ∂qr | ∂qr |
in place of § 2 (10). These equations, together with (28), serve to determine the n co-ordinates q1, q2, ... qn and the m multipliers λ, μ, ....
When t does not occur explicitly in the relations (28) the system is said to be holonomic. The term connotes the existence of integral (as opposed to differential) relations between the co-ordinates, independent of the time.
Again, it may happen that although there are no prescribed relations between the co-ordinates q1, q2, ... qn, yet from the circumstances of the problem certain geometrical conditions are imposed on their variations, thus
A1δq1 + A2δq2 + ... = 0, B1δq1 + B2δq2 + ... = 0, &c.,
where the coefficients are functions of q1, q2, ... qn and (possibly) of t. It is assumed that these equations are not integrable as regards the variables q1, q2, ... qn; otherwise, we fall back on the previous conditions. Cases of the present type arise, for instance, in ordinary dynamics when we have a solid rolling on a (fixed or moving) surface. The six co-ordinates which serve to specify the position of the solid at any instant are not subject to any necessary relation, but the conditions to be satisfied at the point of contact impose three conditions of the form (31). The general equations of motion are obtained, as before, by the method of indeterminate multipliers, thus
| d | ∂T | − | ∂T | = Qr + λAr + μBr + ... | |
| dt | ∂q˙r | ∂qr |
The co-ordinates q1, q2, ... qn, and the indeterminate multipliers λ, μ, ..., are determined by these equations and by the velocity-conditions corresponding to (31). When t does not appear explicitly in the coefficients, these velocity-conditions take the forms
A1q˙1 + A2q˙2 + ... = 0, B1q˙1 + B2q˙2 + ... = 0, &c.
Systems of this kind, where the relations (31) are not integrable, are called non-holonomic.
4. Hamiltonian Equations of Motion.
In the Hamiltonian form of the equations of motion of a conservative system with unvarying relations, the kinetic energy is supposed expressed in terms of the momenta p1, p2, ... and the co-ordinates q1, q2, ..., as in § 1 (19). Since the symbol δ now denotes a variation extending to the co-ordinates as well as to the momenta, we must add to the last member of § 1 (21) terms of the types
| ∂T | δq1 + | ∂T` | δq2 + .... |
| ∂q1 | ∂q2 |
Since the variations δp1, δp2, ... δq1, δq2, ... may be taken to be independent, we infer the equations § 1 (23) as before, together with
| ∂T | = − | ∂T` | , | ∂T | = − | ∂T` | , ..., |
| ∂q1 | ∂q1 | ∂q2 | ∂q2 |
Hence the Lagrangian equations § 2 (14) transform into
| ṗ1 = − | ∂ | (T` + V), ṗ2 = − | ∂ | (T` + V), ... |
| ∂q1 | ∂q2 |
If we write
H = T` + V,
so that H denotes the total energy of the system, supposed expressed in terms of the new variables, we get
| ṗ1 = − | ∂H | , ṗ2 = − | ∂H | , ... |
| ∂q1 | ∂q2 |
If to these we join the equations
| q˙1 = | ∂H | , q˙2 = | ∂H | , ..., |
| ∂p1 | ∂p2 |
which follow at once from § 1 (23), since V does not involve p1, p2, ..., we obtain a complete system of differential equations of the first order for the determination of the motion.
The equation of energy is verified immediately by (5) and (6), since these make
| dH | = | ∂H | ṗ1 + | ∂H | ṗ2 + ... + | ∂H | q˙1 + | ∂H | q˙2 + ... = 0. |
| dt | ∂p1 | ∂p2 | ∂q1 | ∂q2 |
The Hamiltonian transformation is extended to the case of varying relations as follows. Instead of (4) we write
H = p1q˙1 + p2q˙2 + ... − T + V,
and imagine H to be expressed in terms of the momenta p1, p2, ..., the co-ordinates q1, q2, ..., and the time. The internal forces of the system are assumed to be conservative, with the potential energy V. Performing the variation δ on both sides, we find
| δH = q˙1δp1 + ... − | ∂T | δq1 + | ∂V | δq + ..., |
| ∂q1 | ∂q1 |
terms which cancel in virtue of the definition of p1, p2, ... being omitted. Since δp1, δp2, ..., δq1, δq2, ... may be taken to be independent, we infer
| q˙1 = | ∂H | , q˙2 = | ∂H | , ..., |
| ∂p1 | ∂p2 |
and
| ∂ | (T − V) = − | ∂H | , | ∂ | (T − V) = − | ∂H | , .... |
| ∂q1 | ∂q1 | ∂q2 | ∂q2 |
It follows from (11) that
| ṗ1 = − | ∂H | , ṗ2 = − | ∂H | , .... |
| ∂q1 | ∂q2 |
The equations (10) and (12) have the same form as above, but H is no longer equal to the energy of the system.
5. Cyclic Systems.
A cyclic or gyrostatic system is characterized by the following properties. In the first place, the kinetic energy is not affected if we alter the absolute values of certain of the co-ordinates, which we will denote by χ, χ′, χ″, ..., provided the remaining co-ordinates q1, q2, ... qm and the velocities, including of course the velocities χ˙, χ˙′, χ˙″, ..., are unaltered. Secondly, there are no forces acting on the system of the types χ, χ′, χ″, .... This case arises, for example, when the system includes gyrostats which are free to rotate about their axes, the co-ordinates χ, χ′, χ″, ... then being the angular co-ordinates of the gyrostats relatively to their frames. Again, in theoretical hydrodynamics we have the problem of moving solids in a frictionless liquid; the ignored co-ordinates χ, χ′, χ″, ... then refer to the fluid, and are infinite in number. The same question presents itself in various physical speculations where certain phenomena are ascribed to the existence of latent motions in the ultimate constituents of matter. The general theory of such systems has been treated by E.J. Routh, Lord Kelvin, and H.L.F. Helmholtz.
If we suppose the kinetic energy Τ to be expressed, as in Lagrange’s method, in terms of the co-ordinates and Routh’s equations. the velocities, the equations of motion corresponding to χ, χ′, χ″, ... reduce, in virtue of the above hypotheses, to the forms
| d | ∂Τ | = 0, | d | ∂Τ | = 0, | d | ∂Τ | = 0, ..., | |||
| dt | ∂χ˙ | dt | ∂χ˙′ | dt | ∂χ˙″ |
whence
| ∂Τ | = κ, | ∂Τ | = κ′, | ∂Τ | = κ″, ..., |
| ∂χ˙ | ∂χ˙′ | ∂χ˙″ |
where κ, κ′, κ″, ... are the constant momenta corresponding to the cyclic co-ordinates χ, χ′, χ″, .... These equations are linear in χ˙, χ˙′, χ˙″, ...; solving them with respect to these quantities and substituting in the remaining Lagrangian equations, we obtain m differential equations to determine the remaining co-ordinates q1, q2, ... qm. The object of the present investigation is to ascertain the general form of the resulting equations. The retained co-ordinates q1, q2, ... qm may be called (for distinction) the palpable co-ordinates of the system; in many practical questions they are the only co-ordinates directly in evidence.
If, as in § 1 (25), we write
R = T − κχ˙ − κ′χ˙′ − κ″χ˙″ − ...,
and imagine R to be expressed by means of (2) as a quadratic function of q˙1, q˙2, ... q˙m, κ, κ′, κ″, ... with coefficients which are in general functions of the co-ordinates q1, q2, ... qm, then, performing the operation δ on both sides, we find
| ∂R | δq˙1 + ... + | ∂R | δκ + ... + | ∂R | δq1 + ... = | ∂T | δq˙1 + ... + | ∂T | δq1 + ... |
| ∂q˙1 | ∂κ | ∂q1 | ∂q˙1 | ∂q1 |
| + | ∂T | δχ˙ + ... + | ∂T | δq1 + ... − κδχ˙ − χ˙δκ − .... |
| ∂χ˙ | ∂χ1 |
Omitting the terms which cancel by (2), we find
| ∂T | = | ∂R | , | ∂T | = | ∂R | , ..., |
| ∂q˙1 | ∂q˙1 | ∂q˙2 | ∂q˙2 |
| ∂T | = | ∂R | , | ∂T | = | ∂R | , ..., |
| ∂q1 | ∂q1 | ∂q2 | ∂q2 |
| χ˙ = − | ∂R | , χ˙′ = − | ∂R | , χ˙″ = − | ∂R | , ... |
| ∂κ | ∂κ′ | ∂κ″ |
Substituting in § 2 (10), we have
| d | ∂R | − | ∂R | = Q1, | d | ∂R | − | ∂R | = Q2, ... | ||
| dt | ∂q˙1 | ∂q1 | dt | ∂q˙2 | ∂q2 |
These are Routh’s forms of the modified Lagrangian equations. Equivalent forms were obtained independently by Helmholtz at a later date.
The function R is made up of three parts, thus
R = R2, 0 + R1, 1 + R0, 2, ...
where R2, 0 is a homogeneous quadratic function of q˙1, q˙2, ... q˙m, R0, 2 is Kelvin’s equations. a homogeneous quadratic function of κ, κ′, κ″, ..., whilst R1, 1 consists of products of the velocities q˙1, q˙2, ... q˙m into the momenta κ, κ′, κ″.... Hence from (3) and (7) we have
| T = R − (κ | ∂R | + κ′ | ∂R | + κ″ | ∂R | + ...) = R2, 0 − R0, 2. |
| ∂κ | ∂κ′ | ∂κ″ |
If, as in § 1 (30), we write this in the form
Τ = ⅋ + K,
then (3) may be written
R = ⅋ − K + β1q˙1 + β2q˙2 + ...,
where β1, β2, ... are linear functions of κ, κ′, κ″, ..., say
βr = αrκ + α′rκ′ + α″rκ″ + ...,
the coefficients αr, α′r, α″r, ... being in general functions of the co-ordinates q1, q2, ... qm. Evidently βr denotes that part of the momentum-component ∂R / ∂q˙r which is due to the cyclic motions. Now
| d | ∂R | = | d | ( | ∂⅋ | + βr) = | d | ∂⅋ | + | ∂βr | q˙1 + | ∂βr | q˙2+ ..., | ||
| dt | ∂q˙r | dt | ∂q˙r | dt | ∂q˙r | ∂q1 | ∂q2 |
| ∂R | = | ∂⅋ | − | ∂K | + | ∂β1 | q˙1 + | ∂β2 | q˙2 + .... |
| ∂qr | ∂qr | ∂qr | ∂qr | ∂qr |
Hence, substituting in (8), we obtain the typical equation of motion of a gyrostatic system in the form
| d | ∂⅋ | − | ∂⅋ | + (r, 1) q˙1 + (r, 2) q˙2 + ... + (r, s) q˙s + ... + | ∂K | = Qr, | |
| dt | ∂q˙r | ∂qr | ∂qr |
where
| (r, s) = | ∂βr | − | ∂βs | . |
| ∂qs | ∂qr |
This form is due to Lord Kelvin. When q1, q2, ... qm have been determined, as functions of the time, the velocities corresponding to the cyclic co-ordinates can be found, if required, from the relations (7), which may be written
| χ˙ = | ∂K | − α1q˙1 − α2q˙2 − ..., |
| ∂κ |
| χ˙′ = | ∂K | − α′1q˙1 − α′2q˙2 − ..., |
| ∂κ′ |
&c., &c.
It is to be particularly noticed that
(r, r) = 0, (r, s) = −(s, r).
Hence, if in (16) we put r = 1, 2, 3, ... m, and multiply by q˙1, q˙2, ... q˙m respectively, and add, we find
| d | (⅋ + K) = Q1q˙1 + Q2q˙2 + ..., |
| dt |
or, in the case of a conservative system
⅋ + V + K = const.,
which is the equation of energy.
The equation (16) includes § 3 (17) as a particular case, the eliminated co-ordinate being the angular co-ordinate of a rotating solid having an infinite moment of inertia.
In the particular case where the cyclic momenta κ, κ′, κ″, ... are all zero, (16) reduces to
| d | ∂⅋ | − | ∂⅋ | = Qr. | |
| dt | ∂q˙r | ∂qr |
The form is the same as in § 2, and the system now behaves, as regards the co-ordinates q1, q2, ... qm, exactly like the acyclic type there contemplated. These co-ordinates do not, however, now fix the position of every particle of the system. For example, if by suitable forces the system be brought back to its initial configuration (so far as this is defined by q1, q2, ..., qm), after performing any evolutions, the ignored co-ordinates χ, χ′, χ″, ... will not in general return to their original values.
If in Lagrange’s equations § 2 (10) we reverse the sign of the time-element dt, the equations are unaltered. The motion is therefore reversible; that is to say, if as the system is passing through any configuration its velocities q˙1, q˙2, ..., q˙m be all reversed, it will (if the forces be the same in the same configuration) retrace its former path. But it is important to observe that the statement does not in general hold of a gyrostatic system; the terms of (16), which are linear in q˙1, q˙2, ..., q˙m, change sign with dt, whilst the others do not. Hence the motion of a gyrostatic system is not reversible, unless indeed we reverse the cyclic motions as well as the velocities q˙1, q˙2, ..., q˙m. For instance, the precessional motion of a top cannot be reversed unless we reverse the spin.
The conditions of equilibrium of a system with latent cyclic motions Kineto-statics. are obtained by putting q˙1 = 0, q˙2 = 0, ... q˙m = 0 in (16); viz. they are
| Q1 = | ∂K | , Q2 = | ∂K | , ... |
| ∂q1 | ∂q2 |
These may of course be obtained independently. Thus if the system be guided from (apparent) rest in the configuration (q1, q2, ... qm) to rest in the configuration q1 + δq1, q2 + δq2, ..., qm + δqm, the work done by the forces must be equal to the increment of the kinetic energy. Hence
Q1δq1 + Q2δq2 + ... = δK,
which is equivalent to (23). The conditions are the same as for the equilibrium of a system without latent motion, but endowed with potential energy K. This is important from a physical point of view, as showing how energy which is apparently potential may in its ultimate essence be kinetic.
By means of the formulae (18), which now reduce to
| χ˙ = | ∂K | , χ˙′ = | ∂K | , χ˙″ = | ∂K | , ..., |
| ∂κ | ∂κ′ | ∂κ″ |
K may also be expressed as a homogeneous quadratic function of the cyclic velocities χ˙, χ˙′, χ˙″,... Denoting it in this form by Τ0, we have
δ (T0 + K) = 2δK = δ (κχ˙ + κ′χ˙′ + κ″χ˙″ + ...)
Performing the variations, and omitting the terms which cancel by (2) and (25), we find
| ∂Τ0 | = − | ∂K | , | ∂Τ0 | = − | ∂K | , ..., |
| ∂q1 | ∂q1 | ∂q2 | ∂q2 |
so that the formulae (23) become
| Q1 = − | ∂Τ0 | , Q2 = − | ∂Τ0 | , ... |
| ∂q1 | ∂q2 |
A simple example is furnished by the top (Mechanics, § 22). The cyclic co-ordinates being ψ, φ, we find
| 2⅋ = Aθ˙², 2K = | (μ − ν cos θ)² | + | ν² | , |
| A sin² θ | C |
2Τ0 = A sin² θψ˙² + C (φ˙ + ψ cos θ)²,
whence we may verify that ∂Τ0 / ∂θ = −∂K / ∂θ in accordance with (27). And the condition of equilibrium
| ∂K | = − | ∂V |
| ∂θ | ∂θ |
gives the condition of steady precession.
6. Stability of Steady Motion.
The small oscillations of a conservative system about a configuration of equilibrium, and the criterion of stability, are discussed in Mechanics, § 23. The question of the stability of given types of motion is more difficult, owing to the want of a sufficiently general, and at the same time precise, definition of what we mean by “stability.” A number of definitions which have been propounded by different writers are examined by F. Klein and A. Sommerfeld in their work Über die Theorie des Kreisels (1897-1903). Rejecting previous definitions, they base their criterion of stability on the character of the changes produced in the path of the system by small arbitrary disturbing impulses. If the undisturbed path be the limiting form of the disturbed path when the impulses are indefinitely diminished, it is said to be stable, but not otherwise. For instance, the vertical fall of a particle under gravity is reckoned as stable, although for a given impulsive disturbance, however small, the deviation of the particle’s position at any time t from the position which it would have occupied in the original motion increases indefinitely with t. Even this criterion, as the writers quoted themselves recognize, is not free from ambiguity unless the phrase “limiting form,” as applied to a path, be strictly defined. It appears, moreover, that a definition which is analytically precise may not in all cases be easy to reconcile with geometrical prepossessions. Thus a particle moving in a circle about a centre of force varying inversely as the cube of the distance will if slightly disturbed either fall into the centre, or recede to infinity, after describing in either case a spiral with an infinite number of 761 convolutions. Each of these spirals has, analytically, the circle as its limiting form, although the motion in the circle is most naturally described as unstable.
A special form of the problem, of great interest, presents itself in the steady motion of a gyrostatic system, when the non-eliminated co-ordinates q1, q2, ... qm all vanish (see § 5). This has been discussed by Routh, Lord Kelvin and Tait, and Poincaré. These writers treat the question, by an extension of Lagrange’s method, as a problem of small oscillations. Whether we adopt the notion of stability which this implies, or take up the position of Klein and Sommerfeld, there is no difficulty in showing that stability is ensured if V + K be a minimum as regards variations of q1, q2, ... qm. The proof is the same as that of Dirichlet for the case of statical stability.
We can illustrate this condition from the case of the top, where, in our previous notation,
| V + K = Mgh cos θ + | (μ − νcos θ)² | + | ν² | . |
| 2A sin² θ | 2C |
To examine whether the steady motion with the centre of gravity vertically above the pivot is stable, we must put μ = ν. We then find without difficulty that V + K is a minimum provided ν² ≥ 4AMgh. The method of small oscillations gave us the condition ν² > 4AMgh, and indicated instability in the cases ν² ≤ 4AMgh. The present criterion can also be applied to show that the steady precessional motions in which the axis has a constant inclination to the vertical are stable.
The question remains, as before, whether it is essential for stability that V + K should be a minimum. It appears that from the point of view of the theory of small oscillations it is not essential, and that there may even be stability when V + K is a maximum. The precise conditions, which are of a somewhat elaborate character, have been formulated by Routh. An important distinction has, however, been established by Thomson and Tait, and by Poincaré, between what we may call ordinary or temporary stability (which is stability in the above sense) and permanent or secular stability, which means stability when regard is had to possible dissipative forces called into play whenever the co-ordinates q1, q2, ... qm vary. Since the total energy of the system at any instant is given (in the notation of § 5) by an expression of the form ⅋ + V + K, where ⅋ cannot be negative, the argument of Thomson and Tait, given under Mechanics, § 23, for the statical question, shows that it is a necessary as well as a sufficient condition for secular stability that V + K should be a minimum. When a system is “ordinarily” stable, but “secularly” unstable, the operation of the frictional forces is to induce a gradual increase in the amplitude of the free vibrations which are called into play by accidental disturbances.
There is a similar theory in relation to the constrained systems considered in § 3 above. The equation (21) there given leads to the conclusion that for secular stability of any type of motion in which the velocities q˙1, q˙2, ... q˙n are zero it is necessary and sufficient that the function V − Τ0 should be a minimum.
The simplest possible example of this is the case of a particle at the lowest point of a smooth spherical bowl which rotates with constant angular velocity (ω) about the vertical diameter. This position obviously possesses “ordinary” stability. If a be the radius of the bowl, and θ denote angular distance from the lowest point, we have
V − Τ0 = mga(1 − cos θ) − ½mω²a² sin² θ;
this is a minimum for θ = 0 only so long as ω² < g/a. For greater values of ω the only position of “permanent” stability is that in which the particle rotates with the bowl at an angular distance cos−1 (g/ω²a) from the lowest point. To examine the motion in the neighbourhood of the lowest point, when frictional forces are taken into account, we may take fixed ones, in a horizontal plane, through the lowest point. Assuming that the friction varies as the relative velocity, we have
ẍ = −p²x − k (ẋ + ωy),
ÿ = −p²y − k (ẏ − ωx),
where p² = g/a. These combine into
z¨ + kz˙ + (p² − ikω) z = 0,
where z = x + iy, i = √−1. Assuming z = Ceλt, we find
λ = −½k(1 ∓ ω/p) ± ip,
if the square of k be neglected. The complete solution is then
x + iy = C1e−β1t eipt + + C2e−β2t e−ipt,
where
β1 = ½k (1 − ω/p), β2 = ½k (1 + ω/p).
This represents two superposed circular vibrations, in opposite directions, of period 2π/p. If ω < p, the amplitude of each of these diminishes asymptotically to zero, and the position x = 0, y = 0 is permanently stable. But if ω > p the amplitude of that circular vibration which agrees in sense with the rotation ω will continually increase, and the particle will work its way in an ever-widening spiral path towards the eccentric position of secular stability. If the bowl be not spherical but ellipsoidal, the vertical diameter being a principal axis, it may easily be shown that the lowest position is permanently stable only so long as the period of the rotation is longer than that of the slower of the two normal modes in the absence of rotation (see Mechanics, § 13).
7. Principle of Least Action.
The preceding theories give us statements applicable to the system at any one instant of its motion. We now come to a series of theorems relating to the whole motion of the system between any two configurations through which it passes, Stationary Action. viz. we consider the actual motion and compare it with other imaginable motions, differing infinitely little from it, between the same two configurations. We use the symbol δ to denote the transition from the actual to any one of the hypothetical motions.
The best-known theorem of this class is that of Least Action, originated by P.L.M. de Maupertuis, but first put in a definite form by Lagrange. The “action” of a single particle in passing from one position to another is the space-integral of the momentum, or the time-integral of the vis viva. The action of a dynamical system is the sum of the actions of its constituent particles, and is accordingly given by the formula
A = Σ ∫ mvds = Σ ∫ mv²dt = 2 ∫ Τdt.
The theorem referred to asserts that the free motion of a conservative system between any two given configurations is characterized by the property
δA = 0,
provided the total energy have the same constant value in the varied motion as in the actual motion.
If t, t′ be the times of passing through the initial and final configurations respectively, we have
δA = δ ∫t′t Σm (ẋ² + ẏ² + z˙²) dt
= ∫t′t δΤdt + 2Τ′δt′ + 2Τδt,
since the upper and lower limits of the integral must both be regarded as variable. This may be written
δA = ∫t′t δΤdt + ∫t′t Σm (ẋδẋ + ẏδẏ + z˙δz˙) dt + 2Τ′δt′ − 2Τδt
= ∫t′t δΤdt + [ Σm (ẋδx + ẏδy + z˙δz)]t′t
− ∫t′t Σm (ẍδx + ÿδy + z¨δz) dt + 2Τ′δt′ − 2Τδt.
Now, by d’Alembert’s principle,
Σm (ẍδx + ÿδy + z¨δz) = −δV,
and by hypothesis we have
δ(Τ + V) = 0.
The formula therefore reduces to
δA = [Σm (ẋδx + ẏδy + z˙δz)]t′t + 2Τ′δt′ − 2Τδt.
Since the terminal configurations are unaltered, we must have at the lower limit
δx + ẋδt = 0, δy + ẏδt = 0, δz + z˙δt = 0,
with similar relations at the upper limit. These reduce (7) to the form (2).
The equation (2), it is to be noticed, merely expresses that the variation of A vanishes to the first order; the phrase stationary action has therefore been suggested as indicating more accurately what has been proved. The action in the free path between two given configurations is in fact not invariably a minimum, and even when a minimum it need not be the least possible subject to the given conditions. Simple illustrations are furnished by the case of a single particle. A particle moving on a smooth surface, and free from extraneous force, will have its velocity constant; hence the theorem in this case resolves itself into
δ ∫ ds = 0,
i.e. the path must be a geodesic line. Now a geodesic is not necessarily the shortest path between two given points on it; for example, on the sphere a great-circle arc ceases to be the shortest path between its extremities when it exceeds 180°. More generally, taking any surface, let a point P, starting from O, move along a geodesic; this geodesic will be a minimum path from O to P until P passes through a point O′ (if such exist), which is the intersection with a consecutive geodesic through O. After this point the minimum property ceases. On an anticlastic surface two geodesics cannot intersect more than once, and each geodesic is therefore a minimum path between any two of its points. These illustrations are due to K.G.J. Jacobi, who has also formulated the general criterion, applicable to all dynamical systems, as follows:—Let O and P denote any two configurations on a natural path of the system. If this be the sole free path from O to P with the prescribed amount of energy, the action from O to P is a minimum. But if 762 there be several distinct paths, let P vary from coincidence with O along the first-named path; the action will then cease to be a minimum when a configuration O′ is reached such that two of the possible paths from O to O′ coincide. For instance, if O and P be positions on the parabolic path of a projectile under gravity, there will be a second path (with the same energy and therefore the same velocity of projection from O), these two paths coinciding when P is at the other extremity (O′, say) of the focal chord through O. The action from O to P will therefore be a minimum for all positions of P short of O′. Two configurations such as O and O′ in the general statement are called conjugate kinetic foci. Cf. Variations, Calculus of.
Before leaving this topic the connexion of the principle of stationary action with a well-known theorem of optics may be noticed. For the motion of a particle in a conservative field of force the principle takes the form
δ ∫ vds = 0.
On the corpuscular theory of light v is proportional to the refractive index μ of the medium, whence
δ ∫ μds = 0.
In the formula (2) the energy in the hypothetical motion is prescribed, whilst the time of transit from the initial to the final configuration Hamiltonian principle. is variable. In another and generally more convenient theorem, due to Hamilton, the time of transit is prescribed to be the same as in the actual motion, whilst the energy may be different and need not (indeed) be constant. Under these conditions we have
δ ∫t′t (T − V)dt = 0,
where t, t′ are the prescribed times of passing through the given initial and final configurations. The proof of (12) is simple; we have
δ ∫t′t (T − V)dt = ∫t′t (δΤ − δV)dt = ∫t′t {Σm (ẋδẋ + ẏδẏ + z˙δz˙) − δV} dt
= [ Σm (ẋδx + ẏδy + z˙δz)]t′t − ∫t′t {Σm (ẍδx + ÿδy + z¨δz) + δV} dt.
The integrated terms vanish at both limits, since by hypothesis the configurations at these instants are fixed; and the terms under the integral sign vanish by d’Alembert’s principle.
The fact that in (12) the variation does not affect the time of transit renders the formula easy of application in any system of co-ordinates. Thus, to deduce Lagrange’s equations, we have
| ∫t′t (δΤ − δV) dt = ∫t′t { | ∂T | δq˙1 + | ∂T | δq1 + ... − | ∂V | δq1 − ... } dt |
| ∂q˙1 | ∂q1 | ∂q1 |
| = [p1δq1 + p2δq2 + ...]t′t − ∫t′t { [ṗ1 − | ∂T | + | ∂V | ) δq1 + (ṗ2 − | ∂T | + | ∂V | ) δq2 + ...} dt. |
| ∂q1 | ∂q1 | ∂q2 | ∂q2 |
The integrated terms vanish at both limits; and in order that the remainder of the right-hand member may vanish it is necessary that the coefficients of δq1, δq2, ... under the integral sign should vanish for all values of t, since the variations in question are independent, and subject only to the condition of vanishing at the limits of integration. We are thus led to Lagrange’s equation of motion for a conservative system. It appears that the formula (12) is a convenient as well as a compact embodiment of the whole of ordinary dynamics.
The modification of the Hamiltonian principle appropriate to Extension to cyclic systems. the case of cyclic systems has been given by J. Larmor. If we write, as in § 1 (25),
R = Τ − κχ˙ − κ′χ˙′ − κ″χ˙″ − ...,
we shall have
δ ∫t′t (R − V) dt = 0,
provided that the variation does not affect the cyclic momenta κ, κ′, κ″, ..., and that the configurations at times t and t′ are unaltered, so far as they depend on the palpable co-ordinates q1, q2, ... qm. The initial and final values of the ignored co-ordinates will in general be affected.
To prove (16) we have, on the above understandings,
δ ∫t′t (R − V) dt = ∫t′t (δT − κδχ˙ − ... − δV) dt
| = ∫t′t ( | ∂T | δq˙1 + ... + | ∂T | δq1 + ... − δV) dt, |
| ∂q˙1 | ∂q1 |
where terms have been cancelled in virtue of § 5 (2). The last member of (17) represents a variation of the integral
∫t′t (T − V) dt
on the supposition that δX = 0, δX′ = 0, δX″ = 0, ... throughout, whilst δq1, δq2, δqm vanish at times t and t′; i.e. it is a variation in which the initial and final configurations are absolutely unaltered. It therefore vanishes as a consequence of the Hamiltonian principle in its original form.
Larmor has also given the corresponding form of the principle of least action. He shows that if we write
A = ∫ (2T − κχ˙ − κ′χ˙′ − κ″χ˙″ − ...) dt,
then
δA = 0,
provided the varied motion takes place with the same constant value of the energy, and with the same constant cyclic momenta, between the same two configurations, these being regarded as defined by the palpable co-ordinates alone.
§ 8. Hamilton’s Principal and Characteristic Functions.
In the investigations next to be described a more extended meaning is given to the symbol δ. We will, in the first instance, denote by it an infinitesimal variation of the most Principal function. general kind, affecting not merely the values of the co-ordinates at any instant, but also the initial and final configurations and the times of passing through them. If we put
S = ∫t′t (Τ − V) dt,
we have, then,
δS = (T′ − V′) δt′ − (T − V) δt + ∫t′t (δΤ − δV) dt
= (T′ − V′) δt′ − (T − V) δt + [Σm (ẋδx + ẏδy + z˙δz)]t′t.
Let us now denote by x′ + δx′, y′ + δy′, z′ + δz′, the final co-ordinates (i.e. at time t′ + δt′) of a particle m. In the terms in (2) which relate to the upper limit we must therefore write δx′ − ẋ′δt′, δy′ − ẏ′δt′, δz′ − z˙′δt′ for δx, δy, δz. With a similar modification at the lower limit, we obtain
δS = −Hδτ + Σm (ẋ′δx′ + ẏ′δy′ + z˙′δz′) − Σm (ẋδx + ẏδy + z˙δz),
where H (= T + V) is the constant value of the energy in the free motion of the system, and τ (= t′ − t) is the time of transit. In generalized co-ordinates this takes the form
δS = −Hδτ + p′1δq′1 + p′2δq′2 + ... − p1δq1 − p2δq2 − ....
Now if we select any two arbitrary configurations as initial and final, it is evident that we can in general (by suitable initial velocities or impulses) start the system so that it will of itself pass from the first to the second in any prescribed time τ. On this view of the matter, S will be a function of the initial and final co-ordinates (q1, q2, ... and q′1, q′2, ...) and the time τ, as independent variables. And we obtain at once from (4)
| p′1 = | ∂S | , p′2 = | ∂S | , ... , |
| ∂q′1 | ∂q′2 |
| p1 = − | ∂S | , p2 = − | ∂S | , ... , |
| ∂q1 | ∂q2 |
and
| H = − | ∂S | . |
| ∂τ |
S is called by Hamilton the principal function; if its general form for any system can be found, the preceding equations suffice to determine the motion resulting from any given conditions. If we substitute the values of p1, p2, ... and H from (5) and (6) in the expression for the kinetic energy in the form T′ (see § 1), the equation
T¹ + V = H
becomes a partial differential equation to be satisfied by S. It has been shown by Jacobi that the dynamical problem resolves itself into obtaining a “complete” solution of this equation, involving n + 1 arbitrary constants. This aspect of the subject, as a problem in partial differential equations, has received great attention at the hands of mathematicians, but must be passed over here.
There is a similar theory Characteristic function. for the function
A = 2 ∫ Tdt = S + Hτ
It follows from (4) that
δA = τδH + p′1δq′1 + p′2δq′2 + ... − p1δq1 − p2δq2 − ....
This formula (it may be remarked) contains the principle of “least 763 action” as a particular case. Selecting, as before, any two arbitrary configurations, it is in general possible to start the system from one of these, with a prescribed value of the total energy H, so that it shall pass through the other. Hence, regarding A as a function of the initial and final co-ordinates and the energy, we find
| p′1 = | ∂A | , p′2 = | ∂A | , ... , |
| ∂q′1 | ∂q′2 |
| p1 = − | ∂A | , p2 = − | ∂A | , ... , |
| ∂q1 | ∂q2 |
and
| τ = | ∂A | . |
| ∂H |
A is called by Hamilton the characteristic function; it represents, of course, the “action” of the system in the free motion (with prescribed energy) between the two configurations. Like S, it satisfies a partial differential equation, obtained by substitution from (10) in (7).
The preceding theorems are easily adapted to the case of cyclic systems. We have only to write
S = ∫t′t (R − V) dt = ∫t′t (T − κχ˙ − κ′χ˙′ − ... − V) dt
in place of (1), and
A = ∫ (2T − κχ˙ − κ′χ˙′ − ...) dt,
in place of (8); cf. § 7 ad fin. It is understood, of course, that in (12) S is regarded as a function of the initial and final values of the palpable co-ordinates q1, q2, ... qm, and of the time of transit τ, the cyclic momenta being invariable. Similarly in (13), A is regarded as a function of the initial and final values of q1, q2, ... qm, and of the total energy H, with the cyclic momenta invariable. It will be found that the forms of (4) and (9) will be conserved, provided the variations δq1, δq2, ... be understood to refer to the palpable co-ordinates alone. It follows that the equations (5), (6) and (10), (11) will still hold under the new meanings of the symbols.
9. Reciprocal Properties of Direct and Reversed Motions.
We may employ Hamilton’s principal function to prove a very remarkable formula connecting any two slightly disturbed Lagrange’s formula. natural motions of the system. If we use the symbols δ and Δ to denote the corresponding variations, the theorem is
| d | Σ (δpr·Δqr − Δpr·δqr) = 0; |
| dt |
or integrating from t to t′,
Σ (δp′r·Δq′r − Δq′r·δq′r) = Σ (δpr·Δqr − Δpr·δqr).
If for shortness we write
| (r, s) = | ∂²S | , (r, s′) = | ∂²S | , |
| ∂qr∂qs | ∂qr∂q′s |
we have
∂pr = −Σs (r, s) δqs − Σs (r, s′) δq′s
with a similar expression for Δpr. Hence the right-hand side of (2) becomes
− Σr {Σs(r, s) δqs + Σs(r, s′) δq′s} Δqr + Σr {Σs(r, s)Δqs + Σs(r, s′) Δq′s} δqr
= ΣrΣs(r, s′) {δqr·Δq′s − Δqr·δq′s}.
The same value is obtained in like manner for the expression on the left hand of (2); hence the theorem, which, in the form (1), is due to Lagrange, and was employed by him as the basis of his method of treating the dynamical theory of Variation of Arbitrary Constants.
The formula (2) leads at once to some remarkable reciprocal relations which were first expressed, in their complete form, by Helmholtz. Consider any natural motion of a conservative system between two configurations O and O′ Helmholtz’s reciprocal theorems. through which it passes at times t and t′ respectively, and let t′ − t = τ. As the system is passing through O let a small impulse δpr be given to it, and let the consequent alteration in the co-ordinate qs after the time τ be δq′s. Next consider the reversed motion of the system, in which it would, if undisturbed, pass from O′ to O in the same time τ. Let a small impulse δp′s be applied as the system is passing through O′, and let the consequent change in the co-ordinate qr after a time τ be δqr. Helmholtz’s first theorem is to the effect that
δqr : δp′s = δq′s : δpr.
To prove this, suppose, in (2), that all the δq vanish, and likewise all the δp with the exception of δpr. Further, suppose all the Δq′ to vanish, and likewise all the Δp′ except Δp′s, the formula then gives
δpr·Δqr = −Δp′s·δq′s,
which is equivalent to Helmholtz’s result, since we may suppose the symbol Δ to refer to the reversed motion, provided we change the signs of the Δp. In the most general motion of a top (Mechanics, § 22), suppose that a small impulsive couple about the vertical produces after a time τ a change δθ in the inclination of the axis, the theorem asserts that in the reversed motion an equal impulsive couple in the plane of θ will produce after a time τ a change δψ, in the azimuth of the axis, which is equal to δθ. It is understood, of course, that the couples have no components (in the generalized sense) except of the types indicated; for instance, they may consist in each case of a force applied to the top at a point of the axis, and of the accompanying reaction at the pivot. Again, in the corpuscular theory of light let O, O′ be any two points on the axis of a symmetrical optical combination, and let V, V′ be the corresponding velocities of light. At O let a small impulse be applied perpendicular to the axis so as to produce an angular deflection δθ, and let β′ be the corresponding lateral deviation at O′. In like manner in the reversed motion, let a small deflection δθ′ at O′ produce a lateral deviation β at O. The theorem (6) asserts that
| β | = | β′β′ | , |
| V′δθ′ | Vδθ |
or, in optical language, the “apparent distance” of O from O′ is to that of O′ from O in the ratio of the refractive indices at O′ and O respectively.
In the second reciprocal theorem of Helmholtz the configuration O is slightly varied by a change δqr in one of the co-ordinates, the momenta being all unaltered, and δq′s is Helmholtz’s second reciprocal theorem. the consequent variation in one of the momenta after time τ. Similarly in the reversed motion a change δp′s produces after time τ a change of momentum δpr. The theorem asserts that
δp′s : δqr = δpr : δq′s
This follows at once from (2) if we imagine all the δp to vanish, and likewise all the δq save δqr, and if (further) we imagine all the Δp′ to vanish, and all the Δq′ save Δq′s. Reverting to the optical illustration, if F, F′, be principal foci, we can infer that the convergence at F′ of a parallel beam from F is to the convergence at F of a parallel beam from F′ in the inverse ratio of the refractive indices at F′ and F. This is equivalent to Gauss’s relation between the two principal focal lengths of an optical instrument. It may be obtained otherwise as a particular case of (8).
We have by no means exhausted the inferences to be drawn from Lagrange’s formula. It may be noted that (6) includes as particular cases various important reciprocal relations in optics and acoustics formulated by R.J.E. Clausius, Helmholtz, Thomson (Lord Kelvin) and Tait, and Lord Rayleigh. In applying the theorem care must be taken that in the reversed motion the reversal is complete, and extends to every velocity in the system; in particular, in a cyclic system the cyclic motions must be imagined to be reversed with the rest. Conspicuous instances of the failure of the theorem through incomplete reversal are afforded by the propagation of sound in a wind and the propagation of light in a magnetic medium.
It may be worth while to point out, however, that there is no such limitation to the use of Lagrange’s formula (1). In applying it to cyclic systems, it is convenient to introduce conditions already laid down, viz. that the co-ordinates qr are the palpable co-ordinates and that the cyclic momenta are invariable. Special inference can then be drawn as before, but the interpretation cannot be expressed so neatly owing to the non-reversibility of the motion.
Authorities.—The most important and most accessible early authorities are J.L. Lagrange, Mécanique analytique (1st ed. Paris, 1788, 2nd ed. Paris, 1811; reprinted in Œuvres, vols. xi., xii., Paris, 1888-89); Hamilton, “On a General Method in Dynamics,” Phil. Trans. 1834 and 1835; C.G.J. Jacobi, Vorlesungen über Dynamik (Berlin, 1866, reprinted in Werke, Supp.-Bd., Berlin, 1884). An account of the extensive literature on the differential equations of dynamics and on the theory of variation of parameters is given by A. Cayley, “Report on Theoretical Dynamics,” Brit. Assn. Rep. (1857), Mathematical Papers, vol. iii. (Cambridge, 1890). For the modern developments reference may be made to Thomson and Tait, Natural Philosophy (1st ed. Oxford, 1867, 2nd ed. Cambridge, 1879); Lord Rayleigh, Theory of Sound, vol. i. (1st ed. London, 1877; 2nd ed. London, 1894); E.J. Routh, Stability of Motion (London, 1877), and Rigid Dynamics (4th ed. London, 1884); H. Helmholtz, “Über die physikalische Bedeutung des Prinzips der kleinsten Action,” Crelle, vol. c., 1886, reprinted (with other cognate papers) in Wiss. Abh. vol. iii. (Leipzig, 1895); J. Larmor, “On Least Action,” Proc. Lond. Math. Soc. vol. xv. (1884); E.T. Whittaker, Analytical Dynamics (Cambridge, 1904). As to the question of stability, reference may be made to H. Poincaré, “Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation” Acta math. vol. vii. (1885); F. Klein and A. Sommerfeld, Theorie des Kreisels, pts. 1, 2 (Leipzig, 1897-1898); A. Lioupanoff and J. Hadamard, Liouville, 5me série, vol. iii. (1897); T.J.I. Bromwich, Proc. Lond. Math. Soc. vol. xxxiii. (1901). A remarkable interpretation of various dynamical principles is given by H. Hertz in his posthumous work Die Prinzipien der Mechanik (Leipzig, 1894), of which an English translation appeared in 1900.
DYNAMITE (Gr. δύναμις, power), the name given to several explosive preparations containing nitroglycerin (q.v.) which are almost exclusively used for blasting purposes. The first practical application of nitroglycerin in this way was made by A. Nobel in 1863. He soaked gunpowder with the liquid and fired the gunpowder by an ordinary fuse. Later he found that nitroglycerin could be detonated by the explosion of several materials such as fulminate of mercury, the use of which as a detonator he patented in 1867. In 1866-1867 he experimented with charcoal and other substances, and found the infusorial earth known as kieselguhr, which consists mainly of silica (nearly 95%), eminently adapted to the purpose, as it was inert, non-combustible, and after a little heating and preparation very porous, retaining a large amount of nitroglycerin as water is held in a sponge, without very serious exudation on standing. This kieselguhr dynamite is generally made by incorporating three parts of nitroglycerin with one part of the dry earth, the paste being then formed into cylindrical cartridges. This work is done by hand. Generally a small percentage of the kieselguhr is replaced by a mixture containing sodium and ammonium carbonates, talc and ochre. This product is known as dynamite No. 1. Disabilities attaching to kieselguhr dynamite are that when placed in water the nitroglycerin is liable to be exuded or displaced, also that, like nitroglycerin itself, it freezes fairly easily and thawing the frozen cartridges is a dangerous operation. Other substances, e.g. kaolin, tripoli, magnesia alba (magnesium carbonate), alumina, sugar, charcoal, some powdered salts and mixtures of sawdust and salts, have been shown to be absorbents more or less adapted to the purpose of making a dynamite. Charcoal from cork is said to absorb about 90% of its weight of nitroglycerin. With the idea of obtaining greater safety, mixtures have been made of nitroglycerin with wood fibre, charcoal and metallic nitrates. Lithofracteur, for instance, consists of 50% nitroglycerin and a mixture of prepared sawdust, kieselguhr and barium nitrate. Carbonite contains 25% of nitroglycerin, the remainder being a mixture of wood-meal and alkali nitrates, with about 1% of sulphur. Dualin, atlas dynamite and potentite are other modifications.
A convenient form in which nitroglycerin can be made up for blasting purposes, especially in wet ground, is the gelatinous material obtained by the action of nitroglycerin, either alone or with the help of solvents, on low-grade or soluble gun-cottons. It is known as blasting gelatin, and was first made by Nobel by incorporating 6 or 7% of low nitrated cellulose (collodion cotton or soluble gun-cotton) with slightly warmed nitroglycerin. The result is a transparent plastic material, of specific gravity 1.5 to 1.6, which may be kept under water for a long time without appreciable change. It is less sensitive to detonation than ordinary dynamite, and although its explosion is slightly slower it is more powerful than dynamite and much superior to the liquid nitroglycerin. Blasting gelatin also freezes and is sensitive to percussion in this state. Camphor and other substances have been added to blasting gelatin to render it more solid and less sensitive. Some modifications of blasting gelatin, e.g. gelignite, contain wood-meal and such oxygen-containing salts as potassium nitrate. Experience has conclusively shown that dynamites are more satisfactory, quicker, and more intense in action than liquid nitroglycerin.
To prevent nitroglycerin and some of the forms of dynamite from freezing it has been proposed to add to them small quantities of either monochlor-dinitroglycerin or of a nitrated poly-glycerin. The former is obtained by first acting upon glycerin with hydrogen chloride to produce u-chlorhydrin or chlor-propylene glycol, C3H7O2Cl, which is then nitrated as in the case of glycerin. The latter is obtained by heating glycerin for six or seven hours to about 300° C., whereby water is split off in such manner that a diglycerin C6H14O5, for the most part, results. This on nitration in the usual manner gives a product C6H10N4O13, which burns and explodes in a similar manner to ordinary nitroglycerin, but is less sensitive and does not so easily freeze. The mono- and di-nitrates of glycerin have also been proposed as additions to ordinary nitroglycerin (q.v.) for the same purpose.
DYNAMO (a shortened form of “dynamo-electric machine,” from Gr. δύναμις, power), a machine for converting mechanical into electrical energy.
 |
| Fig. 1. |
The dynamo ranks with the telegraph and telephone as one of the three striking applications of electrical and magnetic science to which the material progress that marked the second half of the 19th century was in no small measure due. Since the discovery of the principle of the dynamo by Faraday in 1831 the simple model which he first constructed has been gradually developed into the machines of 5000 horse-power or more which are now built to meet the needs of large cities for electric lighting and power, while at the same time the numbers of dynamos in use have increased almost beyond estimate. Yet such was the insight of Faraday into the fundamental nature of the dynamo that the theory of its action which he laid down has remained essentially unchanged. His experiments on the current which was set up in a coil of wire during its movement across the poles of a magnet led naturally to the explanation of induced electromotive force as caused by the linking or unlinking of magnetic lines of flux with an electric circuit. For the more definite case of the dynamo, however, we may, with Faraday, make the transition from line-linkage to the equivalent conception of “line-cutting” as the source of E.M.F.—in other words, to the idea of electric conductors “cutting” or intersecting1 the lines of flux in virtue of relative motion of the magnetic field and electric circuit. On the 28th of October 1831 Faraday mounted a copper disk so that it could be rotated edgewise between the poles of a permanent horse-shoe magnet. When so rotated, it cut the lines of flux which passed transversely through its lower half, and by means of two rubbing contacts, one on its periphery and the other on its spindle, the circuit was closed through a galvanometer, which indicated the passage of a continuous current so long as the disk was rotated (fig. 1). Thus by the invention of the first dynamo Faraday proved his idea that the E.M.F. induced through the interaction of a magnetic field and an electric circuit was due to the passage of a portion of the electric circuit across the lines of flux, or vice versa, and so could be maintained if the cutting of the lines were made continuous.2 In comparison with Faraday’s results, the subsequent advance is to be regarded as a progressive perfecting of the mechanical and electro-magnetic design, partly from the theoretical and partly from the practical side, rather than as modifying or adding to the idea which was originally present in his mind, and of which he already saw the possibilities.
A dynamo, then, is a machine in which, by means of continuous relative motion, an electrical conductor or system of conductors forming part of a circuit is caused to cut the lines of a magnetic field or fields; the cutting of the magnetic flux induces an electromotive force in the conductors, and when the circuit is closed a current flows, whereby mechanical energy is converted into electrical energy.
Little practical use could be made of electrical energy so long as its only known sources were frictional machines and voltaic batteries. The cost of the materials for producing electrical currents on a large scale by chemical action was prohibitive, while the frictional machine only yielded very small currents at extremely high potentials. In the dynamo, on the other hand, electrical energy in a convenient form could be cheaply and easily obtained by mechanical means, and with its invention the application of electricity to a wide range of commercial purposes became economically possible. As a converter of energy from one form to another it is only surpassed in efficiency by another electrical appliance, namely, the transformer (see Transformers). In this there is merely conversion of electrical energy at a high potential into electrical energy at a low potential, or vice versa, but in the dynamo the mechanical energy which must be applied to maintain the relative movement of magnetic field and conductor is absorbed, and reappears in an electrical form. A true transformation takes place, and the proportion which the rate of 765 delivery of electrical energy bears to the power absorbed, or in other words the efficiency, is the more remarkable. The useful return or “output” at the terminals of a large machine may amount to as much as 95% of the mechanical energy which forms the “input.” Since it needs some prime mover to drive it, the dynamo has not made any direct addition to our sources of energy, and does not therefore rank with the primary battery or oil-engine, or even the steam-engine, all of which draw their energy more immediately from nature. Yet by the aid of the dynamo the power to be derived from waterfalls can be economically and conveniently converted into an electrical form and brought to the neighbouring factory or distant town, to be there reconverted by motors into mechanical power. Over any but very short distances energy is most easily transmitted when it is in an electrical form, and turbine-driven dynamos are very largely and successfully employed for such transmission. Thus by conducing to the utilization of water-power which may previously have had but little value owing to its disadvantageous situation, the dynamo may almost be said to have added another to our available natural resources.
The two essential parts of the dynamo, as required by its definition, may be illustrated by the original disk machine of Faraday. They are (1) the iron magnet, between the poles of which a magnetic field exists, and (2) the electrical conductors, represented by the rotating copper disk. The sector of the disk cutting the lines of the field forms part of a closed electric circuit, and has an E.M.F. induced in it, by reason of which it is no longer simply a conductor, but has become “active.” In its more highly developed form the simple copper disk is elaborated into a system of many active wires or bars which form the “winding,” and which are so interconnected as to add up their several E.M.F.’s. Since these active wires are usually mounted on an iron structure, which may be likened to the keeper or “armature” of a magnet rotating between its poles, the term “armature” has been extended to cover not only the iron core, but also the wires on it, and when there is no iron core it is even applied to the copper conductors themselves. In the dynamo of Faraday the “armature” was the rotating portion, and such is the case with modern continuous-current dynamos; in alternators, however, the magnet, or a portion of it, is more commonly rotated while the armature is stationary. It is in fact immaterial to the action whether the one or the other is moved, or both, so long as their relative motion causes the armature conductors to cut the magnetic flux. As to the ultimate reason why an E.M.F. should be thereby induced, physical science cannot as yet yield any surer knowledge than in the days of Faraday.3 For the engineer, it suffices to know that the E.M.F. of the dynamo is due to the cutting of the magnetic flux by the active wires, and, further, is proportional to the rate at which the lines are cut.4
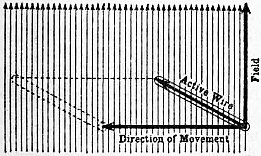 |
| Fig. 2. |
The equation of the electromotive force which is required in order to render this statement quantitative must contain three factors, namely, the density of the flux in the air-gap through which the armature conductors move, the active length of these wires, and the speed of their movement. For given values of the first and third factors and a single straight wire moved parallel to itself through a uniform field, the maximum rate of cutting is evidently obtained when the three directions of the lines of the conductor’s length and of the relative motion are respectively at right angles to each other, as shown by the three co-ordinate axes of fig. 2. The E.M.F. of the single wire is then
E = BgLV × 10−8 volts
where Bg is the density of the flux within the air-gap expressed in C.G.S. lines per square centimetre, L is the active length of the conductor within the field in centimetres, and V is the velocity of movement in centimetres per second. Further, the direction in which the E.M.F. has the above maximum value is along the length of the conductor, its “sense” being determined by the direction of the movement5 in relation to the direction of the field.
The second fundamental equation of the dynamo brings to light its mechanical side, and rests on H.C. Oersted’s discovery of the interaction of a magnetic field and an electric current. If a straight electric conductor through which a current is passing be so placed in a magnetic field that its length is not parallel to the direction of the lines of flux, it is acted on by a force which will move it, if free, in a definite direction relatively to the magnet; or if the conductor is fixed and the magnet is free, the latter will itself move in the opposite direction. Now in the dynamo the active wires are placed so that their length is at right angles to the field; hence when they are rotated and an electric current begins to flow under the E.M.F. which they induce, a mutual force at once arises between the copper conductors and the magnet, and the direction of this force must by Lenz’s law be opposed to the direction of the movement. Thus as soon as the disk of fig. 1 is rotated and its circuit is closed, it experiences a mechanical pull or drag which must be overcome by the force applied to turn the disk. While the magnet must be firmly held so as to remain stationary, the armature must be of such mechanical construction that its wires can be forcibly driven through the magnetic field against the mutual pull. This law of electrodynamic action may be quantitatively stated in an equation of mechanical force, analogous to the equation (I.) of electromotive force, which states the law of electromagnetic induction. If a conductor of length L cm., carrying a current C amperes, is immersed in a field of uniform density Bg, and the length of the conductor is at right angles to the direction of the lines, it is acted on by a force
F = BgLC × 10−1 dynes,
and the direction of this force is at right angles to the conductor and to the field. The rate at which electrical energy is developed, when this force is overcome by moving the conductor as a dynamo through the field, is EC = BgLVC × 10−8 watts, whence the equality of the mechanical power absorbed and the electrical power developed (as required by the law of the conservation of energy) is easily established. The whole of this power is not, however, available at the terminals of the machine; if Ra be the resistance of the armature in ohms, the passage of the current Ca through the armature conductors causes a drop of pressure of CaRa volts, and a corresponding loss of energy in the armature at the rate of Ca²Ra watts. As the resistance of the external circuit Re is lowered, the current C = Ea / (Re + Ra) is increased. The increase of the current is, however, accompanied by a progressive increase in the loss of energy over the armature, and as this is expended in heating the armature conductors, their temperature may rise so much as to destroy the insulating materials with which they are covered. Hence the temperature which the machine may be permitted to attain in its working is of great importance in determining its output, the current which forms one factor therein being primarily limited by the heating which it produces in the armature winding. The lower the resistance of the armature, the less the rise of its temperature for a given current flowing through it; and the reason for the almost universal adoption of copper as the material for the armature conductors is now seen to lie in its high conductivity.6
Since the voltage of the dynamo is the second factor to which its output is proportional, the conditions which render the induced E.M.F. a maximum must evidently be reproduced as far as possible in practice, if the best use is to be made of a given mass of iron and copper. The first problem, therefore, in the construction of the dynamo is the disposition of the wires and field in such a manner that the three directions of field, length of active conductors, and movement are at right angles to one another, and so that the relative motion is continuous. Reciprocating motion, such as would be obtained by direct attachment of the conductors to the piston of a steam-engine, has 766 been successfully employed only in the special case of an “oscillator,”7 producing a small current very rapidly changing in direction. Rotary motion is therefore universally adopted, and with this two distinct cases arise. Either (A) the active length of the wire is parallel to the axis of rotation, or (B) it is at right angles to it.
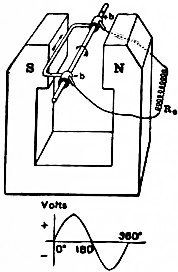 |
| Fig. 3. |
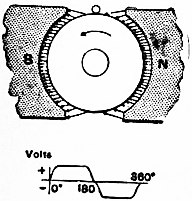 |
| Fig. 4. |
(A) If a conductor is rotated in the gap between the poles of a horse-shoe magnet, and these poles have plane parallel faces opposing one another as in fig. 3, not only is the density of the flux in the interpolar gap small, but the direction of movement is not always at right angles to the direction of the lines, which for the most part pass straight across from one opposing face to the other. When the conductor is midway between the poles (i.e. either at its highest or lowest point), it is at this instant sliding along the lines and does not cut them, so that its E.M.F. is zero. Taking this position as the starting-point, as the conductor moves round, its rate of line-cutting increases to a maximum when it has moved through a right angle and is opposite to the centre of a pole-face (as in fig. 3), from which point onward the rate decreases to zero when it has moved through 180°. Each time the conductor crosses a line drawn symmetrically through the gap between the poles and at right angles to the axis of rotation, the E.M.F. along its length is reversed in direction, since the motion relatively to the direction of the field is reversed. If the ends of the active conductor are electrically connected to two collecting rings fixed upon, but insulated from, the shaft, two stationary brushes bb can be pressed on the rings so as to make a sliding contact. An external circuit can then be connected to the brushes, which will form the “terminals” of the machine, the periodically reversed or alternating E.M.F. induced in the active conductor will cause an alternating current to flow through conductor and external circuit, and the simplest form of “alternator” is obtained. If the field cut by the straight conductor is of uniform density, and all the lines pass straight across from one pole-face to the other (both of which assumptions are approximately correct), a curve connecting the instantaneous values of the E.M.F. as ordinates with time or degrees of angular movement as abscissae (as shown at the foot of fig. 3), will, if the speed of rotation be uniform, be a sine curve. If, however, the conductor is mounted on an iron cylinder (fig. 4),8 a sufficient margin being allowed for mechanical clearance between it and the poles, not only will the reluctance of the magnetic circuit be reduced and the total flux and its density in the air-gap Bg be thereby increased, but the path of the lines will become nearly radial, except at the “fringe” near the edges of the pole-tips; hence the relative directions of the movement and of the lines will be continuously at right angles. The shape of the E.M.F. curve will then be as shown in fig. 4—flat-topped, with rounded corners rapidly sloping down to the zero line.
 |
| Fig. 5. |
But a single wire cannot thus be made to give more than a few volts, and while dynamos for voltages from 5 to 10 are required for certain purposes, the voltages in common use range from 100 to 10,000. It is therefore necessary to connect a number of such wires in series, so as to form an “armature winding.” If several similar conductors are arranged along the length of the iron core parallel to the first (fig. 5), the E.M.F.’s generated in the conductors which at any moment are under the same pole are similarly directed, and are opposite to the directions of the E.M.F.’s in the conductors under the other pole (cf fig. 5 where the dotted and crossed ends of the wires indicate E.M.F.’s directed respectively towards and away from the observer). Two distinct methods of winding thence arise, the similarity of the E.M.F.’s under the same pole being taken advantage of in the first, and the opposite E.M.F.’s under N and S poles in the second.
 |
| Fig. 6. |
1. The first, or ring-winding, was invented by Dr Antonio Pacinotti of Florence9 in 1860, and was subsequently and independently reintroduced in 187010 by the Belgian electrician, Zénobe Théophile Gramme, whence it is also frequently called the “Gramme” winding. By this method the farther end of conductor 1 (fig. 5) is joined in series to the near end of conductor 2; this latter lies next to it on the surface of the core or immediately above it, so that both are simultaneously under the same pole-piece. For this series connexion to be possible, the armature core must be a hollow cylinder, supported from the shaft on an open non-magnetic spider or hub, between the arms of which there is room for the internal wire completing the loop (fig. 6). The end of one complete loop or turn embracing one side of the armature core thus forms the starting-point for another loop, and the process can be continued if required to form a coil of two or more turns. In the ring armature the iron core serves the double purpose of conducting the lines across from one pole to the other, and also of shielding from the magnetic flux the hollow interior through which the connecting wires pass. Any lines which leak across the central space are cut by the internal wires, and the direction of cutting is such that the E.M.F. caused thereby opposes the E.M.F. due to the active conductors proper on the external surface. If, however, the section of iron in the core be correctly proportioned, the number of lines which cross the interior will bear but a small ratio to those which pass entirely through the iron, and the counter E.M.F. of the internal wires will become very small; they may then be regarded simply as connectors for joining the external active wires in series.
 |
| Fig. 7. |
2. The second or drum method was used in the original “shuttle-wound” armatures invented by Dr Werner von Siemens in 1856, and is sometimes called the “Siemens” winding. The farther end of conductor 1 (fig. 5) is joined by a connecting wire to the farther end of another conductor 2’ situated nearly diametrically opposite on the other side of the core and under the opposite pole-piece. The near end of the complete loop or turn is then brought across the end of the core, and can be used as the starting-point for another loop beginning with conductor 2, which is situated by the side of the first conductor. The iron core may now be solid from the surface to the shaft, since no connecting wires are brought through the centre, and each loop embraces the entire armature core (fig. 7). By the formation of two loops in the ring armature and of the single loop in the drum armature, two active wires are placed in series; 767 the curves of instantaneous E.M.F. are therefore similar in shape to that of the single wire (fig. 4), but with their ordinates raised throughout to double their former height, as shown at the foot of fig. 6.
Next, if the free ends of either the ring or drum loops, instead of being connected to two collecting rings, are attached to the two halves of a split-ring insulated from the shaft (as shown in fig. 7 in connexion with a drum armature), and the stationary brushes are so set relatively to the loops that they pass over from the one half of the split-ring to the other half at the moment when the loops are passing the centre of the interpolar gap, and so are giving little or no E.M.F., each brush will always remain either positive or negative. The current in the external circuit attached to the brushes will then have a constant direction, although the E.M.F. in the active wires still remains alternating; the curve of E.M.F. obtained at the brushes is thus (as in fig. 7) entirely above the zero line. The first dynamo of H. Pixii,11 which immediately followed Faraday’s discovery, gave an alternating current, but in 183212 the alternator was converted into a machine giving a unidirected current by the substitution of a rudimentary “commutator” in place of mercury collecting cups.
(B) So far the length of the active wires has been parallel to the axis of rotation, but they may equally well be arranged perpendicularly thereto. The poles will then have plane faces and the active wires will be disposed with their length approximately radial to the axis of the shaft. In order to add their E.M.F.’s in series, two types of winding may be employed, which are precisely analogous in principle to the ring and drum windings under arrangement (A).
3. The discoidal or flat-ring armature is equivalent to a ring of which the radial depth greatly exceeds the length, with the poles presented to one side of the ring instead of embracing its cylindrical surface. A similar set of poles is also presented to the opposite side of the ring, like poles being opposite to one another, so that in effect each polar surface is divided into two halves, and the groups of lines from each side bifurcate and pass circumferentially through the armature core to issue into the adjacent poles of opposite sign.
4. In the disk machine, no iron core is necessary for the armature, the two opposite poles of unlike sign being brought close together, leaving but a short path for the lines in the air-gap through which the active wires are rotated.
 |
| Fig. 8. |
If the above elementary dynamos are compared with fig. 1, it will be found that they all possess a distinctive feature which is not present in the original disk machine of Faraday. In the four types of machine above described each active wire in each revolution first cuts the group of lines forming a field in one direction, and then cuts the same lines again in the opposite direction relatively to the sense of the lines, so that along the length of the wire the E.M.F. alternates in direction. But in the dynamo of fig. 1 the sector of the copper disk which is at any moment moving through the magnetic field and which forms the single active element is always cutting the lines in the same manner, so that the E.M.F. generated along its radial length is continuous and unchanged in direction. This radical distinction differentiates the two classes of heteropolar and homopolar dynamos, Faraday’s disk machine of fig. 1 being the type of the latter class. In it the active element may be arranged either parallel or at right angles to the axis of rotation; but in both cases, in order to increase the E.M.F. by placing two or more elements in series, it becomes necessary either (1) to employ some form of sliding contact by which the current may be collected from the end of one active element and passed round a connecting wire into the next element without again cutting the field in the reverse direction, or (2) to form on the armature a loop of which each side is alternately active and inactive. The first method limits the possibilities of the homopolar machine so greatly when large currents and high voltages are required that it is now only used in rare instances, as e.g. occasionally in dynamos driven by steam-turbines which have a very high speed of rotation. The second alternative may be carried into effect with any of the four methods of armature winding, but is practically confined to the drum and disk types. In its drum form the field is divided into two or more projecting poles, all of the same sign, with intervening neutral spaces of equal width, and the span of the loop in the direction of rotation is at least equal to the width of a polar projection, as in fig. 8, where two polar projections are shown. Each side of the loop then plays a dual part; it first cuts the lines of one polar projection and generates an E.M.F., and next becomes an inactive connecting wire, while the action is taken up by the opposite side of the loop which has previously served as a connector but now cuts the lines of the next polar projection. The E.M.F. is thus always in the same direction along the side which is at any moment active, but alternates round the loop as a whole, and the distinctive peculiarity of the homopolar machine, so soon as any form of “winding” is introduced into its armature, is lost. It results that the homopolar principle, which would prima facie appear specially suitable for the generation of a unidirectional E.M.F. and continuous current, can seldom be used for this purpose and is practically confined to alternators. It may therefore be said that in almost all dynamos, whether they supply an alternating or a continuous current in the external circuit, the E.M.F. and current in the armature are alternating.
Ring winding was largely employed in early continuous-current dynamos and also in the alternators of Gramme and H. Wilde, and later of Auguste de Méritens. Disk winding was also successfully introduced for alternators, as in the magneto-machines of Nollet (1849) and the alternators of Wilde (1866) and Siemens (1878), and its use was continued in the machines of W.M. Mordey and S.Z. Ferranti. But although the ring, discoidal-ring and disk methods of winding deserve mention from their historical importance, experience has shown that drum winding possesses a marked superiority for both electrical and manufacturing reasons; the three former methods have in fact been practically discarded in its favour, so that the drum method will hereafter alone be considered.
The drum coil, composed of several loops wound side by side, may therefore be regarded as the constituent active element out of which the armature winding of the modern dynamo is developed. Its application to the multipolar machine is easily followed from fig. 9, which illustrates the heteropolar type of dynamo. The span of the loops, which is nearly 180° or across the diameter of the two-pole machine, is reduced approximately to 90° in the four-pole or to 60° in the six-pole machine and so on, the curvature of the coil becoming gradually less as the number of poles is increased. The passage of a coil through two magnetic fields of opposite direction yields a complete wave of E.M.F., such as is shown in fig. 6, and the time in seconds taken to pass through such a complete cycle is the “period” of the alternating E.M.F. The number of complete periods through which the E.M.F. of the coil passes per second is called the “periodicity” or “frequency” of the machine. In the bipolar machine this 768 is equal to the number of revolutions per second, and in the multipolar machine it is equal to the number of pairs of fields through which the coil passes in one second; hence in general the periodicity is pN / 60, where N = the number of revolutions per minute and p = the number of pairs of poles, and this holds true of the E.M.F. and current round the coil, even though the E.M.F. and current furnished to the external circuit may be rendered unidirectional or continuous. The only difference on this point is that in the continuous-current machine the poles are usually fewer than in the alternator, and the periodicity is correspondingly lower. Thus in the former case the number of poles ranges from 2 to 12 and the usual frequencies from 5 to 20; but with alternators the frequencies in commercial use range from 25 to 120, and in large machines driven by slow-speed engines the number of poles may even be as high as 96.
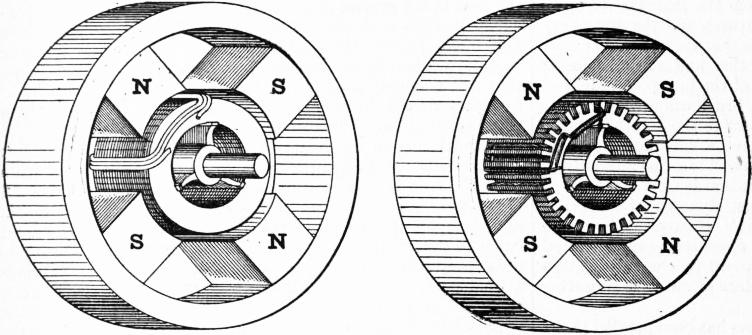 | |
| I. Smooth. | II. Toothed. |
| Fig. 9. | |
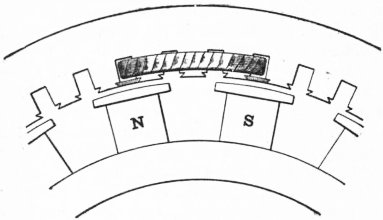 |
| Fig. 10. |
The drum coil may be applied either to the external surface of a rotating armature, the field-magnet being external and stationary (fig. 9), or to the internal surface of a stationary armature (fig. 10), the field-magnet being internal and rotating. While the former combination is universally adopted in the continuous-current dynamo, the latter is more usual in the modern alternator. In either case the iron armature core must be “laminated”; the passage of the lines of the field across its surface sets up E.M.F.’s which are in opposite directions under poles of opposite sign, so that if the core were a solid mass a current-sheet would flow along its surface opposite to a pole, and complete its circuit by passing through the deeper layers of metal or by returning in a sheet under a pole of opposite sign. Such “eddy-currents” can be practically avoided by dividing the metal core into laminations at right angles to the length of the active wires which are themselves arranged to secure the greatest rate of line-cutting and maximum E.M.F. The production of the eddy-current E.M.F. is not thereby prevented, but the paths of the eddy-currents are so broken up that the comparatively high resistance with which they meet reduces their amount very greatly. The laminae must be lightly insulated from one another, right up to their edges, so that the E.M.F.’s which still act across their thickness will not be added up along the length of the core, but will only produce extremely small currents circulating through the interior of the separate laminations. Each thin iron plate is either coated with an insulating varnish or has one of its sides covered with a sheet of very thin paper; the thickness of the laminae is usually about one-fortieth of an inch, and if this is not exceeded the rate at which energy is dissipated by eddy-currents in the core is so far reduced that it does not seriously impair the efficiency of the machine.
Lastly, the drum coils may be either attached to the surface of a smooth armature core (fig. 9, I.), or may be wound through holes formed close to the periphery of the core, or may be embedded in the slots between projecting iron teeth (figs. 9 [II.] and 10). Originally employed by Antonio Pacinotti in connexion with ring winding, the toothed armature was after some considerable use largely discarded in favour of the smooth core; it has, however, been reintroduced with a fuller understanding of the special precautions necessitated in its design, and it is now so commonly used that it may be said to have superseded the smooth-surface armature.
Not only does the toothed armature reduce the length of the air-gap to the minimum permitted by mechanical and magnetic considerations, and furnish better mechanical protection to the armature coils, but it also ensures the positive holding of the active wires against the mechanical drag which they experience as they pass through the magnetic field. Further, the active wires in the toothed armature are relieved of a large proportion of this mechanical drag, which is transferred to the iron teeth. The lines of the field, after passing through the air-gap proper, divide between the teeth and the slots in proportion to their relative permeances. Hence at any moment the active wires are situated in a weak field, and for a given armature current the force on them is only proportional to this weak field. This important result is connected with the fact that when the armature is giving current the distribution of the lines over the face of each tooth is distorted, so that they become denser on the “trailing” side than on the “leading” side;13 the effect of the non-uniform distribution acting on all the teeth is to produce a magnetic drag on the armature core proportional to the current passing through the wires, so that the total resisting force remains the same as if the armature had a smooth core. The amount by which the stress on the active wires is reduced entirely depends upon the degree to which the teeth are saturated, but, since the relative permeability of iron even at a flux density of 20,000 lines per sq. cm. is to that of air approximately as 33 : 1, the embedded wires are very largely relieved of the driving stress. An additional gain is that solid bars of much greater width can be used in the toothed armature than on a smooth core without appreciable loss from eddy-currents within their mass.
A disadvantage of the slotted core is, however, that it usually necessitates the lamination of the pole-pieces. If the top of the slot is open, and its width of opening is considerably greater than the length of the air-gap from the iron of the pole-face to the surface of the teeth, the lines become unequally distributed not only at the surface of the teeth, but also at the face of the pole-pieces; and this massing of the lines into bands causes the density at the pole-face to be rhythmically varied as the teeth pass under it. No such variation can take place in a solid mass of metal without the production of eddy-currents within it; hence if the width of the slot-opening is equal to or exceeds twice the length of the single air-gap, lamination of the pole-pieces in the same plane as that of the armature core becomes advisable.
If the wires are threaded through holes or tunnels pierced close to the periphery of the core, the same advantages are gained as with open slots, and lamination of the pole-pieces is rendered unnecessary. But on the other hand, the process of winding becomes laborious and expensive, while the increase in the inductance of 769 the coils owing to their being surrounded by a closed iron circuit is prejudicial to sparkless commutation in the continuous-current dynamo and to the regulation of the voltage of the alternator. A compromise is found in the half-closed slot, which is not uncommon in alternators, although the open slot is more usual in continuous-current dynamos.
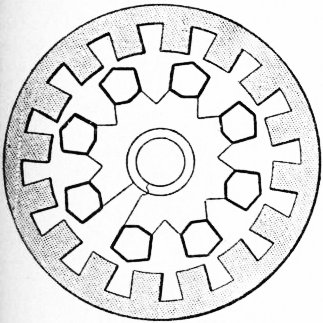 |
| Fig. 11. |
With the addition of more turns to the elementary drum loop or of several complete coils, new questions arise, and in connexion therewith the two great classes of machines, viz. alternators and continuous-current dynamos, which have above been treated side by side, diverge considerably, so that they are best considered separately. The electromotive-force equation of the alternator will be first deduced, and subsequently that of the continuous-current machine.
Corresponding to the number of pairs of poles in the multipolar alternator, it is evident that there may also be an equal number of coils as shown diagrammatically in fig. 11. The additional coils, being similarly situated in respect to other pairs of poles, will exactly reproduce the E.M.F. of the original coil in phase and magnitude, so that when they are connected in series the total E.M.F. will be proportional to the number of coils in series; or if they are connected in parallel, while not adding to the E.M.F., they will proportionately increase the current-carrying capacity of the combination. But within each coil the addition of more loops will not cause an equal increase in the total E.M.F., unless the phases of the component E.M.F.’s due to the several turns are identical, and on this account it becomes necessary to consider the effect of the width of the coil-side.
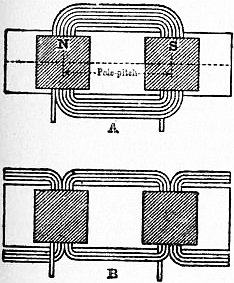 |
| Fig. 12. |
If the additional loops are wound within the same slots as the original loop, the winding is “concentrated,” and each turn will then add the same E.M.F. But if the coil-side is divided between two or more slots, the phase of the E.M.F. yielded by the wires in one slot being different from that of the wires in another neighbouring slot, the sum of all the E.M.F.’s will be less than the E.M.F. of one component loop multiplied by the number of loops or turns in the coil. The percentage reduction in the E.M.F. will depend upon the number of the slots in a coil-side and their distance apart, i.e. on the virtual width of the coil-side expressed as a fraction of the “pole-pitch” or the distance measured along the pitch-line from the centre of one pole to the centre of a neighbouring pole of opposite sign (fig. 12). The winding is now to be regarded as “grouped,” since a small number of distinct phases corresponding to the groups within the two, three or four slots have to be compounded together. As the number of slots per coil-side is increased, an approach is gradually made to the case of “uniform distribution,” such as would obtain in a smooth-core armature in which the turns of the coil are wound closely side by side. Thus in the six-turn coil of fig. 12 A, which represents the development of a two-pole armature when the core is cut down to the shaft and opened out flat, there are in effect six phases compounded together, each of which differs but little from that of its next neighbour. With numerous wires lying still closer together a large number of phases are compounded until the distribution becomes practically uniform; the decrease in the E.M.F., as compared with that of a single turn multiplied by the number in series, is then immediately dependent upon the width of the coil-side relatively to the pole-pitch.
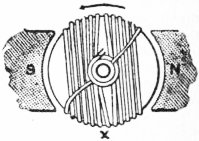 |
| Fig. 13. |
If the width of the inner loop of fig. 12 A is less than that of the pole-face, its two sides will for some portion of each period be moving under the same pole, and “differential action” results, the net E.M.F. being only that due to the difference between the E.M.F.’s of the two sides. The loop of smallest width must therefore exceed the width of pole-face, if direct differential action is to be avoided. The same consideration also determines the width of the outer loop; if this be deducted from twice the pole-pitch, the difference should not be less than the width of the pole-face, so that, e.g., in a bipolar machine the outer loop may stand to the S. pole exactly as the inner loop stands to the N. pole (fig. 13). In other words, the width of the coil-side must not exceed the width of the interpolar gap between two fields. Evidently then if the ratio of the pole-width to the pole-pitch approaches unity, the width of the coil-side must be very small, and vice versa. A compromise between these conflicting considerations is found if the pole is made not much more than half the pole-pitch, and the width of the coil-side is similarly about half the pole-pitch and therefore equal in width to the pole (fig. 13). A single large coil, such as that of fig. 12 A, can, however, equally well be divided into two halves by taking the end-connexions of one half of the turns round the opposite side of the shaft (fig. 12 B), as indeed has already been done in fig. 13. Each sheaf or band of active wires corresponding to a pole is thereby unaffected, but the advantages are gained that the axial length of the end-connexions is halved, and that they have less inductance. Thus if in fig. 11 there are four turns per coil, fig. 14 is electrically equivalent to it (save that the coils are here shown divided into two parallel paths, each carrying half the total current). When the large coils are divided as above described, it results that there are as many coils as there are poles, the outer loop of the small coil having a width equal to the pole-pitch, and the inner a width equal to the pole-face.
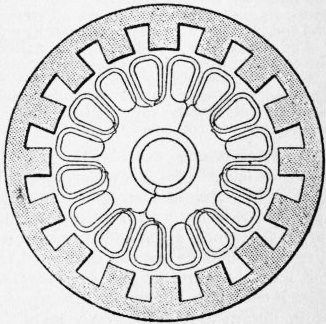 |
| Fig. 14. |
Such is the form which the “single-phase alternator” takes, but since only one-half of the armature core is now covered with winding, an entirely distinct but similar set of coils may be wound to form a second armature circuit between the coils of the first circuit. The phase of this second circuit will differ by 90° or a quarter of a period from that of the first, and it may either be used to feed an entirely separate external circuit possibly at a different pressure or, if it be composed of the same number of turns and therefore gives the same voltage, it may be interconnected with the first circuit to form a “quarter-phase alternator,” as will be more fully described later. By an extension of the same process, if the width of each side of a coil is reduced to one-sixth of the pole-pitch, three armature circuits can be wound on the same core, and a “three-phase alternator,” giving waves of E.M.F. differing in phase by 120°, is obtained.
The fundamental “electromotive-force equation” of the heteropolar alternator can now be given a more definite form. Let Za be the number of C. G. S. lines or the total flux, which issuing from any 770 one pole flows through the armature core, to leave it by another pole of opposite sign. Since each active wire cuts these lines, first as they enter the armature core and then as they emerge from it to enter another pole, the total number of lines cut in one revolution by any one active wire is 2pZa. The time in seconds taken by one revolution is 60/N. The average E.M.F. induced in each active wire in one revolution being proportional to the number of lines cut divided by the time taken to cut them is therefore 2Za (pN / 60) × 10−8 volts. The active wires which are in series and form one distinct phase may be divided into as many bands as there are poles; let each such band contain t active wires, which as before explained may either form one side of a single large coil or the adjacent sides of two coils when the large coil is divided into two halves. Since the wires are joined up into loops, two bands are best considered together, which with either arrangement yield in effect a single coil of t turns. The average E.M.F.’s of all the wires in the two bands when added together will therefore be 4Za (pN / 60)t × 10−8. But unless each band is concentrated within a single slot, there must be some differential action as they cross the neutral line between the poles, so that the last expression is virtually the gross average E.M.F. of the loops on the assumption that the component E.M.F.’s always act in agreement round the coil and do not at times partially neutralize one another. The net average E.M.F. of the coil as a whole, or the arithmetical mean of all the instantaneous values of a half-wave of the actual E.M.F. curve, is therefore reduced to an extent depending upon the amount of differential action and so upon the width of the coil-side when this is not concentrated. Let k′ = the coefficient by which the gross average E.M.F. must be multiplied to give the net average E.M.F.; then k′ may be called the “width-factor,” and will have some value less than unity when the wires of each band are spread over a number of slots. The net average E.M.F. of the two bands corresponding to a pair of poles is thus eav = 4k′Za (pN / 60)t × 10−8.
The shape of the curve of instantaneous E.M.F. of the coil must further be taken into account. The “effective” value of an alternating E.M.F. is equal to the square root of the mean square of its instantaneous values, since this is the value of the equivalent unidirectional and unvarying E.M.F., which when applied to a given resistance develops energy at the same rate as the alternating E.M.F., when the effect of the latter is averaged over one or any whole number of periods. Let k″ = the ratio of the square root of the mean square to the average E.M.F. of the coil, i.e. = effective E.M.F. / average E.M.F. Since it depends upon the shape of the E.M.F. curve, k″ is also known as the “form-factor”; thus if the length of gap between pole-face and armature core and the spacing of the wires were so graduated as to give a curve of E.M.F. varying after a sine law, the form-factor would have the particular value of π/2 √2 = 1.11, and to this condition practical alternators more or less conform. The effective E.M.F. of the two bands corresponding to a pair of poles is thus eeff = 4k′k″Za (pN / 60)t × 10−8.
In any one phase there are p pairs of bands, and these may be divided into q parallel paths, where q is one or any whole number of which p is a multiple. The effective E.M.F. of a complete phase is therefore peeff/q. Lastly, if m = the number of phases into which the armature winding is divided, and τ = the total number of active wires on the armature counted all round its periphery, t = τ / 2pm, and the effective E.M.F. per phase is Ea = 2k′k″Za (pNτ / 60mq) × 10−8.
The two factors k′ and k″ may be united into one coefficient, and the equation then takes its final form
Ea = 2KZa (pNτ / 60mq) × 10−8 volts
In the alternator q is most commonly 1, and there is only one circuit per phase; finally the value of K or the product of the width-factor and the form-factor usually falls between the limits of 1 and 1.25.
We have next to consider the effect of the addition of more armature loops in the case of dynamos which give a unidirectional E.M.F. in virtue of their split-ring collecting device, i.e. of the type shown in fig. 7 with drum armature or its equivalent ring form. As before, if the additional loops are wound in continuation of the first as one coil connected to a single split-ring, this coil must be more or less concentrated into a narrow band; since if the width becomes nearly equal to or exceeds the width of the interpolar gap, the two edges of the coil-side will just as in the alternator act differentially against one another during part of each revolution. The drum winding with a single coil thus gives an armature of the H- or “shuttle” form invented by Dr Werner von Siemens. Although the E.M.F. of such an arrangement may have a much higher maximum value than that of the curve of fig. 7 for a single loop, yet it still periodically varies during each revolution and so gives a pulsating current, which is for most practical uses unsuitable. But such pulsation might be largely reduced if, for example, a second coil were placed at right angles to the original coil and the two were connected in series; the crests of the wave of E.M.F. of the second coil will then coincide with the hollows of the first wave, and although the maximum of the resultant curve of E.M.F. may be no higher its fluctuations will be greatly decreased. A spacial displacement of the new coils along the pole-pitch, somewhat as in a polyphase machine, thus suggests itself, and the process may be carried still further by increasing the number of equally spaced coils, provided that they can be connected in series and yet can have their connexion with the external circuit reversed as they pass the neutral line between the poles.
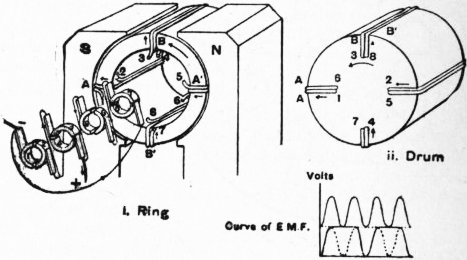 |
| Fig. 15. |
 |
| Fig. 16. |
Given two coils at right angles and with their split-rings displaced through a corresponding angle of 90°, they may be connected in series by joining one brush to the opposite brush of the second coil, the external circuit being applied to the two remaining brushes.14 The same arrangement may again be repeated with another pair of coils in parallel with the first, and we thus obtain fig. 15 with four split-rings, their connexions to the loops being marked by corresponding numerals; the four coils will give the same E.M.F. as the two, but they will be jointly capable of carrying twice the current, owing to their division into two parallel circuits. Now in place of the four split-rings may be employed the greatly simplified four-segment structure shown in fig. 16, which serves precisely the same purpose as the four split-rings but only requires two instead of eight brushes. The effect of joining brush 2 in fig. 15 across to brush 3, brush 4 to brush 5, 5 to 6, &c., has virtually been to connect the end of coil A with the beginning of coil B, and the end of coil B with the beginning of coil A′, and so on, until they form a continuous closed helix. Each sector of fig. 16 will therefore replace two halves of a pair of adjacent split-rings, if the end and beginning of a pair of adjacent coils are connected to it in a regular order of sequence. The four sectors are insulated from one another and from the shaft, and the whole structure is known as the “commutator,”15 its function being not simply to collect the current but also to commute its direction in any coil as it passes the interpolar gap. The principle of the “closed-coil continuous-current armature” is thus reached, in which there are at least two parallel circuits from brush to brush, and from which a practically steady current can be obtained. Each coil is successively short-circuited, as a brush bridges over the insulation between the two sectors which terminate it; and the brushes must be so set that the period of short-circuit takes place when the coil is generating little or no E.M.F., i.e. when it is moving through the zone between the pole-tips. The effect of the four coils in reducing the percentage fluctuation of the E.M.F. is very marked, as shown at the foot of fig. 15 (where the upper curve is the resultant obtained by adding together the separate curves of coils A and B), and the levelling process may evidently be carried still further by the insertion of more coils and more corresponding sectors in the commutator, until the whole 771 armature is covered with winding. For example, figs. 17 and 18 show a ring and a drum armature, each with eight coils and eight commutator sectors; their resultant curve, on the assumption that a single active wire gives the flat-topped curve of fig. 4, will be the upper wavy line of E.M.F. obtained by adding together two of the resultant curves of fig. 15, with a relative displacement of 45°. The amount of fluctuation for a given number of commutator sectors depends upon the shape of the curve of E.M.F. yielded by the separate small sections of the armature winding; the greater the polar arc, the less the fluctuation. In practice, with a polar arc equal to about 0.75 of the pitch, any number of sectors over 32 per pair of poles yields an E.M.F. which is sensibly constant throughout one or any number of revolutions.
 |
| Fig. 17. |
 |
| Fig. 18. |
The fundamental electro-motive-force equation of the continuous-current heteropolar machine is easily obtained by analogy from that of the alternator. The gross average E.W.F. from the two sides of a drum loop without reference to its direction is as before 4Za (pN / 60) × 10−8 volts. But for two reasons its net average E.M.F. may be less; the span of the loop may be less than the pole-pitch, so that even when the brushes are so set that the position of short-circuit falls on the line where the field changes its direction, the two sides of the loop for some little time act against each other; or, secondly, even if the span of the loop be equal to the pole-pitch, the brushes may be so set that the reversal of the direction of its induced E.M.F. does not coincide with reversal of the current by the passage of the coil under the brushes. The net average E.M.F. of the loop is therefore proportional to the algebraic sum of the lines which it cuts in passing from one brush to another, and this is equal to the net amount of the flux which is included within the loop when situated in the position of short-circuit under a brush. The amount of this flux may be expressed as k′Za where k′ is some coefficient, less than unity if the span of the coil be less than the pole-pitch, and also varying with the position of the brushes. The net average E.M.F. of the loop is therefore
4k′Za (pN / 60) × 10−8.
In practice the number of sections of the armature winding is so large and their distribution round the armature periphery is so uniform, that the sum total of the instantaneous E.M.F.’s of the several sections which are in series becomes at any moment equal to the net average E.M.F. of one loop multiplied by the number which are in series. If the winding is divided into q parallel circuits, the number of loops in series is τ/2q, so that the total E.M.F. is Ea = 2(k′ / q) Za (pN / 60)τ × 10−8 volts. Thus as compared with the alternator not only is there no division of the winding into separate phases, but the form-factor k′ disappears, since the effective and average E.M.F.’s are the same. Further whereas in the alternator q may = 1, in the continuous-current closed-coil armature there can never be less than two circuits in parallel from brush to brush, and if more, their number must always be a multiple of two, so that q can never be less than two and must always be an even number. Lastly, the factor k′ is usually so closely equal to 1, that the simplified equation may in practice be adopted, viz.
Ea = (2/q) (ZpN / 60) τ × 10−8 volts.
The fundamental equation of the electromotive force of the dynamo in its fully developed forms (1 a) (and 1 b) may be compared with its previous simple statement (I.). The three variable terms still find their equivalents, but are differently expressed, the density Bg being replaced by the total flux of one field Za, the length L of the single active wire by the total number of such wires τ, and the velocity of movement V by the number of revolutions per second. Even when the speed is fixed, an endless number of changes may be rung by altering the relative values of the remaining two factors; and in successful practice these may be varied between fairly wide limits without detriment to the working or economy of the machine. While it may be said that the equation of the E.M.F. was implicitly known from Faraday’s time onwards, the difficulty under which designers laboured in early days was the problem of choosing the correct relation of Za or τ for the required output; this, again, was due chiefly to the difficulty of predetermining the total flux before the machine was constructed. The general error lay in employing too weak a field and too many turns on the armature, and credit must here be given to the American inventors, E. Weston and T.A. Edison, for their early appreciation of the superiority in practical working of the drum armature, with comparatively few active wires rotating in a strong field.
Continuous-current Dynamos.—On passing to the separate consideration of alternators and continuous-current dynamos, the chief constructive features of the latter will first be taken in greater detail. As already stated in the The armature core. continuous-current dynamo the armature is usually the rotating portion, and the necessity of laminating its core has been generally described. The thin iron stampings employed to build up the core take the form of circular washers or “disks,” which in small machines are strung directly on the shaft; in larger multipolar machines, in which the required radial depth of iron is small relatively to the diameter, a central cast iron hub supports the disks. Since the driving force is transmitted through the shaft to the disks, they must in the former case be securely fixed by keys sunk into the shaft; when a central hub is employed (fig. 19) it is keyed to the shaft, and its projecting arms engage in notches stamped on the inner circumference of the disks, or the latter have dovetailed projections fitting into the arms. The disks are then tightly compressed and clamped between stout end-plates so as to form a nearly solid iron cylinder of axial length slightly exceeding the corresponding dimension of the poles. If the armature is more than 4 ft. in diameter, the disks become too large to be conveniently handled in one piece, and are therefore made in segments, which are built up so as to break joint alternately. Prior to assemblage, the external circumference of each disk is notched in a stamping machine with the required number of slots to receive the armature coils, and the longitudinal grooves thereby formed in the finished core only require to have their sharp edges smoothed off so that there may be no risk of injury to the insulation of the coils.
 |
| Fig. 19. |
With open slots either the armature coils may be encased with wrappings of oiled linen, varnished paper and thin flexible micanite sheeting in order to insulate them electrically from the iron slots in which they are afterwards embedded; Armature winding. or the slots may be themselves lined with moulded troughs of micanite, &c., for the reception of the armature coils, the latter method being necessary with half-closed slots. According to the nature of the coils armatures may be divided into the two classes of coil-wound and bar-wound. In the former class, round copper wire, double-cotton covered, is 772 employed, and the coils are either wound by hand directly on to the armature core, or are shaped on formers prior to being inserted in the armature slots. Hand-winding is now only employed in very small bipolar machines, the process being expensive and accompanied by the disadvantage that if one section requires to be repaired, the whole armature usually has to be dismantled and re-wound. Former-wound coils are, on the other hand, economical in labour, perfectly symmetrical and interchangeable, and can be thoroughly insulated before they are placed in the slots. The shapers employed in the forming process are very various, but are usually arranged to give to the finished coil a lozenge shape, the two straight active sides which fit into the straight slots being joined by V-shaped ends; at each apex of the coil the wire is given a twist, so that the two sides fall into different levels, an upper and a lower, corresponding to the two layers which the coil-sides form on the finished armature. Rectangular wire of comparatively small section may be similarly treated, and if only one loop is required per section, wide and thin strip can be bent into a complete loop, so that the only soldered joints are those at the commutator end where the loops are interconnected. But finally with massive rectangular conductors, the transition must be made to bar-winding, in which each bar is a half-loop, insulated by being taped after it has been bent to the required shape; the separate bars are arranged on the armature in two layers, and their ends are soldered together subsequently to form loops. As a general rule, whether bars or former-wound coils are employed, the armature is barrel-wound, i.e. the end-connexions project outwards from the slots with but little change of level, so that they form a cylindrical mass supported on projections from the end-plates of the core (fig. 19); but, in certain cases, the end-connexions are bent downwards at right angles to the shaft, and they may then consist of separate strips of copper bent to a so-called butterfly or evolute shape.
After the coils or loops have been assembled in the slots on the armature core, and the commutator has been fixed in place on the shaft, the soldering of the ends of the coils proceeds, by which at once the union of the end of one coil with the beginning of the next, and also their connexion to the commutator sectors, is effected, and in this lies the essential part of armature winding.
 |
| Lap-loops Fig. 20. |
The development of the modern drum armature, with its numerous coils connected in orderly sequence into a symmetrical winding, as contrasted with the earlier Siemens armatures, was initiated by F. von Hefner Alteneck (1871), and the laws governing the interconnexion of the coils have now been elaborated into a definite system of winding formulae. Whatever the number of wires or bars in each side of a coil, i.e. whether it consist of a single loop or of many turns, the final connexions of its free ends are not thereby affected, and it may be mentally replaced by a single loop with two active inducing sides. The coil-sides in their final position are thus to be regarded as separate primary elements, even in number, and distributed uniformly round the armature periphery or divided into small, equally spaced groups by being located within the slots of a toothed armature. Attention must then be directed simply to the span of the back connexion between the elements at the end of the armature further from the commutator, and to the span of the front connexion by which the last turn of a coil is finally connected to the first turn of the next in sequence, precisely as if each coil of many turns were reduced to a single loop. In order to avoid direct differential action, the span of the back connexion which fixes the width of the coil must exceed the width of the pole-face, and should not be far different from the pole-pitch; it is usually a little less than the pole-pitch. Taking any one element as No. 1 in fig. 20, where for simplicity a smooth-core bipolar armature is shown, the number of winding-spaces, each to be occupied by an element, which must be counted off in order to find the position of the next element in series, is called the “pitch” of the end-connexion, front or back, as the case may be. Thus the back pitch of the winding as marked by the dotted line in fig. 20 is 7, the second side of the first loop being the element numbered 1 + 7 = 8. In forming the front end-connexion which completes the loop and joins it to the next in succession, two possible cases present themselves. By the first, or “lap-winding,” the front end-connexion is brought backwards, and passing on its way to a junction with a commutator sector is led to a third element lying within the two sides of the first loop, i.e. the second loop starts with the element, No. 3, lying next but one to the starting-point of the first loop. The winding therefore returns backwards on itself to form each front end, but as a whole it works continually forwards round the armature, until it finally “re-enters,” after every element has been traversed. The development of the completed winding on a flat surface shows that it takes the form of a number of partially overlapping loops, whence its name originates. The firm-line portion of fig. 21 gives the development of an armature similar to that of fig. 18 when cut through at the point marked X and opened out; two of the overlapping loops are marked thereon in heavy lines. The multipolar lap-wound armature is obtained by simply repeating the bipolar winding p times, as indicated by the dotted additions of fig. 21 which convert it from a two-pole to a four-pole machine. The characteristic feature of the lap-wound armature is that there are as many parallel paths from brush to brush, and as many points at which the current must be collected, as there are poles. As the bipolar closed-coil continuous-current armature has been shown to consist in reality of two circuits in parallel, each giving the same E.M.F. and carrying half the total current, so the multipolar lap-wound drum consists of p pairs of parallel paths, each giving the same E.M.F. and carrying 1/2p of the total current. Thus in equation 1.b we have q = 2p, and the special form which the E.M.F. equation of the lap-wound armature takes is Ea = Za (N / 60)τ × 10−8 volts. All the brushes which are of the same sign must be connected together in order to collect the total armature current. The several brush-sets of the multipolar lap-wound machine may again be reduced to two by “cross-connexion” of sectors situated 360°/p apart, but this is seldom done, since the commutator must then be lengthened p times in order to obtain the necessary brush contact-surface for the collection of the entire current.
 |
| Fig. 21. |
 |
| Fig. 23. |
 |
| Wave-loops Fig. 22. |
But for many purposes, especially where the voltage is high and the current small, it is advantageous to add together the inductive effect of the several poles of the multipolar machine by throwing the E.M.F’s of half the total number of elements Wave-winding. into series, the number of parallel circuits being conversely again reduced to two. This is effected by the second method of winding the closed-coil continuous current drum, which is known 773 as “wave-winding.” The front pitch is now in the same direction round the armature as the back pitch (fig. 22), so that the beginning of the second loop, i.e. element No. 15, lies outside the first loop. After p loops have been formed and as many elements have been traversed as there are poles, the distance covered either falls short of or exceeds a complete tour of the armature by two winding-spaces, or the width of two elements. A second and third tour are then made, and so on, until finally the winding again closes upon itself. When the completed winding is developed as in fig. 23, it is seen to work continuously forwards round the armature in zigzag waves, one of which is marked in heavy lines, and the number of complete tours is equal to the average of the back and front pitches. Since the number of parallel circuits from brush to brush is q = 2, the E.M.F. equation of the wave-wound drum is Ea = pZa (N / 60)τ × 10−8 volts. Only two sets of brushes are necessary, but in order to shorten the length of the commutator, other sets may also be added at the point of highest and lowest potential up to as many in number as there are poles. Thus the advantage of the wave-wound armature is that for a given voltage and number of poles the number of active wires is only 1/p of that in the lap-wound drum, each being of larger cross-section in order to carry p times as much current; hence the ratio of the room occupied by the insulation to the copper area is less, and the available space is better utilized. A further advantage is that the two circuits from brush to brush consist of elements influenced by all the poles, so that if for any reason, such as eccentricity of the armature within the bore of the pole-pieces, or want of uniformity in the magnetic qualities of the poles, the flux of each field is not equal to that of every other, the equality of the voltage produced by the two halves of the winding is not affected thereby.
In appearance the two classes of armatures, lap and wave, may be distinguished in the barrel type of winding by the slope of the upper layer of back end-connexions, and that of the front connexions at the commutator end being parallel to one another in the latter, and oppositely directed in the former.
 |
| Fig. 24. |
After completion of the winding, the end-connexions are firmly bound down by bands of steel or phosphor bronze binding wire, so as to resist the stress of centrifugal force. In the case of smooth-surface armatures, such bands are also placed at intervals along the length of the armature core, but in toothed armatures, although the coils are often in small machines secured in the slots by similar bands of a non-magnetic high-resistance wire, the use of hard-wood wedges driven into notches at the sides of the slots becomes preferable, and in very large machines indispensable. The external appearance of a typical armature with lap-winding is shown in fig. 24.
A sound mechanical construction of the commutator is of vital importance to the good working of the continuous-current dynamo. The narrow, wedge-shaped sectors of hard-drawn copper, with their insulating strips of thin The commutator. mica, are built up into a cylinder, tightly clamped together, and turned in the lathe; at each end a V-shaped groove is turned, and into these are fitted rings of micanite of corresponding section (fig. 19); the whole is then slipped over a cast iron sleeve, and at either end strong rings are forced into the V-shaped grooves under great pressure and fixed by a number of closely-pitched tightening bolts. In dynamos driven by steam-turbines in which the peripheral speed of the commutator is very high, rings of steel are frequently shrunk on the surface of the commutator at either end and at its centre. But in every case the copper must be entirely insulated from the supporting body of metal by the interposition of mica or micanite and the prevention of any movement of the sectors under frequent and long-continued heating and cooling calls for the greatest care in both the design and the manufacture.
On passing to the second fundamental part of the dynamo, namely, the field-magnet, its functions may be briefly recalled as follows:—It has to supply the magnetic flux; to provide for it an iron path as nearly closed as possible Forms of field-magnet. upon the armature, save for the air-gaps which must exist between the pole-system and the armature core, the one stationary and the other rotating; and, lastly, it has to give the lines such direction and intensity within the air-gaps that they may be cut by the armature wires to the best advantage. Roughly corresponding to the three functions above summarized are the three portions which are more or less differentiated in the complete structure. These are: (1) the magnet “cores” or “limbs,” carrying the exciting coils whereby the inert iron is converted into an electro-magnet; (2) the yoke, which joins the limbs together and conducts the flux between them; and (3) the pole-pieces, which face the armature and transmit the lines from the limbs through the air-gap to the armature core, or vice versa.
 |
| Fig. 25. |
Of the countless shapes which the field-magnet may take, it may be said, without much exaggeration, that almost all have been tried; yet those which have proved economical and successful, and hence have met with general adoption, may be classed under a comparatively small number of types. For bipolar machines the single horse-shoe (fig. 25), which is the lineal successor of the permanent magnet employed in the first magneto-electric machines, was formerly very largely used. It takes two principal forms, according as the pole-pieces and armature are above or beneath the magnet limbs and yoke. The “over-type” form is best suited to small belt-driven dynamos, while the “under-type” is admirably adapted to be directly driven by the steam-engine, the armature shaft being immediately coupled to the crank-shaft of the engine. In the latter case the magnet must be mounted on non-magnetic supports of gun-metal or zinc, so as to hold it at some distance away from the iron bedplate which carries both engine and dynamo; otherwise a large proportion of the flux which passes through the magnet limbs would leak through the bedplate across from pole to pole without passing through the armature core, and so would not be cut by the armature wires.
 |
| Fig. 26. |
Next may be placed the “Manchester” field (fig. 26)—the type of a divided magnetic circuit in which the flux forming one field or pole is divided between two magnets. An exciting coil is placed on each half of the double horse-shoe magnet, the pair being so wound that consequent poles are formed above and below the armature. Each magnet thus carries one-half of the total flux, the lines of the two halves uniting to form a common field where they issue forth into or leave the air-gaps. The pole-pieces may be lighter than in the single horse-shoe type, and the field is much more symmetrical, whence it is well suited to ring armatures of large diameter. Yet these advantages are greatly discounted by the excessive magnetic leakage, and by the increased weight of copper in the exciting coils. Even if the greater percentage which the leakage lines bear to the useful flux is neglected, and the cross sectional area of each magnet core is but half that of the equivalent single horse-shoe, the weight of wire in the double magnet for the same rise of temperature in the coils must be some 40% more than in the single horse-shoe, and the rate at which energy is expended in heating the coils will exceed that of the single horse-shoe in the same proportion.
Thirdly comes the two-pole ironclad type, so called from the exciting coil being more or less encased by the iron yoke; this latter is divided into two halves, which pass on either side of the armature. Unless the yoke be kept well away from the polar edges and armature, the leakage across the air into the yoke becomes considerable, especially if only one exciting coil is used, as in fig. 27 A; it is better, therefore, to divide the excitation between two coils, as in fig. 27 B, when the field also becomes symmetrical.
From this form is easily derived the multipolar type of fig. 28 or fig. 29, which is by far the most usual for any number of poles from four upwards; its leakage coefficient is but small, and it is economical in weight both of iron and copper.
 |
| Fig. 27. |
As regards the materials of which magnets are made, generally speaking there is little difference in the permeability of “wrought iron” or “mild steel forgings” and good “cast steel”; typical 774 Materials of magnets. (B, H) curves connecting the magnetizing force required with different flux-densities for these materials are given under Electromagnetism. On the other hand there is a marked inferiority in the case of “cast iron,” which for a flux-density of B = 8000 C.G.S. lines per sq. cm. requires practically the same number of ampere-turns per centimetre length as steel requires for B = 16,000. Whatever the material, if the flux-density be pressed to a high value the ampere-turns are very largely increased owing to its approaching saturation, and this implies either a large amount of copper in the field coils or an undue expenditure of electrical energy in their excitation. Hence there is a limit imposed by practical considerations to the density at which the magnet should be worked, and this limit may be placed at about B = 16,000 for wrought iron or steel, and at half this value for cast iron. For a given flux, therefore, the cast iron magnet must have twice the sectional area and be twice as heavy, although this disadvantage is partly compensated by its greater cheapness. If, however, cast iron be used for the portion of the magnetic circuit which is covered with the exciting coils, the further disadvantage must be added that the weight of copper on the field-magnet is much increased, so that it is usual to employ forgings or cast steel for the magnet cores on which the coils are wound. If weight is not a disadvantage, a cast iron yoke may be combined with the wrought iron or cast steel magnet cores. An absence of joints in the magnetic circuit is only desirable from the point of view of economy of expense in machining the component parts during manufacture; when the surfaces which abut against each other are drawn firmly together by screws, the want of homogeneity at the joint, which virtually amounts to the presence of a very thin film of air, produces little or no effect on the total reluctance by comparison with the very much longer air-gaps surrounding the armature. In order to reduce the eddy-currents in the pole-pieces, due to the use of toothed armatures with relatively wide slots, the poles themselves must be laminated, or must have fixed to them laminated pole-shoes, built up of thin strips of mild steel riveted together (as shown in fig. 29).
 |
| Fig. 28. |
However it be built up, the mechanical strength of the magnet system must be carefully considered. Any two surfaces between which there exists a field of density Bg experience a force tending to draw them together proportional to the square of the density, and having a value of Bg² / (1.735 × 106) ℔ per sq. in. of surface, over which the density may be regarded as having the uniform value Bg. Hence, quite apart from the torque with which the stationary part of the dynamo tends to turn with the rotating part as soon as current is taken out of the armature, there exists a force tending to make the pole-pieces close on the armature as soon as the field is excited. Since both armature and magnet must be capable of resisting this force, they require to be rigidly held; although the one or the other must be capable of rotation, there should otherwise be no possibility of one part of the magnetic circuit shifting relatively to any other part. An important conclusion may be drawn from this circumstance. If the armature be placed exactly concentric within the bore of the poles, and the two or more magnetic fields be symmetrical about a line joining their centres, there is no tendency for the armature core to be drawn in one direction more than in another; but if there is any difference between the densities of the several fields, it will cause an unbalanced stress on the armature and its shaft, under which it will bend, and as this bending is continually reversed relatively to the fibres of the shaft, they will eventually become weakened and give way. Especially is this likely to take place in dynamos with short air-gaps, wherein any difference in the lengths of the air-gaps produces a much greater percentage difference in the flux-density than in dynamos with long air-gaps. In toothed armatures with short air-gaps the shaft must on this account be sufficiently strong to withstand the stress without appreciable bending.
Reference has already been made to the importance in dynamo design of the predetermination of the flux due to a given number of ampere-turns wound on the field-magnet, or, conversely, of the number of ampere-turns which must The magnetic circuit. be furnished by the exciting coils in order that a certain flux corresponding to one field may flow through the armature core from each pole. An equally important problem is the correct proportioning of the field-magnet, so that the useful flux Za may be obtained with the greatest economy in materials and exciting energy. The key to the two problems is to be found in the concept of a magnetic circuit as originated by H.A. Rowland and R.H.M. Bosanquet;16 and the full solution of both may be especially connected with the name of Dr J. Hopkinson, from his practical application of the concept in his design of the Edison-Hopkinson machine, and in his paper on “Dynamo-Electric Machinery.”17 The publication of this paper in 1886 begins the second era in the history of the dynamo; it at once raised its design from the level of empirical rules-of-thumb to a science, and is thus worthy to be ranked as the necessary supplement of the original discoveries of Faraday. The process of predetermining the necessary ampere-turns is described in a simple case under Electromagnetism. In its extension to the complete dynamo, it consists merely in the division of the magnetic circuit into such portions as have the same sectional area and permeability and carry approximately the same total flux; the difference of magnetic potential that must exist between the ends of each section of the magnet in order that the flux may pass through it is then calculated seriatim for the several portions into which the magnetic circuit is divided, and the separate items are summed up into one magnetomotive force that must be furnished by the exciting coils.
 |
| Fig. 29. |
The chief sections of the magnetic circuit are (1) the air-gaps, (2) the armature core, and (3) the iron magnet.
The air-gap of a dynamo with smooth-core armature is partly filled with copper and partly with the cotton, mica, or other materials used to insulate the core and wires; all these substances are, however, sensibly non-magnetic, so that the whole interferric gap between the iron of the pole-pieces and the iron of the armature may be treated as an air-space, of which the permeability is constant for all values of the flux density, and in the C.G.S. system is unity. Hence if lg and Ag be the length and area of the single air-gap in cm. and sq. cm., the reluctance of the double air-gap is 2lg / Ag, and the difference of magnetic potential required to pass Za lines over this reluctance is Za·2lg / Ag = Bg·2lg; or, since one ampere-turn gives 1.257 C.G.S. units of magnetomotive force, the exciting power in ampere-turns required over the two air-gaps is Xg = Bg·2lg / 1.257 = 0.8Bg·2lg. In the determination of the area Ag small allowance must be made for the fringe of lines which extend beyond the actual polar face. In the toothed armature with open slots, the lines are no longer uniformly distributed over the air-gap area, but are graduated into alternate bands of dense and weak induction corresponding to the teeth and slots. Further, the lines curve round into the sides of the teeth, so that their average length of path in the air and the air-gap reluctance is not so easily calculated. Allowance must be made for this by taking an increased length of air-gap = mlg, where m is the ratio maximum density/mean density, of which the value is chiefly determined by the ratios of the width of tooth to width of slot and of the width of slot to the air-gap between pole-face and surface of the armature core.
The armature core must be divided into the teeth and the core proper below the teeth. Owing to the tapering section of the teeth, the density rises towards their root, and when this reaches a high value, such as 18,000 or more lines per sq. cm., the saturation of the iron again forces an increasing proportion of the lines outwards into the slot. A distinction must then be drawn between the “apparent” induction which would hold if all the lines were concentrated in the teeth, and the “real” induction. The area of the iron is obtained by multiplying the number of teeth under the pole-face by their width and by the net length of the iron core parallel to the axis of rotation. The latter is the gross length of the armature less the space lost through the insulating varnish or paper between the disks or through the presence of ventilating ducts, which are introduced at intervals along the length of the core. The former deduction averages about 7 to 10% of the gross length, while the latter, especially in large multipolar machines, is an even more important item. Alter calculating the density at different sections of the teeth, reference has now to be made to a (B, H) or flux-density curve, from which may be found the number of ampere-turns required per cm. length of path. This number may be expressed as a function of the density in the teeth, and ƒ(Bt) be its average value over the length of a tooth, the ampere-turns of excitation required over the teeth on either side of the core as the lines of one field enter or leave the armature is Xt = ƒ(Bt)·2lt, where lt is the length of a single tooth in cm.
In the core proper below the teeth the length of path continually shortens as we pass from the middle of the pole towards the centre line of symmetry. On the other hand, as the lines gradually accumulate in the core, their density increases from zero midway under the poles until it reaches a maximum on the line of symmetry. The two effects partially counteract one another, and tend to equalize the difference of magnetic potential required over the paths of varying lengths; but since the reluctivity of the iron increases more rapidly than the density of the lines, we may approximately take for the length of path (la) the minimum peripheral distance between the edges of adjacent pole-faces, and then assume the maximum value of the density of the lines as holding throughout this entire path. In ring and drum machines the flux issuing from one pole divides into two halves in the armature core, so that the maximum density of lines in the armature is Ba = Za / 2ab, where a = the radial depth of the disks in centimetres and b = the net length of iron core. The total exciting power required between the pole-pieces is therefore, at no load, Xp = Xg + Xt + Xa, where Xa = ƒ(Ba)·la; in order, however, to allow for the effect of the armature current, which increases with the load, a further term Xb, must be added.
 |
| Fig. 30. |
In the continuous-current dynamo it may be, and usually is, necessary to move the brushes forward from the interpolar line of symmetry through a small angle in the direction of rotation, in order to avoid sparking between the brushes and the commutator (vide infra). When the dynamo is giving current, the wires on either side of the diameter of commutation form a current-sheet flowing along the surface of the armature from end to end, and whatever the actual end-connexions of the wires, the wires may be imagined to be joined together into a system of loops such that the two sides of each loop are carrying current in opposite directions. Thus a number of armature ampere-turns are formed, and their effect on the entire system of magnet and armature must be taken into account. So long as the diameter of commutation coincides with the line of symmetry, the armature may be regarded as a cylindrical electromagnet producing a flux of lines, as shown in fig. 30. The direction of the self-induced flux in the air-gaps is the same as that of the lines of the external field in one quadrant on one side of DC, but opposed to it in the other quadrant on the same side of DC; hence in the resultant field due to the combined action of the field-magnet and armature ampere-turns, the flux is as much strengthened over the one half of each polar face as it is weakened over the other, and the total number of lines is unaffected, although their distribution is altered. The armature ampere-turns are then called cross-turns, since they produce a cross-field, which, when combined with the symmetrical field, causes the leading pole-corners ll to be weakened and the trailing pole-corners tt to be strengthened, the neutral line of zero field being thus twisted forwards in the direction of rotation. But when the brushes and diameter of commutation are shifted forward, as shown in fig. 31, it will be seen that a number of ampere-turns, forming a zone between the lines Dn and mC, are in effect wound immediately on the magnetic circuit proper, and this belt of ampere-turns is in direct opposition to the ampere-turns of the field, as shown by the dotted and crossed wires on the pole-pieces. The armature ampere-turns are then divisible into the two bands, the back-turns, included within twice the angle of lead λ, weakening the field, and the cross-turns, bounded by the lines Dm, nC, again producing distortion of the weakened symmetrical field. If, therefore, a certain flux is to be passed through the armature core in opposition to the demagnetizing turns, the difference of magnetic potential between the pole-faces must include not only Xa, Xt, and Xg, but also an item Xb, in order to balance the “back” ampere-turns of the armature. The amount by which the brushes must be shifted forward increases with the armature current, and in corresponding proportion the back ampere-turns are also increased, their value being cτ2λ / 360°, where c = the current carried by each of the τ active wires. Thus the term Xb, takes into account the effect of the armature reaction on the total flux; it varies as the armature current and angle of lead required to avoid sparking are increased; and the reason for its introduction in the fourth place (Xp = Xg + Xt + Xa + Xb), is that it increases the magnetic difference of potential which must exist between the poles of the dynamo, and to which the greater part of the leakage is due. The leakage paths which are in parallel with the armature across the poles must now be estimated, and so a new value be derived for the flux at the commencement of the iron-magnet path. If P = their joint permeance, the leakage flux due to the difference of potential at the poles is zl = 1.257Xp × P, and this must be added to the useful flux Za, or Zp = Za + Zl. There are also certain leakage paths in parallel with the magnet cores, and upon the permeance of these a varying number of ampere-turns is acting as we proceed along the magnet coils; the magnet flux therefore increases by the addition of leakage along the length of the limbs, and finally reaches a maximum near the yoke. Either, then, the density in the magnet Bm = Zm / Am will vary if the same sectional area be retained throughout, or the sectional area of the magnet must itself be progressively increased. In general, sufficient accuracy will be obtained by assuming a certain number of additional leakage lines zn as traversing the entire length of magnet limbs and yoke (= lm), so that the density in the magnet has the uniform value Bm = (Zp + zn) / Am. The leakage flux added on actually within the length of the magnet core or zn will be approximately equal to half the total M.M.F. of the coils multiplied by the permeance of the leakage paths around one coil. The corresponding value of H can then be obtained from the (B, H) curve of the material of which the magnet is composed, and the ampere-turns thus determined must be added to Xp, or X = Xp + Xm, where Xm = ƒ(Bm)lm. The final equation for the exciting power required on a magnetic circuit as a whole will therefore take the form
X = AT = 0.8Bg·2lg + ƒ(Bt) 2lt + ƒ(Ba) la + Xb + ƒ(Bm) lm.
 |
| Fig. 31. |
If the magnet cores are of wrought iron or cast steel, and the yoke is of cast iron, the last term must be divided into two portions corresponding to the different materials, i.e. into f(Bm)lm + f(By)ly. In the ordinary multipolar machine with as many magnet-coils as there are poles, each coil must furnish half the above number of ampere-turns.
Since no substance is impermeable to the passage of magnetic flux, the only form of magnetic circuit free from leakage is one uniformly wound with ampere-turns over its whole length. The reduction of the magnetic leakage to a minimum in any Magnetic leakage. given type is therefore primarily a question of distributing the winding as far as possible uniformly upon the circuit, and as the winding must be more or less concentrated into coils, it resolves itself into the necessity of introducing as long air-paths as possible between any surfaces which are at different magnetic potentials. No iron should be brought near the machine which does not form part of the magnetic circuit proper, and especially no iron should be brought near the poles, between which the difference of magnetic potential practically reaches its maximum value. In default of a machine of the same size or similar type on which to experiment, the probable direction of the leakage flux must be assumed from the drawing, and the air surrounding the machine must be mapped out into areas, between which the permeances are calculated as closely as possible by means of such approximate formulae as those devised by Professor G. Forbes.
In the earliest “magneto-electric” machines permanent steel magnets, either simple or compound, were employed, and for many years these were retained in certain alternators, some of which are still in use for arc lighting in lighthouses. Excitation of field-magnet. But since the field they furnish is very weak, a great advance was made when they were replaced by soft iron electromagnets, which could be made to yield a much more intense flux. As early as 1831 Faraday18 experimented with electromagnets, and after 1850 they gradually superseded the permanent magnet. When the total ampere-turns required to excite the electromagnet have been determined, it remains to decide how the excitation shall be obtained; and, according to the method 776 adopted, continuous-current machines may be divided into four well-defined classes.
 |
| Fig. 32. |
The simplest method, and that which was first used, is separate excitation from some other source of direct current, which may be either a primary or a secondary battery or another dynamo (fig. 32). But since the armature yields a continuous current, it was early suggested (by J. Brett in 1848 and F. Sinsteden in 1851) that this current might be utilized to increase the flux; combinations of permanent and electromagnets were therefore next employed, acting either on the main armature or on separate armatures, until in 1867 Dr Werner von Siemens and Sir C. Wheatstone almost simultaneously discovered that the dynamo could be made self-exciting through the residual magnetism retained in the soft iron cores of the electromagnet. The former proposed to take the whole of the current round the magnet coils which were in series with the armature and external circuit, while the latter proposed to utilize only a portion derived by a shunt from the main circuit; we thus arrive at the second and third classes, namely, series and shunt machines. The starting of the process of excitation in either case is the same; when the brushes are touching the commutator and the armature is rotated, the small amount of flux left in the magnet is cut by the wires, and a very small current begins to flow round the closed circuit; this increases the flux, which in turn further increases the E.M.F. and current, until, finally, the cumulative effect stops through the increasing saturation of the iron cores. Fig. 33, illustrating the series machine, shows the winding of the exciting coils to be composed of a few turns of thick wire. Since the current is undivided throughout the whole circuit, the resistance of both the armature and field-magnet winding must be low as compared with that of the external circuit, if the useful power available at the terminals of the machine is to form a large percentage of the total electrical power—in other words, if the efficiency is to be high. Fig. 34 shows the third method, in which the winding of the field-magnets is a shunt or fine-wire circuit of many turns applied to the terminals of the machine; in this ease the resistance of the shunt must be high as compared with that of the external circuit, in order that only a small proportion of the total energy may be absorbed in the field.
 | |
| Fig. 33. | Fig. 34. |
Since the whole of the armature current passes round the field-magnet of the series machine, any alteration in the resistance of the external circuit will affect the excitation and also the voltage. A curve connecting together corresponding values of external current and terminal voltage for a given speed of rotation is known as the external-characteristic of the machine; in its main features it has the same appearance as a curve of magnetic flux, but when the current exceeds a certain amount it begins to bend downwards and the voltage decreases. The reason for this will be found in the armature reaction at large loads, which gradually produces a more and more powerful demagnetizing effect, as the brushes are shifted forwards to avoid sparking; eventually the back ampere-turns overpower any addition to the field that would otherwise be due to the increased current flowing round the magnet. The “external characteristic” for a shunt machine has an entirely different shape. The field-magnet circuit being connected in parallel with the external circuit, the exciting current, if the applied voltage remains the same, is in no way affected by alterations in the resistance of the latter. As, however, an increase in the external current causes a greater loss of volts in the armature and a greater armature reaction, the terminal voltage, which is also the exciting voltage, is highest at no load and then diminishes. The fall is at first gradual, but after a certain critical value of the armature current is reached, the machine is rapidly demagnetized and loses its voltage entirely.
 |
| Fig. 35. |
The last method of excitation, namely, compound-winding (fig. 35), is a combination of the two preceding, and was first used by S.A. Varley and by C.F. Brush. If a machine is in the first instance shunt-wound, and a certain number of series-turns are added, the latter, since they carry the external current, can be made to counteract the effect which the increased external current would have in lowering the voltage of the simple shunt machine. The ampere-turns of the series winding must be such that they not only balance the increase of the demagnetizing back ampere-turns on the armature, but further increase the useful flux, and compensate for the loss of volts over their own resistance and that of the armature. The machine will then give for a constant speed a nearly constant voltage at its terminals, and the curve of the external characteristic becomes a straight line for all loads within its capacity. Since with most prime movers an increase of the load is accompanied by a drop in speed, this effect may also be counteracted; while, lastly, if the series-turns are still further increased, the voltage may be made to rise with an increasing load, and the machine is “over-compounded.”
At the initial moment when an armature coil is first short-circuited by the passage of the two sectors forming its ends under the contact surface of a brush, a certain amount of electromagnetic energy is stored up in its magnetic Commutation and sparking at the brushes. field as linked with the ampere-turns of the coil when carrying its full share of the total armature current. During the period of short-circuit this quantity of energy has to be dissipated as the current falls to zero, and has again to be re-stored as the current is reversed and raised to the same value, but in the opposite direction. The period of short-circuit as fixed by the widths of the brush and of the mica insulation between the sectors, and by the peripheral speed of the commutator is extremely brief, and only lasts on an average from 1⁄200th to 1⁄1000th of a second. The problem of sparkless commutation is therefore primarily a question of our ability to dissipate and to re-store the required amount of energy with sufficient rapidity.
An important aid towards the solution of this problem is found in the effect of the varying contact-resistance between the brush and the surfaces of the leading and trailing sectors which it covers. As the commutator moves under the brush, the area of contact which the brush makes with the leading sector diminishes, and the resistance between the two rises; conversely, the area of contact between the brush and the trailing sector increases and the resistance falls. This action tends automatically to bring the current through each sector into strict proportionality to the amount of its surface which is covered by the brush, and so to keep the current-density and the loss of volts over the contacts uniform and constant. As soon as the current-density in the two portions of the brush becomes unequal, a greater amount of heat is developed at the commutator surface, and this in the first place affords an additional outlet for the dissipation of the stored energy of the coil, while after reversal of the current it is the accompaniment of a re-storage of the required energy. This energy, as well as that which is spent in heating the coil, can in fact, in default of other sources, be derived through the action of the unequal current-density from the electrical output of the rest of the armature winding, and so only indirectly from the prime mover.
In practice, when the normal contact-resistance of the brushes is low relatively to the resistance of the coil, as is the case with metal brushes of copper or brass gauze, but little benefit can be obtained from the action of the varying contact-resistance. It exerts no appreciable effect until close towards the end of the period of short-circuit, and then only with such a high-current-density at the trailing edge of the leaving sector that at the moment of parting the brush-tip is fused, or its metal volatilized, and sparking has in fact set in. With such brushes, then, it becomes necessary to call in the aid of a reversing E.M.F. impressed upon the coil by the magnetic field through which it is moving. If such a reversing field comes into action while 777 the current is still unreversed, its E.M.F. is opposed to the direction of the current, and the coil is therefore driving the armature forward as in a motor; it thus affords a ready means of rapidly dissipating part of the initial energy in the form of mechanical work instead of as heat. After the current has been reversed, the converse process sets in, and the prime mover directly expends mechanical energy not only in heating the coil, but also in storing up electromagnetic energy with a rapidity dependent upon the strength of the reversing field. The required direction of external field can be obtained in the dynamo by shifting the brushes forward, so that the short-circuited coil enters into the fringe of lines issuing from the leading pole-tip, i.e. by giving the brushes an “angle of lead.” An objection to this process is that the main flux is thereby weakened owing to the belt of back ampere-turns which arises (v. supra). A still greater objection is that the amount of the angle of lead must be suited to the value of the load, the corrective power of copper brushes being very small if the reversing E.M.F. is not closely adjusted in proportion to the armature current.
On this account metal brushes have been almost entirely superseded by carbon moulded into hard blocks. With these, owing to their higher specific contact-resistance, a very considerable reversing effect can be obtained through the action of unequal current-density, and indeed in favourable cases complete sparklessness can be obtained throughout the entire range of load of the machine with a fixed position of the brushes. Yet if the work which they are called upon to perform exceeds certain limits, they tend to become overheated with consequent glowing or sparking at their tips, so that, wherever possible, it is advisable to reinforce their action by a certain amount of reversing field, the brushes being set so that its strength is roughly correct for, say, half load.
In the case of dynamos driven by steam-turbines, sparkless commutation is especially difficult to obtain owing to the high speed of rotation and the very short space of time in which the current has to be reversed. Special “reversing poles” then become necessary; these are wound with magnetizing coils in series with the main armature current, so that the strength of field which they yield is roughly proportional to the current which has to be reversed. These again may be combined with a “compensating winding” embedded in the pole-faces and carrying current in the opposite direction to the armature ampere-turns, so as to neutralize the cross effect of the latter and prevent distortion of the resultant field.
From the moment that a dynamo begins to run with excited field, heat is continuously generated by the passage of the current through the windings of the field-magnet coils and the armature, as well as by the action of hysteresis and Heating effects. eddy currents in the armature and pole-pieces. Whether the source of the heat be in the field-magnet or in the armature, the mass in which it originates will continue to rise in temperature until such a difference of temperature is established between itself and the surrounding air that the rate at which the heat is carried off by radiation, convection and conduction is equal to the rate at which it is being generated. Evidently, then, the temperature which any part of the machine attains after a prolonged run must depend on the extent and effectiveness of the cooling surface from which radiation takes place, upon the presence or absence of any currents of air set up by the rotation of itself or surrounding parts, and upon the presence of neighbouring masses of metal to carry away the heat by conduction. In the field-magnet coils the rate at which heat is being generated is easily determined, since it is equal to the square of the current passing through them multiplied by their resistance. Further, the magnet is usually stationary, and only indirectly affected by draughts of air due to the rotating armature. Hence for machines of a given type and of similar proportions, it is not difficult to decide upon some method of reckoning the cooling surface of the magnet coils Sc, such that the rise of temperature above that of the surrounding air may be predicted from an equation of the form t° = kW / Sc, where W = the rate in watts at which heat is generated in the coils, and k is some constant depending upon the exact method of reckoning their cooling surface. As a general rule the cooling surface of a field-coil is reckoned as equal to the exposed outer surface of its wire, the influence of the end flanges being neglected, or only taken into account in the case of very short bobbins wound with a considerable depth of wire. In the case of the rotating armature a similar formula must be constructed, but with the addition of a factor to allow for the increase in the effectiveness of any given cooling surface due to the rotation causing convection currents in the surrounding air. Only experiment can determine the exact effect of this, and even with a given type of armature it is dependent on the number of poles, each of which helps to break up the air-currents, and so to dissipate the heat. For example, in two-pole machines with drum bar-armatures, if the cooling surface be reckoned as equal to the cylindrical exterior plus the area of the two ends, the heating coefficient for a peripheral speed of 1500 ft. per minute is less than half of that for the same armature when at rest. A further difficulty still meets the designer in the correct predetermination of the total loss of watts in an armature before the machine has been tested. It is made up of three separate items, namely, the copper loss in the armature winding, the loss by hysteresis in the iron, and the loss by eddy currents, which again may be divided into those in the armature bars and end-connexions, and those in the core and its end-plates. The two latter items are both dependent upon the speed of the machine; but whereas the hysteresis loss is proportional to the speed for a given density of flux in the armature, the eddy current loss is proportional to the square of the speed, and owing to this difference, the one loss can be separated from the other by testing an armature at varying speeds. Thus for a given rise of temperature, the question of the amount of current which can be taken out of an armature at different speeds depends upon the proportion which the hysteresis and eddy watts bear to the copper loss, and the ratio in which the effectiveness of the cooling surface is altered by the alteration in speed. Experimental data, again, can alone decide upon the amount of eddy currents that may be expected in given armatures, and caution is required in applying the results of one machine to another in which any of the conditions, such as the number of poles, density in the teeth, proportions of slot depth to width, &c., are radically altered.
It remains to add, that the rise of temperature which may be permitted in any part of a dynamo after a prolonged run is very generally placed at about 70° Fahr. above the surrounding air. Such a limit in ordinary conditions of working leads to a final temperature of about 170° Fahr., beyond which the durability of the insulation of the wires is liable to be injuriously affected. Upon some such basis the output of a dynamo in continuous working is rated, although for short periods of, say, two hours the normal full-load current of a large machine may be exceeded by some 25% without unduly heating the armature.
For the electro-deposition of metals or the electrolytic treatment of ores a continuous current is a necessity; but, apart from such use, the purposes from which the continuous-current dynamo is well adapted are so numerous that Uses of continuous current dynamos. they cover nearly the whole field of electrical engineering, with one important exception. To meet these various uses, the pressures for which the machine is designed are of equally wide range; for the transmission of power over long distances they may be as high as 3000 volts, and for electrolytic work as low as five. Each electrolytic bath, with its leads, requires on an average only some four or five volts, so that even when several are worked in series the voltage of the dynamo seldom exceeds 60. On the other hand, the current is large and may amount to as much as from 1000 to 14,000 amperes, necessitating the use of two commutators, one at either end of the armature, in order to collect the current without excessive heating of the sectors and brushes. The field-magnets are invariably shunt-wound, in order to avoid reversal of the current through polarization at the electrodes of the bath. For incandescent lighting by glow lamps, the requirements of small isolated installations and of central stations for the distribution of electrical energy over large areas must be distinguished. For the lighting of a private house or small factory, the dynamo giving from 5 to 100 kilo-watts of output is commonly wound for a voltage of 100, and is driven by pulley and belt from a gas, oil or steam-engine; or, if approaching the higher limit above mentioned, it is often directly coupled to the crank-shaft of the steam-engine. If used in conjunction with an accumulator of secondary cells, it is shunt-wound, and must give the higher voltage necessary to charge the battery; otherwise it is compound-wound, in order to maintain the pressure on the lamps constant under all loads within its capacity. The compound-wound dynamo is likewise the most usual for the lighting of steamships, and is then directly coupled to its steam-engine; its output seldom exceeds 100 kilo-watts, at a voltage of 100 or 110. For larger installations a voltage of 250 is commonly used, while for central-station work, economy in the distributing 778 mains dictates a higher voltage, especially in connexion with a three-wire system; the larger dynamos may then give 500 volts, and be connected directly across the two outer wires. A pair of smaller machines coupled together, and each capable of giving 250 volts, are often placed in series across the system, with their common junction connected to the middle wire; the one which at any time is on the side carrying the smaller current will act as a motor and drive the other as a dynamo, so as to balance the system. The directly-coupled steam dynamo may be said to have practically displaced the belt- or rope-driven sets which were formerly common in central stations. The generating units of the central station are arranged in progressive sizes, rising from, it may be, 250 or 500 horse-power up to 750 or 1000, or in large towns to as much as 5000 horse-power. If for lighting only, they are usually shunt-wound, the regulation of the voltage, to keep the pressure constant on the distributing system under the gradual changes of load, being effected by variable resistances in the shunt circuit of the field-magnets.
Generators used for supplying current to electric tramways are commonly wound for 500 volts at no load and are over-compounded, so that the voltage rises to 550 volts at the maximum load, and thus compensates for the loss of volts over the transmitting lines. For arc lighting it was formerly usual to employ a class of dynamo which, from the nature of its construction, was called an “open-coil” machine, and which gave a unidirectional but pulsating current. Of such machines the Brush and Thomson-Houston types were very widely used; their E.M.F. ranged from 2000 to 3000 volts for working a large number of arcs in series, and by means of special regulators their current was maintained constant over a wide range of voltage. But as their efficiency was low and they could not be applied to any other purpose, they have been largely superseded in central stations by closed-coil dynamos or alternators, which can also be used for incandescent lighting. In cases where the central station is situated at some distance from the district to which the electric energy is to be supplied, voltages from 1000 to 2000 are employed, and these are transformed down at certain distributing centres by continuous-current transformers (see Transformers and Electricity Supply). These latter machines are in reality motor-driven dynamos, and hence are also called motor-generators; the armatures of the motor and dynamo are often wound on the same core, with a commutator at either end, the one to receive the high-pressure motor current, and the other to collect the low-pressure current furnished by the dynamo.
In all large central stations it is necessary that the dynamos should be capable of being run in parallel, so that their outputs may be combined on the same “omnibus bars” and thence distributed to the network of feeders. With simple shunt-wound machines this is easily effected by coupling together terminals of like sign when the voltage of the two or more machines are closely equal. With compound-wound dynamos not only must the external terminals of like sign be coupled together, but the junctions of the brush leads with the series winding must be connected by an “equalizing” lead of low resistance; otherwise, should the E.M.F. of one machine for any reason fall below the voltage of the omnibus bars, there is a danger of its polarity being reversed by a back current from the others with which it is in parallel.
Owing to the necessary presence in the continuous-current dynamo of the commutator, with its attendant liability to sparking at the brushes, and further, owing to the difficulty of insulating the rotating armature wires, a pressure of 3000 volts has seldom been exceeded in any one continuous-current machine, and has been given above as the limiting voltage of the class. If therefore it is required to work with higher pressures in order to secure economy in the transmitting lines, two or more machines must be coupled in series by connecting together terminals which are of unlike sign.19 The stress of the total voltage may still fall on the insulation of the winding from the body of the machine; hence for high-voltage transmission of power over very long distances, the continuous-current dynamo in certain points yields in convenience to the alternator. In this there is no commutator, the armature coils may be stationary and can be more thoroughly insulated, while further, if it be thought undesirable to design the machine for the full transmitting voltage, it is easy to wind the armature for a low pressure; this can be subsequently transformed up to a high pressure by means of the alternating-current transformer, which has stationary windings and so high an efficiency that but little loss arises from its use. With these remarks, the transition may be made to the fuller discussion of the alternator.
Alternators.
The frequency employed in alternating-current systems for distributing power and light varies between such wide limits as 25 and 133; yet in recent times the tendency has been towards standard frequencies of 25, 50 Frequency. and 100 as a maximum. High frequencies involve more copper in the magnet coils, owing to the greater number of poles, and a greater loss of power in their excitation, but the alternator as a whole is somewhat lighter, and the transformers are cheaper. On the other hand, high frequency may cause prejudicial effects, due to the inductance and capacity of the distributing lines; and in asynchronous motors used on polyphase systems the increased number of poles necessary to obtain reasonable speeds reduces their efficiency, and is otherwise disadvantageous, especially for small horse-powers. A frequency lower than 40 is, however, not permissible where arc lighting is to form any considerable portion of the work and is to be effected by the alternating current without rectification, since below this value the eye can detect the periodic alteration in the light as the carbons alternately cool and become heated. Thus for combined lighting and power 50 or 60 are the most usual frequencies; but if the system is designed solely or chiefly for the distribution of power, a still lower frequency is preferable. On this account 25 was selected by the engineers for the Niagara Falls power transmission, after careful consideration of the problem, and this frequency has since been widely adopted in similar cases.
The most usual type of heteropolar alternator has an internal rotating field-magnet system, and an external stationary armature, as in fig. 10. The coils of the armature, which must for high voltages be heavily insulated, are then Alternator construction. not subjected to the additional stresses due to centrifugal force; and further, the collecting rings which must be attached to the rotating portion need only transmit the exciting current at a low voltage.
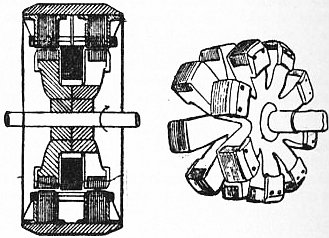 |
| Fig. 36. |
The homopolar machine possesses the advantages that only a single exciting coil is required, whatever the number of polar projections, and that both the armature and field-magnet coils may be stationary. From fig. 8 it will be seen that it is not essential that the exciting coil should revolve with the internal magnet, but it may be supported from the external stationary armature while still embracing the central part of the rotor. The E.M.F. is set up in the armature coils through the periodic variation of the flux through them as the iron projections sweep past, and these latter may be likened to a number of “keepers,” which complete the magnetic circuit. From the action of the rotating iron masses they may also be considered as the inducing elements or “inductors,” and the homopolar machine is thence also known as the “inductor alternator.” If the end of the rotor marked S in fig. 8 is split up into a number of S polar projections similar to the N poles, a second set of armature coils may be arranged opposite to them, and we obtain an inductor 779 alternator with double armature. Or the polar projections at the two ends may be staggered, and a single armature winding be passed straight through the armature, as in fig. 36, which shows at the side the appearance of the revolving inductor with its crown of polar projections in one ring opposite to the gaps between the polar projections of the other ring. But in spite of its advantage of the single stationary exciting coil, the inductor alternator has such a high degree of leakage, and the effect of armature reaction is so detrimental in it, that the type has been gradually abandoned, and a return has been almost universally made to the heteropolar alternator with internal poles radiating outwards from a circular yoke-ring. The construction of a typical machine of this class is illustrated in fig. 37.
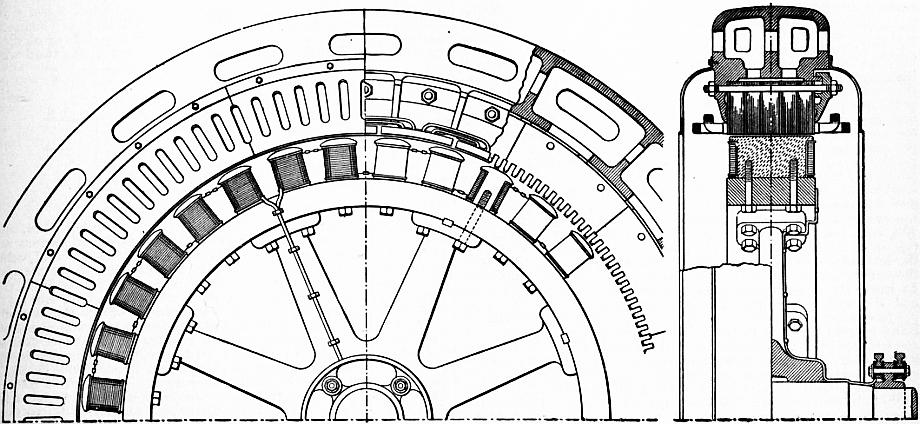 |
| Fig. 37. |
Since the field-magnet coils rotate, they must be carefully designed to withstand centrifugal force, and are best composed of flat copper strip wound on edge with thin insulation between adjacent layers. The coil is secured by the edges of the pole-shoes which overhang the pole and tightly compress the coil against the yoke-ring; the only effect from centrifugal force is then to compress still further the flat turns of copper against the pole-shoes without deformation. The poles are either of cast steel of circular or oblong section, bolted to the rim of the yoke-ring, or are built up of thin laminations of sheet steel. When the peripheral speed is very high, the yoke-ring will be of cast steel or may itself be built up of sheet steel laminations, this material being reliable and easily tested to ensure its sound mechanical strength. If the armature slots are open, the pole-pieces will in any case be laminated to reduce the eddy currents set up by the variation of the flux-density.
Owing to the great number of poles20 of the alternator when driven by a reciprocating steam-engine, the diameter of its rotor is usually larger and its length less than in the continuous-current dynamo of corresponding output. The support of the armature core when of large diameter is therefore a more difficult problem, since, apart from any magnetic strains to which it may be subjected, its own weight tends to deform it. The segmental core-disks are usually secured to the internal circumference of a circular cast iron frame; the latter has a box section of considerable radial depth to give stiffness to it, and the disks are tightly clamped between internal flanges, one being a fixed part of the frame and the other loose, with transverse bolts passing right through from side to side (fig. 37). In order to lessen the weight of the structure and its expense in material, the cast iron frame has in some cases been entirely dispensed with, and braced tie-rods have been used to render the effective iron of the armature core-disks self-supporting.
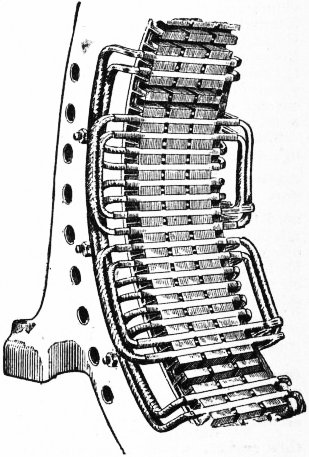 |
| Fig. 38. |
Owing to the high speed of the turbo-alternator, its rotor calls for the utmost care in its design to withstand the effect of centrifugal force without any shifting of the exciting coils, and to secure a perfect balance.
The appearance of the armature of a typical three-phase alternator is illustrated in fig. 38, which shows a portion of the lower half after removal of the field-magnet.
With open slots the coils, after being wound on formers to the required shape, are thoroughly impregnated with insulating compound, dried, and after a further wrapping with several layers of insulating material, finally pressed into the slots together with a sheet of leatheroid or flexible micanite. The end-connexions of each group of coils of one phase project straight out from the slots or are bent upwards alternately with those of the other phases, so that they may clear one another (fig. 37). A wooden wedge driven into a groove at the top of each slot is often used to lock the coil in place. With slots nearly closed at the top, the coils are formed by hand by threading the wire 780 through tubes of micanite or specially prepared paper lining the slots; or with single-turn loops, stout bars of copper of U-shape can be driven through the slots and closed by soldered connexions at the other end.
The first experimental determination of the shape of the E.M.F. curve of an alternator was made by J. Joubert in 1880. A revolving contact-maker charged a condenser with the E.M.F. produced by the armature at a particular instant during Shape of E.M.F. curve. each period. The condenser was discharged through a ballistic galvanometer, and from the measured throw the instantaneous E.M.F. could be deduced. The contact-maker was then shifted through a small angle, and the instantaneous E.M.F. at the new position corresponding to a different moment in the period was measured; this process was repeated until the E.M.F. curve for a complete period could be traced. Various modifications of the same principle have since been used, and a form of “oscillograph” (q.v.) has been perfected which is well adapted for the purpose of tracing the curves both of E.M.F. and of current. The machine on which Joubert carried out his experiments was a Siemens disk alternator having no iron in its armature, and it was found that the curve of E.M.F. was practically identical with a sine curve. The same law has also been found to hold true for a smooth-core ring or drum armature, but the presence of the iron core enables the armature current to produce greater distorting effect, so that the curves under load may vary considerably from their shape at no load. In toothed armatures, the broken surface of the core, and the still greater reaction from the armature current, may produce wide variations from the sine law, the general tendency being to give the E.M.F. curve a more peaked form. The great convenience of the assumption that the E.M.F. obeys the sine law has led to its being very commonly used as the basis for the mathematical analysis of alternator problems; but any deductions made from this premiss require to be applied with caution if they are likely to be modified by a different shape of the curve. Further, the same alternator will give widely different curves even of E.M.F., and still more so of current, according to the nature of the external circuit to which it is connected. As will be explained later, the phase of the current relatively to the E.M.F. depends not only on the inductance of the alternator itself, but also upon the inductance and capacity of the external circuit, so that the same current will produce different effects according to the amount by which it lags or leads. The question as to the relative advantages of differently shaped E.M.F. curves has led to much discussion, but can only be answered by reference to the nature of the work that the alternator has to do—i.e. whether it be arc lighting, motor driving, or incandescent lighting through transformers. The shape of the E.M.F. curve is, however, of great importance in one respect, since upon it depends the ratio of the maximum instantaneous E.M.F. to the effective value, and the insulation of the entire circuit, both external and internal, must be capable of withstanding the maximum E.M.F. While the maximum value of the sine curve is √2 or 1.414 times the effective value, the maximum value of a Λ curve is 1.732 times the effective value, so that for the same effective E.M.F. the armature wires must not only be more heavily insulated than in the continuous-current dynamo, but also the more peaked the curve the better must be the insulation.
Since an alternating current cannot be used for exciting the field-magnet, recourse must be had to some source of a direct current. This is usually obtained from a small auxiliary continuous-current dynamo, called an exciter, which may Excitation. be an entirely separate machine, separately driven and used for exciting several alternators, or may be driven from the alternator itself; in the latter case the armature of the exciter is often coupled directly to the rotating shaft of the alternator, while its field-magnet is attached to the bed-plate. Although separate excitation is the more usual method, the alternator can also be made self-exciting if a part or the whole of the alternating current is “rectified,” and thus converted into a direct current.
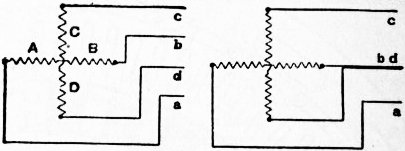 |
| Fig. 39. |
 |
| Fig. 40. |
The general idea of the polyphase alternator giving two or more E.M.F.’s of the same frequency, but displaced in phase, has been already described. The several phases may be entirely independent, and such was the case with the early polyphase Quarter-phase alternators. machines of Gramme, who used four independent circuits, and also in the large two-phase alternators designed by J.E.H. Gordon in 1883. If the phases are thus entirely separate, each requires two collector rings and two wires to its external circuit, i.e. four in all for two-phase and six for three-phase machines. The only advantage of the polyphase machine as thus used is that the whole of the surface of the armature core may be efficiently covered with winding, and the output of the alternator for a given size be thereby increased. It is, however, also possible so to interlink the several circuits of the armature that the necessary number of transmitting lines to the external circuits may be reduced, and also the weight of copper in them for a given loss in the transmission.21 The condition which obviously must be fulfilled, for such interlinking of the phases to be possible, is that in the lines which are to meet at any common junction the algebraic sum of the instantaneous currents, reckoned as positive if away from such junction and as negative if towards it, must be zero. Thus if the phases be diagrammatically represented by the relative angular position of the coils in fig. 39, the current in the coils A and B differs in phase from the current in the coils C and D by a quarter of a period or 90°; hence if the two wires b and d be replaced by the single wire bd, this third wire will serve as a common path for the currents of the two phases either outwards or on their return. At any instant the value of the current in the third wire must be the vector sum of the two currents in the other wires, and if the shape of the curves of instantaneous E.M.F. and current are identical, and are assumed to be sinusoidal, the effective value of the current in the third wire will be the vector sum of the effective values of the currents in the other wires; in other words, if the system is balanced, the effective current in the third wire is √2, or 1.414 times the current in either of the two outer wires. Since the currents of the two phases do not reach their maximum values at the same time, the sectional area of the third wire need not be twice that of the others; in order to secure maximum efficiency by employing the same current density in all three wires, it need only be 40% greater than that of either of the outer wires. The effective voltage between the external leads may in the same way be calculated by a vector diagram, and with the above star connexion the voltage between the outer pair of wires a and c is √2, or 1.414 times the voltage between either of the outer wires and the common wire bd. Next, if the four coils are joined up into a continuous helix, just as in the winding of a continuous-current machine, four wires may be attached to equidistant points at the opposite ends of two diameters at right angles to each other (fig. 40). Such a method is known as the mesh connexion, and gives a perfectly symmetrical four-phase system of distribution. Four collecting rings are necessary if the armature rotates, and there is no saving in copper in the transmitting lines; but the importance of the arrangement lies in its use in connexion with rotary converters, in which it is necessary that the winding of the armature should form a closed circuit. If e = the effective voltage of one phase A, the voltage between any pair of adjacent lines in the diagram is e, and between m and o or n and p is e √2. The current in any line is the resultant of the currents in the two phases connected to it, and its effective value is c √2, where c is the current of one phase.
 |
| Fig. 41. |
When we pass to machines giving three phases differing by 120°, the same methods of star and mesh connexion find their analogies. If the current in coil A (fig. 41) is flowing away from the centre, and has its maximum value, the Three-phase alternators. currents in coils B and C are flowing towards the centre, and are each of half the magnitude of the current in A; the algebraic sum of the currents is therefore zero, and this will also be the case for all other instants. Hence the three coils can be united together at the centre, and three external wires are alone required. In this star or “Y” connexion, if e be the effective voltage of each phase, or the voltage between any one of the three collecting rings and the common connexion, the volts between any pair of transmitting lines will be E = e √3 (fig. 41); if the load be balanced, the effective current C in each of the three lines will be equal, and the total output in watts will be W = 3Ce = 3CE / √3 = 1.732 EC, or 1.732 times the product of the effective voltage between the lines and the current in any single line. Next, if the three coils are closed upon themselves in a mesh or delta fashion (fig. 42), the three transmitting wires may be connected to the junctions of the coils (by means of collecting rings if the armature rotates). The voltage E between any pair of wires is evidently 781 that generated by one phase, and the current in a line wire is the resultant of that in two adjacent phases; or in a balanced system, if c be the current in each phase, the current in the line wire beyond a collecting ring is C = c√3, hence the watts are W = 3cE = 3CE / √3 = 1.732 EC, as before. Thus any three-phase winding may be changed over from the star to the delta connexion, and will then give 1.732 times as much current, but only 1/1.732 times the voltage, so that the output remains the same.
 |
| Fig. 42. |
The “armature reaction” of the alternator, when the term is used in its widest sense to cover all the effects of the alternating current in the armature as linked with a magnetic circuit or circuits, may be divided into three items which are Armature reaction in alternators different in their origin and consequences. In the first place the armature current produces a self-induced flux in local circuits independent of the main magnetic circuit, as e.g. linked with the ends of the coils as they project outwards from the armature core; such lines may be called “secondary leakage,” of which the characteristic feature is that its amount is independent of the position of the coils relatively to the poles. The alternations of this flux give rise to an inductive voltage lagging 90° behind the phase of the current, and this leakage or reactance voltage must be directly counterbalanced electrically by an equal component in the opposite sense in the voltage from the main field. The second and third elements are more immediately magnetic and are entirely dependent upon the position of the coils in relation to the poles and in relation to the phase of the current which they then carry. When the side of a drum coil is immediately under the centre of a pole, its ampere-turns are cross-magnetizing, i.e. produce a distortion of the main flux, displacing its maximum density to one or other edge of the pole. When the coil-side is midway between the poles and the axes of coil and pole coincide, the coil stands exactly opposite to the pole and embraces the same magnetic circuit as the field-magnet coils; its turns are therefore directly magnetizing, either weakening or strengthening the main flux according to the direction of the current. In intermediate positions the ampere-turns of the coil gradually pass from cross to direct and vice versa. When the instantaneous values of either the cross or direct magnetizing effect are integrated over a period and averaged, due account being taken of the number of slots per coil-side and of the different phases of the currents in the polyphase machine, expressions are obtained for the equivalent cross and direct ampere-turns of the armature as acting upon a pair of poles. For a given winding and current, the determining factor in either the one or the other is found to be the relative phase angle between the axis of a coil in its position when carrying the maximum current and the centre of a pole, the transverse reaction being proportional to the cosine of this angle, and the direct reaction to its sine. If the external circuit is inductive, the maximum value of the current lags behind the E.M.F. and so behind the centre of the pole; such a negative angle of lag causes the direct magnetizing turns to become back turns, directly weakening the main field and lowering the terminal voltage. Thus, just as in the continuous-current dynamo, for a given voltage under load the excitation between the pole-pieces Xp must not only supply the net excitation required over the air-gaps, armature core and teeth, but must also balance the back ampere-turns Xb of the armature.
Evidently therefore the characteristic curve connecting armature current and terminal volts will with a constant exciting current depend on the nature of the load, whether inductive or non-inductive, and upon the amount of inductance already possessed by the armature itself. With an inductive load it will fall more rapidly from its initial maximum value, or, conversely, if the initial voltage is to be maintained under an increasing load, the exciting current will have to be increased more than if the load were non-inductive. In practical working many disadvantages result from a rapid drop of the terminal E.M.F. under increasing load, so that between no load and full load the variation in terminal voltage with constant excitation should not exceed 15%. Thus the output of an alternator is limited either by its heating or by its armature reaction, just as is the output of a continuous-current dynamo; in the case of the alternator, however, the limit set by armature reaction is not due to any sparking at the brushes, but to the drop in terminal voltage as the current is increased, and the consequent difficulty in maintaining a constant potential on the external circuit.
The joint operation of several alternators so that their outputs may be delivered into the same external circuit is sharply distinguished from the corresponding problem in continuous-current dynamos by the necessary condition that they The coupling of alternators. must be in synchronism, i.e. not only must they be so driven that their frequency is the same, but their E.M.F.’s must be in phase or, as it is also expressed, the machines must be in step. Although in practice it is impossible to run two alternators in series unless they are rigidly coupled together—which virtually reduces them to one machine—two or more machines can be run in parallel, as was first described by H. Wilde in 1868 and subsequently redemonstrated by J. Hopkinson and W.G. Adams in 1884. Their E.M.F.’s should be as nearly as possible in synchronism, but, as contrasted with series connexion, parallel coupling gives them a certain power of recovery if they fall out of step, or are not in exact synchronism when thrown into parallel. In such circumstances a synchronizing current passes between the two machines, due to the difference in their instantaneous pressures; and as this current agrees in phase more nearly with the leading than with the lagging machine, the former machine does work as a generator on the latter as a motor. Hence the lagging machine is accelerated and the leading machine is retarded, until their frequencies and phase are again the same.
The chief use of the alternator has already been alluded to. Since it can be employed to produce very high pressures either directly or through the medium of transformers, it is specially adapted to the electrical transmission of Uses of alternators. energy over long distances.22 In the early days of electric lighting, the alternate-current system was adopted for a great number of central stations; the machines, designed to give a pressure of 2000 volts, supplied transformers which were situated at considerable distances and spread over large areas, without an undue amount of copper in the transmitting lines. While there was later a tendency to return to the continuous current for central stations, owing to the introduction of better means for economizing the weight of copper in the mains, the alternating current again came into favour, as rendering it possible to place the central station in some convenient site far away from the district which it was to serve. The pioneer central station in this direction was the Deptford station of the London Electric Supply Corporation, which furnished current to the heart of London from a distance of 7 m. In this case, however, the alternators were single-phase and gave the high pressure of 10,000 volts immediately, while more recently the tendency has been to employ step-up transformers and a polyphase system. The advantage of the latter is that the current, after reaching the distant sub-stations, can be dealt with by rotary converters, through which it is transformed into a continuous current. The alternator is also used for welding, smelting in electric furnaces, and other metallurgical processes where heating effects are alone required; the large currents needed therein can be produced without the disadvantage of the commutator, and, if necessary, transformers can be interposed to lower the voltage and still further increase the current. The alternating system can thus meet very various needs, and its great recommendation may be said to lie in the flexibility with which it can supply electrical energy through transformers at any potential, or through rotary converters in continuous-current form.
Authorities.—For the further study of the dynamo, the following may be consulted, in addition to the references already given:—
General: S.P. Thompson, Dynamo-Electric Machinery—Continuous-Current Machines (1904), Alternating-Current Machinery (1905, London); G. Kapp, Dynamos, Alternators and Transformers (London, 1893); Id., Electric Transmission of Energy (London, 1894); Id., Dynamo Construction; Electrical and Mechanical (London, 1899); H.F. Parshall and H.M. Hobart, Electric Generators (London, 1900); C.C. Hawkins and F. Wallis, The Dynamo (London, 1903); E. Arnold, Konstruktionstafeln für den Dynamobau (Stuttgart, 1902); C.P. Steinmetz, Elements of Electrical Engineering (New York, 1901).
Continuous-Current Dynamos: J. Fischer-Hinnen, Continuous-Current Dynamos (London, 1899); E. Arnold, Die Gleichstrommaschine (Berlin, 1902); F. Niethammer, Berechnung und Konstruktion der Gleichstrommaschinen und Gleichstrommotoren (Stuttgart, 1904).
Alternators: D.C. Jackson and J.P. Jackson, Alternating Currents and Alternating Current Machinery (New York, 1903); J.A. Fleming, The Alternate Current Transformer (London, 1899); C.P. Steinmetz, Alternating Current Phenomena (New York, 1900); E. Arnold, Die Wechselstromtechnik (Berlin, 1904); S.P. Thompson, Polyphase Electric Currents (London, 1900); A. Stewart, Modern Polyphase Machinery (London, 1906); M. Oudin, Standard Polyphase Apparatus and Systems (New York, 1904).
1 Experimental Researches in Electricity, series ii. § 6, pars. 256, 259-260, and series xxviii. § 34.
2 Ibid. series i. § 4, pars. 84-90.
3 “On the Physical Lines of Magnetic Force,” Phil. Mag., June 1852.
4 Faraday, Exp. Res. series xxviii. § 34, pars. 3104, 3114-3115.
5 Id., ib. series i. § 4, pars. 114-119.
6 Id., ib. series ii. § 6, pars. 211, 213; series xxviii. § 34, par. 3152.
7 Invented by Nikola Tesla (Elec. Eng. vol. xiii. p. 83. Cf. Brit. Pat. Spec. Nos. 2801 and 2812, 1894). Several early inventors, e.g. Salvatore dal Negro in 1832 (Phil. Mag. third series, vol. i. p. 45), adopted reciprocating or oscillatory motion, and this was again tried by Edison in 1878.
8 The advantage to be obtained by making the poles closely embrace the armature core was first realized by Dr Werner von Siemens in his “shuttle-wound” armature (Brit. Pat. No. 2107, 1856).
9 Nuovo Cimento (1865), 19, 378.
10 Brit. Pat. No. 1668 (1870); Comptes rendus (1871), 73, 175.
11 Ann. Chim. Phys. l. 322.
12 Ibid. li. 76. Since in H. Pixii’s machine the armature was stationary, while both magnet and commutator rotated, four brushes were used, and the arrangement was not so simple as the split-ring described above, although the result was the same. J. Saxton’s machine (1833) and E.M. Clarke’s machine (1835, see Sturgeon’s Annals of Electricity, i. 145) were similar to one another in that a unidirected current was obtained by utilizing every alternate half-wave of E.M.F., but the former still employed mercury collecting cups, while the latter employed metal brushes. W. Sturgeon in 1835 followed Pixii in utilizing the entire wave of E.M.F., and abandoned the mercury cups in favour of metal brushes pressing on four semicircular disks (Scientific Researches, p. 252). The simple split-ring is described by Sir C. Wheatstone and Sir W.F. Cooke in their Patent No. 8345 (1840).
13 By the “leading” side of the tooth or of an armature coil or sector is to be understood that side which first enters under a pole after passing through the interpolar gap, and the edge of the pole under which it enters is here termed the “leading” edge as opposed to the “trailing” edge or corner from under which a tooth or coil emerges into the gap between the poles; cf. fig. 30, where the leading and trailing pole-corners are marked ll and tt.
14 Such was the arrangement of Wheatstone’s machine (Brit. Pat. No. 9022) of 1841, which was the first to give a more nearly “continuous” current, the number of sections and split-rings being five.
15 Its development from the split-ring was due to Pacinotti and Gramme (Brit. Pat. No. 1668, 1870) in connexion with their ring armatures.
16 And extended by G. Kapp, “On Modern Continuous-Current Dynamo-Electric Machines,” Proc. Inst. C.E. vol. lxxxiii. p. 136.
17 Drs J. and E. Hopkinson, “Dynamo-Electric Machinery,” Phil. Trans., May 6, 1886; this was further expanded in a second paper on “Dynamo-Electric Machinery,” Proc. Roy. Soc., Feb. 15, 1892, and both are reprinted in Original Papers on Dynamo-Machinery and Allied Subjects.
18 Exp. Res., series i. § 4, par. 111. In 1845 Wheatstone and Cooke patented the use of “voltaic” magnets in place of permanent magnets (No. 10,655).
19 Between Moutiers and Lyons, a distance of 115 m., energy is transmitted on the Thury direct-current system at a maximum pressure of 60,000 volts. Four groups of machines in series are employed, each group consisting of four machines in series; the rated output of each component machine is 75 amperes at 3900 volts or 400 h.p. A water turbine drives two pairs of such machines through an insulating coupling, and the sub-base of each pair of machines is separately insulated from earth, the foundation being also of special insulating materials.
20 For experiments on high-frequency currents, Nikola Tesla constructed an alternator having 384 poles and giving a frequency of about 10,000 (Journ. Inst. Elec. Eng. 1892, 21, p. 82). The opposite extreme is found in alternators directly coupled to the Parsons steam-turbine, in which, with a speed of 3000 revs. per min., only two poles are required to give a frequency of 50. By a combination of a Parsons steam-turbine running at 12,000 revs. per min. with an alternator of 140 poles a frequency of 14,000 has been obtained (Engineering, 25th of August 1899). For description of an experimental machine for 10,000 cycles per second when running at 3000 revs. per min., see Trans. Amer. Inst. Elect. Eng. vol. xxiii. p. 417.
21 As in the historical transmission of energy from Lauffen to Frankfort (1891).
22 In the pioneer three-phase transmission between Laufen and Frankfort (Electrician, vol. xxvi. p. 637, and xxvii. p. 548), the three-phase current was transformed up from about 55 to 8500 volts, the distance being 110 m. A large number of installations driven by water power are now at work, in which energy is transmitted on the alternating-current system over distances of about 100 m. at pressures ranging from 20,000 to 67,000 volts.
DYNAMOMETER (Gr. δύναμις, strength, and μέτρον, a measure), an instrument for measuring force exerted by men, animals and machines. The name has been applied generally to all kinds of instruments used in the measurement of a force, as for example electric dynamometers, but the term specially denotes apparatus used in connexion with the measurement of work, or in the measurement of the horse-power of engines and motors. If P represent the average value of the component of a force in the direction of the displacement, s, of its point of application, the product Ps measures the work done during the displacement. When the force acts on a body free to turn about a fixed axis only, it is convenient to express the work done by the transformed product Tθ, where T is the average turning moment or torque acting to produce the displacement θ radians. The apparatus used to measure P or T is the dynamometer. The factors s or θ are observed independently. Apparatus is added to some dynamometers by means of which a curve showing the variations of P on a distance base is drawn automatically, the area of the diagram representing the work done; with others, integrating apparatus is combined, from which the work done during a given interval may be read off directly. It is convenient to distinguish between absorption and transmission dynamometers. In the first kind the work done is converted into heat; in the second it is transmitted, after measurement, for use.
Absorption Dynamometers.—Baron Prony’s dynamometer (Ann. Chim. Phys. 1821, vol. 19), which has been modified in various ways, consists in its original form of two symmetrically shaped timber beams clamped to the engine-shaft. When these are held from turning, their frictional resistance may be adjusted by means of nuts on the screwed bolts which hold them together until the shaft revolves at a given speed. To promote smoothness of action, the rubbing surfaces are lubricated. A weight is moved along the arm of one of the beams until it just keeps the brake steady midway between the stops which must be provided to hold it when the weight fails to do so. The general theory of this kind of brake is as follows:-Let F be the whole frictional resistance, r the common radius of the rubbing surfaces, W the force which holds the brake from turning and whose line of action is at a perpendicular distance R from the axis of the shaft, N the revolutions of the shaft per minute, ω its angular velocity in radians per second; then, assuming that the adjustments are made so that the engine runs steadily at a uniform speed, and that the brake is held still, clear of the stops and without oscillation, by W, the torque T exerted by the engine is equal to the frictional torque Fr acting at the brake surfaces, and this is measured by the statical moment of the weight W about the axis of revolution; that is—
T = Fr = WR.
Hence WR measures the torque T.
If more than one force be applied to hold the brake from turning, Fr, and therefore T, are measured by the algebraical sum of their individual moments with respect to the axis. If the brake is not balanced, its moment about the axis must be included. Therefore, quite generally,
T = ΣWR.
The factor θ of the product Tθ is found by means of a revolution counter. The power of a motor is measured by the rate at which it works, and this is expressed by Tω = T2πN / 60 in foot-pounds per second, or T2πN / 33,000 in horse-power units. The latter is commonly referred to as the “brake horse-power.” The maintenance of the conditions of steadiness implied in equation (1) depends upon the constancy of F, and therefore of the coefficient of friction μ between the rubbing surfaces. The heating at the surfaces, the variations in their smoothness, and the variations of the lubrication make μ continuously variable, and necessitate frequent adjustment of W or of the nuts. J.V. Poncelet (1788-1867) invented a form of Prony brake which automatically adjusted its grip as μ changed, thereby maintaining F constant.
The principle of the compensating brake devised by J.G. Appold (1800-1865) is shown in fig. 1. A flexible steel band, lined with wood blocks, is gripped on the motor fly-wheel or pulley by a screw A, which, together with W, is adjusted to hold the brake steady. Compensation is effected by the lever L inserted at B. This has a slotted end, engaged by a pin P fixed to the framing, and it will be seen that its action is to slacken the band if the load tends to rise and to tighten it in the contrary case. The external forces holding the brake from turning are W, distant R from the axis, and the reaction, W1 say, of the lever against the fixed pin P, distant R1 from the axis. The moment of W1 may be positive or negative. The torque T at any instant of steady running is therefore {WR ± W1R1}.
 |
| Fig. 1. |
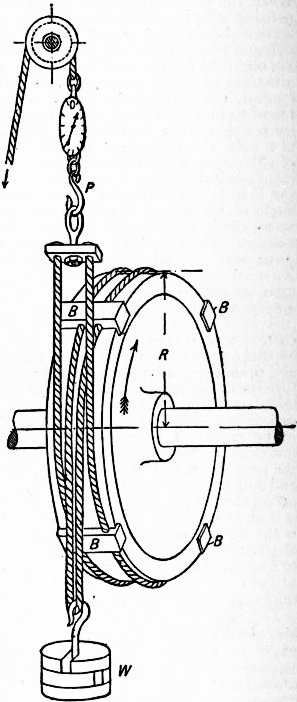 |
| Fig. 2. |
Lord Kelvin patented a brake in 1858 (fig. 2) consisting of a rope or cord wrapped round the circumference of a rotating wheel, to one end of which is applied a regulated force, the other end being fixed to a spring balance. The ropes are spaced laterally by the blocks B, B, B, B, which also serve to prevent them from slipping sideways. When the wheel is turning in the direction indicated, the forces holding the band still are W, and p, the observed pull on the spring balance. Both these forces usually act at the same radius R, the distance from the axis to the centre line of the rope, in which case the torque T is (W − p)R, and consequently the brake horse-power is [(W − p)R × 2πN] / 33,000. When μ changes the weight W rises or falls against the action of the spring balance until a stable condition of running is obtained. The ratio W/p is given by eμθ, where e = 2.718; μ is the coefficient of friction and θ the angle, measured in radians, subtended by the arc of contact between the rope and the wheel. In fig. 2 θ = 2π. The ratio W/p increases very rapidly as θ is increased, and therefore, by making θ sufficiently large, p may conveniently be made a small fraction of W, thereby rendering errors of observation of the spring balance negligible. Thus this kind of brake, though cheap to make, is, when θ is large enough, an exceedingly accurate measuring instrument, readily applied and easily controlled. It has come into very general use in recent years, and has practically superseded the older forms of block brakes.
It is sometimes necessary to use water to keep the brake wheel cool. Engines specially designed for testing are usually provided with a brake wheel having a trough-shaped rim. Water trickles continuously into the trough, and the centrifugal action holds it as an inside lining against the rim, where it slowly evaporates.
Fig. 3 shows a band-brake invented by Professor James Thomson, suitable for testing motors exerting a constant torque (see Engineering, 22nd October 1880). To maintain eμθ constant, compensation for variation of μ is made by inversely varying θ. A and B are fast and loose pulleys, and the brake band is placed partly over the one and partly over the other. Weights W and w are adjusted to the torque. The band turns with the fast pulley if μ increase, thereby slightly turning the loose pulley, otherwise at rest, until θ is adjusted to the new value of μ. This form of brake was also invented independently by J.A.M.L. Carpentier, and the principle has been used in the Raffard brake. A self-compensating brake of another kind, by Marcel Deprez, was described with Carpentier’s in 1880 (Bulletin de la société d’encouragement, Paris). W.E. Ayrton and J. Perry used a band or rope brake in which compensation is effected by the pulley drawing in or letting out a part of the band or rope which has been roughened or in which a knot has been tied.
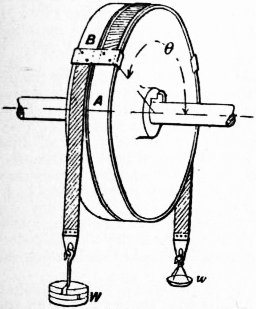 |
| Fig. 3. |
In an effective water-brake invented by W. Froude (see Proc. Inst. M. E. 1877), two similar castings, A and B, each consisting 783 of a boss and circumferential annular channel, are placed face to face on a shaft, to which B is keyed, A being free (fig. 4). A ring tube of elliptical section is thus formed. Each channel is divided into a series of pockets by equally spaced vanes inclined at 45°. When A is held still, and B rotated, centrifugal action sets up vortex currents in the water in the pockets; thus a continuous circulation is caused between B and A, and the consequent changes of momentum give rise to oblique reactions. The moments of the components of these actions and reactions in a plane to which the axis of rotation is at right angles are the two aspects of the torque acting, and therefore the torque acting on B through the shaft is measured by the torque required to hold A still. Froude constructed a brake to take up 2000 H.P. at 90 revs. per min. by duplicating this apparatus. This replaced the propeller of the ship whose engines were to be tested, and the outer casing was held from turning by a suitable arrangement of levers carried to weighing apparatus conveniently disposed on the wharf. The torque corresponding to 2000 H.P. at 90 revs. per min. is 116,772 foot-pounds, and a brake 5 ft. in diameter gave this resistance. Thin metal sluices were arranged to slide between the wheel and casing, and by their means the range of action could be varied from 300 H.P. at 120 revs. per min. to the maximum.
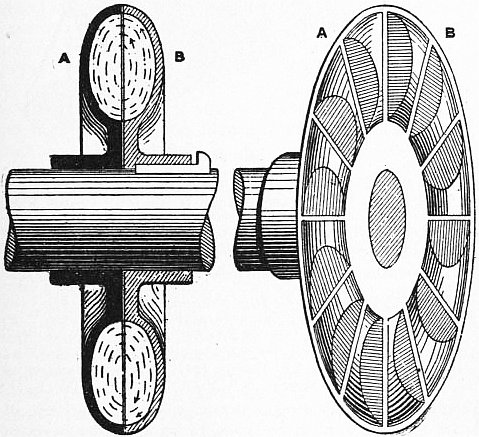 |
| Fig. 4. |
Professor Osborne Reynolds in 1887 patented a water-brake (see Proc. Inst. C.E. 99, p. 167), using Froude’s turbine to obtain the highly resisting spiral vortices, and arranging passages in the casing for the entry of water at the hub of the wheel and its exit at the circumference. Water enters at E (fig. 5), and finds its way into the interior of the wheel, A, driving the air in front of it through the air-passages K, K. Then following into the pocketed chambers V1, V2, it is caught into the vortex, and finally escapes at the circumference, flowing away at F. The air-ways k, k, in the fixed vanes establish communication between the cores of the vortices and the atmosphere. From 1⁄5 to 30 H.P. may be measured at 100 revs. per min. by a brake-wheel of this kind 18 in. in diameter. For other speeds the power varies as the cube of the speed. The casing is held from turning by weights hanging on an attached arm. The cocks regulating the water are connected to the casing, so that any tilting automatically regulates the flow, and therefore the thickness of the film in the vortex. In this way the brake may be arranged to maintain a constant torque, not withstanding variation of the speed. In G.I. Alden’s brake (see Trans. Amer. Soc. Eng. vol. xi.) the resistance is obtained by turning a cast iron disk against the frictional resistance of two thin copper plates, which are held in a casing free to turn upon the shaft, and are so arranged that the pressure between the rubbing surfaces is controlled, and the heat developed by friction carried away, by the regulated flow of water through the casing. The torque required to hold the casing still against the action of the disk measures the torque exerted by the shaft to which the disk is keyed.
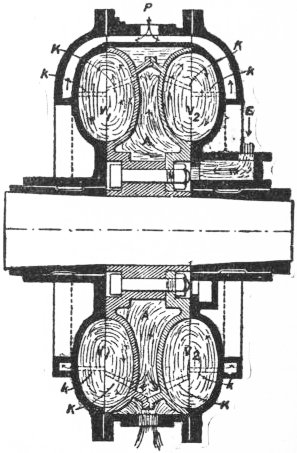 |
| Fig. 5. |
 |
| Fig. 6. |
Transmission Dynamometers.—The essential part of many transmission dynamometers is a spring whose deformation indirectly measures the magnitude of the force transmitted through it. For many kinds of spring the change of form is practically proportional to the force, but the relation should always be determined experimentally. General A.J. Morin (see Notice sur divers appareils dynamométriques, Paris, 1841), in his classical experiments on traction, arranged his apparatus so that the change in form of the spring was continuously recorded on a sheet of paper drawn under a style. For longer experiments he used a “Compteur” or mechanical integrator, suggested by J.V. Poncelet, from which the work done during a given displacement could be read off directly. This device consists of a roller of radius r, pressed into contact with a disk. The two are carried on a common frame, so arranged that a change in form of the spring causes a relative displacement of the disk and roller, the point of contact moving radially from or towards the centre of the disk. The radial distance x is at any instant proportional to the force acting through the spring. The angular displacement, θ, of the disk is made proportional to the displacement, s, of the point of application of the force by suitable driving gear. If dφ is the angular displacement of the roller corresponding to displacements, dθ of the disk, and ds of the point of application of P, a, and C constants, then dφ = xdθ / r = (a/r) P ds = C·P ds, and therefore φ = C ∫S2S1 P ds; that is, the angular displacement of the roller measures the work done during the displacement from s1 to s2. The shaft carrying the roller is connected to a counter so that φ may be observed. The angular velocity of the shaft is proportional to the rate of working. Morin’s dynamometer is shown in fig. 6. The transmitting spring is made up of two flat bars linked at their ends. Their centres s1, s2, are held respectively by the pieces A, B, which together form a sliding pair. The block A carries the disk D, B carries the roller R and counting gear. The pulley E is driven from an axle of the carriage. In a dynamometer used by F.W. Webb to measure the tractive resistance of trains on the London & North-Western railway, a tractive pull or push compresses two spiral springs by a definite amount, which is recorded to scale by a pencil on a sheet of paper, drawn continuously from a storage drum at the rate of 3 in. per mile, by a roller driven from one of the carriage axles. Thus the diagram shows the tractive force at any instant. A second pencil electrically connected to a clock traces a time line on the diagram with a kick at every thirty seconds. A third pencil traces an observation line in which a kick can be made at will by pressing any one of the electrical pushes placed about the car, and a fourth draws a datum line. The spring of the dynamometer car used by W. Dean on the Great Western railway is made up of thirty flat plates, 7 ft. 6 in. long, 5 in. × 5⁄8 in. at the centre, spaced by distance pieces nibbed into the plates at the centre and by rollers at the ends. The draw-bar is connected to the buckle, which is carried on rollers, the ends of the spring resting on plates fixed to the under-frame. The gear operating the paper roll is driven from the axle of an independent wheel which is let down into contact with the rail when required. This wheel serves also to measure the distance travelled. A Morin disk and roller integrator is connected with the apparatus, so that the work done during a journey may be read off. Five lines are traced on the diagram.
 |
| Fig. 7. |
In spring dynamometers designed to measure a transmitted torque, the mechanical problem of ascertaining the change of form of the spring is complicated by the fact that the spring and the whole apparatus are rotating together. In the Ayrton and Perry transmission dynamometer or spring coupling of this type, 784 the relative angular displacement is proportional to the radius of the circle described by the end of a light lever operated by mechanism between the spring-connected parts. By a device used by W.E. Dalby (Proc. Inst.C.E. 1897-1898, p. 132) the change in form of the spring is shown on a fixed indicator, which may be placed in any convenient position. Two equal sprocket wheels Q1, Q2, are fastened, the one to the spring pulley, the other to the shaft. An endless band is placed over them to form two loops, which during rotation remain at the same distance apart, unless relative angular displacement occurs between Q1 and Q2 (fig. 7) due to a change in form of the spring. The change in the distance d is proportional to the change in the torque transmitted from the shaft to the pulley. To measure this, guide pulleys are placed in the loops guided by a geometric slide, the one pulley carrying a scale, and the other an index. A recording drum or integrating apparatus may be arranged on the pulley frames. A quick variation, or a periodic variation of the magnitude of the force or torque transmitted through the springs, tends to set up oscillations, and this tendency increases the nearer the periodic time of the force variation approaches a periodic time of the spring. Such vibrations may be damped out to a considerable extent by the use of a dash-pot, or may be practically prevented by using a relatively stiff spring.
Every part of a machine transmitting force suffers elastic deformation, and the force may be measured indirectly by measuring the deformation. The relation between the two should in all cases be found experimentally. G.A. Hirn (see Les Pandynamomètres, Paris, 1876) employed this principle to measure the torque transmitted by a shaft. Signor Rosio used a telephonic method to effect the same end, and mechanical, optical and telephonic devices have been utilized by the Rev. F.J. Jervis-Smith. (See Phil. Mag. February 1898.)
H. Frahm,1 during an important investigation on the torsional vibration of propeller shafts, measured the relative angular displacement of two flanges on a propeller shaft, selected as far apart as possible, by means of an electrical device (Engineering, 6th of February 1903). These measurements were utilized in combination with appropriate elastic coefficients of the material to find the horse-power transmitted from the engines along the shaft to the propeller. In this way the effective horse-power and also the mechanical efficiency of a number of large marine engines, each of several thousand horse-power, have been determined.
 |
| Fig. 8. |
When a belt, in which the maximum and minimum tensions are respectively P and p ℔, drives a pulley, the torque exerted is (P − p)r ℔ ft., r being the radius of the pulley plus half the thickness of the belt. P and p may be measured directly by leading the belt round two freely hanging guide pulleys, one in the tight, the other in the slack part of the belt, and adjusting loads on them until a stable condition of running is obtained. In W. Froude’s belt dynamometer (see Proc. Inst. M.E., 1858) (fig. 8) the guide pulleys G1, G2 are carried upon an arm free to turn about the axis O. H is a pulley to guide the approaching and receding parts of the belt to and from the beam in parallel directions. Neglecting friction, the unbalanced torque acting on the beam is 4r {P − p} ℔ ft. If a force Q acting at R maintains equilibrium, QR/4 = (P − p)r = T. Q is supplied by a spring, the extensions of which are recorded on a drum driven proportionally to the angular displacement of the driving pulley; thus a work diagram is obtained. In the Farcot form the guide pulleys are attached to separate weighing levers placed horizontally below the apparatus. In a belt dynamometer built for the Franklin Institute from the designs of Tatham, the weighing levers are separate and arranged horizontally at the top of the apparatus. The weighing beam in the Hefner-Alteneck dynamometer is placed transversely to the belt (see Electrotechnischen Zeitschrift, 1881, 7). The force Q, usually measured by a spring, required to maintain the beam in its central position is proportional to (P − p). If the angle θ1 = θ2 = 120°, Q = (P − p) neglecting friction.
When a shaft is driven by means of gearing the driving torque is measured by the product of the resultant pressure P acting between the wheel teeth and the radius of the pitch circle of the wheel fixed to the shaft. Fig. 9, which has been reproduced from J. White’s A New Century of Inventions (Manchester, 1822), illustrates possibly the earliest application of this principle to dynamometry. The wheel D, keyed to the shaft overcoming the resistance to be measured, is driven from wheel N by two bevel wheels L, L, carried in a loose pulley K. The two shafts, though in a line, are independent. A torque applied to the shaft A can be transmitted to D, neglecting friction, without change only if the central pulley K is held from turning; the torque required to do this is twice the torque transmitted.
 |
| Fig. 9. |
The torque acting on the armature of an electric motor is necessarily accompanied by an equal and opposite torque acting on the frame. If, therefore, the motor is mounted on a cradle free to turn about knife-edges, the reacting torque is the only torque tending to turn the cradle when it is in a vertical position, and may therefore be measured by adjusting weights to hold the cradle in a vertical position. The rate at which the motor is transmitting work is then T2πn / 550 H.P., where n is the revolutions per second of the armature.
See James Dredge, Electric Illumination, vol. ii. (London, 1885); W.W. Beaumont, “Dynamometers and Friction Brakes,” Proc. Inst.C.E. vol. xcv. (London, 1889); E. Brauer, “Über Bremsdynamometer and verwandte Kraftmesser,” Zeitschrift des Vereins deutscher Ingenieure (Berlin, 1888); J.J. Flather, Dynamometers and the Measurement of Power (New York, 1893).
1 H. Frahm, “Neue Untersuchungen über die dynamischen Vorgänge in den Wellenleitungen von Schiffsmaschinen mit besonderer Berücksichtigung der Resonanzschwingungen,” Zeitschrift des Vereins deutscher Ingenieure, 31st May 1902.
DYNASTY (Gr. δυναστεία, sovereignty, the position of a δυνάοτης, lord, ruler, from δύνασθαι, to be able, δύναμις, power), a family or line of rulers, a succession of sovereigns of a country belonging to a single family or tracing their descent to a common ancestor. The term is particularly used in the history of ancient Egypt as a convenient means of arranging the chronology.
DYSART, a royal and police burgh and seaport of Fifeshire, Scotland, on the shore of the Firth of Forth, 2 m. N.E. of Kirkcaldy by the North British railway. Pop. (1901) 3562. It has a quaint old-fashioned appearance, many ancient houses in High Street bearing inscriptions and dates. The public buildings include a town hall, library, cottage hospital, mechanics’ institute and memorial hall. Scarcely anything is left of the old chapel dedicated to St Dennis, which for a time was used as a 785 smithy; and of the chapel of St Serf, the patron saint of the burgh, only the tower remains. The chief industries are the manufacture of bed and table linen, towelling and woollen cloth, shipbuilding and flax-spinning. There is a steady export of coal, and the harbour is provided with a wet dock and patent slip. In smuggling days the “canty carles” of Dysart were professed “free traders.” In the 15th and 16th centuries the town was a leading seat of the salt industry (“salt to Dysart” was the equivalent of “coals to Newcastle”), but the salt-pans have been abandoned for a considerable period. Nail-making, once famous, is another extinct industry. During the time of the alliance between Scotland and Holland, which was closer in Fifeshire than in other counties, Dysart became known as Little Holland. To the west of the town is Dysart House, the residence of the earl of Rosslyn. With Burntisland and Kinghorn Dysart forms one of the Kirkcaldy district group of parliamentary burghs. The town is mentioned as early as 874 in connexion with a Danish invasion. Its name is said to be a corruption of the Latin desertum, “a desert,” which was applied to a cave on the seashore occupied by St Serf. In the cave the saint held his famous colloquy with the devil, in which Satan was worsted and contemptuously dismissed. From James V. the town received the rights of a royal burgh. In 1559 it was the headquarters of the Lords of the Congregation, and in 1607 the scene of the meetings of the synod of Fife known as the Three Synods of Dysart. Ravensheugh Castle, on the shore to the west of the town, is the Ravenscraig of Sir Walter Scott’s ballad of “Rosabelle.”
William Murray, a native of the place, was made earl of Dysart in 1643, and his eldest child and heir, a daughter, Elizabeth, obtained in 1670 a regrant of the title, which passed to the descendants of her first marriage with Sir Lionel Tollemache, Bart., of Helmingham; she married secondly the 1st duke of Lauderdale, but had no children by him, and died in 1698. This countess of Dysart (afterwards duchess of Lauderdale) was a famous beauty of the period, and notorious both for her amours and for her political influence. She was said to have been the mistress of Oliver Cromwell, and also of Lauderdale before her first husband’s death, and was a leader at the court of Charles II. Wycherley is supposed to have aimed at her in his Widow Blackacre in the Plain Dealer. Her son, Lionel Tollemache (d. 1727), transmitted the earldom to his grandson Lionel (d. 1770), whose sons Lionel (d. 1799) and Wilbraham (d. 1821) succeeded; they died without issue, and their sister Louisa (d. 1840), who married John Manners, an illegitimate son of the second son of the 2nd duke of Rutland, became countess in her own right, being succeeded by her grandson (d. 1878), and his grandson, the 8th earl.
The earldom of Dysart must not be confounded with that of Desart (Irish), created (barony 1733) in 1793, and held in the Cuffe family, who were originally of Creech St Michael, Somerset, the Irish branch dating from Queen Elizabeth’s time.
DYSENTERY (from the Gr. prefix δυσ-, in the sense of “bad,” and ἔντερον, the intestine), also called “bloody flux,” an infectious disease with a local lesion in the form of inflammation and ulceration of the lower portion of the bowels. Although at one time a common disease in Great Britain, dysentery is now very rarely met with there, and is for the most part confined to warm countries, where it is the cause of a large amount of mortality. (For the pathology see Digestive Organs.)
Recently considerable advance has been made in our knowledge of dysentery, and it appears that there are two distinct types of the disease: (1) amoebic dysentery, which is due to the presence of the amoeba histolytica (of Schaudinn) in the intestine; (2) bacillary dysentery, which has as causative agent two separate bacteria, (a) that discovered by Shiga in Japan, (b) that discovered by Flexner in the Philippine Islands. With regard to the bacillary type, at first both organisms were considered to be identical, and the name bacillus dysenteriae was given to them; but later it was shown that these bacilli are different, both in regard to their cultural characteristics and also in that one (Shiga) gives out a soluble toxin, whilst the other has so far resisted all efforts to discover it. Further, the serum of a patient affected with one of the types has a marked agglutinative power on the variety with which he is infected and not on the other.
Clinically, dysentery manifests itself with varying degrees of intensity, and it is often impossible without microscopical examination to determine between the amoebic and bacillary forms. In well-marked cases the following are the chief symptoms. The attack is commonly preceded by certain premonitory indications in the form of general illness, loss of appetite, and some amount of diarrhoea, which gradually increases in severity, and is accompanied with griping pains in the abdomen (tormina). The discharges from the bowels succeed each other with great frequency, and the painful feeling of pressure downwards (tenesmus) becomes so intense that the patient is constantly desiring to defecate. The matters passed from the bowels, which at first resemble those of ordinary diarrhoea, soon change their character, becoming scanty, mucous or slimy, and subsequently mixed with, or consisting wholly of, blood, along with shreds of exudation thrown off from the mucous membrane of the intestine. The evacuations possess a peculiarly offensive odour characteristic of the disease. Although the constitutional disturbance is at first comparatively slight, it increases with the advance of the disease, and febrile symptoms come on attended with urgent thirst and scanty and painful flow of urine. Along with this the nervous depression is very marked, and the state of prostration to which the patient is reduced can scarcely be exceeded. Should no improvement occur death may take place in from one to three weeks, either from repeated losses of blood, or from gradual exhaustion consequent on the continuance of the symptoms, in which case the discharges from the bowels become more offensive and are passed involuntarily.
When, on the other hand, the disease is checked, the signs of improvement are shown in the cessation of the pain, in the evacuations being less frequent and more natural, and in relief from the state of extreme depression. Convalescence is, however, generally slow, and recovery may be imperfect—the disease continuing in a chronic form, which may exist for a variable length of time, giving rise to much suffering, and not unfrequently leading to an ultimately fatal result.
The dysentery poison appears to exert its effects upon the glandular structures of the large intestine, particularly in its lower part. In the milder forms of the disease there is simply a congested or inflamed condition of the mucous membrane, with perhaps some inflammatory exudation on its surface, which is passed off by the discharges from the bowels. But in the more severe forms ulceration of the mucous membrane takes place. Commencing in and around the solitary glands of the large intestine in the form of exudations, these ulcers, small at first, enlarge and run into each other, till a large portion of the bowel may be implicated in the ulcerative process. Should the disease be arrested these ulcers may heal entirely, but occasionally they remain, causing more or less disorganization of the coats of the intestines, as is often found in chronic dysentery. Sometimes, though rarely, the ulcers perforate the intestines, causing rapidly fatal inflammation of the peritoneum, or they may erode a blood vessel and produce violent haemorrhage. Even where they undergo healing they may cause such a stricture of the calibre of the intestinal canal as to give rise to the symptoms of obstruction which ultimately prove fatal. One of the severest complications of the disease is abscess of the liver, usually said to be solitary, and known as tropical abscess of the liver, but probably is more frequently multiple than is usually thought.
Treatment.—Where the disease is endemic or is prevailing epidemically, it is of great importance to use all preventive measures, and for this purpose the avoidance of all causes likely to precipitate an attack is to be enjoined. Exposure to cold after heat, the use of unripe fruit, and intemperance in eating and drinking should be forbidden; and the utmost care taken as to the quality of the food and drinking water. In houses or hospitals where cases of the disease are under treatment, disinfectants should be freely employed, and the evacuations of the 786 patients removed as speedily as possible, having previously been sterilized in much the same manner as is employed in typhoid fever. In the milder varieties of this complaint, such as those occurring sporadically, and where the symptoms are probably due to matters in the bowels setting up the dysenteric irritation, the employment of diaphoretic medicines is to be recommended, and the administration of such a laxative as castor oil, to which a small quantity of laudanum has been added, will often, by removing the source of the mischief, arrest the attack; but a method of treatment more to be recommended is the use of salines in large doses, such as one drachm of sodium sulphate from four to eight times a day. This treatment may with advantage be combined with the internal administration of ipecacuanha, which still retains its reputation in this disease. Latterly, free irrigation of the bowel with astringents, such as silver nitrate, tannalbin, &c., has been attended with success in those cases which have been able to tolerate the injections. In many instances they cannot be used owing to the extreme degree of irritability of the bowel. The operation of appendicostomy, or bringing the appendix to the surface and using it as the site for the introduction of the irrigating fluid, has been attended with considerable success.
In those cases due to Shiga’s bacillus the ideal treatment has been put at our disposal by the preparation of a specific antitoxin; this has been given a trial in several grave epidemics of late, and may be said to be the most satisfactory treatment and offer the greatest hope of recovery. It is also of great use as a prophylactic.
The preparations of morphia are of great value in the symptomatic treatment of the disease. They may be applied externally as fomentations, for the relief of tormina; by rectal injection for the relief of the tenesmus and irritability of the bowel; hypodermically in advanced cases, for the relief of the general distress. In amoebic dysentery, warm injections of quinine per rectum have proved very efficacious, are usually well tolerated, and are not attended with any ill effects. The diet should be restricted, consisting chiefly of soups and farinaceous foods; more especially is this of importance in the chronic form. For the thirst ice may be given by the mouth. Even in the chronic forms, confinement to bed and restriction of diet are the most important elements of the treatment. Removal from the hot climate and unhygienic surroundings must naturally be attended to.
Bibliography.—Allbutt and Rolleston, System of Medicine, vol. ii. part ii. (1907), “Dysentery,” Drs Andrew Davidson and Simon Flexner; Davidson, Hygiene and Diseases of Warm Climates (Edinburgh, 1903); Fearnside in Ind. Med. Gaz. (July 1905); Ford in Journal of Tropical Medicine (July 15, 1904); Korentchewsky in Bulletin de l’Institut Pasteur (February 1905); Shiga: Osier and M’Crae’s System of Medicine, vol. ii. p. 781 (1907); Skschivan and Stefansky in Berliner klinische Wochenschrift (February 11, 1907); Vaillard and Dopter, on the treatment by antidysenteric serum, Annales de l’Institut Pasteur, No. 5, p. 326 (1906); J.A. Pottinger, “Appendicostomy in Chronic Dysentery,” Lancet (December 28, 1907); Robert Doerr, Das Dysenterietoxin (Gustav Fischer, Jena, 1907); F.M. Sandwith, “Hunterian Lecture on the Treatment of Dysentery,” Lancet (December 7, 1907).
DYSPEPSIA (from the Gr. prefix δυσ-, hard, ill, and πέπτειν, to digest), or indigestion, a term vaguely given to a group of pathological symptoms. There are comparatively few diseases of any moment where some of the phenomena of dyspepsia are not present as associated symptoms, and not infrequently these exist to such a degree as to mask the real disease, of which they are only complications. This is especially the case in many organic diseases of the alimentary canal, in which the symptoms of dyspepsia are often the most prominent. In its restricted meaning, however (and it is to this that the present article applies), the term is used to describe a functional derangement of the natural process of digestion, apart from any structural change in the organs concerned in the act.
The causes of this trouble may be divided into (a) those which concern the food, and (b) those which concern the organism. Among the causes connected with the food are not only the indulgence in indigestible articles of diet, but the too common practice of eating too much of what may be otherwise quite wholesome and digestible; and irregular, too frequent or too infrequent meals. The quantity of food required by different individuals varies between wide limits, but also the quantity required by the same individual varies considerably according to circumstances, more food being needed in cold than in warm weather, and more in an active open-air occupation than in a sedentary one. The thorough mastication of the food is a very important precursor of digestion,1 and this only too often fails, either owing to haste over meals or because of painful or deficient teeth. Again, the quality of the food is of importance, some kinds of flesh being harder and more difficult of mastication than others. This is especially the case with meat that has been smoked or salted, and with that cooked too soon after the death of the animal. Drinks are a common source of dyspepsia. Beer when new and its fermentation not completed is especially bad. Vinegar and acid wines, if taken in large quantities, tend to produce gastric catarrh, and tea is a very fruitful source of this trouble. Even too much water at meal-times may cause indigestion, since the food in the mouth is apt to be softened by the water instead of saliva, and also the gastric juice becomes unduly diluted, rendering the digestion in the stomach too slow and prolonged. Carious teeth and oral sepsis, from whatsoever cause, lead to the same trouble.
Of the causes which concern the organism, nervous influences come first. Bad news may take away all power of digestion and even provoke vomiting, and any worry or mental trouble tends to bring on this condition. General weakness and atony of the body affects the stomach in like degree, and, if the muscles of the abdominal wall be much wasted, they become too weak to support the abdominal viscera in place. Hence results a general tendency for these organs to fall, giving rise to a condition of visceroptosis, of which an obstinate dyspepsia is a very marked feature. Adhesions of the intestines from old inflammatory troubles, floating kidney and bad circulation may each be a cause of painful digestion. Again, a dyspepsia that will not yield to treatment is often one of the symptoms of renal disease, or, in young people of fifteen to twenty years of age, it may be the earliest sign of a gouty diathesis, or even of a more serious condition still—incipient phthisis. Chronic dyspepsia, by weakening the organism, renders it more liable to fall a prey to the attacks of the tubercle bacillus, but, on the other hand, the tuberculous lesion in the lung is often accompanied by a most intractable form of dyspepsia. From this it is clear that any condition which lessens the general well-being of the organism as a whole, apart from its producing any permanent morbid condition in the stomach, may yet interfere with the normal digestive processes and so give rise to dyspepsia.
The symptoms of dyspepsia, even when due to a like cause, are so numerous and diversified in different individuals that probably no description could exactly represent them as they occur in any given case. All that can be here attempted is to mention some of the more prominent morbid phenomena usually present in greater or less degree.
Very briefly, a furred tongue, foul breath, disturbance of appetite, nausea and vomiting, oppression in the chest, pain, flatulence and distension, acidity, pyrosis and constipation or diarrhoea are a few of the commonest symptoms.
When the attack is dependent on some error in diet, and the dyspepsia consequently more of an acute character, there is often pain followed with sickness and vomiting of the offensive matters, after which the patient soon regains his former healthy state. What are commonly known as “bilious attacks” are frequently of this character. In the more chronic cases of dyspepsia the symptoms are somewhat different. A sensation of discomfort comes on shortly after a meal, and is more of the nature of weight and distension in the stomach than of actual pain, although this too may be present. These feelings may come 787 on after each meal, or only after certain meals, and they may arise irrespective of the kind of food taken, or only after certain articles of diet. As in most of such cases the food is long retained in the stomach, it is apt to undergo fermentive changes, one of the results of which is the accumulation of gases which cause flatulence and eructations of an acid or foul character. Occasionally quantities of hot, sour, tasteless or bitter fluid—pyrosis—or mouthfuls of half-digested food, regurgitate from the stomach. Temporary relief may be obtained when another meal is taken, but soon the uncomfortable sensations return as before. The appetite may be craving or deficient, or desirous of abnormal kinds of food. The tongue registers the gastric condition with great delicacy;—a pasty white fur on the tongue is considered a sign of weakness or atony of the digestive tract; a clean pointed tongue with large papillae, and rather red at the edges and tip, is a sign of gastric irritation; and a pale flabby tongue suggests the need of stimulating treatment. Constipation is more common in the chronic forms of dyspepsia, diarrhoea in the acute.
Numerous disagreeable and painful sensations in other parts are experienced, and are indeed often more distressing than the merely gastric symptoms. Pains in the chest, shortness of breathing, palpitation, headache, giddiness, affections of vision, coldness of the extremities, and general languor are common accompaniments of dyspepsia; while the nervous phenomena are specially troublesome in the form of sleeplessness, irritability, despondency and hypochondriasis.
As regards treatment only a few general observations can be made. The careful arrangement of the diet is a matter of first importance. Quantity must be regulated by the digestive capabilities of the individual, his age, and the demands made upon his strength by work. There is little doubt that the danger is in most instances on the side of excess, and the rule which enjoins the cessation from eating before the appetite is satisfied is a safe one for dyspeptics. Due time, too, must be given for the digestion of a meal, and from four to six hours are in general required for this purpose. Long fasts, however, are nearly as hurtful as too frequent meals. Of no less importance is the kind of food taken, and on this point those who suffer from indigestion must ever exercise the greatest care. It must be borne in mind that idiosyncrasy often plays an important part in digestion, some persons being unable to partake without injury of substances which are generally regarded as wholesome and digestible. In most cases it is found very helpful to separate the protein from the farinaceous food, and the more severe the dyspepsia the more thoroughly should this be done, only relaxing as the dyspepsia yields. No fluid should be drunk at meal-times, but from one to two tumblers of hot water should be drunk from an hour to an hour and a half before food. This washes any remnant of the last meal from the stomach, and also supplies material for the free secretion of saliva and gastric juice, thus promoting and accelerating digestion. The only exception to this is in the case of a dilated stomach, when it is wholly contra-indicated. With regard to mastication, Sir Andrew Clark’s rule is a very good one, and is more easily followed than the ideal theory laid down by Horace Fletcher, according to whom any food is digestible if properly treated while still in the mouth. Clark’s rule is that as the mouth normally contains thirty-two teeth, thirty-two bites should be given before the food is swallowed. This, of course, is a practical doctor’s concession to human weakness. Mr Fletcher would train every one to “chew” till the contents of the mouth were swallowed by reflex action without deliberate act; and he applies this theory of mastication and salivation also to drinks (except water). Again, a lack of warmth being a source of dyspepsia, this should be attended to, the back of the neck, the front of the abdomen and the feet being the parts that require special attention. The feet should be raised on a stool, the ankles protected with warm stockings and a woollen “cummerbund” wound two or three times round the body. Experience has shown that in this complaint no particular kind of food or avoidance of food is absolutely to be relied on, but that in general the best diet is one of a mixed animal and vegetable kind, simply but well cooked. The partaking of many dishes, of highly-seasoned or salted meats, raw vegetables, newly-baked bread, pastry and confectionery are all well-known common causes of dyspepsia, and should be avoided. When even the simple diet usually taken is found to disagree, it may be necessary to change it temporarily for a still lighter form, such as a milk diet, and that even in very moderate quantity.
The employment of alcoholic stimulants to assist digestion is largely resorted to, both with and without medical advice. While it seems probable that in certain cases of atonic dyspepsia, particularly in the feeble and aged, the moderate administration of alcohol has the effect of stimulating the secretion of gastric juice, and is an important adjuvant to other remedies, the advantages of its habitual use as an aid to digestion by the young and otherwise healthy, is more than questionable, and it will generally be found that among them, those are least troubled with indigestion who abstain from it. Rest should be taken both before and after food, and general hygienic measures are highly important, since whatever improves the state of the health will have a favourable influence on digestion. Hence regular exercise in the open air, early rising and the cold bath are to be strongly recommended.
The medicinal treatment of dyspepsia can only be undertaken by a physician, but the following is a very brief résumé of the drugs he depends on to-day. Bicarbonate of soda with some bitter, as quassia, gentian or columba, is much in vogue as a direct gastric stimulant. In irritable dyspepsia some form of bismuth in solution or powder; and, to assist digestion through the nervous system, nux vomica and strychnine can be relied on. To give directly digestive material, hydrochloric acid, pepsin and rennet are prescribed in many forms, but where there is much vomiting ingluvin is more efficacious than pepsin. When farinaceous food is badly borne, diastase is helpful, given either before or with the meal. To prevent fermentation, phenol, creasote and sulpho-carbolate of soda are all extremely useful in skilled hands; and for intestinal decomposition and flatulent distension, bismuth salicylate with salol or β-naphthol is much used. Cyllin, and charcoal in many forms, may be taken both for gastric and intestinal flatulence. But all these drugs, of proved value though they are, must be modified and combined to suit the special idiosyncrasy of the patient, and are therefore often worse than useless in inexperienced hands. The condition of the bowels must always have due attention.
See also Digestive Organs; Nutrition and Dietetics.
1 This aspect of the matter—“buccal digestion”—has been specially emphasized in recent years by Horace Fletcher of the United States, whose experience of the results of systematic “chewing,” confirmed by Sir M. Foster, Prof. Chittenden and others, has almost revolutionized the science of dietetics.
DYSTELEOLOGY, a modern word invented by Haeckel (Evolution of Man) for the doctrine of purposelessness, as opposed to the philosophical doctrine of design (Teleology).
DZUNGARIA, Dsongaria, or Jungaria, a former Mongolian kingdom of Central Asia, raised to its highest pitch by Kaldan or Bushtu Khan in the latter half of the 17th century, but completely destroyed by Chinese invasion about 1757-1759. It has played an important part in the history of Mongolia and the great migrations of Mongolian stems westward. Now its territory belongs partly to the Chinese empire (east Turkestan and north-western Mongolia) and partly to Russian Turkestan (provinces of Semiryechensk and Semipalatinsk). It derived its name from the Dsongars, or Songars, who were so called because they formed the left wing (dson, left; gar, hand) of the Mongolian army. Its widest limit included Kashgar, Yarkand, Khotan, the whole region of the T’ien Shan, or Tian-shan, Mountains, and in short the greater proportion of that part of Central Asia which extends from 35° to 50° N. and from 72° to 97° E. The name, however, is more properly applied only to the present Chinese province of T’ien Shan-pei-lu and the country watered by the Ili. As a political or geographical term it has practically disappeared from the map; but the range of mountains stretching north-east along the southern frontier of the Land of the Seven Streams, as the district to the south-east of the Balkhash Lake is called, preserves the name of Dzungarian Range.
E The fifth symbol in the English alphabet occupies also
the same position in Phoenician and in the other
alphabets descended from Phoenician. As the Semitic
alphabet did not represent vowels, E was originally an
aspirate. Its earliest form, while writing is still from right to left,
is  , the upright being continued some distance below the lowest
of the cross-strokes. In some of the Greek alphabets it appears
as
, the upright being continued some distance below the lowest
of the cross-strokes. In some of the Greek alphabets it appears
as 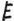 with the upright prolonged at both top and bottom, but
it soon took the form with which we are familiar, though in
the earlier examples of this form the cross-strokes are not
horizontal but drop at an angle,
with the upright prolonged at both top and bottom, but
it soon took the form with which we are familiar, though in
the earlier examples of this form the cross-strokes are not
horizontal but drop at an angle,  . In Corinth and places
under its early influence like Megara, or colonized from it like
Corcyra, the symbol for e takes the form
. In Corinth and places
under its early influence like Megara, or colonized from it like
Corcyra, the symbol for e takes the form  or
or  , while at Sicyon
in the 6th and 5th centuries B.C. it is represented by
, while at Sicyon
in the 6th and 5th centuries B.C. it is represented by  . In
early Latin it was sometimes represented by two perpendicular
strokes of equal length,
. In
early Latin it was sometimes represented by two perpendicular
strokes of equal length,  .
.
In the earliest Greek inscriptions and always in Latin the
symbol  represented both the short and the long e-sound.
In Greek also it was often used for the close long sound which
arose either by contraction of two short e-sounds or by the loss
of a consonant, after a short e-sound, as in φιλεῖτε, “you love,”
for φιλέετε, and φαεινός, “bright,” out of an earlier φαεσνός.
The Ionian Greeks of Asia Minor, who had altogether lost the
aspirate, were the first to use the symbol
represented both the short and the long e-sound.
In Greek also it was often used for the close long sound which
arose either by contraction of two short e-sounds or by the loss
of a consonant, after a short e-sound, as in φιλεῖτε, “you love,”
for φιλέετε, and φαεινός, “bright,” out of an earlier φαεσνός.
The Ionian Greeks of Asia Minor, who had altogether lost the
aspirate, were the first to use the symbol  for the long e-sound,
and in official documents at Athens down to 403 B.C., when the
Greek alphabet as still known was adopted by the state,
for the long e-sound,
and in official documents at Athens down to 403 B.C., when the
Greek alphabet as still known was adopted by the state,  represented ε, η and the sound arising by contraction or consonant
loss as mentioned above which henceforth was written with
two symbols, ει, and being really a single sound is known as
the “spurious diphthong.” There were some minor distinctions
in usage of the symbols
represented ε, η and the sound arising by contraction or consonant
loss as mentioned above which henceforth was written with
two symbols, ει, and being really a single sound is known as
the “spurious diphthong.” There were some minor distinctions
in usage of the symbols  and
and  which need not here be given
in detail. The ancient Greek name was εἶ, not Epsilon as
popularly supposed; the names of the Greek letters are
given from Kallias, an earlier contemporary of Euripides, in
Athenaeus x. p. 453 d.
which need not here be given
in detail. The ancient Greek name was εἶ, not Epsilon as
popularly supposed; the names of the Greek letters are
given from Kallias, an earlier contemporary of Euripides, in
Athenaeus x. p. 453 d.
In Greek the short e-sound to which  was ultimately limited
was a close sound inclining more towards i than a; hence the
representation of the contraction of εε by ει. Its value in
Latin was exactly the opposite, the Latin short e being open,
and the long close. In English there has been a gradual
narrowing of the long vowels, ā becoming approximately ēi
and ē becoming ī (Sweet, History of English Sounds, §§ 781, 817 ff.
2nd ed.). In languages where the diphthong ai has become a
monophthong, the resulting sound is some variety of long e.
Often the gradual assimilation can be traced through the intermediate
stage of ae to ē, as in the Old Latin aidilis, which in
classical Latin is aedilis, and in medieval MSS. edilis.
was ultimately limited
was a close sound inclining more towards i than a; hence the
representation of the contraction of εε by ει. Its value in
Latin was exactly the opposite, the Latin short e being open,
and the long close. In English there has been a gradual
narrowing of the long vowels, ā becoming approximately ēi
and ē becoming ī (Sweet, History of English Sounds, §§ 781, 817 ff.
2nd ed.). In languages where the diphthong ai has become a
monophthong, the resulting sound is some variety of long e.
Often the gradual assimilation can be traced through the intermediate
stage of ae to ē, as in the Old Latin aidilis, which in
classical Latin is aedilis, and in medieval MSS. edilis.
The variety of spelling in English for the long and short e-sounds is conveniently illustrated in Miss Soames’s Introduction to the Study of Phonetics, pp. 16 and 20.
EA (written by means of two signs signifying “house” and “water”), in the Babylonian religion, originally the patron deity of Eridu, situated in ancient times at the head of the Persian Gulf, but now, by reason of the constant accumulation of soil in the Euphrates valley, at some distance from the gulf. Eridu, meaning “the good city,” was one of the oldest settlements in the Euphrates valley, and is now represented by the mounds known as Abu Shahrein. In the absence of excavations on that site, we are dependent for our knowledge of Ea on material found elsewhere. This is, however, sufficient to enable us to state definitely that Ea was a water-deity, and there is every reason to believe that the Persian Gulf was the body of water more particularly sacred to him. Whether Ea (or A-e as some scholars prefer) represents the real pronunciation of his name we do not know. All attempts to connect Ea with Yah and Yahweh are idle conjectures without any substantial basis. He is figured as a man covered with the body of a fish, and this representation, as likewise the name of his temple E-apsu, “house of the watery deep,” points decidedly to his character as a god of the waters (see Oannes). Of his cult at Eridu, which reverts to the oldest period of Babylonian history, nothing definite is known beyond the fact that the name of his temple was E-saggila, “the lofty house”—pointing to a staged tower as in the case of the temple of Bel (q.v.) at Nippur, known as E-Kur, i.e. “mountain house”—and that incantations, involving ceremonial rites, in which water as a sacred element played a prominent part, formed a feature of his worship. Whether Eridu at one time also played an important political rôle is not certain, though not improbable. At all events, the prominence of the Ea cult led, as in the case of Nippur, to the survival of Eridu as a sacred city, long after it had ceased to have any significance as a political centre. Myths in which Ea figures prominently have been found in Assur-bani-pal’s library, indicating that Ea was regarded as the protector and teacher of mankind. He is essentially a god of civilization, and it was natural that he was also looked upon as the creator of man, and of the world in general. Traces of this view appear in the Marduk epic celebrating the achievements of this god, and the close connexion between the Ea cult at Eridu and that of Marduk also follows from two considerations: (1) that the name of Marduk’s sanctuary at Babylon bears the same name, E-saggila, as that of Ea in Eridu, and (2) that Marduk is generally termed the son of Ea, who derives his powers from the voluntary abdication of the father in favour of his son. Accordingly, the incantations originally composed for the Ea cult were re-edited by the priests of Babylon and adapted to the worship of Marduk, and, similarly, the hymns to Marduk betray traces of the transfer of attributes to Marduk which originally belonged to Ea.
It is, however, more particularly as the third figure in the triad, the two other members of which were Anu (q.v.) and Bel (q.v.), that Ea acquires his permanent place in the pantheon. To him was assigned the control of the watery element, and in this capacity he becomes the shar apsi, i.e. king of the Apsu or “the deep.” The Apsu was figured as an ocean encircling the earth, and since the gathering place of the dead, known as Arālu, was situated near the confines of the Apsu, he was also designated as En-Ki, i.e. “lord of that which is below,” in contrast to Anu, who was the lord of the “above” or the heavens. The cult of Ea extended throughout Babylonia and Assyria. We find temples and shrines erected in his honour, e.g. at Nippur, Girsu, Ur, Babylon, Sippar and Nineveh, and the numerous epithets given to him, as well as the various forms under which the god appears, alike bear witness to the popularity which he enjoyed from the earliest to the latest period of Babylonian-Assyrian history. The consort of Ea, known as Damkina, “lady of that which is below,” or Nin-Ki, having the same meaning, or Damgal-nunna, “great lady of the waters,” represents a pale reflection of Ea and plays a part merely in association with her lord.
EABANI, the name of the friend of Gilgamesh, the hero in the Babylonian epic (see Gilgamesh, Epic of). Eabani, whose name signifies “Ea creates,” pointing to the tradition which made the god Ea (q.v.) the creator of mankind, is represented in the epic as the type of the primeval man. He is a wild man who lives with the animals of the field until lured away from his surroundings by the charms of a woman. Created to become a rival to Gilgamesh, he strikes up a friendship with the hero, and together they proceed to a cedar forest guarded by Khumbaba, whom they kill. The goddess Irnina (a form of Ishtar, q.v.) in revenge kills Eabani, and the balance of the epic is taken up with Gilgamesh’s lament for his friend, his wanderings in quest of a remote ancestor, Ut-Napishtim, from whom he hopes to learn how he may escape the fate of Eabani, and his finally learning from his friend of the sad fate in store for all mortals except the favourites of the god, like 789 Ut-Napishtim, to whom immortal life is vouchsafed as a special boon.
EACHARD, JOHN (1636?-1697), English divine, was born in Suffolk, and was educated at Catharine Hall, Cambridge, of which he became master in 1675 in succession to John Lightfoot. He was created D.D. in 1676 by royal mandate, and was twice (in 1679 and 1695) vice-chancellor of the university. He died on the 7th of July 1697. In 1670 he had published anonymously a humorous satire entitled The Ground and Occasions of the Contempt of the Clergy enquired into in a letter to R. L., which excited much attention and provoked several replies, one of them being from John Owen. These were met by Some Observations, &c., in a second letter to R. L. (1671), written in the same bantering tone as the original work. Eachard attributed the contempt into which the clergy had fallen to their imperfect education, their insufficient incomes, and the want of a true vocation. His descriptions, which were somewhat exaggerated, were largely used by Macaulay in his History of England. He gave amusing illustrations of the absurdity and poverty of the current pulpit oratory of his day, some of them being taken from the sermons of his own father. He attacked the philosophy of Hobbes in his Mr Hobb’s State of Nature considered; in a dialogue between Philautus and Timothy (1672), and in his Some Opinions of Mr Hobbs considered in a second dialogue (1673). These were written in their author’s chosen vein of light satire, and Dryden praised them as highly effective within their own range. Eachard’s own sermons, however, were not superior to those he satirized. Swift (Works, xii. 279) alludes to him as a signal instance of a successful humorist who entirely failed as a serious writer.
A collected edition of his works in three volumes, with a notice of his life, was published in 1774. The Contempt of the Clergy was reprinted in E. Arber’s English Garner. A Free Enquiry into the Causes of the very great Esteem that the Nonconforming Preachers are generally in with their Followers (1673) has been attributed to Eachard on insufficient grounds.
EADBALD (d. 640), king of Kent, succeeded to the throne on the death of his father Æthelberht in 616. He had not been influenced by the teaching of the Christian missionaries, and his first step on his accession was to marry his father’s widow. After his subsequent conversion by Laurentius, archbishop of Canterbury, he recalled the bishops Mellitus and Justus, and built a church dedicated to the Virgin at Canterbury. He arranged a marriage between his sister Æthelberg and Edwin of Northumbria, on whose defeat and death in 633 he received his sister and Paulinus, and offered the latter the bishopric of Rochester. Eadbald married Emma, a Frankish princess, and died on the 20th of January 640.
See Bede, Historia ecclesiastica (ed. C. Plummer, Oxford, 1896); Saxon Chronicle (ed. J. Earle and C. Plummer, Oxford, 1899).
EADIE, JOHN (1810-1876), Scottish theologian and biblical critic, was born at Alva, in Stirlingshire, on the 9th of May 1810. Having taken the arts curriculum at Glasgow University, he studied for the ministry at the Divinity Hall of the Secession Church, a dissenting body which, on its union a few years later with the Relief Church, adopted the title United Presbyterian. In 1835 he became minister of the Cambridge Street Secession church in Glasgow, and for many years he was generally regarded as the leading representative of his denomination in Glasgow. As a preacher, though he was not eloquent, he was distinguished by good sense, earnestness and breadth of sympathy. In 1863 he removed with a portion of his congregation to a new church at Lansdowne Crescent. In 1843 Eadie was appointed professor of biblical literature and hermeneutics in the Divinity Hall of the United Presbyterian body. He held this appointment along with his ministerial charge till the close of his life. Though not a profound scholar, he was surpassed by few biblical commentators of his day in range of learning, and in soundness of judgment. In the professor’s chair, as in the pulpit, his strength lay in the tact with which he selected the soundest results of biblical criticism, whether his own or that of others, and presented them in a clear and connected form, with a constant view to their practical bearing. He received the degree of LL.D. from Glasgow in 1844, and that of D.D. from St Andrews in 1850.
His publications were connected with biblical criticism and interpretation, some of them being for popular use and others more strictly scientific. To the former class belong the Biblical Cyclopaedia, his edition of Cruden’s Concordance, his Early Oriental History, and his discourses on the Divine Love and on Paul the Preacher; to the latter his commentaries on the Greek text of St Paul’s epistles to the Ephesians, Colossians, Philippians and Galatians, published at intervals in four volumes. His last work was the History of the English Bible (2 vols., 1876). He rendered good service as one of the revisers of the authorized version. He died at Glasgow on the 3rd of June 1876. His valuable library was bought and presented to the United Presbyterian College.
EADMER, or Edmer (c. 1060-c. 1124), English historian and ecclesiastic, was probably, as his name suggests, of English, and not of Norman parentage. He became a monk in the Benedictine monastery of Christ Church, Canterbury, where he made the acquaintance of Anselm, at that time visiting England as abbot of Bec. The intimacy was renewed when Anselm became archbishop of Canterbury in 1093; thenceforward Eadmer was not only his disciple and follower, but his friend and director, being formally appointed to this position by Pope Urban II. In 1120 he was nominated to the archbishopric of St Andrews, but as the Scots would not recognize the authority of the see of Canterbury he was never consecrated, and soon afterwards he resigned his claim to the archbishopric. His death is generally assigned to the year 1124.
Eadmer left a large number of writings, the most important of which is his Historiae novorum, a work which deals mainly with the history of England between 1066 and 1122. Although concerned principally with ecclesiastical affairs scholars agree in regarding the Historiae as one of the ablest and most valuable writings of its kind. It was first edited by John Selden in 1623 and, with Eadmer’s Vita Anselmi, has been edited by Martin Rule for the “Rolls Series” (London, 1884). The Vita Anselmi, first printed at Antwerp in 1551, is probably the best life of the saint. Less noteworthy are Eadmer’s lives of St Dunstan, St Bregwin, archbishop of Canterbury, and St Oswald, archbishop of York; these are all printed in Henry Wharton’s Anglia Sacra, part ii. (1691), where a list of Eadmer’s writings will be found. The manuscripts of most of Eadmer’s works are preserved in the library of Corpus Christi College, Cambridge.
See M. Rule, On Eadmer’s Elaboration of the first four Books of “Historiae novorum” (1886); and Père Ragey, Eadmer (Paris, 1892).
EADS, JAMES BUCHANAN (1820-1887), American engineer, was born at Lawrenceburg, Indiana, on the 23rd of May 1820. His first engineering work of any importance was in raising sunken steamers. In 1845 he established glass works in St Louis. During the Civil War he constructed ironclad steamers and mortar boats for the Federal government. His next important engineering achievement was the construction of the great steel arch bridge across the Mississippi at St Louis (see Bridge, fig. 29), upon which he was engaged from 1867 till 1874. The work, however, upon which his reputation principally rests was his deepening and fixing the channel at the mouths of the Mississippi by means of jetties, whereby the narrowed stream was made to scour out its own channel and carry the sediment out to sea. Shortly before his death he projected a scheme for a ship railway across the Isthmus of Tehuantepec, in lieu of an isthmian canal. He died at Nassau, in the Bahamas, on the 8th of March 1887.
EAGLE (Fr. aigle, from the Lat. aquila), the name generally given to the larger diurnal birds of prey which are not vultures; but the limits of the subfamily Aquilinae have been very variously assigned by different writers on systematic ornithology, and there are eagles smaller than certain buzzards. By some authorities the Laemmergeier of the Alps, and other high mountains of Europe, North Africa and Asia, is accounted an eagle, but by others the genus Gypaetus is placed with the Vulturidae as its 790 common English name (bearded vulture) shows. There are also other forms, such as the South American Harpyia and its allies, which though generally called eagles have been ranked as buzzards. In the absence of any truly scientific definition of the family Aquilinae it is best to leave these and many other more or less questionable members of the group—such as the genera Spizaetus, Circaetus, Spilornis, Helotarsus, and so forth—and to treat here of those whose position cannot be gainsaid.
 |
| Fig. 1.—Sea-Eagle. |
True eagles inhabit all the regions of the world, and some seven or eight species at least are found in Europe, of which two are resident in the British Islands. In England and in the Lowlands of Scotland eagles only exist as stragglers; but in the Hebrides and some parts of the Highlands a good many may yet be found, and their numbers appear to have rather increased of late years than diminished; for the foresters and shepherds, finding that a high price can be got for their eggs, take care to protect the owners of the eyries, which are nearly all well known, and to keep up the stock by allowing them at times to rear their young. There are also now not a few occupiers of Scottish forests who interfere so far as they can to protect the king of birds.1 In Ireland the extirpation of eagles seems to have been carried on almost unaffected by the prudent considerations which in the northern kingdom have operated so favourably for the race, and except in the wildest parts of Donegal, Mayo and Kerry, eagles in the sister island are almost birds of the past.
Of the two British species the erne (Icel. Œrn) or sea-eagle (by some called also the white-tailed and cinereous eagle)—Haliaetus albicilla—affects chiefly the coast and neighbourhood of inland waters, living in great part on the fish and refuse that is thrown up on the shore, though it not unfrequently takes living prey, such as lambs, hares and rabbits. On these last, indeed, young examples mostly feed when they wander southward in autumn, as they yearly do, and appear in England. The adults (fig. 1) are distinguished by their prevalent greyish-brown colour, their pale head, yellow beak and white tail—characters, however, wanting in the immature, which do not assume the perfect plumage for some three or four years. The eyry is commonly placed in a high cliff or on an island in a lake—sometimes on the ground, at others in a tree—and consists of a vast mass of sticks in the midst of which is formed a hollow lined with Luzula sylvatica (as first observed by John Wolley) or some similar grass, and here are laid the two or three white eggs. In former days the sea-eagle seems to have bred in several parts of England—as the Lake district, and possibly even in the Isle of Wight and on Dartmoor. This species inhabits all the northern part of the Old World from Iceland to Kamchatka, and breeds in Europe so far to the southward as Albania. In the New World, however, it is only found in Greenland, being elsewhere replaced by the white-headed or bald eagle, H. leucocephalus, a bird of similar habits, and the chosen emblem of the United States of America. In the far east of Asia occurs a still larger and finer sea-eagle, H. pelagicus, remarkable for its white thighs and upper wing-coverts. South-eastern Europe and India furnish a much smaller species, H. leucoryphus, which has its representative, H. leucogaster, in the Malay Archipelago and Australia, and, as allies in South Africa and Madagascar, H. vocifer and H. vociferoides respectively. All these eagles may be distinguished by their scaly tarsi, while the group next to be treated of have the tarsi feathered to the toes.
 |
| Fig. 2.—Mountain-Eagle. |
The golden or mountain eagle, Aquila chrysaetus, is the second British species. This also formerly inhabited England, and a nest, found in 1668 in the Peak of Derbyshire, is well described by Willughby, in whose time it was said to breed also in the Snowdon range. It seldom if ever frequents the coast, and is more active on the wing than the sea-eagle, being able to take some birds as they fly, but a large part of its sustenance is the flesh of animals that die a natural death. Its eyry is generally placed and built like that of the other British species,2 but the neighbourhood of 791 water is not requisite. The eggs, from two to four in number, vary from a pure white to a mottled, and often highly coloured, surface, on which appear different shades of red and purple. The adult bird (fig. 2) is of a rich dark brown, with the elongated feathers of the neck, especially on the nape, light tawny, in which imagination sees a “golden” hue, and the tail marbled with brown and ashy-grey. In the young the tail is white at the base, and the neck has scarcely any tawny tint. The golden eagle does not occur in Iceland, but occupies suitable situations over the rest of the Palaearctic Region and a considerable portion of the Nearctic—though the American bird has been, by some, considered a distinct species. Domesticated, it has many times been trained to take prey for its master in Europe, and to this species is thought to belong an eagle habitually used by the Kirghiz Tatars, who call it Bergut or Bearcoot, for the capture of antelopes, foxes and wolves. It is carried hooded on horseback or on a perch between two men, and released when the quarry is in sight. Such a bird, when well trained, is valued, says P.S. Pallas, at the price of two camels. It is quite possible, however, that more than one kind of eagle is thus used, and the services of A. heliaca (which is the imperial eagle of some writers3) and of A. mogilnik—both of which are found in central Asia, as well as in south-eastern Europe—may also be employed.
A smaller form of eagle, which has usually gone under the name of A. naevia, is now thought by the best authorities to include three local races, or, in the eyes of some, species. They inhabit Europe, North Africa and western Asia to India, and two examples of one of them—A. clanga, the form which is somewhat plentiful in north-eastern Germany—have occurred in Cornwall. The smallest true eagle is A. pennata, which inhabits southern Europe, Africa and India. Differing from other eagles of their genus by its wedge-shaped tail, though otherwise greatly resembling them, is the A. audax of Australia. Lastly may be noticed here a small group of eagles, characterized by their long legs, forming the genus Nisaetus, of which one species, N. fasciatus, is found in Europe.
1 Lord Breadalbane (d. 1871) was perhaps the first large landowner who set the example that has been since followed by others. On his unrivalled forest of Black Mount, eagles—elsewhere persecuted to the death—were by him ordered to be unmolested so long as they were not numerous enough to cause considerable depredations on the farmers’ flocks. He thought that the spectacle of a soaring eagle was a fitting adjunct to the grandeur of his Argyllshire mountain scenery, and a good equivalent for the occasional loss of a lamb, or the slight deduction from the rent paid by his tenantry in consequence.
2 As already stated, the site chosen varies greatly. Occasionally placed in a niche in what passes for a perpendicular cliff to which access could only be gained by a skilful cragsman with a rope, the writer has known a nest to within 10 or 15 yds. of which he rode on a pony. Two beautiful views of as many golden eagles’ nests, drawn on the spot by Joseph Wolf, are given in the Ootheca Wolleyana, and a fine series of eggs is also figured in the same work.
3 Which species may have been the traditional emblem of Roman power, and the Ales Jovis, is very uncertain.
EAGLEHAWK, a borough of Bendigo county, Victoria, Australia, 105 m. by rail N.N.W. of Melbourne and 4 m. from Bendigo, with which it is connected by steam tramway. Pop. (1901) 8130. It stands on the Bendigo gold-bearing reef, and its mines are important.
EAGRE (a word of obscure origin; the earliest form seems to be higre, Latinized as higra, which William of Malmesbury gives as the name of the bore in the Severn; the New English Dictionary rejects the usual derivations from the O. Eng. eagor or egor, which is seen in compounds meaning “flood,” and also the connexion with the Norse sea-god Aegir), a tide wave of great height rushing up an estuary (see Bore), used locally of the Humber and Trent.
EAKINS, THOMAS (1844- ), American portrait and figure painter, was born at Philadelphia, on the 25th of July 1844. A pupil of J.L. Gérôme, in the École des Beaux-Arts, Paris, and Also of Léon Bonnat, besides working in the studio of the sculptor Dumont, he became a prolific portrait painter. He also painted genre pictures, sending to the Centennial Exhibition at Philadelphia, in 1876, the “Chess Players,” now in the Metropolitan Museum of Art, New York. A large canvas, “The Surgical Clinic of Professor Gross,” owned by Jefferson Medical College, Philadelphia, contains many life-sized figures. Eakins, with his pupil Samuel Murray (b. 1870), modelled the heroic “Prophets” for the Witherspoon Building, Philadelphia, and his work in painting has a decided sculptural quality. He was for some years professor of anatomy at the schools of the Pennsylvania Academy of Fine Arts in Philadelphia. A man of great inventiveness, he experimented in many directions, depicting on canvas modern athletic sports, the negro, and early American life, but he is best known by his portraits. He received awards at the Columbian (1893), Paris (1900), Pan-American (1900), and the St Louis (1904), Expositions; and won the Temple medal in the Pennsylvania Academy of Fine Arts, and the Proctor prize of the National Academy of Design.
EALING, a municipal borough in the Ealing parliamentary division of Middlesex, England, suburban to London, 9 m. W. of St Paul’s cathedral. Pop. (1891) 23,979; (1901) 33,031. The nucleus of the town, the ancient village, lies south of the highroad to Uxbridge, west of the open Ealing Common. The place is wholly residential. At St Mary’s church, almost wholly rebuilt c. 1870, are buried John Oldmixon, the historian (d. 1742), and Horne Tooke (d. 1812). The church of All Saints (1905) commemorates Spencer Perceval, prime minister, who was assassinated in the House of Commons in 1812. It was erected under the will of his daughter Frederica, a resident of Ealing. Gunnersbury Park, south of Ealing Common, is a handsome Italian mansion. Among former owners of the property was Princess Amelia, daughter of George II., who lived here from 1761 till her death in 1786. The name of Gunnersbury is said to be traceable to the residence here of Gunilda, niece of King Canute. The manor of Ealing early belonged to the see of London, but it is not mentioned in Domesday and its history is obscure.
EAR (common Teut.; O.E. éare, Ger. Ohr, Du. oor, akin to Lat. auris, Gr. οὖς), in anatomy, the organ of hearing. The human ear is divided into three parts—external, middle and internal. The external ear consists of the pinna and the external auditory meatus. The pinna is composed of a yellow fibro-cartilaginous framework covered by skin, and has an external and an internal or cranial surface. Round the margin of the external surface in its upper three quarters is a rim called the helix (fig. 1, a), in which is often seen a little prominence known as Darwin’s tubercle, representing the folded-over apex of a prick-eared ancestor. Concentric with the helix and nearer the meatus is the antihelix (c), which, above, divides into two limbs to enclose the triangular fossa of the antihelix. Between the helix and the antihelix is the fossa of the helix. In front of the antihelix is the deep fossa known as the concha (fig. 1, d), and from the anterior part of this the meatus passes inward into the skull. Overlapping the meatus from in front is a flap called the tragus, and below and behind this is another smaller flap, the antitragus. The lower part of the pinna is the lobule (e), which contains no cartilage. On the cranial surface of the pinna elevations correspond to the concha and to the fossae 792 of the helix and antihelix. The pinna can be slightly moved by the anterior, superior and posterior auricular muscles, and in addition to these there are four small intrinsic muscles on the external surface, known as the helicis major and minor, the tragicus and the antitragicus, and two on the internal surface called the obliquus and transversus. The external auditory meatus (fig. 1, n) is a tube running at first forward and upward, then a little backward and then forward and slightly downward; of course all the time it is also running inward until the tympanic membrane is reached. The tube is about an inch long, its outer third being cartilaginous and its inner two-thirds bony. It is lined by skin in its whole length, the sweat glands of which are modified to secrete the wax or cerumen.
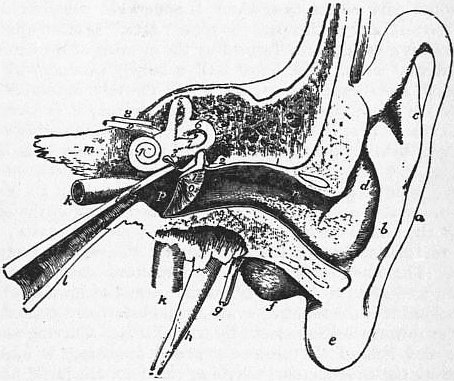 | |
| Fig. 1.—The Ear as seen in Section. | |
|
a, Helix. b, Antitragus. c, Antihelix. d, Concha. e, Lobule. f, Mastoid process. g, Portio dura. h, Styloid process. k, Internal carotid artery. l, Eustachian tube. |
m, Tip of petrous process. n, External auditory meatus. o, Membrana tympani. p, Tympanum. 1, points to malleus. 2, to incus. 3, to stapes. 4, to cochlea. 5, 6, 7, the three semicircular canals. 8 and 9, facial and auditory nerves. |
The middle ear or tympanum (fig. 1, p) is a small cavity in the temporal bone, the shape of which may perhaps be realized by imagining a hock bottle subjected to lateral pressure in such a way that its circular section becomes triangular, the base of the triangle being above. The neck of the bottle, also laterally compressed, will represent the Eustachian tube (fig. 1, l), which runs forward, inward and downward, to open into the naso-pharynx, and so admits air into the tympanum. The bottom of the bottle will represent the posterior wall of the tympanum, from the upper part of which an opening leads backward into the mastoid antrum and so into the air-cells of the mastoid process. Lower down is a little pyramid which transmits the stapedius muscle, and at the base of this is a small opening known as the iter chordae posterius, for the chorda tympani to come through from the facial nerve. The roof is formed by a very thin plate of bone, called the tegmen tympani, which separates the cavity from the middle fossa of the skull. Below the roof the upper part of the tympanum is somewhat constricted off from the rest, and to this part the term “attic” is often applied. The floor is a mere groove formed by the meeting of the external and internal walls. The outer wall is largely occupied by the tympanic membrane (fig. 1, o), which entirely separates the middle ear from the external auditory meatus; it is circular, and so placed that it slopes from above, downward and inward, and from behind, forward and inward. Externally it is lined by skin, internally by mucous membrane, while between the two is a firm fibrous membrane, convex inward about its centre to form the umbo. Just in front of the membrane on the outer wall is the Glaserian fissure leading to the glenoid cavity, and close to this is the canal of Huguier for the chorda tympani nerve. The inner wall shows a promontory caused by the cochlea and grooved by the tympanic plexus of nerves; above and behind it is the fenestra ovalis, while below and behind the fenestra rotunda is seen, closed by a membrane. Curving round, above and behind the promontory and fenestrae, is a ridge caused by the aqueductus Fallopii or canal for the facial nerve. The whole tympanum is about half an inch from before backward, and half an inch high, and is spanned from side to side by three small bones, of which the malleus (fig. 1, 1) is the most external. This is attached by its handle to the umbo of the tympanic membrane, while its head lies in the attic and articulates posteriorly with the upper part of the next bone or incus (fig. 1, 2). The long process of the incus runs downward and ends in a little knob called the os orbiculare, which is jointed on to the stapes or stirrup bone (fig. 1, 3). The two branches of the stapes are anterior and posterior, while the footplate fits into the fenestra ovalis and is bound to it by a membrane. It will thus be seen that the stapes lies nearly at right angles to the long process of the incus. From the front of the malleus a slender process projects forward into the Glaserian fissure, while from the back of the incus the posterior process is directed backward and is attached to the posterior wall of the tympanum. These two processes form a fulcrum by which the lever action of the malleus and incus is brought about, so that when the handle of the malleus is pushed in by the membrane the head moves out; the top of the incus, attached to it, also moves out, and the os orbiculare moves in, and so the stapes is pressed into the fenestra ovalis. The stapedius and tensor tympanic muscles, the latter of which enters the tympanum in a canal just above the Eustachian tube to be attached to the malleus, modify the movements of the ossicles.
The mucous membrane lining the tympanum is continuous through the Eustachian tube with that of the naso-pharynx, and is reflected on to the ossicles, muscles and chorda tympani nerve. It is ciliated except where it covers the membrana tympani, ossicles and promontory; here it is stratified.
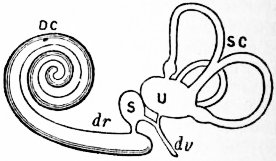 |
| Fig. 2.—Diagram of the Membranous Labyrinth. |
|
DC, Ductus cochlearis. dr, Ductus reuniens. S, Sacculus. U, Utriculus. dv, Ductus endolymphaticus. SC, Semicircular canals. (After Waldeyer.) |
The internal ear or labyrinth consists of a bony and a membranous part, the latter of which is contained in the former. The bony labyrinth is composed of the vestibule, the semicircular canals and the cochlea. The vestibule lies just internal to the posterior part of the tympanum, and there would be a communication between the two, through the fenestra ovalis, were it not that the footplate of the stapes blocks the way. The inner wall of the vestibule is separated from the bottom of the internal auditory meatus by a plate of bone pierced by many foramina for branches of the auditory nerve (fig. 1, 9), while at the lower part is the opening of the aqueductus vestibuli, by means of which a communication is established with the posterior cranial fossa. Posteriorly the three semicircular canals open into the vestibule; of these the external (fig. 1, 7) has two independent openings, but the superior and posterior (fig. 1, 5 and 6) join together at one end and so have a common opening, while at their other ends they open separately. The three canals have therefore five openings into the vestibule instead of six. One end of each canal is dilated to form its ampulla. The superior semicircular canal is vertical, and the two pillars of its arch are nearly external and internal; the external canal is horizontal, its two pillars being anterior and posterior, while the convexity of the arch of the posterior canal is backward and its two pillars are superior and inferior. Anteriorly the vestibule leads into the cochlea (fig. 1, 4), which is twisted two and a half times round a central pillar called the modiolus, the whole cochlea forming a rounded cone something like the shell of a snail though it is only about 5 mm. from base to apex. Projecting from the modiolus is a horizontal plate which runs round it from base to apex like a spiral staircase; this is known as the lamina spiralis, and it stretches nearly half-way across the canal of the cochlea. At the summit it ends in a little hook named the hamulus. The modiolus is pierced by canals which transmit branches of the auditory nerve to the lamina spiralis.
 |
| Fig. 3.—cl, Columnar cells covering the crista acustica; p, peripheral, and c, central processes of auditory cells; n, nerve fibres. (After Rüdinger.) |
The membranous labyrinth lies in the bony labyrinth, but does not fill it; between the two is the fluid called perilymph, while inside the membranous labyrinth is the endolymph. In the bony vestibule lie two membranous bags, the saccule (fig. 2, S) in front, and the utricle (fig. 2, U) behind; each of these has a special patch or macula to which twigs of the auditory nerve are supplied, and in the mucous membrane of which specialized hair cells are found (fig. 3, p).
Attached to the maculae are crystals of carbonate of lime called otoconia. The membranous semicircular canals are very much smaller in section than the bony; in the ampulla of each is a ridge, the crista acustica, which is covered by a mucous 793 membrane containing sensory hair cells like those in the maculae. All the canals open into the utricle. From the lower part of the saccule a small canal called the ductus endolymphaticus (fig. 2, dv) runs into the aqueductus vestibuli; it is soon joined by a small duct from the utricle, and ends, close to the dura mater of the posterior fossa of the cranium, as the saccus endolymphaticus, which may have minute perforations through which the endolymph can pass. Anteriorly the saccule communicates with the membranous cochlea or scala media by a short ductus reuniens (fig. 2, dr). A section through each turn of the cochlea shows the bony lamina spiralis, already noticed, which is continued right across the canal by the basilar membrane (fig. 4, bm), thus cutting the canal into an upper and lower half and connected with the outer wall by the strong spiral ligament (fig. 4, sl). Near the free end of the lamina spiralis another membrane called the membrane of Reissner (fig. 4, mR) is attached, and runs outward and upward to the outer wall, taking a triangular slice out of the upper half of the section. There are now three canals seen in section, the upper of which is the scala vestibuli (fig. 4, SV), the middle and outer the scala media, ductus cochlearis or true membranous cochlea (fig. 4, DC), while the lower is the scala tympani (fig. 4, ST). The scala vestibuli and scala tympani communicate at the apex of the cochlea by an opening known as the helicotrema, so that the perilymph can here pass from one canal to the other. At the base of the cochlea the perilymph in the scala vestibuli is continuous with that in the vestibule, but that in the scala tympani bathes the inner surface of the membrane stretched across the fenestra rotunda, and also communicates with the subarachnoid space through the aqueductus cochleae, which opens into the posterior cranial fossa. The scala media containing endolymph communicates, as has been shown, with the saccule through the canalis reuniens, while, at the apex of the cochlea, it ends in a blind extremity of considerable morphological interest called the lagena.
 | |
| Fig. 4.—Transverse Section through the Tube of the Cochlea. | |
|
m, Modiolus. 0, Outer wall of cochlea. SV, Scala vestibuli. ST, Scala tympani. DC, Ductus cochlearis. mR, Membrane of Reissner. |
bm, Basilar membrane. cs, Crista spiralis. sl, Spiral ligament. sg, Spiral ganglion of auditory nerve. oc, Organ of Corti. |
The scala media contains the essential organ of hearing or organ of Corti (fig. 4, oc), which lies upon the inner part of the basilar membrane; it consists of a tunnel bounded on each side of the inner and outer rods of Corti; on each side of these are the inner and outer hair cells, between the latter of which are found the supporting cells of Deiters. Most externally are the large cells of Hensen. A delicate membrane called the lamina reticularis covers the top of all these, and is pierced by the hairs of the hair cells, while above this is the loose membrana tectoria attached to the periosteum of the lamina spiralis, near its tip, internally, and possibly to some of Deiter’s cells externally. The cochlear branch of the auditory nerve enters the lamina spiralis, where a spiral ganglion (fig. 4, sg) is developed on it; after this it is distributed to the inner and outer hair cells.
 |
| (From R. Howden—Cunningham’s Text-Book of Anatomy.) |
| Fig. 5.—Transverse Section of Corti’s Organ from the Central Coil of Cochlea (Retzius). |
For further details see Text-Book of Anatomy, edited by D.J. Cunningham (Edinburgh, 1906); Quain’s Elements of Anatomy (London, 1893); Gray’s Anatomy (London, 1905); A Treatise on Anatomy, edited by H. Morris (London, 1902); A Text-Book of Human Anatomy, by A. Macalister (London, 1889).
Embryology.—The pinna is formed from six tubercles which appear round the dorsal end of the hyomandibular cleft or, more strictly speaking, pouch. Those for the tragus and anterior part of the helix belong to the first or mandibular arch, while those for the antitragus, antihelix and lobule come from the second or hyoid arch. The tubercle for the helix is dorsal to the end of the cleft where the two arches join. The external auditory meatus, tympanum and Eustachian tube are remains of the hyomandibular cleft, the membrana tympani being a remnant of the cleft membrane and therefore lined by ectoderm outside and entoderm inside. The origin of the ossicles is very doubtful. H. Gadow’s view, which is one of the latest, is that all three are derived from the hyomandibular plate which connects the dorsal ends of the hyoid and mandibular bars (Anatomischer Anzeiger, Bd. xix., 1901, p. 396). Other papers which should be consulted are those of E. Gaupp, Anatom. Hefte, Ergebnisse, Bd. 8, 1898, p. 991, and J.A. Hammar, Archiv f. mikr. Anat. lix., 1902. These papers will give a clue to the immense literature of the subject. The internal ear first appears as a pit from the cephalic ectoderm, the mouth of which in Man and other mammals closes up, so that a pear-shaped cavity is left. The stalk of the pear which is nearest the point of invagination is called the recessus labyrinthi, and this, after losing its connexion with the surface of the embryo, grows backward toward the posterior cranial fossa and becomes the ductus endolymphaticus. The lower part of the vesicle grows forward and becomes the cochlea, while from the upper part three hollow circular plates grow out, the central parts of which disappear, leaving the margin as the semicircular canals. Subsequently constrictions appear in the vesicle marking off the saccule and utricle. From the surrounding 794 mesoderm the petrous bone is formed by a process of chondrification and ossification.
See W. His, Junr., Archiv f. Anat. und Phys., 1889, supplement, p. 1; also Streeter, Am. Journ. of Anat. vi., 1907.
Comparative Anatomy.—The ectodermal inpushing of the internal ear has probably a common origin with the organs of the lateral line of fish. In the lower forms the ductus endolymphaticus retains its communication with the exterior on the dorsum of the head, and in some Elasmobranchs the opening is wide enough to allow the passage of particles of sand into the saccule. It is probable that this duct is the same which, taking a different direction and losing its communication with the skin, abuts on the posterior cranial fossa of higher forms (see Rudolf Krause, “Die Entwickelung des Aq. vestibuli seu d. Endelymphaticus,” Anat. Anzeiger, Bd. xix., 1901, p. 49). In certain Teleostean fishes the swim bladder forms a secondary communication with the internal ear by means of special ossicles (see G. Ridewood, Journ. Anat. & Phys. vol. xxvi.). Among the Cyclostomata the external semicircular canals are wanting; Petromyzon has the superior and posterior only, while in Myxine these two appear to be fused so that only one is seen. In higher types the three canals are constant. Concretions of carbonate of lime are present in the internal ears of almost all vertebrates; when these are very small they are called otoconia, but when, as in most of the teleostean fishes, they form huge concretions, they are spoken of as otoliths. One shark, Squatina, has sand instead of otoconia (C. Stewart, Journ. Linn. Society, xxix. 409). The utricle, saccule, semicircular canals, ductus endolymphaticus and a short lagena are the only parts of the ear present in fish.
The Amphibia have an important sensory area at the base of the lagena known as the macula acustica basilaris, which is probably the first rudiment of a true cochlea. The ductus endolymphaticus has lost its communication with the skin, but it is frequently prolonged into the skull and along the spinal canal, from which it protrudes, through the intervertebral foramina, bulging into the coelom. This is the case in the common frog (A. Coggi, Anat. Anz. 5. Jahrg., 1890, p. 177). In this class the tympanum and Eustachian tube are first developed; the membrana tympani lies flush with the skin of the side of the head, and the sound-waves are transmitted from it to the internal ear by a single bony rod—the columella.
In the Reptilia the internal ear passes through a great range of development. In the Chelonia and Ophidia the cochlea is as rudimentary as in the Amphibia, but in the higher forms (Crocodilia) there is a lengthened and slightly twisted cochlea, at the end of which the lagena forms a minute terminal appendage. At the same time indications of the scalae tympani and vestibuli appear. As in the Amphibia the ductus endolymphaticus sometimes extends into the cranial cavity and on into other parts of the body. Snakes have no tympanic membrane. In the birds the cochlea resembles that of the crocodiles, but the posterior semicircular canal is above the superior where they join one another. In certain lizards and birds (owls) a small fold of skin represents the first appearance of an external ear. In the monotremes the internal ear is reptilian in its arrangement, but above them the mammals always have a spirally twisted cochlea, the number of turns varying from one and a half in the Cetacea to nearly five in the rodent Coelogenys. The lagena is reduced to a mere vestige. The organ of Corti is peculiar to mammals, and the single columella of the middle ear is replaced by the three ossicles already described in Man (see Alban Doran, “Morphology of the Mammalian Ossicula auditus,” Proc. Linn. Soc., 1876-1877, xiii. 185; also Trans. Linn. Soc. 2nd Ser. Zool. i. 371). In some mammals, especially Carnivora, the middle ear is enlarged to form the tympanic bulla, but the mastoid cells are peculiar to Man.
For further details see G. Retzius, Das Gehörorgan der Wirbelthiere (Stockholm, 1881-1884); Catalogue of the Museum of the R. College of Surgeons—Physiological Series, vol. iii. (London, 1906); R. Wiedersheim’s Vergleichende Anatomie der Wirbeltiere (Jena, 1902).
Diseases of the Ear
Modern scientific aural surgery and medicine (commonly known as Otology) dates from the time of Sir William Wilde of Dublin (1843), whose work marked a great advance in the application of anatomical, physiological and therapeutical knowledge to the study of this organ. Less noticeable contributions to the subject had not long before been made by Saunders (1827), Kramer (1833), Pilcher (1841) and Yearsley (1841). The next important event in the history of otology was the publication of J. Toynbee’s book in 1860 containing his valuable anatomical and pathological observations. Von Tröltsch of Würzburg, following on the lines of Wilde and Toynbee, produced two well-known works in 1861 and 1862, laying the foundation of the study in Germany. In that country and in Austria he was followed by Hermann Schwartze, Politzer, Gruber, Weber-Liel, Rüdinger, Moos and numerous others. France produced Itard, de la Charrière, Menière, Loewenberg and Bonnafont; and Belgium, Charles Delstanche, father and son. In Great Britain the work was carried on by James Hinton (1874), Peter Allen (1871), Patterson Cassells and Sir William Dalby. In America we may count among the early otologists Edward H. Clarke (1858), D.B. St John Roosa, H. Knapp, Clarence J. Blake, Albert H. Buck and Charles Burnett. Other workers all over the world are too numerous to mention.
Various Diseases and Injuries.—Diseases of the ear may affect any of the three divisions, the external, middle or internal ear. The commoner affections of the auricle are eczema, various tumours (simple and malignant), and serous and sebaceous cysts. Haematoma auris (othaematoma), or effusion of blood into the auricle, is often due to injury, but may occur spontaneously, especially in insane persons. The chief diseases of the external auditory canal are as follows:—impacted cerumen (or wax), circumscribed (or furuncular) inflammation, diffuse inflammation, strictures due to inflammatory affections, bony growths, fungi (otomycosis), malignant disease, caries and necrosis, and foreign bodies.
Diseases of the middle ear fall into two categories, suppurative and non-suppurative (i.e. with and without the formation of pus). Suppurative inflammation of the middle ear is either acute or chronic, and is in either case accompanied by perforation of the drum head and discharge from the ear. The chief importance of these affections, in addition to the symptoms of pain, deafness, discharge, &c., is the serious complications which may ensue from their neglect, viz. aural polypi, caries and necrosis of the bone, affections of the mastoid process, including the mastoid antrum, paralysis of the facial nerve, and the still more serious intracranial and vascular infective diseases, such as abscess in the brain (cerebrum or cerebellum), meningitis, with subdural and extradural abscesses, septic thrombosis of the sigmoid and other venous sinuses, and pyaemia. It is owing to the possibility of these complications that life insurance companies usually, and rightly, inquire as to the presence of ear discharge before accepting a life. Patterson Cassells of Glasgow urged this special point as long ago as 1877. Acute suppurative disease of the middle ear is often due to the exanthemata, scarlatina, measles and smallpox, and to bathing and diving. It may also be caused by influenza, diphtheria and pulmonary phthisis.
Non-suppurative disease of the middle ear may be acute or chronic. In the acute form the inflammation is less violent than in the acute suppurative inflammation, and is rarely accompanied by perforation. Chronic non-suppurative inflammation may be divided into the moist form, in which the symptoms are improved by inflation of the tympanum through the Eustachian tube, and the dry form (including sclerosis), which is more intractable and in which this procedure has little or no beneficial effect. Diseases of the internal ear may be primary or secondary to an affection of the tympanum or to intracranial disease.
Injuries to any part of the ear may occur, among the commoner being injuries to the auricle, rupture of the drum head (from explosions, blows on the ear or the introduction of sharp bodies into the ear canal), and injuries from fractured skull. Congenital 795 malformations of the ear are most frequently met with in the auricle and external canal.
Methods of Examination.—The methods of examining the ear are roughly threefold:—(1) Testing the hearing with watch, voice and tuning-fork. The latter is especially used to distinguish between disease of the middle ear (conducting apparatus) and that of the internal ear (perceptive apparatus). Our knowledge of the subject has been brought to its present state by the labours of many observers, notably Weber, Rinne, Schwabach, Lucae and Gellé. (2) Examination of the canal and drum-head with speculum and reflector, introduced by Kramer, Wilde and von Tröltsch. (3) Examination of the drum-cavity through the Eustachian tube by the various methods of inflation.
Symptoms.—The chief symptoms of ear diseases are deafness, noises in the ear (tinnitus aurium), giddiness, pain and discharge. Deafness (or other disturbance of hearing) and noises may occur from disease in almost any part of the ear. Purulent discharge usually comes from the middle ear. Giddiness is more commonly associated with affections of the internal ear.
Treatment.—Ear diseases are treated on ordinary surgical and medical lines, due regard being had to the anatomical and physiological peculiarities of this organ of sense, and especially to its close relationship, on the one hand to the nose and naso-pharynx, and on the other hand to the cranium and its contents. The chief advance in aural surgery in recent years has been in the surgery of the mastoid process and antrum. The pioneers of this work were H. Schwartze of Halle, and Stacke of Erfurt, who have been followed by a host of workers in all parts of the world. This development led to increased attention being paid to the intracranial complications of suppurative ear disease, in the treatment of which great strides have been made in the last few years.
Effects of Diseases of the Nose on the Ear.—The influence of diseases of the nose and naso-pharynx on ear diseases was brought out by Loewenberg of Paris, Voltolini of Breslau, and especially by Wilhelm Meyer of Copenhagen, the discoverer of adenoid vegetations of the naso-pharynx (“adenoids”), who recognized the great importance of this disease and gave an inimitable account of it in the Trans. of the Royal Medical and Chirurgical Society of London, 1870, and the Archiv für Ohrenheilkunde, 1873. Adenoid vegetations, which consist of an abnormal enlargement of Luschka’s tonsil in the vault of the pharynx, frequently give rise to ear disease in children, and, if not attended to, lay the foundation of nasal and ear troubles in after life. They are often associated with enlargement of the faucial tonsils.
Journals.—In 1864 the Archiv für Ohrenheilkunde was started by Politzer and Schwartze, and, in 1867, the Monatsschrift für Ohrenheilkunde (a monthly publication) was founded by Voltolini, Gruber, Weber-Liel and Rüdinger. Appearing first as the Archives of Ophthalmology and Otology, simultaneously in English and German, in 1869, the Archives of Otology became a separate publication under the editorship of Knapp, Moos and Roosa in 1879. Amongst other journals now existing are Annales des maladies de l’oreille et du larynx (Paris), Journal of Laryngology (London), Centralblatt für Ohrenheilkunde (Leipzig), &c.
Societies.—The earliest society formed was the American Otological Society (1868), which held annual meetings and published yearly transactions. Flourishing societies for the study of otology (sometimes combined with laryngology) exist in almost all civilized countries, and they usually publish transactions consisting of original papers and cases. The Otological Society of the United Kingdom was founded in 1900.
International Congresses.—International Otological congresses have been held at intervals of about four years at New York, Milan, Basel, Brussels, Florence, London and Bordeaux (1904). The proceedings of the congresses appear as substantial volumes.
Hospitals.—The earliest record of a public institution for the treatment of ear diseases is a Dispensary for Diseases of the Eye and Ear in London, started by Saunders and Cooper, which existed in 1804; the aural part, however, was soon closed, so that the actual oldest institution appears to be the Royal Ear Hospital, London, which was founded by Curtis in 1816. Four years later there was started the New York Eye and Ear Infirmary. At the present time in every large town of Europe and America ear diseases are treated either in separate departments of general hospitals or in institutions especially devoted to the purpose.
For a history of otology from the earliest times refer to A Practical Treatise on the Diseases of the Ear, by D.B. St John Roosa, M.D., LL.D. (6th edition, New York, 1885), and for a general account of the present state of otological science to A Text-Book of the Diseases of the Ear for Students and Practitioners, by Professor Dr Adam Politzer, transl. by Milton J. Ballin, Ph.B., M.D., and Clarence J. Heller, M.D. (4th edition, London, 1902).
EARL, a title and rank of nobility (corresponding to Lat. comes; Fr. comte), now the third in order of the British peerage, and accordingly intervening between marquess and viscount. Earl, however, is the oldest title and rank of English nobles, and was the highest until the year 1337, when the Black Prince was created duke of Cornwall by Edward III.
The nature of a modern earldom is readily understood, since it is a rank and dignity of nobility which, while it confers no official power or authority, is inalienable, indivisible, and descends in regular succession to all the heirs under the limitation in the grant until, on their failure, it becomes extinct.
The title is of Scandinavian origin, and first appears in England under Canute as jarl, which was englished as eorl. Like the ealdorman, whose place he took, the eorl was a great royal officer, who might be set over several counties, but who presided separately in the county court of each with the bishop of the diocese. Although there were counts in Normandy before the Norman Conquest, they differed in character from the English earls, and the earl’s position appears to have been but slightly modified by the Conquest. He was still generally entitled to the “third penny” of the county, but his office tended, under Norman influence, to become an hereditary dignity and his sphere was restricted by the Conqueror to a single county. The right to the “third penny” is a question of some obscurity, but its possession seems to have been deemed the distinctive mark of an earl, while the girding with “the sword of the county” formed the essential feature in his creation or investiture, as it continued to do for centuries later. The fact that every earl was the earl of a particular county has been much obscured by the loose usage of early times, when the style adopted was sometimes that of the noble’s surname (e.g. the Earls Ferrers), sometimes that of his chief seat (e.g. the Earls of Arundel), and sometimes that of the county. Palatine earldoms, or palatinates, were those which possessed regalia, i.e. special privileges delegated by the crown. The two great examples, which dated from Norman times, were Chester and Durham, where the earl and the bishop respectively had their own courts and jurisdiction, and were almost petty sovereigns.
The earliest known charter creating an earl is that by which Stephen bestowed on Geoffrey de Mandeville, in or about 1140, the earldom of Essex as an hereditary dignity. Several other creations by Stephen and the empress Maud followed in quick succession. From at least the time of the Conquest the earl had a double character; he was one of the “barons,” or tenants in chief, in virtue of the fief he held of the crown, as well as an earl in virtue of his “belting” (with the sword) and his “third penny” of the county. His fief would descend to the heirs of his body; and the earliest charters creating earldoms were granted with the same “limitation.” The dignity might thus descend to a woman, and, in that case, like the territorial fief, it would be held by her husband, who might be summoned to parliament in right of it. The earldom of Warwick thus passed through several families till it was finally obtained, in 1449, by the Kingmaker, who had married the heiress of the former earls. But in the case of “co-heiresses” (more daughters than one), the king determined which, if any, should inherit the dignity.
The 14th century saw some changes introduced. The earldom of March, created in 1328, was the first that was not named from a county or its capital town. Under Edward III. also an idea appears to have arisen that earldoms were connected with the tenure of lands, and in 1337 several fresh ones were created and large grants of lands made for their support. The first earldom granted with limitation to the heirs male of the grantee’s body was that of Nottingham in 1383. Another innovation was the grant of the first earldom for life only in 1377. The girding with the sword was the only observance at a creation till the first year of Edward VI., when the imposition of the cap 796 of dignity and a circlet of gold was added. Under James I. the patent of creation was declared to be sufficient without any ceremony. An earl’s robe of estate has three bars of ermine, but possibly it had originally four.
Something should be said of anomalous earldoms with Norman or Scottish styles. The Norman styles originated either under the Norman kings or at the time of the conquest of Normandy by the house of Lancaster. To the former period belonged that of Aumale, which successive fresh creations, under the Latinized form “Albemarle” have perpetuated to the present day (see Albemarle, Earls and Dukes of). The so-called earls of Eu and of Mortain, in that period, were really holders of Norman comtés. Henry V. and his son created five or six, it is said, but really seven at least, Norman countships or earldoms, of which Harcourt (1418), Perche (1419), Dreux (1427) and Mortain (? 1430) were bestowed on English nobles, Eu (1419), and Tankerville (1419) on English commoners, and Longueville (1419) on a foreigner, Gaston de Foix. Of these the earldom of “Eu” was assumed by the earls of Essex till the death of Robert, the parliament’s general (1646), while the title of Tankerville still survives under a modern creation (1714). An anomalous royal licence of 1661 permitted the earl of Bath to use the title of earl of Corbeil by alleged hereditary right. Of Scottish earldoms recognized in the English parliament the most remarkable case is that of the Lords Umfraville, who were summoned for three generations (1297-1380), as earls of Angus; Henry, Lord Beaumont, also was summoned as earl of Buchan from 1334 to 1339.
The earldom of Chester is granted to the princes of Wales on their creation, and the Scottish earldom of Carrick is held by the eldest son of the sovereign under act of parliament.
The premier earldom is that of Arundel (q.v.), but as this is at present united with the dukedom of Norfolk, the oldest earldom not merged in a higher title is that of Shrewsbury (1442), the next in seniority being Derby (1485), and Huntingdon (1529). These three have been known as “the catskin earls,” a term of uncertain origin. The ancient earldom of Wiltshire (1397) was unsuccessfully claimed in 1869 by Mr Scrope of Danby, and that of Norfolk (1312), in 1906, by Lord Mowbray and Stourton.
The premier earldom of Scotland as recognized by the Union Roll (1707), is that of Crawford, held by the Lindsays since its creation in 1398; but it is not one of the ancient “seven earldoms.” The Decreet of Ranking (1606) appears to have recognized the earldom of Sutherland as the most ancient in virtue of a charter of 1347, but the House of Lords’ decision of 1771 recognized it as having descended from at least the year 1275, and it may be as old as 1228. It is at present united with the dukedom of Sutherland. The original “seven earldoms” (of which it was one) represented seven provinces, each of which was under a “mormaer.” This Celtic title was rendered “jarl” by the Norsemen, and under Alexander I. (c. 1115) began to be replaced by earl (comes), owing to Anglo-Norman influence, which also tended to make these earldoms less official and more feudal.
In Ireland the duke of Leinster is, as earl of Kildare, premier earl as well as premier duke.
An earl is “Right Honourable,” and is styled “My Lord.” His eldest son bears his father’s “second title,” and therefore, that second title being in most cases a viscounty, he generally is styled “Viscount”; where, as with Devon and Huntingdon, there is no second title, one may be assumed for convenience; under all circumstances, however, the eldest son of an earl takes precedence immediately after the viscounts. The younger sons of earls are “Honourable,” but all their daughters are “Ladies.” In formal documents and instruments, the sovereign, when addressing or making mention of any peer of the degree of an earl, usually designates him “trusty and well-beloved cousin,”—a form of appellation first adopted by Henry IV., who either by descent or alliance was actually related to every earl and duke in the realm. The wife of an earl is a countess; she is “Right Honourable,” and is styled “My Lady.” For the earl’s coronet see Crown and Coronet.
See Lord’s Reports on the Dignity of a Peer; Pike’s Constitutional History of the House of Lords; Selden’s Titles of Honour; G.E. C(okayne)’s Complete Peerage; Round’s Geoffrey de Mandeville.
EARLE, JOHN (c. 1601-1665), English divine, was born at York about 1601. He matriculated at Christ Church, Oxford, but migrated to Merton, where he obtained a fellowship. In 1631 he was proctor and also chaplain to Philip, earl of Pembroke, then chancellor of the university, who presented him to the rectory of Bishopston in Wiltshire. His fame spread, and in 1641 he was appointed chaplain and tutor to Prince Charles. In 1643 he was elected one of the Assembly of Divines at Westminster, but his sympathies with the king and with the Anglican Church were so strong that he declined to sit. Early in 1643 he was chosen chancellor of the cathedral of Salisbury, but of this preferment he was soon deprived as a “malignant.” After Cromwell’s great victory at Worcester, Earle went abroad, and was named clerk of the closet and chaplain to Charles II. He spent a year at Antwerp in the house of Isaac Walton’s friend, George Morley, who afterwards became bishop of Winchester. He next joined the duke of York (James II.) at Paris, returning to England at the Restoration. He was at once appointed dean of Westminster, and in 1661 was one of the commissioners for revising the liturgy. He was on friendly terms with Richard Baxter. In November 1662 he was consecrated bishop of Worcester, and was translated, ten months later, to the see of Salisbury, where he conciliated the nonconformists. He was strongly opposed to the Conventicle and Five Mile Acts. During the great plague Earle attended the king and queen at Oxford, and there he died on the 17th of November 1665.
Earle’s chief title to remembrance is his witty and humorous work entitled Microcosmographie, or a Peece of the World discovered, in Essayes and Characters, which throws light on the manners of the time. First published anonymously in 1628, it became very popular, and ran through ten editions in the lifetime of the author. The style is quaint and epigrammatic; and the reader is frequently reminded of Thomas Fuller by such passages as this: “A university dunner is a gentlemen follower cheaply purchased, for his own money has hyr’d him.” Several reprints of the book have been issued since the author’s death; and in 1671 a French translation by J. Dymock appeared with the title of Le Vice ridiculé. Earle was employed by Charles II. to make the Latin translation of the Eikon Basilike, published in 1649. A similar translation of R. Hooker’s Ecclesiastical Polity was accidentally destroyed.
“Dr Earle,” says Lord Clarendon in his Life, “was a man of great piety and devotion, a most eloquent and powerful preacher, and of a conversation so pleasant and delightful, so very innocent, and so very facetious, that no man’s company was more desired and loved. No man was more negligent in his dress and habit and mien, no man more wary and cultivated in his behaviour and discourse. He was very dear to the Lord Falkland, with whom he spent as much time as he could make his own.”
See especially Philip Bliss’s edition of the Microcosmographie (London, 1811), and E. Arber’s Reprint (London, 1868).
EARLE, RALPH (1751-1801), American historical and portrait painter, was born at Leicester, Massachusetts, on the 11th of May 1751. Like so many of the colonial craftsmen, Earle was self-taught, and for many years was an itinerant painter. He went with the Governor’s Guard to Lexington and made battle sketches, from which in 1775 he painted four scenes, engraved by Amos Doolittle, which are probably the first historical paintings by an American. After the War of Independence, Earle went to London, entered the studio of Benjamin West, and painted the king and many notables. After his return to America in 1786 he made portraits of Timothy Dwight, Governor Caleb Strong, Roger Sherman, and other prominent men. He also painted a large picture of Niagara Falls. He died at Bolton, Connecticut, on the 16th of August 1801.
EARL MARSHAL, in England, a functionary who ranks as the eighth of the great officers of state. He is the head of the college of arms, and has the appointment of the kings-of-arms, heralds and pursuivants at his discretion. He attends the sovereign in opening and closing the session of parliament, 797 walking opposite to the lord great chamberlain on his or her right hand. It is his duty to make arrangements for the order of all state processions and ceremonials, especially for coronations and royal marriages and funerals. Like the lord high constable he rode into Westminster Hall with the champion after a coronation, till the coronation banquet was abandoned, taking his place on the left hand, and with the lord great chamberlain he assists at the introduction of all newly-created peers into the House of Lords.
The marshal appears in the feudal armies to have been in command of the cavalry under the constable, and to have in some measure superseded him as master of the horse in the royal palace. He exercised joint and co-ordinate jurisdiction with the constable in the court of chivalry, and afterwards became the sole judge of that tribunal till its obsolescence. The marshalship of England was formerly believed to have been inherited from the Clares by the Marshal family, who had only been marshals of the household. It was held, however, by the latter family, as the office of chief (magister) marshal, as early as the days of Henry I. Through them, under Henry III., it passed to the Bigods, as their eldest co-heirs. In 1306 it fell to the crown on the death of the last Bigod, earl of Norfolk, who had made Edward I. his heir, and in 1316 it was granted by Edward II. to his own younger brother, Thomas “of Brotherton,” earl of Norfolk. As yet the style of the office was only “marshal” although the last Bigod holder, being an earl, was sometimes loosely spoken of as the earl marshal. The office, having reverted to the crown, was granted out anew by Richard II., in 1385, to Thomas Mowbray, earl of Nottingham, the representative of Thomas “of Brotherton.” In 1386 the style of “earl marshal” was formally granted to him in addition. After several attainders and partial restorations in the reigns of the Tudors and the Stuarts, the earl marshalship was granted anew to the Howards by Charles II. in 1672 and entailed on their male line, with many specific remainders and limitations, under which settlement it has regularly descended to the present duke of Norfolk. Its holders, however, could not execute the office until the Roman Catholic emancipation, and had to appoint deputies. The duke is styled earl marshal “and hereditary marshal of England,” but the double style would seem to be an error, though the Mowbrays, with their double creation (1385, 1386) might have claimed it. His Grace appends the letters “E.M.” to his signature, and bears behind his shield two batons crossed in saltire, the marshal’s rod (virga) having been the badge of the office from Norman times. There appear to have been hereditary marshals of Ireland, but their history is not well ascertained. The Keiths were Great Marischals of Scotland from at least the days of Robert Bruce, and were created earls marischal in or about 1458, but lost both earldom and office by the attainder of George, the 10th earl, in 1716. (See also Marshal; State, Great Officers of.)
See “The Marshalship of England,” in J.H. Round, Commune of London and Other Studies (London, 1899); G.E. C(okayne)’s Complete Peerage.
EARLOM, RICHARD (1742-1822), English mezzotint engraver, was born and died in London. His natural faculty for art appears to have been first called into exercise by admiration for the lord mayor’s state coach, just decorated by Cipriani. He tried to copy the paintings, and was sent to study under Cipriani. He displayed great skill as a draughtsman, and at the same time acquired without assistance the art of engraving in mezzotint. In 1765 he was employed by Alderman Boydell, then one of the most liberal promoters of the fine arts, to make a series of drawings from the pictures at Houghton Hall; and these he afterwards engraved in mezzotint. His most perfect works as engraver are perhaps the fruit and flower pieces after the Dutch artists Van Os and Van Huysum. Amongst his historical and figure subjects are—“Agrippina,” after West; “Love in Bondage,” after Guido Reni; the “Royal Academy,” the “Embassy of Hyderbeck to meet Lord Cornwallis,” and a “Tiger Hunt,” the last three after Zoffany; and “Lord Heathfield,” after Sir Joshua Reynolds. Earlom also executed a series of 200 facsimiles of the drawings and sketches of Claude Lorraine, which was published in 3 vols. folio, under the title of Liber veritatis (1777-1819).
EARLSTON (formerly Ercildoune, of which it is a corruption), a parish and market town of Berwickshire, Scotland. Pop. (1901) 1049. It is situated on Leader Water in Lauderdale, 72½ m. S.E. of Edinburgh by the North British railway branch line from Reston Junction to St Boswells, and about 4 m. N.E. of Melrose. When the place was a hamlet of rude huts it was called Arcioldun or “Prospect Fort,” with reference to Black Hill (1003 ft.), on the top of which may yet be traced the concentric rings of the British fort by which it was crowned. It is said to be possible to make out the remains of the cave-dwellings of the Ottadeni, the aborigines of the district. In the 12th and 13th centuries the Lindsays and the earls of March and Dunbar were the chief baronial families. The particular link with the remote past, however, is the ivy-clad ruin of the ancient tower, “The Rhymer’s Castle,” the traditional residence of Thomas Learmont, commonly called Thomas of Ercildoune, or Thomas the Rhymer, poet and prophet, and friend of the Fairies, who was born here about 1225. Rhymer’s Tower was crumbling to pieces, and its stones were being used in the erection of dykes, cottages and houses, when the Edinburgh Border Counties Association acquired the relic and surrounding lands in 1895, and took steps to prevent further spoliation and decay. The leading manufactures are ginghams, tweeds and shirtings, and the town is also an important agricultural centre, stock sales taking place at regular intervals and cattle and horse fairs being held every year. Some 3 m. away is the estate of Bemersyde, said to have been in the possession of the Haigs for nearly 1000 years. The prospect from Bemersyde Hill was Sir Walter Scott’s favourite view. The castle at Bemersyde was erected in 1535 to secure the peace of the Border.
EARLY, JUBAL ANDERSON (1816-1894), American soldier and lawyer, was born in Franklin county, Virginia, on the 3rd of November 1816, and graduated at the U.S. Military Academy in 1837. He served in the Seminole War of 1837-38, after which he resigned in order to practise law in Franklin county, Va. He also engaged in state politics, and served in the Mexican War as a major of Virginia volunteers. He was strongly opposed to secession, but thought it his duty to conform to the action of his state. As a colonel in the Confederate army, he rendered conspicuous service at the first battle of Bull Run (q.v.). Promoted brigadier-general, and subsequently major-general, Early served throughout the Virginian campaigns of 1862-63, and defended the lines of Fredericksburg during the battle of Chancellorsville. At Gettysburg he commanded his division of Ewell’s corps. In the campaign of 1864 Early, who had now reached the rank of lieutenant-general, commanded the Confederate forces in the Shenandoah Valley. The action of Lynchburg left him free to move northwards, his opponent being compelled to march away from the Valley. Early promptly utilized his advantage, crossed the Potomac, and defeated, on the Monocacy, all the troops which could be gathered to meet him. He appeared before the lines of Washington, put part of Maryland and Pennsylvania under contribution, and only retired to the Valley when threatened by heavy forces hurriedly sent up to Washington. He then fought a successful action at Winchester, reappeared on the Potomac, and sent his cavalry on a raid into Pennsylvania. A greatly superior army was now formed under General Sheridan to oppose Early. In spite of his skill and energy the Confederate leader was defeated in the battles of Winchester and Fisher’s Hill. Finally, on the 19th of October, after inflicting at first a severe blow upon the Federal army in its camps on Cedar Creek, he was decisively beaten by Sheridan. (See Shenandoah Valley Campaigns.) Waynesboro (March 1865) was his last fight, after which he was relieved from his command. General Early was regarded by many as the ablest soldier, after Lee and Jackson, in the Army of Northern Virginia, and one of the ablest in the whole Confederate army. That he failed to make headway against an army far superior in numbers, and led by a general of the calibre of Sheridan, cannot be held to prove the 798 falsity of this judgment. After the peace he went to Canada, but in 1867 returned to resume the practice of law. For a time he managed in conjunction with General Beauregard the Louisiana lottery. He died at Lynchburg, Va., on the 2nd of March 1894. General Early was for a time president of the Southern Historical Society, and wrote, besides various essays and historical papers, A Memoir of the Last Year of the War, &c. (1867).
EARLY ENGLISH PERIOD, in architecture, the term given by Rickman to the first pointed or Gothic style in England, nominally 1189-1307, which succeeded the Romanesque or Norman period towards the end of the 12th century, and developed into the Decorated period in the commencement of the 14th century. It is chiefly characterized by the almost universal employment of the pointed arch, not only in arches of wide span such as those of the nave arcade, but for doorways and windows. The actual introduction of the pointed arch took place at a much earlier date, as in the nave arcade of the Cistercian Abbey of Buildwas (1140), though the clerestory window above has semicircular arches. It is customary, therefore, to make allowance for a transitional epoch from the middle of the 12th century. Although the pointed arches used are sometimes equilateral and sometimes drop-arches, the lancet-arch is the most characteristic. The period is best recognized in England by the great depth given to the hollows of the mouldings, alternating with fillets and rolls, by the decoration of the hollows with the dog-tooth ornament, by the circular abacus of the capitals, and the employment of slender detached shafts of Purbeck marble which are attached to piers by circular moulded shaft-rings (Fr. anneau).
The arches are sometimes cusped; circles with trefoils, quatrefoils, &c., are introduced into the tracery, and large rose windows in the transept or nave, as at Lincoln (1220). The conventional foliage decorating the capitals is of great beauty and variety, and extends to spandrils, bosses, &c. In the spandrils of the arches of the nave, transept or choir arcades, diaper work is occasionally found, as in the transept of Westminster Abbey. The latter is one of the chief examples of the period, to which must be added the cathedral of Salisbury (except the tower); the Galilee at Ely; nave and transept of Wells (1225-1240); nave of Lincoln; west front of Peterborough; and the minster at Beverley.
EARN, the name of a loch and river in Perthshire, Scotland. The loch, lying almost due east and west, is 6½ m. long and 4⁄5 m. in maximum breadth, 287 ft. deep, with a mean depth of 138 ft., covers an area of nearly 4 sq. m., has a drainage basin of over 54½ sq. m., and stands 317 ft. above the sea. Its waters are said never to freeze. It discharges by the river Earn. The points of interest on its shores are Lochearnhead (at the southern extremity of Glen Ogle), which has a station on the Callander-Oban railway, and the ruins of St Blane’s chapel; Edinample Castle, an old turreted mansion belonging to the marquess of Breadalbane, situated in well-wooded grounds near the pretty falls of the Ample; Ardvorlich House, the original of Darlinvarach in Scott’s Legend of Montrose, and the village of St Fillans at the foot of the loch, once the terminus of the branch of the Caledonian railway from Perth. The river flows out of Loch Earn, pursues an eastward course with a gentle inclination towards the south, and reaches the Firth of Tay, 6½ m. below Perth, after a total run of 49 m. Its chief tributaries on the right are the Ruchil, Machany, Ruthven, May and Farg, and on the left, the Lednock and Turret. It is navigable by vessels of 50 tons as far up as Bridge of Earn, and is a notable fishing stream, abounding with salmon and trout, perch and pike being also plentiful. On the Lednock are the falls of the Devil’s Cauldron and on the Turret and its feeders several graceful cascades. The principal places of interest on the banks of the Earn are Dunira, the favourite seat of Henry Dundas, 1st Viscount Melville, who took the title of his barony from the estate and to whose memory an obelisk was raised on the adjoining hill of Dunmore; the village of Comrie; the town of Crieff; the ruined castle of Innerpeffray, founded in 1610 by the 1st Lord Maderty, close to which is the library founded in 1691 by the 3rd Lord Maderty, containing some rare black-letter books and the Bible that belonged to the marquess of Montrose; Gascon Hall, now in ruins, but with traditions reaching back to the days of Wallace; Dupplin Castle, a fine Tudor mansion, seat of the earl of Kinnoull, who derives from it the title of his viscounty; Aberdalgie, Forgandenny and Bridge of Earn, a health resort situated amidst picturesque surroundings. Strathearn, as the valley of the Earn is called, extending from the loch to the Firth of Tay, is a beautiful and, on the whole, fertile tract, though liable at times to heavy floods. The earl of Perth is hereditary steward of Strathearn.
EARNEST (probably a corruption of the obsolete arles or erles, adapted from Lat. equivalent arrha, due to a confusion with the adjective “earnest,” serious, O. Eng. eornust, cognate with Ger. ernst), the payment of a sum of money by the buyer of goods to the seller on the conclusion of a bargain as a pledge for its due performance. It is almost similar to the arrha of the Roman law, which may be traced back in the history of legal institutions to a period when the validity of a contract depended not so much upon the real intention of the parties, as upon the due observance of a prescribed ceremony. But earnest was never part payment, which arrha might have been. Apart from its survival as a custom, its chief importance in English law is its recognition by the Statute of Frauds as giving validity to contracts for the sale of goods of a value exceeding £10 (see Sale of Goods). It is in that statute clearly distinguished from part payment, consequently any sum, however small, would be sufficient as earnest, being given as a token that the contract is binding and should be expressly stated so by the giver. The giving of earnest, or hand-money, as it is sometimes called, has now fallen into very general disuse.
EAR-RING, an ornament worn pendent from the ear, and generally suspended (especially among the more civilized races) by means of a ring or hook passing through the pendulous lobe of the ear. Among savage races the impulse to decorate, or at any rate to modify the appearance of the ear, is almost universal. With such peoples the ear appendage is chiefly remarkable for its extravagant dimensions. Many examples may be seen in the ethnographic galleries of the British Museum. The Berawan people of Borneo use plugs through the lobe of the ear 3¾ in. in diameter. More extraordinary still is an example of a stone ear-plug worn by a Masai, 4½ in. in diameter and weighing 2 ℔ 14 oz. (Man, 1905, p. 22). It is stated that according to the Masai standard of fashion, the lobes of the ears should be enlarged so as to be capable of meeting above the head. Among the superior races, though ear ornaments of extravagant size and elaboration are not unknown, moderation in size is commonly observed, and greater attention is paid to workmanship and fineness of material.
 |
| From La Grande Encyclopédie. |
| Fig. 1.—Ear-ring from an Assyrian bas relief. |
 |
| From La Grande Encyclopédie. |
| Fig. 2.—Thetis crossing the sea, with the armour of Achilles. Ear-ring from the Crimea, Hermitage museum. |
The general usage appears to have been to have ear-rings worn in pairs, the two ornaments in all respects resembling each other; in ancient times, or more recently among Oriental races, a single ear-ring has sometimes been worn. The use of this kind of ornament, which constantly was of great value, dates from the remotest historical antiquity, the earliest mention of ear-rings occurring in the book of Genesis. It appears probable that the ear-rings of Jacob’s family, which he buried with his strange idols at Bethel, were regarded as amulets or talismans, such unquestionably being the estimation in which some ornaments of this class have been held from a very early period, as they still are held in the East. Thus in New Zealand ear-rings are decorated with the teeth of enemies, and with talismanic sharks’ teeth. Among all the Oriental races of whom we have any accurate knowledge, the Hebrews and Egyptians excepted, ear-rings always have been in general use by both sexes; while in the West, as well as by the Hebrews and Egyptians, as a general rule they have been considered exclusively female ornaments. By the Greeks and Romans also ear-rings were worn only by women, and the wearing of them by a man is often spoken of as distinctively oriental.
In archaic art, ear-rings are frequently represented or their traces are left in the perforated ear lobes of early statues. After the 4th century such perforations occur seldom. In one instance, 799 a Greek inscription records the weight of the detachable gold ornaments on a statue, among which a pair of ear-rings is included. Ear-rings of characteristic form are frequently discovered by excavation. In Egypt, a system of pendent chains is found hanging from a disk. In Assyria the decoration consists of pendants or knobs attached to a rigid ring. In the early civilization represented by Dr Schliemann’s Trojan investigations, pieces of gold plate are suspended by parallel chains. In the Mycenaean period, ear-rings are infrequent in Greece, but have been found in abundance in the Mycenaean finds of Enkomi (Cyprus) in the form of pendent bulls’-heads, or of decorative forms based on the bull’s head. In the tombs of the Greek settlers in the Crimea (4th century B.C.), ear-rings are found of marvellous complexity and beauty. The lexicographer Pollux, speaking of the names given to ear-rings, derived from their forms, mentions caryatids, hippocamps and centauresses. Jewels of the same class, of exquisite beauty and of workmanship that is truly wonderful, have been rescued from the sepulchres of ancient Etruria. Ear-rings of comparatively simple forms, but set with pearls and other stones, were the mode in Rome. In some instances, the stones were of fabulous value. During the Byzantine period they once more attained an extravagant size. Researches among the burial places of Anglo-Saxon Britain have led to the discovery of jewels in considerable numbers, which among their varieties include ear-rings executed in a style that proves the Anglo-Saxons to have made no inconsiderable advances in the arts of civilization.
These same ornaments, which never have fallen into disuse, enjoy at the present day a considerable degree of favour, and the tide of fashion has set towards their increased use. Like all other modern jewels, however, the ear-rings of our own times as works of art can claim no historical attributes, because they consist as well of reproductions from all past ages and of every race as of fanciful productions that certainly can be assigned to no style of art whatever. As one of the curiosities of the subject it may be mentioned that Antonia, wife of Drusus, is said by Pliny to have attached a pair of ear-rings to her pet lamprey.
EARTH (a word common to Teutonic languages, cf. Ger. Erde, Dutch aarde, Swed. and Dan. jord; outside Teutonic it appears only in the Gr. ἔραζε, on the ground; it has been connected by some etymologists with the Aryan root ar-, to plough, which is seen in the Lat. arare, obsolete Eng. “ear,” and Gr. ἀροῦν, but this is now considered very doubtful; see G. Curtius, Greek Etymology, Eng. trans., i. 426; Max Müller, Lectures, 8th ed. i. 294). From early times the word “earth” has been used in several connexions—from that of soil or ground to that of the planet which we inhabit, but it is difficult to trace the exact historic sequence of the diverse usages. In the cosmogony of the Pythagoreans, Platonists and other philosophers, the term or its equivalent denoted an element or fundamental quality which conferred upon matter the character of earthiness; and in the subsequent development of theories as to the ultimate composition of matter by the alchemists, iatrochemists, and early phlogistonists an element of the same name was retained (see Element). In modern chemistry, the common term “earth” is applied to certain oxides:—the ”alkaline earths” (q.v.) are the oxides of calcium (lime), barium (baryta) and strontium (strontia); the ”rare earths” (q.v.) are the oxides of a certain class of rare metals.
The Earth
The terrestrial globe is a member of the Solar system, the third in distance from the Sun, and the largest within the orbit of Jupiter. In the wider sense it may be regarded as composed of a gaseous atmosphere (see Meteorology), which encircles the crust or lithosphere (see Geography), and surface waters or hydrosphere (see Ocean and Oceanography). The description of the surface features is a branch of Geography, and the discussions as to their origin and permanence belongs to Physiography (in the narrower sense), physiographical geology, or physical geography. The investigation of the crust belongs to geology and of rocks in particular to petrology.
In the present article we shall treat the subject matter of the Earth as a planet under the following headings:—(1) Figure and Size, (2) Mass and Density, (3) Astronomical Relations, (4) Evolution and Age. These subjects will be treated summarily, readers being referred to the article Astronomy and to the cross-references for details.
1. Figure and Size.—To primitive man the Earth was a flat disk with its surface diversified by mountains, rivers and seas. In many cosmogonies this disk was encircled by waters, unmeasurable by man and extending to a junction with the sky; and the disk stood as an island rising up through the waters from the floor of the universe, or was borne as an immovable ship on the surface. Of such a nature was the cosmogony of the Babylonians and Hebrews; Homer states the same idea, naming the encircling waters Ὠκεανός; and Hesiod regarded it as a disk midway between the sky and the infernal regions. The theory that the Earth extended downwards to the limit of the universe was subjected to modification when it was seen that the same sun and stars reappeared in the east after their setting in the west. But man slowly realized that the earth was isolated in space, floating freely as a balloon, and much speculation was associated about that which supported the Earth. Tunnels in the foundations to permit the passage of the sun and stars were suggested; the Greeks considered twelve columns to support the heavens, and in their mythology the god Atlas appears condemned to support the columns; while the Egyptians had the Earth supported by four elephants, which themselves stood on a tortoise swimming on a sea. Earthquakes were regarded as due to a movement of these foundations; in Japan this was considered to be due to the motion of a great spider, an animal subsequently replaced by a cat-fish; in Mongolia it is a hog; in India, a mole; in some parts of South America, a whale; and among some of the North American Indians, a giant tortoise.
The doctrine of the spherical form has been erroneously assigned to Thales; but he accepted the Semitic conception of the disk, and regarded the production of springs after earthquakes as due to the inrushing of the waters under the Earth into fissures in the surface. His pupil, Anaximander (610-547), according to Diogenes Laërtius, believed it to be spherical (see The Observatory, 1894, P. 208); and Anaximenes probably held a similar view. The spherical form is undoubtedly a discovery of Pythagoras, and was taught by the Pythagoreans and by the Eleatic Parmenides. The expositor of greatest moment was Aristotle; his arguments are those which we employ to-day:—the ship gradually disappearing from hull to mast as it recedes from the harbour to the horizon; the circular shadow cast by the Earth on the Moon during an eclipse, and the alteration in the appearance of the heavens as one passes from point to point on the Earth’s surface.1 He records attempts made to determine the circumference; but the first scientific investigation in this 800 direction was made 150 years later by Eratosthenes. The spherical form, however, only became generally accepted after the Earth’s circumnavigation (see Geography).
The historical development of the methods for determining the figure of the Earth (by which we mean a theoretical surface in part indicated by the ocean at rest, and in other parts by the level to which water freely communicating with the oceans by canals traversing the land masses would rise) and the mathematical investigation of this problem are treated in the articles Earth, Figure of the, and Geodesy; here the results are summarized. Sir Isaac Newton deduced from the mechanical consideration of the figure of equilibrium of a mass of rotating fluid, the form of an oblate spheroid, the ellipticity of a meridian section being 1/231, and the axes in the ratio 230 : 231. Geodetic measurements by the Cassinis and other French astronomers pointed to a prolate form, but the Newtonian figure was proved to be correct by the measurement of meridional arcs in Peru and Lapland by the expeditions organized by the French Academy of Sciences. More recent work points to an elliptical equatorial section, thus making the earth pear-shaped. The position of the longer axis is somewhat uncertain; it is certainly in Africa, Clarke placing it in longitude 8° 15′ W., and Schubert in longitude 41° 4′ E.; W.J. Sollas, arguing from terrestrial symmetry, has chosen the position lat. 6° N., long. 28° E., i.e. between Clarke’s and Schubert’s positions. For the lengths of the axes and the ellipticity of the Earth, see Earth, Figure of the.
2. Mass and Density.—The earliest scientific investigation on the density and mass of the Earth (the problem is really single if the volume of the Earth be known) was made by Newton, who, mainly from astronomical considerations, suggested the limiting densities 5 and 6; it is remarkable that this prophetic guess should be realized, the mean value from subsequent researches being about 5½, which gives for the mass the value 6 × 1021 tons. The density of the Earth has been determined by several experimenters within recent years by methods described in the article Gravitation; the most probable value is there stated to be 5.527.
3. Astronomical Relations.—The grandest achievements of astronomical science are undoubtedly to be associated with the elucidation of the complex motion of our planet. The notion that the Earth was fixed and immovable at the centre of an immeasurable universe long possessed the minds of men; and we find the illustrious Ptolemy accepting this view in the 2nd century A.D., and rejecting the notion of a rotating Earth—a theory which had been proposed as early as the 5th century B.C. by Philolaus on philosophical grounds, and in the 3rd century B.C. by the astronomer Aristarchus of Samos. He argued that if the Earth rotated then points at the equator had the enormous velocity of about 1000 m. per hour, and as a consequence there should be terrific gales from the east; the fact that there were no such gales invalidated, in his opinion, the theory. The Ptolemaic theory was unchallenged until 1543, in which year the De Revolutionibus orbium Celestium of Copernicus was published. In this work it was shown that the common astronomical phenomena could be more simply explained by regarding the Earth as annually revolving about a fixed Sun, and daily rotating about itself. A clean sweep was made of the geocentric epicyclic motions of the planets which Ptolemy’s theory demanded, and in place there was substituted a procession of planets about the Sun at different distances. The development of the Copernican theory—the corner-stone of modern astronomy—by Johann Kepler and Sir Isaac Newton is treated in the article Astronomy: History; here we shall summarily discuss the motions of our planet and its relation to the solar system.
The Earth has two principal motions—revolution about the Sun, rotation about its axis; there are in addition a number of secular motions.
Revolution.—The Earth revolves about the Sun in an elliptical orbit having the Sun at one focus. The plane of the orbit is termed the ecliptic; it is inclined to the Earth’s equator at an angle termed the obliquity, and the points of intersection of the equator and ecliptic are termed the equinoctial points. The major axis of the ellipse is the line of apsides; when the Earth is nearest the Sun it is said to be in perihelion, when farthest it is in aphelion. The mean distance of the Earth from the Sun is a most important astronomical constant, since it is the unit of linear measurement; its value is about 93,000,000 m., and the difference between the perihelion and aphelion distances is about 3,000,000 m. The eccentricity of the orbit is 0.016751. A tabular comparison of the orbital constants of the Earth and the other planets is given in the article Planet. The period of revolution with regard to the Sun, or, in other words, the time taken by the Sun apparently to pass from one equinox to the same equinox, is the tropical or equinoctial year; its length is 365 d. 5 hrs. 48 m. 46 secs. It is about 20 minutes shorter than the true or sidereal year, which is the time taken for the Sun apparently to travel from one star to it again. The difference in these two years is due to the secular variation termed precession (see below). A third year is named the anomalistic year, which is the time occupied in the passage from perihelion to perihelion; it is a little longer than the sidereal.
Rotation.—The Earth rotates about an axis terminating at the north and south geographical poles, and perpendicular to the equator; the period of rotation is termed the day (q.v.), of which several kinds are distinguished according to the body or point of reference. The rotation is performed from west to east; this daily rotation occasions the diurnal motion of the celestial sphere, the rising of the Sun and stars in the east and their setting in the west, and also the phenomena of day and night. The inclination of the axis to the ecliptic brings about the presentation of places in different latitudes to the more direct rays of the sun; this is revealed in the variation in the length of daylight with the time of the year, and the phenomena of seasons.
Although the rotation of the Earth was an accepted fact soon after its suggestion by Copernicus, an experimental proof was wanting until 1851, when Foucault performed his celebrated pendulum experiment at the Pantheon, Paris. A pendulum about 200 ft. long, composed of a flexible wire carrying a heavy iron bob, was suspended so as to be free to oscillate in any direction. The bob was provided with a style which passed over a table strewn with fine sand, so that the style traced the direction in which the bob was swinging. It was found that the oscillating pendulum never retraced its path, but at each swing it was apparently deviated to the right, and moreover the deviations in equal times were themselves equal. This means that the floor of the Pantheon was moving, and therefore the Earth was rotating. If the pendulum were swung in the southern hemisphere, the deviation would be to the left; if at the equator it would not deviate, while at the poles the plane of oscillation would traverse a complete circle in 24 hours.
The rotation of the Earth appears to be perfectly uniform, comparisons of the times of transits, eclipses, &c., point to a variation of less than 1⁄100th of a second since the time of Ptolemy. Theoretical investigations on the phenomena of tidal friction point, however, to a retardation, which may to some extent be diminished by the accelerations occasioned by the shrinkage of the globe, and some other factors difficult to evaluate (see Tide).
We now proceed to the secular variations.
Precession.—The axis of the earth does not preserve an invariable direction in space, but in a certain time it describes a cone, in much the same manner as the axis of a top spinning out of the vertical. The equator, which preserves approximately the same inclination to the ecliptic (there is a slight variation in the obliquity which we shall mention later), must move so that its intersections with the ecliptic, or equinoctial points, pass in a retrograde direction, i.e. opposite to that of the Earth. This motion is termed the precession of the equinoxes, and was observed by Hipparchus in the 2nd century B.C.; Ptolemy corrected the catalogue of Hipparchus for precession by adding 2° 40′ to the longitudes, the latitudes being unaltered by this motion, which at the present time is 50.26″ annually, the complete circuit being made in about 26,000 years. Owing to precession the signs of the zodiac are traversing paths through the constellations, or, 801 in other words, the constellations are continually shifting with regard to the equinoctial points; at one time the vernal equinox Aries was in the constellations of that name; it is now in Pisces, and will then pass into Aquarius. The pole star, i.e. the star towards which the Earth’s axis points, is also shifting owing to precession; in about 2700 B.C. the Chinese observed α Draconis as the pole star (at present α Ursae minoris occupies this position and will do so until 3500); in 13600 Vega (α Lyrae) the brightest star in the Northern hemisphere, will be nearest.
Precession is the result of the Sun and the Moon’s attraction on the Earth not being a single force through its centre of gravity. If the Earth were a homogeneous sphere the attractions would act through the centre, and such forces would have no effect upon the rotation about the centre of gravity, but the Earth being spheroidal the equatorial band which stands up as it were beyond the surface of a sphere is more strongly attracted, with the result that the axis undergoes a tilting. The precession due to the Sun is termed the solar precession and that due to the Moon the lunar precession; the joint effect (two-thirds of which is due to the Moon) is the luni-solar precession. Solar precession is greatest at the solstices and zero at the equinoxes; the part of luni-solar precession due to the Moon varies with the position of the Moon in its orbit. The obliquity is unchanged by precession (see Precession of the Equinoxes).
Nutation.—In treating precession we have stated that the axis of the Earth traces a cone, and it follows that the pole describes a circle (approximately) on the celestial sphere, about the pole of the ecliptic. This is not quite true. Irregularities in the attracting forces which occasion precession also cause a slight oscillation backwards and forwards over the mean precessional path of the pole, the pole tracing a wavy line or nodding. Both the Sun and Moon contribute to this effect. Solar nutation depends upon the position of the Sun on the ecliptic; its period is therefore 1 year, and in extent it is only 1.2″; lunar nutation depends upon the position of the Moon’s nodes; its period is therefore about 18.6 years, the time of revolution of the nodes, and its extent is 9.2″. There is also given to the obliquity a small oscillation to and fro. Nutation is one of the great discoveries of James Bradley (1747).
Planetary Precession.—So far we have regarded the ecliptic as absolutely fixed, and treated precession as a real motion of the equator. The ecliptic (q.v.), however, is itself subject to a motion, due to the attractions of the planets on the Earth. This effect also displaces the equinoctial points. Its annual value is 0.13″. The term General Precession in longitude is given to the displacement of the intersection of the equator with the apparent ecliptic on the latter. The standard value is 50.2453″, which prevailed in 1850, and the value at 1850 + t, i.e. the constant of precession, is 50.2453″ + 0.0002225″ t. This value is also liable to a very small change. The nutation of the obliquity at time 1850 + t is given by the formula 23° 27′ 32.0″ − 0.47″ t. Complete expressions for these functions are given in Newcomb’s Spherical Astronomy (1908), and in the Nautical Almanac.
The variation of the line of apsides is the name given to the motion of the major axis of the Earth’s orbit along the ecliptic. It is due to the general influence of the planets, and the revolution is effected in 21,000 years.
The variation of the eccentricity denotes an oscillation of the form of the Earth’s orbit between a circle and ellipse. This followed the mathematical researches of Lagrange and Leverrier. It was suggested by Sir John Herschel in 1830 that this variation might occasion great climatic changes, and James Croll developed the theory as affording a solution of the glacial periods in geology (q.v.).
Variation of Latitude.—Another secular motion of the Earth is due to the fact that the axis of rotation is not rigidly fixed within it, but its polar extremities wander in a circle of about 50 ft. diameter. This oscillation brings about a variability in terrestrial latitudes, hence the name. Euler showed mathematically that such an oscillation existed, and, making certain assumptions as to the rigidity of the Earth, deduced that its period was 305 days; S.C. Chandler, from 1890 onwards, deduced from observations of the stars a period of 428 days; and Simon Newcomb explained the deviation of these periods by pointing out that Euler’s assumption of a perfectly rigid Earth is not in accordance with fact. For details of this intricate subject see the articles Latitude and Earth, Figure of the.
4. Evolution and Age.—In its earliest history the mass now consolidated as the Earth and Moon was part of a vast nebulous aggregate, which in the course of time formed a central nucleus—our Sun—which shed its outer layers in such a manner as to form the solar system (see Nebular Theory). The moon may have been formed from the Earth in a similar manner, but the theory of tidal friction suggests the elongation of the Earth along an equatorial axis to form a pear-shaped figure, and that in the course of time the protuberance shot off to form the Moon (see Tide). The age of the Earth has been investigated from several directions, as have also associated questions related to climatic changes, internal temperature, orientation of the land and water (permanence of oceans and continents), &c. These problems are treated in the articles Geology and Geography.
1 Aristotle regarded the Earth as having an upper inhabited half and a lower uninhabited one, and the air on the lower half as tending to flow upwards through the Earth. The obstruction of this passage brought about an accumulation of air within the Earth, and the increased pressure may occasion oscillations of the surface, which may be so intense as to cause earthquakes.
EARTH, FIGURE OF THE. The determination of the figure of the earth is a problem of the highest importance in astronomy, inasmuch as the diameter of the earth is the unit to which all celestial distances must be referred.
Historical.
Reasoning from the uniform level appearance of the horizon, the variations in altitude of the circumpolar stars as one travels towards the north or south, the disappearance of a ship standing out to sea, and perhaps other phenomena, the earliest astronomers regarded the earth as a sphere, and they endeavoured to ascertain its dimensions. Aristotle relates that the mathematicians had found the circumference to be 400,000 stadia (about 46,000 miles). But Eratosthenes (c. 250 B.C.) appears to have been the first who entertained an accurate idea of the principles on which the determination of the figure of the earth really depends, and attempted to reduce them to practice. His results were very inaccurate, but his method is the same as that which is followed at the present day—depending, in fact, on the comparison of a line measured on the earth’s surface with the corresponding arc of the heavens. He observed that at Syene in Upper Egypt, on the day of the summer solstice, the sun was exactly vertical, whilst at Alexandria at the same season of the year its zenith distance was 7° 12′, or one-fiftieth of the circumference of a circle. He assumed that these places were on the same meridian; and, reckoning their distance apart as 5000 stadia, he inferred that the circumference of the earth was 250,000 stadia (about 29,000 miles). A similar attempt was made by Posidonius, who adopted a method which differed from that of Eratosthenes only in using a star instead of the sun. He obtained 240,000 stadia (about 27,600 miles) for the circumference. Ptolemy in his Geography assigns the length of the degree as 500 stadia.
The Arabs also investigated the question of the earth’s magnitude. The caliph Abdallah al Mamun (A.D. 814), having fixed on a spot in the plains of Mesopotamia, despatched one company of astronomers northwards and another southwards, measuring the journey by rods, until each found the altitude of the pole to have changed one degree. But the result of this measurement does not appear to have been very satisfactory. From this time the subject seems to have attracted no attention until about 1500, when Jean Fernel (1497-1558), a Frenchman, measured a distance in the direction of the meridian near Paris by counting the number of revolutions of the wheel of a carriage. His astronomical observations were made with a triangle used as a quadrant, and his resulting length of a degree was very near the truth.
Willebrord Snell1 substituted a chain of triangles for actual linear measurement. He measured his base line on the frozen surface of the meadows near Leiden, and measured the angles of his triangles, which lay between Alkmaar and Bergen-op-Zoom, with a quadrant and semicircles. He took the precaution of 802 comparing his standard with that of the French, so that his result was expressed in toises (the length of the toise is about 6.39 English ft.). The work was recomputed and reobserved by P. von Musschenbroek in 1729. In 1637 an Englishman, Richard Norwood, published a determination of the figure of the earth in a volume entitled The Seaman’s Practice, contayning a Fundamentall Probleme in Navigation experimentally verified, namely, touching the Compasse of the Earth and Sea and the quantity of a Degree in our English Measures. He observed on the 11th of June 1633 the sun’s meridian altitude in London as 62° 1′, and on the 6th of June 1635, his meridian altitude in York as 59° 33′. He measured the distance between these places partly with a chain and partly by pacing. By this means, through compensation of errors, he arrived at 367,176 ft. for the degree—a very fair result.
The application of the telescope to angular instruments was the next important step. Jean Picard was the first who in 1669, with the telescope, using such precautions as the nature of the operation requires, measured an arc of meridian. He measured with wooden rods a base line of 5663 toises, and a second or base of verification of 3902 toises; his triangulation extended from Malvoisine, near Paris, to Sourdon, near Amiens. The angles of the triangles were measured with a quadrant furnished with a telescope having cross-wires. The difference of latitude of the terminal stations was determined by observations made with a sector on a star in Cassiopeia, giving 1° 22′ 55″ for the amplitude. The terrestrial measurement gave 78,850 toises, whence he inferred for the length of the degree 57,060 toises.
Hitherto geodetic observations had been confined to the determination of the magnitude of the earth considered as a sphere, but a discovery made by Jean Richer (d. 1696) turned the attention of mathematicians to its deviation from a spherical form. This astronomer, having been sent by the Academy of Sciences of Paris to the island of Cayenne, in South America, for the purpose of investigating the amount of astronomical refraction and other astronomical objects, observed that his clock, which had been regulated at Paris to beat seconds, lost about two minutes and a half daily at Cayenne, and that in order to bring it to measure mean solar time it was necessary to shorten the pendulum by more than a line (about 1⁄12th of an in.). This fact, which was scarcely credited till it had been confirmed by the subsequent observations of Varin and Deshayes on the coasts of Africa and America, was first explained in the third book of Newton’s Principia, who showed that it could only be referred to a diminution of gravity arising either from a protuberance of the equatorial parts of the earth and consequent increase of the distance from the centre, or from the counteracting effect of the centrifugal force. About the same time (1673) appeared Christian Huygens’ De Horologio Oscillatorio, in which for the first time were found correct notions on the subject of centrifugal force. It does not, however, appear that they were applied to the theoretical investigation of the figure of the earth before the publication of Newton’s Principia. In 1690 Huygens published his De Causa Gravitatis, which contains an investigation of the figure of the earth on the supposition that the attraction of every particle is towards the centre.
Between 1684 and 1718 J. and D. Cassini, starting from Picard’s base, carried a triangulation northwards from Paris to Dunkirk and southwards from Paris to Collioure. They measured a base of 7246 toises near Perpignan, and a somewhat shorter base near Dunkirk; and from the northern portion of the arc, which had an amplitude of 2° 12′ 9″, obtained for the length of a degree 56,960 toises; while from the southern portion, of which the amplitude was 6° 18′ 57″, they obtained 57,097 toises. The immediate inference from this was that, the degree diminishing with increasing latitude, the earth must be a prolate spheroid. This conclusion was totally opposed to the theoretical investigations of Newton and Huygens, and accordingly the Academy of Sciences of Paris determined to apply a decisive test by the measurement of arcs at a great distance from each other—one in the neighbourhood of the equator, the other in a high latitude. Thus arose the celebrated expeditions of the French academicians. In May 1735 Louis Godin, Pierre Bouguer and Charles Marie de la Condamine, under the auspices of Louis XV., proceeded to Peru, where, assisted by two Spanish officers, after ten years of laborious exertion, they measured an arc of 3° 7′, the northern end near the equator. The second party consisted of Pierre Louis Moreau de Maupertuis, Alexis Claude Clairault, Charles Étienne Louis Camus, Pierre Charles Lemonnier, and Reginaud Outhier, who reached the Gulf of Bothnia in July 1736; they were in some respects more fortunate than the first party, inasmuch as they completed the measurement of an arc near the polar circle of 57′ amplitude and returned within sixteen months from the date of their departure.
The measurement of Bouguer and De la Condamine was executed with great care, and on account of the locality, as well as the manner in which all the details were conducted, it has always been regarded as a most valuable determination. The southern limit was at Tarqui, the northern at Cotchesqui. A base of 6272 toises was measured in the vicinity of Quito, near the northern extremity of the arc, and a second base of 5260 toises near the southern extremity. The mountainous nature of the country made the work very laborious, in some cases the difference of heights of two neighbouring stations exceeding 1 mile; and they had much trouble with their instruments, those with which they were to determine the latitudes proving untrustworthy. But they succeeded by simultaneous observations of the same star at the two extremities of the arc in obtaining very fair results. The whole length of the arc amounted to 176,945 toises, while the difference of latitudes was 3° 7′ 3″. In consequence of a misunderstanding that arose between De la Condamine and Bouguer, their operations were conducted separately, and each wrote a full account of the expedition. Bouguer’s book was published in 1749; that of De la Condamine in 1751. The toise used in this measure was afterwards regarded as the standard toise, and is always referred to as the Toise of Peru.
The party of Maupertuis, though their work was quickly despatched, had also to contend with great difficulties. Not being able to make use of the small islands in the Gulf of Bothnia for the trigonometrical stations, they were forced to penetrate into the forests of Lapland, commencing operations at Torneå, a city situated on the mainland near the extremity of the gulf. From this, the southern extremity of their arc, they carried a chain of triangles northward to the mountain Kittis, which they selected as the northern terminus. The latitudes were determined by observations with a sector (made by George Graham) of the zenith distance of α and δ Draconis. The base line was measured on the frozen surface of the river Torneå about the middle of the arc; two parties measured it separately, and they differed by about 4 in. The result of the whole was that the difference of latitudes of the terminal stations was 57′ 29″ .6, and the length of the arc 55,023 toises. In this expedition, as well as in that to Peru, observations were made with a pendulum to determine the force of gravity; and these observations coincided with the geodetic results in proving that the earth was an oblate and not prolate spheroid.
In 1740 was published in the Paris Mémoires an account, by Cassini de Thury, of a remeasurement by himself and Nicolas Louis de Lacaille of the meridian of Paris. With a view to determine more accurately the variation of the degree along the meridian, they divided the distance from Dunkirk to Collioure into four partial arcs of about two degrees each, by observing the latitude at five stations. The results previously obtained by J. and D. Cassini were not confirmed, but, on the contrary, the length of the degree derived from these partial arcs showed on the whole an increase with an increasing latitude. Cassini and Lacaille also measured an arc of parallel across the mouth of the Rhone. The difference of time of the extremities was determined by the observers at either end noting the instant of a signal given by flashing gunpowder at a point near the middle of the arc.
While at the Cape of Good Hope in 1752, engaged in various astronomical observations, Lacaille measured an arc of meridian of 1° 13′ 17″, which gave him for the length of the degree 57,037 803 toises—an unexpected result, which has led to the remeasurement of the arc by Sir Thomas Maclear (see Geodesy).
Passing over the measurements made between Rome and Rimini and on the plains of Piedmont by the Jesuits Ruggiero Giuseppe Boscovich and Giovanni Battista Beccaria, and also the arc measured with deal rods in North America by Charles Mason and Jeremiah Dixon, we come to the commencement of the English triangulation. In 1783, in consequence of a representation from Cassini de Thury on the advantages that would accrue from the geodetic connexion of Paris and Greenwich, General William Roy was, with the king’s approval, appointed by the Royal Society to conduct the operations on the part of England, Count Cassini, Méchain and Delambre being appointed on the French side. A precision previously unknown was attained by the use of Ramsden’s theodolite, which was the first to make the spherical excess of triangles measurable. The wooden rods with which the first base was measured were replaced by glass rods, which were afterwards rejected for the steel chain of Ramsden. (For further details see Account of the Trigonometrical Survey of England and Wales.)
Shortly after this, the National Convention of France, having agreed to remodel their system of weights and measures, chose for their unit of length the ten-millionth part of the meridian quadrant. In order to obtain this length precisely, the remeasurement of the French meridian was resolved on, and deputed to J.B.J. Delambre and Pierre François André Méchain. The details of this operation will be found in the Base du système métrique décimale. The arc was subsequently extended by Jean Baptiste Biot and Dominique François Jean Arago to the island of Iviza. Operations for the connexion of England with the continent of Europe were resumed in 1821 to 1823 by Henry Kater and Thomas Frederick Colby on the English side, and F.J.D. Arago and Claude Louis Mathieu on the French.
The publication in 1838 of Friedrich Wilhelm Bessel’s Gradmessung in Ostpreussen marks an era in the science of geodesy. Here we find the method of least squares applied to the calculation of a network of triangles and the reduction of the observations generally. The systematic manner in which all the observations were taken with the view of securing final results of extreme accuracy is admirable. The triangulation, which was a small one, extended about a degree and a half along the shores of the Baltic in a N.N.E. direction. The angles were observed with theodolites of 12 and 15 in. diameter, and the latitudes determined by means of the transit instrument in the prime vertical—a method much used in Germany. (The base apparatus is described in the article Geodesy.)
The principal triangulation of Great Britain and Ireland, which was commenced in 1783 under General Roy, for the more immediate purpose of connecting the observatories of Greenwich and Paris, had been gradually extended, under the successive direction of Colonel E. Williams, General W. Mudge, General T.F. Colby, Colonel L.A. Hall, and Colonel Sir Henry James; it was finished in 1851. The number of stations is about 250. At 32 of these the latitudes were determined with Ramsden’s and Airy’s zenith sectors. The theodolites used for this work were, in addition to the two great theodolites of Ramsden which were used by General Roy and Captain Kater, a smaller theodolite of 18 in. diameter by the same mechanician, and another of 24 in. diameter by Messrs Troughton and Simms. Observations for determination of absolute azimuth were made with those instruments at a large number of stations; the stars α, δ, and λ Ursae Minoris and 51 Cephei being those observed always at the greatest azimuths. At six of these stations the probable error of the result is under 0.4″, at twelve under 0.5″, at thirty-four under 0.7″: so that the absolute azimuth of the whole network is determined with extreme accuracy. Of the seven base lines which have been measured, five were by means of steel chains and two with Colby’s compensation bars (see Geodesy). The triangulation was computed by least squares. The total number of equations of condition for the triangulation is 920; if therefore the whole had been reduced in one mass, as it should have been, the solution of an equation of 920 unknown quantities would have occurred as a part of the work. To avoid this an approximation was resorted to; the triangulation was divided into twenty-one parts or figures; four of these, not adjacent, were first adjusted by the method explained, and the corrections thus determined in these figures carried into the equations of condition of the adjacent figures. The average number of equations in a figure is 44; the largest equation is one of 77 unknown quantities. The vertical limb of Airy’s zenith sector is read by four microscopes, and in the complete observation of a star there are 10 micrometer readings and 12 level readings. The instrument is portable; and a complete determination of latitude, affected with the mean of the declination errors of two stars, is effected by two micrometer readings and four level readings. The observation consists in measuring with the telescope micrometer the difference of zenith distances of two stars which cross the meridian, one to the north and the other to the south of the observer at zenith distances which differ by not much more than 10′ or 15′, the interval of the times of transit being not less than one nor more than twenty minutes. The advantages are that, with simplicity in the construction of the instrument and facility in the manipulation, refraction is eliminated (or nearly so, as the stars are generally selected within 25° of the zenith), and there is no large divided circle. The telescope, which is counterpoised on one side of the vertical axis, has a small circle for finding, and there is also a small horizontal circle. This instrument is universally used in American geodesy.
The principal work containing the methods and results of these operations was published in 1858 with the title “Ordnance Trigonometrical Survey of Great Britain and Ireland. Account of the observations and calculations of the principal triangulation and of the figure, dimensions and mean specific gravity of the earth as derived therefrom. Drawn up by Captain Alexander Ross Clarke, R.E., F.R.A.S., under the direction of Lieut.-Colonel H. James, R.E., F.R.S., M.R.I.A., &c.” A supplement appeared in 1862: “Extension of the Triangulation of the Ordnance Survey into France and Belgium, with the measurement of an arc of parallel in 52° N. from Valentia in Ireland to Mount Kemmel in Belgium. Published by ... Col. Sir Henry James.”
Extensive operations for surveying India and determining the figure of the earth were commenced in 1800. Colonel W. Lambton started the great meridian arc at Punnae in latitude 8° 9′, and, following generally the methods of the English survey, he carried his triangulation as far north as 20° 30′. The work was continued by Sir George (then Captain) Everest, who carried it to the latitude of 29° 30′. Two admirable volumes by Sir George Everest, published in 1830 and in 1847, give the details of this undertaking. The survey was afterwards prosecuted by Colonel T.T. Walker, R.E., who made valuable contributions to geodesy. The working out of the Indian chains of triangle by the method of least squares presents peculiar difficulties, but, enormous in extent as the work was, it has been thoroughly carried out. The ten base lines on which the survey depends were measured with Colby’s compensation bars.
The survey is detailed in eighteen volumes, published at Dehra Dun, and entitled Account of the Operations of the Great Trigonometrical Survey of India. Of these the first nine were published under the direction of Colonel Walker; and the remainder by Colonels Strahan and St G.C. Gore, Major S.G. Burrard and others. Vol. i., 1870, treats of the base lines; vol. ii., 1879, history and general descriptions of the principal triangulation and of its reduction; vol. v., 1879, pendulum operations (Captains T.P. Basevi and W.T. Heaviside); vols. xi., 1890, and xviii., 1906, latitudes; vols. ix., 1883, x., 1887, xv., 1893, longitudes; vol. xvii., 1901, the Indo-European longitude-arcs from Karachi to Greenwich. The other volumes contain the triangulations.
In 1860 Friedrich Georg Wilhelm Struve published his Arc du méridien de 25° 20′ entre le Danube et la Mer Glaciale mesuré depuis 1816 jusqu’en 1855. The latitudes of the thirteen astronomical stations of this arc were determined partly with vertical circles and partly by means of the transit instrument in the prime vertical. The triangulation, a great part of which, however, is a simple chain of triangles, is reduced by the method of least squares, and the probable errors of the resulting distances of parallels is given; the probable error of the whole arc in length is ± 6.2 toises. Ten base lines were measured. The sum of the 804 lengths of the ten measured bases is 29,863 toises, so that the average length of a base line is 19,100 ft. The azimuths were observed at fourteen stations. In high latitudes the determination of the meridian is a matter of great difficulty; nevertheless the azimuths at all the northern stations were successfully determined,—the probable error of the result at Fuglenaes being ± 0″.53.
Before proceeding with the modern developments of geodetic measurements and their application to the figure of the earth, we must discuss the “mechanical theory,” which is indispensable for a full understanding of the subject.
Mechanical Theory.
Newton, by applying his theory of gravitation, combined with the so-called centrifugal force, to the earth, and assuming that an oblate ellipsoid of rotation is a form of equilibrium for a homogeneous fluid rotating with uniform angular velocity, obtained the ratio of the axes 229:230, and the law of variation of gravity on the surface. A few years later Huygens published an investigation of the figure of the earth, supposing the attraction of every particle to be towards the centre of the earth, obtaining as a result that the proportion of the axes should be 578 : 579. In 1740 Colin Maclaurin, in his De causa physica fluxus et refluxus maris, demonstrated that the oblate ellipsoid of revolution is a figure which satisfies the conditions of equilibrium in the case of a revolving homogeneous fluid mass, whose particles attract one another according to the law of the inverse square of the distance; he gave the equation connecting the ellipticity with the proportion of the centrifugal force at the equator to gravity, and determined the attraction on a particle situated anywhere on the surface of such a body. In 1743 Clairault published his Théorie de la figure de la terre, which contains a remarkable theorem (“Clairault’s Theorem”), establishing a relation between the ellipticity of the earth and the variation of gravity from the equator to the poles. Assuming that the earth is composed of concentric ellipsoidal strata having a common axis of rotation, each stratum homogeneous in itself, but the ellipticities and densities of the successive strata varying according to any law, and that the superficial stratum has the same form as if it were fluid, he proved that
| g′ − g | + e = | 5 | m, |
| g | 2 |
where g, g′ are the amounts of gravity at the equator and at the pole respectively, e the ellipticity of the meridian (or “flattening”), and m the ratio of the centrifugal force at the equator to g. He also proved that the increase of gravity in proceeding from the equator to the poles is as the square of the sine of the latitude. This, taken with the former theorem, gives the means of determining the earth’s ellipticity from observation of the relative force of gravity at any two places. P.S. Laplace, who devoted much attention to the subject, remarks on Clairault’s work that “the importance of all his results and the elegance with which they are presented place this work amongst the most beautiful of mathematical productions” (Isaac Todhunter’s History of the Mathematical Theories of Attraction and the Figure of the Earth, vol. i. p. 229).
The problem of the figure of the earth treated as a question of mechanics or hydrostatics is one of great difficulty, and it would be quite impracticable but for the circumstance that the surface differs but little from a sphere. In order to express the forces at any point of the body arising from the attraction of its particles, the form of the surface is required, but this form is the very one which it is the object of the investigation to discover; hence the complexity of the subject, and even with all the present resources of mathematicians only a partial and imperfect solution can be obtained.
We may here briefly indicate the line of reasoning by which some of the most important results may be obtained. If X, Y, Z be the components parallel to three rectangular axes of the forces acting on a particle of a fluid mass at the point x, y, z, then, p being the pressure there, and ρ the density,
dp = ρ(Xdx + Ydy + Zdz);
and for equilibrium the necessary conditions are, that ρ(Xdx + Ydy + Zdz) be a complete differential, and at the free surface Xdx + Ydy + Zdz = 0. This equation implies that the resultant of the forces is normal to the surface at every point, and in a homogeneous fluid it is obviously the differential equation of all surfaces of equal pressure. If the fluid be heterogeneous then it is to be remarked that for forces of attraction according to the ordinary law of gravitation, if X, Y, Z be the components of the attraction of a mass whose potential is V, then
| Xdx + Ydy + Zdz = | dV | dx + | dV | dy + | dV | dz, |
| dx | dy | dz |
which is a complete differential. And in the case of a fluid rotating with uniform velocity, in which the so-called centrifugal force enters as a force acting on each particle proportional to its distance from the axis of rotation, the corresponding part of Xdx + Ydy + Zdz is obviously a complete differential. Therefore for the forces with which we are now concerned Xdx + Ydy + Zdz = dU, where U is some function of x, y, z, and it is necessary for equilibrium that dp = ρdU be a complete differential; that is, ρ must be a function of U or a function of p, and so also p a function of U. So that dU = 0 is the differential equation of surfaces of equal pressure and density.
We may now show that a homogeneous fluid mass in the form of an oblate ellipsoid of revolution having a uniform velocity of rotation can be in equilibrium. It may be proved that the attraction of the ellipsoid x² + y² + z²(1 + ε²) = c²(1 + ε²); upon a particle P of its mass at x, y, z has for components
X = − Ax, Y = − Ay, Z = − Cz,
where
| A = 2πk²ρ( | 1 + ε² | tan−1ε − | 1 | ), |
| ε³ | ε² |
| C = 4πk²ρ( | 1 + ε² | − | 1 + ε² | tan−1ε), |
| ε² | ε³ |
and k² the constant of attraction. Besides the attraction of the mass of the ellipsoid, the centrifugal force at P has for components + xω², + yω², 0; then the condition of fluid equilibrium is
(A − ω²)xdx + (A − ω²)ydy + Czdz = 0,
which by integration gives
(A − ω²)(x² + y²) + Cz² = constant.
This is the equation of an ellipsoid of rotation, and therefore the equilibrium is possible. The equation coincides with that of the surface of the fluid mass if we make
A − ω² = C / (1 + ε²),
which gives
| ω² | = | 3 + ε² | tan−1ε − | 3 | . |
| 2πk²ρ | ε³ | ε² |
In the case of the earth, which is nearly spherical, we obtain by expanding the expression for ω² in powers of ε², rejecting the higher powers, and remarking that the ellipticity e = ½ε²,
ω² / 2πk²ρ = 4ε² / 15 = 8e / 15.
Now if m be the ratio of the centrifugal force to the intensity of gravity at the equator, and a = c(1 + e), then
m = aω² / 4⁄3πk²ρa, ∴ ω² / 2πk²ρ = 2⁄3m.
In the case of the earth it is a matter of observation that m = 1/289, hence the ellipticity
e = 5m / 4 = 1/231,
so that the ratio of the axes on the supposition of a homogeneous fluid earth is 230 : 231, as stated by Newton.
Now, to come to the case of a heterogeneous fluid, we shall assume that its surfaces of equal density are spheroids, concentric and having a common axis of rotation, and that the ellipticity of these surfaces varies from the centre to the outer surface, the density also varying. In other words, the body is composed of homogeneous spheroidal shells of variable density and ellipticity. On this supposition we shall express the attraction of the mass upon a particle in its interior, and then, taking into account the centrifugal force, form the equation expressing the condition of fluid equilibrium. The attraction of the homogeneous spheroid x² + y² + z²(1 + 2e) = c²(1 + 2e), where e is the ellipticity (of which the square is neglected), on an internal particle, whose co-ordinates are x = f, y = 0, z = h, has for its x and z components
X′ = −4⁄3πk²ρf(1 − 2⁄5e), Z′ = −4⁄3πk²ρh(1 + 4⁄5e),
the Y component being of course zero. Hence we infer that the attraction of a shell whose inner surface has an ellipticity e, and its outer surface an ellipticity e + de, the density being ρ, is expressed by
dX′ = 4⁄3 · 2⁄5πk²ρf de, dZ′ = −4⁄3 · 4⁄5πk²ρh de.
To apply this to our heterogeneous spheroid; if we put c1 for the semiaxis of that surface of equal density on which is situated the attracted point P, and c0 for the semiaxis of the outer surface, the attraction of that portion of the body which is exterior to P, namely, of all the shells which enclose P, has for components
| X0 = 8⁄15πk²f ∫c0c1 ρ | de | dc, Z0 = 16⁄15πk²h ∫c0c1 ρ | de | dc, |
| dc | dc |
both e and ρ being functions of c. Again the attraction of a homogeneous spheroid of density ρ on an external point f, h has the components
X″ = −4⁄3πk²ρfr−3 {c³(1 + 2e) − λec5},
Z″ = −4⁄3πk²ρhr−3 {c³(1 + 2e) − λ′ec5},
where λ = 3⁄5(4h² − f²) / r4, λ′ = 3⁄5(2h² − 3f²) / r4, and r² = f² + h².
Now e being considered a function of c, we can at once express the attraction of a shell (density ρ) contained between the surface defined by c + dc, e + de and that defined by c, e upon an external point; the differentials with respect to c, viz. dX″ dZ″, must then be integrated with ρ under the integral sign as being a function of c. The integration will extend from c = 0 to c = c1. Thus the components of the attraction of the heterogeneous spheroid upon a particle within its mass, whose co-ordinates are f, 0, h, are
| X = −4⁄3πk²f [ | 1 | ∫c10 ρ d{c³(1 + 2e)} − | λ | ∫c10 ρ d(ec5) + 2⁄5 ∫c0c1 ρ de], |
| r3 | r3 |
| Z = −4⁄3πk²h [ | 1 | ∫c10 ρ d{c³(1 + 2e)} − | λ′ | ∫c10 ρ d(ec5) + 4⁄5 ∫c0c1 ρ de]. |
| r3 | r3 |
We take into account the rotation of the earth by adding the centrifugal force fω² = F to X. Now, the surface of constant density upon which the point f, 0, h is situated gives (1 − 2e) fdf + hdh = 0; and the condition of equilibrium is that (X + F)df + Zdh = 0. Therefore,
(X + F) h = Zf (1 − 2e),
which, neglecting small quantities of the order e² and putting ω²t² = 4π²k², gives
| 2e | ∫c10 ρd{c³(1 + 2e)} − | 6 | ∫c10 ρd(ec5) − | 6 | ∫c10 ρde = | 3π | . |
| r³ | 5r5 | 5 | t² |
Here we must now put c for c1, c for r; and 1 + 2e under the first integral sign may be replaced by unity, since small quantities of the second order are neglected. Two differentiations lead us to the following very important differential equation (Clairault):
| d²e | + | 2ρc² | · | de | + ( | 2ρc | − | 6 | ) e = 0. |
| dc² | ∫ρc² dc | dc | ∫ρc² dc | c² |
When ρ is expressed in terms of c, this equation can be integrated. We infer then that a rotating spheroid of very small ellipticity, composed of fluid homogeneous strata such as we have specified, will be in equilibrium; and when the law of the density is expressed, the law of the corresponding ellipticities will follow.
If we put M for the mass of the spheroid, then
| M = | 4π | ∫c0 ρd{c³(1 + 2e)}; and m = | c³ | · | 4π² | , |
| 3 | M | t² |
and putting c = c0 in the equation expressing the condition of equilibrium, we find
| M(2e − m) = | 4 | π · | 6 | ∫c0 ρ d(ec5). |
| 3 | 5c² |
Making these substitutions in the expressions for the forces at the surface, and putting r/c = 1 + e − e(h/c)², we get
| G cos φ = | Mk² | {1 − e − | 3 | m + ( | 5 | m − 2e) | h² | } | f |
| ac | 2 | 2 | c² | c |
| G sin φ = | Mk² | {1 + e − | 3 | m + ( | 5 | m − 2e) | h² | } | h | . |
| ac | 2 | 2 | c² | c |
Here G is gravity in the latitude φ, and a the radius of the equator. Since
sec φ = (c/f){1 + e + (eh²/c²)},
| G = | Mk² | {1 − | 3 | m +( | 5 | m − e) sin² φ}, |
| ac | 2 | 2 |
an expression which contains the theorems we have referred to as discovered by Clairault.
The theory of the figure of the earth as a rotating ellipsoid has been especially investigated by Laplace in his Mécanique celeste. The principal English works are:—Sir George Airy, Mathematical Tracts, a lucid treatment without the use of Laplace’s coefficients; Archdeacon Pratt’s Attractions and Figure of the Earth; and O’Brien’s Mathematical Tracts; in the last two Laplace’s coefficients are used.
In 1845 Sir G.G. Stokes (Camb. Trans. viii.; see also Camb. Dub. Math. Journ., 1849, iv.) proved that if the external form of the sea—imagined to percolate the land by canals—be a spheroid with small ellipticity, then the law of gravity is that which we have shown above; his proof required no assumption as to the ellipticity of the internal strata, or as to the past or present fluidity of the earth. This investigation admits of being regarded conversely, viz. as determining the elliptical form of the earth from measurements of gravity; if G, the observed value of gravity in latitude φ, be expressed in the form G = g(1 + β sin² φ), where g is the value at the equator and β a coefficient. In this investigation, the square and higher powers of the ellipticity are neglected; the solution was completed by F.R. Helmert with regard to the square of the ellipticity, who showed that a term with sin² 2φ appeared (see Helmert, Geodäsie, ii. 83). For the coefficient of this term, the gravity measurements give a small but not sufficiently certain value; we therefore assume a value which agrees best with the hypothesis of the fluid state of the entire earth; this assumption is well supported, since even at a depth of only 50 km. the pressure of the superincumbent crust is so great that rocks become plastic, and behave approximately as fluids, and consequently the crust of the earth floats, to some extent, on the interior (even though this may not be fluid in the usual sense of the word). This is the geological theory of “Isostasis” (cf. Geology); it agrees with the results of measurements of gravity (vide infra), and was brought forward in the middle of the 19th century by J.H. Pratt, who deduced it from observations made in India.
The sin² 2φ term in the expression for G, and the corresponding deviation of the meridian from an ellipse, have been analytically established by Sir G.H. Darwin and E. Wiechert; earlier and less complete investigations were made by Sir G.B. Airy and O. Callandreau. In consequence of the sin² 2φ term, two parameters of the level surfaces in the interior of the earth are to be determined; for this purpose, Darwin develops two differential equations in the place of the one by Clairault. By assuming Roche’s law for the variation of the density in the interior of the Earth, viz. ρ = ρ1 − k(c/c1)², k being a coefficient, it is shown that in latitude 45°, the meridian is depressed about 3¼ metres from the ellipse, and the coefficient of the term sin²φ cos²φ (= ¼ sin²2φ) is −0.0000295. According to Wiechert the earth is composed of a kernel and a shell, the kernel being composed of material, chiefly metallic iron, of density near 8.2, and the shell, about 900 miles thick, of silicates, &c., of density about 3.2. On this assumption the depression in latitude 45° is 2¾ metres, and the coefficient of sin²φ cos²φ is, in round numbers, −0.0000280.2 To this additional term in the formula for G, there corresponds an extension of Clairault’s formula for the calculation of the flattening from β with terms of the higher orders; this was first accomplished by Helmert.
For a long time the assumption of an ellipsoid with three unequal axes has been held possible for the figure of the earth, in consequence of an important theorem due to K.G. Jacobi, who proved that for a homogeneous fluid in rotation a spheroid is not the only form of equilibrium; an ellipsoid rotating round its least axis may with certain proportions of the axes and a certain time of revolution be a form of equilibrium.3 It has been objected to the figure of three unequal axes that it does not satisfy, in the proportions of the axes, the conditions brought out in Jacobi’s theorem (c : a < 1/√2). Admitting this, it has to be noted, on the other hand, that Jacobi’s theorem contemplates a homogeneous fluid, and this is certainly far from the actual condition of our globe; indeed the irregular distribution of continents and oceans suggests the possibility of a sensible divergence from a perfect surface of revolution. We may, however, assume the ellipsoid with three unequal axes to be an interpolation form. More plausible forms are little adapted for computation.4 Consequently we now generally take the ellipsoid of rotation as a basis, especially so because measurements of gravity have shown that the deviation from it is but trifling.
Local Attraction.
In speaking of the figure of the earth, we mean the surface of the sea imagined to percolate the continents by canals. That 806 this surface should turn out, after precise measurements, to be exactly an ellipsoid of revolution is a priori improbable. Although it may be highly probable that originally the earth was a fluid mass, yet in the cooling whereby the present crust has resulted, the actual solid surface has been left most irregular in form. It is clear that these irregularities of the visible surface must be accompanied by irregularities in the mathematical figure of the earth, and when we consider the general surface of our globe, its irregular distribution of mountain masses, continents, with oceans and islands, we are prepared to admit that the earth may not be precisely any surface of revolution. Nevertheless, there must exist some spheroid which agrees very closely with the mathematical figure of the earth, and has the same axis of rotation. We must conceive this figure as exhibiting slight departures from the spheroid, the two surfaces cutting one another in various lines; thus a point of the surface is defined by its latitude, longitude, and its height above the “spheroid of reference.” Calling this height N, then of the actual magnitude of this quantity we can generally have no information, it only obtrudes itself on our notice by its variations. In the vicinity of mountains it may change sign in the space of a few miles; N being regarded as a function of the latitude and longitude, if its differential coefficient with respect to the former be zero at a certain point, the normals to the two surfaces then will lie in the prime vertical; if the differential coefficient of N with respect to the longitude be zero, the two normals will lie in the meridian; if both coefficients are zero, the normals will coincide. The comparisons of terrestrial measurements with the corresponding astronomical observations have always been accompanied with discrepancies. Suppose A and B to be two trigonometrical stations, and that at A there is a disturbing force drawing the vertical through an angle δ, then it is evident that the apparent zenith of A will be really that of some other place A′, whose distance from A is rδ, when r is the earth’s radius; and similarly if there be a disturbance at B of the amount δ′, the apparent zenith of B will be really that of some other place B′, whose distance from B is rδ′. Hence we have the discrepancy that, while the geodetic measurements deal with the points A and B, the astronomical observations belong to the points A′, B′. Should δ, δ′ be equal and parallel, the displacements AA′, BB′ will be equal and parallel, and no discrepancy will appear. The non-recognition of this circumstance often led to much perplexity in the early history of geodesy. Suppose that, through the unknown variations of N, the probable error of an observed latitude (that is, the angle between the normal to the mathematical surface of the earth at the given point and that of the corresponding point on the spheroid of reference) be ε, then if we compare two arcs of a degree each in mean latitudes, and near each other, say about five degrees of latitude apart, the probable error of the resulting value of the ellipticity will be approximately ±1⁄500ε, ε being expressed in seconds, so that if ε be so great as 2″ the probable error of the resulting ellipticity will be greater than the ellipticity itself.
It is necessary at times to calculate the attraction of a mountain, and the consequent disturbance of the astronomical zenith, at any point within its influence. The deflection of the plumb-line, caused by a local attraction whose amount is k²Aδ, is measured by the ratio of k²Aδ to the force of gravity at the station. Expressed in seconds, the deflection Λ is
Λ = 12″.447Aδ / ρ,
where ρ is the mean density of the earth, δ that of the attracting mass, and A = ƒs−3xdv, in which dv is a volume element of the attracting mass within the distance s from the point of deflection, and x the projection of s on the horizontal plane through this point, the linear unit in expressing A being a mile. Suppose, for instance, a table-land whose form is a rectangle of 12 miles by 8 miles, having a height of 500 ft. and density half that of the earth; let the observer be 2 miles distant from the middle point of the longer side. The deflection then is 1″.472; but at 1 mile it increases to 2″.20.
At sixteen astronomical stations in the English survey the disturbance of latitude due to the form of the ground has been computed, and the following will give an idea of the results. At six stations the deflection is under 2″, at six others it is between 2″ and 4″, and at four stations it exceeds 4″. There is one very exceptional station on the north coast of Banffshire, near the village of Portsoy, at which the deflection amounts to 10″, so that if that village were placed on a map in a position to correspond with its astronomical latitude, it would be 1000 ft. out of position! There is the sea to the north and an undulating country to the south, which, however, to a spectator at the station does not suggest any great disturbance of gravity. A somewhat rough estimate of the local attraction from external causes gives a maximum limit of 5″, therefore we have 5″ which must arise from unequal density in the underlying strata in the surrounding country. In order to throw light on this remarkable phenomenon, the latitudes of a number of stations between Nairn on the west, Fraserburgh on the east, and the Grampians on the south, were observed, and the local deflections determined. It is somewhat singular that the deflections diminish in all directions, not very regularly certainly, and most slowly in a south-west direction, finally disappearing, and leaving the maximum at the original station at Portsoy.
The method employed by Dr C. Hutton for computing the attraction of masses of ground is so simple and effectual that it can hardly be improved on. Let a horizontal plane pass through the given station; let r, θ be the polar co-ordinates of any point in this plane, and r, θ, z, the co-ordinates of a particle of the attracting mass; and let it be required to find the attraction of a portion of the mass contained between the horizontal planes z = 0, z = h, the cylindrical surfaces r = r1, r = r2, and the vertical planes θ = θ1, θ = θ2. The component of the attraction at the station or origin along the line θ = 0 is
| k²δ ∫r2r1 ∫θ2θ1 ∫h0 | r²cosθ | dr dθ dz = k²δh (sinθ2 − sinθ1) log{r2 + (r2² + h²)1/2 / r1 + (r1² + h²)1/2}. |
| (r² + z²)3/2 |
By taking r2 − r1, sufficiently small, and supposing h also small compared with r1 + r2 (as it usually is), the attraction is
k²δ (r2 − r1) (sinθ2 − sinθ1) h/r,
where r = ½ (r1 + r2). This form suggests the following procedure. Draw on the contoured map a series of equidistant circles, concentric with the station, intersected by radial lines so disposed that the sines of their azimuths are in arithmetical progression. Then, having estimated from the map the mean heights of the various compartments, the calculation is obvious.
In mountainous countries, as near the Alps and in the Caucasus, deflections have been observed to the amount of as much as 30″, while in the Himalayas deflections amounting to 60″ were observed. On the other hand, deflections have been observed in flat countries, such as that noted by Professor K.G. Schweizer, who has shown that, at certain stations in the vicinity of Moscow, within a distance of 16 miles the plumb-line varies 16″ in such a manner as to indicate a vast deficiency of matter in the underlying strata; deflections of 10″ were observed in the level regions of north Germany.
Since the attraction of a mountain mass is expressed as a numerical multiple of δ : ρ the ratio of the density of the mountain to that of the earth, if we have any independent means of ascertaining the amount of the deflection, we have at once the ratio ρ : δ, and thus we obtain the mean density of the earth, as, for instance, at Schiehallion, and afterwards at Arthur’s Seat. Experiments of this kind for determining the mean density of the earth have been made in greater numbers; but they are not free from objection (see Gravitation).
Let us now consider the perturbation attending a spherical subterranean mass. A compact mass of great density at a small distance under the surface of the earth will produce an elevation of the mathematical surface which is expressed by the formula
y = aμ {(1 − 2u cosθ + u²)−1/2 − 1},
where a is the radius of the (spherical) earth, a (1 − u) the distance 807 of the disturbing mass below the surface, μ the ratio of the disturbing mass to the mass of the earth, and aθ the distance of any point on the surface from that point, say Q, which is vertically over the disturbing mass. The maximum value of y is at Q, where it is y = aμu (1 − u). The deflection at the distance aθ is Λ = μu sinθ (1 − 2u cosθ + u²)−3/2, or since θ is small, putting h + u = 1, we have Λ = μθ (h² + θ²)−3/2. The maximum deflection takes place at a point whose distance from Q is to the depth of the mass as 1 : √2, and its amount is 2μ/3 √3h². If, for instance, the disturbing mass were a sphere a mile in diameter, the excess of its density above that of the surrounding country being equal to half the density of the earth, and the depth of its centre half a mile, the greatest deflection would be 5″, and the greatest value of y only two inches. Thus a large disturbance of gravity may arise from an irregularity in the mathematical surface whose actual magnitude, as regards height at least, is extremely small.
The effect of the disturbing mass μ on the vibrations of a pendulum would be a maximum at Q; if v be the number of seconds of time gained per diem by the pendulum at Q, and σ the number of seconds of angle in the maximum deflection, then it may be shown that v/σ = π√3/10.
The great Indian survey, and the attendant measurements of the degree of latitude, gave occasion to elaborate investigations of the deflection of the plumb-line in the neighbourhood of the high plateaus and mountain chains of Central Asia. Archdeacon Pratt (Phil. Trans., 1855 and 1857), in instituting these investigations, took into consideration the influence of the apparent diminution of the mass of the earth’s crust occasioned by the neighbouring ocean-basins; he concluded that the accumulated masses of mountain chains, &c., corresponded to subterranean mass diminutions, so that over any level surface in a fixed depth (perhaps 100 miles or more) the masses of prisms of equal section are equal. This is supported by the gravity measurements at Moré in the Himalayas at a height of 4696 metres, which showed no deflection due to the mountain chain (Phil. Trans., 1871); more recently, H.A. Faye (Compt. rend., 1880) arrived at the same conclusion for the entire continent.
This compensation, however, must only be regarded as a general principle; in certain cases, the compensating masses show marked horizontal displacements. Further investigations, especially of gravity measurements, will undoubtedly establish other important facts. Colonel S.G. Burrard has recently recalculated, with the aid of more exact data, certain Indian deviations of the plumb-line, and has established that in the region south of the Himalayas (lat. 24°) there is a subterranean perturbing mass. The extent of the compensation of the high mountain chains is difficult to recognize from the latitude observations, since the same effect may result from different causes; on the other hand, observations of geographical longitude have established a strong compensation.5
Meridian Arcs.
The astronomical stations for the measurement of the degree of latitude will generally lie not exactly on the same meridian; and it is therefore necessary to calculate the arcs of meridian M which lie between the latitude of neighbouring stations. If S be the geodetic line calculated from the triangulation with the astronomically determined azimuths α1 and α2, then
| M = S | cos α | {1 + 1⁄12 | S² | sin²α ...}, |
| cos ½Δα | α² |
in which 2α = α1 + α2 − 180°, Δα = α2 − α1 − 180°.
The length of the arc of meridian between the latitudes φ1 and φ2 is
| M = ∫φ2φ1 ρdφ = α ∫φ2φ1 | (1 − e²) dφ |
| (1 − e² sin²φ)3/2 |
where a²e² = a² − b²; instead of using the eccentricity e, put the ratio of the axes b : a = 1 − n : 1 + n, then
| M = ∫φ2φ1 | b (1 + n) (1 − n²) dφ | . |
| (1 + 2n cos2φ + n²)3/2 |
This, after integration, gives
| M/b = (1 + n + | 5 | n² + | 5 | n³)α0 − (3n + 3n² + | 21 | n³)α1 + ( | 15 | n² + | 15 | n³)α2 − ( | 35 | n³)α3, |
| 4 | 4 | 8 | 8 | 8 | 24 |
where
| α0 = φ2 − φ1 α1 = sin (φ2 − φ1) cos (φ2 + φ1) α2 = sin 2(φ2 − φ1) cos 2(φ2 + φ1) α3 = sin 3(φ2 − φ1) cos 3(φ2 + φ1). |
The part of M which depends on n³ is very small; in fact, if we calculate it for one of the longest arcs measured, the Russian arc, it amounts to only an inch and a half, therefore we omit this term, and put for M/b the value
| (1 + n + | 5 | n²)α0 − (3n + 3n²)α1 + ( | 15 | n²)α2. |
| 4 | 8 |
Now, if we suppose the observed latitudes to be affected with errors, and that the true latitudes are φ1 + x1, φ2 + x2; and if further we suppose that n1 + dn is the true value of a − b : a + b, and that n1 itself is merely a very approximate numerical value, we get, on making these substitutions and neglecting the influence of the corrections x on the position of the arc in latitude, i.e. on φ1 + φ2,
| M/b = (1 + n1 + | 5 | n1²)α0 − (3n1 + 3n1²)α1 + ( | 15 | n1²)α2 + { (1 + | 5 | n1)α0 − (3 + 6n1)α1 + ( | 15 | n1)α2 }dn |
| 4 | 8 | 2 | 4 |
| + {1 + n1 − 3n | dα1 | }dα0; |
| dα0 |
here dα0 = x2 − x1; and as b is only known approximately, put b = b1(1 + u); then we get, after dividing through by the coefficient of dα0, which is = 1 + n1 − 3n1 cos(φ2 − φ1) cos(φ2 + φ1), an equation of the form x2 = x1 + h + fu + gv, where for convenience we put v for dn.
Now in every measured arc there are not only the extreme stations determined in latitude, but also a number of intermediate stations so that if there be i + 1 stations there will be i equations
| x2 = x1 + f1u + g1v + h1 x3 = x1 + f2u + g2v + h2 : : : : : : xi = x1 + fiu + giv + hi |
In combining a number of different arcs of meridian, with the view of determining the figure of the earth, each arc will supply a number of equations in u and v and the corrections to its observed latitudes. Then, according to the method of least squares, those values of u and v are the most probable which render the sum of the squares of all the errors x a minimum. The corrections x which are here applied arise not from errors of observation only. The mere uncertainty of a latitude, as determined with modern instruments, does not exceed a very small fraction of a second as far as errors of observation go, but no accuracy in observing will remove the error that may arise from local attraction. This, as we have seen, may amount to some seconds, so that the corrections x to the observed latitudes are attributable to local attraction. Archdeacon Pratt objected to this mode of applying least squares first used by Bessel; but Bessel was right, and the objection is groundless. Bessel found, in 1841, from ten meridian arcs with a total amplitude of 50°.6:
| a = 3272077 toises = 6377397 metres. e (ellipticity) = (a − b) / a ≈ 1/299.15 (prob. error ± 3.2). |
The probable error in the length of the earth’s quadrant is ± 336 m.
We now give a series of some meridian-arcs measurements, which were utilized in 1866 by A.R. Clarke in the Comparisons of the Standards of Length, pp. 280-287; details of the calculations are given by the same author in his Geodesy (1880), pp. 311 et seq.
The data of the French arc from Formentera to Dunkirk are—
| Stations. | Astronomical Latitudes. | Distance of Parallels. | ||
| ° | ′ | ″ | Ft. | |
| Formentera | 38 | 39 | 53.17 | · · |
| Mountjouy | 41 | 21 | 44.96 | 982671.04 |
| Barcelona | 41 | 22 | 47.90 | 988701.92 |
| Carcassonne | 43 | 12 | 54.30 | 1657287.93 |
| Pantheon | 48 | 50 | 47.98 | 3710827.13 |
| Dunkirk | 51 | 2 | 8.41 | 4509790.84 |
The distance of the parallels of Dunkirk and Greenwich, deduced from the extension of the triangulation of England into France, in 1862, is 161407.3 ft., which is 3.9 ft. greater than that obtained from Captain Kater’s triangulation, and 3.2 ft. less than the distance calculated by Delambre from General Roy’s triangulation. The following table shows the data of the English arc with the distances in standard feet from Formentera.
| ° | ′ | ″ | Ft. | |
| Formentera | · · | · · | ||
| Greenwich | 51 | 28 | 38.30 | 4671198.3 |
| Arbury | 52 | 13 | 26.59 | 4943837.6 |
| Clifton | 53 | 27 | 29.50 | 5394063.4 |
| Kellie Law | 56 | 14 | 53.60 | 6413221.7 |
| Stirling | 57 | 27 | 49.12 | 6857323.3 |
| Saxavord | 60 | 49 | 37.21 | 8086820.7 |
The latitude assigned in this table to Saxavord is not the directly observed latitude, which is 60° 49′ 38.58″, for there are here a cluster of three points, whose latitudes are astronomically determined; and if we transfer, by means of the geodesic connexion, the latitude of Gerth of Scaw to Saxavord, we get 60° 49′ 36.59″; and if we similarly transfer the latitude of Balta, we get 60° 49′ 36.46″. The mean of these three is that entered in the above table.
For the Indian arc in long. 77° 40′ we have the following data:—
| ° | ′ | ″ | Ft. | |
| Punnea | 8 | 9 | 31.132 | · · |
| Putchapolliam | 10 | 59 | 42.276 | 1029174.9 |
| Dodagunta | 12 | 59 | 52.165 | 1756562.0 |
| Namthabad | 15 | 5 | 53.562 | 2518376.3 |
| Daumergida | 18 | 3 | 15.292 | 3591788.4 |
| Takalkhera | 21 | 5 | 51.532 | 4697329.5 |
| Kalianpur | 24 | 7 | 11.262 | 5794695.7 |
| Kaliana | 29 | 30 | 48.322 | 7755835.9 |
The data of the Russian arc (long. 26° 40′) taken from Struve’s work are as below:—
| ° | ′ | ″ | Ft. | |
| Staro Nekrasovsk | 45 | 20 | 2.94 | · · |
| Vodu-Luy | 47 | 1 | 24.98 | 616529.81 |
| Suprunkovzy | 48 | 45 | 3.04 | 1246762.17 |
| Kremenets | 50 | 5 | 49.95 | 1737551.48 |
| Byelin | 52 | 2 | 42.16 | 2448745.17 |
| Nemesh | 54 | 39 | 4.16 | 3400312.63 |
| Jacobstadt | 56 | 30 | 4.97 | 4076412.28 |
| Dorpat | 58 | 22 | 47.56 | 4762421.43 |
| Hogland | 60 | 5 | 9.84 | 5386135.39 |
| Kilpi-maki | 62 | 38 | 5.25 | 6317905.67 |
| Torneå | 65 | 49 | 44.57 | 7486789.97 |
| Stuor-oivi | 68 | 40 | 58.40 | 8530517.90 |
| Fuglenaes | 70 | 40 | 11.23 | 9257921.06 |
From the are measured in Cape Colony by Sir Thomas Maclear in long. 18° 30′, we have
| ° | ′ | ″ | Ft. | |
| North End | 29 | 44 | 17.66 | · · |
| Heerenlogement Berg | 31 | 58 | 9.11 | 811507.7 |
| Royal Observatory | 33 | 56 | 3.20 | 1526386.8 |
| Zwart Kop | 34 | 13 | 32.13 | 1632583.3 |
| Cape Point | 34 | 21 | 6.26 | 1678375.7 |
And, finally, for the Peruvian arc, in long. 281° 0′,
| ° | ′ | ″ | Ft. | |
| Tarqui | 3 | 4 | 32.068 | · · |
| Cotchesqui | 0 | 2 | 31.387 | 1131036.3 |
Having now stated the data of the problem, we may seek that oblate ellipsoid (spheroid) which best represents the observations. Whatever the real figure may be, it is certain that if we suppose it an ellipsoid with three unequal axes, the arithmetical process will bring out an ellipsoid, which will agree better with all the observed latitudes than any spheroid would, therefore we do not prove that it is an ellipsoid; to prove this, arcs of longitude would be required. The result for the spheroid may be expressed thus:—
a = 20926062 ft. = 6378206.4 metres.
b = 20855121 ft. = 6356583.8 metres.
b : a = 293.98 : 294.98.
As might be expected, the sum of the squares of the 40 latitude corrections, viz. 153.99, is greater in this figure than in that of three axes, where it amounts to 138.30. For this case, in the Indian arc the largest corrections are at Dodagunta, + 3.87″, and at Kalianpur, − 3.68″. In the Russian arc the largest corrections are + 3.76″, at Torneå, and − 3.31″, at Staro Nekrasovsk. Of the whole 40 corrections, 16 are under 1.0″, 10 between 1.0″ and 2.0″, 10 between 2.0″ and 3.0″, and 4 over 3.0″. The probable error of an observed latitude is ± 1.42″; for the spheroidal it would be very slightly larger. This quantity may be taken therefore as approximately the probable amount of local deflection.
If ρ be the radius of curvature of the meridian in latitude φ, ρ′ that perpendicular to the meridian, D the length of a degree of the meridian, D′ the length of a degree of longitude, r the radius drawn from the centre of the earth, V the angle of the vertical with the radius-vector, then
| Ft. | ||||
| ρ = | 20890606.6 | − | 106411.5 cos 2φ | + 225.8 cos 4φ |
| ρ′ = | 20961607.3 | − | 35590.9 cos 2φ | + 45.2 cos 4φ |
| D = | 364609.87 | − | 1857.14 cos 2φ | + 3.94 cos 4φ |
| D′ = | 365538.48 cos φ | − | 310.17 cos 3φ | + 0.39 cos 5φ |
| Log r/a = | 9.9992645 | + | .0007374 cos 2φ | − .0000019 cos 4φ |
| V = | 700.44″ sin 2φ − 1.19″ sin 4φ. | |||
A.R. Clarke has recalculated the elements of the ellipsoid of the earth; his values, derived in 1880, in which he utilized the measurements of parallel arcs in India, are particularly in practice. These values are:—
a = 20926202 ft. = 6378249 metres,
b = 20854895 ft. = 6356515 metres,
b : a = 292.465 : 293.465.
The calculation of the elements of the ellipsoid of rotation from measurements of the curvature of arcs in any given azimuth by means of geographical longitudes, latitudes and azimuths is indicated in the article Geodesy; reference may be made to Principal Triangulation, Helmert’s Geodasie, and the publications of the Kgl. Preuss. Geod. Inst.:—Lotabweichungen (1886), and Die europ. Längengradmessung in 52° Br. (1893). For the calculation of an ellipsoid with three unequal axes see Comparison of Standards, preface; and for non-elliptical meridians, Principal Triangulation, p. 733.
Gravitation-Measurements.
According to Clairault’s theorem (see above) the ellipticity e of the mathematical surface of the earth is equal to the difference 5⁄2m − β, where m is the ratio of the centrifugal force at the equator to gravity at the equator, and β is derived from the formula G = g(1 + β sin²φ). Since the beginning of the 19th century many efforts have been made to determine the constants of this formula, and numerous expeditions undertaken to investigate the intensity of gravity in different latitudes. If m be known, it is only necessary to determine β for the evaluation of e; consequently it is unnecessary to determine G absolutely, for the relative values of G at two known latitudes suffice. Such relative measurements are easier and more exact than absolute ones. In some cases the ordinary thread pendulum, i.e. a spherical bob suspended by a wire, has been employed; but more often a rigid metal rod, bearing a weight and a knife-edge on which it may oscillate, has been adopted. The main point is the constancy of the pendulum. From the formula for the time of oscillation of the mathematically ideal pendulum, t = 2π√l/G, l being the length, it follows that for two points G1 / G2 = t2² / t1².
In 1808 J.B. Biot commenced his pendulum observations at several stations in western Europe; and in 1817-1825 Captain Louis de Freycinet and L.I. Duperrey prosecuted similar observations far into the southern hemisphere. Captain Henry Kater confined himself to British stations (1818-1819); Captain E. Sabine, from 1819 to 1829, observed similarly, with Kater’s pendulum, at seventeen stations ranging from the West Indies 809 to Greenland and Spitsbergen; and in 1824-1831, Captain Henry Foster (who met his death by drowning in Central America) experimented at sixteen stations; his observations were completed by Francis Baily in London. Of other workers in this field mention may be made of F.B. Lütke (1826-1829), a Russian rear-admiral, and Captains J.B. Basevi and W.T. Heaviside, who observed during 1865 to 1873 at Kew and at 29 Indian stations, particularly at Moré in the Himalayas at a height of 4696 metres. Of the earlier absolute determinations we may mention those of Biot, Kater, and Bessel at Paris, London and Königsberg respectively. The measurements were particularly difficult by reason of the length of the pendulums employed, these generally being second-pendulums over 1 metre long. In about 1880, Colonel Robert von Sterneck of Austria introduced the half-second pendulum, which permitted far quicker and more accurate work. The use of these pendulums spread in all countries, and the number of gravity stations consequently increased: in 1880 there were about 120, in 1900 there were about 1600, of which the greater number were in Europe. Sir E. Sabine6 calculated the ellipticity to be 1/288.5, a value shown to be too high by Helmert, who in 1884, with the aid of 120 stations, gave the value 1/299.26,7 and in 1901, with about 1400 stations, derived the value 1/298.3.8 The reason for the excessive estimate of Sabine is that he did not take into account the systematic difference between the values of G for continents and islands; it was found that in consequence of the constitution of the earth’s crust (Pratt) G is greater on small islands of the ocean than on continents by an amount which may approach to 0.3 cm. Moreover, stations in the neighbourhood of coasts shelving to deep seas have a surplus, but a little smaller. Consequently, Helmert conducted his calculations of 1901 for continents and coasts separately, and obtained G for the coasts 0.036 cm. greater than for the continents, while the value of β remained the same. The mean value, reduced to continents, is
G = 978.03 (1 + 0.005302 sin²φ − 0.000007 sin²2φ) cm/sec².
The small term involving sin² 2φ could not be calculated with sufficient exactness from the observations, and is therefore taken from the theoretical views of Sir G.H. Darwin and E. Wiechert. For the constant g = 978.03 cm. another correction has been suggested (1906) by the absolute determinations made by F. Kühnen and Ph. Furtwängler at Potsdam.9
A report on the pendulum measurements of the 19th century has been given by Helmert in the Comptes rendus des séances de la 13e conférence générale de l’Association Géod. Internationale à Paris (1900), ii. 139-385.
A difficulty presents itself in the case of the application of measurements of gravity to the determination of the figure of the earth by reason of the extrusion or standing out of the land-masses (continents, &c.) above the sea-level. The potential of gravity has a different mathematical expression outside the masses than inside. The difficulty is removed by assuming (with Sir G.G. Stokes) the vertical condensation of the masses on the sea-level, without its form being considerably altered (scarcely 1 metre radially). Further, the value of gravity (g) measured at the height H is corrected to sea-level by + 2gH/R, where R is the radius of the earth. Another correction, due to P. Bouguer, is − 3⁄2gδH/ρR, where δ is the density of the strata of height H, and ρ the mean density of the earth. These two corrections are represented in “Bouguer’s Rule”: gH = gs (1 − 2H/R + 3δH / 2ρR), where gH is the gravity at height H, and gs the value at sea-level. This is supposed to take into account the attraction of the elevated strata or plateau; but, from the analytical method, this is not correct; it is also disadvantageous since, in general, the land-masses are compensated subterraneously, by reason of the isostasis of the earth’s crust.
In 1849 Stokes showed that the normal elevations N of the geoid towards the ellipsoid are calculable from the deviations Δg of the acceleration of gravity, i.e. the differences between the observed g and the value calculated from the normal G formula. The method assumes that gravity is measured on the earth’s surface at a sufficient number of points, and that it is conformably reduced. In order to secure the convergence of the expansions in spherical harmonics, it is necessary to assume all masses outside a surface parallel to the surface of the sea at a depth of 21 km. (= R × ellipticity) to be condensed on this surface (Helmert, Geod. ii. 172). In addition to the reduction with 2gH/R, there still result small reductions with mountain chains and coasts, and somewhat larger ones for islands. The sea-surface generally varies but very little by this condensation. The elevation (N) of the geoid is then equal to
N = R ∫π FG−1Δgψψ,
where ψ is the spherical distance from the point N, and Δgψ denotes the mean value of Δg for all points in the same distance ψ around; F is a function of ψ, and has the following values:—
| Ψ = | 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° | 100° | 110° | 120° | 130° | 140° | 150° | 160° | 170° | 180° |
| F = | 1 | 1.22 | 0.94 | 0.47 | −0.06 | −0.54 | −0.90 | −1.08 | −1.08 | −0.91 | −0.62 | −0.27 | +0.08 | 0.36 | 0.53 | 0.56 | 0.46 | 0.26 | 0 |
H. Poincaré (Bull. Astr., 1901, p. 5) has exhibited N by means of Lamé’s functions; in this case the condensation is effected on an ellipsoidal surface, which approximates to the geoid. This condensation is, in practice, the same as to the geoid itself.
If we imagine the outer land-masses to be condensed on the sea-level, and the inner masses (which, together with the outer masses, causes the deviation of the geoid from the ellipsoid) to be compensated in the sea-level by a disturbing stratum (which, according to Gauss, is possible), and if these masses of both kinds correspond at the point N to a stratum of thickness D and density δ, then, according to Helmert (Geod. ii. 260) we have approximately
| Δg = | 3 | · | g | ( | δD | − N). |
| 2 | R | ρ |
Since N slowly varies empirically, it follows that in restricted regions (of a few 100 km. in diameter) Δg is a measure of the variation of D. By applying the reduction of Bouguer to g, D is diminished by H and only gives the thickness of the ideal disturbing mass which corresponds to the perturbations due to subterranean masses. Δg has positive values on coasts, small islands, and high and medium mountain chains, and occasionally in plains; while in valleys and at the foot of mountain ranges it is negative (up to 0.2 cm.). We conclude from this that the masses of smaller density existing under high mountain chains lie not only vertically underneath but also spread out sideways.
The European Arc of Parallel in 52° Lat.
Many measurements of degrees of longitudes along central parallels in Europe were projected and partly carried out as early as the first half of the 19th century; these, however, only became of importance after the introduction of the electric telegraph, through which calculations of astronomical longitudes obtained a much higher degree of accuracy. Of the greatest moment is the measurement near the parallel of 52° lat., which extended from Valentia in Ireland to Orsk in the southern Ural mountains over 69° long, (about 6750 km.). F.G.W. Struve, who is to be regarded as the father of the Russo-Scandinavian latitude-degree measurements, was the originator of this investigation. Having made the requisite arrangements with the 810 governments in 1857, he transferred them to his son Otto, who, in 1860, secured the co-operation of England. A new connexion of England with the continent, via the English Channel, was accomplished in the next two years; whereas the requisite triangulations in Prussia and Russia extended over several decennaries. The number of longitude stations originally arranged for was 15; and the determinations of the differences in longitude were uniformly commenced by the Russian observers E.I. von Forsch, J.I. Zylinski, B. Tiele and others; Feaghmain (Valentia) being reserved for English observers. With the concluding calculation of these operations, newer determinations of differences of longitudes were also applicable, by which the number of stations was brought up to 29. Since local deflections of the plumb-line were suspected at Feaghmain, the most westerly station, the longitude (with respect to Greenwich) of the trigonometrical station Killorglin at the head of Dingle Bay was shortly afterwards determined.
The results (1891-1894) are given in volumes xlvii. and l. of the memoirs (Zapiski) of the military topographical division of the Russian general staff, volume li. contains a reconnexion of Orsk. The observations made west of Warsaw are detailed in the Die europ. Längengradmessung in 52° Br., i. and ii., 1893, 1896, published by the Kgl. Preuss. Geod. Inst.
The following figures are quoted from Helmert’s report “Die Grösse der Erde” (Sitzb. d. Berl. Akad. d. Wiss., 1906, p. 535):—
Easterly Deviation of the Astronomical Zenith.
| Name. | Longitude. | ||
| ° | ′ | ″ | |
| Feaghmain | −10 | 21 | −3.3 |
| Killorglin | −9 | 47 | +2.8 |
| Haverfordwest | −4 | 58 | +1.6 |
| Greenwich | 0 | 0 | +1.5 |
| Rosendaël-Nieuport | +2 | 35 | −1.7 |
| Bonn | +7 | 6 | −4.4 |
| Göttingen | +9 | 57 | −2.4 |
| Brocken | +10 | 37 | +2.3 |
| Leipzig | +12 | 23 | +2.7 |
| Rauenberg-Berlin | +13 | 23 | +1.7 |
| Grossenhain | +13 | 33 | −2.9 |
| Schneekoppe | +15 | 45 | +0.1 |
| Springberg | +16 | 37 | +0.8 |
| Breslau-Rosenthal | +17 | 2 | +3.5 |
| Trockenberg | +18 | 53 | −0.5 |
| Schönsee | +18 | 54 | −2.9 |
| Mirov | +19 | 18 | +2.2 |
| Warsaw | +21 | 2 | +1.9 |
| Grodno | +23 | 50 | −2.8 |
| Bobruisk | +29 | 14 | +0.5 |
| Orel | +36 | 4 | +4.4 |
| Lipetsk | +39 | 36 | +0.2 |
| Saratov | +46 | 3 | +6.4 |
| Samara | +50 | 5 | −2.6 |
| Orenburg | +55 | 7 | +1.7 |
| Orsk | +58 | 34 | −8.0 |
These deviations of the plumb-line correspond to an ellipsoid having an equatorial radius (a) of nearly 6,378,000 metres (prob. error ± 70 metres) and an ellipticity 1/299.15. The latter was taken for granted; it is nearly equal to the result from the gravity-measurements; the value for a then gives Ση² a minimum (nearly). The astronomical values of the geographical longitudes (with regard to Greenwich) are assumed, according to the compensation of longitude differences carried out by van de Sande Bakhuyzen (Comp. rend, des séances de la commission permanente de l’Association Géod. Internationale à Genève, 1893, annexe A.I.). Recent determinations (Albrecht, Astr. Nach., 3993/4) have introduced only small alterations in the deviations, a being slightly increased.
Of considerable importance in the investigation of the great arc was the representation of the linear lengths found in different countries, in terms of the same unit. The necessity for this had previously occurred in the computation of the figure of the earth from latitude-degree-measurements. A.R. Clarke instituted an extensive series of comparisons at Southampton (see Comparisons of Standards of Length of England, France, Belgium, Prussia, Russia, India and Australia, made at the Ordnance Survey Office, Southampton, 1866, and a paper in the Philosophical Transactions for 1873, by Lieut.-Col. A.R. Clarke, C.B., R.E., on the further comparisons of the standards of Austria, Spain, the United States, Cape of Good Hope and Russia) and found that 1 toise = 6.39453348 ft., 1 metre = 3.28086933 ft.
In 1875 a number of European states concluded the metre
convention, and in 1877 an international weights-and-measures
bureau was established at Breteuil. Until this time the
metre was determined by the end-surfaces of a platinum rod
(mètre des archives); subsequently, rods of platinum-iridium,
of cross-section  , were constructed, having engraved lines at
both ends of the bridge, which determine the distance of a metre.
There were thirty of the rods which gave as accurately as possible
the length of the metre; and these were distributed among the
different states (see Weights and Measures). Careful comparisons
with several standard toises showed that the metre was
not exactly equal to 443,296 lines of the toise, but, in round numbers,
1/75000 of the length smaller. The metre according to the
older relation is called the “legal metre,” according to the new
relation the “international metre.” The values are (see Europ.
Längengradmessung, i. p. 230):—
, were constructed, having engraved lines at
both ends of the bridge, which determine the distance of a metre.
There were thirty of the rods which gave as accurately as possible
the length of the metre; and these were distributed among the
different states (see Weights and Measures). Careful comparisons
with several standard toises showed that the metre was
not exactly equal to 443,296 lines of the toise, but, in round numbers,
1/75000 of the length smaller. The metre according to the
older relation is called the “legal metre,” according to the new
relation the “international metre.” The values are (see Europ.
Längengradmessung, i. p. 230):—
Legal metre = 3.28086933 ft., International metre = 3.2808257 ft.
The values of a given above are in terms of the international metre; the earlier ones in legal metres, while the gravity formulae are in international metres.
The International Geodetic Association (Internationale Erdmessung).
On the proposition of the Prussian lieutenant-general, Johann Jacob Baeyer, a conference of delegates of several European states met at Berlin in 1862 to discuss the question of a “Central European degree-measurement.” The first general conference took place at Berlin two years later; shortly afterwards other countries joined the movement, which was then named “The European degree-measurement.” From 1866 till 1886 Prussia had borne the expense incident to the central bureau at Berlin; but when in 1886 the operations received further extension and the title was altered to “The International Earth-measurement” or “International Geodetic Association,” the co-operating states made financial contributions to this purpose. The central bureau is affiliated with the Prussian Geodetic Institute, which, since 1892, has been situated on the Telegraphenberg near Potsdam. After Baeyer’s death Prof. Friedrich Robert Helmert was appointed director. The funds are devoted to the advancement of such scientific works as concern all countries and deal with geodetic problems of a general or universal nature. During the period 1897-1906 the following twenty-one countries belonged to the association:—Austria, Belgium, Denmark, England, France, Germany, Greece, Holland, Hungary, Italy, Japan, Mexico, Norway, Portugal, Rumania, Russia, Servia, Spain, Sweden, Switzerland and the United States of America. At the present time general conferences take place every three years.10
Baeyer projected the investigation of the curvature of the meridians and the parallels of the mathematical surface of the earth stretching from Christiania to Palermo for 12 degrees of longitude; he sought to co-ordinate and complete the network of triangles in the countries through which these meridians passed, and to represent his results by a common unit of length. This proposition has been carried out, and extended over the greater part of Europe; as a matter of fact, the network has, with trifling gaps, been carried over the whole of western and central Europe, and, by some chains of triangles, over European Russia. Through the co-operation of France, the network has been extended into north Africa as far as the geographical latitude of 32°; in Greece a network, united with those of Italy and Bosnia, has been carried out by the Austrian colonel, Heinrich Hartl; Servia has projected similar triangulations; Rumania has begun to make the triangle measurements, and three base 811 lines have been measured by French officers with Brunner’s apparatus. At present, in Rumania, there is being worked a connexion between the arc of parallel in lat. 47°/48° in Russia (stretching from Astrakan to Kishinev) with Austria-Hungary. In the latter country and in south Bavaria the connecting triangles for this parallel have been recently revised, as well as the French chain on the Paris parallel, which has been connected with the German net by the co-operation of German and French geodesists. This will give a long arc of parallel, really projected in the first half of the 19th century. The calculation of the Russian section gives, with an assumed ellipticity of 1/299.15, the value a = 6377350 metres; this is rather uncertain, since the arc embraces only 19° in longitude.
We may here recall that in France geodetic studies have recovered their former expansion under the vigorous impulse of Colonel (afterwards General) François Perrier. When occupied with the triangulation of Algeria, Colonel Perrier had conceived the possibility of the geodetic junction of Algeria to Spain, over the Mediterranean; therefore the French meridian line, which was already connected with England, and was thus produced to the 60th parallel, could further be linked to the Spanish triangulation, cross thence into Algeria and extend to the Sahara, so as to form an arc of about 30° in length. But it then became urgent to proceed to a new measurement of the French arc, between Dunkirk and Perpignan. In 1869 Perrier was authorized to undertake that revision. He devoted himself to that work till the end of his career, closed by premature death in February 1888, at the very moment when the Dépôt de la guerre had just been transformed into the Geographical Service of the Army, of which General F. Perrier was the first director. His work was continued by his assistant, Colonel (afterwards General) J.A.L. Bassot. The operations concerning the revision of the French arc were completed only in 1896. Meanwhile the French geodesists had accomplished the junction of Algeria to Spain, with the help of the geodesists of the Madrid Institute under General Carlos Ibañez (1879), and measured the meridian line between Algiers and El Aghuat (1881). They have since been busy in prolonging the meridians of El Aghuat and Biskra, so as to converge towards Wargla, through Ghardaïa and Tuggurt. The fundamental co-ordinates of the Panthéon have also been obtained anew, by connecting the Panthéon and the Paris Observatory with the five stations of Bry-sur-Marne, Morlu, Mont Valérien, Chatillon and Montsouris, where the observations of latitude and azimuth have been effected.11
According to the calculations made at the central bureau of the international association on the great meridian arc extending from the Shetland Islands, through Great Britain, France and Spain to El Aghuat in Algeria, a = 6377935 metres, the ellipticity being assumed as 1/299.15. The following table gives the difference: astronomical-geodetic latitude. The net does not follow the meridian exactly, but deviates both to the west and to the east; actually, the meridian of Greenwich is nearer the mean than that of Paris (Helmert, Grösse d. Erde).
West Europe-Africa Meridian-arc.12
| Name. | Latitude. | A.-G. | |
| ° | ′ | ″ | |
| Saxavord | 60 | 49.6 | −4.0 |
| Balta | 60 | 45.0 | −6.1 |
| Ben Hutig | 58 | 33.1 | +0.3 |
| Cowhythe | 57 | 41.1 | +7.3 |
| Great Stirling | 57 | 27.8 | −2.3 |
| Kellie Law | 56 | 14.9 | −3.7 |
| Calton Hill | 55 | 57.4 | +3.5 |
| Durham | 54 | 46.1 | −0.9 |
| Burleigh Moor | 54 | 34.3 | +2.1 |
| Clifton Beacon | 53 | 27.5 | +1.3 |
| Arbury Hill | 52 | 13.4 | −3.0 |
| Greenwich | 51 | 28.6 | −2.5 |
| Nieuport | 51 | 7.8 | −0.4 |
| Rosendaël | 51 | 2.7 | −0.9 |
| Lihons | 49 | 49.9 | +0.5 |
| Panthéon | 48 | 50.8 | −0.0 |
| Chevry | 48 | 0.5 | +2.2 |
| Saligny le Vif | 47 | 2.7 | +3.0 |
| Arpheuille | 46 | 13.7 | +6.3 |
| Puy de Dôme | 45 | 46.5 | +7.0 |
| Rodez | 44 | 21.4 | +1.7 |
| Carcassonne | 43 | 13.3 | +0.7 |
| Rivesaltes | 42 | 45.2 | −0.7 |
| Montolar | 41 | 38.5 | +3.6 |
| Lérida | 41 | 37.0 | −0.2 |
| Javalon | 40 | 13.8 | −0.2 |
| Desierto | 40 | 5.0 | −4.5 |
| Chinchilla | 38 | 55.2 | +2.2 |
| Mola de Formentera | 38 | 39.9 | −1.2 |
| Tetíca | 37 | 15.2 | +3.5 |
| Roldan | 36 | 56.6 | −6.0 |
| Conjuros | 36 | 44.4 | −12.6 |
| Mt. Sabiha | 35 | 39.6 | +6.5 |
| Nemours | 35 | 5.8 | +7.4 |
| Bouzaréah | 36 | 48.0 | +2.9 |
| Algiers (Voirol) | 36 | 45.1 | −9.1 |
| Guelt ès Stel | 35 | 7.8 | −1.0 |
| El Aghuat | 33 | 48.0 | −2.8 |
 |
While the radius of curvature of this arc is obviously not uniform (being, in the mean, about 600 metres greater in the northern than in the southern part), the Russo-Scandinavian meridian arc (from 45° to 70°), on the other hand, is very uniformly curved, and gives, with an ellipticity of 1/299.15, a = 6378455 metres; this arc gives the plausible value 1/298.6 for the ellipticity. But in the case of this arc the orographical circumstances are more favourable.
The west-European and the Russo-Scandinavian meridians indicate another anomaly of the geoid. They were connected at the Central Bureau by means of east-to-west triangle chains (principally by the arc of parallel measurements in lat. 52°); it was shown that, if one proceeds from the west-European meridian arcs, the differences between the astronomical and geodetic latitudes of the Russo-Scandinavian arc become some 4″ greater.13
The central European meridian, which passes through Germany and the countries adjacent on the north and south, is under review at Potsdam (see the publications of the Kgl. Preuss. Geod. Inst., Lotabweichungen, Nos. 1-3). Particular notice must be made of the Vienna meridian, now carried southwards to Malta. The Italian triangulation is now complete, and has been joined with the neighbouring countries on the north, and with Tunis on the south.
The United States Coast and Geodetic Survey has published an account of the transcontinental triangulation and measurement of an arc of the parallel of 39°, which extends from Cape May (New Jersey), on the Atlantic coast, to Point Arena (California), on the Pacific coast, and embraces 48° 46′ of longitude, with a linear development of about 4225 km. (2625 miles). The triangulation depends upon ten base-lines, with an aggregate length of 86 km. the longest exceeding 17 km. in length, which have been measured with the utmost care. In crossing the Rocky Mountains, many of its sides exceed 100 miles in length, and there is one side reaching to a length of 294 km., or 183 miles; the altitude of many of the stations is also considerable, reaching to 4300 metres, or 14,108 ft., in the case of Pike’s Peak, and to 14,421 ft. at Elbert Peak, Colo. All geometrical conditions subsisting in the triangulation are satisfied by adjustment, inclusive of the required accord of the base-lines, so that the same length for any given line is found, no matter from what line one may start.14
Over or near the arc were distributed 109 latitude stations, occupied with zenith telescopes; 73 azimuth stations; and 29 telegraphically determined longitudes. It has thus been possible to study in a very complete manner the deviations of the vertical, which in the mountainous regions sometimes amount to 25 seconds, and even to 29 seconds.
With the ellipticity 1/299.15, a = 6377897 ± 65 metres (prob. error); in this calculation, however, some exceedingly perturbed stations are excluded; for the employed stations the mean perturbation in longitude is ± 4.9″ (zenith-deflection east-to-west ± 3.8″).
The computations relative to another arc, the “eastern oblique arc of the United States,” are also finished.15 It extends from Calais (Maine) in the north-east, to the Gulf of Mexico, and terminates at New Orleans (Louisiana), in the south. Its length is 2612 km. (1623 miles), the difference of latitude 15° 1′, and of longitude 22° 47′. In the main, the triangulation follows the Appalachian chain of mountains, bifurcating once, so as to leave an oval space between the two branches. It includes among its stations Mount Washington (1920 metres) and Mount Mitchell (2038 metres). It depends upon six base-lines, and the adjustment is effected in the same manner as for the arc of the parallel. The astronomical data have been afforded by 71 latitude stations, 17 longitude stations, and 56 azimuth stations, distributed over the whole extent of the arc. The resulting dimensions of an osculating spheroid were found to be
a = 6378157 metres ± 90 (prob. error),
e (ellipticity) = 1/304.5 ± 1.9 (prob. error).
With the ellipticity 1/399.15, a = 6378041 metres ± 80 (prob. er.).
During the years 1903-1906 the United States Coast and Geodetic Survey, under the direction of O.H. Tittmann and the special management of John F. Hayford, executed a calculation of the best ellipsoid of rotation for the United States. There were 507 astronomical determinations employed, all the stations being connected through the net-work of triangles. The observed latitudes, longitude and azimuths were improved by the attractions of the earth’s crust on the hypothesis of isostasis for three depths of the surface of 114, 121 and 162 km., where the isostasis is complete. The land-masses, within the distance of 4126 km., were taken into consideration. In the derivation of an ellipsoid of rotation, the first case proved itself the most favourable, and there resulted:—
a = 6378283 metres ± 74 (prob. er.), ellipticity = 1/297.8 ± 0.9 (prob. er.).
The most favourable value for the depth of the isostatic surface is approximately 114 km.
The measurement of a great meridian arc, in long. 98° W., has been commenced; it has a range of latitude of 23°, and will extend over 50° when produced southwards and northwards by Mexico and Canada. It may afterwards be connected with the arc of Quito. A new measurement of the meridian arc of Quito was executed in the years 1901-1906 by the Service géographique of France under the direction of the Académie des Sciences, the ground having been previously reconnoitred in 1899. The new arc has an amplitude in latitude of 5° 53′ 33″, and stretches from Tulcan (lat. 0° 48′ 25″) on the borders of Columbia and Ecuador, through Columbia to Payta (lat. − 5° 5′ 8″) in Peru. The end-points, at which the chain of triangles has a slight north-easterly trend, show a longitude difference of 3°. Of the 74 triangle points, 64 were latitude stations; 6 azimuths and 8 longitude-differences were measured, three base-lines were laid down, and gravity was determined from six points, in order to maintain indications over the general deformation of the geoid in that region. Computations of the attraction of the mountains on the plumb-line are also being considered. The work has been much delayed by the hardships and difficulties encountered. It was conducted by Lieut.-Colonel Robert Bourgeois, assisted by eleven officers and twenty-four soldiers of the geodetic branch of the Service géographique. Of these officers mention may be made of Commandant E. Maurain, who retired in 1904 after suffering great hardships; Commandant L. Massenet, who died in 1905; and Captains I. Lacombe, A. Lallemand, and Lieut. Georges Perrier (son of General Perrier). It is conceivable that the chain of triangles in longitude 98° in North America may be united with that of Ecuador and Peru: a continuous chain over the whole of America is certainly but a question of time. During the years 1899-1902 the measurement of an arc of meridian was made in the extreme north, in Spitzbergen, between the latitudes 76° 38′ and 80° 50′, according to the project of P.G. Rosén. The southern part was determined by the Russians—O. Bäcklund, Captain D.D. Sergieffsky, F.N. Tschernychev, A. Hansky and others—during 1899-1901, with the aid of 1 base-line, 15 trigonometrical, 11 latitude and 5 gravity stations. The northern part, which has one side in common with the southern part, has been determined by Swedes (Professors Rosén, father and son, E. Jäderin, T. Rubin and others), who utilized 1 base-line, 9 azimuth measurements, 18 trigonometrical, 17 latitude and 5 gravity stations. The party worked under excessive difficulties, which were accentuated by the arctic climate. Consequently, in the first year, little headway was made.16
Sir David Gill, when director of the Royal Observatory, Cape Town, instituted the magnificent project of working a latitude-degree measurement along the meridian of 30° long. This meridian passes through Natal, the Transvaal, by Lake Tanganyika, and from thence to Cairo; connexion with the Russo-Scandinavian meridian arc of the same longitude should be made through Asia Minor, Turkey, Bulgaria and Rumania. With the completion of this project a continuous arc of 105° in latitude will have been measured.17
Extensive triangle chains, suitable for latitude-degree measurements, have also been effected in Japan and Australia.
Besides, the systematization of gravity measurements is of importance, and for this purpose the association has instituted many reforms. It has ensured that the relative measurements made at the stations in different countries should be reduced conformably with the absolute determinations made at Potsdam; the result was that, in 1906, the intensities of gravitation at some 2000 stations had been co-ordinated. The intensity of gravity on the sea has been determined by the comparison of barometric and hypsometric observations (Mohn’s method). The association, at the proposal of Helmert, provided the necessary funds for two expeditions:—English Channel—Rio de Janeiro, and the Red Sea—Australia—San Francisco—Japan. Dr O. Hecker of the central bureau was in charge; he successfully overcame the difficulties of the work, and established the tenability of the isostatic hypothesis, which necessitates that the intensity of gravity on the deep seas has, in general, the same value as on the continents (without regard to the proximity of coasts).18
As the result of the more recent determinations, the ellipticity, compression or flattening of the ellipsoid of the earth may be assumed to be very nearly 1/298.3; a value determined in 1901 by Helmert from the measurements of gravity. The semi-major axis, a, of the meridian ellipse may exceed 6,378,000 inter. metres by about 200 metres. The central bureau have adopted, for practical reasons, the value 1/299.15, after Bessel, for which tables exist; and also the value a = 6377397.155 (1 + 0.0001).
The methods of theoretical astronomy also permit the evaluation of these constants. The semi-axis a is calculable from the parallax of the moon and the acceleration of gravity on the earth; but the results are somewhat uncertain: the ellipticity deduced from lunar perturbations is 1/297.8 ± 2 (Helmert, Geodäsie, ii. pp. 460-473); William Harkness (The Solar Parallax and its related Constants, 1891) from all possible data derived the values: ellipticity = 1/300.2 ± 3, a = 6377972 ± 125 metres. Harkness also considered in this investigation the relation of the ellipticity to precession and nutation; newer investigations of the latter lead to the limiting values 1/296, 1/298 (Wiechert). It was clearly noticed in this method of determination that the influence of the assumption as to the density of the strata in the interior of the earth was but very slight (Radau, Bull. astr. ii. (1885) 157). The deviations of the geoid from the flattened ellipsoid of rotation with regard to the heights (the directions of normals being nearly the same) will scarcely exceed ± 100 metres (Helmert).19
The basis of the degree- and gravity-measurements is actually formed by a stationary sea-surface, which is assumed to be level. However, by the influence of winds and ocean currents the mean surface of the sea near the coasts (which one assumes as the fundamental sea-surface) can deviate somewhat from a level surface. According to the more recent levelling it varies at the most by only some decimeters.20
It is well known that the masses of the earth are continually undergoing small changes; the earth’s crust and sea-surface reciprocally oscillate, and the axis of rotation vibrates relatively to the body of the earth. The investigation of these problems falls in the programme of the Association. By continued observations of the water-level on sea-coasts, results have already been obtained as to the relative motions of the land and sea (cf. Geology); more exact levelling will, in the course of time, provide observations on countries remote from the sea-coast. Since 1900 an international service has been organized between some astronomical stations distributed over the north parallel of 39° 8′, at which geographical latitudes are observed whenever possible. The association contributes to all these stations, supporting four entirely: two in America, one in Italy, and one in Japan; the others partially (Tschardjui in Russia, and Cincinnati observatory). Some observatories, especially Pulkowa, Leiden and Tokyo, take part voluntarily. Since 1906 another station for South America and one for Australia in latitude − 31° 55′ have been added. According to the existing data, geographical latitudes exhibit variations amounting to ± 0.25″, which, for the greater part, proceed from a twelve- and a fourteen-month period.21
1 Eratosthenes Batavus, seu de terrae ambitus vera quantitate suscitatus, a Willebrordo Snellio, Lugduni-Batavorum (1617).
2 O. Callandreau, “Mémoire sur la théorie de la figure des planètes,” Ann. obs. de Paris (1889); G.H. Darwin, “The Theory of the Figure of the Earth carried to the Second Order of Small Quantities,” Mon. Not. R.A.S., 1899; E. Wiechert, “Über die Massenverteilung im Innern der Erde,” Nach. d. kön. G. d. W. zu Gött., 1897.
3 See I. Todhunter, Proc. Roy. Soc., 1870.
4 J.H. Jeans, “On the Vibrations and Stability of a Gravitating Planet,” Proc. Roy. Soc. vol. 71; G.H. Darwin, “On the Figure and Stability of a liquid Satellite,” Phil. Trans. 206, p. 161; A.E.H. Love, “The Gravitational Stability of the Earth,” Phil. Trans. 207, p. 237; Proc. Roy. Soc. vol. 80.
5 Survey of India, “The Attraction of the Himalaya Mountains upon the Plumb Line in India” (1901), p. 98.
6 Account of Experiments to Determine the Figure of the Earth by means of a Pendulum vibrating Seconds in Different Latitudes (1825).
7 Helmert, Theorien d. höheren Geod. ii., Leipzig, 1884.
8 Helmert, Sitzber. d. kgl. preuss. Ak. d. Wiss. zu Berlin (1901), p. 336.
9 “Bestimmung der absoluten Grösse der Schwerkraft zu Potsdam mit Reversionspendeln” (Veröffentlichung des kgl. preuss. Geod. Inst., N.F., No. 27).
10 Die Königl. Observatorien für Astrophysik, Meteorologie und Geodäsie bei Potsdam (Berlin, 1890); Verhandlungen der I. Allgemeinen Conferenz der Bevollmächtigten zur mitteleurop. Gradmessung, October, 1864, in Berlin (Berlin, 1865); A. Hirsch, Verhandlungen der VIII. Allg. Conf. der Internationalen Erdmessung, October, 1886, in Berlin (Berlin, 1887); and Verhandlungen der XI. Allg. Conf. d. I. E., October, 1895, in Berlin (1896).
11 Ibañez and Perrier, Jonction géod. et astr. de l’Algérie avec l’Espagne (Paris, 1886); Mémorial du dépôt général de la guerre, t. xii.: Nouvelle méridienne de France (Paris, 1885, 1902, 1904); Comptes rendus des séances de la 12e-19e conférence générale de l’Assoc. Géod. Internat., 1898 at Stuttgart, 1900 at Paris, 1903 at Copenhagen, 1906 at Budapest (Berlin, 1899, 1901, 1904, 1908); A. Ferrero, Rapport sur les triangulations, prés. à la 12e conf. gén. 1898.
12 R. Schumann, C. r. de Budapest, p. 244.
13 O. and A. Börsch, “Verbindung d. russ.-skandinav. mit der franz.-engl. Breitengradmessung” (Verhandlungen der 9. Allgem. Conf. d. I. E. in Paris, 1889, Ann. xi.).
14 U.S. Coast and Geodetic Survey; H.S. Pritchett, superintendent. The Transcontinental Triangulation and the American Arc of the Parallel, by C.A. Schott (Washington, 1900).
15 U.S. Coast and Geodetic Survey; O.H. Tittmann, superintendent. The Eastern Oblique Arc of the United States, by C.A. Schott (1902).
16 Missions scientifiques pour la mesure d’un arc de méridien au Spitzberg entreprises en 1899-1902 sous les auspices des gouvernements russe et suédois. Mission russe (St Pétersbourg, 1904); Mission suédoise (Stockholm, 1904).
17 Sir David Gill, Report on the Geodetic Survey of South Africa, 1833-1892 (Cape Town, 1896), vol. ii. 1901, vol. iii. 1905.
18 O. Hecker, Bestimmung der Schwerkraft a. d. Atlantischen Ozean (Veröffentl. d. Kgl. Preuss. Geod. Inst. No. 11), Berlin, 1903.
19 F.R. Helmert. “Neuere Fortschritte in der Erkenntnis der math. Erdgestalt” (Verhandl. des VII. Internationalen Geographen-Kongresses, Berlin, 1899), London, 1901.
20 C. Lallemand, “Rapport sur les travaux du service du nivellement général de la France, de 1900 à 1906″ (Comp. rend. de la 14e conf. gén. de l’Assoc. Géod-Intern., 1903, p. 178).
21 T. Albrecht, Resultate des internat. Breitendienstes, i. and ii. (Berlin, 1903 and 1906); F. Klein and A. Sommerfeld, Über die Theorie des Kreisels, iii. p. 672; R. Spitaler, “Die periodischen Luftmassenverschiebungen und ihr Einfluss auf die Lagenänderung der Erdaxe” (Petermanns Mitteilungen, Ergänzungsheft, 137); S. Newcomb, “Statement of the Theoretical Laws of the Polar Motion” (Astronomical Journal, 1898, xix. 158); F.R. Helmert, “Zur Erklärung der beobachteten Breitenänderungen” (Astr. Nachr. No. 3014); J. Weeder, “The 14-monthly period of the motion of the Pole from determinations of the azimuth of the meridian marks of the Leiden observatory” (Kon. Ak. van Wetenschappen to Amsterdam, 1900); A. Sokolof, “Détermination du mouvement du pôle terr. au moyen des mires méridiennes de Poulkovo” (Mél. math. et astr. vii., 1894); J. Bonsdorff, “Beobachtungen von δ Cassiopejae mit dem grossen Zenitteleskop” (Mitteilungen der Nikolai-Hauptsternwarte zu Pulkowo, 1907); J. Larmor and E.H. Hills, “The irregular movement of the Earth’s axis of rotation: a contribution towards the analysis of its causes” (Monthly Notices R.A.S., 1906, lxvii. 22); A.S. Cristie, “The latitude variation Tide” (Phil. Soc. of Wash., 1895, Bull. xiii. 103); H.G. van de Sande Bakhuysen, “Über die Änderung der Polhöhe” (Astr. Nachr. No. 3261); A.V. Bäcklund, “Zur Frage nach der Bewegung des Erdpoles” (Astr. Nachr. No. 3787); R. Schumann, “Über die Polhöhenschwankung” (Astr. Nachr. No. 3873); “Numerische Untersuchung” (Ergänzungshefte zu den Astr. Nachr. No. 11); Weitere Untersuchungen (No. 4142); Bull. astr., 1900, June, report of different theoretical memoirs.
EARTH CURRENTS. After the invention of telegraphy it was soon found that telegraph lines in which the circuit is completed by the earth are traversed by natural electric currents which occasionally interfere seriously with their use, and which are known as “earth currents.”
1. Amongst the pioneers in investigating the subject were several English telegraphists, e.g. W.H. Barlow (1) and C.V. Walker (2), who were in charge respectively of the Midland and South-Eastern telegraph systems. Barlow noticed the existence of a more or less regular diurnal variation, and the result—confirmed by all subsequent investigators—that earth currents proper occur in a line only when both ends are earthed. Walker, as the result of general instructions issued to telegraph clerks, collected numerous statistics as to the phenomena during times of large earth currents. His results and those given by Barlow both indicate that the lines to suffer most from earth currents in England have the general direction N.E. to S.W. As Walker points out, it is the direction of the terminal plates relative to one another that is the essential thing. At the same time he noticed that whilst at any given instant the currents in parallel lines have with rare exceptions the same direction, some lines show normally stronger currents than others, and he suggested that differences in the geological structure of the intervening ground might be of importance. This is a point which seems still somewhat obscure.
Our present knowledge of the subject owes much to practical men, but even in the early days of telegraphy the fact that telegraph systems are commercial undertakings, and cannot allow 814 the public to wait the convenience of science, was a serious obstacle to their employment for research. Thus Walker feelingly says, when regretting his paucity of data during a notable earth current disturbance: “Our clerks were at their wits’ end to clear off the telegrams.... At a time when observations would have been very highly acceptable they were too much occupied with their ordinary duties.” Some valuable observations have, however, been made on long telegraph lines where special facilities have been given.
Amongst these may be mentioned the observations on French lines in 1883 described by E.E. Blavier (3), and those on two German lines Berlin-Thorn and Berlin-Dresden during 1884 to 1888 discussed by B. Weinstein (4).
2. Of the experimental lines specially constructed perhaps the best known are the Greenwich lines instituted by Sir G.B. Airy (5), the lines at Pawlowsk due to H. Wild (6), and those at Parc Saint Maur, near Paris (7).
Experimental Lines.—At Greenwich observations were commenced in 1865, but there have been serious disturbances due to artificial currents from electric railways for many years. There are two lines, one to Dartford distant about 10 m., in a direction somewhat south of east, the other to Croydon distant about 8 m., in a direction west of south.
Information from a single line is incomplete, and unless this is clearly understood erroneous ideas may be derived. The times at which the current is largest and least, or when it vanishes, in an east-west line, tell nothing directly as to the amplitude at the time of the resultant current. The lines laid down at Pawlowsk in 1883 lay nearly in and perpendicular to the geographical meridian, a distinct desideratum, but were only about 1 km. long. The installation at Parc Saint Maur, discussed by T. Moureaux, calls for fuller description. There are three lines, one having terminal earth plates 14.8 km. apart in the geographical meridian, a second having its earth plates due east and west of one another, also 14.8 km. apart, and the third forming a closed circuit wholly insulated from the ground. In each of the three lines is a Deprez d’Arsonval galvanometer. Light reflected from the galvanometer mirrors falls on photographic paper wound round a drum turned by clockwork, and a continuous record is thus obtained.
3. Each galvanometer has a resistance of about 200 ohms, but is shunted by a resistance of only 2 ohms. The total effective resistances in the N.-S. and E.-W. lines are 225 and 348 ohms respectively. If i is the current recorded, L, g and s the resistances of the line, galvanometer and shunt respectively, then E, the difference of potential between the two earth plates, is given by
E = i (1 + g/s) {L + gs / (g + s)}.
To calibrate the record, a Daniell cell is put in a circuit including 1000 ohms and the three galvanometers as shunted. If i′ be the current recorded, e the E.M.F. of the cell, then e = i′ (1 + g/s) {1000 + 3gs / (g + s)}. Under the conditions at Parc Saint Maur we may write 2 for gs / (g + s), and 1.072 for e, and thence we have approximately E = 0.240 (i / i′) for the N.-S. line, and E = −0.371(i / i′) for the E.-W. line.
The method of standardization assumes a potential difference between earth plates which varies slowly enough to produce a practically steady current. There are several causes producing currents in a telegraph wire which do not satisfy this limitation. During thunderstorms surgings may arise, at least in overhead wires, without these being actually struck. Again, if the circuit includes a variable magnetic field, electric currents will be produced independently of any direct source of potential difference. In the third circuit at Parc Saint Maur, where no earth plates exist, the current must be mainly due to changes in the earth’s vertical magnetic field, with superposed disturbances due to atmospheric electricity or aerial waves. Even in the other circuits, magnetic and atmospheric influences play some part, and when their contribution is important, the galvanometer deflection has an uncertain value. What a galvanometer records when traversed by a suddenly varying current depends on other things than its mere resistance.
Even when the current is fairly steady, its exact significance is not easily stated. In the first place there is usually an appreciable E.M.F. between a plate and the earth in contact with it, and this E.M.F. may vary with the temperature and the dryness of the soil. Naturally one employs similar plates buried to the same depth at the two ends, but absolute identity and invariability of conditions can hardly be secured. In some cases, in short lines (8), there is reason to fear that plate E.M.F.’s have been responsible for a good deal that has been ascribed to true earth currents. With deep earth plates, in dry ground, this source of uncertainty can, however, enter but little into the diurnal inequality.
4. Another difficulty is the question of the resistance in the earth itself. A given E.M.F. between plates 10 m. apart may mean very different currents travelling through the earth, according to the chemical constitution and condition of the surface strata.
According to Professor A. Schuster (9), if ρ and ρ’ be the specific resistances of the material of the wire and of the soil, the current i which would pass along an underground cable formed of actual soil, equal in diameter to the wire connecting the plates, is given by i = i′ρ / ρ′, where i′ is the observed current in the wire. As ρ’ will vary with the depth, and be different at different places along the route, while discontinuities may arise from geological faults, water channels and so on, it is clear that even the most careful observations convey but a general idea as to the absolute intensity of the currents in the earth itself. In Schuster’s formula, as in the formulae deduced for Parc Saint Maur, it is regarded as immaterial whether the wire connecting the plates is above or below ground. This view is in accordance with records obtained by Blavier (3) from two lines between Paris and Nancy, the one an air line, the other underground.
5. The earliest quantitative results for the regular diurnal changes in earth currents are probably those deduced by Airy (5) from the records at Greenwich between 1865 and 1867. Airy resolved the observed currents from the two Greenwich lines in and perpendicular to the magnetic meridian (then about 21° to the west of astronomical north). The information given by Airy as to the precise meaning of the quantities he terms “magnetic tendency” to north and to west is somewhat scanty, but we are unlikely to be much wrong in accepting his figures as proportional to the earth currents from magnetic east to west and from magnetic north to south respectively. Airy gives mean hourly values for each month of the year. The corresponding mean diurnal inequality for the whole year appears in Table 1., the unit being arbitrary. In every month the algebraic mean of the 24 hourly values represented a current from north to south in the magnetic meridian, and from east to west in the perpendicular direction; in the same arbitrary units used in Table I. the mean values of these two “constant” currents were respectively 777 and 559.
6. Diurnal Variation.—Probably the most complete records of diurnal variation are those discussed by Weinstein (4), which depend on several years’ records on lines from Berlin to Dresden and to Thorn. Relative to Berlin the geographical co-ordinates of the other two places are:
| Thorn | 0° 29′ N. lat. 5° 12′ E. long. |
| Dresden | 1° 28′ S. lat. 0° 21′ E. long. |
Thus the Berlin-Dresden line was directed about 8½° east of south, and the Berlin-Thorn line somewhat more to the north of east. The latter line had a length about 2.18 times that of the former. The resistances in the two lines were made the same, so if we suppose the difference of potential between earth plates along a given direction to vary as their distance apart, the current observed in the Thorn-Berlin line has to be divided by 2.18 to be comparable with the other. In this way, resolving along and perpendicular to the geographical meridian, Weinstein gives as proportional to the earth currents from east to west and from south to north respectively
J = 0.147i′ + 0.435i, and J′ = 0.989i′ − 0.100i,
where i and i’ are the observed currents in the Thorn-Berlin and Dresden-Berlin lines respectively, both being counted positive when flowing towards Berlin.
It is tacitly assumed that the average earth conductivity is the same between Berlin and Thorn as between Berlin and Dresden. It should also be noticed that local time at Berlin and Thorn differs by fully 20 minutes, while the crests of the diurnal variations in short lines at the two places would probably occur about the same local time. The result is probably a less sharp occurrence of maxima and minima, and a relatively smaller range, than in a short line having the same orientation.
Table I.
| Mean Diurnal Inequalities for the year. | Numerical Values of resultant current. | |||||||||
| Greenwich. | Thorn-Berlin-Dresden. | Thorn-Berlin-Dresden. | ||||||||
| Hour. | North to South (Mag.) | East to West (Mag.) |
Berlin to Dresden. | Thorn to Berlin. |
North to South (Ast.) | East to West (Ast.) |
Mean hourly values from | |||
| Year. | Winter. | Equinox. | Summer. | |||||||
| 1 | −94 | −41 | −17 | −13 | −20 | −10 | 81 | 94 | 51 | 98 |
| 2 | −68 | −24 | −6 | −13 | −9 | −11 | 84 | 115 | 39 | 97 |
| 3 | −44 | −8 | −1 | −1 | −1 | −1 | 84 | 113 | 31 | 108 |
| 4 | −18 | +9 | −20 | +15 | −17 | +17 | 101 | 94 | 58 | 127 |
| 5 | −30 | −1 | −79 | +21 | −74 | +32 | 122 | 58 | 78 | 230 |
| 6 | −63 | −33 | −139 | +5 | −136 | +26 | 148 | 80 | 139 | 225 |
| 7 | −121 | −80 | −138 | −36 | −144 | −14 | 166 | 155 | 206 | 136 |
| 8 | −175 | −123 | −7 | −98 | −28 | −92 | 203 | 152 | 185 | 271 |
| 9 | −156 | −137 | +249 | −156 | +212 | −184 | 305 | 67 | 272 | 575 |
| 10 | −43 | −77 | +540 | −184 | +494 | −254 | 557 | 232 | 628 | 811 |
| 11 | +82 | +1 | +722 | −165 | +678 | −-263 | 728 | 411 | 885 | 887 |
| Noon | +207 | +66 | +673 | −107 | +642 | −200 | 675 | 441 | 848 | 735 |
| 1 | +245 | +94 | +404 | −20 | +395 | −79 | 400 | 284 | 510 | 406 |
| 2 | +205 | +113 | +35 | +55 | +46 | +47 | 98 | 68 | 103 | 125 |
| 3 | +153 | +97 | −261 | +99 | −237 | +132 | 272 | 136 | 355 | 324 |
| 4 | +159 | +108 | −397 | +114 | −368 | +167 | 404 | 218 | 503 | 492 |
| 5 | +167 | +118 | −391 | +108 | −363 | +160 | 397 | 206 | 453 | 532 |
| 6 | +125 | +95 | −311 | +96 | −287 | +137 | 319 | 176 | 333 | 446 |
| 7 | +43 | +55 | −237 | +85 | −216 | +115 | 247 | 180 | 250 | 312 |
| 8 | −22 | +4 | −191 | +74 | −173 | +98 | 201 | 207 | 217 | 181 |
| 9 | −115 | −49 | −168 | +59 | −153 | +81 | 174 | 208 | 194 | 120 |
| 10 | −138 | −74 | −135 | +40 | −125 | +58 | 138 | 155 | 149 | 111 |
| 11 | −136 | −70 | −84 | +18 | −79 | +29 | 89 | 64 | 95 | 107 |
| Midnight | −147 | −80 | −43 | −2 | −43 | +4 | 91 | 42 | 119 | 111 |
It was found that the average current derived from a number of undisturbed days on either line might be regarded as made up of a “constant part” plus a regular diurnal inequality, the constant part representing the algebraic mean value of the 24 hourly readings. In both lines the constant part showed a decided alteration during the third year—changing sign in one line—in consequence, it is believed, of alterations made in the earth plates. The constant part was regarded as a plate effect, and was omitted from further consideration. Table I. shows in terms of an arbitrary unit—whose relation to that employed for Greenwich data is unknown—the diurnal inequality in the currents along the two lines, and the inequalities thence calculated for ideal lines in and perpendicular to the geographical meridian. Currents are regarded as positive when directed from Berlin to Dresden and from north to south, the opposite point of view to that adopted by Weinstein. The table also shows the mean numerical value of the resultant current (the “constant” part being omitted) for each hour of the day, for the year as a whole, and for winter (November to February), equinox (March, April, September, October) and summer (May to August). There is a marked double period in both the N.-S. and E.-W. currents. In both cases the numerically largest currents occur from 10 A.M. to noon, the directions then being from north to south and from west to east. The currents tend to die out and change sign about 2 P.M., the numerical magnitude then rising again rapidly to 4 or 5 P.M. The current in the meridian is notably the larger. The numerical values assigned to the resultant current are arithmetic means from the several months composing the season in question.
7. The mean of the 24 hourly numerical values of the resultant current for each month of the year a deducible from Weinstein’s data—the unit being the same as before—are given in Table II.
Table II.—Mean Numerical Value of Resultant Current.
| Jan. | Feb. | March | April | May | June | July | Aug. | Sep. | Oct. | Nov. | Dec. |
| 152 | 211 | 293 | 328 | 313 | 314 | 337 | 300 | 258 | 235 | 165 | 132 |
There is thus a conspicuous minimum at mid-winter, and but little difference between the monthly means from April to August. This is closely analogous to what is seen in the daily range of the magnetic elements in similar latitudes (see Magnetism, Terrestrial). There is also considerable resemblance between the curve whose ordinates represent the diurnal inequality in the current passing from north to south, and the curve showing the hourly change in the westerly component of the horizontal magnetic force in similar European latitudes.
8. Relations with Sun-spots, Auroras and Magnetic Storms.—Weinstein gives curves representing the mean diurnal inequality for separate years. In both lines the diurnal amplitudes were notably smaller in the later years which were near sun-spot minimum. This raises a presumption that the regular diurnal earth currents, like the ranges of the magnetic elements, follow the 11-year sun-spot period. When we pass to the large and irregular earth currents, which are of practical interest in telegraphy, there is every reason to suppose that the sun-spot period applies. These currents are always accompanied by magnetic disturbances, and when specially striking by brilliant aurora. One most conspicuous example of this occurred in the end of August and beginning of September 1859. The magnetic disturbances recorded were of almost unexampled size and rapidity, the accompanying aurora was extraordinarily brilliant, and E.M.F.’s of 700 and 800 volts are said to have been reached on telegraph lines 500 to 600 km. long. It is doubtful whether the disturbances of 1859 have been equalled since, but earth current voltages of the order of 0.5 volts per mile have been recorded by various authorities, e.g. Sir W.H. Preece (10).
It was the practice for several years to publish in the Ann. du bureau central météorologique synchronous magnetic and earth current curves from Parc Saint Maur corresponding to the chief disturbances of the year. In most cases there is a marked similarity between the curve of magnetic declination and that of the north-south earth current. At times there is also a distinct resemblance between the horizontal force magnetic curve and that of the east-west earth current, but exceptions to this are not infrequent. Similar phenomena appear in synchronous Greenwich records published by Airy in 1868; these show a close accordance between the horizontal force curves and those of the currents from magnetic east to west. Originally it was supposed by Airy that whilst rapid movements in the declination and north-south current curves sometimes 816 occurred simultaneously, there was a distinct tendency for the latter to precede the former. More recent examinations of the Greenwich records by W. Ellis (11), and of the Parc St Maur curves by Moureaux, have not confirmed this result, and it is now believed that the two phenomena are practically simultaneous.
There has also been a conflict of views as to the connexion between magnetic and earth current disturbances. Airy’s observations tended to suggest that the earth current was the primary cause, and the magnetic disturbance in considerable part at least its effect. Others, on the contrary, have supposed earth currents to be a direct effect of changes in the earth’s magnetic field. The prevailing view now is that both the magnetic and the earth current disturbances are due to electric currents in the upper atmosphere, these upper currents becoming visible at times as aurora.
9. There seems some evidence that earth currents can be called into existence by purely local causes, notably difference of level. Thus K.A. Brander (12) has observed a current flowing constantly for a good many days from Airolo (height 1160 metres) to the Hospice St Gotthard (height 2094 metres). In an 8-km. line from Resina to the top of Vesuvius L. Palmieri (13)—observing in 1889 at three-hour intervals from 9 A.M. to 9 P.M.—always found a current running uphill so long as the mountain was quiet. On a long line from Vienna to Graz A. Baumgartner (14) found that the current generally flowed from both ends towards intervening higher ground during the day, but in the opposite directions at night. During a fortnight in September and October 1885 hourly readings were taken of the current in the telegraph cable from Fort-William to Ben Nevis Observatory, and the results were discussed by H.N. Dickson (15), who found a marked preponderance of currents up the line to the summit. The recorded mean data, otherwise regarded, represent a “constant” current, equal to 29 in the arbitrary units employed by Dickson, flowing up the line, together with the following diurnal inequality, + denoting current towards Fort-William (i.e. down the hill, and nearly east to west).
| Hour | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A.M. | −21 | −41 | +13 | +23 | +55 | −3 | +25 | −32 | −59 | −62 | −46 | +6 |
| P.M. | +24 | +18 | +115 | +18 | +75 | −5 | +50 | −9 | −56 | −37 | −28 | −34 |
There is thus a diurnal inequality, which is by no means very irregular considering the limited number of days, and it bears at least a general resemblance to that shown by Weinstein’s figures for an east-west line in Germany. This will serve to illustrate the uncertainties affecting these and analogous observations. A constant current in one direction may arise in whole or part from plate E.M.F.’s; a current showing a diurnal inequality will naturally arise between any two places some distance apart whether they be at different levels or not. Finally, when records are taken only for a short time, doubts must arise as to the generality of the results. During the Ben Nevis observations, for instance, we are told that the summit was almost constantly enveloped in fog or mist. By having three earth plates in the same vertical plane, one at the top of a mountain, the others at opposite sides of it, and then observing the currents between the summit and each of the base stations, as well as directly between the base stations—during an adequate number of days representative of different seasons of the year and different climatic conditions—many uncertainties would soon be removed.
10. Artificial Currents.—The great extension in the applications of electricity to lighting, traction and power transmission, characteristic of the end of the 19th century, has led to the existence of large artificial earth currents, which exert a disturbing influence on galvanometers and magnetic instruments, and also tend to destroy metal pipes. In the former case, whilst the disturbance is generally loosely assigned to stray or “vagabond” earth currents, this is only partly correct. The currents used for traction are large, and even if there were a perfectly insulated return there would be a considerable resultant magnetic field at distances from the track which were not largely in excess of the distance apart of the direct and return currents (16). At a distance of half a mile or more from an electric tram line the disturbance is usually largest in magnetographs recording the vertical component of the earth’s field. The magnets are slightly displaced from the position they would occupy if undisturbed, and are kept in continuous oscillation whilst the trams are running (17). The extent of the oscillation depends on the damping of the magnets.
The distance from an electric tram line where the disturbance ceases to be felt varies with the system adopted. It also depends on the length of the line and its subdivision into sections, on the strength of the currents supplied, the amount of leakage, the absence or presence of “boosters,” and finally on the sensitiveness of the magnetic instruments. At the U.S. Coast and Geodetic Survey’s observatory at Cheltenham the effect of the Washington electric trams has been detected by highly sensitive magnetographs, though the nearest point of the line is 12 m. away (18). Amongst the magnetic observatories which have suffered severely from this cause are those at Toronto, Washington (Naval Observatory), Kew, Paris (Parc St Maur), Perpignan, Nice, Lisbon, Vienna, Rome, Bombay (Colaba) and Batavia. In some cases magnetic observations have been wholly suspended, in others new observatories have been built on more remote sites.
As regards damage to underground pipes, mainly gas and water pipes, numerous observations have been made, especially in Germany and the United States. When electric tramways have uninsulated returns, and the potential of the rails is allowed to differ considerably from that of the earth, very considerable currents are found in neighbouring pipes. Under these conditions, if the joints between contiguous pipes forming a main present appreciable resistance, whilst the surrounding earth through moisture or any other cause is a fair conductor, current passes locally from the pipes to the earth causing electrolytic corrosion of the pipes. Owing to the diversity of interests concerned, the extent of the damage thus caused has been very variously estimated. In some instances it has been so considerable as to be the alleged cause of the ultimate failure of water pipes to stand the pressure they are exposed to.
Bibliography.—See Svante August Arrhenius, Lehrbuch der kosmischen Physik (Leipzig, 1903), pp. 984-990. For lists of references see J.E. Burbank, Terrestrial Magnetism, vol. 10 (1905), p. 23, and P. Bachmetjew (8). For papers descriptive of corrosion of pipes, &c., by artificial currents see Science Abstracts (in recent years in the volumes devoted to engineering) under the heading “Traction, Electric; Electrolysis.” The following are the references in the text:—(1) Phil. Trans. R.S. for 1849, pt. i. p. 61; (2) Phil. Trans. R.S. vol. 151 (1861), p. 89, and vol. 152 (1862), p. 203; (3) Étude des courants telluriques (Paris, 1884); (4) Die Erdströme im deutschen Reichstelegraphengebiet (Braunschweig, 1900); (5) Phil. Trans. R.S. vol. 158 (1868), p. 465, and vol. 160 (1870), p. 215; (6) Mém. de l’Académie St-Pétersbourg, t. 31, No. 12 (1883); (7) T. Moureaux, Ann. du Bureau Central Mét. (Année 1893), 1 Mem. p. B 23; (8) P. Bachmetjew, Mém. de l’Académie St-Pétersbourg, vol. 12, No. 3 (1901); (9) Terrestrial Magnetism, vol. 3 (1898), p. 130; (10) Journal Tel. Engineers (1881); (11) Proc. R.S. vol. 52 (1892), p. 191; (12) Akad. Abhandlung (Helsingfors, 1888); (13) Acad. Napoli Rend. (1890), and Atti (1894, 1895); (14) Pogg. Ann. vol. 76, p. 135; (15) Proc. R.S.E. vol. 13, p. 530; (16) A. Rücker, Phil. Mag. 1 (1901), p. 423, and R.T. Glazebrook, ibid. p. 432; (17) J. Edler, Elektrotech. Zeit. vol. 20 (1899); (18) L.A. Bauer, Terrestrial Magnetism, vol. 11 (1906), p. 53.
EARTH-NUT, the English name for a plant known botanically as Conopodium denudatum (or Bunium flexuosum), a member of the natural order Umbelliferae, which has a brown tuber-like root-stock the size of a chestnut. It grows in woods and fields, has a slender flexuous smooth stem 2 to 3 ft. high, much-divided leaves, and small white flowers in many-rayed terminal compound umbels. Boswell Syme, in English Botany, iv. 114, says: “The common names of this plant in England are various. It is known as earth-nut, pig-nut, ar-nut, kipper-nut, hawk-nut, jar-nut, earth-chestnut and ground-nut. Though really excellent in taste and unobjectionable as food, it is disregarded in England by all but pigs and children, both of whom appreciate it and seek eagerly for it.” Dr Withering describes the roots as little inferior to chestnuts. In Holland 817 and elsewhere on the continent of Europe they are more generally eaten.
EARTH PILLAR, a pillar of soft rock, or earth, capped by some harder material that has protected it from denudation. The “bad lands” of western North America furnish numerous examples. Here “the formations are often beds of sandstone or shale alternating with unindurated beds of clay. A semi-arid climate where the precipitation is much concentrated seems to be most favourable to the development of this type of formation.” The country round the Dead Sea, where loose friable sandy clay is capped by harder rock, produces “bad-land” topography. The cap of hard rock gives way at the joints, and the water making its way downwards washes away the softer material directly under the cracks, which become wider, leaving isolated columns of clay capped with hard sandstone or limestone. These become smaller and fewer as denudation proceeds, the pillars standing a great height at times, until finally they all disappear.
EARTHQUAKE. Although the terrible effects which often accompany earthquakes have in all ages forced themselves upon the attention of man, the exact investigation of seismic phenomena dates only from the middle of the 19th century. A new science has been thus established under the name of seismology (Gr. σεισμός, an earthquake).
History.—Accounts of earthquakes are to be found scattered through the writings of many ancient authors, but they are, for the most part, of little value to the seismologist. There is a natural tendency to exaggeration in describing such phenomena, sometimes indeed to the extent of importing a supernatural element into the description. It is true that attempts were made by some ancient writers on natural philosophy to offer a rational explanation of earthquake phenomena, but the hypotheses which their explanations involved are, as a rule, too fanciful to be worth reproducing at the present day. It is therefore unnecessary to dwell upon the references to seismic phenomena which have come down to us in the writings of such historians and philosophers as Thucydides, Aristotle and Strabo, Seneca, Livy and Pliny. Nor is much to be gleaned from the pages of medieval and later writers on earthquakes, of whom the most notable are Fromondi (1527), Maggio (1571) and Travagini (1679). In England, the earliest work worthy of mention is Robert Hooke’s Discourse on Earthquakes, written in 1668, and read at a later date before the Royal Society. This discourse, though containing many passages of considerable merit, tended but little to a correct interpretation of the phenomena in question. Equally unsatisfactory were the attempts of Joseph Priestley and some other scientific writers of the 18th century to connect the cause of earthquakes with electrical phenomena. The great earthquake of Lisbon in 1755 led the Rev. John Michell, professor of mineralogy at Cambridge, to turn his attention to the subject; and in 1760 he published in the Philosophical Transactions a remarkable essay on the Cause and Phenomena of Earthquakes. A suggestion of much scientific interest was made by Thomas Young, when in his Lectures on Natural Philosophy, published in 1807, he remarked that an earthquake “is probably propagated through the earth nearly in the same manner as a noise is conveyed through the air.” The recognition of the fact that the seismologist has to deal with the investigation of wave-motion in solids lies at the very base of his science. In 1846 Robert Mallet communicated to the Royal Irish Academy his first paper “On the Dynamics of Earthquakes”; and in the following year W. Hopkins, of Cambridge, presented to the British Association a valuable report in which earthquake phenomena were discussed in some detail. Mallet’s labours were continued for many years chiefly in the form of Reports to the British Association, and culminated in his great work on the Neapolitan earthquake of 1857. An entirely new impetus, however, was given to the study of earthquakes by an energetic body of observers in Japan, who commenced their investigations about the year 1880, mainly through the influence of Prof. John Milne, then of Tokyo. Their work, carried on by means of new instruments of precision, and since taken up by observers in many parts of the world, has so extended our knowledge of earthquake-motion that seismology has now become practically a new department of physical science.
It is hardly too much to say, however, that the earliest systematic application of scientific principles to the study of the effects of an earthquake was made by Mallet in his investigation of the Neapolitan earthquake mentioned above. It is true, the great Calabrian earthquake of 1783 had been the subject of careful inquiry by the Royal Academy of Naples, as also by Deodat Dolomieu and some other scientific authorities; but in consequence of the misconception which at that time prevailed with regard to the nature of seismic activity, the results of the inquiry, though in many ways interesting, were of very limited scientific value. It was reserved for Mallet to undertake for the first time an extensive series of systematic observations in an area of great seismic disturbance, with the view of explaining the phenomena by the application of the laws of wave-motion.
The “Great Neapolitan Earthquake,” by which more than 12,300 lives were lost, was felt in greater or less degree over all Italy south of the parallel of 42°, and has been regarded as ranking third in order of severity among the Neapolitan earthquake, 1857. recorded earthquakes of Europe. The principal shock occurred at about 10 P.M. on the 16th of December 1857; but, as is usually the case, it had been preceded by minor disturbances and was followed by numerous after-shocks which continued for many months. Early in 1858, aided by a grant from the Royal Society, Mallet visited the devastated districts, and spent more than two months in studying the effects of the catastrophe, especially examining, with the eye of an engineer, the cracks and ruins of the buildings. His voluminous report was published in 1862, and though his methods of research and his deductions have in many cases been superseded by the advance of knowledge, the report still remains a memorable work in the history of seismology.
Much of Mallet’s labour was directed to the determination of the position and magnitude of the subterranean source from which the vibratory impulses originated. This is known variously as the seismic centre, centrum, hypocentre, origin or focus. It is often convenient to regard this centre theoretically as a point, but practically it must be a locus or space of three dimensions, which in different cases varies much in size and shape, and may be of great magnitude. That part of the surface of the earth which is vertically above the centre is called the epicentre; or, if of considerable area, the epicentral or epifocal tract. A vertical line joining the epicentre and the focus was termed by Mallet the seismic vertical. He calculated that in the case of the Neapolitan earthquake the focal cavity was a curved lamelliform fissure, having a length of about 10 m. and a height of about 3½ m., whilst its width was inconsiderable. The central point of this fissure, the theoretical seismic centre, he estimated to have been at a depth of about 6½ m. from the surface. Dr C. Davison, in discussing Mallet’s data, was led to the conclusion that there were two distinct foci, possibly situated on a fault, or plane of dislocation, running in a north-west and south-east direction. Mallet located his epicentre near the village of Caggiano, not far from Polla, while the other seems to have been in the neighbourhood of Montemurro, about 25 m. to the south-east.
The intensity, or violence, of an earthquake is greatest in or near the epicentre, whence it decreases in all directions. A line drawn through points of equal intensity forms a curve round the epicentre known as an isoseist, an isoseismal or an isoseismic line. If the intensity declined equally in all directions the isoseismals would be circles, but as this is rarely if ever the case in nature they usually become ellipses and other closed curves. The tract which is most violently shaken was termed by Mallet the meizoseismic area, whilst the line of maximum destruction is known as the meizoseismic line. That isoseismal along which the decline of energy is most rapid was called by K. von Seebach a pleistoseist.
In order to determine the position of the seismic centre, Mallet made much use of the cracks in damaged buildings, especially 818 in walls of masonry, holding that the direction of such fractures must generally be at right angles to that in which the normal earthquake-wave reached them. In this way he obtained the “angle of emergence” of the wave. He also assumed that free-falling bodies would be overthrown and projected in the direction of propagation of the wave, so that the epicentre might immediately be found from the intersection of such directions. These data are, however, subject to much error, especially through want of homogeneity in the rocks, but Mallet’s work was still of great value.
A different method of ascertaining the depth of the focus was adopted by Major C.E. Dutton in his investigation of the Charleston earthquake of the 31st of August 1886 for the U.S. Geological Survey. This catastrophe Charleston earthquake, 1886. was heralded by shocks of greater or less severity a few days previously at Summerville, a village 22 m. north-west of Charleston. The great earthquake occurred at 9.51 P.M., standard time of the 75th meridian, and in about 70 seconds almost every building in Charleston was more or less seriously damaged, while many lives were lost. The epicentral tract was mainly a forest region with but few buildings, and the principal records of seismological value were afforded by the lines of railway which traversed the disturbed area. In many places these rails were flexured and dislocated. Numerous fissures opened in the ground, and many of these discharged water, mixed sometimes with sand and silt, which was thrown up in jets rising in some cases to a height of 20 ft. Two epicentres were recognized—one near Woodstock station on the South Carolina railway, and the other, being the centre of a much smaller tract, about 14 m. south-west of the first and near the station of Rantowles on the Charleston and Savannah line. Around these centres and far away isoseismal lines were drawn, the relative intensity at different places being roughly estimated by the effects of the catastrophe on various structures and natural objects, or, where visible records were wanting, by personal evidence, which is often vague and variable. The Rossi-Forel scale was adopted. This is an arbitrary scale formulated by Professor M.S. de Rossi, of Rome, and Dr F.A. Forel, of Geneva, based mostly on the ordinary phenomena observed during an earthquake, and consisting of ten degrees, of which the lowest is the feeblest, viz. I. Microseismic shock; II. Extremely feeble shock; III. Very feeble shock; IV. Feeble; V. Shock of moderate intensity; VI. Fairly strong shock; VII. Strong shock; VIII. Very strong shock; IX. Extremely strong shock; X. Shock of extreme intensity. Other conventional scales, some being less detailed, have been drawn up by observers in such earthquake-shaken countries as Italy and Japan. A curve, or theoretical isoseismal, drawn through certain points where the decline of intensity on receding from the epicentre seems to be greatest was called by Dutton an “index-circle”; and it can be shown that the radius of such a circle multiplied by the square root of 3 gives the focal depth theoretically. In this way it was computed that in the Charleston earthquake the origin under Woodstock must have had a depth of about 12 m. and that near Rantowles a depth of nearly 8 m. The determination of the index-circle presents much difficulty, and the conclusions must be regarded as only approximate.
It is probable, according to R.D. Oldham, that local earthquakes may originate in the “outer skin” of the earth, whilst a large world-shaking earthquake takes its origin in the deeper part of the “crust,” whence such a disturbance is termed a bathyseism. Large earthquakes may have very extended origins, with no definite centre, or with several foci.
The gigantic disaster known as the “Great Indian Earthquake,” which occurred on the 12th of June 1897, was the subject of careful investigation by the Geological Survey of India and was described in detail by the superintendent, Great Indian earthquake, 1897. R.D. Oldham. It is sometimes termed the Assam earthquake, since it was in that province that the effects were most severe, but the shocks were felt over a large part of India, and indeed far beyond its boundaries. Much of the area which suffered most disturbance was a wild country, sparsely populated, with but few buildings of brick or stone from which the violence of the shocks could be estimated. The epicentral tract was of great size, having an estimated area of about 6000 sq. m., but the mischief was most severe in the neighbourhood of Shillong, where the stonework of bridges, churches and other buildings was absolutely levelled to the ground. After the main disturbance, shocks of greater or less severity continued at intervals for many weeks. It is supposed that this earthquake was connected with movement of subterranean rock-masses of enormous magnitude along a great thrust-plane, or series of such planes, having a length of about 200 m. and a maximum breadth of not less than 50 m. It is pointed out by Oldham that this may be compared for size with the great Faille du Midi in Belgium, which is known to extend for a distance of 120 m. The depth of the principal focus, though not actually capable of determination, was probably less than 5 m. from the surface. From the focus many secondary faults and fractures proceeded, some reaching the surface of the ground. Enormous landslips accompanied the earthquake, and as an indirect effect of these slides the form of the water-courses became in certain cases modified. Permanent changes of level were also observed.
Eight years after the great Assam earthquake India was visited by another earthquake, which, though less intense, resulted in the loss of about 20,000 lives. This catastrophe is known as the Kangra earthquake, since its Kangra earthquake, 1905. centre seems to have been located in the Kangra valley, in the north-west Himalaya. It occurred on the 4th of April 1905, and the first great shocks were felt in the chief epifocal district at about 6.9 a.m., Madras time. Although the tract chiefly affected was around Kangra and Dharmsala, there was a subordinate epifocal tract in Dehra Dun and the neighbourhood of Mussoorie, whilst the effects of the earthquake extended in slight measure to Lahore and other cities of the plain. It is estimated that the earthquake was felt over an area of about 1,625,000 m. Immediately after the calamity a scientific examination of its effects was made by the Geological Survey of India, and a report was drawn up by the superintendent, C.S. Middlemiss.
The great earthquake, which, with the subsequent fire, wrought such terrible destruction in and around San Francisco on the 18th of April 1906, was the most disastrous ever recorded in California. It occurred between 10 and 15 minutes California earthquake, 1906. after 5 A.M., standard time of the 120th meridian. The moment at which the disaster began and the duration of the shock varied at different localities in the great area over which the earthquake was felt. At San Francisco the main shock lasted rather more than one minute.
According to the official Report, the earthquake was due to rupture and movement along the plane of the San Andreas fault, one of a series which runs for several hundred miles approximately in a N.W. and S.E. direction near the coast line. Evidence of fresh movement along this plane of dislocation was traced for a distance of 190 m. from San Juan on the south to Point Arena on the north. There the trace of the fault is lost beneath the sea, but either the same fault or another appears 75 m. to the north at Point Delgada. The belt of disturbed country is notoriously unstable, and part of the fault had been known as the “earthquake crack.” The direction is marked by lines of straight cliffs, long ponds and narrow depressions, forming a Rift, or old line of seismic disturbance. According to Dr G.K. Gilbert the earthquake zone has a length of 300 or 400 m. The principal displacement of rock, in 1906, was horizontal, amounting generally to about 10 ft. (maximum 21 ft.), but there was also locally a slight vertical movement, which towards the north end of the fault reached 3 ft. Movement was traced for a distance of about 270 m., and it is estimated that at least 175,000 sq. m. of country must have been disturbed. In estimating the intensity of the earthquake in San Francisco a new scale was introduced by H.O. Wood. The greatest structural damage occurred on soft alluvial soil and “made ground.” Most of the loss of property in San Francisco was 819 due to the terrible fire which followed the earthquake and was beyond control owing to the destruction of the system of water-supply.
Immediately after the catastrophe a California Earthquake Investigation Committee was appointed by the governor of the state; and the American Association for the Advancement of Science afterwards instituted a Seismological Committee. The elaborate Report of the State Investigation Committee, by the chairman, Professor A.C. Lawson, was published in 1908.
On the 17th of August 1906 a disastrous earthquake occurred at Valparaiso, and the year 1906 was marked generally by exceptional seismic activity.
The Jamaica earthquake of the 14th of January 1907 appears to have accompanied movement of rock along an east and west fracture or series of fractures under the sea a few miles from the city of Kingston. The statue of Queen Victoria at Kingston was turned upon its pedestal the eighth of a revolution.
A terrible earthquake occurred in Calabria and Sicily on December 28, 1908, practically destroying Messina and Reggio. According to the official returns the total loss of life was 77,283. Whilst the principal centre seems to Messina earthquake, 1908. have been in the Strait of Messina, whence the disturbance is generally known as the Messina earthquake, there were independent centres in the Calabrian peninsula, a country which had been visited by severe earthquakes not long previously, namely on September 8, 1905, and October 23, 1907. The principal shock of the great Messina earthquake of 1908 occurred at 5.21 A.M. (4.21 Greenwich time), and had a duration of from 30 to 40 seconds. Neither during nor immediately before the catastrophe was there any special volcanic disturbance at Etna or at Stromboli, but it is believed that there must have been movement along a great plane of weakness in the neighbourhood of the Strait of Messina, which has been studied by E. Cortese. The sea-floor in the strait probably suffered great disturbance, resulting in the remarkable movement of water observed on the coast. At first the sea retired, and then a great wave rolled in, followed by others generally of decreasing amplitude, though at Catania the second was said to have been greater than the first. At Messina the height of the great wave was 2.70 metres, whilst at Ali and Giardini it reached 8.40 metres and at San Alessio as much as 11.7 metres. At Malta the tide-gauge recorded a wave of 0.91 metre. The depth of the chief earthquake-centre was estimated by Dr E. Oddone at about 9 kilometres. The earthquake and accompanying phenomena were studied also by Professor A. Riccò, Dr M. Baratta and Professor G. Platania and by Dr F. Omori of Tokyo. After the great disturbance, shocks continued to affect the region intermittently for several months. In certain respects the earthquake of 1908 presented much resemblance to the great Calabrian catastrophe of 1783.
It has been proposed by R.D. Oldham that the disturbance which causes the fracture and permanent displacement of the rocks during an earthquake should be called an “earthshake,” leaving the term earthquake especially for the vibratory motion. The movement of the earthquake is molecular, whilst that of the earthshake is molar. Subsequently he suggested the terms mochleusis and orchesis (μοχλέυω, I heave; ὀρχέομαι, I dance), to denote respectively the molar and the molecular movement, retaining the word earthquake for use in its ordinary sense.
In most earthquakes the proximate cause is generally regarded as the fracture and sudden movement of underground rock-masses. Disturbances of this type are known as “tectonic” earthquakes, since they are connected with the folding and faulting of the rocks of the earth’s crust. They indicate a relief of the strain to which the rock-masses are subjected by mountain-making and other crustal movements, and they are consequently apt to occur along the steep face of a table-land or the margin of a continent with a great slope from land to sea. In many cases the immediate seat of the originating impulse is located beneath the sea, giving rise to submarine disturbances which have been called “seaquakes.” Much attention has been given to these suboceanic disturbances by Professor E. Rudolph.
Professor J.H. Jeans has pointed out that the regions of the earth’s crust most affected by earthquakes lie on a great circle corresponding with the equator of the slightly pear-shaped figure that he assigns to the earth. This would represent a belt of weakness, subject to crushing, from the tendency of the pear to pass into a spherical or spheroidal form under the action of internal stresses. According to the comte de Montessus de Ballore, the regions of maximum seismic instability appear to be arranged on two great circles, inclined to each other at about 67°. These are the Circumpacific and Mediterranean zones.
Maps of the world, showing the origins of large earthquakes each year, accompany the Annual Reports of the Seismological Committee of the British Association, drawn up by Professor Milne. It is important to note that Professor Milne has shown a relationship between earthquake-frequency and the wandering of the earth’s pole from its mean position. Earthquakes seem to have been most frequent when the displacement of the pole has been comparatively great, or when the change in the direction of movement has been marked. Valuable earthquake catalogues have been compiled at various times by Alexis Perrey, R. and J.W. Mallet, John Milne, T. Oldham, C.W.C. Fuchs, F. de Montessus de Ballore and others.
Such earthquakes as are felt from time to time in Great Britain may generally be traced to the formation of faults, or rather to incidents in the growth of old faults. The East Anglian earthquake of the 22nd of April 1884—the British earthquakes. most disastrous that had occurred in the British Isles for centuries—was investigated by Prof. R. Meldola and W. White on behalf of the Essex Field Club. The shocks probably proceeded from two foci—one near the villages of Peldon and Abberton, the other near Wivenhoe and Rowhedge, in N.E. Essex. It is believed that the superficial disturbance resulted from rupture of rocks along a deep fault. An attempt has been made by H. Darwin, for the Seismological Committee of the British Association, to detect and measure any gradual movement of the strata along a fault, by observation at the Ridgeway fault, near Upway, in Dorsetshire. Dr C. Davison in studying the earthquakes which have originated in Britain since 1889 finds that several have been “twins.” A twin earthquake has two maxima of intensity proceeding from two foci, whereas a double earthquake has its successive impulses from what is practically a single focus. The Hereford earthquake of December 1896, which resulted in great structural damage, was a twin, having one epicentre near Hereford and the other near Ross. Davison refers it to a slip along a fault-plane between the anticlinal areas of Woolhope and May Hill; and according to the same authority the Inverness earthquake of the 18th of September 1901 was referable to movement along a fault between Loch Ness and Inverness. The South Wales earthquake of June 27, 1906, was probably due to movement connected with the Armorican system of folds, striking in an east and west direction.
It may be noted that when a slip occurs along a fault, the displacement underground may be but slight and may die out before reaching the surface, so that no scarp is formed. In connexion, however, with a seismic disturbance of the first magnitude the superficial features may be markedly affected. Thus, the great Japan earthquake of October 1891—known often as the Mino-Owari earthquake—was connected with the formation or development of a fault which, according to Professor B. Koto, was traced on the surface for a distance of nearly 50 m. and presented in places a scarp with a vertical throw of as much as 20 ft., while probably the maximum displacement underground was very much greater.
Although most earthquakes seem to be of tectonic type, there are some which are evidently connected, directly or indirectly, with volcanic activity (see Volcano). Such, it is commonly believed, were the earthquakes which disturbed the Isle of Ischia in 1881 and 1883, and were studied by Professor J. Johnston-Lavis and G. Mercalli. In addition to the tectonic and volcanic types, there are occasional earthquakes of minor importance which may be referred to the collapse of the roof of 820 caverns, or other falls of rock in underground cavities at no great depth. According to Prof. T.J.J. See most earthquakes are due, directly or indirectly, to the explosive action of steam, formed chiefly by the leakage of sea-water through the ocean floor.
Whatever the nature of the impulse which originates the earthquake, it gives rise to a series of waves which are propagated through the earth’s substance and also superficially. In one kind, known as normal or condensational waves, Earthquake waves. or waves of elastic compression, the particles vibrate to and from the centre of disturbance, moving in the direction in which the wave travels, and therefore in a way analogous to the movement of air in a sound-wave. Associated with this type are other waves termed transverse waves, or waves of elastic distortion, in which the particles vibrate across or around the direction in which the wave is propagated. The normal waves result from a temporary change of volume in the medium; the transverse from a change of shape. The distance through which an earth-particle moves from its mean position of rest, whether radially or transversely, is called the amplitude of the wave; whilst the double amplitude, or total distance of movement, to and fro or up and down, like the distance from crest to trough of a water wave, may be regarded as the range of the wave. The period of a wave is the time required for the vibrating particle to complete an oscillation. As the rocks of the earth’s crust are very heterogeneous, the earthquake-waves suffer refraction and reflection as they pass from one rock to another differing in density and elasticity. In this way the waves break up and become much modified in course of transmission, thus introducing great complexity into the phenomena. It is known that the normal waves travel more rapidly than the transverse.
Measurements of the surface speed at which earthquake-waves travel require very accurate time-measurers, and these are not generally available in earthquake-shaken regions. Observations during the Charleston earthquake of 1886 were at that time of exceptional value, since they were made over a large area where standard time was kept. Lines drawn through places around the epicentre at which the shock arrives at the same moment are called coseismal lines. The motion of the wave is to be distinguished from the movement of the vibrating particles. The velocity of the earth-particle is its rate of movement, but this is constantly changing during the vibration, and the rate at which the velocity changes is technically called the acceleration of the particle.
Unfelt movements of the ground are registered in the earthquake records, or seismograms, obtained by the delicate instruments used by modern seismologists. From the study of the records of a great earthquake from a distant source, sometimes termed a teleseismic disturbance, some interesting inferences have been drawn with respect to the constitution of the interior of the earth. The complete record shows two phases of “preliminary tremors” preceding the principal waves. It is believed that while the preliminary tremors pass through the body of the earth, the principal waves travel along or parallel to the surface. Probably the first phase represents condensational, and the second phase distortional, waves. Professor Milne concludes from the speed of the waves at different depths that materials having similar physical properties to those at the surface may extend to a depth of about 30 m., below which they pass into a fairly homogeneous nucleus. From the different rates of propagation of the precursors it has been inferred by R.D. Oldham that below the outer crust, which is probably not everywhere of the same thickness, the earth is of practically uniform character to a depth of about six-tenths of the radius, but the remaining four-tenths may represent a core differing physically and perhaps chemically from the outer part. Oldham also suggests, from his study of oceanic and continental wave-paths, that there is probably a difference in the constitution of the earth beneath oceans and beneath continents.
The surface waves, which are waves of great length and long period and are propagated to great distances with practically a constant velocity, have been regarded as quasi-elastic gravitational waves. Further, in a great earthquake the surface of the ground is sometimes visibly agitated in the epifocal district by undulations which may be responsible for severe superficial damage. (See also for elastic waves Elasticity, § 89.)
An old classification of earthquake-shocks, traces of which still linger in popular nomenclature, described them as “undulatory,” when the movement of the ground was mainly in a horizontal direction; “subsultory,” when the motion was vertical, like the effect of a normal wave at the epicentre; and “vorticose,” when the movement was rotatory, apparently due to successive impulses in varying directions.
The sounds which are associated with seismic phenomena, often described as subterranean rumbling and roaring, are not without scientific interest, and have been carefully studied by Davison. “Isacoustic lines” are curves drawn through places where the sound is heard by the same percentage of observers. The sound is always low and often inaudible to many.
The refined instruments which are now used by seismologists for determining the elements of earthquake motion and for recording earthquakes from distant origins are described in the article Seismometer. These instruments were developed as a consequence of the attention given in modern times to the study of earthquakes in the Far East.
Strange as it may appear, the advances that have been made in the study of earthquakes and the world-wide interest shown in their phenomena were initiated in work commenced in Japan. When the Japanese government, Seismology in Japan. desiring to adopt Western knowledge, invited to its shores bodies of men to act as its instructors, the attention of the newcomers was naturally attracted to the frequent shakings of the ground. Interest in these phenomena increased more rapidly than their frequency, and at length it was felt that something should be done for their systematic study. At midnight on the 22nd of February 1880 movements more violent than usual occurred; chimneys were shattered or rotated, tiles slid down from roofs, and in the morning it was seen that Yokohama had the appearance of a city that had suffered a bombardment. The excitement was intense, and before the ruins had been removed a meeting was convened and the Seismological Society of Japan established. The twenty volumes of original papers published by this body summarize to a large extent the results of the later study of seismology.1
The attention of the students of earthquakes in Japan was at first directed almost entirely to seismometry or earthquake measurement. Forms of apparatus which then existed, as for example the seismographs, seismometers and seismoscopes of Mallet, Palmieri and others, were subjected to trial; but inasmuch as they did little more than indicate that an earthquake had taken place—the more elaborate forms recording also the time of its occurrence—they were rapidly discarded, and instruments were constructed to measure earthquake motion. Slightly modified types of the new instruments devised in Japan were adopted throughout the Italian peninsula, and it is fair to say that the seismometry developed in Japan revolutionized the seismometry of the world. The records obtained from the new instruments increased our knowledge of the character of earthquake motion, and the engineer and the architect were placed in a position to construct so that the effects of known movements could be minimized. It was no doubt the marked success, both practical and scientific, attending these investigations that led the Japanese government to establish a chair of seismology at its university, to organize a system of nearly 1000 observing stations throughout the country, and in 1893 to appoint a committee of scientific and practical men to carry out investigations which might palliate the effects of seismic disturbances. In the first year this committee received a grant of £5000, and as liberal sums for the same purpose appear from time to time in the 821 parliamentary estimates, it may be assumed that the work has been fraught with good results. In their publications we find not only records of experiences and experiments in Japan, but descriptions and comments upon earthquake effects in other countries. In two of the volumes there are long and extremely well illustrated accounts of the earthquake which on the 12th of June 1897 devastated Assam, to which country two members of the above-mentioned committee were despatched to gather such information as might be of value to the architect and builder in earthquake-shaken districts.
A great impetus to seismological investigation in Europe and America was no doubt given by the realization of the fact that a large earthquake originating in any one part of the world may be recorded in almost any other. Italy Seismological research. for many years past has had its observatories for recording earthquakes which can be felt, and which are of local origin, but at the present time at all its first-class stations we find instruments to record the unfelt movements due to earthquakes originating at great distances, and as much attention is now paid to the large earthquakes of the world as to the smaller ones originating within Italian territory.2 The Kaiserliche Akademie der Wissenschaften of Vienna established earthquake observatories in Austria,3 and the Central Observatorium of St Petersburg has carried out similar work in Russia. Germany attached a seismological observatory to its university at Strassburg, whilst provision has been made for a professorship of Earth Physics (Geophysik) at Göttingen.4 In accordance with the recommendation of the British Association, seismographs of a similar character have been installed at stations all over the world.5 The principal objects of this extended and still extending system of stations are to determine the velocity with which motion is propagated over the surface and through the interior of the earth, to locate the positions of sub-oceanic earthquake origins, and generally to extend our knowledge respecting the physical nature of the planet on which we live.
We now know that earthquakes are many times more frequent than was previously supposed. In Japan, for example, between 1885 and 1892 no fewer than 8331 were recorded—that is to say, on the average there were during that time Frequency of earthquakes. more than 1000 disturbances per year. Although many of these did not cause a sensible shaking over areas exceeding a few hundred square miles, many of them were sufficiently intense to propagate vibrations round and through the globe. If we pick out the well-marked earthquake districts of the world, and give to each of them a seismicity or earthquake frequency per unit area one-third of that in Japan, the conclusion arrived at is that considerable areas of our planet are on the average shaken every half-hour.
The knowledge which we now possess respecting the localities where earthquakes are frequent and the forms of the foci from which they have spread, enables us to speak definitely respecting the originating causes of many of these Volcanoes and earthquakes. phenomena. It is found, for example, that although in many countries there may be displays of volcanic and seismic activity taking place almost side by side, it is only rarely that there is direct relationship between the two. Now and then, however, before a volcano breaks into eruption there may be a few ineffectual efforts to form a vent, each of which is accompanied by no more than a slight local shaking of the ground. This is true even for the largest and most violent eruptions, when mountains have with practically a single effort blown off their heads and shoulders. Thus the earthquake which accompanied the eruption of Bandaisan, in central Japan, in 1888 was felt only over a radius of 25 m. The analyses of the seismic registers of Japan clearly indicate that comparatively few shakings originate near to the volcanoes of the country, the majority of them, like those of many other countries, coming from regions where volcanic rocks are absent. The greatest number spread inland from the Pacific seaboard, the movement becoming more and more feeble as it approaches the backbone of the country, which is drilled with numerous volcanic vents. What is true for Japan is generally true for the western coasts of North and South America.
Speaking broadly, earthquakes are most frequent along the steeper flexures in the earth’s surface, and in those regions where there is geological evidence to show that slow secular movements in the earth’s crust are possibly yet in Origin of earthquakes. progress. With a unit distance of 2 degrees, or 120 geographical m., we find that the slopes running eastwards from the highlands of Japan and westwards from the Andean ridges down into the Pacific vary from 1 in 20 to 1 in 30, and it is on the faces or near to the bottom of these slopes that seismic efforts are frequent. The slopes running from Australia, eastern America and western Europe into the neighbouring oceans vary between 1 in 70 and 1 in 250, and in these regions earthquakes are of rare occurrence. The seismic activity met with in the Himalayas and the Alps finds its best explanation in the fact that these mountains are geologically recent, and there are no reasons to doubt that the forces which brought their folds into existence are yet in action.
This peculiar association of earthquakes with pronounced topographical configuration and certain geological conditions evidently indicates that the origin of many of them is connected with rock folding. Inasmuch as certain large earthquakes have been accompanied by rock fracture, as for example in 1891, when in central Japan a fault some 50 m. in length was created, whilst the origins of others have been distinctly traced to the line of an existing fault or its continuation, we may conclude that the majority of earthquakes are spasmodic accelerations in the secular movements which are creating (and in some instances possibly obliterating) the more prominent features of the earth’s surface. These secular movements, which include upheavals, subsidences, horizontal displacements—all of which are explained on the assumption of a crust seeking support on a nucleus gradually contracting by loss of heat, are collectively referred to as bradyseismical (βραδύς, slow) movements. To these may be added movements directly attributable to the influence of gravity. Sub-oceanic districts in a state of seismic strain may be so far loaded by the accumulation of sediments that gentle bending may be accompanied by sudden yieldings. This possibly accounts for the frequency of earthquakes off the mouth of the Tonegawa on the eastern side of Japan. The distortions so frequently observed in fossils and pebbles, the varying thickness of contorted strata, and the “creep” in coal-mines, together with other phenomena, indicate that rocks may flow. Observations of this nature lead to the supposition that high plateau-like regions may be gradually subsiding under the influence of their own weight, and that the process of settlement may from time to time be spasmodic in its character. Whether the earthquakes which originate round the submerged basal frontiers of the continents bounding the Pacific are ever attributable to such activities, it is impossible to say. All that we know with certainty is that they are sometimes accompanied by such a vast displacement of material that the ocean has been set into a state of oscillation for periods of 24 hours, that in some instances there have been marked changes in depth, and that enormous sub-oceanic landslips have occurred. These phenomena are, however, equally well explained on the assumption of sudden faulting accompanied by violent shaking, which would dislodge steeply inclined beds of material beneath the ocean as it does upon the land.
Although the proximate cause of earthquake motion is traced to sudden yieldings in the crust of the earth brought about by some form of bradyseismical action, the existence of at least two distinct types of seismic motion Two types of earthquake motion. indicates that the mechanical conditions accompanying the fracturing of rocks are not always identical. 90 or 95% of the earthquakes which can be recorded consist of elastic or quasi-elastic vibrations. The remainder, including the large earthquakes, not only exhibit the elastic movements, but are accompanied by surface undulations which are propagated most certainly for some hundreds of miles round their origin, and then as horizontal movements sweep over the whole surface of the globe. The former of these may accompany the formation of a new fault or the sudden renewal of movement along an old one; they are cracking or rending effects, without any great displacement. The latter are probably fracturings accompanied by vertical and horizontal displacements of masses of the earth’s crust sufficiently great to set up the observed surface undulations. These shocks are so frequently followed a few minutes later by disturbances, which from their similarity to the movements which have preceded them may be called earthquake echoes, that we are led to the speculation that we are here dealing with the caving-in of ill-supported portions of the earth’s crust, the waves from which are radiated to boundaries and then returned to their origin to coalesce and give rise to a second impulse not unlike the primary. Succeeding the first repetition of motion recorded by the seismograph there is often a rhythmical repetition of similar wave groups, suggesting the existence within our earth of phenomena akin to multiple echoes.
The introduction of new methods into seismometry quickly revolutionized our ideas respecting the character of earthquake motion. Although an earthquake may be strongly felt within a distance of 50 m. from its origin, and Character of earthquake motion. although the movements in the upper storeys of buildings within the shaken area may be large, the actual range of the horizontal motion of the ground is usually less than 1⁄10 of an inch. With such earthquakes ordinary seismographs for recording vertical motion do not show any disturbance. When the movement reaches ½ in. it becomes dangerous, and a back-and-forth movement of an inch is usually accompanied by destructive effects. In this latter case the amplitude of the vertical record which indicates the existence of surface waves will vary between ½ and 1⁄100 of an inch. In the earthquake which devastated central Japan on the 26th of October 1891, nearly every building within the epifocal district fell, the ground was fissured, forests slipped down from mountain sides to dam up valleys, whilst the valleys themselves were permanently compressed. The horizontal movements seem to have reached 9 in. or 1 ft., and the surface undulations were visible to the eye.
The rapidity with which the movements are performed varies throughout a disturbance. A typical earthquake usually commences with minute elastic vibrations, the periods of which vary between 1⁄5 and 1⁄20 of a second. These Period and duration. are recorded by seismographs, and are noticed by certain of the lower animals like pheasants, which before the occurrence of movement perceptible to human beings scream as if alarmed. When an earthquake is preceded by a sound we have evidence of preliminary tremors even more rapid than those recorded by seismographs. Following these precursors there is a shock or shocks, the period of which will be 1 or 2 seconds. From this climax the movements, although irregular in character, become slower and smaller until finally they are imperceptible. The duration of a small earthquake usually varies from a few seconds to a minute, but large earthquakes, which are accompanied by surface undulations, may be felt for 2 or 3 minutes, whilst an ordinary seismograph indicates a duration of from 6 to 12 minutes. A free horizontal pendulum tells us that with severe earthquakes the ground comes to rest by a series of more or less rhythmical surgings, continuing over 1 or 2 hours. Although the maximum displacement has a definite direction, the successive vibrations are frequently performed in many different azimuths. The predominating direction at a given station in certain instances is apparently at right angles to the strike of the neighbouring strata, this being the direction of easiest yielding.
Earthquake motion as recorded at stations several thousands of miles distant from its origin exhibits characteristics strikingly different from those just described. The precursors now show periods of from 1 to 5 seconds, whilst the Velocity. largest movements corresponding to the shocks may have periods of from 20 to 40 seconds. The interval of time by which the first tremors have outraced the maximum movement has also become greater. Within a few hundreds of miles from an origin this interval increases steadily, the velocity of propagation of the first movements being about 2 km. per second, whilst that of the latter may be taken at about 1.6 km. per second. Beyond this distance the velocity of transmission of the first movements rapidly increases, and for great distances, as for example from Japan to England, it is higher than we should expect for waves of compression passing through steel or glass. This observation precludes the idea that these preliminary tremors have travelled through the heterogeneous crust of the earth, and since the average velocity of their transmission increases with the length of the path along which they have travelled, and we but rarely obtain certain evidence that a seismograph has been disturbed by waves which have reached it by travelling in opposite directions round the world, we are led to the conclusion that earthquake precursors pass through our earth and not round its surface. The following table relating to earthquakes, which originated off the coast of Borneo on the 20th and 27th of September 1897, is illustrative of the velocities here considered:—
| Localities. | Distance from origin in degrees. |
Velocity in kms. per sec. if on chord. |
¼ √ | Average depth of chord in kms. |
| Nicolaieff | 81° | 8.1 | 8.0 | |
| Potsdam | 92° | 8.4 | 9.1 | |
| Catania, Ischia, Rocca di Papa, Rome | 96° | 9.0 | 9.5 | |
| Isle of Wight | 103° | 9.8 | 10.2 | |
The chords referred to here are those joining the earthquake origins and distant observing stations, and it will be noted that one-quarter of the square root of the average depths at which these run closely corresponds to observed average velocities if wave paths followed chords. This increase of velocity with average depth shows that the paths followed through the earth must be curved with their convexity towards the centre of the earth. These observations do not directly tell us to what extent a true wave path is deflected from the direction of a chord, but they suggest as an extremely plausible assumption that the square of the speed is a linear function of the depth below the surface of the earth. With this assumption Dr C.G. Knott shows that the square of the speed (v²) can be expressed linearly in terms of the average depth of the chord d, thus: v² = 2.9 + .026 d, the units being miles and seconds. The formula applies with fair accuracy to moderate and high values of d, but it gives too high a value for short chords. It follows that the square of the speed increases 0.9% per mile of descent in the earth. The conclusion we arrive at is that the preliminary tremors which pass through the earth do so in the vicinity of their origin at the rate of almost 2.3 km. per second. This velocity increases as the wave path plunges downwards, attaining in the central regions a velocity of 16 to 17 kms., whilst the highest average velocity which is across a diameter lies between 10 and 12 kms. per second.
The large surface waves radiating from an origin to a distant place have velocities lying between 1.6 and 4 kms. per second, and it has been observed that when the higher velocity has been noted this refers to an observation at a station very remote from the origin. One explanation of this is the assumption that only very large waves indicating a large initial disturbance are capable of travelling to great distances, and as pointed out by 823 R.D. Oldham, large waves under the influence of gravity will travel faster than small waves. These waves (which may be gravitational or distortional) are recorded as slow tiltings of the ground measured by angles of 0.5 to 10 or 15 seconds of arc, or as horizontal displacements of 0.5 or several millimetres. Their calculated lengths have reached 50 kms. (31 m.).
In the section of this article relating to the cause of earthquakes a little has been said about their frequency or the number of times these phenomena are repeated during a given interval of time. It has been shown that all countries Frequency. are very often moved by earthquakes which have originated at great distances. Great Britain, for example, is crossed about 100 times a year by earthquake waves having durations of from 3 minutes to 3 hours, whilst the vibratory motions which originate in that country are not only small but of rare occurrence. In the earlier stages of the world’s history, because the contraction of its nucleus was more rapid than it is at present, it is commonly inferred that phenomena accompanying bradyseismical activity must have been more pronounced and have shown themselves upon a grander scale than they do at the present time. Now, although the records of our rocks only carry us back over a certain portion of this history, they certainly represent an interval of time sufficiently long to furnish some evidence of such enfeeblement if it ever existed. So far from this being the case, however, we meet with distinct evidences in the later chapters of geological history of plutonic awakenings much more violent than those recorded at its commencement. During Palaeozoic times many mountain ranges were formed, and accompanying these orogenic processes there was marked volcanic activity. In the succeeding Secondary period plutonic forces were quiescent, but during the formation of the early Tertiaries, when some of the largest mountain ranges were created, they awoke with a vigour greater than had ever been previously exhibited. At this period it is not improbable that Scotland was as remarkable for its volcanoes and its earthquakes as Japan is at the present day. If the statement relating to the general decrease in bradyseismical changes referred merely to their frequency, and omitted reference to their magnitude, the views of the geologist and physicist might harmonize. One explanation for this divergence of opinion may rest on the fact that too little attention has been directed to all the conditions which accompany the adaptation of the earth’s crust to its shrinking nucleus. As the latter grows smaller the puckerings and foldings of the former should grow larger. Each succeeding geological epoch should be characterized by mountain formations more stupendous than those which preceded them, whilst the fracturing, dislocation, caving-in of ill-supported regions, and creation of lines of freedom for the exhibition of volcanic activity which would accompany these changes, would grow in magnitude. The written records of many countries reflect but on a smaller scale the crystallized records in their hills. In 1844, at Comrie, in Perthshire, as many as twelve earthquakes were recorded in a single month, whilst now there are but one or two per year. Earthquake frequency varies with time. A district under the influence of hypogenic activities reaches a condition of seismic strain which usually is relieved rapidly at first, but subsequently more slowly.
The small shocks which follow an initial large disturbance are known as after-shocks. The first shock which in 1891 devastated central Japan was accompanied by the formation of a large fault, and the 3364 small shocks which succeeded this during the following two years are regarded as due to intermittent settlements of disjointed material. The decreasing frequency with which after-shocks occur may be represented by a curve. Dr F. Omori points out that the continuation of such a curve gives the means of determining the length of time which will probably elapse before the region to which it refers will return to the same seismic quiescence that it had prior to the initial disturbance.
The positive results that we have respecting the periodicity of earthquakes are but few. Generally earthquakes are somewhat more frequent during winter than during summer, and this applies to both the northern and southern hemispheres. The Periodicity. annual periodicity, which, however, does not show itself if only destructive earthquakes are considered, finds an explanation, according to Dr Knott, in the annual periodicity of long-continued stresses, as for example those due to the accumulation of snow and to barometric gradients. For certain earthquake regions there appears to be a distinct semi-annual period for which no satisfactory explanation has yet been adduced. Although the elaborate registers of Japan, which have enabled us to group earthquakes according to their respective origins and varying intensities, and to separate after-shocks from initial disturbances, have been subjected by Dr Knott to most careful analysis, with the object of discovering periodicities connected with the ebb and flow of the tides, the lunar day or lunar months, nothing of marked character has been found. Certainly there is slight evidence of a periodicity connected with the times of conjunction and opposition of the sun and moon, and a maximum frequency near the time of perigee, but the effect of lunar stresses is comparatively insignificant. Ordinary earthquakes, and especially after-shocks, show a diurnal period, but we cannot say that there are more earthquakes during the night than during the day.
Many experiments and investigations have been made to determine a possible relationship between earthquakes and electrical phenomena, but beyond drawing attention to the fact that luminous appearances may accompany Magnetic phenomena. the friction of moving masses of rock, and that a temporary current may be established in a line by the disturbance of an earth-plate, these inquiries have yielded but little of importance. The inquiries respecting a possible relationship between adjustments so frequently taking place within and beneath that region called the crust of the earth and magnetic phenomena are, however, of a more promising nature. We have seen that at or near the origin of earthquakes which for several hours disturb continents, and occasionally cause oceans to oscillate for longer periods, we sometimes have direct evidence of the bodily displacement of many cubic miles of material. When this material is volcanic it is almost invariably magnetic, and we perceive in its sudden rearrangement causes which should produce magnetic effects within an epifocal district. In Japan, where attention is being directed to phenomena of this description, not only have such effects been observed, but unusual magnetic disturbances have been noted prior to the occurrence of large earthquakes. These may, of course, be regarded as mere coincidences, but when we consider volcanic and seismic activities as evidences of physical and chemical changes, together with mechanical displacements of a magnetic magma, it is reasonable to suppose that they should have at least a local influence upon magnetic needles. Another form of disturbance to which magnetic needles are subjected is that which accompanies the passage of large earth-waves beneath certain observatories situated at great distances from earthquake origins. At Utrecht, Potsdam and Wilhelmshaven the magnetographs are frequently disturbed by seismic waves, whilst at many other European observatories such effects are absent or only barely appreciable. To explain these marked differences in the behaviour of magnetic needles at different stations we are at present only in a position to formulate hypotheses. They may be due to the fact that different needles have different periodic times of oscillation; it is possible that at one observatory the mechanical movements of the ground are much greater than at others; we may speculate on the existence of materials beneath and around various observatories which are different in their magnetic characters; and, lastly, we may picture a crust of varying thickness, which from time to time is caused to rise and fall upon a magnetic magma, the places nearest to this being the most disturbed.
A subject to which but little attention has been directed is the effect which displays of seismic and volcanic activities have had upon the human mind. The effects are distinctly dual and opposite in character. In countries like Effects on the human mind. England, where earthquakes are seldom experienced, the prevailing idea is that they are associated with all that is baneful. For certain earthquakes, which fortunately are less than 1% of those which are annually recorded, this is 824 partially true. A disastrous shock may unnerve a whole community. Effects of this nature, however, differ in a marked manner with different nationalities. After the shock of 1891, when Japan lost 9960 of its inhabitants, amongst the wounded indications of mental excitement were shown in spinal and other trouble. Notwithstanding the lightheartedness of this particular nation, it is difficult to imagine that the long series of seismic effects chronicled in Japanese history, which culminated in 1896 in the loss of 29,000 lives by sea-waves, has been without some effect upon its mental and moral character. Several earthquakes are annually commemorated by special services at temples. In bygone times governments have recognized earthquakes as visitations of an angry deity, whom they have endeavoured to appease by repealing stringent laws and taxes. In other countries the sermons which have been preached to show that the tremblings of the world were visitations consequent on impiety, and the prayers which have been formulated to ward off disasters in the future, far exceed in number the earthquakes which gave rise to them. In 1755 many of the English clergy held the view that Lisbon was destroyed because its inhabitants were Catholics, whilst the survivors from that disaster attributed their misfortune to the fact that they had tolerated a few Protestant heretics in their midst. To avoid a recurrence of disaster certain of these were baptized by force. In the myths relating to underground monsters and personages that are said to be the cause of earthquakes we see the direct effects which exhibitions of seismic and volcanic activity have produced upon the imagination. The beliefs, or more properly, perhaps, the poetical fancies, thus engendered have exhibited themselves in various forms. Beneath Japan there is said to be a catfish, which in other countries is replaced by a mole, a hog, an elephant or other living creature, which when it is restless shakes the globe. The Kamchadales picture a subterranean deity called Tuil, who in Scandinavian mythology is represented by the evil genius Loki. We have only to think of the reference in the Decalogue forbidding the making of graven images of that which is in the earth beneath, to see in early Biblical history evidence of a subterranean mythology; and it seems probable that the same causes which led to the creation of Pluto, Vulcan and Poseidon gave rise to practices condemned by Moses.
Perhaps the greatest practical benefits derived from seismological investigations relate to important changes and new principles which have been introduced into the arts of the engineer and builder when constructing in earthquake Building to withstand earthquakes. countries. The new rules and formulae, rather than being theoretical deductions from hypotheses, are the outcome of observation and experiment. True measures of earthquake motion have been given to us by modern seismometers, with the result that seismic destructivity can be accurately expressed in mechanical units. From observation we now know the greatest acceleration and maximum velocity of an earth particle likely to be encountered; and these are measures of the destructivity. The engineer is therefore dealing with known forces, and he has to bear in mind that these are chiefly applied in a horizontal direction. A formula connecting the acceleration requisite to overturn bodies of different dimensions has been given. The acceleration which will fracture or shatter a column firmly fixed at its foundation to the moving earth may be expressed as follows:—
| a = | 1 | gFAB | , | |
| 6 | fw |
where
a = the acceleration per sec. per sec.
F = the force of cohesion, or force per unit surface, which when gradually applied produces fracture.
A = area of base fractured.
B = thickness of the column.
f = height of centre of gravity of column above the fractured base.
w = the weight of the portion broken off.
With this formula and its derivatives we are enabled to state the height to which a wall, for example, may be built capable of resisting any assumed acceleration. Experience has shown that yielding first shows itself at the base of a pier, a wall or a building, and it is therefore clear that the lower portion of such structures should be of greater dimensions or stronger than that above. Piers having these increased dimensions below, and tapering upwards in a proper manner, so that every horizontal section is sufficiently strong to resist the effects of the inertia of its superstructure, are employed to carry railways in Japan. In that country cast-iron piers are things of the past, whilst piers of masonry, together with their foundations, no longer follow the rules of ordinary engineering practice.
After flood, fire, earthquake, or when opportunity presents itself, changes are introduced in the construction of ordinary buildings. In a so-called earthquake-proof house, although externally it is similar to other dwellings, we find rafters running from the ridge pole to the floor sills, an exceedingly light roof, iron straps and sockets replacing mortices and tenons, and many other departures from ordinary rules. Masonry arches for bridges or arched openings in walls (unless protected by lintels), heavy gables, ornamental copings, cappings for chimneys, have by their repeated failure shown that they are undesirable features for construction in earthquake countries. As sites for buildings it is well to avoid soft ground, on which the movement is always greater than on hard ground. Excessive movement also takes place along the face of unsupported openings, and for this reason the edges of scarps, bluffs, cuttings and river-banks are localities to be avoided. In short, the rules and precautions which have to be recognized so as to avoid or mitigate the effects of earthquake movement are so numerous that students of engineering and architecture in Japan receive a special course of lectures on this subject. When it is remembered that a large earthquake may entail a loss of life greater than that which takes place in many wars, and that for the reconstruction of ordinary buildings, factories and public works an expenditure of several million pounds sterling is required, the importance of these studies cannot be overrated. Severe earthquakes are fortunately unknown in the British Isles, but we have simply to turn our eyes to earthquake-shaken colonies and lands in close commercial touch with Great Britain to realize the importance of mitigating such disasters as much as possible, and any endeavour to obviate the wholesale destruction of life should appeal to the civilized communities of the world.
An unexpected application of seismometry has been to record the vibration of railway trains, bridges and steamships. An instrument of suitable construction will give records of the more or less violent jolting and vibratory Applications of seismometry. movements of a train, and so localize irregularities due to changes in the character of ballast and sleepers, to variation in gauge, &c. An instrument placed on a locomotive throws considerable light upon the effects due to the methods of balancing the wheels, and by alterations in this respect a saving of fuel of from 1 to 5 ℔ of coal per mile per locomotive has sometimes been effected.
By mapping the centres from which earthquakes originate off the coast of Japan, we have not only determined districts where geological activity is pronounced, but have placed before the cable engineer well-defined localities which it is advisable to avoid; and in the records of unfelt earthquakes which originate far from land similar information is being collected for the deeper parts of the oceans. Occasionally these records have almost immediately made clear the cause of a cable failure. From lack of such information in 1888, when the cables connecting Australia with the outer world were simultaneously broken, the sudden isolation was regarded as a possible operation of war, and the colonists called out their naval and military reserves. Records of earthquakes originating at great distances have also frequently enabled us to anticipate, to correct, to extend, or to disprove telegraphic accounts of the disasters. Whatever information a seismogram may give is certain, whilst the information gathered from telegrams may in the process of transit become exaggerated or minimized. Otherwise unaccountable disturbances in records from magnetographs, barographs and other instruments employed in observatories are frequently 825 explained by reference to the traces yielded by seismometers. Perhaps the greatest triumph in seismological investigation has been the determination of the varying rates at which motion is propagated through the world. These measurements have already thrown new light upon its effective rigidity, and if we assume that the density of the earth increases uniformly from its surface towards its centre, so that its mean density is 5.5, then, according to Knott, the coefficient of elasticity which governs the transmission of preliminary tremors of an earthquake increases at a rate of nearly 1.2% per mile of descent.
Authorities.—J. Milne, Seismology (London, 1898), Earthquakes (London, 1898), Bakerian Lecture, “Recent Advances in Seismology,” Proc. Roy. Soc., 1906, 77, p. 365; J.A. Ewing, Memoir on Earthquake Measurement (Tokyo, 1883); C.E. Dutton, Earthquakes in the Light of the New Seismology (London, 1904); “The Charleston Earthquake of Aug. 31, 1886,” Ninth Annual Report of the United States Geological Survey, 1889; W.H. Hobbs, Earthquakes, an Introduction to Seismic Geology (London, 1908), “The San Francisco Earthquake and Fire, 1906,” Bull. U.S. Geol. Surv. No. 324; “The California Earthquake of Ap. 18, 1906,” Rep. State Earthq. Com. (Washington, D.C., 1908); R.D. Oldham, “Report on the Great Earthquake of 12 June 1897,” Mem. Geol. Surv. India, xxix. 1899, “On the Propagation of Earthquake Motion to great Distances,” Phil. Trans., 1900, A, vol. 194, p. 135, “The Constitution of the Interior of the Earth as revealed by Earthquakes,” Quar. Jour. Geol. Soc., 1906, 62, p. 456; 1907, 63, p. 344; C. Davison, A Study of Recent Earthquakes (London, 1905); The Hereford Earthquake of December 17, 1896 (Birmingham, 1899), “The Investigation of Earthquakes,” Beiträge z. Geophysik, Bd. ix., 1908, p. 201, and papers on British earthquakes in Quart. Jour. Geol. Soc.; T.J.J. See, “The Cause of Earthquakes, Mountain Formation and Kindred Phenomena connected with the Physics of the Earth,” Proc. Amer. Phil. Soc., 1906, 45, p. 273; F. Frech, “Erdbeben und Gebirgsbau,” Petermann’s Mitteilungen, Bd. 53, 1907, p. 245 (with maps); C.G. Knott, The Physics of Earthquake Phenomena (Oxford, 1908); Comte F. de Montessus de Ballore, Les Tremblements de terre: géographie séismologique (Paris, 1906), La Science séismologique (1907); Transactions of the Seismological Society of Japan; Seismological Journal (Yokohama); Bollettino della Società Sismologica Italiana (Rome); Reports of the British Association, containing the annual reports of the Committee for Seismological Investigations; papers in the Beiträge zur Geophysik and the Ergänzungsbände.
1 The publications for 1880-1892 were termed the Transactions of the Seismological Society of Japan, and for 1893-1895 the Seismological Journal of Japan. The observations are now published by the Earthquake Investigation Committee of Japan, and edited by F. Omori, professor of seismology at the university of Tokyo.
2 The chief Italian station is at Rocca di Papa near Rome. It is equipped with delicate instruments designed by its director, Giovanni Agamennone. The records since 1895 are published in the Bollettino della Società Sismologica Italiana, edited by Luigi Palazzo, director of the Central Office for Meteorology and Geodynamics at Rome.
3 The chief Austrian publications are:—Mittheilungen der Erdbebencommission der k. Akad. der Wissen. in Wien (since 1897); Die Erdbebenwarte (1901-1907); and the “Neueste Erdbebennachrichten, Beilage der Monatsschrift Die Erdbebenwarte.”
4 The “International Seismological Association” was founded at Strassburg in 1903, and publishes the Beiträge zur Geophysik, edited by George Gerland, director of the Strassburg station; the papers are printed in several languages.
5 The records of the British Association stations are published (since 1896) in the Reports. Chile has a national earthquake service (founded after the Valparaiso earthquake of August 1906) directed by comte de Montessus de Ballore.
 |
| From Strasburger’s Lehrbuch der Botanik, by permission of Gustav Fischer. |
| Geaster Granulosus, nat. size. |
EARTH-STAR (Geaster), in botany, a kind of puff-ball, with a distinct outer coat which, on separating from the inner, splits into several divisions, which become reflexed and spread like a star. The inner coat enveloping the spores is supported, like a ball, either with or without a stalk on the upper face of the star. The spores escape generally by means of a distinct aperture which appears in the top of the ball. There are several species in Britain found on the ground or on decaying leaves. They are rare or local, but more common in the south or south-east of England than in other parts of Britain.
EARTHWORM, the common name of a chaetopod worm found nearly all over the world. Linnaeus recognized only one species of earthworm and named it Lumbricus terrestris. There are now one thousand well-characterized species known from different parts of the world, and the number increases almost daily. The earthworms of England belong entirely to the three genera Lumbricus, Allolobophora and Allurus, which are further subdivided by some systematists; and these genera form the prevalent earthworm fauna of the Palaearctic region and are also very numerous in the Nearctic region. Elsewhere they do not appear to be indigenous, but are replaced by the numerous other genera of the families enumerated in the article Chaetopoda (q.v.). It is a remarkable fact that these genera, comprizing a separate family Lumbricidae, when introduced into tropical and other countries, thrive abundantly and oust the indigenous forms. In gatherings of earthworms from various extra-European countries it is always found that if the collections have been made in cultivated ground and near the coast the worms are of European species; farther inland the native forms are met with. Inasmuch as in every case the Lumbricidae from non-European countries are identical with European species, since it has been shown that these animals are very readily introduced accidentally with plants, &c., and in view of the fact that they are impatient of sea water, it seems clear that the presence of these Lumbricidae in other continents is due to accidental transportation. Most earthworms live in the soil, which they devour as they burrow through it. A few, like their allies the river worms (Limicolae), habitually frequent streams, lakes, &c. One genus, at any rate, viz. Pontodrilus, seeks an unusual environment, and is found in heaps of sea-weed cast up by the sea. The range of this genus is therefore naturally wider than that of other genera which are confined to land masses and cannot cross the sea by their own efforts. It might be inferred, therefore, and the inference is proved by facts, that truly oceanic islands have no indigenous fauna of earthworms, but are inhabited by forms which are identical with those of neighbouring continents, and doubtless, therefore, accidentally introduced.
Like the leeches the earthworms produce cocoons which are a product of the glandular epithelium of the clitellum. In these cocoons are deposited the eggs together with a certain amount of albumen upon which the developing embryos feed. So far as is known, the production of cocoons is universal among earthworms and the remaining Oligochaeta of aquatic habit. The young leave the cocoon as fully formed earthworms in which, however, the genitalia are not fully developed. There is no free living larval stage. Out of a single cocoon emerge a varying number of young worms, the numbers being apparently characteristic of the species. The work of earthworms in aiding in the production of the subsoil and in levelling the surface was first studied by C. Darwin, and has since been investigated by others. This work is partly carried out beneath the surface and partly on the surface, upon which the worms wander at night and eject the swallowed and triturated earth; frequently castings of some height are formed of coiled ropes of agglutinated particles of mould. The indigenous species of Great Britain, about twenty in number, do not grow to a greater length than some 10 in.; but in several tropical countries there are species which grow to a length of from 3 to 6 ft. Thus we have in Natal the gigantic Microchaeta rappi, in Ceylon Megascolex coeruleus, in Australia Megascolides australis, and an equally large form in South America.
EARWIG, an insect belonging to the Forficulidae, a family usually referred to the Orthoptera, but sometimes regarded as typifying a special order, to which the names Dermaptera, Dermatoptera and Euplexoptera have been given, in allusion to certain peculiarities in the structure of the wings in the species that possess them. The front wings are short and horny and when at rest meet without overlapping in the middle line, like the wing-cases of brachelytrous (cocktail) beetles. The hind wings, on the contrary, are for the most part membranous and, when extended, of large size; each consists of two portions, the distal of which, in virtue of the arrangement and jointing of its nervures, is capable of being both doubled up and folded fanwise beneath the proximal, which is partly horny when the wing is tucked away under the front wing-case of the same side. Apart from these characteristics, the most distinctive feature of earwigs is the presence at the end of the abdomen of a pair of pincers which are in reality modified appendages, known as cercopods, and represent the similar limbs of Japyx and the caudal feelers of Campodea and some other insects.
The Forficulidae are almost cosmopolitan; but the various species and genera differ from each other both in structure and size to a comparatively slight extent. The length and armature of the pincers and the presence or absence of wings are perhaps the most important features used by systematists in distinguishing the various kinds. Of particular zoological interest in this connexion is a Ceylonese genus Dyscritina, in which the cercopods are long, many-jointed and filiform during the early stages of growth, and only assume at the last moult the forcipate structure characteristic of the family. The best known earwig is the common European species, Forficula auricularia. This insect is gregarious and nocturnal. It hides by day under stones or 826 the loosened bark of trees or in any crevice or hole sheltered from the light. At night it crawls about in search of food, which consists to a small extent of dead animal or vegetable matter, but principally, as gardeners are aware, of the petals and other parts of flowers of growing shoots and soft ripe fruit. During the winter earwigs lie dormant; but in the early months of the year females with their eggs may be found in the soil, frequently in deserted earthworm burrows. Maternal instincts are well developed, both the eggs, which number about fifty, and the young being carefully brooded and watched over by the parent. Except for the absence of wings, the young are miniature models of the adult. As growth proceeds the integument is periodically cast; and at the final moult the perfect winged insect appears. Males and females are like each other in size, but may be distinguished by the difference in the number of visible abdominal segments, the male having nine and the female seven. In the male, moreover, the pincers are caliper-like and toothed at the base, whereas in the female they are untoothed and only lightly curved at the tip. These differences suggest that the pincers aid in the pairing of the sexes. However that may be, they are known to be used in the folding of the wings; and their importance as weapons of defence is attested by the precision and effect with which they are wielded against assailants like ants.
EASEMENT (Fr. aise; O. Fr. aisement; Anglo-Lat. aisiamentum, a privilege or convenience), in English law, a species of “servitude” or limited right of use over land belonging to another. It is distinguished from profits à prendre—another species of servitude which involves a right to participate in the profits of the soil of another—since an easement confers merely a convenience (aisiamentum) to be exercised over the land of another (without any participation in the profits of it), i.e. a right to use the soil or produce of the soil in a way tending to the more convenient enjoyment of another piece of land. Thus a right of way is an easement, a right of common is a profit. An easement is distinguishable also from a licence, which, unless it is coupled with a grant, is personal to both grantor and grantee and is neither binding on the licensor, nor, in general, assignable by the licensee; while both the benefit and the burden of an easement are annexed to land (Gale on Easements, 8th ed. p. 2). With easements are sometimes classed certain closely allied “natural rights,” such as a landowner’s right to lateral support for his soil in its natural state, and a riparian owner’s right to the natural flow of a stream.
The essential features of an easement, in the strict sense of the term, are therefore these: (i.) It is an incorporeal right; a right to the use and enjoyment of land—not to the land itself; (ii.) it is imposed upon corporeal property; (iii.) it is a right without profit; (iv.) it requires for its constitution two distinct tenements—the “dominant tenement” which enjoys the right, and the “servient tenement” which submits to it. This last characteristic excludes from the category of easements the so-called “easements in gross,” such as a right of way conferred by grant independently of the possession of any tenement by the grantee. The true easement is an “appendant” or “appurtenant” right, not a “right in gross.”
Further classifications of easements must be noted. They are divided into (a) affirmative or positive, those which authorize the commission of an act by the dominant owner, e.g. rights of way, a right to draw water from a spring, rights of aqueduct, and negative, when the easement restricts the rights of the servient owner over his own property, e.g. prevents him from building on land so as to obstruct ancient lights (cf. also the right to the support of neighbouring soil); (b) continuous, of which the enjoyment may be continual without the interference of man, e.g. access to light, and discontinuous, where there must be a fresh act on each occasion of the exercise of the right, e.g. a right of way, or right to draw water; (c) apparent, where there are visible external signs of the exercise of the right, e.g. a right to dam up a watercourse, and non-apparent, where such signs are absent, e.g. a right to lateral support from land, a prohibition to build above a certain height.
Acquisition of Easements.—Easements may be acquired (a) by express grant, either by statute, or by deed inter vivos, or by will; (b) by an implied grant; (c) by express or implied reservation, e.g. by the owner of land in selling the fee (as to implied reservation, see Gale on Easements, 8th ed. pp. 137 et seq.); (d) by prescription, either at common law or under the Prescription Act 1832. An express grant, or express reservation, of an easement cannot be effected except by deed. An easement arises by implied grant where a man makes one part of his tenement dependent on another, or makes the parts mutually interdependent, and grants any such part with the dependence attaching to it to another person (Innes, Law of Easements, 7th ed. p. 10). For example, a man builds two houses, each of which by the plan of construction receives support from the other; this mutual right of support is a quasi-easement, of which on severance of the tenements the grantee of one will have the benefit; where the enjoyment of the severed tenement could not be had at all without such a right, it is said to be an “easement of necessity.”
Easements are acquired by prescription at common law by proof of “immemorial user” by the dominant owner and those through whom he claims. At one time it was thought that such proof must date back to the first year (1189) of Richard I. (see preamble to Prescription Act 1832). The ground, however, on which prescription was admitted as a means of acquiring easements was the fiction of a “lost grant.” Long enjoyment of the right pointed to its having had a legal origin in a grant from the servient owner, and so any period of reasonably long use came to be accepted. A “lost grant” may be presumed to have been made (the question is one of fact) if 20 years’ uninterrupted enjoyment is shown. To avoid the difficulties of proof of prescriptive right at common law, the Prescription Act 1832 established shorter periods of user. In the case of easements, other than light, the periods of prescription are 20 years for a claim that may be defeated, and 40 years for an indefeasible claim (s. 2). The right of access of light is dealt with under s. 3 (see Ancient Lights). The enjoyment to become prescriptive must be open, i.e. of such a character that the owner of the tenement said to be servient has a reasonable opportunity of becoming aware of the adverse claim (Union Lighterage Co. v. London Graving Dock Co., 1902, 2 Ch. 557); and it must be enjoyed as of right (Gardner v. Hodgson’s Kingston Brewery Co., 1903, A.C. 229) as against the owner of the tenement affected (Kilgour v. Gaddes, 1904, 1 K.B. 457). The periods of prescription are to be reckoned backwards from the time when some suit or matter involving the claim of the dominant owner has arisen (s. 4). Nothing is to be deemed an interruption unless the act of interruption has been submitted to, or acquiesced in, for a year (s. 4).
Easements may be extinguished (i.) by express release—here an instrument under seal is necessary; (ii.) by “merger,” i.e. where both tenements become the property of the same owner; (iii.) by abandonment through non-user. In the case of discontinuous easements, the shortest period of non-user may suffice if there is direct evidence of an intention to abandon.
A word may be added here as to the right to air. It is an actionable nuisance to cause pollution of the air entering a dwelling-house. The owner of a dwelling-house may by prescription acquire a right to the passage of air through it by a defined channel; and the enjoyment without interruption of ventilation by means of air flowing in a definite channel, with the knowledge of the owner and occupier of the adjoining premises, creates a presumption of the grant of such an easement (see Gale on Easements, 8th ed. p. 338).
In Scots Law the term “easement” is unknown. Both the name “servitude” and the main species of servitudes existing in Roman law (q.v.) have been adopted. The classification of servitudes into positive and negative, &c., and the modes of their creation and extinction, are similar to those of English law. The statutory period of prescription is 40 years (Scots Acts 1617, c. 12), or 20 years in the case of enjoyment under any ex facie valid irredeemable title duly recorded in the appropriate register of sasines (Conveyancing [Scotland] Act 1874). There are 827 certain servitudes special to Scots law, e.g. “thirlage,” by which lands are “thirled” or bound to a particular mill, and the possessors obliged to grind their grain there, for payment of certain multures (quantities of grain or meal, payable to the mill-owner) and sequels (small quantities given to the mill servants) as the customary price of grinding. Statutory provision has been made for the commutation of these duties (Thirlage Act 1799), and they have now almost disappeared.
The French Code Civil (Arts. 637 et seq.) and the other European codes (e.g. Belgium, arts. 637 et seq.; Holland, arts. 721 et seq.; Italy, arts. 531 et seq.; Spain, arts. 530 et seq.; Germany, arts. 1018 et seq.) closely follow Roman law. French law is in force in Mauritius, and has been followed in Quebec (Civil Code, arts. 499 et seq.) and St Lucia (Civil Code, arts. 449 et seq.). In India the law is regulated, on English lines, by the Easements Act 1882 (Act v. of 1882). The term “easements,” however, in India includes profits à prendre. In the South African colonies the law of easements is based on the Roman Dutch law (see Maasdorp, Institutes of Cape Law, 1904; Bk. ii. p. 166 et seq.). In most of the other colonies the law of easements is similar to English law. In some, however, it has been provided by statute that rights to the access and use of light or water cannot be acquired by prescription: e.g. Victoria (Water Act 1890, No. 1156, s. 3), Ontario (Real Property Limitation Act, Revised Stats. Ontario, 1897; c. 133, s. 36, light).
In the United States the law of easements is founded upon, and substantially identical with, English law. The English doctrine, however, as to acquisition of right of light and air by prescription is not accepted in most of the States.
Authorities.—English Law: Gale, Law of Easements (8th ed., London, 1908); Goddard, Law of Easements (6th ed., London, 1904); Innes, Digest of the Law of Easements (7th ed., London, 1903). Indian Law: Peacock, Easements in British India (Calcutta, 1904); Hudson and Inman, Law of Light and Air (2nd ed., London, 1905). Scots Law: Erskine, Principles of the Law of Scotland (20th ed., Edinburgh, 1903). American Law: Jones, Law of Easements (New York, 1898); Bouvier, Law Dict. (Boston and London, 1897); Ruling Cases, London and Boston, 1894-1901, tit. Easement (American Notes).
EAST, ALFRED (1849- ), English painter and etcher, was born at Kettering on the 15th of December 1849. One of the most prominent among modern English landscape painters, he received his art education first at the Glasgow School of Art and then in Paris at the École des Beaux-Arts, and under Robert-Fleury and Bouguereau. His landscapes are remarkable for the lyrical use of colour and for the pleasing rhythm of line which is the result of careful selection and building up of the elements that constitute the scene. Based on keen observation of the colour of nature and on careful studies of the details, they are arranged with a rare and by no means obvious sense of balance and compositional beauty which summarily discards all disturbing accidents of nature. He also achieved distinction as an etcher, and published an instructive and useful volume on landscape painting (London, 1906). He began to exhibit at the Royal Academy in 1882, and was elected an associate. In 1906 he became president of the Royal Society of British Artists. Many of his works are to be found in the English provincial galleries; Manchester owns “The Silent Somme” and “Autumn”; Liverpool, “Gibraltar from Algeciras”; Leeds, “The Golden Valley”; Birmingham, “Hayle from Lelant”; Preston, “An Idyll of Spring”; and Hull, “Evening on the Cotswolds.” His “Passing Storm” is at the Luxembourg; “The Nene Valley” at the Venice gallery; and “A Haunt of Ancient Peace” at the National gallery in Budapest. In 1903 he received the order of the Crown of Italy in connexion with his services to the Venice international exhibition; and he was made an honorary member of the Japanese Meiji Bijutsu Kai.
EAST ANGLIA, one of the kingdoms into which Anglo-Saxon Britain was divided. Bede gives no information about its origin except that its earliest settlers were Angles. The kingdom of East Anglia comprised the two counties of Norfolk and Suffolk. With regard to the western boundary we have no accurate information, but it was probably formed by the fens of Cambridgeshire.
This kingdom first appears in Bede’s narrative early in the 7th century, when its power was at its height. Towards the end of the reign of Æthelberht, who died about 616, Rædwald of East Anglia, who had apparently spent some time at the court of Kent, began to win for himself the chief position among the Anglo-Saxon kings of his day. His position was assured, at least temporarily, in 617, when he decided to espouse the cause of the Northumbrian prince Edwin, then a fugitive at his court, and defeated Æthelfrith of Northumbria on the banks of the Idle, a tributary of the Trent, in Mercian territory. Rædwald had been converted to Christianity in Kent, but after his return home he relapsed, according to Bede, owing to the influence of his wife, and there were to be seen in the same building a Christian and a pagan altar. Bede states that Rædwald was the son of Tytili, the son of Wuffa, from whom the East Anglian royal family derived their name Wuffingas. According to the Historia Brittonum Guffa (Wuffa) was the son of (Guecha) Wehha, who first ruled the East Angles in Britain. This would put the organization of the kingdom in the first or second quarter of the 6th century. Eorpwald, the son of Rædwald, was converted to Christianity by Edwin, but was soon afterwards slain by Ricberht (627 or 628), whereupon the kingdom again became pagan for three years, when Sigeberht, the brother of Eorpwald, became king and founded a see for Felix at Dunwich. Sigeberht also founded a school in East Anglia, and on the arrival of an Irish missionary named Furšeus he built him a monastery at Cnobheresburg, perhaps to be identified with Burgh Castle. Before 644, however, Sigeberht resigned the crown in favour of his brother Ecgric and retired to a monastery. Shortly afterwards both brothers were slain by Penda of Mercia in his invasion of East Anglia, and Anna became king. This king was an enthusiastic Christian, and converted Cœnwalh, king of Wessex, who had fled to his court. Two of his daughters, Sæthryth and Æthelberg, took the veil; while another, Sexburg, was married to Earconberht, king of Kent; and a fourth, Æthelthryth, after two marriages, with Tondberht of the South Gyrwe and Ecgfrith of Northumbria, became abbess of Ely. In 654 Anna was slain by Penda of Mercia, and was succeeded by his brother Æthelhere, who was killed in 655 at the Winwaed, fighting for the Mercian king against Oswio of Northumbria. In 673 Archbishop Theodore divided the East Anglian diocese into two, Elmham being the seat of the northern, Dunwich that of the southern bishop. A long blank follows in the history of this kingdom, until in 792 we find Offa of Mercia slaying Æthelberht, king of East Anglia, who is said to have been his son-in-law. East Anglia was subject to the supremacy of the Mercian kings until 825, when its people slew Beornwulf of Mercia, and with their king acknowledged Ecgberht (Egbert) of Wessex as their lord. In 870 Edmund, king of East Anglia, was killed by the Danes under I′varr and Ubbi, the sons of Ragnar Loðbrok.
The following is a list of the kings of East Anglia of whom there is record:—Wehha; Wuffa; Rædwald, son of Tytili and grandson of Wuffa (reigning 617); Eorpwald, son of Rædwald (d. 627 or 628); Sigeberht, brother of Eorpwald; Ecgric, brother of Sigeberht (both slain before 644); Anna, son of Ene and grandson of Tytili (d. 654); Æthelhere, brother of Anna (d. 655); Æthelwald, a third brother; Aldwulf (succ. 663, d. 713), son of Æthelric and grandson of Ene; Elfwald, son of Aldwulf (d. 749); Hun Beonna and Alberht; Æthelberht (792); Edmund (870).
After the death of Ragnar Loðbrok’s sons East Anglia was occupied by the Danish king Guthrum, who made a treaty with Alfred settling their respective boundaries, probably about 880. Guthrum died in 890. A later king named Eohric took up the cause of Æthelwald, the son of Æthelred I., and was slain in the fight with the Kentish army at the Holm in 905. A war broke out with King Edward the Elder in 913; in 921 a king whose name is unknown was killed at the fall of Tempsford, and in the same year the Danes of East Anglia submitted to Edward the Elder. From this time, probably, East Anglia was governed by English earls, the most famous of whom were Æthelstan, surnamed Half-King (932-956) and his sons, 828 Æthelwold (956-962), and Æthelwine, surnamed Dei amicus (962-992).
See Bede, Hist. Eccl. (ed. C. Plummer, Oxford. 1896), ii. 5, 15, iii. 7, 8, 18-20, 22, iv. 3, 5, 23; Saxon Chronicle (ed. Earle and Plummer, Oxford, 1899), s. a. 823, 838, 866, 870, 880, 885, 890, 894, 905, 921; Historia Brittonum (San-Marte, 1844), s. 59; H. Sweet, Oldest English Texts, p. 171 (London, 1885).
EASTBOURNE, a municipal borough (1883) in the Eastbourne parliamentary division of Sussex, England, 61 m. S.S.E. of London by the London, Brighton & South Coast railway. Pop. (1891) 34,969; (1901) 43,344; (local census, 1909) 49,286. It is situated 3 m. N.E. of Beachy Head, the loftiest headland on the English Channel coast. It once consisted of three parts—the village of East Bourne, a mile inland; South Bourne, lying back from the shore; and Seahouses, facing the beach. The church of St Mary, the ancient parish church of East Bourne, is a fine transitional Norman building; and there are numerous modern churches and chapels. The principal buildings and institutions are the town hall and municipal buildings, the Princess Alice Memorial and other hospitals, a free library and, among many high-class schools, Eastbourne College for boys, founded in 1867. There is a fine pier with pavilion, and a marine parade nearly 3 m. in extent, arranged in terraced promenades. Devonshire Park of 13 acres is pleasantly laid out, and contains a pavilion and a theatre. The duke of Devonshire is the principal landowner. Golf links are laid out on the neighbouring downs. A Roman villa was formerly seen close to the shore, but it is not now visible. The corporation consists of a mayor, 8 aldermen and 24 councillors. In 1910 the corporation promoted a bill in parliament to add the Hampden Park district in the parish of Willingdon to the borough and to make Eastbourne, with this extension, a county borough.
EAST CHICAGO, a city of Lake county, Indiana, U.S.A., on Lake Michigan, about 19 m. S.E. of the business centre of Chicago. Pop. (1890) 1255; (1900) 3411 (1331 foreign-born); (1910) 19,098. It is served by several railways, including the Pennsylvania, the Wabash, the Chicago Terminal Transfer (whose shops are here), the Lake Shore & Michigan Southern, the Chicago, Indiana & Southern, and the Indiana Harbor railways. East Chicago covers an area whose greatest dimensions are 4 by 3½ m. That part of the city along the lake, known as Indiana Harbor, dates from 1901 and has grown very rapidly because of its position at the southernmost part of the Calumet District, and because of the meeting here of railway and lake commerce. A good harbour has been constructed, a new ship canal connecting the harbour with the Calumet river. East Chicago is industrially virtually a part of “Greater” Chicago; among its manufactures are iron and steel, cement, lumber, boilers, hay presses, chains, chemicals and foundry products. East Chicago was chartered as a city in 1893.
EASTER, the annual festival observed throughout Christendom in commemoration of the resurrection of Jesus Christ. The name Easter (Ger. Ostern), like the names of the days of the week, is a survival from the old Teutonic mythology. According to Bede (De Temp. Rat. c. xv.) it is derived from Eostre, or Ostâra, the Anglo-Saxon goddess of spring, to whom the month answering to our April, and called Eostur-monath, was dedicated. This month, Bede says, was the same as the mensis paschalis, “when the old festival was observed with the gladness of a new solemnity.”
The name of the festival in other languages (as Fr. pâques; Ital. pasqua; Span. pascua; Dan. paaske; Dutch paasch; Welsh pasg) is derived from the Lat. pascha and the Gr. πάσχα. These in turn come from the Chaldee or Aramaean form פסהא pascha’, of the Hebrew name of the Passover festival פסח pesach, from פסח “he passed over,” in memory of the great deliverance, when the destroying angel “passed over the houses, of the children of Israel in Egypt when he smote the Egyptians” (Exod. xii. 27).
An erroneous derivation of the word pascha from the Greek πάσχειν, “to suffer,” thus connected with the sufferings or passion of the Lord, is given by some of the Fathers of the Church, as Irenaeus, Tertullian and others, who were ignorant of Hebrew. St Augustine (In Joann. Tract. 55) notices this false etymology, shows how similarity of sound had led to it, and gives the correct derivation.
There is no indication of the observance of the Easter festival in the New Testament, or in the writings of the apostolic Fathers. The sanctity of special times was an idea absent from the minds of the first Christians. “The whole of time is a festival unto Christians because of the excellency of the good things which have been given” is the comment of St Chrysostom on 1 Cor. v. 7, which has been erroneously supposed to refer to an apostolic observance of Easter. The ecclesiastical historian Socrates (Hist. Eccl. v. 22) states, with perfect truth, that neither the Lord nor his apostles enjoined the keeping of this or any other festival. He says: “The apostles had no thought of appointing festival days, but of promoting a life of blamelessness and piety”; and he attributes the observance of Easter by the church to the perpetuation of an old usage, “just as many other customs have been established.”
This is doubtless the true statement of the case. The first Christians continued to observe the Jewish festivals, though in a new spirit, as commemorations of events which those festivals had foreshadowed. Thus the Passover, with a new conception added to it of Christ as the true Paschal Lamb and the first fruits from the dead, continued to be observed, and became the Christian Easter.
Although the observance of Easter was at a very early period the practice of the Christian church, a serious difference as to the day for its observance soon arose between the Christians of Jewish and those of Gentile descent, which led to a long and bitter controversy. The point at issue was when the Paschal fast was to be reckoned as ending. With the Jewish Christians, whose leading thought was the death of Christ as the Paschal Lamb, the fast ended at the same time as that of the Jews, on the fourteenth day of the moon at evening, and the Easter festival immediately followed, without regard to the day of the week. The Gentile Christians, on the other hand, unfettered by Jewish traditions, identified the first day of the week with the Resurrection, and kept the preceding Friday as the commemoration of the crucifixion, irrespective of the day of the month. With the one the observance of the day of the month, with the other the observance of the day of the week, was the guiding principle.
Generally speaking, the Western churches kept Easter on the first day of the week, while the Eastern churches followed the Jewish rule, and kept Easter on the fourteenth day. St Polycarp, the disciple of St John the Evangelist and bishop of Smyrna, visited Rome in 159 to confer with Anicetus, the bishop of that see, on the subject; and urged the tradition, which he had received from the apostle, of observing the fourteenth day. Anicetus, however, declined to admit the Jewish custom in the churches under his jurisdiction, but readily communicated with Polycarp and those who followed it. About forty years later (197) the question was discussed in a very different spirit between Victor, bishop of Rome, and Polycrates, metropolitan of proconsular Asia. That province was the only portion of Christendom which still adhered to the Jewish usage, and Victor demanded that all should adopt the usage prevailing at Rome. This Polycrates firmly refused to agree to, and urged many weighty reasons to the contrary, whereupon Victor proceeded to excommunicate Polycrates and the Christians who continued the Eastern usage. He was, however, restrained from actually proceeding to enforce the decree of excommunication, owing to the remonstrance of Irenaeus and the bishops of Gaul. Peace was thus maintained, and the Asiatic churches retained their usage unmolested (Euseb. H.E. v. 23-25). We find the Jewish usage from time to time reasserting itself after this, but it never prevailed to any large extent.
A final settlement of the dispute was one among the other reasons which led Constantine to summon the council of Nicaea in 325. At that time the Syrians and Antiochenes were the solitary champions of the observance of the fourteenth day. The decision of the council was unanimous that Easter was to be kept on Sunday, and on the same Sunday throughout the world, 829 and “that none should hereafter follow the blindness of the Jews” (Socrates, H.E. i. 9). The correct date of the Easter festival was to be calculated at Alexandria, the home of astronomical science, and the bishop of that see was to announce it yearly to the churches under his jurisdiction, and also to the occupant of the Roman see, by whom it was to be communicated to the Western churches. The few who afterwards separated themselves from the unity of the church, and continued to keep the fourteenth day, were named Quartodecimani, and the dispute itself is known as the Quarto-deciman controversy. Although measures had thus been taken to secure uniformity of observance, and to put an end to a controversy which had endangered Christian unity, a new difficulty had to be encountered owing to the absence of any authoritative rule by which the paschal moon was to be ascertained. The subject is a very difficult and complex one (see also Calendar). Briefly, it may be explained here that Easter day is the first Sunday after the full moon following the vernal equinox. This, of course, varies in different longitudes, while a further difficulty occurred in the attempt to fix the correct time of Easter by means of cycles of years, when the changes of the sun and moon more or less exactly repeat themselves. At first an eight years’ cycle was adopted, but it was found to be faulty, then the Jewish cycle of 84 years was used, and remained in force at Rome till the year 457, when a more accurate calculation of a cycle of 532 years, invented by Victorius of Acquitaine, took its place. Ultimately a cycle of 19 years was accepted, and it is the use of this cycle which makes the Golden Number and Sunday Letter, explained in the preface to the Book of Common Prayer, necessary. Owing to this lack of decision as to the accurate finding of Easter, St Augustine tells us (Epist. 23) that in the year 387 the churches of Gaul kept Easter on the 21st of March, those of Italy on the 18th of April, and those of Egypt on the 25th of April; and it appears from a letter of Leo the Great (Epist. 64, ad Marcian.) that in 455 there was a difference of eight days between the Roman and the Alexandrine Easter. Gregory of Tours relates that in 577 “there was a doubt about Easter. In Gaul we with many other cities kept Easter on the fourteenth calends of May, others, as the Spaniards, on the twelfth calends of April.”
The ancient British and Celtic churches followed the cycle of 84 years which they had originally received from Rome, and their stubborn refusal to abandon it caused much bitter controversy in the 8th century between their representatives and St Augustine of Canterbury and the Latin missionaries. These latter unfairly attempted to fix the stigma of the Quartodeciman observance on the British and Celtic churches, and they are even now sometimes ignorantly spoken of as having followed the Asiatic practice as to Easter. This, however, is quite erroneous. The British and Celtic churches always kept Easter according to the Nicene decree on a Sunday. The difference between them and the Roman Church, at this period, was that they still followed the 84 years’ cycle in computing Easter, which had been abandoned at Rome for the more accurate cycle of 532 years. This difference of calculation led to Easter being observed on different Sundays, in certain years, in England, by the adherents of the two churches. Thus Bede records that in a certain year (which must have been 645, 647, 648 or 651) Queen Eanfleda, who had received her instruction from a Kentish priest of the Roman obedience, was fasting and keeping Palm Sunday, while her husband, Oswy, king of Northumbria, following the rule of the British church, was celebrating the Easter festival. This diversity of usage was ended, so far as the kingdom of Northumbria was concerned, by the council of Streaneshalch, or Whitby, in 654. To Archbishop Theodore is usually ascribed the credit of ending the difference in the rest of England in 669.
The Gregorian correction of the calendar in 1582 has once more led to different days being observed. So far as Western Christendom is concerned the corrected calendar is now universally accepted, and Easter is kept on the same day, but it was not until 1752 that the Gregorian reformation of the calendar was adopted in Great Britain and Ireland. Jealousy of everything emanating from Rome still keeps the Eastern churches from correcting the calendar according to the Gregorian reformation, and thus their Easter usually falls before, or after, that of the Western churches, and only very rarely, as was the case in 1865, do the two coincide.
Easter, as commemorating the central fact of the Christian religion, has always been regarded as the chief festival of the Christian year, and according to a regulation of Constantine it was to be the first day of the year. This reckoning of the year as beginning at Easter lingered in France till 1565, when, by an ordinance of Charles IX., the 1st of January finally took its place.
Four different periods may be mentioned as connected with the observance of Easter, viz. (1) the preparatory fast of the forty days of Lent; (2) the fifteen days, beginning with the Sunday before and ending with the Sunday after Easter, during which the ceremonies of Holy Week and the services of the Octave of Easter were observed; this period, called by the French the Quinzaine de Pâques, was specially observed in that country; (3) the Octave of Easter, during which the newly-baptized wore their white garments, which they laid aside on the Sunday after Easter, known as Dominica in albis depositis from this custom; another name for this Sunday was Pascha clausum, or the close of Easter, and from a clipping of the word “close” the English name of “Low” Sunday is believed to be derived; (4) Eastertide proper, or the paschal season beginning at Easter and lasting till Whit Sunday, during the whole of which time the festival character of the Easter season was maintained in the services of the church.
Many ecclesiastical ceremonies, growing up from early times, clustered round the celebration of the Easter festival. One of the most notable of these was the use of the paschal candle. This was a candle of very large dimensions, set in a candlestick big enough to hold it, which was usually placed on the north side, just below the first ascent to the high altar. It was kept alight during each service till Whitsuntide. The Paschal, as it was called at Durham cathedral, was one of the chief sights of that church before the Reformation. It was an elaborate construction of polished brass, and, contrary to the usual custom, seems to have been placed in the centre of the altar-step, long branches stretching out towards the four cardinal points, bearing smaller candles. The central stem of the candlestick was about 38 ft. high, and bore the paschal candle proper, and together they reached a combined height of about 70 ft., the candle being lighted from an opening above. Other paschal candles seem to have been of scarcely less size. At Lincoln, c. 1300, the candle was to weigh three stones of wax; at Salisbury in 1517 it was to be 36 ft. long; and at Westminster in 1558 it weighed no less than 3 cwt. of wax. After Whitsuntide what remained was made into smaller candles for the funerals of the poor. In the ancient churches at Rome the paschal candlesticks were fixtures, but elsewhere they were usually movable, and were brought into the church and set up on the Thursday before Easter. At Winchester the paschal candlestick was of silver, and was the gift of Canute. Others of more or less importance are recorded as having been at Canterbury, Bury St Edmunds, Hereford and York. The burning of the paschal candle still forms part of the Easter ceremonial of the Roman Catholic Church (see Lights, Ceremonial).
The liturgical colour for Easter was everywhere white, as the sign of joy, light and purity, and the churches and altars were adorned with the best ornaments that each possessed. Flowers and shrubs no doubt in early times were also used for this purpose, but what evidence there is goes against the medieval use of such decorations, which are so popular at the present day.
It is not the purpose of this article to enter on the wide subject of the popular observances, such as the giving and sending of Pasch or Easter eggs as presents. For such the reader may consult Brand’s Popular Antiquities, Hone’s Every-Day Book, and Chambers’s Book of Days.
Authorities.—Bingham, Antiquities of the Christian Church; Bede, Ecclesiastical History of England; Procter and Frere, A New History of the Book of Common Prayer (London, 1901); Surtees Society, Rites of Durham, ed. J.T. Fowler (1903); De Morgan, Companion to the Almanac (1845); De Moleon, Voyages liturgiques (Paris, 1718).
EASTER ISLAND (Rapanui, i.e. Great Rapa), an island in the eastern part of the South Pacific ocean, belonging to Chile (since 1888), in 27° 8′ S. and 109° 28′ W., 1400 m. E. of Pitcairn, and 2000 m. from the South American coast. It is roughly triangular in shape, with its hypotenuse 12 m. long running north-east and south-west, and its three angles marked by three volcanic peaks, of which the north-eastern reaches 1768 ft. of altitude. The area of the island is 45 sq. m. The coast has no good natural harbour, and landing is difficult. There is no lack of fertile soil, and the climate is moist enough to make up for the absence of running water. Formerly the island appears to have been wooded, but it now presents only a few bushes (Edwardsia, Broussonetia, &c.), ferns, grasses, sedges, &c. The natives grow bananas in the shelter of artificial pits, also sugar-canes and sweet potatoes, and keep a few goats and a large stock of domestic fowls, and a Tahitian commercial house breeds cattle and sheep on the island.
It is doubtful whether Rapanui was discovered by Davis in 1686, though it is sometimes marked Davis Island on maps. Admiral Roggeveen reached it on Easter day 1722; in 1774 Captain Cook discovered it anew and called it Teapi or Waihu. It was subsequently visited by La Pérouse (1776), Kotzebue (1816), &c. At the time of Roggeveen’s discovery the island probably contained from 2000 to 3000 inhabitants of Polynesian race, who, according to their own tradition, came from Rapa Iti (Little Rapa) or Oparo, one of the Tubuai or Austral group. In 1863 a large proportion of the inhabitants were kidnapped by the Peruvians and transported to work at the guano diggings on the Chincha Islands. The next year a Jesuit mission from Tahiti reached the island and succeeded in the task of civilization. The natives, who number scarcely one hundred, are all Christians.
Easter Island is famous for its wonderful archaeological remains. Here are found immense platforms built of large cut stones fitted together without cement. They are generally built upon headlands, and on the slope towards the sea. The walls on the seaside are, in some of the platforms, nearly 30 ft. high and from 200 to 300 ft. long, by about 30 ft. wide. Some of the squared stones are as much as 6 ft. long. On the land side of the platforms there is a broad terrace with large stone pedestals upon which once stood colossal stone images carved somewhat into the shape of the human trunk. On some of the platforms there are upwards of a dozen images, now thrown from their pedestals and lying in all directions. Their usual height is from 14 to 16 ft., but the largest are 37 ft., while some are only about 4 ft. They are formed from a grey trachytic lava found at the east end of the island. The top of the heads of the images is cut flat to receive round crowns made of a reddish vesicular tuff found at a crater about 8 m. distant from the quarry where the images were cut. A number of these crowns still lie at the crater apparently ready for removal, some of the largest being over 10 ft. in diameter. In the atlas illustrating the voyage of La Pérouse a plan of the island is given, with the position of several of the platforms. Two of the images are also represented in a plate. One statue, 8 ft. in height and weighing 4 tons, was brought to England, and is now in the British Museum. In one part of the island are the remains of stone houses nearly 100 ft. long by about 20 ft. wide. These are built in courses of large flat stones fitted together without cement, the walls being about 5 ft. thick and over 5 ft. high. They are lined on the inside with upright slabs, on which are painted geometrical figures and representations of animals. The roofs are formed by placing slabs so that each course overlaps the lower one until the opening becomes about 5 ft. wide, when it is covered with flat slabs reaching from one side to the other. The lava rocks near the houses are carved into the resemblance of various animals and human faces, forming, probably, a kind of picture writing. Wooden tablets covered with various signs and figures have also been found. The only ancient implement discovered on the island is a kind of stone chisel, but it seems impossible that such large and numerous works could have been executed with such a tool. The present inhabitants of Easter Island know nothing of the construction of these remarkable works; and the entire subject of their existence in this small and remote island is a mystery.
EASTERN BENGAL AND ASSAM, a province of British India, which was constituted out of Assam and the eastern portion of Bengal on the 16th of October 1905. Area 111,569 sq. m.; pop. (1901) 30,961,459. It is situated between 20° 45′ and 28° 17′ N., and between 87° 48′ and 97° 5′ E. The province, as thus reconstituted, consists of the Bengal districts of Dacca, Mymensingh, Faridpur, Backergunje, Tippera, Noakhali, Chittagong, Chittagong Hill Tracts, Rajshahi, Dinajpur, Jalpaiguri, Rangpur, Bogra, Pabna, Malda, and the native states of Kuch Behar and Hill Tippera; and the whole of the former area of Assam consisting of the districts of Goalpara, Kamrup, Darrang, Nowgong, Sibsagar, Lakhimpur, Sylhet, Cachar, Garo Hills, Khasi and Jaintia Hills, Naga Hills and Lushai Hills. It is bounded on the N. by Bhutan, on the W. by Burma, on the S. by Burma and the Bay of Bengal, and on the E. by Bengal. The line of demarcation between Bengal and the new province begins at the frontier of Bhutan, east of Darjeeling, runs south-west to Sahibganj on the Ganges and thence follows the course of the Ganges down to the deltaic branch, called the Haringhata, which leaves the main stream above Goalanda, and the course of the latter, which runs south into the Bay of Bengal. The capital of the province is Dacca, and its chief port is Chittagong.
The Bengal districts which were transferred to Eastern Bengal and Assam comprised northern and eastern Bengal, the most prosperous and least overcrowded portion of Bengal. The land there is less densely populated, wages are higher and food cheaper, and the rainfall more copious and more regular, while the staple crops of jute, tobacco and rice command a higher price relative to the rent of the land than in Behar or other parts of Bengal. The population are largely Mahommedans and of a more virile stock than the Bengali proper. Northern Bengal corresponds almost exactly with the Rajshahi division and lies within the boundaries of the Ganges and Brahmaputra rivers. It contains much high land of a stiff red clay, with an undulating surface covered for the most part with scrub jungle. The inhabitants are Indo-Chinese, not Indo-Aryans as in Bengal proper, and are Mahommedan by religion instead of Hindu. Eastern Bengal consists of the Dacca and Chittagong divisions which are mainly Bengali in race and Hindu in religion. For the Assamese districts see Assam. The province as a whole contains 18,036,688 Mahommedans and 12,036,538 Hindus. In language 27,272,895 of the inhabitants speak Bengali, 1,349,784 speak Assamese, and the remainder Hindi and various hill dialects, Manipuri, Bodo, Khasi and Garo. The administration is in the hands of a lieutenant-governor, assisted by a legislative council of fifteen members. Under him are five commissioners, and financial matters are regulated by a board of revenue consisting of two members.
The constitution of the new province arose out of the fact that Bengal had grown too unwieldy for the administration of a single lieutenant-governor. In 1868 Sir Stafford Northcote drew attention to the greatly augmented demands that the outlying portions of Bengal made on the time and labour of the government. At that time the population of the province was between 40 and 50 millions, and the question was left in abeyance until 1903, when the population had risen to 78½ millions. In the meantime the importance of rendering Assam a self-contained and independent administration with a service of its own, and of providing for its future commercial expansion, had arisen. These two considerations led Lord Curzon to propose that Bengal should be lopped of territory both on its eastern and western borders, and that all the districts east of the Brahmaputra should be constituted into a separate province. This proposal was bitterly opposed by the Hindus of Bengal on the ground that it would destroy the unity of the Bengali race; and their agitation was associated with the Swadeshi (own country) movement for the boycott of British goods.
After the constitution of the province in October 1905, the agitation in Eastern Bengal increased. Public meetings of protest were held, vernacular broadsheets containing scandalous 831 attacks on the British authorities were circulated, schoolboys and others were organized and drilled as so-called “national volunteers,” and employed as pickets to prevent the sale of British goods. Such was the state of things when Sir J. Bampfylde Fuller entered on his office as first lieutenant-governor of Eastern Bengal in January 1906. His reception was ominous. Representative bodies that were dominated by Hindus refused to vote the usual addresses of welcome, and non-official Hindus abstained from paying the customary calls. There were, however, no further overt signs of objection to the lieutenant-governor personally, and after a month or two—in spite of, or perhaps because of, his efforts to restrain sedition and to keep discipline in the schools—there was a decided change in the attitude of Hindu opinion. At Dacca, in July, for instance, the reception at Government House was attended by large numbers of Bengali gentlemen, who assured the lieutenant-governor that “the trouble was nearly ended.” The agitation was, in fact, largely artificial, the work of Calcutta lawyers, journalists and schoolmasters; the mass of the people, naturally law-abiding, was unmoved by it so long as the government showed a firm hand; while the Mussulmans, who formed a large proportion of the whole, saw in the maintenance of the partition and of the prestige of the British government the guarantees of their own security.
All seemed to be going well when an unfortunate difference of opinion occurred between the lieutenant-governor and the central government, resulting in the resignation of Sir Bampfylde Fuller (August 1906) and in ulterior consequences destined to be of far-reaching import. The facts are briefly as follows. Acting on a report of Dr P. Chatterji, inspector of schools, dated January 2, 1906, the lieutenant-governor, on the 10th of February, addressed a letter to the registrar of Calcutta University recommending that the privilege of affiliation to the university should be withdrawn from the Banwarilal and Victoria high schools at Sirajganj in Pabna, as a punishment for the seditious conduct of both pupils and teachers. Apart from numerous cases of illegal interference with trade and of disorder in the streets reported against the students, two specific outrages of a serious character were instanced as having occurred on the 15th of November: the raiding of a cart laden with English cloth belonging to Marwari traders, and a cowardly assault by some 40 or 50 lads on the English manager of the Bank of Bengal. These outrages “were not the result of thoughtlessness or sudden excitement, but were the outcome of a regularly organized scheme, set on foot and guided by the masters of these schools, for employing the students in enforcing a boycott.” All attempts to discover and punish the offenders had been frustrated by the refusal of the school authorities to take action, and in the opinion of the lieutenant-governor the only course open was to apply the remedy suggested in the circular letter addressed to magistrates and collectors (October 10, 1905) by Mr R.W. Carlyle, the officiating chief secretary to the government of Bengal, directing them, in the event of students taking any part in political agitation, boycotting and the like, to inform the heads of schools or colleges concerned that, unless they prevented such action being taken by the boys attending their institutions, their grant-in-aid and the privilege of competing for scholarships and of receiving scholarship-holders would be withdrawn, and that the university would be asked to disaffiliate their institutions.
The reply, dated July 5th, from the secretary in the home department of the government of India, was—to use Sir Bampfylde’s own later expression—to throw him over. It was likely that a difference of opinion in the syndicate of the university would arise as to the degree of culpability that attached to the proprietors of the schools; in the event of the syndicate taking any “punitive action,” the matter was certain to be raised in the senate, and would lead to an acrimonious public discussion, in which the partition of Bengal and the administration of the new province would be violently attacked; and in the actual state of public opinion in Bengal it seemed to the government of India highly inexpedient that such a debate should take place. “Collective punishment,” too, “would be liable to be misconstrued in England,” and the government preferred to rely on the gradual effect of the new university regulations, which aimed “at discouraging the participation of students in political movements by enforcing the responsibility of masters and the managing committees of schools for maintaining discipline.”
On receipt of this communication Sir Bampfylde Fuller at once tendered his resignation to the viceroy (July 15). He pointed out that to withdraw from the position taken up would be “concession, not in the interests of education, but to those people in Calcutta who have been striving to render my government impossible, in order to discredit the partition”; that previous concessions had had merely provocative effects, and that were he to give way in this matter his authority would be so weakened that he would be unable to maintain order in the country. On the 3rd of August, after some days of deliberation, the viceroy telegraphed saying that he was “unable to reconsider the orders sent,” and accepting Sir Bampfylde’s resignation. By the Anglo-Indian press the news was received with something like consternation, the Times of India describing the resignation as one of the gravest blunders ever committed in the history of British rule in India, and as a direct incentive to the forces of disquiet, disturbance and unrest. Equally emphatic was the verdict of the Mussulman community forming two-thirds of the population of Eastern Bengal. On the 7th of August, the day of Sir Bampfylde Fuller’s departure from Dacca, a mass-meeting of 30,000 Mahommedans was held, which placed on record their disapproval of a system of government “which maintains no continuity of policy,” and expressed its feeling that the lowering of British prestige must “alienate the sympathy of a numerically important and loyal section of His Majesty’s subjects”; and many meetings of Mussulmans subsequently passed resolutions to the same general effect. The Akhbar-i-Islam, the organ of Bombay Mussulman opinion, deplored the “unwise step” taken by the government, and ascribed it to Lord Minto’s fear of the Babu press, a display of weakness of which the Babus would not be slow to take advantage.
This latter prophecy was not slow in fulfilling itself. So early as the 8th of August Calcutta was the scene of several large demonstrations at which the Swadeshi vow was renewed, and at which resolutions were passed declining to accept the partition as a settled fact, and resolving on the continuance of the agitation. The tone of the Babu press was openly exultant: “We have read the familiar story of the Russian traveller and the wolves,” said a leading Indian newspaper in Calcutta. “The British government follows a similar policy. First the little babies were offered up in the shape of the Bande Mataram circular and the Carlyle circular. Now a bigger boy has gone in the person of our own Joseph. Courage, therefore, O wolves! Press on and the horse will soon be yours to devour! Afterwards the traveller himself will alone be left.”1 The task before the new lieutenant-governor of Eastern Bengal, the Hon. L. Hare, was obviously no easy one. The encouragement given to sedition by the weakness of the government in this case was shown by later events in Bengal and elsewhere (see India: History, ad fin.).
For the early history of the various portions of the province see Bengal and Assam.
See Sir James Bourdillon, The Partition of Bengal (Society of Arts, 1905); official blue-books on The Reconstitution of the Provinces of Bengal and Assam (Cd. 2658 and 2746), and Resignation of Sir J. Bampfylde Fuller, lieutenant-governor, &c. (Cd. 3242). A long letter from Sir J.B. Fuller, headed J’accuse, attacking the general policy of the Indian government in regard to the seditious propaganda, appeared in The Times of June 6, 1908.
1 Quoted by Mr F.S.P. Lely in The Times of November 22, 1906.
EASTERN QUESTION, THE, the expression used in diplomacy from about the time of the congress of Verona (1822) to comprehend the international problems involved in the decay of the Turkish empire and its supposed impending dissolution. The essential questions that are involved are so old that historians commonly speak of the “Eastern Question” in reference to events that happened long before the actual phrase was coined. But, wherever used, it is always the Turkish Question, the 832 generic term in which subsidiary issues, e.g. the Greek, Armenian or Macedonian questions, are embraced. That a phrase of so wide and loose a nature should have been stereotyped in so narrow a sense is simply the outcome of the conditions under which it was invented. To the European diplomatists of the first half of the 19th century the Ottoman empire was still the only East with which they were collectively brought into contact. The rivalry of Great Britain and Russia in Persia had not yet raised the question of the Middle East; still less any ambitions of Germany in the Euphrates valley. The immense and incalculable problems involved in the rise of Japan, the awakening of China, and their relations to the European powers and to America—known as the Far Eastern Question—are comparatively but affairs of yesterday.
The Eastern Question, though its roots are set far back in history—in the ancient contest between the political and intellectual ideals of Greece and Asia, and in the perennial rivalry of the powers for the control of the great trade routes to the East—dates in its modern sense from the treaty of Kuchuk Kainarji in 1774, which marked the definitive establishment of Russia as a Black Sea power and formed the basis of her special claims to interfere in the affairs of the Ottoman empire. The compact between Napoleon and the emperor Alexander I. at Tilsit (1807) marked a new phase, which culminated in 1812 in the treaty of Bucharest, in which Russia definitely appeared as the protector of the Christian nationalities subject to the Ottoman sultan.
The attitude of the various powers in the Eastern Question was now defined. Russia, apart from her desire to protect the Orthodox nationalities subject to the Ottoman power, aimed at owning or controlling the straits by which alone she could find an outlet to the Mediterranean and the ocean beyond. Austria, once the champion of Europe against the Turk, saw in the Russian advance on the Danube a greater peril than any to be feared from the moribund Ottoman power, and made the maintenance of the integrity of Turkey a prime object of her policy. She was thus brought into line with Great Britain, whose traditional friendship with Turkey was strengthened by the rise of a new power whose rapid advance threatened the stability of British rule in India. But though Austria, Great Britain and presently France, were all equally interested in maintaining the Ottoman empire, the failure of the congress of Vienna in 1815 to take action in the matter of a guarantee of Turkey, and the exclusion of the Sultan from the Holy Alliance, seemed to endorse the claim of Russia to regard the Eastern Question as “her domestic concern” in which “Europe” had no right to interfere. The revolt of the Greeks (1821) put this claim to the test; by the treaty of Adrianople (1829) Russia stipulated for their autonomy as part of the price of peace, but the powers assembled in conference at London refused to recognize this settlement, and the establishment of Greece as an independent kingdom (1832) was really aimed at the pretensions and the influence of Russia. These reached their high-water mark in the treaty of Unkiar Skelessi (July 8th, 1832). It was no longer a question of the partition of Turkey or of a Russian conquest of Constantinople, but of the deliberate degradation by Russia of the Ottoman empire into a weak state wholly dependent upon herself. The ten years’ crisis (1831-1841) evoked by the revolt of Mehemet Ali, pasha of Egypt, thus resolved itself into a diplomatic struggle between Russia and the other powers to maintain or to recover influence at Constantinople. The Russian experiment of maintaining the integrity of Turkey while practically treating her as a vassal state, ended with the compromise of 1841; and the emperor Nicholas I. reverted to the older idea of expelling the Turks from Europe. The Eastern Question, however, slumbered until, in 1851, the matter of the Holy Places was raised by Napoleon III., involving the whole question of the influence in Ottoman affairs of France under the capitulations of 1740 and of Russia under the treaty of 1774. The Crimean War followed and in 1856 the treaty of Paris, by which the powers hoped to stem the tide of Russian advance and establish the integrity of a reformed Ottoman state. Turkey was now for the first time solemnly admitted to the European concert. The next critical phase was opened in 1871, when Russia took advantage of the collapse of France to denounce the Black Sea clauses of the treaty of 1856. The renewal of an aggressive policy thus announced to the world soon produced a new crisis in the Eastern Question, which had meanwhile become complicated by the growth of Pan-Slav ideals in eastern Europe. In 1875 a rising in Herzegovina gave evidence of a state of feeling in the Balkan peninsula which called for the intervention of Europe, if a disastrous war were to be prevented. But this intervention, embodied in the “Andrassy Note” (December 1875) and the Berlin memorandum (May 1876), met with the stubborn opposition of Turkey, where the “young Turks” were beginning to oppose a Pan-Islamic to the Pan-Slav ideal. The Russo-Turkish War of 1877-78 followed, concluded by the treaty of San Stefano, the terms of which were modified in Turkey’s favour by the congress of Berlin (1878), which marks the beginning of the later phase of the Eastern Question. Between Russia and Turkey it interposed, in effect, a barrier of independent (Rumania, Servia) and quasi-independent (Bulgaria) states, erected with the counsel and consent of collective Europe. It thus, while ostensibly weakening, actually tended to strengthen the Ottoman power of resistance.
The period following the treaty of Berlin is coincident with the reign of Sultan Abd-ul-Hamid II. The international position of the Ottoman empire was strengthened by the able, if Machiavellian, statecraft of the sultan; while the danger of disruption from within was lessened by the more effective central control made possible by railways, telegraphs, and the other mechanical improvements borrowed from western civilization. With the spread of the Pan-Islamic movement, moreover, the undefined authority of the sultan as caliph of Islam received a fresh importance even in countries beyond the borders of the Ottoman empire, while in countries formerly, or nominally still, subject to it, it caused, and promised to cause, incalculable trouble.
The Eastern Question thus developed, in the latter years of the 19th century, from that of the problems raised by the impending break-up of a moribund empire, into the even more complex question of how to deal with an empire which showed vigorous evidence of life, but of a type of life which, though on all sides in close touch with modern European civilization, was incapable of being brought into harmony with it. The belief in the imminent collapse of the Ottoman dominion was weakened almost to extinction; so was the belief, which inspired the treaty of 1856, in the capacity of Turkey to reform and develop itself on European lines. But the Ottoman empire remained, the mistress of vast undeveloped wealth. The remaining phase of the Eastern Question, if we except the concerted efforts to impose good government on Macedonia in the interests of European peace, or the side issues in Egypt and Arabia, was the rivalry of the progressive nations for the right to exploit this wealth. In this rivalry Germany, whose interest in Turkey even so late as the congress of Berlin had been wholly subordinate, took a leading part, unhampered by the traditional policies or the humanitarian considerations by which the interests of the older powers were prejudiced. The motives of German intervention in the Eastern Question were ostensibly commercial; but the Bagdad railway concession, postulating for its ultimate success the control of the trade route by way of the Euphrates valley, involved political issues of the highest moment and opened up a new and perilous phase of the question of the Middle East.
This was the position when in 1908 an entirely new situation was created by the Turkish revolution. As the result of the patient and masterly organization of the “young Turks,” combined with the universal discontent with the rule of the sultan and the palace camarilla, the impossible seemed to be achieved, and the heterogeneous elements composing the Ottoman empire to be united in the desire to establish a unified state on the constitutional model of the West. The result on the international situation was profound. Great Britain hastened to re-knit the bonds of her ancient friendship with Turkey; the powers, without exception, professed their sympathy with the new régime. 833 The establishment of a united Turkey on a constitutional and nationalist basis was, however, not slow in producing a fresh complication in the Eastern Question. Sooner or later the issue was sure to be raised of the status of those countries, still nominally part of the Ottoman empire, but in effect independent, like Bulgaria, or subject to another state, like Bosnia and Herzegovina. The cutting of the Gordian knot by Austria’s annexation of Bosnia and Herzegovina, and by the proclamation of the independence of Bulgaria, and of Prince Ferdinand’s assumption of the old title of tsar (king), threatened to raise the Eastern Question once more in its acutest form. The international concert defined in the treaty of Berlin had been rudely shaken, if not destroyed; the denunciation by Austria, without consulting her co-signatories, of the clauses of the treaty affecting herself seemed to invalidate all the rest; and in the absence of the restraining force of a united concert of the great powers, free play seemed likely once more to be given to the rival ambitions of the Balkan nationalities, the situation being complicated by the necessity for the dominant party in the renovated Turkish state to maintain its prestige. During the anxious months that followed the Austrian coup, the efforts of diplomacy were directed to calming the excitement of Servians, Montenegrins and the Young Turks, and to considering a European conference in which the fait accompli should be regularized in accordance with the accepted canons of international law. The long delay in announcing the assembly of the conference proved the extreme difficulty of arriving at any satisfactory basis of settlement; and though the efforts of the powers succeeded in salving the wounded pride of the Turks, and restraining the impetuosity of the Serbs and Montenegrins, warlike preparations on the part of Austria continued during the winter of 1908-1909, being justified by the agitation in Servia, Montenegro and the annexed provinces. It was not till April 1909 (see Europe: ad fin.) that the crisis was ended, through the effectual backing given by Germany to Austria; and Russia, followed by England and France, gave way and assented to what had been done.
See Turkey: History, where cross-references to the articles on the various phases of the Eastern Question will be found, together with a bibliography. See also E. Driault, La Question d’orient depuis son origine (Paris, 1898), a comprehensive sketch of the whole subject, including the Middle and Far East.
EAST GRINSTEAD, a market town in the East Grinstead parliamentary division of Sussex, England, 30 m. S. by E. from London by the London, Brighton & South Coast railway. Pop. of urban district (1901) 6094. St Swithin’s church contains, among numerous ancient memorials, one of the iron memorial slabs (1507) peculiar to certain churches of Sussex, and recalling the period when iron was extensively worked in the district. There may be noticed Sackville College (an almshouse founded in 1608), and St Margaret’s home and orphanage, founded by the Rev. John Mason Neale (1818-1866), warden of Sackville College. Brewing and brick and tile making are carried on. In the vicinity (near Forest Row station) is the golf course of the Royal Ashdown Forest Golf Club.
The hundred of East Grinstead (Grenestede, Estgrensted) was in the possession of the count of Mortain in 1086, but no mention of a vill or manor of East Grinstead is made in the Domesday Survey. In the reign of Henry III. the hundred was part of the honour of Aquila, then in the king’s hands. The honour was granted by him to Peter of Savoy, through whom it passed to his niece Queen Eleanor. In the next reign the king’s mother held the borough of East Grinstead as parcel of the honour of Aquila. East Grinstead was included in a grant by Edward III. to John of Gaunt, duke of Lancaster, and it remained part of the duchy of Lancaster until James I. granted the borough to Sir George Rivers, through whom it was obtained by the Sackvilles, earls of Dorset. East Grinstead was a borough by prescription. In the 16th century it was governed by an alderman, bailiff and constable. It returned two members to parliament from 1307 until 1832, but was disenfranchised by the Reform Act. In 1285 the king ordered that his market at Grenestede should be held on Saturday instead of Sunday, and in 1516 the inhabitants of the town were granted a market each week on Saturday and a fair every year on the eve of St Andrew and two days following. Charles I. granted the earl of Dorset a market on Thursday instead of the Saturday market, and fairs on the 16th of April and the 26th of September every year. Thursday is still the market-day, and cattle-fairs are now held on the 21st of April and the 11th of December.
EAST HAM, a municipal borough in the southern parliamentary division of Essex, England, contiguous to West Ham, and thus forming geographically part of the eastward extension of London. Pop. (1901) 96,018. Its modern growth has been very rapid, the population being in the main of the artisan class. There are some chemical and other factories. The ancient parish church of St Mary Magdalen retains Norman work in the chancel, which terminates in an eastern apse. There is a monument for Edmund Neville who claimed the earldom of Westmorland in the 17th century, and William Stukeley, the antiquary, was buried in the churchyard. East Ham was incorporated in 1904, and among its municipal undertakings is a technical college (1905). The corporation consists of a mayor, 6 aldermen and 18 councillors. Area, 3320½ acres.
EASTHAMPTON, a township of Hampshire county, Mass., U.S.A., in the Connecticut Valley. Pop. (1900) 5603, of whom 1731 were foreign-born; (1905) 6808; (1910) 8524. It is served by the Boston & Maine, and the New York, New Haven & Hartford railways, and by interurban electric railways. The township is generally level, and is surrounded by high hills. In Easthampton are a free public library and Williston Seminary; the latter, one of the oldest and largest preparatory schools in New England, was founded in 1841 by the gifts of Samuel Williston (1795-1874) and Emily Graves Williston (1797-1885). Mr and Mrs Williston built up the industry of covering buttons with cloth, at first doing the work by hand, then (1827) experimenting with machinery, and in 1848 building a factory for making and covering buttons. As the soil was fertile and well watered, the township had been agricultural up to this time. It is now chiefly devoted to manufacturing. Among its products are cotton goods, especially mercerised goods, for the manufacture of which it has one of the largest plants in the country; rubber, thread, elastic fabrics, suspenders and buttons. Parts of Northampton and Southampton were incorporated as the “district” of Easthampton in 1785; it became a township in 1809, and in 1841 and 1850 annexed parts of Southampton.
EAST HAMPTON, a township of Suffolk county, New York, in the extreme S.E. part of Long Island, occupying the peninsula of Montauk, and bounded on the S. and E. by the Atlantic Ocean, and on the N. by Block Island Sound, Gardiner’s Bay and Peconic Bay. Pop. (1900) 3746; (1905) 4303; (1910) 4722. The township, 25 m. long and 8 m. at its greatest width from north to south, has an irregular north coast-line and a very regular south coast-line. The surface is rougher to the west where there are several large lakes, notably Great Pond, 2 m. long. The scenery is picturesque and the township is much frequented by artists. Montauk Lighthouse, on Turtle Hill, was first built in 1795. At Montauk, after the Spanish-American War, was Camp Wikoff, a large U.S. military camp. The township is served by the southern division of the Long Island railway, the terminus of which is Montauk. Other villages of the township, all summer resorts, are: Promised Land, Amagansett, East Hampton and Sag Harbor; the last named, only partly in the township, was incorporated in 1803 and had a population of 1969 in 1900, and 3084 in 1910. Silverware and watch cases are manufactured here. From Sag Harbor, which is a port of entry, a daily steamer runs to New York city. The village received many gifts in 1906-1908 from Mrs Russell Sage. Most of the present township was bought from the Indians (Montauks, Corchaugs and Shinnecocks) in 1648 for about £30, through the governors of Connecticut and New Haven, by nine Massachusetts freemen, mostly inhabitants of Lynn, Massachusetts. With twenty other families they settled here in 1649, calling the place Maidstone, from the old home of some of the settlers in Kent; but as early as 1650 the name East Hampton was used in reference to the earlier settlement of South Hampton. Until 834 1664, when all Long Island passed to the duke of York, the government was by town meeting, autonomous and independent except for occasional appeals to Connecticut. In 1683 Gardiner’s Island, settled by Lion Gardiner in 1639 and so one of the first English settlements in what is now New York state, was made a part of Long Island and of East Hampton township. The English settlements in East Hampton were repeatedly threatened by pirates and privateers, and there are many stories of treasure buried by Captain Kidd on Gardiner’s Island and on Montauk Point. The Clinton Academy, opened in East Hampton village in 1785, was long a famous school. Of the church built here in 1653 (first Congregational and after 1747 Presbyterian in government), Lyman Beecher was pastor in 1799-1810; and in East Hampton were born his elder children. Whale fishing was begun in East Hampton in 1675, when four Indians were engaged by whites in off-shore whaling; but Sag Harbor, which was first settled in 1730 and was held by the British after the battle of Long Island as a strategic naval and shipping point, became the centre of the whaling business. The first successful whaling voyage was made from Sag Harbor in 1785, and although the Embargo ruined the fishing for a time, it revived during 1830-1850. Cod and menhaden fishing, the latter for the manufacture of fish-oil and guano, were important for a time, but in the second half of the 19th century Sag Harbor lost its commercial importance.
EAST INDIA COMPANY, an incorporated company for exploiting the trade with India and the Far East. In the 17th and 18th centuries East India companies were established by England, Holland, France, Denmark, Scotland, Spain, Austria and Sweden. By far the most important of these was the English East India Company, which became the dominant power in India, and only handed over its functions to the British Government in 1858 (see also Dutch East India Company, Ostend Company).
The English East India Company was founded at the end of the 16th century in order to compete with the Dutch merchants, who had obtained a practical monopoly of the trade with the Spice Islands, and had raised the price of English East India Co. pepper from 3s. to 8s. per ℔. Queen Elizabeth incorporated it by royal charter, dated December 31, 1600, under the title of “The Governor and Company of Merchants of London, trading into the East Indies.” This charter conferred the sole right of trading with the East Indies, i.e. with all countries lying beyond the Cape of Good Hope or the Straits of Magellan, upon the company for a term of 15 years. Unauthorized interlopers were liable to forfeiture of ships and cargo. There were 125 shareholders in the original East India Company, with a capital of £72,000: the first governor was Sir Thomas Smythe. The early voyages of the company, from 1601 to 1612, are distinguished as the “separate voyages,” because the subscribers individually bore the cost of each voyage and reaped the whole profits, which seldom fell below 100%. After 1612 the voyages were conducted on the joint stock system for the benefit of the company as a whole. These early voyages, whose own narratives may be read in Purchas, pushed as far as Japan, and established friendly relations at the court of the Great Mogul. In 1610-1611 Captain Hippon planted the first English factories on the mainland of India, at Masulipatam and at Pettapoli in the Bay of Bengal. The profitable nature of the company’s trade had induced James I. to grant subsidiary licences to private traders; but in 1609 he renewed the company’s charter “for ever,” though with a proviso that it might be revoked on three years’ notice if the trade should not prove profitable to the realm.
Meanwhile friction was arising between the English and Dutch East India Companies. The Dutch traders considered that they had prior rights in the Far East, and their ascendancy in the Indian Archipelago was indeed English and Dutch disputes. firmly established on the basis of territorial dominion and authority. In 1613 they made advances to the English company with a suggestion for co-operation, but the offer was declined, and the next few years were fertile in disputes between the armed traders of both nations. In 1619 was ratified a “treaty of defence” to prevent disputes between the English and Dutch companies. When it was proclaimed in the East, hostilities solemnly ceased for the space of an hour, while the Dutch and English fleets, dressed out in all their flags and with yards manned, saluted each other; but the treaty ended in the smoke of that stately salutation, and perpetual and fruitless contentions between the Dutch and English companies went on just as before. In 1623 these disputes culminated in the “massacre of Amboyna,” where the Dutch governor tortured and executed the English residents on a charge of conspiring to seize the fort. Great and lasting indignation was aroused in England, but it was not until the time of Cromwell that some pecuniary reparation was exacted for the heirs of the victims. The immediate result was that the English company tacitly admitted the Dutch claims to a monopoly of the trade in the Far East, and confined their operations to the mainland of India and the adjoining countries.
The necessity of good ships for the East Indian trade had led the company in 1609 to construct their dockyard at Deptford, from which, as Monson observes, dates “the increase of great ships in England.” Down to the middle of the The East Indiamen. 19th century, the famous “East Indiamen” held unquestioned pre-eminence among the merchant vessels of the world. Throughout the 17th century they had to be prepared at any moment to fight not merely Malay pirates, but the armed trading vessels of their Dutch, French and Portuguese rivals. Many such battles are recorded in the history of the East India Company, and usually with successful results.
It was not until it had been in existence for more than a century that the English East India Company obtained a practical monopoly of the Indian trade. In 1635, a year after the Great Mogul had granted it the liberty of trading The acquisition of territory. throughout Bengal, Charles I. issued a licence to Courten’s rival association, known as “the Assada Merchants,” on the ground that the company had neglected English interests. The piratical methods of their rivals disgraced the company with the Mogul officials, and a modus vivendi was only reached in 1649. In 1657 Cromwell renewed the charter of 1609, providing that the Indian trade should be in the hands of a single joint stock company. The new company thus formed bought up the factories, forts and privileges of the old one. It was further consolidated by the fostering care of Charles II., who granted it five important charters. From a simple trading company, it grew under his reign into a great chartered company—to use the modern term—with the right to acquire territory, coin money, command fortresses and troops, form alliances, make war and peace, and exercise both civil and criminal jurisdiction. It is accordingly in 1689, when the three presidencies of Bengal, Madras and Bombay had lately been established, that the ruling career of the East India Company begins, with the passing by its directors of the following resolution for the guidance of the local governments in India:—“The increase of our revenue is the subject of our care, as much as our trade; ’tis that must maintain our force when twenty accidents may interrupt our trade; ’tis that must make us a nation in India; without that we are but a great number of interlopers, united by His Majesty’s royal charter, fit only to trade where nobody of power thinks it their interest to prevent us; and upon this account it is that the wise Dutch, in all their general advices that we have seen, write ten paragraphs concerning their government, their civil and military policy, warfare, and the increase of their revenue, for one paragraph they write concerning trade.” From this moment the history of the transactions of the East India Company becomes the history of British India (see India: History). Here we shall only trace the later changes in the constitution and powers of the ruling body itself.
The great prosperity of the company under the Restoration, and the immense profits of the Indian trade, attracted a number of private traders, both outside merchants and dismissed or retired servants of the company, who came The interlopers. to be known as “interlopers.” In 1683 the case of Thomas Sandys, an interloper, raised the whole question of the 835 royal prerogative to create a monopoly of the Indian trade. The case was tried by Judge Jeffreys, who upheld the royal prerogative; but in spite of his decision the custom of interloping continued and laid the foundation of many great fortunes. By 1691 the interlopers had formed themselves into a new society, meeting at Dowgate, and rivalling the old company; the case was carried before the House of Commons, which declared in 1694 that “all the subjects of England have equal right to trade to the East Indies unless prohibited by act of parliament.” This decision led up to the act of 1698, which created a new East India Company in consideration of a loan of two millions to the state. The old company subscribed £315,000 and became the dominant factor in the new body; while at the same time it retained its charter for three years, its factories, forts and assured position in India. The rivalry between the two companies continued both in England and in India, until they were finally amalgamated by a tripartite indenture between the companies and Queen Anne (1702), which was ratified under the Godolphin Award (1708). Under this award the company was to lend the nation £3,200,000, and its exclusive privileges were to cease at three years’ notice after this amount had been repaid. But by this time the need for permanence in the Indian establishment began to be felt, while parliament would not relinquish its privilege of “milking” the company from time to time. In 1712 an act was passed continuing the privileges of the company even after their fund should be redeemed; in 1730 the charter was prolonged until 1766, and in 1742 the term was extended until 1783 in return for the loan of a million. This million was required for the war with France, which extended to India and involved the English and French companies there in long-drawn hostilities, in which the names of Dupleix and Clive became prominent.
So long as the company’s chief business was that of trade, it was left to manage its own affairs. The original charter of Elizabeth had placed its control in the hands of a governor and a committee of twenty-four, and this The company and the crown. arrangement subsisted in essence down to the time of George III. The chairman and court of directors in London exercised unchecked control over their servants in India. But after Clive’s brilliant victory at Plassey (1757) had made the company a ruling power in India, it was felt to be necessary that the British government should have some control over the territories thus acquired. Lord North’s Regulating Act (1773) raised the governor of Bengal—Warren Hastings—to the rank of governor-general, and provided that his nomination, though made by a court of directors, should in future be subject to the approval of the crown; in conjunction with a council of four, he was entrusted with the power of peace and war; a supreme court of judicature was established, to which the judges were appointed by the crown; and legislative power was conferred on the governor-general and his council. Next followed Pitt’s India Bill (1784), which created the board of control, as a department of the English government, to exercise political, military and financial superintendence over the British possessions in India. This bill first authorized the historic phrase “governor-general in council.” From this date the direction of Indian policy passed definitely from the company to the governor-general in India and the ministry in London. In 1813 Lord Liverpool passed a bill which further gave the board of control authority over the company’s commercial transactions, and abolished its monopoly of Indian trade, whilst leaving it the monopoly of the valuable trade with China, chiefly in tea. Finally, under Earl Grey’s act of 1833, the company was deprived of this monopoly also. Its property was then secured on the Indian possessions, and its annual dividends of ten guineas per £100 stock were made a charge upon the Indian revenue. Henceforward the East India Company ceased to be a trading concern and exercised only administrative functions. Such a position could not, in the nature of things, be permanent, and the great cataclysm of the Indian Mutiny was followed by the entire transference of Indian administration from the company to the crown, on the 2nd of August 1858.
See Purchas his Pilgrimes (ed. 1905), vols. 2, 3, 4, 5, for the charter of Elizabeth and the early voyages; Sir W.W. Hunter, History of British India (1899); Beckles Willson, Ledger and Sword (1903); Sir George Birdwood, Report on the Old Records of the India Office (1879); The East India Company’s First Letter Book (1895), Letters Received by the East India Company from its Servants in the East, ed. Foster, (1896 ff.). See also the interesting memorial volume Relics of the Honourable East India Company (ed. Griggs, 1909), letterpress by Sir G. Birdwood and W. Foster.
EAST INDIES, a name formerly applied vaguely, in its widest sense, to the whole area of India, Further India and the Malay Archipelago, in distinction from the West Indies, which, at the time of their discovery, were taken to be the extreme parts of the Indian region. The term “East Indies” is still sometimes applied to the Malay Archipelago (q.v.) alone, and the phrase “Dutch East Indies” is commonly used to denote the Dutch possessions which constitute the greater part of that archipelago. The Dutch themselves use the term Nederlandsch-Indië.
EASTLAKE, SIR CHARLES LOCK (1793-1865), English painter, was born on the 17th of November 1793 at Plymouth, where his father, a man of uncommon gifts but of indolent temperament, was solicitor to the admiralty and judge advocate of the admiralty court. Charles was educated (like Sir Joshua Reynolds) at the Plympton grammar-school, and in London at the Charterhouse. Towards 1809, partly through the influence of his fellow-Devonian Haydon, of whom he became a pupil, he determined to be a painter; he also studied in the Royal Academy school. In 1813 he exhibited in the British Institution his first picture, a work of considerable size, “Christ restoring life to the Daughter of Jairus.” In 1814 he was commissioned to copy some of the paintings collected by Napoleon in the Louvre; he returned to England in 1815, and practised portrait-painting at Plymouth. Here he saw Napoleon a captive on the “Bellerophon”; from a boat he made some sketches of the emperor, and he afterwards painted, from these sketches and from memory, a life-sized full-length portrait of him (with some of his officers) which was pronounced a good likeness; it belongs to the marquess of Lansdowne. In 1817 Eastlake went to Italy; in 1819 to Greece; in 1820 back to Italy, where he remained altogether fourteen years, chiefly in Rome and in Ferrara.
In 1827 he exhibited at the Royal Academy his picture of the Spartan Isidas, who (as narrated by Plutarch in the life of Agesilaus), rushing naked out of his bath, performed prodigies of valour against the Theban host. This was the first work that attracted much notice to the name of Eastlake, who in consequence obtained his election as A.R.A.; in 1830, when he returned to England, he was chosen R.A. In 1850 he succeeded Shee as president of the Royal Academy, and was knighted. Prior to this, in 1841, he had been appointed secretary to the royal commission for decorating the Houses of Parliament, and he retained this post until the commission was dissolved in 1862. In 1843 he was made keeper of the National Gallery, a post which he resigned in 1847 in consequence of an unfortunate purchase that roused much animadversion, a portrait erroneously ascribed to Holbein; in 1855, director of the same institution, with more extended powers. During his directorship he purchased for the gallery 155 pictures, mostly of the Italian schools. He became also a D.C.L. of Oxford, F.R.S., a chevalier of the Legion of Honour, and member of various foreign academies.
In 1849 he married Miss Elizabeth Rigby, who had already then become known as a writer (Letters from the Baltic, 1841; Livonian Tales, 1846; The Jewess, 1848) and as a contributor to the Quarterly Review. Lady Eastlake (1809-1893) had for some years been interested in art subjects, and after her marriage she naturally devoted more attention to them, translating Waagen’s Treasures of Art in Great Britain (1854-1857), and completing Mrs Jameson’s History of our Lord in Works of Art. In 1865 Sir Charles Eastlake fell ill at Milan; and he died at Pisa on the 24th of December in the same year. Lady Eastlake, who survived him for many years, continued to play an active part as a writer on art (Five Great Painters, 1883, &c.), and had a large circle of friends among the most interesting men and women of the day. In 1880 she published a volume of Letters from France 836 (describing events in Paris during 1789), written by her father, Edward Rigby (1747-1821), a distinguished Norwich doctor who was known also for his practical interest in agriculture, and who is said to have made known the flying shuttle to Norwich manufacturers.
As a painter, Sir Charles Eastlake was gentle, harmonious, diligent and correct; lacking fire of invention or of execution; eclectic, without being exactly imitative; influenced rather by a love of ideal grace and beauty than by any marked bent of individual power or vigorous originality. Among his principal works (which were not numerous, 51 being the total exhibited in the Academy) are: 1828, “Pilgrims arriving in sight of Rome” (repeated in 1835 and 1836, and perhaps on the whole his chef-d’œuvre); 1829, “Byron’s Dream” (in the Tate Gallery); 1834, the “Escape of Francesco di Carrara” (a duplicate in the Tate Gallery); 1841, “Christ Lamenting over Jerusalem” (ditto); 1843, “Hagar and Ishmael”; 1845, “Comus”; 1849, “Helena”; 1851, “Ippolita Torelli”; 1853, “Violante”; 1855, “Beatrice.” These female heads, of a refined semi-ideal quality, with something of Venetian glow of tint, are the most satisfactory specimens of Eastlake’s work to an artist’s eye. He was an accomplished and judicious scholar in matters of art, and published, in 1840, a translation of Goethe’s Theory of Colours; in 1847 (his chief literary work) Materials for a History of Oil-Painting, especially valuable as regards the Flemish school; in 1848, Contributions to the Literature of the Fine Arts (a second series was edited by Lady Eastlake in 1870, and accompanied by a Memoir from her pen); in 1851 and 1855, translated editions of Kugler’s History of the Italian School of Painting, and Handbook of Painting (new edition, by Lady Eastlake, 1874).
See W. Cosmo Monkhouse, Pictures by Sir Charles Eastlake, with biographical and critical Sketch (1875).
EAST LIVERPOOL, a city of Columbiana county, Ohio, U.S.A., on the Ohio river, about 106 m. S.E. of Cleveland. Pop. (1890) 10,956; (1900) 16,485, of whom 2112 were foreign-born; (1910 census) 20,357. It is served by the Pennsylvania railway, by river steamboats, and by interurban electric lines. Next to Trenton, New Jersey, East Liverpool is the most important place in the United States for the manufacture of earthenware and pottery, 4859 out of its 5228 wage-earners, or 92.9%, being employed in this industry in 1905, when $5,373,852 (83.5% of the value of all its factory products) was the value of the earthenware and pottery. No other city in the United States is so exclusively devoted to the manufacture of pottery; in 1908 there were 32 potteries in the city and its immediate vicinity. The manufacture of white ware, begun in 1872, is the most important branch of the industry—almost half of the “cream-coloured,” white granite ware and semivitreous porcelain produced in the United States in 1905 (in value, $4,344,468 out of $9,195,703) being manufactured in East Liverpool. Though there are large clay deposits in the vicinity, very little of it can be used for crockery, and most of the clay used in the city’s potteries is obtained from other states; some of it is imported from Europe. After 1872 a large number of skilled English pottery-workers settled in the city. The city’s product of pottery, terra-cotta and fireclay increased from $2,137,063 to $4,105,200 from 1890 to 1900, and in the latter year almost equalled that of Trenton, N.J., the two cities together producing more than half (50.9%) of the total pottery product of the United States; in 1905 East Liverpool and Trenton together produced 42.1% of the total value of the country’s pottery product. The municipality owns and operates its water-works. East Liverpool was settled in 1798, and was incorporated in 1834.
EAST LONDON, a town of the Cape province, South Africa, at the mouth of the Buffalo river, in 33° 1′ S. 27° 55′ E., 543 m. E.N.E. of Cape Town by sea and 666 m. S. of Johannesburg by rail. Pop. (1904) 25,220, of whom 14,674 were whites. The town is picturesquely situated on both sides of the river, which is spanned by a combined road and railway bridge. The railway terminus and business quarter are on the east side on the top of the cliffs, which rise 150 ft. above the river. In Oxford Street, the chief thoroughfare, is the town hall, a handsome building erected in 1898. Higher up a number of churches and a school are grouped round Vincent Square, a large open space. In consequence of the excellent sea bathing, and the beauty of the river banks above the town, East London is the chief seaside holiday resort of the Cape province. The town is the entrepot of a rich agricultural district, including the Transkei, Basutoland and the south of Orange Free State, and the port of the Cape nearest Johannesburg. It ranks third among the ports of the province. The roadstead is exposed and insecure, but the inner harbour, constructed at a cost of over £2,000,000, is protected from all winds. A shifting sand bar lies at the mouth of the river, but the building of training walls and dredging have increased the minimum depth of water to 22 ft. From the east bank of the Buffalo a pier and from the west bank a breakwater project into the Indian Ocean, the entrance being 450 ft. wide, reduced between the training walls to 250 ft. There is extensive wharf accommodation on both sides of the river, and steamers of over 8000 tons can moor alongside. There is a patent slip capable of taking vessels of 1000 tons dead weight. An aerial steel ropeway from the river bank to the town greatly facilitates the delivery of cargo. The imports are chiefly textiles, hardware and provisions, the exports mainly wool and mohair. The rateable value of the town in 1908 was £4,108,000, and the municipal rate 15⁄8d.
East London owes its foundation to the necessities of the Kaffir war of 1846-1847. The British, requiring a port nearer the scene of war than those then existing, selected a site at the mouth of the Buffalo river, and in 1847 the first cargo of military stores was landed. A fort, named Glamorgan, was built, and the place permanently occupied. Around this military post grew up the town, known at first as Port Rex. Numbers of its inhabitants are descendants of German immigrants who settled in the district in 1857. The prosperity of the town dates from the era of railway and port development in the last decade of the 19th century. In 1875 the value of the exports was £131,803 and that of the imports £552,033. In 1904 the value of the exports was £1,165,938 and that of the imports £4,688,415. In 1907 the exports, notwithstanding a period of severe trade depression, were valued at £1,475,355, but the imports had fallen to £3,354,633.
EASTON, a city and the county-seat of Northampton county, Pennsylvania, U.S.A., at the confluence of the Lehigh river and Bushkill Creek with the Delaware, about 60 m. N. of Philadelphia. Pop. (1890) 14,481; (1900) 25,238, of whom 2135 were foreign-born; (1910 census) 28,523. Easton is served by the Central of New Jersey, the Lehigh Valley, the Lehigh & Hudson River and the Delaware, Lackawanna & Western railways, and is connected by canals with the anthracite coal region to the north-west and with Bristol, Pa. A bridge across the Delaware river connects it with Phillipsburg, New Jersey, which is served by the Pennsylvania railway. The city is built on rolling ground, commanding pleasant views of hill and river scenery. Many fine residences overlook city and country from the hillsides, and a Carnegie library is prominent among the public buildings. Lafayette College, a Presbyterian institution opened in 1832, is finely situated on a bluff north of the Bushkill and Delaware. The college provides the following courses of instruction: graduate, classical, Latin scientific, general scientific, civil engineering, electrical engineering, mining engineering and chemical; in 1908 it had 38 instructors and 442 students, 256 of whom were enrolled in the scientific and engineering courses. Overlooking the Bushkill is the Easton Cemetery, in which is the grave of George Taylor (1716-1781), a signer of the Declaration of Independence, with a monument of Italian marble to his memory. Among the city’s manufactures are silk, hosiery and knit goods, flour, malt liquors, brick, tile, drills, lumber and planing mill products and organs; in 1905 the value of all the factory products was $5,654,594, of which $2,290,598, or 40.5%, was the value of the silk manufactures. Easton is the commercial centre of an important mining region, which produces, in particular, iron ore, soapstone, cement, slate and building stone. The municipality owns and operates an electric-lighting plant. 837 Easton was a garden spot of the Indians, and here, because they would not negotiate elsewhere, several important treaties were made between 1756 and 1762 during the French and Indian War. The place was laid out in 1752, and was made the county-seat of the newly erected county. It was incorporated as a borough in 1789, received a new borough charter in 1823, and in 1887 was chartered as a city. South Easton was annexed in 1898.
EAST ORANGE, a city of Essex county, New Jersey, U.S.A., in the north-eastern part of the state, adjoining the city of Newark, and about 12 m. W. of New York city. Pop. (1890) 13,282; (1900) 21,506, of whom 3950 were foreign-born and 1420 were negroes; (1910 census) 34,371. It is served by the Morris & Essex division of the Delaware, Lackawanna & Western railway and by the Orange branch of the Erie (the former having four stations—Ampere, Grove Street, East Orange and Brick Church), and is connected with Newark, Orange and West Orange by electric line. The city covers an area of about 4 sq. m., and has broad, well-paved streets, bordered with fine shade trees (under the jurisdiction of a “Shade Tree Commission”). It is primarily a residential suburb of New York and Newark, and has many beautiful homes; with Orange, West Orange and South Orange it forms virtually one community, popularly known as “the Oranges.” The public school system is excellent, and the city has a Carnegie library (1903), with more than 22,000 volumes in 1907. Among the principal buildings are several attractive churches, the city hall, and the club-house of the Woman’s Club of Orange. The principal manufactures of East Orange are electrical machinery, apparatus, and supplies (the factory of the Crocker-Wheeler Co. being here—in a part of the city known as “Ampere”) and pharmaceutical materials. The total value of the city’s factory products in 1905 was $2,326,552. East Orange has a fine water-works system, which it owns and operates; the water supply is obtained from artesian wells at White Oaks Ridge, in the township of Milburn (about 10 m. from the city hall); thence the water is pumped to a steel reinforced reservoir (capacity 5,000,000 gallons) on the mountain back of South Orange. In 1863 the township of East Orange was separated from the township of Orange, which, in turn, had been separated from the township of Newark in 1806. An act of the New Jersey legislature in 1895 created the office of township president, with power of appointment and veto. Four years later East Orange was chartered as a city.
See H. Whittemore, The Founders and Builders of the Oranges (Newark, 1896).
EASTPORT, a city and port of entry of Washington county, Maine, U.S.A., co-extensive with Moose Island in Passamaquoddy Bay, about 190 m. E.N.E. of Portland. Pop. (1890) 4908; (1900) 5311 (1554 foreign-born); (1910) 4961. It is served by the Washington County railway, and by steamboat lines to Boston, Portland and Calais. It is the most eastern city of the United States, and is separated from the mainland by a narrow channel, which is spanned by a bridge. The harbour is well protected from the winds, and the tide, which rises and falls here about 25 ft., prevents it from being obstructed with ice. The city is built on ground sloping gently to the water’s edge, and commands delightful views of the bay, in which there are several islands. Its principal industry is the canning of sardines; there are also clam canneries. Shoes, mustard, decorated tin, and shooks are manufactured, and fish and lobsters are shipped from here in the season. The city is the port of entry for the customs district of Passamaquoddy; in 1908 its imports were valued at $994,961, and its exports at $1,155,791. Eastport was first settled about 1782 by fishermen; it became a port of entry in 1790, was incorporated as a town in 1798, and was chartered as a city in 1893. It was a notorious place for smuggling under the Embargo Acts of 1807 and 1808. On the 11th of July 1814, during the war of 1812, it was taken by the British. As the British government claimed the islands of Passamaquoddy Bay under the treaty of 1783, the British forces retained possession of Eastport after the close of the war and held it under martial law until July 1818, when it was surrendered in accordance with the decision rendered in November 1817 by commissioners appointed under Article IV. of the treaty of Ghent (1814), this decision awarding Moose Island, Dudley Island and Frederick Island to the United States and the other islands, including the Island of Grand Manan in the Bay of Fundy, to Great Britain.
EAST PROVIDENCE, a township of Providence county, Rhode Island, U.S.A., on the E. side of Providence river, opposite Providence. Pop. (1890) 8422; (1900) 12,138, of whom 2067 were foreign-born; (1910 census) 15,808. Area, 12½ sq. m. It is served by the New York, New Haven & Hartford railway. It has a rolling surface and contains several villages, one of which, known as Rumford, has important manufactories of chemicals and electrical supplies. South of this village, along the river bank, are several attractive summer resorts, Hunt’s Mills, Silver Spring, Riverside, Vanity Fair, Kettle Point and Bullock’s Point being prominent among them. In 1905 the factory products of the township were valued at $5,035,288. The oyster trade is important. It was within the present limits of this township that Roger Williams established himself in the spring of 1636, until he learned that the place was within the jurisdiction of the Plymouth Colony. About 1644 it was settled by a company from Weymouth as a part of a town of Rehoboth. In 1812 Rehoboth was divided, and the west part was made the township of Seekonk. Finally, in 1861, it was decided that the west part of Seekonk belonged to Rhode Island, and in the following year that part was incorporated as the township of East Providence.
EAST PRUSSIA (Ost-Preussen), the easternmost province of the kingdom of Prussia, bounded on the N. by the Baltic, on the E. and S.W. by Russia and Russian Poland, and on the W. by the Prussian province of West Prussia. It has an area of 14,284 sq. m., and had, in 1905, a population of 2,025,741. It shares in the general characteristics of the great north German plain, but, though low, its surface is by no means absolutely flat, as the southern half is traversed by a low ridge or plateau, which attains a height of 1025 ft. at a point near the western boundary of the province. This plateau, here named the Prussian Seenplatte, is thickly sprinkled with small lakes, among which is the Spirding See, 46 sq. m. in extent and the largest inland lake in the Prussian monarchy. The coast is lined with low dunes or sandhills, in front of which lie the large littoral lakes or lagoons named the Frisches Haff and the Kurisches Haff. The first of these receives the waters of the Nogat and the Pregel, and the other those of the Memel or Niemen. East Prussia is the coldest part of Germany, its mean annual temperature being about 44° F., while the mean January temperature of Tilsit is only 25°. The rainfall is 24 in. per annum. About half the province is under tillage; 18% is occupied by forests, and about 23% by meadows and pastures. The most fertile soil is found in the valleys of the Pregel and the Memel, but the southern slopes of the Baltic plateau and the district to the north of the Memel consist in great part of sterile moor, sand and bog. The chief crops are rye, oats and potatoes, while flax is cultivated in the district of Ermeland, between the Passarge and the upper Alle. East Prussia is the headquarters of the horse-breeding of the country, and contains the principal government stud of Trakehnen; numerous cattle are also fattened on the rich pastures of the river-valleys. The extensive woods in the south part of the province harbour a few wolves and lynxes, and the elk is still preserved in the forest of Ibenhorst, near the Kurisches Haff. The fisheries in the lakes and haffs are of some importance; but the only mineral product of note is amber, which is found in the peninsula of Samland in greater abundance than in any other part of the world. Manufactures are almost confined to the principal towns, though linen-weaving is practised as a domestic industry. Commerce is facilitated by canals connecting the Memel and Pregel and also the principal lakes, but is somewhat hampered by the heavy dues exacted at the Russian frontier. A brisk foreign trade is carried on through the seaports of Königsberg, the capital of the province, and Memel, the exports consisting mainly of timber and grain.
The population of the province was in 1900 1,996,626, and 838 included 1,698,465 Protestants, 269,196 Roman Catholics and 13,877 Jews. The Roman Catholics are mainly confined to the district of Ermeland, in which the ordinary proportions of the confessions are completely reversed. The bulk of the inhabitants are of German blood, but there are above 400,000 Protestant Poles (Masurians or Masovians) in the south part of the province, and 175,000 Lithuanians in the north. As in other provinces where the Polish element is strong, East Prussia is somewhat below the general average of the kingdom in education. There is a university at Königsberg.
See Lohmeyer, Geschichte von Ost- und West-Preussen (Gotha, 1884); Brünneck, Zur Geschichte des Kirchen-Patronats in Ost- und West-Preussen (Berlin, 1902), and Ost-Preussen, Land und Volk (Stuttgart, 1901-1902).
EASTWICK, EDWARD BACKHOUSE (1814-1883), British Orientalist, was born in 1814, a member of an Anglo-Indian family. Educated at Charterhouse and at Oxford, he joined the Bombay infantry in 1836, but, owing to his talent for languages, was soon given a political post. In 1843 he translated the Persian Kessahi Sanján, or History of the Arrival of the Parsees in India; and he wrote a Life of Zoroaster, a Sindhi vocabulary, and various papers in the transactions of the Bombay Asiatic Society. Compelled by ill-health to return to Europe, he went to Frankfort, where he learned German and translated Schiller’s Revolt of the Netherlands and Bopp’s Comparative Grammar. In 1845 he was appointed professor of Hindustani at Haileybury College. Two years later he published a Hindustani grammar, and, in subsequent years, a new edition of the Gulistán, with a translation in prose and verse, also an edition with vocabulary of the Hindi translation by Lallú Lál of Chatur Chuj Misr’s Prem Sagár, and translations of the Bagh-o-Bahar, and of the Anvár-i Suhaili of Bídpáí. In 1851 he was elected a Fellow of the Royal Society. In 1857-1858 he edited The Autobiography of Lútfullah. He also edited for the Bible Society the Book of Genesis in the Dakhani language. From 1860 to 1863 he was in Persia as secretary to the British Legation, publishing on his return The Journal of a Diplomate. In 1866 he became private secretary to the secretary of state for India, Lord Cranborne (afterwards marquess of Salisbury), and in 1867 went, as in 1864, on a government mission to Venezuela. On his return he wrote, at the request of Charles Dickens, for All the Year Round, “Sketches of Life in a South American Republic.” From 1868 to 1874 he was M.P. for Penryn and Falmouth. In 1875 he received the degree of M.A. with the franchise from the university of Oxford, “as a slight recognition of distinguished services.” At various times he wrote several of Murray’s Indian hand-books. His last work was the Kaisarnamah-i-Hind (“the lay of the empress”), in two volumes (1878-1882). He died at Ventnor, Isle of Wight, on the 16th of July 1883.
EATON, DORMAN BRIDGMAN (1823-1899), American lawyer, was born at Hardwick, Vermont, on the 27th of June 1823. He graduated at the university of Vermont in 1848 and at the Harvard Law School in 1850, and in the latter year was admitted to the bar in New York city. There he became associated in practice with William Kent, the son of the great chancellor, an edition of whose Commentaries he assisted in editing. Eaton early became interested in municipal and civil service reform. He was conspicuous in the fight against Tweed and his followers, by one of whom he was assaulted; he required a long period of rest, and went to Europe, where he studied the workings of the civil service in various countries. From 1873 to 1875 he was a member of the first United States Civil Service Commission. In 1877, at the request of President Hayes, he made a careful study of the British civil service, and three years later published Civil Service in Great Britain. He drafted the Pendleton Civil Service Act of 1883, and later became a member of the new commission established by it. He resigned in 1885, but was almost immediately reappointed by President Cleveland, and served until 1886, editing the 3rd and 4th Reports of the commission. He was an organizer (1878) of the first society for the furtherance of civil service reform in New York, of the National Civil Service Reform Association, and of the National Conference of the Unitarian Church (1865). He died in New York city on the 23rd of December 1899, leaving $100,000 each to Harvard and Columbia universities for the establishments of professorships in government. He was a legal writer and editor, and a frequent contributor to the leading reviews. In addition to the works mentioned he published Should Judges be Elected? (1873), The Independent Movement in New York (1880), Term and Tenure of Office (1882), The Spoils System and Civil Service Reform (1882), Problems of Police Legislation (1895) and The Government of Municipalities (1899).
See the privately printed memorial volume, Dorman B. Eaton, 1823-1899 (New York, 1900).
EATON, MARGARET O’NEILL (1796-1879), better known as Peggy O’Neill, was the daughter of the keeper of a popular Washington tavern, and was noted for her beauty, wit and vivacity. About 1823, she married a purser in the United States navy, John B. Timberlake, who committed suicide while on service in the Mediterranean in 1828. In the following year she married John Henry Eaton (1790-1856), a Tennessee politician, at the time a member of the United States Senate. Senator Eaton was a close personal friend of President Jackson, who in 1829 appointed him secretary of war. This sudden elevation of Mrs Eaton into the cabinet social circle was resented by the wives of several of Jackson’s secretaries, and charges were made against her of improper conduct with Eaton previous to her marriage to him. The refusal of the wives of the cabinet members to recognize the wife of his friend angered President Jackson, and he tried in vain to coerce them. Eventually, and partly for this reason, he almost completely reorganized his cabinet. The effect of the incident on the political fortunes of the vice-president, John C. Calhoun, whose wife was one of the recalcitrants, was perhaps most important. Partly on this account, Jackson’s favour was transferred from Calhoun to Martin Van Buren, the secretary of state, who had taken Jackson’s side in the quarrel and had shown marked attention to Mrs Eaton, and whose subsequent elevation to the vice-presidency and presidency through Jackson’s favour is no doubt partly attributable to this incident. In 1836 Mrs Eaton accompanied her husband to Spain, where he was United States minister in 1836-1840. After the death of her husband she married a young Italian dancing-master, Antonio Buchignani, but soon obtained a divorce from him. She died in Washington on the 8th of November 1879.
See James Parton’s Life of Andrew Jackson (New York, 1860).
EATON, THEOPHILUS (c. 1590-1658), English colonial governor in America, was born at Stony Stratford, Buckinghamshire, about 1590. He was educated in Coventry, became a successful merchant, travelled widely throughout Europe, and for several years was the financial agent of Charles I. in Denmark. He subsequently settled in London, where he joined the Puritan congregation of the Rev. John Davenport, whom he had known since boyhood. The pressure upon the Puritans increasing, Eaton, who had been one of the original patentees of the Massachusetts Bay colony in 1629, determined to use his influence and fortune to establish an independent colony of which his pastor should be the head. In 1637 he emigrated with Davenport to Massachusetts, and in the following year (March 1638) he and Davenport founded New Haven. In October 1639 a form of government was adopted, based on the Mosaic Law, and Eaton was elected governor, a post which he continued to hold by annual re-election, first over New Haven alone, and after 1643 over the New Haven Colony or Jurisdiction, until his death at New Haven on the 7th of January 1658. His administration was embarrassed by constantly recurring disputes with the neighbouring Dutch settlements, especially after Stamford (Conn.) and Southold (Long Island) had entered the New Haven Jurisdiction, but his prudence and diplomacy prevented an actual outbreak of hostilities. He was prominent in the affairs of the New England Confederation, of which he was one of the founders (1643). In 1655 he and Davenport drew up the code of laws, popularly known as the “Connecticut Blue Laws,” which were published 839 in London in 1656 under the title New Haven’s Settling in New England and some Lawes for Government published for the Use of that Colony.
A sketch of his life appears in Cotton Mather’s Magnalia (London, 1702); see also J.B. Moore’s “Memoir of Theophilus Eaton” in the Collections of the New York Historical Society, second series, vol. ii. (New York, 1849).
EATON, WILLIAM (1764-1811), American soldier, was born in Woodstock, Connecticut, on the 23rd of February 1764. As a boy he served for a short time in the Continental army. He was a school teacher for several years, graduated at Dartmouth College in 1790, was clerk of the lower house of the Vermont legislature in 1791-1792, and in 1792 re-entered the army as a captain, later serving against the Indians in Ohio and Georgia. In 1797 he was appointed consul to Tunis, where he arrived in February 1799. In March 1799, with the consuls to Tripoli and Algiers, he negotiated alterations in the treaty of 1797 with Tunis. He rendered great service to Danish merchantmen by buying on credit several Danish prizes in Tunis and turning them over to their original owners for the redemption of his notes. In 1803 he quarrelled with the Bey, was ordered from the country, and returned to the United States to urge American intervention for the restoration of Ahmet Karamanli to the throne of Tripoli, arguing that this would impress the Barbary States with the power of the United States. In 1804 he returned to the Mediterranean as United States naval agent to the Barbary States with Barron’s fleet. On the 23rd of February 1805 he agreed with Ahmet that the United States should undertake to re-establish him in Tripoli, that the expenses of the expedition should be repaid to the United States by Ahmet, and that Eaton should be general and commander-in-chief of the land forces in Ahmet’s campaign; as the secretary of the navy had given the entire matter into the hands of Commodore Barron, and as Barron and Tobias Lear (1762-1816), the United States consul-general at Algiers and a diplomatic agent to conduct negotiations, had been instructed to consider the advisability of making arrangements with the existing government in Tripoli, Eaton far exceeded his authority. On the 8th of March he started for Derna across the Libyan desert from the Arab’s Tower, 40 m. W. of Alexandria, with a force of about 500 men, including a few Americans, about 40 Greeks and some Arab cavalry. In the march of nearly 600 m. the camel-drivers and the Arab chiefs repeatedly mutinied, and Ahmet Pasha once put himself at the head of the Arabs and ordered them to attack Eaton. Ahmet more than once wished to give up the expedition. There were practically no provisions for the latter part of the march. On the 27th of April with the assistance of three bombarding cruisers Eaton captured Derna—an exploit commemorated by Whittier’s poem Derne. On the 13th of May and on the 10th of June he successfully withstood the attacks of Tripolitan forces sent to dislodge him. On the 12th of June he abandoned the town upon orders from Commodore Rodgers, for Lear had made peace (4th June) with Yussuf, the de facto Pasha of Tripoli. Eaton returned to the United States, and received a grant of 10,000 acres in Maine from the Massachusetts legislature. According to a deposition which he made in January 1807 he was approached by Aaron Burr (q.v.), who attempted to enlist him in his “conspiracy,” and wished him to win over the marine corps and to sound Preble and Decatur. As he received from the government, soon after making this deposition, about $10,000 to liquidate claims for his expense in Tripoli, which he had long pressed in vain, his good faith has been doubted. At Burr’s trial at Richmond in 1807 Eaton was one of the witnesses, but his testimony was unimportant. In May 1807 he was elected a member of the Massachusetts House of Representatives, and served for one term. He died on the 1st of June 1811 in Brimfield, Massachusetts.
See the anonymously published Life of the Late Gen. William Eaton (Brookfield, Massachusetts, 1813) by Charles Prentiss; C.C. Felton, “Life of William Eaton” in Sparks’s Library of American Biography, vol. ix. (Boston, 1838); and Gardner W. Allen’s Our Navy and the Barbary Corsairs (Boston, 1905).
EATON, WYATT (1849-1896), American portrait and figure painter, was born at Philipsburg, Canada, on the 6th of May 1849. He was a pupil of the schools of the National Academy of Design, New York, and in 1872 went to Paris, where he studied in the École des Beaux-Arts under J.L. Gérôme. He made the acquaintance of J.F. Millet at Barbizon, and was also influenced by his friend Jules Bastien-Lepage. After his return to the United States in 1876 he became a teacher in Cooper Institute and opened a studio in New York city. He was one of the organizers (and the first secretary) of the Society of American Artists. Among his portraits are those of William Cullen Bryant and Timothy Cole, the wood engraver (“The Man with the Violin”). Eaton died at Newport, Rhode Island, on the 7th of June 1896.
EAU CLAIRE, a city and the county-seat of Eau Claire county, Wisconsin, U.S.A., on the Chippewa river, at the mouth of the Eau Claire, about 87 m. E. of St Paul. Pop. (1890) 17,415; (1900) 17,517, of whom 4996 were foreign-born; (1910 census) 18,310. It is served by the Chicago & North-Western, the Chicago, Milwaukee & St Paul, and the Wisconsin Central railways, and is connected by an electric line with Chippewa Falls (12 m. distant). The city has a Carnegie library with 17,200 volumes in 1908, a Federal building, county court house, normal school and insane asylum. It has abundant water-power, and is an important lumber manufacturing centre; among its other manufactures are flour, wooden-ware, agricultural machinery, saw-mill machinery, logging locomotives, wood pulp, paper, linen, mattresses, shoes and trunks. The total value of factory products in 1905 was $3,601,558. The city is the principal wholesale and jobbing market for the prosperous Chippewa Valley. Eau Claire was first settled about 1847, and was chartered as a city in 1872; its growth dates from the development of the north-western lumber trade in the decade 1870-1880. In 1881 a serious strike necessitated the calling out of state militia for its suppression and the protection of property.
EAU DE COLOGNE (Ger. Kölnisches Wasser, “Cologne water”), a perfume, so named from the city of Cologne, where its manufacture was first established by an Italian, Johann (or Giovanni) Maria Farina (1685-1766), who settled at Cologne in 1709. The perfume gained a high reputation by 1766, and Farina associated himself with his nephew, to whose grandson the secret was ultimately imparted; the original perfume is still manufactured by members of this family under the name of the founder. The manufacture is, however, carried on at Cologne, and also in Italy, by other firms bearing the name Farina, and the scent has become part of the regular output of perfumers. The discovery has also been ascribed to a Paul de Feminis, who is supposed to have brought his recipe from Milan to Cologne, of which he became a citizen in 1690, and sold the perfume under the name Eau admirable, leaving the secret at his death to his nephew Johann Maria Farina. Certain of the Farinas claim to use his process. It was originally prepared by making an alcoholic infusion of certain flowers, pot-herbs, drugs and spices, distilling and then adding definite quantities of several vegetable essences. The purity and thorough blending of the ingredients are of the greatest importance. The original perfume is simulated and even excelled by artificial preparations. The oils of lemon, bergamot and orange are employed, together with the oils of neroli and rosemary in the better class. The common practice consists in dissolving the oils, in certain definite proportions based on experience, in pure alcohol and distilling, the distillate being diluted by rose-water.
EAUX-BONNES, a watering-place of south-western France, in the department of Basses-Pyrénées, 3½ m. S.E. of the small town of Laruns, the latter being 24 m. S. of Pau by rail. Pop. (1906) 610. Eaux-Bonnes is situated at a height of 2460 ft. at the entrance of a fine gorge, overlooking the confluence of two torrents, the Valentin and the Sourde. The village is well known for its sulphurous and saline mineral waters (first mentioned in the middle of the 14th century), which are beneficial in affections of the throat and lungs. They vary between 50° and 90° F. in temperature, and are used for drinking and bathing. There are two thermal establishments, a casino and fine promenades.
The watering-place of Les Eaux-Chaudes is 5 m. by road south-west of Eaux-Bonnes, in a wild gorge on the Gave d’Ossau. The springs are sulphurous, varying in temperature from 52° to 97° F., and are used in cases of rheumatism, certain maladies of women, &c. The thermal establishment is a handsome marble building.
There is fine mountain scenery in the neighbourhood of both places, the Pic de Ger near Eaux-Bonnes, commanding an extensive view. The valley of Ossau, one of the most beautiful in the Pyrenees, before the Revolution formed a community which, though dependent on Béarn, had its own legal organization, manners and costumes, the last of which are still to be seen on holidays.
EAVES (not a plural form as is sometimes supposed, but singular; O. Eng. efes, in Mid. High Ger. obse, Gothic ubizwa, a porch; connected with “over”), in architecture, the projecting edge of a sloping roof, which overhangs the face of the wall so as to throw off the water.
EAVESDRIP, or Eavesdrop, that width of ground around a house or building which receives the rain water dropping from the eaves. By an ancient Saxon law, a landowner was forbidden to erect any building at less than 2 ft. from the boundary of his land, and was thus prevented from injuring his neighbour’s house or property by the dripping of water from his eaves. The law of Eavesdrip has had its equivalent in the Roman stillicidium, which prohibited building up to the very edge of an estate.
From the Saxon custom arose the term “eavesdropper,” i.e. any one who stands within “the eavesdrop” of a house, hence one who pries into others’ business or listens to secrets. At common law an eavesdropper was regarded as a common nuisance, and was presentable at the court leet, and indictable at the sheriff’s tourn and punishable by fine and finding sureties for good behaviour. Though the offence of eavesdropping still exists at common law, there is no modern instance of a prosecution or indictment.
EBBW VALE, an urban district in the western parliamentary division of Monmouthshire, England, 21 m. N.W. of Newport on the Great Western, London & North-Western and Rhymney railways. Pop. (1891) 17,312; (1901) 20,994. It lies near the head of the valley of the river Ebbw, at an elevation of nearly 1000 ft., in a wild and mountainous mining district, which contains large collieries and important iron and steel works.
EBEL, HERMANN WILHELM (1820-1875), German philologist, was born at Berlin on the 10th of May 1820. He displayed in his early years a remarkable capacity for the study of languages, and at the same time a passionate fondness for music and poetry. At the age of sixteen he became a student at the university of Berlin, applying himself especially to philology, and attending the lectures of Böckh. Music continued to be the favourite occupation of his leisure hours, and he pursued the study of it under the direction of Marx. In the spring of 1838 he passed to the university of Halle, and there began to apply himself to comparative philology under Pott. Returning in the following year to his native city, he continued this study as a disciple of Bopp. He took his degree in 1842, and, after spending his year of probation at the French Gymnasium of Berlin, he resumed with great earnestness his language studies. About 1847 he began to study Old Persian. In 1852 he accepted a professorship at the Beheim-Schwarzbach Institution at Filehne, which post he held for six years. It was during this period that his studies in the Old Slavic and Celtic languages began. In 1858 he removed to Schneidemühl, and there he discharged the duties of first professor for ten years. He was afterwards called to the chair of comparative philology at the university of Berlin. He died at Misdroy on the 19th of August 1875. The most important work of Dr Ebel in the field of Celtic philology is his revised edition of the Grammatica Celtica of Professor Zeuss, completed in 1871. This had been preceded by his treatises—De verbi Britannici futuro ac conjunctivo (1866), and De Zeussii curis positis in Grammatica Celtica (1869). He made many learned contributions to Kühn’s Zeitschrift für vergleichende Sprachforschung, and to A. Schleicher’s Beiträge zur vergleichenden Sprachforschung; and a selection of these contributions was translated into English by Sullivan, and published under the title of Celtic Studies (1863). Ebel contributed the Old Irish section to Schleicher’s Indogermanische Chrestomathie (1869). Among his other works must be named Die Lehnwörter der deutschen Sprache (1856).
EBEL, JOHANN GOTTFRIED (1764-1830), the author of the first real guide-book to Switzerland, was born at Züllichau (Prussia). He became a medical man, visited Switzerland for the first time in 1790, and became so enamoured of it that he spent three years exploring the country and collecting all kinds of information relating to it. The result was the publication (Zürich, 1793) of his Anleitung auf die nützlichste und genussvollste Art in der Schweitz zu reisen (2 vols.), in which he gave a complete account of the country, the General Information sections being followed by an alphabetically arranged list of places, with descriptions. It at once superseded all other works of the kind, and was the best Swiss guide-book till the appearance of “Murray” (1838). It was particularly strong on the geological and historical sides. The second (1804-1805) and third (1809-1810) editions filled four volumes, but the following (the 8th appeared in 1843) were in a single volume. The work was translated into French in 1795 (many later editions) and into English (by 1818). Ebel also published a work (2 vols., Leipzig, 1798-1802) entitled Schilderungen der Gebirgsvölker der Schweiz, which deals mainly with the pastoral cantons of Glarus and Appenzell. In 1801 he was naturalized a Swiss citizen, and settled down in Zürich. In 1808 he issued his chief geological work, Über den Bau der Erde im Alpengebirge (Zürich, 2 vols.). He took an active share in promoting all that could make his adopted country better known, e.g. Heinrich Keller’s map (1813), the building of a hotel on the Rigi (1816), and the preparation of a panorama from that point (1823). From 1810 onwards he lived at Zürich, with the family of his friend, Conrad Escher von der Linth (1767-1823), the celebrated engineer.
EBER, PAUL (1511-1569), German theologian, was born at Kitzingen in Franconia, and was educated at Nuremberg and Wittenberg, where he became the close friend of Philip Melanchthon. In 1541 he was appointed professor of Latin grammar at Wittenberg, and in 1557 professor of the Old Testament. His range of learning was wide, and he published a handbook of Jewish history, a historical calendar intended to supersede the Roman Saints’ Calendar, and a revision of the Latin Old Testament. In the theological conflict of the time he played a large part, doing what he could to mediate between the extremists. From 1559 to the close of his life he was superintendent-general of the electorate of Saxony. He attained some fame as a hymn-writer, his best-known composition being “Wenn wir in höchsten Nöthen sein.” He died at Wittenberg on the 10th of December 1569.
EBERBACH, a town of Germany, in the grand-duchy of Baden, romantically situated on the Neckar, at the foot of the Katzenbuckel, 19 m. E. of Heidelberg by the railway to Würzburg. Pop. (1900) 5857. It contains an Evangelical and a Roman Catholic church, a commercial and a technical school, and, in addition to manufacturing cigars, leather and cutlery, carries on by water an active trade in timber and wine. Eberbach was founded in 1227 by the German king Henry VII., who acquired the castle (the ruins of which overhang the town) from the bishop of Worms. It became an imperial town and passed later to the Palatinate.
See Wirth, Geschichte der Stadt Eberbach (Stuttgart, 1864).
EBERBACH, a famous Cistercian monastery of Germany, in the Prussian province of Hesse-Nassau, situated near Hattenheim in the Rheingau, 10 m. N.W. from Wiesbaden. Founded in 1116 by Archbishop Adalbert of Mainz, as a house of Augustinian canons regular, it was bestowed by him in 1131 upon the Benedictines, but was shortly afterwards repurchased and conferred upon the Cistercian order. The Romanesque church (consecrated in 1186) contains numerous interesting monuments and tombs, notable among them being those of the archbishop of Mainz, 841 Gerlach (d. 1371) and Adolph II. of Nassau (d. 1475). It was despoiled during the Thirty Years’ War, was secularized in 1803, and now serves as a house of correction. Its cellars contain some of the finest vintages of the Rhine wines of the locality.
See Bär, Diplomatische Geschichte der Abtei Eberbach (Wiesb., 1851-1858 and 1886, 3 vols.), and Schäfer, Die Abtei Eberbach im Mittelalter (Berlin, 1901).
EBERHARD, surnamed Im Bart (Barbatus), count and afterwards duke of Württemberg (1445-1496), was the second son of Louis I., count of Württemberg-Urach (d. 1450), and succeeded his elder brother Louis II. in 1457. His uncle Ulrich V., count of Württemberg-Stuttgart (d. 1480), acted as his guardian, but in 1459, assisted by Frederick I., elector palatine, he threw off this restraint, and undertook the government of the district of Urach as Count Eberhard V. He neglected his duties as a ruler and lived a reckless life until 1468, when he made a pilgrimage to Jerusalem. He visited Italy, became acquainted with some famous scholars, and in 1474 married Barbara di Gonzaga, daughter of Lodovico III., marquis of Mantua, a lady distinguished for her intellectual qualities. In 1482 he brought about the treaty of Münsingen with his cousin Eberhard VI., count of Württemberg-Stuttgart. By this treaty the districts of Urach and Stuttgart into which Württemberg had been divided in 1437 were again united, and for the future the county was declared indivisible, and the right of primogeniture established. The treaty led to some disturbances, but in 1492 the sanction of the nobles was secured for its provisions. In return for this Eberhard agreed to some limitations on the power of the count, and so in a sense founded the constitution of Württemberg. At the diet of Worms in 1495 the emperor Maximilian I. guaranteed the treaty, confirmed the possessions and prerogatives of the house of Württemberg, and raised Eberhard to the rank of duke. Eberhard, although a lover of peace, was one of the founders of the Swabian League in 1488, and assisted to release Maximilian, then king of the Romans, from his imprisonment at Bruges in the same year. He gave charters to the towns of Stuttgart and Tübingen, and introduced order into the convents of his land, some of which he secularized. He took a keen interest in the new learning, founded the university of Tübingen in 1476, befriended John Reuchlin, whom he made his private secretary, welcomed scholars to his court, and is said to have learned Latin in later life. In 1482 he again visited Italy and received the Golden Rose from Pope Sixtus IV. He won the esteem of the emperors Frederick III. and Maximilian I. on account of his wisdom and fidelity, and his people held him in high regard. His later years were mainly spent at Stuttgart, but he died at Tübingen on the 25th of February 1496, and in 1537 his ashes were placed in the choir of the Stiftskirche there. Eberhard left no children, and the succession passed to his cousin Eberhard, who became Duke Eberhard II.
See Rösslin, Leben Eberhards im Barte (Tübingen, 1793); Bossert, Eberhard im Bart (Stuttgart, 1884).
EBERHARD, CHRISTIAN AUGUST GOTTLOB (1769-1845), German miscellaneous writer, was born at Belzig, near Wittenberg, on the 12th of January 1769. He studied theology at Leipzig; but, a story he contributed to a periodical having proved successful, he devoted himself to literature. With the exception of Hannchen und die Küchlein (1822), a narrative poem in ten parts, and an epic on the Creation, Der erste Mensch und die Erde (1828), Eberhard’s work was ephemeral in character and is now forgotten. He died at Dresden on the 13th of May 1845.
His collected works (Gesammelte Schriften) appeared in 20 volumes in 1830-1831.
EBERHARD, JOHANN AUGUSTUS (1739-1809), German theologian and philosopher, was born at Halberstadt in Lower Saxony, where his father was singing-master at the church of St Martin’s, and teacher of the school of the same name. He studied theology at the university of Halle, and became tutor to the eldest son of the baron von der Horst, to whose family he attached himself for a number of years. In 1763 he was appointed con-rector of the school of St Martin’s, and second preacher in the hospital church of the Holy Ghost; but he soon afterwards resigned these offices and followed his patron to Berlin. There he met Nicolai and Moses Mendelssohn, with whom he formed a close friendship. In 1768 he became preacher or chaplain to the workhouse at Berlin and the neighbouring fishing village of Stralow. Here he wrote his Neue Apologie des Socrates (1772), a work occasioned by an attack on the fifteenth chapter of Marmontel’s Belisarius made by Peter Hofstede, a clergyman of Rotterdam, who maintained the patristic view that the virtues of the noblest pagans were only splendida peccata. Eberhard stated the arguments for the broader view with dignity, acuteness and learning, but the liberality of the reasoning gave great offence to the strictly orthodox divines, and is believed to have obstructed his preferment in the church.
In 1774 he was appointed to the living of Charlottenburg. A second volume of his Apologie appeared in 1778. In this he not only endeavoured to obviate some objections which were taken to the former part, but continued his inquiries into the doctrines of the Christian religion, religious toleration and the proper rules for interpreting the Scriptures. In 1778 he accepted the professorship of philosophy at Halle. As an academical teacher, however, he was unsuccessful. His powers as an original thinker were not equal to his learning and his literary gifts, as was shown in his opposition to the philosophy of Kant. In 1786 he was admitted a member of the Berlin Academy of Sciences; in 1805 the king of Prussia conferred upon him the honorary title of a privy-councillor. In 1808 he obtained the degree of doctor in divinity, which was given him as a reward for his theological writings. He died on the 6th of January 1809. He was master of the learned languages, spoke and wrote French with facility and correctness, and understood English, Italian and Dutch. He possessed a just and discriminating taste for the fine arts, and was a great lover of music.
Works:—Neue Apologie des Socrates, &c. (2 vols., 1772-1778); Allgemeine Theorie des Denkens und Empfindens, &c. (Berlin, 1776), an essay which gained the prize assigned by the Royal Society of Berlin for that year; Von dem Begriff der Philosophie und ihren Theilen (Berlin, 1778)—a short essay, in which he announced the plan of his lectures on being appointed to the professorship at Halle; Lobschrift auf Herrn Johann Thunmann Prof. der Weltweisheit und Beredsamkeit auf der Universität zu Halle (Halle, 1779); Amyntor, eine Geschichte in Briefen (Berlin, 1782)—written with the view of counteracting the influence of those sceptical and Epicurean principles in religion and morals then so prevalent in France, and rapidly spreading amongst the higher ranks in Germany; Über die Zeichen der Aufklärung einer Nation, &c. (Halle, 1783); Theorie der schönen Künste und Wissenschaften, &c. (Halle, 1783, 3rd ed. 1790); Vermischte Schriften (Halle, 1784); Neue vermischte Schriften (ib. 1786); Allgemeine Geschichte der Philosophie, &c. (Halle, 1788), 2nd ed. with a continuation and chronological tables (1796); Versuch einer allgemeinen-deutschen Synonymik (Halle and Leipzig, 1795-1802, 6 vols., 4th ed. 1852-1853), long reckoned the best work on the synonyms of the German language (an abridgment of it was published by the author in one large volume, Halle, 1802); Handbuch der Aesthetik (Halle, 1803-1805, 2nd ed. 1807-1820). He also edited the Philosophisches Magazin (1788-1792) and the Philosophisches Archiv (1792-1795).
See F. Nicolai, Gedächtnisschrift auf J.A. Eberhard (Berlin and Stettin, 1810); also K.H. Jördens, Lexicon deutscher Dichter und Prosaisten.
EBERLIN, JOHANN ERNST (1702-1762), German musician and composer, was born in Bavaria, and became afterwards organist in the cathedral at Salzburg, where he died. Most of his compositions were for the church (oratorios, &c.), but he also wrote some important fugues, sonatas and preludes; and his pieces were at one time highly valued by Mozart.
EBERS, GEORG MORITZ (1837-1898), German Egyptologist and novelist, was born in Berlin on the 1st of March 1837. At Göttingen he studied jurisprudence, and at Berlin oriental languages and archaeology. Having made a special study of Egyptology, he became in 1865 docent in Egyptian language and antiquities at Jena, and in 1870 he was appointed professor in these subjects at Leipzig. He had made two scientific journeys to Egypt, and his first work of importance, Ägypten und die Bücher Moses, appeared in 1867-1868. In 1874 he edited the celebrated medical papyrus (“Papyrus Ebers”) which he had discovered in Thebes (translation by H. Joachim, 1890). Ebers early conceived the idea of popularizing Egyptian lore by means of historical romances. Eine ägyptische Königstochter was 842 published in 1864, and obtained great success. His subsequent works of the same kind—Uarda (1877), Homo sum (1878), Die Schwestern (1880), Der Kaiser (1881), of which the scene is laid in Egypt at the time of Hadrian, Serapis (1885), Die Nilbraut (1887), and Kleopatra (1894), were also well received, and did much to make the public familiar with the discoveries of Egyptologists. Ebers also turned his attention to other fields of historical fiction—especially the 16th century (Die Frau Bürgermeisterin, 1882; Die Gred, 1887)—without, however, attaining the success of his Egyptian novels. Apart from their antiquarian and historical interest, Ebers’s books have not a very high literary value. His other writings include a descriptive work on Egypt (Ägypten in Wort und Bild, 2nd ed., 1880), a guide to Egypt (1886) and a life (1885) of his old teacher, the Egyptologist Karl Richard Lepsius. The state of his health led him in 1889 to retire from his chair at Leipzig on a pension. He died at Tutzing in Bavaria, on the 7th of August 1898.
Ebers’s Gesammelte Werke appeared in 25 vols. at Stuttgart (1893-1895). Many of his books have been translated into English. For his life see his Die Geschichte meines Lebens (Stuttgart, 1893); also R. Gosche, G. Ebers, der Forscher und Dichter (2nd ed., Leipzig, 1887).
EBERSWALDE, a town of Germany, in the kingdom of Prussia, 28 m. N.E. of Berlin by rail; on the Finow canal. Pop. (1905) 23,876. The town has a Roman Catholic and two Evangelical churches, a school of forestry, a gymnasium, a higher-grade girls’ school and two schools of domestic economy. It possesses a mineral spring, which attracts numerous summer visitors, and has various industries, which include iron-founding and the making of horse-shoe nails, roofing material and bricks. A considerable trade is carried on in grain, wood and coals. In the immediate neighbourhood are one of the chief brass-foundries in Germany and an extensive government paper-mill, in which the paper for the notes of the imperial bank is manufactured.
Eberswalde received its municipal charter in 1257. It was taken and sacked during the Thirty Years’ War. In 1747 Frederick the Great brought a colony of Thuringian cutlers to the town, but this branch of industry has entirely died out. About 4 m. to the north lies the old Cistercian monastery of Chorin, the fine Gothic church of which contains the tombs of several margraves of Brandenburg.
EBERT, FRIEDRICH ADOLF (1791-1834), German bibliographer, was born at Taucha, near Leipzig, on the 9th of July 1791, the son of a Lutheran pastor. At the age of fifteen he was appointed to a subordinate post in the municipal library of Leipzig. He studied theology for a short time at Leipzig, and afterwards philology at Wittenberg, where he graduated doctor in philosophy in 1812. While still a student he had already published, in 1811, a work on public libraries, and in 1812 another work entitled Hierarchiae in religionem ac literas commoda. In 1813 he was attached to the Leipzig University library, and in 1814 was appointed secretary to the Royal library of Dresden. The same year he published F. Taubmanns Leben und Verdienste, and in 1819 Torquato Tasso, a translation from Pierre Louis Ginguené with annotations. The rich resources open to him in the Dresden library enabled him to undertake the work on which his reputation chiefly rests, the Allgemeines bibliographisches Lexikon, the first volume of which appeared in 1821 and the second in 1830. This was the first work of the kind produced in Germany, and the most scientific published anywhere. From 1823 to 1825 Ebert was librarian to the duke of Brunswick at Wolfenbüttel, but returning to Dresden was made, in 1827, chief librarian of the Dresden Royal library. Among his other works are—Die Bildung des Bibliothekars (1820), Geschichte und Beschreibung der königlichen öffentlichen Bibliothek in Dresden (1822), Zur Handschriftenkunde (1825-1827), and Culturperioden des obersächsischen Mittelalters (1825). Ebert was a contributor to various journals and took part in the editing of Ersch and Gruber’s great encyclopaedia. He died at Dresden on the 13th of November 1834, in consequence of a fall from the ladder in his library.
See the article in Ersch und Grubers Encyclopädie, and that in the Allg. deutsche Biog. by his successor in the post of chief librarian in Dresden, Schnorr von Carolsfeld.
EBINGEN, a town of Germany, in the kingdom of Württemberg, on the Schmiecha, a left-hand tributary of the Danube, 22 m. S. of Tübingen and 37 m. W. of Ulm by rail. It manufactures velvet and cotton-velvet (“Manchester”) goods, stockings, stays, hats, needles, tools, &c. There are also tanneries. Pop. 9000.
EBIONITES (Heb. אביונם, “poor men”), a name given to the ultra-Jewish party in the early Christian church. It is first met with in Irenaeus (Adv. Haer. i. 26. 2), who sheds no light on the origin of the Ebionites, but says that while they admit the world to have been made by the true God (in contrast to the Demiurge of the Gnostics), they held Cerinthian views on the person of Christ, used only the Gospel of Matthew (probably the Gospel according to the Hebrews—so Eusebius), and rejected Paul as an apostate from the Mosaic Law, to the customs and ordinances of which, including circumcision, they steadily adhered. A similar account is given by Hippolytus (Haer. vii. 35), who invents a founder named Ebion. Origen (Contra Celsum, v. 61; In Matt. tom. xvi. 12) divides the Ebionites into two classes according to their acceptance or rejection of the virgin birth of Jesus, but says that all alike reject the Pauline epistles. This is confirmed by Eusebius, who adds that even those who admitted the virgin birth did not accept the pre-existence of Jesus as Logos and Sophia. They kept both the Jewish Sabbath and the Christian Lord’s day, and held extreme millenarian ideas in which Jerusalem figured as the centre of the coming Messianic kingdom. Epiphanius with his customary confusion makes two separate sects, Ebionites and Nazarenes. Both names, however, refer to the same people1 (the Jewish Christians of Syria), the latter going back to the designation of apostolic times (Acts xxiv. 5), and the former being the term usually applied to them in the ecclesiastical literature of the 2nd and 3rd centuries.
The origin of the Nazarenes or Ebionites as a distinct sect is very obscure, but may be dated with much likelihood from the edict of Hadrian which in 135 finally scattered the old church of Jerusalem. While Christians of the type of Aristo of Pella and Hegesippus, on the snapping of the old ties, were gradually assimilated to the great church outside, the more conservative section became more and more isolated and exclusive. “It may have been then that they called themselves the Poor Men, probably as claiming to be the true representatives of those who had been blessed in the Sermon on the Mount, but possibly adding to the name other associations.” Out of touch with the main stream of the church they developed a new kind of pharisaism. Doctrinally they stood not so much for a theology as for a refusal of theology, and, rejecting the practical liberalism of Paul, became the natural heirs of those early Judaizers who had caused the apostle so much annoyance and trouble.
Though there is insufficient justification for dividing the Ebionites into two separate and distinct communities, labelled respectively Ebionites and Nazarenes, we have good evidence, not only that there were grades of Christological thought among them, but that a considerable section, at the end of the 2nd century and the beginning of the 3rd, exchanged their simple Judaistic creed for a strange blend of Essenism and Christianity. These are known as the Helxaites or Elchasaites, for they accepted as a revelation the “book of Elchasai,” and one Alcibiades of Apamea undertook a mission to Rome about 220 to propagate its teaching. It was claimed that Christ, as an angel 96 miles high, accompanied by the Holy Spirit, as a female angel of the same stature, had given the revelation to Elchasai in the 3rd year of Trajan (A.D. 100), but the book was probably quite new in Alcibiades’ time. It taught that Christ was an angel born of human parents, and had appeared both before (e.g. in Adam and Moses) and after this birth in Judea. His coming did not annul the Law, for he was merely a prophet and teacher; Paul was wrong and circumcision still necessary. Baptism must be repeated as a means of purification from sin, and proof against disease; the sinner immerses himself “in the name of the mighty 843 and most high God,” invoking the “seven witnesses” (sky, water, the holy spirits, the angels of prayer, oil, salt and earth), and pledging himself to amendment. Abstinence from flesh was also enjoined, and a good deal of astrological fancy was interwoven with the doctrinal and practical teaching. It is highly probable, too, that from these Essene Ebionites there issued the fantastical and widely read “Clementine” literature (Homilies and Recognitions) of the 3rd century. Ebionite views lingered especially in the country east of the Jordan until they were absorbed by Islam in the 7th century.
In addition to the literature cited see R.C. Ottley, The Doctrine of the Incarnation, part iii. § ii.; W. Moeller, Hist. of the Christian Church, i. 99; art. in Herzog-Hauck, Realencyklopädie, s.v. “Ebioniten”; also Clementine Literature.
1 So A. Harnack, Hist. of Dogma, i. 301, and F.J.A. Hort, Judaistic Christianity, p. 199. Th. Zahn and J.B. Lightfoot (“St. Paul and the Three,” in Commentary on Galatians) maintain the distinction.
EBNER-ESCHENBACH, MARIE, Freifrau von (1830- ), Austrian novelist, was born at Zdislavič in Moravia, on the 13th of September 1830, the daughter of a Count Dubsky. She lost her mother in early infancy, but received a careful intellectual training from two stepmothers. In 1848 she married the Austrian captain, and subsequent field-marshal, Moritz von Ebner-Eschenbach, and resided first at Vienna, then at Klosterbruck, where her husband had a military charge, and after 1860 again at Vienna. The marriage was childless, and the talented wife sought consolation in literary work. In her endeavours she received assistance and encouragement from Franz Grillparzer and Freiherr von Münch-Bellinghausen. Her first essay was with the drama Maria Stuart in Schottland, which Philipp Eduard Devrient produced at the Karlsruhe theatre in 1860. After some other unsuccessful attempts in the field of drama, she found her true sphere in narrative. Commencing with Die Prinzessin von Banalien (1872), she graphically depicts in Božena (Stuttgart, 1876, 4th ed. 1899) and Das Gemeindekind (Berlin, 1887, 4th ed. 1900) the surroundings of her Moravian home, and in Lotti, die Uhrmacherin (Berlin, 1883, 4th ed. 1900), Zwei Comtessen (Berlin, 1885, 5th ed. 1898), Unsühnbar (1890, 5th ed. 1900) and Glaubenslos? (1893) the life of the Austrian aristocracy in town and country. She also published Neue Erzählungen (Berlin, 1881, 3rd ed. 1894), Aphorismen (Berlin, 1880, 4th ed. 1895) and Parabeln, Märchen und Gedichte (2nd ed., Berlin, 1892). Frau von Ebner-Eschenbach’s elegance of style, her incisive wit and masterly depiction of character give her a foremost place among the German women-writers of her time. On the occasion of her seventieth birthday the university of Vienna conferred upon her the degree of doctor of philosophy, honoris causa.
An edition of Marie von Ebner-Eschenbach’s Gesammelte Schriften began to appear in 1893 (Berlin). See A. Bettelheim, Marie von Ebner-Eschenbach: biographische Blätter (Berlin, 1900), and M. Necker, Marie von Ebner-Eschenbach, nach ihren Werken geschildert (Berlin, 1900).
EBOLI (anc. Eburum), a town of Campania, Italy, in the province of Salerno, from which it is 16 m. E. by rail, situated 470 ft. above sea-level, on the S. edge of the hills overlooking the valley of the Sele. Pop. (1901) 9642 (town), 12,423 (commune). The sacristy of St Francesco contains two 14th-century pictures, one by Roberto da Oderisio of Naples. The ancient Eburum was a Lucanian city, mentioned only by Pliny and in inscriptions, not far distant from the Campanian border. It lay above the Via Popillia, which followed the line taken by the modern railway. Some scanty remains of its ancient polygonal walls may still be seen.
EBONY (Gr. ἔβενος), the wood of various species of trees of the genus Diospyros (natural order Ebenaceae), widely distributed in the tropical parts of the world. The best kinds are very heavy, are of a deep black, and consist of heart-wood only. On account of its colour, durability, hardness and susceptibility of polish, ebony is much used for cabinet work and inlaying, and for the manufacture of pianoforte-keys, knife-handles and turned articles. The best Indian and Ceylon ebony is furnished by D. Ebenum, a native of southern India and Ceylon, which grows in great abundance throughout the flat country west of Trincomalee. The tree is distinguished from others by the inferior width of its trunk, and its jet-black, charred-looking bark, beneath which the wood is perfectly white until the heart is reached. The wood is stated to excel that obtained from D. reticulata of the Mauritius and all other varieties of ebony in the fineness and intensity of its dark colour. Although the centre of the tree alone is employed, reduced logs 1 to 3 ft. in diameter can readily be procured. Much of the East Indian ebony is yielded by the species D. Melanoxylon (Coromandel ebony), a large tree attaining a height of 60 to 80 ft., and 8 to 10 ft. in circumference, with irregular rigid branches, and oblong or oblong-lanceolate leaves. The bark of the tree is astringent, and mixed with pepper is used in dysentery by the natives of India. The wood of D. tomentosa, a native of north Bengal, is black, hard and of great weight. D. montana, another Indian species, produces a yellowish-grey soft but durable wood. D. quaesita is the tree from which is obtained the wood known in Ceylon by the name Calamander, derived by Pridham from the Sinhalee kalumindrie, black-flowing. Its closeness of grain, great hardness and fine hazel-brown colour, mottled and striped with black, render it a valuable material for veneering and furniture making. D. Dendo, a native of Angola, is a valuable timber tree, 25 to 35 ft. high, with a trunk 1 to 2 ft. in diameter. The heart-wood is very black and hard and is known as black ebony, also as billet-wood, and Gabun, Lagos, Calabar or Niger ebony. What is termed Jamaica or West Indian ebony, and also the green ebony of commerce, are produced by Brya Ebenus, a leguminous tree or shrub, having a trunk rarely more than 4 in. in diameter, flexible spiny branches, and orange-yellow, sweet-scented flowers. The heart-wood is rich dark brown in colour, heavier than water, exceedingly hard and capable of receiving a high polish.
From the book of Ezekiel (xxvii. 15) we learn that ebony was among the articles of merchandise brought to Tyre; and Herodotus states (iii. 97) that the Ethiopians every three years sent a tribute of 200 logs of it to Persia. Ebony was known to Virgil as a product of India (Georg. ii. 116), and was displayed by Pompey the Great in his Mithradatic triumph at Rome. By the ancients it was esteemed of equal value for durability with the cypress and cedar (see Pliny, Nat. Hist. xii. 9, xvi. 79). According to Solinus (Polyhistor, cap. lv. p. 353, Paris, 1621), it was employed by the kings of India for sceptres and images, also, on account of its supposed antagonism to poison, for drinking-cups. The hardness and black colour of the wood appear to have given rise to the tradition related by Pausanias, and alluded to by Southey in Thalaba, i. 22, that the ebony tree produced neither leaves nor fruit, and was never seen exposed to the sun.
EBRARD, JOHANNES HEINRICH AUGUST (1818-1888), German theologian, was born at Erlangen on the 18th of January 1818. He was educated in his native town and at Berlin, and after teaching in a private family became Privatdocent at Erlangen (1841) and then professor of theology at Zürich (1844). In 1847 he was appointed professor of theology at Erlangen, a chair which he resigned in 1861; in 1875 he became pastor of the French reformed church in the same city. As a critic Ebrard occupied a very moderate standpoint; as a writer his chief works were Christliche Dogmatik (2 vols., 1851), Vorlesungen über praktische Theologie (1864), Apologetik (1874-1875, Eng. trans. 1886). He also edited and completed H. Olshausen’s commentary, himself writing the volumes on the Epistle to the Hebrews, the Johannine Epistles, and Revelation. In the department of belles-lettres he wrote a good deal under such pseudonyms as Christian Deutsch, Gottfried Flammberg and Sigmund Sturm. He died at Erlangen on the 23rd of July 1888.
EBRO (anc. Iberus or Hiberus), the only one of the five great rivers of the Iberian Peninsula (Tagus, Douro, Ebro, Guadalquivir, Guadiana) which flows into the Mediterranean. The Ebro rises at Fuentibre, a hamlet among the Cantabrian Mountains, in the province of Santander; at Reinosa, 4 m. east, it is joined on the right by the Hijar, and thus gains considerably in volume. It flows generally east by south through a tortuous valley as far as Miranda de Ebro, passing through the celebrated Roman bridge known as La Horadada (“the perforated”), near Oña in Burgos. From Miranda it winds south-eastward through 844 the wide basin enclosed on the right by the highlands of Old Castile and western Aragon, and on the left by the Pyrenees. The chief cities on its banks are Logroño, Calahorra, Tudela, Saragossa and Caspe. Near Mora in Catalonia it forces a way through the coastal mountains, and, passing Tortosa, falls into the Mediterranean about 80 m. south-west of Barcelona, after forming by its delta a conspicuous projection on the otherwise regular coast line. In its length, approximately 465 m., the Ebro is inferior to the Tagus, Guadiana and Douro; it drains an area of nearly 32,000 sq. m. Its principal tributaries are—from the right hand the Jalon with its affluent the Jiloca, the Huerva, Aguas, Martin, Guadalope and Matarraña; from the left the Ega, Aragon, Arba, Gallego, and the Segre with its intricate system of confluent rivers. The Ebro and its tributaries have been utilized for irrigation since the Moorish conquest; the main stream becomes navigable by small boats about Tudela; but its value as a means of communication is almost neutralized by the obstacles in its channel, and seafaring vessels cannot proceed farther up than Tortosa. The great Imperial Canal, begun under the emperor Charles V. (1500-1558), proceeds along the right bank of the river from a point about 3 m. below Tudela, to El Burgo de Ebro, 5 m. below Saragossa; the irrigation canal of Tauste skirts the opposite bank for a shorter distance; and the San Carlos or New Canal affords direct communication between Amposta at the head of the delta and the harbour of Los Alfaques. From Miranda to Mora the Bilbao-Tarragona railway follows the course of the Ebro along the right bank.
EBROÏN (d. 681), Frankish “mayor of the palace,” was a Neustrian, and wished to impose the authority of Neustria over Burgundy and Austrasia. In 656, at the moment of his accession to power, Sigebert III., the king of Austrasia, had just died, and the Austrasian mayor of the palace, Grimoald, was attempting to usurp the authority. The great nobles, however, appealed to the king of Neustria, Clovis II., and unity was re-established. But in spite of a very firm policy Ebroïn was unable to maintain this unity, and while Clotaire III., son of Clovis II., reigned in Neustria and Burgundy, he was obliged in 660 to give the Austrasians a special king, Childeric II., brother of Clotaire III., and a special mayor of the palace, Wulfoald. He endeavoured to maintain at any rate the union of Neustria and Burgundy, but the great Burgundian nobles wished to remain independent, and rose under St Leger (Leodegar), bishop of Autun, defeated Ebroïn, and interned him in the monastery of Luxeuil (670). A proclamation was then issued to the effect that each kingdom should keep its own laws and customs, that there should be no further interchange of functionaries between the kingdoms, and that no one should again set up a tyranny like that of Ebroïn. Soon, however, Leger was defeated by Wulfoald and the Austrasians, and was himself confined at Luxeuil in 673. In the same year, taking advantage of the general anarchy, Ebroïn and Leger left the cloister and soon found themselves once more face to face. Each looked for support to a different Merovingian king, Ebroïn even proclaiming a false Merovingian as sovereign. In this struggle Leger was vanquished; he was besieged in Autun, was forced to surrender and had his eyes put out, and, on the 12th of October 678, he was put to death after undergoing prolonged tortures. The church honours him as a saint. After his death Ebroïn became sole and absolute ruler of the Franks, imposing his authority over Burgundy and subduing the Austrasians, whom he defeated in 678 at Bois-du-Fay, near Laon. His triumph, however, was short-lived; he was assassinated in 681, the victim of a combined attack of his numerous enemies. He was a man of great energy, but all his actions seem to have been dictated by no higher motives than ambition and lust of power.
See Liber historiae Francorum, edited by B. Krusch, in Mon. Germ. hist. script. rer. Merov. vol. ii.; Vita sancti Leodegarii, by Ursinus, a monk of St Maixent (Migne, Patr. Latina, vol. xcvi.); “Vita metrica” in Poetae Latini aevi Carolini, vol. iii. (Mon. Germ. hist.); J.B. Pitra, Histoire de Saint Léger (Paris, 1846); and J. Friedrich, “Zur Gesch. des Hausmeiers Ebroïn,” in the Proceedings of the Academy of Munich (1887, pp. 42-61).
EBURĀCUM, or Eborācum (probably a later variant), the Roman name of York (q.v.) in England. Established about A.D. 75-80 as fortress of the Ninth legion and garrisoned (after the annihilation of that legion about A.D. 118) by the Sixth legion, it developed outside its walls a town of civil life, which later obtained Roman municipal rank and in the 4th century was the seat of a Christian bishop. The fortress and town were separated by the Ouse. On the left bank, where the minster stands, was the fortress, of which the walls can still be partly traced, and one corner (the so-called Multangular Tower) survives. The municipality occupied the right bank near the present railway station. The place was important for its garrison and as an administrative centre, and the town itself was prosperous, though probably never very large. The name is preserved in the abbreviated form Ebor in the official name of the archbishop of York, but the philological connexion between Eboracum and the modern name York is doubtful and has probably been complicated by Danish influence.
EÇA DE QUEIROZ, JOSÉ MARIA (1843-1900), Portuguese writer, was born at the northern fishing town of Povoa de Varzim, his father being a retired judge. He went through the university of Coimbra, and on taking his degree in law was appointed Administrador de Concelho at Leiria, but soon tired of the narrow mental atmosphere of the old cathedral town and left it. He accompanied the Conde de Rezende to Egypt, where he assisted at the opening of the Suez Canal, and to Palestine, and on his return settled down to journalism in Lisbon and began to evolve a style, at once magical and unique, which was to renovate his country’s prose. Though he spent much of his days with the philosopher sonneteer Anthero de Quental, and the critic Jayme Batalha Reis, afterwards consul-general in London, he did not restrict his intimacy to men of letters, but frequented all kinds of society, acquiring a complete acquaintance with contemporary Portuguese life and manners. Entering the consular service in 1872, he went to Havana, and, after a tour in the United States, was transferred two years later to Newcastle-on-Tyne and in 1876 to Bristol. In 1888 he became Portuguese consul-general in Paris, and there died in 1900.
Queiroz made his literary début in 1870 by a sensational story, The Mystery of the Cintra Road, written in collaboration with the art critic Ramalho Ortigão, but the first publication which brought him fame was The Farpas, a series of satirical and humorous sketches of various phases of social life, which, to quote the poet Guerra Junqueiro, contain “the epilepsy of talent.” These essays, the joint production of the same partners, criticized and ridiculed the faults and foibles of every class in turn, mainly by a comparison with the French, for the education of Queiroz had made him a Frenchman in ideas and sympathies. His Brazilian friend, Eduardo Prado, bears witness that at this period French literature, especially Hugo’s verse, and even French politics, interested Queiroz profoundly, while he altogether ignored the belles-lettres of his own country and its public affairs. This phase lasted for some years, and even when he travelled in the East he was inclined to see it with the eyes of Flaubert, though the publication of The Relic and that delightful prose poem Sweet Miracle afterwards showed that he had been directly impressed and deeply penetrated by its scenery, poetry and mysticism. The Franco-German War of 1870, however, by lowering the prestige of France, proved the herald of a national Portuguese revival, and had a great influence on Queiroz, as also had his friend Oliveira Martins (q.v.), the biographer of the patriot kings of the Aviz dynasty. He founded the Portuguese Realist-Naturalist school, of which he remained for the rest of his life the chief exponent, by a powerful romance, The Crime of Father Amaro, written in 1871 at Leiria but only issued in 1875. Its appearance then led to a baseless charge that he had plagiarized La Faute de l’Abbé Mouret, and ill-informed critics began to name Queiroz the Portuguese Zola, though he clearly occupied an altogether different plane in the domain of art. During his stay in England he produced two masterpieces, Cousin Basil and The Maias, but they show no traces of English influence, nor again are they French in tone, for, living near to France, his disillusionment progressed and was completed when he went to Paris and had to live under the régime of the Third 845 Republic. Settling at Neuilly, the novelist became chronicler, critic, and letter-writer as well, and in all these capacities Queiroz displayed a spontaneity, power and artistic finish unequalled in the literature of his country since the death of Garrett. A bold draughtsman, he excelled in freshness of imagination and careful choice and collocation of words, while his warmth of colouring and brilliance of language speak of the south. Many of his pages descriptive of natural scenery, such for instance as the episode of the return to Tormes in The City and the Mountains, have taken rank as classic examples of Portuguese prose, while as a creator of characters he stood unsurpassed by any writer of his generation in the same field. He particularly loved to draw and judge the middle class, and he mocks at and chastises its hypocrisy and narrowness, its veneer of religion and culture, its triumphant lying, its self-satisfied propriety, its cruel egotism. But though he manifested a predilection for middle-class types, his portrait gallery comprises men and women of all social conditions. The Maias, his longest book, treats of fidalgos, while perhaps his most remarkable character study is of a servant, Juliana, in Cousin Basil. At least two of his books, this latter and The Crime of Father Amaro, are chroniques scandaleuses in their plots and episodes; these volumes, however, mark not only the high-water line of the Realist-Naturalist school in Portugal, but are in themselves, leaving aside all accidentals, creative achievements of a high order.
Though Queiroz was a keen satirist of the ills of society, his pages show hardly a trace of pessimism. The City and the Mountains, and in part The Relic also, reveal the apostle of Realism as an idealist and dreamer, a true representative of that Celtic tradition which survives in the race and has permeated the whole literature of Portugal. The Mandarin, a fantastic variation on the old theme of a man self-sold to Satan, and The Illustrious House of Ramires, are the only other writings of his that require mention, except The Correspondence of Fradique Mendes. In conjunction with Anthero de Quental and Jayme Batalha Reis, Queiroz invented under that name a smart man of the world who had something of himself and something of Eduardo Prado, and made him correspond on all sorts of subjects with imaginary friends and relatives to the delight of the public, many of whom saw in him a mysterious new writer whose identity they were eager to discover. These sparkling and humorous letters are an especial favourite with admirers of Queiroz, because they reveal so much of his very attractive personality, and perhaps the cleverest of the number, that on Pacheco, has received an English dress. In addition to his longer and more important works, Queiroz wrote a number of short stories, some of which have been printed in a volume under the title of Contos. The gems of this remarkable collection are perhaps The Peculiarities of a Fair-haired Girl, A Lyric Poet, José Matthias, The Corpse, and Sweet Miracle.
Most of his books have gone through many editions, and they are even more appreciated in the Brazils than in Portugal. It should be mentioned that the fourth edition of Father Amaro is entirely different in form and action from the first, the whole story having been rewritten. One of Queiroz’s romances and two of his short stories have been published in English. An unsatisfactory version of Cousin Basil, under the title Dragon’s Teeth, appeared at Boston, U.S.A., in 1889, while Sweet Miracle has had three editions in England and one in America, and there is also a translation of O Defunto (The Corpse) under the name of Our Lady of the Pillar.
An admirable critical study of the work of Queiroz will be found in A Geração Nova—Os Novellistas, by J. Pereira de Sampaio (Bruno), (Oporto, 1886). The Revista moderna of the 20th of November 1897 was entirely devoted to him. Senhor Batalha Reis gives interesting reminiscences of the novelist’s early days in his preface to some prose fragments edited by him and named Prosas Barbaras (Oporto, 1903).
ÉCARTÉ (Fr. for “separated,” “discarded”), a game at cards, of modern origin, probably first played in the Paris salons in the first quarter of the 19th century. It is a development of a very old card game called la triomphe or French-ruff. Écarté is generally played by two persons, but a pool of three may be formed, the player who is out taking the place of the loser, and the winner of two consecutive games winning the pool. At French écarté (but not at English) bystanders who are betting may advise the players, but only by pointing to the cards they desire them to play, and the loser of the game goes out, one of the rentrants taking his place, unless the loser is playing la chouette, i.e. playing single-handed against two, and taking all bets.
The small cards (from the two to the six, both inclusive) are removed from an ordinary pack. The players cut for deal, the highest having the choice. The king is the highest card, the ace ranking after the knave. The dealer gives five cards to his adversary, and five to himself, by two at a time to each and by three at a time to each, or vice versa. The eleventh card is turned up for trumps. If it is a king, the dealer scores one, at any time before the next deal. The non-dealer then looks at his cards. If satisfied with them he plays, and there is no discarding; if not satisfied he “proposes.” The dealer may either accept or refuse. If he accepts, each player discards face downwards as many cards as he thinks fit, and fresh ones are given from the undealt cards or “stock,” first to complete the non-dealer’s hand to five, then to complete the dealer’s. To ask for “a book” is to ask for five cards. Similarly a second proposal may be made, and so on, until one player is satisfied with his hand. If the dealer refuses, the hand is played without discarding. If the non-dealer announces that he holds the king of trumps, he scores one; and similarly, if the dealer holds the king and announces it, he scores one. The announcement must be made before playing one’s first card, or if that card be the king, on playing it. The non-dealer, being satisfied with his hand, leads a card. The dealer plays a card to it, the two cards thus played forming a trick. The winner of the trick leads to the next, and so on. The second to play to a trick must follow suit if able, and must win the trick if he can.
The scores are for the king and for the majority of tricks. The player who wins three tricks scores one for the “point”; if he wins all five tricks, he scores two for the “vole.” If the non-dealer plays without proposing, or the dealer refuses the first proposal, and fails to win three tricks, the adversary scores two, but no more even if he wins the vole. The game is five up. The points are conveniently marked with a three-card and a two-card, as at euchre. The three is put face upwards with the two face downwards on the top of it. When one or two or three points are scored the top card is moved so as to expose them. At four, one pip of the two-card is put under the other card. Games may be recorded similarly.
Hints to Players.—The following hints may be of service to beginners:—
Shuffle thoroughly after every deal.
Do not announce the king until in the act of playing your first card.
The hands which should be played without proposing, called jeux de règle (standard hands), ought to be thoroughly known. They are as follows:—
1. All hands with three or more trumps, whatever the other cards.
2. Hands with two trumps which contain also—
(a) Any three cards of one plain suit;
(b) Two cards of one plain suit, one being as high as a queen;
(c) Two small cards of one suit, the fifth card being a king of another suit;
(d) Three high cards of different suits.
3. Hands with one trump, which contain also—
(a) King, queen, knave of one suit, and a small card of another;
(b) Four cards of one suit headed by king;
(c) Three cards of one suit headed by queen, and queen of another suit.
4. Hands with no trump, which contain three queens or cards of equal value in different suits, e.g., four court cards.
5. Hands from which only two cards can be discarded without throwing a king or a trump.
Holding cards which make the point certain, propose. If you hold a jeu de règle, and one of the trumps is the king, propose, as your adversary cannot then take in the king.
When discarding, throw out all cards except trumps and kings.
If your adversary proposes you should accept, unless you are guarded in three suits (a queen being a sufficient guard), or in two suits with a trump, or in one suit with two trumps. Hence the rule not to discard two cards, unless holding the king of trumps, applies to the dealer.
The hands with which to refuse are the same as those with which to play without proposing, except as follows:—
1. Two trumps and three cards of one plain suit should not be played unless the plain suit is headed by a court card.
2. One trump and a tierce major is too weak, unless the fifth card is a court card. With similar hands weaker in the tierce major suit, accept unless the fifth card is a queen.
3. One trump and four cards of a plain suit is too weak to play.
4. One trump and two queens is too weak, unless both queens are singly guarded.
5. One trump, queen of one suit, and knave guarded of another should not be played unless the queen is also guarded, or the card of the fourth suit is a court card.
6. One trump, a king and a queen, both unguarded, should not be played, unless the fourth suit contains a card as high as an ace.
7. Four court cards without a trump are too weak to play, unless they are of three different suits.
Refuse with three queens, if two are singly guarded; otherwise, accept.
Lead from your guarded suit, and lead the highest.
If the strong suit led is not trumped, persevere with it, unless with king of trumps, or queen (king not having been announced), or knave ace, when lead a trump before continuing your suit.
You should not lead trumps at starting, unless you hold king or queen, knave, or knave ace, with court cards out of trumps.
The score has to be considered. If the dealer is at four, and the king is not in your hand nor turned up, play any cards without proposing which give an even chance of three tricks, e.g. a queen, a guarded knave, and a guarded ten. The same rule applies to the dealer’s refusal.
At the adverse score of four, and king not being in hand or turned up, any hand with one trump should be played, unless the plain cards are very small and of different suits.
If the non-dealer plays without proposing when he is four to three, and the dealer holds the king he ought not to mark it. The same rule applies to the non-dealer after a refusal, if the dealer is four to three.
At the score of non-dealer three, dealer four, the dealer should refuse on moderate cards, as the player proposing at this score must have a very bad hand.
At four a forward game should not be played in trumps, as there is no advantage in winning the vole.
Laws of Écarté.—The following laws are abridged from the revised code adopted by the Turf Club:—A cut must consist of at least two cards. Card exposed in cutting, fresh cut. Order of distribution of cards, whether by three and two, or vice versa, once selected, dealer must not change it during game. Player announcing king when he has not got it, and playing a card without declaring error, adversary may correct score and have hand played over again. If offender wins point or vole that hand, he scores one less than he wins. Proposal, acceptance, or refusal made cannot be retracted. Cards discarded must not be looked at. Cards exposed in giving cards to non-dealer, he has option of taking them or of having next cards; dealer exposing his own cards, no penalty. Dealer turning up top card after giving cards, cannot refuse second discard. Dealer accepting when too few cards in stock to supply both, non-dealer may take cards, and dealer must play his hand. Card led in turn cannot be taken up again. Card played to a lead can only be taken up prior to another lead, to save revoke or to correct error of not winning trick. Card led out of turn may be taken up prior to its being played to. Player naming one suit and leading another, adversary has option of requiring suit named to be led. If offender has none, no penalty. Player abandoning hand, adversary is deemed to win remaining tricks, and scores accordingly. If a player revokes or does not win trick when he can do so, the adversary may correct score and have hand replayed.
See Académie des jeux (various editions after the first quarter of the 19th century); Hoyle’s Games (various editions about the same dates); Ch. Van-Tenac et Louis Delanoue, Traité du jeu de l’écarté (Paris, 1845; translated in Bohn’s Handbook of Games, London, 1850); “Cavendish,” The Laws of Écarté, adopted by the Turf Club, with a Treatise on the Game (London, 1878); Pocket Guide to Écarté (“Cavendish,” 1897); Foster’s Encyclopaedia of Indoor Games (1903).
ECBATANA (Agbatana in Aeschylus, Haňgmatāna in Old Persian, written Agamtanu by Nabonidos, and Agamatanu at Behistun, mod. Hamadān), the capital of Astyages (Istuvegu), which was taken by Cyrus in the sixth year of Nabonidos (549 B.C.). The Greeks supposed it to be the capital of Media, confusing the Manda, of whom Astyages was king, with the Madā or Medes of Media Atropatene, and ascribed its foundation to Deioces (the Daiukku of the cuneiform inscriptions), who is said to have surrounded his palace in it with seven concentric walls of different colours. Under the Persian kings, Ecbatana, situated at the foot of Mount Elvend, became a summer residence; and was afterwards the capital of the Parthian kings. Sir H. Rawlinson attempted to prove that there was a second and older Ecbatana in Media Atropatene, on the site of the modern Takht-i-Suleiman, midway between Hamadan and Tabriz (J.R.G.S. x. 1841), but the cuneiform texts imply that there was only one city of the name, and Takht-i-Suleiman is the Gazaca of classical geography. The Ecbatana at which Cambyses is said by Herodotus (iii. 64) to have died is probably a blunder for Hamath.
See Perrot and Chipiez, History of Art in Persia (Eng. trans., 1892); M. Dieulafoy, L’Art antique de la Perse, pt. i. (1884); J. de Morgan, Mission scientifique en Perse, ii. (1894). See Hamadan and Persia: Ancient History, § v. 2.
ECCARD, JOHANN (1553-1611), German composer of church music, was born at Mühlhausen on the Unstrut, Prussia, in 1553. At the age of eighteen he went to Munich, where he became the pupil of Orlando Lasso. In his company Eccard is said to have visited Paris, but in 1574 we find him again at Mühlhausen, where he resided for four years, and edited, together with Johann von Burgk, his first master, a collection of sacred songs, called Crepundia sacra Helmboldi (1577). Soon afterwards he obtained an appointment as musician in the house of Jacob Fugger, the Augsburg banker. In 1583 he became assistant conductor, and in 1599 conductor, at Königsberg, to Georg Friedrich, margrave of Brandenburg-Anspach, the administrator of Prussia. In 1608 he was called by the elector Joachim Friedrich to Berlin as chief conductor, but this post he held only for three years, owing to his premature death at Königsberg in 1611. Eccard’s works consist exclusively of vocal compositions, such as songs, sacred cantatas and chorales for four or five, and sometimes for seven, eight, or even nine voices. Their polyphonic structure is a marvel of art, and still excites the admiration of musicians. At the same time his works are instinct with a spirit of true religious feeling. His setting of the beautiful words “Ein’ feste Burg ist unser Gott” is still regarded by the Germans as their representative national hymn. Eccard and his school are inseparably connected with the history of the Reformation.
Of Eccard’s songs a great many collections are extant; see K.G.A. von Winterfeld, Der Evangelische Kirchengesang (1843); Döring (Choralkunde, p. 47).
ECCELINO [or Ezzelino] DA ROMANO (1194-1259), Ghibelline leader, and supporter of the emperor Frederick II., was born on the 25th of April 1194. He belonged to a family descended from a German knight named Eccelin, who followed the emperor Conrad II. to Italy about 1036, and received the fief of Romano near Padua. Eccelin’s grandson was Eccelino III., surnamed the Monk, who divided his lands between his two sons in 1223, and died in 1235. The elder of these two sons was Eccelino, who in early life began to take part in family and other feuds, and in 1226, at the head of a band of Ghibellines, seized Verona and became podestà of the city. He soon lost Verona, but regained it in 1230; and about this time came into relations with Frederick II., who in 1232 issued a charter confirming him in his possessions. In 1236 when besieged in Verona he was saved by the advance of the emperor, who in November of the same year took Vicenza and entrusted its government to Eccelino. In 1237 he obtained authority over Padua and Treviso; and on the 27th of November in that year he shared in the victory gained by the emperor over the Lombards at Cortenuova. In 1238 he married Frederick’s natural daughter, Selvaggia; in 1239 was appointed imperial vicar of the march of Treviso; but in the same year was excommunicated by Pope Gregory IX. He was constantly engaged in increasing his possessions; was present at the siege of Parma in 1247, and after Frederick’s death in 1250 he supported his son, the German king Conrad IV. His cruelties had, however, aroused general disgust, and in 1254 he was again excommunicated. In 1256 Pope Alexander IV. proclaimed a crusade against him, and a powerful league was soon formed under the leadership of Philip, archbishop of Ravenna. Padua was taken from Eccelino, but on the 1st of September 1258 he defeated his enemies at Torricella. He then made an attempt on Milan, and the rival forces met at Cassano on the 27th of September 1259, when Eccelino was wounded and taken prisoner. Enraged at his capture, he tore the bandages from his wounds, refused to take nourishment, and died at Soncino on the 7th of October 1259. In the following year his brother Albert was put to death, and the Romano family became 847 extinct. Eccelino, who is sometimes called the tyrant, acquired a terrible reputation on account of his cruelties, a reputation that won for him the immortality of inclusion in Dante’s Inferno; but his unswerving loyalty to Frederick II. forms a marked contrast to the attitude of many of his contemporaries.
Eccelino is the subject of a novel by Cesare Cantu and of a drama by J. Eichendorff.
See J.M. Gittermann, Ezzelino da Romano (Freiburg, 1890); S. Mitis, Storia d’ Ezzelino IV. da Romano (Maddaloni, 1896); and F. Stieve, Ezzelino von Romano (Leipzig, 1909).
ECCENTRIC (from Gr. ἐκ, out of, and κέντρον, centre), literally “out from the centre,” and thus used to connote generally any deviation from the normal. In astronomy the word denotes a circle round which a body revolves, but whose centre is displaced from the visible centre of motion. In the ancient astronomy the ellipses in which it is now known that the planets revolve around the sun could not be distinguished from circles, but the unequal angular motion due to ellipticity was observed. The theory of the eccentric was that the centre of the epicycle of each planet moved uniformly in a circle, the centre of which was displaced from that of the earth by an amount double the eccentricity of the actual ellipse, as the case is now understood. When measured around this imaginary centre, which is so situated on the major axis of the ellipse that the focus, or place of the real sun, is midway between it and the centre of the ellipse, the motion is approximately uniform. In engineering, an eccentric is a mechanical device for converting rotary into reciprocating motion (see Steam-engine). For eccentric angle see Ellipse.
ECCHELLENSIS (or Echellensis), ABRAHAM (d. 1664), a learned Maronite, whose surname is derived from Eckel in Syria, where he was born towards the close of the 16th century. He was educated at the Maronite college in Rome, and, after taking his doctor’s degree in theology and philosophy, returned for a time to his native land. He then became professor of Arabic and Syriac in the college of the Propaganda at Rome. Called to Paris in 1640 to assist Le Jay in the preparation of his polyglot Bible, he contributed to that work the Arabic and Latin versions of the book of Ruth and the Arabic version of the third book of Maccabees. In 1646 he was appointed professor of Syriac and Arabic at the Collège de France. Being invited by the Congregation of the Propaganda to take part in the preparation of an Arabic version of the Bible, Ecchellensis went again in 1652 or 1653 to Rome. He published several Latin translations of Arabic works, of which the most important was the Chronicon Orientale of Ibnar-Rāhib (Paris, 1653), a history of the patriarchs of Alexandria. He was engaged in an interesting controversy with John Selden as to the historical grounds of episcopacy, in the course of which he published his Eutychius vindicatus, sive Responsio ad Seldeni Origines (Rome, 1661). Conjointly with Giovanni Borelli he wrote a Latin translation of the 5th, 6th and 7th books of the Conics of Apollonius of Perga (1661). He died at Rome in 1664.
ECCLES, a municipal borough in the Eccles parliamentary division of Lancashire, England, 4 m. W. of Manchester, of which it forms practically a suburb. Pop. (1901) 34,369. It is served by the London & North-Western railway and by the Birkenhead railway (North-Western and Great Western joint). The Manchester Ship Canal passes through. The church of St Mary is believed to date from the 12th century, but has been enlarged and wholly restored in modern times. There are several handsome modern churches and chapels, a town hall, and numerous cotton mills, while silk-throwing and the manufacture of fustians and ginghams are also among the industries, and there are also large engine works. A peculiar form of cake is made here, taking name from the town, and has a wide reputation. Eccles was incorporated in 1892, and the corporation consists of a mayor, 6 aldermen and 18 councillors. The borough maintains the tramway service, &c., but water and gas are supplied from Manchester and Salford respectively. Area, 2057 acres.
Before the Reformation the monks of Whalley Abbey had a grange here at what is still called Monks’ Hall; and in 1864 many thousands of silver pennies of Henry III. and John of England and William I. of Scotland were discovered near the spot. Robert Ainsworth, the author of the Latin and English dictionary so long familiar to English students, was born at Eccles in 1660; and it was at the vicarage that William Huskisson expired on the 15th of September 1830 from injuries received at the opening of the Liverpool & Manchester railway. From early times “wakes” were held at Eccles, and bull-baiting, bear-baiting and cock-fighting were carried on. Under Elizabeth these festivals, which had become notoriously disorderly, were abolished, but were revived under James I., and maintained until late in the 19th century on public ground. The cockpit remained on the site of the present town hall. A celebration on private property still recalls these wakes.
ECCLESFIELD, a township in the Hallamshire parliamentary division of the West Riding of Yorkshire, England, 5 m. N. of Sheffield, on the Great Central and Midland railways. The church of St Mary is Perpendicular, with a central tower, and contains excellent woodwork. It formerly bore, and must have deserved, the familiar title of the “Minster of the Moors.” Ecclesfield was the seat of a Benedictine priory, which passed to the Carthusians in the 14th century. Cutlery and tools are largely manufactured, and there are coal-mines, paper mills and iron and fire-clay works. After the inclusion within the county borough of Sheffield of part of the civil parish of Ecclesfield in 1901, the population was 18,324.
ECCLESHALL, a market town in the north-western parliamentary division of Staffordshire, England; 7 m. N.W. from Stafford, and 4 W. of Norton Bridge station on the London & North-Western main line. Pop. (1901) 3799. The church of the Holy Trinity, one of the most noteworthy in Staffordshire, is principally Early English, and has fine stained glass. Several bishops of Lichfield are buried here, as Eccleshall Castle was the episcopal residence from the 13th century until 1867. Of this the ancient remains include a picturesque tower and bridge. To the west on the borders of Shropshire is Blore Heath, the scene of a defeat of the Lancastrians by the Yorkists in 1459.
ECCLESIA (Gr. ἐκκλησία, from ἐκ, out, and καλεῖν, to call), in ancient Athens, the general assembly of all the freemen of the state. In the primitive unorganized state the king was theoretically absolute, though his great nobles meeting in the Council (see Boulē) were no doubt able to influence him considerably. There is, however, no doubt that in the earliest times the free people, i.e. the fighting force of the state, were called together to ratify the decisions of the king, and that they were gradually able to enforce their wishes against those of the nobles. In Athens, as in Rome, where the Plebs succeeded in their demand for the codification of the laws (the Twelve Tables), it was no doubt owing to the growing power of the people meeting in the Agora that Draco was entrusted with the task of publishing a code of law and so putting an end to the arbitrary judicature of the aristocratic party. But there is no evidence that the Ecclesia had more than a de facto existence before Solon’s reforms.
The precise powers which Solon gave the people are not known. It is clear that the executive power in the state (see Archon) was still vested in the Eupatrid class. It is obvious, therefore, that a moderate reformer would endeavour to give to the people some control over the magistracy. Now in speaking of the Thetes (the lowest of the four Solonian classes; see Solon), Aristotle’s Constitution of Athens says that Solon gave them merely “a share in the Ecclesia and the Law Courts,” and in the Politics we find that he gave them the right of electing the magistrates and receiving their accounts at the end of the official year. Thus it seems that the “mixed” character of Solon’s constitution consisted in the fact that though the officials of the state were still necessarily Eupatrid, the Ecclesia elected those of the Eupatrids whom they could trust, and further had the right of criticizing their official actions. Secondly, all our accounts agree that Solon admitted the Thetes to the Ecclesia, thus recognizing them as citizens. Under Cleisthenes the Ecclesia remained the sovereign power, but the Council seems to have become to some extent a separate administrative body. The relation of Boulē and Ecclesia in the Cleisthenic democracy was of the 848 greatest importance. The Ecclesia alone, a heterogeneous body of untrained citizens, could not have passed, nor even have drawn up intelligible measures; all the preliminary drafting was done by the small committee of the Boulē which was in session at any particular time. In the 5th century the functions of the Ecclesia and the popular courts of justice were vastly increased by the exigencies of empire. At the beginning of the 4th century B.C. the system of payment was introduced (see below). In 308 B.C. Demetrius of Phalerum curtailed the power of the Ecclesia by the institution of the Nomophylaces (Guardians of the Law), who prevented the Ecclesia from voting on an illegal or injurious motion. Under Roman rule the powers of the Ecclesia and the popular courts were much diminished, and after 48 B.C. (the franchise being frequently sold to any casual alien) the Demos (people) was of no importance. They still assembled to pass psephisms in the theatre and to elect strategi, and, under Hadrian, had some small judicial duties, but as a governing body the Ecclesia died when Athens became a civitas libera under Roman protection.
Constitution and Functions.—Throughout the period of Athenian greatness the Ecclesia was the sovereign power, not only in practice but also in theory. The assembly met in early times near the sanctuary of Aphrodite Pandemus (i.e. south of the Acropolis), but, in the 5th and 4th centuries, the regular place of meeting was the Pnyx. From the 5th century it met sometimes in the theatre, which in the 3rd century was the regular place. From Demosthenes we learn that in his time special meetings were held at Peiraeus, and, in the last centuries B.C., meetings were held at Athens and Peiraeus alternately. Certain meetings, however, for voting ostracism (q.v.) and on questions affecting individual status took place in the Agora. Meetings were (1) ordinary, (2) extraordinary, and (3) convened by special messengers (κύριαι, σύγκλητοι and κατάκλητοι), these last being called when it was desirable that the country people should attend. At ordinary meetings the attendance was practically confined to Athenian residents. According to Aristotle there were four regular meetings in each prytany (see Boulē); probably only the first of these was called κυρία. It is certain, however, that the four meetings did not fall on regular days, owing to the occurrence of feast days on which no meeting could take place. In the κυρία ἐκκλησία of each month took place the Epicheirotonia (monthly inquiry) of the state officials, and if it proved unsatisfactory a trial before the Heliaea was arranged; the council reported on the general security and the corn-supply, and read out lists of vacant inheritances and unmarried heiresses. In the sixth prytany of each year at the κυρία ἐκκλησία the question whether ostracism should take place that year was put to the vote. For all meetings it was usual that the Prytaneis should give five days’ notice in the form of a programma (agenda). On occasions of sudden importance the herald of the council summoned the people with a trumpet, and sometimes special messengers were despatched to “bring in” the country people (κατακαλεῖν).
After the archonship of Solon all Athenians over the age of eighteen were eligible to attend the assembly, save those who for some reason had suffered atimia (loss of civil rights). To prevent the presence of any disqualified persons, six lexiarchs with thirty assistants were present with the deme-rolls in their hands. These officers superintended the payment in the 4th century and probably the toxotae (police) also, whose duty it was before the introduction of pay to drive the people out of the Agora into the Ecclesia with a rope steeped in red dye which they stretched out and used as a draw net (see Aristoph. Acharn. 22 and Eccles. 378). The introduction of pay, which belongs to the early years of the 4th century and by the Constitution (c. 41 ad fin.) is attributed to Agyrrhius, a statesman of the restored democracy, was a device to secure a larger attendance. The rate rose from one to two obols and then to three obols (Aristoph. Eccles. 300 sqq.), while at the time of Aristotle it was one and a half drachmas for the κυρία ἐκκλησία and one drachma for other meetings. Probably those who were late did not receive payment.
Procedure.—The proceedings opened with formalities: the purification by the peristiarchs, who carried round slain sucking pigs; the curse against all who should deceive the people; the appointment (in the 4th century) of the proedri and their epistates (see Boulē); the report as to the weather-omens. The assembly was always dismissed if there were thunder, rain or an eclipse. These formalities over, the Prytaneis communicated the probouleuma of the council, without which the Ecclesia could not debate. This recommendation either submitted definite proposals or merely brought the agenda before the assembly. Its importance lay largely in the fact that it explained the business in hand, which otherwise must often have been beyond the grasp of a miscellaneous assembly. After the reading, a preliminary vote was taken as to whether the council’s report should be accepted en bloc. If it was decided to discuss, the herald called upon people to speak. Any person, without distinction of age or position, might obtain leave to speak, but it seems probable that the man who had moved the recommendation previously in the council would advocate it in the assembly. The council was, therefore, a check on the assembly, but its powers were to some extent illusory, because any member of the assembly (1) might propose an amendment, (2) might draw up a new resolution founded on the principal motion, (3) might move the rejection of the motion and the substitution of another, (4) might bring in a motion asking the council for a recommendation on a particular matter, (5) might petition the council for leave to speak on a given matter to the assembly. Voting usually was by show of hands, but in special cases (ostracism, &c.) by ballot (i.e. by casting pebbles into one of two urns). The decision of the assembly was called a psephism and had absolute validity. These decisions were deposited in the Metroön where state documents were preserved; peculiarly important decrees were inscribed also on a column (stēlē) erected on the Acropolis. It has been shown that the power of the council was far from sufficient. The real check on the vagaries of amateur legislators was the Graphē Paranomōn. Any man was at liberty to give notice that he would proceed against the mover of a given resolution either before or after the voting in the Ecclesia. A trial in a Heliastic court was then arranged, and the plaintiff had to prove that the resolution in question contravened an existing law. If this contention were upheld by the court, when the case was brought to it by the Thesmothetae, the resolution was annulled, and the defendant had to appear in a new trial for the assessment of the penalty, which was usually a fine, rarely death. Three convictions under this law, however, involved a certain loss of rights; the loser could no longer move a resolution in the Ecclesia. After the lapse of a year the mover of a resolution could not be attacked. In the 4th century the Graphē Paranomōn took the place of Ostracism (q.v.). In the 5th century it was merely an arrangement whereby the people sitting as sworn juries ratified or annulled their own first decision in the Ecclesia.
Revision of Laws.—In the 4th century, the assembly annually, on the eleventh day of Hecatombaeon (the first day of the official year), took a general vote on the laws, to decide whether revision was necessary. If the decision was in favour of alteration, it was open to any private citizen to put up notice of amendments. The Nomothetae, a panel selected by the Prytaneis from the Heliaea, heard arguments for and against the changes proposed and voted accordingly. Against all new laws so passed, there lay the Graphē; Paranomōn. Thus the Nomothetae, not the Ecclesia, finally passed the law.
Judicial Functions.—The Ecclesia heard cases of Probolē and Eisangelia (see Greek Law). The Probolē was an action against sycophants and persons who had not kept their promises to the people, or had disturbed a public festival. The verdict went by show of hands, but no legal consequences ensued; if the plaintiff demanded punishment he had to go to the Heliaea which were not at all bound by the previous vote in the Ecclesia. Cases of Eisangelia in which the penalty exceeded the legal competence of the council came before the Ecclesia in the form of a probouleuma. To prevent vexatious accusations, it was 849 (at some date unknown) decided that the accuser who failed to obtain one-fifth of the votes should be fined 1000 drachmas (£40). (For the procedure in case of Ostracism see that article.)
Summary.—Thus it will be seen that the Ecclesia, with no formal organization, had absolute power save for the Graphē Paranomōn (which, therefore, constituted the dicasteries in one sense the sovereign power in the state). It dealt with all matters home and foreign. Every member could initiate legislation, and, as has been shown, the power of the council was merely formal. As against this it must be pointed out that it was by no means a representative assembly in practice. The phrase used to describe a very special assembly (κατάκλητος ἐκκλησία) shows that ordinarily the country members did not attend (κατακαλεῖν always involving the idea of motion from a distance towards Athens), and Thucydides says that 5000 was the maximum attendance, though it must be remembered that he is speaking of the time when the number of citizens had been much reduced owing to the plague and the Sicilian expedition. From this we understand the necessity of payment in the 4th century, although in that period the Ecclesia was supreme (Constitution of Athens, xli. 2). The functions of the Ecclesia thus differed in two fundamental respects from those which are in modern times associated with a popular assembly. (1) It did not exercise, at least in the period as to which we are best instructed, the power of law-making (νομοθεσία) in the strict sense. It must be remembered, however, in qualification of this statement that it possessed the power of passing psephismata which would in many cases be regarded as law in the modern sense. (2) The Ecclesia was principally concerned with the supervision of administration. Much of what we regard as executive functions were discharged by the Ecclesia.
With this article compare those on Solon; Boule; Areopagus; Greek Law, and, for other ancient popular assemblies, Apella; Comitia. See also A.H.J. Greenidge, Handbook of Greek Constitutional History (1896); Gilbert, Greek Constitutional Antiquities (trans. Brooks and Nicklin, 1895); Schömann, De comitiis Atheniensium; L. Schmidt, “De Atheniensis reipublicae indole democratica” in Ind. Lect. (Marburg, 1865); J.W. Headlam, Election by Lot at Athens (Cambridge, 1891). See also the histories of Greece by Meyer, Busolt, Grote, Evelyn Abbott, and J.E. Sandys’ edition of the Constitution of Athens (1892); for a comparative study, E.A. Freeman, Comparative Politics.
ECCLESIASTES (Heb. קהלת, Kohelet, “Koheleth”; Sept. ἐκκλησιαστής; Jerome concionator), one of the Wisdom Books of the Old Testament (see Wisdom Literature). The book, as it stands, is a collection of the discourses, observations and aphorisms of a sage called Koheleth, a term the precise meaning of which is not certain. The Greek ecclesiastes means one who takes part in the deliberations of an assembly (ecclesia), a debater or speaker in an assembly (Plato, Gorgias, 452 E), and this is the general sense of the Hebrew word. Its form (singular feminine) has been supposed to be the adoption or imitation of the Arabic employment of a fem. sing. as the designation of a high official person, as is the case in the title caliph (whence the rendering in the margin of the Revised Version, “Great orator”); but the adoption of an Arabic idiom is not probable. This usage is not Hebrew; it is not found either in the Old Testament or in the later (Mishnaic) Hebrew. The form may have been suggested by that of the Hebrew word for “wisdom.” Koheleth, however, is employed in the book not as a title of wisdom (for “wisdom” is never the speaker), but as the independent name of the sage. It is intended to represent him as a member of an assembly (Kahal)—not the Jewish congregation, but a body of students or inquirers, such as is referred to in xii. 9-11, a sort of collegium, of which he was the head; and as instructor of this body he gives his criticism of life. The author begins, indeed, with identifying his sage with King Solomon (i. 12-ii. 11, 12b); but he soon abandons this literary device, and speaks in his own name. The rendering “preacher” has a misleading connotation.
In the book as we have it there is no orderly exposition of a theory; it rather has the appearance of a collection of remarks jotted down by a pupil (somewhat after the manner of Xenophon’s Memorabilia), or of extracts from a sage’s notebook. It is, however, characterized throughout (except in some scribal additions) by a definite thought, and pervaded by a definite tone of feeling. The keynote is given in the classic phrase with which the discussion opens and with which it closes: “Vanity of vanities (i.e. absolute vanity), all1 is vanity!” Life, says the author, has nothing of permanent value to offer. His attitude is one not of bitterness but of calm hopelessness, with an occasional tinge of disgust or contempt. He fancies that he has tried or observed everything in human experience, and his deliberate conclusion is that nothing is worth doing. He believes in an all-powerful but indifferent God, and is himself an observer of society, standing aloof from its passions and ambitions, and interested only in pointing out their emptiness.
This general view is set forth in a number of particular observations.
1. His fundamental proposition is that there is a fixed, unchangeable order in the world, a reign of inflexible law (i. 4-11, iii. 1-11, 14, 15, vii. 13, viii. 5-9): natural phenomena, such as sunrise and sunset, recur regularly; for everything in human experience a time has been set; birth and death, building up and destroying, laughing and weeping, silence and speech, love and hate, war and peace, are to be regarded not as utterances of a living, self-directing world, but as incidents in the work of a vast machine that rolls on for ever; there is an endless repetition—nothing is new, nothing is lost; if one thinks he has found something new, inquiry shows that it was in existence long ago; God, the author of all, seeks out the past in order to make it once more present; it is impossible to add to or take from the content of the world, impossible to change the nature of things, to effect any radical betterment of life; the result is unspeakable weariness—a depressing series of sights and sounds. No goal or purpose is discoverable in this eternal round; if the sun rises and goes on his journey through the sky, it is merely to come back to the place where he rose; rivers flow for ever into the sea without filling it. To what end was the world created? It is impossible to say. Such is Koheleth’s view of life, and it is obvious that such a conception of an aimless cosmos is thoroughly non-Jewish, if we may judge Jewish thought by the great body of the extant literature.
2. Further, says Koheleth, man is impelled to study the world, but under the condition that he shall never comprehend it (iii. 11, vii. 23, 24, viii. 16, 17). As to the meaning of the Hebrew term olam in iii. 11, there are various opinions, but “world” appears to be the rendering favoured by the connexion: “God has made everything beautiful in its time, and has put the olam into men’s minds, yet so that they cannot understand His work”: the olam, the sum of phenomena, is God’s work. The word is not found in this sense elsewhere in the Old Testament, but it so occurs in the Mishna (Pirke Aboth, iv. 7), and the vocabulary of Ecclesiastes is admittedly similar to that of the Mishna. Only here in the Old Testament does it stand as a simple isolated noun; elsewhere it is the definition of a noun (in “everlasting covenant,” &c.), or it is preceded by a preposition, in the phrases “for ever,” “of old,” or it stands alone (sing. or plur.) in the same adverbial sense, “for ever.” The word means first a remote point in past or future, then a future point without limit of time, then a period of history, and finally the world considered as a mass of human experiences (cf. αἰών). The renderings “eternity” and “future” in the present passage are unsatisfactory; the former has an inappropriate metaphysical connotation, and yields no distinct sense; the latter does not suit the connexion, though there is reference to the future elsewhere (ix. 1). God, the text here declares, has made the world an object of man’s thought, yet so that man can never find out the work that God has done (iii. 11). The reference seems to be not so much to the variety and complexity of phenomena as to the impossibility of construing them rationally or in such a way that man may foresee and provide for his future. Man is in the clutches of fate (ix. 11, 12): there is no observable relation between exertion and result in life: the race is not to the swift nor the battle to the strong; 850 success does not attend wisdom, knowledge and skill; men are like fish taken in a net or birds caught in a snare.
3. Human life, Koheleth declares, is unsatisfying. He inquired, he says, into everything that is done by men under the sun (i. 12-16): God has inflicted on men a restless desire for movement and work2, yet life is but a catalogue of fruitless struggles. He gives a number of illustrations. In his character of king he tried all the bodily pleasures of life (ii. 1-11): he had houses, vineyards, gardens, parks, ponds, forests, servants, flocks and herds, treasures of gold and silver, singers, wives; all these he set himself to enjoy in a rational way—indeed, he found a certain pleasure in carrying out his designs, but, when all was done, he surveyed it only to see that it was weary and unprofitable. Dropping the rôle of Solomon and speaking as an observer of life, the author declares (iv. 4) that the struggle for success is the result of rivalry among men, which has no worthy outcome. The securing of riches is a fallacious achievement, for often wealth perishes by some accident (v. 13 f.), or its possessor is unable to enjoy it (vi. 1-3a), or he has no one to whom to leave it, and he cannot keep it—naked man comes into the world, naked he goes out. He does not consider the possibility of deriving enjoyment from wealth by helping the poor or encouraging learning (this latter, indeed, he looks on as vanity), and in general he recognizes no obligation on the part of a man to his fellows. A noteworthy survival of an old belief is found in vi. 3: though a man have the great good fortune to live long and to have many children, yet, if he have not proper burial the blank darkness of an untimely birth is better than he: this latter is merely the negation of existence; the former, it appears to be held, is positive misfortune, the loss of a desirable place in Sheol, though elsewhere (ix. 5) existence in Sheol is represented as the negation of real life. It is not necessary to suppose that the writer has here any particular case in mind.
If wealth be thus a vain thing, yet a sage might be supposed to find satisfaction in wisdom, that is, practical good sense and sagacity; but this also the author puts aside as bringing no lasting advantage, since a wise man must finally give up the fruit of his wisdom to someone else, who may be a fool, and in any case the final result for both fools and wise men is the same—both are forgotten (ii. 12-23). A particular instance is mentioned (ix. 13-15) of a beleaguered city saved by a wise man; but the man happened to be poor, and no one remembered him. The whole constitution of society, in fact, seems to the sage a lamentable thing: the poor are oppressed, the earth is full of their cries, and there is no helper (iv. 1); strange social upheavals may be seen: the poor3 set in high places, the rich cast down, slaves on horseback, princes on foot (x. 5-7). He permits himself a sweeping generalization (vii. 25-28): human beings as a rule are bad: one may occasionally find a good man, never a good woman—woman is a snare and a curse. He (or an editor) adds (vii. 29) that this condition of things is due to social development: man was created upright (Gen. i. 27; Enoch lxix. 11), but in the course of history has introduced corrupting complications into life.
4. The natural outcome of these experiences of the author is that he cannot recognize a moral government of the world. He finds, like Job, that there are good men who die prematurely notwithstanding their goodness, and bad men who live long notwithstanding their badness (vii. 15), though long life, it is assumed, is one of the great blessings of man’s lot; and in general there is no moral discrimination in the fortunes of men (viii. 14, ix. 2).
5. There is no sacredness or dignity in man or in human life: man has no pre-eminence over beasts, seeing that he and they have the same final fate, die and pass into the dust, and no one knows what becomes of the spirit, whether in man’s case it goes up to heaven, and in the case of beasts goes down into Sheol—death is practically the end-all; and so poor a thing is life that the dead are to be considered more fortunate than the living, and more to be envied than either class is he who never came into existence (iv. 2, 3). It is a special grievance that the wicked when they die are buried with pomp and ceremony, while men who have acted well are forgotten4 in the city (viii. 10).
6. That the author does not believe in a happy or active future life appears in the passage (iv. 2, 3) quoted above. The old Hebrew view of the future excluded from Sheol the common activities of life and also the worship of the national god (Isa. xxxviii. 18); he goes even beyond this in his conception of the blankness of existence in the underworld. The living, he says, at least know that they shall die, but the dead know nothing—the memory of them, their love, hate and envy, perishes, they have no reward, no part in earthly life (ix. 5, 6); there is absolutely no knowledge and no work in Sheol (ix. 10). His conclusion is that men should do now with all their might what they have to do; the future of man’s vital part, the spirit, is wholly uncertain.
7. His conception of God is in accord with these views. God for him is the creator and ruler of the world, but hardly more; he is the master of a vast machine that grinds out human destinies without sympathy with man and without visible regard for what man deems justice—a being to be acknowledged as lord, not one to be loved. There can thus be no social contact between man and God, no communion of soul, no enthusiasm of service. Moral conduct is to be regulated not by divine law (of this nothing is said) but by human experience. The author’s theism is cold, spiritless, without influence on life.
If now the question be asked what purpose or aim a man can have, seeing that there is nothing of permanent value in human work, an answer is given which recurs, like a refrain, from the beginning to the end of the book, and appears to be from the hand of the original author: after every description of the vanity of things comes the injunction to enjoy such pleasures as may fall to one’s lot (ii. 24, 25, iii. 12, 13, 22, v. 18, 19, viii. 15, ix. 7-10, xi. 7-xii. 7). Elsewhere (ii.), it is true, it is said that there is no lasting satisfaction in pleasure; but the sage may mean to point out that, though there is no permanent outcome to life, it is the part of common-sense to enjoy what one has. The opportunity and the power to enjoy are represented as being the gift of God; but this statement is not out of accord with the author’s general position, which is distinctly theistic. All the passages just cited, except the last (xi. 7-xii. 7), are simple and plain, but the bearing of the last is obscured by interpolations. Obviously the purpose of the paragraph is to point out the wisdom of enjoying life in the time of youth while the physical powers are fresh and strong, and the impotency of old age has not yet crept in. Omitting xi. 8c, 9b, 10b, xii. 1a, the passage will read: “Life is pleasant in the bright sunshine—however long a man may live, he must be cheerful always, only remembering that dark days will come. Let the young man enjoy all the pleasures of youth, putting away everything painful, before the time comes when his bodily powers decay and he can enjoy nothing.” To relieve the apparent Epicureanism of this passage, an editor has inserted reminders of the vanity of youthful pleasures, and admonitions to remember God and His judgment. The author, however, does not recommend dissipation, and does not mean to introduce a religious motive—he offers simply a counsel of prudence. The exhortation to remember the Creator in the days of youth, though it is to be retained in the margin as a pious editorial addition, here interrupts the line of thought. In xii. 1a some critics propose to substitute for “remember thy Creator” the expression of xi. 9, “let thy heart cheer thee”; but the repetition is improbable. Others would read: “remember thy cistern” (Bickell), or “thy well” (Haupt), that is, thy wife. The wife is so called in Prov. v. 15-19 in an elaborate poetical figure (the wife as a source of bodily pleasure), in which the reference is clear from the context; but there is no authority, in the Old Testament or in other literature of this period, for 851 taking the term as a simple prose designation of a wife. Nor would this reference to the wife be appropriate in the connexion, since the writer’s purpose is simply to urge men to enjoy life while they can. The paragraph (and the original book) concludes with a sustained and impressive figure, in which the failing body of the old man is compared to a house falling into decay: first, the bodily organs (xii. 3, 4a): the keepers of the house (the arms and hands) tremble, the strong men (the legs and perhaps the backbone) are bent, the grinding women (the teeth) cease to work, those that look out of the windows (the eyes) are darkened, the street-doors are shut, the sound of the mill being low (apparently a summary statement of the preceding details: communication with the outer world through the senses is cut off, the performance of bodily functions being feeble); the rest of v. 4 may refer to the old man’s inability to make or hear music: in the house there is no sound of birds5 or of singers, there are none of the artistic delights of a well-to-do household; further (v. 5a) the inmates of the house fear dangers from all powerful things and persons (the old man is afraid of everything), the almond tree blossoms (perhaps the hair turns white). The two next clauses are obscure.6 Then comes the end: man goes to his everlasting home; the dust (the body) returns to the earth whence it came (Gen. ii. 7), and the breath of life, breathed by God into the body, returns to him who gave it. This last clause does not affirm the immortality of the soul; it is simply an explanation of what becomes of the vital principle (the “breath of life” of Gen. ii. 7); its positive assertion is not in accord with the doubt expressed in iii. 21 (“who knows whether the spirit of man goes upward?”), and it seems to be from another hand than that of the author of the original book.
There are other sayings in the book that appear to be at variance with its fundamental thought. Wisdom is praised in a number of passages (iv. 13, vii. 5, 11, 12, 19, viii. 1, ix. 16, 17, x. 2, 3), though it is elsewhere denounced as worthless. It may be said that the author, while denying that wisdom (practical sagacity and level-headedness) can give permanent satisfaction, yet admits its practical value in the conduct of life. This may be so; but it would be strange if a writer who could say, “in much wisdom is much grief,” should deliberately laud wisdom. The question is not of great importance and may be left undecided. It may be added that there are in the book a number of aphorisms about fools (v. 3[4], vii. 5, 6, x. 1-3, 12-15) quite in the style of the book of Proverbs, some of them contrasting the wise man and the fool; these appear to be the insertions of an editor. Further, it may be concluded with reasonable certainty that the passages that affirm a moral government of the world are additions by pious editors who wished to bring the book into harmony with the orthodox thought of the time. Such assertions as those of ii. 26 (God gives joy to him who pleases him, and makes the sinner toil to lay up for the latter), viii. 12 (it shall be well with those that fear God, but not with the wicked), xii. 13 f. (man’s duty is simply to obey the commands of God, for God will bring everything into judgment) are irreconcilable with the oft-repeated statement that there is no difference in the earthly lots of the righteous and the wicked, and no ethical life after death.
Many practical admonitions and homely aphorisms are scattered through the book: iv. 5, quiet is a blessing; iv. 9-12, two are better than one; iv. 17 (Eng. v. 1), be reverent in visiting the house of God (the temple and the connected buildings)—to listen (to the service of song or the reading of Scripture) is better than to offer a foolish (thoughtless) sacrifice; v. 1 (2), be sparing of words in addressing God; v. 1-5 (2-6), pay your vows—do not say to the priest’s messenger that you made a mistake; vii. 2-4, sorrow is better than mirth; vii. 16-18, be not over-righteous (over-attentive to details of ritual and convention) or over-wicked (flagrantly neglectful of established beliefs and customs); here “righteous” and “wicked” appear to be technical terms designating two parties in the Jewish world of the 2nd and 1st centuries B.C., the observers and the non-observers of the Jewish ritual law; these parties represent in a general way the Pharisees and the Sadducees; viii. 2-4, x. 20, it is well to obey kings and to be cautious in speaking about them, for there are talebearers everywhere; vii. 20, no man is free from sin; vii. 21, do not listen to all that you may overhear, lest you hear yourself ill spoken of; ix. 4, a living dog is better than a dead lion; xi. 1-6, show prudence and decision in business; do not set all your goods on one venture; act promptly and hope for the best. At the close of the book (xii. 9-12) there are two observations that appear to be editorial recommendations and cautions. First, Koheleth is endorsed as an industrious, discriminating and instructive writer. Possibly this is in reply to objections that had been made to what he had written. There follows an obscure passage (v. 11) which seems to be meant as a commendation of the teaching of the sages in general: their words are said to be like goads (inciting to action) and like nails driven in a building (giving firmness to character); they issue from masters of assemblies,7 heads of academies (but not of the Sanhedrin). The succeeding clause “they are given from one shepherd” may refer to a collection or revision by one authoritative person, but its relevancy is not obvious. The “shepherd” cannot be God (Gen. xlix. 24; Ps. xxiii. 1); the poetical use of the word would not be appropriate here. The clause is possibly a gloss, a comment on the preceding expression. A caution against certain books is added (v. 12), probably works then considered harmful (perhaps philosophic treatises), of which, however, nothing further is known.
Composition of the Book.—If the analysis given above is correct, the book is not a unit; it contains passages mutually contradictory and not harmonizable. Various attempts have been made to establish its unity. The hypothesis of “two voices” is now generally abandoned; there is no indication of a debate, of affirmations and responses. A more plausible theory is that the author is an honest thinker, a keen observer and critic of life, who sees that the world is full of miseries and unsolved problems, regards as futile the attempts of his time to demonstrate an ethically active future life, and, recognizing a divine author of all, holds that the only wise course for men is to abandon the attempt to get full satisfaction out of the struggle for pleasure, riches and wisdom, and to content themselves with making the best of what they have. This conception of him is largely true, as is pointed out above, but it does not harmonize the contradictions of the book, the discrepancies between the piety of some passages and the emotional indifference toward God shown in others. Other of the Biblical Wisdom books (Job, Proverbs) are compilations—why not this? It is not necessary to multiply authors, as is done, for example, by Siegfried, who supposes four principal writers (a pessimistic philosopher, an Epicurean glossator, a sage who upholds the value of wisdom, and an orthodox editor) besides a number of annotators; it is sufficient to assume that several conservative scribes have made short additions to the original work. Nor is it worth while to attempt a logical or symmetrical arrangement of the material. It has been surmised (by Bickell) that the sheets of the original codex became disarranged and were rearranged incorrectly;8 by other critics portions of the book are transferred 852 hither and thither; in all cases the critic is guided in these changes by what he conceives to have been the original form of the book. But it is more probable that we have it in the form in which it grew up—a series of observations by the original author with interspersed editorial remarks; and it is better to preserve the existing form as giving a record of the process of growth.
Date.—As to the date of the book, though there are still differences of opinion among scholars, there is a gradual approach to a consensus. The Solomonic authorship has long since been given up: the historical setting of the work and its atmosphere—the silent assumption of monotheism and monogamy, the non-national tone, the attitude towards kings and people, the picture of a complicated social life, the strain of philosophic reflection—are wholly at variance with what is known of the 10th century B.C. and with the Hebrew literature down to the 5th or 4th century B.C. The introduction of Solomon, the ideal of wisdom, is a literary device of the later time, and probably deceived nobody. The decisive considerations for the determination of the date are the language, the historical background and the thought. The language belongs to the post-classical period of Hebrew. The numerous Aramaisms point to a time certainly not earlier than the 4th century B.C., and probably (though the history of the penetration of Aramaic into Hebrew speech is not definitely known) not earlier than the 3rd century. More than this, there are many resemblances between the dialect of Koheleth and that of Mishna. Not only are new words employed, and old words in new significations, but the grammatical structure has a modern stamp—some phrases have the appearance of having been translated out of Aramaic into Hebrew. By about the beginning of our era the Jews had given up Hebrew and wrote in Aramaic; the process of expulsion had been going on, doubtless, for some time; but comparison with the later extant literature (Chronicles, the Hebrew Ecclesiasticus or Ben-Sira, Esther) makes it improbable that such Hebrew as that of Koheleth would have been written earlier than the 2nd century B.C. (for details see Driver’s Introduction). The general historical situation, also, presupposed or referred to, is that of the period from the year 200 B.C. to the beginning of our era; in particular, the familiar references to kings as a part of the social system, and to social dislocations (servants and princes changing places, x. 7), suggest the troublous time of the later Greek and the Maccabean rulers, of which the history of Josephus gives a good picture.
The conception of the world and of human life as controlled by natural law, a naturalistic cosmos, is alien not only to the prophetic and liturgical Hebrew literature but also to Hebrew thought in general. Whether borrowed or not, it must be late; and its resemblance to Greek ideas suggests Greek influence. The supposition of such influence is favoured by some critics (Tyler, Plumptre, Palm, Siegfried, Cheyne in his Jewish Religious Life after the Exile, and others), rejected by some (Zeller, Renan, Kleinert and others). This disagreement comes largely from the attempts made to find definitely expressed Greek philosophical dogmas in the book; such formulas it has not, but the general air of Greek reflection seems unmistakable. The scepticism of Koheleth differs from that of Job in quality and scope: it is deliberate and calm, not wrung out by personal suffering; and it relates to the whole course and constitution of nature, not merely to the injustices of fortune. Such a conception has a Greek tinge, and would be found in Jewish circles, probably, not before the 2nd century B.C.
A precise indication of date has been sought in certain supposed references or allusions to historical facts. The mention of persons who do not sacrifice or take oaths (ix. 2) is held by some to point to the Essenes; if this be so, it is not chronologically precise, since we have not the means of determining the beginning of the movement of thought that issued in Essenism. So also the coincidences of thought with Ben-Sira (Ecclesiasticus) are not decisive: cf. iii. 14 with B.S. xviii. 6; v. 2-6 (3-7) with B.S. xxxiv. 1-7; vii. 19 with B.S. xxxvii. 14; x. 8 with B.S. xxvii. 26a; xi. 10 with B.S. xxx. 21; xii. 10, 11 with B.S. xxxix. 2 ff., xii. 13 with B.S. xliii. 27; if there be borrowing in these passages, it is not clear on which side it lies; and it is not certain that there is borrowing—the thoughts may have been taken independently by the two authors from the same source. In any case, since Ben-Sira belongs to about 180 B.C., the date of Koheleth, so far as these coincidences indicate it, would not be far from 200 B.C. The contrast made in x. 16 f. between a king who is a boy and one who is of noble birth may allude to historical persons. The antithesis is not exact; we expect either “boy and mature man” or “low-born and high-born.” The “child” might be Antiochus V. (164 B.C.), or Ptolemy V., Epiphanes (204 B.C.), but the reference is too general to be decisive. The text of the obscure passage iv. 13-16 is in bad condition, and it is only by considerable changes that a clear meaning can be got from it. The two personages—the “old and foolish king” and the “poor and wise youth”—have been supposed (by Winckler) to be Antiochus Epiphanes (175-164 B.C.) and Demetrius (162-150 B.C.), or (by Haupt) Antiochus and the impostor Alexander Balas (150-146 B.C.), or (by others) Demetrius and Alexander; in favour of Alexander as the “youth” it may be said that he was of obscure origin, was at first popular, and was later abandoned by his friends. Such identifications, however, do not fix the date of the book precisely; the author may have referred to events that happened before his time. The reign of Herod, a period of despotism and terror, and of strife between Jewish religious parties, is preferred by some scholars (Grätz, Cheyne and others) as best answering to the social situation depicted in the book, while still others (as Renan) decide for the reign of Alexander Jannaeus (104-78 B.C.). The data are not numerous and distinct enough to settle the question beyond determining general limits: for reasons given above the book can hardly have been composed before about 200 B.C., and if, as is probable, a Septuagint translation of it was made (though the present Septuagint text shows the influence of Aquila), it is to be put earlier than 50 B.C. Probably also, its different parts are of different dates.
Of the author nothing is known beyond the obvious fact that he was a man of wide observation and philosophic thought, of the Sadducean type in religion, but non-Jewish in his attitude toward life. He was, doubtless, a man of high standing, but neither a king nor a high-priest, certainly not the apostate priest Alcimus (1 Macc. vii. ix.); nor was he necessarily a physician—there are no details in ch. xii. or elsewhere that any man of good intelligence might not know. The book is written in prose, some of which is rhythmical, with bits of verse here and there: thus i. 2-11 is balanced prose, 12-14 plain prose, 15 a couplet, i. 16-ii. 25 simple prose, vii. contains a number of poetical aphorisms, and so on. Some of the verses are apparently from the author, some from editors.
The fortunes of the book are not known in detail, but it is clear that its merciless criticism of life and its literary charm made it popular, while its scepticism excited the apprehensions of pious conservatives. Possibly the Wisdom of Solomon (c. 50 B.C.) was written partly as a reply to it. The claim of sacredness made for it was warmly contested by some Jewish scholars. In spite of the relief afforded by orthodox additions, it was urged that its Epicurean sentiments contradicted the Torah and favoured heresy. Finally, by some process of reasoning not fully recorded, the difficulties were set aside and the book was received into the sacred canon; Jerome (on Eccl. xii. 13, 14) declares that the decisive fact was the orthodox statement at the end of the book: the one important thing is to fear God and keep His commandments. The probability is that the book had received the stamp of popular approbation before the end of the 1st century of our era, and the leading men did not dare to reject it. It is not certain that it is quoted in the New Testament, but it appears to be included in Josephus’ list of sacred books.
Literature.—For the older works see Zöckler (in Lange’s Comm.); for Jewish commentaries see Zedner, Cat. of Heb. books in Libry. of Brit. Mus. (1867), and for the history of the interpretations, C.D. Ginsburg, Coheleth (1861). Introductions of A. Kuenen, S.R. Driver, Cornhill, König. Articles in Herzog-Hauck, Realencykl. (by P. Kleinert); Hastings, Dict. Bible (by A.S. Peake); T.K. Cheyne, 853 Encycl. Bibl. (by A.B. Davidson); Jew. Encycl. (by D.S. Margoliouth). Commentaries: F. Hitzig (1847); C.D. Ginsburg (1861); H. Grätz (1871); Tyler (1874); Delitzsch (1875); E.H. Plumptre (1881); C.H.H. Wright (1883); Nowack, revision of Hitzig (1883); Volck (in Strack u. Zöckler’s Kurzgef. Komm., 1889); Wildeboer (in Marti’s Kurzer Hand-Comm., 1898); C. Siegfried (in W. Nowack’s Handkomm., 1898); Oort (in De Oude Test., 1899). Other works: C. Taylor, Dirge of Koh. (1874); Wünsche, Midrash on Koh. (in his Biblioth. rabbin., 1880); E. Renan, L’Ecclésiaste (1882); Bickell, Der Prediger (1884) and Kohel.-Untersuchungen (1886; Engl. by E.J. Dillon, Sceptics of Old Test., 1895); Schiffer, Das Buch Koh. nach d. Auffass. d. Weisen d. Talmuds, &c. (1884); A. Palm, Qoh. u. d. nach-aristotel. Philosophie (1885) and Die Qoh.-Lit. (1886); E. Pfleiderer, Die Phil. d. Heraklit, &c. (1886); Cheyne, Job and Solomon (1887) and Jew. Relig. Life, &c. (1898); W. Euringer, Der Masorahtext d. Koh. (1890); W.T. Davison, Wisdom-Lit. of Old Test. (1894); H. Winckler, in his Altorient. Forschungen (1898); J.F. Genung, Words of Koh. (Boston, Mass., 1904); P. Haupt, Ecclesiastes (Baltimore, 1905). The rabbinical discussions of the book are mentioned in Shabbath, 30b; Megilla, 7a; Eduyoth, v. 3; Mishna Yadaim, iii. 5, iv. 6; Midrash Koheleth (on xi. 9), Aboth d’ Rab. Nathan, i.
1 The Hebrew has the definite article, “the whole,” τὸ πᾶν.
2 In fact, he suggests, a curse, as in Gen. iii. 17-19, though with a wider sweep than that passage has in mind.
3 The text has “folly,” but the parallelism and v. 7 point to social, not intellectual, conditions, and a slight change (מסכן for הסכל) gives the sense “poor.”
4 The Septuagint has less well: “They (the wicked) are praised in the city.”
5 The clause is obscure; literally “he (or, one) rises at (?) the voice of the bird,” usually understood to refer to the old man’s inability to sleep in the morning; but this is not a universal trait of old age, and besides, a reference to affairs in the house is to be expected; the Hebrew construction also is of doubtful correctness. A change of the Hebrew text seems necessary; possibly we should read ישפל קול, “low is the voice,” instead of יקום לקול “he rises up at the voice.”
6 The second is perhaps to be read: “the caper-berry blooms” (white hair); usually “the caper-berry loses its appetizing power”; Eng. Auth. Vers. “desire shall fail.” For the meaning of the word abyona (“caper-berry,” not “desire” or “poverty”), see art. by G.F. Moore in Journ. of Bibl. Lit. x. 1 (Boston, Mass., 1891).
7 This is the Talmudic understanding of the Hebrew expression (Jerus. Sanhed. 10, 28a, cf. Sanhed. 12a; see Ecclus. xxxix. 2). There is no good authority for the renderings “collectors of maxims,” “collections of maxims.”
8 It is not certain that the codex form was in use in Palestine or in Egypt as early as the 2nd or the 1st century B.C.
ECCLESIASTICAL COMMISSIONERS, in England, a body corporate, whose full title is “Ecclesiastical and Church Estates Commissioners for England,” invested with very important powers, under the operation of which extensive changes have been made in the distribution of the revenues of the Established Church. Their appointment was one of the results of the vigorous movements for the reform of public institutions which followed the Reform Act of 1832. In 1835 two commissions were appointed “to consider the state of the several dioceses of England and Wales, with reference to the amount of their revenues and the more equal distribution of episcopal duties, and the prevention of the necessity of attaching by commendam to bishoprics certain benefices with cure of souls; and to consider also the state of the several cathedral and collegiate churches in England and Wales, with a view to the suggestion of such measures as might render them conducive to the efficiency of the established church, and to provide for the best mode of providing for the cure of souls, with special reference to the residence of the clergy on their respective benefices.” And it was enacted by an act of 1835 that during the existence of the commission the profits of dignities and benefices without cure of souls becoming vacant should be paid over to the treasurer of Queen Anne’s Bounty. In consequence of the recommendation of these commissioners, a permanent commission was appointed by the Ecclesiastical Commissioners Act 1836 for the purpose of preparing and laying before the king in council such schemes as should appear to them to be best adapted for carrying into effect the alterations suggested in the report of the original commission and recited in the act. The new commission was constituted a corporation with power to purchase and hold lands for the purposes of the act, notwithstanding the statutes of mortmain. The first members of the commission were the two archbishops and three bishops, the lord chancellor and the principal officers of state, and three laymen named in the act.
The constitution of the commission was amended by the Ecclesiastical Commissioners Act 1840 and subsequent acts, and now consists of the two archbishops, all the bishops, the deans of Canterbury, St Paul’s and Westminster, the lord chancellor, the lord president of the council, the first lord of the treasury, the chancellor of the exchequer, the home secretary, the lord chief justice, the master of the rolls, two judges of the admiralty division, and certain laymen appointed by the crown and by the archbishop of Canterbury. The lay commissioners are required to be “members of the Church of England, and to subscribe a declaration to that effect.” The crown also appoints two laymen as church estates commissioners, and the archbishop of Canterbury one. These three are the joint treasurers of the commission, and constitute, along with two members appointed by the commission, the church estates committee, charged with all business relating to the sale, purchase, exchange, letting or management of any lands, tithes or hereditaments. The commission has power to make inquiries and examine witnesses on oath. Five commissioners are a quorum for the transaction of business, provided two of them are church estates commissioners; two ecclesiastical commissioners at least must be present at any proceeding under the common seal, and if only two are present they can demand its postponement to a subsequent meeting. The schemes of the commission having, after due notice to persons affected thereby, been laid before the king in council, may be ratified by orders, specifying the times when they shall take effect, and such orders when published in the London Gazette have the same force and effect as acts of parliament.
The recommendations of the commission recited in the act of 1836 are too numerous to be given here. They include an extensive rearrangement of the dioceses, equalization of episcopal income, providing residences, &c. By the act of 1840 the fourth report of the original commissioners, dealing chiefly with cathedral and collegiate churches, was carried into effect, a large number of canonries being suspended, and sinecure benefices and dignities suppressed.
The emoluments of these suppressed or suspended offices, and the surplus income of the episcopal sees, constitute the fund at the disposal of the commissioners. By an act of 1860, on the avoidance of any bishopric or archbishopric, all the land and emoluments of the see, except the patronage and lands attached to houses of residence, become, by order in council, vested in the commissioners, who may, however, reassign to the see so much of the land as may be sufficient to secure the net annual income named for it by statute or order. All the profits and emoluments of the suspended canonries, &c., pass over to the commissioners, as well as the separate estates of those deaneries and canonries which are not suspended. Out of this fund the expenses of the commission are to be paid, and the residue is to be devoted to increasing the efficiency of the church by the augmentation of the smaller bishoprics and of poor livings, the endowment of new churches, and employment of additional ministers.
The substitution of one central corporation for the many local and independent corporations of the church, so far at least as the management of property is concerned, was a constitutional change of great importance, and the effect of it undoubtedly was to correct the anomalous distribution of ecclesiastical revenues by equalizing incomes and abolishing sinecures. At the same time it was regarded as having made a serious breach in the legal theory of ecclesiastical property. “The important principle,” says Cripps, “on which the inviolability of the church establishment depends, that the church generally possesses no property as a corporation, or which is applicable to general purposes, but that such particular ecclesiastical corporation, whether aggregate or sole, has its property separate, distinct and inalienable, according to the intention of the original endowment, was given up without an effort to defend it” (Law Relating to the Church and Clergy, p. 46).
ECCLESIASTICAL JURISDICTION. This phrase in its primary sense imports not jurisdiction over ecclesiastics, but jurisdiction exercised by ecclesiastics over other ecclesiastics and over the laity. “Jurisdiction” is a word borrowed from the jurists which has acquired a wide extension in theology, wherein, for example, it is frequently used in contradistinction to “order,” to express the right to administer sacraments as something superadded to the power to celebrate them. So it is used to express the territorial or other limits of ecclesiastical, executive or legislative authority. Here it is used, in the limited sense defined by an American Court, as “the authority by which judicial officers take cognizance of and decide causes.”
Such authority in the minds of lay Roman lawyers who first used this word “jurisdiction” was essentially temporal in its origin and in its sphere. The Christian Church transferred the notion to the spiritual domain as part of Origin of ecclesiastical jurisdiction. the general idea of a Kingdom of God correlative, on the spiritual side of man upon earth, to the powers, also ordained of God, who had dominion over his temporal estate (see Canon Law). As the Church in the earliest ages had executive and legislative power in its own spiritual sphere, so also it had “judicial officers,” “taking cognizance of and deciding causes.” Only before its union with the State, its power in this direction, as in others, was merely over the spirits of men. Coercive temporal authority over their bodies or estates could only be given by concession from the temporal prince. Moreover, even spiritual authority over members of the Church, i.e. baptized persons, could not be exclusively claimed as of right by the Church tribunals, if the subject matter of the cause were purely temporal. On the other hand, it is clear that all the faithful were subject to these courts (when acting within their own sphere), and that, in the earliest times, no distinction was made in this respect between clergy and laity.
The fundamental principle of ecclesiastical jurisdiction with its 854 “sanction” of excommunication will be found in Christ’s words in Matt. xviii. 15-18. A very early example of criminal spiritual jurisdiction exercised by St Paul is found in the case of the incestuous Corinthian (1 Cor. v.). We find later the same apostle exercising like jurisdiction in the cause of Hymenaeus and Alexander (1 Tim. i. 20). After the time of the Apostles, we find this criminal jurisdiction exercised by the bishops individually over their respective “subjects”—doubtless with the advice of their presbyters according to the precept of St Ignatius (c. 110). As neighbouring dioceses coalesced into “provinces” and provinces into larger districts (corresponding to the civil “dioceses” of the later Roman Empire), the provincial synods of bishops and the synods of the larger districts acquired a criminal jurisdiction, still purely spiritual, of their own. At first this was “original” and mainly (although not exclusively) over bishops (of the province or larger district). The beginnings of an appellate jurisdiction in the cases of clerics and laymen may be traced before the conversion of the Empire. The bishop over whom the synod of neighbouring bishops had exercised jurisdiction had no formal right of appeal; but sometimes bishops in other parts of the Church would refuse to acknowledge the local synodical sentence and would communicate with a bishop whom they deemed unjustly deposed. The theory, as expressed in legal phrase by St Cyprian in the 3rd century, was that the apostolic power of delegated sovereignty from the Lord, alike legislative and judicial, was held in joint-tenancy by the whole body of Catholic bishops. In both capacities, however, a certain undefined pre-eminence was conceded to the occupants of “Apostolic” sees, i.e. sees traditionally founded by Apostles, or of sees with a special secular position.
Even before the edict of Milan, at least as early as the latter half of the 3rd century, the spiritual sentences of deposition from office had sometimes indirect temporal consequences recognized by the secular courts. The classical example is the case of Paul of Samosata, bishop of Antioch. It would seem that, in the intervals of persecution, some rights of property were recognized in the Christian Church and its officers; although the Church was an illegal society. After some previous abortive trials, Paul of Samosata was deposed and excommunicated, in 269, by a great synod of the Antiochene district. Paul, notwithstanding his deposition, kept possession of the episcopal residence. The local church sought recovery of it before the tribunals of the Empire. The judicial authorities requested a rescript from the emperor Aurelian for the decision of the cause. Aurelian referred the matter to the bishop of Rome and the bishops of Italy, who gave their award in favour of the Antiochene Church.
Side by side with this which we may call criminal jurisdiction—none the less real or coercive because its sanctions were purely spiritual—there grew up a quasi-jurisdiction in causes entirely temporal, based upon the free consent of the Temporal Jurisdiction of the Church. parties to accept the arbitration of the bishop. This system had also its roots in the New Testament (see Matt, xviii. 15-17 and 1 Cor. vi. 1-8). In the matter of criminal jurisdiction we paused for a moment at the edict of Milan; but we may at once trace this second or civil branch of episcopal judicature or quasi-judicature down as far as the reign of Charlemagne, when it underwent a fundamental change, and became, if either litigant once chose, no longer a matter of consent but of right.
Constantine decreed that judgment in causes might be passed by bishops when litigants preferred their adjudication to that of the secular courts (see his epistle to the Numidian bishops and Cod. Theodos. Tit. de Episcopis). The episcopal judgment was to be equivalent to that of the emperor and irreversible, and the civil authorities were to see to its execution. Saints Ambrose and Augustine both spent days in deciding temporal causes. Honorius, in the West, at the end of the 4th century, made a constitution providing that if any desired to litigate before the bishops they should not be forbidden, but that in civil matters the prelates should render judgment in the manner of arbitrators by consent (Cod. 1, Tit. iv.). Where the faithful had had recourse to the bishop, no appeal was to be allowed, and the judges were to command execution of the episcopal decree. A quarter of a century later, however, Valentinian III. in the West expressly provided that bishops were not to be permitted to be judges (that is, of course, in temporal causes), save by the consent of the parties. This legislation was, substantially, adopted by Justinian.
On the revival of the Western Empire, however, Charlemagne, in the beginning of the 9th century, under the mistaken belief that he was following the authority of Constantine I. and Theodosius I., took a great step forward, by which the bishop ceased to be a mere legally indicated arbitrator by consent in secular causes, and became a real judge. By a capitulary he provided that either litigant, without the consent of the other party, and not only at the beginning of a suit but at any time during its continuance, might take the cause from lay cognizance and transfer it to the bishop’s tribunal. He re-enacted the prohibition of appeal.
It should be remembered that, from the latter part of the 3rd century, the leading bishops had generally been trained in secular learning. St Cyprian, St Ambrose and St Augustine, St Paulinus of Nola and St John Chrysostom had practised law as teachers or advocates. St Ambrose and St Paulinus had even held high administrative and judicial offices.
To return to the evolution of ecclesiastical jurisdiction from the time of Constantine. With the “Nicene period” came a great development on the criminal side. A system begins to be formed, and the secular arm supports Roman empire from Constantine. the decrees of the Church. The first trace of system is in the limited right of appeal given by the first oecumenical council of Nicaea and its provision that episcopal sentences or those of provincial synods on appeal were to be recognized throughout the world. The fifth canon provides that those, whether clerics or laymen, who are cut off from communion in any particular province are not to be admitted thereto elsewhere. Still examination must be had whether persons have been expelled from the congregation by any episcopal small-mindedness (μικροψυχία), or contentious spirit, or such-like harshness (ἀηδία). That this may be conveniently inquired into, synods are to be held, three in every year, in each province, and questions of this kind examined. There is to be no “stay of execution”; the episcopal sentence is to prevail until the provincial synod otherwise decide. It will be noticed that as yet no provision is made for appeals by bishops from provincial synods sitting in first instance.
The edicts of Milan had only admitted the Christian Church among the number of lawful religions; but the tendency (except in the time of Julian) was towards making it the only lawful religion. Hence the practice, immediately after Nicaea I., of superadding banishment by the emperor to synodical condemnation. The dogmatic decrees of Nicaea I. were at once enforced in this temporal manner. On the other hand, the Arian reaction at court worked its objects (see Pusey, Councils of the Church) by using the criminal spiritual jurisdiction of synods against the Catholics—often packing the synods for the purpose. The acts of councils of this age are full of the trials of bishops not only for heresy but for immorality and common law crimes. The accusations are frequently unfounded; but the trials are already conducted in a certain regular forensic form. The secular authorities follow the precedent of Nicaea I. and intervene to supplement the spiritual sentence by administrative penalties. Sometimes an imperial officer of high rank (as, e.g. a “count”) is present at the synod, as an assessor to maintain order and advise upon points of procedure. Leading examples may be found in the various prosecutions of St Athanasius, in whose case also there is the germ of an appeal, tanquam ab abusu. It has been contended that, according to later and more formulated jurisprudence, such an appeal would have lain, since the trial at Tyre was not concerned with purely spiritual matters (see the case in Hefele, Councils, in loc.).
The trial of St Athanasius led to extensions of the right of appeal. This was favoured by the development of the greater sees into positions of great administrative dignity, shortly to be called “patriarchal.” A synod was held at Rome, attended 855 by bishops from various regions, which reversed the original judgment of the synod of Tyre which had condemned Athanasius. A much larger synod at Antioch, gathered only from the East, on the other hand, confirmed that judgment. This last synod did something to systematize the criminal procedure of the Church, and its legislation has been always received.
This legislation marks another step forward. Deposition of a bishop by a synod, or of a priest or deacon by his bishop, is to take effect even pending an appeal, and a cleric continuing his functions after sentence in first instance is to lose all right of appeal. The appeal given by Nicaea I. to clerics and laymen from episcopal excommunications is extended. The synod may restore them if convinced of the justice of their cause (and not merely in cases of ἀηδία). A bishop may appeal to a great assembly of bishops. Any bishop, priest or deacon “importuning” the emperor, instead of exerting his right of appeal to synods, is to lose all right of appeal and never to be restored or pardoned. If a provincial synod be divided as to the guilt of a bishop, the metropolitan is to convene bishops from the neighbouring provinces to decide the cause jointly with the bishops of the original province.
A few years later, in 347, the council of Sardica, a council of practically the whole West save Africa, reversed Tyre and acquitted St Athanasius after a full judicial inquiry. This council endeavoured to set up a system of appeals in the case of bishops, in which the see of Rome was made to play a great part. “Out of honour to the memory of St Peter,” a condemned bishop may ask the intervention of Rome. If this be done, the synod of first instance is to send letters to Julius, bishop of Rome. If that prelate think the cause should be heard again, he is to appoint judges; if otherwise, the original judgment is to be confirmed. Pending appeal, the appellant’s see is not to be filled up. The judges appointed by the bishop of Rome to hear the appeal are to be from the neighbouring provinces. The appellant may, however, request that bishop to send priests from his side to sit with the synod of appeal. If such priests are sent, they are to preside in the court of appeal. These canons were always repudiated in the East, and when, sixty years afterwards, they were, for the first time, heard of in Africa, they were repudiated there also.
A rescript of Gratian in 378 empowered the bishop of Rome to judge bishops with the assistance of six or seven other bishops or, in the case of a metropolitan, of fifteen comprovincial bishops. A bishop refusing to come to Rome was to be brought there by the civil power. The rescript, however, was not incorporated in the Codes and perhaps was only a temporary measure.
The tendency to give pre-eminence to Rome appears again in an imperial letter to St Flavian, who, in the judgment of the East, was bishop of Antioch, but who was rejected by the West and Egypt, summoning him to Rome to be there judged by the bishops of the imperial city—a summons which St Flavian did not obey (Tillemont, Mém. Ecc.). In Africa in the beginning of the 5th century Apiarius, a priest who had been deposed by the bishop of Sicca for immorality, and whose deposition had been affirmed by the “provincial synod,” instead of further appealing to a general synod of Africa, carried his appeal to Pope Zosimus. The pope received the appeal, absolved him and restored him to the rank of priest, and sent a bishop and two priests as legates to Africa with instructions to them to hear the cause of Apiarius anew and for execution of their sentence to crave the prefect’s aid; moreover, they were to summon the bishop of Sicca to Rome and to excommunicate him, unless he should amend those things which the legates deemed wrong. The upshot of a long conflict was that the papal claim to entertain appeals from Africa by priests and deacons was rejected by the African bishops, who in their final synodical epistle also repudiate in terms any right of appeal by African bishops to “parts beyond the seas” (see Hefele, Councils, bk. viii.).
The story of the administrative development of the Church in the 5th century is mainly the story of the final emergence and constitution of the great “patriarchates,” as authorities superior to metropolitans and provincial synods. In consequence of the occupants of the thrones of Constantinople and Alexandria falling successively into opposite heresies, the question arose how “patriarchs” were to be judged. In both cases, as it seems, an attempt was made by the bishop of Rome to depose the erring patriarch by his authority as primate of Christendom, acting in concert with a Western synod. In both cases, apparently, an oecumenical synod ignored the Roman deposition and judged the alleged offences of the respective patriarchs in first and last instance. The third and fourth oecumenical synods (Ephesus, 431; Chalcedon, 451) were primarily tribunals for the trials of Nestorius and Dioscorus; it was secondarily that they became organs of the universal episcopate for the definition of the faith, or legislative assemblies for the enactment of canons. Nothing is more remarkable than their minute care as to observance of rules of procedure. In both cases, imperial assessors were appointed. At Ephesus the Count Candidian was commissioned to maintain order, but took little part in the proceedings. At Chalcedon, on the other hand, the imperial commissioners decided points of order, kept the synod to the question, took the votes and adjourned the court. But the synod alone judged and pronounced sentence. No oecumenical synod has tried a patriarch of Old Rome while yet in the flesh. The fifth oecumenical council came nearest to so doing, in the case of Vigilius. That pope, although in Constantinople, refused to attend the sittings of the council. He was cited three times, in the canonical manner, and upon not appearing was threatened in the third session with anathema (Hefele, Councils, sect. 268 ad fin.). He was not, however, charged with direct heresy, as were Nestorius and Dioscorus, and the synod seems to have hesitated to deal stringently with the primate of Christendom. In the seventh session it accepted the suggestion of Justinian, merely to order the name of Vigilius to be removed from the liturgical prayers, at the same time expressing its desire to maintain unity with the see of Old Rome (Hefele, sect. 273). After the council, Justinian banished the pope to Egypt, and afterwards to an island, until he accepted the council, which he ultimately did (ib. 276). The sixth oecumenical synod decreed that the dead pope Honorius should be “cast out from the holy Catholic Church of God” and anathematized, a sentence approved by the reigning pope Leo II. and affirmed by the seventh oecumenical synod in 787.
The constitution of the patriarchal system resulted in the recognition of a certain right of appeal to Rome from the larger part of the West. Britain remained outside that jurisdiction, the Celtic churches of the British islands, after those islands were abandoned by the Empire, pursuing a course of their own. In the East, Constantinople, from its principality, acquired special administrative pre-eminence, naturally followed, as in the case of “old Rome,” by judicial pre-eminence. An example of this is found in the ninth canon of Chalcedon, which also illustrates the enforcement upon a clerical plaintiff in dispute with a brother cleric of that recourse to the arbitration of their ecclesiastical superior already mentioned. The canon provides that any clerk having a complaint against another clerk must not pass by his own bishop and turn to secular tribunals, but first lay bare his cause before him, so that by the sentence of the bishop himself the dispute may be settled by arbitrators acceptable to both parties. Any one acting against these provisions shall be subject to canonical penalties. If any clerk have a complaint against his own bishop, he shall have his cause adjudicated upon by the synod of the province. But if a bishop or clerk have a difference with the metropolitan of his province let him bring it before the exarch of the “diocese” (i.e. the larger district answering to the civil “diocese”), or before the royal see of Constantinople, who shall do justice upon it. An “exarch” means properly a superior metropolitan having several provinces under him. In the next century Justinian (Nov. 123, c. 22) put the other patriarchates on the same footing as Constantinople. In c. 21 he gives either plaintiff or defendant an appeal within ten days to the secular judge of the locality from the bishop’s judgment. If there be no appeal, that judge is to give execution to the episcopal award. The growth of a special “original” jurisdiction at Constantinople, which perhaps 856 developed earlier than the corresponding institution at Rome, may be traced to the fact that bishops from all parts were constantly in Constantinople. The bishop of Constantinople, even before he became properly “patriarch,” would often assemble a synod from these visiting bishops, which acquired the technical name of σύνοδος ἐνδημοῦσα, the synod of sojourners. This synod frequently decided questions belonging to other patriarchates.
The criminal jurisdiction thus exercised was generally speaking unlimited. It must be remembered that the forum externum of the ecclesiastical jurisdiction, in the sense in which we now use the phrase, of a judge deciding causes, was not then clearly marked off from the forum internum, or what afterwards came to be called the “tribunal of penance” (see Van Espen, Jus ecc. univ. pars iii. tit. iv. c. 1). Ecclesiastical proceedings by way of prosecution are called “criminal,” but they are primarily pro salute animae; whereas temporal criminal proceedings are primarily for the protection of the state and its citizens. Hence a Christian might be first punished in the civil courts and then put to public penance by the ecclesiastical jurisdiction, or vice versa: an apparently double system of punishment which the medieval Church, when the forum externum had become quite separated from the forum internum, sometimes repudiated (see Maitland, English Canon Law, 138, 139, 144).
Theodosius began the system of giving secular authority to Church tribunals. Thus, in 376, L. 23 Cod. Theodos. de. Episcopis, &c., subjected clerics for small offences pertaining to the observances of religion to bishops and synods. In 399, L. 1 Cod. de Religione provides that, when it is a matter of religion, it beseems the bishop to judge. A rescript of Constantius, in 355, inserted in Cod. Theod. lxii. de Epis. Ecc. et Cler., excluded bishops from accusations before secular judges and commanded such accusations to be speedily brought before the tribunal of other bishops. This law was probably only intended to be of a temporary character. Then comes the law of Gratian already noticed. Then, in 399, a law of Honorius (Cod. Theod. L. 1 de Religione): “As often as it concerns religion, it is meet that the bishops should judge, but other causes which belong to ordinary jurisdiction or to public law are to be heard in the ordinary courts (legibus oportet audiri).” L. 3 de Epis. Jud., at the end of the Theodosian Code, seems spurious (see the comment of Gothofredus in loco). But a constitution of Honorius in 412 (Cod. Theod. L. xli. de Epis. Ecc. et Cler.) provides that clerks are not to be accused except before the bishop. Bishops, priests, deacons, and every other “minister of the Christian law” of inferior degree, are taken from secular jurisdiction in criminal cases. The words are quite general; but it has been contended that they apply only to crimes of an ecclesiastical character (see Gothofredus in loc.; Van Espen, pars iii. tit. iii. c. 1, 10). In 425 a constitution of Theodosius II. provides that a recent decree of the usurper John should be disregarded and that clerks whom he had brought before secular judges should be reserved for the episcopal jurisdictions, “since it is not lawful to subject the ministers of the divine office to the arbitrament of temporal powers.” Justinian has a clearer perception of the demarcation between the spheres of spiritual and temporal law. The 83rd Novell provides that if the offence be ecclesiastical, needing ecclesiastical correction, the bishop shall take cognizance of it. The 123rd Novell (c. 21) provides that if a clerk be accused of a secular crime he shall be accused before his bishop, who may depose him from his office and order, and then the competent judge may take him and deal with him according to the laws. If the prosecutor have first brought him before the civil judge, the evidence is to be sent to the bishop, and the latter, if he thinks the crime has been committed, may deprive him of his office and order, and the judge shall apply to him the proper legal punishment. But if the bishop think the evidence insufficient, the affair shall be referred to the emperor, by way of appeal both from bishop and judge. If the cause be ecclesiastical, the civil judges are to take no part in the inquiry. The law includes with clerics, monks, deaconesses, nuns, ascetics; and the word “clerics” covered persons in minor orders, down to doorkeepers. It will be noticed that Justinian supposes that the prosecutor may begin the proceedings before the civil judge. A constitution of Alexius Comnenus I. seems to send him to the special forum of the accused.
Certain enactments of later Saxon times in England have been sometimes spoken of as though they united together the temporal and spiritual jurisdictions into one mixed tribunal deriving its authority from the State. In the latter Anglo-Saxon courts. part of the 10th century, laws of Edgar provided that the bishop should be at the county court and also the alderman, and that there each of them should put in use both God’s laws and the world’s law (Johnson’s English Canons, i. 411). This probably was, as Johnson suggests, that the bishop might enforce secular laws by ecclesiastical censure and the alderman ecclesiastical laws with secular punishment. But the two jurisdictions were kept separate; for by another law of Edgar (Leges Edg. c. v.) it was provided that “in the most august assembly the bishop and alderman should be present, and the one should interpret to the people the law of God, the other the laws of men.” Edgar, in a speech to St Dunstan and the bishops in synod (in 969), said, “I hold in my hands the sword of Constantine, you that of Peter. Let us join right hands and unite sword to sword” (Hardouin, Conc. tom. vi. p. 1, col. 675). The juxtaposition of the judicatures may, however, have led to some confusion between them.
As to appeals the mixed council of Cliff at Hoo (747) said they should go to the synod of the province. The only appeal to Rome in Saxon times was that of St Wilfrid, bishop of York, who appealed from the division of his see and his deposition for refusing to consent to it, and was heard in a Roman synod under the presidency of Pope Agatho. The synod found him unlawfully deposed and ordered his restoration. Upon his return to England, the Roman judgment was refused recognition and he was for a time imprisoned. Ten years later he was recalled to York, but refusing to consent to the division of his see was again deposed and again appealed to Rome. The appeal was heard at great length, in a synod of 703 under John VI., deputies from the archbishop of Canterbury being present. St Wilfrid was justified and was sent back to his see, with papal letters to the kings of Northumbria and Mercia. The Roman decree was again disregarded. At the council of “Nid” he was reconciled to the other bishops of the province, but not restored. In the end he was brought back to York, but not to the undivided see. The details of the case will be found in Wilkins, Concilia, in Mansi, Concilia, under the various councils named, and in Haddan & Stubbs, Councils and Eccl. Documents, vol. iii.
The penalties which the spiritual court could inflict, in the period between the edict of Milan and c. 854, were properly excommunication whether generally or as exclusion from the sacraments for a term of months or years or Penalties inflicted by ecclesiastical courts. till the day of death and (in the case of clerics) suspension or deposition. Gradually, however, doubtless by way of commutation of excommunication and of penance, temporal penalties were added, as scourging, banishment, seclusion in a monastery, fines. It is difficult to say how far some of these temporal penalties were penitential only or how far they could be inflicted in invitos. But the secular arm, from the time of Nicaea I., was in the habit of aiding spiritual decrees, as by banishing deposed bishops, and gradually by other ways, even with laymen. Scourging (although it had been a well-known punishment of the synagogue) was at first forbidden. Can. 28 (26) of the Apostolic Canons imposes deposition on any bishop, priest or deacon striking the delinquent faithful. In Africa, however, a contrary practice early sprang up (see St Augustine, Epist. clix. ad Marcellum al. cxxxiii.). The small council of Vannes in Brittany in 465 made it an alternative punishment for clerks convicted of drunkenness (Can. 13). Canon 13 of the first council of Orleans, which has been cited in this matter, seems to have no application. St Gregory the Great seems to assume that scourging and seclusion in a monastery are in the discretion of episcopal tribunals (see Epistles, lib. ii. ep. 11, 40, 42, 44, 45; lib. vii. ep. 11, 67; lib. xii. ep. 31, c. 4). The 16th council of Toledo 857 (in 693) has been cited as if it visited certain very great sinners with scourging as an ecclesiastical punishment. In fact, it only approves the punishment as ordered by the Visigothic laws. An alleged decree of a council of Autun in 670 is part of a code of discipline for monasteries (see authorities cited by Hefele, Councils, sect. 290, towards the end). Banishment does not seem to have been inflicted by the spiritual court in invitum. Seclusion in a monastery seems first to have been used by the civil power in aid of the spiritual. The fifth canon of the council of Macon, in 584, forbids clergy to dress like laymen and imposes a penalty of thirty days’ imprisonment on bread and water; but this may be merely penitential. There is little evidence of the imposition of fines as ecclesiastical penalties; but there are references to the practice in the epistles of St Gregory the Great, notably in his instructions to St Augustine. Gregory III. copies from St Gregory I. Probably these also were by way of penance. Isolated examples in the early middle ages of metropolitans dealing with their suffragan bishops by imprisonment in chains were extra-canonical abuses, connected with the perversion of Church law which treated the metropolitan (who originally was merely convener of the provincial synod and its representative during the intervals of sessions) as the feudal “lord” of his comprovincials.
With the later 9th century we enter upon a new epoch, and by the time of Gregory VII., in the 11th century, the tribunals have fallen into the hands of a regular class of canonists who are in fact professional church-lawyers in orders. The changes due to the adoption of the False Decretals by Nicholas I. and the application of their principles by Hildebrand (afterwards Gregory VII.) are discussed in the article Canon Law. The later medieval system, thus inaugurated, may be considered (1) in its hierarchy, (2) in the subject matter of its jurisdiction, (3) in its penalties.
1. (a) It is a system of courts. Much that had been done by bishops, sine strepitu forensi et figura judicii, is now done in the course of regular judicial procedure. Again, the court takes the place of the synod. The diocesan synod Later medieval system. ceases to have judicial work. The court of the metropolitan takes the place of the provincial synod, except possibly for the trial of bishops, and even this becomes doubtful.
(b) At first the bishop was the only judge in the diocesan court and he always remains a judge. But just as the king appoints judges to hear placita coram rege ipso, and the feudal lord appoints his seneschal or steward, so the bishop appoints his official.
(c) The archdeacon acquires a concurrent ordinary jurisdiction with the bishop (see Archdeacon). For some time it was considered that he was a mere office-holder dependent on the will of the bishop with a jurisdiction merely “vicarial”; but by the 13th century it was settled that he held a “benefice” and that his jurisdiction over causes was ordinary and independent of the bishop (Van Espen, pars i. tit. xii. c. 1; Fournier, Les Officialités au moyen âge, p. 134). It was partly in order to counterpoise the power of archdeacons that bishops created officials (Fournier, p. 8). Archdeacons in course of time created officials who presided in court in their stead. The extent of jurisdiction of archdeacons depended much upon local customs. In England the custom was generally in their favour. Ordinarily, the appeal from an archdeacon or his official lay to the court of the bishop; but by custom the appeal might be to the court of the metropolitan: The Constitutions of Clarendon, in 1164, made the appeal from the court of the archdeacon lie to the court of the bishop.
(d) The official of the bishop might be his official principal, who was his alter ego, or a special officer for a particular locality (officialis foraneus). The latter was treated as a mere delegate, from whom an appeal could be made to the bishop. The former had one consistory with the bishop, so that appeals from him had to be made to the court of the metropolitan. How far the official principal had jurisdiction in criminal matters by virtue of his office, how far it was usual to add this jurisdiction by special commission, and what were the respective limits of his office and that of the vicar-general, are questions of some nicety. The emphasis in Italy was on the vicar-general (Sext. de officio Vicarii). In the Low Countries, France and England the jurisdiction of the official principal was wider (Van Espen, pars i. tit. xii. cc. 4, 5; Fournier, p. 21). But he could not try criminal matters unless specially committed to him (Lyndwood, Provinciale, lib. ii. tit. 1). Later in England it became usual to appoint one man to the two offices and to call him chancellor, a word perhaps borrowed from cathedral chapters, and not in use for a diocesan officer till the time of Henry VIII. or later (see Chancellor). In Ireland the title, till the church was disestablished, was vicar-general.
The importance of distinguishing the normal functions of an official principal and a vicar-general lies in this: that it was gradually established that as a king should not hear causes but commit them to his judges, so a bishop should not hear causes but appoint an official to hear them (see Ridley, View of the Civil and Eccl. Law; Ayliffe, Parergon juris ecclesiastici, p. 161; Godolphin, Abridgement of the Laws Ecclesiastical, p. 8). The “parlements” of France were constantly insisting on the independence and irremovability of the official (Fournier, p. 219). But jurisdiction which was not necessarily incident to the office of the official principal, that is to say voluntary jurisdiction, such as the granting of licences and institution to benefices, and criminal jurisdiction over clerks (and probably over laymen), the bishop could reserve to himself. Reservations of this nature are made in many English patents of chancellors and were held good in R. v. Tristram, 1902, 1 K.B. 816.
(e) The ecclesiastical and temporal courts are kept distinct. The charter of William the Conqueror abrogated the laws of Edgar. No bishop or archdeacon “shall any longer hold pleas in the Hundred concerning episcopal law nor draw a cause which concerns the rule of such to the judgment of men of the world” (Stubbs, Select Charters, part iii.). In France, where the bishop was a temporal baron, his feudal and his spiritual courts were kept by distinct officers (Fournier, p. 2).
(f) From the bishop, or his official, appeal lay to the metropolitan, who again could hear causes by his official. The Constitutions of Clarendon recognize this appeal (c. viii.).
(g) An appeal lay from the court of the metropolitan to that of the primate. There were many disputes as to the existence of these primates (see Maitland, Canon Law in the Church of England, p. 121). In England the dispute between Canterbury and York was settled by making them both primates, giving Canterbury the further honour of being primate of all England. In France the primatial sees and the course of appeals to them were well established (Fournier, p. 219).
(h) Several attempts were made by metropolitans and their officials to take causes arising in the dioceses of their comprovincials in the first instance and not by way of appeal. The officials of primates in their turn made similar attempts. After long struggles this was hindered, in France by the bull Romana (Fournier, p. 218), in England by the Bill of Citations, 23 Henry VIII. c. 9, and Canon 94 of the Canons of 1603. The preamble of the “Bill of Citations” is eloquent as to the mischief which it is framed to prevent. There are, however, a few cases in which the metropolitan is still allowed to cite in the first instance. One of them was in cases of “perplexity.” “Perplexity” arose where the suffragans “could not owing to the geographical limitations of their competence do full justice” (Maitland, pp. 118-119). Such was the case of probate where notable goods of the deceased lay in more than one diocese. Hence the origin of the “prerogative court” of Canterbury (cf. Van Espen, pars i. tit. xix.; and for Spain, Covarruvias, Pract. Quaest. c. 9).
(i) Gradually there grew up a mass of peculiar and exempt jurisdictions (Ayliffe, pp. 417, 418; Phillimore, Eccl. Law, pp. 214, 927; de Maillane, Dict. du droit canonique, s.v. “Exemptions”). Exempt jurisdictions began with the monasteries and were matter of vehement discussion in the later middle ages. There were no true exemptions before the 11th century (Van Espen, pars iii. tit. xii.). Peculiar or special jurisdiction, equal to that of the bishop, was given to deans and chapters over the cathedral precincts and in places where they had corporate property (see Parham v. Templer, 3 Phil. Ecc. R. 22). Sometimes it was given to deans alone or to prebendaries in the parishes whence they derived their prebends. Where the archdeacon 858 had a jurisdiction co-ordinate with the bishop, it was called a peculiar. The metropolitans had peculiars within the dioceses of their comprovincials wherever they had residences or manors, and some whose origin is uncertain, e.g. that of the fifteen parishes in the deanery of the Arches. The official administering justice for the metropolitan was usually called a dean. From a peculiar jurisdiction ranking as episcopal the appeal lay to the court of the metropolitan. As to metropolitan peculiars, the metropolitan might give an appeal from the dean to his regular official principal. Thus, in Canterbury there was an appeal from the dean of Arches to the official principal of the Arches court. When peculiars were abolished (vide infra) the dean of Arches disappeared, and his title, in the 19th century, was erroneously given to the official principal. On peculiars in Spain cf. Covarruvias, Works, tit. i. p. 410. The French parlements, after the middle ages, discouraged them. In exempt convents the head of the monastery or priory exercised jurisdiction subject to an appeal to the pope.
(j) It is said that originally a metropolitan had only one official principal, who, like the metropolitan himself, acted both for the diocese and province. Fournier (p. 219) says that in France it was not till the 17th century that there grew up a custom of having different officials for the metropolitan, one for him as bishop, a second as metropolitan, and even a third as primate, with an appeal from one to the other, and that it was an abuse due to the parlements which strove to make the official independent of the bishop. In England there has been, for a long time, a separate diocesan court of Canterbury held before the “commissary.” The word is significant as showing that there was something special and restricted about the position. In York there are two courts, one called the consistory for the diocese, the other called the chancery for the province. But the same person was often official of both courts.
(k) In England the Constitutions of Clarendon added a provision for appeal to the king, “and if the archbishop shall have failed in doing justice recourse is to be had in the last resort (postremo) to our lord the king, that by his writ the controversy may be ended in the court of the archbishop; because there must be no further process without the assent of our lord the king.” The last words were an attempt to limit further appeal to Rome. It will be observed that the king does not hear the cause or adjudicate upon it. He merely corrects slackness or lack of doing justice (Si archiepiscopus defecerit in justitia exhibenda) and by his writ (precepto) directs the controversy to be determined in the metropolitan’s court. As bishop Stubbs says (Report of Eccl. Comm. vol. i. Hist. App. i.): “The appeal to the king is merely a provision for a rehearing before the archbishop, such failure to do justice being not so much applicable to an unfair decision as to the delays or refusal to proceed common at that time” (cf. Joyce, The Sword and the Keys, 2nd ed. pp. 19-20). The recursus ad principem, in some form or other of appeal or application to the sovereign or his lay judges, was at the end of the middle ages well known over western Europe. This recourse in England sometimes took the form of the appeal to the king given by the Constitutions of Clarendon, just mentioned, and later by the acts of Henry VIII.; sometimes that of suing for writs of prohibition or mandamus, which were granted by the king’s judges, either to restrain excess of jurisdiction, or to compel the spiritual judge to exercise jurisdiction in cases where it seemed to the temporal court that he was failing in his duty. The appellatio tanquam ab abusu (appel comme d’abus) in France was an application of a like nature. Such an appeal lay even in cases where there was a refusal to exercise voluntary jurisdiction (de Maillane, Dictionnaire du droit canonique, tit. “Abus,” cf. tit. “Appel”). This writer traces their origin to the 14th century; but the procedure does not seem to have become regularized or common till the reigns of Louis XII. or Francis I. (cf. Dict. eccl., Paris, 1765, titt. “Abus” and “Appel comme d’abus”). On the recursus ad principem and the practice of “cassation” in Belgium, Germany and Spain, cf. Van Espen’s treatise under this title (Works, vol. iv.) and Jus eccles. univ. pars iii. tit. x. c. 4. Louis XIV. forbad the parlements to give judgment themselves in causes upon an appel comme d’abus. They had to declare the proceedings null and abusive and command the court Christian to render right judgment (Edict of 1695, arts. 34, 36, cited in Gaudry, Traité de la législation des cultes, Paris, 1854, tom. i. pp. 368, 369).
In Catalonia “Pragmatics,” letters from the prince, issued to restrain jurisdiction assumed by ecclesiastical judges contrary to the customs of the principality. Thus in 1368 Peter III. evoked to the royal court a prosecution for abduction pending before the archbishop of Tarragona, declaring that the archbishop and the official were incompetent to judge noblemen. See this and other instances collected in Usages y demas derechos de Cataluña, by Vives y Cebriá (Barcelona, 1835), tom. iv. p. 137 et seq.
(l) Lastly there was the appeal to the patriarchs, i.e. in the West to Rome. The distinguishing feature of this appeal was that the rule of the other appeals did not apply to it. In the regular course of those appeals an appellant could not leap the intermediate stages; but he could at any stage go to this final appeal, omisso medio, as it was technically called (see de appell. c. Dilect. iii. for general rule, and c. 3 de appell. in 6 for different rule in case of the pope, and authorities cited in Van Espen, pars iii, tit. x. c. 2, 5). Van Espen says: “The whole right of appeal to the Roman pontiff omisso medio had undoubtedly its origin in this principle, that the Roman pontiff is ordinary of ordinaries, or, in other words, has immediate episcopal authority in all particular churches, and this principle had its own beginning from the False Decretals.”
Appeals to Rome lay from interlocutory as well as final judgments. Causes could even be evoked to Rome before any judgment and there heard in first instance (Van Espen, pars iii. tit. x. c. 1, 8).
There was an alleged original jurisdiction of the pope, which he exercised sometimes by permanent legates, whom Gregory VII. and his successors established in the chief countries of Europe, and to whom were committed the legislative executive and judicial powers of the spiritual “prince” in the districts assigned to them. These Clement IV. likened to “pro-consuls” and declared to have “ordinary” jurisdiction; because they had jurisdiction over every kind of cause, without any special delegation, in a certain defined area or province (c. ii. de Officio Legati in 6). They were expressed to have not merely appellate but original jurisdiction over causes (iii. c. i. de Officio Legati). The occupants of certain sees by a kind of prescription became legates without special appointment, legati nati, as in the case of Canterbury. In the 13th century Archbishop Peckham, says Maitland (p. 117), as archbishop “asserted for himself and his official (1) a general right to entertain in the first instance complaints made against his suffragans’ subjects, and (2) a general right to hear appeals omisso medio.” It was, for the time, determined that the archbishop might himself, in virtue of his legatine authority, entertain complaints from other dioceses in first instance, but that this legatine jurisdiction was not included in the ordinary jurisdiction of his official principal, even if the archbishop had so willed it in his commission. In fact, however, the official did before the end of the later medieval period get the same power as the archbishop (Maitland, pp. 118-120; cf. Lyndwood, lib. v. tit. 1), till it was taken from him by the Bill of Citations.
After legates came special delegates appointed by the pope to hear a particular cause. It was the general practice to appoint two or three to sit together (Van Espen, pars iii. tit. v. c. 2, 37). These might sub-delegate the whole cause or any part of it as they pleased, ibid. 9-18. Dr Maitland (essay on “The Universal Ordinary”) thinks, but without very much foundation, that great numbers especially of the more important causes were tried before these delegates; although the records have largely perished, since they were the records of courts which were dissolved as soon as their single cause had been decided. These courts were convenient, since it was the custom to appoint delegates resident in the neighbourhood, and the power of sub-delegation, general or limited, simplified questions of distance. In Belgium causes 859 appealed to Rome had to be committed to local delegates (Van Espen, pars iii. tit. v. c. 3, tit. x. c. 2).
There could be an appeal from these delegates to the pope and from the pope himself to the pope “better informed” (Van Espen, pars iii. tit. x. c. 2, 12, 13). So personal had the system of jurisdiction become that even the trials of bishops ceased to be necessarily conciliar. Generally they were reserved to the pope (Van Espen, pars iii. tit. iii. c. 5, 17-19); but in England the archbishop, either in synod, or with some of his comprovincial bishops concurring, tried and deposed bishops (see case of Bishop Peacock and the other cases cited in Read v. Bishop of Lincoln, 14 P.D. 148, and Phillimore, Eccl. Law, pp. 66 et seq.).
(m) The jurisdiction of a bishop sede vacante passed, by general law, to the dean and chapter; but in England the metropolitans became “guardians” of the spiritualities and exercised original jurisdiction through the vacant diocese (Phillimore, pp. 62-63), except in the case of Durham, and with a peculiar arrangement as to Lincoln.
If the metropolitan see were vacant the jurisdiction was exercised by the dean and chapter through an official (Rothery, Return of Cases before Delegates, Nos. 4, 5). As to France see Fournier, p. 294.
(n) Officials, even of bishops and metropolitans, need not be in holy orders, though Bishop Stubbs in his paper in the Report of the Commission on Ecclesiastical Courts seems to say so. They had to be clerics, that is, to have received the tonsure. Even papal delegates might be simple clerks (Van Espen, pars iii. tit. v. c. 2, 20).
It came, however, to be the practice to impose some restrictions, as on clerks twice married. Thus Archbishop Chichele provided that no clerk married or bigamous (that is, having had two wives in succession) should exercise spiritual jurisdiction (see Lyndwood, lib. iii. tit. 3). Abroad unsuccessful attempts were made by local councils to enact that officials and vicars-general should be in holy orders (Hefele on Councils of Tortosa in 1429 and Sixth of Milan in 1582). These councils, as will be seen, are late.
(o) With or without the concurrence and goodwill of the national Church, restrictions were imposed by the State on the papal jurisdiction, whether original or appellate. In England the Constitutions of Clarendon (by chap. viii.) prohibited appeals to the pope; but after the murder of St Thomas of Canterbury Henry II. had to promise not to enforce them. The statutes 38 Edw. III. st. 2, 13 Rich. II. st. 2, c. 2, and 16 Rich. II. c. 5 forbid such appeals; but it is suggested that notwithstanding the generality of their language they refer only to cases of temporal cognizance. Cases upon the execution of these statutes are collected in Stillingfleet, On Ecclesiastical Jurisdiction, p. 189; Gibson, Codex, 83. Obstacles were placed in the way of appeals to the pope omisso medio. Thus when a writ of significavit issued on the mandate of a bishop, an appeal to Rome availed not to stay execution; but if there were an appeal to the archbishop it was otherwise. It therefore became the custom to lodge a double appeal: one to the archbishop “for defence,” and the other to the pope as the real appeal (“Hostiensis,” Super Decret. ii. fol. 169; cf. Owen, Institutes of Canon Law, 1884, pt. i. c. 19, 5).
There seems to have been no machinery for assisting the original or appellate jurisdiction of the pope by secular process,—by significavit or otherwise.
The matrimonial cause between Henry VIII. and Catharine of Aragon was the most famous English cause tried by delegates under the “original” jurisdiction of the pope, and was ultimately “evoked” to Rome. The foreseen adverse termination of this long-drawn cause led to Henry’s legislation.
When the temporal courts interfered to prevent excess of jurisdiction, they did so by prohibiting the ecclesiastical court from trying and the suitor from suing in that court. The pope could not be effectively prohibited, and no instance is recorded of a prohibition to papal delegates. But suitors have been prohibited from appealing to the pope (see per Willes, J., in Mayor of London v. Cox, L.R. 2 H.L. 280). Whatever may have been the law, it is certain that, notwithstanding the statutes of Edw. III. and Rich. II., appeals to Rome and original trials by papal delegates did go on, perhaps with the king’s licence; for the statute 24 Hen. VIII. c. 12 recites that the hearing of appeals was an usurpation by the pope and a grievous abuse, and proceeds to take away the appeal in matrimonial, testamentary and tithe causes, and to hinder by forbidding citation and process from Rome, all original hearings also. The statute 25 Hen. VIII. c. 19 follows this up by taking away appeals in all other subjects of ecclesiastical jurisdiction.
In 1438 the council of Basel took away all papal original jurisdiction (save in certain reserved cases—of which infra), evocation of causes to Rome, appeals to Rome omisso medio, and appeals to Rome altogether in many causes. Such appeals when permissible, except the “greater,” were to be tried by delegates on the spot (31st Session; Mansi, Concilia, in loco). These proceedings at Basel were regarded at Rome as of no effect. Nevertheless this decree and others were adopted by a French national council at Bourges and promulgated by the king as a “Pragmatic Sanction” (Migne, Dict. du droit canonique, “Pragmatique Sanction”). The parlements registered the Sanction and the effect was permanent in France. Louis XI. and Charles VIII. sought to revoke it; but both parlements and states-general refused to recognize the revoking decrees. In 1499 Louis XII. ordered the Pragmatic to be inviolably observed. The parlements thereupon condemned several private persons for obtaining bulls from Rome. In 1516 a Concordat between Leo X. and Francis I. settled all these questions in the sense of the Pragmatic, substantially according to the Basel canon. All causes, except the “greater,” were to be terminated in the country where the proper cognizance would lie (Migne, op. cit. “Concordat”). By this Concordat, by an ordinance of Francis I. in 1539, by two or three other royal edicts, and (above all) by the practice of the parlements, explanatory of this legislation, and their arrêts, the conflict of secular and ecclesiastical jurisdictions was settled until the Revolution (Migne, ubi sup.). “Greater causes” came in France to be restricted to criminal prosecutions of bishops. Even in these the original jurisdiction of the pope was taken away. In first instance they were tried by the provincial synod. Thence there was appeal to the pope (de Maillane, op. cit. s.v. “Causes majeures”; Dict. eccl., Paris, 1765, s.v. “Cause”). The only original jurisdiction left to the pope was in the case of the matrimonial causes of princes. But they could only be heard on the spot by judges delegate. Examples are the causes of Louis XII. and Jeanne of France in 1498, and of Henry IV. and Marguerite of Valois in 1599 (Migne, op. cit. s.v. “Causes”). The prohibition of papal interference was enforced if necessary by the appel comme d’abus (vide supra). Out of respect for the pope this appeal was not brought against his decrees but against their execution (Dict. eccl., Paris, 1765, s.v. “Abus”).
Spain appears to have permitted and recognized appeals to the pope. A royal writ of the 16th century cited by Covarruvias (c. xxxv.) prohibits execution of the sentence of a Spanish court Christian pending an appeal to the pope.
2. The subject matter over which the ecclesiastical courts had jurisdiction was no longer purely “criminal” with a civil quasi-jurisdiction by way of arbitration. In the later middle ages these courts had jurisdiction over most questions, Civil jurisdiction. except indeed the then most important ones, those relating to real property. This civil jurisdiction was sometimes concurrent with that of the secular courts, sometimes exclusive. For England it may be thus classified:—
(a) Matrimonial.—This arose naturally from the sacred character of Christian marriage. This jurisdiction was exclusive. From it followed the right of the courts Christian to pronounce upon questions of legitimacy. Upon this right an inroad was early made, in consequence of the question of legitimation by subsequent marriage. In the 12th century the Church’s rule, that subsequent marriage did legitimize previous issue, was settled (c. 6, x. 4, 17). The king’s judges then began to ask the ordinary the specific question whether A. B. was born before 860 or after his parents’ marriage. After the inconclusive proceedings at the realm-council of Merton (1236), when spiritual and temporal lords took opposite views, the king’s judges went a step further and thenceforward submitted this particular question to a jury. All other questions of legitimacy arising in the king’s courts were still sent for trial to the bishop and concluded by his certificate (see Pollock and Maitland, Hist. Eng. Law before Edward I. vol. i. 105-106; Maitland, ubi supra, pp. 53-56).
(b) Testamentary and in regard to succession from intestates.—Real property was not the subject of will or testament in the medieval period. But as to personal property, the jurisdiction of the courts Christian became exclusive in England. The Church, East and West, had long asserted a right to supervise those legacies which were devoted to pious uses, a right recognized by Justinian (Cod. i. 3. 46). The bishop or, failing him, the metropolitan, was to see such legacies properly paid and applied and might appoint persons to administer the funds (Pollock and Maitland, op. cit. ii. 330). This right and duty became a jurisdiction in all testamentary causes. Intestacy was regarded with the greatest horror, because of the danger to the intestate’s soul from a death without a fitting part given to pious uses (Maine, Ancient Law, ed. 1906, note by Pollock, p. 230; cf. Pollock and Maitland, op. cit. ii. 354). Hence came the jurisdiction of the ordinary in intestacy, for the peace of the soul of the departed. This head of ecclesiastical jurisdiction was in England not transferred to the secular court till 1857.
(c) Church Lands.—If undoubtedly held in frankalmoign or “free alms,” by a “spiritual” tenure only, the claim of jurisdiction for the ecclesiastical forum seems to have been at first conceded. But the Constitutions of Clarendon (c. 9) reserved the preliminary question, of “frankalmoign” or not, for a jury in the king’s court. Then, if the tenure were found free alms, the plea was to be heard in the court Christian. From the 13th century, however, inclusive, the king’s courts insisted on their exclusive jurisdiction in regard to all realty, temporal or “spiritual” (Pollock and Maitland, op. cit. i. 106).
(d) Title to present to and possession of benefices.—As to the title to present to benefices, the courts Christian at one time had concurrent jurisdiction with the temporal courts. “Advowsons” were, however, looked upon as a species of “real” property in England, and therefore the king’s court early claimed exclusive jurisdiction in disputes where the title to present was involved. The Constitutions of Clarendon provided that these causes should be heard only in the king’s court (c. 1). This rule was applied even where both litigants were “spiritual.” In the 13th century abbots sue each other in the royal court for advowsons (Selden Soc. Select Civil Pleas, i. pl. 245). In 1231, in such a suit, the bishop of London accepts wager of battle (Pollock and Maitland, op. cit. i. 105). In cases, however, where the title to present was not in question, but the fitness of the clerk presented, or, in cases of election to benefices, the validity of the election, there was jurisdiction in the courts Christian.
(e) The recovery of tithes and church dues, including in England church rates levied to repair or improve churches and churchyards.
(f) Questions concerning fabrics, ornaments, ritual and ceremonial of churches.
(g) Administration of pious gifts and revenues given to prelates or convents.—Their right application could be effectively enforced only in the courts Christian; until the rise in England of the equitable jurisdiction of the court of chancery and the development of the doctrine of “uses” at the end of the middle ages.
(h) Enforcement of contractual promises made by oath or pledge of faith.—The breaking of such a promissory oath was called “perjury” (as in classical Latin and in Shakespeare), contrary to modern usage which confines the word to false evidence before a court of justice. In regard to the execution of these promises, the jurisdiction of the ecclesiastical courts was possibly traversed by c. 15 of the Constitutions of Clarendon; but allowed by the statute 13 Edw. I. st. 4. As just intimated, besides the enforcement of the promise, the “perjury” was treated as an ecclesiastical crime.
The criminal jurisdiction of courts Christian over laymen included, besides these “perjuries,” (a) all sexual offences not punishable on indictment; (b) Defamation of character (the king’s courts came in time to limit this to such defamation as could not be made the subject of a temporal action); (c) Offences by laymen against clerks (i.e. against all “tonsured” persons, supra); (d) Offences in regard to holy places—“brawling” and such like; (e) Heresy, schism, apostasy, witchcraft.
In regard to “clerks,” there was (1) all the criminal jurisdiction which existed over laymen, and (2) criminal jurisdiction in regard to professional misconduct. Concerning “felonious” clerks the great questions discussed were whether the courts Christian had exclusive jurisdiction or the king’s court, or whether there was a concurrent jurisdiction. The subject was dealt with in the Constitutions of Clarendon, formally revoked after the murder of St Thomas of Canterbury. In the 13th century it was recognized that a “clerk” for felony was subject only to ecclesiastical trial and punishment; punishment which might involve lifelong imprisonment. For “misdemeanours,” as yet unimportant, he had no exemption from secular jurisdiction (Pollock and Maitland, op. cit. ch. iv.). At some indeterminate later period, the “clerk” was tried for felony by a jury in the king’s court and then “pleaded his clergy,” after conviction there, and was remitted to the ordinary for ecclesiastical punishment. “Clerks” for the purpose of “benefit of clergy” included not only persons in minor orders, but all “religious” persons, i.e. monks, friars, nuns, &c. Later the custom arose of taking “clerk” to include any “literate,” even if not in orders or “religious” (cf. Stephen, Hist. Crim. Law, i. 461). The statute 4 Hen. VII. c. 13 took away benefit of clergy, if claimed a second time, from persons not “within orders,” in certain bad cases. 4 Hen. VIII. c. 2 (a temporary act) took away “clergy,” in certain heinous crimes, from all persons not in “holy” orders. This statute was partly renewed by 22 Hen. VIII. c. 13. Other changes were introduced by 23 Hen. VIII. c. 1 and later acts. In time, “benefit of clergy” became entirely diverted from its original objects.
In France, till 1329, there seems to have been no clear line of demarcation between secular and ecclesiastical jurisdictions. Beaumanoir (Coutume de Baulvoisis, ch. xi., cited Gaudry, op. cit. i. 22) had laid down the principle that spiritual justice should meddle only with spiritual things. In the year named the secular courts complained to the king, Philip of Valois, of the encroachments of the courts Christian. The “cause” was solemnly argued before that monarch, who decided to leave things as they were (Migne, Dict. du droit canon., s.v. “Officialités”). In 1371 Charles V. forbade spiritual courts to take cognizance of “real” and “possessory” actions even in regard to clerks (Migne, loc. cit.; cf. Gaudry, ubi sup.). From this period the parlements began the procedure which, after the Pragmatic Sanction of Charles VII., in 1438 took regular shape as the appel comme d’ abus (supra; Migne, loc. cit.). Testamentary causes at first were subject to the concurrent jurisdiction of the spiritual and secular courts. After the 14th century, the latter had exclusive jurisdiction (Van Espen, op. cit. lib. iii. tit. ii. cc. 2, 15, 16). In regard to marriage the secular jurists distinguished between the civil contract and the sacrament, for purposes of separating the jurisdiction (Dict. eccl., Paris, 1765, s.v. “Mariage”). The voluntary jurisdiction as regards dispensations was kept for the Church. The contentious jurisdiction of the courts Christian was confined to promises of marriage, nullity of marriage caused by “diriment” impediments only, validity or invalidity of the sacrament, divorce a thoro (ibid.). Questions in regard to the property in a benefice were for the courts Christian; in regard to its possession, for the king’s courts. But if a “possessory” action had been brought in the latter, a subsequent suit in the courts spiritual for the property was deemed “abusive” and restrained (ib., s.v. “Pétitoire”) Breach of faith or of promise confirmed by oath was matter for the court Christian (Fournier, pp. 95, 99, 109, 125). This 861 branch of jurisdiction was larger and more freely used than in England (cf. Pollock and Maitland, op. cit., as to Normandy). The only other remaining civil jurisdiction of the ecclesiastical courts was in personal actions where clerks were defendants (Migne, op. cit., s.v. “Officialités,” Fournier, pp. 65-125); or, after the 14th century, where both parties were clerks. In regard to crimes delicts (délits) were divided into classes for purposes of jurisdiction. Clerks were punishable only in the court Christian, except in cases of grave crimes such as murder, mutilation (Fournier, p. 72), and cases called “royal cases” (vide infra). Laymen were punishable in the court Christian for the délits following: injury to sacred or religious places, sacrilege, heresy (except where it was a “royal case”), sorcery, magic, blasphemy (also punishable in the secular court), adultery, simony, usury and infractions of the truce of God (Fournier, pp. 90-93). What were called “privileged delicts” were judged in the case of the clergy conjointly by the spiritual judge and the king’s judge. Bishops had no exemption (Dict. ecc., s.v. “Délits,” “Cas privilégié,” “Causes majeures”). “Royal cases” included such crimes as touched the prince, as all forms of treason; or the dignity of his officers; or the public safety. In this class were also included such heresies as troubled the state, as by forbidden assemblies, or by teaching prohibited doctrine. Among these heresies were reckoned idolatry, atheism, Protestantism, relapse (ib. et “Cas royaux,” “Hérésie”). These were of exclusive royal jurisdiction as against both spiritual courts and the courts of feudal lords. A similar claim was made by Pombal for Portugal (vide infra).
The parlements, in order to have a ready means of enforcing all these restrictions by appel comme d’abus, compelled the bishops to appoint officials, Frenchmen, graduates, and (as it seems) “seculars” (Dict. eccl., Paris, 1765, s.v. “Official”). This last qualification was disputed (see Fevret, Traité de l’abus).
3. Punishments.—Ecclesiastical sanctions were divided into punishments (poenae), either purely temporal in character or else of a mixed spiritual and temporal character, and censures (censurae), purely spiritual and remedial (see Van Espen, pars iii. tit. xl. cc. 1, 3; Phillimore, Ecclesiastical Law, p. 1064). In the book last cited censurae and poenae are classed together as “censures” (which is the modern use).
Poenae.—(a) Fines sprang from the older custom of directing alms by way of penance in the internal forum (Van Espen, ubi sup. c. 1, 5-10). They were to be applied to pious uses. (b) Reclusion in a monastery continued from former period, and might be either temporary or perpetual (loc. cit. 17-19). (c) Imprisonment, in the bishop’s prison, might be in chains, or on bread and water, and temporary or perpetual. In its severer forms it was only inflicted for more atrocious crimes which the secular law would have punished with death (loc. cit. 21-27). The act 23 Henry VIII. c. 11 made special provision for convicted clerks who broke out of the prisons of the ordinary. (d) Fustigation, as in former period, was hardly an ecclesiastical punishment. If given, it was to be of a paternal character (loc. cit. 39-45). Punishments of a mixed nature were: (e) Suspension either from office alone or from office and benefice; (f) Deprivation of benefice; (g) Deposition or Degradation (a more solemn and ceremonial form) from the ministry; (h) Irregularity—not always a punishment—a state of incapacity to be ordained, or, being ordained, to execute the ministry; this might result from some defect of mind and body, but was also incurred by some grave offences.
Censures were as follows: (i) Suspension from attending divine offices or ab ingressu ecclesiae, more appropriate for a layman. A clerk in like case might be suspended from office. (j) Interdict was another form of partial or total suspension from the benefit of the rites and sacraments of the Church. An interdict might be personal or local (see Interdict). (k) Excommunication was either greater or less. The greater separated entirely from the Church. It might be pronounced under anathema. The less deprived of participation in the sacraments, and made a clerk incapable of taking a benefice.
On the European continent the courts Christian often carried out their decrees by their own apparitors who could levy pecuniary penalties on a defendant’s goods (Van Espen, pars iii. tit. ix. c. 4). They could arrest and imprison. In England, except in the peculiar case of imprisonment pending trial for heresy, or in the case of a clerk convicted of crime, these things could not be. The sentence of the court Christian had in all other cases to be enforced by the secular arm. Early in Henry II.’s time it had become the custom of England for the court Christian to “signify” its sentence of excommunication to the king and to demand from him a writ of significavit to the sheriff, to imprison the person excommunicated. The writ apparently issued for no court inferior to the bishop’s, unless upon the bishop’s request. In some sense the king’s writ of significavit was discretionary; but its issue could be enforced by excommunication or interdict.
In the cases of heresy, apostasy and sorcery, the spiritual courts sought the aid of the secular jurisdiction to superadd the punishment of death. Incorrigible offenders on these matters were “left” to the secular power, to be corrected with due “animadversion.” This provision of the fourth Lateran Council in 1215 was always interpreted to mean death (see Van Espen, Observ. in Conc. Lat. IV. Canones, and the decree in the Sext. ut inquisitionis negotium; and, as to English law and practice, Maitland, op. cit., Essay vi., and pp. 161, 176; 2 Hen. IV. c. 15; Fitzherbert, Natura brevium, 269; 2 Hen. V. st. 1, c. 7). The “capital” punishment was generally (always in England) by burning. Burning was an English punishment for some secular offences.
The Concordat with Francis I. by which the pope gave up the right of hearing appeals from France was not many years before the legislation of Henry VIII. in England. Both monarchs proceeded on the same lines; but Francis I. got the pope’s consent: Henry VIII. acted in invitum, and in time went rather further.
The Statute of Appeals (24 Hen. VIII. c. 12) takes away appeals to Rome in causes testamentary and matrimonial and in regard to right of tithes, oblations and obventions. A final appeal is given to the archbishop of the particular Ecclesiastical jurisdiction in England. province; but in causes touching the king a final appeal is given to the Upper House of Convocation of the province. The statute is aimed at appeals; but the words used in it concerning “citations and all other processes” are wide enough to take away also the “original” jurisdiction of the pope. No appeal was yet given to the crown. Canterbury, York, Armagh, Dublin, Cashel and Tuam are put in the place of Rome. The English and Irish provinces are treated as self-contained. All ends there.
The “Act of Submission of the Clergy” (25 Hen. VIII. c. 19) took away all appeals to Rome and gave a further appeal, “for lack of justice,” from the several courts of the archbishops to the king in chancery. Thence a commission was to issue to persons named therein to determine the appeal definitely. This was copied from the then existent practice in admiralty appeals and was the origin of the so-called court of delegates. It is a moot question whether this statute took away the appeal to the Upper Houses of the various convocations in causes wherein the king was concerned (see Gorham v. Bishop of Exeter, 15 Q.B. 52; Ex parte Bishop of Exeter, 10 C.B. 102; Re Gorham v. Bishop of Exeter, 5 Exch. 630). 37 Hen. VIII. c. 17 provided that married laymen might be judges of the courts Christian if they were doctors of civil law, created in any university. This qualification even was considered unnecessary in Charles I.’s time (Cro. Car. 258). Canon 127 of 1603 provided that the judges must be learned in the civil and ecclesiastical laws and at least masters of arts or bachelors of laws. Canon Law as a study had been practically prohibited at the universities since 1536 (Merriman, Thomas Cromwell, i. 142-143; Cal. State Papers, vol. ix. p. xxix. 117; Owen, Institutes of Canon Law, viii.). The substitution of “civilians,” rather than common lawyers, for canonists (civilians, hitherto, not an important body in England) had important consequences (see Maitland, op. cit. 92 et seq.).
Henry VIII. had exercised his jurisdiction as Supreme Head through a vicar-general. Edward VI. exercised original 862 jurisdiction in spiritual causes by delegated commissions (see Archdeacon Hale, Precedents in Criminal Cases, p. xlviii.). Unless the king was to be regarded as an ecclesiastical person, they were not properly ecclesiastical courts; although spiritual persons might sit in them, for they sat only as royal commissioners. The same point has been taken by large bodies of clergy and laity in regard to the court of final appeal created by 25 Hen. VIII. c. 19 and its present successor the judicial committee of Privy Council (infra: Rep. Com. Ecc. Discipline, pp. 9, 94 et seq.). At any rate the “original” jurisdiction claimed for the monarch personally and his delegates, under Henry VIII. and Edward VI., has not permanently remained. In theory, Hooker’s contentions have been conceded that “kings cannot in their own proper persons decide questions about matters of faith and Christian religion” and that “they have not ordinary spiritual power” (Ecc. Pol. vii. 8, 1, 6; cf. XXXIX. Articles, Art. 37).
Under Henry VIII. a system began of making certain crimes, which previously had been only of spiritual cognizance, felonies (25 Hen. VIII. c. 6), excluding thereby spiritual jurisdiction (Stephen, Hist. Crim. Law, ii. 429). Bigamy (in its modern sense) was thus made felony (1 Jac. I. c. 11). In this reign and the next, temporal courts were sometimes given jurisdiction over purely spiritual offences. A trace of this remains in 1 Edw. VI. c. 1 (still on the statute book; Stephen, Hist. Crim. Law, ii. 439). Other traces occur in the Acts of Uniformity, which make offences of depraving the Book of Common Prayer triable at Assizes (between 23 Eliz. c. 1 and 7 & 8 Vict. c. 102—also at Sessions) as well as in the courts Christian.
During Edward VI.’s time the courts Christian seem practically to have ceased to exercise criminal jurisdiction (Hale, Precedents in Criminal Cases, p. xlix.). But they sat again for this purpose under Mary and Elizabeth and (save between 1640 and 1661) continued regular criminal sessions till towards the end of the 17th century as continuously and constantly as the king’s courts (op. cit.).
The “ordinary” ecclesiastical tribunals of the later middle ages still subsist in England, at least as regards the laity. This is hardly the case elsewhere in the Western Church, though some exceptions are noted below. Nevertheless, their exercise of criminal jurisdiction over the laity is now in practice suspended; although in law it subsists (see Stephen, Hist. Crim. Law; Ray v. Sherwood, 1 Curt. R. 193; 1 Moore P.C.R. 363; the observations of Kelly, C.B., in Mordaunt v. Moncrieffe, L.R. 2 Sc. & Div. 381, and of Lord Coleridge in Martin v. Mackonochie, L.R. 4 Q.B.D. 770, and, on the other hand, of Lord Penzance in Phillimore v. Machon, L.R. 1 P.D. 480). Theoretically still, in cases of sexual immorality, penance may be imposed. Monitions to amend may be decreed and be enforced by significavit and writ de contumace capiendo, or by excommunication with imprisonment not to exceed six months (53 Geo. III. c. 127). The tribunals thus subsisting are the courts of the bishop and archbishop, the latter sometimes called the court of appeal of the province. Peculiar jurisdictions have been gradually taken away under the operation of the acts establishing the ecclesiastical commissioners. The appeal given to delegates appointed by the crown has been transferred, first by 2 & 3 Will. IV. c. 92 to the privy council, and then by 3 & 4 Will. IV. c. 41 to the judicial committee of the privy council. Bishops may now be summoned as assessors by 39 & 40 Vict. c. 59.
There was in the time of Elizabeth, James I. and Charles I. a “Court of High Commission” with jurisdiction over laity and clergy, based on 1 Eliz. c. i. s. 15, which was reckoned as an ecclesiastical judicature (5 R. 1, Cawdrey’s case) concurrent with the ordinary court Christian. It was created by virtue of the royal supremacy, and was taken away by 16 Car. I. c. 11. As to its history see Stephen, Hist. Crim. Law, ii. 414-428.
In regard to clerical offences, 3 & 4 Vict. c. 86 (the “Church Discipline Act”) creates new tribunals; and first a commission of inquiry appointed by the bishop of five persons, of whom the vicar-general, or an archdeacon, or a rural dean of the diocese must be one. If they report a prima facie case, the bishop may (with the consent of parties) proceed to sentence. In the absence of such consent, the bishop may hear the cause with three assessors, of whom one shall be a barrister of seven years’ standing and another the dean of the cathedral, or one of the archdeacons, or the chancellor. This court is called the “consistory” court, but is not the old consistory. Both these tribunals are new. But the bishop may instead send the cause, in first instance, to the old provincial court, to which appeal lies, if it be not so sent.
The Public Worship Regulation Act (37 & 38 Vict. c. 85) gave criminal jurisdiction over beneficed clerks (concurrent with that of the tribunal under 3 & 4 Vict. c. 86) to the judge under the act in matters of the fabric, ornaments, furniture and decorations of churches, and the conduct of divine service, rites and ceremonies. The “judge” under the act is to be a barrister of ten years’ standing, or an ex-judge of a superior secular court, appointed by the archbishops of Canterbury and York, with the approval of the crown, or, if they fail to appoint, by the crown. Proceedings under this act are to be deemed to be taken in the appropriate ancient ecclesiastical courts (Green v. Lord Penzance, 6 A. C. 657). The judge under this act became (upon vacancies occurring) ex officio official principal of the arches court of Canterbury and of the chancery court of York. This provision caused grave doubts to be entertained as to the canonical position of this statutory official principal.
Finally, the Clergy Discipline Act 1892 (55 & 56 Vict. c. 32) creates yet a new court of first instance for the trial of clerical offences against morality in the shape of a consistory court, which is not the old court of that name, but is to comprehend the chancellor and five assessors (three clergymen and two laymen chosen from a prescribed list), with equal power with the chancellor on questions of fact. In many instances the conviction of a temporal court is made conclusive on the bishop without further trial. In regard to moral offences, jurisdiction under this act is exclusive. But it only applies to clerks holding preferment. Under all these three acts there is a final appeal to the judicial committee of the privy council.
None of these acts applies to the trial of bishops, who are left to the old jurisdictions, or whatever may be held to be the old jurisdictions (with that of the Roman See eliminated). As to suffragan bishops in the province of Canterbury, see Read v. Bishop of Lincoln, 13 P.D. 221, 14 P.D. 88. (On general questions see Phillimore, Ecc. Law, 65, 73.) Despite the bishop of Lincoln’s case, the law is in some uncertainty.
Dilapidations are now not made matters of suit before the court, but of administrative action by the bishop.
The subject matter of ecclesiastical jurisdiction has been gradually reduced in England, &c., by various causes. (1) The taking away of all matrimonial, testamentary and ab intestate jurisdiction by 20 & 21 Vict. c. 77 (testamentary, &c., England), c. 79 (testamentary, &c., Ireland), c. 85 (matrimonial, England); 33 & 34 Vict. c. 110 (matrimonial, Ireland). Matrimonial jurisdiction was taken from the bishop of Sodor and Man in 1884. (2) Since 6 & 7 Will. IV. c. 71, tithe has become, except in a few rare cases, tithe rent charge, and its recovery has been entirely an operation of secular law. Most kinds of offerings are now recoverable in secular courts. (3) Administration of pious gifts has passed to the court of chancery. (4) The enforcement of contractual promises has long been abandoned by the courts Christian themselves. (5) Church rates can no longer be enforced by suit (31 & 32 Vict. c. 109). (6) Defamation was taken away in England by 18 & 19 Vict. c. 41, and in Ireland by 23 & 24 Vict. c. 32. (7) Laymen can no longer be tried in the spiritual courts for offences against clerks. (8) The jurisdiction for “brawling” in church, &c., is taken away by 23 & 24 Vict. c. 32 in the case of the laity. In the case of persons in holy orders there is a concurrent jurisdiction of the two tribunals (Valancy v. Fletcher, 1897, 1 Q.B. 265). This was an offence very frequently prosecuted in the courts Christian (see A.J. Stephens, Ecclesiastical Statutes, i. 336).
The existing ecclesiastical jurisdiction in England is therefore now confined to the following points. (1) Discipline of the clergy. (2) Discipline of the laity in respect of sexual offences 863 as already stated. (3) Control of lay office-bearers, church-wardens, sidesmen, organists, parish clerks, sextons. (4) Protection of the fabrics of churches, of churchyards, ornaments, fittings, &c., sanctioning by licence or faculty any additions or alterations, and preventing or punishing unauthorized dealings by proceedings on the criminal side of the courts. (5) Claims by individuals to particular seats in church or special places of sepulture. (6) Rare cases of personal or special tithes, offerings or pensions claimed by incumbents of benefices. In the Isle of Man and the Channel Islands courts Christian have now jurisdiction substantially as in England. In Jersey and in Guernsey there are courts of first instance with appeal to the bishop of Winchester. Ecclesiastical jurisdiction in Ireland was as in England till the Irish Church was disestablished in 1869 by 32 & 33 Vict. c. 42.
The position of a disestablished or an unestablished Church is comparatively modern, and has given rise to new jural conceptions. These Churches are collegia licita and come within the liberty of association so freely conceded in Ecclesiastical jurisdiction in non-established churches. modern times. The relations of their bishops, priests or other ministers and lay office-bearers inter se and to their lay folk depend upon contract; and these contracts will be enforced by the ordinary courts of law. A consensual ecclesiastical jurisdiction is thus created, which has to this extent temporal sanction. In foro conscientiae spiritual censures canonically imposed are as binding and ecclesiastical jurisdiction is as powerful as ever.
Into the British-settled colonies no bishops were sent till 1787; and consequently there were no regular courts Christian. The bishop of London was treated as the diocesan bishop of the colonists in North America; and in order to provide for testamentary and matrimonial jurisdiction it was usual in the letters patent appointing the governor of a colony to name him ordinary. In New York state there is still a court called the surrogates court, surrogate being the regular name for a deputy ecclesiastical judge. In Lower Canada, by treaty, the Roman Catholic Church remained established.
Throughout the United States, whatever may have been the position in some of them before their independence, the Church has now no position recognized by the State, but is just a body of believers whose relations are governed by contract and with whom ecclesiastical jurisdiction is consensual.
The position is the same now through all the British colonies (except, as already mentioned, Lower Canada or Quebec). From 1787 onwards, colonial bishops and metropolitans were appointed by letters patent which purported to give them jurisdiction for disciplinary purposes. But a series of cases, of which the most remarkable was that Re the Bishop of Natal (3 Moore P.C. N.S. A.D. 1864), decided that in colonies possessing self-governing legislatures such letters patent were of no value; and soon after the crown ceased to issue them, even for crown colonies.
In India the metropolitan of Calcutta and the bishops of Madras and Bombay have some very limited jurisdiction which is conferred by letters patent under the authority of the statutes 53 Geo. III. c. 155 and 3 & 4 Will. IV. c. 85. But the other Indian bishops have no position recognized by the State and no jurisdiction, except consensual.
The Church had the same jurisdiction in Scotland, and exercised it through similar courts to those which she had in England and France, till about 1570. As late as 1566 Archbishop Hamilton of Glasgow, upon his appointment, Ecclesiastical jurisdiction in Scotland. had restitution of his jurisdiction in the probate of testaments and other matters (Keith, History of the Scottish Bishops, Edinburgh, 1824, p. 38). There was an interval of uncertainty, with at any rate titular bishops, till 1592. Then parliament enacted a new system of Church courts which, though to some extent in its turn superseded by the revival of episcopacy under James VI., was revived or ratified by the act of 1690, c. 7, and stands to this day. It is a Presbyterian system, and the Scottish Episcopal Church is a disestablished and voluntary body since 1690.
The Presbyterian courts thus created are arranged in ascending order:—
(a) Kirk Session consists of the minister of the parish and the “ruling elders” (who are elected by the session). It has cognizance of scandalous offences by laymen and punishes them by deprivation of religious privileges. It does not judge ministers (Brodie-Innes, Comparative Principles of the Laws of England and Scotland, 1903, p. 144).
(b) The Presbytery has jurisdiction, partly appellate and partly original, over a number of parishes. There are now eighty-four presbyteries. These courts consist of every parochial minister or professor of divinity of any university within the limits, and of an elder commissioned from every kirk session. A minister is elected to preside as moderator. These courts judge ministers in first instance for scandalous conduct. As civil courts they judge in first instance all questions connected with glebes and the erection and repair of churches and manses. They regulate matters concerning public worship and ordinances, and have appellate jurisdiction from the kirk session.
(c) The Provincial Synod consists of a union of three or more presbyteries with the same members. There are now sixteen. They meet twice a year to hear appeals from presbyteries. No appeal can go direct to the General Assembly, omisso medio, unless the presbytery have so expressly directed, or unless there be no meeting of synod after the decision of the presbytery before the meeting of General Assembly.
(d) The General Assembly is the supreme ecclesiastical court of this system. It meets annually. The king’s “lord high commissioner” attends the sittings; but does not intervene or take part in the court’s decisions. The court consists of ministers and elders, elected from the presbyteries in specified proportions, and of commissioners from the four universities, the city of Edinburgh and the royal burghs. The Presbyterian Church in India sends one minister and one elder. The whole Assembly consists of 371 ministers and 333 elders. The jurisdiction is entirely appellate. The Assembly appoints a commission to exercise some of its functions during the intervals of its session. To this commission may be referred the cognizance of particular matters.
Questions of patronage now (by 37 & 38 Vict. c. 82) belong to the Church courts; but not questions of lapse or stipend. Seats, seat rents, pews, the union and disjunction of parishes and formation of district parishes are of secular jurisdiction. Questions of tithes (or “teinds”) and ministers’ stipends were referred to commissioners by acts of the Scots parliaments beginning in 1607. The commissioners of teinds became a species of ecclesiastical court. By Scots act of 1707, c. 9, their powers were transferred to the judges of the court of session, who now constitute a “teind court” (Brodie-Innes, op. cit. pp. 138, 139). Matrimonial matters and those relating to wills and succession (called in Scotland “consistorial” causes) were in 1563 taken from the old bishops’ courts and given to “commissaries” appointed by the crown with an appeal to the court of session, which by act 1609, c. 6, was declared the king’s great consistory. They have remained matters of secular jurisdiction.
The Scots ecclesiastical courts are entitled to the assistance of the secular courts to carry out their jurisdiction by “due assistance.” Within the limits of their jurisdiction they are supreme. But if a court go outside its jurisdiction, or refuse to exercise powers conferred on it by law, the civil court may “reduce” (i.e. set aside) the sentence and award damages to the party aggrieved.
With the Reformation in the 16th century, Church courts properly speaking disappeared from the non-episcopal religious communities which were established in Protestant continental European states. Holland, in the Protestant states of Switzerland and of Germany, and in the then non-episcopal countries of Denmark and Norway.
Discipline over ministers and other office-bearers was exercised by administrative methods in the form of trials before consistories or synods. To this extent ecclesiastical jurisdiction is still exercised in these countries. Consistories and synods have 864 exercised discipline of a penitential kind over their lay members; but in later times their censures have generally ceased to carry temporal consequences. Ecclesiastical jurisdiction on the civil side for the trial of causes soon disappeared. Heresy has been treated as a crime to be tried in and punished by the ordinary courts of the country, as in the cases of Servetus (q.v.) and Grotius (q.v.).
For the episcopal churches of Sweden and Finland the first constitution or “Church order” was formed in 1571. It provided for the visitation of the clergy by the bishop, and for the power of the clergy to exclude their lay folk from the Holy Communion, subject to appeal to the bishop. Both minor and major excommunication had been in use, and for a long time public penance was required. The procedure underwent great modification in 1686; but public penance was not taken away till 1855, and then confession to and absolution by the priest in the presence of witnesses was still required. Civil jurisdiction in causes appears to have been given up early (Cornelius, Svenska Kirkaus Historia, Upsala, 1875, pp. 146, 186, 189, 285).
Over the rest of western continental Europe and in the colonies of Spain, Portugal and France, ecclesiastical jurisdiction remained generally in the state which we have already described till near the end of the 18th century. The council of Roman Catholic countries. Trent took away the jurisdiction of archdeacons in marriage questions. The testamentary jurisdiction disappeared (as already stated) in France. Disputed cases of contract were more often tried in the secular courts. Recourse to the secular prince by way of appel comme d’abus, or otherwise, became more frequent and met with greater encouragement. Kings began to insist upon trying ecclesiastics for treason or other political crimes in secular courts. So under the advice of his minister (the marquis of Pombal), King Joseph of Portugal in 1759-1760 claimed that the pope should give him permission to try in all cases clerics accused of treason, and was not content with the limited permission given to try and execute, if guilty, the Jesuits then accused of conspiring his death (Life of Pombal, by Count da Carnota, 1871, pp. 128, 141). But there was no sudden change in the position of the courts Christian till the French Revolution.
In France a law of the Revolution (September 1790) purported to suppress all ecclesiastical jurisdictions. On the re-establishing of the Catholic religion on the basis of the new Concordat, promulgated 18 Germinal, year X. (April 8, 1802), no express provision was made for ecclesiastical jurisdictions; but several bishops did create new ecclesiastical tribunals, “officialities” (Migne, Dict. de droit canon., s.v.). The government in some cases recognized these tribunals as capable of judging ecclesiastical causes (Migne, ubi sup.). In 1810 the diocesan official of Paris entertained the cause between Napoleon and Josephine, and pronounced a decree of nullity (Migne, ubi sup. s.v. “Causes”). Such litigation as still continued before the spiritual forum was, however, confined (save in the case of the matrimonial questions of princes) to the professional conduct of the clergy.
Such neighbouring countries as were conquered by France or revolutionized after her pattern took the same course of suppressing their ecclesiastical jurisdictions. After 1814, some of these jurisdictions were revived. But the matter is now determined for all countries which have adopted codes, whether after the pattern of the Code Napoléon or otherwise. These countries have created a hierarchy of temporal courts competent to deal with every matter of which law takes cognizance, and a penal code which embraces and deals with all crimes or delicts which the state recognizes as offences. Hence, even in countries where the Roman Church is established, such as Belgium, Italy, the Catholic states of Germany and cantons of Switzerland, most of the Latin republics of America, and the province of Quebec, and a fortiori where this Church is not established, there is now no discipline over the laity, except penitential, and no jurisdiction exercised in civil suits, except possibly the matrimonial questions of princes (of which there was an example in the case of the reigning prince of Monaco). In Spain causes of nullity and divorce a thoro, in Portugal causes of nullity between Catholics, are still for the court Christian. In Peru, the old ecclesiastical matrimonial jurisdiction substantially remains (Lehr, Le Mariage dans les principaux pays, 1899, arts. 362, 797, 772, 781). Otherwise these three countries are Code countries. In Austria, the ancient ecclesiastical jurisdiction was taken away by various acts of legislation from 1781 to 1856; even voluntary jurisdiction as to dispensations. The Concordat of 1856 and consequent legislation restored matrimonial jurisdiction to the courts Christian over marriages between Roman Catholics. In 1868 this was taken away. The Austrian bishops, however, maintain their tribunals for spiritual purposes, and insist that such things as divorce a vinculo must be granted by their authority (Aichner, Compendium juris ecclesiastici, pp. 551-553).
By consent and submission of her members, the Roman Church decides in foro conscientiae questions of marriage, betrothal and legitimacy everywhere; but no temporal consequences follow except in Spain, Portugal and Peru.
The position in France was the same as that in Belgium, Italy, &c., till 1906, when the Church ceased to be established. The only Latin countries in which conflict has not arisen appear to be the principality of Andorra and the republic of San Marino (Giron y Areas, Situación jurídica de la Iglesia Católica, Madrid, 1905, p. 173 et seq.).
Even as to the discipline of the Roman clergy it is only in certain limited cases that one can speak of ecclesiastical jurisdiction. Bishops and beneficed incumbents (curés) must be regularly tried; and where the Church is established the canonical courts are recognized. But the majority of parishes are served by mere desservants or vicaires, who have no rights and can be recalled and dismissed by mere administrative order without trial (Migne, ubi sup. s.v. “Inamovibilité,” “Desservants”).
The Napoleonic legislation re-established the appel comme d’abus (“Articles organiques,” art. 6). The recourse was now to the council of state (see Migne, ubi supra, “Officialité”). But the revocation of a desservant, and the forbidding him the execution of his ministry in the diocese, was not a case in which the council of state would interfere (Migne, ubi sup. “Appel comme d’abus,” “Conseil d’état”).
In those provinces of the Anglican communion where the Church is not established by the state, the tendency is Jurisdiction in Anglican communion. not to attempt any external discipline over the laity; but on the other hand to exercise consensual jurisdiction over the clergy and office-bearers through courts nearly modelled on the old canonical patterns.
In the Roman communion, on the other hand, both where the Church is established and where it is not, the tendency is to reduce the status of curé to that of desservant, and to deal with all members of the priestly or lower orders Modern jurisdiction of Church of Rome. by administrative methods. This practice obtains in all missionary countries, e.g. Ireland and also in Belgium (S.B. Smith, Elements of Ecclesiastical Law, New York, i. 197 et seq.; p. 403 et seq.; Tauber, Manuale juris canonici, Sabariae, 1904, p. 277). In the United States, the 3rd plenary council of Baltimore in 1884 provided that one rector out of ten should be irremovable (Smith, op. cit. i. 197, 419). In England there are few Roman “benefices” (E. Taunton, Law of the Church, London, 1906, s.v. “Benefice”). A desservant has an informal appeal, by way of recourse, to the metropolitan and ultimately to the pope (Smith, op. cit. p. 201). The bishop’s “official” is now universally called his vicar-general (except in France, where sometimes an official is appointed eo nomine), and generally exercises both voluntary and contentious jurisdiction (op. cit. i. 377). As of old, he must be at least tonsured and without a wife living. At the Vatican Council, a desire was expressed that he should be a priest (ib.). He should be a doctor in theology or a licentiate in canon law (ib. p. 378). Whether a bishop is bound to appoint a vicar-general is still disputed (ib. p. 380; cf. supra; contra, Bouix, Inst. Juris Canon. De Judic. i. 405). In 1831 the pope enacted that in all the dioceses of the then Pontifical States, the court of first instance for the criminal causes of ecclesiastics should consist of the ordinary and four other judges. In the diocese of Rome, 865 the court of the cardinal vicar-general consists of such vicar-general and four other prelates (Smith, ubi supra). In the Roman communion in England and the United States, there are commissions of investigation appointed to hear in first instance the criminal causes of clerks. They consist of five, or at least three, priests nominated by the bishop in and with the advice of the diocesan synod. In the United States, since 1884, the bishop presides on these commissions. They report their opinions to the bishop, who passes final sentence (ib. ii. 129-131).
“Exemptions” now include all the regular religious orders, i.e. those orders which have solemn vows. Over the members of these orders their superiors have jurisdiction and not the bishop. Otherwise if they live out of their monastery, or even within that enclosure so notoriously offend as to cause scandal. In the first case, they may be punished by the ordinary of the place, acting as delegate of the pope without special appointment (Conc. Trid. Sess. vi. c. 3). In the second case, the bishop may require the superior to punish within a certain time and to certify the punishment to him; in default he himself may punish (Conc. Trid. Sess. xxv. c. 14, cf. Smith, op. cit. i. 204-206). So, regulars having cure of souls are subject to the jurisdiction of the bishop in matters pertaining thereto (ib. p. 206). The exemption of regular religious orders may be extended to religious societies without solemn vows by special concession of the pope, as in the case of the Passionists and Redemptorists (ib. p. 205; Sanguineti, Juris ecc. inst., Rome, 1800, pp. 393, 394).
Appeal lies, in nearly all cases, to the metropolitan (Smith, op. cit. pp. 219-223). Metropolitans usually now have a metropolitan tribunal distinct from their diocesan court (ib. ii. 141), but constructed on the same lines, with the metropolitan as judge and his vicar-general as vice-judge. In some “missionary” dioceses, the metropolitan, qua metropolitan, has a separate commission of investigation, to try the criminal causes of clerks, sentence being passed by himself or his vicar-general (ib. p. 142).
The next step in the hierarchy, that of “primates” (supra), has “in the present state of the Church” ceased to exist for our purpose (Sanguineti, op. cit. p. 334), as a result of Tridentine legislation. The only appellate jurisdiction from the metropolitans is the Roman See. To it also lies a direct appeal from the court of first instance, omisso medio (Smith, op. cit. i. 224). The pope’s immediate and original jurisdiction in every diocese is now expressly affirmed by the Vatican Council (ib. p. 239). That original jurisdiction he reserves exclusively to himself in causis majoribus (ib. pp. 249-250). These are (1) causes relating to elections, translations and deprivations of, and criminal prosecutions against, bishops, and (2) the matrimonial cases of princes (Taunton, op. cit. s.v. “Cause”).
In the Eastern Church, the early system of ecclesiastical judicature long continued. But a sacred character was ascribed to the emperors. They are “anointed lords like the bishops” (Balsamon, in Conc. Ancyr. Can. xii., representing Eastern Church. the view of the 12th and 13th centuries). Bishops were often deposed by administrative order of the emperor; synods being expected afterwards to confirm, or rather accept, such order. The germ of this dealing with a major causa may be found in the practice of the Arian emperors in the 4th century. The cause of Ignatius and Photius was dealt with in the 9th century by various synods; those in the East agreeing with the emperor’s view for the time being, while those in the West acted with the pope. (The details are in Mansi, Conc. in locis, and in Hefele, Conc. in locis, more briefly. They are summarized in Landon, Manual of Councils, s.v. “Constantinople,” “Rome,” and in E.S. Foulkes, Manual of Ecclesiastical History, s.v. “Century IX.”) Since these transactions patriarchs have been deposed by the Byzantine emperors; and the Turkish sultans since the 15th century have assumed to exercise the same prerogative.
The spiritual courts in the East have permanently acquired jurisdiction in the matrimonial causes of baptized persons; the Mahommedan governments allowing to Christians a personal law of their own. The patriarch of Constantinople is enabled to exercise an extensive criminal jurisdiction over Christians (Neale, Hist. of the Eastern Church, i. 30, 31).
The empire of Russia has in the matter of ecclesiastical jurisdiction partly developed into other forms, partly systematized 4th century and later Byzantine rules. The provincial system does not exist; or it may be said that all Russia is one province. An exception should be made in the case of Georgia, which is governed by an “exarch,” with three suffragans under him. In the remainder of the empire the titles of metropolitan, save in the case of the metropolitan of all Russia, and of archbishop, were and are purely honorary, and their holders have merely a diocesan jurisdiction (see Mouravieff, History of the Russian Church, translated Blackmore, 1842, translator’s notes at pp. 370, 390, 416 et seq.). So in Egypt the bishop or “pope” (afterwards patriarch) of Alexandria was the only true metropolitan (Neale, History of the Eastern Church, Gen. Introd. vol. i. p. 111). The metropolitan of Russia from the time of the conversion (A.D. 988) settled at Kiev, and his province was part of the patriarchate of Constantinople, and appeals lay to Constantinople. Many such appeals were taken, notably in the case of Leon, bishop of Rostov (Mouravieff, op. cit. p. 38). The metropolitical see was for a short time transferred to Vladimir and then finally to Moscow (Mouravieff, chs. iv., v.). After the taking of Constantinople in 1452, the Russian metropolitans were always chosen and consecrated in Russia, appeals ceased, and Moscow became de facto autocephalous (Joyce, ubi sup. p. 379; Mouravieff, op. cit. p. 126). The tsar Theodore in 1587 exercised the power of the Byzantine emperors by deposing the metropolitan, Dionysius Grammaticus (Mouravieff, p. 125). In 1587 the see of Moscow was raised to patriarchal rank with the consent of Constantinople, and the subsequent concurrence of Alexandria, Antioch and Jerusalem (ib. c. vi.). Moscow became the final court, in theory, as it had long been in practice. Certain religious houses, however, had their own final tribunals and were “peculiars,” exempt from any diocesan or patriarchal jurisdiction for at least all causes relating to Church property (ib. p. 131).
The subject matter of ecclesiastical jurisdiction in Russia during the whole patriarchal period included matrimonial and testamentary causes, inheritance and sacrilege, and many questions concerning the Church domains and Church property, as well as spiritual offences of clergy and laity (ib.). The bishops had consistorial courts; the patriarchs, chanceries and consistories (ib.). Bishops were judged in synod (see, e.g. the case of the archbishop of Polotsk in 1622, ib. p. 179) and only lawfully judged in synod (ib. p. 215).
Clerks and the dependants of the metropolitan (afterwards the patriarch) appear to have been immune from secular jurisdiction, except in the case of crimes against life, from the time of Ivan the Terrible (ib. pp. 180-181). The tsar Michael, in the earlier 17th century, confirmed these immunities in the case of the clergy of the patriarch’s own diocese, but provided that in country places belonging to his diocese, monasteries, churches and lands should be judged in secular matters by the Court of the Great Palace, theoretically held before the tsar himself (ib. p. 181). This tsar limited the “peculiar” monasteries to three, and gave the patriarch jurisdiction over them (ib.). The next tsar, Alexis, however, by his code instituted a “Monastery Court,” which was a secular tribunal composed of laymen, to judge in civil suits against spiritual persons, and in matters arising out of their manors and properties (ib. p. 193). This court was not in operation during the time when the patriarch Nikon was also in effect first minister; but upon his decline exercised its full jurisdiction (ib. p. 216). Nikon was himself tried for abdicating his see, causing disorder in the realm, oppression and violence, first before a synod of Moscow composed of his suffragans and some Greek bishops, and afterwards before another synod in which sat the patriarchs of Alexandria and Antioch, the metropolitans of Servia and Georgia, the archbishops of Sinai and Wallachia, and the metropolitans of Nice, Amasis, Iconium, Trebizond, Varna and Scio, besides the Russian bishops. This synod in 1667 deposed Nikon, degraded him from holy orders, and sentenced him to perpetual penance in a monastery (ib. pp. 220-232). The next tsar, Theodore, 866 suppressed the secular “monastery court,” and directed that all suits against spiritual persons should proceed only in the patriarchal “court of requests” (ib. p. 264). There was, however, a species of appel comme d’abus. Causes could be evoked to the tsar himself, “when any partiality of the judges in any affair in which they themselves were interested was discovered” (ib.).
The old system was swept away by Peter the Great, who settled ecclesiastical jurisdiction substantially on its present basis. The patriarchate was abolished and its jurisdiction transferred by a council at St Petersburg in 1721 to a Holy Governing Synod. The change was approved by the four patriarchs of the East in 1723 (ib. chs. xv.-xvii.). Peter permanently transferred to the secular forum the testamentary jurisdiction and that concerning inheritance, as also questions of “sacrilege” (ib. p. 264). As the result of a long series of legislation, beginning with him and ending with Catherine II., all church property of every kind was transferred to secular administration, allowances, according to fixed scales, being made for ministers, monks and fabrics (op. cit. translator’s appendix i. p. 413 et seq.). There remain to the spiritual courts in Russia the purely ecclesiastical discipline of clerks and laity and matrimonial causes.
The court of first instance is the “consistorial court” of the bishop. This consists of a small body of ecclesiastics. Its decisions must be confirmed by the bishop (op. cit. translator’s appendix ii. pp. 422-423). In the more important causes, as divorce (i.e. a vinculo), it only gives a provisional decision, which is reported by the bishop, with his own opinion, for final judgment, to the Most Holy Governing Synod.
The governing synod is the final court of appeal. It consists of a small number of bishops and priests nominated by the tsar, and is assisted by a “procurator,” who is a layman, who explains to it the limits of its jurisdiction and serves as the medium of communication between it and the autocrat and secular authorities. It deals with the secular crimes of spiritual persons, if of importance and if not capital (these last being reserved for the secular forum), and with heresy and schism. It is the only court which can try bishops or decree divorce. The tsar formally confirms its judgments; but sometimes reduces penalties in the exercise of the prerogative of mercy (see Mouravieff, op. cit. ch. xvii. translator’s app. ii.).
The governing synod now sits at St Petersburg, but appoints delegated commissions, with a portion of its jurisdiction, in Moscow and Georgia. The latter commission is presided over by the “exarch” (supra).
Since the War of Independence, the kingdom of Greece has been ecclesiastically organized after the model of Russia, as one autocephalous “province,” separated from its old patriarchate of Constantinople, with an honorary metropolitan and honorary archbishops (Neale, op. cit. Gen. Introd. vol. i.). The Holy Synod possesses the metropolitical jurisdiction. It sits at Athens. The metropolitan of Athens is president, and there are four other members appointed by the government in annual rotation from the senior bishops. There is attached to it a government commissioner, with no vote, but affixing his signature to the synodical judgments (Joyce, op. cit. p. 35).
The subject matter of the jurisdiction of Hellenic courts Christian seems to be confined to strictly spiritual discipline, mainly in regard to the professional misconduct of the clergy. Imprisonment may be inflicted in these last cases (ib.). All matrimonial causes are heard by the secular tribunals (Lehr, op. cit. sec. 587).
The bishop’s consistorial court, consisting of himself and four priests, has a limited jurisdiction in first instance. Such a court can only suspend for seven days unless with the sanction of the Holy Synod (Joyce, op. cit.).
The Holy Synod can only inflict temporary suspension, or imprisonment for fifteen days, unless with the sanction of the King’s ministry. Deprivation, or imprisonment for more than two months, requires the approval of the king (ib.). The king or the ministry do not, however, rehear the cause by way of appeal, but merely restrain severity of sentence (ib.).
The Church of Cyprus has been autocephalous since at any rate the oecumenical synod of Ephesus in 431. The episcopate now consists of an archbishop and three suffragans (Hackett, Orthodox Church in Cyprus, 1901, ch. v. et passim). The final court is the island synod, which consists of the archbishop, his suffragans and four dignified priests. It has original and exclusive cognizance of causes of deposition of bishops (op. cit. pp. 260, 262).
Each bishop is assisted by at least two officers with judicial or quasi-judicial powers, the “archimandrite” who adjudicates upon causes of revenue and the archdeacon who adjudicates on questions between deacons (op. cit. pp. 272-273). The “exarch” of the archbishop, who is a dignitary but not a bishop, has a seat in the provincial synod.
In the Balkan States, the system—inherited from Byzantine and Turkish times—of ecclesiastical jurisdictions prevails, except that they are now autocephalous, and independent of the patriarch of Constantinople. Matrimonial causes in Servia are of ecclesiastical cognizance (Lehr, op. cit. sect. 901).
Authorities.—St Augustine, Epistles; Codex Theodosianus, edited by Th. Mommsen and P.M. Meyer (1905); Code and Novells of Emperor Justinian, ed. J. Gothofredus (1665); T. Balsamon, “In Conc. Ancyr.” in the Corpus juris canonici (1879-1881); “Hostiensis” Super Decretum; W. Lyndwood, Provinciale (Oxford, 1679); Sir A. Fitzherbert, Natura brevium (1534); Sir T. Ridley, View of the Civile and Ecclesiastical Law (1607); J. Ayliffe, Parergon juris ecclesiastici (1726); J. Godolphin, Abridgement of the Laws Ecclesiastical (London, 1687); E. Gibson, Codex juris ecclesiastici (Oxford, 1761); D. Covarruvias, Opera omnia (Antwerp, 1638); Jean Hardouin, Concilia (1715); J.D. Mansi, Concilia (1759-1798); E. Stillingfleet, Ecclesiastical Jurisdiction (1704); L.S. le Nain de Tillemont, Mémoires pour servir à l’histoire ecclésiastique (1701-1712); P.T. Durand de Maillane, Dictionnaire du droit canonique (1761); Dictionnaire ecclésiastique et canonique, par une société de religieux (Paris, 1765); Z.B. van Espen, Jus ecclesiasticum universum (Louvain, 1720), De recursu ad Principem, observationes in Concilium Lateranense iv.; L. Thomassin, Vetus et nova disciplina ecc. (1705-1706); W. Beveridge, Synodicon (Oxford, 1672); J.A.S. da Carnota, Life of Pombal (1843); J.P. Migne, Dictionnaire de droit canon. (Paris, 1844); R. Keith, History of the Scottish Bishops (Edinburgh, 1824); P.N. Vives y Cebriá, Usages y demas derechos de Cataluña (1832); C.A. Cornelius, Svenska Kyrkaus Historia (Upsala, 1875); Mouravieff, History of the Russian Church (trans. Blackmore, 1842); Ffoulkes, Manual of Ecclesiastical History (1851); E.H. Landon, Manual of Councils of the Church (1893); W.H. Hale, Precedents in Criminal Cases (London, 1847); E.B. Pusey, Councils of the Church (Oxford, 1857); C.J. von Hefele, Conciliengeschichte (Freiburg, 1855-1890); M. Gaudry, Traité de la législation des cultes (Paris, 1854); W. Stubbs, Select Charters (Oxford, 1895); A.W. Haddan and W. Stubbs, Councils and Ecclesiastical Documents (Oxford, 1869); A.J. Stephens, Ecclesiastical Statutes (1845); H.C. Rothery, Return of Cases before Delegates (1864); J.W. Joyce, The Sword and the Keys (2nd ed., 1881); Report of Ecclesiastical Courts Commission (1888); P. Fournier, Les Officialités au moyen âge (1880); S.B. Smith, Elements of Ecclesiastical Law (New York, 1889-1890); S. Sanguineti, Juris ecc. inst. (Rome, 1890); J.F. Stephen, History of the Criminal Law of England (London, 1883); Pollock and Maitland, History of English Law before Edward I. (1898); F.W. Maitland, Roman Canon Law in the Church of England (1898); R. Owen, Canon Law (1884); Sir R.J. Phillimore, Ecclesiastical Law (2nd ed., 1895); J.W. Brodie-Innes, Comparative Principles of the Laws of England and Scotland (1903); R.B. Merriman, Life and Letters of Thomas Cromwell (1902); S. Aichner, Compendium juris ecclesiast. (8th ed., Brixen, 1905, especially in regard to Austro-Hungarian Empire); J. Hackett, History of the Orthodox Church in Cyprus (1901); Tauber, Manuale juris canonici (1906); E.L. Taunton, Law of the Church (London, 1906); Report of Royal Commission on Ecclesiastical Discipline (1906).
ECCLESIASTICAL LAW, in its broadest sense, the sum of the authoritative rules governing the Christian Church, whether in its internal polity or in its relations with the secular power. Since there are various churches, widely differing alike in their principles and practice, it follows that a like difference exists in their ecclesiastical law, which is the outcome of their corporate consciousness as modified by their several relations to the secular authority. At the outset a distinction must be made between churches which are “established” and those that are “free.” The ecclesiastical laws of the latter are, like the rules of a private society or club, the concern of the members of the church only, and come under the purview of the state only in so far as they come in conflict with the secular law (e.g. polygamy among the Mormons, or violation of the trust-deeds under which 867 the property of a church is held). In the case of “established” Churches, on the other hand, whatever the varying principle on which the system is based, or the difference in its practical application, the essential conditions are that the ecclesiastical law is also the law of the land, the decisions of the church courts being enforced by the civil power. This holds good both of the Roman Catholic Church, wherever this is recognized as the “state religion,” of the Oriental Churches, whether closely identified with the state itself (as in Russia), or endowed with powers over particular nationalities within the state (as in the Ottoman empire), and of the various Protestant Churches established in Great Britain and on the continent of Europe.
Writers on the theory of ecclesiastical law, moreover, draw a fundamental distinction between that of the Church of Rome and that of the Protestant national or territorial Churches. This distinction is due to the claim of the Roman Catholic Church to be the only Church, her laws being thus of universal obligation; whereas the laws of the various established Protestant Churches are valid—at least so far as legal obligation is concerned—only within the limits of the countries in which they are established. The practical effects of this distinction have been, and still are, of enormous importance. The Roman Catholic Church, even when recognized as the state religion, is nowhere “established” in the sense of being identified with the state, but is rather an imperium in imperio which negotiates on equal terms with the state, the results being embodied in concordats (q.v.) between the state and the pope as head of the Church. The concordats are of the nature of truces in the perennial conflict between the spiritual and secular powers, and imply in principle no surrender of the claims of the one to those of the other. Where the Roman Catholic Church is not recognized as a state religion, as in the United States or in the British Islands, she is in the position of a “free Church,” her jurisdiction is only in foro conscientiae, and her ecclesiastical laws have no validity from the point of view of the state. On the other hand, the root principle of the ecclesiastical law of the established Protestant Churches is the rejection of alien jurisdiction and the assertion of the supremacy of the state. The theory underlying this may vary. The sovereign may be regarded, as in the case of the Russian emperor or of the English kings from the Reformation to the Revolution, as the vicar of God in all causes spiritual as well as temporal within his realm. As the first fervent belief in the divine right of kings faded, however, a new basis had to be discovered for a relation between the spiritual and temporal powers against which Rome had never ceased to protest. This was found in the so-called “collegial” theory of Church government (Kollegialsystem), which assumed a sort of tacit concordat between the state and the religious community, by which the latter vests in the former the right to exercise a certain part of the jus in sacra properly inherent in the Church (see Pufendorf, Samuel). This had great and lasting effects on the development of the theory of Protestant ecclesiastical law on the continent of Europe. In England, on the other hand, owing to the peculiar character of the Reformation there and of the Church that was its outcome, no theory of the ecclesiastical law is conceivable that would be satisfactory at once to lawyers and to all schools of opinion within the Church. This has been abundantly proved by the attitude of increasing opposition assumed by the clergy, under the influence of the Tractarian movement, towards the civil power in matters ecclesiastical, an attitude impossible to justify on any accepted theory of the Establishment (see below).
Protestant ecclesiastical law, then, is distinguished from that of the Roman Catholic Church (1) by being more limited in its scope, (2) by having for its authoritative source, not the Church only or even mainly, but the Church in more or less complete union with or subordination to the State, the latter being considered, equally with the Church, as an organ of the will of God. The ecclesiastical law of the Church of Rome, on the other hand, whatever its origin, is now valid only in so far as it has the sanction of the authority of the Holy See. And here it must be noted that the “canon law” is not identical with the “ecclesiastical law” of the Roman Catholic Church. By the canon law is meant, substantially, the contents of the Corpus juris canonici, which have been largely superseded or added to by, e.g. the canons of the council of Trent and the Vatican decrees. The long projected codification of the whole of the ecclesiastical law of the Church of Rome, a work of gigantic labour, was not taken in hand until the pontificate of Pius X. (See also Canon Law and Ecclesiastical Jurisdiction.)
The ecclesiastical law of England is in complete dependence upon the authority of the state. The Church of England cannot be said, from a legal point of view, to have a corporate existence or even a representative assembly. The Convocation of York and the Convocation of Canterbury are provincial assemblies possessing no legislative or judicial authority; even such purely ecclesiastical questions as may be formally commended to their attention by “letters of business” from the crown can only be finally settled by act of parliament. The ecclesiastical courts are for the most part officered by laymen, whose subordination to the archbishops and bishops is purely formal, and the final court of appeal is the Judicial Committee of the Privy Council. In like manner changes in the ecclesiastical law are made directly by parliament in the ordinary course of legislation, and in point of fact a very large portion of the existing ecclesiastical law consists of acts of parliament.
The sources of the ecclesiastical law of England are thus described by Dr. Richard Burn (The Ecclesiastical Law, 9th ed., 1842):—“The ecclesiastical law of England is compounded of these four main ingredients—the civil law, the canon law, the common law, and the statute law. And from these, digested in their proper rank and subordination, to draw out one uniform law of the church is the purport of this book. When these laws do interfere and cross each other, the order of preference is this:—’The civil law submitteth to the canon law; both of these to the common law; and all three to the statute law. So that from any one or more of these, without all of them together, or from all of them together without attending to their comparative obligation, it is not possible to exhibit any distinct prospect of the English ecclesiastical constitution.’ Under the head of statute law Burn includes ‘the Thirty-nine Articles of Religion, agreed upon in Convocation in the year 1562; and in like manner the Rubric of the Book of Common Prayer, which, being both of them established by Acts of Parliament, are to be esteemed as part of the statute law.’”
The first principle of the ecclesiastical law in England is the assertion of the supremacy of the crown, which in the present state of the constitution means the same thing as the supremacy of parliament. This principle has been maintained ever since the Reformation. Before the Reformation the ecclesiastical supremacy of the pope was recognized, with certain limitations, in England, and the Church itself had some pretensions to ecclesiastical freedom. The freedom of the Church is, in fact, one of the standing provisions of those charters on which the English constitution was based. The first provision of Magna Carta is quod ecclesia Anglicana libera sit. By the various enactments of the period of the Reformation the whole constitutional position of the Church, not merely with reference to the pope but with reference to the state, was definitely fixed. The legislative power of convocation was held to extend to the clergy only, and even to that extent required the sanction and assent of the crown. The common law courts controlled the jurisdiction of the ecclesiastical courts, claiming to have “the exposition of such statutes or acts of parliament as concern either the extent of the jurisdiction of these courts or the matters depending before them. And therefore if these courts either refuse to allow these acts of parliament, or expound them in any other sense than is truly and properly the exposition of them, the king’s great courts of common law may prohibit and control them.”
The design of constructing a code of ecclesiastical laws was entertained during the period of the Reformation, but never carried into effect. It is alluded to in various statutes of the reign of Henry VIII., who obtained power to appoint a commission to examine the old ecclesiastical laws, with a view of deciding which ought to be kept and which ought to be abolished; 868 and in the meantime it was enacted that “such canons, institutions, ordinances, synodal or provincial or other ecclesiastical laws or jurisdictions spiritual as be yet accustomed and used here in the Church of England, which necessarily and conveniently are requisite to be put in ure and execution for the time, not being repugnant, contrarient, or derogatory to the laws or statutes of the realm, nor to the prerogatives of the royal crown of the same, or any of them, shall be occupied, exercised, and put in ure for the time with this realm” (35 Henry VIII. c. 16, 25 c. 19, 27 c. 8).
The work was actually undertaken and finished in the reign of Edward VI. by a sub-committee of eight persons, under the name of the Reformatio legum ecclesiasticarum, which, however, never obtained the royal assent. Although the powers of the 25 Henry VIII. c. 1 were revived by the 1 Elizabeth c. 1, the scheme was never executed, and the ecclesiastical laws remained on the footing assigned to them in that statute—so much of the old ecclesiastical laws might be used as had been actually in use, and was not repugnant to the laws of the realm.
The statement is, indeed, made by Sir R. Phillimore (Ecclesiastical Law, 2nd ed., 1895) that the “Church of England has at all times, before and since the Reformation, claimed the right of an independent Church in an independent kingdom, to be governed by the laws which she has deemed it expedient to adopt.” This position can only be accepted if it is confined, as the authorities cited for it are confined, to the resistance of interference from abroad. If it mean that the Church, as distinguished from the kingdom, has claimed to be governed by laws of her own making, all that can be said is that the claim has been singularly unsuccessful. From the time of the Reformation no change has been made in the law of the Church which has not been made by the king and parliament, sometimes indirectly, as by confirming the resolutions of convocation, but for the most part by statute. The list of statutes cited in Sir R. Phillimore’s Ecclesiastical Law fills eleven pages. It is only by a kind of legal fiction akin to the “collegial” theory mentioned above, that the Church can be said to have deemed it expedient to adopt these laws.
The terms on which the Church Establishment of Ireland was abolished, by the Irish Council Act of 1869, may be mentioned. By sect. 20 the present ecclesiastical law was made binding on the members for the time being of the Church, “as if they had mutually contracted and agreed to abide by and observe the same”; and by section 21 it was enacted that the ecclesiastical courts should cease after the 1st of January 1871, and that the ecclesiastical laws of Ireland, except so far as relates to matrimonial causes and matters, should cease to exist as law. (See also England, Church of; Establishment; &c.)
Authorities.—The number of works on ecclesiastical law is very great, and it must suffice here to mention a few of the more conspicuous modern ones: Ferdinand Walter, Lehrbuch des Kirchenrechts aller christlichen Konfessionen (14th ed., Bonn, 1871); G. Phillips, Kirchenrecht, Bde. i.-vii. (Regensburg, 1845-1872) incomplete; the text-book by Cardinal Hergenröther (q.v.); P. Hinschius, Kirchenrecht der Katholiken und Protestanten in Deutschland, 6 Bde. (Berlin, 1869 sqq.), only the Catholic part, a masterly and detailed survey of the ecclesiastical law, finished; Sir Robert Phillimore, Eccl. Law of the Church of England (2nd ed., edited by Sir Walter Phillimore, 2 vols., London, 1895). For further references see Canon Law, and the article “Kirchenrecht” in Herzog-Hauck, Realencyklopädie (ed. Leipzig, 1901).
ECCLESIASTICUS (abbreviated to Ecclus.), the alternative title given in the English Bible to the apocryphal book otherwise called “The Wisdom of Jesus the son of Sirach.” The Latin word ecclesiasticus is, properly speaking, not a name, but an epithet meaning “churchly,” so that it would serve as a designation of any book which was read in church or received ecclesiastical sanction, but in practice Ecclesiasticus has become a by-name for the Wisdom of Sirach. The true name of the book appears in the authorities in a variety of forms, the variation affecting both the author’s name and the description of his book. The writer’s full name is given in l. 27 (Heb. text) as “Simeon the son of Jeshua (i.e. Jesus) the son of Eleazar the son of Sira.” In the Greek text this name appears as “Jesus son of Sirach Eleazar” (probably a corruption of the Hebrew reading), and the epithet “of Jerusalem” is added, the translator himself being resident in Egypt. The whole name is shortened sometimes to “Son of Sira,” Ben Sira in Hebrew, Bar Sira in Aramaic, and sometimes (as in the title prefixed in the Greek cod. B) to Sirach. The work is variously described as the Words (Heb. text), the Book (Talmud), the Proverbs (Jerome), or the Wisdom of the son of Sira (or Sirach).
Of the date of the book we have only one certain indication. It was translated by a person who says that he “came into Egypt in the 38th year of Euergetes the king” (Ptolemy VII.), i.e. in 132 B.C., and that he executed the work some time later. The translator believed that the writer of the original was his own grandfather (or ancestor, πάππος). It is therefore reasonable to suppose that the book was composed not later than the first half of the 2nd century B.C., or (if we give the looser meaning to πάππος) even before the beginning of the century. Arguments for a pre-Maccabean date may be derived (a) from the fact that the book contains apparently no reference to the Maccabean struggles, (b) from the eulogy of the priestly house of Zadok which fell into disrepute during these wars for independence.
In the Jewish Church Ecclesiasticus hovered on the border of the canon; in the Christian Church it crossed and recrossed the border. The book contains much which attracted and also much which repelled Jewish feeling, and it appears that it was necessary to pronounce against its canonicity. In the Talmud (Sanhedrin 100 b) Rabbi Joseph says that it is forbidden to read (i.e. in the synagogue) the book of ben Sira, and further that “if our masters had not hidden the book (i.e. declared it uncanonical), we might interpret the good things which are in it” (Schechter, J. Q. Review, iii. 691-692). In the Christian Church it was largely used by Clement of Alexandria (c. A.D. 200) and by St Augustine. The lists of the Hebrew canon, however, given by Melito (c. A.D. 180) and by Origen (c. A.D. 230) rightly exclude Ecclesiasticus, and Jerome (c. A.D. 390-400) writes: “Let the Church read these two volumes (Wisdom of Solomon and Ecclesiasticus) for the instruction of the people, not for establishing the authority of the dogmas of the Church” (Praefatio in libros Salomonis). In the chief MS. of the Septuagint, cod. B, Ecclesiasticus comes between Wisdom and Esther, no distinction being drawn between canonical and uncanonical. In the Vulgate it immediately precedes Isaiah. The council of Trent declared this book and the rest of the books reckoned in the Thirty-nine Articles as apocryphal to be canonical.
The text of the book raises intricate problems which are still far from solution. The original Hebrew (rediscovered in fragments and published between 1896 and 1900) has come down to us in a mutilated and corrupt form. The beginning as far as iii. 7 is lost. There is a gap from xvi. 26 to xxx. 11. There are marginal readings which show that two different recensions existed once in Hebrew. The Greek version exists in two forms—(a) that preserved in cod. B and in the other uncial MSS., (b) that preserved in the cursive codex 248 (Holmes and Parsons). The former has a somewhat briefer text, the latter agrees more closely with the Hebrew text. The majority of Greek cursives agree generally with the Latin Vulgate, and offer the fuller text in a corrupt form. The Syriac (Peshitta) version is paraphrastic, but on the whole it follows the Hebrew text. Owing to the mutilation of the Hebrew by the accidents of time the Greek version retains its place as the chief authority for the text, and references by chapter and verse are usually made to it.
Bickell and D.S. Margoliouth have supposed that the Hebrew text preserved in the fragments is not original, but a retranslation from the Greek or the Syriac or both. This view has not commended itself to the majority of scholars, but there is at least a residuum of truth in it. The Hebrew text, as we have it, has a history of progressive corruption behind it, and its readings can often be emended from the Septuagint, e.g. xxxvii. 11 (read ומירא על for the meaningless ומרר אל). The Hebrew marginal readings occasionally seem to be translations from the Greek or Syriac, e.g. xxxviii. 4 (ברא שמים for ἒκτισεν φάρμακα). More frequently, however, strange readings of the Greek and Syriac 869 are to be explained as corruptions of our present Hebrew. Substantially our Hebrew must be pronounced original.
The restoration of a satisfactory text is beyond our hopes. Even before the Christian era the book existed in two recensions, for we cannot doubt, after reading the Greek translator’s preface, that the translator amplified and paraphrased the text before him. It is probable that at least one considerable omission must be laid to his charge, for the hymn preserved in the Hebrew text after ch. li. 12 is almost certainly original. Ancient translators allowed themselves much liberty in their work, and Ecclesiasticus possessed no reputation for canonicity in the 2nd century B.C. to serve as a protection for its text. Much, however, may be done towards improving two of the recensions which now lie before us. The incomplete Hebrew text exists in four different MSS., and the study of the peculiarities of these had already proved fruitful. The Syriac text, made without doubt from the Hebrew, though often paraphrastic is often suggestive. The Greek translation, made within a century or half-century of the writing of the book, must possess great value for the criticism of the Hebrew text. The work of restoring true Hebrew readings may proceed with more confidence now that we have considerable portions of the Hebrew text to serve as a model. For the restoration of the Greek text we have, besides many Greek MSS., uncial and cursive, the old Latin, the Syro-Hexaplar, the Armenian, Sahidic and Ethiopic versions, as well as a considerable number of quotations in the Greek and Latin Fathers. Each of the two recensions of the Greek must, however, be separately studied, before any restoration of the original Greek text can be attempted.
The uncertainty of the text has affected both English versions unfavourably. The Authorized Version, following the corrupt cursives, is often wrong. The Revised Version, on the other hand, in following the uncial MSS. sometimes departs from the Hebrew, while the Authorized Version with the cursives agrees with it. Thus the Revised Version (with codd. א*, A, B, C) omits the whole of iii. 19, which the Authorized Version retains, but for the clause, “Mysteries are revealed unto the meek,” the Authorized Version has the support of the Hebrew, Syriac and cod. 248. Sometimes both versions go astray in places in which the Hebrew text recommends itself as original by its vigour; e.g. in vii. 26, where the Hebrew is,
| Hast thou a wife? abominate her not. Hast thou a hated wife? trust not in her. |
Again in ch. xxxviii. the Hebrew text in at least two interesting passages shows its superiority over the text which underlies both English versions.
| Hebrew. | Revised Version (similarly Authorized Version). | |
| ver. 1. | Acquaint thyself with a physician before thou have need of him. | Honour a physician according to thy need of him with the honours due unto him. |
| ver. 15. | He that sinneth against his Maker will behave himself proudly against a physician. | He that sinneth before his Maker, let him fall into the hands of the physician. |
In the second instance, while the Hebrew says that the man who rebels against his Heavenly Benefactor will a fortiori rebel against a human benefactor, the Greek text gives a cynical turn to the verse, “Let the man who rebels against his true benefactor be punished through the tender mercies of a quack.” The Hebrew text is probably superior also in xliv. 1, the opening words of the eulogy of the Fathers: “Let me now praise favoured men,” i.e. men in whom God’s grace was shown. The Hebrew phrase is “men of grace,” as in v. 10. The Greek text of v. 1, “famous men,” seems to be nothing but a loose paraphrase, suggested by v. 2, “The Lord manifested in them great glory.”
In character and contents Ecclesiasticus resembles the book of Proverbs. It consists mainly of maxims which may be described in turn as moral, utilitarian and secular. Occasionally the author attacks prevalent religious opinions, e.g. the denial of free-will (xv. 11-20), or the assertion of God’s indifference towards men’s actions (xxxv. 12-19). Occasionally, again, Ben Sira touches the highest themes, and speaks of the nature of God: “He is All” (xliii. 27); “He is One from everlasting” (xlii. 21, Heb. text); “The mercy of the Lord is upon all flesh” (xviii. 13). Though the book is imitative and secondary in character it contains several passages of force and beauty, e.g. ch. ii. (how to fear the Lord); xv. 11-20 (on free-will); xxiv. 1-22 (the song of wisdom); xlii. 15-25 (praise of the works of the Lord); xliv. 1-15 (the well-known praise of famous men). Many detached sayings scattered throughout the book show a depth of insight, or a practical shrewdness, or again a power of concise speech, which stamps them on the memory. A few examples out of many may be cited. “Call no man blessed before his death” (xi. 28); “He that toucheth pitch shall be defiled” (xiii. 1); “He hath not given any man licence to sin” (xv. 20); “Man cherisheth anger against man; and doth he seek healing from the Lord?” (xxviii. 3); “Mercy is seasonable ... as clouds of rain” (xxxv. 20); “All things are double one against another: and he hath made nothing imperfect” (xlii. 24, the motto of Butler’s Analogy); “Work your work before the time cometh, and in his time he will give you your reward” (li. 30). In spite, however, of the words just quoted it cannot be said that Ben Sira preaches a hopeful religion. Though he prays, “Renew thy signs, and repeat thy wonders ... Fill Sion with thy majesty and thy Temple with thy glory” (xxxvi. 6, 14 [19], Heb. text), he does not look for a Messiah. Of the resurrection of the dead or of the immortality of the soul there is no word, not even in xli. 1-4, where the author exhorts men not to fear death. Like the Psalmist (Ps. lxxxviii. 10, 11) he asks, “Who shall give praise to the Most High in the grave?” In his maxims of life he shows a somewhat frigid and narrow mind. He is a pessimist as regards women; “From a woman was the beginning of sin; and because of her we all die” (xxv. 24). He does not believe in home-spun wisdom; “How shall he become wise that holdeth the plough?” (xxxviii. 25). Artificers are not expected to pray like the wise man; “In the handywork of their craft is their prayer” (v. 34). Merchants are expected to cheat; “Sin will thrust itself in between buying and selling” (xxvii. 2).
Bibliography.—The literature of Ecclesiaticus has grown very considerably since the discovery of the first Hebrew fragment in 1896. A useful summary of it is found at the end of Israel Levi’s article, “Sirach,” in the Jewish Encyclopedia. Eberhard Nestle’s article in Hastings’s Dictionary of the Bible is important for its bibliographical information as well as in other respects. A complete edition of the Hebrew fragments in collotype facsimile was published jointly by the Oxford and Cambridge Presses in 1901. J.H.A. Hart’s edition of cod. 248 throws much light on some of the problems of this book. It contains a fresh collation of all the chief authorities (Heb., Syr., Syr.-Hex., Lat. and Gr.) for the text, together with a complete textual commentary.
The account given in the Synopsis attributed to Athanasius (Migne, P.G., iv. 375-384) has an interest of its own. The beginning is given in the Authorized Version as “A prologue made by an uncertain author.”
ECGBERT, or Ecgberht (d. 839), king of the West Saxons, succeeded to the throne in 802 on the death of Beorhtric. It is said that at an earlier period in his life he had been driven out for three years by Offa and Beorhtric. The accession of Ecgbert seems to have brought about an invasion by Æthelmund, earl of the Hwicce, who was defeated by Weoxtan, earl of Wiltshire. In 815 Ecgbert ravaged the whole of the territories of the West Welsh, which probably at this time did not include much more than Cornwall. The next important occurrence in the reign was the defeat of Beornwulf of Mercia at a place called Ellandun in 825. After this victory Kent, Surrey, Sussex and Essex submitted to Wessex; while the East Anglians, who slew Beornwulf shortly afterwards, acknowledged Ecgbert as overlord. In 829 the king conquered Mercia, and Northumbria accepted him as overlord. In 830 he led a successful expedition against the Welsh. In 836 he was defeated by the Danes, but in 838 he won a battle against them and their allies the West Welsh at Hingston Down in Cornwall. Ecgbert died in 839, after a reign of thirty-seven years, and was succeeded by his son Æthelwulf. A somewhat difficult question has arisen as to the parentage of Ecgbert. Under the year 825 the Chronicle states 870 that in his eastern conquests Ecgbert recovered what had been the rightful property of his kin. The father of Ecgbert was called Ealhmund, and we find an Ealhmund, king in Kent, mentioned in a charter dated 784, who is identified with Ecgbert’s father in a late addition to the Chronicle under the date 784. It is possible, however, that the Chronicle in 825 refers to some claim through Ine of Wessex from whose brother Ingeld Ecgbert was descended.
See Anglo-Saxon Chronicle, edited by Earle and Plummer (Oxford, 1899); W. de G. Birch, Cartularium Saxonicum (London, 1885-1893). Also a paper by Sir H.H. Howorth in Numismatic Chronicle, third series, vol. xx. pp. 66-87 (reprinted separately, London, 1900), where attention is called to the peculiar dating of several of Ecgbert’s charters, and the view is put forward that he remained abroad considerably later than the date given by the Chronicle for his accession. On the other hand a charter in Birch, Cart. Sax., purporting to date from 799, contains the curious statement that peace was made between Cœnwulf and Ecgbert in that year.
ECGBERT, or Ecgberht (d. 766), archbishop of York, was made bishop of that see in 734 by Ceolwulf, king of Northumbria, succeeding Wilfrid II. on the latter’s resignation. The pall was sent him in 735 and he became the first northern archbishop after Paulinus. He was the brother of Eadberht, who ruled Northumbria 737-758. He was the recipient of the famous letter of Bede, dealing with the evils arising from spurious monasteries. Ecgberht himself wrote a Dialogus Ecclesiasticae Institutionis, a Penitentiale and a Pontificale. He was a correspondent of St Boniface, who asks him to support his censure of Æthelbald of Mercia.
See Bede, Continuatio, sub. ann. 732, 735, 766, and Epistola ad Ecgberctum (Plummer, Oxford, 1896); Chronicle, sub ann. 734, 735, 738, 766 (Earle and Plummer, Oxford, 1899); Haddan and Stubbs, Councils and Ecclesiastical Documents (Oxford, 1869-1878), iii. 403-431; Proceedings of Surtees Society (Durham, 1853).
ECGFRITH (d. 685), king of Northumbria, succeeded his father Oswio in 671. He was married to Æthelthryth, daughter of Anna of East Anglia, who, however, took the veil shortly after Ecgfrith’s accession, a step which possibly led to his long quarrel with Wilfrid archbishop of York. Ecgfrith married a second wife, Eormenburg, before 678, the year in which he expelled Wilfrid from his kingdom. Early in his reign he defeated the Picts who had risen in revolt. Between 671 and 675 Ecgfrith defeated Wulfhere of Mercia and seized Lindsey. In 679, however, he was defeated by Æthelred of Mercia, who had married his sister Osthryth, on the river Trent. Ecgfrith’s brother Ælfwine was killed in the battle, and the province of Lindsey was given up when peace was restored at the intervention of Theodore of Canterbury. In 684 Ecgfrith sent an expedition to Ireland under his general Berht, which seems to have been unsuccessful. In 685, against the advice of Cuthbert, he led a force against the Picts under his cousin Burde, son of Bile, was lured by a feigned flight into their mountain fastnesses, and slain at Nechtanesmere (now Dunnichen) in Forfarshire. Bede dates the beginning of the decline of Northumbria from his death. He was succeeded by his brother Aldfrith.
See Eddius, Vita Wilfridi (Raine, Historians of Church of York, Rolls, Series, London, 1879-1894), 19, 20, 24, 34, 39, 44; Bede, Hist. Eccl. (Plummer, Oxford, 1896), iii. 24, iv. 5, 12, 13, 18, 19, 21, 26.
ECGONINE, in chemistry, C9H15NO3, a cycloheptane derivative with a nitrogen bridge. It is obtained by hydrolysing cocaine with acids or alkalis, and crystallizes with one molecule of water, the crystals melting at 198° to 199° C. It is laevo-rotatory, and on warming with alkalis gives iso-ecgonine, which is dextro-rotatory. It is a tertiary base, and has also the properties of an acid and an alcohol. When boiled with caustic baryta it gives methylamine. It is the carboxylic acid corresponding to tropine, for it yields the same products on oxidation, and by treatment with phosphorus pentachloride is converted into anhydroecgonine, C9H13NO2, which, when heated to 280° C. with hydrochloric acid, splits out carbon dioxide and yields tropidine, C8H13N. Anhydroecgonine melts at 235° C., and has an acid and a basic character. It is an unsaturated compound, and on oxidation with potassium permanganate gives succinic acid. It is apparently a tropidine monocarboxylic acid, for on exhaustive methylation it yields cycloheptatriene-1·3·5-carboxylic acid-7. Sodium in amyl alcohol solution reduces it to hydroecgonidine C9H15NO2, while moderate oxidation by potassium permanganate converts it into norecgonine. The presence of the heptamethylene ring in these compounds is shown by the production of suberone by the exhaustive methylation, &c., of hydroecgonidine ethyl ester (see Polymethylenes and Tropine). The above compounds may be represented as:

ECHEGARAY Y EIZAGUIRRE, JOSÉ (1833- ), Spanish mathematician, statesman and dramatist, was born at Madrid in March 1833, and was educated at the grammar school of Murcia, whence he proceeded to the Escuela de Caminos at the capital. His exemplary diligence and unusual mathematical capacity were soon noticed. In 1853 he passed out at the head of the list of engineers, and, after a brief practical experience at Almería and Granada, was appointed professor of pure and applied mathematics in the school where he had lately been a pupil. His Problemas de geometría analítica (1865) and Teorías modernas de la física unidad de las fuerzas materiales (1867) are said to be esteemed by competent judges. He became a member of the Society of Political Economy, helped to found La Revista, and took a prominent part in propagating Free Trade doctrines in the press and on the platform. He was clearly marked out for office, and when the popular movement of 1868 overthrew the monarchy, he resigned his post for a place in the revolutionary cabinet. Between 1867 and 1874 he acted as minister of education and of finance; upon the restoration of the Bourbon dynasty he withdrew from politics, and won a new reputation as a dramatist.
As early as 1867 he wrote La Hija natural, which was rejected, and remained unknown till 1877, when it appeared with the title of Para tal culpa tal pena. Another play, La Última Noche, also written in 1867, was produced in 1875; but in the latter year Echegaray was already accepted as the successful author of El Libro talonario, played at the Teatro de Apolo on the 18th of February 1874, under the transparent pseudonym of Jorge Hayaseca. Later in the same year Echegaray won a popular triumph with La Esposa del vengador, in which the good and bad qualities—the clever stagecraft and unbridled extravagance—of his later work are clearly noticeable. From 1874 onwards he wrote, with varying success, a prodigious number of plays. Among the most favourable specimens of his talent may be mentioned En el puño de la espada (1875); O locura ó santidad (1877), which has been translated into Swedish and Italian; En el seno de la muerte (1879), of which there exists an admirable German version by Fastenrath. El gran Galeoto (1881), perhaps the best of Echegaray’s plays in conception and execution, has been translated into several languages, and still holds the stage. The humorous proverb, ¿Piensa mal y acertarás? exemplifies the author’s limitations, but the attempt is interesting as an instance of ambitious versatility. His susceptibility to new ideas is illustrated in such pieces as Mariana (1892), Mancha que limpia (1895), El Hijo de Don Juan (1892), and El Loco Dios (1900): these indicate a close study of Ibsen, and El Loco Dios more especially might be taken for an unintentional parody of Ibsen’s symbolism.
Echegaray succeeded to the literary inheritance of López de Ayala and of Tamayo y Baus; and though he possesses neither the poetic imagination of the first nor the instinctive tact of the second, it is impossible to deny that he has reached a larger audience than either. Not merely in Spain, but in every land where Spanish is spoken, and in cities as remote from Madrid as Munich and Stockholm, he has met with an appreciation incomparably beyond that accorded to any other Spanish dramatist of recent years. But it would be more than usually rash to prophesy that this exceptional popularity will endure. There have been signs of a reaction in Spain itself, and Echegaray’s return to politics in 1905 was significant enough. He applies 871 his mathematics to the drama; no writer excels him in artful construction, in the arrangement of dramatic scenes, in mere theatrical technique, in the focusing of attention on his chief personages. These are valuable gifts in their way, and Echegaray has, moreover, a powerful, gloomy imagination, which is momentarily impressive. In the drawing of character, in the invention of felicitous phrase, in the contrivance of verbal music, he is deficient. He alternates between the use of verse and prose; and his hesitancy in choosing a medium of expression is amply justified, for the writer’s prose is not more distinguished than his verse. These serious shortcomings may explain the diminution of his vogue in Spain; they will certainly tell against him in the estimate of posterity.
ÉCHELON (Fr. from échelle, ladder), in military tactics, a formation of troops in which each body of troops is retired on, but not behind, the flank of the next in front, the position of the whole thus resembling the steps of a staircase. To form échelon from line, the parts of the line move off, each direct to its front, in succession, so that when the formation is completed the rightmost body, for example, is farthest advanced, the one originally next on its left is to the left rear, a third is to the left rear of the second, and so on. The word is also used more loosely to express successive lines, irrespective of distances and relative positions, e.g. the “second échelon of ammunition supply,” which is fully a day’s march behind the first.
ECHIDNA, or Porcupine Ant-Eater (Echidna aculeata), one of the few species of Monotremata, the lowest subclass of Mammalia, forming the family Echidnidae. It is a native of Australia, where it chiefly abounds in New South Wales, inhabiting rocky and mountainous districts, where it burrows among the loose sand, or hides itself in crevices of rocks. In size and appearance it bears a considerable resemblance to the hedgehog, its upper surface being covered over with strong spines directed backwards, and on the back inwards, so as to cross each other on the middle line. The spines in the neighbourhood of the tail form a tuft sufficient to hide that almost rudimentary organ. The head is produced into a long tubular snout, covered with skin for the greater part of its length. The opening of the mouth is small, and from it the echidna puts forth its long slender tongue, lubricated with a viscous secretion, by means of which it seizes the ants and other insects on which it feeds. It has no teeth. Its legs are short and strong, and form, with its broad feet and large solid nails, powerful burrowing organs. In common with the other monotremes, the male echidna has its heel provided with a sharp hollow spur, connected with a secreting gland, and with muscles capable of pressing the secretion from the gland into the spur. It is a nocturnal or crepuscular animal, generally sleeping during the day, but showing considerable activity by night. When attacked it seeks to escape either by rolling itself into a ball, its erect spines proving a formidable barrier to its capture, or by burrowing into the sand, which its powerful limbs enable it to do with great celerity. “The only mode of carrying the creature,” writes G. Bennett (Gatherings of a Naturalist in Australasia), “is by one of the hind legs; its powerful resistance and the sharpness of the spines will soon oblige the captor, attempting to seize it by any other part of the body, to relinquish his hold.” In a younger stage of their development, however, the young are carried in a temporary abdominal pouch, to which they are transferred after hatching, and into which open the mammary glands. The echidnas are exceedingly restless in confinement, and constantly endeavour by burrowing to effect their escape. From the quantity of sand and mud always found in the alimentary canal of these animals, it is supposed that these ingredients must be necessary to the proper digestion of their insect food.
There are two varieties of this species, the Port Moresby echidna and the hairy echidna. The last-mentioned is found in south-eastern New Guinea, Australia and Tasmania. In all the spines are mixed with hair; in the Tasmanian race they are nearly hidden by the long harsh fur. Of the three-clawed echidnas (Proechidna) confined to New Guinea there are two species, Bruijn’s echidna (P. bruijnii), discovered in 1877 in the mountains on the north-east coast at an elevation of 3500 ft., and the black-spined echidna (P. nigroaculeata) of larger size—the type specimen measuring 31 in., as against 24 in.—with shorter claws.
End of the Project Gutenberg EBook of Encyclopaedia Britannica, 11th
Edition, Volume 8, Slice 9, by Various
*** END OF THIS PROJECT GUTENBERG EBOOK ENCYCLOPAEDIA BRITANNICA ***
***** This file should be named 34878-h.htm or 34878-h.zip *****
This and all associated files of various formats will be found in:
http://www.gutenberg.org/3/4/8/7/34878/
Produced by Marius Masi, Don Kretz and the Online
Distributed Proofreading Team at http://www.pgdp.net
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
http://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need, are critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at http://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
http://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at http://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit http://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including checks, online payments and credit card donations.
To donate, please visit: http://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart is the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
http://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.