The Project Gutenberg EBook of Encyclopaedia Britannica, 11th Edition,
Volume 8, Slice 4, by Various
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
Title: Encyclopaedia Britannica, 11th Edition, Volume 8, Slice 4
"Diameter" to "Dinarchus"
Author: Various
Release Date: May 30, 2010 [EBook #32607]
Language: English
Character set encoding: ISO-8859-1
*** START OF THIS PROJECT GUTENBERG EBOOK ENCYC. BRITANNICA, VOL 8 SL 4 ***
Produced by Marius Masi, Don Kretz and the Online
Distributed Proofreading Team at https://www.pgdp.net
| Transcriber's note: |
A few typographical errors have been corrected. They
appear in the text like this, and the
explanation will appear when the mouse pointer is moved over the marked
passage. Sections in Greek will yield a transliteration
when the pointer is moved over them, and words using diacritic characters in the
Latin Extended Additional block, which may not display in some fonts or browsers, will
display an unaccented version. Links to other EB articles: Links to articles residing in other EB volumes will be made available when the respective volumes are introduced online. |
Articles in This Slice
DIAMETER (from the Gr. διά, through, μέτρον, measure), in geometry, a line passing through the centre of a circle or conic section and terminated by the curve; the “principal diameters” of the ellipse and hyperbola coincide with the “axes” and are at right angles; “conjugate diameters” are such that each bisects chords parallel to the other. The diameter of a quadric surface is a line at the extremities of which the tangent planes are parallel. Newton defined the diameter of a curve of any order as the locus of the centres of the mean distances of the points of intersection of a system of parallel chords with the curve; this locus may be shown to be a straight line. The word is also used as a unit of linear measurement of the magnifying power of a lens or microscope.
In architecture, the term is used to express the measure of the lower part of the shaft of a column. It is employed by Vitruvius (iii. 2) to determine the height of a column, which should vary from eight to ten diameters according to the intercolumniation: and it is generally the custom to fix the lower diameter of the shaft by the height required and the Order employed. Thus the diameter of the Roman Doric should be about one-eighth of the height, that of the Ionic one-ninth, and of the Corinthian one-tenth (see Order).
DIAMOND, a mineral universally recognized as chief among precious stones; it is the hardest, the most imperishable, and also the most brilliant of minerals.1 These qualities alone have made it supreme as a jewel since early times, and yet the real brilliancy of the stone is not displayed until it has been faceted by the art of the lapidary (q.v.); and this was scarcely developed before the year 1746. The consummate hardness of the diamond, in spite of its high price, has made it most useful for purposes of grinding, polishing and drilling. Numerous attempts have been made to manufacture the diamond by artificial means, and these attempts have a high scientific interest on account of the mystery which surrounds the natural origin of this remarkable mineral. Its physical and chemical properties have been the subject of much study, and have a special interest in view of the extraordinary difference between the physical characters of the diamond and those of graphite (blacklead) or charcoal, with which it is chemically identical, and into which it can be converted by the action of heat or electricity. Again, on account of the great value of the diamond, much of the romance of precious stones has centred round this mineral; and the history of some of the great diamonds of historic times has been traced through many extraordinary vicissitudes.
The name Άδάμας, “the invincible,” was probably applied by the Greeks to hard metals, and thence to corundum (emery) and other hard stones. According to Charles William King, the first undoubted application of the name to the diamond is found in Manilius (a.d. 16),—Sic Adamas, punctum lapidis, pretiosior auro,—and Pliny (a.d. 100) speaks of the rarity of the stone, “the most valuable of gems, known only to kings.” Pliny described six varieties, among which the Indian, having six pointed angles, and also resembling two pyramids (turbines, whip-tops) placed base to base, may probably be identified as the ordinary octahedral crystal (fig. 1). The “diamond” (Yahalom) in the breastplate of the high priest (Ex. xxxix. 11) was certainly some other stone, for it bore the name of a tribe, and methods of engraving the true diamond cannot have been known so early. The stone can hardly have become familiar to the Romans until introduced from India, where it was probably mined at a very early period. But one or other of the remaining varieties mentioned by Pliny (the Macedonian, the Arabian, the Cyprian, &c.) may be the true diamond, which was in great request for the tool of the gem-engraver. Later Roman authors mentioned various rivers in India as yielding the Adamas among their sands. The name Adamas became corrupted into the forms adamant, diamaunt, diamant, diamond; but the same word, owing to a medieval misinterpretation which derived it from adamare (compare the French word aimant), was also applied to the lodestone.
Like all the precious stones, the diamond was credited with many marvellous virtues; among others the power of averting insanity, and of rendering poison harmless; and in the middle ages it was known as the “pietra della reconciliazione,” as the peacemaker between husband and wife.
 | |||
| Fig. 1. | Fig. 2. | Fig. 3. | Fig. 4. |
 |
| Fig. 5. |
 |
| Fig. 6. |
 |
| Fig. 7. |
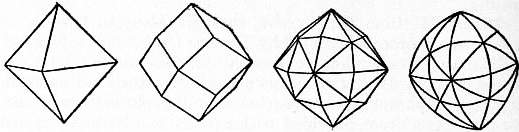
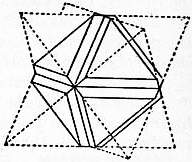
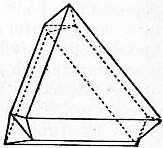
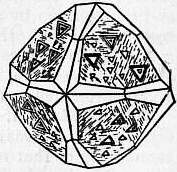
Scientific Characters.—The majority of minerals are found most commonly in masses which can with difficulty be recognized as aggregates of crystalline grains, and occur comparatively seldom as distinct crystals; but the diamond is almost always found in single crystals, which show no signs of previous attachment to any matrix; the stones were, until the discovery of the South African mines, almost entirely derived from sands or gravels, but owing to the hardness of the mineral it is rarely, if ever, water-worn, and the crystals are often very perfect. The crystals belong to the cubic system, generally assuming the form of the octahedron (fig. 1), but they may, in accordance with the principles of crystallography, also occur in other forms symmetrically derived from the octahedron,—for example, the cube, the 12-faced figure known as the rhombic dodecahedron (fig. 2), or the 48-faced figure known as the hexakis-octahedron (fig. 3), or in combinations of these. The octahedron faces are usually smooth; most of the other faces are rounded (fig. 4). The cube faces are rough with protruding points. The cube is sometimes found in Brazil, but is very rare among the S. African stones; and the dodecahedron is perhaps more common in Brazil than elsewhere. There is often a furrow running along the edges of the octahedron, or across the edges of the cube, and this indicates that the apparently simple crystal may really consist of eight individuals meeting at the centre; or, what comes to the same thing, of two individuals interpenetrating and projecting through each other. If this be so the form of the diamond is really the tetrahedron (and the various figures derived symmetrically from it) and not the octahedron Fig. 5 shows how the octahedron with furrowed edge may be constructed from two interpenetrating tetrahedra (shown in dotted lines). If the grooves be left out of account, the large faces which have replaced each tetrahedron corner then make up a figure which has the aspect of a simple octahedron. Such regular interpenetrations are known in crystallography as “twins.” There are also twins of diamond in which two octahedra (fig. 6) are united by contact along a surface parallel to an octahedron face without interpenetration. On account of their resemblance to the twins of the mineral spinel (which crystallizes in octahedra) these are known as “spinel twins.” They are generally flattened along the plane of union. The crystals often display triangular markings, either elevations or pits, upon the octahedron faces; the latter are particularly well defined and have the form of equilateral triangles (fig. 7). They are similar to the “etched figures” produced by moistening an octahedron of alum, and have probably been produced, like them, by the action of some solvent. Similar, but somewhat different markings are produced by the combustion of diamond in oxygen, unaccompanied by any rounding of the edges.
Diamond possesses a brilliant “adamantine” lustre, but this tends to be greasy on the surface of the natural stones and gives 159 the rounded crystals somewhat the appearance of drops of gum. Absolutely colourless stones are not so common as cloudy and faintly coloured specimens; the usual tints are grey, brown, yellow or white; and as rarities, red, green, blue and black stones have been found. The colour can sometimes be removed or changed at a high temperature, but generally returns on cooling. It is therefore more probably due to metallic oxides than to hydrocarbons. Sir William Crookes has, however, changed a pale yellow diamond to a bluish-green colour by keeping it embedded in radium bromide for eleven weeks. The black coloration upon the surface produced by this process, as also by the electric bombardment in a vacuum tube, appears to be due to a conversion of the surface film into graphite. Diamond may break with a conchoidal fracture, but the crystals always cleave readily along planes parallel to the octahedron faces: of this property the diamond cutters avail themselves when reducing the stone to the most convenient form for cutting; a sawing process, has, however, now been introduced, which is preferable to that of cleavage. It is the hardest known substance (though tantalum, or an alloy of tantalum now competes with it) and is chosen as 10 in the mineralogist’s scale of hardness; but the difference in hardness between diamond (10) and corundum (9) is really greater than that between corundum (9) and talc (1); there is a difference in the hardness of the different faces; the Borneo stones are also said to be harder than those of Australia, and the Australian harder than the African, but this is by no means certain. The specific gravity ranges from 3.56 to 3.50, generally about 3.52. The coefficient of expansion increases very rapidly above 750°, and diminishes very rapidly at low temperatures; the maximum density is attained about −42° C.
The very high refractive power (index = 2.417 for sodium light) gives the stone its extraordinary brilliancy; for light incident within a diamond at a greater angle than 24½° is reflected back into the stone instead of passing through it; the corresponding angle for glass is 40½°. The very high dispersion (index for red light = 2.402, for blue light = 2.460) gives it the wonderful “fire” or display of spectral colours. Certain absorption bands at the blue end of the spectrum are supposed to be due to rare elements such as samarium. Unlike other cubic crystals, diamond experiences a diminution of refractive index with increase of temperature. It is very transparent for Röntgen rays, whereas paste imitations are opaque. It is a good conductor of heat, and therefore feels colder to the touch than glass and imitation stones. The diamond has also a somewhat greasy feel. The specific heat increases rapidly with rising temperature up to 60° C., and then more slowly. Crystals belonging to the cubic system should not be birefringent unless strained; diamond often displays double refraction particularly in the neighbourhood of inclusions, both liquid and solid; this is probably due to strain, and the spontaneous explosion of diamonds has often been observed. Diamond differs from graphite in being a bad conductor of electricity: it becomes positively electrified by friction. The electrical resistance is about that of ordinary glass, and is diminished by one-half during exposure by Röntgen rays; the dielectric constant (16) is greater than that which should correspond to the specific gravity.
The phosphorescence produced by friction has been known since the time of Robert Boyle (1663); the diamond becomes luminous in a dark room after exposure to sunlight or in the presence of radium; and many stones phosphoresce beautifully (generally with a pale green light) when subjected to the electric discharge in a vacuum tube. Some diamonds are more phosphorescent than others, and different faces of a crystal may display different tints. The combustibility of the diamond was predicted by Sir Isaac Newton on account of its high refractive power; it was first established experimentally by the Florentine Academicians in 1694. In oxygen or air diamond burns at about 850°, and only continues to do so if maintained at a high temperature; but in the absence of oxidising agents it may be raised to a much higher temperature. It is, however, infusible at the temperature of the electric arc, but becomes converted superficially into graphite. Experiments on the combustion of diamond were made by Smithson Tennant (1797) and Sir Humphry Davy (1816), with the object of proving that it is pure carbon; they showed that burnt in oxygen it yields exactly the same amount of carbon dioxide as that produced by burning the same weight of carbon. Still more convincing experiments were made by A. Krause in 1890. Similarly Guyton de Morveau showed that, like charcoal, diamond converts soft iron into steel. Diamond is insoluble in acid and alkalis, but is oxidised on heating with potassium bichromate and sulphuric acid.
Bort (or Boart) is the name given to impure crystals or fragments useless for jewels; it is also applied to the rounded crystalline aggregates, which generally have a grey colour, a rough surface, often a radial structure, and are devoid of good cleavage. They are sometimes spherical (“shot bort”). Carbonado or “black diamond,” found in Bahia (also recently in Minas Geraes), is a black material with a minutely crystalline structure somewhat porous, opaque, resembling charcoal in appearance, devoid of cleavage, rather harder than diamond, but of less specific gravity; it sometimes displays a rude cubic crystalline form. The largest specimen found (1895) weighed 3078 carats. Both bort and carbonado seem to be really aggregates of crystallized diamond, but the carbonado is so nearly structureless that it was till recently regarded as an amorphous modification of carbon.
Uses of the Diamond.—The use of the diamond for other purposes than jewelry depends upon its extreme hardness: it has always been the only material used for cutting or engraving the diamond itself. The employment of powdered bort and the lapidary’s wheel for faceting diamonds was introduced by L. von Berquen of Bruges in 1476. Diamonds are now employed not only for faceting precious stones, but also for cutting and drilling glass, porcelain, &c,; for fine engraving such as scales; in dentistry for drilling; as a turning tool for electric-light carbons, hard rubber, &c.; and occasionally for finishing accurate turning work such as the axle of a transit instrument. For these tools the stone is actually shaped to the best form: it is now electroplated before being set in its metal mount in order to secure a firm fastening. It is also used for bearings in watches and electric meters. The best glaziers’ diamonds are chosen from crystals such that a natural curved edge can be used. For rock drills, and revolving saws for stone cutting, either diamond, bort or carbonado is employed, set in steel tubes, disks or bands. Rock drilling is the most important industrial application; and for this, owing to its freedom from cleavage, the carbonado is more highly prized than diamond; it is broken into fragments about 3 carats in weight; and in 1905 the value of carbonado was no less than from £10 to £14 a carat. It has been found that the “carbons” in drills can safely be subjected to a pressure of over 60 kilograms per square millimetre, and a speed of 25 metres per second. A recent application of the diamond is for wire drawing; a hole tapering towards the centre is drilled through a diamond, and the metal is drawn through this. No other tool is so endurable, or gives such uniform thickness of wire.
Distribution and Mining.—The most important localities for diamonds have been: (1) India, where they were mined from the earliest times till the close of the 19th century; (2) South America, where they have been mined since the middle of the 18th century; and (3) South Africa, to which almost the whole of the diamond-mining industry has been transferred since 1870.
India.—The diamond is here found in ancient sandstones and conglomerates, and in the river gravels and sands derived from them. The sandstones and conglomerates belong to the Vindhyan formation and overlie the old crystalline rocks: the diamantiferous beds are well defined, often not more than 1 ft. in thickness, and contain pebbles of quartzite, jasper, sandstone, slate, &c. The mines fall into five groups situated on the eastern side of the Deccan plateau about the following places (beginning from the south), the first three being in Madras. (1) Chennur near Cuddapah on the river Pennar. (2) Kurnool near Baneganapalle between the rivers Pennar and Kistna. (3) Kollar near Bezwada on the river Kistna. (4) Sambalpur on the river Mahanadi in the Central Provinces. (5) Panna near Allahabad, in Bundelkhand. The mining has always been carried on by natives of low caste, and by primitive methods which do not differ much from those described by the French merchant Jean Baptiste Tavernier (1605-1689), who paid a prolonged visit to most 160 of the mines between 1638 and 1665 as a dealer in precious stones. According to his description shallow pits were sunk, and the gravel excavated was gathered into a walled enclosure where it was crushed and water was poured over it, and it was finally sifted in baskets and sorted by hand. The buying and selling was at that period conducted by young children. In more modern times there has been the same excavation of shallow pits, and sluicing, sifting and sorting, by hand labour, the only machinery used being chain pumps made of earthen bowls to remove the water from the deeper pits.
At some of the Indian localities spasmodic mining has been carried on at different periods for centuries, at some the work which had been long abandoned was revived in recent times, at others it has long been abandoned altogether. Many of the large stones of antiquity were probably found in the Kollar group, where Tavernier found 60,000 workers in 1645 (?), the mines having, according to native accounts, been discovered about 100 years previously. Golconda was the fortress and the market for the diamond industry at this group of mines, and so gave its name to them. The old mines have now been completely abandoned, but in 1891 about 1000 carats were being raised annually in the neighbourhood of Hyderabad. The Sambalpur group appear to have been the most ancient mines of all, but they were not worked later than 1850. The Panna group were the most productive during the 19th century. India was no doubt the source of all the large stones of antiquity; a stone of 673⁄8 carats was found at Wajra Karur in the Chennur group in 1881, and one of 210½ carats at Hira Khund in 1809. Other Indian localities besides those mentioned above are Simla, in the N.W. Provinces, where a few stones have been found, and a district on the Gouel and the Sunk rivers in Bengal, which V. Ball has identified with the Soumelpour mentioned by Tavernier. The mines of Golconda and Kurnool were described as early as 1677 in the twelfth volume of the Philosophical Transactions of the Royal Society. At the present time very few Indian diamonds find their way out of the country, and, so far as the world’s supply is concerned, Indian mining of diamonds may be considered extinct. The first blow to this industry was the discovery of the Brazilian mines in Minas Geraes and Bahia.
Brazil.—-Diamonds were found about 1725 at Tejuco (now Diamantina) in Minas Geraes, and the mining became important about 1740. The chief districts in Minas Geraes are (1) Bagagem on the W. side of the Serra da Mata da Corda; (2) Rio Abaete on the E. side of the same range; these two districts being among the head waters of the Rio de San Francisco and its tributaries; (3) Diamantina, on and about the watershed separating the Rio de San Francisco from the Rio Jequitinhonha; and (4) Grao Mogul, nearly 200 m. to the N.E. of Diamantina on the latter river.
The Rio Abaete district was worked on a considerable scale between 1785 and 1807, but is now abandoned. Diamantina is at present the most important district; it occupies a mountainous plateau, and the diamonds are found both on the plateau and in the river valleys below it. The mountains consist here of an ancient laminated micaceous quartzite, which is in parts a flexible sandstone known as itacolumite, and in parts a conglomerate; it is interbedded with clay-slate, mica-schist, hornblende-schist and haematite-schist, and intersected by veins of quartz. This series is overlain unconformably by a younger quartzite of similar character, and itself rests upon the crystalline schists. The diamond is found under three conditions: (1) in the gravels of the present rivers, embedded in a ferruginous clay-cemented conglomerate known as cascalho; (2) in terraces (gupiarras) in a similar conglomerate occupying higher levels in the present valleys; (3) in plateau deposits in a coarse surface conglomerate known as gurgulho, the diamond and other heavy minerals being embedded in the red clay which cements the larger blocks. Under all these three conditions the diamond is associated with fragments of the rocks of the country and the minerals derived from them, especially quartz, hornstone, jasper, the polymorphous oxide of titanium (rutile, anatase and brookite), oxides and hydrates of iron (magnetite, ilmenite, haematite, limonite), oxide of tin, iron pyrites, tourmaline, garnet, xenotime, monazite, kyanite, diaspore, sphene, topaz, and several phosphates, and also gold. Since the heavy minerals of the cascalho in the river beds are more worn than those of the terraces, it is highly probable that they have been derived by the cutting down of the older river gravels represented by the terraces; and since in both deposits the heavy minerals are more abundant near the heads of the valleys in the plateau, it is also highly probable that both have really been derived from the plateau deposit. In the latter, especially at São João da Chapada, the minerals accompanying the diamond are scarcely worn at all; in the terraces and the river beds they are more worn and more abundant; the terraces, therefore, are to be regarded as a first concentration of the plateau material by the old rivers; and the cascalho as a second concentration by the modern rivers. The mining is carried on by negroes under the supervision of overseers; the cascalho is dug out in the dry season and removed to a higher level, and is afterwards washed out by hand in running water in shallow wooden basins (bateas). The terraces can be worked at all seasons, and the material is partly washed out by leading streams on to it. The washing of the plateau material is effected in reservoirs of rain water.
It is difficult to obtain an estimate of the actual production of the Minas Geraes mines, for no official returns have been published, but in recent years it has certainly been rivalled by the yield in Bahia. The diamond here occurs in river gravels and sands associated with the same minerals as in Minas Geraes; since 1844 the richest mines have been worked in the Serra de Cincora, where the mountains are intersected by the river Paraguassu and its tributaries; it is said that there were as many as 20,000 miners working here in 1845, and it was estimated that 54,000 carats were produced in Bahia in 1858. The earlier workings were in the Serra de Chapada to the N.W. of the mines just mentioned. In 1901 there were about 5000 negroes employed in the Bahia mines; methods were still primitive; the cascalho was dug out from the river beds or tunnelled out from the valley side, and washed once a week in sluices of running water, where it was turned over with the hoe, and finally washed in wooden basins and picked over by hand; sometimes also the diamantiferous material is scooped out of the bed of the shallow rivers by divers, and by men working under water in caissons. It is almost exclusively in the mines of Bahia, and in particular in the Cincora district, that the valuable carbonado is found. The carbonado and the diamond have been traced to an extensive hard conglomerate which occurs in the middle of the sandstone formation. Diamonds are also mined at Salobro on the river Pardo not far inland from the port of Canavieras in the S.E. corner of Bahia. The enormous development of the South African mines, which supplied in 1906, about 90% of the world’s produce, has thrown into the shade the Brazilian production; but the Bulletin for Feb. 1909 of the International Bureau of American Republics gave a very confident account of its future, under improved methods.
South Africa.—-The first discovery was made in 1867 by Dr W. G. Atherstone, who identified as diamond a pebble obtained from a child in a farm on the banks of the Orange river and brought by a trader to Grahamstown; it was bought for £500 and displayed in the Paris Exhibition of that year. In 1869 a stone weighing 83½ carats was found near the Orange river; this was purchased by the earl of Dudley for £25,000 and became famous as the “Star of South Africa.” A rush of prospectors at once took place to the banks of the Orange and Vaal rivers, and resulted in considerable discoveries, so that in 1870 there was a mining camp of no less than 10,000 persons on the “River Diggings.” In the River Diggings the mining was carried on in the coarse river gravels, and by the methods of the Brazilian negroes and of gold placer-miners. A diggers’ committee limited the size of claims to 30 ft. square, with free access to the river bank; the gravel and sand were washed in cradles provided with screens of perforated metal, and the concentrates were sorted by hand on tables by means of an iron scraper.
But towards the close of 1870 stones were found at Jagersfontein and at Dutoitspan, far from the Vaal river, and led to a second great rush of prospectors, especially to Dutoitspan, and in 1871 to what is now the Kimberley mine in the neighbourhood of the latter. At each of these spots the diamantiferous area was a roughly circular patch of considerable size, and in some occupied the position of one of those depressions or “pans” so frequent in S. Africa. These “dry diggings” were therefore at first supposed to be alluvial in origin like the river gravels; but it was soon discovered that, below the red surface soil and the underlying calcareous deposit, diamonds were also found in a layer of yellowish clay about 50 ft. thick known as “yellow ground.” Below this again was a hard bluish-green serpentinous rock which was at first supposed to be barren bed-rock; but this also contained the precious stone, and has become famous, under the name of “blue ground,” as the matrix of the S. African diamonds. The yellow ground is merely decomposed blue ground. In the Kimberley district five of these round patches of blue ground were found within an area little more than 3 m. in diameter; that at Kimberley occupying 10 acres, that at Dutoitspan 23 acres. There were soon 50,000 workers on this field, the canvas camp was replaced by a town of brick and iron surrounded by the wooden huts of the natives, and Kimberley became an important centre.
It was soon found that each mine was in reality a huge vertical funnel or crater descending to an unknown depth, and filled with diamantiferous blue ground. At first each claim was an independent pit 31 ft. square sunk into the blue ground; the diamantiferous rock was hoisted by bucket and windlass, and roadways were left across the pit to provide access to the claims. But the roadways soon fell in, and ultimately haulage from the claims could only be provided by means of a vast system of wire ropes extending from a triple staging of windlasses erected round the entire edge of the mine, which had by this time become a huge open pit; the ropes from the upper windlasses extended to the centre, and those from the lower tier to the sides of the pit; covering the whole mass like a gigantic cobweb. (See Plate II. fig. 12.) The buckets of blue ground were hauled up these ropes by means of horse whims, and in 1875 steam winding engines began to be employed. By this time also improved methods in the treatment of the blue ground were introduced. It was carried off in carts to open spaces, where an exposure of some weeks to the air was found to pulverize the hard rock far more efficiently than the old method of crushing with mallets. The placer-miner’s cradle and rocking-trough were replaced by puddling troughs stirred by a revolving comb worked by horse power; reservoirs were constructed for the scanty water-supply, bucket elevators were introduced to carry away the tailings; and the natives were confined in compounds. For these improvements co-operation was necessary; the better claims, which in 1872 had risen from £100 to more than £4000 in value, began to be consolidated, and a Mining Board was introduced.
Plate I.
 |
 |
| Fig. 9.—DE BEERS MINE, 1874. | Fig. 10.—KIMBERLEY MINE, 1874. |
 | |
| Fig. 11.—DE BEERS MINE, 1873. (From photographs by C. Evans.) | |
Plate II.
 |
| Fig. 12.—KIMBERLEY MINE, 1874. |
 |
| Fig. 13.—KIMBERLEY MINE, 1902. (From photographs by C. Evans.) |
In a very few years, however, the open pit mining was rendered impossible by the mud rushes, by the falls of the masses of barren rock known as “reef,” which were left standing in the mine, and by landslips from the sides, so that in 1883, when the pit had reached a depth of about 400 ft., mining in the Kimberley crater had become almost impossible. By 1889, in the whole group of mines, Kimberley, Dutoitspan, De Beers and Bultfontein, open pit working was practically abandoned. Meanwhile mining below the bottom of the pits by means of shafts and underground tunnels had been commenced; but the full development of modern methods dates from the year 1889 when Cecil Rhodes and Alfred Beit, who had already secured control of the De Beers mine, acquired also the control of the Kimberley mine, and shortly afterwards consolidated the entire group in the hands of the De Beers Company. (See Kimberley.)
The scene of native mining was now transferred from the open pit to underground tunnels; the vast network of wire ropes (Plate II. fig. 12) with their ascending and descending buckets disappeared, and with it the cosmopolitan crowd of busy miners working like ants at the bottom of the pit. In place of all this, the visitor to Kimberley encounters at the edge of the town only a huge crater, silent and apparently deserted, with no visible sign of the great mining operations which are conducted nearly half a mile below the surface. The aspect of the Kimberley pit in 1906 is shown in fig. 13 of Plate II., which may be compared with the section of fig. 8.
In fig. 13, Plate II., the sequence of the basalt, shale and melaphyre is clearly visible on the sides of the pit; and fig. 8 shows how the crater or “pipe” of blue ground has penetrated these rocks and also the underlying quartzite. The workings at De Beers had extended into the still more deeply seated granite in 1906. Figure 9, Plate I., shows the top of the De Beers’ crater with basalt overlying the shale. Figure 8 also explains the modern system of mining introduced by Gardner Williams. A vertical shaft is sunk in the vicinity of the mine, and from this horizontal tunnels are driven into the pipe at different levels separated by intervals of 40 ft. Through the blue ground itself on each level a series of parallel tunnels about 120 ft. apart are driven to the opposite side of the pipe, and at right angles to these, and 36 ft. apart, another series of tunnels. When the tunnels reach the side of the mine they are opened upwards and sideways so as to form a large chamber, and the overlying mass of blue ground and débris is allowed to settle down and fill up the gallery. On each level this process is carried somewhat farther back than on the level below (fig. 8); material is thus continually withdrawn from one side of the mine and extracted by means of the rock shaft on the opposite side, while the superincumbent débris is continually sinking, and is allowed to fall deeper on the side farthest from the shaft as the blue ground is withdrawn from beneath it. In 1905 the main shaft had been sunk to a depth of 2600 ft. at the Kimberley mine.
For the extraction and treatment of the blue ground the De Beers Company in its great winding and washing plant employs labour-saving machinery on a gigantic scale. The ground is transferred in trucks to the shaft where it is automatically tipped into skips holding 96 cubic ft. (six truck loads); these are rapidly hoisted to the surface, where their contents are automatically dumped into side-tipping trucks, and these in turn are drawn away in a continual procession by an endless wire rope along the tram lines leading to the vast “distributing floors.” These are open tracts upon which the blue ground is spread out and left exposed to sun and rain until it crumbles and disintegrates, the process being hastened by harrowing with steam ploughs; this may require a period of three or six months, or even a year. The stock of blue ground on the floors at one time in 1905 was nearly 4,500,000 loads. The disintegrated ground is then brought back in the trucks and fed through perforated cylinders into the washing pans; the hard blue which has resisted disintegration on the floors, and the lumps which are too big to pass the cylindrical sieves, are crushed before going to the pans. These are shallow cylindrical troughs containing muddy water in which the diamonds and other heavy minerals (concentrates) are swept to the rim by revolving toothed arms, while the lighter stuff escapes near the centre of the pan. The concentrates are then passed over sloping tables (pulsator) and shaken to and fro under a stream of water which effects a second concentration of the heaviest material.
Until recently the final separation of the diamond from the concentrates was made by hand picking, but even this has now been replaced by machinery, owing to the remarkable discovery that a greased surface will hold a diamond while allowing the other heavy minerals to pass over it. The concentrates are washed down a sloping table of corrugated iron which is smeared with grease, and it is found that practically all the diamonds adhere to the table, and the other minerals are washed away. At the large and important Premier mine in the Transvaal the Elmore process, used in British Columbia and in Wales for the separation of metallic ores, has been also introduced. In the Elmore process oil is employed to float off the materials which adhere to it, while the other materials remain in the water, the oil being separated from the water by centrifugal action. The other minerals found in the concentrates are pebbles and fragments of pyrope, zircon, cyanite, chrome-diopside, enstatite, a green pyroxene, mica, ilmenite, magnetite, chromite, hornblende, olivine, barytes, calcite and pyrites.
In all the S. African mines the diamonds are not only crystals of various weights from fractions of a carat to 150 carats, but also occur as microscopic crystals disseminated through the blue ground. In spite of this, however, the average yield in the profitable mines is only from 0.2 carat to 0.6 carat per load of 1600 lb, or on an average about 1½ grs. per ton. The annual output of diamonds from the De Beers mines was valued in 1906 at nearly £5,000,000; the value per carat ranging from about 35s. to 70s.
 |
| From Gardner Williams’s Diamond Mines of South Africa. Fig. 8. |
Pipes similar to those which surround Kimberley have been found in other parts of S. Africa. One of the best known is that of Jagersfontein, which was really the first of the dry diggings (discovered in 1870). This large mine is near Fauresmith and 80 m. to the south of Kimberley. In 1905 the year’s production from the Orange River Colony mines was more than 320,000 carats, valued at £938,000. But by far the largest of all the pipes hitherto discovered is the Premier mine in the Transvaal, about 300 m. to the east of Kimberley. This was discovered in 1902 and occupies an area of about 75 acres. In 1906 it was being worked as a shallow open mine; but the description of the Kimberley methods given above is applicable to the washing plant at that time being introduced into the Premier mine upon a very large scale. Comparatively few of the pipes which have been discovered are at all rich in diamonds, and many are quite barren; some are filled with “hard blue” which even if diamantiferous may be too expensive to work.
The most competent S. African geologists believe all these remarkable pipes to be connected with volcanic outbursts which occurred over the whole of S. Africa during the Cretaceous period (after the deposition of the Stormberg beds), and drilled these enormous craters through all the later formations. With the true pipes are associated dykes and fissures also filled with diamantiferous blue ground. It is only in the more northerly part of the country that the pipes are filled with blue ground (or “kimberlite”), and that they are diamantiferous; but over a great part of Cape Colony have been discovered what are probably similar pipes filled with agglomerates, breccias and tuffs, and some with basic lavas; one, in particular, in the Riversdale Division near the southern coast, being occupied by a melilite-basalt. It is quite clear that the occurrence of the diamond in the S. African pipes is quite different from the occurrences in alluvial deposits which have been described above. The question of the origin of the diamond in S. Africa and elsewhere is discussed below.
The River Diggings on the Vaal river are still worked upon a small scale, but the production from this source is so limited that they are of little account in comparison with the mines in the blue ground. The stones, however, are good; since they differ somewhat from the Kimberley crystals it is probable that they were not derived from the present pipes. Another S. African locality must be mentioned; considerable finds were reported in 1905 and 1906 from gravels at Somabula near Gwelo in Rhodesia where the diamond is associated with chrysoberyl, corundum (both sapphire and ruby), topaz, garnet, ilmenite, staurolite, rutile, with pebbles of quartz, granite, 162 chlorite-schist, &c. Diamond has also been reported from kimberlite “pipes” in Rhodesia.
Other Localities.—In addition to the South American localities mentioned above, small diamonds have also been mined since their discovery in 1890 on the river Mazaruni in British Guiana, and finds have been reported in the gold washings of Dutch Guiana. Borneo has possessed a diamond industry since the island was first settled by the Malays; the references in the works of Garcia de Orta, Linschoten, De Boot, De Laet and others, to Malacca as a locality relate to Borneo. The large Borneo stone, over 360 carats in weight, known as the Matan, is in all probability not a diamond. The chief mines are situated on the river Kapuas in the west and near Bandjarmassin in the south-east of the island, and the alluvial deposits in which they occur are worked by a small number of Chinese and Malays. Australia has yielded diamonds in alluvial deposits near Bathurst (where the first discovery was made in 1851) and Mudgee in New South Wales, and also near Bingara and Inverell in the north of the colony. At Mount Werong a stone weighing 29 carats was found in 1905. At Ruby Hill near Bingara they were found in a breccia filling a volcanic pipe. At Ballina, in New England, diamonds have been found in the sea sand. Other Australian localities are Echunga in South Australia; Beechworth, Arena and Melbourne in Victoria; Freemantle and Nullagine in Western Australia; the Palmer and Gilbert rivers in Queensland. These have been for the most part discoveries in alluvial deposits of the goldfields, and the stones were small. In Tasmania also diamonds have been found in the Corinna goldfields. Europe has produced few diamonds. Humboldt searched for them in the Urals on account of the similarity of the gold and platinum deposits to those of Brazil, and small diamonds were ultimately found (1829) in the gold washings of Bissersk, and later at Ekaterinburg and other spots in the Urals. In Lapland they have been found in the sands of the Pasevig river. Siberia has yielded isolated diamonds from the gold washings of Yenisei. In North America a few small stones have been found in alluvial deposits, mostly auriferous, in Georgia, N. and S. Carolina, Kentucky, Virginia, Tennessee, Wisconsin, California, Oregon and Indiana. A crystal weighing 23¾ carats was found in Virginia in 1855, and one of 21¼ carats in Wisconsin in 1886. In 1906 a number of small diamonds were discovered in an altered peridotite somewhat resembling the S. African blue ground, at Murfreesboro, Pike county, Arkansas. Considerable interest attaches to the diamonds found in Wisconsin, Michigan and Ohio near the Great Lakes, for they are here found in the terminal moraines of the great glacial sheet which is supposed to have spread southwards from the region of Hudson Bay; several of the drift minerals of the diamantiferous region of Indiana have been identified as probably of Canadian origin; no diamonds have however yet been found in the intervening country of Ontario. A rock similar to the blue ground of Kimberley has been found in the states of Kentucky and New York. The occurrence of diamond in meteorites is described below.
Origin of the Diamond in Nature.—It appears from the foregoing account that at most localities the diamond is found in alluvial deposits probably far from the place where it originated. The minerals associated with it do not afford much clue to the original conditions; they are mostly heavy minerals derived from the neighbouring rocks, in which the diamond itself has not been observed. Among the commonest associates of the diamond are quartz, topaz, tourmaline, rutile, zircon, magnetite, garnet, spinel and other minerals which are common accessory constituents of granite, gneiss and the crystalline schists. Gold (also platinum) is a not infrequent associate, but this may only mean that the sands in which the diamond is found have been searched because they were known to be auriferous; also that both gold and diamond are among the most durable of minerals and may have survived from ancient rocks of which other traces have been lost.
The localities at which the diamond has been supposed to occur in its original matrix are the following:—at Wajra Karur, in the Cuddapah district, India, M. Chaper found diamond with corundum in a decomposed red pegmatite vein in gneiss. At Sāo João da Chapada, in Minas Geraes, diamonds occur in a clay interstratified with the itacolumite, and are accompanied by sharp crystals of rutile and haematite in the neighbourhood of decomposed quartz veins which intersect the itacolumite. It has been suggested that these three minerals were originally formed in the quartz veins. In both these occurrences the evidence is certainly not sufficient to establish the presence of an original matrix. At Inverell in New South Wales a diamond (1906) has been found embedded in a hornblende diabase which is described as a dyke intersecting the granite. Finally there is the remarkable occurrence in the blue ground of the African pipes.
There has been much controversy concerning the nature and origin of the blue ground itself; and even granted that (as is generally believed) the blue ground is a much serpentinized volcanic breccia consisting originally of an olivine-bronzite-biotite rock (the so-called kimberlite), it contains so many rounded and angular fragments of various rocks and minerals that it is difficult to say which of them may have belonged to the original rock, and whether any were formed in situ, or were brought up from below as inclusions. Carvill Lewis believed the blue ground to be true eruptive rock, and the carbon to have been derived from the bituminous shales of which it contains fragments. The Kimberley shales, which are penetrated by the De Beers group of pipes, were, however, certainly not the source of the carbon at the Premier (Transvaal) mine, for at this locality the shales do not exist. The view that the diamond may have crystallized out from solution in its present matrix receives some support from the experiments of W. Luzi, who found that it can be corroded by the solvent action of fused blue ground; from the experiments of J. Friedländer, who obtained diamond by dissolving graphite in fused olivine; and still more from the experiments of R. von Hasslinger and J. Wolff, who have obtained it by dissolving graphite in a fused mixture of silicates having approximately the composition of the blue ground. E. Cohen, who regarded the pipes as of the nature of a mud volcano, and the blue ground as a kimberlite breccia altered by hydrothermal action, thought that the diamond and accompanying minerals had been brought up from deep-seated crystalline schists. Other authors have sought the origin of the diamond in the action of the hydrated magnesian silicates on hydrocarbons derived from bituminous schists, or in the decomposition of metallic carbides.
Of great scientific interest in this connexion is the discovery of small diamonds in certain meteorites, both stones and irons; for example, in the stone which fell at Novo-Urei in Penza, Russia, in 1886, in a stone found at Carcote in Chile, and in the iron found at Cañon Diablo in Arizona. Graphitic carbon in cubic form (cliftonite) has also been found in certain meteoric “irons,” for example in those from Magura in Szepes county, Hungary, and Youndegin near York in Western Australia. The latter is now generally believed to be altered diamond. The fact that H. Moissan has produced the diamond artificially, by allowing dissolved carbon to crystallize out at a high temperature and pressure from molten iron, coupled with the occurrence in meteoric iron, has led Sir William Crookes and others to conclude that the mineral may have been derived from deep-seated iron containing carbon in solution (see the article Gem, Artificial). Adolf Knop suggested that this may have first yielded hydrocarbons by contact with water, and that from these the crystalline diamond has been formed. The meteoric occurrence has even suggested the fanciful notion that all diamonds were originally derived from meteorites. The meteoric iron of Arizona, some of which contains diamond, is actually found in and about a huge crater which is supposed by some to have been formed by an immense meteorite penetrating the earth’s crust.
It is, at any rate, established that carbon can crystallize as diamond from solution in iron, and other metals; and it seems that high temperature and pressure and the absence of oxidizing agents are necessary conditions. The presence of sulphur, nickel, &c., in the iron appears to favour the production of the diamond. On the other hand, the occurrence in meteoric stones, and the experiments mentioned above, show that the diamond may also crystallize from a basic magma, capable of yielding some of the metallic oxides and ferro-magnesian silicates; a magma, therefore, which is not devoid of oxygen. This is still more forcibly suggested by the remarkable eclogite boulder found in the blue ground of the Newlands mine, not far from the Vaal river, and described by T. G. Bonney. The boulder is a crystalline rock consisting of pyroxene (chrome-diopside), garnet, and a little olivine, and is studded with diamond crystals; a portion of it is preserved in the British Museum (Natural History). In another eclogite boulder, diamond was found partly embedded in pyrope. Similar boulders have also been found in the blue ground elsewhere. Specimens of pyrope with attached or embedded diamond had previously been found in the blue ground of the De Beers mines. In the Newlands boulder the diamonds have the appearance of being an original constituent of the eclogite. It seems therefore that a holocrystalline pyroxene-garnet rock may be one source of the diamond found in blue ground. On the other hand many tons of the somewhat similar eclogite in the De Beers mine have been crushed and have not yielded diamond. Further, the ilmenite, which is the most characteristic associate of the diamond in blue ground, and other of the accompanying minerals, may have come from basic rocks of a different nature.
The Inverell occurrence may prove to be another example of diamond crystallized from a basic rock.
In both occurrences, however, there is still the possibility that the eclogite or the basalt is not the original matrix, but may have caught up the already formed diamond from some other matrix. Some regard the eclogite boulders as derived from deep-seated crystalline rocks, others as concretions in the blue ground.
None of the inclusions in the diamond gives any clue to its origin; diamond itself has been found as an inclusion, as have also black specks of some carbonaceous materials. Other black specks have been identified as haematite and ilmenite; gold has also been found; other included minerals recorded are rutile, topaz, quartz, pyrites, apophyllite, and green scales of chlorite (?). Some of these are of very doubtful identification; others (e.g. apophyllite and chlorite) may have been introduced along cracks. Some of the fibrous inclusions were identified by H. R. Göppert as vegetable structures and were supposed to point to an organic origin, but this view is no longer held. Liquid inclusions, some of which are certainly carbon dioxide, have also been observed.
Finally, then, both experiment and the natural occurrence in rocks and meteorites suggest that diamond may crystallize not only from iron but also from a basic silicate magma, possibly from various rocks consisting of basic silicates. The blue ground of S. Africa may be 163 the result of the serpentinization of several such rocks, and although now both brecciated and serpentinized some of these may have been the original matrix. A circumstance often mentioned in support of this view is the fact that the diamonds in one pipe generally differ somewhat in character from those of another, even though they be near neighbours.
History.—All the famous diamonds of antiquity must have been Indian stones. The first author who described the Indian mines at all fully was the Portuguese, Garcia de Orta (1565), who was physician to the viceroy of Goa. Before that time there were only legendary accounts like that of Sindbad’s “Valley of the Diamonds,” or the tale of the stones found in the brains of serpents. V. Ball thinks that the former legend originated in the Indian practice of sacrificing cattle to the evil spirits when a new mine is opened; birds of prey would naturally carry off the flesh, and might give rise to the tale of the eagles carrying diamonds adhering to the meat.
The following are some of the most famous diamonds of the world:—
A large stone found in the Golconda mines and said to have weighed 787 carats in the rough, before being cut by a Venetian lapidary, was seen in the treasury of Aurangzeb in 1665 by Tavernier, who estimated its weight after cutting as 280 (?) carats, and described it as a rounded rose-cut-stone, tall on one side. The name Great Mogul has been frequently applied to this stone. Tavernier states that it was the famous stone given to Shah Jahan by the emir Jumla. The Orloff, stolen by a French soldier from the eye of an idol in a Brahmin temple, stolen again from him by a ship’s captain, was bought by Prince Orloff for £90,000, and given to the empress Catharine II. It weighs 194¾ carats, is of a somewhat yellow tinge, and is among the Russian crown jewels. The Koh-i-nor, which was in 1739 in the possession of Nadir Shah, the Persian conqueror, and in 1813 in that of the raja of Lahore, passed into the hands of the East India Company and was by them presented to Queen Victoria in 1850. It then weighed 1861⁄16 carats, but was recut in London by Amsterdam workmen, and now weighs 1061⁄16 carats. There has been much discussion concerning the possibility of this stone and the Orloff being both fragments of the Great Mogul. The Mogul Baber in his memoirs (1526) relates how in his conquest of India he captured at Agra the great stone weighing 8 mishkals, or 320 ratis, which may be equivalent to about 187 carats. The Koh-i-nor has been identified by some authors with this stone and by others with the stone seen by Tavernier. Tavernier, however, subsequently described and sketched the diamond which he saw as shaped like a bisected egg, quite different therefore from the Koh-i-nor. Nevil Story Maskelyne has shown reason for believing that the stone which Tavernier saw was really the Koh-i-nor and that it is identical with the great diamond of Baber; and that the 280 carats of Tavernier is a misinterpretation on his part of the Indian weights. He suggests that the other and larger diamond of antiquity which was given to Shah Jahan may be one which is now in the treasury of Teheran, and that this is the true Great Mogul which was confused by Tavernier with the one he saw. (See Ball, Appendix I. to Tavernier’s Travels (1889); and Maskelyne, Nature, 1891, 44, p. 555.).
The Regent or Pitt diamond is a magnificent stone found in either India or Borneo; it weighed 410 carats and was bought for £20,400 by Pitt, the governor of Madras; it was subsequently, in 1717, bought for £80,000 (or, according to some authorities, £135,000) by the duke of Orleans, regent of France; it was reduced by cutting to 13614⁄16 carats; was stolen with the other crown jewels during the Revolution, but was recovered and is still in France. The Akbar Shah was originally a stone of 116 carats with Arabic inscriptions engraved upon it; after being cut down to 71 carats it was bought by the gaikwar of Baroda for £35,000. The Nizam, now in the possession of the nizam of Hyderabad, is supposed to weigh 277 carats; but it is only a portion of a stone which is said to have weighed 440 carats before it was broken. The Great Table, a rectangular stone seen by Tavernier in 1642 at Golconda, was found by him to weigh 2423⁄16 carats; Maskelyne regards it as identical with the Darya-i-nur, which is also a rectangular stone weighing about 186 carats in the possession of the shah of Persia. Another stone, the Taj-e-mah, belonging to the shah, is a pale rose pear-shaped stone and is said to weigh 146 carats.
Other famous Indian diamonds are the following:—The Sancy, weighing 5312⁄16 carats, which is said to have been successively the property of Charles the Bold, de Sancy, Queen Elizabeth, Henrietta Maria, Cardinal Mazarin, Louis XIV.; to have been stolen with the Pitt during the French Revolution; and subsequently to have been the property of the king of Spain, Prince Demidoff and an Indian prince. The Nassak, 785⁄8 carats, the property of the duke of Westminster. The Empress Eugénie, 51 carats, the property of the gaikwar of Baroda. The Pigott, 49 carats(?), which cannot now be traced. The Pasha, 40 carats. The White Saxon, 48¾ carats. The Star of Este, 2513⁄32 carats.
Coloured Indian diamonds of large size are rare; the most famous are:—a beautiful blue brilliant, 672⁄16 carats, cut from a stone weighing 1123⁄16 carats brought to Europe by Tavernier. It was stolen from the French crown jewels with the Regent and was never recovered. The Hope, 44¼ carats, has the same colour and is probably a portion of the missing stone: it was so-called as forming part of the collection of H. T. Hope (bought for £18,000), and was sold again in 1906 (resold 1909). Two other blue diamonds are known, weighing 13¾ and 1¾ carats, which may also be portions of the French diamond. The Dresden Green, one of the Saxon crown jewels, 40 carats, has a fine apple-green colour. The Florentine, 1331⁄5 carats, one of the Austrian crown jewels, is a very pale yellow.
The most famous Brazilian stones are:—The Star of the South, found in 1853, when it weighed 254½ carats and was sold for £40,000; when cut it weighed 125 carats and was bought by the gaikwar of Baroda for £80,000. Also a diamond belonging to Mr Dresden, 119 carats before, and 76½ carats after cutting.
Many large stones have been found in South Africa; some are yellow but some are as colourless as the best Indian or Brazilian stones. The most famous are the following:—the Star of South Africa, or Dudley, mentioned above, 83½ carats rough, 46½ carats cut. The Stewart, 2883⁄8 carats rough, 120 carats cut. Both these were found in the river diggings. The Porter Rhodes from Kimberley, of the finest water, weighed about 150 carats. The Victoria, 180 carats, was cut from an octahedron weighing 457½ carats, and was sold to the nizam of Hyderabad for £400,000. The Tiffany, a magnificent orange-yellow stone, weighs 125½ carats cut. A yellowish octahedron found at De Beers weighed 428½ carats, and yielded a brilliant of 288½ carats. Some of the finest and largest stones have come from the Jagersfontein mine; one, the Jubilee, found in 1895, weighed 640 carats in the rough and 239 carats when cut. Until 1905 the largest known diamond in the world was the Excelsior, found in 1893 at Jagersfontein by a native while loading a truck. It weighed 971 carats, and was ultimately cut into ten stones weighing from 68 to 13 carats. But all previous records were surpassed in 1905 by a magnificent stone more than three times the size of any known diamond, which was found in the yellow ground at the newly discovered Premier mine in the Transvaal. This extraordinary diamond weighed 3025¾ carats (11⁄3 ℔) and was clear and water white; the largest of its surfaces appeared to be a cleavage plane, so that it might be only a portion of a much larger stone. It was known as the Cullinan Diamond. This stone was purchased by the Transvaal government in 1907 and presented to King Edward VII. It was sent to Amsterdam to be cut, and in 1908 was divided into nine large stones and a number of small brilliants. The four largest stones weigh 516½ carats, 3093⁄16 carats, 92 carats and 62 carats respectively. Of these the first and second are the largest brilliants in existence. All the stones are flawless and of the finest quality.
Bibliography.—Boetius de Boot, Gemmarum et lapidum historia (1609); D. Jeffries, A Treatise on Diamonds and Pearls (1757); J. Mawe, Travels in the Interior of Brazil (1812); Treatise on Diamonds and Precious Stones (1813): Pinder, De adamante (1829); Murray, Memoir on the Nature of the Diamond (1831); C. Zerenner, De adamante dissertatio (1850); H. Emanuel, Diamonds and Precious Stones (1865); A. Schrauf, Edelsteinkunde (1869); N. Jacobs and N. Chatrian, Monographie du diamant (1880); V. Ball, Geology of India (1881); C. W. King, The Natural History of Precious Stones 164 and Precious Metals (1883); M. E. Boutan, Le Diamant (1886); S. M. Burnham, Precious Stones in Nature, Art and Literature (1887); P. Groth, Grundriss der Edelsteinkunde (1887); A. Liversidge, The Minerals of New South Wales (1888); Tavernier’s Travels in India, translated by V. Ball (1889); E. W. Streeter, The Great Diamonds of the World (1896); H. C. Lewis, The Genesis and Matrix of the Diamond (1897); L. de Launay, Les Diamants du Cap (1897); C. Hintze, Handbuch der Mineralogie (1898); E. W. Streeter, Precious Stones and Gems (6th ed., 1898); Dana, System of Mineralogy (1899); Kunz and others, The Production of Precious Stones (in annual, Mineral Resources of the United States); M. Bauer, Precious Stones (trans. L. J. Spencer, 1904); A. W. Rogers, An Introduction to the Geology of Cape Colony (1905); Gardner F. Williams, The Diamond Mines of South Africa (revised edition, 1906); George F. Kunz, “Diamonds, a study of their occurrence in the United States, with descriptions and comparisons of those from all known localities” (U.S. Geol. Survey, 1909); P. A. Wagner, Die Diamantführenden Gesteine Südafrikas (1909).
Among papers in scientific periodicals may be mentioned articles by Adler, Ball, Baumhauer, Beck, Bonney, Brewster, Chaper, Cohen, Crookes, Daubrée, Derby, Des Cloizeaux, Doelter, Dunn, Flight, Friedel, Gorceix, Gürich, Goeppert, Harger, Hudleston, Hussak, Jannettaz, Jeremejew, de Launay, Lewis, Maskelyne, Meunier, Moissan, Molengraaff, Moulle, Rose, Sadebeck, Scheibe, Stelzner, Stow. See generally Hintze’s Handbuch der Mineralogie.
1 Diamonds are invariably weighed in carats and in ½, ¼, 1⁄8, 1⁄16, 1⁄32, 1⁄64 of a carat. One (English) carat = 3.17 grains = .2054 gram. One ounce = 151½ carats. (See Carat.)
DIAMOND NECKLACE, THE AFFAIR OF THE, a mysterious incident at the court of Louis XVI. of France, which involved the queen Marie Antoinette. The Parisian jewellers Boehmer and Bassenge had spent some years collecting stones for a necklace which they hoped to sell to Madame Du Barry, the favourite of Louis XV., and after his death to Marie Antoinette. In 1778 Louis XVI. proposed to the queen to make her a present of the necklace, which cost 1,600,000 livres. But the queen is said to have refused it, saying that the money would be better spent equipping a man-of-war. According to others, Louis XVI. himself changed his mind. After having vainly tried to place the necklace outside of France, the jewellers attempted again in 1781 to sell it to Marie Antoinette after the birth of the dauphin. It was again refused, but it was evident that the queen regretted not being able to acquire it.
At that time there was a personage at the court whom Marie Antoinette particularly detested. It was the cardinal Louis de Rohan, formerly ambassador at Vienna, whence he had been recalled in 1774, having incurred the queen’s displeasure by revealing to the empress Maria Theresa the frivolous actions of her daughter, a disclosure which brought a maternal reprimand, and for having spoken lightly of Maria Theresa in a letter of which Marie Antoinette learned the contents. After his return to France the cardinal was anxious to regain the favour of the queen in order to obtain the position of prime minister. In March 1784 he entered into relations with a certain Jeanne de St Remy de Valois, a descendant of a bastard of Henry II., who after many adventures had married a soi-disant comte de Lamotte, and lived on a small pension which the king granted her. This adventuress soon gained the greatest ascendancy over the cardinal, with whom she had intimate relations. She persuaded him that she had been received by the queen and enjoyed her favour; and Rohan resolved to use her to regain the queen’s good will. The comtesse de Lamotte assured the cardinal that she was making efforts on his behalf, and soon announced to him that he might send his justification to Marie Antoinette. This was the beginning of a pretended correspondence between Rohan and the queen, the adventuress duly returning replies to Rohan’s notes, which she affirmed to come from the queen. The tone of the letters became very warm, and the cardinal, convinced that Marie Antoinette was in love with him, became ardently enamoured of her. He begged the countess to obtain a secret interview for him with the queen, and a meeting took place in August 1784 in a grove in the garden at Versailles between him and a lady whom the cardinal believed to be the queen herself. Rohan offered her a rose, and she promised him that she would forget the past. Later a certain Marie Lejay (renamed by the comtesse “Baronne Gay d’Oliva,” the last word being apparently an anagram of Valoi), who resembled Marie Antoinette, stated that she had been engaged to play the role of queen in this comedy. In any case the countess profited by the cardinal’s conviction to borrow from him sums of money destined ostensibly for the queen’s works of charity. Enriched by these, the countess was able to take an honourable place in society, and many persons believed her relations with Marie Antoinette, of which she boasted openly and unreservedly, to be genuine. It is still an unsettled question whether she simply mystified people, or whether she was really employed by the queen for some unknown purpose, perhaps to ruin the cardinal. In any case the jewellers believed in the relations of the countess with the queen, and they resolved to use her to sell their necklace. She at first refused their commission, then accepted it. On the 21st of January 1785 she announced that the queen would buy the necklace, but that not wishing to treat directly, she left the affair to a high personage. A little while later Rohan came to negotiate the purchase of the famous necklace for the 1,600,000 livres, payable in instalments. He said that he was authorized by the queen, and showed the jewellers the conditions of the bargain approved in the handwriting of Marie Antoinette. The necklace was given up. Rohan took it to the countess’s house, where a man, in whom Rohan believed he recognized a valet of the queen, came to fetch it. Madame de Lamotte had told the cardinal that Marie Antoinette would make him a sign to indicate her thanks, and Rohan believed that she did make him a sign. Whether it was so, or merely chance or illusion, no one knows. But it is certain that the cardinal, convinced that he was acting for the queen, had engaged the jewellers to thank her; that Boehmer and Bassenge, before the sale, in order to be doubly sure, had sent word to the queen of the negotiations in her name; that Marie Antoinette had allowed the bargain to be concluded, and that after she had received a letter of thanks from Boehmer, she had burned it. Meanwhile the “comte de Lamotte” appears to have started at once for London, it is said with the necklace, which he broke up in order to sell the stones.
When the time came to pay, the comtesse de Lamotte presented the cardinal’s notes; but these were insufficient, and Boehmer complained to the queen, who told him that she had received no necklace and had never ordered it. She had the story of the negotiations repeated for her. Then followed a coup de théâtre. On the 15th of August 1785, Assumption day, when the whole court was awaiting the king and queen in order to go to the chapel, the cardinal de Rohan, who was preparing to officiate, was arrested and taken to the Bastille. He was able, however, to destroy the correspondence exchanged, as he thought, with the queen, and it is not known whether there was any connivance of the officials, who did not prevent this, or not. The comtesse de Lamotte was not arrested until the 18th of August, after having destroyed her papers. The police set to work to find all her accomplices, and arrested the girl Oliva and a certain Reteaux de Villette, a friend of the countess, who confessed that he had written the letters given to Rohan in the queen’s name, and had imitated her signature on the conditions of the bargain. The famous charlatan Cagliostro was also arrested, but it was recognized that he had taken no part in the affair. The cardinal de Rohan accepted the parlement of Paris as judges. A sensational trial resulted (May 31, 1786) in the acquittal of the cardinal, of the girl Oliva and of Cagliostro. The comtesse de Lamotte was condemned to be whipped, branded and shut up in the Salpetrière. Her husband was condemned, in his absence, to the galleys for life. Villette was banished.
Public opinion was much excited by this trial. It is generally believed that Marie Antoinette was stainless in the matter, that Rohan was an innocent dupe, and that the Lamottes deceived both for their own ends. People, however, persisted in the belief that the queen had used the countess as an instrument to satisfy her hatred of the cardinal de Rohan. Various circumstances fortified this belief, which contributed to render Marie Antoinette very unpopular—her disappointment at Rohan’s acquittal, the fact that he was deprived of his charges and exiled to the abbey of la Chaise-Dieu, and finally the escape of the comtesse de Lamotte from the Salpetrière, with the connivance, as people believed, of the court. The adventuress, having taken refuge abroad, published Mémoires in which she accused the queen. Her 165 husband also wrote Mémoires, and lived until 1831, after having, it is said, received subsidies from Louis XVIII.
See M. Tourneux, Marie Antoinette devant l’histoire: Essai bibliographique (2nd ed., Paris, 1901); Émile Campardon, Marie Antoinette et le procès du collier (Paris, 1863); P. Audebert, L’Affaire du collier de la reine, d’après la correspondance inédite du chevalier de Pujol (Rouen, 1901); F. d’Albini, Marie Antoinette and the Diamond Necklace from another Point of View (London, 1900); Funck-Brentano, L’Affaire du collier (1903); A. Lang, Historical Mysteries (1904). Carlyle’s essay on The Diamond Necklace (first published in 1837 in Fraser’s Magazine) is of historical literary interest.
DIANA, in Roman mythology, an old Italian goddess, in later times identified with the Greek Artemis (q.v.). That she was originally an independent Italian deity is shown by her name, which is the feminine form of Janus (= Dianus). She is essentially the goddess of the moon and light generally, and presides over wood, plain and water, the chase and war. As the goddess of childbirth, she was known, like Juno, by the name of Lucina, the “bringer to light.” As the moon-goddess she was also identified with Hecate, and invoked as “three-formed” in reference to the phases of the moon. Her most celebrated shrine was in a grove at Aricia (whence her title of Nemorensis) near the modern lake of Nemi. Here she was worshipped side by side with a male deity Virbius, a god of the forest and the chase. This Virbius was subsequently identified with Hippolytus, the favourite of Artemis, who was said to have been brought to life by Aesculapius and conducted by Diana to Aricia (Ovid, Fasti, iii. 263, vi. 731, Metam. xv. 497; Virgil, Aeneid, vii. 761). A barbarous custom, perhaps reminiscent of human sacrifice once offered to her, prevailed in connexion with her ritual here; her priest, called Rex Nemorensis, who was a runaway slave, was obliged to qualify for office by slaying his predecessor in single combat (Strabo v. p. 239; Suetonius, Caligula, 35). This led to the identification of Diana with the Tauric Artemis, whose image was said to have been removed by Orestes to the grove of Aricia (see Aricini).
After the destruction of Alba Longa this grove was for a long time the united sanctuary of the neighbouring Latin and Rutulian cities, until at last it was extinguished beneath the supremacy of Rome. The festival of the goddess was on the ides (13th) of August, the full moon of the hot season. She was worshipped with torches, her aid was sought by women seeking a happy deliverance in childbirth, and many votive offerings have been found on the site. The worship of Diana was brought to Rome by Latin plebeians, and hence she was regarded as the protectress of the lower classes, and especially of slaves. In accordance with this, her most important temple was that on the Aventine, the chief seat of the plebeians, founded by Servius Tullius, originally as a sanctuary of the Latin league (Dion. Halic. iv. 26). No man was allowed to enter the temple, and on the day of its dedication (August 13) the slaves kept holiday (Plutarch, Quaest. Rom. 100). This Diana was identified with the sister of Apollo, and at the secular games she was worshipped simply as Artemis. Another celebrated sanctuary of Diana was that on the slopes of Mount Tifata near Capua (where she was worshipped under the name of Tifatina), a sanctuary specially favoured by Sulla and Vespasian. As Noctiluca (“giving light by night”) she had a sanctuary on the Palatine which was kept illuminated throughout the night (Varro, L.L. v. 68). On the Nemi priesthood see J. G. Frazer, Golden Bough.
DIANA MONKEY, a West African representative of the guenon monkeys taking its name, Cercopithecus diana, from the presence of a white crescent on the forehead; another characteristic feature being the pointed white beard. The general colour of the fur is greyish, with a deep tinge of chestnut from the middle of the back to the root of the tail. Together with C. neglectus of East and Central Africa, C. ignitus of Liberia, and C. roloway of the Gold Coast, the diana represents the special subgenus of guenons known as Pogonocebus. Although the diana monkey is commonly seen in menageries, little is known of its habits in the wild state.
DIANE DE FRANCE (1538-1619), duchess of Montmorency and Angoulême, was the natural daughter of Henry II. of France and a young Piedmontese, Filippe Duc. The constable de Montmorency went so far as to assert that of all the children of Henry II. Diane was the only one who resembled him. Catherine de’ Medici was greatly incensed at this affront, and took her revenge by having the constable disgraced on the death of Henry II. Brantôme is loud in praise of Diane. She was a perfect horsewoman and dancer, played several musical instruments, knew Spanish and Italian, and “estoit très belle de visage et de taille.” Legitimated in 1547, she was married in 1553 to Horace Farnese, second son of the duke of Parma, but her husband was killed soon afterwards at the siege of Hesdin. In order to assure his position, the constable de Montmorency wished to marry her to his eldest son, Francis. This was a romantic adventure, for Francis had clandestinely married Mademoiselle de Piennes. The constable dissolved this union, and after lengthy negotiations obtained the dispensation of the pope. On the 3rd of May 1559 Francis married Diane. A wise and moderate woman, Diane undoubtedly helped to make Francis de Montmorency one of the leaders of the party of the politiques. Again a widow in 1579, she had some influence at the court of Henry III., and negotiated his reconciliation with Henry of Navarre (1588). She retained her influence in the reign of Henry IV., conveyed the bodies of Catherine de’ Medici and Henry III. to St Denis, and died in 1619 at her hôtel of Angoulême.
See Brantôme, ed. by Lalanne, in the Coll de la société d’histoire de France, vol. viii. (1875); J. de Thou, Historia sui temporis... (1733); Matthieu de Morgues, Oraison funèbre de Diane de France (Paris, 1619).
DIANE DE POITIERS (1499-1566), duchess of Valentinois, and mistress of Henry II. of France, was the daughter of Jean de Poitiers, seigneur de St Vallier, who came of an old family of Dauphiné. In 1515 she married Louis de Brézé, grand seneschal of Normandy, by whom she had two daughters. She became a widow in 1533, but soon replaced her husband by a more illustrious lover, the king’s second son, Henry, who became dauphin in 1536. Although he was ten years younger than Diane, she inspired the young prince with a profound passion, which lasted until his death. The accession of Henry II. in 1547 was also the accession of Diane: she was virtual queen, while Henry’s lawful wife, Catherine de’ Medici, lived in comparative obscurity. The part Diane played, however, must not be exaggerated. More rapacious than ambitious, she concerned herself little with government, but devoted her energies chiefly to augmenting her income, and providing for her family and friends. Henry was the most prodigal of lovers, and gave her all rights over the duchy of Valentinois. Although she showed great tact in her dealings with the queen, Catherine drove her from the court after Henry’s death, and forced her to restore the crown jewels and to accept Chaumont in exchange for Chenonceaux. Diane retired to her château at Anet, where she died in 1566.
Several historians relate that she had been the mistress of Francis I. before she became the dauphin’s mistress, and that she gave herself to the king in order to obtain the pardon of her father, who had been condemned to death as an accomplice of the constable de Bourbon. This rumour, however, has no serious foundation. Men vied with each other in celebrating Diane’s beauty, which, if we may judge from her portraits, has been slightly exaggerated. She was a healthy, vigorous woman, and, by dint of great pains, succeeded in retaining her beauty late into life. It is said that even on the coldest mornings she would wash her face with well water. Diane was a patroness of the arts. She entrusted to Philibert de l’Orme the building of her château at Anet, and it was for her that Jean Goujon executed his masterpiece, the statue of Diana, now in the Louvre.
See G. Guiffrey, Lettres inédites de Diane de Poytiers (Paris, 1866) and Procès criminel de Jehan de Poytiers (Paris, 1867); Capefigue, Diane de Poitiers (Paris, 1860); Hay, Madame Dianne de Poytiers (London, 1900).
DIAPASON (Gr. διὰ πασῶν, through all), a term in music, originally for an interval of an octave. The Greek is an abbreviation of ἡ διὰ πασῶν χορδῶν συμφωνία, a consonance through all the tones of the scale. In this sense it is only used now, loosely, for the compass of an instrument or voice, or for a harmonious melody. The name is given to the two 166 foundation stops of an organ, the open and the stopped diapason (see Organ), and to a standard of musical pitch, as in the French diapason normal (see Pitch, Musical).
DIAPER (derived through the Fr, from the Gr. διά, through, and ἄσπρος, white; the derivation from the town of Ypres, “d’Ypres,” in Belgium is unhistorical, as diapers were known for centuries before its existence), the name given to a textile fabric, formerly of a rich and costly nature with embroidered ornament, but now of linen or cotton, with a simple woven pattern; and particularly restricted to small napkins. In architecture, the term “diaper” is given to any small pattern of a conventional nature repeated continuously and uniformly over a surface; the designs may be purely geometrical, or based on floral forms, and in early examples were regulated by the process of their textile origin. Subsequently, similar patterns were employed in the middle ages for the surface decoration of stone, as in Westminster Abbey and Bayeux cathedral in the spandrils of the arcades of the choir and nave; also in mural painting, stained glass, incised brasses, encaustic tiles, &c. Probably in most cases the pattern was copied, so far as the general design is concerned, from the tissues and stuffs of Byzantine manufacture, which came over to Europe and were highly prized as ecclesiastical vestments.
 |
In its textile use, the term diaper was originally applied to silk patterns of a geometrical pattern; it is now almost exclusively used for diamond patterns made from linen or cotton yarns. An illustration of two patterns of this nature is shown in the figure. The floats of the warp and the weft are mostly in three; indeed the patterns are made from a base weave which is composed entirely of floats of this number. It will be seen that both designs are formed of what may be termed concentric figures—alternately black and white. Pattern B differs from pattern A only in that more of these concentric figures are used for the complete figure. If pattern B, which shows only one unit, were extended, the effect would be similar to A, except for the size of the unit. In A there are four complete units, and hence the pattern appears more striking. Again, the repeating of B would cause the four corner pieces to join and to form a diamond similar to the one in the centre. The two diamonds in B would then alternate diagonally to left and right. Special names are given to certain kinds of diapers, e.g. “bird’s-eye,” “pheasant’s-eye”; these terms indicate, to a certain extent, the size of the complete diamond in the cloth—the smaller kind taking the name “bird’s-eye.” The size of the pattern on paper has little connexion with the size of the pattern in the cloth, for it is clearly the number of threads and picks per inch which determine the size of the pattern in the cloth from any given design. Although A is larger than what is usually termed the “bird’s-eye” pattern, it is evident that it may be made to appear as such, provided that the cloth is fine enough. These designs, although adapted mostly for cloths such as nursery-diapers, for pinafores, &c., are sometimes used in the production of towels and table-cloths. In the figure, the first pick in A is identical with the first pick in B, and the part C shows how each interweaves with the twenty-four threads.
DIAPHORETICS (from Gr. διαφορεῖν, to carry through), the name given to those remedies which promote perspiration. In health there is constantly taking place an exhalation of watery vapour from the skin, by which not only are many of the effete products of nutrition eliminated, but the body is kept cool. Under exertion or in a heated atmosphere this natural function of the skin is increased, sweating more or less profuse follows, and, evaporation going on rapidly over the whole surface, little or no rise in the temperature of the body takes place. In many forms of disease, such as fevers and inflammatory affections, the action of the skin is arrested, and the surface of the body feels harsh and dry, while the temperature is greatly elevated. The occurrence of perspiration not unfrequently marks a crisis in such diseases, and is in general regarded as a favourable event. In some chronic diseases, such as diabetes and some cases of Bright’s disease, the absence of perspiration is a marked feature; while, on the other hand, in many wasting diseases, such as phthisis, the action of the skin is increased, and copious exhausting sweating occurs. Many means can be used to induce perspiration, among the best known being baths, either in the form of hot vapour or hot water baths, or in that part of the process of the Turkish bath which consists in exposing the body to a dry and hot atmosphere. Such measures, particularly if followed by the drinking of hot liquids and the wrapping of the body in warm clothing, seldom fail to excite copious perspiration. Numerous medicinal substances have the same effect.
DIAPHRAGM (Gr. διάφραγμα, a partition). The diaphragm or midriff (Anglo-Saxon, mid, middle, hrif, belly) in human anatomy is a large fibro-muscular partition between the cavities of the thorax and abdomen; it is convex toward the thorax, concave toward the abdomen, and consists of a central tendon and a muscular margin. The central tendon (q, fig. 1) is trefoil in shape, its leaflets being right, left and anterior; of these the right is the largest and the left the smallest. The fleshy fibres rise, in front from the back of the xiphoid cartilage of the sternum (d), laterally by six serrations, from the inner surfaces of the lower six ribs, interdigitating with the transversalis, posteriorly from the arcuate ligaments, of which there are five, a pair of external, a pair of internal, and a single median one. The external arcuate ligament (h) stretches from the tip of the twelfth rib (b) to the costal process of the first lumbar vertebra in front of the quadratus lumborum muscle (o), the internal and middle are continuations of the crura which rise from the ventro-lateral aspects of the bodies of the lumbar vertebrae, the right (e) coming from three, the left (f) from two. On reaching the level of the twelfth thoracic vertebra each crus spreads out into a fan-shaped mass of fibres, of which the innermost join their fellows from the opposite crus, in front of the aortic opening (k), to form the middle arcuate ligament; the outer ones (g) arch in front of the psoas muscle (n) to the tip of the costal process of the first lumbar vertebra to form the internal arcuate ligament, while the intermediate ones pass to the central tendon. There are three large openings in the diaphragm; the aortic (k) is behind the middle arcuate ligament and transmits the aorta, the vena azygos major, and the thoracic duct. In the right leaflet is an opening (sometimes called the hiatus quadratus) for the inferior vena cava and a branch of the right phrenic nerve (m), while in front and a little to the left of the aortic opening is one for the oesophagus and the two pneumogastric nerves (l), the left being in front and the right behind. 167 The fleshy fibres on each side of this opening act as a sphincter. Passing between the xiphoid and costal origins in front are the superior epigastric arteries, while the other terminal branches of the internal mammaries, the musculo-phrenics, pass through between two costal origins.
 |
| Fig. 1.—Abdominal Surface of the Diaphragm. |
Through the crura pass the splanchnic nerves, and in addition to these the left crus is pierced by the vena azygos minor. The sympathetic nerves usually enter the abdomen behind the internal arcuate ligaments. The phrenic nerves, which are the main supply of the diaphragm, divide before reaching the muscle and pierce it in a number of places to enter its abdominal surface, but some of the lower intercostal nerves assist in the supply. The last thoracic or subcostal nerves pass behind the external arcuate ligament.
For the action of the diaphragm see Respiratory System.
Embryology.—The diaphragm is at first developed in the neck region of the embryo, and this accounts for the phrenic nerves, which supply it, rising from the fourth and fifth cervical. From the mesoderm on the caudal side of the pericardium is developed the septum transversum, and in this the central tendon is formed. The fleshy portion is developed on each side in two parts, an anterior or sterno-costal which is derived from the longitudinal neck musculature, probably the same layer from which the sternothyroid comes, and a spinal part which is a derivative of the transversalis sheet of the trunk. Between these two parts is at one time a gap, the spino-costal hiatus, and this is obliterated by the growth of the pleuro-peritoneal membrane, which may occasionally fail to close and so may form the site of a phrenic hernia. With the growth of the body and the development of the lungs the diaphragm shifts its position until it becomes the septum between the thoracic and abdominal cavities. (See A. Keith, “On the Development of the Diaphragm,” Jour. of Anat. and Phys. vol. 39.) A. Paterson has recorded cases in which the left half of the diaphragm is wanting (Proceedings of the Anatomical Society of Gt. Britain, June 1900; Jour. of Anat. and Phys. vol. 34), and occasionally deficiencies are found elsewhere, especially in the sternal portion. For further details see Quain’s Anatomy, vol. i. (London, 1908).
Comparative Anatomy.—A complete diaphragm, separating the thoracic from the abdominal parts of the coelom, is characteristic of the Mammalia; it usually has the human structure and relations except that below the Anthropoids it is separated from the pericardium by the azygous lobe of the lung. In some Mammals, e.g. Echidna and Phocoena, it is entirely muscular. In the Cetacea it is remarkable for its obliquity; its vertebral attachment is much nearer the tail than its sternal or ventral one; this allows a much larger lung space in the dorsal than in the ventral part of the thorax, and may be concerned with the equipoise of the animal. (Otto Müller, “Untersuchungen über die Veränderung, welche die Respirationsorgane der Säugetiere durch die Anpassung an das Leben im Wasser erlitten haben,” Jen. Zeitschr. f. Naturwiss., 1898, p. 93.) In the Ungulata only one crus is found (Windle and Parsons, “Muscles of the Ungulata,” Proc. Zool. Soc., 1903, p. 287). Below the Mammals incomplete partitions between the pleural and peritoneal cavities are found in Chelonians, Crocodiles and Birds, and also in Amphibians (Xenopus and Pipa).
DIARBEKR1 (Kara Amid or Black Amid; the Roman Amida), the chief town of a vilayet of Asiatic Turkey, situated on a basaltic plateau on the right bank of the Tigris, which here flows in a deep open valley. The town is still surrounded by the masonry walls of black basalt which give it the name of Kara or Black Amid; they are well built and imposing on the west facing the open country, but almost in ruins where they overlook the river. A mass of gardens and orchards cover the slope down to the river on the S.W., but there are no suburbs outside the walls. The houses are rather crowded but only partially fill the walled area. The population numbers 38,000, nearly half being Christian, comprising Turks, Kurds, Arabs, Turkomans, Armenians, Chaldeans, Jacobites and a few Greeks. The streets are 10 ft. to 15 ft. wide, badly paved and dirty; the houses and shops are low, mostly of stone, and some of stone and mud. The bazaar is a good one, and gold and silver filigree work is made, peculiar in character and design. The cotton industry is declining, but manufacture of silk is increasing. Fruit is good and abundant as the rich volcanic soil is well watered from the town springs. The size of the melons is specially famous. To the south, the walls are some 40 ft. high, faced with large cut stone blocks of very solid construction, with towers and square bastions rising to 500 ft. There are four gates: on the north the Kharput gate, on the west the Rum, on the south the Mardin, and on the east the Yeni Kapu or new gate. A citadel enclosure stands at the N. E. corner and is now partly in ruins, but the interior space is occupied by the government konak. The summer climate in the confined space within the town is excessively hot and unhealthy. Epidemics of typhus are not unknown, as well as ophthalmia. The Diarbekr boil is like the “Aleppo button,” lasting a long time and leaving a deep scar. Winters are frequently severe but do not last long. Snow sometimes lies, and ice is stored for summer use. Scorpions noted for the virulence of their poison abound as well as horse leeches in the tanks. The town is supplied with water both by springs inside the town and by aqueducts from fountains at Ali Punar and Hamervat. The principal exports are wool, mohair and copper ore, and imports are cotton and woollen goods, indigo, coffee, sugar, petroleum, &c.
The Great Mosque, Ulu Jami, formerly a Christian church, occupies the site of a Sassanian palace and was built with materials from an older palace, probably that of Tigranes II. The remains consist of the façades of two palaces 400 ft. apart, each formed by a row of Corinthian columns surmounted by an equal number of a Byzantine type. Kufic inscriptions run across the fronts under the entablature. The court of the mosque is entered by a gateway on which lions and other animals are sculptured. The churches of greatest interest are those of SS. Cosmas and Damian (Jacobite) and the church of St James (Greek). In the 19th century Diarbekr was one of the largest and most flourishing cities of Asia, and as a commercial centre it now stands at the meeting-point of several important routes. It is at the head of the navigation of the Tigris, which is traversed down stream by keleks or rafts supported by inflated skins. There is a good road to Aleppo and Alexandretta on the Mediterranean, and to Samsun on the Black Sea by Kharput, Malatia and Sivas. There are also routes to Mosul and Bitlis.
Diarbekr became a Roman colony in a.d. 230 under the name of Amida, and received a Christian bishop in a.d. 325. It was enlarged and strengthened by Constantius II., in whose reign it was taken after a long siege by Shapur (Sapor) II., king of Persia. The historian Ammianus Marcellinus, who took part in the defence, gives a detailed account of it. In the later wars between the Persians and Romans it more than once changed hands. Though ceded by Jovian to the Persians it again became annexed to the Roman empire, and in the reign of Anastasius (a.d. 502) was once more taken by the Persians, when 80,000 of its inhabitants were slain. It was taken c. 638 by the Arabs, and afterwards passed into the hands of the Seljuks and Persians, from whom it was finally captured by Selim I. in 1515; and since that date it has remained under Ottoman rule. About 2 m. below the town is a masonry bridge over the Tigris; the older portion being probably Roman, and the western part, which bears a Kufic inscription, being Arab.
The vilayet of Diarbekr extends south from Palu on the Euphrates to Mardin and Nisibin on the edge of the Mesopotamian plain, and is divided into three sanjaks—Arghana, Diarbekr and Mardin. The headwaters of the main arm of the Tigris have their source in the vilayet.
Cereals, cotton, tobacco, rice and silk are produced, but most of the fertile lands have been abandoned to semi-nomads, who raise large quantities of live stock. The richest portion of the vilayet lies east of the capital in the rolling plains watered by tributaries of the Tigris. An exceptionally rich copper mine exists at Arghana Maden, but it is very imperfectly worked; galena mineral oil and silicious sand are also found.
1 From Diar, land, and Bekr (i.e. Abu Bekr, the caliph).
DIARRHOEA (from Gr. διά, through, ῥέω, flow), an excessive looseness of the bowels, a symptom of irritation which may be due to various causes, or may be associated with some specific disease. The treatment in such latter cases necessarily varies, since the symptom itself may be remedial, but in ordinary cases depends on the removal of the cause of irritation by the use of aperients, various sedatives being also prescribed. In chronic diarrhoea careful attention to the diet is necessary.
DIARY, the Lat. diarium (from dies, a day), the book in which are preserved the daily memoranda regarding events and actions which come under the writer’s personal observation, or are related to him by others. The person who keeps this record is called a diarist. It is not necessary that the entries in a diary should be made each day, since every life, however full, must contain absolutely empty intervals. But it is essential that the entry should be made during the course of the day to which it refers. When this has evidently not been done, as in the case of Evelyn’s diary, there is nevertheless an effort made to give the memoranda the effect of being so recorded, and in point of fact, even in a case like that of Evelyn, it is probable that what we now read is an enlargement of brief notes jotted down on the day cited. When this is not approximately the case, the diary is a fraud, for its whole value depends on its instantaneous transcript of impressions.
In its primitive form, the diary must always have existed; as soon as writing was invented, men and women must have wished to note down, in some almanac or journal, memoranda respecting their business, their engagements or their adventures. But the literary value of these would be extremely insignificant until the spirit of individualism had crept in, and human beings began to be interesting to other human beings for their own sake. It is not, therefore, until the close of the Renaissance that we find diaries beginning to have literary value, although, as the study of sociology extends, every scrap of genuine and unaffected record of early history possesses an ethical interest. In the 17th century, diaries began to be largely written in England, although in most cases without any idea of even eventual publication. Sir William Dugdale (1605-1686) had certainly no expectation that his slight diary would ever see the light. There is no surviving record of a journal kept by Clarendon, Richard Baxter, Lucy Hutchinson and other autobiographical writers of the middle of the century, but we may take it for granted that they possessed some such record, kept from day to day. Bulstrode Whitelocke (1605-1675), whose Memorials of the English Affairs covers the ground from 1625 to 1660, was a genuine diarist. So was the elder George Fox (1624-1690), who kept not merely “a great journal,” but “the little journal books,” and whose work was published in 1694. The famous diary of John Evelyn (1620-1706) professes to be the record of seventy years, and, although large tracts of it are covered in a very perfunctory manner, while in others many of the entries have the air of having been written in long after the event, this is a very interesting and amusing work; it was not published until 1818. In spite of all its imperfections there is a great charm about the diary of Evelyn, and it would hold a still higher position in the history of literature than it does if it were not overshadowed by what is unquestionably the most illustrious of the diaries of the world, that of Samuel Pepys (1633-1703). This was begun on the 1st of January 1660 and was carried on until the 29th of May 1669. The extraordinary value of Pepys’ diary consists in its fidelity to the portraiture of its author’s character. He feigns nothing, conceals nothing, sets nothing down in malice or insincerity. He wrote in a form of shorthand intelligible to no one but himself, and not a phrase betrays the smallest expectation that any eye but his own would ever investigate the pages of his confession. The importance of this wonderful document, in fact, lay unsuspected until 1819, when the Rev. John Smith of Baldock began to decipher the MS. in Magdalene College, Cambridge. It was not until 1825 that Lord Braybrooke published part of what was only fully edited, under the care of Mr Wheatley, in 1893-1896. In the age which succeeded that of Pepys, a diary of extraordinary emotional interest was kept by Swift from 1710 to 1713, and was sent to Ireland in the form of a “Journal to Stella”; it is a surprising amalgam of ambition, affection, wit and freakishness. John Byrom (1692-1763), the Manchester poet, kept a journal, which was published in 1854. The diary of the celebrated dissenting divine, Philip Doddridge (1702-1751), was printed in 1829. Of far greater interest are the admirably composed and vigorously written journals of John Wesley (1703-1791). But the most celebrated work of this kind produced in the latter half of the 18th century was the diary of Fanny Burney (Madame D’Arblay), published in 1842-1846. It will be perceived that, without exception, these works were posthumously published, and the whole conception of the diary has been that it should be written for the writer alone, or, if for the public, for the public when all prejudice shall have passed away and all passion cooled down. Thus, and thus only, can the diary be written so as to impress upon its eventual readers a sense of its author’s perfect sincerity and courage.
Many of the diaries described above were first published in the opening years of the 19th century, and it is unquestionable that the interest which they awakened in the public led to their imitation. Diaries ceased to be rare, but as a rule the specimens which have hitherto appeared have not presented much literary interest. Exception must be made in favour of the journals of two minor politicians, Charles Greville (1794-1865) and Thomas Creevey (1768-1838), whose indiscretions have added much to the gaiety of nations; the papers of the former appeared in 1874-1887, those of the latter in 1903. The diary of Henry Crabb Robinson (1775-1867), printed in 1869, contains excellent biographical material. Tom Moore’s journal, published in 1856 by Lord John Russell, disappointed its readers. But it is probable, if we reason by the analogy of the past, that the most curious and original diaries of the 19th century are still unknown to us, and lie jealously guarded under lock and key by the descendants of those who compiled them.
It was natural that the form of the diary should appeal to a people so sensitive to social peculiarities and so keen in the observation of them as the French. A medieval document of immense value is the diary kept by an anonymous curé during the reigns of Charles VI. and Charles VII. This Journal d’un bourgeois de Paris was kept from 1409 to 1431, and was continued by another hand down to 1449. The marquis de Dangeau (1638-1720) kept a diary from 1684 till the year of his death; this although dull, and as Saint-Simon said “of an insipidity to make you sick,” is an inexhaustible storehouse of facts about the reign of Louis XIV. Saint-Simon’s own brilliant memoirs, written from 1691 to 1723, may be considered as a sort of diary. The lawyer, Edmond Barbier (1689-1771), wrote a journal of the anecdotes and little facts which came to his knowledge from 1718 to 1762. The studious care which he took to be correct, and his manifest candour, give a singular value to Barbier’s record; his diary was not printed at all until 1847, nor, in its entirety, until 1857. The song-writer, Charles Collé (1709-1783), kept a journal historique from 1758 to 1782; it is full of vivacity, but very scandalous and spiteful. It saw the light in 1805, and surprised those to whom Collé, in his lifetime, had seemed the most placid and good-natured of men. Petit de Bachaumont (1690-1770) had access to remarkable sources of information, and his Mémoires secrets (a diary the publication of which began in 1762 and was continued after Bachaumont’s death, until 1787, by other persons) contains a valuable mass of documents. The marquis d’Argenson (1694-1757) kept a diary, of which a comparatively full text was first published in 1859. In recent times the posthumous publication of the diaries of the Russian artist, Marie Bashkirtseff (1860-1884), produced a great sensation in 1887, and revealed a most remarkable temperament. The brothers Jules and Edmond de Goncourt kept a very minute diary of all that occurred around them in artistic and literary Paris; after the death of Jules, in 1870, this was continued by Edmond, who published the three first volumes in 1888. The publication of this work was continued, and it produced no little scandal. It is excessively ill-natured in parts, but of its vivid picturesqueness, and of its general accuracy as a transcript of conversation, there can be no two opinions.
DIASPORE, a native aluminium hydroxide, AlO(OH), crystallizing in the orthorhombic system and isomorphous with göthite and manganite. It occurs sometimes as flattened crystals, but usually as lamellar or scaly masses, the flattened surface being a direction of perfect cleavage on which the lustre is markedly pearly in character. It is colourless or greyish-white, yellowish, sometimes violet in colour, and varies from translucent to 169 transparent. It may be readily distinguished from other colourless transparent minerals, with a perfect cleavage and pearly lustre—mica, talc, brucite, gypsum—by its greater hardness of 6½-7. The specific gravity is 3.4. When heated before the blowpipe it decrepitates violently, breaking up into white pearly scales; it was because of this property that the mineral was named diaspore by R. J. Hauy in 1801, from διασπείρειν, “to scatter.” The mineral occurs as an alteration product of corundum or emery, and is found in granular limestone and other crystalline rocks. Well-developed crystals are found in the emery deposits of the Urals and at Chester, Massachusetts, and in kaolin at Schemnitz in Hungary. If obtainable in large quantity it would be of economic importance as a source of alumina.
DIASTYLE (from Gr. διά, through, and στῦλος, column), in architecture, a term used to designate an intercolumniation of three or four diameters.
DIATOMACEAE. For the knowledge we possess of these beautiful plants, so minute as to be undiscernible by our unaided vision, we are indebted to the assistance of the microscope. It was not till towards the close of the 18th century that the first known forms of this group were discovered by O. F. Muller. And so slow was the process of discovery in this field of scientific research that in the course of half a century, when Agardh published his Systema algarum in 1824, only forty-nine species included under eight genera had been described. Since that time, however, with modern microscopes and microscopic methods, eminent botanists in all parts of the civilized world have studied these minute plants, with the result that the number of known genera and species has been greatly increased. Over 10,000 species of diatoms have been described, and about 1200 species and numerous varieties occur in the fresh waters and on the coasts of Great Britain and Ireland. Rabenhorst, in the index to his Flora Europaea algarum (1864) enumerated about 4000 forms which had up to that time been discovered throughout the continent of Europe.
 | |
| Fig. 1. | |
| A and B, Melosira arenaria. | C-E, Melosira varians. |
| E, showing formation of auxospore. | |
 |
| Fig. 2. |
The diatoms are more commonly known among systematic botanists as the Bacillarieae, particularly on the continent of Europe, and although such an immense number of very diverse forms are included in it, the group as a whole exhibits a remarkable uniformity of structure. The Bacillarieae is one of the large groups of Algae, placed by some in close proximity to the Conjugatae and by others as an order of the Brown Algae (or Phaeophyceae), but their characters are so distinctive and their structure is so uniform as to warrant the separation of the diatoms as a distinct class. The affinities of the group are doubtful.
 |
| Fig. 3.—Podosphenia Lyngbyii. |
 |
| Fig. 4.—Pleurosigma balticum. |
The diatoms exhibit great variety of form. While some species are circular and more or less disk-shaped, others are oval in outline. Some are linear, as Synedra Ulna (fig. 2), others more or less crescentic; others again are cuneate, as Podosphenia Lyngbyii (fig. 3); some few have a sigmoid outline, as Pleurosigma balticum (fig. 4); but the prevailing forms are naviculoid, as in the large family Naviculaceae, of which the genus Navicula embraces upwards of 1000 species. They vary also in their modes of growth,—some being free-floating, others attached to foreign bodies by simple or branched gelatinous stalks, which in some species are short and thick, while in others they are long and slender. In some genera the forms are simple, while in others the frustules are connected together in ribbon-like filaments, or form, as in other cases, zigzag chains. In some genera the individuals are naked, while in many others they are enclosed in a more or less definite gelatinous investment. The conditions necessary to their growth are moisture and light. Wherever these circumstances coexist, diatomaceous forms will almost invariably be found. They occur mixed with other organisms on the surface of moist rocks; in streamlets and pools, they form a brownish stratum on the surface of the mud, or cover the stems and leaves of water plants or floating twigs with a furry investment. Marine forms are usually attached to various sea-weeds, and many are found in the stomachs of molluscs, holothurians, ascidians and other denizens of the ocean. The fresh-water forms are specifically distinct from those incidental to salt or brackish water,—fresh-water species, however, are sometimes carried some distance into the sea by the force of the current, and in tidal rivers marine forms are carried up by the force of the tide. Some notion may be formed of the extreme minuteness of these forms from the fact that one the length of which is 1⁄200th of an inch may be considered as beyond the medium size. Some few, indeed, are much larger, but by far the greater proportion are of very much smaller dimensions.
 | |
| Fig. 5. | |
| A-C, Tetracyclus lacustris. | D and E, Tabellaria fenestrata. |
| F and G, Tabellaria flocculosa. | |
Diatoms are unicellular plants distinguished from kindred forms by the fact of having their soft vegetative part covered by a siliceous case. Each individual is known as a frustule, and the cell-wall consists of two similar valves nearly parallel to each other, each valve being furnished with a rim (or connecting-band) projecting from it at a right angle.
One of these valves with its rim is slightly smaller than the 170 other, the smaller fitting into the larger pretty much as a pill-box fits into its cover. This peculiarity of structure affords ample scope for the growth of the protoplasmic cell-contents, for as the latter increase in volume the siliceous valves are pushed out, and their corresponding siliceous rims become broader. The connecting-bands although closely fitting their respective valves are distinct from them, and together the two bands form the girdle.
An individual diatom is usually described from two aspects, one in which the surface of the valve is exposed to view—the valve view, and one in which the girdle side is exposed—the girdle view. The valves are thin and transparent, convex on the outside, and generally ornamented with a variety of sculptured markings. These sculptures often present the aspect of striae across the face of the valve, and the best lenses have shown them to consist of a series of small cavities within the siliceous wall of the cell. The valves of some of the marine genera exhibit a beautiful areolated structure due to the presence of larger chambers within the siliceous cell-wall. Many diatoms possess thickenings of the cell-wall, visible in the valve view, in the centre of the valve and at each extremity. These thickenings are known as the nodules, and they are generally connected by a long median line, the raphe, which is a cleft in the siliceous valve, extending at least some part of its length.
The protoplasmic contents of this siliceous box-like unicell are very similar to the contents of many other algal cells. There is a living protoplasmic layer or primordial utricle, connected either by two broad bands or by a number of anastomosing threads with a central mass of protoplasm in which the nucleus is embedded. The greater part of the cavity of the cell is occupied by one or several fluid vacuoles. The characteristic brown colour of diatoms is due to the presence of chromatophores embedded in the lining layer of protoplasm. In number and form these chromatophores are variable. They contain chlorophyll, but the green colour is masked by the presence of diatomin, a brown pigment which resembles that which occurs in the Brown Algae or Phaeophyceae. The chromatophores contain a variable number of pyrenoids, colourless proteid bodies of a crystalloidal character.
One of the first phenomena which comes under the notice of the observer is the extraordinary power of motion with which the frustules are endowed. Some species move slowly backwards and forwards in pretty much the same line, but in the case of Bacillaria paradoxa the motion is very rapid, the frustules darting through the water in a zigzag course. To account for this motion various theories have been suggested, none of which appear to be altogether satisfactory. There is little doubt that the movements are connected with the raphe, and in some diatoms there is much evidence to prove that they are due to an exudation of mucilage.
Classification.—The most natural system of classification of the Bacillarieae is the one put forward by Schütt (1896), and since generally followed by systematists. He separates them into two primary divisions, the ‘Centricae’ and the ‘Pennatae.’ The former includes all those diatoms which in the valve view possess a radial symmetry around a central point, and which are destitute of a raphe (or a pseudoraphe). The latter includes those which are zygomorphic or otherwise irregular, and in which the valve view is generally boat-shaped or needle-shaped, with the markings arranged in a sagittal manner on each side of a raphe or pseudoraphe.
Reproduction.—In the Diatomaceae, as well as in the Desmidieae, the ordinary mode of increase is by simple cell-division. The cell-contents within the enclosure of the siliceous case separate into two distinct masses. As these two daughter-masses become more and more developed, the valves of the mother-cell are pushed more and more widely apart. A new siliceous valve is secreted by each of the two masses on the side opposite to the original valve, the new valves being situated within the girdle of the original frustule. When this process has been completed the girdle of the mother frustule gives way, and two distinct frustules are formed, the siliceous valves in each of these new frustules being one of the valves of the mother-cell, and a newly formed valve similar and more or less parallel to it.
During the life of the plant this process of self-division is continued with an almost incredible rapidity. On this subject the observation of Professor William Smith, writing in 1853, is worthy of special notice:—“I have been unable to ascertain the time occupied in a single act of self-division, but supposing it to be completed in twenty-four hours we should have, as the progeny of a single frustule, the amazing number of 1,000,000,000 in a single month, a circumstance which will in some degree explain the sudden, or at least rapid, appearance of these organisms in localities where they were a short time previously either unrecognized or sparingly diffused” (British Diatomaceae, vol. i. p. 25).
 |
| Fig. 6.—Formation of Auxospores. A. Navicula limosa. B. Achnanthes flexella. C. Navicula Amphisbaena. D. Navicula viridis. |
Individual diatoms when once produced by cell-division are incapable of any increase in size owing to the rigidity of their siliceous cell-walls, and since the new valves are always formed within the girdle of the old ones, it would follow that every succeeding generation is reduced in size by the thickness of the girdle. In some diatoms, however, this is not strictly true as daughter-cells are sometimes produced of larger size than the parent-cells. Thus, the reduction in size of the individuals is not always proportionate to the number of cell-divisions.
On the diminution in size having reached a limit in any species, the maximum size is regained by the formation of an auxospore. There are five known methods of reproduction by auxospores, but it is unnecessary here to enter into details of these methods. Suffice it to say that a normal auxospore is produced by the conjugation of two parent-cells, its distinguishing feature being a rejuvenescence accompanied by a marked increase in size. These auxospores formed without conjugation are parthenogenetic.
Mode of Preparation.—The Diatomaceae are usually gathered in small bottles, and special care should be taken to collect them as free as possible from extraneous matter. A small portion having been examined under the microscope, should the gathering be thought worthy of preservation, some of the material is boiled in acid for the purpose of cleaning it. The acids usually employed are hydrochloric, nitric or sulphuric, according as circumstances require. When the operator considers that by this process all foreign matter has been eliminated, the residuum is put into a precipitating jar of a conical shape, broader at the bottom than at the top, and covered to the brim with filtered or distilled water. When the diatoms have settled in the bottom of the jar, the supernatant fluid is carefully removed by a syringe or some similar instrument, so that the sediment be not disturbed. The jar is again filled with water, and the process repeated till the acid has been completely removed. It is desirable afterwards to boil the sediment for a short time with supercarbonate of soda, the alkali being removed in the same manner as the acid. A small portion may then be placed with a pipette upon a slip of glass, and, when the moisture has been thoroughly evaporated, the film that remains should be covered with dilute Canada balsam, and, a thin glass cover having been gently laid over the balsam, the preparation should be laid aside for a short time to harden, and then is ready for observation.
General Remarks.—Diatoms are most abundant in cold latitudes, having a general preference for cold water. In the pelagic waters of lakes and of the oceans they are often very abundant, and in the cold waters of the Arctic and Antarctic 171 Oceans they exist in prodigious numbers. They thus form a large proportion of both the marine and the fresh-water plankton.
Large numbers of fossil diatoms are known. Not only are these minute plants assisting at the present time in the accumulation of oceanic and lake deposits, but in former ages they have been sufficiently active to give rise to considerable deposits of diatomaceous earths. When the plant has fulfilled its natural course the siliceous covering sinks to the bottom of the water in which it had lived, and there forms part of the sediment. When in the process of ages, as it has often happened, the accumulated sediment has been hardened into solid rock, the siliceous frustules of the diatoms remain unaltered, and, if the rock be disintegrated by natural or artificial means, may be removed from the enveloping matrix and subjected to examination under the microscope. The forms found may from their character help in some degree to illustrate the conditions under which the stratum of rock had been originally deposited. These earths are generally of a white or grey colour. Some of them are hard, but most are soft and friable. Many of them are of economic importance, being used as polishing powders (“Tripoli”), as absorbents for nitroglycerin in the manufacture of dynamite (“Kieselguhr”), as a dentifrice, and more recently they have been used to a large extent in the manufacture of non-conducting and sound-proof materials. Most of these diatomaceous earths are associated with rocks of Tertiary formations, although it is generally regarded that the earliest appearance of diatoms is in the Upper Cretaceous (chalk).
Vast deposits of Diatomaceous earths have been discovered in various parts of the world,—some the deposit of fresh, others of salt water. Of these deposits the most remarkable for extent, as well as for the number and beauty of the species contained in it, is that of Richmond, in Virginia, one of the United States of America. It extends for many miles, and is in some places at least 40 ft. deep. It is a remarkable fact that though the generations of a diatom in the space of a few months far exceed in number the generation of man during the period usually assigned to the existence of the race, the fossil genera and species are in most respects to the most minute details identical with the numerous living representatives of their class.
DIAULOS (from Gr. δι-, double, and αὐλός, pipe), in architecture, the peristyle round the great court of the palaestra, described by Vitruvius (v. II), which measured two stadia (1200 ft.) in length; on the south side this peristyle had two rows of columns, so that in stormy weather the rain might not be driven into the inner part. The word was also used in ancient Greece for a foot-race of twice the usual length.
DIAVOLO, FRA (1771-1806), the popular name given to a famous Italian brigand associated with the political revolutions of southern Italy at the time of the French invasion. His real name was Michele Pezza, and he was born of low parentage at Itri; he had committed many murders and robberies in the Terra di Lavoro, but by good luck combined with audacity he always escaped capture, whence his name of Fra Diavolo, popular superstition having invested him with the characters of a monk and a demon, and it seems that at one time he actually was a monk. When the kingdom of Naples was overrun by the French and the Parthenopaean Republic established (1799), Cardinal Ruffo, acting on behalf of the Bourbon king Ferdinand IV., who had fled to Sicily, undertook the reconquest of the country, and for this purpose he raised bands of peasants, gaol-birds, brigands, &c., under the name of Sanfedisti or bande della Santa Fede (“bands of the Holy Faith”). Fra Diavolo was made leader of one of them, and waged untiring war against the French troops, cutting off isolated detachments and murdering stragglers and couriers. Owing to his unrivalled knowledge of the country, he succeeded in interrupting the enemy’s communications between Rome and Naples. But although, like his fellow-brigands under Ruffo, he styled himself “the faithful servant and subject of His Sicilian Majesty,” wore a military uniform and held military rank, and was even created duke of Cassano, his atrocities were worthy of a bandit chief. On one occasion he threw some of his prisoners, men, women and children, over a precipice, and on another he had a party of seventy shot. His excesses while at Albano were such that the Neapolitan general Naselli had him arrested and imprisoned in the castle of St Angelo, but he was liberated soon after. When Joseph Bonaparte was made king of Naples, extraordinary tribunals were established to suppress brigandage, and a price was put on Fra Diavolo’s head. After spreading terror through Calabria, he crossed over to Sicily, where he concerted further attacks on the French. He returned to the mainland at the head of 200 convicts, and committed further excesses in the Terra di Lavoro; but the French troops were everywhere on the alert to capture him and he had to take refuge in the woods of Lenola. For two months he evaded his pursuers, but at length, hungry and ill, he went in disguise to the village of Baronissi, where he was recognized and arrested, tried by an extraordinary tribunal, condemned to death and shot. In his last moments he cursed both the Bourbons and Admiral Sir Sidney Smith for having induced him to engage in this reckless adventure (1806). Although his cruelty was abominable, he was not altogether without generosity, and by his courage and audacity he acquired a certain romantic popularity. His name has gained a world-wide celebrity as the title of a famous opera by Auber.
The best known account of Fra Diavolo is in Pietro Colletta’s Storia del reame di Napoli (2nd ed., Florence, 1848); B. Amante’s Fra Diavolo e il suo tempo (Florence, 1904) is an attempted rehabilitation; but A. Luzio, whose account in Profili e bozzetti storici (Milan, 1906) gives the latest information on the subject, has demolished Amante’s arguments.
DIAZ, NARCISSE VIRGILIO (1808-1876), French painter, was born in Bordeaux of Spanish parents, on the 25th of August 1808. At first a figure-painter who indulged in strong colour, in his later life Diaz became a painter of the forest and a “tone artist” of the first order. He spent much time at Barbizon; and although he is the least exalted of the half-dozen great artists who are usually grouped round that name, he sometimes produced works of the highest quality. At the age of ten Diaz became an orphan, and misfortune dogged his earlier years. His foot was bitten by a reptile in Meudon wood, near Sèvres, where he had been taken to live with some friends of his mother. The bite was badly dressed, and ultimately it cost him his leg. Afterwards his wooden stump became famous. At fifteen he entered the studios at Sèvres, where the decoration of porcelain occupied him; but tiring of the restraint of fixed hours, he took to painting Eastern figures dressed in richly coloured garments. Turks and Oriental scenes attracted him, and many brilliant gems remain of this period. About 1831 Diaz encountered Théodore Rousseau, for whom he entertained a great veneration, although Rousseau was four years his junior; but it was not until ten years later that the remarkable incident took place of Rousseau teaching Diaz to paint trees. At Fontainebleau Diaz found Rousseau painting his wonderful forest pictures, and determined to paint in the same way if possible. Rousseau, then in poor health, worried at home, and embittered against the world, was difficult to approach. Diaz followed him surreptitiously to the forest,—wooden leg not hindering,—and he dodged round after the painter, trying to observe his method of work. After a time Diaz found a way to become friendly with Rousseau, and revealed his anxiety to understand his painting. Rousseau was touched with the passionate words of admiration, and finally taught Diaz all he knew. Diaz exhibited many pictures at the Paris Salon, and was decorated in 1851. During the Franco-German War he went to Brussels. After 1871 he became fashionable, his works gradually rose in the estimation of collectors, and he worked constantly and successfully. In 1876 he caught cold at his son’s grave, and on the 18th of November of that year he died at Mentone, whither he had gone to recruit his health. Diaz’s finest pictures are his forest scenes and storms, and it is on these, and not on his pretty figures, that his fame is likely to rest. There are several fairly good examples of the master in the Louvre, and three small figure pictures in the Wallace collection, Hertford House. Perhaps the most notable of Diaz’s works are “La Fée aux Perles” (1857), in the Louvre; “Sunset in the Forest” (1868); “The Storm,” 172 and “The Forest of Fontainebleau” (1870) at Leeds. Diaz had no well-known pupils, but Léon Richet followed markedly his methods of tree-painting, and J. F. Millet at one period painted small figures in avowed imitation of Diaz’s then popular subjects.
See A. Hustin, Les Artistes célèbres: Diaz (Paris); D. Croal Thomson, The Barbizon School of Painters (London, 1890); J. W. Mollett, Diaz (London, 1890); J. Claretie, Peintres et sculpteurs contemporains: Diaz (Paris, 1882); Albert Wolff, La Capitale de l’art: Narcisse Diaz (Paris, 1886); Ph. Burty, Maîtres et petit-maîtres: N. Diaz (Paris, 1877).
DIAZ, PORFIRIO (1830- ), president of the republic of Mexico (q.v.), was born in the southern state of Oaxaca, on the 15th of September 1830. His father was an innkeeper in the little capital of that province, and died three years after the birth of Porfirio, leaving a family of seven children. The boy, who had Indian blood in his veins, was educated for the Catholic Church, a body having immense influence in the country at that time and ordering and controlling revolutions by the strength of their filled coffers. Arrived at the age of sixteen Porfirio Diaz threw off the authority of the priests. Fired with enthusiasm by stories told by the revolutionary soldiers continually passing through Oaxaca, and hearing about the war with the United States, a year later he determined to set out for Mexico city and join the National Guard. There being no trains, and he being too poor to ride, he walked the greater part of the 250 m., but arrived there too late, as the treaty of Guadalupe-Hidalgo (1848) had been already signed, and Texas finally ceded to the United States. Thus his entering the army was for the time defeated. Thereupon he returned to his native town and began studying law. He took pupils in order to pay his own fees at the Law Institute, and help his mother. At this time he came under the notice and influence of Don Marcos Pérez and Benito Juárez, the first a judge, the second a governor of the state of Oaxaca, and soon to become famous as the deliverer of Mexico from the priesthood (War of Reform). Diaz continued in his native town until 1854, when, refusing to vote for the dictator, Santa Anna, he was stung by a taunt of cowardice, and hastily pushing his way to the voting place, he recorded his vote in favour of Alvarez and the revolutionists. Orders were given for his arrest, but seizing a rifle and mounting a horse he placed himself at the head of a few revolting peasants, and from that moment became one of the leading spirits in that long struggle for reform, known as the War of Reform, which, under the leadership of Juárez, followed the overthrow of Santa Anna. Promotion succeeded promotion, as Diaz led his troops from victory to victory, amid great privations and difficulties. He was made captain (1856), lieutenant-colonel and colonel (1859), brigadier-general (1861), and general of division for the army (1863). Closely following on civil war, political strife, open rebellion and the great War of Reform, came the French invasion of 1862, and the landing of the emperor Maximilian in 1864. From the moment the French disclosed their intentions of settling in Mexico in 1862, Diaz took a prominent part against the foreign invasion. He was twice seriously wounded, imprisoned on three different occasions, had two hairbreadth escapes, and took part in many daring engagements. So important a personage did he become that both Marshal Bazaine and the emperor Maximilian made overtures to him. At the time of Maximilian’s death (with which Diaz personally had nothing to do) he was carrying on the siege of Mexico city, which ended in the surrender of the town two days after the emperor was shot at Quérétaro between his two leading generals. Diaz at once set to work to pay up arrears due to his soldiers, proclaimed death as the penalty of plunder and theft, and in the few weeks that followed showed his great administrative powers, the officers as well as the rank and file receiving arrears of pay. On the very day that he occupied Mexico city, the great commander of the army of the east, to everyone’s surprise, sent in his resignation. He was, indeed, appointed to the command of the second division of the army by President Juárez in his military reorganization, but Diaz, seeing men who had given great and loyal service to the state dismissed from their positions in the government, and disgusted at this course, retired to the little city of Oaxaca; there he lived, helping in the reorganization of the army but taking no active part in the government until 1871.
On Juárez’ death Lerdo succeeded as president, in 1872. His term of office again brought discord, and when it was known that he was attempting to be re-elected in 1876, the storm broke. Diaz came from retirement, took up the leadership against Lerdo, and after desperate struggles and a daring escape finally made a triumphal entry into Mexico city on the 24th of November 1876, as provisional president, quickly followed by the full presidentship. His term of office marks a prominent change in the history of Mexico; from that date he at once forged ahead with financial and political reform, the scrupulous settlement of all national debts, the welding together of the peoples and tribes (there are 150 different Indian tribes) of his country, the establishment of railroads and telegraphs, and all this in a land which had been upheaved for a century with revolutions and bloodshed, and which had had fifty-two dictators, presidents and rulers in fifty-nine years. In 1880 Diaz was succeeded by Gonzalez, the former minister of war, for four years (owing to the limit of the presidential office), but in 1884 he was unanimously re-elected. The government having set aside the above-mentioned limitation, Diaz was continually re-elected to the presidency. He married twice and had a son and two daughters. His gifted second wife (Carmelita), very popular in Mexico, was many years younger than himself. King Edward VII. made him an honorary grand commander of the Bath in June 1906, in recognition of his wonderful administration as perpetual president for over a quarter of a century.
See also Mrs Alec Tweedie, Porfirio Diaz, Seven Times President of Mexico (1906), and Mexico as I saw it (1901); Dr Noll, From Empire to Republic (1890); Lieut. Seaton Schroeder, Fall of Maximilian’s Empire (New York, 1887); R. de Z. Enriquez, P. Diaz (1908); and an article by Percy Martin in Quarterly Review for October 1909.
DIAZ DE NOVAES, BARTHOLOMEU (fl. 1481-1500), Portuguese explorer, discoverer of the Cape of Good Hope, was probably a kinsman of João Diaz, one of the first Portuguese to round Cape Bojador (1434), and of Diniz Diaz, the discoverer of Cape Verde (1445). In 1478 a Bartholomeu Diaz, probably identical with the discoverer, was exempted from certain customary payments on ivory brought from the Guinea coast. In 1481 he commanded one of the vessels sent by King John II. under Diogo d’Azambuja to the Gold Coast. In 1486 he seems to have been a cavalier of the king’s household, and superintendent of the royal warehouses; on the 10th of October in this year he received an annuity of 6000 reis from King John for “services to come”; and some time after this (probably about July or August 1487, rather than July 1486, the traditional date) he left Lisbon with three ships to carry on the work of African exploration so greatly advanced by Diogo Cão (1482-1486). Passing Cão’s farthest point near Cape Cross (in the modern German South-west Africa and) in 21° 50′ S., he erected a pillar on what is now known as Diaz Point, south of Angra Pequena or Lüderitz Bay, in 26° 38′ S.; of this fragments still exist. From this point (according to De Barros) Diaz ran thirteen days southwards before strong winds, which freshened to dangerous stormy weather, in a comparatively high southern latitude, considerably south of the Cape. When the storm subsided the Portuguese stood east; and failing, after several days’ search, to find land, turned north, and so struck the south coast of Cape Colony at Mossel Bay (Diaz’ Bahia dos Vaqueiros), half way between the Cape of Good Hope and Port Elizabeth (February 3, 1488). Thence they coasted eastward, passing Algoa Bay (Diaz’ Bahia da Roca), erecting pillars (or perhaps wooden crosses), it is said, on one of the islands in this bay and at or near Cape Padrone farther east; of these no traces remain. The officers and men now began to insist on return, and Diaz could only persuade them to go as far as the estuary of the Great Fish River (Diaz’ Rio do Iffante, so named from his colleague, Captain João Iffante). Here, however, half way between Port Elizabeth and East London (and indeed from Cape Padrone), the north-easterly trend of the coast became unmistakable; the way round Africa had been laid open. On his return Diaz perhaps named Cape Agulhas after St Brandan; 173 while on the southernmost projection of the modern Cape peninsula, whose remarkable highlands (Table Mountain, &c.) doubtless impressed him as the practical termination of the continent, he bestowed, says De Barros, the name of Cape of Storms (Cabo Tormentoso) in memory of the storms he had experienced in these far southern waters; this name (in the ordinary tradition) was changed by King John to that of Good Hope (Cabo da Boa Esperança). Some excellent authorities, however, make Diaz himself give the Cape its present name. Hard by this “so many ages unknown promontory” the explorer probably erected his last pillar. After touching at the Ilha do Principe (Prince’s Island, south-west of the Cameroons) as well as at the Gold Coast, he appeared at Lisbon in December 1488. He had discovered 1260 m. of hitherto unknown coast; and his voyage, taken with the letters soon afterwards received from Pero de Covilhão (who by way of Cairo and Aden had reached Malabar on one side and the “Zanzibar coast” on the other as far south as Sofala, in 1487-1488) was rightly considered to have solved the question of an ocean route round Africa to the Indies and other lands of South and East Asia.
No record has yet been found of any adequate reward for Diaz: on the contrary, when the great Indian expedition was being prepared (for Vasco da Gama’s future leadership) Bartolomeu only superintended the building and outfit of the ships; when the fleet sailed in 1497, he only accompanied da Gama to the Cape Verde Islands, and after this was ordered to El Mina on the Gold Coast. On Cabral’s voyage of 1500 he was indeed permitted to take part in the discovery of Brazil (April 22), and thence should have helped to guide the fleet to India; but he perished in a great storm off his own Cabo Tormentoso. Like Moses, as Galvano says, he was allowed to see the Promised Land, but not to enter in.
See João de Barros, Asia, Dec. I. bk. iii. ch. 4; Duarte Pacheco Pereira, Esmeraldo de situ orbis, esp. pp. 15, 90, 92, 94 and Raphael Bastos’s introduction to the edition of 1892 (Pacheco met Diaz, returning from his great voyage, at the Ilha do Principe); a marginal note, probably by Christopher Columbus himself, on fol. 13 of a copy of Pierre d’Ailly’s Imago mundi, now in the Colombina at Seville (the writer of this note fixes Diaz’s return to Lisbon, December 1488, and says he was present at Diaz’s interview with the king of Portugal, when the explorer described his voyage and showed his route upon the chart he had kept); a similar but briefer note in a copy of Pope Pius II.’s Historia rerum ubique gestarum, from the same hand; the Roteiro of Vasco da Gama’s First Voyage (Journal of the First Voyage of ... Da Gama, Hakluyt Soc., ed. E. G. Ravenstein (1898), pp. 9, 14); Ramusio, Navigationi (3rd ed.), vol. i. fol. 144; Castanheda, Historia, bk. i. ch. 1; Galvano, Descobrimentos (Discoveries of the World), Hakluyt Soc. (1862), p. 77; E. G. Ravenstein, “Voyages of ... Cão and ... Dias,” in Geog. Journ. (London, December 1900), vol. xvi. pp. 638-655), an excellent critical summary in the light of the most recent investigations of all the material. The fragments of Diaz’s only remaining pillar (from Diaz Point) are now partly at the Cape Museum, partly at Lisbon: the latter are photographed in Ravenstein’s paper in Geog. Journ. (December 1900, p. 642).
DIAZO COMPOUNDS, in organic chemistry, compounds of the type R·N·2·X (where R = a hydrocarbon radical, and X = an acid radical or a hydroxyl group). These compounds may be divided into two classes, namely, the true diazo compounds, characterized by the grouping −N = N−, and the diazonium compounds, characterized by the grouping N ∶ N <.
The diazonium compounds were first discovered by P. Griess (Ann., 1858, 106, pp. 123 et seq.), and may be prepared by the action of nitrous fumes on a well-cooled solution of a salt of a primary amine,
C6H5NH2·HNO3 + HNO2 = C6H5N2·NO3 + 2H2O,
or, as is more usually the case (since the diazonium salts themselves are generally used only in aqueous solution) by the addition of a well-cooled solution of potassium or sodium nitrite to a well-cooled dilute acid solution of the primary amine. In order to isolate the anhydrous diazonium salts, the method of E. Knoevenagel (Ber., 1890, 23, p. 2094) may be employed. In this process the amine salt is dissolved in absolute alcohol and diazotized by the addition of amyl nitrite; a crystalline precipitate of the diazonium salt is formed on standing, or on the addition of a small quantity of ether. The diazonium salts are also formed by the action of zinc-dust and acids on the nitrates of primary amines (R. Mohlau, Ber., 1883, 16, p. 3080), and by the action of hydroxylamine on nitrosobenzenes. They are colourless crystalline solids which turn brown on exposure. They dissolve easily in water, but only to a slight extent in alcohol and ether. They are very unstable, exploding violently when heated or rubbed. Benzene diazonium nitrate, C6H5N(NO3)∶N, crystallizes in long silky needles. The sulphate and chloride are similar, but they are not quite so unstable as the nitrate. The bromide may be prepared by the addition of bromine to an ethereal solution of diazo-amino-benzene (tribromaniline remaining in solution). By the addition of potassium bromide and bromine water to diazonium salts they are converted into a perbromide, e.g. C6H5N2Br3, which crystallizes in yellow plates.
The diazonium salts are characterized by their great reactivity and consequently are important reagents in synthetical processes, since by their agency the amino group in a primary amine may be exchanged for other elements or radicals. The chief reactions are as follows:—
1. Replacement of -NH2 by -OH:—The amine is diazotized and the aqueous solution of the diazonium salt is heated, nitrogen being eliminated and a phenol formed.
2. Replacement of -NH2 by halogens and by the -CN and -CNO groups:—The diazonium salt is warmed with an acid solution of the corresponding cuprous salt (T. Sandmeyer, Ber., 1884, 17, p. 2650), or with copper powder (L. Gattermann, Ber., 1890, 23, p. 1218; 1892, 25, p. 1074). In the case of iodine, the substitution is effected by adding a warm solution of potassium iodide to the diazonium solution, no copper or cuprous salt being necessary; whilst for the production of nitriles a solution of potassium cuprous cyanide is used. This reaction (the so-called “Sandmeyer” reaction) has been investigated by A. Hantzsch and J. W. Blagden (Ber., 1900, 33, p. 2544), who consider that three simultaneous reactions occur, namely, the formation of labile double salts which decompose in such a fashion that the radical attached to the copper atom wanders to the aromatic nucleus; a catalytic action, in which nitrogen is eliminated and the acid radical attaches itself to the aromatic nucleus; and finally, the formation of azo compounds.
3. Replacement of -NH2 by -NO2:—A well-cooled concentrated solution of potassium mercuric nitrate is added to a cooled solution of benzene diazonium nitrate, when the crystalline salt 2C6H5N2·NO3, Hg(NO2)2 is precipitated. On warming this with copper powder, it gives a quantitative yield of nitrobenzene (A. Hantzsch, Ber., 1900, 33, p. 2551).
4. Replacement of -NH2 by hydrogen:—This exchange is brought about, in some cases, by boiling the diazonium salt with alcohol; but I. Remsen and his pupils (Amer. Chem. Journ., 1888, 9, pp. 389 et seq.) have shown that the main product of this reaction is usually a phenolic ether. This reaction has also been investigated by A. Hantzsch and E. Jochem (Ber., 1901, 34, p. 3337), who arrived at the conclusion that the normal decomposition of diazonium salts by alcohols results in the formation of phenolic ethers, but that an increase in the molecular weight of the alcohol, or the accumulation of negative groups in the aromatic nucleus, diminishes the yield of the ether and increases the amount of the hydrocarbon formed. The replacement is more readily brought about by the use of sodium stannite (P. Friedlander, Ber., 1889, 22, p. 587), or by the use of a concentrated solution of hypophosphorous acid (J. Mai, Ber., 1902, 35, p. 162). A. Hantzsch (Ber., 1896, 29, p. 947; 1898, 31, p. 1253) has shown that the chlor- and brom- diazoniumthiocyanates, when dissolved in alcohol containing a trace of hydrochloric acid, become converted into the isomeric thiocyanbenzene diazonium chlorides and bromides. This change only occurs when the halogen atom is in the ortho- or para- position to the -N2- group.
Metallic Diazo Derivatives.—Benzene diazonium chloride is decomposed by silver oxide in aqueous solution, with the formation of benzene diazonium hydroxide, C6H5·N(OH)∶N. This hydroxide, although possessing powerful basic properties, is unstable in the presence of alkalis and neutralizes them, being converted first into the isomeric benzene-diazotic acid, the potassium salt of which is obtained when the diazonium chloride is added to an excess of cold concentrated potash (A. Hantzsch and W. B. Davidson, Ber., 1898, 31, p. 1612). Potassium benzene diazotate, C6H5N2·OK, crystallizes in colourless silky needles. The free acid is not known; by the addition of the potassium salt to 50% acetic acid at -20° C., the acid anhydride, benzene diazo oxide, (C6H5N2)2O, is obtained as a very unstable, yellow, insoluble compound, exploding spontaneously at 0° C. Strong acids convert it into a diazonium salt, and potash converts it into the diazotate. On the constitution, of these anhydrides see E. Bamberger, Ber., 1896, 29, p. 446, and A. Hantzsch, Ber., 1896, 29, p. 1067; 1898, 31, p. 636. By the addition of the diazonium salts to a hot concentrated solution of a caustic alkali, C. Schraube and C. Schmidt (Ber., 1894, 27, p. 520) obtained an isomer of potassium benzene diazotate. These iso-diazotates are formed much more readily when the aromatic nucleus in the diazonium salt contains negative radicals. Potassium benzene iso-diazotate resembles the normal salt, but is more stable, and is more highly ionized. Carbon dioxide converts it into phenyl nitrosamine, C6H5NH·NO 174 (A. Hantzsch). The potassium salt of the iso-diazo hydroxide yields on methylation a nitrogen ether, R·N(CH3)·NO, whilst the silver salt yields an oxygen ether, R·N:N·OCH3. These results point to the conclusion that the iso-diazo hydroxide is a tautomeric substance. The same oxygen ether is formed by the methylation of the silver salt of the normal diazo hydroxide; this points to the conclusion that the isomeric hydroxides, corresponding with the silver derivatives, have the same structural formulae, namely, R·N:N·OH. These oxygen ethers contain the grouping -N:N-, since they couple very readily with the phenols in alkaline solution to form azo compounds (q.v.) (E. Bamberger, Ber., 1895, 28, p. 225); they are also explosive.
By oxidizing potassium benzene iso-diazotate with alkaline potassium ferricyanide, E. Bamberger (Ber., 1894, 27, p. 914) obtained the diazoic acids, R·NH·NO2, substances which he had previously prepared by similarly oxidizing the diazonium salts, by dehydrating the nitrates of primary amines with acetic anhydride, and by the action of nitric anhydride on the primary amines. Concentrated acids convert them into the isomeric nitro-amines, the -NO2 group going into the nucleus in the ortho- or para- position to the amine nitrogen; this appears to indicate that the compounds are nitramines. They behave, however, as tautomeric substances, since their alkali salts on methylation give nitrogen ethers, whilst their silver salts yield oxygen ethers:
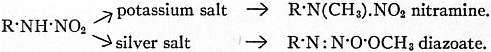
Phenyl nitramine, C6H5NH·NO2, is a colourless crystalline solid, which melts at 46° C. Sodium amalgam in alkaline solution reduces it to phenylhydrazine.
Constitution of the Diazo Compounds.—P. Griess (Ann., 1866, 137, p. 39) considered that the diazo compounds were formed by the addition of complex groupings of the type C6H4N2- to the inorganic acids; whilst A. Kekulé (Zeit. f. Chemie, 1866, 2, p. 308), on account of their ready condensation to form azo compounds and their easy reduction to hydrazines, assumed that they were substances of the type R·N:N·Cl. The constitution of the diazonium group -N2·X, may be inferred from the following facts:—The group C6H5N2- behaves in many respects similarly to an alkali metal, and even more so to the ammonium group, since it is capable of forming colourless neutral salts with mineral acids, which in dilute aqueous solution are strongly ionized, but do not show any trace of hydrolytic dissociation (A. Hantzsch, Ber., 1895, 28, p. 1734). Again, the diazonium chlorides combine with platinic chloride to form difficultly soluble double platinum salts, such as (C6H5N2Cl)2·PtCl4; similar gold salts, C6H5N2Cl·AuCl3, are known. Determinations of the electrical conductivity of the diazonium chloride and nitrate also show that the diazonium radical is strictly comparable with other quaternary ammonium ions. For these reasons, one must assume the existence of pentavalent nitrogen in the diazonium salts, in order to account for their basic properties.
The constitution of the isomeric diazo hydroxides has given rise to much discussion. E. Bamberger (Ber., 1895, 28, pp. 444 et seq.) and C. W. Blomstrand (Journ. prakt. Chem., 1896, 53, pp. 169 et seq.) hold that the compounds are structurally different, the normal diazo-hydroxide being a diazonium derivative of the type R·N(∶N)·OH. The recent work of A. Hantzsch and his pupils seems to invalidate this view (Ber., 1894, 27, pp. 1702 et seq.; see also A. Hantzsch, Die Diazoverbindungen). According to Hantzsch the isomeric diazo hydroxides are structurally identical, and the differences in behaviour are due to stereo-chemical relations, the isomerism being comparable with that of the oximes (q.v.). On such a hypothesis, the relatively unstable normal diazo hydroxides would be the syn-compounds, since here the nitrogen atoms would be more easily eliminated, whilst the stable iso-diazo derivatives would be the anti-compounds, thus:
 | |
| Normal hydroxide (Syn-compound) |
Iso hydroxide (Anti-compound) |
In support of this theory, Hantzsch has succeeded in isolating a series of syn- and anti-diazo-cyanides and -sulphonates (Ber., 1895, 28, p. 666; 1900, 33, p. 2161; 1901, 34, p. 4166). By diazotizing para-chloraniline and adding a cold solution of potassium cyanide, a salt (melting at 29° C.) is obtained, which readily loses nitrogen, and forms para-chlorbenzonitrile on the addition of copper powder. By dissolving this diazocyanide in alcohol and reprecipitating it by water, it is converted into the isomeric diazocyanide (melting at 105-106° C.), which does not yield para-chlorbenzonitrile when treated with copper powder. Similar results have been obtained by using diazotized para-anisidine, a syn- and an anti- compound being formed, as well as a third isomeric cyanide, obtained by evaporating para-methoxy-benzenediazonium hydroxide in the presence of an excess of hydrocyanic acid at ordinary temperatures. This salt is a colourless crystalline substance of composition CH3O·C6H4·N2·CN·HCN·2H2O, and has the properties of a metallic salt; it is very soluble in water and its solution is an electrolyte, whereas the solutions of the syn- and anti- compounds are not electrolytes. The isolation of these compounds is a powerful argument in favour of the Hantzsch hypothesis which requires the existence of these three different types, whilst the Bamberger-Blomstrand view only accounts for the formation of two isomeric cyanides, namely, one of the normal diazonium type and one of the iso-diazocyanide type.
Benzene diazonium hydroxide, although a strong base, reacts with the alkaline hydroxides to form salts with the evolution of heat, and generally behaves as a weak acid. On mixing dilute solutions of the diazonium hydroxide and the alkali together, it is found that the molecular conductivity of the mixture is much less than the sum of the two electrical conductivities of the solutions separately, from which it follows that a portion of the ions present have changed to the non-ionized condition. This behaviour is explained by considering the non-ionized part of the diazonium hydroxide to exist in solution in a hydrated form, the equation of equilibrium being:
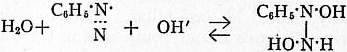
On adding the alkaline hydroxide to the solution, this hydrate is supposed to lose water, yielding the syn-diazo hydroxide, which then gives rise to a certain amount of the sodium salt (A. Hantzsch, Ber., 1898, 31, p. 1612),
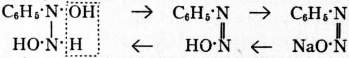
This assumption also shows the relationship of the diazonium hydroxides to other quaternary ammonium compounds, for most of the quaternary ammonium hydroxides (except such as have the nitrogen atom attached to four saturated hydrocarbon radicals) are unstable, and readily pass over into compounds in which the hydroxyl group is no longer attached to the amine nitrogen; thus the syn-diazo hydroxides are to be regarded as pseudo-diazonium derivatives. (A. Hantzsch, Ber., 1899, 32, p. 3109; 1900, 33, p. 278.) It is generally accepted that the iso-diazo hydroxides possess the oxime structure R·N:N·OH.
Hantzsch explains the characteristic reactions of the diazonium compounds by the assumption that an addition compound is first formed, which breaks down with the elimination of the hydride of the acid radical, and the formation of an unstable syn-diazo compound, which, in its turn, decomposes with evolution of nitrogen (Ber., 1897, 30, p. 2548; 1898, 31, p. 2053).
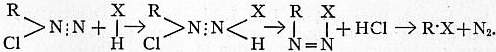
J. Cain (Jour. Chem. Soc., 1907, 91, p. 1049) suggested a quinonoid formula for diazonium salts, which has been combated by Hantzsch (Ber., 1908, 41, pp. 3532 et seq.). G. T. Morgan and F. M. G. Micklethwaite (Jour. Chem. Soc., 1908, 93, p. 617; 1909, 95, p. 1319) have pointed out that the salts may possess a dynamic formula, Cain’s representing the middle stage, thus:
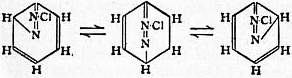
Diazoamines.—The diazoamines, R·N2·NHR, may be prepared by the action of the primary and secondary amines on the diazonium salts, or by the action of nitrous acid on the free primary amine. In the latter reaction it is assumed that the isodiazohydroxide first formed is immediately attacked by a second molecule of the amine. They are yellow crystalline solids, which do not unite with acids. Nitrous acid converts them, in acid solution, into diazonium salts.
C6H5N2·NHC6H5 + 2HCl + HNO2 = 2C6H5N2Cl + 2H2O.
They are readily converted into the isomeric aminoazo compounds, either by standing in alcoholic solution, or by warming with a mixture of the parent base and its hydrochloride; the diazo group preferably going into the para-position to the amino group. When the para-position is occupied, the diazo group takes the ortho-position. H. Goldschmidt and R. U. Reinders (Ber., 1896, 29, p. 1369, 1899) have shown that the transformation is a monomolecular reaction, the velocity of transformation in moderately dilute solution being independent of the concentration, but proportional to the amount of the catalyst present (amine hydrochloride) and to the temperature. It has also been shown that when different salts of the amine are used, their catalytic influence varies in amount and is almost proportional to their degree of ionization in aqueous solution. Diazoaminobenzene, C6H5N2·NHC6H5, crystallizes in golden yellow laminae, which melt at 96° C. and explode at a slightly higher temperature. It is readily soluble in alcohol, ether and benzene. Concentrated hydrochloric acid converts it into chlorbenzene, aniline and nitrogen. Zinc dust and alcoholic acetic acid reduce it to aniline and phenylhydrazine.
Diazoimino compounds, R·N3, may be regarded as derivatives of azoimide (q.v.); they are formed by the action of ammonia on the diazoperbromides, or by the action of hydroxylamine on the diazonium sulphates (J. Mai, Ber., 1892, 25, p. 372; T. Curtius, Ber., 1893, 26, p. 1271). Diazobenzeneimide, C6H5N3, is a yellowish oil of stupefying odour. It boils at 59° C. (12 mm.), and explodes when heated. Concentrated hydrochloric acid decomposes it with formation of 175 chloranilines and elimination of nitrogen, whilst on boiling with sulphuric acid it is converted into aminophenols.
Aliphatic Diazo Compounds.—The esters of the aliphatic amino
acids may be diazotized in a manner similar to the primary aromatic
amines, a fact discovered by T. Curtius (Ber., 1833, 16, p. 2230). The
first aliphatic diazo compound to be isolated was diazoacetic ester,
CH·N2·CO2C2H5, which is prepared by the action of potassium nitrite
on the ethyl ester of glycocoll hydrochloride, HCl·NH2·CH2·CO2C2H5
+ KNO2 = CHN2·CO2C2H5 + KCl + 2H2O. It is a yellowish oil which
melts at -24° C.; it boils at 143-144° C., but cannot be distilled safely
as it decomposes violently, giving nitrogen and ethyl fumarate. It
explodes in contact with concentrated sulphuric acid. On reduction
it yields ammonia and glycocoll (aminoacetic acid). When heated
with water it forms ethyl hydroxy-acetate; with alcohol it yields
ethyl ethoxyacetate. Halogen acids convert it into monohalogen
fatty acids, and the halogens themselves convert it into dihalogen
fatty acids. It unites with aldehydes to form esters of ketonic acids,
and with aniline yields anilido-acetic acid. It forms an addition
product with acrylic ester, which on heating loses nitrogen and leaves
trimethylene dicarboxylic ester. Concentrated ammonia converts
it into diazoacetamide, CHN2·CONH2, which crystallizes in golden
yellow plates which melt at 114° C. For other reactions see
Hydrazine. The constitution of the diazo fatty esters is inferred
from the fact that the two nitrogen atoms, when split off, are
replaced by two monovalent elements or groups, thus leading to
the formula 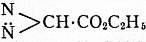 for diazoacetic ester.
for diazoacetic ester.
Diazosuccinic ester, N2·C(CO2C2H5)2, is similarly prepared by the action of nitrous acid on the hydrochloride of aspartic ester. It is decomposed by boiling water and yields fumaric ester.
Diazomethane, CH2N2, was first obtained in 1894 by H. v. Pechmann (Ber., 1894, 27, p. 1888; 1895, 28, p. 855). It is prepared by the action of aqueous or alcoholic solutions of the caustic alkalis on the nitroso-acidyl derivatives of methylamine (such, for example, as nitrosomethyl urethane, NO·N(CH3)·CO2C2H5, which is formed on passing nitrous fumes into an ethereal solution of methyl urethane). E. Bamberger (Ber., 1895, 28, p. 1682) regards it as the anhydride of iso-diazomethane, CH3·N:N·OH, and has prepared it by a method similar to that used for the preparation of iso-diazobenzene. By the action of bleaching powder on methylamine hydrochloride, there is obtained a volatile liquid (methyldichloramine, CH3·N·Cl2), boiling at 58-60° C., which explodes violently when heated with water, yielding hydrocyanic acid (CH3NCl2 = HCN + 2HCl). Well-dried hydroxylamine hydrochloride is dissolved in methyl alcohol and mixed with sodium methylate; a solution of methyldichloramine in absolute ether is then added and an ethereal solution of diazomethane distils over. Diazomethane is a yellow inodorous gas, very poisonous and corrosive. It may be condensed to a liquid, which boils at about 0° C. It is a powerful methylating agent, reacting with water to form methyl alcohol, and converting acetic acid into methylacetate, hydrochloric acid into methyl chloride, hydrocyanic acid into acetonitrile, and phenol into anisol, nitrogen being eliminated in each case. It is reduced by sodium amalgam (in alcoholic solution) to methylhydrazine, CH3·NH·NH2. It unites directly with acetylene to form pyrazole (H. v. Pechmann, Ber., 1898, 31, p. 2950) and with fumaric methyl ester it forms pyrazolin dicarboxylic ester.
See G. T. Morgan, B.A. Rep., 1902; J. Cain, Diazo Compounds, 1908.
DIAZOMATA (Gr. διάζωμα, a girdle), in architecture, the landing places and passages which were carried round the semicircle and separated the upper and lower tiers in a Greek theatre.
DIBDIN, CHARLES (1745-1814), British musician, dramatist, novelist, actor and song-writer, the son of a parish clerk, was born at Southampton on or before the 4th of March 1745, and was the youngest of a family of eighteen. His parents designing him for the church, he was sent to Winchester; but his love of music early diverted his thoughts from the clerical profession. After receiving some instruction from the organist of Winchester cathedral, where he was a chorister from 1756 to 1759, he went to London at the age of fifteen. Here he was placed in a music warehouse in Cheapside, but he soon abandoned this employment to become a singing actor at Covent Garden. On the 21st of May 1762 his first work, an operetta entitled The Shepherd’s Artifice, with words and music by himself, was produced at this theatre. Other works followed, his reputation being firmly established by the music to the play of The Padlock, produced at Drury Lane under Garrick’s management in 1768, the composer himself taking the part of Mungo with conspicuous success. He continued for some years to be connected with Drury Lane, both as composer and as actor, and produced during this period two of his best known works, The Waterman (1774) and The Quaker (1775). A quarrel with Garrick led to the termination of his engagement. In The Comic Mirror he ridiculed prominent contemporary figures through the medium of a puppet show. In 1782 he became joint manager of the Royal circus, afterwards known as the Surrey theatre. In three years he lost this position owing to a quarrel with his partner. His opera Liberty Hall, containing the successful songs “Jock Ratlin,” “The Highmettled Racer,” and “The Bells of Aberdovey,” was produced at Drury Lane theatre on the 8th of February 1785. In 1788 he sailed for the East Indies, but the vessel having put in to Torbay in stress of weather, he changed his mind and returned to London. In a musical variety entertainment called The Oddities, he succeeded in winning marked popularity with a number of songs that included “’Twas in the good ship ‘Rover’,” “Saturday Night at Sea,” “I sailed from the Downs in the ‘Nancy,’” and the immortal “Tom Bowling,” written on the death of his eldest brother, Captain Thomas Dibdin, at whose invitation he had planned his visit to India. A series of monodramatic entertainments which he gave at his theatre, Sans Souci, in Leicester Square, brought his songs, music and recitations more prominently into notice, and permanently established his fame as a lyric poet. It was at these entertainments that he first introduced many of those sea-songs which so powerfully influenced the national spirit. The words breathe the simple loyalty and dauntless courage that are the cardinal virtues of the British sailor, and the music was appropriate and naturally melodious. Their effect in stimulating and ennobling the spirit of the navy during the war with France was so marked as to call for special acknowledgment. In 1803 Dibdin was rewarded by government with a pension of £200 a year, of which he was only for a time deprived under the administration of Lord Grenville. During this period he opened a music shop in the Strand, but the venture was a failure. Dibdin died of paralysis in London on the 25th of July 1814. Besides his Musical Tour through England (1788), his Professional Life, an autobiography published in 1803, a History of the Stage (1795), and several smaller works, he wrote upwards of 1400 songs and about thirty dramatic pieces. He also wrote the following novels:—The Devil (1785); Hannah Hewitt (1792); The Younger Brother (1793). An edition of his songs by G. Hogarth (1843) contains a memoir of his life. His two sons, Charles and Thomas John Dibdin (q.v.), whose works are often confused with those of their father, were also popular dramatists in their day.
DIBDIN, THOMAS FROGNALL (1776-1847), English bibliographer, born at Calcutta in 1776, was the son of Thomas Dibdin, the sailor brother of Charles Dibdin. His father and mother both died on the way home to England in 1780, and Thomas was brought up by a maternal uncle. He was educated at St John’s College, Oxford, and studied for a time at Lincoln’s Inn. After an unsuccessful attempt to obtain practice as a provincial counsel at Worcester, he was ordained a clergyman at the close of 1804, being appointed to a curacy at Kensington. It was not until 1823 that he received the living of Exning in Sussex. Soon afterwards he was appointed by Lord Liverpool to the rectory of St Mary’s, Bryanston Square, which he held until his death on the 18th of November 1847. The first of his numerous bibliographical works was his Introduction to the Knowledge of Editions of the Classics (1802), which brought him under the notice of the third Earl Spencer, to whom he owed much important aid in his bibliographical pursuits. The rich library at Althorp was thrown open to him; he spent much of his time in it, and in 1814-1815 published his Bibliotheca Spenceriana. As the library was not open to the general public, the information given in the Bibliotheca was found very useful, but since its author was unable even to read the characters in which the books he described were written, the work was marred by the errors which more or less characterize all his productions. This fault of inaccuracy however was less obtrusive in his series of playful, discursive works in the form of dialogues on his favourite subject, the first of which, Bibliomania (1809), was republished with large additions in 1811, and was very popular, passing through numerous editions. To the same class belonged the Bibliographical Decameron, a larger work, which appeared in 1817. In 1810 he began the publication of a new and much extended edition of Ames’s Typographical Antiquities. The first volume was a great success, but the publication was checked by the failure of the fourth volume, and was 176 never completed. In 1818 Dibdin was commissioned by Earl Spencer to purchase books for him on the continent, an expedition described in his sumptuous Bibliographical, Antiquarian and Picturesque Tour in France and Germany (1821). In 1824 he made an ambitious venture in his Library Companion, or the Young Man’s Guide and Old Man’s Comfort in the Choice of a Library, intended to point out the best works in all departments of literature. His culture was not broad enough, however, to render him competent for the task, and the work was severely criticized. For some years Dibdin gave himself up chiefly to religious literature. He returned to bibliography in his Bibliophobia, or Remarks on the Present Depression in the State of Literature and the Book Trade (1832), and the same subject furnishes the main interest of his Reminiscences of a Literary Life (1836), and his Bibliographical, Antiquarian and Picturesque Tour in the Northern Counties of England and Scotland (1838). Dibdin was the originator and vice-president, Lord Spencer being the president, of the Roxburghe Club, founded in 1812,—the first of the numerous book clubs which have done such service to literature.
DIBDIN, THOMAS JOHN (1771-1841), English dramatist and song-writer, son of Charles Dibdin, the song-writer, and of Mrs Davenet, an actress whose real name was Harriet Pitt, was born on the 21st of March 1771. He was apprenticed to his maternal uncle, a London upholsterer, and later to William Rawlins, afterwards sheriff of London. He summoned his second master unsuccessfully for rough treatment; and after a few years of service he ran away to join a company of country players. From 1789 to 1795 he played in all sorts of parts; he acted as scene painter at Liverpool in 1791; and during this period he composed more than 1000 songs. He made his first attempt as a dramatic writer in Something New, followed by The Mad Guardian in 1795. He returned to London in 1795, having married two years before; and in the winter of 1798-1799 his Jew and the Doctor was produced at Covent Garden. From this time he contributed a very large number of comedies, operas, farces, &c., to the public entertainment. Some of these brought immense popularity to the writer and immense profits to the theatres. It is stated that the pantomime of Mother Goose (1807) produced more than £20,000 for the management at Covent Garden theatre, and the High-mettled Racer, adapted as a pantomime from his father’s play, £18,000 at Astley’s. Dibdin was prompter and pantomime writer at Drury Lane until 1816, when he took the Surrey theatre. This venture proved disastrous and he became bankrupt. After this he was manager of the Haymarket, but without his old success, and his last years were passed in comparative poverty. In 1827 he published two volumes of Reminiscences; and at the time of his death he was preparing an edition of his father’s sea songs, for which a small sum was allowed him weekly by the lords of the admiralty. Of his own songs “The Oak Table” and “The Snug Little Island” are well-known examples. He died in London on the 16th of September 1841.
DIBRA (Slav. Debra), the capital of a sanjak bearing the same name, in the vilayet of Monastir, eastern Albania, Turkey. Pop. (1900) about 15,000. Dibra occupies a valley enclosed by mountains, and watered by the Tsrni Drin and Radika rivers, which meet 3 m. S. It is a fortified city, and the only episcopal see of the Bulgarian exarchate in Albania; most of the inhabitants are Albanians, but there is a strong Bulgarian colony. The local trade is almost entirely agricultural.
DIBRUGARH, a town of British India, in the Lakhimpur district of eastern Bengal and Assam, of which it is the headquarters, situated on the Dibru river about 4 m. above its confluence with the Brahmaputra. Pop. (1901) 11,227. It is the terminus of steamer navigation on the Brahmaputra, and also of a railway running to important coal-mines and petroleum wells, which connects with the Assam-Bengal system. Large quantities of coal and tea are exported. There are a military cantonment, the headquarters of the volunteer corps known as the Assam Valley Light Horse; a government high school, a training school for masters; and an aided school for girls. In 1900 a medical school for the province was established, out of a bequest left by Brigade-Surgeon J. Berry-White, which is maintained by the government, to train hospital assistants for the tea gardens. The Williamson artisan school is entirely supported by an endowment.
DICAEARCHUS, of Messene in Sicily, Peripatetic philosopher and pupil of Aristotle, historian, and geographer, flourished about 320 b.c. He was a friend of Theophrastus, to whom he dedicated the majority of his works. Of his writings, which comprised treatises on a great variety of subjects, only the titles and a few fragments survive. The most important of them was his βίος τῆς Έλλάδος (Life in Greece), in which the moral, political and social condition of the people was very fully discussed. In his Tripoliticos he described the best form of government as a mixture of monarchy, aristocracy and democracy, and illustrated it by the example of Sparta. Among the philosophical works of Dicaearchus may be mentioned the Lesbiaci, a dialogue in three books, in which the author endeavours to prove that the soul is mortal, to which he added a supplement called Corinthiaci. He also wrote a Description of the World illustrated by maps, in which was probably included his Measurements of Mountains. A description of Greece (150 iambics, in C. Müller, Frag. hist. Graec. i. 238-243) was formerly attributed to him, but, as the initial letters of the first twenty-three lines show, was really the work of Dionysius, son of Calliphon. Three considerable fragments of a prose description of Greece (Müller, i. 97-110) are now assigned to an unknown author named Heracleides. The De re publica of Cicero is supposed to be founded on one of Dicaearchus’s works.
The best edition of the fragments is by M. Fuhr (1841), a work of great learning; see also a dissertation by F. G. Osann, Beiträge zur röm. und griech. Litteratur, ii. pp. 1-117 (1839); Pauly-Wissowa, Realencyclopädie der klass. Altertumswiss. v. pt. 1 (1905).
DICE (plural of die, O. Fr. de, derived from Lat. dare, to give), small cubes of ivory, bone, wood or metal, used in gaming. The six sides of a die are each marked with a different number of incised dots in such a manner that the sum of the dots on any two opposite sides shall be 7. Dice seem always to have been employed, as is the case to-day, for gambling purposes, and they are also used in such games as backgammon. There are many methods of playing, from one to five dice being used, although two or three are the ordinary numbers employed in Great Britain and America. The dice are thrown upon a table or other smooth surface either from the hand or from a receptacle called a dice-box, the latter method having been in common use in Greece, Rome and the Orient in ancient times. Dice-boxes have been made in many shapes and of various materials, such as wood, leather, agate, crystal, metal or paper. Many contain bars within to ensure a proper agitation of the dice, and thus defeat trickery. Some, formerly used in England, were employed with unmarked dice, and allowed the cubes to fall through a kind of funnel upon a board marked off into six equal parts numbered from 1 to 6. It is a remarkable fact, that, wherever dice have been found, whether in the tombs of ancient Egypt, of classic Greece, or of the far East, they differ in no material respect from those in use to-day, the elongated ones with rounded ends found in Roman graves having been, not dice but tali, or knucklebones. Eight-sided dice have comparatively lately been introduced in France as aids to children in learning the multiplication table. The teetotum, or spinning die, used in many modern games, was known in ancient times in China and Japan. The increased popularity of the more elaborate forms of gaming has resulted in the decline of dicing. The usual method is to throw three times with three dice. If one or more sixes or fives are thrown the first time they may be reserved, the other throws being made with the dice that are left. The object is to throw three sixes = 18 or as near that number as possible, the highest throw winning, or, when drinks are to be paid for, the lowest throw losing. (For other methods of throwing consult the Encyclopaedia of Indoor Games, by R. F. Foster, 1903.) The most popular form of pure gambling with dice at the present day, particularly with the lower classes in America, is Craps, or Crap-Shooting, a simple form of Hazard, of French origin. Two dice are used. Each player puts up a stake 177 and the first caster may cover any or all of the bets. He then shoots, i.e. throws the dice from his open hand upon the table. If the sum of the dice is 7 or 11 the throw is a nick, or natural, and the caster wins all stakes. If the throw is either 2, 3 or 12 it is a crap, and the caster loses all. If any other number is thrown it is a point, and the caster continues until he throws the same number again, in which case he wins, or a 7, in which case he loses. The now practically obsolete game of Hazard was much more complicated than Craps. (Consult The Game of Hazard Investigated, by George Lowbut.) Poker dice are marked with ace, king, queen, jack and ten-spot. Five are used and the object is, in three throws, to make pairs, triplets, full hands or fours and fives of a kind, five aces being the highest hand. Straights do not count. In throwing to decide the payment of drinks the usual method is called horse and horse, in which the highest throws retire, leaving the two lowest to decide the loser by the best two in three throws. Should each player win one throw both are said to be horse and horse, and the next throw determines the loser. The two last casters may also agree to sudden death, i.e. a single throw. Loaded dice, i.e. dice weighted slightly on the side of the lowest number, have been used by swindlers from the very earliest times to the present day, a fact proved by countless literary allusions. Modern dice are often rounded at the corners, which are otherwise apt to wear off irregularly.
History.—Dice were probably evolved from knucklebones. The antiquary Thomas Hyde, in his Syntagma, records his opinion that the game of “odd or even,” played with pebbles, is nearly coeval with the creation of man. It is almost impossible to trace clearly the development of dice as distinguished from knucklebones, on account of the confusing of the two games by the ancient writers. It is certain, however, that both were played in times antecedent to those of which we possess any written records. Sophocles, in a fragment, ascribed their invention to Palamedes, a Greek, who taught them to his countrymen during the siege of Troy, and who, according to Pausanias (on Corinth, xx.), made an offering of them on the altar of the temple of Fortune. Herodotus (Clio) relates that the Lydians, during a period of famine in the days of King Atys, invented dice, knucklebones and indeed all other games except chess. The fact that dice have been used throughout the Orient from time immemorial, as has been proved by excavations from ancient tombs, seems to point clearly to an Asiatic origin. Dicing is mentioned as an Indian game in the Rig-veda. In its primitive form knucklebones was essentially a game of skill, played by women and children, while dice were used for gambling, and it was doubtless the gambling spirit of the age which was responsible for the derivative form of knucklebones, in which four sides of the bones received different values, which were then counted, like dice. Gambling with three, sometimes two, dice (κύβοι) was a very popular form of amusement in Greece, especially with the upper classes, and was an almost invariable accompaniment to the symposium, or drinking banquet. The dice were cast from conical beakers, and the highest throw was three sixes, called Aphrodite, while the lowest, three aces, was called the dog. Both in Greece and Rome different modes of counting were in vogue. Roman dice were called tesserae from the Greek word for four, indicative of the four sides. The Romans were passionate gamblers, especially in the luxurious days of the Empire, and dicing was a favourite form, though it was forbidden except during the Saturnalia. The emperor Augustus wrote in a letter to Suetonius concerning a game that he had played with his friends: “Whoever threw a dog or a six paid a denarius to the bank for every die, and whoever threw a Venus (the highest) won everything.” In the houses of the rich the dice-beakers were of carved ivory and the dice of crystal inlaid with gold. Mark Antony wasted his time at Alexandria with dicing, while, according to Suetonius, the emperors Augustus, Nero and Claudius were passionately fond of it, the last named having written a book on the game. Caligula notoriously cheated at the game; Domitian played it, and Commodus set apart special rooms in his palace for it. The emperor Verus, adopted son of Antonine, is known to have thrown dice whole nights together. Fashionable society followed the lead of its emperors, and, in spite of the severity of the laws, fortunes were squandered at the dicing table. Horace derided the youth of the period, who wasted his time amid the dangers of dicing instead of taming his charger and giving himself up to the hardships of the chase. Throwing dice for money was the cause of many special laws in Rome, according to one of which no suit could be brought by a person who allowed gambling in his house, even if he had been cheated or assaulted. Professional gamblers were common, and some of their loaded dice are preserved in museums. The common public-houses were the resorts of gamblers, and a fresco is extant showing two quarrelling dicers being ejected by the indignant host. Virgil, in the Copa generally ascribed to him, characterizes the spirit of that age in verse, which has been Englished as follows:—
| “What ho! Bring dice and good wine! Who cares for the morrow? Live—so calls grinning Death— Live, for I come to you soon!” |
That the barbarians were also given to gaming, whether or not they learned it from their Roman conquerors, is proved by Tacitus, who states that the Germans were passionately fond of dicing, so much so, indeed, that, having lost everything, they would even stake their personal liberty. Centuries later, during the middle ages, dicing became the favourite pastime of the knights, and both dicing schools (scholae deciorum) and gilds of dicers existed. After the downfall of feudalism the famous German mercenaries called landsknechts established a reputation as the most notorious dicing gamblers of their time. Many of the dice of the period were curiously carved in the images of men and beasts. In France both knights and ladies were given to dicing, which repeated legislation, including interdictions on the part of St Louis in 1254 and 1256, did not abolish. In Japan, China, Korea, India and other Asiatic countries dice have always been popular and are so still.
See Foster’s Encyclopaedia of Indoor Games (1903); Raymond’s Illustriertes Knobelbrevier (Oranienburg, 1888); Les Jeux des Anciens, by L. Becq de Fouquières (Paris, 1869); Das Knöchelspiel der Alten, by Bolle (Wismar, 1886); Die Spiele der Griechen und Römer, by W. Richter (Leipzig, 1887); Raymond’s Alte und neue Würfelspiele; Chinese Games with Dice, by Stewart Culin (Philadelphia, 1889); Korean Games, by Stewart Culin (Philadelphia, 1895).
DICETO, RALPH DE (d. c. 1202), dean of St Paul’s, London, and chronicler, is first mentioned in 1152, when he received the archdeaconry of Middlesex. He was probably born between 1120 and 1130; of his parentage and nationality we know nothing. The common statement that he derived his surname from Diss in Norfolk is a mere conjecture; Dicetum may equally well be a Latinized form of Dissai, or Dicy, or Dizy, place names which are found in Maine, Picardy, Burgundy and Champagne. In 1152 Diceto was already a master of arts; presumably he had studied at Paris. His reputation for learning and integrity stood high; he was regarded with respect and favour by Arnulf of Lisieux and Gilbert Foliot of Hereford (afterwards of London), two of the most eminent bishops of their time. Quite naturally, the archdeacon took in the Becket question the same side as his friends. Although his narrative is colourless, and although he was one of those who showed some sympathy for Becket at the council of Northampton (1164), the correspondence of Diceto shows that he regarded the archbishop’s conduct as ill-considered, and that he gave advice to those whom Becket regarded as his chief enemies. Diceto was selected, in 1166, as the envoy of the English bishops when they protested against the excommunications launched by Becket. But, apart from this episode, which he characteristically omits to record, he remained in the background. The natural impartiality of his intellect was accentuated by a certain timidity, which is apparent in his writings no less than in his life. About 1180 he became dean of St Paul’s. In this office he distinguished himself by careful management of the estates, by restoring the discipline of the chapter, and by building at his own expense a deanery-house. A scholar and a man of considerable erudition, he showed a strong preference for historical studies; and about the time when he was preferred to the deanery he began to collect materials for the history of his 178 own times. His friendships with Richard Fitz Nigel, who succeeded Foliot in the see of London, with William Longchamp, the chancellor of Richard I., and with Walter of Coutances, the archbishop of Rouen, gave him excellent opportunities of collecting information. His two chief works, the Abbreviationes Chronicorum and the Ymagines Historiarum, cover the history of the world from the birth of Christ to the year 1202. The former, which ends in 1147, is a work of learning and industry, but almost entirely based upon extant sources. The latter, beginning as a compilation from Robert de Monte and the letters of Foliot, becomes an original authority about 1172, and a contemporary record about 1181. In precision and fulness of detail the Ymagines are inferior to the chronicles of the so-called Benedict and of Hoveden. Though an annalist, Diceto is careless in his chronology; and the documents which he incorporates, while often important, are selected on no principle. He has little sense of style; but displays considerable insight when he ventures to discuss a political situation. For this reason, and on account of the details with which they supplement the more important chronicles of the period, the Ymagines are a valuable though a secondary source.
See W. Stubbs’ edition of the Historical Works of Diceto (Rolls ed. 1876, 2 vols.), and especially the introduction. The second volume contains minor works which are the barest compendia of facts taken from well-known sources. Diceto’s fragmentary Domesday of the capitular estates has been edited by Archdeacon Hale in The Domesday of St Paul’s, pp. 109 ff. (Camden Society, 1858).
DICEY, EDWARD (1832- ), English writer, son of T. E. Dicey of Claybrook Hall, Leicestershire, was born in 1832. Educated at Trinity College, Cambridge, where he took mathematical and classical honours, he became an active journalist, contributing largely to the principal reviews. He was called to the bar in 1875, became a bencher of Gray’s Inn in 1896, and was treasurer in 1903-1904. He was connected with the Daily Telegraph as leader writer and then as special correspondent, and after a short spell in 1870 as editor of the Daily News he became editor of the Observer, a position which he held until 1889. Of his many books on foreign affairs perhaps the most important are his England and Egypt (1884), Bulgaria, the Peasant State (1895), The Story of the Khedivate (1902), and The Egypt of the Future (1907). He was created C.B. in 1886.
His brother Albert Venn Dicey (b. 1835), English jurist, was educated at Balliol College, Oxford, where he took a first class in the classical schools in 1858. He was called to the bar at the Inner Temple in 1863. He held fellowships successively at Balliol, Trinity and All Souls’, and from 1882 to 1909 was Vinerian professor of law. He became Q.C. in 1890. His chief works are the Introduction to the Study of the Law of the Constitution (1885, 6th ed. 1902), which ranks as a standard work on the subject; England’s Case against Home Rule (1886); A Digest of the Law of England with Reference to the Conflict of Laws (1896), and Lectures on the Relation between Law and Public Opinion in England during the 19th century (1905).
DICHOTOMY (Gr. δίχα, apart, τέμνειν, to cut), literally a cutting asunder, the technical term for a form of logical division, consisting in the separation of a genus into two species, one of which has and the other has not, a certain quality or attribute. Thus men may be thus divided into white men, and men who are not white; each of these may be subdivided similarly. On the principle of contradiction this division is both exhaustive and exclusive; there can be no overlapping, and no members of the original genus or the lower groups are omitted. This method of classification, though formally accurate, has slight value in the exact sciences, partly because at every step one of the two groups is merely negatively characterized and therefore incapable of real subdivision; it is useful, however, in setting forth clearly the gradual descent from the most inclusive genus (summum genus) through species to the lowest class (infima species), which is divisible only into individual persons or things. (See further Division.) In astronomy the term is used for the aspect of the moon or of a planet when apparently half illuminated, so that its disk has the form of a semicircle.
DICK, ROBERT (1811-1866), Scottish geologist and botanist, was born at Tullibody, in Clackmannanshire, in January 1811. His father was an officer of excise. At the age of thirteen, after receiving a good elementary education at the parish school, Robert Dick was apprenticed to a baker, and served for three years. In these early days he became interested in wild flowers—he made a collection of plants and gradually acquired some knowledge of their names from an old encyclopaedia. When his time was out he left Tullibody and gained employment as a journeyman baker at Leith, Glasgow and Greenock. Meanwhile his father, who in 1826 had been removed to Thurso, as supervisor of excise, advised his son to set up a baker’s shop in that town. Thither Robert Dick went in 1830, he started in business as a baker and worked laboriously until he died on the 24th of December 1866. Throughout this period he zealously devoted himself to studying and collecting the plants, mollusca and insects of a wide area of Caithness, and his attention was directed soon after he settled in Thurso to the rocks and fossils. In 1835 he first found remains of fossil fishes; but it was not till some years later that his interest became greatly stirred. Then he obtained a copy of Hugh Miller’s Old Red Sandstone (published in 1841), and he began systematically to collect with hammer and chisel the fossils from the Caithness flags. In 1845 he found remains of Holoptychius and forwarded specimens to Hugh Miller, and he continued to send the best of his fossil fishes to that geologist, and to others after the death of Miller. In this way he largely contributed to the progress of geological knowledge, although he himself published nothing and was ever averse from publicity. His herbarium, which consisted of about 200 folios of mosses, ferns and flowering plants “almost unique in its completeness,” is now stored, with many of his fossils, in the museum at Thurso. Dick had a hard struggle for existence, especially through competition during his late years, when he was reduced almost to beggary: but of this few, if any, of his friends were aware until it was too late. A monument erected in the new cemetery at Thurso testifies to the respect which his life-work created, when the merits of this enthusiastic naturalist came to be appreciated.
See Robert Dick, Baker of Thurso, Geologist and Botanist, by Samuel Smiles (1878).
DICK, THOMAS (1774-1857), Scottish writer on astronomy, was born at Dundee on the 24th of November 1774. The appearance of a brilliant meteor inspired him, when in his ninth year, with a passion for astronomy; and at the age of sixteen he forsook the loom, and supported himself by teaching. In 1794 he entered the university of Edinburgh, and set up a school on the termination of his course; then, in 1801, took out a licence to preach, and officiated for some years as probationer in the United Presbyterian church. From about 1807 to 1817 he taught in the secession school at Methven in Perthshire, and during the ensuing decade in that of Perth, where he composed his first substantive book, The Christian Philosopher (1823, 8th ed. 1842). Its success determined his vocation as an author; he built himself, in 1827, a cottage at Broughty Ferry, near Dundee, and devoted himself wholly to literary and scientific pursuits. They proved, however, owing to his unpractical turn of mind, but slightly remunerative, and he was in 1847 relieved from actual poverty by a crown pension of £50 a year, eked out by a local subscription. He died on the 29th of July 1857. His best-known works are: Celestial Scenery (1837), The Sidereal Heavens (1840), and The Practical Astronomer (1845), in which is contained (p. 204) a remarkable forecast of the powers and uses of celestial photography. Written with competent knowledge, and in an agreeable style, they obtained deserved and widespread popularity.
See R. Chambers’s Eminent Scotsmen (ed. 1868); Monthly Notices Roy. Astr. Society, xviii. 98; Athenaeum (1857), p. 1008.
DICKENS, CHARLES JOHN HUFFAM (1812-1870), English novelist, was born on the 7th of February 1812 at a house in the Mile End Terrace, Commercial Road, Landport (Portsea)—a house which was opened as a Dickens Museum on 22nd July 1904. His father John Dickens (d. 1851), a clerk in the navy-pay office 179 on a salary of £80 a year, and stationed for the time being at Portsmouth, had married in 1809 Elizabeth, daughter of Thomas Barrow, and she bore him a family of eight children, Charles being the second. In the winter of 1814 the family moved from Portsea in the snow, as he remembered, to London, and lodged for a time near the Middlesex hospital. The country of the novelist’s childhood, however, was the kingdom of Kent, where the family was established in proximity to the dockyard at Chatham from 1816 to 1821. He looked upon himself in later years as a man of Kent, and his capital abode as that in Ordnance Terrace, or 18 St Mary’s Place, Chatham, amid surroundings classified in Mr Pickwick’s notes as “appearing” to be soldiers, sailors, Jews, chalk, shrimps, officers and dockyard men. He fell into a family the general tendency of which was to go down in the world, during one of its easier periods (John Dickens was now fifth clerk on £250 a year), and he always regarded himself as belonging by right to a comfortable, genteel, lower middle-class stratum of society. His mother taught him to read; to his father he appeared very early in the light of a young prodigy, and by him Charles was made to sit on a tall chair and warble popular ballads, or even to tell stories and anecdotes for the benefit of fellow-clerks in the office. John Dickens, however, had a small collection of books which were kept in a little room upstairs that led out of Charles’s own, and in this attic the boy found his true literary instructors in Roderick Random, Peregrine Pickle, Humphry Clinker, Tom Jones, The Vicar of Wakefield, Don Quixote, Gil Blas and Robinson Crusoe. The story of how he played at the characters in these books and sustained his idea of Roderick Random for a month at a stretch is picturesquely told in David Copperfield. Here as well as in his first and last books and in what many regard as his best, Great Expectations, Dickens returns with unabated fondness and mastery to the surroundings of his childhood. From seven to nine years he was at a school kept in Clover Lane, Chatham, by a Baptist minister named William Giles, who gave him Goldsmith’s Bee as a keepsake when the call to Somerset House necessitated the removal of the family from Rochester to a shabby house in Bayham Street, Camden Town. At the very moment when a consciousness of capacity was beginning to plump his youthful ambitions, the whole flattering dream vanished and left not a rack behind. Happiness and Chatham had been left behind together, and Charles was about to enter a school far sterner and also far more instructive than that in Clover Lane. The family income had been first decreased and then mortgaged; the creditors of the “prodigal father” would not give him time; John Dickens was consigned to the Marshalsea; Mrs Dickens started an “Educational Establishment” as a forlorn hope in Upper Gower Street; and Charles, who had helped his mother with the children, blacked the boots, carried things to the pawnshop and done other menial work, was now sent out to earn his own living as a young hand in a blacking warehouse, at Old Hungerford Stairs, on a salary of six shillings a week. He tied, trimmed and labelled blacking pots for over a year, dining off a saveloy and a slice of pudding, consorting with two very rough boys, Bob Fagin and Pol Green, and sleeping in an attic in Little College Street, Camden Town, in the house of Mrs Roylance (Pipchin), while on Sunday he spent the day with his parents in their comfortable prison, where they had the services of a “marchioness” imported from the Chatham workhouse.
Already consumed by ambition, proud, sensitive and on his dignity to an extent not uncommon among boys of talent, he felt his position keenly, and in later years worked himself up into a passion of self-pity in connexion with the “degradation” and “humiliation” of this episode. The two years of childish hardship which ate like iron into his soul were obviously of supreme importance in the growth of the novelist. Recollections of the streets and the prison and its purlieus supplied him with a store of literary material upon which he drew through all the years of his best activity. And the bitterness of such an experience was not prolonged sufficiently to become sour. From 1824 to 1826, having been rescued by a family quarrel and by a windfall in the shape of a legacy to his father, from the warehouse, he spent two years at an academy known as Wellington House, at the corner of Granby Street and the Hampstead Road (the lighter traits of which are reproduced in Salem House), and was there known as a merry and rather mischievous boy. Fortunately he learned nothing there to compromise the results of previous instruction. His father had now emerged from the Marshalsea and was seeking employment as a parliamentary reporter. A Gray’s Inn solicitor with whom he had had dealings was attracted by the bright, clever look of Charles, and took him into his office as a boy at a salary of thirteen and sixpence (rising to fifteen shillings) a week. He remained in Mr Blackmore’s office from May 1827 to November 1828, but he had lost none of his eager thirst for distinction, and spent all his spare time mastering Gurney’s shorthand and reading early and late at the British Museum. A more industrious apprentice in the lower grades of the literary profession has never been known, and the consciousness of opportunities used to the most splendid advantage can hardly have been absent from the man who was shortly to take his place at the head of it as if to the manner born. Lowten and Guppy, and Swiveller had been observed from this office lad’s stool; he was now greatly to widen his area of study as a reporter in Doctors’ Commons and various police courts, including Bow Street, working all day at law and much of the night at shorthand. Some one asked John Dickens, during the first eager period of curiosity as to the man behind “Pickwick,” where his son Charles was educated. “Well really,” said the prodigal father, “he may be said—haw—haw—to have educated himself.” He was one of the most rapid and accurate reporters in London when, at nineteen years of age, in 1831, he realized his immediate ambition and “entered the gallery” as parliamentary reporter to the True Sun. Later he was reporter to the Mirror of Parliament and then to the Morning Chronicle. Several of his earliest letters are concerned with his exploits as a reporter, and allude to the experiences he had, travelling fifteen miles an hour and being upset in almost every description of known vehicle in various parts of Britain between 1831 and 1836. The family was now living in Bentwick Street, Manchester Square, but John Dickens was still no infrequent inmate of the sponging-houses. With all the accessories of these places of entertainment his son had grown to be excessively familiar. Writing about 1832 to his school friend Tom Mitton, Dickens tells him that his father has been arrested at the suit of a wine firm, and begs him go over to Cursitor Street and see what can be done. On another occasion of a paternal disappearance he observes: “I own that his absence does not give me any great uneasiness, knowing how apt he is to get out of the way when anything goes wrong.” In yet another letter he asks for a loan of four shillings.
In the meanwhile, however, he had commenced author in a more creative sense by penning some sketches of contemporary London life, such as he had attempted in his school days in imitation of the sketches published in the London and other magazines of that day. The first of these appeared in the December number of the Old Monthly Magazine for 1833. By the following August, when the signature “Boz” was first given, five of these sketches had appeared. By the end of 1834 we find him settled in rooms in Furnival’s Inn, and a little later his salary on the Morning Chronicle was raised, owing to the intervention of one of its chiefs, George Hogarth, the father of (in addition to six sons) eight charming daughters, to one of whom, Catherine, Charles was engaged to be married before the year was out. Clearly as his career now seemed designated, he was at this time or a little before it coquetting very seriously with the stage: but circumstances were rapidly to determine another stage in his career. A year before Queen Victoria’s accession appeared in two volumes Sketches by Boz, Illustrative of Everyday Life and Everyday People. The book came from a prentice hand, but like the little tract on the Puritan abuse of the Sabbath entitled “Sunday under three Heads” which appeared a few months later, it contains in germ all, or almost all, the future Dickens. Glance at the headings of the pages. Here we have the Beadle and all connected with him, London streets, theatres, shows, the pawnshop, Doctors’ Commons, Christmas, Newgate, coaching, the 180 river. Here comes a satirical picture of parliament, fun made of cheap snobbery, a rap on the knuckles of sectarianism. And what could be more prophetic than the title of the opening chapter—Our Parish? With the Parish—a large one indeed—Dickens to the end concerned himself; he began with a rapid survey of his whole field, hinting at all he might accomplish, indicating the limits he was not to pass. This year was to be still more momentous to Dickens, for, on the 2nd of April 1836, he was married to George Hogarth’s eldest daughter Catherine. He seems to have fallen in love with the daughters collectively, and, judging by subsequent events, it has been suggested that perhaps he married the wrong one. His wife’s sister Mary was the romance of his early married life, and another sister, Georgina, was the dearest friend of his last ten years.
A few days before the marriage, just two months after the appearance of the Sketches, the first part of The Posthumous Papers of the Pickwick Club was announced. One of the chief vogues of the day was the issue of humorous, sporting or anecdotal novels in parts, with plates, and some of the best talent of the day, represented by Ainsworth, Bulwer, Marryat, Maxwell, Egan, Hook and Surtees, had been pressed into this kind of enterprise. The publishers of the day had not been slow to perceive Dickens’s aptitude for this species of “letterpress.” A member of the firm of Chapman & Hall called upon him at Furnival’s Inn in December 1835 with a proposal that he should write about a Nimrod Club of amateur sportsmen, foredoomed to perpetual ignominies, while the comic illustrations were to be etched by Seymour, a well-known rival of Cruikshank (the illustrator of Boz). The offer was too tempting for Dickens to refuse, but he changed the idea from a club of Cockney sportsmen to that of a club of eccentric peripatetics, on the sensible grounds, first that sporting sketches were stale, and, secondly, that he knew nothing worth speaking of about sport. The first seven pictures appeared with the signature of Seymour and the letterpress of Dickens. Before the eighth picture appeared Seymour had blown his brains out. After a brief interval of Buss, Dickens obtained the services of Hablot K. Browne, known to all as “Phiz.” Author and illustrator were as well suited to one another and to the common creation of a unique thing as Gilbert and Sullivan. Having early got rid of the sporting element, Dickens found himself at once. The subject exactly suited his knowledge, his skill in arranging incidents—nay, his very limitations too. No modern book is so incalculable. We commence laughing heartily at Pickwick and his troupe. The laugh becomes kindlier. We are led on through a tangle of adventure, never dreaming what is before us. The landscape changes: Pickwick becomes the symbol of kindheartedness, simplicity and innocent levity. Suddenly in the Fleet Prison a deeper note is struck. The medley of human relationships, the loneliness, the mystery and sadness of human destinies are fathomed. The tragedy of human life is revealed to us amid its most farcical elements. The droll and laughable figure of the hero is transfigured by the kindliness of human sympathy into a beneficent and bespectacled angel in shorts and gaiters. By defying accepted rules, Dickens had transcended the limited sphere hitherto allotted to his art: he had produced a book to be enshrined henceforth in the inmost hearts of all sorts and conditions of his countrymen, and had definitely enlarged the boundaries of English humour and English fiction. As for Mr Pickwick, he is a fairy like Puck or Santa Claus, while his creator is “the last of the mythologists and perhaps the greatest.”
When The Pickwick Papers appeared in book form at the close of 1837 Dickens’s popular reputation was made. From the appearance of Sam Weller in part v. the universal hunger for the monthly parts had risen to a furore. The book was promptly translated into French and German. The author had received little assistance from press or critics, he had no influential connexions, his class of subjects was such as to “expose him at the outset to the fatal objections of vulgarity,” yet in less than six months from the appearance of the first number, as the Quarterly Review almost ruefully admits, the whole reading world was talking about the Pickwickians. The names of Winkle, Wardle, Weller, Jingle, Snodgrass, Dodson & Fogg, were as familiar as household words. Pickwick chintzes figured in the linendrapers’ windows, and Pickwick cigars in every tobacconist’s; Weller corduroys became the stock-in-trade of every breeches-maker; Boz cabs might be seen rattling through the streets, and the portrait of the author of Pelham and Crichton was scraped down to make way for that of the new popular favourite on the omnibuses. A new and original genius had suddenly sprung up, there was no denying it, even though, as the Quarterly concluded, “it required no gift of prophecy to foretell his fate—he has risen like a rocket and he will come down like the stick.” It would have needed a very emphatic gift of prophecy indeed to foretell that Dickens’s reputation would have gone on rising until at the present day (after one sharp fall, which reached an extreme about 1887) it stands higher than it has ever stood before.
Dickens’s assumption of the literary purple was as amazing as anything else about him. Accepting the homage of the luminaries of the literary, artistic and polite worlds as if it had been his natural due, he arranges for the settlement of his family, decrees, like another Edmund Kean, that his son is to go to Eton, carries on the most complicated negotiations with his publishers and editors, presides and orates with incomparable force at innumerable banquets, public and private, arranges elaborate villegiatures in the country, at the seaside, in France or in Italy, arbitrates in public on every topic, political, ethical, artistic, social or literary, entertains and legislates for an increasingly large domestic circle, both juvenile and adult, rules himself and his time-table with a rod of iron. In his letter-writing alone, Dickens did a life’s literary work. Nowadays no one thinks of writing such letters; that is to say, letters of such length and detail, for the quality is Dickens’s own. He evidently enjoyed this use of the pen. Page after page of Forster’s Life (750 pages in the Letters edited by his daughter and sister-in-law) is occupied with transcription from private correspondence, and never a line of this but is thoroughly worthy of print and preservation. If he makes a tour in any part of the British Isles, he writes a full description of all he sees, of everything that happens, and writes it with such gusto, such mirth, such strokes of fine picturing, as appear in no other private letters ever given to the public. Naturally buoyant in all circumstances, a holiday gave him the exhilaration of a schoolboy. See how he writes from Cornwall, when on a trip with two or three friends, in 1843. “Heavens! if you could have seen the necks of bottles, distracting in their immense variety of shape, peering out of the carriage pockets! If you could have witnessed the deep devotion of the post-boys, the maniac glee of the waiters! If you could have followed us into the earthy old churches we visited, and into the strange caverns on the gloomy seashore, and down into the depths of mines, and up to the tops of giddy heights, where the unspeakably green water was roaring, I don’t know how many hundred feet below.... I never laughed in my life as I did on this journey. It would have done you good to hear me. I was choking and gasping and bursting the buckles off the back of my stock, all the way. And Stanfield”—the painter—“got into such apoplectic entanglements that we were obliged to beat him on the back with portmanteaus before we could recover him.”
The animation of Dickens’s look would attract the attention of any one, anywhere. His figure was not that of an Adonis, but his brightness made him the centre and pivot of every society he was in. The keenness and vivacity of his eye combined with his inordinate appetite for life to give the unique quality to all that he wrote. His instrument is that of the direct, sinewy English of Smollett, combined with much of the humorous grace of Goldsmith (his two favourite authors), but modernized to a certain extent under the influence of Washington Irving, Sydney Smith, Jeffrey, Lamb, and other writers of the London Magazine. He taught himself to speak French and Italian, but he could have read little in any language. His ideas were those of the inchoate and insular liberalism of the ’thirties. His unique force in literature he was to owe to no supreme artistic or intellectual quality, but almost entirely to his inordinate gift of observation, his sympathy with the humble, his power over the emotions and his incomparable endowment of unalloyed human fun. To 181 contemporaries he was not so much a man as an institution, at the very mention of whose name faces were puckered with grins or wreathed in smiles. To many his work was a revelation, the revelation of a new world and one far better than their own. And his influence went further than this in the direction of revolution or revival. It gave what were then universally referred to as “the lower orders” a new sense of self-respect, a new feeling of citizenship. Like the defiance of another Luther, or the Declaration of a new Independence, it emitted a fresh ray of hope across the firmament. He did for the whole English-speaking race what Burns had done for Scotland—he gave it a new conceit of itself. He knew what a people wanted and he told what he knew. He could do this better than anybody else because his mind was theirs. He shared many of their “great useless virtues,” among which generosity ranks before justice, and sympathy before truth, even though, true to his middle-class vein, he exalts piety, chastity and honesty in a manner somewhat alien to the mind of the low-bred man. This is what makes Dickens such a demigod and his public success such a marvel, and this also is why any exclusively literary criticism of his work is bound to be so inadequate. It should also help us to make the necessary allowances for the man. Dickens, even the Dickens of legend that we know, is far from perfect. The Dickens of reality to which Time may furnish a nearer approximation is far less perfect. But when we consider the corroding influence of adulation, and the intoxication of unbridled success, we cannot but wonder at the relatively high level of moderation and self-control that Dickens almost invariably observed. Mr G. K. Chesterton remarks suggestively that Dickens had all his life the faults of the little boy who is kept up too late at night. He is overwrought by happiness to the verge of exasperation, and yet as a matter of fact he does keep on the right side of the breaking point. The specific and curative in his case was the work in which he took such anxious pride, and such unmitigated delight. He revelled in punctual and regular work; at his desk he was often in the highest spirits. Behold how he pictured himself, one day at Broadstairs, where he was writing Chuzzlewit. “In a bay-window in a one-pair sits, from nine o’clock to one, a gentleman with rather long hair and no neckcloth, who writes and grins, as if he thought he was very funny indeed. At one he disappears, presently emerges from a bathing-machine, and may be seen, a kind of salmon-colour porpoise, splashing about in the ocean. After that, he may be viewed in another bay-window on the ground-floor eating a strong lunch; and after that, walking a dozen miles or so, or lying on his back on the sand reading a book. Nobody bothers him, unless they know he is disposed to be talked to, and I am told he is very comfortable indeed. He’s as brown as a berry, and they do say he is as good as a small fortune to the innkeeper, who sells beer and cold punch.” Here is the secret of such work as that of Dickens; it is done with delight—done (in a sense) easily, done with the mechanism of mind and body in splendid order. Even so did Scott write; though more rapidly and with less conscious care: his chapter finished before the world had got up to breakfast. Later, Dickens produced novels less excellent with much more of mental strain. The effects of age could not have shown themselves so soon, but for the unfortunate loss of energy involved in his non-literary labours.
While the public were still rejoicing in the first sprightly runnings of the “new humour,” the humorist set to work desperately on the grim scenes of Oliver Twist, the story of a parish orphan, the nucleus of which had already seen the light in his Sketches. The early scenes are of a harrowing reality, despite the germ of forced pathos which the observant reader may detect in the pitiful parting between Oliver and little Dick; but what will strike every reader at once in this book is the directness and power of the English style, so nervous and unadorned: from its unmistakable clearness and vigour Dickens was to travel far as time went on. But the full effect of the old simplicity is felt in such masterpieces of description as the drive of Oliver and Sikes to Chertsey, the condemned-cell ecstasy of Fagin, or the unforgettable first encounter between Oliver and the Artful Dodger. Before November 1837 had ended, Charles Dickens entered on an engagement to write a successor to Pickwick on similar lines of publication. Oliver Twist was then in mid-career; a Life of Grimaldi and Barnaby Rudge were already covenanted for. Dickens forged ahead with the new tale of Nicholas Nickleby and was justified by the results, for its sale far surpassed even that of Pickwick. As a conception it is one of his weakest. An unmistakably 18th-century character pervades it. Some of the vignettes are among the most piquant and besetting ever written. Large parts of it are totally unobserved conventional melodrama; but the Portsmouth Theatre and Dotheboys Hall and Mrs Nickleby (based to some extent, it is thought, upon Miss Bates in Emma, but also upon the author’s Mamma) live for ever as Dickens conceived them in the pages of Nicholas Nickleby.
Having got rid of Nicholas Nickleby and resigned his editorship of Bentley’s Miscellany, in which Oliver Twist originally appeared, Dickens conceived the idea of a weekly periodical to be issued as Master Humphrey’s Clock, to comprise short stories, essays and miscellaneous papers, after the model of Addison’s Spectator. To make the weekly numbers “go,” he introduced Mr Pickwick, Sam Weller and his father in friendly intercourse. But the public requisitioned “a story,” and in No. 4 he had to brace himself up to give them one. Thus was commenced The Old Curiosity Shop, which was continued with slight interruptions, and followed by Barnaby Rudge. For the first time we find Dickens obsessed by a highly complicated plot. The tonality achieved in The Old Curiosity Shop surpassed anything he had attempted in this difficult vein, while the rich humour of Dick Swiveller and the Marchioness, and the vivid portraiture of the wandering Bohemians, attain the very highest level of Dickensian drollery; but in the lamentable tale of Little Nell (though Landor and Jeffrey thought the character-drawing of this infant comparable with that of Cordelia), it is generally admitted that he committed an indecent assault upon the emotions by exhibiting a veritable monster of piety and long-suffering in a child of tender years. In Barnaby Rudge he was manifestly affected by the influence of Scott, whose achievements he always regarded with a touching veneration. The plot, again, is of the utmost complexity, and Edgar Allan Poe (who predicted the conclusion) must be one of the few persons who ever really mastered it. But few of Dickens’s books are written in a more admirable style.
Master Humphrey’s Clock concluded, Dickens started in 1842 on his first visit to America—an episode hitherto without parallel in English literary history, for he was received everywhere with popular acclamation as the representative of a grand triumph of the English language and imagination, without regard to distinctions of nationality. He offended the American public grievously by a few words of frank description and a few quotations of the advertisement columns of American papers illustrating the essential barbarity of the old slave system (American Notes). Dickens was soon pining for home—no English writer is more essentially and insularly English in inspiration and aspiration than he is. He still brooded over the perverseness of America on the copyright question, and in his next book he took the opportunity of uttering a few of his impressions about the objectionable sides of American democracy, the result being that “all Yankee-doodle-dom blazed up like one universal soda bottle,” as Carlyle said. Martin Chuzzlewit (1843-1844) is important as closing his great character period. His sève originale, as the French would say, was by this time to a considerable extent exhausted, and he had to depend more upon artistic elaboration, upon satires, upon tours de force of description, upon romantic and ingenious contrivances. But all these resources combined proved unequal to his powers as an original observer of popular types, until he reinforced himself by autobiographic reminiscence, as in David Copperfield and Great Expectations, the two great books remaining to his later career.
After these two masterpieces and the three wonderful books with which he made his début, we are inclined to rank Chuzzlewit. Nothing in Dickens is more admirably seen and presented than Todgers’s, a bit of London particular cut out with a knife. Mr 182 Pecksniff and Mrs Gamp, Betsy Prig and “Mrs Harris” have passed into the national language and life. The coach journey, the windy autumn night, the stealthy trail of Jonas, the undertone of tragedy in the Charity and Mercy and Chuffey episodes suggest a blending of imaginative vision and physical penetration hardly seen elsewhere. Two things are specially notable about this novel—the exceptional care taken over it (as shown by the interlineations in the MS.) and the caprice or nonchalance of the purchasing public, its sales being far lower than those of any of its monthly predecessors.
At the close of 1843, to pay outstanding debts of his now lavish housekeeping, he wrote that pioneer of Christmas numbers, that national benefit as Thackeray called it, A Christmas Carol. It failed to realize his pecuniary anticipations, and Dickens resolved upon a drastic policy of retrenchment and reform. He would save expense by living abroad and would punish his publishers by withdrawing his custom from them, at least for a time. Like everything else upon which he ever determined, this resolution was carried out with the greatest possible precision and despatch. In June 1844 he set out for Marseilles with his now rapidly increasing family (the journey cost him £200). In a villa on the outskirts of Genoa he wrote The Chimes, which, during a brief excursion to London before Christmas, he read to a select circle of friends (the germ of his subsequent lecture-audiences), including Forster, Carlyle, Stanfield, Dyce, Maclise and Jerrold. He was again in London in 1845, enjoying his favourite diversion of private theatricals; and in January 1846 he experimented briefly as the editor of a London morning paper—the Daily News. By early spring he was back at Lausanne, writing his customary vivid letters to his friends, craving as usual for London streets, commencing Dombey and Son, and walking his fourteen miles daily. The success of Dombey and Son completely rehabilitated the master’s finances, enabled him to return to England, send his son to Eton and to begin to save money. Artistically it is less satisfactory; it contains some of Dickens’s prime curios, such as Cuttle, Bunsby, Toots, Blimber, Pipchin, Mrs MacStinger and young Biler; it contains also that masterpiece of sentimentality which trembles upon the borderland of the sublime and the ridiculous, the death of Paul Dombey (“that sweet Paul,” as Jeffrey, the “critic laureate,” called him), and some grievous and unquestionable blemishes. As a narrative, moreover, it tails off into a highly complicated and exacting plot. It was followed by a long rest at Broadstairs before Dickens returned to the native home of his genius, and early in 1849 “began to prepare for David Copperfield.”
“Of all my books,” Dickens wrote, “I like this the best; like many fond parents I have my favourite child, and his name is David Copperfield.” In some respects it stands to Dickens in something of the same relation in which the contemporary Pendennis stands to Thackeray. As in that book, too, the earlier portions are the best. They gained in intensity by the autobiographical form into which they are thrown; as Thackeray observed, there was no writing against such power. The tragedy of Emily and the character of Rosa Dartle are stagey and unreal; Uriah Heep is bad art; Agnes, again, is far less convincing as a consolation than Dickens would have us believe; but these are more than compensated by the wonderful realization of early boyhood in the book, by the picture of Mr Creakle’s school, the Peggottys, the inimitable Mr Micawber, Betsy Trotwood and that monument of selfish misery, Mrs Gummidge.
At the end of March 1850 commenced the new twopenny weekly called Household Words, which Dickens planned to form a direct means of communication between himself and his readers, and as a means of collecting around him and encouraging the talents of the younger generation. No one was better qualified than he for this work, whether we consider his complete freedom from literary jealousy or his magical gift of inspiring young authors. Following the somewhat dreary and incoherent Bleak House of 1852, Hard Times (1854)—an anti-Manchester School tract, which Ruskin regarded as Dickens’s best work—was the first long story written for Household Words. About this time Dickens made his final home at Gad’s Hill, near Rochester, and put the finishing touch to another long novel published upon the old plan, Little Dorrit (1855-1857). In spite of the exquisite comedy of the master of the Marshalsea and the final tragedy of the central figure, Little Dorrit is sadly deficient in the old vitality, the humour is often a mock reality, and the repetition of comic catch-words and overstrung similes and metaphors is such as to affect the reader with nervous irritation. The plot and characters ruin each other in this amorphous production. The Tale of Two Cities, commenced in All the Year Round (the successor of Household Words) in 1859, is much better: the main characters are powerful, the story genuinely tragic, and the atmosphere lurid; but enormous labour was everywhere expended upon the construction of stylistic ornament.
The Tale of Two Cities was followed by two finer efforts at atmospheric delineation, the best things he ever did of this kind: Great Expectations (1861), over which there broods the mournful impression of the foggy marshes of the Lower Thames; and Our Mutual Friend (1864-1865), in which the ooze and mud and slime of Rotherhithe, its boatmen and loafers, are made to pervade the whole book with cumulative effect. The general effect produced by the stories is, however, very different. In the first case, the foreground was supplied by autobiographical material of the most vivid interest, and the lucidity of the creative impulse impelled him to write upon this occasion with the old simplicity, though with an added power. Nothing therefore, in the whole range of Dickens surpassed the early chapters of Great Expectations in perfection of technique or in mastery of all the resources of the novelist’s art. To have created Abel Magwitch alone is to be a god indeed, says Mr Swinburne, among the creators of deathless men. Pumblechook is actually better and droller and truer to imaginative life than Pecksniff; Joe Gargery is worthy to have been praised and loved at once by Fielding and by Sterne: Mr Jaggers and his clients, Mr Wemmick and his parent and his bride, are such figures as Shakespeare, when dropping out of poetry, might have created, if his lot had been cast in a later century. “Can as much be said,” Mr Swinburne boldly asks, “for the creatures of any other man or god?”
In November 1867 Dickens made a second expedition to America, leaving all the writing that he was ever to complete behind him. He was to make a round sum of money, enough to free him from all embarrassments, by a long series of exhausting readings, commencing at the Tremont Temple, Boston, on the 2nd of December. The strain of Dickens’s ordinary life was so tense and so continuous that it is, perhaps, rash to assume that he broke down eventually under this particular stress; for other reasons, however, his persistence in these readings, subsequent to his return, was strongly deprecated by his literary friends, led by the arbitrary and relentless Forster. It is a long testimony to Dickens’s self-restraint, even in his most capricious and despotic moments, that he never broke the cord of obligation which bound him to his literary mentor, though sparring matches between them were latterly of frequent occurrence. His farewell reading was given on the 15th of March 1870, at St James’s Hall. He then vanished from “those garish lights,” as he called them, “for evermore.” Of the three brief months that remained to him, his last book, The Mystery of Edwin Drood, was the chief occupation. It hardly promised to become a masterpiece (Longfellow’s opinion) as did Thackeray’s Denis Duval, but contained much fine descriptive technique, grouped round a scene of which Dickens had an unrivalled sympathetic knowledge.
In March and April 1870 Dickens, as was his wont, was mixing in the best society; he dined with the prince at Lord Houghton’s and was twice at court, once at a long deferred private interview with the queen, who had given him a presentation copy of her Leaves from a Journal of our Life in the Highlands with the inscription “From one of the humblest of authors to one of the greatest”; and who now begged him on his persistent refusal of any other title to accept the nominal distinction of a privy councillor. He took for four months the Milner Gibsons’ house at 5 Hyde Park Place, opposite the Marble Arch, where he gave a brilliant reception on the 7th of April. His last public appearance was made at the Royal Academy banquet early in May. 183 He returned to his regular methodical routine of work at Gad’s Hill on the 30th of May, and one of the last instalments he wrote of Edwin Drood contained an ominous speculation as to the next two people to die at Cloisterham: “Curious to make a guess at the two, or say at one of the two.” Two letters bearing the well-known superscription “Gad’s Hill Place, Higham by Rochester, Kent” are dated the 8th of June, and, on the same Thursday, after a long spell of writing in the Châlet where he habitually wrote, he collapsed suddenly at dinner. Startled by the sudden change in the colour and expression of his face, his sister-in-law (Miss Hogarth) asked him if he was ill; he said “Yes, very ill,” but added that he would finish dinner and go on afterwards to London. “Come and lie down,” she entreated; “Yes, on the ground,” he said, very distinctly; these were the last words he spoke, and he slid from her arms and fell upon the floor. He died at 6-10 P.M. on Friday, the 9th of June, and was buried privately in Poets’ Corner, Westminster Abbey, in the early morning of the 14th of June. One of the most appealing memorials was the drawing by his “new illustrator” Luke Fildes in the Graphic of “The Empty Chair; Gad’s Hill: ninth of June, 1870.” “Statesmen, men of science, philanthropists, the acknowledged benefactors of their race, might pass away, and yet not leave the void which will be caused by the death of Charles Dickens” (The Times). In his will he enjoined his friends to erect no monument in his honour, and directed his name and dates only to be inscribed on his tomb, adding this proud provision, “I rest my claim to the remembrance of my country on my published works.”
Dickens had no artistic ideals worth speaking about. The sympathy of his readers was the one thing he cared about and, like Cobbett, he went straight for it through the avenue of the emotions. In personality, intensity and range of creative genius he can hardly be said to have any modern rival. His creations live, move and have their being about us constantly, like those of Homer, Virgil, Chaucer, Rabelais, Cervantes, Shakespeare, Bunyan, Molière and Sir Walter Scott. As to the books themselves, the backgrounds on which these mighty figures are projected, they are manifestly too vast, too chaotic and too unequal ever to become classics. Like most of the novels constructed upon the unreformed model of Smollett and Fielding, those of Dickens are enormous stock-pots into which the author casts every kind of autobiographical experience, emotion, pleasantry, anecdote, adage or apophthegm. The fusion is necessarily very incomplete and the hotch-potch is bound to fall to pieces with time. Dickens’s plots, it must be admitted, are strangely unintelligible, the repetitions and stylistic decorations of his work exceed all bounds, the form is unmanageable and insignificant. The diffuseness of the English novel, in short, and its extravagant didacticism cannot fail to be most prejudicial to its perpetuation. In these circumstances there is very little fiction that will stand concentration and condensation so well as that of Dickens.
For these reasons among others our interest in Dickens’s novels as integers has diminished and is diminishing. But, on the other hand, our interest and pride in him as a man and as a representative author of his age and nation has been steadily augmented and is still mounting. Much of the old criticism of his work, that it was not up to a sufficiently high level of art, scholarship or gentility, that as an author he is given to caricature, redundancy and a shameless subservience to popular caprice, must now be discarded as irrelevant.
As regards formal excellence it is plain that Dickens labours under the double disadvantage of writing in the least disciplined of all literary genres in the most lawless literary milieu of the modern world, that of Victorian England. In spite of these defects, which are those of masters such as Rabelais, Hugo and Tolstoy, the work of Dickens is more and more instinctively felt to be true, original and ennobling. It is already beginning to undergo a process of automatic sifting, segregation and crystallization, at the conclusion of which it will probably occupy a larger segment in the literary consciousness of the English-spoken race than ever before.
Portraits of Dickens, from the gay and alert “Boz” of Samuel Lawrence, and the self-conscious, rather foppish portrait by Maclise which served as frontispiece to Nicholas Nickleby, to the sketch of him as Bobadil by C. R. Leslie, the Drummond and Ary Scheffer portraits of middle age and the haggard and drawn representations of him from photographs after his shattering experiences as a public entertainer from 1856 (the year of his separation from his wife) onwards, are reproduced in Kitton, in Forster and Gissing and in the other biographies. Sketches are also given in most of the books of his successive dwelling places at Ordnance Terrace and 18 St Mary’s Place, Chatham; Bayham Street, Camden Town; 15 Furnival’s Inn; 48 Doughty Street; 1 Devonshire Terrace, Regent’s Park; Tavistock House, Tavistock Square; and Gad’s Hill Place. The manuscripts of all the novels, with the exception of the Tale of Two Cities and Edwin Drood, were given to Forster, and are now preserved in the Dyce and Forster Museum at South Kensington. The work of Dickens was a prize for which publishers naturally contended both before and after his death. The first collective edition of his works was begun in April 1847, and their number is now very great. The most complete is still that of Messrs Chapman & Hall, the original publishers of Pickwick; others of special interest are the Harrap edition, originally edited by F. G. Kitton; Macmillan’s edition with original illustrations and introduction by Charles Dickens the younger; and the edition in the World’s Classics with introductions by G.K. Chesterton. Of the translations the best known is that done into French by Lorain, Pichot and others, with B.H. Gausseron’s excellent Pages Choisies (1903).
Bibliography.—During his lifetime Dickens’s biographer was clearly indicated in his guide, philosopher and friend, John Forster, who had known the novelist intimately since the days of his first triumph with Pickwick, who had constituted himself a veritable encyclopaedia of information about Dickens, and had clung to his subject (in spite of many rebuffs which his peremptory temper found it hard to digest) as tightly as ever Boswell had enveloped Johnson. Two volumes of Forster’s Life of Charles Dickens appeared in 1872 and a third in 1874. He relied much on Dickens’s letters to himself and produced what must always remain the authoritative work. The first two volumes are put together with much art, the portrait as a whole has been regarded as truthful, and the immediate success was extraordinary. In the opinion of Carlyle, Forster’s book was not unworthy to be named after that of Boswell. A useful abridgment was carried out in 1903 by the novelist George Gissing. Gissing also wrote Charles Dickens: A Critical Study (1898), which ranks with G.K. Chesterton’s Charles Dickens(1906) as a commentary inspired by deep insight and adorned by great literary talent upon the genius of the master-novelist. The names of other lives, sketches, articles and estimates of Dickens and his works would occupy a large volume in the mere enumeration. See R.H. Shepherd, The Bibliography of Dickens (1880); James Cooke’s Bibliography of the Writings of Charles Dickens (1879); Dickensiana, by F. G. Kitton (1886); and Bibliography by J.P. Anderson, appended to Sir F.T. Marzials’s Life of Charles Dickens (1887). Among the earlier sketches may be specially cited the lives by J. C. Hotten and G. A. Sala (1870), the Anecdote-Biography edited by the American R. H. Stoddard (1874), Dr A. W. Ward in the English Men of Letters Series (1878), that by Sir Leslie Stephen in the Dictionary of National Biography, and that by Professor Minto in the eighth edition of the Encyclopaedia Britannica. The Letters were first issued in two volumes edited by his daughter and sister-in-law in 1880. For Dickens’s connexion with Kent the following books are specially valuable:—Robert Langton’s Childhood and Youth of Charles Dickens (1883); Langton’s Dickens and Rochester (1880); Thomas Frost’s In Kent with Charles Dickens (1880); F. G. Kitton’s The Dickens Country (1905); H. S. Ward’s The Real Dickens Land (1904); R. Allbut’s Rambles in Dickens Land (1899 and 1903). For Dickens’s reading tours see G. Dolby’s Charles Dickens as I knew him (1884); J. T. Fields’s In and Out of Doors with Charles Dickens (1876); Charles Kent’s Dickens as a Reader (1872). And for other aspects of his life see M. Dickens’s My Father as I recall him (1897); P. H. Fitzgerald’s Life of C. Dickens as revealed in his Writings (1905), and Bozland (1895); F. G. Kitton’s Charles Dickens, his Life, Writings and Personality, a useful compendium (1902); T. E. Pemberton’s Charles Dickens and the Stage, and Dickens’s London (1876); F. Miltoun’s Dickens’s London (1904); Kitton’s Dickens and his Illustrators; W. Teignmouth Shore’s Charles Dickens and his Friends (1904 and 1909); B. W. Matz, Story of Dickens’s Life and Work (1904), and review of solutions to Edwin Drood in The Bookman for March 1908; the recollections of Edmund Yates, Trollope, James Payn, Lehmann, R. H. Horne, Lockwood and many others. The Dickensian, a magazine devoted to Dickensian subjects, was started in 1905; it is the organ of the Dickens Fellowship, and in a sense of the Boz Club. A Dickens Dictionary (by G. A. Pierce) appeared in 1872 and 1878; another (by A. J. Philip) in 1909; and a Dickens Concordance by Mary Williams in 1907.
DICKINSON, ANNA ELIZABETH (1842- ), American author and lecturer, was born, of Quaker parentage, at Philadelphia, Pennsylvania, on the 28th of October 1842. She was educated at the Friends’ Free School in Philadelphia, and was for a time a teacher. In 1861 she obtained a clerkship in the United States mint, but was removed for criticizing General McClellan at a public meeting. She had gradually become widely known as an eloquent and persuasive public speaker, one of the first of her sex to mount the platform to discuss the burning questions of the hour. Before the Civil War she lectured on anti-slavery topics, during the war she toured the country on behalf of the Sanitary Commission, and also lectured on reconstruction, temperance and woman’s rights. She wrote several plays, including The Crown of Thorns (1876); Mary Tudor (1878), in which she appeared in the title rôle; Aurelian (1878); and An American Girl (1880), successfully acted by Fanny Davenport. She also published a novel, Which Answer? (1868); A Paying Investment, a Plea for Education (1876); and A Ragged Register of People, Places and Opinions (1879).
DICKINSON, JOHN (1732-1808), American statesman and pamphleteer, was born in Talbot county, Maryland, on the 8th of November 1732. He removed with his father to Kent county, Delaware, in 1740, studied under private tutors, read law, and in 1753 entered the Middle Temple, London. Returning to America in 1757, he began the practice of law in Philadelphia, was speaker of the Delaware assembly in 1760, and was a member of the Pennsylvania assembly in 1762-1765 and again in 1770-1776.1 He represented Pennsylvania in the Stamp Act Congress (1765) and in the Continental Congress from 1774 to 1776, when he was defeated owing to his opposition to the Declaration of Independence. He then retired to Delaware, served for a time as private and later as brigader-general in the state militia, and was again a member of the Continental Congress (from Delaware) in 1779-1780. He was president of the executive council, or chief executive officer, of Delaware in 1781-1782, and of Pennsylvania in 1782-1785, and was a delegate from Delaware to the Annapolis convention of 1786 and the Federal Constitutional convention of 1787. Dickinson has aptly been called the “Penman of the Revolution.” No other writer of the day presented arguments so numerous, so timely and so popular. He drafted the “Declaration of Rights” of the Stamp Act Congress, the “Petition to the King” and the “Address to the Inhabitants of Quebec” of the Congress of 1774, and the second “Petition to the King”2 and the “Articles of Confederation” of the second Congress. Most influential of all, however, were The Letters of a Farmer in Pennsylvania, written in 1767-1768 in condemnation of the Townshend Acts of 1767, in which he rejected speculative natural rights theories and appealed to the common sense of the people through simple legal arguments. By opposing the Declaration of Independence, he lost his popularity and was never able entirely to regain it. As the representative of a small state, he championed the principle of state equality in the constitutional convention, but was one of the first to advocate the compromise, which was finally adopted, providing for equal representation, in one house and proportional representation in the other. He was probably influenced by Delaware prejudice against Pennsylvania when he drafted the clause which forbids the creation of a new state by the junction of two or more states or parts of states without the consent of the states concerned as well as of congress. After the adjournment of the convention he defended its work in a series of letters signed “Fabius,” which will bear comparison with the best of the Federalist productions. It was largely through his influence that Delaware and Pennsylvania were the first two states to ratify the Constitution. Dickinson’s interests were not exclusively political. He helped to found Dickinson College (named in his honour) at Carlisle, Pennsylvania, in 1783, was the first president of its board of trustees, and was for many years its chief benefactor. He died on the 14th of February 1808 and was buried in the Friends’ burial ground in Wilmington, Del.
See C. J. Stillé, Life and Times of John Dickinson, and P. L. Ford (editor), The Writings of John Dickinson, in vols. xiii. and xiv. respectively of the Memoirs of the Historical Society of Pennsylvania (Philadelphia, 1891 and 1895).
1 Being under the same proprietor and the same governor, Pennsylvania and Delaware were so closely connected before the Revolution that there was an interchange of public men.
2 The “Declaration of the United Colonies of North America ... setting forth the Causes and the Necessity of their Taking up Arms” (often erroneously attributed to Thomas Jefferson).
DICKSON, SIR ALEXANDER (1777-1840), British artillerist, entered the Royal Military Academy in 1793, passing out as second lieutenant in the Royal Artillery in the following year. As a subaltern he saw service in Minorca in 1798 and at Malta in 1800. As a captain he took part in the unfortunate Montevideo Expedition of 1806-07, and in 1809 he accompanied Howorth to the Peninsular War as brigade-major of the artillery. He soon obtained a command in the Portuguese artillery, and as a lieutenant-colonel of the Portuguese service took part in the various battles of 1810-11. At the two sieges of Budazoz, Ciudad Rodrigo, the Salamanca forts and Burgos, he was entrusted by Wellington (who had the highest opinion of him) with most of the detailed artillery work, and at Salamanca battle he commanded the reserve artillery. In the end he became commander of the whole of the artillery of the allied army, and though still only a substantive captain in the British service he had under his orders some 8000 men. At Vitoria, the Pyrenees battles and Toulouse he directed the movements of the artillery engaged, and at the end of the war received handsome presents from the officers who had served under him, many of whom were his seniors in the army list. He was at the disastrous affair of New Orleans, but returned to Europe in time for the Waterloo campaign. He was present at Quatre Bras and Waterloo on the artillery staff of Wellington’s army, and subsequently commanded the British battering train at the sieges of the French fortresses left behind the advancing allies. For the rest of his life he was on home service, principally as a staff officer of artillery. He died, a major-general and G.C.B., in 1840. A memorial was erected at Woolwich in 1847. Dickson was one of the earliest fellows of the Royal Geographical Society.
His diaries kept in the Peninsula were the main source of information used in Duncan’s History of the Royal Artillery.
DICKSON, SIR JAMES ROBERT (1832-1901), Australian statesman, was born in Plymouth on the 30th of November 1832. He was brought up in Glasgow, receiving his education at the high school, and became a clerk in the City of Glasgow Bank. In 1854 he emigrated to Victoria, but after some years spent in that colony and in New South Wales, he settled in 1862 in Queensland, where he was connected with many important business enterprises, among them the Royal Bank of Queensland. He entered the Queensland House of Assembly in 1872, and became minister of works (1876), treasurer (1876-1879, and 1883-1887), acting premier (1884), but resigned in 1887 on the question of taxing land. In 1889 he retired from business, and spent three years in Europe before resuming political life. He fought for the introduction of Polynesian labour on the Queensland sugar plantations at the general election of 1892, and was elected to the House of Assembly in that year and again at the elections of 1893 and 1896. He became secretary for railways in 1897, minister for home affairs in 1898, represented Queensland in the federal council of Australia in 1896 and at the postal conference at Hobart in 1898, and in 1898 became premier. His energies were now devoted to the formation of an Australian commonwealth. He secured the reference of the question to a plebiscite, the result of which justified his anticipations. He resigned the premiership in November 1899, but in the ministry of Robert Philp, formed in the next month, he was reappointed to the offices of chief secretary and vice-president of the executive council which he had combined with the office of premier. He represented Queensland in 1900 at the conference held in London to consider the question of Australian unity, and on his return was appointed minister of defence in the first government of the Australian Commonwealth. He did not long survive the accomplishment of his political aims, dying at Sydney on the 10th of January 1901, in the midst of the festivities attending the inauguration of the new state.
DICOTYLEDONS, in botany, the larger of the two great classes of angiosperms, embracing most of the common flower-bearing plants. The name expresses the most universal character of the class, the importance of which was first noticed by John Ray, namely, the presence of a pair of seed-leaves or cotyledons, in the plantlet or embryo contained in the seed. The embryo is generally surrounded by a larger or smaller amount of foodstuff (endosperm) which serves to nourish it in its development to form a seedling when the seed germinates; frequently, however, as in pea or bean and their allies, the whole of the nourishment for future use is stored up in the cotyledons themselves, which then become thick and fleshy. In germination of the seed the root of the embryo (radicle) grows out to get a holdfast for the plant; this is generally followed by the growth of the short stem immediately above the root, the so-called “hypocotyl,” which carries up the cotyledons above the ground, where they spread to the light and become the first green leaves of the plant. Protected between the cotyledons and terminating the axis of the plant is the first stem-bud (the plumule of the embryo), by the further growth and development of which the aerial portion of the plant, consisting of stem, leaves and branches, is formed, while the development of the radicle forms the root-system. The size and manner of growth of the adult plant show a great variety, from the small herb lasting for one season only, to the forest tree living for centuries. The arrangement of the conducting tissue in the stem is characteristic; a transverse section of the very young stem shows a number of distinct conducting strands—vascular bundles—arranged in a ring round the pith; these soon become united to form a closed ring of bast and wood, separated by a layer of formative tissue (cambium). In perennials the stem shows a regular increase in thickness each year by the addition of a new ring of wood outside the old one—for details of structure see Plants: Anatomy. A similar growth occurs in the root. This increase in the diameter of stem and root is correlated with the increase in leaf-area each season, due to the continued production of new leaf-bearing branches. A characteristic of the class is afforded by the complicated network formed by the leaf-veins,—well seen in a skeleton leaf, from which the soft parts have been removed by maceration. The parts of the flower are most frequently arranged in fives, or multiples of fives; for instance, a common arrangement is as follows,—five sepals, succeeded by five petals, ten stamens in two sets of five, and five or fewer carpels; an arrangement in fours is less frequent, while the arrangement in threes, so common in monocotyledons, is rare in dicotyledons. In some orders the parts are numerous, chiefly in the case of the stamens and the carpels, as in the buttercup and other members of the order Ranunculaceae. There is a very wide range in the general structure and arrangement of the parts of the flower, associated with the means for ensuring the transference of pollen; in the simplest cases the flower consists only of a few stamens or carpels, with no enveloping sepals or petals, as in the willow, while in the more elaborate type each series is represented, the whole forming a complicated structure closely correlated with the size, form and habits of the pollinating agent (see Flower). The characters of the fruit and seed and the means for ensuring the dispersal of the seeds are also very varied (see Fruit).
DICTATOR (from the Lat. dictare, frequentative of dicere, to speak). In modern usage this term is loosely used for a personal ruler enjoying extraordinary and extra-constitutional power. The etymological sense of one who “dictates”—i.e. one whose word (dictum) is law (from which that of one who “dictates,” i.e. speaks for some writer to record, is to be distinguished)—has been assisted by the historical use of the term, in ancient times, for an extraordinary magistrate in the Roman commonwealth. It is unknown precisely how the Roman word came into use, though an explanation of the earlier official title, magister populi, throws some light on the subject. That designation may mean “head of the (infantry) host” as opposed to his subordinate, the magister equitum, who was “head of the cavalry.” If this explanation be accepted, emphasis was thus laid in early times on the military aspect of the dictatorship, and in fact the office seems to have been instituted for the purpose of meeting a military crisis such as might have proved too serious for the annual consuls with their divided command. Later constitutional theory held that the repression of civil discord was also one of the motives for the institution of a dictatorship. Such is the view expressed by Cicero in the De legibus (iii. 3, 9) and by the emperor Claudius in his extant Oratio (i. 28). This function of the office, although it may not have been contemplated at first, is attested by the internal history of Rome. In the crisis of the agitation that gathered round the Licinian laws (367 b.c.) a dictator was appointed, and in 314 b.c. we have the notice of a dictator created for purposes of criminal jurisdiction (quaestionibus exercendis). The dictator appointed to meet the dangers of war, sedition or crime was technically described as “the administrative dictator” (rei gerundae causa). Minor, or merely formal, needs of the state might lead to the creation of other types of this office. Thus we find dictators destined to hold the elections, to make out the list of the senate, to celebrate games, to establish festivals, and to drive the nail into the temple of Jupiter—an act of natural magic which was believed to avert pestilence. These dictators appointed for minor purposes were expected to retire from office as soon as their function was completed. The “administrative dictator” held office for at least six months.
The powers of a dictator were a temporary revival of those of the kings; but there were some limitations to his authority. He was never concerned with civil jurisdiction, and was dependent on the senate for supplies of money. His military authority was confined to Italy; and his power of life and death over the citizens was at an early period limited by law. It was probably the lex Valeria of 300 b.c. that made him subject to the right of criminal appeal (provocatio) within the limits of the city. But during his tenure of power all the magistrates of the people were regarded as his subordinates; and it was even held that the right of assistance (auxilium), furnished by the tribunes of the plebs to members of the citizen body, should not be effectively exercised when the state was under this type of martial law. The dictator was nominated by one of the consuls. But here as elsewhere the senate asserted its authority over the magistrates, and the view was finally held that the senate should not only suggest the need of nomination but also the name of the nominee. After the nomination, the imperium of the dictator was confirmed by a lex curiata (see Comitia). To emphasize the superiority of this imperium over that of the consuls, the dictator might be preceded by twenty-four lictors, not by the usual twelve; and, at least in the earlier period of the office, these lictors bore the axes, the symbols of life and death, within the city walls.
Tradition represents the dictatorship as having a life of three centuries in the history of the Roman state. The first dictator is said to have been created in 501 b.c.; the last of the “administrative” dictators belongs to the year 216 b.c. It was an office that was incompatible both with the growing spirit of constitutionalism and with the greater security of the city; and the epoch of the Second Punic War was marked by experiments with the office, such as the election of Q. Fabius Maximus by the people, and the co-dictatorship of M. Minucius with Fabius, which heralded its disuse (see Punic Wars). The emergency office of the early and middle Republic has few points of contact, except those of the extraordinary position and almost unfettered authority of its holder, with the dictatorship as revised by Sulla and by Caesar. Sulla’s dictatorship was the form taken by a provisional government. He was created “for the establishment of the Republic.” It is less certain whether the dictatorships held by Caesar were of a consciously provisional character. Since the office represented the only supreme Imperium in Rome, it was the natural resort of the founder of a monarchy (see Sulla and Caesar). Ostensibly to prevent its further use for such a purpose, M. Antonius in 44 b.c. carried a law abolishing the dictatorship as a part of the constitution.
Bibliography.—Mommsen, Römisches Staatsrecht, ii. 141 foll. (3rd ed., Leipzig, 1887); Herzog, Geschichte und System der römischen Staatsverfassung, i. 718 foll. (Leipzig, 1884); Pauly-Wissowa, Realencyclopädie, v. 370 foll. (new edition, Stuttgart. 1893, &c.); 186 Lange, Römische Alterthümer, i. 542 foll. (Berlin, 1856, &c.); Daremberg-Saglio, Dictionnaire des antiquités grecques et romaines, ii. 161 foll. (1875, &c.); Haverfield, “The Abolition of the Dictatorship,” in Classical Review, iii. 77.
DICTIONARY. In its proper and most usual meaning a dictionary is a book containing a collection of the words of a language, dialect or subject, arranged alphabetically or in some other definite order, and with explanations in the Definition and history. same or some other language. When the words are few in number, being only a small part of those belonging to the subject, or when they are given without explanation, or some only are explained, or the explanations are partial, the work is called a vocabulary; and when there is merely a list of explanations of the technical words and expressions in some particular subject, a glossary. An alphabetical arrangement of the words of some book or author with references to the places where they occur is called an index (q.v.). When under each word the phrases containing it are added to the references, the work is called a concordance. Sometimes, however, these names are given to true dictionaries; thus the great Italian dictionary of the Accademia della Crusca, in six volumes folio, is called Vocabolario, and Ernesti’s dictionary to Cicero is called Index. When the words are arranged according to a definite system of classification under heads and subdivisions, according to their nature or their meaning, the book is usually called a classed vocabulary; but when sufficient explanations are given it is often accepted as a dictionary, like the Onomasticon of Julius Pollux, or the native dictionaries of Sanskrit, Manchu and many other languages.
Dictionaries were originally books of reference explaining the words of a language or of some part of it. As the names of things, as well as those of persons and places, are words, and often require explanation even more than other classes of words, they were necessarily included in dictionaries, and often to a very great extent. In time, books were devoted to them alone, and were limited to special subjects, and these have so multiplied, that dictionaries of things now rival in number and variety those of words or of languages, while they often far surpass them in bulk. There are dictionaries of biography and history, real and fictitious, general and special, relating to men of all countries, characters and professions; the English Dictionary of National Biography (see Biography) is a great instance of one form of these; dictionaries of bibliography, relating to all books, or to those of some particular kind or country; dictionaries of geography (sometimes called gazetteers) of the whole world, of particular countries, or of small districts, of towns and of villages, of castles, monasteries and other buildings. There are dictionaries of philosophy; of the Bible; of mathematics; of natural history, zoology, botany; of birds, trees, plants and flowers; of chemistry, geology and mineralogy; of architecture, painting and music; of medicine, surgery, anatomy, pathology and physiology; of diplomacy; of law, canon, civil, statutory and criminal; of political and social sciences; of agriculture, rural economy and gardening; of commerce, navigation, horsemanship and the military arts; of mechanics, machines and the manual arts. There are dictionaries of antiquities, of chronology, of dates, of genealogy, of heraldry, of diplomatics, of abbreviations, of useful receipts, of monograms, of adulterations and of very many other subjects. These works are separately referred to in the bibliographies attached to the articles on the separate subjects. And lastly, there are dictionaries of the arts and sciences, and their comprehensive offspring, encyclopaedias (q.v.), which include in themselves every branch of knowledge. Neither under the heading of dictionary nor under that of encyclopaedia do we propose to include a mention of every work of its class, but many of these will be referred to in the separate articles on the subjects to which they pertain. And in this article we confine ourselves to an account of those dictionaries which are primarily word-books. This is practically the most convenient distinction from the subject-book or encyclopaedia; though the two characters are often combined in one work. Thus the Century Dictionary has encyclopaedic features, while the present edition of the Encyclopaedia Britannica, restoring its earlier tradition but carrying out the idea more systematically, also embodies dictionary features.
Dictionarium is a word of low or modern Latinity;1 dictio, from which it was formed, was used in medieval Latin to mean a word. Lexicon is a corresponding word of Greek origin, meaning a book of or for words—a dictionary. A glossary is properly a collection of unusual or foreign words requiring explanation. It is the name frequently given to English dictionaries of dialects, which the Germans usually call idioticon, and the Italians vocabolario. Wörterbuch, a book of words, was first used among the Germans, according to Grimm, by Kramer (1719), imitated from the Dutch woordenboek. From the Germans the Swedes and Danes adopted ordbok, ordbog. The Icelandic ordabôk, like the German, contains the genitive plural. The Slavonic nations use slovar, slovnik, and the southern Slavs ryetshnik, from slovo, ryetsh, a word, formed, like dictionary and lexicon, without composition. Many other names have been given to dictionaries, as thesaurus, Sprachschatz, cornucopia, gazophylacium, comprehensorium, catholicon, to indicate their completeness; manipulus predicantium, promptorium puerorum, liber memorialis, hortus vocabulorum, ionia (a violet bed), alveary (a beehive), kamoos (the sea), haft kulzum (the seven seas), tsze tien (a standard of character), onomasticon, nomenclator, bibliotheca, elucidario, Mundart-sammlung, clavis, scala, pharetra,2 La Crusca from the great Italian dictionary, and Calepino (in Spanish and Italian) from the Latin dictionary of Calepinus.
The tendency of great dictionaries is to unite in themselves all the peculiar features of special dictionaries. A large dictionary is most useful when a word is to be thoroughly studied, or when there is difficulty in making out the meaning of a word or phrase. Special dictionaries are more useful for special purposes; for instance, synonyms are best studied in a dictionary of synonyms. And small dictionaries are more convenient for frequent use, as in translating from an unfamiliar language, for words may be found more quickly, and they present the words and their meanings in a concentrated and compact form, instead of being scattered over a large space, and separated by other matter. Dictionaries of several languages, called polyglots, are of different kinds. Some are polyglot in the vocabulary, but not in the explanation, like Johnson’s dictionary of Persian and Arabic explained in English; some in the interpretation, but not in the vocabulary or explanation, like Calepini octoglotton, a Latin dictionary of Latin, with the meanings in seven languages. Many great dictionaries are now polyglot in this sense. Some are polyglot in the vocabulary and interpretation, but are explained in one language, like Jal’s Glossaire nautique, a glossary of sea terms in many languages, giving the equivalents of each word in the other languages, but the explanation in French. Pauthier’s Annamese Dictionary is polyglot in a peculiar way. It gives the Chinese characters with their pronunciation in Chinese and Annamese. Special dictionaries are of many kinds. There are technical dictionaries of etymology, foreign words, dialects, secret languages, slang, neology, barbarous words, faults of expression, choice words, prosody, pronunciation, spelling, orators, poets, law, music, proper names, particular authors, nouns, verbs, participles, particles, double forms, difficulties and many others. Fick’s dictionary (Göttingen, 1868, 8vo; 1874-1876, 8vo, 4 vols.) is a remarkable attempt to ascertain the common language of the Indo-European nations before each of their great separations. In the second edition of his Etymologische Forschungen (Lemgo and Detmoldt, 1859-1873, 8vo, 7217 pages) Pott gives a comparative lexicon of Indo-European roots, 2226 in number, occupying 5140 pages.
At no time was progress in the making of general dictionaries so rapid as during the second half of the 19th century. It is to be seen in three things: in the perfecting of the theory of what a general dictionary should be; in the elaboration Methods. of methods of collecting and editing lexicographic materials; and in the magnitude and improved quality of the work which has been accomplished or planned. Each of these can best be illustrated from English lexicography, in which the process of development has in all directions been carried farthest. The advance that has been made in theory began with a radical change of opinion with regard to the chief end of the general dictionary of a language. The older view of the matter was that the lexicographer should furnish a standard of usage—should register only those words which are, or at some period of the language have been, “good” from a literary point of view, with their “proper” senses and uses, or should at least furnish the means of determining what these are. In other words, his chief duty was conceived to be to sift and refine, to decide authoritatively questions with regard to good usage, and thus to fix the language as completely as might be possible within the limits determined by the literary taste of his time. Thus the Accademia della Crusca, founded near the close of the 16th century, was established for the purpose of purifying in this way the Italian tongue, and in 1612 the Vocabolario degli Accademici della Crusca, long the standard of that language, was published. The Académie Française, the first edition of whose dictionary appeared in 1694, had a similar origin. In England the idea of constructing a dictionary upon this principle arose during the second quarter of the 18th century. It was imagined by men of letters—among them Alexander Pope—that the English language had then attained such perfection that further improvement was hardly possible, and it was feared that if it were not fixed by lexicographic authority deterioration would soon begin. Since there was no English “Academy,” it was necessary that the task should fall to some one whose judgment would command respect, and the man who undertook it was Samuel Johnson. His dictionary, the first edition of which, in two folio volumes, appeared in 1755, was in many respects admirable, but it was inadequate even as a standard of the then existing literary usage. Johnson himself did not long entertain the belief that the natural development of a language can be arrested in that or in any other way. His work was, however, generally accepted as a final authority, and the ideas upon which it was founded dominated English lexicography for more than a century. The first effective protest in England against the supremacy of this literary view was made by Dean (later Archbishop) Trench, in a paper on “Some Deficiencies in Existing English Dictionaries” read before the Philological Society in 1857. “A dictionary,” he said, “according to that idea of it which seems to me alone capable of being logically maintained, is an inventory of the language; much more, but this primarily.... It is no task of the maker of it to select the good words of the language.... The business which he has undertaken is to collect and arrange all words, whether good or bad, whether they commend themselves to his judgment or otherwise.... He is an historian of [the language], not a critic.” That is, for the literary view of the chief end of the general dictionary should be substituted the philological or scientific. In Germany this substitution had already been effected by Jacob and Wilhelm Grimm in their dictionary of the German language, the first volume of which appeared in 1854. In brief, then, the modern view is that the general dictionary of a language should be a record of all the words—current or obsolete—of that language, with all their meanings and uses, but should not attempt to be, except secondarily or indirectly, a guide to “good” usage. A “standard” dictionary has, in fact, been recognized to be an impossibility, if not an absurdity.
This theoretical requirement must, of course, be modified considerably in practice. The date at which a modern language is to be regarded by the lexicographer as “beginning” must, as a rule, be somewhat arbitrarily chosen; while considerable portions of its earlier vocabulary cannot be recovered because of the incompleteness of the literary record. Moreover, not even the most complete dictionary can include all the words which the records—earlier and later—actually contain. Many words, that is to say, which are found in the literature of a language cannot be regarded as, for lexicographic purposes, belonging to that language; while many more may or may not be held to belong to it, according to the judgment—almost the whim—of the individual lexicographer. This is especially true of the English tongue. “That vast aggregate of words and phrases which constitutes the vocabulary of English-speaking men presents, to the mind that endeavours to grasp it as a definite whole, the aspect of one of those nebulous masses familiar to the astronomer, in which a clear and unmistakable nucleus shades off on all sides, through zones of decreasing brightness, to a dim marginal film that seems to end nowhere, but to lose itself imperceptibly in the surrounding darkness” (Dr J. A. H. Murray, Oxford Dict. General Explanations, p. xvii). This “marginal film” of words with more or less doubtful claims to recognition includes thousands of the terms of the natural sciences (the New-Latin classificatory names of zoology and botany, names of chemical compounds and of minerals, and the like); half-naturalized foreign words; dialectal words; slang terms; trade names (many of which have passed or are passing into common use); proper names and many more. Many of these even the most complete dictionary should exclude; others it should include; but where the line shall be drawn will always remain a vexed question.
Another important principle upon which Trench insisted, and which also expresses a requirement of modern scientific philology, is that the dictionary shall be not merely a record, but also an historical record of words and their uses. From the literary point of view the most important thing is present usage. To that alone the idea of a “standard” has any application. Dictionaries of the older type, therefore, usually make the common, or “proper” or “root” meaning of a word the starting point of its definition, and arrange its other senses in a logical or accidental order commonly ignoring the historical order in which the various meanings arose. Still less do they attempt to give data from which the vocabulary of the language at any previous period may be determined. The philologist, however, for whom the growth, or progressive alteration, of a language is a fact of central importance, regards no record of a language as complete which does not exhibit this growth in its successive stages. He desires to know when and where each word, and each form and sense of it, are first found in the language; if the word or sense is obsolete, when it died; and any other fact that throws light upon its history. He requires, accordingly, of the lexicographer that, having ascertained these data, he shall make them the foundation of his exposition—in particular, of the division and arrangement of his definitions, that sense being placed first which appeared first in order of time. In other words, each article in the dictionary should furnish an orderly biography of the word of which it treats, each word and sense being so dated that the exact time of its appearance and the duration of its use may as nearly as possible be determined. This, in principle, is the method of the new lexicography. In practice it is subject to limitations similar to those of the vocabulary mentioned above. Incompleteness of the early record is here an even greater obstacle; and there are many words whose history is, for one reason or another, so unimportant that to treat it elaborately would be a waste of labour and space.
The adoption of the historical principle involves a further noteworthy modification of older methods, namely, an important extension of the use of quotations. To Dr Johnson belongs the credit of showing how useful, when properly chosen, they may be, not only in corroborating the lexicographer’s statements, but also in revealing special shades of meaning or variations of use which his definitions cannot well express. No part of Johnson’s work is more valuable than this. This idea was more fully developed and applied by Dr Charles Richardson, whose New Dictionary of the English Language ... Illustrated by Quotations from the Best Authors (1835-1836) still remains a most valuable collection of literary illustrations. Lexicographers, however, have, with 188 few exceptions, until a recent date, employed quotations chiefly for the ends just mentioned—as instances of use or as illustrations of correct usage—with scarcely any recognition of their value as historical evidence; and they have taken them almost exclusively from the works of the “best” authors. But since all the data upon which conclusions with regard to the history of a word can be based must be collected from the literature of the language, it is evident that, in so far as the lexicographer is required to furnish evidence for an historical inference, a quotation is the best form in which he can give it. In fact, extracts, properly selected and grouped, are generally sufficient to show the entire meaning and biography of a word without the aid of elaborate definitions. The latter simply save the reader the trouble of drawing the proper conclusions for himself. A further rule of the new lexicography, accordingly, is that quotations should be used, primarily, as historical evidence, and that the history of words and meanings should be exhibited by means of them. The earliest instance of use that can be found, and (if the word or sense is obsolete) the latest, are as a rule to be given; while in the case of an important word or sense, instances taken from successive periods of its currency also should be cited. Moreover, a quotation which contains an important bit of historical evidence must be used, whether its source is “good,” from the literary point of view, or not—whether it is a classic of the language or from a daily newspaper; though where choice is possible, preference should, of course, be given to quotations extracted from the works of the best writers. This rule does not do away with the illustrative use of quotations, which is still recognized as highly important, but it subordinates it to their historical use. It is necessary to add that it implies that the extracts must be given exactly, and in the original spelling and capitalization, accurately dated, and furnished with a precise reference to author, book, volume, page and edition; for insistence upon these requirements—which are obviously important, whatever the use of the quotation may be—is one of the most noteworthy of modern innovations. Johnson usually gave simply the author’s name, and often quoted from memory and inaccurately; and many of his successors to this day have followed—altogether or to some extent—his example.
The chief difficulty in the way of this use of quotations—after the difficulty of collection—is that of finding space for them in a dictionary of reasonable size. Preference must be given to those which are essential, the number of those which are cited merely on methodical grounds being made as small as possible. It is hardly necessary to add that the negative evidence furnished by quotations is generally of little value; one can seldom, that is, be certain that the lexicographer has actually found the earliest or the latest use, or that the word or sense has not been current during some intermediate period from which he has no quotations.
Lastly, a much more important place in the scheme of the ideal dictionary is now assigned to the etymology of words. This may be attributed, in part, to the recent rapid development of etymology as a science, and to the greater abundance of trustworthy data; but it is chiefly due to the fact that from the historical point of view the connexion between that section of the biography of a word which lies within the language—subsequent, that is, to the time when the language may, for lexicographical purposes, be assumed to have begun, or to the time when the word was adopted or invented—and its antecedent history has become more vital and interesting. Etymology, in other words, is essentially the history of the form of a word up to the time when it became a part of the language, and is, in a measure, an extension of the history of the development of the word in the language. Moreover, it is the only means by which the exact relations of allied words can be ascertained, and the separation of words of the same form but of diverse origin (homonyms) can be effected, and is thus, for the dictionary, the foundation of all family history and correct genealogy. In fact, the attention that has been paid to these two points in the best recent lexicography is one of its distinguishing and most important characteristics. Related to the etymology of words are the changes in their form which may have occurred while they have been in use as parts of the language—modifications of their pronunciation, corruptions by popular etymology or false associations, and the like. The facts with regard to these things which the wide research necessitated by the historical method furnishes abundantly to the modern lexicographer are often among the most novel and interesting of his acquisitions.
It should be added that even approximate conformity to the theoretical requirements of modern lexicography as above outlined is possible only under conditions similar to those under which the Oxford New English Dictionary was undertaken (see below). The labour demanded is too vast, and the necessary bulk of the dictionary too great. When, however, a language is recorded in one such dictionary, those of smaller size and more modest pretensions can rest upon it as an authority and conform to it as a model so far as their special limitations permit.
The ideal thus developed is primarily that of the general dictionary of the purely philological type, but it applies also to the encyclopaedic dictionary. In so far as the latter is strictly lexicographic—deals with words as words, and not with the things they denote—it should be made after the model of the former, and is defective to the extent in which it deviates from it. The addition of encyclopaedic matter to the philological in no way affects the general principles involved. It may, however, for practical reasons, modify their application in various ways. For example, the number of obsolete and dialectal words included may be much diminished and the number of scientific terms (for instance, new Latin botanical and zoological names) be increased; and the relative amount of space devoted to etymologies and quotations may be lessened. In general, since books of this kind are designed to serve more or less as works of general reference, the making of them must be governed by considerations of practical utility which the compilers of a purely philological dictionary are not obliged to regard. The encyclopaedic type itself, although it has often been criticized as hybrid—as a mixture of two things which should be kept distinct—is entirely defensible. Between the dictionary and the encyclopaedia the dividing line cannot sharply be drawn. There are words the meaning of which cannot be explained fully without some description of things, and, on the other hand, the description of things and processes often involves the definition of names. To the combination of the two objection cannot justly be made, so long as it is effected in a way—with a selection of material—that leaves the dictionary essentially a dictionary and not an encyclopaedia. Moreover, the large vocabulary of the general dictionary makes it possible to present certain kinds of encyclopaedic matter with a degree of fulness and a convenience of arrangement which are possible in no single work of any other class. In fact, it may be said that if the encyclopaedic dictionary did not exist it would have to be invented; that its justification is its indispensableness. Not the least of its advantages is that it makes legitimate the use of diagrams and pictorial illustrations, which, if properly selected and executed, are often valuable aids to definition.
On its practical side the advance in lexicography has consisted in the elaboration of methods long in use rather than in the invention of new ones. The only way to collect the data upon which the vocabulary, the definitions and the history are to be based is, of course, to search for them in the written monuments of the language, as all lexicographers who have not merely borrowed from their predecessors have done. But the wider scope and special aims of the new lexicography demand that the investigation shall be vastly more comprehensive, systematic and precise. It is necessary, in brief, that, as far as may be possible, the literature (of all kinds) of every period of the language shall be examined systematically, in order that all the words, and senses and forms of words, which have existed during any period may be found, and that enough excerpts (carefully verified, credited and dated) to cover all the essential facts shall be made. The books, pamphlets, journals, newspapers, and so on which must thus be searched will be numbered by thousands, and the quotations selected may (as in the case of the Oxford New English Dictionary) be counted by millions. This task is beyond the powers of any one man, even though he be a Johnson, or a Littré or a Grimm, and it is now 189 assigned to a corps of readers whose number is limited only by the ability of the editor to obtain such assistance. The modern method of editing the material thus accumulated—the actual work of compilation—also is characterized by the application of the principle of the division of labour. Johnson boasted that his dictionary was written with but little assistance from the learned, and the same was in large measure true of that of Littré. Such attempts on the part of one man to write practically the whole of a general dictionary are no longer possible, not merely because of the vast labour and philological research necessitated by modern aims, but more especially because the immense development of the vocabulary of the special sciences renders indispensable the assistance, in the work of definition, of persons who are expert in those sciences. The tendency, accordingly, has been to enlarge greatly the editorial staff of the dictionary, scores of sub-editors and contributors being now employed where a dozen or fewer were formerly deemed sufficient. In other words, the making of a “complete” dictionary has become a co-operative enterprise, to the success of which workers in all the fields of literature and science contribute.
The most complete exemplification of these principles and methods is the Oxford New English Dictionary, on historical principles, founded mainly on materials collected by the Philological Society. This monumental work originated in the suggestion of Trench that an attempt should be made, under the direction of the Philological Society, to complete the vocabulary of existing dictionaries and to supply the historical information which they lacked. The suggestion was adopted, considerable material was collected, and Mr Herbert Coleridge was appointed general editor. He died in 1861, and was succeeded by Dr F. J. Furnivall. Little, however, was done, beyond the collection of quotations—about 2,000,000 of which were gathered—until in 1878 the expense of printing and publishing the proposed dictionary was assumed by the Delegates of the University Press, and the editorship was entrusted to Dr (afterwards Sir) J. A. H. Murray. As the historical point of beginning, the middle of the 12th century was selected, all words that were obsolete at that date being excluded, though the history of words that were current both before and after that date is given in its entirety; and it was decided that the search for quotations—which, according to the original design, was to cover the entire literature down to the beginning of the 16th century and as much of the subsequent literature (especially the works of the more important writers and works on special subjects) as might be possible—should be made more thorough. More than 800 readers, in all parts of the world, offered their aid; and when the preface to the first volume appeared in 1888, the editor was able to announce that the readers had increased to 1300, and that 3,500,000 of quotations, taken from the writings of more than 5000 authors, had already been amassed. The whole work was planned to be completed in ten large volumes, each issued first in smaller parts. The first part was issued in 1884, and by the beginning of 1910 the first part of the letter S had been reached.
The historical method of exposition, particularly by quotations, is applied in the New English Dictionary, if not in all cases with entire success, yet, on the whole, with a regularity and a precision which leave little to be desired. A minor fault is that excerpts from second or third rate authors have occasionally been used where better ones from writers of the first class either must have been at hand or could have been found. As was said above, the literary quality of the question is highly important even in historical lexicography, and should not be neglected unnecessarily. Other special features of the book are the completeness with which variations of pronunciation and orthography (with dates) are given; the fulness and scientific excellence of the etymologies, which abound in new information and corrections of old errors; the phonetic precision with which the present (British) pronunciation is indicated; and the elaborate subdivision of meanings. The definitions as a whole are marked by a high degree of accuracy, though in a certain number of cases (not explicable by the date of the volumes) the lists of meanings are not so good as one would expect, as compared (say) with the Century Dictionary. Work of such magnitude and quality is possible, practically, only when the editor of the dictionary can command not merely the aid of a very large number of scholars and men of science, but their gratuitous aid. In this the New English Dictionary has been singularly fortunate. The conditions under which it originated, and its aim, have interested scholars everywhere, and led them to contribute to the perfecting of it their knowledge and time. The long list of names of such helpers in Sir J. A. H. Murray’s preface is in curious contrast with their absence from Dr Johnson’s and the few which are given in that of Littré. The editor’s principal assistants were Dr Henry Bradley and Dr W. A. Craigie. Of the dictionary as a whole it may be said that it is one of the greatest achievements, whether in literature or science, of modern English scholarship and research.
The New English Dictionary furnishes for the first time data from which the extent of the English word-store at any given period, and the direction and rapidity of its growth, can fairly be estimated. For this purpose the materials furnished by the older dictionaries are quite insufficient, on account of their incompleteness and unhistorical character. For example 100 pages of the New English Dictionary (from the letter H) contain 1002 words, of which, as the dated quotations show, 585 were current in 1750 (though some, of course, were very rare, some dialectal, and so on), 191 were obsolete at that date, and 226 have since come into use. But of the more than 700 words—current or obsolete—which Johnson might thus have recorded, he actually did record only about 300. Later dictionaries give more of them, but they in no way show their status at the date in question. It is worth noting that the figures given seem to indicate that not very many more words have been added to the vocabulary of the language during the past 150 years than had been lost by 1750. The pages selected, however, contain comparatively few recent scientific terms. A broader comparison would probably show that the gain has been more than twice as great as the loss.
In the Deutsches Wörterbuch of Jacob and Wilhelm Grimm the scientific spirit, as was said above, first found expression in general lexicography. The desirability of a complete inventory and investigation of German words was recognized by Leibnitz and by various 18th-century scholars, but the plan and methods of the Grimms were the direct product of the then new scientific philology. Their design, in brief, was to give an exhaustive account of the words of the literary language (New High German) from about the end of the 15th century, including their earlier etymological and later history, with references to important dialectal words and forms; and to illustrate their use and history abundantly by quotations. The first volume appeared in 1854. Jacob Grimm (died 1863) edited the first, second (with his brother, who died in 1859), third and a part of the fourth volumes; the others have been edited by various distinguished scholars. The scope and methods of this dictionary have been broadened somewhat as the work has advanced. In general it may be said that it differs from the New English Dictionary chiefly in its omission of pronunciations and other pedagogic matter; its irregular treatment of dates; its much less systematic and less lucid statement of etymologies; its less systematic and less fruitful use of quotations; and its less convenient and less intelligible arrangement of material and typography.
These general principles lie also at the foundation of the scholarly Dictionnaire de la langue française of E. Littré, though they are there carried out less systematically and less completely. In the arrangement of the definitions the first place is given to the most primitive meaning of the word instead of to the most common one, as in the dictionary of the Academy; but the other meanings follow in an order that is often logical rather than historical. Quotations also are frequently used merely as literary illustrations, or are entirely omitted; in the special paragraphs on the history of words before the 16th century, however, they are put to a strictly historical use. This dictionary—perhaps the greatest ever compiled by one man—was published 1863-1872. (Supplement, 1878.)
The Thesaurus Linguae Latinae, prepared under the auspices of the German Academies of Berlin, Göttingen, Leipzig, Munich and Vienna, is a notable application of the principles and practical co-operative method of modern lexicography to the classical tongues. The plan of the work is to collect quotations which shall register, with its full context, every word (except 190 the most familiar particles) in the text of each Latin author down to the middle of the 2nd century a.d., and to extract all important passages from all writers of the following centuries down to the 7th; and upon these materials to found a complete historical dictionary of the Latin language. The work of collecting quotations was begun in 1894, and the first part of the first volume has been published.
In the making of all these great dictionaries (except, of course, the last) the needs of the general public as well as those of scholars have been kept in view. But the type to which the general dictionary designed for popular use has tended more and more to conform is the encyclopaedic. This combination of lexicon and encyclopaedia is exhibited in an extreme—and theoretically objectionable—form in the Grand dictionnaire universel du XIXe siècle of Pierre Larousse. Besides common words and their definitions, it contains a great many proper names, with a correspondingly large number of biographical, geographical, historical and other articles, the connexion of which with the strictly lexicographical part is purely mechanical. Its utility, which—notwithstanding its many defects—is very great, makes it, however, a model in many respects. Fifteen volumes were published (1866-1876), and supplements were brought out later (1878-1890). The Nouveau Larousse illustré started publication in 1901, and was completed in 1904 (7 vols.). This is not an abridgment or a fresh edition of the Grand Dictionnaire of Pierre Larousse, but a new and distinct publication.
The most notable work of this class, in English, is the Century Dictionary, an American product, edited by Professor W. D. Whitney, and published 1889-1891 in six volumes, containing 7046 pages (large quarto). It conforms to the philological mode in giving with great fulness the older as well as the present vocabulary of the language, and in the completeness of its etymologies; but it does not attempt to give the full history of every word within the language. Among its other more noteworthy characteristics are the inclusion of a great number of modern scientific and technical words, and the abundance of its quotations. The quotations are for the most part provided with references, but they are not dated. Even when compared with the much larger New English Dictionary, the Century’s great merit is the excellent enumeration of meanings, and the accuracy of its explanations; in this respect it is often better and fuller than the New English. In the application of the encyclopaedic method this dictionary is conservative, excluding, with a few exceptions, proper names, and restricting, for the most part, the encyclopaedic matter to descriptive and other details which may legitimately be added to the definitions. Its pictorial illustrations are very numerous and well executed. In the manner of its compilation it is a good example of modern cooperative dictionary-making, being the joint product of a large number of specialists. Next to the New English Dictionary it is the most complete and scholarly of English lexicons.
Bibliography.—The following list of dictionaries (from the 9th edition of this work, with occasional corrections) is given for its historical interest, but in recent years dictionary-making has been so abundant that no attempt is made to be completely inclusive of later works; the various articles on languages may be consulted for these. The list is arranged geographically by families of languages, or by regions. In each group the order, when not alphabetical, is usually from north to south, extinct languages generally coming first, and dialects being placed under their language. Dictionaries forming parts of other works, such as travels, histories, transactions, periodicals, reading-books, &c., are generally excluded. The system here adopted was chosen as on the whole the one best calculated to keep together dictionaries naturally associated. The languages to be considered are too many for an alphabetical arrangement, which ignores all relations both natural and geographical, and too few to require a strict classification by affinities, by which the European languages, which for many reasons should be kept together, would be dispersed. Under either system, Arabic, Persian and Turkish, whose dictionaries are so closely connected, would be widely separated. A wholly geographical arrangement would be inconvenient, especially in Europe. Any system, however, which attempts to arrange in a consecutive series the great network of languages by which the whole world is enclosed, must be open to some objections; and the arrangement adopted in this list has produced some anomalies and dispersions which might cause inconvenience if not pointed out. The old Italic languages are placed under Latin, all dialects of France under French (but Provençal as a distinct language), and Wallachian among Romanic languages. Low German and its dialects are not separated from High German. Basque is placed after Celtic; Albanian, Gipsy and Turkish at the end of Europe, the last being thus separated from its dialects and congeners in Northern and Central Asia, among which are placed the Kazan dialect of Tatar, Samoyed and Ostiak. Accadian is placed after Assyrian among the Semitic languages, and Maltese as a dialect of Arabic; while the Ethiopic is among African languages as it seemed undesirable to separate it from the other Abyssinian languages, or these from their neighbours to the north and south. Circassian and Ossetic are joined to the first group of Aryan languages lying to the north-west of Persia, and containing Armenian, Georgian and Kurd. The following is the order of the groups, some of the more important languages, that is, of those best provided with dictionaries, standing alone:—
Europe: Greek, Latin, French, Romance, Teutonic (Scandinavian and German), Celtic, Basque, Baltic, Slavonic, Ugrian, Gipsy, Albanian.
Asia: Semitic, Armenian, Persian, Sanskrit, Indian, Indo-Chinese, Malay Archipelago, Philippines, Chinese, Japanese, Northern and Central Asia.
Africa: Egypt and Abyssinia, Eastern Africa, Southern, Western, Central, Berber.
Australia and Polynesia.
America: North, Central (with Mexico), South.
EUROPE
Greek.—Athenaeus quotes 35 writers of works, known or supposed to be dictionaries, for, as they are all lost, it is often difficult to decide on their nature. Of these, Anticlides, who lived after the reign of Alexander the Great, wrote Έξηγητικός, which seems to have been a sort of dictionary, perhaps explaining the words and phrases occurring in ancient stories. Zenodotus, the first superintendent of the great library of Alexandria, who lived in the reigns of Ptolemy I. and Ptolemy II., wrote Γλῶσσαι, and also Λέξεις ἐθνικαἰ, a dictionary of barbarous or foreign phrases. Aristophanes of Byzantium, son of Apelles the painter, who lived in the reigns of Ptolemy II. and Ptolemy III., and had the supreme management of the Alexandrian library, wrote a number of works, as Άττικαί Λέξεις, Λακωνικαί Γλῶσσαι which, from the titles, should be dictionaries, but a fragment of his Λέξεις printed by Boissonade, in his edition of Herodian (London, 1869, 8vo, pp. 181-189), is not alphabetical. Artemidorus, a pupil of Aristophanes, wrote a dictionary of technical terms used in cookery. Nicander Colophonius, hereditary priest of Apollo Clarius, born at Claros, near Colophon in Ionia, in reputation for 50 years, from 181 to 135, wrote Γλῶσσαι in at least three books. Parthenius, a pupil of the Alexandrian grammarian Dionysius (who lived in the 1st century before Christ), wrote on choice words used by historians. Didymus, called χαλκένερος, who, according to Athenaeus, wrote 3500 books, and, according to Seneca, 4000, wrote lexicons of the tragic poets (of which book 28 is quoted), of the comic poets, of ambiguous words and of corrupt expressions. Glossaries of Attic words were written by Crates, Philemon, Philetas and Theodorus; of Cretan, by Hermon or Hermonax; of Phrygian, by Neoptolemus; of Rhodian, by Moschus; of Italian, by Diodorus of Tarsus; of foreign words, by Silenus; of synonyms, by Simaristus; of cookery, by Heracleon; and of drinking vessels, by Apollodorus of Cyrene. According to Suidas, the most ancient Greek lexicographer was Apollonius the sophist, son of Archibius. According to the common opinion, he lived in the time of Augustus at Alexandria. He composed a lexicon of words used by Homer, Λέξεις Όμηρικαί, a very valuable and useful work, though much interpolated, edited by Villoison, from a MS. of the 10th century, Paris, 1773, 4to, 2 vols.; and by Tollius, Leiden, 1788, 8vo; ed. Bekker, Berlin, 1833, 8vo. Erotian or Herodian, physician to Nero, wrote a lexicon on Hippocrates, arranged in alphabetical order, probably by some copyist, whom Klein calls “homo sciolus.” It was first published in Greek in H. Stephani Dictionarium Medicum, Paris, 1564, 8vo; ed. Klein, Lipsiae, 1865, 8vo, with additional fragments. Timaeus the sophist, who, according to Ruhnken, lived in the 3rd century, wrote a very short lexicon to Plato, which, though much interpolated, is of great value, 1st ed. Ruhnken, Leiden, 1754; ed. locupletior, Lugd. Bat. 1789, 8vo. Aelius Moeris, called the Atticist, lived about 190 191 a.d., and wrote an Attic lexicon, 1st ed. Hudson, Oxf. 1712, Bekker, 1833. Julius Pollux (Ίούλιος Πολυδεύκης) of Naucratis, in Egypt, died, aged fifty-eight, in the reign of Commodus (180-192), who made him professor of rhetoric at Athens. He wrote, besides other lost works, an Onomasticon in ten books, being a classed vocabulary, intended to supply all the words required by each subject with the usage of the best authors. It is of the greatest value for the knowledge both of language and of antiquities. First printed by Aldus, Venice, 1500, fol.; often afterwards; ed. Lederlinus and Hemsterhuis, Amst. 1706, 2 vols.; Dindorf, 1824, 5 vols., Bethe (1900 f.). Harpocration of Alexandria, probably of the 2nd century, wrote a lexicon on the ten Attic orators, first printed by Aldus, Ven. 1503, fol.; ed. Dindorf, Oxford, 1853, 8vo, 2 vols. from 14 MSS. Orion, a grammarian of Thebes, in Egypt, who lived between 390 and 460, wrote an etymological dictionary, printed by Sturz, Leipzig, 1820, 4to. Helladius a priest of Jupiter at Alexandria, when the heathen temples there were destroyed by Theophilus in 389 or 391 escaped to Constantinople, where he was living in 408. He wrote an alphabetical lexicon, now lost, chiefly of prose, called by Photius the largest (πολυστιχώτατον) which he knew. Ammonius, professor of grammar at Alexandria, and priest of the Egyptian ape, fled to Constantinople with Helladius, and wrote a dictionary of words similar in sound but different in meaning, which has been often printed in Greek lexicons, as Aldus, 1497, Stephanus, and separately by Valckenaer, Lugd. Bat. 1739, 4to, 2 vols., and by others. Zenodotus wrote on the cries of animals, printed in Valckenaer’s Ammonius; with this may be compared the work of Vincentio Caralucci, Lexicon vocum quae a brutis animalibus emittuntur, Perusia, 1779, 12mo. Hesychius of Alexandria wrote a lexicon, important for the knowledge of the language and literature, containing many dialectic and local expressions and quotations from other authors, 1st ed. Aldus, Ven. 1514, fol.; the best is Alberti and Ruhnken, Lugd. Bat. 1746-1766, fol. 2 vols.; collated with the MS. in St Mark’s library, Venice, the only MS. existing, by Niels Iversen Schow, Leipzig, 1792, 8vo; ed. Schmidt, Jena, 1867, 8vo. The foundation of this lexicon is supposed to have been that of Pamphilus, an Alexandrian grammarian, quoted by Athenaeus, which, according to Suidas, was in 95 books from Ε to Ω; Α to Δ had been compiled by Zopirion. Photius, consecrated patriarch of Constantinople, 25th December 857, living in 886, left a lexicon, partly extant, and printed with Zonaras, Lips. 1808, 4to, 3 vols., being vol. iii.; ed. Naber, Leidae, 1864-1865, 8vo, 2 vols. The most celebrated of the Greek glossaries is that of Suidas, of whom nothing is known. He probably lived in the 10th century. His lexicon is an alphabetical dictionary of words including the names of persons and places—a compilation of extracts from Greek writers, grammarians, scholiasts and lexicographers, very carelessly and unequally executed. It was first printed by Demetrius Chalcondylas, Milan, 1499, fol.; the best edition, Bernhardy, Halle, 1853, 4to, 2 vols. John Zonaras, a celebrated Byzantine historian and theologian, who lived in the 12th century, compiled a lexicon, first printed by Tittmann, Lips. 1808. 4to, 2 vols. An anonymous Greek glossary, entitled Έτυμολογικὸν μέγα, Etymologicum magnum, has been frequently printed. The first edition is by Musurus, Venitia, 1499, fol.; the best by Gaisford, Oxonii, 1848, fol. It contains many grammatical remarks by famous authorities, many passages of authors, and mythological and historical notices. The MSS. vary so much that they look like the works of different authors. To Eudocia Augusta of Makrembolis, wife of the emperors Constantine XI. and Romanus IV. (1059 to 1071), was ascribed a dictionary of history and mythology, Ίωνιά (bed of violets), first printed by D’Ansse de Villoison, Anecdota Graeca, Venetiis, 1781, 4to, vol. i. pp. 1-442. It was supposed to have been of much value before it was published. Thomas, Magister Officiorum under Andronicus Palaeologus, afterward called as a monk Theodulus, wrote Έκλογαὶ ὀνομάτων Άττικῶν, printed by Callierges, Romae, 1517, 8vo: Papias, Vocabularium, Mediolani, 1476, fol.: Craston, an Italian Carmelite monk of Piacenza, compiled a Greek and Latin lexicon, edited by Bonus Accursius, printed at Milan, 1478, fol.: Aldus, Venetiis, 1497, fol.: Guarino, born about 1450 at Favora, near Camarino, who called himself both Phavorinus and Camers, published his Thesaurus in 1504. These three lexicons were frequently reprinted. Estienne, Thesaurus, Genevae, 1572, fol., 4 vols.; ed. Valpy, Lond. 1816-1826, 6 vols. fol.; Paris, 1831-1865, 9 vols. fol., 9902 pages: Κιβωτός, the ark, was intended to give the whole language, ancient and modern, but vol. i., Constantinople, 1819, fol., 763 pages, Α to Δ, only appeared, as the publication was put an end to by the events of 1821. English.—Jones, London, 1823, 8vo: Dunbar, Edin. 3rd ed. 1850, 4to: Liddell and Scott, 8th ed. Oxford, 1897, 4to. French.—Alexandre, 12th ed. Paris, 1863, 8vo; 1869-1871, 2 vols: Chassang, ib. 1872, 8vo. Italian.—Camini, Torino, 1865, 8vo, 972 pages: Müller, ib. 1871, 8vo. Spanish.—Diccionario manual, por les padres Esculapios, Madrid, 1859, 8vo. German.—Passow, 5th ed. Leipzig, 1841-1857, 4to: Jacobitz and Seiler, 4th ed. ib. 1856, 8vo: Benseler, ib. 1859, 8vo: Pape, Braunschweig, 1870-1874, 8vo, 4 vols. Prellwitz, Etymologisches Wörterbuch der griechischen Sprache, new edition, 1906: Herwerden, Lexicon Graecum suppletorium et dialecticum, 1902. Dialects.—Attic: Moeris, ed. Pierson, Lugd. Bat. 1759. 8vo. Attic Orators: Reiske, Oxon. 1828, 8vo, 2 vols. Doric: Portus, Franckof. 1605, 8vo. Ionic: Id. ib. 1603, 8vo; 1817; 1825. Prosody.—Morell, Etonae, 1762, 4to; ed. Maltby, Lond. 1830, 4to: Brasse, Lond. 1850, 8vo. Rhetoric.—Ernesti, Lips. 1795, 8vo. Music.—Drieberg, Berlin, 1855. Etymology.—Curtius, Leipzig, 1858-1862: Lancelot, Paris, 1863, 8vo. Synonyms.—Peucer, Dresden, 1766, 8vo: Pillon, Paris, 1847, 8vo. Proper Names.—Pape, ed. Sengebusch, 1866, 8vo, 969 pages. Verbs.—Veitch, 2nd ed. Oxf. 1866. Terminations.—Hoogeveen, Cantab. 1810, 4to: Pape, Berlin, 1836, 8vo. Particular Authors.—Aeschylus: Wellauer, 2 vols. Lips. 1830-1831, 8vo. Aristophanes: Caravella, Oxonii, 1822, 8vo. Demosthenes: Reiske, Lips. 1775, 8vo. Euripides: Beck, Cantab. 1829, 8vo. Herodotus: Schweighäuser, Strassburg, 1824, 8vo, 2 vols. Hesiod: Osoruis, Neapol. 1791, 8vo. Homer: Apollonius Sophista, ed. Tollius, Lugd. Bat., 1788, 8vo: Schaufelberger, Zürich, 1761-1768, 8vo, 8 vols.: Crusius, Hanover, 1836, 8vo: Wittich, London, 1843, 8vo: Döderlein, Erlangen, 8vo, 3 vols.: Eberling, Lipsiae, 1875, 8vo: Autenrieth, Leipzig, 1873, 8vo; London, 1877, 8vo. Isocrates: Mitchell, Oxon. 1828, 8vo. Pindar: Portus, Hanov. 1606, 8vo. Plato: Timaeus, ed. Koch, Lips. 1828, 8vo: Mitchell, Oxon. 1832, 8vo: Ast, Lips. 1835-1838, 8vo, 3 vols. Plutarch: Wyttenbach, Lips. 1835, 8vo, 2 vols. Sophocles: Ellendt, Regiomonti, 1834-1835, 8vo ed.; Genthe, Berlin, 1872, 8vo. Thucydides: Bétant, Geneva, 1843-1847, 8vo, 2 vols. Xenophon: Sturtz, Lips. 1801-1804, 8vo, 4 vols.: Cannesin (Anabasis, Gr.-Finnish), Helsirgissä, 1868, 8vo: Sauppe, Lipsiae, 1869, 8vo. Septuagint: Hutter, Noribergae, 1598, 4to: Biel, Hagae, 1779-1780, 8vo. New Testament: Lithocomus, Colon, 1552, 8vo: Parkhurst, ed. Major, London, 1845, 8vo: Schleusner (juxta ed. Lips. quartam), Glasguae, 1824, 4to.
Medieval and Modern Greek.—Meursius, Lugd. Bat. 1614, 4to: Critopulos, Stendaliae, 1787, 8vo: Portius, Par. 1635, 4to: Du Cange, Paris, 1682, fol., 2 vols.; Ludg. 1688, fol. English.—Polymera, Hermopolis, 1854, 8vo: Sophocles, Cambr. Mass. 1860-1887: Contopoulos, Athens, 1867, 8vo; Smyrna, 1868-1870, 8vo, 2 parts, 1042 pages. French.—Skarlatos, Athens, 1852, 4to: Byzantius, ib. 1856, 8vo, 2 vols.: Varvati, 4th ed. ib., 1860, 8vo. Italian.—Germano, Romae, 1622, 8vo: Somavera, Parigi, 1709, fol., 2 vols.: Pericles, Hermopolis, 1857, 8vo. German.—Schmidt, Lips. 1825-1827, 12mo, 2 vols.: Petraris, Leipz. 1897. Polyglots.—Koniaz (Russian and Fr.), Moscow, 1811, 4to; Schmidt (Fr.-Germ.), Leipzig, 1837-1840, 12mo, 3 vols.: Theocharopulas de Patras (Fr.-Eng.), Munich, 1840, 12mo.
Latin.—Johannes de Janua, Catholicon or Summa, finished in 1286, printed Moguntiæ 1460, fol.; Venice, 1487; and about 20 editions before 1500: Johannes, Comprehensorium, Valentia, 1475, fol.: Nestor Dionysius, Onomasticon, Milan, 1477, fol.: Stephanus, Paris, 1531, fol., 2 vols.: Gesner, Lips. 1749, fol., 4 vols.: Forcellini, Patavii, 1771, fol., 4 vols. Polyglot.—Calepinus, Reggio, 1502, fol. (Aldus printed 16 editions, with the Greek equivalents of the Latin words; Venetiis, 1575, fol., added Italian, French and Spanish; Basileae, 1590, fol., is in 11 languages; several editions, from 1609, are called Octolingue; many of the latter 2 vol. editions were edited by John Facciolati): Verantius (Ital., Germ., Dalmatian, Hungarian), Venetiis, 1595, 4to: Lodereckerus (Ital., Germ., Dalm., Hungar., Bohem., Polish), Pragae, 1605, 4to. English.—Promptorium parvulorum, compiled in 1440 by Galfridus Grammaticus, a Dominican monk of Lynn Episcopi, in Norfolk, was printed by Pynson, 1499; 8 editions, 1508-1528, ed. Way, Camden Society, 1843-1865, 3 vols. 4to; Medulla grammaticis, probably by the same author, MS. written 1483; printed as Ortus vocabulorum, by Wynkyn de Worde, 1500; 13 editions 1509-1523; Sir Thomas Elyot, London, 1538, fol.; 2nd ed. 1543; Bibliotheca Eliotae, ed. Cooper, ib. 1545, fol.: Huloet, Abecedarium, London, 1552, fol.; Dictionarie, 1572, fol.: Cooper, London, 1565, fol.; 4th edition, 1584, fol.: Baret, Alvearie, ib. 1575, fol.; 1580, fol.: Fleming, ib. 1583, fol.: Ainsworth, London, 1736, 4to; ed. Morell, London, 1796, 4to, 2 vols.; ed. Beatson and Ellis, ib. 1860, 8vo: Scheller, translated by Riddle, Oxford, 1835, fol.: Smith, London, 1855, 8vo; 1870: Lewis and Short, Oxford, 1879. Eng.-Latin.—Levins, Manipulus puerorum, Lond. 1570, 4to: Riddle, ib. 1838, 8vo: Smith, ib. 1855, 8vo. French.—Catholicon parvum, Geneva, 1487: Estienne, Dictionnaire, Paris, 1539, fol. 675 pages; enlarged 1549; ed. Huggins, Lond. 1572: Id. Dictionarium Latino-Gallicum, Lutetiae, 1546, fol.; Paris, 1552; 1560: Id., Dictionariolum puerorum, Paris, 1542, 4to: Les Mots français, Paris, 1544, 4to; the copy in the British Museum has the autograph of Queen Catherine Parr: Thierry (Fr.-Lat.), Paris, 1564, fol.: Danet, Ad usum Delphini, Paris, 1700, 4to, 2 vols.; and frequently: Quicherat, 9th ed. Paris, 1857, 8vo: Theil, 3rd ed. Paris, 1863, 8vo: Freund, ib. 1835-1865, 4to, 3 vols. German.—Joh. Melber, of Gerolzhofen, Vocabularius praedicantium, of which 26 editions are described by Hain (Repertorium, No. 11,022, &c.), 15 undated, 7 dated 1480-1495, 4to, and 3 after 1504: Vocabularius gemma gemmarum, Antwerp, 1484, 4to; 1487; 12 editions, 1505-1518: Herman Torentinus, Elucidarius carminum, Daventri, 1501, 4to; 22 editions, 1504-1536: Binnart, Ant. 1649, 8vo: Id., Biglotton, ib. 1661; 4th ed. 1688: Faber, ed. Gesner, Hagae Com. 1735, fol., 2 vols.: Hederick, Lips. 1766, 8vo, 2 vols.: Ingerslev, Braunschweig, 1835-1855, 8vo, 2 vols.: Thesaurus linguae Latinae, Leipzig, 1900: Walde, Lateinisches etymologisches Wörterbuch, 1906. Italian.—Seebar (Sicilian translation of Lebrixa), Venet. 1525, 8vo: Venuti, 1589, 8vo: Galesini, Venez. 1605, 8vo: Bazzarini and Bellini, Torino, 1864, 4to, 2 vols. 3100 pages. Spanish.—Salmanticae, 1494, fol.; Antonio de Lebrixa, Nebrissenis, Compluti, 1520, fol., 2 vols.: Sanchez de la Ballesta, Salamanca, 1587, 4to: Valbuena, Madrid, 1826, fol. Portuguese.—Bluteau, 192 Lisbon, 1712-1728, fol., 10 vols: Fonseca, ib. 1771, fol.: Ferreira, Paris, 1834, 4to; 1852. Romansch.—Promptuario di voci volgari, Valgrisii, 1565, 4to. Vlach.—Divalitu, Bucuresci, 1852, 8vo. Swedish.—Vocabula, Rostock, 1574, 8vo; Stockholm, 1579: Lindblom, Upsala, 1790, 4to. Dutch.—Binnart, Antw. 1649, 8vo: Scheller, Lugd. Bat. 1799, 4to, 2 vols. Flemish.—Paludanus, Gandavi, 1544, 4to. Polish.—Macinius, Königsberg, 1564, fol.: Garszynski, Breslau, 1823, 8vo, 2 vols. Bohemian.—Johannes Aquensis, Pilsnae, 1511, 4to: Reschel, Olmucii, 1560-1562, 4to, 2 vols.: Cnapius, Cracovia, 1661, fol., 3 vols. Illyrian.—Bellosztenecz, Zagrab, 1740, 4to: Jambresich (also Germ. and Hungar.), Zagrab, 1742, 4to. Servian.—Swotlik, Budae, 1721, 8vo. Hungarian.—Molnar, Frankf. a. M. 1645, 8vo: Pariz-Papai, Leutschen, 1708, 8vo; 1767. Finnish.—Rothsen, Helsingissä, 1864, 8vo. Poetic.—Epithetorum et synonymorum thesaurus, Paris, 1662, 8vo, attributed to Chatillon; reprinted by Paul Aler, a German Jesuit, as Gradus ad Parnassum, Paris, 1687, 8vo; many subsequent editions: Schirach, Hal. 1768, 8vo: Noel, Paris, 1810, 8vo; 1826: Quicherat, Paris, 1852, 8vo: Young, London, 1856, 8vo. Erotic.—Rambach, Stuttgart, 1836, 8vo. Rhetorical.—Ernesti, Lips. 1797, 8vo. Civil Law.—Dirksen, Berolini, 1837, 4to. Synonyms.—Hill, Edinb. 1804, 4to: Döderlein, Lips. 1826-1828, 8vo, 6 vols. Etymology.—Danet, Paris, 1677, 8vo: Vossius, Neap. 1762, fol., 2 vols.: Salmon, London, 1796, 8vo, 2 vols.: Nagel, Berlin, 1869, 8vo; Latin roots, with their French and English derivatives, explained in German: Zehetmayr, Vindobonae, 1873, 8vo: Vaniček, Leipz. 1874, 8vo. Barbarous.—Marchellus, Mediol. 1753, 4to; Krebs, Frankf. a. M. 1834, 8vo; 1837. Particular Authors.—Caesar: Crusius, Hanov. 1838, 8vo. Cicero: Nizzoli, Brescia, 1535, fol.; ed. Facciolati, Patavii, 1734, fol.; London, 1820, 8vo, 3 vols.: Ernesti, Lips. 1739, 8vo; Halle, 1831. Cornelius Nepos: Schmieder, Halle, 1798, 8vo; 1816: Billerbeck, Hanover, 1825, 8vo. Curtius Rufus: Crusius, Hanov. 1844, 8vo. Horace: Ernesti, Berlin, 1802-1804, 8vo, 3 vols.: Döring, Leipz. 1829, 8vo. Justin: Meinecke, Lemgo, 1793, 8vo; 2nd ed. 1818. Livy: Ernesti, Lips. 1784, 8vo; ed Schäfer, 1804. Ovid: Gierig, Leipz. 1814: (Metamorphoses) Meinecke, 2nd ed., Lemgo, 1825, 8vo: Billerbeck (Do.), Hanover, 1831, 8vo. Phaedrus: Oertel, Nürnberg, 1798, 8vo: Hörstel, Leipz. 1803, 8vo: Billerbeck Hanover, 1828, 8vo. Plautus: Paraeus, Frankf. 1614, 8vo. Pliny: Denso, Rostock, 1766, 8vo. Pliny, jun.: Wensch, Wittenberg, 1837-1839, 4to. Quintilian: Bonnellus, Leipz. 1834, 8vo. Sallust: Schneider, Leipz. 1834, 8vo: Crusius, Hanover, 1840, 8vo. Tacitus: Bötticher, Berlin, 1830, 8vo. Velleius Paterculus: Koch, Leipz. 1857, 8vo. Virgil: Clavis, London, 1742, 8vo: Braunhard, Coburg, 1834, 8vo. Vitruvius: Rode, Leipz. 1679, 4to, 2 vols.: Orsini, Perugia, 1801, 8vo.
Old Italian Languages.—Fabretti, Torini, 1858, 4to. Umbrian: Huschke, Leipz. 1860, 8vo. Oscan and Sabellian: Id. Elberfeld, 1856, 8vo.
Medieval Latin.—Du Cange, Glossarium, Paris, 1733-1736, fol., 6 vols.; Carpentier, Suppl., Paris, 1766, fol., 4 vols.; ed. Adelung, Halae, 1772-1784, 8vo, 6 vols.; ed. Henschel, Paris, 1840-1850, 4to, 7 vols. (vol. vii. contains a glossary of Old French): Brinckmeier, Gotha, 1850-1863, 8vo, 2 vols.: Hildebrand (Glossarium saec. ix.), Götting. 1854, 4to: Diefenbach, Glossarium, Frankf. 1857, 4to: Id. Gloss. novum, ib. 1867, 4to. Ecclesiastical.—Magri, Messina, 1644, 4to; 8th ed. Venezia, 1732; Latin translation, Magri Hierolexicon, Romae, 1677, fol.; 6th ed. Bologna, 1765, 4to, 2 vols.
Romance Languages.
Romance Languages generally.—Diez, Bonn, 1853, 8vo; 2nd ed. ib. 1861-1862, 8vo, 2 vols.; 3rd ed. ib. 1869-1870, 8vo, 2 vols.; transl. by Donkin, 1864, 8vo.
French.—Ranconet, Thresor, ed. Nicot, Paris, 1606, fol.; ib. 1618, 4to: Richelet, Genève, 1680, fol., 2 vols.; ed. Gattel, Paris, 1840, 8vo, 2 vols.
The French Academy, after five years’ consideration, began their dictionary, on the 7th of February 1639, by examining the letter A, which took them nine months to go through. The word Académie was for some time omitted by oversight. They decided, on the 8th of March 1638, not to cite authorities, and they have since always claimed the right of making their own examples. Olivier justifies them by saying that for eighty years all the best writers belonged to their body, and they could not be expected to cite each other. Their design was to raise the language to its last perfection, and to open a road to reach the highest eloquence. Antoine Furetière, one of their members, compiled a dictionary which he says cost him forty years’ labour for ten hours a day, and the manuscript filled fifteen chests. He gave words of all kinds, especially technical, names of persons and places, and phrases. As a specimen, he published his Essai, Paris, 1684, 4to; Amst. 1685, 12mo. The Academy charged him with using the materials they had prepared for their dictionary, and expelled him, on the 22nd of January 1685, for plagiarism. He died on the 14th of May 1688, in the midst of the consequent controversy and law suit. His complete work was published, with a preface by Bayle, La Haye and Rotterdam, 1690, fol., 3 vols.; again edited by Basnage de Beauval, 1701; La Haye, 1707, fol., 4 vols. From the edition of 1701 the very popular so-called Dictionnaire de Trevoux, Trevoux, 1704, fol., 2 vols., was made by the Jesuits, who excluded everything that seemed to favour the Calvinism of Basnage. The last of its many editions is Paris, 1771, fol., 8 vols. The Academy’s dictionary was first printed Paris, 1694, fol., 2 vols. They began the revision in 1700; second edition 1718, fol., 2 vols.; 3rd, 1740, fol., 2 vols.; 6th, 1835, 2 vols. 4to, reprinted 1855; Supplément, by F. Raymond, 1836, 4to; Complément, 1842, 4to, reprinted 1856; Dictionnaire historique, Paris, 1858-1865, 4to, 2 parts (A to Actu), 795 pages, published by the Institut: Dochez, Paris, 1859, 4to: Bescherelle, ib. 1844, 4to, 2 vols.; 5th ed. Paris, 1857, 4to, 2 vols.; 1865; 1887: Landais, Paris, 1835; 12th ed. ib. 1854, 4to, 2 vols.: Littré, Paris, 1863-1873, 4to, 4 vols. 7118 pages: Supplément, Paris, 1877, 4to: Godefroy (with dialects from 9th to 15th cent.), Paris, 1881-1895, and Complément: Hatzfield, Darmesteter, and Thomas, Paris, 1890-1900: Larive and Fleury, (mots et choses, illustré), Paris, 1884-1891. English.—Palsgrave, Lesclaircissement de la langue francoyse, London, 1530, 4to, 2 parts; 1852: Hollyband, London, 1533, 4to: Cotgrave, ib. 1611, fol.: Boyer, La Haye, 1702, 4to, 2 vols.; 37th ed. Paris, 1851, 8vo, 2 vols.: Fleming and Tibbins, Paris, 1846-1849, 4to, 2 vols.; ib. 1854, 4to, 2 vols.; ib. 1870-1872, 4to, 2 vols.: Tarver, London, 1853-1854, 8vo, 2 vols.; 1867-1872: Bellows, Gloucester, 1873, 16mo; ib. 1876. Ideological, or Analogical.—Robertson, Paris, 1859, 8vo: Boissière, Paris, 1862, 8vo. Etymology.—Lebon, Paris, 1571, 8vo: Ménage, ib. 1650, 4to. Pougens projected a Trésor des origines, his extracts for which, filling nearly 100 volumes folio, are in the library of the Institut. He published a specimen, Paris, 1819, 4to. After his death, Archéologie française, Paris, 1821, 8vo, 2 vols., was compiled from his MSS., which were much used by Littré: Scheler, Bruxelles, 1862, 8vo; 1873: Brachet, 2nd ed. Paris, 1870, 12mo; English trans. Kitchin, Oxf. 1866, 8vo. Greek Words.—Trippault, Orleans, 1580, 8vo: Morin, Paris, 1809, 8vo. German Words.—Atzler, Cöthen, 1867, 8vo. Oriental Words.—Pihan, Paris, 1847, 8vo; 1866: Devic, ib. 1876, 8vo. Neology.—Desfontaines, 3rd ed. Amst. 1728, 12mo: Mercier, Paris, 1801, 8vo, 2 vols.: Richard, ib. 1842, 8vo; 2nd ed. 1845. Poetic.—Dict. des rimes (by La Noue), Geneve, 1596, 8vo; Cologny, 1624, 8vo: Carpentier, Le Gradus français, Paris, 1825, 8vo, 2 vols. Erotic.—De Landes, Bruxelles, 1861, 12mo. Oratory.—Demandre and Fontenai, Paris, 1802, 8vo: Planche, ib. 1819-1820, 8vo, 3 vols. Pronunciation.—Féline, ib. 1857, 8vo. Double Forms.—Brachet, ib. 1871, 8vo. Epithets.—Daire, ib. 1817, 8vo. Verbs.—Bescherelle, ib. 1855, 8vo, 2 vols.: 3rd ed. 1858. Participles.—Id., ib. 1861, 12mo. Difficulties.—Boiste, London, 1828, 12mo: Laveaux, Paris, 1872, 8vo, 843 pages. Synonyms.—Boinvilliers, Paris, 1826, 8vo: Lafaye, ib. 1858, 8vo; 1861; 1869: Guizot, ib. 1809, 8vo; 6th ed. 1863; 1873. Homonyms.—Zlatagorski (Germ., Russian, Eng.), Leipzig, 1862, 8vo, 664 pages. Imitative Words.—Nodier, Onomatopées, ib. 1828, 8vo. Technology.—D’Hautel, ib. 1808, 8vo, 2 vols.: Desgranges, ib. 1821, 8vo: Tolhausen (Fr., Eng., Germ.), Leipz. 1873, 8vo, 3 vols. Faults of Expression.—Roland, Gap, 1823, 8vo: Blondin, Paris, 1823, 8vo. Particular Authors.—Corneille: Godefroy, ib. 1862, 8vo, 2 vols.: Marty-Laveaux, ib. 1868, 8vo, 2 vols. La Fontaine: Lorin, ib. 1852, 8vo. Malherbe: Regnier, ib. 1869, 8vo. Molière: Genin, ib. 1846, 8vo: Marty-Laveaux, ib. 8vo. Racine: Marty-Laveaux, ib. 1873, 8vo, 2 vols. Mme de Sévigné: Sommer, ib. 1867, 8vo, 2 vols. Old French.—La Curne de St Palaye prepared a dictionary, of which he only published Projet d’un glossaire, Paris, 1756, 4to. His MSS. in many volumes are in the National Library, and were much used by Littré. They were printed by L. Favre, and fasciculi 21-30 (tom. iii.), Niort, 4to, 484 pages, were published in February 1877. Lacombe (vieux langage), Paris, 1766, 2 vols. 4to: Kelham (Norman and Old French), London, 1779, 8vo: Roquefort (langue romane), Paris, 1808, 8vo; Supplément, ib. 1820, 8vo: Pougens, Archéologie, ib. 1821, 8vo, 2 vols.: Burguy, Berlin, 1851-1856, 8vo, 3 vols.: Laborde (Notice des émaux ... du Louvre, part ii.), Paris, 1853, 8vo, 564 pages:3 Gachet (rhymed chronicles), Bruxelles, 1859, 4to: Le Héricher (Norman, English and French), Paris, 1862, 3 vols. 8vo: Hippeau (12th and 13th centuries), Paris, 1875, 8vo. Dialects.—Jaubert (central), Paris, 1856-1857, 8vo, 2 vols.: Baumgarten (north and centre), Coblentz, 1870, 8vo: Azais, Idiomes romans du midi, Montpellier, 1877. Austrasian: François. Metz, 1773, 8vo. Auvergne: Mège, Riom, 1861, 12mo. Bearn: Lespi, Pau, 1858, 8vo. Beaucaire: Bonnet (Bouguirén), Nismes, 1840, 8vo. Pays de Bray: Decorde, Neufchâtel, 1852, 8vo. Burgundy: Mignard, Dijon, 1870, 8vo. Pays de Castres: Couzinié, Castres, 1850, 4to. Dauphiné: Champollion-Figeac, Paris, 1809, 8vo: Jules, Valence, 1835, 8vo; Paris, 1840, 4to. Dep. of Doubs: Tissot (Patois des Fourg, arr. de Pontarlier) Besançon, 1865, 8vo. Forez: Gras, Paris, 1864, 8vo; Neolas, Lyon, 1865, 8vo. Franche Comté: Maisonforte, 2nd ed. Besançon, 1753, 8vo. Gascony: Desgrouais (Gasconismes corrigés), Toulouse, 1766, 8vo; 1769; 1812, 12mo, 2 vols.; 1825, 8vo, 2 vols. Dep. of Gers: Cenac-Montaut, Paris, 1863, 8vo. Geneva: Humbert, Geneve, 1820, 8vo. Languedoc: Odde, Tolose, 1578, 8vo: Doujat, Toulouse, 1638, 8vo: De S.[auvages], Nismes, 1756, 2 vols.; 1785; Alais, 1820: Azais, Beziers, 1876, &c., 8vo: Hombres, Alais, 1872, 4to: Thomas (Greek words) Montpellier, 1843, 4to. Liége: Forir, Liége, 1866, 8vo, vol i. 455 pages. Lille: Vermesse, Lille, 1861, 12mo: Debuire du Buc ib., 1867, 8vo. Limousin: Beronie, ed. Vialle (Corrèze), Tulle, 1823, 4to. 193 Lyonnais, Forez, Beaujolais: Onofrio, Lyon, 1864, 8vo. Haut Maine: R[aoul] de M.[ontesson], Paris, 1857; 1859, 503 pages. Mentone: Andrews, Nice, 1877, 12mo. Dep. de la Meuse: Cordier, Paris, 1853, 8vo. Norman: Edélestand and Alfred Duméril, Caen, 1849, 8vo: Dubois, ib. 1857, 8vo: Le Héricher (Philologie topographique), Caen, 1863, 4to: Id. (éléments scandinaves), Avranches, 1861, 12mo: Metivier (Guernsey), London, 1870, 8vo: Vasnier (arrond de Pont Audemer), Rouen, 1861, 8vo: Delboulle (Vallée d’Yères), Le Havre, 1876. Picardy: Corblet, Amiens, 1851, 8vo. Poitou, Saintonge, Aunis: Favre, Niort, 1867, 8vo. Poitou: Beauchet-Filleau, Paris, 1864, 8vo: Levrier, Niort, 1867, 8vo: Lalanne, Poitiers, 1868, 8vo. Saintonge: Boucherie, Angoulême, 1865, 8vo: Jonain, Royan, 1867, 8vo. Savoy: Pont (Terratzu de la Tarantaise), Chambery, 1869, 8vo. La Suisse Romande: Bridel, Lausanne, 1866, 8vo. Dep. of Tarn: Gary, Castre, 1845, 8vo. Dep. of Vaucluse: Barjavel, Carpentras, 1849, 8vo. Walloon (Rouchi): Cambresier, Liége, 1787, 8vo: Grandgagnage, ib. 1845-1850, 8vo. 2 vols.: Chavée, Paris, 1857, 18mo: Vermesse, Doudi, 1867, 8vo. Sigart (Montois), Bruxelles, 1870, 8vo. Slang.—Oudin, Curiositez Françaises, Paris, 1640, 8vo: Baudeau de Saumaise (Précieuses, Langue de Ruelles), Paris, 1660, 12mo; ed. Livet, ib. 1856: Le Roux, Dict. Comique, Amst. 1788, and 6 other editions: Carême Prenant [i.e. Taumaise], (argot réforme), Paris, 1829, 8vo: Larchey (excentricitées du langage), Paris, 1860, 12mo; 5th ed. 1865: Delvau (langue verte, Parisian), Paris, 1867, 8vo: Larchey, Paris, 1873, 4to, 236 pages.
Provençal.—Pallas, Avignon, 1723, 4to: Bastero, La Crusca Provenzale, Roma, 1724, fol. vol. i. only: Raynouard, Paris, 1836-1844, 8vo, 6 vols.: Garcin, Draguignand, 1841, 8vo, 2 vols.: Honnorat, Digne, 1846-1849, 4to, 4 vols. 107,201 words: Id., Vocab. fr. prov., ib. 1848, 12mo, 1174 pages.
Spanish.—Covarruvias Orosco, Madrid, 1611, fol.: ib. 1673-1674, fol. 2 vols.; Academia Española, Madrid, 1726-1739, fol. 6 vols.; 8th ed. 1837: Caballero, Madrid, 1849, fol.; 8th ed. ib. 1860, 4to, 2 vols.: Cuesta, ib. 1872, fol. 2 vols.: Campano, Paris, 1876, 18mo, 1015 pages. Cuervo, 1886-1894; Monlau, 1881; Zerola, Toro y Gomes, and Isaza, 1895; Serrano (encyclopaedic) 1876-1881. English.—Percivall, London, 1591, 4to: Pineda, London, 1740, fol.: Connelly and Higgins, Madrid, 1797-1798, 4to, 4 vols.: Neuman and Baretti, 9th ed. London, 1831, 8vo, 2 vols.; 1874. French.—Oudin, Paris, 1607, 4to, 1660; Gattel, Lyon, 1803, 4to, 2 vols.: Dominguez, Madrid, 1846, 8vo, 6 vols.: Blanc, Paris, 1862, 8vo, 2 vols. German.—Wagener, Hamb. 1801-1805, 8vo, 4 vols.: Seckendorp, ib. 1823, 8vo, 3 vols.: Franceson, 3rd ed. Leipzig, 1862, 8vo, 2 vols. Italian.—Franciosini, Venezia, 1735, 8vo, 2 vols.; Cormon y Manni, Leon, 1843, 16mo, 2 vols.: Romero, Madrid, 1844, 4to. Synonyms.—Diccionario de Sinonimos, Paris, 1853, 4to. Etymology.—Aldrete, Madrid, 1682, fol.: Monlau y Roca, ib. 1856, 12mo; Barcia, 1881-1883. Arabic Words.—Hammer Purgstall, Wien, 1855, 8vo: Dozy and Engelmann, 2d ed. Leiden, 1869, 8vo. Ancient.—Sanchez, Paris, 1842, 8vo. Rhyming.—Garcia de Rengifo (consonancias) Salmantica, 1592, 4to; 1876. Don Quixote.—Beneke (German), Leipzig, 1800, 16mo; 4th ed. Berlin, 1841, 16mo. Dialects.—Aragonese: Peralta, Zaragoza, 1836, 8vo: Borao, ib. 1859, 4to. Catalan: Rocha de Girona (Latin), Barcinone, 1561, fol.: Dictionari Catala (Lat. Fr. Span.), Barcelona, 1642, 8vo: Lacavalleria (Cat.-Lat.), ib. 1696, fol.: Esteve, ed. Belvitges, &c. (Catal.-Sp. Lat.), Barcelona, 1805-1835, fol. 2 vols.: Saura (Cat.-Span.), ib. 1851, 16mo; 2nd ed.(Span.-Cat.), ib. 1854; 3rd ed. (id.) ib. 1862, 8vo: Labernia, ib. 1844-1848, 8vo, 2 vols. 1864. Gallegan: Rodriguez, Coruña, 1863, 4to: Cuveira y Piñol, Madrid, 1877, 8vo. Majorca: Figuera, Palma, 1840, 4to: Amengual, ib. 1845, 4to. Minorca: Diccionario, Madrid, 1848, 8vo. Valencian: Palmyreno, Valentiae, 1569: Ros, Valencia, 1764, 8vo: Fuster, ib. 1827, 8vo: Lamarca, 2nd ed. ib. 1842, 16mo. Cuba: Glossary of Creole Words, London, 1840, 8vo: Pichardo, 1836; 2nd ed. Havana, 1849, 8vo; 3rd ed. ib. 1862, 8vo; Madrid, 1860, 4to.
Portuguese.—Lima, Lisbon, 1783, 4to: Moraes da Silva, ib. 1789, 4to, 2 vols.; 6th ed. 1858: Academia real das Sciencas, ib. 1793, tom. i., ccvi. and 544 pages (A to Azurrar); Faria, ib. 1849, fol. 2 vols.; 3rd ed. ib. 1850-1857, fol. 2 vols. 2220 pages. English.—Vieyra, London, 1773, 2 vols. 4to: Lacerda, Lisboa, 1866-1871, 4to, 2 vols. French.—Marquez, Lisboa, 1756-1761, fol. 2 vols.: Roquette, Paris, 1841, 8vo, 2 vols.; 4th ed. 1860: Marques, Lisbonne, 1875, fol. 2 vols.: Souza Pinto, Paris, 1877, 32mo, 1024 pages. German.—Wagener, Leipzig, 1811-1812, 8vo, 2 vols.: Wollheim, ib. 1844, 12mo, 2 vols.: Bösche, Hamburg, 1858, 8vo, 2 vols. 1660 pages. Italian.—Costa e Sá, Lisboa, 1773-1774, fol. 2 vols. 1652 pages: Prefumo, Lisboa, 1853, 8vo, 1162 pages. Ancient.—Joaquim de Sancta Rosa de Viterbo, ib. 1798, fol. 2 vols.; 1824, 8vo. Arabic Words.—Souza, ib. 1789, 4to; 2nd ed. by S. Antonio Moura, ib. 1830, 224 pages. Oriental and African Words, not Arabic.—Saõ Luiz, ib. 1837, 4to, 123 pages. French Words.—Id., ib. 1827, 4to; 2nd ed. Rio de Janeiro, 1835, 8vo. Synonyms.—Id., ib. 1821, 4to; 2nd ed. ib. 1824-1828, 8vo. Fonseca, Paris, 1833, 8vo; 1859, 18mo, 863 pages. Homonyms.—De Couto, Lisboa, 1842, fol. Poetic.—Luzitano (i.e. Freire), ib. 1765, 8vo, 2 vols.; 3rd ed. ib. 1820, 4to, 2 vols. Rhyming.—Couto Guerreiro, Lisboa, 1763, 4to. Naval.—Tiberghien, Rio de Janeiro, 1870, 8vo. Ceylon-Portuguese.—Fox, Colombo, 1819, 8vo: Callaway, ib. 1823, 8vo.
Italian.—Accarigi, Vocabulario, Cento, 1543, 4to: Alunno, La fabrica del mundo, Vinezia, 1548, fol.: Porccachi, Venetia, 1588, fol.: Accademici della Crusca, Vocabulario, Venez. 1612, fol.; 4th ed. Firenze, 1729-1738, fol. 6 vols.: Costa and Cardinali, Bologna, 1819-1826, 4to, 7 vols.: Tommaseo and Bellini, Torino, 1861, &c., 4to, 4 vols.: Petrocchi, 1884-1891. English.—Thomas, London, 1598, 4to: Florio, London, 1598, 4to, 1611: Baretti, London, 1794, 2 vols.: 1854, 8vo, 2 vols.: Petronj and Davenport, Londra, 1828, 8vo, 3 vols.: Grassi, Leipz. 1854, 12mo: Millhouse, Lond., 1868, 8vo, 2 vols. 1348 pages. French.—Alberti, Paris, 1771, 4to, 2 vols.; Milan, 1862: Barberi, Paris, 1838, 4to, 2 vols.: Renzi, Paris, 1850, 8vo. German.—Libro utilissimo, Venetiis, 1499, 4to: Valentini, Leipzig, 1834-1836, 4to, 4 vols. Etymology.—Menage, Geneva, 1685, fol.: Bolza, Vienna, 1852, 4to. Provençal Words.—Nannucci, Firenze, 1840, 8vo. Synonyms.—Rabbi, Venezia, 1774, 4to; 10th ed. 1817; Tommaseo, Firenze, 1839-1840, 4to, 2 vols.: Milano, 1856, 8vo; 1867. Verbs.—Mastrofini, Roma, 1814, 4to, 2 vols. Select Words and Phrases.—Redi, Brescia, 1769, 8vo. Incorrect Words and Phrases.—Molassi, Parma, 1830-1841, 8vo, 854 pages. Supposed Gallicisms.—Viani, Firenze, 1858-1860, 8vo, 2 vols. Additions To the Dictionaries.—Gherardini, Milano, 1819-1821, 8vo, 2 vols.; ib. 1852-1857, 8vo, 6 vols. Rhyming.—Falco, Napoli, 1535, 4to: Ruscelli, Venetia, 1563, 8vo; 1827: Stigliani, Roma, 1658, 8vo: Rosasco, Padova, 1763, 4to; Palermo, 1840, 8vo. Technical.—Bonavilla-Aquilino, Mil. 1819-1821, 8vo, 5 vols.; 2nd ed. 1829-1831, 4to, 2 vols.: Vogtberg (Germ.), Wein, 1831, 8vo. Particular Authors.—Boccaccio: Aluno, Le ricchezze della lingua volgare, Vinegia, 1543. fol. Dante: Blanc, Leipzig, 1852, 8vo; Firenze, 1859, 8vo. Dialects.—Bergamo: Gasparini, Mediol. 1565: Zappetini, Bergamo, 1859, 8vo: Tiraboschi (anc. and mod.), Turin, 1873, 8vo. Bologna: Bumaldi, Bologna, 1660, 12mo: Ferrari, ib. 1820, 8vo; 1838, 4to. Brescia: Gagliardi, Brescia, 1759, 8vo: Melchiori, ib. 1817-1820, 8vo: Vocabularietto, ib. 1872, 4to. Como: Monti, Milano, 1845, 8vo. Ferrara: Manini, Ferrara, 1805, 8vo: Azzi, ib. 1857, 8vo. Friuli: Scala, Pordenone, 1870, 8vo. Genoa: Casaccia, Gen. 1842-1851, 8vo; 1873, &c.: Paganini, ib. 1857, 8vo. Lombardy: Margharini, Tuderti, 1870, 8vo. Mantua: Cherubini, Milano, 1827, 4to. Milan: Varon, ib. 1606, 8vo: Cherubini, ib. 1814, 8vo, 2 vols.; 1841-1844, 8vo, 4 vols.; 1851-1861, 8vo, 5 vols.: Banfi, ib. 1857, 8vo: 1870, 8vo. Modena: Galvani, Modena, 1868, 8vo. Naples: Galiani, Napoli, 1789, 12mo, 2 vols. Parma: Peschieri, Parma, 1828-1831, 8vo, 3 vols. 1840; Malespina, ib. 1856, 8vo, 2 vols. Pavia: Dizionario domestico pavese, Pavia, 1829, 8vo: Gambini, ib. 1850, 4to, 346 pages. Piacenza: Nicolli, Piacenza, 1832: Foresti, ib. 1837-1838, 8vo, 2 pts. Piedmont: Pino, Torino, 1784, 4to: Capello (Fr.), Turin, 1814, 8vo, 2 pts.: Zalli (Ital. Lat. Fr.), Carmagnola, 1815, 8vo, 2 vols: Sant’ Albino, Torino, 1860, 4to. Reggio: Vocabulario Reggiano, 1832. Romagna: Morri, Fienza, 1840. Rome: Raccolto di voci Romani e Marchiani, Osimo, 1769, 8vo. Roveretano and Trentino: Azzolini, Venezia, 1856, 8vo. Sardinia: Porru, Casteddu, 1832, fol.: Spano, Cagliari, 1851-1852, fol. 3 vols. Sicily: Bono (It. Lat.), Palermo, 1751-1754, 4to, 3 vols.; 1783-1785, 4to, 5 vols.: Pasqualino, ib. 1785-1795, 4to, 5 vols.: Mortillaro, ib. 1853, 4to, 956 pages: Biundi, ib. 1857, 12mo, 578 pages: Traina, ib. 1870, 8vo. Siena: Barbagli, Siena, 1602, 4to. Taranto: Vincentiis, Taranto, 1872, 8vo. Turin: Somis di Chavrie, Torino, 1843, 8vo. Tuscany: Luna, Napoli, 1536, 4to: Politi, Roma, 1604, 8vo; Venezia, 1615; 1628; 1665; Paulo, ib. 1740, 4to. Vaudois: Callet, Lausanne, 1862, 12mo. Venetian: Patriarchi (Veneziano e padevano), Padova, 1755, 4to; 1796, 1821: Boerio, Venezia, 1829, 4to; 1858-1859; 1861. Verona: Angeli, Verona, 1821, 8vo. Vicenza: Conti, Vicenza, 1871, 8vo. Lingua Franca.—Dictionnaire de la langue Franque, ou Petit Mauresque, Marseille, 1830, 16mo, 107 pages. Slang.—Sabio (lingua Zerga), Venetia, 1556, 8vo; 1575: Trattato degli bianti, Pisa, 1828, 8vo.
Romansh.—Promptuario de voci volgari e Latine, Valgrisii, 1565, 4to: Der, die, das, oder Nomenclatura (German nouns explained in Rom.), Scoul, 1744, 8vo: Conradi, Zurich, 1820, 8vo; 1826, 12mo, 2 vols.: Carisch, Chur, 1821, 8vo; 1852, 16mo.
Vlach.—Lesicon Rumanese (Lat. Hung. Germ.), Budae, 1825, 4to: Bobb (Lat. Hung.), Clus, 1822-1823, 4to, 2 vols. French.—Vaillant, Boucoureshti, 1840, 8vo: Poyenar, Aaron and Hill, Boucourest, 1840-1841, 4to, 2 vols.; Jassi, 1852, 16mo, 2 vols.: De Pontbriant, Bucuresci, 1862, 8vo: Cihac, Frankf. 1870, 8vo: Costinescu, Bucuresci, 1870, 8vo, 724 pages: Antonescu, Bucharest, 1874, 16mo, 2 vols. 919 pages. German.—Clemens, Hermanstadt, 1823, 8vo: Isser, Kronstadt, 1850: Polyzu, ib. 1857, 8vo.
Teutonic: (1) Scandinavian.
Icelandic.—Latin.—Andreae, Havniae, 1683, 8vo: Halderson (Lat. Danish), ib. 1814, 4to, 2 vols. English.—Cleasby-Vigfusson, Oxford, 1874, 4to. German.—Dieterich, Stockholm, 1844, 8vo: Möbius, Leipzig, 1866, 8vo. Danish.—Jonssen, Kjöbenhavn, 1863, 8vo. Norwegian.—Kraft, Christiania, 1863, 8vo: Fritzner, Kristiania, 1867, 8vo. Poetic.—Egilsson (Latin), Hafniae, 1860, 8vo; 1864.
Swedish.—Kindblad, Stockholm, 1840, 4to: Almqvist, Örebro, 1842-1844, 8vo: Dalin, Ordbog. Stockholm, 1850-1853, 8vo, 2 vols. 1668 pages; 1867, &c. 4to (vol. i. ii., A to Fjermare, 928 pages): Id., Handordbog, ib. 1868, 12mo, 804 pages; Svenska Academien. Stockholm, 1870, 4to (A) pp. 187. Latin.—Stjernhjelm, Holm, 1643, 4to: Verelius, Upsala, 1691, 8vo: Ihre (Sueo-Gothicum), 194 Upsala, 1769, fol. 2 vols. English.—Serenius, Nyköping, 1757, 4to: Brisnon, Upsala, 1784, 4to: Widegren, Stockholm, 1788, 4to; Brisman, Upsala, 1801, 4to; 3rd ed. 1815, 2 vols.: Deleen Örebro, 1829, 8vo: Granberg, ib. 1832, 12mo: Nilssen, Widmark, &c., Stockholm, 1875, 8vo. French.—Möller, Stockholm, 1745, 4to: Björkengren, ib. 1795, 2 vols.: Nordforss, ib. 1805, 8vo, 2 vols.: 2nd ed. Örebro, 1827, 12mo: West, Stockh. 1807, 8vo: Dalin, ib. 1842-1843, 4to, 2 vols.; 1872. German.—Dähnert, Holmiae, 1746, 4to: Heinrich, Christiansund, 1814, 4to, 2 vols.; 4th ed. Örebro, 1841, 12mo: Helms, Leipzig, 1858, 8vo; 1872. Danish.—Höst, Kjöbenhavn, 1799, 4to: Welander, Stockholm, 1844, 8vo: Dalin, ib. 1869, 16mo: Kaper, Kjöbenhavn, 1876, 16mo. Etymology.—Tamm, Upsala, 1874, &c., 8vo (A and B), 200 pages. Foreign Words.—Sahlstedt, Wästerås, 1769, 8vo: Andersson (20,000), Stockholm, 1857, 16mo: Tullberg, ib. 1868, 8vo: Ekbohrn, ib. 1870, 12mo: Dalin, ib. 1870, &c., 8vo. Synonyms.—Id., ib. 1870, 12mo. Naval.—Ramsten, ib. 1866, 8vo. Technical.—Jungberg, ib. 1873, 8vo. Dialects.—Ihre, Upsala, 1766, 4to: Rietz, Lund, 1862-1867, 4to, 859 pages. Bohuslän: Idioticon Bohusiense, Götaborg, 1776, 4to. Dalecarlia: Arborelius, Upsala, 1813, 4to. Gothland: Hof (Sven), Stockholmiae, 1772, 8vo: Rääf (Ydre), Örebro, 1859, 8vo. Halland: Möller, Lund, 158, 8vo. Helsingland: Lenström, ib. 1841, 8vo: Fornminnessällskap, Hudikswall, 1870, 8vo.
Norwegian.—Jenssen, Kjöbenhavn, 1646, 8vo: Pontoppidan, Bergen, 1749, 8vo: Hanson (German), Christiania, 1840, 8vo: Aasen, ib. 1873, 8vo, 992 pages.
Danish.—Aphelen, Kopenh, 1764, 4to, 2 vols.; 1775, 4to, 3 vols.: Molbech, Kjöbenhavn, 1833, 8vo, 2 vols.: ib. 1859, 2 vols.: Videnskabernes Selskab, ib. 1793-1865, Kalkar. English.—Berthelson (Eng. Dan.), 1754, 4to: Wolff, London, 1779, 4to. Bay, ib. 1807, 8vo, 2 vols.; 1824, 8vo: Hornbeck, ib. 1863, 8vo: Ferrall and Repp, ib. 1814, 16mo; 1873, 8vo: Rosing, Copenhagen, 1869, 8vo: Ancker, ib. 1874, 8vo. French.—Aphelen, 1754, 8vo: Id., ib. 1759, 4to, 2 vols.; 2nd ed. 1772-1777, vol. i. ii. German.—Id., ib. 1764, 4to, 2 vols.: Grönberg, 2nd ed. Kopenh. 1836-1839, 12mo, 2 vols.; 1851, Helms, Leipzig, 1858, 8vo. Synonyms.—Müller, Kjöbenhavn, 1853, 8vo. Foreign Words.—Hansen, Christiania, 1842, 12mo. Naval.—Wilsoet, Copenhagen, 1830, 8vo: Fisker (French), Kjöbenhavn, 1839, 8vo. Old Danish.—Molbech, ib. 1857-1868, 8vo, 2 vols. Dialects.—Id., ib. 1841, 8vo. Bornholm: Adler, ib. 1856, 8vo. South Jutland: Kok, 1867, 8vo. Slang.—Kristiansen (Gadesproget), ib. 1866, 8vo. p. 452.
(2) Germanic.
Teutonic.—Comparative.—Meidinger, Frankf. a. M. 1833, 8vo, 2nd ed. 1836, 8vo.
Gothic.—Junius, Dortrecht, 1665, 4to: 1671; 1684, Diefenbach (comparative), Franckf. a. M. 1846-1851, 2 vols. 8vo: Schulze, Magdeburg, 1848, 4to: 1867, 8vo: Skeat, London, 1868, 4to: Balg (Comparative Glossary), Magvike, Wisconsin, 1887-1889. Ulphilas (editions with dictionaries).—Castilionaeus, Mediol, 1829, 4to: Gabelentz and Löbe, Altenburg, 1836-1843, 4to, 2 vols.: Gaugengigl, Passau, 1848, 8vo: Stamm, Paderborn, 1857: Stamm and Heyne, ib. 1866, 8vo.
Anglo-Saxon.—Latin.—Somner (Lat. Eng.), Oxonii, 1659, fol.: Benson, ib. 1701, 8vo: Lye (A.-S. and Gothic), London, 1772, fol. 2 vols.: Ettmüller, Quedlinburg, 1851, 8vo. 838 pages. English.—Bosworth, London, 1838, 8vo, 721 pages: Id. (Compendious), 1848, 278 pages. Corson (A.-S. and Early English), New York, 1871, 8vo, 587 pages; Toller (based on Bosworth), Oxford, 1882-1898. German.—Bouterwek, Gütersloh, 1850, 8vo, 418 pages: Grein (Poets), Göttingen, 1861-1863, 8vo, 2 vols.: Leo, Halle, 1872, 8vo.
English.—Cockeram, London, 1623, 8vo: 9th ed. 1650: Blount, ib. 1656, 8vo: Philips, The new World of Words, London, 1658, fol.: Bailey, London, 1721, 8vo; 2nd ed. ib. 1736, fol.; 24th ed. ib. 1782, 8vo: Johnson, ib. 1755, fol. 2 vols.; ed. Todd, London, 1818, 4to, 4 vols.; ib. 1827. 4to, 3 vols.; ed. Latham, ib. 1866-1874, 4to, 4 vols. (2 in 4 parts): Barclay, London, 1774, 4to; ed. Woodward, ib. 1848: Sheridan, ib. 1780, 4to, 2 vols.: Webster, New York, 1828, 4to, 2 vols.; London, 1832, 4to, 2 vols.; ed. Goodrich and Porter, 1865, 4to: Richardson, ib. 1836, 4to, 2 vols.; Supplement, 1856: Ogilvie, Imperial Dictionary, Glasgow, 1850-1855, 8vo, 3 vols. (the new edition of Ogilvie by Charles Annandale, 4 vols., 1882, was an encyclopaedic dictionary, which served to some extent as the foundation of the Century Dictionary); Boag, Do., Edinburgh, 1852-1853, 8vo, 2 vols.: Craik, ib. 1856, 8vo: Worcester, Boston, 1863, 4to. Stormouth and Bayne, 1885; Murray and Bradley, The Oxford English Dictionary, 1884- ; Whitney, The Century Dict., New York, 1889-1891; Porter, Webster’s Internat. Dict., Springfield, Massachusetts, 1890; Funk, Standard Dict., New York, 1894; Hunter, The Encyclopaedic Dict., 1879-1888. Etymology.—Skinner, Londini, 1671, fol.: Junius, Oxonii, 1743, fol.: Wedgewood, London, 1859-1865, 3 vols.; ib. 1872, 8vo. Skeat, Oxford, 1881; Fennell (Anglicized words), Camb. 1892. Pronouncing.—Walker, London, 1774, 4to: by Smart, 2nd ed. ib. 1846, 8vo. Pronouncing in German.—Hausner, Frankf. 1793, 8vo; 3rd ed. 1807; Winkelmann, Berlin, 1818, 8vo: Voigtmann, Coburg, 1835, 8vo: Albert, Leipz. 1839, 8vo: Bassler, ib. 1840, 16mo. Analytical.—Booth, Bath, 1836, 4to: Roget, Thesaurus, London, 1852, 8vo; 6th ed. 1857; Boston, 1874. Synonyms.—Piozzi, London, 1794, 8vo, 2 vols.: L. [abarthe], Paris, 1803, 8vo, 2 vols.: Crabb, London, 1823, 8vo; 11th ed. 1859: C. J. Smith, ib. 1871, 8vo, 610 pages. Reduplicated Words.—Wheatley, ib. 1866, 8vo. Surnames.—Arthur, New York, 1857, 12mo, about 2600 names: Lower, ib. 1860, 4to. Particles.—Le Febure de Villebrune, Paris, 1774, 8vo. Rhyming.—Levins, Manipulus Puerorum, London, 1570, 4to; ed. Wheatley, ib. 1867, 8vo: Walker, London, 1775, 8vo; 1865, 8vo. Shakespeare.—Nares, Berlin, 1822, 4to; ed. Halliwell and Wright, London, 1859, 8vo: Schmidt, Berlin, 1874. Old English.—Spelman, London [1626], fol. (A to I only); 1664 (completed); 1687 (best ed.): Coleridge (1250-1300), ib. 1859, 8vo: Stratmann (Early Eng.), Krefeld, 1867, 8vo; 2nd ed. 1873, 4to: Bradley (new edition of Stratman), Oxford, 1891; Matzner and Bieling, Berlin, 1878- . Old and Provincial.—Halliwell, London, 1844-1846, 8vo; 2nd ed. ib. 1850, 2 vols.: 6th ed. 1904: Wright, ib. 1857, 8vo, 2 vols.; 1862. Dialects.—Ray, ib. 1674, 12mo: Grose, ib. 1787, 8vo; 1790: Holloway, Lewes, 1840, 8vo; Wright, Eng. Dialect Dict., London, 1898-1905, 28 vols. Scotch: Jamieson, Edin. 1806, 4to, 2 vols.; Supplement, 1826, 2 vols.; abridged by Johnstone, ib. 1846, 8vo: Brown, Edin, 1845, 8vo: Motherby (German), Königsberg, 1826-1828, 8vo: (Shetland and Orkney), Edmonston, London, 1866, 8vo: (Banffshire), Gregor, ib. 1866, 8vo. North Country: Brockett, London, 1839, 8vo, 2 vols. Berkshire: [Lousley] ib. 1852, 8vo, Cheshire: Wilbraham, ib. 1817, 4to; 1826, 12mo: Leigh, Chester, 1877, 8vo. Cumberland: Glossary, ib. 1851, 12mo: Dickenson, Whitehaven, 1854, 12mo; Supplement, 1867: Ferguson (Scandinavian Words), London, 1856, 8vo. Derbyshire: Hooson (mining), Wrexham, 1747, 8vo: Sleigh, London, 1865, 8vo. Dorset: Barnes, Berlin, 1863, 8vo. Durham: [Dinsdale] (Teesdale), London, 1849, 12mo. Gloucestershire: Huntley (Cotswold), ib. 1868, 8vo. Herefordshire: [Sir George Cornewall Lewis,] London, 1839, 12mo. Lancashire: Nodal and Milner, Manchester Literary Club, 1875, 8vo, Morris (Furness), London, 1869, 8vo: R. B. Peacock (Lonsdale, North and South of the Sands), ib. 1869, 8vo. Leicestershire: A. B. Evans, ib. 1848, 8vo. Lincolnshire: Brogden, ib. 1866, 12mo: Peacock (Manley & Corringham), ib. 1877, 8vo. Norfolk and Suffolk; Forby, London, 1830, 8vo, 2 vols. Northamptonshire: Sternberg, ib. 1851, 8vo: Miss Anne E. Baker, ib. 1866, 8vo, 2 vols. 868 pages. Somersetshire: Jennings, ib. 1869, 8vo: W. P. Williams and W. A. Jones, Taunton, 1873, 8vo. Suffolk: Moor, Woodbridge, 1823, 12mo: Bowditch (Surnames), Boston, U.S., 1851, 8vo; 1858; 3rd ed. London, 1861, 8vo, 784 pages. Sussex: Cooper, Brighton, 1836, 8vo: Parish, Farncombe, 1875, 8vo. Wiltshire: Akerman, London, 1842, 12mo. Yorkshire (North and East), Toone, ib. 1832, 8vo: (Craven), Carr, 2nd ed. London, 1828, 8vo, 2 vols.: (Swaledale), Harland, ib. 1873, 8vo: (Cleveland), Atkinson, ib. 1868, 4to, 653 pages: (Whitby) [F. K. Robinson], ib. 1876, 8vo: (Mid-Yorkshire and Lower Niddersdale), C. Clough Robinson, ib. 1876, 8vo: (Leeds), Id., ib. 1861, 12mo: (Wakefield), Banks, ib. 1865, 16mo: (Hallamshire), Hunter, London, 1829, 8vo. Ireland: (Forth and Bargy, Co. Wexford), Poole, London, 1867, 8vo. America: Pickering, Boston, 1816, 8vo: Bartlett, New York, 1848, 8vo; 3rd ed. Boston, 1860. 8vo; Dutch transl. by Keijzer, Gorinchen, 1854, 12mo; Germ. transl. by Köhler, Leipz. 1868, 8vo. Elwyn, Philadelphia, 1859. 8vo. Negro English: Kingos, St Croix, 1770, 8vo: Focke (Dutch), Leiden, 1855, 8vo: Wullschlaegel, Löbau, 1856, 8vo. 350 pages. Slang.—Grose, London, 1785, 8vo; 1796: Hotten, ib. 1864, 8vo; 1866; Farmer & Henley (7 vols., 1890-1904).
Frisic.—Wassenbergh, Leeuwarden, 1802, 8vo: Franeker, 1806, 8vo: Outzen, Kopenh. 1837, 4to: Hettema (Dutch), Leuwarden, 1832, 8vo; 1874, 8vo, 607 pages: Winkler (Nederdeutsch en Friesch Dialectikon), ’s Gravenhage, 1874, 8vo, 2 vols. 1025 pages. Old Frisic.—Wiarda (Germ.), Aurich, 1786, 8vo: Richthofen, Göttingen, 1840, 4to. North Frisic.—Bendson (Germ.), Leiden, 1860, 8vo: Johansen (Föhringer und Amrumer Mundart), Kiel, 1862, 8vo. East Frisic.—Stürenburg, Aurich, 1857, 8vo. Heligoland.—Oelrichs, s. l., 1836, 16mo.
Dutch.—Kok, 2nd ed. Amst. 1785-1798, 8vo, 38 vols.: Weiland, Amst. 1790-1811, 8vo, 11 vols.: Harrebomée, Utrecht, 1857, 4to; 1862-1870, 8vo, 3 vols.: De Vries and Te Winkel, Gravenh. 1864, &c., 4to (new ed. 1882- ); Dale, ib. 4th ed. 1898; English.—Hexham, ed. Manley, Rotterdam, 1675-1678, 4to: Holtrop, Dortrecht, 1823-1824, 8vo, 2 vols.: Bomhoff, Nimeguen, 1859, 8vo, 2 vols. 2323 pages: Jaeger, Gouda, 1862, 16mo: Calisch, Tiel, 1871, &c., 8vo. French.—Halma, Amst. 1710, 4to; 4th ed. 1761: Marin, ib. 1793, 4to, 2 vols.: Winkelman, ib. 1793, 4to, 2 vols.: Mook, Zutphen, 1824-1825, 8vo, 4 vols.; Gouda, 1857, 8vo, 2 vols. 2818 pages: Kramers, ib. 1859-1862, 2 vols. 16mo. German.—Kramer, Nürnb. 1719, fol.; 1759, 4to, 2 vols.; ed. Titius, 1784, Weiland, Haag, 1812, 8vo: Terwen, Amst. 1844, 8vo. Etymology.—Franck, 1884-1892. Oriental Words.—Dozy, ’s Gravenhage, 1867, 8vo. Genders of Nouns.—Bilderdijk, Amst. 1822, 8vo, 2 vols. Spelling.—Id., ’s Gravenhage, 1829, 8vo. Frequentatives.—De Jager, Gouda, 1875, 8vo, vol. i. Old Dutch.—Suringer, Leyden, 1865, 8vo. Middle Dutch.—De Vries, ’s Gravenhage, 1864, &c., 4to. Verwijs and Verdam, ib. 1885- .
Flemish.—Kilian, Antw. 1511, 8vo; ed. Hasselt, Utrecht, 1777, 4to, 2 vols. French.—Berlemont, Anvers, 1511, 4to: Meurier, ib. 1557, 8vo: Rouxell and Halma, Amst. 1708, 4to; 6th ed. 1821: Van de Velde and Sleeckx, Brux. 1848-1851, 8vo, 2440 pages; ib. 195 1860, 8vo, 2 vols. Ancient Names of Places.—Grandgagnage (East Belgium), Bruxelles, 1859, 8vo.
German.—Josua Pictorius (Maaler), Die teütsch Spraach, Tiguri, 1561, 8vo; Stieler, Nürnb. 1691, 4to: Adelung, Leipz. 1774-1786, 4to, 5 vols.; 1793-1818, 5 vols.: Campe, Braunschweig, 1807-1811, 4to, 5 vols.: Grimm, Leipzig, 1854, &c., 4to: Sanders, ib. 1860-1865, 4to, 3 vols. 1885: Diefenbach and Wülcker (High and Low German, to supplement Grimm), Frankf. a. M. 1874, 1885, 8vo.; Kluge, Strassburg, 1883; Heine, Leipzig, 1890-1895; Weigand, Giessen, 1873. English.—Adelung, 1783-1796, 8vo, 3 vols.: Hilpert, Karlsruhe, 1828-1829, 8vo, 2 vols.; 1845-1846, 4to, 2 vols.: Flügel, Leipz. 1830, 8vo, 2 vols.; London, 1857, 8vo; Leipzig, 1870: Müller, Cöthen, 1867, 8vo, 2 vols. French.—Laveaux, Strassburg, 1812, 4to: Mozin, Stuttgard, 1811-1812, 4to, 4 vols.; 1842-1846, 8vo, 4 vols., 3rd ed. 1850-1851, 8vo: Schuster, Strasb. 1859, 8vo: Daniel, Paris, 1877, 16mo. Old High German.—Haltaeus, Lipsiae, 1758, fol. 2 vols.: Graff, Berlin, 1834-1846, 4to, 7 vols.: Brinckmeier, Gotha, 1850-1863, 4to, 2 vols.: Kehrein (from Latin records), Nordhausen, 1863, 8vo. Schade, Halle, 1872-1882. Middle High German.—Ziemann, Quedlinburg, 1838, 8vo: Benecke, Müller and Zarnche, Leipz. 1854-1866, 8vo, 3 vols.: Lexer, Leipzig, 1870, 8vo. Middle Low German.—Schiller and Lübben, Bremen, 1872, &c., 8vo, in progress. Low German.—Vollbeding, Zerbst, 1806, 8vo: Kosegarten, Griefswald, 1839, 4to; 1856, &c., 4to. Etymology.—Helvigius, Hanov. 1620, 8vo: Wachter, Lipsiae, 1737, fol. 2 vols.: Kaindl, Salzbach, 1815-1830, 8vo, 7 vols.: Heyse, Magdeburg, 1843-1849, 8vo, 3 vols.: Kehrein, Wiesbaden, 1847-1852, 2 vols. Synonyms.—Eberhard, Maas, and Grüber, 4th ed. Leipzig, 1852-1863, 8vo, 4 vols.: Aue (Engl.), Edinb. 1836, 8vo: Eberhard, 11th ed. Berlin, 1854, 12mo: Sanders, Hamburg, 1872, 8vo, 743 pages. Foreign Words.—Campe, Braunschweig, 1813, 4to: Heyse, Fremdwörterbuch, Hannover, 1848, 8vo. Names.—Pott. Leipz. 1853, 8vo: Michaelis (Taufnamen), Berlin, 1856, 8vo: Förstemann (Old Germ.) Nordhausen, 1856-1859, 4to, 2 vols. 1573 pages, 12,000 names: Steub (Oberdeutschen), München, 1871, 8vo. Luther.—Dietz, Leipzig, 1869-1872, 8vo, 2 vols. Dialects.—Popowitsch, Wien, 1780, 8vo: Fulda, Berlin, 1788, 8vo: Klein, Frankf. 1792, 8vo, 2 vols.: Kaltschmidt, Nordlingen, 1851, 4to; 1854, 5th ed. 1865. Aix-la-Chapelle, Müller and Weitz, Aachen, 1836, 12mo. Appenzell: Tobler, Zürich, 1837, 8vo. Austria: Höfer, Linz, 1815, 8vo; Castelli, Wien, 1847, 12mo: Scheuchenstül (mining), ib. 1856, 8vo. Bavaria: Zaupser, München, 1789, 8vo: Deling, ib. 1820, 2 vols.: Schmeller, Stuttg. 1827-1837, 8vo, 4 vols.; 2nd ed. München, 1872, 4to, vol. i. 1799 pages. Berlin: Trachsel. Berlin, 1873, 8vo. Bremen: Bremisch Deutsch Gesellschaft, Bremen, 1767-1771, 1869, 8vo, 6 vols. Oelrich (anc. statutes), Frankf. a. M. 1767, 8vo. Carinthia: Ueberfelder, Klagenfurt, 1862, 8vo: Lexe, Leipzig, 1862, 8vo. Cleves: De Schueren, Teuthonista, Colon, 1477, fol.; Leiden, 1804, 4to. Göttingen: Schambach, Hannover, 1838, 8vo. Hamburg: Richey, Hamb. 1873, 4to; 1755, 8vo. Henneberg: Reinwold, Berlin and Stettin, 1793, 1801, 8vo, 2 vols.: Brückner, Meiningen, 1843, 4to. Hesse: Vilmar, Marburg, 1868, 8vo, 488 pages. Holstein: Schütz Hamb. 1800-1806, 8vo, 4 vols. Hungary: Schoer, Wien, 1858. Livonia: Bergmann, Salisburg, 1785, 8vo: Gutzeit, Riga, 1859-1864, 8vo, 2 parts. Upper Lusatia: Anton, Görlitz, 1825-1839, 13 parts. Luxembourg: Gangler, Lux. 1847, 8vo, 406 pages. Mecklenburg and Western Pomerania: M., Leipzig, 1876, 8vo, 114 pages. Nassau: Kehrein, Weilburg, 1860, 8vo. Osnaburg: Strodtmann, Leipz. 1756, 8vo. Pomerania and Rügen: Dähnert, Stralsund, 1781, 4to. Posen: Bernd, Bonn, 1820, 8vo. Prussia: Bock, Königsb. 1759, 8vo: Hennig, ib. 1785, 8vo. Saxony: Schmeller (from Heliand, &c.), Stuttg. 1840, 4to. Silesia: Berndt, Stendal, 1787, 8vo. Swabia: Schmid, Berlin, 1795, 8vo; Stuttg. 1831, 8vo. Switzerland: Stalder, Aarau, 1807-1813, 8vo, 2 vols. Thuringia: Keller, Jena, 1819, 8vo. Transylvania: Schuller, Prag, 1865, 8vo. Tirol: Schöpf, Innspruck, 1866, 8vo. Venetian Alps: Schmeller, Wien, 1854, 8vo. Vienna: Hugel, ib. 1873, 8vo. Hunting.—Westerwald: Schmidt, Hadamar, 1800, 8vo; Kehrein, Wiesbaden, 1871, 12mo. Slang.—Gauner Sprache: Schott, Erlangen, 1821, 8vo: Grolmann, Giessen, 1822, 8vo: Train, Meissen, 1833, 8vo: Anton, 2nd ed. Magdeburg, 1843, 8vo; 1859: Avé-Lallemant, Das Deutsche Gaunerthun, Leipzig, 1858-1862, 8vo, vol. iv. pp. 515-628. Student Slang: Vollmann (Burschicoses), Ragaz, 1846, 16mo, 562 pages.
Celtic.
Celtic generally.—Lluyd, Archaeologia Britannica, Oxford, 1707, folio: Bullet, Besançon, 1754-1860, fol. 2 vols.
Irish.—Cormac, bishop of Cashel, born 831, slain in battle 903, wrote a Glossary, Sanas Cormaic, printed by Dr Whitley Stokes, London, 1862, 8vo, with another, finished in 1569, by O’Davoren, a schoolmaster at Burren Castle, Co. Clare: O’Clery, Lovanii, 1643, 8vo: MacCuirtin (Eng.-Irish), Paris, 1732, 4to: O’Brien, ib. 1768, 4to; Dublin, 1832, 8vo: O’Reilly, 1817, 4to: 1821; ed. O’Donovan, ib. 1864, 4to, 725 pages: Foley (Eng.-Irish), ib. 1855, 8vo: Connellan (do.), 1863, 8vo.
Gaelic.—Macdonald, Edin. 1741, 8vo: Shaw, London, 1780, 4to, 2 vols.: Allan, Edin. 1804, 4to: Armstrong, London, 1825, 4to: Highland Society, ib. 1828, 4to, 2 vols.: Macleod and Dewar, Glasgow, 1853, 8vo.
Manx.—Cregeen, Douglas, 1835, 8vo: Kelly, ib. 1866, 8vo, 2 vols.
Welsh.—Latin.—Davies, London, 1632, fol.: Boxhornius, Amstelodami, 1654, 4to. English.—Salesbury, London, 1547, 4to: 1551: Richards, Bristol, 1759, 8vo: Owen (W.), London, 1793-1794, 8vo, 2 vols.; 1803, 4to, 3 vols.: Walters, ib. 1794, 4to: Owen-Pughe, Denbigh, 1832, 8vo; 3rd ed. Pryse, ib. 1866, 8vo: D. S. Evans (Eng.-Welsh), ib. 1852-1853, 8vo; 1887.
Cornish.—Pryce, Archaeologia, Sherborne, 1770, 4to: Williams, Llandovery, 1862-1865, 4to. Names.—Bannister (20,000), Truro, 1869-1871, 8vo.
Breton.—Legadeuc, Le Catholicon breton, finished 1464, printed at Lantrequier, 1499, fol. 210 pages; 1501, 4to; L’Orient, 1868, 8vo: Quicquer de Roskoff, Morlaix, 1633, 8vo: Rostrenen, Rennes, 1732, 4to, 978 pages; ed. Jolivet, Guingamps, 1834, 8vo, 2 vols.: l’A.[rmerie], Leyde, 1744, 8vo; La Haye, 1756: Lepelletier, Paris, 1752, fol.: Legonidec, Angouleme, 1821, 8vo; St Brieuc, 1847-1850, 4to, 924 pages. Dialect of Léon.—Troude (Fr.-Bret.), Brest, 1870, 8vo; Id. (Bret.-Fr.), ib. 1876, 8vo, 845 pages. Diocese of Vannes.—Armerie, Leyde, 1774, 8vo.
Basque.
Basque.—Larramendi, St Sebastian, 1745, fol. 2 vols.; ed. Zuazua, ib. 1854, fol.; Chaho, Bayonne, 1856, 4to, 1867: Fabre, ib. 1870, 8vo: Van Eys, Paris, 1873, 8vo: Egúren, Madrid, 1877.
Baltic.
Lithuanian.—Szyrwid, 3rd ed., Vilnae, 1642, 8vo; 5th ed. 1713: Schleicher, Prag, 1856-1857, 8vo, 2 vols.: Kurmin, Wilno, 1858, 8vo: Kurschat, Halle, 1870, &c., 8vo.
Lettic.—Mancelius, Riga, 1638, 4to: Elvers, ib. 1748, 8vo: Lange, Mitau, 1777, 4to: Sjögren, Petersburg, 1861, 4to: Ulmann, ed. Bielenstein, Riga, 1872, &c., 8vo.
Prussian.—Bock, Königsberg, 1759, 8vo: Hennig, ib. 1785, 8vo: Nesselmann, Berlin, 1873, 8vo: Pierson, ib. 1875, 8vo.
Slavonic.
Slavonic generally.—Franta-Sumavski (Russ. Bulg. Old Slav. Boh. Polish), Praga, 1857, 8vo, Miklosich, Wien, 1886.
Old Slavonic.—Beruinda, Kiev, 1627, 8vo; Kuteinsk, 1653, 4to: Polycarpi (Slav. Greek, Latin), Mosque, 1704, 4to: Alexyeev, St Petersb. 1773, 8vo; 4th ed. ib. 1817-1819, 8vo, 5 vols.: Russian Imp. Academy, ib. 1847, 4to, 4 vols.: Miklosich, Vindobonae, 1850: 4to; 1862-1865, 8vo, Mikhailovski, St Petersb. 1875, 8vo: Charkovski, Warschaw, 1873, 8vo.
Russian.—Russian Academy, St Petersburg, 1789-1794, 4to, 6 vols.; 1806-1822, ib. 1869, 8vo, 3 vols.: Dahl, Moskva, 1862-1866, fol. 4 vols.; d., ib. 1873, &c., 4to; a 3rd edition, 1903, &c. French-Germ.-Eng.—Reiff, ib. 1852-1854, 4to. German, Latin.—Holterhof, Moskva, 1778, 8vo, 2 vols.; 3rd ed. 1853-1855, 8vo, 2 vols.: Weismann, ib. 1731, 4to; 1782, and frequently. French, German.—Nordstet, ib. 1780-1782, 4to, 2 vols.: Heym, Moskau, 1796-1805, 4to, 4 vols.: Booch-Arkossi and Frey, Leipzig, 1871, &c., 8vo. English.—Nordstet, London, 1780, 4to: Grammatin and Parenogo, Moskva, 1808-1817, 4to, 4 vols. French.—Tatischeff, 2nd ed. St Petersb. 1798, 8vo, 2 vols.; Moskau, 1816, 4to, 2 vols.: Reiff, St Petersb. 1835-1836, 8vo, 2 vols.: Makaroff, ib. 1872, 8vo, 2 vols, 1110 pages; 1873-1874, 12mo, 2 vols. German.—Pawlowski, Riga, 1859, 8vo: Lenström, Mitau, 1871, 8vo. Swedish.—Geitlin, Helsingfors, 1833, 12mo: Meurmann, ib. 1846, 8vo. Polish.—Jakubowicz, Warszawa, 1825-1828, 8vo, 2 vols.: Amszejewicz, ib. 1866, 8vo: Szlezigier, ib. 1867, 8vo. Technical.—Grakov (Germ.), St Petersb. 1872, 8vo. Naval.—Butakov, ib. 1837. Dialects.—North-west Russia: Gorbachevski (old language, in Russian), Vilna, 1874, 8vo, 418 pages. White Russia: Nosovich (Russian), St Petersburg, 1870, 4to, 760 pages. Red Russia: Patritzkii (German), Lemberg, 1867, 8vo, 2 vols. 842 pages. Ukraine: Piskanov (Russian), Odessa, 1873, 4to, 156 pages.
Polish.—Linde (explained in Lat. Germ. and 13 Slav dialects), Warszawie, 1807-1814, 4to, 6 vols. 4574 pages. English.—[Rykaczewski], Complete Dictionary, Berlin, 1849-1851, 8vo, 2 vols.: Rykaczewski, Berlin, 1866, 16mo, 1161 pages. French and German.—Troc, Leipz. 1742-1764, 8vo, 4 vols.; 4th ed. ib. 1806-1822, 4to, 4 vols.: Bandtke, Breslau, 1806, 8vo, 2 vols.; 1833-1839, 8vo. French.—Schmidt, Leipzig, 1870, 16mo. Russian and German.—Schmidt (J. A. E.), Breslau, 1834, 8vo. German.—Mrongovius, Königsberg, 1765; 1835, 4to; 1837: Troianski, Berlin, 1835-1838, 8vo, 2 vols.: Booch-Arkossi, Leipzig, 1864-1868, 8vo, 2 vols.: Jordan, ib. 1866, 8vo. Italian.—Plazowski, Warszawa, 1860, 8vo. 2 vols. 730 pages. Russian.—Potocki, Lipsk, 1873, &c., 12mo.
Wendish.—Matthäi, Budissen, 1721, 8vo: Bose, Grimma, 1840, 8vo: Pfuhl, w Budzsinje, 1866, 8vo, 1210 pages. Upper Lusatian.—Pfuhl and Jordan, Leipz. 1844, 8vo. Lower Lusatian.—Zwahr, Spremberg, 1847, 8vo.
Czech.—Rohn (Germ. Lat.), Prag, 1780, 4to, 4 vols.: Dobrowski and Hanka, ib. 1802-1821, 4to, 2 vols. Lat. Germ. Hungar.—Jungmann, Praze, 1835-1839, 6 vols. 4to, 5316 pages. German.—Thàm, Prag. 1805-1807, 8vo, 2 vols.: Sumavski, ib. 1844-1846, 8vo, 2 vols.: Koneney, ib. 1855, 18mo, 2 vols.: Rank (Germ. Boh.), ib. 1860, 16mo, 775 pages. Technical.—Spatny, ib. 1864, 8vo: Kheil (names of goods, Germ. Boh.), ib. 1864, 8vo, 432 pages. Hunting.—Spatny, ib. 1870, 8vo, 137 pages.
South Slavic.—Richter and Ballman, Wien, 1839-1840, 8vo, 2 vols. Servian.—Karajić (Germ. Lat.), ib. 1818, 8vo; 1852: Lavrovski (Russian), St Petersb. 1870, 8vo, 814 pages. Bosnian.—Micalia, Laureti, 1649, 8vo. Slovak.—Bernolak (Lat. Germ. Hung.), Budae, 1825-1827, 8vo, 6 vols.: Loos (Hung. and Germ.), Pest, 1869, &c., 3 vols. Slovene.—Gutsmann, Klagenfurt, 1789, 4to: Relkovich, Wien, 1796, 4to, 2 vols.: Murko, Grätz, 1838, 8vo, 2 vols.: Janezić, Klagenfurt, 1851, 12mo. Dalmatian.—Ardelio della Bella, Venezia, 1728, 8vo; 2nd ed. Ragusae, 1785, 4to: Stulli, ib. 1801-1810, 4to, 2 vols. Croatian.—Habdelich, Grätz, 1670, 8vo: Sulek, Agram, 1854-1860, 8vo, 2 vols. 1716 pages. Carinthian.—Lexer, Leipzig, 1862, 8vo. Old Servian.—Danitziye (Servian), Belgrad, 1864, 8vo, 3 vols.
Bulgarian.—Daniel (Romaic, Albanian, Rumanian, and Bulgarian), Moschopolis, 1770; Venice, 1802, 4to. English.—Morse and Vassiliev, Constantinople, 1860, 8vo. Russian.—Borogoff, Vienna, 1872, &c., 8vo.
Ugrian.
Ugrian, Comparative.—Donner, Helsingfors, 1874, 8vo, in progress: Budenz (Ugrian-Magyar), Budapest, 1872-1875, 8vo.
Lappish.—Manuale, Holmiae, 1648, 8vo: Fjellström, ib. 1738, 8vo: Leem and Sandberg, Havn. 1768-1781, 4to, 2 parts: Lindahl and Oehrling, Holm. 1780, 8vo. North Lappish.—Stockfleht, Christiania, 1852, 8vo.
Finnish.—Juslenius, Holmiae, 1745, 4to, 567 pages: Renvall, Aboae, 1826, 4to, 2 vols.: Europaeus, Helsingissä, 1852-1853, 16mo, 2 vols. 742 pages: Lunin, Derpt, 1853, 8vo: Eurén, Tavashuus, 1860, 8vo: Ahlman, ib. 1864, 8vo: Wiedemann, St Petersb. 1869, 4to: Godenhjelm (Germ.), Helsingfors, 1871: Lönnrot, Helsingissä, 1874. Naval.—Stjerncreutz, ib. 1863, 8vo.
Esthonian.—Hupel, Mitau, 1818, 8vo, 832 pages: Körber, Dorpat, 1860, 8vo: Wiedemann, St Petersb. 1869, 4to, 1002 pages: Aminoff (Esth.-Finnish), Helsingissä, 1869, 8vo: Meves (Russian), Riga, 1876, 12mo.
Permian.—Rogord (Russian), St Petersb. 1869, 8vo, 420 pages.
Votiak.—Wiedemann, Reval, 1847, 8vo: Ahlquist, Helsingfors, 1856, 4to.
Cheremiss.—Budenz, Pest, 1866, 8vo.
Ersa-Mordvine.—Wiedemann, St Petersb. 1865, 4to. Moksha-Mordvine.—Ahlquist, ib. 1862, 8vo.
Magyar.—Szabo, Kassan, 1792, 8vo: Guczor and Fogarazi (Hung. Academy), Pesth, 1862, 8vo, in progress. English.—Dallos, Pesth, 1860, 8vo. French.—Kiss, ib. 1844, 12mo, 2 vols.: Karady, Leipz. 1848, 12mo: Mole, Pesth, 1865, 8vo, 2 vols. German.—Schuster, Wien, 1838, 8vo: Bloch, Pesth, 1857, 4to, 2 vols.: Ballagi, ib. 1857, 8vo; 6th ed. 1905, 8vo, 2 vols.: Loos, ib. 1870, 8vo, 914 pages. Etymological.—Dankovsky (Lat.-Germ.), Pressburg, 1853, 8vo: Kresznerics (under roots, in Hung.), Budân, 1831-1832, 4to, 2 vols.: Podhorsky (from Chinese roots, in Germ.), Budapest, 1877, 8vo. New Words.—Kunoss, Pesth, 1836, 8vo; 1844.
Turkish.—Arab. Pers.—Esaad Effendi, Constantinople, 1802, fol. Romaic.—Alexandrides, Vienna, 1812, 4to. Polyglotts.—Pianzola (Ital. Grec. volgare, e Turca), Padova, 1789, 4to: Ciakciak (Ital. Armeno, Turco), Venice, 1804, 4to; 2nd ed. 1829: Azarian (Ellenico, Ital. Arm. Turco), Vienna, 1848, 8vo: Mechitarist Congregation (Ital. Francese, Arm. Turco), ib. 1846, 8vo. Latin.—Mesgnien-Meninski, Viennae, 1680, fol. 3 vols.; ed. Jenisch and Klezl, ib. 1780-1802, fol. 4 vols. English.—Sauerwein, London, 1855, 12mo: Redhouse, ib. 1856, 8vo, 1176 pages: Id., Eng. Turkish, ib. 860, 8vo. French.—Kieffer and Bianchi (Turk.-Fr.), Paris, 1835-1837, 2 vols. 2118 pages: Bianchi (Fr.-Turk.) Paris, 1843-1846, 8vo, 2 vols. 2287 pages; 1850, 8vo, 2 vols.: Mallouf, ib. 1863-1867, 8vo, 2 vols. French and German.—Zenker (Arab. Pers.), Leipz, 1862-1876, 4to, 2 vols, 982 pages. German.—Korabinsky, Pressburg, 1788, 8vo: Vambéry, Constantinople, 1858, 8vo. Italian.—Molina, Roma, 1641, 8vo: Masais, Firenze, 1677, 8vo: Ciadyrgy, Milano, 1832-1834, 4to, 2 vols. Russian.—Budagov (Comparative lexicon of the Turkish-Tartar dialects), St Petersburg, 1869, 8vo, 2 vols.
Gipsy.—Bischoff, Ilmenau, 1827, 8vo: Truxillo, Madrid, 1844, 8vo: Jimenes, Sevilla, 1846, 16mo: Baudrimont, Bordeaux, 1862, 8vo: Vaillant, Paris, 1868, 8vo: Paspati; Constantinople, 1870, 4to: Borrow, Romany Lavo Lil, London, 1874, 8vo: Smart and Crofton, London, 1875, 8vo.
Albanian.—Blanchus, Romae, 1635, 8vo: Kaballioti (Romaic, Wallach. Alb.), Venice, 1770, 8vo: Xylander, Frankfurt a. M. 1835, 8vo: Hahn, Jena, 1854, 4to: Rossi da Montalto, Roma, 1866, 8vo.
ASIA
Semitic.—Polyglotts.—Thurneissius, Berolini, 1585, fol.: Thorndike, London, 1635, fol.: Schindler, Pentaglotton, Frankf, ad M. 1653, fol.: Hottinger, Heptaglotton, ib. 1661, fol.: Castellus, London, 1669, fol. 2 vols. (Hebrew, Chaldaic, Syriac, Samaritan, Aethiopic and Arabic in one alphabet; Persian separately. It occupied him for seventeen years, during which he worked sixteen to eighteen hours a day): Otho, Frankf. a. M. 1702, 4to (the same languages with Rabbinical).
Hebrew.—About 875, Zemaḥ, head of the school of Pumbeditha, wrote a Talmudical dictionary of words and things, arranged in alphabetical order, which is lost. About 880, Jehudah ben ’Alan, of Tiberias, and Jehudah ibn Koreish, of Tahurt, in Morocco wrote Hebrew dictionaries. Saadia ben Joseph (born 892, died 942), of Fayum, in Upper Egypt, wrote ןורגא רפכ, probably a Hebrew-Arabic dictionary. Menaḥem ben Jacob Ibn Sarūq (born 910, died about 970), of Tortosa and Cordova, wrote a copious Hebrew dictionary, first printed by Herschell F. Filipowski, Edinburgh, 1855, 8vo, from five MSS. David ben Abraham, of Fās, wrote, in Arabic, a large Hebrew dictionary, the MS. of which, a quarto of 313 leaves on cotton paper, was found about 1830 by A. Firkowitz, of Eupatoria, in the cellar of a Qaraite synagogue in Jerusalem. The age of this work cannot be ascertained. About 1050, Ali ben Suleiman wrote a dictionary in Arabic, on the plan of that of David ben Abraham. The MS. of 429 leaves belongs to Firkowitz. Haja ben Sherira, the famous teacher of the Academy of Pumbeditha, wrote a Hebrew dictionary in Arabic, called al Ḥāvi (The Gathering), arranged alphabetically in the order of the last radical letter. This dictionary is lost, as well as that of the Spaniard Isaac ben Saul, of Lucena. Iona ibn Ganaḥ, of Cordova, born about 985, wrote a Hebrew dictionary in Arabic called Kitāb al Azul (Book of Roots). This, as well as a Hebrew translation by Samuel ibn Tabōn, is extant in MS., and was used by Gesenius in his Thesaurus. Rabbi David ben Joseph ḳimḥi died soon after 1232. His lexicon of roots, called םישוש, was printed at Naples 1490, fol.; Constantinople, 1513, fol.; Naples, 1491, 8vo; Venice, 1552; Berolini, 1838, 4to. Tishbi (The Tishbite), by Elijah ben Asher, the Levite, so called because it contained 712 roots, was printed at Isny 1541, 8vo and 4to, and often afterwards. Latin.—Münster, Basileae, 1523, 8vo; 5 editions to 1564: Zamora, Compluti, 1526, fol.: Pellicanus, Argentorati, 1540, fol.: Reuchlin, Basil, 1556, fol.: Avenarius, Wittebergae, 1568, fol.; auctus, 1589: Pagnini, Lugd. Bat. 1575, fol.; 1577; Genevae, 1614; Buxtorf, Basil. 1607, 8vo; 1615, and many other editions: Frey (Lat.-Eng.), 2nd ed. London, 1815, 8vo: Gesenius, Thesaurus, Leipz. 1829-1858, 4to, 3 vols. English.—Bale, London, 1767, 4to: Parkhurst, ib. 1792, 4to: Lee, ib. 1840, 8vo: Gesenius, translated by Robinson, ib. 1844, 8vo; by Tregelles, ib. 1846, 4to: Fuerst, 4th ed. transl. by Davidson, ib. 1866, 8vo: 1871, 8vo, 1547 pages. French.—Leigh, Amst. 1703, 4to: Glaire, Paris, 1830, 8vo; 1843. German.—Gesenius, Leipzig, 1810-1812, 8vo, 2 vols.: Fuerst, ib. 1842, 16mo: ib. 1876, 8vo, 2 vols. Italian.—Modena, Venetia, 1612, 4to; 1640; Coen, Reggio, 1811, 8vo: Fontanella, Venezia, 1824, 8vo. Dutch.—Waterman, Rotterdam, 1859, &c., 8vo. Hungarian.—Ehrentheil (Pentateuch), Pest, 1868, 8vo. Romaic.—Loundes, Melité. 1845, 8vo, 987 pages.
Rabbinical and Chaldee.—Nathan ben Yeḥiel of Rome wrote in the beginning of the 12th century a Talmudic dictionary, Aruch, printed 1480 (?), s. l., fol.; Pesaro, 1517, fol.; Venice, 1531; and often: Isaiah ben Loeb, Berlin, wrote a supplement to Aruch, vol. i. Breslau, 1830, 8vo; vol. ii. (ל to ת), Wien, 1859, 8vo: Münster, Basil. 1527, 4to, 1530, fol.: Elijah ben Asher, the Levite, transl. by Fagius, Isnae, 1541, fol.; Venet. 1560: David ben Isaac de Pomis, Zamaḥ David, Venet. 1587, fol.: Buxtorf, Basileae, 1639, fol.: ed. Fischer, Leipz. 1866-1875, 4to: Otho, Geneva, 1675, 8vo; Altona, 1757, 8vo: Zanolini, Patavii, 1747, 8vo: Hornheim, Halle, 1807, 8vo: Landau, Prag, 1819-1824, 8vo, 5 vols.: Dessauer, Erlangen, 1838, 8vo: Nork (i.e. Korn), Grimma, 1842, 4to: Schönhak, Warschau, 1858, 8vo, 2 vols. Targums.—Levy, Leipzig, 1866-68 4to, 2 vols.; 1875: Id. (Eng.), London, 1869, 8vo, 2 vols. Talmud.—Löwy (in Heb.), Wien, 1863, 8vo: Levy, Leipzig, 1876, &c., 4to. Prayer-Book.—Hecht, Kreuznach, 1860, 8vo: Nathan, Berlin, 1854, 12mo. Synonyms.—Pantavitius, Lodevae, 1640, fol. Foreign Words.—Rabeini, Lemberg, 1857, 8vo, &c. Jewish-German.—Callenberg, Halle, 1736, 8vo: Vollbeding, Hamburg, 1808, 8vo: Stern, München, 1833, 8vo, 2 vols.: Theile, Berlin, 1842-1843, 8vo, 2 vols.: Avé-Lallemant, Das deutsche Gaunerthum, Leipzig, 1858, 8vo, 4 vols.; vol. iv. pp. 321-512.
Phœnician.—M. A. Levy, Breslau, 1864, 8vo.
Samaritan.—Crinesius, Altdorphi, 1613, 4to: Morini, Parisiis, 1657, 12mo: Hilligerus, Wittebergae, 1679, 4to: Cellarius, Cizae, 1682, 4to; Frankof. 1705: Uhlemann, Leipsiae, 1837, 8vo: Nicholls, London, 1859, 8vo.
Assyrian.—Norris, London, 1868, 8vo, 3 vols. Proper Names.—Menant, Paris, 1861, 8vo.
Accadian.—Lenormant, Paris, 1875, 8vo.
Syriac.—Joshua ben Ali, a physician, who lived about 885, made a Syro-Arabic lexicon, of which there is a MS. in the Vatican. Hoffmann printed this lexicon from Alif to Mim, from a Gotha MS., Kiel, 1874, 4to. Joshua bar Bahlul, living 963, wrote another, great part of which Castelli put into his lexicon. His MS. is now at Cambridge, and, with those at Florence and Oxford, was used by Bernstein. Elias bar Shinaya, born 975, metropolitan of Nisibis, 1009, wrote a Syriac and Arabic lexicon, entitled Kitāb ūt Tarjuman fi Taalem Loghat es Sūriān (Book called the Interpreter for teaching the Language of the Syrians), of which there is a MS. in the British Museum. It was translated into Latin by Thomas à Novaria, a Minorite friar, edited by Germanus, and published at Rome by Obicinus, 1636, 8vo. It is a classified vocabulary, divided in 30 chapters, each containing several sections. Crinesius, Wittebergae, 197 1612, 4to: Buxforf, Basileae, 1622, 4to: Ferrarius, Romae, 1622, 4to: Trost, Cothenis Anhaltor, 1643, 4to: Gutbir, Hamburgi, 1667, 8vo: Schaaf, Lugd. Bat, 1708, 4to: Zanolini, Patavii, 1742, 4to: Castellus, ed. Michaelis, Göttingen, 1788, 4to, 2 vols.: Bernstein, Berlin, 1857, &c. fol.: Smith (Robt. Paine), Dean of Canterbury, Oxonii, 1868, &c. fol.: fasc. 1-3 contain 538 pages: Zingerle, Romae, 1873, 8vo, 148 pages.
Arabic.—The native lexicons are very many, voluminous and copious. In the preface to his great Arabic-English lexicon, Lane describes 33, the most remarkable of which are-the ’Ain, so called from the letter which begins its alphabet, commonly ascribed to al Khalil (who died before A.H. 175 [a.d. 791], aged seventy-four): the Sihah of Jauhari (died 398 [1003]): the Mohkam of Ibn Sidah the Andalusian, who was blind, and died A.H. 458 [a.d. 1066], aged about sixty: the Asas of Zamakhshari (born 467 [1075], died 538 [1144]), “a most excellent repertory of choice words and phrases”: the Lisān el ’Arab of Ibn Mukarram (born 630 [1232], died 711 [1311]); Lane’s copy is in 28 vols. 4to: the Kamus (The Sea) of Fairuzabadi (born 729 [1328], died 816 [1413]),: the Taj el Arus, by Murtada Ez Zebadi (born a.d. 1732, died 1791)—the copy made for Lane is in 24 vols. thick 4to. The Sihah was printed Hardervici Getorum, 1774, 4to; Bulak, 1865, fol. 2 vols.: Kamus, Calcutta, 1817, fol. 2 vols.; Bombay, 1855, fol. 920 pages: Sirr el Lagal, by Farish esh Shidiac, Tunis, fol. 609 pages: Muhīt al Muhīt, by Beitrus Al Bustani Beirut, 1867-1870, 2 vols. 4to, 2358 pages (abridged as Katr Al Muhit, ib. 1867-1869, 2 vols. 8vo, 2352 pages), is excellent for spoken Arabic. Persian.—The Surah, by Jumal, Calcutta, 1812-1815, 2 vols. 4to: Samachsharii Lexicon, ed. Wetzstein, Leipz. 1845, 4to; 1850: Muntakhal al Loghat, Calcutta, 1808; ib. 1836; Lucknow, 1845; Bombay, 1862, 8vo, 2 vols.: Muntaha l’Arabi, 4 vols. fol. 1840: Shams al Loghat, Bombay, 1860, fol. 2 vols. 509 pages. Turkish.—Achteri Kabir, Constantinople. 1827, fol.: El Kamus, ib. 1816, fol. 3 vols.; translated by Açan Effendi, Bulak, fol. 3 vols.; El Sihah, translated by Al Vani, Constantinople, 1728, fol. 2 vols.: 1755-1756; Scutari, 1802, fol. 2 vols. Latin.—Raphelengius, Leiden, 1613, fol.: Giggeius, Mediolani, 1632, fol. 4 vols.: Golius Lugd. Bat. 1653, fol. (the best before Lane’s): Jahn, Vindobonae, 1802, 8vo: Freytag, Halle, 1830-1838, 4 vols. 4to; abridged, ib. 1837, 4to. English.—Catafago (Arab.-Eng. and Eng.-Arab.), London, 1858, 8vo, 2 vols.; 2nd ed. 1873, 8vo: Lane, London, 1863-1893 (edited after Lane’s death, from 1876, by his grandnephew, Stanley Lane-Poole. The Arabic title is Medd el Kamoos, meaning either the Flow of the Sea, or The Extension of the Kamus. It was undertaken in 1842, at the suggestion and at the cost of the 6th duke of Northumberland, then Lord Prudhoe, by Mr Lane, who returned to Egypt for the purpose, and lived in Cairo for seven years to study, and obtain copies of, the great MS. lexicons in the libraries of the mosques, few of which had ever been seen by a European, and which were so quickly disappearing through decay, carelessness and theft, that the means of composing such a work would not long have existed). Newman (modern), ib. 1872, 8vo, 2 vols. 856 pages. French.—Ruphy (Fr.-Ar.), Paris, 1802, 4to: Bochtor (do.), Paris, 1828, 4to, 2 vols.; 2nd ed. ib. 1850: Roland de Bussy (Algiers, Fr.-Ar.), Alger, 1835, 16mo: Id., 1836, 8vo; 1839: Berggren (Fr.-vulg. Ar., Syria and Egypt.), Upsala, 1844, 4to: Farhat (Germanos), revu par Rochaid ed Dahdah, Marseille, 1849, 4to: Biberstein Kasimirski, Paris, 1846, 8vo, 2 vols.; 1853-1856; 1860, 2 vols. 3032 pages: Marcel (vulgar dialects of Africa), Paris, 1830; 1835, 8vo; 1837; enlarged, 1869, 8vo; Paulmier (Algeria), 2nd ed. Paris, 1860, 8vo, 931 pages; 1872: Bernard (Egypt), Lyon, 1864, 18mo: Cuche, Beirut, 1862, 8vo; 1867: Nar Bey (A. Calfa), 2nd ed. Paris, 1872, 12mo, 1042 pages: Cherbonneau (written language), Paris, 1876, 2 vols. 8vo: Id. (Fr.-Ar.), Paris, 1872, 8vo: Beausier (Algiers, Tunis, legal, epistolary), Alger, 1871, 4to, 764 pages; 1873. German.—Seyfarth (Algeria), Grimma, 1849, 16mo: Wolff (Mod. Ar.), Leipzig, 1867, 8vo: Wahrmund (do.), Giessen, 1870-1875, 8vo, 4 vols. Italian.—Germano, Roma, 1636, 8vo; (Ar. Lat. It.), Romae, 1639, fol.: Dizionario, Bulak. 1824, 4to: Schiaparelli, Firenze, 1871, 4to, 641 pages. Spanish.—Alcala, Grenada, 1505, 4to: Cañes, Madrid, 1787, fol. 3 vols. Sufi Technical Terms.—Abd Errahin, ed. Sprenger, Calcutta, 1845, 8vo. Technical Terms of the Mussulman Sciences.—Abd al Hagg and Gholam Kadir, Calcutta, 1853-1862, 4to, 1593 pages. Medical Terms.—Pharaon and Bertherand, Paris, 1860, 12mo. Materia Medica.—Muhammed Abd Allah Shirazi, Ulfaz Udwiyeh, translated by Gladwin (Eng. Pers. Hindi), Calcutta, 1793, 4to, 1441 words. Noms des Vêtements.—Dozy, Amst. 1845, 8vo. Wörter in entgegengesetzten Bedeutungen.—Redslob, Göttingen, 1873, 8vo. Koran.—Willmet (also in Haririum et vitam Timuri), Lugd. Bat. 1784, 4to; Amst. 1790: Fluegel, Concordantia, Leipz. 1842, 4to: Penrice, Dictionary and Glossary, London, 1873, 4to. El Tabrizi’s Logic.—Mir Abufeth (French), Bulak, 1842, 8vo. Maltese.—Vassali, Romae, 1796, 4to: Falzon (Malt. Ital. Eng.), Malta, s.a. 8vo: Vella, Livorno, 1843, 8vo.
Armenian.—Mechitar, Venice, 1749-1769, 4to, 2 vols.: Avedichiam, Sürmelian and Aucher (Aukerian), ib. 1836-1837, 4to, 2 vols.: Aucher, ib. 1846, 4to. Polyglot.—Villa (Arm.-vulg., litteralis, Lat. Indicae et Gallicae), Romae, 1780. Greek and Latin.—Lazarists, Venice, 1836-1837, 4to, 2 vols. 2217 pages. Latin.—Rivola, Mediolani, 1621, fol.: Nierszesovicz, Romae, 1695, 4to; Villotte, ib. 1714, fol.: Mechitar, Venetiae, 1747-1763, 4to, 2 vols. English.—Aucher, Venice, 1821-1825, 4to, 2 vols. French.—Aucher, Venise, 1812-1817, 8vo, 2 vols.; (Fr.-Arm. Turc.), ib. 1840, 4to: Eminian, Vienna, 1853, 4to: Calfa, Paris, 1861, 8vo, 1016 pages; 1872. Italian.—Ciakciak, Venezia, 1837, 4to. Russian.—Khudobashev [Khutapashian], Moskva, 1838, 8vo, 2 vols. Russ. Arm.—Adamdarov, ib. 1821, 8vo: Popov, ib. 1841, 8vo, 2 vols. Modern Words.—Riggs, Smyrna, 1847, 8vo.
Georgian.—Paolini (Ital.), Roma, 1629, 4to: Klaproth (Fr.), Paris, 1827, 8vo: Tshubinov (Russian, French), St Petersburg, 1840, 4to; 1846, 8vo, 2 vols. 1187 pages.
Circassian.—Loewe, London, 1854, 8vo.
Ossetic.—Sjörgen, St Petersb. 1844, 4to.
Kurd.—Garzoni, Roma, 1787, 8vo: Lerch (German), St Petersburg, 1857, 8vo: Id. (Russian), ib. 1856-1858, 8vo.
Persian.—Burhani Qatiu, arranged by J. Roebuck, Calcutta, 1818, 4to: Burhan i Kati, Bulak, 1836, fol.: Muhammed Kazim, Tabriz, 1844, fol.: Haft Kulzum (The Seven Seas), by Ghazi ed din Haidar, King of Oude, Lucknow, 1822, fol. 7 vols. Arabic.—Shums ul Loghat, Calcutta, 1806, 4to, 2 vols. Turkish.—Ibrahim Effendi, Farhangi Shu’uri, ib. 1742, fol. 2 vols. 22,530 words, and 22,450 poetical quotations: Burhan Kati, by Ibn Kalif, translated by Ahmed Asin Aintabi, ib. 1799, fol.; Bulak, 1836, fol.: Hayret Effendi, ib. 1826, 8vo. Armenian.—Douzean, Constantinople, 1826, fol. Bengali.—Jay Gopal, Serampore, 1818, 8vo. Latin.—Vullers (Zend appendix), Bonnae ad Rhen, 1855-1868, 4to, 2 vols. 2544 pages; Supplement of Roots, 1867, 142 pages. English.—Gladwin, Malda in Bengal, 1780, 4to; Calcutta, 1797: Kirkpatrick, London, 1785, 4to: Moises, Newcastle, 1794, 4to: Rousseau, London, 1802, 8vo; 1810: Richardson (Arab, and Pers.), ib. 1780-1800, fol. 2 vols.; ed. Wilkins, ib. 1806-1810, 4to, 2 vols.; ed Johnson, ib. 1829, 4to: Ramdhen Sen, Calcutta, 1829, 8vo; 1831: Tucker (Eng.-Pers.), London, 1850, 4to: Johnson (Pers. and Arab.), ib. 1852, 4to: Palmer, ib. 1876, 8vo, 726 pages. French.—Handjeri (Pers. Arab. and Turkish), Moscou, 1841, 4to, 3 vols. 2764 pages: Bergé, Leipzig, 1869, 12mo. German.—Richardson, translated by Wahl as Orientalische Bibliotheque, Lemg, 1788-1792, 8vo, 3 vols. Italian.—Angelus a S. Josepho [i.e. Labrosse] (Ital. Lat. Fr.), Amst. 1684, fol.
Old Persian.—(Cuneiform), Benfey (German), Leipzig, 1847, 8vo: Spiegel (id.), ib. 1862, 8vo: Kossovich (Latin), Petropoli, 1872, 8vo.
Zend.—Justi, Leipzig, 1864, 4to: Vullers, Persian Lexicon, Appendix: Lagarde, Leipzig, 1868, 8vo.
Pahlavi.—An old Pahlavi and Pazend Glossary, translated by Destur Hoshengi Jamaspji, ed. Haug, London, 1867, 8vo; 1870, 8vo: West, Bombay, 1874, 8vo.
Indian Terms.—The Indian Vocabulary, London, 1788, 16mo: Gladwin, Calcutta, 1797, 4to: Roberts, London, 1800, 8vo: Rousseau, ib. 1802, 8vo: Roebuck (naval), ib. 1813, 12mo: C. P. Brown, Zillah Dict., Madras, 1852, 8vo: Robinson (Bengal Courts), Calcutta, 1854, 8vo; 1860: Wilson, London, 1855, 4to: Fallon, Calcutta, 1858, 8vo.
Sanskrit.—Amarasimha (lived before a.d. 1000), Amarakosha Calcutta, 1807, 8vo; ib. 1834, 4to; Bombay, 1860, 4to; Lucknow, 1863, 4to; Madras, 1870, 8vo, in Grantha characters; Cottayam, 1873, 8vo, in Malaylim characters; Benares, 1867, fol. with Amaraviveka, a commentary by Mahesvara: Rajah Radhakanta Deva, Sabdakalpadruma, Calcutta, 1821-1857, 4to, 8 vols. 8730 pages: 2nd ed. 1874, &c.: Bhattachdrya, Sabdastoma Mahanidhi, Calcutta, 1869-1870, 8vo, parts i.-vii. 528 pages: Abhidhanaratnamala, by Halayudha, ed. Aufrecht, London, 1861, 8vo: Vachaspatya, by Taranatha Tarkavachaspati, Calcutta, 1873, &c., 4to (parts i.-vii., 1680 pages). Bengali.—Sabdasindhu, Calcutta, 1808: Amarakosa, translated by Ramodoyu Bidjalunker, Calcutta, 1831, 4to: Mathurana Tarkaratna, Sabdasandarbhasindhu, Calcutta, 1863, 4to. Marathi.—Ananta Sastri Talekar, Poona, 1853, 8vo, 495 pages: Madhava Chandora, Bombay, 1870, 4to, 695 pages. Telugu.—Amarakosha, Madras, 1861, ed. Kala, with Gurubalala prabodhika, a commentary, ib. 1861, 4to; with the same, ib. 1875, 4to, 516 pages; with Amarapadaparijata (Sans. and Tel.), by Vavilla Ramasvani Sastri, ib. 1862, 4to; ib. 1863, 8vo; 3rd ed. by Jaganmohana Tarkalankara and Khetramohana, 1872, &c., parts i.-iv. 600 pages: Suria Pracasa Row, Sarva-Sabda-Sambodhini, ib. 1875, 4to, 1064 pages. Tibetan and Mongol.—Schiefner, Buddhistische Triglotte, St Petersburg, 1859, fol., the Vyupatti or Mahavyupatti from the Tanguir, vol. 123 of the Sutra. Latin.—Paulinus a Sancto Bartholomeo, Amarasinha, sectio i. de coelo, Romae, 1798, 4to: Bopp. Berlin, 1828-1830, 4to; 2nd ed. 1840-1844; 3rd, 1866, 4to. English.—Amarakosha, trans. by Colebrooke, Serampore, 1808, 4to; 1845, 8vo: Rousseau, London, 1812, 4to: Wilson, Calcutta, 1819, 4to; 2nd ed. 1832: ed. Goldstücker, Berlin, 1862, &c., folio, to be in 20 parts: Yates, Calcutta, 1846, 4to: Benfey, London, 1865, 8vo: Ram Jasen, Benares, 1871, 8vo, 713 pages: Williams, Oxford, 1872, 4to. English-Sanskrit.—Williams, London, 1851, 4to. French.—Amarakosha, transl. by Loiseleur Deslongchamps, Paris, 1839-1845, 8vo, 2 vols. 796 pages: Burnouf and Leupol, Nancy, 1863-1864, 8vo. German.—Böhtlingk and Roth, St Petersb. 1853, &c., 4to, 7 vols. to 1875. Italian.—Gubernatis, Torino, 1856, &c. 8vo, unfinished, 2 parts. Russian.—Kossovich, St Petersburg, 1859, 198 8vo. Roots.—Wilkins, London, 1815, 4to: Rosen, Berolini, 1827, 8vo: Westergaard, Bonnae, 1840-1841, 8vo: Vishnu Parasurama Sastri Pandita (Sans. and Marathi), Bombay, 1865, 8vo: Taranatha Tarkavachaspati, Dhatupadarsa, Calcutta, 1869, 8vo: Leupol, Paris, 1870, 8vo. Synonyms.—Abhidhanacintamani, by Hemachadra, ed. Colebrooke, Calcutta, 1807, 8vo; translated by Böhtlingk and Rieu (German), St Petersburg, 1847, 8vo. Homonyms.—Medinikara, Medinikosha, Benares, 1865, 4to; Calcutta, 1869, 8vo; ib. 1872, 8vo. Derivatives.—Hirochand and Rooji Rangit, Dhatumanjari, Bombay, 1865, 8vo. Technical Terms of the Nyâya Philosophy.—Nyâyakosa, by Bhimachârya Jhalakîkar (Sanskrit), Bombay, 1875, 8vo, 183 pages. Rig Veda.—Grassmann, Leipzig, 1873-1875, 8vo.
Bengali.—Manoel, Lisboa, 1743, 8vo: Forster, Calcutta, 1799-1802, 4to, 2 vols. 893 pages: Carey, Serampore, 1815-1825, 4to, 2 vols.; ed. Marshman, ib. 1827-1828, 8vo, 2 vols.; 3rd ed. ib. 1864-1867, 8vo; abridged by Marshman, ib. 1865, 8vo; ib. 1871, 8vo, 2 vols. 936 pages: Morton, Calcutta, 1828, 8vo: Houghton, London, 1833, 4to: Adea, Shabdabudhi, Calcutta, 1854, 604 pages. English.—Ram Comul Sen, ib. 1834, 4to, 2 vols.; London, 1835, 4to: D’Rozario, Calcutta, 1837, 8vo: Adea, Abhidan, Calcutta, 1854, 761 pages. English Lat.—Ramkissen Sen, ib. 1821, 4to. Eng.-Beng. and Manipuri.—[Gordon], Calcutta, 1837, 8vo.
Canarese.—Reeve, Madras, 1824-1832, 4to, 2 vols.; ed. Sanderson, Bangalore, 1858, 8vo, 1040 pages; abridged by the same, 1858, 8vo, 276 pages: Dictionarium Canarense, Bengalori, 1855, 8vo: School Dictionary, Mangalore, 1876, 8vo, 575 pages.
Dardic Languages.—Leitner (Astori, Ghilghiti, Chilasi, and dialects of Shina, viz. Arnyia, Khajuna and Kalasha), Lahore, 1868, 4to.
Guzarati.—(English) Mirza Mohammed Cauzim, Bombay, 1846, 4to; Shapurji Edalji, ib. 1868, 8vo, 896 pages: Karsandas Mulji, ib. 1868, 8vo, 643 pages.
Hindi.—Rousseau, London, 1812, 4to: Adam, Calcutta, 1829, 8vo: Thompson, ib. 1846, 8vo: J. D. Bate, London, 1876, 8vo, 809 pages. English.—Adam, Calcutta, 1833, 8vo. English, Urdu and Hindi.—Mathuraprasada Mirsa, Benares, 1865, 8vo, 1345 pages.
Hindustani.—Ferguson, London, 1773, 4to: Gilchrist, Calcutta, 1800, 8vo; ed. Hunter, Edinb. 1810; Lond. 1825: Taylor, Calcutta, 1808, 4to, 2 vols.: Gladwin (Persian and Hind.), Calcutta, 1809, 8vo, 2 vols.: Shakespeare, London, 1817, 4to; 1820; 1834; 1849: Forbes, London, 1847, 8vo; 1857: Bertrand (French), Paris, 1858, 8vo: Brice, London, 1864, 12mo: Fallon, Banaras, 1876, &c., to be in about 25 parts and 1200 pages. English.—Gilchrist, 1787-1780, 4to, 2 parts: Thompson, Serampore, 1838, 8vo.
Kashmiri.—Elmslie, London, 1872, 12mo.
Khassia.—Roberts, Calcutta, 1875, 12mo.
Malayalim.—Fabricius and Breithaupt, Weperg, 1779, 4to: Bailey, Cottayam, 1846, 8vo: Gundert, Mangalore, 1871, 8vo, 1171 pages.
Marathi.—Carey, Serampore, 1810, 8vo: Kennedy, Bombay, 1824, fol.: Jugunnauth Shastri Kramavant, Bombay, 1829-1831, 4to, 3 vols.: Molesworth, ib. 1831, 4to; 2nd ed. 1847, 4to; ed. Candy, Bombay, 1857, 4to, 957 pages; abridged by Baba Padmanji, ib. 1863, 8vo; 2nd ed. (abridged), London, 1876, 8vo, 644 pages. English.—Molesworth, Bombay, 1847, 4to.
Oriya.—Mohunpersaud Takoor, Serampore, 1811, 8vo: Sutton, Cuttack, 1841-1848, 8vo, 3 vols. 856 pages.
Pali.—Clough, Colombo, 1824, 8vo: Moggallana Thero (a Sinhalese priest of the 12th century), Abhidhanappika (Pali, Eng. Sinhalese), ed. Waskeduwe Subheti, Colombo, 1865, 8vo: Childers, London, 1872-1875, 8vo, 658 pages. Roots.—Silavansa, Dhatumanjusa (Pali Sing. and Eng.), Colombo, 1872, 8vo.
Prakrit.—Delius, Radices, Bonnae ad Rh., 1839, 8vo.
Punjabi.—Starkey, 1850, 8vo; Lodiana Mission, Lodiana, 1854-1860, 444 pages.
Pushtu or Afghan.—Dorn, St Petersb. 1845, 4to: Raverty, London, 1860, 4to; 2nd ed. ib. 1867, 4to: Bellew, 1867, 8vo.
Sindhi.—Eastwick, Bombay, 1843, fol. 73 pages: Stack, ib. 1855, 8vo, 2 vols.
Sinhalese.—Clough, Colombo, 1821-1830, 8vo, 2 vols.: Callaway (Eng., Portuguese and Sinhalese), ib. 1818, 8vo: Id., School Dictionary, ib. 1821, 8vo: Bridgenell (Sinh.-Eng.), ib. 1847, 18mo: Nicholson (Eng.-Sinh.), 1864, 32mo, 646 pages.
Tamil.—Provenza (Portug.), Ambalacotae, 1679, 8vo: Sadur Agurardi, written by Beschi in 1732, Madras, 1827, fol.; Pondicherry, 1875, 8vo: Blin (French), Paris, 1834, 8vo: Rottler, Madras, 1834-1841, 4to, 4 vols.: Jaffna Book Society (Tamil), Jaffna, 1842, 8vo, about 58,500 words: Knight and Spaulding (Eng. Tam.), ib. 1844, 8vo; Dictionary, ib. 1852, 4to: Pope, 2nd ed. ib. 1859, 8vo: Winslow, Madras, 1862, 4to, 992 pages, 67,452 words.
Telugu.—Campbell, Madras, 1821, 4to: C. P. Brown, Madras (Eng.-Tel.), 1852, 8vo, 1429 pages: Id. (Tel.-Eng.), ib. 1852, 8vo, 1319 pages. Mixed Telugu.—Id., ib. 1854, 8vo.
Thuggee.—Sleeman, Calcutta, 1830, 8vo, 680 Ramasi words.
Indo-Chinese Languages.—Leyden, Comparative Vocabulary of Barma, Malaya and Thai, Serampore, 1810, 8vo. Annamese: Rhodes (Portug. and Lat.), Romae, 1651, 4to: Pigneaux and Taberd, Fredericinagori, 1838, 4to; Legrand de la Liraye, Paris, 1874, 8vo: Pauthier (Chin. Ann.-Fr. Lat.), Paris, 1867, &c., 8vo. Assamese: Mrs Cutter, Saipur, 1840, 12 mo; Bronson, London, 1876, 8vo, 617 pages. Burmese: Hough (Eng.-Burm.), Serampore, 1825, Moulmain, 1845, 8vo, 2 vols. 955 pages: Judson, Calcutta, 1826, 8vo; (Eng. Burm.), Moulmain, 1849, 4to; (Burm. Eng.), ib. 1852, 8vo; 2nd ed., Rangoon, 1866, 8vo, 2 vols. 968 pages: Lane, Calcutta, 1841, 4to. Cambodian: Aymonier (Fr.-Camb.), Saigon, 1874, 4to; Id. (Camb.-Fr.), ib. 1875, fol. Karen: Sau-kau Too (Karen), Tavoy, 1847, 12mo, 4 vols.: Mason, Tavoy, 1840, 4to. Sgau-Karen: Wade, ib. 1849, 8vo. Siamese (Thai): Pallegoix (Lat. French, Eng.), Paris, 1854, 4to: Dictionarium Latinum Thai, Bangkok, 1850, 4to, 498 pages.
Malay.—Latin.—Haex, Romae, 1631, 4to; Batavia, 1707. Dutch.—Houtmann (Malay and Malagasy), Amst. 1603, 4to; 1673; 1680; 1687; 1703; Batavia, 1707: Wiltens and Dankaarts, Gravenhage, 1623, 4to; Amst. 1650; 1677; Batavia, 1708, 4to: Heurnius, Amst. 1640, 4to: Gueynier, Batavia, 1677, 4to; 1708: Loder, ib. 1707-1708, 4to: Van der Worm, ib. 1708, 4to: Roorda van Eysinga (Low), ib. 1824-1825, 8vo, 2 vols.; 12th ed. ’s Gravenhage, 1863, 8vo; Id. (Hof, Volks en Lagen Taal), ib. 1855, 8vo: Dissel and Lucardie (High Malay), Leiden, 1860, 12mo: Pijnappel, Amst. 1863, 8vo: Badings, Schoonhoven, 1873, 8vo. English.—Houtmann (Malay and Malagasy), translated by A. Spaulding, London, 1614, 4to: Bowrey, ib. 1701, 4to: Howison, ib. 1801, 4to: Marsden, ib. 1812, 4to: Thomsen, Malacca, 1820, 8vo; 1827: Crawford, London, 1851, 8vo, 2 vols. French.—Boze, Paris, 1825, 16mo: Elout (Dutch-Malay and French-Malay), Harlem, 1826, 4to: Bougourd, Le Havre, 1856, 8vo: Richard, Paris, 1873, 8vo, 2 vols.: Favre, Vienna, 1875, 8vo, 2 vols.
Malay Archipelago.—Batak: Van der Tuuk, Amsterdam, 1861, 8vo, 564 pages. Bugis: Mathes, Gravenh. 1874, 8vo, 1188 pages: Thomsen (Eng.-Bugis and Malay), Singapore, 1833, 8vo. Dyak: Hardeland (German), Amst. 1859, 8vo, 646 pages. Javanese: Senerpont Domis, Samarang, 1827, 4to, 2 vols.: Roorda van Eysinga, Kampen, 1834-1835, 8vo, 2 vols.: Gericke, Amst. 1847, 8vo; ed. Taco Roorda, ib. 1871, &c. parts i.-v., 880 pages: Jansz and Klinkert, Samarang, 1851, 8vo; 1865: Favre (French), Vienne, 1870, 8vo. Macassar: Matthes, Amst. 1859, 8vo, 951 pages. Sunda: De Wilde (Dutch, Malay and Sunda), Amsterdam, 1841, 8vo: Rigg (Eng.), Batavia, 1862, 4to, 573 pages. Formosa: Happart (Favorlang dialect, written about 1650), Parrapattan, 1840, 12mo.
Philippines.—Bicol: Marcos, Sampaloc, 1754, fol. Bisaya: Sanchez, Manila, 1711, fol.: Bergaño, ib. 1735, fol.: Noceda, ib. 1841: Mentrida (also Hiliguena and Haraya) ib. 1637, 4to; 1841, fol. 827 pages: Felis de la Encarnacion, ib. 1851, 4to, 2 vols. 1217 pages. Ibanac: Bugarin, ib. 1854, 4to. Ilocana, Carro, ib. 1849, fol. Pampanga: Bergaño, ib. 1732, fol. Tagala: Santos, Toyabas, 1703, fol.; ib. 1835, 4to, 857 pages: Noceda and San Lucar, Manila, 1754, fol.; 1832.
Chinese.—Native Dictionaries are very numerous. Many are very copious and voluminous, and have passed through many editions. Shwo wan, by Hü Shin, is a collection of the ancient characters, about 10,000 in number, arranged under 540 radicals, published 150 b.c., usually in 12 vols.: Yu pien, by Ku Ye Wang, published a.d. 530, arranged under 542 radicals, is the basis of the Chinese Japanese Dictionaries used in Japan: Ping tseu loui pien, Peking, 1726, 8vo, 130 vols.: Pei wan yün fu (Thesaurus of Literary Phrases), 1711, 131 vols. 8vo, prepared by 66 doctors of the Han lin Academy in seven years. It contains 10,362 characters, and countless combinations of two, three or four characters, forming compound words and idioms, with numerous and copious quotations. According to Williams (On the word Shin, p. 79), an English translation would fill 140 volumes octavo of 1000 pages each. Kanghi tsze tien (Kanghi’s Standard or Canon of the Character), the dictionary of Kanghi, the first emperor of the present dynasty, was composed by 30 members of the Han lin, and published in 1716, 40 vols. 4to, with a preface by the emperor. It contains 49,030 characters, arranged under the 214 radicals. It is generally in 12 vols., and is universally used in China, being the standard authority among native scholars for the readings as well as the meanings of characters. Latin.—De Guignes (French, Lat.), Paris, 1813, fol.; Klaproth, Supplément, 1819; ed. Bazil (Latin), Hong-Kong, 1853, 4to: Gonçalves (Lat.-Chin.), Macao, 1841, fol.: Callery, Systema phoneticum, Macao, 1841, 8vo: Schott, Vocabularium, Berlin, 1844, 4to. English.—Raper, London, 1807, fol. 4 vols.: Morrison, Macao, 1815-1823, 4to, 3 parts in 6 vols.: Medhurst, Batavia, 1842-1843, 8vo, 2 vols.: Thom, Canton, 1843, 8vo: Lobscheid, Hong-Kong, 1871, 4to: Williams, Shanghai, 1874, 4to. Eng. Chinese.—Morrison, part iii.: Williams, Macao, 1844, 8vo: Medhurst, Shanghai, 1847-1848, 8vo, 2 vols.: Hung Maou, Tung yung fan hwa (Common words of the Red-haired Foreigners), 1850, 8vo. Doolittle, Foochow, 1872, 4to, vol. i. 550 pages. French,—Callery, Dict. encyclopédique, Macao and Paris, 1845 (radicals 1-20 only): M. A. H., 1876, 8vo, autographié, 1730 pages. French-Chin.—Perny (Fr.-Latin, Spoken Mandarin), Paris, 1869, 4to; Appendice, 1770; Lemaire and Giguel, Shanghai, 1874, 16mo. Portuguese.—Gonçalves (Port.-Chin.), Macao, 1830, 8vo, 2 vols.: Id. (Chin.-Port.), ib. 1833, 8vo. Idioms.—Giles, Shanghai, 1873, 4to. Phrases.—Yaou Pei-keen, Luy yih, 1742-1765, 8vo, 55 vols.: Tseen Ta-hin, Shing luy, 1853, 8vo, 4 vols. Classical Expressions.—Keang Yang and 30 others, Sze Shoo teen Lin, 1795, 8vo, 30 vols. Elegant Expressions.—Chang ting yuh, Fun luy tsze kin, 1722, 199 8vo, 64 vols. Phrases of Three Words.—Julien (Latin), Paris, 1864, 8vo. Poetical.—Pei wan she yun, 1800, 8vo, 5 vols. Proper Names.—F. Porter Smith (China, Japan, Corea, Annam, &c., Chinese-Eng.), Shanghai, 1870, 8vo. Topography.—Williams, Canton, 1841, 8vo. Names of Towns.—Biot, Paris, 1842, 8vo. Ancient Characters.—Foo Lwantseang, Luh shoo fun luy, 1800, 8vo, 12 vols. Seal Character.—Heu Shin, Shwo wan, ed. Seu Heuen, 1527, 8vo, 12 vols. Running Hand.—St Aulaire and Groeneveld (Square Characters, Running Hand; Running, Square), Amst. 1861, 4to, 117 pages. Technical Terms (in Buddhist translations from Sanskrit)—Yuen Ying, Yih ’see king pin e, 1848, 8vo. Dialects.—Amoy: Douglas, London, 1873, 4to, 632 pages: Macgowan, Hong-Kong, 1869, 8vo. Canton: Yu Heo-poo and Wan ke-shih, Keang hoo chih tuh fun yun tso yaou ho tseih, Canton, 1772, 8vo, 4 vols.; 1803, 8vo, 4 vols.; Fuh-shan, 1833, 8vo, 4 vols.: Morrison, Macao, 1828, 8vo: Wan ke shih, Canton, 1856, 8vo: Williams (tonic, Eng.-Chinese), Canton, 1856, 8vo: Chalmers, Hong-Kong, 1859, 12mo; 3rd ed. 1873, 8vo. Changchow in Fuhkeen: Seay Sew-lin, Ya suh tung shih woo yin, 1818, 8vo, 8 vols.; 1820. Foo-chow: Tseih (a Japanese general) and Lin Peih shan, Pa yin ho ting, ed. Tsin Gan, 1841, 8vo: Maclay and Baldwin, Foochow, 1870, 8vo, 1123 pages. Hok-keen: Medhurst, Macao, 1832, 4to: Peking, Stent, Shanghai, 1871, 8vo.
Corean.—Chinese, Corean and Japanese.—Cham Seen Wo Kwo tsze mei, translated by Medhurst, Batavia, 1835, 8vo. Russian.—Putzillo, St Petersburg, 1874, 12mo, 746 pages.
Japanese.—Sio Ken Zi Ko (Examination of Words and Characters), 1608, 8vo, 10 vols.: Wa Kan Won Se Ki Sio Gen Zi Ko, lithographed by Siebold, Lugd. Bat., 1835, fol. Jap.-Chinese.—Faga biki set yo siu. Chinese-Jap.—Kanghi Tse Tein, 30 vols. 12mo: Zi rin gioku ben. Dutch Dictionaries printed by Japanese.—Nieeu verzameld Japansch en Hollandsch Woordenbock, by the interpreter, B. Sadayok, 1810: Minamoto Masataka, Prince of Nakats (Jap. Chinese-Dutch), 5 vols. 4to, printed at Kakats by his servants: Jedo-Halma (Dutch-Jap.), Jedo, 4to, 20 vols.: Nederduitsche taal, Dutch Chinese, for the use of interpreters. Latin and Portuguese.—Calepinus, Dictionarium, Amacusa, 1595, 4to. Latin.—Collado, Compendium, Romae, 1632, 4to: Lexicon, Romae, 1870, 4to, from Calepinus. English.—Medhurst, Batavia, 1830, 8vo: Hepburn, Shanghai, 1867, 8vo; 1872. Eng.-Jap.—Hori Tatnoskoy, Yedo, 1862, 8vo; 2nd ed. Yeddo, 1866, 8vo: Satow and Ishibashi Masakata (spoken language), London, 1876, 8vo. French.—Rosny (Jap. Fr. Eng.), Paris, 1857, 4to, vol. i.: Pagés, Paris, 1869, 4to, translated from Calepinus. Fr.-Jap.—Soutcovey, Paris, 1864, 8vo. Fr. Eng. Jap.—Mermet de Cachon, Paris, 1866, 8vo, unfinished. German.—Pfizmaier (Jap.-Ger., Eng.), Wien, 1851, 4to, unfinished. Spanish.—Vocabulario del Japon, Manila, 1630, 4to, translated from the next. Portuguese.—Vocabulario da Lingua de Japam, Nagasaki, 1603, 4to. Russian.—Goshkevich, St Petersburg, 1857, 8vo, 487 pages. Chinese Characters with Japanese Pronunciation.—Rosny, Paris, 1867, 8vo. Chinese and Japanese Names of Plants.—Hoffmann, Leyde, 1864, 8vo.
Aino.—Pfizmaier, Wien, 1854, 4to.
Northern and Central Asia.—Buriat: Castrén, St Petersburg, 1857, 8vo. Calmuck: Zwick, Villingen, 1853, 4to: Smirnov, Kazan, 1857, 12mo: Jügl, Siddhi Kur, Leipzig, 1866, 8vo. Chuvash: Clergy of the school of the Kazan Eparchia, Kazan, 1836, 8vo, 2481 words: Lyulé (Russ.-Chuv. French), Odessa, 1846, 8vo, 244 pages: Zolotnitski, Kazan, 1875, 8vo, 287 pages. Jagatai: Mir Ali Shir, Abuska, ed. Vámbéry, with Hungarian translation, Pesth, 1862, 8vo: Vámbéry, Leipzig, 1867, 8vo: Pavet de Courteille, Paris, 1870, 8vo. Koibal and Karagas: Castrén, St Petersburg, 1857, 8vo. Manchu: Yutchi tseng ting tsing wen kian (Manchu Chinese), 1771, 4to, 6 vols.: Sze li hoh pik wen kian (Manchu-Mongol, Tibetan, Chinese) 10 vols. 4to, the Chinese pronunciation represented in Manchu: San hoh pien lan (Manchu-Chinese, Mongol), 1792, 8vo, 12 vols.;—all three classed vocabularies: Langlès (French), Paris, 1789-1790, 4to, 3 vols.: Gabelentz (German), Leipzig, 1864, 8vo: Zakharov (Russian), St Petersburg, 1875, 8vo, 1235 pages: Mongol: I. J. Schmidt (German, Russian), St Petersburg, 1835, 4to: Schergin, Kazan, 1841, 8vo: Kovalevski, Kasan, 1844-1849, 4to, 3 vols. 2703 pages. Ostiak: Castrén, St Petersb. 1858, 8vo. Samoyed: Castrén, St Petersb. 1855, 8vo, 308 pages. Tartar: Giganov (Tobolsk), St Petersburg, 1804, 4to; (Russ.-Tartar), ib. 1840, 4to: Troyanski (Karan), Kasan, 1835-1855, 4to. Tibetan: Minggi djamtoo (Tibet-Mongol): Bodschi dajig togpar lama: Kad shi schand scharwi melonggi jige (Manchu-Mongol-Tibetan-Chinese), Kanghi’s Dictionary with the Tibetan added in the reign of Khian lung (1736-1795); Csoma de Körös (Eng.), Calcutta, 1834, 4to: I. J. Schmidt (German), St Petersburg, 1841, 4to: Id. (Russian), ib. 1843, 4to: Jaeschke (Eng.), London, 1870, 8vo, 160 pages: Id. (Germ.), Gnadau, 1871, 658 pages: (Bhotanta), Schroeter, Serampore, 1826, 4to. Tungusian: Castrén, St Petersburg, 1856, 8vo, 632 pages. Uigur: Vámbéry, Innspruck, 1870, 4to. Yakut: Böhtlingk, ib. 1854, 4to, 2 vols. Yenissei Ostiak: Castrén, ib. 1849, 8vo.
AFRICA
Egyptian.—Young (enchorial), London, 1830-1831, 8vo: Sharpe, London, 1837, 4to: Birch, London. 1838, 4to: Champollion (died March 4, 1832), Dictionnaire égyptien, Paris, 1841, 4to: Brugsch, Hieroglyphisch-Demotisches Wörterbuch, Leipzig, 1867-1868, 4to, 4 vols. 1775 pages, nearly 4700 words, arranged according to the hieroglyphic alphabet of 28 letters: Pierret, Vocabulaire hiérog., Paris, 1875, 8vo, containing also names of persons and places: Birch, in vol. v. pp. 337-580 of Bunsen’s Egypt’s Place, 2nd ed. London, 1867, &c. 8vo, 5010 words. Proper Names.—Brugsch, Berlin, 1851, 8vo, 726 names: Parthey, ib. 1864, 8vo, about 1500 names: Lieblein, Christiania, 1871, 8vo, about 3200 from hieroglyphic texts. Book of the Dead.—Id., Paris, 1875, 12mo.
Coptic.—Veyssière de la Croze, Oxon. 1775, 8vo: Rossi, Romae, 1807, 4to: Tattam, Oxon. 1855, 8vo: Peyron, 1835, 4to (the standard): Parthey, Berolini, 1844, 8vo.
Ethiopic.—Wemmer, Romae, 1638, 4to: Ludolf, London, 1661, 4to: Francof. ad M., 1699, fol.: Dillmann (Tigré appendix), Leipzig, 1863-1865, 4to, 828 pages.
Amharic.—Ludolphus, Franc. ad Maenum, 1698, fol.: Isenberg, London, 1841, 4to, 442 pages. Tigré: Munzinger, Leipzig, 1865, 8vo: Beurmann, ib. 1868, 8vo.
East Coast.—Dankali: Isenberg, London, 1840, 12mo. Galla: Krapf, London, 1842, 8vo: Tutschek, München, 1844, 8vo. Engutuk Iloigob: Erhardt, Ludwigsberg, 1857, 8vo. Kisuaheli: Vocabulary of the Soahili, Cambridge, U.S. 1845, 8vo: Steere, London, 1870, 8vo, about 5800 words. Kisuaheli, Kinika, Kikamba, Kipokono, Kikian, Kigalla: Krapf, Tübingen, 1850, 8vo.
Malagasy.—Houtmann (Malaysche en Madagask Talen), Amst. 1603, 2nd ed. Matthysz, ib. 1680, 8vo: Huet de Froberville, Isle de France, fol. 2 vols.: Flacourt, Paris, 1658, 8vo: Challand (Southern), Isle de France, 1773, 4to: Freeman and Johns, London, 1835, 8vo, 2 vols.: Dalmont (Malgache, Salalave, et Betsimara), 1842, 8vo: Kessler, London, 1870, 8vo.
Southern Africa.—Bleek, The Languages of Mozambique, London, 1856, 8vo. Kaffre: Bennie, Lovedale, 1826, 16mo: Ayliffe, Graham’s Town, 1846, 12mo: Appleyard, 1850, 8vo: Bleek, Bonn, 1853, 4to, 646 pages. Zulu-Kaffre: Perrin (Kaffre-Eng.), London, 1855, 24mo, 172 pages: Id. (Eng.-Kaffre), Pietermaritzburg, 1855, 24mo, 227 pages: Id. (Eng.-Zulu), ib. 1865, 12mo, 226 pages: Dohne, Cape Town, 1857, 8vo, 428 pages: Colenso, Pietermaritzburg, 1861, 8vo, 560 pages, about 8000 words. Hottentot: Bleek, Cape Town, 1857, 4to, 261 pages. Namaqua: Tindall, ib. 1852, 8vo: Vocabulary, Barmen, 1854, 8vo: Hahn, Leipzig, 1870, 12mo. Sechuana: Casalis, Paris, 1841, 8vo. Herero: Hahn, Berlin, 1857, 8vo, 207 pages, 4300 words.
Western Africa.—Akra or Ga: Zimmermann, Stuttgart, 1858, 8vo, 690 pages. Ashantee: Christaller (also Akra), Basel, 1874, 8vo, 299 pages. Bullom: Nylander, London, 1814, 12mo. Bunda or Angola: Cannecatim, Lisboa, 1804, 4to, 722 pages. Dualla Grammatical Elements, &c., Cameroons, 1855, 8vo. Efik or Old Calabar: Waddell, Old Calabar, 1846, 16mo, 126 pages; Edinb, 1849, 8vo, 95 pages. Eyo: Raban, London, 1830-1831, 12mo, 2 parts. Grebo: Vocabulary, Cape Palmas, 1837, 8vo; Dictionary, ib. 1839, 8vo, 119 pages. Ifa: Schlegel, Stuttgart, 1857, 8vo. Mpongwe: De Lorme (Franç.-Pongoué), Paris, 1876, 12mo, 354 pages. Oji: Riis, Basel, 1854, 8vo, 284 pages. Sherbro’: Schön, s. a. et l. 8vo, written in 1839, 42 pages. Susu: Brunton, Edinburgh, 1802, 8vo, 145 pages. Vei: Koelle, London, 1854, 8vo, 266 pages. Wolof and Bambarra: Dard, Paris, 1825, 8vo. Wolof: Roger, ib. 1829, 8vo: Missionnaires de S. Esprit, Dakar, 1855, &c. 16mo. Faidherbe (French-Wolof, Poula and Soninke), St Louis, Senegambia, 1860, 12mo. Yoruba: Crowther, London, 1843, 8vo; 1852, 298 pages: Vidal, ib. 1852, 8vo: Bowen, Washington, 1858, 4to.
Central Africa.—Barth, Vocabularies. Gotha, 1862-1866, 4to. Bari: Mitterreutzner, Brixen, 1867, 8vo: Reinisch, Vienna, 1874, 8vo. Dinka: Mitterreutzner, Brixen, 1866, 8vo. Haussa: Schön (Eng.), London, 1843, 8vo.
Berber.—Venture de Paradis, Paris, 1844, 8vo: Brosselard, ib. 1844, 8vo: Delaporte, ib. 1844, 4to, by order of the Minister of War: Creusat, Franç.-Kabyle (Zouaoua), Alger, 1873, 8vo. Siwah: Minutoli, Berlin, 1827, 4to.
AUSTRALIA AND POLYNESIA
Australia.—New South Wales: Threlkeld (Lake Macquarie Language), Sydney, 1834, 8vo. Victoria: Bunce, Melbourne, 1856, 12mo, about 2200 words. South Australia: Williams, South Australia, 1839, 8vo: Teichelmann and Schürmann, Adelaide, 1840, 8vo: Meyer, ib. 1843, 8vo. Murray River: Moorhouse, ib. 1846, 8vo. Parnkalla: Schürmann, Adelaide, 1844, 8vo. Woolner District: Vocabulary, ib. 1869, 12mo. Western Australia: Sir George Grey, Perth, 1839, 4to; London, 1840, 8vo: Moore, ib. 1843: Brady, Roma, 1845, 24mo, 8vo, 187 pages. Tasmania: Millegan, Tasmania, 1857.
Polynesia.—Hale, Grammars and Vocabularies of all the Polynesian Languages, Philadelphia, 1846, 4to. Marquesas, Sandwich Gambier: Mosblech, Paris, 1843, 8vo. Hawaiian: Andrews, Vocabulary, Lahainaluna, 1636, 8vo: Id., Dictionary, Honolulu, 1865, 8vo, 575 pages, about 15,500 words. Marquesas: Pierquin, de Gembloux, Bourges, 1843, 8vo: Buschmann, Berlin, 1843, 8vo. Samoan: Dictionary, Samoa, 1862, 8vo. Tahitian: A Tahitian and English Dictionary, Tahiti, 1851, 8vo, 314 pages. Tonga: Rabone, Vavau, 1845, 8vo. Fijian: Hazlewood (Fiji-Eng.), Vewa. 1850, 200 12mo: Id. (Eng.-Fiji), ib. 1852, 12mo: Id., London, 1872, 8vo. Maori: Kendall, 1820, 12mo: Williams, Paihia, 1844, 8vo; 3rd ed. London, 1871, 8vo: Taylor, Auckland, 1870, 12mo.
AMERICA
North America.—Eskimo: Washington, London, 1850, 8vo: Petitot (Mackenzie and Anderson Rivers), Paris, 1876, 4to. Kinai: Radloff, St Petersburg, 1874, 4to. Greenland: Egede (Gr. Dan. Lat., 3 parts), Hafn, 1750, 8vo; 1760, Fabricius, Kjöbenhavn, 1804, 4to. Hudson’s Bay Indians: Bowrey, London, 1701, fol. Abnaki: Rasles, Cambridge, U.S., 1833, 4to. Chippewa: Baraga, Cincinnati, 1853, 12mo, 622 pages: Petitot, Paris, 1876, 4to, 455 pages. Massachusetts or Natick: Cotton, Cambridge, U.S. 1829, 8vo. Onondaga: Shea (French-Onon.), from a MS. (of 17th century), London, 1860, 4to, 109 pages. Dacota: Riggs, New York, 1851, 4to, 424 pages: Williamson (Eng. Dac.), Santos Agency, Nebraska, 12mo, 139 pages. Mohawk: Bruyas, New York, 1863, 8vo. Hidatsa (Minnetarees, Gros Ventres of the Missouri): Matthews, ib. 1874, 8vo. Choctaw: Byington, ib. 1852, 16mo. Clallam and Lummi: Gibbs, ib. 1863, 8vo. Yakama: Pandosy, translated by Gibbs and Shea, ib. 1862, 8vo. Chinook: Gibbs, New York, 1863, 4to. Chinook Jargon, the trade language of Oregon: Id., ib. 1863, 8vo. Tatche or Telamé: Sitjar, ib. 1841, 8vo.
Mexico and Central America.—Tepehuan: Rinaldini, Mexico, 1743, 4to. Cora: Ortega, Mexico, 1732, 4to. Tarahumara: Steffel, Brünn, 1791, 8vo. Otomi: Carochi, Mexico, 1645, 4to: Neve y Molina, ib. 1767, 8vo: Yepes, ib. 1826, 4to: Piccolomini, Roma, 1841, 8vo. Mexican or Aztec: Molina, Mexico, 1555, 4to; 1571, fol. 2 vols.: Arenas, ib. 1583; 1611, 8vo; 1683; 1725; 1793, 12mo: Biondelli, Milan, 1869, fol. Mexican, Tontonacan, and Huastecan: Olmos, Mexico, 1555-1560, 4to, 2 vols. Huastecan: Tapia Zenteno, ib. 1767, 4to, 128 pages. Opata or Tequima: Lombardo, ib. 1702, 4to. Tarasca: Gilberti, ib. 1559, 4to: Lagunas, ib. 1574, 8vo. Mixtecan: Alvarado, Mexico, 1593, 4to. Zapoteca: Cordova, ib. 1578, 4to. Maya: Beltran de Santa Rosa Maria, ib. 1746, 4to; Merida de Yucatan, 1859, 4to, 250 pages: Brasseur de Bourbourg, Paris, 1874, 8vo, 745 pages. Quiché: Id. (also Cakchiquel and Trutuhil dialects), ib. 1862, 8vo.
South America.—Chibcha: Uricoechea, Paris, 1871, 8vo. Chayma: Tauste, Madrid, 1680, 4to: Yanguas, Burgos, 1683, 4to. Carib: Raymond, Auxerre, 1665-1666, 8vo. Galibi: D.[e]. L.[a] S.[auvage], Paris, 1763, 8vo. Tupi: Costa Rubim, Rio de Janeiro, 1853, 8vo: Silva Guimaräes, Bahia, 1854, 8vo: Diaz, Lipsia, 1858, 16mo. Guarani: Ruiz de Montoyo, Madrid, 1639, 4to; 1640; 1722, 4to; ed. Platzmann, Leipzig, 1876, &c., 8vo, to be in 4 vols. 1850 pages. Moxa: Marban, Lima, 1701, 8vo. Lule: Machoni de Corderia, Madrid, 1732, 12mo. Quichua: Santo Thomas, Ciudad de los Reyes, 1586, 8vo: Torres Rubio, Sevilla, 1603, 8vo; Lima, 1609, 8vo; ed. Figueredo, Lima, 1754, 8vo; Holguin, Ciudad de los Reyes, 1608, 8vo: Tschudi, Wien, 1853, 8vo, 2 vols.: Markham, London, 1864, 8vo: Lopez, Les Races Aryennes de Perou, Paris, 1871, 8vo, comparative vocabulary, pp. 345-421. Aymara: Bertonio, Chicuyto, 1612, 4to, 2 vols. Chileno: Valdivia (also Allentiac and Milcocayac), Lima, 1607, 8vo: Febres, ib. 1765, 12mo; ed. Hernandez y Caluza, Santiago, 1846, 8vo, 2 vols. Tsonecan (Patagonian): Schmid, Bristol, 1860, 12mo.
The above article incorporates the salient features of the 9th-edition article by the Rev. Ponsonby A. Lyons, and the 10th-edition article by Benjamin E. Smith.
1 Joannes de Garlandia (John Garland; fl. 1202-1252) gives the following explanation in his Dictionarius, which is a classed vocabulary:—“Dictionarius dicitur libellus iste a dictionibus magis necessariis, quas tenetur quilibet scolaris, non tantum in scrinio de lignis facto, sed in cordis armariolo firmiter retinere.” This has been supposed to be the first use of the word.
2 An excellent dictionary of quotations, perhaps the first of the kind; a large folio volume printed in Strassburg about 1475 is entitled “Pharetra auctoritates et dicta doctorum, philosophorum, et poetarum continens.”
3 This volume was issued with a new title-page as Glossaire du moyen âge, Paris, 1872.
DICTYOGENS (Gr. δίκτυον, a net, and the termination -γενης, produced), a botanical name proposed by John Lindley for a class including certain families of Monocotyledons which have net-veined leaves. The class was not generally recognized.
DICTYS CRETENSIS, of Cnossus in Crete, the supposed companion of Idomeneus during the Trojan War, and author of a diary of its events. The MS. of this work, written in Phoenician characters, was said to have been found in his tomb (enclosed in a leaden box) at the time of an earthquake during the reign of Nero, by whose order it was translated into Greek. In the 4th century a.d. a certain Lucius Septimius brought out Dictys Cretensis Ephemeris belli Trojani, which professed to be a Latin translation of the Greek version. Scholars were not agreed whether any Greek original really existed; but all doubt on the point was removed by the discovery of a fragment in Greek amongst the papyri found by B. P. Grenfell and A. S. Hunt in 1905-1906. Possibly the Latin Ephemeris was the work of Septimius himself. Its chief interest lies in the fact that (together with Dares Phrygius’s De excidio Trojae) it was the source from which the Homeric legends were introduced into the romantic literature of the middle ages.
Best edition by F. Meister (1873), with short but useful introduction and index of Latinity; see also G. Körting, Diktys und Dares (1874), with concise bibliography; H. Dunger, Die Sage vom trojanischen Kriege in den Bearbeitungen des Mittelalters und ihren antiken Quellen (1869, with a literary genealogical table); E. Collilieux, Étude sur Dictys de Crète et Darès de Phrygie (1887), with bibliography; W. Greif, “Die mittelalterlichen Bearbeitungen der Trojanersage,” in E. M. Stengel’s Ausgaben und Abhandlungen aus dem Gebiete der romanischen Philologie, No. 61 (1886, esp. sections 82, 83, 168-172); F. Colagrosso, “Ditte Cretese” in Atti della r. Accademia di Archeologia (Naples, 1897, vol. 18, pt. ii. 2); F. Noack, “Der griechische Dictys,” in Philologus, supp. vi. 403 ff.; N. E. Griffin, Dares and Dictys, Introduction to the Study of the Medieval Versions of the Story of Troy (1907).
DICUIL (fl. 825), Irish monastic scholar, grammarian and geographer. He was the author of the De mensura orbis terrae, finished in 825, which contains the earliest clear notice of a European discovery of and settlement in Iceland and the most definite Western reference to the old freshwater canal between the Nile and the Red Sea, finally blocked up in 767. In 795 (February 1-August 1) Irish hermits had visited Iceland; on their return they reported the marvel of the perpetual day at midsummer in “Thule,” where there was then “no darkness to hinder one from doing what one would.” These eremites also navigated the sea north of Iceland on their first arrival, and found it ice-free for one day’s sail, after which they came to the ice-wall. Relics of this, and perhaps of other Irish religious settlements, were found by the permanent Scandinavian colonists of Iceland in the 9th century. Of the old Egyptian freshwater canal Dicuil learnt from one “brother Fidelis,” probably another Irish monk, who, on his way to Jerusalem, sailed along the “Nile” into the Red Sea—passing on his way the “Barns of Joseph” or Pyramids of Giza, which are well described. Dicuil’s knowledge of the islands north and west of Britain is evidently intimate; his references to Irish exploration and colonization, and to (more recent) Scandinavian devastation of the same, as far as the Faeroes, are noteworthy, like his notice of the elephant sent by Harun al-Rashid (in 801) to Charles the Great, the most curious item in a political and diplomatic intercourse of high importance. Dicuil’s reading was wide; he quotes from, or refers to, thirty Greek and Latin writers, including the classical Homer, Hecataeus, Herodotus, Thucydides, Virgil, Pliny and King Juba, the sub-classical Solinus, the patristic St Isidore and Orosius, and his contemporary the Irish poet Sedulius;—in particular, he professes to utilize the alleged surveys of the Roman world executed by order of Julius Caesar, Augustus and Theodosius (whether Theodosius the Great or Theodosius II. is uncertain). He probably did not know Greek; his references to Greek authors do not imply this. Though certainly Irish by birth, it has been conjectured (from his references to Sedulius and the caliph’s elephant) that he was in later life in an Irish monastery in the Frankish empire. Letronne inclines to identify him with Dicuil or Dichull, abbot of Pahlacht, born about 760.
There are seven chief MSS. of the De mensura (Dicuil’s tract on grammar is lost); of these the earliest and best are (1) Paris, National Library, Lat. 4806; (2) Dresden, Regius D. 182; both are of the 10th century. Three editions exist: (1) C. A. Walckenaer’s, Paris, 1807; (2) A. Letronne’s, Paris, 1814, best as to commentary; (3) G. Parthey’s, Berlin, 1870, best as to text. See also C. R. Beazley, Dawn of Modern Geography (London, 1897), i. 317-327, 522-523, 529; T. Wright, Biographia Britannica literaria, Anglo-Saxon Period (London, 1842), pp. 372-376.
DIDACHĒ, THE, or Teaching of the (twelve) Apostles,—the most important of the recent recoveries in the region of early Christian literature (see Apocryphal Literature). It was previously known by name from lists of canonical and extra-canonical books compiled by Eusebius and other writers. Moreover, it had come to be suspected by several scholars that a lost book, variously entitled The Two Ways or The Judgment of Peter, had been freely used in a number of works, of which mention must presently be made. In 1882 a critical reconstruction of this book was made by Adam Krawutzcky with marvellous accuracy, as was shown when in the very next year the Greek bishop and metropolitan, Philotheus Bryennius, published The Teaching of the Twelve Apostles from the same manuscript from 201 which he had previously published the complete form of the Epistle of Clement.1
The Didachē, as we now have it in the Greek, falls into two marked divisions: (a) a book of moral precepts, opening with the words, “There are two ways”; (b) a manual of church ordinances, linked on to the foregoing by the words, “Having first said all these things, baptize, &c.” Each of these must be considered separately before we approach the question of the locality and date of the whole book in its present form.
1. The Two Ways.—The author of the complete work, as we now have it, has modified the original Two Ways by inserting near the beginning a considerable section containing, among other matter, passages from the Sermon on the Mount, in which the language of St Matthew’s Gospel is blended with that of St Luke’s. He has also added at the close a few sentences, beginning, “If thou canst not bear (the whole yoke of the Lord), bear what thou canst” (vi. 2); and among minor changes he has introduced, in dealing with confession, reference to “the church” (iv. 14). No part of this matter is to be found in the following documents, which present us in varying degrees of accuracy with The Two Ways: (i.) the Epistle of Barnabas, chaps. xix., xx. (in which the order of the book has been much broken up, and a good deal has been omitted); (ii.) the Ecclesiastical Canons of the Holy Apostles, usually called the Apostolic Church Order, a book which presents a parallel to the Teaching, in so far as it consists first of a form of The Two Ways, and secondly of a number of church ordinances (here, however, as in the Syriac Didascalia, which gives about the same amount of The Two Ways, various sections are ascribed to individual apostles, e.g. “John said, There are two ways,” &c.); (iii.) a discourse of the Egyptian monk Schnudi (d. 451), preserved in Arabic (see Iselin, Texte u. Unters., 1895); (iv.) a Latin version, of which a fragment was published by O. von Gebhardt in 1884, and the whole by J. Schlecht in 1900. When by the aid of this evidence The Two Ways is restored to us free of glosses, it has the appearance of being a Jewish manual which has been carried over into the use of the Christian church. This is of course only a probable inference; there is no prototype extant in Jewish literature, and, comparing the moral (non-doctrinal) instruction for Christian catechumens in Hermas, Shepherd (Mand. i.-ix.), no real need to assume one. There was a danger of admitting Gentile converts to the church on too easy moral terms; hence the need of such insistence on the ideal as in The Two Ways and the Mandates. The recent recovery of the Latin version is of singular interest, as showing that, even without the distinctively Christian additions and interpolations which our full form of the Teaching presents, it was circulating under the title Doctrina apostolorum.2
2. The second part of our Teaching might be called a church directory. It consists of precepts relating to church life, which are couched in the second person plural; whereas The Two Ways uses throughout the second person singular. It appears to be a composite work. First (vii. 1-xi. 2) is a short sacramental manual intended for the use of local elders or presbyters, though such are not named, for they were not yet a distinctive order or clergy. This section was probably added to The Two Ways before the addition of the remainder. It orders baptism in the threefold name, making a distinction as to waters which has Jewish parallels, and permitting a threefold pouring on the head, if sufficient water for immersion cannot be had. It prescribes a fast before baptism for the baptizer as well as the candidate. Fasts are to be kept on Wednesday and Friday, not Monday and Thursday, which are the fast days of “the hypocrites,” i.e. by a perversion of the Lord’s words, the Jews. “Neither pray ye as the hypocrites; but as the Lord commanded in His Gospel.” Then follows the Lord’s Prayer, almost exactly as in St Matthew, with a brief doxology—“for Thine is the power and the glory forever.” This is to be said three times a day. Next come three eucharistic prayers, the language of which is clearly marked off from that of the rest of the book, and shows parallels with the diction of St John’s Gospel. They are probably founded on Jewish thanksgivings, and it is of interest to note that a portion of them is prescribed as a grace before meat in (pseudo-) Athanasius’ De virginitate. A trace of them is found in one of the liturgical prayers of Serapion, bishop of Thmui, in Egypt, but they have left little mark on the liturgies of the church. As in Ignatius and other early writers, the eucharist, a real meal (x. 1) of a family character, is regarded as producing immortality (cf. “spiritual food and drink and eternal life”). None are to partake of it save those who have been “baptized in the name of the Lord” (an expression which is of interest in a document which prescribes the threefold formula). The prophets are not to be confined to these forms, but may “give thanks as much as they will.” This appears to show that a prophet, if present, would naturally preside over the eucharist. The next section (xi. 3-xiii.) deals with the ministry of spiritual gifts as exercised by apostles, prophets and teachers. An apostle is to be “received as the Lord”; but he must follow the Gospel precepts, stay but one or two days, and take no money, but only bread enough for a day’s journey. Here we have that wider use of the term “apostle” to which Lightfoot had already drawn attention. A prophet, on the contrary, may settle if he chooses, and in that case he is to receive tithes and first-fruits; “for they are your high priests.” If he be once approved as a true prophet, his words and acts are not to be criticized; for this is the sin that shall not be forgiven. Next comes a section (xiv., xv.) reflecting a somewhat later development concerning fixed services and ministry; the desire for a stated service, and the need of regular provision for it, is leading to a new order of things. The eucharist is to be celebrated every Lord’s Day, and preceded by confession of sins, “that your sacrifice may be pure ... for this is that sacrifice which was spoken of by the Lord, In every place and time to offer unto Me a pure sacrifice. Appoint therefore unto yourselves bishops and deacons, worthy of the Lord, men meek and uncovetous, and true and approved; for they also minister unto you the ministration of the prophets and teachers. Therefore despise them not; for they are your honoured ones, together with the prophets and teachers.” This is an arrangement recommended by one who has tried it, and he reassures the old-fashioned believer who clings to the less formal régime (and whose protest was voiced in the Montanist movement), that there will be no spiritual loss under the new system. The book closes (chap. xvi.) with exhortations to steadfastness in the last days, and to the coming of the “world-deceiver” or Antichrist, which will precede the coming of the Lord. This section is perhaps the actual utterance of a Christian prophet, and may be of earlier origin than the two preceding sections.
3. It will now be clear that indications of the locality and date of our present Teaching must be sought for only in the second part, and in the Christian interpolations in the first part. We have no ground for thinking that the second part ever existed independently as a separate book. The whole work was in the hands of the writer of the seventh book of the Apostolic Constitutions, who embodies almost every sentence of it, interspersing it with passages of Scripture, and modifying the precepts of the second part to suit a later (4th-century) stage of church development; this writer was also the interpolator of the Epistles of Ignatius, and belonged to the Syrian Church. Whether the second part was known to the writer of the Apostolic Church Order is not clear, as his only quotation of it comes from one of the eucharistic prayers. The allusions of early writers seem to point to Egypt, but their references are mostly to the first part, so that we must be careful how we argue from them as to the provenance of the book as a whole. Against Egypt has been urged the allusion in one of the eucharistic prayers to “corn upon the mountains.” This is found in the Prayer-book of Serapion 202 (c. 350) but omitted in a later Egyptian prayer; the form as we have it in The Didachē may have passed into Egypt with the authority of tradition which was afterwards weakened. The anti-Jewish tone of the second part suggests the neighbourhood of Jews, from whom the Christians were to be sharply distinguished. Either Egypt or Syria would satisfy this condition, and in favour of Syria is the fact that the presbyterate there was to a late date regarded as a rank rather than an office. If we can connect the injunctions (vi. 3) concerning (abstinence from certain) food and that which is offered to idols with the old trouble that arose at Antioch (Acts xv. 1) and was legislated for by the Jerusalem council, we have additional support for the Syrian claim. But all that we can safely say as to locality is that the community here represented seems to have been isolated, and out of touch with the larger centres of Christian life.
This last consideration helps us in discussing the question of date. For such an isolated community may have preserved primitive customs for some time after they had generally disappeared. Certainly the stage of development is an early one, as is shown, e.g., by the prominence of prophets, and the need that was felt for the vindication of the position of the bishops and deacons (there is no mention at all of presbyters); moreover, there is no reference to a canon of Scripture (though the written Gospel is expressly mentioned) or to a creed. On the other hand the “apostles” of the second part are obviously not “the twelve apostles” of the title; and the prophets seem in some instances to have proved unworthy of their high position. The ministry of enthusiasm which they represent is about to give way to the ministry of office, a transition which is reflected in the New Testament in the 3rd Epistle of John. Three of the Gospels have clearly been for some time in circulation; St Matthew’s is used several times, and there are phrases which occur only in St Luke’s, while St John’s Gospel lies behind the eucharistic prayers which the writer has embodied in his work. There are no indications of any form of doctrinal heresy as needing rebuke; the warnings against false teaching are quite general. While the first part must be dated before the Epistle of Barnabas, i.e. before a.d. 90, it seems wisest not to place the complete work much earlier than a.d. 120, and there are passages which may well be later.
A large literature has sprung up round The Didachē since 1884. Harnack’s edition in Texte u. Unters. vol. ii. (1884) is indispensable to the student; and his discussions in Altchristl. Litteratur and Chronologie give clear summaries of his work. Other editions of the text are those of F. X. Funk, Patres Apostolici, vol. i. (Tübingen, 1901); H. Lietzmann (Bonn, 1903; with Latin version). Dr J. E. Odgers has published an English translation with introduction and notes (London, 1906). Dr C. Taylor in 1886 drew attention to some important parallels in Jewish literature; his edition contains an English translation. Dr Rendel Harris published in 1887 a complete facsimile, and gathered a great store of patristic illustration. Text and translation will also be found in Lightfoot’s Apostolic Fathers (ed. min.) The fullest critical treatment in English is by Dr Vernon Bartlet in the extra volume of Hastings’s Dictionary of the Bible; the most complete commentary on the text is by P. Drews in Hennecke’s Handbuch zu den N.T. Apocryphen (1904). Other references to the literature may be found by consulting Harnack’s Altchristl. Litteratur.
1 The MS. was found in the Library of the Jerusalem Monastery of the Most Holy Sepulchre, in Phanar, the Greek quarter of Constantinople. It is a small octavo volume of 120 parchment leaves, written throughout by Leo, “notary and sinner,” who finished his task on the 11th of June 1156. Besides The Didachē and the Epistles of Clement it contains several spurious Ignatian epistles.
2 The word twelve had no place in the original title and was inserted when the original Didachē or Teaching (e.g. The Two Ways) was combined with the church manual which mentions apostles outside of the twelve. It may be noted that the division of the Didachē into chapters is due to Bryennius, that into verses to A. Harnack.
DIDACTIC POETRY, that form of verse the aim of which is, less to excite the hearer by passion or move him by pathos, than to instruct his mind and improve his morals. The Greek word διδακτικός signifies a teacher, from the verb διδάσκειν, and poetry of the class under discussion approaches us with the arts and graces of a schoolmaster. At no time was it found convenient to combine lyrical verse with instruction, and therefore from the beginning of literature the didactic poets have chosen a form approaching the epical. Modern criticism, which discourages the epic, and is increasingly anxious to limit the word “poetry” to lyric, is inclined to exclude the term “didactic poetry” from our nomenclature, as a phrase absurd in itself. It is indeed more than probable that didactic verse is hopelessly obsolete. Definite information is now to be found in a thousand shapes, directly and boldly presented in clear and technical prose. No farmer, however elegant, will, any longer choose to study agriculture in hexameters, or even in Tusser’s shambling metre. The sciences and the professions will not waste their time on methods of instruction which must, from their very nature, be artless, inexact and vague. But in the morning of the world, those who taught with authority might well believe that verse was the proper, nay, the only serious vehicle of their instruction. What they knew was extremely limited, and in its nature it was simple and straightforward; it had little technical subtlety; it constantly lapsed into the fabulous and the conjectural. Not only could what early sages knew, or guessed, about astronomy and medicine and geography be conveniently put into rolling verse, but, in the absence of all written books, this was the easiest way in which information could be made attractive to the ear and be retained by the memory.
In the prehistoric dawn of Greek civilization there appear to have been three classes of poetry, to which the literature of Europe looks back as to its triple fountain-head. There were romantic epics, dealing with the adventures of gods and heroes; these Homer represents. There were mystic chants and religious odes, purely lyrical in character, of which the best Orphic Hymns must have been the type. And lastly there was a great body of verse occupied entirely with increasing the knowledge of citizens in useful branches of art and observation; these were the beginnings of didactic poetry, and we class them together under the dim name of Hesiod. It is impossible to date these earliest didactic poems, which nevertheless set the fashion of form which has been preserved ever since. The Works and Days, which passes as the direct masterpiece of Hesiod (q.v.), is the type of all the poetry which has had education as its aim. Hesiod is supposed to have been a tiller of the ground in a Boeotian village, who determined to enrich his neighbours’ minds by putting his own ripe stores of useful information into sonorous metre. Historically examined, the legend of Hesiod becomes a shadow, but the substance of the poems attributed to him remains. The genuine parts of the Works and Days, which Professor Gilbert Murray has called “a slow, lowly, simple poem,” deal with rules for agriculture. The Theogony is an annotated catalogue of the gods. Other poems attributed to Hesiod, but now lost, were on astronomy, on auguries by birds, on the character of the physical world; still others seem to have been genealogies of famous women. All this mass of Boeotian verse was composed for educational purposes, in an age when even preposterous information was better than no knowledge at all. In slightly later times, as the Greek nation became better supplied with intellectual appliances, the stream of didactic poetry flowed more and more closely in one, and that a theological, channel. The great poem of Parmenides On Nature and those of Empedocles exist only in fragments, but enough remains to show that these poets carried on the didactic method in mythology. Cleostratus of Tenedos wrote an astronomical poem in the 6th century, and Periander a medical one in the 4th, but didactic poetry did not flourish again in Greece until the 3rd century, when Aratus, in the Alexandrian age, wrote his famous Phenomena, a poem about things seen in the heavens. Other later Greek didactic poets were Nicander, and perhaps Euphorion.
It was from the hands of these Alexandrian writers that the genius of didactic poetry passed over to Rome, since, although it is possible that some of the lost works of the early republic, and in particular those of Ennius, may have possessed an educational character, the first and by far the greatest didactic Latin poet known to us is Lucretius. A highly finished translation by Cicero into Latin hexameters of the principal works of Aratus is believed to have drawn the attention of Lucretius to this school of Greek poetry, and it was not without reference to the Greeks, although in a more archaic and far purer taste, that he composed, in the 1st century before Christ, his magnificent De rerum natura. By universal consent, this is the noblest didactic poem in the literature of the world. It was intended to instruct mankind in the interpretation and in the working of the system of philosophy revealed by Epicurus, which at that time was exciting the sympathetic attention of all classes of Roman society. What gave the poem of Lucretius its extraordinary interest, and what has prolonged and even increased its vitality, was the imaginative and illustrative insight of the author, piercing and lighting up the 203 recesses of human experience. On a lower intellectual level, but of a still greater technical excellence, was the Georgics of Virgil, a poem on the processes of agriculture, published about 30 b.c. The brilliant execution of this famous work has justly made it the type and unapproachable standard of all poetry which desires to impart useful information in the guise of exquisite literature. Himself once a farmer on the banks of the Mincio, Virgil, at the apex of his genius, set himself in his Campanian villa to recall whatever had been essential in the agricultural life of his boyish home, and the result, in spite of the ardours of the subject, was what J. W. Mackail has called “the most splendid literary production of the Empire.” In the rest of surviving Latin didactic poetry, the influence and the imitation of Virgil and Lucretius are manifest. Manilius, turning again to Alexandria, produced a fine Astronomica towards the close of the reign of Augustus. Columella, regretting that Virgil had omitted to sing of gardens, composed a smooth poem on horticulture. Natural philosophy inspired Lucilius junior, of whom a didactic poem on Etna survives. Long afterwards, under Diocletian, a poet of Carthage, Nemesianus, wrote in the manner of Virgil the Cynegetica, a poem on hunting with dogs, which has had numerous imitations in later European literatures. These are the most important specimens of didactic poetry which ancient Rome has handed down to us.
In Anglo-Saxon and early English poetic literature, and especially in the religious part of it, an element of didacticism is not to be overlooked. But it would be difficult to say that anything of importance was written in verse with the sole purpose of imparting information, until we reach the 16th century. Some of the later medieval allegories are didactic or nothing. The first poem, however, which we can in any reasonable way compare with the classic works of which we have been speaking is the Hundreth Pointes of Good Husbandrie, published in 1557 by Thomas Tusser; these humble Georgics aimed at a practical description of the whole art of English farming. Throughout the early part of the 17th century, when our national poetry was in its most vivid and brilliant condition, the last thing a poet thought of doing was the setting down of scientific facts in rhyme. We come across, however, one or two writers who were as didactic as the age would permit them to be, Samuel Daniel with his philosophy, Fulke Greville, Lord Brooke with his “treatises” of war and monarchy. After the Restoration, as the lyrical element rapidly died out of English poetry, there was more and more room left for educational rhetoric in verse. The poems about prosody, founded upon Horace, and signed by John Sheffield, 3rd earl of Mulgrave (1648-1721), and Lord Roscommon, were among the earliest purely didactic verse-studies in English. John Philips deserves a certain pre-eminence, as his poem called Cyder, in 1706, set the fashion which lasted all down the 18th century, of writing precisely in verse about definite branches of industry or employment. None of the greater poets of the age of Anne quite succumbed to the practice, but there is a very distinct flavour of the purely didactic about a great deal of the verse of Pope and Gay. In such productions as Gilbert West’s (1703-1756) Education, Dyer’s Fleece, and Somerville’s Chase, we see technical information put forward as the central aim of the poet. Instead of a passionate pleasure, or at least an uplifted enthusiasm, being the poet’s object, he frankly admits that, first and foremost, he has some facts about wool or dogs or schoolmasters which he wishes to bring home to his readers, and that, secondly, he consents to use verse, as brilliantly as he can, for the purpose of gilding the pill and attracting an unwilling attention. As we descend the 18th century, these works become more and more numerous, and more dry, especially when opposed by the descriptive and rural poets of the school of Thomson, the poet of The Seasons. But Thomson himself wrote a huge poem of Liberty (1732), for which we have no name if we must not call it didactic. Even Gray began, though he failed to finish, a work of this class, on The Alliance of Education and Government. These poems were discredited by the publication of The Sugar-Cane (1764), a long verse-treatise about the cultivation of sugar by negroes in the West Indies, by James Grainger (1721-1766), but, though liable to ridicule, such versified treatises continued to appear. Whether so great a writer as Cowper is to be counted among the didactic poets is a question on which readers of The Task may be divided; this poem belongs rather to the class of descriptive poetry, but a strong didactic tendency is visible in parts of it. Perhaps the latest frankly educational poem which enjoyed a great popularity was The Course of Time by Robert Pollok (1798-1827), in which a system of Calvinistic divinity is laid down with severity and in the pomp of blank verse. This kind of literature had already been exposed, and discouraged, by the teaching of Wordsworth, who had insisted on the imperative necessity of charging all poetry with imagination and passion. Oddly enough, The Excursion of Wordsworth himself is perhaps the most didactic poem of the 19th century, but it must be acknowledged that his influence, in this direction, was saner than his practice. Since the days of Coleridge and Shelley it has been almost impossible to conceive a poet of any value composing in verse a work written with the purpose of inculcating useful information.
The history of didactic poetry in France repeats, in great measure, but in drearier language, that of England. Boileau, like Pope, but with a more definite purpose as a teacher, offered instruction in his Art poétique and in his Epistles. But his doctrine was always literary, not purely educational. At the beginning of the 18th century, the younger Racine (1692-1763) wrote sermons in verse, and at the close of it the Abbé Delille (1738-1813) tried to imitate Virgil in poems about horticulture. Between these two there lies a vast mass of verse written for the indulgence of intellect rather than at the dictates of the heart; wherever this aims at increasing knowledge, it at once becomes basely and flatly didactic. There is nothing in French literature of the transitional class that deserves mention beside The Task or The Excursion.
During the century which preceded the Romantic revival of poetry in Germany, didactic verse was cultivated in that country on the lines of imitation of the French, but with a greater dryness and on a lower level of utility. Modern German literature began with Martin Opitz (1597-1639) and the Silesian School, who were in their essence rhetorical and educational, and who gave their tone to German verse. Albrecht von Haller (1708-1777) brought a very considerable intellectual force to bear on his huge poems, The Origin of Evil, which was theological, and The Alps (1729), botanical and topographical. Johann Peter Uz (1720-1796) wrote a Theodicée, which was very popular, and not without dignity. Johann Jacob Dusch (1725-1787) undertook to put The Sciences into the eight books of a great didactic poem. Tiedge (1752-1840) was the last of the school; in a once-famous Urania, he sang of God and Immortality and Liberty. These German pieces were the most unswervingly didactic that any modern European literature has produced. There was hardly the pretence of introducing into them descriptions of natural beauty, as the English poets did, or of grace and wit like the French. The German poets simply poured into a lumbering mould of verse as much solid information and direct instruction as the form would hold.
Didactic poetry has, in modern times, been antipathetic to the spirit of the Latin peoples, and neither Italian nor Spanish literature has produced a really notable work in this class. An examination of the poems, ancient and modern, which have been mentioned above, will show that from primitive times there have been two classes of poetic work to which the epithet didactic has been given. It is desirable to distinguish these a little more exactly. One is the pure instrument of teaching, the poetry which desires to impart all that it knows about the growing of cabbages or the prevention of disasters at sea, the revolution of the planets or the blessings of inoculation. This is didactic poetry proper, and this, it is almost certain, became irrevocably obsolete at the close of the 18th century. No future Virgil will give the world a second Georgics. But there is another species which it is very improbable that criticism has entirely dislodged; that is the poetry which combines, with philosophical instruction, an impetus of imaginative movement, and a certain definite cultivation 204 of fire and beauty. In hands so noble as those of Lucretius and Goethe this species of didactic poetry has enriched the world with durable masterpieces, and, although the circle of readers which will endure scientific disquisition in the bonds of verse grows narrower and narrower, it is probable that the great poet who is also a great thinker will now and again insist on being heard. In Sully-Prudhomme France has possessed an eminent writer whose methods are directly instructive, and both La Justice (1878) and Le Bonheur (1888) are typically didactic poems. Perhaps future historians may name these as the latest of their class.
DIDEROT, DENIS (1713-1784), French man of letters and encyclopaedist, was born at Langres on the 5th of October 1713. He was educated by the Jesuits, like most of those who afterwards became the bitterest enemies of Catholicism; and, when his education was at an end, he vexed his brave and worthy father’s heart by turning away from respectable callings, like law or medicine, and throwing himself into the vagabond life of a bookseller’s hack in Paris. An imprudent marriage (1743) did not better his position. His wife, Anne Toinette Champion, was a devout Catholic, but her piety did not restrain a narrow and fretful temper, and Diderot’s domestic life was irregular and unhappy. He sought consolation for chagrins at home in attachments abroad, first with a Madame Puisieux, a fifth-rate female scribbler, and then with Sophie Voland, to whom he was constant for the rest of her life. His letters to her are among the most graphic of all the pictures that we have of the daily life of the philosophic circle in Paris. An interesting contrast may be made between the Bohemianism of the famous English literary set who supped at the Turk’s Head with the Tory Johnson and the Conservative Burke for their oracles, and the Bohemianism of the French set who about the same time dined once a week at the baron D’Holbach’s, to listen to the wild sallies and the inspiring declamations of Diderot. For Diderot was not a great writer; he stands out as a fertile, suggestive and daring thinker, and a prodigious and most eloquent talker.
Diderot’s earliest writings were of as little importance as Goldsmith’s Enquiry into the State of Polite Learning or Burke’s Abridgement of English History. He earned 100 crowns by translating Stanyan’s History of Greece (1743); with two colleagues he produced a translation of James’s Dictionary of Medicine (1746-1748) and about the same date he published a free rendering of Shaftesbury’s Inquiry Concerning Virtue and Merit (1745), with some original notes of his own. With strange and characteristic versatility, he turned from ethical speculation to the composition of a volume of stories, the Bijoux indiscrets (1748), gross without liveliness, and impure without wit. In later years he repented of this shameless work, just as Boccaccio is said in the day of his grey hairs to have thought of the sprightliness of the Decameron with strong remorse. From tales Diderot went back to the more congenial region of philosophy. Between the morning of Good Friday and the evening of Easter Monday he wrote the Pensées philosophiques (1746), and he presently added to this a short complementary essay on the sufficiency of natural religion. The gist of these performances is to press the ordinary rationalistic objections to a supernatural revelation; but though Diderot did not at this time pass out into the wilderness beyond natural religion, yet there are signs that he accepted that less as a positive doctrine, resting on grounds of its own, than as a convenient point of attack against Christianity. In 1747 he wrote the Promenade du sceptique, a rather poor allegory—pointing first to the extravagances of Catholicism; second, to the vanity of the pleasures of that world which is the rival of the church; and third, to the desperate and unfathomable uncertainty of the philosophy which professes to be so high above both church and world.
Diderot’s next piece was what first introduced him to the world as an original thinker, his famous Lettre sur les aveugles (1749). The immediate object of this short but pithy writing was to show the dependence of men’s ideas on their five senses. It considers the case of the intellect deprived of the aid of one of the senses; and in a second piece, published afterwards, Diderot considered the case of a similar deprivation in the deaf and dumb. The Lettre sur les sourds et muets, however, is substantially a digressive examination of some points in aesthetics. The philosophic significance of the two essays is in the advance they make towards the principle of Relativity. But what interested the militant philosophers of that day was an episodic application of the principle of relativity to the master-conception of God. What makes the Lettre sur les aveugles interesting is its presentation, in a distinct though undigested form, of the modern theory of variability, and of survival by superior adaptation. It is worth noticing, too, as an illustration of the comprehensive freedom with which Diderot felt his way round any subject that he approached, that in this theoretic essay he suggests the possibility of teaching the blind to read through the sense of touch. If the Lettre sur les aveugles introduced Diderot into the worshipful company of the philosophers, it also introduced him to the penalties of philosophy. His speculation was too hardy for the authorities, and he was thrown into the prison of Vincennes. Here he remained for three months; then he was released, to enter upon the gigantic undertaking of his life.
The bookseller Lebreton had applied to him with a project for the publication of a translation into French of Ephraim Chambers’s Cyclopaedia, undertaken in the first instance by an Englishman, John Mills, and a German, Gottfried Sellius (for particulars see Encyclopaedia). Diderot accepted the proposal, but in his busy and pregnant intelligence the scheme became transformed. Instead of a mere reproduction of Chambers, he persuaded the bookseller to enter upon a new work, which should collect under one roof all the active writers, all the new ideas, all the new knowledge, that were then moving the cultivated class to its depths, but still were comparatively ineffectual by reason of their dispersion. His enthusiasm infected the publishers; they collected a sufficient capital for a vaster enterprise than they had at first planned; D’Alembert was persuaded to become Diderot’s colleague; the requisite permission was procured from the government; in 1750 an elaborate prospectus announced the project to a delighted public; and in 1751 the first volume was given to the world. The last of the letterpress was issued in 1765, but it was 1772 before the subscribers received the final volumes of the plates. These twenty years were to Diderot years not merely of incessant drudgery, but of harassing persecution, of sufferings from the cabals of enemies, and of injury from the desertion of friends. The ecclesiastical party detested the Encyclopaedia, in which they saw a rising stronghold for their philosophic enemies. By 1757 they could endure the sight no longer. The subscribers had grown from 2000 to 4000, and this was a right measure of the growth of the work in popular influence and power. To any one who turns over the pages of these redoubtable volumes now, it seems surprising that their doctrines should have stirred such portentous alarm. There is no atheism, no overt attack on any of the cardinal mysteries of the faith, no direct denunciation even of the notorious abuses of the church. Yet we feel that the atmosphere of the book may well have been displeasing to authorities who had not yet learnt to encounter the modern spirit on equal terms. The Encyclopaedia takes for granted the justice of religious tolerance and speculative freedom. It asserts in distinct tones the democratic doctrine that it is the common people in a nation whose lot ought to be the main concern of the nation’s government. From beginning to end it is one unbroken process of exaltation of scientific knowledge on the one hand, and pacific industry on the other. All these things were odious to the old governing classes of France; their spirit was absolutist, ecclesiastical and military. Perhaps the most alarming thought of all was the current belief that the Encyclopaedia was the work of an organized band of conspirators against society, and that a pestilent doctrine was now made truly formidable by the confederation of its preachers into an open league. When the seventh volume appeared, it contained an article on “Geneva,” written by D’Alembert. The writer contrived a panegyric on the pastors of Geneva, of which every word was a stinging reproach to the abbés and prelates of Versailles. At the same moment Helvétius’s book, L’Esprit, 205 appeared, and gave a still more profound and, let us add, a more reasonable shock to the ecclesiastical party. Authority could brook no more, and in 1759 the Encyclopaedia was formally suppressed.
The decree, however, did not arrest the continuance of the work. The connivance of the authorities at the breach of their own official orders was common in those times of distracted government. The work went on, but with its difficulties increased by the necessity of being clandestine. And a worse thing than troublesome interference by the police now befell Diderot. D’Alembert, wearied of shifts and indignities, withdrew from the enterprise. Other powerful colleagues, Turgot among them, declined to contribute further to a book which had acquired an evil fame. Diderot was left to bring the task to an end as he best could. For seven years he laboured like a slave at the oar. He wrote several hundred articles, some of them very slight, but many of them most laborious, comprehensive and ample. He wore out his eyesight in correcting proofs, and he wearied his soul in bringing the manuscript of less competent contributors into decent shape. He spent his days in the workshops, mastering the processes of manufactures, and his nights in reproducing on paper what he had learnt during the day. And he was incessantly harassed all the time by alarms of a descent from the police. At the last moment, when his immense work was just drawing to an end, he encountered one last and crowning mortification: he discovered that the bookseller, fearing the displeasure of the government, had struck out from the proof sheets, after they had left Diderot’s hands, all passages that he chose to think too hardy. The monument to which Diderot had given the labour of twenty long and oppressive years was irreparably mutilated and defaced. It is calculated that the average annual salary received by Diderot for his share in the Encyclopaedia was about £120 sterling. “And then to think,” said Voltaire, “that an army contractor makes £800 in a day!”
Although the Encyclopaedia was Diderot’s monumental work, he is the author of a shower of dispersed pieces that sowed nearly every field of intellectual interest with new and fruitful ideas. We find no masterpiece, but only thoughts for masterpieces; no creation, but a criticism with the quality to inspire and direct creation. He wrote plays—Le Fils naturel (1757) and Le Père de famille (1758)—and they are very insipid performances in the sentimental vein. But he accompanied them by essays on dramatic poetry, including especially the Paradoxe sur le comédien, in which he announced the principles of a new drama,—the serious, domestic, bourgeois drama of real life, in opposition to the stilted conventions of the classic French stage. It was Diderot’s lessons and example that gave a decisive bias to the dramatic taste of Lessing, whose plays, and his Hamburgische Dramaturgie (1768), mark so important an epoch in the history of the modern theatre. In the pictorial art, Diderot’s criticisms are no less rich, fertile and wide in their ideas. His article on “Beauty” in the Encyclopaedia shows that he had mastered and passed beyond the metaphysical theories on the subject, and the Essai sur la peinture was justly described by Goethe, who thought it worth translating, as “a magnificent work, which speaks even more helpfully to the poet than to the painter, though to the painter too it is as a blazing torch.” Diderot’s most intimate friend was Grimm, one of the conspicuous figures of the philosophic body. Grimm wrote news-letters to various high personages in Germany, reporting what was going on in the world of art and literature in Paris, then without a rival as the capital of the intellectual activity of Europe. Diderot helped his friend at one time and another between 1759 and 1779, by writing for him an account of the annual exhibitions of paintings. These Salons are among the most readable of all pieces of art criticism. They have a freshness, a reality, a life, which take their readers into a different world from the dry and conceited pedantries of the ordinary virtuoso. As has been said by Sainte-Beuve, they initiated the French into a new sentiment, and introduced people to the mystery and purport of colour by ideas. “Before Diderot,” Madame Necker said, “I had never seen anything in pictures except dull and lifeless colours; it was his imagination that gave them relief and life, and it is almost a new sense for which I am indebted to his genius.”
Greuze was Diderot’s favourite among contemporary artists, and it is easy to see why. Greuze’s most characteristic pictures were the rendering in colour of the same sentiment of domestic virtue and the pathos of common life, which Diderot attempted with inferior success to represent upon the stage. For Diderot was above all things interested in the life of men,—not the abstract life of the race, but the incidents of individual character, the fortunes of a particular family, the relations of real and concrete motives in this or that special case. He delighted with the enthusiasm of a born casuist in curious puzzles of right and wrong, and in devising a conflict between the generalities of ethics and the conditions of an ingeniously contrived practical dilemma. Mostly his interest expressed itself in didactic and sympathetic form; in two, however, of the most remarkable of all his pieces, it is not sympathetic, but ironical. Jacques le fataliste (written in 1773, but not published until 1796) is in manner an imitation of Tristram Shandy and The Sentimental Journey. Few modern readers will find in it any true diversion. In spite of some excellent criticisms dispersed here and there, and in spite of one or two stories that are not without a certain effective realism, it must as a whole be pronounced savourless, forced, and as leaving unmoved those springs of laughter and of tears which are the common fountain of humour. Le Neveu de Rameau is a far superior performance. If there were any inevitable compulsion to name a masterpiece for Diderot, one must select this singular “farce-tragedy.” Its intention has been matter of dispute; whether it was designed to be merely a satire on contemporary manners, or a reduction of the theory of self-interest to an absurdity, or the application of an ironical clincher to the ethics of ordinary convention, or a mere setting for a discussion about music, or a vigorous dramatic sketch of a parasite and a human original. There is no dispute as to its curious literary flavour, its mixed qualities of pungency, bitterness, pity and, in places, unflinching shamelessness. Goethe’s translation (1805) was the first introduction of Le Neveu de Rameau to the European public. After executing it, he gave back the original French manuscript to Schiller, from whom he had it. No authentic French copy of it appeared until the writer had been nearly forty years in his grave (1823).
It would take several pages merely to contain the list of Diderot’s miscellaneous pieces, from an infinitely graceful trifle like the Regrets sur ma vieille robe de chambre up to Le Rêve de D’Alembert, where he plunges into the depths of the controversy as to the ultimate constitution of matter and the meaning of life. It is a mistake to set down Diderot for a coherent and systematic materialist. We ought to look upon him “as a philosopher in whom all the contradictions of the time struggle with one another” (Rosenkranz). That is to say, he is critical and not dogmatic. There is no unity in Diderot, as there was in Voltaire or in Rousseau. Just as in cases of conduct he loves to make new ethical assumptions and argue them out as a professional sophist might have done, so in the speculative problems as to the organization of matter, the origin of life, the compatibility between physiological machinery and free will, he takes a certain standpoint, and follows it out more or less digressively to its consequences. He seizes a hypothesis and works it to its end, and this made him the inspirer in others of materialist doctrines which they held more definitely than he did. Just as Diderot could not attain to the concentration, the positiveness, the finality of aim needed for a masterpiece of literature, so he could not attain to those qualities in the way of dogma and system. Yet he drew at last to the conclusions of materialism, and contributed many of its most declamatory pages to the Système de la nature of his friend D’Holbach,—the very Bible of atheism, as some one styled it. All that he saw, if we reduce his opinions to formulae, was motion in space: “attraction and repulsion, the only truth.” If matter produces life by spontaneous generation, and if man has no alternative but to obey the compulsion of nature, what remains for God to do?
In proportion as these conclusions deepened in him, the more 206 did Diderot turn for the hope of the race to virtue; in other words, to such a regulation of conduct and motive as shall make us tender, pitiful, simple, contented. Hence his one great literary passion, his enthusiasm for Richardson, the English novelist. Hence, also, his deepening aversion for the political system of France, which makes the realization of a natural and contented domestic life so hard. Diderot had almost as much to say against society as even Rousseau himself. The difference between them was that Rousseau was a fervent theist. The atheism of the Holbachians, as he called Diderot’s group, was intolerable to him; and this feeling, aided by certain private perversities of humour, led to a breach of what had once been an intimate friendship between Rousseau and Diderot (1757). Diderot was still alive when Rousseau’s Confessions appeared, and he was so exasperated by Rousseau’s stories about Grimm, then and always Diderot’s intimate, that in 1782 he transformed a life of Seneca, that he had written four years earlier, into an Essai sur les règnes de Claude et de Néron (1778-1782), which is much less an account of Seneca than a vindication of Diderot and Grimm, and is one of the most rambling and inept productions in literature. As for the merits of the old quarrel between Rousseau and Diderot, we may agree with the latter, that too many sensible people would be in the wrong if Jean Jacques was in the right.
Varied and incessant as was Diderot’s mental activity, it was not of a kind to bring him riches. He secured none of the posts that were occasionally given to needy men of letters; he could not even obtain that bare official recognition of merit which was implied by being chosen a member of the Academy. The time came for him to provide a dower for his daughter, and he saw no other alternative than to sell his library. When the empress Catherine of Russia heard of his straits, she commissioned an agent in Paris to buy the library at a price equal to about £1000 of English money, and then handsomely requested the philosopher to retain the books in Paris until she required them, and to constitute himself her librarian, with a yearly salary. In 1773 Diderot started on an expedition to thank his imperial benefactress in person, and he passed some months at St Petersburg. The empress received him cordially. The strange pair passed their afternoons in disputes on a thousand points of high philosophy, and they debated with a vivacity and freedom not usual in courts. “Fi, donc,” said Catherine one day, when Diderot hinted that he argued with her at a disadvantage, “is there any difference among men?” Diderot returned home in 1774. Ten years remained to him, and he spent them in the industrious acquisition of new knowledge, in the composition of a host of fragmentary pieces, some of them mentioned above, and in luminous declamations with his friends. All accounts agree that Diderot was seen at his best in conversation. “He who only knows Diderot in his writings,” says Marmontel, “does not know him at all. When he grew animated in talk, and allowed his thoughts to flow in all their abundance, then he became truly ravishing. In his writings he had not the art of ensemble; the first operation which orders and places everything was too slow and too painful to him.” Diderot himself was conscious of the want of literary merit in his pieces. In truth he set no high value on what he had done. It is doubtful whether he was ever alive to the waste that circumstance and temperament together made of an intelligence from which, if it had been free to work systematically, the world of thought had so much to hope. He was one of those simple, disinterested and intellectually sterling workers to whom their own personality is as nothing in presence of the vast subjects that engage the thoughts of their lives. He wrote what he found to write, and left the piece, as Carlyle has said, “on the waste of accident, with an ostrich-like indifference.” When he heard one day that a collected edition of his works was in the press at Amsterdam, he greeted the news with “peals of laughter,” so well did he know the haste and the little heed with which those works had been dashed off.
Diderot died on the 30th of July 1784, six years after Voltaire and Rousseau, one year after his old colleague D’Alembert, and five years before D’Holbach, his host and intimate for a lifetime. Notwithstanding Diderot’s peals of laughter at the thought, an elaborate and exhaustive collection of his writings in twenty stout volumes, edited by MM. Assézat and Tourneux, was completed in 1875-1877.
Authorities.—Studies on Diderot by Scherer (1880); by E. Faguet (1890); by Sainte-Beuve in the Causeries du lundi; by F. Brunetière in the Études critiques, 2nd series, may be consulted. In English, Diderot has been the subject of a biography by John Morley [Viscount Morley of Blackburn] (1878). See also Karl Rosenkranz, Diderots Leben und Werke (1866). For a discussion of the authenticity of the posthumous works of Diderot see R. Dominic in the Revue des deux mondes (October 15, 1902).
DIDIUS SALVIUS JULIANUS, MARCUS, Roman emperor for two months (March 28-June 2) during the year a.d. 193. He was the grandson of the famous jurist Salvius Julianus (under Hadrian and the Antonines), and the son of a distinguished general, who might have ascended the throne after the death of Antoninus Pius, had not his loyalty to the ruling house prevented him. Didius filled several civil and military offices with distinguished success, but subsequently abandoned himself to dissipation. On the death of Pertinax, the praetorian guards offered the throne to the highest bidder. Flavius Sulpicianus, the father-in-law of Pertinax and praefect of the city, had already made an offer; Didius, urged on by the members of his family, his freedmen and parasites, hurried to the praetorian camp to contend for the prize. He and Sulpicianus bid against each other, and finally the throne was knocked down to Didius. The senate and nobles professed their loyalty; but the people made no attempt to conceal their indignation at this insult to the state, and the armies of Britain, Syria and Illyricum broke out into open revolt. Septimius Severus, the commander of the Pannonian legions, was declared emperor and hastened by forced marches to Italy. Didius, abandoned by the praetorians, was condemned and executed by order of the senate, which at once acknowledged Severus.
Authorities.—Dio Cassius lxxiii. 11-17, who was actually in Rome at the time; Aelius Spartianus, Didius Julianus; Julius Capitolinus, Pertinax; Herodian ii.; Aurelius Victor, De Caesaribus, 19; Zosimus i. 7; Gibbon, Decline and Fall, chap. 5.
DIDO, or Elissa, the reputed founder of Carthage (q.v.), in Africa, daughter of the Tyrian king Metten (Mutto, Methres, Belus), wife of Acerbas (more correctly Sicharbas; Sychaeus in Virgil), a priest of Hercules. Her husband having been slain by her brother Pygmalion, Dido fled to Cyprus, and thence to the coast of Africa, where she purchased from a local chieftain Iarbas a piece of land on which she built Carthage. The city soon began to prosper and Iarbas sought Dido’s hand in marriage, threatening her with war in case of refusal. To escape from him, Dido constructed a funeral pile, on which she stabbed herself before the people (Justin xviii. 4-7). Virgil, in defiance of the usually accepted chronology, makes Dido a contemporary of Aeneas, with whom she fell in love after his landing in Africa, and attributes her suicide to her abandonment by him at the command of Jupiter (Aeneid, iv.). Dido was worshipped at Carthage as a divinity under the name of Caelestis, the Roman counterpart of Tanit, the tutelary goddess of Carthage. According to Timaeus, the oldest authority for the story, her name was Theiosso, in Phoenician Helissa, and she was called Dido from her wanderings, Dido being the Phoenician equivalent of πλανῆτις (Etymologicum Magnum, s.v.); some modern scholars, however, translate the name by “beloved.” Timaeus makes no mention of Aeneas, who seems to have been introduced by Naevius in his Bellum Poenicum, followed by Ennius in his Annales.
For the variations of the legend in earlier and later Latin authors, see O. Rossbach in Pauly-Wissowa’s Realencyclopädie, v. pt. 1 (1905); O. Meltzer’s Geschichte der Karthager, i. (1879), and his article in Roscher’s Lexikon der Mythologie.
DIDON, HENRI (1840-1900), French Dominican, was born at Trouvet, Isère, on the 17th of March 1840. He joined the Dominicans, under the influence of Lacordaire, in 1858, and completed his theological studies at the Minerva convent at Rome. The influence of Lacordaire was shown in the zeal displayed by Didon in favour of a reconciliation between philosophy and science. In 1871 his fame had so much grown that he was chosen to deliver the funeral oration over the murdered archbishop of Paris, Monseigneur G. Darboy. He also delivered some 207 discourses at the church of St Jean de Beauvais in Paris on the relations between science and religion; but his utterances, especially on the question of divorce, were deemed suspicious by his superiors, and his intimacy with Claude Bernard the physiologist was disapproved. He was interdicted from preaching and sent into retirement at the convent of Corbara in Corsica. After eighteen months he emerged, and travelled in Germany, publishing an interesting work upon that country, entitled Les Allemands (English translation by R. Ledos de Beaufort, London, 1884). On his return to France in 1890 he produced his best known work, Jésus-Christ (2 vols., Paris), for which he had qualified himself by travel in the Holy Land. In the same year he became director of the Collège Albert-le-Grand at Arcueil, and founded three auxiliary institutions, École Lacordaire, École Laplace and École St Dominique. He wrote, in addition, several works on educational questions, and augmented his fame as an eloquent preacher by discourses preached during Lent and Advent. He died at Toulouse on the 13th of March 1900.
See the biographies by J. de Romano (1891), and A. de Coulanges (Paris, 1900); and especially the work of Stanislas Reynaud, entitled Le Père Didon, sa vie et son œuvre (Paris, 1904).
DIDOT, the name of a family of learned French printers and publishers. François Didot (1689-1757), founder of the family, was born at Paris. He began business as a bookseller and printer in 1713, and among his undertakings was a collection of the travels of his friend the Abbé Prévost, in twenty volumes (1747). It was remarkable for its typographical perfection, and was adorned with many engravings and maps. François Ambroise Didot (1730-1804), son of François, made important improvements in type-founding, and was the first to attempt printing on vellum paper. Among the works which he published was the famous collection of French classics prepared by order of Louis XVI. for the education of the Dauphin, and the folio edition of L’Art de vérifier les dates. Pierre François Didot (1732-1795), his brother, devoted much attention to the art of type-founding and to paper-making. Among the works which issued from his press was an edition in folio of the Imitatio Christi (1788). Henri Didot (1765-1852), son of Pierre François, is celebrated for his “microscopic” editions of various standard works, for which he engraved the type when nearly seventy years of age. He was also the engraver of the assignats issued by the Constituent and Legislative Assemblies and the Convention. Didot Saint-Léger, second son of Pierre François, was the inventor of the paper-making machine known in England as the Didot machine. Pierre Didot (1760-1853), eldest son of François Ambroise, is celebrated as the publisher of the beautiful “Louvre” editions of Virgil, Horace and Racine. The Racine, in three volumes folio, was pronounced in 1801 to be “the most perfect typographical production of all ages.” Firmin Didot (1764-1836), his brother, second son of François Ambroise, sustained the reputation of the family both as printer and type-founder. He revived (if he did not invent—a distinction which in order of time belongs to William Ged) the process of stereotyping, and coined its name, and he first used the process in his edition of Callet’s Tables of Logarithms (1795), in which he secured an accuracy till then unattainable. He published stereotyped editions of French, English and Italian classics at a very low price. He was the author of two tragedies—La Reine de Portugal and La Mort d’Annibal; and he wrote metrical translations from Virgil, Tyrtaeus and Theocritus. Ambroise Firmin Didot (1790-1876) was his eldest son. After receiving a classical education, he spent three years in Greece and in the East; and on the retirement of his father in 1827 he undertook, in conjunction with his brother Hyacinthe, the direction of the publishing business. Their greatest undertaking was a new edition of the Thesaurus Graecae linguae of Henri Estienne, under the editorial care of the brothers Dindorf and M. Hase (9 vols., 1855-1859). Among the numerous important works published by the brothers, the 200 volumes forming the Bibliothèque des auteurs grecs, Bibliothèque latine, and Bibliothèque française deserve special mention. Ambroise Firmin Didot was the first to propose (1823) a subscription in favour of the Greeks, then in insurrection against Turkish tyranny. Besides a translation of Thucydides (1833), he wrote the articles “Estienne” in the Nouvelle Biographie générale, and “Typographie” in the Ency. mod., as well as Observations sur l’orthographie française (1867), &c. In 1875 he published a very learned and elaborate monograph on Aldus Manutius. His collection of MSS., the richest in France, was said to have been worth, at the time of his death, not less than 2,000,000 francs.
DIDRON, ADOLPHE NAPOLÉON (1806-1867), French archaeologist, was born at Hautvillers, in the department of Marne, on the 13th of March 1806. At first a student of law, he began in 1830, by the advice of Victor Hugo, a study of the Christian archaeology of the middle ages. After visiting and examining the principal churches, first of Normandy, then of central and southern France, he was on his return appointed by Guizot secretary to the Historical Committee of Arts and Monuments (1835); and in the following years he delivered several courses of lectures on Christian iconography at the Bibliothèque Royale. In 1839 he visited Greece for the purpose of examining the art of the Eastern Church, both in its buildings and its manuscripts. In 1844 he originated the Annales archéologiques, a periodical devoted to his favourite subject, which he edited until his death. In 1845 he established at Paris a special archaeological library, and at the same time a manufactory of painted glass. In the same year he was admitted to the Legion of Honour. His most important work is the Iconographie chrétienne, of which, however, the first portion only, Histoire de Dieu (1843), was published. It was translated into English by E. J. Millington. Among his other works may be mentioned the Manuel d’iconographie chrétienne grecque et latine (1845), the Iconographie des chapiteaux du palais ducal de Venise (1857), and the Manuel des objets de bronze et d’orfèvrerie (1859). He died on the 13th of November 1867.
DIDYMI, or Didyma (mod. Hieronta), an ancient sanctuary of Apollo in Asia Minor situated in the territory of Miletus, from which it was distant about 10 m. S. and on the promontory Poseideion. It was sometimes called Branchidae from the name of its priestly caste which claimed descent from Branchus, a youth beloved by Apollo. As the seat of a famous oracle, the original temple attracted offerings from Pharaoh Necho (in whose army there was a contingent of Milesian mercenaries), and the Lydian Croesus, and was plundered by Darius of Persia. Xerxes finally sacked and burnt it (481 b.c.) and exiled the Branchidae to the far north-east of his empire. This exile was believed to be voluntary, the priests having betrayed their treasures to the Persian; and on this belief Alexander the Great acted 150 years later, when, finding the descendants of the Branchidae established in a city beyond the Oxus, he ordered them to be exterminated for the sin of their fathers (328). The celebrated cult-statue of Apollo by Canachus, familiar to us from reproductions on Milesian coins, was also carried to Persia, there to remain till restored by Seleucus I. in 295, and the oracle ceased to speak for a century and a half. The Milesians were not able to undertake the rebuilding till about 332 b.c., when the oracle revived at the bidding of Alexander. The work proved too costly, and despite a special effort made by the Asian province nearly 400 years later, at the bidding of the emperor Caligula, the structure was never quite finished: but even as it was, Strabo ranked the Didymeum the greatest of Greek temples and Pliny placed it among the four most splendid and second only to the Artemisium at Ephesus. In point of fact it was a little smaller than the Samian Heraeum and the temple of Cybele at Sardis, and almost exactly the same size as the Artemisium. The area covered by the platform measures roughly 360 × 160 ft.
When Cyriac of Ancona visited the spot in 1446, it seems that the temple was still standing in great part, although the cella had been converted into a fortress by the Byzantines: but when the next European visitor, the Englishman Dr Pickering, arrived in 1673, it had collapsed. It is conjectured that the cause was the great earthquake of 1493. The Society of Dilettanti sent two expeditions to explore the ruins, the first in 1764 under Richard Chandler, the second in 1812 under Sir Wm. Gell; and the French 208 “Rothschild Expedition” of 1873 under MM. O. Rayet and A. Thomas sent a certain amount of architectural sculpture to the Louvre. But no excavation was attempted till MM. E. Pontremoli and B. Haussoullier were sent out by the French Schools of Rome and Athens in 1895. They cleared the western façade and the prodomos, and discovered inscriptions giving information about other parts which they left still buried. Finally the site was purchased by, and the French rights were ceded to, Dr Th. Wiegand, the German explorer of Miletus, who in 1905 began a thorough clearance of what is incomparably the finest temple ruin in Asia Minor.
The temple was a decastyle peripteral structure of the Ionic order, standing on seven steps and possessing double rows of outer columns 60 ft. high, twenty-one in each row on the flanks. It is remarkable not only for its great size, but (inter alia) for (1) the rich ornament of its column bases, which show great variety of design; (2) its various developments of the Ionic capital, e.g. heads of gods, probably of Pergamene art, spring from the “eyes” of the volutes with bulls’ heads between them; (3) the massive building two storeys high at least, which served below for prodomos, and above for a dispensary of oracles (χρησμογράφια mentioned in the inscriptions) and a treasury; two flights of stairs called “labyrinths” in the inscriptions, led up to these chambers; (4) the pylon and staircase at the west; (5) the frieze of Medusa heads and foliage. Two outer columns are still erect on the north-east flank, carrying their entablature, and one of the inner order stands on the south-west. The fact that the temple was never finished is evident from the state in which some bases still remain at the west. There were probably no pedimental sculptures. A sacred way led from the temple to the sea at Panormus, which was flanked with rows of archaic statues, ten of which were excavated and sent to the British Museum in 1858 by C. T. Newton. Fragments of architectural monuments, which once adorned this road, have also been found. Modern Hieronta is a large and growing Greek village, the only settlement within a radius of several miles. Its harbour is Kovella, distant about 2½ m., and on the N. of the promontory.
See Dilettanti Society, Ionian Antiquities, ii. (1821); C. T. Newton, Hist. of Discoveries, &c. (1862) and Travels in the Levant, ii. (1865); O. Rayet and A. Thomas, Milet et le Golfe Latmique (1877); E. Pontremoli and B. Haussoullier, Didymes (1904).
DIDYMIUM (from the Gr. διδυμος, twin), the name given to the supposed element isolated by C. G. Mosander from cerite (1839-1841). In 1879, however, Lecoq de Boisbaudran showed that Mosander’s “didymium” contained samarium; while the residual “didymium,” after removal of samarium, was split by Auer v. Welsbach (Monats. f. Chemie, 1885, 6, 477) into two components (known respectively as neodymium and praseodymium) by repeated fractional crystallization of the double nitrate of ammonium and didymium in nitric acid. Neodymium (Nd) forms the chief portion of the old “didymium.” Its salts are reddish violet in colour, and give a characteristic absorption spectrum. It forms oxides of composition Nd2O3 and Nd2O5, the latter being obtained by ignition of the nitrate (B. Brauner). The atomic weight of neodymium is 143.6 (B. Brauner, Proc. Chem. Soc., 1897-1898, p. 70). Praseodymium (Pr) forms oxides of composition Pr2O3, Pr2O5 ,xH2O (B. Brauner), and Pr4O7. The peroxide, Pr4O7, forms a dark brown powder, and is obtained by ignition of the oxalate or nitrate. The sesquioxide, Pr2O3, is obtained as a greenish white mass by the reduction of the peroxide. The salts of praseodymium are green in colour, and give a characteristic spark spectrum. The atomic weight of praseodymium is 140.5.
DIDYMUS (?309-?394), surnamed “the Blind,” ecclesiastical writer of Alexandria, was born about the year 309. Although he became blind at the age of four, before he had learned to read; he succeeded in mastering the whole circle of the sciences then known; and on entering the service of the Church he was placed at the head of the Catechetical school in Alexandria, where he lived and worked till almost the close of the century. Among his pupils were Jerome and Rufinus. He was a loyal follower of Origen, though stoutly opposed to Arian and Macedonian teaching. Such of his writings as survive show a remarkable knowledge of scripture, and have distinct value as theological literature. Among them are the De Trinitate, De Spiritu Sancto (Jerome’s Latin translation), Adversus Manichaeos, and notes and expositions of various books, especially the Psalms and the Catholic Epistles.
See Migne, Patrol. Graec. xxxix.; O. Bardenhewer, Patrologie, pp. 290-293 (Freiburg, 1894).
DIDYMUS CHALCENTERUS (c. 63 b.c.-a.d. 10), Greek scholar and grammarian, flourished in the time of Cicero and Augustus. His surname (Gr. Χαλκέντερος, brazen-bowelled) came from his indefatigable industry; he was said to have written so many books (more than 3500) that he was unable to recollect their names (βιβλιολάθας). He lived and taught in Alexandria and Rome, where he became the friend of Varro. He is chiefly important as having introduced Alexandrian learning to the Romans. He was a follower of the school of Aristarchus, upon whose recension of Homer he wrote a treatise, fragments of which have been preserved in the Venetian Scholia. He also wrote commentaries on many other Greek poets and prose authors. In his work on the lyric poets he treated of the various classes of poetry and their chief representatives, and his lists of words and phrases (used in tragedy and comedy and by orators and historians), of words of doubtful meaning, and of corrupt expressions, furnished the later grammarians with valuable material. His activity extended to all kinds of subjects: grammar (orthography, inflexions), proverbs, wonderful stories, the law-tablets (ἄξονες) of Solon, stones, and different kinds of wood. His polemic against Cicero’s De republica (Ammianus Marcellinus xxii. 16) provoked a reply from Suetonius. In spite of his stupendous industry, Didymus was little more than a compiler, of little critical judgment and doubtful accuracy, but he deserves recognition for having incorporated in his numerous writings the works of earlier critics and commentators.
See M. W. Schmidt, De Didymo Chalcentero (1853) and Didymi Chalcenteri fragmenta (1854); also F. Susemihl, Geschichte der griech. Literatur in der Alexandrinerzeit, ii. (1891); J. E. Sandys, History of Classical Scholarship, i. (1906).
DIE, a town of south-eastern France, capital of an arrondissement in the department of Drôme, 43 m. E.S.E. of Valence on the Paris-Lyon railway. Pop. (1906) 3090. The town is situated in a plain enclosed by mountains on the right bank of the Drôme below its confluence with the Meyrosse, which supplies power to some of the industries. The most interesting structures of Die are the old cathedral, with a porch of the 11th century supported on granite columns from an ancient temple of Cybele; and the Porte St Marcel, a Roman gateway flanked by massive towers. The Roman remains also include the ruins of aqueducts and altars. Die is the seat of a sub-prefect, and of a tribunal of first instance. The manufactures are silk, furniture, cloth, lime and cement, and there are flour and saw mills. Trade is in timber, especially walnut, and in white wine known as clairette de Die. The mulberry is largely grown for the rearing of silkworms. Under the Romans, Die (Dea Augusta Vocontiorum) was an important colony. It was formerly the seat of a bishopric, united to that of Valence from 1276 to 1687 and suppressed in 1790. Previous to the revocation of the edict of Nantes in 1685 it had a Calvinistic university.
DIE (Fr. dé, from Lat. datum, given), a word used in various senses, for a small cube of ivory, &c. (see Dice), for the engraved stamps used in coining money, &c., and various mechanical appliances in engineering. In architecture a “die” is the term used for the square base of a column, and it is applied also to the vertical face of a pedestal or podium.
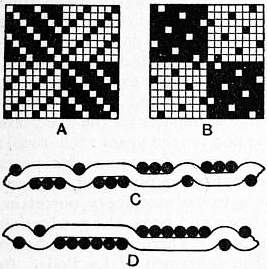 |
The fabrics known as “dice” take their name from the rectangular form of the figure. The original figures would probably be perfectly square, but to-day the same principle of weaving is applied, and the name dice is given to all figures of rectangular form. The different effects in the adjacent squares or rectangles are due to precisely the same reasons as those explained in connexion with the ground and the figure of damasks. The same weaves are used in both damasks and dices, but simpler 209 weaves are generally employed for the commoner classes of the latter. The effect is, in every case, obtained by what are technically called warp and weft float weaves. The illustration B shows the two double damask weaves arranged to form a dice pattern, while A shows a similar pattern made from two four-thread twill weaves. C and D represent respectively the disposition of the threads in A and B with the first pick, and the solid marks represent the floats of warp. The four squares, which are almost as pronounced in the cloth as those of a chess-board, may be made of any size by repeating each weave for the amount of surface required. It is only in the finest cloths that the double damask weaves B are used for dice patterns, the single damask weaves and the twill weaves being employed to a greater extent. This class of pattern is largely employed for the production of table-cloths of lower and medium qualities. The term damask is also often applied to cloths of this character, and especially so when the figure is formed by rectangles of different sizes.
DIEBITSCH, HANS KARL FRIEDRICH ANTON, count von Diebitsch and Narden, called by the Russians Ivan Ivanovich, Count Diebich-Zabalkansky (1785-1831), Russian field-marshal, was born in Silesia on the 13th of May 1785. He was educated at the Berlin cadet school, but by the desire of his father, a Prussian officer who had passed into the service of Russia, he also did the same in 1801. He served in the campaign of 1805, and was wounded at Austerlitz, fought at Eylau and Friedland, and after Friedland was promoted captain. During the next five years of peace he devoted himself to the study of military science, engaging once more in active service in the War of 1812. He distinguished himself very greatly in Wittgenstein’s campaign, and in particular at Polotzk (October 18 and 19), after which combat he was raised to the rank of major-general. In the latter part of the campaign he served against the Prussian contingent of General Yorck (von Wartenburg), with whom, through Clausewitz, he negotiated the celebrated convention of Tauroggen, serving thereafter with Yorck in the early part of the War of Liberation. After the battle of Lützen he served in Silesia and took part in negotiating the secret treaty of Reichenbach. Having distinguished himself at the battles of Dresden and Leipzig he was promoted lieutenant-general. At the crisis of the campaign of 1814 he strongly urged the march of the allies on Paris; and after their entry the emperor Alexander conferred on him the order of St Alexander Nevsky. In 1815 he attended the congress of Vienna, and was afterwards made adjutant-general to the emperor, with whom, as also with his successor Nicholas, he had great influence. By Nicholas he was created baron, and later count. In 1820 he had become chief of the general staff, and in 1825 he assisted in suppressing the St Petersburg émeute. His greatest exploits were in the Russo-Turkish War of 1828-1829, which, after a period of doubtful contest, was decided by Diebitsch’s brilliant campaign of Adrianople; this won him the rank of field-marshal and the honorary title of Zabalkanski to commemorate his crossing of the Balkans. In 1830 he was appointed to command the great army destined to suppress the insurrection in Poland. He won the terrible battle of Gróchow on the 25th of February, and was again victorious at Ostrolenka on the 26th of May, but soon afterwards he died of cholera (or by his own hand) at Klecksewo near Pultusk, on the 10th of June 1831.
See Belmont (Schümberg), Graf Diebitsch (Dresden, 1830); Stürmer, Der Tod des Grafen Diebitsch (Berlin, 1832); Bantych-Kamenski, Biographies of Russian Field-Marshals (in Russian, St Petersburg, 1841).
DIEDENHOFEN (Fr. Thionville), a fortified town of Germany, in Alsace-Lorraine, dist. Lorraine, on the Mosel, 22 m. N. from Metz by rail. Pop. (1905) 6047. It is a railway junction of some consequence, with cultivation of vines, fruit and vegetables, brewing, tanning, &c. Diedenhofen is an ancient Frank town (Theudonevilla, Totonisvilla), in which imperial diets were held in the 8th century; was captured by Condé in 1643 and fortified by Vauban; capitulated to the Prussians, after a severe bombardment, on the 25th of November 1870.
DIEKIRCH, a small town in the grand duchy of Luxemburg, charmingly situated on the banks of the Sûre. Pop. (1905) 3705. Its name is said to be derived from Dide or Dido, granddaughter of Odin and niece of Thor. The mountain at the foot of which the town lies, now called Herrenberg, was formerly known as Thorenberg, or Thor’s mountain. On the summit of this rock rises a perennial stream which flows down into the town under the name of Bellenflesschen. Diekirch was an important Roman station, and in the 14th century John of Luxemburg, the blind king of Bohemia, fortified it, surrounding the place with a castellated wall and a ditch supplied by the stream mentioned. It remained more or less fortified until the beginning of the 19th century when the French during their occupation levelled the old walls, and substituted the avenues of trees that now encircle the town. Diekirch is the administrative centre of one of the three provincial divisions of the grand duchy. It is visited during the summer by many thousand tourists and travellers from Holland, Belgium and Germany.
DIELECTRIC, in electricity, a non-conductor of electricity; it is the same as insulator. The “dielectric constant” of a medium is its specific inductive capacity, and on the electromagnetic theory of light it equals the square of its refractive index for light of infinite wave length (see Electrostatics; Magneto-Optics).
DIELMANN, FREDERICK (1847- ), American portrait and figure painter, was born at Hanover, Germany, on the 25th of December 1847. He was taken to the United States in early childhood; studied under Diez at the Royal Academy at Munich; was first an illustrator, and became a distinguished draughtsman and painter of genre pictures. His mural decorations and mosaic panels for the Congressional library, Washington, are notable. He was elected in 1899 president of the National Academy of Design.
DIEMEN, ANTHONY VAN (1593-1645), Dutch admiral and governor-general of the East Indian settlements, was born at Kuilenburg in 1593. He was educated in commerce, and on entering the service of the East India Company speedily attained high rank. In 1631 he led a Dutch fleet from the Indies to Holland, and in 1636 he was raised to the governor-generalship. He came into conflict with the Portuguese, and took their possessions in Ceylon and Malacca from them. He greatly extended the commercial relationships of the Dutch, opening up trade with Tong-king, China and Japan. As an administrator also he showed ability, and the foundation of a Latin school and several churches in Batavia is to be ascribed to him. Exploring expeditions were sent to Australia under his auspices in 1636 and 1642, and Abel Tasman named after him (Van Diemen’s Land) the island now called Tasmania. Van Diemen died at Batavia on the 19th of April 1645.
DIEPENBECK, ABRAHAM VAN (1599-1675), Flemish painter, was born at Herzogenbusch, and studied painting at Antwerp, where he became one of Rubens’s “hundred pupils.” But he was not one of the cleverest of Rubens’s followers, and he succeeded, at the best, in imitating the style and aping the peculiarities of his master. We see this in his earliest pictures—a portrait dated 1629 in the Munich Pinakothek, and a “Distribution of Alms” of the same period in the same collection. Yet even at this time there were moments when Diepenbeck probably fancied that he might take another path. A solitary copperplate executed with his own hand in 1630 represents a peasant sitting under a tree holding the bridle of an ass, and this is a minute and finished specimen of the engraver’s art which shows that the master might at one time have hoped to rival the animal draughtsmen who flourished in the schools of Holland. However, large commissions now poured in upon him; he was asked for altarpieces, subject-pieces and pagan allegories. He was tempted to try the profession of a glass-painter, and at last he gave up every 210 other occupation for the lucrative business of a draughtsman and designer for engravings. Most of Diepenbeck’s important canvases are in continental galleries. The best are the “Marriage of St Catherine” at Berlin and “Mary with Angels Wailing over the Dead Body of Christ” in the Belvedere at Vienna, the first a very fair specimen of the artist’s skill, the second a picture of more energy and feeling than might be expected from one who knew more of the outer form than of the spirit of Rubens. Then we have the fine “Entombment” at Brunswick, and “St Francis Adoring the Sacrament” at the museum at Brussels, “Clelia and her Nymphs Flying from the Presence and Pursuit of Porsenna” in two examples at Berlin and Paris, and “Neptune and Amphitrite” at Dresden. In all these compositions the drawing and execution are after the fashion of Rubens, though inferior to Rubens in harmony of tone and force of contrasted light and shade. Occasionally a tendency may be observed to imitate the style of Vandyck, for whom, in respect of pictures, Diepenbeck in his lifetime was frequently taken. But Diepenbeck spent much less of his leisure on canvases than on glass-painting. Though he failed to master the secrets of gorgeous tinting, which were lost, apparently for ever in the 16th century, he was constantly employed during the best years of his life in that branch of his profession. In 1635 he finished forty scenes from the life of St Francis of Paula in the church of the Minimes at Antwerp. In 1644 he received payment for four windows in St Jacques of Antwerp, two of which are still preserved, and represent Virgins to whom Christ appears after the Resurrection. The windows ascribed to him at St Gudule of Brussels were executed from the cartoons of Theodore van Thulden. On the occasion of his matriculation at Antwerp in 1638-1639, Diepenbeck was registered in the guild of St Luke as a glass-painter. He resigned his membership in the Artist Club of the Violette in 1542, apparently because he felt hurt by a valuation then made of drawings furnished for copperplates to the engraver Pieter de Jode. The earliest record of his residence at Antwerp is that of his election to the brotherhood (Sodalität) “of the Bachelors” in 1634. It is probable that before this time he had visited Rome and London, as noted in the work of Houbraken. In 1636 he was made a burgess of Antwerp. He married twice, in 1637 and 1652. He died in December 1675, and was buried at St Jacques of Antwerp.
DIEPPE, a seaport of northern France, capital of an arrondissement in the department of Seine-Inférieure, on the English Channel, 38 m. N. of Rouen, and 105 m. N.W. of Paris by the Western railway. Pop. (1906) 22,120. It is situated at the mouth of the river Arques in a valley bordered on each side by steep white cliffs. The main part of the town lies to the west, and the fishing suburb of Le Pollet to the east of the river and harbour. The sea-front of Dieppe, which in summer attracts large numbers of visitors, consists of a pebbly beach backed by a handsome marine promenade. Dieppe has a modern aspect; its streets are wide and its houses, in most cases, are built of brick. Two squares side by side and immediately to the west of the outer harbour form the nucleus of the town, the Place Nationale, overlooked by the statue of Admiral A. Duquesne, and the Place St Jacques, named after the beautiful Gothic church which stands in its centre. The Grande Rue, the busiest and handsomest street, leads westward from the Place Nationale. The church of St Jacques was founded in the 13th century, but consists in large measure of later workmanship and was in some portions restored in the 19th century. The castle, overlooking the beach from the summit of the western cliff, was erected in 1435. The church of Notre-Dame de Bon Secours on the opposite cliff, and the church of St Remy, of the 16th and 17th centuries, are other noteworthy buildings. A well-equipped casino stands at the west end of the sea-front. The public institutions include the subprefecture, tribunals of first instance and commerce, a chamber of commerce, a communal college and a school of navigation.
Dieppe has one of the safest and deepest harbours on the English Channel. A curved passage cut in the bed of the Arques and protected by an eastern and a western jetty gives access to the outer harbour, which communicates at the east end by a lockgate with the Bassin Duquesne and the Bassin Bérigny, and at the west end by the New Channel, with an inner tidal harbour and two other basins. Vessels drawing 20 ft. can enter the new docks at neap tide. A dry-dock and a gridiron are included among the repairing facilities of the port. The harbour railway station is on the north-west quay of the outer harbour alongside which the steamers from Newhaven lie. The distance of Dieppe from Newhaven, with which there has long been daily communication, is 64 m. The imports include silk and cotton goods, thread, oil-seeds, timber, coal and mineral oil; leading exports are wine, silk, woollen and cotton fabrics, vegetables and fruit and flint-pebbles. The average annual value of imports for the five years 1901-1905 was £4,916,000 (£4,301,000 for the years 1896-1900); the exports were valued at £9,206,000 (£7,023,000 for years 1896-1900). The industries comprise shipbuilding, cotton-spinning, steam-sawing, the manufacture of machinery, porcelain, briquettes, lace, and articles in ivory and bone, the production of which dates from the 15th century. There is also a tobacco factory of some importance. The fishermen of Le Pollet, to whom tradition ascribes a Venetian origin, are among the main providers of the Parisian market. The sea-bathing attracts many visitors in the summer. Two miles to the north-east of the town is the ancient camp known as the Cité de Limes, which perhaps furnished the nucleus of the population of Dieppe.
It is suggested on the authority of its name, that Dieppe owed its origin to a band of Norman adventurers, who found its “diep” or inlet suitable for their ships, but it was unimportant till the latter half of the 12th century. Its first castle was probably built in 1188 by Henry II. of England, and it was counted a place of some consideration when Philip Augustus attacked it in 1195. By Richard I. of England it was bestowed in 1197 on the archbishop of Rouen in return for certain territory in the neighbourhood of the episcopal city. In 1339 it was plundered by the English, but it soon recovered from the blow, and in spite of the opposition of the lords of Hantot managed to surround itself with fortifications. Its commercial activity was already great, and it is believed that its seamen visited the coast of Guinea in 1339, and founded there a Petit Dieppe in 1365. The town was occupied by the English from 1420 to 1435. A siege undertaken in 1442 by John Talbot, first earl of Shrewsbury, was raised by the dauphin, afterwards Louis XI., and the day of the deliverance continued for centuries to be celebrated by a great procession and miracle plays. In the beginning of the 16th century Jean Parmentier, a native of the town, made voyages to Brazil and Sumatra; and a little later its merchant prince, Jacques Ango, was able to blockade the Portuguese fleet in the Tagus. Francis I. began improvements which were continued under his successor. Its inhabitants in great number embraced the reformed religion; and they were among the first to acknowledge Henry IV., who fought one of his great battles at the neighbouring village of Arques. Few of the cities of France suffered more from the revocation of the edict of Nantes in 1685; and this blow was followed in 1694 by a terrible bombardment on the part of the English and Dutch. The town was rebuilt after the peace of Ryswick, but the decrease of its population and the deterioration of its port prevented the restoration of its commercial prosperity. During the 19th century it made rapid advances, partly owing to Marie Caroline, duchess of Berry, who brought it into fashion as a watering-place; and also because the establishment of railway communication with Paris gave an impetus to its trade. During the Franco-German War the town was occupied by the Germans from December 1870 till July 1871.
See L. Vitet, Histoire de Dieppe (Paris, 1844); D. Asseline, Les Antiquités et chroniques de la ville de Dieppe, a 17th-century account published at Paris in 1874.
DIERX, LÉON (1838- ), French poet, was born in the island of Réunion in 1838. He came to Paris to study at the Central School of Arts and Manufactures, and subsequently settled there, taking up a post in the education office. He became a disciple of Leconte de Lisle and one of the most distinguished of the Parnassians. In the death of Stéphane Mallarmé in 1898 he was acclaimed “prince of poets” by “les jeunes.” His works include: Poèmes et poésies (1864); 211 Lèvres closes (1867); Paroles d’un vaincu (1871); La Rencontre, a dramatic scene (1875) and Les Amants (1879). His Poésies complètes (1872) were crowned by the French Academy. A complete edition of his works was published in 2 vols., 1894-1896.
DIES, CHRISTOPH ALBERT (1755-1822), German painter, was born at Hanover, and learned the rudiments of art in his native place. For one year he studied in the academy of Dusseldorf, and then he started at the age of twenty with thirty ducats in his pocket for Rome. There he lived a frugal life till 1796. Copying pictures, chiefly by Salvator Rosa, for a livelihood, his taste led him to draw and paint from nature in Tivoli, Albano and other picturesque places in the vicinity of Rome. Naples, the birthplace of his favourite master, he visited more than once for the same reasons. In this way he became a bold executant in water-colours and in oil, though he failed to acquire any originality of his own. Lord Bristol, who encouraged him as a copyist, predicted that he would be a second Salvator Rosa. But Dies was not of the wood which makes original artists. Besides other disqualifications, he had necessities which forced him to give up the great career of an independent painter. David, then composing his Horatii at Rome, wished to take him to Paris. But Dies had reasons for not accepting the offer. He was courting a young Roman whom he subsequently married. Meanwhile he had made the acquaintance of Volpato, for whom he executed numerous drawings, and this no doubt suggested the plan, which he afterwards carried out, of publishing, in partnership with Méchan, Reinhardt and Frauenholz, the series of plates known as the Collection de vues pittoresques de l’Italie, published in seventy-two sheets at Nuremberg in 1799. With so many irons in the fire Dies naturally lost the power of concentration. Other causes combined to affect his talent. In 1787 he swallowed by mistake three-quarters of an ounce of sugar of lead. His recovery from this poison was slow and incomplete. He settled at Vienna, and lived there on the produce of his brush as a landscape painter, and on that of his pencil or graver as a draughtsman and etcher. But instead of getting better, his condition became worse, and he even lost the use of one of his hands. In this condition he turned from painting to music, and spent his leisure hours in the pleasures of authorship. He did not long survive, dying at Vienna in 1822, after long years of chronic suffering. From two pictures now in the Belvedere gallery, and from numerous engraved drawings from the neighbourhood of Tivoli, we gather that Dies was never destined to rise above a respectable mediocrity. He followed Salvator Rosa’s example in imitating the manner of Claude Lorraine. But Salvator adapted the style of Claude, whilst Dies did no more than copy it.
DIEST, a small town in the province of Brabant, Belgium, situated on the Demer at its junction with the Bever. Pop. (1904) 8383. It lies about half-way between Hasselt and Louvain, and is still one of the five fortified places in Belgium. It contains many breweries, and is famous for the excellence of its beer.
DIESTERWEG, FRIEDRICH ADOLF WILHELM (1790-1866), German educationist, was born at Siegen on the 29th of October 1790. Educated at Herborn and Tübingen universities, he took to the profession of teaching in 1811. In 1820 he was appointed director of the new school at Mörs, where he put in practice the methods of Pestalozzi. In 1832 he was summoned to Berlin to direct the new state-schools seminary in that city. Here he proved himself a strong supporter of unsectarian religious teaching. In 1846 he established the Pestalozzi institution at Pankow, and the Pestalozzi societies for the support of teachers’ widows and orphans. In 1850 he retired on a pension, but continued vigorously to advocate his educational views. In 1858 he was elected to the chamber of deputies as member for the city of Berlin, and voted with the Liberal opposition. He died in Berlin on the 7th of July 1866. Diesterweg was a voluminous writer on educational subjects, and was the author of various school text-books.
DIET, a term used in two senses, (1) food or the regulation of feeding (see Dietary and Dietetics), (2) an assembly or council (Fr. diète; It. dieta; Low Lat. diaeta; Ger. Tag). We are here concerned only with this second sense. In modern usage, though in Scotland the term is still sometimes applied to any assembly or session, it is practically confined to the sense of an assembly of estates or of national or federal representatives. The origin of the word in this connotation is somewhat complicated. It is undoubtedly ultimately derived from the Greek δίαιτα (Lat. diaeta), which meant “mode of life” and thence “prescribed mode of life,” the English “diet” or “regimen.” This was connected with the verb διαιτᾶν, in the sense of “to rule,” “to regulate”; compare the office of διαιτητής at Athens, and dieteta, “umpire,” in Late Latin. In both Greek and Latin, too, the word meant “a room,” from which the transition to “a place of assembly” and so to “an assembly” would be easy. In the latter sense the word, however, actually occurs only in Low Latin, Du Cange (Glossarium, s.v.) deriving it from the late sense of “meal” or “feast,” the Germans being accustomed to combine their political assemblies with feasting. It is clear, too, that the word diaeta early became confused with Lat. dies, “day” (Ger. Tag), “especially a set day, a day appointed for public business; whence, by extension, meeting for business, an assembly” (Skeat). Instances of this confusion are given by Du Cange, e.g. diaeta for dieta, “a day’s journey” (also an obsolete sense of “diet” in English), and dieta for “the ordinary course of the church,” i.e. “the daily office,” which suggests the original sense of diaeta as “a prescribed mode of life.”
The word “diet” is now used in English for the Reichstag, “imperial diet” of the old Holy Roman Empire; for the Bundestag, “federal diet,” of the former Germanic confederation; sometimes for the Reichstag of the modern German empire; for the Landtage, “territorial diets” of the constituent states of the German and Austrian empires; as well as for the former or existing federal or national assemblies of Switzerland, Hungary, Poland, &c. Although, however, the word is still sometimes used of all the above, the tendency is to confine it, so far as contemporary assemblies are concerned, to those of subordinate importance. Thus “parliament” is often used of the German Reichstag or of the Russian Landtag, while the Landtag, e.g. of Styria, would always be rendered “diet.” In what follows we confine ourselves to the diet of the Holy Roman Empire and its relation to its successors in modern Germany.
The origin of the diet, or deliberative assembly, of the Holy Roman Empire must be sought in the placitum of the Frankish empire. This represented the tribal assembly of the Franks, meeting (originally in March, but after 755 in May, whence it is called the Campus Maii) partly for a military review on the eve of the summer campaign, partly for deliberation on important matters of politics and justice. By the side of this larger assembly, however, which contained in theory, if not in practice, the whole body of Franks available for war, there had developed, even before Carolingian times, a smaller body composed of the magnates of the Empire, both lay and ecclesiastical. The germ of this smaller body is to be found in the episcopal synods, which, afforced by the attendance of lay magnates, came to be used by the king for the settlement of national affairs. Under the Carolingians it was usual to combine the assembly of magnates with the generalis conventus of the “field of May,” and it was in this inner assembly, rather than in the general body (whose approval was merely formal, and confined to matters momentous enough to be referred to a general vote), that the centre of power really lay. It is from the assembly of magnates that the diet of medieval Germany springs. The general assembly became meaningless and unnecessary, as the feudal array gradually superseded the old levy en masse, in which each freeman had been liable to service; and after the close of the 10th century it no longer existed.
The imperial diet (Reichstag) of the middle ages might sometimes contain representatives of Italy, the regnum Italicum; but it was practically always confined to the magnates of Germany, the regnum Teutonicum. Upon occasion a summons to the diet might be sent even to the knights, but the regular members were the princes (Fürsten), both lay and ecclesiastical. In the 13th 212 century the seven electors began to disengage themselves from the prince as a separate element, and the Golden Bull (1356) made their separation complete; from the 14th century onwards the nobles (both counts and other lords) are regarded as regular members; while after 1250 the imperial and episcopal towns often appear through their representatives. By the 14th century, therefore, the originally homogeneous diet of princes is already, at any rate practically if not yet in legal form, divided into three colleges—the electors, the princes and nobles, and the representatives of the towns (though, as we shall see, the latter can hardly be reckoned as regular members until the century of the Reformation). Under the Hohenstaufen it is still the rule that every member of the diet must attend personally, or lose his vote; at a later date the principle of representation by proxy, which eventually made the diet into a mere congress of envoys, was introduced. By the end of the 13th century the vote of the majority had come to be regarded as decisive; but in accordance with the strong sense of social distinctions which marks German history, the quality as well as the quantity of votes was weighed, and if the most powerful of the princes were agreed, the opinion of the lesser magnates was not consulted. The powers of the medieval diet extended to matters like legislation, the decision upon expeditions (especially the expeditio Romana), taxation and changes in the constitution of the principalities or the Empire. The election of the king, which was originally regarded as one of the powers of the diet, had passed to the electors by the middle of the 13th century.
A new era in the history of the diet begins with the Reformation. The division of the diet into three colleges becomes definite and precise; the right of the electors, for instance, to constitute a separate college is explicitly recognized as a matter of established custom in 1544. The representatives of the towns now become regular members. In the 15th century they had only attended when special business, such as imperial reform or taxation, fell under discussion; in 1500, however, they were recognized as a separate and regular estate, though it was not until 1648 that they were recognized as equal to the other estates of the diet. The estate of the towns, or college of municipal representatives, was divided into two benches, the Rhenish and the Swabian. The estate of the princes and counts, which stood midway between the electors and the towns, also attained, in the years that followed the Reformation, its final organization. The vote of the great princes ceased to be personal, and began to be territorial. This had two results. The division of a single territory among the different sons of a family no longer, as of old, multiplied the voting power of the family; while in the opposite case, the union of various territories in the hands of a single person no longer meant the extinction of several votes, since the new owner was now allowed to give a vote for each of his territories. The position of the counts and other lords, who joined with the princes in forming the middle estate, was finally fixed by the middle of the 17th century. While each of the princes enjoyed an individual vote, the counts and other lords were arranged in groups, each of which voted as a whole, though the whole of its vote (Kuriatstimme) only counted as equal to the vote of a single prince (Virilstimme). There were six of these groups; but as the votes of the whole college of princes and counts (at any rate in the 18th century) numbered 100, they could exercise but little weight.
The last era in the history of the diet may be said to open with the treaty of Westphalia (1648). The treaty acknowledged that Germany was no longer a unitary state, but a loose confederation of sovereign princes; and the diet accordingly ceased to bear the character of a national assembly, and became a mere congress of envoys. The “last diet” which issued a regular recess (Reichsabschied—the term applied to the acta of the diet, as formally compiled and enunciated at its dissolution) was that of Regensburg in 1654. The next diet, which met at Regensburg in 1663, never issued a recess, and was never dissolved; it continued in permanent session, as it were, till the dissolution of the Empire in 1806. This result was achieved by the process of turning the diet from an assembly of principals into a congress of envoys. The emperor was represented by two commissarii; the electors, princes and towns were similarly represented by their accredited agents. Some legislation was occasionally done by this body; a conclusum imperii (so called in distinction from the old recessus imperii of the period before 1663) might slowly (very slowly—for the agents, imperfectly instructed, had constantly to refer matters back to their principals) be achieved; but it rested with the various princes to promulgate and enforce the conclusum in their territories, and they were sufficiently occupied in issuing and enforcing their own decrees. In practice the diet had nothing to do; and its members occupied themselves in “wrangling about chairs”—that is to say, in unending disputes about degrees and precedences.
In the Germanic Confederation, which occupies the interval between the death of the Holy Roman Empire and the formation of the North German Confederation (1815-1866), a diet (Bundestag) existed, which was modelled on the old diet of the 18th century. It was a standing congress of envoys at Frankfort-on-Main. Austria presided in the diet, which, in the earlier years of its history, served, under the influence of Metternich, as an organ for the suppression of Liberal opinion. In the North German Confederation (1867-1870) a new departure was made, which has been followed in the constitution of the present German empire. Two bodies were instituted—a Bundesrat, which resembles the old diet in being a congress of envoys sent by the sovereigns of the different states of the confederation, and a Reichstag, which bears the name of the old diet, but differs entirely in composition. The new Reichstag is a popular representative assembly, based on wide suffrage and elected by ballot; and, above all, it is an assembly representing, not the several states, but the whole Empire, which is divided for this purpose into electoral districts. Both as a popular assembly, and as an assembly which represents the whole of a united Germany, the new Reichstag goes back, one may almost say, beyond the diet even of the middle ages, to the days of the old Teutonic folk-moot.
See R. Schröder, Lehrbuch der deutschen Rechtsgeschichte (1902), pp. 149, 508, 820, 880. Schröder gives a bibliography of monographs bearing on the history of the medieval diet.
DIETARY, in a general sense, a system or course of diet, in the sense of food; more particularly, such an allowance and regulation of food as that supplied to workhouses, the army and navy, prisons, &c. Lowest in the scale of such dietaries comes what is termed “bare existence” diet, administered to certain classes of the community who have a claim on their fellow-countrymen that their lives and health shall be preserved in statu quo, but nothing further. This applies particularly to the members of a temporarily famine-stricken community. Before the days of prison reform, too, the dietary scale of many prisons was to a certain extent penal, in that the food supplied to prisoners was barely sufficient for existence. Nowadays more humane principles apply; there is no longer the obvious injustice of applying the same scale of quantity and quality to all prisoners under varying circumstances of constitution and surroundings, and whether serving long or short periods of imprisonment.
The system of dietary in force in the local and convict prisons of England and Wales is that recommended by the Home Office on the advice of a departmental committee. As to the local prison dietary, its application is based on (1) the principle of variation of diet with length of sentence; (2) the system of progressive dietary; (3) the distinction between hard labour diets and non-hard labour diets; (4) the differentiation of diet according to age and sex. There are three classes of diet, classes A, B and C. Class A diet is given to prisoners undergoing not more than seven days’ imprisonment. The food is good and wholesome, but sufficiently plain and unattractive, so as not to offer temptation to the loafer or mendicant. It is given in quantity sufficient to maintain health and strength during the single week. Prisoners sentenced to more than seven days and not more than fourteen days are given class A diet for the first seven days and class B for the remainder of the sentence. In most of the local prisons in England and Wales prisoners sentenced to hard labour received hard labour diet, although quite 60% were unable to perform the hardest forms of prison labour either through physical defect, age or infirmity. The departmental committee of 1899 in their report recommended that no distinction should be made between hard labour and non-hard labour diets. Class A diet is as follows:—Breakfast, Bread, 8 oz. daily (6 oz. for women and juveniles) with 1 pint of gruel. Juveniles (males and females under 213 sixteen years of age) get, in addition, ½ pint of milk. Dinner, 8 oz. of bread daily, with 1 pint of porridge on three days of the week, 8 oz. of potatoes (representing the vegetable element) on two other days, and 8 oz. of suet pudding (representing the fatty element) on the other two days. Supper, the breakfast fare repeated.
Class B diet, which is also given to (1) prisoners on remand or awaiting trial, (2) offenders of the 1st division who do not maintain themselves, (3) offenders of the 2nd division and (4) debtors, is as shown in Table I.
Table I.
| Men. | Women. | Juveniles. | ||
| Breakfast. | Daily:— | |||
| Bread | 8 oz. | 6 oz. | 6 oz. | |
| Gruel | 1 pt. | 1 pt. | 1 pt. | |
| Milk | · · | · · | ½ pt. | |
| Dinner. | Sunday:— | |||
| Bread | 6 oz. | 6 oz. | ||
| Potatoes | 8 ” | 8 ” | ||
| Cooked meat, preserved by heat | 4 ” | 3 ” | ||
| Monday:— | ||||
| Bread | 6 oz. | 6 oz. | ||
| Potatoes | 8 ” | 8 ” | ||
| Beans | 10 ” | 8 ” | ||
| Fat bacon | 2 ” | 1 ” | ||
| Tuesday:— | ||||
| Bread | 6 oz | 6 oz. | ||
| Potatoes | 8 ” | 8 ” | ||
| Soup | 1 pt. | 1 pt. | ||
| Wednesday:— | ||||
| Bread | 6 oz. | 6 oz. | ||
| Potatoes | 8 ” | 8 ” | ||
| Suet pudding | 10 ” | 8 ” | ||
| Thursday:— | ||||
| Bread | 6 oz. | 6 oz. | ||
| Potatoes | 8 ” | 8 ” | ||
| Cooked beef, without bone | 4 ” | 3 ” | ||
| Friday:— | ||||
| Bread | 6 oz. | 6 oz. | ||
| Potatoes | 8 ” | 8 ” | ||
| Soup | 1 pt. | 1 pt. | ||
| Saturday:— | ||||
| Bread | 6 oz. | 6 oz. | ||
| Potatoes | 8 ” | 8 ” | ||
| Suet pudding | 10 ” | 8 ” | ||
| Supper. | Daily:— | |||
| Bread | 8 oz. | 6 oz. | 6 oz. | |
| Porridge | 1 pt. | |||
| Gruel | 1 pt. | |||
| Cocoa | 1 pt. | |||
Class C diet is class B amplified, and is given to those prisoners serving sentences of three months and over.
The dietary of convict prisons, in which prisoners are all under long sentence, is divided into a diet for convicts employed at hard labour and a diet for convicts employed at sedentary, indoor and light labour. It will be found set forth in the Blue-book mentioned above. The sparest of all prison diets is called “punishment diet,” and is administered for offences against the internal discipline of the prison. It is limited to a period of three days. It consists of 1 ℔ of bread and as much water as the prisoner chooses to drink.
In French prisons the dietary is nearly two pounds weight of bread, with two meals of thin soup (breakfast and dinner) made from potatoes, beans or other vegetables, and on two days a week made from meat. In France the canteen system is in vogue, additional food, such as sausages, cheese, fruit, &c., may be obtained by the prisoner, according to the wages he receives for his labours. The dietary of Austrian prisons is 1½ ℔ of bread daily, a dinner of soup on four days of the week, and of meat on the other three days, with a supper of soup or vegetable stew. Additional food can be purchased by the prisoner out of his earnings.
These dietaries may be taken as more or less typical of the ordinary prison fare in most civilized countries, though in some countries it may err on the side of severity, as in Sweden, prisoners being given only two meals a day, one at mid-day and one at seven p.m., porridge or gruel being the principal element in both meals. On the other hand, the prison dietaries of many of the United States prisons go to the other extreme, fresh fish, green vegetables, even coffee and fruit, figuring in the dietary.
Another class of dietary is that given to paupers. In England, until 1900, almost every individual workhouse had its own special dietary, with the consequence that many erred on the side of scantiness and unsuitability, while others were too lavish. By an order of the Local Government Board of that year, acting on a report of a committee, all inmates of workhouses, with the exception of the sick, children under three years of age, and certain other special cases, are dieted in accordance with certain dietary tables as framed and settled by the board. The order contained a great number of different rations, it being left to the discretion of the guardians as to the final settlement of the tables. For adult inmates the dietary tables are for each sex respectively, two in number, one termed “plain diet” and the other “infirm diet.” All male inmates certified as healthy able-bodied persons receive plain diet only. All inmates, however, in workhouses are kept employed according to their capacity and ability, and this is taken into consideration in giving allowances of food. For instance, for work with sustained exertion, such as stone-breaking, digging, &c., more food is given than for work without sustained exertion, such as wood-chopping, weeding or sewing. Table II. shows an example of a workhouse dietary.
Table II.
| Sun. | Mon. | Tue. | Wed. | Thu. | Fri. | Sat. | |||
| Breakfast. | Bread. | oz. | 8 | 4 | 4 | 4 | 4 | 4 | 4 |
| Porridge. | pt. | * | 1½ | 1½ | 1½ | 1½ | 1½ | 1½ | |
| Dinner. | Bread. | oz. | 4 | 6 | .. | 4 | 4 | 8 | 6 |
| Beef. | oz. | 4½ | .. | .. | .. | 4½ | .. | .. | |
| Vegetables. | oz. | 12 | .. | .. | 12 | 12 | .. | .. | |
| Barley Soup. | pt. | .. | 1½ | .. | .. | .. | .. | .. | |
| Pork. | oz. | .. | .. | 4½ | .. | .. | .. | .. | |
| Beans. | oz. | .. | .. | 12 | .. | .. | .. | .. | |
| Fish. | oz. | .. | .. | .. | 10 | .. | .. | .. | |
| Cheese. | oz. | .. | .. | .. | .. | .. | 3 | .. | |
| Broth. | pt. | .. | .. | .. | .. | .. | 1 | .. | |
| Irish Stew. | pt. | .. | .. | .. | .. | .. | .. | 1 | |
| Supper. | Bread. | oz. | 8 | 6 | 6 | 6 | 8 | 6 | 6 |
| Butter. | oz. | ½ | .. | .. | .. | .. | .. | .. | |
| Tea. | pt. | 1 | .. | .. | .. | .. | .. | .. | |
| Gruel. | pt. | .. | 1½ | 1½ | 1½ | .. | 1½ | 1½ | |
| Broth. | pt. | .. | .. | .. | .. | 1 | .. | .. | |
| Cheese. | oz. | .. | .. | .. | .. | 2 | .. | .. | |
| * On Sundays 1 pint of tea and 2½ oz. of butter are given instead of porridge. | |||||||||
In the casual wards of workhouses the dietary is plainer, consisting of 8 oz. of bread, or 6 oz. of bread and one pint of gruel or broth for breakfast; the same for supper; for dinner 8 oz. of bread and 1½ oz. of cheese or 6 oz. of bread and one pint of soup. The American poor law system is based broadly on that of England, and the methods of relief are much the same. Each state, however, makes its own regulations, and there is considerable diversity in workhouse dietaries in consequence. The German system of poor relief is more methodical than those of England and America. The really deserving are treated 214 with more commiseration, and a larger amount of outdoor relief is given than in England. There is no casual ward, tramps and beggars being liable to penal treatment, but there are “relief stations,” somewhat corresponding to casual wards, where destitute persons tramping from one place to another can obtain food and lodging in return for work done.
In the British navy certain staple articles of diet are supplied to the men to the value approximately of 6d. per diem—the standard government ration—and, in addition, a messing allowance of 4d. per diem, which may either be expended on luxuries in the canteen, or in taking up government provisions on board ship, in addition to the standard ration. The standard ration as recommended in 1907 by a committee appointed to inquire into the question of victualling in the navy is as follows:—
Service Afloat.
| 1 ℔ bread (or ¾ ℔ bread and ¼ ℔ trade flour). ½ ℔ fresh meat. 1 ℔ fresh vegetables. 1⁄8 pint spirit. 4 oz. sugar. ½ oz. tea (or 1 oz. coffee for every ¼ oz. tea). ½ oz. ordinary or soluble chocolate (or 1 oz. coffee). ¾ oz. condensed milk. 1 oz. jam or marmalade. 4 oz. preserved meat on one day of the week in harbour, or on two days at sea. Mustard, pepper, vinegar, and salt as required. |
Substitute for soft bread when the latter is not available—
½ ℔ biscuit (new type) or 1 ℔ flour.
Substitutes for fresh meat when the latter is not available:—
| On alternate days. | (1) Salt pork day:— | |
| ½ ℔ salt pork. | ||
| ¼ ℔ split peas. | ||
| Celery seed, ½ oz. to every 8 ℔ of split peas put into the coppers. | ||
| ½ ℔ potatoes (or 1 oz. compressed vegetables). | ||
| (2) Preserved meat day:— | ||
| 6 oz. preserved meat. | ||
| 8 oz. trade flour | } or 4 oz. rice. | |
| ¾ oz. refined suet | ||
| 2 oz. raisins | ||
| ½ ℔ potatoes (or 1 oz. compressed vegetables). | ||
On shore establishments and depot ships ¼ pt. fresh milk is issued in lieu of the ¾ oz. of condensed milk.
In the United States navy there is more liberality and variety of diet, the approximate daily cost of the rations supplied being 1s. 3d. per head. In the American mercantile marine, too, according to the scale sanctioned by act of Congress (December 21, 1898) for American ships, the seaman is better off than in the British merchant service. The scale is shown in Table III.
Table III.
| Weekly Scale. | Articles. | Weekly Scale. | Articles. |
| 3½ ℔ | Biscuits. | 7⁄8 oz. | Tea. |
| 3¾ ” | Salt beef. | 21 ” | Sugar. |
| 3 ” | “ pork. | 1½ ℔ | Molasses. |
| 1½ ” | Flour. | 9 oz. | Fruits, dried. |
| 2 ” | Meats, preserved. | ¾ pt. | Pickles. |
| 10½ ” | Bread, fresh (8 ℔ flour in lieu). | 1 ” | Vinegar. |
| 1 ” | Fish, dried. | 8 oz. | Corn Meal. |
| 7 ” | Potatoes or yams. | 12 ” | Onions. |
| 1 ” | Tomatoes, preserved. | 7 ” | Lard. |
| 2⁄3 ” | Peas. | 7 ” | Butter. |
| 2⁄3 ” | Calavances. | ¼ ” | Mustard. |
| 2⁄3 ” | Rice. | ¼ ” | Pepper. |
| 5¼ oz. | Coffee, green. | ¼ ” | Salt. |
In the British mercantile marine there is no scale of provisions prescribed by the Board of Trade; there is, however, a traditional scale very generally adopted, having the sanction of custom only and seldom adhered to. The following dietary scale for steerage passengers, laid down in the 12th schedule of the Merchant Shipping Act 1894, is of interest. See Table IV.
Table IV.—Weekly, per Statute Adult.
| Scale A. For voyages not exceeding 84 days for sailing ships or 50 days for steamships. |
Scale B. For voyages exceeding 84 days for sailing ships or 50 days for steamships. | |
| ℔ oz. | ℔ oz. | |
| Bread or biscuit, not inferior to navy biscuit | 3 8 | 3 8 |
| Wheaten flour | 1 0 | 2 0 |
| Oatmeal | 1 8 | 1 0 |
| Rice | 1 8 | 0 8 |
| Peas | 1 8 | 1 8 |
| Beef | 1 4 | 1 4 |
| Pork | 1 0 | 1 0 |
| Butter | · · | 0 4 |
| Potatoes | 2 0 | 2 0 |
| Sugar | 1 0 | 1 0 |
| Tea | 0 2 | 0 2 |
| Salt | 0 2 | 0 2 |
| Pepper (white or black), ground | 0 0½ | 0 0½ |
| Vinegar | 1 gill | 1 gill |
| Preserved meat | · · | 1 0 |
| Suet | 0 6 | |
| Raisins | 0 8 | |
| Lime juice | 0 6 |
Certain substitutions may be made in this scale at the option of the master of any emigrant ship, provided that the substituted articles are set forth in the contract tickets of the steerage passengers.
In the British army the soldier is fed partly by a system of co-operation. He gets a free ration from government of 1 ℔ of bread and ¾ ℔ of meat; in addition there is a messing allowance of 3½d. per man per day. He is able to supplement his food by purchases from the canteen. Much depends on the individual management in each regiment as to the satisfactory expenditure of the messing allowance. In some regiments an allowance is made from the canteen funds towards messing in addition to that granted by the government. The ordinary field ration of the British soldier is 1½ ℔ of bread or 1 ℔ of biscuit; 1 ℔ of fresh, salt or preserved meat; ½ oz. of coffee; 1/6 oz. of tea; 2 oz. of sugar; ½ oz. of salt, 1⁄36 oz. of pepper, the whole weighing something over 2 ℔ 3 oz. This cannot be looked on as a fixed ration, as it varies in different campaigns, according to the country into which the troops may be sent. The Prussian soldier during peace gets weekly from his canteen 11 ℔ 1 oz. of rye bread and not quite 2½ ℔ of meat. This is obviously insufficient, but under
the conscription system it is reckoned that he will be able to make up the deficiency out of his own private means, or obtain charitable contributions from his friends. In the French infantry of the line each man during peace gets weekly 15 ℔ of bread, 33⁄10 ℔ of meat, 2½ ℔ of haricot beans or other vegetables, with salt and pepper, and 1¾ oz. of brandy.
An Austrian under the same circumstances receives 13.9 ℔ of bread, ½ ℔ of flour and 3.3 ℔ of meat.
The Russian conscript is allowed weekly:—
| Black bread | 7 ℔. |
| Meat | 7 ℔. |
| Kvass (beer) | 7.7 quarts. |
| Sour cabbage | 24½ gills = 122½ oz. |
| Barley | 24½ gills = 122½ oz. |
| Salts | 10½ oz. |
| Horse-radish | 28 grains. |
| Pepper | 28 grains. |
| Vinegar | 5½ gills = 26½ oz. |
DIETETICS, the science of diet, i.e. the food and nutrition of man in health and disease (see Nutrition). This article deals mainly with that part of the subject which has to do with the composition and nutritive values of foods and their adaptation to the use of people in health. The principal topics considered are: (1) Food and its functions; (2) Metabolism of matter and energy; (3) Composition of food materials; (4) Digestibility of food; (5) Fuel value of food; (6) Food consumption; (7) Quantities of nutrients needed; (8) Hygienic economy of food; (9) Pecuniary economy of food.
1. Food and its Functions.—For practical purposes, food may be defined as that which, when taken into the body, may be utilized for the formation and repair of body tissue, and the production of energy. More specifically, food meets the requirements of the body in several ways. It is used for the formation of the tissues and fluids of the body, and for the restoration of losses of substance due to bodily activity. The potential energy of the food is converted into heat or muscular work or other forms of energy. In being thus utilized, food protects body substance or previously acquired nutritive material from consumption. When the amount 215 of food taken into the body is in excess of immediate needs, the surplus may be stored for future consumption.
Ordinary food materials, such as meat, fish, eggs, vegetables, &c., consist of inedible materials, or refuse, e.g. bone of meat and fish, shell of eggs, rind and seed of vegetables; and edible material, as flesh of meat and fish, white and yolk of eggs, wheat flour, &c. The edible material is by no means a simple substance, but consists of water, and some or all of the compounds variously designated as food stuffs, proximate principles, nutritive ingredients or nutrients, which are classified as protein, fats, carbohydrates and mineral matters. These have various functions in the nourishment of the body.
The refuse commonly contains compounds similar to those in the food from which it is derived, but since it cannot be eaten, it is usually considered as a non-nutrient. It is of importance chiefly in a consideration of the pecuniary economy of food. Water is also considered as a non-nutrient, because although it is a constituent of all the tissues and fluids of the body, the body may obtain the water it needs from that drunk; hence, that contained in the food materials is of no special significance as a nutrient.
Mineral matters, such as sulphates, chlorides, phosphates and carbonates of sodium, potassium, calcium, &c., are found in different combinations and quantities in most food materials. These are used by the body in the formation of the various tissues, especially the skeletal and protective tissues, in digestion, and in metabolic processes within the body. They yield little or no energy, unless perhaps the very small amount involved in their chemical transformation.
Protein1 is a term used to designate the whole group of nitrogenous compounds of food except the nitrogenous fats. It includes the albuminoids, as albumin of egg-white, and of blood serum, myosin of meat (muscle), casein of milk, globulin of blood and of egg yolk, fibrin of blood, gluten of flour; the gelatinoids, as gelatin and allied substances of connective tissue, collagen of tendon, ossein of bone and the so-called extractives (e.g. creatin) of meats; and the amids (e.g. asparagin) and allied compounds of vegetables and fruits.
The albuminoids and gelatinoids, classed together as proteids, are the most important constituents of food, because they alone can supply the nitrogenous material necessary for the formation of the body tissues. For this purpose, the albuminoids are most valuable. Both groups of compounds, however, supply the body with energy, and the gelatinoids in being thus utilized protect the albuminoids from consumption for this purpose. When their supply in the food is in excess of the needs of the body, the surplus proteids may be converted into body fat and stored.
The so-called extractives, which are the principal constituents of meat extract, beef tea and the like, act principally as stimulants and appetizers. It has been believed that they serve neither to build tissue nor to yield energy, but recent investigations2 indicate that creatin may be metabolized in the body.
The fats of food include both the animal fats and the vegetable oils. The carbohydrates include such compounds as starches, sugars and the fibre of plants or cellulose, though the latter has but little value as food for man. The more important function of both these classes of nutrients is to supply energy to the body to meet its requirements above that which it may obtain from the proteids. It is not improbable that the atoms of their molecules as well as those from the proteids are built up into the protoplasmic substance of the tissues. In this sense, these nutrients may be considered as being utilized also for the formation of tissue; but they are rather the accessory ingredients, whereas the proteids are the essential ingredients for this purpose. The fats in the food in excess of the body requirements may be stored as body fat, and the surplus carbohydrates may also be converted into fat and stored.
To a certain extent, then, the nutrients of the food may substitute each other. All may be incorporated into the protoplasmic structure of body tissue, though only the proteids can supply the essential nitrogenous ingredients; and apart from the portion of the proteid material that is indispensable for this purpose, all the nutrients are used as a source of energy. If the supply of energy in the food is not sufficient, the body will use its own proteid and fat for this purpose. The gelatinoids, fats and carbohydrates in being utilized for energy protect the body proteids from consumption. The fat stored in the body from the excess of food is a reserve of energy material, on which the body may draw when the quantity of energy in the food is insufficient for its immediate needs.
What compounds are especially concerned in intellectual activity is not known. The belief that fish is especially rich in phosphorus and valuable as a brain food has no foundation in observed fact.
2. Metabolism of Matter and Energy.—The processes of nutrition thus consist largely of the transformation of food into body material and the conversion of the potential energy of both food and body material into the kinetic energy of heat and muscular work and other forms of energy. These various processes are generally designated by the term metabolism. The metabolism of matter in the body is governed largely by the needs of the body for energy. The science of nutrition, of which the present subject forms a part, is based on the principle that the transformations of matter and energy in the body occur in accordance with the laws of the conservation of matter and of energy. That the body can neither create nor destroy matter has long been universally accepted. It would seem that the transformation of energy must likewise be governed by the law of the conservation of energy; indeed there is every reason a priori to believe that it must; but the experimental difficulties in the way of absolute demonstration of the principle are considerable. For such demonstration it is necessary to prove that the income and expenditure of energy are equal. Apparatus and methods of inquiry devised in recent years, however, afford means for a comparison of the amounts of both matter and energy received and expended by the body, and from the results obtained in a large amount of such research, it seems probable that the law obtains in the living organism in general.
The first attempt at such demonstration was made by M. Rubner3 in 1894, experimenting with dogs doing no external muscular work. The income of energy (as heat) was computed, but the heat eliminated was measured. In the average of eight experiments continuing forty-five days, the two quantities agreed within 0.47%, thus demonstrating what it was desired to prove—that the heat given off by the body came solely from the oxidation of food within it. Results in accordance with these were reported by Studenski4 in 1897, and by Laulanie5 in 1898.
The most extensive and complete data yet available on the subject have been obtained by W. O. Atwater, F. G. Benedict and associates6 in experiments with men in the respiration calorimeter, in which a subject may remain for several consecutive days and nights. These experiments involve actual weighing and analyses of the food and drink, and of the gaseous, liquid and solid excretory products; determinations of potential energy (heat of oxidation) of the oxidizable material received and given off by the body (including estimation of the energy of the material gained or lost by the body); and measurements of the amounts of energy expended as heat and as external muscular work. By October 1906 eighty-eight experiments with fifteen different subjects had been completed. The separate experiments continued from two to thirteen days, making a total of over 270 days. 216 In some cases the subjects were at rest; in others they performed varying amounts of external muscular work on an apparatus by means of which the amount of work done was measured. In some cases they fasted, and in others they received diets generally not far from sufficient to maintain nitrogen, and usually carbon, equilibrium in the body. In these experiments the amount of energy expended by the body as heat and as external muscular work measured in terms of heat agreed on the average very closely with the amount of heat that would be produced by the oxidation of all the matter metabolized in the body. The variations for individual days, and in the average for individual experiments as well, were in some cases appreciable, amounting to as much as 6%, which is not strange in view of the uncertainties in physiological experimenting; but in the average of all the experiments the energy of the expenditure was above 99.9% of the energy of the income,—an agreement within one part in 1000. While these results do not absolutely prove the application of the law of the conservation of energy in the human body, they certainly approximate very closely to such demonstration. It is of course possible that energy may have given off 217 from the body in other forms than heat and external muscular work. It is conceivable, for example, that intellectual activity may involve the transformation of physical energy, and that the energy involved may be eliminated in some form now unknown. But if the body did give off energy which was not measured in these experiments, the quantity must have been extremely small. It seems fair to infer from the results obtained that the metabolism of energy in the body occurred in conformity with the law of the conservation of energy.
3. Composition of Food Materials.—The composition of food is determined by chemical analyses, the results of which are conventionally expressed in terms of the nutritive ingredients previously described. As a result of an enormous amount of such investigation in recent years, the kinds and proportions of nutrients in our common sorts of food are well known. Average values for percentage composition of some ordinary food materials are shown in Table I. (Table I. also includes figures for fuel value.)
Table I.—Percentage Composition of some Common Food Materials.
| Food Material. | Refuse. | Water. | Protein. | Fat. | Carbo- hydrates. | Mineral Matter. | Fuel Value per ℔ |
| % | % | % | % | % | % | Calories. | |
| Beef, fresh (medium fat)— | |||||||
| Chuck | 16.3 | 52.6 | 15.5 | 15.0 | · · | 0.8 | 910 |
| Loin | 13.3 | 52.5 | 16.1 | 17.5 | · · | 0.9 | 1025 |
| Ribs | 20.8 | 43.8 | 13.9 | 21.2 | · · | 0.7 | 1135 |
| Round | 7.2 | 60.7 | 19.0 | 12.8 | · · | 1.0 | 890 |
| Shoulder | 16.4 | 56.8 | 16.4 | 9.8 | · · | 0.9 | 715 |
| Beef, dried and smoked | 4.7 | 53.7 | 26.4 | 6.9 | · · | 8.9 | 790 |
| Veal— | |||||||
| Leg | 14.2 | 60.1 | 15.5 | 7.9 | · · | 0.9 | 625 |
| Loin | 16.5 | 57.6 | 16.6 | 9.0 | · · | 0.9 | 685 |
| Breast | 21.3 | 52.0 | 15.4 | 11.0 | · · | 0.8 | 745 |
| Mutton— | |||||||
| Leg | 18.4 | 51.2 | 15.1 | 14.7 | · · | 0.8 | 890 |
| Loin | 16.0 | 42.0 | 13.5 | 28.3 | · · | 0.7 | 1415 |
| Flank | 9.9 | 39.0 | 13.8 | 36.9 | · · | 0.6 | 1770 |
| Pork— | |||||||
| Loin | 19.7 | 41.8 | 13.4 | 24.2 | · · | 0.8 | 1245 |
| Ham, fresh | 10.7 | 48.0 | 13.5 | 25.9 | · · | 0.8 | 1320 |
| Ham, smoked and salted | 13.6 | 34.8 | 14.2 | 33.4 | · · | 4.2 | 1635 |
| Fat, salt | · · | 7.9 | 1.9 | 86.2 | · · | 3.9 | 3555 |
| Bacon | 7.7 | 17.4 | 9.1 | 62.2 | · · | 4.1 | 2715 |
| Lard, refined | · · | · · | · · | 100.0 | · · | · · | 4100 |
| Chicken | 25.9 | 47.1 | 13.7 | 12.3 | · · | 0.7 | 765 |
| Turkey | 22.7 | 42.4 | 16.1 | 18.4 | · · | 0.8 | 1060 |
| Goose | 17.6 | 38.5 | 13.4 | 29.8 | · · | 0.7 | 1475 |
| Eggs | 11.2 | 65.5 | 13.1 | 9.3 | · · | 0.9 | 635 |
| Cod, fresh | 29.9 | 58.5 | 11.1 | 0.2 | · · | 0.8 | 220 |
| Cod, salted | 24.9 | 40.2 | 16.0 | 0.4 | · · | 18.5 | 325 |
| Mackerel, fresh | 44.7 | 40.4 | 10.2 | 4.2 | · · | 0.7 | 370 |
| Herring, smoked | 44.4 | 19.2 | 20.5 | 8.8 | · · | 7.4 | 755 |
| Salmon, tinned | · · | 63.5 | 21.8 | 12.1 | · · | 2.6 | 915 |
| Oysters, shelled | · · | 88.3 | 6.0 | 1.3 | 3.3 | 1.1 | 225 |
| Butter | · · | 11.0 | 1.0 | 85.0 | · · | 3.0 | 3410 |
| Cheese | · · | 34.2 | 25.9 | 33.7 | 2.4 | 3.8 | 1885 |
| Milk, whole | · · | 87.0 | 3.3 | 4.0 | 5.0 | 0.7 | 310 |
| Milk, skimmed | · · | 90.5 | 3.4 | 0.3 | 5.1 | 0.7 | 165 |
| Oatmeal | · · | 7.7 | 16.7 | 7.3 | 66.2 | 2.1 | 1800 |
| Corn (maize) meal | · · | 12.5 | 9.2 | 1.9 | 75.4 | 1.0 | 1635 |
| Rye flour | · · | 12.9 | 6.8 | 0.9 | 78.7 | 0.7 | 1620 |
| Buckwheat flour | · · | 13.6 | 6.4 | 1.2 | 77.9 | 0.9 | 1605 |
| Rice | · · | 12.3 | 8.0 | 0.3 | 79.0 | 0.4 | 1620 |
| Wheat flour, white | · · | 12.0 | 11.4 | 1.0 | 75.1 | 0.5 | 1635 |
| Wheat flour, graham | · · | 11.3 | 13.3 | 2.2 | 71.4 | 1.8 | 1645 |
| Wheat, breakfast food | · · | 9.6 | 12.1 | 1.8 | 75.2 | 1.3 | 1680 |
| Wheat bread, white | · · | 35.3 | 9.2 | 1.3 | 53.1 | 1.1 | 1200 |
| Wheat bread, graham | · · | 35.7 | 8.9 | 1.8 | 52.1 | 1.5 | 1195 |
| Rye bread | · · | 35.7 | 9.0 | 0.6 | 53.2 | 1.5 | 1170 |
| Biscuit (crackers) | · · | 6.8 | 9.7 | 12.1 | 69.7 | 1.7 | 1925 |
| Macaroni | · · | 10.3 | 13.4 | 0.9 | 74.1 | 1.3 | 1645 |
| Sugar | · · | · · | · · | · · | 100.0 | · · | 1750 |
| Starch (corn starch) | · · | · · | · · | · · | 90.0 | · · | 1680 |
| Beans, dried | · · | 12.6 | 22.5 | 1.8 | 59.6 | 3.5 | 1520 |
| Peas, dried | · · | 9.5 | 24.6 | 1.0 | 62.0 | 2.9 | 1565 |
| Beets | 20.0 | 70.0 | 1.3 | 0.1 | 7.7 | 0.9 | 160 |
| Cabbage | 50.0 | 4.2 | 0.7 | 0.2 | 4.5 | 0.4 | 100 |
| Potatoes | 20.0 | 62.6 | 1.8 | 0.1 | 14.7 | 0.8 | 295 |
| Sweet potatoes | 20.0 | 55.2 | 1.4 | 0.6 | 21.9 | 0.9 | 440 |
| Tomatoes | · · | 94.3 | 0.9 | 0.4 | 3.9 | 0.5 | 100 |
| Apples | 25.0 | 63.3 | 0.3 | 0.3 | 10.8 | 0.3 | 190 |
| Bananas | 35.0 | 48.9 | 0.8 | 0.4 | 14.3 | 0.6 | 260 |
| Grapes | 25.0 | 58.0 | 1.0 | 1.2 | 14.4 | 0.4 | 295 |
| Strawberries | 5.0 | 85.9 | 0.9 | 0.6 | 7.0 | 0.6 | 150 |
| Almonds | 45.0 | 2.7 | 11.5 | 30.2 | 9.5 | 1.1 | 1515 |
| Brazil nuts | 49.6 | 2.6 | 8.6 | 33.7 | 3.5 | 2.0 | 1485 |
| Chestnuts | 16.0 | 37.8 | 5.2 | 4.5 | 35.4 | 1.1 | 915 |
| Walnuts | 58.1 | 1.0 | 6.9 | 26.6 | 6.8 | 0.6 | 1250 |
It will be observed that different kinds of food materials vary widely in their proportions of nutrients. In general the animal foods contain the most protein and fats, and vegetable foods are rich in carbohydrates. The chief nutrient of lean meat and fish is protein; but in medium fat meats the proportion of fat is as large as that of protein, and in the fatter meats it is larger. Cheese is rich in both protein and fat. Among the vegetable foods, dried beans and peas are especially rich in protein. The proportion in oatmeal is also fairly large, in wheat it is moderate, and in maize meal and rice it is rather small. Oats contain more oil than any of the common cereals, but in none of them is the proportion especially large. The most abundant nutrient in all the cereals is starch, which comprises from two-thirds to three-fourths or more of their total nutritive substance. Cotton-seed is rich in edible oil, and so are olives. Some of the nuts contain fairly large proportions of both protein and fat. The nutrient of potatoes is starch, present in fair proportion. Fruits contain considerable carbohydrates, chiefly sugar. Green vegetables are not of much account as sources of any of the nutrients or energy.
Similar food materials from different sources may also differ considerably in composition. This is especially true of meats. Thus, the leaner portions from a fat animal may contain nearly as much fat as the fatter portions from a lean animal. The data here presented are largely those for American food products, but the available analyses of English food materials indicate that the latter differ but little from the former in composition. The analyses of meats produced in Europe imply that they commonly contain somewhat less fat and more water, and often more protein, than American meats. The meats of English production compare with the American more than with the European meats. Similar vegetable foods from the different countries do not differ so much in composition.
4. Digestibility or Availability of Food Materials.—The value of any food material for nutriment depends not merely upon the kinds and amounts of nutrients it contains, but also upon the ease and convenience with which the nutrients may be digested, and especially upon the proportion of the nutrients that will be actually digested and absorbed. Thus, two foods may contain equal amounts of the same nutrient, but the one most easily digested will really be of most value to the body, because less effort is necessary to utilize it. Considerable study of this factor is being made, and much valuable information is accumulating, but it is of more especial importance in cases of disordered digestion.
The digestibility of food in the sense of thoroughness of digestion, however, is of particular importance in the present discussion. Only that portion of the food that is digested and absorbed is available to the body for the building of tissue and the production of energy. Not all the food eaten is thus actually digested; undigested material is excreted in the faeces. The thoroughness of digestion is determined experimentally by weighing and analysing the food eaten and the faeces pertaining to it. The difference between the corresponding ingredients of the two is commonly considered to represent the amounts of the ingredients digested. Expressed in percentages, these are called coefficients of digestibility. See Table II.
Table II.—Coefficients of Digestibility (or Availability) of Nutrients in Different Classes of Food Materials.
| Kind of Food. | Protein. | Fat. | Carbohydrates. |
| % | % | % | |
| Meats | 98 | 98 | · · |
| Fish | 96 | 97 | · · |
| Poultry | 96 | 97 | · · |
| Eggs | 97 | 98 | · · |
| Dairy products | 97 | 96 | 98 |
| Total animal food of mixed diet | 97 | 97 | 98 |
| Potatoes | 73 | · · | 98 |
| Beets, carrots, &c. | 72 | · · | 97 |
| Cabbage, lettuce, &c. | · · | · · | 83 |
| Legumes | 78 | 90 | 95 |
| Oatmeal | 78 | 90 | 97 |
| Corn meal | 80 | · · | 99 |
| Wheat meals without bran | 83 | · · | 93 |
| Wheat meals with bran | 75 | · · | 92 |
| White bread | 88 | · · | 98 |
| Entire wheat bread | 82 | · · | 94 |
| Graham bread | 76 | · · | 90 |
| Rice | 76 | · · | 91 |
| Fruits and nuts | 80 | 86 | 96 |
| Sugars and starches | · · | · · | 98 |
| Total vegetable food of mixed diet | 85 | 90 | 97 |
| Total food of mixed diet | 92 | 95 | 97 |
Such a method is not strictly accurate, because the faeces do not consist entirely of undigested food but contain in addition to this the so-called metabolic products, which include the residuum of digestive juices not resorbed, fragments of intestinal epithelium, &c. Since there is as yet no satisfactory method of separating these constituents of the excreta, the actual digestibility of the food is not determined. It has been suggested that since these materials must originally come from food, they represent, when expressed in terms of food ingredients, the cost of digestion; hence that the values determined as above explained represent the portion of food available to the body for the building of tissue and the yielding of energy, and what is commonly designated as digestibility should be called availability. Other writers retain the term “digestibility,” but express the results as “apparent digestibility,” until more knowledge regarding the metabolic products of the excreta is available and the actual digestibility may be ascertained.
Experimental inquiry of this nature has been very active in recent years, especially in Europe, the United States and Japan; and the results of considerably over 1000 digestion experiments with single foods or combinations of food materials are available. These were mostly with men, but some were with women and with children. The larger part of these have been taken into account in the following estimations of the digestibility of the nutrients in different classes of food materials. The figures here shown are subject to revision as experimental data accumulate. They are not to be taken as exact measures of the digestibility (or availability) of every kind of food in each given class, but they probably represent fairly well the average digestibility of the classes of food materials as ordinarily utilized in the mixed diet.
5. Fuel Value of Food.—The potential energy of food is commonly measured as the amount of heat evolved when the food is completely oxidized. In the laboratory this is determined by burning the food in oxygen in a calorimeter. The results, which are known as the heat of combustion of the food, are 218 expressed in calories, one calory being the amount of heat necessary to raise the temperature of one kilogram of water one degree centigrade. But it is to be observed that this unit is employed simply from convenience, and without implication as to what extent the energy of food is converted into heat in the body. The unit employed in the measurement of some other form of energy might be used instead, as, for example, the foot-ton, which represents the amount of energy necessary to raise one ton through one foot.
Table III.—Estimates of Heats of Combustion and of Fuel Value of Nutrients in Ordinary Mixed Diet.
| Nutrients. | Heat of Combustion. | Fuel Value. |
| Calories. | Calories. | |
| One gram of protein | 5.65 | 4.05 |
| One gram of fats | 9.40 | 8.93 |
| One gram of carbohydrates | 4.15 | 4.03 |
The amount of energy which a given quantity of food will produce on complete oxidation outside the body, however, is greater than that which the body will actually derive from it. In the first place, as previously shown, part of the food will not be digested and absorbed. In the second place, the nitrogenous compounds absorbed are not completely oxidized in the body, the residuum being excreted in the urine as urea and other bodies that are capable of further oxidation in the calorimeter. The total heat of combustion of the food eaten must therefore be diminished by the heat of combustion of the oxidizable material rejected by the body, to find what amount of energy is actually available to the organism for the production of work and heat. The amount thus determined is commonly known as the fuel value of food.
Rubner’s7 commonly quoted estimates for the fuel value of the nutrients of mixed diet are,—for protein and carbohydrates 4.1, and for fats 9.3 calories per gram. According to the method of deduction, however, these factors were more applicable to digested than to total nutrients. Atwater8 and associates have deduced, from data much more extensive than those available to Rubner, factors for total nutrients somewhat lower than these, as shown in Table III. These estimates seem to represent the best average factors at present available, but are subject to revision as knowledge is extended.
Table IV.—Quantities of Available Nutrients and Energy in Daily Food Consumption of Persons in Different Circumstances.
| Number of Studies. | Nutrients and Energy per Man per Day. | ||||
| Protein. | Fat. | Carbo- hydrates. | Fuel Value. | ||
| Persons with Active Work. | Grams. | Grams. | Grams. | Calories. | |
| English royal engineers | 1 | 132 | 79 | 612 | 3835 |
| Prussian machinists | 1 | 129 | 107 | 657 | 4265 |
| Swedish mechanics | 5 | 174 | 105 | 693 | 4590 |
| Bavarian lumbermen | 3 | 120 | 277 | 702 | 6015 |
| American lumbermen | 5 | 155 | 327 | 804 | 6745 |
| Japanese rice cleaner | 1 | 103 | 11 | 917 | 4415 |
| Japanese jinrikshaw runner | 1 | 137 | 22 | 1010 | 5050 |
| Chinese farm labourers in California | 1 | 132 | 90 | 621 | 3980 |
| American athletes | 19 | 178 | 192 | 525 | 4740 |
| American working-men’s families | 13 | 156 | 226 | 694 | 5650 |
| Persons with Ordinary Work. | |||||
| Bavarian mechanics | 11 | 112 | 32 | 553 | 3060 |
| Bavarian farm labourers | 5 | 126 | 52 | 526 | 3200 |
| Russian peasants | .. | 119 | 31 | 571 | 3155 |
| Prussian prisoners | 1 | 117 | 28 | 620 | 3320 |
| Swedish mechanics | 6 | 123 | 75 | 507 | 3325 |
| American working-men’s families | 69 | 105 | 135 | 426 | 3480 |
| Persons with Light Work. | |||||
| American artisans’ families | 21 | 93 | 107 | 358 | 2880 |
| English tailors (prisoners) | 1 | 121 | 37 | 509 | 2970 |
| German shoemakers | 1 | 99 | 73 | 367 | 2629 |
| Japanese prisoners | 1 | 43 | 6 | 444 | 2110 |
| Professional and Business Men. | |||||
| Japanese professional men | 13 | 75 | 15 | 408 | 2190 |
| Japanese students | 8 | 85 | 18 | 537 | 2800 |
| Japanese military cadets | 11 | 98 | 20 | 611 | 3185 |
| German physicians | 2 | 121 | 90 | 317 | 2685 |
| Swedish medical students | 5 | 117 | 108 | 291 | 2725 |
| Danish physicians | 1 | 124 | 133 | 242 | 2790 |
| American professional and business men and students | 51 | 98 | 125 | 411 | 3285 |
| Persons with Little or no Exercise. | |||||
| Prussian prisoners | 2 | 90 | 27 | 427 | 2400 |
| Japanese prisoners | 1 | 36 | 6 | 360 | 1725 |
| Inmates of home for aged—Germany | 1 | 85 | 43 | 322 | 2097 |
| Inmates of hospitals for insane—America | 49 | 80 | 86 | 353 | 2590 |
| Persons in Destitute Circumstances. | |||||
| Prussian working people | 13 | 63 | 43 | 372 | 2215 |
| Italian mechanics | 5 | 70 | 36 | 384 | 2225 |
| American working-men’s families | 11 | 69 | 75 | 263 | 2085 |
The heats of combustion of all the fats in an ordinary mixed diet would average about 9.40 calories per gram, but as only 95% of the fat would be available to the body, the fuel value per gram would be (9.40 × 0.95 =) 8.93 calories. Similarly, the average heat of combustion of carbohydrates of the diet would be about 4.15 calories per gram, and as 97% of the total quantity is available to the body, the fuel value per gram would be 4.03. (It is commonly assumed that the resorbed fats and carbohydrates are completely oxidized in the body.) The heats of combustion of all the kinds of protein in the diet would average about 5.65 calories per gram. Since about 92% of the total protein would be available to the body, the potential energy of the available protein would be equivalent to (5.65 × 0.92 =) 5.20 calories; but as the available protein is not completely oxidized allowance must be made for the potential energy of the incompletely oxidized residue. This is estimated as equivalent to 1.15 calories for the 0.92 gram of available protein; hence, the fuel value of the total protein is (5.20 − 1.15 =) 4.05 calories per gram. Nutrients of the same class, but from different food materials, vary both in digestibility and in heat of combustion, and hence in fuel value. These factors are therefore not so applicable to the nutrients of the separate articles in a diet as to those of the diet as a whole.
6. Food Consumption.—Much information regarding the food consumption of people in various circumstances in different parts of the world has accumulated during the past twenty years, as a result of studies of actual dietaries in England, Germany, Italy, Russia, Sweden and elsewhere in Europe, in Japan and other oriental countries, and especially in the United States. These studies commonly consist in ascertaining the kinds, amounts and composition of the different food materials consumed by a group of persons during a given period and the number of meals taken by each member of the group, and computing the quantities of the different nutrients in the food on the basis of one man for one day. When the members of the group are of different age, sex, occupation, &c., account must be taken of the effect of these factors on consumption in estimating the value “per man.” Men as a rule eat more than women under similar conditions, women more than children, and persons at active work more than those at sedentary occupation. The navvy, for example, who is constantly using up more nutritive material or body tissue to supply the energy required for his muscular work needs more protein and energy in his food than a bookkeeper who sits at his desk all day.
In making allowance for these differences, the various individuals are commonly compared with a man at moderately active muscular work, who is taken as unity. A man at hard muscular work is reckoned at 1.2 times such an individual; a man with light muscular work or a boy 15-16 years old, .9; a man at sedentary occupation, woman at moderately active muscular work, boy 13-14 or girl 15-16 years old, .8; woman at light work, boy 12 or girl 13-14 years old, .7; boy 10-11 or girl 10-12 years old, .6; child 6-9 years old, .5; child 2-5 years old, .4; child under 2 years, .3. These factors are by no means absolute or final, but are based in part upon experimental data and in part upon arbitrary assumption.
The total number of dietary studies on record is very large, but not all of them are complete enough to furnish reliable data. Upwards of 1000 are sufficiently accurate to be included in statistical averages of food consumed by people in different circumstances, nearly half of which have been made in the United States in the past decade. The number of persons in the individual studies has ranged from one to several hundred. Some typical results are shown in Table IV.
7. Quantities of Nutrients needed.—For the proper nourishment of the body, the important problem is how much protein, fats and carbohydrates, or more simply, what amounts of protein and potential energy are needed under varying circumstances, to build and repair muscular and other tissues and to supply energy for muscular work, heat and other forms of energy. The answer to the problem is sought in the data obtained in dietary studies with considerable numbers of people, and in metabolism experiments with individuals in which the income and expenditure of the body are measured. From the information thus derived, different investigators have proposed so-called dietary standards, such as are shown in the table below, but unfortunately the experimental data are still insufficient for entirely trustworthy figures of this sort; hence the term “standard” as here used is misleading. The figures given are not to be considered as exact and final as that would suggest; they are merely tentative estimates of the average daily amounts of nutrients and energy required. (It is to be especially noted that these are available nutrients and fuel value rather than total nutrients and energy.) Some of the values proposed by other investigators are slightly larger than these, and others are decidedly smaller, but these are the ones that have hitherto been most commonly accepted in Europe and America.
Table V.—Standards for Dietaries. Available Nutrients and Energy per Man per Day.
| Protein. | Fat. | Carbo- hydrates. | Fuel Value. | |
| Voit’s Standards. | Grams.9 | Grams. | Grams. | Calories. |
| Man at hard work | 133 | 95 | 437 | 3270 |
| Man at moderate work | 109 | 53 | 485 | 2965 |
| Atwater’s Standards. | ||||
| Man at very hard muscular work | 161 | · ·10 | · ·10 | 5500 |
| Man at hard muscular work | 138 | · · | · · | 4150 |
| Man at moderately active muscular work | 115 | · · | · · | 3400 |
| Man at light to moderate muscular work | 103 | · · | · · | 3050 |
| Man at “sedentary” or woman at moderately active work | 92 | · · | · · | 2700 |
| Woman at light muscular work, or man without muscular exercise | 83 | · · | · · | 2450 |
8. Hygienic Economy of Food.—For people in good health, there are two important rules to be observed in the regulation of the diet. One is to choose the foods that “agree” with them, and to avoid those which they cannot digest and assimilate without harm; and the other is to use such sorts and quantities of foods as will supply the kinds and amounts of nutrients needed by the body and yet to avoid burdening it with superfluous material to be disposed of at the cost of health and strength.
As for the first-mentioned rule, it is practically impossible to give information that may be of more than general application. There are people who, because of some individual peculiarity, cannot use foods which for people in general are wholesome and nutritious. Some persons cannot endure milk, others suffer if they eat eggs, others have to eschew certain kinds of meat, or are made uncomfortable by fruit; but such cases are exceptions. Very little is known regarding the cause of these conditions. It is possible that in the metabolic processes to which the ingredients of the food are subjected in the body, or even during digestion before the substances are actually taken into the body, compounds may be formed that are in one way or another injurious. Whatever the cause may be, it is literally true in this sense that “what is one man’s meat is another man’s poison,” and each must learn for himself what foods “agree” with him and what ones do not. But for the great majority of people in health, 220 suitable combinations of the ordinary sorts of wholesome food materials make a healthful diet. On the other hand, some foods are of particular value at times, aside from their use for nourishment. Fruits and green vegetables often benefit people greatly, not as nutriment merely, for they may have very little actual nutritive material, but because of fruit or vegetable acids or other substances which they contain, and which sometimes serve a most useful purpose.
Table VI.—Amounts of Nutrients and Energy Furnished for One Shilling in Food Materials at Ordinary Prices.
| Food Materials as Purchased. | Prices per ℔ | One Shilling will buy | ||||
| Total Food materials. | Available Nutrients. | Fuel Value. | ||||
| Protein. | Fat. | Carbo- hydrates. | ||||
| s. d. | ℔ | ℔ | ℔ | ℔ | Calories. | |
| Beef, round | 0 10 | 1.20 | .22 | .14 | · · | 1,155 |
| 0 8½ | 1.41 | .26 | .17 | · · | 1,235 | |
| 0 5 | 2.40 | .44 | .29 | · · | 2,105 | |
| Beef, sirloin | 0 10 | 1.20 | .19 | .20 | · · | 1,225 |
| 0 9 | 1.33 | .21 | .22 | · · | 1,360 | |
| 0 8 | 1.50 | · · | · · | · · | · · | |
| 0 5 | 2.40 | · · | · · | · · | · · | |
| Beef, rib | 0 9 | 1.33 | .19 | .19 | · · | 1,200 |
| 0 7½ | 1.60 | · · | · · | · · | · · | |
| 0 4½ | 2.67 | · · | · · | · · | · · | |
| Mutton, leg | 0 9 | 1.33 | .20 | .20 | · · | 1,245 |
| 0 5 | 2.40 | .37 | .35 | · · | 2,245 | |
| Pork, spare-rib | 0 9 | 1.33 | .17 | .31 | · · | 1,645 |
| 0 7 | 1.71 | .22 | .39 | · · | 2,110 | |
| Pork, salt, fat | 0 7 | 1.71 | .03 | 1.40 | · · | 6,025 |
| 0 5 | 2.40 | .04 | 1.97 | · · | 8,460 | |
| Pork, smoked ham | 0 8 | 1.50 | .20 | .48 | · · | 2,435 |
| 0 4½ | 2.67 | .36 | .85 | · · | 4,330 | |
| Fresh cod | 0 4 | 3.00 | .34 | .01 | · · | 710 |
| 0 3 | 4.00 | .45 | .01 | · · | 945 | |
| Salt cod | 0 3½ | 3.43 | .54 | .07 | · · | 1,370 |
| 0 10 | 1.20 | .07 | .01 | .04 | 275 | |
| Milk, whole, 4d. a qt. | 0 2 | 6.00 | .19 | .23 | .30 | 1,915 |
| ” 3d. a qt. | 0 1½ | 8.00 | .26 | .30 | .40 | 2,550 |
| ” 2d. a qt. | 0 1 | 12.00 | .38 | .46 | .60 | 3,825 |
| Milk, skimmed, 2d. a qt. | 0 1 | 12.00 | .40 | .03 | .61 | 2,085 |
| Butter | 1 6 | .67 | .01 | .54 | · · | 2,320 |
| 1 3 | .80 | .01 | .64 | · · | 2,770 | |
| 1 0 | 1.00 | .01 | .81 | · · | 3,460 | |
| Margarine | 0 4 | 3.00 | · · | 2.37 | · · | 10,080 |
| Eggs, 2s. a dozen | 1 4 | .75 | .10 | .07 | · · | 475 |
| ” 1½s. a dozen | 1 0 | 1.00 | .13 | .09 | · · | 635 |
| ” 1s. a dozen | 0 8 | 1.50 | .19 | .13 | · · | 950 |
| Cheese | 0 8 | 1.50 | .38 | .48 | .04 | 2,865 |
| 0 7 | 1.71 | .43 | .55 | .04 | 3,265 | |
| 0 5 | 2.40 | .60 | .77 | .06 | 4,585 | |
| Wheat bread | 0 11⁄8 | 10.67 | .76 | .13 | 5.57 | 12,421 |
| Wheat flour | 0 13⁄5 | 7.64 | .67 | .07 | 5.63 | 12,110 |
| 0 1½ | 8.16 | .72 | .07 | 6.01 | 12,935 | |
| Oatmeal | 0 12⁄5 | 8.39 | 1.11 | .54 | 5.54 | 14,835 |
| 0 1½ | 8.16 | 1.08 | .53 | 5.39 | 14,430 | |
| Rice | 0 1¾ | 6.86 | .45 | .02 | 5.27 | 10,795 |
| Potatoes | 0 02⁄3 | 18.00 | .25 | .02 | 2.70 | 5,605 |
| 0 0½ | 24.00 | .34 | .02 | 3.60 | 7,470 | |
| Beans | 0 2 | 6.00 | 1.05 | .10 | 3.47 | 8,960 |
| Sugar | 1 ¾ | 6.86 | · · | · · | 6.86 | 12,760 |
The proper observance of the second rule mentioned requires information regarding the demands of the body for food under different circumstances. To supply this information is one purpose of the effort to determine the so-called dietary standards 221 mentioned above. It should be observed, however, that these are generally more applicable to the proper feeding of a group or class of people as a whole than for particular individuals in this class. The needs of individuals will vary largely from the average in accordance with the activity and individuality. Moreover, it is neither necessary nor desirable for the individual to follow any standard exactly from day to day. It is requisite only that the average supply shall be sufficient to meet the demands of the body during a given period.
The cooking of food and other modes of preparing it for consumption have much to do with its nutritive value. Many materials which, owing to their mechanical condition or to some other cause, are not particularly desirable food materials in their natural state, are quite nutritious when cooked or otherwise prepared for consumption. It is also a matter of common experience that well-cooked food is wholesome and appetizing, whereas the same material poorly prepared is unpalatable. There are three chief purposes of cooking; the first is to change the mechanical condition of the food. Heating changes the structure of many food materials very materially, so that they may be more easily chewed and brought into a condition in which the digestive juices can act upon them more freely, and in this way probably influencing the ease and thoroughness of digestion. The second is to make the food more appetizing by improving the appearance or flavour or both. Food which is attractive to the eye and pleasing to the palate quickens the flow of saliva and other digestive juices and thus aids digestion. The third is to kill, by heat, disease germs, parasites or other dangerous organisms that may be contained in food. This is often a very important matter and applies to both animal and vegetable foods. Scrupulous neatness should always be observed in storing, handling and serving food. If ever cleanliness is desirable it must be in the things we eat, and every care should be taken to ensure it for the sake of health as well as of decency. Cleanliness in this connexion means not only absence of visible dirt, but freedom from undesirable bacteria and other minute organisms and from worms and other parasites. If food, raw or cooked, is kept in dirty places, peddled from dirty carts, prepared in dirty rooms and in dirty dishes, or exposed to foul air, disease germs and other offensive and dangerous substances may easily enter it.
9. Pecuniary Economy of Food.—Statistics of economy and of cost of living in Great Britain, Germany and the United States show that at least half, and commonly more, of the income of wage-earners and other people in moderate circumstances is expended for subsistence. The relatively large cost of food, and the important influence of diet upon health and strength, make a more widespread understanding of the subject of dietetics very desirable. The maxim that “the best is the cheapest” does not apply to food. The “best” food, in the sense of that which is the finest in appearance and flavour and which is sold at the highest price, is not generally the most economical.
The price of food is not regulated largely by its value for nutriment. Its agreeableness to the palate or to the buyer’s fancy is a large factor in determining the current demand and market price. There is no more nutriment in an ounce of protein or fat from the tender-loin of beef than from the round or shoulder. The protein of animal food has, however, some advantage over that of vegetable foods in that it is more thoroughly, and perhaps more easily, digested, for which reason it would be economical to pay somewhat more for the same quantity of nutritive material in the animal food. Furthermore, animal foods such as meats, fish and the like, gratify the palate as most vegetable foods do not. For persons in good health, foods in which the nutrients are the most expensive are like costly articles of adornment. People who can well afford them may be justified in buying them, but they are not economical. The most economical food is that which is at the same time most healthful and cheapest.
The variations in the cost of the actual nutriment in different food materials may be illustrated by comparison of the amounts of nutrients obtained for a given sum in the materials as bought at ordinary market prices. This is done in Table VI., which shows the amounts of available nutrients contained in the quantities of different food materials that may be purchased for one shilling at prices common in England.
When proper attention is given to the needs of the body for food and the relation between cost and nutritive value of food materials, it will be found that with care in the purchase and skill in the preparation of food, considerable control may be had over the expensiveness of a palatable, nutritious and healthful diet.
Authorities.—Composition of Foods:—König, Chemie der menschlichen Nahrungs- und Genussmittel; Atwater and Bryant, “Composition of American Food Materials,” Bul. 28, Office of Experiment Stations, U.S. Department of Agriculture. Nutrition and Dietetics:—Armsby, Principles of Animal Nutrition; Lusk, The Science of Nutrition; Burney Yeo, Food in Health and Disease; Munk and Uffelmann, Die Ernährung des gesunden und kranken Menschen; Von Leyden, Ernährungstherapie und Diätetik; Dujardin-Beaumetz, Hygiène alimentaire; Hutchison, Food and Dietetics; R. H. Chittenden, Physiological Economy in Nutrition (1904), Nutrition of Man (1907); Atwater, “Chemistry and Economy of Food,” Bul. 21, Office of Experiment Stations, U.S. Department of Agriculture. See also other Bulletins of the same office on composition of food, results of dietary studies, metabolism experiments, &c., in the United States. General Metabolism:—Voit, Physiologie des allgemeinen Stoffwechsels und der Ernährung; Hermann, Handbuch der Physiologie, Bd. vi.; Von Noorden, Pathologie des Stoffwechsels; Schäfer, Text-Book of Physiology, vol. i.; Atwater and Langworthy, “Digest of Metabolism Experiments,” Bull. 45, Office of Experiment Stations, U.S. Department of Agriculture.
1 The terms applied by different writers to these nitrogenous compounds are conflicting. For instance, the term “proteid” is sometimes used as protein is here used, and sometimes to designate the group here called albuminoids. The classification and terminology here followed are those tentatively recommended by the Association of American Agricultural Colleges and Experiment Stations.
2 Folin, Festschrift für Olaf Hammarsten, iii. (Upsala, 1906).
3 Ztschr. Biol. 30, 73.
4 In Russian. Cited in United States Department of Agriculture, Office of Experiment Stations, Bul. No. 45, A Digest of Metabolism Experiments, by W. O. Atwater and C. F. Langworthy.
5 Arch. physiol. norm. et path. (1894) 4.
6 U.S. Department of Agriculture, Office of Experiment Stations, Bulletins Nos. 63, 69, 109, 136, 175. For a description of the respiration calorimeter here mentioned see also publication No. 42 of the Carnegie Institution of Washington.
7 Ztschr. Biol. 21 (1885), p. 377.
8 Connecticut (Storrs) Agricultural Experiment Station Report (1899), 73.
9 One ounce equals 28.35 grams.
10 As the chief function of both fats and carbohydrates is to furnish energy, their exact proportion in the diet is of small account. The amount of either may vary largely according to taste, available supply, or other condition, as long as the total amount of both is sufficient, together with the protein to furnish the required energy.
DIETRICH, CHRISTIAN WILHELM ERNST (1712-1774), German painter, was born at Weimar, where he was brought up early to the profession of art by his father Johann George, then painter of miniatures to the court of the duke. Having been sent to Dresden to perfect himself under the care of Alexander Thiele, he had the good fortune to finish in two hours, at the age of eighteen, a picture which attracted the attention of the king of Saxony. Augustus II. was so pleased with Dietrich’s readiness of hand that he gave him means to study abroad, and visit in succession the chief cities of Italy and the Netherlands. There he learnt to copy and to imitate masters of the previous century with a versatility truly surprising. Winckelmann, to whom he had been recommended, did not hesitate to call him the Raphael of landscape. Yet in this branch of his practice he merely imitated Salvator Rosa and Everdingen. He was more successful in aping the style of Rembrandt, and numerous examples of this habit may be found in the galleries of St Petersburg, Vienna and Dresden. At Dresden, indeed, there are pictures acknowledged to be his, bearing the fictitious dates of 1636 and 1638, and the name of Rembrandt. Among Dietrich’s cleverest reproductions we may account that of Ostade’s manner in the “Itinerant Singers” at the National Gallery. His skill in catching the character of the later masters of Holland is shown in candlelight scenes, such as the “Squirrel and the Peep-Show” at St Petersburg, where we are easily reminded of Godfried Schalcken. Dietrich tried every branch of art except portraits, painting Italian and Dutch views alternately with Scripture scenes and still life. In 1741 he was appointed court painter to Augustus III. at Dresden, with an annual salary of 400 thalers (£60), conditional on the production of four cabinet pictures a year. This condition, no doubt, accounts for the presence of fifty-two of the master’s panels and canvases in one of the rooms at the Dresden museum. Dietrich, though popular and probably the busiest artist of his time, never produced anything of his own; and his imitations are necessarily inferior to the originals which he affected to copy. His best work is certainly that which he gave to engravings. A collection of these at the British Museum, produced on the general lines of earlier men, such as Ostade and Rembrandt, reveal both spirit and skill. Dietrich, after his return from the Peninsula, generally signed himself “Dietericij,” and with this signature most of his extant pictures are inscribed. He died at Dresden, after he had successively filled the important appointments of director of the school of painting at the Meissen porcelain factory and professor of the Dresden academy of arts.
DIETRICH OF BERN, the name given in German popular poetry to Theodoric the Great. The legendary history of Dietrich differs so widely from the life of Theodoric that it has been suggested that the two were originally unconnected. Medieval 222 chroniclers, however, repeatedly asserted the identity of Dietrich and Theodoric, although the more critical noted the anachronisms involved in making Ermanaric (d. 376) and Attila (d. 453) contemporary with Theodoric (b. 455). That the legend is based on vague historical reminiscences is proved by the retention of the names of Theodoric (Thiuda-reiks, Dietrich) and his father Theudemir (Dietmar), by Dietrich’s connexion with Bern (Verona) and Raben (Ravenna). Something of the Gothic king’s character descended to Dietrich, familiarly called the Berner, the favourite of German medieval saga heroes, although his story did not leave the same mark on later German literature as did that of the Nibelungs. The cycle of songs connected with his name in South Germany is partially preserved in the Heldenbuch (q.v.) in Dietrich’s Flucht, the Rabenschlacht and Alpharts Tod; but it was reserved for an Icelandic author, writing in Norway in the 13th century, to compile, with many romantic additions, a consecutive account of Dietrich. In this Norse prose redaction, known as the Vilkina Saga, or more correctly the Thidrekssaga, is incorporated much extraneous matter from the Nibelungen and Wayland legends, in fact practically the whole of south German heroic tradition.
There are traces of a form of the Dietrich legend in which he was represented as starting out from Byzantium, in accordance with historical tradition, for his conquest of Italy. But this early disappeared, and was superseded by the existing legend, in which, perhaps by an “epic fusion” with his father Theudemir, he was associated with Attila, and then by an easy transition with Ermanaric. Dietrich was driven from his kingdom of Bern by his uncle Ermanaric. After years of exile at the court of Attila he returned with a Hunnish army to Italy, and defeated Ermanaric in the Rabenschlacht, or battle of Ravenna. Attila’s two sons, with Dietrich’s brother, fell in the fight, and Dietrich returned to Attila’s court to answer for the death of the young princes. This very improbable renunciation of the advantages of his victory suggests that in the original version of the story the Rabenschlacht was a defeat. In the poem of Ermenrichs Tod he is represented as slaying Ermanaric, as in fact Theodoric slew Odoacer. “Otacher” replaces Ermanaric as his adversary in the Hildebrandslied, which relates how thirty years after the earlier attempt he reconquered his Lombard kingdom. Dietrich’s long residence at Attila’s court represents the youth and early manhood of Theodoric spent at the imperial court and fighting in the Balkan peninsula, and, in accordance with epic custom, the period of exile was adorned with war-like exploits, with fights with dragons and giants, most of which had no essential connexion with the cycle. The romantic poems of König Laurin, Sigenot, Eckenlied and Virginal are based largely on local traditions originally independent of Dietrich. The court of Attila (Etzel) was a ready bridge to the Nibelungen legend. In the final catastrophe he was at length compelled, after steadily holding aloof from the combat, to avenge the slaughter of his Amelungs by the Burgundians, and delivered Hagen bound into the hands of Kriemhild. The flame breath which anger induced from him shows the influence of pure myth, but the tales of his demonic origin and of his being carried off by the devil in the shape of a black horse may safely be put down to the clerical hostility to Theodoric’s Arianism.
Generally speaking, Dietrich of Bern was the wise and just monarch as opposed to Ermanaric, the typical tyrant of Germanic legend. He was invariably represented as slow of provocation and a friend of peace, but once roused to battle not even Siegfried could withstand his onslaught. But probably Dietrich’s fight with Siegfried in Kriemhild’s rose garden at Worms is a late addition to the Rosengarten myth. The chief heroes of the Dietrich cycle are his tutor and companion in arms, Hildebrand (see Hildebrand, Lay of), with his nephews the Wolfings Alphart and Wolfhart; Wittich, who renounced his allegiance to Dietrich and slew the sons of Attila; Heime and Biterolf.
The contents of the poems dealing with the Dietrich cycle are summarized by Uhland in Schriften zur Geschichte der Dichtung und Sage (Stuttgart, 1873). The Thidrekssaga (ed. C. Unger, Christiania, 1853) is translated into German by F. H. v. der Hagen in Altdeutsche und altnordische Heldensagen (vols. i. and ii. 3rd ed., Breslau, 1872). A summary of it forms the concluding chapter of T. Hodgkin’s Theodoric the Goth (1891). The variations in the Dietrich legend in the Latin historians, in Old and Middle High German literature, and in the northern saga, can be studied in W. Grimm’s Deutsche Heldensage (2nd ed., Berlin, 1867). There is a good account in English in F. E. Sandbach’s Heroic Saga-cycle of Dietrich of Bern (1906), forming No. 15 of Alfred Nutt’s Popular Studies in Mythology, and another in M. Bentinck Smith’s translation of Dr O. L. Jiriczek’s Deutsche Heldensage (Northern Legends, London, 1902). For modern German authorities and commentators see B. Symons, “Deutsche Heldensage” in H. Paul’s Grd. d. german. Phil. (Strassburg, new ed., 1905); also Goedeke, Geschichte der deutschen Dichtung (i. 241-246).
DIEZ, FRIEDRICH CHRISTIAN (1794-1876), German philologist, was born at Giessen, in Hesse-Darmstadt, on the 15th of March 1794. He was educated first at the gymnasium and then at the university of his native town. There he studied classics under Friedrich Gottlieb Welcker (1784-1868) who had just returned from a two years’ residence in Italy to fill the chair of archaeology and Greek literature. It was Welcker who kindled in him a love of Italian poetry, and thus gave the first bent to his genius. In 1813 he joined the Hesse corps as a volunteer and served in the French campaign. Next year he returned to his books, and this short taste of military service was the only break in a long and uneventful life of literary labours. By his parents’ desire he applied himself for a short time to law, but a visit to Goethe in 1818 gave a new direction to his studies, and determined his future career. Goethe had been reading Raynouard’s Selections from the Romance Poets, and advised the young scholar to explore the rich mine of Provençal literature which the French savant had opened up. This advice was eagerly followed, and henceforth Diez devoted himself to Romance literature. He thus became the founder of Romance philology. After supporting himself for some years by private teaching, he removed in 1822 to Bonn, where he held the position of privatdocent. In 1823 he published his first work, An Introduction to Romance Poetry; in the following year appeared The Poetry of the Troubadours, and in 1829 The Lives and Works of the Troubadours. In 1830 he was called to the chair of modern literature. The rest of his life was mainly occupied with the composition of the two great works on which his fame rests, the Grammar of the Romance Languages (1836-1844), and the Lexicon of the Romance Languages—Italian, Spanish and French (1853); in these two works Diez did for the Romance group of languages what Jacob Grimm did for the Teutonic family. He died at Bonn on the 29th of May 1876.
The earliest French philologists, such as Perion and Henri Estienne, had sought to discover the origin of French in Greek and even in Hebrew. For more than a century Ménage’s Etymological Dictionary held the field without a rival. Considering the time at which it was written (1650), it was a meritorious work, but philology was then in the empirical stage, and many of Ménage’s derivations (such as that of “rat” from the Latin “mus,” or of “haricot” from “faba”) have since become bywords among philologists. A great advance was made by Raynouard, who by his critical editions of the works of the Troubadours, published in the first years of the 19th century, laid the foundations on which Diez afterwards built. The difference between Diez’s method and that of his predecessors is well stated by him in the preface to his dictionary. In sum it is the difference between science and guess-work. The scientific method is to follow implicitly the discovered principles and rules of phonology, and not to swerve a foot’s breadth from them unless plain, actual exceptions shall justify it; to follow the genius of the language, and by cross-questioning to elicit its secrets; to gauge each letter and estimate the value which attaches to it in each position; and lastly to possess the true philosophic spirit which is prepared to welcome any new fact, though it may modify or upset the most cherished theory. Such is the historical method which Diez pursues in his grammar and dictionary. To collect and arrange facts is, as he tells us, the sole secret of his success, and he adds in other words the famous apophthegm of Newton, “hypotheses non fingo.” The introduction to the grammar consists of two parts:—the first discusses the Latin, Greek and Teutonic elements common to the Romance languages; the second treats of the six dialects separately, their origin and the elements peculiar to each. The grammar itself is divided into four books, on phonology, on flexion, on the formation of words by composition and derivation, and on syntax.
His dictionary is divided into two parts. The first contains words common to two at least of the three principal groups of Romance:—Italian, Spanish and Portuguese, and Provençal and French. The Italian, as nearest the original, is placed at the head of each article. 223 The second part treats of words peculiar to one group. There is no separate glossary of Wallachian.
Of the introduction to the grammar there is an English translation by C. B. Cayley. The dictionary has been published in a remodelled form for English readers by T. C. Donkin.
DIEZ, a town of Germany, in the Prussian province of Hesse-Nassau, romantically situated in the deep valley of the Lahn, here crossed by an old bridge, 30 m. E. from Coblenz on the railway to Wetzlar. Pop. 4500. It is overlooked by a former castle of the counts of Nassau-Dillenburg, now a prison. Close by, on an eminence above the river, lies the castle of Oranienstein, formerly a Benedictine nunnery and now a cadet school, with beautiful gardens. There are a Roman Catholic and two Evangelical churches. The new part of the town is well built and contains numerous pretty villa residences. In addition to extensive iron-works there are sawmills and tanneries. In the vicinity are Fachingen, celebrated for its mineral waters, and the majestic castle of Schaumburg belonging to the prince of Waldeck-Pyrmont.
DIFFERENCES, CALCULUS OF (Theory of Finite Differences), that branch of mathematics which deals with the successive differences of the terms of a series.
1. The most important of the cases to which mathematical methods can be applied are those in which the terms of the series are the values, taken at stated intervals (regular or irregular), of a continuously varying quantity. In these cases the formulae of finite differences enable certain quantities, whose exact value depends on the law of variation (i.e. the law which governs the relative magnitude of these terms) to be calculated, often with great accuracy, from the given terms of the series, without explicit reference to the law of variation itself. The methods used may be extended to cases where the series is a double series (series of double entry), i.e. where the value of each term depends on the values of a pair of other quantities.
2. The first differences of a series are obtained by subtracting from each term the term immediately preceding it. If these are treated as terms of a new series, the first differences of this series are the second differences of the original series; and so on. The successive differences are also called differences of the first, second, ... order. The differences of successive orders are most conveniently arranged in successive columns of a table thus:—
| Term. | 1st Diff. | 2nd Diff. | 3rd Diff. | 4th Diff. |
| a | ||||
| b − a | ||||
| b | c − 2b + a | |||
| c − b | d − 3c + 3b − a | |||
| c | d − 2c + b | e − 4d + 6c − 4b + a | ||
| d − c | e − 3d + 3c − b | |||
| d | e − 2d + c | |||
| e − d | ||||
| e |
Algebra of Differences and Sums.
 |
| Fig. 1. |
3. The formal relations between the terms of the series and the differences may be seen by comparing the arrangements (A) and (B) in fig. 1. In (A) the various terms and differences are the same as in § 2, but placed differently. In (B) we take a new series of terms α, β, γ, δ, commencing with the same term α, and take the successive sums of pairs of terms, instead of the successive differences, but place them to the left instead of to the right. It will be seen, in the first place, that the successive terms in (A), reading downwards to the right, and the successive terms in (B), reading downwards to the left, consist each of a series of terms whose coefficients follow the binomial law; i.e. the coefficients in b − a, c − 2b + a, d − 3c + 3b − a, ... and in α + β, α + 2β + γ, α + 3β + 3γ + δ, ... are respectively the same as in y − x, (y − x)², (y − x)³, ... and in x + y, (x + y)², (x + y)³,.... In the second place, it will be seen that the relations between the various terms in (A) are identical with the relations between the similarly placed terms in (B); e.g. β + γ is the difference of α + 2β + γ and α + β, just as c − b is the difference of c and b: and d − c is the sum of c − b and d − 2c + b, just as β + 2γ + δ is the sum of β + γ and γ + δ. Hence if we take β, γ, δ, ... of (B) as being the same as b − a, c − 2b + a, d − 3c + 3b − a, ... of (A), all corresponding terms in the two diagrams will be the same.
Thus we obtain the two principal formulae connecting terms and differences. If we provisionally describe b − a, c − 2b + a, ... as the first, second, ... differences of the particular term a (§ 7), then (i.) the nth difference of a is
| l − nk + ... + (-1)n-2 | n·n − 1 | c + (-1)n-1 nb + (-1)n a, |
| 1·2 |
where l, k ... are the (n + 1)th, nth, ... terms of the series a, b, c, ...; the coefficients being those of the terms in the expansion of (y − x)n: and (ii.) the (n + 1)th term of the series, i.e. the nth term after a, is
| a + nβ + | n·n − 1 | γ + ... |
| 1·2 |
where β, γ, ... are the first, second, ... differences of a; the coefficients being those of the terms in the expansion of (x + y)n.
4. Now suppose we treat the terms a, b, c, ... as being themselves the first differences of another series. Then, if the first term of this series is N, the subsequent terms are N + a, N + a + b, N + a + b + c, ...; i.e. the difference between the (n + 1)th term and the first term is the sum of the first n terms of the original series. The term N, in the diagram (A), will come above and to the left of a; and we see, by (ii.) of § 3, that the sum of the first n terms of the original series is
| ( | N + na + | n·n − 1 | β + ... | ) | − N = na + | n·n − 1 | β + | n·n − 1·n − 2 | γ + ... |
| 1·2 | 1·2 | 1 · 2 · 3 |
5. As an example, take the arithmetical series
a, a + p, a + 2p, ...
The first differences are p, p, p, ... and the differences of any higher order are zero. Hence, by (ii.) of § 3, the (n + 1)th term is a + np, and, by § 4, the sum of the first n terms is na + ½n(n − 1)p = ½n{2a + (n − 1)p}.
6 As another example, take the series 1, 8, 27, ... the terms of which are the cubes of 1, 2, 3, ... The first, second and third differences of the first term are 7, 12 and 6, and it may be shown (§ 14 (i.)) that all differences of a higher order are zero. Hence the sum of the first n terms is
| n + 7 | n·n − 1 | + 12 | n·n − 1·n − 2 | + 6 | n·n − 1·n − 2·n − 3 | = ¼n4 + ½n³ + ¼n² = {½n (n + 1)}². |
| 1·2 | 1·2·3 | 1·2·3·4 |
7. In § 3 we have described b − a, c − 2b + a, ... as the first, second, ... differences of a. This ascription of the differences to particular terms of the series is quite arbitrary. If we read the differences in the table of § 2 upwards to the right instead of downwards to the right, we might describe e − d, e − 2d + c, ... as the first, second, ... differences of e. On the other hand, the term of greatest weight in c − 2b + a, i.e. the term which has the numerically greatest coefficient, is b, and therefore c − 2b + a might properly be regarded as the second difference of b, and similarly e − 4d + 6c − 4b + a might be regarded as the fourth difference of c. These three methods of regarding the differences lead to three different systems of notation, which are described in §§ 9, 10 and 11.
Notation of Differences and Sums.
8. It is convenient to denote the terms a, b, c, ... of the series by u0, u1, u2, u3, ... If we merely have the terms of the series, un may be regarded as meaning the (n + 1)th term. Usually, however, the terms are the values of a quantity u, which is a function of another quantity x, and the values of x, to which a, b, c, ... correspond, proceed by a constant difference h. If x0 and u0 are a pair of corresponding values of x and u, and if any other value x0 + mh of x and the corresponding value of u are denoted by xm and um, then the terms of the series will be ... un-2, un-1, un, un+1, un+2 ..., corresponding to values of x denoted by ... xn-2, xn-1, xn, xn+1, xn+2....
9. In the advancing-difference notation un+1 − un is denoted by Δun. The differences Δu0, Δu1, Δu2 ... may then be regarded as values of a function Δu corresponding to values of x proceeding by constant difference h; and therefore Δun+1 − Δun denoted by ΔΔun, or, more briefly, Δ²un; and so on. Hence the table of differences in § 2, with the corresponding values of x and of u placed opposite each other in the ordinary manner of mathematical tables, becomes
| x | u | 1st Diff. | 2nd Diff. | 3rd Diff. | 4th Diff. |
| · | · | · | · | · | · |
| · | · | · | · | · | · |
| · | · | · | · | · | · |
| xn-2 | un-2 | Δ²un-3 | Δ4un-4 ... | ||
| Δun-2 | Δ³un-3 | ||||
| xn-1 | un-1 | Δ²un-2 | Δ4un-3 ... | ||
| Δun-1 | Δ³un-2 | ||||
| xn | un | Δ²un-1 | Δ4un-2 ... | ||
| Δun | Δ³un-1 | ||||
| xn+1 | un+1 | Δ²un | Δ4un-1 ... | ||
| Δun+1 | Δ³un | ||||
| xn+2 | un+2 | Δ²un+1 | Δ4un ... | ||
| · | · | · | · | · | · |
| · | · | · | · | · | · |
| · | · | · | · | · | · |
The terms of the series of which ... un-1, un, un+1, ... are the first differences are denoted by Σu, with proper suffixes, so 224 that this series is ... Σun-1, Σun, Σun+1.... The suffixes are chosen so that we may have ΔΣun = un, whatever n may be; and therefore (§ 4) Σun may be regarded as being the sum of the terms of the series up to and including un-1. Thus if we write Σun-1 = C + un-2, where C is any constant, we shall have
| Σun = Σun-1 + ΔΣun-1 = C + un-2 + un-1, |
| Σun+1 = C + un-2 + un-1 + un, |
and so on. This is true whatever C may be, so that the knowledge of ... un-1, un, ... gives us no knowledge of the exact value of Σun; in other words, C is an arbitrary constant, the value of which must be supposed to be the same throughout any operations in which we are concerned with values of Σu corresponding to different suffixes.
There is another symbol E, used in conjunction with u to denote the next term in the series. Thus Eun means un+1, so that Eun = un + Δun.
10. Corresponding to the advancing-difference notation there is a receding-difference notation, in which un+1 − un is regarded as a difference of un+1, and may be denoted by Δ′un+1, and similarly un+1 − 2un + un-1 may be denoted by Δ′²un+1. This notation is only required for certain special purposes, and the usage is not settled (§ 19 (ii.)).
11. The central-difference notation depends on treating un+1 − 2un − un-1 as the second difference of un, and therefore as corresponding to the value xn; but there is no settled system of notation. The following seems to be the most convenient. Since un is a function of xn, and the second difference un+2 − 2un+1 + un is a function of xn+1, the first difference un+1 − un must be regarded as a function of xn+1/2, i.e. of ½(xn + xn+1). We therefore write un+1 − un = δun+1/2, and each difference in the table in § 9 will have the same suffix as the value of x in the same horizontal line; or, if the difference is of an odd order, its suffix will be the means of those of the two nearest values of x. This is shown in the table below.
In this notation, instead of using the symbol E, we use a symbol μ to denote the mean of two consecutive values of u, or of two consecutive differences of the same order, the suffixes being assigned on the same principle as in the case of the differences. Thus
μun+1/2 = ½(un + un+1, μδun = ½(δun-1/2 + δun+1/2, &c.
If we take the means of the differences of odd order immediately above and below the horizontal line through any value of x, these means, with the differences of even order in that line, constitute the central differences of the corresponding value of u. Thus the table of central differences is as follows, the values obtained as means being placed in brackets to distinguish them from the actual differences:—
| x | u | 1st Diff. | 2nd Diff. | 3rd Diff. | 4th Diff. |
| · | · | · | · | · | · |
| · | · | · | · | · | · |
| · | · | · | · | · | · |
| xn-2 | un-2 | (μδun-2) | δ²un-2 | (μδ³un-2) | δ4un-2 ... |
| δun-3/2 | δ³un-3/2 | ||||
| xn-1 | un-1 | (μδun-1) | δ²un-1 | (μδ³un-1) | δ4un-1 ... |
| δun-1/2 | δ³un-2 | ||||
| xn | un | (μδun) | δ²un | (μδ³un) | δ4un ... |
| δun+1/2 | δ³un+1/2 | ||||
| xn+1 | un+1 | (μδun+1) | δ²un+1 | (μδ³un+1) | δ4un+1 ... |
| δun+3/2 | δ³un+3/2 | ||||
| xn+2 | un+2 | (μδun+2) | δ²un+2 | (μδ³un+2) | δ4un+2 ... |
| · | · | · | · | · | · |
| · | · | · | · | · | · |
| · | · | · | · | · | · |
Similarly, by taking the means of consecutive values of u and also of consecutive differences of even order, we should get a series of terms and differences central to the intervals xn-2 to xn-1, xn-1 to xn, ....
The terms of the series of which the values of u are the first differences are denoted by σu, with suffixes on the same principle; the suffixes being chosen so that δσun shall be equal to un. Thus, if
σun-3/2 = C + un-2,
then
σun-1/2 = C + un-2 + un-1, σn+1/2 = C + un-2 + un-1 + un, &c.,
and also
μσun-1 = C + un-2 + ½un-1, μσun = C + un-2 + un-1 + ½un, &c.,
C being an arbitrary constant which must remain the same throughout any series of operations.
Operators and Symbolic Methods.
12. There are two further stages in the use of the symbols Δ, Σ, δ, σ, &c., which are not essential for elementary treatment but lead to powerful methods of deduction.
(i.) Instead of treating Δu as a function of x, so that Δun means (Δu)n, we may regard Δ as denoting an operation performed on u, and take Δun as meaning Δ.un. This applies to the other symbols E, δ, &c., whether taken simply or in combination. Thus ΔEun means that we first replace un by un+1, and then replace this by un+2 − un+1.
(ii.) The operations Δ, E, δ, and μ, whether performed separately or in combination, or in combination also with numerical multipliers and with the operation of differentiation denoted by D (≡ d/dx), follow the ordinary rules of algebra: e.g. Δ(un + vn) = Δun + Δvn, ΔDun = DΔun, &c. Hence the symbols can be separated from the functions on which the operations are performed, and treated as if they were algebraical quantities. For instance, we have
E·un = un+1 = un + Δun = 1·un + Δ·un,
so that we may write E = 1 + Δ, or Δ = E − 1. The first of these is nothing more than a statement, in concise form, that if we take two quantities, subtract the first from the second, and add the result to the first, we get the second. This seems almost a truism. But, if we deduce En = (1 + Δ)n, Δn = (E-1)n, and expand by the binomial theorem and then operate on u0, we get the general formulae
| un = u0 + nΔu0 + | n·n − 1 | Δ2u0 + ... + Δnu0, |
| 1·2 |
| Δnu0 = un − nun-1 + | n·n − 1 | un-2 + ... + (-1)nu0, |
| 1·2 |
which are identical with the formulae in (ii.) and (i.) of § 3.
(iii.) What has been said under (ii.) applies, with certain reservations, to the operations Σ and σ, and to the operation which represents integration. The latter is sometimes denoted by D-1; and, since ΔΣun = un, and δσun = un, we might similarly replace Σ and σ by Δ-1 and δ-1. These symbols can be combined with Δ, E, &c. according to the ordinary laws of algebra, provided that proper account is taken of the arbitrary constants introduced by the operations D-1, Δ-1, δ-1.
Applications to Algebraical Series.
13. Summation of Series.—If ur, denotes the (r + 1)th term of a series, and if vr is a function of r such that Δvr = ur for all integral values of r, then the sum of the terms um, um+1, ... un is vn+1 − vm. Thus the sum of a number of terms of a series may often be found by inspection, in the same kind of way that an integral is found.
14. Rational Integral Functions.—(i.) If ur is a rational integral function of r of degree p, then Δur, is a rational integral function of r of degree p − 1.
(ii.) A particular case is that of a factorial, i.e. a product of the form (r + a + 1) (r + a + 2) ... (r + b), each factor exceeding the preceding factor by 1. We have
Δ · (r + a + 1) (r + a + 2) ... (r + b) = (b − a)·(r + a + 2) ... (r + b),
whence, changing a into a-1,
Σ(r + a + 1) (r + a + 2) ... (r + b) = const. + (r + a)(r + a + 1) ... (r + b)/(b − a + 1).
A similar method can be applied to the series whose (r + 1)th term is of the form 1/(r + a + 1) (r + a + 2) ... (r + b).
(iii.) Any rational integral function can be converted into the sum of a number of factorials; and thus the sum of a series of which such a function is the general term can be found. For example, it may be shown in this way that the sum of the pth powers of the first n natural numbers is a rational integral function of n of degree p + 1, the coefficient of np+1 being 1/(p + 1).
15. Difference-equations.—The summation of the series ... + un+2 + un-1 + un is a solution of the difference-equation Δvn = un+1, which may also be written (E − 1)vn = un+1. This is a simple form of difference-equation. There are several forms which have been investigated; a simple form, more general than the above, is the linear equation with constant coefficients—
vn+m + a1vn+m-1 + a2vn+m-2 + ... + amvn = N,
where a1, a2, ... am are constants, and N is a given function of n. This may be written
(Em + a1Em-1 + ... + am)vn = N
or
(E − p1)(E − p2) ... (E − pm)vn = N.
The solution, if p1, p2, ... pm are all different, is vn = C1p1n + C2p2n + ... + Cmpmn + Vn, where C1, C2 ... are constants, and vn = Vn is any one solution of the equation. The method of finding a value for Vn depends on the form of N. Certain modifications are required when two or more of the p’s are equal.
It should be observed, in all cases of this kind, that, in describing C1, C2 as “constants,” it is meant that the value of any one, as C1, is the same for all values of n occurring in the series. A “constant” may, however, be a periodic function of n.
Applications to Continuous Functions.
16. The cases of greatest practical importance are those in which u is a continuous function of x. The terms u1, u2 ... of the series then represent the successive values of u corresponding to x = x1, x2.... The important applications of the theory in these cases are to (i.) relations between differences and differential coefficients, (ii.) 225 interpolation, or the determination of intermediate values of u, and (iii.) relations between sums and integrals.
17. Starting from any pair of values x0 and u0, we may suppose the interval h from x0 to x1 to be divided into q equal portions. If we suppose the corresponding values of u to be obtained, and their differences taken, the successive advancing differences of u0 being denoted by ∂u0, ∂²u0 ..., we have (§ 3 (ii.))
| u1 = u0 + q∂u0 + | q·q − 1 | ∂²u0 + .... |
| 1·2 |
When q is made indefinitely great, this (writing ƒ(x) for u) becomes Taylor’s Theorem (Infinitesimal Calculus)
| ƒ(x + h) = ƒ(x) + hƒ′(x) + | h² | ƒ″(x) + ..., |
| 1·2 |
which, expressed in terms of operators, is
| E = 1 + hD + | h² | D² + | h³ | D³ + ... = ehD. |
| 1·2 | 1·2·3 |
This gives the relation between Δ and D. Also we have
| u2 = u0 + 2q∂u0 + | 2q·2q − 1 | ∂²u0 + ... |
| 1·2 | ||
| u3 = u0 + 3q∂u0 + | 3q·3q − 1 | ∂²u0 + ... |
| 1·2 | ||
| · · | ||
| · · | ||
| · · | ||
and, if p is any integer,
| up/q = u0 + p∂u0 + | p·p − 1 | ∂²u0 + .... |
| 1·2 |
From these equations up/q could be expressed in terms of u0, u1, u2, ...; this is a particular case of interpolation (q.v.).
18. Differences and Differential Coefficients.—The various formulae are most quickly obtained by symbolical methods; i.e. by dealing with the operators Δ, E, D, ... as if they were algebraical quantities. Thus the relation E = ehD (§ 17) gives
hD = loge (1 + Δ) = Δ − ½Δ² + 1⁄3Δ³ ...
or
h(du/dx)0 = Δu0 − ½Δ²u0 + 1⁄3Δ³u0 ....
The formulae connecting central differences with differential coefficients are based on the relations μ = cosh ½hD = ½(e1/2hD + e-1/2hD), δ = 2 sinh ½hD − e1/2hD − e-1/2hD, and may be grouped as follows:—
| u0 | = u0 | } |
| μδu0 | = (hD + 1⁄6 h³D³ + 1⁄120 h5D5 + ...)u0 | |
| δ²u0 | = (h²D² + 1⁄12 h4D4 + 1⁄360 h6D6 + ...)u0 | |
| μδ³u0 | = (h³D³ + 1⁄4 h5D5 + ...)u0 | |
| δ4u0 | = (h4D4 + 1⁄6 h6D6 + ...)u0 | |
| · · · | ||
| · · · | ||
| · · · | ||
| μu1/2 | = (1 + 1⁄8 h²D² + 1⁄384 h4D4 + 1⁄46080 h6D6 + ...)u1/2 | } |
| δu1/2 | = (hD + 1⁄24 h³D³ + 1⁄1920 h5D5 + ...)u1/2 | |
| μδ²u1/2 | = (h²D² + 5⁄24 h4D4 + 91⁄5760 h6D6 + ...)u1/2 | |
| δ³u1/2 | = (h³D³ + 1⁄8 h5D5 + ...)u1/2 | |
| μδ4 u1/2 | = (h4D4 + 7⁄24 h6D6 + ...)u1/2 | |
| · · · | ||
| · · · | ||
| · · · | ||
| u0 | = u0 | } |
| hDu0 | = (μδ − 1⁄6 μδ³ + 1⁄30 μδ5 − ...)u0 | |
| h²D²u0 | = (δ² − 1⁄12 δ4 + 1⁄90 δ6 − ...)u0 | |
| h³D³u0 | = (μδ³ − 1⁄4 μδ5 + ...)u0 | |
| h4D4u0 | = (δ4 − 1⁄6 δ6 + ...)u0 | |
| · · · | ||
| · · · | ||
| · · · | ||
| u1/2 | = (μ − 1⁄8 μδ² + 3⁄128 μδ4 − 5⁄1024 μδ6 + ...)u1/2 | } |
| hDu1/2 | = (δ − 1⁄24 δ³ + 3⁄640 δ5 − ...)u1/2 | |
| h²D²u1/2 | = (μδ² − 5⁄24 μδ4 + 259⁄5760 μδ6 − ...)u1/2 | |
| h³D³u1/2 | = (δ³ − 1⁄8 δ5 + ...)u1/2 | |
| h4D4 u1/2 | = (μδ4 − 7⁄24 μδ6 + ...)u1/2 | |
| · · · | ||
| · · · | ||
| · · · | ||
When u is a rational integral function of x, each of the above series is a terminating series. In other cases the series will be an infinite one, and may be divergent; but it may be used for purposes of approximation up to a certain point, and there will be a “remainder,” the limits of whose magnitude will be determinate.
19. Sums and Integrals.—The relation between a sum and an integral is usually expressed by the Euler-Maclaurin formula. The principle of this formula is that, if um and um+1, are ordinates of a curve, distant h from one another, then for a first approximation to the area of the curve between um and um+1 we have ½h(um + um+1), and the difference between this and the true value of the area can be expressed as the difference of two expressions, one of which is a function of xm, and the other is the same function of xm+1. Denoting these by φ(xm) and φ(xm+1), we have
| ∫ | xm+1 | udx = ½h(um + um+1) + φ(xm+1) − φ(xm). |
| xm |
Adding a series of similar expressions, we find
| ∫ | xn | udx = h{½um + um+1 + um+2 + ... + un-1 + ½un} + φ(xn) − φ(xm). |
| xm |
The function φ(x) can be expressed in terms either of differential coefficients of u or of advancing or central differences; thus there are three formulae.
(i.) The Euler-Maclaurin formula, properly so called, (due independently to Euler and Maclaurin) is
| ∫ | xn | udx = h·μσun − 1⁄12 h² | dun | ½ + 1⁄720 h4 | d³un | − 1⁄30240 h6 | d5un | + ... = h·μσun − | B1 | h2 | dun | + | B2 | h4 | d3un | − | B3 | h6 | d5un | + ... |
| dx | dx3 | dx5 | 2! | dx | 4! | dx3 | 6! | dx5 |
where B1, B2, B3 ... are Bernoulli’s numbers.
(ii.) If we express differential coefficients in terms of advancing differences, we get a theorem which is due to Laplace:—
| 1/h | ∫ | xn | udx = μσ(un − u0) − 1⁄12(Δun − Δu0) + 1⁄24(Δ²un − Δ²u0) − 19⁄720(Δ³un − Δ³u0) + 3⁄160(Δ4un − Δ4u0) − ... |
| x0 |
For practical calculations this may more conveniently be written
| 1/h | ∫ | xn | udx = μσ(un − u0) + 1⁄12(Δu0 − ½Δ²u0 + 19⁄60Δ³u0 − ...) + 1⁄12(Δ′ un − ½Δ′ ²un + 19⁄60Δ′ ³un − ...), |
| x0 |
where accented differences denote that the values of u are read backwards from un; i.e. Δ′un denotes un-1 − un, not (as in § 10) un − un-1.
(iii.) Expressed in terms of central differences this becomes
| 1/h | ∫ | xn | udx = μσ(un − u0) − 1⁄12μδun + 11⁄720 μδ³un − ... + 1⁄12μδu0 − 11⁄720 μδ³u0 + ... = μ(σ − 1⁄12δ + 11⁄720δ³ − 191⁄60480δ5 + 2497⁄3628800δ7 − ...)(un − u0). |
| x0 |
(iv.) There are variants of these formulae, due to taking hum+1/2 as the first approximation to the area of the curve between um and um+1; the formulae involve the sum u1/2 + u3/2 + ... + un-1/2 ≡ σ(un − u0) (see Mensuration).
20. The formulae in the last section can be obtained by symbolical methods from the relation
| 1/h | ∫ | udx = 1/h D-1u = 1/hD · u. |
Thus for central differences, if we write θ ≡ ½hD, we have μ = cosh θ, δ = 2 sinh θ, σ = δ-1, and the result in (iii.) corresponds to the formula
sinh θ = θ cosh θ/(1 + 1⁄3 sinh² θ − 2⁄3·5 sinh4 θ + 2·4⁄3·5·7 sinh6 θ − ...).
References.—There is no recent English work on the theory of finite differences as a whole. G. Boole’s Finite Differences (1st ed., 1860, 2nd ed., edited by J. F. Moulton, 1872) is a comprehensive treatise, in which symbolical methods are employed very early. A. A. Markoff’s Differenzenrechnung (German trans., 1896) contains general formulae. (Both these works ignore central differences.) Encycl. der math. Wiss. vol. i. pt. 2, pp. 919-935, may also be consulted. An elementary treatment of the subject will be found in many text-books, e.g. G. Chrystal’s Algebra (pt. 2, ch. xxxi.). A. W. Sunderland, Notes on Finite Differences (1885), is intended for actuarial students. Various central-difference formulae with references are given in Proc. Lond. Math. Soc. xxxi. pp. 449-488. For other references see Interpolation.
DIFFERENTIAL EQUATION, in mathematics, a relation between one or more functions and their differential coefficients. The subject is treated here in two parts: (1) an elementary introduction dealing with the more commonly recognized types of differential equations which can be solved by rule; and (2) the general theory.
Part I.—Elementary Introduction.
Of equations involving only one independent variable, x (known as ordinary differential equations), and one dependent variable, y, and containing only the first differential coefficient dy/dx (and therefore said to be of the first order), the simplest form is that reducible to the type
dy/dx = ƒ(x)/F(y),
leading to the result ƒF(y)dy − ƒƒ(x)dx = A, where A is an arbitrary constant; this result is said to solve the differential equation, the problem of evaluating the integrals belonging to the integral calculus.
Another simple form is
dy/dx + yP = Q,
where P, Q are functions of x only; this is known as the linear equation, since it contains y and dy/dx only to the first degree. If ƒPdx = u, we clearly have
| d | (yeu) = eu | ( | dy | + Py | ) | = euQ, |
| dx | dx |
so that y = e-u(ƒeuQdx + A) solves the equation, and is the only possible solution, A being an arbitrary constant. The rule for the solution of the linear equation is thus to multiply the equation by eu, where u = ƒPdx.
A third simple and important form is that denoted by
y = px + ƒ(p),
where p is an abbreviation for dy/dx; this is known as Clairaut’s form. By differentiation in regard to x it gives
| p = p + x | dp | + ƒ′(p) | dp | , |
| dx | dx |
where
| ƒ′(p) = | d | ƒ(p); |
| dp |
thus, either (i.) dp/dx = 0, that is, p is constant on the curve satisfying the differential equation, which curve is thus any one of the straight lines y = cx = ƒ(c), where c is an arbitrary constant, or else, (ii.) x + ƒ′(p) = 0; if this latter hypothesis be taken, and p be eliminated between x + ƒ′(p) = 0 and y = px + ƒ(p), a relation connecting x and y, not containing an arbitrary constant, will be found, which obviously represents the envelope of the straight lines y = cx + ƒ(c).
In general if a differential equation φ(x, y, dy/dx) = 0 be satisfied by any one of the curves F(x, y, c) = 0, where c is an arbitrary constant, it is clear that the envelope of these curves, when existent, must also satisfy the differential equation; for this equation prescribes a relation connecting only the co-ordinates x, y and the differential coefficient dy/dx, and these three quantities are the same at any point of the envelope for the envelope and for the particular curve of the family which there touches the envelope. The relation expressing the equation of the envelope is called a singular solution of the differential equation, meaning an isolated solution, as not being one of a family of curves depending upon an arbitrary parameter.
An extended form of Clairaut’s equation expressed by
y = xF(p) + ƒ(p)
may be similarly solved by first differentiating in regard to p, when it reduces to a linear equation of which x is the dependent and p the independent variable; from the integral of this linear equation, and the original differential equation, the quantity p is then to be eliminated.
Other types of solvable differential equations of the first order are (1)
M dy/dx = N,
where M, N are homogeneous polynomials in x and y, of the same order; by putting v = y/x and eliminating y, the equation becomes of the first type considered above, in v and x. An equation (aB ≷ bA)
(ax + by + c)dy/dx = Ax + By + C
may be reduced to this rule by first putting x + h, y + k for x and y, and determining h, k so that ah + bk + c = 0, Ah + Bk + C = 0.
(2) An equation in which y does not explicitly occur,
ƒ(x, dy/dx) = 0,
may, theoretically, be reduced to the type dy/dx = F(x); similarly an equation F(y, dy/dx) = 0.
(3) An equation
ƒ(dy/dx, x, y) = 0,
which is an integral polynomial in dy/dx, may, theoretically, be solved for dy/dx, as an algebraic equation; to any root dy/dx = F1(x, y) corresponds, suppose, a solution φ1(x, y, c) = 0, where c is an arbitrary constant; the product equation φ1(x, y, c)φ2(x, y, c) ... = 0, consisting of as many factors as there were values of dy/dx, is effectively as general as if we wrote φ1(x, y, c1)φ2(x, y, c2) ... = 0; for, to evaluate the first form, we must necessarily consider the factors separately, and nothing is then gained by the multiple notation for the various arbitrary constants. The equation φ1(x, y, c)φ2(x, y, c) ... = 0 is thus the solution of the given differential equation.
In all these cases there is, except for cases of singular solutions, one and only one arbitrary constant in the most general solution of the differential equation; that this must necessarily be so we may take as obvious, the differential equation being supposed to arise by elimination of this constant from the equation expressing its solution and the equation obtainable from this by differentiation in regard to x.
A further type of differential equation of the first order, of the form
dy/dx = A + By + Cy²
in which A, B, C are functions of x, will be briefly considered below under differential equations of the second order.
When we pass to ordinary differential equations of the second order, that is, those expressing a relation between x, y, dy/dx and d²y/dx², the number of types for which the solution can be found by a known procedure is very considerably reduced. Consider the general linear equation
| d²y | + P | dy | + Qy = R, |
| dx² | dx |
where P, Q, R are functions of x only. There is no method always effective; the main general result for such a linear equation is that if any particular function of x, say y1, can be discovered, for which
| d²y1 | + P | dy1 | + Qy1 = 0, |
| dx² | dx |
then the substitution y = y1η in the original equation, with R on the right side, reduces this to a linear equation of the first order with the dependent variable dη/dx. In fact, if y = y1η we have
| dy | = y1 | dη | + η | dy1 | and | d²y | = y1 | d²η | + 2 | dy1 | dη | + η | d²y1 | , |
| dx | dx | dx | dx² | dx² | dx | dx | dx² |
and thus
| d²y | + P | dy | + Qy = y1 | d²η | + (2 | dy1 | + Py1) | dη | + ( | d²y1 | + P | dy1 | + Qy1)η; | |
| dx² | dx | dx² | dx | dx | dx² | dx |
if then
| d²y1 | + P | dy1 | + Qy1 = 0, |
| dx² | dx |
and z denote dη/dx, the original differential equation becomes
| y1 | dz | + ( 2 | dy1 | Py1) z = R. |
| dx | dx |
From this equation z can be found by the rule given above for the linear equation of the first order, and will involve one arbitrary constant; thence y = y1 η = y1 ∫ zdx + Ay1, where A is another arbitrary constant, will be the general solution of the original equation, and, as was to be expected, involves two arbitrary constants.
The case of most frequent occurrence is that in which the coefficients P, Q are constants; we consider this case in some detail. If θ be a root of the quadratic equation θ² + θP + Q = 0, it can be at once seen that a particular integral of the differential equation with zero on the right side is y1 = eθx. Supposing first the roots of the quadratic equation to be different, and φ to be the other root, so that φ + θ = -P, the auxiliary differential equation for z, referred to above, becomes dz/dx + (θ − φ)z = Re-θx which leads to ze(θ-φ) = B + ∫ Re-θxdx, where B is an arbitrary constant, and hence to
y = Aeθ x + eθ x ∫ Be(φ-θ) x dx + eθ x ∫ e(φ-θ) x ∫ Re-θ x dxdx,
or say to y = Aeθ x + Ceθ x + U, where A, C are arbitrary constants and U is a function of x, not present at all when R = 0. If the quadratic equation θ² + Pθ + Q = 0 has equal roots, so that 2θ = -P, the auxiliary equation in z becomes dz/dx = Reθ x giving z = B + ∫ Reθ x dx, where B is an arbitrary constant, and hence
y = (A + Bx)eθ x + eθ x ∫ ∫ Re-θ x dxdx,
or, say, y = (A + Bx)eθ x + U, where A, B are arbitrary constants, and U is a function of x not present at all when R = 0. The portion Aeθ x + Beθ x or (A + Bx)eθ x of the solution, which is known as the complementary function, can clearly be written down at once by inspection of the given differential equation. The remaining portion U may, by taking the constants in the complementary function properly, be replaced by any particular solution whatever of the differential equation
| d²v | + P | dy | + Qy = R; |
| dx² | dx |
for if u be any particular solution, this has a form
u = A0 eθ x + B0 eφ x + U,
or a form
u = (A0 + B0x) eθ x + U;
thus the general solution can be written
(A − A0)eθ x + (B − B0)eθ x + u, or {A − A0 + (B − B0)x} eθ x + u,
where A − A0, B − B0, like A, B, are arbitrary constants.
A similar result holds for a linear differential equation of any order, say
| dny | + P1 | dn-1y | + ... + Pny = R, |
| dxn | dxn-1 |
where P1, P2, ... Pn are constants, and R is a function of x. If we form the algebraic equation θn + P1θn-1 + ... + Pn = 0, and all the roots of this equation be different, say they are θ1, θ2, ... θn, the general solution of the differential equation is
y = A1 eθ1 x + A2 eθ2 x + ... + An eθn x + u,
where A1, A2, ... An are arbitrary constants, and u is any 227 particular solution whatever; but if there be one root θ1 repeated r times, the terms A1 eθ1 x + ... + Ar eθr x must be replaced by (A1 + A2x + ... + Arxr-1)eθ1 x where A1, ... An are arbitrary constants; the remaining terms in the complementary function will similarly need alteration of form if there be other repeated roots.
To complete the solution of the differential equation we need some method of determining a particular integral u; we explain a procedure which is effective for this purpose in the cases in which R is a sum of terms of the form eaxφ(x), where φ(x) is an integral polynomial in x; this includes cases in which R contains terms of the form cos bx·φ(x) or sin bx·φ(x). Denote d/dx by D; it is clear that if u be any function of x, D(eaxu) = eaxDu + aeaxu, or say, D(eaxu) = eax(D + a)u; hence D²(eaxu), i.e. d²/dx² (eaxu), being equal to D(eaxv), where v = (D + a)u, is equal to eax(D + a)v, that is to eax(D + a)²u. In this way we find Dn(eaxu) = eax(D + a)nu, where n is any positive integer. Hence if ψ(D) be any polynomial in D with constant coefficients, ψ(D) (eaxu) = eaxψ(D + a)u. Next, denoting ∫ udx by D-1u, and any solution of the differential equation dz/dx + az = u by z = (d + a)-1u, we have D[eax(D + a)-1u] = D(eaxz) = eax(D + a)z = eaxu, so that we may write D-1(eaxu) = eax(D + a)-1u, where the meaning is that one value of the left side is equal to one value of the right side; from this, the expression D-2(eaxu), which means D-1[D-1(eaxu)], is equal to D-1(eaxz) and hence to eax(D + a)-1z, which we write eax(D + a)-2u; proceeding thus we obtain
D-n(eaxu) = eax(D + a)-nu,
where n is any positive integer, and the meaning, as before, is that one value of the first expression is equal to one value of the second. More generally, if ψ(D) be any polynomial in D with constant coefficients, and we agree to denote by [1/ψ(D)]u any solution z of the differential equation ψ(D)z = u, we have, if v = [1/ψ(D + a)]u, the identity ψ(D)(eaxv) = eaxψ(D + a)v = eaxu, which we write in the form
| 1 | (eaxu) = eax | 1 | u. |
| ψ(D) | ψ(D + a) |
This gives us the first step in the method we are explaining, namely that a solution of the differential equation ψ(D)y = eaxu + ebxv + ... where u, v, ... are any functions of x, is any function denoted by the expression
| eax | 1 | u + ebx | 1 | v + .... |
| ψ(D + a) | ψ(D + b) |
It is now to be shown how to obtain one value of [1/ψ(D + a)]u, when u is a polynomial in x, namely one solution of the differential equation ψ(D + a)z = u. Let the highest power of x entering in u be xm; if t were a variable quantity, the rational fraction in t, 1/ψ(t + a) by first writing it as a sum of partial fractions, or otherwise, could be identically written in the form
Krt-r + Kr-1t-r+1 + ... + K1t-1 + H + H1t + ... + Hmtm + tm+1φ(t)/ψ(t + a),
where φ(t) is a polynomial in t; this shows that there exists an identity of the form
1 = ψ(t + a)(Krt−r + ... + K1t−1 + H + H1t + ... + Hmtm) + φ(t)tm+1,
and hence an identity
u = ψ(D + a) [KrD−r + ... + K1D−1 + H + H1D + ... + HmDm] u + φ(D) Dm+1u;
in this, since u contains no power of x higher than xm, the second term on the right may be omitted. We thus reach the conclusion that a solution of the differential equation ψ(D + a)z = u is given by
z = (KrD−r + ... + K1D−1 + H + H1D + ... + HmDm)u,
of which the operator on the right is obtained simply by expanding 1/ψ(D + a) in ascending powers of D, as if D were a numerical quantity, the expansion being carried as far as the highest power of D which, operating upon u, does not give zero. In this form every term in z is capable of immediate calculation.
Example.—For the equation
| d4v | + 2 | d²y | + y = x³ cos x or (D² + 1)²y = x³ cos x, |
| dx4 | dx3 |
the roots of the associated algebraic equation (θ² + 1)² = 0 are θ = ±i, each repeated; the complementary function is thus
(A + Bx)eix + (C + Dx)e−ix,
where A, B, C, D are arbitrary constants; this is the same as
(H + Kx) cos x + (M + Nx) sin x,
where H, K, M, N are arbitrary constants. To obtain a particular integral we must find a value of (1 + D²)−²x³ cos x; this is the real part of (1 + D²)−² eixx³ and hence of eix [1 + (D + i)²]−² x³
or
eix [2iD(1 + ½iD)]−² x³,
or
−¼eix D−² (1 + iD − ¾D² − ½iD³ + 5⁄16D4 + 3⁄16iD5 ...)x³,
or
−¼eix (1⁄20x5 + ¼ix4 − ¾x³ − 3⁄2 ix² + 15⁄8 x + 9⁄8 i);
the real part of this is
−¼ (1⁄20 x5 − ¾x² + 15⁄8x) cos x + ¼ (¼x4 − 3⁄4x² + 9⁄8) sin x.
This expression added to the complementary function found above gives the complete integral; and no generality is lost by omitting from the particular integral the terms −15⁄32x cos x + 9⁄32 sin x, which are of the types of terms already occurring in the complementary function.
The symbolical method which has been explained has wider applications than that to which we have, for simplicity of explanation, restricted it. For example, if ψ(x) be any function of x, and a1, a2, ... an be different constants, and [(t + a1) (t + a2) ... (t + an)]−1 when expressed in partial fractions be written Σcm(t + am)−1, a particular integral of the differential equation (D + a1)(D + a2) ... (D + an)y = ψ(x) is given by
y = Σcm(D + am)−1 ψ(x) = Σcm (D + am)−1 e−amxeamx ψ(x) = Σcme−amxD−1 (eamxψ(x) ) = Σcme−amx ∫ eamxψ(x)dx.
The particular integral is thus expressed as a sum of n integrals. A linear differential equation of which the left side has the form
| xn | dny | + P1xn−1 | dn−1y | + ... + Pn−1x | dy | + Pny, |
| dxn | dxn−1 | dx |
where P1, ... Pn are constants, can be reduced to the case considered above. Writing x = et we have the identity
| xm | dmu | = θ(θ − 1)(θ − 2) ... (θ − m + 1)u, where θ = d/dt. |
| dxm |
When the linear differential equation, which we take to be of the second order, has variable coefficients, though there is no general rule for obtaining a solution in finite terms, there are some results which it is of advantage to have in mind. We have seen that if one solution of the equation obtained by putting the right side zero, say y1, be known, the equation can be solved. If y2 be another solution of
| d²y | + P | dy | + Qy = 0, |
| dx² | dx |
there being no relation of the form my1 + ny2 = k, where m, n, k are constants, it is easy to see that
| d | (y1′y2 − y1y2′) = P(y1′y2 − y1y2′), |
| dx |
so that we have
y1′y2 − y1y2′ = A exp. (∫ Pdx),
where A is a suitably chosen constant, and exp. z denotes ez. In terms of the two solutions y1, y2 of the differential equation having zero on the right side, the general solution of the equation with R = φ(x) on the right side can at once be verified to be Ay1 + By2 + y1u − y2v, where u, v respectively denote the integrals
u = ∫ y2φ(x) (y1′y2 − y2′y1)−1dx, v = ∫ y1φ(x) (y1′y2 − y2′y1)−1dx.
The equation
| d²y | + P | dy | + Qy = 0, |
| dx² | dx |
by writing y = v exp. (-½ ∫ Pdx), is at once seen to be reduced to d²v/dx² + Iv = 0, where I = Q − ½dP/dx − ¼P². If η = − 1/v dv/dx, the equation d²v/dx² + Iv = 0 becomes dη/dx = I + η², a non-linear equation of the first order.
More generally the equation
| dη | = A + Bη + Cη², |
| dx |
where A, B, C are functions of x, is, by the substitution
| η = − | 1 | dy |
| Cy | dx |
reduced to the linear equation
| d²y | − (B + | 1 | dC | ) | dy | + ACy = 0. |
| dx² | C | dx | dx |
The equation
| dη | = A + Bη + Cη², |
| dx |
known as Riccati’s equation, is transformed into an equation of the same form by a substitution of the form η = (aY + b)/(cY + d), where a, b, c, d are any functions of x, and this fact may be utilized to obtain a solution when A, B, C have special forms; in particular if any particular solution of the equation be known, say η0, the 228 substitution η = η0 − 1/Y enables us at once to obtain the general solution; for instance, when
| 2B = | d | log ( | A | ), |
| dx | C |
a particular solution is η0 = √(-A/C). This is a case of the remark, often useful in practice, that the linear equation
| φ(x) | d²y | + ½ | dφ | dy | + μy = 0, |
| dx² | dx | dx |
where μ is a constant, is reducible to a standard form by taking a new independent variable z = ∫ dx[φ(x)]-½.
We pass to other types of equations of which the solution can be obtained by rule. We may have cases in which there are two dependent variables, x and y, and one independent variable t, the differential coefficients dx/dt, dy/dt being given as functions of x, y and t. Of such equations a simple case is expressed by the pair
| dx | = ax + by + c, | dy | a′x + b′y + c′, |
| dt | dt |
wherein the coefficients a, b, c, a′, b′, c′, are constants. To integrate these, form with the constant λ the differential coefficient of z = x + λy, that is dz/dt = (a + λa′)x + (b + λb′)y + c + λc′, the quantity λ being so chosen that b + λb′ = λ(a + λa′), so that we have dz/dt = (a + λa′)z + c + λc′; this last equation is at once integrable in the form z(a + λa′) + c + λc′ = Ae(a + λa′)t, where A is an arbitrary constant. In general, the condition b + λb′ = λ(a + λa′) is satisfied by two different values of λ, say λ1, λ2; the solutions corresponding to these give the values of x +λ1y and x + λ2y, from which x and y can be found as functions of t, involving two arbitrary constants. If, however, the two roots of the quadratic equation for λ are equal, that is, if (a − b′)² + 4a′b = 0, the method described gives only one equation, expressing x + λy in terms of t; by means of this equation y can be eliminated from dx/dt = ax + by + c, leading to an equation of the form dx/dt = Px + Q + Re(a + λa′)t, where P, Q, R are constants. The integration of this gives x, and thence y can be found.
A similar process is applicable when we have three or more dependent variables whose differential coefficients in regard to the single independent variables are given as linear functions of the dependent variables with constant coefficients.
Another method of solution of the equations
dx/dt = ax + by + c, dy/dt = a′x + b′y + c′,
consists in differentiating the first equation, thereby obtaining
| d²x | = a | dx | + b | dy | ; |
| dt² | dt | dx |
from the two given equations, by elimination of y, we can express dy/dt as a linear function of x and dx/dt; we can thus form an equation of the shape d²x/dt² = P + Qx + Rdx/dt, where P, Q, R are constants; this can be integrated by methods previously explained, and the integral, involving two arbitrary constants, gives, by the equation dx/dt = ax + by + c, the corresponding value of y. Conversely it should be noticed that any single linear differential equation
| d²x | = u + vx + w | dx | , |
| dt² | dt |
where u, v, w are functions of t, by writing y for dx/dt, is equivalent with the two equations dx/dt = y, dy/dt = u + vx + wy. In fact a similar reduction is possible for any system of differential equations with one independent variable.
Equations occur to be integrated of the form
Xdx + Ydy + Zdz = 0,
where X, Y, Z are functions of x, y, z. We consider only the case in which there exists an equation φ(x, y, z) = C whose differential
| ∂φ | dx + | ∂φ | dy + | ∂φ | dz = 0 |
| ∂x | ∂y | ∂z |
is equivalent with the given differential equation; that is, μ being a proper function of x, y, z, we assume that there exist equations
| ∂φ | = μX, | ∂φ | = μY, | ∂φ | = μZ; |
| ∂x | ∂y | ∂z |
these equations require
| ∂ | (μY) ≈ | ∂ | (μZ), &c., |
| ∂z | ∂y |
and hence
| X( | ∂Z | − | ∂Y | ) + Y( | ∂X | − | ∂Z | ) + Z( | ∂Y | − | ∂X | ) = 0; |
| ∂y | ∂z | ∂z | ∂x | ∂x | ∂y |
conversely it can be proved that this is sufficient in order that μ may exist to render μ(Xdx + Ydy + Zdz) a perfect differential; in particular it may be satisfied in virtue of the three equations such as
| ∂Z | − | ∂Y | = 0; |
| ∂y | ∂z |
in which case we may take μ = 1. Assuming the condition in its general form, take in the given differential equation a plane section of the surface φ = C parallel to the plane z, viz. put z constant, and consider the resulting differential equation in the two variables x, y, namely Xdx + Ydy = 0; let ψ(x, y, z) = constant, be its integral, the constant z entering, as a rule, in ψ because it enters in X and Y. Now differentiate the relation ψ(x, y, z) = ƒ(z), where ƒ is a function to be determined, so obtaining
| ∂ψ | dx + | ∂ψ | dy + ( | ∂ψ | − | dƒ | ) dz = 0; |
| ∂x | ∂y | ∂z | dz |
there exists a function σ of x, y, z such that
| ∂ψ | = σX, | ∂ψ | = σY, |
| ∂x | ∂y |
because ψ = constant, is the integral of Xdx + Ydy = 0; we desire to prove that ƒ can be chosen so that also, in virtue of ψ(x, y, z) = ƒ(z), we have
| ∂ψ | − | dƒ | = σZ, namely | dƒ | = | ∂ψ | − σZ; |
| ∂z | dz | dz | ∂z |
if this can be proved the relation ψ(x, y, z) − ƒ(z) = constant, will be the integral of the given differential equation. To prove this it is enough to show that, in virtue of ψ(x, y, z) = ƒ(z), the function ∂ψ/∂x − σZ can be expressed in terms of z only. Now in consequence of the originally assumed relations,
| ∂ψ | = μX, | ∂φ | = μY, | ∂φ | = μZ, |
| ∂x | ∂y | ∂z |
we have
| ∂ψ | / | ∂φ | = | σ | = | ∂ψ | / | ∂φ | , |
| ∂x | ∂x | μ | ∂y | ∂y |
and hence
| ∂ψ | ∂φ | − | ∂ψ | ∂φ | = 0; |
| ∂x | ∂y | ∂y | ∂x |
this shows that, as functions of x and y, ψ is a function of φ (see the note at the end of part i. of this article, on Jacobian determinants), so that we may write ψ = F(z, φ), from which
| σ | = | ∂F | ; then | ∂ψ | = | ∂F | + | ∂F | ∂φ | = | ∂F | + | σ | · μZ = | ∂F | + σZ or | ∂ψ | − σZ = | ∂F | ; |
| μ | ∂φ | ∂z | ∂z | ∂φ | ∂z | ∂z | μ | ∂z | ∂z | ∂z |
in virtue of ψ(x, y, z) = ƒ(z), and ψ = F(z, φ), the function φ can be written in terms of z only, thus ∂F/∂z can be written in terms of z only, and what we required to prove is proved.
Consider lastly a simple type of differential equation containing two independent variables, say x and y, and one dependent variable z, namely the equation
| P | ∂z | + Q | ∂z | = R, |
| ∂x | ∂y |
where P, Q, R are functions of x, y, z. This is known as Lagrange’s linear partial differential equation of the first order. To integrate this, consider first the ordinary differential equations dx/dz = P/R, dy/dz = Q/R, and suppose that two functions u, v, of x, y, z can be determined, independent of one another, such that the equations u = a, v = b, where a, b are arbitrary constants, lead to these ordinary differential equations, namely such that
| P | ∂u | + Q | ∂u | + R | ∂u | = 0 and P | ∂v | + Q | ∂v | + R | ∂v | = 0. |
| ∂x | ∂y | ∂z | ∂x | ∂y | ∂z |
Then if F(x, y, z) = 0 be a relation satisfying the original differential equations, this relation giving rise to
| ∂F | + | ∂F | ∂z | = 0 and | ∂F | + | ∂F | ∂z | = 0, we have P | ∂F | + Q | ∂F | + R | ∂F | = 0. |
| ∂x | ∂z | ∂x | ∂y | ∂z | ∂y | ∂x | ∂y | ∂z |
It follows that the determinant of three rows and columns vanishes whose first row consists of the three quantities ∂F/∂x, ∂F/∂y, ∂F/∂z, whose second row consists of the three quantities ∂u/∂x, ∂u/∂y, ∂u/∂z, whose third row consists similarly of the partial derivatives of v. The vanishing of this so-called Jacobian determinant is known to imply that F is expressible as a function of u and v, unless these are themselves functionally related, which is contrary to hypothesis (see the note below on Jacobian determinants). Conversely, any relation φ(u, v) = 0 can easily be proved, in virtue of the equations satisfied by u and v, to lead to
| P | dz | + Q | dz | = R. |
| dx | dx |
The solution of this partial equation is thus reduced to the solution of the two ordinary differential equations expressed by dx/P = dy/Q = dz/R. In regard to this problem one remark may be made which is often of use in practice: when one equation u = a has been found to satisfy the differential equations, we may utilize this to obtain the second equation v = b; for instance, we may, by means of u = a, eliminate z—when then from the resulting equations in x and y a relation v = b has been found containing x and y and a, the substitution a = u will give a relation involving x, y, z.
Note on Jacobian Determinants.—The fact assumed above that the vanishing of the Jacobian determinant whose elements are the partial derivatives of three functions F, u, v, of three variables x, y, z, 229 involves that there exists a functional relation connecting the three functions F, u, v, may be proved somewhat roughly as follows:—
The corresponding theorem is true for any number of variables. Consider first the case of two functions p, q, of two variables x, y. The function p, not being constant, must contain one of the variables, say x; we can then suppose x expressed in terms of y and the function p; thus the function q can be expressed in terms of y and the function p, say q = Q(p, y). This is clear enough in the simplest cases which arise, when the functions are rational. Hence we have
| ∂q | = | ∂Q | ∂p | and | ∂q | = | ∂Q | ∂p | + | ∂Q | ; |
| ∂x | ∂p | ∂x | ∂y | ∂p | ∂y | ∂y |
these give
| ∂p | ∂q | − | ∂p | ∂q | = | ∂p | ∂Q | ; |
| ∂x | ∂y | ∂y | ∂x | ∂x | ∂y |
by hypothesis ∂p/∂x is not identically zero; therefore if the Jacobian determinant of p and q in regard to x and y is zero identically, so is ∂Q/∂y, or Q does not contain y, so that q is expressible as a function of p only. Conversely, such an expression can be seen at once to make the Jacobian of p and q vanish identically.
Passing now to the case of three variables, suppose that the Jacobian determinant of the three functions F, u, v in regard to x, y, z is identically zero. We prove that if u, v are not themselves functionally connected, F is expressible as a function of u and v. Suppose first that the minors of the elements of ∂F/∂x, ∂F/∂y, ∂F/∂z in the determinant are all identically zero, namely the three determinants such as
| ∂u | ∂v | − | ∂u | ∂v | ; |
| ∂y | ∂z | ∂z | ∂y |
then by the case of two variables considered above there exist three functional relations. ψ1(u, v, x) = 0, ψ2(u, v, y) = 0, ψ3(u, v, z) = 0, of which the first, for example, follows from the vanishing of
| ∂u | ∂v | − | ∂u | ∂v | . |
| ∂y | ∂z | ∂z | ∂y |
We cannot assume that x is absent from ψ1, or y from ψ2, or z from ψ3; but conversely we cannot simultaneously have x entering in ψ1, and y in ψ2, and z in ψ3, or else by elimination of u and v from the three equations ψ1 = 0, ψ2 = 0, ψ3 = 0, we should find a necessary relation connecting the three independent quantities x, y, z; which is absurd. Thus when the three minors of ∂F/∂x, ∂F/∂y, ∂F/∂z in the Jacobian determinant are all zero, there exists a functional relation connecting u and v only. Suppose no such relation to exist; we can then suppose, for example, that
| ∂u | ∂v | − | ∂u | ∂v |
| ∂y | ∂z | ∂z | ∂y |
is not zero. Then from the equations u(x, y, z) = u, v(x, y, z) = v we can express y and z in terms of u, v, and x (the attempt to do this could only fail by leading to a relation connecting u, v and x, and the existence of such a relation would involve that the determinant
| ∂u | ∂v | − | ∂u | ∂v |
| ∂y | ∂z | ∂z | ∂y |
was zero), and so write F in the form F(x, y, z) = Φ(u, v, x). We then have
| ∂F | = | ∂Φ | ∂u | + | ∂Φ | ∂v | + | ∂Φ | , | ∂F | = | ∂Φ | ∂u | + | ∂Φ | ∂v | , | ∂F | = | ∂Φ | ∂u | + | ∂Φ | ∂v | ; |
| ∂x | ∂u | ∂x | ∂v | ∂x | ∂x | ∂y | ∂u | ∂y | ∂v | ∂y | ∂z | ∂u | ∂z | ∂v | ∂z |
thereby the Jacobian determinant of F, u, v is reduced to
| ∂Φ | ( | ∂u | ∂v | − | ∂u | ∂v | ); |
| ∂x | ∂y | ∂z | ∂z | ∂y |
by hypothesis the second factor of this does not vanish identically; hence ∂Φ/∂x = 0 identically, and Φ does not contain x; so that F is expressible in terms of u, v only; as was to be proved.
Part II.—General Theory.
Differential equations arise in the expression of the relations between quantities by the elimination of details, either unknown or regarded as unessential to the formulation of the relations in question. They give rise, therefore, to the two closely connected problems of determining what arrangement of details is consistent with them, and of developing, apart from these details, the general properties expressed by them. Very roughly, two methods of study can be distinguished, with the names Transformation-theories, Function-theories; the former is concerned with the reduction of the algebraical relations to the fewest and simplest forms, eventually with the hope of obtaining explicit expressions of the dependent variables in terms of the independent variables; the latter is concerned with the determination of the general descriptive relations among the quantities which are involved by the differential equations, with as little use of algebraical calculations as may be possible. Under the former heading we may, with the assumption of a few theorems belonging to the latter, arrange the theory of partial differential equations and Pfaff’s problem, with their geometrical interpretations, as at present developed, and the applications of Lie’s theory of transformation-groups to partial and to ordinary equations; under the latter, the study of linear differential equations in the manner initiated by Riemann, the applications of discontinuous groups, the theory of the singularities of integrals, and the study of potential equations with existence-theorems arising therefrom. In order to be clear we shall enter into some detail in regard to partial differential equations of the first order, both those which are linear in any number of variables and those not linear in two independent variables, and also in regard to the function-theory of linear differential equations of the second order. Space renders impossible anything further than the briefest account of many other matters; in particular, the theories of partial equations of higher than the first order, the function-theory of the singularities of ordinary equations not linear and the applications to differential geometry, are taken account of only in the bibliography. It is believed that on the whole the article will be more useful to the reader than if explanations of method had been further curtailed to include more facts.
When we speak of a function without qualification, it is to be understood that in the immediate neighbourhood of a particular set x0, y0, ... of values of the independent variables x, y, ... of the function, at whatever point of the range of values for x, y, ... under consideration x0, y0, ... may be chosen, the function can be expressed as a series of positive integral powers of the differences x − x0, y − y0, ..., convergent when these are sufficiently small (see Function: Functions of Complex Variables). Without this condition, which we express by saying that the function is developable about x0, y0, ..., many results provisionally stated in the transformation theories would be unmeaning or incorrect. If, then, we have a set of k functions, ƒ1 ... ƒk of n independent variables x1 ... xn, we say that they are independent when n ≥ k and not every determinant of k rows and columns vanishes of the matrix of k rows and n columns whose r-th row has the constituents dƒr/dx1, ... dƒr/dxn; the justification being in the theorem, which we assume, that if the determinant involving, for instance, the first k columns be not zero for x1 = xº1 ... xn = xºn, and the functions be developable about this point, then from the equations ƒ1 = c1, ... ƒk = ck we can express x1, ... xk by convergent power series in the differences xk+1 − xºk+1, ... xn − xnº, and so regard x1, ... xk as functions of the remaining variables. This we often express by saying that the equations ƒ1 = c1, ... ƒk = ck can be solved for x1, ... xk. The explanation is given as a type of explanation often understood in what follows.
We may conveniently begin by stating the theorem: If each of the n functions φ1, ... φn of the (n + 1) variables x1, ... xnt be developable Ordinary equations of the first order. about the values xº1, ... xn0t0, the n differential equations of the form dx1/dt = φ1(tx1, ... xn) are satisfied by convergent power series
xr = xºr + (t − t0) Ar1 + (t − t0)² Ar2 + ...
reducing respectively to xº1, ... xºn when t = t0; and the only functions satisfying the equations and reducing respectively to xº1, ... xºn when t = t0, are those determined by continuation of these series. If the result of solving these n equations for xº1, ... xºn be written in the form ω1(x1, ... xnt) = xº1, ... ωn(x1, ... xnt) = xºn, Single homogeneous partial equation of the first order. it is at once evident that the differential equation
dƒ/dt + φ1dƒ/dx1 + ... + φndƒ/dxn = 0
possesses n integrals, namely, the functions ω1, ... ωn, which are developable about the values (xº1 ... xn0t0) and reduce respectively to x1, ... xn when t = t0. And in fact it has no other integrals so reducing. Thus this equation also possesses a unique integral reducing when t = t0 to an arbitrary function ψ(x1, ... xn), this integral being. ψ(ω1, ... ωn). Conversely the existence of these principal integrals ω1, ... ωn of the partial equation establishes the existence of the specified solutions of the ordinary equations dxi/dt = φi. The following sketch of the proof of the existence of these principal integrals for the case n = 2 will show the character of more general investigations. Put x for x − x0, &c., and consider the equation a(xyt) dƒ/dx + b(xyt) dƒ/dy = dƒ/dt, wherein the functions a, b are developable about x = 0, y = 0, t = 0; say
a(xyt) = a0 + ta1 + t²a2/2! + ..., b(xyt) = b0 + tb1 + t²b2/2! + ...,
so that
ad/dx + bd/dy = δ0 + tδ1 + ½t²δ2 + ...,
where δ = ard/dx + brd/dy. In order that
ƒ = p0 + tp1 + t²p2/2! + ...
wherein p0, p1 ... are power series in x, y, should satisfy the equation, it is necessary, as we find by equating like terms, that
p1 = δ0p0, p2 = δ0p1 + δ1p0, &c.
and in generalProof of the existence of integrals.
ps+1 = δ0ps + s1δ1ps-1 + s2δ2ps-2 +... + δsp0,
where
sr = (s!)/(r!) (s − r)!
Now compare with the given equation another equation
A(xyt)dF/dx + B(xyt)dF/dy = dF/dt,
wherein each coefficient in the expansion of either A or B is real and positive, and not less than the absolute value of the corresponding coefficient in the expansion of a or b. In the second equation let us substitute a series
F = P0 + tP1 + t²P2/2! + ...,
wherein the coefficients in P0 are real and positive, and each not less than the absolute value of the corresponding coefficient in p0; then putting Δr = Ard/dx + Brd/dy we obtain necessary equations of the same form as before, namely,
P1 = Δ0P0, P2 = Δ0P1 + Δ1P0, ...
and in general Ps+1 = Δ0Ps, + s1Δ1Ps-1 + ... + ΔsP0. These give for every coefficient in Ps+1 an integral aggregate with real positive coefficients of the coefficients in Ps, Ps-1, ..., P0 and the coefficients in A and B; and they are the same aggregates as would be given by the previously obtained equations for the corresponding coefficients in ps+1 in terms of the coefficients in ps, ps-1, ..., p0 and the coefficients in a and b. Hence as the coefficients in P0 and also in A, B are real and positive, it follows that the values obtained in succession for the coefficients in P1, P2, ... are real and positive; and further, taking account of the fact that the absolute value of a sum of terms is not greater than the sum of the absolute values of the terms, it follows, for each value of s, that every coefficient in ps+1 is, in absolute value, not greater than the corresponding coefficient in Ps+1. Thus if the series for F be convergent, the series for ƒ will also be; and we are thus reduced to (1), specifying functions A, B with real positive coefficients, each in absolute value not less than the corresponding coefficient in a, b; (2) proving that the equation
AdF/dx + BdF/dy = dF/dt
possesses an integral P0 + tP1 + t²P2/2! + ... in which the coefficients in P0 are real and positive, and each not less than the absolute value of the corresponding coefficient in p0. If a, b be developable for x, y both in absolute value less than r and for t less in absolute value than R, and for such values a, b be both less in absolute value than the real positive constant M, it is not difficult to verify that we may take A = B = M[1 − (x + y)/r]-1 (1 − t/R)-1, and obtain
| F = r − (r − x − y) [ 1 − | 4MR | (1 − | x + y | ) | −2 | log ( 1 − | t | ) | −1 | ] | 1/2 | , |
| r | r | R |
and that this solves the problem when x, y, t are sufficiently small for the two cases p0 = x, p0 = y. One obvious application of the general theorem is to the proof of the existence of an integral of an ordinary linear differential equation given by the n equations dy/dx = y1, dy1/dx = y2, ...,
dyn-1/dx = p − p1yn-1 − ... − pny;
but in fact any simultaneous system of ordinary equations is reducible to a system of the form
dxi/dt = φi(tx1, ... xn).
Suppose we have k homogeneous linear partial equations of the first order in n independent variables, the general equation being aσ1dƒ/dx1 + ... + aσndƒ/dxn = 0, where σ = 1, ... k, and that Simultaneous linear partial equations. we desire to know whether the equations have common solutions, and if so, how many. It is to be understood that the equations are linearly independent, which implies that k ≤ n and not every determinant of k rows and columns is identically zero in the matrix in which the i-th element of the σ-th row is aσi}(i = 1, ... n, σ = 1, ... k). Denoting the left side of the σ-th equation by Pσƒ, it is clear that every common solution of the two equations Pσƒ = 0, Pρƒ = 0, is also a solution of the equation Pρ(pσƒ), Pσ(pρƒ), We immediately find, however, that this is also a linear equation, namely, ΣHidƒ/dxi = 0 where Hi = Pρaσ − Pσaρ, and if it be not already contained among the given equations, or be linearly deducible from them, it may be added to them, as not introducing any additional limitation of the possibility of their having common solutions. Proceeding thus with every pair of the original equations, and then with every pair of the possibly augmented system so obtained, and so on continually, we shall arrive at a system of equations, linearly independent of each other and therefore not more than n in number, such that the combination, in the way described, of every pair of them, leads to an equation which is linearly deducible from them. If the number of this so-called complete system is n, the equations give dƒ/dx1 = 0 ... dƒ/dxn = 0, leading to the nugatory result ƒ = a constant. Suppose, then, the number of this system to be r < n; suppose, further, that from the Complete systems of linear partial equations. matrix of the coefficients a determinant of r rows and columns not vanishing identically is that formed by the coefficients of the differential coefficients of ƒ in regard to x1 ... xr; also that the coefficients are all developable about the values x1 = xº1, ... xn= xºn, and that for these values the determinant just spoken of is not zero. Then the main theorem is that the complete system of r equations, and therefore the originally given set of k equations, have in common n − r solutions, say ωr+1, ... ωn, which reduce respectively to xr+1, ... xn when in them for x1, ... xr are respectively put xº1, ... xºr; so that also the equations have in common a solution reducing when x1 = xº1, ... xr = xºr to an arbitrary function ψ(xr+1, ... xn) which is developable about xºr+1, ... xºn, namely, this common solution is ψ(ωr+1, ... ωn). It is seen at once that this result is a generalization of the theorem for r = 1, and its proof is conveniently given by induction from that case. It can be verified without difficulty (1) that if from the r equations of the complete system we form r independent linear aggregates, with coefficients not necessarily constants, the new system is also a complete system; (2) that if in place of the independent variables x1, ... xn we introduce any other variables which are independent functions of the former, the new equations also form a complete system. It is convenient, then, from the complete system of r equations to form r new equations by solving separately for dƒ/dx1, ..., dƒ/dxr; suppose the general equation of the new system to be
Qσƒ = dƒ/dxσ + cσjr+1dƒ/dxr+1 + ... + cσndƒ/dxn = 0 (σ = 1, ... r).
Then it is easily obvious that the equation QρQσƒ − QσQρƒ = 0 contains only the differential coefficients of ƒ in regard to xr+1 ... xn; as it is at most a linear function of Q1ƒ, ... Qrƒ, it must be identically zero. So reduced the system is called a Jacobian system. Of this system Q1ƒ=0 has n − 1 principal solutions reducing respectively Jacobian systems. to x2, ... xn when
x1 = xº1,
and its form shows that of these the first r − 1 are exactly x2 ... xr. Let these n − 1 functions together with x1 be introduced as n new independent variables in all the r equations. Since the first equation is satisfied by n − 1 of the new independent variables, it will contain no differential coefficients in regard to them, and will reduce therefore simply to dƒ/dx1 = 0, expressing that any common solution of the r equations is a function only of the n − 1 remaining variables. Thereby the investigation of the common solutions is reduced to the same problem for r − 1 equations in n − 1 variables. Proceeding thus, we reach at length one equation in n − r + 1 variables, from which, by retracing the analysis, the proposition stated is seen to follow.
The analogy with the case of one equation is, however, still closer. With the coefficients cσj, of the equations Qσƒ = 0 in transposed array (σ = 1, ... r, j = r + 1, ... n) we can put down the (n − r) equations, dxj = c1jdx1 + ... + crjdxr, equivalent to System of total differential equations. the r(n − r) equations dxj/dxσ = cσr. That consistent with them we may be able to regard xr+1, ... xn as functions of x1, ... xr, these being regarded as independent variables, it is clearly necessary that when we differentiate cσj in regard to xρ on this hypothesis the result should be the same as when we differentiate cρj, in regard to xσ on this hypothesis. The differential coefficient of a function ƒ of x1, ... xn on this hypothesis, in regard to xρj is, however,
dƒ/dxρ + cρjr+1dƒ/dxr+1 + ... + cρndƒ/dxn,
namely, is Qρƒ. Thus the consistence of the n − r total equations requires the conditions Qρcσj − Qσcρj = 0, which are, however, verified in virtue of Qρ(Qσƒ) − Qσ(Qρƒ) = 0. And it can in fact be easily verified that if ωr+1, ... ωn be the principal solutions of the Jacobian system, Qσƒ = 0, reducing respectively to xr+1, ... xn when x1 = xº1, ... xr = xºr, and the equations ωr+1 = x0r+1, ... ωn = xºn be solved for xr+1, ... xn to give xj = ψj(x1, ... xr, x0r+1, ... xºn), these values solve the total equations and reduce respectively to x0r+1, ... xºn when x1 = xº1 ... xr = xºr. And the total equations have no other solutions with these initial values. Conversely, the existence of these solutions of the total equations can be deduced a priori and the theory of the Jacobian system based upon them. The theory of such total equations, in general, finds its natural place under the heading Pfaffian Expressions, below.
A practical method of reducing the solution of the r equations of a Jacobian system to that of a single equation in n − r + 1 variables may be explained in connexion with a geometrical interpretation which will perhaps be clearer in a particular Geometrical interpretation and solution. case, say n = 3, r = 2. There is then only one total equation, say dz = adz + bdy; if we do not take account of the condition of integrability, which is in this case da/dy + bda/dz = db/dx + adb/dz, this equation may be regarded as defining through an arbitrary point (x0, y0, z0) of three-dimensioned space (about which a, b are developable) a plane, namely, z − z0 = a0(x − x0) + b0(y − y0), and therefore, through this arbitrary point ∞2 directions, namely, all those in the plane. If now there be a surface z = ψ(x, y), satisfying dz = adz + bdy and passing through (x0, y0, z0), this plane will touch the surface, and the operations of passing along the surface from (x0, y0, z0) to
(x0 + dx0, y0, z0 + dz0)
and then to (x0 + dx0, y0 + dy0, Z0 + d1z0), ought to lead to the same value of d1z0 as do the operations of passing along the surface from (x0, y0, z0) to (x0, y0 + dy0, z0 + δz0), and then to
(x0 + dx0, y0 + dy0, z0 + δ1z0),
namely, δ1z0 ought to be equal to d1z0. But we find
| a0dx0 + b0dy0 + dx0dy0( | db | + a0 | db | ), |
| dx0 | dz0 |
and so at once reach the condition of integrability. If now we put 231 x = x0 + t, y = y0 + mt, and regard m as constant, we shall in fact be considering the section of the surface by a fixed plane y − y0 = m(x − x0); along this section dz = dt(a + bm); if we then integrate the equation dx/dt = a + bm, where a, b are expressed as functions of m and t, with m kept constant, finding the solution which reduces to z0 for t = 0, and in the result again replace m by (y − y0)/(x − x0), we shall have the surface in question. In the general case the equations
dxj = cijdx1 + ... crjdxr
similarly determine through an arbitrary point xº1, ... xºn Mayer’s method of integration. a planar manifold of r dimensions in space of n dimensions, and when the conditions of integrability are satisfied, every direction in this manifold through this point is tangent to the manifold of r dimensions, expressed by ωr+1 = x0r+1, ... ω_ = xºn, which satisfies the equations and passes through this point. If we put x1 − xº1 = t, x2 − xº2 = m2t, ... xr − xºr = mrt, and regard m2, ... mr as fixed, the (n − r) total equations take the form dxj/dt = c1j + m2c2j + ... + mrcrj, and their integration is equivalent to that of the single partial equation
| dƒ/dt + Σ | n | (c1j + m2c2j + ... + mrcrj) dƒ/dxj = 0 |
| j=r+1 |
in the n − r + 1 variables t, xr+1, ... xn. Determining the solutions Ωr+1, ... Ωn which reduce to respectively xr+1, ... xn when t = 0, and substituting t = x1 − xº1, m2 = (x2 − xº2)/(x1 − xº1), ... mr = (xr − xºr)/(x1 − xº1), we obtain the solutions of the original system of partial equations previously denoted by ωr+1, ... ωn. It is to be remarked, however, that the presence of the fixed parameters m2, ... mr in the single integration may frequently render it more difficult than if they were assigned numerical quantities.
We have above considered the integration of an equation
dz = adz + bdy
on the hypothesis that the condition
da/dy + bda/dz = db/dz + adb/dz.
It is natural to inquire what relations among x, y, z, if any, Pfaffian Expressions. are implied by, or are consistent with, a differential relation adx + bdy + cdx = 0, when a, b, c are unrestricted functions of x, y, z. This problem leads to the consideration of the so-called Pfaffian Expression adx + bdy + cdz. It can be shown (1) if each of the quantities db/dz − dc/dy, dc/dx − da/dz, da/dy − db/dz, which we shall denote respectively by u23, u31, u12, be identically zero, the expression is the differential of a function of x, y, z, equal to dt say; (2) that if the quantity au23 + bu31 + cu12 is identically zero, the expression is of the form udt, i.e. it can be made a perfect differential by multiplication by the factor 1/u; (3) that in general the expression is of the form dt + u1dt1. Consider the matrix of four rows and three columns, in which the elements of the first row are a, b, c, and the elements of the (r + 1)-th row, for r = 1, 2, 3, are the quantities ur1, ur2, ur3, where u11 = u22 = u33 = 0. Then it is easily seen that the cases (1), (2), (3) above correspond respectively to the cases when (1) every determinant of this matrix of two rows and columns is zero, (2) every determinant of three rows and columns is zero, (3) when no condition is assumed. This result can be generalized as follows: if a1, ... an be any functions of x1, ... xn, the so-called Pfaffian expression a1dx1 + ... + andxn can be reduced to one or other of the two forms
u1dt1 + ... + ukdtk, dt + u1dt1 + ... + uk-1dtk-1,
wherein t, u1 ..., t1, ... are independent functions of x1, ... xn, and k is such that in these two cases respectively 2k or 2k − 1 is the rank of a certain matrix of n + 1 rows and n columns, that is, the greatest number of rows and columns in a non-vanishing determinant of the matrix; the matrix is that whose first row is constituted by the quantities a1, ... an, whose s-th element in the (r + 1)-th row is the quantity dar/dxs − das/dxr. The proof of such a reduced form can be obtained from the two results: (1) If t be any given function of the 2m independent variables u1, ... um, t1, ... tm, the expression dt + u1dt1 + ... + umdtm can be put into the form u′1dt′1 + ... + u′mdt′m. (2) If the quantities u1, ..., u1, t1, ... tm be connected by a relation, the expression n1dt1 + ... + umdtm can be put into the format dt′ + u′1dt′1 + ... + u′m-1dt′m-1; and if the relation connecting u1, um, t1, ... tm be homogeneous in u1, ... um, then t′ can be taken to be zero. These two results are deductions from the theory of contact transformations (see below), and their demonstration requires, beside elementary algebraical considerations, only the theory of complete systems of linear homogeneous partial differential equations of the first order. When the existence of the reduced form of the Pfaffian expression containing only independent quantities is thus once assured, the identification of the number k with that defined by the specified matrix may, with some difficulty, be made a posteriori.
In all cases of a single Pfaffian equation we are thus led to consider what is implied by a relation dt − u1dt1 − ... − umdtm = 0, in which t, u1, ... um, t1 ..., tm are, except for this equation, independent variables. This is to be satisfied in virtue of Single linear Pfaffian equation. one or several relations connecting the variables; these must involve relations connecting t, t1, ... tm only, and in one of these at least t must actually enter. We can then suppose that in one actual system of relations in virtue of which the Pfaffian equation is satisfied, all the relations connecting t, t1 ... tm only are given by
t = ψ(ts+1 ... tm), t1 = ψ1(ts+1 ... tm), ... ts = ψs(ts+1 ... tm);
so that the equation
dψ − u1dψ1 − ... − usdψs − us+1dts+1 − ... − umdtm = 0
is identically true in regard to u1, ... um, ts+1 ..., tm; equating to zero the coefficients of the differentials of these variables, we thus obtain m − s relations of the form
dψ/dtj − u1dψ1/dtj − ... − usdψs/dtj − uj = 0;
these m − s relations, with the previous s + 1 relations, constitute a set of m + 1 relations connecting the 2m + 1 variables in virtue of which the Pfaffian equation is satisfied independently of the form of the functions ψ,ψ1, ... ψs. There is clearly such a set for each of the values s = 0, s = 1, ..., s = m − 1, s = m. And for any value of s there may exist relations additional to the specified m + 1 relations, provided they do not involve any relation connecting t, t1, ... tm only, and are consistent with the m − s relations connecting u1, ... um. It is now evident that, essentially, the integration of a Pfaffian equation
a1dx1 + ... + andxn = 0,
wherein a1, ... an are functions of x1, ... xn, is effected by the processes necessary to bring it to its reduced form, involving only independent variables. And it is easy to see that if we suppose this reduction to be carried out in all possible ways, there is no need to distinguish the classes of integrals corresponding to the various values of s; for it can be verified without difficulty that by putting t′ = t − u1t1 − ... − usts, t′1 = u1, ... t′s = us, u′1 = −t1, ..., u′s = −ts, t′s+1 = ts+1, ... t′m = tm, u′s+1 = us+1, ... u′m = um, the reduced equation becomes changed to dt′ − u′1dt′1 − ... − u′mdt′m = 0, and the general relations changed to
t′ = ψ(t′s+1, ... t′m) − t′1ψ1(t′s+1, ... t′m) − ... − t′sψs(t′s+1, ... t′m), = φ,
say, together with u′1 = dφ/dt′1, ..., u′m = dφ/dt′m, which contain only one relation connecting the variables t′, t′1, ... t′m only.
This method for a single Pfaffian equation can, strictly speaking, be generalized to a simultaneous system of (n − r) Pfaffian equations dxj = c1jdx1 + ... + crjdxr only in the case already treated, Simultaneous Pfaffian equations. when this system is satisfied by regarding xr+1, ... xn as suitable functions of the independent variables x1, ... xr; in that case the integral manifolds are of r dimensions. When these are non-existent, there may be integral manifolds of higher dimensions; for if
dφ = φ1dx1 + ... + φrdxr + φr+1(c1,r+1dx1 + ... + cr,r+1dxr) + φr+2( ) + ...
be identically zero, then φσ + cσ,r+1φr+1 + ... + cσ,nφn ≈ 0, or φ satisfies the r partial differential equations previously associated with the total equations; when these are not a complete system, but included in a complete system of r − μ equations, having therefore n − r − μ independent integrals, the total equations are satisfied over a manifold of r + μ dimensions (see E. v. Weber, Math. Annal. 1v. (1901), p. 386).
It seems desirable to add here certain results, largely of algebraic character, which naturally arise in connexion with the theory of contact transformations. For any two functions of the 2n Contact transformations. independent variables x1, ... xn, p1, ... pn we denote by (φψ) the sum of the n terms such as dφdψ/dpidxi − dψdφ/dpidxi For two functions of the (2n + 1) independent variables z, x1, ... xn, p1, ... pn we denote by φψ the sum of the n terms such as
| dφ | ( | dψ | + pi | dψ | ) − | dψ | ( | dφ | pi | dφ | ). |
| dpi | dxi | dz | dpi | dxi | dz |
It can at once be verified that for any three functions [ƒ[φψ]] + [φ[ψƒ]] + [psi[ƒφ]] = dƒ/dz [φψ] + dφ/dz [ψƒ] + dψ/dz [ƒφ], which when ƒ, φ,ψ do not contain z becomes the identity (ƒ(φψ)) + (phi(ψƒ)) + (ψ(ƒφ)) = 0.Then, if X1, ... Xn, P1, ... Pn be such functions Of x1, ... xn, p1 ... pn that P1dX1 + ... + PndXn is identically equal to p1dx1 + ... + pndxn, it can be shown by elementary algebra, after equating coefficients of independent differentials, (1) that the functions X1, ... Pn are independent functions of the 2n variables x1, ... pn, so that the equations x′i = Xi, p′i = Pi can be solved for x1, ... xn, p1, ... pn, and represent therefore a transformation, which we call a homogeneous contact transformation; (2) that the X1, ... Xn are homogeneous functions of p1, ... pn of zero dimensions, the P1, ... Pn are homogeneous functions of p1, ... pn of dimension one, and the ½n(n − 1) relations (XiXj) = 0 are verified. So also are the n² relations (PiXi = 1, (PiXj) = 0, (PiPj) = 0. Conversely, if X1, ... Xn be independent functions, each homogeneous of zero dimension in p1, ... pn satisfying the ½n(n − 1) relations (XiXj) = 0, then P1, ... Pn can be uniquely determined, by solving linear algebraic equations, such that P1dX1 + ... + PndXn = p1dx1 + ... + pndxn. If now we put n + 1 for n, put z for xn+1, Z for Xn+1, Qi for -Pi/Pn+1, for i = 1, ... n, put qi for -pi/pn+1 and σ for qn+1/Qn+1, and then finally write P1, ... Pn, p1, ... pn for Q1, ... Qn, q1, ... qn, we obtain the following results: If ZX1 ... Xn, P1, ... Pn be functions of z, x1, ... xn, p1, ... pn, such that the expression dZ − P1dX1 − ... − PndXn is identically equal to σ(dz − p1dx1 − ... − pndxn), and σ not zero, then (1) the functions Z, X1, ... Xn, P1, ... Pn are independent functions of z, x1, ... xn, p1, ... pn, so that the equations z′ = Z, x′i = Xi, p′i = Pi can be solved for z, x1, ... xn, p1, ... pn and determine a transformation which we call a (non-homogeneous) contact transformation; (2) the Z, X1, ... Xn verify the ½n(n + 1) 232 identities [ZXi] = 0, [XiXj] = 0. And the further identities
[PiXi] = σ, [PiXj] = 0, [PiZ] = σPi, [PiPj] = 0,
| [Zσ] = σ | dZ | − σ², [Xiσ] = σ | dXi | , [Piσ] = | dPi |
| dz | dz | dz |
are also verified. Conversely, if Z, x1, ... Xn be independent functions satisfying the identities [ZXi] = 0, [XiXj] = 0, then σ, other than zero, and P1, ... Pn can be uniquely determined, by solution of algebraic equations, such that
dZ − P1dX1 − ... − PndXn = σ(dz − p1dx1 − ... − pndxn).
Finally, there is a particular case of great importance arising when σ = 1, which gives the results: (1) If U, X1, ... Xn, P1, ... Pn be 2n + 1 functions of the 2n independent variables x1, ... xn, p1, ... pn, satisfying the identity
dU + P1dx1 + ... + PndXn = p1dx1 + ... + pndxn,
then the 2n functions P1, ... Pn, X1, ... Xn are independent, and we have
(XiXj) = 0, (XiU) = δXi, (PiXi) = 1, (PiXj) = 0, (PiPj) = 0, (PiU) + Pi = δPi,
where δ denotes the operator p1d/dp1 + ... + pnd/dpn; (2) If X1, ... Xn be independent functions of x1, ... xn, p1, ... pn, such that (XiXj) = 0, then U can be found by a quadrature, such that
(XiU) = δXi;
and when Xi, ... Xn, U satisfy these ½n(n + 1) conditions, then P1, ... Pn can be found, by solution of linear algebraic equations, to render true the identity dU + P1dX1 + ... + PndXn = p1dx1 + ... + pndxn; (3) Functions X1, ... Xn, P1, ... Pn can be found to satisfy this differential identity when U is an arbitrary given function of x1, ... xn, p1, ... pn; but this requires integrations. In order to see what integrations, it is only necessary to verify the statement that if U be an arbitrary given function of x1, ... xn, p1, ... pn, and, for r < n, X1, ... Xr be independent functions of these variables, such that (XσU) = δXσ, (XρXσ) = 0, for ρ, σ = 1 ... r, then the r + 1 homogeneous linear partial differential equations of the first order (Uƒ) + δƒ = 0, (Xρƒ) = 0, form a complete system. It will be seen that the assumptions above made for the reduction of Pfaffian expressions follow from the results here enunciated for contact transformations.
We pass on now to consider the solution of any partial differential equation of the first order; we attempt to explain certain ideas relatively to a single equation with any number of independent variables (in particular, an Partial differential equation of the first order. ordinary equation of the first order with one independent variable) by speaking of a single equation with two independent variables x, y, and one dependent variable z. It will be seen that we are naturally led to consider systems of such simultaneous equations, which we consider below. The central discovery of the transformation theory of the solution of an equation F(x, y, z, dz/dx, dz/dy) = 0 is that its solution can always be reduced to the solution of partial equations which are linear. For this, however, we must regard dz/dx, dz/dy, during the process of integration, not as the differential coefficients of a function z in regard to x and y, but as variables independent of x, y, z, the too great indefiniteness that might thus appear to be introduced being provided for in another way. We notice that if z = ψ(x, y) be a solution of the differential equation, then dz = dxdψ/dx + dydψ/dy; thus if we denote the equation by F(x, y, z, p, q,) = 0, and prescribe the condition dz = pdx + qdy for every solution, any solution such as z = ψ(x, y) will necessarily be associated with the equations p = dz/dx, q = dz/dy, and z will satisfy the equation in its original form. We have previously seen (under Pfaffian Expressions) that if five variables x, y, z, p, q, otherwise independent, be subject to dz − pdx − qdy = 0, they must in fact be subject to at least three mutual relations. If we associate with a point (x, y, z) the plane
Z − z = p(X − x) + q(Y − y)
passing through it, where X, Y, Z are current co-ordinates, and call this association a surface-element; and if two consecutive elements of which the point(x + dx, y + dy, z + dz) of one lies on the plane of the other, for which, that is, the condition dz = pdx + qdy is satisfied, be said to be connected, and an infinity of connected elements following one another continuously be called a connectivity, then our statement is that a connectivity consists of not more than ∞² elements, the whole number of elements (x, y, z, p, q) that are possible being called ∞5. The solution of an equation F(x, y, z, dz/dx, dz/dy) = 0 is then to be understood to mean finding in all possible ways, from the ∞4 elements (x, y, z, p, q) which satisfy F(x, y, z, p, q) = 0 a set of ∞² elements forming a connectivity; or, more analytically, finding in all possible ways two relations G = 0, H = 0 connecting x, y, z, p, q and independent of F = 0, so that the three relations together may involve
dz = pdx + qdy.
Such a set of three relations may, for example, be of the form z = ψ(x, y), p = dψ/dx, q = dψ/dy; but it may also, as another case, involve two relations z = ψ(y), x = ψ1(y) connecting x, y, z, the third relation being
ψ′(y) = pψ′1(y) + q,
the connectivity consisting in that case, geometrically, of a curve in space taken with ∞¹ of its tangent planes; or, finally, a connectivity is constituted by a fixed point and all the planes passing through that point. This generalized view of the meaning of a solution of F = 0 is of advantage, moreover, in view of anomalies otherwise arising from special forms of the equation Meaning of a solution of the equation. itself. For instance, we may include the case, sometimes arising when the equation to be solved is obtained by transformation from another equation, in which F does not contain either p or q. Then the equation has ∞² solutions, each consisting of an arbitrary point of the surface F = 0 and all the ∞² planes passing through this point; it also has ∞² solutions, each consisting of a curve drawn on the surface F = 0 and all the tangent planes of this curve, the whole consisting of ∞² elements; finally, it has also an isolated (or singular) solution consisting of the points of the surface, each associated with the tangent plane of the surface thereat, also ∞² elements in all. Or again, a linear equation F = Pp + Qq − R = 0, wherein P, Q, R are functions of x, y, z only, has ∞² solutions, each consisting of one of the curves defined by
dx/P = dy/Q = dz/R
taken with all the tangent planes of this curve; and the same equation has ∞² solutions, each consisting of the points of a surface containing ∞¹ of these curves and the tangent planes of this surface. And for the case of n variables there is similarly the possibility of n + 1 kinds of solution of an equation F(x1, ... xn, z, p1, ... pn) = 0; these can, however, by a simple contact transformation be reduced to one kind, in which there is only one relation z′ = ψ(x′1, ... x′n) connecting the new variables x’1, ... x′n, z′ (see under Pfaffian Expressions); just as in the case of the solution
z = ψ(y), x = ψ1(y), ψ′(y) = pψ′1(y) + q
of the equation Pp + Qq = R the transformation z’ = z − px, x′ = p, p′ = −x, y′ = y, q′ = q gives the solution
z′ = ψ(y′) + x′ψ1(y′), p′ = dz′/dx′, q′ = dz′/dy′
of the transformed equation. These explanations take no account of the possibility of p and q being infinite; this can be dealt with by writing p = -u/w, q = -v/w, and considering homogeneous equations in u, v, w, with udx + vdy + wdz = 0 as the differential relation necessary for a connectivity; in practice we use the ideas associated with such a procedure more often without the appropriate notation.
In utilizing these general notions we shall first consider the theory of characteristic chains, initiated by Cauchy, which shows well the nature of the relations implied by the given differential equation; the alternative ways of carrying Order of the ideas. out the necessary integrations are suggested by considering the method of Jacobi and Mayer, while a good summary is obtained by the formulation in terms of a Pfaffian expression.
Consider a solution of F = 0 expressed by the three independent equations F = 0, G = 0, H = 0. If it be a solution in which there is more than one relation connecting x, y, z, let new variables x′, y′, z′, p′, q′ be introduced, as before explained under Pfaffian Expressions, Characteristic chains. in which z’ is of the form
z′ = z − p1x1 − ... − psxs (s = 1 or 2),
so that the solution becomes of a form z’ = ψ(x′y′), p′ = dψ/dx′, q′ = dψ/dy′, which then will identically satisfy the transformed equations F′ = 0, G′ = 0, H′ = 0. The equation F′ = 0, if x′, y′, z′ be regarded as fixed, states that the plane Z − z′ = p′(X − x′) + q′(Y − y′) is tangent to a certain cone whose vertex is (x′, y′, z′), the consecutive point (x′ + dx′, y′ + dy′, z′ + dz′) of the generator of contact being such that
| dx′/ | dF′ | = dy′/ | dF′ | = dz′/ ( p′ | dF′ | + q′ | dF′ | ). |
| dp′ | dq′ | dp′ | dq′ |
Passing in this direction on the surface z′ = ψ(x′, y′) the tangent 233 plane of the surface at this consecutive point is (p′ + dp′, q′ + dq′), where, since F′(x′, y′, ψ, dψ/dx′, dψ/dy′) = 0 is identical, we have dx′ (dF′/dx′ + p′dF′/dz′) + dp′dF′/dp′ = 0. Thus the equations, which we shall call the characteristic equations,
| dx′/ | dF′ | = dy′/ | dF′ | = dz′/ ( p′ | dF′ | + q′ | dF′ | ) = dp′/ ( − | dF′ | − p′ | dF′ | ) = dq′/ ( − | dF′ | − q′ | dF′ | ) |
| dp′ | dq′ | dp′ | dq′ | dx′ | dz′ | dy′ | dz′ |
are satisfied along a connectivity of ∞¹ elements consisting of a curve on z′ = ψ(x′, y′) and the tangent planes of the surface along this curve. The equation F′ = 0, when p′, q′ are fixed, represents a curve in the plane Z − z′ = p′(X − x′) + q′(Y − y′) passing through (x′, y′, z′); if (x′ + δx′, y′ + δy′, z′ + δz′) be a consecutive point of this curve, we find at once
| δx′( | dF′ | + p′ | dF′ | ) + δy′( | dF′ | q′ | dF′ | ) = 0; |
| dx′ | dz′ | dy′ | dz′ |
thus the equations above give δx′dp′ + δy′dq′ = 0, or the tangent line of the plane curve, is, on the surface z′ = ψ(x′, y′), in a direction conjugate to that of the generator of the cone. Putting each of the fractions in the characteristic equations equal to dt, the equations enable us, starting from an arbitrary element x′0, y′0, z′0, p′0, q′0, about which all the quantities F′, dF′/dp′, &c., occurring in the denominators, are developable, to define, from the differential equation F′ = 0 alone, a connectivity of ∞¹ elements, which we call a characteristic chain; and it is remarkable that when we transform again to the original variables (x, y, z, p, q), the form of the differential equations for the chain is unaltered, so that they can be written down at once from the equation F = 0. Thus we have proved that the characteristic chain starting from any ordinary element of any integral of this equation F = 0 consists only of elements belonging to this integral. For instance, if the equation do not contain p, q, the characteristic chain, starting from an arbitrary plane through an arbitrary point of the surface F = 0, consists of a pencil of planes whose axis is a tangent line of the surface F = 0. Or if F = 0 be of the form Pp + Qq = R, the chain consists of a curve satisfying dx/P = dy/Q = dz/R and a single infinity of tangent planes of this curve, determined by the tangent plane chosen at the initial point. In all cases there are ∞³ characteristic chains, whose aggregate may therefore be expected to exhaust the ∞4 elements satisfying F = 0.
Consider, in fact, a single infinity of connected elements each satisfying F = 0, say a chain connectivity T, consisting of elements specified by x0, y0, z0, p0, q0, which we suppose expressed as Complete integral constructed with characteristic chains. functions of a parameter u, so that
U0 = dz0/du − p0dx0/du − q0dy0/du
is everywhere zero on this chain; further, suppose that each of F, dF/dp, ... , dF/dx + pdF/dz is developable about each element of this chain T, and that T is not a characteristic chain. Then consider the aggregate of the characteristic chains issuing from all the elements of T. The ∞² elements, consisting of the aggregate of these characteristic chains, satisfy F = 0, provided the chain connectivity T consists of elements satisfying F = 0; for each characteristic chain satisfies dF = 0. It can be shown that these chains are connected; in other words, that if x, y, z, p, q, be any element of one of these characteristic chains, not only is
dz/dt − pdx/dt − qdy/dt = 0,
as we know, but also U = dz/du − pdx/du − qdy/du is also zero. For we have
| dU | = | d | ( | dz | − p | dx | − q | dy | ) − | d | ( | dz | − p | dx | − q | dy | ) |
| dt | dt | du | du | du | du | dt | dt | dt |
| = | dp | dx | − | dp | dx | + | dq | dy | − | dq | dy | , |
| du | dt | dt | du | du | dt | dt | du |
which is equal to
| dp | dF | + | dx | ( | dF | + p | dF | ) + | dq | dF | + | dy | ( | dF | + q | dF | ) = − | dF | U. |
| du | dp | du | dx | dz | du | dq | du | dy | dz | dz |
As dF/dz is a developable function of t, this, giving
| U = U0 exp( − ∫ | t | dF | dt ), |
| t0 | dz |
shows that U is everywhere zero. Thus integrals of F = 0 are obtainable by considering the aggregate of characteristic chains issuing from arbitrary chain connectivities T satisfying F = 0; and such connectivities T are, it is seen at once, determinable without integration. Conversely, as such a chain connectivity T can be taken out from the elements of any given integral all possible integrals are obtainable in this way. For instance, an arbitrary curve in space, given by x0 = θ(u), y0 = φ(u), z0 = ψ(u), determines by the two equations F(x0, y0, z0, p0, q0) = 0, ψ′(u) = p0θ′(u) + q0φ′(u), such a chain connectivity T, through which there passes a perfectly definite integral of the equation F = 0. By taking ∞² initial chain connectivities T, as for instance by taking the curves x0 = θ, y0 = φ, z0 = ψ to be the ∞² curves upon an arbitrary surface, we thus obtain ∞² integrals, and so ∞4 elements satisfying F = 0. In general, if functions G, H, independent of F, be obtained, such that the equations F = 0, G = b, H = c represent an integral for all values of the constants b, c, these equations are said to constitute a complete integral. Then ∞4 elements satisfying F = 0 are known, and in fact every other form of integral can be obtained without further integrations.
In the foregoing discussion of the differential equations of a characteristic chain, the denominators dF/dp, ... may be supposed to be modified in form by means of F = 0 in any way conducive to a simple integration. In the immediately following explanation of ideas, however, we consider indifferently all equations F = constant; when a function of x, y, z, p, q is said to be zero, it is meant that this is so identically, not in virtue of F = 0; in other words, we consider the integration of F = a, where a is an arbitrary constant. In the theory of linear partial equations we have seen that the integration Operations necessary for integration of F = a. of the equations of the characteristic chains, from which, as has just been seen, that of the equation F = a follows at once, would be involved in completely integrating the single linear homogeneous partial differential equation of the first order [Fƒ] = 0 where the notation is that explained above under Contact Transformations. One obvious integral is ƒ = F. Putting F = a, where a is arbitrary, and eliminating one of the independent variables, we can reduce this equation [Fƒ] = 0 to one in four variables; and so on. Calling, then, the determination of a single integral of a single homogeneous partial differential equation of the first order in n independent variables, an operation of order n − 1, the characteristic chains, and therefore the most general integral of F = a, can be obtained by successive operations of orders 3, 2, 1. If, however, an integral of F = a be represented by F = a, G = b, H = c, where b and c are arbitrary constants, the expression of the fact that a characteristic chain of F = a satisfies dG = 0, gives [FG] = 0; similarly, [FH] = 0 and [GH] = 0, these three relations being identically true. Conversely, suppose that an integral G, independent of F, has been obtained of the equation [Fƒ] = 0, which is an operation of order three. Then it follows from the identity [ƒ[φψ]] + [φ[ψƒ]] + [ψ[ƒφ]] = dƒ/dz [ψφ] + dφ/dz [ψƒ] + dψ/dz [ƒφ] before remarked, by putting φ = F, ψ = G, and then [Fƒ] = A(ƒ), [Gƒ] = B(ƒ), that AB(ƒ) − BA(ƒ) = dF/dz B(ƒ) − dG/dz A(ƒ), so that the two linear equations [Fƒ] = 0, [Gƒ] = 0 form a complete system; as two integrals F, G are known, they have a common integral H, independent of F, G, determinable by an operation of order one only. The three functions F, G, H thus identically satisfy the relations [FG] = [GH] = [FH] = 0. The ∞² elements satisfying F = a, G = b, H = c, wherein a, b, c are assigned constants, can then be seen to constitute an integral of F = a. For the conditions that a characteristic chain of G = b issuing from an element satisfying F = a, G = b, H = c should consist only of elements satisfying these three equations are simply [FG] = 0, [GH] = 0. Thus, starting from an arbitrary element of (F = a, G = b, H = c), we can single out a connectivity of elements of (F = a, G = b, H = c) forming a characteristic chain of G = b; then the aggregate of the characteristic chains of F = a issuing from the elements of this characteristic chain of G = b will be a connectivity consisting only of elements of
(F = a, G = b, H = c),
and will therefore constitute an integral of F = a; further, it will include all elements of (F = a, G = b, H = c). This result follows also from a theorem given under Contact Transformations, which shows, moreover, that though the characteristic chains of F = a are not determined by the three equations F = a, G = b, H = c, no further integration is now necessary to find them. By this theorem, since identically [FG] = [GH] = [FH] = 0, we can find, by the solution of linear algebraic equations only, a non-vanishing function σ and two functions A, C, such that
dG − AdF − CdH = σ(dz − pdz − qdy);
thus all the elements satisfying F = a, G = b, H = c, satisfy dz = pdx + qdy and constitute a connectivity, which is therefore an integral of F = a. While, further, from the associated theorems, F, G, H, A, C are independent functions and [FC] = 0. Thus C may be taken to be the remaining integral independent of G, H, of the equation [Fƒ] = 0, whereby the characteristic chains are entirely determined.
When we consider the particular equation F = 0, neglecting the case when neither p nor q enters, and supposing p to enter, we may express p from F = 0 in terms of x, y, z, q, and then eliminate it from all other equations. Then instead of the equation [Fƒ] = 0, we have, if F = 0 give p = ψ(x, y, z, q), the equation
| Σƒ = − ( | dƒ | + ψ | dƒ | ) + | dψ | ( | dƒ | + q | dƒ | ) − ( | dψ | + q | dψ | ) | dƒ | = 0, |
| dx | dz | dq | dy | dz | dy | dz | dq |
moreover obtainable by omitting the term in dƒ/dp in [p − ψ, ƒ] = 0. Let x0, y0, z0, q0, be values about which the coefficients in The single equation F = 0 and Pfaffian formulations. this equation are developable, and let ζ, η, ω be the principal solutions reducing respectively to z, y and q when x = x0. Then the equations p = ψ, ζ = z0, η = y0, ω = q0 represent a characteristic chain issuing from the element x0, y0, z0, ψ0, q0; we have seen that the aggregate of such chains issuing from the elements of an arbitrary chain satisfying
dz0 = p0dx0 − q0dy0 = 0
constitute an integral of the equation p = ψ. Let this arbitrary 234 chain be taken so that x0 is constant; then the condition for initial values is only
dz0 − q0dy0 = 0,
and the elements of the integral constituted by the characteristic chains issuing therefrom satisfy
dζ − ωdη = 0.
Hence this equation involves dz − ψdx − qdy = 0, or we have
dz − ψdx − qdy = σ(dζ − ωdη),
where σ is not zero. Conversely, the integration of p = ψ is, essentially, the problem of writing the expression dz − ψdx − qdy in the form σ(dζ − ωdη), as must be possible (from what was said under Pfaffian Expressions).
To integrate a system of simultaneous equations of the first order X1 = a1, ... Xr = ar in n independent variables x1, ... xn and one dependent variable z, we write p1 for dz/dx1, &c., System of equations of the first order. and attempt to find n + 1 − r further functions Z, Xr+1 ... Xn, such that the equations Z = a, Xi = ai,(i = 1, ... n) involve dz − p1dx1 − ... − pndxn = 0. By an argument already given, the common integral, if existent, must be satisfied by the equations of the characteristic chains of any one equation Xi = ai; thus each of the expressions [XiXj] must vanish in virtue of the equations expressing the integral, and we may without loss of generality assume that each of the corresponding ½r(r − 1) expressions formed from the r given differential equations vanishes in virtue of these equations. The determination of the remaining n + 1 − r functions may, as before, be made to depend on characteristic chains, which in this case, however, are manifolds of r dimensions obtained by integrating the equations [X1ƒ] = 0, ... [Xrƒ] = 0; or having obtained one integral of this system other than X1, ... Xr, say Xr+1, we may consider the system [X1ƒ] = 0, ... [Xr+1ƒ] = 0, for which, again, we have a choice; and at any stage we may use Mayer’s method and reduce the simultaneous linear equations to one equation involving parameters; while if at any stage of the process we find some but not all of the integrals of the simultaneous system, they can be used to simplify the remaining work; this can only be clearly explained in connexion with the theory of so-called function groups for which we have no space. One result arising is that the simultaneous system p1 = φ1, ... pr = φr, wherein p1, ... pr are not involved in φ1, ... φr, if it satisfies the ½r(r − 1) relations [pi − φi, pj − φj] = 0, has a solution z = ψ(x1, ... xn), p1 = dψ/dx1, ... pn = dψ/dxn, reducing to an arbitrary function of xr+1, ... xn only, when x1 = xº1, ... xr = xºr under certain conditions as to developability; a generalization of the theorem for linear equations. The problem of integration of this system is, as before, to put
dz − φ1dx1 − ... − φrdxr − pr+1dxr+1 − ... − pndxn
into the form σ(dζ − ωr+1 + dξr+1 − ... − ωndξn); and here ζ, ξr+1, ... ξn, ωr+1, ... ωn may be taken, as before, to be principal integrals of a certain complete system of linear equations; those, namely, determining the characteristic chains.
If L be a function of t and of the 2n quantities x1, ... xn, ẋ1, ... ẋn, where ẋi, denotes dxi/dt, &c., and if in the n equations
| d | ( | dL | ) = | dL |
| dt | dxi | dxi |
we put pi = dL/dẋi, and so express ẋi, ... ẋn in terms of t, xi, ... xn, p1, ... pn, assuming that the determinant of the quantities d²L/dxidẋj is not zero; if, further, H denote the function of t, x1, ... xn, p1, ... pn, numerically equal to p1ẋ1 + ... + pnẋn − L, it is easy Equations of dynamics. to prove that dpi/dt = −dH/dxi, dxi/dt = dH/dpi. These so-called canonical equations form part of those for the characteristic chains of the single partial equation dz/dt + H(t, x1, ... xn, dz/dx1, ..., dz/dxn) = 0, to which then the solution of the original equations for x1 ... xn can be reduced. It may be shown (1) that if z = ψ(t, x1, ... xn, c1, .. cn) + c be a complete integral of this equation, then pi = dψ/dxi, dψ/dci = ei are 2n equations giving the solution of the canonical equations referred to, where c1 ... cn and e1, ... en are arbitrary constants; (2) that if xi = Xi(t, x01, ... pºn), pi = Pi(t, xº1, ... p0n) be the principal solutions of the canonical equations for t = t0, and ω denote the result of substituting these values in p1dH/dp1 + ... + pndH/dpn − H, and Ω = ∫tt0 ωdt, where, after integration, Ω is to be expressed as a function of t, x1, ... xn, xº1, ... xºn, then z = Ω + z0 is a complete integral of the partial equation.
A system of differential equations is said to allow a certain continuous group of transformations (see Groups, Theory of) when the introduction for the variables in the differential equations of the new variables given by the Application of theory of continuous groups to formal theories. equations of the group leads, for all values of the parameters of the group, to the same differential equations in the new variables. It would be interesting to verify in examples that this is the case in at least the majority of the differential equations which are known to be integrable in finite terms. We give a theorem of very general application for the case of a simultaneous complete system of linear partial homogeneous differential equations of the first order, to the solution of which the various differential equations discussed have been reduced. It will be enough to consider whether the given differential equations allow the infinitesimal transformations of the group.
It can be shown easily that sufficient conditions in order that a complete system Π1ƒ = 0 ... Πkƒ = 0, in n independent variables, should allow the infinitesimal transformation Pƒ = 0 are expressed by k equations ΠiPƒ − PΠiƒ = λi1Π1ƒ + ... + λikΠkƒ. Suppose now a complete system of n − r equations in n variables to allow a group of r infinitesimal transformations (P1f, ..., Prƒ) which has an invariant subgroup of r − 1 parameters (P1ƒ, ..., Pr-1ƒ), it being supposed that the n quantities Π1ƒ, ..., Πn-rƒ, P1ƒ, ..., Prƒ are not connected by an identical linear equation (with coefficients even depending on the independent variables). Then it can be shown that one solution of the complete system is determinable by a quadrature. For each of ΠiPσƒ − PσΠif is a linear function of Π1ƒ, ..., Πn-rƒ and the simultaneous system of independent equations Π1ƒ = 0, ... Πn-rƒ = 0, P1ƒ = 0, ... Pr-1ƒ = 0 is therefore a complete system, allowing the infinitesimal transformation Prƒ. This complete system of n − 1 equations has therefore one common solution ω, and Pr(ω) is a function of ω. By choosing ω suitably, we can then make Pr(ω) = 1. From this equation and the n − 1 equations Πiω = 0, Pσω = 0, we can determine ω by a quadrature only. Hence can be deduced a much more general result, that if the group of r parameters be integrable, the complete system can be entirety solved by quadratures; it is only necessary to introduce the solution found by the first quadrature as an independent variable, whereby we obtain a complete system of n − r equations in n − 1 variables, subject to an integrable group of r − 1 parameters, and to continue this process. We give some examples of the application of the theorem. (1) If an equation of the first order y′ = ψ(x, y) allow the infinitesimal transformation ξdƒ/dx + ηdƒ/dy, the integral curves ω(x, y) = y0, wherein ω(x, y) is the solution of dƒ/dx + ψ(x, y) dƒ/dy = 0 reducing to y for x = x0, are interchanged among themselves by the infinitesimal transformation, or ω(x, y) can be chosen to make ξdω/dx + ηdω/dy = 1; this, with dω/dx + ψdω/dy = 0, determines ω as the integral of the complete differential (dy − ψdx)/(η − ψξ). This result itself shows that every ordinary differential equation of the first order is subject to an infinite number of infinitesimal transformations. But every infinitesimal transformation ξdƒ/dx + ηdƒ/dy can by change of variables (after integration) be brought to the form dƒ/dy, and all differential equations of the first order allowing this group can then be reduced to the form F(x, dy/dx) = 0. (2) In an ordinary equation of the second order y” = ψ(x, y, y′), equivalent to dy/dx = y1, dy1/dx = ψ(x, y, y1), if H, H1 be the solutions for y and y1 chosen to reduce to y0 and yº1 when x = x0, and the equations H = y, H1= y1 be equivalent to ω = y0, ω1 = yº1, then ω, ω1 are the principal solutions of Πƒ = dƒ/dx + y1dƒ/dy + ψdƒ/dy1 = 0. If the original equation allow an infinitesimal transformation whose first extended form (see Groups) is Pƒ = ξdƒ/dx + ηdƒ/dy + η1dƒ/dy1, where η1δt is the increment of dy/dx when ξδt, ηδt are the increments of x, y, and is to be expressed in terms of x, y, y1, then each of Pω and Pω1 must be functions of ω and ω1, or the partial differential equation Πƒ must allow the group Pƒ. Thus by our general theorem, if the differential equation allow a group of two parameters (and such a group is always integrable), it can be solved by quadratures, our explanation sufficing, however, only provided the form Πƒ and the two infinitesimal transformations are not linearly connected. It can be shown, from the fact that η1 is a quadratic polynomial in y1, that no differential equation of the second order can allow more than 8 really independent infinitesimal transformations, and that every homogeneous linear differential equation of the second order allows just 8, being in fact reducible to d²y/dx² = 0. Since every group of more than two parameters has subgroups of two parameters, a differential equation of the second order allowing a group of more than two parameters can, as a rule, be solved by quadratures. By transforming the group we see that if a differential equation of the second order allows a single infinitesimal transformation, it can be transformed to the form F(x, dγ/dx, d²γ/dx²); this is not the case for every differential equation of the second order. (3) For an ordinary differential equation of the third order, allowing an integrable group of three parameters whose infinitesimal transformations are not linearly connected with the partial equation to which the solution of the given ordinary equation is reducible, the similar result follows that it can be integrated by quadratures. But if the group of three parameters be simple, this result must be replaced by the statement that the integration is reducible to quadratures and that of a so-called Riccati equation of the first order, of the form dy/dx = A + By + Cy², where A, B, C are functions of x. (4) Similarly for the integration by quadratures of an ordinary equation yn = ψ(x, y, y1, ... yn-1) of any order. Moreover, the group allowed by the equation may quite well consist of extended contact transformations. An important application is to the case where the differential equation is the resolvent equation defining the group of 235 transformations or rationality group of another differential equation (see below); in particular, when the rationality group of an ordinary linear differential equation is integrable, the equation can be solved by quadratures.
Following the practical and provisional division of theories of differential equations, to which we alluded at starting, into transformation theories and function theories, we pass now to give some account of the latter. These are both Consideration of function theories of differential equations. a necessary logical complement of the former, and the only remaining resource when the expedients of the former have been exhausted. While in the former investigations we have dealt only with values of the independent variables about which the functions are developable, the leading idea now becomes, as was long ago remarked by G. Green, the consideration of the neighbourhood of the values of the variables for which this developable character ceases. Beginning, as before, with existence theorems applicable for ordinary values of the variables, we are to consider the cases of failure of such theorems.
When in a given set of differential equations the number of equations is greater than the number of dependent variables, the equations cannot be expected to have common solutions unless certain conditions of compatibility, obtainable by equating different forms of the same differential coefficients deducible from the equations, are satisfied. We have had examples in systems of linear equations, and in the case of a set of equations p1 = φ1, ..., pr = φr. For the case when the number of equations is the same as that of dependent variables, the following is a general theorem which should be referred to: Let there be r equations in r dependent variables z1, ... zr and n independent A general existence theorem. variables x1, ... xn; let the differential coefficient of zσ of highest order which enters be of order hσ, and suppose dhσzσ / dx1hσ to enter, so that the equations can be written dhσzσ / dx1hσ = Φσ, where in the general differential coefficient of zρ which enters in Φσ, say
dk1 + ... + kn zρ / dx1k1 ... dxnkn,
we have k1 < hρ and k1 + ... + kn ≤ hρ. Let a1, ... an, b1, ... br, and bρk1 ... kn be a set of values of
x1, ... xn, z1, ... zr
and of the differential coefficients entering in Φσ about which all the functions Φ1, ... Φr, are developable. Corresponding to each dependent variable zσ, we take now a set of hσ functions of x2, ... xn, say φσ, φσ;(1), ... ,φσh−1 arbitrary save that they must be developable about a2, a3, ... an, and such that for these values of x2, ... xn, the function φρ reduces to bρ, and the differential coefficient
dk2 + ... + kn φρk1 / dx2k2 ... dxnkn
reduces to bρk1 ... kn. Then the theorem is that there exists one, and only one, set of functions z1, ... zr, of x2, ... xn developable about a1, ... an satisfying the given differential equations, and such that for x1 = a1 we have
zσ = φσ, dzσ / dx1 = φσ(1), ... dhσ−1zσ / dhσ−1x1 = φσhσ−1.
And, moreover, if the arbitrary functions φσ, φσ(1) ... contain a certain number of arbitrary variables t1, ... tm, and be developable about the values tº1, ... tºm of these variables, the solutions z1, ... zr will contain t1, ... tm, and be developable about tº1, ... tºm.
The proof of this theorem may be given by showing that if ordinary power series in x1 − a1, ... xn − an, t1 − tº1, ... tm − tºm be substituted in the equations wherein in zσ the coefficients of (x1 − a1)º, x1 − a1, ..., (x1 − a1)hσ−1 are the arbitrary functions φσ, φσ(1), ..., φσh−1, divided respectively by 1, 1!, 2!, &c., then the differential equations determine uniquely all the other coefficients, and that the resulting series are convergent. We rely, in fact, upon the theory of monogenic analytical functions (see Function), a function being determined entirely by its development in the neighbourhood of one set of values of the independent variables, from which all its other values arise by continuation; it being of course understood that the coefficients in the differential equations are to be continued at the same time. But it is to be remarked that there is no ground for believing, if this method of continuation be utilized, that the function is single-valued; we may quite well return to the same values of the independent variables with a different Singular points of solutions. value of the function; belonging, as we say, to a different branch of the function; and there is even no reason for assuming that the number of branches is finite, or that different branches have the same singular points and regions of existence. Moreover, and this is the most difficult consideration of all, all these circumstances may be dependent upon the values supposed given to the arbitrary constants of the integral; in other words, the singular points may be either fixed, being determined by the differential equations themselves, or they may be movable with the variation of the arbitrary constants of integration. Such difficulties arise even in establishing the reversion of an elliptic integral, in solving the equation
(dx/ds)² = (x − a1)(x − a2)(x − a3)(x − a4);
about an ordinary value the right side is developable; if we put x − a1 = t1², the right side becomes developable about t1 = 0; if we put x = 1/t, the right side of the changed equation is developable about t = 0; it is quite easy to show that the integral reducing to a definite value x0 for a value s0 is obtainable by a series in integral powers; this, however, must be supplemented by showing that for no value of s does the value of x become entirely undetermined.
These remarks will show the place of the theory now to be sketched of a particular class of ordinary linear homogeneous Linear differential equations with rational coefficients. differential equations whose importance arises from the completeness and generality with which they can be discussed. We have seen that if in the equations
dy/dx = y1, dy1/dx = y2, ..., dyn−2/dx = yn−1,
dyn−1/dx = any + an−1y1 + ... + a1yn−1,
where a1, a2, ..., an are now to be taken to be rational functions of x, the value x = xº be one for which no one of these rational functions is infinite, and yº, yº1, ..., yºn−1 be quite arbitrary finite values, then the equations are satisfied by
y = yºu + yº1u1 + ... + yºn−1un−1,
where u, u1, ..., un−1 are functions of x, independent of yº, ... yºn−1, developable about x = xº; this value of y is such that for x = xº the functions y, y1 ... yn−1 reduce respectively to yº, yº1, ... yºn−1; it can be proved that the region of existence of these series extends within a circle centre xº and radius equal to the distance from xº of the nearest point at which one of a1, ... an becomes infinite. Now consider a region enclosing xº and only one of the places, say Σ, at which one of a1, ... an becomes infinite. When x is made to describe a closed curve in this region, including this point Σ in its interior, it may well happen that the continuations of the functions u, u1, ..., un−1 give, when we have returned to the point x, values v, v1, ..., vn−1, so that the integral under consideration becomes changed to yº + yº1v1 + ... + yºn−1vn−1. At xº let this branch and the corresponding values of y1, ... yn−1 be ηº, ηº1, ... ηºn−1; then, as there is only one series satisfying the equation and reducing to (ηº, ηº1, ... ηºn−1) for x = xº and the coefficients in the differential equation are single-valued functions, we must have ηºu + ηº1u1 + ... + ηºn−1un−1 = yºv + yº1v1 + ... + yºn−1vn−1; as this holds for arbitrary values of yº ... yºn−1, upon which u, ... un−1 and v, ... vn−1 do not depend, it follows that each of v, ... vn−1 is a linear function of u, ... un−1 with constant coefficients, say vi = Ai1u + ... + Ainun−1. Then
yºv + ... + yºn−1vn−1 = (Σi Ai1 yºi)u + ... + (Σi Ain yºi) un−1;
this is equal to μ(yºu + ... + yºn−1un−1) if Σi Air yºi = μyºr−1; eliminating yº ... yºn−1 from these linear equations, we have a determinantal equation of order n for μ; let μ1 be one of its roots; determining the ratios of yº, y1º, ... yºn−1 to satisfy the linear equations, we have thus proved that there exists an integral, H, of the equation, which when continued round the point Σ and back to the starting-point, becomes changed to H1 = μ1H. Let now ξ be the value of x at Σ and r1 one of the values of (½πi) log μ1; consider the function (x − ξ)−r1H; when x makes a circuit round x = ξ, this becomes changed to
exp (-2πir1) (x − ξ)−r1 μH,
that is, is unchanged; thus we may put H = (x − ξ)r1φ1, φ1 being a function single-valued for paths in the region considered described about Σ, and therefore, by Laurent’s Theorem (see Function), capable of expression in the annular region about this point by a series of positive and negative integral powers of x − ξ, which in general may contain an infinite number of negative powers; there is, however, no reason to suppose r1 to be an integer, or even real. Thus, if all the roots of the determinantal equation in μ are different, we obtain n integrals of the forms (x − ξ)r1φ1, ..., (x − ξ)rnφn. In general we obtain as many integrals of this form as there are really different roots; and the problem arises to discover, in case a root be k times repeated, k − 1 equations of as simple a form as possible to replace the k − 1 equations of the form yº + ... + yºn−1vn−1 = μ(yº + ... + yºn−1un−1) which would have existed had the roots been different. The most natural method of obtaining a suggestion lies probably in remarking that if r2 = r1 + h, there is an integral [(x − ξ)r1 + hφ2 − (x − ξ)r1φ1] / h, where the coefficients in φ2 are 236 the same functions of r1 + h as are the coefficients in φ1 of r1; when h vanishes, this integral takes the form
(x − ξ)r1 [dφ1/dr1 + φ1 log (x − ξ)],
or say
(x − ξ)r1 [φ1 + ψ1 log (x − ξ)];
denoting this by 2πiμ1K, and (x − ξ)r1 φ1 by H, a circuit of the point ξ changes K into
| K′ = | 1 | [e2πir1 (x − ξ)r1 ψ1 + e2πir j (x − ξ)r1 φ1 (2πi + log(x − ξ) )] = μ1K + H. |
| 2πiμ1 |
A similar artifice suggests itself when three of the roots of the determinantal equation are the same, and so on. We are thus led to the result, which is justified by an examination of the algebraic conditions, that whatever may be the circumstances as to the roots of the determinantal equation, n integrals exist, breaking up into batches, the values of the constituents H1, H2, ... of a batch after circuit about x = ξ being H1′ = μ1H1, H2′ = μ1H2 + H1, H3′ = μ1H3 + H2, and so on. And this is found to lead to the forms (x − ξ)r1φ1, (x − ξ)r1 [ψ1 + φ1 log (x − ξ)], (x − ξ)r1 [χ1 + χ2 log (x − ξ) + φ1(log(x − ξ) )²], and so on. Here each of φ1, ψ1, χ1, χ2, ... is a series of positive and negative integral powers of x − ξ in which the number of negative powers may be infinite.
It appears natural enough now to inquire whether, under proper conditions for the forms of the rational functions a1, ... an, it may be possible to ensure that in each of the series φ1, ψ1, [chi]1, ... the number of negative powers shall be finite. Herein Regular equations. lies, in fact, the limitation which experience has shown to be justified by the completeness of the results obtained. Assuming n integrals in which in each of φ1, ψ1, χ1 ... the number of negative powers is finite, there is a definite homogeneous linear differential equation having these integrals; this is found by forming it to have the form
y′ n = (x − ξ)−1 b1y′ (n−1) + (x − ξ)−2 b2y′ (n−2) + ... + (x − ξ)−n bny,
where b1, ... bn are finite for x = ξ. Conversely, assume the equation to have this form. Then on substituting a series of the form (x − ξ)r [1 + A1(x − ξ) + A2(x − ξ)² + ... ] and equating the coefficients of like powers of x − ξ, it is found that r must be a root of an algebraic equation of order n; this equation, which we shall call the index equation, can be obtained at once by substituting for y only (x − ξ)r and replacing each of b1, ... bn by their values at x = ξ; arrange the roots r1, r2, ... of this equation so that the real part of ri is equal to, or greater than, the real part of ri+1, and take r equal to r1; it is found that the coefficients A1, A2 ... are uniquely determinate, and that the series converges within a circle about x = ξ which includes no other of the points at which the rational functions a1 ... an become infinite. We have thus a solution H1 = (x − ξ)r1φ1 of the differential equation. If we now substitute in the equation y = H1∫ηdx, it is found to reduce to an equation of order n − 1 for η of the form
η′ (n−1) = (x − ξ)−1 c1η′ (n−2) + ... + (x − ξ)(n−1) cn−1η,
where c1, ... cn−1 are not infinite at x = ξ. To this equation precisely similar reasoning can then be applied; its index equation has in fact the roots r2 − r1 − 1, ..., rn − r1 − 1; if r2 − r1 be zero, the integral (x − ξ)−1ψ1 of the η equation will give an integral of the original equation containing log (x − ξ); if r2 − r1 be an integer, and therefore a negative integer, the same will be true, unless in ψ1 the term in (x − ξ)r1 − r2 be absent; if neither of these arise, the original equation will have an integral (x − ξ)r2φ2. The η equation can now, by means of the one integral of it belonging to the index r2 − r1 − 1, be similarly reduced to one of order n − 2, and so on. The result will be that stated above. We shall say that an equation of the form in question is regular about x = ξ.
We may examine in this way the behaviour of the integrals at all the points at which any one of the rational functions a1 ... an becomes infinite; in general we must expect that beside these the value x = ∞ will be a singular point for the Fuchsian equations. solutions of the differential equation. To test this we put x = 1/t throughout, and examine as before at t = 0. For instance, the ordinary linear equation with constant coefficients has no singular point for finite values of x; at x = ∞ it has a singular point and is not regular; or again, Bessel’s equation x²y″ + xy′ + (x² − n²)y = 0 is regular about x = 0, but not about x = ∞. An equation regular at all the finite singularities and also at x = ∞ is called a Fuchsian equation. We proceed to examine particularly the case of an equation of the second order
y″ + ay′ + by = 0.
Putting x = 1/t, it becomes
d²y/dt² + (2t−1 − at−2) dy/dt + bt−4 y = 0,
which is not regular about t = 0 unless 2 − at−1 and bt−2, that is, unless ax and bx² are finite at x = ∞; which we thus assume; putting y = tr(1 + A1t + ... ), we find for the index equation at x = ∞ the equation r(r − 1) + r(2 − ax)0 + (bx²)0 = 0. If there be Equation of the second order. finite singular points at ξ1, ... ξm, where we assume m > 1, the cases m = 0, m = 1 being easily dealt with, and if φ(x) = (x − ξ1) ... (x − ξm), we must have a·φ(x) and b·[φ(x)]² finite for all finite values of x, equal say to the respective polynomials ψ(x) and θ(x), of which by the conditions at x = ∞ the highest respective orders possible are m − 1 and 2(m − 1). The index equation at x = ξ1 is r(r − 1) + rψ(ξ1) / φ′ (ξ1) + θ(ξ)1 / [φ′(ξ1)]² = 0, and if α1, β1 be its roots, we have α1 + β1 = 1 − ψ(ξ1) / φ′ (ξ1) and α1β1 = θ(ξ)1 / [φ′(ξ1)]². Thus by an elementary theorem of algebra, the sum Σ(1 − αi − βi) / (x − ξi), extended to the m finite singular points, is equal to ψ(x) / φ(x), and the sum Σ(1 − αi − βi) is equal to the ratio of the coefficients of the highest powers of x in ψ(x) and φ(x), and therefore equal to 1 + α + β, where α, β are the indices at x = ∞. Further, if (x, 1)m−2 denote the integral part of the quotient θ(x) / φ(x), we have Σ αiβiφ′ (ξi) / (x = ξi) equal to −(x, 1)m−2 + θ(x)/φ(x), and the coefficient of xm−2 in (x, 1)m−2 is αβ. Thus the differential equation has the form
y″ + y′Σ (1 − αi − βi) / (x − ξi) + y[(x, 1)m-2 + Σ αiβiφ′(ξi) / (x − ξi)]/φ(x) = 0.
If, however, we make a change in the dependent variable, putting y = (x − ξ1)α1 ... (x − ξm)α mη, it is easy to see that the equation changes into one having the same singular points about each of which it is regular, and that the indices at x = ξi become 0 and βi − αi, which we shall denote by λi, for (x − ξi)αj can be developed in positive integral powers of x − ξi about x = ξi; by this transformation the indices at x = ∞ are changed to
α + α1 + ... + αm, β + β1 + ... + βm
which we shall denote by λ, μ. If we suppose this change to have been introduced, and still denote the independent variable by y, the equation has the form
y″ + y′Σ (1 − λi) / (x − ξi) + y(x, 1)m−2 / φ(x) = 0,
while λ + μ + λ1 + ... + λm = m − 1. Conversely, it is easy to verify that if λμ be the coefficient of xm−2 in (x, 1)m−2, this equation has the specified singular points and indices whatever be the other coefficients in (x, 1)m−2.
Thus we see that (beside the cases m = 0, m = 1) the “Fuchsian equation” of the second order with two finite singular points is distinguished by the fact that it has a definite form when the singular points and the indices are assigned. Hypergeometric equation. In that case, putting (x − ξ1) / (x − ξ2) = t / (t − 1), the singular points are transformed to 0, 1, ∞, and, as is clear, without change of indices. Still denoting the independent variable by x, the equation then has the form
x(1 − x)y″ + y′[1 − λ1 − x(1 + λ + μ)] − λμy = 0,
which is the ordinary hypergeometric equation. Provided none of λ1, λ2, λ − μ be zero or integral about x = 0, it has the solutions
F(λ, μ, 1 − λ1, x), xλ1 F(λ + λ1, μ + λ1, 1 + λ1, x);
about x = 1 it has the solutions
F(λ, μ, 1 − λ2, 1 − x), (1 − x)λ2 F(λ + λ2, μ + λ2, 1 + λ2, 1 − x),
where λ + μ + λ1 + λ2 = 1; about x = ∞ it has the solutions
x−λ F(λ, λ + λ1, λ − μ + 1, x−1), x−μ F(μ, μ + λ1, μ − λ + 1, x−1),
where F(α, β, γ, x) is the series
| 1 + | αβx | + | α(α + 1)β(β + 1)x² | ..., |
| γ | 1·2·γ(γ + 1) |
which converges when |x| < 1, whatever α, β, γ may be, converges for all values of x for which |x| = 1 provided the real part of γ − α − β < 0 algebraically, and converges for all these values except x = 1 provided the real part of γ − α − β > −1 algebraically.
In accordance with our general theory, logarithms are to be expected in the solution when one of λ1, λ2, λ − μ is zero or integral. Indeed when λ1 is a negative integer, not zero, the second solution about x = 0 would contain vanishing factors in the denominators of its coefficients; in case λ or μ be one of the positive integers 1, 2, ... (−λ1), vanishing factors occur also in the numerators; and then, in fact, the second solution about x = 0 becomes xλ1 times an integral polynomial of degree (−λ1) − λ or of degree (−λ1) − μ. But when λ1 is a negative integer including zero, and neither λ nor μ is one of the positive integers 1, 2 ... (−λ1), the second solution about x = 0 involves a term having the factor log x. When λ1 is a positive integer, not zero, the second solution about x = 0 persists as a solution, in accordance with the order of arrangement of the roots of the index equation in our theory; the first solution is then replaced by an integral polynomial of degree -λ or −μ1, when λ or μ is one of the negative integers 0, −1, −2, ..., 1 − λ1, but otherwise contains a logarithm. Similarly for the solutions about x = 1 or x = ∞; it will be seen below how the results are deducible from those for x = 0.
Denote now the solutions about x = 0 by u1, u2; those about x = 1 by v1, v2; and those about x = ∞ by w1, w2; in the region (S0S1) common to the circles S0, S1 of radius 1 whose centres are the points x = 0, x = 1, all the first four are valid, March of the Integral. and there exist equations u1 =Av1 + Bv2, u2 = Cv1 + Dv2 where A, B, C, D are constants; in the region (S1S) lying inside the circle S1 and outside the circle S0, those that are valid are v1, v2, w1, w2, and there exist equations v1 = Pw1 + Qw2, v2 = Rw1 + Tw2, where P, Q, R, T are constants; thus considering any integral whose expression within the circle S0 is au1 + bu2, where a, b are constants, the same integral will be represented within the circle S1 by (aA + bC)v1 + (aB + bD)v2, and outside these circles will be represented by
[aA + bC)P + (aB + bD)R]w1 + [(aA + bC)Q + (aB + bD)T]w2.
A single-valued branch of such integral can be obtained by making a barrier in the plane joining ∞ to 0 and 1 to ∞; for instance, by excluding the consideration of real negative values of x and of real 237 positive values greater than 1, and defining the phase of x and x − 1 for real values between 0 and 1 as respectively 0 and π.
We can form the Fuchsian equation of the second order with three arbitrary singular points ξ1, ξ2, ξ3, and no singular point at x = ∞, and with respective indices α1, β1, α2, β2, α3, β3 such that α1 + β1 + α2 + β2 + α3 + β3 = 1. This equation can then be Transformation of the equation into itself. transformed into the hypergeometric equation in 24 ways; for out of ξ1, ξ2, ξ3 we can in six ways choose two, say ξ1, ξ2, which are to be transformed respectively into 0 and 1, by (x − ξ1)/(x − ξ2) = t(t − 1); and then there are four possible transformations of the dependent variable which will reduce one of the indices at t = 0 to zero and one of the indices at t = 1 also to zero, namely, we may reduce either α1 or β1 at t = 0, and simultaneously either α2 or β2 at t = 1. Thus the hypergeometric equation itself can be transformed into itself in 24 ways, and from the expression F(λ, μ, 1 − λ1, x) which satisfies it follow 23 other forms of solution; they involve four series in each of the arguments, x, x − 1, 1/x, 1/(1 − x), (x − 1)/x, x/(x − 1). Five of the 23 solutions agree with the fundamental solutions already described about x = 0, x = 1, x = ∞; and from the principles by which these were obtained it is immediately clear that the 24 forms are, in value, equal in fours.
The quarter periods K, K′ of Jacobi’s theory of elliptic functions, of which K = ∫π/20 (1 − h sin ²θ)−½dθ, and K′ is the same function of 1-h, can easily be proved to be the solutions of a hypergeometric Inversion. Modular functions. equation of which h is the independent variable. When K, K′ are regarded as defined in terms of h by the differential equation, the ratio K′/K is an infinitely many valued function of h. But it is remarkable that Jacobi’s own theory of theta functions leads to an expression for h in terms of K′/K (see Function) in terms of single-valued functions. We may then attempt to investigate, in general, in what cases the independent variable x of a hypergeometric equation is a single-valued function of the ratio s of two independent integrals of the equation. The same inquiry is suggested by the problem of ascertaining in what cases the hypergeometric series F(α, β, γ, x) is the expansion of an algebraic (irrational) function of x. In order to explain the meaning of the question, suppose that the plane of x is divided along the real axis from -∞ to 0 and from 1 to +∞, and, supposing logarithms not to enter about x = 0, choose two quite definite integrals y1, y2 of the equation, say
y1 = F(λ, μ, 1 − λ1, x), y2 = xλ1 F(λ + λ1, μ + λ1, 1 + λ1, x),
with the condition that the phase of x is zero when x is real and between 0 and 1. Then the value of ς = y2/y1 is definite for all values of x in the divided plane, ς being a single-valued monogenic branch of an analytical function existing and without singularities all over this region. If, now, the values of ς that so arise be plotted on to another plane, a value p + iq of σ being represented by a point (p, q) of this ς-plane, and the value of x from which it arose being mentally associated with this point of the σ-plane, these points will fill a connected region therein, with a continuous boundary formed of four portions corresponding to the two sides of the two barriers of the x-plane. The question is then, firstly, whether the same value of s can arise for two different values of x, that is, whether the same point (p, q) of the ς-plane can arise twice, or in other words, whether the region of the ς-plane overlaps itself or not. Supposing this is not so, a second part of the question presents itself. If in the x-plane the barrier joining -∞ to 0 be momentarily removed, and x describe a small circle with centre at x = 0 starting from a point x = −h − ik, where h, k are small, real, and positive and coming back to this point, the original value s at this point will be changed to a value σ, which in the original case did not arise for this value of x, and possibly not at all. If, now, after restoring the barrier the values arising by continuation from σ be similarly plotted on the ς-plane, we shall again obtain a region which, while not overlapping itself, may quite possibly overlap the former region. In that case two values of x would arise for the same value or values of the quotient y2/y1, arising from two different branches of this quotient. We shall understand then, by the condition that x is to be a single-valued function of x, that the region in the ς-plane corresponding to any branch is not to overlap itself, and that no two of the regions corresponding to the different branches are to overlap. Now in describing the circle about x = 0 from x = −h − ik to −h + ik, where h is small and k evanescent,
ς = xλ1 F(λ + λ1, μ + λ1, 1 + λ1, x) / F(λ, μ, 1 − λ1, x)
is changed to σ = ςe2πiλ1. Thus the two portions of boundary of the s-region corresponding to the two sides of the barrier (−∞, 0) meet (at ς = 0 if the real part of λ1 be positive) at an angle 2πL1, where L1 is the absolute value of the real part of λ1; the same is true for the σ-region representing the branch σ. The condition that the s-region shall not overlap itself requires, then, L1 = 1. But, further, we may form an infinite number of branches σ = ςe2πiλ1, σ1 = e2πiλ1, ... in the same way, and the corresponding regions in the plane upon which y2/y1 is represented will have a common point and each have an angle 2πL1; if neither overlaps the preceding, it will happen, if L1 is not zero, that at length one is reached overlapping the first, unless for some positive integer α we have 2παL1 = 2π, in other words L1 = 1/α. If this be so, the branch σα−1 = ςe2πiαλ1 will be represented by a region having the angle at the common point common with the region for the branch ς; but not altogether coinciding with this last region unless λ1 be real, and therefore = ±1/α; then there is only a finite number, α, of branches obtainable in this way by crossing the barrier (−∞, 0). In precisely the same way, if we had begun by taking the quotient
ς′ = (x − 1)λ2 F(λ + λ2, μ + λ2, 1 + λ2, 1 − x) / F(λ, μ, 1 − λ2, 1 − x)
of the two solutions about x = 1, we should have found that x is not a single-valued function of ς′ unless λ2 is the inverse of an integer, or is zero; as ς′ is of the form (Aσ + B)/(Cς + D), A, B, C, D constants, the same is true in our case; equally, by considering the integrals about x = ∞ we find, as a third condition necessary in order that x may be a single-valued function of ς, that λ − μ must be the inverse of an integer or be zero. These three differences of the indices, namely, λ1, λ2, λ − μ, are the quantities which enter in the differential equation satisfied by x as a function of ς, which is easily found to be
| − | x111 | + | 3x²11 | ½(h − h1 − h2)x−1(x − 1)−1 + ½h1x−2 + ½h2(x − 1)−2, |
| x1³ | 2x14 |
where x1 = dx/dς, &c.; and h1 = 1 − y1², h2 = 1 − λ2², h3 = 1 − (λ − μ)². Into the converse question whether the three conditions are sufficient to ensure (1) that the σ region corresponding to any branch does not overlap itself, (2) that no two such regions overlap, we have no space to enter. The second question clearly requires the inquiry whether the group (that is, the monodromy group) of the differential equation is properly discontinuous. (See Groups, Theory of.)
The foregoing account will give an idea of the nature of the function theories of differential equations; it appears essential not to exclude some explanation of a theory intimately related both to such theories and to transformation theories, which is a generalization of Galois’s theory of algebraic equations. We deal only with the application to homogeneous linear differential equations.
In general a function of variables x1, x2 ... is said to be rational when it can be formed from them and the integers 1, 2, 3, ... by a finite number of additions, subtractions, multiplications and divisions. We generalize this definition. Assume that Rationality group of a linear equation. we have assigned a fundamental series of quantities and functions of x, in which x itself is included, such that all quantities formed by a finite number of additions, subtractions, multiplications, divisions and differentiations in regard to x, of the terms of this series, are themselves members of this series. Then the quantities of this series, and only these, are called rational. By a rational function of quantities p, q, r, ... is meant a function formed from them and any of the fundamental rational quantities by a finite number of the five fundamental operations. Thus it is a function which would be called, simply, rational if the fundamental series were widened by the addition to it of the quantities p, q, r, ... and those derivable from them by the five fundamental operations. A rational ordinary differential equation, with x as independent and y as dependent variable, is then one which equates to zero a rational function of y, the order k of the differential equation being that of the highest differential coefficient y(k) which enters; only such equations are here discussed. Such an equation P = 0 is called irreducible when, firstly, being arranged as an integral polynomial in y(k), this polynomial Irreducibility of a rational equation. is not the product of other polynomials in y(k) also of rational form; and, secondly, the equation has no solution satisfying also a rational equation of lower order. From this it follows that if an irreducible equation P = 0 have one solution satisfying another rational equation Q = 0 of the same or higher order, then all the solutions of P = 0 also satisfy Q = 0. For from the equation P = 0 we can by differentiation express y(k+1), y(k+2), ... in terms of x, y, y(1), ... , y(k), and so put the function Q rationally in terms of these quantities only. It is sufficient, then, to prove the result when the equation Q = 0 is of the same order as P = 0. Let both the equations be arranged as integral polynomials in y(k); their algebraic eliminant in regard to y(k) must then vanish identically, for they are known to have one common solution not satisfying an equation of lower order; thus the equation P = 0 involves Q = 0 for all solutions of P = 0.
Now let y(n) = a1y(n−1) + ... + any be a given rational homogeneous linear differential equation; let y1, ... yn be n particular functions of x, unconnected by any equation with constant coefficients of the form c1y1 + ... + cnyn = 0, all satisfying The variant function for a linear equation. the differential equation; let η1, ... ηn be linear functions of y1, ... yn, say ηi = Ai1y1 + ... + Ainyn, where the constant coefficients Aij have a non-vanishing determinant; write (η) = A(y), these being the equations of a general linear homogeneous group whose transformations may be denoted by A, B, .... We desire to form a rational function φ(η), or say φ(A(y)), of η1, ... η, in which the η² constants Aij shall all be essential, and not reduce effectively to a fewer number, as they would, for instance, if the y1, ... yn were connected by a linear equation with constant coefficients. Such a function is in fact given, if the solutions y1, ... yn be developable 238 in positive integral powers about x = a, by φ(η) = η1 + (x − a)n η2 + ... + (x − a)(n−1)n ηn. Such a function, V, we call a variant.
Then differentiating V in regard to x, and replacing ηi(n) by its value a1η(n−1) + ... + anη, we can arrange dV/dx, and similarly each of d²/dx² ... dNV/dxN, where N = n², as a linear function of the N quantities η1, ... ηn, ... η1(n−1), ... ηn(n−1), and The resolvent eqution. thence by elimination obtain a linear differential equation for V of order N with rational coefficients. This we denote by F = 0. Further, each of η1 ... ηn is expressible as a linear function of V, dV/dx, ... dN−1V / dxN−1, with rational coefficients not involving any of the n² coefficients Aij, since otherwise V would satisfy a linear equation of order less than N, which is impossible, as it involves (linearly) the n² arbitrary coefficients Aij, which would not enter into the coefficients of the supposed equation. In particular, y1 ,.. yn are expressible rationally as linear functions of ω, dω/dx, ... dN−1ω / dxN−1, where ω is the particular function φ(y). Any solution W of the equation F = 0 is derivable from functions ζ1, ... ζn, which are linear functions of y1, ... yn, just as V was derived from η1, ... ηn; but it does not follow that these functions ζi, ... ζn are obtained from y1, ... yn by a transformation of the linear group A, B, ... ; for it may happen that the determinant d(ζ1, ... ζn) / (dy1, ... yn) is zero. In that case ζ1, ... ζn may be called a singular set, and W a singular solution; it satisfies an equation of lower than the N-th order. But every solution V, W, ordinary or singular, of the equation F = 0, is expressible rationally in terms of ω, dω / dx, ... dN−1ω / dxN−1; we shall write, simply, V = r(ω). Consider now the rational irreducible equation of lowest order, not necessarily a linear equation, which is satisfied by ω; as y1, ... yn are particular functions, it may quite well be of order less than N; we call it the resolvent equation, suppose it of order p, and denote it by γ(v). Upon it the whole theory turns. In the first place, as γ(v) = 0 is satisfied by the solution ω of F = 0, all the solutions of γ(v) are solutions F = 0, and are therefore rationally expressible by ω; any one may then be denoted by r(ω). If this solution of F = 0 be not singular, it corresponds to a transformation A of the linear group (A, B, ...), effected upon y1, ... yn. The coefficients Aij of this transformation follow from the expressions before mentioned for η1 ... ηn in terms of V, dV/dx, d²V/dx², ... by substituting V = r(ω); thus they depend on the p arbitrary parameters which enter into the general expression for the integral of the equation γ(v) = 0. Without going into further details, it is then clear enough that the resolvent equation, being irreducible and such that any solution is expressible rationally, with p parameters, in terms of the solution ω, enables us to define a linear homogeneous group of transformations of y1 ... yn depending on p parameters; and every operation of this (continuous) group corresponds to a rational transformation of the solution of the resolvent equation. This is the group called the rationality group, or the group of transformations of the original homogeneous linear differential equation.
The group must not be confounded with a subgroup of itself, the monodromy group of the equation, often called simply the group of the equation, which is a set of transformations, not depending on arbitrary variable parameters, arising for one particular fundamental set of solutions of the linear equation (see Groups, Theory of).
The importance of the rationality group consists in three propositions. (1) Any rational function of y1, ... yn which is unaltered in value by the transformations of the group can be written in rational form. (2) If any rational function be changed The fundamental theorem in regard to the rationality group. in form, becoming a rational function of y1, ... yn, a transformation of the group applied to its new form will leave its value unaltered. (3) Any homogeneous linear transformation leaving unaltered the value of every rational function of y1, ... yn which has a rational value, belongs to the group. It follows from these that any group of linear homogeneous transformations having the properties (1) (2) is identical with the group in question. It is clear that with these properties the group must be of the greatest importance in attempting to discover what functions of x must be regarded as rational in order that the values of y1 ... yn may be expressed. And this is the problem of solving the equation from another point of view.
Literature.—(α) Formal or Transformation Theories for Equations of the First Order:—E. Goursat, Leçons sur l’intégration des équations aux dérivées partielles du premier ordre (Paris, 1891); E. v. Weber, Vorlesungen über das Pfaff’sche Problem und die Theorie der partiellen Differentialgleichungen erster Ordnung (Leipzig, 1900); S. Lie und G. Scheffers, Geometrie der Berührungstransformationen, Bd. i. (Leipzig, 1896); Forsyth, Theory of Differential Equations, Part i., Exact Equations and Pfaff’s Problem (Cambridge, 1890); S. Lie, “Allgemeine Untersuchungen über Differentialgleichungen, die eine continuirliche endliche Gruppe gestatten” (Memoir), Mathem. Annal.xxv. (1885), pp. 71-151; S. Lie und G. Scheffers, Vorlesungen über Differentialgleichungen mit bekannten infinitesimalen Transformationen (Leipzig, 1891). A very full bibliography is given in the book of E. v. Weber referred to; those here named are perhaps sufficiently representative of modern works. Of classical works may be named: Jacobi, Vorlesungen über Dynamik (von A. Clebsch, Berlin, 1866); Werke, Supplementband; G Monge, Application de l’analyse à la géométrie (par M. Liouville, Paris, 1850); J. L. Lagrange, Leçons sur le calcul des fonctions (Paris, 1806), and Théorie des fonctions analytiques (Paris, Prairial, an V); G. Boole, A Treatise on Differential Equations (London, 1859); and Supplementary Volume (London, 1865); Darboux, Leçons sur la théorie générale des surfaces, tt. i.-iv. (Paris, 1887-1896); S. Lie, Théorie der transformationsgruppen ii. (on Contact Transformations) (Leipzig, 1890).
(β) Quantitative or Function Theories for Linear Equations:—C. Jordan, Cours d’analyse, t. iii. (Paris, 1896); E. Picard, Traité d’analyse, tt. ii. and iii. (Paris, 1893, 1896); Fuchs, Various Memoirs, beginning with that in Crelle’s Journal, Bd. lxvi. p. 121; Riemann, Werke, 2r Aufl. (1892); Schlesinger, Handbuch der Theorie der linearen Differentialgleichungen, Bde. i.-ii. (Leipzig, 1895-1898); Heffter, Einleitung in die Theorie der linearen Differentialgleichungen mit einer unabhängigen Variablen (Leipzig, 1894); Klein, Vorlesungen über lineare Differentialgleichungen der zweiten Ordnung (Autographed, Göttingen, 1894); and Vorlesungen über die hypergeometrische Function (Autographed, Göttingen, 1894); Forsyth, Theory of Differential Equations, Linear Equations.
(γ) Rationality Group (of Linear Differential Equations):—Picard, Traité d’Analyse, as above, t. iii.; Vessiot, Annales de l’École Normale, série III. t. ix. p. 199 (Memoir); S. Lie, Transformationsgruppen, as above, iii. A connected account is given in Schlesinger, as above, Bd. ii., erstes Theil.
(δ) Function Theories of Non-Linear Ordinary Equations:—Painlevé, Leçons sur la théorie analytique des équations différentielles (Paris, 1897, Autographed); Forsyth, Theory of Differential Equations, Part ii., Ordinary Equations not Linear (two volumes, ii. and iii.) (Cambridge, 1900); Königsberger, Lehrbuch der Theorie der Differentialgleichungen (Leipzig, 1889); Painlevé, Leçons sur l’intégration des équations differentielles de la mécanique et applications (Paris, 1895).
(ε) Formal Theories of Partial Equations of the Second and Higher Orders:—E. Goursat, Leçons sur l’intégration des équations aux dérivées partielles du second ordre, tt. i. and ii. (Paris, 1896, 1898); Forsyth, Treatise on Differential Equations (London, 1889); and Phil. Trans. Roy. Soc. (A.), vol. cxci. (1898), pp. 1-86.
(ζ) See also the six extensive articles in the second volume of the German Encyclopaedia of Mathematics.
DIFFLUGIA (L. Leclerc), a genus of lobose Rhizopoda, characterized by a shell formed of sand granules cemented together; these are swallowed by the animal, and during the process of bud-fission they pass to the surface of the daughter-bud and are cemented there. Centropyxis (Steia) and Lecqueureuxia (Schlumberg) differ only in minor points.
DIFFRACTION OF LIGHT.—1. When light proceeding from a small source falls upon an opaque object, a shadow is cast upon a screen situated behind the obstacle, and this shadow is found to be bordered by alternations of brightness and darkness, known as “diffraction bands.” The phenomena thus presented were described by Grimaldi and by Newton. Subsequently T. Young showed that in their formation interference plays an important part, but the complete explanation was reserved for A. J. Fresnel. Later investigations by Fraunhofer, Airy and others have greatly widened the field, and under the head of “diffraction” are now usually treated all the effects dependent upon the limitation of a beam of light, as well as those which arise from irregularities of any kind at surfaces through which it is transmitted, or at which it is reflected.
2. Shadows.—In the infancy of the undulatory theory the objection most frequently urged against it was the difficulty of explaining the very existence of shadows. Thanks to Fresnel and his followers, this department of optics is now precisely the one in which the theory has gained its greatest triumphs. The principle employed in these investigations is due to C. Huygens, and may be thus formulated. If round the origin of waves an ideal closed surface be drawn, the whole action of the waves in the region beyond may be regarded as due to the motion continually propagated across the various elements of this surface. The wave motion due to any element of the surface is called a secondary wave, and in estimating the total effect regard must be paid to the phases as well as the amplitudes of the components. It is usually convenient to choose as the surface of resolution a wave-front, i.e. a surface at which the primary vibrations are in one phase. Any obscurity that may hang over Huygens’s principle is due mainly to the indefiniteness of thought and expression which we must be content to put up with if we wish to avoid pledging ourselves as to the character of the vibrations. In the application to sound, where we know what we are dealing with, the matter is simple enough in principle, although mathematical difficulties would often stand in the way of the calculations we might wish to make. 239 The ideal surface of resolution may be there regarded as a flexible lamina; and we know that, if by forces locally applied every element of the lamina be made to move normally to itself exactly as the air at that place does, the external aerial motion is fully determined. By the principle of superposition the whole effect may be found by integration of the partial effects due to each element of the surface, the other elements remaining at rest.
 |
| Fig. 1. |
We will now consider in detail the important case in which uniform plane waves are resolved at a surface coincident with a wave-front (OQ). We imagine a wave-front divided into elementary rings or zones—often named after Huygens, but better after Fresnel—by spheres described round P (the point at which the aggregate effect is to be estimated), the first sphere, touching the plane at O, with a radius equal to PO, and the succeeding spheres with radii increasing at each step by ½λ. There are thus marked out a series of circles, whose radii x are given by x² + r² = (r + ½nλ)², or x² = nλr nearly; so that the rings are at first of nearly equal area. Now the effect upon P of each element of the plane is proportional to its area; but it depends also upon the distance from P, and possibly upon the inclination of the secondary ray to the direction of vibration and to the wave-front.
The latter question can only be treated in connexion with the dynamical theory (see below, § 11); but under all ordinary circumstances the result is independent of the precise answer that may be given. All that it is necessary to assume is that the effects of the successive zones gradually diminish, whether from the increasing obliquity of the secondary ray or because (on account of the limitation of the region of integration) the zones become at last more and more incomplete. The component vibrations at P due to the successive zones are thus nearly equal in amplitude and opposite in phase (the phase of each corresponding to that of the infinitesimal circle midway between the boundaries), and the series which we have to sum is one in which the terms are alternately opposite in sign and, while at first nearly constant in numerical magnitude, gradually diminish to zero. In such a series each term may be regarded as very nearly indeed destroyed by the halves of its immediate neighbours, and thus the sum of the whole series is represented by half the first term, which stands over uncompensated. The question is thus reduced to that of finding the effect of the first zone, or central circle, of which the area is πλr.
We have seen that the problem before us is independent of the law of the secondary wave as regards obliquity; but the result of the integration necessarily involves the law of the intensity and phase of a secondary wave as a function of r, the distance from the origin. And we may in fact, as was done by A. Smith (Camb. Math. Journ., 1843, 3, p. 46), determine the law of the secondary wave, by comparing the result of the integration with that obtained by supposing the primary wave to pass on to P without resolution.
Now as to the phase of the secondary wave, it might appear natural to suppose that it starts from any point Q with the phase of the primary wave, so that on arrival at P, it is retarded by the amount corresponding to QP. But a little consideration will prove that in that case the series of secondary waves could not reconstitute the primary wave. For the aggregate effect of the secondary waves is the half of that of the first Fresnel zone, and it is the central element only of that zone for which the distance to be travelled is equal to r. Let us conceive the zone in question to be divided into infinitesimal rings of equal area. The effects due to each of these rings are equal in amplitude and of phase ranging uniformly over half a complete period. The phase of the resultant is midway between those of the extreme elements, that is to say, a quarter of a period behind that due to the element at the centre of the circle. It is accordingly necessary to suppose that the secondary waves start with a phase one-quarter of a period in advance of that of the primary wave at the surface of resolution.
Further, it is evident that account must be taken of the variation of phase in estimating the magnitude of the effect at P of the first zone. The middle element alone contributes without deduction; the effect of every other must be found by introduction of a resolving factor, equal to cos θ, if θ represent the difference of phase between this element and the resultant. Accordingly, the amplitude of the resultant will be less than if all its components had the same phase, in the ratio
| ∫ | +½π | cos θdθ : π, |
| -½π |
or 2 : π. Now 2 area /π = 2λr; so that, in order to reconcile the amplitude of the primary wave (taken as unity) with the half effect of the first zone, the amplitude, at distance r, of the secondary wave emitted from the element of area dS must be taken to be
dS/λr (1).
By this expression, in conjunction with the quarter-period acceleration of phase, the law of the secondary wave is determined.
That the amplitude of the secondary wave should vary as r-1 was to be expected from considerations respecting energy; but the occurrence of the factor λ-1, and the acceleration of phase, have sometimes been regarded as mysterious. It may be well therefore to remember that precisely these laws apply to a secondary wave of sound, which can be investigated upon the strictest mechanical principles.
The recomposition of the secondary waves may also be treated analytically. If the primary wave at O be cos kat, the effect of the secondary wave proceeding from the element dS at Q is
| dS | cos k(at − ρ + ¼λ) = − | dS | sin k(at − ρ). |
| λρ | λρ |
If dS = 2πxdx, we have for the whole effect
| − | 2π | ∫ | ∞ | sin k(at − ρ)x dx | , |
| λ | 0 | ρ |
or, since xdx = ρdρ, k = 2π/λ,
| −k ∫ | ∞ | sin k(at − ρ)dρ = [ −cos k(at − ρ) ] | ∞ | . | |
| r | r |
In order to obtain the effect of the primary wave, as retarded by traversing the distance r, viz. cos k(at − r), it is necessary to suppose that the integrated term vanishes at the upper limit. And it is important to notice that without some further understanding the integral is really ambiguous. According to the assumed law of the secondary wave, the result must actually depend upon the precise radius of the outer boundary of the region of integration, supposed to be exactly circular. This case is, however, at most very special and exceptional. We may usually suppose that a large number of the outer rings are incomplete, so that the integrated term at the upper limit may properly be taken to vanish. If a formal proof be desired, it may be obtained by introducing into the integral a factor such as e-hρ, in which h is ultimately made to diminish without limit.
When the primary wave is plane, the area of the first Fresnel zone is πλr, and, since the secondary waves vary as r-1, the intensity is independent of r, as of course it should be. If, however, the primary wave be spherical, and of radius a at the wave-front of resolution, then we know that at a distance r further on the amplitude of the primary wave will be diminished in the ratio a : (r + a). This may be regarded as a consequence of the altered area of the first Fresnel zone. For, if x be its radius, we have
{(r + ½λ)² − x²} + √ {a² − x²} = r + a,
so that
x² = λar/(a + r) nearly.
Since the distance to be travelled by the secondary waves is still r, we see how the effect of the first zone, and therefore of the whole series is proportional to a/(a + r). In like manner may be treated other cases, such as that of a primary wave-front of unequal principal curvatures.
The general explanation of the formation of shadows may also be conveniently based upon Fresnel’s zones. If the point under consideration be so far away from the geometrical shadow that a large number of the earlier zones are complete, then the illumination, determined sensibly by the first zone, is the same as if there were no obstruction at all. If, on the other hand, the point be well immersed in the geometrical shadow, the earlier zones are altogether missing, and, instead of a series of terms beginning with finite numerical magnitude and gradually diminishing to zero, we have now to deal with one of which the terms diminish to zero at both ends. The sum of such a series is very approximately zero, each term being neutralized by the halves of its immediate neighbours, which are of the opposite sign. The question of light or darkness then depends upon whether the series begins or ends abruptly. With few exceptions, abruptness can occur only in the presence of the first term, viz. when the secondary wave of least retardation is unobstructed, or when a ray passes through the point under consideration. According to the undulatory theory the light cannot be regarded strictly as travelling along a ray; but the existence of an unobstructed ray implies that the system of Fresnel’s zones can be commenced, and, if a large number of these zones are fully developed and do not terminate abruptly, the illumination is unaffected by the neighbourhood of obstacles. Intermediate cases in which a few zones only are formed belong especially to the province of diffraction.
An interesting exception to the general rule that full brightness requires the existence of the first zone occurs when the obstacle assumes the form of a small circular disk parallel to the plane of the incident waves. In the earlier half of the 18th century R. Delisle found that the centre of the circular shadow was occupied by a bright point of light, but the observation passed into oblivion until S. D. Poisson brought forward as an objection to Fresnel’s theory that it required at the centre of a circular shadow a point as bright as if no obstacle were intervening. If we conceive the primary wave to be broken up at the plane of the disk, a system of Fresnel’s zones can be constructed which begin from the circumference; and the first zone external to the disk plays the part ordinarily taken by the centre of the entire system. The whole effect is the 240 half of that of the first existing zone, and this is sensibly the same as if there were no obstruction.
When light passes through a small circular or annular aperture, the illumination at any point along the axis depends upon the precise relation between the aperture and the distance from it at which the point is taken. If, as in the last paragraph, we imagine a system of zones to be drawn commencing from the inner circular boundary of the aperture, the question turns upon the manner in which the series terminates at the outer boundary. If the aperture be such as to fit exactly an integral number of zones, the aggregate effect may be regarded as the half of those due to the first and last zones. If the number of zones be even, the action of the first and last zones are antagonistic, and there is complete darkness at the point. If on the other hand the number of zones be odd, the effects conspire; and the illumination (proportional to the square of the amplitude) is four times as great as if there were no obstruction at all.
The process of augmenting the resultant illumination at a particular point by stopping some of the secondary rays may be carried much further (Soret, Pogg. Ann., 1875, 156, p. 99). By the aid of photography it is easy to prepare a plate, transparent where the zones of odd order fall, and opaque where those of even order fall. Such a plate has the power of a condensing lens, and gives an illumination out of all proportion to what could be obtained without it. An even greater effect (fourfold) can be attained by providing that the stoppage of the light from the alternate zones is replaced by a phase-reversal without loss of amplitude. R. W. Wood (Phil. Mag., 1898, 45, p 513) has succeeded in constructing zone plates upon this principle.
In such experiments the narrowness of the zones renders necessary a pretty close approximation to the geometrical conditions. Thus in the case of the circular disk, equidistant (r) from the source of light and from the screen upon which the shadow is observed, the width of the first exterior zone is given by
dx = λ(2r)/4(2x),
2x being the diameter of the disk. If 2r = 1000 cm., 2x = 1 cm., λ = 6 × 10-5 cm., then dx = .0015 cm. Hence, in order that this zone may be perfectly formed, there should be no error in the circumference of the order of .001 cm. (It is easy to see that the radius of the bright spot is of the same order of magnitude.) The experiment succeeds in a dark room of the length above mentioned, with a threepenny bit (supported by three threads) as obstacle, the origin of light being a small needle hole in a plate of tin, through which the sun’s rays shine horizontally after reflection from an external mirror. In the absence of a heliostat it is more convenient to obtain a point of light with the aid of a lens of short focus.
The amplitude of the light at any point in the axis, when plane waves are incident perpendicularly upon an annular aperture, is, as above,
cos k(at − r1) − cos k(at − r2) = 2 sin kat sin k(r1 − r2),
r2, r1 being the distances of the outer and inner boundaries from the point in question. It is scarcely necessary to remark that in all such cases the calculation applies in the first instance to homogeneous light, and that, in accordance with Fourier’s theorem, each homogeneous component of a mixture may be treated separately. When the original light is white, the presence of some components and the absence of others will usually give rise to coloured effects, variable with the precise circumstances of the case.
 |
| Fig. 2. |
Although the matter can be fully treated only upon the basis of a dynamical theory, it is proper to point out at once that there is an element of assumption in the application of Huygens’s principle to the calculation of the effects produced by opaque screens of limited extent. Properly applied, the principle could not fail; but, as may readily be proved in the case of sonorous waves, it is not in strictness sufficient to assume the expression for a secondary wave suitable when the primary wave is undisturbed, with mere limitation of the integration to the transparent parts of the screen. But, except perhaps in the case of very fine gratings, it is probable that the error thus caused is insignificant; for the incorrect estimation of the secondary waves will be limited to distances of a few wave-lengths only from the boundary of opaque and transparent parts.
3. Fraunhofer’s Diffraction Phenomena.—A very general problem in diffraction is the investigation of the distribution of light over a screen upon which impinge divergent or convergent spherical waves after passage through various diffracting apertures. When the waves are convergent and the recipient screen is placed so as to contain the centre of convergency—the image of the original radiant point, the calculation assumes a less complicated form. This class of phenomena was investigated by J. von Fraunhofer (upon principles laid down by Fresnel), and are sometimes called after his name. We may conveniently commence with them on account of their simplicity and great importance in respect to the theory of optical instruments.
If ƒ be the radius of the spherical wave at the place of resolution, where the vibration is represented by cos kat, then at any point M (fig. 2) in the recipient screen the vibration due to an element dS of the wave-front is (§ 2)
| − | dS | sin k(at − ρ), |
| λρ |
ρ being the distance between M and the element dS.
Taking co-ordinates in the plane of the screen with the centre of the wave as origin, let us represent M by ξ, η, and P (where dS is situated) by x, y, z.
Then
ρ² = (x − ξ)² + (y − η)² + z², ƒ² = x² + y² + z²;
so that
ρ² = ƒ² − 2xξ − 2yη + ξ² + η².
In the applications with which we are concerned, ξ, η are very small quantities; and we may take
| ρ = ƒ{ 1 − | xξ + yη | }. |
| ƒ² |
At the same time dS may be identified with dxdy, and in the denominator ρ may be treated as constant and equal to ƒ. Thus the expression for the vibration at M becomes
| − | 1 | ∫∫sin k { at − ƒ + | xξ + yη | } dxdy (1); |
| λƒ | ƒ |
and for the intensity, represented by the square of the amplitude,
| I² = | 1 | [ ∫∫ sin k | xξ + yη | dxdy ] | ² | |
| 벃² | ƒ | |||||
| + | 1 | [ ∫∫ cos k | xξ + yη | dxdy ] | ² | (2). |
| 벃² | ƒ |
This expression for the intensity becomes rigorously applicable when ƒ is indefinitely great, so that ordinary optical aberration disappears. The incident waves are thus plane, and are limited to a plane aperture coincident with a wave-front. The integrals are then properly functions of the direction in which the light is to be estimated.
In experiment under ordinary circumstances it makes no difference whether the collecting lens is in front of or behind the diffracting aperture. It is usually most convenient to employ a telescope focused upon the radiant point, and to place the diffracting apertures immediately in front of the object-glass. What is seen through the eye-piece in any case is the same as would be depicted upon a screen in the focal plane.
Before proceeding to special cases it may be well to call attention to some general properties of the solution expressed by (2) (see Bridge, Phil. Mag., 1858).
If when the aperture is given, the wave-length (proportional to k-1) varies, the composition of the integrals is unaltered, provided ξ and η are taken universely proportional to λ. A diminution of λ thus leads to a simple proportional shrinkage of the diffraction pattern, attended by an augmentation of brilliancy in proportion to λ-2.
If the wave-length remains unchanged, similar effects are produced by an increase in the scale of the aperture. The linear dimension of the diffraction pattern is inversely as that of the aperture, and the brightness at corresponding points is as the square of the area of aperture.
If the aperture and wave-length increase in the same proportion, the size and shape of the diffraction pattern undergo no change.
We will now apply the integrals (2) to the case of a rectangular aperture of width a parallel to x and of width b parallel to y. The limits of integration for x may thus be taken to be −½a and +½a, and for y to be −½b, +½b. We readily find (with substitution for k of 2π/λ)
| · | sin² | πaξ | · | sin² | πbη | (3), | ||
| I² = | a²b² | ƒλ | ƒλ | |||||
| ƒ²λ² | π²a²ξ² | π²b²η² | ||||||
| ƒ²λ² | ƒ²λ² | |||||||
as representing the distribution of light in the image of a mathematical point when the aperture is rectangular, as is often the case in spectroscopes.
The second and third factors of (3) being each of the form sin²u/u², we have to examine the character of this function. It vanishes when u = mπ, m being any whole number other than zero. When u = 0, it takes the value unity. The maxima occur when
u = tan u, (4),
and then
sin²u / u² = cos²u (5).
To calculate the roots of (5) we may assume
u = (m + ½)π − y = U − y,
where y is a positive quantity which is small when u is large. Substituting this, we find cot y = U − y, whence
| y = | 1 | (1 + | y | + | y- | + ...) − | y³ | − | 2y5 | − | 17y7 | . |
| U | U | U² | 3 | 15 | 315 |
This equation is to be solved by successive approximation. It will readily be found that
| u = U − y = U − U−1 − | 2 | U−3 − | 13 | U−5 − | 146 | U−7 − ... (6). |
| 3 | 15 | 105 |
In the first quadrant there is no root after zero, since tan u > u, and in the second quadrant there is none because the signs of u and tan u are opposite. The first root after zero is thus in the third quadrant, corresponding to m = 1. Even in this case the series converges sufficiently to give the value of the root with considerable accuracy, while for higher values of m it is all that could be desired. The actual values of u/π (calculated in another manner by F. M. Schwerd) are 1.4303, 2.4590, 3.4709, 4.4747, 5.4818, 6.4844, &c.
Since the maxima occur when u = (m + ½)π nearly, the successive values are not very different from
| 4 | , | 4 | , | 4 | , &c. |
| 9π² | 25π | 49π² |
The application of these results to (3) shows that the field is brightest at the centre ξ = 0, η = 0, viz. at the geometrical image of the radiant point. It is traversed by dark lines whose equations are
ξ = mfλ / a, η = mfλ / b.
Within the rectangle formed by pairs of consecutive dark lines, and not far from its centre, the brightness rises to a maximum; but these subsequent maxima are in all cases much inferior to the brightness at the centre of the entire pattern (ξ = 0, η = 0).
By the principle of energy the illumination over the entire focal plane must be equal to that over the diffracting area; and thus, in accordance with the suppositions by which (3) was obtained, its value when integrated from ξ = ∞ to ξ = +∞, and from η = −∞ to η = +∞ should be equal to ab. This integration, employed originally by P. Kelland (Edin. Trans. 15, p. 315) to determine the absolute intensity of a secondary wave, may be at once effected by means of the known formula
| ∫ | +∞ | sin²u | du = ∫ | +∞ | sin u | du = π. |
| −∞ | u² | −∞ | u |
It will be observed that, while the total intensity is proportional to ab, the intensity at the focal point is proportional to a²b². If the aperture be increased, not only is the total brightness over the focal plane increased with it, but there is also a concentration of the diffraction pattern. The form of (3) shows immediately that, if a and b be altered, the co-ordinates of any characteristic point in the pattern vary as a−1 and b−1.
The contraction of the diffraction pattern with increase of aperture is of fundamental importance in connexion with the resolving power of optical instruments. According to common optics, where images are absolute, the diffraction pattern is supposed to be infinitely small, and two radiant points, however near together, form separated images. This is tantamount to an assumption that λ is infinitely small. The actual finiteness of λ imposes a limit upon the separating or resolving power of an optical instrument.
This indefiniteness of images is sometimes said to be due to diffraction by the edge of the aperture, and proposals have even been made for curing it by causing the transition between the interrupted and transmitted parts of the primary wave to be less abrupt. Such a view of the matter is altogether misleading. What requires explanation is not the imperfection of actual images so much as the possibility of their being as good as we find them.
At the focal point (ξ = 0, η = 0) all the secondary waves agree in phase, and the intensity is easily expressed, whatever be the form of the aperture. From the general formula (2), if A be the area of aperture,
I0² = A² / 벃² (7).
The formation of a sharp image of the radiant point requires that the illumination become insignificant when ξ, η attain small values, and this insignificance can only arise as a consequence of discrepancies of phase among the secondary waves from various parts of the aperture. So long as there is no sensible discrepancy of phase there can be no sensible diminution of brightness as compared with that to be found at the focal point itself. We may go further, and lay it down that there can be no considerable loss of brightness until the difference of phase of the waves proceeding from the nearest and farthest parts of the aperture amounts to ¼λ.
When the difference of phase amounts to λ, we may expect the resultant illumination to be very much reduced. In the particular case of a rectangular aperture the course of things can be readily followed, especially if we conceive ƒ to be infinite. In the direction (suppose horizontal) for which η = 0, ξ/ƒ = sin θ, the phases of the secondary waves range over a complete period when sin θ = λ/a, and, since all parts of the horizontal aperture are equally effective, there is in this direction a complete compensation and consequent absence of illumination. When sin θ = 3⁄2λ/a, the phases range one and a half periods, and there is revival of illumination. We may compare the brightness with that in the direction θ = 0. The phase of the resultant amplitude is the same as that due to the central secondary wave, and the discrepancies of phase among the components reduce the amplitude in the proportion
| 1 | ∫ | +3⁄2π | cos φ dφ: 1 |
| 3π | −3⁄2π |
or -2⁄3π : 1; so that the brightness in this direction is 4⁄9π² of the maximum at θ = 0. In like manner we may find the illumination in any other direction, and it is obvious that it vanishes when sin θ is any multiple of λ/a.
The reason of the augmentation of resolving power with aperture will now be evident. The larger the aperture the smaller are the angles through which it is necessary to deviate from the principal direction in order to bring in specified discrepancies of phase—the more concentrated is the image.
In many cases the subject of examination is a luminous line of uniform intensity, the various points of which are to be treated as independent sources of light. If the image of the line be ξ = 0, the intensity at any point ξ, η of the diffraction pattern may be represented by
| sin² | πaξ | (8), | ||||
| ∫ | +∞ | I²dη = | a²b | λf | ||
| −∞ | λƒ | π²a²ξ² | ||||
| λ²f² | ||||||
the same law as obtains for a luminous point when horizontal directions are alone considered. The definition of a fine vertical line, and consequently the resolving power for contiguous vertical lines, is thus independent of the vertical aperture of the instrument, a law of great importance in the theory of the spectroscope.
The distribution of illumination in the image of a luminous line is shown by the curve ABC (fig. 3), representing the value of the function sin²u/u² from u = 0 to u = 2π. The part corresponding to negative values of u is similar, OA being a line of symmetry.
 |
| Fig. 3. |
Let us now consider the distribution of brightness in the image of a double line whose components are of equal strength, and at such an angular interval that the central line in the image of one coincides with the first zero of brightness in the image of the other. In fig. 3 the curve of brightness for one component is ABC, and for the other OA′C′; and the curve representing half the combined brightnesses is E′BE. The brightness (corresponding to B) midway between the two central points AA’ is .8106 of the brightness at the central points themselves. We may consider this to be about the limit of closeness at which there could be any decided appearance of resolution, though doubtless an observer accustomed to his instrument would recognize the duplicity with certainty. The obliquity, corresponding to u = π, is such that the phases of the secondary waves range over a complete period, i.e. such that the projection of the horizontal aperture upon this direction is one wave-length. We conclude that a double line cannot be fairly resolved unless its components subtend an angle exceeding that subtended by the wave-length of light at a distance equal to the horizontal aperture. This rule is convenient on account of its simplicity; and it is sufficiently accurate in view of the necessary uncertainty as to what exactly is meant by resolution.
If the angular interval between the components of a double line be half as great again as that supposed in the figure, the brightness midway between is .1802 as against 1.0450 at the central lines of each image. Such a falling off in the middle must be more than sufficient for resolution. If the angle subtended by the components of a double line be twice that subtended by the wave-length at a distance equal to the horizontal aperture, the central bands are just clear of one another, and there is a line of absolute blackness in the middle of the combined images.
The resolving power of a telescope with circular or rectangular aperture is easily investigated experimentally. The best object for examination is a grating of fine wires, about fifty to the inch, backed by a sodium flame. The object-glass is provided with diaphragms pierced with round holes or slits. One of these, of width equal, say, to one-tenth of an inch, is inserted in front of the object-glass, and the telescope, carefully focused all the while, is drawn gradually back from the grating until the lines are no longer seen. From a measurement of the maximum distance the least angle between consecutive lines consistent with resolution may be deduced, and a comparison made with the rule stated above.
Merely to show the dependence of resolving power on aperture it is not necessary to use a telescope at all. It is sufficient to look at wire gauze backed by the sky or by a flame, through a piece of blackened cardboard, pierced by a needle and held close to the eye. By varying the distance the point is easily found at which resolution ceases; and the observation is as sharp as with a telescope. The 242 function of the telescope is in fact to allow the use of a wider, and therefore more easily measurable, aperture. An interesting modification of the experiment may be made by using light of various wave-lengths.
Since the limitation of the width of the central band in the image of a luminous line depends upon discrepancies of phase among the secondary waves, and since the discrepancy is greatest for the waves which come from the edges of the aperture, the question arises how far the operation of the central parts of the aperture is advantageous. If we imagine the aperture reduced to two equal narrow slits bordering its edges, compensation will evidently be complete when the projection on an oblique direction is equal to ½λ, instead of λ as for the complete aperture. By this procedure the width of the central band in the diffraction pattern is halved, and so far an advantage is attained. But, as will be evident, the bright bands bordering the central band are now not inferior to it in brightness; in fact, a band similar to the central band is reproduced an indefinite number of times, so long as there is no sensible discrepancy of phase in the secondary waves proceeding from the various parts of the same slit. Under these circumstances the narrowing of the band is paid for at a ruinous price, and the arrangement must be condemned altogether.
A more moderate suppression of the central parts is, however, sometimes advantageous. Theory and experiment alike prove that a double line, of which the components are equally strong, is better resolved when, for example, one-sixth of the horizontal aperture is blocked off by a central screen; or the rays quite at the centre may be allowed to pass, while others a little farther removed are blocked off. Stops, each occupying one-eighth of the width, and with centres situated at the points of trisection, answer well the required purpose.
It has already been suggested that the principle of energy requires that the general expression for I² in (2) when integrated over the whole of the plane ξ, η should be equal to A, where A is the area of the aperture. A general analytical verification has been given by Sir G. G. Stokes (Edin. Trans., 1853, 20, p. 317). Analytically expressed—
| ∫∫ | +∞ | I² dξdη = ∫∫ dxdy = A (9). |
| −∞ |
We have seen that I0² (the intensity at the focal point) was equal to A²/λ²f². If A′ be the area over which the intensity must be I0² in order to give the actual total intensity in accordance with
| A′ I0² = ∫∫ | +∞ | I² dξdη, |
| −∞ |
the relation between A and A′ is AA′ = λ²f². Since A′ is in some sense the area of the diffraction pattern, it may be considered to be a rough criterion of the definition, and we infer that the definition of a point depends principally upon the area of the aperture, and only in a very secondary degree upon the shape when the area is maintained constant.
4. Theory of Circular Aperture.—We will now consider the important case where the form of the aperture is circular.
Writing for brevity
kξ/f = p, kη/f = q, (1),
we have for the general expression (§ 11) of the intensity
λ²f²I² = S² + C² (2),
where
S = ∫∫ sin(px + qy)dx dy, (3),
C = ∫∫ cos(px + qy)dx dy, (4).
When, as in the application to rectangular or circular apertures, the form is symmetrical with respect to the axes both of x and y, S = 0, and C reduces to
C = ∫∫ cos px cos qy dx dy, (5).
In the case of the circular aperture the distribution of light is of course symmetrical with respect to the focal point p = 0, q = 0; and C is a function of p and q only through √(p² + q²). It is thus sufficient to determine the intensity along the axis of p. Putting q = 0, we get
| C = ∫∫ cos px dx dy = 2 ∫ | +R | cos px √(R² − x²) dx, |
| −R |
R being the radius of the aperture. This integral is the Bessel’s function of order unity, defined by
| J1(z) = | z | ∫ | π | cos (z cos φ) sin² φ dφ (6). |
| π | 0 |
Thus, if x = R cos φ,
| C = π²R | 2J1(pR) | (7); |
| pR |
and the illumination at distance r from the focal point is
| · | 4J1² ( | 2πRr | ) | (8). | ||
| I² = | π²R4 | ƒλ | ||||
| λ²f² | ( | 2πRr | ) ² | |||
| ƒλ | ||||||
The ascending series for J1(z), used by Sir G. B. Airy (Camb. Trans., 1834) in his original investigation of the diffraction of a circular object-glass, and readily obtained from (6), is
| J1(z) = | z | − | z³ | + | z5 | − | z7 | + ... (9). |
| 2 | 2²·4 | 2²·4²·6 | 2²·4²·6²·8 |
When z is great, we may employ the semi-convergent series
| J1(z) = √( | 2 | ) sin (z − ¼π) { 1 + | 3·5·1 | ( | 1 | ) | ² | − | 3·5·7·9·1·3·5 | ( | 1 | ) | 4 | + ... } |
| πz | 8·16 | z | 8·16·24·32 | z |
| + √( | 2 | ) cos (z − ¼π) {3/8 · 1/z − | 3·5·7·1·3 | ( | 1 | ) | ³ | + | 3·5·7·9·11·1·3·5·7 | ( | 1 | ) | 5 | − ... } (10). |
| πz | 8·16·24 | z | 8·16·24·32·40 | z |
A table of the values of 2z-1J1(z) has been given by E. C. J. Lommel (Schlömilch, 1870, 15, p. 166), to whom is due the first systematic application of Bessel’s functions to the diffraction integrals.
The illumination vanishes in correspondence with the roots of the equation J1(z) = 0. If these be called z1 z2, z3, ... the radii of the dark rings in the diffraction pattern are
| ƒλz1 | ƒλz2 | , ... | |
| 2πR | 2πR |
being thus inversely proportional to R.
The integrations may also be effected by means of polar co-ordinates, taking first the integration with respect to φ so as to obtain the result for an infinitely thin annular aperture. Thus, if
x = ρ cos φ, y = ρ sin φ,
| C = ∫∫ cos px dx dy = ∫ | R | ∫ | 2π | cos (pρ cos θ) ρdρ dθ. |
| 0 | 0 |
Now by definition
| J0(z) = | 2 | ∫ | ½π | cos (z cos θ) dθ = 1 − | z² | + | z4 | − | z6 | + ... (11). |
| π | 0 | 2² | 2²·4² | 2²·4²·6² |
The value of C for an annular aperture of radius r and width dr is thus
dC = 2 π J0 (pρ) ρ dρ, (12).
For the complete circle,
| C = | 2π | ∫ | pr | J0(z) zdz = | 2π | { | p²R² | − | p4R4 | + | p6R6 | − ...}= πR² · | 2J1(pR) | as before. |
| p² | 0 | p² | 2 | 2²·4² | 2²·4²·6² | pR |
In these expressions we are to replace p by kξ/ƒ, or rather, since the diffraction pattern is symmetrical, by kr/ƒ, where r is the distance of any point in the focal plane from the centre of the system.
The roots of J0(z) after the first may be found from
| z | = i − .25 + | .050561 | − | .053041 | + | .262051 | (13), |
| π | 4i − 1 | (4i − 1)³ | (4i − 1)5 |
and those of J1(z) from
| z | = i + .25 − | .151982 | + | .015399 | − | .245835 | (14), |
| π | 4i + 1 | (4i + 1)³ | (4i + 1)5 |
formulae derived by Stokes (Camb. Trans., 1850, vol. ix.) from the descending series.1 The following table gives the actual values:—
| i | z/π for J0(z) = 0 | z/π for J1(z) = 0 |
| 1 | 7655 | 1 2197 |
| 2 | 1 7571 | 2 2330 |
| 3 | 2 7546 | 3 2383 |
| 4 | 3 7534 | 4 2411 |
| 5 | 4 7527 | 5 2428 |
| 6 | 5 7522 | 6 2439 |
| 7 | 6 7519 | 7 2448 |
| 8 | 7 7516 | 8 2454 |
| 9 | 8 7514 | 9 2459 |
| 10 | 9 7513 | 10 2463 |
In both cases the image of a mathematical point is thus a symmetrical ring system. The greatest brightness is at the centre, where
dC = 2πρ dρ, C = π R².
For a certain distance outwards this remains sensibly unimpaired and then gradually diminishes to zero, as the secondary waves become discrepant in phase. The subsequent revivals of brightness forming the bright rings are necessarily of inferior brilliancy as compared with the central disk.
The first dark ring in the diffraction pattern of the complete circular aperture occurs when
r/ƒ = 1.2197 × λ/2R (15).
We may compare this with the corresponding result for a rectangular aperture of width a,
ξ/ƒ =λ/a;
and it appears that in consequence of the preponderance of the central parts, the compensation in the case of the circle does not set in at so small an obliquity as when the circle is replaced by a rectangular aperture, whose side is equal to the diameter of the circle.
Again, if we compare the complete circle with a narrow annular aperture of the same radius, we see that in the latter case the first dark ring occurs at a much smaller obliquity, viz.
r/ƒ = .7655 × λ/2R.
It has been found by Sir William Herschel and others that the definition of a telescope is often improved by stopping off a part of the central area of the object-glass; but the advantage to be obtained in this way is in no case great, and anything like a reduction of the aperture to a narrow annulus is attended by a development of the external luminous rings sufficient to outweigh any improvement due to the diminished diameter of the central area.2
The maximum brightnesses and the places at which they occur are easily determined with the aid of certain properties of the Bessel’s functions. It is known (see Spherical Harmonics) that
J0′(z) = −J1(z), (16);
J2(z) = (1/z) J1(z) − J1′(z) (17);
J0(z) + J2(z) = (2/z) J1(z) (18).
The maxima of C occur when
| d | ( | J1(z) | ) = | J1′(z) | − | J1(z) | = 0; |
| dz | z | z | z² |
or by 17 when J2(z) = 0. When z has one of the values thus determined,
| 2 | J1(z) = J0(z). |
| z |
The accompanying table is given by Lommel, in which the first column gives the roots of J2(z) = 0, and the second and third columns the corresponding values of the functions specified. If appears that the maximum brightness in the first ring is only about 1⁄57 of the brightness at the centre.
| z | 2z−1J1(z) | 4z−2J1²(z) |
| .000000 | +1.000000 | 1.000000 |
| 5.135630 | − .132279 | .017498 |
| 8.417236 | + .064482 | .004158 |
| 11.619857 | − .040008 | .001601 |
| 14.795938 | + .027919 | .000779 |
| 17.959820 | − .020905 | .000437 |
We will now investigate the total illumination distributed over the area of the circle of radius r. We have
| I² = | π²R4 | · | 4J1²(z) | (19), |
| 벃² | z² |
where
z = 2πRr/λf (20).
Thus
| 2π ∫ I²rdr = | λ²f² | ∫ I²zdz = πR²· 2 ∫ z−1J1²(z)dz. |
| 2πR² |
Now by (17), (18)
z-1J1(z) = J0(z) − J1′(z);
so that
| z-1J1²(z) = − ½ | d | J0² − ½ | d | J1²(z), |
| dz | dz |
and
| 2 ∫ | z | z-1J1²(z)dz = 1 − J0²(z) − J1²(z) (21). |
| 0 |
If r, or z, be infinite, J0(z), J1(z) vanish, and the whole illumination is expressed by πR², in accordance with the general principle. In any case the proportion of the whole illumination to be found outside the circle of radius r is given by
J0²(z) + J1²(z).
For the dark rings J1(z) = 0; so that the fraction of illumination outside any dark ring is simply J0²(z). Thus for the first, second, third and fourth dark rings we get respectively .161, .090, .062, .047, showing that more than 9⁄10ths of the whole light is concentrated within the area of the second dark ring (Phil. Mag., 1881).
When z is great, the descending series (10) gives
| 2J1(z) | = | 2 | √( | 2 | ) sin(z − ¼π) (22); |
| z | z | πz |
so that the places of maxima and minima occur at equal intervals.
The mean brightness varies as z-3 (or as r-3), and the integral found by multiplying it by zdz and integrating between 0 and ∞ converges.
It may be instructive to contrast this with the case of an infinitely narrow annular aperture, where the brightness is proportional to J0²(z). When z is great,
| J0(z) = √( | 2 | ) cos(z-1/4π). |
| πz |
The mean brightness varies as z-1; and the integral ∫∞0 J0²(z)z dz is not convergent.
5. Resolving Power of Telescopes.—The efficiency of a telescope is of course intimately connected with the size of the disk by which it represents a mathematical point. In estimating theoretically the resolving power on a double star we have to consider the illumination of the field due to the superposition of the two independent images. If the angular interval between the components of a double star were equal to twice that expressed in equation (15) above, the central disks of the diffraction patterns would be just in contact. Under these conditions there is no doubt that the star would appear to be fairly resolved, since the brightness of its external ring system is too small to produce any material confusion, unless indeed the components are of very unequal magnitude. The diminution of the star disks with increasing aperture was observed by Sir William Herschel, and in 1823 Fraunhofer formulated the law of inverse proportionality. In investigations extending over a long series of years, the advantage of a large aperture in separating the components of close double stars was fully examined by W. R. Dawes.
The resolving power of telescopes was investigated also by J. B. L. Foucault, who employed a scale of equal bright and dark alternate parts; it was found to be proportional to the aperture and independent of the focal length. In telescopes of the best construction and of moderate aperture the performance is not sensibly prejudiced by outstanding aberration, and the limit imposed by the finiteness of the waves of light is practically reached. M. E. Verdet has compared Foucault’s results with theory, and has drawn the conclusion that the radius of the visible part of the image of a luminous point was equal to half the radius of the first dark ring.
The application, unaccountably long delayed, of this principle to the microscope by H. L. F. Helmholtz in 1871 is the foundation of the important doctrine of the microscopic limit. It is true that in 1823 Fraunhofer, inspired by his observations upon gratings, had very nearly hit the mark.3 And a little before Helmholtz, E. Abbe published a somewhat more complete investigation, also founded upon the phenomena presented by gratings. But although the argument from gratings is instructive and convenient in some respects, its use has tended to obscure the essential unity of the principle of the limit of resolution whether applied to telescopes or microscopes.
 |
| Fig. 4. |
In fig. 4, AB represents the axis of an optical instrument (telescope or microscope), A being a point of the object and B a point of the image. By the operation of the object-glass LL′ all the rays issuing from A arrive in the same phase at B. Thus if A be self-luminous, the illumination is a maximum at B, where all the secondary waves agree in phase. B is in fact the centre of the diffraction disk which constitutes the image of A. At neighbouring points the illumination is less, in consequence of the discrepancies of phase which there enter. In like manner if we take a neighbouring point P, also self-luminous, in the plane of the object, the waves which issue from it will arrive at B with phases no longer absolutely concordant, and the discrepancy of phase will increase as the interval AP 244 increases. When the interval is very small the discrepancy, though mathematically existent, produces no practical effect; and the illumination at B due to P is as important as that due to A, the intensities of the two luminous sources being supposed equal. Under these conditions it is clear that A and P are not separated in the image. The question is to what amount must the distance AP be increased in order that the difference of situation may make itself felt in the image. This is necessarily a question of degree; but it does not require detailed calculations in order to show that the discrepancy first becomes conspicuous when the phases corresponding to the various secondary waves which travel from P to B range over a complete period. The illumination at B due to P then becomes comparatively small, indeed for some forms of aperture evanescent. The extreme discrepancy is that between the waves which travel through the outermost parts of the object-glass at L and L′; so that if we adopt the above standard of resolution, the question is where must P be situated in order that the relative retardation of the rays PL and PL’ may on their arrival at B amount to a wave-length (λ). In virtue of the general law that the reduced optical path is stationary in value, this retardation may be calculated without allowance for the different paths pursued on the farther side of L, L′, so that the value is simply PL − PL′. Now since AP is very small, AL′ − PL′ = AP sin α, where α is the angular semi-aperture L′AB. In like manner PL − AL has the same value, so that
PL − PL′ = 2AP sin α.
According to the standard adopted, the condition of resolution is therefore that AP, or ε, should exceed ½λ/sin α. If ε be less than this, the images overlap too much; while if ε greatly exceed the above value the images become unnecessarily separated.
In the above argument the whole space between the object and the lens is supposed to be occupied by matter of one refractive index, and λ represents the wave-length in this medium of the kind of light employed. If the restriction as to uniformity be violated, what we have ultimately to deal with is the wave-length in the medium immediately surrounding the object.
Calling the refractive index μ, we have as the critical value of ε,
ε = ½λ0 /μ sin α, (1),
λ0 being the wave-length in vacuo. The denominator μ sin α is the quantity well known (after Abbe) as the “numerical aperture.”
The extreme value possible for α is a right angle, so that for the microscopic limit we have
ε = ½λ0/μ (2).
The limit can be depressed only by a diminution in λ0, such as photography makes possible, or by an increase in μ, the refractive index of the medium in which the object is situated.
The statement of the law of resolving power has been made in a form appropriate to the microscope, but it admits also of immediate application to the telescope. If 2R be the diameter of the object-glass and D the distance of the object, the angle subtended by AP is ε/D, and the angular resolving power is given by
λ/2D sin α = λ/2R (3).
This method of derivation (substantially due to Helmholtz) makes it obvious that there is no essential difference of principle between the two cases, although the results are conveniently stated in different forms. In the case of the telescope we have to deal with a linear measure of aperture and an angular limit of resolution, whereas in the case of the microscope the limit of resolution is linear, and it is expressed in terms of angular aperture.
It must be understood that the above argument distinctly assumes that the different parts of the object are self-luminous, or at least that the light proceeding from the various points is without phase relations. As has been emphasized by G. J. Stoney, the restriction is often, perhaps usually, violated in the microscope. A different treatment is then necessary, and for some of the problems which arise under this head the method of Abbe is convenient.
The importance of the general conclusions above formulated, as imposing a limit upon our powers of direct observation, can hardly be overestimated; but there has been in some quarters a tendency to ascribe to it a more precise character than it can bear, or even to mistake its meaning altogether. A few words of further explanation may therefore be desirable. The first point to be emphasized is that nothing whatever is said as to the smallness of a single object that may be made visible. The eye, unaided or armed with a telescope, is able to see, as points of light, stars subtending no sensible angle. The visibility of a star is a question of brightness simply, and has nothing to do with resolving power. The latter element enters only when it is a question of recognizing the duplicity of a double star, or of distinguishing detail upon the surface of a planet. So in the microscope there is nothing except lack of light to hinder the visibility of an object however small. But if its dimensions be much less than the half wave-length, it can only be seen as a whole, and its parts cannot be distinctly separated, although in cases near the border line some inference may be possible, founded upon experience of what appearances are presented in various cases. Interesting observations upon particles, ultra-microscopic in the above sense, have been recorded by H. F. W. Siedentopf and R. A. Zsigmondy (Drude’s Ann., 1903, 10, p. 1).
In a somewhat similar way a dark linear interruption in a bright ground may be visible, although its actual width is much inferior to the half wave-length. In illustration of this fact a simple experiment may be mentioned. In front of the naked eye was held a piece of copper foil perforated by a fine needle hole. Observed through this the structure of some wire gauze just disappeared at a distance from the eye equal to 17 in., the gauze containing 46 meshes to the inch. On the other hand, a single wire 0.034 in. in diameter remained fairly visible up to a distance of 20 ft. The ratio between the limiting angles subtended by the periodic structure of the gauze and the diameter of the wire was (.022/.034) × (240/17) = 9.1. For further information upon this subject reference may be made to Phil. Mag., 1896, 42, p. 167; Journ. R. Micr. Soc., 1903, p. 447.
6. Coronas or Glories.—The results of the theory of the diffraction patterns due to circular apertures admit of an interesting application to coronas, such as are often seen encircling the sun and moon. They are due to the interposition of small spherules of water, which act the part of diffracting obstacles. In order to the formation of a well-defined corona it is essential that the particles be exclusively, or preponderatingly, of one size.
If the origin of light be treated as infinitely small, and be seen in focus, whether with the naked eye or with the aid of a telescope, the whole of the light in the absence of obstacles would be concentrated in the immediate neighbourhood of the focus. At other parts of the field the effect is the same, in accordance with the principle known as Babinet’s, whether the imaginary screen in front of the object-glass is generally transparent but studded with a number of opaque circular disks, or is generally opaque but perforated with corresponding apertures. Since at these points the resultant due to the whole aperture is zero, any two portions into which the whole may be divided must give equal and opposite resultants. Consider now the light diffracted in a direction many times more oblique than any with which we should be concerned, were the whole aperture uninterrupted, and take first the effect of a single small aperture. The light in the proposed direction is that determined by the size of the small aperture in accordance with the laws already investigated, and its phase depends upon the position of the aperture. If we take a direction such that the light (of given wave-length) from a single aperture vanishes, the evanescence continues even when the whole series of apertures is brought into contemplation. Hence, whatever else may happen, there must be a system of dark rings formed, the same as from a single small aperture. In directions other than these it is a more delicate question how the partial effects should be compounded. If we make the extreme suppositions of an infinitely small source and absolutely homogeneous light, there is no escape from the conclusion that the light in a definite direction is arbitrary, that is, dependent upon the chance distribution of apertures. If, however, as in practice, the light be heterogeneous, the source of finite area, the obstacles in motion, and the discrimination of different directions imperfect, we are concerned merely with the mean brightness found by varying the arbitrary phase-relations, and this is obtained by simply multiplying the brightness due to a single aperture by the number of apertures (n) (see Interference of Light, § 4). The diffraction pattern is therefore that due to a single aperture, merely brightened n times.
In his experiments upon this subject Fraunhofer employed plates of glass dusted over with lycopodium, or studded with small metallic disks of uniform size; and he found that the diameters of the rings were proportional to the length of the waves and inversely as the diameter of the disks.
In another respect the observations of Fraunhofer appear at first sight to be in disaccord with theory; for his measures of the diameters of the red rings, visible when white light was employed, correspond with the law applicable to dark rings, and not to the different law applicable to the luminous maxima. Verdet has, however, pointed out that the observation in this form is essentially different from that in which homogeneous red light is employed, and that the position of the red rings would correspond to the absence of blue-green light rather than to the greatest abundance of red light. Verdet’s own observations, conducted with great care, fully confirm this view, and exhibit a complete agreement with theory.
By measurements of coronas it is possible to infer the size of the particles to which they are due, an application of considerable interest in the case of natural coronas—the general rule being the larger the corona the smaller the water spherules. Young employed this method not only to determine the diameters of cloud particles (e.g. 1⁄1000 in.), but also those of fibrous material, for which the theory is analogous. His instrument was called the eriometer (see “Chromatics,” vol. iii. of supp. to Ency. Brit., 1817).
7. Influence of Aberration. Optical Power of Instruments.—Our investigations and estimates of resolving power have thus far proceeded upon the supposition that there are no optical imperfections, whether of the nature of a regular aberration or dependent upon irregularities of material and workmanship. In 245 practice there will always be a certain aberration or error of phase, which we may also regard as the deviation of the actual wave-surface from its intended position. In general, we may say that aberration is unimportant when it nowhere (or at any rate over a relatively small area only) exceeds a small fraction of the wave-length (λ). Thus in estimating the intensity at a focal point, where, in the absence of aberration, all the secondary waves would have exactly the same phase, we see that an aberration nowhere exceeding ¼λ can have but little effect.
The only case in which the influence of small aberration upon the entire image has been calculated (Phil. Mag., 1879) is that of a rectangular aperture, traversed by a cylindrical wave with aberration equal to cx³. The aberration is here unsymmetrical, the wave being in advance of its proper place in one half of the aperture, but behind in the other half. No terms in x or x² need be considered. The first would correspond to a general turning of the beam; and the second would imply imperfect focusing of the central parts. The effect of aberration may be considered in two ways. We may suppose the aperture (a) constant, and inquire into the operation of an increasing aberration; or we may take a given value of c (i.e. a given wave-surface) and examine the effect of a varying aperture. The results in the second case show that an increase of aperture up to that corresponding to an extreme aberration of half a period has no ill effect upon the central band (§ 3), but it increases unduly the intensity of one of the neighbouring lateral bands; and the practical conclusion is that the best results will be obtained from an aperture giving an extreme aberration of from a quarter to half a period, and that with an increased aperture aberration is not so much a direct cause of deterioration as an obstacle to the attainment of that improved definition which should accompany the increase of aperture.
If, on the other hand, we suppose the aperture given, we find that aberration begins to be distinctly mischievous when it amounts to about a quarter period, i.e. when the wave-surface deviates at each end by a quarter wave-length from the true plane.
As an application of this result, let us investigate what amount of temperature disturbance in the tube of a telescope may be expected to impair definition. According to J. B. Biot and F. J. D. Arago, the index μ for air at t° C. and at atmospheric pressure is given by
| μ − 1 = | .00029 | . |
| 1 + .0037 t |
If we take 0° C. as standard temperature,
δμ = -1.1 × 10-6.
Thus, on the supposition that the irregularity of temperature t extends through a length l, and produces an acceleration of a quarter of a wave-length,
¼λ = 1.1 lt × 10-6;
or, if we take λ = 5.3 × 10-5,
lt = 12,
the unit of length being the centimetre.
We may infer that, in the case of a telescope tube 12 cm. long, a stratum of air heated 1° C. lying along the top of the tube, and occupying a moderate fraction of the whole volume, would produce a not insensible effect. If the change of temperature progressed uniformly from one side to the other, the result would be a lateral displacement of the image without loss of definition; but in general both effects would be observable. In longer tubes a similar disturbance would be caused by a proportionally less difference of temperature. S. P. Langley has proposed to obviate such ill-effects by stirring the air included within a telescope tube. It has long been known that the definition of a carbon bisulphide prism may be much improved by a vigorous shaking.
We will now consider the application of the principle to the formation of images, unassisted by reflection or refraction (Phil. Mag., 1881). The function of a lens in forming an image is to compensate by its variable thickness the differences of phase which would otherwise exist between secondary waves arriving at the focal point from various parts of the aperture. If we suppose the diameter of the lens to be given (2R), and its focal length ƒ gradually to increase, the original differences of phase at the image of an infinitely distant luminous point diminish without limit. When ƒ attains a certain value, say ƒ1, the extreme error of phase to be compensated falls to ¼λ. But, as we have seen, such an error of phase causes no sensible deterioration in the definition; so that from this point onwards the lens is useless, as only improving an image already sensibly as perfect as the aperture admits of. Throughout the operation of increasing the focal length, the resolving power of the instrument, which depends only upon the aperture, remains unchanged; and we thus arrive at the rather startling conclusion that a telescope of any degree of resolving power might be constructed without an object-glass, if only there were no limit to the admissible focal length. This last proviso, however, as we shall see, takes away almost all practical importance from the proposition.
To get an idea of the magnitudes of the quantities involved, let us take the case of an aperture of 1⁄5 in., about that of the pupil of the eye. The distance ƒ1, which the actual focal length must exceed, is given by
√ (ƒ1² + R²) − ƒ1 = ¼λ;
so that
ƒ1 = 2R²/λ (1).
Thus, if λ = 1⁄40000, R = 1⁄10, we find
ƒ1 = 800 inches.
The image of the sun thrown upon a screen at a distance exceeding 66 ft., through a hole 1⁄5 in. in diameter, is therefore at least as well defined as that seen direct.
As the minimum focal length increases with the square of the aperture, a quite impracticable distance would be required to rival the resolving power of a modern telescope. Even for an aperture of 4 in., ƒ1 would have to be 5 miles.
A similar argument may be applied to find at what point an achromatic lens becomes sensibly superior to a single one. The question is whether, when the adjustment of focus is correct for the central rays of the spectrum, the error of phase for the most extreme rays (which it is necessary to consider) amounts to a quarter of a wave-length. If not, the substitution of an achromatic lens will be of no advantage. Calculation shows that, if the aperture be 1⁄5 in., an achromatic lens has no sensible advantage if the focal length be greater than about 11 in. If we suppose the focal length to be 66 ft., a single lens is practically perfect up to an aperture of 1.7 in.
Another obvious inference from the necessary imperfection of optical images is the uselessness of attempting anything like an absolute destruction of spherical aberration. An admissible error of phase of ¼λ will correspond to an error of 1⁄8λ in a reflecting and ½λ in a (glass) refracting surface, the incidence in both cases being perpendicular. If we inquire what is the greatest admissible longitudinal aberration (δƒ) in an object-glass according to the above rule, we find
δƒ = λα-2 (2),
α being the angular semi-aperture.
In the case of a single lens of glass with the most favourable curvatures, δƒ is about equal to ᲃ, so that α4 must not exceed λ/ƒ. For a lens of 3 ft. focus this condition is satisfied if the aperture does not exceed 2 in.
When parallel rays fall directly upon a spherical mirror the longitudinal aberration is only about one-eighth as great as for the most favourably shaped single lens of equal focal length and aperture. Hence a spherical mirror of 3 ft. focus might have an aperture of 2½ in., and the image would not suffer materially from aberration.
On the same principle we may estimate the least visible displacement of the eye-piece of a telescope focused upon a distant object, a question of interest in connexion with range-finders. It appears (Phil. Mag., 1885, 20, p. 354) that a displacement δf from the true focus will not sensibly impair definition, provided
δƒ < ƒ²λ/R² (3),
2R being the diameter of aperture. The linear accuracy required is thus a function of the ratio of aperture to focal length. The formula agrees well with experiment.
The principle gives an instantaneous solution of the question of the ultimate optical efficiency in the method of “mirror-reading,” as commonly practised in various physical observations. A rotation by which one edge of the mirror advances ¼λ (while the other edge retreats to a like amount) introduces a phase-discrepancy of a whole period where before the rotation there was complete agreement. A rotation of this amount should therefore be easily visible, but the limits of resolving power are being approached; and the conclusion is independent of the focal length of the mirror, and of the employment of a telescope, provided of course that the reflected image is seen in focus, and that the full width of the mirror is utilized.
 |
| Fig. 5. |
A comparison with the method of a material pointer, attached to the parts whose rotation is under observation, and viewed through a microscope, is of interest. The limiting efficiency of the microscope is attained when the angular aperture amounts to 180°; and it is evident that a lateral displacement of the point under observation through ½λ entails (at the old image) a phase-discrepancy of a whole period, one extreme ray being accelerated and the other retarded by half that amount. We may infer that the limits of efficiency in the two methods are the same when the length of the pointer is equal to the width of the mirror.
We have seen that in perpendicular reflection a surface error not exceeding 1⁄8λ may be admissible. In the case of oblique reflection at an angle φ, the error of retardation due to an elevation BD (fig. 5) is
QQ′ − QS = BD sec φ(1 − cos SQQ′) = BD sec φ (1 + cos 2φ) = 2BD cos φ;
from which it follows that an error of given magnitude in the figure of a surface is less important in oblique than in perpendicular reflection. It must, however, be borne in mind that errors can sometimes be compensated by altering adjustments. If a surface intended to be flat is affected with a slight general curvature, a remedy may be found in an alteration of focus, and the remedy is the less complete as the reflection is more oblique.
The formula expressing the optical power of prismatic spectroscopes may readily be investigated upon the principles of the wave theory. Let A0B0 be a plane wave-surface of the light before it falls upon the prisms, AB the corresponding wave-surface for a particular part of the spectrum after the light has passed the prisms, or after it has passed the eye-piece of the observing telescope. The path of a ray from the wave-surface A0B0 to A or B is determined by the condition that the optical distance, ∫ μ ds, is a minimum; and, as AB is by supposition a wave-surface, this optical distance is the same for both points. Thus
∫ μ ds (for A) = ∫ μ ds (for B) (4).
We have now to consider the behaviour of light belonging to a neighbouring part of the spectrum. The path of a ray from the wave-surface A0B0 to the point A is changed; but in virtue of the minimum property the change may be neglected in calculating the optical distance, as it influences the result by quantities of the second order only in the changes of refrangibility. Accordingly, the optical distance from A0B0 to A is represented by ∫(μ + δμ)ds, the integration being along the original path A0 ... A; and similarly the optical distance between A0B0 and B is represented by ∫ (μ + δμ)ds, the integration being along B0 ... B. In virtue of (4) the difference of the optical distances to A and B is
∫ δμ ds (along B0 ... B) − ∫ δμ ds (along A0 ... A) (5).
The new wave-surface is formed in such a position that the optical distance is constant; and therefore the dispersion, or the angle through which the wave-surface is turned by the change of refrangibility, is found simply by dividing (5) by the distance AB. If, as in common flint-glass spectroscopes, there is only one dispersing substance, ∫ δμ ds = δμ·s, where s is simply the thickness traversed by the ray. If t2 and t1 be the thicknesses traversed by the extreme rays, and a denote the width of the emergent beam, the dispersion θ is given by
θ = δμ(t2 − t1)/a,
or, if t1 be negligible,
θ = δμt/a (6).
The condition of resolution of a double line whose components subtend an angle θ is that θ must exceed λ/a. Hence, in order that a double line may be resolved whose components have indices μ and μ + δμ, it is necessary that t should exceed the value given by the following equation:—
t = λ/δμ (7).
8. Diffraction Gratings.—Under the heading “Colours of Striated Surfaces,” Thomas Young (Phil. Trans., 1802) in his usual summary fashion gave a general explanation of these colours, including the law of sines, the striations being supposed to be straight, parallel and equidistant. Later, in his article “Chromatics” in the supplement to the 5th edition of this encyclopaedia, he shows that the colours “lose the mixed character of periodical colours, and resemble much more the ordinary prismatic spectrum, with intervals completely dark interposed,” and explains it by the consideration that any phase-difference which may arise at neighbouring striae is multiplied in proportion to the total number of striae.
The theory was further developed by A. J. Fresnel (1815), who gave a formula equivalent to (5) below. But it is to J. von Fraunhofer that we owe most of our knowledge upon this subject. His recent discovery of the “fixed lines” allowed a precision of observation previously impossible. He constructed gratings up to 340 periods to the inch by straining fine wire over screws. Subsequently he ruled gratings on a layer of gold-leaf attached to glass, or on a layer of grease similarly supported, and again by attacking the glass itself with a diamond point. The best gratings were obtained by the last method, but a suitable diamond point was hard to find, and to preserve. Observing through a telescope with light perpendicularly incident, he showed that the position of any ray was dependent only upon the grating interval, viz. the distance from the centre of one wire or line to the centre of the next, and not otherwise upon the thickness of the wire and the magnitude of the interspace. In different gratings the lengths of the spectra and their distances from the axis were inversely proportional to the grating interval, while with a given grating the distances of the various spectra from the axis were as 1, 2, 3, &c. To Fraunhofer we owe the first accurate measurements of wave-lengths, and the method of separating the overlapping spectra by a prism dispersing in the perpendicular direction. He described also the complicated patterns seen when a point of light is viewed through two superposed gratings, whose lines cross one another perpendicularly or obliquely. The above observations relate to transmitted light, but Fraunhofer extended his inquiry to the light reflected. To eliminate the light returned from the hinder surface of an engraved grating, he covered it with a black varnish. It then appeared that under certain angles of incidence parts of the resulting spectra were completely polarized. These remarkable researches of Fraunhofer, carried out in the years 1817-1823, are republished in his Collected Writings (Munich, 1888).
The principle underlying the action of gratings is identical with that discussed in § 2, and exemplified in J. L. Soret’s “zone plates.” The alternate Fresnel’s zones are blocked out or otherwise modified; in this way the original compensation is upset and a revival of light occurs in unusual directions. If the source be a point or a line, and a collimating lens be used, the incident waves may be regarded as plane. If, further, on leaving the grating the light be received by a focusing lens, e.g. the object-glass of a telescope, the Fresnel’s zones are reduced to parallel and equidistant straight strips, which at certain angles coincide with the ruling. The directions of the lateral spectra are such that the passage from one element of the grating to the corresponding point of the next implies a retardation of an integral number of wave-lengths. If the grating be composed of alternate transparent and opaque parts, the question may be treated by means of the general integrals (§ 3) by merely limiting the integration to the transparent parts of the aperture. For an investigation upon these lines the reader is referred to Airy’s Tracts, to Verdet’s Leçons, or to R. W. Wood’s Physical Optics. If, however, we assume the theory of a simple rectangular aperture (§ 3); the results of the ruling can be inferred by elementary methods, which are perhaps more instructive.
Apart from the ruling, we know that the image of a mathematical line will be a series of narrow bands, of which the central one is by far the brightest. At the middle of this band there is complete agreement of phase among the secondary waves. The dark lines which separate the bands are the places at which the phases of the secondary wave range over an integral number of periods. If now we suppose the aperture AB to be covered by a great number of opaque strips or bars of width d, separated by transparent intervals of width a, the condition of things in the directions just spoken of is not materially changed. At the central point there is still complete agreement of phase; but the amplitude is diminished in the ratio of a : a + d. In another direction, making a small angle with the last, such that the projection of AB upon it amounts to a few wave-lengths, it is easy to see that the mode of interference is the same as if there were no ruling. For example, when the direction is such that the projection of AB upon it amounts to one wave-length, the elementary components neutralize one another, because their phases are distributed symmetrically, though discontinuously, round the entire period. The only effect of the ruling is to diminish the amplitude in the ratio a : a + d; and, except for the difference in illumination, the appearance of a line of light is the same as if the aperture were perfectly free.
The lateral (spectral) images occur in such directions that the projection of the element (a + d) of the grating upon them is an exact multiple of λ. The effect of each of the n elements of the grating is then the same; and, unless this vanishes on account of a particular adjustment of the ratio a : d, the resultant amplitude becomes comparatively very great. These directions, in which the retardation between A and B is exactly mnλ, may be called the principal directions. On either side of any one of them the illumination is distributed according to the same law as for the central image (m = 0), vanishing, for example, when the retardation amounts to (mn ± 1)λ. In considering the relative brightnesses of the different spectra, it is therefore sufficient to attend merely to the principal directions, provided that the whole deviation be not so great that its cosine differs considerably from unity.
We have now to consider the amplitude due to a single element, which we may conveniently regard as composed of a transparent part a bounded by two opaque parts of width ½d. The phase of the resultant effect is by symmetry that of the component which comes from the middle of a. The fact that the other components have phases differing from this by amounts ranging between ± amπ/(a + d) causes the resultant amplitude to be less than for the central image (where there is complete phase agreement). 247 If Bm denote the brightness of the mth lateral image, and B0 that of the central image, we have
| Bm : B 0 = [∫ | + amπ/(a+d) | cosx dx ÷ | 2amπ | ] | ² | = ( | a + d | ) | ² | sin² | amπ | (1). |
| − amπ/(a+d) | a + d | amπ | a + d |
If B denotes the brightness of the central image when the whole of the space occupied by the grating is transparent, we have
B0 : B = a² : (a + d)²,
and thus
| Bm : B = | 1 | sin² | amπ | (2). |
| m²π² | a + d |
The sine of an angle can never be greater than unity; and consequently under the most favourable circumstances only 1/m²π² of the original light can be obtained in the mth spectrum. We conclude that, with a grating composed of transparent and opaque parts, the utmost light obtainable in any one spectrum is in the first, and there amounts to 1/π², or about 1⁄10, and that for this purpose a and d must be equal. When d = a the general formula becomes
| Bm : B = | sin² ½mπ | (3), |
| m²π² |
showing that, when m is even, Bm vanishes, and that, when m is odd,
Bm : B = 1/m²π².
The third spectrum has thus only 1⁄9 of the brilliancy of the first.
Another particular case of interest is obtained by supposing a small relatively to (a + d). Unless the spectrum be of very high order, we have simply
Bm : B = {a/(a + d)}² (4);
so that the brightnesses of all the spectra are the same.
The light stopped by the opaque parts of the grating, together with that distributed in the central image and lateral spectra, ought to make up the brightness that would be found in the central image, were all the apertures transparent. Thus, if a = d, we should have
1 = ½ + ¼ + 2/π² (1 + 1⁄9 + 1⁄25 + ...),
which is true by a known theorem. In the general case
| a | = ( | a | ) | ² | + | 2 | Σ | m=∞ | 1 | sin²( | mπa | ), |
| a + d | a + d | π² | m=1 | m² | a + d |
a formula which may be verified by Fourier’s theorem.
According to a general principle formulated by J. Babinet, the brightness of a lateral spectrum is not affected by an interchange of the transparent and opaque parts of the grating. The vibrations corresponding to the two parts are precisely antagonistic, since if both were operative the resultant would be zero. So far as the application to gratings is concerned, the same conclusion may be derived from (2).
 |
| Fig. 6. |
From the value of Bm : B0 we see that no lateral spectrum can surpass the central image in brightness; but this result depends upon the hypothesis that the ruling acts by opacity, which is generally very far from being the case in practice. In an engraved glass grating there is no opaque material present by which light could be absorbed, and the effect depends upon a difference of retardation in passing the alternate parts. It is possible to prepare gratings which give a lateral spectrum brighter than the central image, and the explanation is easy. For if the alternate parts were equal and alike transparent, but so constituted as to give a relative retardation of ½λ, it is evident that the central image would be entirely extinguished, while the first spectrum would be four times as bright as if the alternate parts were opaque. If it were possible to introduce at every part of the aperture of the grating an arbitrary retardation, all the light might be concentrated in any desired spectrum. By supposing the retardation to vary uniformly and continuously we fall upon the case of an ordinary prism: but there is then no diffraction spectrum in the usual sense. To obtain such it would be necessary that the retardation should gradually alter by a wave-length in passing over any element of the grating, and then fall back to its previous value, thus springing suddenly over a wave-length (Phil. Mag., 1874, 47, p. 193). It is not likely that such a result will ever be fully attained in practice; but the case is worth stating, in order to show that there is no theoretical limit to the concentration of light of assigned wave-length in one spectrum, and as illustrating the frequently observed unsymmetrical character of the spectra on the two sides of the central image.4
We have hitherto supposed that the light is incident perpendicularly upon the grating; but the theory is easily extended. If the incident rays make an angle θ with the normal (fig. 6), and the diffracted rays make an angle φ (upon the same side), the relative retardation from each element of width (a + d) to the next is (a + d) (sinθ + sinφ); and this is the quantity which is to be equated to mλ. Thus
sinθ + sinφ = 2sin ½(θ + φ) cos ½ (θ − φ) = mλ/(a + d) (5).
The “deviation” is (θ + φ), and is therefore a minimum when θ = φ, i.e. when the grating is so situated that the angles of incidence and diffraction are equal.
 |
| Fig. 7. |
In the case of a reflection grating the same method applies. If θ and φ denote the angles with the normal made by the incident and diffracted rays, the formula (5) still holds, and, if the deviation be reckoned from the direction of the regularly reflected rays, it is expressed as before by (θ + φ), and is a minimum when θ = φ, that is, when the diffracted rays return upon the course of the incident rays.
In either case (as also with a prism) the position of minimum deviation leaves the width of the beam unaltered, i.e. neither magnifies nor diminishes the angular width of the object under view.
From (5) we see that, when the light falls perpendicularly upon a grating (θ = 0), there is no spectrum formed (the image corresponding to m = 0 not being counted as a spectrum), if the grating interval σ or (a + d) is less than λ. Under these circumstances, if the material of the grating be completely transparent, the whole of the light must appear in the direct image, and the ruling is not perceptible. From the absence of spectra Fraunhofer argued that there must be a microscopic limit represented by λ; and the inference is plausible, to say the least (Phil. Mag., 1886). Fraunhofer should, however, have fixed the microscopic limit at ½λ, as appears from (5), when we suppose θ = ½π, φ = ½π.
 |
| Fig. 8. |
We will now consider the important subject of the resolving power of gratings, as dependent upon the number of lines (n) and the order of the spectrum observed (m). Let BP (fig. 8) be the direction of the principal maximum (middle of central band) for the wave-length λ in the mth spectrum. Then the relative retardation of the extreme rays (corresponding to the edges A, B of the grating) is mnλ. If BQ be the direction for the first minimum (the darkness between the central and first lateral band), the relative retardation of the extreme rays is (mn + 1)λ. Suppose now that λ + δλ is the wave-length for which BQ gives the principal maximum, then
(mn + 1)λ = mn(λ + δλ);
whence
δλ/λ = 1/mn (6).
According to our former standard, this gives the smallest difference of wave-lengths in a double line which can be just resolved; and we conclude that the resolving power of a grating depends only upon the total number of lines, and upon the order of the spectrum, without regard to any other considerations. It is here of course assumed that the n lines are really utilized.
In the case of the D lines the value of δλ/λ is about 1/1000; so that to resolve this double line in the first spectrum requires 1000 lines, in the second spectrum 500, and so on.
It is especially to be noticed that the resolving power does not depend directly upon the closeness of the ruling. Let us take the case of a grating 1 in. broad, and containing 1000 lines, and consider the effect of interpolating an additional 1000 lines, so as to bisect the former intervals. There will be destruction by interference of the first, third and odd spectra generally; while the advantage gained in the spectra of even order is not in dispersion, nor in resolving power, but simply in brilliancy, which is increased four times. If we now suppose half the grating cut away, so as to leave 1000 lines in half an inch, the dispersion will not be altered, while the brightness and resolving power are halved.
There is clearly no theoretical limit to the resolving power of gratings, even in spectra of given order. But it is possible that, as suggested by Rowland,5 the structure of natural spectra may be too coarse to give opportunity for resolving powers much higher than those now in use. However this may be, it would always be possible, with the aid of a grating of given resolving power, to construct artificially from white light mixtures of slightly different wave-length whose resolution or otherwise would discriminate between powers inferior and superior to the given one.6
If we define as the “dispersion” in a particular part of the spectrum the ratio of the angular interval dθ to the corresponding increment of wave-length dλ, we may express it by a very simple formula. For the alteration of wave-length entails, at the two limits of a diffracted wave-front, a relative retardation equal to mndλ. Hence, if a be the width of the diffracted beam, and dθ the angle through which the wave-front is turned,
adθ = mn dλ,
or
dispersion = mn/a (7).
The resolving power and the width of the emergent beam fix the optical character of the instrument. The latter element must eventually be decreased until less than the diameter of the pupil of the eye. Hence a wide beam demands treatment with further apparatus (usually a telescope) of high magnifying power.
In the above discussion it has been supposed that the ruling is accurate, and we have seen that by increase of m a high resolving power is attainable with a moderate number of lines. But this procedure (apart from the question of illumination) is open to the objection that it makes excessive demands upon accuracy. According to the principle already laid down it can make but little difference in the principal direction corresponding to the first spectrum, provided each line lie within a quarter of an interval (a + d) from its theoretical position. But, to obtain an equally good result in the mth spectrum, the error must be less than 1/m of the above amount.7
There are certain errors of a systematic character which demand special consideration. The spacing is usually effected by means of a screw, to each revolution of which corresponds a large number (e.g. one hundred) of lines. In this way it may happen that although there is almost perfect periodicity with each revolution of the screw after (say) 100 lines, yet the 100 lines themselves are not equally spaced. The “ghosts” thus arising were first described by G. H. Quincke (Pogg. Ann., 1872, 146, p. 1), and have been elaborately investigated by C. S. Peirce (Ann. Journ. Math., 1879, 2, p. 330), both theoretically and experimentally. The general nature of the effects to be expected in such a case may be made clear by means of an illustration already employed for another purpose. Suppose two similar and accurately ruled transparent gratings to be superposed in such a manner that the lines are parallel. If the one set of lines exactly bisect the intervals between the others, the grating interval is practically halved, and the previously existing spectra of odd order vanish. But a very slight relative displacement will cause the apparition of the odd spectra. In this case there is approximate periodicity in the half interval, but complete periodicity only after the whole interval. The advantage of approximate bisection lies in the superior brilliancy of the surviving spectra; but in any case the compound grating may be considered to be perfect in the longer interval, and the definition is as good as if the bisection were accurate.
 | |||
| Fig. 9.—x². | Fig. 10.—y². | Fig. 11.—x³. | Fig. 12.—xy². |
 |
| Fig. 13.—xy. Fig. 14.—x²y. Fig. 15.—y³. |
The effect of a gradual increase in the interval (fig. 9) as we pass across the grating has been investigated by M. A. Cornu (C.R., 1875, 80, p. 655), who thus explains an anomaly observed by E. E. N. Mascart. The latter found that certain gratings exercised a converging power upon the spectra formed upon one side, and a corresponding diverging power upon the spectra on the other side. Let us suppose that the light is incident perpendicularly, and that the grating interval increases from the centre towards that edge which lies nearest to the spectrum under observation, and decreases towards the hinder edge. It is evident that the waves from both halves of the grating are accelerated in an increasing degree, as we pass from the centre outwards, as compared with the phase they would possess were the central value of the grating interval maintained throughout. The irregularity of spacing has thus the effect of a convex lens, which accelerates the marginal relatively to the central rays. On the other side the effect is reversed. This kind of irregularity may clearly be present in a degree surpassing the usual limits, without loss of definition, when the telescope is focused so as to secure the best effect.
It may be worth while to examine further the other variations from correct ruling which correspond to the various terms expressing the deviation of the wave-surface from a perfect plane. If x and y be co-ordinates in the plane of the wave-surface, the axis of y being parallel to the lines of the grating, and the origin corresponding to the centre of the beam, we may take as an approximate equation to the wave-surface
| z = | x² | + Bxy + | y² | + αx³ + βx²y + γxy² + δy³ + ... (8); |
| 2ρ | 2ρ′ |
and, as we have just seen, the term in x² corresponds to a linear error in the spacing. In like manner, the term in y² corresponds to a general curvature of the lines (fig. 10), and does not influence the definition at the (primary) focus, although it may introduce astigmatism.8 If we suppose that everything is symmetrical on the two sides of the primary plane y = 0, the coefficients B, β, δ vanish. In spite of any inequality between ρ and ρ’, the definition will be good to this order of approximation, provided α and γ vanish. The former measures the thickness of the primary focal line, and the latter measures its curvature. The error of ruling giving rise to α is one in which the intervals increase or decrease in both directions from the centre outwards (fig. 11), and it may often be compensated by a slight rotation in azimuth of the object-glass of the observing telescope. The term in γ corresponds to a variation of curvature in crossing the grating (fig. 12).
When the plane zx is not a plane of symmetry, we have to consider the terms in xy, x²y, and y³. The first of these corresponds to a deviation from parallelism, causing the interval to alter gradually as we pass along the lines (fig. 13). The error thus arising may be compensated by a rotation of the object-glass about one of the diameters y = ± x. The term in x²y corresponds to a deviation from parallelism in the same direction on both sides of the central line (fig. 14); and that in y³ would be caused by a curvature such that there is a point of inflection at the middle of each line (fig. 15).
All the errors, except that depending on α, and especially those depending on γ and δ, can be diminished, without loss of resolving power, by contracting the vertical aperture. A linear error in the spacing, and a general curvature of the lines, are eliminated in the ordinary use of a grating.
The explanation of the difference of focus upon the two sides as due to unequal spacing was verified by Cornu upon gratings purposely constructed with an increasing interval. He has also shown how to rule a plane surface with lines so disposed that the grating shall of itself give well-focused spectra.
 |
| Fig. 16. |
A similar idea appears to have guided H. A. Rowland to his brilliant invention of concave gratings, by which spectra can be photographed without any further optical appliance. In these instruments the lines are ruled upon a spherical surface of speculum metal, and mark the intersections of the surface by a system of parallel and equidistant planes, of which the middle member passes through the centre of the sphere. If we consider for the present only the primary plane of symmetry, the figure is reduced to two dimensions. Let AP (fig. 16) represent the surface of the grating, O being the centre of the circle. Then, if Q be any radiant point and Q’ its image (primary focus) in the spherical mirror AP, we have
| 1 | + | 1 | = | 2cosφ | , |
| v1 | u | a |
where v1 = AQ′, u = AQ, a = OA, φ = angle of incidence QAO, equal to the angle of reflection Q′AO. If Q be on the circle described upon OA as diameter, so that u = a cos φ, then Q′ lies also upon the same circle; and in this case it follows from the symmetry that the unsymmetrical aberration (depending upon a) vanishes.
This disposition is adopted in Rowland′s instrument; only, in addition to the central image formed at the angle φ′ = φ, there are a series of spectra with various values of φ’, but all disposed upon the same circle. Rowland’s investigation is contained in the paper already referred to; but the following account of the theory is in the form adopted by R. T. Glazebrook (Phil. Mag., 1883).
In order to find the difference of optical distances between the courses QAQ′, QPQ′, we have to express QP − QA, PQ′ − AQ′. To find the former, we have, if OAQ = φ, AOP = ω,
QP² = u² + 4a²sin²½ω − 4au sin ½ω sin (½ω − φ)
= (u + a sin φ sin ω)² − a² sin²φ sin²ω + 4a sin² ½ω(a − u cosφ).
Now as far as ω4
4 sin² ½ω = sin²ω + ¼sin4ω,
and thus to the same order
QP² = (u + a sin φ sin ω)²
− a cos φ(u − a cos φ) sin²ω + ¼ a(a − u cos φ) sin4 ω.
pose that Q lies on the circle u = a cos φ, the middle term vanishes, and we get, correct as far as ω4,
| QP = (u + a sin φ sin ω) √ {1 + | a² sin² φ sin4ω | }; |
| 4u |
so that
QP − u = a sin φ sin ω + 1⁄8a sin φ tan φ sin4 ω (9),
in which it is to be noticed that the adjustment necessary to secure the disappearance of sin²ω is sufficient also to destroy the term in sin³ω.
A similar expression can be found for Q’P − Q′A; and thus, if Q′A = v, Q′AO = φ′, where v = a cos φ′, we get
QP + PQ′ − QA -AQ′ = a sin ω (sin φ − sin φ′)
+ 1⁄8a sin4 ω (sin φ tan φ + sin φ′ tan φ′) (10).
If φ′ = φ, the term of the first order vanishes, and the reduction of the difference of path via P and via A to a term of the fourth order proves not only that Q and Q′ are conjugate foci, but also that the foci are exempt from the most important term in the aberration. In the present application φ′ is not necessarily equal to φ; but if P correspond to a line upon the grating, the difference of retardations for consecutive positions of P, so far as expressed by the term of the first order, will be equal to ± mλ (m integral), and therefore without influence, provided
σ (sin φ − sinφ′) = ± mλ (11),
where σ denotes the constant interval between the planes containing the lines. This is the ordinary formula for a reflecting plane grating, and it shows that the spectra are formed in the usual directions. They are here focused (so far as the rays in the primary plane are concerned) upon the circle OQ′A, and the outstanding aberration is of the fourth order.
In order that a large part of the field of view may be in focus at once, it is desirable that the locus of the focused spectrum should be nearly perpendicular to the line of vision. For this purpose Rowland places the eye-piece at O, so that φ = 0, and then by (11) the value of φ′ in the mth spectrum is
σ sin φ’ = ± mλ (12).
If ω now relate to the edge of the grating, on which there are altogether n lines,
nσ = 2a sin ω,
and the value of the last term in (10) becomes
1⁄16 nσsin³ ω sin φ′ tan φ′,
or
1⁄16 mnλ sin³ω tan φ′ (13).
This expresses the retardation of the extreme relatively to the central ray, and is to be reckoned positive, whatever may be the signs of ω, and φ′. If the semi-angular aperture (ω) be 1⁄100, and tan φ′ = 1, mn might be as great as four millions before the error of phase would reach ¼λ. If it were desired to use an angular aperture so large that the aberration according to (13) would be injurious, Rowland points out that on his machine there would be no difficulty in applying a remedy by making σ slightly variable towards the edges. Or, retaining σ constant, we might attain compensation by so polishing the surface as to bring the circumference slightly forward in comparison with the position it would occupy upon a true sphere.
It may be remarked that these calculations apply to the rays in the primary plane only. The image is greatly affected with astigmatism; but this is of little consequence, if γ in (8) be small enough. Curvature of the primary focal line having a very injurious effect upon definition, it may be inferred from the excellent performance of these gratings that γ is in fact small. Its value does not appear to have been calculated. The other coefficients in (8) vanish in virtue of the symmetry.
The mechanical arrangements for maintaining the focus are of great simplicity. The grating at A and the eye-piece at O are rigidly attached to a bar AO, whose ends rest on carriages, moving on rails OQ, AQ at right angles to each other. A tie between the middle point of the rod OA and Q can be used if thought desirable.
The absence of chromatic aberration gives a great advantage in the comparison of overlapping spectra, which Rowland has turned to excellent account in his determinations of the relative wave-lengths of lines in the solar spectrum (Phil. Mag., 1887).
For absolute determinations of wave-lengths plane gratings are used. It is found (Bell, Phil. Mag., 1887) that the angular measurements present less difficulty than the comparison of the grating interval with the standard metre. There is also some uncertainty as to the actual temperature of the grating when in use. In order to minimize the heating action of the light, it might be submitted to a preliminary prismatic analysis before it reaches the slit of the spectrometer, after the manner of Helmholtz.
In spite of the many improvements introduced by Rowland and of the care with which his observations were made, recent workers have come to the conclusion that errors of unexpected amount have crept into his measurements of wave-lengths, and there is even a disposition to discard the grating altogether for fundamental work in favour of the so-called “interference methods,” as developed by A. A. Michelson, and by C. Fabry and J. B. Pérot. The grating would in any case retain its utility for the reference of new lines to standards otherwise fixed. For such standards a relative accuracy of at least one part in a million seems now to be attainable.
Since the time of Fraunhofer many skilled mechanicians have given their attention to the ruling of gratings. Those of Nobert were employed by A. J. Ångström in his celebrated researches upon wave-lengths. L. M. Rutherfurd introduced into common use the reflection grating, finding that speculum metal was less trying than glass to the diamond point, upon the permanence of which so much depends. In Rowland’s dividing engine the screws were prepared by a special process devised by him, and the resulting gratings, plane and concave, have supplied the means for much of the best modern optical work. It would seem, however, that further improvements are not excluded.
There are various copying processes by which it is possible to reproduce an original ruling in more or less perfection. The earliest is that of Quincke, who coated a glass grating with a chemical silver deposit, subsequently thickened with copper in an electrolytic bath. The metallic plate thus produced formed, when stripped from its support, a reflection grating reproducing many of the characteristics of the original. It is best to commence the electrolytic thickening in a silver acetate bath. At the present time excellent reproductions of Rowland’s speculum gratings are on the market (Thorp, Ives, Wallace), prepared, after a suggestion of Sir David Brewster, by coating the original with a varnish, e.g. of celluloid. Much skill is required to secure that the film when stripped shall remain undeformed.
A much easier method, applicable to glass originals, is that of photographic reproduction by contact printing. In several papers dating from 1872, Lord Rayleigh (see Collected Papers, i. 157, 160, 199, 504; iv. 226) has shown that success may be attained by a variety of processes, including bichromated gelatin and the old bitumen process, and has investigated the effect of imperfect approximation during the exposure between the prepared plate and the original. For many purposes the copies, containing lines up to 10,000 to the inch, are not inferior. It is to be desired that transparent gratings should be obtained from first-class ruling machines. To save the diamond point it might be possible to use something softer than ordinary glass as the material of the plate.
9. Talbot’s Bands.—These very remarkable bands are seen under certain conditions when a tolerably pure spectrum is regarded with the naked eye, or with a telescope, half the aperture being covered by a thin plate, e.g. of glass or mica. The view of the matter taken by the discoverer (Phil. Mag., 1837, 10, p. 364) was that any ray which suffered in traversing the plate a retardation of an odd number of half wave-lengths would be extinguished, and that thus the spectrum would be seen interrupted by a number of dark bars. But this explanation cannot be accepted as it stands, being open to the same objection as Arago’s theory of stellar scintillation.9 It is as far as possible from being true that a body emitting homogeneous light would disappear on merely covering half the aperture of vision with a half-wave plate. Such a conclusion would be in the face of the principle of energy, which teaches plainly that the retardation in question leaves the aggregate brightness unaltered. The actual formation of 250 the bands comes about in a very curious way, as is shown by a circumstance first observed by Brewster. When the retarding plate is held on the side towards the red of the spectrum, the bands are not seen. Even in the contrary case, the thickness of the plate must not exceed a certain limit, dependent upon the purity of the spectrum. A satisfactory explanation of these bands was first given by Airy (Phil. Trans., 1840, 225; 1841, 1), but we shall here follow the investigation of Sir G. G. Stokes (Phil. Trans., 1848, 227), limiting ourselves, however, to the case where the retarded and unretarded beams are contiguous and of equal width.
The aperture of the unretarded beam may thus be taken to be limited by x = -h, x = 0, y = -l, y= +l; and that of the beam retarded by R to be given by x = 0, x = h, y= -l, y = +l. For the former (1) § 3 gives
| − | 1 | ∫ | 0 | ∫ | +l | sin k{ at − ƒ + | xξ + yη | }dxdy |
| λƒ | −h | −l | ƒ |
| = − | 2lh | · | ƒ | sin | kηl | · | 2ƒ | sin | kξh | · sin k{at − ƒ − | ξh | } (1), |
| λƒ | kηl | ƒ | kξh | 2ƒ | 2ƒ |
on integration and reduction.
For the retarded stream the only difference is that we must subtract R from at, and that the limits of x are 0 and +h. We thus get for the disturbance at ξ, η, due to this stream
| − | 2lh | · | ƒ | sin | kηl | · | 2ƒ | sin | kξh | · sin k{at − ƒ − R + | ξh | } (2) |
| λƒ | kηl | ƒ | kξh | 2ƒ | 2ƒ |
If we put for shortness π for the quantity under the last circular function in (1), the expressions (1), (2) may be put under the forms u sin τ, v sin (τ − α) respectively; and, if I be the intensity, I will be measured by the sum of the squares of the coefficients of sin τ and cos τ in the expression
u sin τ + v sin (τ − α),
so that
I = u² + v² + 2uv cos α,
which becomes on putting for u, v, and α their values, and putting
| { | ƒ | sin | kηl | } | ² | = Q (3), |
| kηl | ƒ |
| I = Q · | 4l² | sin² | πξh | {2 + 2 cos( | 2πR | − | 2πξh | )} (4). |
| π²ξ² | λƒ | λ | λƒ |
If the subject of examination be a luminous line parallel to η, we shall obtain what we require by integrating (4) with respect to η from −∞ to +∞. The constant multiplier is of no especial interest so that we may take as applicable to the image of a line
| I = | 2 | sin² | πξh | {1 + cos( | 2πR | − | 2πξh | )} (5). |
| ξ² | λƒ | λ | λƒ |
If R = ½λ, I vanishes at ξ= 0; but the whole illumination, represented by ∫+∞−∞ I dξ, is independent of the value of R. If R = 0, I = (1/ξ²) sin² (2πξh/λƒ), in agreement with § 3, where a has the meaning here attached to 2h.
The expression (5) gives the illumination at ξ due to that part of the complete image whose geometrical focus is at ξ = 0, the retardation for this component being R. Since we have now to integrate for the whole illumination at a particular point O due to all the components which have their foci in its neighbourhood, we may conveniently regard O as origin. ξ is then the co-ordinate relatively to O of any focal point O′ for which the retardation is R; and the required result is obtained by simply integrating (5) with respect to ξ from −∞ to +∞. To each value of ξ corresponds a different value of λ, and (in consequence of the dispersing power of the plate) of R. The variation of λ may, however, be neglected in the integration, except in 2πR/λ, where a small variation of λ entails a comparatively large alteration of phase. If we write
ρ = 2πR/λ (6),
we must regard ρ as a function of ξ, and we may take with sufficient approximation under any ordinary circumstances
ρ = ρ′ + ωξ (7),
where ρ′ denotes the value of ρ at O, and ω is a constant, which is positive when the retarding plate is held at the side on which the lue of the spectrum is seen. The possibility of dark bands depends upon ω being positive. Only in this case can
cos {ρ′ + (ω − 2πh/λƒ) ξ}
retain the constant value -1 throughout the integration, and then only when
ω = 2πh / λƒ (8)
and
cos ρ′ = −1 (9).
The first of these equations is the condition for the formation of dark bands, and the second marks their situation, which is the same as that determined by the imperfect theory.
The integration can be effected without much difficulty. For the first term in (5) the evaluation is effected at once by a known formula. In the second term if we observe that
cos {ρ′ +(ω − 2πh/λƒ) ξ} = cos {ρ′ − g1ξ}
= cos ρ′ cos g1ξ + sin ρ′ sin g1ξ,
we see that the second part vanishes when integrated, and that the remaining integral is of the form
| w = ∫ | +∞ | sin² h1ξ cos g1ξ | dξ | , |
| −∞ | ξ² |
where
h1 = πh/λƒ, g1 = ω − 2πh/λƒ (10).
By differentiation with respect to g1 it may be proved that
| w = 0 | from g1 = −∞ | to g1 = −2h1, |
| w = ½π(2h1 + g1) | from g1 = −2h1 | to g1 = 0, |
| w = ½π(2h1 − g1) | from g1 = 0 | to g1 = 2h1, |
| w = 0 | from g1 = 2h1 | to g1 = ∞. |
The integrated intensity, I′, or
2πh1 + 2 cos ρw,
is thus
I′ = 2πh1 (11),
when g1 numerically exceeds 2h1; and, when g1 lies between ±2h1,
I = π{2h1 + (2h1 − √ g1²) cos ρ′} (12).
It appears therefore that there are no bands at all unless ω lies between 0 and +4h1, and that within these limits the best bands are formed at the middle of the range when ω = 2h1. The formation of bands thus requires that the retarding plate be held upon the side already specified, so that ω be positive; and that the thickness of the plate (to which ω is proportional) do not exceed a certain limit, which we may call 2T0. At the best thickness T0 the bands are black, and not otherwise.
The linear width of the band (e) is the increment of ξ which alters ρ by 2π, so that
e = 2π / ω (13).
With the best thickness
ω = 2πh/λƒ (14),
so that in this case
e = λƒ / h (15).
The bands are thus of the same width as those due to two infinitely narrow apertures coincident with the central lines of the retarded and unretarded streams, the subject of examination being itself a fine luminous line.
If it be desired to see a given number of bands in the whole or in any part of the spectrum, the thickness of the retarding plate is thereby determined, independently of all other considerations. But in order that the bands may be really visible, and still more in order that they may be black, another condition must be satisfied. It is necessary that the aperture of the pupil be accommodated to the angular extent of the spectrum, or reciprocally. Black bands will be too fine to be well seen unless the aperture (2h) of the pupil be somewhat contracted. One-twentieth to one-fiftieth of an inch is suitable. The aperture and the number of bands being both fixed, the condition of blackness determines the angular magnitude of a band and of the spectrum. The use of a grating is very convenient, for not only are there several spectra in view at the same time, but the dispersion can be varied continuously by sloping the grating. The slits may be cut out of tin-plate, and half covered by mica or “microscopic glass,” held in position by a little cement.
If a telescope be employed there is a distinction to be observed, according as the half-covered aperture is between the eye and the ocular, or in front of the object-glass. In the former case the function of the telescope is simply to increase the dispersion, and the formation of the bands is of course independent of the particular manner in which the dispersion arises. If, however, the half-covered aperture be in front of the object-glass, the phenomenon is magnified as a whole, and the desirable relation between the (unmagnified) dispersion and the aperture is the same as without the telescope. There appears to be no further advantage in the use of a telescope than the increased facility of accommodation, and for this of course a very low power suffices.
The original investigation of Stokes, here briefly sketched, extends also to the case where the streams are of unequal width h, k, and are separated by an interval 2g. In the case of unequal width the bands cannot be black; but if h = k, the finiteness of 2g does not preclude the formation of black bands.
The theory of Talbot’s bands with a half-covered circular aperture has been considered by H. Struve (St Peters. Trans., 1883, 31, No. 1).
The subject of “Talbot’s bands” has been treated in a very instructive manner by A. Schuster (Phil. Mag., 1904), whose point of view offers the great advantage of affording an instantaneous explanation of the peculiarity noticed by Brewster. A plane pulse, i.e. a disturbance limited to an infinitely thin slice of the medium, is supposed to fall upon a parallel grating, which again may 251 be regarded as formed of infinitely thin wires, or infinitely narrow lines traced upon glass. The secondary pulses diverted by the ruling fall upon an object-glass as usual, and on arrival at the focus constitute a procession equally spaced in time, the interval between consecutive members depending upon the obliquity. If a retarding plate be now inserted so as to operate upon the pulses which come from one side of the grating, while leaving the remainder unaffected, we have to consider what happens at the focal point chosen. A full discussion would call for the formal application of Fourier’s theorem, but some conclusions of importance are almost obvious.
Previously to the introduction of the plate we have an effect corresponding to wave-lengths closely grouped around the principal wave-length, viz. σ sin φ, where σ is the grating-interval and φ the obliquity, the closeness of the grouping increasing with the number of intervals. In addition to these wave-lengths there are other groups centred round the wave-lengths which are submultiples of the principal one—the overlapping spectra of the second and higher orders. Suppose now that the plate is introduced so as to cover naif the aperture and that it retards those pulses which would otherwise arrive first. The consequences must depend upon the amount of the retardation. As this increases from zero, the two processions which correspond to the two halves of the aperture begin to overlap, and the overlapping gradually increases until there is almost complete superposition. The stage upon which we will fix our attention is that where the one procession bisects the intervals between the other, so that a new simple procession is constituted, containing the same number of members as before the insertion of the plate, but now spaced at intervals only half as great. It is evident that the effect at the focal point is the obliteration of the first and other spectra of odd order, so that as regards the spectrum of the first order we may consider that the two beams interfere. The formation of black bands is thus explained, and it requires that the plate be introduced upon one particular side, and that the amount of the retardation be adjusted to a particular value. If the retardation be too little, the overlapping of the processions is incomplete, so that besides the procession of half period there are residues of the original processions of full period. The same thing occurs if the retardation be too great. If it exceed the double of the value necessary for black bands, there is again no overlapping and consequently no interference. If the plate be introduced upon the other side, so as to retard the procession originally in arrear, there is no overlapping, whatever may be the amount of retardation. In this way the principal features of the phenomenon are accounted for, and Schuster has shown further how to extend the results to spectra having their origin in prisms instead of gratings.
10. Diffraction when the Source of Light is not seen in Focus.—The phenomena to be considered under this head are of less importance than those investigated by Fraunhofer, and will be treated in less detail; but in view of their historical interest and of the ease with which many of the experiments may be tried, some account of their theory cannot be omitted. One or two examples have already attracted our attention when considering Fresnel’s zones, viz. the shadow of a circular disk and of a screen circularly perforated.
Fresnel commenced his researches with an examination of the fringes, external and internal, which accompany the shadow of a narrow opaque strip, such as a wire. As a source of light he used sunshine passing through a very small hole perforated in a metal plate, or condensed by a lens of short focus. In the absence of a heliostat the latter was the more convenient. Following, unknown to himself, in the footsteps of Young, he deduced the principle of interference from the circumstance that the darkness of the interior bands requires the co-operation of light from both sides of the obstacle. At first, too, he followed Young in the view that the exterior bands are the result of interference between the direct light and that reflected from the edge of the obstacle, but he soon discovered that the character of the edge—e.g. whether it was the cutting edge or the back of a razor—made no material difference, and was thus led to the conclusion that the explanation of these phenomena requires nothing more than the application of Huygens’s principle to the unobstructed parts of the wave. In observing the bands he received them at first upon a screen of finely ground glass, upon which a magnifying lens was focused; but it soon appeared that the ground glass could be dispensed with, the diffraction pattern being viewed in the same way as the image formed by the object-glass of a telescope is viewed through the eye-piece. This simplification was attended by a great saving of light, allowing measures to be taken such as would otherwise have presented great difficulties.
 |
| Fig. 17. |
In theoretical investigations these problems are usually treated as of two dimensions only, everything being referred to the plane passing through the luminous point and perpendicular to the diffracting edges, supposed to be straight and parallel. In strictness this idea is appropriate only when the source is a luminous line, emitting cylindrical waves, such as might be obtained from a luminous point with the aid of a cylindrical lens. When, in order to apply Huygens’s principle, the wave is supposed to be broken up, the phase is the same at every element of the surface of resolution which lies upon a line perpendicular to the plane of reference, and thus the effect of the whole line, or rather infinitesimal strip, is related in a constant manner to that of the element which lies in the plane of reference, and may be considered to be represented thereby. The same method of representation is applicable to spherical waves, issuing from a point, if the radius of curvature be large; for, although there is variation of phase along the length of the infinitesimal strip, the whole effect depends practically upon that of the central parts where the phase is sensibly constant.10
In fig. 17 APQ is the arc of the circle representative of the wave-front of resolution, the centre being at O, and the radius QA being equal to a. B is the point at which the effect is required, distant a + b from O, so that AB = b, AP = s, PQ = ds.
Taking as the standard phase that of the secondary wave from A, we may represent the effect of PQ by
| cos 2π( | t | − | δ | )· ds, |
| r | λ |
where δ = BP − AP is the retardation at B of the wave from P relatively to that from A.
Now
δ = (a + b) s²/2ab (1),
so that, if we write
| 2πδ | = | π(a + b)s² | = | π | v² (2), |
| λ | abλ | 2 |
the effect at B is
| { | abλ | } | ½ | { cos | 2πt | ∫ cos ½πv²·dv + sin | 2πt | ∫ sin ½πv²·dv } (3) |
| 2(a + b) | τ | τ |
the limits of integration depending upon the disposition of the diffracting edges. When a, b, λ are regarded as constant, the first factor may be omitted,—as indeed should be done for consistency’s sake, inasmuch as other factors of the same nature have been omitted already.
The intensity I², the quantity with which we are principally concerned, may thus be expressed
I²= { ∫ cos ½πv²·dv}² + { ∫ sin ½πv²·dv }² (4).
These integrals, taken from v = 0, are known as Fresnel’s integrals; we will denote them by C and S, so that
| C = ∫ | v | cos ½πv²·dv, S = ∫ | v | sin ½πv²·dv (5). |
| 0 | 0 |
When the upper limit is infinity, so that the limits correspond to the inclusion of half the primary wave, C and S are both equal to ½, by a known formula; and on account of the rapid fluctuation of sign the parts of the range beyond very moderate values of v contribute but little to the result.
Ascending series for C and S were given by K. W. Knockenhauer, and are readily investigated. Integrating by parts, we find
| C + iS = ∫ | v | e | i·½πv² | dv = e | i·½πv² | · v − 1⁄3 iπ ∫ | v | e | i·½πv² | dv³; |
| 0 | 0 |
and, by continuing this process,
| C + iS = e | i·½πv² | { v − | iπ | v³ + | iπ | iπ | v5 − | iπ | iπ | iπ | v7 + ... }. |
| 3 | 3 | 5 | 3 | 5 | 7 |
By separation of real and imaginary parts,
| C = M cos ½πv² − N sin ½πv² | } (6), |
| S = M sin ½πv² − N cos ½πv² |
where
| M = | v | − | π²v5 | + | π4v9 | − ... (7), |
| 1 | 3·5 | 3·5·7·9 |
| N = | πv³ | − | π3v7 | + | π5v11 | ... (8). |
| 1·3 | 1·3·5·7 | 1·3·5·7·9·11 |
These series are convergent for all values of v, but are practically useful only when v is small.
Expressions suitable for discussion when v is large were obtained 252 by L. P. Gilbert (Mem. cour. de l’Acad. de Bruxelles, 31, p. 1). Taking
½πv² = u (9),
we may write
| C + iS = | 1 | ∫ | u | eiudu | (10). |
| √(2π) | 0 | √u |
Again, by a known formula,
| 1 | = | 1 | ∫ | ∞ | e−uxdx | (11). |
| √ u | √π | 0 | √x |
Substituting this in (10), and inverting the order of integration, we get
| C + iS = | 1 | ∫ | ∞ | dx | ∫ | u | e | u(i − x) | dx = | 1 | ∫ | ∞ | dx | eu(i − x) − 1 | (12). |
| π√2 | 0 | √x | 0 | π√2 | √x | i − x |
Thus, if we take
| G = | 1 | ∫ | ∞ | e−ux √x · dx | , H = | 1 | ∫ | ∞ | e−ux dx | (13), |
| π√2 | 0 | 1 + x² | π√2 | 0 | √x · (1 + x²) |
C = ½ − G cos u + H sin u, S = ½ − G sin u − H cos u (14).
The constant parts in (14), viz. ½, may be determined by direct integration of (12), or from the observation that by their constitution G and H vanish when u = ∞, coupled with the fact that C and S then assume the value ½.
Comparing the expressions for C, S in terms of M, N, and in terms of G, H, we find that
G = ½ (cos u + sin u) − M, H = ½ (cos u − sin u) + N (15),
formulae which may be utilized for the calculation of G, H when u (or v) is small. For example, when u = 0, M = 0, N = 0, and consequently G = H = ½.
Descending series of the semi-convergent class, available for numerical calculation when u is moderately large, can be obtained from (12) by writing x = uy, and expanding the denominator in powers of y. The integration of the several terms may then be effected by the formula
| ∫ | ∞ | e−y yq−½dy = Γ(q + ½) = (q − ½)(q − 3⁄2) ... ½ √π; |
| 0 |
and we get in terms of v
| G = | 1 | − | 1·3·5 | + | 1·3·5·9 | − ... (16), |
| π²v³ | π4v7 | π6v11 |
| H = | 1 | − | 1·3 | + | 1·3·5·7 | − ... (17). |
| πv | π³v5 | π5v9 |
The corresponding values of C and S were originally derived by A. L. Cauchy, without the use of Gilbert’s integrals, by direct integration by parts.
From the series for G and H just obtained it is easy to verify that
| dH | = − πvG, | dG | = πvH − 1 (18). |
| dv | dv |
We now proceed to consider more particularly the distribution of light upon a screen PBQ near the shadow of a straight edge A. At a point P within the geometrical shadow of the obstacle, the half of the wave to the right of C (fig. 18), the nearest point on the wave-front, is wholly intercepted, and on the left the integration is to be taken from s = CA to s = ∞. If V be the value of v corresponding to CA, viz.
| V = √{ | 2(a + b) | } · CA, (19), |
| abλ |
we may write
| I² = ( ∫ | ∞ | cos ½πv² · dv ) | ² | + ( ∫ | ∞ | sin ½πv² · dv ) | ² | (20), |
| v | v |
or, according to our previous notation,
I²=(½ − Cv)² + (½ − Sv)² = G² + H² (21).
 |
| Fig. 18. |
Now in the integrals represented by G and H every element diminishes as V increases from zero. Hence, as CA increases, viz. as the point P is more and more deeply immersed in the shadow, the illumination continuously decreases, and that without limit. It has long been known from observation that there are no bands on the interior side of the shadow of the edge.
The law of diminution when V is moderately large is easily expressed with the aid of the series (16), (17) for G, H. We have ultimately G = 0, H = (πV)−1, so that
I² = 1/π²V²,
or the illumination is inversely as the square of the distance from the shadow of the edge.
For a point Q outside the shadow the integration extends over more than half the primary wave. The intensity may be expressed by
I² = (½ + Cv)² + (½ + Sv)² (22);
and the maxima and minima occur when
| (½ + Cv) | dC | + (½ + Sv) | dS | = 0, |
| dV | dV |
whence
sin ½πV² + cos ½πV² = G (23).
When V = 0, viz. at the edge of the shadow, I² = ½; when V = ∞, I² = 2, on the scale adopted. The latter is the intensity due to the uninterrupted wave. The quadrupling of the intensity in passing outwards from the edge of the shadow is, however, accompanied by fluctuations giving rise to bright and dark bands. The position of these bands determined by (23) may be very simply expressed when V is large, for then sensibly G = 0, and
½πV² = ¾π + nπ (24),
n being an integer. In terms of δ, we have from (2)
δ = (3⁄8 + ½n)λ (25).
The first maximum in fact occurs when δ = 3⁄8λ − .0046λ, and the first minimum when δ = 7⁄8λ − .0016λ, the corrections being readily obtainable from a table of G by substitution of the approximate value of V.
The position of Q corresponding to a given value of V, that is, to a band of given order, is by (19)
| BQ = | a + b | AD = V √ { | bλ(a + b) | } (26). |
| a | 2a |
By means of this expression we may trace the locus of a band of given order as b varies. With sufficient approximation we may regard BQ and b as rectangular co-ordinates of Q. Denoting them by x, y, so that AB is axis of y and a perpendicular through A the axis of x, and rationalizing (26), we have
2ax² − V²λy² − V²aλy = 0,
which represents a hyperbola with vertices at O and A.
From (24), (26) we see that the width of the bands is of the order √{bλ(a + b)/a}. From this we may infer the limitation upon the width of the source of light, in order that the bands may be properly formed. If ω be the apparent magnitude of the source seen from A, ωb should be much smaller than the above quantity, or
ω < √{λ(a + b)/ab} (27).
If a be very great in relation to b, the condition becomes
ω < √(λ / b) (28).
so that if b is to be moderately great (1 metre), the apparent magnitude of the sun must be greatly reduced before it can be used as a source. The values of V for the maxima and minima of intensity, and the magnitudes of the latter, were calculated by Fresnel. An extract from his results is given in the accompanying table.
| V | I² | |
| First maximum | 1.2172 | 2.7413 |
| First minimum | 1.8726 | 1.5570 |
| Second maximum | 2.3449 | 2.3990 |
| Second minimum | 2.7392 | 1.6867 |
| Third maximum. | 3.0820 | 2.3022 |
| Third minimum | 3.3913 | 1.7440 |
A very thorough investigation of this and other related questions, accompanied by fully worked-out tables of the functions concerned, will be found in a paper by E. Lommel (Abh. bayer. Akad. d. Wiss. II. CI., 15, Bd., iii. Abth., 1886).
When the functions C and S have once been calculated, the discussion of various diffraction problems is much facilitated by the idea, due to M. A. Cornu (Journ. de Phys., 1874, 3, p. 1; a similar suggestion was made independently by G. F. Fitzgerald), of exhibiting as a curve the relationship between C and S, considered as the rectangular co-ordinates (x, y) of a point. Such a curve is shown in fig. 19, where, according to the definition (5) of C, S,
| x = ∫ | v | cos ½πv²·dv, y = ∫ | v | sin ½πv²·dv (29). |
| 0 | 0 |
The origin of co-ordinates O corresponds to v = 0; and the asymptotic points J, J′, round which the curve revolves in an ever-closing spiral, correspond to v = ±∞.
The intrinsic equation, expressing the relation between the arc σ (measured from O) and the inclination φ of the tangent at any points to the axis of x, assumes a very simple form. For
dx = cos ½πv²·dv, dy = sin ½πv²·dv;
so that
σ = ∫ √(dx² + dy²) = v, (30),
φ = tan−1(dy/dx) = ½πv² (31).
Accordingly,
φ = ½πσ² (32);
and for the curvature,
dφ / dσ = πσ (33).
 |
| Fig. 19. |
Cornu remarks that this equation suffices to determine the general character of the curve. For the osculating circle at any point includes the whole of the curve which lies beyond; and the successive convolutions envelop one another without intersection.
The utility of the curve depends upon the fact that the elements of arc represent, in amplitude and phase, the component vibrations due to the corresponding portions of the primary wave-front. For by (30) dσ = dv, and by (2) dv is proportional to ds. Moreover by (2) and (31) the retardation of phase of the elementary vibration from PQ (fig. 17) is 2πδ/λ, or φ. Hence, in accordance with the rule for compounding vector quantities, the resultant vibration at B, due to any finite part of the primary wave, is represented in amplitude and phase by the chord joining the extremities of the corresponding arc (σ2 − σ1).
In applying the curve in special cases of diffraction to exhibit the effect at any point P (fig. 18) the centre of the curve O is to be considered to correspond to that point C of the primary wave-front which lies nearest to P. The operative part, or parts, of the curve are of course those which represent the unobstructed portions of the primary wave.
Let us reconsider, following Cornu, the diffraction of a screen unlimited on one side, and on the other terminated by a straight edge. On the illuminated side, at a distance from the shadow, the vibration is represented by JJ′. The co-ordinates of J, J′ being (½, ½), (−½, −½), I² is 2; and the phase is 1⁄8 period in arrear of that of the element at O. As the point under contemplation is supposed to approach the shadow, the vibration is represented by the chord drawn from J to a point on the other half of the curve, which travels inwards from J′ towards O. The amplitude is thus subject to fluctuations, which increase as the shadow is approached. At the point O the intensity is one-quarter of that of the entire wave, and after this point is passed, that is, when we have entered the geometrical shadow, the intensity falls off gradually to zero, without fluctuations. The whole progress of the phenomenon is thus exhibited to the eye in a very instructive manner.
We will next suppose that the light is transmitted by a slit, and inquire what is the effect of varying the width of the slit upon the illumination at the projection of its centre. Under these circumstances the arc to be considered is bisected at O, and its length is proportional to the width of the slit. It is easy to see that the length of the chord (which passes in all cases through O) increases to a maximum near the place where the phase-retardation is 3⁄8 of a period, then diminishes to a minimum when the retardation is about 7⁄8 of a period, and so on.
If the slit is of constant width and we require the illumination at various points on the screen behind it, we must regard the arc of the curve as of constant length. The intensity is then, as always, represented by the square of the length of the chord. If the slit be narrow, so that the arc is short, the intensity is constant over a wide range, and does not fall off to an important extent until the discrepancy of the extreme phases reaches about a quarter of a period.
We have hitherto supposed that the shadow of a diffracting obstacle is received upon a diffusing screen, or, which comes to nearly the same thing, is observed with an eye-piece. If the eye, provided if necessary with a perforated plate in order to reduce the aperture, be situated inside the shadow at a place where the illumination is still sensible, and be focused upon the diffracting edge, the light which it receives will appear to come from the neighbourhood of the edge, and will present the effect of a silver lining. This is doubtless the explanation of a “pretty optical phenomenon, seen in Switzerland, when the sun rises from behind distant trees standing on the summit of a mountain.”11
II. Dynamical Theory of Diffraction.—The explanation of diffraction phenomena given by Fresnel and his followers is independent of special views as to the nature of the aether, at least in its main features; for in the absence of a more complete foundation it is impossible to treat rigorously the mode of action of a solid obstacle such as a screen. But, without entering upon matters of this kind, we may inquire in what manner a primary wave may be resolved into elementary secondary waves, and in particular as to the law of intensity and polarization in a secondary wave as dependent upon its direction of propagation, and upon the character as regards polarization of the primary wave. This question was treated by Stokes in his “Dynamical Theory of Diffraction” (Camb. Phil. Trans., 1849) on the basis of the elastic solid theory.
Let x, y, z be the co-ordinates of any particle of the medium in its natural state, and χ, η, ζ the displacements of the same particle at the end of time t, measured in the directions of the three axes respectively. Then the first of the equations of motion may be put under the form
| d²ξ | = b² ( | d²ξ | + | d²ξ | + | d²ξ | ) + (a² − b²) | d² | ( | d²ξ | + | d²η | + | d²ζ | ), |
| dt² | dx² | dy² | dz² | dx | dx² | dy² | dz² |
where a² and b² denote the two arbitrary constants. Put for shortness
| d²ξ | + | d²η | + | d²ζ | ≈ δ (1), |
| dx² | dy² | dz² |
and represent by Δ²χ the quantity multiplied by b². According to this notation, the three equations of motion are
| d²ξ | b²Δ²ξ + (a² − b²) | dδ | } (2). |
| dt² | dx | ||
| d²η | b²Δ²η + (a² − b²) | dδ | |
| dt² | dy | ||
| d²ζ | b²Δ²ζ + (a² − b²) | dδ | |
| dt² | dz |
It is to be observed that S denotes the dilatation of volume of the element situated at (x, y, z). In the limiting case in which the medium is regarded as absolutely incompressible δ vanishes; but, in order that equations (2) may preserve their generality, we must suppose a at the same time to become infinite, and replace a²δ by a new function of the co-ordinates.
These equations simplify very much in their application to plane waves. If the ray be parallel to OX, and the direction of vibration parallel to OZ, we have ξ = 0, η = 0, while ζ is a function of x and t only. Equation (1) and the first pair of equations (2) are thus satisfied identically. The third equation gives
| d²ζ | = b² | d²ζ | (3), |
| dt² | dx² |
of which the solution is
ζ = ƒ(bt − x) (4),
where ƒ is an arbitrary function.
The question as to the law of the secondary waves is thus answered by Stokes. “Let ξ = 0, η = 0, ζ = ƒ(bt − x) be the displacements corresponding to the incident light; let O1 be any point in the plane P (of the wave-front), dS an element of that plane adjacent to O1, and consider the disturbance due to that portion only of the incident disturbance which passes continually across dS. Let O be any point in the medium situated at a distance from the point O1 which is large in comparison with the length of a wave; let O1O = r, and let this line make an angle θ with the direction of propagation of the incident light, or the axis of x, and φ with the direction of vibration, or axis of z. Then the displacement at O will take place in a direction perpendicular to O1O, and lying in the plane ZO1O; and, if ζ′ be the displacement at O, reckoned positive in the direction nearest to that in which the incident vibrations are reckoned positive,
| ζ′ = | dS | (1 + cos θ) sin φ ƒ′(bt − r). |
| 4πr |
In particular, if
| ƒ(bt − x) = c sin | 2π | (bt − x) (5), |
| λ |
we shall have
| ζ′ = | cdS | (1 + cos θ) sin φcos | 2π | (bt − r) (6).” |
| 2λr | λ |
It is then verified that, after integration with respect to dS, (6) gives the same disturbance as if the primary wave had been supposed to pass on unbroken.
The occurrence of sin φ as a factor in (6) shows that the relative intensities of the primary light and of that diffracted in the direction θ depend upon the condition of the former as regards polarization. If the direction of primary vibration be perpendicular to the plane of diffraction (containing both primary and secondary rays), sin φ = 1; but, if the primary vibration be in the plane of diffraction, sin φ = cos θ. This result was employed by Stokes as a criterion of the direction of vibration; and his experiments, conducted with gratings, led him to the conclusion that the vibrations 254 of polarized light are executed in a direction perpendicular to the plane of polarization.
The factor (1 + cos θ) shows in what manner the secondary disturbance depends upon the direction in which it is propagated with respect to the front of the primary wave.
If, as suffices for all practical purposes, we limit the application of the formulae to points in advance of the plane at which the wave is supposed to be broken up, we may use simpler methods of resolution than that above considered. It appears indeed that the purely mathematical question has no definite answer. In illustration of this the analogous problem for sound may be referred to. Imagine a flexible lamina to be introduced so as to coincide with the plane at which resolution is to be effected. The introduction of the lamina (supposed to be devoid of inertia) will make no difference to the propagation of plane parallel sonorous waves through the position which it occupies. At every point the motion of the lamina will be the same as would have occurred in its absence, the pressure of the waves impinging from behind being just what is required to generate the waves in front. Now it is evident that the aerial motion in front of the lamina is determined by what happens at the lamina without regard to the cause of the motion there existing. Whether the necessary forces are due to aerial pressures acting on the rear, or to forces directly impressed from without, is a matter of indifference. The conception of the lamina leads immediately to two schemes, according to which a primary wave may be supposed to be broken up. In the first of these the element dS, the effect of which is to be estimated, is supposed to execute its actual motion, while every other element of the plane lamina is maintained at rest. The resulting aerial motion in front is readily calculated (see Rayleigh, Theory of Sound, § 278); it is symmetrical with respect to the origin, i.e. independent of θ. When the secondary disturbance thus obtained is integrated with respect to dS over the entire plane of the lamina, the result is necessarily the same as would have been obtained had the primary wave been supposed to pass on without resolution, for this is precisely the motion generated when every element of the lamina vibrates with a common motion, equal to that attributed to dS. The only assumption here involved is the evidently legitimate one that, when two systems of variously distributed motion at the lamina are superposed, the corresponding motions in front are superposed also.
The method of resolution just described is the simplest, but it is only one of an indefinite number that might be proposed, and which are all equally legitimate, so long as the question is regarded as a merely mathematical one, without reference to the physical properties of actual screens. If, instead of supposing the motion at dS to be that of the primary wave, and to be zero elsewhere, we suppose the force operative over the element dS of the lamina to be that corresponding to the primary wave, and to vanish elsewhere, we obtain a secondary wave following quite a different law. In this case the motion in different directions varies as cosθ, vanishing at right angles to the direction of propagation of the primary wave. Here again, on integration over the entire lamina, the aggregate effect of the secondary waves is necessarily the same as that of the primary.
In order to apply these ideas to the investigation of the secondary wave of light, we require the solution of a problem, first treated by Stokes, viz. the determination of the motion in an infinitely extended elastic solid due to a locally applied periodic force. If we suppose that the force impressed upon the element of mass D dx dy dz is
DZ dx dy dz,
being everywhere parallel to the axis of Z, the only change required in our equations (1), (2) is the addition of the term Z to the second member of the third equation (2). In the forced vibration, now under consideration, Z, and the quantities ξ, η, ζ, δ expressing the resulting motion, are to be supposed proportional to eint, where i = √(-1), and n = 2π/τ, τ being the periodic time. Under these circumstances the double differentiation with respect to t of any quantity is equivalent to multiplication by the factor -n², and thus our equations take the form
| (b²Δ² + n²)ξ + (a² − b²) | dδ | = 0 | } (7). |
| dx | |||
| (b²Δ² + n²)η + (a² − b²) | dδ | = 0 | |
| dy | |||
| (b²Δ² + n²)ζ + (a² − b²) | dδ | = −Z | |
| dz |
It will now be convenient to introduce the quantities.ω1, ω2, ω3 which express the rotations of the elements of the medium round axes parallel to those of co-ordinates, in accordance with the equations
| ω3 = | dξ | − | dη | , ω1 = | dη | − | dζ | , ω2 | dζ | − | dξ | (8). |
| dy | dx′ | dz | dy′ | dx | dz′ |
In terms of these we obtain from (7), by differentiation and subtraction,
| (b²Δ² + n²) ω3 = 0 | } (9). |
| (b²Δ² + n²) ω1 = dZ/dy | |
| (b²Δ² + n²) ω2 = −dZ/dx |
The first of equations (9) gives
ω3 = 0 (10).
For ω1, we have
| ω1 = | 1 | ∫∫∫ | dZ | e−ikr | dx dy dz (11), |
| 4πb² | dy | r |
where r is the distance between the element dx dy dz and the point where ω1 is estimated, and
k = n/b = 2π/λ (12),
λ being the wave-length.
(This solution may be verified in the same manner as Poisson’s theorem, in which k = 0.)
We will now introduce the supposition that the force Z acts only within a small space of volume T, situated at (x, y, z), and for simplicity suppose that it is at the origin of co-ordinates that the rotations are to be estimated. Integrating by parts in (11), we get
| ∫ | e−ikr | dZ | dy = [ Z | e−ikr | ] − ∫ Z | d | ( | e−ikr | ) dy, |
| r | dy | r | dy | r |
in which the integrated terms at the limits vanish, Z being finite only within the region T. Thus
| ω1 = | 1 | ∫∫∫ Z | d | ( | e−ikr | ) dx dy dz. |
| 4πb² | dy | r |
Since the dimensions of T are supposed to be very small in comparison with λ, the factor d/dy (e−ikr/r) is sensibly constant; so that, if Z stand for the mean value of Z over the volume T, we may write
| ω1 = | TZ | · | y | · | d | ( | e−ikr | ) (13). |
| 4πb² | r | dr | r |
In like manner we find
| ω2 = − | TZ | · | x | · | d | ( | e−ikr | ) (14). |
| 4πb² | r | dr | r |
From (10), (13), (14) we see that, as might have been expected, the rotation at any point is about an axis perpendicular both to the direction of the force and to the line joining the point to the source of disturbance. If the resultant rotation be ω, we have
| ω = | TZ | · | √(x² + y²) | · | d | ( | e−ikr | ) = | TZ sin φ | d | ( | e−ikr | ), |
| 4πb² | r | dr | r | 4πb² | dr | r |
φ denoting the angle between r and z. In differentiating e−ikr/r with respect to r, we may neglect the term divided by r² as altogether insensible, kr being an exceedingly great quantity at any moderate distance from the origin of disturbance. Thus
| ω = | −ik · TZ sin φ | · | e−ikr | (15), |
| 4πb² | r |
which completely determines the rotation at any point. For a disturbing force of given integral magnitude it is seen to be everywhere about an axis perpendicular to r and the direction of the force, and in magnitude dependent only upon the angle (φ) between these two directions and upon the distance (r).
The intensity of light is, however, more usually expressed in terms of the actual displacement in the plane of the wave. This displacement, which we may denote by ζ′, is in the plane containing z and r, and perpendicular to the latter. Its connexion with ωis expressed by ω = dζ′/dr; so that
| ζ′ = | TZ sin φ | · | e′ (at−kr) | (16), |
| 4πb² | r |
where the factor eint is restored.
Retaining only the real part of (16), we find, as the result of a local application of force equal to
DTZ cos nt (17),
the disturbance expressed by
| ζ′ = | TZ sin φ | · | cos (nt − kr) | (18). |
| 4πb² | r |
The occurrence of sin φ shows that there is no disturbance radiated in the direction of the force, a feature which might have been anticipated from considerations of symmetry.
We will now apply (18) to the investigation of a law of secondary disturbance, when a primary wave
ζ = sin(nt − kx) (19)
is supposed to be broken up in passing the plane x = 0. The first step is to calculate the force which represents the reaction between the parts of the medium separated by x = 0. The force operative upon the positive half is parallel to OZ, and of amount per unit of area equal to
−b²D dζ/dx = b²kD cos nt;
and to this force acting over the whole of the plane the actual motion on the positive side may be conceived to be due. The 255 secondary disturbance corresponding to the element dS of the plane may be supposed to be that caused by a force of the above magnitude acting over dS and vanishing elsewhere; and it only remains to examine what the result of such a force would be.
Now it is evident that the force in question, supposed to act upon the positive half only of the medium, produces just double of the effect that would be caused by the same force if the medium were undivided, and on the latter supposition (being also localized at a point) it comes under the head already considered. According to (18), the effect of the force acting at dS parallel to OZ, and of amount equal to
2b²kD dS cos nt,
will be a disturbance
| ζ′ = | dS sin φ | cos (nt − kr) (20), |
| λr |
regard being had to (12). This therefore expresses the secondary disturbance at a distance r and in a direction making an angle φ with OZ (the direction of primary vibration) due to the element dS of the wave-front.
The proportionality of the secondary disturbance to sin φ is common to the present law and to that given by Stokes, but here there is no dependence upon the angle θ between the primary and secondary rays. The occurrence of the factor λr−1, and the necessity of supposing the phase of the secondary wave accelerated by a quarter of an undulation, were first established by Archibald Smith, as the result of a comparison between the primary wave, supposed to pass on without resolution, and the integrated effect of all the secondary waves (§ 2). The occurrence of factors such as sin φ, or ½(1 + cos θ), in the expression of the secondary wave has no influence upon the result of the integration, the effects of all the elements for which the factors differ appreciably from unity being destroyed by mutual interference.
The choice between various methods of resolution, all mathematically admissible, would be guided by physical considerations respecting the mode of action of obstacles. Thus, to refer again to the acoustical analogue in which plane waves are incident upon a perforated rigid screen, the circumstances of the case are best represented by the first method of resolution, leading to symmetrical secondary waves, in which the normal motion is supposed to be zero over the unperforated parts. Indeed, if the aperture is very small, this method gives the correct result, save as to a constant factor. In like manner our present law (20) would apply to the kind of obstruction that would be caused by an actual physical division of the elastic medium, extending over the whole of the area supposed to be occupied by the intercepting screen, but of course not extending to the parts supposed to be perforated.
On the electromagnetic theory, the problem of diffraction becomes definite when the properties of the obstacle are laid down. The simplest supposition is that the material composing the obstacle is perfectly conducting, i.e. perfectly reflecting. On this basis A. J. W. Sommerfeld (Math. Ann., 1895, 47, p. 317), with great mathematical skill, has solved the problem of the shadow thrown by a semi-infinite plane screen. A simplified exposition has been given by Horace Lamb (Proc. Lond. Math. Soc., 1906, 4, p. 190). It appears that Fresnel’s results, although based on an imperfect theory, require only insignificant corrections. Problems not limited to two dimensions, such for example as the shadow of a circular disk, present great difficulties, and have not hitherto been treated by a rigorous method; but there is no reason to suppose that Fresnel’s results would be departed from materially.
1 The descending series for J0(z) appears to have been first given by Sir W. Hamilton in a memoir on “Fluctuating Functions,” Roy. Irish Trans., 1840.
2 Airy, loc. cit. “Thus the magnitude of the central spot is diminished, and the brightness of the rings increased, by covering the central parts of the object-glass.”
3 ”Man kann daraus schliessen, was moglicher Weise durch Mikroskope noch zu sehen ist. Ein mikroskopischer Gegenstand z. B, dessen Durchmesser = (λ) ist, und der aus zwei Theilen besteht, kann nicht mehr als aus zwei Theilen bestehend erkannt werden. Dieses zeigt uns eine Grenze des Sehvermogens durch Mikroskope” (Gilbert’s Ann. 74, 337). Lord Rayleigh has recorded that he was himself convinced by Fraunhofer’s reasoning at a date antecedent to the writings of Helmholtz and Abbe.
4 The last sentence is repeated from the writer’s article “Wave Theory” in the 9th edition of this work, but A. A. Michelson’s ingenious échelon grating constitutes a realization in an unexpected manner of what was thought to be impracticable.—[R.]
5 Compare also F. F. Lippich, Pogg. Ann. cxxxix. p. 465, 1870; Rayleigh, Nature (October 2, 1873).
6 The power of a grating to construct light of nearly definite wave-length is well illustrated by Young’s comparison with the production of a musical note by reflection of a sudden sound from a row of palings. The objection raised by Herschel (Light, § 703) to this comparison depends on a misconception.
7 It must not be supposed that errors of this order of magnitude are unobjectionable in all cases. The position of the middle of the bright band representative of a mathematical line can be fixed with a spider-line micrometer within a small fraction of the width of the band, just as the accuracy of astronomical observations far transcends the separating power of the instrument.
8 “In the same way we may conclude that in flat gratings any departure from a straight line has the effect of causing the dust in the slit and the spectrum to have different foci—a fact sometimes observed.” (Rowland, “On Concave Gratings for Optical Purposes,” Phil. Mag., September 1883).
9 On account of inequalities in the atmosphere giving a variable refraction, the light from a star would be irregularly distributed over a screen. The experiment is easily made on a laboratory scale, with a small source of light, the rays from which, in their course towards a rather distant screen, are disturbed by the neighbourhood of a heated body. At a moment when the eye, or object-glass of a telescope, occupies a dark position, the star vanishes. A fraction of a second later the aperture occupies a bright place, and the star reappears. According to this view the chromatic effects depend entirely upon atmospheric dispersion.
10 In experiment a line of light is sometimes substituted for a point in order to increase the illumination. The various parts of the line are here independent sources, and should be treated accordingly. To assume a cylindrical form of primary wave would be justifiable only when there is synchronism among the secondary waves issuing from the various centres.
11 H. Necker (Phil. Mag., November 1832); Fox Talbot (Phil. Mag., June 1833). “When the sun is about to emerge ... every branch and leaf is lighted up with a silvery lustre of indescribable beauty.... The birds, as Mr Necker very truly describes, appear like flying brilliant sparks.” Talbot ascribes the appearance to diffraction; and he recommends the use of a telescope.
DIFFUSION (from the Lat. diffundere; dis-, asunder, and fundere, to pour out), in general, a spreading out, scattering or circulation; in physics the term is applied to a special phenomenon, treated below.
1. General Description.—When two different substances are placed in contact with each other they sometimes remain separate, but in many cases a gradual mixing takes place. In the case where both the substances are gases the process of mixing continues until the result is a uniform mixture. In other cases the proportions in which two different substances can mix lie between certain fixed limits, but the mixture is distinguished from a chemical compound by the fact that between these limits the composition of the mixture is capable of continuous variation, while in chemical compounds, the proportions of the different constituents can only have a discrete series of numerical values, each different ratio representing a different compound. If we take, for example, air and water in the presence of each other, air will become dissolved in the water, and water will evaporate into the air, and the proportions of either constituent absorbed by the other will vary continuously. But a limit will come when the air will absorb no more water, and the water will absorb no more air, and throughout the change a definite surface of separation will exist between the liquid and the gaseous parts. When no surface of separation ever exists between two substances they must necessarily be capable of mixing in all proportions. If they are not capable of mixing in all proportions a discontinuous change must occur somewhere between the regions where the substances are still unmixed, thus giving rise to a surface of separation.
The phenomena of mixing thus involves the following processes:—(1) A motion of the substances relative to one another throughout a definite region of space in which mixing is taking place. This relative motion is called “diffusion.” (2) The passage of portions of the mixing substances across the surface of separation when such a surface exists. These surface actions are described under various terms such as solution, evaporation, condensation and so forth. For example, when a soluble salt is placed in a liquid, the process which occurs at the surface of the salt is called “solution,” but the salt which enters the liquid by solution is transported from the surface into the interior of the liquid by “diffusion.”
Diffusion may take place in solids, that is, in regions occupied by matter which continues to exhibit the properties of the solid state. Thus if two liquids which can mix are separated by a membrane or partition, the mixing may take place through the membrane. If a solution of salt is separated from pure water by a sheet of parchment, part of the salt will pass through the parchment into the water. If water and glycerin are separated in this way most of the water will pass into the glycerin and a little glycerin will pass through in the opposite direction, a property frequently used by microscopists for the purpose of gradually transferring minute algae from water into glycerin. A still more interesting series of examples is afforded by the passage of gases through partitions of metal, notably the passage of hydrogen through platinum and palladium at high temperatures. When the process is considered with reference to a membrane or partition taken as a whole, the passage of a substance from one side to the other is commonly known as “osmosis” or “transpiration” (see Solution), but what occurs in the material of the membrane itself is correctly described as diffusion.
Simple cases of diffusion are easily observed qualitatively. If a solution of a coloured salt is carefully introduced by a funnel into the bottom of a jar containing water, the two portions will at first be fairly well defined, but if the mixture can exist in all proportions, the surface of separation will gradually disappear; and the rise of the colour into the upper part and its gradual weakening in the lower part, may be watched for days, weeks or even longer intervals. The diffusion of a strong aniline colouring matter into the interior of gelatine is easily observed, and is commonly seen in copying apparatus. Diffusion of gases may be shown to exist by taking glass jars containing vapours of hydrochloric acid and ammonia, and placing them in communication with the heavier gas downmost. The precipitation of ammonium chloride shows that diffusion exists, though the chemical action prevents this example from forming a typical case of diffusion. Again, when a film of Canada balsam is enclosed between glass plates, the disappearance during a few weeks of small air bubbles enclosed in the balsam can be watched under the microscope.
In fluid media, whether liquids or gases, the process of mixing is greatly accelerated by stirring or agitating the fluids, and liquids which might take years to mix if left to themselves can thus be mixed in a few seconds. It is necessary to carefully distinguish the effects of agitation from those of diffusion proper. By shaking up two liquids which do not mix we split them up into a large number of different portions, and so greatly increase the area of the surface of separation, besides decreasing the thicknesses of the various portions. But even when we produce the appearance of a uniform turbid mixture, the small portions remain quite distinct. If however the fluids can really mix, the final process must in every case depend on diffusion, and all we do by shaking is to increase the sectional area, and decrease the thickness of the diffusing portions, thus rendering the completion of the operation more rapid. If a gas is shaken up in a liquid the process of absorption of the bubbles is also accelerated by capillary action, as occurs in an ordinary sparklet bottle. To state the matter precisely, however finely two fluids have been 256 subdivided by agitation, the molecular constitution of the different portions remains unchanged. The ultimate process by which the individual molecules of two different substances become mixed, producing finally a homogeneous mixture, is in every case diffusion. In other words, diffusion is that relative motion of the molecules of two different substances by which the proportions of the molecules in any region containing a finite number of molecules are changed.
In order, therefore, to make accurate observations of diffusion in fluids it is necessary to guard against any cause which may set up currents; and in some cases this is exceedingly difficult. Thus, if gas is absorbed at the upper surface of a liquid, and if the gaseous solution is heavier than the pure liquid, currents may be set up, and a steady state of diffusion may cease to exist. This has been tested experimentally by C. G. von Hüfner and W. E. Adney. The same thing may happen when a gas is evolved into a liquid at the surface of a solid even if no bubbles are formed; thus if pieces of aluminium are placed in caustic soda, the currents set up by the evolution of hydrogen are sufficient to set the aluminium pieces in motion, and it is probable that the motions of the Diatomaceae are similarly caused by the evolution of oxygen. In some pairs of substances diffusion may take place more rapidly than in others. Of course the progress of events in any experiment necessarily depends on various causes, such as the size of the containing vessels, but it is easy to see that when experiments with different substances are carried out under similar conditions, however these “similar conditions” be defined, the rates of diffusion must be capable of numerical comparison, and the results must be expressible in terms of at least one physical quantity, which for any two substances can be called their coefficient of diffusion. How to select this quantity we shall see later.
2 Quantitative Methods of observing Diffusion.—The simplest plan of determining the progress of diffusion between two liquids would be to draw off and examine portions from different strata at some stage in the process; the disturbance produced would, however, interfere with the subsequent process of diffusion, and the observations could not be continued. By placing in the liquid column hollow glass beads of different average densities, and observing at what height they remain suspended, it is possible to trace the variations of density of the liquid column at different depths, and different times. In this method, which was originally introduced by Lord Kelvin, difficulties were caused by the adherence of small air bubbles to the beads.
In general, optical methods are the most capable of giving exact results, and the following may be distinguished, (a) By refraction in a horizontal plane. If the containing vessel is in the form of a prism, the deviation of a horizontal ray of light in passing through the prism determines the index of refraction, and consequently the density of the stratum through which the ray passes, (b) By refraction in a vertical plane. Owing to the density varying with the depth, a horizontal ray entering the liquid also undergoes a small vertical deviation, being bent downwards towards the layers of greater density. The observation of this vertical deviation determines not the actual density, but its rate of variation with the depth, i.e. the “density gradient” at any point, (c) By the saccharimeter. In the cases of solutions of sugar, which cause rotation of the plane of polarized light, the density of the sugar at any depth may be determined by observing the corresponding angle of rotation, this was done originally by W. Voigt.
3. Elementary Definitions of Coefficient of Diffusion.—The simplest case of diffusion is that of a substance, say a gas, diffusing in the interior of a homogeneous solid medium, which remains at rest, when no external forces act on the system. We may regard it as the result of experience that: (1) if the density of the diffusing substance is everywhere the same no diffusion takes place, and (2) if the density of the diffusing substance is different at different points, diffusion will take place from places of greater to those of lesser density, and will not cease until the density is everywhere the same. It follows that the rate of flow of the diffusing substance at any point in any direction must depend on the density gradient at that point in that direction, i.e. on the rate at which the density of the diffusing substance decreases as we move in that direction. We may define the coefficient of diffusion as the ratio of the total mass per unit area which flows across any small section, to the rate of decrease of the density per unit distance in a direction perpendicular to that section.
In the case of steady diffusion parallel to the axis of x, if ρ be the density of the diffusing substance, and q the mass which flows across a unit of area in a plane perpendicular to the axis of x, then the density gradient is -dρ/dx and the ratio of q to this is called the “coefficient of diffusion.” By what has been said this ratio remains finite, however small the actual gradient and flow may be., and it is natural to assume, at any rate as a first approximation, that it is constant as far as the quantities in question are concerned. Thus if the coefficient of diffusion be denoted by K we have q= -K(dρ/dx).
Further, the rate at which the quantity of substance is increasing in an element between the distances x and x+dx is equal to the difference of the rates of flow in and out of the two faces, whence as in hydrodynamics, we have dρ/dt =-dq/dx.
It follows that the equation of diffusion in this case assumes the form
| dρ | = | d | ( K | dρ | ), |
| dt | dx | dx |
which is identical with the equations representing conduction of heat, flow of electricity and other physical phenomena. For motion in three dimensions we have in like manner
| dρ | = | d | ( K | dρ | ) + | d | ( K | dρ | ) + | d | ( K | dρ | ); |
| dt | dx | dx | dy | dy | dz | dz |
and the corresponding equations in electricity and heat for anisotropic substances would be available to account for any parallel phenomena, which may arise, or might be conceived, to exist in connexion with diffusion through a crystalline solid.
In the case of a very dilute solution, the coefficient of diffusion of the dissolved substance can be defined in the same way as when the diffusion takes place in a solid, because the effects of diffusion will not have any perceptible influence on the solvent, and the latter may therefore be regarded as remaining practically at rest. But in most cases of diffusion between two fluids, both of the fluids are in motion, and hence there is far greater difficulty in determining the motion, and even in defining the coefficient of diffusion. It is important to notice in the first instance, that it is only the relative motion of the two substances which constitutes diffusion. Thus when a current of air is blowing, under ordinary circumstances the changes which take place are purely mechanical, and do not depend on the separate diffusions of the oxygen and nitrogen of which the air is mainly composed. It is only when two gases are flowing with unequal velocity, that is, when they have a relative motion, that these changes of relative distribution, which are called diffusion, take place. The best way out of the difficulty is to investigate the separate motions of the two fluids, taking account of the mechanical actions exerted on them, and supposing that the mutual action of the fluids causes either fluid to resist the relative motion of the other.
4. The Coefficient of Resistance.—Let us call the two diffusing fluids A and B. If B were absent, the motion of the fluid A would be determined entirely by the variations of pressure of the fluid A, and by the external forces, such as that due to gravity acting on A. Similarly if A were absent, the motion of B would be determined entirely by the variations of pressure due to the fluid B, and by the external forces acting on B. When both fluids are mixed together, each fluid tends to resist the relative motion of the other, and by the law of equality of action and reaction, the resistance which A experiences from B is everywhere equal and opposite to the resistance which B experiences from A. If the amount of this resistance per unit volume be divided by the relative velocity of the two fluids, and also by the product of their densities, the quotient is called the “coefficient of resistance.” If then ρ1, ρ2 are the densities cf the two fluids, u1, u2 their velocities, C the coefficient of resistance, then the portion of the fluid A contained in a small element of volume v will experience from the fluid B a resistance Cρ1ρ2v(u1 − u2), and the fluid B contained in the same volume element will experience from the fluid A an equal and opposite resistance, Cρ1ρ2v(u2 − u1).
This definition implies the following laws of resistance to diffusion, which must be regarded as based on experience, and not as self-evident truths: (1) each fluid tends to assume, so far as diffusion is concerned, the same equüibrium distribution that it would assume if its motion were unresisted by the presence of the other fluid. (Of course, the mutual attraction of gravitation of the two fluids might affect the final distribution, but this is practically negligible. Leaving such actions as this out of 257 account the following statement is correct.) In a state of equilibrium, the density of each fluid at any point thus depends only on the partial pressure of that fluid alone, and is the same as if the other fluids were absent. It does not depend on the partial pressures of the other fluids. If this were not the case, the resistance to diffusion would be analogous to friction, and would contain terms which were independent of the relative velocity u2 − u1. (2) For slow motions the resistance to diffusion is (approximately at any rate) proportional to the relative velocity. (3) The coefficient of resistance C is not necessarily always constant; it may, for example, and, in general, does, depend on the temperature.
If we form the equations of hydrodynamics for the different fluids occurring in any mixture, taking account of diffusion, but neglecting viscosity, and using suffixes 1, 2 to denote the separate fluids, these assume the form given by James Clerk Maxwell (“Diffusion,” in Ency. Brit., 9th ed.):—
| ρ1 | Du1 | + | dp1 | − X1ρ1 + C12ρ1ρ2(u1 − u2) + &c. = 0, |
| Dt | dx |
where
| Du1 | = | du1 | + u1 | du1 | + v1 | du1 | + w1 | du1 | , |
| Dt | dt | dx | dy | dz |
and these equations imply that when diffusion and other motions cease, the fluids satisfy the separate conditions of equilibrium dp1/dx − X1ρ1 = 0. The assumption made in the following account is that terms such as Du1/Dt may be neglected in the cases considered.
A further property based on experience is that the motions set up in a mixture by diffusion are very slow compared with those set up by mechanical actions, such as differences of pressure. Thus, if two gases at equal temperature and pressure be allowed to mix by diffusion, the heavier gas being below the lighter, the process will take a long time; on the other hand, if two gases, or parts of the same gas, at different pressures be connected, equalization of pressure will take place almost immediately. It follows from this property that the forces required to overcome the “inertia” of the fluids in the motions due to diffusion are quite imperceptible. At any stage of the process, therefore, any one of the diffusing fluids may be regarded as in equilibrium under the action of its own partial pressure, the external forces to which it is subjected and the resistance to diffusion of the other fluids.
5. Slow Diffusion of two Gases. Relation between the Coefficients of Resistance and of Diffusion.—We now suppose the diffusing substances to be two gases which obey Boyle’s law, and that diffusion takes place in a closed cylinder or tube of unit sectional area at constant temperature, the surfaces of equal density being perpendicular to the axis of the cylinder, so that the direction of diffusion is along the length of the cylinder, and we suppose no external forces, such as gravity, to act on the system.
The densities of the gases are denoted by ρ1, ρ2, their velocities of diffusion by u1, u2, and if their partial pressures are p1, p2, we have by Boyle’s law p1 = k1ρ1, p2 = k2ρ2, where k1,k2 are constants for the two gases, the temperature being constant. The axis of the cylinder is taken as the axis of x.
From the considerations of the preceding section, the effects of inertia of the diffusing gases may be neglected, and at any instant of the process either of the gases is to be treated as kept in equilibrium by its partial pressure and the resistance to diffusion produced by the other gas. Calling this resistance per unit volume R, and putting R = Cρ1ρ2(u1 − u2), where C is the coefficient of resistance, the equations of equilibrium give
| dp1 | + Cρ1ρ2(u1 − u2) = 0, and | dp2 | + Cρ1ρ2(u2 − u1) = 0 (1) |
| dx | dx |
These involve
| dp1 | + | dp2 | = 0 or p1 + p2 = P (2) |
| dx | dx |
where P is the total pressure of the mixture, and is everywhere constant, consistently with the conditions of mechanical equilibrium.
Now dp1/dx is the pressure-gradient of the first gas, and is, by Boyle’s law, equal to k1 times the corresponding density-gradient. Again ρ1u1 is the mass of gas flowing across any section per unit time, and k1ρ1u1 or p1u1 can be regarded as representing the flux of partial pressure produced by the motion of the gas. Since the total pressure is everywhere constant, and the ends of the cylinder are supposed fixed, the fluxes of partial pressure due to the two gases are equal and opposite, so that
p1u1 + p2u2 = 0 or k1ρ1u1 + k2ρ2u2 = 0 (3).
From (2) (3) we find by elementary algebra
u1/p2 = −u2/p1 = (u1 − u2)/(p1 + p2) = (u1 − u2)/P,
and therefore
p2u1 = −p2u2 = p1p2(u1 − u2)/P = k1k2ρ1ρ2(u1 − u2)/P
Hence equations (1) (2) gives
| dp1 | + | CP | (p1u1) = 0, and | dp2 | + | CP | (p2u2) = 0; |
| dx | k1k2 | dx | k1k2 |
whence also substituting p1 = k1ρ1, p2 = k2ρ2, and by transposing
| ρ1u1 = − | k1k2 | dρ1 | , and ρ2u2 = − | k1k2 | dρ2 | . |
| CP | dx | CP | dx |
We may now define the “coefficient of diffusion” of either gas as the ratio of the rate of flow of that gas to its density-gradient. With this definition, the coefficients of diffusion of both the gases in a mixture are equal, each being equal to k1k2/CP. The ratios of the fluxes of partial pressure to the corresponding pressure-gradients are also equal to the same coefficient. Calling this coefficient K, we also observe that the equations of continuity for the two gases are
| dρ1 | + | d(ρ1u1) | = 0, and | dρ2 | + | d(ρ2u2) | = 0, |
| dt | dx | dt | dx |
leading to the equations of diffusion
| dρ1 | = | d | (K | dρ1 | ), and | dρ2 | = | d | (K | dρ2 | ), |
| dt | dx | dx | dt | dx | dx |
exactly as in the case of diffusion through a solid.
If we attempt to treat diffusion in liquids by a similar method, it is, in the first place, necessary to define the “partial pressure” of the components occurring in a liquid mixture. This leads to the conception of “osmotic pressure,” which is dealt with in the article Solution. For dilute solutions at constant temperature, the assumption that the osmotic pressure is proportional to the density, leads to results agreeing fairly closely with experience, and this fact may be represented by the statement that a substance occurring in a dilute solution behaves like a perfect gas.
6. Relation of the Coefficient of Diffusion to the Units of Length and Time.—We may write the equation defining K in the form
| −K × | I | dρ | . |
| ρ | dx |
Here −dρ/ρdx represents the “percentage rate” at which the density decreases with the distance x; and we thus see that the coefficient of diffusion represents the ratio of the velocity of flow to the percentage rate at which the density decreases with the distance measured in the direction of flow. This percentage rate being of the nature of a number divided by a length, and the velocity being of the nature of a length divided by a time, we may state that K is of two dimensions in length and −1 in time, i.e. dimensions L²/T.
Example 1. Taking K = 0.1423 for carbon dioxide and air (at temperature 0° C. and pressure 76 cm. of mercury) referred to a centimetre and a second as units, we may interpret the result as follows:—Supposing in a mixture of carbon dioxide and air, the density of the carbon dioxide decreases by, say, 1, 2 or 3% of itself in a distance of 1 cm., then the corresponding velocities of the diffusing carbon dioxide will be respectively 0.01, 0.02 and 0.03 times 0.1423, that is, 0.001423, 0.002846 and 0.004269 cm. per second in the three cases.
Example 2. If we wished to take a foot and a second as our units, we should have to divide the value of the coefficient of diffusion in Example 1 by the square of the number of centimetres in 1 ft., that is, roughly speaking, by 900, giving the new value of K = 0.00016 roughly.
7. Numerical Values of the Coefficient of Diffusion.—The table on p. 258 gives the values of the coefficient of diffusion of several of the principal pairs of gases at a pressure of 76 cm. of mercury, and also of a number of other substances. In the gases the centimetre and second are taken as fundamental units, in other cases the centimetre and day.
8. Irreversible Changes accompanying Diffusion.—The diffusion of two gases at constant pressure and temperature is a good example of an “irreversible process.” The gases always tend to mix, never to separate. In order to separate the gases a change must be effected in the external conditions to which the mixture is subjected, either by liquefying one of the gases, or by separating them by diffusion through a membrane, or by bringing other outside influences to bear on them. In the case of liquids, electrolysis affords a means of separating the constituents of a mixture. Every such method involves some change taking place outside the mixture, and this change may be regarded as a “compensating 258 transformation.” We thus have an instance of the property that every irreversible change leaves an indelible imprint somewhere or other on the progress of events in the universe. That the process of diffusion obeys the laws of irreversible thermodynamics (if these laws are properly stated) is proved by the fact that the compensating transformations required to separate mixed gases do not essentially involve anything but transformation of energy. The process of allowing gases to mix by diffusion, and then separating them by a compensating transformation, thus constitutes an irreversible cycle, the outside effects of which are that energy somewhere or other must be less capable of transformation than it was before the change. We express this fact by stating that an irreversible process essentially implies a loss of availability. To measure this loss we make use of the laws of thermodynamics, and in particular of Lord Kelvin’s statement that “It is impossible by means of inanimate material agency to derive mechanical effect from any portion of matter by cooling it below the temperature of the coldest of the surrounding objects.”
| Substances. | Temp. | K. | Author. |
| Carbon dioxide and air | 0°C. | 0.1423 cm²/sec. | J. Loschmidt. |
| ” ” hydrogen | 0°C. | 0.5558 ” | ” |
| ” ” oxygen | 0°C. | 0.1409 ” | ” |
| ” ” carbon monoxide | 0°C. | 0.1406 ” | ” |
| ” ” marsh gas (methane) | 0°C. | 0.1586 ” | ” |
| ” ” nitrous oxide | 0°C. | 0.0983 ” | ” |
| Hydrogen and oxygen | 0°C. | 0.7214 ” | ” |
| ” ” carbon monoxide | 0°C. | 0.6422 ” | ” |
| ” ” sulphur dioxide | 0°C. | 0.4800 ” | ” |
| Oxygen and carbon monoxide | 0°C. | 0.1802 ” | ” |
| Water and ammonia | 20°C. | 1.250 ” | G. Hüfner. |
| ” ” | 5°C. | 0.822 ” | ” |
| ” common salt (density 1.0269) | 0.355 ” | J. Graham. | |
| ” ” ” | 14.33°C. | 1.020, 0.996, 0.972, 0.932 cm²/day. | F. Heimbrodt. |
| ” zinc sulphate (0.312 gm/cm³) | 0.1162 cm²/day. | W. Seitz. | |
| ” zinc sulphate (normal) | 0.2355 ” | ” | |
| ” zinc acetate (double normal) | 0.1195 ” | ” | |
| ” zinc formate (half normal) | 0.4654 ” | ” | |
| ” cadmium sulphate (double normal) | · · | 0.2456 ” | ” |
| ” glycerin (1⁄8n, ½n, 7⁄8n, 1.5n) | 10.14°C. | 0.356, 0.350, 0.342, 0.315 cm²/day. | F. Heimbrodt. |
| ” urea ” ” | 14.83°C. | 0.973, 0.946, 0.926, 0.883 cm²/day. | ” |
| ” hydrochloric acid | 14.30°C. | 2.208, 2.331, 2.480 cm²/day. | ” |
| Gelatin 20% and ammonia | 17°C. | 127.1 cm²/day. | A. Hagenbach. |
| ” ” carbon dioxide | · · | 0.845 ” | ” |
| ” ” nitrous oxide | · · | 0.509 ” | ” |
| ” ” oxygen | · · | 0.230 ” | ” |
| ” ” hydrogen | · · | 0.0565 ” | ” |
Let us now assume that we have any syste m such as the gases above considered, and that it is in the presence of an indefinitely extended medium which we shall call the “auxiliary medium.” If heat be taken from any part of the system, only part of this heat can be converted into work by means of thermodynamic engines; and the rest will be given to the auxiliary medium, and will constitute unavailable energy or waste. To understand what this means, we may consider the case of a condensing steam engine. Only part of the energy liberated by the combustion of the coal is available for driving the engine, the rest takes the form of heat imparted to the condenser. The colder the condenser the more efficient is the engine, and the smaller is the quantity of waste.
The amount of unavailable energy associated with any given transformation is proportional to the absolute temperature of the auxiliary medium. When divided by that temperature the quotient is called the change of “entropy” associated with the given change (see Thermodynamics). Thus if a body at temperature T receives a quantity of heat Q, and if T0 is the temperature of the auxiliary medium, the quantity of work which could be obtained from Q by means of ideal thermodynamic engines would be Q(1 − T0/T), and the balance, which is QT0/T, would take the form of unavailable or waste energy given to the medium. The quotient of this, when divided by T0, is Q/T, and this represents the quantity of entropy associated with Q units of heat at temperature T.
Any irreversible change for which a compensating transformation of energy exists represents, therefore, an increase of unavailable energy, which is measurable in terms of entropy. The increase of entropy is independent of the temperature of the auxiliary medium. It thus affords a measure of the extent to which energy has run to waste during the change. Moreover, when a body is heated, the increase of entropy is the factor which determines how much of the energy imparted to the body is unavailable for conversion into work under given conditions. In all cases we have
| increase of unavailable energy | = increase of entropy. |
| temperature of auxiliary medium |
When diffusion takes place between two gases inside a closed vessel at uniform pressure and temperature no energy in the form of heat or work is received from without, and hence the entropy gained by the gases from without is zero. But the irreversible processes inside the vessel may involve a gain of entropy, and this can only be estimated by examining by what means mixed gases can be separated, and, in particular, under what conditions the process of mixing and separating the gases could (theoretically) be made reversible.
9. Evidence derived from Liquefaction of one or both of the Gases.—The gases in a mixture can often be separated by liquefying, or even solidifying, one or both of the components. In connexion with this property we have the important law according to which “The pressure of a vapour in equilibrium with its liquid depends only on the temperature and is independent of the pressures of any other gases or vapours which may be mixed with it.” Thus if two closed vessels be taken containing some water and one be exhausted, the other containing air, and if the temperatures be equal, evaporation will go on until the pressure of the vapour in the exhausted vessel is equal to its partial pressure in the other vessel, notwithstanding the fact that the total pressure in the latter vessel is greater by the pressure of the air.
To separate mixed gases by liquefaction, they must be compressed and cooled till one separates in the form of a liquid. If no changes are to take place outside the system, the separate components must be allowed to expand until the work of expansion is equal to the work of compression, and the heat given out in compression is reabsorbed in expansion. The process may be made as nearly reversible as we like by performing the operations so slowly that the substances are practically in a state of equilibrium at every stage. This is a consequence of an important axiom in thermodynamics according to which “any small change in the neighbourhood of a state of equilibrium is to a first approximation reversible.”
Suppose now that at any stage of the compression the partial pressures of the two gases are p1 and p2, and that the volume is changed from V to V − dV. The work of compression is (p1 + p2)dV, and this work will be restored at the corresponding stage if each of the separated gases increases in volume from V − dV to V. The ultimate state of the separated gases will thus be one in which each gas occupies the volume V originally occupied by the mixture.
We may now obtain an estimate of the amount of energy rendered unavailable by diffusion. We suppose two gases occupying volumes V1 and V2 at equal pressure p to mix by diffusion, so that the final volume is V1 + V2. Then if before mixing each gas had been allowed to expand till its volume was V1 + V2, work would have been done in the expansion, and the gases could still have been mixed by a reversal of the process above described. In the actual diffusion this work of expansion is lost, and represents energy rendered unavailable at the temperature at which diffusion takes place. When divided by that temperature the quotient gives the increase of entropy. Thus the irreversible processes, and, in particular, the entropy changes associated with diffusion of two gases at uniform pressure, are the same as would take place if each of the gases in turn were to expand by rushing into a vacuum, till it occupied the whole volume of the mixture. A more rigorous proof involves considerations of the thermodynamic potentials, following the methods of J. Willard Gibbs (see Energetics).
Another way in which two or more mixed gases can be separated is by placing them in the presence of a liquid which can freely absorb one of the gases, but in which the other gas or gases are insoluble. Here again it is found by experience that when equilibrium exists at a given temperature between the dissolved and undissolved portions of the first gas, the partial pressure of that gas in the mixture depends on the temperature alone, and is independent of the partial pressures of the insoluble gases with which it is mixed, so that the conclusions are the same as before.
10. Diffusion through a Membrane or Partition. Theory of the semi-permeable Membrane.—It has been pointed out that diffusion of gases frequently takes place in the interior of solids; moreover, different gases behave differently with respect to the same solid at the same temperature. A membrane or partition formed of such a solid can therefore be used to effect a more or less complete separation of gases from a mixture. This method is employed commercially for extracting oxygen from the atmosphere, in particular for use in projection lanterns where a high degree of purity is not required. A similar method is often applied to liquids and solutions and is known as “dialysis.”
In such cases as can be tested experimentally it has been found that a gas always tends to pass through a membrane from the side where its density, and therefore its partial pressure, is greater to the side where it is less; so that for equilibrium the partial pressures on the two sides must be equal. This result is unaffected by the presence of other gases on one or both sides of the membrane. For example, if different gases at the same pressure are separated by a partition through which one gas can pass more rapidly than the other, the diffusion will give rise to a difference of pressure on the two sides, which is capable of doing mechanical work in moving the partition. In evidence of this conclusion Max Planck quotes a test experiment made by him in the Physical Institute of the university of Munich in 1883, depending on the fact that platinum foil at white heat is permeable to hydrogen but impermeable to air, so that if a platinum tube filled with hydrogen be heated the hydrogen will diffuse out, leaving a vacuum.
The details of the experiment may be quoted here:—“A glass tube of about 5 mm. internal diameter, blown out to a bulb at the middle, was provided with a stop-cock at one end. To the other a platinum tube 10 cm. long was fastened, and closed at the end. The whole tube was exhausted by a mercury pump, filled with hydrogen at ordinary atmospheric pressure, and then closed. The closed end of the platinum portion was then heated in a horizontal position by a Bunsen burner. The connexion between the glass and platinum tubes, having been made by means of sealing-wax, had to be kept cool by a continuous current of water to prevent the softening of the wax. After four hours the tube was taken from the flame, cooled to the temperature of the room, and the stop-cock opened under mercury. The mercury rose rapidly, almost completely filling the tube, proving that the tube had been very nearly exhausted.”
 |
In order that diffusion through a membrane may be reversible so far as a particular gas is concerned, the process must take place so slowly that equilibrium is set up at every stage (see § 9 above). In order to separate one gas from another consistently with this condition it is necessary that no diffusion of the latter gas should accompany the process. The name “semi-permeable” is applied to an ideal membrane or partition through which one gas can pass, and which offers an insuperable barrier to any diffusion whatever of a second gas. By means of two semi-permeable partitions acting oppositely with respect to two different gases A and B these gases could be mixed or separated by reversible methods. The annexed figure shows a diagrammatic representation of the process.
We suppose the gases contained in a cylindrical tube; P, Q, R, S are four pistons, of which P and R are joined to one connecting rod, Q and S to another. P, S are impermeable to both gases; Q is semi-permeable, allowing the gas A to pass through but not B, similarly R allows the gas B to pass through but not A. The distance PR is equal to the distance QS, so that if the rods are pushed towards each other as far as they will go, P and Q will be in contact, as also R and S. Imagine the space RQ filled with a mixture of the two gases under these conditions. Then by slowly drawing the connecting rods apart until R, Q touch, the gas A will pass into the space PQ, and B will pass into the space RS, and the gases will finally be completely separated; similarly, by pushing the connecting rods together, the two gases will be remixed in the space RQ. By performing the operations slowly enough we may make the processes as nearly reversible as we please, so that no available energy is lost in either change. The gas A being at every instant in equilibrium on the two sides of the piston Q, its density, and therefore its partial pressure, is the same on both sides, and the same is true regarding the gas B on the two sides of R. Also no work is done in moving the pistons, for the partial pressures of B on the two sides of R balance each other, consequently, the resultant thrust on R is due to the gas A alone, and is equal and opposite to its resultant thrust on P, so that the connecting rods are at every instant in a state of mechanical equilibrium so far as the pressures of the gases A and B are concerned. We conclude that in the reversible separation of the gases by this method at constant temperature without the production or absorption of mechanical work, the densities and the partial pressures of the two separated gases are the same as they were in the mixture. These conclusions are in entire agreement with those of the preceding section. If this agreement did not exist it would be possible, theoretically, to obtain perpetual motion from the gases in a way that would be inconsistent with the second law of thermodynamics.
Most physicists admit, as Planck does, that it is impossible to obtain an ideal semi-permeable substance; indeed such a substance would necessarily have to possess an infinitely great resistance to diffusion for such gases as could not penetrate it. But in an experiment performed under actual conditions the losses of available energy arising from this cause would be attributable to the imperfect efficiency of the partitions and not to the gases themselves; moreover, these losses are, in every case, found to be completely in accordance with the laws of irreversible thermodynamics. The reasoning in this article being somewhat condensed the reader must necessarily be referred to treatises on thermodynamics for further information on points of detail connected with the argument. Even when he consults these treatises he may find some points omitted which have been examined in full detail at some time or other, but are not sufficiently often raised to require mention in print.
II. Kinetic Models of Diffusion.—Imagine in the first instance that a very large number of red balls are distributed over one half of a billiard table, and an equal number of white balls over the other half. If the balls are set in motion with different velocities in various directions, diffusion will take place, the red balls finding their way among the white ones, and vice versa; and the process will be retarded by collisions between the balls. The simplest model of a perfect gas studied in the kinetic theory of gases (see Molecule) differs from the above illustration in that the bodies representing the molecules move in space instead of in a plane, and, unlike billiard balls, their motion is unresisted, and they are perfectly elastic, so that no kinetic energy is lost either during their free motions, or at a collision.
The mathematical analysis connected with the application of the kinetic theory to diffusion is very long and cumbersome. We shall therefore confine our attention to regarding a medium formed of elastic spheres as a mechanical model, by which the most important features of diffusion can be illustrated. We shall assume the results of the kinetic theory, according to which:—(1) In a dynamical model of a perfect gas the mean kinetic energy of translation of the molecules represents the absolute temperature of the gas. (2) The pressure at any point is proportional to the product of the number of molecules in unit volume about that point into the mean square of the velocity. (The mean square of the velocity is different from but proportional to the square of the mean velocity, and in the subsequent arguments either of these two quantities can generally be taken.) (3) In a gas mixture represented by a mixture of molecules of unequal masses, the mean kinetic energies of the different kinds are equal.
Consider now the problem of diffusion in a region containing two kinds of molecules A and B of unequal mass. The molecules of A in the neighbourhood of any point will, by their motion, spread out in every direction until they come into collision with other molecules of either kind, and this spreading out from every point of the medium will give rise to diffusion. If we imagine the velocities of the A molecules to be equally distributed in all directions, as they would be in a homogeneous mixture, it is obvious that the process of diffusion will be greater, ceteris paribus, the greater the velocity of the molecules, and the greater the length of the free path before a collision takes place. If we assume consistently with this, that the coefficient of diffusion of the gas A is proportional to the mean value of W{a}l{a}, where w{a} is the velocity and l{a} is the length of the path of a 260 molecule of A, this expression for the coefficient of diffusion is of the right dimensions in length and time. If, moreover, we observe that when diffusion takes place in a fixed direction, say that of the axis of x, it depends only on the resolved part of the velocity and length of path in that direction: this hypothesis readily leads to our taking the mean value of 1⁄3wala as the coefficient of diffusion for the gas A. This value was obtained by O. E. Meyer and others.
Unfortunately, however, it makes the coefficients of diffusion unequal for the two gases, a result inconsistent with that obtained above from considerations of the coefficient of resistance, and leading to the consequence that differences of pressure would be set up in different parts of the gas. To equalize these differences of pressure, Meyer assumed that a counter current is set up, this current being, of course, very slow in practice; and J. Stefan assumed that the diffusion of one gas was not affected by collisions between molecules of the same gas. When the molecules are mixed in equal proportions both hypotheses lead to the value 1⁄6([wala] + [wblb]), (square brackets denoting mean values). When one gas preponderates largely over the other, the phenomena of diffusion are too difficult of observation to allow of accurate experimental tests being made. Moreover, in this case no difference exists unless the molecules are different in size or mass.
Instead of supposing a velocity of translation added after the mathematical calculations have been performed, a better plan is to assume from the outset that the molecules of the two gases have small velocities of translation in opposite directions, superposed on the distribution of velocity, which would occur in a medium representing a gas at rest. When a collision occurs between molecules of different gases a transference of momentum takes place between them, and the quantity of momentum so transferred in one second in a unit of volume gives a dynamical measure of the resistance to diffusion. It is to be observed that, however small the relative velocity of the gases A and B, it plays an all-important part in determining the coefficient of resistance; for without such relative motion, and with the velocities evenly distributed in all directions, no transference of momentum could take place. The coefficient of resistance being found, the motion of each of the two gases may be discussed separately.
One of the most important consequences of the kinetic theory is that if the volume be kept constant the coefficient of diffusion varies as the square root of the absolute temperature. To prove this, we merely have to imagine the velocity of each molecule to be suddenly increased n fold; the subsequent processes, including diffusion, will then go on n times as fast; and the temperature T, being proportional to the kinetic energy, and therefore to the square of the velocity, will be increased n² fold. Thus K, the coefficient of diffusion, varies as √T.
The relation of K to the density when the temperature remains constant is more difficult to discuss, but it may be sufficient to notice that if the number of molecules is increased n fold, the chances of a collision are n times as great, and the distance traversed between collisions is (not therefore but as the result of more detailed reasoning) on the average 1/n of what it was before. Thus the free path, and therefore the coefficient of diffusion, varies inversely as the density, or directly as the volume. If the pressure p and temperature T be taken as variables, K varies inversely as p and directly as √T³.
Now according to the experiments first made by J. C. Maxwell and J. Loschmidt, it appeared that with constant density K was proportional to T more nearly than to √T. The inference is that in this respect a medium formed of colliding spheres fails to give a correct mechanical model of gases. It has been found by L. Boltzmann, Maxwell and others that a system of particles whose mutual actions vary according to the inverse fifth power of the distance between them represents more correctly the relation between the coefficient of diffusion and temperature in actual gases. Other recent theories of diffusion have been advanced by M. Thiesen, P. Langevin and W. Sutherland. On the other hand, J. Thovert finds experimental evidence that the coefficient of diffusion is proportional to molecular velocity in the cases examined of non-electrolytes dissolved in water at 18° at 2.5 grams per litre.
Bibliography.—The best introduction to the study of theories of diffusion is afforded by O. E. Meyer’s Kinetic Theory of Gases, translated by Robert E. Baynes (London, 1899). The mathematical portion, though sufficient for ordinary purposes, is mostly of the simplest possible character. Another useful treatise is R. Ruhlmann’s Handbuch der mechanischen Wärmetheorie (Brunswick, 1885). For a shorter sketch the reader may refer to J. C. Maxwell’s Theory of Heat, chaps, xix. and xxii., or numerous other treatises on physics. The theory of the semi-permeable membrane is discussed by M. Planck in his Treatise on Thermodynamics, English translation by A. Ogg (1903), also in treatises on thermodynamics by W. Voigt and other writers. For a more detailed study of diffusion in general the following papers may be consulted:—L. Boltzmann, “Zur Integration der Diffusionsgleichung,” Sitzung. der k. bayer. Akad math.-phys. Klasse (May 1894); T. des Coudres, “Diffusionsvorgänge in einem Zylinder,” Wied. Ann. lv. (1895), p. 213; J. Loschmidt, “Experimentaluntersuchungen über Diffusion,” Wien. Sitz. lxi., lxii. (1870); J. Stefan, “Gleichgewicht und ... Diffusion von Gasmengen,” Wien. Sitz. lxiii., “Dynamische Theorie der Diffusion,” Wien. Sitz. lxv. (April 1872); M. Toepler, “Gas-diffusion,” Wied. Ann. lviii. (1896), p. 599; A. Wretschko, “Experimentaluntersuchungen über die Diffusion von Gasmengen,” Wien. Sitz. lxii. The mathematical theory of diffusion, according to the kinetic theory of gases, has been treated by a number of different methods, and for the study of these the reader may consult L. Boltzmann, Vorlesungen über Gastheorie (Leipzig, 1896-1898); S. H. Burbury, Kinetic Theory of Gases (Cambridge, 1899), and papers by L. Boltzmann in Wien. Sitz. lxxxvi. (1882), lxxxvii. (1883); P. G. Tait, “Foundations of the Kinetic Theory of Gases,” Trans. R.S.E. xxxiii., xxxv., xxvi., or Scientific Papers, ii. (Cambridge, 1900). For recent work reference should be made to the current issues of Science Abstracts (London), and entries under the heading “Diffusion” will be found in the general index at the end of each volume.
DIGBY, SIR EVERARD (1578-1606), English conspirator, son of Everard Digby of Stoke Dry, Rutland, was born on the 16th of May 1578. He inherited a large estate at his father’s death in 1592, and acquired a considerable increase by his marriage in 1596 to Mary, daughter and heir of William Mulsho of Gothurst (now Gayhurst), in Buckinghamshire. He obtained a place in Queen Elizabeth’s household and as a ward of the crown was brought up a Protestant; but about 1599 he came under the influence of the Jesuit, John Gerard, and soon afterwards joined the Roman Catholics. He supported James’s accession and was knighted by the latter on the 23rd of April 1603. In a letter to Salisbury, the date of which has been ascribed to May 1605, Digby offered to go on a mission to the pope to obtain from the latter a promise to prevent Romanist attempts against the government in return for concessions to the Roman Catholics; adding that if severe measures were again taken against them “within brief there will be massacres, rebellions and desperate attempts against the king and state.” Digby had suffered no personal injury or persecution on account of his religion, but he sympathized with his co-religionists; and when at Michaelmas, 1605, the government had fully decided to return to the policy of repression, the authors of the Gunpowder Plot (q.v.) sought his financial support, and he joined eagerly in the conspiracy. His particular share in the plan was the organization of a rising in the Midlands; and on the pretence of a hunting party he assembled a body of gentlemen together at Danchurch in Warwickshire on the 5th of November, who were to take action immediately the news arrived from London of the successful destruction of the king and the House of Lords, and to seize the person of the princess Elizabeth, who was residing in the neighbourhood. The conspirators arrived late on the evening of the 6th to tell their story of failure and disaster, and Digby, who possibly might have escaped the more serious charge of high treason, was persuaded by Catesby, with a false tale that the king and Salisbury were dead, to further implicate himself in the plot and join the small band of conspirators in their hopeless endeavour to raise the country. He accompanied them, the same day, to Huddington in Worcestershire and on the 7th to Holbeche in Staffordshire. The following morning, however, he abandoned his companions, dismissed his servants except two, who declared “they would never leave him but against their will,” and attempted with these to conceal himself in a pit. He was, however, soon discovered and surrounded. He made a last effort to break through his captors on horseback, but was taken and conveyed a prisoner to the Tower. His trial took place in Westminster Hall, on the 27th of January 1606, and alone among the conspirators he pleaded guilty, declaring that the motives of his crime had been his friendship for Catesby and his devotion to his religion. He was condemned to death, and his execution, which took place on the 31st, in St Paul’s Churchyard, was accompanied by all the brutalities exacted by the law.
Digby was a handsome man, of fine presence. Father Gerard 261 extols his skill in sport, his “riding of great horses,” as well as his skill in music, his gifts of mind and his religious devotion, and concludes “he was as complete a man in all things, that deserved estimation or might win affection as one should see in a kingdom.” Some of Digby’s letters and papers, which include a poem before his execution, a last letter to his infant sons and correspondence with his wife from the Tower, were published in The Gunpowder Treason by Thomas Barlow, bishop of Lincoln, in 1679. He left two sons, of whom the elder, Sir Kenelm Digby, was the well-known author and diplomatist.
See works on the Gunpowder Plot; Narrative of Father Gerard, in Condition of the Catholics under James I. by J. Morris (1872), &c. A life of Digby under the title of A Life of a Conspirator, by a Romish Recusant (Thomas Longueville), was published in 1895.
DIGBY, SIR KENELM (1603-1665), English author, diplomatist and naval commander, son of Sir Everard Digby (q.v.), was born on the 11th of July 1603, and after his father’s execution in 1606 resided with his mother at Gayhurst, being brought up apparently as a Roman Catholic. In 1617 he accompanied his cousin, Sir John Digby, afterwards 1st earl of Bristol, and then ambassador in Spain, to Madrid. On his return in April 1618 he entered Gloucester Hall (now Worcester College), Oxford, and studied under Thomas Allen (1542-1632), the celebrated mathematician, who was much impressed with his abilities and called him the Mirandula, i.e. the infant prodigy, of his age.1 He left the university without taking a degree in 1620, and travelled in France, where, according to his own account, he inspired an uncontrollable passion in the queen-mother, Marie de’ Medici, now a lady of more than mature age and charms; he visited Florence, and in March 1623 joined Sir John Digby again at Madrid, at the time when Prince Charles and Buckingham arrived on their adventurous expedition. He joined the prince’s household and returned with him to England on the 5th of October 1623, being knighted by James I. on the 23rd of October and receiving the appointment of gentleman of the privy chamber to Prince Charles. In 1625 he married secretly Venetia, daughter of Sir Edward Hanley of Tonge Castle, Shropshire, a lady of extraordinary beauty and intellectual attainments, but of doubtful virtue. Digby was a man of great stature and bodily strength. Edward Hyde, afterwards earl of Clarendon, who with Ben Jonson was included among his most intimate friends, describes him as “a man of very extraordinary person and presence which drew the eyes of all men upon him, a wonderful graceful behaviour, a flowing courtesy and civility, and such a volubility of language as surprised and delighted.”2 Digby for some time was excluded from public employment by Buckingham’s jealousy of his cousin, Lord Bristol. At length in 1627, on the latter’s advice, Digby determined to attempt “some generous action,” and on the 22nd of December, with the approval of the king, embarked as a privateer with two ships, with the object of attacking the French ships in the Venetian harbour of Scanderoon. On the 18th of January he arrived off Gibraltar and captured several Spanish and Flemish vessels. From the 15th of February to the 27th of March he remained at anchor off Algiers on account of the sickness of his men, and extracted a promise from the authorities of better treatment of the English ships. He seized a rich Dutch vessel near Majorca, and after other adventures gained a complete victory over the French and Venetian ships in the harbour of Scanderoon on the 11th of June. His successes, however, brought upon the English merchants the risk of reprisals, and he was urged to depart. He returned home in triumph in February 1629, and was well received by the king, and was made a commissioner of the navy in October 1630, but his proceedings were disavowed on account of the complaints of the Venetian ambassador. In 1633 Lady Digby died, and her memory was celebrated by Ben Jonson in a series of poems entitled Eupheme, and by other poets of the day. Digby retired to Gresham College, and exhibited extravagant grief, maintaining a seclusion for two years. About this time Digby professed himself a Protestant, but by October 1635, while in France, he had already returned to the Roman Catholic faith.3 In a letter dated the 27th of March 1636 Laud remonstrates with him, but assures him of the continuance of his friendship.4 In 1638 he published A Conference with a Lady about choice of a Religion, in which he argues that the Roman Church, possessing alone the qualifications of universality, unity of doctrine and uninterrupted apostolic succession, is the only true church, and that the intrusion of error into it is impossible. The same subject is treated in letters to George Digby, afterwards 2nd earl of Bristol, dated the 2nd of November 1638 and the 29th of November 1639, which were published in 1651, as well as in a further Discourse concerning Infallibility in Religion in 1652. Returning to England he associated himself with the queen and her Roman Catholic friends, and joined in the appeal to the English Romanists for money to support the king’s Scottish expedition.5 In consequence he was summoned to the bar of the House of Commons on the 27th of January 1641, and the king was petitioned to remove him with other recusants from his councils. He left England, and while at Paris killed in a duel a French lord who had insulted Charles I. in his presence. Louis XIII. took his part, and furnished him with a military escort into Flanders. Returning home he was imprisoned, by order of the House of Commons, early in 1642, successively in the “Three Tobacco Pipes nigh Charing Cross,” where his delightful conversation is said to have transformed the prison into “a place of delight,”6 and at Winchester House. He was finally released and allowed to go to France on the 30th of July 1643, through the intervention of the queen of France, Anne of Austria, on condition that he would neither promote nor conceal any plots abroad against the English government.
Before leaving England an attempt was made to draw from him an admission that Laud, with whom he had been intimate, had desired to be made a cardinal, but Digby denied that the archbishop had any leanings towards Rome. On the 1st of November 1643 it was resolved by the Commons to confiscate his property. He published in London the same year Observations on the 22nd stanza in the 9th canto of the 2nd book of Spenser’s “Faërie Queene,” the MS. of which is in the Egerton collection (British Museum, No. 2725 f. 117 b), and Observations on a surreptitious and unauthorized edition of the Religio Medici, by Sir Thomas Browne, from the Roman Catholic point of view, which drew a severe rebuke from the author. After his arrival in Paris he published his chief philosophical works, Of Bodies and Of the Immortality of Man’s Soul (1644), autograph MSS. of which are in the Bibliothèque Ste Geneviève at Paris, and made the acquaintance of Descartes. He was appointed by Queen Henrietta Maria her chancellor, and in the summer of 1645 he was despatched by her to Rome to obtain assistance. Digby promised the conversion of Charles and of his chief supporters. At first his eloquence made a great impression. Pope Innocent X. declared that he spoke not merely as a Catholic but as an ecclesiastic. But the absence of any warrant from Charles himself roused suspicions as to the solidity of his assurances, and he obtained nothing but a grant of 20,000 crowns. A violent quarrel with the pope followed, and he returned in 1646, having consented in the queen’s name to complete religious freedom for the Roman Catholics, both in England and Ireland, to an independent parliament in Ireland, and to the surrender of Dublin and all the Irish fortresses into the hands of the Roman Catholics, the king’s troops to be employed in enforcing the articles and the pope granting about £36,000 with a promise of further payments in obtaining direct assistance. In February 1649 Digby was invited to come to England to arrange a proposed toleration of the Roman Catholics, but on his arrival in May the scheme had already been abandoned. He was again banished on the 31st of August, and it was not till 1654 that he was allowed by the council of state to return. He now entered into close relations with Cromwell, from whom he hoped to obtain toleration for the Roman Catholics, and whose alliance he desired to secure for France rather than for 262 Spain, and was engaged by Cromwell, much to the scandal of both Royalists and Roundheads, in negotiations abroad, of which the aim was probably to prevent a union between those two foreign powers. He visited Germany, in 1660 was in Paris, and at the Restoration returned to England. He was well received in spite of his former relations with Cromwell, and was confirmed in his post as Queen Henrietta Maria’s chancellor. In January 1661 he delivered a lecture, which was published the same month, at Gresham College, on the vegetation of plants, and became an original member of the Royal Society in 1663. In January 1664 he was forbidden to appear at court, the cause assigned being that he had interposed too far in favour of the 2nd earl of Bristol, disgraced by the king on account of the charge of high treason brought by him against Clarendon into the House of Lords. The rest of his life was spent in the enjoyment of literary and scientific society at his house in Covent Garden. He died on the 11th of June 1665. He had five children, of whom two, a son and one daughter, survived him.
Digby, though he possessed for the time a considerable knowledge of natural science, and is said to have been the first to explain the necessity of oxygen to the existence of plants, bears no high place in the history of science. He was a firm believer in astrology and alchemy, and the extraordinary fables which he circulated on the subject of his discoveries are evidence of anything rather than of the scientific spirit. In 1656 he made public a marvellous account of a city in Tripoli, petrified in a few hours, which he printed in the Mercurius Politicus. Malicious reports had been current that his wife had been poisoned by one of his prescriptions, viper wine, taken to preserve her beauty. Evelyn, who visited him in Paris in 1651, describes him as an “errant mountebank.” Henry Stubbes characterizes him as “the very Pliny of our age for lying,” and Lady Fanshawe refers to the same “infirmity.”7 His famous “powder of sympathy,” which seems to have been only powder of “vitriol,” healed without any contact, by being merely applied to a rag or bandage taken from the wound, and Digby records a miraculous cure by this means in a lecture given by him at Montpellier on this subject in 1658, published in French and English the same year, in German in 1660 and in Dutch in 1663; but Digby’s claim to its original discovery is doubtful, Nathaniel Highmore in his History of Generation (1651, p. 113) calling the powder “Talbot’s powder,” and ascribing its invention to Sir Gilbert Talbot. Some of Digby’s pills and preparations, however, described in The Closet of the Eminently Learned Sir Kenelm Digby Knt. Opened (publ. 1677), are said to make less demand upon the faith of patients, and his injunction on the subject of the making of tea, to let the water “remain upon it no longer than you can say the Miserere Psalm very leisurely,” is one by no means to be ridiculed. As a philosopher and an Aristotelian Digby shows little originality and followed the methods of the schoolmen. His Roman Catholic orthodoxy mixed with rationalism, and his political opinions, according to which any existing authority should receive support, were evidently derived from Thomas White (1582-1676), the Roman Catholic philosopher, who lived with him in France. White published in 1651 Institutionum Peripateticorum libri quinque, purporting to expound Digby’s “peripatetic philosophy,” but going far beyond Digby’s published treatises. Digby’s Memoirs are composed in the high-flown fantastic manner then usual when recounting incidents of love and adventure, but the style of his more sober works is excellent. In 1632 he presented to the Bodleian library a collection of 236 MSS., bequeathed to him by his former tutor Thomas Allen, and described in Catalogi codicum manuscriptorum bibliothecae Bodleianae, by W. D. Macray, part ix. Besides the works already mentioned Digby translated A Treatise of adhering to God written by Albert the Great, Bishop of Ratisbon (1653); and he was the author of Private Memoirs, published by Sir N. H. Nicholas from Harleian MS. 6758 with introduction (1827); Journal of the Scanderoon Voyage in 1628, printed by J. Bruce with preface (Camden Society, 1868); Poems from Sir Kenelm Digby’s Papers... with preface and notes (Roxburghe Club, 1877); in the Add. MSS. 34,362 f. 66 is a poem Of the Miserys of Man, probably by Digby; Choice of Experimental Receipts in Physick and Chirurgery ... collected by Sir K. Digby (1668), and Chymical Secrets and Rare Experiments (1683), were published by G. Hartman, who describes himself as Digby’s steward and laboratory assistant.
See the Life of Sir Kenelm Digby by one of his Descendants (T. Longueville), 1896.
1 Letters by Eminent Persons (Aubrey’s Lives), ii. 324.
2 Life and Continuation.
3 Strafford’s Letters, i. 474.
4 Laud’s Works, vi. 447.
5 Thomason Tracts, Brit. Mus. E 164 (15).
6 Archaeologia Cantiana, ii. 190.
7 Dict. of Nat. Biog. sub “Digby.” See also Robert Boyle’s Works (1744), v. 302.
DIGBY, KENELM HENRY (1800-1880), English writer, youngest son of William Digby, dean of Clonfert, was born at Clonfert, Ireland, in 1800. He was educated at Trinity College, Cambridge, and soon after taking his B.A. degree there in 1819 became a Roman Catholic. He spent most of his life, which was mainly devoted to literary pursuits, in London, where he died on the 22nd of March 1880. Digby’s reputation rests chiefly on his earliest publication, The Broadstone of Honour, or Rules for the Gentlemen of England (1822), which contains an exhaustive survey of medieval customs, full of quotations from varied sources. The work was subsequently enlarged and issued (1826-1827) in four volumes entitled: Godefridus, Tancredus, Morus and Orlandus (numerous re-impressions, the best of which is the edition brought out by B. Quaritch in five volumes, 1876-1877).
Among Digby’s other works are: Mores Catholici, or Ages of Faith (11 vols., London, 1831-1840); Compitum; or the Meeting of the Ways at the Catholic Church (7 vols., London, 1848-1854); The Lovers’ Seat, Kathemérina; or Common Things in relation to Beauty, Virtue and Faith (2 vols., London, 1856). A complete list is given in J. Gillow’s Bibliographical Dictionary of English Catholics, ii. 81-83.
DIGENES ACRITAS, BASILIUS, Byzantine national hero, probably lived in the 10th century. He is named Digenes (of double birth) as the son of a Moslem father and a Christian mother; Acritas (ἄκρα, frontier, boundary), as one of the frontier guards of the empire, corresponding to the Roman milites limitanei. The chief duty of these acritae consisted in repelling Moslem inroads and the raids of the apelatae (cattle-lifters), brigands who may be compared with the more modern Klephts. The original Digenes epic is lost, but four poems are extant, in which the different incidents of the legend have been worked up by different hands. The first of these consists of about 4000 lines, written in the so-called “political” metre, and was discovered in the latter part of the 19th century, in a 16th-century MS., at Trebizond; the other three MSS. were found at Grotta Ferrata, Andros and Oxford. The poem, which has been compared with the Chanson de Roland and the Romance of the Cid, undoubtedly contains a kernel of fact, although it cannot be regarded as in any sense an historical record. The scene of action is laid in Cappadocia and the district of the Euphrates.
Editions of the Trebizond MS. by C. Sathas and E. Legrand in the Collection des monuments pour servir à l’étude de la langue néohellénique, new series, vi. (1875), and by S. Joannides (Constantinople, 1887). See monographs by A. Luber (Salzburg, 1885) and G. Wartenberg (Berlin, 1897). Full information will be found in C. Krumbacher’s Geschichte der byzantinischen Litteratur, p. 827 (2nd ed., 1897); see also G. Schlumberger, L’Épopée Byzantine à la fin du dixième siècle (1897).
DIGEST, a term used generally of any digested or carefully arranged collection or compendium of written matter, but more particularly in law of a compilation in condensed form of a body of law digested in a systematical method; e.g. the Digest (Digesta) or Pandects (Πάνδεκται) of Justinian, a collection of extracts from the earlier jurists compiled by order of the emperor Justinian. The word is also given to the compilations of the main points (marginal or hand-notes) of decided cases, usually arranged in alphabetical and subject order, and published under such titles as “Common Law Digest,” “Annual Digest,” &c.
DIGESTIVE ORGANS (Pathology). Several facts of importance have to be borne in mind for a proper appreciation of the pathology of the organs concerned in digestive processes (for the anatomy see Alimentary Canal and allied articles). In the first place, more than all other systems, the digestive comprises greater range of structure and exhibits wider diversity of function within its domain. Each separate structure and each different function presents special pathological signs and symptoms. Again, the duties imposed upon the system have to be performed 263 notwithstanding constant variations in the work set them. The crude articles of diet offered them vary immensely in nature, bulk and utility, from which they must elaborate simple food-elements for absorption, incorporate them after absorption into complex organic substances properly designed to supply the constant needs of cellular activity, of growth and repair, and fitly harmonized to fulfil the many requirements of very divergent processes and functions. Any form of unphysiological diet, each failure to cater for the wants of any special tissue engaged in, or of any processes of, metabolism, carry with them pathological signs. Perhaps in greater degree than elsewhere are the individual sections of the digestive system dependent upon, and closely correlated with, one another. The lungs can only yield oxygen to the blood when the oxygen is uncombined; no compounds are of use. The digestive organs have to deal with an enormous variety of compound bodies, from which to obtain the elements necessary for protoplasmic upkeep and activity. Morbid lesions of the respiratory and circulatory systems are frequently capable of compensation through increased activity elsewhere, and the symptoms they give rise to follow chiefly along one line; diseases of the digestive organs are more liable to occasion disorders elsewhere than to excite compensatory actions. The digestive system includes every organ, function and process concerned with the utilization of food-stuffs, from the moment of their entrance into the mouth, their preparation in the canal, assimilation with the tissues, their employment therein, up to their excretion or expulsion in the form of waste. Each portion resembles a link of a continuous chain; each link depends upon the integrity of the others, the weakening or breaking of one straining or making impotent the chain as a whole.
The mucous membrane lining the alimentary tract is the part most subject to pathological alterations, and in this connexion it should be remembered that this membrane differs both in structure and functions throughout the tract. Chiefly protective from the mouth to the cardia, it is secretory and absorbent in the stomach and bowel; while the glandular cells forming part of it secrete both acid and alkaline fluids, several ferments or mucus. Over the dorsum of the tongue its modified cells subserve the sense of taste. Without, connected with it by the submucous connective tissue, is placed the muscular coat, and externally over the greater portion of its length the peritoneal serous membrane. All parts are supplied with blood-vessels, lymph-ducts and nerves, the last belonging either to local or to central circuits. Associated with the tract are the salivary glands, the liver and the pancreas; while, in addition, lymphoid tissue is met with diffusely scattered throughout the lining membranes in the tonsils, appendix, solitary glands and Peyer’s patches, and the mesenteric glands. The functions of the various parts of the system in whose lesions we are here interested are many in number, and can only be summarized here. (For the physiology of digestion see Nutrition.) Broadly, they maybe given as: (1) Ingestion and swallowing of food, transmission of it through the tract, and expulsion of the waste material; (2) secretion of acids and alkalis for the performance of digestive processes, aided by (3) elaboration and addition of complex bodies, termed enzymes or ferments; (4) secretion of mucus; (5) protection of the body against organismal infection, and against toxic products; (6) absorption of food elements and reconstitution of them into complex substances fitted for metabolic application; and (7) excretion of the waste products of protoplasmic action. These functions may be altered by disease, singly or in conjunction; it is rare, however, to find but one affected, while an apparently identical disturbance of function may often arise from totally different organic lesions. Another point of importance is seen in the close interdependence which exists between the secretions of acid and those of alkaline reaction. The difference in reaction seems to act mutatis mutandis as a stimulant in each instance.
General Diseases.
In all sections of the alimentary canal actively engaged in the digestion of food, a well-marked local engorgement of the blood-vessels supplying the walls occurs. The hyperaemia abates soon after completion of the special duties of the individual sections. Vascular lesions. This normal condition may be abnormally exaggerated by overstimulation from irritant poisons introduced into the canal; from too rich, too copious or indigestible articles of diet; or from too prolonged an experience of some unvaried kind of food-stuff, especially if large quantities of it are necessary for metabolic needs; entering into the first stage of inflammation, acute hyperaemia. More important, because productive of less tractable lesions, is passive congestion of the digestive organs. Whenever the flow of blood into the right side of the heart is hindered, whether it arise from disease of the heart itself, or of the lungs, or proceed from obstruction in some part of the portal system, the damming-back of the venous circulation speedily produces a more or less pronounced stasis of the blood in the walls of the alimentary canal and in the associated abdominal glands. The lack of a sufficiently vigorous flow of blood is followed by deficient secretion of digestive agents from the glandular elements involved, by decreased motility of the muscular coats of the stomach and bowel, and lessened adaptability throughout for dealing with even slight irregular demands on their powers. The mucous membrane of the stomach and bowel, less able to withstand the effects of irritation, even of a minor character, readily passes into a condition of chronic catarrh, while it frequently is the seat of small abrasions, haemorrhagic erosions, which may cause vomiting of blood and the appearance of blood in the stools. Obstruction to the flow of blood from the liver leads to dilatation of its blood-vessels, consequent pressure upon the hepatic cells adjoining them, and their gradual loss of function, or even atrophy and degeneration. In addition to the results of such passive congestion exhibited by the stomach and bowel as noted above, passive congestion of the liver is often accompanied by varicose enlargement of the abdominal veins, in particular of those which surround the lower end of the oesophagus, the lowest part of the rectum and anus. In the latter position these dilated veins constitute what are known as haemorrhoids or piles, internal or external as their site lies within or outside the anal aperture.
The mucous and serous membranes of the canal and the glandular elements of the associated organs are the parts most subject to inflammatory affections. Among the several sections of the digestive tract itself, the oesophagus and jejunum are singularly exempt from inflammatory processes; the fauces, stomach, caecum and appendix, ileum, mouth and duodenum (including the opening of the common bile-duct), are more commonly involved. Stomatitis, or inflammation of the mouth, Inflammatory lesions. has many predisposing factors, but it has now been definitely determined that its exciting cause is always some form of micro-organism. Any condition favouring oral sepsis, as carious teeth, pyorrhoea alveolaris (a discharge of pus due to inflamed granulations round carious teeth), granulations beneath thick crusts of tartar, or an irritating tooth plate, favours the growth of pyogenic organisms and hence of stomatitis. Many varieties of this disease have been described, but all are forms of “pyogenic” or “septic stomatitis.” This in its mildest form is catarrhal or erythematous, and is attended only by slight swelling tenderness and salivation. In its next stage of acuteness it is known as “membranous,” as a false membrane is produced somewhat resembling that due to diphtheria, though caused by a staphylococcus only. A still more acute form is “ulcerative,” which may go on to the formation of an abscess beneath the tongue. Scarlet fever usually gives rise to a slight inflammation of the mouth followed by desquamation, but more rarely it is accompanied by a most severe oedematous stomatitis with glossitis and tonsillitis. Erysipelas on the face may infect the mouth, and an acute stomatitis due to the diphtheria bacillus, Klebs-Loeffler bacillus, has been described. A distinct and very dangerous form of stomatitis in infants and young children is known as “aphthous stomatitis” or “thrush.” This is caused by the growth of Oidium albicans. It is always preceded by a gastro-enteritis and dry mouth, and if this is not attended to, soon attracts attention by the little white raised patches surrounded by a dusky red zone 264 scattered on tongue and cheeks. Epidemics have occurred in hospitals and orphanages. Mouth breathing is the cause of many ills. As a result of this, the mucous membrane of the tongue, &c., becomes dry, micro-organisms multiply and the mouth becomes foul. Also from disease of the nose, the upper jaw, palate and teeth do not make proper progress in development. There is overgrowth of tonsils, and adenoids, with resulting deafness, and the child’s mental development suffers. An ordinary “sore throat” usually signifies acute catarrh of the fauces, and is of purely organismal origin, “catching cold” being only a secondary and minor cause. In “relaxed throats” there is a chronic catarrhal state of the lining membrane, with some passive congestion. The tonsils are peculiarly liable to catarrhal attacks, as might a priori be expected by reason of their Cerberus-like function with regard to bacterial intruders. Still, acute attacks of tonsillitis appear on good evidence to be more common among individuals predisposed constitutionally to rheumatic manifestations. Cases of acute tonsillitis may or may not go on to suppuration or quinsy; in all there is great congestion of the glands, increased mucus secretion, and often secondary involvement of the lymphatic glands of the neck. Repeated acute attacks often lead to chronic inflammation, in which the glands are enlarged, and often hypertrophied in the true sense of the term. The oesophagus is the seat of inflammation but seldom. In infants and young children thrush due to Oidium albicans may spread from the mouth, and also a diphtheritic inflammation spreads from the fauces into the oesophagus. A catarrhal oesophagitis is rarely seen, but the commonest form is traumatic, due to the swallowing of boiling water, corrosive or irritant substances, &c. A non-malignant ulceration may result which later leads on to an oesophageal stricture. The physical changes presented by the coats of the stomach and the intestine, the subjects of catarrhal attacks, closely resemble one another, but differ symptomatically. Acute catarrh of the stomach is associated with intense hyperaemia of its lining coats, with visible engorgement and swelling of the mucous membrane, and an excessive secretion of mucus. The formation of active gastric juice is arrested, digestion ceases, peristaltic movements are sluggish or absent, unless so over-stimulated that they act in a direction the reverse of the normal, and induce expulsion of the gastric contents by vomiting. The gastric contents, in whatever degree of dilution or concentration they may have been ingested, when ejected are of porridge-thick consistency, and often but slightly digested. Such conditions may succeed a severe alcoholic bout, be caused by irritant substances taken in by the mouth or arise from fermentative processes in the stomach contents themselves. Should the irritating material succeed in passing from the stomach into the bowel, similar physical signs are present; but as the quickest path offered for the expulsion of the offending substances from the body is downwards, peristalsis is increased, the flow of fluid from the intestinal glands is larger in bulk, though of less potency as regards its normal actions, than in health, and diarrhoea, with removal of the irritant, follows. As a general rule, the more marked the involvement of the large bowel, the severer and more fluid is the resultant diarrhoea. Inflammation of the stomach may be due to mechanical injury, thermal or chemical irritants or invasion by micro-organisms. Also all the symptoms of gastric catarrh may be brought on by any acute emotion. The commonest mechanical injury is that due to an excess of food, especially when following on a fast; poisons act as irritants, and also the weevils of cheese and the larvae of insects.
Inflammatory affections of the caecum and its attached appendix vermiformis are very common, and give rise to several special symptoms and signs. Acute inflammatory appendicitis appears to be increasing in frequency, and is associated by many with the modern deterioration in the teeth. Constipation certainly predisposes to it, and it appears to be more prevalent among medical men, commercial travellers, or any engaged in arduous callings, subjected to irregular meals, fatigue and exposure. A foreign body is the exciting cause in many cases, though less commonly so than was formerly imagined. The inflammation in the appendix varies in intensity from a very slight catarrhal or simple form to an ulcerative variety, and much more rarely to the acute fulminating appendicitis in which necrosis of the appendix with abscess formation occurs. It is always accompanied by more or less peritonitis, which is protective in nature, shutting in the inflammatory process. Very similar symptomatically is the condition termed perityphlitis, doubtless in former days frequently due to the appendix, an acute or chronic inflammation of the walls of the caecum often leading to abscess formation outside the gut, with or without direct communication with the canal. The colon is subject to three main forms of inflammation. In simple colitis the mucous membrane of the colon is intensely injected, bright red in colour, and secreting a thick mucus, but there is no accompanying ulceration. It is often found in association with some constitutional disease, as Bright’s disease, and also with cancer of the bowel. But when it has no association with other trouble it is probably bacterial in origin, the Bacillus enteritidis spirogenes having been isolated in many cases. The motions always contain large quantities of mucus and more or less blood. A second very severe form of inflammation of the colon is known as “membranous colitis,” and this may be either dyspeptic, or secondary to other diseases. In this trouble membranes are passed per anum, accompanied by a pain so intense as often to cause fainting. In severe cases complete tubular casts of the intestine have been found. Often the motions contain very little faecal matter, but consist only of membranes, mucus and a little blood. A third form is that known as “ulcerative colitis.” Any part of the large intestine may be affected, and the ulceration shows no special distribution. In severe cases the muscular coat is exposed, and perforation may ensue. The number of ulcers varies from a few to many dozen, and in size from a pea to a five-shilling piece. Like all chronic intestinal ulcers they show a tendency to become transverse.
Chronic catarrhal affections of the stomach are very common, and often follow upon repeated acute attacks. In them the connective tissue increases at the expense of the glandular elements; the mucous membrane becomes thickened and less active in function. Should the muscular coat be involved, the elasticity and contractility of the organ suffer; peristaltic movement is weakened; expulsion of the contents through the pylorus hindered; and, aggravated by these effects, the condition becomes worse, atonic dyspepsia in its most pronounced form results, with or without dilatation. Chronic vascular congestion may occasion in process of time similar signs and symptoms.
Duodenal catarrh is constantly associated with jaundice, indeed is most probably the commonest cause of catarrhal jaundice; often it is accompanied by catarrh of the common bile-duct. Chronic inflammation of the small intestine gives rise to less prominent symptoms than in the stomach. It generally arises from more than one cause; or rather secondary causes rapidly become as important as the primary in its incidence. Chronic congestion and prolonged irritation lead to deficient secretion and sluggish peristalsis; these effects encourage intestinal putrefaction and auto-intoxication; and these latter, in turn, increase the local unrest.
The intestinal mucous membrane, the peritoneum and the mesenteric glands are the chief sites of tubercular infection in the digestive organs. Rarely met with in the gullet and stomach, and comparatively seldom in the mouth and Infective lesions. lips, tubercular inflammation of the small intestine and peritoneum is common. Tubercular enteritis is a frequent accompaniment of phthisis, but may occur apart from tubercle of other organs. Children are especially subject to the primary form. Tubercular peritonitis often is present also. The inflammatory process readily tends towards ulcer formation, with haemorrhage and sometimes perforation. If in the large bowel, the symptoms are usually less acute than those characterizing tubercular inflammation of the small intestine. The appendix has been found to be the seat of tubercular processes; in the rectum they form the general cause of the fistulae and abscesses so commonly met with here. Tubercular peritonitis may be primary or secondary, acute or chronic; occasionally very acute cases are seen running a rapid course; the majority are chronic in type. 265 The tubercles spread over the surface of the serous membrane, and if small and not very numerous may give rise in chronic cases to few symptoms; if larger, and especially when they involve and obstruct the lymph- and blood-vessels, ascites follows. It is hardly possible that tubercular invasion of the mesenteric glands can ever occur unaccompanied by peritoneal infection; but when the infection of the glands constitutes the most prominent sign, the term tabes mesenterica is sometimes employed. Here the glands, enlarged, form a doughy mass in the abdomen, leading to marked protrusion of the abdominal walls, with wasting elsewhere and diarrhoea.
The liver is seldom attacked by tubercle, unless in cases of general miliary tuberculosis. Now and then it contains large caseous tubercular masses in its substance.
An important fact with regard to the tubercular processes in the digestive organs lies in the ready response to treatment shown by many cases of peritoneal or mesenteric invasion, particularly in the young.
The later sequelae of syphilis display a predilection for the rectum and the liver, usually leading to the development of a stricture in the former, to a diffuse hepatitis or the formation of gummata in the second. In inherited syphilis the temporary teeth usually appear early, are discoloured and soon crumble away. The permanent teeth may be sound and healthy, but are often—especially the upper incisors—notched and stunted, when they are known as “Hutchinson’s teeth.” As the result both of syphilis and of tubercle, the tissues of the liver and bowel may present a peculiar alteration; they become amyloid, or lardaceous, a condition in which they appear “waxy,” are coloured dark mahogany brown with dilute iodine solutions, and show degenerative changes in the connective tissue.
The Bacillus typhosus discovered by Eberth is the causal agent of typhoid fever, and has its chief seat of activity in the small intestine, more especially in the lower half of the ileum. Attacking the lymphoid follicles in the mucous membrane, it causes first inflammatory enlargement, then necrosis and ulceration. The adjacent portions of the mucous membrane show acute catarrhal changes. Diarrhoea, of a special “pea-soup” type, may or may not be present; while haemorrhage from the bowel, if ulcers have formed, is common. As the ulcers frequently extend down to the peritoneal coat of the bowel, perforation of this membrane and extravasation into the peritoneal cavity is easily induced by irritants introduced into or elaborated in the bowel, acting physically or by the excitation of hyper-peristalsis.
True Asiatic cholera is due to the comma-bacillus or spirillum of cholera, which is found in the rice-water evacuations, in the contents of the intestine after death, and in the mucous membrane of the intestine just beneath the epithelium. It has not been found in the blood. It produces an intense irritation of the bowel, seldom of the stomach, without giving rise locally to any marked physical change; it causes violent diarrhoea and copious discharges of “rice-water” stools, consisting largely of serum swarming with the organism.
Dysentery gives rise to an inflammation of the large intestine and sometimes of the lower part of the ileum, resulting in extensive ulceration and accompanied by faecal discharges of mucus, muco-pus or blood. In some forms a protozoan, the Amoeba dysenteriae, is found in the stools—this is the amoebic dysentery; in other cases a bacillus, Bacillus dysenteriae, is found—the bacillary dysentery.
Acute parotitis, or mumps, is an infectious disease of the parotid glands, chiefly interesting because of the association between it and the testes in males, inflammation of these glands occasionally following or replacing the affection of the parotids. The causal agent is probably organismal, but has as yet escaped detection.
The relative frequency with which malignant growths occur in the different organs of the digestive system may be gathered from the tabular analysis, on p. 266, of 1768 cases recorded in the books of the Edinburgh Royal Infirmary as having New growths. been treated in the medical and surgical wards between the years 1892 and 1899 inclusive. Of these, 1263, or 71.44%, were males; 505, or 28.56%, females. (See Table I. p. 266.)
If the figures there given be classified upon broader lines, the results are as given in Table II. p. 266, and speak for themselves.
The digestive organs are peculiarly subject to malignant disease, a result of the incessant changes from passive to active conditions, and vice versa, called for by repeated introduction of food; while the comparative frequency with which different parts are attacked depends, in part, upon the degree of irritation or changes of function imposed upon them. Scirrhous, encephaloid and colloid forms of carcinoma occur. In the stomach and oesophagus the scirrhous form is most common, the soft encephaloid form coming next. The most common situation for cancerous growth in the stomach is the pyloric region. Walsh out of 1300 cases found 60.8% near the pylorus, 11.4% over the lesser curvature, and 4.7% more or less over the whole organ. The small intestine is rarely attacked by cancer; the large intestine frequently. The rectum, sigmoid flexure, caecum and colon are affected, and in this order, the cylindrical-celled form being the most common. Carcinoma of the peritoneum is generally colloid in character, and is often secondary to growths in other organs. Cancer of the liver follows cancer of the stomach and rectum in frequency of occurrence, and is relatively more common in females than males. Secondary invasion of the liver is a frequent sequel to gastric cancer. The pancreas occasionally is the seat of cancerous growth.
Sarcomata are not so often met with in the digestive organs. When present, they generally involve the peritoneum or the mesenteric glands. The liver is sometimes attacked, the stomach rarely.
Benign tumours are not of common occurrence in the digestive organs. Simple growths of the salivary glands, cysts of the pancreas and polypoid tumours of the rectum are the most frequent.
The intestinal canal is the habitat of the majority of animal parasites found in man. Frequently their presence leads to no morbid symptoms, local or general; nor are the symptoms, when they do arise, always characteristic of the presence of Animal parasites. parasites alone. Discovery of their bodies, or of their eggs, in the stools is in most instances the only satisfactory proof of their presence. The parasites found in the bowel belong principally to two natural groups, Protozoa and Metazoa. The great class of the Protozoa furnish amoebae, members of Sporozoa and Infusoria. The amoebae are almost invariably found in the large intestine; one species, indeed, is termed Amoeba coli. The frequently observed relation between attacks of dysentery and the presence of amoebae in the stools has led to the proposition that an Amoeba dysenterica exists, causing the disease—a theory supported by the detection of amoebae in the contents of dysenteric abscesses of the liver. No symptoms of injury to health appear to accompany the presence of Sporozoa in the bowel, while the species of Infusoria found in it, the Cercomonas, and Trichomonas intestinalis, and the Balantidium coli, may or may not be guilty of prolonging conditions within the bowel as have previously set up diarrhoea.
The Metazoa supply examples of intestinal parasites from the classes Annuloida and Nematoidea. To the former class belong the various tapeworms found in the small intestine of man. They, like other intestinal parasites, are destitute of any power of active digestion, simply absorbing the nutritious proceeds of the digestive processes of their hosts. Nematode worms infest both the small and large intestine; Ascaris lumbricoides, the common round worm, and the male Oxyuris vermicularis are found in the small bowel, the adult female Oxyuris vermicularis and the Tricocephalus dispar in the large.
The eggs of the Trichina spiralis, when introduced with the food, develop in the bowel into larval forms which invade the tissues of the body, to find in the muscles congenial spots wherein to reach maturity. Similarly, the eggs of the Echinococcus are hatched in the bowel, and the embryos proceed to take up their abode in the tissues of the body, developing into cysts capable of growth into mature worms after their ingestion by dogs.
Numbers of bacterial forms habitually infest the alimentary canal. Many of them are non-pathogenic; some develop pathogenic characters only under provocation or when a suitable environment induces them to act in such a Vegetable parasites. manner; others may form the materies morbi of special lesions, or be casual visitors capable of originating disease if opportunity occurs. Apart from those organisms associated with acute infective diseases, disturbances of function and physical lesions may be the result of abnormal bacterial activity in the canal; and these disturbances may be both local and general. Many of the bacteria commonly present produce putrefactive changes in the contents of the tract by their metabolic processes. They render the medium they grow in alkaline, produce different gases and elaborate more or less virulent toxins. Other species set up an acid fermentation, seldom accompanied by gas or toxin formation. The products of either class are inimical to the free growth of members of the other. The species which produce acids are more resistant to the action of acids. Thus, when the contents of the stomach possess a normal or excessive proportion of free hydrochloric acid, a much larger number of putrefactive and pathogenic organisms in the food are destroyed or inhibited than of the bacteria of acid fermentation. Diminished gastric acidity allows of the entry of a greater number of putrefactive (and pathogenic) types, with, as a consequence, increased facilities for their growth and activity, and the appearance of intestinal derangements.
Table I.
| Males. | Females. | Both Sexes. | |||
| Organ or Tissue in Order of Frequency. | Per- centage |
Organ or Tissue in Order of Frequency. | Per- centage |
Organ or Tissue in Order of Frequency. | Per- centage |
| 1 Stomach | 22.56 | 1 Stomach | 22.37 | 1 Stomach | 22.49 |
| 2 Lip | 12.94 | 2 Rectum | 17.24 | 2 Rectum | 13.12 |
| 3 Rectum | 11.57 | 3 Liver | 15.50 | 3 Liver | 10.02 |
| 4 Tongue | 11.36 | 4 Peritoneum | 7.86 | 4 Lip | 9.89 |
| 5 Oesophagus | 10.90 | 5 Oesophagus | 5.33 | 5 Oesophagus | 9.29 |
| 6 Liver | 7.80 | 6 Sigmoid | 4.53 | 6 Tongue | 8.96 |
| 7 Jaw | 6.38 | 7 Pancreas | 3.52 | 7 Jaw | 5.65 |
| 8 Mouth | 2.88 | 8 Tongue | 3.12 | 8 Peritoneum | 2.94 |
| 9 Tonsils | 2.09 | 9 Omentum | 2.98 | 9 Sigmoid | 2.56 |
| 10 Sigmoid flexure | 1.77 | 10 Lip | 2.57 | 10 Mouth | 2.40 |
| 11 Parotid | 1.10 | 11 Jaw | 1.97 | 11 Pancreas | 1.80 |
| 12 Pancreas | ” | 12 Colon | 1.84 | 12 Tonsils | 1.35 |
| 13 Caecum | 0.94 | 13 Abdomen | ” | 13 Omentum | 1.25 |
| 14 Peritoneum | ” | 14 Intestine | 1.56 | 14 Parotid | 1.12 |
| 15 Colon | 0.89 | 15 Caecum | 1.37 | 15 Colon | ” |
| 16 Pharynx | 0.79 | 16 Mouth | 1.18 | 16 Caecum | 1.08 |
| 17 Intestine (site unknown) | ” | 17 Parotid | ” | 17 Intestine | 1.00 |
| 18 Abdomen | 0.71 | 18 Splenic flexure | 0.98 | 18 Abdomen | ” |
| 19 Mesentery | 0.55 | 19 Jejunum and ileum | 0.78 | 19 Pharynx | 0.62 |
| 20 Omentum | ” | 20 Tonsils | 0.68 | 20 Mesentery | 0.52 |
| 21 Hepatic flexure | 0.39 | 21 Pharynx | 0.40 | 21 Jejunum and ileum | 0.44 |
| 22 Submaxillary gland | 0.31 | 22 Hepatic flexure | ” | 22 Hepatic flexure | ” |
| 23 Jejunum and ileum | ” | 23 Mesentery | ” | 23 Splenic flexure | ” |
| 24 Duodenum | 0.23 | 24 Submaxillary | 0.20 | 24 Submaxillary | 0.28 |
| 25 Splenic flexure | 0.15 | 25 Duodenum | ” | 25 Duodenum | 0.22 |
| Note.—The figures where several organs are bracketed apply to each organ separately. | |||||
In a healthy new-born infant the mouth is free from micro-organisms, and very few are found in a breast-fed baby, but Bacillus lactis may be found where the child is bottle fed. If there is trouble with the first dentition and food is allowed to collect, staphylococci, streptococci, pneumococci and colon bacilli may be present. Even in healthy babies Oidium albicans may be present, and in older children the pseudo-diphtheria bacillus. From carious teeth may be isolated streptothrix, leptothrix, spirilla and fusiform bacilli. Under conditions of health these micro-organisms live in the mouth as saprophytes, and show no virulence when cultivated and injected into animals. The two common pyogenetic organisms, Staphylococcus albus and brevis, show no virulence. Also the pneumococcus, though often present, must be raised in virulence before it can produce untoward results. The foulness of the mouth is supposed to be due to the colon bacillus and its allies, but those obtained from the mouth are innocuous. Also to enable the Oidium albicans to attack the mucous membrane there must be some slight inflammation or injury. The micro-organisms found in the stomach gain access to that organ in the food or by regurgitation from the small intestine. Most are relatively inert, but some have a special fermentative action on the food (see Nutrition). Abelous isolated sixteen distinct species of organism from a healthy stomach, including Sarcinae, B. lactis, pyocyaneus, subtilis, lactis erythrogenes, amylobacter, megatherium, and Vibrio rugula.
Hare-lip, cleft palate, hernia and imperforate anus are physical abnormalities which are interesting to the surgeon rather than to the pathologist. The oesophagus may be the seat of a diverticulum, or blind pouch, usually situated in its lower half, which in Physical abnormalities most instances is probably partly acquired and partly congenital; a local weakness succumbing to pressure. Hypertrophy of the muscular coat of the pyloric region is an infrequent congenital gastric anomaly in infants, preventing the passage of food into the bowel, and causing death in a short time. Incomplete closure of the vitelline duct results in the presence of a diverticulum—Meckel’s—generally connected with the ileum, mainly important by reason of the readiness with which it occasions intestinal obstruction. Idiopathic congenital dilatation of the colon has been described.
Table II.
| Males. | Per- centage. | Females. | Per- centage. | Total. | Per- centage. |
| 1 Mouth and pharynx | 37.85 | 1 Intestines | 28.9 | 1 Oesophagus and stomach | 31.78 |
| 2 Oesophagus and stomach | 33.46 | 2 Oesophagus and stomach | 27.7 | 2 Mouth and pharynx | 30.27 |
| 3 Intestines | 17.04 | 3 Liver | 15.5 | 3 Intestines | 20.42 |
| 4 Liver | 7.8 | 4 Peritoneum | 13.1 | 4 Liver | 10.02 |
| 5 Peritoneum | 2.75 | 5 Mouth and pharynx | 11.3 | 5 Peritoneum | 5.71 |
| 6 Pancreas | 1.1 | 6 Pancreas | 3.5 | 6 Pancreas | 1.80 |
Traction diverticula of the oesophagus not uncommonly occur as sequels to suppurative inflammation of cervical lymphatic glands. More frequently dilatation of a section is met with, due as a rule to the presence of a stricture. The stomach often diverges from the normal in size, shape and position. Normally capable in the adult of containing from fifty to sixty ounces, either by reason of organic disease, or as the result of functional disturbance, its capacity may vary enormously. The writer has seen post mortem a stomach which held a gallon (160 ounces), and again one holding only two ounces. Cancer spread over a large area and cirrhosis of the stomach wall cause diminution in capacity; pyloric obstruction, weakness of the muscular coat, and nervous influences are associated with dilatation. A peculiar distortion of the shape of the stomach follows cicatrization of 267 ulcers of greater or lesser curvature; the gastric cavity becomes “hour-glass” in shape. In addition, the stomach may be displaced downwards as a whole, a condition known as gastroptosis: if the pyloric portion only be displaced, the lesion is termed pyloroptosis. Ptoses of other abdominal organs are described; the liver, transverse colon, spleen and kidneys may be involved. Displacements downwards of the stomach and transverse colon, along with a movable right kidney and associated with dyspepsia and neurasthenia, form the malady termed by Glénard enteroptosis. A general visceroptosis often occurs in those patients who have some tuberculous lesion of the lungs or elsewhere, this disease causing a general weakening and subsequent stretching of all ligaments. Displacements of the abdominal viscera are almost invariably accompanied by symptoms of dyspepsia of a neurotic type. The rectum is liable to prolapse, consequent upon constipation and straining at stool, or following local injuries of the perineal floor.
Every pathological lesion shown by digestive organs is closely associated with the state of the nervous system, general or local; so stoppage of active gastric digestive processes after profound nervous shock, and occurrence of nervous Influence of the nervous system. diarrhoea from the same cause. Gastric dyspepsia of nervous origin presents most varied and contradictory symptoms: diminished acidity of the gastric juice, hyper-acidity, over-production, arrest of secretion, lessened or increased movements, greater sensitiveness to the presence of contents, dilatation or spasm. Often the nervous cause can be traced back farther,—in females, frequently to the pelvic organs; in both sexes, to the condition of the blood, the brain or the bowel. Unhealthy conditions related to evacuation of the bowel-contents commonly induce reflex nervous manifestations of abnormal character referred to the stomach and liver. Gastric disturbances similarly react upon the proper conduct of intestinal functions.
Local Diseases.
The Mouth.—The lining membrane of the cheeks inside the mouth, of the gums and the under-surface and edges of the tongue, is often the seat of small irritable ulcers, usually associated with some digestive derangement. A crop of minute vesicles known as Koplik’s spots over these parts has been lately stated by Koplik to be an early symptom of measles. Xerostomia, or dry mouth, is a rare condition, connected with lack of salivary secretion. Gangrenous stomatitis, cancrum oris, or noma, occasionally attacks debilitated children, or patients convalescing from acute fevers, more especially after measles. It commences in the gums or cheeks, and causes widespread sloughing of the adjacent soft parts—it may be of the bones.
The Stomach.—It were futile to attempt to enumerate all the protean manifestations of disturbance which proceed from a disordered stomach. The possible permutations and combinations of the causes of gastric vagaries almost reach infinity. Idiosyncrasy, past and present gastric education, penury or plethora, actual digestive power, motility, bodily requirements and conditions, environment, mental influences, local or adjacent organic lesions, and, not least, reflex impressions from other organs, all contribute to the variance.
Ulcer of the stomach, however—the perforating gastric ulcer—occupies a unique position among diseases of this organ. Gastric ulcers are circumscribed, punched out, rarely larger than a sixpenny-bit, funnel-shaped, the narrower end towards the peritoneal coat, and distributed in those regions of the stomach wall which are most exposed to the action of the gastric contents. They occur most frequently in females, especially if anaemic, and are usually accompanied by excess of acid, actual or relative to the state of the blood, in the stomach contents. Local pain, dorsal pain, generally to the left of the eighth or ninth dorsal spinous process, and haematernesis and melaena, are symptomatic of it. The amount of blood lost varies with the rapidity of ulcer formation and the size of vessel opened into. Fatal results arise from ulceration into large blood-vessels, followed by copious haemorrhage, or by perforation of the ulcer into the peritoneal cavity. Scars of such ulcers may be found post mortem, although no symptoms of gastric disease have been exhibited during life; gastric ulcers, therefore, may be latent.
Irritation of the sensory nerve-endings in the stomach wall from the presence of an increased proportion of acid, organic or mineral, in the stomach contents is accountable for the well known symptom heartburn. Water-brash is a term applied to eructation of a colourless, almost tasteless fluid, probably saliva, which has collected in the lower part of the oesophagus from failure of the cardiac sphincter of the stomach to relax; reversed oesophageal peristalsis causing regurgitation. A similar reversed action serves in merycism, or rumination, occasionally found in man, to raise part of the food, lately ingested, from the stomach to the mouth. Vomiting also is aided by reversed peristaltic action, both of the stomach and the oesophagus, with the help of the diaphragm and the muscles of the anterior abdominal wall. Emesis may be caused both by local nervous influence, and through the central nervous mechanism either reflexly or from the direct action of substances circulating in the blood. Further, the causal agent acting on the central nervous apparatus may be organic or functional, as well as medicinal. Vomiting without any apparent cause suggests nervous lesions, organic or reflex. The obstinate vomiting of pregnancy is a case in point. Here the primary cause proceeds reflexly from the pelvis. In females the pelvic organs are often the true source of emesis. Haematemesis accompanies gastric ulcer, cancer, chronic congestion with haemorrhagic erosion, congestion of the liver, or may follow violent acts of vomiting. In cases of ulcer the blood is usually bright and in considerable amount; in cancer, darker, like coffee-grounds; and in cases of erosion, in smaller quantity and of bright colour. The reaction of the stomach contents, if the cause be doubtful, yields valuable aid towards a diagnosis. Of increased acidity in gastric ulcer, normal in hepatic congestion, it is diminished in cancer; but as the acid present in cancer is largely lactic, analysis of the gastric contents must often be a sine qua non, because hyperacidity from lactic may obscure hypoacidity of hydrochloric acid.
Flatulence usually results from fermentative processes in the stomach and bowel, as the outcome of bacterial activity. A different form of flatulence is common in neurotic individuals: in such the gas evolved consists simply in carbonic acid liberated from the blood, and its evolution is generally characterized by rapid development and by lack of all fermentative signs.
The Liver.—The liver is an organ frequently libelled for the delinquencies of other organs, and regarded as a common source of ill. In catarrhal jaundice it is in most cases the bowel that is at fault, the liver acting properly, but unable to get rid of all the bile produced. The liver suffers, however, from several diseases of its own. Its fibrous or connective tissue is very apt to increase at the expense of the cellular elements, destroying their functions. This cirrhotic process usually follows long-continued irritation, such as is produced by too much alcohol absorbed from the bowel habitually, the organ gradually becoming harder in texture and smaller in bulk. Hypertrophic cirrhosis of the liver is not uncommonly met with, in which the liver is much increased in size, the “unilobular” form, also of alcoholic origin. In still-born children and in some infants a form of hypertrophic cirrhosis is occasionally seen, probably of hereditary syphilitic origin. Acute congestion of the liver forms an important symptom of malarial fever, and often leads in time to establishment of cirrhotic changes; here the liver is generally enlarged, but not invariably so, and the part played by alcohol in its causation has still to be investigated. Acute yellow atrophy of the liver is a disease sui generis. Of rare occurrence, possibly of toxic origin, it is marked by jaundice, at first of usual type, later becoming most intense; by vomiting; haemorrhages widely distributed; rapid diminution in the size of the liver; the appearance of leucin and tyrosin in the urine, with lessened urea; and in two or three days, death. The liver after death is soft, of a reddish colour dotted with yellow patches, and weighs only about a third part of the normal—about 1½ lb in place of 3¾ lb. A closely analogous affection of the liver, known as Weil’s disease, is of infectious type, and has been noted in 268 epidemic form. In this the spleen and liver are commonly but not always swollen, and the liver is often tender on pressure. As a large proportion of the sufferers from this disease have been butchers, and the epidemics have occurred in the hot season of the year, it probably arises from contact with decomposing animal matter. Hepatic abscess may follow on an attack of amoebic dysentery, and is produced either by infection through the portal vein, or by direct infection from the adjacent colon. In general pyaemia multiple small abscesses may occur in the liver.
The Gall-Bladder.—The formation of biliary calculi in the gall-bladder is the chief point of interest here. At least 75% of such cases occur in women, especially in those who have borne children. Tight-lacing has been stated to act as an exciting cause, owing to the consequent retardation of the flow of bile. Gall-stones may number from one to many thousands. They are largely composed of cholesterin, combined with small amounts of bile-pigments and acids, lime and magnesium salts. Their presence may give rise to no symptoms, or may cause violent biliary colic, and, if the bile-stream be obstructed, to jaundice. Inflammatory processes may be initiated in the gall-bladder or the bile-ducts, catarrhal or suppurative in character.
The Pancreas.—Haemorrhages into the body of the pancreas, acute and chronic inflammation, calculi, cysts and tumours, among which cancer is by far the most common, are recognized as occurring in this organ; the point of greatest interest regarding them lies in the relations established between pancreatic disease and diabetes mellitus, affections of the gland frequently being complicated by, and probably causing, the appearance of sugar in the urine.
The Small Intestine.—Little remains to be added to the account of inflammatory lesions in connexion with the small intestine. It offers but few conditions peculiar to itself, save in typhoid fever, and the ease with which it contrives to become kinked, or intussuscepted, producing obstruction, or to take part in hernial protrusions. The first section, the duodenum, is subject to development of ulcers very similar to those of the gastric mucous membrane. For long duodenal ulceration has been regarded as a complication of extensive burns of the skin, but the relationship between them has not yet been quite satisfactorily explained. The condition of colic in the bowel usually arises from overdistension of some part of the small gut with gas, the frequent sharp turns of the gut facilitating temporary closure of its lumen by pressure of the dilated gut near a curve against the part beyond. In the large bowel accumulations of gas seldom cause such acute symptoms, having a readier exit.
The Large Intestine.—The colon, especially the ascending portion, may become immensely dilated, usually after prolonged constipation and paralysis of the gut; occasionally the condition is congenital. Straining efforts made in defaecation may often account for prolapse of the lower end of the rectum through the anus. Haemorrhage from the bowel is usually a sign of disease situated in the large intestine: if bright in colour, the source is probably low down; if dark, from the caecum or from above the ileo-caecal valve. Blood after a short stay in any section of the alimentary canal darkens, and eventually becomes almost black in colour.
DIGGES, WEST (1720-1786), English actor, made his first stage appearance in Dublin in 1749 as Jaffier in Venice Preserved; and both there and in Edinburgh until 1764 he acted in many tragic rôles with success. He was the original “young Norval” in Home’s Douglas (1756). His first London appearance was as Cato in the Haymarket in 1777, and he afterwards played Lear, Macbeth, Shylock and Wolsey. In 1881 he returned to Dublin and retired in 1784.
DIGIT (Lat. digitus, finger), literally a finger or toe, and so used to mean, from counting on the fingers, a single numeral, or, from measuring, a finger’s breadth. In astronomy a digit is the twelfth part of the diameter of the sun or moon; it is used to express the magnitude of an eclipse.
DIGITALIS. The leaves of the foxglove (q.v.), gathered from wild plants when about two-thirds of their flowers are expanded, deprived usually of the petiole and the thicker part of the midrib, bitter taste; and to preserve their properties they must be kept excluded from light in stoppered bottles. They are occasionally adulterated with the leaves of Inula Conyza, ploughman’s spikenard, which may be distinguished by their greater roughness, their less divided margins, and their odour when rubbed; also with the leaves of Symphytum officinale, comfrey, and of Verbascum Thapsus, great mullein, which unlike those of the foxglove have woolly upper and under surfaces. The earliest known descriptions of the foxglove are those given by Leonhard Fuchs and Tragus about the middle of the 16th century, but its virtues were doubtless known to herbalists at a much remoter period. J. Gerarde, in his Herbal (1597), advocates the use of foxglove for a variety of complaints; and John Parkinson, in the Theatrum Botanicum, or Theater of Plants (1640), and later W. Salmon, in The New London Dispensatory, similarly praised the remedy. Digitalis was first brought prominently under the notice of the medical profession by Dr W. Withering, who, in his Account of the Foxglove (1785), gave details of upwards of 200 cases chiefly dropsical, in which it was used.
Digitalis contains four important glucosides, of which three are cardiac stimulants. The most powerful is digitoxin C34H54O11, an extremely poisonous and cumulative drug, insoluble in water. Digitalin, C35H56O14, is crystalline and is also insoluble in water. Digitalein is amorphous but readily soluble in water. It can therefore be administered subcutaneously, in doses of about one-hundredth of a grain. Digitonin, on the other hand, is a cardiac depressant, and has been found to be identical with saponin, the chief constituent of senega root. There are numerous preparations, patent and pharmacopeial, their composition being extremely varied, so that, unless one has reason to be certain of any particular preparation, it is almost better to use only the dried leaves themselves in the form of a powder (dose ½-2 grains). The pharmacopeial tincture may be given in doses of five to fifteen minims, and the infusion has the unusually small dose of two to four drachms—the dose of other infusions being an ounce or more. The tincture contains a fair proportion of both digitalin and digitoxin.
Digitalis leaves have no definite external action. Taken by the mouth, the drug is apt to cause considerable digestive disturbance, varying in different cases and sometimes so severe as to cause serious difficulty. This action is probably due to the digitonin, which is thus a constituent in every way undesirable. The all-important property of the drug is its action on the circulation. Its first action on any of the body-tissues is upon unstriped muscle, so that the first consequence of its absorption is a contraction of the arteries and arterioles. No other known drug has an equally marked action in contracting the arterioles. As the vaso-motor centre in the medulla oblongata is also stimulated, as well as the contractions of the heart, there is thus trebly caused a very great rise in the blood-pressure.
The clinical influence of digitalis upon the heart is very well defined. After the taking of a moderate dose the pulse is markedly slowed. This is due to a very definite influence upon the different portions of the cardiac cycle. The systole is not altered in length, but the diastole is very much prolonged, and since this is the period not only of cardiac rest but also of cardiac “feeding”—the coronary vessels being compressed and occluded during systole—the result is greatly to benefit the nutrition of the cardiac muscle. So definite is this that, despite a great increase in the force of the contractions and despite experimental proof that the heart does more work in a given time under the influence of digitalis, the organ subsequently displays all the signs of having rested, its improved vigour being really due to its obtaining a larger supply of the nutrient blood. Almost equally striking is the fact that digitalis causes an irregular pulse to become regular. Added to the greater force of cardiac contraction is a permanent tonic contraction of the organ, so that its internal capacity is reduced. The bearing of this fact on cases of cardiac dilatation is evident. In larger doses a remarkable sequel to these actions 269 may be observed. The cardiac contractions become irregular, the ventricle assumes curious shapes—“hour-glass,” &c.—becomes very pale and bloodless, and finally the heart stops in a state of spasm, which shortly afterwards becomes rigor-mortis. Before this final change the heart may be started again by the application of a soluble potassium salt, or by raising the fluid pressure within it. Clinically it is to be observed that the drug is cumulative, being very slowly excreted, and that after it has been taken for some time the pulse may become irregular, the blood-pressure low, and the cardiac pulsations rapid and feeble. These symptoms with more or less gastro-intestinal irritation and decrease in the quantity of urine passed indicate digitalis poisoning. The initial action of digitalis is a stimulation of the cardiac terminals of the vagus nerves, so that the heart’s action is slowed. Thereafter follows the most important effect of the drug, which is a direct stimulation of the cardiac muscle. This can be proved to occur in a heart so embryonic that no nerves can be recognized in it, and in portions of cardiac muscle that contain neither nervecells nor nerve-fibres.
The action of this drug on the kidney is of importance only second to its action on the circulation. In small or moderate doses it is a powerful diuretic. Though Heidenhain asserts that rise in the renal blood-pressure has not a diuretic action per se, it seems probable that this influence of the drug is due to a rise in the general blood-pressure associated with a relatively dilated condition of the renal vessels. In large doses, on the other hand, the renal vessels also are constricted and the amount of urine falls. It is probable that digitalis increases the amount of water rather than that of the urinary solids. In large doses the action of digitalis on the circulation causes various cerebral symptoms, such as seeing all objects blue, and various other disturbances of the special senses. There appears also to be a specific action of lowering the reflex excitability of the spinal cord.
Digitalis is used in therapeutics exclusively for its action on the circulation. In prescribing this drug it must be remembered that fully three days elapse before it gets into the system, and thus it must always be combined with other remedies to tide the patient over this period. It must never be prescribed in large doses to begin with, as some patients are quite unable to take it, intractable vomiting being caused. The three days that must pass before any clinical effect is obtained renders it useless in an emergency. A certain consequence of its use is to cause or increase cardiac hypertrophy—a condition which has its own dangers and ultimately disastrous consequences, and must never be provoked beyond the positive needs of the case. But digitalis is indicated whenever the heart shows itself unequal to the work it has to perform. This formula includes the vast majority of cardiac cases. The drug is contra-indicated in all cases where the heart is already beating too slowly; in aortic incompetence—where the prolongation of diastole increases the amount of the blood that regurgitates through the incompetent valve; in chronic Bright’s disease and in fatty degeneration of the heart—since nothing can cause fat to become contractile.
DIGNE, the chief town of the department of the Basses Alpes, in S.E. France, 14 m. by a branch line from the main railway line between Grenoble and Avignon. Pop. (1906), town, 4628; commune, 7456. The Ville Haute is built on a mountain spur running down to the left bank of the Bléone river, and is composed of a labyrinth of narrow winding streets, above which towers the present cathedral church, dating from the end of the 15th century, but largely reconstructed in modern times, and the former bishop’s palace (now the prison). The fine Boulevard Gassendi separates the Ville Haute from the Ville Basse, which is of modern date. The old cathedral (Notre Dame du Bourg) is a building of the 13th century, but is now disused except for funerals: it stands at the east end of the Ville Basse. The neighbourhood of Digne is rich in orchards, which have long made the town famous in France for its preserved fruits and confections. It is the Dinia of the Romans, and was the capital of the Bodiontii. From the early 6th century at least it has been an episcopal see, which till 1790 was in the ecclesiastical province of Embrun, but since 1802 in that of Aix en Provence. The history of Digne in the middle ages is bound up with that of its bishops, under whom it prospered greatly. But it suffered much during the religious wars of the 16th and 17th centuries, when it was sacked several times. A little way off, above the right bank of the Bléone, is Champtercier, the birthplace of the astronomer Gassendi (1592-1655), whose name has been given to the principal thoroughfare of the little town.
See F. Guichard, Souvenirs historiques sur la ville de Digne et ses environs (Digne, 1847).
DIGOIN, a town of east-central France, in the department of Saône-et-Loire, on the right bank of the Loire, 55 m. W.N.W. of Mâcon on the Paris-Lyon railway. Pop. (1906) 5321. It is situated at the meeting places of the Loire, the Lateral canal of the Loire and the Canal du Centre, which here crosses the Loire by a fine aqueduct. The town carries on considerable manufactures of faience, pottery and porcelain. The port on the Canal du Centre has considerable traffic in timber, sand, iron, coal and stone.
DIJON, a town of eastern France, capital of the department of Côte d’Or and formerly capital of the province of Burgundy, 195 m. S.E. of Paris on the Paris-Lyon railway. Pop. (1906) 65,516. It is situated on the western border of the fertile plain of Burgundy, at the foot of Mont Afrique, the north-eastern summit of the Côte d’Or range, and at the confluence of the Ouche and the Suzon; it also has a port on the canal of Burgundy. The great strategic importance of Dijon as a centre of railways and roads, and its position with reference to an invasion of France from the Rhine, have led to the creation of a fortress forming part of the Langres group. There is no enceinte, but on the east side detached forts, 3 to 4 m. distant from the centre, command all the great roads, while the hilly ground to the west is protected by Fort Hauteville to the N.W. and the “groups” of Motte Giron and Mont Afrique to the S.W., these latter being very formidable works. Including a fort near Saussy (about 8 m. to the N.W.) protecting the water-supply of Dijon, there are eight forts, besides the groups above mentioned. The fortifications which partly surrounded the old and central portion of the city have disappeared to make way for tree-lined boulevards with fine squares at intervals. The old churches and historic buildings of Dijon are to be found in the irregular streets of the old town, but industrial and commercial activity has been transferred to the new quarters beyond its limits. A fine park more than 80 acres in extent lies to the south of the city, which is rich in open spaces and promenades, the latter including the botanical garden and the Promenade de l’Arquebuse, in which there is a black poplar famous for its size and age.
The cathedral of St Bénigne, originally an abbey church, was built in the latter half of the 13th century on the site of a Romanesque basilica, of which the crypt remains. The west front is flanked by two towers and the crossing is surmounted by a slender timber spire. The plan consists of three naves, short transepts and a small choir, without ambulatory, terminating in three apses. In the interior there is a fine organ and a quantity of statuary, and the vaults contain the remains of Philip the Bold, duke of Burgundy, and Anne of Burgundy, daughter of John the Fearless. The site of the abbey buildings is occupied by the bishop’s palace and an ecclesiastical seminary. The church of Notre-Dame, typical of the Gothic style of Burgundy, was erected from 1252 to 1334, and is distinguished for the grace of its interior and the beauty of the western façade. The portal consists of three arched openings, above which are two stages of arcades, open to the light and supported on slender columns. A row of gargoyles surmounts each storey of the façade, which is also ornamented by sculptured friezes. A turret to the right of the portal carries a clock called the Jaquemart, on which the hours are struck by two figures. The church of St Michel belongs to the 15th century. The west façade, the most remarkable feature of the church, is, however, of the Renaissance period. The vaulting of the three portals is of exceptional depth owing to the projection of the lower storey of the façade. Above this storey rise two towers of five stages, the fifth stage being formed by an octagonal cupola. The columns decorating the façade represent all the four orders. The design of this façade is wrongly attributed to Hugues 270 Sambin (fl. c. 1540), a native of Dijon, and pupil of Leonardo da Vinci, but the sculpture of the portals, including “The Last Judgment” on the tympanum of the main portal, is probably from his hand. St Jean (15th century) and St Étienne (15th, 16th and 17th centuries), now used as the exchange, are the other chief churches. Of the ancient palace of the dukes of Burgundy there remain two towers, the Tour de la Terrasse and the Tour de Bar, the guard-room and the kitchens; these now form part of the hôtel de ville, the rest of which belongs to the 17th and 18th centuries. This building contains an archaeological museum with a collection of Roman stone monuments; the archives of the town; and the principal museum, which, besides valuable paintings and other works of art, contains the magnificent tombs of Philip the Bold and John the Fearless, dukes of Burgundy. These were transferred from the Chartreuse of Dijon (or of Champmol), built by Philip the Bold as a mausoleum, now replaced by a lunatic asylum. Relics of it survive in the old Gothic entrance, the portal of the church, a tower and the well of Moses, which is adorned with statues of Moses and the prophets by Claux Sluter (fl. end of 14th century), the Dutch sculptor, who also designed the tomb of Philip the Bold. The Palais de Justice, which belongs to the reign of Louis XII., is of interest as the former seat of the parlement of Burgundy. Dijon possesses several houses of the 15th, 16th and 17th centuries, notably the Maison Richard in the Gothic, and the Hôtel Vogüé in the Renaissance style. St Bernard, the composer J. P. Rameau and the sculptor François Rude have statues in the town, of which they were natives. There are also monuments to those inhabitants of Dijon who fell in the engagement before the town in 1870, and to President Carnot and Garibaldi.
The town is important as the seat of a prefecture, a bishopric, a court of appeal and a court of assizes, and as centre of an académie (educational district). There are tribunals of first instance and of commerce, a board of trade-arbitrators, a chamber of commerce, an exchange (occupying the former cathedral of St Étienne), and an important branch of the Bank of France. Its educational establishments include faculties of law, of science and of letters, a preparatory school of medicine and pharmacy, a higher school of commerce, a school of fine art, a conservatoire of music, lycées and training colleges, and there is a public library with about 100,000 volumes.
Dijon is well known for its mustard, and for the black currant liqueur called cassis de Dijon; its industries include the manufacture of machinery, automobiles, bicycles, soap, biscuits, brandy, leather, boots and shoes, candles and hosiery. There are also flour mills, breweries, important printing works, vinegar works and, in the vicinity, nursery gardens. The state has a large tobacco manufactory in the town. Dijon has considerable trade in cereals and wool, and is the second market for the wines of Burgundy.
Under the Romans Dijon (Divonense castrum) was a vicus in the civitas of Langres. In the 2nd century it was the scene of the martyrdom of St Benignus (Bénigne, vulg. Berin, Berain), the apostle of Burgundy. About 274 the emperor Aurelian surrounded it with ramparts. Gregory of Tours, in the 6th century, comments on the strength and pleasant situation of the place, expressing surprise that it does not rank as a civitas. During the middle ages the fortunes of Dijon followed those of Burgundy, the dukes of which acquired it early in the 11th century. The communal privileges, conferred on the town in 1182 by Hugh III., duke of Burgundy, were confirmed by Philip Augustus in 1183, and in the 13th century the dukes took up their residence there. For the decoration of the palace and other monuments built by them, eminent artists were gathered from northern France and Flanders, and during this period the town became one of the great intellectual centres of France. The union of the duchy with the crown in 1477 deprived Dijon of the splendour of the ducal court; but to counterbalance this loss it was made the capital of the province and seat of a parlement. Its fidelity to the monarchy was tested in 1513, when the citizens were besieged by 50,000 Swiss and Germans, and forced to agree to a treaty so disadvantageous that Louis XII. refused to ratify it. In the wars of religion Dijon sided with the League, and only opened its gates to Henry IV. in 1595. The 18th century was a brilliant period for the city; it became the seat of a bishopric, its streets were improved, its commerce developed, and an academy of science and letters founded; while its literary salons were hardly less celebrated than those of Paris. The neighbourhood was the scene of considerable fighting during the Franco-German War, which was, however, indirectly of some advantage to the city owing to the impetus given to its industries by the immigrants from Alsace.
See H. Chabeuf, Dijon à travers les âges (Dijon, 1897), and Dijon, monuments et souvenirs (Dijon, 1894).
DIKE, or Dyke (Old Eng. dic, a word which appears in various forms in many Teutonic languages, cf. Dutch dijk, German Teich, Danish dige, and in French, derived from Teutonic, digue; it is the same word as “ditch” and is ultimately connected with the root of “dig”), properly a trench dug out of the earth for defensive and other purposes. Water naturally collects in such trenches, and hence the word is applied to natural and artificial channels filled with water, as appears in the proverbial expression “February fill-dyke,” and in the names of many narrow waterways in East Anglia. “Dike” also is naturally used of the bank of earth thrown up out of the ditch, and so of any embankment, dam or causeway, particularly the defensive works in Holland, the Fen district of England, and other low-lying districts which are liable to flooding by the sea or rivers (see Holland and Fens). In Scotland any wall, fence or even hedge, used as a boundary is called a dyke. In geology the term is applied to wall-like masses of rock (sometimes projecting beyond the surrounding surface) which fill up vertical or highly inclined fissures in the strata.
DIKKA, a term in Mahommedan architecture for the tribune raised upon columns, from which the Koran is recited and the prayers intoned by the Imam of the mosque.
DILAPIDATION (Lat. for “scattering the stones,” lapides, of a building), a term meaning in general a falling into decay, but more particularly used in the plural in English law for (1) the waste committed by the incumbent of an ecclesiastical living; (2) the disrepair for which a tenant is usually liable when he has agreed to give up his premises in good repair (see Easement; Flat; Landlord and Tenant). By the general law a tenant for life has no power to cut down timber, destroy buildings, &c., (voluntary waste), or to let buildings fall into disrepair (permissive waste). In the eye of the law an incumbent of a living is a tenant for life of his benefice, and any waste, voluntary or permissive, on his part must be made good by his administrators to his successor in office. The principles on which such dilapidations are to be ascertained, and the application of the money payable in respect thereof, depend partly on old ecclesiastical law and partly on acts of parliament. Questions as to ecclesiastical dilapidations usually arise in respect of the residence house and other buildings belonging to the living. Inclosures, hedges, ditches and the like are included in things “of which the beneficed person hath the burden and charge of reparation.” In a leading case (Ross v. Adcock, 1868, L.R. 3 C.P. 657) it was said that the court was acquainted with no precedent or decision extending the liability of the executors of a deceased incumbent to any species of waste beyond dilapidation of the house, chancel or other buildings or fences of the benefice. And it has been held that the mere mismanagement or miscultivation of the ecclesiastical lands will not give rise to an action for dilapidations. To place the law relating to dilapidations on a more satisfactory footing, the Ecclesiastical Dilapidations Act 1871 was passed. The buildings to which the act applies are defined to be such houses of residence, chancels, walls, fences and other buildings and things as the incumbent of the benefice is by law and custom bound to maintain in repair. In each diocese a surveyor is appointed by the archdeacons and rural deans subject to the approval of the bishop; and such surveyor shall by the direction of the bishop examine the buildings on the following occasions—viz. (1) when the benefice is sequestrated; (2) when it is vacant; (3) at the request of the incumbent or on complaint by the archdeacon, rural dean or patron. The surveyor specifies the works required, and gives an 271 estimate of their probable cost. In the case of a vacant benefice, the new incumbent and the old incumbent or his representatives may lodge objections to the surveyor’s report on any grounds of fact or law, and the bishop, after consideration, may make an order for the repairs and their cost, for which the late incumbent or his representatives are liable. The sum so stated becomes a debt due from the late incumbent or his representatives to the new incumbent, who shall pay over the money when recovered to the governors of Queen Anne’s Bounty. The governors pay for the works on execution on receipt of a certificate from the surveyor; and the surveyor, when the works have been completed to his satisfaction, gives a certificate to that effect, the effect of which, so far as regards the incumbent, is to protect him from liability for dilapidations for the next five years. Unnecessary buildings belonging to a residence house may, by the authority of the bishop and with the consent of the patron, be removed. An amending statute of 1872 (Ecclesiastical Dilapidations Act (1871) Amendment) relates chiefly to advances by the governors of Queen Anne’s Bounty for the purposes of the act.
DILATATION (from Lat. dis-, distributive, and latus, wide), a widening or enlarging; a term used in physiology, &c.
DILATORY (from Lat. dilatus, from differre, to put off or delay), delaying, or slow; in law a “dilatory plea” is one made merely for delaying the suit.
DILEMMA (Gr. δίλημμα, a double proposition, from δί- and λαμβάνειν), a term used technically in logic, and popularly in common parlance and rhetoric. (1) The latter use has no exact definition, but in general it describes a situation wherein from either of two (or more) possible alternatives an unsatisfactory conclusion results. The alternatives are called the “horns” of the dilemma. Thus a nation which has to choose between bankruptcy and the repudiation of its debts is on the horns of a dilemma. (2) In logic there is considerable divergence of opinion as to the best definition. Whately defined it as “a conditional syllogism with two or more antecedents in the major and a disjunctive minor.” Aulus Gellius gives an example as follows:—“Women are either fair or ugly; if you marry a fair woman, she will attract other men; if an ugly woman she will not please you; therefore marriage is absurd.” From either alternative, an unpleasant result follows. Four kinds of dilemma are admitted:—(a) Simple Constructive: If A, then C; if B, then C, but either B or A; therefore C. (b) Simple Destructive: If A is true, B is true; if A is true, C is true; B and C are not both true; therefore A is not true. (c) Complex Constructive: If A, then B; if C, then D; but either A or C; therefore either B or D. (d) Complex Destructive: If A is true, B is true; if C is true, D is true; but B and D are not both true; hence A and C are not both true. The soundness of the dilemmatic argument in general depends on the alternative possibilities. Unless the alternatives produced exhaust the possibilities of the case, the conclusion is invalid. The logical form of the argument makes it especially valuable in public speaking, before uncritical audiences. It is, in fact, important rather as a rhetorical subtlety than as a serious argument.
Dilemmist is also a term used to translate Vaibhashikas, the name of a Buddhist school of philosophy.
DILETTANTE, an Italian word for one who delights in the fine arts, especially in music and painting, so a lover of the fine arts in general. The Ital. dilettare is from Lat. delectare, to delight. Properly the word refers to an “amateur” as opposed to a “professional” cultivation of the arts, but like “amateur” it is often used in a depreciatory sense for one who is only a dabbler, or who only has a superficial knowledge or interest in art. The Dilettanti Society founded in 1733-1734 still exists in England. A history of the society, by Lionel Cust, was published in 1898.
DILIGENCE, in law, the care which a person is bound to exercise in his relations with others. The possible degrees of diligence are of course numerous, and the same degree is not required in all cases. Thus a mere depositary would not be held bound to the same degree of diligence as a person borrowing an article for his own use and benefit. Jurists, following the divisions of the civil law, have concurred in fixing three approximate standards of diligence—viz. ordinary (diligentia), less than ordinary (levissima diligentia) and more than ordinary (exactissima diligentia). Ordinary or common diligence is defined by Story (On Bailments) as “that degree of diligence which men in general exert in respect of their own concerns.” So Sir William Jones:—“This care, which every person of common prudence and capable of governing a family takes of his own concerns, is a proper measure of that which would uniformly be required in performing every contract, if there were not strong reasons for exacting in some of them a greater and permitting in others a less degree of attention” (Essay on Bailments). The highest degree of diligence would be that which only very prudent persons bestow on their own concerns; the lowest, that which even careless persons bestow on their own concerns. The want of these various degrees of diligence is negligence in corresponding degrees. These approximations indicate roughly the greater or less severity with which the law will judge the performance of different classes of contracts; but English judges have been inclined to repudiate the distinction as a useless refinement of the jurists. Thus Baron Rolfe could see no difference between negligence and gross negligence; it was the same thing with the addition of a vituperative epithet. See Negligence.
Diligence, in Scots law, is a general term for the process by which persons, lands or effects are attached on execution, or in security for debt.
DILKE, SIR CHARLES WENTWORTH, Bart. (1810-1869), English politician, son of Charles Wentworth Dilke, proprietor and editor of The Athenaeum, was born in London on the 18th of February 1810, and was educated at Westminster school and Trinity Hall, Cambridge. He studied law, and in 1834 took his degree of LL.B., but did not practise. He assisted his father in his literary work, and was for some years chairman of the council of the Society of Arts, besides taking a prominent part in the affairs of the Royal Horticultural Society and other bodies. He was one of the most zealous promoters of the Great Exhibition (1851), and a member of the executive committee. At the close of the exhibition he was honoured by foreign sovereigns, and the queen offered him knighthood, which, however, he did not accept; he also declined a large remuneration offered by the royal commission. In 1853 Dilke was one of the English commissioners at the New York Industrial Exhibition, and prepared a report on it. He again declined to receive any money reward for his services. He was appointed one of the five royal commissioners for the Great Exhibition of 1862; and soon after the death of the prince consort he was created a baronet. In 1865 he entered parliament as member for Wallingford. In 1869 he was sent to Russia as representative of England at the horticultural exhibition held at St Petersburg. His health, however, had been for some time failing, and he died suddenly in that city, on the 10th of May 1869. A selection from his writings, Papers of a Critic (2 vols., 1875), contains a biographical sketch by his son.
His son, Sir Charles Wentworth Dilke, Bart. (1843- ), became a prominent Liberal politician, as M.P. for Chelsea (1868-1886), under-secretary for foreign affairs (1880-1882), and president of the local government board (1882-1885); and he was then marked out as one of the best-informed and ablest of the advanced Radicals. He was chairman of the royal commission on the housing of the working classes in 1884-1885. But his sensational appearance as co-respondent in a divorce case of a peculiarly unpleasant character in 1885 cast a cloud over his career. He was defeated in Chelsea in 1886, and did not return to parliament till 1892, when he was elected for the Forest of Dean; and though his knowledge of foreign affairs and his powers as a critic and writer on military and naval questions were admittedly of the highest order, his official position in public life could not again be recovered. His military writings are The British Army (1888); Army Reform (1898) and, with Mr Spenser Wilkinson, Imperial Defence (1892). On colonial questions he wrote with equal authority. His Greater Britain (2 vols., 1866-1867) reached a fourth edition in 1868, and was followed by Problems of Greater Britain (2 vols., 1890) and The British Empire (1899). He was twice married, his second wife (née 272 Emilia Frances Strong), the widow of Mark Pattison, being an accomplished art critic and collector. She died in 1904. The most important of her books were the studies on French Painters of the Eighteenth Century (1899) and three subsequent volumes on the architects and sculptors, furniture and decoration, engravers and draughtsmen of the same period, the last of which appeared in 1902. A posthumous volume, The Book of the Spiritual Life (1905), contains a memoir of her by Sir Charles Dilke.
 |
| Dill (Anethum or Peucedanum graveolens), leaf and inflorescence. |
DILL (Anethum or Peucedanum graveolens), a member of the natural botanical order Umbelliferae, indigenous to the south of Europe, Egypt and the Cape of Good Hope. It resembles fennel in appearance. Its root is long and fusiform; the stem is round, jointed and about a yard high; the leaves have fragrant leaflets; and the fruits are brown, oval and concavo-convex. The plant flowers from June till August in England. The seeds are sown, preferably as soon as ripe, either broadcast or in drills between 6 and 12 in. asunder. The young plants should be thinned when 3 or 4 weeks old, so as to be at distances of about 10 in. A sheltered spot and dry soil are needed for the production of the seed in the climate of England. The leaves of the dill are used in soups and sauces, and, as well as the umbels, for flavouring pickles. The seeds are employed for the preparation of dill-water and oil of dill; they are largely consumed in the manufacture of gin, and, when ground, are eaten in the East as a condiment. The British Pharmacopoeia contains the Aqua Anethi or dill-water (dose 1-2 oz.), and the Oleum Anethi, almost identical in composition with caraway oil, and given in doses of ½-3 minims. Dill-water is largely used as a carminative for children, and as a vehicle for the exhibition of nauseous drugs.
DILLEN [Dillenius], JOHANN JAKOB (1684-1747), English botanist, was born at Darmstadt in 1684, and was educated at the university of Giessen, where he wrote several botanical papers for the Ephemerides naturae curiosorum, and printed, in 1719, his Catalogus plantarum sponte circa Gissam nascentium, illustrated with figures drawn and engraved by his own hand, and containing descriptions of many new species. In 1721, at the instance of the botanist William Sherard (1659-1728), he came to England, and in 1724 he published a new edition of Ray’s Synopsis stirpium Britannicarum. In 1732 he published Hortus Elthamensis, a catalogue of the rare plants growing at Eltham, Kent, in the collection of Sherard’s younger brother, James (1666-1738), who, after making a fortune as an apothecary, devoted himself to gardening and music. For this work Dillen himself executed 324 plates, and it was described by Linnaeus, who spent a month with him at Oxford in 1736, and afterwards dedicated his Critica botanica to him, as “opus botanicum quo absolutius mundus non vidit.” In 1734 he was appointed Sherardian professor of botany at Oxford, in accordance with the will of W. Sherard, who at his death in 1728 left the university £3000 for the endowment of the chair, as well as his library and herbarium. Dillen, who was also the author of an Historia muscorum (1741), died at Oxford, of apoplexy, on the 2nd of April 1747. His manuscripts, books and collections of dried plants, with many drawings, were bought by his successor at Oxford, Dr Humphry Sibthorp (1713-1797), and ultimately passed into the possession of the university.
For an account of his collections preserved at Oxford, see The Dillenian Herbaria, by G. Claridge Druce (Oxford, 1907).
DILLENBURG, a town of Germany, in the Prussian province of Hesse-Nassau, delightfully situated in the midst of a well-wooded country, on the Dill, 25 m. N.W. from. Giessen on the railway to Troisdorf. Pop. 4500. On an eminence above it lie the ruins of the castle of Dillenburg, founded by Count Henry the Rich of Nassau, about the year 1255, and the birthplace of Prince William of Orange (1533). It has an Evangelical church, with the vault of the princes of Nassau-Dillenburg, a Roman Catholic church, a classical school, a teachers’ seminary and a chamber of commerce. Its industries embrace iron-works, tanneries and the manufacture of cigars. Owing to its beautiful surroundings Dillenburg has become a favourite summer resort.
DILLENS, JULIEN (1849-1904), Belgian sculptor, was born at Antwerp on the 8th of June 1849, son of a painter. He studied under Eugène Simonis at the Brussels Academy of Fine Arts. In 1877 he received the prix de Rome for “A Gaulish Chief taken Prisoner by the Romans.” At Brussels, in 1881, he executed the groups entitled “Justice” and “Herkenbald, the Brussels Brutus.” For the pediment of the orphanage at Uccle, “Figure Kneeling” (Brussels Gallery), and the statue of the lawyer Metdepenningen in front of the Palais de Justice at Ghent, he was awarded the medal of honour in 1889 at the Paris Universal Exhibition, where, in 1900, his “Two Statues of the Anspach Monument” gained him a similar distinction. For the town of Brussels he executed “The Four Continents” (Maison du Renard, Grand’ Place), “The Lansquenets” crowning the lucarnes of the Maison de Roi, and the “Monument t’ Serclaes” under the arcades of the Maison de l’Etoile, and, for the Belgian government, “Flemish Art,” “German Art,” “Classic Art” and “Art applied to Industry” (all in the Palais des Beaux Arts, Brussels), “The Laurel” (Botanic Garden, Brussels), and the statue of “Bernard van Orley” (Place du petit Sablon, Brussels). Mention must also be made of “An Enigma” (1876), the bronze busts of “Rogier de la Pasture” and “P. P. Rubens” (1879), “Etruria” (1880), “The Painter Leon Frederic” (1888), “Madame Leon Herbo,” “Hermes,” a scheme of decoration for the ogival façade of the hôtel de ville at Ghent (1893), “The Genius of the Funeral Monument of the Moselli Family,” “The Silence of Death” (for the entrance of the cemetery of St Gilles), two caryatides for the town hall of St Gilles, presentation plaquette to Dr Heger, medals of MM. Godefroid and Vanderkindere and of “The Three Burgomasters of Brussels,” and the ivories “Allegretto,” “Minerva” and the “Jamaer Memorial.” Dillens died at Brussels in November 1904.
DILLINGEN, a town of Germany, in the kingdom of Bavaria, on the left bank of the Danube, 25 m. N.E. from Ulm, on the railway to Ingolstadt. Pop. (1905) 6078. Its principal buildings are an old palace, formerly the residence of the bishops of Augsburg and now government offices, a royal gymnasium, a Latin school with a library of 75,000 volumes, seven churches (six Roman Catholic), two episcopal seminaries, a Capuchin monastery, a Franciscan convent and a deaf and dumb asylum. The university, founded in 1549, was abolished in 1804, being converted into a lyceum. The inhabitants are engaged in cattle-rearing, the cultivation of corn, hops and fruit, shipbuilding and the shipping trade, and the manufacture of cloth, paper and cutlery. In the vicinity is the Karolinen canal, which cuts off a bend in the Danube between Lauingen and Dillingen. In 1488 Dillingen became the residence of the bishops of Augsburg; was taken by the Swedes in 1632 and 1648, by the Austrians in 1702, and on the 17th of June 1800 by the French. In 1803 it passed to Bavaria.
DILLMANN, CHRISTIAN FRIEDRICH AUGUST (1823-1894), German orientalist and biblical scholar, the son of a Württemberg schoolmaster, was born at Illingen on the 25th of April 1823. He was educated at Tübingen, where he became a pupil and friend of Heinrich Ewald, and studied under F. C. Baur, though he did not join the new Tübingen school. For a short time he worked as pastor at Gersheim, near his native place, but he soon came to feel that his studies demanded his whole time. He devoted himself to the study of Ethiopic MSS. in the libraries of Paris, London and Oxford, and this work caused a revival of Ethiopic study in the 19th century. In 1847 and 1848 he prepared catalogues of the Ethiopic MSS. in the British Museum and the Bodleian library at Oxford. He then set to work upon an edition of the Ethiopic bible. Returning to Tübingen in 1848, in 1853 he was appointed professor extraordinarius. Subsequently he became 273 professor of philosophy at Kiel (1854), and of theology at Giessen (1864) and Berlin (1869). He died on the 4th of July 1894.
In 1851 he had published the Book of Enoch in Ethiopian (German, 1853), and at Kiel he completed the first part of the Ethiopic bible, Octateuchus Aethiopicus (1853-1855). In 1857 appeared his Grammatik der äthiopischen Sprache (2nd ed. by C. Bezold, 1899); in 1859 the Book of Jubilees; in 1861 and 1871 another part of the Ethiopic bible, Libri Regum; in 1865 his great Lexicon linguae aethiopicae; in 1866 his Chrestomathia aethiopica. Always a theologian at heart, however, he returned to theology in 1864. His Giessen lectures were published under the titles, Ursprung der alttestamentlichen Religion (1865) and Die Propheten des alten Bundes nach ihrer politischen Wirksamkeit (1868). In 1869 appeared his Commentar zum Hiob (4th ed. 1891) which stamped him as one of the foremost Old Testament exegetes. His renown as a theologian, however, was mainly founded by the series of commentaries, based on those of August Wilhelm Knobels’ Genesis (Leipzig, 1875; 6th ed. 1892; Eng. trans, by W. B. Stevenson, Edinburgh, 1897); Exodus und Leviticus, 1880, revised edition by V. Ryssel, 1897; Numeri, Deuteronomium und Josua, with a dissertation on the origin of the Hexateuch, 1886; Jesaja, 1890 (revised edition by Rudolf Kittel in 1898). In 1877 he published the Ascension of Isaiah in Ethiopian and Latin. He was also a contributor to D. Schenkel’s Bibellexikon, Brockhaus’s Conversationslexikon, and Herzog’s Realencyklopädie. His lectures on Old Testament theology, Vorlesungen über Theologie des Allen Testamentes, were published by Kittel in 1895.
See the articles in Herzog-Hauck, Realencyklopädie, and the Allgemeine deutsche Biographie; F. Lichtenberger, History of German Theology in the Nineteenth Century (1889); Wolf Baudissin, A. Dillmann (Leipzig, 1895).
DILLON, ARTHUR RICHARD (1721-1807), French archbishop, was the son of Arthur Dillon (1670-1733), an Irish gentleman who became general in the French service. He was born at St Germain, entered the priesthood and was successively curé of Elan near Mezières, vicar-general of Pontoise (1747), bishop of Evreux (1753) and archbishop of Toulouse (1758), archbishop of Narbonne in 1763, and in that capacity, president of the estates of Languedoc. He devoted himself much less to the spiritual direction of his diocese than to its temporal welfare, carrying out many works of public utility, bridges, canals, roads, harbours, &c.; had chairs of chemistry and of physics created at Montpellier and at Toulouse, and tried to reduce the poverty, especially in Narbonne. In 1787 and in 1788 he was a member of the Assembly of Notables called together by Louis XVI., and in 1788 presided over the assembly of the clergy. Having refused to accept the civil constitution of the clergy, Dillon had to leave Narbonne in 1790, then to emigrate to Coblenz in 1791. Soon afterwards he went to London, where he lived until his death in 1807, never accepting the Concordat, which had suppressed his archiepiscopal see.
See L. Audibret, Le Dernier Président des États du Languedoc, Mgr. Arthur Richard Dillon, archevêque de Narbonne (Bordeaux, 1868); L. de Lavergne, Les Assemblées provinciales sous Louis XVI (Paris, 1864).
DILLON, JOHN (1851- ), Irish nationalist politician, was the son of John Blake Dillon (1816-1866), who sat in parliament for Tipperary, and was one of the leaders of “Young Ireland.” John Dillon was educated at the Roman Catholic university of Dublin, and afterwards studied medicine. He entered parliament in 1880 as member for Tipperary, and was at first an ardent supporter of C. S. Parnell. In August he delivered a speech on the Land League at Kildare which was characterized as “wicked and cowardly” by W. E. Forster; he advocated boycotting, and was arrested in May 1881 under the Coercion Act, and again after two months of freedom in October. In 1883 he resigned his seat for reasons of health, but was returned unopposed in 1885 for East Mayo, which he continued to represent. He was one of the prime movers in the famous “plan of campaign,” which provided that the tenant should pay his rent to the National League instead of the landlord, and in case of eviction be supported by the general fund. Mr Dillon was compelled by the court of queen’s bench on the 14th of December 1886 to find securities for good behaviour, but two days later he was arrested while receiving rents on Lord Clanricarde’s estates. In this instance the jury disagreed, but in June 1888 under the provisions of the new Criminal Law Procedure Bill he was condemned to six months’ imprisonment. He was, however, released in September, and in the spring of 1889 sailed for Australia and New Zealand, where he collected funds for the Nationalist party. On his return to Ireland he was again arrested, but, being allowed bail, sailed to America, and failed to appear at the trial. He returned to Ireland by way of Boulogne, where he and Mr W. O’Brien held long and indecisive conferences with Parnell. They surrendered to the police in February, and on their release from Galway gaol in July declared their opposition to Parnell. After the expulsion of Mr T. M. Healy and others from the Irish National Federation, Mr Dillon became the chairman (February 1896). His early friendship with Mr O’Brien gave place to considerable hostility, but the various sections of the party were ostensibly reconciled in 1900 under the leadership of Mr Redmond. In the autumn of 1896 he arranged a convention of the Irish race, which included 2000 delegates from various parts of the world. In 1897 Mr Dillon opposed in the House the Address to Queen Victoria on the occasion of the Diamond Jubilee, on the ground that her reign had not been a blessing to Ireland, and he showed the same uncompromising attitude in 1901 when a grant to Lord Roberts was under discussion, accusing him of “systematized inhumanity.” He was suspended on the 20th of March for violent language addressed to Mr Chamberlain. He married in 1895 Elizabeth (d. 1907), daughter of Lord justice J. C. Mathew.
DILUVIUM (Lat. for “deluge,” from diluere, to wash away), a term in geology for superficial deposits formed by flood-like operations of water, and so contrasted with alluvium (q.v.) or alluvial deposits formed by slow and steady aqueous agencies. The term was formerly given to the “boulder clay” deposits, supposed to have been caused by the Noachian deluge.
DIME (from the Lat. decima, a tenth, through the O. Fr. disme), the tenth part, the tithe paid as church dues, or as tribute to a temporal power. In this sense it is obsolete, but is found in Wycliffe’s translation of the Bible—“He gave him dymes of alle thingis” (Gen. xiv. 20). A dime is a silver coin of the United States, in value 10 cents (English equivalent about 5d.) or one-tenth of a dollar; hence “dime-novel,” a cheap sensational novel, a “penny dreadful”; also “dime-museum.”
DIMENSION (from Lat. dimensio, a measuring), in geometry, a magnitude measured in a specified direction, i.e. length, breadth and thickness; thus a line has only length and is said to be of one dimension, a surface has length and breadth, and has two dimensions, a solid has length, breadth and thickness, and has three dimensions. This concept is extended to algebra: since a line, surface and solid are represented by linear, quadratic and cubic equations, and are of one, two and three dimensions; a biquadratic equation has its highest terms of four dimensions, and, in general, an equation in any number of variables which has the greatest sum of the indices of any term equal to n is said to have n dimensions. The “fourth dimension” is a type of non-Euclidean geometry, in which it is conceived that a “solid” has one dimension more than the solids of experience. For the dimensions of units see Units, Dimensions of.
DIMITY, derived from the Gr. δίμιτος “double thread,” through the Ital. dimito, “a kind of course linzie-wolzie” (Florio, 1611); a cloth commonly employed for bed upholstery and curtains, and usually white, though sometimes a pattern is printed on it in colours. It is stout in texture, and woven in raised patterns.
DINAJPUR, a town (with a population in 1901 of 13,430) and district of British India, in the Rajshahi division of Eastern Bengal and Assam. The earthquake of the 12th of June 1897 caused serious damage to most of the public buildings of the town. There is a railway station and a government high school. The district comprises an area of 3946 sq. m. It is traversed in every direction by a network of channels and water courses. Along the banks of the Kulik river, the undulating ridges and long lines of 274 mango-trees give the landscape a beauty which is not found elsewhere. Dinajpur forms part of the rich arable tract lying between the Ganges and the southern slopes of the Himalayas. Although essentially a fluvial district, it does not possess any river navigable throughout the year by boats of 4 tons burden. Rice forms the staple agricultural product. The climate of the district, although cooler than that of Calcutta, is very unhealthy, and the people have a sickly appearance. The worst part of the year is at the close of the rains in September and October, during which months few of the natives escape fever. The average maximum temperature is 92.3° F., and the minimum 74.8°. The average rainfall is 85.54 in. In 1901 the population was 1,567,080, showing an increase of 6% in the decade. The district is partly traversed by the main line of the Eastern Bengal railway and by two branch lines. Save between 1404 and 1442, when it was the seat of an independent raj, founded by Raja Ganesh, a Hindu turned Mussulman, Dinajpur has no separate history. Pillars and copper-plate inscriptions have yielded numerous records of the Pal kings who ruled the country from the 9th century onwards, and the district is famous for many other antiquities, some of which are connected by legend with an immemorial past (see Reports, Arch. Survey of India, xv.; Epigraphia Indica, ii.).
DINAN, a town of north-western France, capital of an arrondissement in the department of Côtes-du-Nord, 37 m. E. of St Brieuc on the Western railway. Pop. (1906) 8588. Dinan is situated on a height on the left bank of the Ranee (here canalized), some 17 m. above its mouth at St Malo, with which it communicates by means of small steamers. It is united to the village of Lanvallay on the right bank of the river by a granite viaduct 130 ft. in height. The town is almost entirely encircled by the ramparts of the middle ages, strengthened at intervals by towers and defended on the south by a castle of the late 14th century, which now serves as prison. Three old gateways are also preserved. Dinan has two interesting churches; that of St Malo, of late Gothic architecture, and St Sauveur, in which the Romanesque and Gothic styles are intermingled. In the latter church a granite monument contains the heart of Bertrand Du Guesclin, whose connexion with the town is also commemorated by an equestrian statue. The quaint winding streets of Dinan are often bordered by medieval houses. Its picturesqueness attracts large numbers of visitors and there are many English residents in the town and its vicinity. About three-quarters of a mile from the town are the ruins of the château and the Benedictine abbey at Léhon; near the neighbouring village of St Esprit stands the large lunatic asylum of Les Bas Foins, founded in 1836; and at no great distance is the now dismantled château of La Garaye, which was rendered famous in the 18th century by the philanthropic devotion of the count and countess whose story is told in Mrs Norton’s Lady of La Garaye. Dinan is the seat of a subprefect and has a tribunal of first instance, and a communal college. There is trade in grain, cider, wax, butter and other agricultural products. The industries include the manufacture of leather, farm-implements and canvas.
The principal event in the history of Dinan, which was a stronghold of the dukes of Brittany, is the siege by the English under the duke of Lancaster in 1359, during which Du Guesclin and an English knight called Thomas of Canterbury engaged in single combat.
DINANT, an ancient town on the right bank of the Meuse in the province of Namur, Belgium, connected by a bridge with the left bank, on which are the station and the suburb of St Medard. Pop. (1904) 7674. The name is supposed to be derived from Diana, and as early as the 7th century it was named as one of the dependencies of the bishopric of Tongres. In the 10th century it passed under the titular sway of Liége, and remained the fief of the prince-bishopric till the French revolution put an end to that survival of feudalism. In the middle of the 15th century Dinant reached the height of its prosperity. With a population of 60,000, and 8000 workers in copper, it was one of the most flourishing cities in Walloon Belgium, until it incurred the wrath of Charles the Bold. Belief in the strength of its walls and of the castle that occupied the centre bridge, thus effectually commanding navigation by the river, engendered arrogance and overconfidence, and the people of Dinant thought they could defy the full power of Burgundy. Perhaps they also expected aid from France or Liége. In 1466 Charles, in his father’s name, laid siege to Dinant, and on the 27th of August carried the place by storm. He razed the walls and allowed the women, children and priests to retire in safety to Liége, but the male prisoners he either hanged or drowned in the river by causing them to be cast from the projecting cliff of Bouvignes. In 1675 the capture of Dinant formed one of the early military achievements of Louis XIV., and it remained in the hands of the French for nearly thirty years after that date. The citadel on the cliff, 300 ft. or 408 steps above the town, was fortified by the Dutch in 1818. It is now dismantled, but forms the chief curiosity of the place. The views of the river valley from this eminence are exceedingly fine. Half way up the cliff, but some distance south of the citadel, is the grotto of Montfat, alleged to be the site of Diana’s shrine. The church of Notre Dame, dating from the 13th century, stands immediately under the citadel and flanking the bridge. It has been restored, and is considered by some authorities, although others make the same claim on behalf of Huy, the most complete specimen in Belgium of pointed Gothic architecture. The baptismal fonts date from the 12th century, and the curious spire in the form of an elongated pumpkin and covered with slates gives a fantastic and original appearance to the whole edifice. The present prosperity of Dinant is chiefly derived from its being a favourite summer resort for Belgians as well as foreigners. It has facilities for beating and bathing as well as for trips by steamer up and down the river Meuse. It is also a convenient central point for excursions into the Ardennes. Although there are some indications of increased industrial activity in recent years, the population of Dinant is not one-eighth of what it was at the time of the Burgundians.
DINAPUR, a town and military station of British India, in the Patna district of Bengal, on the right bank of the Ganges, 12 m. W. of Patna city by rail. Pop. (1901) 33,699. It is the largest military cantonment in Bengal, with accommodation for two batteries of artillery, a European and a native infantry regiment. In 1857 the sepoy garrison of the place initiated the mutiny of that year in Patna district, but after a conflict with the European troops were forced to retire from the town, and subsequently laid siege to Arrah.
DINARCHUS, last of the “ten” Attic orators, son of Sostratus (or, according to Suidas, Socrates), born at Corinth about 361 b.c. He settled at Athens early in life, and when not more than twenty-five was already active as a writer of speeches for the law courts. As an alien, he was unable to take part in the debates. He had been the pupil both of Theophrastus and of Demetrius Phalereus, and had early acquired a certain fluency and versatility of style. In 324 the Areopagus, after inquiry, reported that nine men had taken bribes from Harpalus, the fugitive treasurer of Alexander. Ten public prosecutors were appointed. Dinarchus wrote, for one or more of these prosecutors, the three speeches which are still extant—Against Demosthenes, Against Aristogeiton, Against Philocles. The sympathies of Dinarchus were in favour of an Athenian oligarchy under Macedonian control; but it should be remembered that he was not an Athenian citizen. Aeschines and Demades had no such excuse. In the Harpalus affair, Demosthenes was doubtless innocent, and so, probably, were others of the accused. Yet Hypereides, the most fiery of the patriots, was on the same side as Dinarchus.
Under the regency of his old master, Demetrius Phalereus, Dinarchus exercised much political influence. The years 317-307 were the most prosperous of his life. On the fall of Demetrius Phalereus and the restoration of the democracy by Demetrius Poliorcetes, Dinarchus was condemned to death and withdrew into exile at Chalcis in Euboea. About 292, thanks to his friend Theophrastus, he was able to return to Attica, and took up his abode in the country with a former associate, Proxenus. He afterwards brought an action against Proxenus on the ground that he had robbed him of some money and plate. Dinarchus died at Athens about 291.
According to Suidas, Dinarchus wrote 160 speeches; and Dionysius held that, out of 85 extant speeches bearing his name, 58 were genuine,—28 relating to public, 30 to private causes. Although the authenticity of the three speeches mentioned above is generally admitted, Demetrius of Magnesia doubted that of the speech Against Demosthenes, while A. Westermann rejected all three. Dinarchus had little individual style and imitated by turns Lysias, Hypereides and Demosthenes. He is called by Hermogenes ὁ κριθινὸς Δημοσθένης, a metaphor taken from barley compared with wheat, or beer compared with wine,—a Demosthenes whose strength is rougher, without flavour or sparkle.
Editions: (text and exhaustive commentary) E. Mätzner (1842); (text) T. Thalheim (1887), F. Blass (1888); see L.L. Forman, Index Andocideus, Lycurgeus, Dinarcheus (1897); and, in general, F. Blass, Attische Beredsamkeit, iii. There is a valuable treatise on the life and speeches of Dinarchus by Dionysius of Halicarnassus.
End of the Project Gutenberg EBook of Encyclopaedia Britannica, 11th
Edition, Volume 8, Slice 4, by Various
*** END OF THIS PROJECT GUTENBERG EBOOK ENCYC. BRITANNICA, VOL 8 SL 4 ***
***** This file should be named 32607-h.htm or 32607-h.zip *****
This and all associated files of various formats will be found in:
https://www.gutenberg.org/3/2/6/0/32607/
Produced by Marius Masi, Don Kretz and the Online
Distributed Proofreading Team at https://www.pgdp.net
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
https://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH F3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need are critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at https://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
https://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at https://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit https://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including including checks, online payments and credit card
donations. To donate, please visit: https://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart was the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
https://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.