The Project Gutenberg EBook of Encyclopaedia Britannica, 11th Edition,
Volume 6, Slice 1, by Various
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
Title: Encyclopaedia Britannica, 11th Edition, Volume 6, Slice 1
"Châtelet" to "Chicago"
Author: Various
Release Date: February 2, 2010 [EBook #31156]
Language: English
Character set encoding: ISO-8859-1
*** START OF THIS PROJECT GUTENBERG EBOOK ENCYCLOPAEDIA BRITANNICA, VOL 6 SL 1 ***
Produced by Marius Masi, Don Kretz, Juliet Sutherland and
the Online Distributed Proofreading Team at
https://www.pgdp.net
| Transcriber's note: |
A few typographical errors have been corrected. They
appear in the text like this, and the
explanation will appear when the mouse pointer is moved over the marked
passage. Sections in Greek will yield a transliteration
when the pointer is moved over them, and words using diacritic characters in the
Latin Extended Additional block, which may not display in some fonts or browsers, will
display an unaccented version. Links to other EB articles: Links to articles residing in other EB volumes will be made available when the respective volumes are introduced online. |
Table of Contents
CHÂTELET (from Med. Lat. castella), the word, sometimes also written castillet, used in France for a building designed for the defence of an outwork or gate, sometimes of great strength or size, but distinguished from the château, or castle proper, in being purely defensive and not residential. In Paris, before the Revolution, this word was applied both to a particular building and to the jurisdiction of which it was the seat. This building, the original Châtelet, had been first a castle defending the approach to the Cité. Tradition traced its existence back to Roman times, and in the 18th century one of the rooms in the great tower was still called the chambre de César. The jurisdiction was that of the provostship (prévôté) and viscountship of Paris, which was certainly of feudal origin, probably going back to the counts of Paris.
It was not till the time of Saint Louis that, with the appointment of Étienne Boileau, the provostship of Paris became a prévôté en garde, i.e. a public office no longer put up to sale. When the baillis (see Bailiff AND Bailie) were created, the provost of Paris naturally discharged the duties and functions of a bailli, in which capacity he heard appeals from the seigniorial and inferior judges of the city and its neighbourhood, keeping, however, his title of provost. When under Henry II. certain bailliages became presidial jurisdictions (présidiaux), i.e. received to a certain extent the right of judging without appeal, the Châtelet, the court of the provost of Paris, was made a presidial court, but without losing its former name. Finally, various tribunals peculiar to the city of Paris, i.e. courts exercising jurisdictions outside the common law or corresponding to certain cours d’exception which existed in the provinces, were united with the Châtelet, of which they became divisions (chambres). Thus the lieutenant-general of police made it the seat of his jurisdiction, and the provost of the Île de France, who had the same criminal jurisdiction as the provosts of the marshals of France in other provinces, sat there also. As to the personnel of the Châtelet, it was originally the same as in the bailliages, except that after the 14th century it had some special officials, the auditors and the examiners of inquests. Like the baillis, the provost had lieutenants who were deputies for him, and in addition gradually acquired a considerable body of ex officio councillors. This last staff, however, was not yet in existence at the end of the 14th century, for it is not mentioned in the Registre criminel du Châtelet (1389-1392), published by the Société des Bibliophiles Français. In 1674 the whole personnel was doubled, at the time when the new Châtelet was established side by side with the old, the two being soon after amalgamated. On the eve of the Revolution it comprised, beside the provost whose office had become practically honorary, the lieutenant civil, who presided over the chambre de prévôté au parc civil or court of first instance; the lieutenant criminel, who presided over the criminal court; two lieutenants particuliers, who presided in turn over the chambre du présidial or court of appeal from the inferior jurisdictions; a juge auditeur; sixty-four councillors (conseillers); the procureur du roi, four avocats du roi, and eight substituts, i.e. deputies of the procureur (see Procurator), beside a host of minor officials. The history of the Châtelet under the Revolution may be briefly told: the Constituent Assembly empowered it to try cases of lèse-nation, and it was also before this court that was opened the inquiry following on the events of the 5th and 6th of August 1789. It was suppressed by the law of the 16th of August 1790, together with the other tribunals of the ancien régime.
CHÂTELLERAULT, a town of western France, capital of an arrondissement in the department of Vienne, 19 m. N.N.E. of Poitiers on the Orleans railway between that town and Tours. Pop. (1906) 15,214. Châtellerault is situated on the right and eastern bank of the Vienne; it is connected with the suburb of Châteauneuf on the opposite side of the river by a stone bridge of the 16th and 17th centuries, guarded at the western extremity by massive towers. The manufacture of cutlery is carried on on a large scale in villages on the banks of the Clain, south of the town. Of the other industrial establishments the most important is the national small-arms factory, which was established in 1815 in Châteauneuf, and employs from 1500 to 5500 men. Châtellerault (or Châtelherault: Castellum Airaldi) derives its name from a fortress built in the 10th century by Airaud, viscount of its territory. In 1515 it was made a duchy in favour of François de Bourbon, but it was not long after this date that it became reunited to the crown. In 1548 it was bestowed on James Hamilton, 2nd earl of Arran (see Hamilton).
CHATHAM, WILLIAM PITT, 1st Earl of (1708-1778), English statesman, was born at Westminster on the 15th of November 1708. He was the younger son of Robert Pitt of Boconnoc, Cornwall, and grandson of Thomas Pitt (1653-1726), governor of Madras, who was known as “Diamond” Pitt, from the fact of his having sold a diamond of extraordinary size to the regent Orleans for something like £135,000. It was mainly by this fortunate transaction that the governor was enabled to raise his family, which was one of old standing, to a position of wealth and political influence. The latter he acquired by purchasing the burgage tenures of Old Sarum.
William Pitt was educated at Eton, and in January 1727 was entered as a gentleman commoner at Trinity College, Oxford. There is evidence that he was an extensively read, if not a minutely accurate classical scholar; and it is interesting to know that Demosthenes was his favourite author, and that he diligently cultivated the faculty of expression by the practice of translation and re-translation. An hereditary gout, from which 2 he had suffered even during his school-days, compelled him to leave the university without taking his degree, in order to travel abroad. He spent some time in France and Italy; but the disease proved intractable, and he continued subject to attacks of growing intensity at frequent intervals till the close of his life. In 1727 his father had died, and on his return home it was necessary for him, as the younger son, to choose a profession. Having chosen the army, he obtained through the interest of his friends a cornet’s commission in the dragoons. But his military career was destined to be short. His elder brother Thomas having been returned at the general election of 1734 both for Oakhampton and for Old Sarum, and having preferred to sit for the former, the family borough fell to the younger brother by the sort of natural right usually recognized in such cases. Accordingly, in February 1735, William Pitt entered parliament as member for Old Sarum. Attaching himself at once to the formidable band of discontented Whigs known as the Patriots, whom Walpole’s love of exclusive power had forced into opposition under Pulteney, he became in a very short time one of its most prominent members. His maiden speech was delivered in April 1736, in the debate on the congratulatory address to the king on the marriage of the prince of Wales. The occasion was one of compliment, and there is nothing striking in the speech as reported; but it served to gain for him the attention of the house when he presented himself, as he soon afterwards did, in debates of a party character. So obnoxious did he become as a critic of the government, that Walpole thought fit to punish him by procuring his dismissal from the army. Some years later he had occasion vigorously to denounce the system of cashiering officers for political differences, but with characteristic loftiness of spirit he disdained to make any reference to his own case. The loss of his commission was soon made up to him. The heir to the throne, as was usually the case in the house of Hanover, if not in reigning families generally, was the patron of the opposition, and the ex-cornet became groom of the bed-chamber to the prince of Wales. In this new position his hostility to the government did not, as may be supposed, in any degree relax. He had all the natural gifts an orator could desire—a commanding presence, a graceful though somewhat theatrical bearing, an eye of piercing brightness, and a voice of the utmost flexibility. His style, if occasionally somewhat turgid, was elevated and passionate, and it always bore the impress of that intensity of conviction which is the most powerful instrument a speaker can have to sway the convictions of an audience. It was natural, therefore, that in the series of stormy debates, protracted through several years, that ended in the downfall of Walpole, his eloquence should have been one of the strongest of the forces that combined to bring about the final result. Specially effective, according to contemporary testimony, were his speeches against the Hanoverian subsidies, against the Spanish convention in 1739, and in favour of the motion in 1742 for an investigation into the last ten years of Walpole’s administration. It must be borne in mind that the reports of these speeches which have come down to us were made from hearsay, or at best from recollection, and are necessarily therefore most imperfect. The best-known specimen of Pitt’s eloquence, his reply to the sneers of Horatio Walpole at his youth and declamatory manner, which has found a place in so many handbooks of elocution, is evidently, in form at least, the work, not of Pitt, but of Dr Johnson, who furnished the report to the Gentleman’s Magazine. Probably Pitt did say something of the kind attributed to him, though even this is by no means certain in view of Johnson’s repentant admission that he had often invented not merely the form, but the substance of entire debates.
In 1742 Walpole was at last forced to succumb to the long-continued attacks of opposition, and was succeeded as prime minister by the earl of Wilmington, though the real power in the new government was divided between Carteret and the Pelhams. Pitt’s conduct on the change of administration was open to grave censure. The relentless vindictiveness with which he insisted on the prosecution of Walpole, and supported the bill of indemnity to witnesses against the fallen minister, was in itself not magnanimous; but it appears positively unworthy when it is known that a short time before Pitt had offered, on certain conditions, to use all his influence in the other direction. Possibly he was embittered at the time by the fact that, owing to the strong personal dislike of the king, caused chiefly by the contemptuous tone in which he had spoken of Hanover, he did not by obtaining a place in the new ministry reap the fruits of the victory to which he had so largely contributed. The so-called “broad-bottom” administration formed by the Pelhams in 1744, after the dismissal of Carteret, though it included several of those with whom he had been accustomed to act, did not at first include Pitt himself even in a subordinate office. Before the obstacle to his admission was overcome, he had received a remarkable accession to his private fortune. The eccentric duchess of Marlborough, dying in 1744, at the age of ninety, left him a legacy of £10,000 as an “acknowledgment of the noble defence he had made for the support of the laws of England and to prevent the ruin of his country.” As her hatred was known to be at least as strong as her love, the legacy was probably as much a mark of her detestation of Walpole as of her admiration of Pitt. It may be mentioned here, though it does not come in chronological order, that Pitt was a second time the object of a form of acknowledgment of public virtue which few statesmen have had the fortune to receive even once. About twenty years after the Marlborough legacy, Sir William Pynsent, a Somersetshire baronet to whom he was personally quite unknown, left him his entire estate, worth about three thousand a year, in testimony of approval of his political career.
It was with no very good grace that the king at length consented to give Pitt a place in the government, although the latter did all he could to ingratiate himself at court, by changing his tone on the questions on which he had made himself offensive. To force the matter, the Pelhams had to resign expressly on the question whether he should be admitted or not, and it was only after all other arrangements had proved impracticable, that they were reinstated with the obnoxious politician as vice-treasurer of Ireland. This was in February 1746. In May of the same year he was promoted to the more important and lucrative office of paymaster-general, which gave him a place in the privy council, though not in the cabinet. Here he had an opportunity of displaying his public spirit and integrity in a way that deeply impressed both the king and the country. It had been the usual practice of previous paymasters to appropriate to themselves the interest of all money lying in their hands by way of advance, and also to accept a commission of ½% on all foreign subsidies. Although there was no strong public sentiment against the practice, Pitt altogether refused to profit by it. All advances were lodged by him in the Bank of England until required, and all subsidies were paid over without deduction, even though it was pressed upon him, so that he did not draw a shilling from his office beyond the salary legally attaching to it. Conduct like this, though obviously disinterested, did not go without immediate and ample reward, in the public confidence which it created, and which formed the mainspring of Pitt’s power as a statesman.
The administration formed in 1746 lasted without material change till 1754. It would appear from his published correspondence that Pitt had a greater influence in shaping its policy than his comparatively subordinate position would in itself have entitled him to. His conduct in supporting measures, such as the Spanish treaty and the continental subsidies, which he had violently denounced when in opposition, had been much criticized; but within certain limits, not indeed very well defined, inconsistency has never been counted a vice in an English statesman. The times change, and he is not blamed for changing with the times. Pitt in office, looking back on the commencement of his public life, might have used the plea “A good deal has happened since then,” at least as justly as some others have done. Allowance must always be made for the restraints and responsibilities of office. In Pitt’s case, too, it is to be borne in mind that the opposition with which he had acted gradually dwindled away, and that it ceased to have any organized existence after the death of the prince of Wales in 1751. Then in regard to the important question with Spain as to the right of search, 3 Pitt has disarmed criticism by acknowledging that the course he followed during Wapole’s administration was indefensible. All due weight being given to these various considerations, it must be admitted, nevertheless, that Pitt did overstep the limits within which inconsistency is usually regarded as venial. His one great object was first to gain office, and then to make his tenure of office secure by conciliating the favour of the king. The entire revolution which much of his policy underwent in order to effect this object bears too close a resemblance to the sudden and inexplicable changes of front habitual to placemen of the Tadpole stamp to be altogether pleasant to contemplate in a politician of pure aims and lofty ambition. Humiliating is not too strong a term to apply to a letter in which he expresses his desire to “efface the past by every action of his life,” in order that he may stand well with the king.
In 1754 Henry Pelham died, and was succeeded at the head of affairs by his brother, the duke of Newcastle. To Pitt the change brought no advancement, and he had thus an opportunity of testing the truth of the description of his chief given by Sir Robert Walpole, “His name is treason.” But there was for a time no open breach. Pitt continued at his post; and at the general election which took place during the year he even accepted a nomination for the duke’s pocket borough of Aldborough. He had sat for Seaford since 1747. When parliament met, however, he was not long in showing the state of his feelings. Ignoring Sir Thomas Robinson, the political nobody to whom Newcastle had entrusted the management of the Commons, he made frequent and vehement attacks on Newcastle himself, though still continuing to serve under him. In this strange state matters continued for about a year. At length, just after the meeting of parliament in November 1751, Pitt was dismissed from office, having on the debate on the address spoken at great length against a new system of continental subsidies, proposed by the government of which he was a member. Fox, who had just before been appointed secretary of state, retained his place, and though the two men continued to be of the same party, and afterwards served again in the same government, there was henceforward a rivalry between them, which makes the celebrated opposition of their illustrious sons seem like an inherited quarrel.
Another year had scarcely passed when Pitt was again in power. The inherent weakness of the government, the vigour and eloquence of his opposition, and a series of military disasters abroad combined to rouse a public feeling of indignation which could not be withstood, and in December 1756 Pitt, who now sat for Okehampton, became secretary of state, and leader of the Commons under the premiership of the duke of Devonshire. He had made it a condition of his joining any administration that Newcastle should be excluded from it, thus showing a resentment which, though natural enough, proved fatal to the lengthened existence of his government. With the king unfriendly, and Newcastle, whose corrupt influence was still dominant in the Commons, estranged, it was impossible to carry on a government by the aid of public opinion alone, however emphatically that might have declared itself on his side. In April 1757, accordingly, he found himself again dismissed from office on account of his opposition to the king’s favourite continental policy. But the power that was insufficient to keep him in office was strong enough to make any arrangement that excluded him impracticable. The public voice spoke in a way that was not to be mistaken. Probably no English minister ever received in so short a time so many proofs of the confidence and admiration of the public, the capital and all the chief towns voting him addresses and the freedom of their corporations. From the political deadlock that ensued relief could only be had by an arrangement between Newcastle and Pitt. After some weeks’ negotiation, in the course of which the firmness and moderation of “the Great Commoner,” as he had come to be called, contrasted favourably with the characteristic tortuosities of the crafty peer, matters were settled on such a basis that, while Newcastle was the nominal, Pitt was the virtual head of the government. On his acceptance of office he was chosen member for Bath.
This celebrated administration was formed in June 1757, and continued in power till 1761. During the four years of its existence it has been usual to say that the biography of Pitt is the history of England, so thoroughly was he identified with the great events which make this period, in so far as the external relations of the country are concerned, one of the most glorious in her annals. A detailed account of these events belongs to history; all that is needed in a biography is to point out the extent to which Pitt’s personal influence may really be traced in them. It is scarcely too much to say that, in the general opinion of his contemporaries, the whole glory of these years was due to his single genius; his alone was the mind that planned, and his the spirit that animated the brilliant achievements of the British arms in all the four quarters of the globe. Posterity, indeed, has been able to recognize more fully the independent genius of those who carried out his purposes. The heroism of Wolfe would have been irrepressible, Clive would have proved himself “a heaven-born general,” and Frederick the Great would have written his name in history as one of the most skilful strategists the world has known, whoever had held the seals of office in England. But Pitt’s relation to all three was such as to entitle him to a large share in the credit of their deeds. It was his discernment that selected Wolfe to lead the attack on Quebec, and gave him the opportunity of dying a victor on the heights of Abraham. He had personally less to do with the successes in India than with the other great enterprises that shed an undying lustre on his administration; but his generous praise in parliament stimulated the genius of Clive, and the forces that acted at the close of the struggle were animated by his indomitable spirit. Pitt, the first real Imperialist in modern English history, was the directing mind in the expansion of his country, and with him the beginning of empire is rightly associated. The Seven Years’ War might well, moreover, have been another Thirty Years’ War if Pitt had not furnished Frederick with an annual subsidy of £700,000, and in addition relieved him of the task of defending western Germany against France.
Contemporary opinion was, of course, incompetent to estimate the permanent results gained for the country by the brilliant foreign policy of Pitt. It has long been generally agreed that by several of his most costly expeditions nothing was really won but glory. It has even been said that the only permanent acquisition that England owed directly to him was her Canadian dominion; and, strictly speaking, this is true, it being admitted that the campaign by which the Indian empire was virtually won was not planned by him, though brought to a successful issue during his ministry. But material aggrandizement, though the only tangible, is not the only real or lasting effect of a war policy. More may be gained by crushing a formidable rival than by conquering a province. The loss of her Canadian possessions was only one of a series of disasters suffered by France, which radically affected the future of Europe and the world. Deprived of her most valuable colonies both in the East and in the West, and thoroughly defeated on the continent, her humiliation was the beginning of a new epoch in history. The victorious policy of Pitt destroyed the military prestige which repeated experience has shown to be in France as in no other country the very life of monarchy, and thus was not the least considerable of the many influences that slowly brought about the French Revolution. It effectually deprived her of the lead in the councils of Europe which she had hitherto arrogated to herself, and so affected the whole course of continental politics. It is such far-reaching results as these, and not the mere acquisition of a single colony, however valuable, that constitute Pitt’s claim to be considered as on the whole the most powerful minister that ever guided the foreign policy of England.
The first and most important of a series of changes which ultimately led to the dissolution of the ministry was the death of George II. on the 25th of October 1760, and the accession of his grandson, George III. The new king had, as was natural, new counsellors of his own, the chief of whom, Lord Bute, was at once admitted to the cabinet as a secretary of state. Between Bute and Pitt there speedily arose an occasion of serious difference. 4 The existence of the so-called family compact by which the Bourbons of France and Spain bound themselves in an offensive alliance against England having been brought to light, Pitt urged that it should be met by an immediate declaration of war with Spain. To this course Bute would not consent, and as his refusal was endorsed by all his colleagues save Temple, Pitt had no choice but to leave a cabinet in which his advice on a vital question had been rejected. On his resignation, which took place in October 1761, the king urged him to accept some signal mark of royal favour in the form most agreeable to himself. Accordingly he obtained a pension of £3000 a year for three lives, and his wife, Lady Hester Grenville, whom he had married in 1754, was created Baroness Chatham in her own right. In connexion with the latter gracefully bestowed honour it may be mentioned that Pitt’s domestic life was a singularly happy one.
Pitt’s spirit was too lofty to admit of his entering on any merely factious opposition to the government he had quitted. On the contrary, his conduct after his retirement was distinguished by a moderation and disinterestedness which, as Burke has remarked, “set a seal upon his character.” The war with Spain, in which he had urged the cabinet to take the initiative, proved inevitable; but he scorned to use the occasion for “altercation and recrimination,” and spoke in support of the government measures for carrying on the war. To the preliminaries of the peace concluded in February 1763 he offered an indignant resistance, considering the terms quite inadequate to the successes that had been gained by the country. When the treaty was discussed in parliament in December of the preceding year, though suffering from a severe attack of gout, he was carried down to the House, and in a speech of three hours’ duration, interrupted more than once by paroxysms of pain, he strongly protested against its various conditions. The physical cause which rendered this effort so painful probably accounts for the infrequency of his appearances in parliament, as well as for much that is otherwise inexplicable in his subsequent conduct. In 1763 he spoke against the obnoxious tax on cider, imposed by his brother-in-law, George Grenville, and his opposition, though unsuccessful in the House, helped to keep alive his popularity with the country, which cordially hated the excise and all connected with it. When next year the question of general warrants was raised in connexion with the case of Wilkes, Pitt vigorously maintained their illegality, thus defending at once the privileges of Parliament and the freedom of the press. During 1765 he seems to have been totally incapacitated for public business. In the following year he supported with great power the proposal of the Rockingham administration for the repeal of the American Stamp Act, arguing that it was unconstitutional to impose taxes upon the colonies. He thus endorsed the contention of the colonists on the ground of principle, while the majority of those who acted with him contented themselves with resisting the disastrous taxation scheme on the ground of expediency. The Repeal Act, indeed, was only passed pari passu with another censuring the American assemblies, and declaring the authority of the British parliament over the colonies “in all cases whatsoever”; so that the House of Commons repudiated in the most formal manner the principle Pitt laid down. His language in approval of the resistance of the colonists was unusually bold, and perhaps no one but himself could have employed it with impunity at a time when the freedom of debate was only imperfectly conceded.
Pitt had not been long out of office when he was solicited to return to it, and the solicitations were more than once renewed. Unsuccessful overtures were made to him in 1763, and twice in 1765, in May and June—the negotiator in May being the king’s uncle, the duke of Cumberland, who went down in person to Hayes, Pitt’s seat in Kent. It is known that he had the opportunity of joining the marquis of Rockingham’s short-lived administration at any time on his own terms, and his conduct in declining an arrangement with that minister has been more generally condemned than any other step in his public life. In July 1766 Rockingham was dismissed, and Pitt was entrusted by the king with the task of forming a government entirely on his own conditions. The result was a cabinet, strong much beyond the average in its individual members, but weak to powerlessness in the diversity of its composition. Burke, in a memorable passage of a memorable speech, has described this “chequered and speckled” administration with great humour, speaking of it as “indeed a very curious show, but utterly unsafe to touch and unsure to stand on.” Pitt chose for himself the office of lord privy seal, which necessitated his removal to the House of Lords; and in August he became earl of Chatham and Viscount Pitt.
By the acceptance of a peerage the great commoner lost at least as much and as suddenly in popularity as he gained in dignity. One significant indication of this may be mentioned. In view of his probable accession to power, preparations were made in the city of London for a banquet and a general illumination to celebrate the event. But the celebration was at once countermanded when it was known that he had become earl of Chatham. The instantaneous revulsion of public feeling was somewhat unreasonable, for Pitt’s health seems now to have been beyond doubt so shattered by his hereditary malady, that he was already in old age though only fifty-eight. It was natural, therefore, that he should choose a sinecure office, and the ease of the Lords. But a popular idol nearly always suffers by removal from immediate contact with the popular sympathy, be the motives for removal what they may.
One of the earliest acts of the new ministry was to lay an embargo upon corn, which was thought necessary in order to prevent a dearth resulting from the unprecedentedly bad harvest of 1766. The measure was strongly opposed, and Lord Chatham delivered his first speech in the House of Lords in support of it. It proved to be almost the only measure introduced by his government in which he personally interested himself. His attention had been directed to the growing importance of the affairs of India, and there is evidence in his correspondence that he was meditating a comprehensive scheme for transferring much of the power of the company to the crown, when he was withdrawn from public business in a manner that has always been regarded as somewhat mysterious. It may be questioned, indeed, whether even had his powers been unimpaired he could have carried out any decided policy on any question with a cabinet representing interests so various and conflicting; but, as it happened, he was incapacitated physically and mentally during nearly the Whole period of his tenure of office. He scarcely ever saw any of his colleagues though they repeatedly and urgently pressed for interviews with him, and even an offer from the king to visit him in person was declined, though in the language of profound and almost abject respect which always marked his communications with the court. It has been insinuated both by contemporary and by later critics that being disappointed at his loss of popularity, and convinced of the impossibility of co-operating with his colleagues, he exaggerated his malady as a pretext for the inaction that was forced upon him by circumstances. But there is no sufficient reason to doubt that he was really, as his friends represented, in a state that utterly unfitted him for business. He seems to have been freed for a time from the pangs of gout only to be afflicted with a species of mental alienation bordering on insanity. This is the most satisfactory, as it is the most obvious, explanation of his utter indifference in presence of one of the most momentous problems that ever pressed for solution on an English statesman. Those who are able to read the history in the light of what occurred later may perhaps be convinced that no policy whatever initiated, after 1766 could have prevented or even materially delayed the declaration of American independence; but to the politicians of that time the coming event had not yet cast so dark a shadow before as to paralyse all action, and if any man could have allayed the growing discontent of the colonists and prevented the ultimate dismemberment of the empire, it would have been Lord Chatham. The fact that he not only did nothing to remove existing difficulties, but remained passive while his colleagues took the fatal step which led directly to separation, is in itself clear proof of his entire incapacity. The imposition 5 of the import duty on tea and other commodities was the project of Charles Townshend, and was carried into effect in 1767 without consultation with Lord Chatham, if not in opposition to his wishes. It is probably the most singular thing in connexion with this singular administration, that its most pregnant measure should thus have been one directly opposed to the well-known principles of its head.
For many months things remained in the curious position that he who was understood to be the head of the cabinet had as little share in the government of the country as an unenfranchised peasant. As the chief could not or would not lead, the subordinates naturally chose their own paths and not his. The lines of Chatham’s policy were abandoned in other cases besides the imposition of the import duty; his opponents were taken into confidence; and friends, such’ as Amherst and Shelburne, were dismissed from their posts. When at length in October 1768 he tendered his resignation on the ground of shattered health, he did not fail to mention the dismissal of Amherst and Shelburne as a personal grievance.
Soon after his resignation a renewed attack of gout freed Chatham from the mental disease under which he had so long suffered. He had been nearly two years and a half in seclusion when, in July 1769, he again appeared in public at a royal levee. It was not, however, until 1770 that he resumed his seat in the House of Lords. He had now almost no personal following, mainly owing to the grave mistake he had made in not forming an alliance with the Rockingham party. But his eloquence was as powerful as ever, and all its power was directed against the government policy in the contest with America, which had become the question of all-absorbing interest. His last appearance in the House of Lords was on the 7th of April 1778, on the occasion of the duke of Richmond’s motion for an address praying the king to conclude peace with America on any terms. In view of the hostile demonstrations of France the various parties had come generally to see the necessity of such a measure. But Chatham could not brook the thought of a step which implied submission to the “natural enemy” whom it had been the main object of his life to humble, and he declaimed for a considerable time, though with sadly diminished vigour, against the motion. After the duke of Richmond had replied, he rose again excitedly as if to speak, pressed his hand upon his breast, and fell down in a fit. He was removed to his seat at Hayes, where he died on the 11th of May. With graceful unanimity all parties combined to show their sense of the national loss. The Commons presented an address to the king praying that the deceased statesman might be buried with the honours of a public funeral, and voted a sum for a public monument which was erected over his grave in Westminster Abbey. Soon after the funeral a bill was passed bestowing a pension of £4000 a year on his successors in the earldom. He had a family of three sons and two daughters, of whom the second son, William, was destined to add fresh lustre to a name which is one of the greatest in the history of England.
Dr Johnson is reported to have said that “Walpole was a minister given by the king to the people, but Pitt was a minister given by the people to the king,” and the remark correctly indicates Chatham’s distinctive place among English statesmen. He was the first minister whose main strength lay in the support of the nation at large as distinct from its representatives in the Commons, where his personal following was always small. He was the first to discern that public opinion, though generally slow to form and slow to act, is in the end the paramount power in the state; and he was the first to use it not in an emergency merely, but throughout a whole political career. He marks the commencement of that vast change in the movement of English politics by which it has come about that the sentiment of the great mass of the people now tells effectively on the action of the government from day to day,—almost from hour to hour. He was well fitted to secure the sympathy and admiration of his countrymen, for his virtues and his failings were alike English. He was often inconsistent, he was generally intractable and overbearing, and he was always pompous and affected to a degree which, Macaulay has remarked, seems scarcely compatible with true greatness. Of the last quality evidence is furnished in the stilted style of his letters, and in the fact recorded by Seward that he never permitted his under-secretaries to sit in his presence. Burke speaks of “some significant, pompous, creeping, explanatory, ambiguous matter, in the true Chathamic style.” But these defects were known only to the inner circle of his associates. To the outside public he was endeared as a statesman who could do or suffer “nothing base,” and who had the rare power of transfusing his own indomitable energy and courage into all who served under him. “A spirited foreign policy” has always been popular in England, and Pitt was the most popular of English ministers, because he was the most successful exponent of such a policy. In domestic affairs his influence was small and almost entirely indirect. He himself confessed his unfitness for dealing with questions of finance. The commercial prosperity that was produced by his war policy was in a great part delusive, as prosperity so produced must always be, though it had permanent effects of the highest moment in the rise of such centres of industry as Glasgow. This, however, was a remote result which he could have neither intended nor foreseen.
The correspondence of Lord Chatham, in four volumes, was published in 1838-1840; and a volume of his letters to Lord Camelford in 1804. The Rev. Francis Thackeray’s History of the Rt. Hon. William Pitt, Earl of Chatham (2 vols., 1827), is a ponderous and shapeless work. Frederic Harrison’s Chatham, in the “Twelve English Statesmen” series (1905), though skilfully executed, takes a rather academic and modern Liberal view. A German work, William Pitt, Graf von Chatham, by Albert von Ruville (3 vols., 1905; English trans. 1907), is the best and most thorough account of Chatham, his period, and his policy, which has appeared. See also the separate article on William Pitt, and the authorities referred to, especially the Rev. William Hunt’s appendix i. to his vol. x. of The Political History of England (1905).
CHATHAM, also called Miramichi, an incorporated town and port of entry in Northumberland county, New Brunswick, Canada, on the Miramichi river, 24 m. from its mouth and 10 m. by rail from Chatham junction on the Intercolonial railway. Pop. (1901) 5000. The town contains the Roman Catholic pro-cathedral, many large saw-mills, pulp-mills, and several establishments for curing and exporting fish. The lumber trade, the fisheries, and the manufacture of pulp are the chief industries.
CHATHAM, a city and port of entry of Ontario, Canada, and the capital of Kent county, situated 64 m. S.W. of London, and 11 m. N. of Lake Erie, on the Thames river and the Grand Trunk, Canadian Pacific and Lake Erie & Detroit River railways. Pop. (1901) 9068. It has steamboat connexion with Detroit and the cities on Lakes Huron and Erie. It is situated in a rich agricultural and fruit-growing district, and carries on a large export trade. It contains a large wagon factory, planing and flour mills, manufactories of fanning mills, binder-twine, woven wire goods, engines, windmills, &c.
CHATHAM, a port and municipal and parliamentary borough of Kent, England, on the right bank of the Medway, 34 m. E.S.E. of London by the South-Eastern & Chatham railway. Pop. (1891) 31,657; (1901) 37,057. Though a distinct borough it is united on the west with Rochester and on the east with Gillingham, so that the three boroughs form, in appearance, a single town with a population which in 1901 exceeded 110,000. With the exception of the dockyards and fortifications there are few objects of interest. St Mary’s church was opened in 1903, but occupies a site which bore a church in Saxon times, though the previous building dated only from 1786. A brass commemorates Stephen Borough (d. 1584), discoverer of the northern passage to Archangel in Russia (1553). St Bartholomew’s chapel, originally attached to the hospital for lepers (one of the first in England), founded by Gundulph, bishop of Rochester, in 1070, is in part Norman. The funds for the maintenance of the hospital were appropriated by decision of the court of chancery to the hospital of St Bartholomew erected in 1863 within the boundaries of Rochester. The almshouse established in 1592 by Sir John Hawkins for decayed seamen and shipwrights is still extant, the building having been re-erected in the 19th century; but the fund called the Chatham Chest, originated by Hawkins and Drake in 6 1588, was incorporated with Greenwich Hospital in 1802. In front of the Royal Engineers’ Institute is a statue (1890) of General Gordon, and near the railway station another (1888) to Thomas Waghorn, promoter of the overland route to India. In 1905 King Edward VII. unveiled a fine memorial arch commemorating Royal Engineers who fell in the South African War. It stands in the parade ground of the Brompton barracks, facing the Crimean arch. There are numerous brickyards, lime-kilns and flour-mills in the district neighbouring to Chatham; and the town carries on a large retail trade, in great measure owing to the presence of the garrison. The fortifications are among the most elaborate in the kingdom. The so-called Chatham Lines enclose New Brompton, a part of the borough of Gillingham. They were begun in 1758 and completed in 1807, but have been completely modernized. They are strengthened by several detached forts and redoubts. Fort Pitt, which rises above the town to the west, was built in 1779, and is used as a general military hospital. It was regarded as the principal establishment of the kind in the country till the foundation of Netley in Hampshire. The lines include the Chatham, the Royal Marine, the Brompton, the Hut, St Mary’s and naval barracks; the garrison hospital, Melville hospital for sailors and marines, the arsenal, gymnasium, various military schools, convict prison, and finally the extensive dockyard system for which the town is famous. This dockyard covers an area of 516 acres, and has a river frontage of over 3 m. It was brought into its present state by the extensive works begun about 1867. Before that time there was no basin or wet-dock, though the river Medway to some extent answered the same purpose, but a portion of the adjoining salt-marshes was then taken in, and three basins have been constructed, communicating with each other by means of large locks, so that ships can pass from the bend of the Medway at Gillingham to that at Upnor. Four graving docks were also formed, opening out of the first (Upnor) basin. Subsequent improvements included dredging operations in the Medway to improve the approach, and the provision of extra dry-dock accommodation under the Naval Works Acts.
The parliamentary borough returns one member. The town was incorporated in 1890, and is governed by a mayor, six aldermen and eighteen councillors. Area, 4355 acres. The borough includes the suburb (an ecclesiastical parish) of Luton, in which are the waterworks of Chatham and the adjoining towns.
Chatham (Ceteham, Chetham) belonged at the time of the Domesday Survey to Odo, bishop of Bayeux. During the middle ages it formed a suburb of Rochester, but Henry VIII. in founding a regular navy began to establish dockyards, and the harbour formed by the deep channel of the Medway was utilized by Elizabeth, who built a dockyard and established an arsenal here. The dockyard was altered and improved by Charles I. and Charles II., and became the chief naval station of England. In 1708 an act was passed for extending the fortifications of Chatham. During the excavations on Chatham Hill after 1758 a number of tumuli containing human remains, pottery, coins, &c., suggestive of an ancient settlement, were found. Chatham was constituted a parliamentary borough by the Reform Bill of 1832. In the time of Edward III. the lord of the manor had two fairs, one on the 24th of August and the other on the 8th of September. A market to be held on Tuesday, and a fair on the 4th, 5th and 6th of May, were granted by Charles II. in 1679, and another provision market on Saturday by James II. in 1688. In 1738 fairs were held on the 4th of May and the 8th of September, and a market every Saturday.
CHATHAM ISLANDS, a small group in the Pacific Ocean, forming part of New Zealand, 536 m. due E. of Lyttelton in the South Island, about 44° S., 177° W. It consists of three islands, a large one called Whairikauri, or Chatham Island, a smaller one, Rangihaute, or Pitt Island, and a third, Rangatira, or South-east Island. There are also several small rocky islets. Whairikauri, whose highest point reaches about 1000 ft., is remarkable for the number of lakes and tarns it contains, and for the extensive bogs which cover the surface of nearly the whole of the uplands. It is of very irregular form, about 38 m. in length and 25 m. in extreme breadth, with an area of 321 sq. m.—a little larger than Middlesex. The geological formation is principally of volcanic rocks, with schists and tertiary limestone; and an early physical connexion of the islands with New Zealand is indicated by their geology and biology. The climate is colder than that of New Zealand. In the centre of Whairikauri is a large brackish lake called Tewanga, which at the southern end is separated from the sea by a sandbank only 150 yds. wide, which it occasionally bursts through. The southern part of the island has an undulating surface, and is covered either with an open forest or with high ferns. In general the soil is extremely fertile, and where it is naturally drained a rich vegetation of fern and flax occurs. On the north-west are several conical hills of basalt, which are surrounded by oases of fertile soil. On the south-western side is Petre Bay, on which, at the mouth of the river Mantagu, is Waitangi, the principal settlement.
The islands were discovered in 1791 by Lieutenant W.R. Broughton (1762-1821), who gave them the name of Chatham from the brig which he commanded. He described the natives as a bright, pleasure-loving people, dressed in sealskins or mats, and calling themselves Morioris or Maiorioris. In 1831 they were conquered by 800 Maoris who were landed from a European vessel. They were almost exterminated, and an epidemic of influenza in 1839 killed half of those left; ten years later there were only 90 survivors out of a total population of 1200. They subsequently decreased still further. Their language was allied to that of the Maoris of New Zealand, but they differed somewhat from them in physique, and they were probably a cross between an immigrating Polynesian group and a lower indigenous Melanesian stock. The population of the islands includes about 200 whites of various races and the same number of natives (chiefly Maoris). Cattle and sheep are bred, and a trade is carried on in them with the whalers which visit these seas. The chief export from the group is wool, grown upon runs farmed both by Europeans and Morioris. There is also a small export by the natives of the flesh of young albatrosses and other sea-birds, boiled down and cured, for the Maoris of New Zealand, by whom it is reckoned a delicacy. The imports consist of the usual commodities required by a population where little of the land is actually cultivated.
There are no indigenous mammals; the reptiles belong to New Zealand species. The birds—the largest factor in the fauna—have become very greatly reduced through the introduction of cats, dogs and pigs, as well as by the constant persecution of every sort of animal by the natives. The larger bell-bird (Anthornis melanocephala) has become quite scarce; the magnificent fruit-pigeon (Carpophaga chathamensis), and the two endemic rails (Nesolimnas dieffenbachii and Cabalus modestus), the one of which was confined to Whairikauri and the other to Mangare Island, are extinct. Several fossil or subfossil avian forms, very interesting from the point of view of geographical distribution, have been discovered by Dr H.O. Forbes, namely, a true species of raven (Palaeocorax moriorum), a remarkable rail (Diaphorapteryx), closely related to the extinct Aphanapteryx of Mauritius, and a large coot (Palaeolimnas chathamensis). There have also been discovered the remains of a species of swan belonging to the South American genus Chenopis, and of the tuatara (Hatteria) lizard, the unique species of an ancient family now surviving only in New Zealand. The swan is identical with an extinct species found in caves and kitchen-middens in New Zealand, which was contemporaneous with the prehistoric Maoris and was largely used by them for food. One of the finest of the endemic flowering plants of the group is the boraginaceous “Chatham Island lily” (Myositidium nobile), a gigantic forget-me-not, which grows on the shingly shore in a few places only, and always just on the high-water mark, where it is daily deluged by the waves; while dracophyllums, leucopogons and arborescent ragworts are characteristic forms in the vegetation.
See Bruno Weiss, Fünfzig Jahre auf Chatham Island (Berlin, 1900); H.O. Forbes, “The Chatham Islands and their Story,” Fortnightly Review (1893), vol. liii. p. 669, “The Chatham Islands, their relation to a former Southern Continent,” Supplementary 7 Papers, R.G.S., vol. iii. (1893); J.H. Scott, “The Osteology of the Maori and the Moriori,” Trans. New Zealand Institute, vol. xxvi. (1893); C.W. Andrews, “The Extinct Birds of the Chatham Islands,” Novitates Zoologicae, vol. ii. p. 73 (1896).
CHÂTILLON, the name of a French family whose history has furnished material for a large volume in folio by A. du Chesne, a learned Frenchman, published in 1621. But in spite of its merits this book presents a certain number of inaccurate statements, some of which it is important to notice. If, for instance, it be true that the Châtillons came from Châtillon-sur-Marne (Marne, arrondissement of Reims), it is now certain that, since the 11th century, this castle belonged to the count of Champagne, and that the head of the house of Châtillon was merely tenant in that place. One of them, however, Gaucher of Châtillon, lord of Crécy and afterwards constable of France, became in 1290 lord of Châtillon-sur-Marne by exchange, but since 1303 a new agreement allotted to him the countship of Porcien, while Châtillon reverted to the domain of the counts of Champagne. It may be well to mention also that, in consequence of a resemblance of their armorial bearings, du Chesne considered wrongly that the lords of Bazoches and those of Château-Porcien of the 12th and 13th centuries drew their descent from the house of Châtillon.
The most important branches of the house of Châtillon were those of (1) St Pol, beginning with Gaucher III. of Châtillon, who became count of St Pol in right of his wife Isabella in 1205, the last male of the line being Guy V. (d. 1360); (2) Blois, founded by the marriage of Hugh of Châtillon-St Pol (d. 1248) with Mary, daughter of Margaret of Blois (d. 1230),—this branch became extinct with the death of Guy II. in 1397; (3) Porcien, from 1303 to 1400, when Count John sold the countship to Louis, duke of Orleans; (4) Penthièvre, by the marriage of Charles of Blois (d. 1364) with Jeanne (d. 1384), heiress of Guy, count of Penthièvre (d. 1331), the male line becoming extinct in 1457.
See A. du Chesne, Histoire généalogique de la maison de Chastillon-sur-Marne (1621); Anselme, Histoire généalogique de la maison royale de France, vi. 91-124 (1730).
CHÂTILLON-SUR-SEINE, a town of eastern France, capital of an arrondissement in the department of Côte-d’Or, on the Eastern and Paris-Lyon railways, 67 m. N.N.W. of Dijon, between that city and Troyes. Pop. (1906) 4430. It is situated on both banks of the upper Seine, which is swelled at its entrance to the town by the Douix, one of the most abundant springs in France. Châtillon is constructed on ample lines and rendered attractive by beautiful promenades. Some ruins on an eminence above it mark the site of a château of the dukes of Burgundy. Near by stands the church of St Vorle of the l0th century, but with many additions of later date; it contains a sculptured Holy Sepulchre of the 16th century and a number of frescoes. In a fine park stands a modern château built by Marshal Marmont, duke of Ragusa, born at Châtillon in 1774. It was burnt in 1871, and subsequently rebuilt. The town preserves several interesting old houses. Châtillon has a sub-prefecture, tribunals of first instance and of commerce, a school of agriculture and a communal college. Among its industries are brewing, iron-founding and the manufacture of mineral and other blacks. It has trade in wood, charcoal, lithographic and other stone. Châtillon anciently consisted of two parts, Chaumont, belonging to the duchy of Burgundy, and Bourg, ruled by the bishop of Langres; it did not coalesce into one town till the end of the 16th century. It was taken by the English in 1360 and by Louis XI. in 1475, during his struggle with Charles the Bold. Châtillon was one of the first cities to adhere to the League, but suffered severely from the oppression of its garrisons and governors, and in 1595 made voluntary submission to Henry IV. In modern times it is associated with the abortive conference of 1814 between the representatives of Napoleon and the Allies.
CHATSWORTH, a village of Derbyshire, England, containing a seat belonging to the duke of Devonshire, one of the most splendid private residences in England. Chatsworth House is situated close to the left bank of the river Derwent, 2¾ m. from Bakewell. It is Ionic in style, built foursquare, and enclosing a large open courtyard, with a fountain in the centre. In front, a beautiful stretch of lawn slopes gradually down to the riverside, and a bridge, from which may best be seen the grand façade of the building, as it stands out in relief against the wooded ridge of Bunker’s Hill. The celebrated gardens are adorned with sculptures by Gabriel Gibber; Sir Joseph Paxton designed the great conservatory, unrivalled in Europe, which covers an acre; and the fountains, which include one with a jet 260 ft. high, are said to be surpassed only by those at Versailles. Within the house there is a very fine collection of pictures, including the well-known portraits by Reynolds of Georgiana, duchess of Devonshire. Other paintings are ascribed to Holbein, Dürer, Murillo, Jan van Eyck, Dolci, Veronese and Titian. Hung in the gallery of sketches there are some priceless drawings attributed to Michelangelo, Leonardo da Vinci, Raffaelle, Correggio, Titian and other old masters. Statues by Canova, Thorwaldsen, Chantrey and R.J. Wyatt are included among the sculptures. In the state apartments the walls and window-panes are in some cases inlaid with marble or porphyry; the woodcarving, marvellous for its intricacy, grace and lightness of effect, is largely the work of Samuel Watson of Heanor (d. 1715). Chatsworth Park is upwards of 11 m. in circuit, and contains many noble forest-trees, the whole being watered by the Derwent, and surrounded by high moors and uplands. Beyond the river, and immediately opposite the house, stands the model village of Edensor, where most of the cottages were built in villa style, with gardens, by order of the 6th duke. The parish church, restored by the same benefactor, contains an old brass in memory of John Beaton, confidential servant to Mary, queen of Scots, who died in 1570; and in the churchyard are the graves of Lord Frederick Cavendish, murdered in 1882 in Phoenix Park, Dublin, and of Sir Joseph Paxton.
Chatsworth (Chetsvorde, Chetelsvorde, “the court of Chetel”) took its name from Chetel, one of its Saxon owners, who held it of Edward the Confessor. It belonged to the crown and was entrusted by the Conqueror to the custody of William Peverell. Chatsworth afterwards belonged for many generations to the family of Leech, and was purchased in the reign of Elizabeth by Sir William Cavendish, husband of the famous Bess of Hardwick. In 1557 he began to build Chatsworth House, and it was completed after his death by his widow, then countess of Shrewsbury. Here Mary, queen of Scots, spent several years of her imprisonment under the care of the earl of Shrewsbury. During the Civil War, Chatsworth was occasionally occupied as a fortress by both parties. It was pulled down, and the present house begun by William, 1st duke of Devonshire in 1688. The little village consists almost exclusively of families employed upon the estate.
CHATTANOOGA, a city and the county-seat of Hamilton county, Tennessee, U.S.A., in the S.E. part of the state, about 300 m. S. of Cincinnati, Ohio, and 150 m. S.E. of Nashville, Tennessee, on the Tennessee river, and near the boundary line between Tennessee and Georgia. Pop. (1860) 2545; (1870) 6093; (1880) 12,892; (1890) 29,100; (1900) 30,154, of whom 994 were foreign-born and 13,122 were negroes; (U.S. census, 1910) 44,604. The city is served by the Alabama Great Southern (Queen and Crescent), the Cincinnati Southern (leased by the Cincinnati, New Orleans & Texas Pacific railway company), the Nashville, Chattanooga & St Louis (controlled by the Louisville & Nashville), and its leased line, the Western & Atlantic (connecting with Atlanta, Ga.), the Central of Georgia, and the Chattanooga Southern railways, and by freight and passenger steamboat lines on the Tennessee river, which is navigable to and beyond this point during eight months of the year. That branch of the Southern railway extending from Chattanooga to Memphis was formerly the Memphis & Charleston, under which name it became famous in the American Civil War. Chattanooga occupies a picturesque site at a sharp bend of the river. To the south lies Lookout Mountain, whose summit (2126 ft. above the sea; 1495 ft. above the river) commands a magnificent view. To the east rises Missionary Ridge. Fine driveways and electric lines connect with both Lookout Mountain (the summit of which is reached by an inclined plane on which cars are operated by 8 cable) and Missionary Ridge, where there are Federal reservations, as well as with the National Military Park (15 sq. m.; dedicated 1895) on the battlefield of Chickamauga (q.v.); this park was one of the principal mobilization camps of the United States army during the Spanish-American War of 1898. Among the principal buildings are the city hall, the Federal building, the county court house, the public library, the high school and the St Vincent’s and the Baroness Erlanger hospitals. Among Chattanooga’s educational institutions are two commercial colleges, the Chattanooga College for Young Ladies (non-sectarian), the Chattanooga Normal University, and the University of Chattanooga, until June 1907, United States Grant University (whose preparatory department, “The Athens School,” is at Athens, Tenn.), a co-educational institution under Methodist Episcopal control, established in 1867; it has a school of law (1899), a medical school (1889), and a school of theology (1888). East of the city is a large national cemetery containing more than 13,000 graves of Federal soldiers. Chattanooga is an important produce, lumber, coal and iron market, and is the principal trade and jobbing centre for a large district in Eastern Tennessee and Northern Georgia and Alabama. The proximity of coalfields and iron mines has made Chattanooga an iron manufacturing place of importance, its plants including car shops, blast furnaces, foundries, agricultural implement and machinery works, and stove factories; the city has had an important part in the development of the iron and steel industries in this part of the South. There are also flour mills, tanneries (United States Leather Co.), patent medicine, furniture, coffin, woodenware and wagon factories, knitting and spinning mills, planing mills, and sash, door and blind factories—the lumber being obtained from logs floated down the river and by rail. The value of the city’s factory products increased from $10,517,886 in 1900 to $15,193,909 in 1905 or 44.5%.
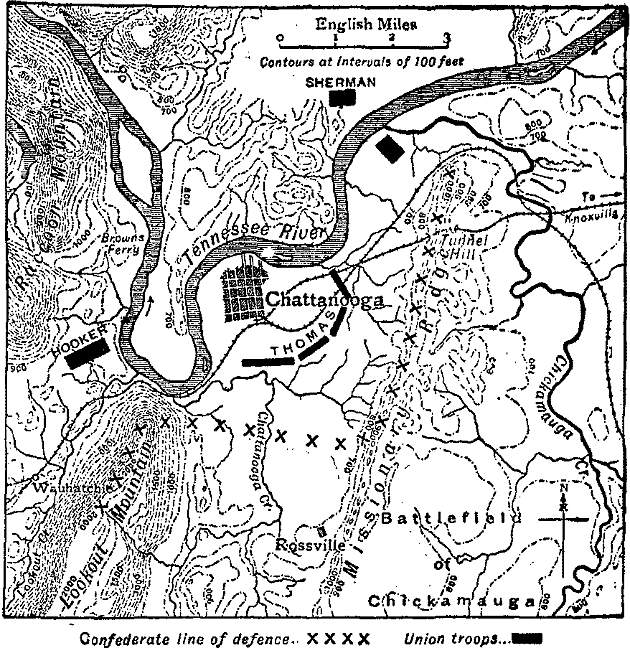
Chattanooga was first settled about 1835, and was long known as Ross’s Landing. It was incorporated in 1851 as Chattanooga, and received a city charter in 1866. Its growth for the three decades after the Civil War was very rapid. During the American Civil War it was one of the most important strategic points in the Confederacy, and in its immediate vicinity were fought two great battles. During June 1862 it was threatened by a Federal force under General O.M. Mitchel, but the Confederate army of General Braxton Bragg was transferred thither by rail from Corinth, Miss., before Mitchel was able to advance. In September 1863, however, General W.S. Rosecrans, with the Union Army of the Cumberland out-manœuvred Bragg, concentrated his numerous columns in the Chickamauga Valley, and occupied the town, to which, after the defeat of Chickamauga (q.v.), he retired.
From the end of September to the 24th of November the Army of the Cumberland was then invested in Chattanooga by the Confederates, whose position lay along Missionary Ridge from its north end near the river towards Rossville, whence their entrenchments extended westwards to Lookout Mountain, which dominates the whole ground, the Tennessee running directly beneath it. Thus Rosecrans was confined to a semicircle of low ground around Chattanooga itself, and his supplies had to make a long and difficult détour from Bridgeport, the main road being under fire from the Confederate position on Lookout and in the Wauhatchie valley adjacent. Bragg indeed expected that Rosecrans would be starved into retreat. But the Federals once more, and this time on a far larger scale, concentrated in the face of the enemy. The XI. and XII. corps from Virginia under Hooker were transferred by rail to reinforce Rosecrans; other troops were called up from the Mississippi, and on the 16th of October the Federal government reconstituted the western armies under the supreme command of General Grant. The XV. corps of the Army of the Tennessee, under Sherman, was on the march from the Mississippi. Hooker’s troops had already arrived when Grant reached Chattanooga on the 23rd of October. The Army of the Cumberland was now under Thomas, Rosecrans having been recalled. The first action was fought at Brown’s Ferry in the Wauhatchie valley, where Hooker executed with complete precision a plan for the revictualling of Chattanooga, established himself near Wauhatchie on the 28th, and repulsed a determined attack on the same night. But Sherman was still far distant, and the Federal forces at Knoxville, against which a large detachment of Bragg’s army under Longstreet was now sent, were in grave danger. Grant waited for Sherman’s four divisions, but prepared everything for battle in the meantime. His plan was that Thomas in the Chattanooga lines should contain the Confederate centre on Missionary Ridge, while Hooker on the right at Wauhatchie was to attack Lookout Mountain, and Sherman farther up the river was to carry out the decisive attack against Bragg’s extreme right wing at the end of Missionary Ridgg. The last marches of the XV. corps were delayed, by stormy weather, Bragg reinforced Longstreet, and telegraphic communication between Grant and the Federals at Knoxville had already ceased. But Grant would not move forward without Sherman, and the battle of Chattanooga was fought more than two months after Chickamauga. On the 23rd of November a forward move of Thomas’s army, intended as a demonstration, developed into a serious and successful action, whereby the first line of the Confederate centre was driven in for some distance. Bragg was now much weakened by successive detachments having been sent to Knoxville, and on the 24th the real battle began. Sherman’s corps was gradually brought over the river near the mouth of Chickamauga Creek, and formed up on the east side.

The attack began at 1 P.M. and was locally a complete success. The heights attacked were in Sherman’s hands, and fortified against counter-attack, before nightfall. Hooker in the meanwhile had fought the “Battle above the Clouds” on the steep face of Lookout Mountain, and though opposed by an equal force of Confederates, had completely driven the enemy from the mountain. The 24th then had been a day of success for the Federals, and the decisive attack of the three armies in concert was to take place on the 25th. But the maps deceived Grant and Sherman as they had previously deceived Rosecrans. Sherman had captured, not the north point of Missionary Ridge, but a detached hill, and a new and more serious action had to be fought for the possession of Tunnel Hill, where Bragg’s right now lay strongly entrenched. The Confederates used every effort to hold the position and all Sherman’s efforts were made in vain. Hooker, who was moving on Rossville, had not progressed far, and Bragg was still free to reinforce his right. Grant therefore directed Thomas to move forward on the centre to relieve the 9 pressure on Sherman. The Army of the Cumberland was, after all, to strike the decisive blow. About 3.30 P.M. the centre advanced on the Confederate’s trenches at the foot of Missionary Ridge. These were carried at the first rush, and the troops were ordered to lie down and await orders. Then occurred one of the most dramatic episodes of the war. Suddenly, and without orders either from Grant or the officers at the front, the whole line of the Army of the Cumberland rose and rushed up the ridge. Two successive lines of entrenchments were carried at once. In a short time the crest was stormed, and after a last attempt at resistance the enemy’s centre fled in the wildest confusion. The pursuit was pressed home by the divisional generals, notably by Sheridan. Hooker now advanced in earnest on Rossville, and by nightfall the whole Confederate army, except the troops on Tunnel Hill, was retreating in disorder. These too were withdrawn in the night, and the victory of the Federals was complete. Bragg lost 8684 men killed, wounded and prisoners out of perhaps 34,000 men engaged; Grant, with 60,000 men, lost about 6000.
CHATTEL (for derivation see Cattle), a term used in English law as equivalent to “personal property,” that is, property which, on the death of the owner, devolves on his executor or administrator to be distributed (unless disposed of by will) among the next of kin according to the Statutes of Distributions. Chattels are divided into chattels real and chattels personal. Chattels real are those interests in land for which no “real action” (see Action) lies; estates which are less than freehold (estates for years, at will, or by sufferance) are chattels real. Chattels personal are such things as belong immediately to the person of the owner, and for which, if they are injuriously withheld from him, he has no remedy other than by a personal action. Chattels personal are divided into choses in possession and choses in action (see Chose).
A chattel mortgage, in United States law, is a transfer of personal property as security for a debt or obligation in such form that the title to the property will pass to the mortgagee upon the failure of the mortgagor to comply with the terms of the contract. At common law a chattel mortgage might be made without writing, and was valid as between the parties, and even as against third parties if accompanied by possession in the mortgagee, but in most states of the Union legislation now requires a chattel mortgage to be in writing and duly recorded in order to be valid against third parties. At common law a mortgage can be given only of chattels actually in existence and belonging to the mortgagor, though if he acquired title afterwards the mortgage would be good as between the parties, but not as against subsequent purchasers or creditors. In equity, on the other hand, a chattel mortgage, though not good as a conveyance, is valid as an executory agreement.
Goods and chattels is a phrase which, in its widest signification, includes any property other than freehold. The two words, however, have come to be synonymous, and the expression, now practically confined to wills, means merely things movable in possession.
CHATTERIS, a market town in the Wisbech parliamentary division of Cambridgeshire, England, 25½ m. N. by W. of Cambridge by the Great Eastern railway. Pop. of urban district (1901) 4711. It lies in the midst of the flat Fen country. The church of St Peter is principally Decorated; and there are fragments of a Benedictine convent founded in the 10th century and rebuilt after fire in the first half of the 14th. The town has breweries, and engineering and rope-making works. To the north runs the great Forty-foot Drain, also called Vermuyden’s, after the Dutch engineer whose name is associated with the fen drainage works of the middle of the 17th century.
CHATTERJI, BANKIM CHANDRA [Bankimachandra ChattĀradh-yĀya] (1838-1894), Indian novelist, was born in the district of the Twenty-four Parganas in Bengal on the 27th of June 1838, and was by caste a Brahman. He was educated at the Hugli College, at the Presidency College in Calcutta, and at Calcutta University, where he was the first to take the degree of B.A. (1858). He entered the Indian civil service, and served as deputy magistrate in various districts of Bengal, his official services being recognized, on his retirement in 1891, by the title of rai bahadur and the C.I.E. He died on the 8th of April 1894.
Bankim Chandra was beyond question the greatest novelist of India during the 19th century, whether judged by the amount and quality of his writings, or by the influence which they have continued to exercise. His education had brought him into touch with the works of the great European romance writers, notably Sir Walter Scott, and he created in India a school of fiction on the European model. His first historical novel, the Durges-Nandini or Chief’s Daughter, modelled on Scott, made a great sensation in Bengal; and the Kapala-Kundala and Mrinalini, which followed it, established his fame as a writer whose creative imagination and power of delineation had never been surpassed in India. In 1872 he brought out his first social novel, the Biska-Brikkha or Poison Tree, which was followed by others in rapid succession. It is impossible to exaggerate the effect they produced; for over twenty years Bankim Chandra’s novels were eagerly read by the educated public of Bengal, including the Hindu ladies in the zenanas; and though numerous works of fiction are now produced year by year in every province of India, his influence has increased rather than diminished. Of all his works, however, by far the most important from its astonishing political consequences was the Ananda Math, which was published in 1882, about the time of the agitation arising out of the Ilbert Bill. The story deals with the Sannyasi (i.e. fakir or hermit) rebellion of 1772 near Purmea, Tirhut and Dinapur, and its culminating episode is a crushing victory won by the rebels over the united British and Mussulman forces, a success which was not, however, followed up, owing to the advice of a mysterious “physician” who, speaking as a divinely-inspired prophet, advises Satyananda, the leader of “the children of the Mother,” to abandon further resistance, since a temporary submission to British rule is a necessity; for Hinduism has become too speculative and unpractical, and the mission of the English in India is to teach Hindus how to reconcile theory and speculation with the facts of science. The general moral of the Ananda Math, then, is that British rule and British education are to be accepted as the only alternative to Mussulman oppression, a moral which Bankim Chandra developed also in his Dharmatattwa, an elaborate religious treatise in which he explained his views as to the changes necessary in the moral and religious condition of his fellow-countrymen before they could hope to compete on equal terms with the British and Mahommedans. But though the Ananda Math is in form an apology for the loyal acceptance of British rule, it is none the less inspired by the ideal of the restoration, sooner or later, of a Hindu kingdom in India. This is especially evident in the occasional verses in the book, of which the Bande Mataram is the most famous.
As to the exact significance of this poem a considerable controversy has raged. Bande Mataram is the Sanskrit for “Hail to thee, Mother!” or more literally “I reverence thee, Mother!”, and according to Dr G.A. Grierson (The Times, Sept. 12, 1906) it can have no other possible meaning than an invocation of one of the “mother” goddesses of Hinduism, in his opinion Kali “the goddess of death and destruction.” Sir Henry Cotton, on the other hand (ib. Sept. 13, 1906), sees in it merely an invocation of the “mother-land” Bengal, and quotes in support of this view the free translation of the poem by the late W.H. Lee, a proof which, it may be at once said, is far from convincing. But though, as Dr Grierson points out, the idea of a “mother-land” is wholly alien to Hindu ideas, it is quite possible that Bankim Chandra may have assimilated it with his European culture, and the true explanation is probably that given by Mr J.D. Anderson in The Times of September 24, 1906. He points out that in the 11th chapter of the 1st book of the Ananda Math the Sannyasi rebels are represented as having erected, in addition to the image of Kali, “the Mother who Has Been,” a white marble statue of “the Mother that Shall Be,” which “is apparently a representation of the mother-land. 10 The Bande Mataram hymn is apparently addressed to both idols.”
The poem, then, is the work of a Hindu idealist who personified Bengal under the form of a purified and spiritualized Kali. Of its thirty-six lines, partly written in Sanskrit, partly in Bengali, the greater number are harmless enough. But if the poet sings the praise of the “Mother”
|
“As Lachmi, bowered in the flower That in the water grows,” |
he also praises her as “Durga, bearing ten weapons,” and lines 10, 11 and 12 are capable of very dangerous meanings in the mouths of unscrupulous agitators. Literally translated these run, “She has seventy millions of throats to sing her praise, twice seventy millions of hands to fight for her, how then is Bengal powerless?” As S.M. Mitra points out (Indian Problems, London, 1908), this language is the more significant as the Bande Mataram in the novel was the hymn by singing which the Sannyasis gained strength when attacking the British forces.
During Bankim Chandra Chatterji’s lifetime the Bande Mataram, though its dangerous tendency was recognized, was not used as a party war-cry; it was not raised, for instance, during the Ilbert Bill agitation, nor by the students who flocked round the court during the trial of Surendra Nath Banerji in 1883. It has, however, obtained an evil notoriety in the agitations that followed the partition of Bengal. That Bankim Chandra himself foresaw or desired any such use of it is impossible to believe. According to S.M. Mitra, he composed it “in a fit of patriotic excitement after a good hearty dinner, which he always enjoyed. It was set to Hindu music, known as the Mallar-Kawali-Tal. The extraordinarily stirring character of the air, and its ingenious assimilation of Bengali passages with Sanskrit, served to make it popular.”
Circumstances have made the Bande Mataram the most famous and the most widespread in its effects of Bankim Chandra’s literary works. More permanent, it may be hoped, was the wholesome influence he exercised on the number of literary men he gathered round him, who have left their impress on the literature of Bengal. In his earlier years he served his apprenticeship in literature under Iswar Chandra Vidyasagar, the chief poet and satirist of Bengal during the earlier half of the 19th century. Bankim Chandra’s friend and colleague, Dina Bandhu Mitra, was virtually the founder of the modern Bengali drama. Another friend of his, Hem Chandra Banerji, was a poet of recognized merit and talent. And among the younger men who venerated Bankim Chandra, and benefited by his example and advice, may be mentioned two distinguished poets, Nalein Chandra Sen and Rabindra Nath Tagore.
Of Bankim Chandra’s novels some have been translated into English by H.A.D. Phillips and by Mrs M.S. Knight.
CHATTERTON, THOMAS (1752-1770), English poet, was born at Bristol on the 20th of November 1752. His pedigree has a curious significance. The office of sexton of St Mary Redcliffe, at Bristol, one of the most beautiful parish churches in England, had been transmitted for nearly two centuries in the Chatterton family; and throughout the brief life of the poet it was held by his uncle, Richard Phillips. The poet’s father, Thomas Chatterton, was a musical genius, somewhat of a poet, a numismatist, and a dabbler in occult arts. He was one of the sub-chanters of Bristol cathedral, and master of the Pyle Street free school, near Redcliffe church. But whatever hereditary tendencies may have been transmitted from the father, the sole training of the boy necessarily devolved on his mother, who was in the fourth month of her widowhood at the time of his birth. She established a girls’ school, took in sewing and ornamental needlework, and so brought up her two children, a girl and a boy, till the latter attained his eighth year, when he was admitted to Colston’s Charity. But the Bristol blue-coat school, in which the curriculum was limited to reading, writing, arithmetic and the Church Catechism, had little share in the education of its marvellous pupil. The hereditary race of sextons had come to regard the church of St Mary Redcliffe as their own peculiar domain; and, under the guidance of his uncle, the child found there his favourite haunt. The knights, ecclesiastics and civic dignitaries, recumbent on its altar tombs, became his familiar associates; and by and by, when he was able to spell his way through the inscriptions graven on their monuments, he found a fresh interest in certain quaint oaken chests in the muniment room over the porch on the north side of the nave, where parchment deeds, old as the Wars of the Roses, long lay unheeded and forgotten. They formed the child’s playthings almost from his cradle. He learned his first letters from the illuminated capitals of an old musical folio, and learned to read out of a black-letter Bible. He did not like, his sister said, reading out of small books. Wayward, as it seems, almost from his earliest years, and manifesting no sympathy with the ordinary pastimes of children, he was regarded for a time as deficient in intellect. But he was even then ambitious of distinction. His sister relates that on being asked what device he would like painted on a bowl that was to be his, he replied, “Paint me an angel, with wings, and a trumpet, to trumpet my name over the world.”
From his earliest years he was liable to fits of abstraction, sitting for hours in seeming stupor, or yielding after a time to tears, for which he would assign no reason. He had no one near him to sympathize in the strange world of fancy which his imagination had already called into being; and circumstances helped to foster his natural reserve, and to beget that love of mystery which exercised so great an influence on the development of his genius. When the strange child had attained his sixth year his mother began to recognize his capacity; at eight he was so eager for books that he would read and write all day long if undisturbed; and in his eleventh year he had become a contributor to Felix Farley’s Bristol Journal. The occasion of his confirmation inspired some religious poems published in this paper. In 1763 a beautiful cross of curious workmanship, which had adorned the churchyard of St Mary Redcliffe for upwards of three centuries, was destroyed by a churchwarden. The spirit of veneration was strong in the boy, and he sent to the local journal on the 7th of January 1764 a clever satire on the parish Vandal. But his delight was to lock himself in a little attic which he had appropriated as his study; and there, with books, cherished parchments, saved from the loot of the muniment room of St Mary Redcliffe, and drawing materials, the child lived in thought with his 15th-century heroes and heroines. The first of his literary mystifications, the duologue of “Elinoure and Juga,” was written before he was twelve years old, and he showed his poem to the usher at Colston’s hospital, Thomas Phillips, as the work of a 15th-century poet.
Chatterton remained an inmate of Colston’s hospital for upwards of six years, and the slight advantages gained from this scanty education are traceable to the friendly sympathy of Phillips, himself a writer of verse, who encouraged his pupils to write. Three of Chatterton’s companions are named as youths whom Phillips’s taste for poetry stimulated to rivalry; but Chatterton held aloof from these contests, and made at that time no confidant of his own more daring literary adventures. His little pocket-money was spent in borrowing books from a circulating library; and he early ingratiated himself with book collectors, by whose aid he found access to Weever, Dugdale and Collins, as well as to Speght’s edition of Chaucer, Spenser and other books.
His “Rowleian” jargon appears to have been chiefly the result of the study of John Kersey’s Dictionarium Anglo-Britannicum, and Prof. W. W. Skeat seems to think his knowledge of even Chaucer was very slight. His holidays were mostly spent at his mother’s house; and much of them in the favourite retreat of his attic study there. He had already conceived the romance of Thomas Rowley, an imaginary monk of the 15th century, and lived for the most part in an ideal world of his own, in that elder time when Edward IV. was England’s king, and Master William Canynge—familiar to him among the recumbent effigies in Redcliffe church—still ruled in Bristol’s civic chair. Canynge is represented as an enlightened patron of literature, and Rowley’s dramatic interludes were written for 11 performance at his house. In order to escape a marriage urged by the king, Canynge retired to the college of Westbury in Gloucestershire, where he enjoyed the society of Rowley, and eventually became dean of the institution. In “The Storie of William Canynge,” one of the shorter pieces of his ingenious romance, his early history is recorded.
|
“Straight was I carried back to times of yore, Whilst Canynge swathed yet in fleshly bed, And saw all actions which had been before, And all the scroll of Fate unravelled; And when the fate-marked babe acome to sight, I saw him eager gasping after light. In all his sheepen gambols and child’s play, In every merrymaking, fair, or wake, I kenn’d a perpled light of wisdom’s ray; He ate down learning with the wastel-cake; As wise as any of the aldermen, He’d wit enow to make a mayor at ten.” |
This beautiful picture of the childhood of the ideal patron of Rowley is in reality that of the poet himself—“the fate-marked babe,” with his wondrous child-genius, and all his romantic dreams realized. The literary masquerade which thus constituted the life-dream of the boy was wrought out by him in fragments of prose and verse into a coherent romance, until the credulous scholars and antiquaries of his day were persuaded into the belief that there had lain in the parish chest of Redcliffe church for upwards of three centuries, a collection of MSS. of rare merit, the work of Thomas Rowley, an unknown priest of Bristol in the days of Henry VI. and his poet laureate, John Lydgate.
Among the Bristol patrons of Chatterton were two pewterers, George Catcott and his partner Henry Burgum. Catcott was one of the most zealous believers in Rowley, and continued to collect his reputed writings long after the death of their real author. On Burgum, who had risen in life by his own exertions, the blue-coat boy palmed off the de Bergham pedigree, and other equally apocryphal evidences of the pewterer’s descent from an ancestry old as the Norman Conquest. The de Bergham quartering, blazoned on a piece of parchment doubtless recovered from the Redcliffe muniment chest, was itself supposed to have lain for centuries in that ancient depository. The pedigree was professedly collected by Chatterton from original records, including “The Rowley MSS.” The pedigree still exists in Chatterton’s own handwriting, copied into a book in which he had previously transcribed portions of antique verse, under the title of “Poems by Thomas Rowley, priest of St. John’s, in the city of Bristol”; and in one of these, “The Tournament,” Syrr Johan de Berghamme plays a conspicuous part. The ennobled pewterer rewarded Chatterton with five shillings, and was satirized for this valuation of a noble pedigree in some of Chatterton’s latest verse.
On the 1st of July 1767, Chatterton was transferred to the office of John Lambert, attorney, to whom he was bound apprentice as a clerk. There he was left much alone; and after fulfilling the routine duties devolving on him, he found leisure for his own favourite pursuits. An ancient stone bridge on the Avon, built in the reign of Henry II., and altered by many later additions into a singularly picturesque but inconvenient thoroughfare, had been displaced by a structure better adapted to modern requirements. In September 1768, when Chatterton was in the second year of his apprenticeship, the new bridge was partially opened for traffic. Shortly afterwards the editor of Felix Farley’s Journal received from a correspondent, signing himself Dunelmus Bristoliensis, a “description of the mayor’s first passing over the old bridge,” professedly derived from an ancient MS. William Barrett, F.S.A., surgeon and antiquary, who was then accumulating materials for a history of Bristol, secured the original manuscript, which is now preserved in the British Museum, along with other Chatterton MSS., most of which were ultimately incorporated by the credulous antiquary into a learned quarto volume, entitled the History and Antiquities of the City of Bristol, published nearly twenty years after the poet’s death. It was at this time that the definite story made its appearance—over which critics and antiquaries wrangled for nearly a century—of numerous ancient poems and other MSS. taken by the elder Chatterton from a coffer in the muniment room of Redcliffe church, and transcribed, and so rescued from oblivion, by his son. The pieces include the “Bristowe Tragedie, or the Dethe of Syr Charles Bawdin,” a ballad celebrating the death of the Lancastrian knight, Charles Baldwin; “Ælla,” a “Tragycal Enterlude,” as Chatterton styles it, but in reality a dramatic poem of sustained power and curious originality of structure; “Goddwyn,” a dramatic fragment; “Tournament,” “Battle of Hastings,” “The Parliament of Sprites,” “Balade of Charitie,” with numerous shorter pieces, forming altogether a volume of poetry, the rare merit of which is indisputable, wholly apart from the fact that it was the production of a mere boy. Unfortunately for him, his ingenious romance had either to be acknowledged as his own creation, and so in all probability be treated with contempt, or it had to be sustained by the manufacture of spurious antiques. To this accordingly Chatterton resorted, and found no difficulty in gulling the most learned of his credulous dupes with his parchments.
The literary labours of the boy, though diligently pursued at his desk, were not allowed to interfere with the duties of Mr Lambert’s office. Nevertheless the Bristol attorney used to search his apprentice’s drawer, and tear up any poems or other manuscripts that he could lay his hands upon; so that it was only during the absences of Mr Lambert from Bristol that he was able to expend his unemployed time in his favourite pursuits. But repeated allusions, both by Chatterton and others, seem to indicate that such intervals of freedom were of frequent occurrence. Some of his modern poems, such as the piece entitled “Resignation,” are of great beauty; and these, with the satires, in which he took his revenge on all the local celebrities whose vanity or meanness had excited his ire, are alone sufficient to fill a volume. The Catcotts, Burgum, Barrett and others of his patrons, figure in these satires, in imprudent yet discriminating caricature, along with mayor, aldermen, bishop, dean and other notabilities of Bristol. Towards Lambert his feelings were of too keen a nature to find relief in such sarcasm.
In December 1768, in his seventeenth year, he wrote to Dodsley, the London publisher, offering to procure for him “copies of several ancient poems, and an interlude, perhaps the oldest dramatic piece extant, wrote by one Rowley, a priest in Bristol, who lived in the reigns of Henry VI. and Edward IV.” To this letter he appended the initials of his favourite pseudonym, Dunelmus Bristoliensis, but directed the answer to be sent to the care of Thomas Chatterton, Redcliffe Hill, Bristol. To this, as well as to another letter enclosing an extract from the tragedy of “Ælla,” no answer appears to have been returned. Chatterton, conceiving the idea of finding sympathy and aid at the hand of some modern Canynge, bethought him of Horace Walpole, who not only indulged in a medieval renaissance of his own, but was the reputed author of a spurious antique in the Castle of Otranto. He wrote to him offering him a document entitled “The Ryse of Peyncteyne yn Englande, wroten by T. Rowleie, 1469, for Mastre Canynge,” accompanied by notes which included specimens of Rowley’s poetry. To this Walpole replied with courteous acknowledgments. He characterized the verses as “wonderful for their harmony and spirit,” and added, “Give me leave to ask you where Rowley’s poems are to be had? I should not be sorry to print them; or at least a specimen of them, if they have never been printed.” Chatterton replied, enclosing additional specimens of antique verse, and telling Walpole that he was the son of a poor widow, and clerk to an attorney, but had a taste for more refined studies; and he hinted a wish that he might help him to some more congenial occupation. Walpole’s manner underwent an abrupt change. The specimens of verse had been submitted to his friends Gray and Mason, the poets, and pronounced modern. They did not thereby forfeit the wonderful harmony and spirit which Walpole had already professed to recognize in them. But he now coldly advised the boy to stick to the attorney’s office; and “when he should have made a fortune,” he might betake himself to more favourite 12 studies, Chatterton had to write three times before he recovered his MSS. Walpole has been loaded with more than his just share of responsibility for the fate of the unhappy poet, of whom he admitted when too late, “I do not believe there ever existed so masterly a genius.”
Chatterton now turned his attention to periodical literature and politics, and exchanged Felix Farley’s Bristol Journal for the Town and County Magazine and other London periodicals. Assuming the vein of Junius—then in the full blaze of his triumph—he turned his pen against the duke of Grafton, the earl of Bute, and the princess of Wales. He had just despatched one of his political diatribes to the Middlesex Journal, when he sat down on Easter Eve, I7th April 1770, and penned his “Last Will and Testament,” a strange satirical compound of jest and earnest, in which he intimated his intention of putting an end to his life the following evening. Among his satirical bequests, such as his “humility” to the Rev. Mr Camplin, his “religion” to Dean Barton, and his “modesty” along with his “prosody and grammar” to Mr Burgum, he leaves “to Bristol all his spirit and disinterestedness, parcels of goods unknown on its quay since the days of Canynge and Rowley.” In more genuine earnestness he recalls the name of Michael Clayfield, a friend to whom he owed intelligent sympathy. The will was probably purposely prepared in order to frighten his master into letting him go. If so, it had the desired effect. Lambert cancelled his indentures; his friends and acquaintance made him up a purse; and on the 25th or 26th of the month he arrived in London.
Chatterton was already known to the readers of the Middlesex Journal as a rival of Junius, under the nom de plume of Decimus. He had also been a contributor to Hamilton’s Town and County Magazine, and speedily found access to the Freeholder’s Magazine, another political miscellany strong for Wilkes and liberty. His contributions were freely accepted; but the editors paid little or nothing for them. He wrote in the most hopeful terms to his mother and sister, and spent his first earnings in buying gifts for them. His pride and ambition were amply gratified by the promises and interested flattery of editors and political adventurers; Wilkes himself had noted his trenchant style, “and expressed a desire to know the author”; and Lord Mayor Beckford graciously acknowledged a political address of his, and greeted him “as politely as a citizen could.” But of actual money he received but little. He was extremely abstemious, his diligence was great, and his versatility wonderful. He could assume the style of Junius or Smollett, reproduce the satiric bitterness of Churchill, parody Macpherson’s Ossian, or write in the manner of Pope, or with the polished grace of Gray and Collins. He wrote political letters, eclogues, lyrics, operas and satires, both in prose and verse. In June 1770—after Chatterton had been some nine weeks in London—he removed from Shoreditch, where he had hitherto lodged with a relative, to an attic in Brook Street, Holborn. But for most of his productions the payment was delayed; and now state prosecutions of the press rendered letters in the Junius vein no longer admissible, and threw him back on the lighter resources of his pen. In Shoreditch, as in his lodging at the Bristol attorney’s, he had only shared a room; but now, for the first time, he enjoyed uninterrupted solitude. His bed-fellow at Mr Walmsley’s, Shoreditch, noted that much of the night was spent by him in writing; and now he could write all night. The romance of his earlier years revived, and he transcribed from an imaginary parchment of the old priest Rowley his “Excelente Balade of Charitie.” This fine poem, perversely disguised in archaic language, he sent to the editor of the Town and County Magazine, and had it rejected.
The high hopes of the sanguine boy had begun to fade. He had not yet completed his second month in London, and already failure and starvation stared him in the face. Mr Cross, a neighbouring apothecary, repeatedly invited him to join him at dinner or supper; but he refused. His landlady also, suspecting his necessity, pressed him to share her dinner, but in vain. “She knew,” as she afterwards said, “that he had not eaten anything for two or three days.” But he was offended at her urgency, and assured her that he was not hungry. The note of his actual receipts, found in his pocket-book after his death, shows that Hamilton, Fell and other editors who had been so liberal in flattery, had paid him at the rate of a shilling for an article, and somewhat less than eightpence each for his songs; while much which had been accepted was held in reserve, and still unpaid for. The beginning of a new month revealed to him the indefinite postponement of the publication and payment of his work. He had wished, according to his foster-mother, to study medicine with Barrett; in his desperation he now reverted to this, and wrote to Barrett for a letter to help him to an opening as a surgeon’s assistant on board an African trader. He appealed also to Mr Catcott to forward his plan, but in vain. On the 24th of August 1770, he retired for the last time to his attic in Brook Street, carrying with him the arsenic which he there drank, after tearing into fragments whatever literary remains were at hand.
He was only seventeen years and nine months old; but the best of his numerous productions, both in prose and verse, require no allowance to be made for the immature years of their author, when comparing him with the ablest of his contemporaries. He pictures Lydgate, the monk of Bury St Edmunds, challenging Rowley to a trial at versemaking, and under cover of this fiction, produces his “Songe of Ælla,” a piece of rare lyrical beauty, worthy of comparison with any antique or modern production of its class. Again, in his “Tragedy of Goddwyn,” of which only a fragment has been preserved, the “Ode to Liberty,” with which it abruptly closes, may claim a place among the finest martial lyrics in the language. The collection of poems in which such specimens occur furnishes by far the most remarkable example of intellectual precocity in the whole history of letters. Collins, Burns, Keats, Shelley and Byron all awaken sorrow over the premature arrestment of their genius; but the youngest of them survived to his twenty-fifth year, while Chatterton was not eighteen when he perished in his miserable garret. The death of Chatterton attracted little notice at the time; for the few who then entertained any appreciative estimate of the Rowley poems regarded him as their mere transcriber. He was interred in a burying-ground attached to Shoe Lane Workhouse, in the parish of St Andrew’s, Holborn, which has since been converted into a site for Farringdon Market. There is a discredited story that the body of the poet was recovered, and secretly buried by his uncle, Richard Phillips, in Redcliffe Churchyard. There a monument has since been erected to his memory, with the appropriate inscription, borrowed from his “Will,” and so supplied by the poet’s own pen—“To the memory of Thomas Chatterton. Reader! judge not. If thou art a Christian, believe that he shall be judged by a Superior Power. To that Power only is he now answerable.”
Bibliography.—Poems supposed to have been written at Bristol by Thomas Rowley and others, in the Fifteenth Century (1777) was edited by Thomas Tyrwhitt; Thomas Warton, in his History of English Poetry (1778), vol. ii. section viii., gives Rowley a place among the 15th century poets; but neither of these critics believed in the antiquity of the poems. In 1782 a new edition of Rowley’s poems appeared, with a “Commentary, in which the antiquity of them is considered and defended,” by Jeremiah Milles, dean of Exeter. The controversy which raged round the Rowley poems is discussed in A. Kippis, Biographia Britannica (vol. iv., 1789), where there is a detailed account by G. Gregory of Chatterton’s life (pp. 573-619). This was reprinted in the edition (1803) of Chatterton’s Works by R. Southey and J. Cottle, published for the benefit of the poet’s sister. The neglected condition of the study of earlier English in the 18th century alone accounts for the temporary success of Chatterton’s mystification. It has long been agreed that Chatterton was solely responsible for the Rowley Poems, but the language and style are analysed in confirmation of this view by Prof. W.W. Skeat in an introductory essay prefaced to vol. ii. of The Poetical Works of Thomas Chatterton (1871) in the “Aldine Edition of the British Poets.” This, which is the most convenient edition, also contains a memoir of the poet by Edward Bell. The spelling of the Rowley poems is there modernized, and many of the archaic words are replaced by modern equivalents provided in many cases from Chatterton’s own notes, the theory being that Chatterton usually composed in modern English, and inserted his peculiar words and his complicated orthography afterwards. For some criticism of Prof. Skeat’s success in the very difficult task of reconstituting the text, see H.B. Forman, Thomas Chatterton and his latest Editor (1874). 13 The Chatterton MSS., originally in the possession of William Barrett of Bristol, were left by his heir to the British Museum in 1800. Others are preserved in the Bristol library.
Chatterton’s genius and his tragic death are commemorated by Shelley in Adonais, by Wordsworth in “Resolution and Independence,” by Coleridge in “A Monody on the Death of Chatterton,” by D.G. Rossetti in “Five English Poets,” and John Keats inscribed Endymion “to the memory of Thomas Chatterton.” Alfred de Vigny’s drama of Chatterton gives an altogether fictitious account of the poet. Herbert Croft (q.v.), in his Love and Madness, interpolated a long and valuable account of Chatterton, giving many of the poet’s letters, and much information obtained from his family and friends (pp. 125-244, letter li.). There is a valuable collection of “Chattertoniana” in the British Museum, consisting of separate works by Chatterton, newspaper cuttings, articles, dealing with the Rowley controversy and other subjects, with MS. notes by Joseph Haslewood, and several autograph letters.
Among biographies of Chatterton may be mentioned Chatterton: A Biographical Study (1869), by Daniel Wilson; Chatterton: A Biography (1899; first printed 1856 in a volume of essays), by D. Masson; “Thomas Chatterton” (1900), by Helene Richter, in Wiener Beiträge zur engl. Philologie; Chatterton, by C.E. Russell (1909).
CHATTI, an ancient German tribe inhabiting the upper reaches of the rivers Weser, Eder, Fulda and Werra, a district approximately corresponding to Hesse-Cassel, though probably somewhat more extensive. They frequently came into conflict with the Romans during the early years of the 1st century. Eventually they formed a portion of the Franks and were incorporated in the kingdom of Clovis probably with the Ripuarii, at the beginning of the 6th century.
Tacitus, Annals, i. 2, II, 12, 13; Germania, 30-31; Strabo p. 291 f.
CHAUCER, GEOFFREY (? 1340-1400), English poet. The name Chaucer, a French form of the Latin calcearius, a shoe-maker, is found in London and the eastern counties as early as the second half of the 13th century. Some of the London Chaucers lived in Cordwainer Street, in the shoemakers’ quarter; several of them, however, were vintners, and among others the poet’s father John, and probably also his grandfather Robert. Legal pleadings inform us that in December 1324 John Chaucer was not much over twelve years old, and that he was still unmarried Life. in 1328, the year which used to be considered that of Geoffrey’s birth.The poet was probably born from eight to twelve years later, since in 1386, when giving evidence in Sir Richard le Scrope’s suit against Sir Robert Grosvenor as to the right to bear certain arms, he was set down as “del age de xl ans et plus, armeez par xxvij ans.” At a later date, and probably at the time of the poet’s birth, his father lived in Thames Street, and had to wife a certain Agnes, niece of Hamo de Compton, whom we may regard as Geoffrey Chaucer’s mother. In 1357 Geoffrey is found, apparently as a lad, in the service of Elizabeth, countess of Ulster, wife of Lionel, duke of Clarence, entries in two leaves of her household accounts, accidentally preserved, showing that she paid in April, May and December various small sums for his clothing and expenses. In 1359, as we learn from his deposition in the Scrope suit, Chaucer went to the war in France. At some period of the campaign he was at “Retters,” i.e. Rethel, near Reims, and subsequently had the ill luck to be taken prisoner. On the 1st of March 1360 the king contributed £16 to his ransom, and by a year or two later Chaucer must have entered the royal service, since on the 20th of June 1367 Edward granted him a pension of twenty marks for his past and future services. A pension of ten marks had been granted by the king the previous September to a Philippa Chaucer for services to the queen as one of her “domicellae” or “damoiselles,” and it seems probable that at this date Chaucer was already married and this Philippa his wife, a conclusion which used to be resisted on the ground of allusions in his early poems to a hopeless love-affair, now reckoned part of his poetical outfit. Philippa is usually said to have been one of two daughters of a Sir Payne Roet, the other being Katherine, who after the death of her first husband, Sir Hugh de Swynford, in 1372, became governess to John of Gaunt’s children, and subsequently his mistress and (in 1396) his wife. It is possible that Philippa was sister to Sir Hugh and sister-in-law to Katherine. In either case the marriage helps to account for the favour subsequently shown to Chaucer by John of Gaunt.
In the grant of his pension Chaucer is called “dilectus vallectus noster,” our beloved yeoman; before the end of 1368 he had risen to be one of the king’s esquires. In September of the following year John of Gaunt’s wife, the duchess Blanche, died at the age of twenty-nine, and Chaucer wrote in her honour The Book of the Duchesse, a poem of 1334 lines in octosyllabic couplets, the first of his undoubtedly genuine works which can be connected with a definite date. In June 1370 he went abroad on the king’s service, though on what errand, or whither it took him, is not known. He was back probably some time before Michaelmas, and seems to have remained in England till the 1st of December 1372, when he started, with an advance of 100 marks in his pocket, for Italy, as one of the three commissioners to treat with the Genoese as to an English port where they might have special facilities for trade. The accounts which he delivered on his return on the 23rd of May 1373 show that he had also visited Florence on the king’s business, and he probably went also to Padua and there made the acquaintance of Petrarch.
In the second quarter of 1374 Chaucer lived in a whirl of prosperity. On the 23rd of April the king granted him a pitcher of wine daily, subsequently commuted for an annuity of 20 marks. From John of Gaunt, who in August 1372 had granted Philippa Chaucer £10 a year, he himself now received (June 13) a like annuity in reward for his own and his wife’s services. On the 8th of June he was appointed Comptroller of the Custom and Subsidy of Wools, Hides and Woodfells and also of the Petty Customs of Wine in the Port of London. A month before this appointment, and probably in anticipation of it, he took (May 10, 1374) a lease for life from the city of London of the dwelling-house above the gate of Aldgate, and here he lived for the next twelve years. His own and his wife’s income now amounted to over £60, the equivalent of upwards of £1000 in modern money. In the next two years large windfalls came to him in the form of two wardships of Kentish heirs, one of whom paid him £104, and a grant of £71: 4: 6; the value of some confiscated wool. In December 1376 he was sent abroad on the king’s service in the retinue of Sir John Burley; in February 1377 he was sent to Paris and Montreuil in connexion probably with the peace negotiations between England and France, and at the end of April (after a reward of £20 for his good services) he was again despatched to France.
On the accession of Richard II. Chaucer was confirmed in his offices and pensions. In January 1378 he seems to have been in France in connexion with a proposed marriage between Richard and the daughter of the French king; and on the 28th of May of the same year he was sent with Sir Edward de Berkeley to the lord of Milan and Sir John Hawkwood to treat for help in the king’s wars, returning on the 19th of September. This was his last diplomatic journey, and the close of a period of his life generally considered to have been so unprolific of poetry that little beyond the Clerk’s “Tale of Grisilde,” one or two other of the stories afterwards included in the Canterbury Tales, and a few short poems, are attributed to it, though the poet’s actual absences from England during the eight years amount to little more than eighteen months. During the next twelve or fifteen years there is no question that Chaucer was constantly engaged in literary work, though for the first half of them he had no lack of official employment. Abundant favour was shown him by the new king. He was paid £22 as a reward for his later missions in Edward III.’s reign, and was allowed an annual gratuity of 10 marks in addition to his pay of £10 as comptroller of the customs of wool. In April 1382 a new comptrollership, that of the petty customs in the Port of London, was given him, and shortly after he was allowed to exercise it by deputy, a similar licence being given him in February 1385, at the instance of the earl of Oxford, as regards the comptrollership of wool. In October 1385 Chaucer was made a justice of the peace for Kent. In February 1386 we catch a glimpse of his wife Philippa being admitted to the fraternity of Lincoln cathedral in the company of Henry, earl of 14 Derby (afterwards Henry IV.), Sir Thomas de Swynford and other distinguished persons. In August 1386 he was elected one of the two knights of the shire for Kent, and with this dignity, though it was one not much appreciated in those days, his good fortune reached its climax. In December of the same year he was superseded in both his comptrollerships, almost certainly as a result of the absence of his patron, John of Gaunt, in Spain, and the supremacy of the duke of Gloucester. In the following year the cessation of Philippa’s pension suggests that she died between Midsummer and Michaelmas. In May 1388 Chaucer surrendered to the king his two pensions of 20 marks each, and they were re-granted at his request to one John Scalby. The transaction was unusual and probably points to a pressing need for ready money, nor for the next fourteen months do we know of any source of income possessed by Chaucer beyond his annuity of £10 from John of Gaunt.
In July 1389, after John of Gaunt had returned to England, and the king had taken the government into his own hands, Chaucer was appointed clerk of the works at various royal palaces at a salary of two shillings a day, or over £31 a year, worth upwards of £500 present value. To this post was subsequently added the charge of some repairs at St George’s Chapel, Windsor. He was also made a commissioner to maintain the banks of the Thames between Woolwich and Greenwich, and was given by the earl of March (grandson of Lionel, duke of Clarence, his old patron) a sub-forestership at North Petherton, Devon, obviously a sinecure. While on the king’s business, in September 1390, Chaucer was twice robbed by highwaymen, losing £20 of the king’s money. In June 1391 he was superseded in his office of clerk of the works, and seems to have suffered another spell of misfortune, of which the first alleviation came in January 1393 when the king made him a present of £10. In February 1394 he was granted a new pension of £20. It is possible, also, that about this time, or a little later, he was in the service of the earl of Derby. In 1397 he received from King Richard a grant of a butt of wine yearly. For this he appears to have asked in terms that suggest poverty, and in May 1398 he obtained letters of protection against his creditors, a step perhaps rendered necessary by an action for debt taken against him earlier in the year. On the accession of Henry IV. a new pension of 40 marks was conferred on Chaucer (13th of October 1399) and Richard II.’s grants were formally confirmed. Henry himself, however, was probably straitened for ready money, and no instalment of the new pension was paid during the few months of his reign that the poet lived. Nevertheless, on the strength of his expectations, on the 24th of December 1399 he leased a tenement in the garden of St Mary’s Chapel, Westminster, and it was probably here that he died, on the 25th of the following October. He was buried in Westminster Abbey, and his tomb became the nucleus of what is now known as Poets’ Corner.
The portrait of Chaucer, which the affection of his disciple, Thomas Hoccleve, caused to be painted in a copy of the latter’s Regement of Princes (now Harleian MS. 4866 in the British Museum), shows him an old man with white hair; he has a fresh complexion, grey eyes, a straight nose, a grey moustache and a small double-pointed beard. His dress and hood are black, and he carries in his hands a string of beads. We may imagine that it was thus that during the last months of his life he used to walk about the precincts of the Abbey.
Henry IV.’s promise of an additional pension was doubtless elicited by the Compleynt to his Purs, in the envoy to which Chaucer addresses him as the “conquerour of Brutes Works. Albioun.” Thus within the last year of his life the poet was still writing. Nevertheless, as early as 1393-1394, in lines to his friend Scogan, he had written as if his day for poetry were past, and it seems probable that his longer poems were all composed before this date. In the preceding fifteen—or, if another view be taken, twenty—years, his literary activity was very great, and with the aid of the lists of his works which he gives in the Legende of Good Women (lines 414-431), and the talk on the road which precedes the “Man of Law’s Tale” (Canterbury Tales, B. 46-76), the order in which his main works were written can be traced with approximate certainty,1 while a few both of these and of the minor poems can be connected with definite dates.
The development of his genius has been attractively summed up as comprised in three stages, French, Italian and English, and there is a rough approximation to the truth in this formula, since his earliest poems are translated from the French or based on French models, and the two great works of his middle period are borrowed from the Italian, while his latest stories have no such obvious and direct originals and in their humour and freedom anticipate the typically English temper of Henry Fielding. But Chaucer’s indebtedness to French poetry was no passing phase. For various reasons—a not very remote French origin of his own family may be one of them—he was in no way interested in older English literature or in the work of his English contemporaries, save possibly that of “the moral Gower.” On the other hand he knew the Roman de la rose as modern English poets know Shakespeare, and the full extent of his debt to his French contemporaries, not merely in 1369, but in 1385 and in 1393 (the dates are approximate), is only gradually being discovered. To be in touch throughout his life with the best French poets of the day was much for Chaucer. Even with their stimulus alone he might have developed no small part of his genius. But it was his great good fortune to add to this continuing French influence, lessons in plot and construction derived from Boccaccio’s Filostrato and Teseide, as well as some glimpses of the higher art of the Divina Commedia. He shows acquaintance also with one of Petrarch’s sonnets, and though, when all is said, the Italian books with which he can be proved to have been intimate are but few, they sufficed. His study of them was but an episode in his literary life, but it was an episode of unique importance. Before it began he had already been making his own artistic experiments, and it is noteworthy that while he learnt so much from Boccaccio he improved on his originals as he translated them. Doubtless his busy life in the service of the crown had taught him self-confidence, and he uses his Italian models in his own way and with the most triumphant and assured success. When he had no more Italian poems to adapt he had learnt his lesson. The art of weaving a plot out of his own imagination was never his, but he could take what might be little more than an anecdote and lend it body and life and colour with a skill which has never been surpassed.
The most direct example of Chaucer’s French studies is his translation of Le Roman de la rose, a poem written in some 4000 lines by Guillaume Lorris about 1237 and extended to over 22,000 by Jean Clopinel, better known as Jean de Meun, forty years later. We know from Chaucer himself that he translated this poem, and the extant English fragment of 7698 lines was generally assigned to him from 1532, when it was first printed, till its authorship was challenged in the early years of the Chaucer Society. The ground of this challenge was its wide divergence from Chaucer’s practice in his undoubtedly genuine works as to certain niceties of rhyme, notable as to not rhyming words ending in -y with others ending -ye. It was subsequently discovered, however, that the whole fragment was divisible linguistically into three portions, of which the first and second end respectively at lines 1705 and 5810, and that in the first of these three sections the variations from Chaucer’s accepted practice are insignificant. Lines 1-1705 have therefore been provisionally accepted as Chaucer’s, and the other two fragments as the work of unknown translators (James I. of Scotland has been suggested as one of them), which somehow came to be pieced together. If, however, the difficulties in the way of this theory are less than those which confront any other, they are still considerable, and the question can hardly be treated as closed.
While our knowledge of Chaucer’s Romaunt of the Rose is in this unsatisfactory state, another translation of his from the French, the Book of the Lyon (alluded to in the “Retraction” found, in some manuscripts, at the end of the Canterbury Tales), which must certainly have been taken from Guillaume 15 Machault’s Le Dit du lion, has perished altogether. The strength of French influence on Chaucer’s early work may, however, be amply illustrated from the first of his poems with which we are on sure ground, the Book of the Duchesse, or, as it is alternatively called, the Deth of Blaunche. Here not only are individual passages closely imitated from Machault and Froissart, but the dream, the May morning, and the whole machinery of the poem are taken over from contemporary French conventions. But even at this stage Chaucer could prove his right to borrow by the skill with which he makes his materials serve his own purpose, and some of the lines in the Deth of Blaunche are among the most tender and charming he ever wrote.
Chaucer’s A.B.C., a poem in honour of the Blessed Virgin, of which the stanzas begin with the successive letters of the alphabet, is another early example of French influence. It is taken from the Pèlerinage de la vie humaine, written by Guillaume de Deguilleville about 1330. The occurrence of some magnificent lines in Chaucer’s version, combined with evidence that he did not yet possess the skill to translate at all literally as soon as rhymes had to be considered, accounts for this poem having been dated sometimes earlier than the Book of the Duchesse, and sometimes several years later. With it is usually moved up and down, though it should surely be placed in the ’seventies, the Compleynt to Pity, a fine poem which yet, from its slight obscurity and absence of Chaucer’s usual ease, may very well some day prove to be a translation from the French.
While Chaucer thus sought to reproduce both the matter and the style of French poetry in England, he found other materials in popular Latin books. Among his lost works are renderings of “Origenes upon the Maudeleyne,” and of Pope Innocent III. on “The Wreced Engendring of Mankinde” (De miseria conditionis humanae). He must have begun his attempts at straightforward narrative with the Lyf of Seynt Cecyle (the weakest of all his works, the second Nun’s Tale in the Canterbury series) from the Legenda Aurea of Jacobus de Voragine, and the story of the patience of Grisilde, taken from Petrarch’s Latin version of a tale by Boccaccio. In both of these he condenses a little, but ventures on very few changes, though he lets his readers see his impatience with his originals. In his story of Constance (afterwards ascribed to the Man of Law), taken from the Anglo-Norman chronicle of Nicholas Trivet, written about 1334, we find him struggling to put some substance into another weak tale, but still without the courage to remedy its radical faults, though here, as with Grisilde, he does as much for his heroine as the conventional exaltation of one virtue at a time permitted. It is possible that other tales which now stand in the Canterbury series were written originally at this period. What is certain is that at some time in the ’seventies three or four Italian poems passed into Chaucer’s possession, and that he set to work busily to make use of them. One of the most interesting of the poems reclaimed for him by Professor Skeat is a fragmentary “Compleynt,” part of which is written in terza rima. While he thus experimented with the metre of the Divina Commedia, he made his first attempt to use the material provided by Boccaccio’s Teseide in another fragment of great interest, that of Quene Anelida and Fals Arcyte. More than a third of this is taken up with another, and quite successful, metrical experiment in Anelida’s “compleynt,” but in the introduction of Anelida herself Chaucer made the first of his three unsuccessful efforts to construct a plot for an important poem out of his own head, and the fragment which begins so well breaks off abruptly at line 357.
For a time the Teseide seems to have been laid aside, and it was perhaps at this moment, in despondency at his failure, that Chaucer wrote his most important prose work, the translation of the De Consolatione Philosophiae of Boethius. Reminiscences of this helped to enrich many of his subsequent poems, and inspired five of his shorter pieces (The Former Age, Fortune, Truth, Gentilesse and Lak of Stedfastnesse), but the translation itself was only a partial success. To borrow his own phrase, his “Englysh was insufficient” to reproduce such difficult Latin. The translation is often barely intelligible without the original, and it is only here and there that it flows with any ease or rhythm.
If Chaucer felt this himself he must have been speedily consold by achieving in Troilus and Criseyde his greatest artistic triumph. Warned by his failure in Anelida and Arcyte, he was content this time to take his plot unaltered from the Filostrato, and to follow Boccaccio step by step through the poem. But he did not follow him as a mere translator. He had done his duty manfully for the saints “of other holinesse” in Cecyle, Grisilde and Constance, whom he was forbidden by the rules of the game to clothe with complete flesh and blood. In this great love-story there were no such restrictions, and the characters which Boccaccio’s treatment left thin and conventional became in Chaucer’s hands convincingly human. No other English poem is so instinct with the glory and tragedy of youth, and in the details of the story Chaucer’s gifts of vivid colouring, of humour and pity, are all at their highest.
An unfortunate theory that the reference in the Legends of Good Women to “al the love of Palamon and Arcyte” is to a hypothetical poem in seven-line stanzas on this theme, which Chaucer is imagined, when he came to plan the Canterbury Tales, to have suppressed in favour of a new version in heroic couplets, has obscured the close connexion in temper and power between what we know as the “Knight’s Tale” and the Troilus. The poem may have been more or less extensively revised before, with admirable fitness, it was assigned to the Knight, but that its main composition can be separated by several years from that of Troilus is aesthetically incredible. Chaucer’s art here again is at its highest. He takes the plot of Boccaccio’s Teseide, but only as much of it as he wants, and what he takes he heightens and humanizes with the same skill which he had shown in transforming the Filostrato. Of the individual characters Theseus himself, the arbiter of the plot, is most notably developed; Emilie and her two lovers receive just as much individuality as they will bear without disturbing the atmosphere of romance. The whole story is pulled together and made more rapid and effective. A comparison of almost any scene as told by the two poets suffices to show Chaucer’s immense superiority. At some subsequent period the “Squire’s Tale” of Cambuscan, the fair Canacee and the Horse of Brass, was gallantly begun in something of the same key, but Chaucer took for it more materials than he could use, and for lack of the help of a leader like Boccaccio he was obliged to leave the story, in Milton’s phrase, “half-told,” though the fragment written certainly takes us very much less than half-way.
Meanwhile, in connexion (as is reasonably believed) with the betrothal or marriage of Anne of Bohemia to Richard II. (i.e. about 1381-1382), Chaucer had brought to a successful completion the Parlement of Foules, a charming sketch of 699 lines, in which the other birds, on Saint Valentine’s day, counsel the “Formel Egle” on her choice of a mate. His success here, as in the case of the Deth of Blaunche the Duchesse, was due to the absence of any need for a climax; and though the materials which he borrowed were mainly Latin (with some help from passages of the Teseide not fully needed for Palamon and Arcyte) his method of handling them would have been quite approved by his friends among the French poets. A more ambitious venture, the Hous of Fame, in which Chaucer imagines himself borne aloft by an eagle to Fame’s temple, describes what he sees and hears there, and then breaks off in apparent inability to get home, shows a curious mixture of the poetic ideals of the Roman de la rose and reminiscences of the Divina Commedia.
As the Hous of Fame is most often remembered and quoted for the personal touches and humour of Chaucer’s conversation with the eagle, so the most-quoted passages in the Prologue to the Legende of Good Women are those in which Chaucer professes his affection for the daisy, and the attack on his loyalty by Cupid and its defence by Alceste. Recent discoveries have shown, however, that (besides obligations to Machault) some of the touches about the daisy and the controversy between the partisans of the Flower and of the Leaf are snatches from poems by his friends Froissart and Deschamps, which Chaucer takes up 16 and returns to them with pretty compliments, and that he was indebted to Froissart for some of the framework of his poem.2 Both of the two versions of the Prologue to the Legende are charming, and some of the tales, notably that of Cleopatra, rank with Chaucer’s best work. When, however, he had written eight and part of the ninth he tired of his scheme, which was planned to celebrate nineteen of Cupid’s faithful “saints,” with Alcestis as their queen. With his usual hopefulness he had overlooked the risk of monotony, which obviously weighed heavily on him ere he broke off, and the loss of the other ten stories is less to be regretted than that of the celebration of Alceste, and a possible epilogue which might have exceeded in charm the Prologue itself.
Chaucer’s failure to complete the scheme of the Legende of Good Women may have been partly due to the attractions of the Canterbury Tales, which were probably taken up in Canterbury Tales. immediate succession to it. His guardianship of two Kentish wards, his justiceship of the peace, his representing the county in the parliament of 1386, his commissionership of the river-bank between Greenwich and Woolwich, all make it easy to understand his dramatic use of the merry crowds he saw on the Canterbury road, without supposing him to have had recourse to Boccaccio’s Decamerone, a book which there is no proof of his having seen. The pilgrims whom he imagines to have assembled at the Tabard Inn in Southwark, where Harry Bailey was host, are said to have numbered “wel nyne and twenty in a company,” and the Prologue gives full-length sketches of a Knight, a Squire (his son), and their Yeoman; of a Prioress, Monk, Friar, Oxford Clerk, and Parson, with two disreputable hangers-on of the church, a Summoner and Pardoner; of a Serjeant-at-Law and a Doctor of Physic, and of a Franklin, or country gentleman, Merchant, Shipman, Miller, Cook, Manciple, Reeve, Ploughman (the Parson’s brother) and the ever-famous Wife of Bath. Five London burgesses are described in a group, and a Nun and Priest3 are mentioned as in attendance on the Prioress. Each of these, with Chaucer himself making the twenty-ninth, was pledged to tell two tales, but including one second attempt and a tale told by the Yeoman of a Canon, who overtakes the pilgrims on the road, we have only twenty finished stories, two unfinished and two interrupted ones. As in the case of the Legende of Good Women, our loss is not so much that of the additional stories as of the completed framework. The wonderful character sketches of the Prologue are carried yet farther by the Talks on the Road which link the different tales, and two of these Talks, in which the Wife of Bath and the Pardoner respectively edify the company, have the importance of separate Tales, but between the Tales that have come down to us there are seven links missing,4 and it was left to a later and weaker hand to narrate, in the “Tale of Beryn,” the adventures of the pilgrims at Canterbury.
The reference to the Lyf of Seynt Cecyle in the Prologue to the Legende of Good Women gives external proof that Chaucer included earlier work in the scheme of the Canterbury Tales, and mention has been made of other stories which are indisputably early. In the absence of any such metrical tests as have proved useful in the case of Shakespeare, the dates at which several of the Tales were composed remain doubtful, while in the case of at least two, the Clerk’s tale of Grisilde and the Monk’s tragedies, there is evidence of early work being revised and supplemented. It is fortunately impossible to separate the prologue to the charmingly told story of “yonge Hugh of Lincoln” from the tale itself, and with the “quod sche” in the second line as proof that Chaucer was here writing specially for his Prioress we are forbidden to limit the new stories to any one metre or tone. There can be no doubt, however, that what may be called the Tales of the Churls (Miller, Reeve, Summoner, Friar, &c.), and the conversational outpourings of the Pardoner and Wife of Bath, form, with the immortal Prologue, the most important and distinctive additions to the older work. In these, and in the Pardoner’s story of Death and the Three Revellers, and the Nun’s Priest’s masterly handling of the fable of the Cock and Fox, both of them free from the grossness which marks the others, Chaucer takes stories which could have been told in a short page of prose and elaborates them with all the skill in narration which he had sedulously cultivated. The conjugal reminiscences of the Wife of Bath and the Reeve’s Tale with its abominable climax (lightened a little by Aleyn’s farewell, lines 316-319) are among the great things in Chaucer, as surely as Troilus, and Palamon and Arcyte and the Prologue. They help notably to give him the width of range which may certainly be claimed for him.
In or soon after 1391 Chaucer wrote in prose for an eleven-year-old reader, whom he addresses as “Litel Lowis my son,” a treatise on the use of the Astrolabe, its short prologue being the prettiest specimen of his prose. The wearisome tale of “Melibee and his wyf Prudence,” which was perhaps as much admired in English as it had been in Latin and French, may have been translated at any time. The sermon on Penitence, used as the Parson’s Tale, was probably the work of his old age. “Envoys” to his friends Scogan and Bukton, a translation of some balades by Sir Otes de Granson, and the Compleynt to his Purs complete the record of his minor poetry. We have his own statement that in his youth he had written many Balades, Roundels and Virelayes in honour of Love, and the two songs embedded respectively in the Parlement of Foules and the Prologue to the Legende of Good Women are charming and musical. His extant shorter poems, however, whether early or late, offer no excuse for claiming high rank for him as a lyrist. He had very little sheer singing power, and though there are fine lines in his short poems, witness the famous “Flee fro the prees and dwell with soothfastnesse,” they lack the sustained concentration of great work. From the drama, again, Chaucer was cut off, and it is idle to argue from the innumerable dramatic touches in his poems and his gift of characterization as to what he might have done had he lived two centuries later. His own age delighted in stories, and he gave it the stories it demanded invested with a humanity, a grace and strength which place him among the world’s greatest narrative poets, and which bring the England of his own day, with all the colour and warmth of life, wonderfully near to all his readers.
The part played by Chaucer in the development of the English language has often been overrated. He neither corrupted it, as used to be said, by introducing French words which Influence. it would otherwise have avoided, nor bore any such part in fixing it as was afterwards played by the translators of the Bible. When he was growing up educated society in England was still bilingual, and the changes in vocabulary and pronunciation which took place during his life were the natural results of a society, which had been bilingual with a bias towards French, giving an exclusive preference to English. The practical identity of Chaucer’s language with that of Gower shows that both merely used the best English of their day with the care and slightly conservative tendency which befitted poets. Chaucer’s service to the English language lies in his decisive success having made it impossible for any later English poet to attain fame, as Gower had done, by writing alternatively in Latin and French. The claim which should be made for him is 17 that, at least as regards poetry, he proved that English was “sufficient.”
Chaucer borrowed both his stanza forms and his “decasyllabic” couplets (mostly with an extra syllable at the end of the line) from Guillaume Machault, and his music, like that of his French master and his successors, depends very largely on assigning to every syllable its full value, and more especially on the due pronunciation of the final -e. The slower movement of change in Scotland allowed time for Chaucer to exercise a potent influence on Scottish poetry, but in England this final -e, to which most of the earlier grammatical forms by Chaucer’s time had been reduced, itself fell rapidly into disuse during the 15th century, and a serious barrier was thus raised to the appreciation of the artistic value of his verse. His disciples, Hoccleve and Lydgate, who at first had caught some echoes of his rhythms, gradually yielded to the change in pronunciation, so that there was no living tradition to hand down his secret, while successive copyists reduced his text to a state in which it was only by accident that lines could be scanned correctly. For fully three centuries his reputation was sustained solely by his narrative power, his warmest panegyrists betraying no consciousness that they were praising one of the greatest technical masters of poetry. Even when thus maimed, however, his works found readers and lovers in every generation, and every improvement in his text has set his fame on a surer basis.
Bibliography.—The Canterbury Tales have always been Chaucer’s most popular work, and, including fragments, upwards of sixty 15th-century manuscripts of it still survive. Two thin volumes of his minor poems were among the little quartos which Caxton printed by way of advertisement immediately on his return to England; the Canterbury Tales and Boethius followed in 1478, Troilus and a second edition of the Tales in 1483, the Hous of Fame in 1484. The Canterbury Tales were subsequently printed in 1492 (Pynson), 1498 (de Worde) and 1526 (Pynson); Troilus in 1517 (de Worde) and 1526 (Pynson); the Hous of Fame in 1526 (Pynson); the Parlement of Foules in 1526 (Pynson) and 1530 (de Worde), and the Mars, “Venus” and Envoy to Bukton by Julyan Notary about 1500. Pynson’s three issues in 1526 almost amounted to a collected edition, but the first to which the title The Workes of Geffray Chaucer was given was that edited by William Thynne in 1532 for Thomas Godfray. Of this there was a new edition in 1542 for John Reynes and William Bonham, and an undated reprint a few years later for Bonham, Kele, Petit and Toye, each of whom put his name on part of the edition. In 1561 a reprint, with numerous additions, edited by John Stowe, was printed by J. Kyngston for J. Wight, and this was re-edited, with fresh additions by Thomas Speght, in 1598 for G. Bishop and again in 1602 for Adam Islip. In 1687 there was an anonymous reprint, and in 1721 John Urry produced the last and worst of the folios. By this time the paraphrasers were already at work, Dryden rewriting the tales of the Knight, the Nun’s Priest and the Wife of Bath, and Pope the Merchant’s. In 1737 (reprinted in 1740) the Prologue and Knight’s Tale were edited (anonymously) by Thomas Morell “from the most authentic manuscripts,” and here, though by dint of much violence and with many mistakes, Chaucer’s lines were for the first time in print given in a form in which they could be scanned. This promise of better things (Morell still thought it necessary to accompany his text with the paraphrases by Betterton and Dryden) was fulfilled by a fine edition of the Canterbury Tales (1775-1778), in which Thomas Tyrwhitt’s scholarly instincts produced a comparatively good text from second-rate manuscripts and accompanied it with valuable illustrative notes. The next edition of any importance was that edited by Thomas Wright for the Percy Society in 1848-1851, based on the erratic but valuable British Museum manuscript Harley 7334, containing readings which must be either Chaucer’s second thoughts or the emendations of a brilliantly clever scribe. In 1866 Richard Morris re-edited this text in a more scholarly manner for the Aldine edition of the British Poets, and in the following year produced for the Clarendon Press Series a school edition of the Prologue and Tales of the Knight and Nun’s Priest, edited with the fulness and care previously bestowed only on Greek and Latin classics.
In 1868 the foundation of the Chaucer Society, with Dr Furnivall as its director and chief worker, and Henry Bradshaw as a leading spirit, led to the publication of a six-text edition of the Canterbury Tales, and the consequent discovery that a manuscript belonging to the Earl of Ellesmere, though undoubtedly “edited,” contained the best available text. The Chaucer Society also printed the best manuscripts of Troilus and Criseyde and of all the minor poems, and thus cleared the way for the “Oxford” Chaucer, edited by Professor Skeat, with a wealth of annotation, for the Clarendon Press in 1894, the text of which was used for the splendid folio printed two years later by William Morris at the Kelmscott Press, with illustrations by Sir Edward Burne-Jones. A supplementary volume of the Oxford edition, entitled Chaucerian and other Pieces, issued by Professor Skeat in 1897, contains the prose and verse which his early publishers and editors, from Pynson and Thynne onwards, included among his Works by way of illustration, but which had gradually come to be regarded as forming part of his text. The reasons for their rejection are fully stated by Professor Skeat in the work named and also in The Chaucer Canon (1900). Many of these pieces have now been traced to other authors, and their exclusion has helped to clear not only Chaucer’s text but also his biography, which used (as in the “Life” published by William Godwin in two quarto volumes in 1803) to be encumbered with inferences from works now known not to be Chaucer’s, notably the Testament of Love written by Thomas Usk. All information about Chaucer’s life available in 1900 will be found summarized by Mr R.E.G. Kirk in Life-Records of Chaucer, part iv., published by the Chaucer Society in that year. See also Chaucer; a Bibliographical Manual, by Eleanor P. Hammond (1909).
1 The positions of the House of Fame and Palamon and Arcyte are still matters of controversy.
2 The French influences on this Prologue, its connexion with the Flower and the Leaf controversy, and the priority of what had previously been reckoned as the second or “B” form of the Prologue over the “A,” were demonstrated in papers by Prof. Kittredge on “Chaucer and some of his Friends” in Modern Philology, vol. i. (Chicago, 1903), and by Mr J. L. Lowes on “The Prologue to the Legend of Good Women” in Publications of the Modern Language Association of America, vol. xix., December 1904.
3 The Talks on the Road show clearly that only one Priest in attendance on the Prioress, and two tales to each narrator, were originally contemplated, but the “Prestes thre” in line 164 of the Prologue, and the bald couplet (line 793 sq.) explaining that each pilgrim was to tell two tales each way, were probably both alterations made by Chaucer in moments of amazing hopefulness. The journey was reckoned a 3½ days’ ride, and eight or nine tales a day would surely have been a sufficient allowance.
4 The absence of these links necessitates the division of the Canterbury Tales into nine groups, to which, for purposes of quotation, the letters A to I have been assigned, the line numeration of the Tales in each group being continuous.
CHAUDESAIGUES, a village of central France, in the department of Cantal, at the foot of the mountains of Aubrac, 19 m. S.S.W. of St Flour by road. Pop. (1906) town, 937; commune, 1558. It is celebrated for its hot mineral springs, which vary in temperature from 135° to 177° Fahr., and at their maximum rank as the hottest in France. The water, which contains bicarbonate of soda, is employed not only medicinally (for rheumatism, &c.), but also for the washing of fleeces, the incubation of eggs, and various other economic purposes; and it furnishes a ready means of heating the houses of the town during winter. In the immediate neighbourhood is the cold chalybeate spring of Condamine. The warm springs were known to the Romans, and are mentioned by Sidonius Apollinaris.
CHAUFFEUR (from Fr. chauffer), to heat, a term primarily used in French of a man in charge of a forge or furnace, and so of a stoker on a locomotive or in a steamship, but in its anglicized sense more particularly confined to a professional driver of a motor vehicle. (See also Brigandage.)
CHAULIEU, GUILLAUME AMFRYE DE (1639-1720), French poet and wit, was born at Fontenay, Normandy, in 1639. His father, maître des comptes of Rouen, sent him to study at the Collège de Navarre. Guillaume early showed the wit that was to distinguish him, and gained the favour of the duke of Vendôme, who procured for him the abbey of Aumale and other benefices. Louis Joseph, duke of Vendôme, and his brother Philippe, grand prior of the Knights of Malta in France, at that time had a joint establishment at the Temple, where they gathered round them a very gay and reckless circle. Chaulieu became the constant companion and adviser of the two princes. He made an expedition to Poland in the suite of the marquis de Béthune, hoping to make a career for himself in the court of John Sobieski; he saw one of the Polish king’s campaigns in Ukraine, but returned to Paris without securing any advancement. Saint-Simon says that the abbé helped his patron the grand prior to rob the duke of Vendôme, and that the king sent orders that the princes should take the management of their affairs from him. This account has been questioned by Sainte-Beuve, who regards Saint-Simon as a prejudiced witness. In his later years Chaulieu spent much time at the little court of the duchesse du Maine at Sceaux. There he became the trusted and devoted friend of Mdlle Delaunay, with whom he carried on an interesting correspondence. Among his poems the best known are “Fontenay” and “La Retraite.” Chaulieu died on the 27th of June 1720.
His works were edited with those of his friend the marquis de la Fare in 1714, 1750 and 1774. See also C.A. Sainte-Beuve, Causeries du lundi, vol. i.; and Lettres inédites (1850), with a notice by Raymond, marquis de Berenger.
CHAUMETTE, PIERRE GASPARD (1763-1794), French revolutionist, was born at Nevers. Until the Revolution he lived a somewhat wandering life, interesting himself particularly in botany. He was a student of medicine at Paris in 1790, became one of the orators of the club of the Cordeliers, and contributed anonymously to the Révolutions de Paris. As member of the insurrectionary Commune of the 10th of August 1792, he was delegated to visit the prisons, with full power to arrest suspects. He was accused later of having taken part in the massacres of September, but was able to prove that at that time he had been sent by the provisional executive council to Normandy to oversee a requisition of 60,000 men. Returning 18 from this mission, he pronounced an eloquent discourse in favour of the republic. His simple manners, easy speech, ardent temperament and irreproachable private life gave him great influence in Paris, and he was elected president of the Commune, defending the municipality in that capacity at the bar of the Convention on the 31st of October 1792. Re-elected in the municipal elections of the 2nd of December 1792, he was soon charged with the functions of procurator of the Commune, and contributed with success to the enrolments of volunteers by his appeals to the populace. Chaumette was one of the ringleaders in the attacks of the 31st of May and of the 2nd of June 1793 on the Girondists, toward whom he showed himself relentless. He demanded the formation of a revolutionary army, and preached the extermination of all traitors. He was one of the promoters of the worship of Reason, and on the 10th of November 1793 he presented the goddess to the Convention in the guise of an actress. On the 23rd of the same month he obtained a decree closing all the churches of Paris, and placing the priests under strict surveillance; but on the 25th he retraced his steps and obtained from the Commune the free exercise of worship. He wished to save the Hébertists by a new insurrection and struggled against Robespierre; but a revolutionary decree promulgated by the Commune on his demand was overthrown by the Convention. Robespierre had him accused with the Hébertists; he was arrested, imprisoned in the Luxembourg, condemned by the Revolutionary tribunal and executed on the 13th of April 1794. Chaumette’s career had its brighter side. He was an ardent social reformer; he secured the abolition of corporal punishment in the schools, the suppression of lotteries, of houses of ill-fame and of obscene literature; he instituted reforms in the hospitals, and insisted on the honours of public burial for the poor.
Chaumette left some printed speeches and fragments, and memoirs published in the Amateur d’autographes. His memoirs on the 10th of August were published by F.A. Aulard, preceded by a biographical study.
CHAUMONT-EN-BASSIGNY, a town of eastern France, capital of the department of Haute-Marne, a railway junction 163 m. E.S.E. of Paris on the main line of the Eastern railway to Belfort. Pop. (1906) 12,089. Chaumont is picturesquely situated on an eminence between the rivers Marne and Suize in the angle formed by their confluence. To the west a lofty viaduct over the Suize carries the railway. The church of St-Jean-Baptiste dates from the 13th century, the choir and lateral chapels belonging to the 15th and 16th. In the interior the sculptured triforium (15th century), the spiral staircase in the transept and a Holy Sepulchre are of interest. The lycée and the hospital have chapels of the 17th and 16th centuries respectively. The Tour Hautefeuille (a keep of the 11th century) is the principal relic of a château of the counts of Champagne; the rest of the site is occupied by the law courts. In the Place de l’Escargot stands a statue of the chemist Philippe Lebon (1767-1804), born in Haute-Marne. Chaumont is the seat of a prefect and of a court of assizes, and has tribunals of first instance and of commerce, a lycée, training colleges, and a branch of the Bank of France. The main industries are glove-making and leather-dressing. The town has trade in grain, iron, mined in the vicinity, and leather. In 1190 it received a charter from the counts of Champagne. It was here that in 1814 Great Britain, Austria, Russia and Prussia concluded the treaty (dated March 1, signed March 9) by which they severally bound themselves not to conclude a separate peace with Napoleon, and to continue the war until France should have been reduced within the boundaries of 1792.
CHAUNCEY, ISAAC (1772-1840), American naval commander, was born at Black Rock, Connecticut, on the 20th of February 1772. He was brought up in the merchant service, and entered the United States navy as a lieutenant in 1798. His first services were rendered against the Barbary pirates. During these operations, more especially at Tripoli, he greatly distinguished himself, and was voted by Congress a sword of honour, which, however, does not appear to have been given him. The most active period of his life is that of his command on the Lakes during the War of 1812. He took the command at Sackett’s Harbor on Lake Ontario in October 1812. There was at that time only one American vessel, the brig “Oneida” (16), and one armed prize, a schooner, on the lake. But Commodore Chauncey brought from 400 to 500 officers and men with him, and local resources for building being abundant, he had by November formed a squadron of ten vessels, with which he attacked the Canadian port, York, taking it in April 1813, capturing one vessel and causing the destruction of another then building. He returned to Sackett’s Harbor. In May Sir James Lucas Yeo (1732-1818) came out from England with some 500 officers and men, to organize a squadron for service on the Lakes. By the end of the month he was ready for service with a squadron of eight ships and brigs, and some small craft. The governor, Sir G. Prevost, gave him no serious support. On the 29th of May, during Chauncey’s absence at Niagara, the Americans were attacked at Sackett’s Harbor and would have been defeated if Prevost had not insisted on a retreat at the very moment when the American shipbuilding yard was in danger of being burnt, with a ship of more than eight hundred tons on the stocks. The retreat of the British force gave Chauncey time to complete this vessel, the “General Pike,” which was so far superior to anything under Yeo’s command that she was said to be equal in effective strength to the whole of the British flotilla. The American commodore was considered by many of his subordinates to have displayed excessive caution. In August he skirmished with Sir James Yeo’s small squadron of six vessels, but made little effective use of his own fourteen. Two of his schooners were upset in a squall, with the loss of all hands, and he allowed two to be cut off by Yeo. Commodore Chauncey showed a preference for relying on his long guns, and a disinclination to come to close quarters. He was described as chasing the British squadron all round the lake, but his encounters did not go beyond artillery duels at long range, and he allowed his enemy to continue in existence long after he might have been destroyed. The winter suspended operations, and both sides made exertions to increase their forces. The Americans had the advantage of commanding greater resources for shipbuilding. Sir James Yeo began by blockading Sackett’s Harbor in the early part of 1814, but when the American squadron was ready he was compelled to retire by the disparity of the forces. The American commodore was now able to blockade the British flotilla at Kingston. When the cruising season of the lake was nearly over he in his turn retired to Sackett’s Harbor, and did not leave it for the rest of the war. During his later years he served as commissioner of the navy, and was president of the board of naval commissioners from 1833 till his death at Washington on the 27th of February 1840.
See Roosevelt’s War of 1812 (1882); and A. T. Mahan, Sea-Power in its Relations to the War of 1812 (1905).
CHAUNCY, CHARLES (1592-1672), president of Harvard College, was born at Yardley-Bury, Hertfordshire, England, in November 1592, and was educated at Trinity College, Cambridge, of which he became a fellow. He was in turn vicar at Ware, Hertfordshire (1627-1633), and at Marston St Lawrence, Northamptonshire (1633-1637). Refusing to observe the ecclesiastical regulations of Archbishop Laud, he was brought before the court of high commission in 1629, and again in 1634, when, for opposing the placing of a rail around the communion table, he was suspended and imprisoned. His formal recantation in February 1637 caused him lasting self-reproach and humiliation. In 1637 he emigrated to America, and from 1638 until 1641 was an associate pastor at Plymouth, where, however, his advocacy of the baptism of infants by immersion caused dissatisfaction. He was the pastor at Scituate, Massachusetts, from 1641 until 1654, and from 1654 until his death was president of Harvard College, as the successor of the first president Henry Dunster (c. 1612-1659). He died on the 19th of February 1672. By his sermons and his writings he exerted a great influence in colonial Massachusetts, and according to Mather was “a most incomparable scholar.” His writings include: The Plain Doctrine of the Justification of a Sinner in the Sight of God (1659) and Antisynodalia Scripta Americana (1662). His son, Isaac 19 Chauncy (1632-1712), who removed to England, was a voluminous writer on theological subjects.
There are biographical sketches of President Chauncy in Cotton Mather’s Magnalia Christi Americana. (London, 1702), and in W.C. Fowler’s Memorials of the Chauncys, including President Chauncy (Boston, 1858).
President Chauncy’s great-grandson, CHARLES CHAUNCY (1705-1787), a prominent American theologian, was born in Boston, Massachusetts, on the 1st of January 1705, and graduated at Harvard in 1721. In 1727 he was chosen as the colleague of Thomas Foxcroft (1697-1769) in the pastorate of the First Church of Boston, continuing as pastor of this church until his death. At the time of the “Great Awakening” of 1740-1743 and afterwards, Chauncy was the leader of the so-called “Old Light” party in New England, which strongly condemned the Whitefieldian revival as an outbreak of emotional extravagance. His views were ably presented in his sermon Enthusiasm and in his Seasonable Thoughts on the State of Religion in New England (1743), written in answer to Jonathan Edwards’s Some Thoughts Concerning the Present Revival of Religion in New England (1742). He also took a leading part in opposition to the projected establishment of an Anglican Episcopate in America, and before and during the American War of Independence he ardently supported the whig or patriot party. Theologically he has been classed as a precursor of the New England Unitarians. He died in Boston on the 10th of February 1787. His publications include: Compleat View of Episcopacy, as Exhibited in the Fathers of the Christian Church, until the close of the Second Century (1771); Salvation of All Men, Illustrated and Vindicated as a Scripture Doctrine (1782); The Mystery Hid from Ages and Generations made manifest by the Gospel-Revelation (1783); and Five Dissertations on the Fall and its Consequences (1785).
See P.L. Ford’s privately printed Bibliotheca Chaunciana (Brooklyn, N.Y., 1884); and Williston Walker’s Ten New England Leaders (New York, 1901).
CHAUNY, a town of northern France in the department of Aisne, 19 m. S. by W. of St Quentin by rail. Pop. (1906) 10,127. The town is situated on the Oise (which here becomes navigable) and at the junction of the canal of St Quentin with the lateral canal of the Oise, and carries on an active trade. It contains mirror-polishing works, subsidiary to the mirror-works of St Gobain, chemical works, sugar manufactories, metal foundries and breweries. Chauny was the scene of much fighting in the Hundred Years’ War.
CHAUTAUQUA, a village on the west shore of Chautauqua Lake in the town of Chautauqua, Chautauqua county, New York, U.S.A. Pop. of the town (1900), 3590; (1905) 3505; (1910) 3515; of the village (1908) about 750. The lake is a beautiful body of water over 1300 ft. above sea-level, 20 m. long, and from a few hundred yards to 3 m. in width. The town of Chautauqua is situated near the north end and is within easy reach by steamboat and electric car connexions with the main railways between the east and the west. The town is known almost solely as being the permanent home of the Chautauqua Institution, a system of popular education founded in 1874 by Lewis Miller (1829-1899) of Akron, Ohio, and Bishop John H. Vincent (b. 1832). The village, covering about three hundred acres of land, is carefully laid out to provide for the work of the Institution.
The Chautauqua Institution began as a Sunday-School Normal Institute, and for nearly a quarter of a century the administration was in the hands of Mr Miller, who was responsible for the business management, and Bishop Vincent, who was head of the instruction department. Though founded by Methodists, in its earliest years it became non-sectarian and has furnished a meeting-ground for members of all sects and denominations. At the very outset the activities of the assembly were twofold: (1) the conducting of a summer school for Sunday-school teachers, and (2) the presentation of a series of correlated lectures and entertainments. Although the movement was and still is primarily religious, it has always been assumed that the best religious education must necessarily take advantage of the best that the educational world can afford in the literatures, arts and sciences. The scope of the plan rapidly broadened, and in 1879 a regular group of schools with graded courses of study was established. At about the same time, also, the Chautauqua Literary and Scientific Circle, providing a continuous home-reading system, was founded. The season lasts during June, July and August. In 1907 some 325 lectures, concerts, readings and entertainments were presented by a group of over 190 lecturers, readers and musicians, while at the same time 200 courses in the summer schools were offered by a faculty of instructors drawn from the leading colleges and normal schools of the country.
The Chautauqua movement has had an immense influence on education in the United States, an influence which is especially marked in three directions: (1) in the establishment of about 300 local assemblies or “Chautauquas” in the United States patterned after the mother Chautauqua; (2) in the promotion of the idea of summer education, which has been followed by the founding of summer schools or sessions at a large number of American universities, and of various special summer schools, such as the Catholic Summer School of America, with headquarters at Cliff Haven, Clinton county, New York, and the Jewish Chautauqua Society, with headquarters at Buffalo, N.Y.; and (3) in the establishment of numerous correspondence schools patterned in a general way after the system provided by the Chautauqua Literary and Scientific Circle.
See John Heyl Vincent, The Chautauqua Movement (Boston, 1886), and Frank C. Bray, A Reading Journey through Chautauqua (Chicago, 1905).
CHAUVELIN, BERNARD FRANÇOIS, Marquis de (1766-1832), French diplomatist and administrator. Though master of the king’s wardrobe in 1789, he joined in the Revolution. He served in the army of Flanders, and then was sent to London in February 1792, to induce England to remain neutral in the war which was about to break out between France and “the king of Bohemia and Hungary.” He was well received at first, but after the 10th of August 1792 he was no longer officially recognized at court, and on the execution of Louis XVI. (21st of January 1793) he was given eight days to leave England. After an unsuccessful embassy in Tuscany, he was imprisoned as a suspect during the Terror, but freed after the 9th Thermidor. Under Napoleon he became a member of the council of state, and from 1812 to 1814 he governed Catalonia under the title of intendant-general, being charged to win over the Catalonians to King Joseph Bonaparte. He remained in private life during the Restoration and the Hundred Days. In 1816 he was elected deputy, and spoke in favour of liberty of the press and extension of the franchise. Though he was again deputy in 1827 he played no part in public affairs, and resigned in 1829.
See G. Pallain, La Mission de Talleyrand à Londres en 1792 (Paris, 1889).
CHAUVIGNY, a town of western France, in the department of Vienne, 20 m. E. of Poitiers by rail. Pop. (1906) 2326. The town is finely situated overlooking the Vienne and a small torrent, and has two interesting Romanesque churches, both restored in modern times. There are also ruins of a château of the bishops of Poitiers, and of other strongholds. Near Chauvigny is the curious bone-cavern of Jioux, the entrance to which is fortified by large blocks of stone. The town carries on lime-burning and plaster-manufacture, and there are stone quarries in the vicinity. Trade is in wool and feathers.
CHAUVIN, ÉTIENNE (1640-1725), French Protestant divine, was born at Nîmes on the 18th of April 1640. At the revocation of the Edict of Nantes he retired to Rotterdam, where he was for some years preacher at the Walloon church; in 1695 the elector of Brandenburg appointed him pastor and professor of philosophy, and later inspector of the French college at Berlin, where he enjoyed considerable reputation as a representative of Cartesianism and as a student of physics. His principal work is a laborious Lexicon Rationale, sive Thesaurus Philosophicus (Rotterdam, 1692; new and enlarged edition, Leuwarden, 1713). 20 He also wrote Theses de Cognitione Dei (1662), and started the Nouveau Journal des Savans (1694-1698).
See E. and E. Haag, La France Protestante, vol. iv. (1884).
CHAUVINISM, a term for unreasonable and exaggerated patriotism, the French equivalent of “Jingoism.” The word originally signified idolatry of Napoleon, being taken from a much-wounded veteran, Nicholas Chauvin, who, by his adoration of the emperor, became the type of blind enthusiasm for national military glory.
CHAUX DE FONDS, LA, a large industrial town in the Swiss canton of Neuchâtel. It is about 19 m. by rail N. W. of Neuchâtel, and stands at a height of about 3255 ft. in a valley (5 m. long) of the same name in the Jura. Pop. (1900) 35,968 (only 13,659 in 1850); (1905) 38,700, mainly French-speaking and Protestants; of the 6114 “Catholics” the majority are “Old Catholics.” It is a centre of the watch-making industry, especially of gold watch cases; about 70% of those manufactured in Switzerland are turned out here. In 1900 it exported watches to the value of nearly £3,000,000 sterling. There is a school of industrial art (engraving and enamelling watch cases) and a school of watch-making (including instruction in the manufacture of chronometers and other scientific instruments of precision). It boasts of being le plus gros village de l’Europe, and certainly has preserved some of the features of a big village. Léopold Robert (1794-1835), the painter, was born here.
CHAVES, a town of northern Portugal, in the district of Villa Real, formerly included in the province of Traz os Montes; 8 m. S. of the Spanish frontier, on the right bank of the river Tamega. Pop. (1900) 6388. Chaves is the ancient Aquae Flaviae, famous for its hot saline springs, which are still in use. A fine Roman bridge of 18 arches spans the Tamega. In the 16th century Chaves contained 20,000 inhabitants; it was long one of the principal frontier fortresses, and in fact derives its present name from the position which makes it the “keys,” or chaves, of the north. One of its churches contains the tomb of Alphonso I. of Portugal (1139-1185). In 1830 the town gave the title of marquess to Pinto da Fonseca, a leader of the Miguelite party.
CHAZELLES, JEAN MATHIEU DE (1657-1710), French hydrographer, was born at Lyons on the 24th of July 1657. He was nominated professor of hydrography at Marseilles in 1685, and in that capacity carried out various coast surveys. In 1693 he was engaged to publish a second volume of the Neptune français, which was to include the hydrography of the Mediterranean. For this purpose he visited the Levant and Egypt. When in Egypt he measured the pyramids, and, finding that the angles formed by the sides of the largest were in the direction of the four cardinal points, he concluded that this position must have been intended, and also that the poles of the earth and meridians had not deviated since the erection of those structures. He was made a member of the Academy in 1695, and died in Paris on the 16th of January 1710.
CHEADLE, a town in the Altrincham parliamentary division of Cheshire, England, 6 m. S. of Manchester, included in the urban district of Cheadle and Gatley. Pop. (1901) 7916. This is one of the numerous townships of modern growth which fringe the southern boundaries of Manchester, and practically form suburbs of that city. Stockport lies immediately to the east. The name occurs in the formerly separate villages of Cheadle Hulme, Cheadle Bulkeley and Cheadle Moseley. There are cotton printing and bleaching works in the locality. The parish church of St Giles, Cheadle, is Perpendicular, containing an altar-tomb of the 15th century for two knights.
CHEADLE, a market town in the Leek parliamentary division of Staffordshire, England, 13 m. N.E. of Stafford, and the terminus of a branch line from Cresswell on the North Staffordshire railway. Pop. (1901) 5186. The Roman Catholic church of St Giles, with a lofty spire, was designed by Pugin and erected in 1846. The interior is lavishly decorated. There are considerable collieries in the neighbourhood, and silk and tape works in the town. In the neighbouring Froghall district limestone is quarried, and there are manufactures of copper. In Cheadle two fairs of ancient origin are held annually.
CHEATING, “the fraudulently obtaining the property of another by any deceitful practice not amounting to felony, which practice is of such a nature that it directly affects, or may directly affect, the public at large” (Stephen, Digest of Criminal Law, chap. xl. §367). Cheating is either a common law or statutory offence, and is punishable as a misdemeanour. An indictment for cheating at common law is of comparatively rare occurrence, and the statutory crime usually presents itself in the form of obtaining money by false pretences (q.v.). The word “cheat” is a variant of “escheat,” i.e. the reversion of land to a lord of the fee through the failure of blood of the tenant. The shortened form “cheater” for “escheator” is found early in the legal sense, and chetynge appears in the Promptorium Parvulorum, c. 1440, as the equivalent of confiscatio. In the 16th century “cheat” occurs in vocabularies of thieves and other slang, and in such works as the Use of Dice-Play (1532). It is frequent in Thomas Harman’s Caveat or Warening for ... Vagabones (1567), in the sense of “thing,” with a descriptive word attached, e.g. smeling chete = nose. In the tract Mihil Mumchance, his Discoverie of the Art of Cheating, doubtfully attributed to Robert Greene (1560-1592), we find that gamesters call themselves cheaters, “borrowing the term from the lawyers.” The sense development is obscure, but it would seem to be due to the extortionate or fraudulent demands made by legal “escheators.”
CHEBICHEV, PAFNUTIY LVOVICH (1821-1894), Russian mathematician, was born at Borovsk on the 26th of May 1821. He was educated at the university of Moscow, and in 1859 became professor of mathematics in the university of St Petersburg, a position from which he retired in 1880. He was chosen a correspondent of the Institute of France in 1860, and succeeded to the high honour of associé étranger in 1874. He was also a foreign member of the Royal Society of London. After N.I. Lobachevskiy he probably ranks as the most distinguished mathematician Russia has produced. In 1841 he published a valuable paper, “Sur la convergence de la serié de Taylor,” in Crelle’s Journal. His best-known papers, however, deal with prime numbers; in one of these (“Sur les nombres premiers,” 1850) he established the existence of limits within which must be comprised the sum of the logarithms of the primes inferior to a given number. Another question to which he devoted much attention was that of obtaining rectilinear motion by linkage. The parallel motion known by his name is a three-bar linkage, which gives a very close approximation to exact rectilinear motion, but in spite of all his efforts he failed to devise one that produced absolutely true rectilinear motion. At last, indeed, he came to the conclusion that to do so was impossible, and in that conviction set to work to find a rigorous proof of the impossibility. While he was engaged on this task the desired linkage, which moved the highest admiration of J.J. Sylvester, was discovered and exhibited to him by one of his pupils, named Lipkin, who, however, it was afterwards found, had been anticipated by A. Peaucellier. Chebichev further constructed an instrument for drawing large circles, and an arithmetical machine with continuous motion. His mathematical writings, which account for some forty entries in the Royal Society’s catalogue of scientific papers, cover a wide range of subjects, such as the theory of probabilities, quadratic forms, theory of integrals, gearings, the construction of geographical maps, &c. He also published a Traité de la théorie des nombres. He died at St Petersburg on the 8th of December 1894.
CHEBOYGAN, a city and the county-seat of Cheboygan county, Michigan, U.S.A., on South Channel (between Lakes Michigan and Huron), at the mouth of Cheboygan river, in the N. part of the lower peninsula. Pop. (1890) 6235; (1900) 6489, of whom 2101 were foreign-born; (1904) 6730; (1910) 6859. It is served by the Michigan Central and the Detroit & Mackinac railways, and by steamboat lines to Chicago, Milwaukee, Detroit, Sault Ste Marie, Green Bay and other lake ports; and is connected by ferry with Mackinac and Pointe aux Pins. During a great part of the year small boats ply between Cheboygan and the head of Crooked Lake, over the “Inland Route.” Cheboygan is situated in a fertile farming region, for 21 which it is a trade centre, and it has lumber mills, tanneries, paper mills, boiler works, and other manufacturing establishments. The water-works are owned and operated by the municipality. The city, at first called Duncan, then Inverness, and finally Cheboygan, was settled in 1846, incorporated as a village in 1871, reincorporated in 1877, and chartered as a city in 1889.
CHECHENZES, Tchetchen, or Khists (Kisti), the last being the name by which they are known to the Georgians, a people of the eastern Caucasus occupying the whole of west Daghestan. They call themselves Nakhtche, “people.” A wild, fierce people, they fought desperately against Russian aggression in the 18th century under Daûd Beg and Oman Khan and Shamyl, and in the 19th under Khazi-Mollah, and even now some are independent in the mountain districts. On the surrender of the chieftain Shamyl to Russia in 1859 numbers of them migrated into Armenia. In physique the Chechenzes resemble the Circassians, and have the same haughtiness of carriage. They are of a generous temperament, very hospitable, but quick to revenge. They are fond of fine clothes, the women wearing rich robes with wide, pink silk trousers, silver bracelets and yellow sandals. Their houses, however, are mere hovels, some dug out of the ground, others formed of boughs and stones. Before their subjection to Russia they were remarkable for their independence of spirit and love of freedom. Everybody was equal, and they had no slaves except prisoners of war. Government in each commune was by popular assembly, and the administration of justice was in the hands of the wronged. Murder and robbery with violence could be expiated only by death, unless the criminal allowed his hair to grow and the injured man consented to shave it himself and take an oath of brotherhood on the Koran. Otherwise the law of vendetta was fully carried out with curious details. The wronged man, wrapped in a white woollen shroud, and carrying a coin to serve as payment to a priest for saying the prayers for the dead, started out in search of his enemy. When the offender was found he must fight to a finish. A remarkable custom among one tribe is that if a betrothed man or woman dies on the eve of her wedding, the marriage ceremony is still performed, the dead being formally united to the living before witnesses, the father, in case it is the girl who dies, never failing to pay her dowry. The religion of the Chechenzes is Mahommedanism, mixed, however, with Christian doctrines and observances. Three churches near Kistin in honour of St George and the Virgin are visited as places of pilgrimage, and rams are there offered as sacrifices. The Chechenzes number upwards of 200,000. They speak a distinct language, of which there are said to be twenty separate dialects.
See Ernest Chanter, Recherches anthropologiques dans le Caucase (Lyon, 1885-1887); D.G. Brinton, Races of Man (1890); Hutchinson, Living Races of Mankind (London, 1901).
CHECKERS, the name by which the game of draughts (q.v.) is known in America. The origin of the name is the same as that of “chess” (q.v.).
CHEDDAR, a small town in the Wells parliamentary division of Somersetshire, England, 22 m. S.W. of Bristol by a branch of the Great Western railway. Pop. (1901) 1975. The town, with its Perpendicular church and its picturesque market-cross, lies below the south-western face of the Mendip Hills, which rise sharply from 600 to 800 ft. To the west stretches the valley of the river Axe, broad, low and flat. A fine gorge opening from the hills immediately upon the site of the town is known as Cheddar cliffs from the sheer walls which flank it; the contrast of its rocks and rich vegetation, and the falls of a small stream traversing it, make up a beautiful scene admired by many visitors. Several stalactitical caverns are also seen, and prehistoric British and Roman relics discovered in and near them are preserved in a small museum. The two caverns most frequently visited are called respectively Cox’s and Gough’s; in each, but especially in the first, there is a remarkable collection of fantastic and beautiful stalactitical forms. There are other caverns of greater extent but less beauty, but their extent is not completely explored. The remains discovered in the caves give evidence of British and Roman settlements at Cheddar (Cedre, Chedare), which was a convenient trade centre. The manor of Cheddar was a royal demesne in Saxon times, and the witenagemot was held there in 966 and 968. It was granted by John in 1204 to Hugh, archdeacon of Wells, who sold it to the bishop of Bath and Wells in 1229, whose successors were overlords until 1553, when the bishop granted it to the king. It is now owned by the marquis of Bath. By a charter of 1231 extensive liberties in the manor of Cheddar were granted to Bishop Joceline, who by a charter of 1235 obtained the right to hold a weekly market and fair. By a charter of Edward III. (1337) Cheddar was removed from the king’s forest of Mendip. The market was discontinued about 1690. Fairs are now held on the 4th of May and the 29th of October under the original grants. The name of Cheddar is given to a well-known species of cheese (see Dairy), the manufacture of which began in the 17th century in the town and neighbourhood.
CHEDUBA, or Man-aung, an island in the Bay of Bengal, situated 10 m. from the coast of Arakan, between 18° 40′ and 18° 56′ N. lat., and between 93° 31′ and 93° 50′ E. long. It forms part of the Kyaukpyu district of Arakan. It extends about 20 m. in length from N. to S., and 17 m. from E. to W., and its area of 220 sq. m. supports a population of 26,899 (in 1901). The channel between the island and the mainland is navigable for boats, but not for large vessels. The surface of the interior is richly diversified by hill and dale, and in the southern portion some of the heights exceed a thousand feet in elevation. There are various indications of former volcanic activity, and along the coast are earthy cones covered with green-sward, from which issue springs of muddy water emitting bubbles of gas. Copper, iron and silver ore have been discovered; but the island is chiefly noted for its petroleum wells, the oil derived from which is of excellent quality, and is extensively used in the composition of paint, as it preserves wood from the ravages of insects. Timber is not abundant, but the gamboge tree and the wood-oil tree are found of a good size. Tobacco, cotton, sugar-cane, hemp and indigo are grown, and the staple article is rice, which is of superior quality, and the chief article of export. The inhabitants of the island are mainly Maghs. Cheduba fell to the Burmese in the latter part of the 18th century. From them it was captured in 1824 by the British, whose possession of it was confirmed in 1826 by the treaty concluded with the Burmese at Yandaboo.
CHEERING, the uttering or making of sounds encouraging, stimulating or exciting to action, indicating approval of acclaiming or welcoming persons, announcements of events and the like. The word “cheer” meant originally face, countenance, expression, and came through the O. Fr. into Mid. Eng. in the 13th century from the Low Lat. cara, head; this is generally referred to the Gr. κάρα. Cara is used by the 6th-century poet Flavius Cresconius Corippus, “Postquam venere verendam Caesaris ante caram” (In Laudem Justini Minoris). “Cheer” was at first qualified with epithets, both of joy and gladness and of sorrow; compare “She thanked Dyomede for alle ... his gode chere” (Chaucer, Troylus) with “If they sing ... ’tis with so dull a cheere” (Shakespeare, Sonnets, xcvii.). An early transference in meaning was to hospitality or entertainment, and hence to food and drink, “good cheer.” The sense of a shout of encouragement or applause is a late use. Defoe (Captain Singleton) speaks of it as a sailor’s word, and the meaning does not appear in Johnson. Of the different words or rather sounds that are used in cheering, “hurrah,” though now generally looked on as the typical British form of cheer, is found in various forms in German, Scandinavian, Russian (urá), French (houra). It is probably onomatopoeic in origin; some connect it with such words as “hurry,” “whirl”; the meaning would then be “haste,” to encourage speed or onset in battle. The English “hurrah” was preceded by “huzza,” stated to be a sailor’s word, and generally connected with “heeze,” to hoist, probably being one of the cries that sailors use when hauling or hoisting. The German hoch, seen in full in hoch lebe der Kaiser, &c., the French vive, Italian and Spanish viva, evviva, are cries rather 22 of acclamation than encouragement. The Japanese shout banzai became familiar during the Russo-Japanese War. In reports of parliamentary and other debates the insertion of “cheers” at any point in a speech indicates that approval was shown by members of the House by emphatic utterances of “hear hear.” Cheering may be tumultuous, or it may be conducted rhythmically by prearrangement, as in the case of the “Hip-hip-hip” by way of introduction to a simultaneous “hurrah.”
Rhythmical cheering has been developed to its greatest extent in America in the college yells, which may be regarded as a development of the primitive war-cry; this custom has no real analogue at English schools and universities, but the New Zealand football team in 1907 familiarized English crowds at their matches with a similar sort of war-cry adopted from the Maoris. In American schools and colleges there is usually one cheer for the institution as a whole and others for the different classes. The oldest and simplest are those of the New England colleges. The original yells of Harvard and Yale are identical in form, being composed of rah (abbreviation of hurrah) nine times repeated, shouted in unison with the name of the university at the end. The Yale cheer is given faster than that of Harvard. Many institutions have several different yells, a favourite variation being the name of the college shouted nine times in a slow and prolonged manner. The best known of these variants is the Yale cheer, partly taken from the Frogs of Aristophanes, which runs thus:
|
“Brekekekéx, ko-áx, ko-áx, Brekekekéx, ko-áx, ko-áx, O-óp, O-óp, parabaloū, Yale, Yale, Yale, Rah, rah, rah, rah, rah, rah, rah, rah, rah, Yale! Yale! Yale!” |
The regular cheer of Princeton is:
|
“H’ray, h’ray, h’ray, tiger, Siss, boom, ah; Princeton!” |
This is expanded into the “triple cheer”:
|
“H’ray, h’ray, h’ray, Tiger, tiger, tiger, Siss, siss, siss, Boom, boom, boom, Ah, ah, ah, Princetón, Princetón, Princetón!” |
The “railroad cheer” is like the foregoing, but begun very slowly and broadly, and gradually accelerated to the end, which is enunciated as fast as possible. Many cheers are formed like that of Toronto University:
|
“Varsitý, varsitý, V-a-r-s-í-t-y (spelled) VARSIT-Y (spelled staccato) Vár-sí-tý, Rah, rah, rah!” |
Another variety of yell is illustrated by that of the School of Practical Science of Toronto University:
|
“Who are we? Can’t you guess? We are from the S.P.S.!” |
The cheer of the United States Naval Academy is an imitation of a nautical syren. The Amherst cheer is:
|
“Amherst! Amherst! Amherst! Rah! Rah! Amherst! Rah! Rah! Rah! Rah! Rah! Rah! Rah! Rah! Amherst!” |
Besides the cheers of individual institutions there are some common to all, generally used to compliment some successful athlete or popular professor. One of the oldest examples of these personal cheers is:
|
“Who was George Washington? First in war, First in peace, Fírst in the heárts of his countrymén,” |
followed by a stamping on the floor in the same rhythm.
College yells are used particularly at athletic contests. In any large college there are several leaders, chosen by the students, who stand in front and call for the different songs and cheers, directing with their arms in the fashion of an orchestral conductor. This cheering and singing form one of the distinctive features of inter-collegiate and scholastic athletic contests in America.
CHEESE (Lat. caseus), a solidified preparation from milk, the essential constituent of which is the proteinous or nitrogenous substance casein. All cheese contains in addition some proportion of fatty matter or butter, and in the more valuable varieties the butter present is often greater in amount than the casein. Cheese being thus a compound substance of no definite composition is found in commerce of many different varieties and qualities; and such qualities are generally recognized by the names of the localities in which they are manufactured. The principal distinctions arise from differences in the composition and condition of the milk operated upon, from variations in the method of preparation and curing, and from the use of the milk of other animals besides the cow, as, for example, the goat and the ewe, from the milk of both of which cheese is manufactured on a commercial scale. For details about different cheeses and cheese-making, see Dairy. From the Urdu chiz (“thing”) comes the slang expression “the cheese,” meaning “the perfect thing,” apparently from Anglo-Indian usage.
A useful summary of the history and manufacture of all sorts of cheeses, under their different names, is given in Bulletin 105 of the Bureau of Animal Industry (United States Dep. of Agriculture), Varieties of Cheese, by C.F. Doane and H.W. Lawson (Washington, 1908).
CHEESE CLOTH, the name given to cloth, usually made from flax or tow yarns, of an open character, resembling a fine riddle or sieve, used for wrapping cheese. A finer quality and texture is made for women’s gowns. A similar cloth is used for inside linings in the upholstery trade, and for the ground of embroidery.
CHEETA (Chita), or Hunting-Leopard (Cynaelurus jubatus, formerly known as Gueparda jubata), a member of the family Felidae, distinguished by its claws being only partially retractile (see Carnivora). The cheeta attains a length of 3 to 4 ft.; it is of a pale fulvous colour, marked with numerous spots of black on the upper surface and sides, and is nearly white beneath. The fur is somewhat crisp, altogether lacking the sleekness which characterizes the fur of the typical cats, and the tail is long and somewhat bushy at the extremity. In confinement the cheeta soon becomes fond of those who are kind to it, and gives evidence of its attachment in an open, dog-like manner. The cheeta is found throughout Africa and southern Asia, and has been employed for centuries in India and Persia in hunting antelopes and other game. According to Sir W. Jones, this mode of hunting originated with Hushing, king of Persia, 865 B.C., and afterwards became so popular that certain of the Mongol emperors were in the habit of being accompanied in their sporting expeditions by a thousand hunting leopards. In prosecuting this sport at the present day the cheeta is conveyed to the field in a low car without sides, hooded and chained like hunting-birds in Europe in the days of falconry. When a herd of deer or antelopes is seen, the car, which bears a close resemblance to the ordinary vehicles used by the peasants, is usually brought within 200 yds. of the game before the latter takes alarm; the cheeta is then let loose and the hood removed from its eyes. No sooner does it see the herd, than dropping from the car on the side remote from its prey, it approaches stealthily, making use of whatever means of concealment the nature of the ground permits, until observed, when making a few gigantic bounds, it generally arrives in the midst of the herd and brings down its victim with a stroke of its paw. The sportsman then approaches, draws off a bowl of the victim’s blood, and puts it before the cheeta, which is again hooded and led back to the car. Should it not succeed in reaching the herd in the first few bounds, it makes no further effort to pursue, but retires seemingly dispirited to the car. In Africa the cheeta is only valued for its skin, which is worn by chiefs and other people of rank. It should be added that in India the name cheeta (chita) is applied also to the leopard.
CHEFFONIER, properly Chiffonier, a piece of furniture differentiated from the sideboard by its smaller size and by the 23 enclosure of the whole of the front by doors. Its name (which comes from the French for a rag-gatherer) suggests that it was originally intended as a receptacle for odds and ends which had no place elsewhere, but it now usually serves the purpose of a sideboard. It is a remote and illegitimate descendant of the cabinet; it has rarely been elegant and never beautiful. It was one of the many curious developments of the mixed taste, at once cumbrous and bizarre, which prevailed in furniture during the Empire period in England. The earliest cheffoniers date from that time; they are usually of rosewood—the favourite timber of that moment; their “furniture” (the technical name for knobs, handles and escutcheons) was most commonly of brass, and there was very often a raised shelf with a pierced brass gallery at the back. The doors were well panelled and often edged with brass-beading, while the feet were pads or claws, or, in the choicer examples, sphinxes in gilded bronze. Cheffoniers are still made in England in cheap forms and in great number.
CHEH-KIANG, an eastern province of China, bounded N. by the province of Kiang-su, E. by the sea, S. by the province of Fu-kien, and W. by the provinces of Kiang-si and Ngan-hui. It occupies an area of about 36,000 sq. m., and contains a population of 11,800,000. With the exception of a small portion of the great delta plain, which extends across the frontier from the province of Kiang-su, and in which are situated the famous cities of Hu Chow, Ka-hing, Hang-chow, Shao-Sing and Ning-po, the province forms a portion of the Nan-shan of south-eastern China, and is hilly throughout. The Nan-shan ranges run through the centre of the province from south-west to north-east, and divide it into a northern portion, the greater part of which is drained by the Tsien-t’ang-kiang, and a southern portion which is chiefly occupied by the Ta-chi basin. The valleys enclosed between the mountain ranges are numerous, fertile, and for the most part of exquisite beauty. The hilly portion of the province furnishes large supplies of tea, and in the plain which extends along the coast, north of Ning-po, a great quantity of silk is produced. In minerals the province is poor. Coal and iron are occasionally met with, and traces of copper ore are to be found in places, but none of these minerals exists in sufficiently large deposits to make mining remunerative. The province, however, produces cotton, rice, ground-nuts, wheat, indigo, tallow and beans in abundance. The principal cities are Hang-chow, which is famed for the beauty of its surroundings, Ning-po, which has been frequented by foreign ships ever since the Portuguese visited it in the 16th century, and Wênchow. Opposite Ning-po, at a distance of about 50 m., lies the island of Chusan, the largest of a group bearing that general name. This island is 21 m. long, and about 50 m. in circumference. It is very mountainous, and is surrounded by numerous islands and islets. On its south side stands the walled town of Ting-hai, in front of which is the principal harbour. The population is returned as 50,000.
CHEKE, SIR JOHN (1514-1557), English classical scholar, was the son of Peter Cheke, esquire-bedell of Cambridge University. He was educated at St John’s College, Cambridge, where he became a fellow in 1529. While there he adopted the principles of the Reformation. His learning gained him an exhibition from the king, and in 1540, on Henry VIII.’s foundation of the regius professorships, he was elected to the chair of Greek. Amongst his pupils at St John’s were Lord Burghley, who married Cheke’s sister Mary, and Roger Ascham, who in The Schoolmaster gives Cheke the highest praise for scholarship and character. Together with Sir Thomas Smith, he introduced a new method of Greek pronunciation very similar to that commonly used in England in the 19th century. It was strenuously opposed in the University, where the continental method prevailed, and Bishop Gardiner, as chancellor, issued a decree against it (June 1542); but Cheke ultimately triumphed. On the 10th of July 1554, he was chosen as tutor to Prince Edward, and after his pupil’s accession to the throne he continued his instructions. Cheke took a fairly active share in public life; he sat, as member for Bletchingley, for the parliaments of 1547 and 1552-1553; he was made provost of King’s College, Cambridge (April 1, 1548), was one of the commissioners for visiting that university as well as Oxford and Eton, and was appointed with seven divines to draw up a body of laws for the governance of the church. On the 11th of October 1551 he was knighted; in 1553 he was made one of the secretaries of state, and sworn of the privy council. His zeal for Protestantism induced him to follow the duke of Northumberland, and he filled the office of secretary of state for Lady Jane Grey during her nine days’ reign. In consequence Mary threw him into the Tower (July 27, 1553), and confiscated his wealth. He was, however, released on the 13th of September 1554, and granted permission to travel abroad. He went first to Basel, then visited Italy, giving lectures in Greek at Padua, and finally settled at Strassburg, teaching Greek for his living. In the spring of 1556 he visited Brussels to see his wife; on his way back, between Brussels and Antwerp, he and Sir Peter Carew were treacherously seized (May 15) by order of Philip of Spain, hurried over to England, and imprisoned in the Tower. Cheke was visited by two priests and by Dr John Feckenham, dean of St Paul’s, whom he had formerly tried to convert to Protestantism, and, terrified by a threat of the stake, he gave way and was received into the Church of Rome by Cardinal Pole, being cruelly forced to make two public recantations. Overcome with shame, he did not long survive, but died in London on the 13th of September 1557, carrying, as T. Fuller says (Church History), “God’s pardon and all good men’s pity along with him.” About 1547 Cheke married Mary, daughter of Richard Hill, sergeant of the wine-cellar to Henry VIII., and by her he had three sons. The descendants of one of these, Henry, known only for his translation of an Italian morality play Freewyl (Tragedio del Libero Arbitrio) by Nigri de Bassano, settled at Pyrgo in Essex.
Thomas Wilson, in the epistle prefixed to his translation of the Olynthiacs of Demosthenes (1570), has a long and most interesting eulogy of Cheke; and Thomas Nash, in To the Gentlemen Students, prefixed to Robert Greene’s Menaphon (1589), calls him “the Exchequer of eloquence, Sir Ihon Cheke, a man of men, supernaturally traded in all tongues.” Many of Cheke’s works are still in MS., some have been altogether lost. One of the most interesting from a historical point of view is the Hurt of Sedition how greueous it is to a Communewelth (1549), written on the occasion of Ket’s rebellion, republished in 1569, 1576 and 1641, on the last occasion with a life of the author by Gerard Langbaine. Others are D. Joannis Chrysostomi homiliae duae (1543), D. Joannis Chrysostomi de providentia Dei (1545), The Gospel according to St Matthew ... translated (c. 1550; ed. James Goodwin, 1843), De obitu Martini Buceri (1551), (Leo VI.’s) de Apparatu bellico (Basel, 1554; but dedicated to Henry VIII., 1544), Carmen Heroicum, aut epitaphium in Antonium Deneium (1551), De pronuntiatione Graecae ... linguae (Basel, 1555). He also translated several Greek works, and lectured admirably upon Demosthenes.
His Life was written by John Strype (1821); additions by J. Gough Nichols in Archaeologia (1860), xxxviii. 98, 127.
CHELLIAN, the name given by the French anthropologist G. de Mortillet to the first epoch of the Quaternary period when the earliest human remains are discoverable. The word is derived from the French town Chelles in the department of Seine-et-Marne. The climate of the Chellian epoch was warm and humid as evidenced by the wild growth of fig-trees and laurels. The animals characteristic of the epoch are the Elephas antiquus, the rhinoceros, the cave-bear, the hippopotamus and the striped hyaena. Man existed and belonged to the Neanderthal type. The implements characteristic of the period are flints chipped into leaf-shaped forms and held in the hand when used. The drift-beds of St Acheul (Amiens), of Menchecourt (Abbeville), of Hoxne (Suffolk), and the detrital laterite of Madras are considered by de Mortillet to be synchronous with the Chellian beds.
See Gabriel de Mortillet, Le Préhistorique (1900); Lord Avebury, Prehistoric Times (1900).
CHELMSFORD, FREDERIC THESIGER, 1st Baron (1794-1878), lord chancellor of England, was the third son of Charles Thesiger, and was born in London on the 15th of April 1794. His father, collector of customs at St Vincent’s, was the son of a Saxon gentleman who had migrated to England and become secretary to Lord Rockingham, and was the brother of Sir Frederic Thesiger, naval A.D.C. to Nelson at Copenhagen. Young Frederic Thesiger was originally destined for a naval 24 career, and he served as a midshipman on board the “Cambrian” frigate in 1807 at the second bombardment of Copenhagen. His only surviving brother, however, died about this time, and he became entitled to succeed to a valuable estate in the West Indies, so it was decided that he should leave the navy and study law, with a view to practising in the West Indies and eventually managing his property in person. Another change of fortune, however, awaited him, for a volcano destroyed the family estate, and he was thrown back upon his prospect of a legal practice in the West Indies. He proceeded to enter at Gray’s Inn in 1813, and was called on the 18th of November 1818, another change in his prospects being brought about by the strong advice of Godfrey Sykes, a special pleader in whose chambers he had been a pupil, that he should remain to try his fortune in England. He accordingly joined the home circuit, and soon got into good practice at the Surrey sessions, while he also made a fortunate purchase in buying the right to appear in the old palace court (see Lord Steward). In 1824 he distinguished himself by his defence of Joseph Hunt when on his trial at Hertford with John Thurtell for the murder of Wm. Weare; and eight years later at Chelmsford assizes he won a hard-fought action in an ejectment case after three trials, to which he attributed so much of his subsequent success that when he was raised to the peerage he assumed the title Lord Chelmsford. In 1834 he was made king’s counsel, and in 1835 was briefed in the Dublin election inquiry which unseated Daniel O’Connell. In 1840 he was elected M.P. for Woodstock. In 1844 he became solicitor-general, but having ceased to enjoy the favour of the duke of Marlborough, lost his seat for Woodstock and had to find another at Abingdon. In 1845 he became attorney-general, holding the post until the fall of the Peel administration on the 3rd of July 1846. Thus by three days Thesiger missed being chief justice of the common pleas, for on the 6th of July Sir Nicholas Tindal died, and the seat on the bench, which would have been Thesiger’s as of right, fell to the Liberal attorney-general, Sir Thomas Wilde. Sir Frederic Thesiger remained in parliament, changing his seat, however, again in 1852, and becoming member for Stamford. During this period he enjoyed a very large practice at the bar, being employed in many causes célèbres. On Lord Derby coming into office for the second time in 1858, Sir Frederic Thesiger was raised straight from the bar to the lord chancellorship (as were Lord Brougham, Lord Selborne and Lord Halsbury). In the following year Lord Derby resigned and his cabinet was broken up. Again in 1866, on Lord Derby coming into office for the third time, Lord Chelmsford became lord chancellor for a short period. In 1868 Lord Derby retired, and Disraeli, who took his place as prime minister, wished for Lord Cairns as lord chancellor. Lord Chelmsford was very sore at his supersession and the manner of it, but, according to Lord Malmesbury he retired under a compact made before he took office. Ten years later Lord Chelmsford died in London on the 5th of October 1878. Lord Chelmsford had married in 1822 Anna Maria Tinling. He left four sons and three daughters, of whom the eldest, Frederick Augustus, 2nd Baron Chelmsford (1827-1905), earned distinction as a soldier, while the third, Alfred Henry Thesiger (1838-1880) was made a lord justice of appeal and a privy councillor in 1877, at the early age of thirty-nine, but died only three years later.
See Lives of the Chancellors (1908), by J.B. Atlay, who has had the advantage of access to an unpublished autobiography of Lord Chelmsford’s.
CHELMSFORD, a market town and municipal borough, and the county town of Essex, England, in the Chelmsford parliamentary division, 30 m. E.N.E. from London by the Great Eastern railway. Pop. (1901) 12,580. It is situated in the valley of the Chelmer, at the confluence of the Cann, and has communication by the river with Maldon and the Blackwater estuary 11 m. east. Besides the parish church of St Mary, a graceful Perpendicular edifice, largely rebuilt, the town has a grammar school founded by Edward VI., an endowed charity school and a museum. It is the seat of the county assizes and quarter sessions, and has a handsome shire hall; the county gaol is near the town. Its corn and cattle markets are among the largest in the county; for the first a fine exchange is provided. In the centre of the square in which the corn exchange is situated stands a bronze statue of Lord Chief-Justice Tindal (1776-1846), a native of the parish. There are agricultural implement and iron foundries, large electric light and engineering works, breweries, tanneries, maltings and extensive corn mills. There is a race-course 2 m. south of the town. The borough is under a mayor, 6 aldermen and 18 councillors. Area 2308 acres.
A place of settlement since Palaeolithic times, Chelmsford (Chilmersford, Chelmeresford, Chelmesford) owed its importance to its position on the road from London to Colchester. It consisted of two manors: that of Moulsham, which remained in the possession of Westminster Abbey from Saxon times till the reign of Henry VIII., when it was granted to Thomas Mildmay; and that of Bishop’s Hall, which was held by the bishops of London from the reign of Edward the Confessor to 1545, when it passed to the crown and was granted to Thomas Mildmay in 1563. The medieval history of Chelmsford centred round the manor of Bishop’s Hall. Early in the 12th century Bishop Maurice built the bridge over the Chelmer which brought the road from London directly through the town, thus making it an important stopping-place. The town was not incorporated until 1888. In 1225 Chelmsford was made the centre for the collection of fifteenths from the county of Essex, and in 1227 it became the regular seat of assizes and quarter-sessions. Edward I. confirmed Bishop Richard de Gravesend in his rights of frank pledge in Chelmsford in 1290, and in 1395 Richard II. granted the return of writs to Bishop Robert de Braybroke. In 1377 writs were issued for the return of representatives from Chelmsford to parliament, but no return of members has been found. In 1199 the bishop obtained the grant of a weekly market at the yearly rent of one palfrey, and in 1201 that of an annual fair, now discontinued, for four days from the feast of St Philip and St James.
CHELSEA, a western metropolitan borough of London, England, bounded E. by the city of Westminster, N.W. by Kensington, S.W. by Fulham, and S. by the river Thames. Pop. (1901) 73,842. Its chief thoroughfare is Sloane Street, containing handsome houses and good shops, running south from Knightsbridge to Sloane Square. Hence King’s Road leads west, a wholly commercial highway, named in honour of Charles II., and recalling the king’s private road from St James’s Palace to Fulham, which was maintained until the reign of George IV. The main roads south communicate with the Victoria or Chelsea, Albert and Battersea bridges over the Thames. The beautiful Chelsea embankment, planted with trees and lined with fine houses and, in part, with public gardens, stretches between Victoria and Battersea bridges. The better residential portion of Chelsea is the eastern, near Sloane Street and along the river; the western, extending north to Fulham Road, is mainly a poor quarter.
Chelsea, especially the riverside district, abounds in historical associations. At Cealchythe a synod was held in 785. A similar name occurs in a Saxon charter of the 11th century and in Domesday; in the 16th century it is Chelcith. The later termination ey or ea was associated with the insular character of the land, and the prefix with a gravel bank (ceosol; cf. Chesil Bank, Dorsetshire) thrown up by the river; but the early suffix hythe is common in the meaning of a haven. The manor was originally in the possession of Westminster Abbey, but its history is fragmentary until Tudor times. It then came into the hands of Henry VIII., passed from him to his wife Catharine Parr, and thereafter had a succession of owners, among whom were the Howards, to whom it was granted by Queen Elizabeth, and the Cheynes, from whom it was purchased in 1712 by Sir Hans Sloane, after which it passed to the Cadogans. The memorials which crowd the picturesque church and churchyard of St Luke near the river, commonly known as the Old Church, to a great extent epitomize the history of Chelsea. Such are those of Sir Thomas More (d. 1535); Lord Bray, lord of the manor (1539), his father and son; Lady Jane Guyldeford, duchess of Northumberland, who died “at her maner of Chelse” 25 in 1555; Lord and Lady Dacre (1594-1595); Sir John Lawrence (1638); Lady Jane Cheyne (1698); Francis Thomas, “director of the china porcelain manufactory, Lawrence Street, Chelsea” (1770); Sir Hans Sloane (1753); Thomas Shadwell, poet laureate (1602); Woodfall the printer of Junius (1844), and many others. More’s tomb is dated 1532, as he set it up himself, though it is doubtful whether he lies beneath it. His house was near the present Beaufort Street. In the 18th and 19th centuries Chelsea, especially the parts about the embankment and Cheyne Walk, was the home of many eminent men, particularly of writers and artists, with whom this pleasant quarter has long been in favour. Thus in the earlier part of the period named, Atterbury and Swift lived in Church Lane, Steele and Smollett in Monmouth House. Later, the names of Turner, Rossetti, Whistler, Leigh Hunt, Carlyle (whose house in Cheyne Row is preserved as a public memorial), Count D’Orsay, and Isambard Brunel, are intimately connected with Chelsea. At Lindsey House Count Zinzendorf established a Moravian Society (c. 1750). Sir Robert Walpole’s residence was extant till 1810; and till 1824 the bishops of Winchester had a palace in Cheyne Walk. Queen’s House, the home of D.G. Rossetti (when it was called Tudor House), is believed to take name from Catharine of Braganza.
Chelsea was noted at different periods for two famous places of entertainment, Ranelagh (q.v.) in the second half of the 18th century, and Cremorne Gardens (q.v.) in the middle of the 19th. Don Saltero’s museum, which formed the attraction of a popular coffee-house, was formed of curiosities from Sir Hans Sloane’s famous collections. It was Sloane who gave to the Apothecaries’ Company the ground which they had leased in 1673 for the Physick Garden, which is still extant, but ceased in 1902 to be maintained by the Company. At Chelsea Sir John Danvers (d. 1655) introduced the Italian style of gardening which was so greatly admired by Bacon and soon after became prevalent in England. Chelsea was formerly famous for a manufacture of buns; the original Chelsea bun-house, claiming royal patronage, stood until 1839, and one of its successors until 1888. The porcelain works existed for some 25 years before 1769, when they were sold and removed to Derby. Examples of the original Chelsea ware (see Ceramics) are of great value.
Of buildings and institutions the most notable is Chelsea Royal Hospital for invalid soldiers, initiated by Charles II. (according to tradition on the suggestion of Nell Gwynne), and opened in 1694. The hospital itself accommodates upwards of 500 men, but a system of out-pensioning was found necessary from the outset, and now relieves large numbers throughout the empire. The picturesque building by Wren stands in extensive grounds, which include the former Ranelagh Gardens. A theological college (King James’s) formerly occupied the site; it was founded in 1610 and was intended to be of great size, but the scheme was unsuccessful, and only a small part of the buildings was erected. In the vicinity are the Chelsea Barracks (not actually in the borough). The Royal Military Asylum for boys, commonly called the Duke of York’s school, founded in 1801 by Frederick, duke of York, for the education of children connected with the army, was removed in 1909 to new quarters at Dover. Other institutions are the Whitelands training college for school-mistresses, in which Ruskin took deep interest; the St Mark’s college for school-masters; the Victoria and the Cheyne hospitals for children, a cancer hospital, the South-western polytechnic, and a public library containing an excellent collection relative to local history.
The parliamentary borough of Chelsea returns one member, and includes, as a detached portion, Kensal Town, north of Kensington. The borough council consists of a mayor, 6 aldermen and 36 councillors. Area, 659.6 acres.
CHELSEA, a city of Suffolk county, Massachusetts, U.S.A., a suburb of Boston. Pop. (1890) 27,909; (1900) 34,072, of whom 11,203 were foreign-born; (1910) 32,452. It is situated on a peninsula between the Mystic and Chelsea rivers, and Charlestown and East Boston, and is connected with East Boston and Charlestown by bridges. It is served by the Boston & Maine and (for freight) by the Boston & Albany railways. The United States maintains here naval and marine hospitals, and the state a soldiers’ home. Chelsea’s interests are primarily industrial. The value of the city’s factory products in 1905 was $13,879,159, the principal items being rubber and elastic goods ($3,635,211) and boots and shoes ($2,044,250.) The manufacture of stoves, and of mucilage and paste are important industries. Flexible tubing for electric wires (first made at Chelsea 1889) and art tiles are important products. The first settlement was established in 1624 by Samuel Maverick (c. 1602-c. 1670), the first settler (about 1629) of Noddle’s Island (or East Boston), and one of the first slave-holders in Massachusetts; a loyalist and Churchman, in 1664 he was appointed with three others by Charles II. on an important commission sent to Massachusetts and the other New England colonies (see Nicolls, Richard), and spent the last years of his life in New York. Until 1739, under the name of Winnisimmet, Chelsea formed a part of Boston, but in that year it was made a township; it became a city in 1857. In May 1775 a British schooner in the Mystic defended by a force of marines was taken by colonial militia under General John Stark and Israel Putnam,—one of the first conflicts of the War of Independence. A terrible fire swept the central part of the city on the 12th of April 1908.
See Mellen Chamberlain (and others), History of Chelsea (2 vols., Boston, 1908), published by the Massachusetts Historical Society.
CHELTENHAM, a municipal and parliamentary borough of Gloucestershire, England, 109 m. W. by N. of London by the Great Western railway; served also by the west and north line of the Midland railway. Pop. (1901) 49,439. The town is well situated in the valley of the Chelt, a small tributary of the Severn, under the high line of the Cotteswold Hills to the east, and is in high repute as a health resort. Mineral springs were accidentally discovered in 1716. The Montpellier and Pittville Springs supply handsome pump rooms standing in public gardens, and are the property of the corporation. The Montpellier waters are sulphated, and are valuable for their diuretic effect, and as a stimulant to the liver and alimentary canal. The alkaline-saline waters of Pittville are efficacious against diseases resulting from excess of uric acid. The parish church of St Mary dates from the 14th century, but is almost completely modernized. The town, moreover, is wholly modern in appearance. Assembly rooms opened in 1815 by the duke of Wellington were removed in 1901. A new town hall, including a central spa and assembly rooms, was opened in 1903. There are numerous other handsome buildings, especially in High Street, and the Promenade forms a beautiful broad thoroughfare, lined with trees. The town is famous as an educational centre. Cheltenham College (1842) provides education for boys in three departments, classical, military and commercial; and includes a preparatory school. The Ladies’ College (1854), long conducted by Miss Beale (q.v.), is one of the most successful in England. The Normal Training College was founded in 1846 for the training of teachers, male and female, in national and parochial schools. A free grammar school was founded in 1568 by Richard Pate, recorder of Gloucester. The art gallery and museum may be mentioned also. The parliamentary borough returns one member. The municipal borough is under a mayor, 6 aldermen and 18 councillors. Area, 4726 acres. The urban district of Charlton Kings (pop. 3806) forms a south-eastern suburb of Cheltenham.
The site of a British village and burying-ground, Cheltenham (Celtanhomme, Chiltham, Chelteham) was a village with a church in 803. The manor belonged to the crown; it was granted to Henry de Bohun, earl of Hereford, late in the 12th century, but in 1199 was exchanged for other lands with the king. It was granted to William de Longespée, earl of Salisbury, in 1219, but resumed on his death and granted in dower to Eleanor of Provence in 1243. In 1252 the abbey of Fécamp purchased the manor, and it afterwards belonged to the priory of Cormeille, but was confiscated in 1415 as the possession of an alien priory, and was granted in 1461 to the abbey of Lyon, by which it was held until, once more returning to the crown at the Dissolution, 26 it was granted to the family of Dutton. The town is first mentioned in 1223, when William de Longespée leased the benefit of the markets, fairs and hundred of Cheltenham to the men of the town for three years; the lease was renewed by Henry III. in 1226, and again in 1230 for ten years. A market town in the time of Camden, it was governed by commissioners from the 18th century in 1876, when it was incorporated; it became a parliamentary borough in 1832. Henry III. in 1230 had granted to the men of Cheltenham a market on each Thursday, and a fair on the vigil, feast and morrow of St James. Although Camden mentions a considerable trade in malt, the spinning of woollen yarn was the only industry in 1779. After the discovery of springs in 1716, and the erection of a pump-room in 1738, Cheltenham rapidly became fashionable, the visit of George III. and the royal princesses in 1788 ensuring its popularity.
See S. Moreau, A Tour to Cheltenham Spa (Bath, 1738).
CHELYABINSK, a town of Russia, in the Orenburg government, at the east foot of the Urals, is the head of the Siberian railway, 624 m. by rail E.N.E. of Samara and 154 m. by rail S.S.E. of Ekaterinburg. Pop. (1900) 25,505. It has tanneries and distilleries, and is the centre of the trade in corn and produce of cattle for the Ural iron-works. The town was founded in 1658.
CHELYS (Gr. χέλυς, tortoise; Lat. testudo), the common lyre of the ancient Greeks, which had a convex back of tortoiseshell or of wood shaped like the shell. The word chelys was used in allusion to the oldest lyre of the Greeks which was said to have been invented by Hermes. According to tradition he was attracted by sounds of music while walking on the banks of the Nile, and found they proceeded from the shell of a tortoise across which were stretched tendons which the wind had set in vibration (Homeric Hymn to Hermes, 47-51). The word has been applied arbitrarily since classic times to various stringed instruments, some bowed and some twanged, probably owing to the back being much vaulted. Kircher (Musurgia, i. 486) applied the name of chelys to a kind of viol with eight strings. Numerous representations of the chelys lyre or testudo occur on the Greek vases, in which the actual tortoiseshell is depicted; a good illustration is given in Le Antichità, di Ercolano (vol. i. pl. 43). Propertius (iv. 6) calls the instrument the lyra testudinea. Scaliger (on Manilius, Astronomicon, Proleg. 420) was probably the first writer to draw attention to the difference, between chelys and cithara (q.v.).
CHEMICAL ACTION, the term given to any process in which change in chemical composition occurs. Such processes may be set up by the application of some form of energy (heat, light, electricity, &c.) to a substance, or by the mixing of two or more substances together. If two or more substances be mixed one of three things may occur. First, the particles may be mechanically intermingled, the degree of association being dependent upon the fineness of the particles, &c. Secondly, the substances may intermolecularly penetrate, as in the case of gas-mixtures and solutions. Or thirdly they may react chemically. The question whether, in any given case, we have to deal with a physical mixture or a chemical compound is often decided by the occurrence of very striking phenomena. To take a simple example:—oxygen and hydrogen are two gases which may be mixed in all proportions at ordinary temperatures, and it is easy to show that the properties of the products are simply those of mixtures of the two free gases. If, however, an electric spark be passed through the mixtures, powerful chemical union ensues, with its concomitants, great evolution of heat and consequent rise of temperature, and a compound, water, is formed which presents physical and chemical properties entirely different from those of its constituents.
In general, powerful chemical forces give rise to the evolution of large quantities of heat, and the properties of the resulting substance differ vastly more from those of its components than is the case with simple mixtures. This constitutes a valuable criterion as to whether mere mixture is involved on the one hand, or strong chemical union on the other. When, however, the chemical forces are weak and the reaction, being incomplete, leads to a state of chemical equilibrium, in which all the reacting substances are present side by side, this criterion vanishes. For example, the question whether a salt combines with water molecules when dissolved in water cannot be said even yet to be fully settled, and, although there can be no doubt that solution is, in many cases, attended by chemical processes, still we possess as yet no means of deciding, with certainty, how many molecules of water have bound themselves to a single molecule of the dissolved substance (solute). On the other hand, we possess exact methods of testing whether gases or solutes in dilute solution react one with another and of determining the equilibrium state which is attained. For if one solute react with another on adding the latter to its solution, then corresponding to the decrease of its concentration there must also be a decrease of vapour pressure, and of solubility in other solvents; further, in the case of a mixture of gases, the concentration of each single constituent follows from its solubility in some suitable solvent. We thus obtain the answer to the question: whether the concentration of a certain constituent has decreased during mixing, i.e. whether it has reacted chemically.
When a compound can be obtained in a pure state, analysis affords us an important criterion of its chemical nature, for unlike mixtures, the compositions of which are always variable within wider or narrower limits, chemical compounds present definite and characteristic mass-relations, which find full expression in the atomic theory propounded by Dalton (see Atom). According to this theory a mixture is the result of the mutual interpenetration of the molecules of substances, which remain unchanged as such, whilst chemical union involves changes more deeply seated, inasmuch as new molecular species appear. These new substances, if well-defined chemical compounds, have a perfectly definite composition and contain a definite, generally small, number of elementary atoms, and therefore the law of constant proportions follows at once, and the fact that only an integral number of atoms of any element may enter into the composition of any molecule determines the law of multiple proportions.
These considerations bring us face to face with the task of more closely investigating the nature of chemical forces, in other words, of answering the question: Nature of chemical forces. what forces guide the atoms in the formation of a new molecular species? This problem is still far from being completely answered, so that a few general remarks must suffice here.
It is remarkable that among the most stable chemical compounds, we find combinations of atoms of one and the same element. Thus, the stability of the di-atomic molecule N2 is so great, that no trace of dissociation has yet been proved even at the highest temperatures, and as the constituent atoms of the molecule N2 must be regarded as absolutely identical, it is clear that “polar” forces cannot be the cause of all chemical action. On the other hand, especially powerful affinities are also at work when so-called electro-positive and electro-negative elements react. The forces which here come into play appear to be considerably greater than those just mentioned; for instance, potassium fluoride is perhaps the most stable of all known compounds.
It is also to be noticed that the combinations of the electro-negative elements (metalloids) with one another exhibit a metalloid character, and also we find, in the mutual combinations of metals, all the characteristics of the metallic state; but in the formation of a salt from a metal and a metalloid we have an entirely new substance, quite different from its components; and at the same time, the product is seen to be an electrolyte, i.e. to have the power of splitting up into a positively and a negatively charged constituent when dissolved in some solvent. These considerations lead to the conviction that forces of a “polar” origin play an important part here, and indeed we may make the general surmise that in the act of chemical combination forces of both a non-polar and polar nature play a part, and that the latter are in all probability identical with the electric forces.
It now remains to be asked—what are the laws which govern 27 the action of these forces? This question is of fundamental importance, since it leads directly to those laws which regulate the chemical process. Besides the already mentioned fundamental law of chemical combination, that of constant and multiple proportions, there is the law of chemical mass-action, discovered by Guldberg and Waage in 1867, which we will now develop from a kinetic standpoint.
Kinetic Basis of the Law of Chemical Mass-action.—We will assume that the molecular species A1, A2, ... A′1, A′2, ... are present in a homogeneous system, where they can react on each other only according to the scheme
A1 + A2 + ... ↔ A′1 + A′2 + ...;
this is a special case of the general equation
n1A1 + n2A2 + ... ↔ n′1A′1 + n′2A′2 + ...,
in which only one molecule of each substance takes part in the reaction. The reacting substances may be either gaseous or form a liquid mixture, or be dissolved in some selected solvent; but in each case we may state the following considerations regarding the course of the reaction. For a transformation to take place from left to right in the sense of the reaction equation, all the molecules A1, A2, ... must clearly collide at one point; otherwise no reaction is possible, since we shall not consider side-reactions. Such a collision need not of course bring about that transposition of the atoms of the single molecules which constitutes the above reaction. Much rather must it be of such a kind as is favourable to that loosening of the bonds that bind the atoms in the separate molecules, which must precede this transposition. Of a large number of such collisions, therefore, only a certain smaller number will involve a transposition from left to right in the sense of the equation. But this number will be the same under the same external conditions, and the greater the more numerous the collisions; in fact a direct ratio must exist between the two. Bearing in mind now, that the number of collisions must be proportional to each of the concentrations of the bodies A1, A2, ..., and therefore, on the whole, to the product of all these concentrations, we arrive at the conclusion that the velocity v of the transposition from left to right in the sense of the reaction equation is v = kc1c2 ..., in which c1, c2, ... represent the spatial concentrations, i.e. the number of gram-molecules of the substances A1, A2, ... present in one litre, and k is, at a given temperature, a constant which may be called the velocity-coefficient.
Exactly the same consideration applies to the molecules A′1, A′2.... Here the velocity of the change from right to left in the sense of the reaction-equation increases with the number of collisions of all these molecules at one point, and this is proportional to the product of all the concentrations. If k’ denotes the corresponding proportionality-factor, then the velocity v’ of the change from right to left in the sense of the reaction-equation is v′ = k′c′1c′2.... These spatial concentrations are often called the “active masses” of the reacting components. Hence the reaction-velocity in the sense of the reaction-equation from left to right, or the reverse, is proportional to the product of the “active-masses” of the left-hand or right-hand components respectively.
Neither v nor v′ can be separately investigated, and the measurements of the course of a reaction always furnish only the difference of these two quantities. The reaction-velocity Law of chemical statics. actually observed represents the difference of these two partial reaction-velocities, whilst the amount of change observed during any period of time is equal to the change in the one direction, minus the change in the opposite direction. It must not be assumed, however, that on the attainment of equilibrium all action has ceased, but rather that the velocity of change in one direction has become equal to that in the opposite direction, with the result that no further total change can be observed, i.e. the system has reached equilibrium, for which the relation v - v′ = 0 must therefore hold, or what is the same thing
kc1c2 ... = k’c’1c’2 ...,
this is the fundamental law of chemical statics.
The conception that the equilibrium is not to be attributed to absolute indifference between the reacting bodies, but that these continue to exert their mutual actions undiminished and the opposing changes now balance, is of fundamental significance in the interpretation of changes of matter in general. This is generally expressed in the form: the equilibrium in this and other analogous cases is not static but dynamic. This conception was a direct result of the kinetic-molecular considerations, and was applied with special success to the development of the kinetic theory of gases. Thus with Clausius, we conceive the equilibrium of water-vapour with water, not as if neither water vaporized nor vapour condensed, but rather as though the two processes went on unhindered in the equilibrium state, i.e. during contact of saturated vapour with water, in a given time, as many water molecules passed through the water surface in one direction as in the opposite direction. This view, as applied to chemical changes, was first advanced by A.W. Williamson (1851), and further developed by C.M. Guldberg and P. Waage and others.
From the previous considerations it follows that the reaction-velocity at every moment, i.e. the velocity with which the chemical process advances towards the Law of chemical kinetics. equilibrium state, is given by the equation
V = v - v′ = kc1c2 ... - k′c′1c′2 ...;
this states the fundamental law of chemical kinetics.
The equilibrium equation is simply a special case of this more general one, and results when the total velocity is written zero, just as in analytical mechanics the equilibrium conditions follow at once by specialization of the general equations of motion.
No difficulty presents itself in the generalization of the previous equations for the reaction which proceeds after the scheme
n1A1 + n2A2 + ... = n′1A′1 + n′2A′2 + ...,
where n1, n2, ..., n′1, n′2, ... denote the numbers of molecules of the separate substances which take part in the reaction, and are therefore whole, mostly small, numbers (generally one or two, seldom three or more). Here as before, v and v′ are to be regarded as proportional to the number of collisions at one point of all molecules necessary to the respective reaction, but now n1 molecules of A1, n2 molecules of A2, &c., must collide for the reaction to advance from left to right in the sense of the equation; and similarly n′1 molecules of A′1, n′2 molecules of A′2, &c., must collide for the reaction to proceed in the opposite direction. If we consider the path of a single, arbitrarily chosen molecule over a certain time, then the number of its collisions with other similar molecules will be proportional to the concentration C of that kind of molecule to which it belongs. The number of encounters between two molecules of the kind in question, during the same time, will be in general C times as many, i.e. the number of encounters of two of the same molecules is proportional to the square of the concentration C; and generally, the number of encounters of n molecules of one kind must be regarded as proportional to the nth power of C, i.e. Cn.
The number of collisions of n1 molecules of A1, n2 molecules of A2 ... is accordingly proportional to C1n1C2n2 ..., and the reaction-velocity corresponding to it is therefore
v = kC1n1C2n2 ...,
and similarly the opposed reaction-velocity is
v′ = k′C′1n′1C′2n′2 ...;
the resultant reaction-velocity, being the difference of these two partial velocities, is therefore
V = v - v′ = kC1n1C2n2 ... - k′C′1n′1C′2n′2 ...
This is the most general expression of the law of chemical mass-action, for the case of homogeneous systems.
Equating V to zero, we obtain the equation for the equilibrium state, viz.
C1n1C2n2 ... / C′1n′1C′2n′2 ... = k / k′ = K;
K is called the “equilibrium-constant.”
These formulae hold for gases and for dilute solutions, but assume the system to be homogeneous, i.e. to be either a homogeneous gas-mixture or a homogeneous dilute solution. Limitations and applications of the laws. The case in which other states of matter share in the equilibrium permits of simple treatment when the substances in question may be regarded as pure, and consequently as possessing definite vapour-pressures or solubilities at a given temperature. In this case the molecular species in question, which is, at the same time, present in excess and is hence usually, called a Bodenkörper, must possess a constant concentration in the gas-space or solution. But since the left-hand side of the last equation contains only variable quantities, it is simplest and most convenient to absorb these constant concentrations into the equilibrium-constant; whence we have the rule: leave the molecular species present as Bodenkörper out of account, when determining the concentration-product. Guldberg and Waage expressed this in the form “the active mass of a solid substance is constant.” The same is true of liquids when these participate in the pure state in the equilibrium, and possess therefore a definite vapour-pressure or solubility. When, finally, we are not dealing with a dilute solution but with any kind of mixture whatever, it is simplest to apply the law of mass-action to the gaseous mixture in equilibrium with this. The composition of the liquid mixture is then determinable when the vapour-pressures of the separate components are known. This, however, is not often the case; but in principle this consideration is important, since it involves the possibility of extending the law of chemical mass-action from ideal gas-mixtures and dilute solutions, for which it primarily holds, to any other system whatever.
The more recent development of theoretical chemistry, as well as the detailed study of many chemical processes which have found technical application, leads more and more convincingly to the recognition that in the law of chemical mass-action we have a law of as fundamental significance as the law of constant and multiple proportions. It is therefore not without interest to briefly touch upon the development of the doctrine of chemical affinity.
Historical Development of the Law of Mass-action.—The theory developed by Torbern Olof Bergman in 1775 must be regarded as the first attempt of importance to account for the mode of action of chemical forces. The essential principle of this may be stated as follows:—The magnitude of chemical affinity may be expressed by a definite number; if the affinity of the substance A is greater for the substance B than for the substance C, then the latter (C) will be completely expelled by B from its compound with A, in the sense of the equation A·C + B = A·B + C. This theory fails, however, to take account of the influence of the relative masses of the reacting substances, and had to be abandoned as soon as such an influence was noticed. An attempt to consider this factor was made by Claude Louis Berthollet (1801), who introduced the conception of chemical equilibrium. The views of this French chemist may be summed up in the following sentence:—Different substances have different affinities for each other, which only come into play on immediate contact. The condition of equilibrium depends not only upon the chemical affinity, but also essentially upon the relative masses of the reacting substances.
Essentially, Berthollet’s idea is to-day the guiding principle of the doctrine of affinity. This is especially true of our conceptions of many reactions which, in the sense of Bergman’s idea, proceed to completion, i.e. until the reacting substances are all used up; but only for this reason, viz. that one or more of the products of the reaction is removed from the reaction mixture (either by crystallization, evaporation or some other process), and hence the reverse reaction becomes impossible. Following Berthollet’s idea, two Norwegian investigators, C.M. Guldberg and Peter Waage, succeeded in formulating the influence of the reacting masses in a simple law—the law of chemical mass-action already defined. The results of their theoretical and experimental studies were published at Christiania in 1867 (Études sur les affinités chimiques); this work marks a new epoch in the history of chemistry. Even before this, formulae to describe the progress of certain chemical reactions, which must be regarded as applications of the law of mass-action, had been put forward by Ludwig Wilhelmy (1850), and by A.G. Vernon-Harcourt and William Esson (1856), but the service of Guldberg and Waage in having grasped the law in its full significance and logically applied it in all directions, remains of course undiminished. Their treatise remained quite unknown; and so it happened that John Hewitt Jellett (1873), J.H. van’t Hoff (1877), and others independently developed the same law. The thermodynamic basis of the law of mass-action is primarily due to Horstmann, J. Willard Gibbs and van’t Hoff.
Applications.—Let us consider, as an example of the application of the law of mass-action, the case of the dissociation of water-vapour, which takes place at high temperatures in the sense of the equation 2H2O = 2H2 + O2. Representing the concentrations of the corresponding molecular species by [H2], &c., the expression [H2]² [O2] / [H2O]² must be constant at any given temperature. This shows that the dissociation is set back by increasing the pressure; for if the concentrations of all three kinds of molecules be increased by strong compression, say to ten times the former amounts, then the numerator is increased one thousand, the denominator only one hundred times. Hence if the original equilibrium-constant is to hold, the dissociation must go back, and, what is more, by an exactly determinable amount. At 2000° C. water-vapour is only dissociated to the extent of a few per cent; therefore, even when only a small excess of oxygen or hydrogen be present, the numerator in the foregoing expression is much increased, and it is obvious that in order to restore the equilibrium state, the concentration of the other component, hydrogen or oxygen as the case may be, must diminish. In the case of slightly dissociated substances, therefore, even a relatively small excess of one component is sufficient to set back the dissociation substantially.
Chemical Kinetics.—It has been already mentioned that the law of chemical mass-action not only defines the conditions for chemical equilibrium, but contains at the same time the principles of chemical kinetics. The previous considerations show indeed that the actual progress of the reaction is determined by the difference of the reaction-velocities in the one and the other (opposed) direction, in the sense of the corresponding reaction-equation. Since the reaction-velocity is given by the amount of chemical change in a small interval of time, the law of chemical mass-action supplies a differential equation, which, when integrated, provides formulae which, as numerous experiments have shown, very happily summarize the course of the reaction. For the simplest case, in which a single species of molecule undergoes almost complete decomposition, so that the reaction-velocity in the reverse direction may be neglected, we have the simple equation
dx/dt = k(a-x)
and if x = 0 when t = 0 we have by integration
k = t-1 log {a / (a-x) }.
We will now apply these conclusions to the theory of the ignition of an explosive gas-mixture, and in particular to the combustion of “knallgas” (a mixture of hydrogen Theory of explosive combustion. and oxygen) to water-vapour. At ordinary temperatures knallgas undergoes practically no change, and it might be supposed that the two gases, oxygen and hydrogen, have no affinity for each other. This conclusion, however, is shown to be incorrect by the observation that it is only necessary to add some suitable catalyst such as platinum-black in order to immediately start the reaction. We must therefore conclude that even at ordinary temperatures strong chemical affinity is exerted between oxygen and hydrogen, but that at low temperatures this encounters great frictional resistances, or in other words that the reaction-velocity is very small. It is a matter of general experience that the resistances which the chemical forces have to overcome diminish with rising temperature, i.e. the reaction-velocity increases with temperature. Therefore, when we warm the knallgas, the number of collisions of oxygen and hydrogen molecules favourable to the formation 29 of water becomes greater and greater, until at about 500° the gradual formation of water is observed, while at still higher temperatures the reaction-velocity becomes enormous. We are now in a position to understand what is the result of a strong local heating of the knallgas, as, for example, by an electric spark. The strongly heated parts of the knallgas combine to form water-vapour with great velocity and the evolution of large amounts of heat, whereby the adjacent parts are brought to a high temperature and into a state of rapid reaction, i.e. we observe an ignition of the whole mixture. If we suppose the knallgas to be at a very high temperature, then its combustion will be no longer complete owing to the dissociation of water-vapour, whilst at extremely high temperatures it would practically disappear. Hence it is clear that knallgas appears to be stable at low temperatures only because the reaction-velocity is very small, but that at very high temperatures it is really stable, since no chemical forces are then active, or, in other words, the chemical affinity is very small.
The determination of the question whether the failure of some reaction is due to an inappreciable reaction-velocity or to absence of chemical affinity, is of fundamental importance, and only in the first case can the reaction be hastened by catalysts.
Many chemical compounds behave like knallgas. Acetylene is stable at ordinary temperatures, inasmuch as it only decomposes slowly; but at the same time it is explosive, for the decomposition when once started is rapidly propagated, on account of the heat evolved by the splitting up of the gas into carbon and hydrogen. At very high temperatures, however, acetylene acquires real stability, since carbon and hydrogen then react to form acetylene.
Many researches have shown that the combustion of an inflammable gas-mixture which is started at a point, e.g. by an electric spark, may be propagated in two essentially Explosion-waves. different ways. The characteristic of the slower combustion consists in this, viz. that the high temperature of the previously ignited layer spreads by conduction, thereby bringing the adjacent layers to the ignition-temperature; the velocity of the propagation is therefore conditioned in the first place by the magnitude of the conductivity for heat, and more particularly, in the second place, by the velocity with which a moderately heated layer begins to react chemically, and so to rise gradually in temperature, i.e. essentially by the change of reaction-velocity with temperature. A second entirely independent mode of propagation of the combustion lies at the basis of the phenomenon that an explosive gas-mixture can be ignited by strong compression or—more correctly—by the rise of temperature thereby produced. The increase of the concentrations of the reacting substances consequent upon this increase of pressure raises the reaction-velocity in accordance with the law of chemical mass-action, and so enormously favours the rapid evolution of the heat of combustion.
It is therefore clear that such a powerful compression-wave can not only initiate the combustion, but also propagate it with extremely high velocity. Indeed a compression-wave of this kind passes through the gas-mixture, heated by the combustion to a very high temperature. It must, however, be propagated considerably faster than an ordinary compression-wave, for the result of ignition in the compressed (still unburnt) layer is the production of a very high pressure, which must in accordance with the principles of wave-motion increase the velocity of propagation. The absolute velocity of the explosion-wave would seem, in the light of these considerations, to be susceptible of accurate calculation. It is at least clear that it must be considerably higher than the velocity of sound in the mass of gas strongly heated by the explosion, and this is confirmed by actual measurements (see below) which show that the velocity of the explosion-wave is from one and a half times to double that of sound-waves at the combustion temperature.
We are now in a position to form the following picture of the processes which follow upon the ignition of a combustible gas-mixture contained in a long tube. First we have the condition of slow combustion; the heat is conveyed by conduction to the adjacent layers, and there follows a velocity of propagation of a few metres per second. But since the combustion is accompanied by a high increase of pressure, the adjacent, still unburnt layers are simultaneously compressed, whereby the reaction-velocity increases, and the ignition proceeds faster. This involves still greater compression of the next layers, and so if the mixture be capable of sufficiently rapid combustion, the velocity of propagation of the ignition must continually increase. As soon as the compression in the still unburnt layers becomes so great that spontaneous ignition results, the now much more pronounced compression-waves excited with simultaneous combustion must be propagated with very great velocity, i.e. we have spontaneous development of an “explosion-wave.” M.P.E. Berthelot, who discovered the presence of such explosion-waves, proved their velocity of propagation to be independent of the pressure, the cross-section of the tubes in which the explosive gas-mixture is contained, as well as of the material of which these are made, and concluded that this velocity is a constant, characteristic of the particular mixture. The determination of this velocity is naturally of the highest interest.
In the following table Berthelot’s results are given along with the later (1891) concordant ones of H.B. Dixon, the velocities of propagation of explosions being given in metres per second.
| Reacting Mixture. | Velocity of Wave in Metres per second. | ||
| Berthelot. | Dixon. | ||
| Hydrogen and oxygen, | H2+O | 2810 | 2821 |
| Hydrogen and nitrous oxide, | H2+N2O | 2284 | 2305 |
| Methane and oxygen, | CH4+4O | 2287 | 2322 |
| Ethylene and oxygen, | C2H4+6O | 2210 | 2364 |
| Acetylene and oxygen, | C2H2+5O | 2482 | 2391 |
| Cyanogen and oxygen, | C2N2+4O | 2195 | 2321 |
| Hydrogen and chlorine, | H2+Cl2 | .. | 1730 |
| Hydrogen and chlorine, | 2H2+Cl2 | .. | 1849 |
The maximum pressure of the explosion-wave possesses very high values; it appears that a compression of from 1 to 30-40 atmospheres is necessary to produce spontaneous ignition of mixtures of oxygen and hydrogen. But since the heat evolved in the path of the explosion causes a rise of temperature of 2000°-3000°, i.e. a rise of absolute temperature about four times that directly following upon the initial compression, we are here concerned with pressures amounting to considerably more than 100 atmospheres. Both the magnitude of this pressure and the circumstance that it so suddenly arises are peculiar to the very powerful forces which distinguish the explosion-wave from the slow combustion-wave.
Nascent State.—The great reactive power of freshly formed or nascent substances (status nascens)may be very simply referred to the principles of mass-action. As is well known, this phenomenon is specially striking in the case of hydrogen, which may therefore be taken as a typical example. The law of mass-action affirms the action of a substance to be the greater the higher its concentration, or, for a gas, the higher its partial-pressure. Now experience teaches that those metals which liberate hydrogen from acids are able to supply the latter under extremely high pressure, and we may therefore assume that the hydrogen which results, for example, from the action of zinc upon sulphuric acid is initially under very high pressures which are then afterwards relieved. Hence the hydrogen during liberation exhibits much more active powers of reduction than the ordinary gas.
A deeper insight into the relations prevailing here is offered from the atomistic point of view. From this we are bound to conclude that the hydrogen is in the first instance evolved in the form of free atoms, and since the velocity of the reaction H + H = H2 at ordinary temperatures, though doubtless very great, is not practically instantaneous, the freshly generated hydrogen will contain a remnant of free atoms, which are able to react both more actively and more rapidly. Similar considerations are of course applicable to other cases.
Ion-reactions.—The application of the law of chemical mass 30 action is much simplified in the case in which the reaction-velocity is enormously great, when practically an instantaneous adjustment of the equilibrium results. Only in this case can the state of the system, which pertains after mixing the different components, be determined merely from knowledge of the equilibrium-constant. This case is realized in the reactions between gases at very high temperatures, which have, however, been little investigated, and especially by the reactions between electrolytes, the so-called ion-reactions. In this latter case, which has been thoroughly studied on account of its fundamental importance for inorganic qualitative and quantitative analysis, the degrees of dissociation of the various electrolytes (acids, bases and salts) are for the most part easily determined by the aid of the freezing-point apparatus, or of measurements of the electric conductivity; and from these data the equilibrium-constant K may be calculated. Moreover, it can be shown that the state of the system can be determined when the equilibrium constants of all the electrolytes which are present in the common solution are known. If this be coupled with the law that the solubility of solid substances, as with vapour-pressures, is independent of the presence of other electrolytes, it is sufficient to know the solubilities of the electrolytes in question, in order to be able to determine which substances must participate in the equilibrium in the solid state, i.e. we arrive at the theory of the formation and solution of precipitates.
As an illustration of the application of these principles, we shall deal with a problem of the doctrine of affinity, namely, that of the relative strengths of acids and bases. It Strength of acids and bases. was quite an early and often repeated observation that the various acids and bases take part with very varying intensity or avidity in those reactions in which their acid or basic nature comes into play. No success attended the early attempts at giving numerical expression to the strengths of acids and bases, i.e. of finding a numerical coefficient for each acid and base, which should be the quantitative expression of the degree of its participation in those specific reactions characteristic of acids and bases respectively. Julius Thomsen and W. Ostwald attacked the problem in a far-seeing and comprehensive manner, and arrived at indisputable proof that the property of acids and bases of exerting their effects according to definite numerical coefficients finds expression not only in salt-formation but also in a large number of other, and indeed very miscellaneous, reactions.
When Ostwald compared the order of the strengths of acids deduced from their competition for the same base, as determined by Thomsen’s thermo-chemical or his own volumetric method, with that order in which the acids arrange themselves according to their capacity to bring calcium oxalate into solution, or to convert acetamide into ammonium acetate, or to split up methyl acetate into methyl alcohol and acetic acid catalytically, or to invert cane-sugar, or to accelerate the mutual action of hydriodic on bromic acid, he found that in all these well-investigated and very miscellaneous cases the same succession of acids in the order of their strengths is obtained, whichever one of the above chemical processes be chosen as measure of these strengths. It is to be noticed that all these chemical changes cited took place in dilute aqueous solution, consequently the above order of acids refers only to the power to react under these circumstances. The order of acids proved to be fairly independent of temperature. While therefore the above investigations afforded a definite qualitative solution of the order of acids according to strengths, the determination of the quantitative relations offered great difficulties, and the numerical coefficients, determined from the separate reactions, often displayed great variations, though occasionally also surprising agreement. Especially great were the variations of the coefficients with the concentration, and in those cases in which the concentration of the acid changed considerably during the reaction, the calculation was naturally quite uncertain. Similar relations were found in the investigation of bases, the scope of which, however, was much more limited.
These apparently rather complicated relations were now cleared up at one stroke, by the application of the law of chemical mass-action on the lines indicated by S. Arrhenius in 1887, when he put forward the theory of electrolytic dissociation to explain that peculiar behaviour of substances in aqueous solution first recognized by van’t Hoff in 1885. The formulae which must be made use of here in the calculation of the equilibrium-relations follow naturally by simple application of the law of mass-action to the corresponding ion-concentrations.
The peculiarities which the behaviour of acids and bases presents, and, according to the theory of Arrhenius, must present—peculiarities which found expression in the very early distinction between neutral solutions on the one hand, and acid or basic ones on the other, as well as in the belief in a polar antithesis between the two last—must now, in the light of the theory of electrolytic dissociation, be conceived as follows:—
The reactions characteristic of acids in aqueous solution, which are common to and can only be brought about by acids, find their explanation in the fact that this class of bodies gives rise on dissociation to a common molecular species, namely, the positively charged hydrogen-ion (H+). The specific chemical actions peculiar to acids are therefore to be attributed to the hydrogen-ion just as the actions common to all chlorides are to be regarded as those of the free chlorine-ions. In like manner, the reactions characteristic of bases in solution are to be attributed to the negatively charged hydroxyl-ions (OH-), which result from the dissociation of this class of bodies.
A solution has an acid reaction when it contains an excess of hydrogen-ions, and a basic reaction when it contains an excess of hydroxyl-ions. If an acid and an alkaline solution be brought together mutual neutralization must result, since the positive H-ions and the negative OH-ions cannot exist together in view of the extremely weak conductivity of pure water and its consequent slight electrolytic dissociation, and therefore they must at once combine to form electrically neutral molecules, in the sense of the equation
H+ + OH- = H2O.
In this lies the simple explanation of the “polar” difference between acid and basic solutions. This rests essentially upon the fact that the ion peculiar to acids and the ion peculiar to bases form the two constituents of water, i.e. of that solvent in which we usually study the course of the reaction. The idea of the “strength” of an acid or base at once arises. If we compare equivalent solutions of various acids, the intensity of those actions characteristic of them will be the greater the more free hydrogen-ions they contain; this is an immediate consequence of the law of chemical mass-action. The degree of electrolytic dissociation determines, therefore, the strength of acids, and a similar consideration leads to the same result for bases.
Now the degree of electrolytic dissociation changes with concentration in a regular manner, which is given by the law of mass-action. For if C denote the concentration of the electrolyte and a its degree of dissociation, the above law states that
C²a²/C(1-a) = Ca²/(1-a) = K.
At very great dilutions the dissociation is complete, and equivalent solutions of the most various acids then contain the same number of hydrogen-ions, or, in other words, are equally strong; and the same is true of the hydroxyl-ions of bases. The dissociation also decreases with increasing concentration, but at different rates for different substances, and the relative “strengths” of acids and bases must hence change with concentration, as was indeed found experimentally. The dissociation-constant K is the measure of the variation of the degree of dissociation with concentration, and must therefore be regarded as the measure of the strengths of acids and bases. So that in this special case we are again brought to the result which was stated in general terms above, viz. that the dissociation-coefficient forms the measure of the reactivity of a dissolved electrolyte. Ostwald’s series of acids, based upon the investigation of the most various reactions, should therefore correspond with the order of their dissociation-constants, and further with the 31 order of their freezing-point depressions in equivalent solutions, since the depression of the freezing-point increases with the degree of electrolytic dissociation. Experience confirms this conclusion completely. The degree of dissociation of an acid, at a given concentration, for which its molecular conductivity is Λ, is shown by the theory of electrolytic dissociation to be a = Λ / Λ∞; Λ∞, the molecular conductivity at very great dilution in accordance with the law of Kohlrausch, is u + v, where u and v are the ionic-mobilities (see Conduction, Electric). Since u, the ionic-mobility of the hydrogen ion, is generally more than ten times as great as v, the ionic-mobility of the negative acid-radical, Λ∞ has approximately the same value (generally within less than 10%) for the different acids, and the molecular-conductivity of the acids in equivalent concentration is at least approximately proportional to the degree of electrolytic dissociation, i.e. to the strength.
In general, therefore, the order of conductivities is identical with that in which the acids exert their specific powers. This remarkable parallelism, first perceived by Arrhenius and Ostwald in 1885, was the happy development which led to the discovery of electrolytic dissociation (see Conduction, Electric; and Solution).
Catalysis.—We have already mentioned the fact, early known to chemists, that many reactions proceed with a marked increase of velocity in presence of many foreign substances. With Berzelius we call this phenomenon “catalysis,” by which we understand that general acceleration of reactions which also progress when left to themselves, in the presence of certain bodies which do not change in amount (or only slightly) during the course of the reaction. Acids and bases appear to act catalytically upon all reactions involving consumption or liberation of water, and indeed that action is proportional to the concentration of the hydrogen or hydroxyl-ions. Further, the decomposition of hydrogen peroxide is “catalysed” by iodine-ions, the condensation of two molecules of benzaldehyde to benzoin by cyanogen-ions. One of the earliest known and technically most important instances of catalysis is that of the oxidation of sulphur dioxide to sulphuric acid by oxygen in the presence of oxides of nitrogen. Other well-known and remarkable examples are the catalysis of the combustion of hydrogen and of sulphur dioxide in oxygen by finely-divided platinum. We may also mention the interesting work of Dixon and Baker, which led to the discovery that a large number of gas-reactions, e.g. the combustion of carbon monoxide, the dissociation of sal-ammoniac vapour, and the action of sulphuretted hydrogen upon the salts of heavy metals, cease when water-vapour is absent, or at least proceed with greatly diminished velocity.
“Negative catalysis,” i.e. the retardation of a reaction by addition of some substance, which is occasionally observed, appears to depend upon the destruction of a “positive catalyte” by the body added.
A catalyte can have no influence, however, upon the affinity of a process, since that would be contrary to the second law of thermodynamics, according to which affinity of an isothermal process, which is measured by the maximum work, only depends upon the initial and final states. The effect of a catalyte is therefore limited to the resistances opposing the progress of a reaction, and does not influence its driving-force or affinity. Since the catalyte takes no part in the reaction its presence has no effect on the equilibrium-constant. This, in accordance with the law of mass-action, is the ratio of the separate reaction-velocities in the two contrary directions. A catalyte must therefore always accelerate the reverse-reaction. If the velocity of formation of a body be increased by addition of some substance then its velocity of decomposition must likewise increase. We have an example of this in the well-known fact that the formation, and no less the saponification, of esters, proceeds with increased velocity in the presence of acids, while the observation that in absence of water-vapour neither gaseous ammonium chloride dissociates nor dry ammonia combines with hydrogen chloride becomes clear on the same grounds.
A general theory of catalytic phenomena does not at present exist. The formation of intermediate products by the action of the reacting substance upon the catalyte has often been thought to be the cause of these. These intervening products, whose existence in many cases has been proved, then split up into the catalyte and the reaction-product. Thus chemists have sought to ascribe the influence of oxides of nitrogen on the formation of sulphuric acid to the initial formation of nitrosyl-sulphuric acid, SO2(OH)(NO2), from the mixture of sulphur dioxide, oxides of nitrogen and air, which then reacted with water to form sulphuric and nitrous acids. When the velocity of such intermediate reactions is greater than that of the total change, such an explanation may suffice, but a more certain proof of this theory of catalysis has only been reached in a few cases, though in many others it appears very plausible. Hence it is hardly possible to interpret all catalytic processes on these lines.
In regard to catalysis in heterogeneous systems, especially the hastening of gas-reactions by platinum, it is very probable that it is closely connected with the solution or absorption of the gases on the part of the metal. From the experiments of G. Bredig it seems that colloidal solutions of a metal act like the metal itself. The action of a colloidal-platinum solution on the decomposition of hydrogen peroxide is still sensible even at a dilution of 1/70,000,000 grm.-mol. per litre; indeed the activity of this colloidal-platinum solution calls to mind in many ways that of organic ferments, hence Bredig has called it an “inorganic ferment.” This analogy is especially striking in the change of their activity with time and temperature, and in the possibility, by means of bodies like sulphuretted hydrogen, hydrocyanic acid, &c., which act as strong poisons upon the latter, of “poisoning” the former also, i.e. of rendering it inactive. In the case of the catalytic action of water-vapour upon many processes of combustion already mentioned, a part of the effect is probably due to the circumstance, disclosed by numerous experiments, that the union of hydrogen and oxygen proceeds, between certain temperature limits at least, after the equation H2 + O2 = H2O2, that is, with the preliminary formation of hydrogen peroxide, which then breaks down into water and oxygen, and further, above all, to the fact that this substance results from oxygen and water at high temperatures with great velocity, though indeed only in small quantities.
The view now suggests itself, that, for example, in the combustion of carbon monoxide at moderately high temperatures, the reaction
| (I.) | 2CO + O2 = 2CO2 |
advances with imperceptible speed, but that on the contrary the two stages
| (II.) | 2H2O + O2 = 2H2O2, |
| (III.) | 2CO + 2H2O2 = 2CO2 + 2H2O, |
which together result in (I.), proceed rapidly even at moderate temperatures.
Temperature and Reaction-Velocity.—There are few natural constants which undergo so marked a change with temperature as those of the velocities of chemical changes. As a rule a rise of temperature of 10° causes a twofold or threefold rise of reaction-velocity.
If the reaction-coefficient k, in the sense of the equation derived above, viz. k = t-1 log {a / (a-x)}, be determined for the inversion of cane-sugar by an acid of given concentration, the following values are obtained:—
| Temperature | = | 25° | 40° | 45° | 50° | 55° |
| k | = | 9.7 | 73 | 139 | 268 | 491; |
here a rise of temperature of only 30° suffices to raise the speed of inversion fifty times.
We possess no adequate explanation of this remarkable temperature influence; but some account of it is given by the molecular theory, according to which the energy of that motion of substances in homogeneous gaseous or liquid systems which constitutes heat increases with the temperature, and hence also the frequency of collision of the reacting substances. When we reflect that the velocity of motion of the molecules of gases, and in all probability those of liquids also, are proportional to the square root of the absolute temperature, and therefore rise by 32 only 1/6% per degree at room-temperature, and that we must assume the number of collisions proportional to the velocity of the molecules, we cannot regard the actually observed increase of reaction-velocity, which often amounts to 10 or 12% per degree, as exclusively due to the quickening of the molecular motion by heat. It is more probable that the increase of the kinetic energy of the atomic motions within the molecule itself is of significance here, as the rise of the specific heat of gases with temperature seems to show. The change of the reaction-coefficient k with temperature may be represented by the empirical equation log k = -AT-1 + B + CT, where A, B, C are positive constants. For low temperatures the influence of the last term is as a rule negligible, whilst for high temperatures the first term on the right side plays a vanishingly small part.
Definition of Chemical Affinity.—We have still to discuss the question of what is to be regarded as the measure of chemical affinity. Since we are not in a position to measure directly the intensity of chemical forces, the idea suggests itself to determine the strength of chemical affinity from the amount of the work which the corresponding reaction is able to do. To a certain extent the evolution of heat accompanying the reaction is a measure of this work, and attempts have been made to measure chemical affinities thermo-chemically, though it may be easily shown that this definition was not well chosen. For when, as is clearly most convenient, affinity is so defined that it determines under all circumstances the direction of chemical change, the above definition fails in so far as chemical processes often take place with absorption of heat, that is, contrary to affinities so defined. But even in those cases in which the course of the reaction at first proceeds in the sense of the evolution of heat, it is often observed that the reaction advances not to completion but to a certain equilibrium, or, in other words, stops before the evolution of heat is complete.
A definition free from this objection is supplied by the second law of thermodynamics, in accordance with which all processes must take place in so far as they are able to do external work. When therefore we identify chemical affinity with the maximum work which can be gained from the process in question, we reach such a definition that the direction of the process is under all conditions determined by the affinity. Further, this definition has proved serviceable in so far as the maximum work in many cases may be experimentally measured, and moreover it stands in a simple relation to the equilibrium constant K. Thermodynamics teaches that the maximum work A may be expressed as A = RT log K, when R denotes the gas-constant, T the absolute temperature. In this it is further assumed that both the molecular species produced as well as those that disappear are present in unit concentration. The simplest experimental method of directly determining chemical affinity consists in the measurement of electromotive force. The latter at once gives us the work which can be gained when the corresponding galvanic element supplies the electricity, and, since the chemical exchange of one gram-equivalent from Faraday’s law requires 96,540 coulombs, we obtain from the product of this number and the electromotive force the work per gram-equivalent in watt-seconds, and this quantity when multiplied by O.23872 is obtained in terms of the usual unit, the gram-calorie. Experience teaches that, especially when we have to deal with strong affinities, the affinity so determined is for the most part almost the same as the heat-evolution, whilst in the case in which only solid or liquid substances in the pure state take part in the reaction at low temperatures, heat-evolution and affinity appear to possess a practically identical value.
Hence it seems possible to calculate equilibria for low temperatures from heats of reaction, by the aid of the two equations
A = Q, A = RT log K;
and since the change of A with temperature, as required by the principles of thermodynamics, follows from the specific heats of the reacting substances, it seems further possible to calculate chemical equilibria from heats of reaction and specific heats. The circumstance that chemical affinity and heat-evolution so nearly coincide at low temperatures may be derived from the hypothesis that chemical processes are the result of forces of attraction between the atoms of the different elements. If we may disregard the kinetic energy of the atoms, and this is legitimate for low temperatures, it follows that both heat-evolution and chemical affinity are merely equal to the decrease of the potential energy of the above-mentioned forces, and it is at once clear that the evolution of heat during a reaction between only pure solid or pure liquid substances possesses special importance.
More complicated is the case in which gases or dissolved substances take part. This is simplified if we first consider the mixing of two mutually chemically indifferent gases. Thermodynamics teaches that external work may be gained by the mere mixing of two such gases (see Diffusion), and these amounts of work, which assume very considerable proportions at high temperatures, naturally affect the value of the maximum work and so also of the affinity, in that they always come into play when gases or solutions react. While therefore we regard as chemical affinity in the strictest sense the decrease of potential energy of the forces acting between the atoms, it is clear that the quantities here involved exhibit the simplest relations under the experimental conditions just given, for when only substances in a pure state take part in a reaction, all mixing of different kinds of molecules is excluded; moreover, the circumstance that the respective substances are considered at very low temperatures reduces the quantities of energy absorbed as kinetic energy by their molecules to the smallest possible amount.
Chemical Resistance.—When we know the chemical affinity of a reaction, we are in a position to decide in which direction the process must advance, but, unless we know the reaction-velocity also, we can in many cases say nothing as to whether or not the reaction in question will progress with a practically inappreciable velocity so that apparent chemical indifference is the result. This question may be stated in the light of the law of mass-action briefly as follows:—From a knowledge of the chemical affinity we can calculate the equilibrium, i.e. the numerical value of the constant K = k / k′; but to be completely informed of the process we must know not only the ratio of the two velocity-constants k and k′, but also the separate absolute values of the same.
In many respects the following view is more comprehensive, though naturally in harmony with the one just expressed. Since the chemical equilibrium is periodically attained, it follows that, as in the case of the motion of a body or of the diffusion of a dissolved substance, it must be opposed by very great friction. In all these cases the velocity of the process at every instant is directly proportional to the driving-force and inversely proportional to the frictional resistance. We hence arrive at the result that an equation of the form
reaction-velocity = chemical force/chemical resistance
must also hold for chemical change; here we have an analogy with Ohm’s law. The “chemical force” at every instant may be calculated from the maximum work (affinity); as yet little is known about “chemical resistance,” but it is not improbable that it may be directly measured or theoretically deduced. The problem of the calculation of chemical reaction-velocity in absolute measure would then be solved; so far we possess indeed only a few general facts concerning the magnitude of chemical resistance. It is immeasurably small at ordinary temperatures for ion-reactions, and, on the other hand, fairly large for nearly all reactions in which carbon-bonds must be loosened (so-called “inertia of the carbon-bond”) and possesses very high values for most gas-reactions also. With rising temperature it always strongly diminishes; on the other hand, at very low temperatures its values are always enormous, and at the absolute zero of temperature may be infinitely great. Therefore at that temperature all reactions cease, since the denominator in the above expression assumes enormous values.
It is a very remarkable phenomenon that the chemical resistance is often small in the case of precisely those reactions in which the affinity is also small; to this circumstance is to be traced the fact that in many chemical changes the most stable condition is not at once reached, but is preceded by the formation 33 of more or less unstable intermediate products. Thus the unstable ozone is very often first formed on the evolution of oxygen, whilst in the reaction between oxygen and hydrogen water is often not at once formed, but first the unstable hydrogen peroxide as an intermediate product.
Let us now consider the chemical process in the light of the equation
reaction-velocity = chemical force/chemical resistance.
Thermodynamics shows that at very low temperatures, i.e. in the immediate vicinity of the absolute zero, there is no equilibrium, but every chemical process advances to completion in the one or the other direction. The chemical forces therefore act in the one direction towards complete consumption of the reacting substance. But since the chemical resistance is now immensely great, they can produce practically no appreciable result.
At higher temperatures the reaction always proceeds, at least in homogeneous systems, to a certain equilibrium, and as the chemical resistance now has finite values this equilibrium will always finally be reached after a longer or shorter time. Finally, at very high temperatures the chemical resistance is in every case very small, and the equilibrium is almost instantaneously reached; at the same time, the affinity of the reaction, as in the case of the mutual affinity between oxygen and hydrogen, may very strongly diminish, and we have then chemical indifference again, not because, as at low temperatures, the denominator of the previous expression becomes very great, but because the numerator now assumes vanishingly small values.
CHEMISTRY (formerly “chymistry”; Gr. χυμεία; for derivation see Alchemy), the natural science which has for its province the study of the composition of substances. In common with physics it includes the determination of properties or characters which serve to distinguish one substance from another, but while the physicist is concerned with properties possessed by all substances and with processes in which the molecules remain intact, the chemist is restricted to those processes in which the molecules undergo some change. For example, the physicist determines the density, elasticity, hardness, electrical and thermal conductivity, thermal expansion, &c.; the chemist, on the other hand, investigates changes in composition, such as may be effected by an electric current, by heat, or when two or more substances are mixed. A further differentiation of the provinces of chemistry and physics is shown by the classifications of matter. To the physicist matter is presented in three leading forms—solids, liquids and gases; and although further subdivisions have been rendered necessary with the growth of knowledge the same principle is retained, namely, a classification based on properties having no relation to composition. The fundamental chemical classification of matter, on the other hand, recognizes two groups of substances, namely, elements, which are substances not admitting of analysis into other substances, and compounds, which do admit of analysis into simpler substances and also of synthesis from simpler substances. Chemistry and physics, however, meet on common ground in a well-defined branch of science, named physical chemistry, which is primarily concerned with the correlation of physical properties and chemical composition, and, more generally, with the elucidation of natural phenomena on the molecular theory.
It may be convenient here to state how the whole subject of chemistry is treated in this edition of the Encyclopaedia Britannica. The present article includes the following sections:—
I. History.—This section is confined to tracing the general trend of the science from its infancy to the foundations of the modern theory. The history of the alchemical period is treated in more detail in the article Alchemy, and of the iatrochemical in the article Medicine. The evolution of the notion of elements is treated under Element; the molecular hypothesis of matter under Molecule; and the genesis of, and deductions from, the atomic theory of Dalton receive detailed analysis in the article Atom.
II. Principles.—This section treats of such subjects as nomenclature, formulae, chemical equations, chemical change and similar subjects. It is intended to provide an introduction, necessarily brief, to the terminology and machinery of the chemist.
III. Inorganic Chemistry.—Here is treated the history of descriptive inorganic chemistry; reference should be made to the articles on the separate elements for an account of their preparation, properties, &c.
IV. Organic Chemistry.—This section includes a brief history of the subject, and proceeds to treat of the principles underlying the structure and interrelations of organic compounds.
V. Analytical Chemistry.—This section treats of the qualitative detection and separation of the metals, and the commoner methods employed in quantitative analysis. The analysis of organic compounds is also noticed.
VI. Physical Chemistry.—This section is restricted to an account of the relations existing between physical properties and chemical composition. Other branches of this subject are treated in the articles Chemical Action; Energetics; Solution; Alloys; Thermochemistry.
I. History
Although chemical actions must have been observed by man in the most remote times, and also utilized in such processes as the extraction of metals from their ores and in the arts of tanning and dyeing, there is no evidence to show that, beyond an unordered accumulation of facts, the early developments of these industries were attended by any real knowledge of the nature of the processes involved. All observations were the result of accident or chance, or possibly in some cases of experimental trial, but there is no record of a theory or even a general classification of the phenomena involved, although there is no doubt that the ancients had a fair knowledge of the properties and uses of the commoner substances. The origin of chemistry is intimately bound up with the arts which we have indicated; in this respect it is essentially an experimental science. A unifying principle of chemical and physical changes was provided by metaphysical conceptions of the structure of matter. We find the notion of “elements,” or primary qualities, which confer upon all species of matter their distinctive qualities by appropriate combination, and also the doctrine that Greek philosophy. matter is composed of minute discrete particles, prevailing in the Greek schools. These “elements,” however, had not the significance of the elements of to-day; they connoted physical appearances or qualities rather than chemical relations; and the atomic theory of the ancients is a speculation based upon metaphysical considerations, having, in its origin, nothing in common with the modern molecular theory, which was based upon experimentally observed properties of gases (see Element; Molecule).
Although such hypotheses could contribute nothing directly to the development of a science which laid especial claim to experimental investigations, yet indirectly they stimulated inquiry into the nature of the “essence” with which the four “elements” were associated. This quinta essentia had been speculated upon by the Greeks, some regarding it as immaterial or aethereal, and others as material; and a school of philosophers termed alchemists arose who attempted the isolation of this essence. The existence of a fundamental principle, unalterable and indestructible, prevailing alike through physical and chemical changes, was generally accepted. Any change which a substance may chance to undergo was simply due to the discarding or taking up of some proportion of the primary “elements” or qualities: of these coverings “water,” “air,” “earth” and “fire” were regarded as clinging most tenaciously to the essence, while “cold,” “heat,” “moistness” and “dryness” were more easily cast aside or assumed. Several origins have been Alchemy. suggested for the word alchemy, and there seems to have been some doubt as to the exact nature and import of the alchemical doctrines. According to M.P.E. Berthelot, “alchemy rested partly on the industrial processes of the ancient Egyptians, partly on the speculative theories of the Greek philosophers, and partly on the mystical reveries of the Gnostics and Alexandrians.” The search for this essence subsequently resolved itself into the desire to effect the transmutation of metals, more especially the base metals, into silver and gold. It seems that this secondary principle became the dominant idea in alchemy, and in this sense the word is used in Byzantine literature of the 4th century; Suidas, writing in 34 the 11th century, defines chemistry as the “preparation of silver and gold” (see Alchemy).
From the Alexandrians the science passed to the Arabs, who made discoveries and improved various methods of separating substances, and afterwards, from the 11th century, became seated in Europe, where the alchemical doctrines were assiduously studied until the 15th and 16th centuries. It is readily understood why men imbued with the authority of tradition should prosecute the search for a substance which would confer unlimited wealth upon the fortunate discoverer. Some alchemists honestly laboured to effect the transmutation and to discover the “philosopher’s stone,” and in many cases believed that they had achieved success, if we may rely upon writings assigned to them. The period, however, is one of literary forgeries; most of the MSS. are of uncertain date and authorship, and moreover are often so vague and mystical that they are of doubtful scientific value, beyond reflecting the tendencies of the age. The retaining of alchemists at various courts shows the high opinion which the doctrines had gained. It is really not extraordinary that Isaac Hollandus was able to indicate the method of the preparation of the “philosopher’s stone” from “adamic” or “virgin” earth, and its action when medicinally employed; that in the writings assigned to Roger Bacon, Raimon Lull, Basil Valentine and others are to be found the exact quantities of it to be used in transmutation; and that George Ripley, in the 15th century, had grounds for regarding its action as similar to that of a ferment.
In the view of some alchemists, the ultimate principles of matter were Aristotle’s four elements; the proximate constituents were a “sulphur” and a “mercury,” the father and mother of the metals; gold was supposed to have attained to the perfection of its nature by passing in succession through the forms of lead, brass and silver; gold and silver were held to contain very pure red sulphur and white quicksilver, whereas in the other metals these materials were coarser and of a different colour. From an analogy instituted between the healthy human being and gold, the most perfect of the metals, silver, mercury, copper, iron, lead and tin, were regarded in the light of lepers that required to be healed.
Notwithstanding the false idea which prompted the researches of the alchemists, many advances were made in descriptive chemistry, the metals and their salts receiving much Iatrochemistry. attention, and several of our important acids being discovered. Towards the 16th century the failure of the alchemists to achieve their cherished purpose, and the general increase of medical knowledge, caused attention to be given to the utilization of chemical preparations as medicines. As early as the 15th century the alchemist Basil Valentine had suggested this application, but the great exponent of this doctrine was Paracelsus, who set up a new definition: “The true use of chemistry is not to make gold but to prepare medicines.” This relation of chemistry to medicine prevailed until the 17th century, and what in the history of chemistry is termed the iatrochemical period (see Medicine) was mainly fruitful in increasing the knowledge of compounds; the contributions to chemical theory are of little value, the most important controversies ranging over the nature of the “elements,” which were generally akin to those of Aristotle, modified so as to be more in accord with current observations. At the same time, however, there were many who, opposed to the Paracelsian definition of chemistry, still laboured at the problem of the alchemists, while others gave much attention to the chemical industries. Metallurgical operations, such as smelting, roasting and refining, were scientifically investigated, and in some degree explained, by Georg Agricola and Carlo Biringuiccio; ceramics was studied by Bernard Palissy, who is also to be remembered as an early worker in agricultural chemistry, having made experiments on the effect of manures on soils and crops; while general technical chemistry was enriched by Johann Rudolf Glauber.1
The second half of the 17th century witnessed remarkable transitions and developments in all branches of natural science, and the facts accumulated by preceding generations Boyle. during their generally unordered researches were replaced by a co-ordination of experiment and deduction. From the mazy and incoherent alchemical and iatrochemical doctrines, the former based on false conceptions of matter, the latter on erroneous views of life processes and physiology, a new science arose—the study of the composition of substances. The formulation of this definition of chemistry was due to Robert Boyle. In his Sceptical Chemist (1662) he freely criticized the prevailing scientific views and methods, with the object of showing that true knowledge could only be gained by the logical application of the principles of experiment and deduction. Boyle’s masterly exposition of this method is his most important contribution to scientific progress. At the same time he clarified the conception of elements and compounds, rejecting the older notions, the four elements of the “vulgar Peripateticks” and the three principles of the “vulgar Stagyrists,” and defining an element as a substance incapable of decomposition, and a compound as composed of two or more elements. He explained chemical combination on the hypotheses that matter consisted of minute corpuscles, that by the coalescence of corpuscles of different substances distinctly new corpuscles of a compound were formed, and that each corpuscle had a certain affinity for other corpuscles.
Although Boyle practised the methods which he expounded, he was unable to gain general acceptance of his doctrine of elements; and, strangely enough, the theory which next dominated chemical thought was an alchemical Phlogistic theory. invention, and lacked the lucidity and perspicuity of Boyle’s views. This theory, named the phlogistic theory, was primarily based upon certain experiments on combustion and calcination, and in effect reduced the number of the alchemical principles, while setting up a new one, a principle of combustibility, named phlogiston (from φλοιστός, burnt). Much discussion had centred about fire or the “igneous principle.” On the one hand, it had been held that when a substance was burned or calcined, it combined with an “air”; on the other hand, the operation was supposed to be attended by the destruction or loss of the igneous principle. Georg Ernst Stahl, following in some measure the views held by Johann Joachim Becher, as, for instance, that all combustibles contain a “sulphur” (which notion is itself of older date than Becher’s terra pinguis), regarded all substances as capable of resolution into two components, the inflammable principle phlogiston, and another element—“water,” “acid” or “earth.” The violence or completeness of combustion was proportional to the amount of phlogiston present. Combustion meant the liberation of phlogiston. Metals on calcination gave calces from which the metals could be recovered by adding phlogiston, and experiment showed that this could generally be effected by the action of coal or carbon, which was therefore regarded as practically pure phlogiston; the other constituent being regarded as an acid. At the hands of Stahl and his school, the phlogistic theory, by exhibiting a fundamental similarity between all processes of combustion and by its remarkable flexibility, came to be a general theory of chemical action. The objections of the antiphlogistonists, such as the fact that calces weigh more than the original metals instead of less as the theory suggests, were answered by postulating that phlogiston was a principle of levity, or even completely ignored as an accident, the change of qualities being regarded as the only matter of importance. It is remarkable that this theory should have gained the esteem of the notable chemists who flourished in the 18th century. Henry Cavendish, a careful and accurate experimenter, was a phlogistonist, as were J. Black, K. W. Scheele, A. S. Marggraf, J. Priestley and many others who might be mentioned.
Descriptive chemistry was now assuming considerable proportions; the experimental inquiries suggested by Boyle were being assiduously developed; and a wealth of observations Lavoisier. was being accumulated, for the explanation of which the resources of the dominant theory were sorely taxed. To quote Antoine Laurent Lavoisier, “... chemists have turned phlogiston into a vague principle, ... which consequently adapts itself to all the explanations for which it may be required. Sometimes this principle has weight, and sometimes it has not; sometimes it is free fire and sometimes it is fire combined with the earthy element; sometimes it passes through the pores of vessels, sometimes these are impervious to it; it explains both causticity and non-causticity, transparency and opacity, colours and their absence; it is a veritable Proteus changing in form at each instant.” Lavoisier may be justly regarded as the founder of modern or quantitative chemistry. First and foremost, he demanded that the balance must be used in all investigations into chemical changes. He established as fundamental that combustion and calcination were attended by an increase of weight, and concluded, as did Jean Rey and John Mayow in the 17th century, that the increase was due to the combination of the metal with the air. The problem could obviously be completely solved only when the composition of the air, and the parts played by its components, had been determined. At all times the air had received attention, especially since van Helmont made his far-reaching investigations on gases. Mayow had suggested the existence of two components, a spiritus nitroaerus which supported combustion, and a spiritus nitri acidi which extinguished fire; J. Priestley and K. W. Scheele, although they isolated oxygen, were fogged by the phlogistic tenets; and H. Cavendish, who had isolated the nitrogen of the atmosphere, had failed to decide conclusively what had really happened to the air which disappeared during combustion.
Lavoisier adequately recognized and acknowledged how much he owed to the researches of others; to himself is due the co-ordination of these researches, and the welding of his results into a doctrine to which the phlogistic theory ultimately succumbed. He burned phosphorus in air standing over mercury, and showed that (1) there was a limit to the amount of phosphorus which could be burned in the confined air, (2) that when no more phosphorus could be burned, one-fifth of the air had disappeared, (3) that the weight of the air lost was nearly equal to the difference in the weights of the white solid produced and the phosphorus burned, (4) that the density of the residual air was less than that of ordinary air. The same results were obtained with lead and tin; and a more elaborate repetition indubitably established their correctness. He also showed that on heating mercury calx alone an “air” was liberated which differed from other “airs,” and was slightly heavier than ordinary air; moreover, the weight of the “air” set free from a given weight of the calx was equal to the weight taken up in forming the calx from mercury, and if the calx be heated with charcoal, the metal was recovered and a gas named “fixed air,” the modern carbon dioxide, was formed. The former experiment had been performed by Scheele and Priestley, who had named the gas “phlogisticated air”; Lavoisier subsequently named it oxygen, regarding it as the “acid producer” (ὀξύς, sour). The theory advocated by Lavoisier came to displace the phlogistic conception; but at first its acceptance was slow. Chemical literature was full of the phlogistic modes of expression—oxygen was “dephlogisticated air,” nitrogen “phlogisticated air,” &c.—and this tended to retard its promotion. Yet really the transition from the one theory to the other was simple, it being only necessary to change the “addition or loss of phlogiston” into the “loss or addition of oxygen.” By his insistence upon the use of the balance as a quantitative check upon the masses involved in all chemical reactions, Lavoisier was enabled to establish by his own investigations and the results achieved by others the principle now known as the “conservation of mass.” Matter can neither be created nor destroyed; however a chemical system be changed, the weights before and after are equal.2 To him is also due a rigorous examination of the nature of elements and compounds; he held the same views that were laid down by Boyle, and with the same prophetic foresight predicted that some of the elements which he himself accepted might be eventually found to be compounds.
It is unnecessary in this place to recapitulate the many results which had accumulated by the end of the 18th century, or to discuss the labours and theories of individual workers since these receive attention under biographical headings; in this article only the salient features in the history of our science can be treated. The beginning of the 19th century was attended by far-reaching discoveries in the nature of the composition of compounds. Investigations proceeded in two directions:—(1) the nature of chemical affinity, (2) the laws Chemical Affinity. of chemical combination. The first question has not yet been solved, although it has been speculated upon from the earliest times. The alchemists explained chemical action by means of such phrases as “like attracts like,” substances being said to combine when one “loved” the other, and the reverse when it “hated” it. Boyle rejected this terminology, which was only strictly applicable to intelligent beings; and he used the word “affinity” as had been previously done by Stahl and others. The modern sense of the word, viz. the force which holds chemically dissimilar substances together (and also similar substances as is seen in di-, tri-, and poly-atomic molecules), was introduced by Hermann Boerhaave, and made more precise by Sir Isaac Newton. The laws of chemical combination were solved, in a measure, by John Dalton, and the solution expressed as Dalton’s “atomic theory.” Lavoisier appears to have assumed that the composition of every chemical compound was constant, and the same opinion was the basis of much experimental inquiry at the hands of Joseph Louis Proust during 1801 to 1809, who vigorously combated the doctrine of Claude Louis Berthollet (Essai de statique chimique, 1803), viz. that fixed proportions of elements and compounds combine only under exceptional conditions, the general rule being that the composition of a compound may vary continuously between certain limits.3
This controversy was unfinished when Dalton published the first part of his New System of Chemical Philosophy in 1808, although the per saltum theory was the most popular. Dalton. Led thereto by speculations on gases, Dalton assumed that matter was composed of atoms, that in the elements the atoms were simple, and in compounds complex, being composed of elementary atoms. Dalton furthermore perceived that the same two elements or substances may combine in different proportions, and showed that these proportions had always a simple ratio to one another. This is the “law of multiple proportions.” He laid down the following arbitrary rules for determining the number of atoms in a compound:—if only one compound of two elements exists, it is a binary compound and its atom is composed of one atom of each element; if two compounds exist one is binary (say A + B) and the other ternary (say A + 2B); if three, then one is binary and the others may be ternary (A + 2B, and 2A + B), and so on. More important is his deduction of equivalent weights, i.e. the relative weights of atoms. He took hydrogen, the lightest substance known, to be the standard. From analyses of water, which he regarded as composed of one atom of hydrogen and one of oxygen, he 36 deduced the relative weight of the oxygen atom to be 6.5; from marsh gas and olefiant gas he deduced carbon = 5, there being one atom of carbon and two of hydrogen in the former and one atom of hydrogen to one of carbon in the latter; nitrogen had an equivalent of 5, and so on.4
The value of Dalton’s generalizations can hardly be overestimated, notwithstanding the fact that in several cases they needed correction. The first step in this direction was effected by the co-ordination of Gay Lussac’s observations on the combining volumes of gases. He discovered that gases always combined in volumes having simple ratios, and that the volume of the product had a simple ratio to the volumes of the reacting gases. For example, one volume of oxygen combined with two of hydrogen to form two volumes of steam, three volumes of hydrogen combined with one of nitrogen to give two volumes of ammonia, one volume of hydrogen combined with one of chlorine to give two volumes of hydrochloric acid. An immediate inference was that the Daltonian “atom” must have parts which enter into combination with parts of other atoms; in other words, there must exist two orders of particles, viz. (1) particles derived by limiting mechanical subdivision, the modern molecule, and (2) particles derived from the first class by chemical subdivision, i.e. particles which are incapable of existing alone, but may exist in combination. Additional evidence as to the structure of the molecule was discussed by Avogadro in 1811, and by Ampere in 1814. From the gas-laws of Boyle and J.A.C. Charles—viz. equal changes in temperature and pressure occasion equal changes in equal volumes of all gases and vapours—Avogadro deduced the law:—Under the same conditions of temperature and pressure, equal volumes of gases contain equal numbers of molecules; and he showed that the relative weights of the molecules are determined as the ratios of the weights of equal volumes, or densities. He established the existence of molecules and atoms as we have defined above, and stated that the number of atoms in the molecule is generally 2, but may be 4, 8, &c. We cannot tell whether his choice of the powers of 2 is accident or design.
Notwithstanding Avogadro’s perspicuous investigation, and a similar exposition of the atom and molecule by A. M. Ampere, the views therein expressed were ignored both by Berzelius. their own and the succeeding generation. In place of the relative molecular weights, attention was concentrated on relative atomic or equivalent weights. This may be due in some measure to the small number of gaseous and easily volatile substances then known, to the attention which the study of the organic compounds received, and especially to the energetic investigations of J. J. Berzelius, who, fired with enthusiasm by the original theory of Dalton and the law of multiple proportions, determined the equivalents of combining ratios of many elements in an enormous number of compounds.5 He prosecuted his labours in this field for thirty years; as proof of his industry it may be mentioned that as early as 1818 he had determined the combining ratios of about two thousand simple and compound substances.
We may here notice the important chemical symbolism or notation
introduced by Berzelius, which greatly contributed to the definite
and convenient representation of chemical composition
Chemical notation.
and the tracing of chemical reactions. The denotation of
elements by symbols had been practised by the alchemists,
and it is interesting to note that the symbols allotted to the well-known
elements are identical with the astrological symbols of the sun and
the other members of the solar system. Gold, the most perfect metal,
had the symbol of the Sun, ☉; silver, the semiperfect metal, had
the symbol of the Moon, ☽; copper, iron and antimony, the
imperfect metals of the gold class, had the symbols of Venus ♀,
Mars ♂, and the Earth ♁; tin and lead, the imperfect metals of
the silver class, had the symbols of Jupiter ♃, and Saturn ♄;
while mercury, the imperfect metal of both the gold and silver
class, had the symbol of the planet, ☿. Torbern Olof Bergman used
an elaborate system in his Opuscula physica et chemica (1783); the
elements received symbols composed of circles, arcs of circles, and
lines, while certain class symbols, such as  for metals,
for metals,  for acids,
for acids,
 for alkalies,
for alkalies,  for salts,
for salts,  for calces, &c., were used. Compounds
were represented by copulating simpler symbols, e.g. mercury calx
was
for calces, &c., were used. Compounds
were represented by copulating simpler symbols, e.g. mercury calx
was  .6 Bergman’s symbolism was obviously cumbrous, and
the system used in 1782 by Lavoisier was equally abstruse, since the
forms gave no clue as to composition; for instance water, oxygen,
and nitric acid were
.6 Bergman’s symbolism was obviously cumbrous, and
the system used in 1782 by Lavoisier was equally abstruse, since the
forms gave no clue as to composition; for instance water, oxygen,
and nitric acid were  , and
, and  .
.
A partial clarification was suggested in 1787 by J.H. Hassenfratz and Adet, who assigned to each element a symbol, and to each compound a sign which should record the elements present and their relative quantities. Straight lines and semicircles were utilized for the non-metallic elements, carbon, nitrogen, phosphorus and sulphur (the “simple acidifiable bases” of Lavoisier), and circles enclosing the initial letters of their names for the metals. The “compound acidifiable bases,” i.e. the hypothetical radicals of acids, were denoted by squares enclosing the initial letter of the base; an alkali was denoted by a triangle, and the particular alkali by inserting the initial letter. Compounds were denoted by joining the symbols of the components, and by varying the manner of joining compounds of the same elements were distinguished. The symbol \/ was used to denote a liquid, and a vertical line to denote a gas. As an example of the complexity of this system we may note the five oxides of nitrogen, which were symbolized as
 and
and  ,
,
the first three representing the gaseous oxides, and the last two the liquid oxides.
A great advance was made by Dalton, who, besides introducing simpler symbols, regarded the symbol as representing not only the element or compound but also one atom of that element or compound; in other words, his symbol denoted equivalent weights.7 This system, which permitted the correct representation of molecular composition, was adopted by Berzelius in 1814, who, having replaced the geometric signs of Dalton by the initial letter (or letters) of the Latin names of the elements, represented a compound by placing a plus sign between the symbols of its components, and the number of atoms of each component (except in the case of only one atom) by placing Arabic numerals before the symbols; for example, copper oxide was Cu+O, sulphur trioxide S+3O. If two compounds combined, the + signs of the free compounds were discarded, and the number of atoms denoted by an Arabic index placed after the elements, and from these modified symbols the symbol of the new compound was derived in the same manner as simple compounds were built up from their elements. Thus copper sulphate was CuO + SO3, potassium sulphate 2SO3 + PoO2 (the symbol Po for potassium was subsequently discarded in favour of K from kalium). At a later date Berzelius denoted an oxide by dots, equal in number to the number of oxygen atoms present, placed over the element; this notation survived longest in mineralogy. He also introduced barred symbols, i.e. letters traversed by a horizontal bar, to denote the double atom (or molecule). Although the system of Berzelius has been modified and extended, its principles survive in the modern notation.
In the development of the atomic theory and the deduction of the atomic weights of elements and the formulae of compounds, Dalton’s arbitrary rules failed to find complete acceptance. Extension of the atomic theory. Berzelius objected to the hypothesis that if two elements form only one compound, then the atoms combine one and one; and although he agreed with the adoption of simple rules as a first attempt at representing a compound, he availed himself of other data in order to gain further information as to the structure of compounds. For example, at first he represented ferrous and ferric oxides by the formulae FeO2, FeO3, and by the analogy of zinc and other basic oxides he regarded these substances as constituted similarly to FeO2, and the acidic oxides alumina and chromium oxide as similar to FeO3. He found, however, that chromic acid, which he had represented as CrO6, neutralized a base containing 1/3 the 37 quantity of oxygen. He inferred that chromic acid must contain only three atoms of oxygen, as did sulphuric acid SO3; consequently chromic oxide, which contains half the amount of oxygen, must be Cr2O3, and hence ferric oxide must be Fe2O3. The basic oxides must have the general formula MO. To these results he was aided by the law of isomorphism formulated by E. Mitscherlich in 1820; and he confirmed his conclusions by showing the agreement with the law of atomic heat formulated by Dulong and Petit in 1819.
While successfully investigating the solid elements and their compounds gravimetrically, Berzelius was guilty of several inconsistencies in his views on gases. He denied that gaseous atoms could have parts, although compound gases could. This attitude was due to his adherence to the “dualistic theory” of the structure of substances, which he deduced from electrochemical researches. From the behaviour of substances on electrolysis (q.v.) he assumed that all substances had two components, one bearing a negative charge, the other a positive charge. Combination was associated with the coalescence of these charges, and the nature of the resulting compound showed the nature of the residual electricity. For example, positive iron combined with negative oxygen to form positive ferrous oxide; positive sulphur combined with negative oxygen to form negative sulphuric acid; positive ferrous oxide combined with negative sulphuric acid to form neutral ferrous sulphate. Berzelius elevated this theory to an important position in the history of our science. He recognized that if an elementary atom had parts, his theory demanded that these parts should carry different electric charges when they entered into reaction, and the products of the reaction should vary according as a positive or negative atom entered into combination. For instance if the reaction 2H2 + O2 = H2O + H2O be true, the molecules of water should be different, for a negative oxygen atom would combine in one case, and a positive oxygen atom in the other. Hence the gaseous atoms of hydrogen and oxygen could not have parts. A second inconsistency was presented when he was compelled by the researches of Dumas to admit Avogadro’s hypothesis; but here he would only accept it for the elementary gases, and denied it for other substances. It is to be noticed that J.B. Dumas did not adopt the best methods for emphasizing his discoveries. His terminology was vague and provoked caustic criticism from Berzelius; he assumed that all molecules contained two atoms, and consequently the atomic weights deduced from vapour density determinations of sulphur, mercury, arsenic, and phosphorus were quite different from those established by gravimetric and other methods.
Chemists gradually tired of the notion of atomic weights on account of the uncertainty which surrounded them; and the suggestion made by W.H. Wollaston as early as 1814 to deal only with “equivalents,” i.e. the amount of an element which can combine with or replace unit weight of hydrogen, came into favour, being adopted by L. Gmelin in his famous text-book.
Simultaneously with this discussion of the atom and molecule, great controversy was ranging over the constitution of compounds, more particularly over the carbon or organic Atomic and molecular weights. compounds. This subject is discussed in section IV., Organic Chemistry.The gradual accumulation of data referring to organic compounds brought in its train a revival of the discussion of atoms and molecules. A. Laurent and C.F. Gerhardt attempted a solution by investigating chemical reactions. They assumed the atom to be the smallest part of matter which can exist in combination, and the molecule to be the smallest part which can enter into a chemical reaction. Gerhardt found that reactions could be best followed if one assumed the molecular weight of an element or compound to be that weight which occupied the same volume as two unit weights of hydrogen, and this assumption led him to double the equivalents accepted by Gmelin, making H = 1, O = 16, and C = 12, thereby agreeing with Berzelius, and also to halve the values given by Berzelius to many metals. Laurent generally agreed, except when the theory compelled the adoption of formulae containing fractions of atoms; in such cases he regarded the molecular weight as the weight occupying a volume equal to four unit weights of hydrogen. The bases upon which Gerhardt and Laurent founded their views were not sufficiently well grounded to lead to the acceptance of their results; Gerhardt himself returned to Gmelin’s equivalents in his Lehrbuch der Chemie (1853) as they were in such general use.
In 1860 there prevailed such a confusion of hypotheses as to the atom and molecule that a conference was held at Karlsruhe to discuss the situation. At the conclusion of the sitting, Lothar Meyer obtained a paper written by Stanislas Cannizzaro in 1858 wherein was found the final link required for the determination of atomic weights. This link was the full extension of Avogadro’s theory to all substances, Cannizzaro showing that chemical reactions in themselves would not suffice. He chose as his unit of reference the weight of an atom of hydrogen, i.e. the weight contained in a molecule of hydrochloric acid, thus differing from Avogadro who chose the weight of a hydrogen molecule. From a study of the free elements Cannizzaro showed that an element may have more than one molecular weight; for example, the molecular weight of sulphur varied with the temperature. And from the study of compounds he showed that each element occurred in a definite weight or in some multiple of this weight. He called this proportion the “atom,” since it invariably enters compounds without division, and the weight of this atom is the atomic weight. This generalization was of great value inasmuch as it permitted the deduction of the atomic weight of a non-gasifiable element from a study of the densities of its gasifiable compounds.
From the results obtained by Laurent and Gerhardt and their predecessors it immediately followed that, while an element could have but one atomic weight, it could have several equivalent weights. From a detailed study of organic compounds Gerhardt had promulgated a “theory of types” which represented a fusion of the older radical and type theories. This theory brought together, as it were, the most varied compounds, and stimulated inquiry into many fields. According to this theory, an element in a compound had a definite saturation capacity, an idea very old in itself, being framed in the law of multiple Valency. proportions. These saturation capacities were assiduously studied by Sir Edward Frankland, who from the investigation, not of simple inorganic compounds, but of the organo-metallic derivatives, determined the kernel of the theory of valency. Frankland showed that any particular element preferentially combined with a definite number (which might vary between certain limits) of other atoms; for example, some atoms always combined with one atom of oxygen, some with two, while with others two atoms entered into combination with one of oxygen. If an element or radical combined with one atom of hydrogen, it was termed monovalent; if with two (or with one atom of oxygen, which is equivalent to two atoms of hydrogen) it was divalent, and so on. The same views were expressed by Cannizzaro, and also by A.W. von Hofmann, who materially helped the acceptance of the doctrine by the lucid exposition in his Introduction to Modern Chemistry, 1865.
The recognition of the quadrivalency of carbon by A. Kekulé was the forerunner of his celebrated benzene theory in particular, and of the universal application of structural formulae to the representation of the most complex organic compounds equally lucidly as the representation of the simplest salts. Alexander Butlerow named the “structure theory,” and contributed much to the development of the subject. He defined structure “as the manner of the mutual linking of the atoms in the molecule,” but denied that any such structure could give information as to the orientation of the atoms in space. He regarded the chemical properties of a substance as due to (1) the chemical atoms composing it, and (2) the structure, and he asserted that while different compounds might have the same components (isomerism), yet only one compound could have a particular structure. Identity in properties necessitated identity in structure.
While the principle of varying valency laid down by Frankland is still retained, Butlerow’s view that structure had no spatial significance has been modified. The researches of L. Pasteur, 38 J.A. Le Bel, J. Wislicenus, van’t Hoff and others showed that substances having the same graphic formulae vary in properties and reactions, and consequently the formulae need modification in order to exhibit these differences. Such isomerism, named stereoisomerism (q.v.), has been assiduously developed during recent years; it prevails among many different classes of organic compounds and many examples have been found in inorganic chemistry.
The theory of valency as a means of showing similarity of properties and relative composition became a dominant feature of chemical theory, the older hypotheses of types, radicals, &c. being more or less discarded. We have seen how its Periodic law. utilization in the “structure theory” permitted great clarification, and attempts were not wanting for the deduction of analogies or a periodicity between elements. Frankland had recognized the analogies existing between the chemical properties of nitrogen, phosphorus, arsenic and antimony, noting that they act as tri- or penta-valent. Carbon was joined with silicon, zirconium and titanium, while boron, being trivalent, was relegated to another group. A general classification of elements, however, was not realized by Frankland, nor even by Odling, who had also investigated the question from the valency standpoint. The solution came about by arranging the elements in the order of their atomic weights, tempering the arrangement with the results deduced from the theory of valencies and experimental observations. Many chemists contributed to the establishment of such a periodicity, the greatest advances being made by John Newlands in England, Lothar Meyer in Germany, and D.J. Mendeléeff in St Petersburg. For the development of this classification see Element.
In the above sketch we have briefly treated the history of the main tendencies of our science from the earliest times to the establishment of the modern laws and principles. We Summary. have seen that the science took its origin in the arts practised by the Egyptians, and, having come under the influence of philosophers, it chose for its purpose the isolation of the quinta essentia, and subsequently the “art of making gold and silver.” This spirit gave way to the physicians, who regarded “chemistry as the art of preparing medicines,” a denotation which in turn succumbed to the arguments of Boyle, who regarded it as the “science of the composition of substances,” a definition which adequately fits the science to-day. We have seen how his classification of substances into elements and compounds, and the definitions which he assigned to these species, have similarly been retained; and how Lavoisier established the law of the “conservation of mass,” overthrew the prevailing phlogistic theory, and became the founder of modern chemistry by the overwhelming importance which he gave to the use of the balance. The development of the atomic theory and its concomitants—the laws of chemical combination and the notion of atoms and equivalents—at the hands of Dalton and Berzelius, the extension to the modern theory of the atom and molecule, and to atomic and molecular weights by Avogadro, Ampère, Dumas, Laurent, Gerhardt, Cannizzaro and others, have been noted. The structure of the molecule, which mainly followed investigations in organic compounds, Frankland’s conception of valency, and finally the periodic law, have also been shown in their chronological order. The principles outlined above constitute the foundations of our science; and although it may happen that experiments may be made with which they appear to be not in complete agreement, yet in general they constitute a body of working hypotheses of inestimable value.
Chemical Education.—It is remarkable that systematic instruction in the theory and practice of chemistry only received earnest attention in our academic institutions during the opening decades of the 19th century. Although for a long time lecturers and professors had been attached to universities, generally their duties had also included the study of physics, mineralogy and other subjects, with the result that chemistry received scanty encouragement. Of practical instruction there was none other than that to be gained in a few private laboratories and in the shops of apothecaries. The necessity for experimental demonstration and practical instruction, in addition to academic lectures, appears to have been urged by the French chemists L.N. Vauquelin, Gay Lussac, Thénard, and more especially by A.F. Fourcroy and G.F. Rouelle, while in England Humphry Davy expounded the same idea in the experimental demonstrations which gave his lectures their brilliant charm. But the real founder of systematic instruction in our science was Justus von Liebig, who, having accepted the professorship at Giessen in 1824, made his chemical laboratory and course of instruction the model of all others. He emphasized that the practical training should include (1) the qualitative and quantitative analysis of mixtures, (2) the preparation of substances according to established methods, (3) original research—a course which has been generally adopted. The pattern set by Liebig at Giessen was adopted by F. Wöhler at Göttingen in 1836, by R.W. Bunsen at Marburg in 1840, and by O.L. Erdmann at Leipzig in 1843; and during the ’fifties and ’sixties many other laboratories were founded. A new era followed the erection of the laboratories at Bonn and Berlin according to the plans of A.W. von Hofmann in 1867, and of that at Leipzig, designed by Kolbe in 1868. We may also mention the famous laboratory at Munich designed by A. von Baeyer in 1875.
In Great Britain the first public laboratory appears to have been opened in 1817 by Thomas Thomson at Glasgow. But the first important step in providing means whereby students could systematically study chemistry was the foundation of the College of Chemistry in 1845. This institution was taken over by the Government in 1853, becoming the Royal College of Chemistry, and incorporated with the Royal School of Mines; in 1881 the names were changed to the Normal School of Science and Royal School of Mines, and again in 1890 to the Royal College of Science. In 1907 it was incorporated in the Imperial College of Science and Technology. Under A.W. von Hofmann, who designed the laboratories and accepted the professorship in 1845 at the instigation of Prince Albert, and under his successor (in 1864) Sir Edward Frankland, this institution became one of the most important centres of chemical instruction. Oxford and Cambridge sadly neglected the erection of convenient laboratories for many years, and consequently we find technical schools and other universities having a far better equipment and offering greater facilities. In the provinces Victoria University at Manchester exercised the greater impetus, numbering among its professors Sir W.H. Perkin and Sir Henry Roscoe.
In America public laboratory instruction was first instituted at Yale College during the professorship of Benjamin Silliman. To the great progress made in recent years F.W. Clarke, W. Gibbs, E.W. Morley, Ira Remsen, and T.W. Richards have especially contributed.
In France the subject was almost entirely neglected until late in the 19th century. The few laboratories existing in the opening decades were ill-fitted, and the exorbitant fees constituted a serious bar to general instruction, for these institutions received little government support. In 1869 A. Wurtz reported the existence of only one efficient laboratory in France, namely the École Normale Supérieure, under the direction of H. Sainte Claire Deville. During recent years chemistry has become one of the most important subjects in the curriculum of technical schools and universities, and at the present time no general educational institution is complete until it has its full equipment of laboratories and lecture theatres.
Chemical Literature.—The growth of chemical literature since the publication of Lavoisier’s famous Traité de chimie in 1789, and of Berzelius’ Lehrbuch der Chemie in 1808-1818, has been enormous. These two works, and especially the latter, were the models followed by Thénard, Liebig, Strecker, Wöhler and many others, including Thomas Graham, upon whose Elements of Chemistry was founded Otto’s famous Lehrbuch der Chemie, to which H. Kopp contributed the general theoretical part, Kolbe the organic, and Buff and Zamminer the physico-chemical. Organic chemistry was especially developed by the publication of Gerhardt’s Traité de chimie organique in 1853-1856, and of Kekulé’s Lehrbuch der organischen Chemie in 1861-1882. General theoretical and physical chemistry was treated with conspicuous acumen by Lothar Meyer in his Moderne Theorien, by W. Ostwald in his Lehrbuch der allgem. Chemie (1884-1887), and by Nernst in his Theoretische Chemie. In English, Roscoe and Schorlemmer’s Treatise on Chemistry is a standard work; it records 39 a successful attempt to state the theories and facts of chemistry, not in condensed epitomes, but in an easily read form. The Traité de chimie minérale, edited by H. Moissan, and the Handbuch der anorganischen Chemie, edited by Abegg, are of the same type. O. Dammer’s Handbuch der anorganischen Chemie and F. Beilstein’s Handbuch der organischen Chemie are invaluable works of reference. Of the earlier encyclopaedias we may notice the famous Handwörterbuch der reinen und angewandten Chemie, edited by Liebig; Frémy’s Encyclopédie de chimie, Wurtz’s Dictionnaire de chimie pure et appliquée, Watts’ Dictionary of Chemistry, and Ladenburg’s Handwörterbuch der Chemie.
The number of periodicals devoted to chemistry has steadily increased since the early part of the 19th century. In England the most important is the Journal of the Chemical Society of London, first published in 1848. Since 1871 abstracts of papers appearing in the other journals have been printed. In 1904 a new departure was made in issuing Annual Reports, containing résumés of the most important researches of the year. The Chemical News, founded by Sir W. Crookes in 1860, may also be noted. In America the chief periodical is the American Chemical Journal, founded in 1879. Germany is provided with a great number of magazines. The Berichte der deutschen chemischen Gesellschaft, published by the Berlin Chemical Society, the Chemisches Centralblatt, which is confined to abstracts of papers appearing in other journals, the Zeitschrift für Chemie, and Liebig’s Annalen der Chemie are the most important of the general magazines. Others devoted to special phases are the Journal für praktische Chemie, founded by Erdmann in 1834, the Zeitschrift für anorganische Chemie and the Zeitschrift für physikalische Chemie. Mention may also be made of the invaluable Jahresberichte and the Jahrbuch der Chemie. In France, the most important journals are the Annales de chimie et de physique, founded in 1789 with the title Annales de chimie, and the Comptes rendus, published weekly by the Académie française since 1835.
II. General Principles
The substances with which the chemist has to deal admit of classification into elements and compounds. Of the former about eighty may be regarded as well characterized, although many more have been described.
Elements.—The following table gives the names, symbols and atomic weights of the perfectly characterized elements:—
International Atomic Weights, 1910.
| Name. | Symbol. | Atomic Weights. O=16. | Name. | Symbol. | Atomic Weights. O=16. | |||
| Aluminium | Al | 27. | 1 | Mercury | Hg | 200. | 0 | |
| Antimony | Sb | 120. | 2 | Molybdenum | Mo | 96. | 0 | |
| Argon | A | 39. | 9 | Neodymium | Nd | 144. | 3 | |
| Arsenic | As | 74. | 96 | Neon | Ne | 20 | ||
| Barium | Ba | 137. | 37 | Nickel | Ni | 58. | 68 | |
| Beryllium or | Be } | 9. | 1 | Nitrogen | N | 14. | 01 | |
| Glucinum | Gl } | Osmium | Os | 190. | 9 | |||
| Bismuth | Bi | 208. | 0 | Oxygen | O | 16. | 00 | |
| Boron | B | 11. | 0 | Palladium | Pd | 106. | 7 | |
| Bromine | Br | 79. | 92 | Phosphorus | P | 31. | 0 | |
| Cadmium | Cd | 112. | 40 | Platinum | Pt | 195. | 0 | |
| Caesium | Cs | 132. | 81 | Potassium | K | 39. | 10 | |
| Calcium | Ca | 40. | 09 | Praseodymium | Pr | 140. | 6 | |
| Carbon | C | 12. | 0 | Radium | Ra | 226. | 4 | |
| Cerium | Ce | 140. | 25 | Rhodium | Rh | 102. | 9 | |
| Chlorine | Cl | 35. | 46 | Rubidium | Rb | 85. | 45 | |
| Chromium | Cr | 52. | 0 | Ruthenium | Ru | 101. | 7 | |
| Cobalt | Co | 58. | 97 | Samarium | Sa | 150. | 4 | |
| Columbium | Cb } | 93. | 5 | Scandium | Sc | 44. | 1 | |
| or Niobium | Nb } | Selenium | Se | 79. | 2 | |||
| Copper | Cu | 63. | 57 | Silicon | Si | 28. | 3 | |
| Dysprosium | Dy | 162. | 5 | Silver | Ag | 107. | 88 | |
| Erbium | Er | 167. | 4 | Sodium | Na | 23. | 0 | |
| Europium | Eu | 152. | 0 | Strontium | Sr | 87. | 62 | |
| Fluorine | F | 19. | 0 | Sulphur | S | 32. | 07 | |
| Gadolinium | Gd | 157. | 3 | Tantalum | Ta | 181. | 0 | |
| Gallium | Ga | 69. | 9 | Tellurium | Te | 127. | 5 | |
| Germanium | Ge | 72. | 5 | Terbium | Tb | 159. | 2 | |
| Gold | Au | 197. | 2 | Thallium | Tl | 204. | 0 | |
| Helium | He | 4. | 0 | Thorium | Th | 232. | 42 | |
| Hydrogen | H | 1. | 008 | Thulium | Tm | 168. | 5 | |
| Indium | In | 114. | 8 | Tin | Sn | 119. | 0 | |
| Iodine | I | 126. | 92 | Titanium | Ti | 48. | 1 | |
| Iridium | Ir | 193. | 1 | Tungsten | W | 184. | 0 | |
| Iron | Fe | 55. | 85 | Uranium | U | 238. | 5 | |
| Krypton | Kr | 83. | 0 | Vanadium | V | 51. | 2 | |
| Lanthanum | La | 139. | 0 | Xenon | Xe | 130. | 7 | |
| Lead | Pb | 207. | 10 | Ytterbium | ||||
| Lithium | Li | 7. | 00 | (Neoytterbium) | Yb | 172 | ||
| Lutecium | Lu | 174 | Yttrium | Y | 89. | 0 | ||
| Magnesium | Mg | 24. | 32 | Zinc | Zn | 65. | 37 | |
| Manganese | Mn | 54. | 93 | Zirconium | Zr | 90. | 6 | |
The elements are usually divided into two classes, the metallic and the non-metallic elements; the following are classed as non-metals, and the remainder as metals:—
| Hydrogen | Oxygen | Boron | Neon |
| Chlorine | Sulphur | Carbon | Krypton |
| Bromine | Selenium | Silicon | Xenon |
| Iodine | Tellurium | Phosphorus | elium |
| Fluorine | Nitrogen | Argon |
Of these hydrogen, chlorine, fluorine, oxygen, nitrogen, argon, neon, krypton, xenon and helium are gases, bromine is a liquid, and the remainder are solids. All the metals are solids at ordinary temperatures with the exception of mercury, which is liquid. The metals are mostly bodies of high specific gravity; they exhibit, when polished, a peculiar brilliancy or metallic lustre, and they are good conductors of heat and electricity; the non-metals, on the other hand, are mostly bodies of low specific gravity, and bad conductors of heat and electricity, and do not exhibit metallic lustre. The non-metallic elements are also sometimes termed metalloids, but this appellation, which signifies metal-like substances (Gr. εἰδος, like), strictly belongs to certain elements which do not possess the properties of the true metals, although they more closely resemble them than the non-metals in many respects; thus, selenium and tellurium, which are closely allied to sulphur in their chemical properties, although bad conductors of heat and electricity, exhibit metallic lustre and have relatively high specific gravities. But when the properties of the elements are carefully contrasted together it is found that no strict line of demarcation can be drawn dividing them into two classes; and if they are arranged in a series, those which are most closely allied in properties being placed next to each other, it is observed that there is a more or less regular alteration in properties from term to term in the series.
When binary compounds, or compounds of two elements, are decomposed by an electric current, the two elements make their appearance at opposite poles. Those elements which are disengaged at the negative pole are termed electro-positive, or positive, or basylous elements, whilst those disengaged at the positive pole are termed electro-negative, or negative, or chlorous elements. But the difference between these two classes of elements is one of degree only, and they gradually merge into each other; moreover the electric relations of elements are not absolute, but vary according to the state of combination in which they exist, so that it is just as impossible to divide the elements into two classes according to this property as it is to separate them into two distinct classes of metals and non-metals. The following, however, are negative towards the remaining elements which are more or less positive:—Fluorine, chlorine, bromine, iodine, oxygen, sulphur, selenium, tellurium.
The metals may be arranged in a series according to their power of displacing one another in salt solutions, thus Cs, Rb, K, Na, Mg, Al, Mn, Zn, Cd, Tl, Fe, Co, Ni, Sn, Pb, (H), Sb, Bi, As, Cu, Hg, Ag, Pd, Pt, Au.
Elements which readily enter into reaction with each other, and which develop a large amount of heat on combination, are said to have a powerful affinity for each other. The tendency of positive elements to unite with positive elements, or of negative elements to unite with negative elements, is much less than that of positive elements to unite with negative elements, and the greater the difference in properties between two elements the more powerful is their affinity for each other. Thus, the affinity of hydrogen and oxygen for each other is extremely powerful, much heat being developed by the combination of these two elements; when binary compounds of oxygen are decomposed by the electric current, the oxygen invariably appears at the positive pole, being negative to all other elements, but the hydrogen of hydrogen compounds is always disengaged at the negative pole. Hydrogen and oxygen are, therefore, of very opposite natures, and this is well illustrated by the circumstance that oxygen combines, with very few exceptions, with all the remaining elements, whilst compounds of only a limited number with hydrogen have been obtained.
Compounds.—A chemical compound contains two or more 40 elements; consequently it should be possible to analyse it, i.e. separate it into its components, or to synthesize it, i.e. build it up from its components. In general, a compound has properties markedly different from those of the elements of which it is composed.
Laws of Chemical Combination.—A molecule may be defined as the smallest part of a substance which can exist alone; an atom as the smallest part of a substance which can exist in combination. The molecule of every compound must obviously contain at least two atoms, and generally the molecules of the elements are also polyatomic, the elements with monatomic molecules (at moderate temperatures) being mercury and the gases of the argon group. The laws of chemical combination are as follows:—
1. Law of Definite Proportions.—The same compound always contains the same elements combined together in the same mass proportion. Silver chloride, for example, in whatever manner it may be prepared, invariably consists of chlorine and silver in the proportions by weight of 35.45 parts of the former and 107.93 of the latter.
2. Law of Multiple Proportions.—When the same two elements combine together to form more than one compound, the different masses of one of the elements which unite with a constant mass of the other, bear a simple ratio to one another. Thus, 1 part by weight of hydrogen unites with 8 parts by weight of oxygen, forming water, and with 16 or 8 × 2 parts of oxygen, forming hydrogen peroxide. Again, in nitrous oxide we have a compound of 8 parts by weight of oxygen and 14 of nitrogen; in nitric oxide a compound of 16 or 8 × 2 parts of oxygen and 14 of nitrogen; in nitrous anhydride a compound of 24 or 8 × 3 parts of oxygen and 14 of nitrogen; in nitric peroxide a compound of 32 or 8 × 4 parts of oxygen and 14 of nitrogen; and lastly, in nitric anhydride a compound of 40 or 8 × 5 parts of oxygen and 14 of nitrogen.
3. Law of Reciprocal Proportions.—The masses of different elements which combine separately with one and the same mass of another element, are either the same as, or simple multiples of, the masses of these different elements which combine with each other. For instance, 35.45 parts of chlorine and 79.96 parts of bromine combine with 107.93 parts of silver; and when chlorine and bromine unite it is in the proportion of 35.45 parts of the former to 79.96 parts of the latter. Iodine unites with silver in the proportion of 126.97 parts to 107.93 parts of the latter, but it combines with chlorine in two proportions, viz. in the proportion of 126.97 parts either to 35.45 or to three times 35.45 parts of chlorine.
There is a fourth law of chemical combination which only applies to gases. This law states that:—gases combine with one another in simple proportions by volume, and the volume of the product (if gaseous) has a simple ratio to the volumes of the original mixtures; in other words, the densities of gases are simply related to their combining weights.
Nomenclature.—If a compound contains two atoms it is termed a binary compound, if three a ternary, if four a quaternary, and so on. Its systematic name is formed by replacing the last syllable of the electro-negative element by ide and prefixing the name of the other element. For example, compounds of oxygen are oxides, of chlorine, chlorides, and so on. If more than one compound be formed from the same two elements, the difference is shown by prefixing such words as mono-, di-, tri-, sesqui-, per-, sub-, &c., to the last part of the name, or the suffixes -ous and -ic may be appended to the name of the first element. For example take the oxides of nitrogen, N2O, NO, N2O3, NO2, N2O5; these are known respectively as nitrous oxide, nitric oxide, nitrogen trioxide, nitrogen peroxide and nitrogen pentoxide. The affixes -ous and sub- refer to the compounds containing more of the positive element, -ic and per- to those containing less.
An acid (q.v.) is a compound of hydrogen, which element can be replaced by metals, the hydrogen being liberated, giving substances named salts. An alkali or base is a substance which neutralizes an acid with the production of salts but with no evolution of hydrogen. A base may be regarded as water in which part of the hydrogen is replaced by a metal, or by a radical which behaves as a metal. (The term radical is given to a group of atoms which persist in chemical changes, behaving as if the group were an element; the commonest is the ammonium group, NH4, which forms salts similar to the salts of sodium and potassium.) If the acid contains no oxygen it is a hydracid, and its systematic name is formed from the prefix hydro- and the name of the other element or radical, the last syllable of which has been replaced by the termination -ic. For example, the acid formed by hydrogen and chlorine is termed hydrochloric acid (and sometimes hydrogen chloride). If an acid contains oxygen it is termed an oxyacid. The nomenclature of acids follows the same general lines as that for binary compounds. If one acid be known its name is formed by the termination -ic, e.g. carbonic acid; if two, the one containing the less amount of oxygen takes the termination -ous and the other the termination -ic, e.g. nitrous acid, HNO2, nitric acid, HNO3. If more than two be known, the one inferior in oxygen content has the prefix hypo- and the termination -ous, and the one superior in oxygen content has the prefix per- and the termination -ic. This is illustrated in the four oxyacids of chlorine, HClO, HClO2, HClO3, HClO4, which have the names hypochlorous, chlorous, chloric and perchloric acids. An acid is said to be monobasic, dibasic, tribasic, &c., according to the number of replaceable hydrogen atoms; thus HNO3 is monobasic, sulphuric acid H2SO4 dibasic, phosphoric acid H3PO4 tribasic.
An acid terminating in -ous forms a salt ending in -ite, and an oxyacid ending in -ic forms a salt ending in -ate. Thus the chlorine oxyacids enumerated above form salts named respectively hypochlorites, chlorites, chlorates and perchlorates. Salts formed from hydracids terminate in -ide, following the rule for binary compounds. An acid salt is one in which the whole amount of hydrogen has not been replaced by metal; a normal salt is one in which all the hydrogen has been replaced; and a basic salt is one in which part of the acid of the normal salt has been replaced by oxygen.
Chemical Formulae.—Opposite the name of each element in the second column of the above table, the symbol is given which is always employed to represent it. This symbol, however, not only represents the particular element, but a certain definite quantity of it. Thus, the letter H always stands for 1 atom or 1 part by weight of hydrogen, the letter N for 1 atom or 14 parts of nitrogen, and the symbol Cl for 1 atom or 35.5 parts of chlorine.8 Compounds are in like manner represented by writing the symbols of their constituent elements side by side, and if more than one atom of each element be present, the number is indicated by a numeral placed on the right of the symbol of the element either below or above the line. Thus, hydrochloric acid is represented by the formula HCl, that is to say, it is a compound of an atom of hydrogen with an atom of chlorine, or of 1 part by weight of hydrogen with 35.5 parts by weight of chlorine; again, sulphuric acid is represented by the formula H2SO4, which is a statement that it consists of 2 atoms of hydrogen, 1 of sulphur, and 4 of oxygen, and consequently of certain relative weights of these elements. A figure placed on the right of a symbol only affects the symbol to which it is attached, but when figures are placed in front of several symbols all are affected by it, thus 2H2SO4 means H2SO4 taken twice.
The distribution of weight in chemical change is readily expressed in the form of equations by the aid of these symbols; the equation
2HCl + Zn = ZnCl2 + H2,
for example, is to be read as meaning that from 73 parts of hydrochloric acid and 65 parts of zinc, 136 parts of zinc chloride and 2 parts of hydrogen are produced. The + sign is invariably employed in this way either to express combination or action upon, the meaning usually attached to the use of the sign = being that from such and such bodies such and such other bodies are formed. 41
Usually, when the symbols of the elements are written or printed with a figure to the right, it is understood that this indicates a molecule of the element, the symbol alone representing an atom. Thus, the symbols H2 and P4 indicate that the molecules of hydrogen and phosphorus respectively contain 2 and 4 atoms. Since, according to the molecular theory, in all cases of chemical change the action is between molecules, such symbols as these ought always to be employed. Thus, the formation of hydrochloric acid from hydrogen and chlorine is correctly represented by the equation
H2 + Cl2 = 2HCl;
that is to say, a molecule of hydrogen and a molecule of chlorine give rise to two molecules of hydrochloric acid; whilst the following equation merely represents the relative weights of the elements which enter into reaction, and is not a complete expression of what is supposed to take place:—
H + Cl = HCl.
In all cases it is usual to represent substances by formulae which to the best of our knowledge express their molecular composition in the state of gas, and not merely the relative number of atoms which they contain; thus, acetic acid consists of carbon, hydrogen and oxygen in the proportion of one atom of carbon, two of hydrogen, and one of oxygen, but its molecular weight corresponds to the formula C2H4O2, which therefore is always employed to represent acetic acid. When chemical change is expressed with the aid of molecular formulae not only is the distribution of weight represented, but by the mere inspection of the symbols it is possible to deduce from the law of gaseous combination mentioned above, the relative volumes which the agents and resultants occupy in the state of gas if measured at the same temperature and under the same pressure. Thus, the equation
2H2 + O2= 2H2O
not only represents that certain definite weights of hydrogen and oxygen furnish a certain definite weight of the compound which we term water, but that if the water in the state of gas, the hydrogen and the oxygen are all measured at the same temperature and pressure, the volume occupied by the oxygen is only half that occupied by the hydrogen, whilst the resulting water-gas will only occupy the same volume as the hydrogen. In other words, 2 volumes of oxygen and 4 volumes of hydrogen furnish 4 volumes of water-gas. A simple equation like this, therefore, when properly interpreted, affords a large amount of information. One other instance may be given; the equation
2NH3 = N2 + 3H2
represents the decomposition of ammonia gas into nitrogen and hydrogen gases by the electric spark, and it not only conveys the information that a certain relative weight of ammonia, consisting of certain relative weights of hydrogen and nitrogen, is broken up into certain relative weights of hydrogen and nitrogen, but also that the nitrogen will be contained in half the space which contained the ammonia, and that the volume of the hydrogen will be one and a half times as great as that of the original ammonia, so that in the decomposition of ammonia the volume becomes doubled.
Formulae which merely express the relative number of atoms of the different elements present in a compound are termed empirical formulae, and the formulae of all compounds whose molecular weights are undetermined are necessarily empirical. The molecular formula of a compound, however, is always a simple multiple of the empirical formula, if not identical with it; thus, the empirical formula of acetic acid is CH2O, and its molecular formula is C2H4O2, or twice CH2O. In addition to empirical and molecular formulae, chemists are in the habit of employing various kinds of rational formulae, called structural, constitutional or graphic formulae, &c., which not only express the molecular composition of the compounds to which they apply, but also embody certain assumptions as to the manner in which the constituent atoms are arranged, and convey more or less information with regard to the nature of the compound itself, viz. the class to which it belongs, the manner in which it is formed, and the behaviour it will exhibit under various circumstances. Before explaining these formulae it will be necessary, however, to consider the differences in combining power exhibited by the various elements.
Valency.—It is found that the number of atoms of a given element, of chlorine, for example, which unite with an atom of each of the other elements is very variable. Thus, hydrogen unites with but a single atom of chlorine, zinc with two, boron with three, silicon with four, phosphorus with five and tungsten with six. Those elements which are equivalent in combining or displacing power to a single atom of hydrogen are said to be univalent or monad elements; whilst those which are equivalent to two atoms of hydrogen are termed bivalent or dyad elements; and those equivalent to three, four, five or six atoms of hydrogen triad, tetrad, pentad or hexad elements. But not only is the combining power or valency (atomicity) of the elements different, it is also observed that one element may combine with another in several proportions, or that its valency may vary; for example, phosphorus forms two chlorides represented by the formulae PCl3 and PCl5, nitrogen the series of oxides represented by the formulae N2O, NO, (N2O3), N2O4, N2O5, molybdenum forms the chlorides MoCl2, MoCl3, MoCl4, MoCl5, MoCl6(?), and tungsten the chlorides WCl2, WCl4, WCl5, WCl6.
In explanation of these facts it is supposed that each element has a certain number of “units of affinity,” which may be entirely, or only in part, engaged when it enters into combination with other elements; and in those cases in which the entire number of units of affinity are not engaged by other elements, it is supposed that those which are thus disengaged neutralize each other, as it were. For example, in phosphorus pentachloride the five units of affinity possessed by the phosphorus atom are satisfied by the five monad atoms of chlorine, but in the trichloride two are disengaged, and, it may be supposed, satisfy each other. Compounds in which all the units of affinity of the contained elements are engaged are said to be saturated, whilst those in which the affinities of the contained elements are not all engaged by other elements are said to be unsaturated. According to this view, it is necessary to assume that, in all unsaturated compounds, two, or some even number of affinities are disengaged; and also that all elements which combine with an even number of monad atoms cannot combine with an odd number, and vice versa,—in other words, that the number of units of affinity active in the case of any given element must be always either an even or an odd number, and that it cannot be at one time an even and at another an odd number. There are, however, a few remarkable exceptions to this “law.” Thus, it must be supposed that in nitric oxide, NO, an odd number of affinities are disengaged, since a single atom of dyad oxygen is united with a single atom of nitrogen, which in all its compounds with other elements acts either as a triad or pentad. When nitric peroxide, N2O4, is converted into gas, it decomposes, and at about 180° C. its vapour entirely consists of molecules of the composition NO2; while at temperatures between this and 0° C. it consists of a mixture in different proportions of the two kinds of molecules, N2O4 and NO2. The oxide NO2 must be regarded as another instance of a compound in which an odd number of affinities of one of the contained elements are disengaged, since it contains two atoms of dyad oxygen united with a single atom of triad or pentad nitrogen. Again, when tungsten hexachloride is converted into vapour it is decomposed into chlorine and a pentachloride, having a normal vapour density, but as in the majority of its compounds tungsten acts as a hexad, we apparently must regard its pentachloride as a compound in which an odd number of free affinities are disengaged. Hitherto no explanation has been given of these exceptions to what appears to be a law of almost universal application, viz. that the sum of the units of affinity of all the atoms in a compound is an even number.
The number of units of affinity active in the case of any particular element is largely dependent, however, upon the nature of the element or elements with which it is associated. Thus, an atom of iodine only combines with one of hydrogen, 42 but may unite with three of chlorine, which never combines with more than a single atom of hydrogen; an atom of phosphorus unites with only three atoms of hydrogen, but with five of chlorine, or with four of hydrogen and one of iodine; and the chlorides corresponding to the higher oxides of lead, nickel, manganese and arsenic, PbO2, Ni2O3, MnO2 and AS2O5 do not exist as stable compounds, but the lower chlorides, PbCl2, NiCl2, MnCl2 and AsCl3, are very stable.
The valency of an element is usually expressed by dashes or Roman numerals placed on the right of its symbol, thus: H′, O′′, B′′′, CIV, PV, MoVI; but in constructing graphic formulae the symbols of the elements are written with as many lines attached to each symbol as the element which it represents has units of affinity.
The periodic law (see Element) permits a grouping of the elements according to their valency as follows:—Group O.: helium, neon, argon, krypton and xenon appear to be devoid of valency. Group I.: the alkali metals Li, Na, K, Rb, Cs, and also Ag, monovalent; Cu, monovalent and divalent; Au, monovalent and trivalent. Group II.: the alkaline earth metals Ca, Sr, Ba, and also Be (Gl), Mg, Zn, Cd, divalent; Hg, monovalent and divalent. Group III.: B, trivalent; Al, trivalent, but possibly also tetra- or penta-valent; Ga, divalent and trivalent; In, mono-, di- and tri-valent; Tl, monovalent and trivalent. Group IV.: C, Si, Ge, Zr, Th, tetravalent; Ti, tetravalent and hexavalent; Sn, Pb, divalent and tetravalent; Ce, trivalent and tetravalent. Group V.: N, trivalent and pentavalent, but divalent in nitric oxide; P, As, Sb, Bi, trivalent and pentavalent, the last being possibly divalent in BiO and BiCl2. Group VI.: O, usually divalent, but tetravalent and possibly hexavalent in oxonium and other salts; S, Se, Te, di-, tetra- and hexa-valent; Cr, di-, tri- and hexa-valent; Mo, W, di-, tri-, tetra-, penta- and hexa-valent. Group VII.: H(?), monovalent; the halogens F, Cl, Br, I, usually monovalent, but possibly also tri- and pentavalent; Mn, divalent and trivalent, and possibly heptavalent in permanganates. Group VIII.: Fe, Co, divalent and trivalent; Ni, divalent; Os, Ru, hexavalent and octavalent; Pd, Pt, divalent and tetravalent; Ir, tri-, tetra- and hexa-valent. (See also Valency.)
Constitutional Formulae.—Graphic or constitutional formulae are employed to express the manner in which the constituent atoms of compounds are associated together; for example, the trioxide of sulphur is usually regarded as a compound of an atom of hexad sulphur with three atoms of dyad oxygen, and this hypothesis is illustrated by the graphic formula

When this oxide is brought into contact with water it combines with it forming sulphuric acid, H2SO4.
In this compound only two of the oxygen atoms are wholly associated with the sulphur atom, each of the remaining oxygen atoms being united by one of its affinities to the sulphur atoms, and by the remaining affinity to an atom of hydrogen; thus—

The graphic formula of a sulphate is readily deduced by remembering that the hydrogen atoms are partially or entirely replaced. Thus acid sodium sulphate, normal sodium sulphate, and zinc sulphate have the formulae

Again, the reactions of acetic acid, C2H4O2, show that the four atoms of hydrogen which it contains have not all the same function, and also that the two atoms of oxygen have different functions; the graphic formula which we are led to assign to acetic acid, viz.

serves in a measure to express this, three of the atoms of hydrogen being represented as associated with one of the atoms of carbon, whilst the fourth atom is associated with an atom of oxygen which is united by a single affinity to the second atom of carbon, to which, however, the second atom of oxygen is united by both of its affinities. It is not to be supposed that there are any actual bonds of union between the atoms; graphic formulae such as these merely express the hypothesis that certain of the atoms in a compound come directly within the sphere of attraction of certain other atoms, and only indirectly within the sphere of attraction of others,—an hypothesis to which chemists are led by observing that it is often possible to separate a group of elements from a compound, and to displace it by other elements or groups of elements.
Rational formulae of a much simpler description than these graphic formulae are generally employed. For instance, sulphuric acid is usually represented by the formula SO2(OH)2, which indicates that it may be regarded as a compound of the group SO2 with twice the group OH. Each of these OH groups is equivalent in combining or displacing power to a monad element, since it consists of an atom of dyad oxygen associated with a single atom of monad hydrogen, so that in this case the SO2 group is equivalent to an atom of a dyad element. This formula for sulphuric acid, however, merely represents such facts as that it is possible to displace an atom of hydrogen and an atom of oxygen in sulphuric acid by a single atom of chlorine, thus forming the compound SO3HCl; and that by the action of water on the compound SO2Cl2 twice the group OH, or water minus an atom of hydrogen, is introduced in place of the two monad atoms of chlorine—
SO2Cl2 + 2HOH = SO2(OH)2 + 2HCl.
Water. Sulphuric acid.
Constitutional formulae like these, in fact, are nothing more than symbolic expressions of the character of the compounds which they represent, the arrangement of symbols in a certain definite manner being understood to convey certain information with regard to the compounds represented.
Groups of two or more atoms like SO2 and OH, which are capable of playing the part of elementary atoms (that is to say, which can be transferred from compound to compound), are termed compound radicals, the elementary atoms being simple radicals. Thus, the atom of hydrogen is a monad simple radical, the atom of oxygen a dyad simple radical, whilst the group OH is a monad compound radical.
It is often convenient to regard compounds as formed upon certain types; alcohol, for example, may be said to be a compound formed upon the water type, that is to say, a compound formed from water by displacing one of the atoms of hydrogen by the group of elements C2H5, thus—
| O | { | H | O | { | C2H5 |
| H | H | ||||
| Water | Alcohol. | ||||
Constitutional formulae become of preponderating importance when we consider the more complicated inorganic and especially organic compounds. Their full significance is treated in the section of this article dealing with organic chemistry, and in the articles Isomerism and Stereo-isomerism.
Chemical Action.—Chemical change or chemical action may be said to take place whenever changes occur which involve an alteration in the composition of molecules, and may be the result of the action of agents such as heat, electricity or light, or of two or more elements or compounds upon each other.
Three kinds of changes are to be distinguished, viz. changes which involve combination, changes which involve decomposition or separation, and changes which involve at the same time both decomposition and combination. Changes of the first and second kind, according to our views of the constitution of molecules, are probably of very rare occurrence; in fact, chemical action appears almost always to involve the occurrence of both these kinds of change, for, as already pointed out, we must assume that the molecules of hydrogen, oxygen and several other elements are diatomic, or that they consist of two atoms. Indeed, it appears probable that with few exceptions the elements 43 are all compounds of similar atoms united together by one or more units of affinity, according to their valencies. If this be the case, however, it is evident that there is no real distinction between the reactions which take place when two elements combine together and when an element in a compound is displaced by another. The combination, as it is ordinarily termed, of chlorine with hydrogen, and the displacement of iodine in potassium iodide by the action of chlorine, may be cited as examples; if these reactions are represented, as such reactions very commonly are, by equations which merely express the relative weights of the bodies which, enter, into reaction, and of the products, thus—
| H | + | Cl | = | HCl |
| Hydrogen. | Chlorine. | Hydrochloric acid. |
| KI | + | Cl | = | KCl | + | I |
| Potassium iodide. | Chlorine. | Potassium chloride. | Iodine. |
they appear to differ in character; but if they are correctly represented by molecular equations, or equations which express the relative number of molecules which enter into reaction and which result from the reaction, it will be obvious that the character of the reaction is substantially the same in both cases, and that both are instances of the occurrence of what is ordinarily termed double decomposition—
| H2 | + | Cl2 | = | 2HCl |
| Hydrogen. | Chlorine. | Hydrochloric acid. |
| 2KI | + | Cl2 | = | 2KCl | + | I2. |
| Potassium iodide. | Chlorine. | Potassium chloride. | Iodine. |
In all cases of chemical change energy in the form of heat is either developed or absorbed, and the amount of heat developed or absorbed in a given reaction is as definite as are the weights of the substance engaged in the reaction. Thus, in the production of hydrochloric acid from hydrogen and chlorine 22,000 calories are developed; in the production of hydrobromic acid from hydrogen and bromine, however, only 8440 calories are developed; and in the formation of hydriodic acid from hydrogen and iodine 6040 calories are absorbed.
This difference in behaviour of the three elements, chlorine, bromine and iodine, which in many respects exhibit considerable resemblance, may be explained in the following manner. We may suppose that in the formation of gaseous hydrochloric acid from gaseous chlorine and hydrogen, according to the equation
H2 + Cl2 = HCl + HCl,
a certain amount of energy is expended in separating the atoms of hydrogen in the hydrogen molecule, and the atoms of chlorine in the chlorine molecule, from each other; but that heat is developed by the combination of the hydrogen atoms with the chlorine atoms, and that, as more energy is developed by the union of the atoms of hydrogen and chlorine than is expended in separating the hydrogen atoms from each other and the chlorine atoms from one another, the result of the action of the two elements upon each other is the development of heat,—the amount finally developed in the reaction being the difference between that absorbed in decomposing the elementary molecules and that developed by the combination of the atoms of chlorine and hydrogen. In the formation of gaseous hydrobromic acid from liquid bromine and gaseous hydrogen—
H2 + Br2 = HBr + HBr,
in addition to the energy expended in decomposing the hydrogen and bromine molecules, energy is also expended in converting the liquid bromine into the gaseous condition, and probably less heat is developed by the combination of bromine and hydrogen than by the combination of chlorine and hydrogen, so that the amount of heat finally, developed is much less than is developed in the formation of hydrochloric acid. Lastly, in the production of gaseous hydriodic acid from hydrogen and solid iodine—
H2 + I2 = HI + HI,
so much energy is expended in the decomposition of the hydrogen and iodine molecules and in the conversion of the iodine into the gaseous condition, that the heat which it may be supposed is developed by the combination of the hydrogen and iodine atoms is insufficient to balance the expenditure, and the final result is therefore negative; hence it is necessary in forming hydriodic acid from its elements to apply heat continuously.
These compounds also afford examples of the fact that, generally speaking, those compounds are most readily formed, and are most stable, in the formation of which the most heat is developed. Thus, chlorine enters into reaction with hydrogen, and removes hydrogen from hydrogenized bodies, far more readily than bromine; and hydrochloric acid is a far more stable substance than hydrobromic acid, hydriodic acid being greatly inferior even to hydrobromic acid in stability. Compounds formed with the evolution of heat are termed exothermic, while those formed with an absorption are termed endothermic. Explosives are the commonest examples of endothermic compounds.
When two substances which by their action upon each other develop much heat enter into reaction, the reaction is usually complete without the employment of an excess of either; for example, when a mixture of hydrogen and oxygen, in the proportions to form water—
2H2 + O2 = 2OH2,
is exploded, it is entirely converted into water. This is also the case if two substances are brought together in solution, by the action of which upon each other a third body is formed which is insoluble in the solvent employed, and which also does not tend to react upon any of the substances present; for instance, when a solution of a chloride is added to a solution of a silver salt, insoluble silver chloride is precipitated, and almost the whole of the silver is removed from solution, even if the amount of the chloride employed be not in excess of that theoretically required.
But if there be no tendency to form an insoluble compound, Or one which is not liable to react upon any of the other substances present, this is no longer the case. For example, when a solution of a ferric salt is added to a solution of potassium thiocyanate, a deep red coloration is produced, owing to the formation of ferric thiocyanate. Theoretically the reaction takes place in the case of ferric nitrate in the manner represented by the equation
| Fe(NO3)3 | + | 3KCNS | = | Fe(CNS)3 | + | 3KNO3; |
| Ferric nitrate. | Potassium thiocyanate. | Ferric thiocyanate. | Potassium nitrate. |
but it is found that even when more than sixty times the amount of potassium thiocyanate required by this equation is added, a portion of the ferric nitrate still remains unconverted, doubtless owing to the occurrence of the reverse change—
Fe(CNS)3 + 3KNO3 = Fe(NO3)3 + 3KCNS.
In this, as in most other cases in which substances act upon one another under such circumstances that the resulting compounds are free to react, the extent to which the different kinds of action which may occur take place is dependent upon the mass of the substances present in the mixture. As another instance of this kind, the decomposition of bismuth chloride by water may be cited. If a very large quantity of water be added, the chloride is entirely decomposed in the manner represented by the equation—
| BiCl3 | + | OH2 | = | BiOCl | + | 2HCl, |
| Bismuth chloride. | Bismuth oxychloride. |
the oxychloride being precipitated; but if smaller quantities of water be added the decomposition is incomplete, and it is found that the extent to which decomposition takes place is proportional to the quantity of water employed, the decomposition being incomplete, except in presence of large quantities of water, because of the occurrence of the reverse action—
BiOCl + 2HCl = BiCl3 + OH2.
Chemical change which merely involves simple decomposition is thus seen to be influenced by the masses of the reacting substances and the presence of the products of decomposition; in other words the system of reacting substances and resultants form a mixture in which chemical action has apparently ceased, or the system is in equilibrium. Such reactions are termed reversible (see Chemical Action). 44
III. Inorganic Chemistry
Inorganic chemistry is concerned with the descriptive study of the elements and their compounds, except those of carbon. Reference should be made to the separate articles on the different elements and the more important compounds for their preparation, properties and uses. In this article the development of this branch of the science is treated historically.
The earliest discoveries in inorganic chemistry are to be found in the metallurgy, medicine and chemical arts of the ancients. The Egyptians obtained silver, iron, copper, lead, zinc and tin, either pure or as alloys, by smelting the ores; mercury is mentioned by Theophrastus (c. 300 B.C.). The manufacture of glass, also practised in Egypt, demanded a knowledge of sodium or potassium carbonates; the former occurs as an efflorescence on the shores of certain lakes; the latter was obtained from wood ashes. Many substances were used as pigments: Pliny records white lead, cinnabar, verdigris and red oxide of iron; and the preparation of coloured glasses and enamels testifies to the uses to which these and other substances were put. Salts of ammonium were also known; while alum was used as a mordant in dyeing. Many substances were employed in ancient medicine: galena was the basis of a valuable Egyptian cosmetic and drug; the arsenic sulphides, realgar and orpiment, litharge, alum, saltpetre, iron rust were also used. Among the Arabian and later alchemists we find attempts made to collate compounds by specific properties, and it is to these writers that we are mainly indebted for such terms as “alkali,” “sal,” &c. The mineral acids, hydrochloric, nitric and sulphuric acids, and also aqua regia (a mixture of hydrochloric and nitric acids) were discovered, and the vitriols, alum, saltpetre, sal-ammoniac, ammonium carbonate, silver nitrate (lunar caustic) became better known. The compounds of mercury attracted considerable attention, mainly on account of their medicinal properties; mercuric oxide and corrosive sublimate were known to pseudo-Geber, and the nitrate and basic sulphate to “Basil Valentine.” Antimony and its compounds formed the subject of an elaborate treatise ascribed to this last writer, who also contributed to our knowledge of the compounds of zinc, bismuth and arsenic. All the commonly occurring elements and compounds appear to have received notice by the alchemists; but the writings assigned to the alchemical period are generally so vague and indefinite that it is difficult to determine the true value of the results obtained.
In the succeeding iatrochemical period, the methods of the alchemists were improved and new ones devised. Glauber showed how to prepare hydrochloric acid, spiritus salis, by heating rock-salt with sulphuric acid, the method in common use to-day; and also nitric acid from saltpetre and arsenic trioxide. Libavius obtained sulphuric acid from many substances, e.g. alum, vitriol, sulphur and nitric acid, by distillation. The action of these acids on many metals was also studied; Glauber obtained zinc, stannic, arsenious and cuprous chlorides by dissolving the metals in hydrochloric acid, compounds hitherto obtained by heating the metals with corrosive sublimate, and consequently supposed to contain mercury. The scientific study of salts dates from this period, especial interest being taken in those compounds which possessed a medicinal or technical value. In particular, the salts of potassium, sodium and ammonium were carefully investigated, but sodium and potassium salts were rarely differentiated.9 The metals of the alkaline-earths were somewhat neglected; we find Georg Agricola considering gypsum (calcium sulphate) as a compound of lime, while calcium nitrate and chloride became known at about the beginning of the 17th century. Antimonial, bismuth and arsenical compounds were assiduously studied, a direct consequence of their high medicinal importance; mercurial and silver compounds were investigated for the same reason. The general tendency of this period appears to have taken the form of improving and developing the methods of the alchemists; few new fields were opened, and apart from a more complete knowledge of the nature of salts, no valuable generalizations were attained.
The discovery of phosphorus by Brand, a Hamburg alchemist, in 1669 excited chemists to an unwonted degree; it was also independently prepared by Robert Boyle and J. Kunckel, Brand having kept his process secret. Towards the middle of the 18th century two new elements were isolated: cobalt by G. Brandt in 1742, and nickel by A.F. Cronstedt in 1750. These discoveries were followed by Daniel Rutherford’s isolation of nitrogen in 1772, and by K. Scheele’s isolation of chlorine and oxygen in 1774 (J. Priestley discovered oxygen independently at about the same time), and his investigation of molybdic and tungstic acids in the following year; metallic molybdenum was obtained by P.J. Hjelm in 1783, and tungsten by Don Fausto d’Elhuyar; manganese was isolated by J.G. Gahn in 1774. In 1784 Henry Cavendish thoroughly examined hydrogen, establishing its elementary nature; and he made the far-reaching discovery that water was composed of two volumes of hydrogen to one of oxygen.
The phlogistic theory, which pervaded the chemical doctrine of this period, gave rise to continued study of the products of calcination and combustion; it thus happened that the knowledge of oxides and oxidation products was considerably developed. The synthesis of nitric acid by passing electric sparks through moist air by Cavendish is a famous piece of experimental work, for in the first place it determined the composition of this important substance, and in the second place the minute residue of air which would not combine, although ignored for about a century, was subsequently examined by Lord Rayleigh and Sir William Ramsay, who showed that it consists of a mixture of elementary substances—argon, krypton, neon and xenon (see Argon).
The 18th century witnessed striking developments in pneumatic chemistry, or the chemistry of gases, which had been begun by van Helmont, Mayow, Hales and Boyle. Gases formerly considered to be identical came to be clearly distinguished, and many new ones were discovered. Atmospheric air was carefully investigated by Cavendish, who showed that it consisted of two elementary constituents: nitrogen, which was isolated by Rutherford in 1772, and oxygen, isolated in 1774; and Black established the presence, in minute quantity, of carbon dioxide (van Helmont’s gas sylvestre). Of the many workers in this field, Priestley occupies an important position. A masterly device, initiated by him, was to collect gases over mercury instead of water; this enabled him to obtain gases previously only known in solution, such as ammonia, hydrochloric acid, silicon fluoride and sulphur dioxide. Sulphuretted hydrogen and nitric oxide were discovered at about the same time.
Returning to the history of the discovery of the elements and their more important inorganic compounds, we come in 1789 to M.H. Klaproth’s detection of a previously unknown constituent of the mineral pitchblende. He extracted a substance to which he assigned the character of an element, naming it uranium (from Οὐρανός, heaven); but it was afterwards shown by E.M. Péligot, who prepared the pure metal, that Klaproth’s product was really an oxide. This element was investigated at a later date by Sir Henry Roscoe, and more thoroughly and successfully by C. Zimmermann and Alibegoff. Pitchblende attained considerable notoriety towards the end of the 19th century on account of two important discoveries. The first, made by Sir William Ramsay in 1896, was that the mineral evolved a peculiar gas when treated with sulphuric acid; this gas, helium (q.v.), proved to be identical with a constituent of the sun’s atmosphere, detected as early as 1868 by Sir Norman Lockyer during a spectroscopic examination of the sun’s chromosphere. The second discovery, associated with the Curies, is that of the peculiar properties exhibited by the impure substance, and due to a constituent named radium. The investigation of this substance and its properties (see Radioactivity) has proceeded so far as to render it probable that the theory of the unalterability 45 of elements, and also the hitherto accepted explanations of various celestial phenomena—the source of solar energy and the appearances of the tails of comets—may require recasting.
In the same year as Klaproth detected uranium, he also isolated zirconia or zirconium oxide from the mineral variously known as zircon, hyacinth, jacynth and jargoon; but he failed to obtain the metal, this being first accomplished some years later by Berzelius, who decomposed the double potassium zirconium fluoride with potassium. In the following year, 1795, Klaproth announced the discovery of a third new element, titanium; its isolation (in a very impure form), as in the case of zirconium, was reserved for Berzelius.
Passing over the discovery of carbon disulphide by W.A. Lampadius in 1796, of chromium by L.N. Vauquelin in 1797, and Klaproth’s investigation of tellurium in 1798, the next important series of observations was concerned with platinum and the allied metals. Platinum had been described by Antonio de Ulloa in 1748, and subsequently discussed by H.T. Scheffer in 1752. In 1803 W.H. Wollaston discovered palladium, especially interesting for its striking property of absorbing (“occluding”) as much as 376 volumes of hydrogen at ordinary temperatures, and 643 volumes at 90°. In the following year he discovered rhodium; and at about the same time Smithson Tennant added two more to the list—iridium and osmium; the former was so named from the changing tints of its oxides (ῒρις, rainbow), and the latter from the odour of its oxide (ὀσμή, smell). The most recently discovered “platinum metal,” ruthenium, was recognized by C.E. Claus in 1845. The great number and striking character of the compounds of this group of metals have formed the subject of many investigations, and already there is a most voluminous literature. Berzelius was an early worker in this field; he was succeeded by Bunsen, and Deville and Debray, who worked out the separation of rhodium; and at a later date by P.T. Cleve, the first to make a really thorough study of these elements and their compounds. Of especial note are the curious compounds formed by the union of carbon monoxide with platinous chloride, discovered by Paul Schützenberger and subsequently investigated by F.B. Mylius and F. Foerster and by Pullinger; the phosphoplatinic compounds formed primarily from platinum and phosphorus pentachloride; and also the “ammino” compounds, formed by the union of ammonia with the chloride, &c., of these metals, which have been studied by many chemists, especially S.M. Jörgensen. Considerable uncertainty existed as to the atomic weights of these metals, the values obtained by Berzelius being doubtful. K.F.O. Seubert redetermined this constant for platinum, osmium and iridium; E.H. Keiser for palladium, and A.A. Joly for ruthenium.
The beginning of the 19th century witnessed the discovery of certain powerful methods for the analysis of compounds and the isolation of elements. Berzelius’s investigation of the action of the electric current on salts clearly demonstrated the invaluable assistance that electrolysis could render to the isolator of elements; and the adoption of this method by Sir Humphry Davy for the analysis of the hydrates of the metals of the alkalis and alkaline earths, and the results which he thus achieved, established its potency. In 1808 Davy isolated sodium and potassium; he then turned his attention to the preparation of metallic calcium, barium, strontium and magnesium. Here he met with greater difficulty, and it is to be questioned whether he obtained any of these metals even in an approximately pure form (see Electrometallurgy). The discovery of boron by Gay Lussac and Davy in 1809 led Berzelius to investigate silica (silex). In the following year he announced that silica was the oxide of a hitherto unrecognized element, which he named silicium, considering it to be a metal. This has proved to be erroneous; it is non-metallic in character, and its name was altered to silicon, from analogy with carbon and boron. At the same time Berzelius obtained the element, in an impure condition, by fusing silica with charcoal and iron in a blast furnace; its preparation in a pure condition he first accomplished in 1823, when he invented the method of heating double potassium fluorides with metallic potassium. The success which attended his experiments in the case of silicon led him to apply it to the isolation of other elements. In 1824 he obtained zirconium from potassium zirconium fluoride; the preparation of (impure) titanium quickly followed, and in 1828 he obtained thorium. A similar process, and equally efficacious, was introduced by F. Wöhler in 1827. It consisted in heating metallic chlorides with potassium, and was first applied to aluminium, which was isolated in 1827; in the following year, beryllium chloride was analysed by the same method, beryllium oxide (berylla or glucina) having been known since 1798, when it was detected by L. N. Vauquelin in the gem-stone beryl.
In 1812 B. Courtois isolated the element iodine from “kelp,” the burnt ashes of marine plants. The chemical analogy of this substance to chlorine was quickly perceived, especially after its investigation by Davy and Gay Lussac. Cyanogen, a compound which in combination behaved very similarly to chlorine and iodine, was isolated in 1815 by Gay Lussac. This discovery of the first of the then-styled “compound radicals” exerted great influence on the prevailing views of chemical composition. Hydrochloric acid was carefully investigated at about this time by Davy, Faraday and Gay Lussac, its composition and the elementary nature of chlorine being thereby established.
In 1817 F. Stromeyer detected a new metallic element, cadmium, in certain zinc ores; it was rediscovered at subsequent dates by other observers and its chemical resemblance to zinc noticed. In the same year Berzelius discovered selenium in a deposit from sulphuric acid chambers, his masterly investigation including a study of the hydride, oxides and other compounds. Selenic acid was discovered by E. Mitscherlich, who also observed the similarity of the crystallographic characters of selenates and sulphates, which afforded valuable corroboration of his doctrine of isomorphism. More recent and elaborate investigations in this direction by A.E.H. Tutton have confirmed this view.
In 1818 L.J. Thénard discovered hydrogen dioxide, one of the most interesting inorganic compounds known, which has since been carefully investigated by H.E. Schöne, M. Traube, Wolfenstein and others. About the same time, J.A. Arfvedson, a pupil of Berzelius, detected a new element, which he named lithium, in various minerals—notably petalite. Although unable to isolate the metal, he recognized its analogy to sodium and potassium; this was confirmed by R. Bunsen and A. Matthiessen in 1855, who obtained the metal by electrolysis and thoroughly examined it and its compounds. Its crimson flame-coloration was observed by C.G. Gmelin in 1818.
The discovery of bromine in 1826 by A.J. Balard completed for many years Berzelius’s group of “halogen” elements; the remaining member, fluorine, notwithstanding many attempts, remained unisolated until 1886, when Henri Moissan obtained it by the electrolysis of potassium fluoride dissolved in hydrofluoric acid. Hydrobromic and hydriodic acids were investigated by Gay Lussac and Balard, while hydrofluoric acid received considerable attention at the hands of Gay Lussac, Thénard and Berzelius. We may, in fact, consider that the descriptive study of the various halogen compounds dates from about this time. Balard discovered chlorine monoxide in 1834, investigating its properties and reactions; and his observations on hypochlorous acid and hypochlorites led him to conclude that “bleaching-powder” or “chloride of lime” was a compound or mixture in equimolecular proportions of calcium chloride and hypochlorite, with a little calcium hydrate. Gay Lussac investigated chloric acid; Stadion discovered perchloric acid, since more fully studied by G.S. Serullas and Roscoe; Davy and Stadion investigated chlorine peroxide, formed by treating potassium chlorate with sulphuric acid. Davy also described and partially investigated the gas, named by him “euchlorine,” obtained by heating potassium chlorate with hydrochloric acid; this gas has been more recently examined by Pebal. The oxy-acids of iodine were investigated by Davy and H.G. Magnus; periodic acid, discovered by the latter, is characterized by the striking complexity of its salts as pointed out by Kimmins.
46 In 1830 N.G. Sefström definitely proved the existence of a metallic element vanadium, which had been previously detected (in 1801) in certain lead ores by A.M. del Rio; subsequent elaborate researches by Sir Henry Roscoe showed many inaccuracies in the conclusions of earlier workers (for instance, the substance considered to be the pure element was in reality an oxide) and provided science with an admirable account of this element and its compounds. B.W. Gerland contributed to our knowledge of vanadyl salts and the vanadic acids. Chemically related to vanadium are the two elements tantalum and columbium or niobium. These elements occur in the minerals columbite and tantalite, and their compounds became known in the early part of the 19th century by the labours of C. Hatchett, A.G. Ekeberg, W.H. Wollaston and Berzelius. But the knowledge was very imperfect; neither was it much clarified by H. Rose, who regarded niobium oxide as the element. The subject was revived in 1866 by C.W. Blomstrand and J.C. Marignac, to whom is due the credit of first showing the true chemical relations of these elements. Subsequent researches by Sainte Claire Deville and L.J. Troost, and by A.G. Krüss and L.E. Nilson, and subsequently (1904) by Hall, rendered notable additions to our knowledge of these elements and their compounds. Tantalum has in recent years been turned to economic service, being employed, in the same manner as tungsten, for the production of the filaments employed in incandescent electric lighting.
In 1833 Thomas Graham, following the paths already traced out by E.D. Clarke, Gay Lussac and Stromeyer, published his masterly investigation of the various phosphoric acids and their salts, obtaining results subsequently employed by J. von Liebig in establishing the doctrine of the characterization and basicity of acids. Both phosphoric and phosphorous acids became known, although imperfectly, towards the end of the 18th century; phosphorous acid was first obtained pure by Davy in 1812, while pure phosphorous oxide, the anhydride of phosphorous acid, remained unknown until T.E. Thorpe’s investigation of the products of the slow combustion of phosphorus. Of other phosphorus compounds we may here notice Gengembre’s discovery of phosphuretted hydrogen (phosphine) in 1783, the analogy of which to ammonia was first pointed out by Davy and supported at a later date by H. Rose; liquid phosphuretted hydrogen was first obtained by Thénard in 1838; and hypophosphorous acid was discovered by Dulong in 1816. Of the halogen compounds of phosphorus, the trichloride was discovered by Gay Lussac and Thénard, while the pentachloride was obtained by Davy. The oxychloride, bromides, and other compounds were subsequently discovered; here we need only notice Moissan’s preparation of the trifluoride and Thorpe’s discovery of the pentafluoride, a compound of especial note, for it volatilizes unchanged, giving a vapour of normal density and so demonstrating the stability of a pentavalent phosphorus compound (the pentachloride and pentabromide dissociate into a molecule of the halogen element and phosphorus trichloride).
In 1840 C.F. Schönbein investigated ozone, a gas of peculiar odour (named from the Gr. ὄζειν, to smell) observed in 1785 by Martin van Marum to be formed by the action of a silent electric discharge on the oxygen of the air; he showed it to be an allotropic modification of oxygen, a view subsequently confirmed by Marignac, Andrews and Soret. In 1845 a further contribution to the study of allotropy was made by Anton Schrötter, who investigated the transformations of yellow and red phosphorus, phenomena previously noticed by Berzelius, the inventor Of the term “allotropy.” The preparation of crystalline boron in 1856 by Wöhler and Sainte Claire Deville showed that this element also existed in allotropic forms, amorphous boron having been obtained simultaneously and independently in 1809 by Gay Lussac and Davy. Before leaving this phase of inorganic chemistry, we may mention other historical examples of allotropy. Of great importance is the chemical identity of the diamond, graphite and charcoal, a fact demonstrated in part by Lavoisier in 1773, Smithson Tennant in 1706, and by Sir George Steuart-Mackenzie (1780-1848), who showed that equal weights of these three substances yielded the same weight of carbon dioxide on combustion. The allotropy of selenium was first investigated by Berzelius; and more fully in 1851 by J.W. Hittorf, who carefully investigated the effects produced by heat; crystalline selenium possesses a very striking property, viz. when exposed to the action of light its electric conductivity increases. Another element occurring in allotropic forms is sulphur, of which many forms have been described. E. Mitscherlich was an early worker in this field. A modification known as “black sulphur,” soluble in water, was announced by F.L. Knapp in 1848, and a colloidal modification was described by H. Debus. The dynamical equilibrium between rhombic, liquid and monosymmetric sulphur has been worked out by H.W. Bakhuis Roozeboom. The phenomenon of allotropy is not confined to the non-metals, for evidence has been advanced to show that allotropy is far commoner than hitherto supposed. Thus the researches of Carey Lea, E.A. Schneider and others, have proved the existence of “colloidal silver”; similar forms of the metals gold, copper, and of the platinum metals have been described. The allotropy of arsenic and antimony is also worthy of notice, but in the case of the first element the variation is essentially non-metallic, closely resembling that of phosphorus. The term allotropy has also been applied to inorganic compounds, identical in composition, but assuming different crystallographic forms. Mercuric oxide, sulphide and iodide; arsenic trioxide; titanium dioxide and silicon dioxide may be cited as examples.
The joint discovery in 1859 of the powerful method of spectrum analysis (see Spectroscopy) by G.R. Kirchhoff and R.W. Bunsen, and its application to the detection and the characterization of elements when in a state of incandescence, rapidly led to the discovery of many hitherto unknown elements. Within two years of the invention the authors announced the discovery of two metals, rubidium and caesium, closely allied to sodium, potassium and lithium in properties, in the mineral lepidolite and in the Dürkheim mineral water. In 1861 Sir William Crookes detected thallium (named from the Gr. θάλλος, a green bud, on account of a brilliant green line in its spectrum) in the selenious mud of the sulphuric acid manufacture; the chemical affinities of this element, on the one hand approximating to the metals of the alkalis, and on the other hand to lead, were mainly established by C.A. Lamy. Of other metals first detected by the spectroscope mention is to be made of indium, determined by F. Reich and H.T. Richter in 1863, and of gallium, detected in certain zinc blendes by Lecoq de Boisbaudran in 1875. The spectroscope has played an all-important part in the characterization of the elements, which, in combination with oxygen, constitute the group of substances collectively named the “rare earths.” The substances occur, in very minute quantity, in a large number of sparingly-distributed and comparatively rare minerals—euxenite, samarksite, cerite, yttrotantalite, &c. Scandinavian specimens of these minerals were examined by J. Gadolin, M.H. Klaproth, and especially by Berzelius; these chemists are to be regarded as the pioneers in this branch of descriptive chemistry. Since their day many chemists have entered the lists, new and powerful methods of research have been devised, and several new elements definitely characterized. Our knowledge on many points, however, is very chaotic; great uncertainty and conflict of evidence circulate around many of the “new elements” which have been announced, so much so that P.T. Cleve proposed to divide the “rare earth” metals into two groups, (1) “perfectly characterized”; (2) “not yet thoroughly characterized.” The literature of this subject is very large. The memorial address on J.C.G. de Marignac, a noted worker in this field, delivered by Cleve, a high authority on this subject, before the London Chemical Society (J.C.S. Trans., 1895, p. 468), and various papers in the same journal by Sir William Crookes, Bohuslav Brauner and others should be consulted for details.
In the separation of the constituents of the complex mixture of oxides obtained from the “rare earth” minerals, the methods 47 generally forced upon chemists are those of fractional precipitation or crystallization; the striking resemblances of the compounds of these elements rarely admitting of a complete separation by simple precipitation and filtration. The extraordinary patience requisite to a successful termination of such an analysis can only be adequately realized by actual research; an idea may be obtained from Crookes’s Select Methods in Analysis. Of recent years the introduction of various organic compounds as precipitants or reagents has reduced the labour of the process; and advantage has also been taken of the fairly complex double salts which these metals form with compounds. The purity of the compounds thus obtained is checked by spectroscopic observations. Formerly the spark- and absorption-spectra were the sole methods available; a third method was introduced by Crookes, who submitted the oxides, or preferably the basic sulphates, to the action of a negative electric discharge in vacuo, and investigated the phosphorescence induced spectroscopically. By such a study in the ultra-violet region of a fraction prepared from crude yttria he detected a new element victorium, and subsequently by elaborate fractionation obtained the element itself.
The first earth of this group to be isolated (although in an impure form) was yttria, obtained by Gadolin in 1794 from the mineral gadolinite, which was named after its discoverer and investigator. Klaproth and Vauquelin also investigated this earth, but without detecting that it was a complex mixture—a discovery reserved for C.G. Mosander. The next discovery, made independently and simultaneously in 1803 by Klaproth and by W. Hisinger and Berzelius, was of ceria, the oxide of cerium, in the mineral cerite found at Ridderhytta, Westmannland, Sweden. These crude earths, yttria and ceria, have supplied most if not all of the “rare earth” metals. In 1841 Mosander, having in 1839 discovered a new element lanthanum in the mineral cerite, isolated this element and also a hitherto unrecognized substance, didymia, from crude yttria, and two years later he announced the determination of two fresh constituents of the same earth, naming them erbia and terbia. Lanthanum has retained its elementary character, but recent attempts at separating it from didymia have led to the view that didymium is a mixture of two elements, praseodymium and neodymium (see Didymium). Mosander’s erbia has been shown to contain various other oxides—thulia, holmia, &c.—but this has not yet been perfectly worked out. In 1878 Marignac, having subjected Mosander’s erbia, obtained from gadolinite, to a careful examination, announced the presence of a new element, ytterbium; this discovery was confirmed by Nilson, who in the following year discovered another element, scandium, in Marignac’s ytterbia. Scandium possesses great historical interest, for Cleve showed that it was one of the elements predicted by Mendeléeff about ten years previously from considerations based on his periodic classification of the elements (see Element). Other elements predicted and characterized by Mendeléeff which have been since realized are gallium, discovered in 1875, and germanium, discovered in 1885 by Clemens Winkler.
In 1880 Marignac examined certain earths obtained from the mineral samarskite, which had already in 1878 received attention from Delafontaine and later from Lecoq de Boisbaudran. He established the existence of two new elements, samarium and gadolinium, since investigated more especially by Cleve, to whom most of our knowledge on this subject is due. In addition to the rare elements mentioned above, there are a score or so more whose existence is doubtful. Every year is attended by fresh “discoveries” in this prolific source of elementary substances, but the paucity of materials and the predilections of the investigators militate in some measure against a just valuation being accorded to such researches. After having been somewhat neglected for the greater attractions and wider field presented by organic chemistry, the study of the elements and their inorganic compounds is now rapidly coming into favour; new investigators are continually entering the lists; the beaten paths are being retravcrsed and new ramifications pursued.
IV. Organic Chemistry
While inorganic chemistry was primarily developed through the study of minerals—a connexion still shown by the French appellation chimie minérale—organic chemistry owes its origin to the investigation of substances occurring in the vegetable and animal organisms. The quest of the alchemists for the philosopher’s stone, and the almost general adherence of the iatrochemists to the study of the medicinal characters and preparation of metallic compounds, stultified in some measure the investigation of vegetable and animal products. It is true that by the distillation of many herbs, resins and similar substances, several organic compounds had been prepared, and in a few cases employed as medicines; but the prevailing classification of substances by physical and superficial properties led to the correlation of organic and inorganic compounds, without any attention being paid to their chemical composition. The clarification and spirit of research so clearly emphasized by Robert Boyle in the middle of the 17th century is reflected in the classification of substances expounded by Nicolas Lémery, in 1675, in his Cours de chymie. Taking as a basis the nature of the source of compounds, he framed three classes: “mineral,” comprising the metals, minerals, earths and stones; “vegetable,” comprising plants, resins, gums, juices, &c.; and “animal,” comprising animals, their different parts and excreta. Notwithstanding the inconsistency of his allocation of substances to the different groups (for instance, acetic acid was placed in the vegetable class, while the acetates and the products of their dry distillation, acetone, &c., were placed in the mineral class), this classification came into favour. The phlogistonists endeavoured to introduce chemical notions to support it: Becher, in his Physica subterranea(1669), stated that mineral, vegetable and animal matter contained the same elements, but that more simple combinations prevailed in the mineral kingdom; while Stahl, in his Specimen Becherianum (1702), held the “earthy” principle to predominate in the mineral class, and the “aqueous” and “combustible” in the vegetable and animal classes. It thus happened that in the earlier treatises on phlogistic chemistry organic substances were grouped with all combustibles.
The development of organic chemistry from this time until almost the end of the 18th century was almost entirely confined to such compounds as had practical applications, especially in pharmacy and dyeing. A new and energetic spirit was introduced by Scheele; among other discoveries this gifted experimenter isolated and characterized many organic acids, and proved the general occurrence of glycerin (Ölsüss) in all oils and fats. Bergman worked in the same direction; while Rouelle was attracted to the study of animal chemistry. Theoretical speculations were revived by Lavoisier, who, having explained the nature of combustion and determined methods for analysing compounds, concluded that vegetable substances ordinarily contained carbon, hydrogen and oxygen, while animal substances generally contained, in addition to these elements, nitrogen, and sometimes phosphorus and sulphur. Lavoisier, to whom chemistry was primarily the chemistry of oxygen compounds, having developed the radical theory initiated by Guyton de Morveau, formulated the hypothesis that vegetable and animal substances were oxides of radicals composed of carbon and hydrogen; moreover, since simple radicals (the elements) can form more than one oxide, he attributed the same character to his hydrocarbon radicals: he considered, for instance, sugar to be a neutral oxide and oxalic acid a higher oxide of a certain radical, for, when oxidized by nitric acid, sugar yields oxalic acid. At the same time, however, he adhered to the classification of Lémery; and it was only when identical compounds were obtained from both vegetable and animal sources that this subdivision was discarded, and the classes were assimilated in the division organic chemistry.
At this time there existed a belief, held at a later date by Berzelius, Gmelin and many others, that the formation of organic compounds was conditioned by a so-called vital force; and the difficulty of artificially realizing this action explained the supposed impossibility of synthesizing organic compounds. 48 This dogma was shaken by Wöhler’s synthesis of urea in 1828. But the belief died hard; the synthesis of urea remained isolated for many years; and many explanations were attempted by the vitalists (as, for instance, that urea was halfway between the inorganic and organic kingdoms, or that the carbon, from which it was obtained, retained the essentials of this hypothetical vital force), but only to succumb at a later date to the indubitable fact that the same laws of chemical combination prevail in both the animate and inanimate kingdoms, and that the artificial or laboratory synthesis of any substance, either inorganic or organic, is but a question of time, once its constitution is determined.10
The exact delimitation of inorganic and organic chemistry engrossed many minds for many years; and on this point there existed considerable divergence of opinion for several decades. In addition to the vitalistic doctrine of the origin of organic compounds, views based on purely chemical considerations were advanced. The atomic theory, and its correlatives—the laws of constant and multiple proportions—had been shown to possess absolute validity so far as well-characterized inorganic compounds were concerned; but it was open to question whether organic compounds obeyed the same laws. Berzelius, in 1813 and 1814, by improved methods of analysis, established that the Daltonian laws of combination held in both the inorganic and organic kingdoms; and he adopted the view of Lavoisier that organic compounds were oxides of compound radicals, and therefore necessarily contained at least three elements—carbon, hydrogen and oxygen. This view was accepted in 1817 by Leopold Gmelin, who, in his Handbuch der Chemie, regarded inorganic compounds as being of binary composition (the simplest being oxides both acid and basic, which by combination form salts also of binary form), and organic compounds as ternary, i.e. composed of three elements; furthermore, he concluded that inorganic compounds could be synthesized, whereas organic compounds could not. A consequence of this empirical division was that marsh gas, ethylene and cyanogen were regarded as inorganic, and at a later date many other hydrocarbons of undoubtedly organic nature had to be included in the same division.
The binary conception of compounds held by Berzelius received apparent support from the observations of Gay Lussac, in 1815, on the vapour densities of alcohol and ether, which pointed to the conclusion that these substances consisted of one molecule of water and one and two of ethylene respectively; and from Pierre Jean Robiquet and Jean Jacques Colin, showing, in 1816, that ethyl chloride (hydrochloric ether) could be regarded as a compound of ethylene and hydrochloric acid.11 Compound radicals came to be regarded as the immediate constituents of organic compounds; and, at first, a determination of their empirical composition was supposed to be sufficient to characterize them. To this problem there was added another in about the third decade of the 19th century—namely, to determine the manner in which the atoms composing the radical were combined; this supplementary requisite was due to the discovery of the isomerism of silver fulminate and silver cyanate by Justus von Liebig in 1823, and to M. Faraday’s discovery of butylene, isomeric with ethylene, in 1825.
The classical investigation of Liebig and Friedrich Wohler on the radical of benzoic acid (“Über das Radikal der Benzoë-säure,” Ann. Chem., 1832, 3, p. 249) is to be regarded as a most important contribution to the radical theory, for it was shown that a radical containing the elements carbon, hydrogen and oxygen, which they named benzoyl (the termination yl coming from the Gr. ὔλη, matter), formed the basis of benzaldehyde, benzoic acid, benzoyl chloride, benzoyl bromide and benzoyl sulphide, benzamide and benzoic ether. Berzelius immediately appreciated the importance of this discovery, notwithstanding that he was compelled to reject the theory that oxygen could not play any part in a compound radical—a view which he previously considered as axiomatic; and he suggested the names “proin” or “orthrin” (from the Gr. πρωί and ὀρθρός, at dawn). However, in 1833, Berzelius reverted to his earlier opinion that oxygenated radicals were incompatible with his electrochemical theory; he regarded benzoyl as an oxide of the radical C14H10, which he named “picramyl” (from πικρός, bitter, and ἀμυγδάλη, almond), the peroxide being anhydrous benzoic acid; and he dismissed the views of Gay Lussac and Dumas that ethylene was the radical of ether, alcohol and ethyl chloride, setting up in their place the idea that ether was a suboxide of ethyl, (C2H5)2O, which was analogous to K2O, while alcohol was an oxide of a radical C2H6; thus annihilating any relation between these two compounds. This view was modified by Liebig, who regarded ether as ethyl oxide, and alcohol as the hydrate of ethyl oxide; here, however, he was in error, for he attributed to alcohol a molecular weight double its true value. Notwithstanding these errors, the value of the “ethyl theory” was perceived; other radicals—formyl, methyl, amyl, acetyl, &c.—were characterized; Dumas, in 1837, admitted the failure of the etherin theory; and, in company with Liebig, he defined organic chemistry as the “chemistry of compound radicals.” The knowledge of compound radicals received further increment at the hands of Robert W. Bunsen, the discoverer of the cacodyl compounds.
The radical theory, essentially dualistic in nature in view of its similarity to the electrochemical theory of Berzelius, was destined to succumb to a unitary theory. Instances had already been recorded of cases where a halogen element replaced hydrogen with the production of a closely allied substance: Gay Lussac had prepared cyanogen chloride from hydrocyanic acid; Faraday, hexachlorethane from ethylene dichloride, &c. Here the electro-negative halogens exercised a function similar to electro-positive hydrogen. Dumas gave especial attention to such substitutions, named metalepsy μετάληψις, exchange); and framed the following empirical laws to explain the reactions:—(1) a body containing hydrogen when substituted by a halogen loses one atom of hydrogen for every atom of halogen introduced; (2) the same holds if oxygen be present, except that when the oxygen is present as water the latter first loses its hydrogen without replacement, and then substitution according to (1) ensues. Dumas went no further that thus epitomizing his observations; and the next development was made in 1836 by Auguste Laurent, who, having amplified and discussed the applicability of Dumas’ views, promulgated his Nucleus Theory, which assumed the existence of “original nuclei or radicals” (radicaux or noyaux fondamentaux) composed of carbon and hydrogen, and “derived nuclei” (radicaux or noyaux dérivés) formed from the original nuclei by the substitution of hydrogen or the addition of other elements, and having properties closely related to the primary nuclei.
Vigorous opposition was made by Liebig and Berzelius, the latter directing his attack against Dumas, whom he erroneously believed to be the author of what was, in his opinion, a pernicious theory. Dumas repudiated the accusation, affirming that he held exactly contrary views to Laurent; but only to admit their correctness in 1839, when, from his own researches and those of Laurent, Malaguti and Regnault, he formulated his type theory. According to this theory a “chemical type” embraced compounds containing the same number of equivalents combined in a like manner and exhibiting similar properties; thus acetic and trichloracetic acids, aldehyde and chloral, marsh gas and chloroform are pairs of compounds referable to the same type. He also postulated, with Regnault, the existence of “molecular or mechanical types” containing substances which, although having the same number of equivalents, are essentially different in characters. His unitary conceptions may be summarized: every chemical compound forms a complete whole, and cannot therefore consist of two parts; and its chemical character depends primarily upon the arrangement and number of the atoms, and, in a lesser degree, upon their chemical nature. 49 More emphatic opposition to the dualistic theory of Berzelius was hardly possible; this illustrious chemist perceived that the validity of his electrochemical theory was called in question, and therefore he waged vigorous war upon Dumas and his followers. But he fought in a futile cause; to explain the facts put forward by Dumas he had to invent intricate and involved hypotheses, which, it must be said, did not meet with general acceptance; Liebig seceded from him, and invited Wöhler to endeavour to correct him. Still, till the last Berzelius remained faithful to his original theory; experiment, which he had hitherto held to be the only sure method of research, he discarded, and in its place he substituted pure speculation, which greatly injured the radical theory. At the same time, however, the conception of radicals could not be entirely displaced, for the researches of Liebig and Wohler, and those made subsequently by Bunsen, demonstrated beyond all doubt the advantages which would accrue from their correct recognition.
A step forward—the fusion of Dumas’, type theory and the radical theory—was made by Laurent and Charles Gerhardt. As early as 1842, Gerhardt in his Précis de chimie organique exhibited a marked leaning towards Dumas’ theory, and it is without doubt that both Dumas and Laurent exercised considerable influence on his views. Unwilling to discard the strictly unitary views of these chemists, or to adopt the copulae theory of Berzelius, he revived the notion of radicals in a new form. According to Gerhardt, the process of substitution consisted of the union of two residues to form a unitary whole; these residues, previously termed “compound radicals,” are atomic complexes which remain over from the interaction of two compounds. Thus, he interpreted the interaction of benzene and nitric acid as C6H6 + HNO3 = C6H5NO2 + H2O, the “residues” of benzene being C6H5 and H, and of nitric acid HO and NO2. Similarly he represented the reactions investigated by Liebig and Wöhler on benzoyl compounds as double decompositions.
This rejuvenation of the notion of radicals rapidly gained favour; and the complete fusion of the radical theory with the theory of types was not long delayed. In 1849 C.A. Wurtz discovered the amines or substituted ammonias, previously predicted by Liebig; A.W. von Hofmann continued the investigation, and established their recognition as ammonia in which one or more hydrogen atoms had been replaced by hydrocarbon radicals, thus formulating the “ammonia type.” In 1850 A.W. Williamson showed how alcohol and ether were to be regarded as derived from water by substituting one or both hydrogen atoms by the ethyl group; he derived acids and the acid anhydrides from the same type; and from a comparison of many inorganic and the simple organic compounds he concluded that this notion of a “water-type” clarified, in no small measure, the conception of the structure of compounds.
These conclusions were co-ordinated in Gerhardt’s “new theory of types.” Taking as types hydrogen, hydrochloric acid, water and ammonia, he postulated that all organic compounds were referable to these four forms: the hydrogen type included hydrocarbons, aldehydes and ketones; the hydrochloric acid type, the chlorides, bromides and iodides; the water type, the alcohols, ethers, monobasic acids, acid anhydrides, and the analogous sulphur compounds; and the ammonia type, the amines, acid-amides, and the analogous phosphorus and arsenic compounds. The recognition of the polybasicity of acids, which followed from the researches of Thomas Graham and Liebig, had caused Williamson to suggest that dibasic acids could be referred to a double water type, the acid radical replacing an atom of hydrogen in each water molecule; while his discovery of tribasic formic ether, CH(OC2H5)3, in 1854 suggested a triple water type. These views were extended by William Odling, and adopted by Gerhardt, but with modifications of Williamson’s aspects. A further generalization was effected by August Kekulé, who rejected the hydrochloric acid type as unnecessary, and introduced the methane type and condensed mixed types. Pointing out that condensed types can only be fused with a radical replacing more than one atom of hydrogen, he laid the foundation of the doctrine of valency, a doctrine of incalculable service to the knowledge of the structure of chemical compounds.
At about the same time Hermann Kolbe attempted a rehabilitation, with certain modifications, of the dualistic conception of Berzelius. He rejected the Berzelian tenet as to the unalterability of radicals, and admitted that they exercised a considerable influence upon the compounds with which they were copulated. By his own investigations and those of Sir Edward Frankland it was proved that the radical methyl existed in acetic acid; and by the electrolysis of sodium acetate, Kolbe concluded that he had isolated this radical; in this, however, he was wrong, for he really obtained ethane, C2H6, and not methyl, CH3. From similar investigations of valerianic acid he was led to conclude that fatty acids were oxygen compounds of the radicals hydrogen, methyl, ethyl, &c., combined with the double carbon equivalent C2. Thus the radical of acetic acid, acetyl,12 was C2H3·C2. (It will be noticed that Kolbe used the atomic weights H=1, C=6, O=8, S=16, &c.; his formulae, however, were molecular formulae, i.e. the molecular weights were the same as in use to-day.) This connecting link, C2, was regarded as essential, while the methyl, ethyl, &c. was but a sort of appendage; but Kolbe could not clearly conceive the manner of copulation.
The brilliant researches of Frankland on the organo-metallic compounds, and his consequent doctrine of saturation capacity or valency of elements and radicals, relieved Kolbe’s views of all obscurity. The doctrine of copulae was discarded, and in 1859 emphasis was given to the view that all organic compounds were derivatives of inorganic by simple substitution processes. He was thus enabled to predict compounds then unknown, e.g. the secondary and tertiary alcohols; and with inestimable perspicacity he proved intimate relations between compounds previously held to be quite distinct. Lactic acid and alanine were shown to be oxy- and amino-propionic acids respectively; glycollic acid and glycocoll, oxy- and amino-acetic acids; salicylic and benzamic acids, oxy- and amino-benzoic acids.
Another consequence of the doctrine of valency was that it permitted the graphic representation of the molecule. The “structure theory” (or the mode of linking of the atoms) of carbon compounds, founded by Butlerow, Kekulé and Couper and, at a later date, marvellously enhanced by the doctrine of stereo-isomerism, due to J.H. van’t Hoff and Le Bel, occupies such a position in organic chemistry that its value can never be transcended. By its aid the molecule is represented as a collection of atoms connected together by valencies in such a manner that the part played by each atom is represented; isomerism, or the existence of two or more chemically different substances having identical molecular weights, is adequately shown; and, most important of all, once the structure is determined, the synthesis of the compound is but a matter of time.
In this summary the leading factors which have contributed to a correct appreciation of organic compounds have so far been considered historically, but instead of continuing this method it has been thought advisable to present an epitome of present-day conclusions, not chronologically, but as exhibiting the principles and subject-matter of our science.
Classification of Organic Compounds.
An apt definition of organic chemistry is that it is “the study of the hydrocarbons and their derivatives.” This description, although not absolutely comprehensive, serves as a convenient starting-point for a preliminary classification, since a great number of substances, including the most important, are directly referable to hydrocarbons, being formed by replacing one or more hydrogen atoms by other atoms or groups. Two distinct types of hydrocarbons exist: (1) those consisting of an open chain of carbon atoms—named the “aliphatic series” (ἄλειφαρ, oil or fat), and (2) those consisting of a closed chain—the “carbocyclic series.” The second series can be further divided 50 into two groups: (1) those exhibiting properties closely analogous to the aliphatic series—the polymethylenes (q.v.), and (2) a series exhibiting properties differing in many respects from the aliphatic and polymethylene compounds, and characterized by a peculiar stability which is to be associated with the disposition of certain carbon valencies not saturated by hydrogen—the “aromatic series.” There also exists an extensive class of compounds termed the “heterocyclic series”—these compounds are derived from ring systems containing atoms other than carbon; this class is more generally allied to the aromatic series than to the aliphatic.
We now proceed to discuss the types of aliphatic compounds; then, the characteristic groupings having been established, an epitome of their derivatives will be given. Carbocyclic rings will next be treated, benzene and its allies in some detail; and finally the heterocyclic nuclei.
Accepting the doctrine of the tetravalency of carbon (its divalency in such compounds as carbon monoxide, various isocyanides, fulminic acid, &c., and its possible trivalency in M. Gomberg’s triphenyl-methyl play no part in what follows), it is readily seen that the simplest hydrocarbon has the formula CH4 named methane, in which the hydrogen atoms are of equal value, and which may be pictured as placed at the vertices of a tetrahedron, the carbon atom occupying the centre. This tetrahedral configuration is based on the existence of only one methylene dichloride, two being necessary if the carbon valencies were directed from the centre of a plane square to its corners, and on the existence of two optical isomers of the formula C.A.B.D.E., C being a carbon atom and A.B.D.E. being different monovalent atoms or radicals (see Stereo-Isomerism). The equivalence of the four hydrogen atoms of methane rested on indirect evidence, e.g. the existence of only one acetic acid, methyl chloride, and other monosubstitution derivatives—until the experimental proof by L. Henry (Zeit. f. Phys. Chem., 1888, 2, p. 553), who prepared the four nitromethanes, CH3NO2, each atom in methane being successively replaced by the nitro-group.
Henry started with methyl iodide, the formula of which we write in the form CIaHbHcHd. This readily gave with silver nitrite a nitromethane in which we may suppose the nitro-group to replace the a iodine atom, i.e. C(NO2)aHbHcHd. The same methyl iodide gave with potassium cyanide, acetonitril, which was hydrolysed to acetic acid; this must be C(COOH)aHbHcHd. Chlorination of this substance gave a monochloracetic acid; we will assume the chlorine atom to replace the b hydrogen atom. This acid with silver nitrite gave nitroacetic acid, which readily gave the second nitromethane, CHa(NO2)bHcHd identical with the first nitromethane. From the nitroacetic acid obtained above, malonic acid was prepared, and from this a monochlormalonic acid was obtained; we assume the chlorine atom to replace the c hydrogen atom. This acid gives with silver nitrite the corresponding nitromalonic acid, which readily yielded the third nitromethane, CHaHb(NO2)cHd, also identical with the first. The fourth nitromethane was obtained from the nitromalonic acid previously mentioned by a repetition of the method by which the third was prepared; this was identical with the other three.
Let us now consider hydrocarbons containing 2 atoms of carbon. Three such compounds are possible according to the number of valencies acting directly between the carbon atoms. Thus, if they are connected by one valency, and the remaining valencies saturated by hydrogen, we obtain the compound H3C·CH3, ethane. This compound may be considered as derived from methane, CH4, by replacing a hydrogen atom by the monovalent group CH3, known as methyl; hence ethane may be named “methylmethane.” If the carbon atoms are connected by two valencies, we obtain a compound H2C:CH2, ethylene; if by three valencies, HC∶CH, acetylene. These last two compounds are termed unsaturated, whereas ethane is saturated. It is obvious that we have derived three combinations of carbon with hydrogen, characterized by containing a single, double, and triple linkage; and from each of these, by the substitution of a methyl group for a hydrogen atom, compounds of the same nature result. Thus ethane gives H3C·CH2·CH3, propane; ethylene gives H2C:CH·CH3, propylene; and acetylene gives HC∶C·CH3, allylene. By continuing the introduction of methyl groups we obtain three series of homologous hydro-carbons given, by the general formulae CnH2n+2, CnH2n, and CnH2n-2, each member differing from the preceding one of the same series by CH2. It will be noticed that compounds containing two double linkages will have the same general formula as the acetylene series; such compounds are known as the “diolefines.” Hydrocarbons containing any number of double or triple linkages, as well as both double and triple linkages, are possible, and a considerable number of such compounds have been prepared.
A more complete idea of the notion of a compound radical follows from a consideration of the compound propane. We derived this substance from ethane by introducing a methyl group; hence it may be termed “methylethane.” Equally well we may derive it from methane by replacing a hydrogen atom by the monovalent group CH2·CH3, named ethyl; hence propane may be considered as “ethylmethane.” Further, since methane may be regarded as formed by the conjunction of a methyl group with a hydrogen atom, it may be named “methyl hydride”; similarly ethane is “ethyl hydride,” propane, “propyl hydride,” and so on. The importance of such groups as methyl, ethyl, &c. in attempting a nomenclature of organic compounds cannot be overestimated; these compound radicals, frequently termed alkyl radicals, serve a similar purpose to the organic chemist as the elements to the inorganic chemist.
In methane and ethane the hydrogen atoms are of equal value, and no matter which one may be substituted by another element or group the same compound will result. In propane, on the other hand, the hydrogen atoms attached to the terminal carbon atoms differ from those joined to the medial atom; we may therefore expect to obtain different compounds according to the position of the hydrogen atom substituted. By introducing a methyl group we may obtain CH3·CH2·CH2·CH3, known as “normal” or n-butane, substitution occurring at a terminal atom, or CH3·CH(CH3)·CH3, isobutane, substitution occurring at the medial atom. From n-butane we may derive, by a similar substitution of methyl groups, the two hydrocarbons: (1) CH3·CH2·CH2·CH2·CH3, and (2) CH3·CH(CH3)·CH2·CH3; from isobutane we may also derive two compounds, one identical with (2.), and a new one (3) CH3(CH3)C(CH3)CH3. These three hydrocarbons are isomeric, i.e. they possess the same formula, but differ in constitution. We notice that they may be differentiated as follows: (1) is built up solely of methyl and ·CH2· (methylene) groups and the molecule consists of a single chain; such hydrocarbons are referred to as being normal; (2) has a branch and contains the group ÷CH (methine) in which the free valencies are attached to carbon atoms; such hydrocarbons are termed secondary or iso-; (3) is characterized by a carbon atom linked directly to four other carbon atoms; such hydrocarbons are known as tertiary.
Deferring the detailed discussion of cyclic or ringed hydrocarbons, a correlation of the various types or classes of compounds which may be derived from hydrocarbon nuclei will now be given. It will be seen that each type depends upon a specific radical or atom, and the copulation of this character with any hydrocarbon radical (open or cyclic) gives origin to a compound of the same class.
It is convenient first to consider the effect of introducing one, two, or three hydroxyl (OH) groups into the -CH3, >CH2, and ->CH groups, which we have seen to characterize the different types of hydrocarbons. It may be noticed here that cyclic nuclei can only contain the groups >CH2 and ->CH, the first characterizing the polymethylene and reduced heterocyclic compounds, the second true aromatic compounds.
Substituting one hydroxyl group into each of these residues, we obtain radicals of the type -CH2·OH, >CH·OH, and ->C·OH; these compounds are known as alcohols (q.v.), and are termed primary, secondary, and tertiary respectively. Polymethylenes can give only secondary and tertiary alcohols, benzene only tertiary; these latter compounds are known as phenols. A second hydroxyl group may be introduced into the residues -CH2·OH and >CH·OH, with the production of radicals of the form -CH(OH)2 and >C(OH)2. Compounds containing these groupings are, however, rarely observed (see Chloral), and it is generally found that when compounds of these types are expected, the elements of water are split off, and the typical groupings are reduced to -CH:O and >C:O. Compounds containing the group -CH:O are known as aldehydes (q.v.), while the group >C:O (sometimes termed the carbonyl or keto group) characterizes the ketones (q.v.). A third hydroxyl group may be 51 introduced into the -CH:O residue with the formation of the radical -C(OH):O; this is known as the carboxyl group, and characterizes the organic acids.
Sulphur analogues of these oxygen compounds are known. Thus the thio-alcohols or mercaptans (q.v.) contain the group -CH2·SH; and the elimination of the elements of sulphuretted hydrogen between two molecules of a thio-alcohol results in the formation of a thio-ether or sulphide, R2S. Oxidation of thio-ethers results in the formation of sulphoxides, R2:S:O, and sulphones, R2:SO2; oxidation of mercaptans yields sulphonic acids, R·SO3H, and of sodium mercaptides sulphinic acids, R·SO(OH). We may also notice that thio-ethers combine with alkyl iodides to form sulphine or sulphonium compounds, R3÷SI. Thio-aldehydes, thio-ketones and thio-acids also exist.
We proceed to consider various simple derivatives of the alcohols, which we may here regard as hydroxy hydrocarbons, R·OH, where R is an alkyl radical, either aliphatic or cyclic in nature.
Of these, undoubtedly the simplest are the ethers (q.v.), formed by the elimination of the elements of water between two molecules of the same alcohol, “simple ethers,” or of different alcohols, “mixed ethers.” These compounds may be regarded as oxides in just the same way as the alcohols are regarded as hydroxides. In fact, the analogy between the alkyl groups and metallic elements forms a convenient basis from which to consider many derivatives. Thus from ethyl alcohol there can be prepared compounds, termed esters (q.v.), or ethereal salts, exactly comparable in structure with corresponding salts of, say, potassium; by the action of the phosphorus haloids, the hydroxyl group is replaced by a halogen atom with the formation of derivatives of the type R·Cl(Br,I); nitric acid forms nitrates, R·O·NO2; nitrous acid, nitrites, R·O·NO; sulphuric acid gives normal sulphates R2SO4, or acid sulphates, R·SO4H. Organic acids also condense with alcohols to form similar compounds: the fats, waxes, and essential oils are naturally occurring substances of this class.
An important class of compounds, termed amines (q.v.), results from the condensation of alcohols with ammonia, water being eliminated between the alcoholic hydroxyl group and a hydrogen atom of the ammonia. Three types of amines are possible and have been prepared: primary, R·NH2; secondary, R2:NH; and tertiary, R3÷N; the oxamines, R3N:O, are closely related to the tertiary ammonias, which also unite with a molecule of alkyl iodide to form salts of quaternary ammonium bases, e.g. R4N·I. It is worthy of note that phosphorus and arsenic bases analogous to the amines are known (see Phosphorus and Arsenic). From the primary amines are derived the diazo compounds (q.v.) and azo compounds (q.v.); closely related are the hydrazines (q.v.). Secondary amines yield nitrosamines, R2N·NO, with nitrous acid. By the action of hydroxylamine or phenylhydrazine on aldehydes or ketones, condensation occurs between the carbonyl oxygen of the aldehyde or ketone and the amino group of the hydroxylamine or hydrazine. Thus with hydroxylamine aldehydes yield aldoximes, R·CH:N·OH, and ketones, ketoximes, R2C:N·OH (see Oximes), while phenyl hydrazine gives phenylhydrazones, R2C:N·NH·C6H5 (see Hydrazones). Oxyaldehydes and oxyketones (viz. compounds containing an oxy in addition to an aldehydic or ketonic group) undergo both condensation and oxidation when treated with phenylhydrazine, forming compounds known as osozones; these are of great importance in characterizing the sugars (q.v.).
The carboxyl group constitutes another convenient starting-point for the orientation of many types of organic compounds. This group may be considered as resulting from the fusion of a carbonyl (:CO) and a hydroxyl (HO·) group; and we may expect to meet with compounds bearing structural resemblances to the derivatives of alcohols and aldehydes (or ketones).
Considering derivatives primarily concerned with transformations of the hydroxyl group, we may regard our typical acid as a fusion of a radical R·CO- (named acetyl, propionyl, butyl, &c., generally according to the name of the hydrocarbon containing the same number of carbon atoms) and a hydroxyl group. By replacing the hydroxyl group by a halogen, acid-haloids result; by the elimination of the elements of water between two molecules, acid-anhydrides, which may be oxidized to acid-peroxides; by replacing the hydroxyl group by the group ·SH, thio-acids; by replacing it by the amino group, acid-amides (q.v.); by replacing it by the group -NH·NH2, acid-hydrazides. The structural relations of these compounds are here shown:
| R·CO·OH; | R·CO·Cl; | (R·CO)2O; | R·CO·SH; |
| acid; | acid-chloride; | acid-anhydride; | thio-acid; |
| R·CO·NH2; | R·CO·NH·NH2. |
| acid-amide; | acid-hydrazide. |
It is necessary clearly to distinguish such compounds as the amino- (or amido-) acids and acid-amides; in the first case the amino group is substituted in the hydrocarbon residue, in the second it is substituted in the carboxyl group.
By transformations of the carbonyl group, and at the same time of the hydroxyl group, many interesting types of nitrogen compounds may be correlated.
Thus from the acid-amides, which we have seen to be closely related to the acids themselves, we obtain, by replacing the carbonyl oxygen by chlorine, the acidamido-chlorides, R·CCl2·NH2, from which are derived the imido-chlorides, R·CCl:NH, by loss of one molecule of hydrochloric acid. By replacing the chlorine in the imido-chloride by an oxyalkyl group we obtain the imido-ethers, R·C(OR’):NH; and by an amino group, the amidines, R·C(NH2):NH. The carbonyl oxygen may also be replaced by the oxime group, :N·OH; thus the acids yield the hydroxamic acids, R·C(OH):NOH, and the acid-amides the amidoximes, R·C(NH2):NOH. Closely related to the amidoximes are the nitrolic acids, R·C(NO2):NOH.
Cyclic Hydrocarbons and Nuclei.
Having passed in rapid review the various types of compounds derived by substituting for hydrogen various atoms or groups of atoms in hydrocarbons (the separate articles on specific compounds should be consulted for more detailed accounts), we now proceed to consider the closed chain compounds. Here we meet with a great diversity of types: oxygen, nitrogen, sulphur and other elements may, in addition to carbon, combine together in a great number of arrangements to form cyclic nuclei, which exhibit characters closely resembling open-chain compounds in so far as they yield substitution derivatives, and behave as compound radicals. In classifying closed chain compounds, the first step consists in dividing them into: (1) carbocyclic, in which the ring is composed solely of carbon atoms—these are also known as homocyclic or isocyclic on account of the identity of the members of the ring—and (2) heterocyclic, in which different elements go to make up the ring. Two primary divisions of carbocyclic compounds may be conveniently made: (1) those in which the carbon atoms are completely saturated—these are known by the generic term polymethylenes, their general formula being (CH2)n: it will be noticed that they are isomeric with ethylene and its homologues; they differ, however, from this series in not containing a double linkage, but have a ringed structure; and (2) those containing fewer hydrogen atoms than suffice to saturate the carbon valencies—these are known as the aromatic compounds proper, or as benzene compounds, from the predominant part which benzene plays in their constitution.
It was long supposed that the simplest ring obtainable contained six atoms of carbon, and the discovery of trimethylene in 1882 by August Freund by the action of sodium on trimethylene bromide, Br(CH2)3Br, came somewhat as a surprise, especially in view of its behaviour with bromine and hydrogen bromide. In comparison with the isomeric propylene, CH3·HC:CH2, it is remarkably inert, being only very slowly attacked by bromine, which readily combines with propylene. But on the other hand, it is readily converted by hydrobromic acid into normal propyl bromide, CH3·CH2·CH2Br. The separation of carbon atoms united by single affinities in this manner at the time the observation was made was altogether without precedent. A similar behaviour has since been noticed in other trimethylene derivatives, but the fact that bromine, which usually acts so much more readily than hydrobromic acid on unsaturated compounds, should be so inert when hydrobromic acid acts readily is one still needing a satisfactory explanation. A great impetus was given to the study of polymethylene derivatives by the important and unexpected observation made by W.H. Perkin, junr., in 1883, that ethylene and trimethylene bromides are capable of acting in such a way on sodium acetoacetic ester as to form tri- and tetra-methylene rings. Perkin has himself contributed largely to our knowledge of such compounds; penta- and hexa-methylene derivatives have also received considerable attention (see Polymethylenes).
A. von Baeyer has sought to explain the variations in stability manifest in the various polymethylene rings by a purely mechanical hypothesis, the “strain” or Spannungs theory (Ber., 1885, p. 2277). Assuming the four valencies of the carbon atom to be directed from the centre of a regular tetrahedron towards its four corners, the angle at which they meet is 109° 28′. Baeyer supposes that in the formation of carbon ~52 “rings” the valencies become deflected from their positions, and that the tension thus introduced may be deduced from a comparison of this angle with the angles at which the strained valencies would meet. He regards the amount of deflection as a measure of the stability of the “ring.” The readiness with which ethylene is acted on in comparison with other types of hydrocarbon, for example, is in harmony, he considers, with the circumstance that the greatest distortion must be involved in its formation, as if deflected into parallelism each valency will be drawn out of its position through ½.109° 28′. The values in other cases are calculable from the formula ½(1O9° 28′ - a), where a is the internal angle of the regular polygon contained by sides equal in number to the number of the carbon atoms composing the ring. These values are:—
| Trimethylene. | Tetramethylene. |
| ½(109° 28′ - 60°) = 24° 44′. | ½(109° 28′ - 90°) = 9° 44′. |
| Pentamethylene. | Hexamethylene. |
| ½(109° 28′ - 108°) = 0° 44′. | ½(109° 28′ - 120°) = -5° 16′. |
The general behaviour of the several types of hydrocarbons is certainly in accordance with this conception, and it is a remarkable fact that when benzene is reduced with hydriodic acid, it is converted into a mixture of hexamethylene and methylpentamethylene (cf. W. Markownikov, Ann., 1898, 302, p. 1); and many other cases of the conversion of six-carbon rings into five-carbon rings have been recorded (see below, Decompositions of the Benzene Ring). Similar considerations will apply to rings containing other elements besides carbon. As an illustration it may be pointed out that in the case of the two known types of lactones—the γ-lactones, which contain four carbon atoms and one oxygen atom in the ring, are more readily formed and more stable (less readily hydrolysed) than the δ-lactones, which contain one oxygen and five carbon atoms in the ring. That the number of atoms which can be associated in a ring by single affinities is limited there can be no doubt, but there is not yet sufficient evidence to show where the limit must be placed. Baeyer has suggested that his hypothesis may also be applied to explain the instability of acetylene and its derivatives, and the still greater instability of the polyacetylene compounds.
Benzene.
The ringed structure of benzene, C6H6, was first suggested in 1865 by August Kekulé, who represented the molecule by six CH groups placed at the six angles of a regular hexagon, the sides of which denoted the valencies saturated by adjacent carbon atoms, the fourth valencies of each carbon atom being represented as saturated along alternate sides. This formula, notwithstanding many attempts at both disproving and modifying it, has well stood the test of time; the subject has been the basis of constant discussion, many variations have been proposed, but the original conception of Kekulé remains quite as convenient as any of the newer forms, especially when considering the syntheses and decompositions of the benzene complex. It will be seen, however, that the absolute disposition of the fourth valency may be ignored in a great many cases, and consequently the complex may be adequately represented as a hexagon. This symbol is in general use; it is assumed that at each corner there is a CH group which, however, is not always written in; if a hydrogen atom be substituted by another group, then this group is attached to the corner previously occupied by the displaced hydrogen. The following diagrams illustrate these statements:—

Benzene. Abbreviated. Oxybenzene. Abbreviated.
From the benzene nucleus we can derive other aromatic nuclei, graphically represented by fusing two or more hexagons along common sides. By fusing two nuclei we obtain the formula of naphthalene, C10H10; by fusing three, the hydrocarbons anthracene and phenanthrene, C14H10; by fusing four, chrysene, C18H12, and possibly pyrene, C16H10; by fusing five, picene, C22H14. But it must be here understood that each member of these condensed nuclei need not necessarily be identical in structure; thus the central nuclei in anthracene and phenanthrene differ very considerably from the terminal nuclei (see below, Condensed Nuclei). Other hydrocarbon nuclei generally classed as aromatic in character result from the union of two or more benzene nuclei joined by one or two valencies with polymethylene or oxidized polymethylene rings; instances of such nuclei are indene, hydrindene, fluorene, and fluor-anthene. From these nuclei an immense number of derivatives may be obtained, for the hydrogen atoms may be substituted by any of the radicals discussed in the preceding section on the classification of organic compounds.
We now proceed to consider the properties, syntheses, decompositions and constitution of the benzene complex. It has already been stated that benzene derivatives may be Distinctions between aliphatic and aromatic compounds. regarded as formed by the replacement of hydrogen atoms by other elements or radicals in exactly the same manner as in the aliphatic series. Important differences, however, are immediately met with when we consider the methods by which derivatives are obtained. For example: nitric acid and sulphuric acid readily react with benzene and its homologues with the production of nitro derivatives and sulphonic acids, while in the aliphatic series these acids exert no substituting action (in the case of the olefines, the latter acid forms an addition product); another distinction is that the benzene complex is more stable towards oxidizing agents. This and other facts connected with the stability of benzenoid compounds are clearly shown when we consider mixed aliphatic-aromatic hydrocarbons, i.e. compounds derived by substituting aliphatic radicals in the benzene nucleus; such a compound is methylbenzene or toluene, C6H5·CH3. This compound is readily oxidized to benzoic acid, C6H5·COOH, the aromatic residue being unattacked; nitric and sulphuric acids produce nitro-toluenes, C6H4·CH3·NO2, and toluene sulphonic acids, C6H4·CH3·SO3H; chlorination may result in the formation of derivatives substituted either in the aromatic nucleus or in the side chain; the former substitution occurs most readily, chlor-toluenes, C6H4·CH3·Cl, being formed, while the latter, which needs an elevation in temperature or other auxiliary, yields benzyl chloride, C6H5·CH2Cl, and benzal chloride, C6H5·CHCl2. In general, the aliphatic residues in such mixed compounds retain the characters of their class, while the aromatic residues retain the properties of benzene.
Further differences become apparent when various typical compounds are compared. The introduction of hydroxyl groups into the benzene nucleus gives rise to compounds generically named phenols, which, although resembling the aliphatic alcohols in their origin, differ from these substances in their increased chemical activity and acid nature. The phenols more closely resemble the tertiary alcohols, since the hydroxyl group is linked to a carbon atom which is united to other carbon atoms by its remaining three valencies; hence on oxidation they cannot yield the corresponding aldehydes, ketones or acids (see below, Decompositions of the Benzene Ring). The amines also exhibit striking differences: in the aliphatic series these compounds may be directly formed from the alkyl haloids and ammonia, but in the benzene series this reaction is quite impossible unless the haloid atom be weakened by the presence of other substituents, e.g. nitro groups. Moreover, while methylamine, dimethylamine, and trimethylamine increase in basicity corresponding to the introduction of successive methyl groups, phenylamine or aniline, diphenylamine, and triphenylamine are in decreasing order of basicity, the salts of diphenylamine being decomposed by water. Mixed aromatic-aliphatic amines, both secondary and tertiary, are also more strongly basic than the pure aromatic amines, and less basic than the true aliphatic compounds; e.g. aniline, C6H5·NH2, monomethyl aniline, C6H5·NH·CH3, and dimethyl aniline, C6H5·N(CH3)2, are in increasing order of basicity. These observations may be summarized by saying that the benzene nucleus is more negative in character than the aliphatic residues.
Isomerism of Benzene Derivatives.—Although Kekulé founded his famous benzene formula in 1865 on the assumptions that the six hydrogen atoms in benzene are equivalent and that the molecule is symmetrical, i.e. that two pairs of hydrogen atoms are symmetrically situated with reference to any specified hydrogen atom, the absolute demonstration of the validity of 53 these assumptions was first given by A. Ladenburg in 1874 (see Ber., 1874, 7, p. 1684; 1875, 8, p. 1666; Theorie der aromatischen Verbindungen, 1876). These results may be graphically represented as follows: numbering the hydrogen atoms in cyclical order from 1 to 6, then the first thesis demands that whichever atom is substituted the same compound results, while the second thesis points out that the pairs 2 and 6, and 3 and 5 are symmetrical with respect to 1, or in other words, the di-substitution derivatives 1.2 and 1.6, and also 1.3 and 1.5 are identical. Therefore three di-derivatives are possible, viz. 1.2 or 1.6, named ortho- (o), 1.3 or 1.5, named meta- (m), and 1.4, named para- compounds (p). In the same way it may be shown that three tri-substitution, three tetra-substitution, one penta-substitution, and one hexa-substitution derivative are possible. Of the tri-substitution derivatives, 1.2.3.-compounds are known as “adjacent” or “vicinal” (v), the 1.2.4 as “asymmetrical” (as), the 1.3.5 as “symmetrical” (s); of the tetra-substitution derivatives, 1.2.3.4-compounds are known as “adjacent,” 1.2.3.5 as “asymmetrical,” and 1.2.4.5 as “symmetrical.”

Here we have assumed the substituent groups to be alike; when they are unlike, a greater number of isomers is possible. Thus in the tri-substitution derivatives six isomers, and no more, are possible when two of the substituents are alike; for instance, six diaminobenzoic acids, C6H3(NH2)2COOH, are known; when all are unlike ten isomers are possible; thus, ten oxytoluic acids, C6H3·CH3·OH·COOH, are known. In the case of tetra-substituted compounds, thirty isomers are possible when all the groups are different.
The preceding considerations render it comparatively easy to follow the reasoning on which the experimental verification of the above statements is based. The proof is divided into two Equivalence of four hydrogen atoms. parts: (1) that four hydrogen atoms are equal, and (2) that two pairs of hydrogen atoms are symmetrical with reference to a specified hydrogen atom. In the first thesis, phenol or oxybenzene, C6H5·OH, in which we will assume the hydroxyl group to occupy position 1, is converted into brombenzene, which is then converted into benzoic acid, C6H5·COOH. From this substance, an oxybenzoic acid (meta-), C6H4·OH·COOH, may be prepared; and the two other known oxybenzoic acids (ortho- and para-) may be converted into benzoic acid. These three acids yield on heating phenol, identical with the substance started with, and since in the three oxybenzoic acids the hydroxyl groups must occupy positions other than 1, it follows that four hydrogen atoms are equal in value.
R. Hübner and A. Petermann (Ann., 1869, 149, p. 129) provided the proof of the equivalence of the atoms 2 and 6 with respect to 1. From meta-brombenzoic acid two nitrobrombenzoic Symmetry of pairs of hydrogen atoms. acids are obtained on direct nitration; elimination of the bromine atom and the reduction of the nitro to an amino group in these two acids results in the formation of the same ortho-aminobenzoic acid. Hence the positions occupied by the nitro groups in the two different nitrobrombenzoic acids must be symmetrical with respect to the carboxyl group. In 1879, Hübner (Ann., 195, p. 4) proved the equivalence of the second pair, viz. 3 and 5, by starting out with ortho-aminobenzoic acid, previously obtained by two different methods. This substance readily yields ortho-oxybenzoic acid or salicylic acid, which on nitration yields two mononitro-oxybenzoic acids. By eliminating the hydroxy groups in these acids the same nitrobenzoic acid is obtained, which yields on reduction an aminobenzoic acid different from the starting-out acid. Therefore there must be another pair of hydrogen atoms, other than 2 and 6, which are symmetrical with respect to 1. The symmetry of the second pair was also established in 1878 by E. Wroblewsky (Ann., 192, p. 196).
Orientation of Substituent Groups.—The determination of the relative positions of the substituents in a benzene derivative constitutes an important factor in the general investigation of such compounds. Confining our attention, for the present, to di-substitution products we see that there are three distinct series of compounds to be considered. Generally if any group be replaced by another group, then the second group enters the nucleus in the position occupied by the displaced group; this means that if we can definitely orientate three di-derivatives of benzene, then any other compound, which can be obtained from or converted into one of our typical derivatives, may be definitely orientated. Intermolecular transformations—migrations of substituent groups from one carbon atom to another—are of fairly common occurrence among oxy compounds at elevated temperatures. Thus potassium ortho-oxybenzoate is converted into the salt of para-oxybenzoic acid at 220°; the three bromphenols, and also the brombenzenesulphonic acids, yield m-dioxybenzene or resorcin when fused with potash. It is necessary, therefore, to avoid reactions involving such intermolecular migrations when determining the orientation of aromatic compounds.
Such a series of typical compounds are the benzene dicarboxylic acids (phthalic acids), C6H4(COOH)2. C. Graebe (Ann., 1869, 149, p. 22) orientated the ortho-compound or phthalic acid from its formation from naphthalene on oxidation; the meta-compound or isophthalic acid is orientated by its production from mesitylene, shown by A. Ladenburg (Ann., 1875, 179, p. 163) to be symmetrical trimethyl benzene; terephthalic acid, the remaining isomer, must therefore be the para-compound.
P. Griess (Ber., 1872, 5, p. 192; 1874, 7, p. 1223) orientated the three diaminobenzenes or phenylene diamines by considering their preparation by the elimination of the carboxyl group in the six diaminobenzoic acids. The diaminobenzene resulting from two of these acids is the ortho-compound; from three, the meta-; and from one the para-; this is explained by the following scheme:—
W. Körner (Gazz. Chem. Ital., 4, p. 305) in 1874 orientated the three dibrombenzenes in a somewhat similar manner. Starting with the three isomeric compounds, he found that one gave two tribrombenzenes, another gave three, while the third gave only one. A scheme such as the preceding one shows that the first dibrombenzene must be the ortho-compound, the second the meta-, and the third the para-derivative. Further research in this direction was made by D.E. Noetling (Ber., 1885, 18, p. 2657), who investigated the nitro-, amino-, and oxy-xylenes in their relations to the three xylenes or dimethyl benzenes.
The orientation of higher substitution derivatives is determined by considering the di- and tri-substitution compounds into which they can be transformed.
Substitution of the Benzene Ring.—As a general rule, homologues and mono-derivatives of benzene react more readily with substituting agents than the parent hydrocarbon; for example, phenol is converted into tribromphenol by the action of bromine water, and into the nitrophenols by dilute nitric acid; similar activity characterizes aniline. Not only does the substituent group modify the readiness with which the derivative is attacked, but also the nature of the product. Starting with a mono-derivative, we have seen that a substituent group may enter in either of three positions to form an ortho-, meta-, or para-compound. Experience has shown that such mono-derivatives as nitro compounds, sulphonic acids, carboxylic acids, aldehydes, and ketones yield as a general rule chiefly the meta-compounds, and this is independent of the nature of the second group introduced; on the other hand, benzene haloids, amino-, homologous-, and hydroxy-benzenes yield principally a mixture of the ortho- and para-compounds. These facts are embodied in the “Rule of Crum Brown and J. Gibson” (Jour. Chem. Soc. 61, p. 367): If the hydrogen compound of the substituent already in the benzene nucleus can be directly oxidized to the corresponding hydroxyl compound, then meta-derivatives predominate on further substitution, if not, then ortho- and para-derivatives. By further substitution of ortho- and para-di-derivatives, in general the same tri-derivative [1.2.4] is formed (Ann., 1878, 192, p. 219); meta-compounds yield [1.3.4] and [1.2.3] tri-derivatives, except in such cases as when both substituent groups are strongly acid, e.g. m-dinitrobenzene, then [1.3.5]-derivatives are obtained.
Syntheses of the Benzene Ring.—The characteristic distinctions 54 which exist between aliphatic and benzenoid compounds make the transformations of one class into the other especially interesting.
In the first place we may notice a tendency of several aliphatic compounds, e.g. methane, tetrachlormethane, &c., to yield aromatic compounds when subjected to a high temperature, the so-called pyrogenetic reactions (from Greek πῦρ, fire, and γεννάω, I produce); the predominance of benzenoid, and related compounds—naphthalene, anthracene, phenanthrene, &c.—in coal-tar is probably to be associated with similar pyrocondensations. Long-continued treatment with halogens may, in some cases, result in the formation of aromatic compounds; thus perchlorbenzene, C6Cl6, frequently appears as a product of exhaustive chlorination, while hexyl iodide, C6H13I, yields perchlor- and perbrom-benzene quite readily.
The trimolecular polymerization of numerous acetylene compounds—substances containing two trebly linked carbon atoms, —C:C—, to form derivatives of benzene is of considerable interest. M.P.E. Berthelot first accomplished the synthesis of benzene in 1870 by leading acetylene, HC÷CH, through tubes heated to dull redness; at higher temperatures the action becomes reversible, the benzene yielding diphenyl, diphenylbenzene, and acetylene. The condensation of acetylene to benzene is also possible at ordinary temperatures by leading the gas over pyrophoric iron, nickel, cobalt, or spongy platinum (P. Sabatier and J.B. Senderens). The homologues of acetylene condense more readily; thus allylene, CH÷C·CH3, and crotonylene, CH3·C∶C·CH3, yield trimethyl- and hexamethyl-benzene under the influence of sulphuric acid. Toluene or mono-methylbenzene results from the pyrocondensation of a mixture of acetylene and allylene. Substituted acetylenes also exhibit this form of condensation; for instance, bromacetylene, BrC∶CH, is readily converted into tribrombenzene, while propiolic acid, HC∶C·COOH, under the influence of sunlight, gives benzene tricarboxylic acid.
A larger and more important series of condensations may be grouped together as resulting from the elimination of the elements of water between carbonyl (CO) and methylene (CH2) groups. A historic example is that of the condensation of three molecules of acetone, CH3·CO·CH3, in the presence of sulphuric acid, to s-trimethylbenzene or mesitylene, C6H3(CH3)3, first observed in 1837 by R. Kane; methylethyl ketone and methyl-n-propyl ketone suffer similar condensations to s-triethylbenzene and s-tri-n-propylbenzene respectively. Somewhat similar condensations are: of geranial or citral, (CH3)2CH·CH2·CH:CH·C(CH3):CH·CHO, to p-isopropyl-methylbenzene or cymene; of the condensation product of methylethylacrolein and acetone, CH3·CH2·CH:C(CH3)·CH:CH·CO·CH3, to [1.3.4]-trimethylbenzene or pseudocumene; and of the condensation product of two molecules of isovaleryl aldehyde with one of acetone, C3H7·CH2·CH:C(C3H7)·CH:CH·CO·CH3, to (1)-methyl-2-4-di-isopropyl benzene. An analogous synthesis is that of di-hydro-m-xylene from methyl heptenone, (CH3)2C:CH·(CH2)2·CO·CH3. Certain a-diketones condense to form benzenoid quinones, two molecules of the diketone taking part in the reaction; thus diacetyl, CH3·CO·CO·CH3, yields p-xyloquinone, C6H2(CH3)2O2 (Ber., 1888, 21, p. 1411), and acetylpropionyl, CH3·CO·CO·C2H5, yields duroquinone, or tetramethylquinone, C6(CH3)4O2. Oxymethylene compounds, characterized by the grouping >C:CH(OH), also give benzene derivatives by hydrolytic condensation between three molecules; thus oxymethylene acetone, or formyl acetone, CH3·CO·CH:CH(OH), formed by acting on formic ester with acetone in the presence of sodium ethylate, readily yields [1.3.5]-triacetylbenzene, C6H3(CO·CH3)3; oxymethylene acetic ester or formyl acetic ester or β-oxyacrylic ester, (HO)CH:CH·CO2C2H5, formed by condensing acetic ester with formic ester, and also its dimolecular condensation product, coumalic acid, readily yields esters of [1.3.5]-benzene tricarboxylic acid or trimesic acid (see Ber., 1887, 20, p. 2930).
In 1890, O. Doebner (Ber. 23, p. 2377) investigated the condensation of pyroracemic acid, CH3·CO·COOH, with various aliphatic aldehydes, and obtained from two molecules of the acid and one of the aldehyde in the presence of baryta water alkylic isophthalic acids: with acetaldehyde [1.3.5]-methylisophthalic acid or uvitic acid, C6H3·CH3·(COOH)2, was obtained, with propionic aldehyde [1.3.5]-ethylisophthalic acid, and with butyric aldehyde the corresponding propylisophthalic acid. We may here mention the synthesis of oxyuvitic ester (5-methyl-4-oxy-1-3-benzene dicarboxylic ester) by the condensation of two molecules of sodium acetoacetic ester with one of chloroform (Ann., 1883, 222, p. 249). Of other syntheses of true benzene derivatives, mention may be made of the formation of orcinol or [3.5]-dioxytoluene from dehydracetic acid; and the formation of esters of oxytoluic acid (5-methyl-3-oxy-benzoic acid), C6H3·CH3·OH·COOH, when acetoneoxalic ester, CH3·CO·CH2·CO·CO·CO2C2H5, is boiled with baryta (Ber., 1889, 22, p. 3271). Of interest also are H.B. Hill and J. Torray’s observations on nitromalonic aldehyde, NO2·CH(CHO)2, formed by acting on mucobromic acid, probably CHO·CBr:CBr:COOH, with alkaline nitrites; this substance condenses with acetone to give p-nitrophenol, and forms [1.3.5]-trinitrobenzene when its sodium salt is decomposed with an acid.
By passing carbon monoxide over heated potassium J. von Liebig discovered, in 1834, an interesting aromatic compound, potassium carbon monoxide or potassium hexaoxybenzene, the nature of which was satisfactorily cleared up by R. Nietzki and T. Benckiser (Ber. 18, p. 499) in 1885, who showed that it yielded hexaoxybenzene, C6(OH)6, when acted upon with dilute hydrochloric acid; further investigation of this compound brought to light a considerable number of highly interesting derivatives (see Quinones). Another hexa-substituted benzene compound capable of direct synthesis is mellitic acid or benzene carboxylic acid, C6(COOH)6. This substance, first obtained from the mineral honeystone, aluminium mellitate, by M.H. Klaproth in 1799, is obtained when pure carbon (graphite or charcoal) is oxidized by alkaline permanganate, or when carbon forms the positive pole in an electrolytic cell (Ber., 1883, 16, p. 1209). The composition of this substance was determined by A. von Baeyer in 1870, who obtained benzene on distilling the calcium salt with lime.
Hitherto we have generally restricted ourselves to syntheses which result in the production of a true benzene ring; but there are many reactions by which reduced benzene rings are synthesized, and from the compounds so obtained true benzenoid compounds may be prepared. Of such syntheses we may notice: the condensation of sodium malonic ester to phloroglucin tricarboxylic ester, a substance which gives phloroglucin or trioxybenzene when fused with alkalis, and behaves both as a triketohexamethylene tricarboxylic ester and as a trioxybenzene tricarboxylic ester; the condensation of succinic ester, (CH2·CO2C2H5)2, under the influence of sodium to succinosuccinic ester, a diketohexamethylene dicarboxylic ester, which readily yields dioxyterephthalic acid and hydroquinpne (F. Herrmann, Ann., 1882, 211, p. 306; also see below, Configuration of the Benzene Complex); the condensation of acetone dicarboxylic ester with malonic ester to form triketohexamethylene dicarboxylic ester (E. Rimini, Gazz. Chem., 1896, 26, (2), p. 374); the condensation of acetone-di-propionic acid under the influence of boiling water to a diketohexamethylene propionic acid (von Pechmann and Sidgwick, Ber., 1904, 37, p. 3816). Many diketo compounds suffer condensation between two molecules to form hydrobenzene derivatives, thus α, γ-di-acetoglutaric ester, C2H5O2C(CH3·CO)CH·CH2·CH(CO·CH3)CO2C2H5, yields a methyl-ketohexamethylene, while γ-acetobutyric ester, CH3CO(CH2)2CO2C2H5, is converted into dihydroresorcinol or m-diketohexamethylene by sodium ethylate; this last reaction is reversed by baryta (see Decompositions of Benzene Ring). For other syntheses of hexamethylene derivatives, see Polymethylenes.
Decompositions of the Benzene Ring.—We have previously alluded to the relative stability of the benzene complex; consequently reactions which lead to its disruption are all the more interesting, and have engaged the attention of many chemists. If we accept Kekulé’s formula for the benzene nucleus, then we may expect the double linkages to be opened up partially, either by oxidation or reduction, with the formation of di-, tetra-, or hexa-hydro derivatives, or entirely, with the production of open chain compounds. Generally rupture occurs at more than one point; and rarely are the six carbon atoms of the complex regained as an open chain. Certain compounds withstand ring decomposition much more strongly than others; for instance, benzene and its homologues, carboxylic acids, and nitro compounds are much more stable towards oxidizing agents than amino- and oxy-benzenes, aminophenols, quinones, and oxy-carboxylic acids.
Strong oxidation breaks the benzene complex into such compounds as carbon dioxide, oxalic acid, formic acid, &c.; such decompositions are of little interest. More important are Kekulé’s Simple oxidation. observations that nitrous acid oxidizes pyrocatechol or [1.2]-dioxybenzene, and protocatechuic acid or [3.4]-dioxybenzoic acid to dioxytartaric acid, (C(OH)2·COOH)2 (Ann., 1883, 221, p. 230); and O. Doebner’s preparation of mesotartaric acid, the internally compensated tartaric acid, (CH(OH)·COOH)2, by oxidizing phenol with dilute potassium permanganate (Ber., 1891, 24, p. 1753).
For many years it had been known that a mixture of potassium chlorate and hydrochloric or sulphuric acids possessed strong oxidizing powers. L. Carius showed that potassium Chlorination and oxidation. chlorate and sulphuric acid oxidized benzene to trichlor-phenomalic acid, a substance afterwards investigated by Kekulé and O. Strecker (Ann., 1884, 223, p. 170), and shown to be β-trichloracetoacrylic acid, CCl3·CO·CH:CH·COOH, which with baryta gave chloroform and maleic acid. Potassium chlorate and hydrochloric acid oxidize phenol, salicylic acid (o-oxybenzoic acid), and gallic acid ([2.3.4] trioxybenzoic acid) to trichlorpyroracemic acid (isotrichlorglyceric acid), CCl3·C(OH)2·CO2H, a substance also obtained from trichloracetonitrile, CCl3·CO·CN, by hydrolysis. We may also notice the conversion of picric acid, ([2.4.6]-trinitrophenol) into chloropicrin, CCl3NO2, by bleaching lime (calcium hypochlorite), and into bromopicrin, CBr3NO2, by bromine water.
55 The action of chlorine upon di-and tri-oxybenzenes has been carefully investigated by Th. Zincke; and his researches have led to the discovery of many chlorinated oxidation products which admit of decomposition into cyclic compounds containing fewer carbon atoms than characterize the benzene ring, and in turn yielding open-chain or aliphatic compounds. In general, the rupture occurs between a-keto group (CO) and a keto-chloride group (CCl2), into which two adjacent carbon atoms of the ring are converted by the oxidizing and substituting action of chlorine. Decompositions of this nature were first discovered in the naphthalene series, where it was found that derivatives of indene (and of hydrindene and indone) and also of benzene resulted; Zincke then extended his methods to the disintegration of the oxybenzenes and obtained analogous results, R-pentene and aliphatic derivatives being formed (R- symbolizing a ringed nucleus).
When treated with chlorine, pyrocatechol (1.2 or ortho-dioxybenzene) (1) yields a tetrachlor ortho-quinone, which suffers further chlorination to hexachlor-o-diketo-R-hexene (2). This substance is transformed into hexachlor-R-pentene oxycarboxylic acid (3) when digested with water; and chromic acid oxidizes this substance to hexachlor-R-pentene (4). The ring of this compound is ruptured by caustic soda with the formation of perchlorvinyl acrylic acid (5), which gives on reduction ethidine propionic acid (6), a compound containing five of the carbon atoms originally in the benzene ring (see Zincke, Ber., 1894, 27, p. 3364) (the carbon atoms are omitted in some of the formulae).

Resorcin (1.3 or meta dioxybenzene) (1) is decomposed in a somewhat similar manner. Chlorination in glacial acetic acid solution yields pentachlor-m-diketo-R-hexene (2) and, at a later stage, heptachlor-m-diketo-R-hexene (3). These compounds are both decomposed by water, the former giving dichloraceto-trichlor-crotonic acid (4), which on boiling with water gives dichlormethyl-vinyl-a-diketone (5). The heptachlor compound when treated with chlorine water gives trichloraceto-pentachlorbutyric acid (6), which is hydrolysed by alkalis to chloroform and pentachlorglutaric acid (7), and is converted by boiling water into tetrachlor-diketo-R-pentene (8). This latter compound may be chlorinated to perchloracetoacrylic chloride (9), from which the corresponding acid (10) is obtained by treatment with water; alkalis hydrolyse the acid to chloroform and dichlormaleic acid (11).
Hydroquinone (1.4 or para-dioxybenzene) (1) gives with chlorine, first, a tetrachlorquinone (2), and then hexachlor-p-diketo-R-hexene (3), which alcoholic potash converts into perchloracroylacrylic acid (4). This substance, and also the preceding compound, is converted by aqueous caustic soda into dichlormaleic acid, trichlorethylene, and hydrochloric acid (5) (Th. Zincke and O. Fuchs, Ann., 1892, 267, p. 1).

Phloroglucin (1.3.5-trioxybenzene) (1) behaves similarly to resorcin, hexachlor [1.3.5] triketo-R-hexylene (2) being first formed. This compound is converted by chlorine water into octachloracetylacetone (3); by methyl alcohol into the ester of dichlormalonic acid and tetrachloracetone (4); whilst ammonia gives dichloracetamide (5) (Th. Zincke and O. Kegel, Ber., 1890, 23, p. 1706).

When phenol is oxidized in acid solution by chlorine, tetrachlorquinone is obtained, a compound also obtainable from hydroquinone. By conducting the chlorination in alkaline solution, Reduction in alkaline solution. A. Hantzsch (Ber., 1889, 22, p. 1238) succeeded in obtaining derivatives of o-diketo-R-hexene, which yield R-pentene and aliphatic compounds on decomposition. When thus chlorinated phenol (1) yields trichlor-o-diketo-R-hexene (2), which may be hydrolysed to an acid (3), which, in turn, suffers rearrangement to trichlor-R-pentene-oxycarboxylic acid (4). Bromine water oxidizes this substance to oxalic acid and tetrabrom-dichloracetone (5).

The reduction of o-oxybenzoic acids by sodium in amyl alcohol solution has been studied by A. Einhorn and J.S. Lumsden (Ann., 1895, 286, p. 257). It is probable that tetrahydro acids are first formed, which suffer rearrangement to orthoketone carboxylic acids. These substances absorb water and become pimelic acids. Thus salicylic acid yields n-pimelic acid, HOOC·(CH2)5·COOH, while o-, m-, and p-cresotinic acids, C6H3(CH3)(OH)(COOH), yield isomeric methylpimelic acids.
Resorcin on reduction gives dihydroresorcin, which G. Merling (Ann., 1894, 278, p. 20) showed to be converted into n-glutaric acid, HOOC·(CH2)3·COOH, when oxidized with potassium permanganate; according to D. Vörlander (Ber., 1895, 28, p. 2348) it is converted into γ-acetobutyric acid, CH3CO·(CH2)3·COOH, when heated with baryta to 150-160°.
Configuration of the Benzene Complex.—The development of the “structure theory” in about 1860 brought in its train an appreciation of the chemical structure of the derivatives of benzene. The pioneer in this field was August Kekulé, who, in 1865 (Ann., 137, p. 129; see also his Lehrbuch der organischen Chemie), submitted his well-known formula for benzene, so founding the “benzene theory” and opening up a problem which, notwithstanding the immense amount of labour since bestowed upon it, still remains imperfectly solved. Arguing from the existence of only one mono-substitution derivative, and of three di-derivatives (statements of which the rigorous proof was then wanting), he was led to arrange the six carbon atoms in a ring, attaching a hydrogen atom to each carbon atom; being left with the fourth carbon valencies, he mutually saturated these in pairs, thus obtaining the symbol I (see below). The value of this ringed structure was readily perceived, but objections were raised with respect to Kekulé’s disposal of the fourth valencies. In 1866 Sir James Dewar proposed an unsymmetrical form (II); while in 1867, A. Claus (Theoretische Betrachtungen und deren Anwendung zur Systematik der organischen Chemie) proposed his diagonal formula (III), and two years later, A. Ladenburg (Ber., 2, p. 140) devised his prism formula (IV), the six carbon atoms being placed at the six corners of a right equilateral triangular prism, with its plane projections (V, VI).

One of the earliest and strongest objections urged against Kekulé’s formula was that it demanded two isomeric ortho-di-substitution derivatives; for if we number the carbon atoms in cyclical Objections to Kekulé’s formula. order from 1 to 6, then the derivatives 1·2 and 1·6 should be different.13 Ladenburg submitted that if the 1·2 and 1·6 compounds were identical, then we should expect the two well-known crotonic acids, CH3·CH:CH·COOH and CH2:CH·CH2·COOH, to be identical. This view was opposed by Victor Meyer and Kekulé. The former pointed out that the supposed isomerism was not due to an arrangement of atoms, but to the disposition of a valency, and therefore it was doubtful whether such a subtle condition could exert any influence on the properties of the substance. Kekulé answered Ladenburg by formulating a dynamic interpretation of valency. He assumed that if we have one atom 56 connected by single bonds to (say) four other atoms, then in a certain unit of time it will collide with each of these atoms in turn. Now suppose two of the attached atoms are replaced by one atom, then this atom must have two valencies directed to the central atom; and consequently, in the same unit of time, the central atom will collide once with each of the two monovalent atoms and twice with the divalent. Applying this notion to benzene, let us consider the impacts made by the carbon atom (1) which we will assume to be doubly linked to the carbon atom (2) and singly linked to (6), h standing for the hydrogen atom. In the first unit of time, the impacts are 2, 6, h, 2; and in the second 6, 2, h, 6. If we represent graphically the impacts in the second unit of time, we perceive that they point to a configuration in which the double linkage is between the carbon atoms 1 and 6, and the single linkage between 1 and 2. Therefore, according to Kekulé, the double linkages are in a state of continual oscillation, and if his dynamical notion of valency, or a similar hypothesis, be correct, then the difference between the 1.2 and 1.6 di-derivatives rests on the insufficiency of his formula, which represents the configuration during one set of oscillations only. The difference is only apparent, not real. An analogous oscillation prevails in the pyrazol nucleus, for L. Knorr (Ann., 1894, 279, p. 188) has shown that 3- and 5-methylpyrazols are identical.
The explanation thus attempted by Kekulé was adversely criticized, more especially by A. Ladenburg, who devoted much attention to the study of the substitution products of benzene, and Ladenburg’s formula. to the support of his own formula. His views are presented in his Pamphlet: Theorie der aromatischen Verbindungen, 1876. The prism formula also received support from the following data: protocatechuic acid when oxidized by nitrous acid gives carboxytartronic acid, which, on account of its ready decomposition into carbon dioxide and tartronic acid, was considered to be HO·C(COOH)3. This implied that in the benzene complex there was at least one carbon atom linked to three others, thus rendering Kekulé’s formula impossible and Ladenburg’s and Claus’ possible. Kekulé (Ann., 1883, 221, p. 230), however, reinvestigated this acid; he showed that it was dibasic and not tribasic; that it gave tartaric acid on reduction; and, finally, that it was dioxytartaric acid, HOOC·C(OH)2·C(OH)2·COOH. The formation of this substance readily follows from Kekulé’s formula, while considerable difficulties are met with when one attempts an explanation based on Ladenburg’s representation. Kekulé also urged that the formation of trichlorphenomalic acid, shown by him and O. Strecker to be trichloracetoacrylic acid, was more favourably explained by his formula than by Ladenburg’s.
Other objections to Ladenburg’s formula resulted from A. von Baeyer’s researches (commenced in 1886) on the reduced phthalic acids. Baeyer pointed out that although benzene derivatives Baeyer’s researches. were obtainable from hexamethylene compounds, yet it by no means follows that only hexamethylene compounds need result when benzene compounds are reduced. He admitted the possibility of the formulae of Kekulé, Claus, Dewar and Ladenburg, although as to the last di-trimethylene derivatives should be possible reduction products, being formed by severing two of the prism edges; and he attempted to solve the problem by a systematic investigation of the reduced phthalic acids.
Ladenburg’s prism admits of one mono-substitution derivative and three di-derivatives. Furthermore, it is in accordance with certain simple syntheses of benzene derivatives (e.g. from acetylene and acetone); but according to Baeyer (Ber., 1886, 19, p. 1797) it fails to explain the formation of dioxyterephthalic ester from succinosuccinic ester, unless we make the assumption that the transformation of these substances is attended by a migration of the substituent groups. For succinosuccinic ester, formed by the action of sodium on two molecules of succinic ester, has either of the formulae (I) or (II); oxidation of the free acid gives dioxyterephthalic acid in which the para-positions must remain substituted as in (I) and (II). By projecting Ladenburg’s prism on a plane and numbering the atoms so as to correspond with Kekulé’s form, viz. that 1.2 and 1.6 should be ortho-positions, 1.3 and 1.5 meta-, and 1.4 para-, and following out the transformation on the Ladenburg formula, then an ortho-dioxyterephthalic acid (IV) should result, a fact denied by experience, and inexplicable unless we assume a wandering of atoms. Kekulé’s formula (III), on the other hand, is in full agreement (Baeyer). This explanation has been challenged by Ladenburg

(Ber., 1886, 19, p. 971; Ber., 1887, 20, p. 62) and by A.K. Miller (J.C.S. Trans., 1887, p. 208). The transformation is not one of the oxidation of a hexamethylene compound to a benzenoid compound, for only two hydrogen atoms are removed. Succinosuccinic ester behaves both as a ketone and as a phenol, thereby exhibiting desmotropy; assuming the ketone formula as indicating the constitution, then in Baeyer’s equation we have a migration of a hydrogen atom, whereas to bring Ladenburg’s formula into line, an oxygen atom must migrate.
The relative merits of the formulae of Kekulé, Claus and Dewar were next investigated by means of the reduction products of benzene, it being Baeyer’s intention to detect whether double linkages were or were not present in the benzene complex.
To follow Baeyer’s results we must explain his nomenclature of the reduced benzene derivatives. He numbers the carbon atoms placed at the corners of a hexagon from 1 to 6, and each side in the same order, so that the carbon atoms 1 and 2 are connected by the side 1, atoms 2 and 3 by the side 2, and so on. A doubly linked pair of atoms is denoted by the sign Δ with the index corresponding to the side; if there are two pairs of double links, then indices corresponding to both sides are employed. Thus Δ1 denotes a tetrahydro derivative in which the double link occupies the side 1; Δ1.3, a dihydro derivative, the double links being along the sides 1 and 3. Another form of isomerism is occasioned by spatial arrangements, many of the reduced terephthalic acids existing in two stereo-isomeric forms. Baeyer explains this by analogy with fumaric and maleic acids: he assumes the reduced benzene ring to lie in a plane; when both carboxyl groups are on the same side of this plane, the acids, in general, resemble maleic acids, these forms he denotes by Γcis-cis, or shortly cis-; when the carboxyl groups are on opposite sides, the acids correspond to fumaric acid, these forms are denoted by Γcis-trans, or shortly trans-.
By reducing terephthalic acid with sodium amalgam, care being taken to neutralize the caustic soda simultaneously formed by passing in carbon dioxide, Δ2.5 dihydroterephthalic acid is obtained; this results from the splitting of a para-linkage. By boiling with water the Δ2.5 acid is converted into the Δ1.5 dihydroterephthalic acid. This acid is converted into the Δ1.4 acid by soda, and into the Δ2 tetrahydro acid by reduction. From this acid the Δ1.3 dihydro and the Δ1 tetrahydro acids may be obtained, from both of which the hexahydro acid may be prepared. From these results Baeyer concluded that Claus’ formula with three para-linkings cannot possibly be correct, for the Δ2.5 dihydroterephthalic acid undoubtedly has two ethylene linkages, since it readily takes up two or four atoms of bromine, and is oxidized in warm aqueous solution by alkaline potassium permanganate. But the formation of the Δ2.5 acid as the first reduction product is not fully consistent with Kekulé’s symbol, for we should then expect the Δ1.3 or the Δ1.5 acid to be first formed (see also Polymethylenes).
The stronger argument against the ethylenoid linkages demanded by Kekulé’s formula is provided by the remarkable stability towards oxidizing and reducing agents which characterizes all benzenoid compounds. From the fact that reduction products containing either one or two double linkages behave exactly as unsaturated aliphatic compounds, being readily reduced or oxidized, and combining with the halogen elements and haloid acids, it seems probable that in benzenoid compounds the fourth valencies are symmetrically distributed in such a manner as to induce a peculiar stability in the molecule. Such a configuration was proposed in 1887 by H.E. Armstrong (J.C.S. Trans., 1887, p. 258), and shortly afterwards by Baeyer (Ann., 1888, 245, p. 103). In this formula, the so-called “centric formula,” the assumption made is that the fourth valencies are simply directed towards the centre of the ring; nothing further is said about the fourth valencies except that they exert a pressure towards the centre. Claus maintained that Baeyer’s view was identical with his own, for as in Baeyer’s formula, the fourth valencies have a different function from the peripheral valencies, being united at the centre in a form of potential union.
It is difficult to determine which configuration most accurately explains the observed facts; Kekulé’s formula undoubtedly explains the synthetical production of benzenoid compounds most satisfactorily, and W. Marckwald (Ann., 1893, 274, p. 331; 1894, 279, p. 14) has supported this formula from considerations based on the syntheses of the quinoline ring. Further researches by Baeyer, and upon various nitrogenous ring systems by E. Bamberger (a strong supporter of the centric formula), have shown that the nature of the substituent groups influences the distribution of the fourth valencies; therefore it may be concluded that in compounds the benzene nucleus appears to be capable of existence in two tautomeric forms, in the sense that each particular derivative possesses a definite constitution. The benzene nucleus presents a remarkable case, which must be considered in the formulation of any complete theory of valency. From a study of the reduction of compounds containing two ethylenic bonds united by a single bond, termed a “conjugated system,” E. Thiele suggested a doctrine of “partial valencies,” 57 which assumes that in addition to the ordinary valencies, each doubly linked atom has a partial valency, by which the atom first interacts. When applied to benzene, a twofold conjugated system is suggested in which the partial valencies of adjacent atoms neutralize, with the formation of a potential double link. The stability of benzene is ascribed to this conjugation.14
Physico-chemical properties have also been drawn upon to decide whether double unions are present in the benzene complex; but here the predilections of the observers Physico-chemical methods. apparently influence the nature of the conclusions to be drawn from such data. It is well known that singly, doubly and trebly linked carbon atoms affect the physical properties of substances, such as the refractive index, specific volume, and the heat of combustion; and by determining these constants for many substances, fairly definite values can be assigned to these groupings. The general question of the relation of the refractive index to constitution has been especially studied by J.W. Brühl, who concluded that benzene contained 3 double linkages; whereas, in 1901, Pellini (Gazetta, 31, i. p. 1) calculated that 9 single linkages were present. A similar contradiction apparently exists with regard to the specific volume, for while benzene has a specific volume corresponding to Claus’ formula, toluene, or methylbenzene, rather points to Kekulé’s. The heat of combustion, as first determined by Julius Thomsen, agreed rather better with the presence of nine single unions. His work was repeated on a finer scale by M.P.E. Berthelot of Paris, and F.C.A. Stohmann of Leipzig; and the new data and the conclusions to be drawn from them formed the subject of much discussion, Brühl endeavouring to show how they supported Kekulé’s formula, while Thomsen maintained that they demanded the benzene union to have a different heat of combustion from the acetylene union. Thomsen then investigated heats of combustion of various benzenoid hydrocarbons—benzene, naphthalene, anthracene, phenanthrene, &c.—in the crystallized state. It was found that the results were capable of expression by the empirical relation CaH2b = 104.3b + 49.09m + 105.47n, where CaH2b denotes the formula of the hydrocarbon, m the number of single carbon linkings and n the number of double linkings, m and n being calculated on the Kekulé formulae. But, at the same time, the constants in the above relation are not identical with those in the corresponding relation empirically deduced from observations on fatty hydrocarbons; and we are therefore led to conclude that a benzene union is considerably more stable than an ethylene union.
Mention may be made of the absorption spectrum of benzene. According to W.N. Hartley (J.C.S., 1905, 87, p. 1822), there are six bands in the ultra-violet, while E.C.C. Baly and J.N. Collie (J.C.S., 1905, 87, p. 1332; 1906, 89, p. 524) record seven. These bands are due to molecular oscillations; Hartley suggests the carbon atoms to be rotating and forming alternately single and double linkages, the formation of three double links giving three bands, and of three single links another three; Baly and Collie, on the other hand, suggest the making and breaking of links between adjacent atoms, pointing out that there are seven combinations of one, two and three pairs of carbon atoms in the benzene molecule.
Stereo-chemical Configurations.—Simultaneously with the discussions of Kekulé, Ladenburg, Claus, Baeyer and others as to the merits of various plane formulae of the benzene complex, there were published many suggestions with regard to the arrangement of the atoms in space, all of which attempted to explain the number of isomers and the equivalence of the hydrogen atoms. The development of stereo-isomerism at the hands of J. Wislicenus, Le Bel and van ’t Hoff has resulted in the introduction of another condition which formulae for the benzene complex must satisfy, viz. that the hydrogen atoms must all lie in one plane. The proof of this statement rests on the fact that if the hydrogen atoms were not co-planar, then substitution derivatives (the substituting groups not containing asymmetric carbon atoms) should exist in enantiomorphic forms, differing in crystal form and in their action on polarized light; such optical antipodes have, however, not yet been separated. Ladenburg’s prism formula would give two enantiomorphic ortho-di-substitution derivatives; while forms in which the hydrogen atoms are placed at the corners of a regular octahedron would yield enantiomorphic tri-substitution derivatives.
The octahedral formula discussed by Julius Thomsen (Ber., 1886, 19, p. 2944) consists of the six carbon atoms placed at the corners of a regular octahedron, and connected together by the full lines as shown in (I); a plane projection gives a hexagon with diagonals (II). Reduction to hexamethylene compounds necessitates the disruption of three of the edges of the octahedron, the diagonal linkings remaining intact, or, in the plane projection, three peripheral linkages, the hexamethylene ring assuming the form (III):
In 1888 J.E. Marsh published a paper (Phil. Mag. [V.], 26, p. 426) in which he discussed various stereo-chemical representations of the benzene nucleus. (The stereo-chemistry of carbon compounds has led to the spatial representation of a carbon atom as being situated at the centre of a tetrahedron, the four valencies being directed towards the apices; see above, and Isomerism.) A form based on Kekulé’s formula consists in taking three pairs of tetrahedra, each pair having a side in common, and joining them up along the sides of a regular hexagon by means of their apices. This form, afterwards supported by Carl Graebe (Ber., 1902, 35, p. 526; see also Marsh’s reply, Journ. Chem. Soc. Trans., 1902, p. 961) shows the proximity of the ortho-positions, but fails to explain the identity of 1·2 and 1·6 compounds. Arrangements connected with Claus’ formula are obtained by placing six tetrahedra on the six triangles formed by the diagonals of a plane hexagon. The form in which the tetrahedra are all on one side, afterwards discussed by J. Loschmidt (Monats., 1890, II, p. 28), would not give stereo-isomers; and the arrangement of placing the tetrahedra on alternate sides, a form afterwards developed by W. Vaubel (Journ. Pr. Chem., 1894[2], 49, p. 308), has the advantage of bringing the meta-positions on one side, and the ortho- and para- on opposite sides, thus exhibiting the similarity actually observed between these series of compounds. Marsh also devised a form closely resembling that of Thomsen, inasmuch as the carbon atoms occupied the angles of a regular octahedron, and the diagonal linkages differed in nature from the peripheral, but differing from Thomsen’s since rupture of the diagonal and not peripheral bonds accompanied the reduction to hexamethylene.
We may also notice the model devised by H. Sachse (Ber., 1888, 21, 2530; Zeit. fur phys. Chem., II, p. 214; 23, p. 2062). Two parallel triangular faces are removed from a cardboard model of a regular octahedron, and on the remaining six faces tetrahedra are then placed; the hydrogen atoms are at the free angles. This configuration is, according to Sachse, more stable than any other form; no oscillation is possible, the molecule being only able to move as a whole. In 1897, J.N. Collie (Journ. Chem. Soc. Trans., p. 1013) considered in detail an octahedral form, and showed how by means of certain simple rotations of his system the formulae of Kekulé and Claus could be obtained as projections. An entirely new device, suggested by B. König (Chem. Zeit., 1905, 29, p. 30), assumed the six carbon atoms to occupy six of the corners of a cube, each carbon atom being linked to a hydrogen atom and by single bonds to two neighbouring carbon atoms, the remaining valencies being directed to the unoccupied corners of the cube, three to each, where they are supposed to satisfy each other.
Condensed Nuclei.
Restricting ourselves to compounds resulting from the fusion of benzene rings, we have first to consider naphthalene, C10H8, which consists of two benzene rings having a pair of carbon atoms in common. The next members are the isomers anthracene and phenanthrene, C14H10, formed from three benzene nuclei. Here we shall only discuss the structure of these compounds in the light of the modern benzene theories; reference should be made 58 to the articles Naphthalene, Anthracene and Phenanthrene for syntheses, decompositions, &c.
Naphthalene.—Of the earlier suggestions for the constitution of naphthalene we notice the formulae of Wreden (1) and (2), Berthelot and Balls (3), R.A.C.E. Erlenmeyer (4) and Adolf Claus (5).

The first suggestion is quite out of the question. C. Graebe in 1866 (Ann. 149, p. 20) established the symmetry of the naphthalene nucleus, and showed that whichever half of the molecule be oxidized the same phthalic acid results. Therefore formula (2), being unsymmetrical, is impossible. The third formula is based on Dewar’s benzene formula, which we have seen to be incorrect. Formula (4) is symmetrical and based on Kekulé’s formula: it is in full accord with the syntheses and decompositions of the naphthalene nucleus and the number of isomers found. In 1882 Claus suggested a combination of his own and Dewar’s benzene formulae. This is obviously unsymmetrical, consisting of an aliphatic and an aromatic nucleus; Claus explained the formation of the same phthalic acid from the oxidation of either nucleus by supposing that if the aromatic group be oxidized, the aliphatic residue assumes the character of a benzene nucleus. Bamberger opposed Claus’ formula on the following grounds:—The molecule of naphthalene is symmetrical, since 2.7 dioxynaphthalene is readily esterified by methyl iodide and sulphuric acid to a dimethyl ether; and no more than two mono-substitution derivatives are known. The molecule is aromatic but not benzenoid; however, by the reduction of one half of the molecule, the other assumes a benzenoid character.
If β-naphthylamine and β-naphthol be reduced, tetrahydro products are obtained in which the amino- or oxy-bearing half of the molecule becomes aliphatic in character. The compounds so obtained, alicyclic-β-tetrahydronaphthylamine and alicyclic-β-tetrahydronaphthol, closely resemble β-aminodiethylbenzene, C6H4(C2H5)·C2H4NH2, and β-oxydiethylbenzene, C6H4(C2H5)·C2H4OH. If α-naphthylamine and α-naphthol be reduced, the hydrogen atoms attach themselves to the non-substituted half of the molecule, and the compounds so obtained resemble aminodiethylbenzene, C6H3·NH2(C2H5)2 and oxydiethylbenzene, C6H3·OH(C2H5)2. Bamberger’s observations on reduced quinoline derivatives point to the same conclusion, that condensed nuclei are not benzenoid, but possess an individual character, which breaks down, however, when the molecule is reduced.
It remains, therefore, to consider Erlenmeyer’s formula and those derived from the centric hypothesis. The former, based on Kekulé’s symbol for benzene, explains the decompositions and syntheses of the ring, but the character of naphthalene is not in keeping with the presence of five double linkages, although it is more readily acted upon than benzene is. On the centric hypothesis two formulae are possible: (i) due to H.E. Armstrong, and (2) due to E. Bamberger.

In the first symbol it is assumed that one of the affinities of each of the two central carbon atoms common to the two rings acts into both rings, an assumption involving a somewhat wide departure from all ordinary views as to the manner in which affinity acts. This symbol harmonizes with the fact that the two rings are in complete sympathy, the one responding to every change made in the other. Then, on account of the relatively slight—because divided—influence which would be exercised upon the two rings by the two affinities common to both, the remaining four centric affinities of each ring would presumably be less attracted into the ring than in the case of benzene; consequently they would be more active outwards, and combination would set in more readily. When, as in the formation of naphthalene tetrachloride, for example, the one ring becomes saturated, the other might be expected to assume the normal centric form and become relatively inactive. This is absolutely the case. On the other hand, if substitution be effected in the one ring, and the affinities in that ring become attracted inwards, as apparently happens in the case of benzene, the adjoining ring should become relatively more active because the common affinities would act less into it. Hence, unless the radical introduced be one which exercises a special attractive influence, substitution should take place in preference in the previously unsubstituted ring. In practice this usually occurs; for example, on further bromination, α-bromonaphthalene yields a mixture of the (1.4) and (1.5) dibromonaphthalenes; and when nitronaphthalene is either brominated, or nitrated or sulphonated, the action is practically confined to the second ring. The centric formula proposed by Bamberger represents naphthalene as formed by the fusion of two benzene rings, this indicates that it is a monocyclic composed of ten atoms of carbon. The formula has the advantage that it may be constructed from tetrahedral models of the carbon atom; but it involves the assumption that the molecule has within it a mechanism, equivalent in a measure to a system of railway points, which can readily close up and pass into that characteristic of benzene.
Anthracene and Phenanthrene.—These isomeric hydrocarbons, of the formula C14H10, are to be regarded as formed by the fusion of three benzenoid rings as represented by the symbols:—

In both cases the medial ring is most readily attacked; and various formulae have been devised which are claimed by their authors to represent this and other facts. According to Armstrong, anthracene behaves unsymmetrically towards substituents, and hence one lateral ring differs from the other; he represents the molecule as consisting of one centric ring, the remaining medial and lateral ring being ethenoid. Bamberger, on the other hand, extends his views on benzene and naphthalene and assumes the molecule to be (1). For general purposes, however, the symbol (2), in which the lateral rings are benzenoid and the medial ring fatty, represents quite adequately the syntheses, decompositions, and behaviour of anthracene.

Phenanthrene is regarded by Armstrong as represented by (3), the lateral rings being benzenoid, and the medial ring fatty; Bamberger, however, regards it as (4), the molecule being entirely aromatic. An interesting observation by Baeyer, viz. that stilbene, C6H5·CH:CH·C6H5, is very readily oxidized, while phenanthrene is not, supports, in some measure, the views of Bamberger.

Heterocyclic Compounds.
During recent years an immense number of ringed or cyclic compounds have been discovered, which exhibit individual characters more closely resembling benzene, naphthalene, &c. than purely aliphatic substances, inasmuch as in general they contain double linkages, yet withstand oxidation, and behave as nuclei, forming derivatives in much the same way as benzene. By reduction, the double linkages become saturated, and compounds result which stand in much about the same relation to the original nucleus as hexamethylene does to benzene. In general, therefore, it may be considered that the double linkages are not of exactly the same nature as the double linkage present in ethylene and ethylenoid compounds, but that they are analogous to the potential valencies of benzene. The centric hypothesis has been applied to these rings by Bamberger and others; but as in the previous rings considered, the ordinary 59 representation with double and single linkages generally represents the syntheses, decompositions, &c.; exceptions, however, are known where it is necessary to assume an oscillation of the double linkage. Five- and six-membered rings are the most stable and important, the last-named group resulting from the polymerization of many substances; three- and four-membered rings are formed with difficulty, and are easily ruptured; rings containing seven or more members are generally unstable, and are relatively little known. The elements which go to form heterocyclic rings, in addition to carbon, are oxygen, sulphur, selenium and nitrogen. It is remarkable that sulphur can replace two methine or CH groups with the production of compounds greatly resembling, the original one. Thus benzene, (CH)6, gives thiophene, (CH)4S, from which it is difficultly distinguished; pyridine, (CH)5N, gives thiazole, (CH)3·N·S, which is a very similar substance; naphthalene gives thionaphthen, C8H6S, with which it shows great analogies, especially in the derivatives. Similarly a CH group may be replaced by a nitrogen atom with the production of compounds of similar stability; thus benzene gives pyridine, naphthalene gives quinoline and isoquinoline; anthracene gives acridine and α and β anthrapyridines. Similarly, two or more methine groups may be replaced by the same number of nitrogen atoms with the formation of rings of considerable stability.
Most of the simple ring systems which contain two adjacent carbon atoms may suffer fusion with any other ring (also containing two adjacent carbon atoms) with the production of nuclei of greater complexity. Such condensed nuclei are, in many cases, more readily obtained than the parent nucleus. The more important types are derived from aromatic nuclei, benzene, naphthalene, &c.; the ortho-di-derivatives of the first named, lending themselves particularly to the formation of condensed nuclei. Thus ortho-phenylene diamine yields the following products:—

In some cases oxidation of condensed benzenoid-heterocyclic nuclei results in the rupture of the heterocyclic ring with the formation of a benzene dicarboxylic acid; but if the aromatic nucleus be weakened by the introduction of an amino group, then it is the benzenoid nucleus which is destroyed and a dicarboxylic acid of the heterocyclic ring system obtained.
Heterocyclic rings may be systematically surveyed from two aspects: (1) by arranging the rings with similar hetero-atoms according to the increasing number of carbon atoms, the so-called “homologous series”; or (2) by first dividing the ring systems according to the number of members constituting the ring, and then classifying these groups according to the nature of the hetero-atoms, the so-called “isologous series.” The second method possesses greater advantages, for rings of approximate stability come in one group, and, consequently, their derivatives may be expected to exhibit considerable analogies.
As a useful preliminary it is convenient to divide heterocyclic ring systems into two leading groups: (1) systems resulting from simple internal dehydration (or similar condensations) of saturated aliphatic compounds—such compounds are: the internal anhydrides or cyclic ethers of the glycols and thioglycols (ethylene oxide, &c.); the cyclic alkyleneimides resulting from the splitting off of ammonia between the amino groups of diamino-paraffins (pyrrolidine, piperazine, &c.); the cyclic esters of oxycarboxylic acids (lactones, lactides); the internal anhydrides of aminocarboxylic acids (lactams, betaines); cyclic derivatives of dicarboxylic acids (anhydrides, imides, alkylen-esters, alkylen-amides, &c.). These compounds retain their aliphatic nature, and are best classified with open-chain compounds, into which, in general, they are readily converted. (2) Systems which are generally unsaturated compounds, often of considerable stability, and behave as nuclei; these compounds constitute a well-individualized class exhibiting closer affinities to benzenoid substances than to the open-chain series.
The transition between the two classes as differentiated above may be illustrated by the following cyclic compounds, each of which contains a ring composed of four carbon atoms and one oxygen atom:

The first four substances are readily formed from, and converted into, the corresponding dihydroxy open-chain compound; these substances are truly aliphatic in character. The fifth compound, on the other hand, does not behave as an unsaturated aliphatic compound, but its deportment is that of a nucleus, many substitution derivatives being capable of synthesis. Reduction, however, converts it into an aliphatic compound. This is comparable with the reduction of the benzene nucleus into hexamethylene, a substance of an aliphatic character.
True ring systems, which possess the characters of organic nuclei, do not come into existence in three-and four-membered rings, their first appearance being in penta-atomic rings. The three primary members are furfurane, thiophene and pyrrol, each of which contains four methine or CH groups, and an oxygen, sulphur and imido (NH) member respectively; a series of compounds containing selenium is also known. The formulae of these substances are:

By substituting one or more CH groups in these compounds by nitrogen atoms, ring-systems, collectively known as azoles, result. Obviously, isomeric ring-systems are possible, since the carbon atoms in the original rings are not all of equal value. Thus furfurane yields the following rings by the introduction of one and two nitrogen atoms:
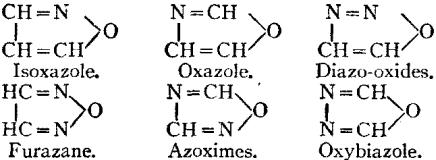
Thiophene yields a similar series: isothiazole (only known as the condensed ring, isobenzothiazole), thiazole, diazosulphides, piazthioles, azosulphimes and thiobiazole (the formulae are easily derived from the preceding series by replacing oxygen by sulphur). Thiophene also gives rise to triazsulphole, three nitrogen atoms being introduced. Selenophene gives the series: selenazole, diazoselenide and piaselenole, corresponding to oxazole, diazo-oxides and furazane. Pyrrol yields an analogous series: pyrazole, imidazole or glyoxaline, azimide or osotriazole, triazole and tetrazole:
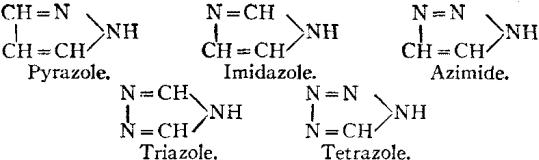
Six-membered ring systems can be referred back, in a manner similar to the above, to pyrone, penthiophene and pyridine, the substances containing a ring of five carbon atoms, and an oxygen, sulphur and nitrogen atom respectively. As before, only true ring nuclei, and not internal anhydrides of aliphatic compounds, will be mentioned. From the pyrone ring the following series of compounds are derived (for brevity, the hydrogen atoms are not printed):

Penthiophene gives, by a similar introduction of nitrogen atoms, penthiazoline, corresponding to meta-oxazine, and para-thiazine, 60 corresponding to paroxazine (para-oxazine). Pyridine gives origin to: pyridazine or ortho-diazine, pyrimidine or meta-diazine, pyrazine or para-diazine, osotriazine, unsymmetrical triazine, symmetrical triazine, osotetrazone and tetrazine. The skeletons of these types are (the carbon atoms are omitted for brevity):

We have previously referred to the condensation of heterocyclic ring systems containing two vicinal carbon atoms with benzene, naphthalene and other nuclei. The more important nuclei of this type have received special and non-systematic names; when this is not the case, such terms as phen-, benzo-, naphtho- are prefixed to the name of the heterocyclic ring. One or two benzene nuclei may suffer condensation with the furfurane, thiophene and pyrrol rings, the common carbon atoms being vicinal to the hetero-atom. The mono-benzo-derivatives are coumarone, benzothiophene and indole; the dibenzo-derivatives are diphenylene oxide, dibenzothiophene or diphenylene sulphide, and carbazole. Typical formulae are (R denoting O, S or NH):

Isomers are possible, for the condensation may be effected on the two carbon atoms symmetrically placed to the hetero-atom; these isomers, however, are more of the nature of internal anhydrides. Benz-oxazoles and -thiazoles have been prepared, benz-isoxazoles are known as indoxazenes; benzo-pyrazoles occur in two structural forms, named indazoles and isindazoles. Derivatives of osotriazol also exist in two forms—azimides and pseudo-azimides.
Proceeding to the six-membered hetero-atomic rings, the benzo-, dibenzo- and naphtho-derivatives are frequently of great commercial and scientific importance, α-pyrone condenses with the benzene ring to form coumarin and isocoumarin; benzo-γ-pyrone constitutes the nucleus of several vegetable colouring matters (chrysin, fisetin, quercetin, &c., which are derivatives of flavone or phenyl benzo-γ-pyrone); dibenzo-γ-pyrone is known as xanthone; related to this substance are fluorane (and fluorescein), fluorone, fluorime, pyronine, &c. The pyridine ring condenses with the benzene ring to form quinoline and isoquinoline; acridine and phenanthridine are dibenzo-pyridines; naphthalene gives rise to α- and β-naphthoquinolines and the anthrapyridines; anthracene gives anthraquinoline; while two pyridine nuclei connected by an intermediate benzene nucleus give the phenanthrolines. Naphthyridines and naphthinolines result from the condensation of two pryridine and two quinoline nuclei respectively; and quino-quinolines are unsymmetrical naphthyridine nuclei condensed with a benzene nucleus. Benzo-orthoxazines, -metoxazines and -paroxazines are known: dibenzoparoxazine or phenoxazine is the parent of a valuable series of dyestuffs; dibenzoparathiazine or thiodiphenylamine is important from the same aspect. Benzo-ortho-diazines exist in two structural forms, cinnolin and phthalazine; benzo-meta-diazines are known as quinazolines; benzo-para-diazines are termed quinoxalines; the dibenzo-compounds are named phenazines, this last group including many valuable dyestuffs—indulines, safranines, &c. In addition to the types of compounds enumerated above we may also notice purin, tropine and the terpenes.
V. ANALYTICAL CHEMISTRY
This branch of chemistry has for its province the determination of the constituents of a chemical compound or of a mixture of compounds. Such a determination is qualitative, the constituent being only detected or proved to be present, or quantitative, in which the amount present is ascertained. The methods of chemical analysis may be classified according to the type of reaction: (1) dry or blowpipe analysis, which consists in an examination of the substance in the dry condition; this includes such tests as ignition in a tube, ignition on charcoal in the blowpipe flame, fusion with borax, microcosmic salt or fluxes, and flame colorations (in quantitative work the dry methods are sometimes termed “dry assaying”); (2) wet analysis, in which a solution of the substance is treated with reagents which produce specific reactions when certain elements or groups of elements are present. In quantitative analysis the methods can be subdivided into: (a) gravimetric, in which the constituent is precipitated either as a definite insoluble compound by the addition of certain reagents, or electrolytically, by the passage of an electric current; (b) volumetric, in which the volume of a reagent of a known strength which produces a certain definite reaction is measured; (c) colorimetric, in which the solution has a particular tint, which can be compared with solutions of known strengths.
Historical.—The germs of analytical chemistry are to be found in the writings of the pharmacists and chemists of the iatrochemical period. The importance of ascertaining the proximate composition of bodies was clearly realized by Otto Tachenius; but the first systematic investigator was Robert Boyle, to whom we owe the introduction of the term analysis. Boyle recognized many reagents which gave precipitates with certain solutions: he detected sulphuric and hydrochloric acids by the white precipitates formed with calcium chloride and silver nitrate respectively; ammonia by the white cloud formed with the vapours of nitric or hydrochloric acids; and copper by the deep blue solution formed by a solution of ammonia. Of great importance is his introduction of vegetable juices (the so-called indicators, q.v.) to detect acids and bases. During the phlogistic period, the detection of the constituents of compounds was considerably developed. Of the principal workers in this field we may notice Friedrich Hoffmann, Andreas Sigismund Marggraf (who detected iron by its reaction with potassium ferrocyanide, and potassium and sodium by their flame colorations), and especially Carl Scheele and Torbern Olof Bergman. Scheele enriched the knowledge of chemistry by an immense number of facts, but he did not possess the spirit of working systematically as Bergman did. Bergman laid the foundations of systematic qualitative analysis, and devised methods by which the metals may be separated into groups according to their behaviour with certain reagents. This subdivision, which is of paramount importance in the analysis of minerals, was subsequently developed by Wilhelm August Lampadius in his Handbuch zur chemischen Analyse der Mineralien (1801) and by John Friedrich A. Göttling in his Praktische Anleitung zur prüfenden und zurlegenden Chemie (1802).
The introduction of the blowpipe into dry qualitative analysis by Axel Fredrik Cronstedt marks an important innovation. The rapidity of the method, and the accurate results which it gave in the hands of a practised experimenter, led to its systematization by Jöns Jakob Berzelius and Johann Friedrich Ludwig Hausmann, and in more recent times by K.F. Plattner, whose treatise Die Probirkunst mit dem Löthrohr is a standard work on the subject. Another type of dry reaction, namely, the flame coloration, had been the subject of isolated notices, as, for example, the violet flame of potassium and the orange flame of sodium observed by Marggraf and Scheele, but a systematic account was wanting until Cartmell took the subject up. His results (Phil. Mag. 16, p. 382) were afterwards perfected by Robert Wilhelm Bunsen and Gustav Merz. Closely related to the flame-colorations, we have to notice the great services rendered by the spectroscope to the detection of elements. Rubidium, caesium, thallium, indium and gallium were first discovered by means of this instrument; the study of the rare earths is greatly facilitated, and the composition of the heavenly bodies alone determinable by it.
Quantitative chemistry had been all but neglected before the time of Lavoisier, for although a few chemists such as Tachenius, Bergman and others had realized the advantages which would accrue from a knowledge of the composition of 61 bodies by weight, and had laid down the lines upon which such determinations should proceed, the experimental difficulties in making accurate observations were enormous, and little progress could be made until the procedure was more accurately determined. Martin Heinrich Klaproth showed the necessity for igniting precipitates before weighing them, if they were not decomposed by this process; and he worked largely with Louis Nicolas Vauquelin in perfecting the analysis of minerals. K.F. Wenzel and J.B. Richter contributed to the knowledge of the quantitative composition of salts. Anton Laurent Lavoisier, however, must be considered as the first great exponent of this branch of chemistry. He realized that the composition by weight of chemical compounds was of the greatest moment if chemistry were to advance. His fame rests upon his exposition of the principles necessary to chemistry as a science, but of his contributions to analytical inorganic chemistry little can be said. He applied himself more particularly to the oxygen compounds, and determined with a fair degree of accuracy the ratio of carbon to oxygen in carbon dioxide, but his values for the ratio of hydrogen to oxygen in water, and of phosphorus to oxygen in phosphoric acid, are only approximate; he introduced no new methods either for the estimation or separation of the metals. The next advance was made by Joseph Louis Proust, whose investigations led to a clear grasp of the law of constant proportions. The formulation of the atomic theory by John Dalton gave a fresh impetus to the development of quantitative analysis; and the determination of combining or equivalent weights by Berzelius led to the perfecting of the methods of gravimetric analysis. Experimental conditions were thoroughly worked out; the necessity of working with hot or cold solutions was clearly emphasized; and the employment of small quantities of substances instead of the large amounts recommended by Klaproth was shown by him to give more consistent results.
Since the time of Berzelius many experimenters have entered the lists, and introduced developments which we have not space to mention. We may, however, notice Heinrich Rose15 and Friedrich Wohler,16 who, having worked up the results of their teacher Berzelius, and combined them with their own valuable observations, exerted great influence on the progress of analytical chemistry by publishing works which contained admirable accounts of the then known methods of analysis. To K.R. Fresenius, the founder of the Zeitschrift für analytische Chemie (1862), we are particularly indebted for perfecting and systematizing the various methods of analytical chemistry. By strengthening the older methods, and devising new ones, he exerted an influence which can never be overestimated. His text-books on the subject, of which the Qualitative appeared in 1841, and the Quantitative in 1846, have a world-wide reputation, and have passed through several editions.
The quantitative precipitation of metals by the electric current, although known to Michael Faraday, was not applied to analytical chemistry until O. Wolcott Gibbs worked out the electrolytic separation of copper in 1865. Since then the subject has been extensively studied, more particularly by Alexander Classen, who has summarized the methods and results in his Quantitative Chemical Analysis by Electrolysis (1903). The ever-increasing importance of the electric current in metallurgy and chemical manufactures is making this method of great importance, and in some cases it has partially, if not wholly, superseded the older methods.
Volumetric analysis, possessing as it does many advantages over the gravimetric methods, has of late years been extensively developed. Gay Lussac may be regarded as the founder of the method, although rough applications had been previously made by F.A.H. Descroizilles and L.N. Vauquelin. Chlorimetry (1824), alkalimetry (1828), and the volumetric determination of silver and chlorine (1832) were worked out by Gay Lussac; but although the advantages of the method were patent, it received recognition very slowly. The application of potassium permanganate to the estimation of iron by E. Margueritte in 1846, and of iodine and sulphurous acid to the estimation of copper and many other substances by Robert Wilhelm Bunsen, marks an epoch in the early history of volumetric analysis. Since then it has been rapidly developed, particularly by Karl Friedrich Mohr and J. Volhard, and these methods rank side by side in value with the older and more tedious gravimetric methods.
The detection of carbon and hydrogen in organic compounds by the formation of carbon dioxide and water when they are burned was first correctly understood by Lavoisier, and as he had determined the carbon and hydrogen content of these two substances he was able to devise methods by which carbon and hydrogen in organic compounds could be estimated. In his earlier experiments he burned the substance in a known volume of oxygen, and by measuring the residual gas determined the carbon and hydrogen. For substances of a difficultly combustible nature he adopted the method in common use to-day, viz. to mix the substance with an oxidizing agent—mercuric oxide, lead dioxide, and afterwards copper oxide—and absorb the carbon dioxide in potash solution. This method has been improved, especially by Justus v. Liebig; and certain others based on a different procedure have been suggested. The estimation of nitrogen was first worked out in 1830 by Jean Baptiste Dumas, and different processes have been proposed by Will and F. Varrentrapp, J. Kjeldahl and others. Methods for the estimation of the halogens and sulphur were worked out by L. Carius (see below, § Organic Analysis).
Only a reference can be made in this summary to the many fields in which analytical chemistry has been developed. Progress in forensic chemistry was only possible after the reactions of poisons had been systematized; a subject which has been worked out by many investigators, of whom we notice K.R. Fresenius, J. and R. Otto, and J.S. Stas. Industrial chemistry makes many claims upon the chemist, for it is necessary to determine the purity of a product before it can be valued. This has led to the estimation of sugar by means of the polarimeter, and of the calorific power of fuels, and the valuation of ores and metals, of coal-tar dyes, and almost all trade products.
The passing of the Food and Drug Acts (1875-1899) in England, and the existence of similar adulteration acts in other countries, have occasioned great progress in the analysis of foods, drugs, &c. For further information on this branch of analytical chemistry, see Adulteration.
There exists no branch of technical chemistry, hygiene or pharmacy from which the analytical chemist can be spared, since it is only by a continual development of his art that we can hope to be certain of the purity of any preparation. In England this branch of chemistry is especially cared for by the Institute of Chemistry, which, since its foundation in 1877, has done much for the training of analytical chemists.
In the preceding sketch we have given a necessarily brief account of the historical development of analytical chemistry in its main branches. We shall now treat the different methods in more detail. It must be mentioned here that the reactions of any particular substance are given under its own heading, and in this article we shall only collate the various operations and outline the general procedure. The limits of space prevent any systematic account of the separation of the rare metals, the alkaloids, and other classes of organic compounds, but sources where these matters may be found are given in the list of references.
Qualitative Inorganic Analysis.
The dry examination of a substance comprises several operations, which may yield definite results if no disturbing element is present; but it is imperative that any inference Dry methods. should be confirmed by other methods.
1. Heat the substance in a hard glass tube. Note whether any moisture condenses on the cooler parts of the tube, a gas is evolved, a sublimate formed, or the substance changes colour.
Moisture is evolved from substances containing water of crystallization or decomposed hydrates. If it possesses an alkaline or acid reaction, it must be tested in the first case for ammonia, and in the second case for a volatile acid, such as sulphuric, nitric, hydrochloric, &c.
62 Any evolved gas must be examined. Oxygen, recognized by its power of igniting a glowing splinter, results from the decomposition of oxides of the noble metals, peroxides, chlorates, nitrates and other highly oxygenized salts. Sulphur dioxide, recognized by its smell and acid reaction, results from the ignition of certain sulphites, sulphates, or a mixture of a sulphate with a sulphide. Nitrogen oxides, recognized by their odour and brown-red colour, result from the decomposition of nitrates. Carbon dioxide, recognized by turning lime-water milky, indicates decomposable carbonates or oxalates. Chlorine, bromine, and iodine, each recognizable by its colour and odour, result from decomposable haloids; iodine forms also a black sublimate. Cyanogen and hydrocyanic acid, recognizable by their odour, indicate decomposable cyanides. Sulphuretted hydrogen, recognized by its odour, results from sulphides containing water, and hydrosulphides. Ammonia, recognizable by its odour and alkaline reaction, indicates ammoniacal salts or cyanides containing water.
A sublimate may be formed of: sulphur—reddish-brown drops, cooling to a yellow to brown solid, from sulphides or mixtures; iodine—violet vapour, black sublimate, from iodides, iodic acid, or mixtures; mercury and its compounds—metallic mercury forms minute globules, mercuric sulphide is black and becomes red on rubbing, mercuric chloride fuses before subliming, mercurous chloride does not fuse, mercuric iodide gives a yellow sublimate; arsenic and its compounds—metallic arsenic gives a grey mirror, arsenious oxide forms white shining crystals, arsenic sulphides give reddish-yellow sublimates which turn yellow on cooling; antimony oxide fuses and gives a yellow acicular sublimate; lead chloride forms a white sublimate after long and intense heating.
If the substance does not melt but changes colour, we may have present: zinc oxide—from white to yellow, becoming white on cooling; stannic oxide—white to yellowish brown, dirty white on cooling; lead oxide—from white or yellowish-red to brownish-red, yellow on cooling; bismuth oxide—from white or pale yellow to orange-yellow or reddish-brown, pale yellow on cooling; manganese oxide—from white or yellowish white to dark brown, remaining dark brown on cooling (if it changes on cooling to a bright reddish-brown, it indicates cadmium oxide); copper oxide—from bright blue or green to black; ferrous oxide—from greyish-white to black; ferric oxide—from brownish-red to black, brownish-red on cooling; potassium chromate—yellow to dark orange, fusing at a red heat.
2. Heat the substance on a piece of charcoal in the reducing flame of the blowpipe.
(α) The substance may fuse and be absorbed by the charcoal; this indicates more particularly the alkaline metals.
(β) An infusible white residue may be obtained, which may denote barium, strontium, calcium, magnesium, aluminium or zinc. The first three give characteristic flame colorations (see below); the last three, when moistened with cobalt nitrate and re-ignited, give coloured masses; aluminium (or silica) gives a brilliant blue; zinc gives a green; whilst magnesium phosphates or arsenate (and to a less degree the phosphates of the alkaline earths) give a violet mass.
A metallic globule with or without an incrustation may be obtained. Gold and copper salts give a metallic bead without an incrustation. If the incrustation be white and readily volatile, arsenic is present, if more difficultly volatile and beads are present, antimony; zinc gives an incrustation yellow whilst hot, white on cooling, and volatilized with difficulty; tin gives a pale yellow incrustation, which becomes white on cooling, and does not volatilize in either the reducing or oxidizing flames; lead gives a lemon-yellow incrustation turning sulphur-yellow on cooling, together with metallic malleable beads; bismuth gives metallic globules and a dark orange-yellow incrustation, which becomes lemon-yellow on cooling; cadmium gives a reddish-brown incrustation, which is removed without leaving a gleam by heating in the reducing flame; silver gives white metallic globules and a dark-red incrustation.
3. Heat the substance with a bead of microcosmic salt or borax on a platinum wire in the oxidizing flame.
(α) The substance dissolves readily and in quantity, forming a bead which is clear when hot. If the bead is coloured we may have present: cobalt, blue to violet; copper, green, blue on cooling; in the reducing flame, red when cold; chromium, green, unaltered in the reducing flame; iron, brownish-red, light-yellow or colourless on cooling; in the reducing flame, red while hot, yellow on cooling, greenish when cold; nickel, reddish to brownish-red, yellow to reddish-yellow or colourless on cooling, unaltered in the reducing flame; bismuth, yellowish-brown, light-yellow or colourless on cooling; in the reducing flame, almost colourless, blackish-grey when cold; silver, light yellowish to opal, somewhat opaque when cold; whitish-grey in the reducing flame; manganese, amethyst red, colourless in the reducing flame. If the hot bead is colourless and remains clear on cooling, we may suspect the presence of antimony, aluminium, zinc, cadmium, lead, calcium and magnesium. When present in sufficient quantity the five last-named give enamel-white beads; lead oxide in excess gives a yellowish bead. If the hot colourless bead becomes enamel-white on cooling even when minute quantities of the substances are employed, we may infer the presence of barium or strontium.
(β) The substance dissolves slowly and in small quantity, and forms a colourless bead which remains so on cooling. Either silica or tin may be present. If silica be present, it gives the iron bead when heated with a little ferric oxide; if tin is present there is no change. Certain substances, such as the precious metals, are quite insoluble in the bead, but float about in it.
4. Hold a small portion of the substance moistened with hydrochloric acid on a clean platinum wire in the fusion zone of the Bunsen burner, and note any colour imparted to the flame.
Potassium gives a blue-violet flame which may be masked by the colorations due to sodium, calcium and other elements. By viewing the flame through an indigo prism it appears sky-blue, violet and ultimately crimson, as the thickness of the prism is increased. Other elements do not interfere with this method. Sodium gives an intense and persistent yellow flame; lithium gives a carmine coloration, and may be identified in the presence of sodium by viewing through a cobalt glass or indigo prism; from potassium it may be distinguished by its redder colour; barium gives a yellowish-green flame, which appears bluish-green when viewed through green glass; strontium gives a crimson flame which appears purple or rose when viewed through blue glass; calcium gives an orange-red colour which appears finch-green through green glass; indium gives a characteristic bluish-violet flame; copper gives an intense emerald-green coloration.
5. Film Reactions.—These reactions are practised in the following manner:—A thread of asbestos is moistened and then dipped in the substance to be tested; it is then placed in the luminous point of the Bunsen flame, and a small porcelain basin containing cold water placed immediately over the asbestos. The formation of a film is noted. The operation is repeated with the thread in the oxidizing flame.
Any film formed in the first case is metallic, in the second it is the oxide. The metallic film is tested with 20% nitric acid and with bleaching-powder solution. Arsenic is insoluble in the acid, but immediately dissolves in the bleaching-powder. The black films of antimony and bismuth and the grey mottled film of mercury are slowly soluble in the acid, and untouched by bleaching-powder. The black films of tin, lead and cadmium dissolve at once in the acid, the lead film being also soluble in bleaching-powder. The oxide films of antimony, arsenic, tin and bismuth are white, that of bismuth slightly yellowish; lead yields a very pale yellow film, and cadmium a brown one; mercury yields no oxide film. The oxide films (the metallic one in the case of mercury) are tested with hydriodic acid, and with ammonium sulphide, and from the changes produced the film can be determined (see F.M. Perkin, Qualitative Chemical Analysis, 1905).
Having completed the dry analysis we may now pass on to the wet and more accurate investigation. It is first necessary to get the substance into solution. Small portions Wet methods. should be successively tested with water, dilute hydrochloric acid, dilute nitric acid, strong hydrochloric acid, and a mixture of hydrochloric and nitric acids, first in the cold and then with warming. Certain substances are insoluble in all these reagents, and other methods, such as the fusion with sodium carbonate and potassium nitrate, and subsequent treatment with an acid, must be employed. Some of these insoluble compounds can be detected by their colour and particular reactions. For further information on this subject, we refer the readers to Fresenius’s Qualitative Analysis.
The procedure for the detection of metals in solution consists of first separating them into groups and then examining each group separately. For this purpose the cold solution is treated with hydrochloric acid, which precipitates lead, silver and mercurous salts as chlorides. The solution is filtered and treated with an excess of sulphuretted hydrogen, either in solution or by passing in the gas; this precipitates mercury (mercuric), any lead left over from the first group, copper, bismuth, cadmium, arsenic, antimony and tin as sulphides. The solution is filtered off, boiled till free of sulphuretted hydrogen, and ammonium chloride and ammonia added. If phosphoric acid is absent, aluminium, chromium and ferric hydrates are precipitated. If, however, phosphoric acid is present in the original substance, we may here obtain a precipitate of the phosphates of the remaining metals, together with aluminium, chromium and ferric hydrates. In this case, the precipitate is dissolved in as little as possible hydrochloric acid and boiled with ammonium acetate, acetic acid and ferric chloride. The phosphates of aluminium, chromium and iron are precipitated, and the solution contains the same metals as if phosphoric acid had been absent. To the filtrate from the aluminium, iron and chromium precipitate, ammonia and ammonium sulphide are added; the precipitate may contain nickel, cobalt, zinc and manganese sulphides. Ammonium carbonate is added to the filtrate; this precipitates calcium, strontium and 63 barium. The solution contains magnesium, sodium and potassium, which are separately distinguished by the methods given under their own headings.
We now proceed with the examination of the various group precipitates. The white precipitate formed by cold hydrochloric acid is boiled with water, and the solution filtered while hot. Any lead chloride dissolves, and may be identified by the yellow precipitate formed with potassium chromate. To the residue add ammonia, shake, then filter. Silver chloride goes into solution, and may be precipitated by dilute nitric acid. The residue, which is black in colour, consists of mercuroso-ammonium chloride, in which mercury can be confirmed by its ordinary tests.
The precipitate formed by sulphuretted hydrogen may contain the black mercuric, lead, and copper sulphides, dark-brown bismuth sulphide, yellow cadmium and arsenious sulphides, orange-red antimony sulphide, brown stannous sulphide, dull-yellow stannic sulphide, and whitish sulphur, the last resulting from the oxidation of sulphuretted hydrogen by ferric salts, chromates, &c. Warming with ammonium sulphide dissolves out the arsenic, antimony and tin salts, which are reprecipitated by the addition of hydrochloric acid to the ammonium sulphide solution. The precipitate is shaken with ammonium carbonate, which dissolves the arsenic. Filter and confirm arsenic in the solution by its particular tests. Dissolve the residue in hydrochloric acid and test separately for antimony and tin. The residue from the ammonium sulphide solution is warmed with dilute nitric acid. Any residue consists of black mercuric sulphide (and possibly white lead sulphate), in which mercury is confirmed by its usual tests. The solution is evaporated with a little sulphuric acid and well cooled. The white precipitate consists of lead sulphate. To the filtrate add ammonia in excess; a white precipitate indicates bismuth; if the solution be blue, copper is present. Filter from the bismuth hydrate, and if copper is present, add potassium cyanide till the colour is destroyed, then pass sulphuretted hydrogen, and cadmium is precipitated as the yellow sulphide. If copper is absent, then sulphuretted hydrogen can be passed directly into the solution.
The next group precipitate may contain the white gelatinous aluminium hydroxide, the greenish chromium hydroxide, reddish ferric hydroxide, and possibly zinc and manganese hydroxides. Treatment with casutic soda dissolves out aluminium hydroxide, which is reprecipitated by the addition of ammonium chloride. The remaining metals are tested for separately.
The next group may contain black nickel and cobalt sulphides, flesh-coloured manganese sulphide, and white zinc sulphide. The last two are dissolved out by cold, very dilute hydrochloric acid, and the residue is tested for nickel and cobalt. The solution is boiled till free from sulphuretted hydrogen and treated with excess of sodium hydrate. A white precipitate rapidly turning brown indicates manganese. The solution with ammonium sulphide gives a white precipitate of zinc sulphide.
The next group may contain the white calcium, barium and strontium carbonates. The flame coloration (see above) may give information as to which elements are present. The carbonates are dissolved in hydrochloric acid, and calcium sulphate solution is added to a portion of the solution. An immediate precipitate indicates barium; a precipitate on standing indicates strontium. If barium is present, the solution of the carbonates in hydrochloric acid is evaporated and digested with strong alcohol for some time; barium chloride, which is nearly insoluble in alcohol, is thus separated, the remainder being precipitated by a few drops of hydrofluosilicic acid, and may be confirmed by the ordinary tests. The solution free from barium is treated with ammonia and ammonium sulphate, which precipitates strontium, and the calcium in the solution may be identified by the white precipitate with ammonium oxalate.
Having determined the bases, it remains to determine the acid radicals. There is no general procedure for these operations, and it is customary to test for the acids separately by special tests; these are given in the articles on the various acids. A knowledge of the solubility of salts considerably reduces the number of acids likely to be present, and affords evidence of great value to the analyst (see A.M. Comey, Dictionary of Chemical Solubilities.) In the above account we have indicated the procedure adopted in the analysis of a complex mixture of salts. It is unnecessary here to dwell on the precautions which can only be conveniently acquired by experience; a sound appreciation of analytical methods is only possible after the reactions and characters of individual substances have been studied, and we therefore refer the reader to the articles on the particular elements and compounds for more information on this subject.
Quantitative Inorganic Analysis.
Quantitative methods are divided into four groups, which we now pass on to consider in the following sequence: (α) gravimetric, (β) volumetric, (γ) electrolytic, (δ) colorimetric.
(α) Gravimetric.—This method is made up of four operations: (1) a weighed quantity of the substance is dissolved in a suitable solvent; (2) a particular reagent is added which precipitates the substance it is desired to estimate; (3) the precipitate is filtered, washed and dried; (4) the filter paper containing the precipitate is weighed either as a tared filter, or incinerated and ignited either in air or in any other gas, and then weighed.
(1) Accurate weighing is all-important: for details of the various appliances and methods see Weighing Machines. (2) No general directions can be given as to the method of precipitation. Sometimes it is necessary to allow the solution to stand for a considerable time either in the warm or cold or in the light or dark; to work with cold solutions and then boil; or to use boiling solutions of both the substance and reagent. Details will be found in the articles on particular metals. (3) The operation of filtration and washing is very important. If the substance to be weighed changes in composition on strong heating, it is necessary to employ a tared filter, i.e. a filter paper which has been previously heated to the temperature at which the substance is to be dried until its weight is constant. If the precipitate settles readily, the supernatant liquor may be decanted through the filter paper, more water added to the precipitate and again decanted. By this means most of the washing, i.e.freeing from the other substances in the solution, can be accomplished in the precipitating vessel. If, however, the precipitate refuses to settle, it is directly transferred to the filter paper, the last traces being removed by washing and rubbing the sides of the vessel with a piece of rubber, and the liquid is allowed to drain through. It is washed by ejecting a jet of water, ammonia or other prescribed liquid on to the side of the filter paper until the paper is nearly full. It can be shown that a more efficient washing results from alternately filling and emptying the funnel than by endeavouring to keep the funnel full. The washing is continued until the filtrate is free from salts or acids. (4) After washing, the funnel containing the filter paper is transferred to a drying oven. In the case of a tared filter it is weighed repeatedly until the weight suffers no change; then knowing the weight of the filter paper, the weight of the precipitate is obtained by subtraction. If the precipitate may be ignited, it is transferred to a clean, weighed and recently ignited crucible, and the filter paper is burned separately on the lid, the ash transferred to the crucible, and the whole ignited. After ignition, it is allowed to cool in a desiccator and then weighed. Knowing the weight of the crucible and of the ash of the filter paper, the weight of the precipitate is determined. The calculation of the percentage of the particular constituent is simple. We know the amount present in the precipitate, and since the same amount is present in the quantity of substance experimented with, we have only to work out a sum in proportion.
(β) Volumetric.—This method is made up of three operations:—(1) preparation of a standard solution; (2) preparation of a solution of the substance; (3) titration, or the determination of what volume of the standard solution will occasion a known and definite reaction with a known volume of the test solution.
(1) In general analytical work the standard solution contains the equivalent weight of the substance in grammes dissolved in a litre of water. Such a solution is known as normal. Thus a normal solution of sodium carbonate contains 53 grammes per litre, of sodium hydrate 40 grammes, of hydrochloric acid 36.5 grammes, and so on. By taking 1/10th or 1/100th of these quantities, decinormal or centinormal solutions are obtained. We see therefore that 1 cubic centimetre of a normal sodium carbonate solution will exactly neutralize 0.049 gramme of sulphuric acid, 0.0365 gramme of hydrochloric acid (i.e. the equivalent quantities), and similarly for decinormal and centinormal solutions. Unfortunately, the term normal is sometimes given to solutions which are strictly decinormal; for example, iodine, sodium thiosulphate, &c. In technical analysis, where a solution is used for one process only, it may be prepared so that 1 cc. is equal to .01 gramme of the substance to be estimated. This saves a certain amount of arithmetic, but when the solution is applied in another determination additional calculations are necessary. Standard solutions are prepared by weighing out the exact amount of the pure substance and dissolving it in water, or by forming a solution of approximate normality, determining its exact strength by gravimetric or other means, and then correcting it for any divergence. This may be exemplified in the case of alkalimetry. Pure sodium carbonate is prepared by igniting the bicarbonate, and exactly 53 grammes are dissolved in water, forming a strictly normal solution. An approximate normal sulphuric acid is prepared from 30 ccs. of the pure acid (1.84 specific gravity) diluted to 1 litre. The solutions are titrated (see below) and the acid solution diluted until equal volumes are exactly equivalent. A standard sodium hydrate solution can be prepared by dissolving 42 grammes of sodium hydrate, making up to a litre, and diluting until one cubic centimetre is exactly equivalent to one cubic centimetre of the sulphuric acid. Similarly, normal solutions of hydrochloric and nitric acids can be prepared. Where a solution is likely to change in composition on keeping, such as potassium permanganate, iodine, 64 sodium hydrate, &c., it is necessary to check or re-standardize it periodically.
(2) The preparation of the solution of the substance consists in dissolving an accurately determined weight, and making up the volume in a graduated cylinder or flask to a known volume.
(3) The titration is conducted by running the standard solution from a burette into a known volume of the test solution, which is usually transferred from the stock-bottle to a beaker or basin by means of a pipette. Various artifices are employed to denote the end of the reaction. These may be divided into two groups: (1) those in which a change in appearance of the reacting mixture occurs; (2) those in which it is necessary to use an indicator which, by its change in appearance, shows that an excess of one reagent is present. In the first group, we have to notice the titration of a cyanide with silver nitrate, when a milkiness shows how far the reaction has gone; the titration of iron with permanganate, when the faint pink colour shows that all the iron is oxidized. In the second group, we may notice the application of litmus, methyl orange or phenolphthalein in alkalimetry, when the acid or alkaline character of the solution commands the colour which it exhibits; starch paste, which forms a blue compound with free iodine in iodometry; potassium chromate, which forms red silver chromate after all the hydrochloric acid is precipitated in solutions of chlorides; and in the estimation of ferric compounds by potassium bichromate, the indicator, potassium ferricyanide, is placed in drops on a porcelain plate, and the end of the reaction is shown by the absence of a blue coloration when a drop of the test solution is brought into contact with it.
(γ) Electrolytic.—This method consists in decomposing a solution of a salt of the metal by the electric current and weighing the metal deposited at the cathode.
It is only by paying great attention to the current density that good results are obtained, since metals other than that sought for may be deposited. In acid copper solutions, mercury is deposited before the copper with which it subsequently amalgamates; silver is thrown down simultaneously; bismuth appears towards the end; and after all the copper has been precipitated, arsenic and antimony may be deposited. Lead and manganese are partially separated as peroxides, but the remaining metals are not deposited from acid solutions. It is therefore necessary that the solution should be free from metals which may vitiate the results, or special precautions taken by which the impurities are rendered harmless. In such cases the simplicity of manipulation and the high degree of accuracy of the method have made it especially valuable. The electrolysis is generally conducted with platinum electrodes, of which the cathode takes the form of a piece of foil bent into a cylindrical form, the necessary current being generated by one or more Daniell cells.
(δ) Colorimetric.—This method is adopted when it is necessary to determine minute traces (as in the liquid obtained in the electrolytic separation of copper) of substances which afford well-defined colour reactions.
The general procedure is to make a series of standard solutions containing definite quantities of the substance which it is desired to estimate; such a series will exhibit tints which deepen as the quantity of the substance is increased. A known weight of the test substance is dissolved and a portion of the solution is placed in a tube similar to those containing the standard solutions. The colour-producing reagent is added and the tints compared. In the case of copper, the colour reactions with potassium ferrocyanide or ammonia are usually employed; traces of ammonia are estimated with Nessler’s reagent; sulphur in iron and steel is determined by the tint assumed by a silver-copper plate suspended in the gases liberated when the metal is dissolved in sulphuric acid (Eggertz’s test) (see W. Crookes, Select Methods in Analytical Chemistry).
Organic Analysis.
The elements which play important parts in organic compounds are carbon, hydrogen, nitrogen, chlorine, bromine, iodine, sulphur, phosphorus and oxygen. We shall here consider the qualitative and quantitative determination of these elements.
Qualitative.—Carbon is detected by the formation of carbon dioxide, which turns lime-water milky, and hydrogen by the formation of water, which condenses on the tube, when the substance is heated with copper oxide. Nitrogen may be detected by the evolution of ammonia when the substance is heated with soda-lime. A more delicate method is that due to J. L. Lassaigne and improved by O. Jacobsen and C. Graebe. The substance is heated with metallic sodium or potassium (in excess if sulphur be present) to redness, the residue treated with water, filtered, and ferrous sulphate, ferric chloride and hydrochloric acid added. A blue coloration indicates nitrogen, and is due to the formation of potassium (or sodium) cyanide during the fusion, and subsequent interaction with the iron salts. The halogens may be sometimes detected by fusing with lime, and testing the solution for a bromide, chloride and iodide in the usual way. F. Beilstein determines their presence by heating the substance with pure copper oxide on a platinum wire in the Bunsen flame; a green coloration is observed if halogens be present. Sulphur is detected by heating the substance with sodium, dissolving the product in water, and adding sodium nitroprusside; a bluish-violet coloration indicates sulphur (H. Vohl). Or we may use J. Horbaczewski’s method, which consists in boiling the substance with strong potash, saturating the cold solution with chlorine, adding hydrochloric acid, and boiling till no more chlorine is liberated, and then testing for sulphuric acid with barium chloride. Phosphorus is obtained as a soluble phosphate (which can be examined in the usual way) by lixiviating the product obtained when the substance is ignited with potassium nitrate and carbonate.
Quantitative.—Carbon and hydrogen are generally estimated by the combustion process, which consists in oxidizing the substance and absorbing the products of combustion in suitable Carbon and hydrogen. apparatus. The oxidizing agent in commonest use is copper oxide, which must be freshly ignited before use on account of its hygroscopic nature. Lead chromate is sometimes used, and many other substances, such as platinum, manganese dioxide, &c., have been suggested. The procedure for a combustion is as follows:—


A hard glass tube slightly longer than the furnace and 12 to 15 mm. in diameter is thoroughly cleansed and packed as shown in fig. 1. The space a must allow for the inclusion of a copper spiral if the substance contains nitrogen, and a silver spiral if halogens be present, for otherwise nitrogen oxides and the halogens may be condensed in the absorption apparatus; b contains copper oxide; c is a space for the insertion of a porcelain or platinum boat containing a weighed quantity of the substance; d is a copper spiral. The end d is connected to an air or oxygen supply with an intermediate drying apparatus. The other end is connected with the absorption vessels, which consist of a tube (e) containing calcium chloride, and a set of bulbs (f) containing potash solution. Various forms of potash bulbs are employed; fig. 2 is Liebig’s, fig. 3 Mohr’s or Geissler’s, fig. 4 is a more recent form, of which special variations have been made by Anderson, Gomberg, Delisle and others. After having previously roasted the tube and copper oxide, and reduced the copper spiral a, the weighed calcium chloride tube and potash bulbs are put in position, the boat containing the substance is inserted (in the case of a difficultly combustible substance it is desirable to mix it with cupric oxide or lead chromate), the copper spiral (d) replaced, and the air and oxygen supply connected up. The apparatus is then tested for leaks. If all the connexions are sound, the copper oxide is gradually heated from the end a, the gas-jets under the spiral d are lighted, and a slow current of oxygen is passed through the tube. The success of the operation depends upon the slow burning of the substance. Towards the end the heat and the oxygen supply are increased. When there is no more absorption in the potash bulbs, the oxygen supply is cut off and air passed through. Having replaced the oxygen in the absorption vessels by air, they are disconnected and weighed, after having cooled down to the temperature of the room. The increase in weight of the calcium chloride tube gives the weight of water formed, and of the potash bulbs the carbon dioxide.
Liquids are amenable to the same treatment, but especial care must be taken so that they volatilize slowly. Difficultly volatile liquids may be weighed directly into the boat; volatile liquids are weighed in thin hermetically sealed bulbs, the necks of which are broken just before they are placed in the combustion tube.
The length of time and other disadvantages attending the combustion method have caused investigators to devise other processes. In 1855 C. Brunner described a method for oxidizing the carbon to carbon dioxide, which could be estimated by the usual methods, by heating the substance with potassium bichromate and sulphuric acid. This process has been considerably developed by J. Messinger, and we may hope that with subsequent improvements it may be adapted to all classes of organic compounds. The oxidation, which is effected by chromic acid and sulphuric acid, is conducted in a flask provided with a funnel and escape tube, and the carbon dioxide formed is swept by a current of dry air, previously freed from carbon dioxide, through a drying tube to a set of potash bulbs and a tube containing soda-lime; if halogens are present, a small wash bottle containing potassium iodide, and a U tube containing glass wool moistened with silver nitrate on one side and strong sulphuric acid on the other, must be inserted between the flask and the drying tube. The increase in weight of the potash bulbs and soda-lime tube gives 65 the weight of carbon dioxide evolved. C.F. Cross and E.J. Bevan collected the carbon dioxide obtained in this way over mercury. They also showed that carbon monoxide was given off towards the end of the reaction, and oxygen was not evolved unless the temperature exceeded 100°.
Methods depending upon oxidation in the presence of a contact substance have come into favour during recent years. In that of M. Dennstedt, which was first proposed in 1902, the substance is vaporized in a tube containing at one end platinum foil, platinized quartz, or platinized asbestos. The platinum is maintained at a bright red heat, either by a gas flame or by an electric furnace, and the vapour is passed over it by leading in a current of oxygen. If nitrogen be present, a boat containing dry lead peroxide and heated to 320° is inserted, the oxide decomposing any nitrogen peroxide which may be formed. The same absorbent quantitatively takes up any halogen and sulphur which may be present. The process is therefore adapted to the simultaneous estimation of carbon, hydrogen, the halogens and sulphur.
Nitrogen is estimated by (1) Dumas’ method, which consists in heating the substance with copper oxide and measuring the volume of nitrogen liberated; (2) by Will and Varrentrapp’s Sidenote: Nitrogen. method, in which the substance is heated with soda-lime, and the ammonia evolved is absorbed in hydrochloric acid, and thence precipitated as ammonium chlorplatinate or estimated volumetrically; or (3) by Kjeldahl’s method, in which the substance is dissolved in concentrated sulphuric acid, potassium permanganate added, the liquid diluted and boiled with caustic soda, and the evolved ammonia absorbed in hydrochloric acid and estimated as in Will and Varrentrapp’s method.
Dumas’ Method.—In this method the operation is carried out in a hard glass tube sealed at one end and packed as shown in fig. 5. The magnesite (a) serves for the generation of carbon dioxide which clears the tube of air before the compound (mixed with fine copper oxide (b)) is burned, and afterwards sweeps the liberated nitrogen into the receiving vessel (e), which contains a strong potash solution; c is coarse copper oxide; and d a reduced copper gauze spiral, heated in order to decompose any nitrogen oxides. Ulrich Kreusler generates the carbon dioxide in a separate apparatus, and in this case the tube is drawn out to a capillary at the end (a). This artifice is specially valuable when the substance decomposes or volatilizes in a warm current of carbon dioxide. Various forms of the absorbing apparatus (e) have been discussed by M. Ilinski (Ber. 17, p. 1347), who has also suggested the use of manganese carbonate instead of magnesite, since the change of colour enables one to follow the decomposition. Substances which burn with difficulty may be mixed with mercuric oxide in addition to copper oxide.
Will and Varrentrapp’s Method.—This method, as originally proposed, is not in common use, but has been superseded by Kjeldahl’s method, since the nitrogen generally comes out too low. It is susceptible of wider application by mixing reducing agents with the soda-lime: thus Goldberg (Ber. 16, p. 2546) uses a mixture of soda-lime, stannous chloride and sulphur for nitro- and azo-compounds, and C. Arnold (Ber. 18, p. 806) a mixture containing sodium hyposulphite and sodium formate for nitrates.
Kjeldahl’s Method.—This method rapidly came into favour on account of its simplicity, both of operation and apparatus. Various substances other than potassium permanganate have been suggested for facilitating the operation; J.W. Gunning (Z. anal. Chem., 1889, p. 189) uses potassium sulphate; Lassar-Cohn uses mercuric oxide. The applicability of the process has been examined by F.W. Dafert (Z. anal. Chem., 1888, p. 224), who has divided nitrogenous bodies into two classes with respect to it. The first class includes those substances which require no preliminary treatment, and comprises the amides and ammonium compounds, pyridines, quinolines, alkaloids, albumens and related bodies; the second class requires preliminary treatment and comprises, with few exceptions, the nitro-, nitroso-, azo-, diazo- and amidoazo-compounds, hydrazines, derivatives of nitric and nitrous acids, and probably cyanogen compounds. Other improvements have been suggested by Dyer (J.C.S. Trans. 67, p. 811). For an experimental comparison of the accuracy of the Dumas, Will-Varrentrapp and Kjeldahl processes see L. L’Hôte, C.R. 1889, p. 817. Debordeaux (C.R. 1904, p. 905) has obtained good results by distilling the substance with a mixture of potassium thiosulphate and sulphide.
The halogens may be estimated by ignition with quicklime, or by heating with nitric acid and silver nitrate in a sealed tube. In the first method the substance, mixed with quicklime free from chlorine, is heated in a tube closed at one end in a combustion furnace. Halogens, sulphur, phosphorus. The product is dissolved in water, and the calcium haloid estimated in the usual way. The same decomposition may be effected by igniting with iron, ferric oxide and sodium carbonate (E. Kopp, Ber. 10, p. 290); the operation is easier if the lime be mixed with sodium carbonate, or a mixture of sodium carbonate and potassium nitrate be used. With iodine compounds, iodic acid is likely to be formed, and hence the solution must be reduced with sulphurous acid before precipitation with silver nitrate. C. Zulkowsky (Ber. 18, R. 648) burns the substance in oxygen, conducts the gases over platinized sand, and collects the products in suitable receivers. The oxidation with nitric acid in sealed tubes at a temperature of 150° to 200° for aliphatic compounds, and 250° to 260° for aromatic compounds, is in common use, for both the sulphur and phosphorus can be estimated, the former being oxidized to sulphuric acid and the latter to phosphoric acid. This method was due to L. Carius (Ann. 136, p. 129). R. Klason (Ber. 19, p. 1910) determines sulphur and the halogens by oxidizing the substance in a current of oxygen and nitrous fumes, conducting the vapours over platinum foil, and absorbing the vapours in suitable receivers. Sulphur and phosphorus can sometimes be estimated by Messinger’s method, in which the oxidation is effected by potassium permanganate and caustic alkali, or by potassium bichromate and hydrochloric acid. A comparison of the various methods for estimating sulphur has been given by O. Hammarsten (Zeit. physiolog. Chem. 9, p. 273), and by Höland (Chemiker Zeitung, 1893, p. 991). H.H. Pringsheim (Ber. 38, p. 1434) has devised a method in which the oxidation is effected by sodium peroxide; the halogens, phosphorus and sulphur can be determined by one operation.
VI. PHYSICAL CHEMISTRY
We have seen how chemistry may be regarded as having for its province the investigation of the composition of matter, and the changes in composition which matter or energy may effect on matter, while physics is concerned with the general properties of matter. A physicist, however, does more than merely quantitatively determine specific properties of matter; he endeavours to establish mathematical laws which co-ordinate his observations, and in many cases the equations expressing such laws contain functions or terms which pertain solely to the chemical composition of matter. One example will suffice here. The limiting law expressing the behaviour of gases under varying temperature and pressure assumes the form pv = RT; so stated, this law is independent of chemical composition and may be regarded as a true physical law, just as much as the law of universal gravitation is a true law of physics. But this relation is not rigorously true; in fact, it does not accurately express the behaviour of any gas. A more accurate expression (see Condensation of Gases and Molecule) is (p + a/v²)(v - b) = RT, in which a and b are quantities which depend on the composition of the gas, and vary from one gas to another.
It may be surmised that the quantitative measures of most physical properties will be found to be connected with the chemical nature of substances. In the investigation of these relations the physicist and chemist meet on common ground; this union has been attended by fruitful and far-reaching results, and the correlation of physical properties and chemical composition is one of the most important ramifications of physical chemistry. This branch receives treatment below. Of considerable importance, also, are the properties of solids, liquids and gases in solution. This subject has occupied a dominant position in physico-chemical research since the investigations of van’t Hoff and Arrhenius. This subject is treated in the article Solution; for the properties of liquid mixtures reference should also be made to the article Distillation.
Another branch of physical chemistry has for its purpose the quantitative study of chemical action, a subject which has brought out in clear detail the analogies of chemical and physical equilibrium (see Chemical Action). Another branch, related to energetics (q.v.), is concerned with the transformation of chemical energy into other forms of energy—heat, light, electricity. Combustion is a familiar example of the transformation of chemical energy into heat and light; the quantitative measures of heat evolution or absorption (heat of combustion or combination), and the deductions therefrom, are treated in the article Thermochemistry. Photography (q.v.) is based on chemical action induced by luminous rays; apart from this practical 66 application there are many other cases in which actinic rays occasion chemical actions; these are treated in the article Photochemistry. Transformations of electrical into chemical energy are witnessed in the processes of electrolysis (q.v.; see also Electrochemistry and Electrometallurgy). The converse is presented in the common electric cell.
Physical Properties and Composition.
For the complete determination of the chemical structure of any compound, three sets of data are necessary: (1) the empirical chemical composition of the molecule; (2) the constitution, i.e. the manner in which the atoms are linked together; and (3) the configuration of the molecule, i.e. the arrangement of the atoms in space. Identity in composition, but difference in constitution, is generally known as “isomerism” (q.v.), and compounds satisfying this relation differ in many of their physical properties. If, however, two compounds only differ with regard to the spatial arrangement of the atoms, the physical properties may be (1) for the most part identical, differences, however, being apparent with regard to the action of the molecules on polarized light, as is the case when the configuration is due to the presence of an asymmetric atom (optical isomerism); or (2) both chemical and physical properties may be different when the configuration is determined by the disposition of the atoms or groups attached to a pair of doubly-linked atoms, or to two members of a ring system (geometrical isomerism or allo-isomerism). Three sets of physical properties may therefore be looked for: (1) depending on composition, (2) depending on constitution, and (3) depending on configuration. The first set provides evidence as to the molecular weight of a substance: these are termed “colligative properties.” The second and third sets elucidate the actual structure of the molecule: these are known as “constitutional properties.”
In any attempts to gain an insight into the relations between the physical properties and chemical composition of substances, the fact must never be ignored that a comparison can only be made when the particular property under consideration is determined under strictly comparable conditions, in other words, when the molecular states of the substances experimented upon are identical. This is readily illustrated by considering the properties of gases—the simplest state of aggregation. According to the law of Avogadro, equal volumes of different gases under the same conditions of temperature and pressure contain equal numbers of molecules; therefore, since the density depends upon the number of molecules present in unit volume, it follows that for a comparison of the densities of gases, the determinations must be made under coincident conditions, or the observations reduced or re-computed for coincident conditions. When this is done, such densities are measures of the molecular weights of the substances in question.
Volume Relations.17—When dealing with colligative properties of liquids it is equally necessary to ensure comparability of conditions. In the article Condensation of Gases (see also Molecule) it is shown that the characteristic equation of gases and liquids is conveniently expressed in the form (p + a/v²)(v - b) = RT. This equation, which is mathematically deducible from the kinetic theory of gases, expresses the behaviour of gases, the phenomena of the critical state, and the behaviour of liquids; solids are not accounted for. If we denote the critical volume, pressure and temperature by Vk, Pk and Tk, then it may be shown, either by considering the characteristic equation as a perfect cube in v or by using the relations that dp/dv = 0, d²p/dv² = 0 at the critical point, that Vk = 3b, Pk = a/27b², Tk = 8a/27b. Eliminating a and b between these relations, we derive PkVk/Tk = (3/8)R, a relation which should hold between the critical constants of any substance. Experiment, however, showed that while the quotient on the left hand of this equation was fairly constant for a great number of substances, yet its value was not (3/8)R but (1/3.7)R; this means that the critical density is, as a general rule, 3.7 times the theoretical density. Deviation from this rule indicates molecular dissociation or association. By actual observations it has been shown that ether, alcohol, many esters of the normal alcohols and fatty acids, benzene, and its halogen substitution products, have critical constants agreeing with this originally empirical law, due to Sydney Young and Thomas; acetic acid behaves abnormally, pointing to associated molecules at the critical point.
The critical volume provides data which may be tested for additive relations. Theoretically the critical volume is three times the volume at absolute zero, i.e. the actual volume of the Volume at critical point and at absolute zero. molecules; this is obvious by considering the result of making T zero in the characteristic equation. Experimentally (by extrapolation from the “law of the rectilinear diameter”) the critical volume is four times the volume at absolute zero (see Condensation of Gases). The most direct manner in which to test any property for additive relations is to determine the property for a number of elements, and then investigate whether these values hold for the elements in combination. Want of data for the elements, however, restricts this method to narrow limits, and hence an indirect method is necessary. It is found that isomers have nearly the same critical volume, and that equal differences in molecular content occasion equal differences in critical volume. For example, the difference due to an increment of CH2 is about 56.6, as is shown in the following table:—
| Name. | Formula. | Crit. Vol. | Vol. per CH2 | |
| Methyl formate | H·CO2CH3 | 171 | ||
| Ethyl formate | H·C02C2H5 | 228 | }227.5 | 56.5 |
| Methyl acetate | CH3·CO2CH3 | 227 | ||
| Propyl formate | H·CO2C3H7 | 284 | }283.3 | 55.8 |
| Ethyl acetate | CH3·C02C2H5 | 285 | ||
| Methyl propionate | C2H5·CO2CH3 | 28l | ||
| Propyl acetate | CH3·CO2C3H7 | 343 | }340.7 | 57.4 |
| Ethyl propionate | C2H5·CO2C2H5 | 343 | ||
| Methyl n-butyrate | }C3H7·CO2CH3 | 339 | ||
| Methyl isobutyrate | 337 | |||
Since the critical volume of normal pentane C5H12 is 307.2, we have H2 = C5H12 - 5CH2 = 307.2 - 5 × 56.6 = 24.2, and C = CH2 - H2 = 32.4. The critical volume of oxygen can be deduced from the data of the above table, and is found to be 29, whereas the experimental value is 25.
The researches of H. Kopp, begun in 1842, on the molecular volumes, i.e. the volume occupied by one gramme molecular weight of a substance, of liquids measured at their boiling-point Volume at boiling-point. under atmospheric pressure, brought to light a series of additive relations which, in the case of carbon compounds, render it possible to predict, in some measure, the composition of the substance. In practice it is generally more convenient to determine the density, the molecular volume being then obtained by dividing the molecular weight of the substance by the density. By the indirect method Kopp derived the following atomic volumes:
| C. | O. | H. | Cl. | Br. | I. | S. |
| 11 | 12.2 | 5.5 | 22.8 | 27.8 | 37.5 | 22.6. |
These values hold fairly well when compared with the experimental values determined from other compounds, and also with the molecular volumes of the elements themselves. Thus the actually observed densities of liquid chlorine and bromine at the boiling-points are 1.56 and 2.96, leading to atomic volumes 22.7 and 26.9, which closely correspond to Kopp’s values deduced from organic compounds.
These values, however, require modification in certain cases, for discrepancies occur which can be reconciled in some cases by assuming that the atomic value of a polyvalent element varies according to the distribution of its valencies. Thus a double bond of oxygen, as in the carbonyl group CO, requires a larger volume than a single bond, as in the hydroxyl group -OH, being about 12.2 in the first case and 7.8 in the second. Similarly, an increase of volume is associated with doubly and trebly linked carbon atoms.
Recent researches have shown that the law originally proposed by Kopp—“That the specific volume of a liquid compound (molecular volume) at its boiling-point is equal to the sum of the specific volumes of its constituents (atomic volumes), and that every element has a definite atomic value in its compounds”—is by no means exact, for isomers have different specific volumes, and the volume for an increment of CH2 in different homologous series is by no means constant; for example, the difference among the esters of the fatty acids is about 57, whereas for the aliphatic aldehydes it is 49. We may therefore conclude that the molecular volume depends more upon the internal structure of the molecule than its empirical content. W. Ostwald (Lehr. der allg. Chem.), after an exhaustive review of the material at hand, concluded that simple additive relations did exist but with considerable deviations, which he ascribed to differences in structure. In this connexion we may notice W. Städel’s determinations:
| CH3CCl3 | 108 | CHClBr·CH3 | 96·5 |
| CH2Cl·CHCl2 | 102.8 | CH2Br·CH2Cl | 88 |
These differences do not disappear at the critical point, and hence the critical volumes are not strictly additive.
Theoretical considerations as to how far Kopp was justified in choosing the boiling-points under atmospheric pressure as being comparable states for different substances now claim our attention. Van der Waal’s equation (p+a/v²)(v-b) = RT contains two constants a and b determined by each particular substance. If we express the pressure, volume and temperature as fractions of the critical constants, then, calling these fractions the “reduced” pressure, volume and temperature, and denoting them by π, φ and θ respectively, the characteristic equation becomes (π+3/φ²)(3φ-1) = 8θ; which has the same form for all substances. Obviously, therefore, liquids are comparable when the pressures, volumes and temperatures are equal fractions of the critical constants. In view of the extremely slight compressibility of liquids, atmospheric pressure may be regarded as a coincident condition; also C.M. Guldberg pointed out that for the most diverse substances the absolute boiling-point is about two-thirds of the critical temperature. Hence within narrow limits Kopp’s determinations were carried out under coincident conditions, and therefore any regularities presented by the critical volumes should be revealed in the specific volumes at the boiling-point.
The connexion between the density and chemical composition of solids has not been investigated with the same completeness as in the case of gases and liquids. The relation between the atomic Volume relations of solids. volumes and the atomic weights of the solid elements exhibits the periodicity which generally characterizes the elements. The molecular volume is additive in certain cases, in particular of analogous compounds of simple constitution. For instance, constant differences are found between the chlorides, bromides and iodides of sodium and potassium:—
| I. | Diff. | II. | Diff. | Diff. I. & II. |
| KCl = 37.4 | 6.9 | NaCl = 27.1 | 6.7 | 10.3 |
| KBr = 44.3 | 9.7 | NaBr = 33.8 | 9.7 | 10.5 |
| KI = 54.0 | NaI = 43.5 | 10.5 |
According to H. Schroeder the silver salts of the fatty acids exhibit additive relations; an increase in the molecule of CH2 causes an increase in the molecular volume of about 15.3.
Thermal Relations.
Specific Heat and Composition.—-The nature and experimental determination of specific heats are discussed in the article CALORIMETRY; here will be discussed the relations existing between the heat capacities of elements and compounds.
In the article Thermodynamics it is shown that the amount of heat required to raise a given weight of a gas through a certain range of temperature is different according as the gas Specific heat of gases. is maintained at constant pressure, the volume increasing, or at constant volume, the pressure increasing. A gas, therefore, has two specific heats, generally denoted by Cp and Cv, when the quantity of gas taken as a unit is one gramme molecular weight, the range of temperature being 1° C. It may be shown that Cp - Cv = R, where R is the gas-constant, i.e. R in the equation PV = RT. From the ratio Cp/Cv conclusions may be drawn as to the molecular condition of the gas. By considerations based on the kinetic theory of gases (see Molecule) it may be shown that when no energy is utilized in separating the atoms of a molecule, this ratio is 5/3 = 1.67. If, however, an amount of energy a is taken up in separating atoms, the ratio is expressible as Cp/Cv = (5+a)/(3+a), which is obviously smaller than 5/3, and decreases with increasing values of a. These relations may be readily tested, for the ratio Cp/Cv is capable of easy experimental determination. It is found that mercury vapour, helium, argon and its associates (neon, krypton, &c.) have the value 1.67; hence we conclude that these gases exist as monatomic molecules. Oxygen, nitrogen, hydrogen and carbon monoxide have the value 1.4; these gases have diatomic molecules, a fact capable of demonstration by other means. Hence it may be inferred that this value is typical for diatomic molecules. Similarly, greater atomic complexity is reflected in a further decrease in the ratio Cp/Cv. The following table gives a comparative view of the specific heats and the ratio for molecules of variable atomic content.
The abnormal specific heats of the halogen elements may be due to a loosening of the atoms, a preliminary to the dissociation into monatomic molecules which occurs at high temperatures. In the more complex gases the specific heat varies considerably with temperature; only in the case of monatomic gases does it remain constant. Le Chatelier (Zeit. f. phys. Chem. i. 456) has given the formula Cp = 6.5 + aT, where a is a constant depending on the complexity of the molecule, as an expression for the molecular heat at constant pressure at any temperature T (reckoned on the absolute scale). For a further discussion of the ratio of the specific heats see Molecule.
| Molecular Content. | Examples. | Cp. | Cv. | Cp/Cv. |
| Monatomic | Hg, Zn, Cd, He, Ar, &c. | 5 | 3 | 1.66 |
| Diatomic | H2, 02, N2 (0°-200°) | 6.83 | 4.83 | 1.41 |
| Cl2, Br2, I2 (0°-200°) | 8.6 | 6.6 | 1.30 | |
| HCl, HBr, HI, NO, CO | . . . | . . . | 1.41 | |
| Triatomic | H2O, H2S, N2O, CO2 | 9.2 | 7.2 | 1.28 |
| Tetratomic | As4, P4 | 13.4 | 11.4 | 1.175 |
| NH3, C2H2 | 11.6 | 9.6 | 1.21 | |
| Pentatomic | CHCl3 | 14 | 12 | 1.17 |
| Hexatomic | C2H4, C2H3Br | 16.4 | 14.4 | 1.14 |
Specific Heats of Solids.—The development of the atomic theory and the subsequent determination of atomic weights in the opening decades of the 19th century inspired A.T. Petit and P.L. Dulong to investigate relations (if any) existing between specific heats and the atomic weight. Their observations on the solid elements led to a remarkable generalization, now known as Dulong and Petit’s law. This states that “the atomic heat (the product of the atomic weight and specific heat) of all elements is a constant quantity.” The value of this constant when H = 1 is about 6.4; Dulong and Petit, using O = 1, gave the value .38, the specific heat of water being unity in both cases. This law—purely empirical in origin—was strengthened by Berzelius, who redetermined many specific heats, and applied the law to determine the true atomic weight from the equivalent weight. At the same time he perceived that specific heats varied with temperature and also with allotropes, e.g. graphite and diamond. The results of Berzelius were greatly extended by Hermann Kopp, who recognized that carbon, boron and silicon were exceptions to the law. He regarded these anomalies as solely due to the chemical nature of the elements, and ignored or regarded as insignificant such factors as the state of aggregation and change of specific heat with temperature.
The specific heats of carbon, boron and silicon subsequently formed the subject of elaborate investigations by H.F. Weber, who showed that with rise of temperature the specific (and atomic) heat increases, finally attaining a fairly constant value; diamond, graphite and the various amorphous forms of carbon having the value about 5.6 at 1000°, and silicon 5.68 at 232°; while he concluded that boron attained a constant value of 5.5. Niison and Pettersson’s observations on beryllium and germanium have shown that the atomic heats of these metals increase with rise of temperature, finally becoming constant with a value 5.6. W.A. Tilden (Phil. Trans., 1900, p. 233) investigated nickel and cobalt over a wide range of temperature (from -182.5° to 100°); his results are:—
| Cobalt. | Nickel. | |
| From -182.5° to -78.4° | 4.1687 | 4.1874 |
| -78.4° to 15° | 5.4978 | 5.6784 |
| 15° to 100° | 6.0324 | 6.3143 |
It is evident that the atomic heats of these intimately associated elements approach nearer and nearer as we descend in temperature, approximating to the value 4. Other metals were tested in order to determine if their atomic heats approximated to this value at low temperatures, but with negative results.
It is apparent that the law of Dulong and Petit is not rigorously true, and that deviations are observed which invalidate the law as originally framed. Since the atomic heat of the same element varies with its state of aggregation, it must be concluded that some factor taking this into account must be introduced; moreover, the variation of specific heat with temperature introduces another factor.
We now proceed to discuss molecular heats of compounds, that is, the product of the molecular weight into the specific heat. The earliest generalization in this direction is associated with F.E. Neumann, who, in 1831, deduced from observations on many carbonates (calcium, magnesium, ferrous, zinc, barium and lead) that stoichiometric quantities (equimolecular weights) of compounds possess the same heat capacity. This is spoken of as “Neumann’s law.” Regnault confirmed Neumann’s observations, and showed that the molecular heat depended on the number of atoms present, equiatomic compounds having the same molecular heat. Kopp systematized the earlier observations, 68 and, having made many others, he was able to show that the molecular heat was an additive property, i.e. each element retains the same heat capacity when in combination as in the free state. This has received confirmation by the researches of W.A. Tilden (Phil. Trans., 1904, 203 A, p.139) for those elements whose atomic heats vary considerably with temperature.
The specific heat of a compound may, in general, be calculated from the specific heats of its constituent elements. Conversely, if the specific heats of a compound and its constituent elements, except one, be known, then the unknown atomic heat is readily deducible. Similarly, by taking the difference of the molecular heats of compounds differing by one constituent, the molecular (or atomic) heat of this constituent is directly obtained. By this method it is shown that water, when present as “water of crystallization,” behaves as if it were ice.
Deductions from Dulong and Petit’s Law.—Denoting the atomic weight by W and the specific heat by s, Dulong and Petit’s law states that 6.4 = Ws. Thus if s be known, an approximate value of W is determinate. In the determination of the atomic weight of an element two factors must be considered: (1) its equivalent weight, i.e. the amount which is equivalent to one part of hydrogen; and (2) a factor which denotes the number of atoms of hydrogen which combines with or is equivalent to one atom of the particular element. This factor is termed the valency. The equivalent weight is capable of fairly ready determination, but the settlement of the second factor is somewhat more complex, and in this direction the law of atomic heats is of service. To take an example: 38 parts of indium combine with 35.4 parts of chlorine; hence, if the formula of the chloride be InCl, InCl2 or InCl3, indium has the atomic weights 38, 76 or 114. The specific heat of indium is 0.057; and the atomic heats corresponding to the atomic weights 38, 76 and 114 are 3.2, 4.3, 6.5. Dulong and Petit’s law thus points to the value 114, which is also supported by the position occupied by this element in the periodic classification. C. Winkler decided the atomic weight of germanium by similar reasoning.
Boiling-Point and Composition.—From the relation between the critical constants PkVk/Tk = (1/3.7)R or Tk/Pk = 3.7Vk/R, and since Vk is proportional to the volume at absolute zero, the ratio Tk/Pk should exhibit additive relations. This ratio, termed by Guye the critical coefficient, has the following approximate values:—
| C. | H. | Cl. | -O-. | =O. | N. | N=. | P. | Double linkage. | Triple linkage. |
| 1.35 | 0.57 | 2.66 | 0.87 | 1.27 | 1.6 | 1.86 | 3.01 | 0.88 | 1.03 |
Since at the boiling-point under atmospheric pressure liquids are in corresponding states, the additive nature of the critical coefficient should also be presented by boiling-points. It may be shown theoretically that the absolute boiling-point is proportional to the molecular volume, and, since this property is additive, the boiling-point should also be additive.
These relations have been more thoroughly tested in the case of organic compounds, and the results obtained agree in some measure with the deductions from molecular volumes. In general, isomers boil at about the same temperature, as is shown by the isomeric esters C9H18O2:—
| Methyl octoate | 192.9° | Amyl butyrate | 184.8° |
| Ethyl heptoate | 187.1° | Heptyl acetate | 191.3° |
| Propyl hexoate | 185.5° | Octyl formate | 198.1° |
| Butyl pentoate | 185.8 |
Equal increments in the molecule are associated with an equal rise in the boiling-point, but this increment varies in different homologous series. Thus in the normal fatty alcohols, acids, esters, nitriles and ketones, the increment per CH2 is 19°-21°; in the aldehydes it is 26°-27°. In the aromatic compounds there is no regularity between the increments due to the introduction of methyl groups into the benzene nucleus or side chains; the normal value of 20°-21° is exhibited, however, by pyridine and its derivatives. The substitution of a hydrogen atom by the hydroxyl group generally occasions a rise in boiling-point at about 100°. The same increase accompanies the introduction of the amino group into aromatic nuclei.
While certain additive relations hold between some homologous series, yet differences occur which must be referred to the constitution of the molecule. As a general rule, compounds formed Constitutive influences. with a great evolution of heat have high boiling-points, and vice versa. The introduction of negative groups into a molecule alters the boiling-point according to the number of negative groups already present. This is shown in the case of the chloracetic acids:
| CH3CO2H = 118° | Diff. | |
| ClCH2·CO2H = 185° | 67° | |
| Cl2CH·CO2H = 195° | 10° | |
| Cl3C·CO2H = 195° | -200° | 3° |
According to van ’t Hoff the substitution of chlorine atoms into a methyl group occasions the following increments:—
| Cl in CH3 | 66° |
| Cl in CH2Cl | 39° |
| Cl in CHCl2 | 13°. |
The introduction of chlorine, however, may involve a fall in the boiling-point, as is recorded by Henry in the case of the chlorinated acetonitriles:—
| NC·CH3. | NC·CH2Cl. | NC·CHC12. | NC·CC13. | |||
| 81° | 123° | 112° | 83° | |||
| 42° | -11° | -29° |
The replacement of one negative group by another is accompanied by a change in the boiling-point, which is independent of the compound in which the substitution is effected, and solely conditioned by the nature of the replaced and replacing groups. Thus bromine and iodine replace chlorine with increments of about 22° and 50° respectively.
A factor of considerable importance in determining boiling-points of isomers is the symmetry of the molecule. Referring to the esters C9H18O2 previously mentioned, it is seen that the highest boiling-points belong to methyl octoate and octyl formate, the least symmetrical, while the minimum belongs to amyl butyrate, the most symmetrical. The isomeric pentanes also exhibit a similar relation CH3(CH2)4CH3 = 38°, (CH3)2CHC2H5 = 30°, (CH3)4C = 9.5°. For a similar reason secondary alcohols boil at a lower temperature than the corresponding primary, the difference being about 19°. A.E. Earp (Phil. Mag., 1893 [5], 35, p. 458) has shown that, while an increase in molecular weight is generally associated with a rise in the boiling-point, yet the symmetry of the resulting molecule may exert such a lowering effect that the final result is a diminution in the boiling-point. The series H2S = -61°, CH3SH = 21°, (CH3)2S = 41° is an example; in the first case, the molecular weight is increased and the symmetry diminished, the increase of boiling-point being 82°; in the second case the molecular weight is again increased but the molecule assumes a more symmetrical configuration, hence the comparatively slight increase of 20°. A similar depression is presented by methyl alcohol (67°) and methyl ether (-23°).
Among the aromatic di-substitution derivatives the ortho compounds have the highest boiling-point, and the meta boil at a higher, or about the same temperature as the para compounds. Of the tri-derivatives the symmetrical compounds boil at the lowest temperature, the asymmetric next, and the vicinal at the highest.
An ethylenic or double carbon union in the aliphatic hydrocarbons has, apparently, the same effect on the boiling-point as two hydrogen atoms, since the compounds CnH2n+2 and CnH2n boil at about the same temperature. An acetylenic or triple linkage is associated with a rise in the boiling-point; for example, propargyl compounds boil about 19.5° higher than the corresponding propyl compound.
Certain regularities attend the corresponding property of the melting-point. A rule applicable to organic compounds, due to Adolf v. Baeyer and supported by F.S. Kipping (Jour. Chem. Soc., 1893, 63, p.465) states, that the melting-point of any odd member of a homologous series is lower than the melting-point of the even member containing one carbon atom less. This is true of the fatty acid series, and the corresponding ketones and alcohols, and also of the succinic acid series. Other regularities exist, but generally with many exceptions. It is to be noted that although the correlation of melting-point with constitution has not been developed to such an extent as the chemical significance of other physical properties, the melting-point is the most valuable test of the purity of a substance, a circumstance due in considerable measure to the fact that impurities always tend to lower the melting-point.
Heat of Combustion and Constitution.—In the article Thermochemistry a general account of heats of formation of chemical compounds is given, and it is there shown that this constant measures the stability of the compound. In organic chemistry it is more customary to deal with the “heat of combustion,” i.e. the heat evolved when an organic compound is completely burned in oxygen; the heat of formation is deduced from the fact that it is equal to the heats of formation of the products of combustion less the observed heat of combustion. The researches of Julius Thomsen and others have shown that in many cases definite conclusions regarding constitution can be drawn from quantitative measurements of the heats of combustion; and in this article a summary of the chief results will be given.
The identity of the four valencies of the carbon atom follows from the fact that the heats of combustion of methane, ethane, propane, trimethyl methane, and tetramethyl methane, have a constant difference in the order given, viz. 158.6 calories; this means 69 that the replacement of a hydrogen atom by a methyl group is attended by a constant increase in the heat of combustion. The same difference attends the introduction of the methyl group into many classes of compounds, for example, the paraffins, olefines, acetylenes, aromatic hydrocarbons, alcohols, aldehydes, ketones and esters, while a slightly lower value (157.1) is found in the case of the halogen compounds, nitriles, amines, acids, ethers, sulphides and nitro compounds. It therefore appears that the difference between the heats of combustion of two adjacent members of a series of homologous compounds is practically a constant, and that this constant has two average values, viz. 158.6 and 157.1.
An important connexion between heats of combustion and constitution is found in the investigation of the effect of single, double and triple carbon linkages on the thermochemical constants. If twelve grammes of amorphous carbon be burnt to carbon dioxide under constant volume, the heat evolved (96.96 cal.) does not measure the entire thermal effect, but the difference between this and the heat required to break down the carbon molecule into atoms. If the number of atoms in the carbon molecule be denoted by n, and the heat required to split off each atom from the molecule by d, then the total heat required to break down a carbon molecule completely into atoms is nd. It follows that the true heat of combustion of carbon, i.e. the heat of combustion of one gramme-atom, is 96.96 + d. The value of d can be evaluated by considering the combustion of amorphous carbon to carbon monoxide and carbon dioxide. In the first case the thermal effect of 58.58 calories actually observed must be increased by 2d to allow for the heat absorbed in splitting off two gramme-atoms of carbon; in the second case the thermal effect of 96.96 must be increased by d as above. Now in both cases one gramme-molecule of oxygen is decomposed, and the two oxygen atoms thus formed are combined with two carbon valencies. It follows that the thermal effects stated above must be equal, i.e. 58.58 + 2d = 96.96 + d, and therefore d = 38.38. The absolute heat of combustion of a carbon atom is therefore 135.34 calories, and this is independent of the form of the carbon burned.
Consider now the combustion of a hydrocarbon of the general formula CnH2m. We assume that each carbon atom and each hydrogen atom contributes equally to the thermal effect. If α be the heat evolved by each carbon atom, and β that by each hydrogen atom, the thermal effect may be expressed as H = nα + 2mβ - A, where A is the heat required to break the molecule into its constituent atoms. If the hydrocarbon be saturated, i.e. only contain single carbon linkages, then the number of such linkages is 2n - m, and if the thermal effect of such a linkage be X, then the term A is obviously equal to (2n - m)X. The value of H then becomes H = nα + 2mβ - (2n - m)X or nξ + mν, where ξ and ν are constants. Let double bonds be present, in number p, and let the energy due to such a bond be Y. Then the number of single bonds is 2n - m - 2p, and the heat of combustion becomes H1 = nξ + mν + p(2X - Y). If triple bonds, q in number, occur also, and the energy of such a bond be Z, the equation for H becomes
H = nξ + mν + p(2X - Y) + q(3X - Z).
This is the general equation for calculating the heat of combustion of a hydrocarbon. It contains four independent constants; two of these may be calculated from the heats of combustion of saturated hydrocarbons, and the other two from the combustion of hydrocarbons containing double and triple linkages. By experiment it is found that the thermal effect of a double bond is much less than the effect of two single bonds, while a triple bond has a much smaller effect than three single bonds. J. Thomsen deduces the actual values of X, Y, Z to be 14.71, 13.27 and zero; the last value he considers to be in agreement with the labile equilibrium of acetylenic compounds. One of the most important applications of these values is found in the case of the constitution of benzene, where Thomsen decides in favour of the Claus formula, involving nine single carbon linkages, and rejects the Kekulé formula, which has three single and three double bonds (see section IV.).
The thermal effects of the common organic substituents have also been investigated. The thermal effect of the “alcohol” group C·OH may be determined by finding the heat of formation of the alcohol and subtracting the thermal effects of the remaining linkages in the molecule. The average value for primary alcohols is 44.67 cal., but many large differences from this value obtain in certain cases. The thermal effects increase as one passes from primary to tertiary alcohols, the values deduced from propyl and isopropyl alcohols and trimethyl carbinol being:—primary = 45.08, secondary = 50.39, tertiary = 60.98. The thermal effect of the aldehyde group has the average value 64.88 calories, i.e. considerably greater than the alcohol group. The ketone group corresponds to a thermal effect of 53.52 calories. It is remarkable that the difference in the heats of formation of ketones and the paraffin containing one carbon atom less is 67.94 calories, which is the heat of formation of carbon monoxide at constant volume. It follows therefore that two hydrocarbon radicals are bound to the carbon monoxide residue with the same strength as they combine to form a paraffin. The average value for the carboxyl group is 119.75 calories, i.e. it is equal to the sum of the thermal effects of the aldehyde and carbonyl groups.
The thermal effects of the halogens are: chlorine = l5.13 calories, bromine = 7.68; iodine = -4.25 calories. It is remarkable that the position of the halogen in the molecule has no effect on the heat of formation; for example, chlorpropylene and allylchloride, and also ethylene dichloride and ethylidene dichloride, have equal heats of formation. The thermal effect of the ether group has an average value of 34.31 calories. This value does not hold in the case of methylene oxide if we assign to it the formula H2C·O·CH2, but if the formula H2C·O·CH2 (which assumes the presence of two free valencies) be accepted, the calculated and observed heats of formation are in agreement.
The combination of nitrogen with carbon may result in the formation of nitriles, cyanides, or primary, secondary or tertiary amines. Thomsen deduced that a single bond between a carbon and a nitrogen gramme-atom corresponds to a thermal effect of 2.77 calories, a double bond to 5.44, and a treble bond to 8.31. From this he infers that cyanogen is C:N·N:C and not N∶C-C∶N, that hydrocyanic acid is HC·N, and acetonitrile CH3·C∶N. In the case of the amines he decides in favour of the formulae

These involve pentavalent nitrogen. These formulae, however, only apply to aliphatic amines; the results obtained in the aromatic series are in accordance with the usual formulae.
Optical Relations.
Refraction and Composition.—Reference should be made to the article Refraction for the general discussion of the phenomenon known as the refraction of light. It is there shown that every substance, transparent to light, has a definite refractive index, which is the ratio of the velocity of light in vacuo to its velocity in the medium to which the refractive index refers. The refractive index of any substance varies with (1) the wave-length of the light; (2) with temperature; and (3) with the state of aggregation. The first cause of variation may be at present ignored; its significance will become apparent when we consider dispersion (vide infra).The second and third causes, however, are of greater importance, since they are associated with the molecular condition of the substance; hence, it is obvious that it is only from some function of the refractive index which is independent of temperature variations and changes of state (i.e. it must remain constant for the same substance at any temperature and in any form) that quantitative relations between refractivity and chemical composition can be derived.
The pioneer work in this field, now frequently denominated “spectro-chemistry,” was done by Sir Isaac Newton, who, from theoretical considerations based on his corpuscular theory of light, determined the function (n²-1), where n is the refractive index, to be the expression for the refractive power; dividing this expression by the density (d), he obtained (n²-1)/d, which he named the “absolute refractive power.” To P.S. Laplace is due the theoretical proof that this function is independent of temperature and pressure, and apparent experimental confirmation was provided by Biot and Arago’s, and by Dulong’s observations on gases and vapours. The theoretical basis upon which this formula was devised (the corpuscular theory) was shattered early in the 19th century, and in its place there arose the modern wave theory which theoretically invalidates Newton’s formula. The question of the dependence of refractive index on temperature was investigated in 1858 by J.H. Gladstone and the Rev. T.P. Dale; the more simple formula (n-1)/d, which remained constant for gases and vapours, but exhibited slight discrepancies when liquids were examined over a wide range of temperature, being adopted. The subject was next taken up by Hans Landolt, who, from an immense number of observations, supported in a general way the formula of Gladstone and Dale. He introduced the idea of comparing the refractivity of equimolecular quantities of different substances by multiplying the function (n-1)/d by the molecular weight (M) of the substance, and investigated the relations of chemical grouping to refractivity. Although establishing certain general relations between atomic and molecular refractions, the results were somewhat vitiated by the inadequacy of the empirical function which he employed, since it was by no means a constant which depended only on the actual composition of the substance and was independent of its physical condition. A more accurate expression (n²-1)/(n²+2)d was 70 suggested in 1880 independently and almost simultaneously by L.V. Lorenz of Copenhagen and H.A. Lorentz of Leiden, from considerations based on the Clausius-Mossotti theory of dielectrics.
Assuming that the molecules are spherical, R.J.E. Clausius and O.F. Mossotti found a relation between the dielectric constant and the space actually occupied by the molecules, viz. K = (1 + 2a)/(1 - a), or a = (K - 1)/(K + 2), where K is the dielectric constant and a the fraction of the total volume actually occupied by matter. According to the electromagnetic theory of light K = N², where N is the refractive index for rays of infinite wave-length. Making this substitution, and dividing by d, the density of the substance, we obtain a/d = (N² - 1)/(N² + 2 )d. Since a/d is the real specific volume of the molecule, it is therefore a constant; hence (N² - 1)/(N² + 2)d is also a constant and is independent of all changes of temperature, pressure, and of the state of aggregation. To determine N recourse must be made to Cauchy’s formula of dispersion (q.v.), n = A + B/λ2 + C/λ4 + ... from which, by extrapolation, λ becoming infinite, we obtain N = A. In the case of substances possessing anomalous dispersion, the direct measurement of the refractive index for Hertzian waves of very long wave-length may be employed.
It is found experimentally that the Lorenz and Lorentz function holds fairly well, and better than the Gladstone and Dale formula. This is shown by the following observations of Rühlmann on water, the light used being the D line of the spectrum:—
| t. | (n - 1)/d. | (n² - 1)/(n² + 2)d. |
| 0 | 0.3338 | 0.2061 |
| 10 | 0.3338 | 0.2061 |
| 20 | 0.3336 | 0.2061 |
| 90 | 0.3321 | 0.2059 |
| 100 | 0.3323 | 0.2061 |
Eykmann’s observations also support the approximate constancy of the Lorenz-Lorentz formula over wide temperature differences, but in some cases the deviation exceeds the errors of observation. The values are for the Hα line:—
| Substance. | Temp. | (n² - 1)/(n² + 2)d. |
| Isosafrol, C10H10O2 | 17.6° | 0.2925 |
| 141.2° | 0.2962 | |
| Diphenyl ethylene, C14H12 | 22° | 0.3339 |
| 143.4° | 0.3382 | |
| Quinoline, C9H7N | 16.2° | 0.3187 |
| 141° | 0.3225 |
The empirical formula (n² - 1)/(n² + 0.4)d apparently gives more constant values with change of temperature than the Lorenz-Lorentz form. The superiority of the Lorenz-Lorentz formula over the Gladstone and Dale formula for changes of state is shown by the following observations of Brühl (Zeit. f. phys. Chem., 1891, 71, p. 4). The values are for the D line:—
| Substance. | Temp. | Gladstone and Dale. | Lorenz and Lorentz. | ||
| Vapour. | Liquid. | Vapour. | Liquid. | ||
| Water | 10° | 0.3101 | 0.3338 | 0.2068 | 0.2061 |
| Carbon disulphide | 10° | 0.4347 | 0.4977 | 0.2898 | 0.2805 |
| Chloroform | 10° | 0.2694 | 0.3000 | 0.1796 | 0.1790 |
Landolt and Gladstone, and at a later date J.W. Brühl, have investigated the relations existing between the refractive power and composition. To Landolt is due the proof that, Additive relations. in general, isomers, i.e. compounds having the same composition, have equal molecular refractions, and that equal differences in composition are associated with equal differences in refractive power. This is shown in the following table (the values are for Hα):—
| Substance. | Mol. Refract. | Substance. | Mol. Refract. | Diff. for CH2. | |
| Ethylene chloride | C2H4Cl2 | 20.96 | Acetic acid | 12.93 | |
| Ethylidene chloride | 21.08 | Propionic acid | 17.42 | 4.49 | |
| Fumaric acid | C4H4O4 | 70.89 | Butyric acid | 22.01 | 4.59 |
| Maleic acid | 70.29 | ||||
| o-Cresol | C7H8O | 32.52 | Acetaldehyde | 11.50 | |
| m-Cresol | 32.56 | Propionaldehyde | 15.93 | 4.43 | |
| p-Cresol | 32.57 | Butylaldehyde | 20.52 | 4.59 | |
Additive relations undoubtedly exist, but many discrepancies occur which may be assigned, as in the case of molecular volumes, to differences in constitution. Atomic refractions may be obtained either directly, by investigating the various elements, or indirectly, by considering differences in the molecular refractions of related compounds. The first method needs no explanation. The second method proceeds on the same lines as adopted for atomic volumes. By subtracting the value for CH2, which may be derived from two substances belonging to the same homologous series, from the molecular refraction of methane, CH4, the value of hydrogen is obtained; subtracting this from CH2, the value of carbon is determined. Hydroxylic oxygen is obtained by subtracting the molecular refractions of acetic acid and acetaldehyde. Similarly, by this method of differences, the atomic refraction of any element may be determined. It is found, however, that the same element has not always the same atomic refraction, the difference being due to the nature of the elements which saturate its valencies. Thus oxygen varies according as whether it is linked to hydrogen (hydroxylic oxygen), to two atoms of carbon (ether oxygen), or to one carbon atom (carbonyl oxygen); similarly, carbon varies according as whether it is singly, doubly, or trebly bound to carbon atoms.
A table of the atomic refractions and dispersions of the principal elements is here given:—
| Element. | Hα | D. | Hγ | Dispersion Hγ - Hα. |
| Hydrogen | 1.103 | 1.051 | 1.139 | 0.036 |
| Oxygen, hydroxyl | 1.506 | 1.521 | 1.525 | 0.019 |
| Oxygen, ether | 1.655 | 1.683 | 1.667 | 0.012 |
| Oxygen, carbonyl | 2.328 | 2.287 | 2.414 | 0.086 |
| Chlorine | 6.014 | 5.998 | 6.190 | 0.176 |
| Bromine | 8.863 | 8.927 | 9.211 | 0.348 |
| Iodine | 13.808 | 14.12 | 14.582 | 0.774 |
| Carbon (singly bound) | 2.365 | 2.501 | 2.404 | 0.039 |
| Double linkage of carbon | 1.836 | 1.707 | 1.859 | 0.23 |
| Triple linkage of carbon | 2.22 | 2.41 | 0.19 | |
| Nitrogen, singly bound and only to carbon | 2.76 | 2.95 | 0.19 |
Dispersion and Composition.—-In the preceding section we have seen that substances possess a definite molecular (or atomic) refraction for light of particular wave-length; the difference between the refractions for any two rays is known as the molecular (or atomic) dispersion. Since molecular refractions are independent of temperature and of the state of aggregation, it follows that molecular dispersions must be also independent of these conditions; and hence quantitative measurements should give an indication as to the chemical composition of substances. This subject has been principally investigated by Brühl; he found that molecular dispersions of liquids and gases were independent of temperature, and fairly independent of the state of aggregation, but that no simple connexion exists between atomic refractions and dispersions (see preceding table). He also showed how changes in constitution effected dispersions to a far greater extent than they did refractions; thus, while the atomic dispersion of carbon is 0.039, the dispersions due to a double and treble linkage is 0.23 and 0.19 respectively.
Colour and Constitution.—In this article a summary of the theories which have been promoted in order to connect the colour of organic compounds with their constitution will be given, and the reader is referred to the article Colour for the physical explanation of this property, and to Vision for the physiological and psychological bearings. A clear distinction must be drawn between colour and the property of dyeing; all coloured substances are not dyes, and it is shown in the article Dyeing that the property of entering into chemical or physical combination with fibres involves properties other than those essential to colour. At the same time, however, all dyestuffs are coloured substances.
A survey of coloured substances led O.N. Witt in 1876 to formulate his “chromophore-auxochrome” theory. On this theory colour is regarded as due to the presence of a “chromophore,” and dyeing power to an “auxochrome”; the latter by itself cannot produce colour or dyeing power, but it is only active in the presence of a chromophore, when it intensifies the colour and confers the property of dyeing. The principal chromophores are the azo, -N=N-, azoxy, =N2O, nitro, -NO2, nitroso, -NO, and carbonyl, =CO, groups. The azo-group is particularly active, both the aliphatic and aromatic compounds being coloured. The simplest aliphatic compounds, such as diazo-methane, diazo-ethane, and azo-formic acid, are yellow; the diamide of the latter acid is orange-red. Of the aromatic compounds azo-benzene is bright orange-red, and α-azo-naphthalene forms red needles or small steel-blue prisms. The azo-group, however, has little or no colouring effect when present in a 71 ring system, such as in cinnolene, phthalazine and tolazone. The nitro group has a very important action mainly on account of the readiness with which it can be introduced into the molecule, but its effect is much less than that of the azo group. The colour produced is generally yellow, which, in accordance with a general rule, is intensified with an increase in the number of groups; compare, for example, mono-, di-and tri-nitrobenzene. The nitroso group is less important. The colour produced is generally of a greenish shade; for example, nitrosobenzene is green when fused or in solution (when crystalline, it is colourless), and dinitrosoresorcin has been employed as a dyestuff under the names “solid green” and “chlorine.” The carbonyl group by itself does not produce colour, but when two adjacent groups occur in the molecule, as for example in the a-diketones (such as di-acetyl and benzil), a yellow colour is produced. It also acts as a chromogenic centre when double bonds or ethylenic linkages are present, as in fluorene ketone or fluorenone.
A more complex chromophoric group is the triple ethylenic grouping
 the introduction of which was rendered necessary
by the discovery of certain coloured hydrocarbons. As a general
rule, hydrocarbons are colourless; the exceptions include the golden
yellow acenaphthylene, the red bidiphenylene-ethylene, and the
derivatives of fulvene
the introduction of which was rendered necessary
by the discovery of certain coloured hydrocarbons. As a general
rule, hydrocarbons are colourless; the exceptions include the golden
yellow acenaphthylene, the red bidiphenylene-ethylene, and the
derivatives of fulvene
 which have been discussed by J. Thiele (Ber., 1900, 33, p. 666).
This grouping is not always colour-producing, since diphenyl is colourless.
which have been discussed by J. Thiele (Ber., 1900, 33, p. 666).
This grouping is not always colour-producing, since diphenyl is colourless.
The most important auxochromes are the hydroxyl (-OH) and amino (-NH2) groups. According to the modern theory of auxochromic action, the introduction of a group into the molecule is accompanied by some strain, and the alteration in colour produced is connected with the magnitude of the strain. The amino group is more powerful than the hydroxyl, and the substituted amino group more powerful still; the repeated substitution of hydroxyl groups sometimes causes an intensification and sometimes a diminution of colour.
We may here notice an empirical rule formulated by Nietzski in 1879:—the simplest colouring substances are in the greenish-yellow and yellow, and with increasing molecular weight the colour passes into orange, red, violet, blue and green. This rule, however, is by no means perfect. Examination of the absorption spectra of coloured compounds shows that certain groupings displace the absorption bands in one direction, and other groupings in the other. If the bands be displaced towards the violet, involving a regression through the colours mentioned above, the group is said to be “hypsochromic”; if the reverse occurs the group is “bathochromic.” It may be generally inferred that an increase in molecular weight is accompanied by a change in colour in the direction of the violet.
Auxochromic groups generally aid one another, i.e. the tint deepens as the number of auxochromes increases. Also the relative position of the auxochrome to the chromophore influences colour, the ortho-position being generally the most powerful. Kauffmann (Ber., 1906, 39, p. 1959) attempted an evaluation of the effects of auxochromic groups by means of the magnetic optical constants. The method is based on the supposition that the magnetic rotation measures the strain produced in the molecule by an auxochrome, and he arranges the groups in the following order:—
| ·OCOCH3 | ·OCH3 | ·NHCOCH3 | ·NH2 | ·N(CH3)2 | ·N(C2H5)2 |
| -0.260 | 1.459 | 1.949 | 3.821 | 8.587 | 8.816 |
The phenomena attending the salt formation of coloured and colouring substances are important. The chromophoric groups are rarely strongly acid or basic; on the other hand, the auxochromes are strongly acid or basic and form salts very readily. Notable differences attend the neutralization of the chromophoric and auxochromic groups. With basic substances, the chromophoric combination with a colourless acid is generally attended by a deepening in colour; auxochromic combination, on the other hand, with a lessening. Examples of the first case are found among the colourless acridines and quinoxalines which give coloured salts; of the second case we may notice the colourless hydrochloride and sulphate of the deep yellow o-aminobenzophenone. With acid substances, the combination with “colourless” metals, i.e. metals producing colourless salts with acids, is attended by colour changes contrary to those given above, auxochromic combination being accompanied by a deepening, and chromophoric by a lessening of the tint.
Mention may be made of the phenomenon of halochromism, the name given to the power of colourless or faintly-coloured substances of combining with acids to form highly-coloured substances without the necessary production of a chromophoric group. The researches of Adolf von Baeyer and Villiger, Kehrmann, Kauffmann and others, show that this property is possessed by very many and varied substances. In many cases it may be connected with basic oxygen, and the salt formation is assumed to involve the passage of divalent into tetravalent oxygen. It seems that intermolecular change also occurs, but further research is necessary before a sound theory can be stated.
Quinone Theory of Colour.—A theory of colour in opposition to the Witt theory was proposed by Henry Armstrong in 1888 and 1892. This assumed that all coloured substances were derivatives of ortho- or para-quinone (see Quinones), and although at the time of its promotion little practical proof was given, yet the theory found wide acceptance on account of the researches of many other chemists. It follows on this theory that all coloured substances contain either of the groupings

the former being a para-quinonoid, the latter an ortho-quinonoid. While very many coloured substances must obviously contain this grouping, yet in many cases it is necessary to assume a simple intermolecular change, while in others a more complex rearrangement of bonds is necessary. Quinone, which is light yellow in colour, is the simplest coloured substance on this theory. Hydrocarbons of similar structure have been prepared by Thiele, for example, the orange-yellow tetraphenyl-para-xylylene, which is obtained by boiling the bromide C6H4[CBr(C6H5)2]2 with benzene and molecular silver. The quinonoid structure of many coloured compounds has been proved experimentally, as, for example, by Hewitt for the benzene-azo-phenols, and Hantzsch for triaminotriphenyl methane and acridine derivatives; but, at the same time, many substances cannot be so explained. A notable example is provided by the phthaleins, which result by the condensation of phthalic anhydride with phenols. In the free state these substances are colourless, and were assumed to have the formula shown in 1. Solution in dilute alkali was supposed to be accompanied by the rupture of the lactone ring with the formation of the quinonoid salt shown in 2.

Baeyer (Ber., 1905, 38, p. 569) and Silberrad (Journ. Chem. Soc., 1906, 89, p. 1787) have disputed the correctness of this explanation, and the latter has prepared melliteins and pyromelliteins, which are highly-coloured compounds produced from mellitic and pyromellitic acids, and which cannot be formulated as quinones. Baeyer has suggested that the nine carbon atom system of xanthone may act as a chromophore. An alternative view, due to Green, is that the oxygen atom of the xanthone ring is tetravalent, a supposition which permits the formulation of these substances as ortho-quinonoids.
The theories of colour have also been investigated by Hantzsch, who first considered the nitro-phenols. On the chromophore-auxochrome theory (the nitro group being the chromophore, and the hydroxyl the auxochrome) it is necessary in order to explain the high colour of the metallic salts and the colourless alkyl and aryl derivatives to assume that the auxochromic action of the hydroxyl group is only brought strongly into evidence by salt formation. Armstrong, on the other hand, assumed an intermolecular change, thus:—

The proof of this was left for Hantzsch, who traced a connexion with the nitrolic acids of V. Meyer, which are formed when nitrous acid acts on primary aliphatic nitro compounds. Meyer formulated these compounds as nitroximes or nitro-isnitroso derivatives, viz. R·C(NO2)(NOH). Hantzsch explains the transformation of the colourless acid into red salts, which on standing yield more stable, colourless salts, by the following scheme:—

He has also shown that the nitrophenols yield, in addition to the
colourless true nitrophenol ethers, an isomeric series of coloured unstable
quinonoid aci-ethers, which have practically the same colour
and yield the same absorption spectra as the coloured metallic
salts. He suggests that the term “quinone” theory be abandoned,
and replaced by the Umlagerungs theory, since this term implies
some intermolecular rearrangement, and does not connote simply
benzenoid compounds as does “quinonoid.” H. von Liebig (Ann.,
1908, 360, p. 128), from a very complete discussion of triphenyl-methane
derivatives, concluded that the grouping
 was the only true organic chromophore, colour production, however,
requiring another condition, usually the closing of a ring.
was the only true organic chromophore, colour production, however,
requiring another condition, usually the closing of a ring.
The views as to the question of colour and constitution may be summarized as follows:—(1) The quinone theory (Armstrong, Gomberg, R. Meyer) regards all coloured substances as having a quinonoid structure. (2) The chromophore-auxochrome theory (Kauffmann) regards colour as due to the entry of an “auxochrome” into a “chromophoric” molecule. (3) If a colourless compound gives a coloured one on solution or by 72 salt-formation, the production of colour may be explained as a particular form of ionization (Baeyer), or by a molecular rearrangement (Hantzsch). A dynamical theory due to E.C.C. Baly regards colour as due to “isorropesis” or an oscillation between the residual affinities of adjacent atoms composing the molecule.
Fluorescence and Constitution.—The physical investigation of the phenomenon named fluorescence—the property of transforming incident light into light of different refrangibility—is treated in the article Fluorescence. Researches in synthetical organic chemistry have shown that this property of fluorescence is common to an immense number of substances, and theories have been proposed whose purpose is to connect the property with constitution.
In 1897 Richard Meyer (Zeit. physik. Chemie, 24, p. 468) submitted the view that fluorescence was due to the presence of certain “fluorophore” groups; such groupings are the pyrone ring and its congeners, the central rings in anthracene and acridine derivatives, and the paradiazine ring in safranines. A novel theory, proposed by J.T. Hewitt in 1900 (Zeit. f. physik. Chemie, 34, p. 1; B.A. Report, 1903, p. 628, and later papers in the Journ. Chem. Soc.), regards the property as occasioned by internal vibrations within the molecule conditioned by a symmetrical double tautomerism, light of one wave-length being absorbed by one form, and emitted with a different wave-length by the other. This oscillation may be represented in the case of acridine and fluorescein as

This theory brings the property of fluorescence into relation with that of colour; the forms which cause fluorescence being the coloured modifications: ortho-quinonoid in the case of acridine, para-quinonoid in the case of fluorescein. H. Kauffmann (Ber., 1900, 33, p. 1731; 1904, 35, p. 294; 1905, 38, p. 789; Ann., 1906, 344, p. 30) suggested that the property is due to the presence of at least two groups. The first group, named the “luminophore,” is such that when excited by suitable aetherial vibrations emits radiant energy; the other, named the “fluorogen,” acts with the luminophore in some way or other to cause the fluorescence. This theory explains the fluorescence of anthranilic acid (o-aminobenzoic acid), by regarding the aniline residue as the luminophore, and the carboxyl group as the fluorogen, since, apparently, the introduction of the latter into the non-fluorescent aniline molecule involves the production of a fluorescent substance. Although the theories of Meyer and Hewitt do not explain (in their present form) the behaviour of anthranilic acid, yet Hewitt has shown that his theory goes far to explain the fluorescence of substances in which a double symmetrical tautomerism is possible. This tautomerism may be of a twofold nature:—(1) it may involve the mere oscillation of linkages, as in acridine; or (2) it may involve the oscillation of atoms, as in fluorescein. A theory of a physical nature, based primarily upon Sir J.J. Thomson’s theory of corpuscles, has been proposed by J. de Kowalski (Compt. rend. 1907, 144, p. 266). We may notice that ethyl oxalosuccinonitrile is the first case of a fluorescent aliphatic compound (see W. Wislicenus and P. Berg, Ber., 1908, 41, p. 3757).
Capillarity and Surface Tension.—Reference should be made to the article Capillary Action for the general discussion of this phenomenon of liquids. It is there shown that the surface tension of a liquid may be calculated from its rise in a capillary tube by the formula γ = ½rhs, where γ is the surface tension per square centimetre, r the radius of the tube, h the height of the liquid column, and s the difference between the densities of the liquid and its vapour. At the critical point liquid and vapour become identical, and, consequently, as was pointed out by Frankenheim in 1841, the surface tension is zero at the critical temperature.
Mendeléeff endeavoured to obtain a connexion between surface energy and constitution; more successful were the investigations of Schiff, who found that the “molecular surface tension,” Relation to molecular weight. which he defined as the surface tension divided by the molecular weight, is constant for isomers, and that two atoms of hydrogen were equal to one of carbon, three to one of oxygen, and seven to one of chlorine; but these ratios were by no means constant, and afforded practically no criteria as to the molecular weight of any substance.
In 1886 R. Eötvös (Wied. Ann. 27, p. 452), assuming that two liquids may be compared when the ratios of the volumes of the liquids to the volumes of the saturated vapours are the same, deduced that γV2/3 (where γ is the surface tension, and V the molecular volume of the liquid) causes all liquids to have the same temperature coefficients. This theorem was investigated by Sir W. Ramsay and J. Shields (Journ. Chem. Soc. 63, p. 1089; 65, p. 167), whose results have thrown considerable light on the subject of the molecular complexity of liquids. Ramsay and Shields suggested that there exists an equation for the surface energy of liquids, analogous to the volume-energy equation of gases, PV = RT. The relation they suspected to be of the form γS = KT, where K is a constant analogous to R, and S the surface containing one gramme-molecule, γ and T being the surface tension and temperature respectively. Obviously equimolecular surfaces are given by (Mv)2/3, where M is the molecular weight of the substance, for equimolecular volumes are Mv, and corresponding surfaces the two-thirds power of this. Hence S may be replaced by (Mv)2/3. Ramsay and Shields found from investigations of the temperature coefficient of the surface energy that T in the equation γ(Mv)2/3 = KT must be counted downwards from the critical temperature T less about 6°. Their surface energy equation therefore assumes the form γ(Mv)2/3 = K(τ - 6°). Now the value of K, γ being measured in dynes and M being the molecular weight of the substance as a gas, is in general 2.121; this value is never exceeded, but in many cases it is less. This diminution implies an association of molecules, the surface containing fewer molecules than it is supposed to. Suppose the coefficient of association be n, i.e. n is the mean number of molecules which associate to form one molecule, then by the normal equation we have γ(Mnv)2/3 = 2.121(τ - 6°); if the calculated constant be K1, then we have also γ(Mv)2/3 = K1(τ-6°). By division we obtain n2/3 = 2.121/K1, or n = (2.121/K1)3/2 the coefficient of association being thus determined.
The apparatus devised by Ramsay and Shields consisted of a capillary tube, on one end of which was blown a bulb provided with a minute hole. Attached to the bulb was a glass rod and then a tube containing iron wire. This tube was placed in an outer tube containing the liquid to be experimented with; the liquid is raised to its boiling-point, and then hermetically sealed. The whole is enclosed in a jacket connected with a boiler containing a liquid, the vapour of which serves to keep the inner tube at any desired temperature. The capillary tube can be raised or lowered at will by running a magnet outside the tube, and the heights of the columns are measured by a cathetometer or micrometer microscope.
Normal values of K were given by nitrogen peroxide, N2O4, sulphur chloride, S2Cl2, silicon tetrachloride, SiCl4, phosphorus chloride, PCl3, phosphoryl chloride, POCl3, nickel carbonyl, Ni(CO)4, carbon disulphide, benzene, pyridine, ether, methyl propyl ketone; association characterized many hydroxylic compounds: for ethyl alcohol the factor of association was 2.74-2-43, for n-propyl alcohol 2.86-2.72, acetic acid 3.62-2.77, acetone 1.26, water 3.81-2.32; phenol, nitric acid, sulphuric acid, nitroethane, and propionitril, also exhibit association.
Crystalline Form and Composition.
The development of the theory of crystal structure, and the fundamental principles on which is based the classification of crystal forms, are treated in the article Crystallography; in the same place will be found an account of the doctrine of isomorphism, polymorphism and morphotropy. Here we shall treat the latter subjects in more detail, viewed from the standpoint of the chemist. Isomorphism may be defined as the existence of two or more different substances in the same crystal form and structure, polymorphism as the existence of the same substance in two or more crystal modifications, and morphotropy (after P. von Groth) as the change in crystal form due to alterations in the molecule of closely (chemically) related substances. In order to permit a comparison of crystal forms, from which we hope to gain an insight into the prevailing molecular conditions, it is necessary that some unit of crystal dimensions must be chosen. A crystal may be regarded as built up of primitive parallelepipeda, the edges of which are in the ratio of the crystallographic axes, and the angles the axial angles of the crystals. To reduce these figures to a common standard, so that the volumes shall contain equal numbers of molecules, the notion of molecular volumes is introduced, the arbitrary values of the crystallographic axes (a, b, c) being replaced by the topic parameters18 (χ,ψ,ω), which are such that, combined with the axial angles, they enclose volumes which contain equal numbers of molecules. The actual values of the topic parameters can then readily be expressed in terms of the elements of the crystals (the axial ratios and angles), the density, and the molecular weight (see Groth, Physikalische Krystallographie, or Chemical Crystallography).
73 Polymorphism.—On the theory that crystal form and structure are the result of the equilibrium between the atoms and molecules composing the crystals, it is probable, a priori, that the same substance may possess different equilibrium configurations of sufficient stability, under favourable conditions, to form different crystal structures. Broadly this phenomenon is termed polymorphism; however, it is necessary to examine closely the diverse crystal modifications in order to determine whether they are really of different symmetry, or whether twinning has occasioned the apparent difference. In the article Crystallography the nature and behaviour of twinned crystals receives full treatment; here it is sufficient to say that when the planes and axes of twinning are planes and axes of symmetry, a twin would exhibit higher symmetry (but remain in the same crystal system) than the primary crystal; and, also, if a crystal approximates in its axial constants to a higher system, mimetic twinning would increase the approximation, and the crystal would be pseudo-symmetric.
In general, polysymmetric and polymorphous modifications suffer transformation when submitted to variations in either temperature or pressure, or both. The criterion whether a pseudo-symmetric form is a true polymorph or not consists in the determination of the scalar properties (e.g. density, specific heat, &c.) of the original and the resulting modification, a change being in general recorded only when polymorphism exists. Change of temperature usually suffices to determine this, though in certain cases a variation in pressure is necessary; for instance, sodium magnesium uranyl acetate, NaMg(UO2)3(C2H3O2)9·9H2O shows no change in density unless the observations are conducted under a considerable pressure. Although many pseudo-symmetric twins are transformable into the simpler form, yet, in some cases, a true polymorph results, the change being indicated, as before, by alterations in scalar (as well as vector) properties.
For example, boracite forms pseudo-cubic crystals which become truly cubic at 265°, with a distinct change in density; leucite behaves similarly at about 560°. Again, the pyroxenes, RSiO3 (R = Fe, Mg, Mn, &c.), assume the forms (1) monoclinic, sometimes twinned so as to become pseudo-rhombic; (2) rhombic, resulting from the pseudo-rhombic structure of (1) becoming ultramicroscopic; and (3) triclinic, distinctly different from (1) and (2); (1) and (2) are polysymmetric modifications, while (3) and the pair (1) and (2) are polymorphs.
While polysymmetry is solely conditioned by the manner in which the mimetic twin is built up from the single crystals, there being no change in the scalar properties, and the vector properties being calculable from the nature of the twinning, in the case of polymorphism entirely different structures present themselves, both scalar and vector properties being altered; and, in the present state of our knowledge, it is impossible to foretell the characters of a polymorphous modification. We may conclude that in polymorphs the substance occurs in different phases (or molecular aggregations), and the equilibrium between these phases follows definite laws, being dependent upon temperature and pressure, and amenable to thermodynamic treatment (cf. Chemical Action and Energetics). The transformation of polymorphs presents certain analogies to the solidification of a liquid. Liquids may be cooled below their freezing-point without solidification, the metastable (after W. Ostwald) form so obtained being immediately solidified on the introduction of a particle of the solid modification; and supersaturated solutions behave in a similar manner. At the same time there may be conditions of temperature and pressure at which polymorphs may exist side by side.

The above may be illustrated by considering the equilibrium between rhombic and monoclinic sulphur. The former, which is deposited from solutions, is transformed into monoclinic sulphur at about 96°, but with great care it is possible to overheat it and even to fuse it (at 113.5°) without effecting the transformation. Monoclinic sulphur, obtained by crystallizing fused sulphur, melts at 119.5°, and admits of undercooling even to ordinary temperatures, but contact with a fragment of the rhombic modification spontaneously brings about the transformation. From Reicher’s determinations, the exact transition point is 95.6°; it rises with increasing pressure about 0.05° for one atmosphere; the density of the rhombic form is greater than that of the monoclinic. The equilibria of these modifications may be readily represented on a pressure-temperature diagram. If OT, OP (fig. 6), be the axes of temperature and pressure, and A corresponds to the transition point (95.6°) of rhombic sulphur, we may follow out the line AB which shows the elevation of the transition point with increasing pressure. The overheating curve of rhombic sulphur extends along the curve AC, where C is the melting-point of monoclinic sulphur. The line BC, representing the equilibrium between monoclinic and liquid sulphur, is thermodynamically calculable; the point B is found to correspond to 131° and 400 atmospheres. From B the curve of equilibrium (BD) between rhombic and liquid sulphur proceeds; and from C (along CE) the curve of equilibrium between liquid sulphur and sulphur vapour. Of especial interest is the curve BD: along this line liquid and rhombic sulphur are in equilibrium, which means that at above 131° and 400 atmospheres the rhombic (and not the monoclinic) variety would separate from liquid sulphur.
Mercuric iodide also exhibits dimorphism. When precipitated from solutions it forms red tetragonal crystals, which, on careful heating, give a yellow rhombic form, also obtained by crystallization from the fused substance, or by sublimation. The transition point is 126.3° (W. Schwarz, Zeit. f. Kryst. 25, p. 613), but both modifications may exist in metastable forms at higher and lower temperatures respectively; the rhombic form may be cooled down to ordinary temperature without changing, the transformation, however, being readily induced by a trace of the red modification, or by friction. The density and specific heat of the tetragonal form are greater than those of the yellow.
Hexachlorethane is trimorphous, forming rhombic, triclinic and cubic crystals; the successive changes occur at about 44° and 71°, and are attended by a decrease in density.
Tetramorphism is exhibited by ammonium nitrate. According to O. Lehmann it melts at 168° (or at a slightly lower temperature in its water of crystallization) and on cooling forms optically isotropic crystals; at 125.6° the mass becomes doubly refracting, and from a solution rhombohedral (optically uniaxial) crystals are deposited; by further cooling acicular rhombic crystals are produced at 82.8°, and at 32.4° other rhombic forms are obtained, identical with the product obtained by crystallizing at ordinary temperatures. The reverse series of transformations occurs when this final modification is heated. M. Bellati and R. Romanese (Zeit. f. Kryst. 14, p. 78) determined the densities and specific heats of these modifications. The first and third transformations (reckoned in order with increasing temperature of the transition point) are attended by an increase in volume, the second with a contraction; the solubility follows the same direction, increasing up to 82.8°, then diminishing up to 125.6°, and then increasing from this temperature upwards.
The physical conditions under which polymorphous modifications are prepared control the form which the substance assumes. We have already seen that temperature and pressure exercise considerable influence in this direction. In the case of separation from solutions, either by crystallization or by precipitation by double decomposition, the temperature, the concentration of the solution, and the presence of other ions may modify the form obtained. In the case of sodium dihydrogen phosphate, NaH2PO4·H2O, a stable rhombic form is obtained from warm solutions, while a different, unstable, rhombic form is obtained from cold solutions. Calcium carbonate separates as hexagonal calcite from cold solutions (below 30°), and as rhombic aragonite from solutions at higher temperatures; lead and strontium carbonates, however, induce the separation of aragonite at lower temperatures. From supersaturated solutions the form unstable at the temperature of the experiment is, as a rule, separated, especially on the introduction of a crystal of the unstable form; and, in some cases, similar inoculation of the fused substance is attended by the same result. Different modifications may separate and exist side by side at one and the same time from a solution; e.g. telluric acid forms cubic and monoclinic crystals from a hot nitric acid solution, and ammonium fluosilicate gives cubic and hexagonal forms from aqueous solutions between 6° and 13°.
A comparison of the transformation of polymorphs leads to a twofold classification: (1) polymorphs directly convertible in a reversible manner—termed “enantiotropic” by O. Lehmann and (2) polymorphs in which the transformation proceeds in one direction only—termed “monotropic.” In the first class 74 are included sulphur and ammonium nitrate; monotropy is exhibited by aragonite and calcite.
It is doubtful indeed whether any general conclusions can yet be drawn as to the relations between crystal structure and scalar properties and the relative stability of polymorphs. As a general rule the modification stable at higher temperatures possesses a lower density; but this is by no means always the case, since the converse is true for antimonious and arsenious oxides, silver iodide and some other substances. Attempts to connect a change of symmetry with stability show equally a lack of generality. It is remarkable that a great many polymorphous substances assume more symmetrical forms at higher temperatures, and a possible explanation of the increase in density of such compounds as silver iodide, &c., may be sought for in the theory that the formation of a more symmetrical configuration would involve a drawing together of the molecules, and consequently an increase in density. The insufficiency of this argument, however, is shown by the data for arsenious and antimonious oxides, and also for the polymorphs of calcium carbonate, the more symmetrical polymorphs having a lower density.
Morphotropy.—Many instances have been recorded where substitution has effected a deformation in one particular direction, the crystals of homologous compounds often exhibiting the same angles between faces situated in certain zones. The observations of Slavik (Zeit. f. Kryst., 1902, 36, p. 268) on ammonium and the quaternary ammonium iodides, of J.A. Le Bel and A. Ries (Zeit. f. Kryst., 1902, 1904, et seq.) on the substituted ammonium chlorplatinates, and of G. Mez (ibid., 1901, 35, p. 242) on substituted ureas, illustrate this point.
Ammonium iodide assumes cubic forms with perfect cubic cleavage; tetramethyl ammonium iodide is tetragonal with perfect cleavages parallel to {100} and {001}—a difference due to the lengthening of the a axes; tetraethyl ammonium iodide also assumes tetragonal forms, but does not exhibit the cleavage of the tetramethyl compound; while tetrapropyl ammonium iodide crystallizes in rhombic form. The equivalent volumes and topic parameters are tabulated:
| NH4I. | NMe4I. | NEt4I. | NPr4I. | |
| V | 57.51 | 108.70 | 162.91 | 235.95 |
| χ | 3.860 | 5.319 | 6.648 | 6.093 |
| ψ | 3.860 | 5.319 | 6.648 | 7.851 |
| ω | 3.860 | 3.842 | 3.686 | 4.933 |
From these figures it is obvious that the first three compounds form a morphotropic series; the equivalent volumes exhibit a regular progression; the values of χ and ψ, corresponding to the a axes, are regularly increased, while the value of ω, corresponding to the c axis, remains practically unchanged. This points to the conclusion that substitution has been effected in one of the cube faces. We may therefore regard the nitrogen atoms as occupying the centres of a cubic space lattice composed of iodine atoms, between which the hydrogen atoms are distributed on the tetrahedron face normals. Coplanar substitution in four hydrogen atoms would involve the pushing apart of the iodine atoms in four horizontal directions. The magnitude of this separation would obviously depend on the magnitude of the substituent group, which may be so large (in this case propyl is sufficient) as to cause unequal horizontal deformation and at the same time a change in the vertical direction.
The measure of the loss of symmetry associated with the introduction of alkyl groups depends upon the relative magnitudes of the substituent group and the rest of the molecule; and the larger the molecule, the less would be the morphotropic effect of any particular substituent. The mere retention of the same crystal form by homologous substances is not a sufficient reason for denying a morphotropic effect to the substituent group; for, in the case of certain substances crystallizing in the cubic system, although the crystal form remains unaltered, yet the structures vary. When both the crystal form and structure are retained, the substances are said to be isomorphous.
Other substituent groups exercise morphotropic effects similar to those exhibited by the alkyl radicles; investigations have been made on halogen-, hydroxy-, and nitro-derivatives of benzene and substituted benzenes. To Jaeger is due the determination of the topic parameters of certain haloid-derivatives, and, while showing that the morphotropic effects closely resemble those occasioned by methyl, he established the important fact that, in general, the crystal form depended upon the orientation of the substituents in the benzene complex.
Benzoic acid is pseudo-tetragonal, the principal axis being remarkably long; there is no cleavage at right angles to this axis. Direct nitration gives (principally) m-nitrobenzoic acid, also pseudo-tetragonal with a much shorter principal axis. From this two chlornitrobenzoic acids [COOH·NO2·Cl = 1.3.6 and 1.3.4] may be obtained. These are also pseudotetragonal; the (1.3.6) acid has nearly the same values of χ and ψ as benzoic acid, but ω is increased; compared with m-nitrobenzoic acid, χ and ψ have been diminished, whereas ω is much increased; the (1.3.4) acid is more closely related to m-nitrobenzoic acid, χ and ψ being increased, ω diminished. The results obtained for the (1.2) and (1.4) chlorbenzoic acids also illustrate the dependence of crystal form and structure on the orientation of the molecule.
The hydroxyl group also resembles the methyl group in its morphotropic effects, producing, in many cases, no change in symmetry but a dimensional increase in one direction. This holds for benzene and phenol, and is supported by the observations of Gossner on [1.3.5] trinitrobenzene and picric acid (1.3.5-trinitro, 2 oxybenzene); these last two substances assume rhombic forms, and picric acid differs from trinitrobenzene in having ω considerably greater, with χ and ψ slightly less. A similar change, in one direction only, characterizes benzoic acid and salicylic acid.
The nitro group behaves very similarly to the hydroxyl group. The effect of varying the position of the nitro group in the molecule is well marked, and conclusions may be drawn as to the orientation of the groups from a knowledge of the crystal form; a change in the symmetry of the chemical molecule being often attended by a loss in the symmetry of the crystal.
It may be generally concluded that the substitution of alkyl, nitro, hydroxyl, and haloid groups for hydrogen in a molecule occasions a deformation of crystal structure in one definite direction, hence permitting inferences as to the configuration of the atoms composing the crystal; while the nature and degree of the alteration depends (1) upon the crystal structure of the unsubstituted compound; (2) on the nature of the substituting radicle; (3) on the complexity of the substituted molecule; and (4) on the orientation of the substitution derivative.
Isomorphism.—It has been shown that certain elements and groups exercise morphotropic effects when substituted in a compound; it may happen that the effects due to two or more groups are nearly equivalent, and consequently the resulting crystal forms are nearly identical. This phenomenon was first noticed in 1822 by E. Mitscherlich, in the case of the acid phosphate and acid arsenate of potassium, KH2P(As)O4, who adopted the term isomorphism, and regarded phosphorus and arsenic as isomorphously related elements. Other isomorphously related elements and groups were soon perceived, and it has been shown that elements so related are also related chemically.
Tutton’s investigations of the morphotropic effects of the metals potassium, rubidium and caesium, in combination with the acid radicals of sulphuric and selenic acids, showed that the replacement of potassium by rubidium, and this metal in turn by caesium, was accompanied by progressive changes in both physical and crystallographical properties, such that the rubidium salt was always intermediate between the salts of potassium and caesium (see table; the space unit is taken as a pseudo-hexagonal prism). This fact finds a parallel in the atomic weights of these metals.
| V | χ | ψ | ω | |
| K2SO4 | 69.42 | 4.464 | 4.491 | 4.997 |
| Rb2SO4 | 73.36 | 4.634 | 4.664 | 5.237 |
| Cs2SO4 | 83.64 | 4.846 | 4.885 | 5.519 |
| K2SeO4 | 71.71 | 4.636 | 4.662 | 5.118 |
| Rb2SeO4 | 79.95 | 4.785 | 4.826 | 5.346 |
| Cs2SeO4 | 91.16 | 4.987 | 5.035 | 5.697 |
By taking appropriate differences the following facts will be observed: (1) the replacement of potassium by rubidium occasions an increase in the equivalent volumes by about eight units, and of rubidium by caesium by about eleven units; (2) replacement in the same order is attended by a general increase in the three topic parameters, a greater increase being met with in the replacement of rubidium by caesium; (3) the parameters χ and ψ are about equally increased, while the increase in ω is always the greatest. Now consider the effect of replacing sulphur by selenium. It will be seen that (1) the increase in equivalent volume is about 6.6; (2) all the topic parameters are increased; (3) the greatest increase is effected in the parameters χ and ψ, which are equally lengthened.
These observations admit of ready explanation in the following
75
manner. The ordinary structural formula of potassium sulphate is
 If the crystal structure be regarded as composed of
three interpenetrating point systems, one consisting of sulphur
atoms, the second of four times as many oxygen atoms, and the
third of twice as many potassium atoms, the systems being so arranged
that the sulphur system is always centrally situated with respect
to the other two, and the potassium system so that it would affect
the vertical axis, then it is obvious that the replacement of potassium
by an element of greater atomic weight would specially increase the
length of ω (corresponding to the vertical axis), and cause a smaller
increase in the horizontal parameters χ and ψ; moreover, the
increments would advance with the atomic weight of the replacing
metal. If, on the other hand, the sulphur system be replaced by a
corresponding selenium system, an element of higher atomic weight,
it would be expected that a slight increase would be observed in the
vertical parameter, and a greater increase recorded equally in the
horizontal parameters.
If the crystal structure be regarded as composed of
three interpenetrating point systems, one consisting of sulphur
atoms, the second of four times as many oxygen atoms, and the
third of twice as many potassium atoms, the systems being so arranged
that the sulphur system is always centrally situated with respect
to the other two, and the potassium system so that it would affect
the vertical axis, then it is obvious that the replacement of potassium
by an element of greater atomic weight would specially increase the
length of ω (corresponding to the vertical axis), and cause a smaller
increase in the horizontal parameters χ and ψ; moreover, the
increments would advance with the atomic weight of the replacing
metal. If, on the other hand, the sulphur system be replaced by a
corresponding selenium system, an element of higher atomic weight,
it would be expected that a slight increase would be observed in the
vertical parameter, and a greater increase recorded equally in the
horizontal parameters.
Muthmann (Zeit. f. Kryst., 1894), in his researches on the tetragonal potassium and ammonium dihydrogen phosphates and arsenates, found that the replacement of potassium by ammonium was attended by an increase of about six units in the molecular volume, and of phosphorus by arsenic by about 4.6 units. In the topic parameters the following changes were recorded: replacement of potassium by ammonium was attended by a considerable increase in ω, χ and ψ being equally, but only slightly, increased; replacement of phosphorus by arsenic was attended by a considerable increase, equally in χ and ψ, while ω suffered a smaller, but not inconsiderable, increase. It is thus seen that the ordinary plane representation of the structure of compounds possesses a higher significance than could have been suggested prior to crystallographical researches.

Identity, or approximate identity, of crystal form is not in itself sufficient to establish true isomorphism. If a substance deposits itself on the faces of a crystal of another substance of similar crystal form, the substances are probably isomorphous. Such parallel overgrowths, termed episomorphs, are very common among the potassium and sodium felspars; and K. von Hauer has investigated a number of cases in which salts exhibiting episomorphism have different colours, thereby clearly demonstrating this property of isomorphism. For example, episomorphs of white potash alum and violet chrome alum, of white magnesium sulphate and green nickel sulphate, and of many other pairs of salts, have been obtained. More useful is the property of isomorphous substances of forming mixed crystals, which are strictly isomorphous with their constituents, for all variations in composition. In such crystals each component plays its own part in determining the physical properties; in other words, any physical constant of a mixed crystal can be calculated as additively composed of the constants of the two components.
Fig. 7 represents the specific volumes of mixtures of ammonium and potassium sulphates; the ordinates representing specific volumes, and the abscissae the percentage composition of the mixture. Fig. 8 shows the variation of refractive index of mixed crystals of potash alum and thallium alum with variation in composition.
In these two instances the component crystals are miscible in all proportions; but this is by no means always the case. It may happen that the crystals do not form double salts, and are only miscible in certain proportions. Two cases then arise: (1) the properties may be expressed as linear functions of the composition, the terminal values being identical with those obtained for the individual components, and there being a break in the curve corresponding to the absence of mixed crystals; or (2) similar to (1) except that different values must be assigned to the terminal values in order to preserve collinearity. Fig. 9 illustrates the first case: the ordinates represent specific volumes, and the abscissae denote the composition of isomorphous mixtures of ammonium and potassium dihydrogen phosphates, which mutually take one another up to the extent of 20% to form homogeneous crystals. The second case is illustrated in fig. 10. Magnesium sulphate (orthorhombic) takes up ferrous sulphate (monoclinic) to the extent of 19%, forming isomorphous orthorhombic crystals; ferrous sulphate, on the other hand, takes up magnesium sulphate to the extent of 54% to form monoclinic crystals. By plotting the specific volumes of these mixed crystals as ordinates, it is found that they fall on two lines, the upper corresponding to the orthorhombic crystals, the lower to the monoclinic. From this we may conclude that these salts are isodimorphous: the upper line represents isomorphous crystals of stable orthorhombic magnesium sulphate and unstable orthorhombic ferrous sulphate, the lower line isomorphous crystals of stable monoclinic ferrous sulphate and unstable monoclinic magnesium sulphate.

An important distinction separates true mixed crystals and crystallized double salts, for in the latter the properties are not linear functions of the properties of the components; generally there is a contraction in volume, while the refractive indices and other physical properties do not, in general, obey the additive law.
Isomorphism is most clearly discerned between elements of analogous chemical properties; and from the wide generality of such observations attempts have been made to form a classification of elements based on isomorphous replacements. The following table shows where isomorphism may be generally expected. The elements are arranged in eleven series, and the series are subdivided (as indicated by semicolons) into groups; these groups exhibit partial isomorphism with the other groups of the same series (see W. Nernst, Theoretical Chemistry).
| Series | 1. Cl, Br, I, F; Mn (in permanganates). 2. S, Se; Te (in tellurides); Cr, Mn, Te (in the acids H2RO4); As, Sb (in the glances MR2). 3. As, Sb, Bi; Te (as an element); P, Vd (in salts); N, P (in organic bases). 4. K, Na, Cs, Rb, Li; Tl, Ag. 5. Ca, Ba, Sr, Pb; Fe, Zn, Mn, Mg; Ni, Co, Cu; Ce, La, Di, Er, Y, Ca; Cu, Hg, Pb; Cd, Be, In, Zn; Tl, Pb. 6. Al, Fe, Cr, Mn; Ce, U (in sesquioxides). 7. Cu, Ag (when monovalent); Au. 8. Pt, Ir, Pd, Rh, Ru, Os; Au, Fe, Ni; Sn, Te. 9. C, Si, Ti, Zr, Th, Sn; Fe, Ti. 10. Ta, Cb (Nb). 11. Mo, W, Cr. |
For a detailed comparison of the isomorphous relations of the elements the reader is referred to P. von Groth, Chemical Crystallography. Reference may also be made to Ida Freund, The Study of Chemical Composition; and to the Annual Reports of the Chemical Society for 1908, p. 258.
Bibliography.—History: F. Hoefer, Histoire de la chimie (2nd ed., 1866-1869); Hermann Kopp, Geschichte der Chemie (1869), Entwickelung der Chemie in d. neueren Zeit (1871-1874); E. von Meyer, Geschichte der Chemie (3rd ed., 1905, Eng. trans.); A. Ladenburg, Entwickelungsgeschichte der Chemie (4th ed., 1907); A. Stange, Die Zeitalter der Chemie (1908). Reference may also be made to M.M. Pattison Muir, History of Chemical Theories and Laws (1907); Ida Freund, Study of Chemical Composition (1904); T.E. Thorpe, Essays in Historical Chemistry (2nd ed., 1902). See also the article Alchemy.
Principles and Physical.—W. Ostwald, Principles of Inorganic Chemistry (3rd Eng. ed., 1908), Outlines of General Chemistry, Lehrbuch der allgemeinen Chemie; W. Nernst, Theoretische Chemie (4th ed., 1907, Eng. trans.); J.H. van’t Hoff, Lectures on Theoretical and Physical Chemistry; J. Walker, Introduction to Physical Chemistry (4th ed., 1907); H.C. Jones, Outlines of Physical Chemistry (1903); D. Mendeléeff, Principles of Chemistry (3rd ed., 1905).
Inorganic.—Roscoe and Schorlemmer, Inorganic Chemistry (3rd ed., Non-metals, 1905; Metals, 1907); R. Abegg, Handbuch der anorganischen Chemie; Gmelin-Kraut, Handbuch der anorganischen Chemie; O. Dammer, Handbuch der anorganischen Chemie; H. Moissan, Chimie minérale.
Organic.—F. Beilstein, Handbuch der organischen Chemie; M.M. Richter, Lexikon der Kohlenstoffverbindungen (these are primarily works of reference); V. Meyer and P.H. Jacobson, Lehrbuch der organischen Chemie; Richter-Anschutz, Organische Chemie (11th ed., 76 vol. i., 1909, Eng. trans.); G.K. Schmidt, Kurzes Lehrbuch der organischen Chemie; A. Bernthsen, Organische Chemie (Eng. trans.). Practical methods are treated in Lassar-Cohn, Arbeitsmethoden für organisch-chemische Laboratorien (4th ed., 1906-1907). Select chapters are treated in A. Lachmann, Spirit of Organic Chemistry; J.B. Cohen, Organic Chemistry (1908); A.W. Stewart, Recent Advances in Organic Chemistry (1908); and in a series of pamphlets issued since 1896 with the title Sammlung chemischer und chemisch-technischer Vorträge.
Analytical.—For Blowpipe Analysis: C.F. Plattner, Probirkunst mit dem Löthrohr. For General Analysis: C.R. Fresenius, Qualitative and Quantitative Analysis, Eng. trans, by C.E. Groves (Qualitative, 1887) and A.I. Cohn (Quantitative, 1903); F.P. Treadwell, Kurzes Lehrbuch der analytischen Chemie (1905); F. Julian, Textbook of Quantitative Chemical Analysis (1904); A. Classen, Ausgewählte Methoden der analytischen Chemie (1901-1903); W. Crookes, Select Methods in Chemical Analysis (1894). Volumetric Analysis: F. Sutton, Systematic Handbook of Volumetric Analysis (1904); F. Mohr, Lehrbuch der chemisch-analytischen Titrirmethode (1896). Organic Analysis: Hans Meyer, Analyse und Konstitutionsermittlung organischer Verbindungen (1909); Wilhelm Vaubel, Die physikalischen und chemischen Methoden der quantitativen Bestimmung organischer Verbindungen. For the historical development of the proximate analysis of organic compounds see M.E.H. Dennstedt, Die Entwickelung der organischen Elementaranalyse (1899).
Encyclopaedias.—The early dictionaries of Muspratt and Watts are out of date; there is a later edition of the latter by H.F. Morley and M.M.P. Muir. A. Ladenburg, Handwörterbuch der Chemie, A. Wurtz, Dictionnaire de chimie, and F. Selmi, Enciclopedia di chimica, are more valuable; the latter two are kept up to date by annual supplements.
1 The more notable chemists of this period were Turquet de Mayerne (1573-1665), a physician of Paris, who rejected the Galenian doctrines and accepted the exaggerations of Paracelsus; Andreas Libavius (d. 1616), chiefly famous for his Opera Omnia Medicochymica (1595); Jean Baptiste van Helmont (1577-1644), celebrated for his researches on gases; F. de la Boë Sylvius (1614-1672), who regarded medicine as applied chemistry; and Otto Tachenius, who elucidated the nature of salts.
2 This dictum was questioned by the researches of H. Landolt, A. Heydweiller and others. In a series of 75 reactions it was found that in 61 there was apparently a diminution in weight, but in 1908, after a most careful repetition and making allowance for all experimental errors, Landolt concluded that no change occurred (see ELEMENT).
3 The theory of Berthollet was essentially mechanical, and he attempted to prove that the course of a reaction depended not on affinities alone but also on the masses of the reacting components. In this respect his hypothesis has much in common with the “law of mass-action” developed at a much later date by the Swedish chemists Guldberg and Waage, and the American, Willard Gibbs (see Chemical Action). In his classical thesis Berthollet vigorously attacked the results deduced by Bergman, who had followed in his table of elective attractions the path traversed by Stahl and S. F. Geoffroy.
4 Dalton’s atomic theory is treated in more detail in the article ATOM.
5 Berzelius, however, appreciated the necessity of differentiating the atom and the molecule, and even urged Dalton to amend his doctrine, but without success.
6 The following symbols were also used by Bergman:—

which represented zinc, manganese, cobalt, bismuth, nickel, arsenic, platinum, water, alcohol, phlogiston.
7 The following are the symbols employed by Dalton:—

which represent in order, hydrogen, nitrogen, carbon, oxygen, phosphorus, sulphur, magnesia, lime, soda, potash, strontia, baryta, mercury; iron, zinc, copper, lead, silver, platinum, and gold were represented by circles enclosing the initial letter of the element.
8 Approximate values of the atomic weights are employed here.
9 The definite distinction between potash and soda was first established by Duhamel de Monceau (1700-1781).
10 The reader is specially referred to the articles ALIZARIN; INDIGO; PURIN and TERPENES for illustrations of the manner in which chemists have artificially prepared important animal and vegetable products.
11 These observations were generalized by J.B. Dumas and Polydore Boullay (1806-1835) in their “etherin theory” (vide infra).
12 This must not be confused with the modern acetyl, CH3·CO, which at that time was known as acetoxyl.
13 It is now established that ortho compounds do exist in isomeric forms, instances being provided by chlor-, brom-, and amino-toluene, chlorphenol, and chloraniline; but arguments, e.g. E. Knoevenagel’s theory of “motoisomerism,” have been brought forward to cause these facts to support Kekulé.
14 Victor Meyer and G. Heyl (Ber., 1895, 28, p. 2776) attempted a solution from the following data. It is well known that di-ortho-substituted benzoic acids are esterified with difficulty. Two acids corresponding to the formula of Kekulé and Claus are triphenyl acrylic acid, (C6H5)2C:C(COOH)·C6H5, and triphenyl acetic acid, (C6H5)3C·COOH. Experiments showed that the second acid was much more difficult to esterify than the first, pointing to the conclusion that Claus’ formula for benzene was more probable than Kekulé’s.
15 H. Rose, Ausführliches Handbuch der analytischen Chemie (1851).
16 F. Wöhler, Die Mineralanalyse in Beispielen (1861).
17 For the connexion between valency and volume, see Valency.
18 This was done simultaneously in 1894 by W. Muthmann and A. E. H. Tutton, the latter receiving the idea from F. Becke (see Journ. Chem. Soc., 1896, 69, p. 507; 1905, 87, p. 1183).
CHEMNITZ (or Kemnitz), MARTIN (1522-1586), German Lutheran theologian, third son of Paul Kemnitz, a cloth-worker of noble extraction, was born at Treuenbrietzen, Brandenburg, on the 9th of November 1522. Left an orphan at the age of eleven, he worked for a time at his father’s trade. A relative at Magdeburg put him to school there (1539-1542). Having made a little money by teaching, he went (1543) to the university of Frankfort-on-Oder; thence (1545) to that of Wittenberg. Here he heard Luther preach, but was more attracted by Melanchthon, who interested him in mathematics and astrology. Melanchthon gave him (1547) an introduction to his son-in-law, Georg Sabinus, at Königsberg, where he was tutor to some Polish youths, and rector (1548) of the Kneiphof school. He practised astrology; this recommended him to Duke Albert of Prussia, who made him his librarian (1550). He then turned to Biblical, patristic and kindred studies. His powers were first brought out in controversy with Osiander on justification by faith. Osiander, maintaining the infusion of Christ’s righteousness into the believer, impugned the Lutheran doctrine of imputation; Chemnitz defended it with striking ability. As Duke Albert sided with Osiander, Chemnitz resigned the librarianship. Returning (1553) to Wittenberg, he lectured on Melanchthon’s Loci Communes, his lectures forming the basis of his own Loci Theologici (published posthumously, 1591), which constitute probably the best exposition of Lutheran theology as formulated and modified by Melanchthon. His lectures were thronged, and a university career of great influence lay before him, when he accepted a call to become coadjutor at Brunswick to the superintendent, Joachim Mörlin, who had known him at Königsberg. He removed to Brunswick on the 15th of December 1554, and there spent the remainder of his life, refusing subsequent offers of important offices from various Protestant princes of Germany. Zealous in the duties of his pastoral charge, he took a leading part in theological controversy. His personal influence, at a critical period, did much to secure strictness of doctrine and compactness of organization in the Lutheran Church. Against Crypto-Calvinists he upheld the Lutheran view of the eucharist in his Repetitio sanae doctrinae de Vera Praesentia (1560; in German, 1561). To check the reaction towards the old religion he wrote several works of great power, especially his Theologiae Jesuitarum praecipua capita (1562), an incisive attack on the principles of the society, and the Examen concilii Tridentini (four parts, 1565-66-72-73), his greatest work. His Corpus doctrinae Prutenicum (1567), drawn up in conjunction with Mörlin, at once acquired great authority. In the year of its publication he became superintendent of Brunswick, and in effect the director of his church throughout Lower Saxony. His tact was equal to his learning. In conjunction with Andreä and Selnecker he induced the Lutherans of Saxony and Swabia to adopt the Formula Concordiae and so become one body. Against lax views of Socinian tendency he directed his able treatise De duabus naluris in Christo (1570). Resigning office in infirm health (1584) he survived till the 8th of April 1586.
Lives of Chemnitz are numerous, e.g. by T. Gasmerus (1588), T. Pressel (1862), C.G.H. Lentz (1866), H. Hachfeld (1867), H. Schmid in J.J. Herzog’s Realencyklopädie (1878), T. Kunze in A. Hauck’s Realencyklop. für prot. Theol. und Kirche (1897); that by Hausle, in I. Goschler’s Dict. encyclopédique de la théol. cath. (1858), gives a Roman Catholic view.
CHEMNITZ, a town of Germany, in the kingdom of Saxony, the capital of a governmental district, 50 m. W.S.W. of Dresden and 51 S.E. of Leipzig by rail. Pop. (1885) 110,817; (1895) 161,017; (1905) 244,405. It lies 950 ft. above the sea, in a fertile plain at the foot of the Erzgebirge, watered by the river Chemnitz, an affluent of the Mulde. It is the chief manufacturing town in the kingdom, ranks next to Dresden and Leipzig in point of population, and is one of the principal commercial and industrial centres of Germany. It is well provided with railway communication, being directly connected with Berlin and with the populous and thriving towns of the Erzgebirge and Voigtland. Chemnitz is in general well built, the enormous development of its industry and commerce having of late years led to the laying out of many fine streets and to the embellishing of the town with handsome buildings. The centre is occupied by the market square, with the handsome medieval Rathaus, now superseded for municipal business by a modern building in the Post-strasse. In this square are monuments to the emperor William I., Bismarck and Moltke. The old inner town is surrounded by pleasant promenades, occupying the site of the old fortifications, and it is beyond these that industrial Chemnitz lies, girdling the old town on all sides with a thick belt of streets and factories, and ramifying far into the country. Chemnitz has eleven Protestant churches, among them the ancient Gothic church of St James, with a fine porch, and the modern churches of St Peter, St Nicholas and St Mark. There are also a synagogue and chapels of various sects. The industry of Chemnitz has gained for the town the name of “Saxon Manchester.” First in importance are its locomotive and engineering works, which give employment to some 20,000 hands in 90 factories. Next come its cotton-spinning, hosiery, textile and glove manufactures, in which a large trade is done with Great Britain and the United States. It is also the seat of considerable dyeworks, bleachworks, chemical and woollen factories, and produces leather and straps, cement, small vehicles, wire-woven goods, carpets, beer and bricks. The town is well provided with technical schools for training in the various industries, including commercial, public, economic and agricultural schools, and has a chamber of commerce. There are also industrial and historical museums, and collections of painting and natural history. The local communications are maintained by an excellent electric tramway system. To the northwest of the town is the Gothic church of a former Benedictine monastery, dating from 1514-1525, with a tower of 1897. Chemnitz is a favourite tourist centre for excursions into the Erzgebirge, the chain of mountains separating Saxony from Bohemia.
Chemnitz (Kaminizi) was originally a settlement of the Serbian Wends and became a market town in 1143. Its municipal constitution dates from the 14th century, and it soon became the most important industrial centre in the mark of Meissen. A monopoly of bleaching was granted to the town, and thus a considerable trade in woollen and linen yarns was attracted to Chemnitz; paper was made here, and in the 16th century the manufacture of cloth was very flourishing. In 1539 the Reformation was introduced, and in 1546 the Benedictine monastery, founded about 1136 by the emperor Lothair II. about 2 m. north of the town, was dissolved. During the Thirty Years’ War Chemnitz was plundered by all parties and its trade was completely ruined, but at the beginning of the 18th century it had begun to recover. Further progress in this direction was made 77 during the 19th century, especially after 1834 when Saxony joined the German Zollverein.
See Zöllner, Geschichte der Fabrik- und Handelsstadt Chemnitz (1891); and Straumer, Die Fabrik- und Handelsstadt Chemnitz (1892).
CHEMOTAXIS (from the stem of “chemistry” and Gr. τάξις, arrangement), a biological term for the attraction exercised on living or growing organisms or their members by chemical substances; e.g. the attraction of the male cells of ferns or mosses by an organic acid or sugar-solution.
CHENAB (the Greek Acesines), one of the “Five rivers” of the Punjab, India. It rises in the snowy Himalayan ranges of Kashmir, enters British territory in the Sialkot district, and flows through the plains of the Punjab, forming the boundary between the Rechna and the Jech Doabs. Finally it joins the Jhelum at Trimmu.
The Chenab Colony, resulting from the great success of the Chenab Canal in irrigating the desert of the Bar, was formed out of the three adjacent districts of Gujranwala, Jhang, and Montgomery in 1892, and contained in 1901 a population of 791,861. It lies in the Rechna Doab between the Chenab and Ravi rivers in the north-east of the Jhang district, and is designed to include an irrigated area of 2½ million acres. The Chenab Canal (opened 1887) is the largest and most profitable perennial canal in India. The principal town is Lyallpur, called after Sir J. Broad wood Lyall, lieutenant-governor of the Punjab 1887-1892, which gives its name to a district created in 1904.
CHÊNEDOLLÉ, CHARLES JULIEN LIOULT DE (1769-1833), French poet, was born at Vire (Calvados) on the 4th of November 1769. He early showed a vocation for poetry, but the outbreak of the Revolution temporarily diverted his energy. Emigrating in 1791, he fought two campaigns in the army of Conde, and eventually found his way to Hamburg, where he met Antoine de Rivarol, of whose brilliant conversation he has left an account. He also visited Mme de Staël in her retreat at Coppet. On his return to Paris in 1799 he met Chateaubriand and his sister Lucile (Mme de Caud), to whom he became deeply attached. After her death in 1804, Chênedollé returned to Normandy, where he married and became eventually inspector of the academy of Caen (1812-1832). With the exception of occasional visits to Paris, he spent the rest of his life in his native province. He died at the château de Coisel on the 2nd of December 1833. He published his Genie de l’Homme in 1807, and in 1820 his Études poétiques, which had the misfortune to appear shortly after the Méditations of Lamartine, so that the author did not receive the credit of their real originality. Chênedollé had many sympathies with the romanticists, and was a contributor to their organ, the Muse française. His other works include the Esprit de Rivarol (1808) in conjunction with F.J.M. Fayolle.
The works of Chênedollé were edited in 1864 by Sainte-Beuve, who drew portraits of him in his Chateaubriand et son groupe and in an article contributed to the Revue des deux mondes (June 1849). See also E. Helland, Étude biographique et littéraire sur Chênedollé (1857); Cazin, Notice sur Chênedollé (1869).
CHENERY, THOMAS (1826-1884), English scholar and editor of The Times, was born in 1826 at Barbados. He was educated at Eton and Caius College, Cambridge. Having been called to the bar, he went out to Constantinople as The Times correspondent just before the Crimean War, and it was under the influence there of Algernon Smythe (afterwards Lord Strangford) that he first turned to those philological studies in which he became eminent. After the war he returned to London and wrote regularly for The Times for many years, eventually succeeding Delane as editor in 1877. He was then an experienced publicist, particularly well versed in Oriental affairs, an indefatigable worker, with a rapid and comprehensive judgment, though he lacked Delane’s intuition for public opinion. It was as an Orientalist, however, that he had meantime earned the highest reputation, his knowledge of Arabic and Hebrew being almost unrivalled and his gift for languages exceptional. In 1868 he was appointed Lord Almoner’s professor of Arabic at Oxford, and retained his position until he became editor of The Times. He was one of the company of revisers of the Old Testament. He was secretary for some time to the Royal Asiatic Society, and published learned editions of the Arabic classic The Assemblies of Al-Harirī and of the Machberoth Ithiel. He died in London on the 11th of February 1884.
CHENG, Tscheng or Tschiang (Ger. Scheng), an ancient Chinese wind instrument, a primitive organ, containing the principle of the free reed which found application in the accordion, concertina and harmonium. The cheng resembles a tea-pot filled with bamboo pipes of graduated lengths. It consists of a gourd or turned wooden receptacle acting as wind reservoir, in the side of which is inserted an insufflation tube curved like a swan’s neck or the spout of a tea-pot. The cup-shaped reservoir is closed by means of a plate of horn pierced with seventeen round holes arranged round the edge in an unfinished circle, into which fit the bamboo pipes. The pipes are cylindrical as far as they are visible above the plate, but the lower end inserted in the wind reservoir is cut to the shape of a beak, somewhat like the mouthpiece of the clarinet, to receive the reed. The construction of the free reed is very simple: it consists of a thin plate of metal—gold according to the Jesuit missionary Joseph Amiot,1 but brass in the specimens brought to Europe—of the thickness of ordinary paper. In this plate is cut a rectangular flap or tongue which remains fixed at one end, while at the other the tongue is filed so that, instead of closing the aperture, it passes freely through, vibrating as the air is forced through the pipe (see Free-Reed Vibrator). The metal plate is fastened with wax longitudinally across the diameter of the beak end of the pipe, a little layer of wax being applied also to the free end of the vibrating tongue for the purpose of tuning by adding weight and impetus. About half an inch above the horn plate a small round hole or stop is bored through the pipe, which speaks only when this hole is covered by the finger. A longitudinal aperture about an inch long cut in the upper end of the bamboo pipe serves to determine the length of the vibrating column of air proper to respond to the vibrations of the free reed. The length of the bamboo above this opening is purely ornamental, as are also four or five of the seventeen pipes which have no reeds and do not speak, being merely inserted for the purposes of symmetry in design. The notes of the cheng, like those of the concertina, speak either by inspiration or expiration of air, the former being the more usual method. Mahillon states that performers on the cheng in China are rare, as the method of playing by inspiration induces inflammation of the throat.2 Amiot, who gives a description of the instrument with illustrations showing the construction, states that in the great Chinese encyclopaedia Eulh-ya, articles Yu and Ho, the Yu of ancient China was the large cheng with nineteen free reeds (twenty-four pipes), and the Ho the small cheng with thirteen reeds or seventeen pipes described in this article. The compass of the latter is given by him as the middle octave with chromatic intervals, the thirteenth note giving the octave of the first. Mahillon gives the compass of a modern cheng as follows:

E.F.F. Chladni,3 who examined a cheng sent from China to Herr Müller, organist of the church of St Nicholas, Leipzig, at the beginning of the 19th century, gives an excellent description of the instrument, reproducing in illustration a plate from Giulio Ferrario’s work on costume.4 Müller’s cheng had the same compass as Mahillon’s. Chladni’s article was motived by the publication of an account of the exhibition of G.J. Grenié’s Orgue expressif, invented about 1810, in the Conservatoire of 78 Paris.5 Grenié’s invention, perfected by Alexandre and Debain about 1840, produced the harmonium. Kratzenstein (see under Harmonium) of St Petersburg was the first to apply the free reed to the organ in the second half of the 18th century. Inventions of similar instruments, which after a short life were relegated to oblivion, followed at the beginning of the 19th century. An interesting reproduction of a Persian cheng dating from the 10th or 11th century is to be seen on a Persian vase described and illustrated together with a shawm in the Gazette archéologique (tome xi., 1886).
1 Mémoire sur la musique des Chinois (Paris, 1779), pp. 78 and 82, pl. vi., or Mémoire sur les Chinois, tome vi. pl. vi.
2 Catalogue descriptif, vol. ii. (Ghent, 1896), p. 91; also vol. i. (1880), pp. 29, 44, 154.
3 “Weitere Nachrichten von dem ... chinesischen Blasinstrumente Tscheng oder Tschiang,” in Allgemeine musikalische Zeitung (Leipzig, 1821), Bd. xxiii. No. 22, pp. 369, 374 et seq., and illustration appendix ii.
4 Il Costume anticho e moderno (Milan, 1816), pl. 66, vol. i.
5 See Allg. mus. Zt. (Leipzig, 1821), Bd. xxiii. Nos. 9 and 10, pp. 133 and 149 et seq.
CHÊN-HAI [Chinhai], a district town of China, in the province of Cheh-kiang, at the mouth of the Yung-kiang, 12 m. N.E. of Ningpo, in 29° 58′ N., 121° 45′ E. It lies at the foot of a hill on a tongue of land, and is partly protected from the sea on the N. by a dike about 3 m. long, composed entirely of large blocks of hewn granite. The walls are 20 ft. high and 3 m. in circumference. The defences were formerly of considerable strength, and included a well-built but now dismantled citadel on a precipitous cliff, 250 ft. high, at the extremity of the tongue of land on which the town is built. In the neighbourhood an engagement took place between the English and Chinese in 1841.
CHÉNIER, ANDRÉ DE (1762-1794), French poet, was born at Constantinople on the 30th of October 1762. His father, Louis Chénier, a native of Languedoc, after twenty years of successful commerce in the Levant as a cloth-merchant, was appointed to a position equivalent to that of French consul at Constantinople. His mother, Elisabeth Santi-Lomaca, whose sister was grandmother of A. Thiers, was a Greek. When the poet was three years old his father returned to France, and subsequently from 1768 to 1775 served as consul-general of France in Morocco. The family, of which André was the third son, and Marie-Joseph (see below) the fourth, remained in France; and after a few years, during which André ran wild with “la tante de Carcasonne,” he distinguished himself as a verse-translator from the classics at the Collège de Navarre (the school in former days of Gerson and Bossuet) in Paris. In 1783 he obtained a cadetship in a French regiment at Strassburg. But the glamour of the military life was as soon exhausted by Chénier as it was by Coleridge. He returned to Paris before the end of the year, was well received by his family, and mixed in the cultivated circle which frequented the salon of his mother, among them Lebrun-Pindaré, Lavoisier, Lesueur, Dorat, Parmy, and a little later the painter David. He was already a poet by predilection, an idyllist and steeped in the classical archaism of the time, when, in 1784, his taste for the antique was confirmed by a visit to Rome made in the company of two schoolfellows, the brothers Trudaine. From Naples, after visiting Pompeii, he returned to Paris, his mind fermenting with poetical images and projects, few of which he was destined to realize. For nearly three years, however, he was enabled to study and to experiment in verse without any active pressure or interruption from his family—three precious years in which the first phase of his art as a writer of idylls and bucolics, imitated to a large extent from Theocritus, Bion and the Greek anthologists, was elaborated. Among the poems written or at least sketched during this period were L’Oaristys, L’Aveugle, La Jeune Malade, Bacchus, Euphrosine and La Jeune Tarentine, the last a synthesis of his purest manner, mosaic though it is of reminiscences of at least a dozen classical poets. As in glyptic so in poetic art, the Hellenism of the time was decadent and Alexandrine rather than Attic of the best period. But Chénier is always far more than an imitator. La Jeune Tarentine is a work of personal emotion and inspiration. The colouring is that of classic mythology, but the spiritual element is as individual as that of any classical poem by Milton, Gray, Keats or Tennyson. Apart from his idylls and his elegies, Chénier also experimented from early youth in didactic and philosophic verse, and when he commenced his Hermès in 1783 his ambition was to condense the Encyclopédie of Diderot into a poem somewhat after the manner of Lucretius. This poem was to treat of man’s position in the Universe, first in an isolated state, and then in society. It remains fragmentary, and though some of the fragments are fine, its attempt at scientific exposition approximates too closely to the manner of Erasmus Darwin to suit a modern ear. Another fragment called L’Invention sums Chénier’s Ars Poetica in the verse “Sur des pensers nouveaux, faisons des vers antiques.” Suzanne represents the torso of a Biblical poem on a very large scale, in six cantos.
In the meantime, André had published nothing, and some of these last pieces were in fact not yet written, when in November 1787 an opportunity of a fresh career presented itself. The new ambassador at the court of St James’s, M. de la Luzerne, was connected in some way with the Chénier family, and he offered to take André with him as his secretary. The offer was too good to be refused, but the poet hated himself on the banks of the fière Tamise, and wrote in bitter ridicule of
|
“Ces Anglais. Nation toute à vendre à qui peut la payer. De contrée en contrée allant au monde entier, Offrir sa joie ignoble et son faste grossier.” |
He seems to have been interested in the poetic diction of Milton and Thomson, and a few of his verses are remotely inspired by Shakespeare and Gray. To say, however, that he studied English literature would be an exaggeration. The events of 1789 and the startling success of his younger brother, Marie-Joseph, as political playwright and pamphleteer, concentrated all his thoughts upon France. In April 1790 he could stand London no longer, and once more joined his parents at Paris in the rue de Cléry.
The France that he plunged into with such impetuosity was upon the verge of anarchy. A strong constitutionalist, Chénier took the view that the Revolution was already complete and that all that remained to be done was the inauguration of the reign of law. Moderate as were his views and disinterested as were his motives, his tactics were passionately and dangerously aggressive. From an idyllist and elegist we find him suddenly transformed into an unsparing master of poetical satire. His prose Avis au peuple français (August 24, 1790) was followed by the rhetorical Jeu de paume, a somewhat declamatory moral ode addressed “à Louis David, peintre.” In the meantime he orated at the Feuillants Club, and contributed frequently to the Journal de Paris from November 1791 to July 1792, when he wrote his scorching Iambes to Collot d’Herbois, Sur les Suisses révoltés du regiment de Châteauvieux. The 10th of August uprooted his party, his paper and his friends, and the management of relatives who kept him out of the way in Normandy alone saved him from the massacre of September. In the month following these events his democratic brother, Marie-Joseph, had entered the Convention. André’s sombre rage against the course of events found vent in the line on the Maenads who mutilated the king’s Swiss Guard, and in the Ode à Charlotte Corday congratulating France that “Un scélérat de moins rampe dans cette fange.” At the express request of Malesherbes he furnished some arguments to the materials collected for the defence of the king. After the execution he sought a secluded retreat on the Plateau de Satory at Versailles and took exercise after nightfall. There he wrote the poems inspired by Fanny (Mme Laurent Lecoulteux), including the exquisite Ode à Versailles, one of his freshest, noblest and most varied poems.
His solitary life at Versailles lasted nearly a year. On the 7th of March 1794 he was taken at the house of Mme Piscatory at Passy. Two obscure agents of the committee of public safety were in search of a marquise who had flown, but an unknown stranger was found in the house and arrested on suspicion. This was André, who had come on a visit of sympathy. He was taken to the Luxembourg and afterwards to Saint-Lazare. During the 140 days of his imprisonment there he wrote the marvellous Iambes (in alternate lines of 12 and 8 syllables), which hiss and stab like poisoned bullets, and which were transmitted to his family by a venal gaoler. There he wrote the best known of all his verses, the pathetic Jeune captive, a poem at once of enchantment and of despair. Suffocating in an atmosphere of cruelty and baseness, Chénier’s agony found expression almost to the last in these murderous Iambes which he launched against the 79 Convention. Ten days before the end, the painter J.B. Suvée executed the well-known portrait. He might have been overlooked but for the well-meant, indignant officiousness of his father. Marie-Joseph had done his best to prevent this, but he could do nothing more. Robespierre, who was himself on the brink of the volcano, remembered the venomous sallies in the Journal de Paris. At sundown on the 25th of July 1794, the very day of his condemnation on a bogus charge of conspiracy, André Chénier was guillotined. The record of his last moments by La Touche is rather melodramatic and is certainly not above suspicion.
Incomplete as was his career—he was not quite thirty-two—his life was cut short in a crescendo of all its nobler elements. Exquisite as was already his susceptibility to beauty and his mastership of the rarest poetic material, we cannot doubt that Chénier was preparing for still higher flights of lyric passion and poetic intensity. Nothing that he had yet done could be said to compare in promise of assured greatness with the Iambes, the Odes and the Jeune Captive. At the moment he left practically nothing to tell the world of his transcendent genius, and his reputation has had to be retrieved from oblivion page by page, and almost poem by poem. During his lifetime only his Jeu de paume (1791) and Hymne sur les Suisses (1792) had been given to the world. The Jeune Captive appeared in the Décade philosophique, Jan. 9, 1795; La Jeune Tarentine in the Mercure of March 22, 1801. Chateaubriand quoted three or four passages in his Génie du christianisme. Fayette and Lefeuvre-Deumier also gave a few fragments; but it was not until 1819 that a first imperfect attempt was made by H. de la Touche to collect the poems in a substantive volume. Since the appearance of the editio princeps of Chénier’s poems in La Touche’s volume, many additional poems and fragments have been discovered, and an edition of the complete works of the poet, collated with the MSS. bequeathed to the Bibliothèque Nationale by Mme Elisa de Chénier in 1892, has been edited by Paul Dimoff and published by Delagrave. During the same period the critical estimates of the poet have fluctuated in a truly extraordinary manner. Sainte-Beuve in his Tableau of 1828 sang the praises of Chénier as an heroic forerunner of the Romantic movement and a precursor of Victor Hugo. Chénier, he said, had “inspired and determined” Romanticism. This suggestion of modernity in Chénier was echoed by a chorus of critics who worked the idea to death; in the meantime, the standard edition of Chénier’s works was being prepared by M. Becq de Fouquières and was issued in 1862, but rearranged and greatly improved by the editor in 1872. The same patient investigator gave his New Documents on André Chénier to the world in 1875.
In the second volume of La Vie littéraire Anatole France contests the theory of Sainte-Beuve. Far from being an initiator, he maintains that Chénier’s poetry is the last expression of an expiring form of art. His matter and his form belong of right to the classic spirit of the 18th century. He is a contemporary, not of Hugo and Leconte de Lisle, but of Suard and Morellet. M. Faguet sums up on the side of M. France in his volume on the 18th century (1890). Chénier’s real disciples, according to the latest view, are Leconte de Lisle and M. de Heredia, mosaïstes who have at heart the cult of antique and pagan beauty, of “pure art” and of “objective poetry.” Heredia himself reverted to the judgment of Sainte-Beuve to the effect that Chénier was the first to make modern verses, and he adds, “I do not know in the French language a more exquisite fragment than the three hundred verses of the Bucoliques.” Chénier’s influence has been specially remarkable in Russia, where Pushkin imitated him, Kogloff translated La Jeune Captive, La jeune Tarentine and other famous pieces, while the critic Vesselovsky pronounces “Il a rétabli le lyrisme pur dans la poésie française.” The general French verdict on his work is in the main well summed by Morillot, when he says that, judged by the usual tests of the Romantic movement of the ’twenties (love for strange literatures of the North, medievalism, novelties and experiments), Chénier would inevitably have been excluded from the cénacle of 1827. On the other hand, he exhibits a decided tendency to the world-ennui and melancholy which was one of the earlier symptoms of the movement, and he has experimented in French verse in a manner which would have led to his excommunication by the typical performers of the 18th century. What is universally admitted is that Chénier was a very great artist, who like Ronsard opened up sources of poetry in France which had long seemed dried up. In England it is easier to feel his attraction than that of some far greater reputations in French poetry, for, rhetorical though he nearly always is, he yet reveals something of that quality which to the Northern mind has always been of the very essence of poetry, that quality which made Sainte-Beuve say of him that he was the first great poet “personnel et rêveur” in France since La Fontaine. His diction is still very artificial, the poetic diction of Delille transformed in the direction of Hugo, but not very much. On the other hand, his descriptive power in treating of nature shows far more art than the Trianin school ever attained. His love of the woodland and his political fervour often remind us of Shelley, and his delicate perception of Hellenic beauty, and the perfume of Greek legend, give us almost a foretaste of Keats. For these reasons, among others, Chénier, whose art is destined to so many vicissitudes of criticism in his own country, seems assured among English readers of a place among the Dii Majores of French poetry.
The Chénier literature of late years has become enormous. His fate has been commemorated in numerous plays, pictures and poems, notably in the fine epilogue of Sully Prudhomme, the Stello of A. de Vigny, the delicate statue by Puech in the Luxembourg, and the well-known portrait in the centre of the “Last Days of the Terror.” The best editions are still those of Becq de Fouquières (Paris, 1862, 1872 and 1881), though these are now supplemented by those of L. Moland (2 vols., 1889) and R. Guillard (2 vols., 1899).
CHÉNIER, MARIE-JOSEPH BLAISE DE (1764-1811), French poet, dramatist and politician, younger brother of André de Chénier, was born at Constantinople on the 11th of February 1764.1 He was brought up at Carcassonne, and educated in Paris at the Collège de Navarre. Entering the army at seventeen, he left it two years afterwards; and at nineteen he produced Azémire, a two-act drama (acted in 1786), and Edgar, ou le page supposé, a comedy (acted in 1785), which were failures. His Charles IX was kept back for nearly two years by the censor. Chénier attacked the censorship in three pamphlets, and the commotion aroused by the controversy raised keen interest in the piece. When it was at last produced on the 4th of November 1789, it achieved an immense success, due in part to its political suggestion, and in part to Talma’s magnificent impersonation of Charles IX. Camille Desmoulins said that the piece had done more for the Revolution than the days of October, and a contemporary memoir-writer, the marquis de Ferrière, says that the audience came away “ivre de vengeance et tourmenté d’une soif de sang.” The performance was the occasion of a split among the actors of the Comédie Française, and the new theatre in the Palais Royal, established by the dissidents, was inaugurated with Henri VIII (1791), generally recognized as Chénier’s masterpiece; Jean Calas, ou l’école des juges followed in the same year. In 1792 he produced his Caius Gracchus, which was even more revolutionary in tone than its predecessors. It was nevertheless proscribed in the next year at the instance of the Montagnard deputy Albitte, for an anti-anarchical hemistich (Des lois et non du sang!); Fénelon (1793) was suspended after a few representations; and in 1794 his Timoléon, set to Étienne Méhul’s music, was also proscribed. This piece was played after the fall of the Terror, but the fratricide of Timoléon became the text for insinuations to the effect that by his silence Joseph de Chénier had connived at the judicial murder of André, whom Joseph’s enemies alluded to as Abel. There is absolutely nothing to support the calumny, which has often been repeated since. In fact, after some fruitless attempts to save his brother, variously related by his biographers, Joseph became aware that André’s only chance of safety lay in being forgotten by the authorities, and that ill-advised intervention would only hasten the end. Joseph Chénier had been a member of the Convention and of 80 the Council of Five Hundred, and had voted for the death of Louis XVI.; he had a seat in the tribunate; he belonged to the committees of public instruction, of general security, and of public safety. He was, nevertheless, suspected of moderate sentiments, and before the end of the Terror had become a marked man. His purely political career ended in 1802, when he was eliminated with others from the tribunate for his opposition to Napoleon. In 1801 he was one of the educational jury for the Seine; from 1803 to 1806 he was inspector-general of public instruction. He had allowed himself to be reconciled with Napoleon’s government, and Cyrus, represented in 1804, was written in his honour, but he was temporarily disgraced in 1806 for his Épître à Voltaire. In 1806 and 1807 he delivered a course of lectures at the Athénée on the language and literature of France from the earliest years; and in 1808 at the emperor’s request, he prepared his Tableau historique de l’état et du progrès de la littérature française depuis 1789 jusqu’à 1808, a book containing some good criticism, though marred by the violent prejudices of its author. He died on the 10th of January 1811. The list of his works includes hymns and national songs—among others, the famous Chant du départ; odes, Sur la mort de Mirabeau, Sur l’oligarchie de Robespierre, &c.; tragedies which never reached the stage, Brutus et Cassius, Philippe deux, Tibère; translations from Sophocles and Lessing, from Gray and Horace, from Tacitus and Aristotle; with elegies, dithyrambics and Ossianic rhapsodies. As a satirist he possessed great merit, though he sins from an excess of severity, and is sometimes malignant and unjust. He is the chief tragic poet of the revolutionary period, and as Camille Desmoulins expressed it, he decorated Melpomene with the tricolour cockade.
See the Œuvres complètes de Joseph Chénier (8 vols., Paris, 1823-1826), containing notices of the poet by Arnault and Daunou; Charles Labitte, Études litteraires (1846); Henri Welschinger, Le Théâtre révolutionnaire, 1789-1799 (1881); and A. Lieby, Étude sur le théâtre de Marie-Joseph Chénier(1902).
1 This is the date given by G. de Chénier in his La Vérité sur la famille de Chénier (1844).
CHENILLE (from the Fr. chenille, a hairy caterpillar), a twisted velvet cord, woven so that the short outer threads stand out at right angles to the central cord, thus giving a resemblance to a caterpillar. Chenille is used as a trimming for dress and furniture.
CHENONCEAUX, a village of central France, in the department of Indre-et-Loire, on the right bank of the Cher, 20 m. E. by S. of Tours on the Orléans railway. Pop. (1906) 216. Chenonceaux owes its interest to its chateau (see Architecture: Renaissance Architecture in France), a building in the Renaissance style on the river Cher, to the left bank of which it is united by a two-storeyed gallery built upon five arches, and to the right by a drawbridge flanked by an isolated tower, part of an earlier building of the 15th century. Founded in 1515 by Thomas Bohier (d. 1523), financial minister in Normandy, the château was confiscated by Francis I. in 1535. Henry II. presented it to his mistress Diane de Poitiers, who on his death was forced to exchange it for Chaumont-sur-Loire by Catherine de’ Medici. The latter built the gallery which leads to the left bank of the Cher. Chenonceaux passed successively into the hands of Louise de Vaudémont, wife of Henry III., the house of Vendôme, and the family of Bourbon-Condé. In the 18th century it came into the possession of the farmer-general Claude Dupin (1684-1769), who entertained the most distinguished people in France within its walls. In 1864 it was sold to the chemist Théophile Pélouze, whose wife executed extensive restorations. It subsequently became the property of the Crédit Foncier, and again passed into private occupancy.
CHENOPODIUM, or Goose-foot, a genus of erect or prostrate herbs (natural order Chenopodiaceae), usually growing on the seashore or on waste or cultivated ground. The green angular stem is often striped with white or red, and, like the leaves, often more or less covered with mealy hairs. The leaves are entire, lobed or toothed, often more or less deltoid or triangular in shape. The minute flowers are bisexual, and borne in dense axillary or terminal clusters or spikes. The fruit is a membranous one-seeded utricle often enclosed by the persistent calyx. Ten species occur in Britain, one of which, C. Bonus-Henricus, Good King Henry, is cultivated as a pot-herb, in lieu of asparagus, under the name mercury, and all-good.
CHEOPS, in Herodotus, the name of the king who built the Great Pyramid in Egypt. Following on a period of good rule and prosperity under Rhampsinitus, Cheops closed the temples, abolished the sacrifices and made all the Egyptians labour for his monument, working in relays of 100,000 men every three months (see Pyramid). Proceeding from bad to worse, he sacrificed the honour of his daughter in order to obtain the money to complete his pyramid; and the princess built herself besides a small pyramid of the stones given to her by her lovers. Cheops reigned 50 years and was succeeded by his brother, Chephren, who reigned 56 years and built the second pyramid. During these two reigns the Egyptians suffered every kind of misery and the temples remained closed. Herodotus continues that in his own day the Egyptians were unwilling to name these oppressors and preferred to call the pyramids after a shepherd named Philition, who pastured his flocks in their neighbourhood. At length Mycerinus, son of Cheops and successor of Chephren, reopened the temples and, although he built the Third Pyramid, allowed the oppressed people to return to their proper occupations.
heops, Chephren and Mycerinus are historical personages of the fourth Egyptian dynasty, in correct order, and they built the three pyramids attributed to them here. But they are wholly misplaced by Herodotus. Rhampsinitus, the predecessor of Cheops, appears to represent Rameses III. of the twentieth dynasty, and Mycerinus in Herodotus is but a few generations before Psammetichus, the founder of the twenty-sixth dynasty. Manetho correctly places the great Pyramid kings in Dynasty IV. In Egyptian the name of Cheops (Chemmis or Chembis in Diodorus Siculus, Suphis in Manetho) is spelt Hwfw (Khufu), but the pronunciation, in late times perhaps Khöouf, is uncertain. The Greeks and Romans generally accepted the view that Herodotus supplies of his character, and moralized on the uselessness of his stupendous work; but there is nothing else to prove that the Egyptians themselves execrated his memory. Modern writers rather dwell on the perfect organization demanded by his scheme, the training of a nation to combined labour, the level attained here by art and in the fitting of masonry, and finally the fact that the Great Pyramid was the oldest of the seven wonders of the ancient world and now alone of them survives. It seems that representations of deities, and indeed any representations at all, were rare upon the polished walls of the great monuments of the fourth dynasty, and Petrie thinks that he can trace a violent religious revolution with confiscation of endowments at this time in the temple remains at Abydos; but none the less the wants of the deities were then attended to by priests selected from the royal family and the highest in the land. Khufu’s work in the temple of Bubastis is proved by a surviving fragment, and he is figured slaying his enemy at Sinai before the god Thoth. In late times the priests of Denderah claimed Khufu as a benefactor; he was reputed to have built temples to the gods near the Great Pyramids and Sphinx (where also a pyramid of his daughter Hentsen is spoken of), and there are incidental notices of him in the medical and religious literature. The funerary cult of Khufu and Khafrē was practised under the twenty-sixth dynasty, when so much that had fallen into disuse and been forgotten was revived. Khufu is a leading figure in an ancient Egyptian story (Papyrus Westcar), but it is unfortunately incomplete. He was the founder of the fourth dynasty, and was probably born in Middle Egypt near Beni Hasan, in a town afterwards known as “Khufu’s Nurse,” but was connected with the Memphite third dynasty. Two tablets at the mines of Wadi Maghara in the peninsula of Sinai, a granite block from Bubastis, and a beautiful ivory statuette found by Petrie in the temple at Abydos, are almost all that can be definitely assigned to Khufu outside the pyramid at Giza and its ruined accompaniments. His date, according to Petrie, is 3969-3908 B.C., but in the shorter chronology of Meyer, Breasted and others he reigned (23 years) about a thousand years later, c. 2900 B.C.
See Herodotus ii. 124; Diodorus Siculus i. 64; Sethe in Pauly-Wissowa’s Realencyclopädie, s.v.; W.M.F. Petrie, History of Egypt, vol. i., and Abydos, part ii. p. 48; J.H. Breasted, History.
CHEPSTOW, a market town and river-port in the southern parliamentary division of Monmouthshire, England, on the Wye, 2 m. above its junction with the Severn, and on the Great Western railway. Pop. of urban district (1901) 3067. It occupies the slope of a hill on the western (left) bank of the river, and is environed by beautiful scenery. The church of St Mary, originally the conventual chapel of a Benedictine priory of Norman foundation, has remains of that period in the west front and the nave, but a rebuilding of the chancel and transepts was effected in the beginning of the 19th century. The church contains many interesting monuments. The castle, still a magnificent pile, was founded in the 11th century by William Fitz-Osbern, earl of Hereford, but was almost wholly rebuilt in the 13th. There are, however, parts of the original building in the keep. The castle occupies a splendid site on the summit of a cliff above the Wye, and covers about 3 acres. The river is crossed by a fine iron bridge of five arches, erected in 1816, and by a tubular railway bridge designed by Sir Isambard Brunel. There is a free passage on the Wye for large vessels as far as the bridge. From the narrowness and depth of the channel the tide rises suddenly and to a great height, forming a dangerous bore. The exports are timber, bark, iron, coal, cider and millstones. Some shipbuilding is carried on.
As the key to the passage of the Wye, Chepstow (Estrighorel, Striguil) was the site successively of British, Roman and Saxon fortifications. Domesday Book records that the Norman castle was built by William Fitz-Osbern to defend the Roman road into South Wales. On the confiscation of his son’s estates, the castle was granted to the earls of Pembroke, and after its reversion to the crown in 1306, Edward II. in 1310 granted it to his half-brother Thomas de Brotherton. On the latter’s death it passed, through his daughter Margaret, Lady Segrave, to the dukes of Norfolk, from whom, after again reverting to the crown, it passed to the earls of Worcester. It was confiscated by parliament and settled on Oliver Cromwell, but was restored to the earls in 1660. The borough must have grown up between 1310, when the castle and vill were granted to Thomas de Brotherton, and 1432, when John duke of Norfolk died seised of the castle, manor and borough of Struguil. In 1524 Charles, first earl of Worcester and then lord of the Marches, granted a new charter of incorporation to the bailiffs and burgesses of the town, which had fallen into decay. This was sustained until the reign of Charles II., when, some dispute arising between the earl of Bridgwater and the burgesses, no bailiff was appointed and the charter lapsed. Chepstow was afterwards governed by a board of twelve members. A port since early times, when the lord took dues of ships going up to the forest of Dean, Chepstow had no ancient market and no manufactures but that of glass, which was carried on for a short time within the ruins of the castle.
CHEQUE, or CHECK, in commercial law, a bill of exchange drawn on a banker and signed by the drawer, requiring the banker to pay on demand a certain sum in money to or to the order of a specified person or to bearer. In this, its most modern sense, the cheque is the outcome of the growth of the banking system of the 19th century. For details see Banks and Banking: Law, and Bill of Exchange. The word check,1 of which “cheque” is a variant now general in English usage, signified merely the counterfoil or indent of an exchequer bill, or any draft form of payment, on which was registered the particulars of the principal part, as a check to alteration or forgery. The check or counterfoil parts remained in the hands of the banker, the portion given to the customer being termed a “drawn note” or “draft.” From the beginning of the 19th century the word “cheque” gradually became synonymous with “draft” as meaning a written order on a banker by a person having money in the banker’s hands, to pay some amount to bearer or to a person named. Ultimately, it entirely superseded the word “draft,” and has now a statutory definition (Bills of Exchange Act 1882, s. 73)—” a bill of exchange drawn on a banker payable on demand.” The word “draft” has come to have a wider meaning, that of a bill drawn by one person on another for a sum of money, or an order (whether on a banker or other) to pay money. The employment of cheques as a method of payment offering greater convenience than coin is almost universal in Great Britain and the United States. Of the transactions through the banks of the United Kingdom between 86 and 90% are conducted by means of cheques, and an even higher proportion in the United States. On the continent of Europe the use of cheques, formerly rare, is becoming more general, particularly in France, and to some extent in Germany.
1 The original meaning of “check” is a move in the game of chess which directly attacks the king; the word comes through the Old Fr. eschec, eschac, from the Med. Lat. form scaccus of the Persian shāh, king, i.e. the king in the game of chess; cf. the origin of “mate” from the Arabic shah-mat, the king is dead. The word was early used in a transferred sense of a stoppage or rebuff, and so is applied to anything which stops or hinders a matter in progress, or which controls or restrains anything, hence a token, ticket or counterfoil which serves as a means of identification, &c.
CHER, a department of central France, embracing the eastern part of the ancient province of Berry, and parts of Bourbonnais, Nivernais and Orléanais, bounded N. by the department of Loiret, W. by Loir-et-Cher and Indre, S. by Allier and Creuse, and E. by Nièvre. Pop. (1906) 343,484. Area 2819 sq. m. The territory of the department is elevated in the south, where one point reaches 1654 ft., and in the east. The centre is occupied by a wide calcareous table-land, to the north of which stretches the plain of Sologne. The principal rivers, besides the Cher and its tributaries, are the Grande Sauldre and the Petite Sauldre on the north, but the Loire and Allier, though not falling within the department, drain the eastern districts, and are available for navigation. The Cher itself becomes navigable when it receives the Arnon and Yèvre, and the communications of the department are greatly facilitated by the Canal du Berry, which traverses it from east to west, the lateral canal of the Loire, which follows the left bank of that river, and the canal of the Sauldre. The climate is temperate, and the rainfall moderate. Except in the Sologne, the soil is generally fertile, but varies considerably in different localities. The most productive region is that on the east, which belongs to the valley of the Loire; the central districts are tolerably fertile but marshy, being often flooded by the Cher; while in the south and south-west there is a considerable extent of dry and fertile land. Wheat and oats are largely cultivated, while hemp, vegetables and various fruits are also produced. The vine flourishes chiefly in the east of the arrondissement of Sancerre. The department contains a comparatively large extent of pasturage, which has given rise to a considerable trade in horses, cattle, sheep and wool for the northern markets. Nearly one-fifth of the whole area consists of forest. Mines of iron are worked, and various sorts of stone are quarried. Brick, porcelain and glassworks employ large numbers of the inhabitants. There are also flour-mills, distilleries, oil-works, saw-mills and tanneries. Bourges and Vierzon are metallurgical and engineering centres. Coal and wine are leading imports, while cereals, timber, wool, fruit and industrial products are exported. The department is served by the Orléans railway, and possesses in all more than 300 m. of navigable waterways. It is divided into three arrondissements (29 cantons, 292 communes) cognominal with the towns of Bourges, Saint-Amand-Mont-Rond, and Sancerre, of which the first is the capital, the seat of an archbishop and of a court of appeal and headquarters of the VIII. army-corps. The department belongs to the académie (educational division) of Paris. Bourges, Saint-Amand-Mont-Rond, Vierzon and Sancerre (q.v.) are the principal towns. Méhun-sur-Yèvre (pop. 5227), a town with an active manufacture of porcelain, has a Romanesque church and a château of the 14th century. Among the other interesting churches of the department, that at St Satur has a fine choir of the 14th and 15th centuries; those of Dun-sur-Auron, Plaimpied, Aix d’Angillon and Jeanvrin are Romanesque in style, while Aubigny-Ville has a church of the 12th, 13th and 82 15th centuries and a château of later date. Drevant, built on the site of a Roman town, preserves ruins of a large theatre and other remains. Among the megalithic monuments of Cher, the most notable is that at Villeneuve-sur-Cher, known as the Pierre-de-la-Roche.
CHERAT, a hill cantonment and sanatorium in the Peshawar district of the North-West Frontier Province, India, 34 m. S.E. of Peshawar. It is situated at an elevation of 4500 ft, on the west of the Khattak range, which divides the Peshawar from the Kohat district. It was first used in 1861, and since then has been employed during the hot weather as a health station for the British troops quartered in the hot and malarious vale of Peshawar.
CHERBOURG, a naval station, fortified town and seaport of north-western France, capital of an arrondissement in the department of Manche, on the English Channel, 232 m. W.N.W. of Paris on the Ouest-État railway. Pop. (1906) town, 35,710; commune, 43,827. Cherbourg is situated at the mouth of the Divette, on a small bay at the apex of the indentation formed by the northern shore of the peninsula of Cotentin. Apart from a fine hospital and the church of La Trinité dating from the 15th century, the town has no buildings of special interest. A rich collection of paintings is housed in the hôtel de ville. A statue of the painter J.F. Millet, born near Cherbourg, stands in the public garden, and there is an equestrian statue of Napoleon I. in the square named after him. Cherbourg is a fortified place of the first class, headquarters of one of the five naval arrondissements of France, and the seat of a sub-prefect. It has tribunals of first instance and of commerce, a chamber of commerce, a lycée and a naval school. The chief industries of the town proper are fishing, saw-milling, tanning, leather-dressing, ship-building, iron and copper-founding, rope-making and the manufacture of agricultural implements. There are stone quarries in the environs, and the town has trade in farm produce.
Cherbourg derives its chief importance from its naval and commercial harbours, which are distant from each other about half a mile. The former consists of three main basins cut out of the rock, and has an area of 55 acres. The minimum depth of water is 30 ft. Connected with the harbour are dry docks, the yards where the largest ships in the French navy are constructed, magazines, rope walks, and the various workshops requisite for a naval arsenal of the first class. The works and town are carefully guarded on every side by redoubts and fortifications, and are commanded by batteries on the surrounding hills. There is a large naval hospital close to the harbour. The commerical harbour at the mouth of the Divette communicates with the sea by a channel 650 yds. long. It consists of two parts, an outer and tidal harbour 17½ acres in extent, and an inner basin 15 acres in extent, with a depth on sill at ordinary spring tide of 25 ft. Outside these harbours is the triangular bay, which forms the roadstead of Cherbourg. The bay is admirably sheltered by the land on every side but the north. On that side it is sheltered by a huge breakwater, over 2 m. in length, with a width of 650 ft. at its base and 30 ft. at its summit, which is protected by forts, and leaves passages for vessels to the east and west. These passages are guarded by forts placed on islands intervening between the breakwater and the mainland, and themselves united to the land by breakwaters. The surface within these barriers amounts to about 3700 acres. Cherbourg is a port of call for the American, North German Lloyd and other important lines of transatlantic steamers. The chief exports are stone for road-making, butter, eggs and vegetables; the chief imports are coal, timber, superphosphates and wine from Algeria. Great Britain is the principal customer.
Cherbourg is supposed by some investigators to occupy the site of the Roman station of Coriallum, but nothing definite is known about its origin. The name was long regarded as a corruption of Caesaris Burgus (Caesar’s Borough). William the Conqueror, under whom it appears as Carusbur, provided it with a hospital and a church; and Henry II. of England on several occasions chose it as his residence. In 1295 it was pillaged by an English fleet from Yarmouth; and in the 14th century it frequently suffered during the wars against the English. Captured by the English in 1418 after a four months’ siege, it was recovered by Charles VII. of France in 1450. An attempt was made under Louis XIV. to construct a military port; but the fortifications were dismantled in 1688, and further damage was inflicted by the English in 1758. In 1686 Vauban planned harbour-works which were begun under Louis XVI. and continued by Napoleon I. It was left, however, to Louis Philippe, and particularly to Napoleon III., to complete them, and their successful realization was celebrated in 1858, in the presence of the queen of England, against whose dominions they had at one time been mainly directed. At the close of 1857, £8,000,000, of which the breakwater cost over £2,500,000, had been expended on the works; in 1889 a further sum of £680,000 was voted by the Chamber of Deputies for the improvement of the port.
CHERBULIEZ, CHARLES VICTOR (1829-1899), French novelist and miscellaneous writer, was born on the 19th of July 1829, at Geneva, where his father, André Cherbuliez (1795-1874), was a classical professor at the university. He was descended from a family of Protestant refugees, and many years later Victor Cherbuliez resumed his French nationality, taking advantage of an act passed in the early days of the Revolution. Geneva was the scene of his early education; thence he proceeded to Paris, and afterwards to the universities of Bonn and Berlin. He returned to his native town and engaged in the profession of teaching. After his resumption of French citizenship he was elected a member of the Academy (1881), and having received the Legion of Honour in 1870, he was promoted to be officer of the order in 1892. He died on the 1st of July 1899. Cherbuliez was a voluminous and successful writer of fiction. His first book, originally published in 1860, reappeared in 1864 under the title of Un Cheval de Phidias: it is a romantic study of art in the golden age of Athens. He went on to produce a series of novels, of which the following are the best known:—Le Comte Kostia (1863), Le Prince Vitale (1864), Le Roman d’une honnête femme (1866), L’Aventure de Ladislas Bolski (1869), Miss Ravel (1875), Samuel Brohl et Cie (1877), L’Idée de Jean Teterol (1878), Noirs et rouges (1881), La Vocation du Comte Ghislain (1888), Une Gageure (1890), Le Secret du précepteur (1893), Jacquine Vanesse (1898), &c. Most of these novels first appeared in the Revue des deux mondes, to which Cherbuliez also contributed a number of political and learned articles, usually printed with the pseudonym G. Valbert. Many of these have been published in collected form under the titles L’Allemagne politique (1870), L’Espagne politique (1874), Profils étrangers (1889), L’Art et la nature (1892), &c. The volume Études de littérature et d’art (1873) includes articles for the most part reprinted from Le Temps. The earlier novels of Cherbuliez have been said with truth to show marked traces of the influence of George Sand; and in spite of modification, his method was that of an older school. He did not possess the sombre power or the intensely analytical skill of some of his later contemporaries, but his books are distinguished by a freshness and honesty, fortified by cosmopolitan knowledge and lightened by unobtrusive humour, which fully account for their wide popularity in many countries besides his own. His genius was the reverse of dramatic, and attempts to present two of his stories on the stage have not succeeded. His essays have all the merits due to liberal observation and thoroughness of treatment; their style, like that of the novels, is admirably lucid and correct.
CHERCHEL, a seaport of Algeria, in the arrondissement and department of Algiers, 55 m. W. of the capital. It is the centre of an agricultural and vine-growing district, but is commercially of no great importance, the port, which consists of part only of the inner port of Roman days, being small and the entry difficult. The town is chiefly noteworthy for the extensive ruins of former cities on the same site. Of existing buildings the most remarkable is the great Mosque of the Hundred Columns, now used as a military hospital. The mosque contains 89 columns of diorite, surmounted by a variety of capitals brought from other buildings. 83 The population of the town in 1906 was 4733; of the commune of which Cherchel is the centre 11,088.
Cherchel was a city of the Carthaginians, who named it Jol. Juba II. (25 B.C.) made it the capital of the Mauretanian kingdom under the name of Caesarea. Juba’s tomb, the so-called Tombeau de la Chrétienne (see Algeria), is 7½ m. E. of the town. Destroyed by the Vandals, Caesarea regained some of its importance under the Byzantines. Taken by the Arabs it was renamed by them Cherchel. Khair-ed-Din Barbarossa captured the city in 1520 and annexed it to his Algerian pashalik. In the early years of the 18th century it was a commercial city of some importance, but was laid in ruins by a terrible earthquake in 1738. In 1840 the town was occupied by the French. The ruins suffered greatly from vandalism during the early period of French rule, many portable objects being removed to museums in Paris or Algiers, and most of the monuments destroyed for the sake of their stone. Thus the dressed stones of the ancient theatre served to build barracks; the material of the hippodrome went to build the church; while the portico of the hippodrome, supported by granite and marble columns, and approached by a fine flight of steps, was destroyed by Cardinal Lavigerie in a search for the tomb of St Marciana. The fort built by Arouj Barbarossa, elder brother of Khair-ed-Din, was completely destroyed by the French. There are many fragments of a white marble temple. The ancient cisterns still supply the town with water. The museum contains some of the finest statues discovered in Africa. They include colossal figures of Aesculapius and Bacchus, and the lower half of a seated Egyptian divinity in black basalt, bearing the cartouche of Tethmosis (Thothmes) I. This statue was found at Cherchel, and is held by some archaeologists to indicate an Egyptian settlement here about 1500 B.C.
See Africa, Roman, and the description of the museum by P. Gauckler in the Musées et collections archéologiques de l’Algérie.
CHERCHEN, a town of East Turkestan, situated at the northern foot of the Altyn-tagh, a range of the Kuen-lun, in 85° 35′ E., and on the Cherchen-darya, at an altitude of 4100 ft. It straggles mostly along the irrigation channels that go off from the left side of the river, and in 1900 had a population of about 2000. The Cherchen-darya, which rises in the Arka-tagh, a more southerly range of the Kuen-lun, in 87° E. and 36° 20′ N., flows north until it strikes the desert below Cherchen, after which it turns north-east and meanders through a wide bed (300-400 ft.), beset with dense reeds and flanked by older channels. It is probable that anciently it entered the disused channel of the Ettek-tarim, but at present it joins the existing Tarim in the lake of Kara-buran, a sort of lacustrine “ante-room” to the Kara-koshun (N.M. Przhevalsky’s Lop-nor). At its entrance into the former lake the Cherchen-darya forms a broad delta. The river is frozen in its lower course for two to three months in the winter. From the foot of the mountains to the oasis of Cherchen it has a fall of nearly 4000 ft., whereas in the 300 m. or so from Cherchen to the Kara-buran the fall is 1400 ft. The total length is 500-600 m., and the drainage basin measures 6000-7000 sq. m.
See Sven Hedin, Scientific Results of a Journey in Central Asia, 1899-1902, vols. i. and ii. (1905-1906); also Takla-Makan.
CHEREMISSES, or Tcheremisses, a Finnish people living in isolated groups in the governments of Kazan, Viatka, Novgorod, Perm, Kostroma and Ufa, eastern Russia. Their name for themselves is Mori or Mari (people), possibly identifiable with the ancient Merians of Suzdalia. Their language belongs to the Finno-Ugrian family. They number some 240,000. There are two distinct physical types: one of middle height, black-haired, brown skin and flat-faced; the other short, fair-haired, white skinned, with narrow eyes and straight short noses. Those who live on the right bank of the Volga are sometimes known as Hill Cheremis, and are taller and stronger than those who inhabit the swamps of the left bank. They are farmers and herd horses and cattle. Their religion is a hotchpotch of Shamanism, Mahommedanism and Christianity. They are usually monogamous. The chief ceremony of marriage is a forcible abduction of the bride. The women, naturally ugly, are often disfigured by sore eyes caused by the smoky atmosphere of the huts. They wear a head-dress, trimmed with glass jewels, forming a hood behind stiffened with metal. On their breasts they carry a breastplate formed of coins, small bells and copper disks.
See Smirinov, Mordres et Tcheremisses (Paris, 1895); J. Abercromby, Pre- and Proto-historic Finns (London, 1898).
CHERIBON, a residency of the island of Java, Dutch East Indies, bounded S. and W. by the Preanger regencies, N.W. by Krawang, N. by the Java Sea, and E. by the residencies of Tegal and Banyumas. Pop. (1897) 1,577,521, including 867 Europeans, 21,108 Chinese, and 2016 Arabs and other Asiatic foreigners. The natives consist of Middle Javanese in the north and Sundanese in the south. Cheribon has been for many centuries the centre of Islamism in western Java, and is also the seat of a fanatical Mahommedan sect controlled from Mecca. The native population is on the whole orderly and prosperous. The northern half of the residency is flat and marshy in places, especially in the north-western corner, while the southern half is mountainous. In the middle stands the huge volcano Cherimai, clad with virgin forest and coffee plantations, and surrounded at its foot by rice fields. South-south-west of Cherimai on the Preanger border is the Sawal volcano, at whose foot is the beautiful Penjalu lake. Sulphur and salt springs occur on the slopes of Cherimai, and near Palimanan there is a cavernous hole called Guwagalang (or Payagalang), which exhales carbonic acid gas, and is considered holy by the natives and guarded by priests. There is a similar hole in the Preanger. The principal products of cultivation are sugar, coffee, rice and also tea and pulse (rachang), the plantations being for the most part owned by Europeans. The chief towns are Cheribon, a seaport and capital of the residency, the seaport of Indramaya, Palimanan, Majalengka, Kuningan and Chiamis. Cheribon has a good open roadstead. The town is very old and irregularly built, and the climate is unhealthy; nevertheless it has a lively export trade in sugar and coffee and is a regular port of call. In 1908 the two descendants of the old sultans of Cheribon still resided there in their respective Kratons or palaces, and each received an annual income of over £1500 for the loss of his privileges. A country residence belonging to one of the sultans is situated close to Cheribon and is much visited on account of its fantastic architecture. Indramaya was a considerable trading place in the days of the early Portuguese and Dutch traders. Kuningan is famous for a breed of small but strong horses.
CHERKASY (Polish, Czerkasy), a town of Russia, in the government of Kiev, 96 m. S.E. of Kiev, on the right bank of the Dnieper. Pop. (1883) 15,740; (1897) 26,619. The inhabitants (Little Russians) are mostly employed in agriculture and gardening; but sugar and tobacco are manufactured and spirits distilled. Cherkasy was an important town of the Ukraine in the 15th century, and remained so, under Polish rule, until the revolt of the Cossack hetman Chmielnicki (1648). It was annexed by Russia in 1795.
CHERNIGOV, a government of Little Russia, on the left bank of the Dnieper, bounded by the governments of Mogilev and Smolensk on the N., Orel and Kursk on the E., Poltava on the S., and Kiev and Minsk on the W. Area, 20,233 sq. m. Its surface is an undulating plain, 650 to 750 ft. high in the north and 370 to 600 ft. in the south, deeply grooved by ravines and the valleys of the rivers. In the north, beyond the Desna river, about one-third of the area is under forest (rapidly disappearing), and marshes occur along the courses of the rivers; while to the south of the Desna the soil is dry and sometimes sandy, and gradually it assumes the characters of a steppe-land as one proceeds southward. The government is drained by the Dnieper, which forms its western boundary for 180 m., and by its tributary the Desna. The latter, which flows through Chernigov for nearly 350 m., is navigable, and timber is brought down its tributaries. The climate is much colder in the wooded tracts of the north than in the south; the average yearly temperature at the city of Chernigov is 44.4° F. (January, 23°; July 68.5°).
The population reached 1,996,250 in 1883, 2,316,818 in 1897, 84 and 2,746,300 (estimate) in 1906. It is chiefly Little Russian (85.6%); but Great Russians (6.1%), mostly Raskolniks, i.e. nonconformists, and White Russians (5.6%) inhabit the northern districts. There are, besides, some Germans, as well as Greeks, at Nyezhin. Agriculture is the principal occupation; in the north, however, many of the inhabitants are engaged in the timber trade, and in the production of tar, pitch, wooden wares, leather goods and so forth. Cattle-breeding is carried on in the central districts. Beet is extensively cultivated. The cultivation of tobacco is increasing. Hemp is widely grown in the north, and the milder climate of the south encourages gardening. Bee-keeping is extensively carried on by the Raskolniks. Limestone, grindstones, china-clay and building-stone are quarried. Manufactures have begun to develop rapidly of late, the most important being sugar-works, distilleries, cloth-mills and glass-works. The government is divided into fifteen districts, their chief towns being Chernigov (q.v.), Borzna (pop. 12,458 in 1897), Glukhov (14,856), Gorodnya (4197), Konotop (23,083), Kozelets (5160), Krolevets (10,375), Mglin (7631), Novgorod-Syeversk (9185), Novozybkov (15,480), Nyezhin (32,481), Oster (5384), Sosnitsa (2507), Starodub (12,451) and Surazh (4004).
CHERNIGOV, a town of Russia, capital of the above government, on the right bank of the Desna, nearly half a mile from the river, 141 m. by rail N.E. of Kiev on a branch line. Pop. (1897) 27,006. It is an archiepiscopal see and possesses a cathedral of the 11th century. In 907 the city is mentioned in the treaty of Oleg as next in importance to Kiev, and in the 11th century it became the capital of the principality of Syeversk and an important commercial city. The Mongol invasion put an end to its prosperity in 1239. Lithuania annexed it in the 14th century, but it was soon seized by Poland, which held it until the 17th century. In 1686 it was definitely annexed to Russia.
CHEROKEE (native Tsalagi, “cave people”), a tribe of North American Indians of Iroquoian stock. Next to the Navaho they are the largest tribe in the United States and live mostly in Oklahoma (formerly Indian territory). Before their removal they possessed a large tract of country now distributed among the states of Alabama, Georgia, Mississippi, Tennessee and the west of Florida. Their chief divisions were then settled around the head-waters of the Savannah and Tennessee rivers, and were distinguished as the Elati Tsalagi or Lower Cherokees, i.e. those in the plains, and Atali Tsalagi or Upper Cherokees, i.e. those on the mountains. They were further divided into seven exogamous clans. Fernando de Soto travelled through their country in 1540, and during the next three centuries they were important factors in the history of the south. They attached themselves to the English in the disputes and contests which arose between the European colonizers, formally recognized the English king in 1730, and in 1755 ceded a part of their territory and permitted the erection of English forts. Unfortunately this amity was interrupted not long after; but peace was again restored in 1761. When the revolutionary war broke out they sided with the royalist party. This led to their subjugation by the new republic, and they had to surrender that part of their lands which lay to the south of the Savannah and east of the Chattahoochee. Peace was made in 1781, and in 1785 they recognized the supremacy of the United States and were confirmed in their possessions. In 1820 they adopted a civilized form of government, and in 1827, as a “Nation,” a formal constitution. The gradual advance of white immigration soon led to disputes with the settlers, who desired their removal, and exodus after exodus took place; a small part of the tribe agreed (1835) to remove to another district, but the main body remained. An appeal was made by them to the United States government; but President Andrew Jackson refused to interfere. A force of 2000 men, under the command of General Winfield Scott, was sent in 1838, and the Cherokees were compelled to emigrate to their present position. After the settlement various disagreements between the eastern and western Cherokees continued for some time, but in 1839 a union was effected. In the Civil War they all at first sided with the South; but before long a strong party joined the North, and this led to a disastrous internecine struggle. On the close of the contest they were confirmed in the possession of their territory, but were forced to give a portion of their lands to their emancipated slaves. Their later history is mainly a story of hopeless struggle to maintain their tribal independence against the white man. In 1892 they sold their western territory known as the “Cherokee outlet.” Until 1906, when tribal government virtually ceased, the “nation” had an elected chief, a senate and house of representatives. Many of them have become Christians, schools have been established and there is a tribal press. Those in Oklahoma still number some 26,000, though most are of mixed blood. A group, known as the Eastern Band, some 1400 strong, are on a reservation in North Carolina. Their language consists of two dialects—a third, that of the “Lower” branch, having been lost. The syllabic alphabet invented in 1821 by George Guess (Sequoyah) is the character employed.
See also Handbook of American Indians(Washington, 1907); T.V. Parker, Cherokee Indians (N.Y., 1909); and Indians, North American.
CHEROOT, or Sheroot (from the Tamil word “shuruttu,” a roll), a cigar made from tobacco grown in southern India and the Philippine Islands. It was once esteemed very highly for its delicate flavour. A cheroot differs from other cigars in having both ends cut square, instead of one being pointed, and one end considerably larger than the other.
CHERRAPUNJI, a village in the Khasi hills district of Assam. It is notable as having the heaviest known rainfall in the world. In 1861 it registered a total of 905 in., and its annual average is 458 in. This excessive rainfall is caused by the fact that Cherrapunji stands on the edge of the plateau overlooking the plains of Bengal, where it catches the full force of the monsoon as it rises from the sea. There is a good coal-seam in the vicinity.
CHERRY. As a cultivated fruit-tree the cherry is generally supposed to be of Asiatic origin, whence, according to Pliny, it was brought to Italy by Lucullus after his defeat of Mithradates, king of Pontus, 68 B.C. As with most plants which have been long and extensively cultivated, it is a matter of difficulty, if not an impossibility, to identify the parent stock of the numerous cultivated varieties of cherry; but they are generally referred to two species: Prunus Cerasus, the wild or dwarf cherry, the origin of the morello, duke and Kentish cherries, and P. Avium, the gean, the origin of the geans, hearts and bigarreaus. Both species grow wild through Europe and western Asia to the Himalayas, but the dwarf cherry has the more restricted range of the two in Britain, as it does not occur in Scotland and is rare in Ireland. The cherries form a section Cerasus of the genus Prunus; and they have sometimes been separated as a distinct genus from the plums proper; both have a stone-fruit or drupe, but the drupe of the cherry differs from that of the plum in not having a waxy bloom; further, the leaves of the plum are rolled (convolute) in the bud, while those of the cherry are folded (conduplicate).
The cherries are trees of moderate size and shrubs, having smooth, serrate leaves and white flowers. They are natives of the temperate regions of both hemispheres; and the cultivated varieties ripen their fruit in Norway as far as 63° N. The geans are generally distinguished from the common cherry by the greater size of the trees, and the deeper colour and comparative insipidity of the flesh in the ripe fruit, which adheres firmly to the “nut” or stone; but among the very numerous cultivated varieties specific distinctions shade away so that the fruit cannot be ranged under these two heads. The leading varieties are recognized as bigarreaus, dukes, morellos and geans. Several varieties are cultivated as ornamental trees and on account of their flowers.
The cherry is a well-flavoured sub-acid fruit, and is much esteemed for dessert. Some of the varieties are particularly selected for pies, tarts, &c., and others for the preparation of preserves, and for making cherry brandy. The fruit is also very extensively employed in the preparation of the liqueurs known as kirschwasser, ratafia and maraschino. Kirschwasser is made 85 chiefly on the upper Rhine from the wild black gean, and in the manufacture the entire fruit-flesh and kernels are pulped up and allowed to ferment. By distillation of the fermented pulp the liqueur is obtained in a pure, colourless condition. Ratafia is similarly manufactured, also by preference from a gean. Maraschino, a highly valued liqueur, the best of which is produced at Zara in Dalmatia, differs from these in being distilled from a cherry called marasca, the pulp of which is mixed with honey, honey or sugar being added to the distillate for sweetening. It is also said that the flavour is heightened by the use of the leaves of the perfumed cherry, Prunus Mahaleb, a native of central and southern Europe.
The wood of the cherry tree is valued by cabinetmakers, and that of the gean tree is largely used in the manufacture of tobacco pipes. The American wild cherry, Prunus serotina, is much sought after, its wood being compact, fine-grained, not liable to warp, and susceptible of receiving a brilliant polish. The kernels of the perfumed cherry, P. Mahaleb, are used in confectionery and for scent. A gum exudes from the stem of cherry trees similar in its properties to gum arabic.
The cherry is increased by budding on the wild gean, obtained by sowing the stones of the small black or red wild cherries. To secure very dwarf trees the Prunus Mahaleb has been used for the May duke, Kentish, morello and analogous sorts, but it is not adapted for strong-growing varieties like the bigarreaus. The stocks are budded, or, more rarely, grafted, at the usual seasons. The cherry prefers a free, loamy soil, with a well-drained subsoil. Stiff soils and dry gravelly subsoils are both unsuitable, though the trees require a large amount of moisture, particularly the large-leaved sorts, such as the bigarreaus. For standard trees, the bigarreau section should be planted 30 ft. apart, or more, in rich soil, and the May duke, morello and similar varieties 20 or 25 ft. apart; while, as trained trees against walls and espaliers, from 20 to 24 ft. should be allowed for the former, and from 15 to 20 ft. for the latter. In forming the stems of a standard tree the temporary side-shoots should not be allowed to attain too great a length, and should not be more than two years old when they are cut close to the stem. The first three shoots retained to form the head should be shortened to about 15 in., and two shoots from each encouraged, one at the end, and the other 3 or 4 in. lower down. When these have become established, very little pruning will be required, and that chiefly to keep the principal branches as nearly equal in strength as possible for the first few years. Espalier trees should have the branches about a foot apart, starting from the stem with an upward curve, and then being trained horizontally. In summer pruning the shoots on the upper branches must be shortened at least a week before those on the lower ones. After a year or two clusters of fruit buds will be developed on spurs along the branches, and those spurs will continue productive for an indefinite period. For wall trees any form of training may be adopted; but as the fruit is always finest on young spurs, fan-training is probably the most advantageous. A succession of young shoots should be laid in every year. The morello, which is of twiggy growth and bears on the young wood, must be trained in the fan form, and care should be taken to avoid the very common error of crowding its branches.
Forcing.—The cherry will not endure a high temperature nor close atmosphere. A heat of 45° at night will be sufficient at starting, this being gradually increased during the first few weeks to 55°, but lowered again when the blossom buds are about to open. After stoning the temperature may be again gradually raised to 60°, and may go up to 70° by day, or 75° by sun heat, and 60° at night. The best forcing cherries are the May duke and the royal duke, the duke cherries being of more compact growth than the bigarreau tribe and generally setting better; nevertheless a few of the larger kinds, such as bigarreau Napoléon, black tartarian and St Margaret’s, should be forced for variety. The trees may be either planted out in tolerably rich soil, or grown in large pots of good turfy friable calcareous loam mixed with rotten dung. If the plants are small, they may be put into 12-in. pots in the first instance, and after a year shifted into 15-in. pots early in autumn, and plunged in some loose or even very slightly fermenting material. The soil of the pots should be protected from snow-showers and cold rains. Occasionally trees have been taken up in autumn with balls, potted and forced in the following spring; but those which have been established a year in the pots are to be preferred. Such only as are well furnished with blossom-buds should be selected. The trees should be removed to the forcing house in the beginning of December, if fruit be required very early in the season. During the first and second weeks it may be kept nearly close; but, as vegetation advances, air becomes absolutely necessary during the day, and even at night when the weather will permit. If forcing is commenced about the middle or third week of December, the fruit ought to be ripe by about the end of March. After the fruit is gathered, the trees should be duly supplied with water at the root, and the foliage kept well syringed till the wood is mature. (See also Fruit and Flower Farming.)
CHERRYVALE, a city of Montgomery county, Kansas, U.S.A., about 140 m. S.S.E. of Kansas City. Pop. (1890) 2104; (1900) 3472, including 180 negroes; (1905, state census) 5089; (1910) 4304. It is served by the Atchison, Topeka & Santa Fé, and the main line and a branch (of which it is a terminus) of the St Louis & San Francisco railways. It is in a farming district and in the Kansas natural-gas and oil-field, and has large zinc smelters, an oil refinery, and various manufactures, including vitrified brick, flour, glass, cement and ploughs. Cherryvale was laid out in 1871 by the Kansas City, Lawrence & South Kansas Railway Company (later absorbed by the Atchison, Topeka & Santa Fé). The main part of the town was destroyed by fire in 1873, but was soon rebuilt, and in 1880 Cherryvale became a city of the third and afterwards of the second class. Natural gas, which is used as a factory fuel and for street and domestic lighting, was found here in 1889, and oil several years later.
CHERRY VALLEY, a village of Otsego county, New York, U.S.A., in a township of the same name, 68 m. N.W. of Albany. Pop. (1890) 685; (1900) 772; (1905) 746; (1910) 792; of the township (1910) 1706. It is served by the Delaware & Hudson railway. Cherry Valley is in the centre of a rich farming and dairying region, has a chair factory, and is a summer resort with sulphur and lithia springs. It was the scene of a terrible massacre during the War of Independence. The village was attacked on the 11th of November 1778 by Walter Butler (d. 1781) and Joseph Brant with a force of 800 Indians and Tories, who killed about 50 men, women and children, sacked and burned most of the houses, and carried off more than 70 prisoners, who were subjected to the greatest cruelties and privations, many of them dying or being tomahawked before the Canadian settlements were reached. Cherry Valley was incorporated in 1812.
CHERSIPHRON, a Cretan architect, the traditional builder (with his son Metagenes) of the great Ionic temple of Artemis at Ephesus set up by the Greeks in the 6th century. Some remains of this temple were found by J.T. Wood and brought to the British Museum. In connexion with the pillars, which are adorned with archaic reliefs, a fragmentary inscription has been found, recording that they were presented by King Croesus, as indeed Herodotus informs us. This temple was burned on the day on which Alexander the Great was born.
CHERSO, an island in the Adriatic Sea, off the east coast of Istria, from which it is separated by the channel of Farasina. Pop. (1900) 8274. It is situated in the Gulf of Quarnero, and is connected with the island of Lussin, lying on the S.W. by a turn bridge over the small channel of Ossero, and with the island of Veglia, lying on the E. by the Canale di Mezzo. These three are the principal islands of the Quarnero group, and form together the administrative district of Lussin in the Austrian crownland of Istria. Cherso is an elongated island about 40 m. long, 1¼ to 7 m. wide, and has an area of 150 sq. m. It is traversed by a range of mountains, which attain in the peak of Syss an altitude of 2090 ft. and form natural terraces, planted with vines and olive trees, specially in the middle and southern parts of the island. The northern part is covered with bushes of laurel 86 and mastic, but there are scarcely any large trees. There is a scarcity of springs, and the houses are generally furnished with cisterns for rain water. In the centre of the island is an interesting lake called the Vrana or Crow’s Lake, situated at an altitude of 40 ft. above, the level of the sea, 3¾ m. long, 1 m. wide and 184 ft. deep. This lake is in all probability fed by subterranean sources, The chief town of the island is Cherso, situated on the west coast. It possesses a good harbour and is provided with a shipwright’s wharf.
CHERSONESE, Chersonesus, or Cherronesus (Gr. χἐρσος, dry, and νῆσος, island), a word equivalent to “peninsula.” In ancient geography the Chersonesus Thracica, Chersonesus Taurica or Scythica, and Chersonesus Cimbrica correspond to the peninsulas of the Dardanelles, the Crimea and Jutland; and the Golden Chersonese is usually identified with the peninsula of Malacca. The Tauric Chersonese was further distinguished as the Great, in contrast to the Heracleotic or Little Chersonese at its S.W. corner, where Sevastopol now stands.
The Tauric Chersonese1 (from 2nd century A.D. called Cherson) was a Dorian colony of Heraclea in Bithynia, founded in the 5th century B.C. in the Crimea about 2 m. S. of the modern Sevastopol. After defending itself against the kingdom of Bosporus (q.v.), and the native Scythians and Tauri, and even extending its power over the west coast of the peninsula, it was compelled to call in the aid of Mithradates VI. and his general Diophantus, c. 110 B.C., and submitted to the Pontic dynasty. On regaining a nominal independence, it came more or less under the Roman suzerainty. In the latter part of the 1st century A.D., and again in the succeeding century, it received a Roman garrison and suffered much interference in its internal affairs. In the time of Constantine, in return for assistance against the Bosporans and the native tribes, it regained its autonomy and received special privileges. It must, however, have been subject to the Byzantine authorities, as inscriptions testify to restorations of its walls by Byzantine officials. Under Theophilus the central government sent out a governor to take the place of the elected magistrate. Even so it seems to have preserved a measure of self-government and may be said to have been the last of the Greek city states. Its ruin was brought about by the commercial rivalry of the Genoese, who forbade the Greeks to trade there and diverted its commerce to Caffa and Sudak. Previous to this it had been the main emporium of Byzantine commerce upon the N. coast of the Euxine. Through it went the communications of the empire with the Petchenegs and other native tribes, and more especially with the Russians. The commerce of Cherson is guaranteed in the early treaties between the Greeks and Russians, and it was in Cherson, according to Ps. Nestor’s chronicle, that Vladimir was baptized in 988 after he had captured the city. The constitution of the city was at first democratic under Damiorgi, a senate and a general assembly. Latterly it appears to have become aristocratic, and most of the power was concentrated in the hands of the first archon or Proteuon, who in time was superseded by the strategus sent out from Byzantium. Its most interesting political document is the form of oath sworn to by all the citizens in the 3rd century B.C.
The remains of the city occupy a space about two-thirds of a mile long by half a mile broad. They are enclosed by a Byzantine wall. Foundations and considerable remains of a Greek wall going back to the 4th century B.C. have been found beneath this in the eastern or original part of the site. Many Byzantine churches, both cruciform and basilican, have been excavated. The latter survived here into the 13th century when they had long been extinct in other Greek-speaking lands. The churches were adorned with frescoes, wall and floor mosaics, some well preserved, and marble carvings similar to work found at Ravenna. The fact that the site has not been inhabited since the 14th century makes it important for our knowledge of Byzantine life. The city was used by the Romans as a place of banishment: St Clement of Rome was exiled hither and first preached the Gospel; another exile was Justinian II., who is said to have destroyed the city in revenge. We have a considerable series of coins from the 3rd century B.C. to about A.D. 200, and also some of Byzantine date.
See B. Koehne, Beiträge zur Geschichte von Cherronesus in Taurien (St Petersburg, 1848); art. “Chersonesos” (20) by C.G. Brandis in Pauly-Wissowa, Realencydopädie, vol. iii. 221; A. A. Bobrinskoj, Chersonesus Taurica (St Petersburg, 1905) (Russian); V. V. Latyshev, Inscrr. Orae Septentr. Ponti Euxini, vols. i. and iv. Reports of excavations appear in the Compte rendu of the Imperial Archaeological Commission of St Petersburg from 1888 and in its Bulletin. See E. H. Minns, Scythians and Greeks (Cambridge, 1907).
1 In Pliny “Heraclea Chersonesus,” probably owing to a confusion with the name of the mother city.
CHERTSEY, a market town in the Chertsey parliamentary division of Surrey, England, 22 m. W.S.W. from London by the London & South-Western railway. Pop. of urban district (1901) 12,762. It is pleasantly situated on the right bank of the Thames, which is crossed by a bridge of seven arches, built of Purbeck stone in 1785. The parish church, rebuilt in 1808, contains a tablet to Charles James Fox, who resided at St Anne’s Hill in the vicinity, and another to Lawrence Tomson, a translator of the New Testament in the 17th century. Hardly any remains are left of a great Benedictine abbey, whose buildings at one time included an area of 4 acres. They fell into almost complete decay in the 17th century, and a “fair house” was erected out of the ruins by Sir Nicholas Carew of Beddington. The ground-plan can be traced; the fish-ponds are complete; and carved stones, coffins and encaustic tiles of a peculiar manufacture are frequently exhumed. Among the abbots the most famous was John de Rutherwyk, who was appointed in 1307, and continued, till his death in 1346, to carry on a great system of alteration and extension, which almost made the abbey a new building. The house in which the poet Cowley spent the last years of his life remains, and the chamber in which he died is preserved unaltered. The town is the centre of a large residential district. Its principal trade is in produce for the London markets.
The first religious settlement in Surrey, a Benedictine abbey, was founded in 666 at Chertsey (Cerotesei, Certesey), the manor of which belonged to the abbot until 1539, since when it has been a possession of the crown. In the reign of Edward the Confessor Chertsey was a large village and was made the head of Godley hundred. The increase of copyhold under Abbot John de Rutherwyk led to discontent, the tenants in 1381 rising and burning the rolls. Chertsey owed its importance primarily to the abbey, but partly to its geographical position. Ferries over the Redewynd were subjects of royal grant in 1340 and 1399; the abbot built a new bridge over the Bourne in 1333, and wholly maintained the bridge over the Thames when it replaced the 14th century ferry. In 1410 the king gave permission to build a bridge over the Redewynd. As the centre of an agricultural district the markets of Chertsey were important and are still held. Three days’ fairs were granted to the abbots in 1129 for the feast of St Peter ad Vincula by Henry III. for Holy Rood day; in 1282 for Ascension day; and a market on Mondays was obtained in 1282. In 1590 there were many poor, for whose relief Elizabeth gave a fair for a day in Lent and a market on Thursdays. These fairs still survive.
See Lucy Wheeler, Chertsey Abbey (London, 1905); Victoria County History, Surrey.
CHERUBIM, the Hebrew plural of “cherub” (kěrūb), imaginary winged animal figures of a sacred character, referred to in the description of Solomon’s temple (1 Kings vi. 23-35, vii. 29, viii. 6, 7), and also in that of the ark of the tabernacle (Ex. xxv. 18-22, xxvi. 1, 31, xxxvii. 7-9). The cherub-images, where such occur, represent to the imagination the supernatural bearers of Yahweh’s throne or chariot, or the guardians of His abode; the cherub-carvings at least symbolize His presence, and communicate some degree of His sanctity. In Gen. iii. 24 the cherubim are the guards of Paradise; Ezek. xxviii. 14, 16 cannot be mentioned here, the text being corrupt. We also find (1 Sam. iv. 4; 2 Sam. vi. 2) as a divine title “that sitteth upon the cherubim”; here it is doubted whether the cherubim are the material ones in the temple, or those which faith assumes and 87 the artist tries to represent—the supernatural steeds upon which Yahweh issues forth to interfere in human affairs. In a poetic theophany (Ps. xviii. 10) we find “upon a cherub” parallel to “upon the wings of the wind” (cp. Isa. xix. 1; Ps. civ. 3). One naturally infers from this that the “cherub” was sometimes viewed as a bird. For the clouds, mythologically, are birds. “The Algonkins say that birds always make the winds, that they create the waterspouts, and that the clouds are the spreading and agitation of their wings.” “The Sioux say that the thunder is the sound of the cloud-bird flapping his wings.” If so, Ps. xviii. 10 is a solitary trace of the archaic view of the cherub. The bird, however, was probably a mythic, extra-natural bird. At any rate the cherub was suggested by and represents the storm-cloud, just as the sword in Gen. iii. 24 corresponds to the lightning. In Ezek. i. the four visionary creatures are expressly connected with a storm-wind, and a bright cloud (ver. 4). Elsewhere (xli. 18) the cherub has two faces (a man’s and a bird’s), but in i. 10 and x. 14 each cherub has four faces, a view tastefully simplified in the Johannine Apocalypse (Rev. iv. 7).
It is best, however, to separate Ezekiel from other writers, since he belongs to what may be called a great mythological revival. Probably his cherubim are a modification of older ones, which may well have been of a more sober type. His own accounts, as we have seen, vary. Probably the cherub has passed through several phases. There was a mythic bird-cherub, and then perhaps a winged animal-form, analogous to the winged figures of bulls and lions with human faces which guarded Babylonian and Assyrian temples and palaces. Another analogy is furnished by the winged genii represented as fertilizing the sacred tree—the date-palm (Tylor); here the body is human, though the face is sometimes that of an eagle. It is perhaps even more noteworthy that figures thought to be cherubs have been found at Zenjirli, within the ancient North Syrian kingdom of Ya’di (see Jeremias, Das Alte Testament im Lichte des Alten Orients, pp. 350 f.); we may combine this with the fact that one of the great gods of this kingdom was called Rakab’el or Rekūb’el (also perhaps Rakab or Rekūb). A Sabaean (S. Arabian) name Karab’el also exists. The kerubim might perhaps be symbolic representatives of the god Rakab’el or Rek#363;b’el, probably equivalent to Hadad, whose sacred animal was the bull. That the figures symbolic of Rakab or Hadad were compounded or amalgamated by the Israelites with those symbolic of Nergal (the lion-god) and Ninib (the eagle-god), is not surprising.
See further “Cherubim,” in Ency. Bib. and Hast. D.B.; Cheyne, Genesis; Tylor, Proc. Soc. Bibl. Arch. xii. 383 ff.; Zimmern, Die Keilinschriften und das Alte Testament, pp. 529 f., 631 f.; Dibelius, Die Lade Jahves (1906), pp. 72-86.
CHERUBINI, MARIA LUIGI CARLO ZENOBIO SALVATORE (1760-1842), Italian musical composer, was born at Florence on the 14th of September 1760, and died on the 15th of March 1842 in Paris. His father was accompanist (Maestro al Cembalo) at the Pergola theatre. Cherubini himself, in the preface of his autograph catalogue of his own works, states, “I began to learn music at six and composition at nine, the former from my father, the latter from Bartolomeo and Alessandro Felici, and, after their death, from Bizzarri and J Castrucci.” By the time he was sixteen he had composed a great deal of church music, and in 1777 he went to Bologna, where for four years he studied under Sarti. This deservedly famous master well earned the gratitude which afterwards impelled Cherubini to place one of his double choruses by the side of his own Et Vitam Venturi as the crown of his Treatise on Counterpoint and Fugue, though the juxtaposition is disastrous for Sarti. But besides grounding Cherubini in the church music for which he had early shown so special a bent, Sarti also trained him in dramatic composition; sometimes, like the great masters of painting, entrusting his pupil with minor parts of his own works. From 1780 onwards for the next fourteen years dramatic music occupied Cherubini almost entirely. His first complete opera, Quinto Fabio, was produced in 1780, and was followed in 1782 by Armida, Adriano in Siria, and other works. Between 1782 and 1784 the successful production of five operas in four different towns must have secured Cherubini a dignified position amongst his Italian contemporaries; and in 1784 he was invited to London to produce two works for the Italian opera there, one of which, La Finta Frincipessa, was favourably received, while the other, Giulio Sabino, was, according to a contemporary witness, “murdered” by the critics.
In 1786 he left London for Paris, which became his home after a visit to Turin in 1787-1788 on the occasion of the production there of his Ifigenia in Aulide. With Cherubini, as with some other composers first trained in a school where the singer reigned supreme, the influence of the French dramatic sensibility prpved decisive, and his first French opera, Démophon (1788), though not a popular success, already marks a departure from the Italian style, which Cherubini still cultivated in the pieces he introduced into the works of Anfossi, Paisiello and Cimarosa, produced by him as director of the Italian opera in Paris (established in 1789). As in Paris Gluck realized his highest ambitions, and even Rossini awoke to a final effort of something like dramatic life in Guillaume Tell, so in Paris Cherubini became a great composer. If his melodic invention had been as warm as Gluck’s, his immensely superior technique in every branch of the art would have made him one of the greatest composers that ever lived. But his personal character shows in quaint exaggeration the same asceticism that in less sour and more negative form deprives even his finest music of the glow of that lofty inspiration that fears nothing.
With Lodoiska (1791) the series of Cherubim’s masterpieces begins, and by the production of Médée (1797) his reputation was firmly established. The success of this sombre classical tragedy, which shows Cherubini’s genius in its full power, is an honour to the Paris public. If Cherubini had known how to combine his high ideals with an urbane tolerance of the opinions of persons of inferior taste, the severity of his music would not have prevented his attaining the height of prosperity. But Napoleon Bonaparte irritated him by an enthusiasm for the kind of Italian music against which his whole career, from the time he became Sarti’s pupil, was a protest. When Cherubini said to Napoleon, “Citoyen Général, I perceive that you love only that music which does not prevent you thinking of your politics,” he may perhaps have been as firmly convinced of his own conciliatory manner as he was when many years afterwards he “spared the feelings” of a musical candidate by “delicately” telling him that he had “a beautiful voice and great musical intelligence, but was too ugly for a public singer.” Napoleon seems to have disliked opposition in music as in other matters, and the academic offices held by Cherubini under him were for many years far below his deserts. But though Napoleon saw no reason to conceal his dislike of Cherubini, his appointment of Lesueur in 1804 as his chapelmaster must not be taken as an evidence of his hostility. Lesueur was not a great genius, but, although recommended for the post by the retiring chapelmaster, Paesiello (one of Napoleon’s Italian favourites), he was a very meritorious and earnest Frenchman whom the appointment saved from starvation. Cherubini’s creative genius was never more brilliant than at this period, as the wonderful two-act ballet, Anacreon, shows; but his temper and spirits were not improved by a series of disappointments which culminated in the collapse of his prospects of congenial success at Vienna, where he went in 1805 in compliance with an invitation to compose an opera for the Imperial theatre. Here he produced, under the title of Der Wasserträger, the great work which, on its first production on the 7th of January 1801 (26 Nivôse, An8) as Les Deux Journées, had thrilled Paris with the accents of a humanity restored to health and peace. It was by this time an established favourite in Austria. On the 25th of February Cherubini produced Faniska, but the war between Austria and France had broken out immediately after his arrival, and public interest in artistic matters was checked by the bombardment and capitulation of Vienna. Though the meeting between Cherubini and the victorious Napoleon was not very friendly, he was called upon to direct the music at Napoleon’s soirées at Schönbrunn. But this had not been his object in coming to Vienna, and he soon returned to a retired and gloomy life in Paris.
His stay at Vienna is memorable for his intercourse with Beethoven, who had a profound admiration for him which he could neither realize nor reciprocate. It is too much to expect that the mighty genius of Beethoven, which broke through all rules in vindication of the principles underlying them, would be comprehensible to a mind like Cherubini’s, in which, while the creative faculties were finely developed, the critical faculty was atrophied and its place supplied by a mere disciplinary code inadequate even as a basis for the analysis of his own works. On the other hand, it would be impossible to exaggerate the influence Les Deux Journées had on the lighter parts of Beethoven’s Fidelio. Cherubini’s librettist was also the author of the libretto from which Fidelio was adapted, and Cherubini’s score was a constant object of Beethoven’s study, not only before the production of the first version of Fidelio, as Leonore, but also throughout Beethoven’s life. Cherubini’s record of his impressions of Beethoven as a man is contained in the single phrase, “Il était toujours brusque,” which at least shows a fine freedom from self-consciousness on the part of the man whose only remark on being told of the death of Brod, the famous oboist, was, “Ah, he hadn’t much tone” (“Ah, petit son”). Of the overture to Leonore Cherubini only remarked that he could not tell what key it was in, and of Beethoven’s later style he observed, “It makes me sneeze.” Beethoven’s brusqueness, notorious as it was, did not prevent him from assuring Cherubini that he considered him the greatest composer of the age and that he loved him and honoured him. In 1806 Haydn had just sent out his pathetic “visiting card” announcing that he was past work; Weber was still sowing wild oats, and Schubert was only nine years old. We need not, then, be surprised at Beethoven’s judgment. And though we must regret that Cherubini’s disposition prevented him from understanding Beethoven, it would be by no means true to say that he was uninfluenced at least by the sheer grandeur of the scale which Beethoven had by that time established as the permanent standard for musical art. Grandeur of proportion was, in fact, eminently characteristic of both composers, and the colossal structure of such a movement as the duet Perfides ennemis in Médée is almost inconceivable without the example of Beethoven’s C minor trio, op. 1, No. 3, published two years before it; while the cavatina Eterno iddio in Faniska is not only worthy of Beethoven but surprisingly like him in style.
After Cherubini’s disappointing visit to Vienna he divided his time between teaching at the conservatoire and cutting up playing-cards into figures and landscapes, which he framed and placed round the walls of his study. Not until 1809 was he aroused from this morbid indolence. He was staying in retirement at the country seat of the prince de Chimay, and his friends begged him to write some music for the consecration of a church there. After persistent refusals he suddenly surprised them with a mass in F for three-part chorus and orchestra. With this work the period of his great church music may be said to begin; although it was by no means the end of his career as an opera writer, which, in fact, lasted as late as his seventy-third year. This third period is also marked by some not unimportant instrumental compositions. An early event in the annals of the Philharmonic Society was his invitation to London in 1815 to produce a symphony, an overture and a vocal piece. The symphony (in D) was afterwards arranged with a new slow movement as the string quartet in C (1829), a fact which, taken in connexion with the large scale of the work, illustrates Cherubini’s deficient sense of style in chamber music. Nevertheless all the six string quartets written between 1814 and 1837 are interesting works performed with success at the present day, though the last three, discovered in 1880, are less satisfactory than the earlier ones. The requiem in C minor (1817) caused Beethoven to declare that if he himself ever wrote a requiem Cherubini’s would be his model.
At the eleventh hour Cherubini received recognition from Napoleon, who, during the Hundred Days, made him chevalier of the Legion of Honour. Then, with the restoration of the Bourbons, the very fact that Cherubini had not been persona grata with Napoleon brought him honour and emoluments. He was appointed, jointly with Lesueur, as composer and conductor to the Chapel Royal, and in 1822 he obtained the permanent directorship of the conservatoire. This brought him into contact, for the most part unfriendly, with all the most talented musicians of the younger generation. It is improbable that Berlioz would have been an easy subject for the wisest and kindest of spiritual guides; but no influence, repellent or attractive, could have been more disastrous for that passionate, quick-witted and yet eminently puzzle-headed mixture of Philistine and genius, than the crabbed old martinet whose regulations forbade the students access to Gluck’s scores in the library, and whose only theory of art (as distinguished from his practice) is accurately formulated in the following passage from Berlioz’s Grande Traité de l’instrumentation et d’orchestration: “It was no use for the modern composer to say, ‘But do just listen! See how smoothly this is introduced, how well motived, how deftly connected with the context, and how splendid it sounds!’ He was answered, ‘That is not the point. This modulation is forbidden; therefore it must not be made.’” The lack of really educative teaching, and the actual injustice for which Cherubini’s disciplinary methods were answerable, did much to weaken Berlioz’s at best ill-balanced artistic sense, and it is highly probable that, but for the kindliness and comparative wisdom of his composition master, Lesueur, he would have broken down from sheer lack of any influence which could command the respect of an excitable youth starving in the pursuit of a fine art against the violent opposition of his family. Only when Mendelssohn, at the age of seventeen, visited Paris in 1825, did Cherubini startle every one by praising a young composer to his face.
In 1833 Cherubini produced his last work for the stage, Ali Baba, adapted (with new and noisy features which excited Mendelssohn’s astonished disgust) from a manuscript opera, Koukourgi, written forty years earlier. It is thus, perhaps, not a fair illustration of the vigour of his old age; but the requiem in D minor (for male voices), written in 1836, is one of his greatest works, and, though not actually his last composition, is a worthy close to the long career of an artist of high ideals who, while neither by birth nor temperament a Frenchman, must yet be counted with a still greater foreigner, Gluck, as the glory of French classical music. In this he has no parallel except his friend and contemporary, Méhul, to whom he dedicated Médée, and who dedicated to him the beautiful Ossianic one-act opera Uthal. The direct results of his teaching at the conservatoire were the steady, though not as yet unhealthy, decline of French opera into a lighter style, under the amiable and modest Boieldieu and the irresponsible and witty Auber; for, as we have seen, Cherubini was quite incapable of making his ideals intelligible by any means more personal than his music; and the crude grammatical rules which he mistook for the eternal principles of his own and of all music had not the smallest use as a safeguard against vulgarity and pretentiousness.
Lest the passage above quoted from Berlioz should be suspected of bias or irrelevance, we cite a few phrases from Cherubini’s Treatise on Counterpoint and Fugue, of which, though the letter-press is by his favourite pupil, Halévy, the musical examples and doctrine are beyond suspicion his own. Concerning the 16th-century idiom, incorrectly but generally known as the “changing note” (an idiom which to any musical scholar is as natural as “attraction of the relative” is to a Greek scholar), Cherubini remarks, “No tradition gives us any reason why the classics thus faultily deviated from the rule.” Again, he discusses the use of “suspensions” in a series of chords which without them would contain consecutive fifths, and after making all the observations necessary for the rational conclusion that the question whether the fifths are successfully disguised or not depends upon the beauty and force of the suspensions, he merely remarks that “The opinion of the classics appears to me erroneous, notwithstanding that custom has sanctioned it, for, on the principle that the discord is a mere suspension of the chord, it should not affect the nature of the chord. But since 89 the classics have pronounced judgment we must of course submit.” In the whole treatise not one example is given from Palestrina or any other master who handled as a living language what are now the forms of contrapuntal discipline. As a dead language Cherubini brought counterpoint up to date by abandoning the church modes; but in true severity of principle, as in educational stimulus, his treatise shows a deplorable falling off from the standard set a hundred years before in Fux’s Gradus ad Panassum with its delightful dialogues between master and pupil and its continual appeal to artistic experience. Whatever may have been Cherubini’s success in imparting facility and certainty to his light-hearted pupils who established 19th-century French opera as a refuge from the terrors of serious art, there can be no doubt that his career as a teacher did more harm than good. In it the punishment drill of an incompetent schoolmaster was invested with the authority of a great composer, and by it the false antithesis between the “classical” and the “romantic” was erected into a barrier which many critics still find an insuperable obstacle to the understanding of the classical spirit. And yet as a composer Cherubini was no pseudo-classic but a really great artist, whose purity of style, except at rare moments, just failed to express the ideals he never lost sight of, because in his love of those ideals there was top much fear.
His principal works are summarized by Fetis as thirty-two operas, twenty-nine church compositions, four cantatas and several instrumental pieces, besides the treatise on counterpoint and fugue.
Good modern full scores of the two Requiems and of Les Deux Journées(the latter unfortunately without the dialogue, which, however, is accessible in its fairly good German translation in the Reclam Bibliolhek), and also of ten opera overtures, are current in the Peters edition. Vocal scores of some of the other operas are not difficult to get. The great Credo is in the Peters edition, but is becoming scarce. The string quartets are in Payne’s Miniature Scores.It is very desirable that the operas, from Démophon onwards, should be republished in full score.
See also E. Bellasis, Cherubini (1874); and an article with personal reminiscences by the composer Ferdinand Hiller, in Macmillan’s Magazine(1875). A complete catalogue of his compositions (1773-1841) was edited by Bottée du Toulmon.
CHÉRUEL, PIERRE ADOLPHE (1800-1891), French historian, was born at Rouen on the 17th of January 1809. He was educated at the École Normale Supérieure, and became a fellow (agrégé) in 1830. His early studies were devoted to his native town. His Histoire de Rouen sous la domination anglaise au XVe siecle(1840) and Histoire de Rouen pendant l’époque comunale, 1150-1382(Rouen, 1843-1844), are meritorious productions for a time when the archives were neither inventoried nor classified, and contain useful documents previously unpublished. His theses for the degree of doctor, De l’administration de Louis XIV d’après les Mémoires inédits d’Olivier d’Ormesson and De Maria Stuarta et Henrico III. (1849), led him to the study of general history. The former was expanded afterwards under the title Histoire de l’administration monarchique en France depuis l’avènement de Philippe-Auguste jusqu’à la mort de Louis XIV(1855), and in 1855 he also published his Dictionnaire historique des institutions, mœurs et coutumes de la France, of which many editions have appeared. These works may still be consulted for the 17th century, the period upon which Chéruel concentrated all his scientific activity. He edited successively the Journal d’Olivier Lefèvre d’Ormesson(1860-1862), interesting for the history of the parlement of Paris during the minority of Louis XIV.; Lettres du cardinal Mazarin pendant son ministère (6 vols., 1870-1891), continued by the vicomte G. d’Avenel; and Memoires du duc de Saint-Simon, published for the first time according to the original MSS. (2 editions, 1856-1858 and 1878-1881). To Saint-Simon also he devoted two critical studies, which are acute but not definitive: Saint-Simon considéré comme historien de Louis XIV (1865) and Notice sur la vie et sur les mémoires du duc de Saint-Simon(1876). The latter may be considered as an introduction to the famous Mémoires. Among his later writings may be mentioned the Histoire de la France pendant la minorité de Louis XIV (4 vols., 1880) and Histoire de la France sous le ministère de Mazarin (3 vols., 1882-1883). These two works are valuable for abundance of facts, precision of details, and clear and intelligent arrangement, but are characterized by a slightly frigid style. In their compilation Chéruel used a fair number of unpublished documents. To the student of the second half of the 17th century in France the works of Chéruel are a mine of information. He died in Paris on the 1st of May 1891.
CHERUSCI, an ancient German tribe occupying the basin of the Weser to the north of the Chatti. Together with the other tribes of western Germany they submitted to the Romans in 11-9 B.C., but in A.D. 9 Arminius, one of their princes, rose in revolt, and defeated and slew the Roman general Quintilius Varus with his whole army. Germanicus Caesar made several unsuccessful attempts to bring them into subjection again. By the end of the 1st century the prestige of the Cherusci had declined through unsuccessful warfare with the Chatti. Their territory was eventually occupied by the Saxons.
Tacitus, Annals, i.2, 11, 12, 13; Germania, 36; Strabo, p. 291 f.; E. Devrient, in Neue Jahrb. f. d. klass. Alter. (1900), p. 517.
CHESELDEN, WILLIAM (1688-1752), English surgeon, was born at Somerby, Leicestershire, on the 19th of October 1688. He studied anatomy in London under William Cowper (1666-1709), and in 1713 published his Anatomy of the Human Body, which achieved great popularity and went through thirteen editions. In 1718 he was appointed an assistant surgeon at St Thomas’s hospital (London), becoming full surgeon in the following year, and he was also chosen one of the surgeons to St George’s hospital on its foundation in 1733. He retired from St Thomas’s in 1738, and died at Bath on the 10th of April 1752. Cheselden is famous for his “lateral operation for the stone,” which he first performed in 1727. He also effected a great advance in ophthalmic surgery by his operation of iridectomy, described in 1728, for the treatment of certain forms of blindness by the production of an “artificial pupil.” He attended Sir Isaac Newton in his last illness, and was an intimate friend of Alexander Pope and of Sir Hans Sloane.
CHESHAM, a market town in the Aylesbury parliamentary division of Buckinghamshire, England, 26 m. W.N.W. of London by the Metropolitan railway. Pop. of urban district (1901) 7245. It is pleasantly situated in the narrow valley of the river Chess, closely flanked by low wooded hills. The church of St Mary is cruciform and mainly Perpendicular. Some ancient frescoes and numerous monuments are preserved. All sorts of small dairy utensils, chairs, malt-shovels, &c., are made of beech, the growth of which forms a feature of the surrounding country. Shoemaking is also carried on. In Waterside hamlet, adjoining the town, are flour-mills, duck farms, and some of the extensive watercress beds for which the Chess is noted, as it is also for its trout-fishing.
CHESHIRE, a north-western county of England, bounded N. by Lancashire, N.E. by Yorkshire and Derbyshire, S.E. by Staffordshire, S. by Shropshire, W. by Denbighshire and Flint, and N.W. by the Irish Sea. Its area is 1027.8 sq. m. The coast-line is formed by the estuaries of the Dee and the Mersey, which are separated by the low rectangular peninsula of Wirral. The estuary of the Dee is dry at low tide on the Cheshire shore, but that of the Mersey bears upon its banks the ports of Liverpool (in Lancashire) and Birkenhead (on the Wirral shore). The Dee forms a great part of the county boundary with Denbighshire and Flint, and the Mersey the boundary along the whole of the northern side. The principal river within the county is the Weaver, which crosses it with a north-westerly course, and, being joined by the Dane at Northwich, discharges into the estuary of the Mersey south of Runcorn. The surface of Cheshire is mostly low and gently undulating or flat; but the broken line of the Peckforton hills, seldom exceeding 600 ft. in height, runs north and south flanking the valley of the Weaver on the west. A low narrow gap in these hills is traversed by the small river Gowy, which rises to the east but has the greater part of its course to the west of them. Commanding this gap on the west, the Norman castle of Beeston stands on an isolated eminence. The northern part of the hills coincides approximately with the district still called Delamere Forest, formerly a chase of the earls of Chester, and finally disforested in 1812. 90 In certain sequestered parts the forest has not wholly lost its ancient character. On the east Cheshire includes the western face of the broad belt of high land which embraces the Peak district of Derbyshire; these hills rise sharply to the east of Congleton, Macclesfield and Hyde, reaching a height of about 1800 ft. within Cheshire. Distributed over the county, but principally in the eastern half, are many small lakes or meres, such as Combermere, Tatton, Rostherne, Tabley, Doddington, Marbury and Mere, and it was a common practice among the gentry of the county to build their mansions on the banks of these waters. The meres form one of the most picturesque features of the county.
Geology.—With the exception of a small area of Carboniferous rocks on the eastern border, and a small patch of Lower Lias near Audlem, the whole country is occupied by Triassic strata. The great central plain is covered by red and mottled Keuper Marls. From these marls salt is obtained; there are many beds of rock-salt, mostly thin; two are much thicker than the others, being from 75 ft. to over 100 ft. thick. Thin beds and veins of gypsum are common in the marls. The striking features of the Peckforton Hills are due to the repeated faulting of the Lower Keuper Sandstone, which lies upon beds of Bunter Sandstone. Besides forming this well-marked ridge, the Lower Keuper Sandstones or “Waterstones” form several ridges north-west of Macclesfield and appear along most of the northern borders of the county and in the neighbourhood of New Brighton and Birkenhead. The Lower Keuper Sandstone is quarried near the last-named place, also at Storeton, Delamere and Manley. This is a good building stone and an important water-bearing stratum; it is often ripple-marked, and bears the footprints of the Cheirotherium. At Alderley Edge ores of copper, lead and cobalt are found. West of the Peckforton ridge, Bunter Sandstones and pebble beds extend to the border. They also form low foothills between Cheadle and Macclesfield. They fringe the northern boundary and appear on the south-eastern boundary as a narrow strip of hilly ground near Woore. The oldest rock exposed in the county is the small faulted anticline of Carboniferous limestone at Astbury, followed in regular succession eastward by the shale, and thin limestones and sandstones of the Pendleside series. These rocks extend from Congleton Edge to near Macclesfield, where the outcrop bends sharply eastward and runs up the Goyt valley. Some hard quartzites in the Pendleside series, known locally as “Crowstones,” have contributed to the formation of the high Bosley Min and neighbouring hills. East of Bosley Min, on either side of the Goyt valley, are the Millstone Grits and Shales, forming the elevated moorland tracts. Cloud Hill, a striking feature near Congleton, is capped by the “Third Grit,” one of the Millstone Grit series. From Macclesfield northward through Stockport is a narrow tongue of Lower and Middle Coal-Measures—an extension of the Lancashire coalfield. Coal is mined at Neston in the Wirral peninsula from beneath the Trias; it is a connecting link between the Lancashire and Flintshire coalfields. Glacial drift is thickly spread over all the lower ground; laminated red clays, stiff clay with northern erratics and lenticular sand masses with occasional gravels, are the common types. At Crewe the drift is over 400 ft. thick. Patches of Drift sand, with marine shells, occur on the high ground east of Macclesfield at an elevation of 1250 ft.
Agriculture and Industries.—The climate is temperate and rather damp; the soil is varied and irregular, but a large proportion is a thin-skinned clay. More than four-fifths of the total area is under cultivation. The crop of wheat is comparatively insignificant; but a large quantity of oats is grown, and a great proportion of the cultivated land is in permanent pasture. The vicinity of such populous centres as Liverpool and Manchester, as well as the several large towns within the county, makes cattle and dairy-farming profitable. Cheese of excellent quality is produced, the name of the county being given to a particular brand (see Dairy). Potatoes are by far the most important green crop. Fruit-growing is carried on in some parts, especially the cultivation of stone fruit and, among these, damsons; while the strawberry beds near Farndon and Holt are celebrated. In the first half of the 19th century the condition of agriculture in Cheshire was notoriously backward; and in 1865-1866 the county suffered with especial severity from a visitation of cattle plague. The total loss of stock amounted to more than 66,000 head, and it was necessary to obtain from the Treasury a loan of £270,000 on the security of the county rate, for purposes of relief and compensation. The cheese-making industry naturally received a severe blow, yet to agriculture at large an ultimate good resulted as the possibility and even the necessity of new methods were borne in upon the farmers.
The industries of the county are various and important. The manufacture of cotton goods extends from its seat in Lancashire into Cheshire, at the town of Stockport and elsewhere in the north-east. Macclesfield and Congleton are centres of silk manufacture. At Crewe are situated the great workshops of the London & North-Western railway company, the institution of which actually brought the town in to being. Another instance of the modern creation of a town by an individual industrial corporation is seen in Port Sunlight on the Mersey, where the soap-works of Messrs Lever are situated. On the Mersey there are shipbuilding yards, and machinery and iron works. Other important manufactures are those of tools, chemicals, clothing and hats, and there are printing, bleaching and dye works, and metal foundries. Much sandstone is quarried, but the mineral wealth of the county lies in coal and salt. The second is a specially important product. Some rock-salt is obtained at Northwich and Winsford, but most of the salt is extracted from brine both here and at Lawton, Wheelock and Middlewich. At Northwich and other places in the locality curious accidents frequently occur owing to the sinking of the soil after the brine is pumped out; walls crack and collapse, and houses are seen leaning far out of the perpendicular. A little copper and lead are found.
Communications.—The county is well served with railways. The main line of the London & North-Western railway, passing north from Crewe to Warrington in Lancashire, serves no large town, but from Crewe branches diverge fanwise to Manchester, Chester, North Wales and Shrewsbury. The Great Western railway, with a line coming northward from Wrexham, obtains access through Cheshire to Liverpool and Manchester. These two companies jointly work the Birkenhead railway from Chester to Birkenhead. The heart of the county is traversed by the Cheshire Lines, serving the salt district, and reaching Chester from Manchester by way of Delamere Forest. In the east the Midland and Great Central systems enter the county, and the North Staffordshire line serves Macclesfield. The Manchester, South Junction & Altrincham and the Wirral railways are small systems serving the localities indicated by their names. The river Weaver is locked as far up as Winsford, and the transport of salt is thus expedited. The profits of the navigation, which was originally undertaken in 1720 by a few Cheshire squires, belong to the county, and are paid annually to the relief of the county rates. In the salt district through which the Weaver passes subsidence of the land has resulted in the formation of lakes of considerable extent, which act as reservoirs to supply the navigation. There are further means of inland navigation by the Grand Trunk, Shropshire Union and other canals, and many small steamers are in use. The Manchester Ship Canal passes through a section of north Cheshire, being entered from the estuary of the Mersey by locks near Eastham, and following its southern shore up to Runcorn, after which it takes a more direct course than the river.
Population and Administration.—The ancient county, which is a county palatine, has an area of 657,783 acres, with a population in 1891 of 730,058 and in 1901 of 815,099. Cheshire has been described as a suburb of Liverpool, Manchester and the Potteries of Staffordshire, and many of those whose business lies in these centres have colonized such districts as Bowdon, Alderley, Sale and Marple near Manchester, the Wirral, and Alsager on the Staffordshire border, until these localities have come to resemble the richer suburban districts of London. On the short seacoast of the Wirral are found the popular resorts of New Brighton and Hoylake. This movement and importance of its industries have given the county a vast increase of population in modern times. In 1871 the population was 561,201; from 1801 until that year it had increased 191%. The area of the administrative county is 654,825 acres. The county contains 7 hundreds. The municipal boroughs are Birkenhead (pop. 110,915), Chester (38,309), Congleton (10,707), Crewe (42,074), Dukinfield (18,929), Hyde (32,766), Macclesfield (34,624), Stalybridge (27,673), Stockport (92,832). Chester, the county town, is a city, county of a city, and county borough, and Birkenhead and Stockport are county 91 boroughs. The other urban districts with their populations are as follows:—
| Alderley Edge (a) | 2,856 | Hoylake and West Kirkby (b) | 10,911 |
| Alsager | 2,597 | Knutsford (a) | 5,172 |
| Altrincham (a) | 16,831 | Lower Bebington (b) | 8,398 |
| Ashton-upon-Mersey (a) | 5,563 | Lymm (a) | 4,707 |
| Bollington (a) | 5,245 | Marple (a) | 5,595 |
| Bowdon (a) | 2,788 | Middlewich | 4,669 |
| Bredbury and Romiley (a) | 7,087 | Mottram-in-Longdendale (a) | 3,128 |
| Bromborough (b) | 1,891 | Nantwich | 7,722 |
| Buglawton (Congleton) | 1,452 | Neston and Parkgate (b) | 4,154 |
| Cheadle and Gatley (a) | 7,916 | Northwich | 17,611 |
| Compstall (a) | 875 | Runcorn | 16,491 |
| Ellesmere Port and Whitby (b) | 4,082 | Sale (a) | 12,088 |
| Hale (a) | 4,562 | Sandbach | 5,558 |
| Handforth (a) | 911 | Tarporley | 2,644 |
| Hazel Grove and Bramhall (a) | 7,934 | Wallasey (b) | 53,579 |
| Higher Bebington (b) | 1,540 | Wilmslow (a) | 7,361 |
| Hollingworth (a) | 2,447 | Winsford | 10,382 |
| Hoole (Chester) | 5,341 | Yeardsley-cum-Whaley (a) | 1,487 |
Of the townships in this table, those marked (a) are within a radius of about 15 m. from Manchester (Knutsford being taken as the limit), while those marked (b) are in the Wirral. The localities of densest population are thus clearly illustrated.
The county is in the North Wales and Chester circuit, and assizes are held at Chester. It has one court of quarter sessions, and is divided into fourteen petty sessional divisions. The boroughs already named, excepting Dukinfield, have separate commissions of the peace, and Birkenhead and Chester have separate courts of quarter sessions. There are 464 civil parishes. Cheshire is almost wholly in the diocese of Chester, but small parts are in those of Manchester, St Asaph or Lichfield. There are 268 ecclesiastical parishes or districts wholly or in part within the county. There are eight parliamentary divisions, namely, Macclesfield, Crewe, Eddisbury, Wirral, Knutsford, Altrincham, Hyde and Northwich, each returning one member; the county also includes the parliamentary borough of Birkenhead returning one member, and parts of the borough of Stockport, which returns two members, and of Ashton-under-Lyne, Chester, Stalybridge, and Warrington, which return one member each.
History.—The earliest recorded historical fact relating to the district which is now Cheshire is the capture of Chester and destruction of the native Britons by the Northumbrian king Æthelfrith about 614. After a period of incessant strife between the Britons and their Saxon invaders the district was subjugated by Ecgbert in 830 and incorporated in the kingdom of Mercia. During the 9th century. Æthelwulf held his parliament at Chester, and received the homage of his tributary kings from Berwick to Kent, and in the 10th century Æthelflæd rebuilt the city, and erected fortresses at Eddisbury and Runcorn. Edward the Elder garrisoned Thelwall and strengthened the passages of the Mersey and the Irwell. On the splitting up of Mercia in the 10th century the dependent districts along the Dee were made a shire for the fortress of Chester. The shire is first mentioned in the Abingdon Chronicle, which relates that in 980 Cheshire was plundered by a fleet of Northmen. At the time of the Domesday Survey the county was divided into twelve hundreds, exclusive of the six hundreds between the Ribble and the Mersey, now included in Lancashire, but then a part of Cheshire. These divisions have suffered great modification, both in extent and in name, and of the seven modern hundreds Bucklow alone retains its Domesday appellation. The hundreds of Atiscross and Exestan have been transferred to the counties of Flint and Denbigh, with the exception of a few townships now in the hundred of Broxton. The prolonged resistance of Cheshire to the Conqueror was punished by ruthless harrying and sweeping confiscations of property, and no Englishman retained estates of importance after the Conquest. In order that the shire might be relieved of all obligations beyond the ever-pressing necessity of defending its borders against the inroads of hostile neighbours, it was constituted a county palatine which the earl of Chester “held as freely by his sword as the king held England by his crown.” The County had its independent parliament consisting of the barons and clergy, and courts, and all lands except those of the bishop were held of the earl. The court of exchequer was presided over by a chamberlain, a vice-chamberlain, and a baron of the exchequer. It was principally a court of revenue, but probably a court of justice also, before that of the justiciary was established, and had besides the functions of a chancery court, with an exclusive jurisdiction in equity. Other officers of the palatinate were the constable, high-steward and the Serjeants of the peace and of the forests. The abbots of St Werburgh and Combermere and all the eight barons held courts, in any of which cases of capital felony might be tried.
During the 12th and 13th centuries the county was impoverished by the constant inroads of the Welsh. In 1264 the castle and city of Chester were granted to Simon de Montfort, and in 1267 the treaty of Shrewsbury procured a short interval of peace. Richard II., in return for the loyal support furnished him by the county, made it a principality, but the act was revoked in the next reign. In 1403 Cheshire was the headquarters of Hotspur, who roused the people by telling them that Richard II. was still living. At the beginning of the Wars of the Roses Margaret collected a body of supporters from among the Cheshire gentry, and Lancastrian risings occurred as late as 1464. At the time of the Civil War feeling was so equally divided that an attempt was made to form an association for preserving internal peace. In 1643, however, Chester was made the headquarters of the royalist forces, while Nantwich was garrisoned for the parliament, and the county became the scene of constant skirmishes until the surrender of Chester in 1646 put an end to the struggle.
From the number of great families with which it has been associated Chester has been named “the mother and nurse of English gentility.” Of the eight baronies of the earldom none survives, but the title of that of Kinderton was bestowed in 1762 on George Venables-Vernon, son of Anne, sister of Peter Venables, last baron of Kinderton, from whom the present Lord Vernon of Kinderton is descended. Other great Domesday proprietors were William FitzNigel, baron of Halton, ancestor of the Lacys; Hugh de Mara, baron of Montalt, ancestor of the Ardens; Ranulph, ancestor of the Mainwarings; and Hamo de Massey. The Davenports, Leighs and Warburtons trace their descent back to the 12th century, and the Grosvenors are descended from a nephew of Hugh Lupus.
In the reign of Henry VIII. the distinctive privileges of Cheshire as a county palatine were considerably abridged. The right of sanctuary attached to the city of Chester was abolished; justices of the peace were appointed as in other parts of the kingdom, and in 1542 it was enacted that in future two knights for the shire and two burgesses for the city of Chester should be returned to parliament. After the Reform Act of 1832 the county returned four members from two divisions, and Macclesfield and Stpckport returned two members each. Birkenhead secured representation in 1859. From 1868 until the Redistribution Act of 1885 the county returned six members from three divisions.
From earliest times the staple products of Cheshire have been salt and cheese. The salt-pits of Nantwich, Middlewich and Northwich were in active operation at the time of Edward the Confessor, and at that date the mills and fisheries on the Dee also furnished a valuable source of revenue. Twelfth century writers refer to the excellence of Cheshire cheese, and at the time of the Civil War three hundred tons at £33 per ton were ordered in one year for the troops in Scotland. The trades of tanners, skinners and glove-makers existed at the time of the Conquest, and the export trade in wool in the 13th and 14th centuries was considerable. The first bed of rock-salt was discovered in 1670. Weaving and wool-combing were introduced in 1674.
Antiquities.—The main interest in the architecture of the 92 county lies in the direction of domestic buildings rather than ecclesiastical. Old half-timbered houses are common in almost every part of the county; many of these add to the picturesqueness of the streets in the older towns, as in the case of the famous Rows in Chester, while in the country many ancient manor-houses remain as farm-houses. Among the finest examples are Bramhall Hall, between Stockport and Macclesfield, and Moreton Old Hall, near Congleton (see House, Plate IV., fig. 13). The first, occupying three sides of a quadrangle (formerly completed by a fourth side), dates from the 13th and 14th centuries, and contains a splendid panelled hall and other rooms. Of Moreton Hall, which is moated, only three sides similarly remain; its date is of the 16th century. Other buildings of the Elizabethan period are not infrequent, such as Brereton and Dorfold Halls, while more modern mansions, set in fine estates, are numerous. Crewe Hall is a modern building on an ancient site, and Vale Royal near Winsford incorporates fragments of a Cistercian monastery founded in 1277. A noteworthy instance of the half-timbered style applied to an ecclesiastical building is found in the church of Lower Peover near Knutsford, of which only the tower is of stone. The church dates from the 13th century, and was carefully restored in 1852. Cheshire has no monastic remains of importance, save those attached to the cathedral of Chester, nor are its village churches as a rule of special interest. There is, however, a fine late Perpendicular church (with earlier portions) at Astbury near Congleton, and of this style and the Decorated the churches of Bunbury and Malpas may be noticed as good illustrations. In Chester, besides the cathedral, there is the massive Norman church of St John; and St Michael’s church and the Rivers chapel at Macclesfield are noteworthy. No more remarkable religious monuments remain in the county than the two sculptured Saxon crosses in the market-place at Sandbach. Ruins of two Norman castles exist in Beeston and Halton.
Authorities.—Sir John Doddridge, History of the Ancient and Modern State of the Principality of Wales, Duchy of Cornwall, and Earldom of Chester (London, 1630; 2nd ed., 1714); D. King, The Vale-Royall of England, or the County Palatine of Cheshire Illustrated, 4 parts (London, 1656); D. and S. Lysons, Magna Britannia, vol. ii. pt. ii. (London, 1810); J. H. Hanshall, History of the County Palatine of Chester (Chester, 1817-1823); J.O. Halliwell, Palatine Anthology (London, 1850); G. Ormerod, History of the County Palatine and City of Chester (London, 1819; new ed., London, 1875-1882); J.P. Earwaker, East Cheshire (2 vols., London, 1877); R. Wilbraham, Glossary (London, 1820; 2nd ed., London, 1826); and Glossary founded on Wilbraham by E. Leigh (London, 1877); J. Croston, Historic Sites of Cheshire (Manchester, 1883); and County Families of Cheshire (Manchester, 1887); W.E.A. Axon, Cheshire Gleanings (Manchester, 1884); Holland, Glossary of Words used in the County of Cheshire (London, 1884-1886); N.G. Philips, Views of Old Halls in Cheshire (London, 1893); Victoria County History, Cheshire. See also various volumes of the Chetham Society and of the Record Society of Manchester, as well as the Proceedings of the Cheshire Antiquarian Society, and Cheshire Notes and Queries.
CHESHUNT, an urban district in the Hertford parliamentary division of Hertfordshire, England, on the Lea, 14 m. N. of London by the Great Eastern railway. Pop. (1891) 9620; (1901) 12,292. The church of St Mary is Perpendicular and has been enlarged in modern times. A college was founded, for the education of young men to the ministry of the Connexion, by Selina countess of Huntingdon in 1768 at Trevecca-isaf near Talgarth, Brecknockshire. In 1792 it was moved to Cheshunt, and became known as Cheshunt College. In 1904, as it was felt that the college was unable properly to carry on its work under existing conditions, it was proposed to amalgamate it with Hackney College, but the Board of Education refused to sanction any arrangement which would set aside the requirements of the deed of foundation, namely that the officers and students of Cheshunt College should subscribe the fifteen articles appended to the deed, and should take certain other obligations. In 1905 it was decided by the board to reorganize the college and remove it to Cambridge.
Nursery and market gardening, largely under glass, brick-making and saw-mills are the chief industries of Cheshunt. Roman coins and other remains have been found at this place, and an urn appears built into the wall of an inn. A Romano-British village or small town is indicated. There was a Benedictine nunnery here in the 13th century. Of several interesting mansions in the vicinity one, the Great House, belonged to Cardinal Wolsey, and a former Pengelly House was the residence of Richard Cromwell the Protector after his resignation. Theobalds Park was built in the 18th century, but the original mansion was acquired by William Cecil, Lord Burghley, in 1561; being taken in 1607 by James I. from Robert Cecil, first earl of Salisbury, in exchange for Hatfield House. James died here in 1625, and Charles I. set out from here for Nottingham in 1642 at the outset of the Civil War. One of the entrances to Theobalds Park is the old Temple Bar, removed from Fleet Street, London, in 1878.
CHESIL BANK (A.S. ceosol, pebble bank), a remarkable beach of shingle on the coast of Dorsetshire, England. It is separated from the mainland for 8 m. by an inlet called the Fleet, famous for its swannery, and continues in all for 18 m. south-eastward from Abbotsbury, terminating at the so-called Isle of Portland. The height of the bank at the Portland end is 35 ft. above spring-tide level, and its breadth 200 yds. The greater height at this end accords with the general-movement of shingle along this coast from west to east; and for the same reason the pebbles of the bank decrease in size from 1 to 3 in. in diameter at Portland to the size of peas at the western end, where the breadth is only 170 yds.
CHESNELONG, PIERRE CHARLES (1820-1894), French politician, was born at Orthez in the department of the Basses-Pyrénées, on the 14th of April 1820. In 1848 he proclaimed himself a Republican; but after the establishment of the Second Empire he changed his views, and in 1865 was returned to the chamber as the official candidate for his native place. He at once became conspicuous, both for his eloquence and for his uncompromising clericalism, especially in urging the necessity for maintaining the temporal power of the papacy. In 1869 he was again returned, and, devoting himself with exceptional ability to financial questions, was in 1870 appointed to report the budget. During and after the war, for which he voted, he retired for a while into private life; but in 1872 he was again elected deputy, this time as a Legitimist, and took his seat among the extreme Right. He was the soul of the reactionary opposition that led to the fall of Thiers; and in 1873 it was he who, with Lucien Brun, carried to the comte de Chambord the proposals of the chambers. Through some misunderstanding, he reported on his return that the count had accepted all the terms offered, including the retention of the tricolour flag; and the count published a formal denial. Chesnelong now devoted himself to the establishment of Catholic universities and to the formation of Catholic working-men’s clubs. In 1876 he was again returned for Orthez, but was unseated, and then beaten by the republican candidate. On the 24th of November, however, he was elected to a seat in the senate, where he continued his vigorous polemic against the progressive attempts of the republican government to secularize the educational system of France until his death in 1894.
CHESNEY, CHARLES CORNWALLIS (1826-1876), British soldier and military writer, the third son of Charles Cornwallis Chesney, captain on the retired list of the Bengal Artillery, and nephew of General F.R. Chesney, was born in Co. Down, Ireland, on the 29th of September 1826. Educated at Blundell’s school, Tiverton, and afterwards at the Royal Military Academy, Woolwich, he obtained his first commission as second lieutenant of engineers in 1845, passing out of the academy at the head of his term. His early service was spent in the ordinary course of regimental duty at home and abroad, and he was stationed in New Zealand during the Crimean War. Among the various reforms in the British military system which followed from that war was the impetus given to military education; and in 1858 Captain Chesney was appointed professor of military history at Sandhurst. In 1864 he succeeded Colonel (afterwards Sir Edward) Hamley in the corresponding chair at the Staff College. The writings of these two brilliant officers had a great influence not only at home, but on the continent and in America. Chesney’s 93 first published work (1863) was an account of the Civil War in Virginia, which went through several editions. But the work which attained the greatest reputation was his Waterloo Lectures (1868), prepared from the notes of lectures orally delivered at the Staff College. Up to that time the English literature on the Waterloo campaign, although voluminous, was made up of personal reminiscences or of formal records, useful materials for history rather than history itself; and the French accounts had mainly taken the form of fiction. In Chesney’s lucid and vigorous account of the momentous struggle, while it illustrates both the strategy and tactics which culminated in the final catastrophe, the mistakes committed by Napoleon are laid bare, and for the first time an English Writer is found to point out that the dispositions of Wellington were far from faultless. And in the Waterloo Lectures the Prussians are for the first time credited by an English pen with their proper share in the victory. The work attracted much attention abroad as well as at home, and French and German translations were published.
Chesney was for many years a constant contributor to the newspaper press and to periodic literature, devoting himself for the most part to the critical treatment of military operations, and professional subjects generally. Some of his essays on military biography, contributed mainly to the Edinburgh Review, were afterwards published separately (1874). In 1868 he was appointed a member of the royal commission on military education, under the presidency first of Earl De Grey and afterwards of Lord Dufferin, to whose recommendations were due the improved organization of the military colleges, and the development of military education in the principal military stations of the British army. In 1871, on the conclusion of the Franco-German War, he was sent on a special mission to France and Germany, and furnished to the government a series of valuable reports on the different siege operations which had been carried out during the war, especially the two sieges of Paris. These reports were published in a large volume, which was issued confidentially. Never seeking regimental or staff preferment, Colonel Chesney never obtained any, but he held at the time of his death a unique position in the army, altogether apart from and above his actual place in it. He was consulted by officers of all grades on professional matters, and few have done more to raise the intellectual standard of the British officer. Constantly engaged in literary pursuits, he was nevertheless laborious and exemplary in the discharge of his public duties, while managing also to devote a large part of his time to charitable and religious offices. He was abstemious to a fault; and, overwork of mind and body telling at last on a frail constitution, he died after a short illness on the 19th of March 1876. He had become lieutenant-colonel in 1873, and at the time of his death he was commanding Royal Engineer of the London district. He was buried at Sandhurst.
CHESNEY, FRANCIS RAWDON (1789-1872), British general and explorer, was the son of Captain Alexander Chesney, an Irishman of Scottish descent who, having emigrated to South Carolina in 1772, did brilliant service under Lord Rawdon (afterwards marquess of Hastings) in the War of Independence, and subsequently received an appointment as coast officer at Annalong, Co. Down, Ireland. There F.R. Chesney was born on the 16th of March 1789. Lord Rawdon gave the boy a cadetship at Woolwich, and he was gazetted to the Royal Artillery in 1805. But though he rose to be lieutenant-general and colonel-commandant of the 14th brigade Royal Artillery (1864), and general in 1868, Chesney’s memory lives not for his military record, but for his connexion with the Suez Canal, and with the exploration of the Euphrates valley, which started with his being sent out to Constantinople in the course of his military duties in 1829, and his making a tour of inspection in Egypt and Syria. His report in 1830 on the feasibility of making the Suez Canal was the original basis of Lesseps’ great undertaking (in 1869 Lesseps greeted him in Paris as the “father” of the canal); and in 1831 he introduced to the home government the idea of opening a new overland route to India, by a daring and adventurous journey (for the Arabs were hostile and he was ignorant of the language) along the Euphrates valley from Anah to the Persian Gulf. Returning home, Colonel Chesney (as he then was) busied himself to get support for the latter project, to which the East India Company’s board was favourable; and in 1835 he was sent out in command of a small expedition, for which parliament voted £20,000, in order to test the navigability of the Euphrates. After encountering immense difficulties, from the opposition of the Egyptian pasha, and from the need of transporting two steamers (one of which was lost) in sections from the Mediterranean over the hilly country to the river, they successfully arrived by water at Bushire in the summer of 1836, and proved Chesney’s view to be a practicable one. In the middle of 1837 he returned to England, and was given the Royal Geographical Society’s gold medal, having meanwhile been to India to consult the authorities there; but the preparation of his two volumes on the expedition (published in 1850) was interrupted by his being ordered out in 1843 to command the artillery at Hong Kong. In 1847 his period of service was completed, and he went home to Ireland, to a life of retirement; but both in 1856 and again in 1862 he went out to the East to take a part in further surveys and negotiations for the Euphrates valley railway scheme, which, however, the government would not take up, in spite of a favourable report from the House of Commons committee in 1871. In 1868 he published a further volume of narrative on his Euphrates expedition. He died on the 30th of January 1872.
His Life, edited by Stanley Lane Poole, appeared in 1885.
CHESNEY, SIR GEORGE TOMKYNS (1830-1895), English general, brother of Colonel C.C. Chesney, was born at Tiverton, Devonshire, on the 30th of April 1830. Educated at Blundell’s school, Tiverton, and at Addiscombe, he entered the Bengal Engineers as second lieutenant in 1848. He was employed for some years in the public works department and, on the outbreak of the Indian Mutiny in 1857, joined the Ambala column, was field engineer at the battle of Badli-ke-serai, brigade-major of engineers throughout the siege of Delhi, and was severely wounded in the assault (medal and clasp and a brevet majority). In 1860 he was appointed head of a new department in connexion with the public works accounts. His work on Indian Polity (1868), dealing with the administration of the several departments of the Indian government, attracted wide attention and remains a permanent text-book. The originator of the Royal Indian Civil Engineering College at Cooper’s Hill, Staines, he was also its first president (1871-1880). In 1871 he contributed to Blackwood’s Magazine, “The Battle of Dorking,” a vivid account of a supposed invasion of England by the Germans after their victory over France. This was republished in many editions and translations, and produced a profound impression. He was promoted lieutenant-colonel, 1869; colonel, 1877; major-general, 1886; lieutenant-general, 1887; colonel-commandant of Royal Engineers, 1890; and general, 1892. From 1881 to 1886 he was secretary to the military department of the government of India, and was made a C.S.I, and a C.I.E. From 1886 to 1892, as military member of the governor-general’s council, he carried out many much-needed military reforms. He was made a C.B. at the jubilee of 1887, and a K.C.B. on leaving India in 1892. In that year he was returned to parliament, in the Conservative interest, as member for Oxford, and was chairman of the committee of service members of the House of Commons until his death on the 31st of March 1895. He wrote some novels, The Dilemma, The Private Secretary, The Lesters, &c., and was a frequent contributor to periodical literature.
CHESS, once known as “checker,” a game played with certain “pieces” on a special “board” described below. It takes its name from the Persian word shah, a king, the name of one of the pieces or men used in the game. Chess is the most cosmopolitan of all games, invented in the East (see History, below), introduced into the West and now domiciled in every part of the world. As a mere pastime chess is easily learnt, and a very moderate amount of study enables a man to become a fair player, but the higher ranges of chess-skill are only attained by persistent labour. The real proficient or “master” not merely must know 94 the subtle variations in which the game abounds, but must be able to apply his knowledge in the face of the enemy and to call to his aid, as occasion demands, all that he has of foresight, brilliancy and resource, both in attack and in defence. Two chess players fighting over the board may fitly be compared to two famous generals encountering each other on the battlefield, the strategy and the tactics being not dissimilar in spirit.
The Board, Pieces and Moves.—The chessboard is divided (see accompanying diagrams) into sixty-four chequered squares. In diagram 1, the pieces, or chess-men, are arranged for the beginning of a game, while diagram 2 shows the denomination of the squares according to the English and German systems of notation. Under diagram 1 are the names of the various “pieces”—each side, White or Black, having a King, a Queen, two Rooks (or Castles), two Knights, and two Bishops. The eight men in front are called Pawns. At the beginning of the game the queen always stands upon a square of her own colour. The board is so set that each player has a white square at the right hand end of the row nearest to him. The rook, knight and bishop on the right of the king are known as King’s rook, King’s knight, and King’s bishop; the other three as Queen’s rook, Queen’s knight, and Queen’s bishop.
Briefly described, the powers of the various pieces and of the pawns are as follows.
The king may move in any direction, only one square at a time, except in castling. Two kings can never be on adjacent squares.
 |
| Diagram 1.—Showing the arrangement of the pieces at the commencement of a game. |
The queen moves in any direction square or diagonal, whether forward or backward. There is no limit to her range over vacant squares; an opponent she may take; a piece of her own colour stops her. She is the most powerful piece on the board, for her action is a union of those of the rook and bishop. The rooks (from the Indian rukh and Persian rokh, meaning a soldier or warrior) move in straight lines—forward or backward—but they cannot move, diagonally. Their range is like the queen’s, unlimited, with the same exceptions.
The bishops move diagonally in any direction whether backward or forward. They have an unlimited range, with the same exceptions.
The knights’ moves are of an absolutely different kind. They move from one corner of any rectangle of three squares by two to the opposite corner; thus, in diagram 3, the white knight can move to the square occupied by the black one, and vice versa, or a knight could move from C to D, or D to C. The move may be made in any direction. It is no obstacle to the knight’s move if squares A and B are occupied. It will be perceived that the knight always moves to a square of a different colour.
The king, queen, rooks and bishops may capture any foeman which stands anywhere within their respective ranges; and the knights can capture the adverse men which stand upon the squares to which they can leap. The piece which takes occupies the square of the piece which is taken, the latter being removed from the board. The king cannot capture any man which is protected by another man.
The moves and capturing powers of the pawns are as follows:—Each pawn for his first move may advance either one or two squares straight forward, but afterwards one square only, and this whether upon starting he exercised his privilege of moving two squares or not. A pawn can never move backwards. He can capture only diagonally—one square to his right or left front. A pawn moves like a rook, captures like a bishop, but only one square at a time. When a pawn arrives at an eighth square, viz. at the extreme limit of the board, he may, at the option of his owner, be exchanged for any other piece, so that a player may, e.g., have two or more queens on the board at once.

Diagram 2.—Showing English and German Methods of Notation.
“Check and Checkmate.” The king can never be captured, but when any piece or pawn attacks him, he is said to be “in check,” and the fact of his being so attacked should be announced by the adverse player saying “check,” whereupon the king must move from the square he occupies, or be screened from check by the interposition of one of his own men, or the attacking piece must be captured. If, however, when the king is in check, none of these things can be done, it is “checkmate” (Persian, shah mat, the king is dead), known generally as “mate,” whereupon the game terminates, the player whose king has been thus checkmated being the loser. When the adversary has only his king left, it is very easy to checkmate him with only a queen and king, or only a rook and king. The problem is less easy with king and two bishops, and still less easy with king, knight and bishop, in which case the opposing king has to be driven into a corner square whose colour corresponds with the bishop’s, mate being given with the bishop. A king and two knights cannot mate. To mate with king and rook the opposing king must be driven on to one of the four side files and kept there with the rook on the next file, till it is held by the other king, when the rook mates.
The pawn gives check in the same way as he captures, viz. diagonally. One king cannot give check to another, nor may a king be moved into check.
 |
| Knight’s move. |
“Check by discovery” is given when a player, by moving one of his pieces, checks with another of them. “Double check” means attacking the king at once with two pieces—one of the pieces in this case giving check by discovery.
“Perpetual check” occurs when one player, seeing that he cannot win the game, finds the men so placed that he can give check ad infinitum, while his adversary cannot possibly avoid it. The game is then drawn. A game is also drawn “if, before touching a man, the player whose turn it is to play, claims that the game be treated as drawn, and proves that the existing position existed, in the game and at the commencement of his turn of play, twice at least before the present turn.”
“Stalemate.” When a king is not in check, but his owner has no move left save such as would place the king in check, it is “stalemate,” and the game is drawn.
“Castling.” This is a special move permitted to the king once only in the game. It is performed in combination with either rook, the king being moved two squares laterally, while the rook towards which he is moved (which must not have previously 95 moved from its square) is placed next him on the other side; the king must be touched first. The king cannot castle after having been once moved, nor when any piece stands between him and the rook, nor if he is in check, nor when he has to cross a square commanded by an adverse piece or pawn, nor into check. It will be perceived that after castling with the king’s rook the latter will occupy the KB square, while the king stands on the KKt square, and if with the queen’s rook, the latter will occupy the queen’s square while the king stands on the QB square.
“Taking en passant.” This is a privilege possessed by any of the pawns under the following circumstances:—If a pawn, say of the white colour, stands upon a fifth square, say upon K5 counting from the white side, and a black pawn moves from Q2 or KB2 to Q4 or KB4 counting from the black side, the white pawn can take the black pawn en passant. For the purposes of such capture the latter is dealt with as though he had only moved to Q3 or KB3, and the white pawn taking him diagonally then occupies the square the captured pawn would have reached had he moved but one square. The capture can be made only on the move immediately succeeding that of the pawn to be captured.
“Drawn Game.” This arises from a stalemate (noticed above), or from either player not having sufficient force wherewith to effect checkmate, as when there are only two kings left on the board, or king and bishop against king, or king with one knight, or two knights against king, or from perpetual check. One of the players can call upon the other to give checkmate in fifty moves, the result of failure being that the game is drawn. But, if a pawn is moved, or a piece is captured, the counting must begin again.
A “minor piece” means either a knight or a bishop. “Winning the exchange” signifies capturing a rook in exchange for a minor piece. A “passed pawn” is one that has no adverse pawn either in front or on either of the adjoining files. A “file” is simply a line of squares extending vertically from one end of the board to the other. An “open file” is one on which no piece or pawn of either colour is standing. A pawn or piece is en prise when one of the enemy’s men can capture it. “Gambit” is a word derived from the Ital. gambetto, a tripping up of the heels; it is a term used to signify an opening in which a pawn or piece is sacrificed at the opening of a game to obtain an attack. An “opening,” or début, is a certain set method of commencing the game. When a player can only make one legal move, that move is called a “forced move.”
Value of the Pieces.—The relative worth of the chess-men cannot be definitely stated on account of the increase or decrease of their powers according to the position of the game and the pieces, but taking the pawn as the unit the following will be an estimate near enough for practical purposes:—pawn 1, bishop 3.25, knight 3.25, rook 5, queen 9.50. Three minor pieces may more often than not be advantageously exchanged for the queen. The knight is generally stronger than the bishop in the end game, but two bishops are usually stronger than two knights, more especially in open positions.
Laws.—The laws of chess differ, although not very materially, in different countries. Various steps have been taken, but as yet without success, to secure the adoption of a universal code. In competitions among English players the particular laws to be observed are specially agreed upon,—the regulations most generally adopted being those laid down at length in Staunton’s Chess Praxis, or the modification of the Praxis laws issued in the name of the British Chess Association in 1862.
First Move and Odds.—To decide who moves first, one player conceals a white pawn in one hand and a black pawn in the other, his adversary not seeing in which hand the different pawns are put. The other holds out his hands with the pawns concealed, and his adversary touches one. If that contains the white pawn, he takes the white men and moves first. If he draws the black pawn his adversary has the first move, since white, by convention, always plays first. Subsequently the first move is taken alternately. If one player, by way of odds, “gives” his adversary a pawn or piece, that piece is removed before play begins. If the odds are “pawn and move,” or “pawn and two,” a black pawn, namely, the king’s bishop’s pawn, is removed and white plays one move, or any two moves in succession. “Pawn and two” is generally considered to be slightly less in point of odds than to give a knight or a bishop; to give a knight and a bishop is to give rather more than a rook; a rook and bishop less than a queen; two rooks rather more than a queen. The odds of “the marked pawn” can only be given to a much weaker player. A pawn, generally KB’s pawn, is marked with a cap of paper. If the pawn is captured its owner loses the game; he can also lose by being checkmated in the usual way, but he cannot give mate to his adversary with any man except the marked pawn, which may not be moved to an eighth square and exchanged for a piece.
Rules.—If a player touch one of his men he must move it, unless he says j’adoube (I adjust), or words of a similar meaning, to the effect that he was only setting it straight on its square. If he cannot legally move a touched piece, he must move his king, if he can, but may not castle; if not, there is no penalty. He must say j’adoube before touching his piece. If a player touch an opponent’s piece, he must take it, if he can: if not, move his king. If he can do neither, no penalty. A move is completed and cannot be taken back, as soon as a player, having moved a piece, has taken his hand off it. If a player is called upon to mate under the fifty-move rule, “fifty moves” means fifty moves and the forty-nine replies to them. A pawn that reaches an eighth square must be exchanged for some other piece, the move not being complete until this is done; a second king cannot be selected.
Modes of Notation.—The English and German methods of describing the moves made in a game are different. According to the English method each player counts from his own side of the board, and the moves are denoted by the names of the files and the numbers of the squares. Thus when a player for his first move advances the king’s pawn two squares, it is described as follows:—“1. P-K4.” The following moves, with the aid of diagram 2, will enable the reader to understand the principles of the British notation. The symbol x is used to express “takes”; a dash—to express “to.”
| White. | Black. |
| 1. P-K4 | 1. P-K4 |
| 2. KKt-KB3 (i.e. King’s Knight to the third square of the King’s Bishop’s file) | 2. QKt-QB3 (i.e. Queen’s Knight to the third square of the Queen’s Bishop’s file) |
| 3. KB-QB4 (King’s Bishop to the fourth square of the Queen’s Bishop’s file) | 3. KB-QB4 |
| 4. P-QB3 | 4. KKt-KB3 |
| 5. P-Q4 | 5. P takes P (or PxP) (King’s pawn takes White’s Queen’s pawn) |
| 6. P takes P (or PxP) (Queen’s Bishop’s pawn takes pawn: no other pawn has a pawn en prise) | 6. KB-QKt5 (ch., i.e. check) |
It is now usual to express the notation as concisely as possible; thus, the third moves of White and Black would be given as 3. B-B4, because it is clear that only the fourth square of the queen’s bishop’s file is intended.
The French names for the pieces are, King, Roi; Queen, Dame; Rook, Tour; Knight, Cavalier; Pawn, Pion; for Bishop the French substitute Fou, a jester. Chess is Les Échecs.
The German notation employs the alphabetical characters a, b, c, d, e, f, g and h, proceeding from left to right, and the numerals 1, 2, 3, 4, 5, 6, 7 and 8, running upwards, these being always calculated from the white side of the board (see diagram 2). Thus the White Queen’s Rook’s square is a1, the White Queen’s square is d1; the Black Queen’s square, d8; the White King’s square, e1; the Black King’s square, e8, and so with the other pieces and squares. The German names of the pieces are as follows:—King, König; Queen, Dame; Rook, Turm; Bishop, Läufer; Knight, Springer; Pawn, Bauer; Chess, Schach.
The initials only of the pieces are given, the pawns (Bauern) being understood. The Germans use the following signs in their notation, viz.:—for “check” (†); “checkmate” (‡); “takes” (:); “castles on king’s side” (0-0); “castles on queen’s side” (0-0-0); for “best move” a note of admiration (!); for “weak move” a note of interrogation (?). The opening moves just given in the English will now be given in the German notation:—
| White. | Black. |
| 1. e2 - e4 | 1. e7 - e5 |
| 2. S g1 - f3 | 2. S b8 - c6 |
| 3. L f1 - c4 | 3. L f8 - c5 |
| 4. c2 - c3 | 4. S g8 - f6! |
| 5. d2 - d4 | 5. e5 - d4: |
| 6. c3 - d4: | 6. L cs - b4† |
In both notations the moves are often given in a tabular form, thus:—
| 1. | P - K4 | 1. | e2 - e4 | , |
| P - K4 | e7 - e5 |
the moves above the line being White’s and below the line Black’s.
Illustrative Games.—The text-books should be consulted by students who wish to improve their game. The following are some of the leading openings:—
Giuoco Piano.
| White. | Black. |
| 1. P - K4 | 1. P - K4 |
| 2. KKt - B3 | 2. QKt - B3 |
| 3. B - B4 | 3. B - B4 |
| 4. P - B3 | 4. Kt - KB3 |
| 5. P - Q4 | 5. P × P |
| 6. P × P | 6. B - Kt5 (ch) |
| 7. B - Q2 | 7. B × B (ch) |
| 8. QKt × B | 8. P - Q4 |
| 9. P × P | 9. KKt × P |
| 10. Q - Kt3 | 10. QKt - K2 |
| 11. Castles (K’s side) | 11. Castles |
Even game.
Ruy Lopez.
| White. | Black. |
| 1. P - K4 | 1. P - K4 |
| 2. KKt - B3 | 2. QKt - B3 |
| 3. B - Kt5 | 3. P - QR3 |
| 4. B - R4 | 4. Kt - B3 |
| 5. P - Q4 | 5. P × P |
| 6. P - K5 | 6. Kt - K5 |
| 7. Castles | 7. B - K2 |
| 8. R - K sq | 8. Kt - B4 |
| 9. B × Kt | 9. QP × B |
| 10. Kt × P | 10. Castles |
| 11. Kt - QB3 | 11. P - KB3 |
Even game.
Scotch Gambit.
| White. | Black. |
| 1. P - K4 | 1. P - K4 |
| 2. KKt - B3 | 2. QKt - B3 |
| 3. P - Q4 | 3. P × P |
| 4. B - QB4 | 4. B - B4 |
| 5. P - B3 | 5. Kt - B3 |
| 6. P × P |
The position here arrived at is the same as in the Giuoco Piano opening above.
Evans Gambit.
| White. | Black. |
| 1. P - K4 | 1. P - K4 |
| 2. KKt - B3 | 2. QKt - B3 |
| 3. B - B4 | 3. B - B4 |
| 4. P - QKt4 | 4. B × KtP |
| 5. P - B3 | 5. B - B4 |
| 6. P - Q4 | 6. P × P |
| 7. Castles | 7. P - Q3 |
| 8. P × P | 8. B - Kt3 |
White has for its ninth move three approved continuations, viz. B-Kt2, P-Q5, and Kt-B3. To take one of them:—
| 9. P - Q5 | 9. Kt - R4 |
| 10. B - Kt2 | 10. Kt - K2 |
| 11. B - Q3 | 11. Castles |
| 12. Kt - B3 | 12. Kt - Kt3 |
| 13. Kt - K2 | 13. P - QB4 |
| 14. Q - Q2 | 14. P - B3 |
| 15. K - R sq | 15. B - B2 |
| 16. QR - B sq | 16. R - Kt sq |
This game may be considered about even.
King’s Knight’s Gambit (Proper).
| White. | Black. |
| 1. P - K4 | 1. P - K4 |
| 2. P - KB4 | 2. P × P |
| 3. KKt - B3 | 3. P - KKt4 |
| 4. B - B4 | 4. B - Kt2 |
| 5. Castles | 5. P - Q3 |
| 6. P - Q4 | 6. P - KR3 |
| 7. P - B3 | 7. Kt - K2 |
Black has the advantage.
Allgaier-kieseritzki Gambit.
| White. | Black. |
| 1. P - K4 | 1. P - K4 |
| 2. P - KB4 | 2. P × P |
| 3. Kt - KB3 | 3. P - KKt4 |
| 4. P - KR4 | 4. P - Kt5 |
| 5. Kt - K5 | 5. KKt - B3 |
| 6. B - B4 | 6. P - Q4 |
| 7. P × P | 7. B - Kt2 |
| 8. P - Q4 | 8. Castles |
| 9. B × P | 9. Kt × P |
| 10. B × Kt | 10. Q × B |
| 11. Castles | 11. P - QB4 |
Black has the better game.
King’s Bishop’s Gambit.
| White. | Black. |
| 1. P - K4 | 1. P - K4 |
| 2. P - KB4 | 2. P × P |
| 3. B - B4 | 3. P - Q4 |
| 4. B × P | 4. Q - R5 (ch) |
| 5. K - B sq | 5. P - KKt4 |
| 6. KKt - B3 | 6. Q - R4 |
| 7. P - Q4 | 7. B - Kt2 |
| 8. P - KR4 | 8. P - KR3 |
| 9. Kt - B3 | 9. Kt - K2 |
| 10. K - Kt sq | 10. P - Kt5 |
| 11. Kt - K5 | 11. B × Kt |
| 12. P × B | 12. Q × KP |
| 13. Q - B sq | 13. P - B6 |
| 14. P - P | 14. Q - Kt6 (ch) |
| 15. Q - Kt2 |
Drawn game.
Salvio Gambit.
| White. | Black. |
| 1. P - K4 | 1. P - K4 |
| 2. P - KB4 | 2. P × P |
| 3. KKt - B3 | 3. P - KKt4 |
| 4. B - B4 | 4. P - Kt5 |
| 5. Kt - K5 | 5. Q - R5 (ch) |
| 6. K - B sq | 6. Kt - KR3 |
| 7. P - Q4 | 7. P - B6 |
| 8. Kt - QB3 | 8. P - Q3 |
| 9. Kt - Q3 | 9. P × P (ch) |
| 10. K × P | 10. B - Kt2 |
| 11. Kt - KB4 | 11. Kt - B3 |
| 12. B - K3 | 12. Castles |
| 13. QKt - Q5 | 13. Q - Q sq |
| 14. P - B3 |
White has a slight advantage.
Muzio Gambit.
| 1. | P - K4 | 2. | P - KB4 | 3. | KKt - B3 | 4. | B - B4 |
| P - K4 | P × P | P - KKt4 | P - Kt5 |
| White. | Black. |
| 5. Castles | 5. P × Kt |
| 6. Q × P | 6. Q - B3 |
| 7. P - K5 | 7. Q × P |
| 8. P - Q3 | 8. B - R3 |
| 9. B - Q2 | 9. Kt - K2 |
| 10. Kt - B3 | 10. QKt - B3 |
| 11. QR - K sq | 11. Q - KB4 |
| 12. R - K4 | 12. Castles |
| 13. QB × P | 13. B - Kt2 |
| 14. Q - K2 | 14. P - Q4 |
| 15. B × BP | 15. Q - Kt4 |
| 16. P - KR4 | 16. Q - Kt3 |
| 17. Kt × P | 17. Kt × Kt |
| 18. B × Kt | 18. B - B4 |
| 19. QR - KB4 | 19. B - K3 |
| 20. B × B | 20. P × B |
| 21. R - K4 | 21. R × R (ch) |
| 22. K × R | 22. R - B sq (ch) |
| 23. K - Kt sq | 23. Kt - Q5 |
And Black has the better game.
Queen’s Gambit.
| White. | Black. |
| 1. P - Q4 | 1. P - Q4 |
| 2. P - QB4 | 2. P × P |
| 3. P - K3 | 3. P - K4 |
| 4. B × P | 4. P × P |
| 5. P × P | 5. B - Q3 |
| 6. Kt - KB3 | 6. Kt - KB3 |
| 7. Castles | 7. Castles |
| 8. P - KR3 | 8. P - KR3 |
| 9. Kt - QB3 | 9. P - QB3 |
The game is about equal, though White has a somewhat freer position.
The following is a selection of noteworthy games played by great masters:—
King’s Bishop’s Gambit.
| White. Anderssen. | Black. Kieseritzki. |
| 1. P - K4 | 1. P - K4 |
| 2. P - KB4 | 2. P × P |
| 3. B - B4 | 3. Q - R5 (ch) |
| 4. K - B sq | 4. P - QKt4 |
| 5. B × KtP | 5. Kt - KB3 |
| 6. Kt - KB3 | 6. Q - R3 |
| 7. P - Q3 | 7. Kt - R4 |
| 8. Kt - R4 | 8. Q - Kt4 |
| 9. Kt - B5 | 9. P - QB3 |
| 10. P - KKt4 | 10. Kt - B3 |
| 11. R - Kt sq | 11. P × B |
| 12. P - KR4 | 12. Q - Kt3 |
| 13. P - R5 | 13. Q - Kt4 |
| 14. Q - B3 | 14. Kt - Kt sq |
| 15. B × P | 15. Q - B3 |
| 16. Kt - B3 | 16. B - B4 |
| 17. Kt - Q5 | 17. Q × KtP |
| 18. B - Q6 | 18. Q × R (ch) |
| 19. K - K2 | 19. B × R |
| 20. P - K5 | 20. Kt - QR3 |
White mates in three moves.
Philidor’S Defence.
| White. Barnes. | Black. Morphy. |
| 1. P - K4 | 1. P - K4 |
| 2. Kt - KB3 | 2. P - Q3 |
| 3. P - Q4 | 3. P - KB4 |
| 4. P × KP | 4. BP × P |
| 5. Kt - Kt5 | 5. P - Q4 |
| 6. P - K6 | 6. B - QB4 |
| 7. Kt - B7 | 7. Q - B3 |
| 8. B - K3 | 8. P - Q5 |
| 9. B - KKt5 | 9. Q - B4 |
| 10. Kt × R | 10. Q × B |
| 11. B - B4 | 11. Kt - QB3 |
| 12. Kt - B7 | 12. Q × P |
| 13. R - B sq | 13. Kt - B3 |
| 14. P - KB3 | 14. Kt - QKt5 |
| 15. Kt - QR3 | 15. B × P |
| 16. B × B | 16. Kt - Q6 (ch) |
| 17. Q × Kt | 17. P × Q |
| 18. Castles | 18. B × Kt |
| 19. B - Kt3 | 19. P - Q7 (ch) |
| 20. K - Kt sq | 20. B - B4 |
| 21. Kt - K5 | 21. K - B sq |
| 22. Kt - Q3 | 22. R - K sq |
| 23. Kt × B | 23. Q × R |
And White resigns.
BISHOP’S GAMBIT.
| White. Charousek. | Black. Tchigorin. |
White. Charousek. | Black. Tchigorin. |
| 1. P - K4 | P - K4 | 13. Q × P (ch) | K - K2 |
| 2. P - KB4 | P × P | 14. Kt × P | Kt × Kt |
| 3. B - B4 | Kt - QB3 | 15. B × Kt | P - R3 |
| 4. P - Q4 | Kt - B3 | 16. Kt - B3 | B - B5 |
| 5. P - K5 | P - Q4 | 17. P - K6 | R - B sq |
| 6. B - Kt3 | B - Kt5 | 18. B - B7 | P × P |
| 7. Q - Q3 | Kt - KR4 | 19. B × Q (ch) | R × B |
| 8. Kt - KR3 | Kt - Kt5 | 20. Q - Kt7 (ch) | R - Q2 |
| 9. Q - QB3 | Kt - R3 | 21. R - B7 (ch) | K × R |
| 10. Castles | B - K7 | 22. Q × R (ch) | B - K2 |
| 11. B - R4 (ch) | P - B3 | 23. R - K sq | R - K sq |
| 12. B × P (ch) | P × B | 24. P - QKt3 | Resigns. |
This pretty game was played in the tie match for first prize at the Budapest tournament, 1896.
Queen’s Gambit Declined.
| White. W. Steinitz. | Black. Dr E. Lasker. |
White. W. Steinitz. | Black. Dr E. Lasker. |
| 1. P - Q4 | P - Q4 | 21. Kt - B3 | Kt - Q5 |
| 2. P - QB4 | P - K3 | 22. Q × P | Kt × B (ch) |
| 3. Kt - QB3 | Kt - KB3 | 23. P × Kt | R - Kt sq |
| 4. B - B4 | B - K2 | 24. Q × P | R - Kt3 |
| 5. P - K3 | Castles | 25. Q - B4 | R × P |
| 6. R - B sq | P - B4 | 26. P - KR4 | B - R2 |
| 7. QP × P | B × P | 27. B - K4 | Q - Q3 |
| 8. P × P | P × P | 28. P - B4 | Q - Q2 |
| 9. Kt - B3 | Kt - B3 | 29. B - Kt2 | Q - Kt5 |
| 10. B - Q3 | P - Q5 | 30. Q - Q3 | Kt - B4 |
| 11. P × P | Kt × P | 31. Kt - K4 | B - K6 |
| 12. Castles | B - KKt5 | 32. R - B3 | R × B |
| 13. Kt - QKt5 | B × Kt | 33. K × R | Kt × P (ch) |
| 14. P - B | Kt - K3 | 34. K - R2 | Kt × R (ch) |
| 15. B - K5 | Kt - R4 | 35. K - Kt2 | Kt - R5 (ch) |
| 16. K - R sq | Q - Kt4 | 36. K - R2 | Kt - B4 |
| 17. B - Kt3 | QR - Q sq | 37. R - QKt sq | P - R4 |
| 18. Q - B2 | Q - R3 | 38. R - Kt5 | R - R sq |
| 19. QR - Q sq | R - B sq | 39. P - R3 | R × P |
| 20. Q - Kt3 | P - R3 | Resigns. |
This game was played in the St Petersburg tournament, 1895, a fine specimen of Lasker’s style. The final attack, beginning with 21. with Kt - Q5, furnishes a gem of an ending.
Rice Gambit.
| White. Professor Rice. | Black. Major Hanham. |
White. Professor Rice. | Black. Major Hanham. |
| 1. P - K4 | P - K4 | 15. Q - R3 | Kt - B7 |
| 2. P - KB4 | P × P | 16. R × B (ch) | B - K3 |
| 3. Kt - KB3 | P - KKt4 | 17. K - B sq | Q - R8 (ch) |
| 4. P - KR4 | P - Kt5 | 18. Kt - Kt sq | Kt - R6 |
| 5. Kt - K5 | Kt - KB3 | 19. P × Kt | P - B6 |
| 6. B - B4 | P - Q4 | 20. B - Kt5 | Q - Kt7 (ch) |
| 7. P × P | B - Q3 | 21. K - K sq | P - B7 (ch) |
| 8. Castles | B × Kt | 22. K - Q2 | P - B8=Kt (ch) |
| 9. R - K sq | Q - K2 | 23. K - Q3 | K - Q2 |
| 10. P - B3 | P - Kt6 | 24. P × B (ch) | K - B2 |
| 11. P - Q4 | Kt - Kt5 | 25. Q - K7 (ch) | K - Kt3 |
| 12. Kt - Q2 | Q × P | 26. Q - Q8 (ch) | R × Q |
| 13. Kt - B3 | Q - R3 | 27. B × Q and mates | |
| 14. Q - R4 (ch) | P - B3 |
The Rice Gambit (so called after its inventor, Prof. Isaac L. Rice of New York), whether right or not, is only possible if Black plays 7. B - Q3. Paulsen’s 7. B - Kt2 is better, and avoids unnecessary complications. 8. P - Q4 is the usual move. Leaving the knight en prise, followed by 9. R - K sq, constitutes the Rice Gambit. The interesting points in the game are that White subjects himself to a most violent attack with impunity, for in the end Black could not save the game by 22. P - B8 claiming a second queen with a discovered check, nor by claiming a knight with double check, as it is equally harmless to White.
Giuoco Piano.
| White. Steinitz. | Black. Bardeleben. |
White. Steinitz. | Black. Bardeleben. |
| 1. P - K4 | P - K4 | 14. R - K sq | P - KB3 |
| 2. Kt - KB3 | Kt - QB3 | 15. Q - K2 | Q - Q2 |
| 3. B - B4 | B - B4 | 16. QR - B sq | P - B3 |
| 4. P - B3 | Kt - B3 | 17. P - Q5 | P × P |
| 5. P - Q4 | P × P | 18. Kt - Q4 | K - B2 |
| 6. P × P | B - Kt5 (ch) | 19. Kt - K6 | KR - QB sq |
| 7. Kt - B3 | P - Q4 | 20. Q - Kt4 | P - KKt3 |
| 8. P × P | KKt × P | 21. Kt - Kt5 (ch) | K - K sq |
| 9. Castles | B - K3 | 22. R × Kt (ch) | K - B sq |
| 10. B - KKt5 | B - K2 | 23. R - B7 (ch) | K - Kt sq |
| 11. B × Kt | QB × B | 24. R - Kt7 (ch) | K - R sq |
| 12. Kt × B | Q × Kt | 25. R × P (ch) | Resigns. |
| 13. B × B | Kt × B |
As a matter of fact, Bardeleben left the board here, and lost the game by letting his clock run out the time-limit; but Steinitz, who remained at the board, demonstrated afterwards the following variation leading to a forced win:—
| White. Steinitz. | Black. Bardeleben. |
White. Steinitz. | Black. Bardeleben. |
| 25. . . . . . . | K - Kt sq | 31. Q - Kt8 (ch) | K - K2 |
| 26. R - Kt7 (ch) | K - R sq | 32. Q - B7 (ch) | K - Q sq |
| 27. Q - R4 (ch) | K × R | 33. Q - B8 (ch) | Q - K sq |
| 28. Q - R7 (ch) | K - B sq | 34. Kt - B7 (ch) | K - Q2 |
| 29. Q - R8 (ch) | K - K2 | 35. Q - Q6 mate. | |
| 30. Q - Kt7 (ch) | K - K sq |
This game was awarded the prize for “brilliancy” at the Hastings tournament, 1895.
Ruy Lopez.
| White. Halprin. | Black. Pillsbury. |
White. Halprin. | Black. Pillsbury. |
| 1. P - K4 | P - K4 | 14. P - Kt6 | BP × P |
| 2. Kt - KB3 | Kt - QB3 | 15. Kt - Q5 | P × Kt |
| 3. B - Kt5 | Kt - B3 | 16. KR - K sq (ch) | K - B sq |
| 4. Castles | Kt × P | 17. R - R3 | Kt - K4 |
| 5. P - Q4 | Kt - Q3 | 18. R × Kt | P × R |
| 6. P × P | Kt × B | 19. R - B3 (ch) | K - Kt sq |
| 7. P - QR4 | P - Q3 | 20. B - R6 | Q - K2 |
| 8. P - K6 | P × P | 21. B × P | K × B |
| 9. P × Kt | Kt - K2 | 22. R - Kt3 (ch) | K - B sq |
| 10. Kt - B3 | Kt - Kt3 | 23. R - B3 (ch) | K - Kt2 |
| 11. Kt - Kt5 | B - K2 | 24. R - Kt3 (ch) | K - B sq |
| 12. Q - R5 | B × Kt | 25. R - B3 (ch) | K - Kt sq |
| 13. B × B | Q - Q2 | Draw. | |
This brilliant game, played at the Munich tournament, 1900, would be unique had the combinations occurred spontaneously in the game. As a matter of fact, however, the whole variation had been elaborated by Maroczy and Halprin previously, on the chance of Pillsbury adopting the defence in the text. The real merit belongs to Pillsbury, who had to find the correct defence to an attack which Halprin had committed to memory and simply had to be careful to make the moves in regular order.
Sicilian Defence.
| White. Pillsbury. | Black. Mieses. |
White. Pillsbury. | Black. Mieses. |
| 1. P - K4 | P - QB4 | 16. P × P | Kt - Q5 |
| 2. Kt - KB3 | P - K3 | 17. B × R | K × B |
| 3. P - Q4 | P × P | 18. R - R2 | B - K3 |
| 4. Kt × P | Kt - KB3 | 19. R - Q2 | R - K sq |
| 5. Kt - QB3 | Kt - B3 | 20. Castles | B - Kt6 |
| 6. KKt - Kt5 | B - Kt5 | 21. Q - Kt sq | B - Q4 |
| 7. P - QR3 | B × Kt (ch) | 22. B - Q sq | B × P |
| 8. Kt × B | P - Q4 | 23. K × B | Q - Kt4 (ch) |
| 9. P × P | P × P | 24. K - R sq | Q × R |
| 10. B - KKt5 | Castles | 25. B - Kt4 | Q - B5 |
| 11. B - K2 | P - Q5 | 26. R - Kt sq | P - B4 |
| 12. Kt - K4 | Q - R4 (ch) | 27. B - R5 | Kt - B6 |
| 13. P - Kt4 | Q - K4 | 28. B × Kt | Q × B (ch) |
| 14. Kt × Kt (ch) | P × Kt | 29. R - Kt2 | R - K7 |
| 15. B - R6 | P - Q6 | 30. Q - QB sq | Q × QP |
Drawn eventually.
This brilliant game occurred at the Paris tournament, 1900.
Evans Gambit.
| White. Anderssen. | Black. Dufresne. |
White. Anderssen. | Black. Dufresne. |
| 1. P - K4 | P - K4 | 13. Q - R4 | B - Kt3 |
| 2. Kt - KB3 | Kt - QB3 | 14. QKt - Q2 | B - Kt2 |
| 3. B - B4 | B - B4 | 15. Kt - K4 | Q - B4 |
| 4. P - QKt4 | B × P | 16. B × P | Q - R4 |
| 5. P - B3 | B - R4 | 17. Kt - B6 (ch) | P × Kt |
| 6. P - Q4 | P × P | 18. P × P | R - Kt sq |
| 7. Castles | P - Q6 | 19. QR - Q sq | Q × Kt |
| 8. Q - Kt3 | Q - B3 | 20. R × Kt (ch) | Kt × R |
| 9. P - K5 | Q - Kt3 | 21. Q × P (ch) | K × Q |
| 10. R - K sq | KKt - K2 | 22. B - B5 (ch) | K - K sq |
| 11. B - R3 | P - Kt4 | 23. B - Q7 (ch) | K moves |
| 12. Q × P | R - QKt sq | 24. B × Kt mate. |
This game is most remarkable and brilliant. The coup de repos of 19. QR - Q sq is the key - move to the brilliant final combination, the depth and subtlety of which have never been equalled, except perhaps in the following game between Zukertort and Blackburne:—
English Opening.
| White. Zukertort. | Black. Blackburne. |
White. Zukertort. | Black. Blackburne. |
| 1. P - QB4 | P - K3 | 18. P - K4 | QR - QB sq |
| 2. P - K3 | Kt - KB3 | 19. P - K5 | Kt - K sq |
| 3. Kt - KB3 | P - QKt3 | 20. P - B4 | P - Kt3 |
| 4. B - K2 | B - Kt2 | 21. R - K3 | P - B4 |
| 5. Castles | P - Q4 | 22. P × P e.p. | Kt × P |
| 6. P - Q4 | B - Q3 | 23. P - B5 | Kt - K5 |
| 7. Kt - B3 | Castles | 24. B × Kt | P × B |
| 8. P - QKt3 | QKt - Q2 | 25. P × KtP | R - B7 |
| 9. B - Kt2 | Q - K2 | 26. P × P (ch) | K - R sq |
| 10. Kt - QKt5 | Kt - K5 | 27. P - Q5 dis. (ch) | P - K4. |
| 11. Kt × B | P × Kt | 28. Q - Kt4 | QR - B4 |
| 12. Kt - Q2 | QKt - B3 | 29. R - B8 (ch) | K × P |
| 13. P - B3 | Kt × Kt | 30. Q × P (ch) | K - Kt2 |
| 14. Q × Kt | P × P | 31. B × P (ch) | K × R |
| 15. B × P | P - Q4 | 32. B - Kt7 (ch) | K - Kt sq |
| 16. B - Q3 | KR - B sq | 33. Q × Q | Resigns. |
| 17. QR - K sq | R - B2 |
This game, played in the London tournament, 1883, is one of the most remarkable productions of modern times, neither surpassed nor indeed equalled hitherto.
End Games.—A game of chess consists of three branches—the opening, the middle and the end game. The openings have been analysed and are to be acquired by the study of the books on the subject. The middle game can only be acquired practically. The combinations being inexhaustible in their variety, individual ingenuity has its full scope. Those endowed with a fertile imagination will evolve plans and combinations leading to favourable issues. The less endowed player, however, is not left quite defenceless; he has necessarily to adopt a different system, namely, to try to find a weak point in the arrangement of his opponent’s forces and concentrate his attack on that weak spot. As a matter of fact, in a contest between players of equal strength, finding the weak point in the opponent’s armour is the only possible plan, and this may be said to be the fundamental principle of the modern school. In the good old days the battles were mostly fought in the neighbourhood of the king, each side striving for a checkmate. Nowadays the battle may be fought anywhere. It is quite immaterial where the advantage is gained be it ever so slight. Correct continuation will necessarily increase it, and the opponent may be compelled to surrender in the end game without being checkmated, or a position may be reached when the enemies, in consequence of the continual fight, are so reduced that the kings themselves have to take the field—the end game. The end game, therefore, requires a special study. It has its special laws and the value of the pieces undergoes a considerable change. The kings leave their passive rôle and become attacking forces. The pawns increase in value, whilst that of the pieces may diminish in certain cases. Two knights, for instance, without pawns, become valueless, as no checkmate can be effected with them. In the majority of cases the players must be guided by general principles, as the standard examples do not meet all-cases.
The handbooks as a rule give a sprinkling of elementary endings, such as to checkmate with queen, rook, bishop and knight, two bishops, and pawn endings pure and simple, as well as pawns in connexion with pieces in various forms. Towards the end of the 19th century a valuable work on end games was published in England by the late B. Horwitz; thus for the first time a theoretical classification of the art was given. This was followed by a more comprehensive work by Professor J. Berger of Gratz, which was translated a few years later by the late Mr Freeborough.
A few specimens of the less accessible positions are given below:—
Position from a Game played by the late J.G. Campbell in 1863.

Obviously White has to lose the game, not being able to prevent the pawns from queening. By a remarkably ingenious device White averts the loss of the game by stalemating himself as follows:—
1. B - Q2, P - Kt7; 2. B - R5, P - Kt8 = Q; 3. P - Kt4 stalemate.
| Position by Sarratt, 1808. |
 |
White wins as follows:—
1. P - Kt6, RP × P; 2. P - B6, P(Kt2) × P; 3. P - R6 and wins by queening the pawn. If 1. ... BPXP then 2. P - R6, KtPXP; 3-P-B6 and queens the pawn.
Problems.—A chess problem1 has been described as “merely a position supposed to have occurred in a game of chess, being none other than the critical point where your antagonist announces checkmate in a given number of moves, no matter what defence you play,” but the above description conveys no idea of the degree to which problem-composing has become a specialized study. Owing its inception, doubtless, to the practice of recording critical phases from actual play, the art of problem composition has so grown in favour as to earn the title of the “poetry” of the game.
| Position by B. Horwitz. |
 |
As a rule the game should be drawn. Supposing by a series of checks White were to compel Black to abandon the pawn, he would move K - R8; Q × P and Black is stale-mate. Therefore the ingenious way to win is:—
1. K - B4, P - B8 = Q ch; K - Kt3 and wins. Or 1. ... K - R8 (threatening P - B8 = Kt); then 2. Q - Q2 preliminary to K - Kt3 now wins.
| Position by B. Horwitz. |
 |
Without Black’s pawn White could only draw. The pawn being on the board, White wins as follows:—
1. Kt - B4, K - Kt sq; 2. Kt (B4) - K3, K - R sq; 3. K - Kt4, K - Kt sq; 4. K - R3, K - R sq; 5. Kt - B4, K - Kt sq; 6. Kt (B4) - Q2, K - R sq; 7. Kt - Kt3 ch, K - Kt sq; 8. Kt - B3 mate.
| Position by B. Horwitz. |
 |
White wins with two pieces against one—a rare occurrence.
1. Kt - K6, B - R3; 2. B - Q4 ch, K - R2; 3. B - B3, B moves anywhere not en prise; 4. B - Kt7 and Kt mates.
| Position by O. Schubert. |
 |
White wins as follows:—
1. P - Kt5, Kt - Kt5; 2. K - B3, Kt - K6; 3. B - K6, Kt - B8; 4. B × P, Kt - Q7 ch; 5. K - Kt4, Kt × P; 6. P - Kt6, Kt - B3, ch; 7. K - Kt5, P - K5; 8. K × Kt, P - K6; 9. B - B4, K × B; 10. P - Kt7, P - K7; 11. P - Kt8 = Q ch, and wins by the simple process of a series of checks so timed that the king may approach systematically. The fine points in this instructive ending are the two bishop’s moves, 3. B - K6, and 9. B - B4, the latter move enabling White to queen the pawn with a check.
| Position by F. Amelung. |
 |
White with the inferior position saves the game as follows:—
1. P-R6, P × P; 2. K-B3 dis. ch, K moves; 3. R-R2, or Kt2 ch, K × R; 4. K-Kt2 and draw, as Black has to give up the rook, and the RP cannot be queened, the Black bishop having no power on the White diagonal. Extremely subtle.
| Position by B. Horwitz. |
 |
The main idea being to checkmate with the bishop, this is accomplished thus:—1. B-K4 ch, K - R4; 2. Q × R, Q × Q; 3. K - B7, Q - B sq ch; 4. K × Q, BXP; 5. K - B7, B × P; 6. B - Kt6 mate.
| Position by A. Troitzky. |
 |
White wins as follows:—
1. P-R8=Q, R - R7 ch; 2. K - Kt5, R × Q; 3. Kt - Q7 ch, K - Kt2; 4. P - B6 ch, K - R2; 5. QP × Kt, R - R sq; 6. Kt - B8 ch, R × Kt; 7. P × R=Kt mate.
| Position by Hoffer. |
 |
A position from actual play. White plays 1. R-B5 threatening to win a piece. Black replies with the powerful Kt-Kt5, threatening two mates, and finally White (Mr Hoffer) finds an ingenious sacrifice of the Queen—the saving clause.
The following are the moves:—
1. R - B5, Kt - Kt5; 2. Q - Kt8 ch, K - Kt3; 3. Q - K6 ch, K - R2; 4. Q - Kt8 ch, and drawn by perpetual check, as Black cannot capture the Queen with K or R without losing the game.
A good chess problem exemplifies chess strategy idealized and concentrated. In examples of actual play there will necessarily remain on the board pieces immaterial to the issue (checkmate), whereas in problems the composer employs only indispensable force so as to focus attention on the idea, avoiding all material which would tend to “obscure the issue.” Hence the first object in a problem is to extract the maximum of finesse with a sparing use of the pieces, but “economy of force” must be combined with “purity of the mate.” A very common mistake, until comparatively recent years, was that of appraising the “economy” of a position according to the slenderness of the force used, but economy is not a question of absolute values. The true criterion is the ratio of the force employed to the skill demanded. The earliest composers strove to give their productions every appearance of real play, and indeed their compositions 100 partook of the nature of ingenious end-games, in which it was usual to give Black a predominance of force, and to leave the White king in apparent jeopardy. From this predicament he was extricated by a series of checking moves, usually involving a number of brilliant sacrifices. The number of moves was rarely less than five. In the course of time the solutions were reduced to shorter limits and the beauty of quiet (non-checking) moves began to make itself felt. The early transition school, as it has been called, was the first to recognize the importance of economy, i.e. the representation of the main strategic point without any extraneous force. The mode of illustrating single-theme problems, often of depth and beauty, was being constantly improved, and the problems of C. Bayer, R. Willmers, S. Loyd, J.G. Campbell, F. Healey, “J.B.” of Bridport, and W. Grimshaw are, of their kind, unsurpassed. In the year 1845 the “Indian” problem attracted much notice, and in 1861 appeared Healey’s famous “Bristol” problem. To this period must be ascribed the discovery of most of those clever ideas which have been turned to such good account by the later school. In an article written in 1899 F.M. Teed mentions the fact that his incomplete collection of “Indians” totalled over three hundred.
In 1870 or thereabouts, the later transition period, a more general tendency was manifest to illustrate two or more finished ideas in a single problem with strict regard to purity and economy, the theory of the art received greater attention than before and the essays of C. Schwede, Kohtz and Kockelkorn, Lehner and Gelbfuss, helped to codify hitherto unwritten rules of taste. The last quarter of the 19th century, and its last decade especially, saw a marked advance in technique, until it became a common thing to find as much deep and quiet play embodied in a single first-class problem as in three or four of the old-time problems, and hence arose the practice of blending several distinct ideas in one elaborate whole.
In the composition of “two-movers” it is customary to allow greater elasticity and a less rigorous application of the principles of purity and economy. By this means a greater superficial complexity is attained; but the Teutonic and Bohemian schools, and even English and American two-move specialists, recognize that complexity, if it involves the sacrifice of first principles, is liable to abuse. The blind master, A.F. Mackenzie of Jamaica, however, with a few others (notably T. Taverner, W. Gleave, H. and E. Bettman and P.F. Blake) have won some of their greatest successes with problems which, under stricter ruling, would not be allowed.
Bohemian (Czech) composers have long stood unrivalled as exponents of that blending of ideas which is the distinguishing trait of the later problem. Such is their skill in construction that it is rare to find in a problem of the Bohemian school fewer than three or four lines of play which, in economy and purity, are unimpeachable. Amongst the earliest composers of this class Anton König, the founder of the school, Makovky, Drtina, Palct and Pilnacek deserve to be honourably mentioned, but it was not until the starting of a chess column in the weekly journal Svetozor that the merits of the new school were fully asserted. It was in 1871 that Jan Dobrusky contributed his first composition to that paper: he was followed by G. Chocholous, C. Kondelik, Pospisil, Dr Mazel, Kviciala, Kesl, Tuzar, Musil and J. Kotrc; and later still, Havel, Traxler and Z. Mach were no unworthy followers of Dobrusky.
The faculty for blending variations is not without “the defects of its qualities,” and consequently among the less able composers a certain tendency to repeat combinations of similar companion ideas is discernible at times, while the danger that facile construction might usurp the place of originality and strategy was already apparent to Chocholous when, in an article on the classification of chess problems (Deutsche Schachzeitung, 1890), he warned the younger practitioners of the Bohemian school against what has been dubbed by H. Von Gottschall Varianten-leierei, or “the grinding out of variations.” When this one reservation is made few will be inclined to dispute the pre-eminence of the Bohemian school. To some tastes, however, a greater appeal is made by the deeper play of the older German school, the quaint fancy of the American composer Samuel Loyd, or the severity and freedom from “duals” which mark the English composers.
The idea of holding a problem competition open to the world was first mooted in connexion with the chess congress of 1851, but it was in 1854 that a tourney (confined to British composers) was first held. Since then a number of important problem tournaments have been held.
History of Chess.
The origin of chess is lost in obscurity. Its invention has been variously ascribed to the Greeks, Romans, Babylonians, Scythians, Egyptians, Jews, Persians, Chinese, Hindus, Arabians, Araucanians, Castilians, Irish and Welsh. Some have endeavoured to fix upon particular individuals as the originators of the game; amongst others upon Japheth, Shem, King Solomon, the wife of Ravan, king of Ceylon, the philosopher Xerxes, the Greek chieftain Palamedes, Hermes, Aristotle, the brothers Lydo and Tyrrhene, Semiramis, Zenobia, Attalus (d. c. 200 B.C.), the mandarin Hansing, the Brahman Sissa and Shatrenscha, stated to be a celebrated Persian astronomer. Many of these ascriptions are fabulous, others rest upon little authority, and some of them proceed from easily traceable errors, as where the Roman games of Ludus Latrunculorum and Ludus Calculorum, the Welsh recreation of Tawlbwrdd (throw-board) and the ancient Irish pastime of Fithcheall are assumed to be identical with chess; so far as the Romans and Welsh are concerned, the contrary can be proved, while from what little is known of the Irish game it appears not to have been a sedentary game at all. The claims of the Chinese were advocated in a letter addressed by Mr Eyles Irwin in 1793 to the earl Charlemont. This paper was published in the Transactions of the Royal Irish Academy, and its purport was that chess, called in the Chinese tongue chong-ki (the “royal game”) was invented in the reign of Kao-Tsu, otherwise Lin-Pang, then king, but afterwards emperor of Kiang-Nang, by a mandarin named Han-sing, who was in command of an army invading the Shen-Si country, and who wanted to amuse his soldiers when in winter quarters. This invasion of the Shen-Si country by Han-Sing took place about 174 B.C. Capt. Hiram Cox states that the game is called by the Chinese choke-choo-hong ki, “the play of the science of war.” (See also a paper published by the Hon. Daines Barrington in the 9th vol. of the Archaeologia.) Mr N. Bland, M.R.A.S., in his Persian Chess (London, 1850), endeavours to prove that the Persians were the inventors of chess, and maintains that the game, born in Persia, found a home in India, whence after a series of ages it was brought back to its birthplace. The view, however, which has obtained the most credence, is that which attributes the origin of chess to the Hindus. Dr Thomas Hyde of Oxford, writing in 1694 (De Ludis Orientalibus), seems to have been the first to propound this theory, but he appears to have been ignorant of the game itself, and the Sanskrit records were not accessible in his time. About 1783-1789 Sir William Jones, in an essay published in the 2nd vol. of Asiatic Researches, argued that Hindustan was the cradle of chess, the game having been known there from time immemorial by the name of chaturanga, that is, the four angas, or members of an army, which are said in the Amarakosha to be elephants, horses, chariots and foot soldiers. As applicable to real armies, the term chaturanga is frequently used by the epic poets of India. Sir William Jones’s essay is substantially a translation of the Bhawishya Purana, in which is given a description of a four-handed game of chess played with dice. A pundit named Rhadhakant informed him that this was mentioned in the oldest law books, and also that it was invented by the wife of Ravan, king of Lanka (Ceylon), in the second age of the world in order to amuse that monarch while Rama was besieging his metropolis. This account claims for chess an existence of 4000 or 5000 years. Sir William, however, grounds his opinions as to the Hindu origin of chess upon the testimony of the Persians and not upon the above manuscript, while he considers the game described therein to be more modern than the Persian game. Though sure that the latter came from India and was invented there, he admits that he could not find any account 101 of it in the classical writings of the Brahmans. He lays it down that chess, under the Sanskrit name chaturanga, was exported from India into Persia in the 6th century of our era; that by a natural corruption the old Persians changed the name into chatrang, but when their country was soon afterwards taken possession of by the Arabs, who had neither the initial nor final letter of the word in their alphabet, they altered it further into shatranj, which name found its way presently into modern Persian and ultimately into the dialects of India.
Capt. Hiram Cox, in a letter upon Burmese chess, written in 1799 and published in the 7th vol. of Asiatic Researches, refers to the above essay, and considers the four-handed game described in the Sanskrit manuscript to be the most ancient form of chess, the Burmese and Persian games being second and third in order of precedence. Later, in the 11th and 24th vols. of the Archaeologia, Mr Francis Douce and Sir Frederick Madden expressed themselves in favour of the views held by Hyde and his followers.
In Professor Duncan Forbes’s History of Chess (1860) Capt. Cox’s views, as founded upon Sir William Jones’s Sanskrit manuscript, are upheld and are developed into an elaborate theory. Professor Forbes holds that the four-handed game of chaturanga described in the Bhawishya Purana was the primeval form of chess; that it was invented by a people whose language was Sanskrit (the Hindus); and that it was known and practised in India from a time lost in the depths of a remote antiquity, but for a period the duration of which may have been from 3000 to 4000 years before the 6th century of the Christian era. He endeavours to show, but adduces no proof, how the four armies commanded by four kings in Sir William Jones’s manuscript became converted into two opposing armies, and how two of the kings were reduced to a subordinate position, and became “monitors” or “counsellors,” one standing by the side of the White and the other of the Black king, these counsellors being the farzins from which we derive our “queens.” Among other points he argues, apparently with justice, that chaturanga was evidently the root of shatranj, the latter word being a mere exotic in the language of the inhabitants of Persia.
Van der Linde, in his exhaustive work, Geschichte und Litteratur des Schachspiels (Berlin, 1874), has much to say of the origin-theories, nearly all of which he treats as so many myths. He agrees with those who consider that the Persians received the game from the Hindus; but the elaborate chaturanga theories of Forbes receive but scant mercy. Van der Linde argues that chaturanga is always used by the old Indian poets of an army and never of a game, that all Sanskrit scholars are agreed that chess is not mentioned in really ancient Hindu records; that the Puranas generally, though formerly considered to be extremely old, are held in the light of modern research to reach no farther back than the 10th century—while the copies of the Bhawishya Purana in the British Museum and the Berlin Library do not contain the extract relied upon by Forbes, though it is to be found in the Raghunandana, which was translated by Weber in 1872, and is stated by Bühler to date from the 16th century. The outcome of van der Linde’s studies appears to be that chess certainly existed in Hindustan in the 8th century, and that probably that country is the land of its birth. He inclines to the idea that the game originated among the Buddhists, whose religion was prevalent in India from the 3rd to the 9th century. According to their ideas, war and the slaying of one’s fellow-men, for any purposes whatever, is criminal, and the punishment of the warrior in the next world will be much worse than that of the simple murderer; hence chess was invented as a substitute for war. In opposition to Forbes, therefore, and in agreement with Sir William Jones, van der Linde takes the view that the four-handed game of the original manuscript is a comparatively modern adaptation of the Hindu chess, and he altogether denies that there is any proof that any form of the game has the antiquity attributed to it. Internal evidence certainly seems to contradict the theory that Sir William Jones’s manuscript is very ancient testimony; for it mentions two great sages, Vyasa and Gotama, the former as teaching chaturanga to Prince Yudhishthira, and the other as giving an opinion upon certain principles of the game; but this could not well be, seeing that it was played with dice, and that all games of hazard were positively forbidden by Manu. It would appear also that Indian manuscripts are not absolutely trustworthy as evidence of the antiquity of their contents; for the climate has the effect of destroying such writings in a period of 300 or 400 years. They must, therefore, be recopied from time to time and in this way later interpolations may easily creep in.
Von der Lasa, who had, in an article prefixed to the Handbuch in 1864, accepted Forbes’s views, withdrew his support in a review of the work just noticed, published in the September and November numbers of the Deutsche Schachzeitung, 1874, and expressed his adherence to the opinions of van der Linde.
Altogether, therefore, we find the best authorities agreeing that chess existed in India before it is known to have been played anywhere else. In this supposition they are strengthened by the names of the game and of some of the pieces. Shatranj, as Forbes has pointed out, is a foreign word among the Persians and Arabians, whereas its natural derivation from the term chaturanga is obvious. Again al-fil, the Arabic name of the bishop, means the elephant, otherwise alephhind, the Indian ox. Our earliest authority on chess is Masudi, an Arabic author who wrote about A.D. 950. According to him, shatranj had existed long before his time; and though he may speak not only for his own generation but for a couple of centuries before, that will give to chess an existence of over a thousand years.
Early and Medieval Times.—The dimness which shrouds the origin of chess naturally obscures also its early history. We have seen that chess crossed over from India into Persia, and became known in the latter country by the name of shatranj. Some have understood that word to mean “the play of the king”; but undoubtedly Sir William Jones’s derivation carries with it the most plausibility. How and when the game was introduced into Persia we have no means of knowing. The Persian poet Firdusi, in his historical poem, the Shahnama, gives an account of the introduction of shatranj into Persia in the reign of Chosroes I. Anushirwan, to whom came ambassadors from the sovereign of Hind (India), with a chessboard and men asking him to solve the secrets of the game, if he could, or pay tribute. Chosroes I. was the contemporary of Justinian, and reigned in the 6th century A.D. Professor Forbes seems to think that this poem may be looked upon as an authentic history. This appears, however, to be somewhat dangerous, especially as Firdusi lived some 450 years after the supposed event took place; but since other Persian and Arabian writers state that shatranj came into Persia from India, there appears to be a consensus of opinion that may be considered to settle the question. Thus we have the game passing from the Hindus to the Persians and thence to the Arabians, after the capture of Persia by the Caliphs in the 7th century, and from them, directly or indirectly, to various parts of Europe, at a time which cannot be definitely fixed, but either in or before the 11th century. That the source of the European game is Arabic is clear enough, not merely from the words “check” and “mate,” which are evidently from Shah mat (“the king is dead”), but also from the names of some of the pieces. There are various chess legends having reference to the 7th and 8th centuries, but these may be neglected as historically useless; and equally useless appear the many oriental and occidental romances which revolve around those two great central figures, Harun al-Rashid and Charlemagne. There is no proof that either of them knew anything of chess or, so far as the latter is concerned, that it had been introduced into Europe in his time. True, there is an account given in Gustavus Selenus, taken from various old chronicles, as to the son of Prince Okar or Otkar of Bavaria having been killed by a blow on the temple, struck by a son of Pippin after a game of chess; and there is another well-known tradition as to the magnificent chess-board and set of men said to have been sent over as a present by the empress Irene to Charlemagne. But both tales are not less mythical than the romance which relates how the great Frankish monarch lost his kingdom over a game of chess to Guérin de Montglave; for van der Linde shows that there was no Bavarian prince of the name of Okar or Otkar at the period alluded to, and as ruthlessly shatters the 102 tradition about Irene’s chessmen. With respect to Harun al-Rashid, among the various stories told which connect him with chess, there is one that at first sight may seem entitled to some degree of credit. In the annals of the Moslems by Abulfeda (Abu’l Fida), there is given a copy of a letter stated to be “From Nicephorus, emperor of the Romans, to Harun, sovereign of the Arabs,” which (using Professor Forbes’s translation) after the usual compliments runs thus:—“The empress (Irene) into whose place I have succeeded, looked upon you as a Rukh and herself as a mere Pawn; therefore she submitted to pay you a tribute more than the double of which she ought to have exacted from you. All this has been owing to female weakness and timidity. Now, however, I insist that you, immediately on reading this letter, repay to me all the sums of money you ever received from her. If you hesitate, the sword shall settle our accounts.” Harun’s reply, written on the back of the Byzantine emperor’s letter, was terse and to the point. “In the name of God the merciful and gracious. From Harun, the commander of the faithful, to the Roman dog Nicephorus. I have read thine epistle, thou son of an infidel mother; my answer to it thou shalt see, not hear.” Harun was as good as his word, for he marched immediately as far as Heraclea, devastating the Roman territories with fire and sword, and soon compelled Nicephorus to sue for peace. Now the points which give authority to this narrative and the alleged correspondence are that the relations which they assume between Irene and Nicephorus on the one hand and the warlike caliph on the other are confirmed by the history of those times, while, also, the straightforward brevity of Harun’s reply commends itself as what one might expect from his soldier-like character. Still, the fact must be remembered that Abulfeda lived about five centuries after the time to which he refers. Perhaps we may assume that it is not improbable that the correspondence is genuine; but that the words rukh and pawn may have been substituted for other terms of comparison originally used.
As to how chess was introduced into western and central Europe nothing is really known. The Spaniards very likely received it from their Moslem conquerors, the Italians not improbably from the Byzantines, and in either case it would pass northwards to France, going on thence to Scandinavia and England. Some say that chess was introduced into Europe at the time of the Crusades, the theory being that the Christian warriors learned to play it at Constantinople. This is negatived by a curious epistle of St Peter Damian, cardinal bishop of Ostia, to Pope Alexander II., written about A.D. 1061, which, assuming its authenticity, shows that chess was known in Italy before the date of the first crusade. The cardinal, as it seems, had imposed a penance upon a bishop whom he had found diverting himself at chess; and in his letter to the pope he repeats the language he had held to the erring prelate, viz. “Was it right, I say, and consistent with thy duty, to sport away thy evenings amidst the vanity of chess, and defile the hand which offers up the body of the Lord, and the tongue that mediates between God and man, with the pollution of a sacrilegious game?” Following up the same idea that statutes of the church of Elna, in the 3rd vol. of the Councils of Spain, say, “Clerks playing at dice or chess shall be ipso facto excommunicated.” Eudes de Sully, bishop of Paris under Philip Augustus, is stated in the Ordonn. des Rois de France to have forbidden clerks to play the game, and according to the Hist. Eccles. of Fleury, St Louis, king of France, imposed a fine on all who should play it. Ecclesiastical authorities, however, seemed to have differed among themselves upon the question whether chess was or was not a lawful game according to the canons, and Peirino (De Proelat. chap. 1) holds that it was permissible for ecclesiastics to play thereat. Among those who have taken an unfavourable view of the game may be mentioned John Huss, who, when in prison, deplored his having played at chess, whereby he had lost time and run the risk of being subject to violent passions. Among authentic records of the game may be quoted the Alexiad of the princess Anna Comnena, in which she relates how her father, the emperor Alexius, used to divert his mind from the cares of state by playing at chess with his relatives. This emperor died in 1118.
Concerning chess in England there is the usual confusion between legend and truth. Snorre Sturleson relates that as Canute was playing at chess with Earl Ulf, a quarrel arose, which resulted in the upsetting of the board by the latter, with the further consequence of his being murdered in church a few days afterwards by Canute’s orders. Carlyle, in The Early Kings of Norway, repeats this tale, but van der Linde treats it as a myth. The Ramsey Chronicle relates how bishop Utheric, coming to Canute at night upon urgent business, found the monarch and his courtiers amusing themselves at dice and chess. There is nothing intrinsically improbable in this last narrative; but Canute died about 1035, and the date, therefore, is suspiciously early. Moreover, allowance must be made for the ease with which chroniclers described other games as chess. William the Conqueror, Henry I., John and Edward I. are variously stated to have played at chess. It is generally supposed that the English court of exchequer took its name from the cloth, figured with squares like a chess-board, which covered the table in it (see Exchequer). An old writer says that at the coronation of Richard I. in 1189, six earls and barons carried a chess-board with the royal insignia to represent the exchequer court. According to Edmonson’s Heraldry, twenty-six English families bore chess rooks in their coats of arms.
As regards the individual pieces, the king seems to have had the same move as at present; but it is said he could formerly be captured. His “castling” privilege is a European invention; but he formerly leaped two and even three squares, and also to his Kt 2nd. Castling dates no farther back than the first half of the 16th century. The queen has suffered curious changes in name, sex and power. In shatranj the piece was called farz or firz (also farzan, farzin and farzi), signifying a “counsellor,” “minister” or “general.” This was latinized into farzia or fercia. The French slightly altered the latter form into fierce, fierge, and as some say, vierge, which, if true, might explain its becoming a female. Another and much more probable account has it that whereas formerly a pawn on reaching an eighth square became a farzin, and not any other piece, which promotion was of the same kind as at draughts (in French, dames), so she became a dame or queen as in the latter game, and thence dama, donna, &c. There are old Latin manuscripts in which the terms ferzia and regina are used indifferently. The queen formerly moved only one square diagonally and was consequently the weakest piece on the board. The immense power she now possesses seems to have been conferred upon her so late as about the middle of the 15th century. It will be noticed that under the old system the queens could never meet each other, for they operated on diagonals of different colours. The bishop’s scope of action was also very limited formerly; he could only move two squares diagonally, and had no power over the intermediate square, which he could leap over whether it was occupied or not. This limitation of their powers prevailed in Europe until the 15th century. This piece, according to Forbes, was called among the Persians pil, an elephant, but the Arabs, not having the letter p in their alphabet, wrote it fil, or with their definite article al-fil, whence alphilus, alfinus, alifiere, the latter being the word used by the Italians; while the French perhaps get their fol and fou from the same source. The pawns formerly could move only one square at starting; their powers in this respect were increased about the early part of the 16th century. It was customary for them on arriving at an eighth square to be exchanged only for a farzin (queen), and not any other piece; the rooks (so called from the Indian rukh and Persian rokh, meaning “a soldier”) and the knights appear to have always had the same powers as at present. As to the chessboards, they were formerly uncoloured, and it is not until the 13th century that we hear of checkered boards being used in Europe.
Development in Play.—The change of shatranj into modern chess took place most probably first in France, and thence made its way into Spain early in the 15th century, where the new game was called Axedrez de la dama, being also adopted by the Italians 103 under the name of scacci alla rabiosa. The time of the first important writer on modern chess, the Spaniard Ruy Lopez de Segura (1561), is also the period when the latest improvement, castling, was introduced, for his book (Libra de la invention liberal y arte del juego del Axedrez), though treating of it as already in use, also gives the old mode of play, which allowed the king a leap of two or three squares. Shortly afterwards the old shatranj disappears altogether. Lopez was the first who merits the name of chess analyst. At this time flourished the flower of the Spanish and Italian schools of chess—the former represented by Lopez, Ceron, Santa Maria, Busnardo and Avalos; the latter by Giovanni Leonardo da Cutri (il Puttino) and Paolo Boi (il Syracusano). In the years 1562-1575 both Italian masters visited Spain and defeated their Spanish antagonists. During the whole 17th century we find but one worthy to be mentioned, Giacchino Greco (il Calabrese). The middle of the 18th century inaugurates a new era in chess. The leading man of this time was François André Danican Philidor. He was born in 1726 and was trained by M. de Kermur, Sire de Légal, the star of the Cafe de la Régence in Paris, which has been the centre of French chess ever since the commencement of the 18th century. In 1747 Philidor visited England, and defeated the Arabian player, Phillip Stamma, by 8 games to 1 and 1 draw. In 1749 he published his Analyse des échecs, a book which went through more editions and was more translated than any other work upon the game. During more than half a century Philidor travelled much, but never went to Italy, the only country where he could have found opponents of first-rate skill. Italy was represented in Philidor’s time by Ercole del Rio, Lolli and Ponziani. Their style was less sound than that of Philidor, but certainly a much finer and in principle a better one. As an analyst the Frenchman was in many points refuted by Ercole del Rio (“the anonymous Modenese”). Blindfold chess-play, already exhibited in the 11th century by Arabian and Persian experts, was taken up afresh by Philidor, who played on many occasions three games simultaneously without sight of board or men. These exhibitions were given in London, at the Chess Club in St James’s Street, and Philidor died in that city in 1795. As eminent players of this period must be mentioned Count Ph.J. van Zuylen van Nyevelt (1743-1826), and the German player, J. Allgaier (1763-1823). after whom a well-known brilliant variation of the King’s Gambit is named. Philidor was succeeded by Alexandre Louis Honoré Lebreton Deschapelles (1780-1847), who was also a famous whist player. The only player who is known to have fought Deschapelles not unsuccessfully on even terms is John Cochrane. He also lost a match (1821) to W. Lewis, to whom he conceded the odds of “pawn and move,” the Englishman winning one and drawing the two others. Deschapelles’ greatest pupil, and the strongest player France ever possessed, was Louis Charles Mahé de la Bourdonnais, who was born in 1797 and died in 1840. His most memorable achievement was his contest with the English champion, Alexander Macdonnell, the French player winning in the proportion of three to two.
The English school of chess began about the beginning of the 19th century, and Sarratt was its first leader. He flourished from 1808 to 1821, and was followed by his great pupil, W. Lewis, who will be principally remembered for his writings. His literary career belongs to the period from 1818 to 1848 and he died in 1869. A. Macdonnell (1798-1835) has been already mentioned. To the same period belong also Captain Evans, the inventor of the celebrated “Evans Gambit” (1828), who died at a very advanced age in 1873; Perigal, who participated in the correspondence matches against Edinburgh and Paris; George Walker, for thirty years chess editor of Bell’s Life in London; and John Cochrane, who met every strong player from Deschapelles downwards. In the same period Germany possessed but one good player, J. Mendheim of Berlin. The fifth decade of the 19th century is marked by the fact that the leadership passed from the French school to the English. After the death of la Bourdonnais, Fournié de Saint-Amant became the leading player in France; he visited England in the early part of 1843, and successfully met the best English players, including Howard Staunton (q.v.); but the latter soon took his revenge, for in November and December 1843 a great match between Staunton and Saint-Amant took place in Paris, the English champion winning by 11 games to 6 with 4 draws. During the succeeding eight years Staunton maintained his reputation by defeating Popert, Horwitz and Harrwitz. Staunton was defeated by Anderssen at the London tournament in 1851, and this concluded his match-playing career. Among the contemporaries of Staunton may be mentioned Henry Thomas Buckle, author of the History of Civilization, who defeated Kieseritzki, Anderssen and Löwenthal.
In the ten years 1830-1840 a new school arose in Berlin, the seven leaders of which have been called “The Pleiades.” These were Bledow (1795-1846), Bilguer (1815-1840), Hanstein (1810-1850), Mayet (1810-1868), Schorn (1802-1850), B. Horwitz (b. 1809) and von Heydebrandt und der Lasa, once German ambassador at Copenhagen. As belonging to the same period must be mentioned the three Hungarian players, Grimm, Szen and J. Löwenthal.
Among the great masters since the middle of the 19th century Paul Morphy (1837-1884), an American, has seldom been surpassed as a chess player. His career was short but brilliant. Born in New Orleans in 1837, he was taught chess by his father when only ten years of age, and in two years’ time became a strong player. When not quite thirteen he played three games with Löwenthal, and won two of them, the other being drawn. He was twenty years of age when he competed in the New York congress of 1857, where he won the first prize. In 1858 he visited England, and there defeated Boden, Medley, Mongrédien, Owen, Bird and others. He also beat Löwenthal by 9 games to 3 and 2 drawn. In the same year he played a match at Paris with Harrwitz, winning by 5 to 2 and 1 drawn; and later on he obtained a victory over Anderssen. On two or three occasions he played blindfold against eight strong players simultaneously, each time with great success. He returned to America in 1859 and continued to play, but with decreasing interest in the game, until 1866. He died in 1884.
Wilhelm Steinitz (b. 1836) took the sixth prize at the London congress of 1862. He defeated Blackburne in a match by 7 to 1 and 2 drawn. In 1866 he beat Anderssen in a match by 8 games to 6. In 1868 he carried off the first prize in the British Chess Association handicap, and in 1872 in the London grand tourney, also defeating Zukertort in a match by 7 games to 1 and 4 drawn. In 1873 he carried off the first prize at the Vienna congress; and in 1876 he defeated Blackburne, winning 7 games right off. In 1872-1874, in conjunction with W.N. Potter, he conducted and won a telegraphic correspondence match for London against Vienna. In Philidor’s age it was considered almost incredible that he should be able to play three simultaneous games without seeing board or men, but Paulsen, Blackburne and Zukertort often played 10 or 12 such games, while as many as 14 and 15 have been so played.
In 1876 England was in the van of the world’s chess army. English-born players then were Boden, Burn, Macdonnell, Bird, Blackburne and Potter; whilst among naturalized English players were Löwenthal, Steinitz, Zukertort, who died in 1888, and Horwitz. This illustrious contingent was reinforced in 1878 by Mason, an Irish-American, who came over for the Paris tournament; by Gunsberg, a Hungarian; and later by Teichmann, who also made England his home. English chess flourished under the leadership of these masters, the chief prizes in tournaments being consistently carried off by the English representatives.
To gauge the progress made by the game since about 1875 it will suffice to give the following statistics. In London Simpson’s Divan was formerly the chief resort of chess players; the St George’s Chess Club was the principal chess club in the West End, and the City of London Chess Club in the east. About a hundred or more clubs are now scattered all over the city. Formerly only the British Chess Association existed; after its dissolution the now defunct Counties’ Chess Association took 104 its place, and this was superseded by the re-establishment by Mr Hoffer of the British Chess Association, which again fell into abeyance after having organized three international tournaments—London, 1886; Bradford, 1888; and Manchester, 1890—and four national tournaments. There were various reasons why the British Chess Association ceased to exercise its functions, one being that minor associations did not feel inclined to merge their identity in a central association. The London League was established, besides the Northern Chess Union, the Southern Counties’ Chess Union, the Midland Counties’ Union, the Kent County Association; and there are associations in Surrey, Sussex, Essex, Hampshire, Wiltshire, Gloucestershire, Somersetshire, Cambridgeshire, Herefordshire, Leicestershire, Northamptonshire, Staffordshire, Worcestershire and Lancashire. All these associations are supported by the affiliated chess clubs of the respective counties. Scotland (which has its own association), Wales and Ireland have also numerous clubs.
Still, England did not produce one new eminent player between 1875 and 1905. First-class chess remained in the hands of the veterans Burn, Blackburne, Mason and Bird. The old amateurs passed away, their place being taken by a new generation of powerful amateurs, so well equipped that Great Britain could hold its own in an amateur contest against the combined forces of Germany, Austria, Holland and Russia. The terms master and amateur are not used in any invidious sense, but simply as designating, in the former case, first-class players, and in the latter, those just on the borderland of highest excellence. The professional element as it existed in the heydey of Simpson’s Divan almost disappeared, the reason being the increased number of chess clubs, where enthusiasts and students might indulge in their favourite pastime to their heart’s content, tournaments with attractive prizes being arranged during the season. The former occupation of the masters vanished in consequence; the few who remained depended upon the passing visitors from the provinces who were eager to test their strength by the standard of the master. Blackburne visited the provinces annually, keeping the interest in first-class chess alive by his simultaneous play and his extraordinary skill as a blindfold player—unsurpassed until the advent of Harry Nelson Pillsbury (1872-1906), the leading American master since Morphy.
Germany has produced great chess players in Tarrasch, E. Lasker, Lipke, Fritz, Bardeleben, Walbrodt and Mieses, besides a goodly number of amateurs. Austria produced Max Weiss, Schlechter, Marco and Hruby, to say nothing of such fine players as the Fleissigs, Dr Mertner, Dr Kaufmann, Fahndrich, Jacques Schwarz and others. Hungary was worthily represented by Maroczy, Makovetz and Brody, Maroczy being the best after Charousek’s death. Russia, having lost Jaenisch, Petroff and Schumoff, discovered Tchigorin, Janowsky, Schiffers, Alapin, Winawer and Taubenhaus. France showed a decline for many years, having only the veteran M. Arnous de Rivière and the naturalized M. Rosenthal left, followed by Goetz and two good amateurs, MM. Didier and Billecard. Italy had only Signer Salvioli, although Signer Reggio came to the fore. Holland had a fair number of players equal to the English amateurs, but no master since the promising young van Lennep died.
The first modern International Chess Tournament held in London in 1851 was the forerunner of various similar contests of which the following is a complete table:—
Tournaments.
1851. London. 1 Anderssen, 2 Wyvill, 3 Williams.
1857. Manchester. 1 Lowenthal, 2 Anderssen.
1857. New York. 1 Morphy, 2 L. Paulsen.
1858. Birmingham. 1 Lowenthal, 2 Falkbeer.
1860. Cambridge. 1 Kolisch, 2 Stanley.
1861. Bristol, 1 L. Paulsen, 2 Boden.
1862. London, 1 Anderssen, 2 L. Paulsen, 3 Owen.
1865. Dublin. 1 Steinitz, 2 MacDonnell.
1866. Redcar. De Vere.
1866. English Championship Cup. De Vere.
1866. British Chess Association. 1 Steinitz, 2 Green.
1867. Paris. 1 Kolisch, 2 Winawer, 3 Steinitz.
1867. Dundee. 1 Neumann, 2 Steinitz, 3 De Vere and MacDonnell.
1868. English Championship Cup. 1 Blackburne, 2 De Vere.
1868. British Chess Association Handicap. 1 Steinitz, 2 Wisker, 3 Blackburne.
1870. Baden-Baden. 1 Anderssen, 2 Steinitz, 3 Blackburne and Neumann.
1870. English Championship Cup. 1 Wisker, 2 Burn.
1870-1871. City of London Handicap. 1 Potter, 2 De Vere.
1871-1872. City of London Handicap. 1 Steinitz, 2 Keats.
1872. London. 1 Steinitz, 2 Blackburne, 3 Zukertort.
1872. English Championship Cup. 1 Wisker (becoming permanent holder of the cup), 2 De Vere.
1873. Vienna. 1 Steinitz, 2 Blackburne, 3 Anderssen.
1876. London. 1 Blackburne, 2 Zukertort, 3 Potter.
1878. Paris. 1 Zukertort, 2 Winawer (after a tie with Zukertort), 3 Blackburne.
1880. Wiesbaden. 1, 2, and 3, a tie between Blackburne, Englisch and A. Schwarz.
1881. Berlin. 1 Blackburne, 2 Zukertort, 3 Tchigorin and Winawer. Tchigorin made his first public appearance in this contest.
1882. Vienna. 1 Steinitz and Winawer, 3 Mason.
1883. London. 1 Zukertort, 2 Steinitz, 3 Blackburne.
1883. Nuremberg. 1 Winawer, 2 Blackburne, 3 Mason. This tournament is a milestone in modern chess history. The prizes being comparatively small, it was thought that it necessarily must be a failure, the munificently endowed London tournament having just been completed. But, strange to say, whilst in London fourteen players competed, there were nineteen entries in Nuremberg. Winawer, not placed in the former, won the first prize in the latter.
1885. Hamburg. 1 Gunsberg; the next prizes were divided by Blackburne, Mason, Englisch, Tarrasch and Weiss.
1885. Hereford. 1 Blackburne, 2 and 3 Bird and Schallopp.
1886. London. 1 Blackburne, 2 Burn, 3 Gunsberg and Taubenhaus.
1886. Nottingham. 1 Burn, 2 Schallopp, 3 Gunsberg and Zukertort.
1887. Frankfort. 1 Mackenzie, 2 Blackburne and Weiss.
1888. Bradford. 1 Gunsberg, 2 Mackenzie, 3 Mason and Bardeleben.
1889. New York. 1 Tchigorin and Weiss, 3 Gunsberg.
1889. Breslau. 1 Tarrasch, 2 Burn, 3 Weiss.
1890. Amsterdam. 1 Burn, 2 Lasker, 3 Mason. There were only nine competitors, Lasker unexpectedly losing to van Vliet by a trap.
1890. Manchester. 1 Tarrasch, 2 Blackburne, 3 Bird and Mackenzie.
1892. Dresden. 1 Tarrasch, 2 Makovetz and Forges. Blackburne received a special prize.
1894. Leipzig. 1 Tarrasch, 2 Lipke and Teichmann.
1895. Hastings. 1 Pillsbury, 2 Tchigorin, 3 Lasker. This tournament is historical for the first appearance of Pillsbury, the American champion, and Maroczy, the Hungarian champion.
1896. Nuremberg. 1 Lasker, 2 Maroczy, 3 Pillsbury and Tarrasch.
1896. Budapest. 1 Tchigorin, 2 Charousek, 3 Pillsbury.
1897. Berlin. 1 Charousek, 2 Walbrodt, 3 Blackburne. Englisch had to abandon the tournament and return to Vienna ill. He never recovered and died a few weeks later.
1898. Vienna. 1 Tarrasch, 2 Pillsbury, 3 Janowsky. Tarrasch achieved a remarkable victory in this important tournament. Pillsbury’s chances were better than his, but he managed to run him neck and neck and beat him in the tie match which followed.
1898. Cologne. 1 Burn, 2 Charousek, Cohn and Tchigorin.
1899. London. 1 Lasker, 2 Janowsky, Maroczy and Pillsbury. Janowsky sacrificed the second prize by trying to win a game against Steinitz when with an easy draw in hand he could have secured the second place for himself alone.
1900. Munich. Tie between Maroczy, Pillsbury and Schlechter for three chief prizes.
1900. Paris, 1 Lasker, 2 Pillsbury, 3 Maroczy and Marshall.
1901. Monte Carlo. 1 Janowsky, 2 Schlechter, 3 Scheve and Tehigorin. A novel rule was introduced at this tournament, viz. the first drawn game to count ¼ to each player, to be replayed, and in case of a draw again to count ¼ each, and in case of win ½ to the winner. Theoretically this seems logical, but in practice it did not work well.
1902. Monte Carlo. 1 Pillsbury and Maroczy, 3 Janowsky.
1902. Hanover. 1 Janowsky, 2 Pillsbury, 3 Atkins.
1903. Monte Carlo. 1 Tarrasch, 2 Maroczy, 3 Pillsbury.
1904. Monte Carlo. 1 Maroczy, 2 Schlechter, 3 Marshall.
1904. Cambridge Springs, 1 Marshall, 2 Lasker and Janowsky.
1905. Ostend. 1 Maroczy, 2 Tarrasch and Janowsky.
1905. Scheveningen. 1 Marshall, 2 Leussen, 3 Spielmann.
1906. Stockholm. 1 Schlechter and Bernstein, 3 Mieses.
1906. Ostend. 1 Schlechter, 2 Maroczy, 3 Rubenstein.
1906. Nuremberg, 1 Marshall, 2 Duras, 3 Schlechter and Fleischmann.
1907. Vienna, 1 Mieses, 2 Duras, 3 Maroczy and Vidmare.
1907. Ostend. 1 Bernstein and Rubenstein, 3 Mieses.
1907. Ostend. 1 Tarrasch, 2 Schlechter, 3 Janowsky and Marshall.
1907. Carlsbad. 1 Rubenstein, 2 Maroczy, 3 Niemzowitch and Leonhardt.
In the absence of any recognized authority to confer the title 105 of chess champion of the world, it has usually been appropriated by the most successful competitor in tournaments. On this ground Tarrasch claimed the title in 1907, although Lasker, who had twice beaten Steinitz, the previous champion, in championship matches, in addition to such masters as Bird, Blackburne, Mieses and Marshall, was well qualified to assume it. Accordingly in arranging the programme for the tournament at Ostend in 1907 it was agreed that the winner of this contest should receive the title of tournament champion, and should play a match with Lasker for the championship of the world. Tarrasch having proved successful at Ostend, the match between him and Lasker was played at Munich in September 1908, and resulted in the victory of Lasker by 8 games to 3 and 5 draws.
Chess has developed various schools of play from time to time. The theory of the game, however, did not advance in proportion to the enormous strides in its popularity. Formerly the theory of play had been enriched by such enthusiasts as Dr Max Lange, Louis Paulsen, Professor Anderssen, Neumann, Dr Suhle, Falkbeer, Kieseritzki, Howard Staunton, Dr Zukertort, W. N. Potter and Steinitz, foremost amongst them being Louis Paulsen. The openings were thoroughly overhauled, new variations discovered and tested in practical play over the board. These are now things of the past. The masters who find flaws in old variations and discover new ones bring them to light only in matches or tournaments, as new discoveries have now a market value and may gain prizes in matches or tournaments. The old “romantic” school consequently became extinct, and the eliminating process resulted in the retention of a small répertoire only, sufficient for practical purposes in important contests. Gambits and kindred openings containing elements of chance were avoided, and the whole stock which a first-class player requires is a thorough knowledge of the “Ruy Lopez,” the “Queen’s Pawn Openings,” and the “French” and “Sicilian Defences”—openings which contain the least element of chance. The répertoire being restricted it necessarily follows that the scope for grand combinations is also diminished and only strategy or position play remains. The “romantic” school invariably aimed at an attack on the king’s position at any cost; nowadays the struggle is to obtain a minute advantage, and the whole plan consists in finding or creating a weak spot in the opponent’s arrangement of forces; such is the theory of the modern school, conceived and advocated by Steinitz. But it is a curious fact that Steinitz founded the modern school rather late in life. He felt his powers of combination waning, and being the world’s champion and eager to retain that title, he started the new theory. This novel departure revolutionized chess entirely. The attacking and combination style was sacrificed to a sound, sober and dry method; but Steinitz, strange to say, was not even the best exponent of his own theory, this position falling to younger players, Siegbert Tarrasch, Schlechter, Amos Burn and Emanuel Lasker. Pillsbury and Janowsky adhered to both styles, the former in a high degree, and so did Zukertort and Charousek; Tchigorin being a free-lance with a style of his own. The old charm of the game disappeared—in match and tournament play at least—and beauty was sacrificed to exact calculation and to scoring points. This is to be regretted, for the most beautiful games still occur when a player resorts to the gambits. One of the finest games in the Hastings tournament was played by Tchigorin against Pillsbury, and this was a “King’s Gambit Declined.” Charousek won a “Bishop’s Gambit” against Dr Lasker in the Nuremberg tournament; and some brilliant games occur in the “Queen’s Gambit Declined,” if either White or Black sacrifices the KP. Another reason why gambits should be adopted by players in tournaments is that competitors would necessarily be readily prepared for the regulation openings, so that the gambits might take them by surprise. After all, the new school is a natural consequence of the progress of the game. Paulsen, Anderssen and Tchigorin devoted a lifetime to the Evans Gambit, volumes of analyses were written on it, and then Lasker revives an obsolete defence, and the Evans Gambit disappears! Zukertort achieved a great success with “1. Kt to KB3” in the London tournament, 1883, and this, or the kindred “1. P to Q4” opening, has since become the trusty weapon in serious encounters. Lasker wrote Common Sense in Chess, and gave the best defences of the Ruy Lopez (a certain form of it); but the “common sense” was demolished in the Paris and Nuremberg tournaments, and old forms of that remarkable opening have to be refurbished. These instances will suffice to show the reason for the cautious style of modern times. The Moltkes have replaced the Napoleons.
The old versatility of style could be revived if club tournaments were organized differently. The players might be compelled to adopt one single opening only in a two-round contest, each player thus having attack and defence in turn. The next season another opening would form the programme, and so on. Even in international tournaments this condition might be imposed; the theory would be enriched; full scope would be given to power of combination and ingenuity; whilst the game would be more interesting.
There are still amateurs who devote their energies to the theory of the game; but so long as innovations or new discoveries are not tested by masters in serious games, they are of no value. Steinitz used to keep a number of new discoveries ready to be produced in masters’ contests, the result being that his novelties were regularly demolished when it came to a practical test. The mistake was that he did not try his novelties over the board with an opponent of equal strength, instead of trusting to his own judgment alone.
The British Chess Federation was instituted in 1904, its first congress being held at Hastings in that year, when a British championship, a ladies’ championship and a first-class amateur tournament were played. These competitions have been continued annually at the congresses of the federation, with the following results:—
British Championship.
1904, Hastings, 1 H.E. Atkins and W.E. Napier, 3 J.H. Blackburne.
1905. Southport. 1 H.E. Atkins, 2 G.E.H. Bellingham and J.H. Blackburne.
1906. Shrewsbury. 1 H.E. Atkins, 2 R.P. Michell, 3 G.E. Wainwright.
1907. Crystal Palace. 1 H.E. Atkins, 2 J.H. Blackburne, R.P. Michell, E. G. Sergeant and G. E. Wainwright.
Ladies’ Championship.
1904. Hastings. 1 Miss Finn, 2 Mrs Anderson and Mrs Herring.
1905. Southport. 1 Miss Finn. 2 Mrs Anderson and Mrs Houlding.
1906. Shrewsbury. 1 Mrs Herring, 2 Mrs Anderson, 3 Miss Ellis and Mrs Houlding.
1907. Crystal Palace. 1 Mrs Herring and Mrs Houlding, 3 Mrs Anderson.
First Class Amateur Tournament.
1904. Hastings Section A. 1 W.H. Gunston, 2 H.F. Cheshire and F. Brown.
Section B. 1 G.E. Wainwright and C.H. Sherrard, 3 W.P. M’Bean.
1905. Southport Section A. 1 Dr Holmes, 2 J. Mortimer, 3 H.G. Cole and J.E. Purry.
Section B. 1 F.E. Hammond, 2 F. Brown. T.J. Kelly and C.H. Wallwork.
1906. Shrewsbury. 1 G. Shories, J. F. Allcock, P. W. Fairweather and E. D. Palmer.
In 1896 and following years matches between representative players of Great Britain and the United States respectively were played by cable, with the following results:—
| 1896. America | won by | 4½ | games to | 3½ |
| 1897. Great Britain | " | 5½ | " | 4½ |
| 1898. Great Britain | " | 5½ | " | 4½ |
| 1899. America | " | 6 | " | 4 |
| 1900. America | " | 6 | " | 4 |
| 1901. Drawn | ||||
| 1902. America | " | 5½ | " | 4½ |
| 1903. America | " | 5½ | " | 4½ |
| 1907. Great Britain | " | 5½ | " | 4½ |
| 1908. America | " | 6½ | " | 3½ |
| 1909. Great Britain | " | 6 | " | 4 |
Since 1899 cable matches have also been played annually between representatives of English and American universities; of the first six three were won by England, the remaining three 106 being drawn. In England chess matches have been played annually since 1873 between the universities of Oxford and Cambridge, seven players on each side. Up to 1907 Oxford won eleven matches, Cambridge twenty-one, and three were drawn.
Literature of the Game.—The first known writer on chess was Jacobus de Cessolis (Jacopo Dacciesole), whose main object, however, though he gives the moves, &c., was to teach morals rather than chess. He was a Dominican friar, and his treatise, Solatium Ludi Scacchorum, scilicet, Libellus de Moribus Hominum et Officiis Nobilium, was written before the year 1200. It was afterwards translated into French, and in the year 1474 Caxton, under the title of The Game and Playe of Chesse, printed an English translation of the French version.
In 1490 we have the Göttinger Handschrift, a work containing nine different openings and fifty problems. The author of this manuscript is not known. Then comes Vicent, a Spanish writer, whose book bears date 1495. Only the title-page has been preserved, the rest of the work having been lost in the first Carlist war. Of Lucena, another Spanish author who wrote in or about 1497, we are better informed. His treatise, Repeticion des Amores y Arte de Axedres, comprises various practical chess matters, including 150 positions, illustrated by 160 well-executed woodcuts. Various of these positions are identical with those in the Göttinger Handschrift.In the 16th century works upon the game were written by Damiano, Ruy Lopez and Horatio Gianutio della Mantia; in the 17th century by Salvio, Polerio, Gustavus Selenus, Carrera, Greco, Fr. Antonio and the authors of the Traité de Lausanne; in the 18th century by Bertin, Stamma, Ercole del Rio, Lolli, Cozio, Philidor, Ponziani, Stein, van Nyevelt, Allgaier and Peter Pratt; in the 19th century by J.F.W. Koch and C.F. Koch, Sarratt, John Cochrane, Wm. Lewis, Silberschmidt, Ghulam Kassim and James Cochrane, George Walker, A. MacDonnell, Jaenisch, Petroff, von Bilguer, von der Lasa, Staunton, Kling and Horwitz, Bledow, Dubois, Kieseritzki, Max Lange, Löwenthal, Dufresne, Neumann, Suhle, Zukertort, Preti and others.
English chess owes much to W. Lewis and George Walker. But to Howard Staunton must be ascribed the most important share in creating the later popularity which the game achieved in England. Staunton’s first work, The Chess Player’s Handbook, was published in 1847, and again (revised) in 1848. For want of further adequate revision many of its variations are now out of date; but taking the handbook as it was when issued, very high praise must be bestowed upon the author. His other works are: The Chess Player’s Text-Book and The Chess Player’s Companion (1849) (the latter being a collection of his own games), the Chess Praxis (1860), republished in 1903, his posthumous Work, Chess Theory and Practice, edited by R.B. Wormald (1876), and various smaller treatises. The laws of the game as laid down in the Praxis formed the basis of the rules adopted by the British Chess Association in 1862. Besides editing The Chess Player’s Chronicle and The Chess World, he was the chess editor of The Illustrated London News from 1844 till his death in 1874.
Among continental chess authorities von Heydebrandt und der Lasa (more usually known by his second title) stood pre-eminent. The German Handbuch was completed in 1843 by von Bilguer, who died before the first edition was completed. The second, third, fourth and fifth editions (the last published in 1874) were edited and revised by von der Lasa.
Among the more important modern works the following may be mentioned: Vasquez, El Ajedrez de memoria; La Odisea de Pablo Morphy (Havana, 1893); Bauer, Schachlexikon (Leipzig, 1893); Jean Dufresne, Kleines Lehrbuch des Schachspiels (6th ed., Leipzig, 1893); E. Freeborough and Rev. C.E. Ranken, Chess Openings, Ancient and Modern; Arnelung, Baltische Schachblätter, &c. (Berlin, 1893); Bachman, Geistreiche Schachpartien (containing a number of brilliant games) (Ansbach, 1893-1899); E.H. Bird, Chess History and Reminiscences (London, 1893); The Steinitz-Lasker Match (1894); Chess Novelties (1895); Max Lange, Paul Morphy (1894); C. Bardeleben and J. Mieses, Lehrbuch des Schachspiels (very useful); Jas. Mason, The Principles of Chess in Theory and Practice (1894); The Art of Chess (1895); Social Chess (Horace Cox, London); Dr Tarrasch, Dreihundert Schachpartien (Leipzig, 1895); Dr Eugen V. Schmidt, Syslematische Anordung von Schacheröffnungen (Veit & Co., Leipzig, 1895); Numa Preti, A B C des échecs (Paris, 1895); C. Salvioli, Teoria generate del giuoco degli Scacchi (Livorno, 1895): W. Steinitz, Modern Chess Instructor (New York, 1895); L. Hoffer, Chess (Routledge); E. Freeborough, Select Chess End-Games (London, 1895); Euclid, The Chess Ending King and Queen against King and Rook (London, 1895); Tassilo von Heydebrandt und der Laaa, Leitfaden des Schachspiels and Zur Geschichte und Literatur des Schachspiels (Leipzig, 1897); Dr. Lasker, Common Sense in Chess (London, 1896); Oscar Cordel, Neuester Leitfaden des Schachspiels (Berlin, 1896); and a vast number of other publications.
Further, The London Tournament Book (1883); Twelve Tournament Books of the German Chess Association (Veit & Co., Leipzig); The Hastings Tournament Book (London, 1896); The Vienna Tournament Book, by Halprin and Marco (1900); The Nuremberg Tournament Book, by Dr Tarrasch; The Book of the London Congress, by L. Hoffer (Longman, 1899); The Paris Tournament Book (Paris, 1900), by Rosenthal, &c.
The following are some of the best works in English on chess problems:—“J. B.” of Bridport, Chess Strategy (1865); F. Healey, A Collection of 200 Chess Problems (1866); English Chess Problems, edited by James and W.T. Pierce (1876); H.J.C. Andrews, E.N. Frankenstein, B.G. Laws, and C. Planck, The Chess Problem Text-Book (1887); A.F. Mackenzie, Chess: its Poetry and its Prose (Jamaica, 1887); J.A. Miles, Chess Stars (self-mates), (1888); James Rayner, Chess Problems (1890); B.G. Laws, The Two-Move Chess Problem (1890); The Chess Bouquet, compiled by F.R. Gittins (1897); Mr and Mrs T.B. Rowland, The Problem Art (2nd ed., 1898); E.B. Cook, T. Henery and C.A. Gilberg, American Chess-Nuts (1868); Samuel Loyd, Chess Strategy (1878); W.H. Lyons, Chess-Nut Burrs and how to open them (1886); C.A. Gilberg, Crumbs from the Chess Board (1890); Canadian Chess Problems, edited by C.F. Stubbs (1890); W. Pulitzer, Chess Harmonies (1894); G.E. Carpenter (N. Preti of Paris), 200 Chess Problems (1900).
1 The earliest known problem is ascribed to an Arabian caliph of the 9th century. The first known collection is in a manuscript (in the British Museum) of King Alphonso of Castile, dated 1250; it contains 103 problems. The collection of Nicolas of Lombardy, dated 1300, comprises 192 problems.
CHEST (Gr. κίστη, Lat. cista, O. Eng. cist, cest,&c.), a large box of wood or metal with a hinged lid. The term is also used of a variety of kinds of receptacle; and in anatomy is transferred to the portion of the body covered by the ribs and breastbone (see Respiratory System). In the more ordinary meaning chests are, next to the chair and the bed, the most ancient articles of domestic furniture. The chest was the common receptacle for clothes and valuables, and was the direct ancestor of the “chest of drawers,” which was formed by enlarging the chest and cutting up the front. It was also frequently used as a seat. Indeed, in its origin it took in great measure the place of the chair, which, although familiar enough to the ancients, had become a luxury in the days when the chest was already an almost universal possession. The chief use of chests was as wardrobes, but they were also often employed for the storing of valuables. In the early middle ages the rich possessed them in profusion, used them as portmanteaux, and carried them about from castle to castle. These portable receptacles were often covered with leather and emblazoned with heraldic designs. As houses gradually became less sparsely furnished, chests and beds and other movables were allowed to remain stationary, and the chest lost its covered top, and took the shape in which we best know it—that of an oblong box standing upon raised feet. As a rule it was made of oak, but it was sometimes of chestnut or other hard wood.
There are, properly speaking, three types of chest—the domestic, the ecclesiastical and the strong box or coffer. Old domestic chests still exist in great number and some variety, but the proportion of those earlier than the latter part of the Tudor period is very small; most of them are Jacobean in date. Very frequently they were made to contain the store of house-linen which a bride took to her husband upon her marriage. In the 17th century Boulle and his imitators glorified the marriage-coffer until it became a gorgeous casket, almost indeed a sarcophagus, inlaid with ivory and ebony and precious woods, and enriched with ormolu, supported upon a stand of equal magnificence. The Italian marriage-chests (cassone) were also of a richness which was never attempted in England. The main characteristics of English domestic chests (which not infrequently are carved with names and dates) are panelled fronts and ends, the feet being formed from prolongations of the “stiles” or side posts. There were, however, exceptions, and a certain number of 17th-century chests have separate feet, either circular or shaped after the indications of a somewhat later style. There is usually a strong architectural feeling about the chest, the front being divided into panels, which are plain in the more ordinary examples, and richly carved in the choicer ones. The plinth and frieze are often of well-defined guilloche work, or are carved with arabesques or conventionalized flowers. Architectural detail, especially the detail of wainscoting, has indeed been followed with considerable fidelity, many of the earlier chests being carved in the linenfold pattern, while the Jacobean examples are often mere reproductions of the pilastered and recessed oaken mantelpieces of the period. Occasionally a chest is seen which is inlaid with coloured woods, or with 107 geometrical parquetry. Perhaps the most elaborate type of English parquetry chest is that named after the vanished Palace of Nonesuch. Such pieces are, however, rarely met with. The entire front of this type is covered with a representation of the palace in coloured woods. Another class of chest is incised, sometimes rather roughly, but often with considerable geometrical skill. The more ordinary variety has been of great value to the forger of antique furniture, who has used its carved panels for conversion into cupboards and other pieces, the history of which is not easily unravelled by the amateur who collects old oak without knowing much about it. Towards the end of the 17th century chests were often made of walnut, or even of exotic woods such as cedar and cypress, and were sometimes clamped with large and ornamental brass bands and hinges. The chests of the 18th century were much larger than those of the preceding period, and as often as not were furnished with two drawers at the bottom—an arrangement but rarely seen in those of the 17th century—while they were often fitted with a small internal box fixed across one end for ready access to small articles. The chest was not infrequently unpanelled and unornamented, and in the latter period of its history this became the ruling type. It will not have been forgotten that it was in an old oak chest that the real or mythical heroine of the pathetic ballad of “The Mistletoe Bough” concealed herself, to her undoing.
Ecclesiastical chests appear to have been used almost entirely as receptacles for vestments and church plate, and those which survive are still often employed for the preservation of parish documents. A considerable variety of these interesting and often exceedingly elaborate chests are still left in English churches. They are usually of considerable size, and of a length disproportionate to their depth. This no doubt was to facilitate the storage of vestments. Most of them are of great antiquity. Many go back to the 14th century, and here and there they are even earlier, as in the case of the coffer in Stoke d’Abernon church, Surrey, which is unquestionably 13th-century work. One of the most remarkable of these early examples is in Newport church, Essex. It is one of the extremely rare painted coffers of the 13th century, the front carved with an upper row of shields, from which the heraldic painting has disappeared, and a lower row of roundels. Between is a belt of open tracery, probably of pewter, and the inside of the lid is decorated with oil paintings representing the Crucifixion, the Virgin Mary, St Peter, St John and St Paul. The well-known “jewel chest” in St Mary’s, Oxford, is one of the earliest examples of 14th century work. Many of these ecclesiastical chests are carved with architectural motives—traceried windows most frequently, but occasionally with the iinenfold pattern. There is a whole class of chests known as “tilting coffers,” carved with representations of tournaments or feats of arms, and sometimes with a grotesque admixture of chivalric figures and mythical monsters. Only five or six examples of this type are known still to exist in England, and two of them are now in the Victoria and Albert Museum. It is not certain that even these few are of English origin—indeed, very many of the chests and coffers of the 16th and 17th centuries are of foreign make. They were imported into England chiefly from Flanders, and were subsequently carved by native artisans, as was the case with other common pieces of furniture of those periods. The huche or “hutch” was a rough type of household chest.
The word “coffer” is properly applied to a chest which was intended for the safe keeping of valuables. As a rule the coffer is much more massive in construction than the domestic chest; it is clamped by iron bands, sometimes contains secret receptacles opening with a concealed spring, and is often furnished with an elaborate and complex lock, which occupies the whole of the underside of the lid. Pieces of this type are sometimes described as Spanish chests, from the belief that they were taken from ships belonging to the Armada. It is impossible to say that this may not sometimes have been the case, but these strong boxes are frequently of English origin, although the mechanism of the locks may have been due to the subtle skill of foreign locksmiths. A typical example of the treasure chest is that which belonged to Sir Thomas Bodley, and is preserved in the Bodleian library at Oxford. The locks of this description of chest are of steel, and are sometimes richly damascened. It was for being implicated in the breaking open and robbing of just such a chest as this, to which the Collège de Navarre had confided coin to the value of 500 ecus, that François Villon was hanged on the gibbet of Montfaucon.
CHESTER, EARLS OF. The important palatine earldom of Chester was first held by a certain Fleming named Gherbod (fl. 1070), and then by Hugh of Avranches (d. 1101), a son of Richard, viscount of Avranches. Hugh, who was probably one of William the Conqueror’s companions, was made earl of Chester in 1071; he had special privileges in his earldom, and he held land in twenty counties. He was called Le Gros on account of his great bulk and Lupus on account of his ferocity. However, he regarded St Anselm as his friend, and he showed the customary liberality to religious houses. His life was mainly spent in fighting the Welsh and in Normandy, and he died on the 27th of July 1101. Hugh’s only son Richard, who was childless, was drowned in the White Ship in November 1120. Among subsequent holders were Ralph, or Randulph, de Gernon (d. 1153), who took a prominent part in the civil wars of the reign of Stephen, fighting first on one side and then on the other; and his son Hugh de Kevelioc (1147-1181), who shared in the rising against Henry II. in 1173. But perhaps the most celebrated of the early earls was Ralph, Ranulf, or Randulph, de Blundevill (c. 1172-1232), who succeeded his father Hugh de Kevelioc as earl in 1181, and was created earl of Lincoln in 1217. Ranulf married Constance, widow of Henry II.’s son, Geoffrey of Brittany, and is sometimes called duke of Brittany and earl of Richmond. He fought in Wales, was on the side of John during his struggle with the barons over Magna Carta, and was one of this king’s executors; he also fought for the young king Henry III. against the French invaders and their allies. In 1218 he went on crusade to the Holy Land and took part in the capture of Damietta; then returning to England he died at Wallingford in October 1232. After speaking of Ranulf’s unique position in the kingdom, which “fitted him for the part of a leader of opposition to royal or ministerial tyranny,” Stubbs sums up his character in these words: “On more than one occasion he refused his consent to taxation which he deemed unjust; his jealousy of Hubert (de Burgh), although it led him to join the foreign party in 1223, did not prevent him from more than once interposing to prevent his overthrow. He was, moreover, almost the last relic of the great feudal aristocracy of the Conquest.” Although twice married he left no children, and his immense possessions passed to his four sisters. The earl’s memory remained green for a long time, and in the Vision of Piers Plowman his name is linked with that of Robin Hood. In November 1232 the earldom of Chester was granted to his nephew John the Scot, earl of Huntingdon (c. 1207-1237), and in 1246, nine years after John had died childless, it was annexed to the English crown “lest so fair a dominion should be divided among women.”
In 1254 Prince Edward, afterwards King Edward I., was created earl of Chester, and since this date the earldom has always been held by the heirs apparent to the English crown with the single exception of Simon de Montfort, earl of Leicester. Since 1399 the earls of Chester have been also princes of Wales, although the act of Richard II. (1398), which created Chester into a principality to be held by the king’s eldest son, was revoked by Henry IV.
CHESTER, an episcopal city and county of a city, municipal, county and parliamentary borough, and the county town of Cheshire, England, 179 m. N.W. of London. Pop. (1901) 38,309. It lies in a low plain on the Dee, principally on the north (right) bank, 6 m. above the embouchure of the river into its wide, shallow estuary. It is an important railway centre, the principal lines serving it being the London & North-Western, Great Western, Cheshire Lines and Great Central. The city is divided into four principal blocks by the four principal streets—Northgate Street, Eastgate Street, Bridge Street and Watergate Street, which radiate at right angles from the Cross, and terminate in 108 the four gates. These four streets exhibit in what are called “the Rows” a characteristic feature of the city. Their origin is a mystery, and has given rise to much controversy. In Eastgate Street, Bridge Street and Watergate Street, the Rows exist on each side of the street throughout the greater part of its length, and may be described as continuous galleries open to the street, over and under which the houses lining the streets project, and which are formed as it were out of the front first-floor of the houses, approached by flights of steps from the roadway. The Rows are flagged or boarded under foot and ceiled above, thus forming a covered way, standing in the same relation to the shops, which are at their back, as the foot pavement does in other towns. In Northgate Street, on the other hand, the Row on the west side is formed as it were out of the ground floor of the houses, having cellars beneath, while on the east side the Row is formed at the same elevation as in the other three principal streets. In these streets are several examples of old timbered houses and some good modern imitations of them,—all combining to give a picturesque and individual character to the city. Among the most interesting of the ancient houses are Derby House, bearing the date 1591, Bishop Lloyd’s house, and God’s Providence House in Watergate Street, and the Bear and Billet in Lower Bridge Street; the three last date from the 17th century. There is also a chamber with stone groined roof of the 14th century in the basement of a house in Eastgate Street, and another of a similar character in Watergate Street. A mortuary chapel of the early part of the 13th century exists in the basement of a house in Bridge Street.
Chester is the only city in England that still possesses its walls perfect in their entire circuit of 2 m. The gateways have all been rebuilt at various dates; the north and east gates on the site of the Roman gates. The Grosvenor bridge, a single span of stone 200 ft. in length, said to be the largest save one in Europe, carries the road to Wrexham and Shrewsbury over the Dee on the south-west; while the old bridge of seven arches is interesting on account of its antiquity and picturesqueness. The castle, with the exception of “Caesar’s Tower,” and a round tower with adjacent buildings, in the upper ward, was taken down towards the end of the 18th century, and replaced by a gateway, barracks, county hall, gaol and assize courts.
The cathedral church of Christ and the Virgin Mary, which stands towards the north of the city within the walls, rose on the site of a church of extreme antiquity. It appears that the dedication of this church was altered, perhaps in the reign of Athelstan, from St. Peter and St Paul to St Werburgh and St Oswald, St Werburgh being a niece of St Etheldreda of Ely. In 1093 Hugh Lupus, earl of Chester, richly endowed the foundation as a Benedictine monastery. The bishops of Mercia had apparently a seat at Chester, but the city had ceased to be episcopal, until in 1075 Peter, bishop of Lichfield, removed his seat thence to Chester, having for his cathedral the collegiate church of St John. The seat of the see, however, was quickly removed again to Coventry (1102), but Cheshire continued subject to Lichfield until in 1541 Chester was erected into a bishopric by Henry VIII., the church of the dissolved abbey of St Werburgh becoming the cathedral. The diocese covers nearly the whole of Cheshire, with very small portions of Lancashire and Staffordshire. The cathedral does not rank among the most splendid English churches, but possesses certain details of the highest interest, and gains in beauty from the tones of its red sandstone walls and the picturesque close in which it stands. It is cruciform with a central tower 127 ft. high. The south transept is larger than the north. The nave is short (145 ft.), being of six bays; the southern arcade is Decorated, while the northern, which differs in detail, is of uncertain date. The basement of the north-western tower—all that remains of it, now used as a baptistery—is Norman, and formed part of Hugh Lupus’ church; and the fabric of the north wall is also of this period. The north transept also retains Norman work, and its size shows the original plan, as the existence of the conventual buildings to the north probably rendered its extension undesirable. The south transept has aisles, with Decorated and Perpendicular windows. The fine organ stands on a screen across the north transept; but some of its pipes are upon the choir screen, both screens being the work of Sir Gilbert Scott. The style of the choir is transitional from Early English to Decorated, and its length is 125 ft. It is a fine example, and its beauty is enhanced by the magnificent series of ancient carved wooden stalls unsurpassed in England. The Lady Chapel, east of the choir, is of rich Early English workmanship. Of the conventual buildings the cloisters are Perpendicular. The chapter-house, entered by a beautiful vestibule from the east cloister, and lined with cases containing the chapter library, is Early English (c. 1240). The refectory, adjoining the north cloister, is of the same period, with Perpendicular insertions; it has been curtailed in size, but retains its beautiful Early English lector’s pulpit. An early Norman chamber, with massive pillars and vaulting, adjoins the west cloister, and may be the substructure of the abbot’s house. The abbey gateway is of the 14th century.
Within the walls there are several churches of ancient foundation; thus St Peter’s is said to occupy the site of a church erected by Æthelflæd, queen of Mercia, and St Mary’s dates from the 12th century. None, however, is of any special interest; but the church of St John, outside the walls, which as already stated became the cathedral in 1075, is a massive early Norman structure, with later additions, and, especially as regards the exterior, considerably restored in modern times. Its fine tower fell in 1881. It was a collegiate church until 1547, and there are some remains of the adjoining buildings. Among numerous modern churches there may be mentioned St Mary’s without the walls, built in 1887 by the duke of Westminster, of red sandstone, with a fine spire’ and peal of bells.
Among the chief secular buildings, the town hall replaced in 1869 the old exchange, which had been burnt down in 1862. The Grosvenor Museum and School of Art, the foundation of which was suggested by Charles Kingsley the novelist, when canon of Chester cathedral, contains many local antiquities, along with a fine collection of the fauna of Cheshire and the neighbourhood. The King’s school was founded by Henry VIII. (1541), who provided that twenty-four poor scholars should be taught free of cost. It was reorganized as a public school in 1873, and possesses twelve king’s scholarships tenable in the school, and close scholarships tenable at the universities. Among other schools may be mentioned the blue-coat school (1700), the Queen’s school for girls (1878), the girls’ school attached to the Roman Catholic convent, and the diocesan training college for schoolmasters. For recreation provision is made by the New Grosvenor Park, presented to the city in 1867 by the marquess of Westminster; Handbridge Park, opened in 1892; and the Roodee, a level tract by the river at the base of the city wall, appropriated as a race-course. An annual race-meeting is held in May and attendedby thousands. The chief event is the race for the Chester Cup, which dates from 1540, when a silver bell was given as the prize by the Saddlers’ Company. Pleasure vessels ply on the Dee in summer, and an annual regatta is held, at which all the principal northern rowing-clubs are generally represented. The town gains in prosperity from its large number of visitors. The principal industries are carried on without the walls, where there are lead, shot and paint works, leather and tobacco factories, and iron foundries. The trade gilds number twenty-four. There is a considerable amount of shipping on the Dee, the navigation having been much improved in modern times. The parliamentary borough returns one member. The municipal council consists of a mayor, 10 aldermen and 30 councillors. Area, 2862 acres.
History.—Setting aside the numerous legends with regard to the existence of a British city on the site now occupied by Chester, the earliest authentic information relating to its history is furnished by the works of Ptolemy and Antoninus. As the Roman station of Deva it was probably founded about A.D. 48 by Ostorius Scapula, and from its advantageous position, both as the key to communication with Ireland and as a bulwark against the hostile tribes of the north, it became a military and commercial centre of considerable importance. In A.D. 78-79 109 it was the winter-quarters of Agricola, and later became illustrious as the permanent headquarters of Legio XX. Valeria Victrix. Many inscriptions and remains of the Roman military occupation have been found, and the north and east walls stand in great part on Roman foundations. The Saxon form of the name was Leganceaster. About 614 the city was captured and destroyed by Æthelfrith, and henceforth lay in ruins until Æthelflæd in 907 rebuilt the walls, restored the monastery of St Werburgh, and made the city “nigh two such as it was before.” In the reign of Æthelstan a mint was set up at Chester, and in 973 it was the scene of Edgar’s truimph when, it is said, he was rowed on the Dee by six subject kings. Chester opposed a determined resistance to the Conqueror, and did not finally surrender until 1070. On the erection of Cheshire to a county palatine after the Conquest, Chester became the seat of government of the palatine earls. The Domesday account of the city includes a description of the Saxon laws under which it had been governed in the time of Edward the Confessor. All the land, except the bishop’s borough, was held of the earl, and assessed at fifty hides. There were seven mint-masters and twelve magistrates, and the city paid a fee-farm rent of £45. It had been much devastated since the time of Edward the Confessor, and the number of houses reduced by 205.
The earliest extant charter, granted by Henry II. in 1160, empowered the burgesses to trade with Durham as freely as they had done in the reign of Henry I. From this date a large collection of charters enumerates privileges granted by successive earls and later sovereigns. One from Ralph or Ranulf de Blundevill, granted between 1190 and 1211, confirms to the citizens a gild merchant and all liberties and free customs, and three from John protect their privilege of trading with Ireland. Edward I. empowered the citizens to elect coroners and to hold courts of justice, and granted them the fee-farm of the city at a yearly rent of £100. In the 14th century Chester began to lose its standing as a port through the gradual silting up of the estuary of the Dee, and the city was further impoverished by the inroads of the Welsh and by the necessity of rebuilding the Dee bridge, which had been swept away by an unusually high tide. In consideration of these misfortunes Richard II. remitted part of the fee-farm. Continued misfortunes led to a further reduction of the farm to £50 for a term of fifty years by Henry VI., who also made a grant for the completion of a new Dee bridge. Henry VII. reduced the fee-farm to £20, and in 1506 granted to the citizens what is known as “the Great Charter.” This charter constituted the city a county by itself, and incorporated the governing body under the style of a mayor, twenty-four aldermen and forty common councilman; it also instituted two sheriffs, two coroners and a recorder, and the mayor, the ex-mayors and the recorder were appointed justices of the peace. This charter was confirmed by James I. and Charles II. A charter of George III. in 1804 instituted the office of deputy-mayor. The charter of Hugh Lupus to the abbey of St Werburgh includes a grant of the tolls of the fair at the feast of St Werburgh for three days, and a subsequent charter from Ranulf de Blundevill (12th century) licensed the abbot and monks to hold their fairs and markets before the abbey gates. A charter of John the Scot, earl of Chester, mentions fairs at the feasts of the Nativity of St John Baptist and St Michael. For many centuries the rights claimed by the abbot in connexion with the fairs gave rise to constant friction with the civic authorities, which lasted until, in the reign of Henry VIII., it was decreed that the right of holding fairs was vested exclusively in the citizens. Charles II. in 1685 granted a cattle-fair to be held on the first Thursday in February.
In 1553 Chester first returned two members to parliament, having hitherto been represented solely in the parliament of the palatinate. By the Redistribution Act of 1885 the representation was reduced to one member. The trades of tanners, skinners and glove-makers existed at the time of the Conquest, and the importation of marten skins is mentioned in Domesday. In the 14th century the woollen trade was considerable, and in 1674 weavers and wool-combers were introduced into Chester from Norwich. The restoration of the channel of the Dee opened up a flourishing trade in Irish linen, which in 1786 was at its height, but from that date gradually diminished.
See Victoria County History, Cheshire; R. H. Morris, Chester in the Plantagenet and Tudor Reigns (Chester, 1894); Joseph Hemingway, History of the City of Chester (2 vols., Chester, 1831).
CHESTER, a city of Delaware county, Pennsylvania, U.S.A., on the Delaware river, about 13 m. S.W. of Philadelphia. Pop. (1800) 20,226; (1900) 33,988, of whom 5074 were foreign-born and 44O3 were negroes; (U. S. census, 1910) 38,537. It is served by the Baltimore & Ohio and the Philadelphia & Reading railways, by the Philadelphia, Baltimore & Washington division of the Pennsylvania system, and by steamboat lines. Chester has several interesting buildings dating from early in the 18th century—among them the city hall (1724), one of the oldest public buildings in the United States, and the house (1683) occupied for a time by William Penn. It is the seat of the Pennsylvania Military College (1862); and on the border of Chester, in the borough of Upland (pop. in 1900, 2131), is the Crozer Theological Seminary (Baptist), which was incorporated in 1867, opened in 1868, and named after John P. Crozer (1793-1866), by whose family it was founded. Chester has a large shipbuilding industry, and manufactories of cotton and worsted goods, iron and steel, the steel-casting industry being especially important, and large quantities of wrought iron and steel pipes being manufactured. Dye-stuffs and leather also are manufactured. The value of the city’s factory products in 1905 was $16,644,842. Chester is the oldest town in Pennsylvania. It was settled by the Swedes about 1645, was called Upland and was the seat of the Swedish courts until 1682, when William Penn, soon after his landing at a spot in the town now marked by a memorial stone, gave it its present name. The first provincial assembly was convened here in December of the same year. After the battle of Brandywine in the War of Independence, Washington retreated to Chester, and in the “Washington House,” still standing, wrote his account of the battle. Soon afterwards Chester was occupied by the British. In 1701 it was incorporated as a borough; in 1795 and again in 1850 it received a new borough charter; and in 1866 it was chartered as a city. For a long time it was chiefly a small fishing settlement, its population as late as 1820 being only 657; but after the introduction of large manufacturing interests in 1850, when its population was only 1667, its growth was rapid.
See H. G. Ashmead, Historical Sketch of Chester (Chester, 1883).
CHESTERFIELD, PHILIP DORMER STANHOPE, 4th Earl of (1694-1773), son of Philip Stanhope, third earl (1673-1726), and Elizabeth Savile, daughter of George Savile, marquess of Halifax, was born in London on the 22nd of September 1694; Philip, the first earl (1584-1656), son of Sir John Stanhope of Shelford, was a royalist who in 1616 was created Baron Stanhope of Shelford, and in 1628 earl of Chesterfield; and his grandson the 2nd earl (1633-1714) was grandfather of the 4th earl. Deprived at an early age of his mother, the care of the boy devolved upon his grandmother, the marchioness of Halifax, a lady of culture and connexion, whose house was frequented by the most distinguished Whigs of the epoch. He soon began to prove himself possessed of that systematic spirit of conduct and effort which appeared so much in his life and character. His education, begun under a private tutor, was continued (1712) at Trinity Hall, Cambridge; here he remained little more than a year and seems to have read hard, and to have acquired a considerable knowledge of ancient and modern languages. The great orators of all times were a special object of study with him, and he describes his boyish pedantry pleasantly enough, but by no means without a touch of self-satisfaction in the memory. His university training was supplemented (1714) by a continental tour, untrammelled by a governor; at the Hague his ambition for the applause awarded to adventure made a gamester of him, and at Paris he began, from the same motive, that worship of the conventional Venus, the serious inculcation of which has earned for him the largest and most unenviable part of his reputation.
110 The death of Anne and the accession of George I. opened up a career for him and brought him back to England. His relative James Stanhope (afterwards first Earl Stanhope), the king’s favourite minister, procured for him the place of gentleman of the bedchamber to the prince of Wales. In 1715 he entered the House of Commons as Lord Stanhope of Shelford and member for St Germans, and when the impeachment of James, duke of Ormonde, came before the House, he used the occasion (5th of August 1715) to put to proof his old rhetorical studies. His maiden speech was youthfully fluent and dogmatic; but on its conclusion the orator was reminded with many compliments, by an honourable member, that he wanted six weeks of his majority, and consequently that he was amenable to a fine of £500 for speaking in the House. Lord Stanhope quitted the Commons with a low bow and started for the continent. From Paris he rendered the government important service by gathering and transmitting information respecting the Jacobite plot; and in 1716 he returned to England, resumed his seat, and took frequent part in the debates. In that year came the quarrel between the king and the heir apparent. Stanhope, whose politic instinct obliged him to worship the rising rather than the setting sun, remained faithful to the prince, though he was too cautious to break entirely with the king’s party. He was on friendly terms with the prince’s mistress, Henrietta Howard, afterwards countess of Suffolk. He maintained a correspondence with this lady which won for him the hatred of the princess of Wales (afterwards Queen Caroline). In 1723 a vote for the government got him the place of captain of the Gentlemen Pensioners. In January 1725, on the revival of the Bath, the red riband was offered to him, but was declined.
In 1726 his father died, and Lord Stanhope became earl of Chesterfield. He took his seat in the Upper House, and his oratory, never effective in the Commons by reason of its want of force and excess of finish, at once became a power. In 1728 Chesterfield was sent to the Hague as ambassador. In this place his tact and temper, his dexterity and discrimination, enabled him to do good service, and he was rewarded with Walpole’s friendship, a Garter and the place of lord high steward. In 1732 there was born to him, by a certain Mlle du Bouchet, the son, Philip Stanhope, for whose advice and instruction were afterwards written the famous Letters. He negotiated the second treaty of Vienna in 1731, and in the next year, being somewhat broken in health and fortune, he resigned his embassy and returned to England.
A few months’ rest enabled him to resume his seat in the Lords, of which he was one of the acknowledged leaders. He supported the ministry, but his allegiance was not the blind fealty Walpole exacted of his followers. The Excise Bill, the great premier’s favourite measure, was vehemently opposed by him in the Lords, and by his three brothers in the Commons. Walpole bent before the storm and abandoned the measure; but Chesterfield was summarily dismissed from his stewardship. For the next two years he led the opposition in the Upper House, leaving no stone unturned to effect Walpole’s downfall. In 1741 he signed the protest for Walpole’s dismissal and went abroad on account of his health. He visited Voltaire at Brussels and spent some time in Paris, where he associated with the younger Crebillon, Fontenelle and Montesquieu. In 1742 Walpole fell, and Carteret was his real, though not his nominal successor. Although Walpole’s administration had been overthrown largely by Chesterfield’s efforts the new ministry did not count Chesterfield either in its ranks or among its supporters. He remained in opposition, distinguishing himself by the courtly bitterness of his attacks on George II., who learned to hate him violently. In 1743 a new journal, Old England; or, the Constitutional Journal appeared. For this paper Chesterfield wrote under the name of “Jeffrey Broadbottom.” A number of pamphlets, in some of which Chesterfield had the help of Edmund Waller, followed. His energetic campaign against George II. and his government won the gratitude of the dowager duchess of Marlborough, who left him £20,000 as a mark of her appreciation. In 1744 the king was compelled to abandon Carteret, and the coalition or “Broad Bottom” party, led by Chesterfield and Pitt, came into office. In the troublous state of European politics the earl’s conduct and experience were more useful abroad than at home, and he was sent to the Hague as ambassador a second time. The object of his mission was to persuade the Dutch to join in the War of the Austrian Succession and to arrange the details of their assistance. The success of his mission was complete; and on his return a few weeks afterwards he received the lord-lieutenancy of Ireland—a place he had long coveted.
Short as it was, Chesterfield’s Irish administration was of great service to his country, and is unquestionably that part of his political life which does him most honour. To have conceived and carried out a policy which, with certain reservations, Burke himself might have originated and owned, is indeed no small title to regard. The earl showed himself finely capable in practice as in theory, vigorous and tolerant, a man to be feared and a leader to be followed; he took the government entirely into his own hands, repressed the jobbery traditional to the office, established schools and manufactures, and at once conciliated and kept in check the Orange and Roman Catholic factions. In 1746, however, he had to exchange the lord-lieutenancy for the place of secretary of state. With a curious respect for those theories his familiarity with the secret social history of France had caused him to entertain, he hoped and attempted to retain a hold over the king through the influence of Lady Yarmouth, though the futility of such means had already been demonstrated to him by his relations with Queen Caroline’s “ma bonne Howard.” The influence of Newcastle and Sandwich, however, was too strong for him; he was thwarted and over-reached; and in 1748 he resigned the seals, and returned to cards and his books with the admirable composure which was one of his most striking characteristics. He declined any knowledge of the Apology for a late Resignation, in a Letter from an English Gentleman to his Friend at The Hague, which ran through four editions in 1748, but there is little doubt that he was, at least in part, the author.
The dukedom offered him by George II., whose ill-will his fine tact had overcome, was refused. He continued for some years to attend the Upper House, and to take part in its proceedings. In 1751, seconded by Lord Macclesfield, president of the Royal Society, and Bradley, the eminent mathematician, he distinguished himself greatly in the debates on the calendar, and succeeded in making the new style a fact. Deafness, however, was gradually affecting him, and he withdrew little by little from society and the practice of politics. In 1755 occurred the famous dispute with Johnson over the dedication to the English Dictionary. In 1747 Johnson sent Chesterfield, who was then secretary of state, a prospectus of his Dictionary, which was acknowledged by a subscription of £10. Chesterfield apparently took no further interest in the enterprise, and the book was about to appear, when he wrote two papers in the World in praise of it. It was said that Johnson was kept waiting in the anteroom when he called while Cibber was admitted. In any case the doctor had expected more help from a professed patron of literature, and wrote the earl the famous letter in defence of men of letters. Chesterfield’s “respectable Hottentot,” now identified with George, Lord Lyttelton, was long supposed, though on slender grounds, to be a portrait of Johnson. During the twenty years of life that followed this episode, Chesterfield wrote and read a great deal, but went little into society.
In 1768 died Philip Stanhope, the child of so many hopes. The constant care bestowed by his father on his education resulted in an honourable but not particularly distinguished career for young Stanhope. His death was an overwhelming grief to Chesterfield, and the discovery that he had long been married to a lady of humble origin must have been galling in the extreme to his father after his careful instruction in worldly wisdom. Chesterfield, who had no children by his wife, Melusina von Schulemberg, illegitimate daughter of George I., whom he married in 1733, adopted his godson, a distant cousin, named Philip Stanhope (1755-1815), as heir to the title and estates. His famous jest (which even Johnson allowed to have merit)—“Tyrawley 111 and I have been dead these two years, but we don’t choose to have it known”—is the best description possible of his humour and condition during the latter part of this period of decline. To the deafness was added blindness, but his memory and his fine manners only left him with life; his last words (“Give Dayrolles a chair”) prove that he had neither forgotten his friend nor the way to receive him. He died on the 24th of March 1773.
Chesterfield was selfish, calculating and contemptuous; he was not naturally generous, and he practised dissimulation till it became part of his nature. In spite of his brilliant talents and of the admirable training he received, his life, on the whole, cannot be pronounced a success. His anxiety and the pains he took to become an orator have been already noticed, and Horace Walpole, who had heard all the great orators, preferred a speech of Chesterfield’s to any other; yet the earl’s eloquence is not to be compared with that of Pitt. Samuel Johnson, who was not perhaps the best judge in the world, pronounced his manners to have been “exquisitely elegant”; yet as a courtier he was utterly worsted by Robert Walpole, whose manners were anything but refined, and even by Newcastle. He desired to be known as a protector of letters and literary men; and his want of heart or head over the Dictionary dedication, though explained and excused by Croker, none the less inspired the famous change in a famous line—“Toil, envy, want, the patron, and the jail.” His published writings have had with posterity a very indifferent success; his literary reputation rests on a volume of letters never designed to appear in print. The son for whom he worked so hard and thought so deeply failed especially where his father had most desired he should succeed.
As a politician and statesman, Chesterfield’s fame rests on his short but brilliant administration of Ireland. As an author he was a clever essayist and epigrammatist. But he stands or falls by the Letters to his Son, first published by Stanhope’s widow in 1774, and the Letters to his Godson (1890). The Letters are brilliantly written—full of elegant wisdom, of keen wit, of admirable portrait-painting, of exquisite observation and deduction. Against the charge of an undue insistence on the external graces of manner Chesterfield has been adequately defended by Lord Stanhope (History, iii. 34). Against the often iterated accusation of immorality, it should be remembered that the Letters reflected the morality of the age, and that their author only systematized and reduced to writing the principles of conduct by which, deliberately or unconsciously, the best and the worst of his contemporaries were governed.
The earldom of Chesterfield passed at his death to his godson, already mentioned, as 5th earl, and so to the latter’s son and grandson. On the death of the latter unmarried in 1871, it passed in succession to two collateral heirs, the 8th and 9th earls, and so in 1887 to the latter’s son as 10th earl.
See Chesterfield’s Miscellaneous Works (London, 1777, 2 vols. 4to); Letters to his Son, &c., edited by Lord Mahon (London, 1845-1853, 5 vols.); and Letters to his Godson (1890) (edited by the earl of Carnarvon). There are also editions of the first series of letters by J. Bradshaw (3 vols., 1892) and Mr C. Strachey (2 vols., 1901). In 1893 a biography, including numerous letters first published from the Newcastle Papers, was issued by Mr W. Ernst; and in 1907 appeared an elaborate Life by W.H. Craig.
CHESTERFIELD, a market town and municipal borough in the Chesterfield parliamentary division of Derbyshire, England, 24 m. N. by E. of Derby, on the Midland and the Great Central railways. Pop. (1891) 22,009; (1901) 27,185. It lies at the junction of two streams, the Rother and Hipper, in a populous industrial district. It is irregularly built, with narrow streets, but has a spacious market-place. The church of St Mary and All Saints is a large and beautiful cruciform building principally of the Decorated period. Its central tower carries a remarkable twisted spire of wood covered with lead, 230 ft. high; the distortion has evidently taken place through the use of unseasoned timber and consequent warping of the woodwork. The church, which contains numerous interesting monuments, possesses also the unusual feature of an apsidal Decorated chapel. There is an example of flamboyant tracery in one of the windows. Among public buildings, the Stephenson memorial hall (1879), containing a free library, art and science class-rooms, a theatre and the rooms of the Chesterfield Institute, commemorates George Stephenson, the engineer, who resided at Tapton House, close to Chesterfield, in his later life; he died here in 1848, and was buried in Trinity church. Chesterfield grammar school was founded in 1574. The industries of the town include manufactures of cotton, silk, earthenware, machinery and tobacco, with brass and iron founding; while slate and stone are quarried, and there are coal, iron and lead mines in the neighbourhood. The town is governed by a mayor, 6 aldermen and 18 councillors. Area, 1216 acres. In the immediate neighbourhood of Chesterfield on the west is the urban district of Brampton and Walton (pop. 2698), to the south-east is Hasland (7427), and to the north-east Brimington (4569).
In spite of the Roman origin suggested by its name, so few remains have been found here that it is doubtful whether Chesterfield was a Roman station. Chesterfield (Cestrefeld) owes its present name to the Saxons. It is mentioned in Domesday only as a bailiwick of Newbold belonging to the king, and granted to William Peverell. In 1204 John gave the manor to William Bruere and granted to the town all the privileges of a free borough which were enjoyed by Nottingham and Derby; but before this it seems to have had prescriptive borough rights. Later charters were granted by various sovereigns, and it was incorporated by Elizabeth in 1598 under the style of a mayor, 6 brethren and 12 capital burgesses. This charter was confirmed by Charles II. (1662), and the town was so governed till the Municipal Act 1835 appointed a mayor, 3 aldermen and 12 councillors. In 1204 John granted two weekly markets, on Tuesday and Saturday, and an annual fair of eight days at the feast of the Exaltation of the Holy Cross (Sept. 14). This fair, which is still held, and another on Palm Tuesday, are mentioned in the Quo Warranto roll of 1330. The Tuesday market has long been discontinued. That Chesterfield was early a thriving centre is shown by the charter of John Lord Wake, lord of the manor, granting a gild merchant to the town. In 1266 the town was the scene of a battle between the royal forces and the barons, when Robert de Ferrers, earl of Derby, was taken prisoner. In 1586 there was a terrible visitation of the plague; and the parliamentarian forces were overthrown here in the Civil War. With the development of cotton and silk industries the town has increased enormously, and is now second in importance only to Derby among the towns of the county. There is no record that it ever returned representatives to parliament.
See Stephen Glover, History and Gazetteer of the County of Derby (Derby, 1831-1833); J. Pym Yeatman, Records of the Borough of Chesterfield (Chesterfield and Sheffield, 1884); Thomas Ford, History of Chesterfield (London, 1839).
CHESTER-LE-STREET, a town in the Chester-le-Street parliamentary division of Durham, England, near the river Wear, 6 m. N. of the city of Durham on the North-Eastern railway. Pop. (1901) 11,753. The parish church of St Mary and St Cuthbert is an interesting building, formerly collegiate, with a tower 156 ft. high, and a remarkable series of monumental tombs of the Lumley family, collected here from Durham cathedral and various ruined monasteries, and in some cases remade. About 1 m. along the river is Lumley Castle, the seat of the earl of Scarborough, and about 2 m. north lies Lambton Castle, the residence of the earl of Durham, built in 1797 on the site of the old House of Harraton. Collieries and iron-works employ the industrial population. Chester-le-Street is a place of considerable antiquity. It lies on a branch of the Roman north road, on which it was a station, but the name is not known. Under the name of Cunecastre it was made the seat of a bishop in 882, and continued to be the head of the diocese till the Danish invasion of 995. During that time the church was the repository of the shrine of St Cuthbert, which was then removed to Durham.
CHESTERTON, GILBERT KEITH (1874- ), English journalist and author, who came of a family of estate-agents, was born in London on the 29th of May 1874. He was educated 112 at St Paul’s school, which he left in 1891 with the idea of studying art. But his natural bent was literary, and he devoted himself mainly to cultivating that means of expression, both in prose and verse; he did occasional reviewing, and had some experience in a publisher’s office. In 1900, having already produced a volume of clever poems, The Wild Knight, he definitely took to journalism as a career, and became a regular contributor of signed articles to the Liberal journals, the Speaker and Daily News. He established himself from the first as a writer with a distinct personality, combative to a swashbuckling degree, unconventional and dogmatic; and the republication of much of his work in a series of volumes (e.g. Twelve Types, Heretics, Orthodoxy), characterized by much acuteness of criticism, a pungent style, and the capacity of laying down the law with unflagging impetuosity and humour, enhanced his reputation. His powers as a writer are best shown in his studies of Browning (in the “English Men of Letters” series) and of Dickens; but these were only rather more ambitious essays among a medley of characteristic utterances, ranging from fiction (including The Napoleon of Notting-hill) to fugitive verse, and from artistic criticism to discussions of ethics and religion. The interest excited by his work and views was indicated and analysed in an anonymous volume (G.K. Chesterton: a Criticism) published in 1908.
CHESTERTON, an urban district in the Chesterton parliamentary division of Cambridgeshire, England, 1½ m. N. from Cambridge station, on the north bank of the Cam. Pop. (1901) 9591. The church of St Andrew is Decorated and Perpendicular, retaining ancient woodwork and remains of fresco painting. Along the river are several boat-houses erected by the Cambridge University Boat Club. Boat-building and tile manufacture are local industries.
CHESTNUT (nux Castanea), the common name given to two sorts of trees and their fruit, (1) the so-called “horse-chestnut,” and (2) the sweet or “Spanish” chestnut.
(1) The common horse-chestnut, Aesculus Hippocastanum (Ger. Rosskastanie; Fr. marronnier d’Inde), has been stated to be a native of Tibet, and to have been brought thence to England in 1550; it is now, however, thought to be indigenous in the mountains of northern Greece, where it occurs wild at 3000 to 4000 ft. above sea-level. Matthiolus, who attributes the origin of the name of the tree to the use of the nuts by the inhabitants of Constantinople for the relief of short-windedness and cough in horses, remarks that no ancient writer appears to have made mention of the horse-chestnut. Clusius (Rariorum plantarum hist. i. p. 8, 1601) describes it as a vegetable curiosity, of which in 1588 he had left in Vienna a living specimen, but of which he had not yet seen either the flowers or recent fruit. The dry fruit, he says, had frequently been brought from Constantinople into Europe.
The tree grows rapidly; it flourishes best in a sandy, somewhat moist loam, and attains a height of 50 to 60 or more ft., assuming a pyramidal outline. Its boughs are strong and spreading. The buds, conspicuous for their size, are protected by a coat of a glutinous substance, which is impervious to water; in spring this melts, and the bud-scales are then cast off. The leaves are composed of seven radiating leaflets (long-wedge-shaped); when young they are downy and drooping. From the early date of its leafing year by year, a horse-chestnut in the Tuileries is known as the “Marronnier du 20 mars.” The flowers of the horse-chestnut, which are white dashed with red and yellow, appear in May, and sometimes, but quite exceptionally, again in autumn; they form a handsome erect panicle, but comparatively few of them afford mature fruit. The fruit is ripe in or shortly before the first week in October, when it falls to the ground, and the three-valved thorny capsule divides, disclosing the brown and at first beautifully glossy seeds, the so-called nuts, having a resemblance to sweet chestnuts, and commonly three or else two in number. For propagation of the tree, the seeds may be sown either when fresh, or, if preserved in sand or earth, in spring. Drying by exposure to the air for a month has been found to prevent their germination. Rooks are wont to remove the nuts from the tree just before they fall, and to disperse them in various directions. The tree is rarely planted in mixed plantations where profit is an object; it interferes with its neighbours and occupies too much room. It is generally introduced near mansion-houses for ornament and shade, and the celebrated avenues at Richmond and Bushey Park in England are objects of great beauty at the time of flowering.
The bark of the horse-chestnut contains a greenish oil, resin, a yellow body, a tannin, C26H24O12, existing likewise in the seeds and various parts of the tree, and decomposable into phloroglucin and aesciglyoxalic acid, C7H5O3, also aesculetin hydrate, and the crystalline fluorescent compound aesculin, of the formula C21H24O13 (Rochleder and Schwarz), with which occurs a similar substance fraxin, the paviin of Sir G.G. Stokes (Q.J. Chem. Soc. xi. 17, 1859; xii. 126, 1860), who suggests that its presence may perhaps account for the discrepancies in the analyses of aesculin given by different authors. From the seeds have been obtained starch (about 14%), gum, mucilage, a non-drying oil, phosphoric acid, salts of calcium, saponin, by boiling which with dilute hydrochloric or sulphuric acid aesculic acid is obtained, quercitrin, present also in the fully developed leaves, aescigenin, C12H26O2, and aesculetin, C9H6O4, which is procurable also, but in small quantity only, from the bark. Friedrich Rochleder has described as constituent principles of the cotyledons aphrodaescin, C52H82O23, a bitter glucoside, argyraescin, C27H42O12, aescinic acid, C24H40O12, and queraescitrin, C41H46O25, found also in the leaves. To prepare pure starch from the seeds, Flandin (Compt. rend. xxvii. 391, 1848; xxviii. 138, 1849) recommends kneading them, when peeled and bruised, in an aqueous solution of 1/100 to 1/60 of their weight of sodium carbonate. E. Staffel (Ann. d. Chem. u. Pharm. lxxvi., 1850, p. 379) after drying found, in spring and autumn respectively, 10.9 and 3.38% of ash in the wood, 8.68 and 6.57 in the bark, and 7.68 and 7.52 in the leaves of the horse-chestnut. The ash of the unripe fruit contains 58.77, that of the ripe kernel 61.74, and that of the green shell 75.91% of potash (E. Wolff).
The wood of the horse-chestnut is soft, and serves only for the making of water-pipes, for turner’s work and common carpentry, as a source of charcoal for gunpowder, and as fuel. Newly cut it weighs 60 ℔, and dry 35 ℔ per cub. ft. approximately. The bark has been employed for dyeing yellow and for tanning, and was formerly in popular repute as a febrifuge and tonic. The powder of the dried nuts was at one time prescribed as a sternutatory (to encourage sneezing) in the Edinburgh Pharmacopoeia. It is stated to form with alum-water a size or cement highly offensive to vermin, and with two parts of wheaten flour the material for a strong bookbinder’s paste. Infusion of horse-chestnuts is found to expel worms from soil, and soon to kill them if they are left in it. The nuts furthermore have been applied to the manufacture of an oil for burning, cosmetic preparations and starch, and in Switzerland, France and Ireland, when rasped on ground, to the bleaching of flax, hemp, silk and wool. In Geneva horse-chestnuts are largely consumed by grazing stock, a single sheep receiving 2 ℔ crushed morning and evening. Given to cows in moderate quantity, they have been found to enhance both the yield and flavour of milk. Deer readily eat them, and, after a preliminary steeping in lime-water, pigs also. For poultry they should be used boiled, and mixed with other nourishment. The fallen leaves are relished by sheep and deer, and afford a good litter for flocks and herds.
One variety of the horse-chestnut has variegated leaves, and another double flowers. Darwin observed that Ae. Pavia, the red buckeye of North America, shows a special tendency, under unfavourable conditions, to be double-blossomed. The seeds of this species are used to stupefy fish. The scarlet-flowered horse-chestnut, Ae. rubicunda, is a handsome tree, less in height and having a rounder head than the common form; it is a native of North America. Another species, possessing flowers with the lower petals white with a red tinge, and the upper yellow and red with a white border, and fruit unarmed, is Ae. indica, a native of the western Himalayas. Among the North American species are the foetid or Ohio buckeye, Ae. glabra, and Ae. flava, the sweet 113 buckeye. Ae. californica, when full-grown and in flower, is a beautiful tree, but its leaves often fall before midsummer.
(2) The Spanish or sweet chestnut, Castanea sativa (natural order, Fagaceae), is a stately and magnificent tree, native of the countries bordering on the Mediterranean, but also ripening its fruit in sheltered situations as far north as Scotland. It lives very long, and attains a large size, spreading its branches widely. It has large glossy lanceolate leaves with a toothed margin. The flowers, which appear in early summer, are in pendulous, slender yellowish catkins, which bear a number of staminate flowers with a few pistillate flowers at the base. The staminate contain 8 to 20 stamens which produce an enormous amount of dusty yellow pollen, some of which gets carried by wind to the protruding stigmas of the pistillate flowers. The latter are borne three together, invested by a cupule of four green bracts, which, as the fruit matures, grow to form the tough green prickly envelope surrounding the group of generally three nuts. The largest known chestnut tree is the famous Castagno di cento cavalli, or the chestnut of a hundred horses, on the slopes of Mount Etna, a tree which, when measured about 1780 by Count Borch, was found to have a circumference of 190 ft. The timber bears a striking resemblance to that of the oak, which has been mistaken for chestnut; but it may be distinguished by the numerous fine medullary rays. Unlike oak, the wood is more valuable while young than old. When not more than fifty years old it forms durable posts for fences and gates; but at that age it often begins to deteriorate, having ring-shakes and central hollows. In a young state, when the stems are not above 2 in. in diameter at the ground, the chestnut is found to make durable hoops for casks and props for vines; and of a larger size it makes good hop-poles.
Chestnuts (the fruit of the tree) are extensively imported into Great Britain, and are eaten roasted or boiled, and mashed or otherwise as a vegetable. In a raw state they have a sweet taste, but are difficult of digestion. The trees are very abundant in the south of Europe, and chestnuts bulk largely in the food resources of the poor in Spain, Italy, Switzerland and Germany. In Italy the kernels are ground into meal, and used for thickening soups, and even for bread-making. In North America the fruits of an allied species, C. americana, are eaten both raw and cooked.
CHETTLE, HENRY (1564?-1607?), English dramatist and miscellaneous writer, was the son of Robert Chettle, a London dyer. He was apprenticed in 1577 to a stationer, and in 1591 became a partner with William Hoskins and John Danter. In 1592 he published Robert Greene’s Groatsworth of Wit. In the preface to his Kind Herts Dreame (end of 1592) he found it necessary to disavow any share in that pamphlet, and incidentally he apologized to three persons (one of them commonly identified with Shakespeare) who had been abused in it. Piers Plainnes Seaven Yeres Prentiship, the story of a fictitious apprenticeship in Crete and Thrace, appeared in 1595. As early as 1598 Francis Meres includes him in his Palladis Tamia as one of the “best for comedy,” and between that year and 1603 he wrote or collaborated in some forty-nine pieces. He seems to have been generally in debt, judging from numerous entries in Henslowe’s diary of advances for various purposes, on one occasion (17th of January 1599) to pay his expenses in the Marshalsea prison, on another (7th of March 1603) to get his play out of pawn. Of the thirteen plays usually attributed to Chettle’s sole authorship only one was printed. This was The Tragedy of Hoffmann: or a Revenge for a Father (played 1602; printed 1631), a share in which Mr Fleay assigns to Thomas Heywood. It has been suggested that this piece was put forward as a rival to Shakespeare’s Hamlet. Among the plays in which Chettle had a share is catalogued The Danish Tragedy, which was probably either identical with Hoffmann or another version of the same story. The Pleasant Comedie of Patient Grissill (1599), in which he collaborated with Thomas Dekker and William Haughton, was reprinted by the Shakespeare Society in 1841. It contains the lyric “Art thou poor, yet hast thou golden slumbers,” which is probably Dekker’s. In November 1599 Chettle receives ten shillings for mending the first part of “Robin Hood,” i.e. The Downfall of Robert, Earl of Huntingdon, by Anthony Munday; and in the second part, which followed soon after and was printed in 1601, The Death of Robert, Earle of Huntingdon, he collaborated with Munday. Both plays are printed in Dodsley’s Select Collection of Old English Plays (ed. W. C. Hazlitt, vol. viii.). In 1603 Chettle published England’s Mourning Garment, in which are included some verses alluding to the chief poets of the time. His death took place before the appearance of Dekker’s Knight’s Conjurer in 1607, for he is there mentioned as a recent arrival in limbo.
Hoffmann was edited by H. B(arrett) L(ennard) (1852) and by Richard Ackermann (Bamberg, 1894).
CHEVALIER, ALBERT (1861- ), English comedian, began a connexion with the stage while still a child. In 1877 he was engaged as an actor under the Bancrofts in London, and for some years played “legitimate” parts at the Court theatre and elsewhere. In 1891, however, he began a successful music-hall career as a singer of coster songs of his own invention, a new type in which he had an immediate success, both in England and America. He subsequently organized an entertainment of his own, with sketches and songs, with which he went on tour, establishing a wide popularity as an original artist in his special line.
CHEVALIER, MICHEL (1806-1879), French economist, was born at Limoges on the 13th of January 1806. In his early manhood, while employed as an engineer, he became a convert to the theories of Saint Simon; these he ardently advocated in the Globe, the organ of the Saint Simonians, which he edited until his arrest in 1832 on a charge of outraging public morality by its publication. He was sentenced to a year’s imprisonment, but was released in six months through the intervention of Thiers, who sent him on a special mission to the United States to study the question of land and water transport. In 1836 he published, in two volumes, the letters he wrote from America to the Journal des débats. These attracted so much attention that he was sent in the same year on an economic mission to England, which resulted in his publication (in 1838) of Des intérêts matériels de la France. The success of this made his position secure, and in 1840 he was appointed professor of political economy in the Collège de France. He sat for a short time (1845-1846) as a member of the Chamber of Deputies, but lost his seat owing to his enthusiastic adoption of the principles of free trade. Under Napoleon III. he was restored to the position of which the revolution of 1848 had temporarily deprived him. In 1850 he became a member of the Institute, and in the following year published an important work in favour of free trade, under the title of Examen du système commercial connu sous le nom de système protecteur. His chief public triumph was the important part he played in bringing about the conclusion of the commercial treaty between France and Great Britain in 1860. Previously to this he had served, in 1855, upon the commission for organizing the Exhibition of 1855, and his services there led to his forming one of the French jury of awards in the London Exhibition of 1862. He was created a member of the Senate in 1860, and continued for some years to take an active part in its discussions. He retired from public life in 1870, but was unceasingly industrious with his pen. He became grand officer of the Legion of Honour in 1861, and during the later years of his life received from many quarters public recognition of his eminence as a political economist. He died at his château near Montpellier (Hérault) on the 28th of November 1879. Many of his works have been translated into English and other languages. Besides those already mentioned the more important are: Cours d’économie politique (1842-1850); Essais de politique industrielle (1843); De la baisse probable d’or(1859, translated into English by Cobden, On the Probable Fall of the Value of Gold, Manchester, 1859); L’Expédition du Mexique (1862); Introduction aux rapports du jury international (1868).
CHEVALIER, ULYSSE (1841- ), French bibliographer, was born at Rambouillet on the 24th of February 1841. He published a great number of documents relating to the history of Dauphiné, e.g. the cartularies of the church and the town of Die (1868), of the abbey of St André le-Bas at Vienne (1869), of the abbey of Notre Dame at Bonnevaux in the diocese of Vienne (1889), of the abbey of St Chaffre at Le Monestier (1884), the 114 inventories and several collections of archives of the dauphins of Viennais, and a Bibliothèque liturgique in six volumes (1893-1897), the third and fourth volumes of which constitute the Repertorium hymnologicum, containing more than 20,000 articles. But his principal work is the Répertoire des sources historiques du moyen âge. The first part, Bio-bibliographie (1877-1886; 2nd ed., 1905), contains the names of all the historical personages alive between the years 1 and 1500 who are mentioned in printed books, together with the precise indication of all the places where they are mentioned. The second part, Topo-bibliographie (1894-1903), contains not only the names of places mentioned in books on the history of the middle ages, but, in a general way, everything not included in the Bio-bibliographie. The Répertoire as a whole contains an enormous mass of useful information, and is one of the most important bibliographical monuments ever devoted to the study of medieval history. Though a Catholic priest and professor of history at the Catholic university of Lyons, the Abbé (afterwards Canon) Chevalier knew how to maintain an independent critical attitude even in religious questions. In the controversy on the authenticity of the Holy Shroud (sudario) at Turin, he worked in the true scientific spirit by tracing back the history of that piece of stuff, which was undoubtedly used as a shroud, but which was not produced before the 14th century and is probably no older (See Le Saint Suaire de Lirey-Chambéry-Turin et les défenseurs de son authenticité). Similarly, in Notre Dame de Lorette; étude critique sur l’authenticité de la Santa Casa (1906), he dissipated by the aid of authentic documents the legend which had embellished and falsified the primitive history of that sanctuary.
CHEVAUX-DE-FRISE (French for “Friesland horses”; the Dutch Vriesse ruyters, “Frisian horsemen,” and German Spanische Reiter, “Spanish horsemen”), a military obstacle, originating apparently in the Dutch War of Independence, and used to close the breach of a fortress, streets, &c. It was formerly often used in field operations as a defence against cavalry; hence the name, as the Dutch were weak in the mounted arm and had therefore to check the enemy’s cavalry by an artificial obstacle. Chevaux-de-frise consist of beams in which are fixed a number of spears, sword-blades, &c., with the points projecting outwards on all sides.
CHEVERUS, JEAN LOUIS ANNE MAGDELEINE LEFEBVRE DE (1768-1836), French ecclesiastic, was born on the 28th of January 1768, in Mayenne, France, where his father was general civil judge and lieutenant of police. He studied at the college of Mayenne, received the tonsure when twelve, became prior of Torbechet while still little more than a child, thence derived sufficient income for his education, entered the College of Louis le Grand in 1781, and after completing his theological studies at the Seminary of St Magloire, was ordained deacon in October 1790, and priest by special dispensation on the 18th of December. He was immediately made canon of the cathedral of Le Mans and began to act as vicar to his uncle in Mayenne, who died in 1792. Owing to the progress of the Revolution he emigrated in 1792 to England, and thence in 1796 to America, settling in Boston, Mass. His interest had been aroused by François Antoine Matignon, a former professor at Orleans, now in charge under Bishop John Carroll of all the Catholic churches and missions in New England. Cheverus, although at first appointed to an Indian mission in Maine, remained in Boston for nearly a year, and returned thither after several months in the Penobscot and Passamaquoddy missions and visits to scattered Catholic families along the way. During the epidemic of yellow fever in 1798 he won great praise and respect for his courage and charity; and his preaching was listened to by many Protestants—indeed the subscriptions for the Church of the Holy Cross which he founded in 1803 were largely from non-Catholics. In 1808 the papal brief was issued making Boston a bishopric, suffragan to Baltimore, and Cheverus its bishop. He was consecrated on All Saints’ day in 1810, at St Peter’s, Baltimore, by Archbishop Carroll. On the death of the latter his assistant bishop, Neale, urged the appointment of Cheverus as assistant to himself; Cheverus refused and warmly asserted his desire to remain in Boston; but, much broken by the death of Matignon in 1818 and with impaired health, he soon found it necessary to leave the seat of his bishopric. In 1823, Louis XVIII. having insisted on his return to France, Cheverus became bishop of Montauban, where his tolerance captivated the Protestant clergy and laymen of the city. He was made archbishop of Bordeaux in 1826; and on the 1st of February 1836, in accordance with the wish of Louis Philippe, he was made a cardinal. He died in Bordeaux on the 19th of July 1836. To Cheverus, more than to any other, is due the position that Boston now holds in the Roman Catholic Church of America, as well as the general growth of that church in New England. His character was essentially lovable: the Jews of Bordeaux and Protestants everywhere delighted to honour him.
See the rather extravagant biography by J. Huen-Dubourg, Vie du cardinal de Cheverus (Bordeaux, 1838; English version by E. Stewart, Boston, 1839).
CHEVET, the term employed in French architecture to distinguish the apsidal end of a church, in which the apses or chapels radiate round the choir aisle. The two earliest examples (11th and 12th century) are found in the churches of St Hilaire, Poitiers, and Notre Dame-du-Port, Clermont, where there are four apses. A more usual number is five, and the central apse, being of larger dimensions, becomes the Lady chapel. This was the case in Westminster Abbey, where Henry III. introduced the chevet into England; Henry VII.’s chapel is built on the site of the original Lady chapel, which must have been of exceptional size, as it extended the whole length of the present structure. In Solignac, Fontevrault and Paray-le-Monial there are only three, in these cases sufficiently distant one from the other to allow of a window between. The usual number in all the great cathedrals of the 13th century, as in Bourges, Chartres, Reims, Troyes, Tours, Bayeux, Antwerp and Bruges, is five. In Beauvais, Amiens and Cologne there are seven apsidal chapels, and in Clairvaux nine radiating but rectangular chapels. In the 14th and 15th centuries the central apse was increased in size and dedicated to the Virgin Mary, as in St Ouen at Rouen.
CHEVIOT HILLS, a range forming about 35 m. of the border between England and Scotland. The boundary generally follows the line of greatest elevation, but as the slope is more gradual southward and northward the larger part of the range is in Northumberland, England, and the lesser in Roxburghshire, Scotland. The axis runs from N.E. to S.W., with a northward tendency at the eastern end, where the ridge culminates in the Cheviot, 2676 ft. Its chief elevations from this point south-westward fall abruptly to 2034 ft. in Windygate Hill, and then more gradually to about 1600 ft. above the pass, followed by a high road from Redesdale. Beyond this are Carter Fell (1815) and Peel Fell (1964), after which two lines of lesser elevation branch westward and southward to enclose Liddesdale. The hills are finely grouped, of conical and high-arched forms, and generally grass-covered. Their flanks are scored with deep narrow glens in every direction, carrying the headwaters of the Till, Coquet and North Tyne on the south, and tributaries of the Tweed on the north. The range is famous for a valuable breed of sheep, which find abundant pasture on its smooth declivities. In earlier days it was the scene of many episodes of border warfare, and its name is inseparably associated with the ballad of Chevy Chase. The main route into Scotland from England lies along the low coastal belt east of the Till; the Till itself provided another, and Redesdale a third. There are numerous ruins of castles and “peel towers” or forts on the English side in this district.
Geology.—The rocks entering into the geological structure of the Cheviots belong to the Silurian, Old Red Sandstone and Carboniferous systems. The oldest strata, which are of Upper Silurian age, form inliers that have been exposed by the denudation of the younger palaeozoic rocks. One of these which occurs high up on the slopes of the Cheviots is drained by the Kale Water and the river Coquet and is covered towards the north by the Old Red Sandstone volcanic series and on the south by Carboniferous strata. Another area is traversed by the Jed Water and the Edgerston Burn and is surrounded by rocks of Old Red Sandstone age. The strata consist of greywackes, flags and shales with seams and zones of graptolite shale which yield fossils sparingly.
On the upturned and denuded edges of the Silurian strata a great pile of contemporaneous volcanic rocks of Lower Old Red Sandstone age rests unconformably, which consists chiefly of lavas with thin partings of tuff. A striking feature is the absence of coarse sediments, thus indicating prolonged volcanic activity. They cover an area of about 230 sq. m. in the eastern part of the Cheviots and rise to a height of 2676 ft. above the sea. The lavas comprise dark pitchstone, resembling that at Kirk Yetholm, and porphyritic and amygdaloidal andesites and basalts. This volcanic platform is pierced by a mass of granite about 20 sq. m. in extent, which forms the highest peak in the Cheviot range. It has been described by Dr Teall as an augite-biotite-granite having strong affinities with the augite-bearing granitites of Laveline and Oberbrück in the Vosges. Both the granite and the surrounding lavas are traversed by dykes arid sills of intermediate and acid types represented by mica-porphyrites and quartz-felsites.
On their north-west margin the Lower Old Red volcanic rocks are covered unconformably by the upper division of that system composed of red sandstones and conglomerates, which, when followed westwards, rest directly on the Silurian platform. Towards the south and east the volcanic pile is overlaid by Carboniferous strata, thus indicating a prolonged interval of denudation.
On the northern slopes of the western part of the Cheviots the representatives of the Cementstone group of the Carboniferous system come to the surface, where they consist of shales, clays, mudstones, sandstones with cementstones and occasional bands of marine limestone. These are followed in normal order by the Fell Sandstone group, comprising a succession of sandstones with intercalations of red and green clays and impure cementstone bands. They form the higher part of the Larriston Fells and are traceable eastwards to Peel Fell, where there is evidence of successive land surfaces in the form of dirt beds. They are succeeded by the Lewisburn coal-bearing group, which represents the Scremerston coals.
CHEVREUL, MICHEL EUGÈNE (1786-1889), French chemist, was born, on the 31st of August 1786, at Angers, where his father was a physician. At about the age of seventeen he went to Paris and entered L.N. Vauquelin’s chemical laboratory, afterwards becoming his assistant at the natural history museum in the Jardin des Plantes. In 1813 he was appointed professor of chemistry at the Lycée Charlemagne, and subsequently undertook the directorship of the Gobelins tapestry works, where he carried out his researches on colour contrasts (De la loi du contraste simultané des couleurs, 1839). In 1826 he became a member of the Academy of Sciences, and in the same year was elected a foreign member of the Royal Society of London, whose Copley medal he was awarded in 1857. He succeeded his master, Vauquelin, as professor of organic chemistry at the natural history museum in 1830, and thirty-three years later assumed its directorship also; this he relinquished in 1879, though he still retained his professorship. In 1886 the completion of his hundredth year was celebrated with public rejoicings; and after his death, which occurred in Paris on the 9th of April 1889, he was honoured with a public funeral. In 1901 a statue was erected to his memory in the museum with which he was connected for so many years. His scientific work covered a wide range, but his name is best known for the classical researches he carried out on animal fats, published in 1823 (Recherches sur les corps gras d’origine animale). These enabled him to elucidate the true nature of soap; he was also able to discover the composition of stearin and olein, and to isolate stearic and oleic acids, the names of which were invented by him. This work led to important improvements in the processes of candle-manufacture. Chevreul was a determined enemy of charlatanism in every form, and a complete sceptic as to the “scientific” psychical research or spiritualism which had begun in his time (see his De la baguette divinatoire, et des tables tournantes, 1864).
CHEVRON (Fr. from chévre, a goat), in architecture, the beams or rafters in the roofs of a building, meeting in an angle with a fancied resemblance to the horns of a butting goat; in heraldry a bent bar on a shield, used also as a distinguishing badge of rank on the sleeves of non-commissioned officers in most armies and navies and by police and other organized bodies wearing uniform, and as a mark of good conduct in the army and navy. Chevron is also an architectural term for an inflected ornament, called also “zig-zag,” found largely in romanesque architecture in France, England and Sicily. It is one of the most common decorations found in the voussoirs of the Norman arch, and was employed also on shafts, as in the cloisters of Monreale near Palermo, those of St Paul outside Rome, and many churches in Germany. Its earliest appearance was in the tomb of Agamemnon at Mycenae, where the shafts flanking the entrance doorway have nine decorative chevron bands; in this case there is no doubt it was derived from the metal casing of the early wood columns.
CHEVROTAIN, a name taken from the French to designate the various representatives of the mammalian ungulate family Tragulidae. These tiny animals, commonly known as mouse-deer, are in no wise nearly related to the true deer, but constitute by themselves a special section of artiodactyle ungulates known as Tragulina, for the characteristics of which see Artiodactyla. The typical genus Tragulus, which is Asiatic, contains the smallest representatives of the family, the animals having more of the general aspects and habits of some rodents, such as the agoutis, than of other ruminants. The longest-known species are T. javanicus, T. napu, T. kanchil, T. stanleyanus and T. memmina; but a number of other forms, best regarded for the most part as races, have been named. Of those mentioned, the first four are from the Malay Peninsula or the islands of the Indo-Malay Archipelago, the last from Ceylon and India. Kanchil and napu (or napoh) are the Malay names of the species with those specific titles. The second genus, Dorcatherium (or Hyomoschus), is African, and distinguished chiefly by the feet being stouter and shorter, the outer toes better developed, and the two middle metacarpals not welded together. Its dental formula (as that of Tragulus) is i.0/3, c.1/1, p.8/3, m.3/3=34. Vertebrae: C. 7, D. 13, L. 6, S. 5, Ca. 12-13. The only existing species, D. aquaticum (fig.), in type is rather larger than any of the Asiatic chevrotains, which it otherwise much resembles, but is said to frequent the banks of streams, and have much the habits of pigs. It is of a rich brown colour, with back and sides spotted and striped with white; and it is evidently the survivor of an ancient form, as remains of a species only differing in size (D. crassum) have been found in the Miocene deposits of France. For long this species was supposed to be restricted to West Africa, but it has recently been obtained in East Central Africa, where it is represented by a local race.

African Water Chevrotain (Dorcatherium aquaticum).
CHEYENNE (Sioux for “of alien speech”), a tribe of North American Indians of Algonquian stock. They formerly lived on the Cheyenne river, North Dakota. Driven west by the Dakotas, they were found by early explorers at the eastern base of the Black Hills, South Dakota. Part of them later moved south and allied themselves with the Arapahoes. Their whole history has been one of war with their red and white neighbours. They are a powerful athletic race, mentally superior to the average American Indian. They are divided into eleven subdivisions and 116 formerly had a council of chiefs. They number some 3000, and are divided into northern and southern Cheyennes; the former being on a reservation in Montana, the latter in Oklahoma. In 1878-79 a band of the former revolted, and some seventy-five of them were killed.
See Handbook of American Indians (Washington, 1907); also Indians, North American.
CHEYENNE, the chief city and capital of Wyoming, U.S.A., and county-seat of Laramie county, on Crow Creek, about 106 m. N. of Denver. Pop. (1890) 11,690; (1900) 14,087, of whom 1691 were foreign-born; (1905) 13,656; (1910) 11,320. It is served by the Union Pacific, the Chicago, Burlington & Quincy, and the Colorado & Southern railways. It is situated near the southern boundary of the state, on the high plains near the E. foot of the Laramie range, at an altitude of 6050 ft.; the surrounding country is given up to mining (lignite and iron), grazing and dry-farming. Among the principal buildings are the capitol, modelled after the National Capitol at Washington; the United States government building, the Soldiers’ and Sailors’ Home, the Union Pacific depôt, the high school, the Carnegie library, St Mary’s cathedral (Roman Catholic), the Convent of the Holy Child Jesus, the Masonic Temple and the Elks’ clubhouse. The city has two parks, and is connected by a boulevard with Fort D.A. Russell, an important United States military post, 4 m. north of the city, established in 1867 and named in honour of Major-General David Allen Russell (1820-1864) of the Union army, who was killed at Opequan, Virginia. The industrial prosperity of Cheyenne is largely due to the extensive railway shops of the Union Pacific situated here; but the city is also an important cattle market and has stock-yards. In 1905 the value of the city’s factory products ($924,697) was almost one-fourth the total value of the factory products of the state. Cheyenne, settled in 1867, when the Union Pacific reached here, was named from the Cheyenne Indians. It was chosen as the site for the capital of the territory in 1869, and was incorporated in the same year.
CHEYNE, THOMAS KELLY (1841- ), English divine and Biblical critic, was born in London, and educated at Merchant Taylors’ School and Oxford. Subsequently he studied German theological methods at Göttingen. He was ordained in 1864, and held a fellowship at Balliol College, Oxford, 1868-1882. During the earlier part of this period he stood alone in the university as a teacher of the main conclusions of modern Old Testament criticism. In 1881 he was presented to the rectory of Tendring, in Essex, and in 1884 he was made a member of the Old Testament revision company. He resigned the living of Tendring in 1885 on his appointment to the Oriel professorship, which carried with it a canonry at Rochester. In 1889 he delivered the Bampton lectures at Oxford. In 1908 he resigned his professorship. He consistently urged in his writings the necessity of a broad and comprehensive study of the Scriptures in the light of literary, historical and scientific considerations. His publications include commentaries on the Prophets and Hagiographa, and lectures and addresses on theological subjects. He was a joint editor of the Encyclopaedia Biblica (London, 1899-1903), a work embodying the more advanced conclusions of English biblical criticism. In the introduction to his Origin of the Psalter (London, 1891) he gave an account of his development as a critical scholar.
CHÉZY, ANTOINE LÉONARD DE (1773-1832), French orientalist, was born at Neuilly on the 15th of January 1773. His father, Antoine de Chézy (1718-1798), was an engineer who finally became director of the École des Fonts et Chaussées. The son was intended for his father’s profession; but in 1799 he obtained a post in the oriental department of the national library. About 1803 he began the study of Sanskrit, though he possessed neither grammar nor dictionary, and by great labour he obtained sufficient knowledge of the language to be able to compose in it verses said to possess great elegance. He was the first professor of Sanskrit appointed in the Collège de France (1815), a chevalier of the Legion of Honour, and a member of the Académie des Inscriptions. He died in 1832. Among his works were Medjouin et Leila (1807), from the Persian; Yadjanadatta Badha (1814) and La Reconnaissance de Sacountala (1830), from the Sanskrit; L’Anthologie érotique d’Amrou (1831), published under the pseudonym d’Apudy.
See the Mémoires of the Académie des Inscriptions (new series, vol. xii.), where there is a notice of Chézy by Silvestre de Sacy.
CHHATARPUR, a native state in the Bundelkhand agency of Central India. Area, 1118 sq. m.; pop. (1901) 156,139; estimated revenue, £16,000. The chief, whose hereditary title is raja, is a Rajput of the Ponwar clan, whose ancestor dispossessed the descendant of Chhatar Sal, the founder of Bundelkhand independence, towards the end of the 18th century. The state was guaranteed to Kunwar Suni Singh Ponwar in 1806. In 1854 it would have lapsed to the British government for want of direct heirs, but was conferred on Jagat Raj as a special act of grace. The town of CHHATARPUR, which is named after Chhatar Sal, and contains his cenotaph, is 70 m. by road S.W. of Banda. Pop. (1901) 10,029. There are manufactures of paper and coarse cutlery, and a high school. The state also contains the British cantonment of Nowgong.
CHHATTISGARH, a division of the Central Provinces of India, comprising a British division (21,240 sq. m.) and two small feudatory states, Raigarh (1486 sq. m.) and Sarangarh (540 sq. m.). In 1905 the five Oriya states of Bamra, Rairakhol, Sonpur, Patna and Kalahandi were transferred from the Central Provinces to Bengal. Chhattisgarh, or “the thirty-six forts,” is a low-lying plain, enclosed on every side by hills and forests, while a rocky barrier shuts it off from the Nagpur plain on the west. Two great rivers, the Nerbudda and Sone, take their rise at the side of the Amarkantak hill in the north-west corner of the division, the Nerbudda flowing nearly due west to the Bombay coast, the Sone ultimately falling into the Ganges in Lower Bengal. Protected on both sides by ranges of hills, the district was, until late years, the least known portion of the most obscure division of India, but recently it has been opened up by the Bengal-Nagpur railway, and has developed into a great grain-producing country. Its population is almost pure Hindu, except in the two great tracts of hill and forest, where the aboriginal tribes retired before the Aryan invasion. It remained comparatively unaffected either by the Oriya immigration on the east, or by the later influx of Mahrattas on the west. For though the Mahrattas conquered and governed the country for a period, they did not take possession of the land. In 1901 the population of the two remaining feudatory states was 125,281, Raigarh having 86,543 and Sarangarh 38,738. Much of the soil is still covered with forest, but it includes fertile rice land.
The British division of Chhattisgarh comprises the three districts of Drug (created in 1906), Raipur and Bilaspur. In 1905 the district of Sambalpur, together with the five feudatory states, was transferred to Bengal. In 1901 the population of the reduced area was 2,642,983.
CHHINDWARA, a town and district of British India, in the Nerbudda division of the Central Provinces. The site of the town is 2200 ft. above sea-level, and is surrounded by ranges of low hills. The European station extends for nearly 2 m. and is well wooded. It is considered very healthy, and forms a resort for European visitors from Nagpur and Kampti during the hot weather.
The area of the District of Chhindwara is 4631 sq. m. It has two natural subdivisions—the hill country above the slopes of the Satpura mountains, called the Balaghat, and a tract of low land to the south called the Zerghat. The high tableland of the Balaghat lies for the most part upon the great basaltic formation which stretches across the Satpuras as far east as Jubbulpore. The country consists of a regular succession of hills and fertile valleys, formed by the small ranges which cross its surface east and west. The average height of the uplands is 2500 ft., but there are many points of greater elevation. The appearance of the Zerghat below the hills is generally open and undulating. The country is intersected by several streams, of which the Kanhan is the most considerable. Near the hills and along the streams are strips and patches of jungle; the villages are usually surrounded 117 with picturesque groves of tamarind, mango and other shade-giving trees. In the hill-country the climate is temperate and healthy. In the cold season ice is frequently seen in the small tanks at an elevation of about 2000 ft. Until May the hot wind is little felt, while during the rains the weather is cool and agreeable. The average annual rainfall amounts to 36 in. Pop. (1901) 407,927. There are manufactures of cotton cloth and brassware. Coal in this neighbourhood began to be worked after the opening of a branch of the Bengal-Nagpur railway to Chhindwara and the coalfields to the north in 1905.
Chhindwara formed part of the dominions of the ancient Gond dynasty of Chhindwara and Nagpur, whose seat was at Deogarh until, in the 18th century, it was removed by Chand Sultan, son of Bakht Buland (founder of the short-lived greatness of the dynasty, and of the city of Nagpur) to Nagpur (see Gondwana and Nagpur).
CHIABRERA, GABRIELLO (1552-1637), Italian poet, sometimes called the Italian Pindar, was of patrician descent, and was born at Savona, a little town in the domain of the Genoese republic, twenty-eight years after the birth of Ronsard, with whom he has far more in common than with the great Greek whose echo he sought to make himself. As he has told in the pleasant fragment of autobiography prefixed to his works, in which, like Caesar, he speaks of himself in the third person, he was a posthumous child; he went to Rome at the age of nine years, under the care of his uncle Giovanni. There he read with a private tutor, suffered severely from two fevers in succession, and was sent at last, for the sake of society, to the Jesuits’ College, where he remained till his twentieth year, studying philosophy, as he says, “più per trattenimento che per apprendere,”—rather for occupation than for learning’s sake. Losing his uncle about this time, Chiabrera returned to Savona, “again to see his own and be seen by them.” In a little while, however, he returned to Rome, and entered the household of a cardinal, where he remained for several years, frequenting the society of Paulus Manutius and of Sperone Speroni, the dramatist and critic of Tasso, and attending the lectures and hearing the conversation of Mureto. His revenge of an insult offered him obliged him to betake himself once more to Savona, where, to amuse himself, he read poetry, and particularly Greek. The poets of his choice were Pindar and Anacreon, and these he studied till it grew to be his ambition to reproduce in his own tongue their rhythms and structures, and so to enrich his country with a new form of verse—in his own words, “like his countryman, Columbus, to find a new world or drown.” His reputation was made at once; but he seldom quitted Savona, though often invited to do so, saving for journeys of pleasure, in which he greatly delighted, and for occasional visits to the courts of princes whither he was often summoned, for his verse’s sake, and in his capacity as a dramatist. At the ripe age of fifty he took to himself a wife, one Lelia Pavese, by whom he had no children. After a simple and blameless life, during which he produced a vast quantity of verse—epic, tragic, pastoral, lyrical and satirical—he died in 1637, at the patriarchal age of eighty-five. An epitaph was written for him in elegant Latin by Urban VIII.; but on his tombstone are graven two quaint Italian hexameters of his own, in which the gazer is warned from the poet’s own example not to prefer Parnassus to Calvary.
A maker of odes in all their elaborate pomp of strophe and antistrophe, a master of new and complex rhythms, a coiner of ambitious words and composite epithets, an employer of audacious transpositions and inversions, and the inventor of a new system of poetic diction,—it is not surprising that Chiabrera should have been compared with Ronsard. Both were destined to suffer eclipse as great and sudden as had been their glory. Ronsard was succeeded by Malherbe and by French literature, properly so-called; Chiabrera was the last of the great Italians, and after him literature languished till the second renaissance under Manzoni. Chiabrera, however, was a man of merit, apart from that of the mere innovator. Setting aside his epics and dramas (one of the latter received the honours of translation at the hands of Nicolas Chrétien, a sort of scenic du Bartas), much of his work remains yet readable and pleasant. His grand Pindarics are dull, it is true, but some of his Canzonette, like the anacreontics of Ronsard, are exceedingly elegant and graceful. His autobiographical sketch is also extremely interesting. The simple old poet, with his adoration of Greek (when a thing pleased him greatly he was wont to talk of it as “Greek Verse”), his delight in journeys and sight-seeing, his dislike for literary talk save with intimates and equals, his vanities and vengeances, his pride in the memory of favours bestowed on him by popes and princes, his “infinita maraviglia” over Virgil’s versification and metaphor, his fondness for masculine rhymes and blank verse, his quiet Christianity, is a figure deserving perhaps of more study than is likely to be bestowed on that “new world” of art which it was his glory to fancy his own, by discovery and by conquest.
The best editions of Chiabrera are those of Rome (1718, 3 vols. 8vo); of Venice (1731, 4 vols. 8vo); of Leghorn (1781, 5 vols. 12mo); and of Milan (1807, 3 vols. 8vo). These only contain his lyric work; all the rest he wrote has been long forgotten.
CHIANA (anc. Clanis), a river of Tuscany, which rises in the Apennines S. of Arezzo, runs through the valley of Chiusi, and after receiving the Paglia just below Orvieto, falls into the Tiber after a course of 60 m. In Roman times its waters ran entirely into the Tiber. It often caused considerable floods in the valley of Clusium (Chiusi) which were noticeable even in Rome itself, and in A.D. 15 it was proposed to divert part of its waters into the Arnus, a project which was abandoned owing to the opposition of the Florentines (Tac. Ann. i. 76, 79). In the middle ages the whole of its valley from Arezzo to Chiusi was an uninhabitable swamp; but at the end of the 18th century the engineer Count Fossombroni took the matter in hand, and moved the watershed some 25 m. farther south, so that its waters now flow partly into the Arno and partly into the Tiber.
CHIAPAS, a Pacific coast state of southern Mexico on the Guatemalan frontier, bounded by the states of Tabasco on the N. and Vera Cruz and Oaxaca on the W. Pop. (1895) 318,730; (1900) 360,799, a large proportion of which are Indians; area, 27,222 sq.m. largely forested. The Sierra Madre crosses the southern part of the state parallel with the coast, separating the low, humid, forested districts on the frontier of Tabasco from the hot, drier, coastal plain on the Pacific. The mountain region includes a plateau of great fertility and temperate climate, which is one of the best parts of Mexico and contains the larger part of the population of the state. But isolation and lack of transportation facilities have retarded its development. The extension of the Pan-American railway across the state, from San Gerommo, on the Tehuantepec National line, to the Guatemalan frontier, is calculated to improve the industrial and social conditions of the people. The principal industries are agriculture, which is very backward, stock-raising, timber-cutting, fruit-farming and salt-making. Coffee-planting is a new industry on the Pacific slope of the Sierra Madre at elevations of 2000 to 4000 ft., and has met with considerable success. Rubber plantations have also been laid out, principally by American companies, the Castilloa elastica doing well. The exports include cattle, hides, coffee, rubber, fruit and salt. The mineral resources include gold, silver, copper and petroleum, but no mines were in operation in 1906. The capital, Tuxtla Gutierrez (pop. 9395 in 1900), is on the plateau, 3½ m. from the Rio Sabinas, and 138 m. N.E. of the Pacific port of Tonala. The former capital, San Cristobal (pop. about 5000 in 1895), about 40 m. E. of Tuxtla, is an interesting old town and the seat of the bishopric of Chiapas, founded in 1525 and made famous through its associations with Las Casas. Tapachula (pop. in 1895, 6775), the capital of the department of Soconusco, 18 m. from the Guatemalan frontier, is a rising commercial town of the new coffee district. It is 24 m. inland from the small port of San Benito, is 559 ft. above sea-level, and has a healthy climate. Other prominent towns with their populations in 1895, are Comitan, or Comitlan (9316), on the Rio Grijalva about 40 m. S.E. of San Cristobal, and chiefly distinguished for its fine church and convent dedicated to San Domingo; Pichucalco 118 (8549), Tenejapa (7036), San Antonio (6715), Cintalape (6455), La Concordia (6291), San Carlos (5977), and Ococingo (5667).
CHIAROSCURO (from the Ital. chiaro, light or brightness, and oscuro, darkness or shade), the disposition of light and shade in a painting; the term is applied to an early method of printing wood-engravings from several blocks, and also to a picture in black and white, or brown and white only.
CHIAVARI, a town of Liguria, Italy, in the province of Genoa, 24 m. S.E. by rail from the town of Genoa. Pop. (1901) 10,397 (town), 12,689 (commune). It is situated near the mouth of the Entella, in the centre of a fertile plain surrounded by mountains except on the S.W., where it comes down to the sea. Its buildings are mostly modern, but it has a ruined castle of 1147. It has an active trade in agricultural products, and manufactures lace, light wicker-seated bentwood chairs, silk, &c.
CHIAVENNA (anc. Clavenna), a town of Lombardy, Italy, in the province of Sondrio, 17 m. by rail N. of Colico which lies at the N. end of the lake of Como. Pop. (1901) town 3140, commune 4732. It is well situated on the right bank of the Mera, at the mouth of the Val Bregaglia, through which the road to the Maloja Pass and the Engadine runs to the east. This line was partly followed by a Roman road, which at Casaccia, just below the last ascent to the Maloja Pass, diverged to the N. by the Septimer Pass, joining the Julier route to Coire (anc. Curia) at Stalla. The Splügen route, which was also used by the Romans, runs N. from Chiavenna to Coire: the modern road was constructed by the Austrians in 1819-1821. Chiavenna is crowned by a ruined castle, once an important strategic point, and the seat of the counts who ruled the valley from the time of the Goths till 1194, when the district was handed over to the bishops of Coire. In the 14th century the Visconti, having become masters of the Valtellina, bought the “county” (contado or contea) of Chiavenna from the bishop of Coire; but it was taken by the canton of the Grisons in 1525, and the castle dismantled. In 1797 Chiavenna became part of the Cisalpine republic, and thenceforward followed the fortunes of Lombardy. The church of S. Lorenzo is baroque in style, but its baptistery contains a font of 1206 with reliefs. Chiavenna has cotton factories and breweries, and is a depot for the wine of the district.
CHIBOUQUE, or Chibouk (the Fr. form of the Turk, chib#363;k, literally a stick), a long pipe, often ornamented with precious stones, smoked by the Turks.
CHIC (a French word, either a shortened form of chicane, or derived from the Ger. Schick, tact or skill), a term properly used, in French artistic slang, of a work of art possessing brilliant but superficial technical ability, or of one executed without reference to a model or study of nature. The use of the word in French dates from the reign of Louis XIV. and then denoted a lawyer who was master of “chicane.” “Chic,” in general use, now connotes “smartness,” in dress, speech, &c.
CHICACOLE, a town of British India in the Ganjam district of Madras, situated on the right bank of the river Languliya, here crossed by a bridge, 4 m. from the sea. Pop. (1901) 18,196. Under Mahommedan rule it was the capital of one of the Northern Circars, and afterwards of a British district. Several old mosques remain. The town was famous for its muslins, but the industry is now decayed. The roadstead and lighthouse of Calingapatam are about 16 m. to the north, and the East Coast railway has a station 9 m. inland.
CHICAGO, a city, a port of entry and the county-seat of Cook county, Illinois, U.S.A., the second city of the United States in population, commerce and manufactures; pop. (1900) 1,698,575; and (1910) 2,185,283. It is situated at the south-west corner of Lake Michigan (lat. 41° 50′, long. 87° 38′ W.), about 913 m. distant by railway from New York, 912 m. from New Orleans, 2265 m. from Los Angeles, and 2330 m. from Seattle. The climate is very changeable and is much affected by the lake; changes of more than thirty degrees in temperature within 24 hours are not at all rare, and changes of twenty are common. The city is the greatest railway centre of the United States, and was for several decades practically the only commercial outlet of the great agricultural region of the northern Mississippi Valley. Trunk lines reach E. to Montreal, Boston, New York, Philadelphia, Baltimore (the nearest point on the Atlantic coast, 854 m.); S. to Charleston, Savannah, Florida, Mobile, New Orleans, Port Arthur and Galveston; W. to the Pacific at Los Angeles, San Francisco, Seattle and Vancouver, and to most of these by a variety of routes. In 1905 about 14% of the world’s railway mileage centred in Chicago.
With its suburbs Chicago stretches along the shore of Lake Michigan about 40 m. (the city proper 26.5), and the city in 1910 had a total area of 191.4 sq.m.1 It spreads loosely and irregularly backward from the lake over a shallow alluvial basin, which is rimmed to the W. by a low moraine water-parting2 that separates the drainage of the lake from that of the Mississippi Valley. The city site has been built up out of the “Lake Chicago” of glacial times, which exceeded in size Lake Michigan. Three lakes—Calumet, 3122 acres; Hyde; and part of Wolf—with a water-surface of some 4100 acres, lie within the municipal limits. The original elevation of what is now the business heart of the city was only about 7 ft. above the lake, but the level was greatly raised—in some places more than 10 ft.—over a large area, between 1855 and 1860. The West Side, especially in the north-west near Humboldt Park, is much higher (extreme 75 ft.). A narrow inlet from the lake, the Chicago river, runs W. from its shore about a mile, dividing then into a north and a south branch, which run respectively to the N.W. and the S.W., thus cutting the city into three divisions known as the North, the West and the South “Sides,” which are united by three car-tunnels beneath the river as well as by the bridges across it.3 The river no longer empties into Lake Michigan since the completion of the drainage canal. Its commercial importance is very great: indeed it is probably the most important non-tidal stream of its length in the world, or if it be regarded as a harbour, one of the greatest; the tonnage of its yearly commerce far exceeds that of the Suez Canal and almost equals the tonnage of the foreign trade (the domestic excluded) of the Thames or the Mersey. The increase in size of the newer freighters that ply on the Great Lakes4 has proved one serious difficulty, and the bridges and the river tunnels, which hinder the deeper cutting of the channel, are others. The improvement of the outer harbour by the national government was begun in 1833. Great breakwaters protect the river mouth from the silting shore currents of the lake and afford secure shelter in an outer roadstead from its storms, and there is a smaller inner-basin (about 450 acres, 16 ft. depth) as well. But the river itself which has about 15 m. of navigable channel, in part lined with docks, is the most important part of the harbour. Its channel has been repeatedly deepened, and in rectnt years—especially since 1896, after its control as a navigable stream passed (1890) to the federal government—widened and straightened by the removal of jutting building constructions along its shores. Grain elevators of enormous size, coal yards, lumber yards and grimy warehouses or factories crowd close upon it. The shipping facilities on the river are not so good in some ways, however, as on the Calumet in southeastern (or South) Chicago, whither there has been a strong movement of manufactures and heavy commerce.
The plan of the city is in general “regular,” i.e. rigidly rectangular, and the streets are in general wide. The evenness of the plain has saved Chicago from most of the vast expense, incurred by some American cities (notably Boston and San Francisco) in the extension or levelling of their sites and the removal of obstructions unfavourable to their development. The business district is concentrated in a small area of the South Side, just below the main river and between the south branch and the lake. A number of the railway terminals, almost all the great wholesale and retail houses, the leading hotels and 119 public buildings are crowded within an area of about 1.5 sq.m. The congestion of the streets—considerably lessened since the freight-subways have reduced the amount of heavy trucking—is proportionately great, and their din and crush is characteristic of the city. The residential districts, on the other hand, are unevenly and loosely spread; many areas well within the city are only sparsely settled. A belt of “bad lands”—occupied by factories, shanties, &c.—partially surrounds the best business district. The smoke resulting from the use of soft coal has given a drab and dingy colour-tone to the buildings. The low and even relief of the site and the long vistas of the streets do not lend themselves to the picturesque; yet this quality may be claimed for the high and broken skyline, varied colour, massiveness, bustle and impressive commercialism of the business district. Chicago is generally credited with being the original home of the steel-frame “sky-scraper,”5 though there are now higher buildings elsewhere in America. The unstable soil of sand, clay and boulders that underlies the city is unfavourable to tall constructions, and necessitates extraordinary attention to foundations. The bed-rock lies, on an average, 50 ft. below the level of the lake (in places more than a hundred). To the rock the foundations are often sunk in caissons, the buildings restingon monster columns of concrete and steel.6 In other cases great “pads” of the same materials, resting or “floating” upon the clay, sustain and distribute the weight of the building. The small extent of the business quarter adds to the effect of its tall structures. The Auditorium (1889; cost, $3,500,000), a huge building containing a hotel and a theatre (5000 seats), is one of the most massive commercial structures of the country. The Masonic Temple (cost, $3,000,000) is the tallest in the city (302 ft.). In 1909 there were some 475 structures ten or more storeys high. Not a few are noteworthy, whether for size—as the Monadnock office building of 16 storeys, with some 6000 occupants, and the new Northwestern Railway station; or for the luxury of their interior fittings—as the La Salle, Blackstone and Sherman hotels; or for boldness and originality in the treatment of the steel-frame type; or for association with the city’s life—as the Fine Arts building, given over to varied purposes of public amusement and artistic or intellectual improvement, or the Railway Exchange (cased in tiles), the University Club, the Chamber of Commerce and the Board of Trade; and many others are handsome and dignified examples of architecture. The Marquette building, consistently and handsomely decorated with works of art, is one of the finest office-buildings in the country. There are a number of enormous retail stores. The largest, and one of the finest in the world, is that of Marshall Field. The wholesale establishment of the same firm is the work of H.H. Richardson, considered one of his best, and one of the most admirable examples among American commercial buildings. The city hall and county court house (cost, $4,500,000) is an enormous double building in a free French Renaissance style, with columned facades. The new Federal building (finished in 1905; cost, $4,750,000) is a massive edifice (a low rectangle surmounted by a higher inner cross and crowned with a dome). The public library (1893-1897, $2,125,000), constructed of dark granite and limestone, with rich interior decorations of varied frescoes, mosaics, ornamental bronze and iron-work, and mottoes, is one of the handsomest libraries of the country. The Chicago Art Institute (1892-1893; Italian Renaissance), the Chicago Orchestra building (1904), and the Commercial National Bank, are also noteworthy. The finest residence streets are the Lake Shore Drive of the North Side and the “boulevards”—broad parkways that connect the parks of the city—of which Michigan Avenue, Drexel and Grand are the finest. The city’s environs are not of particular beauty, but there are bluffs on the lake to the north, and woods to the south-west, and a fair variety of pretty hill and plain; and though the Calumet and Chicago rivers have been given over to commerce, the valley of the Desplaines will be preserved in the park system. On the South Side are the Union Stockyards, established in 1865, by far the largest in the world. They cover about 500 acres, have about 45 m. of feeding and watering troughs, and can accommodate at one time more than 400,000 hogs, cattle, sheep and horses.
Public Works and Communications.—Local transit is provided for by the suburban service of the steam railways, elevated electric roads, and a system of electric surface cars. Two great public works demand notice: the water system and the drainage canal. Water is pumped from Lake Michigan through several tunnels connecting with “cribs” located from 2 to 5 m. from shore. The “cribs” are heavy structures of timber and iron loaded with stone and enclosing the in-take cylinders, which join with the tunnels well below the bottom of the lake. The first tunnel was completed in 1867. The capacity of the tunnels was estimated in 1900 by two very competent authorities at 528 and 615 million gallons daily, respectively. The average daily supply in 1909 was 475,000,000 gallons; there were then 16.6 m. of tunnels below the lake. The wastes of the city—street washings, building sewage, the offal of slaughter-houses, and wastes of distilleries and rendering houses—were originally turned into the lake, but before 1870 it was discovered that the range of impurity extended already a mile into the lake, half-way to the water “crib,” and it became evident that the lake could not be indefinitely contaminated. The Illinois and Michigan Canal, for which the right of way was granted in 1821 and which was built in 1836-1841 and 1845-1848, and opened in 1848 (cost, $6,557,681), was once thought to have solved the difficulty; it is connected with the main (southern) branch of the Chicago river, 5 m. from its mouth, with the Illinois river at La Salle, the head of steamer navigation on the Illinois river, and is the natural successor in the evolution of transportation of the old Chicago portage, ½ m. in length, between the Chicago river and the headwaters of the Kankakee; it was so deepened as to draw water out from the lake, whose waters thus flowed toward the Gulf of Mexico. It is about 96 m. long, 40-42 ft. wide, and 4-7 ft. deep, but proved inadequate for the disposal of sewage. A solution of the problem was imperative by 1876, but almost all the wastes of the city continued nevertheless to be poured into the lake. In 1890 a sanitary district, including part of the city and certain suburban areas to be affected, was organized, and preparations made for building a greater canal that should do effectively the work it was once thought the old canal could do. The new drainage canal, one of the greatest sanitary works of the world, constructed between 1892 and 1900 under the control of the trustees of the Sanitary District of Chicago (cost up to 1901, $35,448,291), joins the south branch of the Chicago with the Desplaines river, and so with the Illinois and Mississippi, and is 28.5 m. long,7 of which 15 m. were cut through rock; it is 22 ft. deep and has a minimum width of 164 ft. The canal, or sewer, is flushed with water from Lake Michigan, and its waters are pure within a flow of 150 m.8 Its capacity, which was not at first fully utilized, is 600,000 cub. ft. per minute, sufficient entirely to renew the water of the Chicago river daily. A system of intercepting sewers to withdraw drainage into the lake was begun in 1898; and the construction of a canal to drain the Calumet region was begun in 1910. The Illinois and Michigan canal is used by small craft, and the new drainage canal also may be used for shipping in view of the Federal government’s improvements of the rivers connecting it with the Mississippi for the construction of a ship-canal for large vessels. The canal also made possible the development (begun in 1903) of enormous 120 hydraulic power for the use of the city. The Illinois and Michigan Canal has been supplemented by the Illinois and Mississippi Canal, commonly known as “the Hennepin,” from its starting at the great bend of the Illinois river 1¾ m. above Hennepin, not far below La Salle; the first appropriation for it was made in 1890, and work was begun in 1892 and completed in October 1907. Its course from Hennepin is by the Bureau Creek valley to the mouth of Queen river on the Rock river, thence by the Rock river and a canal around its rapids at Milan to its mouth at Rock Island on the Mississippi river. This barge canal is 80 ft. wide at water-line, 52 ft. wide at the bottom, and 7 ft. deep. Its main feeder is the Rock river, dammed by a dam nearly 1500 ft. long between Sterling and Rock Falls, Illinois, where the opening of the canal was celebrated on the 24th of October 1907.
Beginning with 1892 steam railways began the elevation (or depression) of their main tracks, of which there were in 1904 some 838 m. within the city. Another great improvement was begun in 1901 by a private telephone company. This is an elaborate system of freight subways, more than 65 m. of which, underlying the entire business district, had been constructed before 1909. It is the only subway system in the world that seeks to clear the streets by the lessening of trucking, in place of devoting itself to the transportation of passengers. Direct connexion is made with the freight stations of all railways and the basements of important business buildings, and coal, building materials, ashes and garbage, railway luggage, heavy mail and other kinds of heavy freight are expeditiously removed and delivered. Telegraph and telephone wires are carried through the tunnel, and can be readily repaired. The subway was opened for partial operation in 1905.9
Parks.—The park system may be said to have been begun in 1869, and in 1870 aggregated 1887 acres. Chicago then acquired the name of “The Garden City,” which still clings to her. But many other cities have later passed her (until in 1904, though the second largest of the country, she ranked only thirty-second in her holdings of park area per capita among American cities of 100,000 population). In 1908 the acreage of the municipal parks was 3179 acres, and there were 61.4 m. of boulevards. After 1900 another period of ambitious development began. The improvement of old and the creation of new “internal” parks, i.e. within the cordon of those older parks and boulevards that once girdled the city but have been surrounded in its later growth; the creation of a huge metropolitan ring—similar to that of Boston but vaster (35,000 acres)—of lake bluffs, hills, meadows, forests and river valley; and a great increase of “neighbourhood parks” in the poor districts, are included in the new undertakings. The neighbourhood park, usually located near a school, is almost all-inclusive in its provision for all comers, from babyhood to maturity, and is open all day. There are sand gardens and wading ponds and swings and day nurseries, gymnasiums, athletic fields, swimming pools and baths, reading-rooms—generally with branches of the city library—lunch counters, civic club rooms, frequent music, assembly halls for theatricals, lectures, concerts, or meetings, penny savings banks, and in the winter skating ponds. These social centres have practically all been created since about 1895. There are also municipal baths on the lake front and elsewhere. The older parks include several of great size and beauty. Lincoln Park (area 552 acres), on the lake shore of the North Side, has been much enlarged by an addition reclaimed from the lake. It has fine monuments, conservatories, the only zoological garden in the city, and the collections of the Academy of Sciences. A breakwater carriage drive connects with a boulevard to Fort Sheridan (27 m.) up the lake. Jackson Park (542 acres), on the lake shore of the South Side, was the main site of the World’s Columbian Exposition of 1893, and contains the Field Columbian Museum, occupying the art building of the exposition. It is joined with Washington Park (371 acres) by the Midway Plaisance, a wide boulevard, intended to be converted into a magnificent sunken water-course connecting the lagoons of the two parks with Lake Michigan. Along the Midway are the greystone buildings of the University of Chicago, and of its (Blaine) School of Education. On the West Side are three fine parks—Douglas, Garfield (with a fine conservatory), and Humboldt, which has a remarkable rose garden (respectively 182, 187 and 206 acres), and in the extreme South Side several others, including Calumet (66 acres), by the lake side, and Marquette (322 acres), Jackson Boulevard, Western Avenue Boulevard and Marshall Boulevard join the South and the West Park systems. Neither New York nor Boston has preserved as has Chicago the beauty of its water front. The shore of the North Side is quite free, and beginning a short distance above the river is skirted for almost 30 m. by the Lake Shore Drive, Lincoln Park and the Sheridan Drive. The shore of the South Side is occupied by railway tracks, but they have been sunk and the shore otherwise improved. In addition to Calumet and Jackson parks there was another just below the river, Lake Park, which has since been included in Grant Park, mostly reclaimed from the water. Here are the public library and the building of the Art Institute (opened in 1893); the park had also been proposed as the site of a new building for the Field Museum of Natural History. The park and boulevards along the lake in 1905 stretched 10.78 m., within the city limits, or almost half the total frontage.10 The inner “boulevards” are broad parked ways, 150 to 300 ft. wide, joining the parks; Chicago was the first American city to adopt this system.
Art.—Among the monuments erected in public places are a Columbus by D.C. French and a bronze replica of French’s equestrian statue of Washington in Paris; statues of John A. Logan and Abraham Lincoln by St Gaudens; monuments commemorating the Haymarket riot and the Fort Dearborn massacres; statues of General Grant, Stephen A. Douglas, La Salle, Schiller, Humboldt, Beethoven and Linnaeus. There is also a memorial to G.B. Armstrong (1822-1871), a citizen of Chicago, who founded the railway mail service of the United States. A city art commission approves all works of art before they become the property of the city, and at the request of the mayor acts in various ways for the city’s aesthetic betterment. The Architectural Club labours for the same end. A Municipal Art League (organized in 1899) has done good work in arousing civic pride; it has undertaken, among other things, campaigns against bill-board advertisements,11 and against the smoke nuisance.
The Art Institute of Chicago contains valuable collections of paintings, reproductions of bronzes and sculpture, architectural casts, and other objects of art. Connected with it is the largest and most comprehensive art school of the county—including newspaper illustration and a normal school for the training of teachers of drawing in the public schools. The institute was incorporated in 1879, though its beginnings go back to 1866, while the school dates from 1878. The courses in architecture are given with the co-operation of the Armour Institute of Technology. There are also a number of notable private art collections in the city. In 1894 the Chicago Public School Art Society was founded to secure the placing of good works of art in the public schools. Picture collections are also exchanged among the neighbourhood-park homes.
Music in Chicago owes much to the German element of the population. Especially noteworthy among musical organizations 121 are the Apollo Musical Club (1872) and The Theodore Thomas orchestra, which has disputed with the Boston Orchestra the claim to artistic primacy in the United States. Its leader from its organization in 1891 until his death in 1905 was Theodore Thomas, who had long been identified with summer orchestral concerts in the city. In 1904 a fund was gathered by public subscription to erect a handsome building and endow the orchestra.
The Field Museum of Natural History, established (1894) largely by Marshall Field, is mainly devoted to anthropology and natural history. The nucleus of its great collection was formed by various exhibits of the Columbian Exposition which were presented to it. Its collections of American ethnology, of exceptional richness and value, are constantly augmented by research expeditions. In addition to an original endowment of $1,000,000, Mr Field bequeathed to the museum $8,000,000, Lo be utilized in part for the new building which is being erected in Jackson Park.
Libraries.—At the head of the libraries of the city stands the public library12 (established 1872; opened 1874), supported by taxation, which on the 1st of June 1910 had 402,848 volumes, and in the year 1910 circulated 1,805,012 volumes. In 1889 John Crerar (1827-1889), a wealthy manufacturer of railroad supplies, left to the city for the endowment of a non-circulating library funds which in 1907 were estimated to amount to $3,400,000. The library was incorporated in 1894 and was opened in 1897; in February 1908 it had 216,000 volumes and 60,000 pamphlets. It occupies a floor in the Marshall Field Building on Wabash Avenue. Another reference library was established (opened in 1887) with a bequest (1868) of Walter L. Newberry. It has a rich endowment, and in February 1908 had 191,644 volumes and 43,644 pamphlets. By a plan of co-operation each of these three libraries devotes itself primarily to special fields: the John Crerar is best for the natural, physical and social sciences; the Newberry is particularly strong in history, music, medicine, rare books and fine editions; the public library covers the whole range of general literature. The library of the University of Chicago contained in 1908 some 450,000 titles. Among other collections are those of the Chicago Historical Society (1856; about 150,000 titles in 1908), the Athenaeum (1871); the Law Institute and Library (1857), which in 1908 had about 46,500 volumes; the Art Institute, the Field Museum of Natural History, the Academy of Sciences (1857) and the libraries of various schools.
Universities and Colleges.—There are three universities situated wholly or in part in the city. The leading institution is the University of Chicago (see Chicago, University of). The professional department of North-Western University is in Chicago, while its academic department is in the suburb of Evanston. North-Western University was organized in 1851 and is under Methodist Episcopal control. Its students in 1908 (exclusive of pupils in “co-operating” theological schools) numbered 3850; the best equipped departments are those of dentistry, medicine and pharmacy. There are two Roman Catholic colleges in Chicago: Loyola University (chartered in 1870), with a department of law, called Lincoln College (1908), and a medical department; and St. Stanislaus College (1870). The College of Physicians and Surgeons is the medical department of the University of Illinois, at Champaign-Urbana. Theological schools independent of the universities include the McCormick Theological Seminary (Presbyterian); the Chicago Theological Seminary (Congregational, opened 1858, and including German, Danish-Norwegian and Swedish Institutes); the Western Episcopal Theological Seminary; a German Lutheran theological seminary, and an Evangelical Lutheran theological seminary. There are a number of independent medical schools and schools of dentistry and veterinary surgery. The Lewis Institute (bequest 1877, opened 1896), designed to give a practical education to boys and girls at a nominal cost, and the Armour Institute of Technology, one of the best technical schools of the country, provide technical education and are well endowed. The Armour Institute was founded in 1892 by Philip D. Armour, and was opened in 1893. It comprises the College of Engineering, including, besides the usual departments, a department of chemical engineering and a department of fire protection engineering, a department of “commercial tests,” and the Armour Scientific Academy (preparatory). In 1907 the Institute had 1869 students. The Chicago Academy of Science (1857) has a handsome building and museum collections in Lincoln Park.
The leading daily newspapers are the Record-Herald, Evening Post, News (evening) and Journal (evening), all Independent; the Inter-Ocean and Tribune, Republican; and the Evening American and Examiner, both Democratic. There are several journals in German, Bohemian, Polish, Swedish, Norwegian and Danish. Many trade papers are published in the city, which is also a centre for much of the religious publishing of the Middle West. Chicago’s position in the labour world has made it the home of several socialist and anarchistic periodicals.
Industry and Commerce.—Chicago’s situation at the head of the most south-western of the Great Lakes has given it great importance in trade and industry. The development of its extraordinary railway facilities was a recognition of its supreme advantages as the easiest outlet for the products of the Middle West, on whose wealth its prosperity is founded. The growth of its trade has been marvellous. The last years of the 19th century showed, however, an inevitable loss to Chicago in the growth of Duluth, Kansas City and other rivals in strategic situations. In particular, the struggle of the North and South railway lines in the Mississippi Valley to divert to ports on the Gulf of Mexico grain and other freight caused great losses to Chicago. An enormous increase in the cereal trade of Philadelphia, Baltimore, Newport News and Norfolk was partly due to the traffic eastward over lines S. of Chicago. The traffic of the routes through Duluth and Canada does not, indeed, represent in the main actual losses, for the traffic is largely a new growth; but there has been nevertheless a considerable drain to these routes from American territory once tributary to Chicago. Altogether the competition of the Gulf roads and the lines running S.W. from Duluth had largely excluded Chicago by 1899 (according to her Board of Trade) from the grain trade W. of the Missouri river, and in conjunction with southerly E. and W. routes had made serious inroads upon trade E. of that river. Its facilities for receiving and distributing remain nevertheless unequalled, and it still practically monopolizes the traffic between the northern Atlantic seaboard and the West. New York alone, among American cities, has a greater trade. Chicago is the greatest railway centre, the greatest grain market, the greatest live-stock market and meat-packing centre, and the greatest lumber market of the world. The clearings of her ‘associated banks amounted to $13,781,843,612 in the year 1909. The wholesale trade was estimated in 1875 at $293,900,000 and in 1905 at $1,781,000,000. The average annual grain receipts (including flour in wheat equivalent) in the five years 1900-1904 amounted to 265,500,000 bu. (12,902,310 in 1854; 72,369,194 in 1875), and the shipments to 209,862,966 bu. The first shipment of wheat was of 78 bu. in 1838. The grain elevators are among the sights of Chicago. They are enormous storehouses into which the grain is elevated from ships and cars, sorted into grades and reloaded for shipment; all the work is done by machinery. Their capacity in 1904 was 65,140,000 bu.13 In the same quinquennial period, 1900-1904, the average yearly receipts of lumber aggregated 1,807,066,000 ft.,14 and of shingles, 410,711 thousand; of cattle, 3,078,734; of hogs, 8,334,904; of sheep, 3,338,291; of butter, 239,696,921 ℔; the exports of hides, 167,442,077 ℔; of dressed beef, 1,126,995,490 ℔; of 122 lard, 410,688,319 ℔; of pork, 191,371 bbl.; of other hog products, 600,503,394 ℔. The combined tonnage in and out averaged 14,135,406 tons.15 There is a large direct trade with Europe, mainly in goods that come in bond by rail from Atlantic ports. In 1907 the value of Chicago’s imports was $27,058,662, and of its exports, $5,643,302.
The value of manufactures (from establishments under the “factory system”) in 1900 was $797,879,141, 71.2% of all those of Illinois, and in 1905 was $955,036,277, 67.7% of all those of the state; in both these years Chicago was second only to New York City. Wholesale slaughtering and meat-packing (not including many by-products), valued at $256,527,949 (32.2% of the city’s total) in 1900 and at $269,581,486 (28.2% of the total) in 1905, are the most important of the city’s industries; in 1905 the product value in Chicago was 29.5% of that for the slaughtering and meat-packing of the entire United States. Other important manufactures are foundry and machine shop products, $44,561,071 in 1900, and $51,774,695 in 1905; and other iron and steel products, $35,058,700 in 1900 and $27,074,307 in 1905; clothing ($58,093,572 in 1900, and $64,913,481 in 1905); cars and other railway construction, $28,369,956 in 1900 and $36,080,210 in 1905; malt liquors ($14,956,865 in 1900, and $16,983,421 in 1905), and furniture ($12,344,510 in 1900 and $17,488,257 in 1905). The Illinois Steel Company has the largest rolling mills in the world. The McCormick Harvesting Machine Company is the largest concern in the world manufacturing agricultural implements. Pullman in southern Chicago, in the sparsely settled outskirts of the city, is a model little “labour town,” planned and constructed with regard for both appearances and conveniences by the Pullman Palace Car Company, which has its works here. The town consists mainly of workmen’s cottages. Most of the population are dependent upon the car works. The Pullman Company owns and operates dining and sleeping cars on practically all the railways of the country. In addition to its own cars it builds ordinary passenger and freight cars on contract.
Meat-packing is the greatest local industry and is that for which Chicago is best known. In the enormous stock-yards from two-thirds to four-fifths of the cattle and hogs received are killed, and sent out in various forms of prepared meats and by-products (lard, fertilizers, glue, butterine, soap, candles, &c).16 This industry is remarkable for the extraordinary division of labour in its processes. In the preparation of a bullock more than thirty specialties are involved, and some twenty different rates of pay. This system enabled the packing companies, until checked by the development of labour unions, to save money not only by paying low wages for crude labour and high for skilled, but to develop wonderful expertness in every line, and so “speed up” the workmen to a remarkable pace.17 No more interesting field can be found for the study of the qualities of foreign races. The introduction of the refrigerator railway car in the ’seventies of the 19th century, making possible the distant marketing of dressed meats, enormously increased the business. The workmen of the yards were organized in a national union of meat packers in 1897, and all the different classes of workmen have their separate organizations, formed mainly between 1900 and 1902. The number of women employed more than doubled in the decade 1891-1900, constituting probably about 9% of the total in the latter year.
Administration.—Chicago is governed under a general city-charter law of Illinois of 1870, accepted by the city in 1875. In November 1904 the people of Illinois adopted a constitutional amendment authorizing the legislature of the state to provide a complete new system of local government for Chicago, but the old system continued and is here described, the new charter, from which so much had been hoped, being rejected by the voters of the city by an overwhelming majority in September 1907. A common council chosen by wards and renewed in half each year controls the budget, police, liquor licences, city contracts and the granting of franchises; it also confirms appointments made by the mayor and by a vote of two-thirds may pass legislation over his veto. The mayor, chosen for four years, is the executive head of the city, and has large power of appointment and removal, limited by a civil service law, under which he must submit reasons for removals, while two-thirds of the council may prevent them. On the other hand the mayor can veto separate items in the council’s budget. The administrative departments are generally headed by single commissioners; but those of elections, education and the public library are exceptions. The council was once all important, but as early as the charter of 1851 it began to lose power to the mayor, whose directive and executive powers have steadily increased, beginning first in the financial department. Administration was once performed entirely by boards as in other American cities: every specific problem or demand for municipal activity was met by an appeal to the state legislature for special legislation and the creation of a board. The substitution of single commissioners began in 1876. The state constitution of 1870 forbade special legislation, prescribed a general city charter law and forbade special amendatory acts for Chicago. This stopped grave abuses, but because a large part of the state has not been interested in Chicago’s special needs and demands for betterment it also saddled upon the city an organization which in 1901 remained practically the same as in 1870, when Chicago was an overgrown town of 300,000 inhabitants. Chicago was the only large city of the state, and a charter generalized from village experience was unsuitable for it. The parts of Cook county outside the city have also been very jealous of forwarding its reorganization, important features of which must be either, the complete absorption of the county or at least the reconstitution of the county government,18 which the constitution left unchanged, and which, with the city’s growth, has caused clash of interests and authority. Nor is this dual government—though the city has above nine-tenths of the population and pays ninetenths of the taxes of the county—the only anomaly. Illinois has had since 1848 a modified New England “township” local-government system, and various townships have been absorbed by Chicago, yet they all retained till after 1900 their political structure and some of their functions. There are three park commissions, two appointed by the governor and one by circuit court judges, created for different parts of the old city, differently constituted and all independent of the city; their jurisdiction was not enlarged as the city grew, so large portions remained free of charges for parks and boulevards. A special park commission now supplements them and lessens this anomaly though increasing administrative diversity. A sanitary and drainage district, not larger than the city area but quite different from it, was created in 1886 (present form 1890) to carry through the drainage canal. The school board has been nominally separate from and almost independent of the city government in power since 1857. The courts of law are courts of the state of Illinois, but a certain number of justices of the peace are designated by the mayor to act as police magistrates. The initiative and referendum in local matters has been made possible under a state law, and has been several times exercised in important questions. Financial arrangements have been loose and inefficient. Independent taxing power has been lavishly granted. State, county, city, three park boards, the school board, the public library board, the drainage board, and as late as 1903 ten townships,19 exercised this sovereign right within the municipal area. Tax assessment 123 valuations have been excessively irregular (e.g. the “equalized” value for 1875 was $55,000,000 greater than that for 1892), and apparently very low. The average assessment valuation for the years from 1904 to 1908 was $438,729,897 (403.28 millions in 1904, and 477.19 millions in 1908), and in 1907 the highest taxing rate was 8%. The bonded debt in 1908 was $25,157,400, about half of it old ($11,362,726 in 1870; 4.5 millions contracted to aid the World’s Fair of 1893). In the early years following 1900 the city paid more than half of its income on police; this expenditure, per capita of population, was not high (in 1901 Boston $5.03, New York $3.21, Chicago $2.19), and the results were not exactly efficient. The difficulty is that the city is poor and can pay only for strict necessities. Its poverty is due mainly to state laws. The taxation limit on property is 1% on the cash value, thus compelling special dependence upon all sorts of indirect taxes; the debt limit is 5% on the assessed valuation. Since 1900 relief has been given by state law in some matters, such as for the park system. The water system has been operated by the city since 1851, and has been financially very successful from the beginning: rates are far lower than in the other great cities of the country, and a handsome net revenue accrues to the treasury.20 A municipal electric-lighting plant (1887), which was paid for gradually out of the general tax levy and was not built by the sale of bonds, gave excellent results in the city service. The city, like the state, has power to regulate the price of gas sold by private companies. The elevation of the railway tracks within the city was begun in 1892; at the close of 1908 the railway companies had accepted ordinances of the City Council for the elevation of 192.77 m. of main tracks and 947.91 m. of all tracks, and the construction of 724 subways, at an estimated cost of $65,000,000; at that time the railway companies had completed the elevation of 133.83 m. of main tracks and 776 m. of all tracks, and had constructed 567 subways, at a total expense of $52,500,000. The system of intercepting sewers begun in 1898 to complete the service of the drainage canal has been constructed with the profits of the water system.
In addition to the movement for a new charter to remove the anomalies and ease the difficulties already referred to, two great problems have been in the forefront in recent years: the lessening of municipal corruption and the control of local transit agencies.
The traction question may be said to have begun in 1865, in which year, and again in 1883, public opinion was bitterly aroused against an attempt of the traction companies to secure a ninety-nine year extension of franchises. Following 1883 all lines were consolidated and enormously over-capitalized (in 1905 about $150,000,000 of stocks and bonds on a 6% basis, two-thirds of which rested only on the franchise). In 1895-1897 bold attempts to secure a 50-year extension of franchises were defeated by Governor John P. Altgeld (1847-1902), by the formation of a Municipal Voters’ League, and by a representative committee of 100 sent from Chicago to attend the legislature at Springfield. The transit service of the city had for years been antiquated and inadequate. At the mayor’s elections in 1897, 1899, 1901 and 1903 the victory lay with the opponents of the companies, and in 1905 the successful party stood for immediate municipal acquisition of all roads. Meanwhile, under the state referendum act, the city in 1902 voted overwhelmingly for municipal ownership and operation (142,826 to 27,990); the legislature in 1903 by the Mueller law gave the city the requisite powers; the people accepted the law, again declared for municipal ownership, and for temporary compulsion of adequate service, and against granting any franchise to any company, by four additional votes similarly conclusive. At last, after tedious negotiations, a definite agreement was reached in 1906 assuring an early acquisition of all roads by the city. The issue of bonds for municipal railways was, however, declared unconstitutional that year; and at the municipal elections of 1907 there was a complete reversal of policy; a large majority voted this time against municipal ownership in favour of leaving the working of the street railways in private hands, and strengthening the powers of municipal control.
The active campaign for the improvement of municipal service and politics may be said to have begun in 1896. A civil service system was inaugurated in 1895. The salaries of the councilmen were raised with good effect. Numerous reform associations were started to rouse public opinion, such as the Citizens’ Association of Chicago, organized in 1874, the Civic Federation (1894), the Municipal Voters’ League (1896), the Legislative Voters’ League (1901), the Municipal Lecture Association (1902), the Referendum League of Illinois (1901), the Civil Service Reform Association of Chicago, the Civil Service Reform Association of Illinois (1902), the Merchants’ Club, the City Club (1903), the Law and Order League (1904), Society of Social Hygiene (1906), and many of the women’s clubs took an active part. They stood for the real enforcement of the laws, sanitation, pure food, public health, the improvement of the schools and the widening of their social influence, and (here especially the women’s clubs) aesthetic, social and moral progress. The Merchants’ Club reformed the city’s book-keeping, and secured the establishment (1899) of the first state pawnbrokers’ society. The Civic Federation demonstrated (1896) that it could clean the central streets for slightly over half what the city was paying (the city has since saved the difference); it originated the movement for vacation schools and other educational advances, and started the Committee of One Hundred (1897), from which sprang various other reform clubs. The Municipal Voters’ League investigated and published the records of candidates for the city council, and recommended their election or defeat as the case may be. Moreover, a “Municipal Museum” was organized in 1905, mainly supported by private aid, but in part by the board of education, in order to collect and make educational use of materials illustrating municipal administration and conditions, physical and social.
Education and Charity.—The school board is appointed by the mayor. Since 1904 a merit system has been applied in the advancement of teachers; civil service rules cover the rest of the employees. Kindergartens were maintained without legal sanction in connexion with the public schools for several years, and for more than twenty-five years as private schools, before their legal establishment as a part of the system in 1899. Free evening schools, very practical in their courses, are utilized mainly by foreigners. Vacation schools were begun in 1896. So far as possible the school buildings are kept open for school, lectures and entertainments, serving thus as wholesome social centres; and a more adequate use is made of the large investment (in 1908 about $44,500,000) which they represent. In all the public schools manual training, household arts and economy, and commercial studies are a regular part of the curriculum. A department of scientific pedagogy and child study (1900) seeks to secure a development of the school system in harmony with the results of scientific study of children (the combination of hand and brain training, the use of audito-visual methods, an elastic curriculum during the adolescent period, &c.). The expenditure for all purposes by the city in 1903 for every dollar expended for schools was only $1.713; a ratio paralleled in only a few cities of the country.
Hospitals, infirmaries, dispensaries, asylums, shelters and homes for the defective, destitute, orphaned, aged, erring, friendless and incurably diseased; various relief societies, and associations that sift the good from the bad among the mendicant, the economically inefficient, and the viciously pauper, represent the charity work of the city. Among public institutions are the Cook County hospital (situated in the “Medical District” of the West Side, where various hospitals and schools are gathered near together), asylum and poor house. Since 1883 a Lincoln Park Sanitarium has been maintained for infants and small children during warm weather. Two legal-aid societies, the Chicago Bureau of Justice (1888) and the Protective Agency for Women and Children, collect small wage claims and otherwise aid the poor or helpless. The most important charitable societies of the city are the United Charities of Chicago (1909), the United Hebrew Charities (1857), and the Associated Jewish Charities (1900). The first is the union of the Relief and Aid Society (1857) and the Bureau of Charities (1894), 124 and tries to prevent overlapping of efforts and to weed out fraud. Following the gradual development of New York state laws on behalf of children was enacted the Illinois Juvenile Court Law, which came into force on the 1st of July 1899 and was largely the result of Chicago’s interest in juvenile reform. Much philanthropic work centres in the West Side with its heterogeneous population. A famous institution is Hull House, a social settlement of women, which aims to be a social, charitable, and educational neighbourhood centre. It was established in 1889 by Miss Jane Addams, who became the head-worker, and Miss Ellen Gates Starr. It includes an art building, a free kindergarten, a fine gymnasium, a crèche, and a diet kitchen; and supports classes, lectures and concerts. It has had a very great influence throughout the United States. The Armour mission (1886) for the poor is organized with similar breadth of scope.
Population.—Of the total population in 1900 not less than 34.6% were foreign-born; the number of persons either born abroad, or born in the United States of foreign parentage (i.e. father or both parents foreign), was 77.4% of the population, and in the total number of males of voting age the foreign-born predominated (53.4%). Of the latter category 68.2% were already citizens by naturalization. 3.9% of the inhabitants of ten years of age or upward were illiterate (unable to write), while the percentage of foreign-born whites was 8.2% (93.9% of illiterate males of voting age). Germans, Irish, Poles, Swedes and Bohemians made up respectively 29.1, 12.6, 8.6, 8.3 and 6.2% of the foreign-born population. It was estimated in 1903 by a very competent authority that above 500,000 persons spoke German, 125,000 Polish, 100,000 Swedish, 90,000 Bohemian, 50,000 Norwegian, 50,000 Yiddish, 35,000 Dutch, 25,000 Italian, 20,000 Danish, 17,000 French and 12,000 Irish (Celtic), and that each of fourteen foreign languages was spoken by more than 10,000 people: “Newspapers appear regularly in 10 languages, and church-services may be heard in about 20 languages. Chicago is the second largest Bohemian city of the world, the third Swedish, the fourth Norwegian, the fifth Polish, the fifth German (New York being the fourth). In all there are some 40 languages spoken by ... over one million” persons.21 The death-rate of Chicago is the lowest of the great cities of the country. Births are but slightly in excess of deaths, so that the growth of the city is almost wholly from immigration. The death-rate is the lowest of the great cities of the country (16.2 in 1900; New York, 20.4; Boston, 20.1, &c.).
The growth of Chicago has been remarkable even for American cities. Any resident of four-score years living in 1900 had seen it grow from a settlement of fourteen houses, a frontier military post among the Indians, to a great metropolis, fifth in size among the cities of the world. In 1828 what is now the business centre was fenced in as a pasture; in 1831 the Chicago mail was deposited in a dry-goods box; the tax-levy of 1834 was $48.90, and a well that constituted the city water-works was sunk at a cost of $95.50; in 1843 hogs were barred from the town streets. Such facts impress upon one, as nothing else can, the marvellously rapid growth of the city. In 1830 with a population of less than 100, in 1840 with 4479, the increase by percentages in succeeding decades was as follows: 507.3, 264.6, 173.6, 68.3, 118.6 and 54.4; an increase equivalent to 8.6% annually, compounded. Such a continuous “boom” no other American city has ever known.
History.—The river Chicago (an Indian name of uncertain meaning, but possibly from Ojibwa she-kag-ong, “wild onion place”) was visited by Joliet and Marquette in 1673, and later by La Salle and others. It became a portage route of some importance, used by the French in passing to the lower Illinois country. In 1804 the United States established here Fort Dearborn. In 1812, during the Indian War of Tecumseh, the garrison and settlers, who had abandoned the fort and were retreating toward safety, were attacked and overpowered by the savages at a point now well within the city. The fort was re-established and fitfully occupied until its final abandonment in 1837. When Cook county was organized in 1831, Chicago, then a tiny village, became the seat of justice. It became a town in 1833 and a city in 1837. By that time Chicago was confident of its future. The federal government had begun the improvement of the harbour, and the state had started the Illinois and Michigan canal. There was a federal land-office also, and the land speculator and town promoter had opened a chapter of history more picturesque, albeit sordid, than in any of the old French days. The giant growth of the lake trade had drawn attention before railway connexion was secure with the East in 1852, making progress even more rapid thereafter. During the Civil War a large prison-camp for Confederate prisoners, Camp Douglas, was maintained at Chicago. In 1870 the city had 306,605 inhabitants and was already a commercial centre of immense importance.
In 1871 it suffered a terrible calamity. On the 8th of October a fire broke out near the lumber district on the West Side. Two-thirds of the city’s buildings were wood, and the summer had been excessively dry, while to make conditions worse a high and veering wind fanned the flames. The conflagration leaped the river to the South and finally to the North Side, burned over an area of 31⁄3 sq. m., destroyed 17,450 buildings and property valued at $196,000,000,22 and rendered almost 100,000 people homeless; 250 lost their lives. The flames actually travelled 2¼ m. in an air-line within 6½ hours. Thousands of persons, fleeing before the flames and fire-brands, sought refuge on the shore and even in the waters of the lake. Robbery, pillage, extortion, orgies and crime added to the general horror. In the South Side the fire was checked on the 9th by the use of gunpowder; in the North (where the water-works were early destroyed) it had extended almost to the prairie when rainfall finally ended its ravages, after about twenty-seven hours of destruction. With the exception of the San Francisco fire of 1906 this was the greatest fire of modern times. A vast system of relief was organized and received generous aid from all parts of the world. The money contributions from the United States and abroad were $4,996,782; of this foreign countries contributed nearly $1,000,000 (England half of this). These funds, which were over and above gifts of food, clothing and supplies, were made to last till the close of 1876. Out of them temporary homes were provided for nearly 40,000 people; barracks and better houses were erected, workmen were supplied with tools, and women with sewing-machines; the sick were cared for and the dead buried; and the poorer classes of Chicago were probably never so comfortable as during the first two or three years after the fire. The rebuilding of the city was accomplished with wonderful rapidity. Work was begun before the cinders were cold. The business district was largely rebuilt within a year, and within three there were hardly scars of the calamity. Wood was barred from a large area (and subsequently from the entire city), and a new Chicago of brick and stone, larger, finer and wealthier, had taken the place of the old. Business and population showed no set-back in their progress. The solidity and permanence of this prosperity were confirmed during the financial panic of 1873, when Chicago banks alone, among those of the large cities of the country, continued steadily to pay out current funds.
In its later history certain special factors stand out, apart from continued commercial progress.
Chicago has been a storm centre of labour troubles, some of them of a specially spectacular character. There were great strikes in the packing industry in 1886, 1894 and 1904. But more noteworthy are the railway strike of 1894 and the unsuccessful teamsters’ strike of 1905. The former began in the works of the Pullman Car Company, and its leader was Eugene Victor Debs (b. 1855). When the contentions of the Pullman employees were taken up by the American Railway Union the strike immediately extended to tremendous proportions. Union men 125 throughout the country refused to handle Pullman cars, and since Pullman cars are almost invariably attached to mail trains the transportation of the United States mail was thus obstructed. Chicago, as the greatest railway centre of the country and the home of the strike, was naturally the seat of the most serious complications. There was much rioting and destruction of property, and the railway service was completely disorganized. President Cleveland, on the ground of preventing obstruction of the mail service, and of protecting other federal interests, ordered a small number of federal troops to Chicago. Those interests were, he contended, menaced by “domestic violence” evidently beyond the control of the state power. Governor Altgeld denied the inability of the state to deal with the difficulty, and entered a strong protest against Federal interference; but he himself did nothing to put down the disorder. Federal troops entered the state, and almost immediately the strike collapsed. The high officials of the Railway Union, for ignoring a court injunction restraining them from interfering with the movement of the mails, were imprisoned for long terms for contempt of court.
Out of a strike in the McCormick works in 1886 there sprang another famous incident in Chicago’s history. The “international” anarchists of Chicago had been organized in “groups” about two years earlier, and were very active. They were advocating a “general strike” for an eight-hour day, and the tense excitement among the labourers of the city, owing to the McCormick strike, induced unusually ultra utterances. There was a riot at the McCormick works on the 3rd of May, in which several men were killed by the police. An anarchist meeting was called for the next day at the Haymarket, a square in Randolph Street, and when the authorities judged that the speeches were too revolutionary to be allowed to continue, the police undertook to disperse the meeting. A bomb was thrown, and many policemen were injured, seven fatally. No person could be proved to have thrown the bomb, or to have been directly implicated in its throwing; but on the ground that they were morally conspirators and accomplices in the killing, because they had repeatedly and publicly advocated such acts against the servants of government, seven anarchists were condemned to death. An application to the United States Supreme Court for a writ of error was unanimously refused.23
The four-hundredth anniversary of the discovery of America was commemorated by a World’s Columbian Exposition held at Chicago. The site was in Jackson Park and the adjoining Midway, and included 686 acres, of which 188 were covered by buildings. On the 21st of October 1892—corresponding to the 12th of October 1492, O.S.—the grounds were formally dedicated, and on the following 1st of May opened to the public, continuing open for six months. The number of paid admissions was 21,500,000; of total admissions 27,539,521. The buildings, planned by a commission of architects—among whom John W. Root and Daniel H. Burnbam of Chicago were responsible for the general scheme—formed a collection of remarkable beauty, to which the grounds, planned by F.L. Olmsted, intersected by lagoons and bordered by the lake, lent an appropriate setting. The entire cost of the fair is variously estimated at from 33 to 43 million dollars, according to the inclusiveness of the estimate; the local cost may be put at $28,151,169. Of this Chicago gave about 10½ millions, in addition to a preparatory house-cleaning that cost 3½ millions; and finally a very small dividend was paid to stockholders. The whole undertaking, carried through with remarkable enterprise, was an artistic and educational triumph of the first order.
Owing to its position Chicago has long been a favourite convention city. Lincoln (1860), Grant (1868), Garfield (1880), Cleveland (1884 and 1892), Harrison (1888), Roosevelt (1904), and Taft (1908) were all nominated here for president; and in addition not a few candidates who were unsuccessful. A national peace jubilee was held here in 1898.
AUTHORITIES.—See the annual reports of city officials, board of trade, park commissions, sanitary board, &c.; A.T. Andreas, History of Chicago (Chicago, 3 vols., 1884-1886); R. Blanchard, Discovery and Conquest of the North-West with the History of Chicago (Chicago, 2 vols., 1898-1903); J. Kirkland, Story of Chicago (Chicago, 1892); issues of the Fergus Historical Series (1876, ff.); T.J. Riley, A Study of the Higher Life of Chicago (Chicago University, doctoral dissertation, 1905); S.E. Sparling, Municipal History and Present Organization of the City of Chicago (University of Wisconsin, doctoral dissertation, Madison, 1898). Periodical literature contains a vast amount of information on Chicago’s progress and conditions that is elsewhere unobtainable; exact references may be obtained in Poole’s Index to Periodical Literature.
1 In 1889 the total area (land and water) was increased from 43.8 to 169.9 sq.m.; in 1890 the land area was 163.49 sq.m.
2 About 15 ft. in elevation; hence the possibility of the drainage canal.
3 Among the last are many swing and “jack-knife” bridges, bascules, and a lift-bridge that can be lifted bodily 155 ft. above the channel. Steam, compressed air and electricity are used as power.
4 By 1900 almost all were being built of a length exceeding 400 ft.
5 The highest value ever paid in Chicago for land actually sold, up to 1901, was $250 per sq. ft. (1892); a few rental contracts have been based upon an assumed higher value. A municipal ordinance placing the extreme construction at 150 ft. was repealed in 1902.
6 This is true of all the new large buildings. The “old” post office, completed in 1880 at a cost of $5,375,000, was practically a crumbling ruin within fifteen years; its foundations were inadequate. Years were spent in sinking the foundation of the new Federal building that replaced the old.
7 Total excavation, 42,397,904 cub. yds.; of solid rock, 12,265,000.
8 It has been conclusively proved that the Illinois is purer than the Mississippi at their junction. The undiluted sewage of the old canal drove the fish from, the river, but they have come back since the opening of the new canal.
9 The cut was almost entirely through firm clay. It was estimated (1905) that the total freight handled weekly in the business district was nearly 500,000 tons, and the subway was designed to handle this amount when completed. The tunnels are 12.75 x 14 and 7.5 x 6 ft., all concrete. The cars are drawn by trolley wire locomotives on a track of 2 ft. gauge.
10 The Illinois Central enters the business centre by tracks laid along the lake shore. Certain rights as to reclaiming land were granted it in 1852, but the railway extended its claims indefinitely to whatever land it might reclaim. In 1883 began a great legal struggle to determine the respective rights of the United States, the state of Illinois, Chicago, and the Illinois Central in the reclaimed lands and the submerged lands adjacent. The outcome was favourable to the city.
11 There were 50 m. of them in 1904.
12 Thomas Hughes was a leader in gathering English gifts for such a library immediately after the "great fire." A nucleus of 10,500 volumes—7000 from England and 3500 from other countries, especially Germany—was thus secured.
13 In 1900-1904 the average freight rate per bushel of wheat to New York was $0.04998 by the all-water; $0.10554 by the all-rail route. In 1859 it cost $0.1575 to send a bushel of corn to Buffalo by water; in 1890, $0.019.
14 It has been above 1,000,000,000 ft. since 1870, and has in some years risen to 2,000,000,000.
15 This is for the entire Chicago customs district, including Waukegan and Michigan City.
16 The number of hogs packed yearly averaged 7,255,245 in 1900-1904; the cattle packed, 1,955,765; the sheep shipped (partly live), 616,476 (one-fifth those received).
17 e.g. in the most skilled labour, the speed was increased 87.5% from 1884-1894. In 1905 a gang of 230 men would dispose of 105 animals hourly; equivalent to 131 minutes for one man in taking the animal from pen to refrigerator; the average wage was $0.21 per hour (highest 0.50) and the average cost per bullock, $0.46.
18 Cook county is Republican in politics generally, the rural districts being so strongly so as often to overbalance the normal Democratic plurality in Chicago. Thus another ground of jealousy is found In the distribution of county offices.
19 An amendment of 1904 provided that the legislature should enact the consolidation of the townships with the city in matters of taxation, but no further steps had been taken to the end of 1907.
20 The net revenue per million gallons in 1890-1899 was $35.04.
21 Prof. C.D. Buck in Decennial Publications of the University of Chicago (1903, vol. 6).
22 There was an insurance of $88,634,122 on the losses, of which about a half was recovered. F.L. Olmsted estimated that one-third of the roof surface and one-half the cubic contents of the city’s buildings were destroyed.
23 Four were hanged, 1 committed suicide, 2 had their death sentence commuted to life-imprisonment, the eighth was sentenced to imprisonment for 15 years. 981 men were panelled in selecting the jury. Governor J.P. Altgeld in 1893 pardoned the three in prison on the ground that the jury was "packed" and consequently incompetent, that no evidence connected the prisoners with the crime, and that the presiding judge was prejudiced. See an article by Judge J.E. Gary, who presided at the trial, in the Century Magazine (April 1893).
End of the Project Gutenberg EBook of Encyclopaedia Britannica, 11th
Edition, Volume 6, Slice 1, by Various
*** END OF THIS PROJECT GUTENBERG EBOOK ENCYCLOPAEDIA BRITANNICA, VOL 6 SL 1 ***
***** This file should be named 31156-h.htm or 31156-h.zip *****
This and all associated files of various formats will be found in:
https://www.gutenberg.org/3/1/1/5/31156/
Produced by Marius Masi, Don Kretz, Juliet Sutherland and
the Online Distributed Proofreading Team at
https://www.pgdp.net
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
https://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH F3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need are critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at https://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
https://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at https://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit https://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including including checks, online payments and credit card
donations. To donate, please visit: https://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart was the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
https://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.