The Project Gutenberg EBook of Scientific American Supplement, No. 633, February 18, 1888, by Various This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Scientific American Supplement, No. 633, February 18, 1888 Author: Various Release Date: November 27, 2005 [EBook #17167] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK SCIENTIFIC AMERICAN *** Produced by Juliet Sutherland and the Online Distributed Proofreading Team at www.pgdp.net
Last year the whole of the lighting of the Newcastle Exhibition was effected by the agency of seventeen of these motors, of which four were spare, giving in the aggregate 280 electrical horse power. As the steam was provided by the authorities of the exhibition, it was good proof to the public that they had satisfied themselves that the consumption would not be extravagant as however favorable might be the terms on which the manufacturers would be willing to lend their engines, they could scarcely be sufficiently tempting to compensate for an outrageous consumption of coal, even in Newcastle. At the time we gave an account of the result of the test, showing that the steam used was 65 lb. per electrical horse power, a very satisfactory result, and equal to 43 lb. per indicated horse power if compared with an ordinary engine driving a generator through a belt. Recently Mr. Parsons has given an account of the theory and construction of his motor before the Northeast Coast Institution, and has quoted 52 lb. of steam per electric horse power as the best result hitherto attained with a steam pressure of 90 lb. As now made there are forty-five turbines through which the steam passes in succession, expanding in each, until it is finally exhausted.
THE COMPOUND STEAM TURBINE.The theoretical efficiency of a motor of this kind is arrived at by Mr. Parsons in the following manner:
The efflux of steam flowing from a vessel at 15.6 lb. per square inch absolute pressure through an orifice into another vessel at 15 lb. pressure absolute is 366 ft. per second, the drop of pressure of 0.6 lb. corresponding to a diminution of volume of 4 per cent. in the opposite direction. The whole 45 turbines are so proportioned that each one, starting from the steam inlet, has 4 per cent. more blade area or capacity than that preceding it. Taking the pressure at the exhaust end to be 15 lb. absolute, that at the inlet end will be 69 lb. above the atmosphere. The steam enters from the steam pipe at 69 lb. pressure, and in passing through the first turbine it falls 2.65 lb. in pressure, its velocity due to the fall being 386 ft. per second, and its increase of volume 3.85 per cent. of its original volume. It then passes through the second turbine, losing 2.55 lb. in pressure, and gaining 3.85 per cent. in volume, and so on until it reaches the last turbine, when its pressure is 15.6 lb. before entering, and 15 lb. on leaving. The velocity due to the last drop is 366 ft. per second. The velocity of the wheels at 9,200 revolutions per minute is 150 ft. per second, or 39.9 per cent. of the mean velocity due to the head throughout the turbines. Comparing this velocity with the results of a series of experiments made by Mr. James B. Francis on a Tremont turbine at Lowell, Mass., it appears that there should be an efficiency of 72 per cent. if the blades be equally well shaped in the steam as in the water turbine, and that the clearances be kept small and the steam dry. Further, as each turbine discharges without check into the next, the residual energy after leaving the blades is not lost as it is in the case of the water turbine, but continues into the next guide blades, and is wholly utilized there. This gain should be equal to 3 to 5 per cent.
As each turbine of the set is assumed to give 72.5 per cent. efficiency, the total number may be assumed to give the same result, or, in other words, over 72 per cent. of the power derived from using the steam in a perfect engine, without losses due to condensation, clearances, friction, and such like. A perfect engine working with 90 lb. boiler pressure, and exhausting into the atmosphere, would consume 20.5 lb. of steam per hour for each horse power. A motor giving 70 per cent. efficiency would, therefore, require 29.29 lb. of steam per horse power per hour. The best results hitherto attained have been 52 lb. of steam per hour per electrical horse power, as stated above, but it is anticipated that higher results will be attained shortly. Whether that be so or not, the motor has many advantages to recommend it, and among these is the increased life of the lamps due to the uniform rotation of the dynamo. At the Phœnix Mills, Newcastle, an installation of 159 Edison-Swan lamps has been running, on an average, eleven hours a day for two years past, yet in that time only 94 lamps have failed, the remaining 65 being in good condition after 6,500 hours' service. Now, if the lamps had only lasted 1,000 hours on the average, as is commonly assumed, the renewals would have amounted to double the year's cost of fuel, as at present consumed.
The present construction of the motor and dynamo is shown in the figures.
Figs. 1 though 6Fig. 2 shows the arrangement of 90 complete turbines, 45 lying on each side of the central steam inlet. The guide blades, R, are cut on the internal periphery of brass rings, which are afterward cut in halves and held in the top and bottom halves of the cylinder by feathers. The moving blades, S, are cut on the periphery of brass rings, which are afterward threaded and feathered on to the steel shaft, and retained there by the end rings, which form nuts screwed on to the spindle. The whole of this spindle with its rings rotate together in bearings, shown in enlarged section, Fig. 3. Steam entering at the pipe, O, flows all round the spindle and passes along right and left, first through the guide blades, R, by which it is thrown on to the moving blades, S, then back on to the next guide blades, and so on through the whole series on each hand, and escapes by the passages, P, at each end of the cylinder connected to the exhaust pipe at the back of cylinder. The bearings, Fig. 3, consist of a brass bush, on which is threaded an arrangement of washers, each successive washer alternately fitting to the bush and the block, while being alternately 1/32 smaller than the block outside and 1/32 larger than the bush in the hole. One broad washer at the end holds the bearings central. These washers are pressed together by a spiral spring, N, and nut, and, by friction against each other, steady or damp any vibration in the spindle that may be set up by want of balance or other cause at the high rate of speed that is necessary for economical working.
The bearings are oiled by a small screw propeller, I, attached to the shaft. The oil in the drain pipes, D and F, and the oil tank, D, lies at a lower level than the screw, but the suction of the fan, K, raises it up into the stand pipe, H, over and around the screw, which gripes it and circulates it along the pipes to the bearings. The course of the oil is as follows: The oil is forced by the propeller, I, and oils the bearing, A. The greater part passes along the pipe, E, to the end bearing, C; some after oiling the bearing, C, drains back by the pipe, F, to the reservoir, D; the remaining oil passes along through the armature spindle, oils the bearings, B, and drains into the reservoir, D, from which the oil is again drawn along the pipe, G, into the stand pipe, H, by the suction of the fan, K. The suction of the fan is also connected to the diaphragm, L, and forms, with it and the spring, M, the principal part of the governor which actuates the throttle valve, V. Fig. 4 is the electrical control governor, which will be further described in connection with the dynamo. It acts directly upon the controlling diaphragm, L, by admitting or closing a large access of air to it, and thus exercises a controlling influence upon it.
The dynamo which forms the other portion of the electric generator, Fig. 1, is coupled to the motor spindle by a square tube coupling fitted on to the square spindle ends. The armature is of the drum type. The body is built up of thin iron disks threaded on to the spindle and insulated from each other by tracing paper. This iron body is turned up and grooves milled out to receive the conducting wires. For pressures of 60 to 80 volts there are fifteen convolutions of wire, or 30 grooves. The wire starting at b, Fig. 6, is led a quarter of a turn spirally, c, round the cylindrical portion, a, then passing along a groove longitudinally is again led a quarter turn spirally, d, round the cylindrical portion, a, then through the end washer, and back similarly a quarter turn, e, then led along the diametrically opposite groove, and lastly a little over a quarter turn, f, back to g, where it is coupled to the next convolution. The commutator is formed of rings of sections. Each section is formed of short lengths. Each length is dovetailed and interlocked between conical steel rings. The whole is insulated with asbestos, and, when screwed up by the end nut, forms, with the steel bush, a compact whole. There are fifteen sections in the commutator, and each coupling is connected to a section. The whole armature is bound externally from end to end with brass or pianoforte steel wire. The magnets are of soft cast iron and of the horseshoe type. They are shunt-wound only.
On the top of the magnet yoke is the electrical control governor, Fig. 4. It consists of one moving spindle on which are keyed a small soft iron bar, and also a double finger, T. There is also a spiral spring, X, attached at one end to the spindle, and at the other to an adjustable top head and clamping nut, Y. The double finger, T, covers or opens a small hole in the face, U, communicating by the pipe, W, to the diaphragm, L. The action of the magnet yoke is to attract the needle toward the poles of the magnet, while by turning the head the spiral spring, X, is brought into tension to resist and balance this force, and can be set and adjusted to any degree of tension. The double finger, T, turns with the needle, and, by more or less covering the small air inlet hole, U, it regulates the access of air to the regulating diaphragm, L. The second finger is for safety in case the brushes get thrown off, or the magnet circuit be broken, in which case the machine would otherwise gain a considerable increase of speed before the diaphragm would act. In these cases, however, the needle ceases to be attracted, falls back, and the safety finger closes the air inlet hole.
There is no resistance to the free movement of this regulator. A fraction of a volt increase or decrease of potential produces a considerable movement of the finger, sufficient to govern the steam pressure, and in ordinary work it is found possible to maintain the potential within one volt of the standard at all loads within the capacity of the machine, excepting only a slight momentary variation when a large portion of the load is switched on or off.
The resistance of the armature from brush to brush is only 0.0032 ohm, the resistance of the field magnets is only 17.7 ohms, while the normal output of the dynamo is 200 amperes at 80 volts. This, excluding other losses, gives an efficiency of 97 per cent. The other losses are due to eddy currents throughout the armature, magnetic retardation, and bearing friction. They have been carefully measured. By separately exciting the field magnets from another dynamo, and observing the increased steam pressure required to maintain the speed constant, the corresponding power was afterward calculated in watts.
The commercial efficiency of this dynamo, after allowing for all losses, is a little over 90 per cent. In the larger sizes it rises to 94 per cent. Assuming the compound steam turbine to give a return of 70 per cent. of the total mechanical energy of the steam, and the dynamos to convert 90 per cent of this into electrical output, gives a resulting efficiency of 63 per cent. As steam at 90 lb. pressure above the atmosphere will with a perfect non-condensing engine give a horse power for every 20.5 lb. of steam consumed per hour, it follows that an electrical generator of 63 per cent. efficiency will consume 32.5 lb. of steam for every electrical horse power per hour.
Again, with steam at 150 lb. pressure above the atmosphere, a generator of the same efficiency would consume only 22.2 lb. of steam per electrical horse power per hour.
The results so far actually obtained are a consumption of 52 lb. per hour of steam for each electrical horse power with a steam pressure of 90 lb. above the atmosphere.—Engineering.
From the researches and investigations of Carnot, Joule, Rankine, Clausius, and Sir William Thomson, the science of thermo-dynamics has not only been brought into existence, but fully matured. We learn from it that whereas in the steam engine, on account of the limited range of temperature in the working cylinder and the rapid conduction of steam during condensation, no combination of cylinders can materially affect its present efficiency, internally fired engines, such as gas and caloric engines—being, as it were, less fettered—can have their already high efficiency increased by simply overcoming mechanical difficulties. To this fact is no doubt due the recent remarkable development of gas and caloric engines. The first caloric or hot air engine was invented by Sir George Cayley in 1807, and in 1827 Dr. Robert Stirling, a Scotch minister, took out his first patent for a hot air engine, which was the foundation of many subsequent machines, and by the invention of the regenerator he converted what was practically a scientific toy into an efficient machine.
One of the most ardent workers in this field at the present time is Mr. James Hargreaves, of Widnes, who, with a thorough theoretical knowledge of the subject has, after many years of patient perseverance, over come many of the mechanical difficulties, and designed the engine of which the above is an illustration.
The sectional elevation, shown in Fig. 1, is an expanded view of the machine, shown thus to enable the action of the machine to be more clearly understood; the relative position of the different parts, as actually made, is shown in the side elevation (Fig. 4). The principal working parts of the machine are the combustion chamber, D, which is of the form shown, lined with fire brick, and having an entrance, with the door screwed down like a manhole lid; the working cylinder, A, surrounded by the water casing, K; the piston, B, with a water lining, and coupled to the end of the working beam by a parallel motion, the beam being supported by two rocking columns, Z, as in engines of the "grasshopper" type; the air compressor, C, coupled directly to the piston of the working cylinder; the injection pump, F, for supplying the fuel—creosote or coal tar—to the combustion chamber; the regenerator E; the receiver and separator, V Y; the feed and exhaust valves, M.
Fig. 1—SECTIONAL ELEVATION—HARGREAVES'
THERMO-MOTOR.
Fig. 2.The action of the machine is as follows: Assuming the engine to be in condition for starting, the sides of the combustion chamber, D, are red hot, the chamber charged with air, and the spray of creosote, injected by the pump, F, is ignited; the expansion of the gases produced by the combustion acts upon the bottom of the piston, B, forcing it to the top of the cylinder, and thus, by intermediate mechanism, causing the crank shaft to revolve. By the same stroke a charge of air is forced by the compressor, C, into the receiver through the pipe, R. The cylinder is, of course, single acting, and on the down stroke of the piston, B—which falls by its own weight and the momentum of the fly wheel—the exhaust gases are forced through the regenerator, E, which absorbs most of their heat; they then pass through the exhaust valve, placed immediately under the feed valve, M, along the pipe, Q, up through the pipes, T, fitted into the receiver, V, down the pipes, T, fitted into the saturator, Y, and out of the funnel fixed to the bottom of Y.
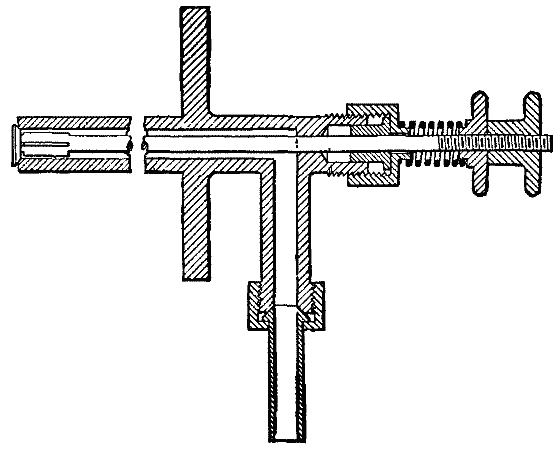Fig. 3.
Fig. 4.The charge of air for supplying the combustion chamber is forced by the compressor, C, through the pipe, R, outside the tubes, T, in the chambers, V and Y, along the pipe, P, through the feed valve, M, and the regenerator, E, into the combustion chamber. In its passage from the compressor, it first picks up the residual heat of the exhaust gases in the tubes, T, and finally the heat absorbed by the regenerator, E, thus entering the combustion chamber in a highly heated state. Having described generally the passage of the air from the compressor to the working cylinder, and back again to the funnel, we will now describe the details. The working cylinder, A, is fitted into the casting which forms the water casing, K, a space being left between the bottom of the cylinder and the casing, which is filled with a non-conducting mixture of asbestos to protect it from the heat of combustion; the bottom of the piston, B, has a similar protection, and the regenerator has a lining of the same mixture, to prevent any heat from escaping through the casting which holds it. The water in the casing, K, and in the piston, B, is supplied by a small pump, G, which forces the water through the pipe, P4, into the telescopic pipe, L either into the piston, B, or through the pipe, P6, into the casing, K—the bottom of the casing being connected by the pipe, P10, with the auxiliary boiler, W. The steam generated in the casing, K, is carried to the boiler, W, by the pipe, P3, and from the boiler it passes along the pipe, P2, through the valve, A2, into the chamber, V, thus giving up its heat to the incoming air, with which it mixes. The vapor gradually condenses at the bottom of the vessel, Y, and the water so formed is drawn by the pump, J, along the suction pipe, P9, and forced through the pipe, P8, back to the chamber, Y, through the valve, A1, and in the form of spray plays on the tubes, T, and absorbing any residual heat. The heat generated by compression in the cylinder, C, is absorbed by a spray of water from the pump, H, the vapor being carried along with the air through the pipe, R, to the chamber, Y, where it is separated, and falling to the bottom is circulated, as just described, by the pump, J. X is a small auxiliary air compressor, to obtain the necessary compression to start the engine, and is worked from the boiler, W. In future engines this compressor will be superseded by a specially designed injector, which will produce the necessary pressure at a considerable reduction in cost. When once the engine is started, the fire of the auxiliary boiler can, of course, be drawn, as the main engine afterward makes its own steam. The regenerator, E, has circular ends of fire clay perforated, the body being filled with fire clay spirals of the shape clearly shown in elevation in Fig. 2. The injector valve for the creosote is shown to a larger scale in Fig. 3. This valve has, however, been since considerably modified and improved. The feed and exhaust valves, M, are actuated by cams keyed to a countershaft driven by bevel wheels from the main shaft. The creosote pump, F, is also worked by a cam on the same shaft, but the pumps, G H J, are worked by eccentrics. A stop valve, N, is fixed to the supply pipe, P, under which is place a back pressure valve to retain the pressure in the combustion chamber. The engine is regulated by an ordinary Porter governor actuating the throttle valve, O. An engine, as described, has been constructed by Messrs. Adair & Co., engineers, Waterloo Road, Liverpool, and has been running most satisfactorily for several weeks, the results being clearly shown by the indicator diagrams (Figs. 5 and 6). The results obtained by this motor are very remarkable, and are a long way in advance of any previous performance, as only a little over ½ lb. of fuel is used per i.h.p. per hour. It may be mentioned that the temperature of the combustion chamber is calculated to be about 2,500°F., and that of the exhaust gases does not exceed 180°F.—Industries.
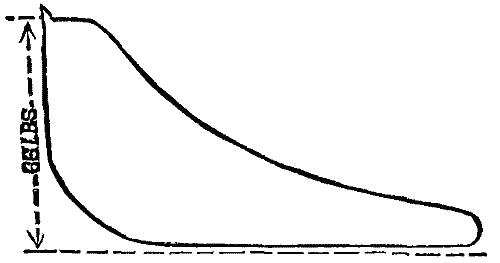
Diagram from cylinder—25 in. diam, 18 in. stroke. I.H.P., 63. Scale, 1/30 in. Mean pressure, 28.2 lb..
Fig. 5.
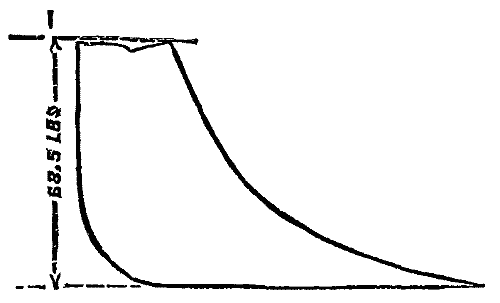
Diagram from air pump—15 in. diam., 18 in. stroke. I.H.P., 23. Scale, 1/30 in—Mean pressure, 28.5 lb.
Fig. 6.
DIAGRAMS FROM CYLINDER AND AIR PUMP.
Net indicated horse power, 40; revolutions per minute, 100; coal tar consumed per hour, 20.5 lb.; coal tar per I.H.P. per hour, 0.512 lb.
Determination of the Influence of Internal Stresses on the Strength of Materials.—We call internal stresses those which exist within the mass of any hollow cylinder or other body, when it appears to be in a state of repose, or not under the influence of external forces. When pressure is applied to a hollow cylinder, either externally or internally, the interior layers into which its walls may be conceived to be divided are subjected to a new series of stresses, the magnitude of which is independent of those already existing. These additional stresses combine with the former in such a manner that at every point of the thickness of the cylinder they have common resultants acting in various directions. Thus, if we call t the internal stress existing at a distance rx from the axis of the cylinder, and in a direction tangential to its cross section, and T the additional stress due to pressure inside the cylinder acting at the same point and in the same direction, then the newly developed stress will be t + T.
If R and r0 be the external and internal radii of the cylinder, and if we suppose the external pressure nil, then, if the pressure inside the bore be P0, the stress on the radius rx is determined by the following expression deduced from the well-known fundamental formulæ of Lame:1
| T = | P0 | r02 ———— R2-r02 |
· | R2 + rx2 ———— rx2 |
From which we see that T is a maximum when rx = r0, i.e., for the layer immediately next to the bore of the cylinder. Calling t0 the internal stress in this layer, and T0 the stress resulting from the action inside the bore of the pressure P0, and allowing that the sum of both these quantities must not exceed the elastic limit U of the material, we have—T0 = U - t0. And for this value of T0, the corresponding pressure inside the bore will be
| P = (U - t0) | P0 | R2 - r02
———— R2 + r02 |
This pressure increases with the term (U-t0). With t0 positive, i.e., when the internal stresses in the thickness of the hollow cylinder are such that the metal of the layers nearest to the bore is in a state of tension and that of the outer layers in a state of compression, then the cylinder will have the least strength when t0 has the greatest numerical value. Such stresses are termed injurious or detrimental stresses. With t0 negative, the strength of the cylinder increases with the numerical value of t0, and those stresses which cause compression in the layers nearest to the bore of the cylinder and tension in the outer layers are termed beneficial or useful stresses.
For these reasons, and in order to increase the power of resistance of a cylinder, it is necessary to obtain on the inner layer a state of initial compression approaching as nearly as possible to the elastic limit of the metal. This proposition is in reality no novelty, since it forms the basis of the theory of hooped guns, by means of which the useful initial stresses which should be imparted to the metal throughout the gun can be calculated, and the extent to which the gun is thereby strengthened determined. The stresses which arise in a hollow cylinder when it is formed of several layers forced on one upon another, with a definite amount of shrinkage, we call the stress of built-up cylinders, in order to distinguish them from natural stresses developed in homogeneous masses, and which vary in character according to the conditions of treatment which the metal has undergone. If we conceive a hollow cylinder made up of a great number of very thin layers—for instance, of wire wound on with a definite tension—in which case the inner layer would represent the bore of the gun, then the distribution of the internal stresses and their magnitude would very nearly approach the ideally perfect useful stresses which should exist in a homogeneous cylinder; but in hollow cylinders built up of two, three, and four layers of great thickness, there would be a considerable deviation from the conditions which should be aimed at.
The magnitude of the stresses in built-up cylinders is determined by calculation, on the presumption that initial stresses do not exist in the respective layers of the tube and of the hoops which make up the walls of the cylinder. Nevertheless, Rodman, as early as the year 1857, first drew attention to the fact that when metal is cast and then cooled, under certain conditions, internal stresses are necessarily developed; and these considerations led him, in the manufacture of cast iron guns, to cool the bore with water and to heat the outside of the moulds after casting. Although Rodman's method was adopted everywhere, yet up to the present time no experiments of importance have been made with the view of investigating the internal stresses which he had drawn attention to, and in the transition from cast iron to steel guns the question has been persistently shelved, and has only very lately attracted serious attention. With the aid of the accepted theory relating to the internal stresses in the metal of hooped guns, we can form a clear idea of the most advantageous character for them to assume both in homogeneous and in built-up hollow cylinders. In proof of this, we can adduce the labors of Colonels Pashkevitch and Duchene, the former of whom published an account of his investigations in the Artillery Journal for 1884—St. Petersburg—and the latter in a work entitled "Basis of the Theory of Hooped Guns," from which we borrow some of the following information.
The maximum resistance of a tube or hollow cylinder to external stresses will be attained when all the layers are expanded simultaneously to the elastic limit of the material employed. In that case, observing the same notation as that already adopted, we have—
| P0 = T | R - r0
——— r0 |
(1) |
But since the initial internal stresses before firing, that is previous to the action of the pressure inside the bore, should not exceed the elastic limit,2 the value of R will depend upon this condition.
In a hollow cylinder which in a state of rest is free from initial stresses, the fiber of which, under fire, will undergo the maximum extension, will be that nearest to the internal surface, and the amount of extension of all the remaining layers will decrease with the increase of the radius. This extension is thus represented—
| tx1 = P0 | r02
———— R2 - r02 |
· | rx2 + R2
———— rx2 |
Therefore, to obtain the maximum resistance in the cylinder, the value tx of the initial stress will be determined by the difference T - t'x, and since P0 is given by Equation (1), then
| tx = T | ( | 1 - | r0 ——— R0 + r0 |
· | rx2 + R2 ———— rx2 |
) | (2) |
The greatest value tx = t0 corresponds to the surface of the bore and must be t0 =-T, therefore
| r02 + R2 ———— r0 (R + r0) |
= 2 |
whence P0 = T √2 = 1.41 T.
From the whole of the preceding, it follows that in a homogeneous cylinder under fire we can only attain simultaneous expansion of all the layers when certain relations between the radii obtain, and on the assumption that the maximum pressure admissible in the bore does not exceed 1.41 U.
Equation (2) may be written thus—
| tx = T | R ——— R + r0 |
· | rx - Rr ———— rx2 |
(3) |
Substituting successively rx = r0 and rx = R, we obtain expressions for the stresses on the external and internal radii—
| tR = T | R - r0 ——— R + r0 |
and | tr0 = - T | R — r0 |
R - r0 —— R + r0 |
Therefore, in a homogeneous hollow cylinder, in which the internal stresses are theoretically most advantageous, the layer situated next to the bore must be in a state of compression, and the amount of compression relative to the tension in the external layer is measured by the inverse ratio of the radii of these layers. It is further evident that the internal stresses will obey a definite but very simple law, namely, there will be in the hollow cylinder a layer whose radius is √R r0, in which the stress is nil; from this layer the stresses increase toward the external and the internal radii of the cylinder, where they attain a maximum, being in compression in the internal layers and in tension in the external ones.
The internal pressures corresponding to these stresses may be found by means of very simple calculations. The expression for this purpose, reduced to its most convenient form, is as follows:
| px = T | R ——— R + r0 |
( | R — rx | - 1 | ) | ( | 1 - | r0 — rx |
) | (4) |
In order to represent more clearly the distribution of stresses and pressures in the metal of a homogeneous ideally perfect hollow cylinder, let us take, as an example, the barrel of a 6 in. gun—153 mm. Let us suppose T = 3,000 atmospheres; therefore, under the most favorable conditions, P0 = 1.41 T, or 4,230 atmospheres. From Equation (1) we determine R = 184.36 mm. With these data were calculated the internal stresses and the pressures from which the curve represented in Fig. 1 is constructed. The stresses developed under fire with a pressure in the bore of 4,230 atmospheres are represented by a line parallel to the axis of the abscissæ, since their value is the same throughout all the layers of metal and equal to the elastic limit, 3,000 atmospheres. If, previous to firing, the metal of the tube were free from any internal stresses, then the resistance of the tube would be
| P0 = U | R2 - r20 ———— R2 + r20 |
or 2,115 atmospheres—that is, one-half that in the ideally perfect cylinder. From this we perceive the great advantage of developing useful initial stresses in the metal and of regulating the conditions of manufacture accordingly. Unless due attention be paid to such precautions, and injurious stresses be permitted to develop themselves in the metal, then the resistance of the cylinder will always be less than 2,115 atmospheres; besides which, when the initial stresses exceed a certain intensity, the elastic limit will be exceeded, even without the action of external pressures, so that the bore of the gun will not be in a condition to withstand any pressure because the tensile stress due to such pressure, and which acts tangentially to the circumference, will increase the stress, already excessive, in the layers of the cylinder; and this will occur, notwithstanding the circumstance that the metal, according to the indications of test pieces taken from the bore, possessed the high elastic limit of 3,000 atmospheres.
Fig. 1In order to understand more thoroughly the difference of the law of distribution of useful internal stresses as applied to homogeneous or to built-up cylinders, let us imagine the latter having the external and internal radii of the same length as in the first case, but as being composed of two layers—that is to say, made up of a tube with one hoop shrunk on under the most favorable conditions—when the internal radius of the hoop = √R v0 or 118.7 mm., Fig. 2, has been traced, after calculating, by means of the usual well known formulæ, the amount of pressure exerted by the hoop on the tube, as well as the stresses and pressures inside the tube and the hoop, before and after firing. A comparison of these curves with those on Fig. 1 will show the difference between the internal stresses in a homogeneous and in a built-up cylinder. In the case of the hooped gun, the stresses in the layers before firing, both in the tube and in the hoop, diminish in intensity from the inside of the bore outward; but this decrease is comparatively small. In the first place, the layer in which the stresses are = 0 when the gun is in a state of rest does not exist. Secondly, under the pressure produced by the discharge, all the layers do not acquire simultaneously a strain equal to the elastic limit. Only two of them, situated on the internal radii of the tube and hoop, reach such a stress; whence it follows that a cylinder so constructed possesses less resistance than one which is homogeneous and at the same time endowed with ideally perfect useful initial stresses. The work done by the forces acting on a homogeneous cylinder is represented by the area a b c d, and in a built-up cylinder by the two areas a' b' c' d' and a" b" c" d". Calculation shows also that the resistance of the built-up cylinder is only 3,262 atmospheres, or 72 per cent. of the resistance of a homogeneous cylinder. By increasing the number of layers or rows of hoops shrunk on, while the total thickness of metal and the caliber of the gun remains the same, we also increase the number of layers participating equally in the total resistance to the pressure in the bore, and taking up strains which are not only equal throughout, but are also the greatest possible. We see an endeavor to realize this idea in the systems advocated by Longridge, Schultz, and others, either by enveloping the inner tubes in numerous coils of wire, or, as in the later imitations of this system, by constructing guns with a greater number of thin hoops shrunk on in the customary manner. But in wire guns, as well as in those with a larger number of hoops—from four to six rows and more—the increase in strength anticipated is acknowledged to be obtained in spite of a departure from one of the fundamental principles of the theory of hooping, since in the majority of guns of this type the initial compression of the metal at the surface of the bore exceeds its elastic limit.3 We have these examples of departure from first principles, coupled with the assumption that initial stresses do not exist in any form in the metal of the inner tube previous to the hoops having been shrunk on; but if the tube happen to be under the influence of the most advantageous initial stresses, and we proceed either to hoop it or to envelope it with wire, according to the principles at present in vogue, then, without doubt, we shall injure the metal of the tube; its powers of resistance will be diminished instead of increased, because the metal at the surface of the bore would be compressed to an amount exceeding twice its elastic limit. An example of injury inflicted in this way is to be found in the method adopted for hooping cast iron tubes cast by Rodman's process. If we take into consideration the undoubted fact of the existence to a considerable extent of useful initial stresses in these tubes, then the hoops should be put on them either with very little shrinkage or none at all, whereas ordnance authorities everywhere have applied to this case methods which are only correct for tubes which are free from initial stresses.
Fig. 2During the process of hooping guns it is very important to know how to take into account the value and mode of distribution of the prejudicial stresses in the inner tube, should such exist. Knowing these stresses, it is possible, by regulating the tension of the hoops, to reduce the compression of the metal at the surface of the bore to the proper extent, thus doing away with the previously existing tension, and by that means removing a source of weakness in the tube. In precisely the same way in the shrinkage of gun hoops attention must be paid to the character and value of the stresses which arise in the course of their manufacture; otherwise it will be impossible to hoop the barrel throughout in a proper manner. If prejudicial stresses exist in the metal of a hoop before it is put in its place, then, when the gun is fired, if it had been shrunk on with the degree of tension usually allowed, the layer situated in the internal radius will be extended beyond admissible limits, thereby causing the resistance of the gun to be less than that prescribed.4
It is evident, from what has been said, that in order to determine precisely the resistance of hollow cylinders to internal pressures, and to make the correct calculations for hooping tubes, it is absolutely necessary to know whether internal initial stresses exist in the tube and in the hoops, and to ascertain what their nature and intensity may be—that is to say, whether they are useful or detrimental; yet it is incontestable that in the construction of modern ordnance no attention has been paid to the investigations indicated. If it be possible to ignore these considerations in the manufacture of guns of small caliber, and where the thickness of metal is not sufficiently great to admit of strongly developed internal stresses, such is by no means the case with the colossal and costly weapons of the present day. In these the thickness of metal in the tube and hoops is very great; hence the extreme probability of very considerable internal stresses developing themselves. That the strength of large guns is often far below that anticipated is demonstrated, year by year, by the repeated cases of failure. Consciousness as to the want of strength in such guns is made evident by the precautionary measures as to their use everywhere adopted. The heavy artillery produced in the gun factories of Europe is constructed with all the skill, science, and experience which engineers and artillerists can command, and therefore it would seem that instances of defective strength should not arise. Such cases, however, do occur everywhere, and irresistibly give rise to the suspicion that not only is the system of construction of guns of large caliber faulty, but also that the conditions of their manufacture must be considered as defective. Bearing in mind the enormous sums of money expended by every nation in order to secure an armament of completely trustworthy guns, this question demands speedy and searching investigation. The first step in this direction is the study of the internal stresses inherent in the metal; because, if such exist, and are capable of attaining, under certain conditions, considerable magnitudes, then it is absolutely necessary to take advantage of them in order to increase the resistance of the metal, instead of allowing them to act to its detriment.
The study of natural internal stresses is of importance, not only with reference to gun making, but also in respect of other structures where great resistance is required. All have heard of the sudden failure of crank shafts and piston rods, of the bursting of boiler shells and tubes, of the breaking of tires, etc. In the majority of cases the investigations into the causes of such sudden failures have not led to any definite results. It has usually been found that the metal possessed a satisfactory elastic resistance, and satisfied all the conditions set down in the specifications. Had attention been paid during these investigations to the state of the internal stresses in the metal, the cause of unlooked-for accidents might have been explained, and steps would consequently have been taken to avoid them in future.
We are also familiar with the development of considerable internal stresses in various kinds of steel articles which are subjected to hardening and tempering; for example, as dies, tools of various description, sword blades, and thin plates rolled at a low temperature or subjected to cold hammering. In the foundry the appearance of internal stresses is of still more frequent occurrence. The neglect of certain practical rules in casting, and during the subsequent cooling, leads to the spontaneous breakage of castings after a few hours or days, although taken out of the sand apparently perfectly sound. Projectiles for penetrating armor plate, and made of cast steel, as well as shells which have been forged and hardened, and in which the metal possessed an ultimate resistance of over twelve thousand (12,000) atmospheres, with an elastic limit of more than six or seven thousand atmospheres, will crack to a serious extent, and even break up in the lathe, while the recess for the copper ring is being turned out. In shell of this nature, as well as in chilled cast iron shell, the heads are apt to fly off spontaneously either while they are lying in store or during transport. Such phenomena, it seems to me, demonstrate the existence of internal stresses of considerable magnitude in the metal of the projectiles, and it is highly probable that the manufacture of many articles would have approached nearer to perfection had more attention been bestowed upon the study of the internal stresses which they were liable to. Having thus explained the nature and importance of the subject, I will proceed to describe the experiments which I have made with a view to its illustration.—London Engineer.
Lame holds that in a homogeneous tube subjected to the action of two pressures, external and internal, the difference between the tension and the compression developed at any point of the thickness of the tube is a constant quantity, and that the sum of these two stresses is inversely proportional to the square of the radius of the layer under consideration. Let r0, R, and rx be the respective radii, p0, p1, and px the corresponding pressures, and T0, T1, and Tx, the tensions, then we have:
| T0 - p0 = Tx - px | (1) |
| (T0 + p0)r02 = (Tx + px)rx2 | (2) |
| Tx - px = T1 - p1 | (3) |
| (Tx + px)rx2 = (T1 + P1)R2 | (4) |
if the radii are known and p and p1 be given, then deducing from the above equations the values T0 and T1, and also the variable pressure px, we determine—
| Tx = | p0 r02(R2 + rx2) - p1 R2(rx2+r02)
—————————————— (R2 + r02)rx2 |
This is the formula of Lame, from which, making p1=0, we obtain the expression in the text.
We must, however, remark that in a built-up hollow cylinder the compression of the metal at the surface of the bore may exceed the elastic limit. This cannot occur in the case of natural stresses.
In certain cases this, of course, may be an advantage, as, for instance, when the inner tube is under injurious initial stresses; but then, in order to be able to apply the necessary shrinkage, we must know the magnitude of these stresses.
When the inner tube is strengthened by means of wire, the initial or natural stresses in the latter may be neglected on account of its thinness; but when the thickness of the hoops is reduced, and the number of layers thereby increased, then the value of the initial stresses in these hoops is a very important factor with respect to the decrease or increase Of the powers of resistance of the gun.
Judging from the nature of the correspondence on architecture and the duty of architects which is frequently seen in the columns of the daily papers, the Times especially, it would seem that the popular notion of architecture now is that it is a study mainly of things connected with sanitary engineering—of the best forms of drain pipes and intercepting traps. This is indeed a very important part of sound building, and it is one that has been very much neglected, and has been, in fact, in a comparatively primitive state until very recent times; and therefore it is not surprising that there should be a reaction in regard to it, and that newspapers which follow every movement of public opinion, and try to keep pace with it, should speak as if the drain pipe were the true foundation of architecture. I have a great respect for the drain pipe, and wish to see it as well laid and "intercepted" as possible; but I think, for all that, that there is something in architecture higher than sanitary engineering. I wish to consider it in these lectures as what I think it essentially is, what it has evidently been in the eyes of all those of past days who have produced what we now regard as great architectural monuments, namely, as an intellectual art, the object of which is to so treat the buildings which we are obliged to raise for shelter and convenience as to render them objects of interest and beauty, and not mere utilitarian floors, walls, and roofs to shelter a race who care nothing for beauty, and who only want to have their physical comfort provided for.
Architecture, then, from the point of view from which I am asking you to regard it—and the only point of view in which it is worth the serious regard of thoughtful people—is the art of erecting expressive and beautiful buildings. I say expressive and beautiful, and I put expressive first, because it is the characteristic which we can at least realize even when we cannot realize what can fairly be called beauty, and it is the characteristic which comes first in the order of things. A building may be expressive and thereby have interest, without rising into beauty; but it can never be, architecturally speaking, beautiful unless it has expression. And what do we mean by expression in a building? That brings us to the very pith of the matter.
We know pretty well what we mean when we say that a painted or sculptured figure is expressive. We mean that, while correctly representing the structure of the human figure, it also conveys to our minds a distinct idea of a special emotion or sentiment, such as human beings are capable of feeling and expressing by looks and actions. Expression in this sense a building cannot be said to have. It is incapable of emotion, and it has no mobility of surface or feature. Yet I think we shall see that it is capable of expression in more senses than one. It may, in the first place, express or reflect the emotion of those who designed it, or it may express the facts of its own internal structure and arrangement. The former, however, can only, I think, be said to be realized in the case of architecture of the highest class, and when taken collectively as a typical style. For instance, we can all pretty well agree that the mediæval cathedral expresses an emotion of aspiration on the part of its builders. The age that built the cathedrals longed to soar in some way, and this was the way then open to it, and it sent up its soul in spreading vaults, and in pinnacles and spires. So also we can never look at Greek architecture without seeing in it the reflection of a nature refined, precise, and critical; loving grace and finish, but content to live with the graces and the muses without any aspirations that spurned this earth. We can hardly go further than this in attributing emotional expression to architecture. But in a more restricted sense of the word expression, a building may express very definitely its main constructive facts, its plan and arrangement, to a certain extent even its purpose, so far at least that we may be able to identify the class of structure to which it belongs. It not only may, but it ought to do this, unless the architecture is to be a mere ornamental screen for concealing the prosaic facts of the structure. There is a good deal of architecture in the world which is in fact of this kind—an ornamental screen unconnected with the constructional arrangement of the building. Nor is such architecture to be entirely scouted. It may be a very charming piece of scenery in itself, and you may even make a very good theoretical defense for it, from a certain point of view. But on the whole, architecture on that principle becomes uninteresting. You very soon tire of it. It is a mask rather than a countenance, and tends to the production of a dull uniformity of conventional design.
For we must remember that architecture, although a form of artistic expression, is not, like painting and sculpture, unfettered by practical considerations. It is an art inextricably bound up with structural conditions and practical requirements. A building is erected first for convenience and shelter; secondly only for appearance, except in the case of such works as monuments, triumphal arches, etc., which represent architectural effect pure and simple, uncontrolled by practical requirements. With such exceptions, therefore, a building ought to express in its external design its internal planning and arrangement; in other words, the architectural design should arise out of the plan and disposition of the interior, or be carried on concurrently with it, not designed as a separate problem. Then a design is dependent on structural conditions also, and if these are not observed, the building does not stand, and hence it is obvious that the architectural design must express these structural conditions. It must not appear to stand or be constructed in a way in which it could not stand (like the modern shops which are supposed to stand on sheets of plate glass), and its whole exterior appearance ought to be in accordance with, and convey the idea of, the manner and principle on which it is constructed. The most important portions of the interior must be shown as such externally by the greater elaboration and emphasis of their architectural treatment. If the general arrangement of the plan is symmetrical, on either side of a center (which, however, it cannot often be except in the largest type of monumental or public buildings), the architectural treatment must be symmetrical. If the building is necessarily arranged, in accordance with the requirements of the plan, unsymmetrically, the architectural treatment must follow suit, and the same principle must be carried out through all the details.
Now this dependence of architectural design upon plan and construction is one of the conditions which is often overlooked by amateurs in forming a judgment upon architectural design; and the overlooking of this is one reason of the uncertainty of opinion about architecture as compared with such arts as sculpture and painting. Few people know or care much about the structure and planning of buildings except those whose business it is to care about this; and consequently they do not realize what it is which they should look for in the architectural design. They like it or do not like it, and they regard this as what is called a mere question of taste, which, according to the proverb, is not to be disputed about. In fact, however, the good or bad taste of an architectural design, say, if you like, its correctness or incorrectness, is to a considerable extent a matter of logical reasoning, of which you must accurately know the premises before you can form a just conclusion. But there is another reason for this prevalent uncertainty and vagueness of opinion, arising out of the very nature of architectural art itself, as compared with the imitative arts. A painting of a figure on a landscape is primarily a direct imitation of the physical facts of nature. I do not for a moment say it is only that, for there is far more involved in painting than the imitation of nature; but the immediate reference to nature does give a standard of comparison which to a certain extent every eye can appreciate. But architecture is not an art which imitates natural forms at all, except as minor decorations, and it then does so, or should do so, only in a conventionalized manner, for reasons which we shall consider later on. Architecture is, like music, a metaphysical art. It deals with the abstract qualities of proportion, balance of form, and direction of line, but without any imitation of the concrete facts of nature. The comparison between architecture and music is an exercise of the fancy which may indeed be pushed too far, but there is really a definite similarity between them which it is useful to notice. For instance, the regular rhythm, or succession of accentuated points in equal times, which plays so important a part in musical form, is discernible in architecture as a rhythm in space. We may treat a cottage type of design, no doubt, with a playful irregularity, especially if this follows and is suggested by an irregularity, of plan. But in architecture on a grand scale, whether it be in a Greek colonnade or a Gothic arcade, we cannot tolerate irregularity of spacing except where some constructive necessity affords an obvious and higher reason for it. Then, again, we find the unwritten law running throughout all architecture that a progress of line in one direction requires to be stopped in a marked and distinct manner when it has run its course, and we find a similarly felt necessity in regard to musical form. The repetition so common at the close of a piece of music of the same chord several times in succession is exactly analogous to the repetition of cross lines at the necking of a Doric column to stop the vertical lines of the fluting, or to the strongly marked horizontal lines of a cornice which form the termination of the height or upward progress of an architectural design. The analogy is here very close. A less close analogy may also be felt between an architectural and a musical composition regarded as a whole. A fugue of Bach's is really a built-up structure of tones (as Browning has so finely put it in his poem, "Abt Vogler"), in accordance with certain ideas of relation and proportion, just as a temple or a cathedral is a built-up structure of lines and spaces in accordance with ideas of relation and proportion. Both appeal to the same sense of proportion and construction in the brain; the one through the ear, the other through the eye. Then, in regard to architecture again, we have further limiting conditions arising not only out of the principle of construction employed, but out of the physical properties of the very material we employ. A treatment that is suitable and expressive for a stone construction is quite unsuitable for a timber construction. Details which are effective and permanent in marble are ineffective and perishable in stone, and so; on and the outcome of all this is that all architectural design has to be judged, not by any easy and ready reference to exterior physical nature, with which it has nothing to do, but by a process of logical reasoning as to the relation of the design to the practical conditions, first, which are its basis, and as to the relation of the parts to each other. Of course beyond all this there is in architecture, as in music, something which defies analysis, which appeals to our sense of delight we know not how or why, and probably we do not want to know; the charm might be dissolved if we did. But up to this point architectural design and expression are based on reasoning from certain premises. The design is good or bad as it recognizes or ignores the logic of the case, and the criticism of it must rest on a similar basis. It is a matter of thought in both cases, and without thought it can neither be designed nor appreciated to any purpose, and this is the leading idea which I wish to urge and to illustrate in these lectures.
You may say: May not a design satisfy all these logical conditions, and yet be cold and uninteresting, and give one no pleasure? Certainly it may. Indeed, we referred just now to that last element of beauty which is beyond analysis. But, if we cannot analyze the result, I rather think we can express what it is which the designer must evince, beyond clear reasoning, to give the highest interest to his architecture. He must have taken an interest in it himself. That seems a little thing to say, but much lies in it. As Matthew Arnold has said of poetry:
"What poets feel not, when they make
A pleasure in creating,
The world, in its turn, will not take
Pleasure in contemplating."
The truth runs through all art. There are, alas, so many people who do not seem to have the faculty of taking pleasure, and there is so much architecture about our streets which it is impossible to suppose any one took "pleasure in creating." When a feature is put into a design, not because the designer liked it, but because it is the usual thing and it saves trouble, it always proclaims that melancholy truth. But where something is designed because the designer liked doing it, and was trying to please his own fancy instead of copying what a hundred other men have done before, it will go hard but he will give some pleasure to the spectator. It is from this blessed faculty that a design becomes inspired with what is best described as "character." It is not the same thing as style. I have something to say in my next lecture as to what I think style means, but it is certain that a building may have style and yet want character, and it may have a good deal of character and yet be faulty or contradictory in style. We cannot define "character," but when we feel that it is present we may rely upon it that it is because the designer took interest and pleasure in his work, was not doing it merely scholastically—in short, he put something of his own character into it, which means that he had some to put.
Figs. 1 through 3Now, coming back to the axiom before mentioned, that architectural design should express and emphasize the practical requirements and physical conditions of the building, let us look a little more in detail into the manner in which this may be done. We will take, to begin with, the very simplest structure we can possibly build—a plain wall (Fig. 1).2 Here there is no expression at all; only stones piled one on another, with sufficient care in coursing and jointing to give stability to the structure. It is better for the wall, constructively, however, that it should have a wider base, to give it more solidity of foundation, and that the coping should project beyond the face of the wall, in order to throw the rain off, and these two requirements may be treated so as to give architectural expression to our work (Fig. 2). It now consists of three distinct portions—a plinth, or base, a superficies of wall, and a coping. We will mark the thickening at the base by a moulding, which will give a few horizontal lines (at B), and the coping in the same way. The moulding of the coping must also be so designed as to have a hollow throating, which will act as a drip, to keep the rain from running round the under side of the coping and down the wall. We may then break up the superficies by inserting a band of single ornament in one course of this portion of the wall—not half way, for to divide any portion of a building into mere "halves" has usually a weak and monotonous effect, but about two thirds of the distance from the base line; and this band of ornament not only breaks up the plain surface a little, but also, by carrying another horizontal line along the wall, emphasizes its horizontality. Always emphasize that which is the essential characteristic of your structure. A wall of this kind is essentially a long horizontal boundary. Emphasize its length and horizontality.
If we are millionaires, and can afford to spend a great deal on a wall, we may not only (Fig. 3) carry further the treatment of the coping and base, by giving them ornamental adjuncts as well as mouldings, but we might treat the whole wall superficies as a space for surface carving, not mechanically repeated, but with continual variation of every portion, so as to render our wall a matter of interest and beauty while retaining all its usefulness as a boundary, observing that such surface ornament should be designed so as to fulfill a double object: 1, to give general relief to the surface of the wall; 2, to afford matter of interest to the eye on close inspection and in detail.
That is the double function of nearly all architectural ornament. It is, in the first place, to aid the general expression and balance of the building, and give point and emphasis where needed; and, in the second place, to furnish something to the eye for study on its own account when viewed more closely.
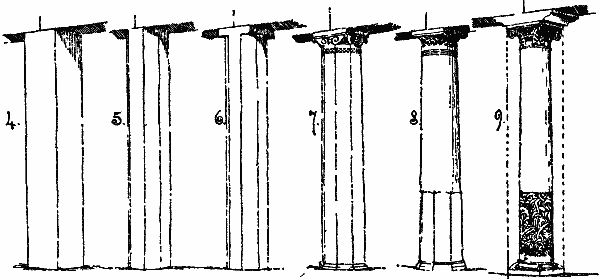Figs. 4 through 9We will take another typical and simple erection, a stone pillar to support the ends of two lintels or beams. This may be simply a long squared piece set on end (Fig. 4), and will perform its constructive functions perfectly well in that form; but it is not only absolutely expressionless, but is in one sense clumsy and inconvenient, as taking up more space than need be, presenting an unwieldy-looking mass when viewed at an angle, and shutting out a good deal of light (if that happen to be a matter of practical consequence in the case). Cutting off the angles (Fig. 5) does not weaken it much, and renders it much less unwieldy-looking, besides giving it a certain degree of verticality of expression, and rendering it more convenient as taking up less room and obstructing less light. But though the column is quite strong enough, the octagonal top does not make so good a seat or bearing for the ends of the lintels. We will therefore put a flat square stone on the top of it (Fig. 6), which will serve as a bed for the lintels to rest on securely. But the angles of this bed plate, where they project beyond the face of the column, appear rather weak, and are so actually to some extent—a double defect, for it is not enough in architecture that a thing should be strong enough, it is necessary that it should appear so, architecture having to do with expression as well as with fact. We will, therefore, strengthen this projecting angle, and correct the abruptness of transition between the column and the bed plate, by brackets (Fig. 7) projecting from the alternate faces of the column to the angles of the bed plates. As this rather emphasizes four planes of the octagon column at the expense of the other four, we will bind the whole together just under the brackets by a thin band of ornament constituting a necking, and thus we have something like a capital developed, a definitely designed finish to our column, expressive of its purpose. This treatment of the upper end, however, would make the lower end rising abruptly from the ground seem very bare. We will accordingly emphasize the base of the column, just as we emphasized the base of the wall, by a projecting moulding, not only giving expression to this connection of the column with the ground, but also giving it the appearance, and to some extent the reality, of greater stability, by giving it a wider and more spreading base to rest on. We have here still left the lines of one column vertically parallel, and there is no constructive reason why they should not remain so. There is, however, a general impression to the eye both of greater stability and more grace arising from a slight diminution upward. It is difficult to account for this on any metaphysical principle, but the fact has been felt by most nations which have used a columnar architecture, and we will accept it and diminute (so to speak) our column (Fig. 8). We have here taken a further step by treating the shaft of the column in two heights, keeping the lower portion octagonal and reducing the upper portion to a circle, and we now find it easier to treat the capital so as to have a direct and complete connection with the column, the capital being here merely a spreading out of the column into a bracket form all round, running it into the square of the bed plate.3 The spreading portion is emphasized by surface ornament, and the necking is again emphasized, this time more decisively, by a moulding, forming a series of parallel rings round the column. If we wish to give our column an expression of more grace and elegance, we can further reduce the thickness of it (Fig. 9), and give more spread to the capital, always taking care to be sure that the strength of the column is not reduced below what the weight which it has to carry requires. In this case a bracket is shown above the capital, projecting longitudinally only (in the direction of the lintel bearing), a method of giving a larger bearing surface for the ends of the lintels, shortening their actual bearing4 (in other words, widening the space which can be bridged between column and column) and giving a workmanlike appearance of stability to the construction at this point. The idea of the division of the column into two sections, suggested in Fig. 8, is kept up in Fig. 9 by treating the lower portion up to the same height with incised decorative carving. The dotted lines on each side in Fig. 9 give the outline of the original square column as shown in Fig. 4. The finished column was within that block; it is the business of the architectural designer to get it out.5
Fig. 10Let us see if we can apply the same kind of process of evolving expression in regard to a building. We will take again the very simplest form of building (Fig. 10), a square house with a door in the center and uniform rows of windows. There cannot be said to be any architectural expression in this. There is no base or plinth at all, no treatment of the wall. The slight projection at the eaves is only what is necessary to keep the rain from running down the walls, and facilitate the emptying of the gutters, and the even spacing of the windows is essential for constructive reasons, to keep the masses of wall over each other, and keep the whole in a state of equally balanced pressure. The first thing we should do in endeavoring to give some expression to the building would be to give it a base or plinth (Fig. 11), and to mark that and the cornice a little more decidedly by mouldings and a line of paneling at the plinth.
Fig. 11The house being obviously in three stories, we should give it some echo externally of this division into horizontal stages by horizontal mouldings, or what are called in architectural phraseology "string courses," not necessarily exactly at the floor levels, but so as to convey the idea of horizontal division; observing here, as in the case of the wall and column, that we should take care not to divide the height into equal parts, which is very expressionless. In this case we will keep the lower string close down on the ground floor windows, and keep these rather low, thus showing that the ground floor apartments are not the most important; while the fact that the first floor ones are so is conversely made apparent by keeping these windows rather higher, putting a double string course over them, and a slight extra depth of moulding, forming a kind of cornice over each.
The space left between these and the roof, in which the attic windows are placed, is treated with a series of mullions and panelings, into which the attic windows are worked, as part of the series of openings; this gives a little richness of effect to the top story, and a continuity of treatment, which binds the whole series of windows together. To have treated the whole of the walls and windows in this way would have been merely throwing away labor; what little effect it has consists in the "character" given by the contrast of this top story treatment with the plain wall surfaces below.
The last thing is to emphasize the door, as the principal opening in the walls, and quite distinct in use and meaning from the other openings, by giving it a little architectural frame or setting, which may be done in many ways, but in this case is done by the old fashioned device (not very logical certainly) of putting a little entablature over it, and a column on either side; there is, however, this to be said for it, that the projecting tablature forms a semi-porch, protecting those at the door somewhat from rain; it must be carried in some way, and columns are the readiest and most seemly manner of doing it, and they also form, practically, something of a weather screen; the bases on which they stand also form a framework or inclosing wall for the steps, which are thus made part of the architectural design, instead of standing out as an eyesore, as on Fig. 10. We have now given the house a little general expression, but it still is vague in its design as far as regards the distribution of the interior; we do not know whether the first floor, for instance, is one large room, or two or more rooms, or how they are divided; and the little house is very square and prim in effect.
Let us try grouping the windows a little, and at the same time breaking up the flat surface of the front wall (Fig. 12). Here, as before, we have divided the building by a horizontal string, but only by one main one on the first floor level, keeping the same contrast, however, between a richer portion above and a plainer portion below; we have divided the building vertically, also, by two projecting bays finishing in gables, thus breaking also the skyline of the roof, and giving it a little picturesqueness, and we have grouped the windows, instead of leaving them as so many holes in the wall at equal distances. The contrast between the ground and first floor windows is more emphatic; and it is now the more evident that the upper floor rooms are the best apartments, from their ample windows; it is also pretty evident that the first floor is divided into two main rooms with large bay windows, and a smaller room or a staircase window, between them; the second floor windows are also shifted up higher, the two principal ones going in to the gables, showing that the rooms below them have been raised in height. Windows carried up the full height of these rooms, however, might be too large either for repose internally or for appearance externally, so the wall intervening between the top of these and the sill of the gables is a good field for some decorative treatment, confined to the bays, so as to assist in separating them from the straight wall which forms the background to them.
Fig. 12So far we have treated our building only as a private house. Without altering its general scale and shape we may suggest something entirely different from a private house. On Fig. 13, we have tried to give a municipal appearance to it, as if it were the guild hall of a small country town. The plain basement and the wide principal doorway, and the row of three very large equal-spaced windows above, render it unquestionable that this is a building with a low ground story, and one large room above. A certain "public building" effect is given to it by the large and enriched cornice with balustrade above and paneling below, and by the accentuation of the angles by projecting piers, and by the turrets over them, which give it quite a different character from that of a private house.
Fig. 13If, on the other hand, the building were the free library and reading room of the same small country town, we should have little doubt of this if we saw it as in Fig. 14, with the walls all blank (showing that they are wanted for ranging something against, and cannot be pierced for windows), and windows only in the upper portion. Similarly, if we want to build it as the country bank, we should have to put the large windows on the ground floor, bank clerks wanting plenty of light, and the ground story being always the principal one; and we might indulge the humor of giving it a grim fortress-like strength by a rusticated plinth (i.e., stones left or worked rough and rock-like) and by very massive piers between the windows, and a heavy cornice over them; the residential upper floor forming a low story subordinate to the bank story. It is true this would not satisfy a banker, who always wants classic pilasters stuck against the walls, that being his hereditary idea of bank expression in architecture.
Fig. 14
Fig. 15Now if we proceed to take to pieces the idea of architectural design, and consider wherein the problem of it consists, we shall find that it falls into a fourfold shape. It consists first in arranging the plan; secondly, in carrying up the boundary lines of this plan vertically in the shape of walls; thirdly, in the method of covering in the space which we have thus defined and inclosed; and, fourthly, in the details of ornamentation which give to it the last and concluding grace and finish. All building, when it gets beyond the mere wall with which we began, is really a method of covering in a space, or, if we may put it so, a collection of spaces, marked out and arranged for certain purposes. The first thing that the architect has to do is to arrange these spaces on the ground so that they may conveniently meet the necessary requirements of the building. Convenience and practical usefulness come first; but in any building which is worth the name of architecture something more than mere convenience has to be kept in mind, even in the arrangement of the plan upon the site. It is to be a combination of convenience with effectiveness of arrangement. We shall probably find that some one compartment of the plan is of paramount importance. We have to arrange the interior so that this most important compartment shall be the climax of the plan.
The entrance and the other subsidiary compartments must be kept subordinate to it, and must lead up to it in such a manner that the spectator shall be led by a natural gradation from the subsidiary compartments up to the main one, which is the center and raison d'etre of the whole—everything in the lines of the plan should point to that. This is the great crux in the planning of complicated public buildings. A visitor to such a building, unacquainted with it previously, ought to have no difficulty in finding out from the disposition of the interior which are the main lines of route, and when he is on the line leading him up to the central feature of the plan. There are public buildings to be found arranged on what may be called the rabbit warren system, in which perhaps a great number of apartments are got upon the ground, but which the visitor is obliged laboriously to learn before he can find his way about them. That is not only inconvenient but inartistic planning, and shows a want of logic and consideration, and, in addition to this, a want of feeling for artistic effect. I saw not long ago, for instance, in a set of competitive designs for an important public building, a design exhibiting a great deal of grace and elegance in the exterior architectural embellishment, but in which the principal entrance led right up to a blank wall facing the entrance, and the spectator had to turn aside to the left and then to the right before finding himself on the principal axis of the plan. That is what I should call inartistic or unarchitectural planning. The building may be just as convenient when you once know its dodges, but it does not appear so, and it loses the great effect of direct vista and climax.
An able architect, who had given much thought to a plan of a large building of this kind, said to me, in showing me his plan, with a justifiable gratification in it, "It has cost me endless trouble, but it is a satisfaction to feel that you have got a plan with backbone in it." That is a very good expression of what is required in planning a complicated building, but few outsiders have any notion of the amount of thought and contrivance which goes to the production of a plan "with backbone;" a plan in which all the subordinate and merely practical departments shall be in the most convenient position in regard to each other, and yet shall all appear as if symmetrically and naturally subordinate to the central and leading feature; and if the public had a little more idea what is the difficulty of producing such a plan, they would perhaps do a little more justice to the labors of the man who contrives the plan, which they think such an easy business; and no doubt it may appear an easy business, because the very characteristic of a really good plan is that it should appear as if it were quite a natural and almost inevitable arrangement.
Just as it is said in regard to literature that easy writing is hard reading, so, in regard to planning, it is the complicated and rabbit warren plans that are the easiest to make, because it is just doing what you please; it is the apparently perfectly simple and natural plan which springs from thought and contrivance. Then there is the next step of raising the walls on the plan, and giving them architectural expression. This must not be thought of as an entirely separate problem, for no truly architectural intellect will ever arrange a plan without seeing generally, in his mind's eye, the superstructure which he intends to rear upon it; but the detailed treatment of this forms a separate branch of the design. Then comes the third and very important problem—the covering in of the space. Next to the plan, this is the most important. All building is the covering over of a space, and the method of covering it over must be foreseen and provided for from the outset. It largely influences the arrangement of the plan. If there were no roofing, you could arrange the walls and carry them up pretty much as you chose, but the roofing of a large space is another matter. It requires extra strength at certain points, where the weight of the roof is concentrated, and it has to be determined whether you will employ a method of roofing which exercises only a vertical pressure on the walls, like the lid of a box, or one which, like an arch, or a vault, or a dome, is abutting against the walls, and requires counterforts to resist the outward thrust of the roof. We shall come upon this subject of the influence of the roof on the design of the substructure more in detail later on. Then, if the plan is convenient and effective, the walls carried up with the architectural expression arising from the placing and grouping of the openings, and the proper emphasizing of the base and the cornice, and the horizontal stages (if any) of the structure, and the roof firmly and scientifically seated on the walls; after all these main portions of the structure are designed logically and in accordance with one another and with the leading idea of the building, then the finishing touches of expression and interest are given by well designed and effective ornamental detail. Here the designer may indulge his fancy as he pleases, as far as the nature of the design is concerned, but not, if you please, as far as its position and distribution are concerned. There the logic of architecture still pursues us.
We may not place ornament anywhere at haphazard on a building simply because it looks pretty. At least, to do so is to throw away great part of its value. For everything in architectural design is relative; it is to be considered in relation to the expression and design of the whole, and ornament is to be placed where it will emphasize certain points or certain features of the building. It must form a part of the grouping of the whole, and be all referable to a central and predominating idea. A building so planned, built, and decorated becomes, in fact, what all architecture—what every artistic design in fact should be—an organized whole, of which every part has its relation to the rest, and from which no feature can be removed without impairing the unity and consistency of the design. You may have a very good, even an expressive, building with no ornament at all if you like, but you may not have misplaced ornament. That is only an excrescence on the design, not an organic portion of it.
I have thought that it would be of use to those who are unacquainted with architectural procedure in delineating architecture by geometrical drawings if I took the opportunity of illustrating very briefly the philosophy of elevations, plans, and sections, which many non-professional people certainly do not understand.
Figs. 16 through 25A simple model of a building, like that in Fig. 16, will serve the purpose, as the principle is the same in the most complicated as in the simplest building. It must be remembered that the object of architectural drawings on the geometrical system is not to show a picture of the building, but to enable the designer to put together his design accurately in all its parts, according to scale, and to convey intelligible and precise information to those who have to erect the building. A perspective drawing like Fig. 16 is of no use for this purpose. It shows generally what the design is, but it is impossible to ascertain the size of any part by scale from it, except that if the length of one line were given it would be possible, by a long process of projection and calculation, to ascertain the other sizes. The rationale of the architect's geometrical drawings is that on them each plane of the building (the front, the side, the plan, etc.) is shown separately and without any distortion by perspective, and in such a manner that every portion is supposed to be opposite to the eye at once. Only the width of any object on one side can be shown in this way at one view; for the width of the return side you have to look to another drawing; you must compare the drawings in order to find out those relative proportions which the perspective view indicates to the eye at a glance; but each portion of each side can be measured by reference to a scale, and its precise size obtained, which can only be guessed at roughly from the perspective drawing. Thus the side of the model is shown in Fig. 19, the end in Fig. 17; the two together give the precise size and proportions of everything outside to scale, except the projection of the pilasters. This has to be got at from the plan and section. Everything being drawn on one plane, of course surfaces which are sloping on one elevation are represented as flat in the other. For instance, on No. 17 the raking line of the sloping roof is shown at N. So we know the slope of the roof, but we do not know to what length it extends the other way. This is shown on Fig. 19, where the portion showing the roof is also marked N, and it will be seen that the surface which is sloping in Fig. 17 is seen in the side elevation only as a space between a top and bottom line. We see the length of the roof here, and its height, but for its slope we go to the end elevation. Neither elevation tells us, however, what is inside the building; but the section (Fig. 18) shows us that it has an arched ceiling, and two stories, a lower and a higher one. The section is the building cut in half, showing the end of the walls, the height and depth of the window openings, the thickness of the floor, etc., and as all parts which are opposite the eye are shown in the drawing, the inside of the cross wall at the end of the building is shown as a part of the section drawing, between the sectional walls. In Fig. 23 the section is sketched in perspective, to show more clearly what it means. Another section is made lengthwise of the building (Fig. 20). It is customary to indicate on the plan by dotted lines the portion through which the section is supposed to be made. Thus on the plans the lines A B and C D are drawn, and the corresponding sections are labeled with the same lines. As with the elevation, one section must be compared with another to get the full information from them. Thus in Fig. 18, the ceiling, M, is shown as a semicircle; in Fig. 20, it is only a space between the top and bottom lines. It is, certainly, shaded here to give the effect of rotundity, but that is quite a superfluity. On Fig. 18 the height of the side windows is shown at F, and the thickness of the wall in which they are made. In Fig. 20 (F) their width and spacing are shown. In Fig. 18 some lines drawn across, one over the other, are shown at H. These are the stairs, of which in this section we see only the fronts, or risers, so that they appear merely as lines (showing the edge of each step) drawn one over the other. At H on the plan, Fig. 21, we again see them represented as a series of lines, but here we are looking down on the top of them, and see only the upper surfaces, or "treads," the edges again appearing as a series of lines. At H on the longitudinal section, we see the same steps in section, and consequently their actual slope, which, however, could have been calculated from Figs. 18 and 21, by putting the heights shown in section with the width shown in plan. The plan, Fig. 21, shows the thickness and position on the floor of the pillars, G G. Their height is shown in the sections. The plan of a building is merely a horizontal section, cutting off the top, and looking down on the sectional top of the walls, so as to see all their thicknesses. I have drawn (Fig. 24) a perspective sketch of one end of the plan (Fig. 22) of the building, on the same principle as was done with the section (Fig. 23), in order to show more intelligibly exactly what it is that a plan represents—the building with the upper part lifted off.
Returning for a moment to the subject of the relation between the plan and the exterior design, it should be noted that the plan of a building being practically the first consideration, and the basis of the whole design, the latter should be in accordance with the principle of disposition of the plan. For example, if we have an elevation (shown in diagram) showing two wings of similar design on either side of a center, designed so as to convey the idea of a grand gallery, with a suite of apartments on either side of similar importance—if the one side only of the plan contains such a suite, and the opposite side is in reality divided up into small and inferior rooms, filled in as well as may be behind the architectural design—the whole design is in that case only a blind or screen, giving a false exterior symmetry to a building which is not so planned. This is an extreme case (or might be called so if it were not actually of pretty frequent occurrence); but it illustrates in a broad sense a principle which must be carried out in all cases, if the architecture is to be a real expression of the facts of the building.
In this lecture, which is concerned with general principles, a word may fittingly be said as to the subject of proportion, concerning which there are many misapprehensions. The word may be, and is, used in two senses, first in regard to the general idea suggested in the words "a well proportioned building." This expression, often vaguely used, seems to signify a building in which the balance of parts is such as to produce an agreeable impression of completeness and repose. There is a curious kind of popular fallacy in regard to this subject, illustrated in the remark which used to be often made about St. Peter's, that it is so well proportioned that you are not aware of its great size, etc.—a criticism which has been slain over and over again, but continues to come to life again. The fact that this building does not show its size is true. But the inference drawn is the very reverse of the truth. One object in architectural design is to give full value to the size of a building, even to magnify its apparent size; and St. Peter's does not show its size, because it is ill proportioned, being merely like a smaller building, with all its parts magnified. Hence the deception to the eye, which sees details which it is accustomed to see on a smaller scale, and underrates their actual size, which is only to be ascertained by deliberate investigation. This confusion as to scale is a weakness inherent in the classical forms of columnar architecture, in which the scale of all the parts is always in the same proportion to each other and to the total size of the building so that a large Doric temple is in most respects only a small one magnified. In Gothic architecture the scale is the human figure, and a larger building is treated, not by magnifying its parts, but by multiplying them. Had this procedure been adopted in the case of St. Peter's, instead of merely treating it with a columnar order of vast size, with all its details magnified in proportion, we should not have the fault to find with it that it does not produce the effect of its real size. In another sense, the word "proportion" in architecture refers to the system of designing buildings on some definite geometrical system of regulating the sizes of the different parts. The Greeks certainly employed such a system, though there are not sufficient data for us to judge exactly on what principle it was worked out. In regard to the Parthenon, and some other Greek buildings, Mr. Watkiss Lloyd has worked out a very probable theory, which will be found stated in a paper in the "Transactions of the Institute of Architects."
Vitruvius gives elaborate directions for the proportioning of the size of all the details in the various orders; and though we may doubt whether his system is really a correct representation of the Greek one, we can have no doubt that some such system was employed by them. Various theorists have endeavored to show that the system has prevailed of proportioning the principal heights and widths of buildings in accordance with geometrical figures, triangles of various angles especially; and very probably this system has from time to time been applied, in Gothic as well as in classical buildings. This idea is open to two criticisms, however. First, the facts and measurements which have been adduced in support of it, especially in regard to Gothic buildings, are commonly found on investigation to be only approximately true. The diagram of the section of the building has nearly always, according to my experience, to be "coaxed" a little in order to fit the theory; or it is found that though the geometrical figure suggested corresponds exactly with some points on the plan or section, these are really of no more importance than other points which might just as well have been taken. The theorist draws our attention to those points in the building which correspond with his geometry, and leaves on one side those which do not. Now it may certainly be assumed that any builders intending to lay out a building on the basis of a geometrical figure would have done so with precise exactitude, and that they would have selected the most obviously important points of the plan or section for the geometrical spacing. In illustration of this point, I have given (Fig. 25) a skeleton diagram of a Roman arch, supposed to be set out on a geometrical figure. The center of the circle is on the intersection of lines connecting the outer projection of the main cornice with the perpendiculars from those points on the ground line. This point at the intersection is also the center of the circle of the archway itself. But the upper part of the imaginary circle beyond cuts the middle of the attic cornice. If the arch were to be regarded as set out in reference to this circle, it should certainly have given the most important line—the top line, of the upper cornice, not an inferior and less important line; and that is pretty much the case with all these proportion theories (except in regard to Greek Doric temples); they are right as to one or two points of the building, but break down when you attempt to apply them further. It is exceedingly probable that many of these apparent geometric coincidences really arise, quite naturally, from the employment of some fixed measure of division in setting out buildings. Thus, if an apartment of somewhere about 30 feet by 25 feet is to be set out, the builder employing a foot measure naturally sets out exactly 30 feet one way and 25 feet the other way. It is easier and simpler to do so than to take chance fractional measurements. Then comes your geometrical theorist, and observes that "the apartment is planned precisely in the proportion of six to five." So it is, but it is only the philosophy of the measuring-tape, after all. Secondly, it is a question whether the value of this geometrical basis is so great as has sometimes been argued, seeing that the results of it in most cases cannot be judged by the eye. If, for instance, the room we are in were nearly in the proportion of seven in length to five in width, I doubt whether any of us here could tell by looking at it whether it were truly so or not, or even, if it were a foot out one way or the other, in which direction the excess lay; and if this be the case, the advantage of such a geometrical basis must be rather imaginary than real.
Figs. 26 through 28Having spoken of plan as the basis of design, I should wish to conclude this lecture by suggesting also, what has never to my knowledge been prominently brought forward, that the plan itself, apart from any consideration of what we may build up upon it, is actually a form of artistic thought, of architectural poetry, so to speak. If we take three such plans as those shown in Figs. 26, 27, and 28, typical forms respectively of the Egyptian, Greek, and Gothic plans, we certainly can distinguish a special imaginative feeling or tendency in each of them. In the Egyptian, which I have called the type of "mystery," the plan continually diminishes as we proceed inward. In the third great compartment the columns are planted thick and close, so as to leave no possibility of seeing through the building except along a single avenue of columns at a time. The gloom and mystery of a deep forest are in it, and the plan finally ends, still lessening as it goes, in the small and presumably sacred compartment to which all this series of colonnaded halls leads up. In the Greek plan there is neither climax nor anti-climax, only the picturesque feature of an exterior colonnade encircling the building and surrounding a single oblong compartment. It is a rationalistic plan, aiming neither at mystery nor aspiration. In the plan of Rheims (Fig. 28) we have the plan of climax or aspiration; as in the Egyptian, we approach the sacred portion through a long avenue of piers; but instead of narrowing, the plan extends as we approach the shrine. I think it will be recognized, putting aside all considerations of the style of the superstructure on these plans, that each of them in itself represents a distinct artistic conception. So in the plan of the Pantheon (Fig. 29), this entrance through a colonnaded porch into a vast circular compartment is in itself a great architectural idea, independently of the manner in which it is built up.
Figs. 29 through 34We may carry out this a little further by imagining a varied treatment on plan of a marked-out space of a certain size and proportion, on which a church of some kind, for instance, is to be placed. The simplest idea is to inclose it round with four walls as a parallelogram (Fig. 30), only thickening the walls where the weight of the roof principals comes. But this is a plan without an idea in it. The central or sacred space at the end is not expressed in the plan, but is merely a railed-off portion of the floor. The entrance is utterly without effect as well as without shelter. If we lay out our plan as in Fig. 31, we see that there is now an idea in it. The two towers, as they must evidently be, form an advanced guard of the plan, the recessed central part connecting them gives an effective entrance to the interior; the arrangement in three aisles gives length, the apse at the end incloses and expresses the sacrarium, which is the climax and object of the plan. The shape of the ground, however, is not favorable to the employment of a long or avenue type of plan, it is too short and square; let us rather try a plan of the open area order, such as Fig 32. This is based on the short-armed Greek cross, with an open center area; again there is an "advanced guard" in the shape of an entrance block with a porch; and the three apses at the end give architectural emphasis to the sacrarium. Fig. 35 is another idea, the special object of which is to give an effect of contrast between the entrance, approached first through a colonnaded portico, then through an internal vestibule, lighted from above, and flanked by rows of small coupled columns; then through these colonnaded entrances, the inner one kept purposely rather dark, we come into an interior expanding in every direction; an effect of strong contrast and climax. If our plot of ground again be so situated that one angle of it is opposite the vista of two or more large streets, there and nowhere else will be the salient angle, so to speak, of the plan, and we can place there a circular porch—which may, it is evident, rise into a tower—and enter the interior at the angle instead of in the center; not an effective manner of entering as a rule, but quite legitimate when there is an obvious motive for it in the nature and position of the site. A new feature is here introduced in the circular colonnade dividing the interior into a central area and an aisle. Each of these plans might be susceptible of many different styles of architectural treatment; but quite independently of that, it will be recognized that each of them represents in itself a distinct idea or invention, a form of artistic arrangement of spaces, which is what "plan," in an architectural sense, really means.
Delivered before the Society of Arts, London, November 28, 1887. From the Journal of the Society.
The dark shaded portion in this and the next two diagrams show the "section" of the wall as seen if we cut it through and look at it endwise.
This is the feature called "abacus" (i.e., "tile") in Greek architecture, but I am here considering it apart from any special style or nomenclature.
"Bearing," in building language, is used in a double sense, for the distance between the points of support, and the extent to which the beam rests on the walls. Thus a beam which extends 20 feet between the points of support is a beam of 20 feet bearing. If the beam is 22 feet long, so that 1 foot rests on the walls at each end, it has "1 foot bearing on the wall."
None of the forms of column sketched here have any existence in reality. They are purposely kept apart from imitation of accepted forms to get rid of the idea that architecture consists in the acceptance of any particular form sanctioned by precedent.
This burner is in the form of a cylinder made of a composition in which magnesium predominates, and gives a light of 210 candle power with a consumption of three and one-half cubic feet of gas per hour.
The cylinder to be heated to incandescence is firmly held in place on a metal spindle, which is slowly revolved by means of an ingenious clock-work in the base of the fixture. The arrangement is such that by turning off the gas the clock-work is stopped, and by the turning on of the gas, it is again set in motion. The movement of the spindle is so slow that a casual observer would not notice it, there being only one revolution made in twenty-four hours. The object of this movement is to continually present new surface to be heated, as that which is exposed to the high temperature wears away, similarly to the carbons used in electric lighting, though much more slowly.
These burners can be made of 2,000 candle power, down to fifty candle power.
Pure oxygen can now be obtained from the atmosphere at a cost of about twenty-five cents per 1,000 cubic feet, and the small amount required to supplement the fuel water gas in producing this light can be supplied under proper pressure from a very small pipe, which can be laid in the same trench with the fuel gas pipe, at much less cost than is required to carry an electric wire to produce an equal amount of light.
The oxygen pipe necessary to carry the gas under pressure need not exceed an inch and a half in diameter to supply 5,000 lamps of 2,000 candle power each. The only reason why this burner has not been further perfected and placed upon the market is because of the continual preoccupation of Prof. Lowe in other lines of invention, and the amount of attention required by his large business interests. Besides, the field for its usefulness has been limited, as cheap fuel gas has only just begun to be generally introduced. Now, however, that extensive preparations are being made for the rapid introduction of the Lowe fuel gas system into various cities, this burner will receive sufficient attention to shortly complete it for general use in large quantities. It is a more powerful and at the same time a softer light than is the electric incandescent or the arc light. The light-giving property of a burner of 1,000 candle power would not cost more than one cent for ten hours' lighting, and the cylinder would only require to be changed once a week; whereas the carbons of arc lights are changed daily. The cost of the gas required to maintain such a lamp ten hours would be six cents, allowing the same profit on the gas as when it is sold for other heating purposes. The lamps complete will cost much less than the present electric lamps, and after allowing a large profit to companies supplying them, will not cost consumers more than one-fourth as much as arc lamps, and will give a much clearer and steadier light.
Since Prof. Lowe perfected his first incandescent burner great progress has been made in this line of invention, and it is no wonder that the attention of the whole gas fraternity of the country has been drawn to the subject of cheap fuel water gas, which is so admirably adapted to all purposes of heat, light, and power.
While there is no doubt that light can be more cheaply produced by incandescence obtained by the use of fuel water gas than by any other means, still a large amount of electric lighting will continue to hold its position, and the electric system will gain ground for many uses. But the electric light also can be more economically produced when fuel water gas is used as power to revolve the dynamos. Therefore, we believe it to be for the best interests of every gas company that would move in the line of progress to commence without delay to make preparations for the introduction of fuel water gas, if, at first, only as supplementary to their present illuminating gas business.-Progressive Age.
We are indebted to Prof. E.B. Cowgill, of Kansas, for a copy of his recent report to the Kansas State Board of Agriculture concerning the operations of the Parkinson Sugar Works, at Fort Scott, Kansas. The report contains an interesting historical sketch of the various efforts heretofore made to produce sugar from sorghum, none of which proved remunerative until 1887, when the persevering efforts of a few energetic individuals, encouraged and assisted by a small pecuniary aid from government, were crowned with success, and gave birth, it may justly be said, to a new industry which seems destined shortly to assume gigantic proportions and increase the wealth of the country.
We make the following abstracts from the report:
The sorghum plant was introduced into the United States in 1853-54, by the Patent Office, which then embraced all there was of the United States Department of Agriculture. Its juice was known to be sweetish, and chemists were not long in discovering that it contained a considerable percentage of some substance giving the reactions of cane sugar. The opinion that the reactions were due to cane sugar received repeated confirmations in the formation of true cane sugar crystals in sirups made from sorghum. Yet the small amounts that were crystallized, compared with the amounts present in the juices as shown by the analyses, led many to believe that the reactions were largely due to some other substance than cane sugar.
During the years 1878 to 1882, inclusive, while Dr. Peter Collier was chief chemist of the Department of Agriculture, much attention was given to the study of sorghum juices from canes cultivated in the gardens of the department at Washington. Dr. Collier became an enthusiastic believer in the future greatness of sorghum as a sugar producing plant, and the extensive series of analyses published by him attracted much attention.
As a result large sugar factories were erected and provided with costly appliances. Hon. John Bennyworth erected one of these at Larned, in Kansas. S.A. Liebold & Co. subsequently erected one at Great Bend.
Sterling and Hutchinson followed with factories which made considerable amounts of merchantable sugar at no profit.
The factory at Sterling was erected by R.M. Sandy & Co., of New Orleans, and while the sirup produced paid the expenses of the factory, not a crystal of sugar was made. The factory then, in 1883, changed hands, and passed under the superintendency of Prof. M.A. Scovell, then of Champaign, Illinois, who, with Prof. Webber, had worked out, in the laboratories of the Illinois Industrial University, a practical method for obtaining sugar from sorghum in quantities which at prices then prevalent would pay a profit on the business. But prices declined, and after making sugar for two years in succession, the Sterling factory succumbed.
The Hutchinson factory at first made no sugar, but subsequently passed under the management of Prof. M. Swenson, who had successfully made sugar in the laboratory of the University of Wisconsin. Large amounts of sugar were made at a loss, and the Hutchinson factory closed its doors. In 1884, Hon. W.L. Parkinson fitted up a complete sugar factory at Ottawa, and for two years made sugar at a loss. Mr. Parkinson was assisted during the first year by Dr. Wilcox, and during the second year by Prof. Swenson.
Much valuable information was developed by the experience in those several factories, but the most important of all was the fact that, with the best crushers, the average extraction did not exceed half of the sugar contained in the cane. It was known to scientists and well informed sugar makers in this country that the process of diffusion was theoretically efficient for the extraction of sugar from plant cells, and that it had been successfully applied by the beet sugar makers of Europe for this purpose.
In 1883, Prof. H.W. Wiley, chief chemist of the Department of Agriculture, made an exhaustive series of practical experiments in the laboratories of the department on the extraction of the sugars from sorghum by the diffusion process, by which the extraction of at least 85 per cent. of the total sugars present was secured.
The Kansas delegation in Congress became interested. Senator Plumb made a thorough study of the entire subject, and, with the foresight of statesmanship, gave his energies to the work of securing an appropriation of $50,000 for the development of the sugar industry, which was granted in 1884, and fifty thousand dollars more was added in 1885 to the agricultural appropriation bill. This was expended at Ottawa, Kansas, and in Louisiana.
In that year Judge Parkinson, at Fort Scott, organized the Parkinson Sugar Company. Taking up the work when all others had failed, this company has taken a full share of the responsibilities and losses, until it has at last seen the Northern sugar industry made a financial success.
The report of 1895 showed such favorable results that in 1886 the House made an appropriation of $90,000, to be used in Louisiana, New Jersey, and Kansas. A new battery and complete carbonatation apparatus were erected at Fort Scott. About $60,000 of the appropriation was expended here in experiments in diffusion and carbonatation.
Last year (1887) the Fort Scott management made careful selection of essential parts of the processes already used, omitted non-essential and cumbrous processes, availed themselves of all the experience of the past in this country, and secured a fresh infusion of experience from the beet sugar factories of Germany, and attained the success which finally places sorghum sugar making among the profitable industries of the country.
The success has been due, first, to the almost complete extraction of the sugars from the cane by the diffusion process; second, the prompt and proper treatment of the juice in defecating and evaporating; third, the efficient manner in which the sugar was boiled to grain in the strike pan.
| Total number tons of | cane bought | 3,840 |
| " | seed tops bought | 437 |
| ——— | ||
| Total number tons of field cane | 4,277 | |
There was something over 500 acres planted. Some of it failed to come at all, some "fell upon the rocky places, where they had not much earth, and when the sun was risen they were scorched;" so that, as nearly as we can estimate, about 450 acres of cane were actually harvested and delivered at the works. This would make the average yield of cane 9½ tons per acre, or $19 per acre in dollars and cents.
TOTAL PRODUCT OF THE SEASON, 1887.
| Sugar, | 235,826 lb., @ 5¾c | $13,559 98 | |
| " | State bounty, @ 2c | 4,716 53 | |
| ———— | $17,276 50 | ||
| Sirups, | 51,000 gals,(estimated) @ 20c. | 10,200 00 | |
| Seed (estimated) | 7,000 00 | ||
| Value of total product | $34,476 50 | ||
TOTAL COST.
| Cane, 3,840 tons,@ $2 | $7,680 | |
| Seed, 967 tons, @ $3 | 1,934 | |
| ——— | $9,614 00 | |
| Labor bill from August 15 to October 15, including labor for department experiments | 5,737 16 | |
| Coal, including all experiments | 1,395 77 | |
| Salaries, etc. | 3,500 00 | |
| Insurance, sundries, etc. | 1,500 00 | |
| ———— | ||
| Total | $21,746 93 | |
| ========== | ||
| Total value | $34,476 50 | |
| Total cost | 31,248 93 | |
| ———— | ||
| Net | $13,329 57 | |
| To be paid by the department | 6,534 75 | |
| ———— | ||
| Total profit for season's work, 1887 | $19,764 32 | |
As now developed, the processes of making sugar from sorghum are as follows:
First, The topped cane is delivered at the factory by the farmers who can grow it.
Second, The cane is cut by a machine into pieces about one and a quarter inches long.
Third, The leaves and sheaths are separated from the cut cane by fanning mills.
Fourth, The cleaned cane is cut into fine bits called chips.
Fifth, The chips are placed in iron tanks, and the sugar "diffused," soaked out with hot water.
Sixth, The juice obtained by diffusion has its acids nearly or quite neutralized with milk of lime, and is heated and skimmed.
Seventh, The defecated or clarified juice is boiled to a semi-sirup in vacuum pans.
Eighth, The semi-sirup is boiled "to grain" in a high vacuum in the "strike pan."
Ninth, The mixture of sugar and molasses from the strike pan is passed through a mixing machine into centrifugal machines which throw out the molasses and retain the sugar.
The process of the formation of sugar in the cane is not fully determined, but analyses of canes made at different stages of growth show that the sap of growing cane contains a soluble substance having a composition and giving reactions similar to starch. As maturity approaches, grape sugar is also found in the juice. A further advance toward maturity discloses cane sugar with the other substances, and at full maturity perfect canes contain much cane sugar and little grape sugar and starchy matter.
In sweet fruits the change from grape sugar to cane sugar does not take place, or takes place but sparingly. The grape sugar is very sweet, however.
Cane sugar, called also sucrose or crystallizable sugar, when in dilute solution is changed very readily into grape sugar or glucose, a substance which is much more difficult than cane sugar to crystallize. This change, called inversion, takes place in over-ripe canes. It sets in very soon after cutting in any cane during warm weather; it occurs in cane which has been injured by blowing down, or by insects, or by frost, and it probably occurs in cane which takes a second growth after nearly or quite reaching maturity.
To insure a successful outcome from the operations of the factory, the cane must be so planted, cultivated and matured as to make the sugar in its juice. It must be delivered to the factory very soon after cutting, and it must be taken care of before the season of heavy frosts.
The operations of the factory are illustrated in the large diagram. The first cutting is accomplished in the ensilage or feed cutter at E. This cutter is provided with three knives fastened to the three spokes of a cast iron wheel which makes about 250 revolutions per minute, carrying the knives with a shearing motion past a dead knife. By a forced feed the cane is so fed as to be cut into pieces about one and a quarter inches long. This cutting frees the leaves and nearly the entire sheaths from the pieces of cane. By a suitable elevator, F, the pieces of cane, leaves and sheaths are carried to the second floor.
The elevator empties into a hopper, below which a series of four or five fans, G, is arranged one below the other. By passing down through these fans the cane is separated from the lighter leaves, much as grain is separated from chaff. The leaves are blown away, and finally taken from the building by an exhaust fan. This separation of the leaves and other refuse is essential to the success of the sugar making, for in them the largest part of the coloring and other deleterious matters are contained. If carried into the diffusion battery, these matters are extracted (see reports of Chemical Division, U.S. Department of Agriculture), and go into the juice with the sugar. As already stated, the process of manufacturing sugar is essentially one of separation. The mechanical elimination of these deleterious substances at the outset at once obviates the necessity of separating them later and by more difficult methods, and relieves the juice of their harmful influences. From the fans the pieces of cane are delivered by a screw carrier to an elevator which discharges into the final cutting machine on the third floor. This machine consists of an eight inch cast iron cylinder, with knives like those of a planing machine. It is really three cylinders placed end to end in the same shaft, making the entire length eighteen inches. The knives are inserted in slots and held in place with set screws. The cylinder revolves at the rate of about twelve hundred per minute, carrying the knives past an iron dead knife, which is set so close that no cane can pass without being cut into fine chips. From this cutter the chips of cane are taken by an elevator and a conveyer, K, to cells, MM, of the diffusion battery. The conveyer passes above and at one side of the battery, and is provided with an opening and a spout opposite each cell of the battery. The openings are closed at pleasure by a slide. A movable spout completes the connection with any cell which it is desired to fill with chips.
The condition in which the sugars and other soluble substances exist in the cane is that of solution in water. The sweetish liquid is contained, like the juices of plants generally, in cells. The walls of these cells are porous. It has long been known that if a solution of sugar in water be placed in a porous or membraneous sack, and the sack placed on water, an action called osmosis, whereby the water from the outside and the sugar solution from the inside of the sack each pass through, until the liquids on the two sides of the membrane are equally sweet. Other substances soluble in water behave similarly, but sugar and other readily crystallizable substances pass through much more readily than uncrystallizable or difficultly crystallizable. To apply this properly to the extraction of sugar, the cane is first cut into fine chips, as already described, and put into the diffusion cells, where water is applied and the sugar is displaced.
as used at the Parkinson factory, consists of twelve iron tanks. (See diagram.) They are arranged in a line, as shown in diagram, Fig. 1. Each has a capacity of seventy-five cubic feet, and by a little packing holds a ton of cane chips. The cells are supported by brackets near the middle, which rest on iron joists. Each cell is provided with a heater, through which the liquid is passed in the operation of the battery. The cells are so connected by pipes and valves that the liquid can be passed into the cells, and from cell to cell, at the pleasure of the operator. The bottom of each cell consists of a door, which closes on an annular rubber hose placed in a groove, and filled with water, under a pressure greater than that ever given to the liquids in the cell. This makes a water tight joint whenever the trap door bottom is drawn up firmly against it. The upper part is of cast iron and is jug shaped, and is covered with a lid which is held with a screw on rubber packing. In the jug neck and near the bottom the sides are double, the inner plates being perforated with small holes to let water in and out. The bottoms are double, the inner plates being perforated like the neighboring sides, and for the same purpose. The cells, of whose appearance a fair idea may be had from diagram, Fig. 2, are connected with a water pipe, a juice pipe, a compressed air pipe, and the heaters, by suitable valves. The heaters are connected with a steam pipe. This, and the compressed air pipe, are not shown in the diagram. The water pipe is fed from an elevated tank, which gives a pressure of twelve pounds per square inch The valve connections enable the operator to pass water into the cells at either the top or the bottom; to pass the liquid from any cell to the next, or to the juice pipe through the heater; to separate any cell from any or all others, and to turn in compressed air.
Now let the reader refer to Fig. 2.
Fig. 2—DIFFUSION PROCESS—MANUFACTURE OF SORGHUM
SUGAR.The cutters are started, and cell 1 is filled with chips. This done, the chips from the cutters are turned into cell 2; cell 1 is closed, and cut off from the others, and water is turned into it by opening valve, c, of cell 1 (see Fig. 2) until it is filled with water among the chips. When 2 is filled with chips, its valve, a, is raised to allow the liquid to pass down into the juice pipe. Valve a of 3 is also raised. Now the juice pipe fills, and when it is full the liquid flows through valve, a, of 3, and into the heater between 2 and 3, and into the bottom of 2, until 2 is full of water among the chips. (This may be understood by following the course of the arrows shown in the diagrams of 9 and 10). Valve a of 2 is now screwed down; c is down and b is opened. It will be readily seen by attention to the diagram that this changes the course of the flow so that it will no longer enter at the bottom, but at the top of 2, as shown by the arrows at cell 2.
It is to be observed that the water is continually pressing in at the top of 1, and driving the liquid forward whenever a valve is opened to admit it to another cell, heater, or pipe. When cell 3 is full of chips, its valves are manipulated just as were those of 2. So as each succeeding cell is filled, the manipulation of valves is repeated until cell 6 is filled with liquid. After passing through six cells of fresh chips, this liquid is very sweet, and is drawn off into the measuring tank shown at p in diagram, Fig. 1, and is thence conveyed for subsequent treatment in the factory. To draw this juice from 6, valve a of 7 is raised to connect the heater between 6 and 7 with the juice pipe. A gate valve in the juice pipe is opened into the measuring tank, and the pressure of water into the top of 1 drives the liquid forward through the bottom of 1, through the heater, into the top of 2, out from the bottom of 2, through the heater into the top of 3, out from the bottom of 3, through the heater into the top of 4, out from the bottom of 4, through the heater, into the top of 5, out from the bottom of 5, through the heater, into the top of 6, and now out from the bottom of 6, through the heater, into the juice pipe, and from the juice pipe into the measuring tank. It will be understood that the liquid which is drawn from 6 is chiefly that which was passed into 1 when it was filled with chips. There is doubtless a little mixing as the pressure drives the liquid forward. But the lighter liquid is always pressed in at the top of the cells, so that the mixing is the least possible. The amount of liquid, now called juice, which is drawn from 6 is 1,110 liters, or 291 gallons. When this quantity has been drawn into the measuring tank, the gate valve is closed, and the valves connecting with 7 are manipulated as were those of 6, a measure of juice being drawn in the same way. All this time the water has been passed into the top of 1, and this is continued until the juice has been drawn from 9. Valve c to cell 1 is now closed, and compressed air is turned into the top of 1 to drive the liquid forward into 10. After the water has thus been nearly all expelled from 1, valve a of cell 2 is lowered so as to shut off communication with the juice pipe, and b, of cell 2 is closed. a and b of cell 1 have, it will be observed, been closed or down from the beginning. Cell 1 is now isolated from all others. Its chips have been exhausted of sugar, and are ready to be thrown out. The bottom of 1 is opened, and the chips fall out into the car, o (see diagram, Fig. 1), and are conveyed away. Immediately on closing valves a and b of cell 2, c is opened, and the water presses into the top of 2, as before into the top of 1, and the circulation is precisely similar to that already described, 2 having taken the place of 1, 3 of 2, and so on.
When 2 is emptied, 3 takes the first place in the series and so on. When 12 has been filled, it takes the l3th place. (The juice pipe returns from the termination of the series, and connects with 1, making the circuit complete.) The process is continuous, and the best and most economical results are obtained if there is no intermission.
One cell should be filled and another emptied every eight minutes, so that in twenty-four hours the number of cells diffused should be one hundred and eighty.
For the purpose of illustration, let us assume that when it has been filled with chips just as much water is passed into the cell as there was juice in the chips. The process of osmosis or diffusion sets in, and in a few minutes there is as much sugar in the liquid outside of the cane cells as in the juice in these cane cells; i.e., the water and the juice have divided the sugar between them, each taking half.
Again, assume that as much liquid can be drawn from 1 as there was water added. It is plain that if the osmotic action is complete, the liquid drawn off will be half as sweet as cane juice. It has now reached fresh chips in 2, and again equalization takes place. Half of the sugar from 1 was brought into 2, so that it now contains one and a half portions of sugar, dissolved in two portions of liquid, or the liquid has risen to three quarters of the strength of cane juice. This liquid having three fourths strength passes to 3, and we have in 3 one and three fourths portions of liquid, or after the action has taken place the liquid in 3 is seven eighths strength. One portion of this liquid passes to 4, and we have one and seven eighths portions of sugar in two portions of liquid, or the liquid becomes 15/16 strength. One portion of this liquid passes to 5, and we have in 5 one and fifteen sixteenths portions of sugar in two portions of liquid, or the liquid is 31/32 strength. It is now called juice. From this time forward a cell is emptied for every one filled.
Throughout the operation, the temperature is kept as near the boiling point as can be done conveniently without danger of filling some of the cells with steam. Diffusion takes place more rapidly at high than at low temperatures, and the danger of fermentation, with the consequent loss of sugar, is avoided.
By the first action of water in 1, ½ of the sugar was left in cell 1; by the second ¼ was left, by the third 1/8 was left, by the fourth 1/16 was left, by the fifth 1/32 was left, by the sixth 1/64 was left, by the seventh 1/128 was left, by the eighth 1/256 was left, by the ninth 1/512 was left. The fractions representing the strength of the juice on the one hand and the sugar left in each cell on the other hand, after the battery is fully in operation, are not so readily deduced. The theory is easily understood, however, although the computation is somewhat intricate. Those who desire to follow the process by mathematical formula are referred to pages 9 and 10, Bulletin No. 2, Chemical Division U.S. Department of Agriculture, where will be found the formula furnished by Professor Harkness, of the U.S. Naval Observatory.
For the sake of simplifying the explanation, it was assumed that the water added is equal in volume to the juice in a cellful of cane chips. In practice more water is added, to secure more perfect exhaustion of the chips, and with the result of yielding about thirteen volumes of juice for every nine volumes as it exists in the cane, and of extracting 92.04 per cent. of all the sugars from the cane, as shown by the report of Dr. C.A. Crampton, Assistant Chemist of the U.S. Department of Agriculture.
In the experiments at Fort Scott in 1886, much difficulty was experienced on account of inversion of the sugar in the diffusion battery. The report shows that this resulted from the use of soured cane and from delays in the operation of the battery on account of the imperfect working of the cutting and elevating machinery, much of which was there experimental. Under the circumstances, however, it became a matter of the gravest importance to find a method of preventing this inversion without in any manner interfering with the other processes. On the suggestion of Prof. Swenson, a portion of freshly precipitated carbonate of lime was placed with the chips in each cell.1 In the case of soured cane, this took up the acid which otherwise produced inversion. In case no harmful acids were present, this chalk was entirely inactive. Soured canes are not desirable to work under any circumstances, and should be rejected by the chemist, and not allowed to enter the factory. So, also, delays on account of imperfect machinery are disastrous to profitable manufacturing, and must be avoided. But for those who desired to experiment with deteriorated canes and untried cutting machines, the addition of the calcium carbonate provides against disastrous results which would otherwise be inevitable.
Immediately after it is drawn from the diffusion battery the juice is taken from the measuring tanks into the defecating tanks or pans. These are large, deep vessels, provided with copper steam coils in the bottom for the purpose of heating the juice. Sufficient milk of lime is added here to nearly or quite neutralize the acids in the juice, the test being made with litmus paper. The juice is brought to the boiling point, and as much of the scum is removed as can be taken quickly. The scum is returned to the diffusion cells, and the juice is sent by a pump to the top of the building, where it is boiled and thoroughly skimmed. These skimmings are also returned to the diffusion cells.
This method of disposing of the skimmings was suggested by Mr. Parkinson. It is better than the old plan of throwing them away to decompose and create a stench about the factory. Probably a better method would be to pass these skimmings through some sort of filter, or, perhaps better still, to filter the juice and avoid all skimming. After this last skimming the juice is ready to be boiled down to a thin sirup in
These consist of two large closed pans provided within with steam pipes of copper, whereby the liquid is heated. They are also connected with each other and with pumps in such a way as to reduce the pressure in the first to about three fifths and in the second to about one fifth the normal atmospheric pressure.
The juice boils rapidly in the first at somewhat below the temperature of boiling water, and in the second at a still lower temperature. The exhaust steam from the engines is used for heating the first pan, and the vapor from the boiling juice in the first pan is hot enough to do all the boiling in the second, and is taken into the copper pipes of the second for this purpose. In this way the evaporation is effected without so great expenditure of fuel as is necessary in open pans, or in single effect vacuum pans, and the deleterious influences of long continued high temperature on the crystallizing powers of the sugar are avoided.
From the double effects the sirup is stored in tanks ready to be taken into the strike pan, where the sugar is crystallized.
At this point the juice has just reached a condition in which it will keep. From the moment the cane is cut in the fields until now, every delay is liable to entail loss of sugar by inversion. After the water is put into the cells of the battery with the chips, the temperature is carefully kept above that at which fermentation takes place most readily, and the danger of inversion is thereby reduced. But with all the precautions known to science up to this point the utmost celerity is necessary to secure the best results. There is here, however, a natural division in the process of sugar making, which will be further considered under the heading of "Auxiliary Factories." Any part of the process heretofore described may be learned in a few days by workmen of intelligence and observation who will give careful attention to their respective duties.
This operation is the next in course, and is performed in what is known at the sugar factory as the strike pan, a large air tight iron vessel from which the air and vapor are almost exhausted by means of a suitable pump and condensing apparatus. As is the case with the saccharine juices of other plants, the sugar from sorghum crystallizes best at medium temperature.
The process of boiling to grain may be described as follows: A portion of the sirup is taken into the pan, and boiled rapidly in vacuo to the crystallizing density. If in a sirup the molecules of sugar are brought sufficiently near to each other through concentration—the removal of the dissolving liquid—these molecules attract each other so strongly as to overcome the separating power of the solvent, and they unite to form crystals. Sugar is much more soluble at high than at low temperatures, the heat acting in this as in almost all cases as a repulsive force among the molecules. It is therefore necessary to maintain a high vacuum in order to boil at a low temperature, in boiling to grain. When the proper density is reached the crystals sometimes fail to appear, and a fresh portion of cold sirup is allowed to enter the pan. This must not be sufficient in amount to reduce the density of the contents of the pan below that at which crystallization may take place. This cold sirup causes a sudden though slight reduction in temperature, which may so reduce the repulsive forces as to allow the attraction among the molecules to prevail, resulting in the inception of crystallization. To discover this requires the keenest observation. When beginning to form, the crystals are too minute to show either form or size, even when viewed through a strong magnifying glass. There is to be seen simply a very delicate cloud. The inexperienced observer would entirely overlook this cloud, his attention probably being directed to some curious globular and annular objects, which I have nowhere seen explained. Very soon after the sample from the pan is placed upon glass for observation, the surface becomes cooled and somewhat hardened. As the cooling proceeds below the surface, contraction ensues, and consequently a wrinkling of the surface, causing a shimmer of the light in a very attractive manner. This, too, is likely to attract more attention than the delicate, thin cloud of crystals, and may be even confounded with the reflection and refraction of light, by which alone the minute crystals are determined. The practical operator learns to disregard all other attractions, and to look for the cloud and its peculiarities. When the contents of the pan have again reached the proper density, another portion of sirup is added. The sugar which this contains is attracted to the crystals already formed, and goes to enlarge these rather than to form new crystals, provided the first are sufficiently numerous to receive the sugar as rapidly as it can crystallize.
The contents of the pan are repeatedly brought to the proper density, and fresh sirup added as above described until the desired size of grain is obtained, or until the pan is full. Good management should bring about these two conditions at the same time. If a sufficient number of crystals has not been started at the beginning of the operation to receive the sugar from the sirup added, a fresh crop of crystals will be started at such time as the crystallization becomes too rapid to be accommodated on the surfaces of the grain already formed. The older and larger crystals grow more rapidly, by reason of their greater attractive force, than the newer and smaller ones on succeeding additions of sirup, so that the disparity in size will increase as the work proceeds. This condition is by all means to be avoided, since it entails serious difficulties on the process of separating the sugar from the molasses. In case this second crop of crystals, called "false grain" or "mush sugar" has appeared, the sugar boiler must act upon his judgment, guided by his experience as to what is to be done. He may take enough thin sirup into the pan to dissolve all of the crystals and begin again, or, if very skillful, he may so force the growth of the false grain as to bring it up to a size that can be worked.
The completion of the work in the strike pan leaves the sugar mixed with molasses. This mixture is called malada or masscuite. It may be drawn off into iron sugar wagons and set in the hot room above mentioned, in which case still more of the sugar which remains in the uncrystallized state generally joins the crystals, somewhat increasing the yield of "first sugars." At the proper time these sugar wagons are emptied into a mixing machine, where the mass is brought to a uniform consistency. If the sugar wagons are not used, the strike pan is emptied directly into the mixer.
From the mixer the melada is drawn into the centrifugal machines. These consist, first, of an iron case resembling in form the husk of mill stones. A spout at the bottom of the husk connects with a molasses tank. Within this husk is placed a metallic vessel with perforated sides. This vessel is either mounted or hung on a vertical axis, and is lined with wire cloth. Having taken a proper portion of the melada into the centrifugal, the operator starts it to revolving, and by means of a friction clutch makes such connection with the engine as gives it about 1,500 revolutions per minute. The centrifugal force developed drives the liquid molasses through the meshes of the wire cloth, and out against the husk, from which it flows off into a tank. The sugar, being solid, is retained by the wire cloth. If there is in the melada the "false grain" already mentioned, it passes into the meshes of the wire cloth, and prevents the passage of the molasses. After the molasses has been nearly all thrown out, a small quantity of water is sprayed over the sugar while the centrifugal is in motion. This is forced through the sugar, and carries with it much of the molasses which would otherwise adhere to the sugar, and discolor it. If the sugar is to be refined, this washing with water is omitted. When the sugar has been sufficiently dried, the machine is stopped, the sugar taken out, and put into barrels for market.
Simple as the operation of the centrifugals is, the direction of the sugar boiler as to the special treatment of each strike is necessary, since he, better than any one else, knows what difficulties are to be expected on account of the condition in which the melada left the strike pan.
A plant having a battery like that at Fort Scott, in which the cells are each capable of containing a ton of cane chips, should have a capacity of 180 tons of cleaned cane, or 200 tons of cane with leaves, or 240 tons of cane as it grows in the field, per day of twenty-four hours. Those who have given most attention to the subject think that a battery composed of one and a half ton cells may be operated quite as successfully as a battery of one ton cells. Such a battery would have a capacity of 360 tons of field cane per day.
This consists of modifications of appliances which have long been used. Simple as it is, and presenting only mechanical problems, the cutting, cleaning, and evaporating apparatus is likely to be the source of more delays and perplexities in the operation of the sugar factory than any other part.
The diffusion battery in good hands works perfectly; the clarification of the juice causes no delays; the concentration to the condition of semi-sirup may be readily, rapidly, and surely effected in apparatus which has been brought to great perfection by long experience, and in many forms; the work at the strike pan requires only to be placed in the hands of an expert; the mixer never fails to do its duty; there are various forms of centrifugal machines on the market, some of which are nearly perfect. If, then, the mechanical work of delivering, cutting, cleaning, and elevating the cane can be accomplished with regularity and rapidity, the operation of a well adjusted sugar factory should proceed without interruption or delay from Monday morning to Saturday night.
An acre of land cultivated in sorghum yields a greater tonnage of valuable products than in any other crop, with the possible exception of hay. Under ordinary methods of cultivation, ten tons of cleaned cane per acre is somewhat above the average, but under the best cultivation the larger varieties often exceed twelve, while the small early amber sometimes goes below eight tons per acre. Let seven and a half tons of cleaned cane per acre be assumed for the illustration. This corresponds to a gross yield of ten tons for the farmer, and at two dollars per ton gives him twenty dollars per acre for his crop. These seven and a half tons of clean cane will yield:
750 pounds of sugar.
1,000 pounds of molasses.
900 pounds of seed.
1,500 pounds of fodder (green leaves).
1,500 pounds of exhausted chips (dried). A total of 5,650 pounds.
The first three items, which are as likely to be transported as wheat or corn, aggregate 2,650 pounds per acre.
Sorghum will yield seven and a half tons of cleaned cane per acre more surely than corn will yield thirty bushels or wheat fifteen bushels per acre.
In the comparison, then, of products which bear transportation, these crops stand as follows:
Sorghum, at 7½ tons, 2,650 pounds per acre.
Corn, at 30 bushels, 1,680 pounds per acre.
Wheat, at 15 bushels, 900 pounds per acre.
The sugar from the sorghum is worth say 5 cents per pound; the molasses, 1¾ cents per pound; the seed, ½ cent per pound.
The sorghum products give market values as follows:
750 pounds sugar at say 5 cents,2 $37.50.
1,000 pounds molasses at say 1¾ cents,2 $17.50.
900 pounds seed at say ½ cent,2 $4.50.
Total value of sorghum, less fodder, $59.50.
The corn crop gives 1,680 pounds, at ½ cent $8.40.
The wheat crop gives 900 pounds, at 1 cent, $9.
Thus it will be seen that the sorghum yields to the farmer more than twice as much per acre as either of the leading cereals, and as a gross product of agriculture and manufacture on our own soil more than six times as much per acre as is usually realized from either of these standard crops.
For this improvement Prof. Swenson obtained a patent Oct. 11, 1887, the grant of which was recently made the subject of congressional inquiry.
The sugar sold this year at 5¾ cents per pound, the molasses at 20 cents per gallon, and the seed at —— per bushel of 56 pounds. The seed is of about equal value with corn for feeding stock.
A new process for producing iron and steel direct from the ore has been brought out in Russia. Under the new process iron ore, after being submitted to the smelting processes, is taken direct from the furnace to the rolling mill and turned into thin sheets of the finest charcoal iron. At present the process has only been commercially applied with charcoal fuel, but experiments are stated to have shown that equal success can be obtained with coke. The secret of the process lies in the construction of the furnace, which is said to be simple and inexpensive.
We have received from M. Menges (of the Hague) a most interesting description of an apparatus on which he has been at work for some time past, with the object of generating electricity by the direct conversion of heat, or, as it might be more accurately described, by a more direct conversion than that of an ordinary dynamo. M. Menges' apparatus depends, like that of Edison, upon the fact that the magnetic metals lose their magnetic permeability at a certain temperature.
It differs greatly, however, from its predecessor in important points, especially in the fact that it does not require the aid of any external source of motive power.
In Edison's pyromagnetic dynamo it will be remembered that it is necessary to provide some small amount of motive power from an extraneous source in order to revolve the shield by which the heat is alternately directed on one half or the other of the armature cores. M. Menges' apparatus is, on the contrary, wholly automatic.
We proceed to give a free translation of the description furnished us by the inventor.
In attempting to employ the thermo-magnetic properties of iron or nickel in the construction of machines for the generation of electricity upon an industrial scale, we are met with the difficulty that the heating and cooling of large masses of metal not only involves great loss of heat, but also requires much time. Hence, to obtain a useful effect of any importance, it would appear necessary to employ machines of dimensions altogether impracticable. By the device and method of construction now to be explained this difficulty has, however, been completely overcome.
The action of a magnetic pole diminishes so rapidly with the increase of distance that it may suffice to remove the armature to a distance relatively small compared with its own dimensions, or with those of the magnet, in order to reduce the action to a negligible value. But if the magnet, N S, and the armature, A, being at a certain distance, we bring between them a piece of iron or nickel, d, then the magnetic force upon A is immediately and very considerably increased. In modern language, the resistance of the magnetic circuit has been reduced by the introduction of a better magnetic conductor, and the number of lines of force passing through A is proportionately increased. The mass of the piece, d, may, moreover, be relatively small compared with that of N S and A. If d be again withdrawn, the magnetic resistance is increased, and the lines through A are again a minimum.
Now, it is evident that we can also obtain the same effect by sufficiently heating and cooling the intermediate piece, d; and again, with a broad field we can alter the distribution of the lines at will by heating or cooling one side of this piece or the other. For this reason we will call the piece d the thermo-magnetic distributor, or, briefly, the distributor.
We will now describe the manner in which this principle has been realized in the practical construction of both a thermo-magnetic generator and motor.
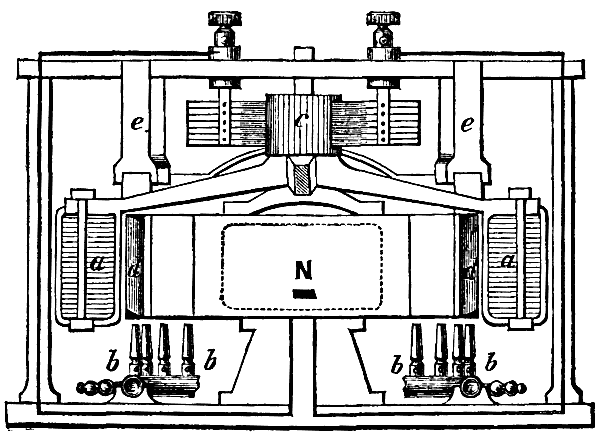Fig. 1.Fig. 1 shows an elevation and part section of one of the arrangements employed. Fig. 2 is a plan of the same machine (in the latter the ring, a a, appearing on a higher plane than it actually occupies).
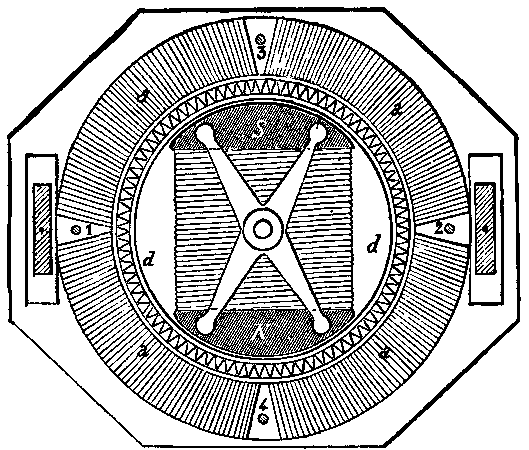Fig. 2.N S is an electro-magnet, a a the armature, wound as a Gramme ring, and fixed to a frame with four arms, which can turn freely upon a pivot midway between the poles. The cross arms of the frame are attached at 1, 2, 3, 4, Fig. 2. Between the magnets and the armature is placed the distributor, d d, where it occupies an annular space open above and below. Both the magnets and the armature are coated on the sides facing the distributor with mica or some other non-conductor of heat and electricity. The distributor is attached to and supported by the cross arms, so that it turns with the armature.
The distributor is composed of a ribbon of iron or nickel, bent into a continuous zigzag. This form has the advantage of presenting, in the cool part of the distributor, an almost direct road for the lines of force between the poles and the armature, thus diminishing the magnetic resistance as far as possible. At the same time the Foucault currents are minimized. To the same end it is useful to slit the ribbon, as in Fig. 3. This also facilitates the folding into zigzags.
Fig. 3.The distributor is heated at two opposite points on a diameter by the burners, b b, above which are the chimneys, e e. The cooling of the alternate section is aided by the circulation of cold air, which is effected by means of the draught in the chimneys, e e. At the points of lowest temperature a jet of air or water is maintained. The cross arms are insulated with mica or asbestos at the points where they extend from the armature to the distributor.
It will now be evident that while the distributor is entirely cool, many of the lines of force pass from N to S without entering the armature core; but if heat is applied at the points 1 and 2 in the figure, so as to increase the magnetic resistance at these points, then a great portion of the lines will leave the distributor, and pass through the armature core. Under these conditions, so long as heat is applied at two points equidistant from N and S, we might, if we so pleased, cause the armature to be rotated by an external source of power, and we should then have an E.M.F. generated in the armature coils—that is to say, the machine would work as an ordinary dynamo, and the power expended in driving the armature would be proportionate to the output.
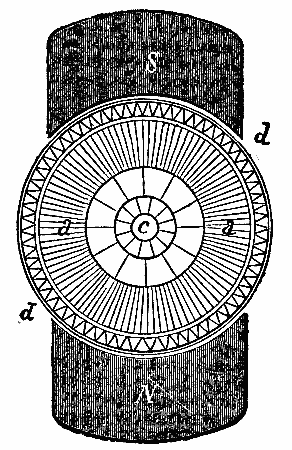Fig. 4.Suppose next that the points of heating, and with them the alternate points of cooling 90 deg. apart, are shifted round about 45 deg., so that the two hot regions are no longer symmetrically situated in respect to each pole of the field. The distribution of the magnetization has therefore become unsymmetrical, and the iron core is no longer in equilibrium in the magnetic field. We have, in fact, the conditions of Schwedoff's experiment upon a larger scale, and if the forces are sufficient to overcome the frictional resistance, a rotation of the ring ensues in the endeavor to restore equilibrium. The regions of heating and cooling being fixed in space, this rotation is continuous so long as the difference of temperature is maintained. The ring in rotating carries with it the armature coils, and of course an E.M.F. is generated in the same way as if the motive power came from an external source. In this respect the machine therefore resembles a motor generator, and the rotation is entirely automatic.
The armature coils are connected with a commutator in the usual way, and the field may, of course, be excited either in shunt or in series. M. Menges says that the residual magnetization is sufficient in his machine to start the rotation by itself.
When the machine is to be used as a motor, it is evident that the windings on the armature core need only be sufficient to supply current to excite the field, or by the use of permanent magnets they may be dispensed with altogether.
M. Menges has further designed a large number of variations on the original type, varying the arrangement of the several parts, and employing armatures and fields of many different types, such as are already in use for dynamos.
In Fig. 4 a machine is represented in which the field is external to the armature.
In Fig. 5 we have a thermo-magnetic generator, which corresponds to the disk machine in dynamos. Similar parts are indicated by the same letters in each of these figures, so that no further detailed description is necessary.
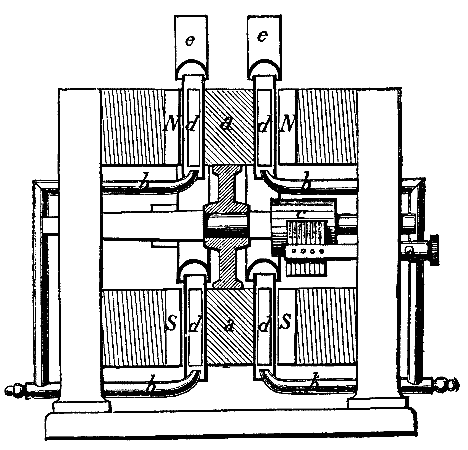Fig. 5.In another modification M. Menges proposes to rotate the burners and leave the armature and distributor at rest. But in this case it is evident that the E.M.F. produced would be much less, because the magnetization of the core would only undergo a variation of intensity, and would nowhere be reversed, except, perhaps, just in front of the poles. In machines modeled on the Brush type it is evident that the distributor need not be continuous.
Enough has, however, been said to indicate the extent of the field upon which the principle may be applied.—The Electrician.
I will try to give a short report of some experiments I have made during the last year in regard to atmospheric electricity. It was formerly uncertain whether the electrostatic potential would increase by rising from the surface of the earth to more elevated region of the atmosphere or not, and also whether the potential in a normal—that is, cloudless—state of the atmosphere was always positive or sometimes negative. Sir William Thomson found by exact methods of measuring that the increase of the potential with elevation is very important, and values about 100 volts per meter. That fact is proved by many other observers, especially lately by Mr. F. Exner, at Vienna, who found an increase of 60 to 600 volts per meter. The observations were made by means of an electrometer. In respect of many inconveniences which are connected with the use of an electrometer, I have tried the measurements with a very sensitive galvanometer. In this case it is necessary to apply a separating air exhaust apparatus, for example flame, or a system of points at the upper end of the conductor, which is elevated in the atmosphere. In order to get a constant apparatus, I have used 400 of the finest needles inserted in a metallic ribbon. This system I have raised in the air by means of a captive balloon, or by a kite, which was attached to a conductor of twine or to a twisted line of the finest steel wire. In this way I have attained a height of 100 to 300 meters. When the lower end of the kite line was communicating with the galvanometer whose other terminal was in contact with the earth, a current passed through the galvanometer. For determining the strength of this current I proposed to called a micro-ampere the 10-9 part of an ampere. At the height of about 100 meters in the average the current begins to be regular, and increases at the height of 300 meters to 4,000 or 5,000 of these units. The increase is very regular, and seems to be a linear function of the height. I have, nevertheless, found the smallest quantities of dust contained in the atmosphere or the lightest veil of cirrus disturbed the measurement very materially, and generally made the potential lower. In negative experiments of this nature I have made at Breslau, at the Sohneekoppe, and at the "Reisengebirge," especially at the last station, an increase of potential was observed, not only by reason of the perpendicular height, but also by reaching such regions of the atmosphere as were situated horizontally to about 200 meters from the utmost steep of the same mountain, Sohneekoppe. Therefore it must, according to Mr. Exner, be assumed that the surface of the air presents a surface of equal potential, and that the falling surfaces of high potential were stretched parallel over the plane contours of the air, and more thinly or narrow lying over all the elevated points, as, for example, mountains, church towers, etc. On the basis of these facts I think it easy to explain the electricity of thunder storm clouds, in fact every cloud, or every part of a cloud, may be considered as a leading conductor, such clouds as have for the most part perpendicular height. After being induced the change results by supposing the conduction of electricity either from the upper or from the lower side, according to greater or smaller speed of the air in the height. In the first case the clouds will be charged positive, in the other negative. I am inclined, therefore, to state that the electricity of thunder storm clouds must be considered as a special but disturbed case of the normal electric state of the atmosphere, and that all attempts to explain thunder storm electricity must be based on the study of the normal electric state of the atmosphere.
Abstract of a paper read before the British Association meeting at Manchester, September, 1887.
At intervals in the history of science, long periods of comparative inertia have attended the death of its more distinguished workers. As time progresses and the number of workers increases, there is a corresponding increase in the number of men whose labors merit distinction in the literature of every language; but as these accessions necessitate in most cases further division of the honors, many names conspicuously identified with modern science fail of their just relative rank, and fade into unmerited obscurity. Thus the earlier workers in science, like Scheele, Liebig, Humboldt, and others of that and later periods, have won imperishable fame, to which we all delight to pay homage, while others of more recent times, whose contributions have perhaps been equally valuable for their respective periods, are given stinted recognition of their services, if indeed their names are not quite forgotten. Nothing illustrates so clearly the steps in the evolution of science as a review of the relative status of its representatives. As in the political history of the world an epoch like that of the French revolution stands out like a mountain peak, so in the history of science an epoch occurs rather by evolution than revolution, when a hitherto chaotic, heterogeneous mass of knowledge is rapidly given shape and systematized. Previous to the seventeenth century an immense mass of facts had accumulated through the labors of investigators working under the Baconian philosophy, but these facts had been thrown together in a confused, unsystematic manner. A man of master mind was then needed to grasp the wonders of nature and formulate the existing knowledge of them into a scientific system with a natural basis. Such a system was given by Linnæus, and so great were its merits that it continues the foundation of all existing systems of classification.
Charles Linnæus was born May 13, 1707, in a country place named Roshult in Smaland, near Skane, Sweden. He was called Charles after the well known Swedish knight errant, King Charles XII., then at the height of his renown.
The natural beauty of his native place, with its verdure-clad hills, its stately trees, and sparkling brooks fringed with mosses and flowers, inspired the boy Linnæus with a love of nature and a devotion to her teachings which tinged the current of his whole life. He was destined by his parents for the ministry, and in accordance with their wish was sent to the Vexio Academy ("gymnasium"). Here the dull theological studies interfered so much with his study of nature that he would have felt lost but for the sympathy of Dr. Rothman, one of his teachers, a graduate of Harderwyk University, Holland, who had been a pupil of Boerhaave (the most eminent physician and scientist of his day), and been much impressed by his scientific teachings.
Dr. Rothman took a great interest in Linnæus, and assured his father that he would prove a great success financially and otherwise as a physician (an occupation whose duties then included a study of all existing sciences). The father was satisfied, but dreaded the effect the announcement of such a career would have on the mother, whose ambition had been to see her son's name among the long list of clergymen of the family who had been ministers to the neighboring church of Stentrohult. She finally yielded, and the best possible use was made by Linnæus of Dr. Rothman's tuition. Latin, then the mother tongue of all scientists and scholars, he wrote and spoke fluently.
At the age of twenty Linnæus entered the University of Lund, and remained there a year. Here he formed the acquaintance of a medical man, a teacher in the university, who opened his home and his library to him, and took him on his botanical excursions and professional visits. Some time later, on Dr. Rothman's advice, Linnæus entered the University of Upsala, then the most celebrated university of Northern Europe. His parents were able to spare him but one hundred silver thalers for his expenses. At the end of a year his money was spent, his clothing and shoes were worn out, and he was without prospects of obtaining a scholarship. When things were at their gloomiest he accidentally entered into a discussion with a stranger in the botanical garden, who turned out to be a clergyman scientist named Celsius. Celsius, while staying at Upsala, had conceived the plan of given a botanical description of biblical plants. Having learned that Linnæus had a herbarium of 600 plants, he took the young man under his protection, and opened up to him his home and library.
While studying in this library, his observations regarding the sexes in plants, hitherto in a chaotic state, took form, stimulated by an abstract published in a German journal of Vaillant's views, and before the end of 1729 the basis of the sexual system had appeared in manuscript. This treatise having been seen by a member of the university faculty, Linnæus was invited to fill a temporary vacancy, and lectured with great success therein one and a half years. Meanwhile the foundation of the celebrated treatises afterward published on the sexual system of classification and on plant nomenclature had been laid.
As in the history of most great men, a seemingly great misfortune proved to be a turning point in his career. The position he had temporarily filled with such credit to himself and profit to the students was claimed by its regular occupant, and, despite the opposition of the faculty, Linnæus had to relinquish it. The two subsequent years were spent in botanical investigations under the patronage of various eminent men. During one of these he traveled through Lapland to the shores of the Polar Sea, and the results of this expedition were embodied in his "Lapland Flora," the first flora founded on the sexual system. He delivered a peripatetic course of lectures, and during one of these he formed the acquaintance of Dr. Moræus, a pupil of the great Boerhaave. Dr. Moræus took Linnæus into partnership with him. Here again a seeming misfortune proved to be a great advantage. Linnæus fell in love with the eldest daughter of Dr. Moræus, but was denied her hand until he should graduate in medicine. Linnæus, to complete his studies as a physician, then entered the University of Harderwyk, Holland, the alma mater of his first benefactor, Dr. Rothman, and of the great Boerhaave.
After two years' study he was graduated in medicine with high honors. His thesis, "The Cause of Chills," received special commendation. He visited all the botanical gardens and other scientific institutions for which Holland was then renowned. A learned and wealthy burgomaster, Gronovius, having read his "Systema Naturæ" in manuscript, not only defrayed the cost of its publication, but secured him the high honor of an interview with the great Boerhaave—an honor for which even the Czar Peter the Great had to beg.
Boerhaave's interest was at once awakened, and he gave Linnæus so strong a recommendation to Dr. Burman, of Amsterdam, that the influence of the scientific circles of the Dutch metropolis was exerted in behalf of Linnæus, and he was soon offered the position of physician superintendent of a magnificent botanical garden owned by a millionaire horticultural enthusiast, Clifford, a director of the Dutch East India Company. Linnæus' financial and scientific future was now secure. Publication of his works was insured, and his position afforded him every opportunity for botanical research. After five years' residence in Holland, during which he declined several positions of trust, he determined to return to Sweden. His fame had become so widespread in Western Europe that his system was already adopted by scientists and made the basis of lectures at the Dutch universities. In the French metropolis he was greatly esteemed, and during a visit thereto he was a highly distinguished guest.
ROSHULT, SWEDEN, BIRTHPLACE OF LINNÆUS.His reception in Sweden was rather frigid, and but for the hearty welcome by his family and betrothed he would probably have returned to Holland. His amour propre was also doubtless wounded, and he determined to remain and fight his way into the magic circle of the gilt-edged aristocracy which then monopolized all scientific honors in Stockholm and the universities. He acquired a great reputation for the treatment of lung disease, and was popularly credited with the ability to cure consumption. This reached the ears of the queen (a sufferer from the disease), who directed one of her councilors to send for Linnæus. He soon recognized the name of Linnæus as one of great renown on the Continent, and at once took him under his protection.
The star of Linnæus was now in the ascendant. He was soon delegated to various pleasant duties, among which was the delivery of lectures on botany and mineralogy in the "auditorium illustre" at Stockholm. He at this time founded the "Swedish Scientific Academy," and was its first president. In 1741 he was elected professor of medicine in Upsala University, which chair he exchanged for that of botany and the position of director of the botanical garden. This opened up a new era for science in Sweden. He who was regarded as the world's greatest botanist abroad had at last been similarly acknowledged in his native land.
With the indomitable courage and tact characteristic of the man, he set on foot a gigantic scientific popular educational project. The government, under his direction, established a system of exploring expeditions into the fauna, flora, and mineralogy of the whole Swedish peninsula, partly for the purpose of developing the resources of the country, partly in the interest of science, but more especially to interest the mass of the people in scientific research. The vast majority of the people of Sweden, like those of other countries, were dominated by fetichic superstitions and absurd notions about plants and vegetables, which were indorsed to a certain extent by popular handbooks devoted more to the dissemination of marvels than facts. A popular clergyman, for instance, stated in a description of the maritime provinces that "certain ducks grew upon trees." The vast stride which was made by the populace in the knowledge of nature was due to these efforts of Linnæus, who, in order to further popularize science, established and edited, in conjunction with Salvius, a journal devoted to the discussion of natural history.
During this period, on the first of May, semi-weekly excursions were made from the university, the public being invited to attend. The people came to these excursions by hundreds, and all classes were represented in them—physicians, apothecaries, preachers, merchants, and mechanics, all joined the procession, which left the university at seven in the morning, to return at eve laden with zoological, botanical, and mineralogical specimens.
A man who could thus arouse popular enthusiasm for science a century and a half ago must have been a remarkable genius. Trusted students of Linnæus were sent on botanical exploring expeditions throughout the world. The high renown in which Linnæus was held was shown in the significant title, almost universally bestowed upon him, of "The Flower King."—Western Druggist.
For the illustrations and many facts in the life of Linnæus we are indebted to the Illustrated Tidning, Stockholm.
The first actual attempt to make the wave length of sodium light a standard of length was made by Peirce.1 This method involves two distinct measurements: first, that of the angular displacement of the image of a slit by a diffraction grating, and, second, that of the distance between the lines of the grating. Both of these are subject to errors due to changes of temperature and to instrumental errors. The results of this work have not as yet been published; but it is not probable that the degree of accuracy attained is much greater than one part in fifty or a hundred thousand. More recently, Mr. Bell, of the Johns Hopkins University, using Rowland's gratings, has made a determination of the length of the wave of sodium light which is claimed to be accurate to one two hundred thousandth part2. If this claim is justified, it is probably very near the limit of accuracy of which the method admits. A short time before this, another method was proposed by Mace de Lepinay.3 This consists in the calculation of the number of wave lengths between two surfaces of a cube of quartz. Besides the spectroscopic observations of Talbot's fringes, the method involves the measurement of the index of refraction and of the density of quartz, and it is not surprising that the degree of accuracy attained was only one in fifty thousand.
Several years ago, a method suggested itself which seemed likely to furnish results much more accurate than either of the foregoing, and some preliminary experiments made in June have confirmed the anticipation. The apparatus for observing the interference phenomena is the same as that used in the experiments on the relative motion of the earth and the luminiferous ether.
Light from the source at s (Fig. 1), a sodium flame, falls on the plane parallel glass, a, and is divided, part going to the plane mirror, c, and part to the plane mirror, b. These two pencils are returned along cae and bae, and the interference of the two is observed in the telescope at e. If the distances, ac and ab, are made equal, the plane, c, made parallel with that of the image of b, and the compensating glass, d, interposed, the interference is at once seen. If the adjustment be exact, the whole field will be dark, since one pencil experiences external reflection and the other internal.
If now b be moved parallel with itself a measured distance by means of the micrometer screw, the number of alternations of light and darkness is exactly twice the number of wave lengths in the measured distance. Thus the determination consists absolutely of a measurement of a length and the counting of a number.
The degree of accuracy depends on the number of wave lengths which it is possible to count. Fizeau was unable to observe interference when the difference of path amounted to 50,000 wave lengths. It seemed probable that with a smaller density of sodium vapor this number might be increased, and the experiment was tried with metallic sodium in an exhausted tube provided with aluminum electrodes. It was found possible to increase this number to more than 200,000. Now it is very easy to estimate tenths or even twentieths of a wave length, which implies that it is possible to find the number of wave lengths in a given fixed distance between two planes with an error less than one part in two millions and probably one in ten millions. But the distance corresponding to 400,000 wave lengths is roughly a decimeter, and this cannot be determined or reproduced more accurately than say to one part in 500,000. So it would be necessary to increase this distance. This can be done by using the same instrument together with a comparer.
The intermediate standard decimeter, lm (Fig. 2), is put in place of the mirror, b. It consists of a prism of glass one decimeter long with one end, l, plane, and the other slightly convex, so that when it touches the plane, m, Newton's rings appear, and these serve to control any change in the distance, lm, which has been previously determined in wave lengths.
The end, l, is now adjusted so that colored fringes appear in white light. These can be measured to within one-twentieth of a wave length, and probably to within one-fiftieth. The piece, lm, is then moved forward till the fringes again appear at m. Then the refractometer is moved in the same direction till the fringes appear again at l, and so on till the whole meter has been stepped off. Supposing that in this operation the error in the setting of the fringes is always in the same direction, the whole error in stepping off the meter would be one part in two millions. By repetition this could of course be reduced. A microscope rigidly attached to the carriage holding the piece, lm, would serve to compare, and a diamond attached to the same piece would be used to produce copies. All measurements would be made with the apparatus surrounded by melting ice, so that no temperature corrections would be required.
Probably there would be considerable difficulty in actually counting 400,000 wave lengths, but this can be avoided by first counting the wave lengths and fractions in a length of one millimeter and using this to step off a centimeter. This will give the nearest whole number of wave-lengths, and the fractions may be observed directly. The centimeter is then used in the same way to step off a decimeter, which again determines the nearest whole number, the fraction being observed directly as before.
The fractions are determined as follows: The fringes observed in the refractometer under the conditions above mentioned can readily be shown to be concentric circles. The center has the minimum intensity when the difference in the distances, ab, ac, is an exact number of wave lengths. The diameters of the consecutive circles vary as the square roots of the corresponding number of waves. Therefore, if x is the fraction of a wave length to be determined, and y the diameter of the first dark ring, d being the diameter of the ring corresponding to one wave length, then x = y2/d2.
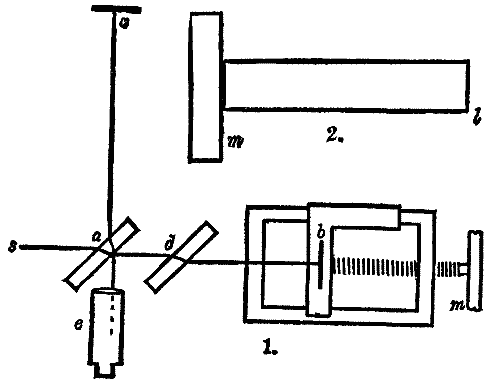
There is a slight difficulty to be noted in consequence of the fact that there are two series of waves in sodium light. The result of this superposition of these is that as the difference of path increases, the interference becomes less distinct and finally disappears, reappears, and has a maximum of distinctness again, when the difference of path is an exact multiple of both wave lengths. Thus there is an alternation of distinct interference fringes with uniform illumination. If the length to be measured, the centimeter for instance, is such that the interference does not fall exactly at the maximum—to one side by, say, one-tenth the distance between two maxima, there would be an error of one-twentieth of a wave length requiring an arithmetical correction.
Among other substances tried in the preliminary experiments were thallium, lithium, and hydrogen. All of these gave interference up to fifty to one hundred thousand wave lengths, and could therefore all be used as checks on the determination with sodium. It may be noted that in case of the red hydrogen line, the interference phenomena disappeared at about 15,000 wave lengths, and again at about 45,000 wave lengths; so that the red hydrogen line must be a double line with the components about one-sixtieth as distant as the sodium lines.—Amer. Jour. Science.
Nature, xx, 99, 1879; this Journal, III, xviii, 51, 1879.
On the absolute wave lengths of light, this Journal, III, xxxiii, 167, 1887.
Comptes Rendus, cii, 1153, 1886; Journal, de Phys., II, v, 411, 1886.
[RURAL NEW YORKER]
Upon this subject I am able to speak with the freedom habitually enjoyed by some voluminous agricultural writers—my imagination will not be hampered by my knowledge.
In debatable climates, like Ohio, Illinois, Kansas and southward, it is conceded that a great point would be gained by the discovery of some plan—not too expensive—that would make it safe to put away potatoes in the summer, as soon as ripe, so that they would go through the winter without sprouting and preserve their eating qualities till potatoes come again. As it is, digging must be deferred till late, for fear of rot; the fields of early varieties grow up with weeds after they are "laid by." In the spring a long interregnum is left between old potatoes fit to eat and the new crop, and the seed stock of the country loses much of its vigor through sprouting in cellars and pits. Most farmers have had occasion to notice the difference between the yield from crisp, unsprouted seed potatoes and that from the wilted, sprouted tubers so often used. Some years ago Professor Beal made a test of this difference. I speak from recollection, but think I am right in saying that, according to the published account which I saw, he found one sprouting of seed potatoes lowered the yield 10 per cent.; each additional sprouting still further reduced the crop, till finally there was no yield at all. Even a 10 per cent. shrinkage in all that portion of the annual potato crop grown from sprouted seed would result in an aggregate loss of millions of bushels. The question how to store potatoes and not have them sprout I have seen answered in the papers by recommending a "cold" cellar, of about 40 degrees temperature. If there are cellars that are cold in warm weather, without the use of some artificial process, I have not seen them. The temperature of well water is about 45 degrees only, and anybody knows how much colder a well is than a cellar. But the greatest difficulty comes in from the fact that potatoes are such a prolific source of heat in themselves.
If a 40 degree cellar could be found and be filled with potatoes, the temperature would at once begin to rise, and the later in the season, the faster it would go up. I repeat that a cellar filled with potatoes will have a much higher temperature than the same cellar would have if empty. This I have learned as Nimbus learned tobacco growing—"by 'sposure." I hope I won't be asked "why." I don't know. The reason is unimportant. The remedy is the thing. The only help for it that I know of is to give the cellar plenty of ventilation, put the potatoes in as clean as possible, and then shovel them over every month or two. This will keep the sprouting tendency in check very largely; but it won't make it practicable to begin storing potatoes in July or cause them to keep in good flavor till June.
Several years ago I placed some barrels of early Ohio potatoes in the Kansas City cold storage warehouses from March till July. They were kept in a temperature of 38 degrees, and came out crisp and very little sprouted. The plan of this structure was very simple: a three-story brick building so lined with matched lumber and tarred paper as to make three air-spaces around the wall. In the top story was a great bulk of ice, which was freely accessible to the air that, when cooled, passed through ducts to the different "cool rooms." The results were satisfactory, but the system seemed too expensive for potatoes. I have wondered whether it was necessary for potatoes to be kept as cold as 38 degrees. Would not a current of air passing through pipes showered with well water keep them cold enough? Wine vaults, I believe, are sometimes cooled by air currents forced through a cold water spray. If the air blast of well water temperature would be sufficient, the apparatus for producing it would be comparatively inexpensive—or at least much cheaper than those plans of cold storage where ice is stored in quantity over the cool room. However, any process that could be devised would probably be unprofitable to the small cropper, and the larger the business done, the less the cost per bushel. If it should be found that individual operators could not reach such an improvement on a profitable scale, why could not several of them pool their issues sufficiently to build, jointly, a potato elevator? There are at least 50,000 bushels of potatoes held in store by farmers within three miles of where I live. It seems to me there would be many advantages and economies in having that large stock under one roof, one insurance, one management; on a side track where they could be loaded in any weather or state of the roads, besides the great item that the temperature could be controlled, by artificial means, in one large building much cheaper than in several small ones.
EDWIN TAYLOR.
Edwardsville, Kans.
[KNOWLEDGE.]
The figure illustrating this article is taken from L'Astronomie, and represents the remarkable southern comet of January, 1887, as drawn on successive days by Mr. Finlay, of Cape Town.
The comet was first seen by a farmer and a fisherman of Blauwberg, near Cape Town, on the night of January 18-19. The same night it was seen at the Cordoba Observatory by M. Thome. On the next Mr. Todd discovered it independently at the Adelaide Observatory, and watched it till the 27th. On the 22d Mr. Finlay detected the comet, and was able to watch it till the 29th. At Rio de Janeiro M. Cruls observed it from the 23d to the 25th; and at Windsor, New South Wales, Mr. Tebbutt observed the comet on the 28th and 30th. Moonlight interfered with further observations.
The comet's appearance was remarkable. Its tail, long and straight, extended over an arc of 30 degrees, but there was no appreciable condensation which could be called the comet's head. The long train of light, described as nearly equal in brightness to the Magellanic clouds, seemed to be simply cut off at that end where in most comets a nucleus and coma are shown.
This comet has helped to throw light on one of the most perplexing puzzles which those most perplexing of all the heavenly bodies, comets, have presented to astronomers.
In the year 1668 a comet was seen in the southern skies which attracted very little notice at the time, and would probably have been little thought of since had not attention been directed to it by the appearance and behavior of certain comets seen during the last half century. Visible for about three weeks, and discovered after it had already passed the point of its nearest approach to the sun, the comet of 1668 was not observed so satisfactorily that its orbit could be precisely determined. In fact, two entirely different orbits would satisfy the observations fairly, though one only could be regarded as satisfying them well.
This orbit, however, was so remarkable that astronomers were led to prefer the other, less satisfactory though it was, in explaining the observed motions of the comet. For the orbit which best explained the comet's movements carried the comet so close to the sun as actually to graze his visible surface.
Moreover, there was this remarkable, and, indeed, absolutely unique peculiarity about the orbit thus assigned: the comet (whose period of revolution was to be measured by hundreds of years) actually passed through the whole of that part of its course during which it was north of our earth's orbit plane in less than two hours and a half! though this part of its course is a half circuit around the sun, so far as direction (not distance of travel) is concerned. That comet, when at its nearest to the sun, was traveling at the rate of about 330 miles per second. It passed through regions near the sun's surface commonly supposed to be occupied by atmospheric matter.
Now, had the comet been so far checked in its swift rush through those regions as to lose one thousandth part of its velocity, it would have returned in less than a year. But the way in which the comet retreated showed that nothing of this sort was to be expected. I am not aware, indeed, that any anticipations were ever suggested in regard to the return of the comet of 1668 to our neighborhood. It was not till the time of Halley's comet, 1682, that modern astronomy began to consider the question of the possibly periodic character of cometic motions with attention. (For my own part, I reject as altogether improbable the statement of Seneca that the ancient Chaldean astronomers could calculate the return of comets.) The comet of 1680, called Newton's, was the very first whose orbital motions were dealt with on the principles of Newtonian astronomy, and Halley's was the first whose periodic character was recognized.
In 1843 another comet came up from the south, and presently returned thither. It was, indeed, only seen during its return, having, like the comet of 1668, been only discovered a day or two after perihelion passage. Astronomers soon began to notice a curious resemblance between the orbits of the two comets. Remembering the comparative roughness of the observations made in 1668, it may be said that the two comets moved in the same orbit, so far as could be judged from observation. The comet of 1843 came along a path inclined at apparently the same angle to the earth's orbit plane, crossed that plane ascendingly at appreciably the same point, swept round in about two hours and a half that part of its angular circuit which lay north of the earth's orbit plane, and, crossing that plane descendingly at the same point as the comet of 1668, passed along appreciably the same course toward the southern stellar regions! The close resemblance of two paths, each so strikingly remarkable in itself, could not well be regarded as a mere accidental coincidence.
The Constellations, though unnamed, can readily be
identified, when it is noted that the Comet's course, as here
represented, began in the constellation of the Crane.
However, at that time no very special attention was directed to the resemblance between the paths of the comets of 1843 and 1668. It was not regarded as anything very new or striking that a comet should return after making a wide excursion round the sun; and those who noticed that the two comets really had traversed appreciably the same path around the immediate neighborhood of the sun, simply concluded that the comet of 1668 had come back in 1843, after 175 years, and not necessarily for the first time.
It must be noticed, however, before leaving this part of the record, that the comet of 1843 was suspected of behaving in a rather strange way when near the sun. For the first observation, made rather roughly, indeed, with a sextant, by a man who had no idea of the interest his observation might afterward have, could not be reconciled by mathematicians (including the well-known mathematician, Benjamin Pierce) with the movement of the comet as subsequently observed. It seemed as though when in the sun's neighborhood the comet had undergone some disturbance, possibly internal, which had in slight degree affected its subsequent career.
According to some calculations, the comet of 1843 seemed to have a period of about thirty-five years, which accorded well with the idea that it was the comet of 1668, returned after five circuits. Nor was it deemed at all surprising that the comet, conspicuous though it is, had not been detected in 1713, 1748, 1783, and 1818, for its path would carry it where it would be very apt to escape notice except in the southern hemisphere, and even there it might quite readily be missed. The appearance of the comet of 1668 corresponded well with that of the comet of 1843. Each was remarkable for its extremely long tail and for the comparative insignificance of its head. In the northern skies, indeed, the comet of 1843 showed a very straight tail, and it is usually depicted in that way, whereas the comet of 1668 had a tail showing curvature. But pictures of the comet of 1843, as seen in the southern hemisphere, show it with a curved tail, and also the tail appeared forked toward the end during that part of the comet's career.
However, the best observations, and the calculations based on them, seemed to show that the period of the comet of 1843 could not be less than 500 years.
Astronomers were rather startled, therefore, when, in 1880, a comet appeared in the southern skies which traversed appreciably the same course as the comets of 1668 and 1843. When I was in Australia, in 1880, a few months after the great comet had passed out of view, I met several persons who had seen both the comet of that year and the comet of 1843. They all agreed in saying that the resemblance between the two comets was very close. Like the comet of 1843, that of 1880 had a singularly long tail, and both comets were remarkable for the smallness and dimness of their heads. One observer told me that at times the head of the comet of 1880 could barely be discerned.
Like the comets of 1668 and 1843, the comet of 1880 grazed close past the sun's surface. Like them, it was but about two hours and a half north of the earth's orbit place. Had it only resembled the other two in these remarkable characteristics, the coincidence would have been remarkable. But of course the real evidence by which the association between the comets was shown was of a more decisive kind. It was not in general character only, but in details, that the path of the comet of 1880 resembled those on which the other two comets had traveled. Its path had almost exactly the same slant to the earth's orbit plane as theirs, crossed that plane ascendingly and descendingly at almost exactly the same points, and made its nearest approach to the sun at very nearly the same place. To the astronomer such evidence is decisive. Mr. Hind, the superintendent of the "Nautical Almanac," and as sound and cautious a student of cometic astronomy as any man living, remarked, so soon as the resemblance of these comets' paths had been ascertained, that if it were merely accidental, the case was most unusual; nay, it might be described as unique. And, be it noticed, he was referring only to the resemblance between the comets of 1880 and 1843. Had he recalled at the time the comet of 1668, and its closely similar orbit, he would have admitted that the double coincidence could not possibly be merely casual.
But this was by no means the end of the matter. Indeed, thus far, although the circumstances were striking, there was nothing to prevent astronomers from interpreting them as other cases of coincident, or nearly coincident, cometic paths had been interpreted. Hind and others, myself included, inferred that the comets of 1880, 1843, and 1668 were simply one and the same comet, whose return in 1880 probably followed the return in 1843 after a single revolution.
In 1882, however, two years and a half after the appearance of the comet of 1880, another comet came up from the south, which followed in the sun's neighborhood almost the same course as the comets of 1668, 1843, and 1880. The path it followed was not quite so close to those followed by the other three as these had been to each other, but yet was far too close to indicate possibly a mere casual resemblance; on the contrary, the resemblance in regard to shape, slope, and those peculiarities which render this family of comets unique in the cometary system, was of the closest and most striking kind.
Many will remember the startling ideas which were suggested, by Professor Piazzi Smyth respecting the portentous significance of the comet of 1882. He regarded it as confirming the great pyramid's teaching (according to the views of orthodox pyramidalists) respecting the approaching end of the Christian dispensation. It was seen under very remarkable circumstances, blazing close by the sun, within a fortnight or three weeks of the precise date which had been announced as marking that critical epoch in the history of the earth.
Moreover, even viewing the matter from a scientific standpoint, Professor Smyth (who, outside his pyramidal paradoxes, is an astronomer of well deserved repute) could recognize sufficient reason for regarding the comet as portentous.
Many others, indeed, both in America and in Europe, shared his opinion in this respect. A very slight retardation of the course of the comet of 1880, during its passage close by the surface of the sun, would have sufficed to alter its period of revolution from the thirty-seven years assigned on the supposition of its identity with the comet of 1843 to the two and a half years indicated by its apparent return in 1882, and if this had occurred in 1880, a similar interruption in 1832 would have caused its return in less than two and a half years.
Thus, circling in an ever narrowing (or rather shortening) orbit, it would presently, within a quarter of a century or so perhaps, have become so far entangled among the atmospheric matter around the sun that it would have been unable to resist absolute absorption. What the consequences to the solar system might have been, none ventured to suggest. Newton had expressed his belief that the effects of such absorption would be disastrous, but the physicists of the nineteenth century, better acquainted with the laws associating heat and motion, were not so despondent. Only Professor Smyth seems to have felt assured (not being despondent, but confident) that the comet portended, in a very decisive way, the beginning of the end.
However, we were all mistaken. The comet of 1882 retreated on such a course, and with such variation of velocity, as to show that its real period must be measured, not by months, as had been supposed, nor even by years, but by centuries. Probably it will not return till 600 or 700 years have passed. Had this not been proved, we might have been not a little perplexed by the return of apparently the same comet in this present year. A comet was discovered in the south early in January, whose course, dealt with by Professor Kruger, one of the most zealous of our comet calculators, is found to be partially identical with that of the four remarkable comets we have been considering. Astronomers have not been moved by this new visitant on the well-worn track as we were by the arrival of the comet of 1882, or as we should have been if either the comet of 1882 had never been seen or its path had not been shown to be so wide ranging. Whatever the comet of the present year may be, it was not the comet of 1882 returned. No one even supposes that it was the comet of 1880, or 1843, or 1668. Nevertheless, rightly apprehended, the appearance of a comet traveling on appreciably the same track as those four other comets is of extreme interest, and indeed practically decisive as to the interpretation we must place on these repeated coincidences.
Observe, we are absolutely certain that the five comets are associated together in some way; but we are as absolutely certain that they are not one and the same comet which had traveled along the same track and returned after a certain number of circuits. We need not trouble ourselves with the question whether two or more of the comets may not have been in reality one and the same body at different returns. It suffices that they all five were not one; since we deduce precisely the same conclusion whether we regard the five as in reality but four or three or two. But it may be mentioned in passing as appearing altogether more probable, when all the evidence is considered, that there were no fewer than five distinct comets, all traveling on what was practically the selfsame track when in the neighborhood of the sun.
There can be but one interpretation of this remarkable fact—a fact really proved, be it noticed (as I and others have maintained since the retreat of the comet of 1882), independently of the evidence supplied by the great southern comet of the present year. These comets must all originally have been one comet, though now they are distinct bodies. For there is no reasonable way (indeed, no possible way) of imagining the separate formation of two or more comets at different times which should thereafter travel in the same path.
No theory of the origin of comets ever suggested, none even which can be imagined, could account for such a peculiarity. Whereas, on the other hand, we have direct evidence showing how a comet, originally single, may be transformed into two or more comets traveling on the same, or nearly the same, track.
The comet called Biela's, which had circuited as a single comet up to the year 1846 (during a period of unknown duration in the past—probably during millions of years), divided then into two, and has since broken up into so many parts that each cometic fragment is separately undiscernible. The two comets into which Biela's divided, in 1846, were watched long enough to show that had their separate existence continued (visibly), they would have been found, in the fullness of time, traveling at distances very far apart, though on nearly the same orbit. The distance between them, which in 1846 had increased only to about a quarter of a million of miles, had in 1852 increased to five times that space.
Probably a few thousands of years would have sufficed to set these comets so far apart (owing to some slight difference of velocity, initiated at the moment of their separation) that when one would have been at its nearest to the sun, the other would have been at its farthest from him. If we could now discern the separate fragments of the comet, we should doubtless recognize a process in progress by which, in the course of many centuries, the separate cometic bodies will be disseminated all round the common orbit. We know, further, that already such a process has been at work on portions removed from the comet many centuries ago, for as our earth passes through the track of this comet she encounters millions of meteoric bodies which are traveling in the comet's orbit, and once formed part of the substance of a comet doubtless much more distinguished in appearance than Biela's.
There can be little doubt that this is the true explanation of the origin of that family of comets, five of whose members returned to the neighborhood of the sun (possibly their parent) in the years 1668, 1843, 1880, 1882, and 1887.1
But it is not merely as thus explaining what had been a most perplexing problem that I have dealt with the evidence supplied by the practical identity of these five comets' orbits. When once we recognize that this, and this only, can be the explanation of the associated group of five comets, we perceive that very interesting and important light has been thrown on the subject of comets generally. To begin with: what an amazing comet that must have been from which these five, and we know not how many more, were formed by disaggregative processes—probably by the divellent action of repulsive forces exerted by the sun! Those who remember the comets of 1843 and 1882 as they appeared when at their full splendor will be able to imagine how noble an appearance a comet would present which was formed of these combined together in one. But the comet of 1880 was described by all who saw it in the southern hemisphere as most remarkable in appearance, despite the faintness of its head. The great southern comet of the present year was a striking object in the skies, though it showed the same weakness about the head. That of 1668 was probably as remarkable in appearance as even the comet of 1882. A comet formed by combining all these together would certainly surpass in magnificence all the comets ever observed by astronomers.
And then, what enormous periods of time must have been required to distribute the fragments of a single comet so widely that one would be found returning to its perihelion more than two centuries after another! When I spoke of one member of the Biela group being in aphelion when another would be in perihelion, I was speaking of a difference of only three and one-third years in time; and even that would require thousands of years. But the scattered cometic bodies which returned to the sun's neighborhood in 1668 and 1887 speak probably of millions of years which have passed since first this comet was formed. It would be a matter of curious inquiry to determine what may have been the condition of our sun, what even his volume, at that remote epoch in history.
It may be interesting to compare the orbital elements of the five comets above dealt with. They may be presented as follows; but it should be noticed that the determinations must be regarded as rough in the case of Comets I. and V., as the observations were insufficient for exact determination of the elements:
| I. | II. | III. | IV. | V. | |
| 1668. | 1843. | 1880. | 1882. | 1887. | |
| Perih. Passage. | Feb. 29 | Feb. 27 | Jan. 27 | Sep. 17 | Jan. 11 |
| Log. Per. Dist. | 7.6721 | 7.8395 | 7.7714 | 7.8895 | 8.1644 |
| Long. Per. | 80° 15' | 73° 30' 46" | 74° 11' 13" | 55° 37' 29" | 89° 41' |
| Long. Node. | 357° 17' | 355° 46' 48" | 356° 17' 4" | 346° 1' 27" | 359° 41' |
| Inclination. | 125° 58' | 143° 1' 31" | 143° 7' 31" | 141° 59' 40" | 141° 16' |
| Eccentricity. | 0.9999 | 0.9991 | 0.9995 | 0.999 | ...... |
| Calculator. | Henderson | Plantamour | Meyer | Kreutz | Finlay |
The element fluorine has at last been successfully isolated, and its chief chemical and physical properties determined. Many chemists, notably Faraday, Gore, Pflaunder, and Brauner, have endeavored to prepare this element in the free state, but all attempts have hitherto proved futile. M. Moissau, after a long series of researches with the fluorides of phosphorus, and the highly poisonous arsenic trifluoride, has finally been able to liberate fluorine in the gaseous state from anhydrous hydrofluoric acid by electrolysis. This acid in the pure state is not an electrolyte, but when potassium fluoride is dissolved in it, a current from ninety Bunsen elements decomposes it, evolving hydrogen from the negative and fluoride from the positive electrode.
The apparatus employed in this process is constructed of platinum, and is made in the form of a U tube, as shown in the accompanying illustration, with fluorspar stoppers, through which the battery terminals, made of platinum iridium alloy, are led. The gas is liberated at about the rate of two liters per hour, and has very powerful chemical properties. It smells somewhat like hypochlorous acid, etches dry glass, and decomposes water, liberating ozone, and forming hydrofluoric acid. The non-metallic elements, with the exception of chlorine, oxygen, nitrogen, and carbon, combine directly with it, evolving in most cases both light and heat. It combines with hydrogen, even in the dark, without the addition of any external energy, and converts most metals into their fluorides. Gold and platinum are not attacked in the cold, but when gently heated are easily corroded. Mercury readily dissolves the gas, forming the protochloride; iron wire also completely absorbs the gas, while powdered antimony and lead take fire in it. It is necessary in the electrolysis of the liquid hydrofluoric acid to cool the electrolytic cell by means of methyl chloride to -50° C. Fluorine appears to thus fully confirm the predictions which have been made by chemists concerning its properties. It is by far the, most energetic of all the known elements, and its position in the halogen series is established by its property of not liberating iodine from the iodides of potassium, mercury, and lead, and also of setting free chlorine from potassium chloride. With iodine it appears to form a fluoride. No compound with oxygen has yet been obtained.—Industries.
Having had occasion to prepare a quantity of sulphurous anhydride, for the purpose of reducing chromates previous to their analysis, I made use of the following apparatus, as represented in the accompanying figure. It consists of a glass vessel, A, provided with three tubulars, otherwise resembling a large Wolff bottle, the large tube, B, being provided with a stopper for the purpose of introducing pieces of sulphur from time to time into the small dish, C, intended for its reception, and fed with air by means of the delivery tube, D, thus allowing the stream of gas caused by the consumption of the sulphur to escape by means of the exit tube, E, to the vessel desired to receive it.
In using the apparatus the sulphur is first kindled by introducing a red hot wire through the tube, B, and replacing the stopper that has been momentarily removed for the introduction of the same. A slight blast is now maintained from the bellows that are in connection with the pipe, D, until the whole of the sulphur is thoroughly kindled, when a somewhat more powerful blast may be applied. When the apparatus above described is in full working order, from 2 to 3 lb. of sodium carbonate may be converted into sodium sulphite in less than half an hour, or several gallons of water saturated. I have also on connecting the apparatus with a powerful refrigerator obtained in a short time a large quantity of liquid SO2. It will be found advantageous, however, during the preparation of sulphurous anhydride, to employ a layer of water covering the bottom of the vessel to about 1 inch in depth. Carbonic anhydride and phosphoric anhydride may also be readily obtained in any desired quantity by slight alteration; but in case of phosphorus the air must be allowed to enter only gently, since a rapid current would at all times determine the fracture of the vessel.—Chem. News.
The expression "chemical structure," as commonly used by chemists, has, as is well known, nothing to do with the arrangement of atoms in space. The structural formula does not profess to represent spatial relations, but simply the connections which, after a careful study of the transformations and modes of formation of the compound represented, are believed to exist between the atoms. Nevertheless, although we do not commonly consider the question of space relations, it is clear that atoms must have some definite positions in space in the molecules, and the only reason why we do not represent these positions is because we know practically nothing about them. The most definite suggestion concerning space relations of atoms which has been made is that of Le Bel and Van't Hoff. The well known hypothesis of these authors was put forward to account for a certain kind of so-called physical isomerism which shows itself in the action of substances upon polarized light. Since this hypothesis was proposed, the number of cases of "abnormal isomerism," that is to say, of cases of isomerism which cannot be accounted for by the commonly accepted method of explaining structure, has increased to a considerable extent, and the necessity for some new hypothesis, or for some modification of the old ones, has come to be pretty generally recognized. Among the cases of isomerism which it is at least difficult to explain by the aid of the prevailing views are those of maleic and fumaric acids; citraconic and mesaconic acids; certain halogen derivatives of crotonic acid and of cinnamic acid; and coumaric and coumarinic acids.
More than one hypothesis has been proposed to account for these cases of isomerism, but no one has shown itself to be entirely satisfactory. Quite recently Johannes Wislicenus, Professor of Chemistry in the University of Liepsic, has made what has the appearance of being an important contribution toward the solution of the problem referred to. The author shows that many of the facts known in regard to the relations between maleic and fumaric acids, and the other substances which furnish examples of "abnormal isomerism," may be explained by the aid of an extension of the Le Bel-Van't Hoff hypothesis. It is difficult without the aid of models to give a clear idea concerning the hypothesis of Wislicenus, but some idea of it may be gained from the following. If we suppose a carbon atom to exert its affinities in the directions of the solid angles of a tetrahedron, as is done in the Le Bel-Van't Hoff hypothesis, then, when two carbon atoms unite, as in ethane, the union will be between two solid angles of two tetrahedrons. If the two carbon atoms unite by the ethylene kind of union, the union will be along a line corresponding to one of the edges of each tetrahedron. In the former case, in which single union exists, the two parts of the molecule represented by the two tetrahedrons can be supposed to be capable of revolving around an axis either in the same direction or in opposite directions. This axis corresponds to the straight line joining the two carbon atoms. In the case in which double union exists no such revolution is possible. Again, if, by addition to an unsaturated compound like ethylene, a saturated compound is formed, the kind of union between the carbon atoms is changed, and the possibility of revolution of the two parts of the compound is given. Whether such revolution take place or not will be determined largely by the structure of the compound. The tendency will be for those parts of the molecule which have the greatest specific affinity for one another to take those positions in which they are nearest to one another. Thus, suppose that chlorine is added to ethylene. By following the change on the model, it is seen that in the resulting figure the two chlorine atoms in ethylene chloride are situated at angles of the two tetrahedrons which are nearest each other. But chlorine has a stronger affinity for hydrogen than it has for chlorine, and therefore each chlorine atom would tend to get as near a hydrogen atom as possible. This involves a partial revolution of the two tetrahedrons in opposite directions around their common axis. So also hydrogen would tend to take a position as near as possible to hydroxyl and to carboxyl, while hydroxyl would avoid hydroxyl, and carboxyl would avoid carboxyl. These views are suggested as a result of a careful application of the original Le Bel-Van't Hoff hypothesis, and are, of course, of little value unless they can be shown to be in accordance with the facts.
The chief merit of the work of Wislicenus consists in the fact that he has shown that a large number of phenomena which have been observed in the study of such cases of isomerism as were mentioned above find a ready explanation in terms of the new hypothesis, whereas for most of these phenomena no explanation whatever has thus far been presented. The most marked case presented is that of maleic and fumaric acids. One by one, the author discusses the transformations of these acids and their substitution products, and becomes to this conclusion: "There is not to my knowledge a single fact known in regard to the relations between fumaric and maleic acids which is not explained by the aid of the above geometrical considerations, not one which does not clearly support the new hypothesis." Among the facts which he discusses in the light of the hypothesis are these: The formation of fumaric and maleic acids from malic acid; the quantitative transformation of maleic into fumaric acid by contact with strong acids; the transformation of the ethereal salts of maleic acid into those of fumaric acid by the action of a minute quantity of free iodine; the formation of brommaleic acid and hydrobromic acid from the dibromsuccinic acid formed by the addition of two bromine atoms to fumaric acid; the formation of dibromsuccinic acid from brommaleic acid and of isodibromsuccinic acid from bromfumaric acid by the action of fuming hydrobromic acid; the conversion of brommaleic acid into fumaric and then into succinic acid by the action of sodium amalgam; the formation of one and the same tribromsuccinic acid by the action of bromine on brommaleic and on bromfumaric acid; and finally, the conversion of maleic into inactive tartaric acid, and of fumaric into racemic acid by potassium permanganate. All these facts are shown to find a ready explanation by the aid of the new hypothesis. Further, it is shown that the decompositions of the salts of certain halogen derivatives of organic acids, which give up halogen salt and carbon dioxide, as well as the formation of lactones and of anhydrides of dibasic acids, are in perfect harmony with the hypothesis. But the only way to get a clear conception in regard to the mass of material which the author has brought together and which he has shown to support his hypothesis is by a careful study of the original paper, and the object of this notice is mainly to call the attention of American chemists to it.
As to the question what value to attach to the speculations which Wislicenus has brought to our notice, it is difficult to give any but a general answer. No one can well have a greater fear of mere speculation, which is indulged in independently of the facts, than the writer of this notice. Great harm has been done chemistry, and probably every other branch of knowledge, by unwarranted speculation, and every one who has looked into the matter knows how extremely difficult it is to emancipate one's self from the influence of a plausible hypothesis, even when it can be shown that it is not in accordance with the facts. It behooves every one, therefore, before accepting a new hypothesis, no matter how fascinating it may appear at first sight, to look carefully into the facts, and to endeavor to determine independently whether it is well founded or not. On the other hand, there is some danger to be apprehended from a tendency, sometimes observed, to denounce everything speculative, no matter how broad the basis of facts upon which it rests may be. Without legitimate speculation, it is clear that there could be no great progress in any subject. As far as the hypothesis under consideration is concerned, the writer is firmly of the opinion that it is likely to prove of great value in dealing with a large number of chemical facts, and that, as it suggests many lines of research, it will undoubtedly in the course of a few years exert a profound influence on chemistry. Whether the evidence which will be accumulated will or will not confirm the view that the tetrahedron form is characteristic of the simplest molecules of carbon compounds is not the most important question to be asked under the circumstances. We should rather ask whether the testing of the hypothesis is or is not likely to bring us nearer to the truth. It is a proposition that admits of no denial that a hypothesis which can be tested by experiment, and which suggests lines of work and stimulates workers to follow them, is a gain to science, no matter what the ultimate fate of the hypothesis may be.—Amer. Chem. Jour.
Ueber die raumliche Anordnung der Atome in organischen Molekulen, and ihre Bestimmung in geometrisch-isomeren ungesattigten Verbindungen. Von Johannes Wislicenus.—Abhandlungen der mathemalisch-physischen Klasse der Konigl. Sachsischen Gesellschaft der Wissenechaften. Band XIV., No. 1.
It should be thoroughly understood by all that any common paper, coarse wrapping paper, new or old newspapers, etc., are admirable to keep out cold or keep in warmth. The blood of all domestic animals, as well as of human beings, must be always kept very near 98 degrees, just as much in winter as in summer. And this heat always comes from within the body, whenever the atmosphere is not above 98 degrees temperature. So long as the air is cooler than this, the heat produced inside the body is escaping. Heat seeks a level. If there is more in one of two bodies or substances side by side, the heat will pass from the warmer into the colder, until they are both of the same temperature.
Moving air carries away vastly more heat than still air. The thin film of air next to the body soon gets warm from it. But if that air is moved along, slowly or swiftly, by a breeze, be it ever so gentle, new cooler air takes its place, and abstracts more heat from the body. Anything that keeps the air next to the bodies of men and of animals from moving, checks the escape of heat.
The thinnest paper serves to keep the air quiet. A newspaper laid on a bed acts much as a coverlid to keep a film or layer of air quiet, and thus less heat escapes from the bodies of the sleepers. If paper is pasted up over the cracks of a house, or of a barn or stable, or under the joists of a house floor, it has just the same effect. Every person who keeps animals will find it a wonderful and paying protection to them, to put against the walls one, two, three, or more layers of newspapers during cold weather. If a person in riding finds his garments too cool, a newspaper placed under the coat or vest, or under or over the trousers, even if only on the side next the wind, will do a great deal to check the outflow of heat, and keep him warm. Two or three thicknesses of newspaper crumpled a little, and put under the coat or overcoat, are almost as effective in keeping in warmth as an extra garment. A slight crumpling keeps them a little separate, and makes additional thin layers of air.
Further: Heat does not pass through films of still air. Fibrous woolens, furs, loosely woven cotton, down, and the like, contain a great deal of air confined in the meshes, and are therefore excellent conservers of heat. Double walls of stone, brick, or wood, or even of wall or roofing paper, double glass, double layers of anything that will have thin layers of still air between them, prevent the escape of heat greatly.
$2.50 a Year. Single Copies, 25 cts.
This is a Special Edition of the Scientific American, issued monthly—on the first day of the month. Each number contains about forty large quarto pages, equal to about two hundred ordinary book pages, forming, practically, a large and splendid Magazine of Architecture, richly adorned with elegant plates in colors and with fine engravings, illustrating the most interesting examples of modern Architectural Construction and allied subjects.
A special feature is the presentation in each number of a variety of the latest and best plans for private residences, city and country, including those of very moderate cost as well as the more expensive. Drawings in perspective and in color are given, together with full Plans, Specifications, Costs, Bills of Estimate, and Sheets of Details.
No other building paper contains so many plans, details, and specifications regularly presented as the Scientific American. Hundreds of dwellings have already been erected on the various plans we have issued during the past year, and many others are in process of construction.
Architects, Builders, and Owners will find this work valuable in furnishing fresh and useful suggestions. All who contemplate building or improving homes, or erecting structures of any kind, have before them in this work an almost endless series of the latest and best examples from which to make selections, thus saving time and money.
Many other subjects, including Sewerage, Piping, Lighting, Warming, Ventilating, Decorating, Laying out of Grounds, etc., are illustrated. An extensive Compendium of Manufacturers' Announcements is also given, in which the most reliable and approved Building Materials, Goods, Machines, Tools, and Appliances are described and illustrated, with addresses of the makers, etc.
The fullness, richness, cheapness, and convenience of this work have won for it the Largest Circulation of any Architectural publication in the world.
MUNN & CO., Publishers,
361 Broadway, New York.
A Catalogue of valuable books on Architecture, Building, Carpentry, Masonry, Heating, Warming, Lighting, Ventilation, and all branches of industry pertaining to the art of Building, is supplied free of charge, sent to any address.
In connection with the publication of the Building Edition of the Scientific American, Messrs. Munn & Co. furnish plans and specifications for buildings of every kind, including Churches, Schools, Stores, Dwellings, Carriage Houses, Barns, etc.
In this work they are assisted by able and experienced architects. Full plans, details, and specifications for the various buildings illustrated in this paper can be supplied.
Those who contemplate building, or who wish to alter, improve, extend, or add to existing buildings, whether wings, porches, bay windows, or attic rooms, are invited to communicate with the undersigned. Our work extends to all parts of the country. Estimates, plans, and drawings promptly prepared. Terms moderate. Address
MUNN & CO., 361 Broadway, New York.
PUBLISHED WEEKLY.
Terms of Subscription, $5 a year.
Sent by mail, postage prepaid, to subscribers in any part of the United States or Canada. Six dollars a year, sent, prepaid, to any foreign country.
All the back numbers of The Supplement, from the commencement, January 1, 1876, can be had. Price, 10 cents each.
All the back volumes of The Supplement can likewise be supplied. Two volumes are issued yearly. Price of each volume, $2.50 stitched in paper, or $3.50 bound in stiff covers.
Combined Rates.—One copy of Scientific American and one copy of Scientific American Supplement, one year, postpaid, $7.00.
A liberal discount to booksellers, news agents, and canvassers.
MUNN & CO., Publishers,
361 Broadway, New York, N.Y.
In connection with the Scientific American, Messrs. MUNN & CO. are solicitors of American and Foreign Patents, have had 42 years' experience, and now have the largest establishment in the world. Patents are obtained on the best terms.
A special notice is made in the Scientific American of all inventions patented through this Agency, with the name and residence of the Patentee. By the immense circulation thus given, public attention is directed to the merits of the new patent, and sales or introduction often easily effected.
Any person who has made a new discovery or invention can ascertain, free of charge, whether a patent can probably be obtained, by writing to MUNN & CO.
We also send free our Hand Book about the Patent Laws, Patents, Caveats, Trade Marks, their costs, and how procured. Address
MUNN & CO.,
361 Broadway, New York.
Branch Office, 622 and 624 F St., Washington, D.C.
End of the Project Gutenberg EBook of Scientific American Supplement, No.
633, February 18, 1888, by Various
*** END OF THIS PROJECT GUTENBERG EBOOK SCIENTIFIC AMERICAN ***
***** This file should be named 17167-h.htm or 17167-h.zip *****
This and all associated files of various formats will be found in:
https://www.gutenberg.org/1/7/1/6/17167/
Produced by Juliet Sutherland and the Online Distributed
Proofreading Team at www.pgdp.net
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
https://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH F3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need, is critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at https://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
https://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at https://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit https://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including including checks, online payments and credit card
donations. To donate, please visit: https://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart was the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
https://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.