Fig. 1.
The Project Gutenberg EBook of Some Mooted Questions in Reinforced
Concrete Design, by Edward Godfrey
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
Title: Some Mooted Questions in Reinforced Concrete Design
American Society of Civil Engineers, Transactions, Paper
No. 1169, Volume LXX, Dec. 1910
Author: Edward Godfrey
Release Date: November 23, 2005 [EBook #17137]
Language: English
Character set encoding: ISO-8859-1
*** START OF THIS PROJECT GUTENBERG EBOOK REINFORCED CONCRETE DESIGN ***
Produced by Juliet Sutherland, Taavi Kalju and the Online
Distributed Proofreading Team at https://www.pgdp.net
Not many years ago physicians had certain rules and practices by which they were guided as to when and where to bleed a patient in order to relieve or cure him. What of those rules and practices to-day? If they were logical, why have they been abandoned?
It is the purpose of this paper to show that reinforced concrete engineers have certain rules and practices which are no more logical than those governing the blood-letting of former days. If the writer fails in this, by reason of the more weighty arguments on the other side of the questions he propounds, he will at least have brought out good reasons which will stand the test of logic for the rules and practices which he proposes to condemn, and which, at the present time, are quite lacking in the voluminous literature on this comparatively new subject.
Destructive criticism has recently been decried in an editorial in an engineering journal. Some kinds of destructive criticism are of the highest benefit; when it succeeds in destroying error, it is reconstructive. No reform was ever accomplished without it, and no[Pg 55] reformer ever existed who was not a destructive critic. If showing up errors and faults is destructive criticism, we cannot have too much of it; in fact, we cannot advance without it. If engineering practice is to be purged of its inconsistencies and absurdities, it will never be done by dwelling on its excellencies.
Reinforced concrete engineering has fairly leaped into prominence and apparently into full growth, but it still wears some of its swaddling-bands. Some of the garments which it borrowed from sister forms of construction in its short infancy still cling to it, and, while these were, perhaps, the best makeshifts under the circumstances, they fit badly and should be discarded. It is some of these misfits and absurdities which the writer would like to bring prominently before the Engineering Profession.
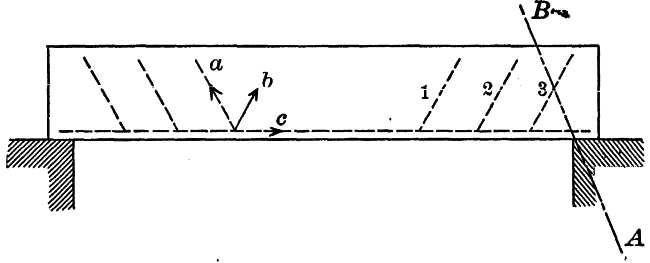
The first point to which attention is called, is illustrated in Fig. 1. It concerns sharp bends in reinforcing rods in concrete. Fig. 1 shows a reinforced concrete design, one held out, in nearly all books on the subject, as a model. The reinforcing rod is bent up at a sharp angle, and then may or may not be bent again and run parallel with the top of the beam. At the bend is a condition which resembles that of a hog-chain or truss-rod around a queen-post. The reinforcing rod is the hog-chain or the truss-rod. Where is the queen-post? Suppose this rod has a section of 1 sq. in. and an inclination of 60° with the horizontal, and that its unit stress is 16,000 lb. per sq. in. The forces, a and b, are then 16,000 lb. The force, c, must be also 16000 lb. What is to take this force, c, of 16,000 lb.? There is nothing but concrete. At 500 lb. per sq. in., this force would require an area of 32 sq. in. Will some advocate of this type of design please state where this area can be found? It must, of necessity, be in contact with the rod, and, for structural reasons, because of the lack of stiffness in the rod, it would have to be close to the point of bend. If analogy to the queen-[Pg 56]post fails so completely, because of the almost complete absence of the post, why should not this borrowed garment be discarded?
If this same rod be given a gentle curve of a radius twenty or thirty times the diameter of the rod, the side unit pressure will be from one-twentieth to one-thirtieth of the unit stress on the steel. This being the case, and being a simple principle of mechanics which ought to be thoroughly understood, it is astounding that engineers should perpetrate the gross error of making a sharp bend in a reinforcing rod under stress.
The second point to which attention is called may also be illustrated by Fig. 1. The rod marked 3 is also like the truss-rod of a queen-post truss in appearance, because it ends over the support and has the same shape. But the analogy ends with appearance, for the function of a truss-rod in a queen-post truss is not performed by such a reinforcing rod in concrete, for other reasons than the absence of a post. The truss-rod receives its stress by a suitable connection at the end of the rod and over the support of the beam. The reinforcing rod, in this standard beam, ends abruptly at the very point where it is due to receive an important element of strength, an element which would add enormously to the strength and safety of many a beam, if it could be introduced.
Of course a reinforcing rod in a concrete beam receives its stress by increments imparted by the grip of the concrete; but these increments can only be imparted where the tendency of the concrete is to stretch. This tendency is greatest near the bottom of the beam, and when the rod is bent up to the top of the beam, it is taken out of the region where the concrete has the greatest tendency to stretch. The function of this rod, as reinforcement of the bottom flange of the beam, is interfered with by bending it up in this manner, as the beam is left without bottom-flange reinforcement, as far as that rod is concerned, from the point of bend to the support.
It is true that there is a shear or a diagonal tension in the beam, and the diagonal portion of the rod is apparently in a position to take this tension. This is just such a force as the truss-rod in a queen-post truss must take. Is this reinforcing rod equipped to perform this office? The beam is apt to fail in the line, A B. In fact, it is apt to crack from shrinkage on this or almost any other line, and to leave the strength dependent on the reinforcing steel. Suppose such a crack[Pg 57] should occur. The entire strength of the beam would be dependent on the grip of the short end of Rod 3 to the right of the line, A B. The grip of this short piece of rod is so small and precarious, considering the important duty it has to perform, that it is astounding that designers, having any care for the permanence of their structures, should consider for an instant such features of design, much less incorporate them in a building in which life and property depend on them.
The third point to which attention is called, is the feature of design just mentioned in connection with the bent-up rod. It concerns the anchorage of rods by the embedment of a few inches of their length in concrete. This most flagrant violation of common sense has its most conspicuous example in large engineering works, where of all places better judgment should prevail. Many retaining walls have been built, and described in engineering journals, in papers before engineering societies of the highest order, and in books enjoying the greatest reputation, which have, as an essential feature, a great number of rods which cannot possibly develop their strength, and might as well be of much smaller dimensions. These rods are the vertical and horizontal rods in the counterfort of the retaining wall shown at a, in Fig. 2. This retaining wall consists of a front curtain wall and a horizontal slab joined at intervals by ribs or counterforts. The manifest and only function of the rib or counterfort is to tie together the curtain wall and the horizontal slab. That it is or should be of concrete is because the steel rods which it contains, need protection. It is clear that failure of the retaining wall could occur by rupture through the Section A B, or through B C. It is also clear that, apart from the cracking of the concrete of the rib, the only thing which would produce this rupture is the pulling out of the short ends of these reinforcing rods. Writers treat the triangle, A B C, as a beam, but there is absolutely no analogy between this triangle and a beam. Designers seem to think that these rods take the place of so-called shear rods in a beam, and that the inclined rods are equivalent to the rods in a tension flange of a beam. It is hard to understand by what process of reasoning such results can be attained. Any clear analysis leading to these conclusions would certainly be a valuable contribution to the literature on the subject. It is scarcely possible, however, that such analysis will be brought forward, for it is the apparent policy of[Pg 58] the reinforced concrete analyst to jump into the middle of his proposition without the encumbrance of a premise.
There is positively no evading the fact that this wall could fail, as stated, by rupture along either A B or B C. It can be stated just as positively that a set of rods running from the front wall to the horizontal slab, and anchored into each in such a manner as would be adopted were these slabs suspended on the rods, is the only rational and the only efficient design possible. This design is illustrated at b in Fig. 2.
The fourth point concerns shear in steel rods embedded in concrete. For decades, specifications for steel bridges have gravely given a unit shear to be allowed on bridge pins, and every bridge engineer knows or ought to know that, if a bridge pin is properly proportioned for bending and bearing, there is no possibility of its being weak from shear. The centers of bearings cannot be brought close enough together to reduce the size of the pin to where its shear need be considered, because of the width required for bearing on the parts. Concrete is about one-thirtieth as strong as steel in bearing. There is, therefore, somewhat less than one-thirtieth of a reason for specifying any shear on steel rods embedded in concrete.
The gravity of the situation is not so much the serious manner in which this unit of shear in steel is written in specifications and building codes for reinforced concrete work (it does not mean anything in specifications for steelwork, because it is ignored), but it is apparent when designers soberly use these absurd units, and proportion shear rods accordingly.
Many designers actually proportion shear rods for shear, shear in the steel at units of 10,000 or 12,000 lb. per sq. in.; and the blame for this dangerous practice can be laid directly to the literature on reinforced concrete. Shear rods are given as standard features in the design of reinforced concrete beams. In the Joint Report of the Committee of the various engineering societies, a method for proportioning shear members is given. The stress, or shear per shear member, is the longitudinal shear which would occur in the space from member to member. No hint is given as to whether these bars are in shear or tension; in fact, either would be absurd and impossible without greatly overstressing some other part. This is just a sample of the state of the literature on this important subject. Shear bars will be taken up more fully in subsequent paragraphs.
The fifth point concerns vertical stirrups in a beam. These stirrups are conspicuous features in the designs of reinforcing concrete beams. Explanations of how they act are conspicuous in the literature on reinforced concrete by its total absence. By stirrups are meant the so-called shear rods strung along a reinforcing rod. They are usually U-shaped and looped around the rod.
It is a common practice to count these stirrups in the shear, taking the horizontal shear in a beam. In a plate girder, the rivets connecting the flange to the web take the horizontal shear or the increment to the flange stress. Compare two 3/4-in. rivets tightly driven into holes in a steel angle, with a loose vertical rod, 3/4 in. in diameter, looped around a reinforcing rod in a concrete beam, and a correct comparison of methods of design in steel and reinforced concrete, as they are commonly practiced, is obtained.
These stirrups can take but little hold on the reinforcing rods—and this must be through the medium of the concrete—and they can take but little shear. Some writers, however, hold the opinion that the stirrups are in tension and not in shear, and some are bold enough to compare them with the vertical tension members of a Howe truss.[Pg 60] Imagine a Howe truss with the vertical tension members looped around the bottom chord and run up to the top chord without any connection, or hooked over the top chord; then compare such a truss with one in which the end of the rod is upset and receives a nut and large washer bearing solidly against the chord. This gives a comparison of methods of design in wood and reinforced concrete, as they are commonly practiced.
Anchorage or grip in the concrete is all that can be counted on, in any event, to take up the tension of these stirrups, but it requires an embedment of from 30 to 50 diameters of a rod to develop its full strength. Take 30 to 50 diameters from the floating end of these shear members, and, in some cases, nothing or less than nothing will be left. In any case the point at which the shear member, or stirrup, is good for its full value, is far short of the centroid of compression of the beam, where it should be; in most cases it will be nearer the bottom of the beam. In a Howe truss, the vertical tension members having their end connections near the bottom chord, would be equivalent to these shear members.
The sixth point concerns the division of stress into shear members. Briefly stated, the common method is to assume each shear member as taking the horizontal shear occurring in the space from member to member. As already stated, this is absurd. If stirrups could take shear, this method would give the shear per stirrup, but even advocates of this method acknowledge that they can not. To apply the common analogy of a truss: each shear member would represent a tension web member in the truss, and each would have to take all the shear occurring in a section through it.
If, for example, shear members were spaced half the depth of a beam apart, each would take half the shear by the common method. If shear members take vertical shear, or if they take tension, what is between the two members to take the other half of the shear? There is nothing in the beam but concrete and the tension rod between the two shear members. If the concrete can take the shear, why use steel members? It is not conceivable that an engineer should seriously consider a tension rod in a reinforced concrete beam as carrying the shear from stirrup to stirrup.
The logical deduction from the proposition that shear rods take tension is that the tension rods must take shear, and that they must[Pg 61] take the full shear of the beam, and not only a part of it. For these shear rods are looped around or attached to the tension rods, and since tension in the shear rods would logically be imparted through the medium of this attachment, there is no escaping the conclusion that a large vertical force (the shear of the beam) must pass through the tension rod. If the shear member really relieves the concrete of the shear, it must take it all. If, as would be allowable, the shear rods take but a part of the shear, leaving the concrete to take the remainder, that carried by the rods should not be divided again, as is recommended by the common method.
Bulletin No. 29 of the University of Illinois Experiment Station shows by numerous experiments, and reiterates again and again, that shear rods do not act until the beam has cracked and partly failed. This being the case, a shear rod is an illogical element of design. Any element of a structure, which cannot act until failure has started, is not a proper element of design. In a steel structure a bent plate which would straighten out under a small stress and then resist final rupture, would be a menace to the rigidity and stability of the structure. This is exactly analogous to shear rods which cannot act until failure has begun.
When the man who tears down by criticism fails to point out the way to build up, he is a destructive critic. If, under the circumstances, designing with shear rods had the virtue of being the best thing to do with the steel and concrete disposed in a beam, as far as experience and logic in their present state could decide, nothing would be gained by simply criticising this method of design. But logic and tests have shown a far simpler, more effective, and more economical means of disposing of the steel in a reinforced concrete beam.
In shallow beams there is little need of provision for taking shear by any other means than the concrete itself. The writer has seen a reinforced slab support a very heavy load by simple friction, for the slab was cracked close to the supports. In slabs, shear is seldom provided for in the steel reinforcement. It is only when beams begin to have a depth approximating one-tenth of the span that the shear in the concrete becomes excessive and provision is necessary in the steel reinforcement. Years ago, the writer recommended that, in such beams, some of the rods be curved up toward the ends of the span and anchored over the support. Such reinforcement completely[Pg 62] relieves the concrete of all shearing stress, for the stress in the rod will have a vertical component equal to the shear. The concrete will rest in the rod as a saddle, and the rod will be like the cable of a suspension span. The concrete could be in separate blocks with vertical joints, and still the load would be carried safely.
By end anchorage is not meant an inch or two of embedment in concrete, for an iron vise would not hold a rod for its full value by such means. Neither does it mean a hook on the end of the rod. A threaded end with a bearing washer, and a nut and a lock-nut to hold the washer in place, is about the only effective means, and it is simple and cheap. Nothing is as good for this purpose as plain round rods, for no other shape affords the same simple and effective means of end connection. In a line of beams, end to end, the rods may be extended into the next beam, and there act to take the top-flange tension, while at the same time finding anchorage for the principal beam stress.
The simplicity of this design is shown still further by the absence of a large number of little pieces in a beam box, as these must be held in their proper places, and as they interfere with the pouring of the concrete.
It is surprising that this simple and unpatented method of design has not met with more favor and has scarcely been used, even in tests. Some time ago the writer was asked, by the head of an engineering department of a college, for some ideas for the students to work up for theses, and suggested that they test beams of this sort. He was met by the astounding and fatuous reply that such would not be reinforced concrete beams. They would certainly be concrete beams, and just as certainly be reinforced.
Bulletin 29 of the University of Illinois Experiment Station contains a record of tests of reinforced concrete beams of this sort. They failed by the crushing of the concrete or by failure in the steel rods, and nearly all the cracks were in the middle third of the beams, whereas beams rich in shear rods cracked principally in the end thirds, that is, in the neighborhood of the shear rods. The former failures are ideal, and are easier to provide against. A crack in a beam near the middle of the span is of little consequence, whereas one near the support is a menace to safety.
The seventh point of common practice to which attention is called, is the manner in which bending moments in so-called continuous beams[Pg 63] are juggled to reduce them to what the designer would like to have them. This has come to be almost a matter of taste, and is done with as much precision or reason as geologists guess at the age of a fossil in millions of years.
If a line of continuous beams be loaded uniformly, the maximum moments are negative and are over the supports. Who ever heard of a line of beams in which the reinforcement over the supports was double that at mid-spans? The end support of such a line of beams cannot be said to be fixed, but is simply supported, hence the end beam would have a negative bending moment over next to the last support equal to that of a simple span. Who ever heard of a beam being reinforced for this? The common practice is to make a reduction in the bending moment, at the middle of the span, to about that of a line of continuous beams, regardless of the fact that they may not be continuous or even contiguous, and in spite of the fact that the loading of only one gives quite different results, and may give results approaching those of a simple beam.
If the beams be designed as simple beams—taking the clear distance between supports as the span and not the centers of bearings or the centers of supports—and if a reasonable top reinforcement be used over these supports to prevent cracks, every requirement of good engineering is met. Under extreme conditions such construction might be heavily stressed in the steel over the supports. It might even be overstressed in this steel, but what could happen? Not failure, for the beams are capable of carrying their load individually, and even if the rods over the supports were severed—a thing impossible because they cannot stretch out sufficiently—the beams would stand.
Continuous beam calculations have no place whatever in designing stringers of a steel bridge, though the end connections will often take a very large moment, and, if calculated as continuous, will be found to be strained to a very much larger moment. Who ever heard of a failure because of continuous beam action in the stringers of a bridge? Why cannot reinforced concrete engineering be placed on the same sound footing as structural steel engineering?
The eighth point concerns the spacing of rods in a reinforced concrete beam. It is common to see rods bunched in the bottom of such a beam with no regard whatever for the ability of the concrete to grip the steel, or to carry the horizontal shear incident to their stress, to[Pg 64] the upper part of the beam. As an illustration of the logic and analysis applied in discussing the subject of reinforced concrete, one well-known authority, on the premise that the unit of adhesion to rod and of shear are equal, derives a rule for the spacing of rods. His reasoning is so false, and his rule is so far from being correct, that two-thirds would have to be added to the width of beam in order to make it correct. An error of 66% may seem trifling to some minds, where reinforced concrete is considered, but errors of one-tenth this amount in steel design would be cause for serious concern. It is reasoning of the most elementary kind, which shows that if shear and adhesion are equal, the width of a reinforced concrete beam should be equal to the sum of the peripheries of all reinforcing rods gripped by the concrete. The width of the beam is the measure of the shearing area above the rods, taking the horizontal shear to the top of the beam, and the peripheries of the rods are the measure of the gripping or adhesion area.
Analysis which examines a beam to determine whether or not there is sufficient concrete to grip the steel and to carry the shear, is about at the vanishing point in nearly all books on the subject. Such misleading analysis as that just cited is worse than nothing.
The ninth point concerns the T-beam. Excessively elaborate formulas are worked out for the T-beam, and haphazard guesses are made as to how much of the floor slab may be considered in the compression flange. If a fraction of this mental energy were directed toward a logical analysis of the shear and gripping value of the stem of the T-beam, it would be found that, when the stem is given its proper width, little, if any, of the floor slab will have to be counted in the compression flange, for the width of concrete which will grip the rods properly will take the compression incident to their stress.
The tenth point concerns elaborate theories and formulas for beams and slabs. Formulas are commonly given with 25 or 30 constants and variables to be estimated and guessed at, and are based on assumptions which are inaccurate and untrue. One of these assumptions is that the concrete is initially unstressed. This is quite out of reason, for the shrinkage of the concrete on hardening puts stress in both concrete and steel. One of the coefficients of the formulas is that of the elasticity of the concrete. No more variable property of concrete is known than its coefficient of elasticity, which may vary from 1,000,000[Pg 65] to 5,000,000 or 6,000,000; it varies with the intensity of stress, with the kind of aggregate used, with the amount of water used in mixing, and with the atmospheric condition during setting. The unknown coefficient of elasticity of concrete and the non-existent condition of no initial stress, vitiate entirely formulas supported by these two props.
Here again destructive criticism would be vicious if these mathematical gymnasts were giving the best or only solution which present knowledge could produce, or if the critic did not point out a substitute. The substitute is so simple of application, in such agreement with experiments, and so logical in its derivation, that it is surprising that it has not been generally adopted. The neutral axis of reinforced concrete beams under safe loads is near the middle of the depth of the beams. If, in all cases, it be taken at the middle of the depth of the concrete beam, and if variation of intensity of stress in the concrete be taken as uniform from this neutral axis up, the formula for the resisting moment of a reinforced concrete beam becomes extremely simple and no more complex than that for a rectangular wooden beam.
The eleventh point concerns complex formulas for chimneys. It is a simple matter to find the tensile stress in that part of a plain concrete chimney between two radii on the windward side. If in this space there is inserted a rod which is capable of taking that tension at a proper unit, the safety of the chimney is assured, as far as that tensile stress is concerned. Why should frightfully complex formulas be proposed, which bring in the unknowable modulus of elasticity of concrete and can only be solved by stages or dependence on the calculations of some one else?
The twelfth point concerns deflection calculations. As is well known, deflection does not play much of a part in the design of beams. Sometimes, however, the passing requirement of a certain floor construction is the amount of deflection under a given load. Professor Gaetano Lanza has given some data on recorded deflections of reinforced concrete beams.[B] He has also worked out the theoretical deflections on various assumptions. An attempt to reconcile the observed deflections with one of several methods of calculating stresses led him to the conclusion that:
"The observations made thus far are not sufficient to furnish the means for determining the actual distribution of the stresses, and[Pg 66] hence for the deduction of reliable formulæ for the computation of the direct stresses, shearing stresses, diagonal stresses, deflections, position of the neutral axis, etc., under a given load."
Professor Lanza might have gone further and said that the observations made thus far are sufficient to show the hopelessness of deriving a formula that will predict accurately the deflection of a reinforced concrete beam. The wide variation shown by two beam tests cited by him, in which the beams were identical, is, in itself, proof of this.
Taking the data of these tests, and working out the modulus of elasticity from the recorded deflections, as though the beams were of plain concrete, values are found for this modulus which are not out of agreement with the value of that variable modulus as determined by other means. Therefore, if the beams be considered as plain concrete beams, and an average value be assumed for the modulus or coefficient of elasticity, a deflection may be found by a simple calculation which is an average of that which may be expected. Here again, simple theory is better than complex, because of the ease with which it may be applied, and because it gives results which are just as reliable.
The thirteenth point concerns the elastic theory as applied to a reinforced concrete arch. This theory treats a reinforced concrete arch as a spring. In order to justify its use, the arch or spring is considered as having fixed ends. The results obtained by the intricate methods of the elastic theory and the simple method of the equilibrium polygon, are too nearly identical to justify the former when the arch is taken as hinged at the ends.
The assumption of fixed ends in an arch is a most extravagant one, because it means that the abutments must be rigid, that is, capable of taking bending moments. Rigidity in an abutment is only effected by a large increase in bulk, whereas strength in an arch ring is greatly augmented by the addition of a few inches to its thickness. By the elastic theory, the arch ring does not appear to need as much strength as by the other method, but additional stability is needed in the abutments in order to take the bending moments. This latter feature is not dwelt on by the elastic theorists.
In the ordinary arch, the criterion by which the size of abutment is gauged, is the location of the line of pressure. It is difficult and[Pg 67] expensive to obtain depth enough in the base of the abutment to keep this line within the middle third, when only the thrust of the arch is considered. If, in addition to the thrust, there is a bending moment which, for many conditions of loading, further displaces the line of pressure toward the critical edge, the difficulty and expense are increased. It cannot be gainsaid that a few cubic yards of concrete added to the ring of an arch will go much further toward strengthening the arch than the same amount of concrete added to the two abutments.
In reinforced concrete there are ample grounds for the contention that the carrying out of a nice theory, based on nice assumptions and the exact determination of ideal stresses, is of far less importance than the building of a structure which is, in every way, capable of performing its function. There are more than ample grounds for the contention that the ideal stresses worked out for a reinforced concrete structure are far from realization in this far from ideal material.
Apart from the objection that the elastic theory, instead of showing economy by cutting down the thickness of the arch ring, would show the very opposite if fully carried out, there are objections of greater weight, objections which strike at the very foundation of the theory as applied to reinforced concrete. In the elastic theory, as in the intricate beam theory commonly used, there is the assumption of an initial unstressed condition of the materials. This is not true of a beam and is still further from the truth in the case of an arch. Besides shrinkage of the concrete, which always produces unknown initial stresses, there is a still more potent cause of initial stress, namely, the settlement of the arch when the forms are removed. If the initial stresses are unknown, ideal determinations of stresses can have little meaning.
The elastic theory stands or falls according as one is able or unable to calculate accurately the deflection of a reinforced concrete beam; and it is an impossibility to calculate this deflection even approximately. The tests cited by Professor Lanza show the utter disagreement in the matter of deflections. Of those tested, two beams which were identical, showed results almost 100% apart. A theory grounded on such a shifting foundation does not deserve serious consideration. Professor Lanza's conclusions, quoted under the twelfth point, have special meaning and force when applied to a reinforced concrete arch;[Pg 68] the actual distribution of the stresses cannot possibly be determined, and complex cloaks of arithmetic cannot cover this fact. The elastic theory, far from being a reliable formula, is false and misleading in the extreme.
The fourteenth point refers to temperature calculations in a reinforced concrete arch. These calculations have no meaning whatever. To give the grounds for this assertion would be to reiterate much of what has been said under the subject of the elastic arch. If the unstressed shape of an arch cannot be determined because of the unknown effect of shrinkage and settlement, it is a waste of time to work out a slightly different unstressed shape due to temperature variation, and it is a further waste of time to work out the supposed stresses resulting from deflecting that arch back to its actual shape.
If no other method of finding the approximate stresses in an arch existed, the elastic theory might be classed as the best available; but this is not the case. There is a method which is both simple and reliable. Accuracy is not claimed for it, and hence it is in accord with the more or less uncertain materials dealt with. Complete safety, however, is assured, for it treats the arch as a series of blocks, and the cementing of these blocks into one mass cannot weaken the arch. Reinforcement can be proportioned in the same manner as for chimneys, by finding the tension exerted to pull these blocks apart and then providing steel to take that tension.
The fifteenth point concerns steel in compression in reinforced concrete columns or beams. It is common practice—and it is recommended in the most pretentious works on the subject—to include in the strength of a concrete column slender longitudinal rods embedded in the concrete. To quote from one of these works:
"The compressive resistance of a hooped member exceeds the sum of the following three elements: (1) The compressive resistance of the concrete without reinforcement. (2) The compressive resistance of the longitudinal rods stressed to their elastic limit. (3) The compressive resistance which would have been produced by the imaginary longitudinals at the elastic limit of the hooping metal, the volume of the imaginary longitudinals being taken as 2.4 times that of the hooping metal."
This does not stand the test, either of theory or practice; in fact, it is far from being true. Its departure from the truth is great[Pg 69] enough and of serious enough moment to explain some of the worst accidents in the history of reinforced concrete.
It is a nice theoretical conception that the steel and the concrete act together to take the compression, and that each is accommodating enough to take just as much of the load as will stress it to just the right unit. Here again, initial stress plays an important part. The shrinkage of the concrete tends to put the rods in compression, the load adds more compression on the slender rods and they buckle, because of the lack of any adequate stiffening, long before the theorists' ultimate load is reached.
There is no theoretical or practical consideration which would bring in the strength of the hoops after the strength of the concrete between them has been counted. All the compression of a column must, of necessity, go through the disk of concrete between the two hoops (and the longitudinal steel). No additional strength in the hoops can affect the strength of this disk, with a given spacing of the hoops. It is true that shorter disks will have more strength, but this is a matter of the spacing of the hoops and not of their sectional area, as the above quotation would make it appear.
Besides being false theoretically, this method of investing phantom columns with real strength is wofully lacking in practical foundation. Even the assumption of reinforcing value to the longitudinal steel rods is not at all borne out in tests. Designers add enormously to the calculated strength of concrete columns when they insert some longitudinal rods. It appears to be the rule that real columns are weakened by the very means which these designers invest with reinforcing properties. Whether or not it is the rule, the mere fact that many tests have shown these so-called reinforced concrete columns to be weaker than similar plain concrete columns is amply sufficient to condemn the practice of assuming strength which may not exist. Of all parts of a building, the columns are the most vital. The failure of one column will, in all probability, carry with it many others stronger than itself, whereas a weak and failing slab or beam does not put an extra load and shock on the neighboring parts of a structure.
In Bulletin No. 10 of the University of Illinois Experiment Station,[C] a plain concrete column, 9 by 9 in. by 12 ft., stood an ultimate crushing load of 2,004 lb. per sq. in. Column 2, identical in[Pg 70] size, and having four 5/8-in. rods embedded in the concrete, stood 1,557 lb. per sq. in. So much for longitudinal rods without hoops. This is not an isolated case, but appears to be the rule; and yet, in reading the literature on the subject, one would be led to believe that longitudinal steel rods in a plain concrete column add greatly to the strength of the column.
A paper, by Mr. M.O. Withey, before the American Society for Testing Materials, in 1909, gave the results of some tests on concrete-steel and plain concrete columns. (The term, concrete-steel, is used because this particular combination is not "reinforced" concrete.) One group of columns, namely, W1 to W3, 10-1/2 in. in diameter, 102 in. long, and circular in shape, stood an average ultimate load of 2,600 lb. per sq. in. These columns were of plain concrete. Another group, namely, E1 to E3, were octagonal in shape, with a short diameter (12 in.), their length being 120 in. These columns contained nine longitudinal rods, 5/8 in. in diameter, and 1/4-in. steel rings every foot. They stood an ultimate load averaging 2,438 lb. per sq. in. This is less than the column with no steel and with practically the same ratio of slenderness.
In some tests on columns made by the Department of Buildings, of Minneapolis, Minn.[D], Test A was a 9 by 9-in. column, 9 ft. 6 in. long, with ten longitudinal, round rods, 1/2 in. in diameter, and 1-1/2-in. by 3/16-in. circular bands (having two 1/2-in. rivets in the splice), spaced 4 in. apart, the circles being 7 in. in diameter. It carried an ultimate load of 130,000 lb., which is much less than half "the compressive resistance of a hooped member," worked out according to the authoritative quotation before given. Another similar column stood a little more than half that "compressive resistance." Five of the seventeen tests on the concrete-steel columns, made at Minneapolis, stood less than the plain concrete columns. So much for the longitudinal rods, and for hoops which are not close enough to stiffen the rods; and yet, in reading the literature on the subject, any one would be led to believe that longitudinal rods and hoops add enormously to the strength of a concrete column.
The sixteenth indictment against common practice is in reference to flat slabs supported on four sides. Grashof's formula for flat plates has no application to reinforced concrete slabs, because it is derived[Pg 71] for a material strong in all directions and equally stressed. The strength of concrete in tension is almost nil, at least, it should be so considered. Poisson's ratio, so prominent in Grashof's formula, has no meaning whatever in steel reinforcement for a slab, because each rod must take tension only; and instead of a material equally stressed in all directions, there are generally sets of independent rods in only two directions. In a solution of the problem given by a high English authority, the slab is assumed to have a bending moment of equal intensity along its diagonal. It is quite absurd to assume an intensity of bending clear into the corner of a slab, and on the very support equal to that at its center. A method published by the writer some years ago has not been challenged. By this method strips are taken across the slab and the moment in them is found, considering the limitations of the several strips in deflection imposed by those running at right angles therewith. This method shows (as tests demonstrate) that when the slab is oblong, reinforcement in the long direction rapidly diminishes in usefulness. When the ratio is 1:1-1/2, reinforcement in the long direction is needless, since that in the short direction is required to take its full amount. In this way French and other regulations give false results, and fail to work out.
If the writer is wrong in any or all of the foregoing points, it should be easy to disprove his assertions. It would be better to do this than to ridicule or ignore them, and it would even be better than to issue reports, signed by authorities, which commend the practices herein condemned.
[A] Presented at the meeting of March 16th, 1910.
[B] "Stresses in Reinforced Concrete Beams," Journal, Am. Soc. Mech. Engrs., Mid-October, 1909.
[C] Page 14, column 8.
[D] Engineering News, December 3d, 1908.
Joseph Wright, M. Am. Soc. C. E. (by letter).—If, as is expected, Mr. Godfrey's paper serves to attract attention to the glaring inconsistencies commonly practiced in reinforced concrete designs, and particularly to the careless detailing of such structures, he will have accomplished a valuable purpose, and will deserve the gratitude of the Profession.
No engineer would expect a steel bridge to stand up if the detailing were left to the judgment or convenience of the mechanics of the shop, yet in many reinforced concrete designs but little more thought is given to the connections and continuity of the steel than if it were an unimportant element of the structure. Such examples, as illustrated by the retaining wall in Fig. 2, are common, the reinforcing bars of the counterfort being simply hooked by a 4-in. U-bend around those of the floor and wall slabs, and penetrating the latter only from 8 to 12 in. The writer can cite an example which is still worse—that of a T-wall, 16 ft. high, in which the vertical reinforcement of the wall slab consisted of 3/4-in. bars, spaced 6 in. apart. The wall slab was 8 in. thick at the top and only 10 in. at the bottom, yet the 3/4-in. vertical bars penetrated the floor slab only 8 in., and were simply hooked around its lower horizontal bars by 4-in. U-bends. Amazing as it may appear, this structure was designed by an engineer who is well versed in the theories of reinforced concrete design. These are only two examples from a long list which might be cited to illustrate the carelessness often exhibited by engineers in detailing reinforced concrete structures.
In reinforced concrete work the detailer has often felt the need of some simple and efficient means of attaching one bar to another, but, in its absence, it is inexcusable that he should resort to such makeshifts as are commonly used. A simple U-hook on the end of a bar will develop only a small part of the strength of the bar, and, of course, should not be relied on where the depth of penetration is inadequate; and, because of the necessity of efficient anchorage of the reinforcing bars where one member of a structure unites with another, it is believed that in some instances economy might be subserved by the use of shop shapes and shop connections in steel, instead of the ordinary reinforcing bars. Such cases are comparatively few, however, for the material in common use is readily adapted to the design, in the ordinary engineering structure, and only requires that its limitations be observed, and that the designer be as conscientious and consistent in detailing as though he were designing in steel.
This paper deserves attention, and it is hoped that each point therein will receive full and free discussion, but its main purport is a plea for simplicity, consistency, and conservatism in design, with which the writer is heartily in accord.
S. Bent Russell, M. Am. Soc. C. E. (by letter).—The author has given expression in a forcible way to feelings possessed no doubt by many careful designers in the field in question. The paper will serve a useful purpose in making somewhat clearer the limitations of reinforced concrete, and may tend to bring about a more economical use of reinforcing material.
It is safe to say that in steel bridges, as they were designed in the beginning, weakness was to be found in the connections and details, rather than in the principal members. In the modern advanced practice of bridge design the details will be found to have some excess of strength over the principal members. It is probable that the design of reinforced concrete structures will take the same general course, and that progress will be made toward safety in minor details and economy in principal bars.
Many of the author's points appear to be well taken, especially the first, the third, and the eighth.
In regard to shear bars, if it is assumed that vertical or inclined bars add materially to the strength of short deep beams, it can only be explained by viewing the beam as a framed structure or truss in which the compression members are of concrete and the tension members of steel. It is evident that, as generally built, the truss will be found to be weak in the connections, more particularly, in some cases, in the connections between the tension and compression members, as mentioned in the author's first point.
It appears to the writer that this fault may be aggravated in the case of beams with top reinforcement for compression; this is scarcely touched on by the author. In such a case the top and bottom chords are of steel, with a weakly connected web system which, in practice, is usually composed of stirrup rods looped around the principal bars and held in position by the concrete which they are supposed to strengthen.
While on this phase of the subject, it may be proper to call attention to the fact that the Progress Report of the Special Committee on Concrete and Reinforced Concrete[E] may well be criticised for its scant attention to the case of beams reinforced on the compression side. No limitations are specified for the guidance of the designer, but approval is given to loading the steel with its full share of top-chord stress.[F]
In certain systems of reinforcement now in use, such as the Kahn and Cummings systems, the need for connections between the web system and the chord member is met to some degree, as is generally known. On the other hand, however, these systems do not provide for such intensity of pressure on the concrete at the points of connection as must occur by the author's demonstration in his first point. The author's criticisms on some other points would also apply to such[Pg 74] systems, and it is not necessary to state that one weak detail will limit the strength of the truss.
The author has only condemnation for the use of longitudinal rods in concrete columns (Point 15). It would seem that if the longitudinal bars are to carry a part of the load they must be supported laterally by the concrete, and, as before, in the beam, it may be likened to a framed structure in which the web system is formed of concrete alone, or of a framework of poorly connected members, and the concrete and steel must give mutual support in a way not easy to analyze. It is scarcely surprising that the strength of such a structure is sometimes less than that shown by concrete alone.
In the Minneapolis tests, quoted by the author, there are certain points which should be noted, in fairness to columns reinforced longitudinally. Only four columns thus reinforced failed below the strength shown by concrete alone, and these were from 52 to 63 days old only, while the plain concrete was 98 days old. There was nothing to hold the rods in place in these four columns except the concrete and the circular hoops surrounding them. On the other hand, all the columns in which the hooping was hooked around the individual rods showed materially greater strength than the plain concrete, although perhaps one should be excepted, as it was 158 days old and showed a strength of only 2,250 lb. per sq. in., or 12% more than the plain concrete.[G]
In considering a column reinforced with longitudinal rods and hoops, it is proper to remark that the concrete not confined by the steel ought not to be counted as aiding the latter in any way, and that, consequently, the bond of the outside bars is greatly weakened.
In view of these considerations, it may be found economical to give the steel reinforcement of columns some stiffness of its own by sufficiently connected lateral bracing. The writer would suggest, further, that in beams where rods are used in compression a system of web members sufficiently connected should be provided, so that the strength of the combined structure would be determinate.
To sum up briefly, columns and short deep beams, especially when the latter are doubly reinforced, should be designed as framed structures, and web members should be provided with stronger connections than have been customary.
J.R. Worcester, M. Am. Soc. C. E. (by letter).—This paper is of value in calling attention to many of the bad practices to be found in reinforced concrete work, and also in that it gives an opportunity for discussing certain features of design, about which engineers do not agree. A free discussion of these features will tend to unify methods. Several of the author's indictments, however, hit at practices which were discarded long ago by most designers, and are not recommended[Pg 75] by any good authorities; the implication that they are in general use is unwarranted.
The first criticism, that of bending rods at a sharp angle, may be said to be of this nature. Drawings may be made without indicating the curve, but in practice metal is seldom bent to a sharp angle. It is undoubtedly true that in every instance a gradual curve is preferable.
The author's second point, that a suitable anchorage is not provided for bent-up rods at the ends of a beam, may also be said to be a practice which is not recommended or used in the best designs.
The third point, in reference to the counterforts of retaining walls, is certainly aimed at a very reprehensible practice which should not be countenanced by any engineer.
The fourth, fifth, and sixth items bring out the fact that undoubtedly there has been some confusion in the minds of designers and authors on the subject of shear in the steel. The author is wholly justified in criticising the use of the shearing stress in the steel ever being brought into play in reinforced concrete. Referring to the report of the Special Committee on Concrete and Reinforced Concrete, on this point, it seems as if it might have made the intention of the Committee somewhat clearer had the word, tensile, been inserted in connection with the stress in the shear reinforcing rods. In considering a beam of reinforced concrete in which the shearing stresses are really diagonal, there is compression in one case and tension in another; and, assuming that the metal must be inserted to resist the tensile portion of this stress, it is not essential that it should necessarily be wholly parallel to the tensile stress. Vertical tensile members can prevent the cracking of the beam by diagonal tension, just as in a Howe truss all the tensile stresses due to shear are taken in a vertical direction, while the compressive stresses are carried in the diagonal direction by the wooden struts. The author seems to overlook the fact, however, that the reinforced concrete beam differs from the Howe truss in that the concrete forms a multiple system of diagonal compression members. It is not necessary that a stirrup at one point should carry all the vertical tension, as this vertical tension is distributed by the concrete. There is no doubt about the necessity of providing a suitable anchorage for the vertical stirrups, and such is definitely required in the recommendations of the Special Committee.
The cracks which the author refers to as being necessary before the reinforcing material is brought into action, are just as likely to occur in the case of the bent-up rods with anchors at the end, advocated by him. While his method may be a safe one, there is also no question that a suitable arrangement of vertical reinforcement may be all that is necessary to make substantial construction.
With reference to the seventh point, namely, methods of calculating moments, it might be said that it is not generally considered good[Pg 76] practice to reduce the positive moments at the center of a span to the amount allowable in a beam fully fixed at the end, and if provision is made for a negative moment over supports sufficient to develop the stresses involved in complete continuity, there is usually a considerable margin of safety, from the fact of the lack of possible fixedness of the beams at the supports. The criticism is evidently aimed at practice not to be recommended.
As to the eighth point, the necessary width of a beam in order to transfer, by horizontal shear, the stress delivered to the concrete from the rods, it might be well worth while for the author to take into consideration the fact that while the bonding stress is developed to its full extent near the ends of the beam, it very frequently happens that only a portion of the total number of rods are left at the bottom, the others having been bent upward. It may be that the width of a beam would not be sufficient to carry the maximum bonding stress on the total number of rods near its center, and yet it may have ample shearing strength on the horizontal planes. The customary method of determining the width of the beams so that the maximum horizontal shearing stress will not be excessive, seems to be a more rational method than that suggested by Mr. Godfrey.
Referring to the tenth and fourteenth points, it would be interesting to know whether the author proportions his steel to take the remaining tension without regard to the elongation possible at the point where it is located, considering the neutral axis of the section under the combined stress. Take, for instance, a chimney: If the section is first considered to be homogeneous material which will carry tension and compression equally well, and the neutral axis is found under the combined stresses, the extreme tensile fiber stress on the concrete will generally be a matter of 100 or 200 lb. Evidently, if steel is inserted to replace the concrete in tension, the corresponding stress in the steel cannot be more than from 1,500 to 3,000 lb. per sq. in. If sufficient steel is provided to keep the unit stress down to the proper figure, there can be little criticism of the method, but if it is worked to, say, 16,000 lb. per sq. in., it is evident that the result will be a different position for the neutral axis, invalidating the calculation and resulting in a greater stress in compression on the concrete.
L.J. Mensch, M. Am. Soc. C. E. (by letter).—Much of the poor practice in reinforced concrete design to which Mr. Godfrey calls attention is due, in the writer's opinion, to inexperience on the part of the designer.
It is true, however, that men of high standing, who derided reinforced concrete only a few years ago, now pose as reinforced concrete experts, and probably the author has the mistakes of these men in mind.
The questions which he propounds were settled long ago by a great many tests, made in various countries, by reliable authorities, although[Pg 77] the theoretical side is not as easily answered; but it must be borne in mind that the stresses involved are mostly secondary, and, even in steel construction, these are difficult of solution. The stresses in the web of a deep steel girder are not known, and the web is strengthened by a liberal number of stiffening angles, which no expert can figure out to a nicety. The ultimate strength of built-up steel columns is not known, frequently not even within 30%; still less is known of the strength of columns consisting of thin steel casings, or of the types used in the Quebec Bridge. It seems to be impossible to solve the problem theoretically for the simplest case, but had the designer of that bridge known of the tests made by Hodgkinson more than 40 years ago, that accident probably would not have happened.
Practice is always ahead of theory, and the writer claims that, with the great number of thoroughly reliable tests made in the last 20 years, the man who is really informed on this subject will not see any reason for questioning the points brought out by Mr. Godfrey.
The author is right in condemning sharp bends in reinforcing rods. Experienced men would not think of using them, if only for the reason that such sharp bends are very expensive, and that there is great likelihood of breaking the rods, or at least weakening them. Such sharp bends invite cracks.
Neither is there any question in regard to the advantage of continuing the bent-up rods over the supports. The author is manifestly wrong in stating that the reinforcing rods can only receive their increments of stress when the concrete is in tension. Generally, the contrary happens. In the ordinary adhesion test, the block of concrete is held by the jaws of the machine and the rod is pulled out; the concrete is clearly in compression.
The underside of continuous beams is in compression near the supports, yet no one will say that steel rods cannot take any stress there. It is quite surprising to learn that there are engineers who still doubt the advisability of using bent-up bars in reinforced concrete beams. Disregarding the very thorough tests made during the last 18 years in Europe, attention is called to the valuable tests on thirty beams made by J.J. Harding, M. Am. Soc. C. E., for the Chicago, Milwaukee and St. Paul Railroad.[H] All the beams were reinforced with about 3/4% of steel. Those with only straight rods, whether they were plain or patented bars, gave an average shearing strength of 150 lb. per sq. in. Those which had one-third of the bars bent up gave an average shearing strength of 200 lb. per sq. in., and those which had nearly one-half of the rods bent up gave an average shearing strength of 225 lb. per sq. in. Where the bent bars were continued over the supports, higher ultimate values were obtained than where some of the rods were stopped off near the supports; but in every case bent-up bars showed a greater carrying capacity than straight rods.[Pg 78] The writer knows also of a number of tests with rods fastened to anchor-plates at the end, but the tests showed that they had only a slight increase of strength over straight rods, and certainly made a poorer showing than bent-up bars. The use of such threaded bars would increase materially the cost of construction, as well as the time of erection.
The writer confesses that he never saw or heard of such poor practices as mentioned in the author's third point. On the other hand, the proposed design of counterforts in retaining walls would not only be very expensive and difficult to install, but would also be a decided step backward in mechanics. This proposition recalls the trusses used before the introduction of the Fink truss, in which the load from the upper chord was transmitted by separate members directly to the abutments, the inventor probably going on the principle that the shortest way is the best. There are in the United States many hundreds of rectangular water tanks. Are these held by any such devices? And as they are not thus held, and inasmuch as there is no doubt that they must carry the stress when filled with water, it is clear that, as long as the rods from the sides are strong enough to carry the tension and are bent with a liberal radius into the front wall and extended far enough to form a good anchorage, the connection will not be broken. The same applies to retaining walls. It would take up too much time to prove that the counterfort acts really as a beam, although the forces acting on it are not as easily found as those in a common beam.
The writer does not quite understand the author's reference to shear rods. Possibly he means the longitudinal reinforcement, which it seems is sometimes calculated to carry 10,000 lb. per sq. in. in shear. The writer never heard of such a practice.
In regard to stirrups, Mr. Godfrey seems to be in doubt. They certainly do not act as the rivets of a plate girder, nor as the vertical rods of a Howe truss. They are best compared with the dowel pins and bolts of a compound wooden beam. The writer has seen tests made on compound concrete beams separated by copper plates and connected only by stirrups, and the strength of the combination was nearly the same as that of beams made in one piece.
Stirrups do not add much to the strength of the beams where bent bars are used, but the majority of tests show a great increase of strength where only straight reinforcing bars are used. Stirrups are safeguards against poor concrete and poor workmanship, and form a good connection where concreting is interrupted through inclemency of weather or other causes. They absolutely prevent shrinkage cracks between the stem and the flange of T-beams, and the separation of the stem and slab in case of serious fires. For the latter reason, the writer condemns the use of simple U-bars, and arranges all his stirrups so that they extend from 6 to 12 in. into the slabs. Engineers[Pg 79] are warned not to follow the author's advice with regard to the omission of stirrups, but to use plenty of them in their designs, or sooner or later they will thoroughly repent it.
In regard to bending moments in continuous beams, the writer wishes to call attention to the fact that at least 99% of all reinforced structures are calculated with a reduction of 25% of the bending moment in the center, which requires only 20% of the ordinary bending moment of a freely supported beam at the supports. There may be some engineers who calculate a reduction of 33%; there are still some ultra-confident men, of little experience, who compute a reduction of 50%; but, inasmuch as most designers calculate with a reduction of only 25%, too great a factor of safety does not result, nor have any failures been observed on that account.
In the case of slabs which are uniformly loaded by earth or water pressure, the bending moments are regularly taken as (w l2)/24 in the center and (w l2)/12 at the supports. The writer never observed any failure of continuous beams over the supports, although he has often noticed failures in the supporting columns directly under the beams, where these columns are light in comparison with the beams. Failure of slabs over the supports is common, and therefore the writer always places extra rods over the supports near the top surface.
The width of the beams which Mr. Godfrey derives from his simple rule, that is, the width equals the sum of the peripheries of the reinforcing rods, is not upheld by theory or practice. In the first place, this width would depend on the kind of rods used. If a beam is reinforced by three 7/8-in. round bars, the width, according to his formula, would be 8.2 in. If the beam is reinforced by six 5/8-in. bars which have the same sectional area as the three 7/8-in. bars, then the width should be 12 in., which is ridiculous and does not correspond with tests, which would show rather a better behavior for the six bars than for the three larger bars in a beam of the same width.
It is surprising to learn that there are engineers who still advocate such a width of the stem of T-beams that the favorable influence of the slab may be dispensed with, although there were many who did this 10 or 12 years ago.
It certainly can be laid down as an axiom that the man who uses complicated formulas has never had much opportunity to design or build in reinforced concrete, as the design alone might be more expensive than the difference in cost between concrete and structural steel work.
The author attacks the application of the elastic theory to reinforced concrete arches. He evidently has not made very many designs in which he used the elastic theory, or he would have found that the[Pg 80] abutments need be only from three to four times thicker than the crown of the arch (and, therefore, their moments of inertia from 27 to 64 times greater), when the deformation of the abutments becomes negligible in the elastic equations. Certainly, the elastic theory gives a better guess in regard to the location of the line of pressure than any guess made without its use. The elastic theory was fully proved for arches by the remarkable tests, made in 1897 by the Austrian Society of Engineers and Architects, on full-sized arches of 70-ft. span, and the observed deflections and lateral deformations agreed exactly with the figured deformation.
Tests on full-sized arches also showed that the deformations caused by temperature changes agree with the elastic theory, but are not as great for the whole mass of the arch as is commonly assumed. The elastic theory enables one to calculate arches much more quickly than any graphical or guess method yet proposed.
Hooped columns are a patented construction which no one has the right to use without license or instructions from M. Considère, who clearly states that his formulas are correct only for rich concrete and for proper percentages of helical and longitudinal reinforcement, which latter must have a small spacing, in order to prevent the deformation of the core between the hoops. With these limitations his formulas are correct.
Mr. Godfrey brings up some erratic column tests, and seems to have no confidence in reinforced concrete columns. The majority of column tests, however, show an increase of strength by longitudinal reinforcement. In good concrete the longitudinal reinforcement may not be very effective or very economical, but it safeguards the strength in poorly made concrete, and is absolutely necessary on account of the bending stresses set up in such columns, due to the monolithic character of reinforced concrete work.
Mr. Godfrey does not seem to be familiar with the tests made by good authorities on square slabs of reinforced concrete and of cast iron, which latter material is also deficient in tensile strength. These tests prove quite conclusively that the maximum bending moment per linear foot may be calculated by the formulas, (w l2)/32 or (w l2)/20, according to the degree of fixture of the slabs at the four sides. Inasmuch as fixed ends are rarely obtained in practice, the formula, (w l2)/24, is generally adopted, and the writer cannot see any reason to confuse the subject by the introduction of a new method of calculation.
Walter W. Clifford, Jun. Am. Soc. C. E. (by letter).—Some of Mr. Godfrey's criticisms of reinforced concrete practice do not seem to be well taken, and the writer begs to call attention to a few points which seem to be weak. In Fig. 1, the author objects to the use of[Pg 81] diagonal bars for the reason that, if the diagonal reinforcement is stressed to the allowable limit, these bars bring the bearing on the concrete, at the point where the diagonal joins the longitudinal reinforcement, above a safe value. The concrete at the point of juncture must give, to some extent, and this would distribute the bearing over a considerable length of rod. In some forms of patented reinforcement an additional safeguard is furnished by making the diagonals of flat straps. The stress in the rods at this point, moreover, is not generally the maximum allowable stress, for considerable is taken out of the rod by adhesion between the point of maximum stress and that of juncture.
Mr. Godfrey wishes to remedy this by replacing the diagonals by rods curved to a radius of from twenty to thirty times their diameter. In common cases this radius will be about equal to the depth of the beam. Let this be assumed to be true. It cannot be assumed that these rods take any appreciable vertical shear until their slope is 30° from the horizontal, for before this the tension in the rod would be more than twice the shear which causes it. Therefore, these curved rods, assuming them to be of sufficient size to take, as a vertical component, the shear on any vertical plane between the point where it slopes 30° and its point of maximum slope, would need to be spaced at, approximately, one-half the depth of the beam. Straight rods of equivalent strength, at 45° with the axis of the beam, at this same spacing (which would be ample), would be 10% less in length.
Mr. Godfrey states:
"Of course a reinforcing rod in a concrete beam receives its stress by increments imparted by the grip of the concrete; but these increments can only be imparted where the tendency of the concrete is to stretch."
He then overlooks the fact that at the end of a beam, such as he has shown, the maximum tension is diagonal, and at the neutral axis, not at the bottom; and the rod is in the best position to resist failure on the plane, AB, if its end is sufficiently well anchored. That this rod should be anchored is, as he states, undoubtedly so, but his implied objection to a bent end, as opposed to a nut, seems to the writer to be unfounded. In some recent tests, on rods bent at right angles, at a point 5 diameters distant from the end, and with a concrete backing, stress was developed equal to the bond stress on a straight rod embedded for a length of about 30 diameters, and approximately equal to the elastic limit of the rod, which, for reinforcing purposes, is its ultimate stress.
Concerning the vertical stirrups to which Mr. Godfrey refers, there is no doubt that they strengthen beams against failure by diagonal tension or, as more commonly known, shear failures. That they are not effective in the beam as built is plain, for, if one con[Pg 82]siders a vertical plane between the stirrups, the concrete must resist the shear on this plane, unless dependence is placed on that in the longitudinal reinforcement. This, the author states, is often done, but the practice is unknown to the writer, who does not consider it of any value; certainly the stirrups cannot aid.
Suppose, however, that the diagonal tension is above the ultimate stress for the concrete, failure of the concrete will then occur on planes perpendicular to the line of maximum tension, approximately 45° at the end of the beam. If the stirrups are spaced close enough, however, and are of sufficient strength so that these planes of failure all cut enough steel to take as tension the vertical shear on the plane, then these cracks will be very minute and will be distributed, as is the case in the center of the lower part of the beam. These stirrups will then take as tension the vertical shear on any plane, and hold the beam together, so that the friction on these planes will keep up the strength of the concrete in horizontal shear. The concrete at the end of a simple beam is better able to take horizontal shear than vertical, because the compression on a horizontal plane is greater than that on a vertical plane. This idea concerning the action of stirrups falls under the ban of Mr. Godfrey's statement, that any member which "cannot act until failure has started, is not a proper element of design," but this is not necessarily true. For example, Mr. Godfrey says "the steel in the tension side of the beam should be considered as taking all the tension." This is undoubtedly true, but it cannot take place until the concrete has failed in tension at this point. If used, vertical tension members should be considered as taking all the vertical shear, and, as Mr. Godfrey states, they should certainly have their ends anchored so as to develop the strength for which they have been calculated.
The writer considers diagonal reinforcement to be the best for shear, and it should be used, especially in all cases of "unit" reinforcement; but, in some cases, stirrups can and do answer in the manner suggested; and, for reasons of practical construction, are sometimes best with "loose rod" reinforcement.
J.C. Meem, M. Am. Soc. C. E. (by letter).—The writer believes that there are some very interesting points in the author's somewhat iconoclastic paper which are worthy of careful study, and, if it be shown that he is right in most of, or even in any of, his assumptions, a further expression of approval is due to him. Few engineers have the time to show fully, by a process of reductio ad absurdum, that all the author's points are, or are not, well considered or well founded, but the writer desires to say that he has read this paper carefully, and believes that its fundamental principles are well grounded. Further, he believes that intricate mathematical formulas have no place in practice. This is particularly true where these elaborate mathematical calculations[Pg 83] are founded on assumptions which are never found in practice or experiment, and which, even in theory, are extremely doubtful, and certainly are not possible within those limits of safety wherein the engineer is compelled to work.
The writer disagrees with the author in one essential point, however, and that is in the wholesale indictment of special reinforcement, such as stirrups, shear rods, etc. In the ordinary way in which these rods are used, they have no practical value, and their theoretical value is found only when the structure is stressed beyond its safe limits; nevertheless, occasions may arise when they have a definite practical value, if properly designed and placed, and, therefore, they should not be discriminated against absolutely.
Quoting the author, that "destructive criticism is of no value unless it offers something in its place," and in connection with the author's tenth point, the writer offers the following formula which he has always used in conjunction with the design of reinforced concrete slabs and beams. It is based on the formula for rectangular wooden beams, and assumes that the beam is designed on the principle that concrete in tension is as strong as that in compression, with the understanding that sufficient steel shall be placed on the tension side to make this true, thus fixing the neutral axis, as the author suggests, in the middle of the depth, that is, M = (1/6)b d2 S, M, of course, being the bending moment, and b and d, the breadth and depth, in inches. S is usually taken at from 400 to 600 lb., according to the conditions. In order to obtain the steel necessary to give the proper tensile strength to correspond with the compression side, the compression and tension areas of the beam are equated, that is
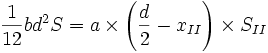 |
, |
where
a = the area of steel per linear foot,
xII = the distance from the center of the steel to the outer fiber, and
SII = the strength of the steel in tension.
Then for a beam, 12 in. wide,
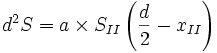 |
, |
or
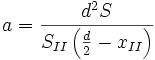 |
. |
Carrying this to its conclusion, we have, for example, in a beam 12 in. deep and 12 in. wide,
| S | = 500, |
| SII | = 15,000, |
| xII | = 2-1/2 in. |
| a | = 1.37 sq. in. per ft. |
The writer has used this formula very extensively, in calculating new work and also in checking other designs built or to be built, and he believes its results are absolutely safe. There is the further fact to its credit, that its simplicity bars very largely the possibility of error from its use. He sees no reason to introduce further complications into such a formula, when actual tests will show results varying more widely than is shown by a comparison between this simple formula and many more complicated ones.
George H. Myers, Jun. Am. Soc. C. E. (by letter).—This paper brings out a number of interesting points, but that which strikes the writer most forcibly is the tenth, in regard to elaborate theories and complicated formulas for beams and slabs. The author's stand for simplicity in this regard is well taken. A formula for the design of beams and slabs need not be long or complicated in any respect. It can easily be obtained from the well-known fact that the moment at any point divided by the distance between the center of compression and the center of tension at that point gives the tension (or compression) in the beam.
The writer would place the neutral axis from 0.42 to 0.45 of the effective depth of the beam from the compression side rather than at the center, as Mr. Godfrey suggests. This higher position of the neutral axis is the one more generally shown by tests of beams. It gives the formula M = 0.86 d As f, or M = 0.85 d As f, which the writer believes is more accurate than M = 5/6 d As f, or 0.83-1/3 d As f, which would result if the neutral axis were taken at the center of the beam.
d = depth of the beam from the compression side to the center
of the steel;
As = the area of the steel;
and f = the allowable stress per square inch in the steel.
The difference, however, is very slight, the results from the two formulas being proportional to the two factors, 83-1/3 and 85 or 86. This formula gives the area of steel required for the moment. The percentage of steel to be used can easily be obtained from the allowable stresses in the concrete and the steel, and the dimensions of the beam can be obtained in the simplest manner. This formula is used with great success by one of the largest firms manufacturing reinforcing materials and designing concrete structures. It is well-known to the Profession, and the reason for using any other method, involving the Greek alphabet and many assumptions, is unknown to the writer. The only thing to assume—if it can be called assuming when there are so many tests to locate it—is the position of the neutral axis. A slight difference in this assumption affects the resulting design very little, and is inappreciable, from a practical point of view. It can be[Pg 85] safely said that the neutral axis is at, or a little above, the center of the beam.
Further, it would seem that the criticism to the effect that the initial stress in the concrete is neglected is devoid of weight. As far as the designer is concerned, the initial stress is allowed for. The values for the stresses used in design are obtained from tests on blocks of concrete which have gone through the process of setting. Whatever initial stress exists in concrete due to this process of setting exists also in these blocks when they are tested. The value of the breaking load on concrete given by any outside measuring device used in these tests, is the value of that stress over and above this initial stress. It is this value with which we work. It would seem that, if the initial stress is neglected in arriving at a safe working load, it would be safe to neglect it in the formula for design.
Edwin Thacher, M. Am. Soc. C. E. (by letter).—The writer will discuss this paper under the several "points" mentioned by the author.
First Point.—At the point where the first rod is bent up, the stress in this rod runs out. The other rods are sufficient to take the horizontal stress, and the bent-up portion provides only for the vertical and diagonal shearing stresses in the concrete.
Second Point.—The remarks on the first point are also applicable to the second one. Rod 3 provides for the shear.
Third Point.—In a beam, the shear rods run through the compression parts of the concrete and have sufficient anchorage. In a counterfort, the inclined rods are sufficient to take the overturning stress. The horizontal rods support the front wall and provide for shrinkage. The vertical rods also provide for shrinkage, and assist the diagonal rods against overturning. The anchorage is sufficient in all cases, and the proposed method is no more effective.
Fourth Point.—In bridge pins, bending and bearing usually govern, but, in case a wide bar pulled on a pin between the supports close to the bar, as happens in bolsters and post-caps of combination bridges and in other locations, shear would govern. Shear rods in concrete-steel beams are proportioned to take the vertical and diagonal shearing stresses. If proportioned for less stress per square inch than is used in the bottom bars, this cannot be considered dangerous practice.
Fifth Point.—Vertical stirrups are designed to act like the vertical rods in a Howe truss. Special literature is not required on the subject; it is known that the method used gives good results, and that is sufficient.
Sixth Point.—The common method is not "to assume each shear member as taking the horizontal shear occurring in the space from[Pg 86] member to member," but to take all the shear from the center of the beam up to the bar in question.
Cracks do not necessarily endanger the safety of a beam. Any device that will prevent the cracks from opening wide enough to destroy the beam, is logical. By numerous experiments, Mr. Thaddeus Hyatt found that nuts and washers at the ends of reinforcing bars were worse than useless, and added nothing to the strength of the beams.
Seventh Point.—Beams can be designed, supported at the ends, fully continuous, or continuous to a greater or less extent, as desired. The common practice is to design slabs to take a negative moment over the supports equal to one-half the positive moment at the center, or to bend up the alternate rods. This is simple and good practice, for no beam can fail as long as a method is provided by which to take care of all the stresses without overstraining any part.
Eighth Point.—Bars in the bottom of a reinforced concrete beam are often placed too close to one another. The rule of spacing the bars not less than three diameters apart, is believed to be good practice.
Ninth Point.—To disregard the theory of T-beams, and work by rule-of-thumb, can hardly be considered good engineering.
Tenth Point.—The author appears to consider theories for reinforced concrete beams and slabs as useless refinements, but as long as theory and experiment agree so wonderfully well, theories will undoubtedly continue to be used.
Eleventh Point.—Calculations for chimneys are somewhat complex, but are better and safer than rule-of-thumb methods.
Twelfth Point.—Deflection is not very important.
Thirteenth Point.—The conclusion of the Austrian Society of Engineers and Architects, after numerous experiments, was that the elastic theory of the arch is the only true theory. No arch designed by the elastic theory was ever known to fail, unless on account of insecure foundations, therefore engineers can continue to use it with confidence and safety.
Fourteenth Point.—Calculations for temperature stresses, as per theory, are undoubtedly correct for the variations in temperature assumed. Similar calculations can also be made for shrinkage stresses, if desired. This will give a much better idea of the stresses to be provided for, than no calculations at all.
Fifteenth Point.—Experiments show that slender longitudinal rods, poorly supported, and embedded in a concrete column, add little or nothing to its strength; but stiff steel angles, securely latticed together, and embedded in the concrete column, will greatly increase its strength, and this construction is considered the most desirable when the size of the column has to be reduced to a minimum.
Sixteenth Point.—The commonly accepted theory of slabs supported on four sides can be correctly applied to reinforced concrete slabs, as it is only a question of providing for certain moments in the slab. This theory shows that unless the slab is square, or nearly so, nothing is to be gained by such construction.
C.A.P. Turner, M. Am. Soc. C. E. (by letter).—Mr. Godfrey has expressed his opinion on many questions in regard to concrete construction, but he has adduced no clean-cut statement of fact or tests, in support of his views, which will give them any weight whatever with the practical matter-of-fact builder.
The usual rules of criticism place the burden of proof on the critic. Mr. Godfrey states that if his personal opinions are in error, it should be easy to prove them to be so, and seems to expect that the busy practical constructor will take sufficient interest in them to spend the time to write a treatise on the subject in order to place him right in the matter.
The writer will confine his discussion to only a few points of the many on which he disagrees with Mr. Godfrey.
First, regarding stirrups: These may be placed in the beam so as to be of little practical value. They were so placed in the majority of the tests made at the University of Illinois. Such stirrups differ widely in value from those used by Hennebique and other first-class constructors.
Mr. Godfrey's idea is that the entire pull of the main reinforcing rod should be taken up apparently at the end. When one frequently sees slabs tested, in which the steel breaks at the center, with no end anchorage whatever for the rods, the soundness of Mr. Godfrey's position may be questioned.
Again, concrete is a material which shows to the best advantage as a monolith, and, as such, the simple beam seems to be decidedly out of date to the experienced constructor.
Mr. Godfrey appears to consider that the hooping and vertical reinforcement of columns is of little value. He, however, presents for consideration nothing but his opinion of the matter, which appears to be based on an almost total lack of familiarity with such construction.
The writer will state a few facts regarding work which he has executed. Among such work have been columns in a number of buildings, with an 18-in. core, and carrying more than 500 tons; also columns in one building, which carry something like 1100 tons on a 27-in. core. In each case there is about 1-1/2 in. of concrete outside the core for a protective coating. The working stress on the core, if it takes the load, is approximately equal to the ultimate strength of the concrete in cubes, to say nothing of the strength of cylinders fifteen times their diameter in height. These values have been used with[Pg 88] entire confidence after testing full-sized columns designed with the proper proportions of vertical steel and hooping, and are regarded by the writer as having at least double the factor of safety used in ordinary designs of structural steel.
An advantage which the designer in concrete has over his fellow-engineer in the structural steel line, lies in the fact that, with a given type of reinforcement, his members are similar in form, and when the work is executed with ordinary care, there is less doubt as to the distribution of stress through a concrete column, than there is with the ordinary structural steel column, since the core is solid and the conditions are similar in all cases.
Tests of five columns are submitted herewith. The columns varied little in size, but somewhat in the amount of hooping, with slight differences in the vertical steel. The difference between Columns 1 and 3 is nearly 50%, due principally to the increase in hooping, and to a small addition in the amount of vertical steel. As to the efficiency of hooping and vertical reinforcement, the question may be asked Mr. Godfrey, and those who share his views, whether a column without reinforcement can be cast, which will equal the strength of those, the tests of which are submitted.
Marks on column—none.
Reinforcement—eight 1-1/8-in. round bars vertically.
Band spacing—- 9 in. vertically.
Hooped with seven 32-in. wire spirals about 2-in. raise.
Outside diameter of hoops—14-1/2 in.
Total load at failure—1,360,000 lb.
Remarks.—Point of failure was about 22 in. from the top. Little indication of failure until ultimate load was reached.
Some slight breaking off of concrete near the top cap, due possibly to the cap not being well seated in the column itself.
Marks on column—Box 4.
Reinforcement—eight 1-1/8-in. round bars vertically.
Band spacing about 13 in. vertically.
Wire spiral about 3-in. pitch.
Point of failure about 18 in. from top.
Top of cast-iron cap cracked at four corners.
Ultimate load—1,260,000 lb.
Remarks.—Both caps apparently well seated, as was the case with all the subsequent tests.
Marks on column—4-B.
Reinforcement—eight 7/8-in. round bars vertically.
Hoops—1-3/4 in. × 3/16 in. × 14 in. outside diameter.
Band spacing—13 in. vertically.
Ultimate load—900,000 lb.
Point of failure about 2 ft. from top.
Remarks.—Concrete, at failure, considerably disintegrated, probably due to continuance of movement of machine after failure.
Marks on column—Box 4.
Reinforcement—eight 1-in. round bars vertically.
Hoops spaced 8 in. vertically.
Wire spirals as on other columns.
Total load at failure—1,260,000 lb.
Remarks.—First indications of failure were nearest the bottom end of the column, but the total failure was, as in all other columns, within 2 ft. of the top. Large cracks in the shell of the column extended from both ends to very near the middle. This was the most satisfactory showing of all the columns, as the failure was extended over nearly the full length of the column.
Marks on column—none.
Reinforcement—eight 7/8-in. bars vertically.
Hoops spaced 10 in. vertically.
Outside diameter of hoops—14-1/2 in.
Wire spiral as before.
Load at failure—1,100,000 lb.
Ultimate load—1,130,000 lb.
Remarks.—The main point of failure in this, as in all other columns, was within 2 ft. of the top, although this column showed some scaling off at the lower end.
In these tests it will be noted that the concrete outside of the hooped area seems to have had very little value in determining the ultimate strength; that, figuring the compression on the core area and deducting the probable value of the vertical steel, these columns exhibited from 5,000 to 7,000 lb. per sq. in. as the ultimate strength of the hooped area, not considering the vertical steel. Some of them run over 8,000 lb.
The concrete mixture was 1 part Alpena Portland cement, 1 part sand, 1-1/2 parts buckwheat gravel and 3-1/2 parts gravel ranging from 1/4 to 3/4 in. in size.
The columns were cast in the early part of December, and tested in April. The conditions under which they hardened were not particularly favorable, owing to the season of the year.
The bands used were 1-3/4 by 1/4 in., except in the light column, where they were 1-3/4 by 3/16 in.
In his remarks regarding the tests at Minneapolis, Minn., Mr. Godfrey has failed to note that these tests, faulty as they undoubtedly were, both in the execution of the work, and in the placing of the reinforcement, as well as in the character of the hooping used, were sufficient to satisfy the Department of Buildings that rational design took into consideration the amount of hooping and the amount of vertical[Pg 90] steel, and on a basis not far from that which the writer considers reasonable practice.
Again, Mr. Godfrey seems to misunderstand the influence of Poisson's ratio in multiple-way reinforcement. If Mr. Godfrey's ideas are correct, it will be found that a slab supported on two sides, and reinforced with rods running directly from support to support, is stronger than a similar slab reinforced with similar rods crossing it diagonally in pairs. Tests of these two kinds of slabs show that those with the diagonal reinforcement develop much greater strength than those reinforced directly from support to support. Records of small test slabs of this kind will be found in the library of the Society.
Mr. Godfrey makes the good point that the accuracy of an elastic theory must be determined by the elastic deportment of the construction under load, and it seems to the writer that if authors of textbooks would pay some attention to this question and show by calculation that the elastic deportment of slabs is in keeping with their method of figuring, the gross errors in the theoretical treatment of slabs in the majority of works on reinforced concrete would be remedied.
Although he makes the excellent point noted, Mr. Godfrey very inconsistently fails to do this in connection with his theory of slabs, otherwise he would have perceived the absurdity of any method of calculating a multiple-way reinforcement by endeavoring to separate the construction into elementary beam strips. This old-fashioned method was discarded by the practical constructor many years ago, because he was forced to guarantee deflections of actual construction under severe tests. Almost every building department contains some regulation limiting the deflection of concrete floors under test, and yet no commissioner of buildings seems to know anything about calculating deflections.
In the course of his practice the writer has been required to give surety bonds of from $50,000 to $100,000 at a time, to guarantee under test both the strength and the deflection of large slabs reinforced in multiple directions, and has been able to do so with accuracy by methods which are equivalent to considering Poisson's ratio, and which are given in his book on concrete steel construction.
Until the engineer pays more attention to checking his complicated theories with facts as determined by tests of actual construction, the view, now quite general among the workers in reinforced concrete regarding him will continue to grow stronger, and their respect for him correspondingly less, until such time as he demonstrates the applicability of his theories to ordinary every-day problems.
Paul Chapman, Assoc. M. Am. Soc. C. E. (by letter).—Mr. Godfrey has pointed out, in a forcible manner, several bad features of text-book design of reinforced concrete beams and retaining walls. The practical engineer, however, has never used such methods of construc[Pg 91]tion. Mr. Godfrey proposes certain rules for the calculation of stresses, but there are no data of experiments, or theoretical demonstrations, to justify their use.
It is also of the utmost importance to consider the elastic behavior of structures, whether of steel or concrete. To illustrate this, the writer will cite a case which recently came to his attention. A roof was supported by a horizontal 18-in. I-beam, 33 ft. long, the flanges of which were coped at both ends, and two 6 by 4-in. angles, 15 ft. long, supporting the same, were securely riveted to the web, thereby forming a frame to resist lateral wind pressure. Although the 18-in. I-beam was not loaded to its full capacity, its deflection caused an outward flexure of 3/4 in. and consequent dangerous stresses in the 6 by 4-in. angle struts. The frame should have been designed as a structure fixed at the base of the struts. The importance of the elastic behavior of a structure is forcibly illustrated by comparing the contract drawings for a great cantilever bridge which spans the East River with the expert reports on the same. Due to the neglect of the elastic behavior of the structure in the contract drawings, and another cause, the average error in the stresses of 290 members was 18-1/2%, with a maximum of 94 per cent.
Mr. Godfrey calls attention to the fact that stringers in railroad bridges are considered as simple beams; this is theoretically proper because the angle knees at their ends can transfer practically no flange stress. It is also to be noted that when stringers are in the plane of a tension chord, they are milled to exact lengths, and when in the plane of a compression chord, they are given a slight clearance in order to prevent arch action.
The action of shearing stresses in concrete beams may be illustrated by reference to the diagrams in Fig. 3, where the beams are loaded with a weight, W. The portion of W traveling to the left support, moves in diagonal lines, varying from many sets of almost vertical lines to a single diagonal. The maximum intensity of stress probably would be in planes inclined about 45°, since, considered independently, they produce the least deflection. While the load, W, remains relatively small, producing but moderate stresses in the steel in the bottom flange, the concrete will carry a considerable portion of the bottom flange tension; when the load W is largely increased, the coefficient of elasticity of the concrete in tension becomes small, or zero, if small fissures appear, and the concrete is unable to transfer the tension[Pg 92] in diagonal planes, and failure results. For a beam loaded with a single load, W, the failure would probably be in a diagonal line near the point of application, while in a uniformly loaded beam, it would probably occur in a diagonal line near the support, where the shear is greatest.
It is evident that the introduction of vertical stirrups, as at b, or the more rational inclined stirrups, as at c, influences the action of the shearing forces as indicated, the intensity of stress at the point of connection of the stirrups being high. It is advisable to space the stirrups moderately close, in order to reduce this intensity to reasonable limits. If the assumption is made that the diagonal compression in the concrete acts in a plane inclined at 45°, then the tension in the vertical stirrups will be the vertical shear times the horizontal spacing of the stirrups divided by the distance, center to center, of the top and bottom flanges of the beam. If the stirrups are inclined at 45°, the stress in them would be 0.7 the stress in vertical stirrups with the same spacing. Bending up bottom rods sharply, in order to dispense with suspenders, is bad practice; the writer has observed diagonal cracks in the beams of a well-known building in New York City, which are due to this cause.
In several structures which the writer has recently designed, he has been able to dispense with stirrups, and, at the same time, effect a saving in concrete, by bending some of the bottom reinforcing rods and placing a bar between them and those which remain horizontal. A typical detail is shown in Fig. 4. The bend occurs at a point where the vertical component of the stress in the bent bars equals the vertical shear, and sufficient bearing is provided by the short cross-bar. The bars which remain horizontal throughout the beam, are deflected at the center of the beam in order to obtain the maximum effective depth. There being no shear at the center, the bars are spaced as closely as possible, and still provide sufficient room for the concrete to flow to the soffit of the beam. Two or more adjacent beams are readily made continuous by extending the bars bent up from each span, a distance along the top flanges. By this system of construction one avoids stopping a bar where the live load unit stress in adjoining bars is high, as their continual lengthening and shortening under stress would cause severe shearing stresses in the concrete surrounding the end of the short bar.
The beam shown in Fig. 5 illustrates the principles stated in the foregoing, as applied to a heavier beam. The duty of the short cross-bars in this case is performed by wires wrapped around the longitudinal rods and then continued up in order to support the bars during erection. This beam, which supports a roof and partitions, etc., has supported about 80% of the load for which it was calculated, and no hair cracks or noticeable deflection have appeared. If the method of calculation suggested by Mr. Godfrey were a correct criterion of the actual stresses, this particular beam (and many others) would have shown many cracks and noticeable deflection. The writer maintains that where the concrete is poured continuously, or proper bond is provided, the influence of the slab as a compression flange is an actual condition, and the stresses should be calculated accordingly.
In the calculation of continuous T-beams, it is necessary to consider the fact that the moment of inertia for negative moments is small because of the lack of sufficient compressive area in the stem or web. If Mr. Godfrey will make proper provision for this point, in studying the designs of practical engineers, he will find due provision made for negative moments. It is very easy to obtain the proper amount of steel for the negative moment in a slab by bending up the bars and letting them project into adjoining spans, as shown in Figs. 4 and 5 (taken from actual construction). The practical engineer does not find, as Mr. Godfrey states, that the negative moment is double the positive moment, because he considers the live load either on one span only, or on alternate spans.
In Fig. 6 a beam is shown which has many rods in the bottom flange, a practice which Mr. Godfrey condemns. As the structure, which has about twenty similar beams, is now being built, the writer would be thankful for his criticism. Mr. Godfrey states that longitudinal steel in columns is worthless, but until definite tests are made,[Pg 94] with the same ingredients, proportions, and age, on both plain concrete and reinforced concrete columns properly designed, the writer will accept the data of other experiments, and proportion steel in accordance with recognized formulas.
Mr. Godfrey states that the "elastic theory" is worthless for the design of reinforced concrete arches, basing his objections on the shrinkage of concrete in setting, the unreliability of deflection formulas for beams, and the lack of rigidity of the abutments. The writer, noting that concrete setting in air shrinks, whereas concrete setting in water expands, believes that if the arch be properly wetted until the setting up of the concrete has progressed sufficiently, the effect of shrinkage, on drying out, may be minimized. If the settlement of the forms themselves be guarded against during the construction of an arch, the settlement of the arch ring, on removing the forms, far from being an uncertain element, should be a check on the accuracy of the calculations and the workmanship, since the weight of the arch ring should produce theoretically a certain deflection. The unreliability of deflection formulas for beams is due mainly to the fact that the neutral axis of the beam does not lie in a horizontal plane throughout, and that the shearing stresses are neglected therein. While there is necessarily bending in an arch ring due to temperature, loads, etc., the extreme flanges sometimes being in tension, even in a properly designed arch, the compression exceeds the tension to such an extent that comparison to a beam does not hold true. An arch should not be used where the abutments are unstable, any more than a suspension bridge should be built where a suitable anchorage cannot be obtained.
The proper design of concrete slabs supported on four sides is a complex and interesting study. The writer has recently designed a floor construction, slabs, and beams, supported on four corners, which is simple and economical. In Fig. 7 is shown a portion of a proposed[Pg 95] twelve-story building, 90 by 100 ft., having floors with a live-load capacity of 250 lb. per sq. ft. For the maximum positive bending in any panel the full load on that panel was considered, there being no live load on adjoining panels. For the maximum negative bending moment all panels were considered as loaded, and in a single line. "Checker-board" loading was considered too improbable for consideration. The flexure curves for beams at right angles to each other were similar (except in length), the tension rods in the longer beams being placed underneath those in the shorter beams. Under full load, therefore, approximately one-half of the load went to the long-span girder and the other half to the short-span girder. The girders were the same depth as the beams. For its depth the writer found this system to be the strongest and most economical of those investigated.
E.P. Goodrich, M. Am. Soc. C. E.—The speaker heartily concurs with the author as to the large number of makeshifts constantly used by a majority of engineers and other practitioners who design and construct work in reinforced concrete. It is exceedingly difficult for the human mind to grasp new ideas without associating them with others in past experience, but this association is apt to clothe the new idea (as the author suggests) in garments which are often worse than "swaddling-bands," and often go far toward strangling proper growth.
While the speaker cannot concur with equal ardor with regard to all the author's points, still in many, he is believed to be well grounded in his criticism. Such is the case with regard to the first point mentioned—that of the use of bends of large radius where the main tension rods are bent so as to assist in the resistance of diagonal tensile stresses.
As to the second point, provided proper anchorage is secured in the top concrete for the rod marked 3 in Fig. 1, the speaker cannot see why the concrete beneath such anchorage over the support does not act exactly like the end post of a queen-post truss. Nor can he understand the author's statement that:
"A reinforcing rod in a concrete beam receives its stress by increments imparted by the grip of the concrete; but these increments can only be imparted where the tendency of the concrete is to stretch."
The latter part of this quotation has reference to the point questioned by the speaker. In fact, the remainder of the paragraph from which this quotation is taken seems to be open to grave question, no reason being evident for not carrying out the analogy of the queen-post truss to the extreme. Along this line, it is a well-known fact that the bottom chords in queen-post trusses are useless, as far as resistance to tension is concerned. The speaker concurs, however, in the author's criticism as to the lack of anchorage usually found in most reinforcing rods, particularly those of the type mentioned in the author's second point.
This matter of end anchorage is also referred to in the third point, and is fully concurred in by the speaker, who also concurs in the criticism of the arrangement of the reinforcing rods in the counterforts found in many retaining walls. The statement that "there is absolutely no analogy between this triangle [the counterfort] and a beam" is very strong language, and it seems risky, even for the best engineer, to make such a statement as does the author when he characterizes his own design (Diagram b of Fig. 2) as "the only rational and the only efficient design possible." Several assumptions can be made on which to base the arrangement of reinforcement in the counterfort of a retaining wall, each of which can be worked out with equal logic and with results which will prevent failure, as has been amply demonstrated by actual experience.
The speaker heartily concurs in the author's fourth point, with regard to the impossibility of developing anything like actual shear in the steel reinforcing rods of a concrete beam; but he demurs when the author affirms, as to the possibility of so-called shear bars being stressed in "shear or tension," that "either would be absurd and impossible without greatly overstressing some other part."
As to the fifth point, reference can be given to more than one place in concrete literature where explanations of the action of vertical stirrups may be found, all of which must have been overlooked by the author. However, the speaker heartily concurs with the author's criticism as to the lack of proper connection which almost invariably exists between vertical "web" members and the top and bottom chords of the imaginary Howe truss, which holds the nearest analogy to the conditions existing in a reinforced concrete beam with vertical "web" reinforcement.
The author's reasoning as to the sixth point must be considered as almost wholly facetious. He seems to be unaware of the fact that concrete is relatively very strong in pure shear. Large numbers of tests seem to demonstrate that, where it is possible to arrange the reinforcing members so as to carry largely all tensile stresses developed through shearing action, at points where such tensile stresses cannot be carried by the concrete, reinforced concrete beams can be designed of ample strength and be quite within the logical processes developed by the author, as the speaker interprets them.
The author's characterization of the results secured at the University of Illinois Experiment Station, and described in its Bulletin No. 29, is somewhat misleading. It is true that the wording of the original reference states in two places that "stirrups do not come into action, at least not to any great extent, until a diagonal crack has formed," but, in connection with this statement, the following quotations must be read:
"The tests were planned with a view of determining the amount of stress (tension and bond) developed in the stirrups. However, for[Pg 97] various reasons, the results are of less value than was expected. The beams were not all made according to the plans. In the 1907 tests, the stirrups in a few of the beams were poorly placed and even left exposed at the face of the beam, and a variation in the temperature conditions of the laboratory also affected the results. It is evident from the results that the stresses developed in the stirrups are less than they were calculated to be, and hence the layout was not well planned to settle the points at issue. The tests, however, give considerable information on the effectiveness of stirrups in providing web resistance."
"A feature of the tests of beams with stirrups is slow failure, the load holding well up to the maximum under increased deflection and giving warning of its condition."
"Not enough information was obtained to determine the actual final occasion of failure in these tests. In a number of cases the stirrups slipped, in others it seemed that the steel in the stirrups was stretched beyond its elastic limit, and in some cases the stirrups broke."
"As already stated, slip of stirrups and insufficient bond resistance were in many cases the immediate cause of diagonal tension failures, and therefore bond resistance of stirrups may be considered a critical stress."
These quotations seem to indicate much more effectiveness in the action of vertical stirrups than the author would lead one to infer from his criticisms. It is rather surprising that he advocates so strongly the use of a suspension system of reinforcement. That variety has been used abroad for many years, and numerous German experiments have proved with practical conclusiveness that the suspension system is not as efficient as the one in which vertical stirrups are used with a proper arrangement. An example is the conclusion arrived at by Mörsch, in "Eisenbetonbau," from a series of tests carried out by him near the end of 1906:
"It follows that with uniform loads, the suspended system of reinforcement does not give any increase of safety against the appearance of diagonal tension cracks, or the final failure produced by them, as compared with straight rods without stirrups, and that stirrups are so much the more necessary."
Again, with regard to tests made with two concentrated loads, he writes:
"The stirrups, supplied on one end, through their tensile strength, hindered the formation of diagonal cracks and showed themselves essential and indispensable elements in the * * * [suspension] system. The limit of their effect is, however, not disclosed by these experiments. * * * In any case, from the results of the second group of experiments can be deduced the facts that the bending of the reinforcement according to the theory concerning the diagonal tensile stress * * * is much more effective than according to the suspension theory, in this case the ultimate loads being in the proportion of 34: 23.4: 25.6."
It is the speaker's opinion that the majority of the failures described in Bulletin No. 29 of the University of Illinois Experiment Station, which are ascribed to diagonal tension, were actually due to deficient anchorage of the upper ends of the stirrups.
Some years ago the speaker demonstrated to his own satisfaction, the practical value of vertical stirrups. Several beams were built identical in every respect except in the size of wire used for web reinforcement. The latter varied from nothing to 3/8-in. round by five steps. The beams were similarly tested to destruction, and the ultimate load and type of failure varied in a very definite ratio to the area of vertical steel.
With regard to the author's seventh point, the speaker concurs heartily as far as it has to do with a criticism of the usual design of continuous beams, but his experience with beams designed as suggested by the author is that failure will take place eventually by vertical cracks starting from the top of the beams close to the supports and working downward so as to endanger very seriously the strength of the structures involved. This type of failure was prophesied by the speaker a number of years ago, and almost every examination which he has lately made of concrete buildings, erected for five years or longer and designed practically in accord with the author's suggestion, have disclosed such dangerous features, traceable directly to the ideas described in the paper. These ideas are held by many other engineers, as well as being advocated by the author. The only conditions under which the speaker would permit of the design of a continuous series of beams as simple members would be when they are entirely separated from each other over the supports, as by the introduction of artificial joints produced by a double thickness of sheet metal or building paper. Even under these conditions, the speaker's experience with separately moulded members, manufactured in a shop and subsequently erected, has shown that similar top cracking may take place under certain circumstances, due to the vertical pressures caused by the reactions at the supports. It is very doubtful whether the action described by the author, as to the type of failure which would probably take place with his method of design, would be as described by him, but the beams would be likely to crack as described above, in accordance with the speaker's experience, so that the whole load supported by the beam would be carried by the reinforcing rods which extend from the beam into the supports and are almost invariably entirely horizontal at such points. The load would thus be carried more nearly by the shearing strength of the steel than is otherwise possible to develop that type of stress. In every instance the latter is a dangerous element.
This effect of vertical abutment action on a reinforced beam was very marked in the beam built of bricks and tested by the speaker, as described in the discussion[J] of the paper by John S. Sewell, M. Am,[Pg 99] Soc. S. E., on "The Economical Design of Reinforced Concrete Floor Systems for Fire-Resisting Structures." That experiment also went far toward showing the efficacy of vertical stirrups.
The same discussion also contains a description of a pair of beams tested for comparative purposes, in one of which adhesion between the concrete and the main reinforcing rods was possible only on the upper half of the exterior surfaces of the latter rods except for short distances near the ends. Stirrups were used, however. The fact that the beam, which was theoretically very deficient in adhesion, failed in compression, while the similar beam without stirrups, but with the most perfect adhesion, and anchorage obtainable through the use of large end hooks, failed in bond, has led the speaker to believe that, in affording adhesive resistance, the upper half of a bar is much more effective than the lower half. This seems to be demonstrated further by comparisons between simple adhesion experiments and those obtained with beams.
The speaker heartily concurs with the author's criticism of the amount of time usually given by designing engineers to the determination of the adhesive stresses developed in concrete beams, but, according to the speaker's recollection, these matters are not so poorly treated in some books as might be inferred by the author's language. For example, both Bulletin No. 29, of the University of Illinois, and Mörsch, in "Eisenbetonbau," give them considerable attention.
The ninth point raised by the author is well taken. Too great emphasis cannot be laid on the inadequacy of design disclosed by an examination of many T-beams.
Such ready concurrence, however, is not lent to the author's tenth point. While it is true that, under all usual assumptions, except those made by the author, an extremely simple formula for the resisting moment of a reinforced concrete beam cannot be obtained, still his formula falls so far short of fitting even with approximate correctness the large number of well-known experiments which have been published, that a little more mathematical gymnastic ability on the part of the author and of other advocates of extreme simplicity would seem very necessary, and will produce structures which are far more economical and amply safe structurally, compared with those which would be produced in accordance with his recommendations.
As to the eleventh point, in regard to the complex nature of the formulas for chimneys and other structures of a more or less complex beam nature, the graphical methods developed by numerous German and Italian writers are recommended, as they are fully as simple as the rather crude method advocated by the author, and are in almost identical accord with the most exacting analytical methods.
With regard to the author's twelfth point, concerning deflection calculations, it would seem that they play such a small part in reinforced concrete design, and are required so rarely, that any engineer[Pg 100] who finds it necessary to make analytical investigations of possible deflections would better use the most precise analysis at his command, rather than fall back on simpler but much more approximate devices such as the one advocated by the author.
Much of the criticism contained in the author's thirteenth point, concerning the application of the elastic theory to the design of concrete arches, is justified, because designing engineers do not carry the theory to its logical conclusion nor take into account the actual stresses which may be expected from slight changes of span, settlements of abutments, and unexpected amounts of shrinkage in the arch ring or ribs. Where conditions indicate that such changes are likely to take place, as is almost invariably the case unless the foundations are upon good rock and the arch ring has been concreted in relatively short sections, with ample time and device to allow for initial shrinkage; or unless the design is arranged and the structure erected so that hinges are provided at the abutments to act during the striking of the falsework, which hinges are afterward wedged or grouted so as to produce fixation of the arch ends—unless all these points are carefully considered in the design and erection, it is the speaker's opinion that the elastic theory is rarely properly applicable, and the use of the equilibrium polygon recommended by the author is much preferable and actually more accurate. But there must be consistency in its use, as well, that is, consistency between methods of design and erection.
The author's fourteenth point—the determination of temperature stresses in a reinforced concrete arch—is to be considered in the same light as that described under the foregoing points, but it seems a little amusing that the author should finally advocate a design of concrete arch which actually has no hinges, namely, one consisting of practically rigid blocks, after he has condemned so heartily the use of the elastic theory.
A careful analysis of the data already available with regard to the heat conductivity of concrete, applied to reinforced concrete structures like arches, dams, retaining walls, etc., in accordance with the well-known but somewhat intricate mathematical formulas covering the laws of heat conductivity and radiation so clearly enunciated by Fourier, has convinced the speaker that it is well within the bounds of engineering practice to predict and care for the stresses which will be produced in structures of the simplest forms, at least as far as they are affected by temperature changes.
The speaker concurs with the author in his criticism, contained in the fifteenth point, with regard to the design of the steel reinforcement in columns and other compression members. While there may be some question as to the falsity or truth of the theory underlying certain types of design, it is unquestioned that some schemes of arrangement undoubtedly produce designs with dangerous properties. The speaker[Pg 101] has several times called attention to this point, in papers and discussions, and invariably in his own practice requires that the spacing of spirals, hoops, or ties be many times less than that usually required by building regulations and found in almost every concrete structure. Mörsch, in his "Eisenbetonbau," calls attention to the fact that very definite limits should be placed on the maximum size of longitudinal rods as well as on their minimum diameters, and on the maximum spacing of ties, where columns are reinforced largely by longitudinal members. He goes so far as to state that:
"It is seen from * * * [the results obtained] that an increase in the area of longitudinal reinforcement does not produce an increase in the breaking strength to the extent which would be indicated by the formula. * * * In inexperienced hands this formula may give rise to constructions which are not sufficiently safe."
Again, with regard to the spacing of spirals and the combination with them of longitudinal rods, in connection with some tests carried out by Mörsch, the conclusion is as follows:
"On the whole, the tests seem to prove that when the spirals are increased in strength, their pitch must be decreased, and the cross-section or number of the longitudinal rods must be increased."
In the majority of cases, the spiral or band spacing is altogether too large, and, from conversations with Considère, the speaker understands that to be the inventor's view as well.
The speaker makes use of the scheme mentioned by the author in regard to the design of flat slabs supported on more than two sides (noted in the sixteenth point), namely, that of dividing the area into strips, the moments of which are determined so as to produce computed deflections which are equal in the two strips running at right angles at each point of intersection. This method, however, requires a large amount of analytical work for any special case, and the speaker is mildly surprised that the author cannot recommend some simpler method so as to carry out his general scheme of extreme simplification of methods and design.
If use is to be made at all of deflection observations, theories, and formulas, account should certainly be taken of the actual settlements and other deflections which invariably occur in Nature at points of support. These changes of level, or slope, or both, actually alter very considerably the stresses as usually computed, and, in all rigorous design work, should be considered.
On the whole, the speaker believes that the author has put himself in the class with most iconoclasts, in that he has overshot his mark. There seems to be a very important point, however, on which he has touched, namely, the lack of care exercised by most designers with regard to those items which most nearly correspond with the so-called "details" of structural steel work, and are fully as important in rein[Pg 102]forced concrete as in steel. It is comparatively a small matter to proportion a simple reinforced concrete beam at its intersection to resist a given moment, but the carrying out of that item of the work is only a start on the long road which should lead through the consideration of every detail, not the least important of which are such items as most of the sixteen points raised by the author.
The author has done the profession a great service by raising these questions, and, while full concurrence is not had with him in all points, still the speaker desires to express his hearty thanks for starting what is hoped will be a complete discussion of the really vital matter of detailing reinforced concrete design work.
Albin H. Beyer, Esq.—Mr. Goodrich has brought out very clearly the efficiency of vertical stirrups. As Mr. Godfrey states that explanations of how stirrups act are conspicuous in the literature of reinforced concrete by their absence, the speaker will try to explain their action in a reinforced concrete beam.
It is well known that the internal static conditions in reinforced concrete beams change to some extent with the intensity of the direct or normal stresses in the steel and concrete. In order to bring out his point, the speaker will trace, in such a beam, the changes in the internal static conditions due to increasing vertical loads.
Let Fig. 8 represent a beam reinforced by horizontal steel rods of such diameter that there is no possibility of failure from lack of adhesion of the concrete to the steel. The beam is subjected to the vertical loads, Σ P. For low unit stresses in the concrete, the neutral surface, n n, is approximately in the middle of the beam. Gradually increase the loads, Σ P, until the steel reaches an elongation of from 0.01 to 0.02 of 1%, corresponding to tensile stresses in the steel of from 3,000 to 6,000 lb. per sq. in. At this stage plain concrete would have reached its ultimate elongation. It is known, however, that reinforced concrete, when well made, can sustain without rupture much greater elongations; tests have shown that its ultimate elongation may be as high as 0.1 of 1%, corresponding to tensions in steel of 30,000 lb. per sq. in.
Reinforced concrete structures ordinarily show tensile cracks at very much lower unit stresses in the steel. The main cause of these cracks is as follows: Reinforced concrete setting in dry air undergoes considerable shrinkage during the first few days, when it has very little resistance. This tendency to shrink being opposed by the reinforcement at a time when the concrete does not possess the necessary strength or ductility, causes invisible cracks or planes of weakness in the concrete. These cracks open and become visible at very low unit stresses in the steel.
Increase the vertical loads, Σ P, and the neutral surface will rise and small tensile cracks will appear in the concrete below the neutral surface (Fig. 8). These cracks are most numerous in the central part of the span, where they are nearly vertical. They decrease in number at the ends of the span, where they curve slightly away from the perpendicular toward the center of the span. The formation of these tensile cracks in the concrete relieves it at once of its highly stressed condition.
It is impossible to predict the unit tension in the steel at which these cracks begin to form. They can be detected, though not often visible, when the unit tensions in the steel are as low as from 10,000 to 16,000 lb. per sq. in. As soon as the tensile cracks form, though invisible, the neutral surface approaches the position in the beam assigned to it by the common theory of flexure, with the tension in the concrete neglected. The internal static conditions in the beam are now modified to the extent that the concrete below the neutral surface is no longer continuous. The common theory of flexure can no longer be used to calculate the web stresses.
To analyze the internal static conditions developed, the speaker will treat as a free body the shaded portion of the beam shown in Fig. 8, which lies between two tensile cracks.
In Fig. 9 are shown all the forces which act on this free body, C b b' C'.
At any section, let
| C or C' | represent the total concrete compression; |
| T or T' | represent the total steel tension; |
| J or J' | represent the total vertical shear; |
| P | represent the total vertical load for the length, b - b'; |
and let Δ T = T' - T = C' - C represent the total transverse shear for the length, b - b'.
Assuming that the tension cracks extend to the neutral surface, n n, that portion of the beam C b b' C', acts as a cantilever fixed at[Pg 104] a b and a' b', and subjected to the unbalanced steel tension, Δ T. The vertical shear, J, is carried mainly by the concrete above the neutral surface, very little of it being carried by the steel reinforcement. In the case of plain webs, the tension cracks are the forerunners of the sudden so-called diagonal tension failures produced by the snapping off, below the neutral surface, of the concrete cantilevers. The logical method of reinforcing these cantilevers is by inserting vertical steel in the tension side. The vertical reinforcement, to be efficient, must be well anchored, both in the top and in the bottom of the beam. Experience has solved the problem of doing this by the use of vertical steel in the form of stirrups, that is, U-shaped rods. The horizontal reinforcement rests in the bottom of the U.
Sufficient attention has not been paid to the proper anchorage of the upper ends of the stirrups. They should extend well into the compression area of the beam, where they should be properly anchored. They should not be too near the surface of the beam. They must not be too far apart, and they must be of sufficient cross-section to develop the necessary tensile forces at not excessive unit stresses. A working tension in the stirrups which is too high, will produce a local disintegration of the cantilevers, and give the beam the appearance of failure due to diagonal tension. Their distribution should follow closely that of the vertical or horizontal shear in the beam. Practice must rely on experiment for data as to the size and distribution of stirrups for maximum efficiency.
The maximum shearing stress in a concrete beam is commonly computed by the equation:
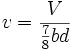 |
(1) |
Where d is the distance from the center of the reinforcing bars to the surface of the beam in compression:
b = the width of the flange, and
V = the total vertical shear at the section.
This equation gives very erratic results, because it is based on a continuous web. For a non-continuous web, it should be modified to
 |
(2) |
In this equation K b d represents the concrete area in compression. The value of K is approximately equal to 0.4.
Three large concrete beams with web reinforcement, tested at the University of Illinois[K], developed an average maximum shearing resistance of 215 lb. per sq. in., computed by Equation 1. Equation 2 would give 470 lb. per sq. in.
Three T-beams, having 32 by 3-1/4-in. flanges and 8-in. webs, tested at the University of Illinois, had maximum shearing resistances of 585, 605, and 370 lb. per. sq. in., respectively.[L] They did not fail in shear, although they appeared to develop maximum shearing stresses which were almost three times as high as those in the rectangular beams mentioned. The concrete and web reinforcement being identical, the discrepancy must be somewhere else. Based on a non-continuous concrete web, the shearing resistances become 385, 400, and 244 lb. per sq. in., respectively. As none of these failed in shear, the ultimate shearing resistance of concrete must be considerably higher than any of the values given.
About thirteen years ago, Professor A. Vierendeel[M] developed the theory of open-web girder construction. By an open-web girder, the speaker means a girder which has a lower and upper chord connected by verticals. Several girders of this type, far exceeding solid girders in length, have been built. The theory of the open-web girder, assuming the verticals to be hinged at their lower ends, applies to the concrete beam reinforced with stirrups. Assuming that the spaces between the verticals of the girder become continually narrower, they become the tension cracks of the concrete beam.[N]
John C. Ostrup, M. Am. Soc. C. E.—The author has rendered a great service to the Profession in presenting this paper. In his first point he mentions two designs of reinforced concrete beams and, inferentially, he condemns a third design to which the speaker will refer later. The designs mentioned are, first, that of a reinforced concrete beam arranged in the shape of a rod, with separate concrete blocks placed on top of it without being connected—such a beam has its strength only in the rod. It is purely a suspension, or "hog-chain" affair, and the blocks serve no purpose, but simply increase the load on the rod and its stresses.
The author's second design is an invention of his own, which the Profession at large is invited to adopt. This is really the same system as the first, except that the blocks are continuous and, presumably, fixed at the ends. When they are so fixed, the concrete will take compressive stresses and a certain portion of the shear, the remaining shear being transmitted to the rod from the concrete above it, but only through friction. Now, the frictional resistance between a steel rod and a concrete beam is not such as should be depended on in modern engineering designs.
The third method is that which is used by nearly all competent designers, and it seems to the speaker that, in condemning the general practice of current reinforced designs in sixteen points, the author[Pg 106] could have saved himself some time and labor by condemning them all in one point.
What appears to be the underlying principle of reinforced concrete design is the adhesion, or bond, between the steel and the concrete, and it is that which tends to make the two materials act in unison. This is a point which has not been touched on sufficiently, and one which it was expected that Mr. Beyer would have brought out, when he illustrated certain internal static conditions. This principle, in the main, will cover the author's fifth point, wherein stirrups are mentioned, and again in the first point, wherein he asks: "Will some advocate of this type of design please state where this area can be found?"
To understand clearly how concrete acts in conjunction with steel, it is necessary to analyze the following question: When a steel rod is embedded in a solid block of concrete, and that rod is put in tension, what will be the stresses in the rod and the surrounding concrete?
The answer will be illustrated by reference to Fig. 10. It must be understood that the unit stresses should be selected so that both the concrete and the steel may be stressed in the same relative ratio. Assuming the tensile stress in the steel to be 16,000 lb. per sq. in., and the bonding value 80 lb., a simple formula will show that the length of embedment, or that part of the rod which will act, must be equal to 50 diameters of the rod.
When the rod is put in tension, as indicated in Fig. 10, what will be the stresses in the surrounding concrete? The greatest stress will come on the rod at the point where it leaves the concrete, where it is a maximum, and it will decrease from that point inward until the total stress in the steel has been distributed to the surrounding concrete. At that point the rod will only be stressed back for a distance equal in length to 50 diameters, no matter how far beyond that length the rod may extend.
The distribution of the stress from the steel rod to the concrete can be represented by a cone, the base of which is at the outer face of the block, as the stresses will be zero at a point 50 diameters back, and will increase in a certain ratio out toward the face of the block, and will also, at all intermediate points, decrease radially outward from the rod.
The intensity of the maximum stress exerted on the concrete is represented by the shaded area in Fig. 10, the ordinates, measured perpendicularly to the rod, indicating the maximum resistance offered by the concrete at any point.
If the concrete had a constant modulus of elasticity under varying stress, and if the two materials had the same modulus, the stress triangle would be bounded by straight lines (shown as dotted lines in Fig. 10); but as this is not true, the variable moduli will modify the stress triangle in a manner which will tend to make the boundary lines resemble parabolic curves.
A triangle thus constructed will represent by scale the intensity of the stress in the concrete, and if the ordinates indicate stresses greater than that which the concrete will stand, a portion will be destroyed, broken off, and nothing more serious will happen than that this stress triangle will adjust itself, and grip the rod farther back. This process keeps on until the end of the rod has been reached, when the triangle will assume a much greater maximum depth as it shortens; or, in other words, the disintegration of the concrete will take place here very rapidly, and the rod will be pulled out.
In the author's fourth point he belittles the use of shear rods, and states: "No hint is given as to whether these bars are in shear or in tension." As a matter of fact, they are neither in shear nor wholly in tension, they are simply in bending between the centers of the compressive resultants, as indicated in Fig. 12, and are, besides, stressed slightly in tension between these two points.
In Fig. 10 the stress triangle indicates the distribution and the intensity of the resistance in the concrete to a force acting parallel to the rod. A similar triangle may be drawn, Fig. 11, showing the resistance of the rod and the resultant distribution in the concrete to a force perpendicular to the rod. Here the original force would cause plain shear in the rod, were the latter fixed in position. Since this cannot be the case, the force will be resolved into two components, one of which will cause a tensile stress in the rod and the other will pass through the centroid of the compressive stress area. This is indicated in Fig. 11, which, otherwise, is self-explanatory.
Rods are not very often placed in such a position, but where it is unavoidable, as in construction joints in the middle of slabs or beams, they serve a very good purpose; but, to obtain the best effect from them, they should be placed near the center of[Pg 108] the slab, as in Fig. 12, and not near the top, as advocated by some writers.
If the concrete be overstressed at the points where the rod tends to bend, that is, if the rods are spaced too far apart, disintegration will follow; and, for this reason, they should be long enough to have more than 50 diameters gripped by the concrete.
This leads up to the author's seventh point, as to the overstressing of the concrete at the junction of the diagonal tension rods, or stirrups, and the bottom reinforcement.
Analogous with the foregoing, it is easy to lay off the stress triangles and to find the intensity of stress at the maximum points, in fact at any point, along the tension rods and the bottom chord. This is indicated in Fig. 13. These stress triangles will start on the rod 50 diameters back from the point in question and, although the author has indicated in Fig. 1 that only two of the three rods are stressed, there must of necessity also be some stress in the bottom rod to the left of the junction, on account of the deformation which takes place in any beam due to bending. Therefore, all three rods at the point where they are joined, are under stress, and the triangles can be laid off accordingly.
It will be noticed that the concrete will resist the compressive components, not at any specific point, but all along the various rods, and with the intensities shown by the stress triangles; also, that some of these triangles will overlap, and, hence, a certain readjustment, or superimposition, of stresses takes place.
The portion which is laid off below the bottom rods will probably not act unless there is sufficient concrete below the reinforcing bars and on the sides, and, as that is not the case in ordinary construction, it is very probable, as Mr. Goodrich has pointed out, that the concrete below the rods plays an unimportant part, and that the triangle which is now shown below the rod should be partially omitted.
The triangles in Fig. 13 show the intensity of stress in the concrete at any point, or at any section where it is wanted. They show conclusively where the components are located in the concrete, their relation to the tensile stresses in the rods, and, furthermore, that they act only in a general way at right angles to one another. This is in[Pg 109] accordance with the theory of beams, that at any point in the web there are tensile and compressive stresses of equal intensity, and at right angles to one another, although in a non-homogeneous web the distribution is somewhat different.
After having found at the point of junction the intensity of stress, it is possible to tell whether or not a bond between the stirrups and the bottom rods is necessary, and it would not seem to be where the stirrups are vertical.
It would also seem possible to tell in what direction, if any, the bend in the inclined stirrups should be made. It is to be assumed, although not expressly stated, that the bends should curve from the center up toward the end of the beam, but an inspection of the stress triangles, Fig. 13, will show that the intensity of stress is just as great on the opposite side, and it is probable that, if any bends were required to reduce the maximum stress in the concrete, they should as likely be made on the side nearest the abutment.
From the stress triangles it may also be shown that, if the stirrups were vertical instead of inclined, the stress in the concrete on both sides would be practically equal, and that, in consequence, vertical stirrups are preferable.
The next issue raised by the author is covered in his seventh point, and relates to bending moments. He states: "* * * bending moments in so-called continuous beams are juggled to reduce them to what the designer would like to have them. This has come to be almost a matter of taste, * * *."
The author seems to imply that such juggling is wrong. As a matter of fact, it is perfectly allowable and legitimate in every instance of beam or truss design, that is, from the standpoint of stress distribution, although this "juggling" is limited in practice by economical considerations.
In a series of beams supported at the ends, bending moments range from (w l2)/8 at the center of each span to zero at the supports, and, in a series of cantilevers, from zero at the center of the span to (w l2)/8 at the supports. Between these two extremes, the designer can divide, adjust, or juggle them to his heart's content, provided that in his design he makes the proper provision for the corresponding shifting of the points of contra-flexure. If that were not the case, how could ordinary bridge trusses, which have their maximum bending at the center, compare with those which, like arches, are assumed to have no bending at that point?
In his tenth point, the author proposes a method of simple designing by doing away with the complicated formulas which take account of the actual co-operation of the two materials. He states that an ideal[Pg 110] design can be obtained in the same manner, that is, with the same formulas, as for ordinary rectangular beams; but, when he does so, he evidently fails to remember that the neutral axis is not near the center of a reinforced concrete beam under stress; in fact, with the percentage of reinforcement ordinarily used in designing—varying between three-fourths of 1% to 1-1/2%—the neutral axis, when the beam is loaded, is shifted from 26 to 10% of the beam depth above the center. Hence, a low percentage of steel reinforcement will produce a great shifting of the neutral axis, so that a design based on the formulas advocated by the author would contain either a waste of materials, an overstress of the concrete, or an understress of the steel; in fact, an error in the design of from 10 to 26 per cent. Such errors, indeed, are not to be recommended by good engineers.
The last point which the speaker will discuss is that of the elastic arch. The theory of the elastic arch is now so well understood, and it offers such a simple and, it might be said, elegant and self-checking solution of the arch design, that it has a great many advantages, and practically none of the disadvantages of other methods.
The author's statement that the segments of an arch could be made up of loose blocks and afterward cemented together, cannot be endorsed by the speaker, for, upon such cementing together, a shifting of the lines of resistance will take place when the load is applied. The speaker does not claim that arches are maintained by the cement or mortar joining the voussoirs together, but that the lines of pressure will be materially changed, and the same calculations are not applicable to both the unloaded and the loaded arch.
It is quite true, as the author states, that a few cubic yards of concrete placed in the ring will strengthen the arch more than a like amount added to the abutments, provided, however, that this material be placed properly. No good can result from an attempt to strengthen a structure by placing the reinforcing material promiscuously. This has been tried by amateurs in bridge construction, and, in such cases, the material either increased the distance from the neutral axis to the extreme fibers, thereby reducing the original section modulus, or caused a shifting of the neutral axis followed by a large bending moment; either method weakening the members it had tried to reinforce. In other words, the mere addition of material does not always strengthen a structure, unless it is placed in the proper position, and, if so placed, it should be placed all over commensurately with the stresses, that is, the unit stresses should be reduced.
The author has criticized reinforced concrete construction on the ground that the formulas and theories concerning it are not as yet fully developed. This is quite true, for the simple reason that there are so many uncertain elements which form their basis: First, the variable quantity of the modulus of elasticity, which,[Pg 111] in the concrete, varies inversely as the stress; and, second, the fact that the neutral axis in a reinforced concrete beam under changing stress is migratory. There are also many other elements of evaluation, which, though of importance, are uncertain.
Because the formulas are established on certain assumptions is no reason for condemning them. There are, the speaker might add, few formulas in the subject of theoretical mechanics which are not based on some assumption, and as long as the variations are such that their range is known, perfectly reliable formulas can be deduced and perfectly safe structures can be built from them.
There are a great many theorists who have recently complained about the design of reinforced concrete. It seems to the speaker that such complaints can serve no useful purpose. Reinforced concrete structures are being built in steadily increasing numbers; they are filling a long needed place; they are at present rendering great service to mankind; and they are destined to cover a field of still greater usefulness. Reinforced concrete will undoubtedly show in the future that the confidence which most engineers and others now place in it is fully merited.
Harry F. Porter, Jun. Am. Soc. C. E. (by letter).—Mr. Godfrey has brought forward some interesting and pertinent points, which, in the main, are well taken; but, in his zealousness, he has fallen into the error of overpersuading himself of the gravity of some of the points he would make; on the other hand, he fails to go deeply enough into others, and some fallacies he leaves untouched. Incidentally, he seems somewhat unfair to the Profession in general, in which many earnest, able men are at work on this problem, men who are not mere theorists, but have been reared in the hard school of practical experience, where refinements of theory count for little, but common sense in design counts for much—not to mention those self-sacrificing devotees to the advancement of the art, the collegiate and laboratory investigators.
Engineers will all agree with Mr. Godfrey that there is much in the average current practice that is erroneous, much in textbooks that is misleading if not fallacious, and that there are still many designers who are unable to think in terms of the new material apart from the vestures of timber and structural steel, and whose designs, therefore, are cumbersome and impractical. The writer, however, cannot agree with the author that the practice is as radically wrong as he seems to think. Nor is he entirely in accord with Mr. Godfrey in his "constructive criticism" of those practices in which he concurs, that they are erroneous.
That Mr. Godfrey can see no use in vertical stirrups or U-bars is surprising in a practical engineer. One is prompted to ask: "Can the holder of this opinion ever have gone through the experience of[Pg 112] placing steel in a job, or at least have watched the operation?" If so, he must have found some use for those little members which he professes to ignore utterly.
As a matter of fact, U-bars perform the following very useful and indispensable services:
(1).—If properly made and placed, they serve as a saddle in which to rest the horizontal steel, thereby insuring the correct placing of the latter during the operation of concreting, not a mean function in a type of construction so essentially practical. To serve this purpose, stirrups should be made as shown in Plate III. They should be restrained in some manner from moving when the concrete strikes them. A very good way of accomplishing this is to string them on a longitudinal rod, nested in the bend at the upper end. Mr. Godfrey, in his advocacy of bowstring bars anchored with washers and nuts at the ends, fails to indicate how they shall be placed. The writer, from experience in placing steel, thinks that it would be very difficult, if not impractical, to place them in this manner; but let a saddle of U-bars be provided, and the problem is easy.
(2).—Stirrups serve also as a tie, to knit the stem of the beam to its flange—the superimposed slab. The latter, at best, is not too well attached to the stem by the adhesion of the concrete alone, unassisted by the steel. T-beams are used very generally, because their construction has the sanction of common sense, it being impossible to cast stem and slab so that there will be the same strength in the plane at the junction of the two as elsewhere, on account of the certainty of unevenness in settlement, due to the disproportion in their depth. There is also the likelihood that, in spite of specifications to the contrary, there will be a time interval between the pouring of the two parts, and thus a plane of weakness, where, unfortunately, the forces tending to produce sliding of the upper part of the beam on the lower (horizontal shear) are a maximum. To offset this tendency, therefore, it is necessary to have a certain amount of vertical steel, disposed so as to pass around and under the main reinforcing members and reach well up into the flange (the slab), thus getting a grip therein of no mean security. The hooking of the U-bars, as shown in Plate III, affords a very effective grip in the concrete of the slab, and this is still further enhanced by the distributing or anchoring effect of the longitudinal stringing rods. Thus these longitudinals, besides serving to hold the U-bars in position, also increase their effectiveness. They serve a still further purpose as a most convenient support for the slab bars, compelling them to take the correct position over the supports, thus automatically ensuring full and proper provision for reversed stresses. More than that, they act in compression within the middle half, and assist in tension toward the ends of the span.
Thus, by using U-bars of the type indicated, in combination with[Pg 113] longitudinal bars as described, tying together thoroughly the component parts of the beam in a vertical plane, a marked increase in stiffness, if not strength, is secured. This being the case, who can gainsay the utility of the U-bar?
Of course, near the ends, in case continuity of action is realized, whereupon the stresses are reversed, the U-bars need to be inverted, although frequently inversion is not imperative with the type of U-bar described, the simple hooking of the upper ends over the upper horizontal steel being sufficient.
As to whether or not the U-bars act with the horizontal and diagonal steel to form truss systems is relatively unessential; in all probability there is some such action, which contributes somewhat to the total strength, but at most it is of minor importance. Mr. Godfrey's points as to fallacy of truss action seem to be well taken, but his conclusions in consequence—that U-bars serve no purpose—are impractical.
The number of U-bars needed is also largely a matter of practice, although subject to calculation. Practice indicates that they should be spaced no farther apart than the effective depth of the member, and spaced closer or made heavier toward the ends, in order to keep pace with cumulating shear. They need this close spacing in order to serve as an adequate saddle for the main bars, as well as to furnish, with the lighter "stringing" rods, an adequate support to the slab bars. They should have the requisite stiffness in the bends to carry their burden without appreciable sagging; it will be found that 5/16 in. is about the minimum practical size, and that 1/2 in. is as large as will be necessary, even for very deep beams with heavy reinforcement.
If the size and number of U-bars were to be assigned by theory, there should be enough of them to care for fully 75% of the horizontal shear, the adhesion of the concrete being assumed as adequate for the remainder.
Near the ends, of course, the inclined steel, resulting from bending up some of the horizontal bars, if it is carried well across the support to secure an adequate anchorage, or other equivalent anchorage is provided, assists in taking the horizontal shear.
The embedment, too, of large stone in the body of the beam, straddling, as it were, the neutral plane, and thus forming a lock between the flange and the stem, may be considered as assisting materially in taking horizontal shear, thus relieving the U-bars. This is a factor in the strength of actual work which theory does not take into account, and by the author, no doubt, it would be regarded as insignificant; nevertheless it is being done every day, with excellent results.
The action of these various agencies—the U-bars, diagonal steel, and embedded stone—in a concrete beam, is analogous to that of bolts or keys in the case of deepened timber beams. A concrete beam may[Pg 114] be assumed, for the purposes of illustration, to be composed of a series of superimposed layers; in this case the function of the rigid material crossing these several layers normally, and being well anchored above and below, as a unifier of the member, is obvious—it acts as so many bolts joining superimposed planks forming a beam. Of course, no such lamination actually exists, although there are always incipient forces tending to produce it; these may and do manifest themselves on occasion as an actual separation in a horizontal plane at the junction of slab and stem, ordinarily the plane of greatest weakness—owing to the method of casting—as well as of maximum horizontal shear. Beams tested to destruction almost invariably develop cracks in this region. The question then naturally arises: If U-bars serve no purpose, what will counteract these horizontal cleaving forces? On the contrary, T-beams, adequately reinforced with U-bars, seem to be safeguarded in this respect; consequently, the U-bars, while perhaps adding little to the strength, as estimated by the ultimate carrying capacity, actually must be of considerable assistance, within the limit of working loads, by enhancing the stiffness and ensuring against incipient cracking along the plane of weakness, such as impact or vibratory loads might induce. Therefore, U-bars, far from being superfluous or fallacious, are, practically, if not theoretically, indispensable.
At present there seems to be considerable diversity of opinion as to the exact nature of the stress action in a reinforced concrete beam. Unquestionably, the action in the monolithic members of a concrete structure is different from that in the simple-acting, unrestrained parts of timber or structural steel construction; because in monolithic members, by the law of continuity, reverse stresses must come into play. To offset these stresses reinforcement must be provided, or cracking will ensue where they occur, to the detriment of the structure in appearance, if not in utility. Monolithic concrete construction should be tied together so well across the supports as to make cracking under working loads impossible, and, when tested to destruction, failure should occur by the gradual sagging of the member, like the sagging of an old basket. Then, and then only, can the structure be said to be adequately reinforced.
In his advocacy of placing steel to simulate a catenary curve, with end anchorage, the author is more nearly correct than in other issues he makes. Undoubtedly, an attempt should be made in every concrete structure to approximate this alignment. In slabs it may be secured simply by elevating the bars over the supports, when, if pliable enough, they will assume a natural droop which is practically ideal; or, if too stiff, they may be bent to conform approximately to this position. In slabs, too, the reinforcement may be made practically continuous, by using lengths covering several spans, and, where ends occur, by gener[Pg 115]ous lapping. In beams the problem is somewhat more complicated, as it is impossible, except rarely, to bow the steel and to extend it continuously over several supports; but all or part of the horizontal steel can be bent up at about the quarter point, carried across the supports into the adjacent spans, and anchored there by bending it down at about the same angle as it is bent up on the approach, and then hooking the ends.

It is seldom necessary to adopt the scheme proposed by the author, namely, a threaded end with a bearing washer and a nut to hold the washer in place, although it is sometimes expedient, but not absolutely necessary, in end spans, where prolongation into an adjacent span is out of the question. In end spans it is ordinarily sufficient to give the bars a double reverse bend, as shown in Plate III, and possibly to clasp hooks with the horizontal steel. If steel be placed in this manner, the catenary curve will be practically approximated, the steel will be fairly developed throughout its length of embedment, and the structure will be proof against cracking. In this case, also, there is much less dependence on the integrity of the bond; in fact, if there were no bond, the structure would still develop most of its strength, although the deflection under heavy loading might be relatively greater.
The writer once had an experience which sustains this point. On peeling off the forms from a beam reinforced according to the method indicated, it was found that, because of the crowding together of the bars in the bottom, coupled with a little too stiff a mixture, the beam had hardly any concrete on the underside to grip the steel in the portion between the points of bending up, or for about the middle half of the member; consequently, it was decided to test this beam. The actual working load was first applied and no deflection, cracking, or slippage of the bars was apparent; but, as the loading was continued, deflection set in and increased rapidly for small increments of loading, a number of fine cracks opened up near the mid-section, which extended to the neutral plane, and the steel slipped just enough, when drawn taut, to destroy what bond there was originally, owing to the contact of the concrete above. At three times the live load, or 450 lb. per sq. ft., the deflection apparently reached a maximum, being about 5/16 in. for a clear distance, between the supports, of 20 ft.; and, as the load was increased to 600 lb. per sq. ft., there was no appreciable increase either in deflection or cracking; whereupon, the owner being satisfied, the loading was discontinued. The load was reduced in amount to three times the working load (450 lb.) and left on over night; the next morning, there being no detectable change, the beam was declared to be sound. When the load was removed the beam recovered all but about 1/8 in. of its deflection, and then repairs were made by attaching light expanded metal to the exposed bars and plastering up to form. Although nearly three years have elapsed, there have been[Pg 116] no unfavorable indications, and the owner, no doubt, has eased his mind entirely in regard to the matter. This truly remarkable showing can only be explained by the catenary action of the main steel, and some truss action by the steel which was horizontal, in conjunction with the U-bars, of which there were plenty. As before noted, the clear span was 20 ft., the width of the bay, 8 ft., and the size under the slab (which was 5 in. thick) 8 by 18 in. The reinforcement consisted of three 1-1/8-in. round medium-steel bars, with 3/8-in. U-bars placed the effective depth of the member apart and closer toward the supports, the first two or three being 6 in. apart, the next two or three, 9 in., the next, 12 in., etc., up to a maximum, throughout the mid-section, of 15 in. Each U-bar was provided with a hook at its upper end, as shown in Plate III, and engaged the slab reinforcement, which in this case was expanded metal. Two of the 1-1/8-in. bars were bent up and carried across the support. At the point of bending up, where they passed the single horizontal bar, which was superimposed, a lock-bar was inserted, by which the pressure of the bent-up steel against the concrete, in the region of the bend, was taken up and distributed along the horizontal bar. This feature is also shown in Fig. 14. The bars, after being carried across the support, were inclined into the adjacent span and provided with a liberal, well-rounded hook, furnishing efficient anchorage and provision for reverse stresses. This was at one end only, for—to make matters worse—the other end was a wall bearing; consequently, the benefit of continuity was denied. The bent-up bars were given a double reverse bend, as already described, carrying them around, down, in, and up, and ending finally by clasping them in the hook of the horizontal bar. This apparently stiffened up the free end, for, under the test load, its action was similar to that of the completely restrained end, thus attesting the value of this method of end-fixing.
The writer has consistently followed this method of reinforcement, with unvaryingly good results, and believes that, in some measure, it approximates the truth of the situation. Moreover, it is economical, for with the bars bent up over the supports in this manner, and positively anchored, plenty of U-bars being provided, it is possible to remove the forms with entire safety much sooner than with the ordinary methods which are not as well stirruped and only partially tied across the supports. It is also possible to put the structure into use at an earlier date. Failure, too, by the premature removal of the centers, is almost impossible with this method. These considerations more than compensate for the trouble and expense involved in connection with such reinforcement. The writer will not attempt here a theoretical analysis of the stresses incurred in the different parts of this beam, although it might be interesting and instructive.
The concrete, with the reinforcement disposed as described, may be[Pg 117][Pg 118] regarded as reposing on the steel as a saddle, furnishing it with a rigid jacket in which to work, and itself acting only as a stiff floor and a protecting envelope. Bond, in this case, while, of course, an adjunct, is by no means vitally important, as is generally the case with beams unrestrained in any way and in which the reinforcement is not provided with adequate end anchorage, in which case a continuous bond is apparently—at any rate, theoretically—indispensable.
An example of the opposite extreme in reinforced concrete design, where provision for reverse stresses was almost wholly lacking, is shown in the Bridgeman Brothers' Building, in Philadelphia, which collapsed while the operation of casting the roof was in progress, in the summer of 1907. The engineering world is fairly familiar with the details of this disaster, as they were noted both in the lay and technical press. In this structure, not only were U-bars almost entirely absent, but the few main bars which were bent up, were stopped short over the support. The result was that the ties between the rib and the slab, and also across the support, being lacking, some of the beams, the forms of which had been removed prematurely, cracked of their own dead weight, and, later, when the roof collapsed, owing to the deficient bracing of the centers, it carried with it each of the four floors to the basement, the beams giving way abruptly over the supports. Had an adequate tie of steel been provided across the supports, the collapse, undoubtedly, would have stopped at the fourth floor. So many faults were apparent in this structure, that, although only half of it had fallen, it was ordered to be entirely demolished and reconstructed.
The cracks in the beams, due to the action of the dead weight alone, were most interesting, and illuminative of the action which takes place in a concrete beam. They were in every case on the diagonal, at an angle of approximately 45°, and extended upward and outward from the edge of the support to the bottom side of the slab. Never was the necessity for diagonal steel, crossing this plane of weakness, more emphatically demonstrated. To the writer—an eye-witness—the following line of thought was suggested:
Should not the concrete in the region above the supports and for a distance on either side, as encompassed by the opposed 45° lines (Fig. 14), be regarded as abundantly able, of and by itself, and without reinforcing, to convey all its load into the column, leaving only the bending to be considered in the truncated portion intersected? Not even the bending should be considered, except in the case of relatively shallow members, but simply the tendency on the part of the wedge-shaped section to slip out on the 45° planes, thereby requiring sufficient reinforcement at the crossing of these planes of principal weakness to take the component of the load on this portion, tending to shove it out. This reinforcement, of course, should be anchored securely both ways; in mid-span by extending it clear through, forming a suspensory, and,[Pg 119] in the other direction, by prolonging it past the supports, the concrete, in this case, along these planes, being assumed to assist partly or not at all.
This would seem to be a fair assumption. In all events, beams designed in this manner and checked by comparison with the usual methods of calculation, allowing continuity of action, are found to agree fairly well. Hence, the following statement seems to be warranted: If enough steel is provided, crossing normally or nearly so the 45° planes from the edge of the support upward and outward, to care for the component of the load on the portion included within a pair of these planes, tending to produce sliding along the same, and this steel is adequately anchored both ways, there will be enough reinforcement for every other purpose. In addition, U-bars should be provided for practical reasons.
The weak point of beams, and slabs also, fully reinforced for continuity of action, is on the under side adjacent to the edge of the support, where the concrete is in compression. Here, too, the amount of concrete available is small, having no slab to assist it, as is the case within the middle section, where the compression is in the top. Over the supports, for the width of the column, there is abundant strength, for here the steel has a leverage equal to the depth of the column; but at the very edge and for at least one-tenth of the span out, conditions are serious. The usual method of strengthening this region is to subpose brackets, suitably proportioned, to increase the available compressive area to a safe figure, as well as the leverage of the steel, at the same time diminishing the intensity of compression. Brackets, however, are frequently objectionable, and are therefore very generally omitted by careless or ignorant designers, no especial compensation being made for their absence. In Europe, especially in Germany, engineers are much more careful in this respect, brackets being nearly always included. True, if brackets are omitted, some compensation is provided by the strengthening which horizontal bars may give by extending through this region, but sufficient additional compressive resistance is rarely afforded thereby. Perhaps the best way to overcome the difficulty, without resorting to brackets, is to increase the compressive resistance of the concrete, in addition to extending horizontal steel through it. This may be done by hooping or by intermingling scraps of iron or bits of expanded metal with the concrete, thereby greatly increasing its resistance. The experiments made by the Department of Bridges of the City of New York, on the value of nails in concrete, in which results as high as 18,000 lb. per sq. in. were obtained, indicate the availability of this device; the writer has not used it, nor does he know that it has been used, but it seems to be entirely rational, and to offer possibilities.
Another practical test, which indicates the value of proper reinforce[Pg 120]ment, may be mentioned. In a storage warehouse in Canada, the floor was designed, according to the building laws of the town, for a live load of 150 lb. per sq. ft., but the restrictions being more severe than the standard American practice, limiting the lever arm of the steel to 75% of the effective depth, this was about equivalent to a 200-lb. load in the United States. The structure was to be loaded up to 400 or 500 lb. per sq. ft. steadily, but the writer felt so confident of the excess strength provided by his method of reinforcing that he was willing to guarantee the structure, designed for 150 lb., according to the Canadian laws, to be good for the actual working load. Plain, round, medium-steel bars were used. A 10-ft. panel, with a beam of 14-ft. span, and a slab 6 in. thick (not including the top coat), with 1/2-in. round bars, 4 in. on centers, was loaded to 900 lb. per sq. ft., at which load no measurable deflection was apparent. The writer wished to test it still further, but there was not enough cement—the material used for loading. The load, however, was left on for 48 hours, after which, no sign of deflection appearing, not even an incipient crack, it was removed. The total area of loading was 14 by 20 ft. The beam was continuous at one end only, and the slab only on one side. In other parts of the structure conditions were better, square panels being possible, with reinforcement both ways, and with continuity, both of beams and slabs, virtually in every direction, end spans being compensated by shortening. The method of reinforcing was as before indicated. The enormous strength of the structure, as proved by this test, and as further demonstrated by its use for nearly two years, can only be explained on the basis of the continuity of action developed and the great stiffness secured by liberal stirruping. Steel was provided in the middle section according to the rule, (w l)/8, the span being taken as the clear distance between the supports; two-thirds of the steel was bent up and carried across the supports, in the case of the beams, and three-fourths of the slab steel was elevated; this, with the lap, really gave, on the average, four-thirds as much steel over the supports as in the center, which, of course, was excessive, but usually an excess has to be tolerated in order to allow for adequate anchorage. Brackets were not used, but extra horizontal reinforcement, in addition to the regular horizontal steel, was laid in the bottom across the supports, which, seemingly, was satisfactory. The columns, it should be added, were calculated for a very low value, something like 350 lb. per sq. in., in order to compensate for the excess of actual live load over and above the calculated load.
This piece of work was done during the winter, with the temperature almost constantly at +10° and dropping below zero over night. The precautions observed were to heat the sand and water, thaw out the concrete with live steam, if it froze in transporting or before it was[Pg 121] settled in place, and as soon as it was placed, it was decked over and salamanders were started underneath. Thus, a job equal in every respect to warm-weather installation was obtained, it being possible to remove the forms in a fortnight.


In another part of this job (the factory annex) where, owing to the open nature of the structure, it was impossible to house it in as well as the warehouse which had bearing walls to curtain off the sides, less fortunate results were obtained. A temperature drop over night of nearly 50°, followed by a spell of alternate freezing and thawing, effected the ruin of at least the upper 2 in. of a 6-in. slab spanning 12 ft. (which was reinforced with 1/2-in. round bars, 4 in. on centers), and the remaining 4 in. was by no means of the best quality. It was thought that this particular bay would have to be replaced. Before deciding, however, a test was arranged, supports being provided underneath to prevent absolute failure. But as the load was piled up, to the extent of nearly 400 lb. per sq. ft., there was no sign of giving (over this span) other than an insignificant deflection of less than 1/4 in., which disappeared on removing the load. This slab still performs its share of the duty, without visible defect, hence it must be safe. The question naturally arises: if 4 in. of inferior concrete could make this showing, what must have been the value of the 6 in. of good concrete in the other slabs? The reinforcing in the slab, it should be stated, was continuous over several supports, was proportioned for (w l)/8 for the clear span (about 11 ft.), and three-fourths of it was raised over the supports. This shows the value of the continuous method of reinforcing, and the enormous excess of strength in concrete structures, as proportioned by existing methods, when the reverse stresses are provided for fully and properly, though building codes may make no concession therefor.
Another point may be raised, although the author has not mentioned it, namely, the absurdity of the stresses commonly considered as occurring in tensile steel, 16,000 lb. per sq. in. for medium steel being used almost everywhere, while some zealots, using steel with a high elastic limit, are advocating stresses up to 22,000 lb. and more; even the National Association of Cement Users has adopted a report of the Committee on Reinforced Concrete, which includes a clause recommending the use of 20,000 lb. on high steel. As theory indicates, and as F.E. Turneaure, Assoc. M. Am. Soc. C. E., of the University of Wisconsin, has proven by experiment, failure of the concrete encircling the steel under tension occurs when the stress in the steel is about 5,000 lb. per sq. in. It is evident, therefore, that if a stress of even 16,000 lb. were actually developed, not to speak of 20,000 lb. or more, the concrete would be so replete with minute cracks on the tension side as to expose the embedded metal in innumerable places. Such[Pg 122] cracks do not occur in work because, under ordinary working loads, the concrete is able to carry the load so well, by arch and dome action, as to require very little assistance from the steel, which, consequently, is never stressed to a point where cracking of the concrete will be induced. This being the case, why not recognize it, modify methods of design, and not go on assuming stresses which have no real existence?
The point made by Mr. Godfrey in regard to the fallacy of sharp bends is patent, and must meet with the agreement of all who pause to think of the action really occurring. This is also true of his points as to the width of the stem of T-beams, and the spacing of bars in the same. As to elastic arches, the writer is not sufficiently versed in designs of this class to express an opinion, but he agrees entirely with the author in his criticism of retaining-wall design. What the author proposes is rational, and it is hard to see how the problem could logically be analyzed otherwise. His point about chimneys, however, is not as clear.
As to columns, the writer agrees with Mr. Godfrey in many, but not in all, of his points. Certainly, the fallacy of counting on vertical steel to carry load, in addition to the concrete, has been abundantly shown. The writer believes that the sole legitimate function of vertical steel, as ordinarily used, is to reinforce the member against flexure, and that its very presence in the column, unless well tied across by loops of steel at frequent intervals, so far from increasing the direct carrying capacity, is a source of weakness. However, the case is different when a large amount of rigid vertical steel is used; then the steel may be assumed to carry all the load, at the value customary in structural steel practice, the concrete being considered only in the light of fire-proofing and as affording lateral support to the steel, increasing its effective radius of gyration and thus its safe carrying capacity. In any event the load should be assumed to be carried either by the concrete or by the steel, and, if by the former, the longitudinal and transverse steel which is introduced should be regarded as auxiliary only. Vertical steel, if not counted in the strength, however, may on occasion serve a very useful practical purpose; for instance, the writer once had a job where, owing to the collection of ice and snow on a floor, which melted when the salamanders were started, the lower ends of several of the superimposed columns were eaten away, with the result that when the forms were withdrawn, these columns were found to be standing on stilts. Only four 1-in. bars were present, looped at intervals of about 1 ft., in a column 12 ft. in length and having a girth of 14 in., yet they were adequate to carry both the load of the floor above and the load incidental to construction. If no such reinforcement had been provided, however, failure would have been inevitable. Thus, again, it is shown that, where theory and experiment may fail to justify certain practices, actual experience does, and emphatically.
Mr. Godfrey is absolutely right in his indictment of hooping as usually done, for hoops can serve no purpose until the concrete contained therein is stressed to incipient rupture; then they will begin to act, to furnish restraint which will postpone ultimate failure. Mr. Godfrey states that, in his opinion, the lamina of concrete between each hoop is not assisted; but, as a matter of fact, practically regarded, it is, the coarse particles of the aggregate bridging across from hoop to hoop; and if—as is the practice of some—considerable longitudinal steel is also used, and the hoops are very heavy, so that when the bridging action of the concrete is taken into account, there is in effect a very considerable restraining of the concrete core, and the safe carrying capacity of the column is undoubtedly increased. However, in the latter case, it would be more logical to consider that the vertical steel carried all the load, and that the concrete core, with the hoops, simply constituted its rigidity and the medium of getting the load into the same, ignoring, in this event, the direct resistance of the concrete.
What seems to the writer to be the most logical method of reinforcing concrete columns remains to be developed; it follows along the lines of supplying tensile resistance to the mass here and there throughout, thus creating a condition of homogeneity of strength. It is precisely the method indicated by the experiments already noted, made by the Department of Bridges of the City of New York, whereby the compressive resistance of concrete was enormously increased by intermingling wire nails with it. Of course, it is manifestly out of the question, practically and economically, to reinforce column concrete in this manner, but no doubt a practical and an economical method will be developed which will serve the same purpose. The writer knows of one prominent reinforced concrete engineer, of acknowledged judgment, who has applied for a patent in which expanded metal is used to effect this very purpose; how well this method will succeed remains to be seen. At any rate, reinforcement of this description seems to be entirely rational, which is more than can be said for most of the current standard types.
Mr. Godfrey's sixteenth point, as to the action in square panels, seems also to the writer to be well taken; he recollects analyzing Mr. Godfrey's narrow-strip method at the time it appeared in print, and found it rational, and he has since had the pleasure of observing actual tests which sustained this view. Reinforcement can only be efficient in two ways, if the span both ways is the same or nearly so; a very little difference tends to throw the bulk of the load the short way, for stresses know only one law, namely, to follow the shortest line. In square panels the maximum bending comes on the mid-strips; those adjacent to the margin beams have very little bending parallel to the beam, practically all the action being the other way; and there are all gradations between. The reinforcing, therefore, should be spaced the[Pg 124] minimum distance only in the mid-region, and from there on constantly widened, until, at about the quarter point, practically none is necessary, the slab arching across on the diagonal from beam to beam. The practice of spacing the bars at the minimum distance throughout is common, extending the bars to the very edge of the beams. In this case about half the steel is simply wasted.
In conclusion, the writer wishes to thank Mr. Godfrey for his very able paper, which to him has been exceedingly illuminative and fully appreciated, even though he has been obliged to differ from its contentions in some respects. On the other hand, perhaps, the writer is wrong and Mr. Godfrey right; in any event, if, through the medium of this contribution to the discussion, the writer has assisted in emphasizing a few of the fundamental truths; or if, in his points of non-concordance, he is in coincidence with the views of a sufficient number of engineers to convince Mr. Godfrey of any mistaken stands; or, finally, if he has added anything new to the discussion which may help along the solution, he will feel amply repaid for his time and labor. The least that can be said is that reform all along the line, in matters of reinforced concrete design, is insistent.
John Stephen Sewell, M. Am. Soc. C. E. (by letter).—The author is rather severe on the state of the art of designing reinforced concrete. It appears to the writer that, to a part of the indictment, at least, a plea of not guilty may properly be entered; and that some of the other charges may not be crimes, after all. There is still room for a wide difference of opinion on many points involved in the design of reinforced concrete, and too much zeal for conviction, combined with such skill in special pleading as this paper exhibits, may possibly serve to obscure the truth, rather than to bring it out clearly.
Point 1.—This is one to which the proper plea is "not guilty." The writer does not remember ever to have seen just the type of construction shown in Fig. 1, either used or recommended. The angle at which the bars are bent up is rarely as great as 45°, much less 60 degrees. The writer has never heard of "sharp bends" being insisted on, and has never seen them used; it is simply recommended or required that some of the bars be bent up and, in practice, the bend is always a gentle one. The stress to be carried by the concrete as a queen-post is never as great as that assumed by the author, and, in practice, the queen-post has a much greater bearing on the bars than is indicated in Fig. 1.
Point 2.—The writer, in a rather extensive experience, has never seen this point exemplified.
Point 3.—It is probable that as far as Point 3 relates to retaining walls, it touches a weak spot sometimes seen in actual practice, but necessity for adequate anchorage is discussed at great length in accepted literature, and the fault should be charged to the individual[Pg 125] designer, for correct information has been within his reach for at least ten years.
Point 4.—In this case it would seem that the author has put a wrong interpretation on what is generally meant by shear. However, it is undoubtedly true that actual shear in reinforcing steel is sometimes figured and relied on. Under some conditions it is good practice, and under others it is not. Transverse rods, properly placed, can surely act in transmitting stress from the stem to the flange of a T-beam, and could properly be so used. There are other conditions under which the concrete may hold the rods so rigidly that their shearing strength may be utilized; where such conditions do not obtain, it is not ordinarily necessary to count on the shearing strength of the rods.
Point 5.—Even if vertical stirrups do not act until the concrete has cracked, they are still desirable, as insuring a gradual failure and, generally, greater ultimate carrying capacity. It would seem that the point where their full strength should be developed is rather at the neutral axis than at the centroid of compression stresses. As they are usually quite light, this generally enables them to secure the requisite anchorage in the compressed part of the concrete. Applied to a riveted truss, the author's reasoning would require that all the rivets by which web members are attached to the top chord should be above the center of gravity of the chord section.
Point 6.—There are many engineers who, accepting the common theory of diagonal tension and compression in a solid beam, believe that, in a reinforced concrete beam with stirrups, the concrete can carry the diagonal compression, and the stirrups the tension. If these web stresses are adequately cared for, shear can be neglected.
The writer cannot escape the conclusion that tests which have been made support the above belief. He believes that stirrups should be inclined at an angle of 45° or less, and that they should be fastened rigidly to the horizontal bars; but that is merely the most efficient way to use them—not the only way to secure the desired action, at least, in some degree.
The author's proposed method of bending up some of the main bars is good, but he should not overlook the fact that he is taking them away from the bottom of the beam just as surely as in the case of a sharp bend, and this is one of his objections to the ordinary method of bending them up. Moreover, with long spans and varying distances of the load, the curve which he adopts for his bars cannot possibly be always the true equilibrium curve. His concrete must then act as a stiffening truss, and will almost inevitably crack before his cable can come into action as such.
Bulletin No. 29 of the University of Illinois contains nothing to indicate that the bars bent up in the tests reported were bent up in any other than the ordinary way; certainly they could not be con[Pg 126]sidered as equivalent to the cables of a suspension bridge. These beams behaved pretty well, but the loads were applied so as to make them practically queen-post trusses, symmetrically loaded. While the bends in the bars were apparently not very sharp, and the angle of inclination was much less than 60°, or even 45°, it is not easy to find adequate bearings for the concrete posts on theoretical grounds, yet it is evident that the bearing was there just the same. The last four beams of the series, 521-1, 521-2, 521-5, 521-6, were about as nearly like Fig. 1 as anything the writer has ever seen in actual practice, yet they seem to have been the best of all. To be sure, the ends of the bent-up bars had a rather better anchorage, but they seem to have managed the shear question pretty much according to the expectation of their designer, and it is almost certain that the latter's assumptions would come under some part of the author's general indictment. These beams would seem to justify the art in certain practices condemned by the author. Perhaps he overlooked them.
Point 7.—The writer does not believe that the "general" practice as to continuity is on the basis charged. In fact, the general practice seems to him to be rather in the reverse direction. Personally, the writer believes in accepting continuity and designing for it, with moments at both center and supports equal to two-thirds of the center movement for a single span, uniformly loaded. He believes that the design of reinforced concrete should not be placed on the same footing as that of structural steel, because there is a fundamental difference, calling for different treatment. The basis should be sound, in both cases; but what is sound for one is not necessarily so for the other. In the author's plan for a series of spans designed as simple beams, with a reasonable amount of top reinforcement, he might get excessive stress and cracks in the concrete entirely outside of the supports. The shear would then become a serious matter, but no doubt the direct reinforcement would come into play as a suspension bridge, with further cracking of the concrete as a necessary preliminary.
Unfortunately, the writer is unable to refer to records, but he is quite sure that, in the early days, the rivets and bolts in the upper part of steel and iron bridge stringer connections gave some trouble by failing in tension due to continuous action, where the stringers were of moderate depth compared to the span. Possibly some members of the Society may know of such instances. The writer's instructors in structural design warned him against shallow stringers on that account, and told him that such things had happened.
Is it certain that structural steel design is on such a sound basis after all? Recent experiences seem to cast some doubt on it, and we may yet discover that we have escaped trouble, especially in buildings, because we almost invariably provide for loads much greater than are ever actually applied, and not because our knowledge and practice are especially exact.
Point 8.—The writer believes that this point is well taken, as to a great deal of current practice; but, if the author's ideas are carried out, reinforced concrete will be limited to a narrow field of usefulness, because of weight and cost. With attached web members, the writer believes that steel can be concentrated in heavy members in a way that is not safe with plain bars, and that, in this way, much greater latitude of design may be safely allowed.
Point 9.—The writer is largely in accord with the author's ideas on the subject of T-beams, but thinks he must have overlooked a very careful and able analysis of this kind of member, made by A.L. Johnson, M. Am. Soc. C. E., a number of years ago. While too much of the floor slab is still counted on for flange duty, it seems to the writer that, within the last few years, practice has greatly improved in this respect.
Point 10.—The author's statement regarding the beam and slab formulas in common use is well grounded. The modulus of elasticity of concrete is so variable that any formulas containing it and pretending to determine the stress in the concrete are unreliable, but the author's proposed method is equally so. We can determine by experiment limiting percentages of steel which a concrete of given quality can safely carry as reinforcement, and then use empirical formulas based on the stress in the steel and an assumed percentage of its depth in the concrete as a lever arm with more ease and just as much accuracy. The common methods result in designs which are safe enough, but they pretend to determine the stress in concrete; the writer does not believe that that is possible within 30% of the truth, and can see no profit in making laborious calculations leading to such unreliable results.
Point 11.—The writer has never designed a reinforced concrete chimney, but if he ever has to do so, he will surely not use any formula that is dependent on the modulus of elasticity of concrete.
Points 12, 13, and 14.—The writer has never had to consider these points to any extent in his own work, and will leave discussion to those better qualified.
Point 15.—There is much questionable practice in regard to reinforced concrete columns; but the matter is hardly disposed of as easily as indicated by the author. Other engineers draw different conclusions from the tests cited by the author, and from some to which he does not refer. To the writer it appears that here is a problem still awaiting solution on a really satisfactory basis. It seems incredible that the author would use plain concrete in columns, yet that seems to be the inference. The tests seem to indicate that there is much merit in both hooping and longitudinal reinforcement, if properly designed; that the fire-resisting covering should not be integral with the columns proper; that the high results obtained by M. Considère in testing small specimens cannot be depended on in practice, but that the[Pg 128] reinforcement is of great value, nevertheless. The writer believes that when load-carrying capacity, stresses due to eccentricity, and fire-resisting qualities are all given due consideration, a type of column with close hooping and longitudinal reinforcement provided with shear members, will finally be developed, which will more than justify itself.
Point 16.—The writer has not gone as deeply into this question, from a theoretical point of view, as he would like; but he has had one experience that is pertinent. Some years ago, he built a plain slab floor supported by brick walls. The span was about 16 ft. The dimensions of the slab at right angles to the reinforcement was 100 ft. or more. Plain round bars, 1/2 in. in diameter, were run at right angles to the reinforcement about 2 ft. on centers, the object being to lessen cracks. The reinforcement consisted of Kahn bars, reaching from wall to wall. The rounds were laid on top of the Kahn bars. The concrete was frozen and undeniably damaged, but the floors stood up, without noticeable deflection, after the removal of the forms. The concrete was so soft, however, that a test was decided on. An area about 4 ft. wide, and extending to within about 1 ft. of each bearing wall, was loaded with bricks piled in small piers not in contact with each other, so as to constitute practically a uniformly distributed load. When the total load amounted to much less than the desired working load for the 4-ft. strip, considerable deflection had developed. As the load increased, the deflection increased, and extended for probably 15 or 20 ft. on either side of the loaded area. Finally, under about three-fourths of the desired breaking load for the 4-ft. strip, it became evident that collapse would soon occur. The load was left undisturbed and, in 3 or 4 min., an area about 16 ft. square tore loose from the remainder of the floor and fell. The first noticeable deflection in the above test extended for 8 or 10 ft. on either side of the loaded strip. It would seem that this test indicated considerable distributing power in the round rods, although they were not counted as reinforcement for load-carrying purposes at all. The concrete was extremely poor, and none of the steel was stressed beyond the elastic limit. While this test may not justify the designer in using lighter reinforcement for the short way of the slab, it at least indicates a very real value for some reinforcement in the other direction. It would seem to indicate, also, that light steel members in a concrete slab might resist a small amount of shear. The slab in this case was about 6 in. thick.
Sanford E. Thompson, M. Am. Soc. C. E. (by letter).—Mr. Godfrey's sweeping condemnation of reinforced concrete columns, referred to in his fifteenth point, should not be passed over without serious criticism. The columns in a building, as he states, are the most vital portion of the structure, and for this very reason their design should be governed by theoretical and practical considerations based on the most comprehensive tests available.
The quotation by Mr. Godfrey from a writer on hooped columns is certainly more radical than is endorsed by conservative engineers, but the best practice in column reinforcement, as recommended by the Joint Committee on Concrete and Reinforced Concrete, which assumes that the longitudinal bars assist in taking stress in accordance with the ratio of elasticity of steel to concrete, and that the hooping serves to increase the toughness of the column, is founded on the most substantial basis of theory and test.
In preparing the second edition of "Concrete, Plain and Reinforced," the writer examined critically the various tests of concrete columns in order to establish a definite basis for his conclusions. Referring more particularly to columns reinforced with vertical steel bars, an examination of all the tests of full-sized columns made in the United States appears to bear out the fact very clearly that longitudinal steel bars embedded in concrete increase the strength of the column, and, further, to confirm the theory by which the strength of the combination of steel and concrete may be computed and is computed in practice.
Tests of large columns have been made at the Watertown Arsenal, the Massachusetts Institute of Technology, the University of Illinois, by the City of Minneapolis, and at the University of Wisconsin. The results of these various tests were recently summarized by the writer in a paper presented at the January, 1910, meeting of the National Association of Cement Users[O]. Reference may be made to this paper for fuller particulars, but the averages of the tests of each series are worth repeating here.
In comparing the averages of reinforced columns, specimens with spiral or other hooping designed to increase the strength, or with horizontal reinforcement placed so closely together as to prevent proper placing of the concrete, are omitted. For the Watertown Arsenal tests the averages given are made up from fair representative tests on selected proportions of concrete, given in detail in the paper referred to, while in other cases all the corresponding specimens of the two types are averaged. The results are given in Table 1.
The comparison of these tests must be made, of course, independently in each series, because the materials and proportions of the concrete and the amounts of reinforcement are different in the different series. The averages are given simply to bring out the point, very definitely and distinctly, that longitudinally reinforced columns are stronger than columns of plain concrete.
A more careful analysis of the tests shows that the reinforced columns are not only stronger, but that the increase in strength due to the reinforcement averages greater than the ordinary theory, using a ratio of elasticity of 15, would predicate.
Certain of the results given are diametrically opposed to Mr. God[Pg 130]frey's conclusions from the same sets of tests. Reference is made by him, for example (page 69), to a plain column tested at the University of Illinois, which crushed at 2,001 lb. per sq. in., while a reinforced column of similar size crushed at 1,557 lb. per sq. in.,[P] and the author suggests that "This is not an isolated case, but appears to be the rule." Examination of this series of tests shows that it is somewhat more erratic than most of those made at the University of Illinois, but, even from the table referred to by Mr. Godfrey, pursuing his method of reasoning, the reverse conclusion might be reached, for if, instead of selecting, as he has done, the weakest reinforced column in the entire lot and the strongest plain column, a reverse selection had been made, the strength of the plain column would have been stated as 1,079 lb. per sq. in. and that of the reinforced column as 3,335 lb. per sq. in. If extremes are to be selected at all, the weakest reinforced column should be compared with the weakest plain column, and the strongest reinforced column with the strongest plain column; and the results would show that while an occasional reinforced column may be low in strength, an occasional plain column will be still lower, so that the reinforcement, even by this comparison, is of marked advantage in increasing strength. In such cases, however, comparisons should be made by averages. The average strength of the reinforced columns, even in this series, as given in Table 1, is considerably higher than that of the plain columns.
| Location of test. |
Average strength of plain columns. |
Average strength of longitudinally reinforced columns. |
Reference. |
| Watertown Arsenal. |
1,781 | 2,992 | Taylor and Thompson's "Concrete, Plain and Reinforced" (2nd edition), p. 493. |
| Massachusetts Institute of Technology. |
1,750 | 2,370 | Transactions, Am. Soc. C. E., Vol. L, p. 487. |
| University of Illinois. |
1,550 | 1,750 | Bulletin No. 10. University of Illinois, 1907. |
| City of Minneapolis. |
2,020 | 2,300 | Engineering News, Dec. 3d, 1908, p. 608. |
| University of Wisconsin. |
2,033 | 2,438 | Proceedings, Am. Soc. for Testing Materials, Vol. IX, 1909, p. 477. |
In referring, in the next paragraph, to Mr. Withey's tests at the University of Wisconsin, Mr. Godfrey selects for his comparison two groups of concrete which are not comparable. Mr. Withey, in the paper describing the tests, refers to two groups of plain concrete[Pg 131] columns, A1 to A4, and W1 to W3. He speaks of the uniformity in the tests of the former group, the maximum variation in the four specimens being only 2%, but states, with reference to columns, W1 to W3, that:
"As these 3 columns were made of a concrete much superior to that in any of the other columns made from 1:2:4 or 1:2:3-1/2 mix, they cannot satisfactorily be compared with them. Failures of all plain columns were sudden and without any warning."
Now, Mr. Godfrey, instead of taking columns A1 to A3, selects for his comparison W1 to W3, made, as Mr. Withey distinctly states, with an especially superior concrete. Taking columns, A1 to A3, for comparison with the reinforced columns, E1 to E3, the result shows an average of 2,033 for the plain columns and 2,438 for the reinforced columns.
Again, taking the third series of tests referred to by Mr. Godfrey, those at Minneapolis, Minn., it is to be noticed that he selects for his criticism a column which has this note as to the manner of failure: "Bending at center (bad batch of concrete at this point)." Furthermore, the column is only 9 by 9 in., and square, and the stress referred to is calculated on the full section of the column instead of on the strength within the hooping, although the latter method is the general practice in a hooped column. The inaccuracy of this is shown by the fact that, with this small size of square column, more than half the area is outside the hooping and never taken into account in theoretical computations. A fair comparison, as far as longitudinal reinforcement is concerned, is always between the two plain columns and the six columns, E, D, and F. The results are so instructive that a letter[Q] by the writer is quoted in full as follows:
"Sir:—
"In view of the fact that the column tests at Minneapolis, as reported in your paper of December 3, 1908, p. 608, are liable because of the small size of the specimens to lead to divergent conclusions, a few remarks with reference to them may not be out of place at this time.
"1. It is evident that the columns were all smaller, being only 9 in. square, than is considered good practice in practical construction, because of the difficulty of properly placing the concrete around the reinforcement.
"2. The tests of columns with flat bands, A, B, and C, in comparison with the columns E, D and F, indicate that the wide bands affected the placing of the concrete, separating the internal core from the outside shell so that it would have been nearly as accurate to base the strength upon the material within the bands, that is, upon a section of 38 sq. in., instead of upon the total area of 81 sq. in. This set of tests, A, B and C, is therefore inconclusive except as showing the practical difficulty in the use of bands in small columns, and the[Pg 132] necessity for disregarding all concrete outside of the bands when computing the strength.
"3. The six columns E, D and F, each of which contained eight 5/8-in. rods, are the only ones which are a fair test of columns longitudinally reinforced, since they are the only specimens except the plain columns in which the small sectional area was not cut by bands or hoops. Taking these columns, we find an average strength 38% in excess of the plain columns, whereas, with the percentage of reinforcement used, the ordinary formula for vertical steel (using a ratio of elasticity of steel to concrete of 15) gives 34% as the increase which might be expected. In other words, the actual strength of this set of columns was in excess of the theoretical strength. The wire bands on these columns could not be considered even by the advocates of hooped columns as appreciably adding to the strength, because they were square instead of circular. It may be noted further in connection with these longitudinally reinforced columns that the results were very uniform and, further, that the strength of every specimen was much greater than the strength of the plain columns, being in every case except one at least 40% greater. In these columns the rods buckled between the bands, but they evidently did not do so until their elastic limit was passed, at which time of course they would be expected to fail.
"4. With reference to columns, A, B, C and L, which were essentially hooped columns, the failure appears to have been caused by the greater deformation which is always found in hooped columns, and which in the earlier stages of the loading is apparently due to lack of homogeneity caused by the difficulty in placing the concrete around the hooping, and in the later stage of the loading to the excessive expansion of the concrete. This greater deformation in a hooped column causes any vertical steel to pass its elastic limit at an earlier stage than in a column where the deformation is less, and therefore produces the buckling between the bands which is noted in these two sets of columns. This excessive deformation is a strong argument against the use of high working stresses in hooped columns.
"In conclusion, then, it may be said that the columns reinforced with vertical round rods showed all the strength that would be expected of them by theoretical computation. The hooped columns, on the other hand, that is, the columns reinforced with circular bands and hoops, gave in all cases comparatively low results, but no conclusions can be drawn from them because the unit-strength would have been greatly increased if the columns had been larger so that the relative area of the internal core to the total area of the column had been greater."
From this letter, it will be seen that every one of Mr. Godfrey's comparisons of plain versus reinforced columns requires explanations which decidedly reduce, if they do not entirely destroy, the force of his criticism.
This discussion can scarcely be considered complete without brief reference to the theory of longitudinal steel reinforcement for columns. The principle[R] is comparatively simple. When a load is placed on a[Pg 133] column of any material it is shortened in proportion, within working limits, to the load placed upon it; that is, with a column of homogeneous material, if the load is doubled, the amount of shortening or deformation is also doubled. If vertical steel bars are embedded in concrete, they must shorten when the load is applied, and consequently relieve the concrete of a portion of its load. It is therefore physically impossible to prevent such vertical steel from taking a portion of the load unless the steel slips or buckles.
As to the possible danger of the bars in the concrete slipping or buckling, to which Mr. Godfrey also refers, again must tests be cited. If the ends are securely held—and this is always the case when bars are properly butted or are lapped for a sufficient length—they cannot slip. With reference to buckling, tests have proved conclusively that vertical bars such as are used in columns, when embedded in concrete, will not buckle until the elastic limit of the steel is reached, or until the concrete actually crushes. Beyond these points, of course, neither steel nor concrete nor any other material is expected to do service.
As proof of this statement, it will be seen, by reference to tests at the Watertown Arsenal, as recorded in "Tests of Metals," that many of the columns were made with vertical bar reinforcement having absolutely no hoops or horizontal steel placed around them. That is, the bars, 8 ft. long, were placed in the four corners of the column—in some tests only 2 in. from the surface—and held in place simply by the concrete itself.[S] There was no sign whatever of buckling until the compression was so great that the elastic limit of the steel was passed, when, of course, no further strength could be expected from it.
To recapitulate the conclusions reached as a result of a study of the tests: It is evident that, not only does theory permit the use of longitudinal bar reinforcement for increasing the strength of concrete columns, whenever such reinforcement is considered advisable, but that all the important series of column tests made in the United States to date show a decisive increase in strength of columns reinforced with longitudinal steel bars over those which are not reinforced. Furthermore, as has already been mentioned, without treating the details of the proof, it can be shown that the tests bear out conclusively the conservatism of computing the value of the vertical steel bars in compression by the ordinary formulas based on the ratio of the moduli of elasticity of steel to concrete.
Edward Godfrey, M. Am. Soc. C. E. (by letter).—As was to be expected, this paper has brought out discussion, some of which is favorable and flattering; some is in the nature of dust-throwing to obscure the force of the points made; some would attempt to belittle the importance of these points; and some simply brings out the old[Pg 134] and over-worked argument which can be paraphrased about as follows: "The structures stand up and perform their duty, is this not enough?"
The last-mentioned argument is as old as Engineering; it is the "practical man's" mainstay, his "unanswerable argument." The so-called practical man will construct a building, and test it either with loads or by practical use. Then he will modify the design somewhere, and the resulting construction will be tested. If it passes through this modifying process and still does service, he has something which, in his mind, is unassailable. Imagine the freaks which would be erected in the iron bridge line, if the capacity to stand up were all the designer had to guide him, analysis of stresses being unknown. Tests are essential, but analysis is just as essential. The fact that a structure carries the bare load for which it is computed, is in no sense a test of its correct design; it is not even a test of its safety. In Pittsburg, some years ago, a plate-girder span collapsed under the weight of a locomotive which it had carried many times. This bridge was, perhaps, thirty years old. Some reinforced concrete bridges have failed under loads which they have carried many times. Others have fallen under no extraneous load, and after being in service many months. If a large number of the columns of a structure fall shortly after the forms are removed, what is the factor of safety of the remainder, which are identical, but have not quite reached their limit of strength? Or what is the factor of safety of columns in other buildings in which the concrete was a little better or the forms have been left in a little longer, both sets of columns being similarly designed?
There are highway bridges of moderately long spans standing and doing service, which have 2-in. chord pins; laterals attached to swinging floor-beams in such a way that they could not possibly receive their full stress; eye-bars with welded-on heads; and many other equally absurd and foolish details, some of which were no doubt patented in their day. Would any engineer with any knowledge whatever of bridge design accept such details? They often stand the test of actual service for years; in pins, particularly, the calculated stress is sometimes very great. These details do not stand the test of analysis and of common sense, and, therefore, no reputable engineer would accept them.
Mr. Turner, in the first and second paragraphs of his discussion, would convey the impression that the writer was in doubt as to his "personal opinions" and wanted some free advice. He intimates that he is too busy to go fully into a treatise in order to set them right. He further tries to throw discredit on the paper by saying that the writer has adduced no clean-cut statement of fact or tests in support of his views. If Mr. Turner had read the paper carefully, he would not have had the idea that in it the hooped column is condemned. As[Pg 135] to this more will be said later. The paper is simply and solely a collection of statements of facts and tests, whereas his discussion teems with his "personal opinion," and such statements as "These values * * * are regarded by the writer as having at least double the factor of safety used in ordinary designs of structural steel"; "On a basis not far from that which the writer considers reasonable practice." Do these sound like clean-cut statements of fact, or are they personal opinions? It is a fact, pure and simple, that a sharp bend in a reinforcing rod in concrete violates the simplest principles of mechanics; also that the queen-post and Pratt and Howe truss analogies applied to reinforcing steel in concrete are fallacies; that a few inches of embedment will not anchor a rod for its value; that concrete shrinks in setting in air and puts initial stress in both the concrete and the steel, making assumed unstressed initial conditions non-existent. It is a fact that longitudinal rods alone cannot be relied on to reinforce a concrete column. Contrary to Mr. Turner's statement, tests have been adduced to demonstrate this fact. Further, it is a fact that the faults and errors in reinforced concrete design to which attention is called, are very common in current design, and are held up as models in nearly all books on the subject.
The writer has not asked any one to believe a single thing because he thinks it is so, or to change a single feature of design because in his judgment that feature is faulty. The facts given are exemplifications of elementary mechanical principles overlooked by other writers, just as early bridge designers and writers on bridge design overlooked the importance of calculating bridge pins and other details which would carry the stress of the members.
A careful reading of the paper will show that the writer does not accept the opinions of others, when they are not backed by sound reason, and does not urge his own opinion.
Instead of being a statement of personal opinion for which confirmation is desired, the paper is a simple statement of facts and tests which demonstrate the error of practices exhibited in a large majority of reinforced concrete work and held up in the literature on the subject as examples to follow. Mr. Turner has made no attempt to deny or refute any one of these facts, but he speaks of the burden of proof resting on the writer. Further, he makes statements which show that he fails entirely to understand the facts given or to grasp their meaning. He says that the writer's idea is "that the entire pull of the main reinforcing rod should be taken up apparently at the end." He adds that the soundness of this position may be questioned, because, in slabs, the steel frequently breaks at the center. Compare this with the writer's statement, as follows:
"In shallow beams there is little need of provision for taking shear by any other means than the concrete itself. The writer has seen[Pg 136] a reinforced slab support a very heavy load by simple friction, for the slab was cracked close to the supports. In slabs, shear is seldom provided for in the steel reinforcement. It is only when beams begin to have a depth approximating one-tenth of the span that the shear in the concrete becomes excessive and provision is necessary in the steel reinforcement. Years ago, the writer recommended that, in such beams, some of the rods be curved up toward the ends of the span and anchored over the support."
It is solely in providing for shear that the steel reinforcement should be anchored for its full value over the support. The shear must ultimately reach the support, and that part which the concrete is not capable of carrying should be taken to it solely by the steel, as far as tensile and shear stresses are concerned. It should not be thrown back on the concrete again, as a system of stirrups must necessarily do.
The following is another loose assertion by Mr. Turner:
"Mr. Godfrey appears to consider that the hooping and vertical reinforcement of columns is of little value. He, however, presents for consideration nothing but his opinion of the matter, which appears to be based on an almost total lack of familiarity with such construction."
There is no excuse for statements like this. If Mr. Turner did not read the paper, he should not have attempted to criticize it. What the writer presented for consideration was more than his opinion of the matter. In fact, no opinion at all was presented. What was presented was tests which prove absolutely that longitudinal rods without hoops may actually reduce the strength of a column, and that a column containing longitudinal rods and "hoops which are not close enough to stiffen the rods" may be of less strength than a plain concrete column. A properly hooped column was not mentioned, except by inference, in the quotation given in the foregoing sentence. The column tests which Mr. Turner presents have no bearing whatever on the paper, for they relate to columns with bands and close spirals. Columns are sometimes built like these, but there is a vast amount of work in which hooping and bands are omitted or are reduced to a practical nullity by being spaced a foot or so apart.
A steel column made up of several pieces latticed together derives a large part of its stiffness and ability to carry compressive stresses from the latticing, which should be of a strength commensurate with the size of the column. If it were weak, the column would suffer in strength. The latticing might be very much stronger than necessary, but it would not add anything to the strength of the column to resist compression. A formula for the compressive strength of a column could not include an element varying with the size of the lattice. If the lattice is weak, the column is simply deficient; so a formula for a hooped column is incorrect if it shows that the strength of the column varies with the section of the hoops, and, on this account, the common formula is incorrect. The hoops might be ever so strong,[Pg 137] beyond a certain limit, and yet not an iota would be added to the compressive strength of the column, for the concrete between the hoops might crush long before their full strength was brought into play. Also, the hoops might be too far apart to be of much or any benefit, just as the lattice in a steel column might be too widely spaced. There is no element of personal opinion in these matters. They are simply incontrovertible facts. The strength of a hooped column, disregarding for the time the longitudinal steel, is dependent on the fact that thin discs of concrete are capable of carrying much more load than shafts or cubes. The hoops divide the column into thin discs, if they are closely spaced; widely spaced hoops do not effect this. Thin joints of lime mortar are known to be many times stronger than the same mortar in cubes. Why, in the many books on the subject of reinforced concrete, is there no mention of this simple principle? Why do writers on this subject practically ignore the importance of toughness or tensile strength in columns? The trouble seems to be in the tendency to interpret concrete in terms of steel. Steel at failure in short blocks will begin to spread and flow, and a short column has nearly the same unit strength as a short block. The action of concrete under compression is quite different, because of the weakness of concrete in tension. The concrete spalls off or cracks apart and does not flow under compression, and the unit strength of a shaft of concrete under compression has little relation to that of a flat block. Some years ago the writer pointed out that the weakness of cast-iron columns in compression is due to the lack of tensile strength or toughness in cast iron. Compare 7,600 lb. per sq. in. as the base of a column formula for cast iron with 100,000 lb. per sq. in. as the compressive strength of short blocks of cast iron. Then compare 750 lb. per sq. in., sometimes used in concrete columns, with 2,000 lb. per sq. in., the ultimate strength in blocks. A material one-fiftieth as strong in compression and one-hundredth as strong in tension with a "safe" unit one-tenth as great! The greater tensile strength of rich mixtures of concrete accounts fully for the greater showing in compression in tests of columns of such mixtures. A few weeks ago, an investigator in this line remarked, in a discussion at a meeting of engineers, that "the failure of concrete in compression may in cases be due to lack of tensile strength." This remark was considered of sufficient novelty and importance by an engineering periodical to make a special news item of it. This is a good illustration of the state of knowledge of the elementary principles in this branch of engineering.
Mr. Turner states, "Again, concrete is a material which shows to the best advantage as a monolith, and, as such, the simple beam seems to be decidedly out of date to the experienced constructor." Similar things could be said of steelwork, and with more force. Riveted trusses are preferable to articulated ones for rigidity. The stringers[Pg 138] of a bridge could readily be made continuous; in fact, the very riveting of the ends to a floor-beam gives them a large capacity to carry reverse moments. This strength is frequently taken advantage of at the end floor-beam, where a tie is made to rest on a bracket having the same riveted connection as the stringer. A small splice-plate across the top flanges of the stringers would greatly increase this strength to resist reverse moments. A steel truss span is ideally conditioned for continuity in the stringers, since the various supports are practically relatively immovable. This is not true in a reinforced concrete building where each support may settle independently and entirely vitiate calculated continuous stresses. Bridge engineers ignore continuity absolutely in calculating the stringers; they do not argue that a simple beam is out of date. Reinforced concrete engineers would do vastly better work if they would do likewise, adding top reinforcement over supports to forestall cracking only. Failure could not occur in a system of beams properly designed as simple spans, even if the negative moments over the supports exceeded those for which the steel reinforcement was provided, for the reason that the deflection or curving over the supports can only be a small amount, and the simple-beam reinforcement will immediately come into play.
Mr. Turner speaks of the absurdity of any method of calculating a multiple-way reinforcement in slabs by endeavoring to separate the construction into elementary beam strips, referring, of course, to the writer's method. This is misleading. The writer does not endeavor to "separate the construction into elementary beam strips" in the sense of disregarding the effect of cross-strips. The "separation" is analogous to that of considering the tension and compression portions of a beam separately in proportioning their size or reinforcement, but unitedly in calculating their moment. As stated in the paper, "strips are taken across the slab and the moment in them is found, considering the limitations of the several strips in deflection imposed by those running at right angles therewith." It is a sound and rational assumption that each strip, 1 ft. wide through the middle of the slab, carries its half of the middle square foot of the slab load. It is a necessary limitation that the other strips which intersect one of these critical strips across the middle of the slab, cannot carry half of the intercepted square foot, because the deflection of these other strips must diminish to zero as they approach the side of the rectangle. Thus, the nearer the support a strip parallel to that support is located, the less load it can take, for the reason that it cannot deflect as much as the middle strip. In the oblong slab the condition imposed is equal deflection of two strips of unequal span intersecting at the middle of the slab, as well as diminished deflection of the parallel strips.
In this method of treating the rectangular slab, the concrete in tension is not considered to be of any value, as is the case in all accepted methods.
Some years ago the writer tested a number of slabs in a building, with a load of 250 lb. per sq. ft. These slabs were 3 in. thick and had a clear span of 44 in. between beams. They were totally without reinforcement. Some had cracked from shrinkage, the cracks running through them and practically the full length of the beams. They all carried this load without any apparent distress. If these slabs had been reinforced with some special reinforcement of very small cross-section, the strength which was manifestly in the concrete itself, might have been made to appear to be in the reinforcement. Magic properties could be thus conjured up for some special brand of reinforcement. An energetic proprietor could capitalize tension in concrete in this way and "prove" by tests his claims to the magic properties of his reinforcement.
To say that Poisson's ratio has anything to do with the reinforcement of a slab is to consider the tensile strength of concrete as having a positive value in the bottom of that slab. It means to reinforce for the stretch in the concrete and not for the tensile stress. If the tensile strength of concrete is not accepted as an element in the strength of a slab having one-way reinforcement, why should it be accepted in one having reinforcement in two or more directions? The tensile strength of concrete in a slab of any kind is of course real, when the slab is without cracks; it has a large influence in the deflection; but what about a slab that is cracked from shrinkage or otherwise?
Mr. Turner dodges the issue in the matter of stirrups by stating that they were not correctly placed in the tests made at the University of Illinois. He cites the Hennebique system as a correct sample. This system, as the writer finds it, has some rods bent up toward the support and anchored over it to some extent, or run into the next span. Then stirrups are added. There could be no objection to stirrups if, apart from them, the construction were made adequate, except that expense is added thereby. Mr. Turner cannot deny that stirrups are very commonly used just as they were placed in the tests made at the University of Illinois. It is the common practice and the prevailing logic in the literature of the subject which the writer condemns.
Mr. Thacher says of the first point:
"At the point where the first rod is bent up, the stress in this rod runs out. The other rods are sufficient to take the horizontal stress, and the bent-up portion provides only for the vertical and diagonal shearing stresses in the concrete."
If the stress runs out, by what does that rod, in the bent portion, take shear? Could it be severed at the bend, and still perform its office? The writer can conceive of an inclined rod taking the shear of a beam if it were anchored at each end, or long enough somehow to have a grip in the concrete from the centroid of compression up[Pg 140] and from the center of the steel down. This latter is a practical impossibility. A rod curved up from the bottom reinforcement and curved to a horizontal position and run to the support with anchorage, would take the shear of a beam. As to the stress running out of a rod at the point where it is bent up, this will hardly stand the test of analysis in the majority of cases. On account of the parabolic variation of stress in a beam, there should be double the length necessary for the full grip of a rod in the space from the center to the end of a beam. If 50 diameters are needed for this grip, the whole span should then be not less than four times 50, or 200 diameters of the rod. For the same reason the rod between these bends should be at least 200 diameters in length. Often the reinforcing rods are equal to or more than one-two-hundredth of the span in diameter, and therefore need the full length of the span for grip.
Mr. Thacher states that Rod 3 provides for the shear. He fails to answer the argument that this rod is not anchored over the support to take the shear. Would he, in a queen-post truss, attach the hog-rod to the beam some distance out from the support and thus throw the bending and shear back into the very beam which this rod is intended to relieve of bending and shear? Yet this is just what Rod 3 would do, if it were long enough to be anchored for the shear, which it seldom is; hence it cannot even perform this function. If Rod 3 takes the shear, it must give it back to the concrete beam from the point of its full usefulness to the support. Mr. Thacher would not say of a steel truss that the diagonal bars would take the shear, if these bars, in a deck truss, were attached to the top chord several feet away from the support, or if the end connection were good for only a fraction of the stress in the bars. Why does he not apply the same logic to reinforced concrete design?
Answering the third point, Mr. Thacher makes more statements that are characteristic of current logic in reinforced concrete literature, which does not bother with premises. He says, "In a beam, the shear rods run through the compression parts of the concrete and have sufficient anchorage." If the rods have sufficient anchorage, what is the nature of that anchorage? It ought to be possible to analyze it, and it is due to the seeker after truth to produce some sort of analysis. What mysterious thing is there to anchor these rods? The writer has shown by analysis that they are not anchored sufficiently. In many cases they are not long enough to receive full anchorage. Mr. Thacher merely makes the dogmatic statement that they are anchored. There is a faint hint of a reason in his statement that they run into the compression part of the concrete. Does he mean that the compression part of the concrete will grip the rod like a vise? How does this comport with his contention farther on that the beams are continuous? This would mean tension in the upper part of the beam. In any beam[Pg 141] the compression near the support, where the shear is greatest, is small; so even this hint of an argument has no force or meaning.
In this same paragraph Mr. Thacher states, concerning the third point and the case of the retaining wall that is given as an example, "In a counterfort, the inclined rods are sufficient to take the overturning stress." Mr. Thacher does not make clear what he means by "overturning stress." He seems to mean the force tending to pull the counterfort loose from the horizontal slab. The weight of the earth fill over this slab is the force against which the vertical and inclined rods of Fig. 2, at a, must act. Does Mr. Thacher mean to state seriously that it is sufficient to hang this slab, with its heavy load of earth fill, on the short projecting ends of a few rods? Would he hang a floor slab on a few rods which project from the bottom of a girder? He says, "The proposed method is no more effective." The proposed method is Fig. 2, at b, where an angle is provided as a shelf on which this slab rests. The angle is supported, with thread and nut, on rods which reach up to the front slab, from which a horizontal force, acting about the toe of the wall as a fulcrum, results in the lifting force on the slab. There is positively no way in which this wall could fail (as far as the counterfort is concerned) but by the pulling apart of the rods or the tearing out of this anchoring angle. Compare this method of failure with the mere pulling out of a few ends of rods, in the design which Mr. Thacher says is just as effective. This is another example of the kind of logic that is brought into requisition in order to justify absurd systems of design.
Mr. Thacher states that shear would govern in a bridge pin where there is a wide bar or bolster or a similar condition. The writer takes issue with him in this. While in such a case the center of bearing need not be taken to find the bending moment, shear would not be the correct governing element. There is no reason why a wide bar or a wide bolster should take a smaller pin than a narrow one, simply because the rule that uses the center of bearing would give too large a pin. Bending can be taken in this, as in other cases, with a reasonable assumption for a proper bearing depth in the wide bar or bolster. The rest of Mr. Thacher's comment on the fourth point avoids the issue. What does he mean by "stress" in a shear rod? Is it shear or tension? Mr. Thacher's statement, that the "stress" in the shear rods is less than that in the bottom bars, comes close to saying that it is shear, as the shearing unit in steel is less than the tensile unit. This vague way of referring to the "stress" in a shear member, without specifically stating whether this "stress" is shear or tension, as was done in the Joint Committee Report, is, in itself, a confession of the impossibility of analyzing the "stress" in these members. It gives the designer the option of using tension or shear, both of which are absurd in the ordinary method of design. Writers of books are[Pg 142] not bold enough, as a rule, to state that these rods are in shear, and yet their writings are so indefinite as to allow this very interpretation.
Mr. Thacher criticises the fifth point as follows:
"Vertical stirrups are designed to act like the vertical rods in a Howe truss. Special literature is not required on the subject; it is known that the method used gives good results, and that is sufficient."
This is another example of the logic applied to reinforced concrete design—another dogmatic statement. If these stirrups act like the verticals in a Howe truss, why is it not possible by analysis to show that they do? Of course there is no need of special literature on the subject, if it is the intention to perpetuate this senseless method of design. No amount of literature can prove that these stirrups act as the verticals of a Howe truss, for the simple reason that it can be easily proven that they do not.
Mr. Thacher's criticism of the sixth point is not clear. "All the shear from the center of the beam up to the bar in question," is what he says each shear member is designed to take in the common method. The shear of a beam usually means the sum of the vertical forces in a vertical section. If he means that the amount of this shear is the load from the center of the beam to the bar in question, and that shear members are designed to take this amount of shear, it would be interesting to know by what interpretation the common method can be made to mean this. The method referred to is that given in several standard works and in the Joint Committee Report. The formula in that report for vertical reinforcement is:
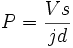 |
, |
in which P = the stress in a single reinforcing member, V = the proportion of total shear assumed as carried by the reinforcement, s = the horizontal spacing of the reinforcing members, and j d = the effective depth.
Suppose the spacing of shear members is one-half or one-third of the effective depth, the stress in each member is one-half or one-third of the "shear assumed to be carried by the reinforcement." Can Mr. Thacher make anything else out of it? If, as he says, vertical stirrups are designed to act like the vertical rods in a Howe truss, why are they not given the stress of the verticals of a Howe truss instead of one-half or one-third or a less proportion of that stress?
Without meaning to criticize the tests made by Mr. Thaddeus Hyatt on curved-up rods with nuts and washers, it is true that the results of many early tests on reinforced concrete are uncertain, because of the mealy character of the concrete made in the days when "a minimum amount of water" was the rule. Reinforcement slips in such concrete when it would be firmly gripped in wet concrete. The writer has been unable to find any record of the tests to which[Pg 143] Mr. Thacher refers. The tests made at the University of Illinois, far from showing reinforcement of this type to be "worse than useless," showed most excellent results by its use.
That which is condemned in the seventh point is not so much the calculating of reinforced concrete beams as continuous, and reinforcing them properly for these moments, but the common practice of lopping off arbitrarily a large fraction of the simple beam moment on reinforced concrete beams of all kinds. This is commonly justified by some virtue which lies in the term monolith. If a beam rests in a wall, it is "fixed ended"; if it comes into the side of a girder, it is "fixed ended"; and if it comes into the side of a column, it is the same. This is used to reduce the moment at mid-span, but reinforcement which will make the beam fixed ended or continuous is rare.
There is not much room for objection to Mr. Thacher's rule of spacing rods three diameters apart. The rule to which the writer referred as being 66% in error on the very premise on which it was derived, namely, shear equal to adhesion, was worked out by F.P. McKibben, M. Am. Soc. C. E. It was used, with due credit, by Messrs. Taylor and Thompson in their book, and, without credit, by Professors Maurer and Turneaure in their book. Thus five authorities perpetrate an error in the solution of one of the simplest problems imaginable. If one author of an arithmetic had said two twos are five, and four others had repeated the same thing, would it not show that both revision and care were badly needed?
Ernest McCullough, M. Am. Soc. C. E., in a paper read at the Armour Institute, in November, 1908, says, "If the slab is not less than one-fifth of the total depth of the beam assumed, we can make a T-section of it by having the narrow stem just wide enough to contain the steel." This partly answers Mr. Thacher's criticism of the ninth point. In the next paragraph, Mr. McCullough mentions some very nice formulas for T-beams by a certain authority. Of course it would be better to use these nice formulas than to pay attention to such "rule-of-thumb" methods as would require more width in the stem of the T than enough to squeeze the steel in.
If these complex formulas for T-beams (which disregard utterly the simple and essential requirement that there must be concrete enough in the stem of the T to grip the steel) are the only proper exemplifications of the "theory of T-beams," it is time for engineers to ignore theory and resort to rule-of-thumb. It is not theory, however, which is condemned in the paper, it is complex theory; theory totally out of harmony with the materials dealt with; theory based on false assumptions; theory which ignores essentials and magnifies trifles; theory which, applied to structures which have failed from their own weight, shows them to be perfectly safe and correct in design; half-baked theories which arrogate to themselves a monopoly on rationality.
To return to the spacing of rods in the bottom of a T-beam; the[Pg 144] report of the Joint Committee advocates a horizontal spacing of two and one-half diameters and a side spacing of two diameters to the surface. The same report advocates a "clear spacing between two layers of bars of not less than 1/2 in." Take a T-beam, 11-1/2 in. wide, with two layers of rods 1 in. square, 4 in each layer. The upper surface of the upper layer would be 3-1/2 in. above the bottom of the beam. Below this surface there would be 32 sq. in. of concrete to grip 8 sq. in. of steel. Does any one seriously contend that this trifling amount of concrete will grip this large steel area? This is not an extreme case; it is all too common; and it satisfies the requirements of the Joint Committee, which includes in its make-up a large number of the best-known authorities in the United States.
Mr. Thacher says that the writer appears to consider theories for reinforced concrete beams and slabs as useless refinements. This is not what the writer intended to show. He meant rather that facts and tests demonstrate that refinement in reinforced concrete theories is utterly meaningless. Of course a wonderful agreement between the double-refined theory and test can generally be effected by "hunching" the modulus of elasticity to suit. It works both ways, the modulus of elasticity of concrete being elastic enough to be shifted again to suit the designer's notion in selecting his reinforcement. All of which is very beautiful, but it renders standard design impossible.
Mr. Thacher characterizes the writer's method of calculating reinforced concrete chimneys as rule-of-thumb. This is surprising after what he says of the methods of designing stirrups. The writer's method would provide rods to take all the tensile stresses shown to exist by any analysis; it would give these rods unassailable end anchorages; every detail would be amply cared for. If loose methods are good enough for proportioning loose stirrups, and no literature is needed to show why or how they can be, why analyze a chimney so accurately and apply assumptions which cannot possibly be realized anywhere but on paper and in books?
It is not rule-of-thumb to find the tension in plain concrete and then embed steel in that concrete to take that tension. Moreover, it is safer than the so-called rational formula, which allows compression on slender rods in concrete.
Mr. Thacher says, "No arch designed by the elastic theory was ever known to fail, unless on account of insecure foundations." Is this the correct way to reach correct methods of design? Should engineers use a certain method until failures show that something is wrong? It is doubtful if any one on earth has statistics sufficient to state with any authority what is quoted in the opening sentence of this paragraph. Many arches are failures by reason of cracks, and these cracks are not always due to insecure foundations. If Mr. Thacher means by insecure foundations, those which settle, his assertion, assuming it to be true,[Pg 145] has but little weight. It is not always possible to found an arch on rock. Some settlement may be anticipated in almost every foundation. As commonly applied, the elastic theory is based on the absolute fixity of the abutments, and the arch ring is made more slender because of this fixity. The ordinary "row-of-blocks" method gives a stiffer arch ring and, consequently, greater security against settlement of foundations.
In 1904, two arches failed in Germany. They were three-hinged masonry arches with metal hinges. They appear to have gone down under the weight of theory. If they had been made of stone blocks in the old-fashioned way, and had been calculated in the old-fashioned row-of-blocks method, a large amount of money would have been saved. There is no good reason why an arch cannot be calculated as hinged ended and built with the arch ring anchored into the abutments. The method of the equilibrium polygon is a safe, sane, and sound way to calculate an arch. The monolithic method is a safe, sane, and sound way to build one. People who spend money for arches do not care whether or not the fancy and fancied stresses of the mathematician are realized; they want a safe and lasting structure.
Of course, calculations can be made for shrinkage stresses and for temperature stresses. They have about as much real meaning as calculations for earth pressures behind a retaining wall. The danger does not lie in making the calculations, but in the confidence which the very making of them begets in their correctness. Based on such confidence, factors of safety are sometimes worked out to the hundredth of a unit.
Mr. Thacher is quite right in his assertion that stiff steel angles, securely latticed together, and embedded in the concrete column, will greatly increase its strength.
The theory of slabs supported on four sides is commonly accepted for about the same reason as some other things. One author gives it, then another copies it; then when several books have it, it becomes authoritative. The theory found in most books and reports has no correct basis. That worked out by Professor W.C. Unwin, to which the writer referred, was shown by him to be wrong.[T] An important English report gave publicity and much space to this erroneous solution. Messrs. Marsh and Dunn, in their book on reinforced concrete, give several pages to it.
In referring to the effect of initial stress, Mr. Myers cites the case of blocks and says, "Whatever initial stress exists in the concrete due to this process of setting exists also in these blocks when they are tested." However, the presence of steel in beams and columns puts internal stresses in reinforced concrete, which do not exist in an isolated block of plain concrete.
Mr. Meem, while he states that he disagrees with the writer in one essential point, says of that point, "In the ordinary way in which these rods are used, they have no practical value." The paper is meant to be a criticism of the ordinary way in which reinforced concrete is used.
While Mr. Meem's formula for a reinforced concrete beam is simple and much like that which the writer would use, he errs in making the moment of the stress in the steel about the neutral axis equal to the moment of that in the concrete about the same axis. The actual amount of the tension in the steel should equal the compression in the concrete, but there is no principle of mechanics that requires equality of the moments about the neutral axis. The moment in the beam is, therefore, the product of the stress in steel or concrete and the effective depth of the beam, the latter being the depth from the steel up to a point one-sixth of the depth of the concrete beam from the top. This is the method given by the writer. It would standardize design as methods using the coefficient of elasticity cannot do.
Professor Clifford, in commenting on the first point, says, "The concrete at the point of juncture must give, to some extent, and this would distribute the bearing over a considerable length of rod." It is just this local "giving" in reinforced concrete which results in cracks that endanger its safety and spoil its appearance; they also discredit it as a permanent form of construction.
Professor Clifford has informed the writer that the tests on bent rods to which he refers were made on 3/4-in. rounds, embedded for 12 in. in concrete and bent sharply, the bent portion being 4 in. long. The 12-in. portion was greased. The average maximum load necessary to pull the rods out was 16,000 lb. It seems quite probable that there would be some slipping or crushing of the concrete before a very large part of this load was applied. The load at slipping would be a more useful determination than the ultimate, for the reason that repeated application of such loads will wear out a structure. In this connection three sets of tests described in Bulletin No. 29 of the University of Illinois, are instructive. They were made on beams of the same size, and reinforced with the same percentage of steel. The results were as follows:
Beams 511.1, 511.2, 512.1, 512.2: The bars were bent up at third points. Average breaking load, 18,600 lb. All failed by slipping of the bars.
Beams 513.1, 513.2: The bars were bent up at third points and given a sharp right-angle turn over the supports. Average breaking load, 16,500 lb. The beams failed by cracking alongside the bar toward the end.
Beams 514.2, 514.3: The bars were bent up at third points and had anchoring nuts and washers at the ends over the supports. Average breaking load, 22,800 lb. These failed by tension in the steel.
By these tests it is seen that, in a beam, bars without hooks were stronger in their hold on the concrete by an average of 13% than those with hooks. Each test of the group of straight bars showed that they were stronger than either of those with hooked bars. Bars anchored over the support in the manner recommended in the paper were nearly 40% stronger than hooked bars and 20% stronger than straight bars. These percentages, furthermore, do not represent all the advantages of anchored bars. The method of failure is of greatest significance. A failure by tension in the steel is an ideal failure, because it is easiest to provide against. Failures by slipping of bars, and by cracking and disintegrating of the concrete beam near the support, as exhibited by the other tests, indicate danger, and demand much larger factors of safety.
Professor Clifford, in criticizing the statement that a member which cannot act until failure has started is not a proper element of design, refers to another statement by the writer, namely, "The steel in the tension side of the beam should be considered as taking all the tension." He states that this cannot take place until the concrete has failed in tension at this point. The tension side of a beam will stretch out a measurable amount under load. The stretching out of the beam vertically, alongside of a stirrup, would be exceedingly minute, if no cracks occurred in the beam.
Mr. Mensch says that "the stresses involved are mostly secondary." He compares them to web stresses in a plate girder, which can scarcely be called secondary. Furthermore, those stresses are carefully worked out and abundantly provided for in any good design. To give an example of how a plate girder might be designed: Many plate girders have rivets in the flanges, spaced 6 in. apart near the supports, that is, girders designed with no regard to good practice. These girders, perhaps, need twice as many rivets near the ends, according to good and acceptable practice, which is also rational practice. The girders stand up and perform their office. It is doubtful whether they would fail in these rivet lines in a test to destruction; but a reasonable analysis shows that these rivets are needed, and no good engineer would ignore this rule of design or claim that it should be discarded because the girders do their work anyway. There are many things about structures, as every engineer who has examined many of those erected without engineering supervision can testify, which are bad, but not quite bad enough to be cause for condemnation. Not many years ago the writer ordered reinforcement in a structure designed by one of the best structural engineers in the United States, because the floor-beams had sharp bends in the flange angles. This is not a secondary matter, and sharp bends in reinforcing rods are not a secondary matter. No amount of analysis can show that these rods or flange angles will perform their full duty. Something else must[Pg 148] be overstressed, and herein is a violation of the principles of sound engineering.
Mr. Mensch mentions the failure of the Quebec Bridge as an example of the unknown strength of steel compression members, and states that, if the designer of that bridge had known of certain tests made 40 years ago, that accident probably would not have happened. It has never been proven that the designer of that bridge was responsible for the accident or for anything more than a bridge which would have been weak in service. The testimony of the Royal Commission, concerning the chords, is, "We have no evidence to show that they would have actually failed under working conditions had they been axially loaded and not subject to transverse stresses arising from weak end details and loose connections." Diagonal bracing in the big erection gantry would have saved the bridge, for every feature of the wreck shows that the lateral collapse of that gantry caused the failure. Here are some more simple principles of sound engineering which were ignored.
It is when practice runs "ahead of theory" that it needs to be brought up with a sharp turn. It is the general practice to design dams for the horizontal pressure of the water only, ignoring that which works into horizontal seams and below the foundation, and exerts a heavy uplift. Dams also fail occasionally, because of this uplifting force which is proven to exist by theory.
Mr. Mensch says:
"The author is manifestly wrong in stating that the reinforcing rods can only receive their increments of stress when the concrete is in tension. Generally, the contrary happens. In the ordinary adhesion test, the block of concrete is held by the jaws of the machine and the rod is pulled out; the concrete is clearly in compression."
This is not a case of increments at all, as the rod has the full stress given to it by the grips of the testing machine. Furthermore, it is not a beam. Also, Mr. Mensch is not accurate in conveying the writer's meaning. To quote from the paper:
"A reinforcing rod in a concrete beam receives its stress by increments imparted by the grip of the concrete, but these increments can only be imparted where the tendency of the concrete is to stretch."
This has no reference to an adhesion test.
Mr. Mensch's next paragraph does not show a careful perusal of the paper. The writer does not "doubt the advisability of using bent-up bars in reinforced concrete beams." What he does condemn is bending up the bars with a sharp bend and ending them nowhere. When they are curved up, run to the support, and are anchored over the support or run into the next span, they are excellent. In the tests mentioned by Mr. Mensch, the beams which had the rods bent up and "continued over the supports" gave the highest "ultimate values." This is exactly[Pg 149] the construction which is pointed out as being the most rational, if the rods do not have the sharp bends which Mr. Mensch himself condemns.
Regarding the tests mentioned by him, in which the rods were fastened to anchor-plates at the end and had "slight increase of strength over straight rods, and certainly made a poorer showing than bent-up bars," the writer asked Mr. Mensch by letter whether these bars were curved up toward the supports. He has not answered the communication, so the writer cannot comment on the tests. It is not necessary to use threaded bars, except in the end beams, as the curved-up bars can be run into the next beam and act as top reinforcement while at the same time receiving full anchorage.
Mr. Mensch's statement regarding the retaining wall reinforced as shown at a, Fig. 2, is astounding. He "confesses that he never saw or heard of such poor practices." If he will examine almost any volume of an engineering periodical of recent years, he will have no trouble at all in finding several examples of these identical practices. In the books by Messrs. Reid, Maurer and Turneaure, and Taylor and Thompson, he will find retaining walls illustrated, which are almost identical with Fig. 2 at a. Mr. Mensch says that the proposed design of a retaining wall would be difficult and expensive to install. The harp-like reinforcement could be put together on the ground, and raised to place and held with a couple of braces. Compare this with the difficulty, expense and uncertainty of placing and holding in place 20 or 30 separate rods. The Fink truss analogy given by Mr. Mensch is a weak one. If he were making a cantilever bracket to support a slab by tension from the top, the bracket to be tied into a wall, would he use an indiscriminate lot of little vertical and horizontal rods, or would he tie the slab directly into the wall by diagonal ties? This is exactly the case of this retaining wall, the horizontal slab has a load of earth, and the counterfort is a bracket in tension; the vertical wall resists that tension and derives its ability to resist from the horizontal pressure of the earth.
Mr. Mensch states that "it would take up too much time to prove that the counterfort acts really as a beam." The writer proposes to show in a very short time that it is not a beam. A beam is a part of a structure subject to bending strains caused by transverse loading. This will do as a working definition. The concrete of the counterfort shown at b, Fig. 2, could be entirely eliminated if the rods were simply made to run straight into the anchoring angle and were connected with little cast skewbacks through slotted holes. There would be absolutely no bending in the rods and no transverse load. Add the concrete to protect the rods; the function of the rods is not changed in the least. M.S. Ketchum, M. Am. Soc. C. E.,[U] calculates the counterfort as a beam, and the six 1-in. square bars which he uses diagonally do not[Pg 150] even run into the front slab. He states that the vertical and horizontal rods are to "take the horizontal and vertical shear."
Mr. Mensch says of rectangular water tanks that they are not held (presumably at the corners) by any such devices, and that there is no doubt that they must carry the stress when filled with water. A water tank,[V] designed by the writer in 1905, was held by just such devices. In a tank[W] not held by any such devices, the corner broke, and it is now held by reinforcing devices not shown in the original plans.
Mr. Mensch states that he "does not quite understand the author's reference to shear rods. Possibly he means the longitudinal reinforcement, which it seems is sometimes calculated to carry 10,000 lb. per sq. in. in shear;" and that he "never heard of such a practice." His next paragraph gives the most pointed out-and-out statement regarding shear in shear rods which this voluminous discussion contains. He says that stirrups "are best compared with the dowel pins and bolts of a compound wooden beam." This is the kernel of the whole matter in the design of stirrups, and is just how the ordinary designer considers stirrups, though the books and reports dodge the matter by saying "stress" and attempting no analysis. Put this stirrup in shear at 10,000 lb. per sq. in., and we have a shearing unit only equalled in the cheapest structural work on tight-fitting rivets through steel. In the light of this confession, the force of the writer's comparison, between a U-stirrup, 3/4-in. in diameter, and two 3/4-in. rivets tightly driven into holes in a steel angle, is made more evident, Bolts in a wooden beam built up of horizontal boards would be tightly drawn up, and the friction would play an important part in taking up the horizontal shear. Dowels without head or nut would be much less efficient; they would be more like the stirrups in a reinforced concrete beam. Furthermore, wood is much stronger in bearing than concrete, and it is tough, so that it would admit of shifting to a firm bearing against the bolt. Separate slabs of concrete with bolts or dowels through them would not make a reliable beam. The bolts or dowels would be good for only a part of the safe shearing strength of the steel, because the bearing on the concrete would be too great for its compressive strength.
Mr. Mensch states that at least 99% of all reinforced structures are calculated with a reduction of 25% of the bending moment in the center. He also says "there may be some engineers who calculate a reduction of 33 per cent." These are broad statements in view of the fact that the report of the Joint Committee recommends a reduction of 33% both in slabs and beams.
Mr. Mensch's remarks regarding the width of beams omit from[Pg 151] consideration the element of span and the length needed to develop the grip of a rod. There is no need of making a rod any less in diameter than one-two-hundredth of the span. If this rule is observed, the beam with three 7/8-in. round rods will be of longer span than the one with the six 5/8-in. rods. The horizontal shear of the two beams will be equal to the total amount of that shear, but the shorter beam will have to develop that shear in a shorter distance, hence the need of a wider beam where the smaller rods are used.
It is not that the writer advocates a wide stem in the T-beam, in order to dispense with the aid of the slab. What he desires to point out is that a full analysis of a T-beam shows that such a width is needed in the stem.
Regarding the elastic theory, Mr. Mensch, in his discussion, shows that he does not understand the writer's meaning in pointing out the objections to the elastic theory applied to arches. The moment of inertia of the abutment will, of course, be many times that of the arch ring; but of what use is this large moment of inertia when the abutment suddenly stops at its foundation? The abutment cannot be anchored for bending into the rock; it is simply a block of concrete resting on a support. The great bending moment at the end of the arch, which is found by the elastic theory (on paper), has merely to overturn this block of concrete, and it is aided very materially in this by the thrust of the arch. The deformation of the abutment, due to deficiency in its moment of inertia, is a theoretical trifle which might very aptly be minutely considered by the elastic arch theorist. He appears to have settled all fears on that score among his votaries. The settlement of the abutment both vertically and horizontally, a thing of tremendously more magnitude and importance, he has totally ignored.
Most soils are more or less compressible. The resultant thrust on an arch abutment is usually in a direction cutting about the edge of the middle third. The effect of this force is to tend to cause more settlement of the abutment at the outer, than at the inner, edge, or, in other words, it would cause the abutment to rotate. In addition to this the same force tends to spread the abutments apart. Both these efforts put an initial bending moment in the arch ring at the springing; a moment not calculated, and impossible to calculate.
Messrs. Taylor and Thompson, in their book, give much space to the elastic theory of the reinforced concrete arch. Little of that space, however, is taken up with the abutment, and the case they give has abutments in solid rock with a slope about normal to the thrust of the arch ring. They recommend that the thrust be made to strike as near the middle of the base of the abutment as possible.
Malverd A. Howe, M. Am. Soc. C. E., in a recent issue of Engineering News, shows how to find the stresses and moments in an[Pg 152] elastic arch; but he does not say anything about how to take care of the large bending moments which he finds at the springing.
Specialists in arch construction state that when the centering is struck, every arch increases in span by settlement. Is this one fact not enough to make the elastic theory a nullity, for that theory assumes immovable abutments?
Professor Howe made some recent tests on checking up the elastic behavior of arches. He reports[X] that "a very slight change at the support does seriously affect the values of H and M." The arch tested was of 20-ft. span, and built between two heavy stone walls out of all proportion to the magnitude of the arch, as measured by comparison with an ordinary arch and its abutment. To make the arch fixed ended, a large heavily reinforced head was firmly bolted to the stone wall. Practical fixed endedness could be attained, of course, by means such as these, but the value of such tests is only theoretical.
Mr. Mensch says:
"The elastic theory was fully proved for arches by the remarkable tests, made in 1897 by the Austrian Society of Engineers and Architects, on full-sized arches of 70-ft. span, and the observed deflections and lateral deformations agreed exactly with the figured deformation."
The writer does not know of the tests made in 1897, but reference is often made to some tests reported in 1896. These tests are everywhere quoted as the unanswerable argument for the elastic theory. Let us examine a few features of those tests, and see something of the strength of the claim. In the first place, as to the exact agreement between the calculated and the observed deformations, this exact agreement was retroactive. The average modulus of elasticity, as found by specimen tests of the concrete, did not agree at all with the value which it was necessary to use in the arch calculations in order to make the deflections come out right.
As found by tests on blocks, the average modulus was about 2,700,000; the "practical" value, as determined from analysis of a plain concrete arch, was 1,430,000, a little matter of nearly 100 per cent. Mansfield Merriman, M. Am. Soc. C. E., gives a digest of these famous Austrian tests.[Y] There were no fixed ended arches among them. There was a long plain concrete arch and a long Monier arch. Professor Merriman says, "The beton Monier arch is not discussed theoretically, and, indeed, this would be a difficult task on account of the different materials combined." And these are the tests which the Engineering Profession points to whenever the elastic theory is questioned as to its applicability to reinforced concrete arches. These are the tests that "fully prove" the elastic theory for arches. These are the tests on the basis of which fixed ended reinforced concrete arches[Pg 153] are confidently designed. Because a plain concrete bow between solid abutments deflected in an elastic curve, reinforced concrete arches between settling abutments are designed with fixed ends. The theorist has departed about as far as possible from his premise in this case. On an exceedingly slender thread he has hung an elaborate and important theory of design, with assumptions which can never be realized outside of the schoolroom or the designer's office. The most serious feature of such theories is not merely the approximate and erroneous results which they give, but the extreme confidence and faith in their certainty which they beget in their users, enabling them to cut down factors of safety with no regard whatever for the enormous factor of ignorance which is an essential accompaniment to the theory itself.
Mr. Mensch says, "The elastic theory enables one to calculate arches much more quickly than any graphical or guess method yet proposed." The method given by the writer[Z] enables one to calculate an arch in about the time it would take to work out a few of the many coefficients necessary in the involved method of the elastic theory. It is not a graphic method, but it is safe and sound, and it does not assume conditions which have absolutely no existence.
Mr. Mensch says that the writer brings up some erratic column tests and seems to have no confidence in reinforced concrete columns. In relation to this matter Sanford E. Thompson, M. Am. Soc. C. E., in a paper recently read before the National Association of Cement Users, takes the same sets of tests referred to in the paper, and attempts to show that longitudinal reinforcement adds much strength to a concrete column. Mr. Thompson goes about it by means of averages. It is not safe to average tests where the differences in individual tests are so great that those of one class overlap those of the other. He includes the writer's "erratic" tests and some others which are "erratic" the other way. It is manifestly impossible for him to prove that longitudinal rods add any strength to a concrete column if, on one pair of columns, identically made as far as practicable, the plain concrete column is stronger than that with longitudinal rods in it, unless the weak column is defective. It is just as manifest that it is shown by this and other tests that the supposedly reinforced concrete column may be weaker.
The averaging of results to show that longitudinal rods add strength, in the case of the tests reported by Mr. Withey, includes a square plain concrete column which naturally would show less compressive strength in concrete than a round column, because of the spalling off at the corners. This weak test on a square column is one of the slender props on which is based the conclusion that longitudinal rods add to the strength of a concrete column; but the weakness of the square concrete column is due to the inherent weakness of brittle[Pg 154] material in compression when there are sharp corners which may spall off.
Mr. Worcester says that several of the writer's indictments hit at practices which were discarded long ago, but from the attitude of their defenders this does not seem to be true. There are benders to make sharp bends in rods, and there are builders who say that they must be bent sharply in order to simplify the work of fitting and measuring them.
There are examples in engineering periodicals and books, too numerous to mention, where no anchorage of any kind is provided for bent-up rods, except what grip they get in the concrete. If they reached beyond their point of usefulness for this grip, it would be all right, but very often they do not.
Mr. Worcester says: "It is not necessary that a stirrup at one point should carry all the vertical tension, as this vertical tension is distributed by the concrete." The writer will concede that the stirrups need not carry all the vertical shear, for, in a properly reinforced beam, the concrete can take part of it. The shear reinforcement, however, should carry all the shear apportioned to it after deducting that part which the concrete is capable of carrying, and it should carry it without putting the concrete in shear again. The stirrups at one point should carry all the vertical tension from the portion of shear assumed to be taken by the stirrups; otherwise the concrete will be compelled to carry more than its share of the shear.
Mr. Worcester states that cracks are just as likely to occur from stress in curved-up and anchored rods as in vertical reinforcement. The fact that the vertical stretching out of a beam from the top to the bottom, under its load, is exceedingly minute, has been mentioned. A curved-up bar, anchored over the support and lying near the bottom of the beam at mid-span, partakes of the elongation of the tension side of the beam and crosses the section of greatest diagonal tension in the most advantageous manner. There is, therefore, a great deal of difference in the way in which these two elements of construction act.
Mr. Worcester prefers the "customary method" of determining the width of beams—so that the maximum horizontal shearing stress will not be excessive—to that suggested by the writer. He gives as a reason for this the fact that rods are bent up out of the bottom of a beam, and that not all of them run to the end. The "customary method" must be described in literature for private circulation. Mention has been made of a method which makes the width of beam sufficient to insert the steel. Considerations of the horizontal shear in a T-beam, and of the capacity of the concrete to grip the steel, are conspicuous by their absence in the analyses of beams. If a reinforcing rod is curved up and anchored over the support, the concrete is relieved of the shear, both horizontal and vertical, incident to the[Pg 155] stress in that rod. If a reinforcing rod is bent up anywhere, and not carried to the support, and not anchored over it, as is customary, the shear is all taken by the concrete; and there is just the same shear in the concrete as though the rods were straight.
For proper grip a straight rod should have a diameter of not more than one two-hundredth of the span. For economy of material, it should not be much smaller in diameter than this. With this balance in a beam, assuming shear equal to bond, the rods should be spaced a distance apart, equal to their perimeters. This is a rational and simple rule, and its use would go a long way toward the adoption of standards.
Mr. Worcester is not logical in his criticism of the writer's method of reinforcing a chimney. It is not necessary to assume that the concrete is not stressed, in the imaginary plain concrete chimney, beyond that which plain concrete could take in tension. The assumption of an imaginary plain concrete chimney and determinations of tensile stresses in the concrete are merely simplified methods of finding the tensile stress. The steel can take just as much tensile stress if its amount is determined in this way as it can if any other method is used. The shifting of the neutral axis, to which Mr. Worcester refers, is another of the fancy assumptions which cannot be realized because of initial and unknown stresses in the concrete and steel.
Mr. Russell states that the writer scarcely touched on top reinforcement in beams. This would come in the class of longitudinal rods in columns, unless the reinforcement were stiff members. Mr. Russell's remarks, to the effect that columns and short deep beams, doubly reinforced, should be designed as framed structures, point to the conclusion that structural beams and columns, protected with concrete, should be used in such cases. If the ruling motive of designers were uniformly to use what is most appropriate in each particular location and not to carry out some system, this is just what would be done in many cases; but some minds are so constructed that they take pleasure in such boasts as this: "There is not a pound of structural steel in that building." A broad-minded engineer will use reinforced concrete where it is most appropriate, and structural steel or cast iron where these are most appropriate, instead of using his clients' funds to carry out some cherished ideas.
Mr. Wright appreciates the writer's idea, for the paper was not intended to criticize something which is "good enough" or which "answers the purpose," but to systematize or standardize reinforced concrete and put it on a basis of rational analysis and common sense, such a basis as structural designing has been or is being placed on, by a careful weeding out of all that is irrational, senseless, and weak.
Mr. Chapman says that the practical engineer has never used such methods of construction as those which the writer condemns. The[Pg 156] methods are common enough; whether or not those who use them are practical engineers is beside the question.
As to the ability of the end connection of a stringer carrying flange stress or bending moments, it is not uncommon to see brackets carrying considerable overhanging loads with no better connection. Even wide sidewalks of bridges sometimes have tension connections on rivet heads. While this is not to be commended, it is a demonstration of the ability to take bending which might be relied on, if structural design were on as loose a basis as reinforced concrete.
Mr. Chapman assumes that stirrups are anchored at each end, and Fig. 3 shows a small hook to effect this anchorage. He does not show how vertical stirrups can relieve a beam of the shear between two of these stirrups.
The criticism the writer would make of Figs. 5 and 6, is that there is not enough concrete in the stem of the T to grip the amount of steel used, and the steel must be gripped in that stem, because it does not run to the support or beyond it for anchorage. Steel members in a bridge may be designed in violation of many of the requirements of specifications, such as the maximum spacing of rivets, size of lattice bars, etc.; the bridge will not necessarily fail or show weakness as soon as it is put into service, but it is faulty and weak just the same.
Mr. Chapman says: "The practical engineer does not find * * * that the negative moment is double the positive moment, because he considers the live load either on one span only, or on alternate spans." It is just in such methods that the "practical engineer" is inconsistent. If he is going to consider the beams as continuous, he should find the full continuous beam moment and provide for it. It is just this disposition to take an advantage wherever one can be taken, without giving proper consideration to the disadvantage entailed, which is condemned in the paper. The "practical engineer" will reduce his bending moment in the beam by a large fraction, because of continuity, but he will not reinforce over the supports for full continuity. Reinforcement for full continuity was not recommended, but it was intimated that this is the only consistent method, if advantage is taken of continuity in reducing the principal bending moment.
Mr. Chapman says that an arch should not be used where the abutments are unstable. Unstable is a relative and indefinite word. If he means that abutments for arches should never be on anything but rock, even such a foundation is only quite stable when the abutment has a vertical rock face to take horizontal thrusts. If arches could be built only under such conditions, few of them would be built. Some settlement is to be expected in almost any soil, and because of horizontal thrusts there is also a tendency for arch abutments to rotate. It is this tendency which opens up cracks in spandrels of arches, and makes the assumption of a fixed tangent at the springing line, commonly made by the elastic theorist, absolute foolishness.
Mr. Beyer has developed a novel explanation of the way stirrups act, but it is one which is scarcely likely to meet with more serious consideration than the steel girder to which he refers, which has neither web plate nor diagonals, but only verticals connecting the top and bottom flanges. This style of girder has been considered by American engineers rather as a curiosity, if not a monstrosity. If vertical stirrups acted to reinforce little vertical cantilevers, there would have to be a large number of them, so that each little segment of the beam would be insured reinforcement.
The writer is utterly at a loss to know what Professor Ostrup means by his first few paragraphs. He says that in the first point two designs are mentioned and a third condemned. The second design, whatever it is, he lays at the writer's door in these words: "The author's second design is an invention of his own, which the Profession at large is invited to adopt." In the first point sharp bends in reinforcing rods are condemned and curves recommended. Absolutely nothing is said of "a reinforced concrete beam arranged in the shape of a rod, with separate concrete blocks placed on top of it without being connected."
In reply to Professor Ostrup, it should be stated that the purpose of the paper is not to belittle the importance of the adhesion or grip of concrete on steel, but to point out that the wonderful things this grip is supposed to do, as exhibited by current design, will not stand the test of analysis.
Professor Ostrup has shown a new phase of the stress in shear rods. He says they are in bending between the centers of compressive resultants. We have been told in books and reports that these rods are in stress of some kind, which is measured by the sectional area of the rod. No hint has been given of designing stirrups for bending. If these rods are not in shear, as stated by Professor Ostrup, how can they be in bending in any such fashion as that indicated in Fig. 12?
Professor Ostrup's analysis, by which he attempts to justify stirrups and to show that vertical stirrups are preferable, merely treats of local distribution of stress from short rods into concrete. Apparently, it would work the same if the stirrups merely touched the tension rod. His analysis ignores the vital question of what possible aid the stirrup can be in relieving the concrete between stirrups of the shear of the beam.
The juggling of bending moments in beams is not compensating. The following is a concrete example. Some beams of a span of about 20 ft., were framed into double girders at the columns. The beams were calculated as partly continuous, though they were separated at their ends by about 1-1/2 or 2 ft., the space between the girders. The beams had 1-1/8-in. tension rods in the bottom. At the supports a short 1/4-in. rod was used near the top of the beam for continuity. Does this[Pg 158] need any comment? It was not the work of a novice or of an inexperienced builder.
Professor Ostrup's remarks about the shifting of the neutral axis of a beam and of the pressure line of an arch are based on theory which is grounded in impossible assumptions. The materials dealt with do not justify these assumptions or the hair-splitting theory based thereon. His platitudes about the danger of misplacing reinforcement in an arch are hardly warranted. If the depth and reinforcement of an arch ring are added to, as the inelastic, hinge-end theory would dictate, as against the elastic theory, it will strengthen the arch just as surely as it would strengthen a plate girder to thicken the web and flange angles.
The writer's complaint is not that the theories of reinforced concrete are not fully developed. They are developed too highly, developed out of all comparison with the materials dealt with. It is just because reinforced concrete structures are being built in increasing numbers that it behooves engineers to inject some rationality (not high-strung theory) into their designs, and drop the idea that "whatever is is right."
Mr. Porter has much to say about U-bars. He states that they are useful in holding the tension bars in place and in tying the slab to the stem of a T-beam. These are legitimate functions for little loose rods; but why call them shear rods and make believe that they take the shear of a beam? As to stirrups acting as dowel pins, the writer has already referred to this subject. Answering a query by Mr. Porter, it may be stated that what would counteract the horizontal cleaving force in a beam is one or more rods curved up to the upper part of the beam and anchored at the support or run into the next span. Strangely enough, Mr. Porter commends this very thing, as advocated in the paper. The excellent results shown by the test referred to by him can well be contrasted with some of the writer's tests. This floor was designed for 250 lb. per sq. ft. When that load was placed on it, the deflection was more than 1 in. in a span of 20 ft. No rods were curved up and run over the supports. It was a stirrup job.
Mr. Porter intimates that the correct reinforced concrete column may be on lines of concrete mixed with nails or wires. There is no doubt but that such concrete would be strong in compression for the reason that it is strong in tension, but a column needs some unifying element which is continuous. A reinforced column needs longitudinal rods, but their office is to take tension; they should not be considered as taking compression.
Mr. Goodrich makes this startling remark: "It is a well-known fact that the bottom chords in queen-post trusses are useless, as far as resistance to tension is concerned." The writer cannot think that he means by this that, for example, a purlin made up of a 3 by 2-in. angle and a 5/8-in. hog-rod would be just as good with the rod omitted. If[Pg 159] queen-post trusses are useless, some hundreds of thousands of hog-rods in freight cars could be dispensed with.
Mr. Goodrich misunderstands the reference to the "only rational and only efficient design possible." The statement is that a design which would be adopted, if slabs were suspended on rods, is the only rational and the only efficient design possible. If the counterfort of a retaining wall were a bracket on the upper side of a horizontal slab projecting out from a vertical wall, and all were above ground, the horizontal slab being heavily loaded, it is doubtful whether any engineer would think of using any other scheme than diagonal rods running from slab to wall and anchored into each. This is exactly the condition in this shape of retaining wall, except that it is underground.
Mr. Goodrich says that the writer's reasoning as to the sixth point is almost wholly facetious and that concrete is very strong in pure shear. The joke, however, is on the experimenters who have reported concrete very strong in shear. They have failed to point out that, in every case where great strength in shear is manifested, the concrete is confined laterally or under heavy compression normal to the sheared plane. Stirrups do not confine concrete in a direction normal to the sheared plane, and they do not increase the compression. A large number of stirrups laid in herring-bone fashion would confine the concrete across diagonal planes, but such a design would be wasteful, and the common method of spacing the stirrups would not suggest their office in this capacity.
As to the writer's statements regarding the tests in Bulletin No. 29 of the University of Illinois being misleading, he quotes from that bulletin as follows:
"Until the concrete web has failed in diagonal tension and diagonal cracks have formed there must be little vertical deformation at the plane of the stirrups, so little that not much stress can have developed in the stirrups." * * * "It is evident, then, that until the concrete web fails in diagonal tension little stress is taken by the stirrups." * * * "It seems evident from the tests that the stirrups did not take much stress until after the formation of diagonal cracks." * * * "It seems evident that there is very little elongation in stirrups until the first diagonal crack forms, and hence that up to this point the concrete takes practically all the diagonal tension." * * * "Stirrups do not come into action, at least not to any great extent, until the diagonal crack has formed."
In view of these quotations, the misleading part of the reference to the tests and their conclusion is not so evident.
The practical tests on beams with suspension rods in them, referred to by Mr. Porter, show entirely different results from those mentioned by Mr. Goodrich as being made by Mörsch. Tests on beams of this sort, which are available in America, seem to show excellent results.
Mr. Goodrich is somewhat unjust in attributing failures to designs which are practically in accordance with the suggestions under Point Seven. In Point Seven the juggling of bending moments is condemned—it is condemnation of methods of calculating. Point Seven recommends reinforcing a beam for its simple beam moment. This is the greatest bending it could possibly receive, and it is inconceivable that failure could be due to this suggestion. Point Seven recommends a reasonable reinforcement over the support. This is a matter for the judgment of the designer or a rule in specifications. Failure could scarcely be attributed to this. It is the writer's practice to use reinforcement equal to one-half of the main reinforcement of the beam across the support; it is also his practice to curve up a part of the beam reinforcement and run it into the next span in all beams needing reinforcement for shear; but the paper was not intended to be a treatise on, nor yet a general discussion of, reinforced concrete design.
Mr. Goodrich characterizes the writer's method of calculating reinforced concrete chimneys as crude. It is not any more crude than concrete. The ultra-theoretic methods are just about as appropriate as calculations of the area of a circle to hundredths of a square inch from a paced-off diameter. The same may be said of deflection calculations.
Mr. Goodrich has also appreciated the writer's spirit in presenting this paper. Attention to details of construction has placed structural steel designing on the high plane on which it stands. Reinforced concrete needs the same careful working out of details before it can claim the same recognition. It also needs some simplification of formulas. Witness the intricate column formulas for steelwork which have been buried, and even now some of the complex beam formulas for reinforced concrete have passed away.
Major Sewell, in his discussion of the first point, seems to object solely to the angle of the bent-up portion of the rod. This angle could have been much less, without affecting the essence of the writer's remarks. Of course, the resultant, b, would have been less, but this would not create a queen-post at the sharp bend of the bar. Major Sewell says that he "does not remember ever to have seen just the type of construction shown in Fig. 1, either used or recommended." This type of beam might be called a standard. It is almost the insignia of a reinforced concrete expert. A little farther on Major Sewell says that four beams tested at the University of Illinois were about as nearly like Fig. 1 as anything he has ever seen in actual practice. He is the only one who has yet accused the writer of inventing this beam.
If Major Sewell's statement that he has never seen the second point exemplified simply means that he has never seen an example of the bar bent up at the identical angle given in the paper, his criticism has not much weight.
Major Sewell's comment on the retaining wall begs the question. Specific references to examples have been given in which the rods of a counterfort are not anchored into the slabs that they hold by tension, save by a few inches of embedment; an analysis has also been cited in which the counterfort is considered as a beam, and ties in the great weight of the slab with a few "shear rods," ignoring the anchorage of either horizontal, vertical, or diagonal rods. It is not enough that books state that rods in tension need anchorage. They should not show examples of rods that are in pure tension and state that they are merely thrown in for shear. Transverse rods from the stem to the flange of a T-beam, tie the whole together; they prevent cracking, and thereby allow the shearing strength of the concrete to act. It is not necessary to count the rods in shear.
Major Sewell's comparison of a stirrup system and a riveted truss is not logical. The verticals and diagonals of a riveted truss have gusset plates which connect symmetrically with the top chord. One line of rivets or a pin in the center line of the top chord could be used as a connection, and this connection would be complete. To distribute rivets above and below the center line of the top chord does not alter the essential fact that the connection of the web members is complete at the center of the top chord. The case of stirrups is quite different. Above the centroid of compression there is nothing but a trifling amount of embedment of the stirrup. If 1/2-in. stirrups were used in an 18-in. beam, assuming that 30 diameters were enough for anchorage, the centroid of compression would be, say, 3 in. below the top of the beam, the middle point of the stirrup's anchorage would be about 8 in., and the point of full anchorage would be about 16 in. The neutral axis would come somewhere between. These are not unusual proportions. Analogy with a riveted truss fails; even the anchorage above the neutral axis is far from realization.
Major Sewell refers to shallow bridge stringers and the possibility of failure at connections by continuity or deflection. Structural engineers take care of this, not by reinforcement for continuity but by ample provision for the full bending moment in the stringer and by ample depth. Provision for both the full bending moment and the ample depth reduces the possibilities of deflection at the floor-beams.
Major Sewell seems also to have assumed that the paper was a general discussion on reinforced concrete design. The idea in pointing out that a column having longitudinal rods in it may be weaker than a plain concrete column was not to exalt the plain concrete column but to degrade the other. A plain concrete column of any slenderness would manifestly be a gross error. If it can be shown that one having only longitudinal rods may be as bad, or worse, instead of being greatly strengthened by these rods, a large amount of life and property may be saved.
A partial reply to Mr. Thompson's discussion will be found in the writer's response to Mr. Mensch. The fault with Mr. Thompson's conclusions lies in the error of basing them on averages. Average results of one class are of little meaning or value when there is a wide variation between the extremes. In the tests of both the concrete-steel and the plain concrete which Mr. Thompson averages there are wide variations. In the tests made at the University of Illinois there is a difference of almost 100% between the minimum and maximum results in both concrete-steel and plain concrete columns.
Average results, for a comparison between two classes, can mean little when there is a large overlap in the individual results, unless there is a large number of tests. In the seventeen tests made at the University of Illinois, which Mr. Thompson averages, the overlap is so great that the maximum of the plain columns is nearly 50% greater than the minimum of the concrete-steel columns.
If the two lowest tests in plain concrete and the two highest in concrete-steel had not been made, the average would be in favor of the plain concrete by nearly as much as Mr. Thompson's average now favors the concrete-steel columns. Further, if these four tests be eliminated, only three of the concrete-steel columns are higher than the plain concrete. So much for the value of averages and the conclusions drawn therefrom.
It is idle to draw any conclusions from such juggling of figures, except that the addition of longitudinal steel rods is altogether problematical. It may lessen the compressive strength of a concrete column. Slender rods in such a column cannot be said to reinforce it, for the reason that careful tests have been recorded in which columns of concrete-steel were weaker than those of plain concrete.
In the averages of the Minneapolis tests Mr. Thompson has compared the results on two plain concrete columns with the average of tests on an indiscriminate lot of hooped and banded columns. This method of boosting the average shows anything but "critical examination" on his part.
Mr. Thompson, on the subject of Mr. Withey's tests, compares plain concrete of square cross-section with concrete-steel of octagonal section. As stated before, this is not a proper comparison. In a fragile material like concrete the corners spall off under a compressive load, and the square section will not show up as well as an octagonal or round one.
Mr. Thompson's contention, regarding the Minneapolis tests, that the concrete outside of the hoops should not be considered, is ridiculous. If longitudinal rods reinforce a concrete column, why is it necessary to imagine that a large part of the concrete must be assumed to be non-existent in order to make this reinforcement manifest? An imaginary core could be assumed in a plain concrete column and any desired results could be obtained. Furthermore, a properly hooped[Pg 163] column does not enter into this discussion, as the proposition is that slender longitudinal rods do not reinforce a concrete column; if hoops are recognized, the column does not come under this proposition.
Further, the proposition in the writer's fifteenth point does not say that the steel takes no part of the compression of a column. Mr. Thompson's laborious explanation of the fact that the steel receives a share of the load is needless. There is no doubt that the steel receives a share of the load—in fact, too great a share. This is the secret of the weakness of a concrete column containing slender rods. The concrete shrinks, the steel is put under initial compression, the load comes more heavily on the steel rods than on the concrete, and thus produces a most absurd element of construction—a column of slender steel rods held laterally by a weak material—concrete. This is the secret of nearly all the great wrecks in reinforced concrete: A building in Philadelphia, a reservoir in Madrid, a factory in Rochester, a hotel in California. All these had columns with longitudinal rods; all were extensive failures—probably the worst on record; not one of them could possibly have failed as it did if the columns had been strong and tough. Why use a microscope and search through carefully arranged averages of tests on nursery columns, with exact central loading, to find some advantage in columns of this class, when actual experience is publishing in bold type the tremendously important fact that these columns are utterly untrustworthy?
It is refreshing to note that not one of the writer's critics attempts to defend the quoted ultimate strength of a reinforced concrete column. Even Mr. Thompson acknowledges that it is not right. All of which, in view of the high authority with whom it originated, and the wide use it has been put to by the use of the scissors, would indicate that at last there is some sign of movement toward sound engineering in reinforced concrete.
In conclusion it might be pointed out that this discussion has brought out strong commendation for each of the sixteen indictments. It has also brought out vigorous defense of each of them. This fact alone would seem to justify its title. A paper in a similar strain, made up of indictments against common practices in structural steel design, published in Engineering News some years ago, did not bring out a single response. While practice in structural steel may often be faulty, methods of analysis are well understood, and are accepted with little question.
[E] Transactions, Am. Soc. C. E., Vol. LXVI, p. 431.
[F] Loc. cit., p. 448.
[G] Engineering News, Dec. 3d, 1908.
[H] Journal of the Western Society of Engineers, 1905.
[I] Tests made for C.A.P. Turner, by Mason D. Pratt, M. Am. Soc. C. E.
[J] Transactions, Am. Soc. C. E., Vol. LVI, p. 343.
[K] Bulletin No. 28, University of Illinois.
[L] Bulletin No. 12, University of Illinois, Table VI, page 27.
[M] Professeur de Stabilité a l'Université de Louvain.
[N] A translation of Professor Vierendeel's theory may be found in Beton und Eisen, Vols. X, XI, and XII, 1907.
[O] Cement, March, 1910, p. 343; and Concrete Engineering, May, 1910, p. 113.
[P] The correct figures from the Bulletin are 1,577 lb.
[Q] Engineering News, January 7th, 1909, p. 20.
[R] For fuller treatment, see the writer's discussion in Transactions, Am. Soc. C. E., Vol. LXI, p. 46.
[S] See "Tests of Metals," U.S.A., 1905, p. 344.
[T] The Engineering Record, August 17th, 1907.
[U] "The Design of Walls, Bins and Elevators."
[V] Engineering News, September 28th, 1905.
[W] The Engineering Record, June 26th, 1909.
[X] Railroad Age Gazette, March 26th, 1909.
[Y] Engineering News, April 9th, 1896.
[Z] "Structural Engineering: Concrete."
End of the Project Gutenberg EBook of Some Mooted Questions in Reinforced
Concrete Design, by Edward Godfrey
*** END OF THIS PROJECT GUTENBERG EBOOK REINFORCED CONCRETE DESIGN ***
***** This file should be named 17137-h.htm or 17137-h.zip *****
This and all associated files of various formats will be found in:
https://www.gutenberg.org/1/7/1/3/17137/
Produced by Juliet Sutherland, Taavi Kalju and the Online
Distributed Proofreading Team at https://www.pgdp.net
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
https://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH F3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need, is critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at https://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
https://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at https://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit https://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including including checks, online payments and credit card
donations. To donate, please visit: https://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart was the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Most people start at our Web site which has the main PG search facility:
https://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.