
The Project Gutenberg EBook of Scientific American Supplement, Vol. XXI., No. 531, March 6, 1886, by Various This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: Scientific American Supplement, Vol. XXI., No. 531, March 6, 1886 Author: Various Release Date: February 29, 2004 [EBook #11383] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK SCIENTIFIC AMERICAN SUPP. 531 *** Produced by Produced by Josephine Paolucci, Don Kretz, Juliet Sutherland, Charles Franks and the DP Team
Roumania is thinking of protecting a portion of the artillery of the forts surrounding her capital by metallic cupolas. But, before deciding upon the mode of constructing these formidable and costly affairs, and before ordering them, she has desired to ascertain their efficacy and the respective merits of the chilled iron armor which was recently in fashion and of rolled iron, which looks as if it were to be the fashion hereafter.
FIG. 1.--MOUGIN'S ROLLED IRON TURRET.
The Krupp works have recommended and constructed a cupola of casehardened iron, while the Saint Chamond works have offered a turret of rolled iron. Both of these recommend themselves by various merits, and by remarkably ingenious arrangements, and it only remains to be seen how they will behave under the fire of the largest pieces of artillery.
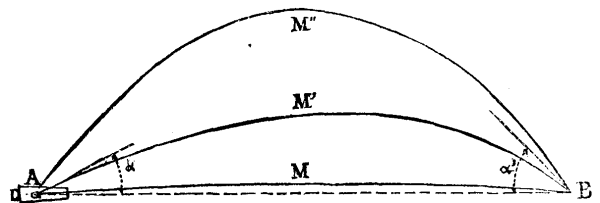
FIG. 2.
We are far in advance of the time when cannons with smooth bore were obliged to approach to within a very short range of a scarp in order to open a breach, and we are far beyond that first rifled artillery which effected so great a revolution in tactics.
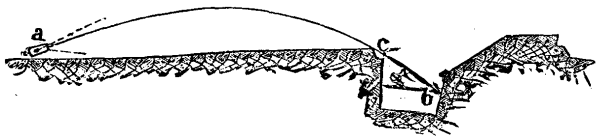
FIG. 3.
To-day we station the batteries that are to tear open a rampart at distances therefrom of from 1,000 to 2,000 yards, and the long, 6 inch cannon that arms them has for probable deviations, under a charge of 20 pounds of powder, and at a distance of 1,000 yards, 28 feet in range, 16 inches in direct fire and 8 inches in curved.
The weight of the projectile is 88 pounds, and its remanent velocity at the moment of impact is 1,295 feet. Under this enormous live force, the masonry gradually crumbles, and carries along the earth of the parapet, and opens a breach for the assaulting columns.
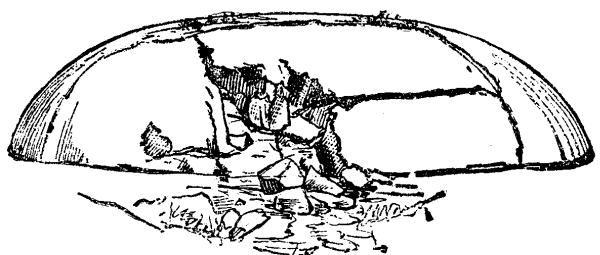
FIG. 4--STATE OF A CUPOLA AFTER THE
ACTION OF THIRTY-SEVEN 6 IN. PROJECTILES.
In order to protect the masonry of the scarp, engineers first lowered the cordon to the level of the covert-way. Under these circumstances, the enemy, although he could no longer see it, reached it by a curved or "plunging" shot. When, in fact, for a given distance we load a gun with the heaviest charge that it will stand, the trajectory, AMB (Fig. 2), is as depressed as possible, and the angles, a and a', at the start and arrival are small, and we have a direct shot. If we raise the chase of the piece, the projectile will describe a curve in space which would be a perfect parabola were it not for the resistance of the air, and the summit of such curve will rise in proportion as the angle so increases. So long as the falling angle, a, remains less than 45°, we shall have a curved shot. When the angle exceeds this, the shot is called "vertical." If we preserve the same charge, the parabolic curve in rising will meet the horizontal plane at a greater distance off. This is, as well known, the process employed for reaching more and more distant objects.

Fig. 5.--STATE OF A CAST-IRON CUPOLA
AFTER THE BREAKAGE OF A VOUSSOIR.
The length of a gun depends upon the maximum charge burned in it, since the combustion must be complete when the projectile reaches the open air. It results from this that although guns of great length are capable of throwing projectiles with small charges, it is possible to use shorter pieces for this purpose--such as howitzers for curved shots and mortars for vertical ones. The curved shot finds one application in the opening of breaches in scarp walls, despite the existence of a covering of great thickness. If, from a point, a (Fig. 3), we wish to strike the point, b, of a scarp, over the crest, c, of the covert-way, it will suffice to pass a parabolic curve through these three points--the unknown data of the problem, and the charge necessary, being ascertained, for any given piece, from the artillery tables. In such cases it is necessary to ascertain the velocity at the impact, since the force of penetration depends upon the live force (mv²) of the projectile, and the latter will not penetrate masonry unless it have sufficient remanent velocity. Live force, however, is not the sole factor that intervenes, for it is indispensable to consider the angle at which the projectile strikes the wall. Modern guns, such as the Krupp 6 inch and De Bange 6 and 8 inch, make a breach, the two former at a falling angle of 22°, and the latter at one of 30°. It is not easy to lower the scarps enough to protect them from these blows, even by narrowing the ditch in order to bring them near the covering mass of the glacis.
The same guns are employed for dismounting the defender's pieces, which he covers as much as possible behind the parapet. Heavy howitzers destroy the materiel, while shrapnel, falling nearly vertically, and bursting among the men, render all operations impossible upon an open terre-plein.
FIG. 6.--STATE OF A CHILLED IRON CUPOLA
BROKEN BY A 12 INCH BALL.
The effect of 6 and 8 inch rifled mortars is remarkable. The Germans have a 9 inch one that weighs 3,850 pounds, and the projectile of which weighs 300. But French mortars in nowise cede to those of their neighbors; Col. De Bange, for example, has constructed a 10½ inch one of wonderful power and accuracy.
Seeing the destructive power of these modern engines of war, it may well be asked how many pieces the defense will be able to preserve intact for the last period of a siege--for the very moment at which it has most need of a few guns to hold the assailants in check and destroy the assaulting columns. Engineers have proposed two methods of protecting these few indispensable pieces. The first of these consists in placing each gun under a masonry vault, which is covered with earth on all sides except the one that contains the embrasure, this side being covered with armor plate.
The second consists in placing one or two guns under a metallic cupola, the embrasures in which are as small as possible. The cannon, in a vertical aim, revolves around the center of an aperture which may be of very small dimensions. As regards direct aim, the carriages are absolutely fixed to the cupola, which itself revolves around a vertical axis. These cupolas may be struck in three different ways: (1) at right angles, by a direct shot, and consequently with a full charge--very dangerous blows, that necessitate a great thickness of the armor plate; (2) obliquely, when the projectile, if the normal component of its real velocity is not sufficient to make it penetrate, will be deflected without doing the plate much harm; and (3) by a vertical shot that may strike the armor plate with great accuracy.
General Brialmont says that the metal of the cupola should be able to withstand both penetration and breakage; but these two conditions unfortunately require opposite qualities. A metal of sufficient ductility to withstand breakage is easily penetrated, and, conversely, one that is hard and does not permit of penetration does not resist shocks well. Up to the present, casehardened iron (Gruson) has appeared to best satisfy the contradictory conditions of the problem. Upon the tempered exterior of this, projectiles of chilled iron and cast steel break upon striking, absorbing a part of their live force for their own breakage.
In 1875 Commandant Mougin performed some experiments with a chilled iron turret established after these plans. The thickness of the metal normally to the blows was 23½ inches, and the projectiles were of cast steel. The trial consisted in firing two solid 12 in. navy projectiles, 46 cylindrical 6 in. ones, weighing 100 lb., and 129 solid, pointed ones, 12 in. in diameter. The 6 inch projectiles were fired from a distance of 3,280 feet, with a remanent velocity of 1,300 feet. The different phases of the experiment are shown in Figs. 4, 5, and 6. The cupola was broken; but it is to be remarked that a movable and well-covered one would not have been placed under so disadvantageous circumstances as the one under consideration, upon which it was easy to superpose the blows. An endeavor was next made to substitute a tougher metal for casehardened iron, and steel was naturally thought of. But hammered steel broke likewise, and a mixed or compound metal was still less successful. It became necessary, therefore, to reject hard metals, and to have recourse to malleable ones; and the one selected was rolled iron. Armor plate composed of this latter has been submitted to several tests, which appear to show that a thickness of 18 inches will serve as a sufficient barrier to the shots of any gun that an enemy can conveniently bring into the field.

FIG. 7.--CASEMATE OF CHILLED IRON AFTER
RECEIVING NINETY-SIX SHOTS.
Armor Plated Casemates.--Fig. 7 shows the state of a chilled iron casemate after a vigorous firing. The system that we are about to describe is much better, and is due to Commandant Mougin.
FIG. 8.--MOUGIN'S ARMOR-PLATE CASEMATE.
The gun is placed under a vault whose generatrices are at right angles to the line of fire (Fig. 8), and which contains a niche that traverses the parapet. This niche is of concrete, and its walls in the vicinity of the embrasure are protected by thick iron plate. The rectangular armor plate of rolled iron rests against an elastic cushion of sand compactly rammed into an iron plate caisson. The conical embrasure traverses this cushion by means of a cast-steel piece firmly bolted to the caisson, and applied to the armor through the intermedium of a leaden ring. Externally, the cheeks of the embrasure and the merlons consist of blocks of concrete held in caissons of strong iron plate. The surrounding earthwork is of sand. For closing the embrasure, Commandant Mougin provides the armor with a disk, c, of heavy rolled iron, which contains two symmetrical apertures. This disk is movable around a horizontal axis, and its lower part and its trunnions are protected by the sloping mass of concrete that covers the head of the casemate. A windlass and chain give the disk the motion that brings one of its apertures opposite the embrasure or that closes the latter. When this portion of the disk has suffered too much from the enemy's fire, a simple maneuver gives it a half revolution, and the second aperture is then made use of.
The Schumann-Gruson Chilled Iron Cupola.--This cupola (Fig. 9) is dome-shaped, and thus offers but little surface to direct fire; but it can be struck by a vertical shot, and it may be inquired whether its top can withstand the shock of projectiles from a 10 inch rifled mortar. It is designed for two 6 inch guns placed parallel. Its internal diameter is 19½ feet, and the dome is 8 inches in thickness and has a radius of 16½ feet. It rests upon a pivot, p, around which it revolves through the intermedium of rollers placed in a circle, r. The dome is of relatively small bulk--a bad feature as regards resistance to shock. To obviate this difficulty, the inventor partitions it internally in such a way as to leave only sufficient space to maneuver the guns. The partitions consist of iron plate boxes filled with concrete. The form of the dome has one inconvenience, viz., the embrasure in it is necessarily very oblique, and offers quite an elongated ellipse to blows, and the edges of the bevel upon a portion of the circumference are not strong enough. In order to close the embrasure as tightly as possible, the gun is surrounded with a ring provided with trunnions that enter the sides of the embrasure. The motion of the piece necessary to aim it vertically is effected around this axis of rotation. The weight of the gun is balanced by a system of counterpoises and the chains, l, and the breech terminates in a hollow screw, f, and a nut, g, held between two directing sectors, h. The cupola is revolved by simply acting upon the rollers.
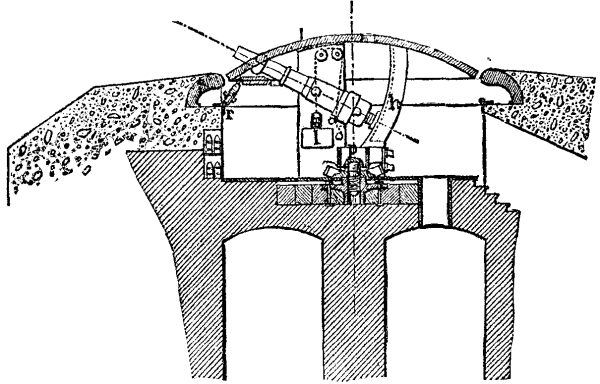
FIG. 9.--THE SCHUMANN-GRUSON CUPOLA.
Mougin's Rolled Iron Cupola.--The general form of this cupola (Fig. 1) is that of a cylindrical turret. It is 12¾ feet in diameter, and rises 3¼ feet above the top of the glacis. It has an advantage over the one just described in possessing more internal space, without having so large a diameter; and, as the embrasures are at right angles with the sides, the plates are less weakened. The turret consists of three plates assembled by slit and tongue joints, and rests upon a ring of strong iron plate strengthened by angle irons. Vertical partitions under the cheeks of the gun carriages serve as cross braces, and are connected with each other upon the table of the hydraulic pivot around which the entire affair revolves. This pivot terminates in a plunger that enters a strong steel press-cylinder embedded in the masonry of the lower concrete vault.
The iron plate ring carries wheels and rollers, through the intermedium of which the turret is revolved. The circular iron track over which these move is independent of the outer armor.
The whole is maneuvered through the action of one man upon the piston of a very small hydraulic press. The guns are mounted upon hydraulic carriages. The brake that limits the recoil consists of two bronze pump chambers, a and b (Fig. 10). The former of these is 4 inches in diameter, and its piston is connected with the gun, while the other is 8 inches in diameter, and its piston is connected with two rows of 26 couples of Belleville springs, d. The two cylinders communicate through a check valve.
When the gun is in battery, the liquid fills the chamber of the 4 inch pump, while the piston of the 8 inch one is at the end of its stroke. A recoil has the effect of driving in the 4 inch piston and forcing the liquid into the other chamber, whose piston compresses the springs. At the end of the recoil, the gunner has only to act upon the valve by means of a hand-wheel in order to bring the gun into battery as slowly as he desires, through the action of the springs.
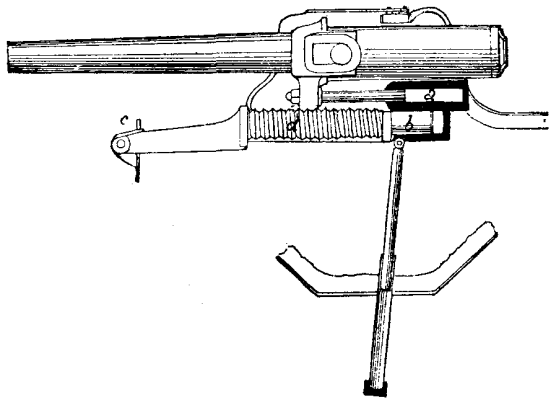
FIG. 10.--MOUGIN'S HYDRAULIC GUN
CARRIAGE.
For high aiming, the gun and the movable part of its carriage are capable of revolving around a strong pin, c, so placed that the axis of the piece always passes very near the center of the embrasure, thus permitting of giving the latter minimum dimensions. The chamber of the 8 inch pump is provided with projections that slide between circular guides, and carries the strap of a small hydraulic piston, p, that suffices to move the entire affair in a vertical plane, the gun and movable carriage being balanced by a counterpoise, q.
The projectiles are hoisted to the breech of the gun by a crane.
Between the outer armor and turret sufficient space is left for a man to enter, in order to make repairs when necessary.
Each of the rolled iron plates of which the turret consists weighs 19 tons. The cupolas that we have examined in this article have been constructed on the hypothesis than an enemy will not be able to bring into the field guns of much greater caliber than 6 inches.--Le Genie Civil.
To the Editor of the Scientific American:
Although not a naval engineer, I wish to reply to some arguments advanced by Capt. Giles, and published in the SCIENTIFIC AMERICAN of Jan. 2, 1886, in regard to high speed on the ocean.
Capt. Giles argues that because quadrupeds and birds do not in propelling themselves exert their force in a direct line with the plane of their motion, but at an angle to it, the same principle would, if applied to a steamship, increase its speed. But let us look at the subject from another standpoint. The quadruped has to support the weight of his body, and propel himself forward, with the same force. If the force be applied perpendicularly, the body is elevated, but not moved forward. If the force is applied horizontally, the body moves forward, but soon falls to the ground, because it is not supported. But when the force is applied at the proper angle, the body is moved forward and at the same time supported. Directly contrary to Capt. Giles' theory, the greater the speed of the quadruped, the nearer in a direct line with his motion does he apply the propulsive force, and vice versa. This may easily be seen by any one watching the motions of the horse, hound, deer, rabbit, etc., when in rapid motion. The water birds and animals, whose weight is supported by the water, do not exert the propulsive force in a downward direction, but in a direct line with the plane of their motion. The man who swims does not increase his motion by kicking out at an angle, but by drawing the feet together with the legs straight, thus using the water between them as a double inclined plane, on which his feet and legs slide and thus increase his motion. The weight of the steamship is already supported by the water, and all that is required of the propeller is to push her forward. If set so as to act in a direct line with the plane of motion, it will use all its force to push her forward; if set so as to use its force in a perpendicular direction, it will use all its force to raise her out of the water. If placed at an angle of 45° with the plane of motion, half the force will be used in raising the ship out of the water, and only half will be left to push her forward.
ENOS M. RICKER.
Park Rapids, Minn., Jan. 23, 1886.
On appearing for the first time before this Association, which, as I am informed, comprises the faculty and the entire body of students of the Sibley College of Mechanical Engineering and the Mechanic Arts, a reminiscence of the founder of this College suggests itself to me, in the relation of which I beg first to be indulged.
In the years 1847-8-9 I lived in Rochester, N.Y., and formed a slight acquaintance with Mr. Sibley, whose home was then, as it has ever since been, in that city. Nearly twelve years afterward, in the summer of 1861, which will be remembered as the first year of our civil war, I met Mr. Sibley again. We happened to occupy a seat together in a car from New York to Albany. He recollected me, and we had a conversation which made a lasting impression on my memory. I said we had a conversation. That reminds me of a story told by my dear friend, of precious memory, Alexander L. Holley. One summer Mr. Holley accompanied a party of artists on an excursion to Mt. Katahdin, which, as you know, rises in almost solitary grandeur amid the forests and lakes of Maine. He wrote, in his inimitably happy style, an account of this excursion, which appeared some time after in Scribner's Monthly, elegantly illustrated with views of the scenery. Among other things, Mr. Holley related how he and Mr. Church painted the sketches for a grand picture of Mt. Katahdin. "That is," he explained, "Mr. Church painted, and I held the umbrella."
This describes the conversation which Mr. Sibley and I had. Mr. Sibley talked, and I listened. He was a good talker, and I flatter myself that I rather excel as a listener. On that occasion I did my best, for I knew whom I was listening to. I was listening to the man who combined bold and comprehensive grasp of thought, unerring foresight and sagacity, and energy of action and power of accomplishment, in a degree not surpassed, if it was equaled, among men.
Some years before, Mr. Sibley had created the Western Union Telegraph Company. At that time telegraphy was in a very depressed state. The country was to a considerable extent occupied by local lines, chartered under various State laws, and operated without concert. Four rival companies, organized under the Morse, the Bain, the House, and the Hughes patents, competed for the business. Telegraph stock was nearly valueless. Hiram Sibley, a man of the people, a resident of an inland city, of only moderate fortune, alone grasped the situation. He saw that the nature of the business, and the demands of the country, alike required that a single organization, in which all interests should be combined, should cover the entire land with its network, by means of which every center and every outlying point, distant as well as near, could communicate with each other directly, and that such an organization must be financially successful. He saw all this vividly, and realized it with the most intense earnestness of conviction. With Mr. Sibley, to be convinced was to act; and so he set about the task of carrying this vast scheme into execution. The result is well known. By his immense energy, the magnetic power with which he infused his own convictions into other minds, the direct, practical way in which he set about the work, and his indomitable perseverance, Mr. Sibley attained at last a phenomenal success.
But he was not then telling me anything about this. He was telling me of the construction of the telegraph line to the Pacific Coast. Here again Mr. Sibley had seen that which was hidden from others. This case differed from the former one in two important respects. Then Mr. Sibley had been dependent on the aid and co-operation of many persons; and this he had been able to secure. Now, he could not obtain help from a human being; but he had become able to act independently of any assistance.
He had made a careful study of the subject, in his thoroughly practical way, and had become convinced that such a line was feasible, and would be remunerative. At his instance a convention of telegraph men met in the city of New York, to consider the project. The feeling in this convention was extremely unfavorable to it. A committee reported against it unanimously, on three grounds--the country was destitute of timber, the line would be destroyed by the Indians, and if constructed and maintained, it would not pay expenses. Mr. Sibley found himself alone. An earnest appeal which he made from the report of the committee was received with derisive laughter. The idea of running a telegraph line through what was then a wilderness, roamed over for between one and two thousand miles of its breadth by bands of savages, who of course would destroy the line as soon as it was put up, and where repairs would be difficult and useless, even if the other objections to it were out of the way, struck the members of the convention as so exquisitely ludicrous that it seemed as if they would never be done laughing about it. If Mr. Sibley had advocated a line to the moon, they would hardly have seen in it greater evidence of lunacy. When he could be heard, he rose again and said: "Gentlemen, you may laugh, but if I was not so old, I would build the line myself." Upon this, of course, they laughed louder than ever. As they laughed, he grew mad, and shouted: "Gentlemen, I will bar the years, and do it." And he did it. Without help from any one, for every man who claimed a right to express an opinion upon it scouted the project as chimerical, and no capitalist would put a dollar in it, Hiram Sibley built the line of telegraph to San Francisco, risking in it all he had in the world. He set about the work with his customary energy, all obstacles vanished, and the line was completed in an incredibly short time. And from the day it was opened, it has proved probably the most profitable line of telegraph that has ever been constructed. There was the practicability, and there was the demand and the business to be done, and yet no living man could see it, or could be made to see it, except Hiram Sibley. "And to-day," he said, with honest pride, "to-day in New York, men to whom I went almost on my knees for help in building this line, and who would not give me a dollar, have solicited me to be allowed to buy stock in it at the rate of five dollars for one."
"But how about the Indians?" I asked. "Why," he replied, "we never had any trouble from the Indians. I knew we wouldn't have. Men who supposed I was such a fool as to go about this undertaking before that was all settled didn't know me. No Indian ever harmed that line. The Indians are the best friends we have got. You see, we taught the Indians the Great Spirit was in that line; and what was more, we proved it to them. It was, by all odds, the greatest medicine they ever saw. They fairly worshiped it. No Indian ever dared to do it harm."
"But," he added, "there was one thing I didn't count on. The border ruffians in Missouri are as bad as anybody ever feared the Indians might be. They have given us so much trouble that we are now building a line around that State, through Iowa and Nebraska. We are obliged to do it."
This opened another phase of the subject. The telegraph line to the Pacific had a value beyond that which could be expressed in money. It was perhaps the strongest of all the ties which bound California so securely to the Union, in the dark days of its struggle for existence. The secession element in Missouri recognized the importance of the line in this respect, and were persistent in their efforts to destroy it. We have seen by what means their purpose was thwarted.
I have always felt that, among the countless evidences of the ordering of Providence by which the war for the preservation of the Union was signalized, not the least striking was the raising up of this remarkable man, to accomplish alone, and in the very nick of time, a work which at once became of such national importance.
This is the man who has crowned his useful career, and shown again his eminently practical character and wise foresight, by the endowment of this College, which cannot fail to be a perennial source of benefit to the country whose interests he has done so much to promote, and which his remarkable sagacity and energy contributed so much to preserve.
We have an excellent rule, followed by all successful designers of machinery, which is, to make provision for the extreme case, for the most severe test to which, under normal conditions, and so far as practicable under abnormal conditions also, the machinery can be subjected. Then, of course, any demands upon it which are less than the extreme demand are not likely to give trouble. I shall apply this principle in addressing you to-day. In what I have to say, I shall speak directly to the youngest and least advanced minds among my auditors. If I am successful in making an exposition of my subject which shall be plain to them, then it is evident that I need not concern myself about being understood by the higher class men and the professors.
The subject to which your attention is now invited is
This is a subject with which every one who expects to be concerned with machinery, either as designer or constructor, ought to be familiar. The principles which underlie it are very simple, but in order to be of use, these need to be thoroughly understood. If they have once been mastered, made familiar, incorporated into your intellectual being, so as to be readily and naturally applied to every case as it arises, then you occupy a high vantage ground. In this particular, at least, you will not go about your work uncertainly, trying first this method and then that one, or leaving errors to be disclosed when too late to remedy them. On the contrary, you will make, first your calculations and then your plans, with the certainty that the result will be precisely what you intend.
Moreover, when you read discussions on any branch of this subject, you will not receive these into unprepared minds, just as apt to admit error as truth, and possessing no test by which to distinguish the one from the other; but you will be able to form intelligent judgments with respect to them. You will discover at once whether or not the writers are anchored to the sure holding ground of sound principles.
It is to be observed that I do not speak of balancing bodies, but of balancing forces. Forces are the realities with which, as mechanical engineers, you will have directly to deal, all through your lives. The present discussion is limited also to those forces which are developed in moving bodies, or by the motion of bodies. This limitation excludes the force of gravity, which acts on all bodies alike, whether at rest or in motion. It is, indeed, often desirable to neutralize the effect of gravity on machinery. The methods of doing this are, however, obvious, and I shall not further refer to them.
Two very different forces, or manifestations of force, are developed by the motion of bodies. These are
The first of these forces is exerted by every moving body, whatever the nature of the path in which it is moving, and always in the direction of its motion. The latter force is exerted only by bodies whose path is a circle, or a curve of some form, about a central body or point, to which it is held, and this force is always at right angles with the direction of motion of the body.
Respecting momentum, I wish only to call your attention to a single fact, which will become of importance in the course of our discussion. Experiments on falling bodies, as well as all experience, show that the velocity of every moving body is the product of two factors, which must combine to produce it. Those factors are force and distance. In order to impart motion to the body, force must act through distance. These two factors may be combined in any proportions whatever. The velocity imparted to the body will vary as the square root of their product. Thus, in the case of any given body,
Let force 1, acting through distance 1, impart velocity 1.
Then " 1, " " " 4, will " " 2, or
" 2, " " " 2, " " " 2, or
" 4, " " " 1, " " " 2;
And " 1, " " " 9, " " " 3, or
" 3, " " " 3, " " " 3, or
" 9, " " " 1, " " " 3.
This table might be continued indefinitely. The product of the force into the distance will always vary as the square of the final velocity imparted. To arrest a given velocity, the same force, acting through the same distance, or the same product of force into distance, is required that was required to impart the velocity.
The fundamental truth which I now wish to impress upon your minds is that in order to impart velocity to a body, to develop the energy which is possessed by a body in motion, force must act through distance. Distance is a factor as essential as force. Infinite force could not impart to a body the least velocity, could not develop the least energy, without acting through distance.
This exposition of the nature of momentum is sufficient for my present purpose. I shall have occasion to apply it later on, and to describe the methods of balancing this force, in those cases in which it becomes necessary or desirable to do so. At present I will proceed to consider the second of the forces, or manifestations of force, which are developed in moving bodies--centrifugal force.
This force presents its claims to attention in all bodies which revolve about fixed centers, and sometimes these claims are presented with a good deal of urgency. At the same time, there is probably no subject, about which the ideas of men generally are more vague and confused. This confusion is directly due to the vague manner in which the subject of centrifugal force is treated, even by our best writers. As would then naturally be expected, the definitions of it commonly found in our handbooks are generally indefinite, or misleading, or even absolutely untrue.
Before we can intelligently consider the principles and methods of balancing this force, we must get a correct conception of the nature of the force itself. What, then, is centrifugal force? It is an extremely simple thing; a very ordinary amount of mechanical intelligence is sufficient to enable one to form a correct and clear idea of it. This fact renders it all the more surprising that such inaccurate and confused language should be employed in its definition. Respecting writers, also, who use language with precision, and who are profound masters of this subject, it must be said that, if it had been their purpose to shroud centrifugal force in mystery, they could hardly have accomplished this purpose more effectually than they have done, to minds by whom it was not already well understood.
Let us suppose a body to be moving in a circular path, around a center to which it is firmly held; and let us, moreover, suppose the impelling force, by which the body was put in motion, to have ceased; and, also, that the body encounters no resistance to its motion. It is then, by our supposition, moving in its circular path with a uniform velocity, neither accelerated nor retarded. Under these conditions, what is the force which is being exerted on this body? Clearly, there is only one such force, and that is, the force which holds it to the center, and compels it, in its uniform motion, to maintain a fixed distance from this center. This is what is termed centripetal force. It is obvious, that the centripetal force, which holds this revolving body to the center, is the only force which is being exerted upon it.
Where, then, is the centrifugal force? Why, the fact is, there is not any such thing. In the dynamical sense of the term "force," the sense in which this term is always understood in ordinary speech, as something tending to produce motion, and the direction of which determines the direction in which motion of a body must take place, there is, I repeat, no such thing as centrifugal force.
There is, however, another sense in which the term "force" is employed, which, in distinction from the above, is termed a statical sense. This "statical force" is the force by the exertion of which a body keeps still. It is the force of inertia--the resistance which all matter opposes to a dynamical force exerted to put it in motion. This is the sense in which the term "force" is employed in the expression "centrifugal force." Is that all? you ask. Yes; that is all.
I must explain to you how it is that a revolving body exerts this resistance to being put in motion, when all the while it is in motion, with, according to our above supposition, a uniform velocity. The first law of motion, so far as we now have occasion to employ it, is that a body, when put in motion, moves in a straight line. This a moving body always does, unless it is acted on by some force, other than its impelling force, which deflects it, or turns it aside, from its direct line of motion. A familiar example of this deflecting force is afforded by the force of gravity, as it acts on a projectile. The projectile, discharged at any angle of elevation, would move on in a straight line forever, but, first, it is constantly retarded by the resistance of the atmosphere, and, second, it is constantly drawn downward, or made to fall, by the attraction of the earth; and so instead of a straight line it describes a curve, known as the trajectory.
Now a revolving body, also, has the same tendency to move in a straight line. It would do so, if it were not continually deflected from this line. Another force is constantly exerted upon it, compelling it, at every successive point of its path, to leave the direct line of motion, and move on a line which is everywhere equally distant from the center to which it is held. If at any point the revolving body could get free, and sometimes it does get free, it would move straight on, in a line tangent to the circle at the point of its liberation. But if it cannot get free, it is compelled to leave each new tangential direction, as soon as it has taken it.
This is illustrated in the above figure. The body, A, is supposed to be revolving in the direction indicated by the arrow, in the circle, A B F G, around the center, O, to which it is held by the cord, O A. At the point, A, it is moving in the tangential direction, A D. It would continue to move in this direction, did not the cord, O A, compel it to move in the arc, A C. Should this cord break at the point, A, the body would move; straight on toward D, with whatever velocity it had.
You perceive now what centrifugal force is. This body is moving in the direction, A D. The centripetal force, exerted through the cord, O A, pulls it aside from this direction of motion. The body resists this deflection, and this resistance is its centrifugal force.
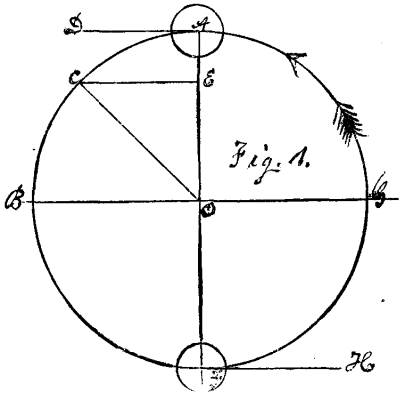
Fig. 1
Centrifugal force is, then, properly defined to be the disposition of a revolving body to move in a straight line, and the resistance which such a body opposes to being drawn aside from a straight line of motion. The force which draws the revolving body continually to the center, or the deflecting force, is called the centripetal force, and, aside from the impelling and retarding forces which act in the direction of its motion, the centripetal force is, dynamically speaking, the only force which is exerted on the body.
It is true, the resistance of the body furnishes the measure of the centripetal force. That is, the centripetal force must be exerted in a degree sufficient to overcome this resistance, if the body is to move in the circular path. In this respect, however, this case does not differ from every other case of the exertion of force. Force is always exerted to overcome resistance: otherwise it could not be exerted. And the resistance always furnishes the exact measure of the force. I wish to make it entirely clear, that in the dynamical sense of the term "force," there is no such thing as centrifugal force. The dynamical force, that which produces motion, is the centripetal force, drawing the body continually from the tangential direction, toward the center; and what is termed centrifugal force is merely the resistance which the body opposes to this deflection, precisely like any other resistance to a force.
The centripetal force is exerted on the radial line, as on the line, A O, Fig. 1, at right angles with the direction in which the body is moving; and draws it directly toward the center. It is, therefore, necessary that the resistance to this force shall also be exerted on the same line, in the opposite direction, or directly from the center. But this resistance has not the least power or tendency to produce motion in the direction in which it is exerted, any more than any other resistance has.
We have been supposing a body to be firmly held to the center, so as to be compelled to revolve about it in a fixed path. But the bond which holds it to the center may be elastic, and in that case, if the centrifugal force is sufficient, the body will be drawn from the center, stretching the elastic bond. It may be asked if this does not show centrifugal force to be a force tending to produce motion from the center. This question is answered by describing the action which really takes place. The revolving body is now imperfectly deflected. The bond is not strong enough to compel it to leave its direct line of motion, and so it advances a certain distance along this tangential line. This advance brings the body into a larger circle, and by this enlargement of the circle, assuming the rate of revolution to be maintained, its centrifugal force is proportionately increased. The deflecting power exerted by the elastic bond is also increased by its elongation. If this increase of deflecting force is no greater than the increase of centrifugal force, then the body will continue on in its direct path; and when the limit of its elasticity is reached, the deflecting bond will be broken. If, however, the strength of the deflecting bond is increased by its elongation in a more rapid ratio than the centrifugal force is increased by the enlargement of the circle, then a point will be reached in which the centripetal force will be sufficient to compel the body to move again in the circular path.
Sometimes the centripetal force is weak, and opportunity is afforded to observe this action, and see its character exhibited. A common example of weak centripetal force is the adhesion of water to the face of a revolving grindstone. Here we see the deflecting force to become insufficient to compel the drops of water longer to leave their direct paths, and so these do not longer leave their direct paths, but move on in those paths, with the velocity they have at the instant of leaving the stone, flying off on tangential lines.
If, however, a fluid be poured on the side of the revolving wheel near the axis, it will move out to the rim on radial lines, as may be observed on car wheels universally. The radial lines of black oil on these wheels look very much as if centrifugal force actually did produce motion, or had at least a very decided tendency to produce motion, in the radial direction. This interesting action calls for explanation. In this action the oil moves outward gradually, or by inconceivably minute steps. Its adhesion being overcome in the least possible degree, it moves in the same degree tangentially. In so doing it comes in contact with a point of the surface which has a motion more rapid than its own. Its inertia has now to be overcome, in the same degree in which it had overcome the adhesion. Motion in the radial direction is the result of these two actions, namely, leaving the first point of contact tangentially and receiving an acceleration of its motion, so that this shall be equal to that of the second point of contact. When we think about the matter a little closely, we see that at the rim of the wheel the oil has perhaps ten times the velocity of revolution which it had on leaving the journal, and that the mystery to be explained really is, How did it get that velocity, moving out on a radial line? Why was it not left behind at the very first? Solely by reason of its forward tangential motion. That is the answer.
When writers who understand the subject talk about the centripetal and centrifugal forces being different names for the same force, and about equal action and reaction, and employ other confusing expressions, just remember that all they really mean is to express the universal relation between force and resistance. The expression "centrifugal force" is itself so misleading, that it becomes especially important that the real nature of this so-called force, or the sense in which the term "force" is used in this expression, should be fully explained.[1] This force is now seen to be merely the tendency of a revolving body to move in a straight line, and the resistance which it opposes to being drawn aside from that line. Simple enough! But when we come to consider this action carefully, it is wonderful how much we find to be contained in what appears so simple. Let us see.
[Footnote 1: I was led to study this subject in looking to see what had become of my first permanent investment, a small venture, made about thirty-five years ago, in the "Sawyer and Gwynne static pressure engine." This was the high-sounding name of the Keely motor of that day, an imposition made possible by the confused ideas prevalent on this very subject of centrifugal force.]
FIRST.--I have called your attention to the fact that the direction in which the revolving body is deflected from the tangential line of motion is toward the center, on the radial line, which forms a right angle with the tangent on which the body is moving. The first question that presents itself is this: What is the measure or amount of this deflection? The answer is, this measure or amount is the versed sine of the angle through which the body moves.
Now, I suspect that some of you--some of those whom I am directly addressing--may not know what the versed sine of an angle is; so I must tell you. We will refer again to Fig. 1. In this figure, O A is one radius of the circle in which the body A is revolving. O C is another radius of this circle. These two radii include between them the angle A O C. This angle is subtended by the arc A C. If from the point O we let fall the line C E perpendicular to the radius O A, this line will divide the radius O A into two parts, O E and E A. Now we have the three interior lines, or the three lines within the circle, which are fundamental in trigonometry. C E is the sine, O E is the cosine, and E A is the versed sine of the angle A O C. Respecting these three lines there are many things to be observed. I will call your attention to the following only:
First.--Their length is always less than the radius. The radius is expressed by 1, or unity. So, these lines being less than unity, their length is always expressed by decimals, which mean equal to such a proportion of the radius.
Second.--The cosine and the versed sine are together equal to the radius, so that the versed sine is always 1, less the cosine.
Third.--If I diminish the angle A O C, by moving the radius O C toward O A, the sine C E diminishes rapidly, and the versed sine E A also diminishes, but more slowly, while the cosine O E increases. This you will see represented in the smaller angles shown in Fig. 2. If, finally, I make O C to coincide with O A, the angle is obliterated, the sine and the versed sine have both disappeared, and the cosine has become the radius.
Fourth.--If, on the contrary, I enlarge the angle A O C by moving the radius O C toward O B, then the sine and the versed sine both increase, and the cosine diminishes; and if, finally, I make O C coincide with O B, then the cosine has disappeared, the sine has become the radius O B, and the versed sine has become the radius O A, thus forming the two sides inclosing the right angle A O B. The study of this explanation will make you familiar with these important lines. The sine and the cosine I shall have occasion to employ in the latter part of my lecture. Now you know what the versed sine of an angle is, and are able to observe in Fig. 1 that the versed sine A E, of the angle A O C, represents in a general way the distance that the body A will be deflected from the tangent A D toward the center O while describing the arc A C.
The same law of deflection is shown, in smaller angles, in Fig. 2. In this figure, also, you observe in each of the angles A O B and A O C that the deflection, from the tangential direction toward the center, of a body moving in the arc A C is represented by the versed sine of the angle. The tangent to the arc at A, from which this deflection is measured, is omitted in this figure to avoid confusion. It is shown sufficiently in Fig. 1. The angles in Fig. 2 are still pretty large angles, being 12° and 24° respectively. These large angles are used for convenience of illustration; but it should be explained that this law does not really hold in them, as is evident, because the arc is longer than the tangent to which it would be connected by a line parallel with the versed sine. The law is absolutely true only when the tangent and arc coincide, and approximately so for exceedingly small angles.
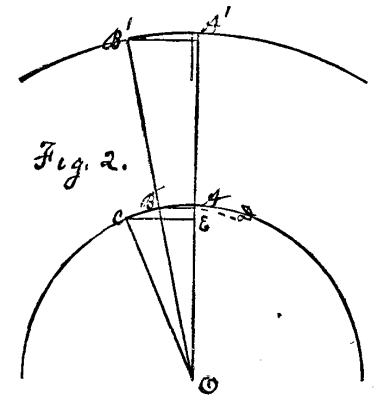
Fig. 2
In reality, however, we have only to do with the case in which the arc and the tangent do coincide, and in which the law that the deflection is equal to the versed sine of the angle is absolutely true. Here, in observing this most familiar thing, we are, at a single step, taken to that which is utterly beyond our comprehension. The angles we have to consider disappear, not only from our sight, but even from our conception. As in every other case when we push a physical investigation to its limit, so here also, we find our power of thought transcended, and ourselves in the presence of the infinite.
We can discuss very small angles. We talk familiarly about the angle which is subtended by 1" of arc. On Fig. 2, a short line is drawn near to the radius O A'. The distance between O A' and this short line is 1° of the arc A' B'. If we divide this distance by 3,600, we get 1" of arc. The upper line of the Table of versed sines given below is the versed sine of 1" of arc. It takes 1,296,000 of these angles to fill a circular space. These are a great many angles, but they do not make a circle. They make a polygon. If the radius of the circumscribed circle of this polygon is 1,296,000 feet, which is nearly 213 geographical miles, each one of its sides will be a straight line, 6.283 feet long. On the surface of the earth, at the equator, each side of this polygon would be one-sixtieth of a geographical mile, or 101.46 feet. On the orbit of the moon, at its mean distance from the earth, each of these straight sides would be about 6,000 feet long.
The best we are able to do is to conceive of a polygon having an infinite number of sides, and so an infinite number of angles, the versed sines of which are infinitely small, and having, also, an infinite number of tangential directions, in which the body can successively move. Still, we have not reached the circle. We never can reach the circle. When you swing a sling around your head, and feel the uniform stress exerted on your hand through the cord, you are made aware of an action which is entirely beyond the grasp of our minds and the reach of our analysis.
So always in practical operation that law is absolutely true which we observe to be approximated to more and more nearly as we consider smaller and smaller angles, that the versed sine of the angle is the measure of its deflection from the straight line of motion, or the measure of its fall toward the center, which takes place at every point in the motion of a revolving body.
Then, assuming the absolute truth of this law of deflection, we find ourselves able to explain all the phenomena of centrifugal force, and to compute its amount correctly in all cases.
We have now advanced two steps. We have learned the direction and the measure of the deflection, which a revolving body continually suffers, and its resistance to which is termed centrifugal force. The direction is toward the center, and the measure is the versed sine of the angle.
SECOND.--We next come to consider what are known as the laws of centrifugal force. These laws are four in number. They are, that the amount of centrifugal force exerted by a revolving body varies in four ways.
First.--Directly as the weight of the body.
Second.--In a given circle of revolution, as the square of the speed or of the number of revolutions per minute; which two expressions in this case mean the same thing.
Third.--With a given number of revolutions per minute, or a given angular velocity[1] directly as the radius of the circle; and
Fourth.--With a given actual velocity, or speed in feet per minute, inversely as the radius of the circle.
[Footnote 1: A revolving body is said to have the same angular velocity, when it sweeps through equal angles in equal times. Its actual velocity varies directly as the radius of the circle in which it is revolving.]
Of course there is a reason for these laws. You are not to learn them by rote, or to accept them on any authority. You are taught not to accept any rule or formula on authority, but to demand the reason for it--to give yourselves no rest until you know the why and wherefore, and comprehend these fully. This is education, not cramming the mind with mere facts and rules to be memorized, but drawing out the mental powers into activity, strengthening them by use and exercise, and forming the habit, and at the same time developing the power, of penetrating to the reason of things.
In this way only, you will be able to meet the requirement of a great educator, who said: "I do not care to be told what a young man knows, but what he can do." I wish here to add my grain to the weight of instruction which you receive, line upon line, precept on precept, on this subject.
The reason for these laws of centrifugal force is an extremely simple one. The first law, that this force varies directly as the weight of the body, is of course obvious. We need not refer to this law any further. The second, third, and fourth laws merely express the relative rates at which a revolving body is deflected from the tangential direction of motion, in each of the three cases described, and which cases embrace all possible conditions.
These three rates of deflection are exhibited in Fig. 2. An examination of this figure will give you a clear understanding of them. Let us first suppose a body to be revolving about the point, O, as a center, in a circle of which A B C is an arc, and with a velocity which will carry it from A to B in one second of time. Then in this time the body is deflected from the tangential direction a distance equal to A D, the versed sine of the angle A O B. Now let us suppose the velocity of this body to be doubled in the same circle. In one second of time it moves from A to C, and is deflected from the tangential direction of motion a distance equal to A E, the versed sine of the angle, A O C. But A E is four times A D. Here we see in a given circle of revolution the deflection varying as the square of the speed. The slight error already pointed out in these large angles is disregarded.
The following table will show, by comparison of the versed sines of very small angles, the deflection in a given circle varying as the square of the speed, when we penetrate to them, so nearly that the error is not disclosed at the fifteenth place of decimals.
The versed sine of 1" is 0.000,000,000,011,752 " " " " 2" is 0.000,000,000,047,008 " " " " 3" is 0.000,000,000,105,768 " " " " 4" is 0.000,000,000,188,032 " " " " 5" is 0.000,000,000,293,805 " " " " 6" is 0.000,000,000,423,072 " " " " 7" is 0.000,000,000,575,848 " " " " 8" is 0.000,000,000,752,128 " " " " 9" is 0.000,000,000,951,912 " " " " 10" is 0.000,000,001,175,222 " " " " 100" is 0.000,000,117,522,250
You observe the deflection for 10" of arc is 100 times as great, and for 100" of arc is 10,000 times as great as it is for 1" of arc. So far as is shown by the 15th place of decimals, the versed sine varies as the square of the angle; or, in a given circle, the deflection, and so the centrifugal force, of a revolving body varies as the square of the speed.
The reason for the third law is equally apparent on inspection of Fig. 2. It is obvious, that in the case of bodies making the same number of revolutions in different circles, the deflection must vary directly as the diameter of the circle, because for any given angle the versed sine varies directly as the radius. Thus radius O A' is twice radius O A, and so the versed sine of the arc A' B' is twice the versed sine of the arc A B. Here, while the angular velocity is the same, the actual velocity is doubled by increase in the diameter of the circle, and so the deflection is doubled. This exhibits the general law, that with a given angular velocity the centrifugal force varies directly as the radius or diameter of the circle.
We come now to the reason for the fourth law, that, with a given actual velocity, the centrifugal force varies inversely as the diameter of the circle. If any of you ever revolved a weight at the end of a cord with some velocity, and let the cord wind up, suppose around your hand, without doing anything to accelerate the motion, then, while the circle of revolution was growing smaller, the actual velocity continuing nearly uniform, you have felt the continually increasing stress, and have observed the increasing angular velocity, the two obviously increasing in the same ratio. That is the operation or action which the fourth law of centrifugal force expresses. An examination of this same figure (Fig. 2) will show you at once the reason for it in the increasing deflection which the body suffers, as its circle of revolution is contracted. If we take the velocity A' B', double the velocity A B, and transfer it to the smaller circle, we have the velocity A C. But the deflection has been increasing as we have reduced the circle, and now with one half the radius it is twice as great. It has increased in the same ratio in which the angular velocity has increased. Thus we see the simple and necessary nature of these laws. They merely express the different rates of deflection of a revolving body in these different cases.
THIRD.--We have a coefficient of centrifugal force, by which we are enabled to compute the amount of this resistance of a revolving body to deflection from a direct line of motion in all cases. This is that coefficient. The centrifugal force of a body making one revolution per minute, in a circle of one foot radius, is 0.000341 of the weight of the body.
According to the above laws, we have only to multiply this coefficient by the square of the number of revolutions made by the body per minute, and this product by the radius of the circle in feet, or in decimals of a foot, and we have the centrifugal force, in terms of the weight of the body. Multiplying this by the weight of the body in pounds, we have the centrifugal force in pounds.
Of course you want to know how this coefficient has been found out, and how you can be sure it is correct. I will tell you a very simple way. There are also mathematical methods of ascertaining this coefficient, which your professors, if you ask them, will let you dig out for yourselves. The way I am going to tell you I found out for myself, and that, I assure you, is the only way to learn anything, so that it will stick; and the more trouble the search gives you, the darker the way seems, and the greater the degree of perseverance that is demanded, the more you will appreciate the truth when you have found it, and the more complete and permanent your possession of it will be.
The explanation of this method may be a little more abstruse than the explanations already given, but it is very simple and elegant when you see it, and I fancy I can make it quite clear. I shall have to preface it by the explanation of two simple laws. The first of these is, that a body acted on by a constant force, so as to have its motion uniformly accelerated, suppose in a straight line, moves through distances which increase as the square of the time that the accelerating force continues to be exerted.
The necessary nature of this law, or rather the action of which this law is the expression, is shown in Fig. 3.
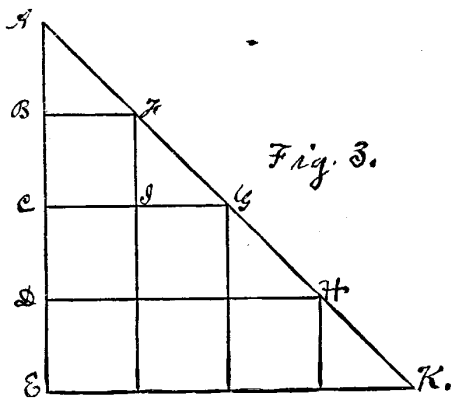
Fig. 3
Let the distances A B, B C, C D, and D E in this figure represent four successive seconds of time. They may just as well be conceived to represent any other equal units, however small. Seconds are taken only for convenience. At the commencement of the first second, let a body start from a state of rest at A, under the action of a constant force, sufficient to move it in one second through a distance of one foot. This distance also is taken only for convenience. At the end of this second, the body will have acquired a velocity of two feet per second. This is obvious because, in order to move through one foot in this second, the body must have had during the second an average velocity of one foot per second. But at the commencement of the second it had no velocity. Its motion increased uniformly. Therefore, at the termination of the second its velocity must have reached two feet per second. Let the triangle A B F represent this accelerated motion, and the distance, of one foot, moved through during the first second, and let the line B F represent the velocity of two feet per second, acquired by the body at the end of it. Now let us imagine the action of the accelerating force suddenly to cease, and the body to move on merely with the velocity it has acquired. During the next second it will move through two feet, as represented by the square B F C I. But in fact, the action of the accelerating force does not cease. This force continues to be exerted, and produces on the body during the next second the same effect that it did during the first second, causing it to move through an additional foot of distance, represented by the triangle F I G, and to have its velocity accelerated two additional feet per second, as represented by the line I G. So in two seconds the body has moved through four feet. We may follow the operation of this law as far as we choose. The figure shows it during four seconds, or any other unit, of time, and also for any unit of distance. Thus:
Time 1 Distance 1
" 2 " 4
" 3 " 9
" 4 " 16
So it is obvious that the distance moved through by a body whose motion is uniformly accelerated increases as the square of the time.
But, you are asking, what has all this to do with a revolving body? As soon as your minds can be started from a state of rest, you will perceive that it has everything to do with a revolving body. The centripetal force, which acts upon a revolving body to draw it to the center, is a constant force, and under it the revolving body must move or be deflected through distances which increase as the squares of the times, just as any body must do when acted on by a constant force. To prove that a revolving body obeys this law, I have only to draw your attention to Fig. 2. Let the equal arcs, A B and B C, in this figure represent now equal times, as they will do in case of a body revolving in this circle with a uniform velocity. The versed sines of the angles, A O B and A O C, show that in the time, A C, the revolving body was deflected four times as far from the tangent to the circle at A as it was in the time, A B. So the deflection increased as the square of the time. If on the table already given, we take the seconds of arc to represent equal times, we see the versed sine, or the amount of deflection of a revolving body, to increase, in these minute angles, absolutely so far as appears up to the fifteenth place of decimals, as the square of the time.
The standard from which all computations are made of the distances passed through in given times by bodies whose motion is uniformly accelerated, and from which the velocity acquired is computed when the accelerating force is known, and the force is found when the velocity acquired or the rate of acceleration is known, is the velocity of a body falling to the earth. It has been established by experiment, that in this latitude near the level of the sea, a falling body in one second falls through a distance of 16.083 feet, and acquires a velocity of 32.166 feet per second; or, rather, that it would do so if it did not meet the resistance of the atmosphere. In the case of a falling body, its weight furnishes, first, the inertia, or the resistance to motion, that has to be overcome, and affords the measure of this resistance, and, second, it furnishes the measure of the attraction of the earth, or the force exerted to overcome its resistance. Here, as in all possible cases, the force and the resistance are identical with each other. The above is, therefore, found in this way to be the rate at which the motion of any body will be accelerated when it is acted on by a constant force equal to its weight, and encounters no resistance.
It follows that a revolving body, when moving uniformly in any circle at a speed at which its deflection from a straight line of motion is such that in one second this would amount to 16.083 feet, requires the exertion of a centripetal force equal to its weight to produce such deflection. The deflection varying as the square of the time, in 0.01 of a second this deflection will be through a distance of 0.0016083 of a foot.
Now, at what speed must a body revolve, in a circle of one foot radius, in order that in 0.01 of one second of time its deflection from a tangential direction shall be 0.0016083 of a foot? This decimal is the versed sine of the arc of 3°15', or of 3.25°. This angle is so small that the departure from the law that the deflection is equal to the versed sine of the angle is too slight to appear in our computation. Therefore, the arc of 3.25° is the arc of a circle of one foot radius through which a body must revolve in 0.01 of a second of time, in order that the centripetal force, and so the centrifugal force, shall be equal to its weight. At this rate of revolution, in one second the body will revolve through 325°, which is at the rate of 54.166 revolutions per minute.
Now there remains only one question more to be answered. If at 54.166 revolutions per minute the centrifugal force of a body is equal to its weight, what will its centrifugal force be at one revolution per minute in the same circle?
To answer this question we have to employ the other extremely simple law, which I said I must explain to you. It is this: The acceleration and the force vary in a constant ratio with each other. Thus, let force 1 produce acceleration 1, then force 1 applied again will produce acceleration 1 again, or, in other words, force 2 will produce acceleration 2, and so on. This being so, and the amount of the deflection varying as the squares of the speeds in the two cases, the centrifugal force of a body making one revolution per minute in a circle of
1²
one foot radius will be ---------- = 0.000341
54.166²
--the coefficient of centrifugal force.
There is another mode of making this computation, which is rather neater and more expeditious than the above. A body making one revolution per minute in a circle of one foot radius will in one second revolve through an arc of 6°. The versed sine of this arc of 6° is 0.0054781046 of a foot. This is, therefore, the distance through which a body revolving at this rate will be deflected in one second. If it were acted on by a force equal to its weight, it would be deflected through the distance of 16.083 feet in the same time. What is the deflecting force actually exerted upon it? Of
0.0054781046
course, it is ------------.
16.083
This division gives 0.000341 of its weight as such deflecting force, the same as before.
In taking the versed sine of 6°, a minute error is involved, though not one large enough to change the last figure in the above quotient. The law of uniform acceleration does not quite hold when we come to an angle so large as 6°. If closer accuracy is demanded, we can attain it, by taking the versed sine for 1°, and multiplying this by 6². This gives as a product 0.0054829728, which is a little larger than the versed sine of 6°.
I hope I have now kept my promise, and made it clear how the coefficient of centrifugal force may be found in this simple way.
We have now learned several things about centrifugal force. Let me recapitulate. We have learned:
1st. The real nature of centrifugal force. That in the dynamical sense of the term force, this is not a force at all: that it is not capable of producing motion, that the force which is really exerted on a revolving body is the centripetal force, and what we are taught to call centrifugal force is nothing but the resistance which a revolving body opposes to this force, precisely like any other resistance.
2d. The direction of the deflection, to which the centrifugal force is the resistance, which is straight to the center.
3d. The measure of this deflection; the versed sine of the angle.
4th. The reason of the laws of centrifugal force; that these laws merely express the relative amount of the deflection, and so the amount of the force required to produce the deflection, and of the resistance of the revolving body to it, in all different cases.
5th. That the deflection of a revolving body presents a case analogous to that of uniformly accelerated motion, under the action of a constant force, similar to that which is presented by falling bodies;[1] and finally,
6th. How to find the coefficient, by which the amount of centrifugal force exerted in any case may be computed.
[Footnote 1: A body revolving with a uniform velocity in a horizontal plane would present the only case of uniformly accelerated motion that is possible to be realized under actual conditions.]
I now pass to some other features.
First.--You will observe that, relatively to the center, a revolving body, at any point in its revolution, is at rest. That is, it has no motion, either from or toward the center, except that which is produced by the action of the centripetal force. It has, therefore, this identity also with a falling body, that it starts from a state of rest. This brings us to a far more comprehensive definition of centrifugal force. This is the resistance which a body opposes to being put in motion, at any velocity acquired in any time, from a state of rest. Thus centrifugal force reveals to us the measure of the inertia of matter. This inertia may be demonstrated and exhibited by means of apparatus constructed on this principle quite as accurately as it can be in any other way.
Second.--You will also observe the fact, that motion must be imparted to a body gradually. As distance, through which force can act, is necessary to the impartation of velocity, so also time, during which force can act, is necessary to the same result. We do not know how motion from a state of rest begins, any more than we know how a polygon becomes a circle. But we do know that infinite force cannot impart absolutely instantaneous motion to even the smallest body, or to a body capable of opposing the least resistance. Time being an essential element or factor in the impartation of velocity, if this factor be omitted, the least resistance becomes infinite.
We have a practical illustration of this truth in the explosion of nitro-glycerine. If a small portion of this compound be exploded on the surface of a granite bowlder, in the open air, the bowlder will be rent into fragments. The explanation of this phenomenon common among the laborers who are the most numerous witnesses of it, which you have doubtless often heard, and which is accepted by ignorant minds without further thought, is that the action of nitro-glycerine is downward. We know that such an idea is absurd.
The explosive force must be exerted in all directions equally. The real explanation is, that the explosive action of nitro-glycerine is so nearly instantaneous, that the resistance of the atmosphere is very nearly equal to that of the rock; at any rate, is sufficient to cause the rock to be broken up. The rock yields to the force very nearly as readily as the atmosphere does.
Third. An interesting solution is presented here of what is to many an astronomical puzzle. When I was younger than I am now, I was greatly troubled to understand how it could be that if the moon was always falling to the earth, as the astronomers assured us it was, it should never reach it, nor have its falling velocity accelerated. In popular treatises on astronomy, such for example as that of Professor Newcomb, this is explained by a diagram in which the tangential line is carried out as in Fig. 1, and by showing that in falling from the point A to the earth as a center, through distances increasing as the square of the time, the moon, having the tangential velocity that it has, could never get nearer to the earth than the circle in which it revolves around it. This is all very true, and very unsatisfactory. We know that this long tangential line has nothing to do with the motion of the moon, and while we are compelled to assent to the demonstration, we want something better. To my mind the better and more satisfactory explanation is found in the fact that the moon is forever commencing to fall, and is continually beginning to fall in a new direction. A revolving body, as we have seen, never gets past that point, which is entirely beyond our sight and our comprehension, of beginning to fall, before the direction of its fall is changed. So, under the attraction of the earth, the moon is forever leaving a new tangential direction of motion at the same rate, without acceleration.
(To be continued.)
In the article on "Gas, Air, and Water Power" in the Journal for Dec. 8 last, you state that you await with some curiosity my reply to certain points in reference to the compressed air power schemes alluded to in that article. I now, therefore, take the liberty of submitting to you the arguments on my side of the question (which are substantially the same as those I am submitting to Mr. Hewson, the Borough Engineer of Leeds). The details and estimates for the Leeds scheme are not yet in a forward enough state to enable me to give them at present; but the whole case is sufficiently worked out for Birmingham to enable a fair deduction to be made therefrom as regards the utility of the system in other towns. In Birmingham, progress has been delayed owing to difficulties in procuring a site for the works, and other matters of detail. We have, however, recently succeeded in obtaining a suitable place, and making arrangements for railway siding, water supply, etc.; and we hope to be in a position to start early in the present year.
I inclose (1) a tabulated summary of the estimates for Birmingham divided into stages of 3,000 gross indicated horse power at a time; (2) a statement showing the cost to consumers in terms of indicated horse power and in different modes, more or less economical, of applying the air power in the consumers' engines; (3) a tracing showing the method of laying the mains; (4) a tracing showing the method of collecting the meter records at the central station, by means of electric apparatus, and ascertaining the exact amount of leakage. A short description of the two latter would be as well.
TABLE I.--Showing the Progressive Development of the Compressed Air System in stages of 3000 Indicated Horse Power (gross) at a Time, and the Profits at each Stage
_____________________________________________________________________________
Gross | 3000 | 6000 | 9000 | 12,000 | 15,000 | Indicated | Ind. | Ind. | Ind. | Ind. | Ind. | Horse Power | H.P. | H.P. | H.P. | H.P. | H.P. | at Central | | | | | | Works: | | | | | | -----------------------------------------------------------------------------
Thousands of | 1,080,000 | 2,160,000 |3,240,000 | 4,320,000 |5,400,000 | Cubic Feet at 45 | | | | | | lbs. pressure | | | | | | at engines | | | | | | Deduction for | 17,928 | 70,927 | 154,429 | 267,529 | 409,346 | friction and | | | | | | leakage | | | | | | Estimated net | 1,062,072 | 2,089,073 |3,085,571 | 4,052,471 |4,990,654 | delivery | | | | | | -----------------------------------------------------------------------------
CAPITAL | | | | | | EXPENDITURE-- | | | | | | Purchase and pre-| £12,500 | (amounts below apply to extension of works) | paration of land | | | | | | Machinery | 27,854 | £25,595 | £25,595 | £25,595 | £25,595 | Mains | 10,328 | 10.328 | 10,328 | 10,328 | 10,328 | Buildings | 8,505 | 4,516 | 4,632 | 4,614 | 4,594 | Parlimentary and | | | | | | general expenses,| 20,000 | .. | .. | .. | .. | royalty, &c. | | | | | | Engineering | 3,268 | 1,820 | 1,825 | 1,824 | 8,823 | Previous Capit-| | 82,455 | 124,714 | 167,094 | 209,455 | al Expenditure | .. | | | | | Total Cap. Exp. | £82,455 | £124,714 | £167,094 | £209,455 | £251,795 | -----------------------------------------------------------------------------
ANNUAL CHARGES-- | | | | | | Salaries, wages, | | | | | | & general working| £6,405 | £7,855 | £9,305 | £10,955 | £12,480 | expenses | | | | | | Repairs, renewals| 2,780 | 5,198 | 7,622 | 10,045 | 12,467 | &c.(reserve fund)| | | | | | Coal, water, &c. | 1,950 | 3,900 | 5,850 | 7,800 | 9,750 | Rates | 370 | 674 | 980 | 1,285 | 1,585 | Contingencies of | | | | | | horse power = 5 | 575 | 881 | 1,187 | 1,504 | 1,814 | per cent on above| | | | | | Total Ann. Exp. | £12,080 | £18,508 | £24,944 | £31,589 | £38,096 | -----------------------------------------------------------------------------
Revenue at 5d. | | | | | | per 1000 cub. ft.| 22,126 | 43,522 | 64,282 | 84,426 | 103,971 | (average) | | | | | | Profit |12.18 p.ct.|20.06 p.ct.|23.54 p.ct.|25.22 p.ct.|26.16 p.ct.| |= 10,046 | = 25,014 | = 39,338 | = 52,837 | = 65,875 | -----------------------------------------------------------------------------
TABLE II.--Cost of Air Power in Terms of Indicated Horse Power.
Abbreviated column headings:
Qty. Air: Quantity of Air at 45 lbs. Pressure required per Ind. H.P. per Hour.
Cost/Hr.: Cost per Hour at 5d. per 1000 Cubic Feet.
Cost/Hr. w/rebate: Cost per Hour with Rebate when Profits reach 26 per Cent.
Cost/Yr.: Cost per Annum (2700 Hours) at 5d. per 1000 Cubic Feet.
Cost/Yr. w/rebate: Cost per Annum with Rebate when Profits reach 26 per Cent.
Abbreviated row headings:
CASE 1.--Where air at 45 lbs. pressure is re-heated to 320° Fahr., and expanded to atmospheric pressure.
CASE 2.--Where air at 45 lbs. pressure is heated by boiling water to 212° Fahr., and expanded to atmospheric pressure.
CASE 3.--Where air is used expansively without re-heating, whereby intensely cold air is exhausted, and may be used for ice making, &c.
CASE 4.--Where air is heated to 212° Fahr., and the terminal pressure is 11.3 lbs. above that of the atmosphere
CASE 5.--Where the air is used without heating, and cut off at one-third of the stroke, as in ordinary slide-valve engines
CASE 6.--Where the air is used without re-heating and without expansion.
_____________________________________________________________________
| Qty. Air | Cost/Hr. | Cost/Hr. | Cost/Yr. | Cost/Yr. |
| | | w/rebate | | w/rebate |
| Cub. Ft. | d. | d. | £ s. d. | £ s. d.|
---------------------------------------------------------------------
CASE 1 | 125.4 | 0.627 | 0.596 | 7 1 1 | 6 14 0½|
CASE 2 | 140.4 | 0.702 | 0.667 | 7 17 11 | 7 10 0 |
CASE 3 | 178.2 | 0.891 | 0.847 | 10 0 5½ | 9 10 5½|
CASE 4 | 170.2 | 0.851 | 0.809 | 9 11 5½ | 9 1 10½|
CASE 5 | 258.0 | 1.290 | 1.226 | 14 10 3 | 13 15 9 |
CASE 6 | 331.8 | 1.659 | 1.576 | 18 13 3 | 17 14 7 |
_____________________________________________________________________
The great thing to guard against is leakage. If the pipes were simply buried in the ground, it would be almost impossible to trace leakage, or even to know of its existence. The income of the company might be wasting away, and the loss never suspected until the quarterly returns from the meters were obtained from the inspectors. Only then would it be discovered that there must be a great leak (or it might be several leaks) somewhere. But how would it be possible to trace them among 20 or 30 miles of buried pipes? We cannot break up the public streets. The very existence of the concern depends upon (1) the daily checking of the meter returns, and comparison with the output from the air compressors, so as to ascertain the amount of leakage; (2) facility for tracing the locality of a leak; and (3) easy access to the mains with the minimum of disturbance to the streets. It will be readily understood, from the drawings, how this is effected. First, the pipes are laid in concrete troughs, near the surface of the road, with removable concrete covers strong enough to stand any overhead traffic. At intervals there are junctions for service connections, with street boxes and covers serving as inspection chambers. These chambers are also provided over the ball-valves, which serve as stop-valves in case of necessity, and are so arranged that in case of a serious breach in the portion of main between any two of them, the rush of air to the breach will blow them up to the corresponding seats and block off the broken portion of main. The air space around the pipe in the concrete trough will convey for a long distance the whistling noise of a leak; and the inspectors, by listening at the inspection openings, will thus be enabled to rapidly trace their way almost to the exact spot where there is an escape. They have then only to remove the top surface of road metal and the concrete cover in order to expose the pipe and get at the breach. Leaks would mostly be found at joints; and, by measuring from the nearest street opening, the inspectors would know where to break open the road to arrive at the probable locality of the leak. A very slight leak can be heard a long way off by its peculiar whistling sound.
COMPRESSED AIR POWER
The next point is to obtain a daily report of the condition of the mains and the amount of leakage. It would be impracticable to employ an army of meter inspectors to take the records daily from all the meters in the district. We therefore adopt the method of electric signaling shown in the second drawing. In the engineer's office, at the central station, is fixed the dial shown in Fig. 1. Each consumer's meter is fitted with the contact-making apparatus shown in Pig. 4, and in an enlarged form in Figs. 5 and 6, by which a current is sent round the electro-magnet, D (Fig. 1), attracting the armature, and drawing the disk forward sufficiently for the roller at I to pass over the center of one of the pins, and so drop in between that and the next pin, thus completing the motion, and holding the disk steadily opposite the figure. This action takes place on any meter completing a unit of measurement of (say) 1,000 cubic feet, at which point the contact makers touch. But suppose one meter should be moving very slowly, and so retaining contact for some time, while other meters were working rapidly; the armature at D would then be held up to the magnet by the prolonged contact maintained by the slow moving meter, and so prevent the quick working meters from actuating it; and they would therefore pass the contact points without recording. A meter might also stop dead at the point of contact on shutting off the air, and so hold up the armature; thus preventing others from acting. To obviate this, we apply the disengaging apparatus shown at L (Fig. 4). The contact maker works on the center, m, having an armature on its opposite end. On contact being made, at the same time that the magnet, D, is operated, the one at L is also operated, attracting the armature, and throwing over the end of the contact maker, l¹, on to the non-conducting side of the pin on the disk. Thus the whole movement is rendered practically instantaneous, and the magnet at D is set at liberty for the next operation. A resistance can be interposed at L, if necessary, to regulate the period of the operation. The whole of the meters work the common dial shown in Fig. 1, on which the gross results only are recorded; and this is all we want to know in this way. The action is so rapid, owing to the use of the magnetic disengaging gear, that the chances of two or more meters making contact at the same moment are rendered extremely small. Should such a thing happen, it would not matter, as it is only approximate results that we require in this case; and the error, if any, would add to the apparent amount of leakage, and so be on the right side. Of course, the record of each consumer's meter would be taken by the inspector at the end of every quarter, in order to make out the bill; and the totals thus obtained would be checked by the gross results indicated by the main dial. In this way, by a comparison of these results, a coefficient would soon be arrived at, by which the daily recorded results could be corrected to an extremely accurate measurement. At the end of the working day, the engineer has merely to take down from the dial in his office the total record of air measured to the consumers, also the output of air from the compressors, which he ascertains by means of a continuous counter on the engines, and the difference between the two will represent the loss. If the loss is trifling, he will pass it over; if serious, he will send out his inspectors to trace it. Thus there could be no long continued leakage, misuse, or robbery of the air, without the company becoming aware of the fact, and so being enabled to take measures to stop or prevent it. The foregoing are absolutely essential adjuncts to any scheme of public motive power supply by compressed air, without which we should be working in the dark, and could never be sure whether the company were losing or making money. With them, we know where we are and what we are doing.
Referring to the estimates given in Table I., I may explain that the item of repairs and renewals covers 10 per cent. on boilers and gas producers, 5 per cent. on engines, 5 per cent. on buildings, and 5 per cent. on mains. Considering that the estimates include ample fitting shops, with the best and most suitable tools, and that the wages list includes a staff of men whose chief work would be to attend to repairs, etc., I think the above allowances ample. Each item also includes 5 per cent. for contingencies.
I have commenced by giving all the preceding detail, in order to show the groundwork on which I base the estimate of the cost of compressed air power to consumers, in terms of indicated horse power per annum, as given in Table II. I may say that, in estimating the engine power and coal consumption, I have not, as in the original report, made purely theoretical calculations, but have taken diagrams from engines in actual use (although of somewhat smaller size than those intended to be employed), and have worked out the results therefrom. It will, I hope, be seen that, with all the safeguards we have provided, we may fairly reckon upon having for sale the stated quantity of air produced by means of the plant, as estimated, and at the specified annual cost; and that therefore the statement of cost per indicated horse power per annum may be fairly relied upon. Thus the cost of compressed air to the consumer, based upon an average charge of 5d. per 1,000 cubic feet, will vary from £6 14s. per indicated horse power per annum to £18 13s. 3d., according to circumstances and mode of application.
A compressed air motor is an exceedingly simple machine--much simpler than an ordinary steam engine. But the air may also be used in an ordinary steam engine; and in this case it can be much simplified in many details. Very little packing is needed, as there is no nuisance from gland leakage; the friction is therefore very slight. Pistons and glands are packed with soapstone, or other self-lubricating packing; and no oil is required except for bearings, etc. The company will undertake the periodical inspection and overhauling of engines supplied with their power, all which is included in the estimates. The total cost to consumers, with air at an average of 5d. per 1,000 cubic feet, may therefore be fairly taken as follows:
Min. Max.
Cost of air used £6 14 0½ £18 13 3
Oil. waste, packing, etc. 1 0 0 1 0 0
Interest, depreciation,
etc., 12½ per cent. on
£10, the cost of engine
per indicated
horse power 1 5 0 1 5 0
-------- ---------
£8 19 0½ £20 18 3
The maximum case would apply only to direct acting engines, such as Tangye pumps, air power hammers, etc., where the air is full on till the end of the stroke, and where there is no expansion. The minimum given is at the average rate of 5d. per 1,000 cubic feet; but as there will be rates below this, according to a sliding scale, we may fairly take it that the lowest charge will fall considerably below £6 per indicated horse power per annum.--Journal of Gas Lighting.
An endeavor has often been made to construct a canoe that a person can easily carry overland and put into the water without aid, and convert into a sailboat. The system that we now call attention to is very well contrived, very light, easily taken apart, and for some years past has met with much favor.

FIG. 1.--BERTHON COLLAPSIBLE CANOE AFLOAT.
Mr. Berthon's canoes are made of impervious oil-skin. Form is given them by two stiff wooden gunwales which are held in position by struts that can be easily put in and taken out. The model shown in the figure is covered with oiled canvas, and is provided with a double paddle and a small sail. Fig. 2 represents it collapsed and being carried overland.

FIG. 2.--THE SAME BEING CARRIED OVERLAND.
Mr. Berthon is manufacturing a still simpler style, which is provided with two oars, as in an ordinary canoe. This model, which is much used in England by fishermen and hunters, has for several years past been employed in the French navy, in connection with movable defenses. At present, every torpedo boat carries one or two of these canoes, each composed of two independent halves that may be put into the water separately or be joined together by an iron rod.
These boats ride the water very well, and are very valuable for exploring quarters whither torpedo boats could not adventure without danger.[1]--La Nature.
[Footnote 1: For detailed description see SUPPLEMENT, No. 84.]
There was great excitement in Nürnberg on the 7th of December, 1835, on which day the first German railroad was opened. The great square on which the buildings of the Nürnberg and Furth "Ludwig's Road" stood, the neighboring streets, and, in fact, the whole road between the two cities, was filled with a crowd of people who flocked from far and near to see the wonderful spectacle. For the first time, a railroad train filled with passengers was to be drawn from Nürnberg to Furth by the invisible power of the steam horse. At eight o'clock in the morning, the civil and military authorities, etc., who took part in the celebration were assembled on the square, and the gayly decorated train started off to an accompaniment of music, cannonading, cheering, etc. Everything passed off without an accident; the work was a success. The engraving in the lower right-hand corner represents the engine and cars of this road.
It will be plainly seen that such a revolution could not be accomplished easily, and that much sacrifice and energy were required of the leaders in the enterprise, prominent among whom was the merchant Johannes Scharrer, who is known as the founder of the "Ludwig's Road."
One would naturally suppose that such an undertaking would have met with encouragement from the Bavarian Government, but this was not the case. The starters of the enterprise met with opposition on every side; much was written against it, and many comic pictures were drawn showing accidents which would probably occur on the much talked of road. Two of these pictures are shown in the accompanying large engraving, taken from the Illustrirte Zeitung. As shown in the center picture, right hand, it was expected by the railway opponents that trains running on tracks at right angles must necessarily come in collision. If anything happened to the engine, the passengers would have to get out and push the cars, as shown at the left.
JUBILEE CELEBRATION OF THE FIFTIETH ANNIVERSARY OF
THE OPENING OF THE FIRST STEAM RAILWAY IN GERMANY--
AT NURNBERG
Much difficulty was experienced in finding an engineer capable of attending to the construction of the road; and at first it was thought that it would be best to engage an Englishman, but finally Engineer Denis, of Munich, was appointed. He had spent much time in England and America studying the roads there, and carried on this work to the entire satisfaction of the company.
All materials for the road were, as far as possible, procured in Germany; but the idea of building the engines and cars there had to be given up, and, six weeks before the opening of the road, Geo. Stephenson, of London, whose engine, Rocket, had won the first prize in the competitive trials at Rainhill in 1829, delivered an engine of ten horse power, which is still known in Nürnberg as "Der Englander."
Fifty years have passed, and, as Johannes Scharrer predicted, the Ludwig's Road has become a permanent institution, though it now forms only a very small part of the network of railroads which covers every portion of Germany. What changes have been made in railroads during these fifty years! Compare the present locomotives with the one made by Cugnot in 1770, shown in the upper left-hand cut, and with the work of the pioneer Geo. Stephenson, who in 1825 constructed the first passenger railroad in England, and who established a locomotive factory in Newcastle in 1824. Geo. Stephenson was to his time what Mr. Borsig, whose great works at Moabit now turn out from 200 to 250 locomotives a year, is to our time.
Truly, in this time there can be no better occasion for a celebration of this kind than the fiftieth anniversary of the opening of the first German railroad, which has lately been celebrated by Nürnberg and Furth.
The lower left-hand view shows the locomotive De Witt Clinton, the third one built in the United States for actual service, and the coaches. The engine was built at the West Point Foundry, and was successfully tested on the Mohawk and Hudson Railroad between Albany and Schenectady on Aug. 9, 1831.
An illustration of a new coal elevator is herewith presented, which presents advantages over any incline yet used, so that a short description may be deemed interesting to those engaged in the coaling and unloading of vessels. The pen sketch shows at a glance the arrangement and space the elevator occupies, taking less ground to do the same amount of work than any other mode heretofore adopted, and the first cost of erecting is about the same as any other.
When the expense of repairing damages caused by the ravages of winter is taken into consideration, and no floats to pump out or tracks to wash away, the advantages should be in favor of a substantial structure.
The capacity of this hoist is to elevate 80,000 bushels in ten hours, at less than one-half cent per bushel, and put coal in elevator, yard, or shipping bins.
IMPROVED COAL ELEVATOR.
The endless wire rope takes the cars out and returns them, dispensing with the use of train riders.
A floating elevator can distribute coal at any hatch on steam vessels, as the coal has to be handled but once; the hoist depositing an empty car where there is a loaded one in boat or barge, requiring no swing of the vessel.
Mr. J.R. Meredith, engineer, of Pittsburg, Pa., is the inventor and builder, and has them in use in the U.S. engineering service.--Coal Trade Journal.
The practice of carrying melted cast iron direct from the blast furnace to the Siemens hearth or the Bessemer converter saves both money and time. It has rendered necessary the construction of special plant in the form of ladles of dimensions hitherto quite unknown. Messrs. Stevenson & Co., of Preston, make the construction of these ladles a specialty, and by their courtesy, says The Engineer, we are enabled to illustrate four different types, each steel works manager, as is natural, preferring his own design. Ladles are also required in steel foundry work, and one of these for the Siemens-Martin process is illustrated by Fig. 1. These ladles are made in sizes to take from five to fifteen ton charges, or larger if required, and are mounted on a very strong carriage with a backward and forward traversing motion, and tipping gear for the ladle. The ladles are butt jointed, with internal cover strips, and have a very strong band shrunk on hot about half way in the depth of the ladle. This forms an abutment for supporting the ladle in the gudgeon band, being secured to this last by latch bolts and cotters. The gearing is made of cast steel, and there is a platform at one end for the person operating the carriage or tipping the ladle. Stopper gear and a handle are fitted to the ladles to regulate the flow of the molten steel from the nozzle at the bottom.
LADLES FOR CARRYING MOLTEN IRON AND STEEL.
Fig. 2 shows a Spiegel ladle, of the pattern used at Cyfarthfa. It requires no description. Fig. 3 shows a tremendous ladle constructed for the North-Eastern Steel Company, for carrying molten metal from the blast furnace to the converter. It holds ten tons with ease. It is an exceptionally strong structure. The carriage frame is constructed throughout of 1 in. wrought-iron plated, and is made to suit the ordinary 4 ft. 8½ in. railway gauge. The axle boxes are cast iron, fitted with gun-metal steps. The wheels are made of forged iron, with steel tires and axles. The carriage is provided with strong oak buffers, planks, and spring buffers; the drawbars also have helical compression springs of the usual type. The ladle is built up of ½ in. wrought-iron plates, butt jointed, and double riveted butt straps. The trunnions and flange couplings are of cast steel. The tipping gear, clearly shown in the engraving, consists of a worm and wheel, both of steel, which can be fixed on either side of the ladle as may be desired. From this it will be seen that Messrs. Stevenson & Co. have made a thoroughly strong structure in every respect, and one, therefore, that will commend itself to most steel makers. We understand that these carriages are made in various designs and sizes to meet special requirements. Thus, Fig. 4 shows one of different design, made for a steel works in the North. This is also a large ladle. The carriage is supported on helical springs and solid steel wheels. It will readily be understood that very great care and honesty of purpose is required in making these structures. A breakdown might any moment pour ten tons of molten metal on the ground, with the most horrible results.
Mr. K.L. Bauer, of Carlsruhe, has just constructed a very simple and ingenious apparatus which permits of demonstrating that electricity develops only on the surface of conductors. It consists (see figure) essentially of a yellow-metal disk, M, fixed to an insulating support, F, and carrying a concentric disk of ebonite, H. This latter receives a hollow and closed hemisphere, J, of yellow metal, whose base has a smaller diameter than that of the disk, H, and is perfectly insulated by the latter. Another yellow-metal hemisphere, S, open below, is connected with an insulating handle, G. The basal diameter of this second hemisphere is such that when the latter is placed over J its edge rests upon the lower disk, M. These various pieces being supposed placed as shown in the figure, the shell, S, forms with the disk, M, a hollow, closed hemisphere that imprisons the hemisphere, J, which is likewise hollow and closed, and perfectly insulated from the former.
The shell, S, is provided internally with a curved yellow-metal spring, whose point of attachment is at B, and whose free extremity is connected with an ebonite button, K, which projects from the shell, S. By pressing this button, a contact may be established between the external hemisphere (formed of the pieces, S and M), and the internal one, J. As soon as the button is left to itself, the spring again begins to bear against the interior surface of S, and the two hemispheres are again insulated.
The experiment is performed in this wise: The shell, S, is removed. Then a disk of steatite affixed to an insulating handle is rubbed for a few instants with a fox's "brush," and held near J until a spark occurs. Then the apparatus is grasped by the support, F, and an elder-pith ball suspended by a flaxen thread from a good conducting support is brought near J. The ball will be quickly repelled, and care must be taken that it does not come into contact with J. After this the apparatus is placed upon a table, the shell, S, is taken by its handle, G, and placed in the position shown in the figure, and a momentary contact is established between the two hemispheres by pressing the button, K. Then the shell, S, is lifted, and the disk, M, is touched at the same time with the other hand. If, now, the pith ball be brought near S, it will be quickly repelled, while it will remain stationary if it be brought near J, thus proving that all the electricity passed from J to S at the moment of contact.--La Lumiere Electrique.
This apparatus has recently been the object of some experiments which resulted in its being finally adopted in the army. We think that our readers will read a description of it with interest. Its mode of construction is based upon a theoretic conception of the lines of force, which its inventor explains as follows in his Elementary Treatise on Electricity:
"To every position of the disk of a magnetic telephone with respect to the poles of the magnet there corresponds a certain distribution of the lines of force, which latter shift themselves when the disk is vibrating. If the bobbin be met by these lines in motion, there will develop in its wire a difference of potential that, according to Faraday's law, will be proportional to their number. All things equal, then, a telephone transmitter will be so much the more potent in proportion as the lines set in motion by the vibrations of the disk and meeting the bobbin wire are greater in number. In like manner, a receiver will be so much the more potent in proportion as the lines of force, set in motion by variations in the induced currents that are traversing the bobbin and meeting the disk, are more numerous. It will consequently be seen that, generally speaking, it is well to send as large a number of lines of force as possible through the bobbin."

FIG. 1.--THE COLSON TELEPHONE.
In order to obtain such a result, the thin tin-plate disk has to be placed between the two poles of the magnet. The pole that carries the fine wire bobbin acts at one side and in the center of the disk, while the other is expanded at the extremity and acts upon the edge and the other side. This pole is separated from the disk by a copper washer, and the disk is thus wholly immersed in the magnetic field, and is traversed by the lines of force radiatingly.
This telephone is being constructed by Mr. De Branville, with the greatest care, in the form of a transmitter (Fig. 2) and receiver (Fig. 3). At A may be seen the magnet with its central pole, P, and its eccentric one, P'. This latter traverses the vibrating disk, M, through a rubber-lined aperture and connects with the soft iron ring, F, that forms the polar expansion. These pieces are inclosed in a nickelized copper box provided with a screw cap, C. The resistance of both the receiver and transmitter bobbin is 200 ohms.

FIG. 2.--TRANSMITTER TAKEN APART.
The transmitter is 3½ in. in diameter, and is provided with a re-enforcing mouthpiece. It is regulated by means of a screw which is fixed in the bottom of the box, and which permits of varying the distance between the disk and the core that forms the central pole of the magnet. The regulation, when once effected, lasts indefinitely. The regulation of the receiver, which is but 2¼ in. in diameter, is performed once for all by the manufacturer. One of the advantages of this telephone is that its regulation is permanent. Besides this, it possesses remarkable power and clearness, and is accompanied with no snuffling sounds, a fact doubtless owing to all the molecules of the disk being immersed in the magnetic field, and to the actions of the two poles occurring concentrically with the disk. As we have above said, this apparatus is beginning to be appreciated, and has already been the object of several applications in the army. The transmitter is used by the artillery service in the organization of observatories from which to watch firing, and the receiver is added to the apparatus pertaining to military telegraphy. The two small receivers are held to the lens of the operator by the latter's hat strap, while the transmitter is suspended in a case supported by straps, with the mouthpieces near the face (Fig. 1).
In the figure, the case is represented as open, so as to show the transmitter. The empty compartment below is designed for the reception and carriage of the receivers, straps, and flexible cords. This arrangement permits of calling without the aid of special apparatus, and it has also the advantage of giving entire freedom to the man on observation, this being something that is indispensable in a large number of cases.
FIG. 3.--RECEIVER TAKEN APART.
In certain applications, of course, the receivers may be combined with a microphone; yet on an aerial as well as on a subterranean line the transmitter produces effects which, as regards intensity and clearness, are comparable with those of a pile transmitter.
Stations wholly magnetic may be established by adding to the transmitter and two receivers a Sieur phonic call, which will actuate them powerfully, and cause them to produce a noise loud enough for a call. It would be interesting to try this telephone on a city line, and to a great distance on those telegraph lines that are provided with the Van Rysselberghe system. Excellent results would certainly be obtained, for, as we have recently been enabled to ascertain, the voice has a remarkable intensity in this telephone, while at the same time perfectly preserving its quality.--La Nature.
[NATURE.]
The apparatus which I propose to call by the above name (μελδω, to melt) consists of an adjunct to the mineralogical microscope, whereby the melting-points of minerals may be compared or approximately determined and their behavior watched at high temperatures either alone or in the presence of reagents.
As I now use it, it consists of a narrow ribbon of platinum (2 mm. wide) arranged to traverse the field of the microscope. The ribbon, clamped in two brass clamps so as to be readily renewable, passes bridgewise over a little scooped-out hollow in a disk of ebony (4 cm. diam.). The clamps also take wires from a battery (3 Groves cells); and an adjustable resistance being placed in circuit, the strip can be thus raised in temperature up to the melting-point of platinum.
The disk being placed on the stage of the microscope the platinum strip is brought into the field of a 1" objective, protected by a glass slip from the radiant heat. The observer is sheltered from the intense light at high temperatures by a wedge of tinted glass, which further can be used in photometrically estimating the temperature by using it to obtain extinction of the field. Once for all approximate estimations of the temperature of the field might be made in terms of the resistance of the platinum strip, the variation of such resistance with rise of temperature being known. Such observations being made on a suitably protected strip might be compared with the wedge readings, the latter being then used for ready determinations. Want of time has hindered me from making such observations up to this.
The mineral to be experimented on is placed in small fragments near the center of the platinum ribbon, and closely watched while the current is increased, till the melting-point of the substance is apparent. Up to the present I have only used it comparatively, laying fragments of different fusibilities near the specimen. In this way I have melted beryl, orthoclase, and quartz. I was much surprised to find the last mineral melt below the melting-point of platinum. I have, however, by me as I write, a fragment, formerly clear rock-crystal, so completely fused that between crossed Nicols it behaves as if an amorphous body, save in the very center where a speck of flashing color reveals the remains of molecular symmetry. Bubbles have formed in the surrounding glass.
Orthoclase becomes a clear glass filled with bubbles: at a lower temperature beryl behaves in the same way.
Topaz whitens to a milky glass--apparently decomposing, throwing out filmy threads of clear glass and bubbles of glass which break, liberating a gas (fluorine?) which, attacking the white-hot platinum, causes rings of color to appear round the specimen. I have now been using the apparatus for nearly a month, and in its earliest days it led me right in the diagnosis of a microscopical mineral, iolite, not before found in our Irish granite, I think. The unlooked-for characters of the mineral, coupled with the extreme minuteness of the crystals, led me previously astray, until my meldometer fixed its fusibility for me as far above the suspected bodies.
Carbon slips were at first used, as I was unaware of the capabilities of platinum.
A form of the apparatus adapted, at Prof. Fitzgerald's suggestion, to fit into the lantern for projection on the screen has been made for me by Yeates. In this form the heated conductor passes both below and above the specimen, which is regarded from a horizontal direction.
J. JOLY.
Physical Laboratory, Trinity College, Dublin.
[AMERICAN ANNALS OF THE DEAF AND DUMB.]
Progress in electrical science is daily causing the world to open its eyes in wonder and the scientist to enlarge his hopes for yet greater achievements. The practical uses to which this subtile fluid, electricity, is being put are causing changes to be made in time-tested methods of doing things in domestic, scientific, and business circles, and the time has passed when startling propositions to accomplish this or that by the assistance of electricity are dismissed with incredulous smiles. This being the case, no surprise need follow the announcement of a device to facilitate the imparting of instruction to deaf children which calls into requisition some service from electricity.
The sense of touch is the direct medium contemplated, and it is intended to convey, with accuracy and rapidity, messages from the operator (the teacher) to the whole class simultaneously by electrical transmission.[1]
[Footnote 1: By the same means two deaf-mutes, miles apart, might converse with each other, and the greatest difficulty in the way of a deaf-mute becoming a telegraph operator, that of receiving messages, would be removed. The latter possibilities are incidentally mentioned merely as of scientific interest, and not because of their immediate practical value. The first mentioned use to which the device may be applied is the one considered by the writer as possibly of practical value, the consideration of which suggested the appliance to him.]
An alphabet is formed upon the palm of the left hand and the inner side of the fingers, as shown by the accompanying cut, which, to those becoming familiar with it, requires but a touch upon a certain point of the hand to indicate a certain letter of the alphabet.
A rapid succession of touches upon various points of the hand is all that is necessary in spelling a sentence. The left hand is the one upon which the imaginary alphabet is formed, merely to leave the right hand free to operate without change of position when two persons only are conversing face to face.
The formation of the alphabet here figured is on the same principle as one invented by George Dalgarno, a Scottish schoolmaster, in the year 1680, a cut of which maybe seen on page 19 of vol. ix. of the Annals, accompanying the reprint of a work entitled "Didascalocophus." Dalgarno's idea could only have been an alphabet to be used in conversation between two persons tête à tête, and--except to a limited extent in the Horace Mann School and in Professor Bell's teaching--has not come into service in the instruction of deaf-mutes or as a means of conversation. There seems to have been no special design or system in the arrangement of the alphabet into groups of letters oftenest appearing together, and in several instances the proximity would seriously interfere with distinct spelling; for instance, the group "u," "y," "g," is formed upon the extreme joint of the little finger. The slight discoverable system that seems to attach to his arrangement of the letters is the placing of the vowels in order upon the points of the fingers successively, beginning with the thumb, intended, as we suppose, to be of mnemonic assistance to the learner. Such assistance is hardly necessary, as a pupil will learn one arrangement about as rapidly as another. If any arrangement has advantage over another, we consider it the one which has so grouped the letters as to admit of an increased rapidity of manipulation. The arrangement of the above alphabet, it is believed, does admit of this. Yet it is not claimed that it is as perfect as the test of actual use may yet make it. Improvements in the arrangement will, doubtless, suggest themselves, when the alterations can be made with little need of affecting the principle.
In order to transmit a message by this alphabet, the following described appliance is suggested: A matrix of cast iron, or made of any suitable material, into which the person receiving the message (the pupil) places his left hand, palm down, is fixed to the table or desk. The matrix, fitting the hand, has twenty-six holes in it, corresponding in position to the points upon the hand assigned to the different letters of the alphabet. In these holes are small styles, or sharp points, which are so placed as but slightly to touch the hand. Connected with each style is a short line of wire, the other end of which is connected with a principal wire leading to the desk of the operator (the teacher), and there so arranged as to admit of opening and closing the circuit of an electric current at will by the simple touch of a button, and thereby producing along the line of that particular wire simultaneous electric impulses, intended to act mechanically upon all the styles connected with it. By these impulses, produced by the will of the sender, the styles are driven upward with a quick motion, but with only sufficient force to be felt and located upon the hand by the recipient. Twenty-six of these principal or primary wires are run from the teacher's desk (there connected with as many buttons) under the floor along the line of pupils' desks. From each matrix upon the desk run twenty-six secondary wires down to and severally connecting with the twenty-six primary wires under the floor. The whole system of wires is incased so as to be out of sight and possibility of contact with foreign substances. The keys or buttons upon the desk of the teacher are systematically arranged, somewhat after the order of those of the type writer, which allows the use of either one or both hands of the operator, and of the greatest attainable speed in manipulation. The buttons are labeled "a," "b," "c," etc., to "z," and an electric current over the primary wire running from a certain button (say the one labeled "a") affects only those secondary wires connected with the styles that, when excited, produce upon the particular spot of the hands of the receivers the tactile impression to be interpreted as "a." And so, whenever the sender touches any of the buttons on his desk, immediately each member of the class feels upon the palm of his hand the impression meant to be conveyed. The contrivance will admit of being operated with as great rapidity as it is probable human dexterity could achieve, i.e., as the strokes of an electric bell. It was first thought of conveying the impressions directly by slight electric shocks, without the intervention of further mechanical apparatus, but owing to a doubt as to the physical effect that might be produced upon the persons receiving, and as to whether the nerves might not in time become partly paralyzed or so inured to the effect as to require a stronger and stronger current, that idea was abandoned, and the one described adopted. A diagram of the apparatus was submitted to a skillful electrical engineer and machinist of Hartford, who gave as his opinion that the scheme was entirely feasible, and that a simple and comparatively inexpensive mechanism would produce the desired result.
TOUCH TRANSMISSION BY ELECTRICITY.
The matter now to consider, and the one of greater interest to the teacher of deaf children, is, Of what utility can the device be in the instruction of deaf-mutes? What advantage is there, not found in the prevailing methods of communication with the deaf, i.e., by gestures, dactylology, speech and speech-reading, and writing?
I. The language of gestures, first systematized and applied to the conveying of ideas to the deaf by the Abbe de l'Epee during the latter part of the last century, has been, in America, so developed and improved upon by Gallaudet, Peet, and their successors, as to leave but little else to be desired for the purpose for which it was intended. The rapidity and ease with which ideas can be expressed and understood by this "language" will never cease to be interesting and wonderful, and its value to the deaf can never fail of being appreciated by those familiar with it. But the genius of the language of signs is such as to be in itself of very little, if any, direct assistance in the acquisition of syntactical language, owing to the diversity in the order of construction existing between the English language and the language of signs. Sundry attempts have been made to enforce upon the sign-language conformity to the English order, but they have, in all cases known to the writer, been attended with failure. The sign-language is as immovable as the English order, and in this instance certainly Mahomet and the mountain will never know what it is to be in each other's embrace. School exercises in language composition are given with great success upon the basis of the sign-language. But in all such exercises there must be a translation from one language to the other. The desideratum still exists of an increased percentage of pupils leaving our schools for the deaf, possessing a facility of expression in English vernacular. This want has been long felt, and endeavoring to find a reason for the confessedly low percentage, the sign-language has been too often unjustly accused. It is only when the sign-language is abused that its merit as a means of instruction degenerates. The most ardent admirers of a proper use of signs are free to admit that any excessive use by the pupils, which takes away all opportunities to express themselves in English, is detrimental to rapid progress in English expression.
II. To the general public, dactylology or finger spelling is the sign-language, or the basis of that language, but to the profession there is no relation between the two methods of communication. Dactylology has the advantage of putting language before the eye in conformity with English syntax, and it has always held its place as one of the elements of the American or eclectic method. This advantage, however, is not of so great importance as to outweigh the disadvantages when, as has honestly been attempted, it asserts its independence of other methods. Very few persons indeed, even after long practice, become sufficiently skillful in spelling on the fingers to approximate the rapidity of speech. But were it possible for all to become rapid spellers, another very important requisite is necessary before the system could be a perfect one, that is, the ability to read rapid spelling. The number of persons capable of reading the fingers beyond a moderate degree of rapidity is still less than the number able to spell rapidly. While it is physically possible to follow rapid spelling for twenty or thirty minutes, it can scarcely be followed longer than that. So long as this is true, dactylology can hardly claim to be more than one of the elements of a system of instruction for the deaf.
III. Articulate speech is another of the elements of the eclectic method, employed with success inversely commensurate with the degree of deficiency arising from deafness. Where the English order is already fixed in his mind, and he has at an early period of life habitually used it, there is comparatively little difficulty in instructing the deaf child by speech, especially if he have a quick eye and bright intellect. But the number so favored is a small percentage of the great body of deaf-mutes whom we are called upon to educate. When it is used as a sole means of educating the deaf as a class its inability to stand alone is as painfully evident as that of any of the other component parts of the system. It would seem even less practicable than a sole reliance upon dactylology would be, for there can be no doubt as to what a word is if spelled slowly enough, and if its meaning has been learned. This cannot be said of speech. Between many words there is not, when uttered, the slightest visible distinction. Between a greater number of others the distinction is so slight as to cause an exceedingly nervous hesitation before a guess can be given. Too great an imposition is put upon the eye to expect it to follow unaided the extremely circumscribed gestures of the organs of speech visible in ordinary speaking. The ear is perfection as an interpreter of speech to the brain. It cannot correctly be said that it is more than perfection. It is known that the ear, in the interpretation of vocal sounds, is capable of distinguishing as many as thirty-five sounds per second (and oftentimes more), and to follow a speaker speaking at the rate of more than two hundred words per minute. If this be perfection, can we expect the eye of ordinary mortal to reach it? Is there wonder that the task is a discouraging one for the deaf child?
But it has been asserted that while a large percentage (practically all) of the deaf can, by a great amount of painstaking and practice, become speech readers in some small degree, a relative degree of facility in articulation is not nearly so attainable. As to the accuracy of this view, the writer cannot venture an opinion. Judging from the average congenital deaf-mute who has had special instruction in speech, it can safely be asserted that their speech is laborious, and far, very far, from being accurate enough for practical use beyond a limited number of common expressions. This being the case, it is not surprising that as an unaided means of instruction it cannot be a success, for English neither understood when spoken, nor spoken by the pupil, cannot but remain a foreign language, requiring to pass through some other form of translation before it becomes intelligible.
There are the same obstacles in the use of the written or printed word as have been mentioned in connection with dactylology, namely, lack of rapidity in conveying impressions through the medium of the English sentence.
I have thus hastily reviewed the several means which teachers generally are employing to impart the use of English to deaf pupils, for the purpose of showing a common difficulty. The many virtues of each have been left unnoticed, as of no pertinence to this article.
The device suggested at the beginning of this paper, claiming to be nothing more than a school room appliance intended to supplement the existing means for giving a knowledge and practice of English to the deaf, employs as its interpreter a different sense from the one universally used. The sense of sight is the sole dependence of the deaf child. Signs, dactylology, speech reading, and the written and printed word are all dependent upon the eye for their value as educational instruments. It is evident that of the two senses, sight and touch, if but one could be employed, the choice of sight as the one best adapted for the greatest number of purposes is an intelligent one; but, as the choice is not limited, the question arises whether, in recognizing the superior adaptability to our purpose of the one, we do not lose sight of a possibly important, though secondary, function in the other. If sight were all-sufficient, there would be no need of a combination. But it cannot be maintained that such is the case. The plan by which we acquire our vernacular is of divine, and not of human, origin, and the senses designed for special purposes are not interchangeable without loss. The theory that the loss of a certain sense is nearly, if not quite, compensated for by increased acuteness of the remaining ones has been exploded. Such a theory accuses, in substance, the Maker of creating something needless, and is repugnant to the conceptions we have of the Supreme Being. When one sense is absent, the remaining senses, in order to equalize the loss, have imposed upon them an unusual amount of activity, from which arises skill and dexterity, and by which the loss of the other sense is in some measure alleviated, but not supplied. No additional power is given to the eye after the loss of the sense of hearing other than it might have acquired with the same amount of practice while both faculties were active. The fact, however, that the senses, in performing their proper functions, are not overtaxed, and are therefore, in cases of emergency, capable of being extended so as to perform, in various degrees, additional service, is one of the wise providences of God, and to this fact is due the possibility of whatever of success is attained in the work of educating the deaf, as well as the blind.
In the case of the blind, the sense of touch is called into increased activity by the absence of the lost sense; while in the case of the deaf, sight is asked to do this additional service. A blind person's education is received principally through the two senses of hearing and touch. Neither of these faculties is so sensible to fatigue by excessive use as is the sense of sight, and yet the eye has, in every system of instruction applied to the deaf, been the sole medium. In no case known to the writer, excepting in the celebrated case of Laura Bridgman and a few others laboring under the double affliction of deafness and blindness, has the sense of touch been employed as a means of instruction.[1]
[Footnote 1: This article was written before Professor Bell had made his interesting experiments with his "parents' class" of a touch alphabet, to be used upon the pupil's shoulder in connection with the oral teaching.--E.A.F.]
Not taking into account the large percentage of myopes among the deaf, we believe there are other cogent reasons why, if found practicable, the use of the sense of touch may become an important element in our eclectic system of teaching. We should reckon it of considerable importance if it were ascertained that a portion of the same work now performed by the eye could be accomplished equally as well through feeling, thereby relieving the eye of some of its onerous duties.
We see no good reason why such accomplishment may not be wrought. If, perchance, it were discovered that a certain portion could be performed in a more efficient manner, its value would thus be further enhanced.
In theory and practice, the teacher of language to the deaf, by whatever method, endeavors to present to the eye of the child as many completed sentences as are nominally addressed to the ear--having them "caught" by the eye and reproduced with as frequent recurrence as is ordinarily done by the child of normal faculties.
In our hasty review of the methods now in use we noted the inability to approximate this desirable process as a common difficulty. The facility now ordinarily attained in the manipulation of the type writer, and the speed said to have been reached by Professor Bell and a private pupil of his by the Dalgarno touch alphabet, when we consider the possibility of a less complex mechanism in the one case and a more systematic grouping of the alphabet in the other, would lead us to expect a more rapid means of communication than is ordinarily acquired by dactylology, speech (by the deaf), or writing. Then the ability to receive the communication rapidly by the sense of feeling will be far greater. No part of the body except the point of the tongue is as sensible to touch as the tips of the fingers and the palm of the hand. Tactile discrimination is so acute as to be able to interpret to the brain significant impressions produced in very rapid succession. Added to this advantage is the greater one of the absence of any more serious attendant physical or nervous strain than is present when the utterances of speech fall upon the tympanum of the ear. To sum up, then, the advantages of the device we find--
First. A more rapid means of communication with the deaf by syntactic language, admitting of a greater amount of practice similar to that received through the ear by normal children.
Second. Ability to receive this rapid communication for a longer duration and without ocular strain.
Third. Perfect freedom of the eye to watch the expression on the countenance of the sender.
Fourth. In articulation and speech-reading instruction, the power to assist a class without distracting the attention of the eye from the vocal organs of the teacher.
Fifth. Freedom of the right hand of the pupil to make instantaneous reproduction in writing of the matter being received through the sense of feeling, thereby opening the way for a valuable class exercise.
Sixth. The possible mental stimulus that accompanies the mastery of a new language, and the consequent ability to receive known ideas through a new medium.
Seventh. A fresh variety of class exercises made possible.
The writer firmly believes in the good that exists in all methods that are, or are to be; in the interdependence rather than the independence of all methods; and in all school-room appliances tending to supplement or expedite the labors of the teacher, whether they are made of materials delved from the earth or snatched from the clouds.
S. TEFFT WALKER,
Superintendent of the Kansas Institution, Olathe, Kans.
In order to approximately ascertain the relative reducing action of water gas, carbon monoxide, and superheated steam on iron ore, the author decided to have carried out the following experiments, which were conducted by Mr. Carl J. Sandahl, of Stockholm, who also carried out the analyses. The ore used was from Bilbao, and known as the Ruby Mine, and was a good average hematite. The carbonaceous material was the Trimsaran South Wales anthracite, and contained about 90 per cent. of carbon.
A small experimental furnace was constructed of the form shown by illustration, about 4 ft. 6 in. high and 2 ft. 3 in. wide at the base, and gradually swelling to 2 ft. 9 in. at the top, built entirely of fireclay bricks. Two refractory tubes, 2 in. square internally, and the height of the furnace, were used for the double purpose of producing the gas and reducing the ore.
The end of the lower tube rested on a fireclay ladle nozzle, and was properly jointed with fireclay; through this nozzle the steam or air was supplied to the inside of the refractory tubes. In each experiment the ore and fuel were raised to the temperature "of from 1,800 to 2,200 deg. Fahr." by means of an external fire of anthracite. Great care was taken to prevent the contact of the solid carbonaceous fuel with the ore. In each experiment in which steam was used, the latter was supplied at a temperature equivalent to 35 lb. to the square inch.
The air for producing the carbon monoxide (CO) gas was used at the temperature of the atmosphere. As near as possible, the same conditions were obtained in each experiment, and the equivalent weight of air was sent through the carbon to generate the same weight of CO as that generated when steam was used for the production of water gas.
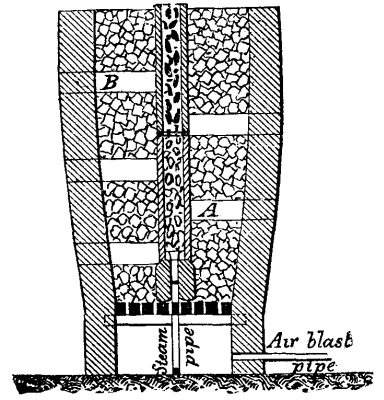
First Experiment, Steam (per se).--Both tubes, A and B, were filled with ore broken to the size of nuts. The tube, A, was heated to about 2,000 deg. Fahr., the upper one to about 1,500 deg.
NOTE.--In this experiment, part of the steam was dissociated in passing through the turned-up end of the steam supply pipe, which became very hot, and the steam would form with the iron the magnetic oxide (Fe3O4). The reduction would doubtless be due to this dissociation. The pieces of ore found on lowest end of the tube, A, were dark colored and semi-fused; part of one of these pieces was crushed fine, and tested; see column I. The remainder of these black pieces was mixed with the rest of the ore contained in tube, A, and ground and tested; see column II. The ore in upper tube was all broken up together and tested; see column III. When finely crushed, the color of No. I. was bluish black; No. II., a shade darker red; No. III., a little darker than the natural color of the ore. The analyses gave:
-----------------------------+---------+---------+---------
| I. | II. | III.
+---------+---------+---------
|per cent.|per cent.|per cent.
Ferric oxide (Fe_{2}O_{3}). | 68.55 | 76.47 | 84.81
Ferrous oxide (FeO). | 16.20 | 9.50 | 1.50
+---------+---------+---------
Total. | 84.75 | 85.97 | 86.31
+---------+---------+---------
Calculated: | | |
Ferric oxide (Fe_{2}O_{3}). | 32.55 | 55.36 | 81.47
Magnetic oxide (Fe_{3}O_{4}).| 52.20 | 30.61 | 4.84
Ferrous oxide (FeO). | | |
+---------+---------+---------
Total. | 84.75 | 85.97 | 86.31
+---------+---------+---------
Percentage of total
oxygen reduced. | 6.93 | 4.02 | 1.07
Metallic iron. | 60.59 | 60.92 | 60.54
-----------------------------+---------+---------+---------
Second Experiment, Water Gas.--The tube, A, was filled with small pieces of anthracite, and heated until all the volatile matter had been expelled. The tube, B, was then placed in tube, A, the joint being made with fireclay, and to prevent the steam from carrying small particles of solid carbon into ore in the upper tube, the anthracite was divided from the ore by means of a piece of fine wire gauze. The steam at a pressure of about 35 lb. to the square inch was passed through the anthracite. The tube, A, was heated to white heat, the tube, B, at its lower end to bright red, the top to cherry red.
------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ Experiment. | 1st. | 2d. | 3d. | ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ Number. | I. | II. | III.| I. | II. | III.| IV. | I. | II. | III.| ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ Total Iron. |60.59|60.92|60.54|65.24|61.71|61.93|57.23|59.73|57.93|55.54| ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+
Iron occurring as ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ FeO. |12.60| 7.39| 1.17|46.98|18.59| 4.03| 0.84|29.45| 2.69| 1.12 Fe_{2}O_{3} |47.99|53.33|59.37|18.26|43.12|57.90|56.39|30.28|55.24|54.42 ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+
Per cent. of Oxides. | ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ FeO. |16.20| 9.50| 1.50|60.40|23.90| 5.18| 1.08|37.86| 3.46| 1.44 Fe_{2}O_{3}. |68.55|76.47|84.81|26.08|61.60|82.71|80.55|43.26|78.91|77.74 Total. |84.75|85.97|86.31|86.48|85.50|87.89|81.63|81.12|82.37|79.18 ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+
Oxygen in Ore. ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ Before experiment.|25.97|26.10|26.05|27.96|26.45|26.54|24.52|25.60|24.81|23.80 After experiment. |24.16|25.05|25.77|21.24|23.79|25.96|24.40|21.39|24.44|23.64 Difference. | 1.81| 1.05| 0.28| 6.72| 2.66| 0.58| 0.12| 4.21| 0.37| 0.16 ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+
Per cent. of oxygen reduced. ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ oxygen reduced. | 6.93| 4.02| 1.07|24.03|10.02| 2.18| 0.49|16.44| 1.49| 0.42 ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+
Degree of Oxidation of the Ore after the Experiment. ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+ FeO. | ... | ... | ... |84.66| ... | ... | ... |18.40| ... | ... | Fe_{3}O_{4}. |52.20|30.61| 4.84|37.82|77.01|28.12| 3.88|62.72|11.14| 4.64| Fe_{2}O_{3}. |32.55|55.36|81.47| ... | 8.49|59.77|77.75| ... |71.23|74.54| Total. |84.75|85.97|85.97|85.97|85.97|85.97|85.97|85.97|85.97|85.97| ------------------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----+
------------------+-----------------+-----------------------+-----------------+ The ore having | | | | been exposed to | Steam. | Water gas. | Carbon monoxide.| ------------------+-----------------+-----------------------+-----------------+
Four Samples were Tested.--I. The bottom layer, 1¼ in. thick; the color of ore quite black, with small particles of reduced spongy metallic iron. II. Layer above I., 4¼ in. thick; the color was also black, but showed a little purple tint. III. Layer above II., 5 in. thick; purple red color. IV. Layer above III., ore a red color. The analyses gave:
-----------------------------+---------+---------+---------+---------
| I. | II. | III. | IV.
+---------+---------+---------+---------
|per cent.|per cent.|per cent.|per cent.
Ferric oxide (Fe_{2}O_{3}). | 26.08 | 61.60 | 82.71 | 80.55
Ferrous oxide (FeO). | 60.40 | 23.90 | 5.18 | 1.08
+---------+---------+---------+---------
Total. | 86.48 | 85.50 | 87.89 | 81.63
+---------+---------+---------+---------
Calculated: | | | |
Ferric oxide (Fe_{2}O_{3}). | ... | 8.49 | 59.77 | 77.75
Magnetic oxide (Fe_{3}O_{4}).| 37.82 | 77.01 | 28.12 | 3.88
Ferrous oxide (FeO). | 48.66 | | |
+---------+---------+---------+---------
Total. | 86.48 | 85.41 | 87.89 | 81.63
+---------+---------+---------+---------
Percentage of total
oxygen reduced. | 24.03 | 10.02 | 2.26 | 0.49
Metallic iron. | 65.24 | 61.71 | 61.93 | 57.23
-----------------------------+---------+---------+---------+---------
NOTE.--All the carbon dioxide (CO2) occurring in the ore as calcic carbonate was expelled.
Third Experiment, Carbon monoxide (CO).--The tube A was filled with anthracite in the manner described for the second experiment, and heated to drive off the volatile matter, before the ore was placed in the upper tube, B, and the anthracite was divided from the ore by means of a piece of fine wire gauze. The lower tube, A, was heated to the temperature of white heat, the upper one, B, to a temperature of bright red. I. Layer, 1 in. thick from the bottom; ore dark brownish colored. II. Layer 4 in. thick above I.; ore reddish brown. III. Layer 11 in. thick above II.; ore red color. The analyses gave:
-----------------------------+---------+---------+---------
| I. | II. | III.
+---------+---------+---------
|per cent.|per cent.|per cent.
Ferric oxide (Fe_{2}O_{3}). | 43.26 | 78.91 | 77.74
Ferrous oxide (FeO). | 37.86 | 3.46 | 1.44
+---------+---------+---------
Total. | 81.12 | 82.37 | 79.18
+---------+---------+---------
Calculated: | | |
Ferric oxide (Fe_{2}O_{3}). | ... | 71.23 | 74.54
Magnetic oxide (Fe_{3}O_{4}).| 62.72 | 11.14 | 4.64
Ferrous oxide (FeO). | 18.40 | |
+---------+---------+---------
Total. | 81.12 | 82.37 | 79.18
+---------+---------+---------
Percentage of total
oxygen reduced. | 16.44 | 1.49 | 0.42
Metallic iron. | 59.73 | 57.93 | 55.54
-----------------------------+---------+---------+---------
NOTE.--The carbon monoxide (CO) had failed to remove from the ore the carbon dioxide existing as calcic carbonate. The summary of experiments in the following table appears to show that the water gas is a more powerful reducing agent than CO in proportion to the ratio of as
4.21 x 100
4.21 : 6.72, or ------------ = 52 per cent.
72
Mr. B.D. Healey, Assoc. M. Inst. C.E., and the author are just now constructing large experimental plant in which water gas will be used as the reducing agent. This plant would have been at work before this but for some defects in the valvular arrangements, which will be entirely removed in the new modifications of the plant.
Where an antiseptic mouth wash is needed, Mr. Sewill prescribes the use of perchloride of mercury in the following form: One grain of the perchloride and 1 grain of chloride of ammonium to be dissolved in 1 oz. of eau de Cologne or tincture of lemons, and a teaspoonful of the solution to be mixed with two-thirds of a wineglassful of water, making a proportion of about 1 of perchloride in 5,000 parts.--Chemist and Druggist.
[Footnote: Read at an evening meeting of the North British Branch of the Pharmaceutical Society, January 21.]
The subject which I have the honor to bring shortly before your notice this evening is one that formed the basis of some instructive remarks by Dr. Redwood in November, 1855, and also of a paper by Dr. Hassall, read before the Society in London in January, 1856, which latter gave rise to an animated discussion. The work detailed below was well in hand when Mr. MacEwan drew my attention to these and kindly supplied me with the volume containing reports of them. Unfortunately, they deal principally with the adulterations, while I was more particularly desirous to learn the composition in a general way, and especially the percentage of coloring resin, the important constituent in commercial annatto. Within the last few years it was one of the articles in considerable demand in this part of the country; now it is seldom inquired for. This, certainly, is not because butter coloring has ceased to be employed, and hence the reason for regretting that the percentage of resin was not dealt with in the articles referred to, so that a comparison could have been made between the commercial annatto of that period and that which exists now. In case some may not be in possession of literature bearing on it--which, by the way, is very meager--it may not be out of place to quote some short details as to its source, the processes for obtaining it, the composition of the raw material, and then the method followed in the present inquiry will be given, together with the results of the examination of ten samples; and though the subject doubtless has more interest for the country than for the town druggist, still, I trust it will have points of interest for both.
Annatto is the coloring matter derived from the seeds of an evergreen plant, Bixa Orellana, which grows in the East and West Indian Islands and South America, in the latter of which it is principally prepared. Two kinds are imported, Spanish annatto, made in Brazil, and flag or French, made mostly in Cayenne. These differ considerably in characters and properties, the latter having a disagreeable putrescent odor, while the Spanish is rather agreeable when fresh and good. It is, however, inferior to the flag as a coloring or dyeing agent. The seeds from which the substance is obtained are red on the outside, and two methods are followed in order to obtain it. One is to rub or wash off the coloring matter with water, allow it to subside, and to expose it to spontaneous evaporation till it acquires a pasty consistence. The other is to bruise the seeds, mix them with water, and allow fermentation to set in, during which the coloring matter collects at the bottom, from which it is subsequently removed and brought to the proper consistence by spontaneous evaporation. These particulars, culled from Dr. Redwood's remarks, may suffice to show its source and the methods for obtaining it.
Dr. John gives the following as the composition of the pulp surrounding the seeds: Coloring resinous matter, 28; vegetable gluten, 26.5; ligneous fiber, 20; coloring, 20; extractive matter, 4; and a trace of spicy and acid matter.
It must be understood, however, that commercial annatto, having undergone processes necessary to fit it for its various uses, as well as to preserve it, differs considerably from this; and though it may not be true, as some hint, that manufacturing in this industry is simply a term synonymous with adulterating, yet results will afterward be given tending to show that there are articles in the market which have little real claim to the title. I tried, but failed, to procure a sample of raw material on which to work, with a view to learn something of its characters and properties in this state, and thus be able to contrast it with the manufactured or commercial article. The best thing to do in the circumstances, I thought, was to operate on the highest priced sample at disposal, and this was done in all the different ways that suggested themselves. The extraction of the resin by means of alcohol--the usual way, I believe--was a more troublesome operation than it appeared to be, as the following experiment will show: One hundred grains of No. 8 were taken, dried thoroughly, reduced to fine powder, and introduced into a flask containing 4 ounces of alcohol in the form of methylated spirit, boiled for an hour--the flask during the operation being attached to an inverted condenser--filtered off, and the residue treated with a smaller amount of the spirit and boiled for ten minutes. This was repeated with diminishing quantities until in all 14 ounces had been used before the alcoholic solution ceased to turn blue on the addition to it of strong sulphuric acid, or failed to give a brownish precipitate with stannous chloride. As the sample contained a considerable quantity of potassium carbonate, in which the resin is soluble, it was thought that by neutralizing this it might render the resin more easy of extraction. This was found to be so, but it was accompanied by such a mass of extractive as made it in the long run more troublesome, and hence it was abandoned. Thinking the spirit employed might be too weak, an experiment with commercial absolute alcohol was carried out as follows: One hundred grains of a red sample, No. 4, were thoroughly dried, powdered finely, and boiled in 2 ounces of the alcohol, filtered, and the residue treated with half an ounce more. This required to be repeated with fresh half ounces of the alcohol until in all 7½ were used; the time occupied from first to last being almost three hours. This was considered unsatisfactory, besides being very expensive, and so it, also, was set aside, and a series of experiments with methylated spirit alone was set in hand. The results showed that the easiest and most satisfactory way was to take 100 grains (this amount being preferred, as it reduces error to the minimum), dry thoroughly, powder finely, and macerate with frequent agitation for twenty-four hours in a few ounces of spirit, then to boil in this spirit for a short time, filter, and repeat the boiling with a fresh ounce or so; this, as a rule, sufficing to completely exhaust it of its resin. Wynter Blyth says that the red resin, or bixin, is soluble in 25 parts of hot alcohol. It appears from these experiments that much more is required to dissolve it out of commercial annatto.
The full process followed consisted in determining the moisture by drying 100 grains at 212° F. till constant, and taking this dried portion for estimation of the resin in the way just stated. The alcoholic extract was evaporated to dryness over a water-bath, the residue dissolved in solution of sodium carbonate, and the resin precipitated by dilute sulphuric acid (these reagents being chosen as the best after numerous trials with others), added in the slightest possible excess. The resin was collected on a tared double filter paper, washed with distilled water until the washings were entirely colorless, dried and weighed.
The ash was found in the usual way, and the extractive by the difference. In the ash the amount soluble was determined, and qualitatively examined, as was the insoluble portion in most of them.
The results are as follows:
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10.
Moisture | 21.75| 21.60| 20.39| 69.73| 18.00| 18.28| 15.71| 38.18| 19.33| 22.50
Resin | 3.00| 2.90| 1.00| 8.80| 3.00| 1.80| 5.40| 12.00| 5.90| 9.20
Extrac-
tive | 57.29| 59.33| 65.00| 19.47| 58.40| 65.67| 26.89| 20.82| 23.77| 28.50
Ash | 17.96| 16.17| 13.61| 2.00| 20.60| 14.25| 52.00| 29.00| 51.00| 39.80
-------------------------------------------------------------------------------
|100.00|100.00|100.00|100.00|100.00|100.00|100.00|100.00|100.00|100.00
-------------------------------------------------------------------------------
Ashes: | | | |Almost| | | | | |
Soluble | 13.20| 12.57| 7.50|wholly| 10.0| 11.75| 18.5 | 20.0 | 15.0 | 13.8
Insoluble| 4.76| 3.60| 6.11| NaCl.| 10.6| 2.50| 33.5 | 9.0 | 36.0 | 26.0
The first six are the ordinary red rolls, with the exception of No. 4, which is a red mass, the only one of this class direct from the manufacturers. The remainder are brown cakes, all except No. 7 being from the manufacturers direct. The ash of the first two was largely common salt; that of No. 3 contained, besides this, iron in some quantity. No. 4 is unique in many respects. It was of a bright red color, and possessed a not disagreeable odor. It contained the largest percentage of moisture and the lowest of ash; had, comparatively, a large amount of coloring matter; was one of the cheapest, and in the course of some dairy trials, carried out by an intelligent farmer, was pronounced to be the best suited for coloring butter. So far as my experience goes, it was a sample of the best commercial excellence, though I fear the mass of water present and the absence of preserving substances will assist in its speedy decay. Were such an article easily procured in the usual way of business, there would not be much to complain of, but it must not be forgotten that it was got direct from the manufacturers--a somewhat suggestive fact when the composition of some other samples is taken into account. No. 5 emitted a disagreeable odor during ignition. The soluble portion of the ash was mostly common salt, and the insoluble contained three of sand--the highest amount found, although most of the reds contained some. No. 6 was a vile-looking thing, and when associated in one's mind with butter gave rise to disagreeable reflections. It was wrapped in a paper saturated with a strongly smelling linseed oil. When it was boiled in water and broken up, hairs, among other things, were observed floating about. It contained some iron. The first cake, No. 7, gave off during ignition an agreeable odor resembling some of the finer tobaccos, and this is characteristic more or less of all the cakes. The ash weighed 52 per cent., the soluble part of which, 18.5, was mostly potassium carbonate, with some chlorides and sulphates; the insoluble, mostly chalk with iron and alumina. No. 8--highest priced of all--had in the mass an odor which I can compare to nothing else than a well rotted farmyard manure. Twenty parts of the ash were soluble and largely potassium carbonate, the insoluble being iron for the most part. The mineral portions of Nos. 9 and 10 closely resemble No. 7.
On looking over the results, it is found that the red rolls contained starchy matters in abundance (in No. 4 the starch was to a large extent replaced by water), and an ash, mostly sodium chloride, introduced no doubt to assist in its preservation as well as to increase the color of the resin--a well known action of salt on vegetable reds. The cakes, which are mostly used for cheese coloring, I believe, all appeared to contain turmeric, for they gave a more or less distinct reaction with the boric acid test, and all except No. 8 contained large quantities of chalk. These results in reference to extractive, etc., reveal nothing that has not been known before. Wynter Blyth, who gives the only analyses of annatto I have been able to find, states that the composition of a fair commercial sample (which I take to mean the raw article) examined by him was as follows: water, 24.2; resin, 28.8; ash, 22.5; and extractive, 24.5; and that of an adulterated (which I take to mean a manufactured) article, water, 13.4; resin, 11.0; ash (iron, silica, chalk, alumina, and common salt), 48.3; and extractive. 27.3. If this be correct, it appears that the articles at present in the market, or at least those which have come in my way, have been wretched imitations of the genuine thing, and should, instead of being called adulterated annatto, be called something else adulterated, but not seriously, with annatto. I have it on the authority of the farmer previously referred to, that ¼ of an ounce of No. 4 is amply sufficient to impart the desired cowslip tint to no less than 60 lb. of butter. When so little is actually required, it does not seem of very serious importance whether the adulterant or preservative be flour, chalk, or water, but it is exasperating in a very high degree to have such compounds as Nos. 3 and 6 palmed off as decent things when even Nos. 1, 2, and 5 have been rejected by dairymen as useless for the purpose. In conclusion, I may be permitted to express the hope that others may be induced to examine the annatto taken into stock more closely than I was taught to do, and had been in the habit of doing, namely, to see if it had a good consistence and an odor resembling black sugar, for if so, the quality was above suspicion.
Professor P. Cohn has recently described the mode in which he has manufactured the Japanese sake or rice wine in the laboratory. The material used was "Tane Kosi," i.e., grains of rice coated with the mycelium, conidiophores, and greenish yellow chains of conidia of Aspergillus Oryzoe. The fermentation is caused by the mycelium of this fungus before the development of the fructification. The rice is first exposed to moist air so as to change the starch into paste, and then mixed with grains of the "Tane Kosi." The whole mass of rice becomes in a short time permeated by the soft white shining mycelium, which imparts to it the odor of apple or pine-apple. To prevent the production of the fructification, freshly moistened rice is constantly added for two or three days, and then subjected to alcoholic fermentation from the Saccharomyces, which is always present in the rice, but which has nothing to do with the Aspergillus. The fermentation is completed in two or three weeks, and the golden yellow, sherry-like sake is poured off. The sample manufactured contained 13.9 per cent. of alcohol. Chemical investigation showed that the Aspergillus mycelium transforms the starch into glucose, and thus plays the part of a diastase.
Another substance produced from the Aspergillus rice is the soja sauce. The soja leaves, which contain little starch, but a great deal of oil and casein, are boiled, mixed with roasted barley, and then with the greenish yellow conidia powder of the Aspergillus. After the mycelium has fructified, the mass is treated with a solution of sodium chloride, which kills the Aspergillus, another fungus, of the nature of a Chalaza, and similar to that produced in the fermentation of "sauerkraut," appearing in its place. The dark-brown soja sauce then separates.
[Footnote: Annual address delivered by President J.A. Price before the meeting of the Scranton Board of Trade, Monday, January 18, 1886.]
Iron is the basis of our civilization. Its supremacy and power it is impossible to overestimate; it enters every avenue of development, and it may be set down as the prime factor in the world's progress. Its utility and its universality are hand in hand, whether in the magnificent iron steamship of the ocean, the network of iron rail upon land, the electric gossamer of the air, or in the most insignificant articles of building, of clothing, and of convenience. Without it, we should have miserably failed to reach our present exalted station, and the earth would scarcely maintain its present population; it is indeed the substance of substances. It is the Archimedean lever by which the great human world has been raised. Should it for a moment forget its cunning and lose its power, earthquake shocks or the wreck of matter could not be more disastrous. However axiomatic may be everything that can be said of this wonderful metal, it is undoubtedly certain that it must give way to a metal that has still greater proportions and vaster possibilities. Strange and startling as may seem the assertion, yet I believe it nevertheless to be true that we are approaching the period, if not already standing upon the threshold of the day, when this magical element will be radically supplanted, and when this valuable mineral will be as completely superseded as the stone of the aborigines. With all its apparent potency, it has its evident weaknesses; moisture is everywhere at war with it, gases and temperature destroy its fiber and its life, continued blows or motion crystallize and rob it of its strength, and acids will devour it in a night. If it be possible to eliminate all, or even one or more, of these qualities of weakness in any metal, still preserving both quantity and quality, that metal will be the metal of the future.
The coming metal, then, to which our reference is made is aluminum, the most abundant metal in the earth's crust. Of all substances, oxygen is the most abundant, constituting about one-half; after oxygen comes silicon, constituting about one-fourth, with aluminum third in all the list of substances of the composition. Leaving out of consideration the constituents of the earth's center, whether they be molten or gaseous, more or less dense as the case may be, as we approach it, and confining ourselves to the only practical phase of the subject, the crust, we find that aluminum is beyond question the most abundant and the most useful of all metallic substances.
It is the metallic base of mica, feldspar, slate, and clay. Professor Dana says: "Nearly all the rocks except limestones and many sandstones are literally ore-beds of the metal aluminum." It appears in the gem, assuming a blue in the sapphire, green in the emerald, yellow in the topaz, red in the ruby, brown in the emery, and so on to the white, gray, blue, and black of the slates and clays. It has been dubbed "clay metal" and "silver made from clay;" also when mixed with any considerable quantity of carbon becoming a grayish or bluish black "alum slate."
This metal in color is white and next in luster to silver. It has never been found in a pure state, but is known to exist in combination with nearly two hundred different minerals. Corundum and pure emery are ores that are very rich in aluminum, containing about fifty-four per cent. The specific gravity is but two and one-half times that of water; it is lighter than glass or as light as chalk, being only one-third the weight of iron and one-fourth the weight of silver; it is as malleable as gold, tenacious as iron, and harder than steel, being next the diamond. Thus it is capable of the widest variety of uses, being soft when ductility, fibrous when tenacity, and crystalline when hardness is required. Its variety of transformations is something wonderful. Meeting iron, or even iron at its best in the form of steel, in the same field, it easily vanquishes it at every point. It melts at 1,300 degrees F., or at least 600 degrees below the melting point of iron, and it neither oxidizes in the atmosphere nor tarnishes in contact with gases. The enumeration of the properties of aluminum is as enchanting as the scenes of a fairy tale.
Before proceeding further with this new wonder of science, which is already knocking at our doors, a brief sketch of its birth and development may be fittingly introduced. The celebrated French chemist Lavoisier, a very magician in the science, groping in the dark of the last century, evolved the chemical theory of combustion--the existence of a "highly respirable gas," oxygen, and the presence of metallic bases in earths and alkalies. With the latter subject we have only to do at the present moment. The metallic base was predicted, yet not identified. The French Revolution swept this genius from the earth in 1794, and darkness closed in upon the scene, until the light of Sir Humphry Davy's lamp in the early years of the present century again struck upon the metallic base of certain earths, but the reflection was so feeble that the great secret was never revealed. Then a little later the Swedish Berzelius and the Danish Oersted, confident in the prediction of Lavoisier and of Davy, went in search of the mysterious stranger with the aggressive electric current, but as yet to no purpose. It was reserved to the distinguished German Wohler, in 1827, to complete the work of the past fifty years of struggle and finally produce the minute white globule of the pure metal from a mixture of the chloride of aluminum and sodium, and at last the secret is revealed--the first step was taken. It took twenty years of labor to revolve the mere discovery into the production of the aluminum bead in 1846, and yet with this first step, this new wonder remained a foetus undeveloped in the womb of the laboratory for years to come.
Returning again to France some time during the years between 1854 and 1858, and under the patronage of the Emperor Napoleon III., we behold Deville at last forcing Nature to yield and give up this precious quality as a manufactured product. Rose, of Berlin, and Gerhard, in England, pressing hard upon the heels of the Frenchman, make permanent the new product in the market at thirty-two dollars per pound. The despair of three-quarters of a century of toilsome pursuit has been broken, and the future of the metal has been established.
The art of obtaining the metal since the period under consideration has progressed steadily by one process after another, constantly increasing in powers of productivity and reducing the cost. These arts are intensely interesting to the student, but must be denied more than a reference at this time. The price of the metal may be said to have come within the reach of the manufacturing arts already.
A present glance at the uses and possibilities of this wonderful metal, its application and its varying quality, may not be out of place. Its alloys are very numerous and always satisfactory; with iron, producing a comparative rust proof; with copper, the beautiful golden bronze, and so on, embracing the entire list of articles of usefulness as well as works of art, jewelry, and scientific instruments.
Its capacity to resist oxidation or rust fits it most eminently for all household and cooking utensils, while its color transforms the dark visaged, disagreeable array of pots, pans, and kitchen implements into things of comparative beauty. As a metal it surpasses copper, brass, and tin in being tasteless and odorless, besides being stronger than either.
It has, as we have seen, bulk without weight, and consequently may be available in construction of furniture and house fittings, as well in the multitudinous requirements of architecture. The building art will experience a rapid and radical change when this material enters as a component material, for there will be possibilities such as are now undreamed of in the erection of homes, public buildings, memorial structures, etc. etc., for in this metal we have the strength, durability, and the color to give all the variety that genius may dictate.
And when we take a still further survey of the vast field that is opening before us, we find in the strength without size a most desirable assistant in all the avenues of locomotion. It is the ideal metal for railway traffic, for carriages and wagons. The steamships of the ocean of equal size will double their cargo and increase the speed of the present greyhounds of the sea, making six days from shore to shore seem indeed an old time calculation and accomplishment. A thinner as well as a lighter plate; a smaller as well as a stronger engine; a larger as well as a less hazardous propeller; and a natural condition of resistance to the action of the elements; will make travel by water a forcible rival to the speed attained upon land, and bring all the distant countries in contact with our civilization, to the profit of all. This metal is destined to annihilate space even beyond the dream of philosopher or poet.
The tensile strength of this material is something equally wonderful, when wire drawn reaches as high as 128,000 pounds, and under other conditions reaches nearly if not quite 100,000 pounds to the square inch. The requirements of the British and German governments in the best wrought steel guns reach only a standard of 70,000 pounds to the square inch. Bridges may be constructed that shall be lighter than wooden ones and of greater strength than wrought steel and entirely free from corrosion. The time is not distant when the modern wonder of the Brooklyn span will seem a toy.
It may also be noted that this metal affords wide development in plumbing material, in piping, and will render possible the almost indefinite extension of the coming feature of communication and exchange--the pneumatic tube.
The resistance to corrosion evidently fits this metal for railway sleepers to take the place of the decaying wooden ties. In this metal the sleeper may be made as soft and yielding as lead, while the rail may be harder and tougher than steel, thus at once forming the necessary cushion and the avoidance of jar and noise, at the same time contributing to additional security in virtue of a stronger rail.
In conductivity this metal is only exceeded by copper, having many times that of iron. Thus in telegraphy there are renewed prospects in the supplanting of the galvanized iron wire--lightness, strength, and durability. When applied to the generation of steam, this material will enable us to carry higher pressure at a reduced cost and increased safety, as this will be accomplished by the thinner plate, the greater conductivity of heat, and the better fiber.
It is said that some of its alloys are without a rival as an anti-friction metal, and having hardness and toughness, fits it remarkably for bearings and journals. Herein a vast possibility in the mechanic art lies dormant--the size of the machine may be reduced, the speed and the power increased, realizing the conception of two things better done than one before. It is one of man's creative acts.
From other of its alloys, knives, axes, swords, and all cutting implements may receive and hold an edge not surpassed by the best tempered steel. Hulot, director in the postage stamp department, Paris, asserts that 120,000 blows will exhaust the usefulness of the cushion of the stamp machine, and this number of blows is given in a day; and that when a cushion of aluminum bronze was substituted, it was unaffected after months of use.
If we have found a metal that possesses both tensile strength and resistance to compression; malleability and ductility--the quality of hardening, softening, and toughening by tempering; adaptability to casting, rolling, or forging; susceptibility to luster and finish; of complete homogeneous character and unusually resistant to destructive agents--mankind will certainly leave the present accomplishments as belonging to an effete past, and, as it were, start anew in a career of greater prospects.
This important material is to be found largely in nearly all the rocks, or as Prof. Dana has said, "Nearly all rocks are ore-beds of the metal." It is in every clay bank. It is particularly abundant in the coal measures and is incidental to the shales or slates and clays that underlie the coal. This under clay of the coal stratum was in all probability the soil out of which grew the vegetation of the coal deposits. It is a compound of aluminum and other matter, and, when mixed with carbon and transformed by the processes of geologic action, it becomes the shale rock which we know and which we discard as worthless slate. And it is barely possible that we have been and are still carting to the refuse pile an article more valuable than the so greatly lauded coal waste or the merchantable coal itself. We have seen that the best alumina ore contains only fifty-four per cent. of metal.
The following prepared table has been furnished by the courtesy and kindness of Mr. Alex. H. Sherred, of Scranton.
ALUMINA.
Blue-black shale, Pine Brook drift 27.36
Slate from Briggs' Shaft coal 15.93
Black fire clay, 4 ft. thick, Nos. 4 and 5 Rolling Mill mines 23.53
First cut on railroad, black clay above Rolling Mill 32.60
G vein black clay, Hyde Park mines 28.67
It will be seen that the black clay, shale, or slate, has a constituent of aluminum of from 15.93 per cent., the lowest, to 32.60 per cent., the highest. Under every stratum of coal, and frequently mixed with it, are these under deposits that are rich in the metal. When exposed to the atmosphere, these shales yield a small deposit of alum. In the manufacture of alum near Glasgow the shale and slate clay from the old coal pits constitute the material used, and in France alum is manufactured directly from the clay.
Sufficient has been advanced to warrant the additional assertion that we are here everywhere surrounded by this incomparable mineral, that it is brought to the surface from its deposits deep in the earth by the natural process in mining, and is only exceeded in quantity by the coal itself. Taking a columnar section of our coal field, and computing the thickness of each shale stratum, we have from twenty-five to sixty feet in thickness of this metal-bearing substance, which averages over twenty-five per cent. of the whole in quantity in metal.
It is readily apparent that the only task now before us is the reduction of the ore and the extraction of the metal. Can this be done? We answer, it has been done. The egg has stood on end--the new world has been sighted. All that now remains is to repeat the operation and extend the process. Cheap aluminum will revolutionize industry, travel, comfort, and indulgence, transforming the present into an even greater civilization. Let us see.
We have seen the discovery of the mere chemical existence of the metal, we have stood by the birth of the first white globule or bead by Wohler, in 1846, and witnesssed its introduction as a manufactured product in 1855, since which time, by the alteration and cheapening of one process after another, it has fallen in price from thirty-two dollars per pound in 1855 to fifteen dollars per pound in 1885. Thirty years of persistent labor at smelting have increased the quantity over a thousandfold and reduced the cost upward of fifty per cent.
All these processes involve the application of heat--a mere question of the appliances. The electric currents of Berzelius and Oersted, the crucible of Wohler, the closed furnaces and the hydrogen gas of the French manufacturers and the Bessemer converter apparatus of Thompson, all indicate one direction. This metal can be made to abandon its bed in the earth and the rock at the will of man. During the past year, the Messrs. Cowles, of Cleveland, by their electric smelting process, claim to have made it possible to reduce the price of the metal to below four dollars per pound; and there is now erecting at Lockport, New York, a plant involving one million of capital for the purpose.
Turning from the employment of the expensive reducing agents to the simple and sole application of heat, we are unwilling to believe that we do not here possess in eminence both the mineral and the medium of its reduction. Whether the electric or the reverberatory or the converter furnace system be employed, it is surely possible to produce the result.
To enter into consideration of the details of these constructions would involve more time than is permitted us on this occasion. They are very interesting. We come again naturally to the limitless consideration of powdered fuel, concerning which certain conclusions have been reached. In the dissociation of water into its hydrogen and oxygen, with the mingled carbon in a powdered state, we undoubtedly possess the elements of combustion that are unexcelled on earth, a heat-producing combination that in both activity and power leaves little to be desired this side of the production of the electric force and heat directly from the carbon without the intermediary of boilers, engines, dynamos, and furnaces.
In the hope of stimulating thought to this infinite question of proper fuel combustion, with its attendant possibilities for man's gratification and ambition, this advanced step is presented. The discussion of processes will require an amount of time which I hope this Board will not grudgingly devote to the subject, but which is impossible at present. Do not forget that there is no single spot on the face of the globe where nature has lavished more freely her choicest gifts. Let us be active in the pursuit of the treasure and grateful for the distinguished consideration.
On January 9, Professor Dewar delivered the sixth and last of his series of lectures at the Royal Institution on "The Story of a Meteorite." [For the preceding lectures, see SUPPLEMENTS 529 and 580.] He said that cosmic dust is found on Arctic snows and upon the bottom of the ocean; all over the world, in fact, at some time or other, there has been a large deposit of this meteoric dust, containing little round nodules found also in meteorites. In Greenland some time ago numbers of what were supposed to be meteoric stones were found; they contained iron, and this iron, on being analyzed at Copenhagen, was found to be rich in nickel. The Esquimaux once made knives from iron containing nickel; and as any such alloy they must have found and not manufactured, it was supposed to be of meteoric origin. Some young physicists visited the basaltic coast in Greenland from which some of the supposed meteoric stones had been brought, and in the middle of the rock large nodules were found composed of iron and nickel; it, therefore, became evident that the earth might produce masses not unlike such as come to us as meteorites. The lecturer here exhibited a section of the Greenland rock containing the iron, and nickel alloy, mixed with stony crystals, and its resemblance to a section of a meteorite was obvious. It was 2½ times denser than water, yet the whole earth is 5½ times denser than water, so that if we could go deep enough, it is not improbable that our own globe might be found to contain something like meteoric iron. He then called attention to the following tables:
Elementary Substances found in Meteorites.
Hydrogen. Chromium. Arsenic. Lithium. Manganese. Vanadium? Sodium. Iron. Phosphorus. Potassium. Nickel. Sulphur. Magnesium. Cobalt. Oxygen. Calcium. Copper. Silicon. Aluminum. Tin. Carbon. Titanium. Antimony. Chlorine.
Density of Meteorites.
Carbonaceous (Orgueil, etc.) 1.9 to 3 Aluminous (Java) 3.0 " 3.2 Peridotes (Chassigny, etc.) 3.5 " -- Ordinary type (Saint Mes) 3.1 " 3.8 Rich in iron (Sierra de Chuco) 6.5 " 7.0 Iron with stone (Krasnoyarsk) 7.1 " 7.8 True irons (Caille) 7.0 " 8.0
Interior of the Earth
Parts of the radius. Density. 0.0 11.0 0.1 10.3 0.2 9.6 0.3 8.9 0.4 8.3 0.5 7.8 0.6 7.4 0.7 7.1 0.8 6.2 0.9 5.0 1.0 2.6
Twice a year, said Professor Dewar, what are called "falling stars" maybe plentifully seen; the times of their appearance are in August and November. Although thousands upon thousands of such small meteors have passed through our atmosphere, there is no distinct record of one having ever fallen to the earth during these annual displays. One was said to have fallen recently at Naples, but on investigation it turned out to be a myth. These annual meteors in the upper air are supposed to be only small ones, and to be dissipated into dust and vapor at the time of their sudden heating; so numerous are they that 40,000 have been counted in one evening, and an exceptionally great display comes about once in 33¼ years. The inference from their periodicity is, that they are small bodies moving round the sun in orbits of their own, and that whenever the earth crosses their orbits, thereby getting into their path, a splendid display of meteors results. A second display, a year later, usually follows the exceptionally great display just mentioned, consequently the train of meteors is of great length. Some of these meteors just enter the atmosphere of the earth, then pass out again forever, with their direction of motion altered by the influence of the attraction of the earth. He here called attention to the accompanying diagram of the orbits of meteors.
The lecturer next invited attention to a hollow globe of linen or some light material; it was about 2 ft. or 2 ft. 6 in. in diameter, and contained hidden within it the great electro-magnet, weighing 2 cwt., so often used by Faraday in his experiments. He also exhibited a ball made partly of thin iron; the globe represented the earth, for the purposes of the experiment, and the ball a meteorite of somewhat large relative size. The ball was then discharged at the globe from a little catapult; sometimes the globe attracted the ball to its surface, and held it there, sometimes it missed it, but altered its curve of motion through the air. So was it, said the lecturer, with meteorites when they neared the earth. Photographs from drawings, by Professor A. Herschel, of the paths of meteors as seen by night were projected on the screen; they all seemed to emanate from one radiant point, which, said the lecturer, is a proof that their motions are parallel to each other; the parallel lines seem to draw to a point at the greatest distance, for the same reason that the rails of a straight line of railway seem to come from a distant central point. The most interesting thing about the path of a company of meteors is, that a comet is known to move in the same orbit; the comet heads the procession, the meteors follow, and they are therefore, in all probability, parts of comets, although everything about these difficult matters cannot as yet be entirely explained; enough, however, is known to give foundation for the assumption that meteorites and comets are not very dissimilar.
The light of a meteorite is not seen until it enters the atmosphere of the earth, but falling meteorites can be vaporized by electricity, and the light emitted by their constituents be then examined with the spectroscope. The light of comets can be directly examined, and it reveals the presence in those bodies of sodium, carbon, and a few other well-known substances. He would put a piece of meteorite in the electric arc to see what light it would give; he had never tried the experiment before. The lights of the theater were then turned down, and the discourse was continued in darkness; among the most prominent lines visible in the spectrum of the meteorite, Professor Dewar specified magnesium, sodium, and lithium. "Where do meteorites come from?" said the lecturer. It might be, he continued, that they were portions of exploded planets, or had been ejected from planets. In this relation, he should like to explain the modern idea of the possible method of construction of our own earth. He then set forth the nebular hypothesis that at some long past time our sun and all his planets existed but as a volume of gas, which in contracting and cooling formed a hot volume of rotating liquid, and that as this further contracted and cooled, the planets, and moons, and planetary rings fell off from it and gradually solidified, the sun being left as the solitary comparatively uncooled portion of the original nebula. In partial illustration of this, he caused a little globe of oil, suspended in an aqueous liquid of nearly its own specific gravity, to rotate, and as it rotated it was seen, by means of its magnified image upon the screen, to throw off from its outer circumference rings and little globes.
One of the most picturesque objects that meet the eye of the traveler over the great plains of the southern portion of California and New Mexico is the candelabra cactus. Systematically it belongs to the Cereus family, in which the notable Night-blooming Cereus also is naturally included. In tropical or semi-tropical countries these plants thrive, and grow to enormous size. For example, the Cereus that bears those great flowers, and blooms at night, exhaling powerful perfume, as we see them in hothouses in our cold climate, are even in the semi-tropical region of Key West, on the Florida Reef, seen to grow enormously in length.
THE CANDELABRA CACTUS--CEREUS GIGANTEUS.
We cultivated several species of the more interesting forms during a residence on the reef. Our brick house, two stories in height, was entirely covered on a broad gable end, the branches more than gaining the top. There is a regular monthly growth, and this is indicated by a joint between each two lengths. Should the stalk be allowed to grow without support, it will continue growing without division, and exhibit stalks five or six feet in length, when they droop, and fall upon the ground.
Where there is a convenient resting place on which it can spread out and attach itself, the stalk throws out feelers and rootlets, which fasten securely to the wall or brickwork; then, this being a normal growth, there is a separation at intervals of about a foot. That is, the stalk grows in one month about twelve inches, and if it has support, the middle woody stalk continues to grow about an inch further, but has no green, succulent portion, in fact, looks like a stem; then the other monthly growth takes place, and ends with a stem, and so on indefinitely. Our house was entirely covered by the stems of such a plant, and the flowers were gorgeous in the extreme. The perfume, however, was so potent that it became a nuisance. Such is the Night-blooming Cereus in the warm climates, and similarly the Candelabra Cereus grows in stalks, but architecturally erect, fluted like columns. The flowers are large, and resemble those of the night-blooming variety. Some columns remain single, and are amazingly artificial appearing; others throw off shoots, as seen in the picture. There are some smaller varieties that have even more of a candelabra look, there being clusters of side shoots, the latter putting out from the trunk regularly, and standing up parallel to each other. The enormous size these attain is well shown in the picture.
Whenever the great stalks of these cacti die, the succulent portion is dried, and nothing is left but the woody fiber. They are hollow in places, and easily penetrated. A species of woodpecker, Melanerpes formicivorus, is found to have adopted the use of these dry stalks for storing the winter's stock of provisions. There are several round apertures seen on the stems in the pictures, which were pecked by this bird. This species of woodpecker is about the size of our common robin or migratory thrush, and has a bill stout and sharp. The holes are pecked for the purpose of storing away acorns or other nuts; they are just large enough to admit the fruit, while the cup or larger end remains outside. The nuts are forced in, so that it requires considerable wrenching to dislodge them. In many instances the nuts are so numerous, the stalk has the appearance of being studded with bullets. This appearance is more pronounced in cases where the dead trunk of an oak is used. There are some specimens of the latter now owned by the American Museum of Natural History, which were originally sent to the Centennial Exhibition at Philadelphia. They were placed in the department contributed by the Pacific Railroad Company, and at that time were regarded as some of the wonders of that newly explored region through which the railroad was then penetrating. Some portions of the surface of these logs are nearly entirely occupied by the holes with acorns in them. The acorns are driven in very tightly in these examples; much more so than in the cactus plants, as the oak is nearly round, and the holes were pecked in solid though dead wood. One of the most remarkable circumstances connected with this habit of the woodpecker is the length of flight required and accomplished. At Mount Pizarro, where such storehouses are found, the nearest oak trees are in the Cordilleras, thirty miles distant; thus the birds are obliged to make a journey of sixty miles to accomplish the storing of one acorn. At first it seemed strange that a bird should spend so much labor to place those bits of food, and so far away. De Saussure, a Swiss naturalist, published in the Bibliotheque Universelle, of Geneva, entertaining accounts of the Mexican Colaptes, a variety of the familiar "high hold," or golden winged woodpecker. They were seen to store acorns in the dead stalks of the maguey (Agave Americana). Sumichrast, who accompanied him to Central America, records the same facts. These travelers saw great numbers of the woodpeckers in a region on the slope of a range of volcanic mountains. There was little else of vegetation than the Agave, whose barren, dead stems were studded with acorns placed there by the woodpeckers.
The maguey throws up a stalk about fifteen feet in height yearly, which, after flowering, grows stalky and brittle, and remains an unsightly thing. The interior is pithy, but after the death of the stalk the pith contracts, and leaves the greater portion of the interior hollow, as we have seen in the case of the cactus branches. How the birds found that these stalks were hollow is a problem not yet solved, but, nevertheless, they take the trouble to peck away at the hard bark, and once penetrated, they commence to fill the interior; when one space is full, the bird pecks a little higher up, and so continues.
Dr. Heerman, of California, describes the California Melanerpes as one of the most abundant of the woodpeckers; and remarks that it catches insects on the wing like a flycatcher. It is well determined that it also eats the acorns that it takes so much pains to transport.

FLOWER OF CEREUS GIGANTEUS.
It seems that these birds also store the pine trees, as well as the oaks. It is not quite apparent why these birds exhibit such variation in habits; they at times select the more solid trees, where the storing cannot go on without each nut is separately set in a hole of its own. There seems an instinct prompting them to do this work, though there may not be any of the nuts touched again by the birds. Curiously enough, there are many instances of the birds placing pebbles instead of nuts in holes they have purposely pecked for them. Serious trouble has been experienced by these pebbles suddenly coming in contact with the saw of the mill through which the tree is running. The stone having been placed in a living tree, as is often the case, its exterior had been lost to sight during growth.
Some doubt has been entertained about the purpose of the bird in storing the nuts in this manner. De Saussure tells us he has witnessed the birds eating the acorns after they had been placed in holes in trees, and expresses his conviction that the insignificant grub which is only seen in a small proportion of nuts is not the food they are in search of.
C.W. Plass, Esq., of Napa City, California, had an interesting example of the habits of the California Melanerpes displayed in his own house. The birds had deposited numbers of acorns in the gable end. A considerable number of shells were found dropped underneath the eaves, while some were found in place under the gable, and these were perfect, having no grubs in them.
The picture shows a very common scene in New Mexico. The columns, straight and angular, are often sixty feet in height. It is called torch cactus in some places. There are many varieties, and as many different shapes. Some lie on the ground; others, attached to trunks of trees as parasites, hang from branches like great serpents; but none is so majestic as the species called systematically Cereus giganteus, most appropriately. The species growing pretty abundantly on the island of Key West is called candle cactus. It reaches some ten or twelve feet, and is about three inches in diameter. The angles are not so prominent, which gives the cylinders a roundish appearance. They form a pretty, rather picturesque feature in the otherwise barren undergrowth of shrubbery and small trees. Accompanied by a few flowering cocoa palms, the view is not unpleasing. The fiber of these plants is utilized in some coarse manufactures. The maguey, or Agave, is used in the manufacture of fine roping. Manila hemp is made from a species. The species whose dried stalks are used by the woodpeckers for their winter storage was cultivated at Key West, Florida, during several years before 1858. Extensive fields of the Agave stood unappropriated at that period. Considerable funds were dissipated on this venture. Extensive works were established, and much confidence was entertained that the scheme would prove a paying one, but the "hemp" rope which this was intended to rival could be made cheaper than this. The great Agave plants, with their long stalks, stand now, increasing every year, until a portion of the island is overrun with them.
This wonderful cactus, its colossal proportions, and weird, yet grand, appearance in the rocky regions of Mexico and California, where it is found in abundance, have been made known to us only through books of travel, no large plants of it having as yet appeared in cultivation in this country. It is questionable if ever the natural desire to see such a vegetable curiosity represented by a large specimen in gardens like Kew can be realized, owing to the difficulty of importing large stems in a living condition; and even if successfully brought here, they survive only a very short time. To grow young plants to a large size seems equally beyond our power, as plants 6 inches high and carefully managed are quite ten years old. When young, the stem is globose, afterward becoming club-shaped or cylindrical. It flowers at the height of 12 feet, but grows up to four or five times that height, when it develops lateral branches, which curve upward and present the appearance of an immense candelabrum, the base of the stem being as thick as a man's body. The flower, of which a figure is given here, is about 5 inches long and wide, the petals cream colored, the sepals greenish white. Large clusters of flowers are developed together near the top of the stem. A richly colored edible fruit like a large fig succeeds each flower, and this is gathered by the natives and used as food under the name of saguarro. A specimen of this cactus 3 feet high may be seen in the succulent house at Kew.--B., The Garden.
[Footnote: Read at a meeting of the Chemists' Assistants' Association. December 16, 1885.]
In two previous papers read before this Association I have tried to condense into as small a space as I could the processes of the nutrition and of the growth of plants; in the present paper I want to set before you the broad lines of the methods by which plants are reproduced.
Although in the great trees of the conifers and the dicotyledons we have apparently provision for growth for any number of years, or even centuries, yet accident or decay, or one of the many ills that plants are heirs to, will sooner or later put an end to the life of every individual plant.
Hence the most important act of a plant--not for itself perhaps, but for its race--is the act by which it, as we say, "reproduces itself," that is, the act which results in the giving of life to a second individual of the same form, structure, and nature as the original plant.
The methods by which it is secured that the second generation of the plant shall be as well or even better fitted for the struggle of life than the parent generation are so numerous and complicated that I cannot in this paper do more than allude to them; they are most completely seen in cross fertilization, and the adaptation of plant structures to that end.
What I want to point out at present are the principles and not so much the details of reproduction, and I wish you to notice, as I proceed, what is true not only of reproduction in plants but also of all processes in nature, namely, the paucity of typical methods of attaining the given end, and the multiplicity of special variation from those typical methods. When we see the wonderfully varied forms of plant life, and yet learn that, so to speak, each edifice is built with the same kind of brick, called a cell, modified in form and function; when we see the smallest and simplest equally with the largest and most complicated plant increasing in size subject to the laws of growth by intussusception and cell division, which are universal in the organic world; we should not be surprised if all the methods by which plants are reproduced can be reduced to a very small number of types.
The first great generalization is into--
1. The vegetative type of reproduction, in which one or more ordinary cells separate from the parent plant and become an independent plant; and--
2. The special-cell type of reproduction, in which either one special cell reproduces the plant, or two special cells by their union form the origin of the new plant; these two modifications of the process are known respectively as asexual and sexual.
The third modification is a combination of the two others, namely, the asexual special cell does not directly reproduce its parent form, but gives rise to a structure in which sexual special cells are developed, from whose coalescence springs again the likeness of the original plant. This is termed alternation of generations.
The sexual special cell is termed the spore.
The sexual special cells are of one kind or of two kinds.
Those which are of one kind may be termed, from their habit of yoking themselves together, zygoblasts, or conjugating cells.
Those which are of two kinds are, first, a generally aggressive and motile fertilizing or so-called "male cell," called in its typical form an antherozoid; and, second, a passive and motionless receptive or so-called "female cell," called an oosphere.
The product of the union of two zygoblasts is termed a zygospore.
The product of the union of an antherozoid and an oosphere is termed an oospore.
In many cases the differentiation of the sexual cells does not proceed so far as the formation of antherozoids or of distinct oospheres; these cases I shall investigate with the others in detail presently.
First, then, I will point out some of the modes of vegetative reproduction.
The commonest of these is cell division, as seen in unicellular plants, such as protococcus, where the one cell which composes the plant simply divides into two, and each newly formed cell is then a complete plant.
The particular kind of cell division termed "budding" here deserves mention. It is well seen in the yeast-plant, where the cell bulges at one side, and this bulge becomes larger until it is nipped off from the parent by contraction at the point of junction, and is then an independent plant.
Next, there is the process by which one plant becomes two by the dying off of some connecting portion between two growing parts.
Take, for instance, the case of the liverworts. In these there is a thallus which starts from a central point and continually divides in a forked or dichotomous manner. Now, if the central portion dies away, it is obvious that there will be as many plants as there were forkings, and the further the dying of the old end proceeds, the more young plants will there be.
Take again, among higher plants, the cases of suckers, runners, stolons, offsets, etc. Here, by a process of growth but little removed from the normal, portions of stems develop adventitious roots, and by the dying away of the connecting links may become independent plants.
Still another vegetative method of reproduction is that by bulbils or gemmæ.
A bulbil is a bud which becomes an independent plant before it commences to elongate; it is generally fleshy, somewhat after the manner of a bulb, hence its name. Examples occur in the axillary buds of Lilium bulbiferum, in some Alliums, etc.
The gemma is found most frequently in the liverworts and mosses, and is highly characteristic of these plants, in which indeed vegetative reproduction maybe said to reach its fullest and most varied extent.
Gemmæ are here formed in a sort of flat cup, by division of superficial cells of the thallus or of the stem, and they consist when mature of flattened masses of cells, which lie loose in the cup, so that wind or wet will carry them away on to soil or rock, when, either by direct growth from apical cells, as with those of the liverworts, or with previous emission of thread-like cells forming a "protonema," in the case of the mosses, the young plant is produced from them.
The lichens have a very peculiar method of gemmation. The lichen-thallus is composed of chains or groups of round chlorophyl-containing cells, called "gonidia," and masses of interwoven rows of elongated cells which constitute the hyphæ. Under certain conditions single cells of the gonidia become surrounded with a dense felt of hyphæ, these accumulate in numbers below the surface of the thallus, until at last they break out, are blown or washed away, and start germination by ordinary cell division, and thus at once reproduce a fresh lichen-thallus. These masses of cells are called soredia.
Artificial budding and grafting do not enter into the scope of this paper.
As in the general growth and the vegetative reproduction of plants cell-division is the chief method of cell formation, so in the reproduction of plants by special cells the great feature is the part played by cells which are produced not by the ordinary method of cell division, but by one or the other processes of cell formation, namely, free-cell formation or rejuvenescence.
If we broaden somewhat the definition of rejuvenescence and free-cell formation, and do not call the mother-cells of spores of mosses, higher cryptogams, and also the mother-cells of pollen-grains, reproductive cells, which strictly speaking they are not, but only producers of the spores or pollen-grains, then we may say that cell-division is confined to vegetative processes, rejuvenescence and free-cell formation are confined to reproductive processes.
Rejuvenescence may be defined as the rearrangement of the whole of the protoplasm of a cell into a new cell, which becomes free from the mother-cell, and may or may not secrete a cell-wall around it.
If instead of the whole protoplasm of the cell arranging itself into one mass, it divides into several, or if portions only of the protoplasm become marked out into new cells, in each case accompanied by rounding off and contraction, the new cells remaining free from one another, and usually each secreting a cell wall, then this process, whose relation to rejuvenescence is apparent, is called free-cell formation.
The only case of purely vegetative cell-formation which takes place by either of these processes is that of the formation of endosperm in Selaginella and phanerogams, which is a process of free-cell formation.
On the other hand, the universal contraction and rounding off of the protoplasm, and the formation by either rejuvenescence or free-cell formation, distinctly mark out the special or true reproductive cell.
Examples of reproductive cells formed by rejuvenescence are:
1. The swarm spores of many algæ, as Stigeoclonium (figured in Sachs' "Botany"). Here the contents of the cell contract, rearrange themselves, and burst the side of the containing wall, becoming free as a reproductive cell.
2. The zygoblasts of conjugating algæ, as in Spirogyra. Here the contents of a cell contract and rearrange themselves only after contact of the cell with one of another filament of the plant. This zygoblast only becomes free after the process of conjugation, as described below.
3. The oosphere of characeæ, mosses and liverworts, and vascular cryptogams, where in special structures produced by cell-divisions there arise single primordial cells, which divide into two portions, of which the upper portion dissolves or becomes mucilaginous, while the lower contracts and rearranges itself to form the oosphere.
4. Spores of mosses and liverworts, of vascular cryptogams, and pollen cells of phanerogams, which are the analogue of the spores.
The type in all these cases is this: A mother-cell produces by cell-division four daughter-cells. This is so far vegetative. Each daughter-cell contracts and becomes more or less rounded, secretes a wall of its own, and by the bursting or absorption of the wall of its mother-cell becomes free. This is evidently a rejuvenescence.
Examples of reproductive cells formed by free-cell formation are:
1. The ascospores of fungi and algæ.
2. The zoospores or mobile spores of many algæ and fungi.
3. The germinal vesicles of phanerogams.
The next portion of my subject is the study of the methods by which these special cells reproduce the plant.
1st. Asexual methods.
1. Rejuvenescence gives rise to a swarm-spore or zoospore. The whole of the protoplasm of a cell contracts, becomes rounded and rearranged, and escapes into the water, in which the plant floats as a mass of protoplasm, clear at one end and provided with cilia by which it is enabled to move, until after a time it comes to rest, and after secreting a wall forms a new plant by ordinary cell-division. Example: Oedogonium.
2. Free-cell formation forms swarm-spores which behave as above. Example: Achlya.
3. Free-cell formation forms the typical motionless spore of algæ and fungi. For instance, in the asci of lichens there are formed from a portion of the protoplasm four or more small ascospores, which secrete a cell-wall and lie loose in the ascus. Occasionally these spores may consist of two or more cells. They are set free by the rupture of the ascus, and germinate by putting out through their walls one or more filaments which branch and form the thallus of a new individual. Various other spores formed in the same way are known as tetraspores, etc.
4. Cell-division with rejuvenescence forms the spores of mosses and higher cryptogams.
To take the example of moss spores:
Certain cells in the sporogonium of a moss are called mother-cells. The protoplasm of each one of these becomes divided into four parts. Each of these parts then secretes a cell-wall and becomes free as a spore by the rupture or absorption of the wall of the mother-cell. The germination of the spores I shall describe later.
5. A process of budding which in the yeast plant and in mosses is merely vegetatively reproductive, in fungi becomes truly reproductive, namely, the buds are special cells arising from other special cells of the hyphæ.
For example, the so-called "gills" of the common mushroom have their surface composed of the ends of the threads of cells constituting the hyphæ. Some of these terminal cells push out a little finger of protoplasm, which swells, thickens its wall, and becomes detached from the mother-cell as a spore, here called specially a basidiospore.
Also in the common gray mould of infusions and preserves, Penicillium, by a process which is perhaps intermediate between budding and cell-division, a cell at the end of a hypha constricts itself in several places, and the constricted portions become separate as conidiospores.
Teleutospores, uredospores, etc., are other names for spores similarly formed.
These conidiospores sometimes at once develop hyphæ, and sometimes, as in the case of the potato fungus, they turn out their contents as a swarm-spore, which actively moves about and penetrates the potato leaves through the stomata before they come to rest and elongate into the hyphal form.
So far for asexual methods of reproduction.
I shall now consider the sexual methods.
The distinctive character of these methods is that the cell from which the new individual is derived is incapable of producing by division or otherwise that new individual without the aid of the protoplasm of another cell.
Why this should be we do not know; all that we can do is to guess that there is some physical or chemical want which is only supplied through the union of the two protoplasmic masses. The process is of benefit to the species to which the individuals belong, since it gives it a greater vigor and adaptability to varying conditions, for the separate peculiarities of two individuals due to climatic or other conditions are in the new generation combined in one individual.
The simplest of the sexual processes is conjugation. Here the two combining cells are apparently of precisely similar nature and structure. I say apparently, because if they are really alike it is difficult to see what is gained by the union.
Conjugation occurs in algæ and fungi. A typical case is that of Spirogyra. This is an alga with its cells in long filaments. Two contiguous cells of two parallel filaments push each a little projection from its cell-wall toward the other. When these meet, the protoplasm of each of the two cells contracts, and assumes an elliptical form--it undergoes rejuvenescence. Next an opening forms where the two cells are in contact, and the contents of one cell pass over into the other, where the two protoplasmic bodies coalesce, contract, and develop a cell-wall. The zygospore thus formed germinates after a long period and forms a new filament of cells.
Another example of conjugation is that of Pandorina, an alga allied to the well-known volvox. Here the conjugating cells swim free in water; they have no cell-wall, and move actively by cilia. Two out of a number approach, coalesce, contract, and secrete a cell-wall. After a long period of rest, this zygospore allows the whole of its contents to escape as a swarm-spore, which after a time secretes a gelatinous wall, and by division reproduces the sixteen-celled family.
We now come to fertilization, where the uniting cells are of two kinds.
The simplest case is that of Vaucheria, an alga. Here the vegetative filament puts out two protuberances, which become shut off from the body of the filament by partitions. The protoplasm in one of these protuberances arranges itself into a round mass--the oosphere or female cell. The protoplasm of the other protuberance divides into many small masses, furnished with cilia, the spermatozoids or male cells. Each protuberance bursts, and some of the spermatozoids come in contact with and are absorbed by the oosphere, which then secretes a cell-wall, and after a time germinates.
The most advanced type of fertilization is that of angiosperms.
In them there are these differences from the above process: the contents of the male cell, represented by the pollen, are not differentiated into spermatozoids, and there is no actual contact between the contents of the pollen tube and the germinal vesicle, but according to Strashurger, there is a transference of the substance of the nucleus of the pollen cell to that of the germinal vesicle by osmose. The coalescence of the two nuclei within the substance of the germinal vesicle causes the latter to secrete a wall, and to form a new plant by division, being nourished the while by the mother plant, from whose tissues the young embryo plant contained in the seed only becomes free when it is in an advanced stage of differentiation.
Perhaps the most remarkable cases of fertilization occur in the Florideæ or red seaweeds, to which class the well-known Irish moss belongs.
Here, instead of the cell which is fertilized by the rounded spermatozoid producing a new plant through the medium of spores, some other cell which is quite distinct from the primarily fertilized cell carries on the reproductive process.
If the allied group of the Coleochæteæ is considered together with the Florideæ, we find a transition between the ordinary case of Coleochæte and that of Dudresnaya. In Coleochæte, the male cell is a round spermatozoid, and the female cell an oosphere contained in the base of a cell which is elongated into an open and hair-like tube called the trichogyne. The spermatozoid coalesces with the oosphere, which secretes a wall, becomes surrounded with a covering of cells called a cystocarp, which springs from cells below the trichogyne, and after the whole structure falls from the parent plant, spores are developed from the oospore, and from them arises a new generation.
In Dudresnaya, on the other hand, the spermatozoid coalesces indeed with the trichogyne, but this does not develop further. From below the trichogyne, however, spring several branches, which run to the ends of adjacent branches, with the apical cells of which they conjugate, and the result of this conjugation is the development of a cystocarp similar to that of Coleochæte. The remarkable point here is the way in which the effect of the fertilizing process is carried from one cell to another entirely distinct from it.
Thus I have endeavored to sum up the processes of asexual and of sexual reproduction. But it is a peculiar characteristic of most classes of plants that the cycle of their existence is not complete until both methods of reproduction have been called into play, and that the structure produced by one method is entirely different from that produced by the other method.
Indeed, it is only in some algæ and fungi that the reproductive cells of one generation produce a generation similar to the parent; in all other plants a generation A produces are unlike generation B, which may either go on to produce another generation, C, and then back to A, or it may go on producing B's until one of these reproduces A, or again it may directly reproduce; A. Thus we have the three types:
1. A-B-C.--A-B-C.--A..................... etc. 2. A-B-B.--B-B...................B--A ... etc. 3. A B A B A............................. etc.
The first case is not common, the usual number of generations being two only; but a typical example of the occurrence of three generations is in such fungi as Puccinia Graminis. Here the first generation grows on barberry leaves, and produces a kind of spore called an æcidium spore. These æcidium spores germinate only on a grass stem or leaf, and a distinct generation is produced, having a particular kind of spore called an uredospore. The uredospore forms fresh generations of the same kind until the close of the summer, when the third generation with another kind of spore, called a teleutospore, is produced.
The teleutospores only germinate on barberry leaves, and there reproduce the original æcidium generation.
Thus we have the series A.B.B.B ... BCA
In this instance all the generations are asexual, but the most common case is for the sexual and the asexual generations to alternate. I will describe as examples the reproduction of a moss, a fern, and a dicotyledon.
In such a typical moss as Funaria, we have the following cycle of developments: The sexual generation is a dioecious leafy structure, having a central elongated axis, with leaves arranged regularly around and along it. At the top of the axis in the male plant rise the antheridia, surrounded by an envelope of modified leaves called the perigonium. The antheridia are stalked sacs, with a single wall of cells, and the spiral antherozoids arise by free-cell formation from the cells of the interior. They are discharged by the bursting of the antheridium, together with a mucilage formed of the degraded walls of their mother cells.
In the female plant there arise at the apex of the stem, surrounded by an envelope of ordinary leaves, several archegonia. These are of the ordinary type of those organs, namely, a broad lower portion, containing a naked oosphere and a long narrow neck with a central canal leading to the oosphere. Down this canal pass one or more antherozoids, which become absorbed into the oosphere, and this then secretes a wall, and from it grows the second or asexual generation. The peculiarity of this asexual or spore-bearing plant is that it is parasitic on the sexual plant; the two generations, although not organically connected, yet remain in close contact, and the spore-bearing generation is at all events for a time nourished by the leafy sexual generation.
The spore-bearing generation consists of a long stalk, closely held below by the cells of the base of the archegonium; this supports a broadened portion which contains the spores, and the top is covered with the remains of the neck of the archegonium forming the calyptra.
The spores arise from special or mother-cells by a process of division, or it may be even termed free-cell formation, the protoplasm of each mother-cell dividing into four parts, each of which contracts, secretes a wall, and thus by rejuvenescence becomes a spore, and by the absorption of the mother-cells the spores lie loose in the spore sac. The spores are set free by the bursting of their chamber, and each germinates, putting out a branched thread of cells called a protonema, which may perhaps properly be termed a third generation in the cycle of the plant; for it is only from buds developed on this protonema that the leafy sexual plant arises.
The characteristics, then, of the mosses are, that the sexual generation is leafy, the one or two asexual generations are thalloid, and that the spore-bearing generation is in parasitic connection with the sexual generation.
In the case of the fern, these conditions are very different.
The sexual generation is a small green thalloid structure called a prothallium, which bears antheridia and archegonia, each archegonium having a neck-canal and oosphere, which is fertilized just as in the moss.
But the asexual generation derived from the oospore only for a short while remains in connection with the prothallium, which, of course, answers to the leafy portion of the moss. What is generally known as the fern is this asexual generation, a great contrast to the small leafless moss fruit or sporogonium as it is called, to which it is morphologically equivalent. On the leaves of this generation arise the sporangia which contain the spores. The spores are formed in a manner very similar to those of the mosses, and are set free by rupture of the sporangium.
The spore produces the small green prothallium by cell-division in the usual way, and this completes the cycle of fern life.
The alternation of generations, which is perhaps most clear and typical in the case of the fern, becomes less distinctly marked in the plants of higher organization and type.
Thus in the Rhizocarpæ there are two kinds of spores, microspores and macrospores, producing prothallia which bear respectively antheridia and archegonia; in the Lycopodiaceæ, the two kinds of spores produce very rudimentary prothallia; in the cycads and conifers, the microspore or pollen grain only divides once or twice, just indicating a prothallium, and no antheridia or antherozoids are formed. The macrospore or embryo-sac produces a prothallium called the endosperm, in which archegonia or corpuscula are formed; and lastly, in typical dicotyledons it is only lately that any trace of a prothallium from the microspore or pollen cell has been discovered, while the macrospore or embryo-sac produces only two or three prothallium cells, known as antipodal cells, and two or three oospheres, known as germinal vesicles.
This description of the analogies of the pollen and embryo-sac of dicotyledons assumes that the general vegetative structure of this class of plants is equivalent to the asexual generation of the higher cryptogams. In describing their cycle of reproduction I will endeavor to show grounds for this assumption.
We start with the embryo as contained in the seed. This embryo is the product of fertilization of a germinal vesicle by a pollen tube. Hence, by analogy with the product of fertilization of rhizocarp's, ferns, and mosses, it should develop into a spore bearing plant. It does develop into a plant in which on certain modified leaves are produced masses of tissue in which two kinds of special reproductive cells are formed. This is precisely analogous to the case of gymnosperms, lycopods, etc., where on leaf structures are formed macro and micro sporangia.
To deal first with the microsporangium or pollen-sac. The pollen cells are formed from mother cells by a process of cell division and subsequent setting free of the daughter cells or pollen cells by rejuvenescence, which is distinctly comparable with that of the formation of the microspores of Lycopodiaceæ, etc. The subsequent behavior of the pollen cell, its division and its fertilization of the germinal vesicle or oosphere, leave no doubt as to its analogy with the microspore of vascular cryptogams.
Secondly, the nucleus of the ovule corresponds with the macrosporangium of Selaginella, through the connecting link of the conifers, where the ovule is of similar origin and position to the macrosporangium of the Lycopodiaceæ. But the formation of the macrospore or embryo-sac is simpler than the corresponding process in cryptogams. It arises by a simple enlargement of one cell of the nucleus instead of by the division of one cell into four, each thus becoming a macrospore. At the top of this macrospore or embryo-sac two or three germinal vesicles are formed by free cell formation, and also two or three cells called antipodal cells, since they travel to the other end of the embryo-sac; these latter represent a rudimentary prothallium. This formation of germinal vesicles and prothallium seems very different from the formation of archegonia and prothallium in Selaginella, for instance; but the link which connects the two is in the gymnosperms, where distinct archegonia in a prothallium are formed.
Thus we see that the flowering plant is essentially the equivalent of the asexual fern, and of the sporogonium of the moss, and the pollen cell and the embryo-sac represent the two spores of the higher cryptogams, and the pollen tube and the germinal vesicles and antipodal cells are all that remain of the sexual generation, seen in the moss as a leafy plant, and in the fern as a prothallium. Indeed, when a plant has monoecious or dioecious flowers, the distinction between the asexual and the sexual generation has practically been lost, and the spore-bearing generation has become identified with the sexual generation.
Having now described the formation of the pollen and the germinal vesicles, it only remains to show how they form the embryo. The pollen cell forms two or three divisions, which are either permanent or soon absorbed; this, as before stated, is the rudimentary male prothallium. Then when it lies on the stigma it develops a long tube, which passes down the style and through the micropyle of the ovule to the germinal vesicles, one of which is fertilized by what is probably an osmotic transference of nuclear matter. The germinal vesicle now secretes a wall, divides into two parts, and while the rest of the embyro-sac fills with endosperm cells, it produces by cell division from the upper half a short row of cells termed a suspensor, and from the lower half a mass of cells constituting the embryo. Thus while in the moss the asexual generation or sporogonium is nourished by the sexual generation or leafy plant, and while in the fern each generation is an independent structure, here in the dicotyledon, on the other hand, the asexual generation or embryo is again for a time nourished in the interior of the embryo-sac representing the sexual generation, and this again derives its nourishment from the previous asexual generation, so that as in the moss, there is again a partial parasitism of one generation on the other.
To sum up the methods of plant reproduction: They resolve themselves into two classes.
1st. Purely vegetative.
2d. Truly reproductive by special cells.
In the second class, if we count conjugation as a simple form of fertilization, there are only two types of reproductive methods.
1st. Reproduction from an asexual spore.
2d. Reproduction from an oospore formed by the combination of two sexual cells.
In the vast majority of plant species these two types are used by the individuals alternately.
The extraordinary similarity of the reproductive process, as shown in the examples I have given, Achlya, Spirogyra, and Vaucheria among algæ, the moss, the fern, and the flowering plant, a similarity which becomes the more marked the more the details of each case and of the cases of plants which form links between these great classes are studied, points to a community of origin of all plants in some few or one primeval ancestor. And to this inference the study of plant structure and morphology, together with the evidence of palæobotany among other circumstances, lends confirmatory evidence, and all modern discoveries, as for instance that of the rudimentary prothallium formed by the pollen of angiosperms, tend to the smoothing of the path by which the descent of the higher plants from simpler types will, as I think, be eventually shown.
A catalogue, containing brief notices of many important scientific papers heretofore published in the SUPPLEMENT, may be had gratis at this office.
Terms of Subscription, $5 a Year.
Sent by mail, postage prepaid, to subscribers in any part of the United States or Canada. Six dollars a year, sent, prepaid, to any foreign country.
All the back numbers of THE SUPPLEMENT, from the commencement, January 1, 1876, can be had. Price, 10 cents each.
All the back volumes of THE SUPPLEMENT can likewise be supplied. Two volumes are issued yearly. Price of each volume, $2.50, stitched in paper, or $3.50, bound in stiff covers.
COMBINED RATES--One copy of SCIENTIFIC AMERICAN and one copy of SCIENTIFIC AMERICAN SUPPLEMENT, one year, postpaid, $7.00.
A liberal discount to booksellers, news agents, and canvassers.
MUNN & CO., Publishers,
361 Broadway, New York, N. Y.
In connection with the Scientific American, Messrs. MUNN & Co. are Solicitors of American and Foreign Patents, have had 42 years' experience, and now have the largest establishment in the world. Patents are obtained on the best terms.
A special notice is made in the Scientific American of all Inventions patented through this Agency, with the name and residence of the Patentee. By the immense circulation thus given, public attention is directed to the merits of the new patent, and sales or introduction often easily effected.
Any person who has made a new discovery or invention can ascertain, free of charge, whether a patent can probably be obtained, by writing to MUNN & Co.
We also send free our Hand Book about the Patent Laws, Patents, Caveats, Trade Marks, their costs, and how procured. Address
MUNN & CO., 361 Broadway, New York.
Branch Office, 622 and 624 F St., Washington, D.C.
End of the Project Gutenberg EBook of Scientific American Supplement, Vol.
XXI., No. 531, March 6, 1886, by Various
*** END OF THIS PROJECT GUTENBERG EBOOK SCIENTIFIC AMERICAN SUPP. 531 ***
***** This file should be named 11383-h.htm or 11383-h.zip *****
This and all associated files of various formats will be found in:
https://www.gutenberg.org/1/1/3/8/11383/
Produced by Produced by Josephine Paolucci, Don Kretz, Juliet Sutherland,
Charles Franks and the DP Team
Updated editions will replace the previous one--the old editions
will be renamed.
Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties. Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark. Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission. If you
do not charge anything for copies of this eBook, complying with the
rules is very easy. You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research. They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks. Redistribution is
subject to the trademark license, especially commercial
redistribution.
*** START: FULL LICENSE ***
THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK
To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
https://gutenberg.org/license).
Section 1. General Terms of Use and Redistributing Project Gutenberg-tm
electronic works
1.A. By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement. If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.
1.B. "Project Gutenberg" is a registered trademark. It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement. There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement. See
paragraph 1.C below. There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works. See paragraph 1.E below.
1.C. The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works. Nearly all the individual works in the
collection are in the public domain in the United States. If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed. Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work. You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.
1.D. The copyright laws of the place where you are located also govern
what you can do with this work. Copyright laws in most countries are in
a constant state of change. If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work. The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.
1.E. Unless you have removed all references to Project Gutenberg:
1.E.1. The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:
This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever. You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org
1.E.2. If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges. If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.
1.E.3. If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder. Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.
1.E.4. Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.
1.E.5. Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.
1.E.6. You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form. However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form. Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.
1.E.7. Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.
1.E.8. You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that
- You pay a royalty fee of 20% of the gross profits you derive from
the use of Project Gutenberg-tm works calculated using the method
you already use to calculate your applicable taxes. The fee is
owed to the owner of the Project Gutenberg-tm trademark, but he
has agreed to donate royalties under this paragraph to the
Project Gutenberg Literary Archive Foundation. Royalty payments
must be paid within 60 days following each date on which you
prepare (or are legally required to prepare) your periodic tax
returns. Royalty payments should be clearly marked as such and
sent to the Project Gutenberg Literary Archive Foundation at the
address specified in Section 4, "Information about donations to
the Project Gutenberg Literary Archive Foundation."
- You provide a full refund of any money paid by a user who notifies
you in writing (or by e-mail) within 30 days of receipt that s/he
does not agree to the terms of the full Project Gutenberg-tm
License. You must require such a user to return or
destroy all copies of the works possessed in a physical medium
and discontinue all use of and all access to other copies of
Project Gutenberg-tm works.
- You provide, in accordance with paragraph 1.F.3, a full refund of any
money paid for a work or a replacement copy, if a defect in the
electronic work is discovered and reported to you within 90 days
of receipt of the work.
- You comply with all other terms of this agreement for free
distribution of Project Gutenberg-tm works.
1.E.9. If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark. Contact the
Foundation as set forth in Section 3 below.
1.F.
1.F.1. Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection. Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.
1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH F3. YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.
1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from. If you
received the work on a physical medium, you must return the medium with
your written explanation. The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund. If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund. If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.
1.F.4. Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS' WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.
1.F.5. Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law. The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.
1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.
Section 2. Information about the Mission of Project Gutenberg-tm
Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers. It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.
Volunteers and financial support to provide volunteers with the
assistance they need, is critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come. In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at https://www.pglaf.org.
Section 3. Information about the Project Gutenberg Literary Archive
Foundation
The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service. The Foundation's EIN or federal tax identification
number is 64-6221541. Its 501(c)(3) letter is posted at
https://pglaf.org/fundraising. Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.
The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations. Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
business@pglaf.org. Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at https://pglaf.org
For additional contact information:
Dr. Gregory B. Newby
Chief Executive and Director
gbnewby@pglaf.org
Section 4. Information about Donations to the Project Gutenberg
Literary Archive Foundation
Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment. Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.
The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States. Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements. We do not solicit donations in locations
where we have not received written confirmation of compliance. To
SEND DONATIONS or determine the status of compliance for any
particular state visit https://pglaf.org
While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.
International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States. U.S. laws alone swamp our small staff.
Please check the Project Gutenberg Web pages for current donation
methods and addresses. Donations are accepted in a number of other
ways including including checks, online payments and credit card
donations. To donate, please visit: https://pglaf.org/donate
Section 5. General Information About Project Gutenberg-tm electronic
works.
Professor Michael S. Hart was the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone. For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.
Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included. Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.
Each eBook is in a subdirectory of the same number as the eBook's
eBook number, often in several formats including plain vanilla ASCII,
compressed (zipped), HTML and others.
Corrected EDITIONS of our eBooks replace the old file and take over
the old filename and etext number. The replaced older file is renamed.
VERSIONS based on separate sources are treated as new eBooks receiving
new filenames and etext numbers.
Most people start at our Web site which has the main PG search facility:
https://www.gutenberg.org
This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.
EBooks posted prior to November 2003, with eBook numbers BELOW #10000,
are filed in directories based on their release date. If you want to
download any of these eBooks directly, rather than using the regular
search system you may utilize the following addresses and just
download by the etext year.
https://www.gutenberg.org/etext06
(Or /etext 05, 04, 03, 02, 01, 00, 99,
98, 97, 96, 95, 94, 93, 92, 92, 91 or 90)
EBooks posted since November 2003, with etext numbers OVER #10000, are
filed in a different way. The year of a release date is no longer part
of the directory path. The path is based on the etext number (which is
identical to the filename). The path to the file is made up of single
digits corresponding to all but the last digit in the filename. For
example an eBook of filename 10234 would be found at:
https://www.gutenberg.org/1/0/2/3/10234
or filename 24689 would be found at:
https://www.gutenberg.org/2/4/6/8/24689
An alternative method of locating eBooks:
https://www.gutenberg.org/GUTINDEX.ALL