[403]
AMERICAN SOCIETY OF CIVIL ENGINEERS
INSTITUTED 1852
TRANSACTIONS
Paper No. 1192
EXPERIMENTS ON RETAINING WALLS AND PRESSURES ON TUNNELS.
The most extended experiments relating to retaining walls are those pertaining to retaining walls proper and the more elaborate ones on small rotating retaining boards. The results referring to the former agree fairly well with a rational theory, especially when the walls are several feet in height; but with the latter, many discrepancies occur, for which, hitherto, no explanation has been offered.
It will be the main object of this paper to show that the results of these experiments on small retaining boards can be harmonized with theory by including the influence of cohesion, which is neglected in deducing practical formulas. It will be found that the influence of cohesion is marked, because of the small size of the boards. This information should prove of value to future experimenters, for it will be shown that, as the height of the board or wall increases, the influence of cohesion becomes less and less, so that (for the usual dry sand filling) for heights, say, from 5 to 10 ft., it can be neglected altogether.
The result of the investigation will then be to give to the practical constructor more confidence in the theory of the sliding prism, which serves as the basis of the methods to follow.
[404]
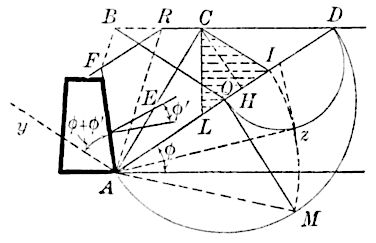
As, in the course of this investigation, certain well-known constructions
for ascertaining the pressure of any granular material
against retaining walls will be needed, it is well to group them here.
The various figures are supposed to represent sections at right angles
to the inner faces of the walls with their backings of granular material.
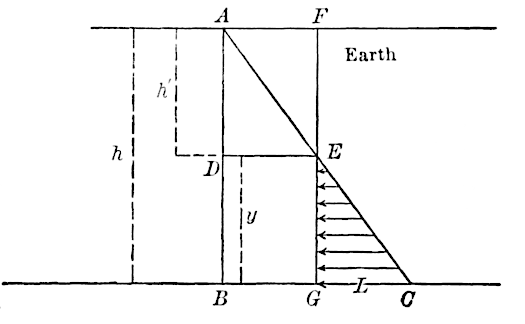
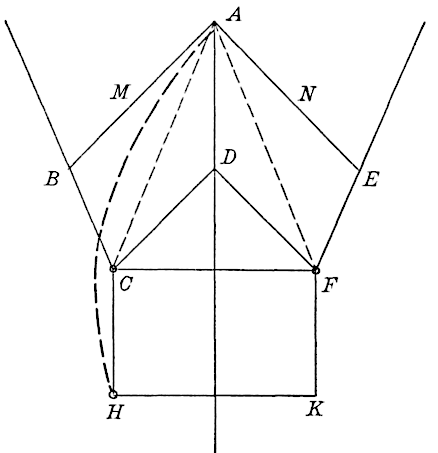
In the surcharged wall, Fig. 1, produce the inner face of the wall to
meet the surface of the surcharge at . It is desired to find the
thrust against the plane,
, for 1 lin. ft. of the wall. Draw
through
, the foot of the wall, making the angle of repose,
, of the
earth with the horizontal and meeting the upper surface at
. Since
any possible prism of rupture, as
, in tending to move downward,
develops friction against both surfaces,
and
, the earth
thrust on the wall will make an angle,
, with the normal to
,
where
is the angle of friction of the earth on the wall. As the earth
settles more than the wall, this friction
will always be exerted. Again,
as the wall, from its elasticity and
that of the foundation, will tend to
move over at the top on account of
the earth thrust, the earth, with its
frictional grip on the wall, will tend
to prevent this, so that the friction is
exerted downward in either case, and the direction of the earth thrust,
, on
is as given in Fig. 1.
However, if , a thin slice of earth will move with the wall,
and the rubbing will be that of earth on earth, so that
in this case
must be replaced by
. This rule will apply in all cases that follow,
without further remark, wherever
is mentioned.
Now draw , making the angle,
, with
, as shown; then
draw
parallel to
, to the intersection,
, with
produced.
From
a parallel to
is constructed, meeting
at
.
Since theory gives the relation: , two constructions follow, by geometry,
for locating the point,
. By the first, a
semicircle is described on
as a diameter; at the point,
, a perpendicular
is erected to
, meeting the semicircle in
; then
is
laid off equal to the chord,
. By the second construction, a semicircle
is described on
as a diameter, a tangent to it,
, from
is drawn,
limited by the perpendicular radius, and finally
is laid off
equal to
.
[405]
The point, , having been thus found by either construction, draw
parallel to
to the intersection,
, with
.
is the plane of
rupture. On laying off
, and dropping the perpendicular,
,
from
on
, the earth pressure,
, on
is given by
,
where
is the weight of a cubic unit of the earth; otherwise, the value
of
is given by
times the area of the shaded triangle,
. If the
dimensions are in feet, and
is in pounds per cubic foot, the thrust,
,
will be given in pounds.
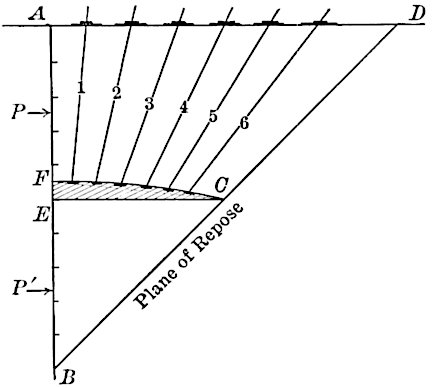
In Figs. 2 and 3, the retaining boards, , are vertical, and
is drawn, making the angle,
, with the vertical,
. The
upper surface of the earth is
, and the constructions for locating
and
are the same as for Fig. 1.
, in all the figures, represents
the plane of rupture.[Footnote 1]
In all cases, the earth thrust found as above
is supposed to make the angle,
(as shown), with the normal to the
inner wall surface.
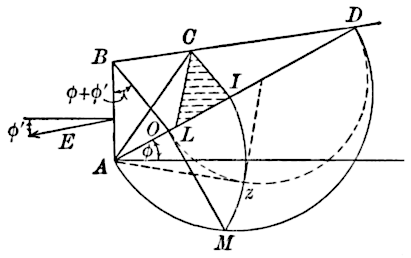
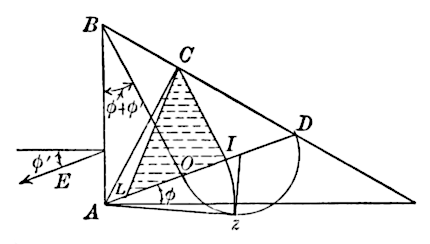
In the Rankine theory, pertaining, say, to Fig. 2, the earth thrust
on a vertical plane, , is always taken as acting parallel to the top
slope. This is true for the pressure on a vertical plane in the
interior of a mass of earth of indefinite extent, but it is not true
generally for the pressure against a retaining wall. Thus, when
,
Fig. 2, is horizontal, Rankine’s thrust on
would be taken as horizontal,
which entirely ignores the friction of the earth on the wall.
The two theories agree when
and
slopes at the angle of
repose, in which case, as
is parallel to
, there is no intersection,
. It is a limiting case in which, to compute the thrust,
can be
laid off from any point in
, on drawing
parallel to
, etc. As
approaches the natural slope, the point,
, recedes indefinitely to
[406]
the right, and it is seen that the plane of rupture,
, approaches
indefinitely the line,
, or the natural slope. This limiting case,
on account of the excessive thrust corresponding, will be examined
more carefully in the sequel.
If the height of the wall,
, in feet, and
the weight of
a cubic foot of earth, in pounds, then when
, and the surface
, Fig. 2, slopes at the angle of repose, the earth thrust, in pounds,
is given by the equation:
If, however, is not equal to
, then
is directed at the angle,
, to the normal to the wall, and the thrust is:
The foregoing constructions, and the corresponding equations, are
all derived from the theory of the sliding prism. The wedge, ,
Figs. 2 and 3, is treated as an invariable solid, tending to slide down
the two faces,
and
, at once, thus developing the full friction
that can be exerted on these faces. In the case of actual rotation of
the board,
, it is found by experiment that each particle of earth
in the prism,
, moves parallel to
, each layer parallel to
moving over the layer just beneath it.
A similar motion is observed if the board, , is moved horizontally
to the left. However, in the first case (of rotation) the
particles at
do not move at all, whereas in the second (of sliding
motion) the particles about
move, rubbing over the floor, which thus
resists the motion by friction. A thrust, thus recorded by springs or
other device, in the case where the wall moves horizontally, would
give an undervaluation at the lower part of
and consequently the
computed center of pressure on
would be too high. On that
account, only the experiments on rotating boards will be considered in
this paper.
The theory of the sliding wedge, however, is justified, because no
motion of either kind is actually supposed. The wedge, , is supposed
to be just on the point of motion, it being in equilibrium under
the action of its weight, the normal components of the reactions of the
wall, and the plane,
, and all the friction that can be exerted along
and
. These forces remain the same, whatever incipient motion
[407]
is supposed. The hypothesis of a plane surface of rupture, however, is
not exactly realized, experiment showing that the earth breaks along a
slightly curved surface convex to the moving mass. For the sake of
simplicity, the theory neglects the cohesion acting, not only along
, but possibly to a small extent along
. This additional force
will be included in certain investigations to be given later.
These preliminary observations having been disposed of, the results of certain experiments on retaining walls at the limit of stability will now be given.

Figs. 4, 5, 6, and 7 refer to vertical rectangular walls backed by
sand, except in the case of Fig. 5, where the filling was macadam
screenings. The surface of the filling was horizontal in each case.
To give briefly in detail the quantities pertaining to each wall, the
following symbols will be used:
and
are positive when the resultant on the base strikes within
the base, otherwise they are negative.
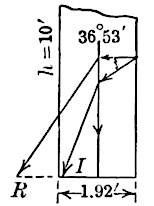
Fig. 4 represents Lieut. Hope’s wall of bricks laid in wet sand:
,
,
,
,
. It was
20 ft. long, and was backed by earth level with its top.
,
. The overhang, at the moment of failure, was probably
4 in. Including this,
.
[408]
Fig. 5 shows Baker’s wall of pitch-pine blocks, backed by macadam
screenings, the level surface of which was 0.25 ft. below the top of
the wall; ,
,
,
,
,
,
the assumed angle of friction of timber on stone,
,
.
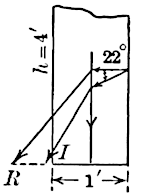
Trautwine’s experimental wall is shown in Fig. 6. Only the ratio
of base to height, 0.35, was given by the author, but J. C. Trautwine,
Jr., Assoc. Am. Soc. C. E., assures the writer that the walls were
probably 6 in. in height, though certain notes refer to walls varying
from about 4 to 9 in. ,
,
,
(assumed)
,
,
.
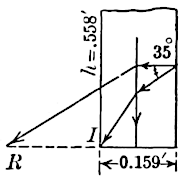
The wall of Curie, Fig. 7, was of wood coated on the back by sand,
so that . Also,
ft.,
ft.,
,
,
.
These walls were all at the limit of stability, and the first two are of appreciable height, 10 ft. and 4 ft., respectively.
The figures show that the theory, including
the whole of the wall friction,
agrees fairly well with experiment, but
that the Rankine theory does not thus
agree. In both theories, the thrust, , is
supposed to act at one-third of the height
from the base of the wall to the surface of
the filling; but, in the Rankine theory, this thrust is assumed to act
horizontally, whereas, in the other theory, it is supposed to act in a
direction making the angle,
, below the normal to the wall.
On combining the thrusts with the weight of the wall, as usual,
the resultant strikes the base produced, at in the first case (Rankine
theory), but at
in the second case. Figs. 4 to 7 present a striking
object lesson as to the inaccuracy of the Rankine method of treating
experimental retaining walls.
In the next experiments, however, referring to a retaining structure
consisting of two boards, hinged at the top, Fig. 8, and backed by sand
level at the top, the Rankine theory is applicable when the board, ,
is placed either at or below the plane of rupture, on the left of
.
The thrust on
is then assumed to act horizontally, at
above
, and is combined with the weight of the sand,
, to find the
[409]
resultant on the board. If the board is at the plane of rupture, this
resultant will make the angle
below the normal to
; hence, if
one assumes a less thrust on
, especially if inclined downward, the
new resultant on
will make an angle greater than
with the
normal to
, which is inconsistent with stability.[Footnote 2]
The same reasoning
applies when
lies below the plane of rupture.[Footnote 3]
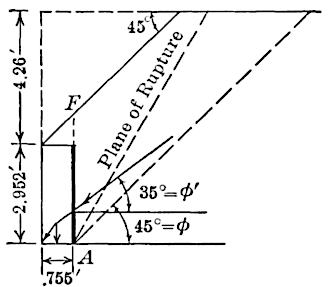
The retaining board, 1 m. square, was coated with sand, so that
for damp sand. Hence, for a horizontal thrust on
,
the plane of rupture (which bisects the angle between the vertical and
the natural slope) makes an angle of
with the vertical. The
board,
, was set at this angle to the vertical, sand was filled in level
with the top, and it was found that the structure was at the limit of
stability when
m. In the meantime, however, the sand had
dried out, so that
was
; hence,
strictly, the construction of Fig. 1 (for
earth level with top of wall) applies; but,
as the results can only differ inappreciably,
the thrust on
, acting horizontally, was
computed for
and combined
with the weight of sand,
, and the
weight of structure, both acting through
their centers of gravity, to find the resultant
on the base,
. It was found to cut it 0.11 of its width
from the outer toe,
; therefore
.
In the next experiment, the angle, , was 55°,
m.
and
. Pursuing the same method, it is found that
,
or the resultant on the base passes practically through
. The third
experiment was on a smaller retaining board. Here
m.,
,
, and
.
In Fig. 9 is shown a surcharged wall of Curie’s, just at the limit
of stability, having ft.,
ft. and the level upper
surface of the surcharge being 4.26 ft. above the top of the wall. The
surcharge extended over the wall at the angle,
, corresponding
to damp sand. Experiment gave
. The wall was of brick in
Portland cement. The ratio,
. It was found, using the
[410]
construction of Fig. 1, that taking the thrust,
, as acting 1.24 ft.
above the base, or at one-third of the height of the surface,
, that
; and further, that if
acts 1.303 ft. above the base, the
resultant on the base passes exactly through the outer toe of the wall.
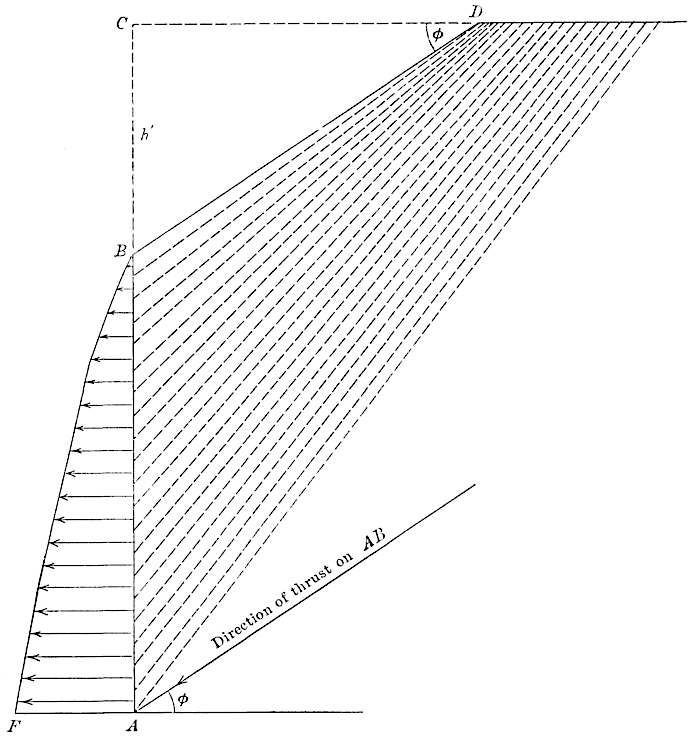
As the true position of the center of pressure on a surcharged wall has never been ascertained, as far as the writer knows, he has made a number of constructions, after the method illustrated in Fig. 1, in order to find it.
In place of making the construction for the special case above, it
was thought that the results would be more generally useful if the
natural slope was taken with a base of 3 and a rise of 2, and ,
therefore
. The wall,
, Fig. 10, was taken
vertical and 20 ft. high. The surcharge sloped from
at the angle
[411]
of repose to a point,
, 10 ft. above
, from which point the surface
of the earth was horizontal. The face of the wall,
, was divided
into twenty equal parts, 1 ft. each; and, by the construction of Fig. 1,
the thrusts (inclined at the angle,
, below the normal to the wall)
were found for the successive heights of wall of 1, 2, 3, ... 20, ft.,
respectively, taking the weight of 1 cu. ft. of earth equal to unity.
The successive planes of rupture are shown by the dotted lines in
Fig. 10. On the original scale (2 ft. to 1 in.), the upper plane of
rupture (for a height of wall = 1 ft.) was found to pass slightly to
the right of
.
On subtracting successive thrusts, the thrusts on each foot of wall were obtained. These were plotted as horizontal ordinates at the center of each foot division of the wall, and the “peaks” were slightly rounded off, as shown on the figure. Since, with all care, mistakes amounting to 1% of the total thrusts can easily be made, it was proper to adjust the results in this manner to give the most probable unit pressures on the successive divisions of the wall. The centers of pressure, for heights of the wall varying from 5 to 20 ft., were easily obtained by taking moments about some convenient point; the results are given in Table 1.
Call the height of wall, measured from
downward, and
, the height of surcharge above the top of the wall; also, let
the ratio of the distance from the foot of the wall considered to
the center of pressure, to the height of the wall. The values of
, for
various ratios,
, are given in Table 1.
| 0.333 | 1.00 | 0.364 | |
| ... | ... | 0.75 | 0.364 |
| 2.00 | 0.353 | 0.50 | 0.364 |
| 1.50 | 0.356 | ... | ... |
| 1.25 | 0.360 | 0.00 | 0.333 |
| 1.11 | 0.362 |
It is seen, as diminishes, that
increases, until for
, the
maximum value for
, 0.364, is attained and remains the same up to
, after which it probably diminishes, because, for
,
.
[412]
When some other flatter slope is given to , doubtless these
values of
will be altered, but, for the case supposed, they should prove
serviceable in practice.
Although the earth thrusts on successive portions of are
really inclined at
below the normal to
, they are laid off here
at right angles to it, so that the area,
, is equal to the total
thrust on
. If the unit pressures varied as the ordinates to the
straight line,
, as for a uniformly sloping earth surface, then, as is
well known,
. The area to the left of
gives the excess thrust
which causes
to exceed
.
Making use of the results of the table as approximately applicable
in the foregoing example (Fig. 9), and taking the center of pressure
on as
above the base, the resultant there is found to
pass 0.02 outside of the base, therefore
. This experiment
on a surcharged wall, of the kind shown, is particularly valuable as
being the only one of which any account has been given, as far as
the writer knows.
Recurring once more to Fig. 10, it may be recalled that some
authors have assumed the unit pressures on to vary as the ordinates
to a trapezoid, so that the unit pressure at
was not zero (as it
should be), but an amount assumed somewhat arbitrarily. In particular,
Scheffler derived in this way
as an upper practical limit,
and used it in making tables for use in practice.
A remark must now be added (relative to all the experimental walls previously mentioned, except Trautwine’s), that the friction of the backing on the sides of the box in which the sand was contained has been uniformly neglected. Where the wall is long, this can have little influence, but where the length is not much greater than the height, as in the experiments, this side friction becomes appreciable.
Darwin, as well as Leygue, endeavored to estimate the amount the full thrust (with no side friction) was reduced, by experimenting with sand behind a retaining board, or wall, enclosed in a box as usual, when a partition board was placed perpendicular to the wall and centrally in the mass, and comparing results with those found when the partition board was omitted. Leygue thus found, for walls having a length of twice the height, that the true or full thrust was diminished about 5% from the side friction, for level-topped earth, and as much as 15% for the surface sloping at the angle of repose. [413] If this is true, then the experimental walls just considered would have to be thicker to withstand the actual thrust; or, to put it another way, for the given thickness, the theoretical thrust, including the side friction, would have to be made (as a rough average) about 5% less for the level-topped earth and (roughly) 15% less for the earth sloping at the angle of repose. From the figures it is seen that this will modify the results but slightly, not enough to alter the general conclusion that the theory advocated (including the wall friction) is practically sustained by the experiments, and that the Rankine theory is not thus sustained.
Trautwine’s wall consisted of a central portion of uniform height, from which it tapered to the ends, the upper surface being at the angle of repose for the tapered ends. In this case no side friction was developed. The results agree in a general way with the others.
In the many experiments on high grain bins, the enormous influence of the friction of the grain against the vertical walls or sides of the bin has been observed. In fact, the greater part of the weight of grain, even when running out, is sustained by the walls through this side friction. This furnishes another argument for including wall friction in retaining-wall design.
In connection with this subject, it may be observed that many experiments, made to determine the actual lateral pressure of sand or its internal friction angle, are inconclusive, because an unknown part of the vertical pressure applied to the sand in the vertical cylinder or box was sustained by the sides of the cylinder or box. The ratio of lateral to vertical pressures, or the friction angle, cannot be precisely found until the proportion of the load sustained by the sides of the containing vessel has been ascertained experimentally. The writer is of the opinion that the best experiments to aid in the design of retaining walls are those relating to the rotation of retaining walls or boards. The few given herein are the best recorded, though some of them were on models which were too small. In fact, for the small models of Leygue and others, the effect of cohesion is so pronounced that some of the results are very misleading.
As the experiments by Leygue[Footnote 4] were very extensive, and evidently made with great care, they will be considered carefully in what follows.
[414]
As preliminary to the discussion, however, it is well to give the
essentials of Leygue’s experimental proof that cohesion and friction
exist at the same time. A box without a bottom, about 4 in. square
in cross-section and 4 in. high, was made into a little carriage by the
addition of four wheels. The latter ran on the sides of a trough
filled with sand which the bottom of the box nearly touched. The
box was partly filled with sand, and the trough and box were then
inclined at the angle at which motion of the box just began, the
sand in the box resting on the sand in the trough, developing friction
or cohesion or both, just before motion began. Only friction
was exerted after motion began. The solution involves the theory of
the inclined plane, but, to explain the principles of the method,
it will suffice to suppose the trough and the sand in it to be horizontal,
and that the bottomless box filled with sand is just on the
point of moving, due to a horizontal force applied to it. The weight
of the box and a part of the weight of the sand in it held up by
the friction of the sides, is directly supported by the wheels resting
on the sides of the trough; so that only a fraction of the weight, ,
of the sand in the box is supported directly by the sand in the trough.
Call this amount
. Then, for equilibrium, calling
the horizontal force, less the resistance of the carriage wheels, we have,[Footnote 5]
The value of was found by weighing: For the dry sand it varied
from 0.79 to 0.65, for heights of the sand in the box varying from
1.2 to 3.5 in. For the damp sand and fresh earth (slightly moistened
and slightly rammed) which can stand with a vertical face for the
height of the box, the filling was loosened by many blows on the box,
and
was taken equal to 1.
Three suppositions were made: (1) that both cohesion and friction
acted at the same time before motion; (2) that friction alone acted
(); (3) that cohesion alone acted (
).
[415]
The results for various heights of sand in the box are given in
Table 2.
| (1) | (2) | (3) | ||
|---|---|---|---|---|
| Dry sand | 7 | 0.70 | 0.80 to 0.96 | 26 to 56 |
| Wet sand | 40 | 0.85 | 1.20 " 1.90 | 73 " 133 |
| Very wet sand | 31 | 1.70 | 2.00 " 2.40 | 107 " 226 |
| Fresh earth | 90 | 1.63 | 2.60 " 4.40 | 150 " 242 |
The values of are given in kilogrammes per square meter. It
is seen that suppositions (2) and (3) give discordant results, whereas
(1), for each kind of filling, gave identical values of
and of
for
various heights; hence it may fairly be concluded that, before motion,
cohesion and friction both acted at the same time. As to the high
values found for
, for the coherent fresh earth, Leygue states that
Collin found, by an independent method, for clayey earth and clay
of little consistency,
and
, respectively. As a further
verification of the values of
and
given in (1), it is found that,
on using them in the formula for computing the height at which
the wet sand or earth will stand vertically, the results agree with
experiments.
The values of , in pounds per square foot, given in Column (1),
with the values of
corresponding to the
given, are as follows:
It is possible that the method used by Leygue may prove of service to experimenters in obtaining more accurately than hitherto the coefficient of internal friction. Increasing pressures could be obtained by adding weights on top of the sand in the box; but, unless the total weight sustained by friction along the sides of the box is determined carefully for each weight used, the results can have but little value. Further, for coherent earths, the method of Leygue is open to objections.
[416]
Admitting the hypothesis that cohesion and friction act at the same
time, a general graphical method[Footnote 6]
will now be given to find the thrust
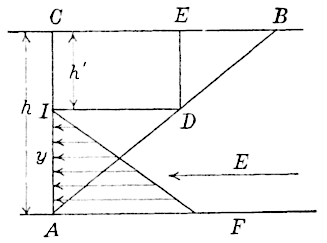
against the inner face, , of a retaining wall or board, Fig. 11,
caused by the earth,
, tending to slide down some plane of
rupture,
,
, ..., the resistance along this plane being due
both to friction and cohesion.
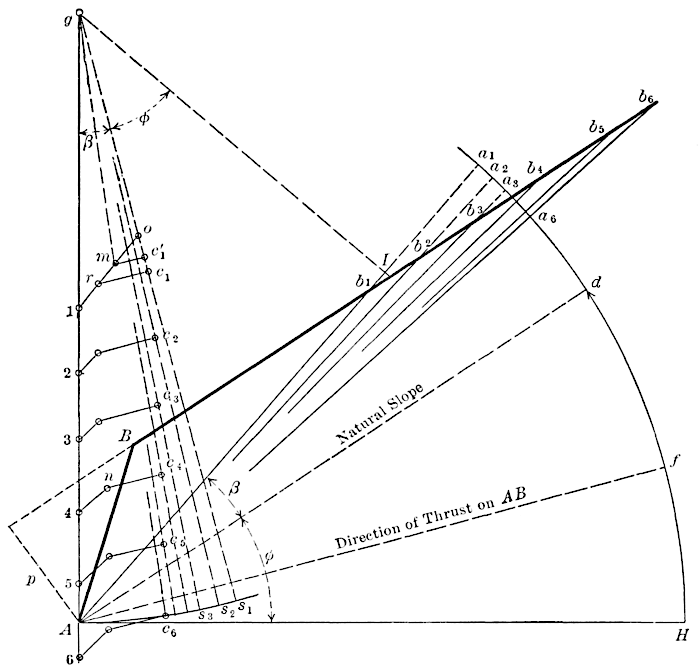
Suppose to be the plane of rupture, and call the weight of the
prism of rupture,
, for a thickness of one unit,
. The weight
of the prism causes the tendency to slide along the planes,
and
. This tendency is resisted by the reactions of the wall,
, and
the plane,
. The reaction of the wall consists of the normal
component,
, acting to the right, and the friction resistance,
, acting up. The resultant of these two forces,
, which is
equal and opposed to the earth thrust on
, thus makes the angle,
,
[417]
with the normal to the wall. Its direction is given by
in Fig. 11.
The reaction of
is made up of the cohesion,
, acting up along
, the normal component,
, acting up, and the friction,
,
acting up along
. The two forces,
and
when combined,
give a resultant,
, making an angle
with the normal,
, to
. Hence, if the angle,
, then
gives the
direction of the resultant,
.
The prism, , is thus in equilibrium under its own weight,
, the cohesive force,
, acting up along
, the reaction,
, of
,
acting to the right, and the force,
, acting up. On drawing, to the
scale of force,
vertical and equal to
; then
parallel to
and equal to
; then
parallel to
to the intersection with
,
the sides of the closed polygon,
, in order, will represent the
four forces,
,
,
, and
, in equilibrium.
A similar investigation pertains to any other supposed prism of
rupture. To find the true one, a number of trial planes of rupture,
,
, ..., are assumed, and each is treated in turn as a true
one (though there can be only one true one). As seen above, the
resultant of the normal reaction and friction on any trial plane of
rupture must be inclined below the normal to the plane at the angle,
.
To lay off the directions of these resultants, from any convenient
point,
, say, in the vertical through
, as a center, describe an arc,
, with a convenient radius,
. With the same radius and
as a
center, describe the arc,
, cutting the trial planes (produced
if necessary) at
,
, ...,
. Let
be the point where the line of
natural slope from
cuts the arc,
. On laying off the chords,
,
, ..., equal to the chords,
,
, ..., respectively, it
will follow that
,
, ..., will make angles,
, below the
normals to the planes,
,
, ..., respectively. To prove this,
take any trial plane, as
, which makes the angle,
, with
,
and drop a perpendicular,
, from
on
(produced if necessary);
then, because the sides of the angles are perpendicular,
,
and if
, it follows that
, as was to be
proved. Hence the chord,
the chord,
,
, etc., as
stated.
The weights, in pounds, of the prisms, ,
, ..., are,
,
, ..., respectively, where
is the length of the
perpendicular from
upon
(produced if necessary), the foot
[418]
being the unit of length and
being the weight, in pounds, of
1 cu. ft. of earth. The prisms are supposed to be 1 ft. in length
perpendicular to the plane of the paper.
These weights are now laid off to the scale of force, vertically
downward from , to points 1, 2, 3, ..., and from these points, lines
are drawn parallel to
,
,
, ..., respectively, of lengths
equal to
,
, ..., to represent the forces of cohesion,
acting upward along
,
, ..., where
the force of cohesion,
in pounds per square foot. From the extremities of these lines, lines
are drawn parallel to the direction of the earth thrust on
(inclined
at the angle,
, below the normal to
), to the intersections,
,
,
, ..., with
,
,
, ..., respectively. With dividers,
it is found, for this figure, that
is the longest of these lines;
whence
, to the scale of force, measures the earth thrust against
, in pounds. This follows, because, for any less thrust, since
is
fixed, when
becomes less,
falls to the left of the first position,
and the new
, representing the thrust on
, due to the normal
reaction on it and friction only, will make a greater angle than
to
the normal to
, which is inconsistent with the laws of stability
of a granular mass. In fact, if
is the normal component of the thrust
on the plane,
,
is all the friction that can be exerted
on it. The resultant of
and
thus makes an angle,
, with
, and this angle cannot be exceeded. The true thrust on the wall,
, is thus the greatest of the trial thrusts,
. The prism of
rupture,
, is in equilibrium under the four forces represented by
the sides of the closed polygon,
;
, representing its weight;
, the cohesion acting along
;
, the reaction of
(opposed
and equal to the earth thrust); and
the reaction of the plane,
, due to the normal component and friction on it only. The
full reaction of the plane can be found by combining the forces, given
in magnitude and direction by
and
, but it is not needed.
It is to be noted that is the least thrust for which equilibrium
is possible. The other trial thrusts should now be lengthened to equal
, since this is the true thrust or reaction of the wall,
. All
the new points,
,
,
,
,
, will now lie to the right of the old
points; hence the new
,
,
,
,
, will all make less angles
than
with the normals to the planes,
, etc.; hence stability everywhere
in the earth mass is assured.
[419]
The solution represented by Fig. 11 is general, and applies whether
is inclined to the right or left of the vertical through
or
coincides with it, and whether the earth surface
is horizontal or
inclined above or below the horizontal. It can likewise be easily
adapted to the case shown in Fig. 1.[Footnote 7]
The construction of Fig. 11
has been used in evaluating the thrust and determining (approximately)
the plane of rupture in the experiments (recorded below) of Leygue
on retaining boards,
, that could be rotated about
, and thus
placed at any inclination to the vertical. In all the experiments, the
vertical height of
was 0.656 ft.; the length of the board was 1.3 ft.
The value of the moment of the earth thrust about
was found by use
of suitable apparatus, corresponding
to dry sand with a natural slope of
3 base to 2 rise, or
,
, and
lb. per cu. ft. By
use of the partition board mentioned
previously, the side friction of the
sand on the glass sides of the box
containing it was estimated, and the
moments corrected, so as to give the
true moment when there is no side friction. The notation used to
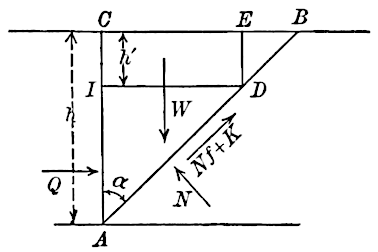
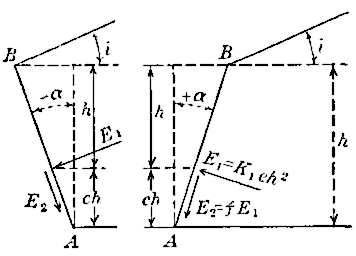
express results is partly given in Fig. 12, for the general case where,
[420]
The resultant, , of
and
, evidently makes the angle,
, with
the normal to
, The moment of this resultant about
, if we put
.
From the last formula, it is seen that
is the moment of the thrust
about
, for
; also from
, it follows that
is the normal component of the thrust for
.
When cohesion is included, is not exactly
, but it is very slightly
less for
or 2. It will be assumed at
, and, from the values
of
given by Leygue,
will be derived from the formula above,
Thus, for the case represented by Fig. 11, , therefore
,
;
. Experiment gave
,
therefore
.
Neglecting cohesion, theory gives , or twice the amount
given by experiment. If, however, the construction of Fig. 11 is made
for the actual height of the retaining board,
ft.,
,
(cohesion, in pounds per square foot), we find
. On
substituting this in the formula,
, we have,
By a comparison of the values, it is evident that, if the cohesion
was assumed at a little less than 1 lb. per sq. ft., the theoretical and
experimental values could be made to agree exactly. The case just
examined exhibits the most pronounced difference between the ordinary
theory (corresponding to ) and experiment, of any shown in
Table 3. Further, it will be observed, that, for an assumed cohesion
of about 1 lb. per sq. ft., the theoretical and experimental values for all
the cases given by Leygue very nearly agree.
The value, , in place of Leygue’s,
, was used, which
would alter the results somewhat, but not the general conclusions. The
construction of Fig. 11 will give
and its normal component,
,
with practical accuracy, but it is not readily adaptable in finding the
plane of rupture. In most of the drawings a small scale was used, in
order to limit the drawing to a sheet of writing paper, hence, on both
accounts,
cannot be counted on to nearer than 1° or 2°, except for
, when
was found by computation, or by the construction
of Fig. 1.
TABLE 3.
| Cohesion, in pounds per square foot. | Angle of rupture with the horizontal, | Coefficient normal component of the thrust | ||||
|---|---|---|---|---|---|---|
| Theory. | Experiment. | Theory. | Experiment. | |||
| +⅓ | 0 | 0 | 50° 12′ | 0.060 | ||
| 1 | 51° | 51° 30′ | 0.042 | 0.043 | ||
| 2 | 52° 30′ | 0.026 | ||||
| +⅓ | ⅔ | 0 | 33° 41′ | 0.182 | ||
| 1 | 44° | 47° | 0.084 | 0.091 | ||
| 2 | 49° | 0.043 | ||||
| 0 | 0 | 0 | 56° 36′ | 0.111 | ||
| 1 | 57° | 56° 30′ | 0.093 | 0.090 | ||
| 2 | 58° | 0.077 | ||||
| 3 | 58° 30′ | 0.062 | ||||
| 0 | ½ | 0 | 47° 30′ | 0.178 | ||
| 1 | 50° | 51° | 0.148 | 0.141 | ||
| 2 | 53° | 0.121 | ||||
| 3 | 55° | 0.098 | ||||
| 0 | ⅔ | 0 | 33° 41′ | 0.345 | ||
| 1 | 44° | 49° | 0.205 | 0.195 | ||
| 2 | 46° 30′ | 0.150 | ||||
| 3 | 50° | 0.111 | ||||
| –⅓ | 0 | 0 | 60° 21′ | 0.185 | ||
| 1 | 63° | 61° | 0.171 | 0.179 | ||
| 2 | 63° | 0.155 | ||||
| –⅓ | ⅔ | 0 | 33° 41′ | 0.660 | ||
| 1 | 57° | 57° | 0.267 | 0.387 | ||
| 2 | 50° | 0.236 | ||||
The results in Table 3 are remarkable, and explain quite satisfactorily how Leygue, Darwin, and others found, by experiments on small models, results differing so much from the ordinary theory, where cohesion is neglected.
It should be remarked that the values of given in Table 3 under
“Experiment,” are not exactly those given by Leygue in his tables, but
are the averages obtained from the two sets of drawings given by him
in the plates, and represent the inclinations of the chords of the really
curved surfaces of rupture. His experiments with the spring apparatus
[422]
are not considered, as the results are open to doubt, because the prism
of rupture, in descending, could not slide down freely, but as it
advanced would rub over the floor, thus lessening the thrust there
considerably.
From Table 3, the results given by experiment are seen to differ
widely from the ordinary theory in which .
The discrepancies are largely, or almost entirely, due to the very
small models used, as will be evident from the following considerations:
Suppose the height, , of the wall,
, to be 10 times the
height given in Fig. 11, or 6.56 ft.; then, as the areas of triangles such
as
, etc., vary as the squares of the heights, but the lengths of
sides, as
etc., vary only as the first power of the heights, the
weights of the successive trial prisms of rupture will be
or 100
times as great as before, whereas the corresponding cohesive forces,
acting along the planes,
, etc., will be only 10 times the first values.
Hence, if we use a scale of force
of the former scale, the weights of
the prisms,
,
, etc., will be represented, as before, by
,
,
etc., but the lines representing the cohesive forces will be only
of
the former lengths. Thus the new
, Fig. 11, will be laid off from
4 only
of the length shown in the figure.
The relative decrease in the lines representing cohesive forces
will be still more marked for a wall ft. high, the
weights of prisms being 400 times as great, but the cohesive forces
only 20 times as great as before. It is evident from this reasoning
that, for
, the cohesive forces are practically negligible for walls,
say, 10 ft. high, especially if the earth surface is level. In fact, a
little examination of the original drawings showed, for walls about
6 ft. high, that the earth thrust, neglecting cohesion, was only from
1 to 5% in excess over that for
. The smaller percentages
referring to
, or
, while the larger percentages
referred to
, for earth surface horizontal or sloping
at the angle of repose.
Such results should be of great service to future experimenters as proving two things: (1) that dry sand, with as small a coefficient of cohesion as possible, should be used (perhaps grain would be a more suitable material), and (2) that no experimental wall should be less than from 6 to 10 ft. high.
Even if the wall is, say, 6 ft. high, if damp clayey earth is used
[423]
as the filling, with a coefficient of adhesion, , then all the diagrams
of forces, as in Fig. 11, will be the same as before, or similar
figures, and the discrepancies noted in Table 3, will be as pronounced
as ever. All the experiments on retaining boards, except some of
Curie’s, have been with very small models, and the results have brought
the common theory under suspicion, if not into disrepute.
The writer hopes that the foregoing investigation and results may be instrumental in establishing more confidence in the theory, and in showing when cohesive forces may be practically neglected and when they must be included.
As an illustration, the results for a vertical wall 10 ft. high are
presented in Table 4, taking and
. In the first
wall, the surface of the earth was horizontal; in the second wall its
slope was 1 rise to 2 base.
| 0 | 0 | 0 | 56°36′ | 0.111 |
| 1 | 56° | 0.110 | ||
| 5 | 57° | 0.101 | ||
| 10 | 57° | 0.096 | ||
| 1 | ½ | 0 | 47°30′ | 0.178 |
| 1 | 49° | 0.176 | ||
| 5 | 49° | 0.165 | ||
| 10 | 49° | 0.155 |
In Table 4 the results for and
are practically the same,
but
for
is 13% less than for
. If the value,
,
for fresh earth slightly damp and lightly rammed, given by Leygue
above, is even approximately correct, it is seen that, for such a filling,
the effect of cohesion must be included to get results at all agreeable
with experience or experiment.
Recurring to the experimental retaining walls proper, Figs. 4 to 9,
it is evident from the foregoing, that cohesion will affect the results
inappreciably, except perhaps in the case of Figs. 6 and 7, where
the height was about 0.6 ft. Assuming , it seems to be probable,
from the results of Table 4, that the thrust should be decreased in
the ratio of 93:111. Effecting the construction for the new thrust,
it is found that the point, I, falls within the base, 0.03 of its width for
Fig. 6 (Trautwine’s wall), and 0.02 of its width for Fig. 7 (Curie’s
wall).
[424]
The theory advocated is thus practically sustained by all the experiments
given above, either on retaining boards or retaining walls proper,
when a coefficient of cohesion of about for dry sand is used.
The method of evaluating the thrust, given in Fig. 11, is as valid
when , or cohesion is neglected, as in the ordinary theory. The
lines parallel to the thrust are now drawn directly from 1, 2, ...,
to the intersection with
,
, ..., and the greatest one is taken
for the true thrust. Although the writer expressly disclaims any
great accuracy in the values of
in Table 4, on account of the small
scale of the drawings, nevertheless, the results by the construction for
and
or ½, were found to differ from computed
values only 2, 3, 0, and 1% for the different cases, which should give
confidence in the general conclusions, at least.
The diagram, Fig. 11, with a slight modification, can be utilized to
find the coefficient of cohesion, , at which the bank of earth will
stand without a retaining board. Thus, let each line, as
, representing
the cohesive force acting along its proper plane, be extended to
meet the corresponding
; any such line measured to the scale of
force and then divided by the length of the plane along which it
acts, will give the cohesive force, in pounds per square foot, corresponding
to no thrust on
, for the particular plane considered.
The greatest of these values is evidently the value of
for which
the filling will stand without a retaining board. The work can be
much abbreviated by using a well-known principle, that the plane
along which the unit cohesion is greatest (the plane of rupture)
bisects the angle,
, between the surface,
, and the line of
natural slope. Suppose
to be this plane, then we have only to
extend
to meet
, at 0, measure 10 to the scale of force, and
divide by the length of
, to the scale of distance, to find the
coefficient desired. By either method it was found that a cohesive
force of 7 lb. per sq. ft. was required to sustain a mass of earth with
a vertical face,
ft. high, when
was horizontal.
It was stated, in connection with Equations (1) and (2), referring
to the thrust on a vertical wall of height, , with the earth surface sloping
at the angle of repose, that this particular case would be discussed
later. To show the influence of cohesion, the planes of rupture for
such a wall, 2.4 ft. high, for various values of
(in pounds per square
[425]
foot), are given in Fig. 13. The values of
(for
and
) are as follows:
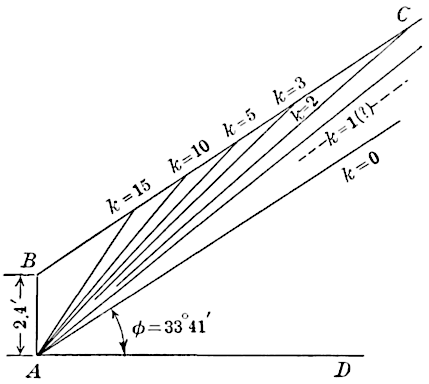
The first value was found by computation, the others by construction.
As is well known, the theoretical plane of rupture approaches
indefinitely the natural slope as approaches zero. For appreciable
cohesion (and there is always some cohesion) the plane of rupture lies
above the natural slope, with very materially decreasing normal
components to the thrust as
increases. As the height of wall
increases, the influence of cohesion diminishes. Thus, as shown above,
for a wall 5 times 2.4 ft., or 12 ft.
high, the weights of the prisms,
, etc., are 25 times the former
values, but the cohesive forces,
which vary directly as
, etc.,
are only 5 times the first values.
Hence, if the former values of
are
multiplied by 5, the new diagram
of forces, Fig. 11, will be similar
to the old one. Thus, for the wall
12 ft. high, the plane of rupture
and the value of
, for
,
correspond to the old values for
, for
, to the old values for
. For fresh earth filling, slightly packed, it is possible that the
values,
,
, may be reached, with a material reduction
in
from the values given by Equations (1) and (2). As the height
of the wall increases, say to 25 or 50 ft., the influence of cohesion, in
diminishing the thrust, becomes very small, and it is better to ignore
it altogether. In fact, as we know very little, and that imperfectly,
of the coefficients of cohesion, it is perhaps safer, at present, to use
Equations (1) and (2) in all cases. It is very evident, though, that
for most cases in practice, the formulas give a very appreciable excess
over the true thrust, and that the true plane of rupture never
coincides with the natural slope.
[426]
From all that precedes, it is seen that the results of experiments on
small models in the past have proved to be very misleading, and
that experiments on large models are desirable, and can alone give
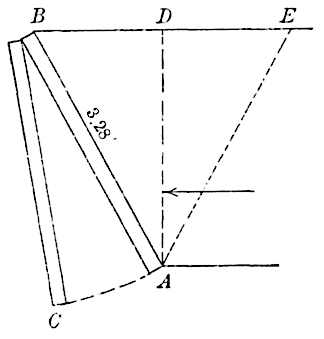
confidence. Leygue has made such experiments on retaining boards,
from 1 to 2 m. (3.28 to 6.56 ft.) in height, simply to determine the surface
of rupture. This is really the essential thing, for, as soon as the
prism of rupture is known, the thrust is easily found. In a general
way, the results agree with theory when the cohesion is neglected,
though the curved surfaces of rupture were very irregular, particularly
for the stone filling. The first two experiments were made with
both dry and damp sand as a filling; the next six, with stones varying
from 1.5 to 20 in. in diameter. In another series of five experiments,
sand was used. In all the foregoing experiments, the surface of the
material was horizontal. In three additional experiments, the walls
were surcharged with sand as a filling. In one experiment, the wall
was 6.56 ft. high and the surcharge was 3.28 ft.; in another experiment,
the wall was 3.28 ft. high, and the sand, sloping from its top
at the angle of repose, as in the former case, extended to 3.28 ft.
above the wall, where the surface was horizontal.
Applying the construction of Fig. 1, it was found that the plane of rupture passed, say, 2° above that given by experiment in the first case and about 3° below in the second. It will be evident from the construction of Fig. 11, omitting cohesion, that trial planes of rupture differing by 2 or 3° from the true one, give nearly the same thrust. Taking the average, these experiments on large models, tend, in a general way, to sustain the theory.
In a paper by the late Sir Benjamin Baker, Hon. M. Am. Soc. C. E., “The Actual Lateral Pressure of Earthwork,”[Footnote 8] two experiments by Lieut. Hope and one by Col. Michon, on counterforted walls, are given. Although such walls do not admit of precise computation, on account of the unknown weight of earth carried by the counterforts, through friction caused by the thrust of the earth in a direction perpendicular to the counterforts, still the computation was made, as the conclusions are interesting. Therefore, the first vertical wall of Lieut. Hope was examined, especially as Mr. Baker, using the Rankine theory, found, for this wall, the greatest divergence between the actual and the Rankine thrust, of any retaining wall examined.
[427]
At the moment of failure, the wall was 12 ft. 10 in. high, the
thickness of the panel was 18 in., and the counterforts were 10 ft.
from center to center, projecting 27 in. from the wall, or 3 ft. 9 in.
from the face, as inferred from the next example. As it is stated that the
wall had the same volume as the 10-ft. wall previously examined in
this paper (Fig. 4), the counterforts must have been 2 ft. thick.
Assuming these dimensions, and using the values given; ,
or
(say
),
weight of a cubic foot
of earth, and
weight of a cubic foot of masonry, we
first compute
lb., the normal component of the earth
thrust on a length of 1 ft. of wall. The normal thrust on the panel
is thus
and on the counterfort
. The friction (acting vertically
downward) caused by this thrust is
on the panel and
on the counterfort. The moment of these forces about
the outer toe of the wall, totals 39 800 ft‑lb. The resisting moment of
10 ft. in length of combined panel and counterfort, about the outer
toe, assuming the wall to be vertical, is 29 800 ft‑lb. If, to the latter,
we add the moment of 17% of the weight of earth between the counterforts,
supposed to be held up by the sides of the latter, the total
moment exactly equals the first. However, at the moment of failure
by overturning, the panels had bulged 4½ in. and the overhang at the
top was 7½ in. Taking the moment of stability of the wall at 26 000 ft‑lb.
(Mr. Baker’s figure), it is found that, for equilibrium, 24% of
the weight of earth between the counterforts must be carried by them,
When the earth was 8 ft. high, a heavy rain was recorded, so that,
doubtless, some appreciable cohesion was exerted, though necessarily
omitted in the computation.
The experimental wall of Col. Michon was 40 ft. high, with very deep counterforts, only 5 ft. from center to center. The very heavy and wet filling between the counterforts, being treated as a part of the wall, a construction (made on the printed drawing) shows that the resultant of earth thrust and weight of wall passes through the outer toe. Doubtless the cohesion factor in this wall was large. In the paper mentioned, the details as to Gen. Burgoyne’s experimental walls are given. There were four of these walls, each 20 ft. long, 20 ft. high, and with a mean thickness of 3 ft. 4 in. Two of the walls were perfectly stable, as in fact theory indicates for all four walls if they were monolithic. The other two walls fell, one bursting out [428] at 5 ft. 6 in. from the base, and the other (a vertical wall), breaking across, as it were, at about one-fourth of its height. As these walls consisted of rough granite blocks laid dry, it is highly probable that the breaks were due to sliding, owing to the imperfect construction; besides, “the filling was of loose earth filled in at random without ramming or other precautions during a very wet winter.”
From a consideration of all the observations and experiments (some of them unintentional), Mr. Baker concludes that the theoretical thrust is often double the actual lateral pressure. He used the old theory, which neglects both cohesion and wall friction. If he had included them, the resulting theory would not have been so deficient “in the most vital elements existent in fact” as he charges against the “textbook” theory.
However, the writer must be clearly understood as not recommending that cohesive forces be considered in designing a retaining wall backed by a granular material, such as fresh earth, sand, gravel, or ballast. It has been the main object of this paper to show that, although cohesive forces must be included in interpreting properly the results on small models and many retaining walls, yet, for walls more than 6 or 10 ft. in height, backed with dry fresh material, not consolidated, the cohesive forces can be practically neglected in design. Hence, experimenters are strongly advised to leave small models severely alone and confine their experiments to walls from 6 to 10 ft. high, backed by a truly granular material, such as dry sand, coal, grain, gravel, or ballast, where the cohesive forces will not affect the results materially. Further, it is evident that walls of brick in wet sand, or walls of granite blocks, etc., laid dry, are very imperfect walls. The overhang, just before falling, is large, and the base is often imperfect. For precise measurements, a light but strong timber wall on a firm foundation, seems to be best; and the triangular frame of Fig. 8 seems to meet the required conditions very well, especially if the framing is an open one, with a retaining board only on one leg. The base thus becomes wider, and the overhang less, than with any rectangular wall.
When the design of a wall to sustain the pressure of consolidated earth is in question, even if a perfect mathematical theory existed, it would still prove of little or no practical value, because the coefficients of friction and cohesion are unknown. The coefficient of friction at the surface can be easily found, but it is a difficult matter to find the [429] coefficient of cohesion, which doubtless varies greatly throughout the mass.
Mr. W. Airy, in his discussion of Mr. Baker’s paper, states that
he found the tensile strength of a block of ordinary brick clay to be
168 and of a certain shaley clay 800 lb. per sq. ft., the coefficients of
friction for the two materials being 1.15 and 0.36, respectively.
Cohesive resistance is more analogous to shear, but such figures indicate
the wide variations to be expected, particularly in , the coefficient of
cohesion. If this coefficient is to be guessed at, in order to substitute
it in the supposed perfect formula, then it is plainly better to guess at
the thickness of the wall in the first instance.
As an illustration, consider the well-known equation:[Footnote 9]
which gives the height, , of vertical trench that will stand without
any sheeting.
In this equation,
Thus, if , whence
, the equation reduces to
As certain trenches with vertical sides have been observed to stand
unsupported for heights of 15 or even 25 ft., the equation would seem
to indicate that cohesive or shearing resistances of about 200 to
300 lb. per sq. ft. were required to cause equilibrium. If friction is
not supposed to be exerted, then and
; and, for the
same unsupported heights, the cohesion would be about doubled.
[430]
Evidently, if cohesion, which (to judge from Mr. Airy’s experiments) may
vary from one to several hundred pounds per square foot, has to be
guessed at in order to determine
, it is plainly better to guess at
at once.
The foregoing equation cannot be regarded as giving very accurate
results, mainly because a plane surface of rupture is assumed, whereas,
from both theory and observation, this surface is known to be very
much curved; besides, the cohesion and friction along the ends of the
break have been neglected. However, the hypothesis of a plane surface
of rupture, the ends being supposed to be included, gives a greater
value to than the true one, whereas, neglecting the influence of the
ends, it tends in the other direction; so that the equation may not
err so greatly.
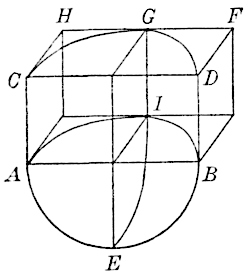
In the discussion of the paper[Footnote 10]
by J. C. Meem, M. Am. Soc. C. E.,
E. G. Haines, M. Am. Soc. C. E., states that where breaks occur
in the sides of an unsupported trench, the solid
of rupture often approximates to a quarter sphere,
surmounted by a half-cylinder of the same
height, the radii of the sphere and cylinder
being equal. In Fig. 14, let represent the
quarter-sphere,
the half-cylinder, and
the face of the trench. According to
the observations of Mr. Haines, when the part,
, of the side of the trench is supported by
sheeting and bracing, it sometimes happens that a part of the quarter-sphere,
, breaks out, so that the semi-cylinder above would
descend but for the bracing, the thrust of which, it is supposed,
induces arch action in the earth.
This is possible; but, if so, as the sheeting is not supposed to be
carried to the bottom of the trench, there can be no vertical component
in its reaction, and the thrust, , of the braces and sheeting, acting
on
, must be horizontal; further, the earth cannot act as a
series of independent arches devoid of frictional resistance between
them, but must act as a whole.
Another way of explaining the phenomena is to suppose the horizontal
thrust of the braces, , on the exposed face,
, to cause
[431]
friction at the back of the break of sufficient intensity to prevent the
semi-cylinder from descending, just as a book can be held against a
vertical wall by a horizontal push.
To illustrate the principle, it will suffice to replace the semi-cylinder
by the circumscribing parallelopiped, , and suppose it to be held up by the friction on the back face, with possibly cohesion
acting on the three interior vertical faces. Thus, let
,
and
; then the friction on the back face is
, the cohesion
on the three faces is
, and the weight of earth,
, equals
. Hence, as friction and cohesion always act opposite
to the incipient motion, or vertically upward in this case,
Evidently, the value of , derived from this equation, gives an
extreme upper limit, which is doubtless never attained, as there is
nearly always some support from the earth which has not broken out
below the level of
.
Where the sheeting and bracing are of sufficient size, are tightly keyed up, and extend to the bottom of the trench, or where the bank is supported by a retaining wall, the earth near the bottom cannot break out, and the equation is not valid.
However, if, from any cause, such as insufficient sheeting, the
break has taken place over even a part of , the mass,
, above
will tend to tip over at the top, giving the greatest pressure on the top
braces. This appears to explain the phenomena observed by Mr. Meem
and others in connection with some trenches.
With regard to tunnel linings, as is well known, the vertical pressure on the top is generally small, the great mass of earth vertically over the tunnel being largely held up by the friction of the earth (caused by the earth thrust) on its vertical sides, exactly as in the case of tall bins, where most of the weight of the grain is held up by the sides of the bin, the theory being very similar in the two cases. In consolidated earth, cohesion assists very materially in this action.
It might be inferred, from the facts of observation, that consolidated earth acts as a solid, though, of course, it differs from a solid in this: that its physical constants (cohesion, friction, etc.) vary enormously with the degree of moisture. It is likely that these constants alter with the depth, and likewise are subject to changes from shocks.
[432]
It is a question too, whether, as is the case with loosely granular
materials, friction acts (before rupture) at the same time with shear
or cohesion in consolidated earth. From the interesting remarks[Footnote 11]
of Mansfield Merriman, M. Am. Soc. C. E., on internal friction,
it seems probable that friction and shear exist at the same time in
a solid; but, to reach sound conclusions, as he states, “further studies
on internal friction and on internal molecular forces are absolutely
necessary.”
From the present state of our knowledge with respect to the theory and physical constants pertaining to consolidated earth, it would seem that experience must largely be the guide in dealing with it. The facts are supreme—the rational theory may come later.
Similarly, for retaining walls backed by loosely aggregated, granular materials, the facts are supreme, and, on that account, they have been presented very fully in this paper; further, a theory has been found to interpret them properly. It is true that the fresh earth, from the time that it is deposited behind a retaining wall, begins to change to a consolidated earth, from the action of rains, the compression due to gravity, and the influence of those cohesive and chemical affinities which manufacture solid earths and clays out of loosely aggregated materials, and even cause the backing sometimes to shrink away from the wall intended to support it; but it is plain that the wall should be designed for the greatest thrust that can come on it at any time, and this, in the great majority of cases, will occur when the earth has been recently deposited.
The cases which have been observed where the bank has shrunk away from the wall and afterward ruptured (after saturation, perhaps) are too few in number to warrant including in a general scheme of design, even supposing that a rational theory existed for such cases. A few remarks on the theory pertaining to the design of retaining walls may not be inappropriate. From the discussion of all the experiments referred to in this paper, the conclusion may be fairly drawn that the sliding wedge theory, involving wall friction, is a practical one for granular materials of any kind subjected to a static load. In practical design, however, vibration due to a moving load has to be allowed for; also the effect of heavy rains. Both these influences tend generally to lower the coefficients of friction and add to the weight of the filling. Mr. Baker says:
[433]
“Granite blocks, which will start on nothing flatter than 1.4 to 1,
will continue in motion on an incline of 2.2 to 1,[Footnote 12]
and, for similar
reasons, earthwork will assume a flatter slope and exert a greater
lateral pressure under vibration than when at rest.”
Instances of slips in railway cuttings, caused by the vibration set
up by passing trains, have been given by many engineers. The effect
of vibration is most pronounced near the top of a retaining wall,
and is evidently greater for a low wall than for a high one. All the
influences cited can only be included under the factor of safety, and
the writer recommends for walls from 10 to 20 ft. in height a factor
of 3. This may be increased to 3.5 for walls 6 ft. high and decreased
to 2.5 for walls 50 ft. high, or those with very high surcharges. In
the application, the normal component of the earth thrust on the
wall, , will alone be multiplied by the factor, the friction,
,
exerted downward along the back of the wall,
being unchanged. This allows very materially
for a decrease in
due to rains and
vibration, as well as for an increase in the
thrust, due to
becoming less.
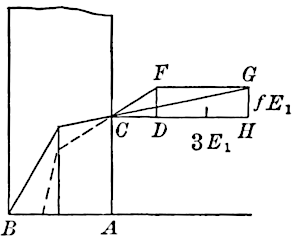
The effect is illustrated in Fig. 15, where
a retaining wall is supposed to be subjected
to the earth thrust, , making an angle
with the normal to the face,
, of the wall. The component of
normal to
is
, the component acting downward
along
is represented in magnitude and direction by
, which
equals
. Suppose the factor of safety to be 3, then
is
extended to
, making
;
is drawn equal and parallel
to
; whence
will represent the thrust, which, combined with
the weight of the wall, acting through its center of gravity, must pass
through the outer toe of the wall.
To see what thickness of a vertical rectangular wall corresponds
to this factor of safety, 3, for , or a natural slope
of 3 base to 2 rise, let it be assumed that the weights per cubic
foot of earth and cut-stone masonry in mortar are in the ratio of 2:3;
then, for level-topped earth, a computation shows that, for the factor,
3, the base of the wall must be
. If the earth slopes indefinitely
at the angle of repose from the top of the back of the wall, and a
factor 2.5 is used, then the thickness will be
.
[434]
For brick masonry in mortar, the specific weight of which is
of that of the filling, the foregoing thickness would be changed
to
and
, respectively,
being equal to the height of the
wall.
It must be noted especially, however, that if the original earth
thrust, when combined as usual with the weight of wall, gives a
resultant which passes outside of the middle third of the base of
the wall as computed above, then the thickness must be increased,
so that the resultant will at least pass through the outer middle-third
limit. This ensures compression over the whole base and
no opening of part of the joint under normal conditions. With regard
to the thickness above of about one-third of the height, Mr. Baker
states that hundreds of brick revetments have been built by the Royal
Engineer officers, with a thickness of only for a vertical wall.
He advises, as the result of his own extensive experience, that the
thickness be made one-third of the height for level-topped earth of
average character, and that the wall be battered 1½ in. to the foot.
He states, further, that, under no ordinary conditions of surcharge
on heavy backing is it necessary to make the thickness of a retaining
wall on a solid foundation more than one-half the height. The
thicknesses computed above agree fairly well with those recommended
by Mr. Baker, and it would seem that a table of thicknesses computed
on the above basis should correspond to safe walls under ordinary
conditions.
It has been noted above that Equation (1), corresponding to a slope of indefinite extent, probably gives too great a thrust; besides, there are no embankments with such a slope. An embankment from 100 to 150 ft. high, supported by a low wall, may approximate the conditions assumed, but, before it is finished, the earth has consolidated to such an extent that the actual thrust is doubtless much less than the computed one. The truth is that, in nearly all back-filling of ordinary earth, the cohesive and chemical affinities commence their work very soon after the filling is deposited, and consolidation is gradually effected; so that, as has been stated, the actual thrust is often much less than is estimated in the design of the wall, where cohesive forces are neglected. In many old walls, as has been observed, the consolidation has gone so far that the backing has shrunk away from the wall altogether. It would be hazardous, though, [435] to allow for cohesion, in a wall backed by fresh earth, unless the surcharge was high and was a long time in building. Finally, it should be observed that the footing of a retaining wall should be wide, and should always be tilted at such an angle that sliding is impossible.
A glance at Figs. 4, 5, and 6, will make it apparent that the Rankine and other theories differ in their results mainly because of the assumed difference of inclination of the earth thrust. In the design of walls, however, the method proposed (Fig. 15) will approximate in results those given by the Rankine theory, where, say, the earth thrust, whether inclined or not, is multiplied by the factor of safety. The writer does not advocate the middle-third limit method in design, as it gives variable factors of safety for different types of walls. Besides, if the actual resultant on the base passes one-third of its width from the outer toe, there is no pressure at the inner toe, and the unit pressure at the outer toe is double the average. If vibration or other cause increases the thrust, the joint at the inner toe opens, and the pressure is concentrated too much near the outer toe. In the reinforced concrete wall, the earth thrust on a vertical plane through the inner toe is required. As this plane lies well within the earth mass, the thrust on it must be taken as acting parallel to the top slope, and its amount will be the same as that given by the Rankine theory.
Although it is highly desirable to have more precise experiments on large models in order to draw sure conclusions, yet, as far as the experiments go—those which have been analyzed and discussed in this paper—the following conclusions may be stated:
1.—When wall friction and cohesion are included, the sliding-wedge theory is a reliable one, when the filling is a loosely aggregated granular material, for any height of wall.
2.—For experimental walls, from 6 to 10 ft. high, and greater, backed by sand or any granular material possessing little cohesion, the influence of cohesion can be neglected in the analysis. Hence, further experiments should be made only on walls at least 6 ft., and preferably 10 ft., high.
3.—The many experiments that have been made on retaining boards less than 1 ft. high, have been analyzed by their authors on the supposition that cohesion could be neglected. This hypothesis is so far from the truth that the deductions are very misleading.
[436]
4.—As it is difficult to ascertain accurately the coefficient of cohesion,
and as it varies with the amount of moisture in the material,
small models should be discarded altogether in future experiments,
and attention should be confined to large ones. Such walls should be
made as light, and with as wide a base, as possible. A triangular
frame of wood on an unyielding foundation seems to meet the conditions
for precise measurements.
5.—The sliding-wedge theory, omitting cohesion but including wall friction, is a good practical one for the design of retaining walls backed by fresh earth, when a proper factor of safety is used.
As the subject of pressures on the roof and sides of a tunnel lining has received much attention of late, the writer has concluded to extend this paper, so as to give a development of a theory, based on the grain-bin theory of Janssen, but modified to include the cohesive or shearing resistances of the earth in addition to the frictional resistances.

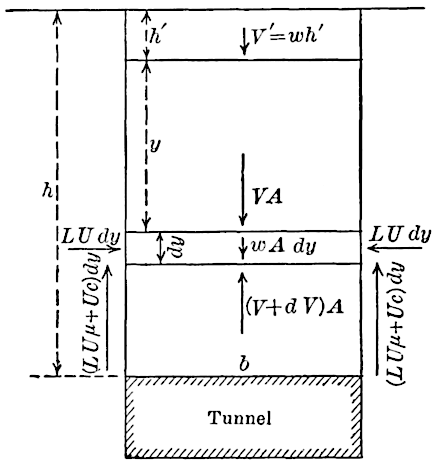
Fig. 16 is a vertical transverse section of a
tunnel, , and the earth,
, extending
over it
feet. If this tunnel has been driven by
the use of a shield or poling boards, the ground
will tend to settle over it, and part of the weight
of
will be sustained by cohesion and friction
(resulting from the lateral thrust) exerted
along the sides, vertically upward. The earth will
probably arch itself, or form a series of domes superposed one upon
the other, but the external forces acting on such domes will be the same
as those acting on a corresponding horizontal lamina, and the theory,
given in full in the Appendix, begins with the considerations pertaining
to the equilibrium of such a lamina.
If there was no settlement of the earth, , in relation to
, then the vertical pressure per square foot on
would be
(
being the weight of a cubic foot of the earth in pounds), but,
as most of the weight of
is carried by the sides, in case of
sufficient settlement, the vertical unit pressure,
, on
, will be
much less than
. Also, the lateral unit pressure,
, at the level,
, will be much less where settlement occurs. From the equations
for
and
, given in the Appendix, the diagrams, Figs. 17 and 18,
have been constructed.
[437]
In both diagrams, the weight of the earth was taken at lb.
per cu. ft., and the cohesion of the earth at
lb. per sq. ft. In
Fig. 17,
and the curves for
and
were laid off for a width
of tunnel,
, of 15 ft. and also for 30 ft. In Fig. 18,
, and
curves are given for
and
, also for
ft. and 30 ft. for various
heights,
.
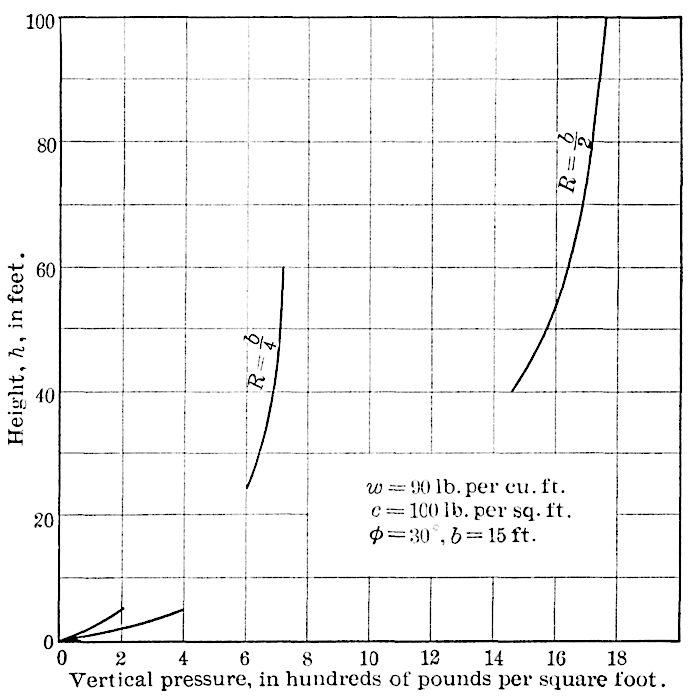
It will be perceived, in both figures, that when certain heights
are attained, both and
cease to increase perceptibly, so that such
values may be taken as corresponding to
indefinitely large.
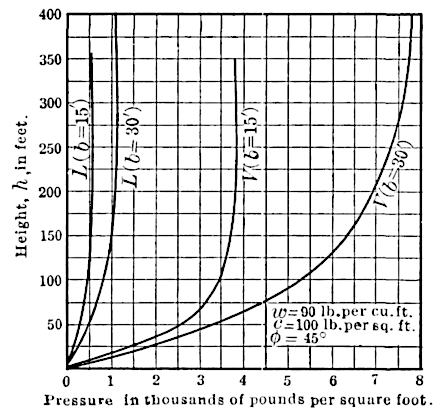
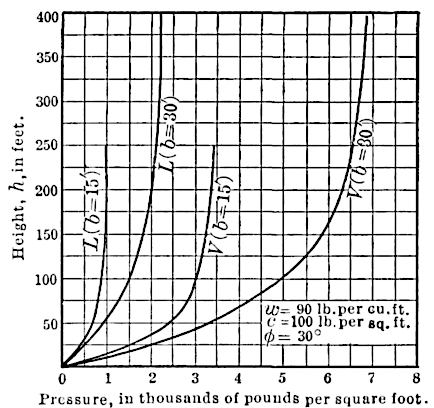
A simple way of deriving these extreme values is given in the
Appendix. The values of ,
and
have been taken here the same
as those used by Mr. Meem, in framing his table of pressures,[Footnote 13]
which may be supposed to embody, in part, practical experience. The results
found from Figs. 17 and 18 by the writer, for a depth of covering of
several hundred feet, are uniformly much larger than those given by
Mr. Meem. Are they too large for safety? In answering this question,
it must be remembered that, of the weight of earth directly over
the tunnel, all has been transferred to the sides that it was possible
to transfer, for the coefficients of friction and cohesion given. We
know scarcely anything of the cohesion coefficients, so that the value
assumed,
lb. per sq. ft., may not be near the truth. Certainly
it must appear plain from this discussion that the values of
and
must be better known, for all kinds of earth, before reliable results
can be attained. The results are submitted for discussion, in the
hope that engineers will give their experience relative to the pressures
[438]
realized in the timbering of tunnels, particularly through sand or
earth not thoroughly consolidated.
The value of , in Figs. 17 and 18, is the average vertical unit
pressure at the top of the tunnel. Experiments on grain bins lead
to the inference that the pressure at the middle of the roof is greater
than that at the sides, but no law of variation can be stated.
The lateral unit pressure on the vertical sides of the tunnel lining
at the top is given by the equation for , or by the corresponding
diagram. The variation in this lateral pressure over the sides of
the tunnel cannot be easily formulated, as so much of the weight of
the earth, directly over the tunnel, has been transferred by a kind of
arch action to the sides. Experience would better speak here.
Table 5 gives the values of and
for
ft. The figures
in Columns
are taken from Mr. Meem’s table, previously referred
to; those for Columns
are from the diagrams, Figs. 17 and 18.
In quoting Mr. Meem’s figures, the writer must not be understood as endorsing in any way his theory; but the results are of interest as embodying the conclusions of a practical engineer of large experience.
foot. | foot. | ||||
|---|---|---|---|---|---|
| 15 | 45° | 1 485 | 2 300 | 405 | 300 |
| 15 | 30° | 1 035 | 2 100 | 540 | 600 |
| 30 | 45° | 3 240 | 2 800 | 450 | 400 |
| 30 | 30° | 2 325 | 2 600 | 450 | 750 |
If the height, , of earth covering is 200 or 300 ft., the values
given by Figs. 17 and 18 are much larger than those given in Columns
, which presumably represent Mr. Meem’s pressures for any height
greater than 40 ft.
In saturated earth, it has been customary, perhaps, to regard the
earth as if it were gravel composed of solid spheres, like marbles,
so that the water has free access in any direction. Thus, in the
case of a retaining wall backed by such material, the water has full
access practically to every part of the wall, and the wall is subjected
to the full water pressure corresponding to its depth. It is
likewise subjected to a thrust from the earth, corresponding to and
, for the saturated material, but with a weight per cubic foot equal
to that of the earth in air less the buoyant effect of the water. Thus,
[439]
if a cubic foot of the porous earth, in air weighed 90 lb., and if the
voids were 40%, then 1 cu. ft. of earth contains 0.6 cu. ft. of solids
and the buoyant effect of the water is the weight of an equal volume
of water or
lb. Hence, the weight per cubic foot
of earth in water is
lb.
Similarly, for the pressures, and
, at the top of a tunnel,
must be replaced by 52.5, and
and
must be found for the
saturated material and these values substituted in Equations (5) and
(6) of the Appendix. To these pressures must be added the corresponding
water pressures for the full height of water, supposing it
to have free communication everywhere, as in the case of the gravel
filling. However, with sand, or earth with much fine material, the
pores are more or less clogged up and there is perhaps intimate contact
of a part of the earth with the roof of the tunnel, so that the
water cannot get under it to produce a lifting effect, and if such
intimate contact is found along any horizontal or vertical section,
of the earth on either side of the section, it is plain that the buoyant
effort of the water on a cubic foot of material will be much diminished.
Mr. Meem deserves great credit, not only for calling attention
to this, but especially for performing certain experiments to prove
it.[Footnote 14]
The experiments were on sand, and only on a small scale,
but the practical conclusion drawn from them is that the water pressure
transmitted through sand having 40% voids is diminished about
40% in intensity. This occurs for a depth of only a few inches
of sand, and presumably the diminution would be greater for sand
several feet in depth. Of course, before definite values can be stated,
experiments on a large scale should be made on every kind of material
usually met; but, as a numerical illustration of the application, for
the diminution mentioned—which is assumed to extend through the
mass—it is seen that, in the examples of the retaining wall and also
the tunnel, the weight per cubic foot of the earth in water must now
be taken at lb. per cu. ft.
This value replaces the in Equations (5) and (6) from which
the
and
for the top of the tunnel are found. To these values,
add
, for the water pressure, where the surface of the
water extends a height,
, above the top of the tunnel. Similarly, in
the case of the retaining wall, add 0.4 of the full water thrust on
the wall to that given by the earth, weighing only 75 lb. per cu. ft.
[440]
As a numerical illustration, take ft.,
,
in air
lb.,
ft.,
ft.; but we must now replace
by the
weight in water, 75 lb., as found above. The values of
and
are
now found, by Equations (5) and (6) (Appendix), to be 1 917 and
246 lb. per sq. ft., respectively, for the saturated earth alone. To these
values add
lb. per sq. ft., water pressure,
giving a total of 3 417 and 1 746 lb. per sq. ft., respectively, for the
vertical and horizontal unit pressures at the top of the tunnel lining.
In connection with this subject of underground pressures, it may not be inappropriate to make some concluding remarks on the maximum vertical pressures to which culverts may be subjected.
Let Fig. 16 now represent a longitudinal vertical section along
the axis of a road embankment, built over an arch culvert or box-drain,
, the line,
, passing through the summit of the arch
or the top of the covering stone of the box-drain, and the lines,
and
, coinciding in part with the exterior sides of the abutments.
There is a horizontal thrust of the earth on the medial plane,
, acting at right angles to the plane of the paper, which tends to
distribute the weight of the central portion partly toward the sides;
but, ignoring this, it is seen that, if the earth everywhere settles uniformly,
the maximum pressure per square unit at the top of the
culvert is
, and the total vertical pressure on the culvert is the
weight of the earth vertically above it.
If, however, the earth outside the abutment walls settles more than
the walls (a case which may occur), then part of its weight, and
that of the earth vertically above it, will be transferred, through
friction and cohesion, along the planes, and
, to the culvert,
and thus the vertical pressure on the top of the culvert will be greater
than in the first supposed case; but, if the reverse obtains, or if the
culvert settles more than the earth outside the lines,
and
, or
if the arch or covering stone descends in the middle relatively to the
abutments, then part of the weight of the earth vertically over the
culvert is transferred to the sides. For a comparatively rigid arch,
the settlement is perhaps not enough to warrant us in making the
maximum unit pressure less than
. Exactly what settlement would
warrant the use of the theory set forth in the Appendix it is impossible
to say. If the unit pressure is taken as
, we can rest
assured that in most cases the real pressure is materially less.
[Footnote 1: The writer refers to his “Retaining Walls,” Van Nostrand’s Science Series, No. 3, for the demonstrations pertaining to the above constructions, and to the derivations of formulas.] Return to text
[Footnote 2: A full discussion may be found in the writer’s “Retaining Walls.”] Return to text
[Footnote 3: The experiments pertaining to Figs. 7, 8, and 9 are due to Curie. See Curie’s “Poussée des Terres” and “Trois Notes,” Gauthier-Villars, Paris. They are of especial interest in that they were undertaken to attempt to overthrow the theory advocated above.] Return to text
[Footnote 4: All the experiments of Leygue referred to in what follows may be found in Annales des Ponts et Chaussées, November, 1885.] Return to text
[Footnote 5: We can suppose, here, the horizontal force to be the pull of a cord extending horizontally
from the box and passing over a fixed pulley, and that at the free end of the cord a
weight is applied. The friction of the pulley and carriage wheels could be found experimentally
and allowed for, so that some fraction of this weight would equal .]
Return to text
[Footnote 6: This method is an extension of that given by Professor H. T. Eddy in his treatment of earth thrust, in “Researches in Graphical Statics.”] Return to text
[Footnote 7: To attain the greatest accuracy, in constructions like that shown in Fig. 11, the scale
should be as large as possible; the arcs of circles, especially, must be drawn with a large
radius, and the points, ,
, etc., determined with care. The angle,
, can be computed
and laid off by aid of a table of chords. The construction in this figure corresponds
to a vertical height of
ft.,
,
. The value of the component,
, perpendicular
to
, is now to be found, by drawing lines from
and
, perpendicular and
parallel to
, to intersection, and measuring the component to scale. For
, it is
found that
is the plane of rupture. The line,
, through the new
, representing
the thrust, is very small; but it can be easily magnified by laying off the polygon,
, to a scale two or three times as large, and thus the thrust can be found as accurately
as before.]
Return to text
[Footnote 8: Minutes of Proceedings, Inst. C. E., Vol. LXV. p. 140: reprinted in Van Nostrand’s Science Series.] Return to text
[Footnote 9: In reference to this equation, see Appendix.] Return to text
[Footnote 10: “The Bracing of Trenches and Tunnels, With Practical Formulas for Earth Pressures.” Transactions, Am. Soc. C. E., Vol. LX. p. 1. A number of important facts brought out in this paper are of vital importance to constructors.] Return to text
[Footnote 11: “Mechanics of Materials,” Tenth Edition, p. 381.] Return to text
[Footnote 12: Perhaps this may be accounted for by supposing cohesion between the blocks at rest, which is destroyed by the motion, when only friction acts.] Return to text
[Footnote 13: Transactions, Am. Soc. C. E., Vol. LXX, p. 387.] Return to text
[Footnote 14: Transactions, Am. Soc. C. E., Vol. LXX, pp. 365–368.] Return to text