
Title: A Class Room Logic
Author: George Hastings McNair
Release date: September 16, 2018 [eBook #57912]
Language: English
Credits: Produced by Richard Hulse and the Online Distributed
Proofreading Team at http://www.pgdp.net (This file was
produced from images generously made available by The
Internet Archive)

Transcriber’s Notes
The cover image was provided by the transcriber and is placed in the public domain.
Punctuation has been standardized.
Most abbreviations have been expanded in tool-tips for screen-readers and may be seen by hovering the mouse over the abbreviation.
The under bracket in the original text has been replaced by a standard underline.
This book was written in a period when many words had not become standardized in their spelling. Words may have multiple spelling variations or inconsistent hyphenation in the text. These have been left unchanged unless indicated with a Transcriber’s Note.
Index references have not been checked for accuracy.
Footnotes are identified in the text with a superscript number and have been accumulated in a table at the end of the text.
Transcriber’s Notes are used when making corrections to the text or to provide additional information for the modern reader. These notes have been accumulated in a table at the end of the book and are identified in the text by a dotted underline and may be seen in a tool-tip by hovering the mouse over the underline.
This treatise is an outgrowth of our class room work in logic.
It has been published in the hope of removing some of the difficulties which handicap the average student.
We trust that the language is simple and definite and that the illustrative exercises and diagrams may be helpful in making clear some of the more abstruse topics.
If a speedy review for examination is necessary, it is recommended that the briefer course as outlined on page 493 be followed and that the summaries closing each chapter be carefully read.
Only the fundamentals of deductive and inductive logic have received attention. Moreover emphasis has been given to those phases which appear to commend themselves because of their practical value.
Further than this we trust that the book may fulfill in some small way the larger mission of inspiring better thinking and, in consequence, of leading to a more serviceable citizenship.
Surely as civilization advances it is with the expectation of giving greater significance to the assumption “that man is a rational animal.”
I am indebted to a number of writers on logic, notably to Mill, Lotze, Keynes, Hibben, Fowler, Aikins, Hyslop, Creighton and Jevons. I am likewise under obligation to that large body of students who, by frankly revealing their difficulties, have given me a different point of view.
For constructive criticism and definite encouragement I owe a personal debt of gratitude to Prof. Charles Gray Shaw of New York University, to Prof. Frank D. Blodgett of the Oneonta Normal School and to Prin. A. C. MacLachlan of the Jamaica Training School for Teachers.
G. H. McN.
City Training School for Teachers,
Jamaica, N. Y. City.
October 3, 1914.
| CHAPTER 1.—THE SCOPE AND NATURE OF LOGIC. | |
| 1. | The Mind. |
| 2. | Logic Related to Other Subjects. |
| 3. | Logic Defined. |
| 4. | The Value of Logic to the Student. |
| 5. | Outline. |
| 6. | Summary. |
| 7. | Review Questions. |
| 8. | Questions for Original Thought and Investigation |
| CHAPTER 2.—THOUGHT AND ITS OPERATION. | |
| 1. | The Knowing Mind Compared with the Thinking Mind. |
| 2. | Knowing by Intuition. |
| 3. | The Thinking Process. |
| 4. | Notions, Individual and General. |
| 5. | Knowledge and Idea as Related to the Notion. |
| 6. | The Logic of the Psychological Terms Involved in the Notion. |
| 7. | Thought in the Sensation and Percept. |
| 8. | Evolution and the Thinking Mind. |
| 9. | The Concept as a Thought Product. |
| 10. | The Judgment as a Thought Product. |
| 11. | Inference as a Thought Product. |
| 12. | Thinking and Apprehension. |
| 13. | Stages in Thinking. |
| 14. | Outline. |
| 15. | Summary. |
| 16. | Review Questions. |
| 17. | Questions for Original Thought and Investigation. |
| CHAPTER 3.—THE PRIMARY LAWS OF THOUGHT. | |
| 1. | Two Fundamental Laws. |
| 2. | The Law of Identity. |
| 3. | The Law of Contradiction. |
| 4. | The Law of Excluded Middle. |
| 5. | The Law of Sufficient Reason. |
| 6. | Unity of Primary Laws of Thought. |
| 7. | Outline. |
| 8. | Summary. |
| 9. | Illustrative Exercises. |
| 10. | Review Questions. |
| 11. | Questions for Original Thought and Investigation. |
| CHAPTER 4.—LOGICAL TERMS. | |
| 1. | Logical Thought and Language Inseparable. |
| 2. | Meaning of Term. |
| 3. | Categorematic and Syncategorematic Words. |
| 4. | Singular Terms. |
| 5. | General Terms. |
| 6. | Collective and Distributive Terms. |
| 7. | Concrete and Abstract Terms. |
| 8. | Connotative and Non-connotative Terms. |
| 9. | Positive and Negative Terms. |
| 10. | Contradictory and Opposite Terms. |
| 11. | Privative and Nego-positive Terms. |
| 12. | Absolute and Relative Terms. |
| 13. | Outline. |
| 14. | Summary. |
| 15. | Illustrative Exercises. |
| 16. | Review Questions. |
| 17. | Questions for Original Thought and Investigation. |
| CHAPTER 5.—THE EXTENSION AND INTENSION OF TERMS. | |
| 1. | Two-fold Function of Connotative Terms. |
| 2. | Extension and Intension Defined. |
| 3. | Extended Comparison of Extension and Intension. |
| 4. | A List of Connotative Terms Used in Extension and Intension. |
| 5. | Other Forms of Expression for Extension and Intension. |
| 6. | Law of Variation in Extension and Intension. |
| 6a. | Important Facts in Law of Variation. |
| 6b. | Law of Variation Diagrammatically Illustrated. |
| 7. | Outline. |
| 8. | Summary. |
| 9. | Illustrative Exercises. |
| 10. | Review Questions. |
| 11. | Questions for Original Thought and Investigation. |
| CHAPTER 6.—DEFINITION. | |
| 1. | Importance. |
| 2. | The Predicables. |
| 3. | The Nature of a Definition. |
| 4. | Definition and Division Compared. |
| 5. | The Kinds of Definitions. |
| 6. | When the Three Kinds of Definitions are Serviceable. |
| 7. | The Rules of Logical Definition. |
| 8. | Terms Which Cannot be Defined Logically. |
| 9. | Definitions of Common Educational Terms. |
| 10. | Outline. |
| 11. | Summary. |
| 12. | Illustrative Exercises. |
| 13. | Review Questions. |
| 14. | Questions for Original Thought and Investigation. |
| CHAPTER 7.—LOGICAL DIVISION AND CLASSIFICATION. | |
| 1. | Nature of Logical Division. |
| 2. | Logical Division Distinguished from Enumeration. |
| 3. | Logical Division as Partition. |
| 4. | Four Rules of Logical Division. |
| 5. | Dichotomy. |
| 6. | Classification Compared with Division. |
| 7. | Kinds of Classification. |
| 8. | Two Rules of Classification. |
| 9. | Use of Division and Classification. |
| 10. | Outline. |
| 11. | Summary. |
| 12. | Review Questions. |
| 13. | Questions for Original Thought and Investigation. |
| CHAPTER 8.—LOGICAL PROPOSITIONS. | |
| 1. | The Nature of Logical Propositions. |
| 2. | Kinds of Logical Propositions. |
| 3. | The Four Elements of a Categorical Proposition. |
| 4. | Logical and Grammatical Subject and Predicate Distinguished. |
| 5. | The Four Kinds of Categorical Propositions. |
| 6. | Propositions which do not Conform to Logical Type. |
| 7. | Propositions not Necessarily Illogical. |
| 8. | The Relation between Subject and Predicate. |
| 9. | Outline. |
| 10. | Summary. |
| 11. | Illustrative Exercises. |
| 12. | Review Questions. |
| 13. | Questions for Original Thought and Investigation. |
| CHAPTER 9.—IMMEDIATE INFERENCE—OPPOSITION. | |
| 1. | The Nature of Inference. |
| 2. | Immediate and Mediate Inference. |
| 3. | The Forms of Immediate Inference. |
| (1) Opposition. | |
| CHAPTER 10.—IMMEDIATE INFERENCE (Continued). | |
| (2) Immediate Inference by Obversion. | |
| (3) Immediate Inference by Conversion. | |
| (4) Immediate Inference by Contraversion. | |
| 4. | Epitome of the Four Processes of Immediate Inference. |
| ◆ Inference by Inversion. | |
| 5. | Outline. |
| 6. | Summary. |
| 7. | Illustrative Exercises. |
| 8. | Review Questions. |
| 9. | Problems for Original Thought and Investigation. |
| CHAPTER 11.—MEDIATE INFERENCE—THE SYLLOGISM. | |
| 1. | Inference and Reasoning. |
| 2. | The Syllogism. |
| 3. | The Rules of the Syllogism. |
| 4. | Rules of Syllogism Explained. |
| 5. | Aristotle’s Dictum. |
| 6. | Canons of the Syllogism. |
| 7. | Mathematical Axioms. |
| 8. | Outline. |
| 9. | Summary. |
| 10. | Illustrative Exercises. |
| 11. | Review Questions. |
| 12. | Questions for Original Thought and Investigation. |
| CHAPTER 12.—FIGURES AND MOODS OF THE SYLLOGISM. | |
| 1. | The Four Figures of the Syllogism. |
| 2. | The Moods of the Syllogism. |
| 3. | Testing the Validity of the Moods. |
| 4. | Special Canons of the Four Figures. |
| 5. | Special Canons Related. |
| 6. | Mnemonic Lines. |
| 7. | Relative Value of the Four Figures. |
| 8. | Outline. |
| 9. | Summary. |
| 10. | Illustrative Exercises. |
| 11. | Review Questions. |
| 12. | Questions for Original Thought and Investigation. |
| CHAPTER 13.—INCOMPLETE SYLLOGISMS AND IRREGULAR ARGUMENTS. | |
| 1. | Enthymeme. |
| 2. | Epicheirema. |
| 3. | Polysyllogisms. Prosyllogism—Episyllogism. |
| 4. | Sorites. |
| 5. | Irregular Arguments. |
| 6. | Outline. |
| 7. | Summary. |
| 8. | Review Questions. |
| 9. | Questions for Original Thought and Investigation. |
| CHAPTER 14.—CATEGORICAL ARGUMENTS TESTED ACCORDING TO FORM. | |
| 1. | Arguments of Form and Matter. |
| 2. | Order of Procedure in a Formal Testing of Arguments. |
| 3. | Illustrative Exercise in Testing Arguments which are Complete and whose Premises are Logical. |
| 4. | Illustrative Exercise in Testing Completed Arguments, one or both of whose Premises are Illogical. |
| 5. | Incomplete and Irregular Arguments. |
| 6. | Common Mistakes of the Student. |
| 7. | Outline. |
| 8. | Summary. |
| 9. | Review Questions. |
| 10. | Questions for Original Thought and Investigation. |
| CHAPTER 15.—HYPOTHETICAL AND DISJUNCTIVE ARGUMENTS INCLUDING THE DILEMMA. | |
| 1. | Three Kinds of Arguments. |
| 2. | Hypothetical Arguments. |
| 3. | Antecedent and Consequent. |
| 4. | Two Kinds of Hypothetical Arguments. |
| 5. | Rule and Two Fallacies of Hypothetical Argument. |
| 6. | Hypothetical Arguments Reduced to Categorical Form. |
| 7. | Illustrative Exercises Testing Hypothetical Arguments of All Kinds. |
| 8. | Disjunctive Arguments. |
| 9. | Two Kinds of Disjunctive Arguments. |
| 10. | First Disjunctive Rule. |
| 11. | Second Disjunctive Rule. |
| 12. | Reduction of Disjunctive Argument. |
| 13. | The Dilemma. |
| 14. | Four Forms of Dilemmatic Arguments. |
| 15. | The Rule of Dilemma. |
| 16. | Illustrative Exercises Testing Disjunctive and Dilemmatic Argument. |
| 17. | Ordinary Experiences Related to Disjunctive Proposition and Hypothetical Argument. |
| 18. | Outline. |
| 19. | Summary. |
| 20. | Review Questions. |
| 21. | Questions for Original Thought and Investigation. |
| CHAPTER 16.—THE LOGICAL FALLACIES OF DEDUCTIVE REASONING. | |
| 1. | A Negative Aspect. |
| 2. | Paralogism and Sophism. |
| 3. | A Division of the Deductive Fallacies. |
| 4. | General Divisions Explained. |
| 5. | Fallacies of Immediate Inference. |
| 6. | Fallacies in Language (Equivocation). |
| 7. | Fallacies in Thought (Assumption). |
| 8. | Outline. |
| 9. | Summary. |
| 10. | Illustrative Exercises in Testing Arguments in Both Form and Meaning. |
| 11. | Review Questions. |
| 12. | Questions for Original Thought and Investigation. |
| CHAPTER 17.—INDUCTIVE REASONING. | |
| 1. | Inductive and Deductive Reasoning Distinguished. |
| 2. | The “Inductive Hazard.” |
| 3. | Complexity of the Problem of Induction. |
| 4. | Various Conceptions of Induction. |
| 5. | Induction and Deduction Contiguous Processes |
| 6. | Induction an Assumption. |
| 7. | Universal Causation. |
| 8. | Uniformity of Nature. |
| 9. | Inductive Assumptions Justified. |
| 10. | Three Forms of Inductive Research. |
| 11. | Induction by Simple Enumeration. |
| 12. | Induction by Analogy. |
| 13. | Induction by Analysis. |
| 14. | Perfect Induction. |
| 15. | Traduction. |
| 16. | Outline. |
| 17. | Summary. |
| 18. | Review Questions. |
| 19. | Questions for Original Thought and Investigation. |
| CHAPTER 18.—MILL’S FIVE SPECIAL METHODS OF OBSERVATION AND EXPERIMENT. | |
| 1. | Aim of Five Methods. |
| 2. | Method of Agreement. |
| 3. | Method of Difference. |
| 4. | The Joint Method of Agreement and Difference. |
| 5. | The Method of Concomitant Variations. |
| 6. | The Method of Residues. |
| 7. | General Purpose and Unity of Five Methods. |
| 8. | Outline. |
| 9. | Summary. |
| 10. | Review Questions. |
| 11. | Questions for Original Thought and Investigation. |
| CHAPTER 19.—AUXILIARY ELEMENTS IN INDUCTION. OBSERVATION—EXPERIMENT—HYPOTHESIS. | |
| 1. | Foundation of Inductive Generalizations. |
| 2. | Observation. |
| 3. | Experiment. |
| 4. | Rules for Logical Observation and Experiment. |
| 5. | Common Errors of Observation and Experiment. |
| 6. | The Hypothesis. |
| 7. | Induction and Hypothesis Distinguished. |
| 8. | Hypothesis and Theory Distinguished. |
| 9. | The Requirements of a Permissible Hypothesis. |
| 10. | Uses of Hypothesis. |
| 11. | Characteristics Needed by Scientific Investigators |
| 12. | Outline. |
| 13. | Summary. |
| 14. | Review Questions. |
| 15. | Questions for Original Thought and Investigation. |
| CHAPTER 20.—LOGIC IN THE CLASS ROOM. | |
| 1. | Thought is King. |
| 2. | Special Functions of Induction and Deduction. |
| 3. | Two Types of Minds. |
| 4. | Conservatism in School. |
| 5. | The Method of the Discoverer. |
| 6. | Real Inductive Method not in Vogue in Class Room Work |
| 7. | As a Method of Instruction, Deduction Superior. |
| 8. | Conquest, not Knowledge, the Desideratum. |
| 9. | Motivation as Related to Spirit of Discovery. |
| 10. | Discoverer’s Method Adapted to Class Room Work. |
| 11. | Question and Answer Method not Necessarily One of Discovery. |
| 12. | Outline. |
| 13. | Summary. |
| 14. | Review Questions. |
| 15. | Questions for Original Thought and Investigation. |
| CHAPTER 21.—LOGIC AND LIFE. | |
| 1. | Logic Given a Place in a Secondary Course. |
| 2. | Man’s Supremacy Due to Power of Thought. |
| 3. | Importance of Progressive Thinking. |
| 4. | Necessity of Right Thinking. |
| 5. | Indifferent and Careless Thought. |
| 6. | The Rationalization of the World of Chance. |
| 7. | The Rationalization of Business and Political Sophistries. |
| 8. | The Rationalization of the Spirit of Progress. |
| 9. | A Rationalization of the Attitude Toward Work. |
| 10. | The Logic of Success. |
| 11. | Outline. |
| 12. | Summary. |
| 13. | Review Questions. |
| 14. | Questions for Original Thought and Investigation. |
| GENERAL EXERCISES IN TESTING CATEGORICAL ARGUMENTS. | |
| GENERAL EXERCISES IN TESTING HYPOTHETICAL, DISJUNCTIVE AND DILEMMATIC ARGUMENTS. | |
| EXAMINATION QUESTIONS FOR TRAINING SCHOOLS AND COLLEGES. | |
| BIBLIOGRAPHY. | |
| OUTLINE OF BRIEFER COURSE. | |
| INDEX. | |
As to the true conception of matter the world is ignorant. Yet when asked, “What does matter do?” the reply is, “Matter moves, matter vibrates.” Moreover, relative to the exact nature of mind, the world is likewise ignorant. But to the question, “What does mind do?” the response comes, “The Mind knows, the mind feels, the mind wills.” The mind has ever manifested itself in these three ways. Because of this three-fold function it is easy to think of the mind as being separated into distinct compartments, each constituting an independent activity. This is erroneous. The mind is a living unit having three sides but never acting one side at a time. When the mind knows it also feels in some way and wills to some extent. To illustrate: Music is heard and one knows it to be Rubinstein’s Melody in F. The execution being good one feels pleasure. That the pleasurable state may be augmented one wills a listening attitude. For analytical purposes the psychologists have a way of naming the state of mind from the predominating manifestation.
What the mind is may in time be answered satisfactorily by philosophy; what the mind does is described by psychology; what the mind knows is treated by logic. Again: the mind as a whole furnishes the subject matter for psychology, whereas logic is concerned with the mind knowing, aesthetics with the mind feeling, and ethics with the mind willing. Ethics attempts to answer the question, “What is right?” aesthetics, “What is beautiful?” and logic, “What is true?”
Though both psychology and logic treat of the knowing aspect of the mind, yet the fields are not identical. The former deals with the process of the knowing mind as a whole, while the latter is concerned mainly with the product of the knowing mind when it thinks. To be specific: The mind knows when it becomes aware of anything, moreover, this condition of awareness appears in two ways: first, immediately or by intuition; second, after deliberation or by thinking. For example, one may know immediately or by intuition that the object in the hand is a lead pencil, but when requested to state the length of the pencil there is deliberation involving a comparison of the unknown length with a definite measure. It may now finally be asserted that the pencil is six inches long. When we know without hesitation the process involved is intuition, whereas when the knowledge comes after some sort of comparison the mental act is called thinking. It, therefore, becomes the business of psychology to deal with both intuition and thinking while logic devotes its attention to thinking only, and even in this field the work of logic is more or less indirect. The specific scope of logic is the product of thinking or thought.1 What are the forms of thought? What are the laws of thought? Are the several thoughts true? These are the questions which logic is supposed to answer.
For the logician thought has two sources, his own mind and the mind of others. In the latter case thought becomes accessible through the medium of language. There is in consequence a close connection between logic, the science of thought, and grammar, the science of language. Because of this near relation logic is sometimes called the “grammar of thought.”
To study any science properly one must have thoughts and since logic is the science of all thought the subject may be regarded as the science of sciences.
“Logic is the science of thought.” This definition commonly given is too brief to be helpful. Should not a definition of any subject represent a working basis upon which one may build with some knowledge of what the structure is to be? The following, a little out of the ordinary, seems to supply this condition: Logic as a science makes known the laws and forms of thought and as an art suggests conditions which must be fulfilled to think rightly.
In justification of the latter definition it may be argued that it covers the topics usually treated by logicians. It is said that a science teaches us to know while an art teaches us to do. As a science logic teaches us to know certain laws which underlie right thinking. For example, the law of identity which makes possible all affirmative judgments, such as “Some men are wise,” “All metals are elements,” etc. Likewise as a science logic acquaints us with certain universal forms to which thought shapes itself, such as definitions, classifications, inductions, deductions. Further, logic lays down definite rules which lead to right thinking. To wit: Because it is true of a part of a class it should not be assumed that it is true of the whole of that class: or, in short, do not distribute an undistributed term.
A possible profit to the student may result from a study of certain authentic definitions herewith subjoined:
(1) “Logic is the science of the laws of thought.” Jevons.
(2) “Logic is the science which investigates the process of thinking.” Creighton.
(3) “Logic as a science aims to ascertain what are the laws of thought; as an art it aims to apply these laws to the detection of fallacies or for the determination of correct reasoning.” Hyslop.
(4) “Logic is the art of thinking.” Watts.
(5) “Logic is the science and also the art of thinking.” Whateley.
(6) “Logic is the science of the formal and necessary laws of thought.” Hamilton.
(7) “Logic is the science of the regulative laws of the human understanding.” Ueberweg.
(8) “Logic treats of the nature and of the laws of thought.” Hibben.
(9) “Logic may be defined as the science of the conditions on which correct thoughts depend, and the art of attaining to correct and avoiding incorrect thoughts.” Fowler.
(10) “Logic is the science of the operations of the understanding which are subservient to the estimation of evidence.” Mill.
(11) “Logic may be briefly described as a body of doctrines and rules having reference to truth.” Bain.
It would seem as if there were as many different definitions as there are books on the subject. This is due partly to the disposition of the older logicians to ignore the art of logic and partly to the difficulty of giving in a few words a satisfactory description of a broad subject. In the fundamentals of logical doctrine present-day authorities virtually agree.
Logic is rapidly coming into favor as a major subject in institutions devoted to educational theory. Some of the reasons for this change of attitude are herewith subjoined:
(1) Logic should stimulate the thought powers. This is the age of the survival of the thinker. The fact that the man who thinks best is the man who thinks much and carefully will be accepted by those who believe that practice makes perfect. “One needs only to observe the average commuter to conclude that a large percent. of our business men read too much and think too little.” “Much readee and no thinkee” was the reply of a Chinaman when asked his opinion of the doings of the average American. “We as a people are newspaper mad, reading for entertainment, seldom for mental improvement.”
(2) Logic aims to secure correct thought. Are not many of the sins and most of the failures in this world due to incorrect thinking?
(3) Logic should train to clear thinking. It would be difficult to estimate the loss of energy to the brain worker because he has not the power to think clearly. Maximum efficiency is impossible with a befogged brain. How discouraging it is to the student to attempt to get from the paragraph the thought of the author, who in trying to be profound succeeds in being profoundly abstruse. There is a probable need for broad, deep thoughts, but these when placed in a text book should be sharpened to a point.
(4) Logic should aid one to estimate aright the statements and arguments of others. This is of especial value to the teacher who is constrained to teach largely from text books. Because it is found in a book is not proof positive that it is true. Why should we assume that the book is infallible when we know that the man behind the book is fallible?
(5) Logic insists on definite, systematic procedure. To be logical is to be businesslike. A study of logic would, no doubt, benefit our churches and parliamentary orders as well as our schools.
(6) Logic demands lucid, pointed, accurate expression. How we would increase our working efficiency could we but express our thoughts in an attractive and interesting manner. To listen to the speeches of some of our great and good men who are concerned in directing the “ship of state” is sufficient argument that the American schools need more logic.
(7) Logic is especially adapted to a general mental training. Despite the swing of the pendulum of public opinion toward the bread-and-butter side of life, there are many of high repute who claim that for the sake of that mental acumen which distinguished the Greek from his contemporaries we cannot afford to sacrifice everything on the altar of commercialism.
(8) Logic worships at the shrine of truth and adds to our store of knowledge. What has aided the world more in its march onward than this deep-seated passion for truth and what has impeded it more than that vain and wanton indifference to truth which brought to the world its darkest age?
THE SCOPE AND NATURE OF LOGIC.
(1) The Mind.
Three aspects.
Unity of.
(2) Logic Related to Other Subjects.
Mental philosophy, psychology, logic.
Psychology, logic, aesthetics, ethics.
Two ways of knowing.
Special province of logic.
Logic and language.
A science of sciences.
(3) Logic Defined.
A general definition.
A more satisfactory definition.
A list of authentic definitions.
(4) The Value of Logic to the Student.
Eight reasons for its study.
(1) The aspects of the mind are knowing, feeling and willing.
The mind is a living unit and never knows without feeling in some way and willing to some extent.
(2) What the mind is must be answered by philosophy; what the mind does by psychology and what the mind knows by logic.
Psychology treats of the mind as a whole, logic of the mind knowing, aesthetics of the mind feeling and ethics of the mind willing. Ethics answers the question, What is right? Aesthetics, What is beautiful? Logic, What is true?
The standpoint of logic is not identical with any particular portion of psychology.
The mind knows in two ways: (a) by intuition, (b) by thinking. Thinking is a process—thought a product. Logic deals indirectly with the former and directly with the latter.
Generally speaking, logic is a systematic study of thought. For the logician thought has two sources: (a) his own mind and (b) spoken or written language.
Because of the ambiguity of language logic has much to do with it as a faulty vehicle of thought.
(3) Logic as a science makes known the laws and forms of thought and as an art suggests conditions which must be fulfilled to think rightly. Author.
“Logic may be defined as the science of the conditions on which correct thoughts depend, and the art of attaining to correct and avoiding incorrect thoughts.” Fowler.
In the fundamentals of logical doctrine present day logicians virtually agree.
(4) Logic should stimulate the thought powers; secure correct and clear thinking; aid in the estimation of arguments; inspire definite, systematic procedure; demand lucid, pointed, accurate expression and be especially adapted to general mental discipline.
Logic adds to our store of knowledge and develops a passion for the truth.
(1) Explain and illustrate the three ways in which the mind may manifest itself.
(2) Illustrate the fact that the mind acts in unity.
(3) Show briefly how logic is related to mental philosophy, psychology, aesthetics, ethics and grammar.
(4) Illustrate the two ways of knowing.
(5) Distinguish between thinking and thought.
(6) Give a general definition of logic. Why is this definition unsatisfactory?
(7) What are the two sources of thought?
(8) Why are logic and language so closely related?
(9) Give that definition of logic which best satisfies you.
(10) Summarize the benefits which you hope to derive from your study of logic.
(11) Why should teachers be clear thinkers?
(12) Why should teachers be especially on guard against incorrect statements of all kinds?
(13) Show how logic might be of assistance to the business man.
(1) Prove that there is nothing real in the world save the mind itself.
(2) “Logic is concerned primarily with how we ought to think and only in a secondary way with how we actually think.” Explain this quotation.
(3) Prove that there is no such thing as intuitive knowing.
(4) Is there any difference between knowledge and thoughts? Illustrate.
(5) Show by illustrations that the English language is ambiguous.
(6) Prove by concrete illustration that this is the age of the survival of the thinker.
(7) Which is the more harmful: falsehood mixed with truth or unadulterated falsehood? Give reasons.
(8) Give a concrete example of incorrect thinking.
(9) Show that wrong thinking leads to wrong doing.
(10) To be worth while must every subject have a practical value?
(11) “The 20th century virtue is a passion for truth.” Prove the truth of this.
In the preceding chapter we were told that the mind may know in two ways (1) by intuition and (2) by thinking. It is thus implied that the knowing mind includes the thinking mind plus intuition. Thinking always involves knowing, but knowing need not involve thinking, and when some logicians maintain that to know a thing one must think it, there is danger of being misled. They mean by this that in order to know anything in a permanent and highly serviceable way one must think it. All animals know, even such a stupid one as the oyster, and yet one would hardly give an oyster credit for thinking. Only the higher orders of animal life think. Some argue that the power is confined exclusively to the human family. This opinion is debatable. If the claimant means by thinking, reasoning then his ground is well taken. But if he is willing to give to thinking a broader content, then he has little defense for his stand. However, attach as broad a meaning to thinking as the derivation of the word will permit and even then it is a narrower term than knowing. Thinking plus intuition equals knowing, and in intuition there is probably no thinking.
It has been affirmed that intuition is the process involved when the mind knows instantly.2
ILLUSTRATIONS:
(1) As I raise my eyes a figure comes to view. My mind knows instantly that it is the figure three. (2) The ear catches immediately a tune which is being sung in the room below. Without deliberation the mind recognizes the tune as America. The mind may thus know by intuition through any one of the five senses. These are the wires of connection between the outer world and the mind within and transmission over these wires may be instantaneous or intuitive. This is not all. (3) My mind may center its attention on itself and may recognize there a mental picture or image of a pet dog. Since this activity is without any apparent deliberation the process must be intuitive. To define intuitive knowledge as that which comes to the mind through the senses only is incorrect, as it leaves out altogether the knowledge the mind may obtain of its own activity as in illustration “(3).”
Knowledge is anything known. Intuitive knowledge is knowledge which comes to the mind immediately by direct observation. The field for intuitive knowledge may be the external world or the internal world though, of course, the former is the more common ground. It is here that the mind by intuition secures the most of its raw material which, through the process of thinking, is worked over into a connected, unified system of lasting value.
The intuitions are the beginning and the basis of all knowledge, and knowledge gained by intuition is the basis of all thinking.
It is claimed that think comes from the same root as thick. From this one would conclude that the process of thinking is virtually a process of thickening. Surely as one thinks he enriches or thickens his knowledge. As one thinks percepts into concepts and concepts into judgments he makes richer in meaning the various notions concerned. Thinking is largely a matter of pressing many into one: of linking together the disconnected fragments of the conscious field.
DEFINITION:
Thinking is the deliberative process of affirming or denying connections.
The same idea may be expressed in a variety of ways as the following indicate.
(1) “Thinking is the conscious adjustment of a means to an end in problematic situations.” Miller.
(2) “To think is to designate an object through a mark or attribute or what is the same thing, to determine a subject through a predicate.” Bowen.
(3) “Thought is the comprehension of a thing under a general notion or attribute.” Wm. Hamilton.
(4) “To think is to make clear through concepts the perceived objects.” Dressler.
In the foregoing definitions it is implied that thinking is a connecting or thickening process. In all forms of thinking from the simplest to the most complex the knowing mind hunts for some basis of connection and having found it thinks the relationship into a unified whole.
The thinking process is the digestive process of the mind. Much as the digestive organs assimilate the food stuff of the physical world, so the thinking organ assimilates the food stuff of the mental world.
ILLUSTRATIONS OF THE THINKING PROCESS:
(1) The child is unable to explain the meaning of “hocus-pocus” as it occurs in the question, “What hocus-pocus is this?” The child mind is unable to establish any connection between the word and its real meaning. In short, is unable to think into it a meaning; it therefore becomes necessary for the teacher to establish some basis of connection and this he does by suggesting nonsense as a synonym.
(2) The teacher holds before the class an Egyptian house god and asks, “What is it?” After a moment of hesitation some child who has seen pictures of “his satanic majesty” avers that the object is a “little devil.” Thus has a connection been established between the idol and pictures of satan.
(3) John is unable to solve the following problem as he can discern no connection between the data given and the data required. Problem. 3⁄4 of my salary is $900, what is my salary?
Data. Given: 3⁄4 of salary = $900.
Required: 4⁄4 of salary = ?
In order that John may think a solution the teacher must lead him to see some connection between 3⁄4 and 4⁄4. With this in mind the form of the data is changed to
Given: 3-fourths = $900
Required: 4-fourths = ?
or
Given: 3 parts = $900
Required: 4 parts = ?
John now notes that 4 parts is 4⁄3 times 3 parts and consequently writes 4⁄3 of $900, which is $1,200 as the answer. Or he may find the value of 1 part and then of 4 parts.
A notion is any product of the knowing mind—anything which the mind notes or becomes aware of.
But the mind knows in two ways, by intuition and by thinking. In consequence the mind has two kinds of notions, those which are intuitive or individual notions and those which originally result from thinking or general notions.
An individual notion is a notion of one thing. A general notion is a notion of a class of things.
Note. Here it is necessary to distinguish between a thing and an object. An object is a thing which occupies space such as a pencil or a book. “Thing” is, therefore, a broader term than “object.” “A thing is that which has individual existence.” From the viewpoint of logic “thing” includes objects, qualities, relations, spiritual entities. Gravitation is a thing but not an object. A tree is both an object and a thing.
ILLUSTRATIONS OF NOTIONS.
My notion of the pencil with which I am writing is an individual notion, but my notion of pencil as a class name is general. My yellow dog, the honesty of Lincoln, Albert White, New York City, are individual notions, while dog, honesty, man, city, are general notions.
A sure way to determine whether the notion is individual or general is to attempt to divide it into its kinds. Only general notions may be subdivided.
Knowledge is anything known, while anything of which the mind becomes aware is a notion. Notions are always bits of knowledge, but knowledge is not always a notion. Notions are mental products belonging to the mind which thinks them, while knowledge, though it must first be a mental product of someone’s mind, may not necessarily be a product of yours or mine. Notions are always found in the mind, while knowledge may be found in books, but not necessarily in some individual mind. Knowledge stands for everything known, the notion, for everything noted. The Egyptians may have possessed much knowledge of which we may never become aware. Much of their knowledge may never become notions of the American people. A notion is an existing state of consciousness. Said notion may be committed to paper, and then it may give way to another notion. It now ceases to be your notion, but remains on the printed page, as a bit of knowledge.
“Idea,” because of its ambiguity, really has no place in logic. The term is frequently restricted to a reproduced percept. To illustrate: When the pencil is before me the mental product is a percept, but when the pencil is withdrawn and I try to think of it, then have I an idea of “pencil.” Probably idea is most commonly associated with meaning and belief. To illustrate: What is your idea as to the meaning of homogeny? or What are your ideas on the tariff?
Concerning the knowing mind the psychologist classifies its activities and their products as follows:
| Activity | Product | ||||
| (1) | Presentative | ||||
| (1) | Sensation | Sensation | |||
| (2) | Perception | Percept | |||
| (2) | Representative | ||||
| (1) | Imagination |
 |
Image | ||
| (2) | Memory | ||||
| (3) | Thinking | ||||
| (1) | Conception | Concept | |||
| (2) | Judging | Judgment | |||
| (3) | Reasoning | Inference | |||
The notion as any product of the knowing mind includes the six products as indicated by the psychologist.
The individual notion which is intuitive includes the sensation, percept and image; the general notion which is a thought product stands for the concept, judgment and inference. To put it mathematically—
| Individual notion | = |
 |
sensation percept image |
 |
= | intuitive products |
 |
notion |
| General notion | = |
 |
concept judgment inference |
 |
= | thought products |
As we shall have occasion frequently to refer to these psychological terms it may be well to define them.
| Psychological Definition. | Logical Definition. |
| A sensation is the first and simplest mental result of the stimulation of an incarrying nerve. | A sensation is a vague, unlocalized mental product of the knowing mind. |
| A percept is a mental product which results from a consciousness of particular material things present to the sense. | A percept is a consciously localized group of sensations. |
| An image is a mental product which results from particular material things not present to the sense. | An image is a reproduced percept. |
| A concept is a representation in our minds answering to a general name. | A concept is a mental product arising from thinking many notions into one class. |
| A judgment is the result of asserting an agreement or disagreement between two ideas. | A judgment is the mental product arising from conjoining or disjoining notions. |
| An inference is a judgment derived from perceiving relations between other judgments. | An inference is a judgment derived from antecedent judgments. |
It is seen that the sensations furnish the raw material. Ignoring the few exceptions we may then say that a percept is a made-over group of sensations; a concept a thought-made group of percepts; a judgment a thought-made group of concepts; an inference a judgment derived from other judgments.
Developed thinking is first found in the concept, and as we study the thought products, “concept,” “judgment” and “inference,” the truth is forced upon us that thinking as a process aims to group the many into one. From many percepts is built the one concept, from two concepts is built the one judgment and from two judgments is built the one inference.3
Speaking figuratively, thinking is a matter of picking up the fragments along the shore of consciousness and tying them into bundles.
So far in this discussion it has been assumed that there is no thinking involved in the sensation or the percept. There are good authorities, however, who insist on dignifying the sensation, even with a crude form of thinking. To illustrate: One may be reading an interesting novel. The mind is being entertained and ignores the activities of the objective world, yet we cannot say that the mind is dead to the world outside. There is a dim consciousness of certain noises without. These unlocalized sounds are sensations; but how is the mind able to recognize them as sounds or noises? To interpret the noises is it not necessary for the mind to affirm a connection between them and some past mental experience? Is it possible for the mind to know anything without establishing some kind of connection between the outside occurrence and an inner situation? If this is granted then in sensation there must be implicit thinking.
As the percept is a localized group of sensations then there must be involved in perception a more complex form of thinking, since in grouping sensations there is a recognition of connections.
If there is thinking in the sensation which is the simplest and lowest form of the knowing-mind then thinking conditions all knowledge and really is the basic elemental cell of all knowing.
On the other hand there are those who maintain that the sensation and percept are mere reflections of consciousness; the sensation being a reflected quality and the percept a reflected object. These mental situations come into being instantly—there is no time for thought and we all know that thought requires time. (“As quick as thought” is misleading, since light travels more rapidly by many times than the agencies of thought.)
It will probably never be settled to the satisfaction of all just when thinking commences. The question is as difficult as some others which have never been solved. For example: Where does life commence? When does the plant merge into the animal? Which was first the egg or the hen? Does the objective world really exist or is it only a mental interpretation of vibrations? etc.
Logically considered the question is immaterial. All will agree that developed thought is involved in the concept, judgment and inference, while, if it appears at all in the percept and sensation, it is more or less undeveloped and consequently lies quite without the province of the logical field.
Speaking in general terms evolution is a development from a lower to a higher state. Thus have come the various species of the vegetable and animal world. The lower orders of life are simple in structure and function. In the one-celled animate form a single organ performs all of the work needed to maintain life and perpetuate the species. If these simple life-forms are cut in two, life continues in the two parts as if nothing had happened. Aside from their simplicity there is little of interdependence of function and little of co-ordination of organs in the lowest life-forms. In short there is no division of labor; “each cell is a world unto itself.”
An analogous development is seen in the thinking mind. The little child thinks in lumps, and these lumps are only faultily linked together, but the adult thinks in terms of the grains of the lump, each grain having its place, which it must occupy for the sake of all the other grains as well as the entire lump. The child’s thinking is vague, general and inaccurate, while the adult’s thinking should be definite, specialized and accurate. Thinking in the lump means little discrimination and very faulty integration or unity, while thinking in terms of the grains means detailed discrimination and perfect integration. To illustrate: The child sees a dog trotting along the side walk which, according to the suggestion of his mother, he learns to call “bow-wow.” Later he observes a cat and at once says “bow-wow,” because all that the child notes is that something with legs, ears and a tail is trotting along the side walk. Anything which fits these general marks is a “bow-wow.” Similarly when a child first observes a robin perched on a gate post he fails to distinguish between the two—it is all bird from the top of the robin’s head to the bottom of the gate post.
Progress in thinking is measured by progress in discrimination. The skilled thinker divides the large unit into very small units, compares these with each other and then reunites them into a more perfect and unified whole. First there is an analysis and then a synthesis. Like a shuttle the power of thought works in and out; it goes in to separate, it comes out to unify.
There is another aspect in the analogy between the life of the physical and mental worlds. Somewhere in the order of progress there is a connecting link between the mineral and vegetable kingdoms, likewise between the vegetable and animal kingdoms. The sensation is as much a state of feeling as an act of knowing and consequently is the connecting link between the feeling mind and the knowing mind. If the percept is the result of thinking as well as intuition then it may stand for the dividing line between the knowing4 mind and the thinking mind.
Conception is the process of thinking many notions into one class. The product of such a process is called a concept. (1) The concept may stand for a group of concrete general notions—as the concept man, which stands for the five general notions: Caucasian, Mongolian, Ethiopian, Malay and American Indian. (2) The concept may stand for a group of concrete individual notions. For example, the same concept man represents all of the individual men of the world. (3) The concept may stand for a group of abstract general notions. To wit: Virtue represents such general notions as honesty, justice, industry, purity, etc. (These are general notions because they admit of a subdivision into kinds. Industry, for instance, may be divided into two kinds: mental industry and physical industry.) (4) The concept may stand for a group of abstract individual notions. To illustrate: Blueness stands for the various shades of blue, as sky blue, bird’s egg blue, navy blue, etc.
Thus does the concept stand for a group of all kinds of notions, individual and general, abstract and concrete.
THE PROCESS OF CONCEPTION ILLUSTRATED.
I see for the first time in my life a pencil. In other words I become conscious of a localized group of sensations—this is a percept. I am told that the name of that which I see is pencil. I note that this particular pencil has a thread of black lead encased in a cylindrical strip of wood which is brown in color. A second object is presented which I recognize as a pencil though the shape is prismatic rather than cylindrical and the color green rather than brown. But I call it a pencil because it has a thread of black lead encased in a strip of wood. The notion which I now have in mind stands for two pencils and is therefore represented by a class name. As I observe other pencils of various shapes, made of wood and paper with threads of different colored lead, my notion of pencil broadens till finally it stands for all pencils. This is the process of conception according to the definition, namely: “The process of thinking many notions into one class.” In this case the notions are individual.
An examination of conception makes evident two distinct characteristics. First, I may be able to recognize each individual pencil because of the two common qualities, a thread of lead and an encasement of some kind. This process of the knowing mind whereby it recognizes and affirms connections is called thinking as we have already learned. Here is the thinking aspect of conception. Second, as the instances of the observed objects are multiplied, my notion of pencil is broadened. It is a building process where many are cemented into one; like the blocks of a cement wall. Here we find the characteristic which enables us to call the process conception. This is the mark which distinguishes conception from all the other thought processes.
Judging is the process of conjoining and disjoining notions. The product of judging is the judgment and all judgments are expressed by means of propositions. A proposition consists of one subject and one predicate connected by some form of the verb be or its equivalent.
(1) A judgment may conjoin or disjoin two individual notions.
To wit: Conjoined—This pencil belongs to Albert White.
Disjoined—This pencil does not belong to Mary Smith.
(2) A judgment may conjoin or disjoin two general notions.
Conjoined—Some men are virtuous.
Disjoined—Some men are not virtuous.
(3) A judgment may conjoin or disjoin a general and an individual notion.
Conjoined—Abraham Lincoln was virtuous.
Disjoined—Edgar Allen Poe was not temperate.
In order that the knowing mind may conjoin notions it must recognize some mark of similarity or connection. This is the thinking aspect of the judgment. It is likewise to a certain degree the judging aspect as the latter is simply a matter of affirming or denying connections between notions. But thinking is a broader term than judging. There may be connections established between a name and a notion. For example in the case of the dog which the child sees trotting along the sidewalk and which the mother refers to as a “bow-wow”; the term “bow-wow” is not a percept and has no meaning independent of its association with the dog, hence it is not a notion, yet some connection has been made in the child’s mind between “bow-wow” and his notion of dog. This is a simple form of thinking, but not of judging, as the latter affirms or denies connections between notions only.
The fact that judging and thinking so closely resemble each other has given just cause for some logicians to designate judging as the most fundamental element in all thinking. “The simplest form of thinking,” says Creighton, “is judging.” In order to think many notions into one class it is necessary to conjoin notions. To illustrate: The child who has a general notion of man sees for the first time a negro. If he recognizes the negro as a colored man he must conjoin his general notion of man with this individual notion. In short, a concept is built by means of a series of judgments. It may be said further that an inference is simply a made-over judgment. It is thus evident that judging appears in both the thought processes of conception and inference and, therefore, as a final conclusion it may be affirmed that judging, though perhaps not the simplest form of thinking, is the basic element of developed thought.
Reasoning is the process of deriving a new judgment from a consideration of other judgments. The product of any reasoning process may be called an inference, although, as will appear in a later chapter, inference is commonly used as indicating the process as well as the product.
Often reasoning may assume a syllogistic form with the inference as its conclusion. A syllogism is an arrangement of three propositions using three different terms. The following are syllogisms:
(1) All children should play.
Mary is a child.
Hence, Mary should play.
(2) No teacher should judge hastily.
You are a teacher.
Hence, you should not judge hastily.
In the second syllogism the inference, “you should not judge hastily,” is derived from the other two judgments by merely eliminating the common term teacher and disjoining the remaining two terms. The inference is consequently a new judgment. Therefore, reasoning is only a matter of judging carried to a more complex stage.
To summarize—conception is largely a matter of conjoining a general notion with an individual notion, judging of conjoining and disjoining all kinds of notions and inference of conjoining and disjoining judgments. All three processes go to form the larger process of thinking. The concept, the judgment and the inference are products arising from conjoining and disjoining notions.
Says Jevons: “Simple apprehension is the act of the mind by which we merely become aware of something, or have an idea or impression of it brought into the mind;” while Hyslop states that “The process of knowledge which gives us percepts is apprehension.” It is obvious that the idea of the latter is that apprehension yields individual notions only, while Jevons, in citing the term iron as an illustration of his definition, would infer that the general notion is the product of apprehension. The term is strikingly ambiguous and will not be referred to often in this treatise. If the student desires a definition this will cover the concensus of opinion on the meaning of apprehension. Apprehension is that process of the knowing mind which yields the percept and concept. Some logicians give to the thinking mind the three aspects of apprehension, judging and reasoning.
In all thinking there are three steps or stages which may be termed discrimination, comparison, integration.
In the case of the two pencils held in the hand, it is noted that one is longer than the other. Let us analyze the process which made possible this conclusion. Step one—Attention is given first to one pencil and then to the other. In each case the pencils are distinguished from the hand and the other surrounding objects. This is discrimination. Step two—The pencils are compared in length. Step three—The two notions are united in the judgment, “Pencil number one is longer than pencil number two.” This is integration.
Another illustration. The child is requested to solve this problem: If 8 tons of hay cost $165, what will 16 tons cost?
Statement: Given: 8 tons cost $165.
Required: 16 tons cost?
Discrimination. The child notes that 8 tons cost $165 and at this rate he is required to find the cost of 16 tons.
Comparison. The child perceives that 16 tons is twice 8 tons.
Integration. The child concludes that the cost of 16 tons will be twice the cost of 8 tons or $330.
When we think, we first tear to pieces that we may become acquainted with every part. This may be called analysis. Then we put the related pieces together again. This may be called synthesis. Before, however, the parts are re-united a certain amount of comparison is necessary. The three stages of thought might thus be denominated: (1) analysis, (2) comparison, (3) synthesis.
After the synthesis or integration it is necessary to name the result, consequently a fourth step is sometimes given, namely denomination.
THOUGHT AND ITS OPERATION.
(1) The Knowing Mind Compared with the Thinking Mind.
(2) Knowing by Intuition.
(3) The Thinking Process.
Defined.
Other definitions.
(4) Notions.
Individual.
General.
Thing and object distinguished.
(5) Knowledge and Idea as Related to the Notion.
(6) The Logic of Psychological Terms Involved in the Notion.
The sensation
The percept
The image
 Individual
Individual
notions.
The concept
The judgment
The inference
 General
General
notions.
Terms defined.
(7) Thought and the Sensation and Percept.
(8) Evolution and the Thinking Mind.
(9) The Concept as a Thought Product.
(10) The Judgment as a Thought Product.
The simplest form of thinking.
(11) Inference as a Thought Product.
(12) Thinking and Apprehension.
(13) Stages in Thinking.
Discrimination.
Comparison.
Integration.
(Denomination.)
(1) Knowing is a broader term than thinking as the former equals the latter plus intuition.
(2) Intuitive knowledge is that which comes to the mind immediately by direct observation.
Although intuitive knowledge comes to the mind without thought, yet such knowledge is essential to all thinking. Intuitive knowledge is the foundation upon which the thinking mind builds.
(3) Thinking is the deliberative process of affirming and denying connections. Thinking is a “thickening process,” the smaller units being pressed together to make a larger. Thinking is chiefly a matter of reducing plurality to unity.
(4) A notion is any product of the knowing mind.
An individual notion is the notion of one thing.
A general notion is a notion of a class of things.
A thing includes objects, qualities, relations or any existing entity. A thing is that which has individual existence.
(5) A bit of knowledge must have been a notion of some one’s mind, but may not necessarily be a notion of your mind. Knowledge may be found in books, but a notion is a mental product found only in the mind. Idea is ambiguous, though its meaning is usually restricted to an image, a meaning or a belief.
(6) The products of the knowing mind are the sensation, the image, percept, concept, judgment, inference.
The sensation, image and percept are individual notions, while the concept, judgment and inference are general notions.
A sensation is a vague, unlocalized product of the knowing mind.
A percept is a consciously localized group of sensations.
An image is a reproduced percept.
A concept is a mental product arising from thinking many notions into one class.
A judgment is a mental product arising from conjoining and disjoining notions.
An inference is a judgment derived from antecedent judgments.
The developed thought processes are the concept, the judgment and the inference.
(7) Just where the simplest form of thinking appears in the various activities of the knowing mind is still an undecided question. It is agreed that thinking in its developed and more complex form is found in conception, judging and reasoning.
(8) Thinking evolves from the simple to the more complex, just as life has evolved.
The child thinks in vague, indefinite wholes, while the adult thinks in clear, definite parts. The child discriminates very imperfectly while the adult discriminates accurately.
The sensation seems to be the connecting link between the feeling mind and the knowing mind, while the percept links together the knowing mind and the thinking mind.
(9) Conception is the process of thinking many notions into one class. The product of such a process is a concept. The concept stands for groups of all kinds of objects.
Conception has the two aspects of affirming connections and of building many into one. The first is the thinking side of the process and the second is the mark which distinguishes conception from the other thought processes.
(10) Judging is the process of conjoining or disjoining notions. Judgment is the product of judging.
Judgments conjoin and disjoin all kinds of notions.
Judging and thinking, though they closely resemble each other, are not synonomous terms. Thinking is a broader term in that connections may be established between a notion and a name for that notion.
Judging is the most fundamental of all thinking, as the concept is built from a series of judgments and an inference is simply a made-over judgment.
(11) Inference.
Reasoning is the process of deriving a new judgment from a consideration of antecedent judgments. This derived judgment may be called an inference. Sometimes the term inference denotes the process of reasoning as well as the product.
Reasoning often takes the form of a syllogism.
The concept, the judgment and the inference are products arising from conjoining and disjoining notions.
(12) Some give to the thinking mind the three aspects, apprehension, judging and reasoning. Apprehension is another word for the two processes, perception and conception.
(13) The three important stages in thinking are discrimination, comparison, integration; or analysis, comparison and synthesis.
(1) Show the difference between the knowing mind and the thinking mind.
(2) Describe the process known as intuition.
(3) What is intuitive knowledge?
(4) Is the assumption that think comes from the same root as thick a feasible one? Explain.
(5) Define thinking in at least two ways.
(6) “Inability to think is due to inability to note connections.” Show this by making use of some problem in arithmetic.
(7) Distinguish between individual and general notions.
(8) Which is the broader term, object or thing? Explain.
(9) What kind of notions only admit of subdivisions? Illustrate.
(10) What is the difference between knowledge and notions? Explain.
(11) Explain and illustrate the meaning of idea.
(12) Classify the various activities of the knowing mind and define each.
(13) Explain by definition and illustration the products of the knowing mind.
(14) Relate the general notion to the psychological products of the knowing mind.
(15) “The thinking mind is a unit.” Explain fully.
(16) Trace the analogy between the evolution of the physical world and the evolution of thought.
(17) Show that the sensation and the percept may be regarded as connecting links between lower and higher states.
(18) Define and illustrate conception.
(19) Show that the concept stands for all kinds of notions.
(20) Point out the thinking aspect of conception as distinguished from the activity which gives the process its name.
(21) Define the judgment. Illustrate two kinds.
(22) Show that the concept is built by means of a series of judgments.
(23) Show that judging is the fundamental element in the thought products.
(24) Define and illustrate reasoning.
(25) Describe the syllogism.
(26) Explain the use of apprehension.
(27) What are the stages in thinking? Illustrate fully.
(28) Show that thinking is a matter of analysis and synthesis.
(1) Give your argument in favor of the statement, “Dogs think, but do not reason.”
(2) Show by illustration that thinking would be impossible without intuition.
(3) “Thinking is the conscious adjustment of a means to an end in problematic situations.” Illustrate this.
(4) The class is unable to solve the following problem: “I sell my house for $12,000, which is a gain of 25% on the cost. Find the cost.” What is the trouble? State the problem so that some connection is apparent.
(5) “Two-thirds of my salary is $2,400. What is my salary?” A child solves this by dividing $2,400 by two and multiplying this result by three. Illustrate a plan for establishing right connections.
(6) May a judgment express a general notion? Illustrate.
(7) Is a thought a thing? Illustrate.
(8) Show the illogic of dividing notions into individual, general and abstract.
(9) Show that goodness is a general notion.
(10) Is the concept an idea? Explain.
(11) Prove that a mental image is always an individual notion.
(12) “In sensation is there implicit thinking?” Argue both sides of the question.
(13) Show that the concept, the judgment and the inference are products of the thinking mind.
(14) Show by illustration where perception ceases and conception begins.
(15) Is there actually any difference between thinking and judging? Illustrate.
(16) “Reasoning is controlled thought.” Explain.
(17) Of the three stages in thinking which one most concerns the teacher? Illustrate.
The elemental form of evolved thought is the judgment. The laws or axioms of thought may, therefore, be discovered by studying the judgment.
Judging is the process of conjoining and disjoining notions. When these notions are conjoined the judgment is affirmative; when disjoined the judgment is negative. To illustrate: “Some men are wise,” is an affirmative judgment, while “Some men are not wise,” is a negative judgment. All judgments are either affirmative or negative and this suggests that there may be but two fundamental laws or axioms underlying judging or all forms of developed thinking. One law would condition the affirmative judgment; the other the negative. Such is actually the case. The law which permits the affirmative judgment is called the law of identity, while the law which allows a negative judgment is known as the law of contradiction. There is a third law termed the law of excluded middle, which is in reality a combination of the other two.
In general the law of identity implies a certain permanency throughout the material world. That door is a door and always will be a door till the conditions change. If it were not for this law, that everything is permanently identical with itself, it would be impossible to think at all. For example: Take away the notion of permanency from the door and thought becomes at once ridiculous. Suppose that while we are asserting that the object is a door, it changes to a tree, and while we insist that the object is now a tree, it changes to a cow, etc. We can readily see that it would hardly be worth while to think at all.
The law of identity may be stated in three ways: (1) Whatever is, is; (2) Everything remains identical with itself; (3) The same is the same.
ABSOLUTE IDENTITY—COMPLETE AND INCOMPLETE.
Applying the law of identity to the affirmative judgment expressed in the form of a proposition, we find two kinds of identity, absolute and relative. In the propositions, “Socrates is Socrates,” “dogs are dogs,” “honesty is honesty,” the subject is absolutely identical with the predicate—the same in form and meaning. If we were to illustrate the subject and predicate by two circles they would be of the same size and shape, the one coinciding with the other point to point.
This kind of absolute identity which makes possible all truisms we may term, for want of a better name, complete absolute identity. This would imply that there is an incomplete absolute identity and such seems to be the case. Examining the definition, “A man is a rational animal,” we observe that the notion man has the same content or meaning as the notion rational animal. In meaning, then, the two notions are absolutely identical. The one includes just as many objects or qualities as the other, and if we were to draw two circles representing them, they would be of the same size. In form, in mode of expression, however, the notions differ and the circles, though coinciding, would need to differ in form, the boundary of one might be a solid line, the other a dotted. This we may call incomplete absolute identity. All logical definitions illustrate identities of this kind.
RELATIVE IDENTITY.
Relative identity is best understood by thinking of it as partial identity, just as we may think of absolute identity as total identity. In relative identity the whole of one notion may be affirmed of a part of another notion; or a part of one notion may be affirmed of a part of another notion. To illustrate: (1) All men are mortal; (2) Some men are wise. These and their like are made possible because of the law of relative identity. In the first proposition all of the “men” class is identical with a part of the “mortal” class. If we were to represent this relation by circles, the “men” circle would be made smaller than the “mortal” circle and placed inside it, as in Fig. 1.
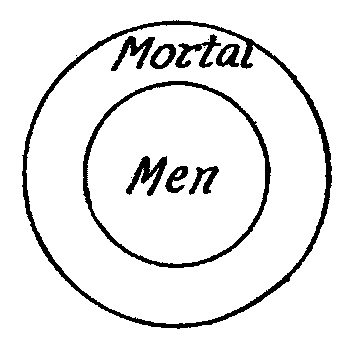
Fig. 1.
Be it remembered that circles are surfaces, and in Fig. 1 the men circle is identical with that portion of the mortal circle which is immediately underneath it.
The same relation may be indicated by a small pad being placed on top of a larger pad. Then the whole of the smaller pad could be thought of as being identical with that part of the larger pad which is immediately underneath.
In the case of the second proposition a part of the “men” class is identical with a portion of the “wise” class. The two circles indicating this relation must intersect each other so that a portion of each may be common ground, as in Fig. 2 where the shaded part represents the identity.

Fig. 2.
Thus we see that the law of identity underlies all affirmative propositions. Absolute identity making possible the truism and definition, and relative identity conditioning all the universal and particular affirmative propositions which are neither truisms nor definitions.
The three forms may be symbolized as follows:
(1) A is A—Absolute complete
(2) A is A—Absolute incomplete
(3) A is B—Relative.
The student will note that the “A’s” of absolute incomplete differ in form.
The law of contradiction underlies all negative propositions. It is the mission of this law to tear down or to be destructive in nature; while the law of identity builds up or is constructive in nature.
The law of contradiction may be stated in this way: It is impossible for the same thing to be and not to be at the same time and in the same place. Or better, it is impossible for the same thing to be itself and its contradictory at the same time. Bringing out a further aspect, no thing can have and not have the same attributes at the same time.
The little word not bisects the universe. All the people in the world are either honest or not honest, virtuous or not virtuous. These are contradictory statements and what is comprehended by the one cannot be comprehended by the other at the same time, any more than a man can shake his head and nod his head at the same time.
If we assert the identity between two notions then we cannot in the same breath deny their identity.
ILLUSTRATIONS:
(1) A red flower cannot be a red flower and not a red flower at the same time.
(2) No man can be guilty and not guilty at the same time.
(3) A boy cannot be working and not working at the same time.
If I assert that the flower is red, then I cannot affirm in the same breath that the flower is not red.
TWO USES OF NOT.
The word not when used with the copula of a given proposition makes that proposition negative, as (1) “Some men are not wise.” But when not is attached to the predicate by a hyphen, the predicate is made negative, not the proposition, as (2) “Some men are not-wise.” Here the predicate not-wise is negative, but the proposition in which it appears is affirmative. It is obvious that the proposition “Some men are not wise” illustrates the law of contradiction, since the some men referred to are contradicted of all which is wise. Whereas the proposition “Some men are not-wise” illustrates relative identity, since the subject “some men” is affirmed of a part of the predicate “not-wise.” The student may be led to see these relations by drawing circles, the one to represent the subject, the other the predicate. (See page 141.)
FURTHER ILLUSTRATIONS:
| Some teachers are wise |
 |
Illustrate the law of identity. |
| Some teachers are not-wise | ||
| Some teachers are unwise | ||
| Some teachers are not wise |
 |
Illustrate the law of contradiction. |
| Some teachers are not not-wise | ||
| Some teachers are not unwise |
The student must understand that a term and its contradictory destroy each other. If we affirm something of the one, then we must deny it of the other, or we undermine the integrity of both. If it is affirmed of teachers A, B and C that they are wise, then it must be denied that they are not-wise.
ILLUSTRATIONS:
| A, B and C are wise. |
 |
These are mutually destructive. |
| A, B and C are not-wise. | ||
| A, B and C are wise. |
 |
These are not mutually destructive, but virtually mean the same thing. |
| A, B and C are not not-wise. |
SYMBOLIZATION OF THE LAW OF CONTRADICTION.
| A is not not-A. | or | A is not B. |
| (As A is always A it would be absurd to say that A is not A.) | or | |
| A is not not-B. |
CONTRADICTORY AND OPPOSITE TERMS.
It is easy to use opposite terms in a contradictory sense. This leads to serious error. “Not-guilty” is the contradictory of “guilty,” while “innocent” is the opposite of “guilty.” We could hardly say that the water must either be cold or hot, as it might be warm. “Not-hot” is the only term which contradicts “hot.” The law of contradiction has nothing to do with opposites.
Further, it is dangerous to regard words with the negative prefix as being contradictory of the affirmative form. For example: Valuable and invaluable are not contradictory. There is likewise some doubt as to the contradictory nature of such words as agreeable and disagreeable, though we are sure that agreeable and not-agreeable contradict each other. To use the “not” with a hyphen is safer than to depend upon some prefix which is supposed to mean “not.”
ILLUSTRATIONS OF CONTRADICTORY AND OPPOSITE TERMS.
| Opposite. | Contradictory. | |||
| bad | good | bad | not-bad | |
| soft | hard | soft | not-soft | |
| cold | hot | cold | not-cold | |
| rough | smooth | rough | not-rough | |
| good | evil | good | not-good | |
| warm | cool | warm | not-warm | |
| weak | strong | weak | not-weak | |
The law of excluded middle may be considered as a combination of identity and contradiction. Identity gives the proposition, “John Doe is honest.” Contradiction, “John Doe is not honest.” Combine the two using either and or and we have the excluded middle proposition, “Either John Doe is honest or he is not honest.”
Excluded middle explains itself. Of the two contradictory notions it must be either the one or the other. There is no “go-between” notion.
The law may be stated in many ways, as will be seen by the following: (1) Everything must either be or not be. (2) Either a given judgment is true or its contradictory is true; there is no middle ground. (3) Of two contradictory judgments one must be true. (4) Every predicate may be affirmed or denied of every subject.
ILLUSTRATIONS:
(1) A man is either mortal or he is not mortal. (2) John Doe is either honest or not-honest. (3) Either you are going or you are not going.
SYMBOLIZATION OF EXCLUDED MIDDLE.
A is either A or not-A
or
A is either B or not-B.
The law may be stated in this wise. Every phenomenon, event or relation must have a sufficient reason for being what it is. To illustrate: (1) If Venus is the evening star, there must be a sufficient reason. (2) If the ground is wet, there must be a cause. Many logicians argue that this law has no place in logic, its field being that of the physical sciences. The laws of identity, contradiction and excluded middle are, however, universally regarded as the Primary Laws of thought.
| (1) Absolute Symbols | Relative Symbols. |
| Excluded middle. | |
| A is either A or not-A. | A is either B or not-B. |
| Contradiction. | |
| A is not not-A. | A is not B or A is not not-B. |
| Identity. | |
| A is A. | A is not-B or A is B. |
| (2) Propositions made to fit symbols. | |
| Excluded middle. | |
| A man is either a man or a not-man. | A man is either honest or not-honest. |
| Contradiction. | |
| A man is not a not-man. | A man is not honest, or a man is not not-honest. |
| Identity. | |
| A man is a man. | A man is not-honest, or a man is honest. |
The “excluded middle” propositions of the foregoing express alternatives which are mutually contradictory. There is no middle ground. The “contradictory propositions” contradict the identity of the subject with one alternative, while the “identity” propositions affirm the identity of the subject with the other alternative. This is made possible because of the principle, “Of two mutually contradictory terms, if one is true the other must be false.” The foregoing scheme shows how closely “contradictory” and “identity” propositions are related to “excluded middle” propositions. Expressed mathematically: excluded middle = contradiction + identity.
PRIMARY LAWS OF THOUGHT.
(1) Two fundamental laws.
Identity, contradiction.
(2) Law of identity.
Absolute—complete, incomplete.
Relative.
(3) Law of contradiction.
Two uses of not.
Contradictory and opposite terms.
(4) Law of excluded middle.
(5) Law of sufficient reason.
(6) Unity of primary laws of thought.
(1) The elemental forms of evolved thought are the affirmative and negative judgments. This suggests two fundamental laws of thought, the law of identity and the law of contradiction. The former conditions the affirmative judgment, the latter the negative.
(2) The law of identity implies a permanency of being. “Everything remains identical with itself,” is a statement of identity.
Absolute identity may be divided into complete and incomplete identity.
In complete absolute identity the subject is the same as the predicate in both form and meaning. Truisms illustrate this.
In incomplete absolute identity the subject is identical with the predicate in meaning only. Illustrated by definitions.
In relative identity the whole of the subject may be affirmed of a part of the predicate or a part of the subject may be affirmed of a part of the predicate.
(3) “It is impossible for the same thing to be itself and its contradictory at the same time,” is a statement of the law of contradiction. Identity is constructive while contradiction is destructive in nature. To make the proposition negative the word not must be used with the copula. “Not” attached to the predicate with a hyphen makes the predicate negative, but not the proposition.
To use opposite terms in a contradictory sense leads to serious error.
The safest way of making a positive term a contradictory negative term is to prefix “not” with a hyphen or use “non.”
(4) The law of excluded middle is virtually a combination of identity and contradiction. It may be stated as follows: “A thing must either be itself or its contradictory.”
(5) “Every condition must have a sufficient reason for its existence,” is the law of sufficient reason. Its distinct province is physical science rather than logic.
(6) The laws may be expressed mathematically: excluded middle = identity + contradiction.
SCHEMATIC STATEMENT OF PRIMARY LAWS.
| Name | Stated | Symbolized | Illustrated |
|---|---|---|---|
| Absolute identity | Whatever is, is | A is A | Work is work |
| Relative identity | The whole is identical with a part or a part is identical with a part |
All A is B
Some A is B |
Work is a blessing
Some play is a blessing |
| Contradiction | Nothing can both be and not be at the same time |
A is not not-A
or
A is not B
or
A is not
not-B |
Work is not
not-work John is not honest Albert is not
not-honest |
| Excluded middle | Everything must either be or not be |
A is either A or
not-A
or
A is either B or
not-B |
Fair play is either fair play or
not-fair play This man is either educated or
not-educated |
(1a) Each of the following propositions is made possible because of the existence of which law of thought?
In answering this question I summarize in my mind the meaning of each law of thought. Viz.:
(1) In complete absolute identity the subject and predicate are the same in form and meaning.
(2) In incomplete absolute identity the subject and predicate are the same in meaning, but not in form.
(3) In relative identity either the whole or a part of the subject is identical with a part of the predicate.
(4) The law of contradiction always denies the identity between subject and predicate.
(5) Excluded middle conditions all alternative expressions.
THE PROPOSITIONS.
(1) “A thief is a thief.” Complete absolute identity.
(2) “Thinking is the process of affirming or denying connections.” Incomplete absolute identity.
(3) “All good men are wise.” Relative identity.
(4) “No triangle has interior angles whose sum is greater than two right angles.” Contradiction.
(5) “A stitch in time saves nine.” Relative identity.
(6) “Judging is the process of conjoining and disjoining notions.” Incomplete absolute identity.
(7) “You are either a voter in this district or you are not a voter in this district.” Excluded middle.
(8) “Some people do not know how to live.” Contradiction.
(9) “All is well that ends well.” Incomplete absolute identity.
(10) “Some men teach school.” Relative identity.
(11) “None of the planets are as large as the sun.” Contradictory.
(12) “All the trees in this grove are maple.” Relative identity.
(1b) Indicate the law which conditions each of the following propositions:
(1) “He who laughs last laughs best.”
(2) “Perfect is perfect.”
(3) “He is a wolf in sheep’s clothing.”
(4) “Either your memory is poor or you are telling a deliberate falsehood.”
(5) “Some of our greatest teachers thought they were failures.”
(6) “No man of sense would ever try to get something for nothing.”
(7) “Failure is not to try.”
(8) “Success is the right man in the right place doing his best.”
(9) “Every man is insane on some topic.”
(10) “Some pupils are not industrious.”
(11) “You are either a genius or a successful fakir.”
(12) “Honesty is the best policy.”
(1) How many kinds of judgments are there? Illustrate.
(2) Name the fundamental laws of thought and explain how they are related to the kinds of judgments.
(3) Show that it would be impossible to think at all were it not for the law of identity.
(4) State the law of identity in three ways.
(5) Explain the kinds of absolute identity. Illustrate by propositions and by circles.
(6) Explain by word and by diagrammatical illustration relative identity.
(7) Symbolize the three forms of identity. Fit words to these symbols.
(8) State in three ways the law of contradiction.
(9) Show by illustration that not bisects the world.
(10) Explain the uses of not.
(11) Prove that “John Doe is not-honest,” illustrates identity and not contradiction.
(12) Symbolize in three ways contradiction. Fit words to these symbols.
(13) Illustrate contradictory and opposite terms.
(14) Show that words with negative prefixes are not necessarily the contradictory of the corresponding affirmative forms.
(15) State and explain the law of excluded middle.
(16) Symbolize the law of excluded middle.
(17) State the law of sufficient reason. Illustrate.
(18) Illustrate the unity of the three primary laws of thought.
(1) Prove that the judgment is the elemental form of evolved thought.
(2) What is meant by evolved thought?
(3) Show that “Whatever is, is” is a statement of complete absolute identity only.
(4) State incomplete absolute identity.
(5) By means of one proposition state relative identity.
(6) Show that incomplete absolute identity is a term more or less illogical.
(7) Show that these statements are exact expressions of relative identity:
All men are some wise.
Some men are some wise.
(8) Why is the law of contradiction so named?
(9) Show that space may be bisected by drawing a circle upon the black board.
(10) Show that there is a difference in meaning between “You are not honest” and “You are not-honest.”
(11) Is there any difference in meaning between disagreeable and not agreeable?
(12) Which is the stronger term not-just or unjust? Why?
(13) Give a list of words in which the contradictory forms are expressed by the ordinary prefixes.
(14) Illustrate by circles the law of excluded middle.
(15) Illustrate by a line-diagram the difference between contradictory and opposite terms.
(16) Show that the province of the law of sufficient reason is physical science.
Any impression upon the mind tends to manifest itself in some form of expression. Impression which arouses thought tends to expression in the form of symbols. Thought and symbol go hand in hand. Expression, taking the form of word-symbols, constitutes a word-language.
It is commonly supposed that language is serviceable mainly in communicating one’s thoughts to others, but language does service in another way which is quite as important. It tends to clarify and make definite all thought. Without a word-language thinking would lack continuity; would be vague, loose, illogical. The right use of a word-language, therefore, is a necessary adjunct to logical thought. The basic element of a word-language is the logical term.
A notion has been referred to as any product of the knowing mind. When we express these notions in words such expressions may be called logical terms.
Definition. A logical term is a word or a group of words denoting a definite notion. Illustrations: Honesty, Chicago, tree, walking, the man who was ill, beautiful roses. This is a list of logical terms, because each word or group of words denotes a notion of some kind. It is now evident that any subject or predicate with its modifiers constitutes a logical term. In the proposition, “The beautiful red house on the hill, owned by Mr. Jones, has burned,” the term used as the subject consists of eleven words. The reader must not confuse logical terms with grammatical parts of speech. “Of” is a preposition but not a logical term, as no definite notion is indicated.
There are some words which, when used alone, denote definite notions, such as man, tree, dog, justice. On the other hand there are other words which, when used alone, do not stand for a definite notion, such as up, beautifully, a, and.
Words like those in the first list are called categorematic words, while those in the second list illustrate syncategorematic words.
DEFINITION.
A categorematic word is one which forms a logical term unaided by other words. A syncategorematic word is one which must be used with other words to form a logical term.
Any word or group of words which can be used as either subject or predicate of a proposition is a logical term. If the one word in question can be used as either subject or predicate of a proposition then it must be a categorematic word. If it is impossible to use the one word as either subject or predicate of a proposition then this is a sure indication that such a word is syncategorematic. For example, there is no sense in the expressions, “_And_ is honest,” “_Of_ is not true”; hence _and_ and _of_ are syncategorematic.
We may conclude from this that nouns, descriptive adjectives and verbs may be categorematic words, while adverbs, prepositions and conjunctions are syncategorematic words.
A singular term is a term which denotes one object or one attribute.
Proper nouns, when they stand for individuals, are singular terms, such as John Adams, Mississippi River, Socrates. Some proper names stand for a class of objects, as the Caesars, the Mephistopheles, the Napoleons. But when thus used they lose their character as proper names. Such names, therefore, are general terms, not singular.
Common nouns may be made singular by some modifying word, as the first man, the pole star, the highest good, my pet dog, etc.
Certain attributes which imply a oneness or a distinct individuality are singular, such as absolute justice, birds-egg blue, perfect happiness, etc.
Some claim that terms like water, air, salt, etc., are singular, as they stand for one thing. This, however, cannot be if such terms admit the possibility of classification as: hard water, soft water, mineral water.
A general term is one which denotes an indefinite number of objects or attributes.
Class-names are general terms, such as men, chair, tree, army, nation. Words like redness, sweetness, justice, are probably general in that they denote a combination of qualities or may be subdivided into kinds.
The way the term is employed in the proposition should determine its singular or general nature.
A collective term is a general term which indicates an indefinite number of objects as one whole. Such words as class, crowd, army, forest, nation, are collective.
A distributive term is a general term which indicates an indefinite number of objects as a whole, and also may be used to refer to each one of the group separately. Such as man, pupil, tree, book.
It is easy to distinguish collective from distributive terms when we attempt to use them in the designation of individuals. Pointing to a body of troops, one may remark, “There is the regiment.” But when pointing to one man in the regiment, he could hardly say, “There is the regiment.” “Regiment” is therefore collective because it may be used with reference to the whole body of troops but cannot be used in connection with any individual of that body. On the other hand in the sentence, “Man is mortal,” “man” refers to the whole family of men. It also indicates any one of them. As, “This man, John Doe, is mortal.” Thus “man” is distributive. The distributive term, therefore, can be used in a two-fold sense; namely, to denote the whole or to denote each.
It must be noted that, viewed from a different standpoint, some collective terms become distributive in nature. As for example in the proposition, “The army of the world is composed of able bodied men,” army is used with reference to all armies. While it may be used to designate some particular army, as The American army.
Collective terms have been classified as general terms. It must be borne in mind, however, that such may be made singular by some modifying word. For example, people is a general term, but American people is a singular term in that it refers to one people, being thus limited by the word American.
A concrete term is a term which denotes a thing; e. g., this man, that tree, John Doe, denote in each case a thing. Man and tree, denote many things. All are concrete.
An abstract term is a term which denotes an attribute of a thing; e. g., whiteness, patience, squareness, are abstract terms.
Such words as red, honest, just, are concrete; while redness, honesty, justice, are abstract.
On first thought it might be inferred that “red” is the name of an attribute just as much as “redness.” This is a mistaken thought, however, as when we use the word red we mean red something—an object which is red in color, not the color itself. For example, in saying the house is red, we refer to the thing that is red, not to the color redness.
Descriptive adjectives, because they describe things, are concrete. They do not alone name qualities of things, hence they are not abstract.
A connotative term is one which denotes a subject and at the same time implies an attribute. (A subject is anything which possesses attributes.)
All concrete general terms are connotative because they denote subjects and at the same time stand for certain attributes; e. g., “man” denotes many subjects; in fact, it stands for all the men in the world; it also implies rationality, the power of speech, power of locomotion, etc. “Triangle” stands for all plane figures of three sides; it likewise stands for the qualities, three-sided, three-cornered, etc. Both “man” and “triangle” are connotative.
A non-connotative term is one which denotes a subject only, or implies an attribute only. Such words as Boston, Columbus, The Elizabeth White, denote a subject only. “Blueness,” “justice,” “width,” imply an attribute only. All these terms are non-connotative. The words blue, just, wide, are connotative. “Blue,” for example, denotes all blue things, as the blue sky, the blue sea; at the same time “blue” implies that something possesses the quality, blueness.
Generally speaking, proper and abstract nouns are non-connotative; though such proper nouns as Mount Washington, Mississippi River, are, no doubt, connotative, as they denote an object and imply at least one attribute. In the case of Mount Washington an object is surely denoted, and the attribute mountainous is implied. Any proper noun which conveys definite information is connotative. It may be claimed that all proper nouns give information. For example, to many Boston indicates not only an object, but the qualities common to a city. In reply it may be said that “Boston” might indicate a boat, or a dog, or almost any individual object.
A positive term is one which signifies the possession of certain attributes; e. g., metal, man, teacher, happy, honest.
A negative term is one which signifies the absence of certain attributes; e. g., inorganic, unhappy, non-metallic.
Terms which have the prefix not, non, un, in, dis, etc., or the affix less, are usually considered negative. The fact that there are some exceptions to this must not be overlooked. For example, unloosed, invaluable, are positive terms.
In theory every positive term has its corresponding negative; as pure, impure; organic, inorganic; metal, non-metal; good, not-good.
In some instances the language does not supply the word with the negative prefix because no need of it has been felt. The only way to express the negative of such words as good, table, etc., is to prefix “not” or “non.”
Positive terms with their negatives have contradictory meanings and therefore are referred to as contradictory terms. For example, honest and not-honest, metallic and non-metallic, perfect and imperfect, are contradictory terms. Such terms are mutually destructive. When we assert the truth of one we also imply the falsity of the other. If, for example, we assert that Abraham Lincoln was honest, we carry with this assertion the implication that Lincoln was not not-honest, or that any statement to the effect that he was not honest is false.
Contradictory terms, when used in a sentence, illustrate the law of excluded middle, as in the statements: “John’s recitation is either perfect or imperfect.” “This teacher is either just or not-just.” There is no middle ground in such propositions.
When contradictory terms are used in classification the whole is divided into but two classes; e. g.:
| honest | not-honest |
| agreeable | not-agreeable |
| metallic | non-metallic |
| perfect | imperfect |
| pure | impure |
| organic | inorganic |
All the men in the world are either honest or not-honest. All the substances in existence are either organic or inorganic, etc.
It will also be seen from this list that the contradictory of the positive form is not always indicated by using the prefix. Honest and dishonest, or agreeable and disagreeable, are not contradictory terms. In the case of agreeable and disagreeable, there seems to be the middle ground of absolute indifference. For example: the music of the orchestra is agreeable while the humming of the enthusiast back of me is decidedly disagreeable; but as to the noise upon the street, it is neither agreeable nor disagreeable as long practice has made me indifferent to it.
When there is any doubt as to the terms being contradictory, the safest plan is to prefix “not” or “non” to the positive form.
Terms which oppose each other but do not contradict are said to be opposite or contrary terms. The following list illustrate opposite terms:
| hot | cold |
| cool | warm |
| less | greater |
| wise | foolish |
| bitter | sweet |
| soft | hard |
| tall | short |
| agreeable | disagreeable |
All these terms admit of a medium. In the case of hot or cold, for example, a substance need not necessarily be either. It may be warm or cool.
Terms seem to be contradictory when it is a matter of quality, but opposite when it is a question of quantity or degree.
A privative term is one which is positive in form but negative in meaning. Such words as blind, deaf, dumb, dead, maimed, orphaned, are privative terms, in that there is no negative prefix or suffix and yet they denote the absence of certain qualities. “Blind,” for example, is positive in form, but denotes absence of sight.
A nego-positive term is one which is negative in form but positive in meaning. Such terms as invaluable, unloosed, immoral, indwell, are nego-positive because, though they have negative prefixes, yet they possess a certain positive meaning. “Invaluable,” for instance, does not mean not-valuable, but very valuable.
An absolute term is one whose meaning becomes intelligible without reference to other terms. Automobile, water, tree, house, book, are absolute terms. Any of them may be made clear to a child or a foreigner without special reference to other terms. For example, the child will recognize from certain common marks the automobile every time he sees it. The marks of tree, house, flower, are apparent to every one.
A relative term is one which derives its meaning from its relation to some other term. Parent, teacher, shepherd, monarch, eldest, cause, commander, are relative terms. For example, in explaining the meaning of “parent” to a foreigner, reference must be made to “child.” The pairs of terms thus associated are spoken of as correlatives. Parent and child, teacher and pupil, shepherd and flock, monarch and subject, eldest and youngest, cause and effect, commander and army, are correlative terms. Either one of each pair is the correlate to the other, and every relative term needs its correlate to make its meaning clear. To say that a relative term denotes an object which cannot be thought of without reference to some other object, is confusing, as it is quite impossible to think of any object without calling to mind some other object or notion. Fire calls to mind water; tree suggests shade, etc.
LOGICAL TERMS.
(1) Meaning of term.
(2) Categorematic and syncategorematic words.
(3) Kinds of terms.
Singular terms.
General terms.
(a) Collective terms.
(b) Distributive terms.
Concrete and abstract terms.
Connotative and non-connotative terms.
Positive and negative terms.
Contradictory and opposite terms.
Privative and nego-positive terms.
Absolute and relative terms.
A logical term is a word or group of words denoting a definite notion.
A singular term is a term which denotes one object or one attribute.
A general term is a term which denotes an indefinite number of objects or attributes.
General terms are collective or distributive.
A collective term is a general term which indicates an indefinite number of objects considered as one whole.
A distributive term is a general term which indicates an indefinite number of objects as a whole and also may be used to refer to each one of the group separately.
A concrete term is a term which denotes a thing.
An abstract term is a term which denotes the attribute of a thing.
A connotative term is one which denotes a subject and at the same time implies an attribute.
A non-connotative term is one which denotes a subject only or implies an attribute only.
A positive term is one which signifies the possession of certain attributes.
A negative term is one which signifies the absence of certain attributes.
In theory every positive term has its negative. As related to each other positive and negative terms are said to be contradictory. If one denotes a true notion then the other denotes a false notion.
Some terms oppose each other but do not flatly contradict. As related to each other such terms are said to be opposite.
A privative term is one which is positive in form but negative in meaning.
A nego-positive term is one which is negative in form but positive in meaning.
An absolute term is one whose meaning becomes intelligible without reference to other terms.
A relative term is one which derives its meaning from its relation to some other term.
(1a) The words in italics are categorematic.
(1) “Honesty is the best policy.”
(2) “A wise teacher never scolds.”
(3) “The woodcock has a long bill and eyes high up on the head.”
NOTE—If there is any doubt as to such words as never, on, etc., being syncategorematic, attempt to use them as subject or predicate of a proposition; e. g., John is never.
(1b) Underscore the categorematic words in the following:
(1) “Socrates was the greatest teacher of pagan times.”
(2) “Play is nature’s way of teaching a child how to work.”
(3) “A man may be what he chooses if he is willing to pay the price.”
(2a) In the following, words enclosed in parentheses are logical terms:
(1) (“All men) are (mortal.”)
(2) (“The law of identity) is (one of the primary laws of thought.”)
(3) (“Judging) is (the process of conjoining and disjoining notions.”)
(2b) Indicate the logical terms in the sentences under 1b.
(3a) The logical characteristics of the term teacher are
(1) general term,
(2) distributive term,
(3) concrete term,
(4) connotative term,
(5) positive term,
(6) relative term.
(3b) The logical characteristics of other terms are as follows:
(1) Goodness—general, abstract, non-connotative, positive, abstract.
(2) Soft—general, concrete, non-connotative, positive, “hard” is its opposite, “not-soft” is its contradictory, absolute.
(3) Disagreeable—general, concrete, non-connotative, “agreeable” is its opposite, “not-disagreeable” is its contradictory, nego-positive, absolute.
(4) Aristotle—singular, concrete, non-connotative, positive, absolute.
(5) Class—general, collective, concrete, connotative, positive, relative.
(3c) Give the logical characteristics of the following terms: justice, Abraham Lincoln, tree, library, America, president, principle, sympathy, dumb, nation.
(1) What is the connection between logical thinking and language?
(2) Why is man a categorematic word?
(3) Why is beautifully syncategorematic?
(4) Distinguish between singular and general terms.
(5) Show how a collective term may be used in a distributive sense.
(6) Why are the words tree and book distributive?
(7) Distinguish between concrete and abstract terms.
(8) Define and illustrate a non-connotative term.
(9) Why are concrete general terms connotative?
(10) Distinguish between positive and privative terms.
(11) Why is not the word immoral negative?
(12) Give the opposite of “hot.” What is the contradictory of “hot”?
(13) Distinguish by definition and illustration between relative and absolute terms.
(14) What is the correlate of the word effect?
(1) Is it possible to think independent of language?
(2) May words be spoken or written without thought? Illustrate.
(3) Are categorematic words always logical terms?
(4) Must all the words of a logical term be categorematic?
(5) Are pronouns and auxiliary verbs categorematic?
(6) Indicate the logical connection between the terms of a proposition and the termini of a railroad.
(7) Show that attribute is a broader term than quality.
(8) Is the word Washington general or singular? Give reasons.
(9) Make the word dog a singular term.
(10) Give an illustration where the word class would not be collective.
(11) “All the members of the baseball team are star players.” How has the term star players been used, collectively or distributively?
(12) Why may the term New York City be connotative to a New Yorker and non-connotative to a Patagonian?
(13) So far as your present knowledge of the martyred president Abraham Lincoln is concerned, is the term Abraham Lincoln connotative or non-connotative?
(14) Are non-connotative terms always singular? Illustrate.
(15) Are singular terms always non-connotative?
(16) What is the difference in meaning between immoral and unmoral, disagreeable and not-agreeable?
(17) Why is immoral a nego-positive term while unmoral is negative?
(18) What is the contradictory of the opposite of wise?
(19) Show that there is some ground for believing all terms to be relative.
(20) Is army a relative term? If “army” were used so as to be distributive in nature would it then be general or collective?
(21) Why should the pronoun be ignored by the logician?
(22) Show the difference between thing and subject.
(23) Argue to the effect that no term can be non-connotative.
It has been indicated that a connotative term is one which possesses the double function of signifying a subject as well as an attribute. It may be observed here that an attribute of a notion is any mark, property or characteristic of that notion. Attribute, then, represents quality, relation or quantity. By a subject is meant anything which possesses attributes. Most subjects stand for objects and most attributes are qualities; consequently, for the sake of simplicity, we may use subject and object interchangeably; likewise, attribute and quality.
A connotative term, therefore, denotes an object at the same time it implies a quality. To illustrate: The symbol man stands for the various individual men of the world, such as Lincoln, Washington, Alfred the Great, etc., or for certain qualities like rationality, power of speech and power of locomotion. The connotative term teacher may be used to denote Socrates, Pestalozzi, Thomas Arnold, or connote such qualities as ability to instruct, sympathy, and scholarship. The term planet stands for such objects as Venus, Earth, and Mars, and for such qualities as rotation upon axis, revolution about sun, and opaque or semi-opaque bodies. In each of the three illustrations the term is employed in the two-fold sense of denoting objects and of implying qualities.
This double function of connotative terms furnishes an important topic for the student of logic—the Extension and Intension of Terms. In short, some authorities claim that to master the extension and intension of terms is virtually to master the entire subject of logic. Though this position may be an exaggerated one, yet it tends to emphasize the importance of the topic.
A term is used in extension when it is employed with reference to the objects for which the term stands.
When the term triangle is used to refer to the objects isosceles triangle, scalene triangle, right triangle, it is employed in extension.
A term is used in intension when it is employed with reference to the attributes for which the term stands.
The term triangle is employed in intension when we use it to refer to the qualities, three sided and three angled.
A connotative term seems to be two dimensional—it has extent or length and intent or depth.
“Extension consists of the things to which the term applies,” while “intension consists of the properties which the term implies.”
Extension is quantitative, while intension is qualitative. An extensional use means to point out or number objects, while an intensional use means to describe by naming qualities. To name is to use a term in extension—to describe is to use a term in intension.
To divide a term into its kinds we must regard it in an extensional sense; e. g., the term man may be divided into Caucasian, Mongolian, Malay, Ethiopian, American Indian.
To define a term we must regard it in an intensional sense; e. g., man is a rational animal.
Etymologically considered extension means to stretch out, intension, to stretch within. To use a term extensionally one must look out. To use a term intensionally one must look in.
In attempting to use a term in extension we may ask ourselves the question, “What are the kinds?” or “To what objects may the term be applied?” While if we would use a term in intension the question should be, “What does it mean?” or “What are the qualities?” Let us, for example, use the term metal in the two senses, first in extension, second in intension. Question: To what objects may the term metal be applied? Answer: Metal may be applied to the objects silver, gold and iron. Thus has metal been employed in extension.
Question: What are the qualities of metal? Answer: The qualities are element, metallic lustre, good conductor of heat and electricity. Thus has metal been used in intension.
NOTE. Since an attribute is anything which belongs to a subject, then the parts of a subject must be classed as attributes. Hence, a term is used intensionally when reference is made to its parts.
| The Term. | Extensional Use. | Intensional Use. | |
| tree. | maple, oak, beech. |
 |
roots, branches, trunk. |
| or | |||
| woody-fiber, sap, bark. | |||
| house. | stone, brick, cement. | foundation, frame-work, roof. | |
| dog. | shepherd, fox terrier, bull. | carnivorous, quadruped, propensity to bark. | |
| book. | textbook, dictionary, encyclopaedia. | cover, leaves, binding. | |
| quadrilateral. | trapezium, trapezoid, parallelogram. | four sides, four angles, limited plane. | |
| logic. | theoretical logic, applied logic, educational logic. | science of thinking, art of right thinking, treats of laws of thought. | |
| star. | Sirius, Arcturus, Vega. | heavenly body, gives light and heat, twinkles. | |
| force. | gravitation, molecular, atomic. |
 |
produces motion |
| changes motion | |||
| destroys motion. | |||
| term. | general, singular, non-connotative. | word or group of words, definite idea. | |
| government. | monarchy, aristocracy, democracy. | body of people, established form of law, banded together for mutual protection. | |
| bird. | crow, robin, pigeon. | biped, feathered, winged. |
| Extension. | Intension. |
| comprehension | content |
| extent | intent |
| breadth | depth |
| denotation | connotation |
| application | implication |
Formerly the words extension and intension were applied to concepts while denotation and connotation were applied to terms representing the concepts, but now the words are interchangeable. Denotation, the noun, and denote, the verb, signify, etymologically, a marking off. To denote is to mark off or indicate the objects or classes of objects for which the term stands. Connotation, the noun, and connote, the verb, signify to mark along with. To connote is to mark along with the object, its attributes.
The terms which should be remembered are
| extension |
 |
and |
 |
intension |
| or | or | |||
| denotation | connotation |
It has been noted that the intension of a term has reference to its qualities while extension considers its application to various objects. It may be wise to experiment with the extension and the intension of certain terms as types with a view of ascertaining how the two ideas are related to each other. For the sake of definiteness let us make use of the following scheme:
| I. | ||||
|---|---|---|---|---|
| Intensional | Extensional | |||
|
(1) four sides
(2) parallel sides
(3) equal sides
(4) right angles |
 |
common qualities of |
 |
(1) squares |
|
(1) four sides
(2) parallel sides
(3) equal sides |
 |
common qualities of |
 |
(1) squares (2) rhombs |
|
(1) four sides
(2) parallel sides |
 |
common qualities of |
 |
(1) squares (2) rhombs (3) rectangles (4) rhomboids |
|
(1) four sides |
 |
common qualities of |
 |
(1) squares (2) rhombs (3) rectangles (4) rhomboids (5) trapezoids (6) trapeziums |
| II. | ||||
|
(1) heavenly body |
 |
common qualities of |
 |
(1) nebulae (2) fixed stars (3) sun (4) comets (5) meteors (6) moon |
|
(1) heavenly body
(2) self-luminous |
 |
common qualities of |
 |
(1) nebulae (2) fixed stars (3) sun (4) comets |
|
(1) heavenly body
(2) self-luminous
(3) fixed |
 |
common qualities of |
 |
(1) nebulae (2) fixed stars (3) sun |
|
(1) heavenly body
(2) self-luminous
(3) fixed
(4) twinkle |
 |
common qualities of |
 |
(1) nebulae (2) fixed stars |
|
(1) heavenly body
(2) self-luminous
(3) fixed
(4) twinkle
(5) foggy |
 |
common qualities of |
 |
(1) nebulae |
In considering the first illustration we observe that as the number of qualities is decreased, the number of objects increases. While in the second example as the qualities are increased, the number of objects decreases. It would appear from this that the intension and extension of a term are inversely related to each other. As the one increases the other decreases and vice versa. It is customary to state this relation in the form of a law known as the law of variation. “As the intension of a term is increased its extension is decreased and vice versa,” or the extension and intension of a term vary in an inverse ratio to each other. To further illustrate: this book refers to a large number of objects; add to the qualities of book those of text book and the application is much reduced. In other words as we increase the intension, the extension is diminished. Increase the intension further by adding the quality English text book and the extension becomes still less.
In studying the law of variation two facts are especially evident. (1) The law applies only to a series of terms representing notions of the same family. The extension and intension of “text book,” for example, could not be compared with the extension and intension of “house” as they belong to a different class of words, the genus of text book being book, while the genus of house is building.
To illustrate the law of variation, determine upon any class name, then think of its proximate genus (the next higher-up class to which it belongs). Continue this till the series is sufficiently complete to illustrate the law. Or proceed in the opposite direction. That is, after selecting the class name think of the next lower term in the class and thus continue till series is complete. Illustration: The class name man is determined upon; the proximate genus of man is biped, the proximate genus of biped is animal, and so on. Or thinking downward: a proximate species of man is white man, of white man. European, etc.
Thus the series:
animal
biped
man
white man
European
(2) As a second fact: the increase and decrease is not a mathematical one. That is, by doubling the extension the intension is not halved. Or if the intension is decreased by one quality the extension is not necessarily increased by one object. Thus “man” stands for one billion seven hundred million beings or objects. Decrease the intension of “man” by the one quality of rationality and the extension would include all bipeds—many billion objects.
In a general way lines may be used to represent the variation in extension and intension. For example: we may let a line an inch long represent the extension of man, one two inches long represent the extension of biped, three inches long represent the extension of animal, etc. While on the other hand, if a line an inch long represents the intension of man, a line one-half inch long may be used to represent the intension of biped, one a quarter of an inch long to represent the intension of animal, etc. The following illustrates this scheme in connection with another series of words:
| Extension | Intension | |
| ―― | barn | ―――――――― |
| ―――― | building | ―――――― |
| ―――――― | structure | ―――― |
| ―――――――― | object | ―― |
In the foregoing scheme building refers to a greater number of objects than barn, hence the line under extension representing building should be longer than the line for barn. Likewise structure, referring to a greater number of objects than building, is represented by a longer line. Thus when the series is viewed from top to bottom a gradual increase in extension is noted. Giving attention to the intensional use of the series we note that building has fewer qualities than barn, structure fewer than building and object fewer than structure. Therefore, from top to bottom, the intension of the terms gradually decreases.
The variation may be made still more apparent if triangles are used, one triangle being placed upon the other, vertex to base, like the following:
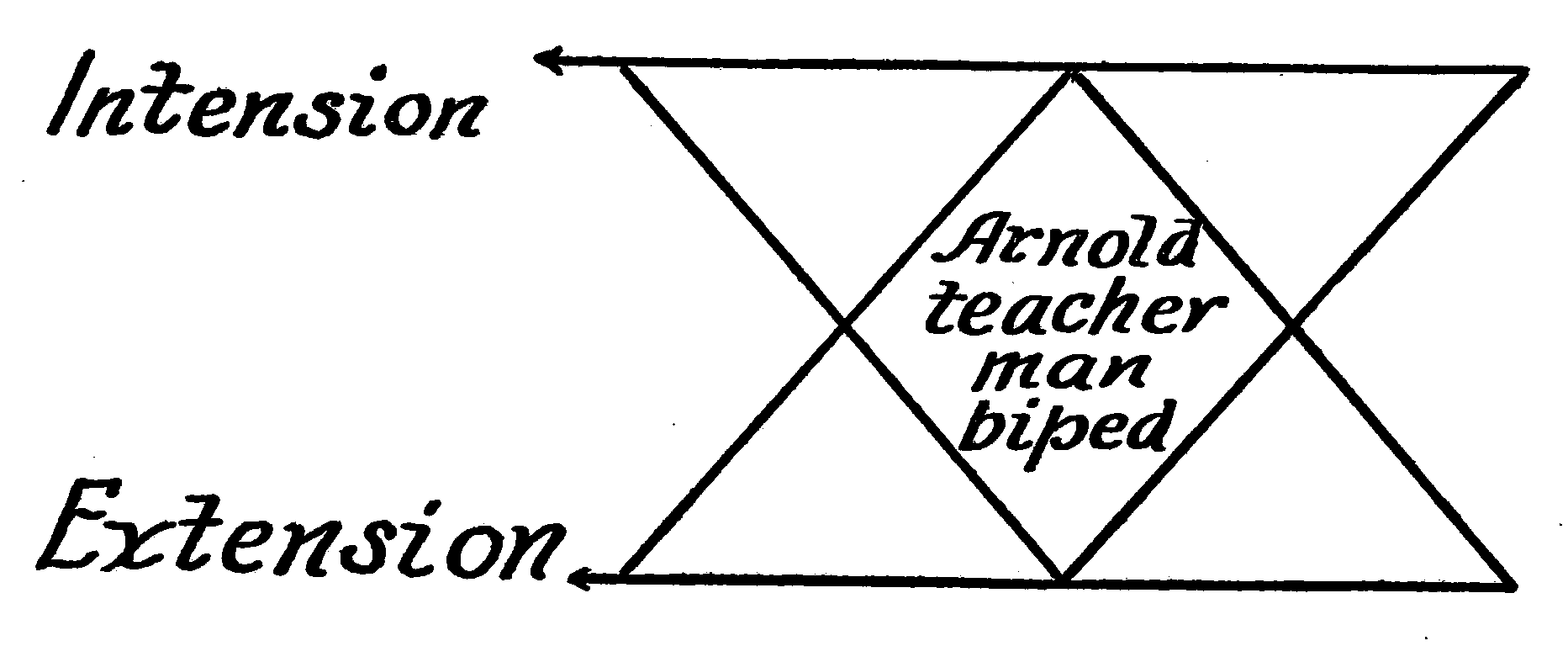
“Biped” is written near the base or in the broadest part of the extension triangle because it denotes the greatest number of objects, and is, therefore, broadest in extension. “Man” occupies a narrower part of the extension triangle because it refers to fewer objects or is narrower in extension than “biped.” “Arnold” occupies the narrowest part of the extension triangle because it is the narrowest in extension. On the other hand “Arnold” occupies the broadest part of the intension triangle because intensionally it possesses more qualities than the others, while “biped,” having the least depth in intension or possessing the fewest qualities, occupies the narrowest portion of the intension triangle.
THE EXTENSION AND INTENSION OF TERMS.
1. Two-fold Function of Connotative Terms.
2. Extension and Intension Defined.
3. Extended Comparison of Extension and Intension.
4. A List of Connotative Terms used in Extension and Intension.
5. Other Forms of Expression for Extension and Intension.
6. Law of Variation in Extension and Intension.
6a. Two Important Facts in the Law of Variation.
6b. The Law of Variation Diagrammatically Illustrated.
1. Connotative terms are used in a two-fold sense: first, to denote objects; second, to imply qualities.
2. A term is used in extension when it is employed with reference to the objects for which the term stands. A term is used in intension when it is employed with reference to the qualities for which the term stands.
3. The answer to either of the following questions will lead one to use any term in extension: First, what are the kinds? or second, to what objects may the term be applied?
The answer to either of the following questions will lead to the use of any term in intension: First, what does it mean? or second, what are the qualities?
4. To illustrate extension and intension it is best to use the class-names in every day speech.
5. The word denotation is commonly used for extension and connotation for intension.
6. “As the intension of a term is increased its extension is decreased and vice versa,” is a statement of the Law of Variation in the extension and intension of terms.
6a. The law of variation applies only to a series of terms representing notions of the same class or family, the words being arranged in a species-genus order. The increase and decrease of the extension and intension of a series is not proportional.
6b. The law of variation is best explained by using two triangles, one super-imposed upon the other vertex to base and base to vertex.
1a. Employ the following terms in extension—European, flower, term, truth.
| European |
 |
Russian Englishman Scotchman |
| flower |
 |
lily rose pansy |
| term |
 |
singular distributive collective |
| truth |
 |
Truth has no extension. Since it refers to a quality only, it is non-connotative. |
1b. Employ the following in extension—grain, rock, soil, precious stone.
2a. Use intensionally bird, quadruped, letter, John.
| bird |
 |
two feet ability to fly feathers |
| quadruped |
 |
four feet back bone hairy covering |
| letter |
 |
heading body complimentary close |
| John |
 |
John has no intension. Since it refers to an object only, it is non-connotative. |
2b. Use the following in intension—word, table, purity, government.
3a. The use of a term in extension follows when attempting to answer two questions: First, what are the kinds? Second, to what objects may the term be applied? Make application of this with reference to the term man.
1. What are the kinds of men? Caucasian, Malay, Mongolian, Ethiopian, Redman.
2. To what objects does the term man refer? George Washington, Chas. Hughes, John Smith.
In both 1 and 2 the word man is used to denote objects, hence it is employed in extension.
3b. Use the term vegetable in extension by answering the two questions in 3a.
4a. Decrease one by one the qualities of some common object with a view of noting how when the intension is decreased the extension is increased.
| Intension | Extension | |||
|
binding
leaves
cover
printed matter
designed for instruction
instruction in arithmetic |
 |
 |
school arithmetic | |
|
binding
leaves
cover
printed matter
designed for instruction |
 |
 |
school arithmetic
school grammar
school speller,
etc. | |
|
binding
leaves
cover
printed matter |
 |
 |
school arithmetic
school grammar
school speller,
etc.
encyclopaedia
novel | |
|
binding
leaves
cover |
 |
 |
school arithmetic
school grammar
school speller,
etc.
encyclopaedia
novel
note book | |
4b. With a view of noting how when the intension is decreased the extension is increased, decrease one by one the common qualities of peach tree.
5a. In the following series what word could be substituted for “mammal” and why? Being, organized being, animal, vertebrate, mammal. Answer: Fish, reptile, or bird; because there are at least seven classes of animals which belong to the vertebrate family, any one of which could be used to complete the series.
5b. Form a series of which “Baldwin apple” has the narrowest extension. What terms may be substituted for “Baldwin apple?”
6a. In a series of which “pupil” is a member show that the increase and decrease is not proportional. The series: logic pupil, pupil, youth, human being, being. In decreasing the intension of “logic pupil” by dropping the one quality, logic, the extension is made larger by many more than one, as “pupil” represents many more objects than “logic pupil.” Therefore, the increase is not in proportion to the decrease.
6b. In a series in which “ruler” appears, show that the increase and decrease is not proportional.
7. From the following list select the proper words of the series; arrange them; draw and name the triangles: Caesar, brute, man, Roman, American, biped, sensuous being, animal, individual.
1. What is a connotative term? Illustrate.
2. Which is the broader term, quality or attribute? Why?
3. When is a term used in extension?
4. Use the term triangle in intension.
5. As an aid to using a term in extension or intension what questions may one ask himself?
6. By asking these questions use the term clock in both extension and intension.
7. By experimenting with the qualities of a rectangle show that as the intension is decreased the extension is increased.
8. Write a list of five connotative terms. Prove that they are connotative by illustrating their extension and intension.
9. The term metal
 denotes
denotes
connotes
 such qualities as element, metallic lustre, conductor of heat and electricity. In the foregoing which of the two words following the brace should be used? Give reasons.
such qualities as element, metallic lustre, conductor of heat and electricity. In the foregoing which of the two words following the brace should be used? Give reasons.
10. State the law of variation in two ways.
11. As one studies the law of variation what two facts are especially evident? Explain fully.
12. For the purpose of illustrating the law of variation form a series of which desk is a member. Draw and name the triangles.
1. Which is the broader term, subject or object? Prove it.
2. If a term like Caesar is given extension does it become a general term? Why?
3. Using “man” as a member of each, arrange at least three different series.
4. Why may it be said that a connotative term is two dimensional?
5. Is there a word which has a broader extension than “being”? Why?
6. Prove that youth has less intension than human being.
7. Devise a series of words in which the variation is proportional.
8. Advance arguments supporting the hypothesis that the term John has neither extension nor intension.
9. Suggest arguments to prove that “George Washington” has both extension and intension.
To be clear, cogent, concise and consistent is to be logical. Reference has been made to a striking tendency on the part of writers and speakers to use words loosely. It is a noticeable fact that scholars generally aim to be profound rather than clear, philosophical rather than pointed.
In the use of text books more or less pedagogical these are the common complaints: “I don’t understand what he means” or “You have to read so much to get so little.” This condition gives to the topic of definition a prominence which cannot be overlooked by those who are seeking the truth; because the definition is the clearest, briefest and altogether the most satisfactory way of describing an idea. Likewise the habit of defining any doubtful term reduces to a minimum the possibility of misunderstanding.
The subject must appeal strongly to the instructor, as he, above all others, should make his work stand for clearness, pointedness and continuity.
A predicable is a term which can be affirmed or predicated of any subject. In the proposition, “A man is a rational animal,” the term “rational animal” is a predicable, because it can be affirmed of the subject man.
To gain a clear knowledge of the definition it is quite necessary to understand the five predicables which we shall consider in the following order:
1. Genus.
2. Species.
3. Differentia (difference).
4. Property.
5. Accident.
(1) Genus and (2) Species.
Genus and species are relative terms and can best be defined together.
A genus is a term which stands for two or more subordinate classes.
A species is a term which represents one of the subordinate classes.
The genus may be subdivided into species; the species together form the genus.
To illustrate: The term man stands for five subordinate classes or species, as white, black, brown, yellow and red. “Man” is, therefore, a genus, while “white man” and “black man,” etc., are species. The term “polygon” is a genus with reference to “trigon,” “tetragon,” “pentagon,” etc., while “trigon” is a species of “polygon.”
Any given genus may be a species of some higher class. That is, “man,” which is a genus with reference to the kinds of men, is a species of the higher class “biped,” while “biped” is a species of “animal,” “animal” a species of “organized being,” “organized being” of “material being,” “material being” of “being.” But here we stop, as there is no higher grade to which “being” can be referred. This highest genus takes the name of summum genus.
Similarly any given species may be a genus of some lower class. “White man,” for example, which is a species of “man,” is a genus of “American,” “Englishman,” “German,” “Frenchman,” etc. “American” is a genus of “New Yorker,” “Californian,” etc., while “New Yorker” is a genus of “Smith of Jamaica.” This last term is an individual and cannot be subdivided. It represents the lowest possible species and is referred to in logic as infima species.
It is obvious that the highest genus cannot become a species, neither can the lowest species become a genus.
PROXIMATE GENUS.
The proximate genus is the next class above. To illustrate: “Animal” is a genus of “man,” but “biped” is the proximate genus of “man.” “Quadrilateral” is the genus of “square,” but “rectangle” is the proximate genus. The next class above “trigon” is polygon not figure. Hence “polygon” is the proximate genus of “trigon.”
GENUS AND SPECIES OF NATURAL HISTORY.
In natural history the following terms are used to denote the various grades of kinship in any scheme of classification: (1) kingdom, (2) class, (3) order, (4) family, (5) genus, (6) species, (7) variety, (8) the individual thing. Here “genus” and “species” are absolute not relative and occupy a fixed place in the scheme, while from a logical viewpoint any of the grades indicated between the lowest and highest would be the species of the next higher grade or a genus of the next lower; e. g., order is a species of “class,” while it is the genus of “family.”
GENUS, A DOUBLE MEANING.
We recall that any class name or genus has a double use, extensional and intensional. When considered from the standpoint of its extension, a genus represents a group of objects or is mathematical in its application, but when used in an intensional sense it represents a group of qualities or is logical in its application.
Considered extensionally the genus refers to a larger number of objects than the species. But when viewed intensionally the species refers to more qualities than the genus. This was made clear when discussing the law of variation in the extension and intension of terms.
(3) Differentia.
The differentia of a term is that attribute which distinguishes a given species from all the other species of the genus.
It has been observed that the species refers to more qualities than the genus. In fact, it represents all the attributes of the genus plus those which distinguish the particular species from the other species of the genus. These additional qualities are the differentiæ of the particular species.
TO ILLUSTRATE:
The attribute which distinguishes man from the other bipeds of the world is his rationality. That which distinguishes the rectangle from the other parallelograms is its four right angles. The attributes rationality and right angles are differentiae.
(4) Property.
A property of a term is any attribute which helps to make the term what it is. Thus “consciousness” is a property of man, “binding” a property of book, “angles” a property of triangle. Deprive the terms of these attributes and their true nature is altered.
A differentia is a property according to the foregoing definition. However, Jevons defines “property” as “Any quality which is common to the whole of a class, but is not necessary to mark out the class from other classes.” This viewpoint excludes “differentia” from the notion of property. The difference in opinion is of slight importance.
(5) Accident.
An accident of a term is any attribute which does not help to make the term what it is. It may indifferently belong or not belong to the term. Deprive a term of an accident and the nature of the term remains unchanged. Thus, a teacher’s position, a man’s watch, the fact that the angle is one of 80° are all accidents.
It is obvious that a property is a constant attribute while an accident is variable. This gives to the former a universal validity while the latter is more or less shifting and uncertain. All triangles must have three angles (property) while the value of each angle in degrees (accident) admits of unlimited variation.
Some logicians divide accidents into separable and inseparable. A man’s hat would be a separable accident while his birthplace would be an inseparable accident.
FIVE PREDICABLES ILLUSTRATED.
In the following brief descriptions the five predicables are designated:
(1) This
(species)
rectangle
is a
(genus)
parallelogram
with
(differentia)
four right angles
its longer sides being
(accident)
ten inches.
(2) This
(species)
man
is a
(differentia)
rational
(prox. genus)
biped
with the
(property)
power of locomotion
and a (accident)
ruddy complexion.
(3) A
(species)
trigon
is a
(genus)
polygon
of
(differentia)
three sides
and
(property)
three angles,
(accident)
the sum of the angles being equal to two right angles.
It will be remembered that an individual notion is a notion of a single thing or attribute, while a general notion is a notion of a class of things or a group of attributes. A term which represents an individual notion is known as a singular term, while a term which stands for a general notion is referred to as a general term.
One may explain the meaning of a singular term which stands for one thing by enumerating its various attributes. For example, such attributes as a piercing bark, a yellow color, intelligent, companionable, a strong liking for sweetmeats, explain the meaning of the singular term “Fido.” Likewise we may explain the meaning of a general term by enumerating its attributes. To illustrate: power of speech, rationality, ability to laugh, etc., explain the meaning of the general term man. The explanation of the singular term fits only Fido. There is probably no other dog in the world just like Fido. But the explanation of the general term man may be applied to all men.
A brief enumeration of attributes which may be applied to a class of things often takes the form of a definition. The word definition comes from the word definire, meaning to limit or fix the bounds of.
A definition, then, consists of the enumeration of such attributes as distinguish a term from all other terms. In this sense it would seem that the singular term Fido, as well as the general term man, admits of definition, but it is usual for logicians to confine definition to the general term. Singular terms may be described; general terms, defined.
A DEFINITION OF DEFINITION.
A definition of a term is a statement of its meaning by enumerating its characteristic attributes.
That the enumeration must be in terms of its distinguishing or characteristic attributes is implied in the derivation of the term definition. The attributes must establish limits or bounds, just as a line fence limits a land owner’s possessions. To indicate that man is a creature possessing the power of locomotion, sense of sight and ability to eat, is surely not a definition, as the marks are not characteristic of men only. These attributes set no boundary between man and horse, consequently the statement is a faulty description of man, not a definition. But when the enumeration includes such attributes as power of speech, rationality and ability to laugh, then does the description become a definition. To put it differently: A definition is a description of a term by means of its distinguishing attributes. This statement may be considered a definition of man, though somewhat faulty: “A man is a creature who is rational and who possesses the power of speech and ability to laugh.”
We have learned that general terms when connotative may be used extensionally or intensionally.
A definition indicates the intensional nature of a term, while a statement which points out the extensional nature of a term is known as logical division. More briefly: A definition is an intensional statement of the nature of the term, while logical division is an extensional statement of the nature of the term.
To illustrate: The following statements are definitions:
(1) A dog is a domesticated quadruped of the genus canis and given to barking.
(2) A quadrilateral is a rectilinear figure of four sides.
(3) Soil is a substance composed of pulverized rock and decayed vegetable matter in which plants will grow.
The following represent Logical Division:
(1) Dogs are divided into hounds, terriers, bull, etc.
(2) The kinds of quadrilaterals are trapeziums, trapezoids and parallelograms.
(3) The various soils are loam, sand, clay, muck, etc.
Generally speaking there are three kinds of definitions, namely, (1) Etymological, (2) Descriptive, (3) Logical.5
(1) An etymological definition is one based upon the derivation of the term.
This kind of a definition, which gives merely the meaning of the symbol, is sometimes called a nominal or verbal definition; while a real definition is regarded as one which gives the meaning of the notion for which the symbol stands. The modern logician is inclined to ignore this classification on the argument that to make a distinction between a symbol and the notion it symbolizes is simply to misunderstand the relation which exists between them. If the definition does not agree with the thing then it cannot correctly explain the term which represents the thing. Define correctly the term and one has defined correctly the notion signified by the term.
The attributes of a term may be separated into three classes: differentia, property and accident. It would appear possible, therefore, to define a term by enumerating the accidents only or by enumerating the properties, or, finally, by stating the differentiae. But if the enumeration is confined to accidents the chances are that the statement will be a description, not a definition, as accidents are seldom sufficiently characteristic to determine the boundaries of a term. This leaves open two distinct ways of defining a term: First, by naming the properties or properties and accidents only; second, by stating the differentiæ only. The former kind is the so-called descriptive definition, while the latter is the logical.
(2) A descriptive definition of a term is a description of its nature by means of its properties and accidents.
(3) A logical definition of a term is a description of its nature by means of its differentiæ.
THE THREE KINDS OF DEFINITIONS ILLUSTRATED AND COMPARED.
Etymological Definition of Trigon.
A trigon is a figure of three corners.
Descriptive:
A trigon is a figure which has three sides and three angles, the sum of the latter being equal to two right angles.
Logical:
A trigon is a polygon of three angles.
It is seen that an etymological definition is simply a root-word analysis. In the case of trigon, the prefix comes from the Greek, meaning three, while the root-word comes from the Greek meaning corner.
The descriptive definition of trigon names the properties, “three sides and three angles” (differentiæ) and the accident, “the sum of the angles of which equals two right angles.”
The logical definition of trigon simply states the proximate genus, “polygon,” and the differentia, “three angles.”
The etymological definition is helpful in furnishing a cue for remembering the descriptive and logical definitions. It also leads to precision of expression—the right word in the right place. Here is where the knowledge of a foreign language, particularly Latin, is helpful.
The descriptive definition is best adapted to the child-mind. Children think in the large; are not given to hair-splitting discriminations, and, therefore, many characteristic marks must be mentioned in order to insure a mastery of the content. With children the logical definition is often too brief to be clear. For example, it is easy to see which of the following definitions would be better adapted to the child-mind. Logical: A square is an equilateral rectangle. Descriptive: A square is a figure of four equal sides and four right angles.
The logical definition may be introduced to the student of the secondary school.
Few exercises are better adapted to the development of powers of discrimination and precision than practice in defining logically the common terms of every-day life. For example: “A book is a pack of paper-sheets bound together.” “A chair is a piece of furniture with back and seat, designed for the seating of one person.” “A lead pencil is a cylindrical writing implement with lead through the center.” “A door is an obstacle designed to swing in and out to open and close an entrance.” “An eraser is an implement made to rub out written or printed characters.”
These definitions, coming from training school students, are not above criticism, yet they illustrate the point in hand.
Five rules summarize the requirements to which a logical definition must conform.
FIRST RULE.
A logical definition should state the essential attributes of the species defined.
This means that a logical definition should contain the species, the proximate genus and the differentia. As the terms species, genus and differentia have been explained, it will be sufficient to briefly illustrate this rule.
Logical According to the First Rule.
(1) A
species
bird
is a
genus
biped
with differentia
feathers.
(2) A
species
mascot
is a
genus
person
differentia
supposed to bring good luck.
(3)
species
Religion
is a
genus
system
of
differentia
faith and worship.
(4) A
species
moonbeam
is a
genus
ray of light
differentia
from the moon.
Illogical According to the First Rule.
(1) A man is a rational animal.
(“Biped” is the proximate genus, not “animal.”)
(2) A Connotative term always denotes both an object and an attribute.
(No genus.)
(3) A trigon is a polygon.
(No differentia.)
(4) It is a term which denotes an indefinite number of objects or attributes.
(No species.)
The Foregoing Illogical Definitions Made Logical.
(1) A man is a rational biped.
(2) A Connotative term is a term which denotes both an object and an attribute.
(3) A trigon is a polygon of three angles.
(4) A general term is a term which denotes an indefinite number of objects or attributes.
SECOND RULE.
A logical definition should be exactly equivalent to the species defined.
This means that the species must equal the genus plus the differentia or the subject and predicate of the definition must be co-extensive—of the same bigness. The subject must refer to the same number of objects as the predicate.
A man upon the witness stand makes the declaration that he will testify to the truth, the whole truth and nothing but the truth. A logical definition must contain the species, the whole species and nothing but the species. If the definition does not include all the species, it is too narrow; while on the other hand, if it includes other species of the genus it is too broad.
An excellent test of this second requirement is to interchange subject and predicate. If the interchanged proposition means the same as the original then the conditions have been met. To illustrate: Original—A trigon is a polygon of three angles. Interchanged—A polygon of three angles is a trigon.
The very best way of making the definition conform to this rule is to put to oneself these three questions: 1. Does it include all of the species? 2. Does it exclude all other species of the genus? 3. Has it any unnecessary marks?
To exemplify: Let us ask the three questions relative to the following logical definitions:
(1) A parallelogram is a quadrilateral whose opposite sides are parallel.
(2) A bird is a biped with feathers.
Questions:
(1) Does the definition include all the parallelograms? Yes. Does it exclude all other quadrilaterals? Yes. Are there any unnecessary marks? No.
(2) Does it include all birds? Yes. Does it exclude all other bipeds? Yes. Any unnecessary marks? No.
Illogical According to the Second Rule.
(1) A man is a vertebrate animal.
(Too broad. Does not exclude other species of the genus, such as horses, dogs, etc.)
(2) A barn is a building where horses are kept.
(Too narrow. Does not include all of the species, such as cow barn.)
(3) An equilateral triangle is a triangle all of whose sides and angles are equal.
(Equal angles is an unnecessary mark.)
The Foregoing Definitions Made Logical.
(1) A man is a rational biped. (Proximate genus.)
(2) A barn is a building where horses and cattle are kept and hay and grain are stored.
(3) An equilateral triangle is a triangle all of whose sides are equal.
THIRD RULE.
A definition must not repeat the name to be defined nor contain any synonym of it.
A violation of this rule is known as “a circle in defining” (circulus in definiendo).
There are some exceptions to this rule, as in the case of compound words and a species which takes its name from its proximate genus. To say that a hobby-horse is a horse, or that an equilateral triangle is a triangle, is not only allowable but necessary, that the proximate genus may be used.
The following definitions are illogical according to the third rule:
(1) A teacher is one who teaches.
(2) Life is the sum of the vital functions.
(3) A sensation is that which comes to the mind through the senses.
FOURTH RULE.
A definition must not be expressed in obscure, figurative or ambiguous language.
A violation of this rule is referred to in logic as “defining the unknown by the still more unknown” (ignotum per ignotius).
It is known that the purpose of definition is to make clear some obscure term, consequently unless every word used is understood the chief aim of the definition has been defeated.
From this it must not be inferred that all definitions should be free from technical terms. Such a restriction would make the defining of many terms unsatisfactory and in a few cases practically impossible. To the student of evolution the following definition by Spencer is intelligible while to the uninitiated it would appear obscure: “Evolution is a continuous change from an indefinite, incoherent homogeneity to a definite coherent heterogeneity through successive differentiations and integrations.”
This rule insists upon simple language when it is possible to use such in giving an accurate and comprehensive meaning to the term defined.
Illogical Definitions According to the Fourth Rule.
(1) “A net is something which is reticulated and decussated, with interstices between the intersections.” Dr. Johnson.
(2) “Thought is only a cognition of the necessary relations of our concepts.”
(3) “The soul is the entelechy, or first form of an organized body which has potential life.” Aristotle.
FIFTH RULE.
When possible the definition must be affirmative rather than negative.
The fact that there are a considerable number of terms which admit of a negative definition only, takes from the force of this rule. Such terms as deafness, inexpressible, infidel and the like can best be defined negatively.
It likewise happens that when words are used in pairs it is expedient to define one affirmatively and the other negatively. Recall, for example, the definitions of relative and absolute terms: “A relative term is one which needs another term to make its meaning clear.” “An absolute term is one which does not need another term to make its meaning clear.”
Illogical Definitions According to the Fifth Rule.
(1) A gentleman is a man who is not rude.
(2) An element is a substance which is not a compound.
(3) An univocal term is a term which does not have more than one meaning.
A logical definition insists upon a proximate genus and differentia. But as there is no genus higher than the highest genus (summum genus) then surely such cannot be defined logically. The words being and thing illustrate terms of this class. Moreover, it is impossible to give a satisfactory definition of an individual (infima species) as no attributes can be mentioned which will distinguish definitely and permanently the individual from others of the class. We may perceive the attributes but not those that are possessed solely by the individual. To say that Abraham Lincoln was a man who was simple and honest is not a definition, as other men have had the same characteristics.
Again there are a few terms such as life, death, time and space which cannot be defined satisfactorily. These terms seem to be in a class by themselves or of their own genus (sui generis).
Since a definition of a term is a brief explanation of it by means of its attributes, it follows that collective terms and terms standing for a single attribute are incapable of definition. Such terms as group, pain, attribute, belong to this class.
We may say, then, that there are some terms too high, some too low and some too peculiar to come within the province of logical definition. In short, “summum genus,” “infima species” and “sui generis” are incapable of definition.
(1) Development is the process whereby the latent possibilities of an individual are unfolded or the invisible conditions of a situation are made apparent.
Development means expansion according to principle, while unfolding may or may not involve a principle.
(2) Education is the process employed in developing systematically, symmetrically and progressively all of the capabilities of a single life; or
(3) Education is the process of modifying experience in order to make the life as valuable as it ought to be.
(4) Teaching is the art of occasioning those activities which result in knowledge, power and skill.
It is the duty of the true teacher to inspire the child to activity along right lines. Through his own activity the child shapes his inner world which is sometimes termed character.
Knowledge is anything known, power is ability to act, skill is a readiness of action.
(5) Instruction is the art of occasioning those activities which result in knowledge.
Instruction develops the understanding; teaching develops character.
(6) Training is the occasioning of those activities which, by means of directed exercise, result in power and skill.
Training and education are not interchangeable. Training implies an outside authority, while education, which involves inner development, may proceed without supervision.
(7) Knowledge is anything acquired by the act of knowing.
(8) Learning is the act of acquiring knowledge or skill.
(9) Instruction, training, teaching, learning and education all involve activity.
Instruction arouses activity which results in knowledge; training directs activity which produces power and skill; teaching includes both instruction and training. Learning is an activity which results in knowledge and skill, while education is a developing process which involves all the others.
(10) A science is knowledge classified for the purpose of discovering general truths.
(11) An art is a skillful application of knowledge and power to practice.
“A science teaches us to know, an art to do.”
(12) A fact is a single, individual, particular thing made or done.
A truth is general knowledge which exactly conforms to the facts.
A truth may be a definition, rule, law, or principle.
(13) A fact as opposed to hypothesis is an occurrence which is true beyond doubt.
An hypothesis is a supposition advanced to explain an occurrence or a group of occurrences.
A theory is a general hypothesis which has been partly verified.
(14) Theory as opposed to practice means general knowledge, while practice involves the putting into operation one’s theories.
(15) A fact as opposed to phenomenon is something accomplished. A phenomenon is something shown.
(16) A method-whole is any subdivision of the matter for instruction which leads to a generalization.
(17) Method is an orderly procedure according to a recognized system of rules and principles.
As the term is commonly used it includes not only the arrangement of the subject matter for instruction but the mode of presenting the same to the mind.
(18) Induction is the process of proceeding from the less general to the more general.
Deduction is the process of proceeding from the more general to the less general.
(19) The terms induction and deduction may have reference to forms of reasoning or to methods of teaching.
The inductive method is the method of deriving a general truth from individual instances.
The deductive method is the method of applying a general truth to individual instances.
The inductive method is objective, while the deductive method is subjective. Induction is the method of discovery; deduction is the method of instruction.
(20) Analysis is the process of separating a whole into its related parts.
Synthesis is the process of uniting the related parts to form the whole.
(21) The analytic method is the method of proceeding from the whole to the related parts.
The synthetic method is the method of proceeding from the related parts to the completed whole.
(22) Analysis and synthesis deal with single things, while induction and deduction are concerned with classes of things.
(23) The complete method consists of three elements: (1) induction, (2) deduction, (3) verification or proof.
When the emphasis is placed on the inductive phase, the complete method is sometimes termed the development method.
DEFINITION.
(1) Importance.
(2) The Predicables.
Genus—species—summum genus—infima species.
Proximate Genus.
Genus and Species of Natural History.
Genus, Double meaning of
Differentia.
Property.
Accident.
Separable, Inseparable.
(3) Nature of Definition.
(4) Definition and Division Compared.
(5) The Kinds of Definitions.
(1) Etymological.
(2) Descriptive.
(3) Logical.
THREE KINDS ILLUSTRATED AND COMPARED.
(6) When the Three Kinds are Serviceable.
(7) The Rules of Logical Definition.
(1) Essentials.
(2) Same size.
(3) Do not repeat.
(4) Unambiguous.
(5) Language affirmative.
(8) Terms Which Cannot be Defined Logically.
Summum genus.
Infima species.
Sui generis.
Collective terms.
A single attribute.
(1) To be logical one must acquire the habit of accurate definition.
This topic ought to appeal strongly to the school teacher, who should above all others make his work stand for clearness, pointedness and continuity.
(2) A predicable is a term which can be affirmed or predicated of any subject.
The five predicables are Genus, Species, Differentia, Property and Accident.
(1) A Genus is a term which stands for two or more subordinate classes.
(2) A Species is a term which represents one of the subordinate classes.
The proximate genus of a species is the next class above the species, while the summum genus is the highest possible class in any graded series of terms. The lowest class is the infima species of that series. The lowest class may be individual.
In natural history genus and species are not relative terms, but absolute, having a fixed place in the series of gradations.
The term genus possesses a double meaning: it may be used to represent objects (extensionally) or qualities (intensionally).
(3) The differentia is that attribute which distinguishes a given species from all the other species of the genus.
(4) A property of a term is any attribute which helps to make that term what it is.
Differentia is a property according to definition. Some logicians would not include the differentia in the content of the term property.
(5) An accident of a term is any attribute which does not help to make it what it is. Some authorities divide accidents into separable and inseparable.
(3) A definition of a term is a statement of its meaning by enumerating its characteristic attributes.
(4) Definitions explain a term intensionally, while logical division explains a term extensionally.
(5) There are three kinds of definitions: (1) etymological, (2) descriptive, (3) logical.
An etymological definition is based upon the derivation of the term; a descriptive definition states the characteristic properties and accidents of a term, while a logical definition is simply a statement of the differentia of a term.
(6) The etymological definition leads to precision of expression, the descriptive definition is best adapted to the child-mind, while the logical definition belongs to the realm of secondary education.
(7) Five rules summarize the requirements to which a logical definition must conform. In a word or two these five rules are: Every logical definition must (1) state the genus and differentia, (2) be equivalent to the species defined, (3) not repeat the name to be defined, (4) not be expressed in obscure language, (5) commonly be affirmative.
(8) Some terms are too high (summum genus), some too low (infima species), some too peculiar (sui generis) to come within the province of logical definition.
1a. The italicized words in the following propositions are predicables because they are affirmed of the subject:
(1) “This man weighs one hundred fifty pounds.”
(2) “A bird is a feathered biped.”
(3) “The earnest teacher is an indefatigable worker.”
(4) “Walking is the most beneficial outdoor exercise.”
1b. Underscore the predicables in the following:
(1) “All men are rational.”
(2) “Teachers must be just.”
(3) “Every form of unhappiness springs from a wrong condition of the mind.”
(4) “Calmness of mind is one of the beautiful jewels of wisdom.”
2a. To clarify our ideas it is an excellent plan to select a group of words belonging to the same genus with a view of defining them as simply and expeditiously as possible. As an illustration building may be selected as a genus. The word kind will suggest to us the species, such as dwelling, church, theatre, school, barn, bird-house, granary and smoke-house. Next it is necessary to discover the basis of distinction. This seems to be the use to which the building is put. Now we are ready for the definitions:
| Species | Genus | Differentia | |
| A | dwelling | is a building | where people live. |
| A | church | is a building | where people worship. |
| A | theatre | is a building | where people act. |
| A | school | is a building | where children are taught. |
| A | barn | is a building | where domestic animals, hay and grain are kept. |
| A | bird-house | is a building | designed for birds. |
| A | granary | is a building | where grain is stored. |
| A | smoke-house | is a building | where meat is smoked. |
2b. By selecting man as the genus, define the terms Caucasian, Mongolian, Ethiopian, Malay and American Indian. Treat the term chair in the same manner.
3a. One may easily distinguish a property from an accident by asking himself the question, “Would subtracting the attribute from the term alter its identity”? For example in the following, I find that the words italicized are properties because subtracting each from the term changes its identity:
| Term | Attributes |
| man | age, rationality, possessions. |
| book | binding, leaves, size, color, contents. |
| radium | emits intense light and heat, costs a million dollars a pound. |
| snail | air-breathing mollusk, moves slowly. |
| slush | soft mud and snow, six inches deep. |
3b. Indicate the common attributes of the following terms, underscoring the properties: Tree, teacher, garden, house, river.
4. The rules summarize well the essentials of the subject matter of the logical definition. Therefore, it is highly important for the student to have these rules at the “tip of the tongue.” With this in view a device of this nature may be helpful. Make each letter of the word rules stand for the initial letter of a suggestive word in each of the five rules. For example: r (repeat), u (unambiguous), l (language affirmative), e (essential), s (same size).
With a little study “r and repeat,” “u and unambiguous,” “l and language affirmative,” “e and essential,” “s and same size” may be firmly linked together in the memory. Repeat suggests the third rule, do not repeat the name, etc.; unambiguous, the fourth rule, not ambiguous language, etc.; language affirmative, the fifth rule; essentials, the first rule; same size, the second rule, subject and predicate must be of same size. The fact that the rules are not recalled in order of treatment is inconsequential.
It is the writer’s experience that fifteen minutes of concentrated study upon this device or one similar to it will indelibly stamp upon the mind these troublesome rules.
The student may be able to devise a more helpful keyword.
(1) Why should the subject of definition appeal strongly to the school teacher?
(2) Define a predicable.
(3) Name in order the five predicables.
(4) Define and illustrate the terms genus and species.
(5) Explain the terms summum genus, infima species, sui generis.
(6) Illustrate proximate genus.
(7) Explain the terms genus and species as used in natural history.
(8) Exemplify the double meaning of the genus man.
(9) Define and illustrate differentia.
(10) In what sense is the species a richer term than the genus?
(11) Distinguish between property and accident.
(12) Illustrate separable and inseparable accidents.
(13) Give descriptive definitions of the following, indicating the five predicables: logic, general term, non-connotative term, obversion.
(14) Define definition; illustrate.
(15) Distinguish between definition and division.
(16) Name, define and illustrate the three kinds of definitions.
(17) Distinguish between real and verbal definitions.
(18) Define in three ways the following: king, government, city, metal.
(19) State the rules of logical definition.
(20) What words may be used as cues to aid in recalling the rules for logical definition?
(21) Under what circumstances will the wise teacher make use of each of three kinds of definitions?
(22) Relative to the second rule for logical definition what are the three questions that one should ask himself?
(23) Explain the exceptions to the third rule.
(24) In connection with the fourth rule what may be said as to the use of technical terms?
(25) What facts take from the force of the fifth rule?
(26) What classes of words do not admit of logical definition? Illustrate.
(27) Define education, teaching, instruction, training.
(28) Distinguish by illustration between induction and synthesis; deduction and analysis.
(1) Why should the scholar be tempted to speak and write illogically?
(2) Name the parts of speech that may be classed as predicables.
(3) Explain the ten categories as given by Aristotle.
(4) Show that genus and species are relative terms.
(5) Why should the definition be needed most in the abstract sciences, such as theology, ethics, political economy, juris-prudence and psychology?
(6) Define sin, life, wrong, personality, habit, character.
(7) From the viewpoint of natural history find the species in the series of terms of which polygon is a member.
(8) What is the plural of differentia?
(9) Why should logic insist upon the proximate genus?
(10) (a) Man is a rational animal.
(b) Man is a rational biped (proximate genus).
In the case of the immature mind the first definition would be clearer. Why?
(11) “A property of a term is any mark or characteristic which belongs to that term.” Is this definition logical? Give reasons.
(12) What is the difference between the logical and the popular conception of property?
(13) Is there any difference between the logical and popular conception of accidents?
(14) “The term conferentia might be used to stand for the essence of the genus, as the term differentia represents the essence of the species.”6 Explain this.
(15) John Stuart Mill affirms that there is no such thing as a real definition. Discuss this.
(16) In your opinion, of the five rules of logical definition what one is violated most by the average teacher? Give reasons.
(17) Distinguish between symbol and content.
(18) Why are descriptive definitions best for young children? What educational principle is involved?
(19) From the standpoint of the five rules for logical definition criticise the following:
(1) A man is a reasonable vertebrate.
(2) A gentleman is a man with no visible means of support.
(3) A man is an organized entity whose cognitive powers function rationally.
(4) A metal is an element with a metallic luster.
(5) A triangle is a figure of three sides.
(6) A teacher is one who imparts knowledge.
(7) Education is the process of drawing out all that is beautiful in the body and noble in the soul.
(8) A democrat is a man who believes in free trade.
(9) A government is a commonwealth controlled by direct vote of the people.
(20) Write the foregoing definitions in logical form.
(21) Since man is the only animal given to laughter, why is not the following a logical definition: “Man is a laughing animal.”
(22) “A logical definition should contain the species, the genus and the appropriate differentia.” Is there any reason for using the term appropriate?
(23) In connection with genus and species explain subaltern.
(24) Is laughter a property of human being or an accident?
(25) Show how a pedagogue may be an instructor but not a teacher.
(26) Illustrate the complete method.
(27) Show that induction may consist of a series of analyses; also a series of syntheses.
The term genus is used for any class name which stands for two or more subordinate classes while the term species is made to stand for any one of the subordinate classes.
The proximate genus of any species is the next class above. For example the proximate genus of man is biped, not animal.
Logical division is the process of separating a proximate genus into its co-ordinate species.
ILLUSTRATIONS:
| Genus | Species | |
| (1) Heavenly bodies |
 |
Fixed stars Planets Satellites Comets Meteors Nebulae |
| (2) Vertebrates |
 |
Leptocardians Fishes Amphibians Reptiles Birds Mammals |
| (3) Man |
 |
Caucasian Mongolian Malay Ethiopian American Indian |
| (4) Government |
 |
Monarchy Aristocracy Democracy |
When the genus is separated at once into individual objects the process is not logical division, but simple enumeration. Logical division implies a separating into smaller class terms, each term being a genus of still smaller subdivisions. This process may be continued till the last division gives individuals as species. Enumeration takes place when the first subdivision results in a list of individuals. To illustrate:
| Logical Division. | ||
| Teacher |
 |
Science teacher Mathematics teacher English teacher Modern language teacher |
| Enumeration. | ||
| Teacher |
 |
John J. Brown H. G. White Mary Jones Alice Smith |
Partition is the process of separating an individual thing into its parts.
The partition is quantitative or mathematical when the separation is in terms of space or time, but when otherwise the partition becomes qualitative or logical. Or to put it in another way, the partition is mathematical when the separation gives parts and logical when the separation gives ingredients.
To illustrate:
| (1) Tree |
 |
quantitative or mathematical |
 |
branches leaves roots trunk |
|
qualitative or (logical) |
 |
woody fibre capillary attraction sap chlorophyll | ||
| (2) House |
 |
quantitative or mathematical |
 |
roof frame-work foundation |
|
qualitative or (logical) |
 |
wood iron stone plaster |
An easy way to determine that the separation involves logical division proper and not partition is to affirm the connection between a class and a sub-class. To wit: A man is a biped; a square is a rectangle; a Caucasian is a man, etc. If such an affirmation cannot be made then the separation involved is not properly logical division but probably partition. For example it cannot be said that a roof is a house, or that sap is a tree. It is seen, then, that a logical division of any genus may be summarized in the form of a series of judgments of which a species is the subject and the genus is the predicate. For example, by a logical division quadrilaterals may be divided into trapeziums, trapezoids and parallelograms; this process may then be summarized in a series of three judgments: (1) A trapezium is a quadrilateral; (2) A trapezoid is a quadrilateral; (3) A parallelogram is a quadrilateral.
When the logical division of a genus is under consideration there are four rules which should be observed.
FIRST RULE. There must be but one principle of division (fundamentum divisionis). To divide mankind into white man, Australian, yellow man, African and red man is a violation of this rule as the two principles of color and geographical location are involved. A division in which more than one principle is used is sometimes referred to as cross division because the various species cross each other. For example in the foregoing there are many white men who are Australians.
This rule applies only to one division. Where there is a series of divisions a new principle may be employed in each division. For example, in dividing triangles into scalene, isosceles and equilateral, the equality of sides is the principle involved, but, in subdividing isosceles triangles into right angled and oblique angled, the principle employed concerns the nature of the angle.
SECOND RULE. The co-ordinate species must be mutually exclusive. There must be no overlapping. The illustration given in the first rule is likewise a violation of this rule. Another example in which this second rule is not obeyed may be found in most geometries where triangles are divided into scalene, isosceles and equilateral. Here the second and third classes are not mutually exclusive since all equilateral triangles are isosceles according to the usual definition, “An isosceles triangle is a triangle having two equal sides.” All equilateral triangles have two equal sides.
THIRD RULE. The division must be exhaustive. That is, the species taken together must equal the whole genus. The sum of the species must be co-extensive with the genus.
Dividing man into Caucasian, Ethiopian and Mongolian would be a violation of this rule, as there are at least two other species of man, Malay and American Indian.
A distinction should be made between an exhaustive division and a complete division as the latter is not a logical requirement. To divide government into monarchy, aristocracy and democracy is exhaustive but incomplete. Exhaustive because there is no other kind of government, all the species are included; but incomplete in that monarchy may be divided into absolute and limited; democracy into pure and representative.
FOURTH RULE. The division must proceed from the proximate genus to the immediate species. There should be no sudden jumps from a high genus to a low species. The division must be gradual and continuous; step by step. To divide government into limited monarchy, absolute monarchy, pure democracy and representative democracy would be a violation of this rule, as government is the proximate genus of monarchy, not of limited monarchy, therefore one step has been omitted. Such an omission involves a step from grandfather to grandchild, so to speak, the generation of father having been left out.
A violation of this rule is most insidious when some of the species of a subdivision are immediate while others are not. To wit: dividing government into monarchy, aristocracy, pure democracy and republic, or dividing quadrilaterals into trapeziums, trapezoids, rectangles, squares, rhomboids and rhombs.
Dichotomy comes from the Greek, meaning to cut in two. Dichotomy is a continual division of a genus into two species which are contradictory in nature.
Contradictory terms are such as admit of no middle ground. They divide the whole universe of thought into two classes. For example, honest and not-honest, pure and impure, perfect and imperfect, are contradictory terms. Dichotomy thus affords an easy opportunity for an exhaustive division as in the use of contradictories nothing in the universe need be omitted.
An historical illustration of dichotomy is the “Tree of Porphyry” named after Porphyrius, a Neo-Platonic philosopher of the third century.
This kind of division is not altogether satisfactory as the negative side is too indefinite. On the other hand, if both subdivisions are made positive then there is danger of making the opposing terms contrary rather than contradictory. This, of course, would be a serious logical fallacy, as contrary terms admit of middle ground while contradictory terms give no choice, it is either the one or the other.
The use of dichotomy becomes evident in situations where new and unexpected discoveries may be made. Without disturbing the classification the new species may be appended to the negative side of the division. The following illustrates:
Classification is the process of grouping notions according to their resemblances or connections.
So far as results are concerned there is no difference between logical division and classification. Both processes may give us the same orderly scheme of heads and subheads. The difference lies in the process itself. Division is deductive in nature as it proceeds from the more general genus to the less general species. While classification is inductive as it groups the less general species under the more general genus. Division differentiates unity into multiplicity, while classification reduces multiplicity to unity. It follows that the one is the inverse of the other. The difference in the mode of procedure may be illustrated by using the common classification or division of triangles. For example:
Without any knowledge of the kinds of triangles the student discovers by examining the various shapes of many triangles that there is a group in which none of the sides are equal. For the lack of a better name he terms these non-equilateral (scalene). Further observation discloses another group in which two of the sides are equal. These he names bi-equilateral (isosceles). Finally a third group is designated as tri-equilateral (equilateral). This process is classification. Division would consist in separating the genus triangle into the three kinds—scalene, isosceles, equilateral.
An artificial classification is one in which the grouping is made on the basis of some arbitrary connection. Cataloguing alphabetically the books in a library illustrates this kind of classification. Likewise the arrangement of the names in a directory or a telephone book. The connecting mark being the initial letter of the title or name. The reason why Mills and Meyers are put in the same group is that both names happen to commence with the letter M.
Artificial classifications are resorted to for some special purpose, designed by man, not by nature. Consequently artificial classifications are sometimes called special or working classifications.
A natural classification is one in which the grouping is made on the basis of some inherent mark of resemblance.
Classifications in animal and plant life are the best illustrations of this kind. Such classifications are suggested by nature and not by man, and may, therefore, be called general or scientific. The main aim of natural classification is to derive general truths and arrange knowledge so that it may be easily remembered.
The rules of logical division are applicable in the making of a logical classification. In addition to these an artificial classification should be made to conform to the one rule: The classification must be appropriate to the purpose in hand. Likewise a natural classification should be made to conform to the rule: Every classification should afford opportunity for the greatest possible number of general assertions.
It has been stated that classification and division aim at the same result. Classification reduces multiplicity to unity while division differentiates unity into multiplicity. In short, division is deductive while classification is inductive in mode of procedure. Therefore, classification should be used in those situations which call for induction and division in cases where deduction is the better method.
Speaking generally, classification should be used with small children when the essential thing is to present the concrete facts with a view of leading the children to discover for themselves the truths contained therein.
With older pupils division may be used, if the purpose is to set in order facts which are already known.
LOGICAL DIVISION AND CLASSIFICATION.
(1) Nature of Logical Division.
Genus—species.
Illustrations.
(2) Logical Division Distinguished from Enumeration.
Illustrations.
(3) Logical Division and Partition.
Quantitative—qualitative.
How summarized.
(4) Four Rules of Logical Division.
(1) One principle—cross division.
(2) Mutually exclusive.
(3) Exhaustive—complete.
(4) Immediate species.
(5) Dichotomy.
Contradictory terms.
Tree of Porphyry.
Use illustrated.
(6) Classification Compared with Division.
(7) Kinds. Artificial—Natural.
(8) Two Rules of Classification.
(1) Appropriate.
(2) Afford many Assertions.
(9) Use of Division and Classification.
(1) Logical division is the process of separating a proximate genus into its co-ordinate species.
(2) The first subdivision in a logical division gives class terms, while the first subdivision in an enumeration gives individual objects.
(3) Partition is the process of separating an individual thing into its parts. These parts may be either quantitative or qualitative.
A logical division of any genus may be summarized in a series of judgments of which a species is the subject and the genus is the predicate.
(4) The four rules of logical division are: the division must (1) be based on one principle, (2) have species mutually exclusive, (3) be exhaustive and (4) proceed from proximate genus to immediate species.
A violation of the first rule gives a cross division.
Exhaustive division is easily confused with a complete or finished division.
(5) Dichotomy is a continual division of a genus into two species which are contradictory in nature.
An historical illustration of dichotomy is the Tree of Porphyry.
Dichotomy is of service in the field of new and unexpected discoveries.
(6) Classification is the process of grouping notions according to their resemblances or connections.
Classification is inductive in nature, division deductive. Classification unifies, division differentiates.
(7) An artificial classification is made on the basis of some arbitrary connection; a natural classification, on some inherent mark of resemblance.
(8) The rules of logical division are applicable in any classification. In addition to these a classification should (1) be appropriate and (2) afford opportunity for the greatest possible number of assertions.
(9) Classification should be the mode of procedure in the lower grades, division in the higher grades.
(1) Define and illustrate logical division.
(2) What is the meaning of proximate genus?
(3) How does logical division differ from enumeration? Illustrate.
(4) Distinguish between logical division, and physical division or partition.
(5) Illustrate a quantitative partition; a qualitative partition.
(6) Illustrate how a logical division may be summarized in the form of a series of judgments.
(7) State and explain the rules of logical division.
(8) State the rules violated in the following divisions, explaining in full:
| (1) Education |
 |
Primary Secondary Collegiate Technical Scientific Professional |
| (2) Life |
 |
Infancy Childhood Youth Old age |
| (3) Man |
 |
Caucasian Ethiopian Malay Mongolian American |
| (4) Buildings |
 |
Cement Frame Stone Dwellings Barns Churches |
(9) Show the difference between contradictory and opposite terms.
(10) Define dichotomy.
(11) Illustrate the Tree of Porphyry and indicate its use to scientists.
(12) Illustrate the difference between classification and division.
(13) Why should classification be the mode of procedure when dealing with immature minds?
(14) Illustrate the difference between an artificial and a natural classification.
(15) State and explain the two rules of classification.
(16) Show which of the following divisions are logical and which are not:
(1) The manifestations of the mind into knowing, thinking and feeling.
(2) Books into mathematical and non-mathematical.
(3) Students into those who are industrious, athletic and shiftless.
(4) Flowers into roses, carnations and lilies.
(5) Planets into those which are larger than the earth and those which are smaller.
(1) Analyze by mathematical partition the terms world, plant, book.
(2) Analyze by logical partition the terms granite, water, air.
(3) What rule is violated if the logical division is applied to the genus rather than the proximate genus?
(4) Divide logically the following terms: school, religion, book, vegetable, life.
(5) “Each new subdivision may adopt a new principle of division.” Illustrate this.
(6) Explain and illustrate the meaning of the terms super-ordinate, sub-ordinate and co-ordinate.
(7) Define and illustrate metaphysical division and verbal division.
(8) Give a definition of an isosceles triangle which will make logical the division of triangles into scalene, isosceles and equilateral.
(9) “The evolution of all truth develops progressively through three stages.” “The first is the thesis; the second is the antithesis; the third is the synthesis.” Explain this in terms of trichotomy.
(10) Illustrate the difference between a complete division and an exhaustive division.
(11) Show in what ways, if any, the following divisions violate the rules of logical division.
| Human Learning (by Bacon) |
 |
1 Memory (History) 2 Imagination (Poetry) 3 Reason (Philosophy) or (the Sciences) |
| Sciences (by Comte) |
 |
1 Mathematics 2 Astronomy 3 Physics 4 Chemistry 5 Biology 6 Sociology 7 Morals |
Judging has been defined as the process of conjoining or disjoining notions. This may be put in another way: “Judging is the process of asserting or denying the agreement between two notions.” The product of the act of judging is a judgment and when judgments are put in word-form such expressions are called logical propositions.
Definition: A logical proposition is a judgment expressed in words. Just as percept and concept notions are expressed by means of logical terms so judgment notions may be expressed by logical propositions.
To illustrate: The terms the squirrel and cracking a nut express two notions, and when an agreement between them is asserted and the product is expressed in word form, then such an expression becomes the logical proposition, “The squirrel is cracking a nut.”
The following being expressed judgments are logical propositions:
(1) All men are mortal.
(2) Some men are wise.
(3) No men are immortal.
(4) Some men are not wise.
(5) No sane person is a lover of vice.
(6) Some good orators are not good statesmen.
(7) Every man is fallible.
(8) If it rains, I shall not go.
(9) He is either sane or insane.
There are three kinds of logical propositions; namely, categorical, hypothetical and disjunctive.
A categorical proposition is one in which the assertion is made unconditionally. An hypothetical proposition is one in which the assertion depends upon a condition. A disjunctive proposition is one which asserts an alternative.
THE THREE KINDS ILLUSTRATED:
(1) “Every dog has his day.” Categorical.
(2) “If you do your best, success will reward you.” Hypothetical.
(3) “He is either stupid or indolent.” Disjunctive.
(4) “All vices are reprehensible.” Categorical.
(5) “Either you are very talented or very industrious.” Disjunctive.
(6) “If capital punishment does not aid society, it should be abolished.” Hypothetical.
(7) “You may go provided your teacher is willing.” Hypothetical.
(8) “No intelligent man can ignore the practice of temperance.” Categorical.
By studying the illustrations it will be observed that the categorical propositions are direct, bold, assertive statements, whereas the hypothetical are limited by conditions which make them less forceful. In the second proposition, for example, “success will reward you,” is limited by the condition, “If you do your best.” The disjunctive may be regarded as categorical in form, but hypothetical in meaning, because in such a proposition as, “He is either, stupid or indolent,” a direct assertion is made which suggests the categorical, and yet it may be implied that, if he is stupid then he is not indolent; this is indicative of the hypothetical.
Some logicians classify propositions as categorical and conditional, the conditional being subdivided into hypothetical and disjunctive. The first classification seems preferable, however, as it conforms to the three modes of reasoning.
The common word-signs of the categorical proposition are all, every, each, any, no and some, while those of the hypothetical are if, even if, unless, although, though, provided that, when, or any word or group of words denoting a condition. The disjunctive symbols are either—or.
Every categorical proposition should have four elements; namely, the quantity sign, the logical subject, the copula and the logical predicate. In the foregoing categorical propositions the quantity signs are respectively, every, all and no. In any case the quantity sign is always attached to the subject and indicates its breadth or extension. For example, in the two propositions, “All men are mortal” and “Some men are wise,” the quantity sign all makes the term man much broader than does the quantity sign some.
The logical subject of a categorical proposition is the term of which something is affirmed or denied, whereas the logical predicate of a categorical proposition is the term which is affirmed or denied of the subject. In the two propositions, “All men are mortal” and “No men are immortal,” the term about which something is affirmed or denied is men, while the terms which are affirmed and denied of the subject are respectively mortal and immortal. “Men” is, therefore, the logical subject of each proposition, while “mortal” is the logical predicate of the first and “immortal” the logical predicate of the second. The copula is the connecting word between the logical subject and predicate and denotes whether or not the latter is affirmed or denied of the former. The copula is always some form of “to be” or its equivalent. When the predicate is denied of the subject, “not” may be used with the copula and considered a part of it. To illustrate: in the logical proposition, “Some men are not wise,” “are not” may be regarded as the copula.
The four elements are indicated in the following categorical propositions:
| Quantity sign | Logical subject | Copula | Logical predicate |
| All | fixed stars | are | self-luminous |
| No | wise man | is | going to steal |
| Some | quadrupeds | are | domestic animals |
| Some | glittering things | are not | gold |
| Some | boys | are not | discreet |
| A few | men | are | multi-millionaires |
| Every | citizen | is | duty-bound to vote |
The student must ever keep in mind the fact that to be absolutely logical all categorical propositions must be expressed in terms of the four elements. However, life is too short and man is too busy to speak always in terms of the four elements. Moreover, to be logical may often compel an awkwardness of expression and a lack of euphony which could hardly be tolerated. For these reasons the utterances in ordinary conversation are frequently illogical so far as the four elements are concerned, though not necessarily illogical in meaning. When it is desired to test the validity of any series of statements leading up to some generalization, it may become necessary to express the statement in terms of the four elements. The student should gain some facility in this, otherwise he may be readily led into fallacious reasoning.
The following statements taken at random from newspapers are given in the original and then expressed in terms of the four elements:
| The Original | In Terms of the Four Elements |
| (1) You came too late. | (1) The person is one who came too late. |
| (2) I saw the swell turnout coming along. | (2) The man was one who saw the swell turnout coming along. |
| (3) All of the men walked. | (3) All of the men were those who walked. |
| (4) The robbers cut a hole in this floor. | (4) All the robbers were the ones who cut a hole in this floor. |
| (5) Some of these flew away. | (5) Some birds were those which flew away. |
| (6) The rain interfered with the attendance. | (6) The rain was that which interfered with the attendance. |
| (7) Our habits make or unmake us. | (7) All our habits are forces which make or unmake us. |
| (8) We all had a fine time. | (8) All the party were those who had a fine time. |
In argumentative discourse it is often sufficient to “think the proposition” in terms of the four elements without taking the time to actually express it.
The grammatical subject is one word while the logical subject is the grammatical subject with all its modifiers except the quantity sign. For example: in the proposition, “All white men are Caucasians,” men is the grammatical subject, while white men is the logical subject. All being the quantity sign simply indicates the extension of men and is not a part of the logical subject.
The grammatical predicate is the verb-form together with any predicate noun or adjective, while the logical predicate is the predicate word or words and all its modifiers. The grammatical predicate includes the copula, but the logical predicate never includes the copula. The grammatical predicate does not include the object, while the logical predicate always includes what is equivalent to the object and all its modifiers. To illustrate: in the proposition, “Some men are wise,” are wise is the grammatical predicate, while wise is the logical predicate. And in the proposition, “He burned the red house on the hill,” burned is the grammatical predicate, while the one who burned the red house on the hill is the logical predicate.
Categorical propositions are divided according to their quantity into Universal and Particular and according to their quality into Affirmative and Negative.
A universal proposition is one in which the predicate refers to the whole of the logical subject.
ILLUSTRATIONS:
(1) All men are mortal.
(2) All civilized men cook their food.
(3) No dogs are immortal.
(4) Every man was once a boy.
Considering the first proposition, “mortal,” the logical predicate, refers to the whole of the logical subject “men.” Similarly “cook their food” refers to the whole of the term “civilized men”; “immortal” to the whole of the term “dogs,” and “once a boy” to the whole of the term “man.”
In considering the definition of a universal proposition it is necessary to keep in mind the distinction between a logical and a grammatical subject, as in the second proposition the logical predicate, “cook their food,” refers to only a part of the grammatical subject, men, and, therefore, the proposition might fallaciously be termed a particular proposition rather than a universal.
A particular proposition is one in which the predicate refers to only a part of the logical subject.
ILLUSTRATIONS:
(1) Some men are wise.
(2) Some animals are not quadrupeds.
(3) Most elements are metals.
(4) Many children are mischievous.
In the foregoing propositions some, most and many are quantity signs and, therefore, must not be considered as a part of the logical subjects. Considering the logical subjects and predicates in order, the term wise refers to only a part of the men in the world, quadrupeds to only a part of the animals, metals to only a part of the elements and mischievous to only a part of the children.
An affirmative proposition is one which expresses an agreement between subject and predicate.
A negative proposition is one which expresses a disagreement between subject and predicate.
Affirmative propositions conjoin terms, negative propositions disjoin terms. In the first the agreement is affirmed; in the second the agreement is denied.
ILLUSTRATIONS:
None of the captives escaped. Negative.
Some teachers are just. Affirmative.
All trees grow towards heaven. Affirmative.
Some people are not companionable. Negative.
No person is above criticism. Negative.
Dividing both universal and particular propositions as to quality, gives four kinds; namely, universal affirmative, universal negative, particular affirmative and particular negative. No topic in logic demands greater familiarity than these four types, as every proposition must be reduced to one of the four before it can be used as a basis of reasoning.
For the sake of brevity the symbols A, E, I and O are used to designate respectively the universal affirmative, the universal negative, the particular affirmative and the particular negative. A and I, symbolizing the affirmative propositions, are the first and second vowels in Affirmo, while E and O, symbolizing the negatives, are the vowels in Nego. The common sign of the universal affirmative, or the A proposition is all; of the universal negative, or E proposition no; of the particular affirmative, or I proposition some; of the particular negative, or O proposition some with not as a part of the copula. The accompanying classification summarizes these facts, S and P being used to symbolize the terms “subject” and “predicate.”
| Illustrations | |||||
| Categorical Propositions |
 |
Universal |
 |
Affirmative-A | All S is P |
| Negative-E | No S is P | ||||
| Particular |
 |
Affirmative-I | Some S is P | ||
| Negative-O | Some S is not P | ||||
Henceforth the symbols A, E, I, O will be used to designate the four kinds of categorical propositions. The propositions have other quantity signs aside from the ones used above. These may be summarized:
| Quantity signs of |
 |
A—all, every, each, any, whole. |
| E—no, none, all-not. | ||
| I—some, certain, most, a few, many, the greatest part, any number. | ||
| O—some - - not, few. |
It has been observed that all expressed judgments must be reduced to one of the four logical types A, E, I or O, before they can be used argumentatively. Logic insists upon definiteness and clearness—there must be no ambiguity, no opportunity for a wrong interpretation. From this viewpoint the four types fulfill every requirement. Their meaning cannot be misunderstood. To any one with normal intelligence their significance may be made perfectly clear. Any argument when once put in terms of the four types may be spelled out with mathematical precision. In consequence it is of prime importance that the four types not only be well understood, but that a certain facility be gained in reducing ordinary conversation to some one of these types.
(1) Indefinite and Elliptical Propositions.
It is known that every logical proposition must be expressed in terms of the four elements—quantity sign, logical subject, copula and logical predicate, consequently the four types A, E, I and O which epitomize every form of logical proposition, are expressed in terms of these four elements. But in common conversation often the quantity sign, as well as the copula, is omitted. See section 3.
Propositions without the quantity sign are called indefinite, while those with the suppressed copula may be termed elliptical propositions. Both may be made logical as the attending illustrations will indicate:
| Illogical | Logical |
| Indefinite | |
| Men are fighting animals. | All men are fighting animals. (A) |
| Lilies are not roses. | No lilies are roses. (E) |
| Good is the object of moral approbation. | All good is the object of moral approbation. (A) |
| Perfect happiness is impossible. | In all cases perfect happiness is impossible. (A) |
| Elliptical | |
| Fashion rules the world. | All fashions are ruling the world. (A) |
| Trees grow. | All trees are plants which grow. (A) |
| Children play. | All children are playful. (A) |
| Some men cheat. | Some men are persons who cheat. (I) |
Here it is noted that the logical form of some propositions is not always the most forceful. Often the logical form gives an awkward construction and should be resorted to only for purposes of logical argument.
The reduction of either kind to the logical form must be determined by the meaning of the proposition. As a usual thing the indefinite is universal (either an A or an E) in meaning, while the problem of the elliptical is to give it in terms of the copula, expressed with as little awkwardness as possible.
General truths, because attended with no quantity sign, might be classed as indefinite propositions, though their universality is so apparent that they may be unhesitatingly classed as universals.
ILLUSTRATIONS:
“Things equal to the same thing are equal to each other.”
“Trees grow in direct opposition to gravity.”
“Honesty is the best policy.”
“A stitch in time saves nine.”
Because the indefinite proposition is so frequently of a general nature, it is sometimes classed as general rather than indefinite.
Sir William Hamilton would class the indefinite as an indesignate proposition.
(2) Grammatical Sentences.
The grammarian divides sentences into five kinds; namely, declarative, interrogative, imperative, optative, exclamatory. But logic recognizes only the declarative, as it has already been seen that the four logical types are declarative in nature. A logical proposition, then, is always a sentence, but all sentences are not logical propositions. The four kinds of sentences which are not logical propositions may be usually reduced to one of the four types as the attending illustrations will indicate:
| Illogical | Logical |
| Interrogative. Do men have the power of reason? | The question is asked, Do men have the power of reason?7 (A) |
| Imperative. “Thou shalt not steal.” | All men are commanded not to steal, or you are one who should not steal. (E) |
| Optative. “I would I had a million.” | I am one who desires a million dollars. (A) |
| Exclamatory. “Oh, how you frightened me!” | You are one who frightened me. (A) |
(3) Individual Propositions.
An individual proposition is one which has a singular subject; e. g., Abraham Lincoln was an honest man. Peter the Great was Russia’s greatest ruler. The maple tree in my yard is dying of old age. These propositions, having a singular term as subject, are individual or singular in nature. As the predicate refers to the whole of the logical subject, individual propositions are classed as universal.
(4) Plurative Propositions.
Plurative propositions are those introduced by “most,” “few,” “a few,” or equivalent quantity signs. For example, “Most birds are useful to man”; “Few men know how to live”; “A few of the prisoners escaped,” are plurative propositions. “Most” means more than half, while “few” and “a few” mean less than half. In either case the proposition is particular. Stated logically, the illustrative propositions would take the form of “Some birds are useful to man”; “Some men do not know how to live”; “Some of the prisoners escaped.”
The reader will observe the difference in significance between few and a few. The former is negative in character and when introducing a proposition makes it a particular negative (O). The latter always introduces a particular affirmative (I).
(5) Partitive Propositions.
Partitive propositions are particulars which imply a complementary opposite. These arise through the ambiguous use of all-not, some and few. All-not may sometimes be interpreted as not all and sometimes as no. To illustrate: The proposition, “All men are not mortal,” is distinctly a universal negative or an E, while the proposition, “All that glitters is not gold,” is a particular negative or an O. The logical form of the first is, “No men are mortal,” and of the second, “Some glittering things are not gold.” When used in the “not-all” sense, the proposition is partitive because if the O-meaning is intended the I is implied. For example, “All that glitters is not gold,” is partitive because the statement implies that some glittering things are gold (I) as well as the complement, “Some glittering things are not gold” (O). A knowledge of both the affirmative and negative aspects is taken for granted in the statement of either the one or the other.
“All-not,” then, is negative in any case, but universal when it means no and particular when it means not all. Any proposition is partitive in nature when the quantity sign is not all, or all-not interpreted as the equivalent of not all.
It may be observed here that all has two distinct uses. First, it may be used in a collective sense; second, in a distributive sense. For example: All is used in the collective sense in such propositions as, “All the members of the football team weighed exactly one ton,” or “All the angles of the triangle are equal to two right angles.” Using all in the distributive sense would make true these: “All the members of the football team weigh more than 140 pounds”; “All the angles of a triangle are less than two right angles.” All is used collectively when reference is made to an aggregate, but distributively when reference is made to each.
The quantity sign some is likewise ambiguous, as it may mean (1) some only—some, but not all, or (2) some at least—some, it may be all or not all. When “some” is used as the quantity sign of any particular proposition which has been accepted as logical, the second meaning, “some at least,” is always implied. This interpretation of “some” will be explained more in detail in a succeeding section.
When some is used in the sense of some only, the partitive nature of the proposition is apparent, as both I and O are implied. For example, with reference to the human family, to say that “some only are wise” necessitates an investigation, which leads to the discovery that some are wise, while others are not wise. If the proposition be an I, then its complementary O is implied, or if it be an O, the I is implied.
Few given as a sign of a plurative proposition also serves as a sign of the partitive. The plurative aspect is prominent when it is said that “Few men can be millionaires” and emphasis is placed upon the meaning that “Most men cannot be millionaires.” But when emphasis is given to “few,” as meaning few only rather than the most are not, then the I and the O are both implied; e. g., Some men become millionaires, but the most do not.
To put it in a word, “all-not,” “some” and “few” introduce partitive propositions when the meaning implies both an I and an O. When treating such in logic the meaning which seems to be given the greater prominence must be accepted. Surely in the statement, “All that glitters is not gold,” the O-interpretation is the one intended; namely, “Some things which glitter are not gold.”
ILLUSTRATIONS:
(1) “All men are not honest.”
(2) “Few men live to be a hundred.”
(3) “Some men are consistent.”
The first proposition with the emphasis placed upon all suggesting that some men are not honest, is the intended proposition while some men are honest is the implied. In reducing it to the logical form the intended proposition is the one which should be used.
With the emphasis upon few and some, the second and third propositions may be interpreted as follows: (2) Intended proposition, Some men do not live to be a hundred. Implied proposition, Some men do live to be a hundred. (3) Intended proposition, Some men are consistent. Implied proposition, Some men are not consistent.
(6) Exceptive Propositions.
These are introduced by such signs as all except, all but, all save. To wit: (1) “All except James and John may be excused”; (2) “All but a few of the culprits have been arrested”; (3) “All birds save the English sparrow are serviceable to man” are exceptive propositions.
Exceptive propositions are universal when the exceptions are mentioned. Universal propositions necessitate a subject more or less definite, as the predicate of such must refer to the whole of a definite subject. It follows that in exceptive statements definiteness is secured when the exceptions are mentioned, therefore it becomes clear how all such propositions must be universal. Of the illustrations, the first and third propositions are universal. Any exceptive proposition is particular when the exceptions are referred to in general terms or when the subject is followed by et cetera. The second illustrative proposition is particular.
(7) Exclusive Propositions.
Of all propositions which vary from the logical form the exclusive is the most misleading. Exclusives are accompanied by such words as “only,” “alone,” “none but,” and “except.” Their peculiarity rests in the fact that reference is made to the whole of the predicate, but only to a part of the subject. For example, in the exclusive proposition, “Only elements are metals,” metals is referred to as a whole while elements is considered only in part. The true meaning is “Some elements are all metals,” or to put it in logical form, “All metals are elements.” The easiest way to deal with an exclusive is to interchange subject and predicate (convert simply) and call the proposition an A.
PROCESS ILLUSTRATED:
| Exclusive Proposition | Reduced to Logical Form |
| 1. None but high school graduates may enter Training School. | All who enter Training School must be high school graduates. |
| 2. Only first-class passengers are allowed in parlor cars. | All parlor cars are for first-class passengers. |
| 3. Residents alone are licensed to teach. | All who are licensed to teach are residents. |
| 4. No admittance except on business. | All who have business may be admitted. |
| 5. Only bad men are not-wise. | All who are not-wise are bad men. |
| 6. Only some men are wise. | All who are wise are men. |
It is claimed by good authority that the real nature of the exclusive is best expressed by negating the subject and calling the proposition an E; e. g., exclusive: “Only elements are metals”; logical form: “No not-elements are metals” (E). In a succeeding chapter it is explained how an E admits of first simple conversion and then obversion. The following illustrate these two processes:
Original E: “No not-elements are metals.”
Simple conversion: “No metals are not-elements.”
Obversion: “All metals are elements.”
From this it may be seen that the statement, “The easiest way to deal with an exclusive is to interchange subject and predicate and call the proposition an A,” is substantially correct.
(8) Inverted Propositions.
The poet often employs the inverted proposition, illustrated by the following: “Blessed are the merciful;” “Great is this man of war.” An interchanging of subject and predicate makes these poetical constructions logical; e. g., “All the merciful are blessed;” “This man of war is great.”
NOTE.—The student should not be misled by the relative clause. Often it may be interpreted as a part of the predicate rather than the subject. To wit: “No man is a friend who betrays a confidence”; clearly the logical subject is no man who betrays a confidence.
(1) Analytic and Synthetic Propositions.
An analytic proposition is one in which the predicate gives information already implied in the subject. Thus, “Fire burns,” “Water is wet,” “A triangle has three angles” are analytic propositions because the predicates do not give added information to one who has any conception of the subjects. Because the attribute mentioned by the predicate is an essential one, analytic propositions are sometimes termed essential propositions. Other names for the same kind of proposition are verbal and explicative.
A synthetic proposition is one in which the predicate gives information not necessarily implied in the subject. “Fire protects men from the wild animal.” “A cubic foot of water weighs 621⁄2 lbs.” “The sum of the interior angles of a triangle is equal to two right angles.” These are synthetic because a common conception of the meaning of the subject would not need to include the information given by the predicate. Other names for synthetic propositions are accidental, real and ampliative.
The distinction between analytic and synthetic propositions is not so clear as would on first thought appear. “Fire burns” might give added information to the child or savage who knows only of the light emitted by fire. To them, then, the proposition would be synthetic. The distinction must be based upon the assumption that the same words mean about the same thing to people in general.
This analytic-synthetic division of propositions finds a significance in the domain of philosophy. To the logician the distinction is of slight importance save in the so-called verbal disputes, viz.: disputes which turn on the meaning of words.
(2) Modal and Pure Propositions.
A modal proposition states the mode or manner in which the predicate belongs to the subject. The signs of modal propositions are the adverbs of time, place, degree, manner. Illustrations: “James is walking rapidly.” “Honesty is always the best policy.” “Aristotle was probably the greatest thinker of ancient times.”
A pure proposition simply states that the predicate belongs, or does not belong, to the subject. Illustrations: “James is walking.” “Honesty is the best policy.” “Aristotle was the greatest thinker of ancient times.”
Some logicians refer to modal propositions as being such as indicate degrees of belief. Such words as “probably,” “certainly,” etc., would indicate their modality.
As logic has to do with the pure proposition and not the modal, the difference of opinion is of little import.
(3) Truistic Propositions.
A truistic proposition is one in which the predicate repeats the words and the meaning of the subject. Illustrations: “A man is a man,” “A beast is a beast,” “A traitor is a traitor,” “What I have done I have done.”
The truistic proposition is of little importance except in cases where the subject is used extensionally while the predicate is used intensionally. In the illustration, “A man is a man,” the subject merely stands for a member of the man family, while the predicate may indicate certain manly qualities. Against such ambiguities the logician must be on guard.
In Chapter 5 the extension and intension of terms was explained. The student recalls, for instance, that the term “man” may be used to denote objects, as “white man,” “black man,” “red man,” etc. In this sense the term “man” is used extensionally. But when made to stand for the attributes “rationality,” “power of speech,” etc., the term “man” is used intensionally.
In considering the relation between subject and predicate it is customary to employ the terms in an extensional sense only, since such a restriction serves the purpose of syllogistic reasoning and conversion.
Let us, then, give attention to the extension of the subject and predicate of the categorical propositions A, E, I, O.
(1) The Universal Affirmative or A Proposition.
All S is P symbolizes the A proposition. This may be interpreted as meaning that all of the subject belongs to a part of the predicate, or that all of the subject belongs to all of the predicate. The first interpretation is the usual one and may be illustrated by the following propositions:
1. “All men are mortal.”
2. “All trees grow.”
3. “All metals are elements.”
It is obvious that the subjects of these propositions include every specimen of the particular class mentioned. For example: The subject all men includes every specimen of the human family; all trees includes every object of that class; all metals covers everything which the scientist classes as such. In the three propositions, then, reference is made to the whole subject but to only a part of the predicate, as other beings beside men, such as the horse, are mortal; and other plants aside from trees, such as the sun flower, grow; other substances, namely oxygen, are elements.
For the sake of making the logical meaning of the four propositions clearer, recourse may be made to Euler’s diagrams, so named because the Swiss mathematician and logician, Leonhard Euler, first used them.
The first illustration of the A proposition, “All men are mortal,” may be represented by two circles, a larger circle standing for the predicate, mortal, and a smaller circle entirely inside the larger representing the subject, men. Thus:

FIG. 1.
It is evident that all of the smaller circle belongs to the larger. This diagram will then fit any proposition where it may be said that all of the subject belongs to a part of the predicate, or which may be symbolized as “All S is some P.” (All the subject is some of the predicate.)
The student knows that circles are plane surfaces and when such a statement as “All men are mortal” is given, reference is made to only that part of the “mortal” circle which is directly underneath the “men” circle. Nothing has been said relative to the remaining part of the “mortal” circle.
“A” propositions which may be interpreted as meaning “All S is all P” are called co-extensive A’s because the subject and predicate are exactly equal in extension. Such propositions are best illustrated by definitions; e. g.:
1. “A man is a rational biped.”
2. “A trigon is a polygon of three sides.”
3. “Teaching is the art of occasioning those activities which result in knowledge, power and skill.”
To represent the meaning of the co-extensive A by the Euler diagram, two circles of the same size may be drawn, one coinciding at every point with the other. If the first circle is drawn heavily in black and the second dotted in red, it will make clear to the eye that there are two circles.
(2) The Universal Negative or E Proposition.
“No S is P” best symbolizes the E proposition, though sometimes the universal negative is written “All S is not P.” This latter form, as has been explained, is ambiguous and therefore illogical.
“No S is P” surely means that no part of the subject belongs to any part of the predicate and no part of the predicate belongs to any part of the subject. The subject and predicate are mutually exclusive.
The following illustrate the E proposition:
1. “No man is immortal.”
2. “No true teacher works for money.”
3. “No thorough student can remain unwise.”
The E proposition may be represented by two circles, the one entirely without the other as in Fig. 2:

FIG. 2.
(3) The Particular Affirmative or I Proposition.
This may be symbolized as “Some S is P,” and considered as meaning that a part of the subject belongs to a part of the predicate. It has already been noted that “some” is ambiguous and that its logical signification is “some at least.” (It may be all or it may not be all.) For example, the only logical interpretation which can be placed on “Some men are wise” is, that the investigation has resulted in finding only a part of the man family wise. Whether or not all are wise is unknown as the entire field has not received attention. In no case can it be assumed that all the others are not wise.
The I proposition illustrated:
1. “Some men are wise.”
2. “Some animals are vertebrates.”
3. “Some teachers are inspiring.”
The meaning of the I proposition may be represented by two circles intersecting each other:

FIG. 3.
The significant feature of the diagram is the shaded part which represents a part of the “men” circle as belonging to a part of the “wise” circle. The unshaded part of each circle is the unknown field.
(4) The Particular Negative or O Proposition.
The common symbolization of the O is “Some S is not P.” Put in statement form: Some of the subject is excluded from the whole of the predicate. Here, as in the I, the same logical import must be given to some; e. g., in the proposition, “Some men are not wise,” our knowledge is confined to the group who are not wise. Whether or not the others are wise or not-wise is unknown.
Illustrations of the O proposition:
1. “Some men are not wise.”
2. “Some laws are not just.”
3. “Some novels are not helpful.”
The significance of the O proposition may be shown by two intersecting circles as in Fig. 4:

FIG. 4.
A similar diagram represents the I proposition, the only difference being in the part shaded. In the O proposition the investigated field is all of the “men” circle outside of the “wise” circle, while in the I proposition the known field is that part of the “men” circle inside the “wise” circle.
In comparing the four diagrams the student will note that the affirmative propositions are inclusive, while the negative propositions are exclusive.
(5) The Distribution of Subject and Predicate.
A term is said to be distributed when it is referred to as a definite whole.
In the proposition, “All men are mortal,” the subject all men is considered as a whole. “All men” stands for every specimen of the human race; not a single one has been left out. Again, the whole is definite; any one, if he were given the time and opportunity, could ascertain by actual count just how many “all men” represented.
It should be observed that if the word definite is not incorporated in the definition of a distributed term, there is afforded an opportunity for error. The attending illustrations will make this clear:
1. “All the students except John and James are dismissed.”
2. “All the students except John, James, etc., are dismissed.”
The subject of the first proposition is distributed, while the subject of the second is undistributed. Reasons: The first subject, “All the students except John and James,” is referred to as a whole and that whole is definite, therefore, it is distributed; the second subject, “All the students except John, James, etc.,” is referred to as a whole, but as the whole is not definite, the term is not distributed. Because all is the quantity sign of the second subject the casual observer might easily be misled in designating it as a distributed term.
Here it may be well to explain that when reference is made to subject or predicate the logical subject or predicate is meant. Unless this is constantly kept in mind error results; e. g., in the proposition, “All white men are Caucasians,” the logical subject is “white men,” not “men.” If the subject were “men,” it would be undistributed, as the whole of the man family is not considered, but the actual subject, being “white men,” is distributed because the predicate refers to all white men.
Recurring to the illustration, “All men are mortal,” we have concluded that the subject “all men” is distributed. The predicate, “mortal,” however, is undistributed, as reference is made to it only in part; i. e., there are other beings aside from men that are mortal, such as “trees,” “horses,” “dogs,” etc. In all A propositions of the type of “all men are mortal,” the subject is distributed while the predicate is undistributed. This relation is clearly shown by the diagrammatical illustration, Fig. 1. Here all of the “men” circle is identical with only a part of the “mortal” circle. In other words, the whole of the “men” circle is considered, while reference is made to only a part of the “mortal” circle.
In the case of the co-extensive A both subject and predicate are distributed. Relative to the co-extensive “All men are rational animals,” it could likewise be said that “all rational animals are men,” or that “all men are all of the rational animals.” Reference is thus made to all of the definite predicate as well as to all of the definite subject.
In the E propositions, such as “No men are immortal,” the whole of the subject is excluded from the whole of the predicate. This makes evident the fact that both terms are distributed. See Fig. 2.
The I proposition, such as “Some men are wise,” concerns itself with only a part of the subject and only a part of the predicate, consequently neither subject nor predicate is distributed. This relation is verified by the representation, Fig. 3.
In the O proposition the subject is undistributed, while the predicate is distributed. For example, in the proposition, “Some men are not wise,” “some men” would indicate that only a part of the logical subject is under consideration. But the predicate is distributed because “some men” is denied of the whole of the predicate, “wise.” This may become clear by studying Fig. 4. Here all of the shaded part which stands for the subject, “some men,” is excluded from the whole of the “wise” circle. But all of the shaded part is only a part of the entire “men” circle, consequently the subject which the shaded part represents (some men) is undistributed. The predicate, “wise,” however, is distributed, as the subject is excluded from every part of it. It is well to remember that not, when used with the copula, distributes the predicate which follows it.
If the student is to succeed in testing the value of arguments, he must ever have “at the tip of his tongue” his knowledge of the distribution of the terms of the four logical propositions. With this in view the following schemes are offered:
| I. | ||
|---|---|---|
| Subject | Predicate | |
| A | distributed | undistributed |
| E | distributed | distributed |
| I | undistributed | undistributed |
| O | undistributed | distributed |
| II. | ||
| A | distributed | undistributed |
| O | undistributed | distributed |
| E | distributed | distributed |
| I | undistributed | undistributed |
| III. | ||
| A | All S is P | |
| E | No S is P | |
| I | Some S is P | |
| O | Some S is not P | |
Referring to scheme II it may be observed that A and O contradict each other; i. e., where A is distributed O is undistributed and vice versa. A similar relation exists between E and I.
In scheme III the underline under the symbol indicates the term which is distributed.
IV. As a fourth scheme a “key word” might be adopted. Any of these three might be used: (1) saepeo, or (2) asebinop, or (3) uaesneop. The significance of “saepeo” is this: “s” stands for subject distributed, “p” for predicate distributed, “a” “e” “o” for the logical propositions where any distribution occurs. Putting the letters together gives this: subject distributed of propositions A and E, predicate distributed of propositions E and O.
Similarly, “asebinop” stands for this: “as,” a distributes its subject; “eb” e distributes both; “in,” i distributes neither; “op,” o distributes the predicate.
In the coined word “uaesneop” appear six letters which compose “saepeo,” and the letters have the same significance. The two additional letters, u and n, stand for universal and negative. The interpretation of the entire word, therefore, is this: “uaes,” the universals a and e distribute their subjects; neop, the negatives e and o distribute their predicates.
It seems to me that the last word is the most helpful as it emphasizes the two facts which are the most used; namely, (1) Only the universals distribute their subjects; (2) Only the negatives distribute their predicates.
If the student will visualize “uaesneop” so thoroughly as never to forget it, he will not experience difficulty in determining the distribution of the terms of the four logical propositions.
LOGICAL PROPOSITIONS.
(1) The nature of logical propositions.
(2) Kinds of logical propositions.
Categorical
Hypothetical
Disjunctive
(3) The four elements of a categorical proposition.
(4) Logical and grammatical subject and predicate distinguished.
(5) The four kinds of categorical propositions.
| Universal affirmative | A |
| Universal negative | E |
| Particular affirmative | I |
| Particular negative | O |
(6) Propositions which do not conform to the logical type.
Indefinite and elliptical
Grammatical sentences
Individual
Plurative
Partitive
Exceptive
Exclusive
Inverted
(7) Propositions not necessarily illogical.
Analytic and synthetic
Modal and pure
Truistic
(8) The relation between subject and predicate of the four logical propositions.
Euler’s diagrams
Distribution of subject and predicate
Uaesneop
Asebinop
Saepeo
(1) A logical proposition is a judgment expressed in words.
(2) The three kinds of logical propositions are categorical, hypothetical, disjunctive.
A categorical proposition is one in which the assertion is made unconditionally.
A hypothetical proposition is one in which the assertion depends upon a condition.
A disjunctive proposition is one which asserts an alternative.
The most common word-signs of the categorical proposition are “all,” “no,” “some” and “some-not,” of the hypothetical, “if” and of the disjunctive, “either-or.”
(3) Every logical categorical proposition has the four elements: quantity sign, subject, copula and predicate.
The quantity sign indicates the extension of the proposition; the logical subject is that of which something is affirmed or denied; the logical predicate is the term which is affirmed or denied of the subject; the copula is always some form of “to be” and is used to connect subject and predicate. “Not” is sometimes used with the copula.
The statements of ordinary conversation are usually not expressed in terms of the four elements, but must be, before they can be used in testing arguments.
(4) One word usually constitutes the grammatical subject while a word with all its modifiers goes to make up the logical subject. The verb with any predicate word is the grammatical predicate. The logical predicate is all which follows the copula—it may include the predicate-word and all its modifiers as well as the modified object.
(5) Categorical propositions are divided into four kinds; universal affirmative (A), universal negative (E), particular affirmative (I), particular negative (O). For the sake of brevity these four are respectively denoted by the vowels A, E, I, O.
An A proposition is one in which the predicate affirms something of all of the logical subject.
An E proposition is one in which the predicate denies something of all of the logical subject.
An I proposition is one in which the predicate affirms something of a part of the logical subject.
An O proposition is one in which the predicate denies something of a part of the logical subject.
Every proposition must be reduced to one of the four types before it can be used as a basis of argumentation.
It is incumbent on the student to recognize these four types with precision and accuracy.
(6) There are a few proposition types which are recognized as being illogical in form. These may be defined as follows:
(1) An indefinite proposition is one without the quantity sign. It usually may be classed as universal.
(2) An elliptical proposition is one in which the copula is suppressed.
(3) An individual proposition is one which has a singular subject. It is universal in content.
(4) Plurative propositions are those introduced by “most,” “a few” or some equivalent quantity sign. These are particular in meaning.
(5) Partitive propositions are particulars which imply a complementary opposite. These arise through the ambiguous use of “all-not,” “some” and “few.”
“All-not” sometimes means “no,” while at other times it may mean “not-all.” If the quantity sign means the latter, then it introduces a partitive proposition.
“Some” may mean “some only,” or “some at least.” The latter is the logical meaning. The former interpretation makes the proposition partitive. When “few” means “few only,” it is partitive in nature.
(6) Exceptive propositions are those introduced by such signs as “all except,” “all but,” “all save,” etc. They are universal only when the exceptions are mentioned.
(7) Exclusive propositions are those introduced by such words as “only,” “alone,” “none but” and “except.” In an exclusive the predicate and not the subject is distributed. Consequently the easiest way to make an exclusive logical is to interchange subject and predicate and call it an A.
(8) An inverted proposition is one where the predicate precedes the subject. Interchanging them gives the logical form.
Of the grammatical sentences only the declarative is logical.
The relative clause, though out of place, must be used with the word it modifies.
(7) There are other propositions, though not illogical, to which the logician usually gives some attention. These may be defined as follows:
(1) An analytical proposition is one in which the predicate gives information already implied in the subject.
(2) A synthetic proposition is one in which the predicate gives information not implied in the subject.
(3) A modal proposition is one which states the manner in which the predicate belongs to the subject. The adverbs of time, place, degree and manner are the signs of the modal proposition.
(4) A pure proposition simply states that the predicate belongs or does not belong to the subject.
(5) A truistic or tautologous proposition is one in which the predicate repeats the words and meaning of the subject.
(8) In considering the relation which may exist between subject and predicate, the two terms are employed in extension only, as this use best serves the interests of inference.
The extensional relation between subject and predicate of the four logical propositions may be stated as follows:
Ordinary A—All of the subject belongs to a part of the predicate.
Co-extensive A—All of the subject belongs to all of the predicate.
E—None of the subject belongs to any part of the predicate.
I—Some of the subject belongs to some of the predicate.
O—Some of the subject is excluded from the whole of the predicate.
In general it may be said that the affirmative propositions are inclusive while the negatives are exclusive.
A term is said to be distributed when it is referred to as a definite whole.
“A” distributes the logical subject only, “E” both logical subject and logical predicate, “I” neither logical subject nor logical predicate, “O” the logical predicate only. The co-extensive “A” distributes both subject and predicate.
It is essential that the student know by heart the distribution of the terms of the logical propositions. Some keyword like uaesneop may be used as an aid to the memory. This means the universals A and E distribute their subjects, while the negatives E and O distribute their predicates.
(1a) Examine the following list of propositions with a view to classifying them as “A’s,” “E’s,” “I’s” or “O’s.”
E 1. “None of the inmates voted.”
A 2. “Benj. Franklin was the best educated American.”
I 3. “Some doctors deem it right to lie to their patients.”
A 4. “All earnest teachers need to observe the teaching of others.”
I 5. “Some politicians are honest.”
A 6. “Fools rush in where angels fear to tread.”
O 7. “Some proverbs are not true to life.”
E 8. “No man should infringe upon the rights of others.”
I recall that an affirmative proposition in which the predicate refers to the whole of the subject is an A, while one where the predicate refers to only a part of the subject is an I. Further, a negative proposition where the predicate refers to the whole of the subject is an E, while one in which the predicate refers to only a part of the subject is an O. With these facts in mind, I classify the propositions as indicated.
(1b) In a similar manner classify as to quantity and quality the following:
(1) “All worthy workers grow to look like their work.”
(2) “Every dog has his day.”
(3) “Some of the presidents were not popular.”
(4) “No unskilled laborer can afford to own an automobile.”
(5) “Some of the ‘election prophets’ were sadly mistaken.”
(2a) Classify the following propositions and make the illogical, logical:
(1) “Only first-class passengers may ride in parlor cars.”
(2) “Haste makes waste.”
(3) “Few men know how to act under stress.”
(4) “All which seems to ring true is not true.”
(5) “Members alone are admitted.”
(6) “None but men of integrity need apply.”
(7) “Horses trot.”
(8) “Blessed are they which are persecuted for righteousness sake.”
The first proposition is an exclusive and may be made logical by converting and calling it an A, viz.: “All who ride in parlor cars are first-class passengers.” (A)
The second is indefinite and elliptical and is made logical by prefixing the universal quantity sign and expressing in terms of the four elements. The logical form is, “All who make haste are those who are wasteful.” (A)
The third is plurative in nature and means, “Most men do not know how to act under stress.” It would be classed as an O.
The fourth is partitive in nature because of the ambiguous use of “all—not.” It means, “Some who seem to ring true are not true.” (O)
The fifth is an exclusive. By converting and changing to an A the proposition takes the logical form, “All who are admitted are members.”
The sixth is likewise an exclusive, the logical form being, “All who apply must be men of integrity.”
The seventh is an elliptical proposition. Logical form: “All horses are trotting animals.”
The eighth is an inverted or poetical proposition. It is made logical by interchanging subject and predicate. Logical form: “Those who are persecuted for righteousness sake are blessed.”
(2b) Classify the attending propositions and change to the logical form, if necessary:
(1) “Only truthful men are honest.”
(2) “The stokers alone were saved.”
(3) “All who run do not think.”
(4) “Honesty is the best policy.”
(5) “They laugh that win.”
(6) “The good alone are happy.”
(7) “Knowledge is power.”
(8) “Only the actions of the just smell sweet and blossom in the dust.”
(1) Define and illustrate logical propositions.
(2) Define and exemplify the three kinds of logical propositions.
(3) What are the usual quantity signs of the four kinds of propositions?
(4) Name and define the four elements of a logical proposition.
(5) Select from the printed page five propositions which are not expressed in terms of the four elements, and so express them.
(6) Distinguish between logical and grammatical subject; likewise between logical and grammatical predicate.
(7) Define and illustrate the four kinds of categorical propositions.
(8) What makes an understanding of the four logical propositions so important?
(9) Give the unusual quantity signs of the logical propositions.
(10) What should guide one in making an indefinite proposition logical?
(11) How are general truths usually classified?
(12) Change birds fly to the logical form.
(13) How many and what kinds of grammatical sentences are logical?
(14) How would the logician deal with interrogative sentences?
(15) Give illustrations of individual propositions. How are they usually classified?
(16) Explain the logical mode of dealing with the plurative proposition.
(17) Exemplify the ambiguity of “all-not,” “some” and “few.”
(18) Why are propositions introduced by “all-not,” “some” and “few” called partitive?
(19) Use “all” in both a partitive and collective sense. Which signification has logic adopted?
(20) When are exceptive propositions universal and when particular?
(21) What is an exclusive proposition?
(22) Explain by circles the exclusive.
(23) Tell in full how to change an exclusive to logical form.
(24) Tell how the logician would deal with such poetical expressions as “Blessed are the pure in heart,” “Tell me not in mournful numbers,” “Strenuous is the man of state.”
(25) What distinction does the logician make between analytic and synthetic propositions?
(26) Illustrate the difference between the so-called modal and pure propositions.
(27) Explain and illustrate the truistic proposition.
(28) Show by circles the relation existing between the subject and predicate of all the logical propositions.
(29) State in good English the relation between the subject and predicate of all the logical propositions.
(30) Relative to the distribution of terms apply the words “uaesneop” and “asebinop.” Which one is the more serviceable?
(31) Distinguish between the grammatical and logical subject.
(32) Explain by circles the distribution of the terms of the four logical propositions.
(33) The statement, “A part of the subject is excluded from the whole of the predicate,” describes which proposition? Explain how it indicates that the predicate is distributed.
(1) Show that a judgment may be an individual notion as well as a general notion.
(2) Many logicians classify logical propositions in this wise:
| Proposition |
 |
Categorical |
| Conditional |
 |
Hypothetical |
| Disjunctive |
Give arguments for and against such a classification.
(3) “All men are bipeds” is a judgment of extension, while “Man is wise” is a judgment of intension. Explain.
(4) “To be logical is to be pedantic.” Discuss this.
(5) Why is the proposition, “He runs,” illogical? Make it logical.
(6) Point out the reasons for calling, “White men are Caucasians,” a particular proposition.
(7) What makes it necessary to change the propositions of ordinary conversation to those of the four logical types?
(8) Some would call the individual proposition particular. Argue the question.
(9) Make a list of five propositions in common speech and show how their partitive implication may mislead.
(10) Explain by circles some only and some at least.
(11) Explain how “et cetera” may change a universal to a particular proposition.
(12) “The real nature of an exclusive is best shown by negating the subject and calling the proposition an E.” Give arguments for and against this statement.
(13) Show that with the immature mind all propositions must be synthetical.
(14) Explain how a proposition may be truistic in form but not in meaning.
(15) Show by the Euler diagram how easy it is for the careless student to think that an “O” does not distribute its predicate.
(16) Explain by the use of two pads (a small yellow one and a large white one) the distribution of terms.
(17) When the logician makes reference to the subject of a proposition, show that he should exercise care in designating it as the logical subject.
Inference is the thought process of deriving a judgment from one or two antecedent judgments.
The process is simply a matter of expressing explicitly in a final judgment, a truth that was implied in one or two previous judgments. To exemplify: From the antecedent truth, that “All teachers should be fair minded,” one may derive a consequent truth that “This teacher, Albert White, should be fair minded.” Or from the statement, “All men are mortal,” one may derive the judgment, “No men are immortal.” Because the ground is wet we conclude that it has rained. If all dogs are quadrupeds then surely some dogs are quadrupeds. Finally from the two propositions, “All training school students are high school graduates,” and “Mary Jones is a training school student,” we are led to conclude that “Mary Jones is a high school graduate.”
It has been noted that a truth may be derived from a consideration of one or two antecedent judgments. To illustrate further: From the judgment, “All men are fallible,” we may derive the conclusion that “No men are infallible”; or, from the two judgments, “All men are fallible,” and “Socrates was a man,” we may readily infer that “Socrates was fallible.” These two modes of inference take the names of immediate inference and mediate inference. Let us express these two kinds in equation form:
| I. | |
|---|---|
| Ordinary Form. |
Equation Form, Using Initial Letters. |
| Antecedent judgment: All men are fallible. | All m are f |
| Conclusion: No men are infallible. | No m are i |
| II. | |
| First antecedent judgment: All men are fallible. | All m are f |
| Second antecedent judgment: Socrates was a man. | S was m |
| Conclusion: Socrates was fallible. | ∴ S was f |
Giving attention to the antecedent judgments of the second argument it is noted that the terms “f” and “S” are referred to the common term “m.” In logic this common term is known as the middle term. As there is but one antecedent judgment in the first argument there can be no common or middle term. The first argument is an illustration of immediate inference; the second of mediate inference. This suggests the definitions:
Immediate inference is inference without the use of a middle term.
Mediate inference is inference by means of a middle term.
Many logicians recognize four forms of immediate inference. These four forms are (1) opposition, (2) obversion, (3) conversion, (4) contraversion.8
(1) IMMEDIATE INFERENCE BY OPPOSITION.
We have learned that to be logical all categorical assertions must be reduced to some one of the four propositions, A, E, I, O. If these four logical propositions be given the same subject and predicate, certain definite relations will become evident; therefore, Opposition is said to exist between propositions which are given the same subject and predicate, but differ in quality, or in quantity, or in both.
The following illustrative outline will make this clear:
1.
Original Proposition.
I. All men are mortal. (A)
II. No men are immortal. (E)
III. Some men are wise. (I)
IV. Some men are mortal. (I)
V. Some men are not wise. (O)
VI. Some men are not immortal. (O)
2.
Opposite in Quantity.
I. Some men are mortal. (I)
II. Some men are not immortal. (O)
III. All men are wise. (A)
IV. All men are mortal. (A)
V. No men are wise. (E)
VI. No men are immortal. (E)
3.
Opposite in Quality.
I. No men are mortal. (E)
II. All men are immortal. (A)
III. Some men are not wise. (O)
IV. Some men are not mortal. (O)
V. Some men are wise. (I)
VI. Some men are immortal. (I)
4.
Opposite in Both.
I. Some men are not mortal. (O)
II. Some men are immortal. (I)
III. No men are wise. (E)
IV. No men are mortal. (E)
V. All men are wise. (A)
VI. All men are immortal. (A)
Granting the truth of the propositions in the first column, it follows that those in the second column differ in quantity. That is, in “Some men are mortal” a smaller number of men is referred to than in “All men are mortal.” A similar variation in quantity obtains with the other propositions in the second column. Moreover, the propositions in the third column are the negative of the corresponding ones in the first; while the fourth column propositions differ from the first in both quantity and quality. Thus opposition exists to a greater or less degree between all. We may now ask ourselves the question, “When the propositions are related to each other in opposition which ones are true and which ones are false?” Giving attention to the propositions in row “I,” we note that if the universal affirmative, “All men are mortal,” is true, then the particular affirmative, “Some men are mortal,” is likewise true; because of the principle, “What is true of the whole of the class is true of a part of that class.” But the universal negative, “No men are mortal,” and the particular negative, “Some men are not mortal,” are both false. Briefly stated: If A is true, then I is true, but, both E and O are false.
Regarding row “II” we may conclude that if E is true, then O is likewise true, but both A and I are false.
As to rows “III” and “IV,” granting the truth of the I propositions, “Some men are wise” and “Some men are mortal,” we are able to assert that of the two A propositions, “All men are wise,” and “All men are mortal,” the first is false while the second is true. A is, therefore, indeterminate, or doubtful. Of the O propositions, “Some men are not wise,” is true while, “Some men are not mortal,” is false. Therefore, O is doubtful. Both of the E propositions are false. Hence, the conclusion relative to rows “III” and “IV” is: If I is true, A and O are doubtful, while E is false.
Concerning rows “V” and “VI” it will be seen without further explanation that if O is true, then E and I are doubtful and A is false.
THE SCHEME OF OPPOSITION.
The conditions of opposition are easily comprehended and remembered when recourse is made to the following scheme:
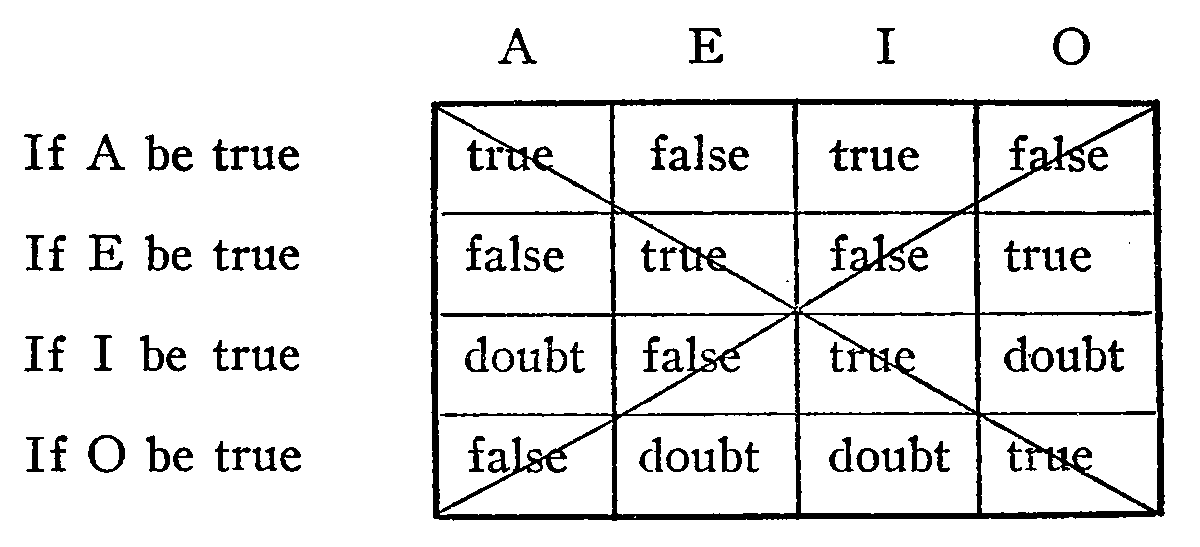
To use the above scheme, read horizontally from left to right. For example: If A be true, then all in the row opposite obtains; that is, A is true, E is false, I is true, and O is false. (We take it for granted that the student will see that the first column belongs to A, the second to E, the third to I, and the fourth to O.) If E be true, then A is false, E is true, I is false, O is true, etc.
The whole of opposition is comprehended in two facts which are based upon one principle. This is the principle: Whatever may be said of the entire class may be said of a part of that class. To put it in another way: Whatever is affirmed of all may be affirmed of some, or, Whatever is denied of all may be denied of some. To illustrate:
Accepted truth: All planets rotate. (A)
Accepted inference: Some planets rotate. (I)
or
Accepted truth: No planet is a sun. (E)
Accepted inference: Some planets are not suns. (O)
These are the two facts: First, a particular affirmative may be derived from a universal affirmative. Second, a particular negative may be derived from a universal negative. Or, more briefly: An I may be derived from an A, and an O from an E.
SQUARE OF OPPOSITION.
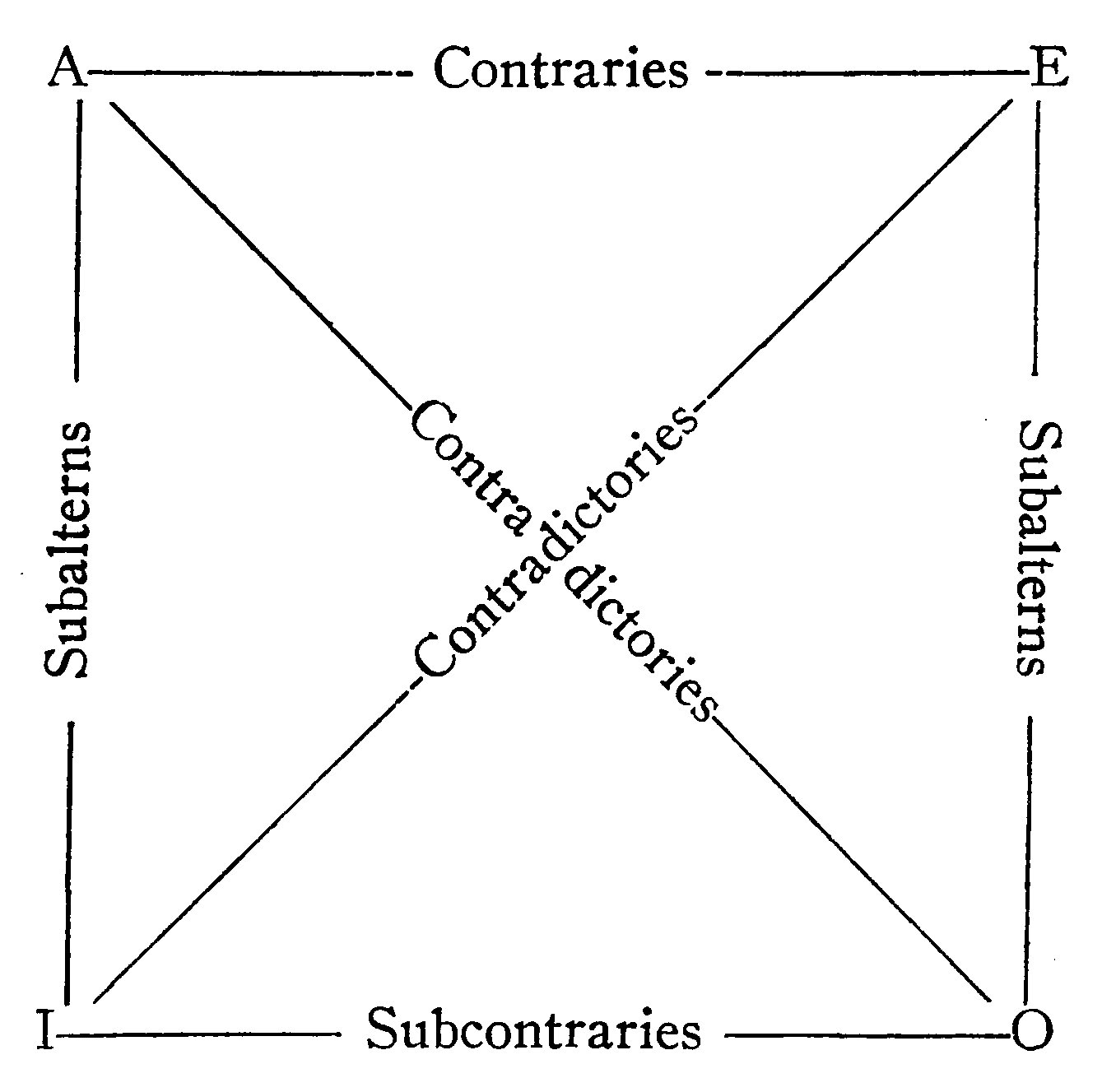
Aristotle represented the relations of the four logical propositions by what is termed the square of opposition. Viewed from the standpoint of the square, the relations may be summed up as follows:
1. Contrary Propositions.
Why so named.
As related to each other, A and E are said to be contrary because they seem to express contrariety to the greatest degree.
Relation stated.
If one is true, the other must be false, but both may be false.
Illustrations.
(1) If one is true, the other must be false; e. g., if A is true, as “All metals are elements,” then E is false, as “No metals are elements.” Or, if E is true, as “No birds are quadrupeds,” then A is false, as “All birds are quadrupeds.”
(2) Both may be false. If A is false, as “All men are wise,” then E may be false, as “No men are wise.”
2. Subcontrary Propositions.
Why so named.
Propositions I and O are said to be related to each other in a subcontrary manner because they are contrary as to each other and “under” their universals A and E.
Relation stated.
If one is false, the other must be true, or, both may be true.
Illustrations.
(1) If one is false, the other must be true.
If I is false, as “Some metals are compounds,” then, O is true, as “Some metals (at least) are not compounds.” Or, if O is false, as “Some metals are not elements,” then I is true, as “Some metals are elements.”
(2) Both may be true.
If I is true, as “Some men are wise,” then O also may be true, as “Some men are not wise.”
3. Subalterns.
Why so named.
Etymologically considered subaltern means under the one, thus proposition I is under A, and O is under E.
Relation stated.
First Relation.
Subalterns are related to each other as are the universals and particulars; hence,
(1) If the universal is true, the particular under it is also true; while if the particular is true, the corresponding universal may, or, may not, be true.
Illustrations.
(a) If the universal is true, the particular under it is true.
If A is true, as “All metals are elements,” then I is true, as “Some metals are elements.” Or, if E is true, as “No metals are compounds,” then, O is also true, as “Some metals (at least) are not compounds.”
(b) If the particular is true, the corresponding universal may, or, may not, be true.
If I is true, as “Some men are wise,” or, “Some men are mortal,” then A may be false, as “All men are wise,” or, A may be true, as “All men are mortal.” Or, if O is true, as “Some men are not wise,” or, “Some men are not immortal,” then E may be false, as “No men are wise”; or, true, as “No men are immortal.”
Second Relation.
(2) If the universal is false, the particular under it may or may not be true, but, if the particular is false, the universal above it must be false.
Illustrations.
(a) If the universal is false, the particular under it may or may not be true.
If A is false, as “All metals are compounds,” or “All men are wise,” then I may be false, as “Some metals are compounds,” or, I may be true, as “Some men are wise.” Or, if E is false, as “No men are mortal,” or, “No men are wise,” then O may be false, as “Some men are not mortal,” or, O may be true, as “Some men are not wise.”
(b) If the particular is false, the universal above it must be false.
If I is false, as “Some men are trees,” then A is false, as “All men are trees.” Or, if O is false, as “Some men are not bipeds,” then E is also false, as “No men are bipeds.”
4. Contradictory Propositions.
Why so named.
The propositions A and O, likewise E and I, are called contradictory propositions because they oppose each other in both quantity and quality. They are mutually opposed to each other or absolutely contradictory.
Relation stated.
If one is true the other must be false.
Illustrations.
(1) A and O compared.
If A is true, as “All metals are elements,” then, O is false, as “Some metals are not elements.” Or, if O is true, as “Some metals are not compounds,” then A is false, as “All metals are compounds.”
(2) E and I compared.
If E is true, as “No birds are quadrupeds,” then I is false, as “Some birds are quadrupeds.” Or, if I is true, as “Some birds are bipeds,” then E is false, as “No birds are bipeds.”
The chief value of the square of opposition springs from the contradictory propositions. The square shows conclusively that any universal affirmative assertion (an A) may best be contradicted by proving a particular negative (an O). For example: To satisfactorily refute the statement that, in this section, all birds migrate to the south in winter, it would be sufficient to prove that the English sparrow and starling do not migrate to the south. The square likewise makes evident that any universal negative (an E) may be conclusively denied by establishing the truth of a particular affirmative (an I). To illustrate: The easiest way to prove the falsity of “No trusts are honest” is to present facts showing that at least trusts A and B are honest.
The Individual Proposition.
An individual proposition is one with an individual subject such as “Aristotle was wise.” In logic, the individual proposition is classed as a universal. This seems to be a bit irregular, as with the individual proposition there is no particular, while, the strictly logical universal always implies a particular. Because of this variation from the true logical form the relations, as indicated by the square of opposition, do not apply to the individual proposition. For example: According to the square A and E are contrary, but, when individual, A and E contradict each other, as “Aristotle was wise” (A)—“Aristotle was not wise” (E).
(2) IMMEDIATE INFERENCE BY OBVERSION.
Obversion is the process of changing a proposition from the affirmative form to its equivalent negative or from the negative form to its equivalent affirmative.
Some authorities refer to this process as “Inference by Privitive Conception,” but Obversion seems to be a better term.
Obversion is based upon the principle that two negatives are equivalent to one affirmative. With this double negative principle in mind let us experiment with the four logical propositions, A, E, I, O.
The A Proposition.
Example: “All thoughtful men are wise.” Insert the double negative and the proposition reads: “All thoughtful men are not not-wise.” Changed to the logical form this becomes: “No thoughtful men are not-wise.” Simplified and we have, finally: “No thoughtful men are unwise.” Thus by the process of obversion we have passed from the original proposition, “All thoughtful men are wise,” to “No thoughtful men are unwise.” In the first proposition the subject “thoughtful men” is denied of the predicate “unwise.” Assuming that “unwise” is the contradictory of “wise,” then: “What is affirmed of a predicate may be denied of its contradictory.” Recourse to circles will make this clearer. In the previous chapter it has been suggested that not bisects the world. For example: What can not be included in the wise class may be placed under the not-wise or unwise class. Likewise a circle bisects space—there is the space inside the circle and the space outside the circle. Let the space inside the circle represent all wise beings, then the space outside the circle would represent all not-wise or unwise beings; e. g.,

FIG. 5.
Now representing thoughtful men by a smaller circle and placing it inside the larger we have,

FIG. 6.
Referring to Fig. 6 we note that all of the smaller circle belongs to the larger or that none of the smaller circle belongs to the space outside of the larger. Hence the two propositions: “All thoughtful men are wise” (A), and “No thoughtful men are unwise” (E) have virtually the same meaning though the same subject is related to different predicates.
The use of the positive or negative form depends upon circumstances. Often the negative puts the thought in a more forceful way.
In passing from, “All thoughtful men are wise,” to “No thoughtful men are unwise,” it was necessary to prefix not to the predicate wise and substitute for not its equivalent un. If the original predicate were unwise or not-wise, then the reverse order of dropping the un or not could be followed. This process of prefixing the not to an affirmative predicate or of dropping the not from a negative predicate is referred to as negating the predicate. Before substituting in, im, un, etc., for not, one must make sure that the substitution really gives the contradictory; there are some logicians who claim that unwise, for instance, is not the contradictory of wise.
In comparing the first proposition with the second it is observed that the first is an A, while the second is an E, also that the predicate of the first was negated to form the predicate of the second. Thus the rule: Negate the predicate and change A to E.
To sum up:
The obversion of an A proposition.
1. Principle:
Two negatives are equivalent to one affirmative.
2. Rule:
Negate the predicate and change the A to an E by using the sign no instead of all.
3. Process illustrated.
| The Original Proposition (A) | The Obverse (E) |
| All men are mortal. | No men are immortal. |
| All maples are trees. | No maples are not-trees. |
| All teachers should be sympathetic. | No teacher should be un-sympathetic. |
| All pain is unpleasant. | No pain is pleasant. |
| All men are imperfect. | No men are perfect. |
| All birds are feathered animals. | No birds are non-feathered animals. |
| All men are not-trees. | No men are trees. |
| All scalene triangles are non-equilateral. | No scalene triangles are equilateral. |
The E Proposition.
It is obvious that the process of obverting an E is simply the reverse of obverting an A. Consequently, the same principle obtains; whereas the process may be illustrated by reading the foregoing illustrations reversely.
The rule for obverting E is: Negate the predicate and change the E to an A by changing the sign no to all.
The I Proposition.
Let us note the result when the double negative principle is applied to the I proposition.
Original: “Some men are wise.”
Adding two negatives: “Some men are not not-wise.”
The foregoing simplified: “Some men are not unwise.”
In comparing the first proposition with the last it is observed that the first is an I while the last is an O; it is also observed that the predicate of the first was negated in order to form the predicate of the last. Thus the rule: “Negate the predicate and change the I to an O.”
The use of circles may make this clearer:

FIG. 7.
The significant part of Fig. 7 is that which is inked. Here we have represented the part of the “men” circle which is common to the “wise” circle. Thus the inked part represents “Some men are wise.” If the inked part is entirely inside of the “wise” circle, no part of it can belong to the “unwise” space without. Thus the obverse, “Some men are not unwise.”
Summary.
The obversion of an I proposition.
1. Principle:
Same as with A.
2. Rule:
Negate the predicate and change the I to an O.
3. Process illustrated.
| The Original Proposition (I) | The Obverse (O) |
| Some water is pure. | Some water is not impure. |
| Some curves are perfect. | Some curves are not imperfect. |
| Some friends are loyal. | Some friends are not disloyal. |
| Some men are true. | Some men are not not-true. |
| Some precious stones are imperfect. | Some precious stones are not perfect. |
| Some plants are not-trees. | Some plants are not trees. |
| Some boys are not-honest. | Some boys are not honest. |
It must be borne in mind that when “not” is used without the hyphen it makes the proposition negative, because when “unhyphened,” “not” must be thought of in connection with the copula and not in connection with the predicate; while “not” attached to the predicate with a hyphen simply makes the predicate negative without affecting the quality of the proposition; e. g., “Some plants are not trees” is a negative proposition, while “Some plants are not-trees” is an affirmative proposition with a negative predicate.
It may not be clearly seen how it is possible, by following the rule given, to pass from such a proposition as “Some plants are not-trees,” to “Some plants are not trees.” Let us illustrate the steps:
1. The original: “Some plants are not-trees.”
2. Negating predicate: “Some plants are trees.”
3. Changing to an O: “Some plants are not trees.”
Dropping the not from “1” and then adding it again to “2” is simply putting into operation the double negative idea, so that there is no violation of the principle.
The O Proposition.
O bears the same relation to I that E bears to A. The principle involved is the same. The process is illustrated by reading reversely the scheme of illustrations under I. The rule is as follows: To obvert an O negate the predicate and change the O to an I by eliminating the not.
Summary of Obverting the Four Logical Propositions.
1. Principle:
Two negatives are equivalent to one affirmative.
2. Rules:
| Negate the predicate and change |
 |
(1) A to E |
| (2) E to A | ||
| (3) I to O | ||
| (4) O to I |
(3) IMMEDIATE INFERENCE BY CONVERSION.
Conversion is the process of inferring from a given proposition another which has, as its subject, the predicate of the given proposition, and, as its predicate, the subject of the given proposition. It is simply a matter of transposing subject and predicate. The original proposition is called the convertend while the derived proposition is named the converse.
The process of conversion is limited by two rules. First rule. No term must be distributed in the converse which is not distributed in the convertend. Second rule. The quality of the converse must be the same as that of the convertend. More briefly: (1) Do not distribute an undistributed term. (2) Do not change the quality.
We recall that a term is distributed when it is referred to as a definite whole. An undistributed term is referred to only in part. The principle underlying rule “1,” therefore, is the one which forms the basis of inference by opposition; namely, “Whatever may be said of the entire class may be said of a part of that class.” The converse of this is not true, that is, “What is said of part of a class cannot be said of the whole of that class.” When we distribute an undistributed term we are saying of the whole class what was said only of a part of that class. This is fallacious. On the other hand, we may say of a part what was said of the whole, or “undistribute” a distributed term.
We recall that the conclusion of the whole matter of inference by opposition was, that only an I could be inferred from an A and only an O from an E, or to put it in another way: Only an affirmative from an affirmative and only a negative from a negative. This establishes the truth of the second rule in conversion: “Do not change the quality.”
Let us apply the two rules to the four logical propositions.
Converting an A proposition.
Take as a type, “All horses are quadrupeds.” Here the subject “horses” is distributed, but the predicate “quadrupeds” is undistributed. In transposing subject and predicate we cannot distribute the term “quadrupeds,” according to the rule which says, “Do not distribute an undistributed term.” Hence in interchanging subject and predicate we cannot say, “All quadrupeds are horses,” but must limit the assertion to, “Some quadrupeds are horses.” Logicians call this process Conversion by Limitation.
Conversion by Limitation Exemplified Further.
| Convertend. | Converse. |
| All metals are elements. | Some elements are metals. |
| All bees buzz. | Some buzzing insects are bees. |
| All men are fallible. | Some fallible beings are men. |
| All good teachers are sympathetic. | Some sympathetic persons are good teachers. |
The conclusions from the foregoing are these: First, the usual mode of converting an A is to interchange subject and predicate, limiting the latter by the word “some” or a word of similar significance. Second, this mode is called conversion by limitation. Third, the converse of an A is an I.
The Co-extensive A.
In the conversion of A propositions there is the one exception of “co-extensive A’s,” such as truisms and definitions. It will be remembered that with these both subject and predicate are distributed; hence, they may be interchanged without limiting the predicate by “some.” To illustrate: The converse of the truism, “A man is a man.” is “A man is a man,” while the converse of the definition, “A man is a rational animal,” is “A rational animal is a man.” This mode of interchanging subject and predicate without limiting the latter is called Simple Conversion. The ordinary A proposition is thus converted by limitation, while the co-extensive A is converted simply.
Converting an E proposition.
As both terms of the E proposition are distributed it is not possible to violate the rule of distribution. It is to be remembered that no fallacy is committed by “undistributing” a term which is already distributed.
Illustrations.
| Convertend. | Converse. |
| No men are immortal. | No immortals are men. Simply. |
| No birds are quadrupeds. | No quadrupeds are birds. Simply. |
| No metals are compounds. | No compounds are metals. Simply. |
| No men are immortal. | Some immortals (at least) are not men. Limitation. |
| No birds are quadrupeds. | Some quadrupeds are not birds. Limitation. |
| No metals are compounds. | Some compounds are not metals. Limitation. |
Three facts are evident relative to the converting of an E. First: An E proposition may be converted either simply or by limitation. Second: E may be converted into either E or O. Third: If the converse is an O then is the inference a weakened one, being particular when it could just as well be universal.
Converting an I proposition.
With an I proposition neither term is distributed. Thus care must be used lest an undistributed term in the convertend be distributed in the converse. Illustrations:
| Convertend. | Converse. |
| Some men are wise. | Some wise beings are men. |
| Some teachers scold. | Some who scold are teachers. |
| Some high school graduates enter college. | Some who enter college are high school graduates. |
| Some Americans live simply. | Some who live simply are Americans. |
From the foregoing we conclude first, that I is converted simply; second, that I is converted into I.
The O Proposition.
With an O proposition the subject is undistributed while the predicate is distributed. This condition presents a peculiar difficulty. Consider, for example, the O proposition, “Some men are not wise.” Convert this into, “Some wise beings are not men,” and the undistributed subject of the convertend, which is “men,” becomes the distributed predicate of the converse. Thus the O proposition cannot be converted without violating the rule for distribution.
A Summary of How the Four Logical Propositions May be Converted.
1. A. The ordinary A proposition may be converted by limitation only. The co-extensive A may be converted simply.
2. E. The E proposition is converted simply. The E may also be converted by limitation, but the inference thus obtained is weakened.
3. I. The I proposition may be converted simply only.
4. O. The O proposition cannot be converted.
(4) INFERENCE BY CONTRAVERSION. (Contraposition).
This mode of inference is usually referred to as inference by contraposition, but contraversion, indicating more definitely the nature of the process, is a better term. Contraversion involves two steps: First, obversion; second, conversion. The same principles and rules evident in these two processes obtain in inference by contraversion. The following scheme, therefore, ought to be sufficient to make the matter clear:
Inference by Contraversion.
| 1. | The Given Proposition. | 2. | Obverted. |
| A. | All men are mortal. | No men are immortal. | |
| All trees are plants. | No trees are not-plants. | ||
| E. | No men are infallible. | All men are fallible. | |
| No men are trees. | All men are not-trees. | ||
| I. | Some men are wise. | Some men are not not-wise. | |
| O. | Some water is not pure. | Some water is impure. | |
| Some houses are not white. | Some houses are not-white. |
3. Converted; giving the contraverse of the original proposition.
No immortals are men.
No not-plants are trees.
Some fallible beings are men.
Some not-trees are men.
An O cannot be converted, consequently the contraversion of an I is impossible.
Some impure liquids are water.
Some not-white buildings are houses.
It is indicated in the foregoing scheme that “I” cannot be contraverted. This is due to the fact that the obverse of an I is an O, and it will be remembered that “O” cannot be converted. All the other propositions admit of contraversion.
| * | Proposition symbolized | Name of Process | Inference symbolized | Principle involved |
| A | All S is P† | Opposition | Some S is P (I) | What is said of all may be said of some. |
| Obversion | No S is not-P (E) | Two negatives are equivalent to one affirmative. | ||
| Conversion by Limitation | Some P is S (I) | An undistributed term cannot be distributed. | ||
| Contraversion | No not-P is S (E) | Same principles which obtain in obverting A and converting E. | ||
| E | No S is P | Opposition | Some S is not P (O) | What is said of all may be said of some. |
| Obversion | All S is not-P (A) | Two negatives are equivalent to one affirmative. | ||
| Simple Conversion | No P is S (E) | Distribution not affected. | ||
| Contraversion | Some not-P is S (I) | An undistributed term cannot be distributed. | ||
| I | Some S is P | Opposition | Doubtful | None. |
| Obversion | Some S is not not-P (O) | Two negatives are equivalent to one affirmative. | ||
| Conversion | Some P is S (I) | Distribution not affected. | ||
| Contraversion | Impossible | None. | ||
| O | Some S is not P | Opposition | Doubtful | None. |
| Obversion | Some S is not-P (I) | Two negatives are equivalent to one affirmative. | ||
| Conversion | Impossible | None. | ||
| Contraversion | Some not-P is S (I) | Same as in obversion of O and conversion of I. |
* – Name of proposition
† – “S” represents any subject and “P” any predicate.
INFERENCE BY INVERSION.
Some logicians treat of a form of immediate inference known as inversion though it is of small importance and of little practical value.
The process can be applied only to propositions A and E. In the one case the contradictory subject is limited by “some” and then denied of the predicate, whereas, in the other case, the contradictory subject is merely affirmed of the predicate.
Illustrations.
| The Given Proposition. | The Inverse. | |
| I. | All S is P. (A) | Some not-S is not P. (O) |
| All planets rotate. | Some not-planets do not rotate. | |
| II. | No S is P. (E) | Some not-S is P. (I) |
| No men are immortal. | Some not-men are immortal. |
From the foregoing we are able to conclude that the inverse of “A” is found by negating the subject and changing to an “O”; while the inverse of “E” is found by negating the subject and changing to an “I.”
IMMEDIATE INFERENCE—OPPOSITION—OBVERSION, CONVERSION, CONTRAVERSION AND INVERSION.
1. The Nature of Inference.
2. Immediate and Mediate Inference.
3. The Forms of Immediate Inference.
(1) Opposition.
(a) Scheme of Opposition.
(b) Square of Opposition.
(2) Obversion.
(3) Conversion.
(a) Simply.
(b) By Limitation.
(4) Contraversion.
Inversion.
1. Inference is the thought process of deriving a judgment from one or two antecedent judgments.
2. Immediate inference is inference without the use of a middle term. Mediate inference is inference by means of a middle term.
3. The four common forms of immediate inference are (1) opposition, (2) obversion, (3) conversion, (4) contraversion.
(1) The name opposition stands for certain definite relations which exist between the logical propositions when they are given the same subject and predicate. The one principle underlying opposition is: Whatever is said of the entire class may be said of a part of that class. The two statements which sum up opposition are first, an I may be derived from an A; and second, an O may be derived from an E.
The crucial fact made obvious by the square of opposition is that A and O are mutually contradictory; likewise E and I.
(2) Obversion is the process of passing from an affirmative to its equivalent negative or from a negative to its equivalent affirmative. “Two negatives are equivalent to one affirmative,” is the basic principle of obversion.
The proposition A may be obverted by negating the predicate and changing to an E. “E” is obverted by negating the predicate and changing to an A. “I” is obverted by negating the predicate and changing to an O. “O” is obverted by negating the predicate and changing to an I.
(3) Conversion is the process of inferring from a given proposition another which has as its subject the predicate of the given proposition and as its predicate the subject of the given proposition.
Conversion is limited by the two rules, (1) do not distribute an undistributed term; (2) do not change the quality.
To convert an A interchange subject and predicate, limiting the latter by some, or a word of like significance. This is called conversion by limitation.
The co-extensive A may be converted without limiting the predicate. This is called simple conversion.
An E proposition may be converted either simply or by limitation. When converted by limitation the inference is a weakened one.
An I proposition is converted simply only.
The O proposition does not admit of conversion.
(4) Immediate inference by contraversion is a process involving first obversion and then conversion.
“A,” “E” and “O” may be contraverted; “I” cannot be contraverted.
(1a) From the antecedent judgment, “All weeds are plants,” I am able to derive by immediate inference these judgments: (1) “All weeds are not not-plants,” or “No weeds are not plants.” (2) “No not-plants are weeds.” (3) “Some plants are weeds.” (4) “Some weeds are plants.”
(1b) “All vertebrates have a backbone.” From the foregoing judgment derive immediately five different conclusions.
(2a) “All good citizens try to vote,”
“Albert White is a good citizen,”
Hence, “Albert White will try to vote.”
I know that the above is an example of mediate inference because the two antecedent judgments make use of the middle term, “good citizen.”
(2b) Why is the following illustrative of mediate inference?
“All wise men are close observers,”
“All wise men are thoughtful,”
Hence, “Some thoughtful men are close observers.”
(3a) Derive immediate inferences by opposition from the following:
(1) “Good men are wise.”
(2) “No teacher can afford to be unjust.”
(3) “All birds fly.”
(4) “None of the inner planets are as large as the earth.”
I first determine that “1” and “3” are A propositions, while “2” and “4” are E’s. Then I recall that by opposition an I may be derived from an A and an O from an E. Hence, the inferences are:
(1) “Some good men are wise.”
(2) “Some teachers cannot afford to be unjust.”
(3) “Some birds fly.”
(4) “Some of the inner planets are not so large as the earth.”
(3b) Derive by opposition inferences from the following:
(1) “No true woman will neglect her home for society.”
(2) “All patriotic men love the flag.”
(3) “Fools rush in where angels fear to tread.”
(4a) Obvert the following:
(1) “All earnest teachers are diligent students.”
(2) “No self-respecting man can afford to be careless in his personal appearance.”
(3) “Some of the great teachers of the past did not practice what they preached.”
(4) “Some weeds are beautiful.”
I determine first the logical character of each proposition, finding the first to be an A, the second an E, the third an O and the fourth an I. Then I recall that in obversion the predicate must always be negated and an A must be changed to an E or an E to an A; also an I must be changed to an O or an O to an I. Hence, the obverse of each proposition is:
(1) “No earnest teacher is a not-diligent student.”
(2) “All self-respecting men can afford to be not-careless (careful) in their personal appearance.”
(3) “Some of the great teachers of the past did not-practice (failed to practice) what they preached.”
(4) “Some weeds are not not-beautiful.”
(4b) Infer by obversion from the following:
(1) “All roses are beautiful.”
(2) “None of the members of the stock exchange are dishonest.”
(3) “Some pupils are not industrious.”
(4) “Some teachers are tactful.”
(5a) Convert the following:
(1) “All that glitters is not gold.”
(2) “All good men are wise.”
(3) “Some books are to be chewed and digested.”
(4) “No man is perfectly happy.”
It is first necessary to determine the logical character of each proposition. Carelessness might lead one to call the first proposition an A because it is introduced by the quantity sign “all.” But on second thought we note that the meaning is to the effect that some glittering things are not gold; this is an O. It is clear that the second is an A, the third an I and the fourth an E. It is now expedient to recall the rules regarding conversion. These are, (1) do not distribute an undistributed term; (2) do not change the quality. We may now attempt to interchange the subject and predicate of each proposition, with the following results:
(1) Conversion impossible.
(2) “Some wise men are good men.”
(3) “Some things to be chewed and digested are books.”
(4) “No perfectly happy being is a man.”
When attempting to convert proposition (1), I find that the subject which is undistributed becomes distributed, hence the rule pertaining to distribution is violated. This conclusion is verified by recalling the fact that an O proposition cannot be converted. The second proposition, being an A, is converted by limitation; while the third and fourth are converted simply, as is the natural procedure with all I’s and E’s.
(5b) Convert these propositions:
(1) “Blessed are the meek.” (All the meek are blessed.)
(2) “None but material bodies gravitate.” (All gravitating bodies are material.)
(3) “Gold is not a compound substance.”
(4) “Usually cruel men are cowards.”
NOTE.—The first proposition is poetical while the second is an exclusive.
(6a) Contravert the following propositions:
(1) “All virtue is praiseworthy.”
(2) “Some teachers are not tactful.”
(3) “A man who lies is not to be trusted.”
Contraversion consists in obverting first, and then converting; consequently, the contraverse of the three propositions is as follows:
(1) “No unpraiseworthy deed is virtue.”
(2) “Some not-tactful persons are teachers.”
(3) “Some untrustworthy men are those who lie.”
(6b) Write the contraverse of the following:
(1) “All honest men pay their debts.”
(2) “All men are rational.”
(3) “Nearly all the troops have left the town.”
(4) “Some teachers are not patient.”
(7a) The attending scheme indicates the logical process and rule involved in passing from one proposition to another:
A. “All men are imperfect.”
Process: Obversion.
Rule: Negate predicate and change to E.
E. “No men are perfect.”
Process: Simple Conversion.
Rule: Interchange subject and predicate.
E. “No perfect beings are men.”
Process: Contraversion.
Rule: Obvert and then convert.
I. “Some not-men are perfect beings.”
(7b) Treat in a manner similar to the above the proposition, “All horses are quadrupeds.”
(1) What is inference?
(2) What is the meaning of antecedent?
(3) Define (1) judging, (2) a judgment.
(4) All roses are beautiful,
This flower is a rose,
This flower is beautiful.
Write this example of mediate inference in equation form. Name the middle term.
(5) Define immediate inference. Illustrate.
(6) Define mediate inference. Illustrate.
(7) Name the five forms of immediate inference.
(8) What principle is involved in inference by opposition?
(9) Draw the scheme of opposition.
(10) Make use of this scheme in deriving inferences from the following propositions:
(a) “Good men are wise.”
(b) “No king is infallible.”
(c) “Cattle are ruminants.”
(d) “All who cheat the railroads are not honest.”
(11) What are contradictory propositions? Illustrate.
(12) What would be the simplest way of disproving the statement that “No great religious teacher has been consistent?”
(13) Why are A and E said to be contrary propositions?
(14) Define obversion.
(15) By what other name is obversion known?
(16) State the basic principle of obversion.
(17) Illustrate the process known as negating the predicate.
(18) State the rule for obverting an A proposition.
(19) Obvert the following:
(1) “All the boys in my room are industrious.”
(2) “Honesty is the best policy.”
(3) “Only the industrious are truly successful.”
(20) First state the rule and then obvert the following:
(1) “Some plants are biennial.”
(2) “Planets are not suns.”
(3) “Blessed are the merciful.”
(4) “These samples are not perfect.”
(21) Define conversion.
(22) State and illustrate the rules which condition the process of conversion.
(23) Convert, if possible, the following:
(1) “Some men practice sophistry.”
(2) “Few men know how to live.”
(3) “Some of the inhabitants are not civilized.”
(4) “All the world is a stage.”
(5) “None of my pupils failed.”
(6) “Experience is a hard taskmaster.”
(24) Why may co-extensive propositions be converted simply?
(25) Describe the process of inference by contraversion.
(1) What ground is there for the belief that immediate inference, so called, is merely a matter of the interpretation of propositions?
(2) Is there any difference between reasoning and inference?
(3) When the conclusion is reached that two rooms are of the same width, because each is five yards wide, what is the middle term?
(4) Put in equation form:
All teachers instruct,
John Jones is a teacher,
John Jones instructs.
Show that the equations are not absolutely true.
(5) Indicate the true relation between the subjects and predicates of the foregoing by using the algebraic signs > and <.
(6) Why cannot an A be derived from an I?
(7) Why cannot an O be derived from an A?
(8) The basic principle of obversion is “Two negatives are equivalent to one affirmative.” Show by means of circles that this is not absolutely true; take as an illustrative proposition, “No men are not mortal.”
(9) Show that agreeable and disagreeable are not contradictory terms.
(10) Why should the logician class individual propositions as universal?
(11) Show by circles that there is a difference in signification between, “Some men are not wise” and “Some men are not-wise.”
(12) Show by circles that the O proposition cannot be converted.
(13) “The I proposition cannot be contraverted.” Make this clear.
(14) Is there any difference in meaning between, “All illogical work is unscholarly” and “No illogical work is scholarly?” Explain by circles.
(15) State the logical process involved in passing from each proposition to its succeeding one:
(1) “All men are imperfect.”
(2) “No men are perfect.”
(3) “No perfect beings are men.”
(4) “Some not-men are perfect beings.”
(5) “Some perfect beings are not-men.”
(6) “Some perfect beings are not men.”
(16) It is sometimes said that in sub-contraries there is really no opposition. Do you agree? Give arguments.
Inference has been defined as both a product and a process. When used to indicate a process the term inference becomes synonomous with reasoning. If logicians could agree to confine inference to the product and reasoning to the process, it would remove an ambiguity which is more or less misleading. But since this has not become the custom, we shall use inference as indicating the process as well as the product.
Definitions—Middle Term Explained.
Inference is the thought process of deriving a judgment from one or two antecedent judgments.
Mediate inference is inference by means of a middle term.
Reasoning of this nature involves three terms, two of which are compared with a third or middle term, and then related to each other to form a new judgment. The middle term is the common unit, or the standard by which the other terms are measured. To illustrate: If John and James are each six feet tall, then plainly, they are of the same height. The standard, or middle term, is “six feet tall.”
Just as the judgment is expressed by means of the proposition, so mediate inference is best expressed by means of the syllogism.9 The following are syllogisms:
(1) James is six feet tall,
John is six feet tall,
Hence James is as tall as John.
(2) All true teachers are just,
You are a true teacher,
Hence you are just.
(3) All men are mortal,
You are a man,
Hence you are mortal.
All syllogistic reasoning is conditioned by the following eight rules:
(1) A syllogism must have three, and only three, different terms.
(2) A syllogism must have three, and only three, propositions.
(3) The middle term must be distributed at least once.
(4) No term must be distributed in the conclusion which is not also distributed in a premise.
(5) No conclusion can be drawn from two negative premises.
(6) If one premise be negative, the conclusion must be negative; and conversely, to prove a negative conclusion, one of the premises must be negative.
(7) No conclusion can be drawn from two particular premises.
(8) If one premise be particular, the conclusion must be particular.
These rules are exceedingly important, as their observance is necessary in all mediate reasoning. The student needs, not only to understand the meaning of these rules, but he needs to commit them to memory so thoroughly that they may be recalled without hesitation or mistake. To aid the memory, the eight rules may be divided into these four groups:
I. Rules one and two relate to the composition of the syllogism.
II. Rules three and four pertain to the distribution of terms.
III. Rules five and six have reference to negative premises.
IV. Rules seven and eight concern particular premises.
(1) A syllogism must have three and only three terms.
It is common to represent the various syllogistic forms by symbols, the same symbols always standing for the same terms. In this treatment we shall let capital G stand for the major term, as “major” means greater; capital S for the minor term, as “minor” means smaller, and capital M for the middle term. G, S and M, the initial letters of greater (major), smaller (minor) and middle, will be the constant symbols for these terms; just as A, E, I and O are used as the constant symbols for the four logical propositions.
Illustration.
Syllogism written in full:
All men are mortal,
Socrates is a man,
(Therefore) Socrates is mortal.
Syllogism symbolized:
All M is G
S is M
∴ S is G
The major term is always the predicate and the minor term the subject of the conclusion. The conclusion of the foregoing syllogism is, “Socrates is mortal.” Since G stands for the predicate of every conclusion, then it stands for “mortal,” the predicate of the above conclusion. For a similar reason, S stands for the subject, namely, “Socrates”; while M represents the middle term, “man.”
Since every syllogism must have three propositions, and since it takes two terms to form a proposition, then it follows that every syllogism must contain six terms. But, as no syllogism can have more than three different terms, we conclude that each term of the syllogism must be used twice. In the foregoing example, G thus appears, not only in the last proposition, or conclusion, but in the first proposition also. Similarly, both S and M occur twice. Every logical syllogism, then, contains first, a major term, which is always the predicate of the conclusion and appears once in the premises; second, a minor term, which is always the subject of the conclusion and appears once in the premises; and third, a middle term to which the other two terms are referred.
There are two ways of locating the middle term; first, it is the term which is used in both the premises; second, it is the term which never appears in the conclusion. Likewise, there are two ways of locating the major and minor terms; first, the major term is always the predicate and the minor term the subject of the conclusion; second, the major term is usually the broader and the minor term the narrower of the two. If the major and minor terms seem to be of about the same extension or breadth, then the term in the first proposition, which is not the middle term, is the major.
In the attending syllogisms the three terms are designated:
(1) All
(middle)
|
true teachers
are (major)
|
sympathetic,
(minor)
|
You
are a (middle)
|
true teacher,
∴ (minor)
|
You
are (major)
|
sympathetic.
(2) No
(major)
|
shell fish
are (middle)
|
vertebrates,
All (minor)
|
trout
are (middle)
|
vertebrates,
∴ No (minor)
|
trout
are (major)
|
shell fish.
The necessity of having but three different terms in any syllogism may be understood by supposing that there are four different terms; then it would follow that there could be no standard or common link. In the axiom, “Things equal to the same thing are equal to each other,” the same thing is the common standard or link. Two things which equal two different things are not equal to each other.
The impossibility of reasoning from four terms may be shown by circles.
All men are mortal.
All trees grow.

FIG. 8.
These circles show that no connection can be established between either group. Using four terms in any syllogism is known as the fallacy of four terms.
(2) A syllogism must have three and only three propositions. The proposition containing the major term is called the major premise, while the one containing the minor term is called the minor premise. In a strictly logical syllogism the major premise is written first, the minor premise second and the conclusion third. In common parlance, however, the minor premise or even the conclusion may appear first.
The conclusion of a syllogism is always preceded by therefore, or its equivalent, which may be written or understood. The premises always answer the question, Why is the conclusion true? The premises are often preceded by such words as for and because.
The attending irregular syllogisms are arranged logically and the premises and conclusions indicated:
(1a) Illogical.
“You must take an examination because all who enter the school are examined and you, as I understand it, are planning to enter.”
(2a) “Some of these books are not well bound, for they are going to pieces as no well bound book would do.”
(1b) Logical.
All who enter this school are examined, Major premise.
You are planning to enter this school, Minor premise.
You must be examined. Conclusion.
(2b) No well bound book goes to pieces, Major premise.
Some of these books are going to pieces, Minor premise.
Some of these books are not well bound. Conclusion.
The fact that all syllogisms must have three and only three premises follows from rule “1.” One premise must compare the middle term with the “major”; another premise must compare the middle term with the “minor”; while the conclusion links together the “major” and the “minor.”
(3) The middle term must be distributed at least once. The rule is usually given in this way, “The middle term must be distributed once at least, and must not be ambiguous.” In this treatment the last part of the rule has been omitted because it must be apparent to the student that a middle term used in two senses is virtually equivalent to two different terms; such an “ambiguous middle” would, in consequence, give a syllogism of four terms.
Rules 3 and 4 are of greater importance than the others because they are more frequently violated. If the middle term is not distributed at least once, the fallacy is referred to as “undistributed middle.” If the distributed major term of the conclusion is not distributed in the major premise, then the fallacy is called, “illicit process of the major term”; and finally, if the distributed minor term of the conclusion is not distributed in the minor premise the fallacy is denominated an “illicit process of the minor term.” These two illicit processes may be abbreviated to illicit major and illicit minor.
Recall that any term is distributed when it is referred to as a definite whole. Unless the whole of the middle term is considered it fails to become a common standard of comparison. This becomes clear when recourse is made to the circles.
Illustration.
Syllogism in which the middle term is not distributed:
All men are mortal,
All trees are mortal,
∴ All trees are men.
All the propositions are A’s and consequently the predicates of each are undistributed, as A distributes the subject only. Therefore the middle term, “mortal,” is not distributed in either of the premises and thus the fallacy.
Fallacy shown by circles:
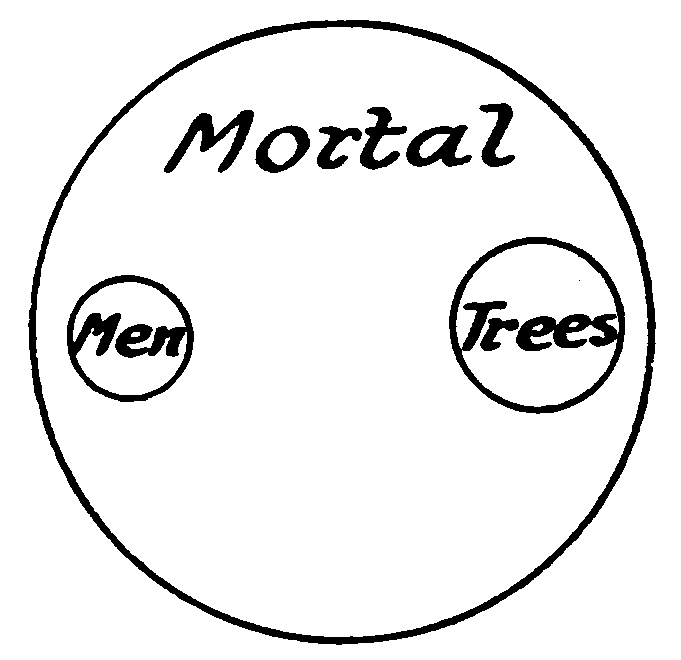
FIG. 9.
These circles indicate the correct meaning of the two premises. By them it is seen that all of the “men” circle belongs to the “mortal” circle and all of the “tree” circle belongs to the “mortal” circle, but in this case there is no connection between the “men” and “tree” circles. Thus, to say that “All trees are men,” is fallacious. We have no right to either affirm or deny the connection between men and trees. If “mortal” were distributed we would have this right as the following will make clear:
All men are mortal,
No stones are mortal,
∴ No stones are men.
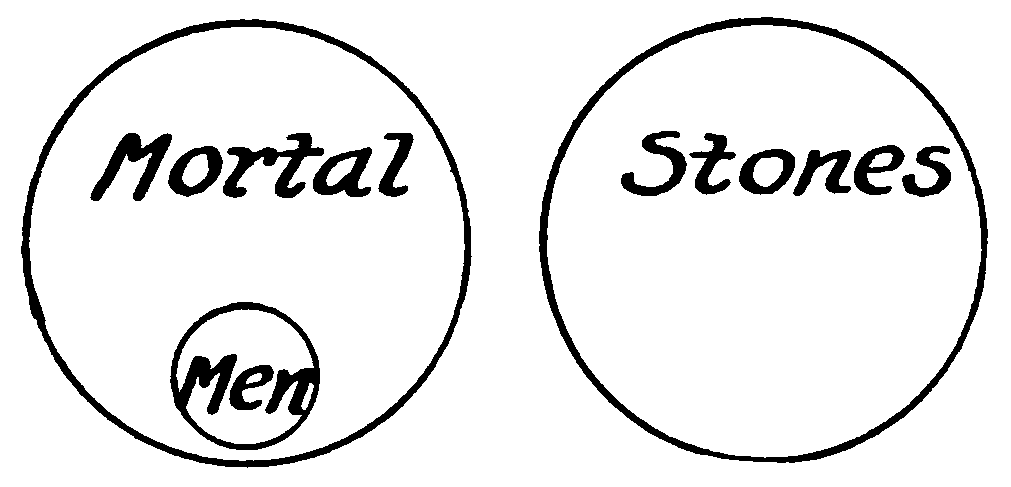
FIG. 10.
Here the middle term mortal is distributed in the second premise as in it the subject “stones” is excluded from the entire mortal territory. This conclusion is verified by the formal statement that “E” distributes both subject and predicate. Since all of the “men” circle belongs to the “mortal” circle and none of the “stones” circle belongs to the “mortal” circle then none of the “stones” circle can belong to the “men” circle.
(4) No term must be distributed in the conclusion which is not also distributed in its premise.
It has been affirmed that a term is distributed when it is referred to as a definite whole. To put it in another way, a term is distributed when it is employed in its fullest sense. It is obvious that we should not employ a term in its fullest sense in the conclusion when it has been used only in a partial sense in its premise. What is said of the part cannot necessarily be said of the whole. For example: Because some men are honest it does not follow that all men are honest. Of course the converse of this is true, namely, if it could be proved that all men are honest then surely it would follow that some of the men are honest. To put it briefly: What is true of all is true of some but what is true of some is not necessarily true of all.
To distribute a term in the conclusion when it is not distributed in the premise where it occurs is equivalent to saying, “what is true of some is true of all.” This error which violates rule “4” leads to the two fallacies of illicit process of the major and minor terms. The following illustrate the two fallacies.
Syllogism illustrating illicit major:
All trees grow,
No men are trees,
∴ No men grow.
The first premise is an A and consequently its subject is distributed. The second premise and conclusion being E’s have both subject and predicate distributed. Thus grow, as used in the conclusion, is distributed, but, as used in the major premise, it is not distributed. Fallacy shown by circles:
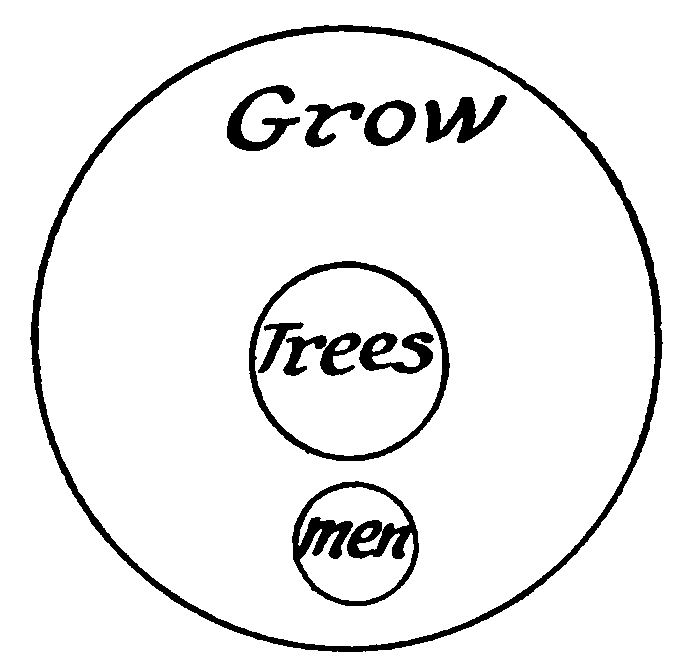
FIG. 11.
Here all of the “tree” circle belongs to the “grow” circle and none of the “men” circle belongs to the “tree” circle, hence the diagram correctly represents the meaning of the two premises and shows the fallacy of concluding that no men grow. The “men” circle, being entirely within the “grow” circle, indicates that all men grow. Syllogism illustrating illicit minor:
All true teachers are just,
All true teachers are sympathetic,
∴ All the sympathetic are just.
Each proposition being an A distributes its subject. But the subject of the conclusion which is “the sympathetic” is not distributed in the minor premise, as an A proposition distributes its subject only. Hence the fallacy of illicit minor.
Fallacy shown by circles:

FIG. 12.
The diagram correctly represents the two premises since all of the “true teacher” circle belongs to both the “just” and “sympathetic” circles. But all of the “sympathetic” circle does not belong to the “just” circle. Hence the fallacy.
(5) No conclusion can be drawn from two negative premises.
When two terms are both denied of a third term, it is quite impossible to draw any conclusion relative to the two terms, as the absolute exclusion of the third term eliminates any possibility of a common link or standard.
The circles will make this apparent:
No men are immortal,
No trees are immortal,

FIG. 13.
“No trees are men” is the conclusion represented by Fig. 13.
Other possible conclusions are, “All trees are men,” “All men are trees” and “Some men are trees.”
It is thus seen that no definite conclusion can be drawn. It may now be said that when the major and minor terms are used in two negative premises the connection between them is indeterminate. This violation of rule “5” may be termed the fallacy of two negatives.
(6) If one premise be negative the conclusion must be negative; and conversely, to prove a negative conclusion one of the premises must be negative.
Referring to the first part of this rule, it may be said of two terms that if one is affirmed and the other denied of a third term, then the two terms must be denied of each other. The attending syllogism and its “circled” representation will throw light upon this:
No men are immortal,
All Americans are men,
∴ No Americans are immortal.
FIG. 14.
Since none of the “men” circle belongs to the “immortal” circle and all of the “American” circle is inside the “men” circle, it is evident that none of the “American” circle can belong to any part of the “immortal” circle. Thus it is manifest that an affirmative conclusion like, “All Americans are immortal,” is invalid.
The converse of rule 6, “To prove a negative conclusion, one of the premises must be negative,” may be explained by the general principle in logic that when two terms are known to disagree, one must agree with a third term while the other must disagree. If both agreed with a third, then the conclusion would of necessity be affirmative. If both disagreed no conclusion could be drawn. A violation of rule 6 may be called the fallacy of negative conclusion.
(7) No conclusion can be drawn from two particular premises. Proof:
(1) All the possible combinations of the two particular premises I and O are, (1) IO, (2) OI, (3) II, (4) OO.
“IO” considered.
(2) Since O is a negative premise the conclusion would have to be negative according to rule 6. (If one premise is negative, the conclusion must be negative.)
(3) If the conclusion is negative, then its predicate, which is the major term, must be distributed. (All negative propositions distribute their predicates.)
(4) If the major term is distributed in the conclusion, it must be distributed in the major premise, rule 4. (No term must be distributed in the conclusion, which is not also distributed in one of the premises.)
(5) Hence two terms must be distributed in the premises, the major term according to (4) and the middle term according to rule 3.
(6) But I distributes neither term and O distributes its predicate only; I and O together, then, distribute but one term.
(7) To draw a negative conclusion the premises must distribute two terms, the middle and the major, according to the foregoing.
(8) Hence a conclusion from I and O is untenable. The same may be said of “OI.”
“II” considered.
(1) The I proposition distributes neither subject nor predicate, hence the premises “II” would distribute no term.
(2) But the middle term must be distributed at least once according to rule 3.
(3) Therefore no conclusion can be drawn from “II.”
A valid conclusion from “OO” is impossible according to rule 5.
(8) If one premise be particular the conclusion must be particular. Proof: The possible combinations conditioned by rule 8 are AI, AO, EI, EO, IO, II, OO.
“AI” considered.
(1) Proposition A distributes its subject, proposition I neither; hence “AI” together distribute but one term.
(2) According to rule 3 this one term must be the middle term.
(3) The minor term must, therefore, be undistributed in the minor premise, and in consequence undistributed in the conclusion.
(4) But this undistributed minor term is the subject of the conclusion; hence said conclusion must be particular, as only particulars have an undistributed subject.
“AO” and “EI” considered.
Proof:
(1) “AO” distribute two terms; so do “EI.”
(2) Both “AO” and “EI” must have negative conclusions according to rule 6.
(3) A negative conclusion distributes its predicate which is the major term.
(4) The major term and the middle term must be distributed in the premises. Rules 4 and 3.
(5) Thus the third term, which is the minor, cannot be distributed in the minor premise and, consequently, the minor cannot be distributed in the conclusion.
(6) This necessitates a particular conclusion.
Premises EO and OO, being negative, cannot yield a conclusion according to rule 5; similarly, neither can the particulars IO and II because of rule 7.
Aristotle gives an axiom on which all syllogistic inference is based. Indeed from this fundamental principle the significant rules of the syllogism could be derived. The dictum is stated in this wise: “Whatever is predicated, whether affirmatively or negatively, of a term distributed may be predicated in the manner of everything contained under it.” The following statements represent various ways of explaining this dictum:
(1) Whatever is said of a term used in its fullest sense may likewise be said of that term when used only in a partial sense.
(2) What is true of the whole is true of the part.
(3) “What pertains to the higher class pertains also to the lower.” Since this dictum is the basic principle underlying the important rules of the syllogism, it is unnecessary to dwell longer upon it; because an explanation of the rules is, virtually, an explanation of the dictum.
The dictum of Aristotle is ostensibly a self-evident truth, and some logicians have put this truth in the form of three axiomatic statements which are known as the canons of the syllogism. These are as follows:
(1) “Two terms agreeing with one and the same third term agree with each other.”
(2) “Two terms of which one agrees and the other does not agree with one and the same third term, do not agree with each other.”
(3) “Two terms both disagreeing with one and the same third term may or may not agree with each other.”
Making use of the symbols as explained on a previous page of this chapter, it will be seen that the first canon conforms to this syllogistic type:
All M is G
All S is M
∴ All S is G
The two terms are S and G, while M is the third term.
The attending symbolizations illustrate, respectively, the second and third canons:
No M is G
All S is M
∴ No S is G
No M is G
No S is M
Conclusion indeterminate.
Analogous to the three canons treated in “6,” there are certain mathematical axioms which are here stated:
(1) “Things equal to the same thing are equal to each other.”
(2) “One thing equal to and the other thing not equal to the same third thing are not equal to each other.”
(3) “Things not equal to the same thing may or may not equal each other.”
Illustrations of the three axioms:
(1) If x equals 5, and y equals 5, then x equals y.
(2) If x equals 5, and y does not equal 5, then x does not equal y.
(3) If x does not equal 5, and y does not equal 5, then x may or may not equal y.
MEDIATE INFERENCE.
(1) Inference and reasoning.
Definitions. Middle term explained.
(2) The analogy between the judgment and the syllogism.
(3) Rules of the syllogism given. Eight in number.
(4) Rules of the syllogism explained:
Rule 1. Syllogistic symbols.
Major, minor, and middle terms; how found.
Fallacy of four terms.
Rule 2. Major and minor premises and conclusion, how determined.
Logical arrangement.
Reason for three propositions.
Rule 3. Reason for omitting “ambiguous middle” from rule.
Undistributed and distributed middle explained.
Rule 4. Illicit major and minor explained and illustrated.
Rule 5. Fallacy of two negatives.
Rule 6. Fallacy of negative conclusion.
Rule 7. Fallacy of two particulars.
Rule 8. Fallacy of particular conclusion.
(5) Aristotle’s dictum.
(6) Canons of the syllogism.
(7) Mathematical axioms.
(1) Inference is a term used to denote a process as well as a product. As a process reasoning and inference are in reality synonomous terms.
Inference is a thought process of deriving a judgment from one or two antecedent judgments.
Mediate inference is inference by means of a middle term. Mediate inference makes use of three terms, two of which are compared with a third term as a standard. This third term is called the middle term.
(2) The syllogism is the common mode of expression for mediate inference.
(3) Valid syllogistic reasoning is conditioned by eight rules. The first and second relate to the composition of the syllogism; the third and fourth to the distribution of terms; the fifth and sixth to negative premises; the seventh and eighth to particular premises.
(4) All syllogisms must have three terms: the major, the minor, and the middle. The middle term occurs twice in the premises but never appears in the conclusion. The minor term is always the subject, and the major term the predicate of the conclusion. The major term is usually broader than the minor.
No conclusion can be drawn from four terms. To attempt this gives rise to the fallacy of four terms.
All syllogisms must have three propositions, the major and the minor premises, and the conclusion. The major premise first and the minor second is the more logical arrangement, although the common conversational form is to use the minor premise first.
Ambiguous middle amounts to the fallacy of four terms.
Unless the middle term is distributed at least once in the syllogism, it fails to become a common standard.
Distributing a term in the conclusion, without its being distributed in its premise, is equivalent to asserting that, “What is true of a part is true of the whole.” This error results in the fallacies of illicit major and minor.
A conclusion from two negatives is impossible, because of the total exclusion of the middle term.
Of two terms, if one is affirmed and the other denied of a third term, then they must be denied of each other; and, conversely, if two terms are to be denied of each other, one must be affirmed and the other denied of a given third term. This fundamental principle necessitates deriving a negative conclusion from two premises when one is negative. It, likewise, compels the converse of this.
A valid conclusion from two particulars is untenable because of the two negative fallacies, or some fallacy relative to the distribution of terms.
One particular premise forces a particular conclusion because of the fallacies of two negatives, two particulars, and illicit minor.
(5) Aristotle’s dictum simplified means, “What is true of the whole is true of the part.”
(6) The canons of the syllogism, three in number, are:
(1) “Two terms agreeing with one and the same third term agree with each other.”
(2) “Two terms of which one agrees and the other does not agree with one and the same third term do not agree with each other.”
(3) “Two terms both disagreeing with one and the same third term may or may not agree with each other.”
(7) The foregoing canons may be stated as mathematical axioms.
(1a) Make use of the proper symbols and indicate the three terms of each of the attending syllogisms:
(1) All fixed stars twinkle,
Vega is a fixed star,
∴ Vega twinkles.
(2) All men are rational beings,
No tree is a rational being,
∴ No trees are men.
(3) All good citizens are law abiding,
All good citizens vote,
∴ Some who vote are law abiding.
I recall that the three terms are the middle, the major and the minor, and that the “middle” does not occur in the conclusion, whereas the “major” is always the predicate and the “minor” the subject of the conclusion. The symbols M, G and S being the initial letters of middle, greater and smaller, I make use of these in designating the three terms, as the following will illustrate:
(1) All M
fixed stars G
twinkle,
S
Vega
is a M
fixed star,
∴ S
Vega G
twinkles.
“Twinkles” being the predicate of the conclusion is designated as being the major term by putting the letter G above it. Then “G” is placed above the term “twinkle” in the first premise.
“S” is placed above the subject of the conclusion to indicate that it is the minor term. “S” is also placed above “Vega,” the minor term, as found in the second premise.
The remaining term, “fixed stars,” must be the middle term, therefore I place “M” above it. The fact that “fixed star” does not occur in the conclusion verifies this.
Using only the symbols, the syllogism takes this form:
All M is G
S is M
∴ S is G
Using the symbols to represent the other syllogisms, we have
(2) All G is M
No S is M
∴ No S is G
(3) All M is G
All M is S
∴ Some S is G
(1b) Indicate by symbols the three terms of the following syllogisms:
(1) No trees are men,
All rational beings are men,
∴ No rational being is a tree.
(2) All men have the power of speech,
You are a man,
∴ You have the power of speech.
(3) Some men are wise,
All men are rational,
∴ Some rational beings are wise.
(2a) Illustrate by syllogism the fallacy of undistributed middle. An easy way is to use the middle term as the predicate of two A premises. This yields the fallacy because an A proposition does not distribute the predicate.
The illustration: distributed terms underscored.
All true teachers are students,
All scholars are students,
―――――――――――――――
∴ All scholars are true teachers.
(2b) Give two illustrations of undistributed middle.
(3a) Give syllogistic illustrations of the fallacies of illicit major and minor.
Illicit Major.
Use the middle term as the subject of an A proposition, and then as the predicate of an E proposition. This would necessitate a negative conclusion in which the major term is distributed. But the major term is not distributed in the major premise, hence the fallacy.
Illustration in which the distributed terms are underscored:
All men are mortal,
No trees are men,
――――――――――
∴ No trees are mortal.
Illicit Minor.
To illustrate this fallacy one may use the middle term as the subject of two A premises. This would give an A conclusion in which the subject is distributed. But this same term is not distributed in its premise because here it is used as the predicate of an A. Illustration:
All earnest students study,
All earnest students desire to succeed,
―――――――――――――――――――
∴ All who desire to succeed study.
(1) Distinguish between inference and reasoning.
(2) Define inference. Mediate inference.
(3) Illustrate the difference between mediate and immediate inference.
(4) Explain by illustration the use of the middle term.
(5) Exemplify the syllogism.
(6) State the rules of the syllogism.
(7) From the attending syllogisms select the three terms:
(1) All patriotic citizens vote,
You are a patriotic citizen,
∴ You should vote.
(2) No honest man would misrepresent,
(but) John Smith did misrepresent,
∴ John Smith is not honest.
(8) Symbolize the foregoing syllogisms.
(9) Illustrate by syllogisms the fallacy of four terms.
(10) Indicate by circles that a valid conclusion cannot be drawn from four terms.
(11) Why must a syllogism have three and only three propositions?
(12) Indicate how the three propositions of an argument may be designated. What is the logical arrangement?
(13) Show that an ambiguous middle amounts to a fallacy of four terms.
(14) Explain and illustrate undistributed middle, illicit major, illicit minor.
(15) Exemplify the fallacies of question “14” by using circles.
(16) Explain by circles why a conclusion cannot be drawn from two negatives.
(17) Make clear that a negative conclusion must follow, if one premise be negative.
(18) State and explain the principle which underlies the rule, “If the conclusion is negative one premise must be negative.”
(19) Prove by the process of elimination that no conclusion can be drawn from two particulars.
(20) In a way similar to that of question “19” show that if one premise be particular the conclusion must be particular.
(21) State and explain Aristotle’s dictum.
(22) State the canons of the syllogism.
(23) Symbolize and explain by circles the three canons.
(24) Illustrate the three mathematical axioms which the canons suggest.
(1) Give an illustration of a valid conclusion being drawn from four terms.
(2) Explain by circles the foregoing.
(3) From three different business transactions, select the middle term of comparison.
(4) Why should not those who are given to much which is argumentative, speak in syllogistic terms?
(5) “He is a man of high ideals, and you know him to be strictly honest, therefore you have no excuse for not voting for him.” Recast this quotation with a view of making a logical syllogism.
(6) Show by circles that there may be a vital difference between a syllogism of three terms and an equation of three terms.
(7) Indicate by illustration that in conversational argumentation the minor premise naturally comes first.
(8) Show by circles the meaning of “indeterminate conclusion.”
(9) Rule five states that no conclusion can be drawn from two negatives. Defend this rule in connection with the following syllogism, which seems to contain a valid conclusion:
Any statement which is not true cannot be accepted,
This statement is not true,
∴ It cannot be accepted.
(10) If the conclusion is particular, must one premise be particular? Explain.
By a figure of a syllogism is meant some particular arrangement of the three terms in the two premises. The conclusion is eliminated from this discussion, because in it the arrangement of the terms is constant, the major term always being used as the predicate of the conclusion and the minor as the subject. Using the symbols M, G and S, we find that there are four possible arrangements and, therefore, but four figures. These may be represented as follows:
| First figure |
Second figure |
Third figure |
Fourth figure |
|---|---|---|---|
| M ― G | G ― M | M ― G | G ― M |
| S ― M | S ― M | M ― S | M ― S |
| S ― G | S ― G | S ― G | S ― G |
No matter what the syllogism, if it is to be proved “logical,” it should be made to fit one of the four figure-types. To be sure, it may fit the figure without being logical, but it cannot be strictly logical without fitting the figure. The following valid syllogisms conform to the four figures as will be seen by the symbolized terms:
First figure: All M
men
are G
mortal,
S
Socrates
is a M
man,
∴ S
Socrates
is G
mortal.
M ― G
S ― M
S ― G
Second figure: All
G
good citizens
love their M
country,
No S
criminal
loves his M
country,
∴ No S
criminal
is a G
good citizen.
G ― M
S ― M
S ― G
Third figure: All
M
good citizens
are G
law abiding,
All M
good citizens S
vote,
∴ Some who S
vote
are G
law abiding.
M ― G
M ― S
S ― G
Fourth figure: Some
G
teachers
are M
fair minded,
All who are M
fair minded
are S
just,
∴ Some S
just persons
are G
teachers.
G ― M
M ― S
S ― G
Here, then, are the types that represent all the syllogisms which mediate inference may use. Logic recognizes no other. Since every successful student of logic must be familiar with the four figures, the following may be used as a suggestive aid to reproducing the figures at will:
First. It is easy for any one to remember this syllogism:
All men are mortal,
Socrates is a man,
∴ Socrates is mortal.
In fact, it comes down to us from the time of Aristotle, and is therefore a patriot of many generations to whom the faithful should touch their hats. Let us, then, be ready to reproduce this syllogism with automatic precision, since it will enable us to know at once the position of the terms in the first figure. Second. Converting the terms of the major premise of the first figure gives the second figure, as, e. g.:
| First figure. | Second figure. | |
|---|---|---|
| M ― G | (Convert) | G ― M |
| S ― M | S ― M | |
| S ― G | S ― G |
Third. Converting the terms of the minor premise of the first figure gives the third figure, as, e. g.:
| First figure. | Third figure. | |
|---|---|---|
| M ― G | M ― G | |
| S ― M | (Convert) | M ― S |
| S ― G | S ― M |
Fourth. Converting the terms of both the major and minor premises of the first figure gives the fourth, as, e. g.:
| First figure. | Fourth figure. | |
|---|---|---|
| M ― G | (Convert) | G ― M |
| S ― M | (Convert) | M ― S |
| S ― G | S ― G |
To summarize: The second, third and fourth figures may be derived from the first. Converting the major premise of the first figure gives the second figure; converting the minor premise gives the third figure; and converting both premises gives the fourth figure.
By the mood of a syllogism is meant some particular arrangement of the propositions which compose the syllogisms. “Mood” stands for an arrangement of the propositions, while “figure” represents an arrangement of the terms in any syllogism.
Combining any three of the four logical propositions gives a mood, as, e. g.,
(1) E
A
E
(2) A
I
I
(3) E
I
O.
are moods. The first one has an E proposition for the major premise, an A for the minor and an E for the conclusion. This syllogism represents the first mood given above:
E No men are trees,
A All Americans are men,
E ∴ No Americans are trees.
It would not be difficult to determine by actual experiment, just how many moods could be formed, and of these, how many would admit of valid conclusions. It may be seen that there are sixty-four permutations of the four logical propositions, taken three at a time. These are in part:
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
| A | A | A | A | A | A | A | A |
| A | A | A | A | E | E | E | E |
| A | E | I | O | A | E | I | O |
| (9) | (10) | (11) | (12) | (13) | (14) | (15) | (16) |
| A | A | A | A | A | A | A | A |
| I | I | I | I | O | O | O | O |
| A | E | I | O | A | E | I | O |
And so the permutations could be continued. Substituting E for the major premise of the above group would give another group of sixteen, while a like substitution of I and O would result in two more groups, sixteen in each. This gives sixty-four in all.10
In order to put the moods to good use, it is necessary to ascertain which ones yield a valid conclusion in any figure. If each were valid in all of the four figures, there would be 256. But it is obvious that such is not the case.
Referring to the sixteen permutations given above, we find that the “negative-conclusion” rule makes invalid 2, 4, 5, 7, 10, 12, 13 and 15; whereas the rule for particulars throws out 9 and 14. This leaves the following as the probable valid moods in one or more of the figures: 1, 3, 6, 8, 11, 16. But to be certain of this the investigation must be continued. The mood A
A
A
has stood the test of the rules for negative and particular conclusions; now let us test this mood from the standpoint of the distribution of terms, using it in all four figures:
| First | Second | Third | Fourth | ||||
| A | M ― G | G ― M | M ― G | G ― M | |||
| A | S ― M | S ― M | M ― S | M ― S | |||
| A | S ― G | S ― G | S ― G | S ― G |
As an A proposition distributes its subject only, we underscore the subject of each proposition in all the figures. (This underscoring is a simple way to indicate distribution.)
We now find that the mood is valid in the first figure, because the middle term is distributed at least once; namely, in the major premise, and there is no term distributed in the conclusion which is not already distributed in the premise where it occurs. On the other hand, the mood A
A
A
is invalid in the second, because of “undistributed middle,” and invalid in the third and fourth, because S is distributed in the conclusion but not distributed in the premise where it occurs (illicit minor).
Let us try AII in the four figures:
| A | M ― G | G ― M | M ― G | G ― M | |||
| I | S ― M | S ― M | M ― S | M ― S | |||
| I | S ― G | S ― G | S ― G | S ― G |
We underscore the subject of the A proposition in each of the four figures. As I distributes neither subject nor predicate, no other term should be underscored. It is now evident that A
I
I
is not valid in figures two and four, because in both figures the middle term is undistributed (undistributed middle).
In a like manner all the other moods might be tested. Logicians, who have done this, have found 24 to be valid. Five of these have weakened conclusions;
i. e.,
a particular conclusion when it could just as well be universal. A
E
O
illustrates this as the conclusion could be E. This syllogism exemplifies the weakened conclusion:
A All trees grow,
E No sticks are trees,
O ∴ Some sticks do not grow.
This conclusion is true, since “some” means “some at least.” Yet the conclusion is weak, because there is nothing to interfere with the broader and stronger conclusion that, “No sticks grow.” There are, therefore, only 19 valid and serviceable moods. These are as follows:
| (1) | (2) | (3) | (4) | (5) | (6) | ||||
| First figure |
 |
A A A |
E A E |
A I I |
E I O |
― ― ― |
― ― ― |
 |
4 |
| Second figure |
 |
E A E |
A E E |
A O O |
E I O |
― ― ― |
― ― ― |
 |
8 |
| Third figure |
 |
A A I |
I A I |
A I I |
E A O |
O A O |
E I O |
 |
14 |
| Fourth figure |
 |
A A I |
A E E |
I A I |
E A O |
E I O |
― ― ― |
 |
19 |
Of these nineteen moods it is not much of a tax to remember that
A
A
A
is valid only in the first figure; whereas
E
A
E
is valid in the first and second figures;
A
I
I
in the first and third; while
E
I
O
is valid in all. This knowledge, however, should be used only as one would employ the answers in arithmetic. Testing the validity of a mood in the four figures is an exceedingly valuable thought-exercise, which a knowledge of the final result might easily vitiate. It is, no doubt, best to test the value of any mood without such knowledge, and then compare the result by referring to the foregoing list of valid moods. It is not always wise to work with the answer in mind, yet it is most satisfying to know of a certainty that one’s reasoning has led to a truth which others have verified.
As a deductive exercise in clear, logical thought, the indirect proof involved in establishing certain principles underlying the four figures, is of immense value. On no account should this section be omitted. The mere fact that it appears to be a difficult section is proof positive that the student is in need of just such exercises.
Canons of the first figure.
(1) The minor premise must be affirmative.
(2) The major premise must be universal.
Problem: The minor premise must be affirmative.
Data: Given the form of the first figure, which is,
M ― G
S ― M
S ― G
Proof: (1) If the minor premise is not affirmative then it must be negative; because affirmative and negative propositions, being contradictory in nature, admit of no middle ground.
(2) If the minor premise is negative, the conclusion must be negative; for the reason that a negative premise necessitates a negative conclusion.
(3) If the conclusion is negative then its predicate, G, must be distributed; since all negatives distribute their predicates.
(4) If the predicate of the conclusion, which is the major term, is distributed, then it must be distributed in the premise where it occurs, which is the major premise; for any term which is distributed in the conclusion must be distributed in the premise where it occurs.
(5) If the major term, which is the predicate of the major premise, is distributed, then the major premise must be negative; because only negatives distribute their predicates.
(6) The result of this argument, then, gives two negative premises, and we know from rule 3 that a conclusion from two negatives is untenable.
(7) Since the minor premise cannot be negative, it must be affirmative.
Problem: To prove that the major premise must be universal.
Data: Given the form of the first figure:
M ― G
S ― M
S ― G
Proof: (1) The predicate of the minor premise, M, which is the middle term, is undistributed; because no affirmative proposition distributes its predicate.
(2) The middle term must be distributed in the major premise; since in any syllogism the middle term must be distributed at least once.
(3) As the middle term, M, used as the subject of the major premise, must be distributed, then the major premise must be universal; because only universals distribute their subjects.
Epitome.
In the first figure, the minor premise must be affirmative, since making it negative necessitates making the major premise negative also; the major premise must be universal in order to distribute the middle term at least once.
Special canons of the second figure.
(1) One premise must be negative.
(2) The major premise must be universal.
Problem: To prove that one premise must be negative.
Data: Given the form of the second figure:
G ― M
S ― M
S ― G
Proof: (1) The middle term, M, is the predicate of both premises.
(2) The middle term must be distributed at least once, according to rule 3.
(3) Hence one premise must be negative; since only negatives distribute their predicates.
Problem: To prove that the major premise must be universal.
Data: Given the form of the second figure:
G ― M
S ― M
S ― G
Proof: (1) As one premise must be negative, it follows that the conclusion must be negative according to rule 6.
(2) If the conclusion is negative, then its predicate, G, the major term, must be distributed; since all negatives distribute their predicates.
(3) When distributed in the conclusion, the major term, G, must also be distributed in the major premise, where it is used as the subject. See rule 4.
(4) Hence the major premise must be universal; for only universals distribute their subjects.
Epitome.
In the second figure one premise must be negative in order to distribute the middle term at least once; and the major premise must be universal that the major term, which is distributed in the conclusion, may be distributed in the premise where it occurs.
Canons of the third figure.
(1) The minor premise must be affirmative.
(2) The conclusion must be particular.
Problem: To prove that the minor premise must be affirmative.
Data: Given the form of the third figure, which is,
M ― G
M ― S
S ― G
Proof: (1) Suppose the minor premise were negative, then the conclusion would have to be negative, and this would distribute the predicate G.
(2) A distributed predicate would necessitate its being distributed in the major premise.
(3) But G, being the conclusion of the major premise, could be distributed only by a negative proposition.
(4) This would result in two negatives; therefore no conclusion could be drawn, if the minor premise were negative.
Problem: To prove that the conclusion must be particular.
Data: Given the form of the third figure:
M ― G
M ― S
S ― G
Proof: (1) The minor term, which is the predicate of the affirmative minor premise, is undistributed; because no affirmative distributes its predicate.
(2) If undistributed in the premise, then the minor term must remain undistributed in the conclusion, where it is used as the subject.
(3) The conclusion must, then, be particular; since all universals distribute their subjects.
Epitome.
In the third figure, unless the minor premise be affirmative, there can be no conclusion; since a negative minor would necessitate a negative major. An affirmative minor compels a particular conclusion, in order that the minor term, in the conclusion, may remain undistributed.
Canons of the fourth figure.
(1) If the major premise is affirmative, the minor premise must be universal.
(2) If the minor premise is affirmative, the conclusion must be particular.
(3) If either premise is negative, the major must be universal.
Problem: To prove that if the major is affirmative, the minor must be universal.
Data: Given the form of the fourth figure:
G ― M
M ― S
S ― G
Proof: (1) If the major premise is affirmative, then its predicate which is the middle term, M, is undistributed; for no affirmative distributes its predicate.
(2) The middle term must then be distributed in the “minor” according to rule 3.
(3) Then the “minor” must be universal; since only universals distribute their subjects.
Problem: To prove that if the minor is affirmative, the conclusion must be particular.
Data: Given the form of the fourth figure:
G ― M
M ― S
S ― G
Proof: (1) If the minor premise be affirmative, then S, its predicate, must be undistributed; because no affirmative distributes its predicate.
(2) Since S is undistributed in the minor premise, it must remain undistributed in the conclusion where it is used as the subject.
Problem: To prove that if either premise is negative, the major must be universal.
Data: Given the form of the fourth figure:
G ― M
M ― S
S ― G
Proof: (1) If one of the premises is negative, then the conclusion must be negative according to rule 6.
(2) If the conclusion is negative, then the predicate, G, must be distributed.
(3) If G is distributed in the conclusion, it must be distributed in the major premise.
(4) The major premise must be universal; as G is used as its subject, and only universals distribute their subjects.
Epitome.
In the fourth figure, if the “major” is affirmative, the “minor” must be universal in order to distribute the middle term. If the minor is affirmative, the conclusion must be particular; otherwise the fallacy of illicit minor would result. If either premise is negative, the major must be universal to avoid the fallacy of illicit major.
After a particular mood has been tested in the regular way, it has been intimated that the student may refer to the tabulated list of valid moods to ascertain, with a certainty, the validity of his reasoning. This is equivalent to referring to the answers in arithmetic; for if the student is unable to find the mood in the figure in which he has proved it valid, then he knows that he has made some mistake in his reasoning. A second check, though not absolute, is to recall the special canons of section four. If, for example, our reasoning has led us to believe that
A
E
E
is valid in the first figure, we may recall that the minor premise of the first figure must be affirmative and therefore AEE cannot be valid.
A few suggestions relative to memorizing the special canons may not be out of place. The two canons of the first figure must be committed, and then it may be remembered that the second figure is the negative figure of logic. Other figures may yield a negative conclusion, but the second must yield a negative conclusion. Since a negative conclusion necessitates a negative premise, it follows that the second figure must always appear with one premise negative. The other canon which pertains to the major premise is the same as the “major premise” canon of the first figure.
The third figure is the particular figure of logic. Other figures may yield particular conclusions, but the third must do so. This helps us to remember the canon that the conclusion of the third figure must be particular. The other canon which relates to the minor premise is the same as the “minor premise” canon of the first figure. The canons of the fourth figure are in reality a summary of the canons of the other three figures.
As a device for remembering the 19 valid moods, the logicians of an earlier day originated a combination of coined words which, though rather unscientific, may be easily committed to memory. Since, however, it is of much more value to test the moods by means of the general rules of the syllogism than it is to try to remember these moods, the mnemonic lines are of slight value. They are treated here merely as an item of historical interest.
(1) Barbara, Celarent, Darii, Ferioque prioris;
(2) Cesare, Camestres, Festino, Baroko, secundæ;
(3) Tertia, Darapti, Disamis, Datisi, Felapton, Bokardo, Ferison, habet; Quarta insuper addit
(4) Bramantip, Camenes, Dimaris, Fesapo, Fresison.
The only letters in these lines which mean nothing are l, n, r, t and small b and d; all the others have a signification. For example, the vowels of the italicized words signify the various valid moods, as e. g., the first line indicates the moods AAA, EAE, AII, EIO. The Latin words, printed in ordinary type, are intended to make evident that the moods indicated by the artificial italicized words of the first line, belong to the first figure; that the moods of the next four words, belong to the second figure; while the third figure includes the next six, and the fourth figure the last five. It is now seen that Festino, for example, stands for that mood of the second figure which has an E for its major premise, an I for its minor premise, and an O for its conclusion.
The first figure was called by Aristotle the perfect figure, whereas the second and third were the imperfect figures. The fourth figure was given no place in the works of Aristotle; its discovery is credited to Galen, a celebrated teacher of medicine of the second century. According to Aristotle, the first figure is the most serviceable and the most convincing and, therefore, as a final test of their validity, the moods of the other figures should be changed to the first. This process in logic is termed Reduction. In this reduction of the imperfect figures to the perfect, the capital letters of the artificial words, together with s, p, m, and k, have a definite meaning. The capital letters indicate that certain moods of the imperfect figures can be reduced to the corresponding moods of the first figure;
e. g.,
Festino (eio) of the second figure, Felapton (eao) of the third figure, and Fesapo (eao) of the fourth figure may all be reduced to Ferio (eio) of the first figure. This is known because F is the initial letter of each word. s signifies that the proposition denoted by the preceding vowel is to be converted simply. To illustrate: s in Fesapo means that the major premise E of the mood
E
A
O
of the fourth figure must be converted simply in order to change the mood to Ferio of the first figure. p indicates that the proposition represented by the vowel which precedes p must be converted by limitation (per accidens). m (mutare) makes evident that the premises are to be interchanged, the major of the old becoming the minor of the new, and the minor of the old becoming the major of the new. k denotes that the mood, such as Baroko, must be reduced by a special process known as indirect reduction. These directions may now be followed as illustrative of the process of reduction.
(1) Given: A syllogism in Darapti
A
A
I
A All
M
true teachers
are G
just,
A All
M
true teachers
are S
sympathetic,
I ∴ Some
S
sympathetic persons
are G
just.
The symbols indicate that the mood is
A
A
I
or is in Darapti and that this mood is used in the third figure.
Problem: To reduce
A
A
I
of the third figure to some mood of the first figure.
Process: D, being the initial letter of Darapti, suggests that its mood must be reduced to one indicated by a word of the first figure whose initial letter is D. This mood is in Darii, or
is A
I
I.
The p in Darapti indicates that the proposition represented by the preceding vowel must be converted by limitation. This proposition is the minor premise; converting it by limitation gives: “Some sympathetic persons are true teachers.” As there are no other significant letters the reduction is complete and we have this:
A All
M
true teachers
are G
just,
I Some
S
sympathetic persons
are M
true teachers,
I ∴ Some
S
sympathetic persons
are G
just.
The symbolization indicates that the mood is
A
I
I
of the first figure, or is in Darii.
(2) Given: A syllogism in Camestres A
E
E
A All
G
true teachers
are M
just,
E No
S
one
who shows partiality is M
just,
E ∴ No
S
one
who shows partiality is a G
true teacher.
The symbols show that the mood is AEE of the second figure or in Camestres. Judging from the initial letter C, the mood in Camestres must be reduced to the mood in Celarent
E
A
E.
The letter m between a and e indicates that the major and minor premises of the given syllogism must be interchanged. The letters following both e’s suggest that the minor premise and the conclusion of the syllogism must be converted simply.
This is the resulting syllogism:
E No
M
just person
shows G
partiality,
A All
S
true teachers
are M
just persons,
E ∴ No
S
true teacher
shows G
partiality.
Here, then, is the
E
A
E
of the first figure or the mood in Celarent.
According to the ancient theory, reduction is necessary as a matter of final and absolute proof that the conclusion follows from the given premises. But, as this claim has been satisfactorily refuted by modern logicians, we need not give more space to the process. The meaning of k, as related to “indirect reduction,” is explained in most of the earlier works on logic. See Hyslop, page 193.
The first figure.
The first figure is known as the perfect figure; because it is the only one which proves all of the four logical propositions. Recalling the moods of the first figure makes this evident:
| A | E | A | E |
| A | A | I | I |
| A | E | I | O |
It is likewise the more natural figure; because it is the only one which uses both the subject and predicate of the conclusion in the same relative places as they appear in the premises. Symbolizing the figure makes this apparent:
M ― G
S ― M
S ― G
The first figure, being the only figure which proves a “universal affirmation” (A), is used most by the scientist; as the object of science is to establish universal affirmative truths.
The second figure.
As the second figure conditions negative conclusions only, it is called the figure of disproof, or the exclusive figure. It is easy to see how negative conclusions may be used to narrow the inquiry down to one definite theory. For example, suppose it is desired to ascertain which boy of the five broke the window; by a series of deductions the teacher may be able to prove that the culprit is not A, not B, not C and not D; hence the guilty one must be E. This figure is virtually the one used in diagnosing most diseases.
The third figure.
The third figure admits of particular conclusions only, and in consequence is of little value to the scientist. Since, however, the easiest way to contradict a universal affirmative (A) or a universal negative (E), is to prove the truth, respectively, of a particular negative (O) and a particular affirmative (I), it follows that the third figure serves a purpose.
The fourth figure.
This figure is so nearly like the first that it is of little value; in fact, it may be changed to the first by simply interchanging the major and minor premises. Some authorities refuse to recognize the fourth figure.
FIGURES AND MOODS OF THE SYLLOGISM.
(1) The four figures of the syllogism.
Definition—symbolization.
Illustrations—device for remembering.
(2) The moods of the syllogism.
Twenty-four valid.
(3) Testing the validity of the moods.
Application of the general rules of the syllogism.
Weakened conclusion—five.
Nineteen useful moods.
A thought exercise.
(4) Special canons of the four figures.
Proof of the two canons of the first figure.
Proof of the two canons of the second figure.
Proof of the two canons of the third figure.
Proof of the three canons of the fourth figure.
(5) Special canons related.
Used as checks.
(6) Mnemonic lines.
Their use explained.
Reduction.
(7) Relative value of the four figures.
(1) By a syllogistic figure is meant some particular arrangement of the three terms in the two premises.
This arrangement yields four figures which are designated by the position of the middle term.
To be logical, any syllogism must conform to one of the four figures. The first figure is suggested by the position of the terms of the “Socrates is mortal” syllogism. The second is derived by converting the major premise of the first; while the third figure results from converting the minor premise of the first, and the fourth by converting both major and minor of the first.
(2) By a mood of a syllogism is meant some particular arrangement of the propositions which compose it.
There are 64 moods but only 24 are valid.
(3) The validity of the various moods may be tested by applying to them the rules of the syllogism. No mood is valid if it violates any one of the eight rules.
A “weakened conclusion” is a particular conclusion which could just as well be universal.
Of the 24 valid moods five have weakened conclusions. This leaves but 19 useful moods.
Testing the validity of the various moods in the four figures is a most valuable thought exercise.
(4) The deductive exercise involved in establishing certain special canons of the four figures is of immense value and should not be omitted.
In the first figure it may be proved (1) that the minor premise must be affirmative; since making it negative necessitates making the major premise negative, and no conclusion can be drawn from two negatives; (2) that the major premise must be universal in order to distribute the middle term at least once.
In the second figure it may be proved (1) that one premise must be negative in order to distribute the middle term; (2) that the major premise must be universal in order to distribute its subject, which is distributed in the negative conclusion where it appears as the predicate.
In the third figure it may be proved (1) that the minor premise must be affirmative in order to prevent the “two negative” fallacy; (2) that an affirmative minor necessitates a particular conclusion, because the minor term in the conclusion must remain undistributed.
In the fourth figure it may be proved (1) that if the major is affirmative, the minor must be universal in order to distribute the middle term; (2) that if the minor is affirmative, the conclusion must be particular in order to avoid committing the fallacy of illicit minor; (3) that if either premise is negative, the major must be universal to avoid the fallacy of illicit major.
(5) A knowledge of the special canons is helpful in that it may be used to check fallacious reasoning.
(6) Certain mnemonic lines were used by the Schoolmen as an aid in recalling the nineteen valid moods, and also as a suggestive device to aid in the process known as Reduction.
The process of reduction is merely a matter of changing to the first figure the moods of the other figures. This process is no longer thought to be necessary.
(7) The first figure, called the perfect figure, is the one used most by scientists, as it is the only figure which proves a universal affirmative truth. The second figure is the negative, or figure of disproof, and is used mainly for the purpose of eliminating all the conditions of the inquiry save one. The third figure serves a purpose in affording an easy way to contradict a universal assertion; this is the figure of particulars. The fourth figure, because it so closely resembles the first, is of little value.
Question 1a. By making use of the rules for negatives and particulars, test the validity of the following moods: O
I
A A
I
A A
A
I.
Answer: The first mood has the negative O as its major premise, and the affirmative A as its conclusion; the mood is thus invalid; because a negative premise necessitates a negative conclusion according to rule 6.
The second mood contains the particular proposition I as its minor premise, and thus should have a particular conclusion according to rule 8. But the conclusion A is universal and, therefore, the mood is invalid.
The premises of the third mood are universal and the conclusion particular. The mood, however, is valid, because rule 8 does not work both ways, as does rule 6. When a universal can just as well be drawn, then the particular becomes a weakened conclusion.
(1b) Using the rules for negatives and particulars, test the validity of the following: A
A
E E
O
O E
O
O.
(2a) Paying no regard to “figure,” derive as many conclusions as possible from the following sets of premises: E
I A
E.
Answer:
E
I.
The major premise of this mood, being negative, necessitates a negative conclusion, according to rule 6, and the minor premise, being particular, compels a particular conclusion, according to rule 8. Since the conclusion must be negative and particular, then O is the only one which can be drawn. The completed mood
is E
I
O.
A
E.
This mood must have a negative conclusion, because the minor premise is negative; this would necessitate either E or O; but O as a conclusion would be, in this case, a weakened one; since E distributing both terms would necessarily distribute the minor; which fact would permit the minor to be distributed in the conclusion. Thus the conclusion could just as well be universal as particular. The completed mood
is A
E
E.
(2b) From the following sets of premises derive as many conclusions as possible paying no attention to figure: E
A A
A O
A.
(3a) Making use of all the general rules of the syllogism, test the validity of the following mood in all the
figures: A
A
I.
Answer:
| 1 | 2 | 3 | 4 | ||||
| A | M ― G | G ― M | M ― G | G ― M | |||
| A | S ― M | S ― M | M ― S | M ― S | |||
| I | S ― G | S ― G | S ― G | S ― G |
An underscored symbol indicates a distributed term. Since A distributes its subject, the subjects of both premises are underscored in all the figures. No term is underscored in the conclusions; since I distributes neither term. In the first figure the middle term is distributed in the major premise, and no term is distributed in the conclusion. Since both premises are affirmative, the rules for negatives are not applicable; and as a particular may be drawn from two universals, if there is no violation of the rules for distribution, this mood seems to be valid in the first figure. It is, however, a weakened conclusion; since an A could just as well be drawn. The mood is invalid in the second figure because of undistributed middle, but valid in both the third and fourth; since in both cases the middle term is distributed at least once.
(3b) Determine the validity of the attending moods in all the figures giving reasons: I
A
I A
O
O E
A
O.
(1) Define a logical figure and illustrate by means of some ordinary syllogistic argument.
(2) Symbolize the four figures and give suggestions for remembering them.
(3) Write syllogisms which illustrate each of the four figures.
(4) Define mood as it is used in logic. Illustrate.
(5) How many moods are valid?
(6) Explain by illustration a “weakened conclusion.”
(7) Test the validity of
A
E
E
in the third figure; of E
I
O
in the third.
(8) Independent of all helps, prove the truth of the canons of the first figure.
(9) In a similar way prove the canons of the second, third and fourth figures.
(10) So far as testing arguments is concerned, what use may be made of the special canons of the syllogism?
(11) Offer a few suggestions for remembering the special canons.
(12) Why did Aristotle attach so much importance to reduction in logic?
(13) Justify calling the first figure the “perfect figure,” and the others the “imperfect figures.”
(14) Treat of the relative value of the four figures.
(15) Show by illustration that the second figure is the exclusive figure.
(16) Test the following moods in all the figures: E
I
A
O
A
O
I
A
I
A
E
O
E
I
O
E
A
O
A
E
O
A
I
E
E
E
I
A
O
I
A
A
I
A
I
I.
(1) Give an illustration of a syllogism in the fourth figure which might just as well be written in the first figure.
(2) May a syllogism, which is invalid in the fourth figure, be made valid by writing it in the form of the first figure? Prove it.
(3) Show why it is impossible to apply all the rules of the ***
(4) Show the difference between a direct and an indirect proof.
(5) Show that A
A
O
is valid in the first figure when the major premise (A) is co-extensive.
(6) The third figure is known as the figure of particular conclusions. Why should not the second canon of that figure be, “One premise must be particular” rather than “The conclusion must be particular?”
(7) Show that there is some ground for thinking that, as a final test, moods in the other figures should be reduced to the first.
(8) Illustrate the fact that the second figure is the figure of disproof; whereas the third is the figure of contradictions.
(9) “To be logical a syllogism must conform to one of the four figures, but this does not mean, necessarily, that all arguments must conform to some figure.” Explain this.
An enthymeme is a syllogism in which one of the three propositions is omitted.
Suppressing the major premise gives an enthymeme of the first order; whereas if the minor premise be suppressed, the enthymeme becomes one of the second order; while omitting the conclusions gives an enthymeme of the third order.
Illustrations:
Complete syllogism.
All true teachers are just,
You are a true teacher,
(Hence) You are just.
Enthymeme of first order; major premise omitted.
..........................
You are a true teacher,
(Hence) You are just.
Enthymeme of second order; minor premise omitted.
All true teachers are just,
..........................
(Hence) You are just.
Enthymeme of the third order; conclusion omitted.
All true teachers are just,
(And) You are a true teacher,
..........................
To argue in terms of the complete syllogism is the unusual, not the usual method. We have a way of abbreviating our remarks; expressing only the necessary and leaving the obvious to be taken for granted. Thus the enthymeme becomes the natural form of expression. But the mere fact that a part of the argument is omitted, makes it more essential for the student to think clearly and with careful continuity, that no error may intrude itself.
Probably the most common enthymemes are those of the first order. This may be explained by the fact that the major premise is usually the most universal of the three propositions, and, in consequence, the one which would be the most generally understood. The following represent enthymemes of this order, gleaned from the ordinary conversation of ordinary people:
(1) “Your beets won’t grow, because you are planting them in the wrong time of the moon.”
(2) “You, being a member of the Sunday School, should be ashamed of such language.”
(3) “Being the son of your father, you ought to have some pride in this matter.”
(4) “We are going to have an open winter, because I have observed that the hornets’ nests are near the ground.”
(5) “You had better put in lots of coal, for I have noticed that the squirrels have gathered in more nuts than usual.”
Judging from these enthymemes, it would seem to be more natural to assert the conclusion and follow this by a reason in the form of a minor premise, leaving the major to the intelligence of the auditor.
The enthymeme of the second order occurs only infrequently, since it seems to be an unnatural mode of expression, though sometimes it appears to lend emphasis to the conclusion; e. g., “All untrustworthy boys come to a bad end, and I predict that you will come to a bad end.”
Enthymemes of the third order are commonly used for the sake of emphasis, as the following make evident:
(1) “No business man wants an indolent boy, and you are indolent.”
(2) “All successful teachers are interested in their work, and you plan to be a successful teacher.”
(3) “Humility is a sign of greatness, and Lincoln possessed this quality.”
An epicheirema is a syllogism in which one or both of the premises is an enthymeme. To put it in another way: An epicheirema is a syllogism in which one or both of the premises is supported by a reason.
When one premise is an enthymeme the syllogism is termed a single epicheirema; whereas when both premises are enthymemes it becomes a double epicheirema.
Single epicheirema.
All men are mortal, because all men die,
Socrates was a man,
∴ Socrates was mortal.
Double epicheirema.
All men are mortal, because all men die,
Socrates was a man, because he was a rational animal,
∴ Socrates was mortal.
It is obvious that supporting each premise with a reason lends strength to the argument. This justifies the use of the epicheirema.
A polysyllogism is a series of syllogisms in which the conclusion of a preceding syllogism becomes a premise of a succeeding one.
The syllogism in the series whose conclusion becomes a premise of the succeeding syllogism is termed a prosyllogism; while the syllogism which uses as one of its premises the conclusion of the preceding syllogism is called an episyllogism.
Illustrations.
| Polysyllogism |
 |
A quadruped is an animal, |
 |
Prosyllogism | |
| A dog is a quadruped, | |||||
| ∴ A dog is an animal. |
 | ||||
| Fido is a dog, | Episyllogism | ||||
| ∴ Fido is an animal. | |||||
| Polysyllogism |
 |
All who libel an associate are unprofessional, |
 |
Prosyllogism | |
| This teacher has libelled her associate, | |||||
| ∴ This teacher is unprofessional. |
 | ||||
| All who are unprofessional should be disciplined, | Episyllogism | ||||
| ∴ This teacher should be disciplined. |
A sorites is a series of syllogisms in which all of the conclusions are omitted except the last one.
Just as the epicheirema is a combination of enthymemes of the first and second orders, so the sorites is a combination of enthymemes of the third order. If each conclusion were written, the sorites would take the form of prosyllogisms and episyllogisms. Two forms of the sorites are recognized by logicians. These are the progressive or Aristotelian, and the regressive or Goclenian.
Illustrations.
Progressive
Symbolized. Put in Word Form.
All A is B Thomas Arnold was a teacher,
All B is C A teacher is a man,
All C is D A man is a biped,
All D is E A biped is an animal,
Hence all A is E Hence Thomas Arnold was an animal.
Regressive
All A is B A biped is an animal,
All C is A A man is a biped,
All D is C A teacher is a man,
All E is D Thomas Arnold was a teacher,
Hence all E is B Hence Thomas Arnold was an animal.
When regarded from the viewpoint of extension, the progressive sorites proceeds from the smaller to the larger while the regressive is the converse of this. The point may be illustrated by circles:

FIG. 15.
Circle 1 stands for Thomas Arnold.
Circle 2 stands for teacher.
Circle 3 stands for man.
Circle 4 stands for biped.
Circle 5 stands for animal.
The progressive sorites proceeds from the smaller circle to the larger, thus:
All of circle 1 belongs to 2
All of circle 2 belongs to 3
All of circle 3 belongs to 4
All of circle 4 belongs to 5
Hence, All of circle 1 belongs to 5
The regressive sorites proceeds from the larger to the smaller; i. e.:
All of circle 4 belongs to 5
All of circle 3 belongs to 4
All of circle 2 belongs to 3
All of circle 1 belongs to 2
Hence, All of circle 1 belongs to 5
Other differences become apparent when the omitted conclusions are expressed.
Progressive
Symbolized Word Form
All A is B T. Arnold was a teacher, (A)
All B is C A teacher is a man, (A)
∴ All A is C ∴ T. Arnold was a man. (A)
All C is D A man is a biped, (A)
∴ All A is D ∴ T. Arnold was a biped. (A)
All D is E A biped is an animal, (A)
∴ All A is E ∴ T. Arnold was an animal. (A)
In the three completed syllogisms it becomes evident that the progressive sorites uses the minor as its first premise and in consequence takes the form of the fourth figure, though the reasoning is according to the first figure.
The progressive sorites must conform to the following rules:
(1) The first premise may be universal or particular, all the others must be universal.
(2) The last premise may be affirmative or negative; all the others must be affirmative.
A violation of the first rule would result in undistributed middle; whereas a violation of the second rule would give illicit major. These rules may be illustrated by giving attention to the symbols of the foregoing completed syllogisms.
The first completed syllogism of the sorites is:
All A is B
All B is C
∴ All A is C
Securing a logical arrangement by interchanging the major and minor premises gives:
(A)
All
(M)
B
is (G)
C
(First premise universal)
(A)
All
(S)
A
is (M)
B
(A)
∴ All
(S)
A
is (G)
C
Applying the rules we find this syllogism valid, or we may recall that
A
A
A
is valid in the first figure.
Let us now make the first premise of the sorites particular and test.
Some A is B
All B is C
∴ Some A is C
Arranged logically:
(A)
All
(M)
B
is (G)
C
(I)
Some
(S)
A
is (M)
B
(I)
∴ Some
(S)
A
is (G)
C
Proof:
Since one premise is particular the conclusion must be particular. (Rule 7) As there are no negatives in the argument, only one conclusion is possible; namely, a particular affirmative (I). Thus, instead of the conclusion, “All A is C,” which is an (A), it must be, “Some A is C,” or an (I). Underscoring the distributed term, it is seen that the middle term is distributed in the major premise and that no term is distributed in the conclusion. Thus the mood is valid. This is “checked” when we recall that AII is always valid in the first figure. We have now shown that the first premise of a progressive sorites may be universal or particular. Let us further proceed to prove that all the other premises must be universal.
Data: Given the first completed syllogism of the sorites:
All A is B
All B is C
∴ All A is C
Proof: Let any other premise, such as the second, be particular; this gives the following:
All A is B
Some B is C
∴ Some A is C
Arranged logically: Mood, figure, and distribution indicated.
(I)
Some
(M)
B
is (G)
C
(A)
All
(S)
A
is (M)
B
(I)
∴ Some
(S)
A
is (G)
C
We note at once that the middle term is undistributed, hence the mood I
A
I
is invalid in the first figure; reference to the valid moods in figure one “checks” this conclusion. Since no premise, other than the first, can be particular, then all save the first must be universal.
The truth of the first rule has been demonstrated, and now we may follow a similar plan to prove the truth of the second rule.
Problem: To prove that the last premise may be negative.11
Data: Given the last completed syllogism:
 All A is D
All A is D
All D is E
∴ All A is E
Let us make the last premise negative (E) and test the result. (As all but the first must be universal we cannot use an O.)
All A is D
No D is E
∴ No A is E
Arranged logically and symbolized:
(E)
No
(M)
D
is (G)
E
(A)
All
(S)
A
is (M)
D
(E)
∴ No
(S)
A
is (G)
E
Proof: Negative premise; negative conclusion. No particulars. Middle term distributed in major premise. No term distributed in conclusion which is not distributed in premise where it occurs. Syllogism valid. We must now prove that all the other premises must be affirmative.
Problem: To prove that no other premise can be negative, or that all others must be affirmative.
Data: Given last syllogism of sorites with the first premise negative. (Any other may be taken.)
No A is D
All D is E
∴ No A is E
Arranged logically and symbolized:
(A)
∴ All
(M)
D
is (G)
E
(E)
No
(S)
A
is (M)
D
(E)
∴ No
(S)
A
is (G)
E
Proof: “G” is distributed in the conclusion but not in the major premise. Fallacy of illicit major. Hence no other premise can be negative.
We may now consider the completed syllogisms of the regressive sorites.
All A is B
All C is A
∴ All C is B
All D is C
∴ All D is B
All E is D
∴ All E is B
By examining the foregoing it becomes apparent that the regressive sorites, both in form and in the reasoning, adapts itself to the first figure.
The rules of the regressive sorites are just the reverse of the progressive. These are:
(1) The first premise may be negative; all the others must be affirmative.
(2) The last premise may be particular; all the others must be universal.
It would be a valuable exercise for the student to test these rules according to the plan pursued in treating the progressive sorites.
It has been intimated that a syllogistic argument, in order to be logical, should be made to conform to the rules of the syllogism. It must not be inferred from this, however, that all deductive reasoning is included by the logical forms here treated. There seem to be arguments which yield valid conclusions, and yet which are not logical in the strict sense of the word. The following illustrate some of these forms:
(1) Quantitative Arguments.
John is taller than James,
Albert is taller than John,
∴ Albert is taller than James.
Here, apparently, is a fallacy of four terms: these four terms are (1) John, (2) taller than James, (3) Albert, (4) taller than John. Yet we know that the argument is valid. There is not a particle of doubt in the mind relative to the truth of the conclusion that “Albert is taller than James.” We are consequently forced to the inference that such quantitative arguments lie outside the field of syllogistic reasoning. The argument involves this new principle, “Whatever is greater than a second thing which is greater than a third thing is itself greater than a third thing.”
There are many other arguments similar to this which are not syllogistic in nature. To wit: A equals B, B equals C, C equals D; A equals D. A is a brother of B, B is a brother of C, C is a brother of D; A is a brother of D. A is west of B, B is west of C, C is west of D; A is west of D.
(2) Plurative Arguments.
These are arguments in which the propositions are introduced by more or most; e. g.:
Most (more than half) of the team are seniors,
Most (at least half) of the team are under twenty,
∴ Some students under twenty are seniors.
Here we have an
I
I
I
which is evidently valid. No term distributed and yet the conclusion is unquestionably true. This is due to the fact that the propositions are so worded as to force an overlapping of the major and minor terms. The student may illustrate this relation by circles.
INCOMPLETE SYLLOGISMS AND IRREGULAR ARGUMENTS.
(1) Enthymeme.
First, second and third orders.
Natural form.
(2) Epicheirema.
Single, double.
(3) Polysyllogism.
Prosyllogism, episyllogism.
(4) Sorites.
Progressive, regressive.
Two rules of each.
(5) Irregular Arguments.
Quantitative, plurative.
(1) An enthymeme is a syllogism in which one of the three propositions is omitted. Suppressing the major premise gives an enthymeme of the first order; omitting the minor gives one of the second order; while omitting the conclusion gives one of the third order.
The enthymeme is really the natural form of expression. Enthymemes of the first order are the most common while those of the third order are the most emphatic.
(2) An epicheirema is a syllogism in which one or more of the premises is an enthymeme. An epicheirema is said to be single when but one premise is an enthymeme, and double when both premises are enthymemes.
(3) A polysyllogism is a series of syllogisms in which the conclusion of the preceding syllogism becomes a premise of the succeeding one. The one of the series whose conclusion becomes a premise is termed a prosyllogism; while the one which uses the conclusion as a premise is called an episyllogism.
(4) A sorites is a series of syllogisms in which all the conclusions are omitted except the last one.
The two kinds of sorites are the progressive and regressive. The progressive uses the “minor” as its first premise and adopts the form of the fourth figure, whereas the regressive uses the “major” as its first premise and adopts the form of the first figure.
The two rules of the progressive sorites are, (1) “The first premise may be particular, all the others must be universal”; (2) “The last premise may be negative, all the others must be affirmative.”
The two rules of the regressive are, (1) “The first premise may be negative, all the others must be affirmative”; (2) “The last premise may be particular, all the others must be universal”.
(5) Irregular arguments are such as yield valid conclusions and yet do not conform to the syllogistic rules.
The quantitative argument expresses quantity and contains four terms. This argument is based on the principle, “What ever is greater than a second thing which is greater than a third thing is itself greater than a third thing.”
Plurative arguments are introduced by “more” or “most” and give in consequence a valid conclusion from two particulars. This is due to the overlapping of the major and minor terms.
(1) Define and illustrate an enthymeme.
(2) Illustrate the enthymemes of the three orders and point out their distinct uses.
(3) Why should the enthymeme demand closer thought than the ordinary syllogism?
(4) Define and illustrate the epicheirema.
(5) Of what use is the epicheirema? Illustrate.
(6) Define and illustrate a prosyllogism and an episyllogism.
(7) Why are polysyllogisms so called?
(8) Define and illustrate the sorites.
(9) Relate the sorites and the epicheirema to the enthymeme.
(10) Illustrate the two forms of sorites.
(11) Explain the two forms of sorites by means of a diagram.
(12) Prove the truth of the two rules of the progressive sorites.
(13) Illustrate two kinds of irregular arguments and show that they are valid.
(14) Complete the five enthymemes of page 248 and indicate their mood and figure.
(1) Why should enthymemes of the second order be less common than those of the first?
(2) You desire to make it evident to a child that a small beginning often leads to a momentous ending; do so in terms of the enthymeme of the first order.
(3) Show that prosyllogism and episyllogism are relative terms.
(4) When the common premise of the “pro” and “epi” syllogism is omitted what abbreviated form results?
(5) From the viewpoint of your definition criticise this: “A sorites is a series of prosyllogisms and episyllogisms in which all of the conclusions are suppressed except the last.”
(6) Prove the truth of the two rules of the regressive sorites.
(7) Show that the prosyllogism and the episyllogism may be progressive or regressive.
(8) “Reasoning from cause to effect”—is such progressive or regressive? Explain.
(9) Which is inductive in nature, the progressive form of reasoning or the regressive? Explain.
(10) Test the validity of the enthymemes on pages 248 and 249.
(11) “A sorites is at least as immediately convincing as the chain of syllogisms into which it can be decomposed.” Discuss this.
The matter relative to the syllogism treated in chapters 11, 12 and 13 is given primarily to enable the reader to test the validity of categorical arguments. Such arguments must be viewed from the two standpoints of form and matter, since it is one of the chief purposes of logic to enable the student to detect fallacious reasoning, no matter how subtly it may be concealed. Therefore, that one may gain marked facility in this kind of work, it becomes necessary to proceed with thoroughness and confidence. The meaning of arguments and the various material fallacies may be treated later; but we are now equipped with sufficient knowledge and experience to test the validity of arguments from the viewpoint of form.
In testing categorical arguments three things are essential; first, to follow a definite plan; second, to give reasons; third, to give the author the benefit of the doubt. In view of these essentials, we suggest this outline which may be helpful to the inexperienced:
(1) Arrange logically and complete the syllogism.
(2) Determine the figure and mood by using symbols.
(3) Apply the rules for negatives and particulars.
(4) Indicate the distribution by underscoring the terms distributed.
(5) Apply the rules for distribution.
(6) Name fallacies, if any, giving reasons.
We recall that to be strictly logical any categorical argument must take this form: first, major premise; second, minor premise; third, conclusion. Often in common conversation either the minor premise or conclusion is given first. Illustrations of this: (1) “He cannot be a gentleman (conclusion); for no gentleman would do such a thing (major premise), and there is no doubt but that he did it” (minor premise). (2) “He has the making of a good teacher (conclusion); because he not only knows, but he knows how to impart what he knows (minor premise), and this is a sure sign of a good teacher” (major premise). When the argument appears in this illogical form, the first duty of the student is to arrange it logically. To do this he must be able to recognize readily the premises and the conclusion. To this end these facts may be of assistance:
(1) A premise always answers the question “Why”, and is often introduced by such words as “for,” “because,” “since,” and the like.
(2) The conclusion is usually introduced by “therefore,” “hence,” “it follows,” etc.
(3) When there are no word-signs those mentioned in the foregoing may be inserted with a view of determining which is the conclusion, and which are the premises.
Suggestions relative to completing abbreviated arguments:
(1) If the conclusion is to be supplied, select the term used twice in the premises; this, the middle term, must not appear in the conclusion. The other two terms may now be connected (copulated) to form the conclusion, the narrower term (minor) being used as the subject, unless it occurs in what clearly seems to be the major premise. (2) If either premise is to be supplied, unite the middle term with the subject of the conclusion for the minor premise, and with the predicate of the conclusion for the major premise. (3) In supplying any missing proposition, care should be taken to make the argument valid, if this can be done in conformity with good English, good sense, and the rules of logic.
As regards the determination of the figure it is well to locate the middle term first, placing above it the symbol M. Then “G” (greater) may be placed above the major term and “S” (smaller) above the minor.
(1)
A
All
M
dogs
are G
quadrupeds,
A
All
S
greyhounds
are M
dogs,
A
∴ All
S
greyhounds
are G
quadrupeds.
This argument is in the first figure, the mood being
 A
A
A
A.
All the propositions are affirmative and universal, consequently the rules pertaining to negatives and particulars are inapplicable. “A” distributes the subject only, hence all the subjects are underscored. The middle term “dog” is distributed in the major premise, and the minor term “greyhound,” which is distributed in the conclusion, is likewise distributed in the minor premise. The argument is, therefore, valid in form. This may be verified by referring to a list of valid moods in the first figure.
(2)
E
No
G
prejudiced person
is M
open to conviction,
A
All
S
fair minded persons
are M
open to conviction,
E
∴ No
S
fair minded person
is G
prejudiced.
The argument is in the second figure; mood
 E
E
A
E.
There is one negative premise and the conclusion is negative; no particulars. “E” distributes both terms, “A” the subject only. The middle term is distributed in the major premise. Both major and minor terms are distributed in the conclusion, but they are likewise distributed in the premises where they are used. The argument is, therefore, valid. Reference to the valid moods of the second figure confirms this conclusion.
(3)
A
All
M
good citizens
G
vote,
A
All
M
good citizens
S
obey the law,
A
∴ All
S
who obey the law
G
vote.
The mood is
 A
A
A
A
used in the third figure. All the propositions are A’s, hence the negative and particular rules are inapplicable. “A” distributes its subject. The middle term is distributed in both premises. “All who obey the law” is distributed in the conclusion but not in the premise where it is used. Therefore the argument is invalid. The fallacy being illicit minor.
 A
A
A
A
is not found in the third figure’s list of valid moods.
(4)
A
All
M
good citizens
G
vote,
E
No
S
criminal
is a M
good citizen,
E
∴ No
S
criminal
G
votes.
The mood of this argument is
 A
A
E
E
used in the first figure. One premise negative; conclusion negative; no particulars. “A” distributes the subject only; “E” both subject and predicate. The middle term, “good citizens,” is distributed in both premises. The major term, “votes,” is distributed in the conclusion but not in the premise where it is used. The argument is invalid, the fallacy being illicit major.
 A
A
E
E
is not found in the first figure’s list of valid moods.
(5)
A
All
G
true teachers
are M
sympathetic,
A
All
S
lovers of children
are M
sympathetic,
A
∴ All
S
lovers of children
are G
true teachers.
The mood of this argument is
 A
A
A
A
used in the second figure. There are no negatives and no particulars. “A” distributes its subject only. The middle term, “sympathetic,” is distributed in neither premise, hence the argument is invalid. Fallacy of undistributed middle. Referring to the list of valid moods, we do not find
 A
A
A
A
in the second figure.
(6)
A
All
M
thoughtful men
are G
humane,
A
All
S
good citizens
are M
thoughtful men,
I
∴ Some
S
good citizens
are G
humane.
The mood is
 A
A
A
I
in the first figure. No negatives; no particulars. “A” distributes its subject only; “I” distributes neither term. Middle term, distributed in the major premise; no term distributed in the conclusion. The argument is, therefore, valid. The conclusion is weakened as it could just as well be an A. The mood
 A
A
A
I
in the first figure is valid, but of little value because of the weakened conclusion.
Arguments containing exclusive propositions.
(1) Only first class passengers may ride in the parlor car,
All these are first class passengers,
∴ They may ride in the parlor car.
Propositions introduced by such words as only, none but, alone and their equivalents are exclusive propositions. Since these distribute their predicates, but do not distribute their subjects, the most convenient way of dealing with them is to interchange subject and predicate and then regard them as “A” propositions. As the first proposition of the argument is an exclusive, we must deal with it accordingly. Interchanging subject and predicate and introducing it with all places the argument in this form:
A
(All)
The G
parlor car
is reserved for M
first class passengers,
A
All S
these
are M
first class passengers,
A
∴ All
S
these
may ride in the G
parlor car.
The mood of this argument is
 A
A
A
A
in the second figure. No negatives; no particulars. “A” distributes its subject only; the middle term is thus undistributed. The argument is invalid, the fallacy being that of undistributed middle.
(2) “No one but a thief would take these books without asking for them, and it has been proved that you took the books; that is the reason I have called you a thief.”
It is clear that “no one but” is equivalent to “only.” Thus the first proposition of the argument is an exclusive, and may be made logical by interchanging subject and predicate and calling it an “A.” As a result of this the argument takes the following form:
A
(All)
These M
books
were taken by a G
thief,
A
S
You
took these M
books,
A
∴ S
You
are a G
thief.
We have now had sufficient experience to recognize the validity of mood AAA in the first figure.
(3) “None but the brave deserve the fair,
And you are not fair.”
Making the exclusive logical and completing gives:
A
(All)
The M
fair
deserve the G
brave,
E
S
You
are not M
fair,
E
∴ S
You
do not deserve the G
brave.
The mood of this argument is
 A
A
E
E
used in the first figure. There is a negative premise, also a negative conclusion; no particulars. The middle term is distributed twice. The major term “brave” is distributed in the conclusion but not in the major premise; hence the argument is invalid, the fallacy being illicit major.
NOTE.—There may be some doubt in the student’s mind as to the proposition “None but the brave deserve the fair,” really meaning “All the fair deserve the brave.” This doubt may be better satisfied by treating the exclusive in the second way as indicated on page 137, to wit: Negate the subject of the exclusive, then give it the form of the regular “E.” This results in “No not-brave persons deserve the fair,” which, after first converting and then obverting becomes, “All the fair deserve the brave.”
Arguments Containing Individual Propositions.
(4) “George Washington never told a lie, but you, when tempted, yielded with no qualms of conscience.”
Completing, and arranging logically gives:
E George Washington never told a lie,
A You did tell a lie,
E ∴ You (in this respect) are not like George Washington.
Treated properly this argument proves to be valid; the student, however, is apt to deal with such in this wise:
O George Washington never told a lie,
I You did tell a lie,
O ∴ You (in this respect) are not like George Washington.
When placed in this mood the argument is invalid; since the major term, which is distributed in the conclusion, is not distributed in the premise where it occurs (illicit major). It is the tendency on the part of students to classify as particular, a proposition which has as its subject a singular term. Such propositions we have learned to call individual. The cause of this tendency is easily explained: Consider the propositions, (1) “This man is mortal”; (2) “Some men are mortal”; (3) “All men are mortal.” In the first instance “mortal” refers to the subject “man” which is narrower in significance than “some men” to which “mortal” of the second proposition refers. In consequence, it is very natural to infer that if, “Some men are mortal,” is particular, then, “This man is mortal,” is likewise particular. The error springs from a wrong conception of particular as used in logic; the content of the term has little to do with extension, but is chiefly concerned with indefiniteness. A particular proposition is one in which the predicate refers to only a part of an indefinite subject. If the subject is referred to as a whole, and this whole is more or less definite, then the proposition is universal. Since “mortal” refers to the whole of the definite term “this man,” as positively as it refers to the whole of “all men,” there is as much justification in calling the first proposition universal as there is in calling the third universal. It may be remembered, then, that logicians class as universal all individual propositions.
Arguments Containing Partitive Propositions.
(5) All that glitters is not gold,
Tinsel glitters,
∴ Tinsel is not gold.
The quantity sign “all” when used with “not” is ambiguous; it may mean “no” or “some-not.” The only way to determine which meaning is intended is to try both these quantity signs, selecting the one which seems to fit best the author’s meaning. When “all-not” means “some-not” the proposition which it introduces is called a partitive proposition; since such always suggests a complementary proposition. (See page 133.) For example, “Some glittering things are not gold,” suggests its complement, “Some glittering things are gold.” In testing the foregoing argument it is clear that “All that glitters is not gold” does not mean “No glittering thing is gold,” so much as it implies “Some glittering things are not gold.” Thus the argument takes this form:
O
Some
M
glittering things
are not G
gold,
A
S
Tinsel
M
glitters,
E
∴ S
Tinsel
is not G
gold.
The mood is
 O
O
A
E
in the first figure. There is one negative premise (O), and the conclusion is negative. There is one particular premise (O), but the conclusion is not particular. This makes the argument invalid according to rule 8;
viz.:
“A particular premise necessitates a particular conclusion.” Carrying the test still further it will be seen that there is likewise the fallacy of undistributed middle.
Other arguments where one of the premises is partitive.
“All scholars are not wise and, therefore, Aristotle was not wise.” “All democrats are not free-traders, but most of the men of this particular club are democrats, and hence they are of a different faith (not free-traders).”
“All the members of the club are not good players, and James belongs to the club.”
“All educated men do not write good English; therefore, you ought not to express surprise when informed that X, though an educated man, uses poor English.”
The major premise in each of the foregoing is partitive in nature and should be changed to the following form before the argument is tested; taking these in order we have: “Some scholars are not wise”; “Some democrats are not free-traders”; “Some of the members of the club are not good players”; “Some educated men do not write good English.” Let us test the validity of the last one:
(6) O Some educated men do not write good English,
A X is an educated man,
E ∴ X does not write good English (uses poor English).
Like the first one of the list, this is invalid inasmuch as a particular premise should yield a particular conclusion, not one which is universal. The argument also contains the fallacy of undistributed middle.
Arguments Containing Inverted Propositions.
(7) “Blessed are the merciful: for they shall obtain mercy.” The first proposition, being poetical in construction, is typical of the inverted form. These are usually made logical by simple conversion. Since premises usually follow “for,” or equivalent word-signs, it is easy to see that “for they shall obtain mercy” is one of the premises; while the other, the broader of the two, is understood.
Arranged logically the argument assumes this form:
A
Those
who M
obtain mercy
are G
blessed,
A
The
S
merciful
shall M
obtain mercy,
A
∴ The
S
merciful
are G
blessed.
Here we have the mood
 A
A
A
A
in the first figure, which we know to be valid.
Other arguments where one of the propositions is inverted.
“Blessed are the pure in heart: for they shall see God.”
“To thine own self be true, and it must follow, as the night the day, thou canst not then be false to any man.”
“A king thou art and, therefore, thy commands shall be, yea, must be obeyed.”
Taking the inverted propositions in order and making each logical, the following is the result: “The pure in heart are blessed”; “You be true to yourself, and....”; “You are a king, therefore....”
(1) “He must be a star player; for he played fullback on the team which won the championship.”
(2) “The man is not to be trusted; because he served a term of 90 days in jail.”
(3) “Only material bodies gravitate, and ether does not gravitate.”
(4) “If only fools despise knowledge, this man cannot be a fool.”
(5) “A charitable man has no merit in relieving distress; because he merely does what is pleasing to himself.”
(6) “It is evident that all who get justice buy it; since only the rich get it.”
The above arguments thrown into logical form and validity or invalidity stated: (The student should test these in detail.)
(1)
A
All
M
belonging to the team which won the championship
were star G
players,
A
S
He
played with the M
team
which won the championship,
A
∴ G
He
is a star player. Valid in form.
(2)
E
M
One who serves a term of 90 days in jail
is not to be G
trusted,
A
This
S
man
served a M
term
of 90 days in jail,
E
∴ This
S
man
is not to be G
trusted.
Valid in form.
(3)
A
All
M
gravitating bodies
are G
material,
E
S
Ether
does not M
gravitate,
E
∴ S
Ether
is not G
material. Illicit major.
(4)
A
All
M
who despise knowledge
are G
fools,
E
This
S
man
does not M
despise knowledge,
E
∴ This
S
man
is not a G
fool. Illicit major.
(5)
E
No
M
one who merely does what is pleasing to himself
has G
merit in relieving distress,
A
A
S
charitable man
merely does what is M
pleasing to himself,
E
∴ No
S
charitable man
has G
merit in relieving distress.
Valid in form.
(6)
A
All
M
the rich
buy G
justice,
A
All
S
who get justice
are M
rich,
A
∴ All
S
who get justice
buy G
it.
Valid in form.
In supplying suppressed premises the critic is duty bound to give the author the benefit of the doubt, if by so doing no principle in logic is violated and the proposition conforms to good English and good sense. Often it is not easy to perceive in the abbreviated argument the meaning intended; in such instances all legitimate effort should be directed to making the argument valid. To illustrate: In supplying the major premise of argument “6” it would be easy to make it, “All justice is bought by the rich”; in consequence the critic could pronounce the argument invalid as the middle term would be undistributed.
Before asserting that an argument is fallacious because it has four terms rather than three, the student must make sure that there are no synonyms or equivalents used. In argument “4,” for instance, there are apparently the four terms: (1) “foolish,” (2) “despise knowledge,” (3) “man,” (4) “fool”; but to regard “foolish” and “fool” as synonyms does not seem like undue liberty. The following arguments further illustrate this need of recognizing synonyms:
“Human beings are accountable for their conduct; brutes, not being human, are therefore free from responsibility.” (Not accountable for their conduct.)
“Not all educated men spell correctly; because one often finds mistakes in the writings of college graduates.” (Educated men.)
“Modern education is not popular in this state; for it increases the tax rate, and the popularity of everything, which touches the pocket of these frugal Yankees, (increases the tax rate) is very short lived.” (Not popular.) In common parlance the use of synonyms is so prevalent that ready ability to substitute equivalents in word, phrase, and clause form is needed by him who would be skillful in testing all kinds of arguments.
It has already become apparent to the student that the number of the noun or the tense of the verb is of small logical consequence. A very large proportion of the formal fallacies in argumentation concern the rules of distribution which are summarized in the dictum “What may be said of the whole may be said of part of that whole.”
The most common mistakes made by the student when testing arguments are as follows: (1) Using the exclusive as an “A” without interchanging subject and predicate; e. g., interpreting the proposition, “Only high school graduates may enter the training school,” as meaning “All high school graduates may enter the training school.” (2) Calling individual propositions particular; e. g., interpreting “Socrates is mortal” as an “I” rather than an “A.” (3) Signifying that partitive propositions are “A’s” rather than “O’s”; e. g., “All that glitters is not gold” interpreted as meaning that “All glittering things are gold,” rather than “Some glittering things are not gold.” (A). (4) Concluding that a fallacy of four terms has been committed when two terms are synonomous. (5) Failing to interchange the subject and predicate of inverted propositions.
CATEGORICAL ARGUMENTS TESTED ACCORDING TO FORM.
(1) Arguments of form and matter.
(2) Order of procedure in the formal testing of arguments.
The outline.
Determining premises and conclusion.
Completing abbreviated arguments.
(3) Illustrative exercises in testing arguments which are complete and whose premises are logical.
(4) Illustrative exercises in testing completed arguments, one or both of whose premises are illogical.
Exclusive premises, individual premises, partitive premises, inverted premises.
(5) Incomplete and irregular arguments.
(6) Common mistakes of the student.
(1) In determining their validity, arguments must be tested from the two viewpoints of form and matter.
(2) In testing categorical arguments it is quite necessary to be definite, to give reasons, and to give the author the benefit of the doubt.
With this in view the attending outline is suggestive:
1. Arrange logically and complete.
2. Determine the figure and mood.
3. Apply rules for negatives and particulars.
4. Indicate distribution.
5. Apply rules for distribution.
6. Name fallacies, if any, giving reasons.
The logical arrangement of syllogistic arguments is
1. Major premise.
2. Minor premise.
3. Conclusion.
Any proposition in a syllogism which answers the question “Why?” is a premise, whereas the conclusion follows “therefore”, or its equivalent either written or understood. If a conclusion is to be supplied, unite the two terms which are used but once in the premises, using the “minor premise term” as the subject. If a premise is to be supplied, unite the middle term with the “minor” to form the minor premise and with the “major” to form the major premise.
(3) Arguments which are regular, complete, and logically arranged, may be tested by symbolizing the mood and figure, underscoring the distributed terms, and then applying the general rules of the syllogism.
(4) Arguments with illogical premises may not be tested with impunity till the faulty premises are made logical. The exclusive, an illogical proposition introduced by only, alone, none but, and the like, may be made logical by interchanging subject and predicate and calling the proposition an A. The individual proposition is one with a singular subject. In testing, individual propositions are classed as universal. Propositions introduced by “all-not” are usually given the significance of “some-not”. These are called partitive propositions, which in the testing, should be denominated “O’s”.
Inverted propositions when subjected to the test for validity must be converted simply and then classified. (Usually as A’s.)
(5) In supplying propositions which are taken for granted, the aim should be to make the argument valid, provided this can be done without violating the rules of logic, English, and common sense.
Ability to substitute equivalent words, phrases, or clauses is demanded of the student of logic, inasmuch as such substitution is frequently needed in the testing of arguments.
Number and tense have little significance in dealing with arguments.
(6) The common mistakes of students made in testing arguments concern exclusive, partitive and inverted propositions, and an inability to recognize expressions equivalent in meaning.
(1) Name and explain the two standpoints from which all arguments must be viewed.
(2) Give an outline of procedure which may be serviceable in the testing of categorical arguments.
(3) Give illustrations showing that the logical order of categorical arguments is not the usual mode of procedure in common parlance.
(4) Offer suggestions which may aid in designating a premise; a conclusion.
(5) How would you proceed in forming any one of the three propositions of a syllogism when the other two are given?
(6) Designate the premises and the conclusion in the following, supplying any proposition which may be omitted, also arrange logically and test the validity.
(1) “The people of this country are suffering from an overdose of prosperity; consequently a period of hard times will be a valuable lesson.” (The conclusion should be recast so as to read, “A period of hard times will cure the people of this country.” The minor premise is, “Those who suffer from an overdose of prosperity may be cured by a period of hard times.”)
(2) “I am a teacher; you are not what I am; hence you are not a teacher.”
(3) “To kill a man is murder, therefore war is murder.”
(4) “You have not adopted the best policy since honesty has always been and will always be the best policy.”
(5) “Since the road is criminally mismanaged, why should not the authorities be indicted as criminals?”
(6) “Early to bed and early to rise makes a man healthy, wealthy and wise. I am none of these; hence my sleeping hours have been wrong.”
(7) Illustrate a weakened conclusion.
(8) Explain the exclusive proposition and indicate how the logician should treat it.
(9) Arrange logically and test the following:
(1) Only weak men become intemperate, and Edgar Allen Poe was surely intemperate.
(2) No admittance except on business; hence you cannot be admitted.
(3) Virtuous acts are praiseworthy, and indiscriminate giving is not a virtuous act.
(10) Explain why individual propositions are classed as universal.
(11) Write an argument whose major premise is a partitive proposition; arrange logically and test validity.
(12) Arrange and test this argument: “Blessed are the poor in spirit: for theirs is the kingdom of heaven.”
(13) Complete, arrange and test.
(1) “The object of war is to settle disputes; hence soldiers are the best peacemakers.”
(2) “The various species of brutes being created to prey upon one another proves that man is intended to prey upon them.”
(3) “The end of everything is its perfection; death being the end of life is its perfection.”
(4) “All the trees of the yard make a thick shade and this is one of them.”
(5) “Minds of moderate caliber ordinarily condemn everything which is beyond their range, and his is such a mind.”
(6) “The best of all medicines are fresh air and sleep, and you are sorely in need of both.”
(7) “Every hen comes from an egg; every egg comes from a hen; therefore every egg comes from an egg.”
(8) “He cannot have been there—otherwise I should have seen him.”
(14) “It is fair to give the author the benefit of the doubt when we set ourselves up as censors worthy of the name.” Explain this.
(15) Illustrate by citing arguments the need of detecting terms which are equivalents in signification.
(16) How does the logician look upon number and tense as treated in grammar?
(17) Illustrate and test an argument in which one of the premises is elliptical.
(18) Summarize the most common mistakes made by students in the testing of categorical arguments; illustrate these mistakes and then write in logical form.
(1) Give illustrations of arguments which are valid in form but invalid in meaning. Explain.
(2) May an argument be valid in meaning but invalid in form? Exemplify.
(3) Put a simple problem in arithmetic in syllogistic form and show that the minor premise naturally comes first.
(4) In the practice of law is there any custom analogous to giving the author the benefit of the doubt in logical argumentation?
(5) Test in detail the following arguments:
(1) “All wise presidents strive to give heed to the demands of the people, but this president has not done so.”
(2) “The existence of God is not universally believed, hence it cannot be true.”
(3) “The institution has prospered under the present régime therefore why change it?”
(4) “The man is guilty because seven out of the nine witnesses so testified.”
(5) “I know three men who cleared not less than ten thousand dollars in this business; and why cannot I do as much?”
(6) “Only members may vote and, since you are not a member, you will not be allowed to vote.” Change the exclusive in this argument in the two ways suggested in Chapter 8, page 126. Test the argument in both cases.
(7) Show by illustration that the quantity sign “all” when used with “not” may in some cases mean “no” and in others “some-not”.
(8) Make two selections from some poet of authority representing arguments with an inverted premise.
(9) Select from news papers three arguments which seem to illustrate the fallacy of four terms but which in reality do not. Explain.
(10) Wherein could the elliptical proposition lead to error?
(11) Put the following in syllogistic form and test:
(1) “That persons may reason without language is proven by the circumstances that infants reason and yet have no language.”
(2) “The scriptures cannot come from God because they contain some things which cannot be comprehended by man.”
(3) “When Columbus was sailing the ocean in search of a new world, he fell in with a flock of land birds and concluded that he could not be far from land.”
(4) “Bolingbroke in arguing against the truth of the Christian religion shows that the Christian religion has bred contentions.” “Burke answered him by showing that civil government had bred contentions.”
The proposition, constituting the basic unit of the argument, would of necessity be indicative of the nature of said argument; therefore the three general kinds of propositions, categorical, hypothetical and disjunctive, suggest the three kinds of arguments which are in turn categorical, hypothetical and disjunctive. Categorical arguments are those in which all of the propositions are categorical. Since this kind has been treated, it remains for us to consider the other two.
We have observed that a hypothetical proposition is one in which the assertion depends on a condition; for example, in the proposition, “If it is pleasant, I will call on you to-morrow,” the calling depends on the state of the weather. “I will call on you to-morrow,” is the assertion which is limited by the condition, “If the weather is pleasant.” Definition:
The hypothetical argument or syllogism is one in which the major premise is hypothetical and the minor premise categorical.
ILLUSTRATION:
If the people are right more than half of the time, the world will progress;
And the people are right more than half of the time,
Hence the world will progress.
In contradistinction to disjunctives, hypothetical propositions and hypothetical syllogisms are frequently referred to as “conjunctive.”
Facility in detecting the antecedent and consequent of hypotheticals is required in order to deal intelligently with the argument. The hypothetical proposition has been defined as one in which the assertion is limited by a condition. The consequent is the assertion and usually follows (though not always) the antecedent which is the limiting condition. First the antecedent and then the consequent is the logical order as the derivative meaning of the words antecedent and consequent would indicate. The antecedent is introduced by such words as “if,” “though,” “unless,” “suppose,” “granted that,” “when,” etc.
ILLUSTRATIONS:
| Antecedent. | Consequent. |
| 1. If you study, | you will pass. |
| 2. If it rains, | it is cloudy. |
| 3. If two is added to three, | the result is five. |
| 4. If you are temperate, | you will live to a ripe old age. |
| Consequent. | Antecedent. |
| 5. I will go, | unless you wire me to the contrary. |
| 6. I will pay you, | when you present your bill. |
| 7. I shall make the trip in ten hours, | granted that I have no accidents. |
| 8. My overcoat would not have been stolen, | if the door had been locked. |
The two kinds of hypothetical syllogisms are the constructive and destructive.
A constructive hypothetical syllogism is one in which the minor premise affirms the antecedent.
A destructive hypothetical syllogism is one in which the minor premise denies the consequent.
The constructive hypothetical is sometimes referred to as the “modus ponens”; whereas the destructive hypothetical is called the “modus tollens.”
ILLUSTRATIONS:
| Constructive Hypothetical Syllogisms. | |
| Symbols. | Words. |
| If A is B, C is D | If you are diligent, you will succeed; |
| A is B | And you are diligent, |
| ∴ C is D | Therefore you will succeed. |
| Destructive Hypothetical Syllogisms. | |
| If A is B, C is D | If you had been diligent, you would have succeeded; |
| C is not D | But you did not succeed, |
| ∴ A is not B | Therefore you were not diligent. |
From a given hypothetical proposition it is possible to construct four different hypothetical syllogisms, as the attending illustrations make evident:
Consider the hypothetical proposition “If it has rained, the ground is damp.”
(1) Minor premise affirms antecedent.
If it has rained, the ground is damp;
It has rained,
Therefore the ground is damp.
(2) Minor premise denies antecedent.
If it has rained, the ground is damp;
It has not rained,
Therefore the ground is not damp.
(3) Minor premise affirms consequent.
If it has rained, the ground is damp;
The ground is damp,
Therefore it has rained.
(4) Minor premise denies the consequent.
If it has rained, the ground is damp;
The ground is not damp,
Therefore it has not rained.
Without any knowledge of the rules of the hypothetical syllogism let us strive to determine how many of the foregoing are valid. Relative to the first, it would be impossible for any rain to fall without making the ground somewhat damp; a few drops would be sufficient. In short, if the antecedent happens, the consequent must follow. It seems, therefore, that the first argument is valid. Considering the second: rain is not the only cause for the dampness of the ground, as it might result from the falling of dew, or from a dense fog; no rain does not necessarily mean no dampness. It is clear that if the antecedent does not happen, the consequent may or may not follow. Thus it appears that the second argument is invalid. Attention to the third makes evident a condition similar to the second: the ground may be made damp by agencies other than rain, such as fog and dew. Thus the third argument is likewise invalid. But in the fourth argument it is obvious that if the ground is not damp, then there could have been neither rain, nor fog, nor dew. No dampness shuts out all of the conditions, including the rain. Therefore the fourth argument is valid.
This investigation suggests a rule for hypothetical arguments. Since only the first and fourth arguments are valid, this is the rule which must obtain: The minor premise should either affirm the antecedent or deny the consequent.
Any violation of this rule would result in the fallacies of denying the antecedent or affirming the consequent.
There is one exception to this rule which must not be overlooked; viz.: If the antecedent and consequent of the hypothetical proposition are co-extensive then both may be either affirmed or denied.
ILLUSTRATIONS:
(1) If the rectangle is equilateral, then it is a square;
The rectangle is equilateral,
∴ It is a square.
(2) If the rectangle is equilateral, then it is a square;
The rectangle is not equilateral,
∴ The rectangle is not a square.
(3) If the rectangle is equilateral, then it is a square;
It is a square,
∴ The rectangle is equilateral.
(4) If the rectangle is equilateral, then it is a square;
It is not a square,
∴ The rectangle is not equilateral.
The hypothetical syllogism so closely resembles the categorical that it may be changed to it by a slight alteration in the wording. After testing the hypothetical by its own rule, it may be expedient to reduce the argument to the categorical form, and subject it to a second test in which the categorical rules are applied. This reduction usually necessitates two steps; first, change the propositions which represent the antecedent and consequent to a subject term and a predicate term respectively and then unite them to form the major premise; second, supply a new minor term, if necessary.
Illustrations of Reduction; and Comparison of Hypothetical and Categorical Fallacies:
Hypothetical Form:
(1) If it has rained, the ground is damp;
It has rained,
∴ The ground is damp.
Categorical Form:
A
M
The falling rain
makes the G
ground damp,
A
S
In this case rain
has M
fallen,
A
∴ S
In this case the ground
is G
damp ground.
It is seen that the argument in the hypothetical form is valid as the minor premise affirms the antecedent. Reducing to the categorical gives to the argument the mode
 A
A
A
A
in the first figure which we know to be valid.
Hypothetical:
(2) If one were wise, he would study;
But you will not study,
∴ You are not wise.
Categorical:
A
A
G
wise person
would M
study,
E
∴ S
You
will not M
study,
E
∴ S
You
are not G
wise.
In the hypothetical form the argument is valid since the minor premise denies the consequent. Reducing to the categorical gives mood
 A
A
E
E
in the second figure. This is valid.
Hypothetical:
(3) If the wind blows from the south, it will rain;
But the wind is not blowing from the south,
Hence it is not going to rain.
Categorical:
A
M
South wind
brings G
rain,
E
S
This wind
is not a M
south wind,
E
∴ S
This wind
will not G
bring rain.
Hypothetically considered, the minor premise denies the antecedent and consequently the argument is invalid. Reducing to the categorical form, it is found that the major term is distributed in the conclusion, but is not distributed in the major premise; hence the fallacy of illicit major is committed.
Hypothetical:
(4) If a man is just, he will obey the golden rule;
This judge has obeyed the golden rule,
Hence he is just.
Categorical:
A
A
G
just man
will obey the M
golden rule,
A
This
S
judge
has obeyed the M
golden rule,
A
∴ This
S
judge
is a G
just man.
Hypothetically considered, the minor premise affirms the consequent and thus the argument is fallacious; when changed to the categorical we find the fallacy of undistributed middle. If other examples were taken, it could be proved that the hypothetical fallacy of denying the antecedent is usually equivalent to the categorical fallacy of illicit major; whereas the hypothetical fallacy of affirming the consequent amounts to undistributed middle.
In reducing some hypotheticals it is necessary to make use of such expressions as, “the case of” or “the circumstances that.” The attending argument will illustrate this:
If Jefferson was right, man was created free and equal;
(but) Man was not created free and equal,
∴ Jefferson was not right.
Reduced to the categorical:
The
G
case of Jefferson being right
is the case of man being created
M
free and equal;
S
Man
was not created M
free and equal,
∴ A
Jefferson
(this man) was not G
right.
The argument is valid in both cases.
The following brief outline may be followed in testing hypothetical arguments:
1. Arrange logically.
2. Determine antecedent and consequent.
3. Apply the hypothetical rule; name fallacies giving reasons.
4. Reduce to categorical form.
5. Apply the categorical rules, giving fallacies with reasons.
(1) If a man is properly educated, he will not despise manual labor;
therefore I conclude that you have not been properly educated,
since you dislike to work with your hands.
Arranged logically and antecedent and consequent indicated:
If a man is properly educated (antecedent), he will not despise manual labor (consequent);
You despise manual labor (dislike to work with your hands),
∴ You have not been properly educated.
The minor premise denies the consequent, hence the argument is valid according to the rule, “The minor premise must affirm the antecedent or deny the consequent.” The student should note that the consequent is negative and therefore its denial must be an affirmative proposition.
Reduced to the categorical:
E
A
G
properly educated man
will not M
despise manual labor;
A
S
You
despise M
manual labor,
E
∴ S
You
have not been G
properly educated.
Regarded categorically this is valid. Why?
(2) “If one believes in the tenets of the democratic party, then he should vote for its candidates; and since A does believe in them I have asked him to vote for me.”
Arranged, and antecedent and consequent indicated.
If one believes in the tenets of the democratic party (antecedent), then he should vote for its candidates (consequent);
And A does believe in these tenets,
∴ He should vote for its candidates (I have asked him to vote for me).
The minor premise affirms the antecedent and thus the argument is valid according to rule.
Reduced to the categorical:
A
M
One who believes in the tenets of the democratic party
should vote for its M
candidates,
A
S
A
believes in these M
tenets,
A
∴ S
A
should vote for its G
candidates.
Reduced to the categorical gives mood
 A
A
A
A
in the first figure and this we know to be valid.
(3) “If the weather had not been pleasant, I could not have come; but as the weather is pleasant, here I am.”
Arranged and antecedent and consequent indicated:
If the weather had not been pleasant (antecedent), I could not have come (consequent);
The weather is pleasant,
∴ I have come (here I am).
The minor premise denies the antecedent and consequently the argument is invalid according to the rule. (An affirmative minor premise denies a negative antecedent.)
Reduced to the categorical:
E Unpleasant weather would not permit me to come,
E This weather is not unpleasant,
A ∴ This weather enabled me to come.
Fallacy of two negative premises.
(4) “If one pays his debts, he will not be ‘black-listed’; but since you are ‘black-listed,’ I conclude that you have not paid your debts.”
Arranged logically and antecedent and consequent indicated:
If one pays his debts (antecedent), he will not be “black-listed” (consequent);
You are “black-listed,”
∴ You have not paid your debts.
The minor premise denies the consequent hence the argument is valid.
Reduced to categorical form:
E
No
G
one who pays his debts
is M
black listed,
A
S
You
are M
black listed,
E
∴ S
You
have not G
paid your debts.
The mood
 E
E
A
E
in the second figure is valid.
(5) “Men would do right for the sake of themselves, if they appreciated the law of retribution; but they never think of that.”
Arranged, completed, and tested:
If they appreciated the law of retribution (antecedent), men would do right for the sake of themselves (consequent);
But they do not appreciate the law of retribution (never think of that),
Hence they do not do right for the sake of themselves.
Fallacy of denying the antecedent.
Reduced to the categorical:
A
The
case of M
men appreciating the law of retribution,
is the case of G
men
doing right for the sake of themselves;
E
But
S
men
do not M
appreciate the law of retribution,
E
∴ S
Men
do not do G
right for the sake of themselves.
Fallacy of illicit major.
(6) “If an animal is a vertebrate, then it must have a backbone; but the books say that this animal is not a vertebrate, hence it cannot have a backbone.”
Since the minor premise denies the antecedent it would appear that the argument is invalid; yet common knowledge and common sense dictate that the conclusion is true. Surely no invertebrate can have a backbone. As a matter of fact the antecedent and consequent are co-extensive and therefore the hypothetical rule is not applicable.
Reduced to the categorical:
A
M
Vertebrates
must have G
a backbone
(Co-extensive),
E
This
S
animal
is not a M
vertebrate,
E
∴ This
S
animal
cannot have G
a backbone.
As co-extensive A’s distribute their predicates the possibility of there being a fallacy of illicit major is forestalled.
Categorically considered the argument is likewise valid.
It has been observed that a disjunctive proposition is one which expresses an alternative. A disjunctive syllogism is one in which the major premise is a disjunctive proposition.
ILLUSTRATION:
The boy is either honest or dishonest,
He is honest,
∴ He is not dishonest.
The two forms of disjunctive arguments are the one which by affirming denies and the one which by denying affirms. The former is known by the Latin words “modus ponendo tollens”; while the latter is termed the “modus tollendo ponens.”
ILLUSTRATIONS:
(1) By affirming denies.
The defendant is either guilty or innocent,
He is guilty,
∴ He is not innocent.
or
The defendant is either guilty or innocent,
He is innocent,
∴ He is not guilty.
(2) By denying affirms.
The defendant is either guilty or innocent,
He is not guilty,
∴ He is innocent.
or
The defendant is either guilty or innocent,
He is not innocent,
∴ He is guilty.
It may be said that disjunctive arguments depend on two rules. This is the first: The major premise must assert a logical disjunction. A logical disjunction involves two requisites; first, the alternatives must be mutually exclusive; second, the enumeration must be complete.
Illustrations of illogical major premise.
Terms not mutually exclusive:
This boy is either inattentive or indolent,
He is not inattentive,
∴ He is indolent.
It is obvious that the boy might be both inattentive and indolent. Experience teaches that the qualities are usually concurrent, and to assume that the boy must be either one or the other is a clear case of “begging the question.”
Some logicians maintain that “either—or” signify that both alternatives cannot be false, but that both may be true. If this viewpoint were adopted, the major premise of the illustration would not be a case of begging the question. It is unnecessary to argue the point, if it is made perfectly clear which view is to obtain in this discussion. Briefly stated the two points are these. First opinion: “Either—or” when used logically, mean that if the first alternative is false the second must be true, or if the first alternative is true the second must be false. Second opinion: “Either—or” when used logically mean that if the first alternative is false, the second must be true; but if the first alternative is true, the other may or may not be true. This treatise adopts the first opinion. With us all alternative arguments to be logical must be mutually contradictory; i. e., when one is false, the other must be true and when one is true the other must be false; both cannot be false, neither can both be true. When it is intended that this implication should not obtain, then the expressed alternative will take this form, “The boy is either inattentive or indolent or both.”
Other examples where the terms of the disjunctive may not be mutually exclusive:
(1) “Lord Bacon was either exceedingly studious or phenomenally bright.” (Undoubtedly he was both.)
(2) “This teacher is a graduate either of Harvard or of Yale.” (Perhaps both.)
(3) “The defendant is either a liar or a thief.” (The one often leads to the other.)
(4) “To succeed one must either seize the opportunity as it passes or make his own.” (The best success results from doing both.)
Incomplete enumeration:
The cause of the disease was either the water or the milk,
It was not the milk,
∴ It was the water.
When such an argument as this is advanced, it must be with the knowledge that every other alternative has received satisfactory investigation. Without this assurance one could justly claim that the disease might have been caused by the meat or fish supply. Complete enumeration means that the investigation has narrowed the facts to the boundary of the field covered by the alternatives. The fallacy of incomplete enumeration is also one of “begging the question.”
Other examples of a possible incomplete enumeration:
(1) “Jones lives either in Boston or New York.”
(2) “Mary is studying either algebra or geometry.”
(3) “He either committed suicide or was lynched.”
(4) “Either the Giants or the Boston Americans will win the pennant.”
The second rule is made so self evident by the first that there is little need of a detailed discussion concerning it. The rule is this: When the minor premise affirms or denies one of the alternatives of a logical disjunction, the conclusion must, in order, deny or affirm all of the others. To put it differently: When the “minor” affirms, the conclusion must deny every other alternative, and vice versa. When there are but two alternatives reference to any of the foregoing disjunctive arguments will make the rule clear. There may be, however, more than two alternatives. In such a case, if the first rule is observed then the second becomes applicable.
ILLUSTRATIONS:
(1) John Doe lives either in Boston, Albany, or New York;
He lives in New York,
∴ He does not live in either Boston or Albany.
or
He does not live in New York,
∴ He lives in either Boston or Albany.
(2) The season must have been either summer, or autumn, or winter, or spring;
It was neither autumn, nor winter, nor spring,
∴ It must have been summer.
or
It was either autumn, or winter, or spring,
∴ It could not have been summer.
It would seem that the laws of the disjunctive contradict those of the categorical syllogism; for we apparently derive from two affirmatives a negative conclusion, and we also derive an affirmative conclusion when one premise is negative. This objection is seen to be nugatory when the disjunctive is reduced to the categorical form. The reduction involves the two steps of first changing the disjunctive to the hypothetical form and then to the categorical form. The following illustrations will suffice to make the matter clear:
(1) Disjunctive.
A is either B or C
A is B
∴ A is not C
Hypothetical.
If A is B, then A is not C
A is B
∴ A is not C
Categorical.
The case of A being B is the case of A not being C
In this case A is B
∴ A is not C
(2) Disjunctive.
The defendant is either guilty or innocent;
He is not innocent,
∴ He is guilty.
Hypothetical.
If the defendant is guilty, then he is not innocent;
But he is guilty,
∴ He is not innocent.
Categorical.
The case of the defendant being guilty is the case of the defendant not being innocent,
In this case the defendant is guilty,
∴ In this case the defendant is not innocent.
The majority of us are acquainted with the dilemma as related to the activities of life. One is in a dilemma when there are two courses open to him but neither is particularly enticing. One is placed in a dilemma when he is forced to choose the lesser of two evils. For example, one may, without the proper equipment, be overtaken by a heavy rain storm; he seeks the shelter of a wayside shed; the rain continues so that he is forced either to miss his train, or to endure the discomfort of a drenching. Thus the logical dilemma limits one to a choice between alternatives, either one of which might well be avoided.
Definition.
The dilemma is a syllogism in which the major premise consists of two or more hypothetical propositions, while the minor premise is a disjunctive proposition.
It being a combination of hypothetical and disjunctive propositions the dilemma is sometimes appropriately referred to as the “hypothetico-disjunctive” argument. The order of the premises is indifferent, yet it seems to be more natural to use the hypothetical first; thus the definition.
The four forms of the dilemma are the simple constructive, the simple destructive, the complex constructive, and the complex destructive. The following symbolizations illustrate these four kinds:
Simple Constructive Dilemma.
If A is B, W is X; and if C is D, W is X,
But either A is B or C is D,
Hence W is X.
This is termed a simple dilemma because there is but one consequent; namely, W is X. The conclusion being affirmative makes it constructive.
Simple Destructive Dilemma.
If A is B, W is X; and if A is B, Y is Z,
But either W is not X or Y is not Z,
Hence A is not B.
This is simple because there is but one antecedent, A is B, and destructive because the conclusion is negative.
Complex Constructive Dilemma.
If A is B, W is X; and if C is D, Y is Z,
But either A is B or C is D,
Hence either W is X or Y is Z.
This is complex because there are two antecedents and two consequents; constructive, inasmuch as the conclusion is affirmative.
Complex Destructive Dilemma.
If A is B, W is X; and if C is D, Y is Z,
But either W is not X or Y is not Z,
Hence either A is not B or C is not D.
This is complex because there are two antecedents as well as two consequents, and destructive because the conclusion is negative. Briefly: (1) A simple dilemma is one where either the antecedent or consequent is repeated; whereas if neither is repeated the dilemma is complex. (2) A constructive dilemma contains an affirmative conclusion; while a destructive dilemma uses a negative conclusion. (3) A simple dilemma has as its conclusion a categorical proposition; whereas the conclusion of a complex dilemma is always disjunctive.
If the number of antecedents and consequents be increased, a trilemma, tetralemma, etc., may result.
ILLUSTRATION—Trilemma.
If A is B, W is X; and if C is D, Y is Z; and if E is F, U is V,
But either A is B, or C is D, or E is F,
Hence either W is X, or Y is Z, or U is V.
Some authorities define a dilemma as a syllogism in which the “major-hypothetical” has more than one antecedent while the “minor” must be disjunctive. This viewpoint necessarily excludes the second form or the simple destructive dilemma. The weight of authority, however, appears to favor the classification here recommended.
Since the major premise of the dilemma is hypothetical, the rule for testing such would of necessity be the hypothetical rule; namely, “The minor premise must either affirm the antecedent or deny the consequent.” As this rule and the fallacies incident to it have been treated in detail, further discussion is unnecessary.
(1) If the arithmetic contains useful facts, it will help to good citizenship; and if it trains the powers of reason, it will help to good citizenship,
But the arithmetic either contains useful facts or trains the powers of reason,
Hence it will help to good citizenship.
This is a simple constructive dilemma in which the minor premise affirms the antecedents. The argument is, therefore, valid since it conforms to the rules of the hypothetical syllogism. The fact that the minor premise may not be a perfect disjunctive does not invalidate the conclusion, inasmuch as it is perfectly obvious that if the arithmetic fulfilled both the requirements of the antecedents, the conclusion would still obtain. It may, therefore, be inferred that if the dilemma conforms to the rules of the hypothetical argument, it is valid, though the disjunctive proposition which it contains may not be strictly logical.
(2) A man is either temperate or intemperate; and, as I have seen you drunk several times, I conclude that you are intemperate.
Arranged logically.
A man is either temperate or intemperate,
You are not temperate,
∴ You are intemperate.
It would seem that the major premise is a logical disjunctive, since temperate and intemperate indicate that the alternatives are mutually exclusive and the enumeration complete. And since the minor premise denies one alternative while the conclusion affirms the other, we may infer that the argument is valid.
(3) If a man is honest, he will either pay his debts or explain; but this fellow paid no heed to the repeated notifications.
Arranged logically.
If a man is honest, he will pay his debts; and if he is honest, he will explain in case he cannot pay,
This man neither paid his debt, nor explained,
∴ This man is not honest.
This is a simple destructive dilemma, and since the minor premise denies the consequents it is valid.
(4) A voter must either favor protection or free trade; and since you do not favor protection, you must be a free trader. The disjunctive is not logical as one might believe in universal reciprocity. The argument is, therefore, invalid. Why?
(5) If a man were loyal, he would not be unduly critical; and if he were wise, he would not be too loquacious; but I find this clerk has been both unduly critical and too loquacious; hence I consider that he has been not only unwise but strikingly disloyal.
This complex dilemma is valid since the minor premise denies the two consequents.
(1) One desires to take a certain trip which involves various routes; information from time tables reveals the fact that there are three routes A, B, and C. Concerning the conditions of the journey the most important factor is the matter of comfort. Further investigation makes evident that route B will be the most comfortable one, and consequently is the route selected. Putting this ordinary experience in argumentative form gives the following:
The route is to be either A, or B, or C;
I will take route A; if it is the most comfortable; (co-extensive)
A is not the most comfortable route,
Hence I will not take route A.
If B is the most comfortable route, I will take it;
B is the most comfortable route,
Hence I will take route B.
(2) The symptoms suggest either malarial or typhoid fever; the physician is undecided till a blood test makes evident that it is not typhoid.
Considered argumentatively.
This disease is either malarial or typhoid fever;
If it is typhoid, the blood will reveal certain evidences;
But the blood does not reveal these evidences,
Hence the disease is not typhoid.
(3) The natural bent of the youth suggests the profession of either the ministry or teaching. He finally decides to follow the one in which he can best serve his fellows. This, after mature deliberation, appears to him to be the work of the teacher. Thrown into the form of an argument the following results:
I am best fitted for either the pulpit or the schoolroom;
If the schoolroom furnishes the richest field for helping my fellows, I will choose that work;
The schoolroom does appear to furnish such a field,
Hence I will choose the work of the teacher.
It would appear from these ordinary experiences that frequently we are brought face to face with a choice of alternatives which are not unattractive, as in the case of the dilemma. Moreover, some condition suggests itself which, if proved or disproved, will lead to a choice of one of these alternatives. Such circumstances when thrown into the form of an argument present a disjunctive proposition followed by a hypothetical argument. To put it differently: Often in our daily affairs a most prominent limiting condition induces us to select one out of several alternatives. These alternatives are not dilemmatic in nature.
HYPOTHETICAL ARGUMENTS, AND DISJUNCTIVE ARGUMENTS INCLUDING THE DILEMMA.
(1) Three kinds of arguments
Categorical, hypothetical, disjunctive.
(2) Hypothetical arguments
Defined, illustrated.
(3) Antecedent and consequent.
How determined, illustrations.
(4) Two kinds of hypothetical arguments
Constructive, destructive, illustrations.
(5) Rule and two fallacies of the hypothetical argument.
Illustrations and application of rules.
Fallacy of denying antecedent.
Fallacy of affirming consequent.
Co-extensive hypotheticals.
(6) Hypothetical arguments reduced to the categorical form.
Rule, illustrations.
Hypothetical and categorical arguments compared.
(7) Illustrative exercises testing hypothetical arguments of all kinds.
(8) Disjunctive arguments.
Defined, illustrated.
(9) Two kinds of disjunctive arguments.
By “affirming denies,” by “denying affirms.” Illustration.
(10) First rule.
Stated, illustrated.
(11) Second rule
Stated, illustrated.
(12) Reduction of disjunctive argument
Two steps.
(13) The dilemma
Definition.
(14) Four forms of dilemmatic arguments
Simple constructive, simple destructive,
Complex constructive, complex destructive.
Illustrations.
(15) The rule.
(16) Illustrative exercises testing disjunctive and dilemmatic arguments.
(17) Ordinary experiences related to the disjunctive proposition and hypothetical argument.
(1) Just as there are three kinds of propositions so there are three kinds of arguments; namely, categorical, hypothetical, disjunctive.
(2) Categorical syllogistic arguments are those in which all of the propositions are categorical.
Hypothetical syllogistic arguments are those in which the major premise is hypothetical.
In contradistinction to disjunctives, hypothetical arguments may be referred to as “conjunctive”.
(3) The hypothetical proposition is composed of antecedent and consequent; the former being the limiting condition; while the latter is the direct assertion. As the words indicate the antecedent usually precedes the consequent. The signs of the antecedent are “if,” “though,” “unless,” “suppose,” “granted that,” “when,” etc.
(4) The two kinds of hypothetical syllogisms are the constructive and destructive; the former is involved when the minor premise affirms the antecedent; the latter when the minor premise denies the consequent. These two kinds are sometimes referred to as “modus ponens” and “modus tollens” respectively.
(5) Out of the four possible hypothetical syllogisms only two are valid as investigation proves this rule: The minor premise must affirm the antecedent or deny the consequent. In the case of the hypothetical proposition being co-extensive, the rule does not apply.
(6) Hypothetical arguments may be reduced to the categorical by contracting the antecedent of the hypothetical proposition to form the subject-term, and by contracting the consequent of the hypothetical proposition to form the predicate-term of the major premise of the categorical syllogism. If it is necessary, supply a new minor term.
Denying the antecedent is a matter of illicit major; whereas affirming the consequent is equivalent to undistributed middle.
(7) Hypothetical arguments may be tested by following this outline:
(1) Arrange logically.
(2) Determine antecedent and consequent.
(3) Apply hypothetical rule.
(4) Reduce to categorical form.
(5) Apply categorical rules.
(8) A disjunctive syllogism is one in which the major premise is a disjunctive proposition.
(9) The two kinds of disjunctives are those which “by affirming deny” and those which “by denying affirm.”
(10) In testing disjunctive arguments there are two rules involved: First, “The major premise must assert a logical disjunction.” This necessitates the two requisites “the alternatives must be mutually exclusive” and the “enumeration must be complete.” The two opinions relative to the nature of an alternative assertion are, first, if one is false, the other must be true and vice versa; and second, if one is false, the other must be true, but both may be true. The first is adopted in this discussion.
Second. The second rule involved is “When the minor premise affirms or denies one of the alternatives of a logical disjunctive the conclusion must deny or affirm all of the others.”
(11) Subjecting the disjunctive arguments to the categorical test gives evidence to the close relation existing between the two forms. A logical disjunctive proves to be logical when reduced to the categorical. The reduction entails the two steps, first, reduce to the hypothetical; second, reduce to the categorical.
(12) The logical meaning of the dilemma is suggested by the popular conception. One is said to be in a dilemma when two courses are open to him, neither of which is specially attractive.
A logical dilemma presents two alternatives either one of which might well be avoided.
The major premise of the dilemma is hypothetical; while the minor is disjunctive.
(13) The four forms of the dilemma are the simple constructive, the simple destructive, the complex constructive and the complex destructive.
(14) The dilemma is subject to the hypothetical rule which is, “The minor premise must either affirm the antecedent or deny the consequent.”
(15) The minor premise need not be a logical disjunctive provided the major conforms to the hypothetical rule.
(16) Frequently when ordinary experiences are reduced to augmentative form they present a disjunctive proposition followed by a hypothetical argument.
(1) Relate the three kinds of arguments to the three general kinds of propositions.
(2) Define and illustrate the hypothetical argument.
(3) Explain the term conjunctive with reference to hypothetical arguments.
(4) Explain and illustrate antecedent and consequent in hypothetical arguments.
(5) Select from the following the antecedent and consequent:
(1) “I usually succeed when I try.”
(2) “I will not undertake it unless you guarantee half of the sum needed.”
(3) “Though I speak with the tongues of men and of angels, and have not charity, I am become as sounding brass or a tinkling cymbal.”
(6) Illustrate the two kinds of hypothetical syllogisms which are valid.
(7) State and explain the rule to which hypothetical arguments must conform.
(8) State and exemplify the one exception to the hypothetical rule.
(9) Explain how hypothetical arguments may be reduced to the categorical form. Illustrate.
(10) Show by illustration that denying the antecedent is equivalent to illicit major, while affirming the consequent is equivalent to undistributed middle.
(11) Reduce to the categorical form and test:
“If Napoleon had possessed more of the spirit of Washington, he would have been less famous but a better man than he was; but he did not possess the spirit of the ‘Father of His Country.’”
(12) Test according to outline the following hypothetical arguments:
(1) “If it be a good thing to have faith, then certainly he who believes in the bible of a pagan has faith and must have a good thing.”
(2) “If a 10-inch charge burst inside of a tank, there would be nothing left of the tank. It would be blown into small pieces.”
(3) “If the plate found had been originally on the outside of the ship, I should have judged that there must be green paint on it, but I could not find green paint on that part of the ship.”
(4) “If I mistake not, you are the man who did not pay me for that pair of shoes. I am sure that you are the man as I never forget a face.”
(5) “If the maxim ‘Early to bed and early to rise makes one healthy, wealthy and wise’ were true, I would have been a millionaire long ago.”
(13) Define and illustrate a disjunctive argument.
(14) Exemplify the two kinds of disjunctive arguments.
(15) What is meant by a logical disjunction?
(16) “The alternatives must be mutually exclusive.” Explain this, illustrating fully.
(17) Cite cases where the enumeration is not complete.
(18) State in complete form both of the rules to which all disjunctive arguments must conform.
(19) Show by illustration how the disjunctive syllogism may be reduced to the categorical.
(20) Define and illustrate the dilemma.
(21) Give examples, using symbols, of the four dilemmatic forms. Explain why these forms are so named.
(22) Why does the hypothetical rule apply to the dilemmatic syllogism?
(23) Test the validity of the following: Give reasons.
(1) “If a substance is solid it possesses elasticity and so also it does if it be a liquid or gaseous; but all substances are either solid, liquid or gaseous; therefore, all substances possess elasticity.”
(2) “If men were prudent, they would act morally for their own good; if benevolent, for the good of others. But many men will not act morally, either for their own good or that of others; such men, therefore, are not prudent or benevolent.”
(3) “If the majority of those who use public houses are prepared to close them, legislation is unnecessary; but if they are not prepared for such a measure, then to force it upon them by outside pressure is both dangerous and unjust.”
(4) “The man is either a liar or a fool and in either case he is beneath my attention.”
(5) “Either he is sincere or else he is the most astute impostor the world has ever produced; for me I prefer to think him sincere.”
(24) Explain the relation that many experiences appear to bear toward an argument introduced by a disjunctive proposition and followed by a hypothetical syllogism. Illustrate.
(1) May both premises of a hypothetical argument be hypothetical propositions? Explain. See Fowler p. 115.
(2) Which of the two is valid? Explain.
(1) If A is B, C is D
If A is B, E is F
∴ If C is D, E is F
(2) If A is B, C is D
If C is D, E is F
∴ If A is B, E is F
(3) Show by circles that two of the possible four hypothetical arguments are invalid.
(4) What categorical rules does the hypothetical argument seem to violate? Explain.
(5) Originate a hypothetical syllogism whose antecedent and consequent are both negative. Test its validity.
(6) Originate a co-extensive hypothetical argument and show that four valid syllogisms may be derived from it.
(7) Explain by word and illustration the two meanings which may be attached to “either-or.”
(8) If we accepted the opinion that both alternates of a disjunctive may be true, which kind of disjunctive argument would it invalidate?
(9) In a logical disjunction what law of thought is involved? Explain.
(10) Why do the laws of the disjunctive seem to contradict the categorical rules? Explain fully.
(11) Show by drawing on common experience that a logical dilemma is closely related to the popular conception of dilemma.
(12) Illustrate by symbols and then place in good English a pentalemma.
(13) State a definition of a dilemma which excludes the simple destructive form.
(14) Give a common experience which, when thrown into argumentative form, results in a disjunctive proposition followed by a hypothetical syllogism. Coin a name for such a combination.
It has been remarked that “Logic as a science makes known the laws and forms of thought and as an art suggests conditions which must be fulfilled to think rightly.” In recent chapters we have discussed the second aspect of the definition; in these we have attempted to answer the question, “What rules must be followed in order to reason correctly?” We are now ready to treat the same aspect from a negative point of view namely, what errors must be avoided in order to reason correctly? What are the fallacies which we must strive to avoid in our own thinking, and attempt to correct in the thinking of others?
“Fallacy” comes from the Latin fallacia, meaning deceptive or erroneous, and therefore a fallacy in logic is any error in reasoning which has an appearance of correctness. If the writer or speaker is himself deceived by the fallacy, then such is called a Paralogism; but if the fallacy is committed by him for the expressed purpose of deceiving others, then such becomes a Sophism. During the time of the Schoolmen the Sophism was in such high repute that it required even a Socrates to puncture this ignominious bubble of vain trickery. In fact, Socrates, the greatest of all pagan educators, led the crusade which has relegated to the “logical dust bin” the notion that skill in the art of framing sophisms is a scholarly accomplishment. Many believe modern sophistry to be the chief social and commercial evil of the day, and to Socrates must be given the credit for teaching us to look upon those who would practice sophism with righteous indignation and pronounced disgust. However, paralogism and not sophism is the more legitimate field for the student of logic; his problem being, “What are the common errors which I, as a writer and speaker, must strive to avoid?”
The mistakes of induction will occupy our attention in a later chapter. We are now concerned with the fallacies of deduction. Any classification or division of the deductive fallacies must of necessity be faulty. Even the labors of Aristotle in this regard are now pronounced crude and unsatisfactory. This is due to the divergence of opinion as to the signification of some of the fallacies, as well as to the fact that no division is free from the fault of an overlapping of the species. As a result of this lack of unanimity in definition and lack of ability in making the species mutually exclusive, any division of the deductive fallacies must be more or less illogical.
Aristotle divides the fallacies of deduction into two groups: (1) Fallacies in dictione, or formal fallacies. (2) Fallacies extra dictionem, or material fallacies. This division has received universal approval and though many distinctions made by him have been abandoned, yet most logicians retain his phraseology. Since many of the technical terms which Aristotle used have lived through the generations under the conventional meaning which he assigned to them, it becomes less confusing to adhere as closely as possible to these terms. Therefore, in the attending division only those changes have been made which progress and experience have forced upon us. What remains of this chapter will be devoted to explaining these fallacies as they appear in this division. For the sake of clearness and definiteness it is strongly recommended that the student study the outline extensively enough to be able to reproduce it.
| Formal (In dictione) | ||
|---|---|---|
| 1. Immediate inference |
 |
1. Opposition |
| 2. Obversion | ||
| 3. Conversion | ||
| 4. Contraversion | ||
| 2. Categorical arguments |
 |
5. Four terms |
| 6. Undistributed middle | ||
| 7. Illicit major | ||
| 8. Illicit minor | ||
| 9. Negative premises | ||
| 10. Particular premises | ||
| 3. Hypothetical arguments |
 |
11. Denying the antecedent |
| 12. Affirming the consequent | ||
| 4. Disjunctive arguments |
 |
13. Illogical disjunction |
| Material (In dictionem) | ||
| 1. In Language Equivocation |
 |
1. Ambiguous middle |
| 2. Amphibology | ||
| 3. Accent | ||
| 4. Composition | ||
| 5. Division | ||
| 6. Figure of speech | ||
| 2. In Thought Assumption |
 |
1. Accident |
| 2. Converse accident | ||
| 3. Irrelevant conclusion | ||
| 4. Non sequitur | ||
| 5. False cause | ||
| 6. Complex question | ||
| 7. Begging the question | ||
The formal fallacies are those which concern the form of the argument rather than the meaning. These fallacies arise from an improper use of words as arbitrary signs of thought, not from any inconsistency in the thought itself. To commit a formal fallacy we must violate one of the specific rules of logic. For this reason the formal fallacies are easier of comprehension. Moreover, because of this definiteness logicians are better able to come to some agreement as to their content and import. Classing the fallacies of immediate inference as formal is somewhat of an innovation; but since they occur because of the breaking of certain definite rules, and since immediate inference is a matter of changing the form without altering the meaning, we believe there is some justification for this position. Some would class “immediate inference” fallacies with the material fallacies of language.
The material fallacies are fallacies of meaning and not of form. They are those arising from inconsistency in thought, and from imperfect ways of interpreting this thought as it appears in language. No very specific rules of logic are violated by them and for this reason there are those who would entirely eliminate the material fallacies from the field of logic. But since thought is even more subtle than form in its deceitful machinations, we believe that the material fallacy calls for special attention on the part of the logician.
Material fallacies are divided into two kinds. First, those which have reference to wrong thinking, or fallacies in thought; and, second, those which are due mainly to an incorrect interpretation of words, or fallacies in language. The former result from inconsistency and unreasonableness in thought, whereas the latter come from lack of precision in expression.
Fallacies of immediate inference arise from some violation of the rules which this topic enunciates.
(1) Opposition.
Among other statements opposition posits these two: (1) When the particular is true its opposing universal is indeterminate; (2) A universal negative does not necessarily contradict a universal affirmative.
These signify that neither an A nor an E must be assumed to be true when the corresponding I or O is true, and that E may not always contradict A, nor O contradict I.
ILLUSTRATIONS OF FALLACIES OF OPPOSITION.
(1) Since some men are wise, then I may conclude that all men are wise.
(2) I have contradicted his statement “all men are honest” by proving that no men are honest.
There is little difference between fallacies like (1) and fallacies of converse accident. Concerning illustration (2), both statements are false; but to contradict we know that if one is false, the other must be true.
(2) Obversion.
“Two negatives are equivalent to one affirmative,” is the principle underlying obversion. The most common fallacy in obversion springs from using one negative instead of two.
ILLUSTRATIONS OF FALLACIOUS OBVERSION.
(a) Original: Some men are not wise. Obverse: (incorrect) Some men are wise.
(b) Original: All true teachers are just. Obverse: (incorrect) All true teachers are not just.
(3) Conversion.
Conversion involves the interchanging of the subject and predicate of a proposition without affecting the distribution; in consequence the usual fallacy incident to this interchange is distributing an undistributed term.
ILLUSTRATIONS OF FALLACY OF CONVERSION.
(a) Original: All fixed stars are heavenly bodies. Converted: (incorrectly) All heavenly bodies are fixed stars.
(b) Original: Some men are not wise. Converted: (incorrectly) Some wise beings are not men.
(4) Contraversion.
As this process involves the two steps of obversion and conversion, fallacies appertaining to contraversion would relate to these two steps.
ILLUSTRATIONS OF FALLACIES OF CONTRAVERSION.
(a) Original: No honest man fails to pay his debts. Contraverted: (incorrectly) Some who do not pay their debts are honest men.
(b) Original: Some animals are quadrupeds. Contraverted: (incorrectly) Some not-quadrupeds are not animals.
The formal fallacies of categorical, hypothetical, and disjunctive arguments have received detailed treatment in chapters 11, 14 and 15; we may, therefore, devote our attention to the material fallacies without further delay.
These are the fallacies of double meaning. It is known that an equivocal term is one which permits two or more interpretations; similarly a proposition which admits of two or more interpretations may be denominated equivocal. Thus the term equivocation has come to stand for all errors in language resulting from a possibility of more than one interpretation. This justifies the position of referring to all of the six fallacies in language as fallacies also of equivocation.
(1) Ambiguous middle.
Ambiguous middle explains itself. It is the fallacy of giving to the middle term a double meaning. In form the argument may contain but three terms, yet in meaning there are in reality four terms. For this reason ambiguous middle and the fallacy of four terms appear to be about one and the same thing; but in this treatment we shall regard them as mutually exclusive, and this is the distinction:
Invalid arguments of “ambiguous middle” have only three terms in form but four terms in meaning. This signifies that the middle term though identical in form is given a double meaning.
Invalid arguments of “four terms” always have four terms in both form and meaning; they are “logical quadrupeds” in every sense of the word.
ILLUSTRATIONS.
Ambiguous middle.
(a) “Necessity is the mother of invention,”
Bread is a necessity,
∴ Bread is the mother of invention.
(b) “Nothing is better than wisdom,”
Dry bread is better than nothing,
∴ Dry bread is better than wisdom.
(c) A church is a force for good in any community,
A slate roof is good for a church,
∴ A slate roof is a force for good in any community.
Fallacies of four terms.
(a) All true teachers are just,
John Doe is an educator,
∴ John Doe is just.
(b) Milk is nourishing,
This substance is a white fluid,
∴ This substance is nourishing.
(c) Thieves should be imprisoned,
This man has taken what does not belong to him,
∴ This man should be imprisoned.
In the “four-term” fallacies, observe that the four terms occur in the premises. When a fourth term is introduced in the conclusion, the material fallacy of non sequitur has been committed.
(2) Amphibology (or amphiboly).
Amphibology is a fallacy resulting from an ambiguous proposition rather than from the ambiguity of any particular term. The fallacy of amphibology is committed when the spoken or written proposition conveys more than one meaning. The ancient oracles indulged in this sort of fallacy, the reason for such indulgence being obvious; the oracles were not too positive as to the outcome of their prognostications, and therefore were especially careful to cover every emergency.
A careless use of relative clauses and prepositional phrases often results in the fallacy of amphibology.
ILLUSTRATIONS OF THE FALLACY OF AMPHIBOLOGY.
(a) “You the enemy will slay.”
(b) “The Duke yet lives that Henry shall depose.”
(c) “Wanted a piano by a young lady made of mahogany.”
(d) “You your father will punish.”
(3) Accent.
This fallacy springs from placing undue emphasis on some word or group of words. Naturally such accentuation may convey a meaning entirely foreign to the author’s intent. Newspapers are guilty of this fallacy when they select a few words from a speech and use them as headlines without further explanation. A politician may quote a sentence uttered by an opponent and fail to relate it to what preceded or followed. A cartoonist may arouse the prejudice of public opinion by giving ridiculous emphasis to some idiosyncracy possessed by the subject of his attack.
ILLUSTRATIONS OF FALLACIES OF ACCENT.
(a) “Thou shalt not bear false witness against thy neighbor.”
By giving undue emphasis to neighbor, the notion is clearly conveyed that one may bear false witness against all who are not neighbors.
(b) “You must not crib when taking my examinations.”
(c) What the “Spellbinder” said.
“I may say, as a side remark, that the labor unions are guilty of developing a nation of shirks, when they prohibit a phenomenally efficient workman from doing his best.” “I do not wish to be misunderstood in this.” “I believe in labor unions but in this particular they are dead wrong.”
What the newspaper reported.
(Headline) “The Labor Union Scored as a Training School for Shirks.” “―――― said in his speech in ―――― Hall that the Union was responsible for the development of a nation of shirks.” “A good man,” said he, “is not permitted to do his best work.”
(4) Composition.
The fallacy of composition is committed when it is assumed that what is true distributively is likewise true collectively. A term is used in a distributive sense when it is applied to each individual of the class; whereas a term is used in a collective sense when it is applied to the class considered as one whole. “All” meaning each one considered separately and “all” meaning the whole furnishes a frequent pitfall for this fallacy.
ILLUSTRATIONS OF THE FALLACY OF COMPOSITION.
(a) “Every member of the team is a star player; hence I expect that the entire aggregation will be a winner.”
(b) “All the men of the jury are fair minded; therefore we have good reason for supposing that the jury’s verdict will be in accord with the rules of justice.”
(c) “Thirteen and twenty-three are odd numbers; thirty-six is equal to thirteen and twenty-three; hence thirty-six is an odd number.”
(d) “All the angles of a triangle are less than two right angles; hence the angles X, Y and Z are less than two right angles.”
(e) In governmental affairs the assumption, that a law which benefits one section will benefit all, is a fallacy of composition.
(5) Division.
The fallacy of division is committed when it is assumed that what is true collectively is true distributively. Division is the converse of composition. Composition is a fallacious procedure from a distributive to a collective use; while division is a fallacious procedure from a collective to a distributive use. The fallacy of division may be illustrated by giving the converse of the illustrations under composition:
(a) “The team is a star playing team; and since Smith is the ‘first baseman’ of the team, he must be a star player.”
(b) “The jury rendered a just decision; hence the foreman is a fair minded man.”
(c) Thirty-seven is an odd number,
Nine and twenty-eight are thirty-seven,
∴ Nine and twenty-eight are odd numbers.
(d) All the angles of a triangle are equal to two right angles,
A is an angle of a triangle,
∴ A is equal to two right angles.
(6) Figure of Speech.
This fallacy results from assuming that words of the same root have the same meaning. Since the same root-word may be used as a noun, verb, adjective, etc., it does not follow that in these various forms it retains a common meaning. “Address” as a noun and “address” as a verb convey two distinct meanings.
The following are examples of this fallacy:
(a) No designing person should be trusted,
This architect is a designer,
∴ This architect should not be trusted.
(b) Justifiable investigation is wise,
This man is a just investigator,
∴ This man is wise.
These fallacies are not classed as those of “four terms” because two terms so closely resemble each other in form, and yet they are not fallacies of ambiguous middle; since the middle terms are not identical in form.
The fallacies in thought arise through a tendency to assume as true that which demands further proof. Any one who is more anxious to be right than to win will make sure that nothing has been taken for granted which should receive further investigation, or that no truth has been given a presumptuous twist in order to make it fit the particular case under discussion. Because these errors in thought may be attributed chiefly to undue assumptions, we may denominate them as the fallacies of assumption.
(1) Accident.
The fallacy of accident occurs when one reasons from a general truth to an accidental case. Doctrinaires and theoretic enthusiasts are partial to this fallacy. It is so easy to lay down a general formula or remedy and then attempt to apply it to every accidental circumstance. Grandmother with her catnip tea and mustard plaster, however we may cherish the memory of the dear old soul, was nevertheless guilty of the fallacy of accident. Applying maxims and proverbs to particular instances is still another way of committing the fallacy.
EXAMPLES OF FALLACIES OF ACCIDENT.
(a) “Honesty is the best policy,” thinks the physician as he reveals the cold, hard truth to his patient and thus shortens the patient’s life.
(b) Spirituous liquor in excess acts as a poison, and therefore should not be used to resuscitate an extreme case.
(c) “What is bought in the market is eaten; raw meat is bought in the market; therefore it is eaten.”
(d) “Early to bed and early to rise makes one healthy, wealthy and wise.” I shall practice this for ten years and by that time hope to be healthy, wealthy and wise.
(e) John has earned the enviable (?) reputation of being the “worst boy in school,” hence he is going to be the worst boy in “my grade.”
(f) Mary is an inveterate whisperer; and since I know that some one is whispering, I am sure that that some one is Mary.
(g) Being a convict, he is not to be trusted.
(2) Converse Accident.
As the title implies this is the fallacy of reasoning from an accidental case to a general truth. Illustrations:
(a) “John has been a bad boy to-day; and hence he is going to make trouble during the entire term.”
(b) “This food is good for hens; and hence it is good for all domestic fowls.”
(c) “I know of several men who have been phenomenally serviceable to mankind, and none of these men were college trained; hence I conclude that college education is not essential to the attainment of the highest state of efficiency.”
Relative to both accident and converse accident, it may be said that they obtain because all general truths, such as rules, principles, definitions, maxims, etc., have their exceptions; and it is through these exceptions that the two fallacies are made possible.
Accident and Converse Accident Distinguished from Division and Composition.
The fallacy of accident, we have learned, occurs when one reasons from a general truth to an accidental case; whereas the fallacy of division obtains when one reasons from a collective use of a term to a distributive use; in both cases the procedure is from a larger unit to a smaller unit. Moreover, with converse accident and composition, the movement is from the smaller unit to the larger. Because of this similarity there is danger of confusing the two kinds of fallacies. As a matter of distinction between the fallacies of accident, and composition and division the attending comparative résumé may be of value:
(1) Division is similar in movement to accident, while composition resembles converse accident.
(2) A valuable cue for remembering which way division and accident move, is to recall that division in arithmetic is a procedure from the larger unit to the smaller, and therefore that division in logic would have the same signification.
(3) Division and composition pertain to mathematical wholes; while accident and converse accident relate to logical wholes.
(4) The aggregates of division and composition may be counted or enumerated easily; while the accident and converse accident aggregates (or generals) are not easily enumerated.
(5) Division and composition relate to logical terms, whereas accident and converse accident relate to general truths.
(6) Division and composition use a term in a collective sense and then in a separate or distributive sense, or vice versa; accident and converse accident use a thought in a general and then in an accidental sense, or vice versa.
Irrelevant Conclusion (Ignoratio Elenchi).
The fallacy of irrelevant conclusion results when the argument does not squarely meet the point at issue. It is the fallacy of arguing to the wrong point either purposely or through ignorance. One in defense, who has a weak case, may be tempted to divert attention from the point in hand, realizing that a close analysis of the matter in dispute will tend to his undoing. In such instances (1) the lawyer will abuse the plaintiff, (2) the demagogue will tell humorous stories, (3) the teacher will take advantage of the ignorance of the pupil, (4) the scholar will refer to authority and (5) the magnate will fall back upon the power of position and wealth. These forms of “rhetorical thinking” are as harmful as they are popular, and furnish one of the chief reasons for giving to the common people a better understanding of “how to think” as well as “how not to think.”
Definite names have been given to the various forms of irrelevant conclusion which may be summarized as follows:
Argumentum ad populum.
This is the fallacy of appealing to the feelings, passions and prejudices of an audience rather than to their good sense and powers of reason. It is probably the most common of the group. To excite sympathy, the lawyer for the defense may speak feelingly of the suffering that an unfavorable verdict will bring to the wife and children of the accused.
Argumentum ad hominem.
Here the character of the opponent is defamed with a view of discrediting him with the court or audience. “Mud throwing” in times of political agitation is a good example of this fallacy.
Argumentum ad ignorantiam.
This fallacy comes from taking advantage of the ignorance of the opponent; the fallacy assumes that the original supposition has been proved if one is unable to prove the contradictory of the original. Illustration: Mars is inhabited because no one is able to prove that Mars is not inhabited.
Argumentum ad baculum.
In this all argumentation is made to give way to the forces of personal opposition and to the power of money. Illustration: A political committee seating those delegates only, who will vote their way; and, doing this, not from the merits of the case, but because said committee happen to have a sufficient number of votes to “put the thing through.”
Argumentum ad verecundiam.
This fallacy comes from supposing that the whole thing may be settled by citing some noted authority who apparently substantiates the argument advanced.
Epitome of five forms of Irrelevant Conclusion:
(1) Appealing to the audience.
(2) Defaming the character of the opponent.
(3) Inability to prove the contradictory.
(4) Gaining the point by force.
(5) Citing authority.
Non Sequitur (False Consequent).
This is the fallacy of deriving a conclusion which does not follow from the premises. The fallacy obtains whenever material appears in the conclusion, which has no bearing on the case under discussion. “Irrelevant conclusion” pertains to the establishment of the premises while “non sequitur” is concerned with the conclusion only. We know that a logical thinker constructs the conclusion from material already presented by the premises; “Non sequitur” uses material in the conclusion which is found in neither premise.
“Non sequitur” differs from the fallacy of four terms in that the latter uses the fourth term in the premises while the former introduces the fourth term in the conclusion, and in a form so well obscured that it sometimes escapes notice. Illustration:
All men are thinking animals,
Socrates was a man,
∴ Socrates was a scholar.
It does not follow that because a man is a thinking animal that he will become scholarly.
False Cause.
This is the fallacy of assuming that because two happenings have occurred together several times, the one is the cause of the other. This very common fallacy is due to lack of discrimination, and to the exaggerations incident to fear and superstition. Illustrations:
(a) Planting vegetables which grow down, such as the beet, during the last two days of the waxing moon in order to have a larger yield. So far as we know the moon has no influence over growing vegetables.
(b) Thirteen seated at a table is an indication that one of the number will die during the year. This is one of the most absurd fallacies that has ever been visited upon an intelligent people.
It is seen that “False Cause” is closely related to “Non Sequitur.”
Complex Question (Double Question).
This fallacy obtains when an assumption is put in the form of a question.
ILLUSTRATIONS:
(a) A wise father who did not want to tempt beyond the yielding point his three-year-old son, asked, pointing to the scratches on the new mahogany piano, “Freddie, did you do that last night or this morning?”
(b) What caused you to desist from slandering your neighbors; New Year’s resolutions or the preaching of Dominie X?
(c) A daily paper anecdote:
“Charles Bradlaugh, the noted English free-thinker, once engaged in a discussion with a dissenting minister. He insisted that the minister should answer questions by a simple yes or no, asserting that every question should be replied to in that manner.” The reverend gentleman arose and said, “Mr. Bradlaugh, will you allow me to ask you a question on these terms?” “Certainly,” said Mr. Bradlaugh. “Then, may I ask, have you given up beating your wife?”
Begging the Question (Petitio Principii).
This is a fallacy of deriving a conclusion from notions which in themselves demand proof.
The fallacy is not committed when the assertion is self-evident. It is easy to claim that our opponent is begging the question as soon as we see that he is getting the better of us. One may himself beg the question by being too ready to charge others with begging the question. When the opponent adopts premises which are commonly accepted, he does not beg the question. One commits the fallacy when he seems to prove the conclusion more satisfactorily than he really does. This he may accomplish by covertly taking for granted the truth of notions which have not the stamp of universal approval. The fallacy of begging the question assumes three forms:
(1) The assumption of an unproved premise (assumptio non probata).
In this either the major or the minor premise, or both may demand more substantial proof. It must be borne in mind, however, that the disputant must not ask for further proof after he has once accepted the premises, or after the opponent has met his demands to the satisfaction of commonly accepted authority.
Examples of begging the question by assuming unproved premises:
(a) All patriotic citizens are honest at heart,
This man charged with graft is a patriotic citizen,
∴ This man charged with graft is honest at heart.
“All patriotic citizens are honest at heart,” is not an accepted truth and thus demands proof.
(b) A famous sophism of the Greek philosopher by which he proved that motion was impossible, is an excellent illustration of an assumed premise:
“If motion is possible, a body must move either in the place where it is, or in the place where it is not;
But a body cannot move in the place where it is; and of course it cannot move where it is not,
Therefore, motion is impossible.”
Referring to this, De Morgan claims “Movement is change, and so a body requires two places in order to move.” A body cannot move in the place where it is, but must be moved from place to place. The major premise being assumed, this sophism illustrates the fallacy of begging the question.
(c) The most subtle form of begging the question is an enthymeme where the suppressed premise is the one assumed; e. g., “You, being a teacher, should not do as other people do.”
Completed and arranged the argument becomes:
No teacher should do as other people do,
You are a teacher,
∴ You should not do as other people do.
Surely the major premise demands proof.
(2) Reasoning in a Circle (Circulus in probando).
This form of begging the question occurs, “When a conclusion is based upon a premise which in an earlier stage of the argument was itself based upon this very conclusion.” To put it in another way: Reasoning in a circle involves proving the truth of a conclusion by using a particular premise, and then proving the truth of the particular premise by using the conclusion. From premise to conclusion and from conclusion to premise completes the circle.
Examples of begging the question by reasoning in a circle:
(a) It is wrong because my conscience pricks me, and my conscience pricks me because it is wrong.
(b) “The effeminate walk shows a lack of force; because no forceful man walks that way.”
(c) Says Hamilton, “Plato, in his Phoedo, demonstrates the immortality of the soul from its simplicity; and in the Republic, he demonstrates its simplicity from its immortality.”
(3) Question Begging Epithets and Appellations.
This is the fallacy of assuming the point at issue by means of a carefully selected epithet.
Scientists sometimes assume to clarify an inexplicable phenomenon by giving it a technical name. Politicians are exceedingly free with their epithets and appellations, and the records of religious disputes prove that the theologian often resorted to this device.
Examples of begging the question by using epithets and appellations:
(a) We must attribute the disease to heredity.
(b) The candidate for governor is an animated feather duster.
(c) They call him Blue Charlie.
(d) It is the policy of the big stick.
(e) The muck-raker seldom makes an efficient servant of the people.
It is seen that the use of these epithets and appellations is simply a rhetorical device for the purpose of creating either a favorable or unfavorable impression.
THE LOGICAL FALLACIES OF DEDUCTIVE REASONING.
(1) A negative aspect of definition of logic.
(2) Paralogism and sophism.
Distinguished. Mission of Socrates.
(3) A division of the deductive fallacies.
More or less faulty. Aristotle’s phraseology retained.
Division given.
(4) General divisions explained.
Formal and material. Material fallacies in language and in thought.
(5) Fallacies of immediate inference.
Opposition, obversion, conversion, contraversion.
(6) Fallacies in language (also fallacies of equivocation).
Ambiguous middle—distinguished from four terms.
Amphibology.
Accent.
Composition—“all” a pitfall.
Division.
Figure of speech.
(7) Fallacies in thought—(also fallacies of assumption).
Accident.
Converse accident. Made possible by exceptions.
Accident and converse accident distinguished from composition and division.
Comparative résumé.
Irrelevant conclusion (ignoratio elenchi).
Argumentum ad populum.
Argumentum ad hominem.
Argumentum ad ignorantiam.
Argumentum ad baculum.
Argumentum ad verecundiam.
Non sequitur (false consequent).
False cause.
Complex question.
Begging the question (petitio principii).
Assumption of premise.
Reasoning in a circle.
Question begging epithets and appellations.
(1) Logic as a science makes known the laws and forms of thought and as an art suggests conditions which must be fulfilled in order to think rightly.
A discussion of the second phase of the definition would be incomplete without a consideration of the negative aspect as well as the positive. Such a viewpoint makes evident the question “What errors must be avoided in order to reason correctly?” An answer to this question is given under the caption of Logical Fallacies.
(2) A logical fallacy is any error in reasoning which has the appearance of correctness.
A fallacy which deceives the writer or speaker himself is termed a paralogism, whereas a fallacy formed for the express purpose of deceiving another is denominated a sophism.
It was the pagan teacher Socrates who taught modern thought to frown upon all forms of sophism; these exist to-day much as they did in the olden time.
(3) Because of disagreement as to definition, and because of inability to prevent an overlapping of species, any logical division of the deductive fallacies must be faulty.
In the division of the deductive fallacies, this treatise retains the phraseology and form worked out by Aristotle, so far as such retention is consistent with the changes incident to the advances of time.
(4) Formal fallacies occur because of careless and improper use of words as arbitrary signs. Formal fallacies are definite and easy of comprehension.
The material fallacies are due to certain inconsistencies in thought and to imperfect ways of interpreting language. They are more subtle and thus more difficult of comprehension than the formal fallacies.
There are material fallacies in thought and material fallacies in language; the former are due to looseness in thinking and the latter to lack of precision in expression.
(5) Fallacies of opposition result most frequently from deriving universals from their corresponding particulars, and from assuming to contradict affirmative universals by negative universals and affirmative particulars by negative particulars.
The common fallacy in the process of obversion consists in using one negative instead of two, whereas the ordinary error of conversion is a matter of distributing an undistributed term.
Fallacies of contraversion must involve either those of obversion or conversion since the process is a combination of the two.
(6) Fallacies in language, because they result from permitting more than one interpretation, may be also denominated fallacies of equivocation.
(1) Ambiguous middle is the fallacy of giving to the middle term a double meaning.
The fallacy of four terms, as the name signifies, exists when the argument has four terms in both form and meaning. Ambiguous middle is a matter of four terms in meaning but only three in form.
(2) The fallacy of amphibology is committed when the given proposition conveys more than one meaning. In order to maintain their prestige the ancient oracles made use of this fallacy.
(3) The fallacy of accent springs from placing undue emphasis on some word or group of words. Newspaper and demagogues are prone to this error, that they may thus create an unfavorable impression towards those whom they oppose.
(4) The fallacy of composition is committed when it is assumed that what is true distributively is likewise true collectively. “All” meaning each one and “all” meaning the whole class often leads to the fallacy of composition.
(5) The fallacy of division is committed when it is assumed that what is true collectively is true distributively.
Division is the converse of composition.
(6) The fallacy of figure of speech is occasioned by assuming that words of the same root have the same meaning.
(7) Fallacies in thought are likewise called fallacies of assumption, because of the tendency to assume as true something which demands further proof.
(1) The fallacy of accident occurs when one reasons from a general truth to an accident case. It is the favored fallacy of the doctrinaire, the reformer and the vender of “cure-alls.”
(2) The fallacy of converse accident occurs when one reasons from an accidental case to a general truth.
Both accident and converse accident are made possible because rules, definitions, maxims, etc., have exceptions. It is easy to confuse division and composition with the fallacies of accident. Division and composition are concerned with the collective and distributive use of terms, whereas the fallacies of accident involve the use of notions in a general and accidental sense. The former represent notions which may be counted or enumerated while the latter concern notions which are logical rather than numerical. Composition and division involve “number of,” accident, “meaning of.”
(3) The fallacy of irrelevant conclusion results when the argument does not squarely meet the point at issue. It is the fallacy of arguing to the wrong point either purposely or ignorantly. This may be accomplished by (1) appealing to sympathy of audience, (2) defaming character of opponent, (3) assuming that the fact is true because of inability to prove the contradictory, (4) gaining point by force, (5) citing authority.
(4) “Non sequitur” is the fallacy of deriving a conclusion which does not follow from the premises. It involves introducing new material in the conclusion.
(5) “False cause” is the fallacy of assuming that because two happenings have occurred together several times the one is the cause of the other. The fallacy is due largely to the exaggerations of fear and superstition.
(6) The fallacy of complex question consists in putting an assumption in the form of a question.
(7) Begging the question is the fallacy of deriving a conclusion from notions which in themselves demand proof.
This fallacy takes the three forms of (1) the assumption of an unproved premise, (2) reasoning in a circle, (3) question begging epithets and appellations.
(1a) He who wilfully takes the life of another should be electrocuted,
This sharp shooter has wilfully taken the life of another,
Hence he should be electrocuted.
In form we know this argument to be valid since it is in mood
 A
A
A
A
of the first figure. But as the conclusion does not meet with our approval, we are forced to the belief that there must be a material fallacy. Such proves to be the case. In the first instance, “Wilfully takes the life of another” is used in a personal, individual, selfish sense, whereas in the second instance the expression is used in a general, “servant-of-the-government” signification. The argument is, therefore, invalid, the fallacy being ambiguous middle.
(1b) From the viewpoint of both form and meaning test the following: “Events which are not probable happen almost every day; but what happens every day are very probable events; therefore events which are not probable are very probable.”
(2a) The planets have those attributes needed in the support of life,
Mars is a planet,
Hence Mars has those attributes needed in the support of life.
This is valid in form
 A
A
A
A
in the first figure. The major premise posits a fact which has not been proved; the argument is therefore invalid in meaning, the fallacy being that of begging the question.
(2b) “The end of a thing is its perfection; death is the end of life, therefore death is the perfection of life.”
Indicate the fallacy in the foregoing, giving reasons.
(3a) The countries of Europe abound in beggars,
France is a country in Europe,
∴ France abounds in beggars.
“The countries of Europe” in the major premise is used in a collective sense, while the same expression in the minor premise is used in a distributive sense. The argument is, therefore, invalid in meaning; fallacy of division.
(3b) State and explain the material fallacy in the following:
The states believe in the income tax principle; hence Vermont’s vote will be favorable to this.
(4a) “On general principles I believe that one is better off when he abstains from both tea and coffee; and this is the reason why I offer you a cup of hot water.”
The individual to whom the hot water was offered might have been in great need of a mild stimulant. Here, then, is an exception to the general principle and the fallacy committed is clearly that of accident.
(4b) “Books are a source both of instruction and amusement; a table of logarithms is a book; therefore it is a source both of instruction and amusement.” Jevons.
Designate with explanations the fallacy in the above argument.
(5) “Twice have I started out on Friday and both times I had tire trouble.” Fallacy of false cause.
(6) “Where do you spend your vacation, in Palestine or Rome?” Fallacy of complex question.
(7) “Of all the men of that department he seemed to be the most trustworthy, and I pride myself on my ability to judge men in this regard; but now even the police cannot find him.”
The fact that the police cannot find him has nothing to do with the argument. The fallacy is that of non sequitur.
(8) “You must not whisper in my classes.” Fallacy of accent.
(9) “I am a Progressive because I believe in progress.” Fallacy of figure of speech.
(10) “I know it is true because I found it in our text book.” Fallacy of irrelevant conclusion.
(1) Give the negative aspect of the second part of the definition of logic.
(2) Define and illustrate the term fallacy as it is used in logic.
(3) Distinguish between a paralogism and a sophism.
(4) Tell of the mission of Socrates.
(5) What reasons may be given for such a divergence of opinion on a proper classification of the fallacies of deduction?
(6) Give a complete outline, without explanation, of the deductive fallacies.
(7) Distinguish between formal and material fallacies.
(8) Explain the two kinds of material fallacies.
(9) Illustrate the fallacies of immediate inference.
(10) Why should the fallacies in language be likewise termed fallacies of equivocation?
(11) Explain and illustrate ambiguous middle.
(12) Illustrate the fallacy of amphibology.
(13) Explain by illustration the fallacy of accent.
(14) Explain and exemplify the fallacies of composition and division.
(15) Illustrate the fallacy of figure of speech.
(16) Give reasons for denominating the fallacies in thought as fallacies also of assumption.
(17) Define and illustrate the fallacies of accident and converse accident.
(18) Distinguish between the fallacies of composition and division and the two fallacies of accident.
(19) “Every rule has its exception,” what has this to do with the fallacies of accident?
(20) Explain and illustrate the fallacy of irrelevant conclusion.
(21) Name the various ways in which irrelevant conclusion may be committed.
(22) Illustrate the fallacy of non sequitur.
(23) Explain the fallacy of false cause.
(24) Give examples of the complex question.
(25) How may the teacher use the complex question to advantage?
(26) Explain the fallacy of begging the question.
(27) Illustrate the three forms of begging the question.
(28) From the viewpoint of form and meaning, test the validity of the following:
(1) “No soldiers should be brought into the field who are not well qualified to perform their part; none but veterans are well qualified to perform their part, therefore, none but veterans should be brought into the field.” Whately.
(2) “For the proverb is true, ‘That light gains make heavy purses;’ for light gains come thick, whereas great gains come but now and then.” Bacon.
(3) “Whatever is given on the evidence of sense may be taken as a fact; the existence of God, therefore, is not a fact, for it is not evident to sense.” St. Andrew. 1896.
(4) “All the trees in the park make a thick shade; this is one of them, therefore this tree makes a thick shade.” Jevons.
(5) “What we eat grew in the field; loaves of bread are what we eat; therefore loaves of bread grew in the fields.” Jevons.
(6) “Who is most hungry eats most; who eats least is most hungry; therefore who eats least eats most.” Jevons.
(7) “Great talkers should be cropped, for they have no need of ears.” Franklin.
(8) “Love your enemies, for they tell you your faults.” Franklin.
(9) “All the works of Shakespeare cannot be read in a day; therefore the play of Hamlet, being one of the works of Shakespeare, cannot be read in a day.” Jevons.
(10) “Logic as it was cultivated by the schoolmen proved a fruitless study; therefore logic as it is cultivated at the present day must be a fruitless study likewise.” Jevons.
(1) Is there any difference in content between error and fallacy? Illustrate.
(2) In what ways do trusts indulge in sophisms?
(3) May the sophism be used conscientiously by the country doctor? Explain.
(4) Give in substance Aristotle’s classification of fallacies.
(5) Select the fallacies which could with justice be called fallacies of interpretation. See Creighton.
(6) Explain in full the popular conception of equivocation.
(7) Indicate the marks which distinguish the following: Ambiguous middle, fallacy of four terms, non sequitur, figure of speech.
(8) “Why should Jeremy Bentham employ a person to read to him who habitually read in a monotonous tone of voice?” Jevons—Hill.
(9) Originate a sentence of about ten words and through the fallacy of accent secure as many different meanings as possible.
(10) Show that the fallacy of figure of speech might be classed as a fallacy of four terms.
(11) To what fallacies, in your opinion, are teachers especially given?
(12) Show that the fallacy of accident could be classed as one of ambiguous middle.
(13) “When the Puritan settlers in New England passed their three famous resolutions—Resolved, first, that the earth is the Lord’s and the fullness thereof; secondly, that he hath given it to his Saints; thirdly, that we are his Saints. What fallacy did the Puritan Fathers commit?” Ryland.
(14) A Dutchman afflicted with pneumonia arises at midnight and eats a large quantity of sauerkraut. The Dutchman gets well, whereat his physician writes in his little book on remedies, “Sauerkraut sure cure for pneumonia.” The physician was guilty of what fallacy? Why?
(15) De Morgan quotes from Boccaccio this: “A servant who was roasting a stork for his master was prevailed upon by his sweetheart to cut off a leg for her to eat. When the bird came upon the table the master desired to know what had become of the other leg. The man answered that storks never had more than one leg. The master, very angry, but determined to strike his servant dumb before he punished him, took him next day into the fields where they saw storks, standing each on one leg, as storks do. The servant turned triumphantly to his master; on which the latter shouted, and the birds put down their other legs and flew away. Ah, sir, said the servant, you did not shout to the stork at dinner yesterday; if you had done so he would have shown his other leg.” What fallacy does this quotation from Boccaccio illustrate?
(16) Why should begging the question and irrelevant conclusion be classed as fallacies of the “forgotten issue?”
(17) From the standpoint of both form and meaning test the validity of the following:
(1) “Virtue is the child of knowledge and vice of ignorance; therefore education, periodical literature, traveling, ventilation, drainage and the arts of life, when fully carried out, serve to make a population moral and happy.” Hibben.
(2) “The civil power has the right of ecclesiastical jurisdiction and administration, therefore parliament may impose articles of faith on the church or suppress dioceses.” Hibben.
(3) “Seeing that abundance of work is a sure sign of industrial prosperity, it follows that fire and hurricane benefit industry, because they undoubtedly create work.” St. Andrews—1895.
(4) “Riches are for spending, and spending for honor and good action; therefore, extraordinary expense must be limited by the worth of the occasion.” Bacon.
(5) “And let a man beware how he keepeth company with choleric and quarrelsome persons; for they will engage him into their own quarrels.” Bacon.
(6) “He that resteth upon gains certain, shall hardly grow to great riches; and he that puts all upon adventures, doth oftentimes break and come to poverty. It is good, therefore, to guard adventures with certainties that they may uphold losses.” Bacon.
It has been remarked that inference is the process of deriving a judgment from one or two antecedent judgments, and that mediate inference is inference by means of a middle term. But to reason by means of a middle term necessitates two judgments; hence mediate inference might be defined as the process of deriving a judgment from two antecedent judgments. In this treatment mediate inference and reasoning have been used interchangeably. This, then, becomes our definition for reasoning: Reasoning is the process of deriving a judgment from two antecedent judgments.
The syllogism results when the process of reasoning is formally clothed in words. Moreover, the conclusion of the syllogism may be more general than the premises or less general. This suggests the two important kinds of reasoning; namely, inductive and deductive. Inductive reasoning is reasoning from less general premises to a more general conclusion. Deductive reasoning is reasoning from more general premises to a less general conclusion.
ILLUSTRATION:
| Inductive Syllogism. | Deductive Syllogism. |
|
The robin, crow, sparrow, etc. have wings, The robin, crow, sparrow, etc. are birds, ∴ All birds have wings. |
All birds have wings, The robin, crow, sparrow, etc. are birds, ∴ The robin, crow, sparrow, etc. have wings. |
|
Iron, silver, gold, etc. are elements, Iron, silver, gold, etc. are metals, ∴ All metals are elements. |
All metals are elements, Iron, silver, gold, etc. are metals, ∴ Iron, silver, gold, etc. are elements. |
|
Boston, New York, Chicago, etc. have fine harbors, Boston, New York, Chicago, etc. are large cities, ∴ All large cities have fine harbors. |
All large cities have fine harbors, Boston, New York, Chicago, etc. are large cities, ∴ Boston, New York, Chicago, etc. have fine harbors. |
The student who is sufficiently familiar with the canons of the deductive syllogism will at once detect the fallacy of illicit minor in the foregoing inductive syllogisms; i. e., “birds” when used as the predicate of the minor premise of the first syllogism is undistributed, but as the subject of the conclusion “birds” is distributed. The same might be said concerning the terms “metals” and “large cities.” A portion of this chapter will be devoted to answering this criticism. At this point it may be stated that the inductive syllogism is not supposed to conform perfectly to the canons of the deductive syllogism.
Referring to the first inductive syllogism of section one, it is assumed that the robin, crow and sparrow are representative birds, and that we are thus justified in concluding that if these type birds have wings, then all birds must have wings. Of course this is more or less of a conjecture or “a hazard”; since birds without wings may exist in some undiscovered corner of the globe. However, inasmuch as the generalization concerns a representative quality, we deem the assumption fairly well founded. The logical right to take this “leap into the unknown” will be discussed later. It will profit us at this time to realize more fully how essential the “inductive hazard” is to the progress of the world. When the Schoolmen of mediæval time refused to venture, they failed to progress, and thus came the dark days. Whenever man has ignored this God given instinct which leads to discovery, the world has stood still. This willingness to “take a leap into the dark” with the hope of finding, in the shadow, truth which would enhance man’s power and increase his serviceableness, has given to the world about all that is worth while. It was the spirit of the hazard which pushed Columbus to the discovery of a new world; which gave Newton the secrets of the motions of the universe; which enabled Edison to harness a multitude of lurking forces; and Morse and Bell to reduce distance to its lowest terms. In ordinary affairs with ordinary men those succeed best who manifest most a safe, steady, persistent spirit of discovery. Here, then, in the “inductive hazard” have we a most important phase of school life which, in this day of making the work easy, is being sadly neglected. On the other hand, an unregulated and insane spirit of venture may result in a great waste of energy, and in the development of low ideals of recklessness and inaccuracy. The “inductive hazard” must be cultivated; yet it must be regulated as well, and, as the reader already realizes, logic needs to concern itself mainly with this regulative aspect.
The problem of induction is much more complex than that of deduction because of these reasons: First. Deduction as a process of reasoning was the only kind discussed by the logicians for two thousand years. Aristotle is called the father of deductive logic and this Intellectual Giant, the greatest of ancient time and possibly of all time, so perfected the form of deductive reasoning that, up to the time of Francis Bacon, no scholar possessed the temerity to gainsay its supremacy in the field of logical reasoning. For twenty centuries Aristotle’s Deductive Logic was the Logicians’ Bible. On the other hand, inductive reasoning, though it was briefly discussed by Aristotle, received little attention till the versatile Francis Bacon placed it upon the stage of the thinking world. This makes deduction nearly two thousand years older than induction. Time, by eliminating the personal equation and exposing in various ways fallacious thinking, tends to unify and universalize truth. Hence, logicians are agreed so far as the fundamentals of deductive logic are concerned, but are still at odds over the true conception and use of inductive logic.
A second reason for this confused status in the field of inductive logic is the fact of its being more closely related to the events of every day living. Induction is the natural method of childhood; the popular method of the school room; and the most used method of common life. In consequence its ramifications are so varied and multitudinous, that it will take centuries of thinking to reduce the doctrine of induction to that uniformity and definiteness which so distinguishes deduction.
The attending quotations will give the student a fair idea of the leading conceptions concerning induction:
(1) “Induction is the process by which we conclude that what is true of certain individuals of a class is true of the whole class, or that what is true at certain times will be true under similar circumstances at all times.” “Induction, as above defined, is a process of inference; it proceeds from the known to the unknown.” “Any process in which what seems the conclusion is no wider than the premises from which it is drawn, does not fall within the meaning of the term.”—J. S. Mill, A System of Logic, 1892, p. 175.
(2) “An induction is a generalization or an inference based upon propositions that state observed facts.” “The truth inferred may be general or particular, but it must be one which we cannot perceive in a single act of observation.”—Ballentine’s Inductive Logic, 1896, p. 14.
(3) “Induction is the process of inference by which we get at general truths from particular facts or cases.”—Ryland’s Logic, 1900, p. 148.
(4) “Induction may be defined as the legitimate inference of the general from the particular, or, of the more general from the less general.”—Fowler, 1905, p. 10, Vol. 2.
(5) “The term induction has been used by logicians to denote this leap of the mind from the limitations of its positive knowledge to belief in universal laws.” “In pedagogy, however, the term is applied to the whole process of arriving at general truths or principles.”—Salisbury’s Theory of Teaching, p. 156.
If there is one thing above another which modern logic is emphasizing it is the unity of the mind and the contiguity of thinking. Induction and deduction are dove-tailed processes which characterize all thinking worthy of the name. Where induction ceases, deduction commences, and vice versa. It becomes the function of inductive thinking to establish a connection between what has been experienced and what has not been experienced. Therefore, the conclusion of an induction must always contain more than is implied in the premises. The premises denote facts which have been observed; whereas the conclusion denotes the observed facts of the premises plus analogous facts which have not been observed. Inductive thought ventures into the unknown, and attempts to establish a bond of connection between it and something already known. Induction seeks new knowledge, and does so by taking that “leap into the dark” already referred to as the “inductive hazard.”
As soon as the mind reaches a universal truth, it sets to work to clarify this truth. Such is accomplished by reference to other facts which the universal is supposed to include; and this application of the general to the particular is deduction. Induction discovers the new knowledge while deduction clarifies it.
In this treatment induction as a general process has been subdivided into induction as a mode of inference and induction as a method. Induction as a mode of inference is the process of reasoning from less general premises to a more general conclusion; whereas induction as a method is a procedure from the observation of individual facts to a realization of a universal truth. In either case the conclusion of an inductive process always implies more than is contained in the premises. This gives to the conclusion an uncertainty. No induction is absolutely free from doubt except the so-called perfect induction, which form will receive attention in a later section.
All inductive assumptions are made possible because of two laws—universal causation and uniformity of nature.
The law of universal causation may be stated in this wise: Nothing can occur without a cause and every cause has its effect. “It is a universal truth, that every fact which has a beginning has a cause.”—Mill.
SIMPLE ILLUSTRATIONS OF UNIVERSAL CAUSATION.
The sun rises in the east. The boy throws a stone through the window. A democratic wave sweeps the country. Prices of food stuff are high. The bullet, shot out into space, finally falls to the earth. Each one of these occurrences has a cause.12
That universal causation is a fundamental condition of all induction may be further illustrated. The astronomer notes that the stars in the vicinity of Vega seem to be moving outward from a common center; whereas in the opposite part of the sky the stars seem to be moving inward toward a common center. Having observed this phenomenon, the astronomer at once looks for a cause. Finally he decides that the phenomenon is due to the fact that the sun, with his attending family, is moving towards Vega. Arranged, the argument may take this form:
The stars in the vicinity of Vega seem to be moving outward from a common center, whereas in the opposite part of the sky the stars seem to be moving inward, When descending a mountain the trees at the foot seem to move outward from, and those at the top inward toward, a common center, When riding on the train the ties in front seem to move outward while those in the rear seem to move inward. From this we conclude that the sun with the Earth and other planets is moving toward a spot in the sky near Vega. Were it not for the assumption that the phenomenon relative to the stars had a cause there could have been no induction. Moreover, any investigation concerning “democratic waves,” “prices of food stuffs,” etc., must assume as a starting point that these phenomena have causes.
It would appear that the mind is not satisfied with a mere passive observation of the occurrences of the world but is inclined to reach out for the “whys and wherefores.” Due partly to this reason, “universal causation” is often referred to as an a priori law; meaning that it is a law which cannot be proved, but must be assumed in all thinking.
Law stated: The same antecedents are invariably followed by the same consequents. “That the course of nature is uniform is the fundamental principle of induction.”—Mill. “It is not enough to feel assured that nothing can happen without a cause (causation); I must also feel assured that the same cause will invariably be followed by the same effect.”—Fowler.
Referring to the observed phenomenon of the outward movement of the stars about Vega, the astronomer might advance as an hypothesis the fact of the solar system’s movement toward Vega. Having done this he could then experiment with a view of verifying this hypothesis. In this experiment he would attempt to introduce the same cause surrounded by similar circumstances, and then watch for the same effect. To make it concrete: suppose the astronomer paints the side of a barn dark blue and bedecks this with stars of white. Then taking a position as far removed from the blue surface as his eyesight will permit, he runs toward the barn watching the apparent movement of the artificial stars. A similar experiment could be performed by substituting for the starred barn, the stumps on a side hill. In both experiments he assumes that like conditions will be followed by constant results. That is, in these particular cases, advancing toward a group of objects is always followed by an apparent separation of said objects.
This law of uniformity of nature not only underlies inductive thinking but it really conditions all thinking. It implies that the universe is a rational system functioning in a uniform manner. Moreover, it suggests that the interpretations of the mind are likewise uniform and whenever the mind proves a fact to be a universal truth, this truth will always remain a truth unless the conditions change. In fact were it not for the uniformity of nature, all activity whatsoever would be rendered nugatory. Because of this law we have a right to assume that grinding a knife under right conditions will always tend to sharpen it; that surrounding a live seed with a proper environment will result in growth; that water at the same altitude will boil at a constant temperature, etc., etc.
The student will discern the close connection between these two laws and the laws of thought. There is really no distinctive mark between the law of causation and the law of sufficient reason, while “uniformity of nature” includes identity as one of its distinctive features. The laws differ, however, in their application, “causation” and “uniformity of nature” conditioning inductive thinking, while the others are concerned with deductive thinking.
Because “uniformity of nature” expresses facts of experience, it is regarded as an empirical law, as contrasted with the law of causation, which is supposed to be based upon an innate mental conception or is an a priori law.
The function of induction seems to be to universalize particulars. The mind of man has ever been engaged in establishing connections among the concrete experiences of daily life. This ability of his to generalize his individual experiences has been one of the chief agencies in elevating him to the position of “King of the animal world.” In this disposition to generalize man has taken it for granted that nature is honest; that what she tells him under given conditions, she will tell him again under identical conditions. To put it in logical terms man can depend upon the invariability of nature’s activities, or upon the uniformity of nature. Here, then, is one of the most fundamental laws not only of induction but of all activity. But this law implies a second quite as fundamental. If every cause is invariably followed by the same effect under like conditions, then it is thereby implied that every cause has an affect and every event is due to some cause. This, too, is invariable. In consequence of these facts man is justified in thinking that nature is not only honest and therefore “she gives me confidence, but her every activity means something and therefore she arouses my curiosity.” “Uniformity of nature” engenders confidence, “universal causation” inspires the spirit of discovery and with these two weapons man is willing to venture into the jungle of the unknown. Why is man eager to undertake the “inductive hazard?” Because, through the laws of universal causation and uniformity of nature, his curiosity is aroused, and he is given confidence in nature’s activities.
Induction is a matter of universalizing less universal experiences. In this the process may assume any one of three forms, namely: (1) Induction by simple enumeration; (inductio per enumerationem); (2) Induction by analogy; (3) Induction by analysis.
THREE FORMS ILLUSTRATED:
(1) Simple enumeration.
Having observed a few instances the generalization is, “All birds have wings.” The certitude of this may now be strengthened by observing more birds and finding without exception that each has wings.
(2) Analogy.
By noting on Mars geometric markings which resemble canals, the generalization is vouchsafed that Mars is inhabited by human beings. Other similarities in atmospheric conditions, existence of land and water, etc., tend to make this generalization more plausible.
(3) Analysis.
By analyzing water taken from a certain spring, it is found to contain hydrogen and oxygen in the proportion of 1 to 8; in consequence a generalization to this effect is posited. Analyses of specimens from other sources yield similar results and thus the generalization is given greater certitude.
As a usual thing the particular form which the induction assumes depends on the nature of the topic under investigation and also on the mental make-up of the investigator. The general statement that all birds have wings could hardly be derived by means of analogy or analysis, but is a matter of a casual observation of many instances. Moreover, that mind given to accurate observation, but not inclined to note resemblances or to carry on experiments, would naturally follow the first inductive type. On the other hand, simple enumeration would be impossible in questions like the habitability of Mars, and would yield no results in cases requiring definite scientific experimentation like electrolysis.
It is worthy of note that some topics lend themselves to all three modes of procedure. To wit: (1) Enumeration. Without being taught the rule the child is given a list of examples involving the dividing of a decimal by a decimal and is asked to solve them. By comparing his answers with those in the book, he somewhat accidentally discovers what seems to be the correct rule for pointing off in the quotient. By following this rule and each time comparing answers he establishes the truth. (2) Analogy. If .24 ÷ .6 is the first example, the child may resort to the well known process of dividing a common fraction by a common fraction, (
24
100 ÷
60
100 =
24
60 =
4
10,
) then, because of their close resemblance, he may reason that decimal fractions should yield the same result. (3) Analysis. Here the child reasons that since division of decimals is the inverse of multiplication of decimals, the rule for pointing off might be the inverse of the multiplication rule. By trying this out and proving his answer in each example, he becomes convinced of the correctness of his reasoning.
As its name implies this type of inductive research consists in observing many instances which may exemplify the particular uniformity under consideration. The process is quantitative rather than qualitative, the certitude of the generalization depending on the mass of facts collected rather than on any striking resemblance or any detailed analysis. The aim is to observe, accurately if not scientifically, instance after instance until all doubt is removed. The outcome of such observation may be three fold. (1) The enumeration may be complete. This gives the so-called “perfect induction” which will receive attention later. (2) The enumeration may be incomplete and without exceptions; generalizing in this way from uncontradicted experience gives what are termed “empirical” truths. (3) The enumeration may be incomplete with exceptions. It is obvious that this type of induction could give no valid generalization; but the result may be put in the form of a ratio between the uniformities and the exceptions. Such a procedure is a mere “calculation of chances” and the result simply an expressed probability.
THE THREE KINDS OF SIMPLE ENUMERATION ILLUSTRATED.
The subject to receive investigation is a school examination.
(1) Complete enumeration. Every paper is read and marked; this leads to the generalization, “All the class have passed.”
(2) Incomplete enumeration with no exceptions. Representative papers are read and marked in which no failures are found. Generalization, “Probably all of the class have passed.”
(3) Incomplete enumeration with exceptions. Representative papers are read and marked in which there are 20 failures out of the hundred papers examined. Generalization, “Probably about 80% of the class have passed.”
Briefly, simple enumeration may take the form of (1) a perfect induction, (2) a probable induction, (3) a mere calculation of chances. The first necessitates completed experience, the second uncontradicted experience and the third contradicted experience.
Induction by analogy assumes that if two (or more) things resemble each other in certain respects, they belong to the same type, and, therefore, any fact known of the one may be affirmed of the other.
THE TYPE.
As the definition implies, analogy involves an extensive use of types; let us, therefore, become better acquainted with them as instruments in analogical inductions. A type is one of a group which embodies the essential characteristics of that group. How easy and natural it is to dismiss a complex topic with the citing of an example which may be regarded as a type; how common is the use of examples in the school room! On second thought it becomes apparent that analogical induction by example or type is the most common of all forms of induction either as a method or a mode of inference. Analogy by example (or type) assumes that if two or more things are of the same type, they resemble each other in every essential property.
Illustrations of analogical inductions by example or type.
(1) Mathematics.
Example: a + b
a + b
―――――――
a2 + ab
+ ab + b2
―――――――
a2 + 2ab + b2
Inductive Inference: The square of the sum of two quantities is equal to the square of the first, plus twice the first by the second, plus the square of the second.
(2) Nature.
This corn sent me as a sample produced heavy, full ears, and many of them; hence (inductive inference), if I plant corn like this sample under like conditions, I will receive in return heavy, full ears, and many of them.
(3) Geography.
Cities like New York, located on the coast, possess a larger foreign element than the inland cities like Philadelphia.
(4) Grammar.
A noun is the name of anything, as the examples, “George Washington” and “house” would indicate.
In deriving a generalization from one or two examples the prime essential is to select types which are truly representative. Often the example used is a special type and in consequence does not exemplify all of the essential characteristics of the group. To teach the nature of a parallelogram by using a rectangle only, is an easy way to commit this error; or one may affirm that the class can easily cover the work, when the judgment is based entirely on knowledge concerning the brightest one of the grade.
Type work when judicially used is a positive time saver and a very present help in times of perplexity. Let the skillful teacher use types and examples extensively yet cautiously.
THE MARK OF SIMILARITY.
As opposed to analogy by type there is a second form; namely, analogy by one or more similar marks or qualities. This form is best described by the definition: When two things resemble each other in a few marks or qualities they resemble each other in other marks or qualities.
Illustrations of analogy by marks.
(1) Noting that two students have the same surname, I infer that they are brothers.
(2) A man with a book under his arm rings the door bell and asks to see “the lady of the house.” At once the conclusion is drawn that the caller is a book agent.
(3) Two automobiles, resembling each other in shape of body, force one to the conclusion that the machines are of the same make.
THE ERRORS OF ANALOGY BY MARKS OF SIMILARITY.
It follows that analogy by example gives generalizations of much greater certitude than analogy by one or two marks of resemblance. Here is a field bespattered from boundary to boundary with erroneous thinking. The principle of resemblance being an innate tendency, this form of error is most common with the immature. The child reasons by analogy when he invests the poodle with the despised cognomen of “kitty”; or honors every man who wears glasses with “papa.” In the childhood of the race natural events were interpreted by means of analogy. The wind blowing through the trees made sounds much like the human voice; hence these noises were attributed to spirits. Primeval man was led to believe by analogy that everything which moved was alive. We may, therefore, think of our revered forbear as engaged in the undignified task of running after his shadow, or chasing a leaf around a stump.
THE VALUE OF ANALOGY.
Analogy being rich in its suggestions is the favored process of the scientist and inventor. Newton reasoned by analogy when he tentatively affirmed of the moon what he positively knew of the apple. Franklin’s reasoning was analogical when he discovered the identity of the electric spark and lightning. Because this form of induction so often leads to error and at best involves a degree of probability far below induction by analysis, some logicians are inclined to ignore its generalizations altogether. Others deem this a mistake because of these reasons: First. Analogy is serviceable to a high degree in suggesting hypotheses which may be advanced either for the purpose of explanation or verification. It has already been indicated that analogy is the common instrument used by the inventor and discoverer. Second. The principle of analogy, in reality, lies at the basis of classification; because in this, things are grouped according to their resemblances. Third. Analogical induction affords valuable training in originality and initiative. A mind which easily and naturally discerns analogies is “fertile in new ideas.”
REQUIREMENTS OF A TRUE ANALOGY.
It has been remarked that the certitude of an induction by simple enumeration depends upon the number of uncontradicted instances. In analogy the case is different as the process emphasizes the weight of the points of resemblance rather than the number. In substance the requirements of a logical analogy are three.
First. The points of resemblance must be representative and not exceptional. For example: The argument that Mars is inhabited because it has two moons is of little worth, since we have no proof that moonshine is essential to life; this point of resemblance is not representative. On the other hand, if the basis of argument is the fact that Mars has an atmosphere, the conclusion carries some weight; as air seems to be essential to life.
Second. The points of resemblance must outweigh the points of difference. That is, the ratio of probability must always be in favor of the resembling instances. Since it is not a matter of numbers but of weight, a numerical proportion like this would be misleading: Resemblances: Differences = 10:6. It is obvious that the six differences might more than outweigh the ten resemblances. The safer way, if it were possible, would be to attach a value to each point of resemblance or difference, and then express the proportion in terms of the sums of these values.
Third. There must be no difference which is absolutely incompatible with the affirmation which we wish to prove. For example, the fact that the moon has no atmosphere renders nugatory any attempt to prove the habitability of the moon.
This, the third form of inductive research, is by far the most important. Simple enumeration, because it depends upon the number of observed instances, consumes much time; while we have already noted how easy it is for analogy to lead to error. At the best, the conclusion of these methods must be subjected to analytic investigation, if we are seeking universal validity. Induction by analysis is superior to the other forms because it secures a higher degree of probability and is a positive time saver.
Defined. We have learned that analysis is the process of separating a whole into its related parts. We thus define induction by analysis as the process of separating a whole into its parts with a view of deriving a generalization relative to the nature and causal connection of these parts.
ILLUSTRATIONS:
(1) Concerning the generalization that “all birds have wings,” it becomes possible to observe in detail the nature of the wings and advance the hypothesis that these wings are designed for aërial navigation. This hypothesis may then be strengthened by observing that the entire structure of the bird is adapted to flying.
(2) If it were possible to analyze the atmosphere, water, and soil of Mars, and should such analysis reveal a composition similar to that of the earth, it would illustrate well not only the method of analysis but also its superiority over the other methods of investigation.
(3) The physician, in diagnosing a “case,” observes that the symptoms resemble those of typhoid; but to be positive of the truth of his diagnosis, he takes a blood test. Noting the resemblances is induction by analogy; but the blood test involves induction by analysis.
Induction by analysis concerns hypothesis, observation, and experiment, including Mill’s experimental methods. These topics will receive due attention in the chapters which follow. It will be sufficient to close this discussion with a brief treatment of perfect induction, and traduction.
As has been indicated under simple enumeration, a perfect induction is one in which the premises enumerate all the instances denoted by the conclusion.
ILLUSTRATIONS:
(1) A, B, C, D, and E are all Reactionaries,
(All) The members of the committee are A, B, C, D, and E,
∴ (All) The members of the committee are Reactionaries.
(2) John, James, Albert, and Peter all have perfect eyesight,
John, James, Albert, and Peter are all the boys of my family,
∴ All the boys of my family have perfect eyesight.
(3) The first, second, and third groups are up to grade,
The first, second, and third groups include all of the children in my room,
Hence all the children in my room are up to grade.
Because the conclusion of a perfect induction gives nothing new—nothing but what is found in the premises, some claim that the process is practically valueless. From the viewpoint of the discoverer this position is well taken; yet to universalize particular observations puts the knowledge in compact, usable form, and saves one the trouble of returning each time to the consideration of each particular. Thus as a process which leads to verified universals, perfect induction is a time saver. In the second place it was the method used by Socrates when he desired to lead up to a definition or some other general truth. The Sophists were given to a careless use of the “inductive hazard”; they were prone to generalize from one or two particulars, or what is worse, to establish a generalization and then attempt to fit the particular instances to it. This led to a superficiality which the Great Pagan Educator abhorred. The fact that perfect induction was the method used by Socrates to counteract the teachings of the Sophists, is sufficient vindication for its use in discouraging the indefensible assumptions of to-day, and in inspiring warrantable generalizations based on accurate observation.
In the school room with classes addicted to careless, inaccurate work, to accept nothing but a perfectly induced generalization, when this is feasible, is a most valuable lesson. For example, the teacher may not accept the generalization that all of the “first class” cities of the U. S. are located on navigable waterways, until the pupils have investigated the waterway conditions of every city belonging to the class. On the other hand, there may be individual cases of “cocksureness” which need attention. The teacher can do little for the “know-it-all youngster” until he pricks the bubble of conceit. This may be accomplished by allowing the youth to draw a generalization, which seems to meet all the requirements of truth arrived at by means of an imperfect induction; then without warning let the teacher give an instance which will show the generalization to be false. This involves what Socrates termed the “torpedo’s shock.” To illustrate: Consider the “prime number” formula given by Jevons. In deriving this, direct the class to add 2 to its square, and to this sum add 41. Give similar directions relative to numbers 3, 4, 7 and 10. Indicating the work as directed, would give the following:
(1) 2 + 2² + 41 = 47
(2) 3 + 3² + 41 = 53
(3) 4 + 4² + 41 = 61
(4) 7 + 7² + 41 = 97
(5) 10 + 10² + 41 = 151
A question or two will make apparent the fact that all the results are prime numbers, and then the generalization may be drawn; namely, X + X² + 41 = prime number. Now without warning, but under the assumption that you desire to test deductively the general formula, let X = 40. This gives (40 + 40² + 41) 1681, which is the square of 41 and is, therefore, not a prime number.
It may have been noted by the student that “perfect induction” is not induction at all according to the definition; viz.: Inductive reasoning is reasoning from less general premises to a more general conclusion. Referring to the first illustration of the previous section it is apparent that the conclusion is no broader than the premises. Ostensibly, the conclusion is a mere summary, or a generalization of the facts mentioned in the premises. Moreover perfect induction does not readily conform to the definition of deductive reasoning, as in this the movement must be from the more general to the less. We are thus forced to the conclusion that perfect induction is a form of a third type of reasoning which is known under the cognomen of traduction. This is from the Latin trans, and ducere meaning to lead across. Definition: Traductive reasoning is reasoning to a conclusion which is neither less general nor more general than the premises.
Aside from the case of perfect induction there are other types which well illustrate traduction. These are: First. Reasoning from particular (or individuals) to particular (or individuals).
ILLUSTRATION:
Highland Street is the longest street in Jamaica,
Highland Street is not so long as Broadway of New York City,
∴ The longest street of Jamaica is not so long as Broadway of New York City.
Second. Reasoning from general to general.
ILLUSTRATION:
All growing things die,
All living things are growing things,
∴ All living things die.
It may be observed that all of the propositions in traduction are co-extensive “A’s” or “E’s”; hence all the terms are distributed. This eliminates any possibility of committing fallacies of distribution. Further, the propositions may be interchanged at will, without invalidating the particular conclusion selected. To illustrate we may change the last argument to this:
All growing things are living things,
All things that die are growing things,
∴ All things that die are living things.
From the viewpoint of authenticity traduction is the most, and induction the least dependable; whereas the certitude of deductive reasoning lies somewhere between the two. On the other hand, when looked at from the ground of serviceableness the order is reversed, induction being the most useful form of inference and traduction the least.
INDUCTIVE REASONING.
(1) Inductive and Deductive Reasoning Distinguished.
(2) The “Inductive Hazard.”
Essential in world’s progress.
Cultivated and regulated in school.
(3) Complexity of the Problem of Induction.
(4) Various Conceptions of Induction.
Quotations from prominent authorities.
(5) Induction and Deduction Contiguous Processes.
(6) Induction an Assumption.
A mode of inference; A method.
(7) Universal Causation.
Law stated and illustrated.
Conditions all induction.
(8) Uniformity of Nature.
Defined and illustrated.
Conditions all induction.
Empirical.
(9) Inductive Assumptions Justified.
(10) Three Forms of Inductive Research.
(1) Enumeration (2) Analogy (3) Analysis.
Illustrated.
Conditions determine form followed.
(11) Induction by Simple Enumeration.
Defined and illustrated.
Outcome threefold—these illustrated.
(12) Induction by Analogy.
Two conceptions.
Analogy by type or example. Illustrations representative.
Error of analogy.
Suggestiveness of analogy.
Value of analogy.
Requirements of a true analogy. Three.
(13) Induction by Analysis.
Importance.
Defined and illustrated.
(14) Perfect Induction.
Defined and illustrated.
Its use.
Method of Socrates.
(15) Traduction.
Defined and illustrated.
Three methods compared.
(1) Reasoning is the process of deriving a judgment from two antecedent judgments. The syllogism is a common form of expressing the process of reasoning.
Inductive reasoning is reasoning from less general premises to a more general conclusion.
Deductive reasoning is reasoning from more general premises to a less general conclusion.
The inductive syllogism is not supposed to conform to the canons of the deductive syllogism.
(2) Positing in the conclusion more than is indicated in the premises involves what is known as the “inductive hazard.”
The inductive hazard which is another expression for the spirit of discovery, should be fostered in the school room since it has been one of the great forces in human progress; but this venturesome spirit must be regulated by rules, principles, and systematic procedure, or low ideals of recklessness and inaccuracy will result.
(3) The problem of induction is more complex than that of deduction; because the former is a comparatively new subject, and also is more closely related to the activities of life.
(4) The opinion relative to the exact nature of induction, though varied, may be summed up in the thought of its being the process which leads to general truths, derived from the observation of individual facts.
(5) Induction and deduction are contiguous processes which go to make up the more general process of thinking. Where induction ceases, deduction naturally commences; induction discovers new knowledge, deduction clarifies it.
(6) Induction as a general process may be treated as a mode of inference or as a method. In either case the conclusion comprehends more than is contained in the premises.
Since no imperfect induction is absolutely free from doubt, on what ground are we justified in making any inductive assumptions? The answer follows:
(7 and 8) “Nothing can occur without a cause and every cause has its effect,” is the law of universal causation; while the law of the uniformity of nature is “the same antecedents are universally followed by the same consequents.” These two laws justify inductive assumptions, and, in a sense, condition all thinking.
(9) Uniformity of nature gives man confidence, while universal causation arouses his curiosity. With these two weapons he is willing to “march into the unknown.”
(10) As the process of universalizing individual experiences, induction assumes the three forms of simple enumeration, analogy and analysis. The form adopted is not always elective but is controlled largely by the exigency of the case. Some topics lend themselves to all three modes.
(11) Induction by simple enumeration consists in observing many instances which exemplify the uniformity under consideration. Complete enumeration gives the so called perfect inductive inference; incomplete but uncontradicted enumeration leads to empirical truths; while incomplete and contradictive enumeration involves a mere calculation of chances.
(12) Induction by analogy assumes that if two (or more) things resemble each other in certain respects, they belong to the same type, and, therefore, any fact known of the one, may be affirmed of the other.
A most common form of analogy is reasoning by type or example. In this it is assumed that if two or more things are of the same type, they resemble each in every essential property. The type must be truly representative. A second form of analogy is reasoning by marks of resemblance. This second form often leads to egregious error.
Analogy is especially valuable in suggesting hypotheses and in giving training in originality and initiative.
A true analogy demands that the points of resemblance be representative; that they outweigh the points of difference, and that no disagreement be incompatible.
(13) Induction by analysis is the process of dividing a whole into its parts with a view of deriving a generalization relative to the nature and causal connection of these parts.
Induction by analysis makes use of the hypothesis, of observation and experiment, including Mill’s five methods.
(14) A perfect induction is one in which the premises enumerate all of the instances denoted by the conclusion. It is serviceable in inspiring care and accuracy in the establishment of generalizations.
(15) Traduction is the process of reasoning to a conclusion which is neither less general nor more general than the premises.
Traduction includes reasoning from particular to particular or from general to general. Perfect induction is in reality a form of traduction.
Induction, though the most useful form of inference, is the most untrustworthy; whereas traduction is just the reverse of this.
(1) Define and illustrate reasoning.
(2) Distinguish by definition and illustration between inductive and deductive reasoning.
(3) Explain the “inductive hazard” and show its use to man.
(4) “For twenty centuries Aristotle’s Deductive Logic was the logician’s bible.” Explain this.
(5) Show that induction and deduction are contiguous processes.
(6) Distinguish between induction as a mode of inference and induction as a method.
(7) State and explain the law of universal causation. Illustrate fully.
(8) Make evident that a cause may involve many antecedents.
(9) State and explain by illustration the law of uniformity of nature.
(10) Verify by illustration the notion that the “fact of causation” conditions all induction.
(11) Which of the two laws is empirical, “causation” or “uniformity”? Why?
(12) Show that induction is a form of thinking.
(13) Why should the law of uniformity of nature convince man that nature is honest? Illustrate.
(14) Show that the law of universal causation stirs the spirit of discovery.
(15) Name and illustrate the three forms of induction.
(16) Why is it that the tendencies of the investigator often determine the inductive form which he adopts?
(17) Explain by illustration the three-fold outcome of induction by simple enumeration.
(18) Selecting some class room experience, illustrate analogy by example or type.
(19) Define and exemplify types as used in logic.
(20) Remark upon the errors incident to analogy.
(21) Summarize the advantages which induction by analogy offers.
(22) State and exemplify the requirements of true analogies.
(23) Indicate the superiority of induction by analysis over the other two forms. Illustrate.
(24) Define and illustrate perfect induction.
(25) Under what circumstances is perfect induction justified?
(26) Define and illustrate traduction.
(27) Indicate the various forms of traduction.
(1) Show the connection between illicit minor and the “inductive hazard.”
(2) Show by illustration that time tends to universalize truth.
(3) “Induction and not deduction is the natural method of the child mind.” Prove the correctness of this statement.
(4) “Induction is the process of inference by which we get at general truths from particular facts or cases.” Prove that this is not strictly correct according to definition.
(5) As related to establishing general truths, what are the special functions of induction and deduction?
(6) Show that an inductive inference must of necessity be more or less uncertain.
(7) Is there any distinction between the laws of universal causation and sufficient reason? Hyslop’s Elements of Logic, page 329.
(8) Show that universal causation and uniformity of nature are complementary laws. Hyslop, p. 330.
(9) Relate the “fact of causation” to the laws of thought.
(10) Distinguish between empirical and “a priori” laws.
(11) When Harvey discovered the circulation of the blood, what form of induction did he use?
(12) What form of reasoning did Columbus follow in proving that the earth is spherical?
(13) “It is said that the greatness of Darwin was due largely to his habit of never ignoring an exception.” Justify by illustration the truth of this assertion.
(14) In analogical reasoning by example, under what conditions would one illustration be as convincing as many?
(15) “Considering the similarities and differences, the weight of the argument favors Mars’ habitability.” Suppose the proportion of probability were something like this—Resemblances: Differences = 8:7; wherein might the conclusion be erroneous?
(16) Mention a mark or characteristic which would make the habitability of Mars incompatible?
(17) Select a topic for investigation which is peculiarly adapted to enumeration; to analogy; to analysis.
(18) “The uniformities we expect to find in the world take two main aspects, one of which is indicated by the term thing and the other by the term circumstance.” Aikin’s Principles of Logic, 1905; p. 233. In the light of the two fundamental laws of universal causation and uniformity of nature explain and illustrate the quotation.
(19) Explain the principle of teleology as related to analogy. Hibben, 1908; p. 317.
The primary forms of induction have been divided into simple enumeration, analogy and analysis. Conditioning these forms are the two laws, uniformity of nature and universal causation. Since these laws are always concerned with causes, we may refer to them as together expressing the fundamental “fact of causation.” Wherever there is a causal connection, no matter how slight, these laws obtain.
Though “the fact of causation” probably conditions all forms of induction, it is most conspicuous in the third form; namely, Analysis. Here the main aim is to establish a causal connection of some kind; an aim which may be accomplished through the medium of observation and experiment. Incident to this notion, John Stewart Mill formulated five experimental methods of induction. These are known according to the following distinctive titles:
1. The Method of Agreement.
2. The Method of Difference.
3. The Joint Method of Agreement and Difference.
4. The Method of Concomitant Variations.
5. The Method of Residues.
(1) Principle stated. As stated by Mill the principle of the Method of Agreement is this: “If two or more instances of the phenomenon under investigation have only one circumstance in common, the circumstances in which alone all the instances agree is the cause (or effect) of the given phenomenon.”
This notion is given in clearer terms by Jevons and Creighton. Viz.: “The sole invariable antecedent of a phenomenon is probably its cause”; and “The sole invariable consequent of a phenomenon is probably its effect.”
It is known that an antecedent is anything which precedes; while a consequent is anything which follows. To be regarded as a cause, an antecedent must be invariable, and to be regarded as an effect, a consequent must likewise be invariable. Antecedents and consequents which are in no way constant could hardly have any causal connection.
(2) Method symbolized. Let P₁, P₂, P₃, P₄, etc., represent the phenomenon as it may appear the first, second, third, fourth, etc., times, and let A, B, C, etc., stand for the various antecedents, or the various consequents as the case may demand. These two forms may now be used to illustrate the two statements which summarize Agreement:
First statement.
Antecedents. Consequents.
A B C D — P₁
A D E F — P₂
A L M N — P₃
A O P Q — P₄
Second statement.
P₁ — A B C D
P₂ — A D E F
P₃ — A L M N
P₄ — A O P Q
In the first case, the sole invariable antecedent is A, and, therefore, we infer that A is probably the cause of P. In the second case, the invariable consequent being A, is probably the effect of P.
(3) Concrete examples illustrating first statement.
The Problem: Cause of John’s tardiness.
On investigation the various antecedents are these: (1) John has his breakfast at seven; (2) after breakfast he carries his father’s dinner to him and (3) feeds the hens; and then (4) goes to school by the path through the woods and around the mill pond.
Phenomenon as a consequent. John is tardy. Determining to do away with the tardiness, the teacher brings about a variation in the antecedents, varying one at a time taken in the order indicated above.
To wit: (1) Varying the first antecedent.
John breakfasts at 6:30;
Other antecedents the same;
(Phenomenon) But John is tardy.
(2) Varying the second antecedent.
The younger brother carries the dinner;
Other antecedents the same;
(Phenomenon) John is tardy.
(3) Varying the third antecedent.
Another brother cares for the hens;
Other antecedents the same;
(Phenomenon) John is still tardy.
The teacher is now quite certain that the tardiness is due to the route through the woods and around the pond.
Using, as symbols, the initial letters of the italicized “key-words” of the antecedents as stated above, the case of tardiness may be symbolized as follows:
Key words Symbols
seven s
dinner d
hens h
woods w
tardy t₁, t₂, t₃
Antecedents Phenomenon
s d h w t₁
e d h w t₂
s b h w t₃
s d a w t₄
“w” standing for route through the woods, is seen to be the invariable antecedent.
(4) Concrete example illustrating the second statement.
The Problem: To determine the effect of direct primaries.
| First trial. | ||
|---|---|---|
| Antecedent | Consequents | |
| Direct primary |
 |
1. Greater expense to candidate, |
| 2. Greater interest shown, | ||
| 3. Better men nominated, | ||
| 4. “Bumper” crops. | ||
| Second trial. | ||
| Direct primary |
 |
1. Greater expense to candidate, |
| 2. Greater interest shown, | ||
| 3. Better men nominated, | ||
| 4. Crops below average. | ||
| Third trial. | ||
| Direct primary |
 |
1. No greater expense, |
| 2. Greater interest shown, | ||
| 3. Better men nominated, | ||
| 4. Crops average. | ||
| Fourth trial. | ||
| Direct primary |
 |
1. No greater expense, |
| 2. No greater interest, | ||
| 3. Better men nominated, | ||
| 4. Crops average. | ||
It is seen that the invariable consequent is, “Better men nominated.” We may, therefore, conclude that this is a probable effect of “Direct primaries.”
(5) Distinguishing features of method of agreement. The essential characteristics of the method of agreement are three:
First, The phenomenon always occurs.
Second, There is at least one invariable antecedent.
Third, The other antecedents vary.
Giving attention to the attending symbolized illustrations it may be noted that “P,” the phenomenon, always happens; while in the case of the first symbolization, “D” is the invariable antecedent and “A, B, C, E, G, L, M, F, I” are the variable antecedents. “K” is the invariable antecedent of the second and “H, I, L, T, M, W, X, Y, Z, S” are the variable antecedents.
Antecedents Consequents
1. A B C D E ― P₁
A B C D G ― P₂
L B C D M ― P₃
A F G D M ― P₄
L B C D I ― P₅
2. H I K L T ― P₁
K L M T W ― P₂
M T L K W ― P₃
X H K Y Z ― P₄
T W L K S ― P₅
(6) A Matter of Observation and Experiment.
On studying the problem relative to the tardiness of John, it appears that in obtaining the various antecedents the work would be largely a matter of observation. Carrying the father’s dinner, the route through the woods, etc., are facts which observation would make evident. However, when it becomes necessary to vary these antecedents with a view to finding the invariable one, the procedure is experimental as well as a matter of casual observation. Moreover, in connection with the direct primary problem the question would be largely a matter of experiment; though observation would obtain as a subsidiary condition. We may conclude from this that the method of agreement involves both observation and experiment; and since the student will discover that the other methods impose similar demands, we are justified in designating these five special methods of induction as those of observation as well as of experiment.
(7) Advantages and Disadvantages of the Method of Agreement.
The concrete cases given to illustrate the method of agreement present a simple combination of antecedents and consequents. In life, however, such simplicity does not usually obtain and in consequence the method of agreement gives rise to a few serious difficulties. These may be summarized as (a) Plurality of causes; (b) Immaterial antecedents; (c) Complexity of phenomena; (d) Uncertainty of conclusion.
(a) Plurality of causes is mentioned by Mill as constituting the “characteristic imperfection” of the method of agreement. As the term signifies, plurality of causes represents a condition where a given phenomenon has more than one cause, or where different causes produce the same effect. For example, “A poor crop” may be due to drought, neglect, pests, etc.; heat may be caused by friction, electricity, combustion. Unfavorable home conditions; ill health; dislike for teacher—any one of these might be followed by irregular attendance.
(b) Immaterial antecedents are those which precede a given phenomenon and yet, under the most favorable situations, have no causal connection with said phenomenon. For example, the various antecedents of the heavy rain may have been a south wind, forgetting to take an umbrella, missing the car and having to walk, etc. Clearly these antecedents, with the exception of the first, are immaterial.
(c) The law of agreement demands that all the material antecedents receive consideration, but often the situation is too complex to make this possible; a fair illustration of such would be an attempt to ascertain all of the antecedents of “the high cost of living.”
(d) The law of agreement never precludes the possibility of error; as it is quite impossible to carry the analysis to the point of absolute certainty. Of all the methods, “agreement” is the least reliable. Despite the foregoing objections, however, the method is of positive value because of its suggestiveness; opening the door to plausible hypotheses it gives the investigators a working basis.
(1) Principle stated.
Says Mill, “If an instance in which the phenomenon under investigation occurs, and an instance in which it does not occur, have every circumstance in common save one, that one occurring only in the former; the circumstance in which alone the two instances differ is the effect or the cause of an indispensable part of the cause, of the phenomenon.”
To put this in simple terms: Whatever is invariably present when the phenomenon occurs and invariably absent when the phenomenon does not occur, other circumstances remaining the same, is probably the cause or the effect of the phenomenon.
(2) Method symbolized.
Using the same symbols as were used in “Agreement.”
Antecedents Consequents
A B C D P
‒ B C D ‒
or
P A B C D
‒ ‒ B C D
In the first instance A is probably the cause of the phenomenon, since it is present when the phenomenon occurs and absent when it does not occur. For a similar reason, A is the effect in the second case.
(3) Concrete illustrations.
(A) A wise teacher in ascertaining the cause of John’s tardiness would have suggested at once a change of route. Using as symbols the initial letters of the key-words of the antecedents in the case, the following results:
s d h w t
s d h − ‒
(B) First trial.
Problem: Unprepared home work.
| Antecedents | Consequents | |
| 1. Length of lesson, |
 |
Work not properly prepared. |
| 2. Definiteness of lesson, | ||
| 3. Amount of interest shown, | ||
| 4. Physical condition the same. |
Second trial.
| 1. Length of lesson the same, |
 |
Work properly prepared. |
| 2. Lesson made more definite, | ||
| 3. Interest the same, | ||
| 4. Physical condition the same. |
The foregoing symbolized:
L D I C W
L ‒ I C —
It is seen that indefiniteness of lesson assignment is the cause of the unprepared home work.
(4) Advantages and disadvantages of the Method of Difference.
The main difficulty attending the use of the method of difference is the complexity of phenomenon. The very nature of the method insists as an essential requirement that only one material antecedent shall be varied at a time. In life the variations are more or less confused, and it is often not only impossible to observe cases of a single variation, but frequently error comes through overlooking antecedents which are material to the case under investigation. For these reasons the Method of Difference is more a method of experiment than it is a method of observation. By controlling the circumstances it becomes possible to vary but one antecedent at a time, and also to bring into prominence all of the material antecedents.
Bacon claims that all “crucial instances” are merely applications of the Method of Difference. By crucial instance he means any fact which will enable us to determine at once which supposition is the correct one. For example, the physician may not know whether it is malaria or typhoid fever till he takes a blood test; such a test typifies “crucial instances.” The various tests in chemistry are likewise cases of crucial instances, and, in consequence, this science makes use of “Difference” more than any other method.
(5) Characteristic features of Method of Difference.
There are three distinguishing marks of the Method of Difference: these are, (1) The phenomenon does not always happen; (2) One antecedent is variable; (3) The other antecedents are more or less invariable.
The following symbolizations will make these three characteristics evident:
| Antecedents | Consequents | |
| (1) | A B C | P |
| A ‒ C | ‒ | |
| (2) | ‒ B C | ‒ |
| X B C | P | |
| (3) | L M T K | P |
| L M ‒ K | ‒ |
AGREEMENT AND DIFFERENCE COMPARED.
(a) The methods of Agreement and Difference are complementary as may be discerned by comparing their characteristic features: In Agreement the phenomenon always occurs; in Difference the phenomenon does not always occur: In Agreement there is one invariable antecedent; whereas in Difference there is one variable antecedent: In Agreement the other antecedents are more or less variable; but in Difference the other antecedents are more or less invariable.
(b) According to Mill the Method of Agreement insists that what can be eliminated is not connected; whereas the Method of Difference implies that what cannot be eliminated is connected.
(c) The Method of Agreement is more a method of observation, since it is chiefly concerned with the discovery of causes. The Method of Difference is distinctly a method of experiment, because its usual aim is to discover effects.
(d) The Method of Agreement is so called because the object is to compare several instances to determine in what respect they agree; but in the case of Difference instances are compared to determine in what respects they differ.
(e) The conclusions of the Method of Difference involve greater certainty than those of Agreement and, therefore, the former method should be adopted when there is a choice.
(1) Principle stated.
The uncertainty of the conclusions of Agreement and the impossibility at times of employing directly the Method of Difference, give rise to the use of the combination of Agreement and Difference known as the Joint Method. As stated by Mill, the principle conditioning the Joint Method is this: “If two or more instances in which the phenomenon occurs have only one circumstance in common, while two or more instances in which it does not occur have nothing in common save the absence of that circumstance, the circumstance in which alone the two sets of instances differ is the effect or the cause or an indispensable part of the cause, of the phenomenon.” More briefly the notion may be stated in this wise: Among many instances, if one circumstance is invariably present when the phenomenon occurs, and invariably absent when the phenomenon does not occur this circumstance is probably the cause or the effect of the phenomenon.
This principle differs from the one underlying the Method of Difference in that the instances considered are more varied and more numerous. The principle of Difference requires but two sets of instances, while the Joint Method demands at least three; two when the phenomenon occurs and one when it does not occur. A study of the symbolizations and illustrations will clarify this distinction.
(2) Joint Method symbolized.
If we use circumstances and phenomenon in place of antecedents and consequent, then one symbolization may be made to stand for ascertaining either the invariable antecedent, or the invariable consequent.
| Circumstances | Phenomenon | |
| 1. | A B C D | P₁ |
| 2. | A D E F | P₂ |
| 3. | A L M N | P₃ |
| 4. | A O P Q | P₄ |
| 5. | O P Q | ― |
| 6. | L M N | ― |
| 7. | D E F | ― |
| 8. | B C D | ― |
It is obvious that the first, second, third and fourth groups of instances illustrate the principle of Agreement; whereas the first and eighth, the second and seventh, the third and sixth, and the fourth and fifth illustrate in each case, the principle of Difference.
(3) Concrete Examples illustrating Joint Method.
The problem: Too much whispering.
| Antecedents | Consequent | ||
| 1. | Insufficient work, |
 |
Much whispering. |
| Lack of interest, | |||
| Seated near a friend. | |||
| 2. | More work, |
 |
Much whispering. |
| Lack of interest, | |||
| Seated near a friend. | |||
| 3. | More work, |
 |
Much whispering. |
| More interest, | |||
| Seated near a friend. | |||
| 4. | More work, |
 |
Not much whispering. |
| More interest, | |||
| Not seated near friend. | |||
| 5. | More work, |
 |
Not much whispering. |
| Lack of interest, | |||
| Not seated near friend. | |||
| 6. | Insufficient work, |
 |
Not much whispering. |
| Lack of interest, | |||
| Not seated near friend. |
From this it may be concluded that the undue amount of whispering is caused by seating particular friends near each other.
The problem: Poor recitations.
| Antecedents | Consequent | ||
| 1. | Long lesson, |
 |
Poor recitation. |
| Faulty assignment of lesson, | |||
| Fear of teacher. | |||
| 2. | Lesson made shorter, |
 |
Poor recitation. |
| Faulty assignment, | |||
| Fear of teacher. | |||
| 3. | Lesson made shorter, |
 |
Poor recitation. |
| A more careful assignment, | |||
| Fear of teacher. | |||
| 4. | Lesson made shorter, |
 |
Good recitation. |
| A more careful assignment, | |||
| Removal of fear of teacher. | |||
| 5. | Lesson made shorter, |
 |
Good recitation. |
| Faulty assignment, | |||
| No fear of teacher. | |||
| 6. | Lesson long, |
 |
Good recitation. |
| Faulty assignment, | |||
| No fear of teacher. |
Fear of teacher is the cause of the poor recitation.
(4) Distinguishing features.
Being a combination of Agreement and Difference the Joint Method possesses the characteristics of each, though more or less modified. The distinguishing marks may be summarized as follows:
(1) Of the first group of instances:
(1) The phenomenon must always occur,
(2) One antecedent must be invariable,
(3) The other antecedents must be more or less variable.
(2) Of the second group of instances:
(1) The phenomenon must never occur,
(2) One antecedent must be variable,
(3) The other antecedents must be more or less invariable.
Briefly, the one principle concerned is this: There must be an invariable conjunction between the phenomenon involved and the antecedent suspected of being the cause.
(5) Advantages and Disadvantages of the Joint Method.
Since the Joint Method permits a consideration of the negative aspect of the question as well as the affirmative, the opportunities for testing the many instances concerned are doubled. In consequence, the conclusions of the Joint Method are more positive than those of the other methods. It follows that this same opportunity to multiply the instances would tend to lessen the other objections raised against the Method of Agreement; viz., plurality of causes, immaterial antecedents, complexity of phenomenon.
The student must regard the given illustrative symbolizations and concrete examples as being of the simplest form; in life such are the exceptions rather than the rule. When investigating questions, like the cause of the high cost of living, the effect of high tariff, the reason for the typhoid epidemic, etc., there is often a confusion of circumstances which makes the Joint Method unsatisfactory, even though it furnishes a larger opportunity for the multiplication of instances.
The strongest case which the Joint Method is able to present is when the negative instances repeat the positive in every detail, with the one exception of the variable antecedent. To wit:
| Strong Argument: | ||
| Circumstances | Phenomenon | |
| A B C | P₁ | |
| A L M | P₂ | |
| ‒ L M | ― | |
| ‒ B C | ― | |
| Weak Argument: | ||
| A B C | P₁ | |
| A L M | P₂ | |
| ‒ R S | ― | |
| ‒ T K | ― | |
Despite the disadvantages, the conditions of the Joint Method are more or less ideal; since the positive branch of the argument suggests the hypothesis, while the negative branch proves the accuracy or inaccuracy of such.
(1) Principle stated.
Mill’s statement is this: “Whatever phenomenon varies in any manner whenever another phenomenon varies in a particular manner, is either a cause or an effect of that phenomenon, or is connected with it through some fact of causation.”
To put it differently: If when one phenomenon varies alone, another also varies alone, the one is either the cause or the effect of the other.
(2) Concomitant Variations symbolized.
| Circumstances | Phenomenon |
| A | P |
| A + a | P + p |
| (A + a) − a | (P + p) − p |
It is evident from this that little “a” is the cause or the effect of little “p.” To put it in concrete form:
Let A = X number of calories of heat,
And P = 68° F., the original temperature of room,
And a = candle burning in room for ½ hour,
And p = 2° F.
Then
| Antecedents | Consequent |
| X no. of cal. of heat in room | = 68° F. temp. of room |
| X no. of cal. of heat + burning candle | = 68° + 2° = 70° |
| X (no. of cal. of heat + burning candle) − burning candle | = (68° + 2°) − 2° = 68° |
As large “A” is increased and decreased by little “a” so large “P” appears to be increased and decreased by little “p.” This strongly suggests a causal connection between little “a” and little “p.”
(3) Other concrete illustrations.
Problem: To ascertain nature of sound.
| Antecedent | Consequent |
| Bell rung when within a glass jar filled with air, | Loud sound. |
| Some of the air pumped out of the jar, | Sound not so loud. |
| More air pumped into jar again, | Sound louder again. |
The conclusion must be that air has something to do with the production of sound.
Problem: To find best feed for egg production.
| 100 lbs. beef scraps, |
 |
30 doz. eggs. |
| 100 lbs. wheat, | ||
| 100 lbs. oats, | ||
| 100 lbs. corn, | ||
| 50 lbs. beef scraps, |
 |
27 doz. eggs. |
| 100 lbs. wheat, | ||
| 100 lbs. oats, | ||
| 100 lbs. corn, | ||
| 90 lbs. beef scraps, |
 |
28 doz. eggs. |
| 100 lbs. wheat, | ||
| 100 lbs. oats, | ||
| 100 lbs. corn, |
Since the variation in the amount of beef scraps is accompanied by a like variation in the number of eggs produced, it may be assumed that beef scraps are essential to large egg production.
(4) Distinguishing features.
The phenomenon always occurs but in varying degrees;
One antecedent varies in degree;
The other antecedents are invariable.
(5) Advantages and disadvantages.
Concomitant Variations is applicable in cases when it is impossible to use Difference. Recourse is made to the latter when the phenomenon can be made to appear or disappear at will, but there are times when it is impossible to cause the phenomenon to disappear altogether. For example, in the case of the varying degrees of heat in the room it would be scientifically impossible to take all of the heat out of the room; or in experimenting with gravitation, to do away with its influence entirely, is beyond the power of man. It is thus evident that Concomitant Variations may be used in cases where the conditions forbid doing away entirely with the phenomenon.
The special function of Concomitant Variations seems to be to establish the exact quantitative relation between the varying cause and the varying effect. To illustrate: As a general law it is known that bodies attract each other in varying degrees according to their distances apart and according to their relative sizes; by Concomitant Variations this law has been given definite quantitative value and reads like this: “Bodies attract each other directly as the product of their masses, and inversely as the square of the distance between them.” This illustration suggests that the variation between antecedent and consequent may be direct or inverse.
The error most common in this method is the assumption that the quantitative relation between two varying phenomena will always be according to a constant ratio. For example, when being reduced from a high temperature to 391⁄5° F., water steadily contracts; but at 391⁄5° F. it commences to expand until it becomes ice. Thus the ratio of contraction of water is constant only within certain limits. In any event the established ratio of variation can with absolute safety be applied only to the instances investigated. Another disadvantage incident to this method, is the situation of two elements varying together constantly, and yet having no causal connection whatever.
(1) Principle stated.
As stated by Mill the principle of residue is this: “Subtract from any phenomenon such part as is known by previous inductions to be the effect of certain antecedents, and the residue of the phenomenon is the effect of the remaining antecedents.”
In simpler form the notion is this: Subtract from any phenomenon those parts of it which are known to be the effect of certain antecedents, and what is left of the phenomenon is the effect of the remaining antecedents.
(2) Principle symbolized.
| Antecedent | Consequent |
| A | x |
| B | y |
| C | z |
The total cause of the phenomenon xyz is ABC. But it is known that the cause of x is the antecedent A; whereas the cause of y is the antecedent B; hence it is concluded that the cause of z is the antecedent C.
(3) Concrete illustrations.
Problem: To find the weight of coal.
| Antecedents | Consequents | ||||||
| Weight of driver, |
 |
= | 4200 lbs. | ||||
| Weight of wagon, | |||||||
| Weight of coal. | |||||||
| Weight of driver, |
 |
= |
 |
200 lbs. |
 |
= 2200 lbs. | |
| Weight of wagon. | 2000 lbs. | ||||||
Hence we may conclude that the weight of coal is 4200 lbs. − 2200 lbs., or 2000 lbs.
Perhaps the most noted instance in history of the application of this method, was the one which resulted in the discovery of Neptune. In calculating the orbit of Uranus, it was found that the combined attractions of the sun and the known planets did not account for the path which Uranus took. There was some unknown influence at work. Assuming that this unaccountable attraction was due to the presence of another planet beyond the orbit of Uranus, an Englishman by the name of Adams, and later the Frenchman Leverrier, were able to indicate by the principle of Residues, the spot where this planet should be. By directing the telescope toward this point, Neptune was discovered.
(4) Distinguishing features:
The phenomenon always occurs,
The antecedents are usually invariable,
Some of the antecedents are known to be the cause of a part of the phenomenon.
(5) Advantages and disadvantages.
The Method of Residues gives three distinct results: First, it tells what is left over after all the other parts of the phenomenon have been explained. Second, it tells how much is left over, and third, it calls attention to the unexplained parts of the phenomenon. For example, in the first concrete illustration, by subtracting the known quantities from the total quantity, what is left over is found to be coal; not only so but we are able to calculate the exact amount of coal. This illustrates the first and second results of the Method of Residues. (Like concomitant variations it is seen that residues is serviceable in given definite quantitative values.) The discovery of Neptune illustrates well the third result of this method; i. e., after accounting for every other force, it was found that there was yet a force at work which had never been explained. It is this third feature of unexplained residues which has placed “Science in its present advanced state.” “Most of the phenomena which nature presents are complicated; and when the effects of all known causes are estimated with exactness, and subducted, the residual facts are constantly appearing in the form of phenomena altogether new, and leading to the most important conclusions.” So says John Herschel. Almost all of the discoveries in astronomy have come about in this way. If a heavenly body does not behave as it should according to the established theory, then either the theory is wrong or there is some residual phenomenon which needs to be explained. Its suggestiveness is, therefore, the most important function of this method, though this very feature is the one which makes evident its greatest disadvantage. The unexplained residual phenomenon may be very complex and, therefore, a careless observer is apt to overlook a lurking element which in reality is the true cause.
Thinking has been defined as the deliberative process of affirming and denying connections. It is obvious that these five methods are a matter of affirming and denying connections between antecedents and consequents. As soon as the looked for connections are established, the antecedents and consequents are known to be related to each other as causes and effects. In this attempt to find and prove connections the Method of Agreement is chiefly valuable in suggesting workable hypotheses, and the method of difference in verifying, through experiment, the correctness or incorrectness of these hypotheses.
In substance the principle conditioning both methods is this: “If a single antecedent is invariably present when the phenomenon is present and invariably absent when the phenomenon is absent then this antecedent is the cause of the phenomenon.” To put it still more briefly: Between two phenomena there is a causal connection, if the conjunction between the two is invariable. It is the business of Agreement to single out the one antecedent and of Difference to show, by presenting the negative as well as the affirmative side of the case, that the conjunction of the one antecedent and the particular phenomenon is invariable. The Joint Method is merely a combination of Agreement and Difference carried into more varied and complex situations. The methods of Concomitant Variations and Residues are merely modifications of Difference; the former being used when the chief feature is the fluctuation of the phenomenon, and the latter when it is desired to find what is left over.
Agreement suggests the hypothesis, “difference” proves it; the joint method is “difference” more or less complicated, concomitant variations is “difference” applied to fluctuating phenomena, residues is “difference” used to find what and how much is left over.
Agreement is the method of observation and belongs to the physician and nature student. Difference and the Joint Method are experimental devices which are used by the physicist and chemist. Concomitant Variations is the method of unstable phenomena and naturally attaches itself to the economist and statistician. Residues is the method of “lurking exceptions” and is favored by the astronomer and mathematician. Residues, being the method of “what is left over,” is the most common in daily affairs.14
All the five methods are forms of inductive thinking which lead to the establishment of causal connections by means of the principle of the invariable conjunction of phenomena.
THE FIVE SPECIAL METHODS OF OBSERVATION AND EXPERIMENT.
(1) Aim of Five Methods.
Fundamental fact of causation.
Aim of analysis.
Methods of
 agreement
agreement
difference
joint
concomitant variations
residues
(2) Method of Agreement.
Principle stated
Method symbolized
Method illustrated
Distinguishing features of method
A matter of observation and experiment
Advantages and disadvantages
(3) Method of Difference.
Principle stated
Method symbolized
Method illustrated
Advantages and disadvantages
Characteristic features
Agreement and Difference compared
(4) The Joint Method of Agreement and Difference
Principle stated
Method symbolized
Concrete illustrations
Distinguishing features
Advantages and disadvantages
(5) Method of Concomitant Variations
Principle stated
Method symbolized
Concrete illustrations
Distinguishing features
Advantages and disadvantages
(6) The Method of Residues
Principle stated
Method symbolized
Concrete illustrations
Distinguishing features
Advantages and disadvantages
(7) General Purpose and Unity of Five Methods
One fundamental principle
(1) The fundamental fact of causation underlies the three forms of induction, but is most conspicuous in the method of analysis and may be ascertained by recourse to one of the experimental methods.
(2) The principle of the method of agreement may be summed up in the two statements: The sole invariable antecedent of a phenomenon is probably its cause and the sole invariable consequent of a phenomenon is probably its effect. These two statements may be symbolized and illustrated.
The essential characteristics of the method of agreement are the phenomenon always occurs; there is at least one invariable antecedent; the other antecedents vary.
The method of agreement together with the other four methods may justly be termed methods of experiment as well as methods of observation.
The difficulties of the method of agreement are in the main plurality of causes, immaterial antecedents, complexity of phenomenon and uncertainty of conclusion. These difficulties may be summarized as involving a phenomenon which may have several causes; may be preceded by conditions of no causal consequence; may be so involved as to prevent exhaustive examination; and may give unreliable conclusions.
Agreement is valuable chiefly in furnishing to the investigator plausible hypotheses.
(3) The principle of difference is this: “Whatever is invariably present when the phenomenon occurs and invariably absent when the phenomenon does not occur, other circumstances remaining the same, is probably the cause or the effect of the phenomenon.”
Like agreement, difference admits of symbolization and illustration by concrete examples.
The chief difficulties attending difference are: in nature varying one antecedent at a time is infrequent, and it is easy to overlook antecedents which are closely related to the case under investigation.
Difference is the most common method of the experimental sciences. The characteristic features of difference are, the phenomenon does not always occur, one antecedent is variable, while the others are invariable.
The methods of agreement and difference are complementary processes. Agreement attempts to eliminate all the antecedents but one, while difference aims to eliminate one only. Agreement is a method of observation, while difference is a method of experiment. The conclusion of the method of difference gives greater certainty than that of the method of agreement.
(4) The joint method may be stated in this way: Among many instances if one circumstance is invariably present when the phenomenon occurs and invariably absent when the phenomenon does not occur, this circumstance is probably the cause or the effect of the phenomenon.
The instances of the joint method are more numerous and more varied than those of either agreement or difference.
The joint method has the distinguishing characteristics of both agreement and difference.
Because it furnishes greater opportunities for multiplying and varying the instances involved, the joint method presents fewer objections than either of the two separate methods.
The positive branch of the joint method suggests the hypothesis, while the negative branch proves it. This makes the method somewhat ideal.
(5) The principle of concomitant variations may be stated as follows: If when one phenomenon varies alone, and another also varies alone, the one is either the cause or the effect of the other. This is the method of fluctuation, and is used when it is impossible to make the phenomenon disappear altogether, as in the case of difference.
The chief function of concomitant variations is to establish exact quantitative relations between cause and effect.
(6) The principle of residues is this: Subtract from any phenomenon those parts of it which are known to be the effect of certain antecedents, and what is left of the phenomenon is the effect of the remaining antecedent.
The most valuable feature of residues is its suggestiveness; an attempt to explain the “residual phenomenon” has led to many important scientific discoveries.
(7) The five methods are concerned with the establishment of causal connections between phenomena. Agreement suggests the connection while difference proves it. The other methods are modified applications of difference, necessitated by some peculiar form which the phenomenon may take. A statement of the one principle involved is: “If the conjunction between two phenomena is invariable then there is a causal connection.”
All of the methods are forms of inductive thinking.
(1) Explain “the fundamental fact of causation.”
(2) Show that the fact of causation is most conspicuous in induction by analysis.
(3) Name the five special inductive methods of observation and experiment.
(4) State, symbolize, and illustrate the method of agreement.
(5) Give examples of antecedents which do not function as causes.
(6) Show that the “special methods” are a matter of both observation and experiment.
(7) Give the distinguishing features of the method of agreement; illustrate by reference to the symbols.
(8) Exemplify the plurality of causes; immaterial antecedents; complexity of phenomenon.
(9) Show that the conclusions of agreement are largely hypothetical.
(10) State, symbolize, and illustrate the method of difference.
(11) Show by illustration that, in the method of difference, only one antecedent should be varied at a time.
(12) Show that difference is naturally a method of experiment.
(13) Explain Bacon’s use of the term “crucial instances.”
(14) Name and explain the characteristic features of the method of difference.
(15) Show that agreement and difference are complementary.
(16) Explain and illustrate the joint method.
(17) What inference may be drawn from the following instances:
| Antecedents | Consequents |
| A L M T | p q r g |
| B L M E | z q r x |
| B C M E | r z x y |
| A M T H | p q g o |
(18) “Mr. Darwin, in his experiment on cross and self fertilization in the vegetable kingdom, placed a net about one hundred flower heads, thus protecting them from the bees. He at the same time placed one hundred other flower heads of the same variety of plant where they would be exposed to the bees. He obtained the following result: The protected flowers failed to yield a single seed. The others yielded about 2,720 seeds. Thus cross-fertilization was proved.” (Hibben).
What method did Darwin employ? Symbolize the experiment.
(19) Summarize the distinguishing marks of the joint method.
(20) Show that the joint method is more ideal than either agreement or difference.
(21) State and give concrete illustrations of the law of concomitant variations.
(22) What is the chief function of concomitant variations? Illustrate.
(23) Give instances where it would be impossible to use difference, but easy to use concomitant variations.
(24) Explain this: “The quantitative variation between antecedent and consequent may be either direct or inverse.”
(25) State and explain by illustration the method of residues.
(26) What are the advantages and disadvantages of the principle of residues?
(27) State the principle which virtually sums up the five methods.
(28) Write briefly on the practical applications of the five methods to the ordinary walks of life.
(1) Trace the connection between the method of agreement and induction by simple enumeration.
(2) Show that Mill’s methods may properly be termed “Inductive Methods of Scientific Investigation.”
(3) How may it be shown by “agreement” that the high cost of living is due to the tendency to spend more than we earn?
(4) Assume that you are a member of the Board of Health, and that you desire to ascertain the cause of the diphtheria epidemic by means of the principle of agreement.
(5) What is the error involved in coming to the conclusion that to sit at table where there are thirteen, may mean the death of one of the thirteen before the end of the year.
(6) Indicate how it could be shown, by the method of difference, that the mosquito is responsible for the propagation of yellow fever.
(7) “Another experiment similar to this was tried by Plateau, who put some food of which cockroaches are fond on a table and surrounded it with a low circular wall of cardboard. He then put some cockroaches on the table; they evidently scented the food, and made straight for it. He then removed their antennae.” (Hibben). Complete and give with explanations the method used.
(8) “In some cases it is impossible to remove an element which is supposed to be the cause of an effect under investigation.” Explain and illustrate.
(9) “Extreme care must be taken that, in the withdrawing of any element, no other element is inadvertently introduced.” Tyndale supposed he had proved spontaneous generation, when, after sealing in a jar of boiled water a wisp of baked hay, he found, after many days, indications of life within the bottle. In transferring the hay to the bottle, he carried the former across the room. What element was inadvertently introduced?
(10) “The attempt to determine the numerical relations according to which two phenomena vary, requires the utmost caution as soon as our inference outsteps the limits of our observations.” (Fowler). Explain this in connection with the law of concomitant variations.
(11) “When the effects of all known causes are estimated with exactness and subducted, the residual facts are constantly appearing in the form of phenomena altogether new, and leading to the most important conclusions.” Make clear by illustration this quotation which has reference to the principle of residues.
(12) Explain “invariable conjunction of phenomena.”
(13) Investigate by means of one of the five methods the following problems:
(1) “All vegetables which grow to root should be planted during the last two days of the waxing moon.”
(2) “In this section the south wind is the storm wind.”
(3) “Mischief is the outcome of misdirected energy.”
(4) “Bad boys usually receive unjust treatment.”
(5) “An ounce of prevention is worth a pound of cure.”
Induction is the process of universalizing particular facts. The starting point is the fact. Through observation the investigator gathers facts, and then works them over with a view of finding uniformities. The mind cannot build inductive generalizations without facts any more than a mason can build a brick wall without the bricks.
A fact is any particular thing made or done or is that which may be acquired by means of the presentative (perception and imagination) powers of the mind. The state of awareness which results from the observation of facts is an individual notion. This presents another aspect of the inductive process; namely, “It is a matter of building general notions from individual notions, acquired by the observation of facts.” To illustrate: I note that A, B, C and D are honest in their dealings with me, hence I come to the conclusion that some men are honest. A fact is something done, consequently the actual doing of the honest things by A, B, C and D are facts. Each state of awareness of each fact is an individual notion. The mind now discerns a uniformity in these facts and derives the general notion that “some men are honest.”
Facts are acquired by means of observation. When the mind fixes the attention upon any phenomenon it observes it. The term observation means “to watch for” and may be defined as the act of watching for phenomena as they may occur. The observation may be only casual, or it may be willed or rational. It is the latter aspect which most concerns the logician. In this sense observation means careful, painstaking, systematic perception. It involves the concentration of consciousness upon the case in hand, or the actual giving of attention. The thing observed may be external, when the observation takes the form of sense-perception; or it may be internal, when the observation becomes a matter of introspection.
In observation we simply watch the phenomenon; in experiment we make it. In experiment we not only observe, but we manipulate the circumstances so as to present the phenomenon under the most favorable conditions for observation. “In observation,” says Mill, “we find an instance in nature suited to our purposes”; whilst in experiment, by an artificial arrangement of circumstances, we make an instance suited to our purpose. In observation we watch for causes; in experiment we work for effects. We may thus define experiment as the act of making phenomena occur for the purpose of watching for effects. In experiment there is much which is merely observation. In fact experiment is observation in which the phenomenon is artificially produced. For the sake of definiteness, however, any observation which involves a manipulation of circumstances, may be designated as experimental.
To the uninitiated, the matter of observation seems an easy task, and yet when one hears two honest men swear to diametrically opposite facts which have come to them from observing the same phenomenon, his faith is shaken. “Eyes have they but see not” is a logical truth as well as a moral one. Only the observation of the trained can be depended upon; and yet this should not discourage the layman, for even he, by a little conscientious effort towards careful observation, may greatly increase his store of accurate knowledge and add to the joy of living.
The attending rules are usually heeded by the trained scientist in matters of observation and experiment:
First Rule. The observations should be precise. The time, the place, the surrounding conditions must be accurately noted. Many artificial contrivances have been devised because of the desire of the scientist to be precise. Instruments like the balance, the thermometer, the microscope, etc., has he invented, and various devices and methods has he adopted for the sake of precision. A common method is to take an average of observations. For example, to estimate justly the class work of a student, the teacher should not be content with the ratings of one or two recitations, but must average the ratings of many recitations. Again, a child may be led to discover approximately the value of the sum of the interior angles of a triangle by measuring the angles of many triangles and then striking an average; assume that the following results are obtained by such a procedure: (1) 178, (2) 181, (3) 179, (4) 180, (5) 182; adding these and dividing by 5 gives 180.
Second Rule. The observations should concern only the material circumstances of the case in hand. All the non essentials may be ignored, as they serve only to distract attention. For example, (1) in order to get the “right count” all other sounds must be ignored save that of the fire gong; (2) in finding the depth of the water for the building of a dam, soundings ten miles away from the objective point could be of little value. On the other hand, it is easy to overlook certain lurking essentials. To observe such, it is necessary to resort to what the psychologist terms a “preadjustment of attention.” We must know with exactness what we are looking for. We must have a mental image of what we wish to see. The astronomer in the discovery of a new planet must know the exact spot where it ought to be, and have a clear mental image of its appearance. This expectant attention is a necessity in the case of the physician who is anxious to make no mistakes in his diagnosis. If he is looking for pneumonia, he must have a very distinct auditory image of the sound of an affected lung. It should be remarked, however, that this very preadjustment of attention, with the untrained, frequently leads to illusion. We are so anxious to see what we are looking for that nine-tenths of what we believe we see is only inference. How easy it is to read into a phenomenon something that is entirely foreign to it; to read between the lines; to see only the reflection of our own ideas. “Verily the mental picture of what we wish to see becomes so vivid that we are positive of the thing being external.” Thus the drunkard sees snakes and the superstitious see ghosts. Reading into the external what is only vividly internal is probably the most common error with the untrained observer.
Third Rule. The observed circumstances should be varied as much as possible. To observe a fact from a different viewpoint may not only broaden the original notion, but it may change it entirely. In order to gain a true notion of the effect of a particular nostrum on the human organism, it becomes necessary to experiment with persons of different ages, living under different environments, and inheriting different constitutions. Those who are noted for pronouncing broad, safe and sane judgments upon momentous questions are those who are “all-angled observers.”
Fourth Rule. The observed phenomenon should, if possible, be isolated from all interfering phenomena.
In studying the action of a drug or a food, all other drugs or foods must be eliminated. The effect of gravitation on a body cannot be recorded accurately unless the experiments are made in a vacuum. When studying the deflections of the compass, all magnetic substances must be removed from the field.
The rules for scientific observation have suggested certain common errors which may now be considered.
(1) Preconceived ideas.
There is not an unholy belief nor an unwholesome theory which cannot be bolstered up by means of apparent facts. For example, that monstrosity of Puritan thought known as “Salem Witchcraft” was substantiated by facts honestly observed. Again, having made up his mind that it is going to be “so and so,” the statistician goes out into the highways and byways and gathers the facts which vindicate his judgment. Further, the democrat finds that the majority of the voters are democrats; while the republican is confident that two-thirds of the voters are for republicanism. Here again is the fallacy springing from a preadjustment of attention. We see what we want to see. Only the highly trained observer is able, with impunity, to make use of preadjusted attention, and even with him, it is not easy to remove from the situation belief and prejudice.
The true observer undertakes his work with his mind open to anything which the eye may bring him, though it may topple into the dust his dearest theory and most cherished belief; he proceeds—the mind a “clean white page.”
(2) The “observed” and the “inferred” confused.
This error has already received some attention. It may be remarked further, however, that, psychologically considered, observation is a matter of interpreting the new by means of the old. Of necessity the interpretation, whatever it may be, will assume the complexion of the particular “old knowledge” which the mind is able to use. In short, a man will see what his previous environment has trained him to see; the conscientious gardener sees the weeds, whilst the artist may see nothing but the flowers. It follows, therefore, that all observation must be largely a matter of inference based on experience. In looking at the moon, for example, all I actually see is a patch of color; the form and distant location of the moon being a matter of experience.
The inference referred to in this heading is not that which is necessary for perception, but that which is suggested by perception. To illustrate: It is icy; three men are running for a car; Smith raises his arm; Jones slips to the ground; and Brown testifies, that “Smith knocked Jones down.” Brown observed, that Smith assumed the proper attitude and that Jones conveniently went down at the right time; and then inferred the rest.
(3) Ignoring the exceptions.
This comes through an over anxiety to prove our theory. With this mental attitude, the observations which are corroborative will so completely fill the mental field, that the exceptions are made to seem of no consequence. This accounts for the superstition attached to thirteen. As a coincidence some one at some time died who had previously eaten at a table where there were thirteen. Perhaps during the life of the superstitious one this happened on two or three occasions, but the fact so impresses the subject that he ignores the dozen times when death did not follow. Other generalizations belonging to this class are (1) people never die at flood tide; (2) there must be three accidents in succession; (3) the first sight of the new moon over the right shoulder is a good omen; (4) seeds which grow to root do best when planted during the last days of the waxing moon; (5) horse chestnut in pocket guards against sore throat, etc.
(4) Sympathy and undue interest.
The influence of the heart over the brain is well known. A physician is liable to this error when he attempts to prescribe for one of his own family. Sympathy not only warps the judgment but it may actually interfere with the accuracy of an honest observer’s perceptive powers.
(5) Inattention and a fallible memory.
These short comings are too apparent to demand discussion.
Having observed the facts, the mind naturally seeks for explanation of the same. Hence taking the facts as a cue and bringing into play a constructive imagination, a plausible supposition is advanced, which is then proved or disproved. Such a supposition is known as an hypothesis.
Definition. An hypothesis is a supposition advanced for purposes of explanation and proof.
First illustration. The facts are known that light travels from the sun to the earth, and at the rate of 186 thousand miles per second. These facts suggest the problems: (1) How does the light reach the earth? (2) Why this rate of speed; why so much faster than the rate at which sound travels? To solve these problems, or to explain the facts, the “ether” hypothesis is advanced: viz., “A rare medium called ether pervades space and transmits the light and heat of the sun.” This hypothesis has never been conclusively proved.
Second illustration. Fact: The child leans forward and squints his eyes, when attempting to read work which has been placed on the black board; hypothesis: The child is near sighted.
Induction is a matter of realizing generalizations from the observation of facts. The product of such is an induction, but we know that an hypothesis is likewise a generalization based upon facts. What is the difference? An induction, as such, is a broader term than hypothesis. As soon as the hypothesis is proved or disproved, it ceases to be an hypothesis, but still remains an induction. An hypothesis, being advanced for purposes of explanation ceases to be an hypothesis when, in the last analysis, it fails to explain. Moreover, as soon as the hypothesis is shown to be an undoubted truth, it also loses its distinctive hypothetic marks. An hypothesis is merely a tentative induction.
ILLUSTRATIONS:
(1) The hypothesis is advanced that the fire started from the coal range in the kitchen. After the incendiary is caught, this supposition ceases to be an hypothesis.
(2) It is suspected, that my insomnia is due to the three cups of strong coffee indulged in at the evening meal. As soon as this supposition is proved by experimental means (law of difference), it ceases to be an hypothesis and becomes an unpopular inductive truth.
In common parlance hypothesis and theory are used interchangeably. We refer to the “nebular hypothesis” or the “nebular theory”; to the “hypothesis of the sun’s heat” or “the theory of the sun’s heat.” On the other hand, we say “the theory of gravitation,” “the theory of evolution,” etc., with certain uniformity. From these observations we may infer that hypothesis and theory may be used interchangeably when the facts are of a low probability; but when the facts have undergone cogent verification, it is more correct to use theory in their designation rather than hypothesis. “A theory is a partially verified hypothesis.” It has been remarked that theory has a second signification of being a term which stands for “any body of acquired truth.” It is unfortunate that its use could not be confined to this latter conception.
Any hypothesis should be made to conform to the following requisites: (1) The hypothesis must be conceivable. The hypothetic generalizations of primeval days were mere fancy. For example, the loud noise from the clouds on dark days was the angry voice of the God of the skies. Even in this day when a complex situation cannot be explained there comes the temptation to draw entirely upon the imagination, and advance an hypothesis which is absurd in every sense of the word. The permissible hypothesis demands that there be some ground for the conjecture. A fact or two at least must be used as the foundation for whatever the constructive imagination may build. On the other hand the past has taught us that we cannot afford to be too exacting in the enforcement of this rule. The ideas of Copernicus, Newton, Harvey, Darwin, and many another of the world’s best thinkers, were looked upon at first as being ridiculous. There is always a bare possibility of a “lurking truth” in the conjecture, and no broad minded and sanely educated man can afford to scoff blindly at something which may seem to him mere fancy. Prejudice and a willful blindness to truth, have ever been imminent stumbling blocks in the path of progress.
(2) The hypothesis must be capable of proof or disproof. This means, that where it is possible the hypothesis should touch, in one form or another, our experience. If the hypothesis is wholly unlike any experience we may have had, it becomes impossible to ascertain, whether it agrees or disagrees with the facts, which it is supposed to explain. A legitimate hypothesis must furnish some opportunity for securing facts to prove or disprove it. For example, to advance an hypothesis relative to the conditions of the next world is hardly permissible, as “spirit-facts” are entirely without our field of experience. Surely, one returning from Heaven could give us no conception of it; because there is nothing in the carnal mind that may be used to interpret the experiences that must function in the Celestial City.
(3) The hypothesis must be adequate. It should take into consideration all the known facts. It stands to reason that, if one known fact is ignored, the entire procedure is thus vitiated. It would be absurd to suppose the moon to be inhabited without giving heed to the fact of its having no atmosphere.
(4) The hypothesis must be as simple as possible. We must, of course, recognize situations which in themselves are too complex to admit of simple conjectures. The purport of the fourth rule is, that the hypothesis should not be made unnecessarily complex.
(5) The hypothesis should not contradict any verified truth. Any conjecture which opposed the law of gravitation would be out of place. Of course it is possible to have only apparent conflicts between the new hypothesis and the old law. Further observation should show that no such clash exists.
The hypothesis is serviceable mainly in these particulars:
(1) As a working basis.
When one is confronted with a huge mass of facts it becomes necessary to start somewhere, and with as little waste of time and energy as possible. Almost anything is better than a haphazard floundering which reaches “nowhere.” So the investigator hazards a tentative theory, which he at once proceeds to verify. If verification fails, then he may discard this first hypothesis for a better one.
(2) As a guide to ultimate truth.
Much might be said relative to the use of rejected hypotheses. By means of these, science has advanced step by step towards the full light of perfect knowledge. As has been remarked, no true scientist cares to overlook the opportunity for suggestive inspiration which some forsaken hypothesis may afford him. Just as the individual attains the best success by using his failures as stepping stones, so the true scientific discoverer climbs up to the light on the stairway of discarded hypotheses. By testing and rejecting the false hypotheses, the situation becomes more definite and the problem more accurately defined. “Kepler himself tried no less than nineteen different hypotheses before he hit upon the right one, and his ultimate success was doubtless in no slight degree due to his unsuccessful efforts.”
(3) As a discoverer of immediate truth.
Often, moreover, the hypothesis leads directly to positive verification. The supposition advanced may hit the truth squarely; and may be of such peculiar nature as to lead easily to clear and conclusive proof.
(4) As affording a probable explanation of a problem which will not lend itself to an entirely satisfactory solution.
The theory of evolution may illustrate this fourth use; while the history of the discovery of Neptune illustrates the third.
The hypothesis is referred to “as the great instrument of science.” The greatest thinkers of time have possessed the courage and the conscience to step from the known to the unknown; to hazard a guess as to the meaning of what they saw, and then subject their guess to a rigorous test. This procedure involves three elements on the part of the investigator: (1) Power of accurate observation. (2) Constructive imagination. (3) A passion for truth.
(1) An hypothesis formed without an accurate knowledge of facts is not only useless, but often it may work positive harm. To advance serviceable suppositions which are not grounded on fact, is as impossible, as it is to build a house without a foundation. The hypothesis is an image of the constructive imagination, but the pedestal of this image must rest on the ground of fact. The investigator who would be scientific must exercise scrupulous care in securing his facts through observation and experiment. The rules and errors involved in such a procedure have received sufficient attention.
(2) After the investigator has his facts to build upon; and these may be few or many—sometimes even a single fact is sufficient—then may he theorize as to a possible explanation of them. Here is where the real work of the born genius tells. To some the facts are nothing but words, to others they mean universal laws and great inventions. Who but a Newton could have seen the law of gravitation in the falling apple? Who but an Edison could have seen the phonograph in the sound wave and wax? It must be recognized that this remarkable imaginative insight is inborn in some cases; and yet this does not preclude the necessity for cultivating this power, though it may be only in a rudimentary state. Here is another opportunity for the school teacher; namely, to train in every legitimate way the constructive imagination.
(3) Having once constructed the hypothesis, the honest scientific investigator at once proceeds to subject it to a series of most rigorous tests. It is well to see big things in a little fact; to have a mind as fertile in new ideas as a watered garden—this is genius! But is it not more incumbent to have a conscience so keen, that nothing will be allowed to pass for truth which has not received ample verification? Intellectual dishonesty is quite as common as moral dishonesty. Moreover, one must maintain an open mind, absolute candor, and a willingness to abandon the most cherished theory. Often it is much easier to explain away contradictory facts than it is to forsake a pet theory.
THE AUXILIARY ELEMENTS IN INDUCTION—OBSERVATION—EXPERIMENT—HYPOTHESIS.
(1) The Foundation of Inductive Generalizations.
(2) Observation. Defined.
(3) Experiment. Defined.
Compared with Observation.
(4) Rules for Logical Observation and Experiment.
Their need.
First Rule.
Second Rule.
Third Rule.
Fourth Rule.
(5) Common Errors of Observation and Experiment.
(1) Preconceived Ideas.
(2) Confusing the Observed with the Inferred.
(3) Ignoring the Exceptions.
(4) Sympathy and Undue Interest.
(5) Inattention and a Fallible Memory.
(6) The Hypothesis.
Defined and Illustrated.
(7) Induction and Hypothesis Distinguished.
(8) Hypothesis and Theory Distinguished.
(9) The Requirements of a Permissible Hypothesis.
(1) Conceivable,
(2) Capable of proof or disproof,
(3) Adequate,
(4) Simple,
(5) Not contradictory.
(10) Uses of Hypothesis.
(1) A working basis,
(2) Guide to ultimate truth,
(3) Discoverer of immediate truth,
(4) Probable explanation.
(11) Characteristics Required by Scientific Investigators.
(1) Accurate observer,
(2) Constructive imagination,
(3) Passion for truth.
(1) Facts are the foundation of all inductive generalizations. Induction is largely a matter of building general notions from individual notions derived from the observation of facts.
(2) Observation is the act of watching the phenomena as they may occur. It involves the voluntary concentration of consciousness on the case in hand.
(3) Experiment is the act of making phenomena occur for the purpose of watching for effects. It is in reality a form of observation which necessitates a manipulation of circumstances.
(4) The average man is not given to careful observation. The rules adopted by scientific observers are: (1) The observation should be precise; (2) should concern only the material circumstances; (3) should be varied; (4) should be isolated.
For the sake of precision many instruments have been invented and methods devised; notably instruments for accurate measurements, such as the balance and thermometer, and methods like the method of averages.
Frequently a situation may be so complicated as to demand a “preadjustment of attention.” With the untrained this very preadjustment may lead to serious error.
An “all-angled observer” is the most trustworthy.
(5) Errors in observation come from preconceived ideas; confusing perception with inference; ignoring the exceptions; sympathy; inattention; and a fallible memory.
(6) An hypothesis is a supposition advanced for purposes of explanation and proof.
(7) An hypothesis is a tentative induction. As soon as it is deprived of its tentative nature it ceases to be an hypothesis.
(8) Hypothesis and theory are often used interchangeably when reference is made to phenomena of low probability. Theory should be used only in instances of high probability.
(9) A permissible hypothesis must be (1) conceivable; (2) capable of proof or disproof; (3) adequate; (4) simple; (5) must not contradict any verified truth.
(10) The hypothesis is especially serviceable in these four particulars: (1) as a working basis; (2) as a guide to ultimate truth; (3) as a discoverer of immediate truth; (4) as affording probable explanations.
(11) There are certain characteristics which an honest and courageous investigator needs to possess. These are: (1) undoubted ability as an accurate observer of facts, (2) a constructive imagination, (3) a passion for truth.
To build an acceptable hypothesis without fact is as impossible as it is to build a house without a foundation.
The genius, because of his imaginative insight, transforms the simple fact into a complex invention or law.
A prevailing “intellectual dishonesty” suggests the need of “a greater passion for truth.”
(1) Show that facts are the raw material of induction.
(2) Define and illustrate a fact.
(3) Define induction in terms of the notion.
(4) Define and illustrate observation.
(5) Define and illustrate experiment.
(6) Show the difference between observation and experiment.
(7) State and exemplify the rules for logical observation and experiment.
(8) Illustrate the method of averaging observations.
(9) Explain “preadjustment of attention.”
(10) What is the most common error with the untrained observer? Explain and illustrate.
(11) Explain the expression “all-angled observer.”
(12) State and exemplify the errors of observation and experiment.
(13) To what error in observation are superstitions generally due?
(14) Define and illustrate hypothesis.
(15) Indicate the difference between an hypothesis and an ordinary induction.
(16) When may theory and hypothesis be used interchangeably? Illustrate.
(17) Show by illustration that the term theory is ambiguous.
(18) Summarize the requirements of a permissible hypothesis. Illustrate.
(19) Select some school room experience with a view of making it conform to the requirements of a permissible hypothesis.
(20) Explain and illustrate the uses of hypothesis.
(21) “The scientific discoverer climbs up to the light on the stairway of discarded hypotheses.” Explain.
(22) Write a short theme on “Characteristics Required by Scientific Investigators.”
(1) “Land and sea breezes are due to a difference in temperature.” Is this a fact or a law? Explain your position.
(2) Give three different definitions of induction. Which one have you adopted? Defend your position.
(3) Define and illustrate observation.
(4) Distinguish between observation and attention.
(5) “In observation we find, in experiment we make.” What is meant by this?
(6) Give illustrations of falsehood due to careless observation.
(7) Argue for and against the use of “expectant attention” in observation.
(8) “Nine-tenths of what we see comes from within.” Do you believe this? Labor the question.
(9) Offer suggestions which, if followed, should lead to scientific observation.
(10) “One must be just before he is sympathetic.” Relate this to the fine art of accurate observation.
(11) Is an hypothesis a generalization? Explain.
(12) Give school room examples of hypotheses which lead to injustice.
(13) “An hypothesis is merely a tentative induction.” Make clear this assertion.
(14) Illustrate inconceivable hypotheses by drawing on your knowledge of ancient history.
(15) “Prejudice and willful blindness to truth have ever been imminent stumbling blocks in the path of progress.” Expatiate upon this.
(16) Are the hypotheses advanced concerning communications from the spiritual world capable of proof or disproof? Give reasons.
(17) Show by historical examples the use of discarded hypotheses.
(18) “Genius is another name for hard work.” Do you agree? Defend your position.
(19) “The man to whom nothing ever occurs is unlikely to make any important discoveries.” Discuss this.
“Our habits make or unmake us.” “In a thoughtless hour a groove is imbedded in the nerve substance, and thereafter, nine-tenths of the life flows through that groove.” Habit is, indeed, a most powerful and a most tyrannical master; and yet it has come within the observation and even the experience of many, that thought is even more masterful than habit. Appearing at the psychological moment and in a pedagogical way, a thought may be made to possess the mind with force sufficient to break almost any habit. From an ethical point of view, the exceptions to this are due to an inability to arouse thought of sufficient strength. Moreover, mental reactions which result in habit are originally brought about through some thought process. Speaking in general terms, it may be affirmed that thought makes habit and if sufficiently strong breaks habit. That our habits make or unmake us may be true, but is it not likewise true that our thoughts make or unmake our habits?
Thought is king; thought has made man king of the animal kingdom, and if thought has figured so largely in the evolution of the human animal in past ages, may we not assume that it will sway the future ages in like manner? Thought is a product of the class room. Here thoughts which make habits, and thoughts which break habits have full sway. As the children of the American schools think to-day, so will the men of American life think on the morrow; and as America thinks so will she ultimately do. This lends vital import to any object which may either inspire or regulate thought.
As commonly treated logic is a regulative subject. This implies the two aspects of direction and correction. Logic directs by means of the laws and forms of thought, and corrects by means of the rules of right thinking. To a certain degree both departments of logic are directive as well as corrective; but it is worthy of remark that inductive logic emphasizes the former, while deductive logic lays stress upon the latter. It is inductive logic which shows how man has acquired new knowledge; inductive logic explains the mode of procedure adopted by the discoverer and the inventor. On the other hand, deductive logic is distinctly a science of criticism. Induction directs to new truth; deduction aims to modify and correct new truth.
Though there are many special forms of thought, yet there are but two general forms; namely, induction and deduction. Inductive thought seeks the new; deductive thought corrects the old. Similarly, there are two types of mind: the inductive type and the deductive type. The former reaches out for new things, the latter is satisfied with ordering the old. In politics the man with the inductive type of mind becomes a “Liberal” or a “Progressive”; while the man with the deductive type of mind becomes a “Conservative” or a “Standpatter.” It must be conceded that both are needed in the development of the best form of Democracy. We need an unfettered freedom as advocated by Jefferson; but we also need an ordered freedom as taught by Hamilton.
Since the beginning these two mental types have been in evidence—the liberal who wants to do things, and the conservative who wants to weigh things. With the liberal, it is fight whether or no; with the conservative, it is fight provided the enemy is not too formidable. The one dares; the other cautions: both are needed to balance the world.
Liberalism and conservatism may be fostered in the school room, and to maintain a true balance each must receive its share of attention. Is such the case? The passing of “district-school-individualism” and the coming of “graded-school-collectism” has transferred the emphasis from liberalism to conservatism—from the inductive type to the deductive type. In this day it seems to be more important to have the child’s work orderly, than to have it original. In the main, examination papers call for correct knowledge and not for thought; in the main, promotions are based on accuracy, not on initiative. The conservative type being in control, the schools are sending out too many “Deductives,” not enough “Inductives.” The world needs more Columbuses and Edisons.
A change must come. The methods of instruction are too didactic and not sufficiently inspirational. Greater attention must be given to the spirit of discovery and less to the spirit of correction. The teacher must lead less and follow more; must correct less and suggest more; must tell less and direct more. If we are to give greater attention to the training of discoverers, logic may aid in this crusade by calling attention to the common mode of procedure which the discoverers of the past have adopted. This is a legitimate topic for the logician, since induction, deduction, hypothesis, and proof have ever been common tools in the discoverer’s workshop. With a view to becoming better acquainted with the common mode of procedure of the man who seeks for new truth, let us study two typical instances:
(1) The Discovery of Neptune.
The discovery of Neptune was a double one. Early in the present century it was found that Uranus was straying widely from his theoretic positions, and the cause of this deviation was for a long time unsuspected. Two astronomers, Adams in England and Leverrier in France, the former in 1843 and the latter in 1845, undertook to find out the cause of this perturbation, on the supposition of an undiscovered planet beyond Uranus. Adams reached his result first, and the English astronomers began to search for the suspected planet with their telescopes, by first making a careful map of all the stars in that part of the sky. But Leverrier, on reaching the conclusion of his search, sent his result to the Berlin observatory, where it chanced that an accurate map had just been formed of all the stars in the suspected region. On comparing this with the sky, the new planet, afterward called Neptune, was at once discovered, 23d September, 1846.
(2) Bees are guided in their flight by a knowledge of their surroundings, not by a general sense of direction.
“M. Romanes took a score of bees in a box out to sea, where there could be no landmarks to guide the insects home. None of them returned home. Then he liberated a second lot of bees on the seashore and none of these returning, he liberated another lot on the lawn between the shore and the house. None of these returned, although the distance from the lawn to the hive was not more than two hundred yards. Lastly he liberated bees in different parts of the flower garden on either side of the house, and these at once returned to the hive.” (Hibben.)
A multiplication of instances would only give stronger evidence to the fact that the mode of procedure adopted by the discoverer and inventor conforms to these three general steps: (1) antecedent facts, (2) forming an hypothesis, (3) verification. It will be to our advantage to study somewhat in detail these three steps.
(1) Antecedent facts.
In the discovery of Neptune the decisive or crucial fact was the knowledge that Uranus deviated from his true path about the sun. This knowledge was obtained through observation and mathematical calculation. But the hypothesis of the existence of another planet could not have been formed had it not been for the more fundamental facts of inertia, gravitation, falling bodies, etc. For the sake of definiteness antecedent facts may thus be divided into foundation facts and crucial or decisive facts. The latter are an outgrowth of the former. The foundation fact of the second illustration is Romanes’ knowledge of animal instinct; while the crucial fact is, no doubt, the observation that bees fly in a circle before starting for home. In the case of Newton’s discovery of the law of gravitation, the falling of the apple was the crucial fact; while his knowledge of terrestrial gravity proved to be the vital foundation fact.
A crucial fact is one which leads immediately to the formation of a reasonable hypothesis. It is not to be inferred from this that the same fact becomes a crucial one to all alike. The falling of the apple was only crucial to a genius like Newton. With the average only extraordinary facts become crucial; but with the genius any ordinary fact may become crucial. Both the scholar and the genius may have the foundation facts, but only the latter may be able to read into a dry fact or event, a new world of truth.
(2) Forming an Hypothesis.
From the viewpoint of logical correctness, the matter of hypothesis has received due attention in an antecedent chapter; we need now to look at the subject through the eyes of the discoverer, not the logician. The crucial fact at first creates an intellectual perplexity which is accompanied with an uneasy, dissatisfied state of mind. This unsatisfied feeling drives the intellect to protracted thought. As a final result some hypothesis is constructed which seems to explain the crucial fact. Here is where analogy functions in a most vital manner. No hypothesis is forthcoming unless it resembles the crucial fact. It has been remarked elsewhere that analogy is the basic element in the forming of hypotheses. So it transpires, that the protracted thought referred to, is virtually a mental effort to detect significant resemblances between the well known crucial fact, and some hypothetical fact which the imagination may picture. To put it differently: The crucial fact arouses a mental state of unrest which in turn drives the mind to a “still hunt” for relations. The establishment of the hypothesis is simply a makeshift, designed to satisfy this “mental urge.” In the discovery of Neptune the crucial fact, the deviation of Uranus, produced a state of uneasiness in the minds of the astronomers. Surely something was wrong. This urged them to further meditation, which finally resulted in the hypothesis that there must be an unknown planet beyond the orbit of Uranus. They assumed, of course, that the relation between this supposed planet and Uranus was analogous to the relation between any two of the known planets. In the case of Newton the falling apple stirred his astute mind to the assumption that the same force which pulled the apple, likewise pulled the moon towards the earth. Here we have again (1) the crucial fact, (2) the mental urge, (3) the analogous hypothesis.
(3) Verification.
Forming an hypothesis only partly fulfills the demands of an unsatisfied intellect. The true discoverer, being possessed with a passion for truth, seeks for “the truth, the whole truth, and nothing but the truth.” In consequence the hypothesis is subjected to tests which may lead to its confirmation, its rejection, or its modification.
The two possible modes of verification are recourse to experience and appeal to reason; or empirical proofs and rational proofs. In the former the hypothesis is compared with facts by means of further observation and experiment. M. Romanes’ experience with the bees is a fair illustration of this form. Possibly the student has already noted that Romanes’ mode of procedure conforms to the “joint method of agreement and difference.” In the case of rational proofs the hypothesis is subjected to deductive demonstration, either of the form of syllogistic argument or mathematical calculation. A fair sample of this kind of verification is Newton’s discovery of universal gravitation. When he decided that the moon and the apple might be controlled by the same universal force, he undertook to establish his hypothesis by mathematical calculation. At first his figures seemed to disprove his theory, but after a wait of ten years, new data relative to the diameter of the earth, removed the apparent discrepancy. In the case of the discovery of Neptune, the verification was both rational and empirical. Mathematical (rational) calculation led to the assumption that the new planet must be at such a point. With this knowledge the observer was enabled to turn his telescope to the spot indicated and there, true to the calculations, was Neptune (empirical).
To summarize: The method of the discoverer involves a knowledge of certain fundamental facts; the observation of crucial facts; a mental unrest; the constructing of an hypothesis through analogy; and finally verification by either appeal to experience, or mathematical demonstration.
It has been remarked elsewhere that there are two general mind types, the liberal and the conservative. Also that the natural method of thought animating the former is inductive; while the natural method of thought of the latter is deductive. The “liberal” is the apostle of new truth; the “conservative” an apostle of safe truth. Both types are needed; the one to balance the other. In consequence both methods are of service in the class room; here each should be given its proportionate place. That this condition does not obtain may not be apparent, since much attention is being given to certain inductive forms, such as “proceeding from the concrete to the abstract,” “from the particular to the general,” “from the known to the related unknown,” etc. Likewise the courses of study and the various text books, claim to advocate the use of the inductive process. Seemingly these facts point toward a very general observance of the inductive tenets. This is true with one vital exception: Induction is the natural method of the discoverer. With it he acquires knowledge; but in the class room induction is used to impart knowledge. In life the discoverer takes the initiative, thinks his own thoughts first hand; but in the school room, above the kindergarten, the child is not allowed to take the initiative, not even in his play. All is planned for him, all doled out, not in the raw, but partially made over. The teacher must impart a certain amount of knowledge in a given time, and consequently she must “set the pace” in this race for second hand facts. To allow the child to lead; to give him the benefit of his own individuality; to permit him to use the God given spirit of discovery which clamors for recognition; would be suicidal according to our present standards. If the plan of the discoverer were followed, the course of study could not be covered; children would fail of promotion; and criticism would be forthcoming from both principal and parent.
In the average class room of the day the inductive FORM prevails but the SPIRIT is not in evidence. Like a wolf in sheep’s clothing induction has entered the class room to devour that primal force in the child’s make-up, which has raised his race above his simian ancestors. Our class room methods, being inductive in form but deductive in spirit, may train the youngster to be a camp follower but never a leader in thought and action. The call of the day is for more initiative; for more originality; for more individuality; for more enthusiasm. There is too much form without the spirit; so much that bespeaks system and refinement without those native impulses and native abilities which mark one child from another. Like the books of a library our children are classified and labeled, and when more come in the others are dusted and placed on the next higher shelf. How many more centuries must we wait before the schools will adopt, in spirit as well as in form, the pedagogical principles of life? Will the time ever come when it may be said that all our leaders in thought and action are college graduates?
The inductive method is pre-eminently the method of the discoverer only when it involves both the form, which he follows, and the spirit, which he evinces. The so-called method of the school room is inductive in form, as the procedure is from particular facts to general truths; but deductive in spirit, as it is used to impart knowledge. If it were inductive in spirit, the child would be allowed to acquire knowledge entirely through his own initiative. Deduction is the method of instruction, whereas induction is the method of discovery. That the child of the school is instructed or better “deducted” and not generally allowed to discover, is a situation so apparent that we need not labor the point further.
Because the inductive process has been made a method of instruction, it has been robbed of its chief advantage over deduction. Indeed, as a method of instruction, deduction is really the superior method. It requires less time, demands greater concentration, often arouses more interest, and creates situations which are less involved.
In all great inventions, man has taken his cue from nature. In inventing the telescope, his model was the eye; in building his house, his inspiration was the cave. In reality man has accepted nature’s suggestions, and then attempted to improve upon them. In this he has met with success. From the crab apple tree, he has developed the northern spy; from the wild hen which laid 25 eggs a year, he has evolved the modern hen which produces 225 eggs a year. Moreover, man has attained his greatest successes by enlarging upon the thoughts of nature and not by unmixed substitutions. Burbank, through a long process of years, has changed the color of a flower, but in accomplishing this did he not use some hidden tendency of nature? Burbank, with all his wisdom, cannot give a flower color unaided by “Dame Nature.”
When man commenced to study nature’s mode of education, he saw that fearful sacrifices were entailed, both in time and in energy as well as in life itself; and so he evolved a more economical way of leading the child through the experiences of the race. In consequence, he has developed the present splendid system of education.
In the evolution of all great institutions, there are in evidence crucial weaknesses, and in the evolution of man’s educational system it appears that he has erred in adopting nature’s form of education without her spirit of education. In his anxiety to have the young acquire as much as possible, man has overshot nature’s true purpose. For example, the big word in man’s educational system is knowledge; but the big word in nature’s educational system is conquest. Nature gives man knowledge simply to reward him for his effort; but man would give to his fellow the reward without the effort. According to nature, the strongest men are those who overcome most; according to man, the strongest men are those who know most. The common educational principles, such as, “From the concrete to the abstract and from the known to the related unknown,” etc., are interpreted by man from the viewpoint of knowledge; whereas nature would teach that these are a feasible way to develop power—to grow manhood. It is seen that nature uses knowledge only as a means to an end, and therefore when man uses knowledge as an end only, he is trying to substitute a plan of his own for nature’s plan. The best results can be secured only when man co-operates with nature in developing, and at the same time regulating, the spirit of conquest.
It has been remarked in this chapter, that the “crucial fact” serves to stir the mind of the natural born discoverer to an activity raised to the nth power of effectiveness. Naturally, the intent of such activity is to solve the mysteries which the crucial fact may suggest. This passion of the mind to “know more about it” is appropriately termed “the mental urge.” From the viewpoint of the pedagogue, the “mental urge” is simply an intrinsic interest in the situation at hand; an interest born of an innate or acquired passion to know the truth.
With the average child, the “mental urge” is strong only when the situations appeal to some immediate need or vital experience. The attempt to make the school work concrete and vital; to make it answer the child’s natural curiosities and real necessities, is dignified with the name “motivation.” It is obvious that this is a new term for an old condition. To motivate the work, means to give to it an attractiveness which any situation might have for the true born discoverer and inventor. If we would use the discoverer’s method successfully, we must learn the art of motivating the work. This may be accomplished by appealing to the play instincts, to the business instincts, and to the vital interests of every day life.
A revolt has already set in against this insatiate desire to teach knowledge, rather than to teach the child. Many schools are permitting a study of those topics which vitally concern every day life. Less attention is being given to formal discipline, and more attention to self activity. Gradually will the scheme of education be directed toward fitting the school work to the child, rather than fitting the child to the school work. When this new thought in education is fully upon us, then will every device and method be directed toward giving full scope to the spirit of inquiry, which so completely possesses every normal child.
It now remains for us to indicate ways in which the spirit of inquiry, or the “discoverer’s method,” may be adapted to school room work. In the first illustration, we shall outline the topic as it is generally given in the average school where attention is paid to development work. This will then be followed by a second outline which may be suggestive of the discoverer’s mode of procedure.
First illustration. School Room Method.
I. Aim: To teach addition of business fractions.
II. Preparation: (Only type examples given).
| (1) | (2) | (3) | |
| 3 bushels | 3 parts | Rule: | Only like numbers |
| + 5 bushels | + 5 parts | can be added. | |
| 8 bushels | 8 parts | ||
III. Presentation:
| (1) | (2) |
| 3 ninths | 3/9 |
| + 5 ninths | + 5/9 |
| 8 ninths | 8/9 |
| (3) | (4) |
| 2/3 = 4/6 | 2/3 = 8/12 |
| 1/6 = + 1/6 | 3/4 = + 9/12 |
| 5/6 | 17/12 |
IV. Summary:
(1) Only like fractions can be added.
(2) Change unlike fractions to like fractions.
(3) Add the numerators, placing the sum over the common denominator.
V. Application:
Examples and problems involving similar and dissimilar fractions.
Before undertaking to illustrate the discoverer’s method, it may be well to designate in order the evident steps as they would appear to the pedagogue:
(1) Motivate the topic to be presented.
(2) Bring to mind appropriate “foundation facts.”
(3) Make evident the “crucial fact.”
(4) Lead to the forming of an hypothesis through analogy.
(5) Afford ample opportunity to prove the hypothesis.
Discoverer’s Method Adapted.
Lesson Plan.
I. Aim: (1) By playing upon the curiosity or by exposing a vital need, create a strong desire to know how to add business fractions. (Motivate the topic.)
Curiosity: “We all know what a fraction is and we know, too, how to change fractions to higher or lower terms.” “Now I wonder how many know how to add fractions, such as 2/5 and 1/5?” “Don’t you tell any one, Mary, but just write your answer on a piece of paper and show it to me.” (Mary’s answer shows that she has thought correctly, but figured incorrectly. John, after having raised his hand, shows his answer to the teacher.) “John has the right answer.” “That’s fine, but let us keep the secret, John.” “I wonder how many others there are in this class who will find the right way?” etc., or
Vital need: Discuss with the class the various occupations of life and secure expressions of preference. Some may plan to be real estate agents, others contractors or book keepers, etc. “George, you plan to be a book keeper.” “Let us suppose that I have given you the job of book keeper in my factory.” “Show that you are worth your wages by adding these numbers: 1243⁄4, 6472⁄3.” “What! can’t do it?” “Then I don’t want you!” etc.
II. Preparation:
(2) Bring to the foreground the necessary foundational knowledge. Suggestions:
| 4 bushels | 8 parts |
| + 3 bushels | + 2 parts |
| 7 bushels | 10 parts |
III. Presentation:
(3) Make evident the crucial fact. Suggestions:
| Add | 2 fifths | 3 eighths | 3/8 |
| + 1 fifth | + 1 eighth | + 1/8 | |
| 3 fifths | 4 eighths |
(4) Without further suggestion, give the young discoverer suitable opportunity for finding the sum of 3/8 and 1/8. In the act of discovering, an implicit hypothesis takes form in the mind through analogous reasoning. This point marks the climax of the lesson—the supreme moment, when the skill and tact of the teacher is assessed to the limit. Just here the child must have a comfortable environment where perfect concentration is possible. Nothing must be forced; and there should be nothing suggestive of disgrace or shame, if the youthful Columbus is unsuccessful. The first attempt should be without books. If more help is needed, access to books may be given. If the investigation is still without definite result, then as a last resort the teacher may, in the presence of the child, add fractions, solving with deliberation example after example, until the child believes he has discovered the process.
(5) Stimulate a desire to verify the facts discovered.
Suggestions leading to verification: Afford opportunity for mathematical demonstration. Illustrations: The fractions 1/4 and 3/8 have been added in this way—
1/4 = 2/8
3/8 = + 3/8
5/8
Use is now made of the crucial fact, when the example assumes this form—
2 eighths
+ 3 eighths
5 eighths
Or if the class has been trained in the use of the diagram the following may be the form of proof:
1⁄4
 ━━━━━━━━━━
━━━━━━━━━━
──────────
━━━━━━━━━━
──────────
━━━━━━━━━━
3⁄8
 ──────────
──────────
━━━━━━━━━━
──────────
━━━━━━━━━━
Explanation from diagram. I see that 1⁄4 equals 2 parts and 3⁄8 equals 3 parts; the sum of 3 parts and 2 parts are 5 parts. But the name of the part is eighths; hence the answer 5 parts may be written 5 eighths, or 5⁄8. Thus the final form is
2 parts
+ 3 parts
5 parts = 5⁄8
Give opportunity to consult answers in text books as further verification.
The summary and application of adding fractions according to the “discoverer’s method,” are virtually the same as the corresponding steps in the “school room method.”
Second Illustration of Discoverer’s Method.
David P. Page in his Theory and Practice of Teaching well illustrates the discoverer’s method in conducting a general exercise in nature study. We cannot do better than to quote from him:
“It is the purpose of the following remarks to give a specimen of the manner of conducting exercises with reference to waking up the mind in the school and also in the district. Let us suppose that the teacher has promised that on the next day, at ten minutes past ten o’clock, he shall request the whole school to give their attention five minutes to something that he may have to show them. This very announcement will excite an interest both in school and at home (playing upon the curiosity); and when the children come in the morning they will be more wakeful than usual till the fixed time arrives. At the precise time, the teacher gives the signal agreed upon, and all the pupils drop their studies and sit erect. When there is perfect silence and strict attention by all, he takes from his pocket an ear of corn and in silence holds it up before the school. The children smile, for it is a familiar object (foundational knowledge already in hand); and they probably did not suspect they were to be fed with corn.”
Teacher. “Now, children,” addressing himself to the youngest, “I am going to ask you only one question about this ear of corn. If you can answer it, I shall be very glad. As soon as I ask the question, those who are under seven years old, and think they can give an answer, may raise their hand. What is this ear of corn for?”
Several of the children raise their hands, and the teacher points to one after another in order, and they rise and give their answers.
Mary. It is to feed the geese with.
John. Yes, and the hens, too, and the pigs.
Sarah. My father gives corn to the cows.
Laura. It is good to eat. They shell it from the cobs and send it to the mill, and it is ground into meal. They make bread of the meal and we eat it.
“I am sorry to tell you that none of you have mentioned the use I was thinking of, though, I confess, I expected it every minute. I shall now put the ear of corn in my desk, and no one of you must speak to me about it till to-morrow. You may now take your studies.”
The consequence of this would be that various families, father, mother and older brothers and sisters, would resolve themselves into a committee of the whole on the ear of corn: and by the next morning several children would have something further to communicate on the subject. The hour would this day be awaited with great interest and the first signal would produce perfect silence.
The teacher now takes the ear of corn from the desk and displays it before the school; and quite a number of hands are instantly raised as if eager to be the first to tell what other use they have discovered for it.
The teacher now says pleasantly, “The use I am thinking of you have all observed, I have no doubt; it is a very important use, indeed; but as it is a little out of the common course (crucial facts) I shall not be surprised if you cannot give it. However, you may try.”
“It is good to boil,” says little Susan, almost springing from the floor as she speaks. “And it is for squirrels to eat,” says little Samuel. “I saw one carry away a whole mouthful yesterday from the cornfield.”
Others still mention other uses. Perhaps, however, none will name the one the teacher has in his own mind; he should cordially welcome the answer if perchance it is given. (Supposing that it has not been given.) “I have told you that the answer I was thinking of was a very simple one; it is something you have all observed and you may be a little disappointed when I tell you. The use I have been thinking of for the ear of corn is this: It is to plant. It is for seed, to propagate that species of plant called corn.” (Verification.) Here the children may look disappointed as much as to say, We knew that before. The teacher continues: “And this is a very important use for the corn; for if for one year none should be planted, and all the ears that grew the year before should be consumed, we should have no more corn. The other uses you have named were merely secondary. But I mean to make something more of my ear of corn. My next question is: Do other plants have seed?” Here is a new field of inquiry, etc., etc.
From the standpoint of “the greatest amount of knowledge in the shortest possible time,” this mode of presentation consumes an inexcusable amount of time and is, therefore, “impracticable.” But when viewed from the ground of interest, originality, initiative, and conquest—the watchwords of the “new thought in education”; there is no real waste in either time or energy. The spirit and method of the discoverer will no doubt be the educational slogan of the future age.
Epitome of Discoverer’s Method, adapted to the class room:
(1) Motivate the topic to be presented.
(2) Bring to mind, if necessary, the “foundational facts.”
(3) Make evident the “crucial fact.”
(4) Furnish every opportunity for a first-hand discovery of the “lesson-point” (establishing hypothesis through analogy).
(5) Let the hypothesis be verified.
The entire situation must be one of freedom, zeal, originality, and initiative.
No one mode of presentation is more universally used than the “question and answer.” The advantages of this mode are many and the teacher who is an adept in the art of questioning, from the standpoint of knowledge, is generally efficient. The common error, however, incident to much questioning, is that of asking “telling questions.” By the use of such, the class is forced along the desired channel of thought so rigorously as to have a condition where the spirit of inquiry is entirely wanting. It is possible to conform to the rules of good questioning, and yet rob the class of all originality and initiative. From the teacher’s viewpoint, the discoverer’s method demands few questions; it is the method of suggestion rather than one of questions. Avowedly in this method, the children should ask and answer their own questions. Viewed from the ground of discovery there are three modes of presentation which may represent a progressive series. These are (1) the lecture mode, (2) the question and answer mode, (3) the mode by suggestion. In the first there is little of the spirit of the discoverer; in the second there is a trifle more of the spirit of the discoverer; while in the third there is much of this spirit. The student is advised to select some class room topic with a view to illustrating these three modes of presentation.
LOGIC IN THE CLASS ROOM.
(1) Thought is king.
(2) Special functions of induction and deduction.
(3) Two types of mind.
Inductive or liberal.
Deductive or conservative.
(4) Too much conservatism in school.
(5) The method of the discoverer.
Three steps
| 1. Antecedent facts |
 |
1. Foundational |
| 2. Crucial | ||
| 2. Forming hypothesis |
 |
1. “Mental urge” |
| 2. Analogy | ||
| 3. Verification |
 |
1. Empirical |
| 2. Rational |
(6) The real inductive method or Discoverer’s Method not in vogue in class room work.
(7) As a method of instruction, deduction is superior to induction.
(8) Conquest, not knowledge, the desideratum.
(9) Motivation as related to the spirit of discovery.
(10) Discoverer’s method or the real inductive method adapted to class room work.
School room method.
Discoverer’s method.
Epitome.
(11) Question and answer method not necessarily one of discovery.
(1) Thought is king in that it is the ruling factor in the making and breaking of habit. This lends import to logic, which is the science of thought.
(2) The chief function of induction is to discover new truth; whereas deduction aims at clarifying and correcting new truth. Inductive logic makes known the special forms of thought which the discoverer uses; while deductive logic tends to show how he verifies the truth thus obtained.
(3) Just as there are two general forms of thinking, inductive and deductive; so there are two general types of mind, the inductive and the deductive; the former leads to liberalism, the latter to conservatism. Both types are needed to maintain a safe balance.
(4) The schools of the day are emphasizing the deductive phase of work to the sacrifice of the inductive. They are neglecting the Columbuses and the Edisons of the class. The course of study makes for a conservatism, which “nips in the bud” any marked tendency to discover and invent.
(5) Logic may aid in the crusade against the ultra conservative tendency of class method, by giving emphasis to the method of the discoverer and inventor. An analysis of this method reveals these three steps: antecedent facts, forming an hypothesis and verification. Antecedent facts may be divided into foundational and crucial. A crucial fact leads immediately to the formation of the hypothesis; whereas the foundational facts represent that body of knowledge which makes it possible to interpret the crucial fact. The crucial fact creates an unsatisfied state of mind, which, in turn, urges the discoverer to construct some satisfactory hypothesis. Inference by analogy is the process used in such a construction. The two modes of verification are recourse to experience, or empirical; and appeal to reason, or rational.
(6) In the class room, induction is used in form, not in spirit; in consequence we are neglecting the generals for the camp followers.
(7) The inductive method is logically the method of discovery, while the deductive method is the method of instruction. In the class room, both methods have been devoted to the matter of instruction. Because of this, induction has been robbed of its chief advantage over deduction.
(8) Man has attained his greatest success by enlarging upon the thoughts of nature and not by an absolute substitution. In enlarging upon nature’s way of educating the child, man has adopted her form of procedure, but has lost her spirit of work. In his scheme of education, man’s watchword is knowledge, while nature’s is conquest. To seek knowledge without inspiring the spirit of conquest is man’s way; whereas nature’s way is to encourage the spirit of conquest by using knowledge as a reward. Man must co-operate with nature, if the best results are to be secured.
(9) In the case of the true discoverer, it is not necessary to endow the object of his thought with added attractiveness; but with the child enthusiasm may need to be stimulated by “motivating” the subject in hand. This may be accomplished by appealing directly to the vital needs, worldly necessities, and innate cravings of the child mind.
(10) A revolt is in evidence against that insatiate desire to teach knowledge, which has been so marked in the past. Already schools are introducing departments of work which look toward conquest rather than knowledge.
When adapted to the school room the discoverer’s method naturally resolves itself into these five steps:
(1) “Motivate” the topic for presentation.
(2) Bring to mind “foundational facts.”
(3) Vividly make evident the “crucial fact.”
(4) Lead to discovery of “lesson-point.”
(5) Afford opportunity for verification.
(11) The question and answer method of presenting work, does not necessarily give full scope to the spirit of inquiry as emulated by the true born discoverer.
As a matter of affording opportunity for the development of the spirit of discovery, there are three modes of presentation which may be arranged in a progressive series:
(1) The lecture mode in which there is little opportunity for discovery.
(2) The question and answer mode which permits some opportunity for discovery.
(3) The mode by suggestion which permits ample opportunity for discovery.
(1) Show that thought may be made to make and break habit.
(2) “Induction directs to new truth, deduction aims to modify and correct new truth.” Explain and illustrate this.
(3) Relate radicalism and conservatism to induction and deduction.
(4) Show that in the present day school situations, the spirit of deduction prevails.
(5) Describe a discovery which is a typical illustration of the discoverer’s method.
(6) Indicate with explanation the general steps in the discoverer’s method.
(7) Show by illustration the difference between “foundational facts” and “crucial facts.”
(8) Explain how the “crucial fact” leads to the construction of an hypothesis.
(9) Explain and illustrate the two ways of verification.
(10) Distinguish between the inductive method as it is used in the class room, and the inductive method as used by the discoverer.
(11) Show that in his inventions, man enlarges upon the thoughts of nature.
(12) Explain “motivation” and show that it is a new name for an old situation.
(13) In adapting the discoverer’s method to class work, what are the successive steps to be followed?
(14) Show by illustration that the question and answer method is not necessarily one which encourages the spirit of discovery.
(1) “Our pet thoughts control us.” Discuss this.
(2) Select some class room experience for the purpose of showing that induction is especially directive in nature, whereas deduction is more or less corrective in nature.
(3) “There are just two kinds of people in the world, the Inductives and the Deductives.” Explain.
(4) Are the schools sending out too many Deductives? Argue the question.
(5) “It is the business of the teacher to teach himself out of the business.” Explain.
(6) Look up the discovery of the laws of the pendulum, with a view of showing that the event well illustrates the fact of the three general steps in the discoverer’s method.
(7) “With the average, only extraordinary facts become crucial; but with the genius any ordinary fact may become crucial.” Make this clear.
(8) Explain “mental urge.” Illustrate.
(9) Illustrate “empirical proof,” also “rational proof.”
(10) Show by illustration that the inductive method as used in the class room, falls far short of being the method of the discoverer.
(11) Indicate by citing historical examples, that conquest rather than knowledge makes for manhood.
(12) Show how you would motivate a topic in geography.
(13) Outline a plan for teaching some topic in nature according to the discoverer’s method.
(14) Select a topic in arithmetic, for the purpose of giving a comparative illustration of the “question and answer mode” of presentation, and the “mode by suggestion.”
“To prepare for complete living” seems to be the ultimate aim of education, and any school subject which does not aid to this end must be eliminated from the courses of study. “Knowledge for the sake of knowledge” will not do in this age of practical efficiency. A subject in order to survive must show indications of doing its share in this larger business of man building. If it can be made evident that logic lends itself in no undecided terms to such an aim, then may its incorporation in a secondary course of study be not only justified but more highly appreciated.
That man is the supreme agent of intelligent progress is due to three factors: First, to the existence of the natural world; second, to the existence of man himself; third, to man’s ability to think. Given life and the world as a place to evolve that life, and it is barely possible that man might have survived, but without thought he could never have become supreme. Man is king of the animal kingdom because of his power of thought. Let us illustrate:
Ages ago when England was a part of the main land; when there was no North Sea nor English Channel; we are told that there lived in the forest tracts there about many large and ferocious animals; such as the elephant, the lion, and the tiger. There lived also in the region a smaller and apparently a weaker animal. This creature had no tusks to hook with, no great jaws to crunch with, and no claws to tear with; and an eye witness would have said “Such a weakling has no possible chance against these enemies of his; he and his descendants will succumb and the species will become extinct.” The region was tropical; but, of a sudden, a cataclysmic twist changed the temperature from a torrid to a frigid state. What happened? The large and ferocious animals either migrated to the south or froze to death; but this weakling put on furs, built fires, and remained in the jungle as its king. His name was man, and though he had no horns to hook with, he possessed a brain to think with; this gave him supremacy over the forces of nature.
From the beginning the adaptation of the lower animals has been physical; whereas man’s has been more or less intellectual. By means of deliberative thought man made the bow and arrow which could kill at a distance of 200 yards; then he invented the repeating rifle which may kill a mile away. Thought has taught man to harness the forces of nature in the form of all kinds of invention. Thought has given man the power to build bridges and palaces, to paint pictures, to chisel angels. Thought has pierced the fog of ignorance and brought light to the dark spots of the globe. Thought has build nations and established the spirit of good will on earth. Through the long years, thought has been the one tool of conquest which has enabled man to build for himself, out of the furnishings of nature, a heaven on earth.
Can you recall a department of life which thought has not embellished? Can you recall a single factor that has been raised to the nth power of efficiency without thought? Steam and electricity plus thought lights the world, unites the world, feeds and clothes the world. To-day, as in the olden time, men who think are ever at a premium. This holds true from the Shopkeeper to the Magnate of Wall Street; from Basil, the Blacksmith, to Edison, the King Inventor; from Reuben, the Farmer, to Burbank, the Wizard.
Man not only thinks but he thinks progressively. The average horse of to-day, for example, is probably no more intelligent than was the average equine of the time of Alexander the Great, whose war horse, Bucephalus, attained historical fame. Yet, intellectually, the average man of to-day is far above the average man of Alexander’s time. “Horse-knowledge” is more or less stationary. Through instinct each generation makes use of the knowledge of its ancestors without any noticeable accretions. But “man-knowledge” is a growing product of progressive thought. Man appropriates all the knowledge of his forbears, and then adds to this a bit of his own. By being able to think progressively, man is enabled to stand upon the shoulders of his ancestors and thus to take advantage of a broader vision.
We are now led to the conclusion that man’s supremacy is due not only to his ability to think, but to his power of progressive thought.
In the main, man’s thinking has been for his good, that is, in the long run, it has contributed to his general progress. If this had not been so, long since would he have dropped back to the level of the non-thinking animals.
Thinking has been defined as the process of affirming or denying connections. Right thinking is, therefore, a matter of affirming the right connections or denying the wrong connections. To put it differently: right thinking is the process of adjusting the best means to a right end; whereas wrong thinking is a matter of overlooking the best means, or directing improper means to a wrong end. Right thinking involves proper adjustment; wrong thinking improper adjustment. In the intellectual world as in the physical, improper adjustment means extinction. Illustrations of this:
(1) A contractor undertakes to build a skyscraper. In the excavation an old wall is discovered. The thought of the contractor is, “I must make a pot of money out of this job, and since this old wall is in the right spot I will build on it, and thus save me ‘five hundred’.” In the course of ten years, without warning, the building topples over and fifty women and children are killed. The contractor is convicted and sent to prison for life. If the builder had thought the right thought; namely, “I want to put up a building that will stand for generations,” he would have survived the competition of his fellows and entered his long home with success etched upon his soul.
(2) Two school teachers, A and B, are working in the same system. A’s ambition is to be promoted and she uses “pull” as the means. For a time she succeeds in pulling the wires, and likewise in pulling the “wool” over the eyes of the Board of Education. B aspires to professional growth, using as the means every opportunity for genuine improvement. In time both are known as they really are, not as they seem to be. A is denominated a “shirk,” a politician, a mere school keeper; whereas B is looked up to as the best equipped worker in the building, a real school teacher.
There may seem to be many exceptions to this point of view, and yet in the last analysis we find that these exceptions are only apparent. When we maintain that right thinking means survival and wrong thinking extinction, we assume that the standard adopted is genuine efficiency and not a certain money basis. High positions may be secured through wrong thinking, but these cannot be filled creditably without the preponderance of right thinking.
It may be advanced as a plausible hypothesis that man, especially if he is an American, finds much trouble for himself, and makes much trouble for the world because of his indifference to thought. To leap first and look afterwards is the spirit of youth, and America is young. Think twice before you look and look twice before you leap is sound logical doctrine. A logically minded man rationalizes every new proposition before he adopts it. He marshals before the mind the favorable points and then bombards them with every conceivable objection. With the steady eye of an honest, earnest, open minded critic, he weighs the unfavorable against the favorable and then accepts the indications of the balance unequivocally. If logic did nothing else save to inspire young people to thus rationalize every doubtful undertaking, it would do its share toward world betterment.
Man seems to be a natural born gambler. He loves to “take a chance” and herein lies much of his unhappiness. Without discussing the evils of the stock exchange, the horrors of the gambling den, and the unbusiness like procedure of the race track, we may merely attempt here to show how the rationalization of the conception of chance may be instrumental in dimming the glare of gambling to the average youth.
(1) The meaning of the term chance.
The term chance implies an inability to find a cause for any particular event. Whenever we trust to luck, we do so through ignorance. In reality every thing in this world is ordered according to law, and if we possessed infinite knowledge concerning these laws, then, for us, the word “chance” would have no meaning. One accomplishment of knowledge has been to rationalize superstition and chance. “Not a grain of sand lies upon the beach, but infinite knowledge would account for its lying there; and the cause of every falling leaf is guided by the same principles of mechanics as rule the motions of the heavenly bodies.”—Jevon’s Prin. of Science, vol. I, p. 225.
That chance is a literal confession of ignorance, is a wholesome truth for all to bear in mind. If we were not so ignorant of atmospheric conditions, we would never be caught in the rain without an umbrella; if we knew perfectly the laws of mechanics, we would not speed our car and trust to luck that the car would hold together.
(2) Chance mathematically considered.
The principle of the “calculation of chances” has been discussed elsewhere. It will be sufficient here to illustrate the principle from a mathematical point of view.
Suppose that a jeweller desires to dispose of a ten-dollar watch by a raffle. He may place a hundred numbers in a box, one of which corresponds to the number on the watch. My chance of drawing the right number is one out of a hundred and may be expressed by the fraction 1⁄100. The fact that I may draw the right number on the first trial or on the last trial is immaterial. The real meaning of the ratio “one out of a hundred” is, that in the long run, I shall lose 99 times where I gain but once. This implies, that if I pay 25 cents for each draw, I shall in the end pay 99 times 25 cents for the watch, or I will have paid $24.75 for a ten dollar watch.
(3) Chance and gambling.
In all forms of gambling no wealth is produced. What one man gains the other man loses. In addition to this the institution which projects the gambling scheme must be supported. In consequence, more money must be lost than can possibly be gained. This leads to the conclusion that on the basis of averages he who would gamble must terminate his career “behind the game.” Statistics verify this conclusion.
(4) Chance and investments.
Interest, which is money paid for the use of money, is high when the demand for money exceeds the supply and low when the supply equals or exceeds the demand. The fact that the supply is short is largely due to the lack of confidence on the part of the investor. This means that he is unwilling to take the risk. Thus the principle: “High rate of interest, great risk; low rate of interest, little risk.”
“Win right or wrong” is a nut shell statement of modern sophistry. Corollaries to this are such aphorisms as “Of two evils choose the lesser”; “Do evil that good may come,” etc. Armed with these platitudes the modern business and political octopus will play the bully and squeeze the life out of the little fellow in the name of economy; will pay for editorials to elect the “right man”; will evade bad laws so-called; institute lobbies; buy votes; and perpetrate a thousand other immoral deeds in the name of “good business” or of “party loyalty.”
Half truths are the most atrocious of all kinds of fallacies in that they are the most misleading. “Do evil that good may come” is but half of the whole truth “Do evil that good may come, provided there is no other way open.” Again, “Of two evils choose the lesser, if a complete enumeration has shown that there is not a third course.”
A development of a finer ability of discernment under right influence should lead the common citizen to see through these various sophistries practiced by corporate greed, and should enable him by means of the ballot to “blaze a better way.”
The “public is a blunderbuss” because the average man either cannot, or will not, think his own thoughts. By developing greater skill and arousing greater interest in the thinking process, the crowd of camp followers will be reduced; selfish bossism will die; and a truer and more efficient democracy will reign supreme.
Genuine progress comes through a happy combination of the old with the new. A love for the old only, means ultra conservatism; whereas a love for the new only, means ultra radicalism; a love for both means rational liberalism.
That people love the old way may be attributed to two forces which will receive attention here.
(1) Race instinct.
It may be said that “life is a brief space between two eternities—a path between infinity and infinitude.” “Man is a pedestrian who perambulates along the way.” The eternities concern him not so much as the path which stretches between them. In a former day, one of the striking characteristics of the western plain was the beaten path stretching out along the table-land like an elongated, dust colored serpent; and often following this path would be a herd of buffalo winding its way in single file around boulder and ant hill till shut from view by the distant horizon. Thus has man travelled along the beaten path, following the “foot prints of the ages.” Here and there and everywhere do we see signs of those who have gone on before; father, grandfather, great grandfather; yes, even to the toe marks of those primeval ancestors of ours who shambled along the way, nobody knows how many years ago. From the dark recesses of the cave, have our forbears thrown a lasso of blood about our necks, and it seems as if we must follow the old, old way. “Being acorns of the ancestral oak,” we grow similar oak tree tendencies, living over again the life of our progenitors. “There lies in every soul the history of the universe.”
(2) Imitation.
But there is another reason for this ultra conservative spirit and it is that nature’s chief mode of instruction is by means of imitation. To every living thing of wood or field nature seems to say, “Your parents are always right, do as they do for this is the best way to learn the lessons of life.” A man thinks, feels and wills his way through life in a certain manner largely because his father did likewise. Moreover, we not only imitate those who have gone on before, but we counterfeit each other; fashion is another name for world wide mimicry. We imitate our friends and those whom we admire; we talk like them, we walk like them, we live like them.
It now appears that we are held to the path of the past by means of race instinct and the power of imitation, and we are thus prone to believe that the old way is good enough. It is evident that to get out of the beaten path is dangerous. The wild animal that deserts the habits of the race dies a premature death, and the man who possesses the temerity to struggle through the thicket of new things must, of necessity, shorten his span of life. To follow the “same old rut” is easiest for the teacher; to be loyal to the “grand old party” is safest for the politician. But to the contrary, if every man of every generation had followed the beaten path blindly—without deviation, the human race would now be a horde of simians. Because man has possessed the power of progressive thought, he has developed the spirit of radicalism and has thereby made himself supreme.
“The old way anyway—the old way right or wrong” has been the world’s biggest stumbling block. Every innovation must fight for its life. Every good thing has to be condemned in its day and generation. It is Huxley who suggests three stages for the course of a new idea: First, it is revolutionary; second, it will make little difference; third, I have always believed in it. On the other hand, the new way anyway; “we must have a change whether or no”; “we must have something different despite the cost,” have ever been the slogans of waste and destitution. The wars which have not resulted from the prejudice of ultra conservatism have been brought about through the thoughtlessness of ultra radicalism. The revolutionist, the freak and the anarchist, products of impulse and the spirit of discontent, spring from an unwise love of change.
The world needs conservatism and radicalism not so much as it needs rationalism. It needs men who can hold to the good of the old and adopt the best of the new; men who neither “rust out” nor “waste out”; but wear out. That rational progress may obtain, there must be a perfect dovetailing of the old with the new. Man must leave the beaten path not altogether, but at times. He needs to blaze out a new way not so much as he needs to straighten the bends, tunnel through the mountains, and fill in the swamps of the old way. A rational “liberalism” implies a willingness to follow the old path with a view to improving the imperfections thereof.
On the assumption that true happiness is the ultimate aim of life, we may conclude that anything which does not contribute to this end functions as a curse and not as a blessing. Happiness involves physical comfort and mental joy. To have comfort of the body implies moderate means. The poor cannot be happy because of bodily want. When “physical-man” is not given proper nourishment for healthy growth, then does he goad “spiritual-man” with the pricks of appetite and pain till his wants are appeased. This is a law of nature. On the other hand happiness is not attained through acquisition; neither the millionaires, nor the scholars, nor the famous are the happiest. This is a fact apparent to all. Over worry and over excitement follow closely the heels of much money and high position. Too little brings unhappiness through want; too much brings unhappiness through worry. Therefore man is cursed by his work when the remuneration is not enough for comfort of body, or when the income is too much for poise of mind.
Unless the organs of the body are used they atrophy. Every cell of the physical makeup demands exercise. Work which is not drudgery; work which causes the organs of the body and the powers of the mind to function normally; work which gives comfort without luxury; work which forces one to the highest actualization of his physical and spiritual powers is man’s greatest blessing. In and through such work will man attain his highest state of happiness.
We may now hope to show that material aggrandizement, the adopted standard of success, is one of the illogical factors of modern life.
The tree of the forest always grows toward the light. It pushes its way through the darkness of the soil into the shadow of the underbrush and finally out into the unobstructed light of the sun. This parallels the progress of the race. From the darkness of savagery into the shadow of barbarism, and finally out into the full light of civilization. Thus has man grown steadily and continually toward better things. But “better things” is a relative term and has changed with the development of the race. “A good healthy idea may not live longer than twenty years.” In consequence growth toward the light has been in accordance with man’s conception of a higher and a better life; which conception is ever changing.
Moreover, growth toward the best is always rewarded by real happiness. It therefore follows that the right road to real happiness extends along the way of better things as conceived by the traveller, man.
Any force which tends to lift the world up toward more light is a blessing, and any personality which contributes to this end is a success. When one drops a pin it falls down toward the earth, at the same time the earth comes up to meet the pin. This is according to the universal law of gravitation. It is true that the earth moves the pin through a much greater space than the pin moves the earth, and yet the fact remains that the pin does move the earth. The extent to which the smaller body is able to move the larger, depends on the two factors of weight and relative position. If the pin were lighter or farther away it would influence the earth so much the less. In like manner does the “pin-man” influence the “human-world.” The extent of this influence is controlled by man’s weight, or his “lifting power,” and the position which he occupies; just as the attraction of the pin for the earth is controlled by weight and position.
The facts of history have proved that man’s power to lift depends not so much upon what he has as upon what he is. In short, lifting power is directly in proportion to personal worth. Moreover, man’s ability to draw humanity up may be increased or decreased by the position which he occupies. Such a position must function for the best good of the world, and at the same time must elicit the highest development of the man.
TO SUMMARIZE:
Individual success involves these three elements:
First—A man of personal worth.
Second—A position which draws out the best in the man.
Third—A work which definitely contributes to the uplift of the world.
A definition is now in order:
Success is the right man in the right place doing his best for the highest good of the world.
LOGIC AND LIFE.
(1) Logic given a place in a secondary course.
(2) Man’s supremacy due to power of thought.
(3) Importance of progressive thinking.
(4) Necessity of right thinking.
(5) Indifferent and careless thought.
(6) The rationalization of the world of chance.
(1) Meaning of the term chance.
(2) Chance mathematically considered.
(3) Chance and gambling.
(4) Chance and investments.
(7) The rationalization of business and political sophistries.
(8) The rationalization of the spirit of progress.
(9) A rationalization of the attitude toward work.
(10) The logic of success.
(1) To justify its having a place in any course of study, logic must lend itself to character building.
(2) Man is king of the animal kingdom because of his power of thought. From the beginning his adaption has been more or less intellectual and his chief weapon of conquest has ever been his thinking brain.
(3) Man’s supremacy has been due not only to his ability to think, but also to his power of progressive thought.
(4) Right thinking is the process of adjusting the best means to a right end. Wrong thinking involves improper adjustment, which in turn results in extinction.
(5) A “logically-minded” man rationalizes every new proposition before he adopts it. That is, he analyzes with the utmost care and with unprejudiced frankness all the favorable and unfavorable situations; he then throws them into the balance of honest judgment and adopts the indications of said balance, unequivocally.
(6) Chance is a confession of ignorance. If man possessed infinite knowledge, the term chance would have no place in his vocabulary.
The games of chance are money making schemes supported by the gambling fraternity. On the basis of averages, the gambler, in the long run, must terminate his career “behind the game.”
High rate of interest implies great risk; low rate of interest little risk.
(7) “Win right or wrong” epitomizes the teachings of modern sophistry. With the coming of better thinking, a more efficient democracy will obtain.
(8) Rational progress combines the best of the old with what seems to be the best of the new.
Blind love for the old, or ultra conservatism, is due to the two forces of race instinct and power of imitation.
An adherence to the “old way anyway” may mean retrogression; whereas following the new way, simply because of its newness, may involve unnecessary waste.
(9) Work which is not drudgery; work which causes the organs of the body and the powers of the mind to function normally; work which gives comfort without luxury; work which forces one to the highest actualization of his physical and spiritual powers is man’s greatest blessing.
(10) Logically considered personal aggrandizement is not a true standard of success. Success involves personal worth rather than personal holding.
Success is measured by man’s ability to help the world on toward better things.
Success is the right man in the right place doing his best for the highest good of the world.
(1) What is the ultimate aim of education? Show that logic contributes to this end.
(2) Prove that man’s power of thought has ever been his best weapon of conquest.
(3) Exemplify the distinction between non-progressive and progressive thinking.
(4) Define right thinking. Illustrate.
(5) “A logically-minded man rationalizes every new project before undertaking it.” Give a concrete instance in explanation of this.
(6) “Chance is a literal confession of ignorance.” Demonstrate this.
(7) Give a mathematical illustration proving that schemes of chance are simply money making devices for the benefit of those who project them.
(8) The average gambler must terminate his career behind the game. Prove this.
(9) Why should high rate of interest imply great risk?
(10) Show that a half truth is a most misleading fallacy.
(11) Illustrate a business sophistry. Explain.
(12) Write a brief theme on “The Rationalization of the Spirit of Progress.”
(13) Under what conditions may work become man’s greatest blessing?
(14) Define success. Illustrate.
(15) In the light of your definition of success discuss the following: “The only failure is not to try.”
(1) “To prepare for complete living” is the end of education. Interpret and discuss this quotation from Spencer.
(2) Mention some discovery or invention which represents the power of progressive thought.
(3) “Man’s adaptation has been largely intellectual while the adaptation of the camel has been physical.” Explain.
(4) Interpret the expression, “The son stands upon the shoulders of the father.”
(5) Illustrate instances where man’s thinking has not been for his best interests.
(6) Indicate how wrong thinking led to the Civil War.
(7) Distinguish between legitimate speculation and gambling.
(8) Name and explain the logical elements involved in a low rate of interest.
(9) How may training in right thinking lead to more efficient citizenship?
(10) “There lies in every soul a history of the universe.” Show the truth of this.
(11) Show by illustration that imitation is one of nature’s chief modes of instruction.
(12) Explain the meaning of drudgery.
(13) Mention instances where work is a curse.
(14) Is success possible when the right man is found doing his best in the wrong place?
(15) Whom do you consider the most successful American? Give reasons.
Let the student give attention to the fallacies in meaning as well as to the fallacies in form.
1. None but those who are contented with their lot in life can justly be considered happy. But the truly wise man will always make himself contented with his lot in life, and, therefore he may justly be considered happy. Keynes.
2. Suffering is a title to an excellent inheritance; for God chastens every son whom he receives. Keynes.
3. No young man is wise; for only experience can give wisdom, and experience comes only with age. Keynes.
4. Dr. Johnson remarked that “a man who sold a penknife was not necessarily an iron-monger.” Against what logical fallacy was this remark directed? Explain. Keynes.
5. This pamphlet contains seditious doctrines, the spread of which may be dangerous to the state; hence the pamphlet must be suppressed. Keynes.
6. Good workmen do not complain of their tools: my pupils do not complain of their tools; therefore, my pupils are probably good workmen. Keynes.
7. Knowledge gives power; consequently, since power is desirable, knowledge is desirable. Keynes.
8. Some who are truly wise are not learned; but the virtuous alone are truly wise; the learned, therefore, are not always virtuous. Keynes.
9. The spread of education among the lower orders will make them unfit for their work; for it has always had that effect on those among them who happen to have acquired it in previous times. Keynes.
10. Slavery is a natural institution and therefore ought not to be abolished. Russell.
11. The yardstick of success is the dollar, and you have made your millions.
12. “All who talk well are not necessarily intelligent, and A is certainly a spell-binder.”
13. Gold and silver are the wealth of a country; consequently, the diminution of gold and silver by exportation must mean the diminution of the wealth of a country. Russell.
14. A miracle is unbelievable, because it fails to conform to known laws of nature.
15. Improbable events happen every day; now, what happens every day is a probable event; therefore, improbable events are probable events.
16. What fallacy did Columbus commit when he made the egg stand on end by breaking one end?
17. Some holder of a ticket is sure to draw the prize; and, as I am a ticket holder, I am sure to draw the prize. Russell.
18. All the members of the jury are just men, hence you may trust the foreman.
19. Select the star players of the country and you will have a team which cannot be beaten.
20. All the houses on this street present a pretty picture; this house, therefore, which is on this street, will make a fine picture.
21. What is the good of all your teaching, for every day we hear of wrong doing made possible by education.
22. You are not what I am; I am a teacher; hence you are not a teacher.
23. The student of history is compelled to admit the law of progress, for he finds that society has never stood still. Russell.
24. This bill must have been designed to bleed the people because it is supported by the grafters of the state.
25. “To close the saloons on Sunday is contrary to the wishes of the people of the city; hence those ‘farmer legislators’ should keep hands off.”
26. Success is the right man in the right place doing his best, and you are working to the limit.
27. Early to bed and early to rise, makes one healthy, wealthy and wise. It is, therefore, easy enough to get rich.
28. Honesty being the best policy, I must tell the truth to my patient, though to tell him that he cannot live will shorten his life many days.
29. A stitch in times saves nine, hence an ounce of prevention is worth a pound of cure.
30. The richest man I know used to sweep his office every morning, hence it pays to commence at the bottom.
31. Cramming is an injurious habit, since it makes the building of logical memories practically impossible.
32. A strong will means a trained will; struggle is an indication of weakness.
33. There is no such thing as a national or state conscience; therefore, no judgments can fall upon a sinful nation. Hibben.
34. The principles of justice are variable; the appointments of nature are invariable; therefore, the principles of justice are no appointment of nature. Aristotle.
35. Intelligence and not sex should be the standard; therefore, let the women have their way.
36. “War by killing off the men of the country gives the living a better opportunity to succeed because of reduced competition.”
37. Since you deem yourself a misfit, in the name of common sense, why do you not change your occupation?
38. The conquest of America by Europeans has been a good thing for the world; since no eminent historian doubts it.
The student must remember to give attention to the fallacies in meaning as well as to the fallacies in form.
1. If I speak at length, he is bored; if I speak briefly, he is offended; therefore I will not speak at all.
2. If virtue is involuntary, vice is also involuntary; but vice is voluntary, hence virtue is also.
3. If a man cannot make progress toward perfection, he must either be a brute or a divinity; but no man is either; therefore every man is capable of such progress. Fowler.
4. If education is popular, compulsion is unnecessary; if unpopular, compulsion will not be tolerated. Fowler.
5. If you are to recover from this illness, then you will. If you are not to recover, then you will not, hence what is the use of calling in a physician?
6. If your act was right, your conscience will approve it; if wrong, your conscience will prick you. Either your act was right or wrong, so you can depend upon your conscience.
7. If he is intoxicated then he is not responsible, but he acts like a sober man.
8. If the Elixir of Life is of any value, those who take it will improve in health; now my friend who has been taking it has improved in health, and therefore the elixir is of value as a curative agent. Hyslop.
9. If you will settle down to business, you may still win out, because I am confident it is not too late for hard work to be effective.
10. If the end justifies the means then money used for any object of charity may be secured in any way.
11. If might is right then money talks, but I find that occasionally money proves ineffective.
12. If the majority of those who use public houses are prepared to close them, legislation is unnecessary, but if they are not prepared for such a measure, then to force it on them by outside pressure is both dangerous and unjust. Hyslop.
13. If the conscience is infallible in matters of right and wrong, then sin is just one thing; namely, doing that which is contrary to one’s conscience. We believe that an educated conscience is infallible.
14. If the earth were of equal density throughout, it would be about 2½ times as dense as water; but it is about 5½ times as dense; therefore the earth must be of unequal density. Hyslop.
15. The end of human life is either perfection or happiness; death is the end of human life, therefore death is either perfection or happiness. Creighton.
16. That chauffeur either lost his head or was drunk because no sane man would deliberately run down an innocent child.
17. If you argue on a subject which you do not understand, you will prove yourself a fool; for this is a mistake which fools always make. Keynes.
18. If you are a man of your word, you will live up to your agreement, or if you have any self respect, you will do the manly thing. Now your neighbors tell me that you are a man in the habit of making good your promises.
Answer ten questions. Time, 2 hours.
Set I.
1. Define and illustrate obversion and state the principle which conditions the process.
2. Give directions for making the following propositions logical:
(1) Only first class passengers may ride in parlor cars.
(2) All who claim to be pious are not pious.
(3) “Blessed are the merciful.”
3. Write a theme of 200 words on “Logic and Life.”
4. Put into syllogistic form and test the validity of this argument. “We are going to have an open winter because the hornets’ nests are near the ground.”
5. Justify the teaching of logic in an institution which offers courses in Educational Theory.
6. Correct the following definitions, stating the rules violated:
(1) A man is an organized entity whose cognitive powers function rationally.
(2) A bird is an animal that flies.
(3) A scholar is an educated man with scholarly attainments.
7. Prove that in the first figure the minor premise must be affirmative.
8. Investigate a case of habitual tardiness by making use of the canon of difference.
9. Describe with illustrations the various ways of begging the question.
10. Why should classification rather than logical division be the mode of procedure in the case of small children? Illustrate.
11. Illustrate the following:
(1) non connotative term,
(2) undistributed middle,
(3) fallacy of accident.
Set II.
Answer ten questions. Time, 2 hours.
Throw the following into the form of a syllogism and criticise, giving reasons:
1. “I do not know how to teach school as I have had no experience.”
2. “Only the honest should be in business and you are not honest.”
3. Why should all teachers study logic? Give arguments in full.
4. Describe Mill’s methods of induction and illustrate one.
5. Give and explain the rules of logical definition.
6. Explain the distribution of terms and illustrate by circles the meaning of the four logical propositions.
7. Define the following:
(1) teaching,
(2) extension of terms,
(3) obversion,
(4) hypothesis,
(5) relative term.
8. Give a class room illustration of the Complete Method.
9. Distinguish between
(1) distributive and collective terms,
(2) analysis and deduction,
(3) logical division and classification.
10. Illustrate the following:
(1) contradictory proposition,
(2) analogy,
(3) law of identity,
(4) singular term,
(5) univocal term.
11. Convert, if possible, the following:
(1) Some men are honest.
(2) All that glitters is not gold.
(3) All kings are fallible.
Set III.
Answer ten questions. Time, 2 hours.
1. Investigate by the Joint Method of Induction this question: “Why is John absent so often?”
2. Explain and illustrate:
(1) contradictory propositions,
(2) illicit middle,
(3) obversion,
(4) contraversion,
(5) synthesis.
3. State and exemplify the rules of logical division.
4. Write a theme of at least 150 words on one of the following:
(1) Induction as the Discoverer’s Method.
(2) A Rational View of Success.
5. Define logically:
(1) teaching,
(2) deduction,
(3) education,
(4) analysis,
(5) money.
6. Distinguish between the extension and intension of terms.
7. Exemplify:
(1) an absolute term,
(2) the complete method,
(3) non connotative terms,
(4) fallacy of accident,
(5) hypothesis.
8. “Educated among savages, he could not be expected to know the customs of polite society.” Is this valid? Reasons.
9. “The signs indicate that you are either stupid or unprepared; but the past proves that you are not the former.” Test the validity.
10. Discuss comprehensively one of the following topics:
(1) The Fallacies.
(2) Thinking.
(3) Abbreviated Arguments.
Set IV.
Answer ten questions. Time, 2 hours.
1. Exemplify:
(1) the law of variation in the extension and intension of terms,
(2) a distributed predicate.
2. Indicate with explanation the logical errors:
(1) A teacher assumes that the “bad boy of the school” is going to cause trouble in her room.
(2) All the men of the Commission are fair minded men, hence they will render a fair decision.
3. What experimental method of induction is the most positive in its conclusion? Illustrate this method.
4. State and illustrate the rules of logical definition.
5. Obvert each of the four logical propositions. Explain the principle involved.
Test the validity of the following arguments:
6. “Horses, not being human, cannot reason.”
7. “Only the industrious deserve to succeed and you have never done a hard day’s work in your life.”
8. “If you had been wise, you would have refused to stoop to the methods of the firm, but you were not wise.”
9. From this premise construct a valid syllogism: “All large cities owe their size to some commercial advantage.”
10. Define and illustrate the following: analogy, hypothesis, thinking, connotative term, relative term.
11. Distinguish between:
(1) Analysis and deduction.
(2) Logical division and classification.
(3) Relative and absolute identity.
Set V.
Answer ten questions. Time, 2 hours.
Test the validity, giving reasons:
1. All successful teachers are industrious, but you are not industrious because you are not successful.
2. John was a troublesome boy in the first and second grades, therefore he is going to make trouble for the third grade teacher.
3. Teaching is the art of imparting knowledge. Criticise, giving reasons. Define correctly, pointing out the essentials.
4. Explain the extensional and intensional use of terms and illustrate the law of variation.
5. Describe Mill’s experimental methods of induction. Symbolize the joint method.
6. Define the following: analysis, law of identity, obversion.
7. Illustrate the laws of thought.
8. Write on one of the following topics:
(1) Complete Method,
(2) Right Thinking.
9. “The science of logic never made a man reason rightly.” Discuss this question.
10. Explain and illustrate the enthymeme.
Set VI.
Answer ten questions. Time, 2 hours.
1. Exemplify the following:
(1) illicit minor,
(2) begging the question,
(3) law of excluded middle,
(4) inductive method.
2. Write a short theme on one of these topics:
(1) Thinking.
(2) Logical Terms.
Test the validity of the attending arguments, giving reasons:
3. “He who talks much usually says little and you are certainly a great talker.”
4. “You must be industrious, since only such truly succeed.”
5. Illustrate and give the characteristic marks of the joint method of induction.
6. Summarize the benefits to be derived from a study of logic.
7. State and illustrate the rules of logical definition.
8. Distinguish between
(1) extension and intension,
(2) opposite and contradictory terms,
(3) analysis and synthesis.
9. Define and illustrate hypothesis, obversion, sorites, hypothetical argument.
10. Explain and illustrate the three forms of induction.
11. Distinguish logically between a teacher and an instructor.
Aikins. The Principles of Logic. Henry Holt and Co., New York. 1905.
Bain. Logic, Inductive and Deductive. Longmans, Green and Co. 1902.
Bosanquet. The Essentials of Logic. The MacMillan Co., London. 1910.
Bradley. The Principles of Logic. London. 1886.
Creighton. Introductory Logic. The MacMillan Co., New York. 1905.
Dewey. Studies in Logical Theory. The University of Chicago Press. 1903.
Fowler. The Elements of Deductive and Inductive Logic. Oxford. 1905.
Hibben. Logic, Deductive and Inductive. Chas. Scribner’s Sons, New York. 1906.
Hyslop. Elements of Logic. Chas. Scribner’s Sons, New York. 1905.
Jevons-Hill. Elements of Logic. American Book Co., New York. 1883.
Keynes. Formal Logic. The MacMillan Co., London. 1906.
Lotze. Logic. Translated by B. Bosanquet, 2 vols. Oxford. 1888.
McCosh. Laws of Discursive Thought. Chas. Scribner’s Sons. 1906.
Mill. A System of Logic, 2 vols. Longmans, Green and Co., London. 1904.
Russell. Elementary Logic. The MacMillan Co., New York. 1908.
Ryland. Logic. George Bell and Sons, London. 1900.
Sigwart. Logic. Translated by Helen Dendy, 2 vols. The MacMillan Co. 1895.
Swinburne. Picture Logic. Longmans, Green and Co., London. 1904.
Taylor. Elementary Logic. Chas. Scribner’s Sons, New York. 1911.
Venn. The Logic of Chance. The MacMillan Co., New York.
Subject
I. THOUGHT AND ITS LAWS
⭘ Logic Defined
⭘ The Thinking Process.
⭘ Stages in Thinking
⭘ The Law of Identity
⭘ The Law of Contradiction
⭘ The Law of Excluded Middle
II. LOGICAL TERMS
⭘ All of Chapter 4
III. EXTENTSION AND INTENSION OF TERMS
⭘ All of Chapter 5
IV. DEFINITION
⭘ All of Chapter 6
V. LOGICAL DIVISION AND CLASSIFICATION
⭘ All of Chapter 7
VI. LOGICAL PROPOSITIONS
⭘ All of Chapter 8 Except Section 7
VII. IMMEDIATE INFERENCE
⭘ All of Chapter 10
VIII. MEDIATE INFERENCE
⭘ All of Chapter 11 Except Section 8
IX. FIGURES AND MOODS
⭘ The Four Figures of the Syllogism
⭘ The Moods of the Syllogism
⭘ Testing the Validity of the Moods
X. INCOMPLETE SYLLOGISMS
⭘ Enthymeme
⭘ Polysyllogisms
⭘ Sorites
XI. CATEGORICAL ARGUMENTS TESTED
⭘ All of Chapter 14
XII. HYPOTHETICAL AND DISJUNCTIVE ARGUMENTS
⭘ All of Chapter 15 except Sections 13,14, 15 and 17
XIII. LOGICAL FALLACIES
⭘ All of Chapter 16
XIV. INDUCTIVE REASONING
⭘ All of Chapter 17 Except Sections 3, 4, 7, 8 and 9
XV. MILL’S METHODS OF OBSERVATION AND EXPERIMENT
⭘ All of Chapter 18
XVI. OBSERVATION, EXPERIMENT AND HYPOTHESIS
⭘ All of Chapter 19
A
Absolute Terms, 56.
Abstract Terms, 51.
Accent, Fallacy of, 330.
Accident, 81;
Fallacy of, 334.
Affirmative Proposition, 127.
Agreement, Method of, 387.
All—not, Some, Few, Logical Significance of, 133.
Ambiguous Middle, 328.
Amphibology, 329.
Analogy, 368.
Analysis, Definition of, 97;
As a Method, 97;
Induction by, 373.
Analytic Propositions, 138;
Method, 97.
Antecedent, 289.
Apprehension and Thinking, 24.
Arguments, Irregular, 258;
Testing of Categorical, 263;
Incomplete, 247;
General Exercises, 481;
Mistakes of Students in Connection with, 281;
Hypothetical, 288;
Disjunctive, 302;
Dilemmatic, 308.
Argumentum ad populum, 338;
ad hominem, 338;
ad ignorantiam, 338;
ad baculum, 338;
ad verecundiam, 339.
Aristotle’s Dictum, 208.
Art, Definition of, 96.
Auxiliary Elements of Induction, 418.
B
Bain Quoted, 12.
Ballentine Quoted, 359.
Barbara, Celarent, etc., 234.
Begging the Question, 341.
Bibliography, 492.
Bowen Quoted, 12.
Briefer Course, Outline of, 493.
C
Canons of Syllogism, 209;
of Four Figures, 226.
Categorematic Words, 48.
Categorical Arguments, 263;
Tested, 263;
General Exercises, 481.
Categorical Propositions Defined, 121;
Four Elements, 122;
Four Kinds, 126;
Classification of, 128.
Cause, Fallacy of False, 340.
Chance, Rationalization of, 468.
Child, Thinking of, 20.
Circulus in Probando, 343.
Classification Compared with Division, 112;
Kinds, 113;
Rules of, 114;
Use, 114.
Co-extensive Propositions, 142.
Collective Terms, 50.
Comparison, Stages in Thinking, 25.
Complete Method, Three Elements, 97.
Composition, Fallacy of, 331.
Concept, Definition of, 17;
a Thought Product, 21.
Concomitant Variations, 402.
Concrete Terms, 51.
Connotative Terms, Two-fold Function of, 62;
Definition of, 52;
a List of, 65.
Conquest the Desideratum, 447.
Consequent, 289;
Fallacy of False, 339.
Contradiction, Law of, 35.
Contradictory Terms, 53;
Propositions, 167.
Contrary Propositions, 165.
Contraversion, 181;
Fallacies of, 327.
Converse Accident, Fallacy of, 335.
Conversion, 176;
by Limitation, 178;
Simply, 179;
Fallacies of, 327.
Copula, 123.
Creighton Quoted, 4, 387, 485.
D
Deduction, Defined, 96;
as a Method, 97;
Special Function of, 438.
Definition, Importance of, 77;
the Predicables, 77;
Nature of, 82;
Definition of, 83;
Compared with Division, 84;
Kinds of, 85;
When Serviceable, 87;
Rules of, 88;
Terms which Cannot be Defined, 93;
of Common Educational Terms, 94.
Denomination, Stages in Thought, 26.
Denotation and Connotation of Terms, 66.
Descriptive Definition, 86.
Development, Definition of, 94.
Dichotomy, 110.
Difference, Method of, 393.
Differentia, 80.
Dilemma, 308.
Discoverer’s Method, 440.
Disjunctive Arguments, 302;
Rules of, 303;
Logical Disjunction, 303;
Reduction of, 307.
Distribution of Subject and Predicate of Propositions, 145;
Schemes for Remembering, 148.
Division, Definition of Logical, 105;
As Partition, 107;
Compared with Definition, 84;
Distinguished from Enumeration, 106;
Rules of, 108;
Compared with Classification, 112;
Use of, 114;
Fallacy of, 332.
Dressler Quoted, 12.
E
Education, Defined, 94;
Compared with Instruction, 95.
Educational Terms Defined, 94.
Elements of the Logical Proposition, 123.
Elliptical Propositions, 129.
Enthymeme, 247.
Epicheirema, 249.
Episyllogism, 250.
Epithets, Question Begging, 343.
Essential Attributes of Definition, 88.
Etymological Definition, 85.
Euler’s Diagrams, 141.
Evolution and the Thinking Mind, 19.
Examination Questions, 486.
Exceptive Propositions, 135.
Excluded Middle, Law of, 39.
Exclusive Propositions, 136.
Exercises, Testing Arguments, 481.
Experiment as an Element in Induction, 419.
Extension and Intension of Terms, Defined, 63;
Compared, 63;
Used in Comparison, 65;
Other Forms of Expression for, 66;
Law of Variation in, 66.
F
Fact, Defined, 96.
Fallacies, of Deductive Reasoning, 322;
Paralogism and Sophism, 322;
Division of, 323;
of Immediate Inference, 326;
Hypothetical, 291;
Disjunctive, 303;
of Language, 328;
in Thought, 334.
False Cause, 340.
False Consequent, Fallacy of, 339.
Figure of Speech, Fallacy of, 333.
Figures of Syllogism, 218;
Special Canons of, 226;
Perfect and Imperfect, 235;
Reduction, 235;
Relative Value of, 239.
Four Terms, Fallacy of, 329.
Fundamentum Divisionis, 108.
G
General Exercises in Testing Arguments, 481.
General Terms, 49.
Genus and Species, 78.
Grammatical Subject and Predicate, 125.
Grammatical Sentences, 131.
H
Huxley Quoted, 473.
Hypothetical Arguments, 288;
Kinds, 290;
Rules and Fallacies, 291;
Reduced to Categorical, 293;
Illustrative Exercise in Testing, 297;
General Exercises, 484.
and Theory, 427;
Requirements of, 427;
Uses of, 429.
I
Identity, Law of, 32;
Absolute, 33;
Complete and Incomplete, 33;
Relative, 34.
Illicit Major and Minor, 199;
Illustration of, 215.
Image, Definition of, 17.
Immediate Inference, 159;
by Obversion, 170;
by Opposition, 161;
by Conversion, 176;
by Contraversion, 181;
Epitome of Four Processes, 182;
by Inversion, 183;
Fallacies of, 326.
Imperfect Induction, 361.
Indefinite Propositions, 129.
Individual Proposition, Nature of, 132;
in Opposition, 168.
Induction, Defined, 96;
as a Method, 97;
Reasoning, 355;
and the Hazard, 356;
the Three Forms of, 365;
Perfect, 375;
Special Function of, 438.
Inference, Definition of, 18;
a Thought Product, 24;
Immediate, 159;
Mediate, 192.
Infima Species, 79.
Instruction Defined, 95.
Intension of Terms, 63.
Integration, a Stage in Thought, 26.
Inversion, 183.
Inverted Proposition, 137.
Irregular Arguments, 258.
Irrelevant Conclusion, 337.
J
Jevons Quoted, 4, 25, 387, 468.
Joint Method of Agreement and Difference, 397.
Judgment, Definition of, 17;
a Thought Product, 22;
Most Fundamental Element in Thinking, 23.
K
Kinds of Definitions, 85.
Knowing, by Intuition and by Thinking, 2;
Knowing and Thinking Compared, 10;
by Intuition, 11;
Habitual, 11.
Knowledge, Defined, 95;
Intuitive, 11.
L
Language and Thought Inseparable, 47.
Law of Variation in Extension and Intension, Stated, 66;
Two Important Facts in, 69;
Diagrammatically Illustrated, 70, 71.
Laws of Sufficient Reason, 40;
of Universal Causation, 361;
of Uniformity of Nature, 362.
Laws of Thought, 32;
Unity of, 40;
Schematic Statement of, 43.
Learning, Defined, 95.
Logic, Defined, 3;
Authentic Definitions of, 4;
Grammar of Thought, 3;
Science of Sciences, 3;
the Value of to the Student, 5;
Related to Other Subjects, 1;
Specific Scope, 2.
Logic in the Class Room, 437.
Logic and Life, 463.
Logic of Success, 475.
Logical Disjunction, 303.
Logical Subject and Predicate, 125.
M
Major Term, 196.
Material Fallacies, 323, 324, 325, 328.
Mediate Inference, 192;
the Syllogism, 192;
Rules of Syllogism, 193.
Method Defined, 96;
Inductive and Deductive, 97;
Complete, 97.
Method-Whole Defined, 96.
Mill Quoted, 5, 359, 361, 387, 393, 397, 402, 406.
Mill’s Experimental Methods, 386.
Miller Quoted, 12.
Mind, the Unity of, 1;
Knowing and Thinking Compared, 10.
Minor Term, 196.
Mnemonic Lines, 234.
Modal Proposition, 139.
Modus Ponendo Tollens, etc., 302.
Moods of Syllogism, 221;
Testing Validity of, 223.
Motivation as Related to Spirit of Discovery, 449.
N
Negative Proposition, 127.
Negative Terms, 53.
Nego-positive Terms, 55.
Non-connotative Terms, 52.
Non Sequitur, Fallacy of, 339.
Not, Bisects the World, 36;
Two Uses of, 36.
Notion, Definition, 14;
Individual, 14;
General, 14;
Distinguished from Knowledge, 15;
Distinguished from Idea, 16;
Psychological Terms Involved in, 16.
O
Observation, 419;
Rules of, 420;
Errors of, 423.
Obversion, Definition of, 170;
Fallacies of, 326.
Opposite Terms, 53.
Opposition, Nature of, 161;
Scheme of, 163;
Square of, 164.
Outline of Briefer Course, 493.
P
Page Quoted, 453.
Particular Propositions, 126;
Affirmative, 143;
Negative, 144.
Partition, 107.
Partitive Propositions, 133.
Percept, Definition of, 17;
Related to Thought, 18.
Perfect Induction, 375.
Petitio Principii, 341.
Plurative Propositions, 132.
Polysyllogism, 250.
Porphyry, Tree of, 111.
Positive Terms, 53.
Predicables. Defined, 77;
Named, 78;
Illustrated, 82.
Predicate, Grammatical and Logical, 125;
Distribution of, 145.
Primary Laws of Thought, 32.
Privative Terms, 55.
Progressive Thought, 465.
Property, 81.
Propositions, Definition of Logical, 120.
Prosyllogism, 250.
Proximate Genus, 79.
Pure Proposition, 139.
Q
Quantity Signs, 123.
Quantity and Quality of Propositions, 126.
Question and Answer, not a Method of Discovery, 457.
Question Begging Epithets, 343.
Question, Complex, 340.
R
Rationalization, of Chance, 468;
of Political and Business Sophistries, 470;
of the Spirit of Progress, 471;
of the Attitude toward Work, 474.
Inductive, 355;
Deductive, 355.
Reduction of Figures, 235.
Relation between Subject and Predicate, 140.
Relative Terms, 56.
Residues, Method of, 406.
Right Thinking, 466.
Rules, of Logical Definition, 88;
of Logical Division, 108;
of Classification, 114;
of the Syllogism, 193;
of the Hypothetical Argument, 291;
of the Disjunctive, 303.
S
Salisbury Quoted, 360.
Science, Defined, 95.
Sensation, Defined, 17;
Related to Thought, 18.
Simple Conversion, 179.
Simple Enumeration, 367.
Singular Terms, 49.
Socrates, 322.
Sorites, 251.
Species, 78.
Square of Opposition, 164.
Subaltern Propositions, 164.
Subcontrary Propositions, 164.
Subject, Logical, 123;
Grammatical and Logical Distinguished, 125;
Distribution of, 145.
Success, Logic of, 475.
Sufficient Reason, Law of, 40.
Summum Genus, 79.
Syllogism, a Product of Inference, 24;
Nature of, 192;
Rules of, 193;
Undistributed Middle, 199;
Illicit Major, 199;
Illicit Minor, 199;
Aristotle’s Dictum, 208;
Canons of, 209;
Mathematical Axioms of, 210;
Four Figures of, 218;
Moods of, 221;
Incomplete, 247.
Syncategorematic Words, 48.
Synthesis, Defined, 97;
as a Method, 97.
Synthetic Proposition, 138.
T
Teaching, Defined, 94;
Compared with Instruction and Education, 95.
Terms, Extension and Intension of, 63;
Used in Extension and Intension, 65;
which Cannot be Defined, 93;
Contradictory and Opposite, 38;
Logical, 47;
Singular and General, 49;
Collective and Distributive, 50;
Concrete and Abstract, 51;
Connotative and Non-connotative, 52;
Positive and Negative, 53;
Contradictory and Opposite, 53;
Privative and Nego-positive, 55;
Absolute and Relative, 56.
Theory Defined, 96.
Thinking, Definition of, 12;
Illustration of Process, 13;
Compared with Knowing, 10;
Compared with Intuition, 2;
the Process, 12;
Groups Many Into One, 18;
in the Sensation and Percept, 18;
Evolution and Thinking Mind, 19;
of the Child, 20;
of the Adult, 20;
and the Concept, 21;
and the Judgment, 22;
and Apprehension, 24;
Stages in, 25;
in the Inference, 24;
Laws of, 32;
Unity of Laws, 40;
Progressive, 465;
Right, Necessity of, 466;
Indifferent and Careless, 467.
Thought and Language, 47.
Thought is King, 437.
Traduction, 377.
Training, Definition of, 95.
Tree of Porphyry, 111.
Truistic Proposition, 139.
Truth Defined, 96.
U
Uberweg Quoted, 4.
Undistributed Middle, 199;
Illustration of, 214.
Uniformity of Nature, 362.
Universal Affirmative Proposition, 140.
Universal Causation, 361.
Universal Negative Proposition, 142.
Universal Propositions, 126.
V
Variations, Method of Concomitant, 402.
W
Watts Quoted, 4.
Weakened Conclusion, 224.
Whately Quoted, 4.
Word-signs of Categorical Propositions, 122.
| 1 – | NOTE. Sometimes thinking and thought are used interchangeably. This is confusing. Properly, “thinking” is always a process of the knowing mind while “thought” is the product of this process, just as the flour of the gristmill is the product of the grinding process. |
| 2 – | Intuitive knowing might be termed habitual knowing. |
| 3 – | Mediate Inference. |
| 4 – | Intuitive Knowing. |
| 5 – | Hyslop’s Elements of Logic (1901), page 100. |
| 6 – | Hyslop. |
| 7 – | Men do have the power of reason. |
| 8 – | Sometimes called contraposition. |
| 9 – | From the Greek meaning to reason with. |
| 10 – | The student may be sufficiently interested to complete the list. |
| 11 – | The student should prove that the last premise may be affirmative. |
| 12 – | This cause, however, need not be a single antecedent, in fact it seldom is. “This cause, philosophically speaking, is the sum total of the conditions, positive and negative, taken together.”—Mill. The cause of the price of food stuff being high, involves many conditions, or antecedents, so interwoven that it is impossible to designate any one as being the chief factor concerned. |
| 13 – | Those might be named the Five Special Methods of Induction by Analysis. |
| 14 – | All cases of finding the net proceeds are examples of the law of residue. |
| The following corrections have been made in the text: | |
| ⭘ – |
‘recignize’ replaced with ‘recognize’ (able to recognize each) |
| ⭘ – |
‘differenece’ replaced with ‘difference’ (the difference in meaning) |
| ⭘ – |
‘non-contotative’ replaced with ‘non-connotative’ (can be non-connotative.) |
| ⭘ – |
‘digerentiæ’ replaced with ‘differentiæ’ (by means of its differentiæ.) |
| ⭘ – |
‘comfined’ replaced with ‘confined’ (knowledge is confined to) |
| ⭘ – |
‘nagtive’ replaced with ‘negative’ (one premise be negative) |
| ⭘ – |
‘affirmavite’ replaced with ‘affirmative’ (and a particular affirmative) |
| ⭘ – | Printer error: lost end of point (3) and duplicated part of point (4) |
| ⭘ – |
‘agruments’ replaced with ‘arguments’ |
| ⭘ – |
‘analagous’ replaced with ‘analogous’ (custom analogous to giving) |
| ⭘ – |
‘(4)’ missing from text ((4) “The man is guilty) |
| ⭘ – |
‘abitrary’ replaced with ‘arbitrary’ (words as arbitrary signs) |
| ⭘ – |
‘fallicies’ replaced with ‘fallacies’ (and fallacies of converse) |
| ⭘ – |
‘sirname’ replaced with ‘surname’ (have the same surname,) |
| ⭘ – |
‘generalziation’ replaced with ‘generalization’ (perfectly induced generalization,) |
| ⭘ – |
‘uncontradiced’ replaced with ‘uncontradicted’ (incomplete but uncontradicted) |
| ⭘ – |
‘prenomenon’ replaced with ‘phenomenon’ (entirely with the phenomenon.) |
| ⭘ – |
‘vivdly’ replaced with ‘vividly’ (what is only vividly internal) |