
Title: The Practical Astronomer
Author: Thomas Dick
Release date: March 24, 2017 [eBook #54420]
Most recently updated: October 23, 2024
Language: English
Credits: Produced by Chris Curnow, Wayne Hammond and the Online
Distributed Proofreading Team at http://www.pgdp.net (This
file was produced from images generously made available
by The Internet Archive)

ii

THE AUTHOR’S OBSERVATORY.
iii
iv
v
PRINTED BY L. SEELEY.
The following work was announced several years ago in the preface to the volume on “The Sidereal Heavens;” since which time numerous enquiries have been made after it by correspondents in England, the West Indies, and America. It was nearly ready for publication three years ago; but circumstances over which the Author had no controul, prevented its appearance at that period. This delay, however, has enabled him to introduce descriptions of certain instruments and inventions which were partly unknown at the time to which he refers.
The title “Practical Astronomer” has been fixed upon, as the shortest that could be selected, although the volume does not comprise a variety of topics and discussions generally comprehended in this department of astronomy. The work is intended for the information of general readers, especially for those who have acquired a relish for astronomical pursuits, and who wish to become acquainted with the instruments by which celestial observations are made, and to apply their mechanical skill to the construction of some of those which they may wish to possess. With this view the Author has entered into a variety of minute details, in reference to the construction and practical application of all kinds vi of telescopes, &c. which are not to be found in general treatises on Optics and Astronomy.
As Light is the foundation of astronomical science, and of all the instruments used for celestial observation, a brief description is given of the general properties of light—of the laws by which it is refracted and reflected when passing through different mediums—and of the effects it produces in the system of nature—in order to prepare the way for a clear understanding of the principles on which optical instruments are constructed, and the effects they produce.
As this, as well as every other physical subject, forms a part of the arrangements of the Creator throughout the material system—the Author has occasionally taken an opportunity of directing the attention of the reader to the Wisdom and Beneficence of the Great First Cause, and of introducing those moral reflections which naturally flow from the subject.
The present is the ninth volume which the Author has presented to the public, and he indulges the hope that it will meet with the same favourable reception which his former publications have uniformly experienced. It was originally intended to conclude the volume with a few remarks on the utility of astronomical studies, and their moral and religious tendency, but this has been prevented, for the present, in consequence of the work having swelled to a greater size than was anticipated. Should he again appear before the public as an author, the subject of discussion and illustration will have a more direct bearing than the present on the great objects of religion and a future world.
Broughty Ferry, near Dundee, August, 1845. vii
| PART I. ON LIGHT. |
|---|
| INTRODUCTION. |
| Necessity of light to the knowledge and happiness of all sentient beings—Its beautiful and enlivening effects—An emblem of the Deity—Provision made for its universal diffusion |
| CHAPTER I. |
| General Properties of Light. |
| Interesting nature of this study—Different hypotheses which have been formed respecting the nature of light—It radiates in straight lines—Moves with amazing velocity—Flows in all directions from luminous bodies—Duration of its impressions on the eye—Supposed to have a certain degree of force or momentum—Experiments in relation to this point—Its intensity diminished in proportion to the square of the distance—Its reflection from opake bodies renders objects visible—Intensity of reflected light—Subject to the law of attraction—Forms a constituent part of certain bodies—Solar phosphori, and the phenomena they exhibit—Produces certain effects on planets and flowers, exemplified in a variety of instances—Supposed to have an influence on the propagation of sound viii |
| Reflections on the nature of light, and the multifarious effects it produces throughout the universe—A representation of the Divinity—Wisdom and Goodness of God displayed in its formation |
| CHAPTER II. |
| On the Refraction of Light. |
| Nature of refraction—Illustrated by experiments—Angle of refraction—Familiar
experiments illustrative of refraction—Refraction
explains the causes of many curious and interesting phenomena—Its
effect on the heavenly bodies—On the twilight—Illustrated by
figures |
| EXTRAORDINARY CASES OF REFRACTION IN RELATION TO TERRESTRIAL OBJECTS. |
| Extraordinary appearance of the coast of France from Hastings—Appearance
of a ship seen by Captain Colby, beyond the coast of
Caithness—Scoresby’s view of his father’s ship when beyond the
horizon—Phenomenon near the Himalaya mountains—Bell Rock
light-house—Summary statement of the diversified effects of refraction—Reflections
on the beneficent and diversified effects produced
by the law of refraction—It increases the length of the day,
particularly in the polar regions—Is the cause of that splendour
which appears in the objects around us—Quantity of refraction in
respect to terrestrial objects, and its utility—Its effects may be
more diversified in other worlds |
| CHAPTER III. |
| On the Refraction of Light through Spherical Transparent Substances, or Lenses. |
| Refraction the foundation of optical instruments—Various forms of lenses—Parallel, converging, and diverging rays—Illustrated by diagrams—Concave lenses, their effects, and how to find their focal distances—Images formed by convex lenses—Illustrated by experiments—Principles in relation to images formed by lenses—Their magnifying powers, &c. |
| REFLECTIONS DEDUCED FROM THE PRECEDING SUBJECT. |
| Property of the rays of light in forming images of objects—Wonderful results and discoveries which have flowed from this property—in ix relation to our knowledge of the scenery of the heavens and the minute parts of nature—and of our views of the attributes of Deity |
| CHAPTER IV. |
| On the Reflection of Light. |
| Nature of reflection—Plane, convex, and concave speculums—Angle of reflection—Reflection of objects from plane mirrors, illustrated by figures—Reflection by Convex and Concave mirrors—Properties of convex mirrors, and the purposes to which they are applied. Properties of concave speculums, and their utility—Of the images formed by concave speculums—Illustrated by a variety of figures and experiments—Their power of magnifying and burning—Amusing deceptions produced by—Resemblance between the properties of convex lenses, and concave mirrors—Quantity of light reflected by polished surfaces |
| UNCOMMON APPEARANCES OF NATURE PRODUCED BY THE COMBINED INFLUENCE OF REFLECTION AND REFRACTION. |
| Fata Morgana—The Mirage—Inverted images of ships seen in the horizon—Appearance of Dover castle at Ramsgate—Spectre of the Brocken—Scenes in the Highlands of Scotland—Large cross seen at Migné in France—Dr. Wollaston’s illustrations of such phenomena—Utility of science in dissipating superstitious fears |
| REMARKS AND REFLECTIONS IN REFERENCE TO THE PHENOMENA DESCRIBED ABOVE. |
| Light, the beauty of the universe, and a symbol of the Divinity—In other worlds it may produce an infinite variety of sublime scenery |
| CHAPTER V. |
| Sect. 1.—On the Colours of Light. |
| Colours, the beauty of nature—Opinions which were formerly entertained respecting their cause—Sir I. Newton’s experiments with the Prism—Colours and phenomena produced by the prism—Imperfection of optic lenses—Various illustrations—Differently coloured rays have not the same illuminating power—Heating and x chemical properties of some of the rays of the solar spectrum—property of communicating the Magnetic power—Fraunhofer, and his discoveries in reference to the spectrum—Experiments on white and coloured light |
| Sect. 2.—on the colours of natural objects. |
| Colours not in the objects themselves, but in the light which falls upon them—Illustrations of this position—Atmosphere the source of a variety of colours—Various natural phenomena, in relation to colour, explained |
| Sect. 3.—phenomena of the rainbow. |
| Rainbow described—Experiments to illustrate its cause—Descriptions of its various phenomena, and optical explanations of their causes—Rainbows exhibiting complete circles—Their appearance in different countries—Summary view of the principal facts respecting the rainbow—Lunar rainbows—Scriptural allusions to the rainbow—Whether there was any rainbow before the deluge |
| Sect. 4.—reflections on the beauty and utility of colours. |
| Beauty and variety derived from colours in the scenery of nature—Colours produced by the atmosphere in different countries—What would be the aspect of nature, in heaven and on earth, were there only one colour—How it would affect the common intercourse and employments of society—Wisdom and Beneficence of the Creator displayed in the diversity of colours—Throughout all the systems of the universe, a diversity of colours prevails—This subject has a tendency to inspire us with gratitude |
| PART II. |
| ON TELESCOPES. |
| CHAPTER I. |
| History of the Invention of Telescopes. |
| The telescope a noble instrument—Effects it produces—Whether known to the ancients—Friar Bacon’s ideas respecting telescopes—First xi constructed in Holland—The invention claimed by different persons—Galileo’s account of the construction of his telescope—Discoveries which he made with this instrument—How his discoveries were received by the learned—Specimens of learned nonsense brought forward by pretended philosophers—Supposed length of Galileo’s telescope—Various claimants to the invention of this instrument |
| CHAPTER II. |
| Of the Camera Obscura. |
| Appearance of objects in a camera obscura—The dark chamber—This instrument serves to explain the nature of a refracting telescope—Particulars to be attended to, in exhibiting objects with the Camera—It illustrates the nature of vision—Revolving camera obscura—Portable camera |
| The Daguerreotype. |
| An important discovery for fixing the images produced by the camera—Description of the Daguerreotype process—Preparation of the plate, fixing the impression, &c.—Preparation of photogenic paper—Beneficial effects which this art may produce—Representations of objects in the heavens, &c. |
| CHAPTER III. |
| On the Optical Angle, and the Apparent Magnitude of Objects. |
| Various illustrations of the apparent magnitude of objects—Fallacies in relation to apparent magnitudes—Apparent magnitudes in the heavens—Difference between absolute and apparent magnitudes |
| CHAPTER IV. |
| On the Different Kinds of Refracting Telescopes. |
| Sect. 1.—The Galilean Telescope. |
| Construction and peculiar properties of this instrument xii |
| Sect. 2.—The Common Astronomical Refracting Telescope. |
| Description of its nature and construction—How its magnifying power is determined. Table of the linear aperture, magnifying powers, &c., of astronomical telescopes from 1 to 120 feet in length—Summary view of the properties of this telescope |
| Sect. 3.—The Aerial Telescope. |
| This telescope is used without a tube—Description of the apparatus connected with it, illustrated with figures—Huygens’ Hartsocker’s and Cassini’s large telescopes |
| Sect. 4.—The Common Refracting Telescope for Terrestrial Objects. |
| Arrangement of its lenses—Magnifying power—Manner in which the rays of light are refracted through the telescopes now described |
| Sect. 5.—Telescope Formed by a Single Lens. |
| Various experiments in relation to this point—Experiments with a lens 26 focal distance, and 11½ inches diameter |
| Sect. 6.—The Achromatic Telescope. |
| Imperfections of common refracting telescopes—Dollond’s discovery—Newton’s error—Explanation of the principle of achromatic telescopes—Combination of lenses—Difficulties in the construction of such instruments—Difficulty in procuring large disks of flint glass—Guinaud’s experiments |
| NOTICES OF SOME LARGE ACHROMATIC TELESCOPES ON THE CONTINENT, AND IN GREAT BRITAIN. |
| The Dorpat telescope—Sir J. South’s telescope—Captain Smyth’s—Rev. Dr. Pearson’s—Mr. Lawson’s—Mr. Cooper’s—Mr. Bridges’, &c.,—Achromatics in Cambridge and Paris observatories |
| ACHROMATIC TELESCOPES OF A MODERATE SIZE, WITH THEIR PRICES, AS SOLD BY LONDON OPTICIANS. |
| The 2½ feet Achromatic—The 3½ feet—The powers applied to it—and xiii the views it gives of the heavenly bodies—The 5 feet achromatic—Stands for telescopes, illustrated by engravings |
| PROPORTIONS OR CURVATURE OF THE LENSES WHICH FORM AN ACHROMATIC OBJECT-GLASS. |
| Various tables and explanations |
| ACHROMATIC TELESCOPES COMPOSED OF FLUID LENSES. |
| Blair’s fluid telescope, with an account of its performance—Barlow’s large refracting telescope with a fluid concave lens—Its construction, and the effect it produces on double stars, &c.—Rogers’ achromatic telescope on a new plan—Wilson’s telescope, &c. |
| CHAPTER V. |
| On Reflecting Telescopes. |
| Sect. 1.—History of the Invention, and a General Description of the Construction of These Instruments. |
| Gregory’s Reflector—Newtonian Reflector—Cassegrainian Reflector—Magnifying powers of reflectors—Short’s Reflectors—Their powers and prices—General remarks on Gregorian reflectors—Apertures and magnifying powers of Newtonian telescopes—Prices of Reflecting telescopes |
| Sect. 2.—The Herschelian Telescope. |
| Description of Sir W. Herschel’s 40 feet telescope, with its machinery,
apparatus, and the discoveries made by it—Sir J. Herschel’s 20 feet
reflector |
| Sect. 3.—Ramage’s Large Reflecting Telescope. |
| Sect. 4.—The Aerial Reflector—constructed by the Author. |
| Construction of this telescope, and the manner of using it—Illustrated xiv by figures—Its properties and advantages—Tube not necessary in reflecting telescopes—How a large reflector might be constructed without a tube—How the form of a telescope may be used for viewing perspectives |
| Sect. 4.—Earl of Rosse’s Reflecting Telescopes. |
| His mode of forming a large speculum, &c., see also, Appendix |
| Sect. 5.—Reflecting Telescopes With Glass Specula. |
| Various experiments on this subject, with their results |
| Sect. 6.—A Reflecting Telescope With a Single Mirror and No Eye-piece. |
| Experiments illustrative of this construction |
| ON THE EYE-PIECES OF TELESCOPES. ASTRONOMICAL EYE-PIECES. |
| Huygenian eye-piece—Ramsden’s eye-piece—Aberration of lenses—Celestial eye-pieces with variable powers. Diagonal eye-pieces—Various forms of them described—Various aspects in which objects may be viewed by them |
| TERRESTRIAL EYE-PIECES. |
| Eye-pieces with four lenses—Proportions of the focal lengths of these lenses—Dimensions and powers of several eye-pieces stated |
| DESCRIPTION OF AN EYE-PIECE, &C., OF AN OLD DUTCH ACHROMATIC TELESCOPE. |
| This telescope supposed to have been invented in Holland before Dollond’s discovery was known—Peculiarity of its eye-piece |
| DESCRIPTION OF THE PANCRATIC EYE-TUBE. |
| CHAPTER VI. |
| Miscellaneous Remarks in Relation to Telescopes. |
| 1. Adjustments requisite to be attended to in the use of telescopes—2. xv State of the atmosphere most proper for observing terrestrial and celestial objects—Average number of hours in the year fit for celestial observations.—3. On the magnifying powers requisite for observing the phenomena of the different planets—Comets—Double stars, &c.—Illustrated at large from p. 369-380.—4. Mode of exhibiting the solar spots—Eye-pieces best adapted for this purpose—How they may be exhibited to a large company—Mode in which their dimensions may be determined.—5. On the space-penetrating power of telescopes—Herschel’s observations on space-penetrating powers—Comparison of achromatic and Gregorian reflectors.—6. On choosing telescopes, and ascertaining their properties—Various modes of ascertaining the goodness of telescopes—General remarks and cautions on this point—A circumstance which requires to be attended to in using achromatics.—7. On the mode of determining the magnifying power of telescopes—Various experiments in relation to this point.—8. On cleaning the lenses of telescopes |
| ON MEGALASCOPES, OR TELESCOPES FOR VIEWING VERY NEAR OBJECTS. |
| Mode of adapting a telescope for this purpose—objects to which they may be applied |
| REFLECTIONS ON LIGHT AND VISION, AND ON THE NATURE AND UTILITY OF TELESCOPES. |
| Wonderful and mysterious nature of light—The organ of vision, and its expansive range—Wonderful nature of the telescope, and the objects it has disclosed to view—No boundaries should be set to the discoveries of science and the improvement of art—The telescope is a machine which virtually transports us to the distant regions of space—It enlarges our views of the sublime scenes of creation—It has tended to amplify our conceptions of the empire and the attributes of the Deity—Various uses of this instrument in relation to science and common life |
| CHAPTER VII. |
| On the Method of Grinding and Polishing Optical Lenses and Specula. |
| 1. Directions for grinding lenses for eye-glasses, microscopes, &c.—2. Method of casting and grinding the specula of reflecting telescopes—Compositions for speculum metal—To try the figure of the metal—To adjust the eye-hole of Gregorian reflectors—To center the specula—To center lenses. xvi |
| PART III. ON VARIOUS ASTRONOMICAL INSTRUMENTS. |
| CHAPTER I. |
| On Micrometers. |
| Various descriptions of micrometers—Cavallo’s micrometer described—To ascertain the value of its divisions—Practical uses of this micrometer—Problems which may be solved by it—Tables for facilitating its use |
| CHAPTER II. |
| On the Equatorial Telescope, or Portable Observatory. |
| History of equatorials—Description of one of the simplest construction of these instruments—To adjust the equatorial for observation—To adjust the line of sight—Description of the nonius—To find the meridian line by one observation—Manner of observing stars and planets in the day-time |
| OBSERVATIONS, BY THE AUTHOR, ON THE FIXED STARS AND PLANETS, MADE IN THE DAY-TIME, BY THE EQUATORIAL. |
| Object of these observations—stars of the first and second magnitudes—General deductions from these observations |
| OBSERVATIONS ON THE PLANETS IN THE DAY-TIME. |
| Series of observations on Venus, when near the sun—Seen at the time of her superior conjunction in 1843—Conclusions deduced from these observations—phenomena observed during these observations—Remarkable phenomenon during an eclipse of the sun xvii |
| OBSERVATIONS ON JUPITER AND OTHER PLANETS. |
| General conclusions, &c. |
| UTILITY OF CELESTIAL DAY OBSERVATIONS. |
| ON THE ASTRONOMICAL QUADRANT. |
| THE ASTRONOMICAL CIRCLE. |
| THE TRANSIT INSTRUMENT. |
| CHAPTER III. |
| On Observatories. |
| Leading features of a spot adapted for celestial observations—Public and private observatories—Greenwich observatory—Instruments with which an observatory should be furnished—The Author’s private observatory—Revolving domes for observatories—Cautions to be attended to in celestial observations |
| CHAPTER IV. |
| On Orreries or Planetariums. |
| History of such machines—Sphere of Archimedes and Posidonius—Dr. Long’s Uranium—Wheel-work of the common Planetarium—Figure representing this machine—Problems which may be performed by it |
| DR. HENDERSON’S PLANETARIUM. |
| Section of its wheel-work—Number of teeth in the wheels and pinions which move the different planets—Extreme accuracy of these movements. |
| ON THE VARIOUS OPINIONS WHICH WERE ORIGINALLY FORMED OF SATURN’S RING, ILLUSTRATED WITH 13 VIEWS. |
| When and by whom its true figure was discovered. xviii |
| ON THE SUPPOSED DIVISION OF THE EXTERIOR RING OF SATURN. |
| Kater’s, Short’s, Quetelet’s and Decuppis’s observations |
| APPENDIX. |
| 1. Description of the Earl of Rosse’s Largest Telescope. |
| Composition of the speculum, and the process of casting it—Mode of grinding and polishing it—Manner in which it is filled up—Expenses incurred in its construction—Results of observations which have been made with it—Two views representing this instrument and the buildings connected with it—Sir J. South’s remarks and anticipations |
| 2. Hints to amateurs in astronomy respecting the construction of telescopes. |
xix
| Figure | Page | |
| 1. | Representation of the diminution of the intensity of light. | 22 |
| 2. | Illustrative of the refraction of light. | 43 |
| 3. | Representing the angles of incidence and refraction. | 44 |
| 4. | The refraction of the atmosphere. | 51 |
| 5. | Various forms of lenses. | 65 |
| 6, | 7, 8. Parallel, converging, and diverging rays. | 66 |
| 9, | 10, 11. Passage of parallel, diverging, and converging rays through convex lenses. | 67 |
| 12. | Passage of parallel rays through concave lenses. | 69 |
| 13. | Images formed by convex lenses. | 71 |
| 14. | Angle of incidence and reflection. | 83 |
| 15. | Images as reflected from a plane mirror. | 84 |
| 16. | Illustrative of reflections from a plane mirror. | 85 |
| 17. | Shewing how the image in a plane mirror is twice the length of the object. | 86 |
| 18. | Reflection from concave mirrors. | 87 |
| 19. | Reflection from convex mirrors. | 89 |
| 20. | Parallel rays as reflected from concave mirrors. | 91 |
| 21. | Diverging rays as reflected from concave mirrors. | 91 |
| 22. | Images formed before concave mirrors. | 93 |
| 23. | Images formed behind concave mirrors. | 96 |
| 24. | Illustrating the magnifying power of concave mirrors. | 97 |
| 25. | Inverted images formed in the front of concave mirrors. | 98 |
| 26. | Illustrative of deceptions produced by concave mirrors. | 100 |
| 27, | 28. Experiment with a bottle half filled with water. | 101 |
| 29. | Effect of extraordinary refraction on ships at sea. | 109 |
| 30. | Experiment for illustrating the causes of uncommon refraction. | 117 |
| 31. | Prismatic spectrum. | 127 |
| 32. | Different foci of coloured rays in convex lenses. | 129 |
| 33. | Experiment to show the different foci of red and violet rays. | 129 |
| 34. | Illustrative of the prismatic colours. | 136 |
| 35. | Explanatory of refraction and reflection from drops of rain. | 147 |
| 36. | Explanatory of the rainbow. | 149 |
| 37. | Images of objects formed in a dark chamber. | 187 |
| 38. | The revolving Camera Obscura. | 194xx |
| 39, | 40. The portable Camera Obscura. | 195, 196 |
| 40,* | 41, 42. Illustrative of the angle of vision, and the apparent magnitude of objects. | 206, 207, 208 |
| 43. | The Galilean telescope. | 215 |
| 44. | The astronomical telescope. | 218 |
| 45, | 46. The aerial refracting telescope. | 226 |
| 47. | The common refracting telescope. | 228 |
| 48, | 49, 50. Manner in which the rays of light are refracted in telescopes. | 231 |
| 51. | Telescope with a single lens. | 234 |
| 52. | Illustrative of spherical aberration. | 236 |
| 53. | Illustrative of the principle of achromatic telescopes. | 241 |
| 54, | 55. Double and treble achromatic object-glass. | 242 |
| 57. | Common stand for achromatic telescopes. | 260 |
| 58. | Equatorial stand for achromatic telescopes. | 262 |
| 59. | Dollond’s stand for achromatic telescopes. | 264 |
| 60. | Blair’s fluid achromatic object-glass. | 271 |
| 61. | Barlow’s fluid telescope. | 274 |
| 62, | 63, 64, 65, 66. Various forms of reflecting telescopes. | 288 |
| 67. | Gregorian reflecting telescope. | 293 |
| 69. | The aerial reflector. | 313 |
| 70. | Front view of the aerial reflector. | 314 |
| 71. | Construction of large reflecting telescope. | 322 |
| 72. | Reflecting telescope with a single mirror. | 332 |
| 73. | Huygenian eye-piece. | 336 |
| 74. | Ramsden’s eye-piece. | 339 |
| 75, | 76. Combination of lenses for achromatic eye-pieces. | 340 |
| 77, | 78. Diagonal eye-pieces. | 344, 345 |
| 79. | Terrestrial eye-piece with four lenses. | 349 |
| 80. | Eye-piece of an old Dutch achromatic telescope. | 356 |
| 81. | Pancratic eye-piece. | 359 |
| 82. | Manner of exhibiting the solar spots. | 384 |
| 84. | Mode of measuring distances from one station. | 430 |
| 85. | Cavallo’s micrometer. | 446 |
| 86. | The equatorial telescope, or portable observatory. | 455 |
| 87. | Figure to illustrate the principle of the quadrant. | 491 |
| 88. | The astronomical quadrant. | 493 |
| 89. | The astronomical circle. | 496 |
| 90. | The transit instrument. | 502 |
| 91. | Plan of a private observatory. | 511 |
| 92. | Rotatory dome for an observatory. | 513 |
| 93. | Wheel-work of a planetarium. | 521 |
| 94. | Perspective view of a planetarium. | 522 |
| 95. | Apparatus for exhibiting the retrograde motions of the planets. | 525 |
| 96. | Section of the wheel-work of Dr. Henderson’s planetarium. | 528 |
| 97. | Thirteen views of the supposed form of Saturn’s ring. | 539 |
| 98. | Earl of Rosse’s Great Telescope. | 559 |
| 99. | Section of the machinery connected with the telescope. | 560 |
| 100. | Perspective view of the author’s observatory—to front the title. |
1
THE
PRACTICAL ASTRONOMER.
Light is that invisible etherial matter which renders objects perceptible by the visual organs. It appears to be distributed throughout the immensity of the universe, and is essentially requisite to the enjoyment of every rank of perceptive existence. It is by the agency of this mysterious substance, that we become acquainted with the beauties and sublimities of the universe, and the wonderful operations of the Almighty Creator. Without its universal influence, an impenetrable veil would be thrown over the distant scenes of creation; the sun, the moon, the planets, and the starry orbs, would be shrouded in the deepest darkness, and the variegated surface of the globe on which we dwell, would be almost unnoticed and unknown. Creation would disappear, a mysterious gloom would surround the mind of every 2 intelligence, all around would appear a dismal waste, and an undistinguished chaos. To whatever quarter we might turn, no form nor comeliness would be seen, and scarcely a trace of the perfections and agency of an All Wise and Almighty Being could be perceived throughout the universal gloom. In short, without the influence of light, no world could be inhabited, no animated being could subsist in the manner it now does, no knowledge could be acquired of the works of God, and happiness, even in the lowest degree, could scarcely be enjoyed by any organized intelligence.
We have never yet known what it is to live in a world deprived of this delightful visitant; for in the darkest night we enjoy a share of its beneficial agency, and even in the deepest dungeon its influence is not altogether unfelt.1 The blind, indeed, do not directly enjoy the advantages of light, but its influence is reflected upon them, and their knowledge is promoted through the medium of those who enjoy the use of their visual organs. Were all the inhabitants of the world deprived of their eye-sight, neither knowledge nor happiness, such as we now possess, could possibly be enjoyed.
There is nothing which so strikingly displays the beneficial and enlivening effects of light, as the dawn of a mild morning after a night of darkness and tempest. All appears gloom and desolation, in our terrestrial abode, till a faint light begins to whiten the eastern horizon. Every succeeding 3 moment brings along with it something new and enlivening. The crescent of light towards the east, now expands its dimensions and rises upwards towards the cope of heaven; and objects, which a little before were immersed in the deepest gloom, begin to be clearly distinguished. At length the sun arises, and all nature is animated by his appearance; the magnificent scene of creation, which a little before was involved in obscurity, opens gradually to view, and every object around excites sentiments of wonder, delight, and adoration. The radiance which emanates from this luminary, displays before us a world strewed with blessings and embellished with the most beautiful attire. It unveils the lofty mountains and the forests with which they are crowned—the fruitful fields with the crops that cover them—the meadows, with the rivers which water and refresh them—the plains adorned with verdure, the placid lake and the expansive ocean. It removes the curtain of darkness from the abodes of men, and shows us the cities, towns and villages, the lofty domes, the glittering spires, and the palaces and temples with which the landscape is adorned. The flowers expand their buds and put forth their colours, the birds awake to melody, man goes forth to his labour, the sounds of human voices are heard, and all appears life and activity, as if a new world had emerged from the darkness of Chaos.
The whole of this splendid scene, which light produces, may be considered as a new creation, no less grand and beneficent than the first creation, when the command was issued, “Let there be light, and light was.” The aurora and the rising sun cause the earth and all the objects which adorn its surface, to arise out of that profound 4 darkness and apparent desolation which deprived us of the view of them, as if they had been no more. It may be affirmed, in full accordance with truth, that the efflux of light in the dawn of the morning, after a dark and cloudy night, is even more magnificent and exhilarating than at the first moment of its creation. At that period, there were no spectators on earth to admire its glorious effects; and no objects, such as we now behold, to be embellished with its radiance. The earth was a shapeless chaos, where no beauty or order could be perceived; the mountains had not reared their heads; the seas were not collected into their channels; no rivers rolled through the valleys, no verdure adorned the plains; the atmosphere was not raised on high to reflect the radiance, and no animated beings existed to diversify and enliven the scene. But now, when the dawning of the morning scatters the darkness of the night, it opens to view a scene of beauty and magnificence. The heavens are adorned with azure, the clouds are tinged with the most lively colours, the mountains and plains are clothed with verdure, and the whole of this lower creation stands forth arrayed with diversified scenes of beneficence and grandeur, while the contemplative eye looks round and wonders.
Such, then, are the important and beneficent effects of that light which every moment diffuses its blessings around us. It may justly be considered as one of the most essential substances connected with the system of the material universe, and which gives efficiency to all the other principles and arrangements of nature. Hence we are informed, in the sacred history, that light was the first production of the Almighty Creator, and the first born of created beings; for without it the 5 universe would have presented nothing but an immense blank to all sentient existences. Hence, likewise, the Divine Being is metaphorically represented under the idea of light, as being the source of knowledge and felicity to all subordinate intelligences: “God is light, and in Him is no darkness at all;” and he is exhibited as “dwelling in light unapproachable and full of glory, whom no man hath seen or can see.” In allusion to these circumstances, Milton, in his Paradise Lost, introduces the following beautiful apostrophe:—
As light is an element of so much importance and utility in the system of nature, so we find that arrangements have been made for its universal diffusion throughout all the worlds in the universe. The sun is one of the principal sources of light to this earth on which we dwell, and to all the other planetary bodies. And, in order that it may be equally distributed over every portion of the surfaces of these globes, to suit the exigencies of their inhabitants, they are endowed with a motion of rotation, by which every part of their surfaces is alternately turned towards the source of light; and when one hemisphere is deprived of the direct influence of the solar rays, its inhabitants derive a portion of light from luminaries in more distant regions, and have their views directed to other suns and systems dispersed, in 6 countless numbers, throughout the remote spaces of the universe. Around several of the planets, satellites, or moons, have been arranged for the purpose of throwing light on their surfaces in the absence of the sun, while at the same time the primary planets themselves reflect an effulgence of light upon their satellites. All the stars which our unassisted vision can discern in the midnight sky, and the millions more which the telescope alone enables us to descry, must be considered as so many fountains of light, not merely to illuminate the voids of immensity, but to irradiate with their beams surrounding worlds with which they are more immediately connected, and to diffuse a general lustre throughout the amplitudes of infinite space. And, therefore, we have every reason to believe, that, could we fly, for thousands of years, with the swiftness of a seraph, through the spaces of immensity, we should never approach a region of absolute darkness, but should find ourselves, every moment encompassed with the emanations of light, and cheered with its benign influences. That Almighty Being who inhabiteth immensity and “dwells in light inaccessible,” evidently appears to have diffused light over the remotest spaces of his creation, and to have thrown a radiance upon all the provinces of his wide and eternal empire, so that every intellectual being, wherever existing, may feel its beneficent effects, and be enabled, through its agency, to trace his wonderful operations, and the glorious attributes with which he is invested.
As the science of astronomy depends solely on the influence of light upon the organ of vision, which is the most noble and extensive of all our senses; and as the construction of telescopes and other astronomical instruments is founded upon 7 our knowledge of the nature of light and the laws by which it operates—it is essentially requisite, before proceeding to a description of such instruments, to take a cursory view of its nature and properties, in so far as they have been ascertained, and the effects it produces when obstructed by certain bodies, or when passing through different mediums. 8
It is not my intention to discuss the subject of light in minute detail—a subject which is of considerable extent, and which would require a separate treatise to illustrate it in all its aspects and bearings. All that I propose is to offer a few illustrations of its general properties, and the laws by which it is refracted and reflected, so as to prepare the way for explaining the nature and construction of telescopes, and other optical instruments.
There is no branch of natural science more deserving of our study and investigation than that which relates to light—whether we consider its beautiful and extensive effects—the magnificence and grandeur of the objects it unfolds to view—the numerous and diversified phenomena it exhibits—the optical instruments which a knowledge of its properties has enabled us to construct—or the daily advantages we derive, as social beings, from its universal diffusion. If air, which serves as the medium of sound, and the vehicle of speech, enables us to carry on an interchange of thought and affection with our fellow-men; how much 9 more extensively is that intercourse increased by light, which presents the images of our friends and other objects as it were immediately before us, in all their interesting forms and aspects—the speaking eye—the rosy cheeks—the benevolent smile, and the intellectual forehead! The eye, more susceptible of multifarious impressions than the other senses, ‘takes in at once the landscape of the world,’ and enables us to distinguish, in a moment, the shapes and forms of all its objects, their relative positions, the colours that adorn them, their diversified aspect, and the motions by which they are transported from one portion of space to another. Light, through the medium of the eye, not only unfolds to us the persons of others, in all their minute modifications and peculiarities, but exhibits us to ourselves. It presents to our own vision a faithful portrait of our peculiar features behind reflecting substances, without which property we should remain entirely ignorant of those traits of countenance which characterize us in the eyes of others.
But, what is the nature of this substance we call light, which thus unfolds to us the scenes of creation? On this subject two leading opinions have prevailed in the philosophical world. One of those opinions is, that the whole sphere of the universe is filled with a subtle matter, which receives from luminous bodies an agitation which is incessantly continued, and which, by its vibratory motion, enables us to perceive luminous bodies. According to this opinion, light may be considered as analogous to sound, which is conveyed to the ear by the vibratory motions of the air. This was the hypothesis of Descartes, which was adopted, with some modifications, by the celebrated Euler, Huygens, Franklin, and other philosophers, 10 and has been admitted by several scientific gentlemen of the present day. The other opinion is, that light consists of the emission or emanation of the particles of luminous bodies, thrown out incessantly on all sides, in consequence of the continued agitation it experiences. This is the hypothesis of the illustrious Newton, and has been most generally adopted by British philosophers.
To the first hypothesis, it is objected that, if true, ‘light would not only spread itself in a direct line, but its motion would be transmitted in every direction like that of sound, and would convey the impression of luminous bodies in the regions of space beyond the obstacles that intervene to stop its progress.’ No wall or other opaque body could obstruct its course, if it undulated in every direction like sound; and it would be a necessary consequence, that we should have no night, nor any such phenomena as eclipses of the sun or moon, or of the satellites of Jupiter and Saturn. This objection has never been very satisfactorily answered. On the other hand, Euler brings forward the following objections against the Newtonian doctrine of emanation. 1. That, were the sun emitting continually, and in all directions, such floods of luminous matter with a velocity so prodigious, he must speedily be exhausted, or at least, some alteration must, after the lapse of so many ages, be perceptible. 2. That the sun is not the only body that emits rays, but that all the stars have the same quality; and as every where the rays of the sun must be crossing the rays of the stars, their collision must be violent in the extreme, and that their direction must be changed by such a collision.2 11
To the first of these objections it is answered—that so vast is the tenuity of light, that it utterly exceeds the power of conception: the most delicate instrument having never been certainly put in motion by the impulse of the accumulated sun-beams. It has been calculated that in the space of 385,130,000 Egyptian years, (of 360 days,) the sun would lose only the 1/1,217,420th of his bulk from the continual efflux of his light. And, therefore, if in 385 millions of years the sun’s diminution would be so extremely small, it would be altogether insensible during the comparatively short period of five or six thousand years. To the second objection it is replied—that the particles of light are so extremely rare that their distance from one another is incomparably greater than their diameters—that all objections of this kind vanish when we attend to the continuation of the impression upon the retina, and to the small number of luminous particles which are on that account necessary for producing constant vision. For it appears, from the accurate experiments of M. D’Arcy, that the impression of light upon the retina continues eight thirds, and as a particle of light would move through 26,000 miles in that time, constant vision would be maintained by a succession of luminous particles twenty-six thousand miles distant from each other.
Without attempting to decide on the merits of these two hypotheses, I shall leave the reader to adopt that opinion which he may judge to be attended with the fewest difficulties, and proceed to illustrate some of the properties of light:—and in the discussion of this subject, I shall generally adhere to the terms employed by those who have adopted the hypothesis of the emanation of light. 12
1. Light emanates or radiates from luminous bodies in a straight line. This property is proved by the impossibility of seeing light through bent tubes, or small holes pierced in metallic plates placed one behind another, except the holes be placed in a straight line. If we endeavour to look at the sun or a candle through the bore of a bended pipe, we cannot perceive the object, nor any light proceeding from it, but through a straight pipe the object may be perceived. This is likewise evident from the form of the rays of light that penetrate a dark room, which proceed straight forward in lines proceeding from the luminous body; and from the form of the shadows which bodies project, which are bounded by right lines passing from the luminous body, and meeting the lines which terminate the interposing body. This property may be demonstrated to the eye, by causing light to pass through small holes into a dark room filled with smoke or dust. It is to be understood, however, that in this case, the rays of light are considered as passing through the same medium; for when they pass from air into water, glass, or other media, they are bent at the point where they enter a different medium, as we shall afterwards have occasion to explain.
2. Light moves with amazing velocity. The ancients believed that it was propagated from the sun and other luminous bodies instantaneously; but the observations of modern astronomers have demonstrated that this is an erroneous hypothesis, and that light, like other projectiles, occupies a certain time in passing from one part of space to another. Its velocity, however, is prodigious, and exceeds that of any other body with which we are acquainted. It flies across the earth’s orbit—a space 190 millions of miles in extent, in the 13 course of sixteen and a half minutes, which is at the rate of 192,000 miles every second, and more than a million of times swifter than a cannon ball flying with its greatest velocity. It appears from the discoveries of Dr. Bradley, respecting the aberration of the stars, that light flies from those bodies, with a velocity similar, if not exactly the same; so that the light of the sun, the planets, the stars, and every luminous body in the universe is propagated with uniform velocity.3 But, if the velocity of light be so very great, it may be asked, how does it not strike against all objects with a force equal to its velocity? If the finest sand were thrown against our bodies with the hundredth part of this velocity, each grain would pierce us as certainly as the sharpest and swiftest arrows from a bow. It is a principle in mechanics that the force with which all bodies strike, is in proportion to the size of these bodies, or the quantity of matter they contain, multiplied by the velocity with which they move. Therefore if the particles of light were not almost infinitely small, they would, of necessity prove destructive in the highest degree. If a particle of light were equal in size to the twelve hundred thousandth part of a small grain of sand,—supposing light to be material—we should be no more able to withstand its force than we should that of sand shot point blank from the mouth of a cannon. Every object would be battered and perforated by such celestial artillery, till our world were laid in ruins, and every living being destroyed. And herein are the wisdom and benevolence of the Creator displayed 14 in making the particles of light so extremely small as to render them in some degree proportionate to the greatness of the force with which they are impelled; otherwise, all nature would have been thrown into ruin and confusion, and the great globes of the universe shattered to atoms.
We have many proofs, besides the above, that the particles of light are next to infinitely small. We find that they penetrate with facility the hardest substances, such as crystal, glass, various kinds of precious stones, and even the diamond itself, though among the hardest of stones; for such bodies could not be transparent, unless light found an easy passage through their pores. When a candle is lighted in an elevated situation, in the space of a second or two, it will fill a cubical space (if there be no interruption) of two miles around it, in every direction, with luminous particles, before the least sensible part of its substance is lost by the candle:—that is, it will in a short instant, fill a sphere four miles in diameter, twelve and a half miles in circumference, and containing thirty-three and a half cubical miles with particles of light; for an eye placed in any part of this cubical space would perceive the light emitted by the candle. It has been calculated that the number of particles of light contained in such a space cannot be less than four hundred septillions—a number which is six billions of times greater than the number of grains of sand which could be contained in the whole earth considered as a solid globe, and supposing each cubic inch of it to contain ten hundred thousand grains. Such is the inconceivable tenuity of that substance which emanates from all luminous bodies, and which gives beauty and splendour to the universe! This may also be evinced by the following experiment. Make a 15 small pin-hole in a piece of black paper, and hold the paper upright facing a row of candles placed near each other, and at a little distance behind the black paper, place a piece of white pasteboard. On this pasteboard the rays which flow from all the candles through the small hole in the black paper, will form as many specks of light as there are candles, each speck being as clear and distinct as if there were only one speck from a single candle. This experiment shows that the streams of light from the different candles pass through the small hole without confusion, and consequently, that the particles of light are exceedingly small. For the same reason we can easily see through a small hole not more than 1/100th of an inch in diameter, the sky, the trees, houses, and nearly all the objects in an extensive landscape, occupying nearly an entire hemisphere, the light of all which may pass through this small aperture.
3. Light is sent forth in all directions from every visible point of luminous bodies. If we hold a sheet of paper before a candle, or the sun, or any other source of light, we shall find that the paper is illuminated in whatever position we hold it, provided the light is not obstructed by its edge or by any other body. Hence, wherever a spectator is placed with regard to a luminous body, every point of that part of its surface which is toward him will be visible, when no intervening object intercepts the passage of the light. Hence, likewise, it follows, that the sun illuminates, not only an immense plane extending along the paths of the planets, from the one side of the orbit of Uranus to the other, but the whole of that sphere, or solid space, of which the distance of Uranus is the radius. The diameter of this sphere is three 16 thousand six hundred millions of miles, and it, consequently, contains about 24,000,000,000,000,000,000,000,000,000, or twenty-four thousand quartillions of cubical miles,—every point of which immense space is filled with the solar beams. Not only so, but the whole cubical space which intervenes between the sun and the nearest fixed stars is more or less illuminated by his rays. For, at the distance of Sirius, or any other of the nearest stars, the sun would be visible, though only as a small twinkling orb; and consequently, his rays must be diffused, however faint, throughout the most distant spaces whence he is visible. The diameter of this immense sphere of light cannot be less than forty billions of miles, and its solid contents 33,500,000,000,000,000,000,000,000,000,000,000,000,000 or, thirty-three thousand, five hundred sextillions of cubical miles. All this immense, and incomprehensible space is filled with the radiations of the solar orb; for were an eye placed in any one point of it, where no extraneous body interposed, the sun would be visible either as a large luminous orb, or as a small twinkling star. But he can be visible only by the rays he emits, and which enter the organs of vision. How inconceivably immense, then, must be the quantity of rays which are thrown off in all directions from that luminary which is the source of our day! Every star must likewise be considered as emitting innumerable streams of radiance over a space equally extensive, so that no point in the universe can be conceived where absolute darkness prevails, unless in the interior regions of planetary bodies.
4. The effect of light upon the eye is not instantaneous, but continues for a short space of time. This may be proved and illustrated by the following 17 examples:—If a stick—or a ball connected with a string—be whirled round in a circle, and a certain degree of velocity given it, the object will appear to fill the whole circle it describes. If a lighted firebrand be whirled round in the same rapid manner, a complete circle of light will be exhibited. This experiment obviously shows that the impression made on the eye by the light from the ball or the firebrand—when in any given point of the circle—is sufficiently lasting to remain till it has described the whole circle, and again renews its effect, as often as the circular motion is continued. The same is proved by the following considerations:—We are continually shutting our eyes, or winking; and, during the time our eyes are shut, on such occasions, we should lose the view of surrounding objects, if the impression of light did not continue a certain time while the eye-lid covers the pupil; but experience proves that during such vibrations of the eye-lids, the light from surrounding objects is not sensibly intercepted. If we look for some time steadily at the light of a candle, and particularly, if we look directly at the sun, without any interposing medium, or if we look for any considerable time at this luminary, through a telescope with a coloured glass interposed—in all these cases, if we shut our eyes immediately after viewing such objects, we shall still perceive a faint image of the object, by the impression which its light has made upon our eyes.
‘With respect to the duration of the impression of light, it has been observed that the teeth of a cog-wheel in a clock were still visible in succession, when the velocity of rotation brought 246 teeth through a given fixed point in a second. In this case it is clear that if the impression made on the 18 eye by the light reflected from any tooth, had lasted without sensible diminution for the 246th part of a second, the teeth would have formed one unbroken line, because a new tooth would have continually arrived in the place of the interior one before its image could have disappeared. If a live coal be whirled round, it is observed that the luminous circle is complete, when the rotation is performed in the (8½)/60th of a second. In this instance we see that the impression was much more durable than the former. Lastly, if an observer sitting in a room direct his sight through a window, to any particular object out of doors, for about half a minute, and then shut his eyes and cover them with his hands, he will still continue to see the window, together with the outline of the terrestrial objects bordering on the sky. This appearance will remain for near a minute, though occasionally vanishing and changing colour in a manner that brevity forbids our minutely describing. From these facts we are authorized to conclude, that all impressions of light on the eye, last a considerable time, that the brightest objects make the most lasting impressions; and that, if the object be very bright, or the eye weak, the impression may remain for a time so strong, as to mix with and confuse the subsequent impressions made by other objects. In the last case the eye is said to be dazzled by the light.’4
The following experiment has likewise been suggested as a proof of the impression which light makes upon the eye. If a card, on both sides of which a figure is drawn, for example, a bird and a cage, be made to revolve rapidly on the straight line which divides it symmetrically, the eye will perceive both 19 figures at the same time, provided they return successively to the same place. M. D’Arcy found by various experiments, that, in general, the impression which light produces on the eye, lasts about the eighth of a second. M. Plateau, of Brussels, found that the impression of different colours lasted the following periods; the numbers here stated being the decimal parts of a second. Flame, 0.242. or nearly one fourth of a second; Burning coal, 0.229; White, 0.182, or, a little more than one sixth of a second; Blue, 0.186; Yellow, 0.173; Red, 0.184.
5. Light, though extremely minute, is supposed to have a certain degree of force or momentum. In order to prove this, the late ingenious Mr. Mitchell contrived the following experiment. He constructed a small vane in the form of a common weather-cock, of a very thin plate of copper, about an inch square, and attached to one of the finest harpsicord wires, about ten inches long, and nicely balanced at the other end of the wire, by a grain of very small shot. The instrument had also fixed to it in the middle, at right angles to the length of the wire, and in an horizontal direction, a small bit of a very slender sewing needle, about half an inch long, which was made magnetical. In this state the whole instrument might weigh about ten grains. The vane was supported in the manner of the needle in the mariner’s compass, so that it could turn with the greatest ease; and to prevent its being affected by the vibrations of the air, it was enclosed in a glass case or box. The rays of the sun were then thrown upon the broad part of the vane or copper plate, from a concave mirror of about two feet diameter, which, passing through the front glass of the box, were collected into the focus of the 20 mirror upon the copper plate. In consequence of this the plate began to move with a slow motion of about an inch in a second of time, till it had moved through a space of about two inches and a half, when it struck against the back of the box. The mirror being removed, the instrument returned to its former situation, and the rays of the sun being again thrown upon it, it again began to move, and struck against the back of the box as before. This was repeated three or four times with the same success.
On the above experiment, the following calculation has been founded: If we impute the motion produced in this experiment to the impulse of the rays of light, and suppose that the instrument weighed ten grains, and acquired a velocity of one inch in a second, we shall find that the quantity of matter contained in the rays falling upon the instrument in that time amounted to no more than one twelve hundred-millionth part of a grain, the velocity of light exceeding the velocity of one inch in a second in the proportion of about 12,000,000,000 to 1. The light in this experiment was collected from a surface of about three square feet, which reflecting only about half what falls upon it, the quantity of matter contained in the rays of the sun incident upon a foot and a half of surface in one second of time, ought to be no more than the twelve hundred-millionth part of a grain. But the density of the rays of light at the surface of the sun is greater than that at the earth in the proportion of 45,000 to 1; there ought therefore to issue from one square foot of the sun’s surface in one second of time, in order to supply the waste by light 1/45,000th part of a grain of matter, that is, a little more than two grains a day, or about 21 4,752,000 grains, or 670 pounds avoirdupoise, nearly, in 6,000 years, a quantity which would have shortened the sun’s diameter no more than about ten feet, if it were formed of the density of water only.
If the above experiment be considered as having been accurately performed, and if the calculations founded upon it be correct, it appears that there can be no grounds for apprehension that the sun can ever be sensibly diminished by the immense and incessant radiations proceeding from his body on the supposition that light is a material emanation. For the diameter of the sun is no less than 880,000 miles; and, before this diameter could be shortened, by the emission of light, one English mile, it would require three millions, one hundred and sixty-eight thousand years, at the rate now stated; and, before it could be shortened ten miles, it would require a period of above thirty-one millions of years. And although the sun were thus actually diminished, it would produce no sensible effect or derangement throughout the planetary system. We have no reason to believe that the system, in its present state and arrangements, was intended to endure for ever, and before that luminary could be so far reduced, during the revolutions of eternity, as to produce any irregularities in the system, new arrangements and modifications might be introduced by the hand of the All Wise and Omnipotent Creator. Besides, it is not improbable that a system of means is established by which the sun and all the luminaries in the universe receive back again a portion of the light which they are continually emitting, either from the planets from whose surfaces it is reflected, or from the millions of stars whose rays are continually traversing the 22 immense spaces of creation, or from some other sources to us unknown.
6. The intensity of light is diminished in proportion to the square of the distance from the luminous body. Thus, a person at two feet distance from a candle, has only the fourth part of the light he would have at one foot, at three feet distance the ninth part, at four feet the sixteenth part, at five feet the twenty fifth part, and so on for other distances. Hence the light received by the planets of the Solar system decreases in proportion to the squares of the distances of these bodies from the sun. This may be illustrated by the following figure,
Figure 1.
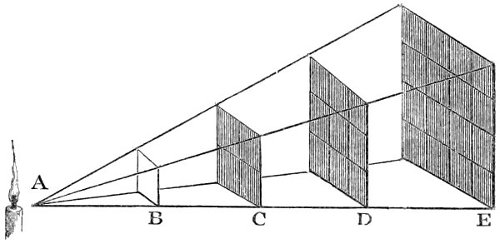
Suppose the light which flows from a point A, and passes through a square hole B, is received upon a plane C, parallel to the plane of the hole—or, let the figure C be considered as the shadow of the plane B. When the distance of C is double of B, the length and breadth of the shadow C will be each double of the length and breadth of the plane B, and treble when AD is treble of AB, and so on, which may be easily 23 examined by the light of a candle placed at A. Therefore the surface of the shadow C, at the distance AC—double of AB, is divisible into four squares, and at a treble distance, into nine squares, severally equal to the square B, as represented in the figure. The light, then, which falls upon the plane B being suffered to pass to double that distance, will be uniformly spread over four times the space, and consequently will be four times thinner in every part of that space. And at a treble distance it will be nine times thinner, and at a quadruple distance sixteen times thinner than it was at first. Consequently the quantities of this rarified light received upon a surface of any given size and shape when removed successively to these several distances, will be but one-fourth, one-ninth, one-sixteenth, of the whole quantity received by it at the first distance AB.
In conformity with this law, the relative quantities of light on the surfaces of the planets may be easily determined, when their distances from the sun are known. Thus, the distance of Uranus from the sun is 1,800,000,000 miles, which is about nineteen times greater than the distance of the earth from the same luminary. The square of 19 is 361; consequently the earth enjoys 361 times the intensity of light when compared with that of Uranus; in other words, this distant planet enjoys only the 1/361 part of the quantity of light which falls upon the earth. This quantity, however, is equivalent to the light we should enjoy from the combined effulgence of 348 full moons; and if the pupils of the eyes of the inhabitants of this planet be much larger than ours, and the retina of the eye be endued with a much greater degree of nervous sensibility, they may perceive objects with as great a degree of splendour 24 as we perceive on the objects which surround us in this world. Following out the same principle, we find that the quantity of light enjoyed by the planet Mercury is nearly seven times greater than that of the Earth, and that of Venus nearly double of what we enjoy—that Mars has less than the one half—Jupiter the one twenty-seventh part—and Saturn only the one ninetieth part of the light which falls upon the Earth. That the light of these distant planets, however, is not so weak as we might at first imagine appears from the brilliancy they exhibit, when viewed in our nocturnal sky, either with the telescope or with the unassisted eye—and likewise from the circumstance that a very small portion of the Sun—such as the one fortieth or one fiftieth part diffuses a quantity of light sufficient for most of the purposes of life, as is found in the case of total eclipses of the Sun, when his western limb begins to be visible, only like a fine luminous thread, for his light is then sufficient to render distinctly visible all the parts of the surrounding landscape.
7. It is by light reflected from opake bodies that most of the objects around us are rendered visible. When a lighted candle is brought into a dark room, not only the candle but all other bodies in the room become visible. Rays of the sun passing into a dark room render luminous a sheet of paper on which they fall, and this sheet in its turn enlightens, to a certain extent, the whole apartment, and renders objects in it visible, so long as it receives the rays of the sun. In like manner, the moon and the planets are opake bodies, but the light of the sun falling upon them, and being reflected from their surfaces, renders them visible. Were no light to fall on them from the sun, or were they not endued with a power of 25 reflecting it, they would be altogether invisible to our sight. When the moon comes between us and the sun, as in a total eclipse of that luminary, as no solar light is reflected from the surface next the earth, she is invisible—only the curve or outline of her figure being distinguished by her shadow. In this case, however, there is a certain portion of reflected light on the lunar hemisphere next the earth, though not distinguishable during a solar eclipse. The earth is enlightened by the sun, and a portion of the rays which fall upon it is reflected upon the dark hemisphere of the moon which is then towards the earth. This reflected light from the earth is distinctly perceptible, when the moon appears as a slender crescent, two or three days after new moon—when the earth reflects its light back on the moon, in the same manner as the full moon reflects her light on the earth. Hence, even at this period of the moon, her whole face becomes visible to us, but its light is not uniform or of equal intensity. The thin crescent on which the full blaze of the solar light falls, is very brilliant and distinctly seen, while the other part, on which falls only a comparatively feeble light from the earth, appears very faint, and is little more than visible to the naked eye, but with a telescope of moderate power,—if the atmosphere be very clear—it appears beautifully distinct, so that the relative positions of many of the lunar spots may be distinguished.
The intensity of reflected light is very small, when compared with that which proceeds directly from luminous bodies. M. Bouguer, a French philosopher, who made a variety of experiments to ascertain the proportion of light emitted by the heavenly bodies, concluded from these experiments, that the light transmitted from the sun to 26 the earth is at least 300,000 times as great as that which descends to us from the full moon—and that, of 300,000 rays which the moon receives, from 170,000 to 200,000 are absorbed. Hence we find that, however brilliant the moon may appear at night—in the day time she appears as obscure as a small portion of dusky cloud to which she happens to be adjacent, and reflects no more light than a portion of whitish cloud of the same size. And as the full moon fills only the ninety thousandth part of the sky, it would require at least ninety thousand moons to produce as much light as we enjoy in the day-time under a cloudy sky.
As the moon and the planets are rendered visible to us only by light reflected from their surfaces, so it is in the same way that the images of most of the objects around us are conveyed to our organs of vision. We behold all the objects which compose an extensive landscape,—the hills and vales, the woods and lawns, the lakes and rivers, and the habitations of man—in consequence of the capacity with which they are endued of sending forth reflected rays to the eye, from every point of their surfaces and in all directions. In connection with the reflection of light, the following curious observation may be stated. Baron Funk, visiting some silver mines in Sweden, observed, that, 27‘in a clear day, it was as dark as pitch underground in the eye of a pit, at sixty or seventy fathoms deep; whereas, in a cloudy or rainy day, he could see to read even at 106 fathoms deep. Enquiring of the miners, he was informed that this is always the case; and reflecting upon it, he imagined it arose from this circumstance, that when the atmosphere is full of clouds, light is reflected from them into the pit in all directions, and that thereby a considerable proportion of the rays are reflected perpendicularly upon the earth: whereas when the atmosphere is clear, there are no opaque bodies to reflect the light in this manner, at least in a sufficient quantity; and rays from the sun himself can never fall perpendicularly in that country.’—The reason here assigned is, in all probability, the true cause of the phenomenon now described.
8. It is supposed by some philosophers that light is subject to the same laws of attraction that govern all other material substances—and that it is imbibed and forms a constituent part of certain bodies. This has been inferred from the phenomena of the Bolognian stone, and what are generally called the solar phosphori. The Bolognian stone was first discovered about the year 1680, by Leascariolo, a shoe-maker of Bologna. Having collected together some stones of a shining appearance at the bottom of Monte Paterno, and being in quest of some alchemical secret, he put them into a crucible to calcine them—that is, to reduce them to the state of cinders. Having taken them out of the crucible, and exposed them to the light of the sun, he afterwards happened to carry them into a dark place, when to his surprise, he observed that they possessed a self-illuminating power, and continued to emit faint rays of light for some hours afterwards. In consequence of this discovery, the Bolognian spar came into considerable demand among natural philosophers and the curious in general; and the best way of preparing it seems to have been hit upon by the family of Zagoni, who supplied all Europe with Bolognian phosphorus, till the discovery of more powerful phosphoric substances put an end to their monopoly.—In the year 1677, Baldwin, a native 28 of Misnia, observed that chalk dissolved in aqua-fortis exactly resembled the Bolognian stone in its property of imbibing light, and emitting it after it was brought into the dark ; and hence it has obtained the name of Baldwin’s phosphorus.
In 1730 M. du Fay directed his attention to this subject, and observed that all earthy substances susceptible of calcination, either by mere fire, or when assisted by the previous action of nitrous acid, possessed the property of becoming more or less luminous, when calcined and exposed for a short time in the light—that the most perfect of these phosphori were limestones, and other kinds of carbonated lime, gypsum, and particularly the topaz, and that some diamonds were also observed to be luminous by simple exposure to the sun’s rays. Sometime afterwards, Beccaria discovered that a great variety of other bodies were convertible into phosphori by exposure to the mere light of the sun, such as, organic animal remains, most compound salts, nitre and borax—all the farinaceous and oily seeds of vegetable substances, all the gums and several of the resins—the white woods and vegetable fibre, either in the form of paper or linen; also starch and loaf-sugar proved to be good phosphori, after being made thoroughly dry, and exposed to the direct rays of the sun. Certain animal substances by a similar treatment were also converted into phosphori; particularly bone, sinew, glue, hair, horn, hoof, feathers, and fish-shells. The same property was communicated to rock crystal and some other of the gems, by rubbing them against each other so as to roughen their surfaces, and then placing them for some minutes in the focus of a lens, by which the rays of light were concentrated upon 29 them, at the same time that they were also moderately heated.
In the year 1768 Mr. Canton contributed some important facts in relation to solar phosphori, and communicated a method of preparing a very powerful one, which, after the inventor, is usually called Canton’s phosphorus. He affirms that his phosphorus, enclosed in a glass flask, and hermetically sealed, retains its property of becoming luminous for at least four years, without any apparent decrease of activity. It has also been found that, if a common box smoothing-iron, heated in the usual manner, be placed for half a minute on a sheet of dry, white paper, and the paper be then exposed to the light, and afterwards examined in a dark closet, it will be found that the whole paper will be luminous, that part, however, on which the iron had stood being much more shining than the rest.
From the above facts it would seem that certain bodies have the power of imbibing light and again emitting it, in certain circumstances, and that this power may remain for a considerable length of time. It is observed that the light which such bodies emit bears an analogy to that which they have imbibed. In general, the illuminated phosphorus is reddish; but when a weak light only has been admitted to it, or when it has been received through pieces of white paper, the emitted light is pale or whitish.—Mr. Morgan, in the seventy-fifth volume of the Philosophical Transactions, treats the subject of light at considerable length; and as a foundation for his reasoning, he assumes the following data:—1. That light is a body, and like all others, subject to the laws of attraction. 2. That light is a heterogeneous body; and that the same attractive power operates with different 30 degrees of force on its different parts. To the principle of attraction, likewise, Sir Isaac Newton has referred the most extraordinary phenomena of light, Refraction and Inflection. He has also endeavoured to show that light is not only subject to the law of attraction but of repulsion also, since it is repelled or reflected from certain bodies. If such principles be admitted, then, it is highly probable that the phosphorescent bodies to which we have adverted have a power of attracting or imbibing the substance of light, and of retaining or giving it out under certain circumstances, and that the matter of light is incorporated at least with the surface of such bodies. But on this subject, as on many others, there is a difference of opinion among philosophers.5 31
9. Light is found to produce a remarkable effect on Plants and Flowers, and other vegetable productions. Of all the phenomena which living vegetables exhibit there are few that appear more extraordinary than the energy and constancy with which their stems incline toward the light. Most of the discous flowers follow the sun in his course. They attend him to his evening retreat, and meet his rising lustre in the morning with the same unerring law. They unfold their flowers on the approach of this luminary; they follow his course by turning on their stems, and close them as soon as he disappears. If a plant, also, is shut up in a dark room, and a small hole afterwards opened by which the light of the sun may enter, the plant will turn towards that hole, and even alter its own shape in order to get near it; so that though it was straight before, it will in time become crooked, that it may get near the light. Vegetables placed in rooms where they receive light only in one direction, always extend themselves in that direction. If they receive light in two directions, they direct their course towards that which is strongest. It is not the heat but the light of the sun which the plant thus covets; for, though a fire be kept in the room, capable of giving a much stronger heat than the sun, the plant will turn away from the fire in order to enjoy the solar light. Trees growing in thick forests, where they only receive light from above, direct their shoots almost invariably upwards, and therefore become much taller and less spreading than such as stand single.
The green colour of plants is likewise found to depend on the sun’s light being allowed to shine on them; for without the influence of the solar light, they are always of a white colour. It is found by experiment that, if a plant which has 32 been reared in darkness be exposed to the light of day, in two or three days it will acquire a green colour perceptibly similar to that of plants which have grown in open day-light. If we expose to the light one part of the plant, whether leaf or branch, this part alone will become green. If we cover any part of a leaf with an opake substance, this place will remain white, while the rest becomes green. The whiteness of the inner leaves of cabbages is a partial effect of the same cause, and many other examples of the same kind might easily be produced. M. Decandolle, who seems to have paid particular attention to this subject, has the following remarks: ‘It is certain, that between the white state of plants vegetating in darkness, and complete verdure, every possible intermediate degree exists, determined by the intensity of the light. Of this any one may easily satisfy himself by attending to the colour of a plant exposed to the full day-light; it exhibits in succession all the degrees of verdure. I had already seen the same phenomenon, in a particular manner, by exposing plants reared in darkness to the light of lamps. In these experiments, I not only saw the colour come on gradually, according to the continuance of the exposure to light; but I satisfied myself, that a certain intensity of permanent light never gives to a plant more than a certain degree of colour. The same fact readily shows itself in nature, when we examine the plants that grow under shelter or in forests, or when we examine in succession the state of the leaves that form the heads of cabbages.’6
It is likewise found that the perspiration of vegetables is increased or diminished, in a certain measure by the degree of light which falls upon 33 them. The experiments of Mr. P. Miller and others, prove that plants uniformly perspire most in the forenoon, though the temperature of the air in which they are placed should be unvaried. M. Guettard likewise informs us that a plant exposed to the rays of the sun, has its perspiration increased to a much greater degree than if it had been exposed to the same heat under the shade. Vegetables are likewise found to be indebted to light for their smell, taste, combustibility, maturity, and the resinous principle, which equally depend upon this fluid. The aromatic substances, resins, and volatile oil are the productions of southern climates, where the light is more pure, constant, and intense. In fine, another remarkable property of light on the vegetable kingdom is that, when vegetables are exposed to open day-light, or to the sun’s rays, they emit oxygen gas or vital air. It has been proved that, in the production of this effect, the sun does not act as a body that heats. The emission of the gas is determined by the light: pure air is therefore separated by the action of light, and the operation is stronger as the light is more vivid. By this continual emission of vital air, the Almighty incessantly purifies the atmosphere, and repairs the loss of pure air occasioned by respiration, combustion, fermentation, putrefaction, and numerous other processes which have a tendency to contaminate this fluid so essential to the vigor and comfort of animal life; so that, in this way, by the agency of light, a due equilibrium is always maintained between the constituent parts of the atmosphere.
In connection with this subject the following curious phenomenon may be stated, as related by M. Haggern, a Lecturer on Natural History in Sweden. One evening he perceived a faint flash 34 of light repeatedly dart from a marigold. Surprised at such an uncommon appearance, he resolved to examine it with attention; and, to be assured it was no deception of the eye, he placed a man near him, with orders to make a signal at the moment when he observed the light. They both saw it constantly at the same moment. The light was most brilliant on marigolds of an orange or flame colour, but scarcely visible on pale ones. The flash was frequently seen on the same flower two or three times in quick succession; but more commonly at intervals of several minutes; and when several flowers in the same place emitted their light together, it could be observed at a considerable distance. The phenomenon was remarked in the months of July and August at sun-set, and for half an hour when the atmosphere was clear; but after a rainy day, or when the air was loaded with vapours, nothing of it was seen. The following flowers emitted flashes more or less vivid, in this order:—1. The Marigold, 2. Monk’s hood, 3. The Orange Lily, 4. The Indian Pink. As to the cause of this phenomenon, different opinions may be entertained. From the rapidity of the flash and other circumstances, it may be conjectured that electricity is concerned in producing this appearance. M. Haggern, after having observed the flash from the orange lily, the antheræ of which are at considerable distance from the petals, found that the light proceeded from the petals only; whence he concludes, that this electrical light is caused by the pollen which, in flying off, is scattered on the petals. But, perhaps, the true cause of it still remains to be ascertained.
10. Light has been supposed to produce a certain degree of influence on the PROPAGATION OF SOUND?—M. Parolette, in a long paper in the 35 ‘Journal de Physique,’ vol. 68, which is copied into ‘Nicholson’s Philosophical Journal,’ vol. 25, pp. 28-39,—has offered a variety of remarks, and detailed a number of experiments on this subject. The author states the following circumstances as having suggested the connection between light and sound. ‘In 1803, I lived in Paris, and being accustomed to rise before day to finish a work on which I had long been employed, I found myself frequently disturbed by the sound of carriages, as my windows looked into one of the most frequented streets in that city. This circumstance which disturbed me in my studies every morning, led me to remark, that the appearance of day-break peculiarly affected the propagation of the sound: from dull and deep, which it was before day, it seemed to me to acquire a more sonorous sharpness in the period that succeeded the dissipation of darkness. The rolling of the wheels seemed to announce the friction of some substances grown more elastic; and my ear on attending to it perceived this difference diminish, in proportion as the sound of wheels was confounded with those excited by the tumult of objects quitting their nocturnal silence. Struck with this observation, I attempted to discover whether any particular causes had deceived my ears. I rose several times before day for this purpose alone, and was every time confirmed in my suspicion, that light must have a peculiar influence on the propagation of sound. This variation, however, in the manner in which the air gave sounds might be the effect of the agitation of the atmosphere produced by the rarefaction the presence of the sun occasioned; but the situation of my windows, and the usual direction of the morning breeze, militated against this argument.’ 36
The author then proceeds to give a description of a very delicate instrument, and various apparatus for measuring the propagation and intensity of sound, and the various experiments both in the dark, and in day-light, and likewise under different changes of the atmosphere, which were made with his apparatus—all of which tended to prove that light had a sensible influence in the propagation of sound. But the detail of these experiments and their several results would be too tedious to be here transcribed.—The night has generally been considered as more favourable than the day for the transmission of sound. ‘That this is the case (says Parolette) with respect to our ears cannot be doubted; but this argues nothing against my opinion. We hear further by night on account of the silence, and this always contributes to it, while the noise of a wind favourable to the propagation of a sound, may prevent the sound from being heard.’ In reference to the cause which produces the effect now stated, he proposes the following queries. ‘Is the atmospheric air more dense on the appearance of light than in darkness? Is this greater density of the air or of the elastic fluid that is subservient to the propagation of sound, the effect of aeriform substances kept in this state through the medium of light?’ He is disposed, on the whole, to conclude, that the effect in question is owing to the action of light upon the oxygen of the atmosphere, since oxygen gas is found by experiment to be best adapted to the transmission of sound.
Our author concludes his communication with the following remarks:—‘Light has a velocity 900,000 times as rapid as that of sound. Whether it emanate from the sun and reach to our earth, or act by means of vibrations agitating the 37 particles of a fluid of a peculiar nature—the particles of this fluid must be extremely light, elastic and active. Nor does it appear to me unreasonable, to ascribe to the mechanical action of these particles set in motion by the sun, the effects its presence occasions in the vibrations that proceed from sonorous bodies. The more deeply we investigate the theory of light, the more we must perceive, that the powers by which the universe is moved reside in the imperceptible particles of bodies; and that the grand results of nature are but an assemblage of an order of actions that take place in its infinitely small parts; consequently, we cannot institute a series of experiments more interesting than those which tend to develope the properties of light. Our organs of sense are so immediately connected with the fluid that enlightens us, that the notion of having acquired an idea of the mode of action of this fluid presents itself to our minds, as the hope of a striking advance in the knowledge of what composes the organic mechanism of our life, and of that of beings which closely follow the rank assigned to the human species.’
Such is a brief description of some of the leading properties of light. Of all the objects that present themselves to the philosophic and contemplative mind, light is one of the noblest and most interesting. The action it exerts on all the combinations of matter, its extreme divisibility, the rapidity of its propagation, the sublime wonders it reveals, and the office it performs in what constitutes the life of organic beings, lead us to consider it as a substance acting the first part in the economy of nature. The magic power which this emanation from the heavens exerts on our organs 38 of vision, in exhibiting to our view the sublime spectacle of the universe, cannot be sufficiently admired. Nor is its power confined to the organs of sight; all our senses are, in a greater or less degree, subjected to the action of light, and all the objects in this lower creation—whether in the animal, the vegetable, or the mineral kingdoms—are, to a certain extent, susceptible of its influence. Our globe appears to be little more than an accumulation of terrestrial materials introduced into the boundless ocean of the solar light, as a theatre on which it may display its exhaustless power and energy, and give animation, beauty and sublimity to every surrounding scene—and to regulate all the powers of nature, and render them subservient to the purposes for which they were ordained. This elementary substance appears to be universal in its movements, and in its influence. It descends to us from the solar orb. It wings its way through the voids of space, along a course of ninety-five millions of miles, till it arrives at the outskirts of our globe; it passes freely through the surrounding atmosphere, it strikes upon the clouds and is reflected by them; it irradiates the mountains, the vales, the forests, the rivers, the seas, and all the productions of the vegetable kingdom, and adorns them with a countless assemblage of colours. It scatters and disperses its rays from one end of creation to another, diffusing itself throughout every sphere of the universe. It flies without intermission from star to star, and from suns to planets, throughout the boundless sphere of immensity, forming a connecting chain and a medium of communication among all the worlds and beings within the wide empire of Omnipotence.
When the sun is said “to rule over the day,” it 39 is intimated that he acts as the vicegerent of the Almighty, who has invested him with a mechanical power of giving light, life and motion to all the beings susceptible of receiving impressions from his radiance. As the servant of his creator he distributes blessings without number among all the tribes of sentient and intelligent existence. When his rays illumine the eastern sky in the morning, all nature is enlivened with his presence. When he sinks beneath the western horizon, the flowers droop, the birds retire to their nests, and a mantle of darkness is spread over the landscape of the world. When he approaches the equinox in spring, the animal and vegetable tribes revive, and nature puts on a new and a smiling aspect. When he declines towards the winter solstice, dreariness and desolation ensue, and a temporary death takes place among the tribes of the vegetable world.—This splendid luminary, whose light embellishes the whole of this lower creation, forms the most lively representation of Him who is the source and the centre of all beauty and perfection. “God is a sun,” the sun of the moral and spiritual universe, from whom all the emanations of knowledge, love and felicity descend. “He covereth himself with light as with a garment.” and “dwells in light inaccessible and full of glory.” The felicity and enjoyments of the future world are adumbrated under the ideas of light and glory. “The glory of God enlightens the celestial city,” its inhabitants are represented as “the saints in light,” it is declared that “their sun shall no more go down,” and that “the Lord God is their everlasting light.” So that light not only cheers and enlivens all beings throughout the material creation, but is the emblem of the Eternal Mind, and of all that is delightful and transporting in the scenes of a blessed immortality. 40
In the formation of light, and the beneficent effects it produces, the wisdom and goodness of the Almighty are conspicuously displayed. Without the beams of the sun and the influence of light, what were all the realms of this world, but an undistinguished chaos and so many dungeons of darkness? In vain should we roll our eyes around to behold, amidst the universal gloom, the flowery fields, the verdant plains, the flowing streams, the expansive ocean, the moon walking in brightness, the planets in their courses, or the innumerable host of stars. All would be lost to the eye of man, and the “blackness of darkness” would surround him for ever. And with how much wisdom has every thing been arranged in relation to the motion and minuteness of light? Were it capable of being transformed into a solid substance, and retain its present velocity, it would form the most dreadful and appalling element in nature, and produce universal terror and destruction throughout the universe. That this is not impossible, and could easily be effected by the hand of Omnipotence, appears from such substances as phosphorus, where light is supposed to be concentrated in a solid state. But in all its operations and effects, as it is now directed by unerring wisdom and beneficence, it exhibits itself as the most benign and delightful element connected with the constitution of the material system, diffusing splendour and felicity wherever its influence extends. 41
Refraction is the turning or bending of the rays of light out of their natural course.
Light, when proceeding from a luminous body—without being reflected from any opake substance or inflected by passing near one—is invariably found to proceed in straight lines without the least deviation. But if it happens to pass obliquely from one medium to another, it always leaves the direction it had before and assumes a new one. This change of direction, or bending of the rays of light, is what is called Refraction—a term which probably had its origin from the broken appearance which a staff or a long pole exhibits, when a portion of it is immersed in water—the word, derived from the Latin frango, literally signifying breaking or bending.
When light is thus refracted, or has taken a new direction, it then proceeds invariably in a straight line till it meets with a different medium,7 when it is again turned out of its course. It must be observed, however, that though we may by this means cause the rays of light to make any number of angles in their course, it is impossible 42 for us to make them describe a curve, except in one single case, namely, where they pass through a medium, the density of which either uniformly increases or diminishes. This is the case with the light of the celestial bodies, which passes downwards through our atmosphere, and likewise with that which is reflected upwards through it by terrestrial objects. In both these cases it describes a curve of the hyperbolic kind; but at all other times, it proceeds in straight lines, or in what may be taken for straight lines without any sensible error.
There are two circumstances essential to refraction. 1. That the rays of light shall pass out of one medium into another of a different density, or of a greater or less degree of resistance. 2. That they pass in an oblique direction. The denser the refracting medium, or that into which the ray enters, the greater will be its refracting power; and of two refracting mediums of the same density, that which is of an oily or inflammable nature will have a greater refracting power than the other. The nature of refraction may be more particularly explained and illustrated by the following figure and description.
Let ADHI fig. 2, be a body of water, AD its surface, C a point in which a ray of light BC enters from the air into the water. This ray, by the greater density of the water, instead of passing straight forward in its first direction to K, will be bent at the point C, and pass along in the direction CE, which is called the refracted ray. Let the line FG be drawn perpendicular to the surface of the water in C, then it is evident that the ray BC, in passing out of air, a rare medium, into a dense medium, as water, is refracted into a ray CE which is nearer to the perpendicular CG than the incident ray BC, and on the contrary, the ray EC 43 passing out of a denser medium into a rarer will be refracted into CB, which is farther from the perpendicular.
figure 2.
The same thing may be otherwise illustrated as follows:—suppose a hole made in one of the sides of the vessel as at a, and a lighted candle placed within two or three feet of it, when empty, so that its flame may be at L, a ray of light proceeding from it will pass through the hole a in a straight line LBCK till it reach the bottom of the vessel at K, where it will form a small circle of light. Having put a mark at the point K, pour water into the vessel till it rise to the height AD, and the round spot that was formerly at K, will appear at E; that is, the ray which went straight forward, when the vessel was empty, to K, has been bent at the point C, where it falls into the the water, into the line CE. In this experiment it is necessary that the front of the vessel should be of glass, in order that the course of the ray may be seen; and if a little soap be mixed with the water so as to give it a little mistiness, the ray CE will be distinctly perceived. If, in place of fresh water we pour in salt water, it will be found that the ray BC is more bent at C. In like manner 44 alcohol will refract the ray BC more than salt water, and oil more than alcohol, and a piece of solid glass, of the shape of the water, would refract the light still more than the oil.
The angle of refraction depends on the obliquity of the rays falling on the refracting surface being always such, that the sine of the incident angle is to the sine of the refracted angle, in a given proportion. The incident angle is the angle made by a ray of light and a line drawn perpendicular to the refracting surface, at the point where the light enters the surface. The refracted angle is the angle made by the ray in the refracting medium with the same perpendicular produced. The sine of the angle is a line which serves to measure the angle, being drawn from a point in one leg perpendicular to the other. The following figure (fig. 3.) will tend to illustrate these definitions.
figure 3.

In this figure BC is the incident ray, CE the refracted ray, DG the perpendicular, AD the sine 45 of the angle of incidence ACD, and HR the sine of the angle of refraction GCE. Now, it is a proposition in optics that,—the sine AD of the angle of incidence BCD is either accurately or very nearly in a given proportion to the sine HR of the angle of refraction GCE. This ratio of the sines is as four to three, when the refraction is made out of air into water, that is AD is to HR as four to three. When the refraction is out of air into glass, the proportion is about as thirty-one to twenty, or nearly as three to two. If the refraction be out of air into diamond it is as five to two, that is AD : HR :: 5 : 2. The denser the medium is, the less is the angle and sine of refraction. If a ray of light MC, were to pass from air into water, or from empty space into air, in the direction MC perpendicular to the plane NO which separates the two mediums, it would suffer no refraction, because one of the essentials to that effect is wanting, namely, the obliquity of the incidence.
It may be also proper to remark, that a ray of light cannot pass out of a denser medium into a rarer, if the angle of incidence exceed a certain limit. Thus a ray of light will not pass out of glass into air, if the angle of incidence exceed 40° 11´; or out of glass into water, if the angle of incidence exceed 59° 20´. In such cases refraction will be changed into reflection.
The following common experiments, which are easily performed, will illustrate the doctrine of refraction. Put a shilling or any other small object which is easily distinguished, into a bason or any other similar vessel, and then retire to such a distance as that the edge of the vessel shall just hide it from your sight. If then you cause another person to fill the vessel with water, you will then 46 find that the shilling is rendered perfectly visible, although you have not in the slightest degree changed your position. The reason of this is, that the rays of light, by which it is rendered visible, are bent out of their course. Thus, suppose the shilling to have been placed in the bottom of the bason at E, (fig. 2.) the ray of light BC which passes obliquely from the air into water at C, instead of continuing its course to K, takes the direction CE, and consequently an object at E would be rendered visible by rays proceeding in that direction, when they would not have touched it had they proceeded in their direct course.
The same principle is illustrated by the following experiment. Place a bason or square box on a table, and a candle at a small distance from it; lay a small rod or stick across the sides of the bason, and mark the place where the extremity of the shadow falls, by placing a shilling or other object at the point; then let water be poured into the bason, and the shadow will then fall much nearer to the side next the candle than before. This experiment may likewise be performed by simply observing the change produced on the shadow of the side of the bason itself. Again, put a long stick obliquely into deep water, and the stick will seem to be broken at the point where it appears at the surface of the water—the part which is immersed in the water appearing to be bent upwards. Hence every one must have observed that, in rowing a boat, the ends of the oars appear bent or broken every time they are immersed in the water, and their appearance at such times is a representation of the course of the refracted rays. Again, fill a pretty deep jar with water, and you will observe the bottom of the jar considerably elevated, so that it appears much shallower than it 47 did before the water was poured in, in the proportion of nearly a third of its depth, which is owing to the same cause as that which makes the end of a stick immersed in water appear more elevated than it would do if there were no refraction. Another experiment may be just mentioned. Put a sixpence in a wine-glass, and pour upon it a little water. When viewed in a certain position, two sixpences will appear in the glass—one image of the sixpence from below, which comes directly to the eye, and another which appears considerably raised above the other, in consequence of the rays of light rising through the water, and being refracted. In this experiment the wine-glass should not be more than half filled with water.
The refraction of light explains the causes of many curious and interesting phenomena both in the heavens and on the earth. When we stand on the banks of a river, and look obliquely through the waters to its bottom, we are apt to think it is much shallower than it really is. If it be eight feet deep in reality, it will appear from the bank to be only six feet; if it be five feet and a half deep, it will appear only about four feet. This is owing to the effects of refraction, by which the bottom of the river is apparently raised by the refraction of the light passing through the water into air, so as to make the bottom appear higher than it really is, as in the experiment with the jar of water. This is a circumstance of some importance to be known and attended to in order to personal safety. For many school-boys and other young persons have lost their lives by attempting to ford a river, the bottom of which appeared to be within their reach, when they viewed it from its banks: and even adult travellers on horseback have sometimes fallen victims to this optical deception; 48 and this is not the only case in which a knowledge of the laws of nature may be useful in guarding us against dangers and fatal accidents.
It is likewise owing to this refractive power in water, that a skilful marksman who wishes to shoot fish under water, is obliged to take aim considerably below the fish as it appears, because it seems much nearer the top of the water than it really is. An acquaintance with this property of light is particularly useful to divers, for, in any of their movements or operations, should they aim directly at the object, they would arrive at a point considerably beyond it; whereas, by having some idea of the depth of the water, and the angle which a line drawn from the eye to the object makes with its surface, the point at the bottom of the water, between the eye and the object at which the aim is to be taken, may be easily determined. For the same reason, a person below water does not see objects distinctly. For, as the aqueous humour of the eye has the same refractive power as water, the rays of light from any object under water will undergo no refraction in passing through the cornea, and aqueous humour, and will therefore meet in a point far behind the retina. But if any person accustomed to go below water should use a pair of spectacles, consisting of two convex lenses, the radius of whose surface is three tenths of an inch—which is nearly the radius of the convexity of the cornea—he will see objects as distinctly below water as above it.
It is owing to refraction, that we cannot judge so accurately of magnitudes and distances in water as in air. A fish looks considerably larger in water than when taken out of it. An object plunged vertically into water always appears contracted, and the more so as its upper extremity 49 approaches nearer the surface of the water. Every thing remaining in the same situation, if we take the object gradually out of the water, and it be of a slender form, we shall see it become larger and larger, by a rapid developement, as it were, of all its parts. The distortion of objects, seen through a crooked pane of glass in a window, likewise arises from its unequal refraction of the rays that pass through it. It has been calculated that in looking through the common glass of a window, objects appear about the one thirtieth of an inch out of their real place, by means of the refraction.
Refraction likewise produces an effect upon the heavenly bodies, so that their apparent positions are generally different from their real. By the refractive power of the atmosphere, the sun is seen before he comes to the horizon in the morning, and after he sinks beneath it in the evening; and hence this luminary is never seen in the place in which it really is, except when it passes the zenith at noon, to places within the torrid zone. The sun is visible, when actually thirty-two minutes of a degree below the horizon, and when the opake rotundity of the earth is interposed between our eye and that orb, just on the same principle as, in the experiment with the shilling and basin of water, the shilling was seen when the edge of the basin interposed between it and the sight. The refractive power of the atmosphere has been found to be much greater, in certain cases, than what has been now stated. In the year 1595 a company of Dutch sailors having been wrecked on the shores of Nova Zembla, and having been obliged to remain in that desolate region during a night of more than three months—beheld the sun make his appearance in the horizon about sixteen days before the time in which he 50 should have risen according to calculation, and when his body was actually more than four degrees below the horizon; which circumstance has been attributed to the great refractive power of the atmosphere in those intensely cold regions. This refraction of the atmosphere, which renders the apparent rising and setting of the sun both earlier and later than the real, produces at least one important beneficial effect. It procures for us the benefit of a much longer day, at all seasons of the year, than we should enjoy, did not this property of the atmosphere produce this effect. It is owing to the same cause that the disks of the sun and moon appear elliptical or oval, when seen in the horizon, their horizontal diameters appearing longer than their vertical—which is caused by the greater refraction of the rays coming from the lower limb, which is immersed in the densest part of the atmosphere.
The illumination of the heavens which precedes the rising of the sun, and continues sometime after he is set—or, what is commonly called the morning and evening twilight—is likewise produced by the atmospherical refraction—which circumstance forms a very pleasing and beneficial arrangement in the system of nature. It not only prolongs to us the influence of the solar light, and adds nearly two hours to the length of our day, but prevents us from being transported all at once from the darkness of midnight to the splendour of noon-day, and from the effulgence of day to the gloom and horrors of the night—which would bewilder the traveller and navigator in their journeys by sea or land, and strike the living world with terror and amazement.
The following figure will illustrate the position now stated, and the manner in which the refraction 51 of the atmosphere produces these effects. Let A a C, fig. 4, represent one half of our globe, and the dark space between that curve and B r D, the atmosphere. A person standing on the earth’s surface at a would see the sun rise at b, when that luminary was in reality only at c—more than half a degree below the horizon. When the rays of the sun, after having proceeded in a straight line through empty space, strike the upper part of the atmosphere at the point d, they are bent out of their right-lined course, by the refraction of the atmosphere, into the direction d a, so that the body of the sun, though actually intercepted by the curve of the earth’s convexity consisting of a dense mass of land or water, is actually beheld by the spectator at a. The refractive power of the atmosphere gradually diminishes from the horizon to the zenith, and increases from the zenith to the horizon, in proportion to the density of its different strata, being densest at its lower extremity next the earth, and more rare towards its higher regions. If a person at a had the sun, e, in his 52 zenith, he would see him where he really is; for his rays coming perpendicularly through the atmosphere, would be equally attracted in all directions, and would therefore suffer no inflection. But, about two in the afternoon, he would see the sun at i, though, in reality, he was at k, thirty-three seconds lower than his apparent situation. At about four in the afternoon he would see him at m, when he is at n, one minute and thirty-eight seconds from his apparent situation. But at six o’clock, when we shall suppose he sets, he will be seen at o, though he is at that time at p, more than thirty-two minutes below the horizon. These phenomena arise from the different refractive powers of the atmosphere at different elevations, and from the obliquity with which the rays of light fall upon it; for we see every object along that line in which the rays from it are directed by the last medium through which they passed.
figure 4.
The same phenomena happen in relation to the moon, the planets, the comets, the stars, and every other celestial body, all of which appear more elevated, especially when near the horizon, than their true places. The variable and increasing refraction from the zenith to the horizon, is a source of considerable trouble and difficulty in making astronomical observations, and in nautical calculations. For, in order to determine the real altitudes of the heavenly bodies, the exact degree of refraction, at the observed elevation, must be taken into account. To the same cause we are to ascribe a phenomenon that has sometimes occurred—namely, that the moon has been seen rising totally eclipsed, while the sun was still visible in the opposite quarter of the horizon. At the middle of a total eclipse of the moon, the sun and moon are in opposition, or 180 degrees asunder; and, therefore, 53 were no atmosphere surrounding the earth, these luminaries, in such a position, could never be seen above the horizon at the same time. But, by the refraction of the atmosphere near the horizon, the bodies of the sun and moon are raised more than 32 minutes above their true places, which is equal, and sometimes more than equal to the apparent diameters of these bodies.
In consequence of the accidental condensation of certain strata of the atmosphere, some very singular effects have been produced in the apparent elevation of terrestrial objects to a position much beyond that in which they usually appear. The following instance is worthy of notice. It is taken from the Philosophical Transactions of London for 1798, and was communicated by W. Latham, Esq., F.R.S., who observed the phenomenon from Hastings, on the south coast of England:—‘On July 26, 1797, about five o’clock in the afternoon, as I was sitting in my dining-room in this place, which is situated upon the Parade, close to the sea-shore, nearly fronting the south, my attention was excited by a number of people running down to the sea-side. Upon inquiring the reason, I was informed, that the coast of France was plainly to be distinguished by the naked eye. I immediately went down to the shore, and was surprised to find that, even without the assistance of a telescope, I could very plainly see the cliffs on the opposite coast, which, at the nearest part, are between forty and fifty miles distant, and are not to be discerned from that low situation by the aid of the best glasses. They appeared to be only a few 54 miles off, and seemed to extend for some leagues along the coast. I pursued my walk along the shore eastward, close to the water’s edge, conversing with the sailors and fishermen upon the subject. They at first would not be persuaded of the reality of the appearance; but they soon became so thoroughly convinced by the cliffs gradually appearing more elevated, and approaching nearer, as it were, that they pointed out and named to me the different places they had been accustomed to visit, such as the Bay, the Old Head, or Man, the Windmill, &c. at Boulogne, St. Vallery, and other places on the coast of Picardy, which they afterwards confirmed, when they viewed them through their telescopes. Their observations were, that the places appeared as near as if they were sailing, at a small distance, into the harbours. The day on which this phenomenon was seen was extremely hot; it was high water at Hastings about two o’clock, P.M., and not a breath of wind was stirring the whole day.’ From the summit of an adjacent hill, a most beautiful scene is said to have presented itself. At one glance the spectators could see Dungeness, Dover Cliffs, and the French coast, all along from Calais to St. Vallery, and, as some affirmed, as far to the westward as Dieppe, which could not be much less than eighty or ninety miles. By the telescope, the French fishing-boats were plainly seen at anchor, and the different colours of the land on the heights, with the buildings, were perfectly discernible.
This singular phenomenon was doubtless occasioned by an extraordinary refraction produced either by an unusual expansion, or condensation of the lower strata of the atmosphere, arising from circumstances connected with the extreme heat of the season. The objects seem to have been apparently 55 raised far above their natural positions; for, from the beach at Hastings, a straight line drawn across towards the French coast, would have been intercepted by the curve of the waters. They seem also to have been magnified by the refraction, and brought apparently four or five times nearer the eye than in the ordinary state of the atmosphere.
The following are likewise instances of unusual refraction:—When Captain Colby was ranging over the coast of Caithness, with the telescope of his great Theodolite, on the 21st of June, 1819, at eight o’clock, P.M. from Corryhabbie Hill, near Mortlich, in Banffshire, he observed a brig over the land of Caithness, sailing to the westward in the Pentland Frith, between the Dunnet and Duncansby heads. Having satisfied himself as to the fact, he requested his assistants, Lieutenants Robe and Dawson, to look through the telescope, which they immediately did, and observed the brig likewise. It was very distinctly visible for several minutes, while the party continued to look at it, and to satisfy themselves as to its position. The brig could not have been less than from ninety to one hundred miles distant; and, as the station on Corryhabbie is not above 850 yards above the sea, the phenomenon is interesting. The thermometer was at 44°. The night and day preceding the sight of the brig had been continually rainy and misty, and it was not till 7 o’clock of the evening of the 21st that the clouds cleared off the hill.8
Captain Scoresby relates a singular phenomenon of this kind, which occurred while he was traversing the Polar seas. His ship had been separated by the ice from that of his father for a considerable 56 time, and he was looking out for her every day, with great anxiety. At length, one evening, to his utter astonishment, he saw her suspended in the air, in an inverted position, traced on the horizon in the clearest colours, and with the most distinct and perfect representation. He sailed in the direction in which he saw this visionary phenomenon, and actually found his father’s vessel by its indication. He was divided from him by immense masses of icebergs, and at such a distance, that it was quite impossible to have seen the ship in her actual situation, or to have seen her at all, if her spectrum had not been thus raised several degrees above the horizon into the sky by this extraordinary refraction. She was reckoned to be seventeen miles beyond the visible horizon, and thirty miles distant.
Mrs. Somerville states, that a friend of her’s, while standing on the plains of Hindostan, saw the whole upper chain of the Himalaya mountains start into view, from a sudden change in the density of the air, occasioned by a heavy shower, after a long course of dry and hot weather. In looking at distant objects through a telescope, over the top of a ridge of hills, about two miles distant, I have several times observed, that some of the more distant objects which are sometimes hid by the interposition of a ridge of hills, are, at other times, distinctly visible above them. I have sometimes observed, that objects near the middle of the field of view of a telescope, which was in a fixed position, have suddenly appeared to descend to the lower part, or ascend to the upper part of the field, while the telescope remained unaltered. I have likewise seen, with a powerful telescope, the Bell Rock Lighthouse, at the distance of about twenty miles, to appear as if contracted to less than two-thirds 57 of its usual apparent height, while every part of it was quite distinct and well-defined, and in the course of an hour or less, it appeared to shoot up to its usual apparent elevation—all which phenomena are evidently produced by the same cause to which we have been adverting.
Such are some of the striking effects produced by the refraction of light. It enables us to see objects in a direction where they are not; it raises, apparently, the bottoms of lakes and rivers: it magnifies objects when their light passes through dense mediums: it makes the sun appear above the horizon, when he is actually below it, and thus increases the length of our day: it produces the Aurora and the evening twilight, which forms, in many instances, the most delightful part of a summer day: it prevents us from being involved in total darkness, the moment after the sun has descended beneath the horizon: it modifies the appearances of the celestial bodies, and the directions in which they are beheld: it tinges the sun, moon, and stars, as well as the clouds, with a ruddy hue, when near the horizon: it elevates the appearance of terrestrial objects, and, in certain extraordinary cases, brings them nearer to our view, and enables us to behold them when beyond the line of our visible horizon. In combination with the power of reflection, it creates visionary landscapes, and a variety of grotesque and extraordinary appearances, which delight and astonish, and sometimes appal the beholders. In short,—as we shall afterwards see more particularly—the refraction of light through glasses of different figures, forms the principle on which telescopes and microscopes are constructed, by which both the remote and the minute wonders of creation have been disclosed to view. So that had there been no bodies 58 capable of refracting the rays of light, we should have remained for ever ignorant of many sublime and august objects in the remote regions of the universe, and of the admirable mechanism and the countless variety of minute objects which lie beyond the range of the unassisted eye in our lower creation, all of which are calculated to direct our views, and to enlarge our conceptions of the Almighty Creator.
In the operation of the law of refraction in these and numerous other instances, we have a specimen of the diversified and beneficent effects which the Almighty can produce by the agency of a single principle in nature. By the influence of the simple law of gravitation, the planets are retained in their orbits, the moon directed in her course around the earth, and the whole of the bodies connected with the sun preserved in one harmonious system. By the same law the mountains of our globe rest on a solid basis, the rivers flow through the plains toward the seas, the ocean is confined to its prescribed boundaries, and the inhabitants of the earth are retained to its surface and prevented from flying upwards through the voids of space. In like manner the law by which light is refracted produces a variety of beneficial effects essential to the present constitution of our world and the comfort of its inhabitants. When a ray of light enters obliquely into the atmosphere, instead of passing directly through, it bends a little downwards, so that the greater portion of the rays which thus enter the atmospheric mass, descend by inflection to the earth. We then enjoy the benefit of that light which would otherwise have been totally lost. We perceive the light of day an hour before the solar orb makes its appearance, and a portion of its light is still retained 59 when it has descended nearly eighteen degrees below our horizon. We thus enjoy, throughout the year, seven hundred and thirty hours of light which would have been lost, had it not been refracted down upon us from the upper regions of the atmosphere. To the inhabitants of the polar regions this effect is still more interesting and beneficial. Were it not for their twilight, they would be involved, for a much longer period than they now are, in perpetual darkness; but by the powerful refraction of light which takes place in the frigid zones, the day sooner makes its appearance towards spring, and their long winter nights are, in certain cases, shortened by a period of thirty days. Under the poles, where the darkness of night would continue six months without intermission, if there were no refraction, total darkness does not prevail during the one half of this period. When the sun sets, at the North pole about the 23rd of September, the inhabitants (if any) enjoy a perpetual aurora, till he has descended 18 degrees below the horizon. In his course through the ecliptic the sun is two months before he can reach this point, during which time there is a perpetual twilight. In two months more he arrives again at the same point, namely 18 degrees below the horizon, when a new twilight commences, which is continually increasing in brilliancy, for other two months, at the end of which the body of this luminary is seen rising in all its glory. So that, in this region, the light of day is enjoyed, in a greater or less degree, for ten months without interruption, by the effects of atmospheric refraction; and, during the two months when the influence of the solar light is entirely withdrawn, the moon is shining above the horizon for two half months without intermission; 60 and thus it happens, that no more than two separate fortnights are passed in absolute darkness; and this darkness is alleviated by the light of the stars and the frequent coruscations of the Aurora Borealis. Hence, it appears, that there are no portions of our globe that enjoy, throughout the year, so large a portion of the solar light, as these northern regions, which is chiefly owing to the refraction of the atmosphere.
The refraction of light by the atmosphere, combined with its power of reflecting it, is likewise the cause of that universal light and splendour which appears on all the objects around us. Were the earth disrobed of its atmosphere, and exposed naked to the solar beams—in this case, we might see the sun without having day, strictly so called. His rising would not be preceded by any twilight as it now is. The most intense darkness would cover us till the very moment of his rising; he would then suddenly break out from under the horizon with the same splendour he would exhibit at the highest part of his course, and would not change his brightness till the very moment of his setting, when in an instant all would be black as the darkest night. At noon day we should see the sun like an intensely brilliant globe shining in a sky as black as ebony, like a clear fire in the night seen in the midst of an extensive field, and his rays would show us the adjacent objects immediately around us; but the rays which fall on the objects remote from us would be for ever lost in the expanse of the heavens. Instead of the beautiful azure of the sky, and the colours which distinguish the face of nature by day, we should see nothing but an abyss of darkness, and the stars shining from a vault as dark as chaos. Thus there would be no day, such 61 as we now enjoy, without the atmosphere: since it is by the refraction and reflections connected with this aerial fluid that light is so modified and directed, as to produce all that beauty, splendour and harmony, which appear on the concave of the sky, and on the objects which diversify our terrestrial abode.
The effect of refraction, in respect to terrestrial objects, is likewise of a beneficial nature. The quantity of this refraction is estimated by Dr. Maskelyne at one-tenth of the distance of the object observed, expressed in degrees of a great circle. Hence, if the distance be 10,000 fathoms, its tenth part 1000 fathoms, is the sixtieth part of a degree, or one minute, which is the refraction in altitude. Le Gendre estimates it at one fourteenth; De Lambre at one eleventh; and others at a twelfth of the distance; but it must be supposed to vary at different times and places according to the varying state of the atmosphere. This refraction, as it makes objects appear to be raised higher than they really are, enlarges the extent of our landscapes, and enables us to perceive distant objects which would otherwise have been invisible. It is particularly useful to the navigator at sea. It is one important object of the mariner when traversing his course, to look out for capes and headlands, rocks and islands, so as to descry them as soon as they are within the reach of his eye. Now, by means of refraction, the tops of hills and the elevated parts of coasts, are apparently raised into the air, so that they may be discovered several leagues further off on the sea than they would be, did no such refractive power exist. This circumstance is therefore a considerable benefit to the science of navigation, in enabling the mariner to steer his course aright, and to give him the most 62 early warning of the track he ought to take, or of the dangers to which he may be exposed.
In short, the effects produced by the refraction and reflection of light on the scenery connected with our globe, teach us that these principles, in the hand of the Almighty, might be so modified and directed, as to produce the most picturesque, the most glorious and wonderful phenomena, such as mortal eyes have never yet seen, and of which human imagination can form no conception; and in other worlds, more resplendent and magnificent than ours, such scenes may be fully realized, in combination with the operation of physical principles and agents, with which we are at present unacquainted. From what we already know of the effects of the reflection and the refraction of light, it is not beyond the bounds of probability to suppose, that in certain regions of the universe, light may be reflected and refracted through different mediums, in such a manner, as to present to the view of their inhabitants the prominent scenes connected with distant systems and worlds, and to an extent, as shall infinitely surpass the effects produced by our most powerful telescopes. 63
It is to the refraction of light that we are indebted for the use of lenses or artificial glasses to aid the powers of vision. It lays the foundation of telescopes, microscopes, camera obscuras, phantasmagorias, and other optical instruments, by which so many beautiful, useful, and wonderful effects have been produced. In order therefore to illustrate the principles on which such instruments are constructed, it is necessary to explain the manner in which the rays of light are refracted and modified, when passing through spherical mediums of different forms. I do not intend however to enter into the minutiæ of this subject, nor into any abstract mathematical demonstrations, but shall simply offer a few explanations of general principles, and several experimental illustrations, which may enable the general reader to understand the construction of the optical instruments to be afterwards described.
A lens is a transparent substance of a different density from the surrounding medium, and terminating in two surfaces, either both spherical, or one 64 spherical and the other plain. It is usually made of glass, but may also be formed of any other transparent substance, as ice, crystal, diamond, pebbles, or by fluids of different densities and refractive powers, enclosed between concave glasses. Lenses are ground into various forms, according to the purpose they are intended to serve. They may be generally distinguished as being either convex or concave. A convex glass is thickest in the middle, and thinner towards the edges. A concave glass is thin in the middle, and thicker towards the extremities. Of these there are various forms, which are represented in fig. 5. A, is a plano-convex lens, which has one side plane, and the other spherical or convex. B, is a plano-concave, which is plane on the one side and concave on the other. C, is a double-convex, or one which is spherical on both sides. D, a double-concave, or concave on both sides. E, is called a meniscus, which is convex on one side and concave on the other. F, is a concavo-convex, the convex side of which is of a smaller sphere than the concave. In regard to the degree of convexity or concavity in lenses, it is evident that there may be almost an infinite variety. For every convex surface is to be considered as the segment of a circle, the diameter and radius of which may vary to almost any extent. Hence, lenses have been formed by opticians, varying from one-fiftieth of an inch in radius, to two hundred feet. When we speak of the length of the radius of a lens,—as for instance, when we say that a lens is two inches or forty inches radius, we mean, that the convex surface of the glass is the part of a circle the radius of which, or half the diameter is two inches or forty inches; or in other words, were the portion of the sphere on which it is ground formed into a globe of corresponding convexity, 65 it would be four inches or eighty inches in diameter.
figure 5.
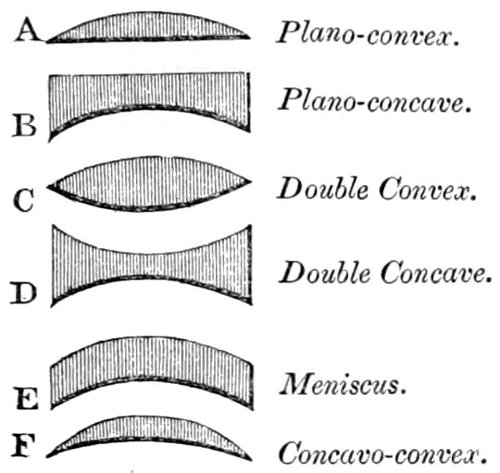
| figure 6. | 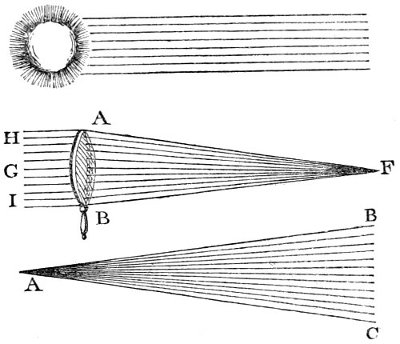 |
| figure 7. | |
| figure 8. |
The axis of a lens is a straight line drawn through the center of its spherical surface; and as the spherical sides of every lens are arches of circles the axis of the lens would pass through the centre of that circle of which its sides are segments. Rays are those emanations of light which proceed from a luminous body, or from a body that is illuminated. The Radiant is that body or object which emits the rays of light—whether it be a self-luminous body, or one that only reflects the rays of light. Rays may proceed from a Radiant in different directions. They may be either parallel, converging, or diverging. Parallel rays are those which proceed equally distant from each other through their whole course. Rays proceeding from the sun, the planets, the stars, and distant terrestrial objects are considered as parallel, as in fig. 6. Converging rays are such as, proceeding from a body, approach nearer and nearer in their progress, tending to a certain point where they all unite. Thus, the rays proceeding 66 from the object AB, (fig. 7.) to the point F, are said to converge towards that point. All convex glasses cause parallel rays, which fall upon them to converge in a greater or less degree; and they render converging rays still more convergent. If AB, fig. 7. represent a convex lens, and H G I parallel rays falling upon it, they will be refracted and converge towards the point F, which is called the focus, or burning point; because, when the sun’s rays are thus converged to a point by a large lens, they set on fire combustible substances. In this point the rays meet and intersect each other. Diverging rays are those which, proceeding from any point as A, fig. 8, continually recede from each other as they pass along in their course towards BC. All the rays which proceed from near objects as a window in a room, or an adjacent house or garden are more or less divergent. The following figures show the effects of 67 parallel, converging and diverging rays in passing through a double convex lens.
| figure 11. | figure 9. | figure 10. |
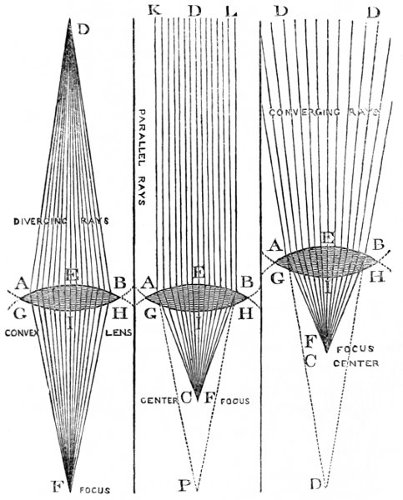 |
||
Fig. 9, shows the effects of parallel rays, KA, DE, LB, falling on a convex glass AB. The rays which fall near the extremities at A and B, are bent or refracted towards CF, the focus, and centre of convexity. It will be observed, that they are less refracted as they approach the center of the lens, and the central ray DEC, which is called the axis of the lens, and which passes through its center, suffers no refraction. Fig. 10, 68 exhibits the course of converging rays, when passing through a similar lens. In this case the rays converge to a focus nearer to the lens than the center; for a convex lens uniformly increases the convergence of converging rays. The converging rays here represented, may be conceived as having been refracted by another convex lens of a longer focus, and, passing on towards a point of convergence, were intercepted by the lens AB. The point D is the place where the rays would have converged to a focus, had they not been thus intercepted. Fig. 11, represents the course of diverging rays when falling on a double convex glass. In this case the rays D B, D A, &c., after passing through the lens, converge to a focus at a point considerably farther from the lens than its centre, as at F. Such rays must be considered as proceeding from near objects, and the fact may be illustrated by the following experiment. Take a common reading-glass, and hold it in the rays of the sun, opposite a sheet of writing-paper or a white wall, and observe at what distance from the glass the rays on the paper converge to a small distinct white spot. This distance gives the focal length of the lens by parallel rays. If now, we hold the glass within a few feet of a window, or a burning candle, and receive its image on the paper, the focal distance of the image from the glass will be found to be longer. If, in the former case, the focal distance was twelve inches,—in the latter case it will be thirteen, fifteen, or sixteen inches, according to the distance of the window or the candle from the glass.
If the lens A B, fig. 9, on which parallel rays are represented as falling, were a plano-convex, as represented at A, fig, 5, the rays would converge to a point P, at double the radius, or the 69 whole diameter of the sphere of which it is a segment. If the thickness of a plano-convex be considered, and if it be exposed on its convex side to parallel rays, as those of the sun, the focus will be at the distance of twice the radius, wanting two-thirds of the thickness of the lens. But if the same lens be exposed with its plane side to parallel rays, the focus will then be precisely at the distance of twice the radius from the glass.
The effects of concave lenses are directly opposite to those of convex. Parallel rays, striking one of those glasses, instead of converging towards a point, are made to diverge. Rays already divergent are rendered more so, and convergent rays are made less convergent. Hence objects seen through concave glasses appear considerably smaller and more distant than they really are. The following diagram, fig. 12, represents the course of parallel rays through a double concave lens, where the parallel rays T A, D E, I B, &c., when passing through the concave glass A B, diverge into the rays G L, E C, H P, &c., as if they proceeded from F, a point before the lens, which is the principal focus of the lens.
figure 12.
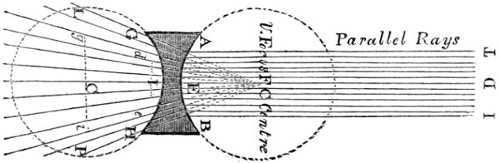
The principal focal distance E F, is the same as in convex lenses. Concave glasses are used to correct the imperfect vision of short-sighted persons. 70 As the form of the eye of such persons is too convex, the rays are made to converge before they reach the optic nerve; and therefore a concave glass, causing a little divergency, assists this defect of vision, by diminishing the effect produced by the too great convexity of the eye, and lengthening its focus. These glasses are seldom used, in modern times, in the construction of optical instruments, except as eye-glasses for small pocket perspectives, and opera glasses.
To find the focal distance of a concave glass. Take a piece of paste-board or card paper, and cut a round hole in it, not larger than the diameter of the lens; and, on another piece of paste-board, describe a circle whose diameter is just double the diameter of the hole. Then apply the piece with the hole in it to the lens, and hold them in the sun-beams, with the other piece at such a distance behind, that the light proceeding from the hole may spread or diverge so as precisely to fill the circle; then the distance of the circle from the lens is equal to its virtual focus, or to its radius, if it be a double concave, and to its diameter, if a plano-concave. Let d, e, (fig. 12,) represent the diameter of the hole, and g, i, the diameter of the circle, then the distance C, I, is the virtual focus of the lens.9
The meniscus represented at E, fig. 5, is like the crystal of a common watch, and as the convexity is the same as the concavity, it neither magnifies 71 nor diminishes. Sometimes, however, it is made in the form of a crescent, as at F, fig. 5, and is called a concavo-convex lens; and, when the convexity is greater than the concavity, or, when it is thickest in the middle, it acts nearly in the same way as a double or plano-convex lens of the same focal distance.
It is a remarkable circumstance, and which would naturally excite admiration, were it not so common and well known, that when the rays of light from any object are refracted through a convex lens, they paint a distinct and accurate picture of the object before it, in all its colours, shades, and proportions. Previous to experience, we could have had no conception that light, when passing through such substances, and converging to a point, could have produced so admirable an effect,—an effect on which the construction and utility of all our optical instruments depend. The following figure will illustrate this position. Let L, N, represent a double convex lens, A, C, 72 a, its axis, and OB, an object perpendicular to it. A ray passing from the extremity of the object at O, after being refracted by the lens at F, will pass on in the direction FI, and form an image of that part of the object at I. This ray will be the axis of all the rays which fall on the lens from the point O, and I will be the focus where they will all be collected. In like manner BCM, is the axis of that parcel of rays which proceed from the extremity of the object B, and their focus will be at M; and since all the points in the object between O, and B, must necessarily have their foci between I and M, a complete picture of the points from which they come will be depicted, and consequently an image of the whole object OB.
figure 13.
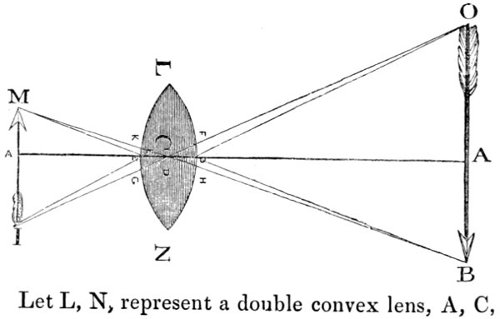
It is obvious, from the figure, that the image of the object is formed in the focus of the lens, in an inverted position. It must necessarily be in this position, as the rays cross at C, the centre of the lens; and as it is impossible that the rays from the upper part of the object O, can be carried by refraction to the upper end of the image at M. This is a universal principle in relation to convex lenses of every description, and requires to be attended to in the construction and use of all kinds of telescopes and microscopes. It is easily illustrated by experiment. Take a convex lens of eight, twelve, or fifteen inches focal distance, such as a reading glass, or the glass belonging to a pair of spectacles, and holding it, at its focal distance from a white wall, in a line with a burning candle, the flame of the candle will be seen depicted on the wall in an inverted position, or turned upside down. The same experiment may be performed with a window-sash, or any other bright object. But, the most beautiful exhibition of the images of objects formed by convex lenses, is made 73 by darkening a room, and placing a convex lens of a long focal distance in a hole cut out of the window-shutter; when a beautiful inverted landscape, or picture of all the objects before the window, will be painted on a white paper or screen placed in the focus of the glass. The image thus formed exhibits not only the proportions and colours, but also the motions of all the objects opposite the lens, forming as it were a living landscape. This property of lenses lays the foundation of the camera obscura, an instrument to be afterwards described.
The following principles in relation to images formed by convex lenses may be stated. 1. That the image subtends the same angle at the centre of the glass as the object itself does. Were an eye placed at C, the centre of the lens LN, fig. 13, it would see the object OB, and the image IM under the same optical angle, or, in other words, they would appear equally large. For, whenever right lines intersect each other, as OI and BM, the opposite angles are always equal, that is, the angle MCI is equal to the angle OCB. 2. The length of the image formed by a convex lens, is to the length of the object, as the distance of the image is to the distance of the object from the lens: that is, MI is to OB :: as Ca to CA. Suppose the distance of the object CA from the lens, to be forty-eight inches, the length of the object OB = sixteen inches, and the distance of the image from the lens, six inches, then the length of the image will be found by the following proportion, 48 : 16 :: 6 : 2, that is, the length of the image, in such a case, is two inches. 3. If the object be at an infinite distance, the image will be formed exactly in the focus. 4. If the object be at the same distance from the lens as its focus, the image 74 is removed to an infinite distance on the opposite side; in other words, the rays will proceed in a parallel direction. On this principle, lamps on the streets are sometimes directed to throw a bright light along a foot-path where it is wanted, when a large convex glass is placed at its focal distance from the burner; and on the same principle, light is thrown to a great distance from lighthouses, either by a very large convex lens of a short focal distance, or by a concave reflector. 5. If the object be at double the distance of the focus from the glass, the image will also be at double the distance of the focus from the glass. Thus, if a lens of six inches focal distance be held at twelve inches distance from a candle, the image of the candle will be formed at twelve inches from the glass on the other side. 6. If the object be a little further from the lens than its focal distance, an image will be formed, at a distance from the object, which will be greater or smaller in proportion to the distance. For example, if a lens five inches focus, be held at a little more than five inches from a candle, and a wall or screen at five feet six inches distant, receive the image, a large and inverted image of the candle will be depicted, which will be magnified in proportion as the distance of the wall from the candle exceeds the distance of the lens from the candle. Suppose the distance of the lens to be five and a half inches, then the distance of the wall where the image is formed, being twelve times greater, the image of the candle will be magnified twelve times. If MI (fig. 13.) be considered as the object, then OB will represent the magnified image on the wall. On this principle the image of the object is formed by the small object glass of a compound microscope. On the same principle the large pictures are formed by 75 the Magic Lantern and the Phantasmagoria; and in the same way small objects are represented in a magnified form, on a sheet or wall by the Solar microscope. 7. All convex lenses magnify the objects seen through them, in a greater or less degree. The shorter the focal distance of the lens, the greater is the magnifying power. A lens four inches focal distance, will magnify objects placed in the focus, two times in length and breadth; a lens two inches focus will magnify four times, a lens one inch focus eight times; a lens half an inch focus sixteen times, &c. supposing eight inches to be the least distance at which we see near objects distinctly. In viewing objects with small lenses, the object to be magnified should be placed exactly at the focal distance of the lens, and the eye at about the same distance on the other side of the lens. When we speak of magnifying power, as, for example, that a lens one inch focal distance magnifies objects eight times, it is to be understood of the lineal dimensions of the object. But as every object at which we look has breadth as well as length, the surface of the object is in reality magnified sixty-four times, or the square of its lineal dimensions; and for the same reason a lens half an inch focal distance magnifies the surfaces of objects 256 times.
Such are some of the leading principles which require to be recognised in the construction of refracting telescopes, microscopes, and other dioptric instruments whose performance chiefly depends on the refraction of light.—It is worthy of particular notice that all the phenomena of optical lenses now described, depend upon that 76 peculiar property which the Creator has impressed upon the rays of light, that, when they are refracted to a focus by a convex transparent substance, they depict an accurate image of the objects whence they proceed. This, however common, and however much overlooked by the bulk of mankind, is indeed a very wonderful property with which light has been endued. Previous to experience we could have had no conception that such an effect would be produced; and, in the first instance, we could not possibly have traced it to all its consequences. All the objects in creation might have been illuminated as they now are, for aught we know, without sending forth either direct or reflected rays with the property of forming exact representations of the objects whence they proceeded. But this we find to be a universal law in regard to light of every description, whether as emanating directly from the sun, or as reflected from the objects he illuminates, or as proceeding from bodies artificially enlightened. It is a law or a property of light not only in our own system, but throughout all the systems of the universe to which mortal eyes have yet penetrated. The rays from the most distant star which astronomers have descried, are endued with this property, otherwise they could never have been perceived by means of our optical instruments; for it is by the pictures or images formed in these instruments that such distant objects are brought to view. Without this property of light, therefore, we should have had no telescopes, and consequently we could not have surveyed, as we can now do, the hills and vales, the deep caverns, the extensive plains, the circular ranges of mountains, and many other novel scenes which diversify the surface of our moon. We should have known 77 nothing of the stupendous spots which appear on the surface of the sun—of the phases of Venus—of the satellites and belts of Jupiter—of the majestic rings of Saturn—of the existence of Uranus and his six moons,—or of the planets Vesta, Juno, Ceres, and Pallas, nor could the exact bulks of any of these bodies have been accurately determined. But, above all, we should have been entirely ignorant of the wonderful phenomena of double stars—which demonstrate that suns revolve around suns—of the thousands and millions of stars which crowd the profundities of the Milky Way and other regions of the heavens—of the thousands of Nebulæ or starry systems which are dispersed throughout the immensity of the firmament, and many other objects of sublimity and grandeur, which fill the contemplative mind with admiration and awe, and raise its faculties to higher conceptions than it could otherwise have formed of the omnipotence and grandeur of the Almighty Creator.
Without this property of the rays of light we should likewise have wanted the use of the microscope—an instrument which has disclosed a world invisible to common eyes, and has opened to our view the most astonishing exhibitions of Divine mechanism, and of the wisdom and intelligence of the Eternal Mind. We should have been ignorant of those tribes of living beings, invisible to the unassisted eye, which are found in water, vinegar, and many other fluids—many of which are twenty thousand times smaller than the least visible point, and yet display the same admirable skill and contrivance in their construction, as are manifested in the formation of the larger animals. We should never have beheld the purple tide of life, and even the globules of the blood rolling 78 with swiftness through veins and arteries smaller than the finest hair; or had the least conception that numberless species of animated beings, so minute that a million of them are less than a grain of sand, could have been rendered visible to human eyes, or that such a number of vessels, fluids, movements, diversified organs of sensation, and such a profusion of the richest ornaments and the gayest colours could have been concentrated in a single point. We should never have conceived that even the atmosphere is replenished with invisible animation, that the waters abound with countless myriads of sensitive existence, that the whole earth is full of life, and that there is scarcely a tree, plant, or flower, but affords food and shelter to a species of inhabitants peculiar to itself, which enjoy the pleasures of existence and share in the bounty of the Creator. We could have formed no conception of the beauties and the varieties of mechanism which are displayed in the scenery of that invisible world to which the microscope introduces us—beauties and varieties, in point of ornament and delicate contrivance, which even surpass what is beheld in the visible operations and aspect of nature around us. We find joints, muscles, a heart, stomach, entrails, veins, arteries, a variety of motions, a diversity of forms, and a multiplicity of parts and functions—in breathing atoms. We behold in a small fibre of a peacock’s feather, not more than one-eighth of an inch in length, a profusion of beauties no less admirable than is presented by the whole feather to the naked eye—a stem sending out multitudes of lateral branches, each of which emits numbers of little sprigs, which consist of a multitude of bright shining globular parts, adorned with a rich variety of colours. In the sections of plants, we see 79 thousands and ten thousands of tubes and pores, and other vessels for the conveyance of air and juices for the sustenance of the plant; in some instances, more than ten hundred thousand of these being compressed within the space of a quarter of an inch in diameter, and presenting to the eye the most beautiful configurations. There is not a weed, nor a moss, nor the most insignificant vegetable, which does not show a multiplicity of vessels disposed in the most curious manner for the circulation of sap for its nourishment, and which is not adorned with innumerable graces for its embellishment. All these and ten thousands of other wonders which lie beyond the limits of natural vision, in this new and unexplored region of the universe, would have been for ever concealed from our view, had not the Creator endued the rays of light with the power of depicting the images of objects, when refracted by convex transparent substances.
In this instance, as well as in many others, we behold a specimen of the admirable and diversified effects, which the Creator can produce from the agency of a single principle in nature. By means of optical instruments, we are now enabled to take a more minute and expansive view of the amazing operations of nature, both in heaven and on earth, than former generations could have surmised. These views tend to raise our conceptions of the attributes of that Almighty Being, who presides over all the arrangements of the material system, and to present them to our contemplation in a new, a more elevated, and expansive point of view. There is, therefore, a connection which may be traced between the apparently accidental principle of the rays of light forming images of objects, and the comprehensive views we are now enabled to 80 take of the character and perfections of the Divinity. Without the existence of the law or principle alluded to, we could not, in the present state, have formed precisely the same conceptions either of the Omnipotence, or of the wisdom and intelligence of the Almighty. Had no microscope ever been invented, the idea never could have entered into the mind of man, that worlds of living beings exist beyond the range of natural vision, that organized beings possessed of animation exist, whose whole bulk is less than the ten hundred thousandth part of the smallest grain of sand; that, descending from a visible point to thousands of degrees beyond it, an invisible world exists, peopled with tribes of every form and size, the extent of which, and how far it verges towards infinity downwards, mortals have never yet explored, and perhaps will never be able to comprehend. This circumstance alone presents before us the perfections of the divinity in a new aspect, and plainly intimates that it is the will and the intention of the Deity, that we should explore his works, and investigate the laws by which the material world is regulated, that we may acquire more expansive views of his character and operations. The inventions of man in relation to art and science, are not therefore to be considered as mere accidental occurrences, but as special arrangements in the divine government, for the purpose of carrying forward the human mind to more clear and ample views of the scenes of the universe, and of the attributes and the agency of Him “who is wonderful in counsel and excellent in working.” 81
The reflection of the rays of light is that property by which—after approaching the surfaces of bodies, they are thrown back, or repelled. It is in consequence of this property that all the objects around us, and all the diversified landscapes on our globe, are rendered visible. It is by light reflected from their surfaces that we perceive the planetary bodies and their satellites, the belts of Jupiter, the rings of Saturn, the various objects which diversify the surface of the Moon, and all the bodies in the universe which have no light of their own. When the rays of light fall upon rough and uneven surfaces, they are reflected very irregularly and scattered in all directions, in consequence of which thousands of eyes, at the same time, may perceive the same objects, in all their peculiar colours, aspects, and relations. But, when they fall upon certain smooth and polished surfaces, they are reflected with regularity, and according to certain laws. Such surfaces, when highly polished, are called Mirrors or Speculums; and it is to the reflection of light from such surfaces, and the 82 effects it produces, that I am now to direct the attention of the reader.
Mirrors or Specula, may be distinguished into three kinds, plane, concave, and convex, according as they are bounded by plane or spherical surfaces. These are made either of metal or of glass, and have their surfaces highly polished for the purpose of reflecting the greatest number of rays. Those made of glass are foliated or quicksilvered on one side; and the metallic specula are generally formed of a composition of different metallic substances, which, when accurately polished, is found to reflect the greatest quantity of light. I shall, in the first place, illustrate the phenomena of reflection produced by plane-mirrors.
When light impinges, or falls, upon a polished flat surface, rather more than the half of it is reflected, or thrown back in a direction similar to that of its approach; that is to say, if it fall perpendicularly on the polished surface, it will be perpendicularly reflected; but if it fall obliquely, it will be reflected with the same obliquity. Hence, the following fundamental law, regarding the reflection of light, has been deduced both from experiment and mathematical demonstration, namely, that the angle of reflection is, in all cases, exactly equal to the angle of incidence. This is a law which is universal in all cases of reflection, whether it be from plane or spherical surfaces, or whether these surfaces be concave or convex, and which requires to be recognized in the construction of all instruments which depend on the reflection of the rays of light. The following figure (fig. 14) will illustrate the position now stated.
Let AB represent a plane mirror, and CD a line or ray of light perpendicular to it. Let FD represent the incident ray from any object, then 83 DE will be the reflected ray, thrown back in the direction from D to E, and it will make with the perpendicular CD the same angle which the incident ray FD did with the same perpendicular, that is, the angle FDC will be equal to the angle EDC, in all cases of obliquity. The incident ray of light may be considered as rebounding from the mirror, like a tennis ball from a marble pavement, or the wall of a court.
figure 14.
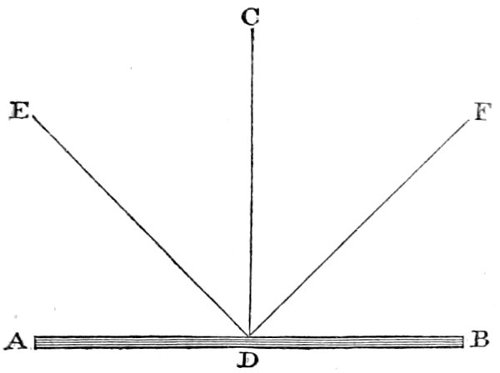
In viewing objects by reflection we see them in a different direction from that in which they really are, namely, along the line in which the rays come to us last. Thus, if AB (fig. 15) represent a plane mirror, the image of an object C appears to the eye at E behind the mirror, in the direction EG, and always in the intersection G of the perpendicular CG, and the reflected ray EG—and consequently at G as far behind the mirror, as the object C is before it. We therefore see the image in the line EG, the direction in which the reflected rays proceed. A plane mirror does not alter the figure or size of objects; but the whole image is 84 equal and similar to the whole object, and has a like situation with respect to one side of the plane, that the object has with respect to the other.
figure 15.

Mr. Walker illustrates the manner in which we see our faces in a mirror by the following figure (16). AB represents a mirror, and OC, a person looking into it. If we conceive a ray proceeding from the forehead CE, it will be sent to the eye at O, agreeably to the angle of incidence and reflection. But the mind puts CEO into one line, and the forehead is seen at H, as if the lines CEO had turned on a hinge at E.—It seems a wonderful faculty of the mind to put the two oblique lines CE and OE into one straight line OH, yet it is seen every time we look at a mirror. For the ray has really travelled from C to E, and from E to O, and it is that journey which determines the distance of the object; and hence we see ourselves as far beyond the mirror as we stand from it. Though a ray is here taken only from one part of the face, it may be easily 85 conceived that rays from every other part of the face must produce a similar effect.
figure 16.
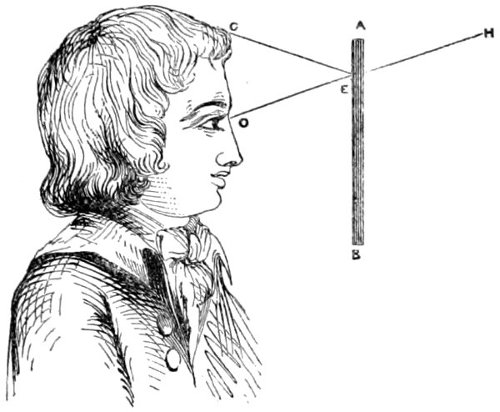
In every plain mirror, the image is always equal to the object, at what distance soever it may be placed; and as the mirror is only at half the distance of the image from the eye, it will completely receive an image of twice its own length. Hence a man six feet high may view himself completely in a looking glass of three feet in length, and half his own breadth; and this will be the case at whatever distance he may stand from the glass. Thus, the man AC (fig. 17) will see the whole of his own image in the glass AB, which is but one half as large as himself. The rays from the head pass to the mirror in the line Aa, perpendicular to the mirror, and are returned to the eye in the same line; consequently, having travelled twice the length Aa, the man must see his head at B. From his feet C rays will be sent to the bottom of the mirror at B; these will be reflected at an equal angle to the eye in the direction BA, as if they had proceeded in the direction DbA, so that the 86 man will see his foot at D, and consequently his whole figure at BD.
figure 17.
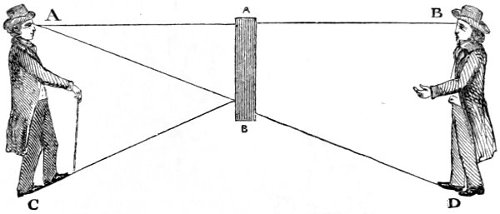
A person when looking into a mirror, will always see his own image as far beyond the mirror as he is before it, and as he moves to or from it, the image will, at the same time, move towards or from him on the other side; but apparently with a double velocity, because the two motions are equal and contrary. In like manner, if while the spectator is at rest, an object be in motion, its image behind the mirror will be seen to move at the same time. And if the spectator moves, the images of objects that are at rest will appear to approach, or recede from him, after the same manner as when he moves towards real objects; plane mirrors reflecting not only the object, but the distance also, and that exactly in its natural dimensions—The following principle is sufficient for explaining most of the phenomena seen in a plane mirror, namely;—That the image of an object seen in a plane mirror, is always in a perpendicular to the mirror joining the object and the image, and that the image is as much on one side the mirror, as the object is on the other. 87
Both convex and concave mirrors are formed of portions of a sphere. A convex speculum is ground and polished in a concave dish or tool which is a portion of a sphere, and a concave speculum is ground upon a convex tool. The inner surface of a sphere brings parallel rays to a focus at one fourth of its diameter, as represented in the following figure, where C is the centre of the sphere on which the concave speculum AB is formed, and F the focus where parallel rays from a distant object would be united, after reflection, that is, at one half the radius, or one fourth of the diameter from the surface of the speculum. Were a speculum of this kind presented to the sun, F 88 would be the point where the reflected rays would be converged to a focus, and set fire to combustible substances if the speculum be of a large diameter, and of a short focal distance. Were a candle placed in that focus, its light would be reflected parallel as represented in the figure. These are properties of concave specula which require to be particularly attended to in the construction of reflecting telescopes. It follows, from what has been now stated, that if we intend to form a speculum of a certain focal distance,—for example, two feet, it is necessary that it should be ground upon a tool whose radius is double that distance, or four feet.
figure 18.
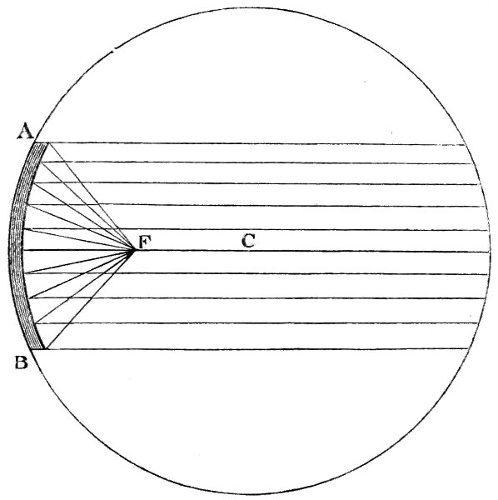
From a convex surface, parallel rays when reflected are made to diverge; convergent rays are reflected less convergent; and divergent rays are rendered more divergent. It is the nature of all convex mirrors and surfaces to scatter or disperse the rays of light, and in every instance to impede their convergence. The following figure shows the course of parallel rays as reflected from a convex mirror. AEB is the convex surface of the mirror; and KA, IE, LB, parallel rays falling upon it. These rays, when they strike the mirror, are made to diverge in the direction AG, BH, &c. and both the parallel and divergent rays are here represented as they appear in a dark chamber, when a convex mirror is presented to the solar rays. The dotted lines denote only the course or tendency of the reflected rays, towards the virtual focus F, were they not intercepted by the mirror. This virtual focus is just equal to half the radius CE. 89
figure 19.
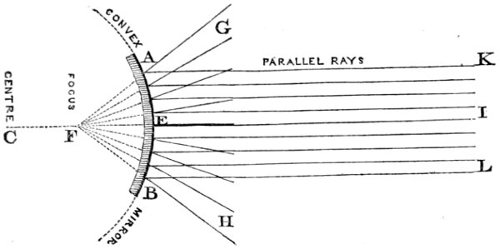
The following are some of the properties of convex mirrors: 1. The image appears always erect, and behind the reflecting surface. 2. The image is always smaller than the object, and the diminution is greater in proportion as the object is further from the mirror, but if the object touch the mirror, the image at the point of contact is of the same size as the object. 3. The image does not appear so far behind the reflecting surface as in a plain mirror. 4. The image of a straight object, placed either parallel or oblique to the mirror is seen curved in the mirror; because the different points of the object are not all at an equal distance from the surface of the mirror. 5. Concave mirrors have a real focus where an image is actually formed; but convex specula have only a virtual focus, and this focus is behind the mirror; no image of any object being formed before it.
The following are some of the purposes to which convex mirrors are applied. They are frequently employed by painters for reducing the proportions of the objects they wish to represent, as the images of objects diminish in proportion to the smallness of the radius of convexity, and to 90 the distances of objects from the surface of the mirror. They form a fashionable part of modern furniture, as they exhibit a large company assembled in a room, with all the furniture it contains, in a very small compass, so that a large hall with all its objects, and even an extensive landscape, being reduced in size, may be seen from one point of view. They are likewise used as the small specula of those reflecting telescopes which are fitted up on the Cassegrainian plan, and in the construction of Smith’s Reflecting Microscope. But on the whole, they are very little used in the construction of optical instruments.
Concave specula have properties very different from those which are convex; they are of more importance in the construction of reflecting telescopes and other optical instruments; and therefore require more minute description and illustration. Concave mirrors cause parallel rays to converge; they increase the convergence of rays that are already converging; they diminish the divergence of diverging rays; and, in some cases, render them parallel and even convergent; which effects are all in proportion to the concavity of the mirror. The following figures show the course of diverging and parallel rays as reflected from concave mirrors.
Fig. 20 represents the course of parallel rays, and AB, the concave mirror on which they fall. In this case, they are reflected so as to unite at F, which point is distant from its surface one fourth of the diameter of the sphere of the mirror. This point is called the focus of parallel rays, or the true focus of the mirror. And, since the sun 91 beams are parallel among themselves, if they are received on a concave mirror, they will all be reflected to that point, and there burn in proportion to the quantity of rays collected by the mirror. Fig. 21. shows the direction of diverging rays, or those which proceed from a near object. These rays proceeding from an object further from the mirror than the true focal point, as from D to A and to B, are reflected converging and meet at a point F, further from the mirror than the focal point of parallel rays. If the distance of the radiant, 92 or object D, be equal to the radius CE, then will the focal distance be likewise equal to the radius: That is, if an object be placed in the center of a concave speculum, the image will be reflected upon the object, or they will seem to meet and embrace each other in the centre. If the distance of the radiant be equal to half the radius, its image will be reflected to an infinite distance, for the rays will then be parallel. If, therefore, a luminous body be placed at half the radius from a concave speculum, it will enlighten places directly before it at great distances. Hence their use when placed behind a candle in a common lantern; hence their utility in throwing light upon objects in the Magic Lantern and Phantasmagoria, and hence the vast importance of very large mirrors of this description, as now used in most of our Light Houses, for throwing a brilliant light to great distances at sea to guide the mariner when directing his course under the cloud of night.
figure 20.
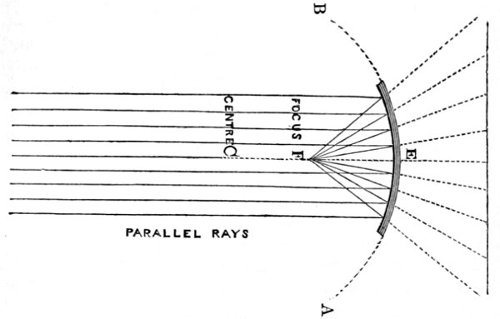
figure 21.
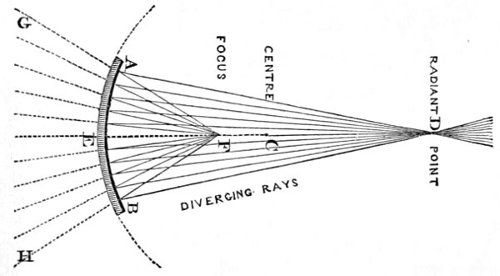
When converging rays fall upon a concave mirror, they are reflected more converging and unite at a point between the focus of parallel rays and the mirror; that is, nearer the mirror than one half the radius; and their precise degree of convergency will be greater than that wherein they converged before reflection.
If rays proceeding from a distant object fall upon a concave speculum, they will paint an image or representation of the object on its focus before the mirror. This image will be inverted, because the rays cross at the points where the image is formed. We have already seen that a convex glass forms an image of an object behind it; the rays of light 93 from objects pass through the glass, and the picture is formed on the side farthest from the object. But in concave mirrors the images of distant objects—and of all objects that are farther from its surface than its principal focus—are formed before the mirror, or on the same side as the object. In almost every other respect, however, the effect of a concave mirror is the same as that of a convex lens, in regard to the formation of images, and the course pursued by the rays of light, except that the effect is produced in the one case by refraction, and in the other by reflection. The following figure represents the manner in which images are formed by concave mirrors. GF represents the reflecting surface of the mirror; OAB, the object; and IAM, the image formed by the mirror. The rays proceeding from O, will be carried to the mirror, in the direction OG, and according to the law that the angle of incidence is equal to the angle of reflection, will be reflected to I, in the direction GI. In like manner the rays 94 from B, will be reflected from F to M, the rays from A, will be reflected to a, and so of all the intermediate rays, so that an inverted image of the object OB, will be formed at IM. If the rays proceeded from objects at a very great distance the image would be formed in the real focus of the mirror, or at one-fourth the diameter of the sphere from its surface; but near objects, which send forth diverging rays, will have their images formed a little farther from the surface of the mirror.
figure 22.
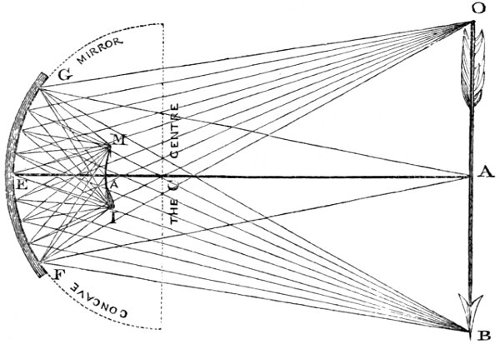
If we suppose a real object placed at IM, then OB will represent its magnified image, which will be larger than the object, in proportion to its distance from the mirror. This may be experimentally illustrated by a concave mirror and a candle. Suppose a concave mirror whose focal distance is five inches, and that a candle is placed before it, at a little beyond its focus, (as at IM)—suppose at five and a half inches,—and that a wall or white screen receives the image, at the distance of five feet six inches from the mirror, an image of the candle will be formed on the wall which will be twelve times longer and broader than the candle itself. In this way concave mirrors may be made to magnify the images of objects to an indefinite extent. This experiment is an exact counterpart of what is effected in similar circumstances by a convex lens, as described p. 74; the mirror performing the same thing by reflection, as the lens did by refraction.
From what has been stated in relation to concave mirrors it will be easily understood how they make such powerful burning-glasses. Suppose the focal distance of a concave mirror to be twelve inches, and its diameter or breadth twelve inches. When the sun’s rays fall on such a mirror, they 95 form an image of the sun at the focal point whose diameter is found to be about one-tenth of an inch. All the rays which fall upon the mirror are converged into this small point; and consequently their intensity is in proportion as the square of the surface of the mirror is to the square of the image. The squares of these diameters are as 14,400 to 1; and consequently the density of the sun’s rays, in the focus, is to their density on the surface of the mirror as 14,400 to 1. That is, the heat of the solar rays in the focus of such a mirror will be fourteen thousand four hundred times greater than before—a heat which is capable of producing very powerful effects in melting and setting fire to substances of almost every description.
Were we desirous of forming an image by a concave speculum which shall be exactly equal to the object, the object must be placed exactly in the centre; and, by an experiment of this kind, the centre of the concavity of a mirror may be found.
In the cases now stated, the images of objects are all formed in the front of the mirror, or between it and the object. But there is a case in which the image is formed behind the mirror. This happens when the object is placed between the mirror and the focus of parallel rays, and then the image is larger than the object. In fig. 23, GF is a concave mirror, whose focus of parallel rays is at E. If an object OB be placed a little within this focus, as at A, a large image IM will be seen behind the mirror, somewhat curved and erect, which will be seen by an eye looking directly into the front of the mirror. Here the image appears at a greater distance behind the mirror than the object is before it, and the object appears magnified in proportion to its distance from the focus 96 and the mirror. If the mirror be one inch focal distance, and the object be placed eight-tenths of an inch from its surface, the image would be five times as large as the object in length and breadth, and consequently twenty-five times larger in surface. In this way small objects may be magnified by reflection, as such objects are magnified by refraction, in the case of deep convex lenses. When such mirrors are large, for example six inches diameter, and eight or ten inches focal distance, they exhibit the human face as of an enormous bulk. This is illustrated by the following figure. Let C N, Fig. 24, represent the surface of a concave mirror, and A a human face looking into it, the face will appear magnified as represented by the image behind the mirror D Q. Suppose a ray A C proceeding from the forehead, and another M N from the chin; these rays are reflected to the person’s eye at O, which consequently sees the image in the lines of reflection O D, O Q, and in the angle 97 D O Q, and consequently magnified much beyond the natural size, and at a small distance behind the mirror.
figure 23.
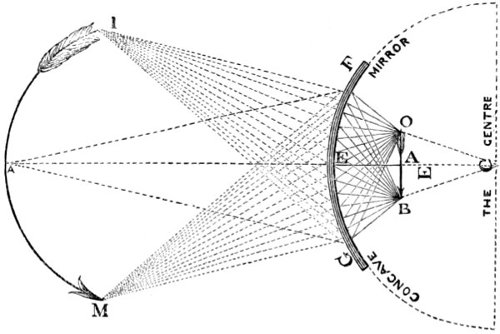
figure 24.
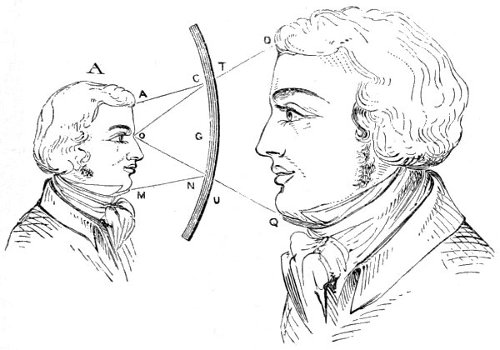
If we suppose the side T U to represent a convex mirror, and the figure D Q a head of an ordinary size, then the figure A will represent the diminished appearance which a person’s face exhibits, when viewed in such a mirror. It will not only appear reduced, but somewhat distorted; because from the form of the mirror, one part of the object is nearer to it than another, and consequently will be reflected under a different angle.
The effect we have now mentioned as produced by concave mirrors, will only take place when the eye is nearer the mirror than its principal focus. If the spectator retire beyond this focus—suppose to the distance of five or six feet, he will not see the image behind the mirror; but he will see his image in a diminished form, hanging upside down, and suspended in the air, in a line between his 98 eye and the mirror. In this case, his image is formed before the mirror as represented at IM fig. 22. In this situation, if you hold out your hand towards the mirror, the hand of the image will come out towards your hand, and, when at the centre of concavity, it will be of an equal size with it, and you may shake hands with this aerial image. If you move your hand farther, you will find the hand of the image pass by your hand, and come between it and your body. If you move your hand towards either side, the hand of the image will move towards the other side; the image moving always in a contrary direction to the object. All this while the by-standers, if any, see nothing of the image, because none of the reflected rays that form it can enter their eyes.—The following figure represents a phenomenon produced in the same manner. A B is a concave mirror of a large size; C represents a hand presented before the mirror, at a point farther distant than its focus. In this case, an inverted image of the hand is formed which is seen hanging in the air at M. The 99 rays C and D go diverging from the two opposite points of the object, and by the action of the mirror, they are again made to converge to points at O and S where they cross, form an image, and again proceed divergent to the eye.10
figure 25.
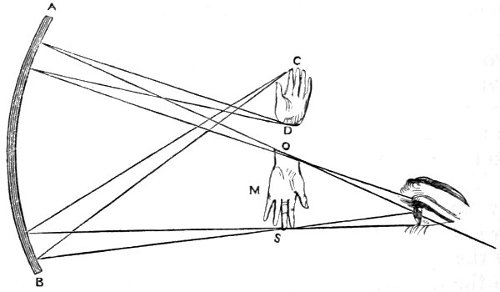
In consequence of the properties of concave mirrors, now described, many curious experiments and optical deceptions have been exhibited. The appearance of images in the air, suspended between the mirror and the object, have sometimes been displayed with such dexterity and an air of mystery, as to have struck with astonishment those who were ignorant of the cause. In this way birds, flying angels, spectres and other objects have been exhibited, and when the hand attempts to lay hold on them, it finds them to be nothing, and they seem to vanish into air. An apple or a beautiful flower is presented, and when a spectator attempts to touch it, it instantly vanishes, and a death’s head immediately appears, and seems to snap at his fingers. A person with a drawn sword appears before him, in an attitude as if about to run him through, or one terrific phantom starts up after another, or sometimes the resemblances of deceased persons are made to appear, as if, by the art of conjuration, they had been forced to return from the world of spirits. In all such exhibitions, a very large concave mirror is requisite, a brilliant light must be thrown upon the objects, and every 100 arrangement is made, by means of partitions, &c., to prevent either the light, the mirror, or the object from being seen by the spectators. The following representation (fig. 26.) shows one of the methods by which this is effected: A is a large concave mirror, either of metal or of glass, placed on the back part of a dark box, D is the performer, concealed from the spectators by the cross partition C; E is a strong light, which is likewise concealed by the partition I, which is thrown upon the actor D, or upon any thing he may hold in his hand. If he hold a book, as represented in the figure, the light reflected from it will pass between the partitions C and I to the mirror, and will be reflected from thence to Z, where the image of the book will appear so distinct and tangible, that a 101 spectator looking through the opening at X, will imagine that it is in his power to take hold of it. In like manner, the person situated at D, may exhibit his own head or body—a portrait, a painting, a spectre, a landscape, or any object or device which he can strongly illuminate.
figure 26.
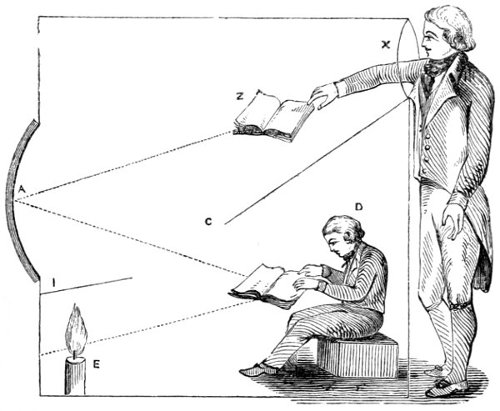
figure 27.
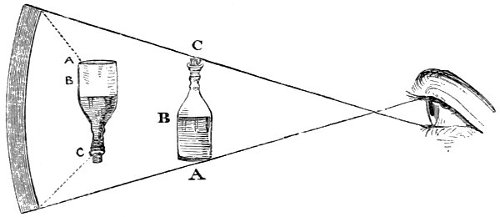
figure 28.
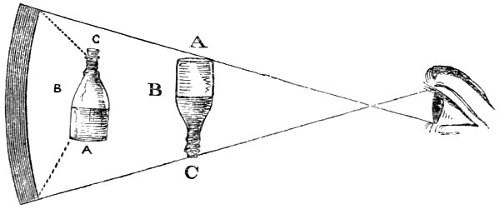
There is another experiment, made with a concave mirror, which has somewhat puzzled philosophers to account for the phenomena. Take a glass bottle AC, (fig. 27) and fill it with water to the point B; leave the upper part BC empty, and cork it in the common manner. Place this bottle opposite a concave mirror, and beyond its focus, that it may appear reversed, and, before the mirror place yourself still further distant from the bottle, and it will appear in the situation A B C. Now, it 102 is remarkable in this apparent bottle, that the water, which, according to the laws of catoptrics, should appear at A B, appears on the contrary at B C, and consequently, the part A B appears empty. If the bottle be inverted and placed before the mirror, its image will appear in its natural erect position, and the water which is in reality at BC (fig. 28) is seen at A B. If while the bottle is inverted, it be uncorked, and the water run gently out, it will appear, that, while the part BC is emptying, that of A B in the image is filling, and, what is remarkable, as soon as the bottle is empty, the illusion ceases, the image also appearing entirely empty.—The remarkable circumstances in this experiment are, first, not only to see the object where it is not, but also where its image is not; and secondly, that of two objects which are really in the same place, as the surface of the bottle and the water it contains, the one is seen at one place, and the other at another; and to see the bottle in the place of its image, and the water where neither it nor its image are.
The following experiments are stated by Mr. Ferguson in his “Lectures on select Subjects,” &c. 103“If a fire be made in a large room, and a smooth mahogany table be placed at a good distance near the wall, before a large concave mirror, so placed that the light of the fire may be reflected from the mirror to its focus upon the table; if a person stand by the table, he will see nothing upon it but a longish beam of light: but if he stand at a distance toward the fire, not directly between the fire and mirror, he will see an image of the fire upon the table, large and erect. And if another person who knows nothing of the matter beforehand should chance to come into the room, and should look from the fire toward the table, he would be startled at the appearance; for the table would seem to be on fire, and by being near the wainscot, to endanger the whole house. In this experiment there should be no light in the room but what proceeds from the fire; and the mirror ought to be at least fifteen inches in diameter. If the fire be darkened by a screen, and a large candle be placed at the back of the screen, a person standing by the candle will see the appearance of a very fine large star, or rather planet, upon the table, as bright as Venus or Jupiter. And if a small wax taper—whose flame is much less than the flame of the candle—be placed near the candle, a satellite to the planet will appear on the table; and if the taper be moved round the candle, the satellite will go round the planet.”
Many other illustrations of the effects of concave specula might have been given, but I shall conclude this department by briefly stating some of the general properties of speculums.
1. There is a great resemblance between the properties of convex lenses and concave mirrors. They both form an inverted focal image of any remote object, by the convergence of the pencil of rays. In those instruments whose performances are the effects of reflection, as reflecting telescopes, the concave mirror is substituted in the place of the convex lens. The whole effect of these instruments, in bringing to view remote objects in heaven and on earth, entirely depends on the property of a concave mirror in forming images of objects in its focus. 2. The image of an object placed beyond the centre, is less than the object; if the object be placed between the principal focus and the centre, the image is greater than the object. In both cases the image is inverted. 3. When the object is placed between the focus and the 104 mirror, the image situated behind the mirror is greater than the object, and it has the same direction: in proportion as the object approaches the focus, the image becomes larger and more distant. These and similar results are proved by placing a lighted candle at different distances from a concave mirror. 4. An eye cannot see an image in the air except it be placed in the diverging rays; but if the image be received on a piece of white paper, it may be seen in any position of the eye, as the rays are then reflected in every direction. 5. If a picture drawn according to the rules of perspective, be placed before a large concave speculum, a little nearer than its principal focus, the image of the picture will appear extremely natural, and very nearly like the real objects whence it was taken. Not only are the objects considerably magnified, so as to approach to their natural size, but they have also different apparent distances, as in nature, so that the view of the inside of a church appears very like what it is in reality, and representations of landscapes appear very nearly, as they do from the spot whence they were taken. In this respect a large concave speculum may be made to serve nearly the same purpose, as the Optical Diagonal Machine, in viewing perspective prints. 6. The concave speculum is that alone which is used as the great mirror which forms the first image in reflecting telescopes; and it is likewise the only kind of speculum used as the small mirror, in that construction of the instrument called the Gregorian Reflector.
As this is a circumstance connected with the construction of reflecting telescopes, it may not be 105 improper, in this place, to state some of the results of the accurate experiments of M. Bonguer on this subject. This philosopher ascertained that of the light reflected from mercury, or quicksilver, more than one-fourth is lost, though it is probable that no substances reflect more light than this. The rays were received at an angle of eleven and a half degrees of incidence, measured from the surface of the reflecting body, and not from the perpendicular. The reflection from water was found to be almost as great as that of quicksilver; so that in very small angles it reflects nearly three-fourths of the direct light. This is the reason why so strong a reflection appears on water, when one walks, in still weather, on the brink of a lake opposite to the sun. The direct light of the sun diminishes gradually as it approaches the horizon, while the reflected light at the same time grows stronger; so that there is a certain elevation of the sun in which the united force of the direct and reflected light will be the greatest possible, and this is when he is twelve or thirteen degrees in altitude. On the other hand, light reflected from water at great angles of incidence is extremely small. When the light was perpendicular, it reflected no more than the thirty-seventh part which mercury does in the same circumstances, and only the fifty-fifth part of what fell upon it in this case.
Using a smooth piece of glass, one line in thickness, he found that, when it was placed at an angle of fifteen degrees with the incident rays, it reflected 628 parts of 1000 which fell upon it; at the same time, a metallic mirror which he tried in the same circumstances, reflected only 561 of them. At a less angle of incidence much more light was reflected; so that at an angle of three degrees, the glass reflected 700 parts, and the metal something 106 less, as in the former case. The most striking observations made by this experimenter relate to the very great difference in the quantity of light reflected at different angles of incidence. He found that for 1000 incident rays, the reflected rays, at different angles of incidence, were as follows.
| Angles of incidence | Rays reflected by water | Rays reflected by glass |
|---|---|---|
| 5° | 501 | 549 |
| 10 | 333 | 412 |
| 15 | 211 | 299 |
| 30 | 65 | 112 |
| 50 | 22 | 34 |
| 70 | 18 | 25 |
| 90 | 18 | 25 |
With regard to such mirrors as the specula of reflecting telescopes, it will be found, in general, that they reflect little more than the one half of the rays which fall upon them.
The reflection and refraction of the rays of light frequently produce phenomena which astonish the beholders, and which have been regarded by the ignorant and the superstitious, as the effects of supernatural agency. Of these phenomena I shall state a few examples.
One of the most striking appearances of this kind is what has been termed the Fata Morgana, or optical appearances of figures in the sea and the air, as seen in the Faro of Messina. The following account is translated from a work of Minasi, who witnessed the phenomenon, and wrote a dissertation 107 on the subject. “When the rising sun shines from that point whence its incident ray forms an angle of about forty-five degrees to the sea of Riggio, and the bright surface of the water in the bay is not disturbed either by the wind or the current, the spectator being placed on an eminence of the city, with his back to the sun and his face to the sea;—on a sudden there appear on the water, as in a catoptric theatre, various multiplied objects, that is to say, numberless series of pilasters, arches, castles well delineated, regular columns, lofty towers, superb palaces, with balconies and windows, extended alleys of trees, delightful plains with herds and flocks, armies of men on foot and horseback, and many other strange images, in their natural colours and proper actions, passing rapidly in succession along the surface of the sea, during the whole of the short period of time, while the above mentioned causes remain.—But, if in addition to the circumstances now described, the atmosphere be highly impregnated with vapour and dense exhalations, not previously dispersed by the winds or the sun, it then happens that, in this vapour, as in a curtain extended along the channel, at the height of about thirty palms, and nearly down to the sea, the observer will behold the scene of the same objects, not only reflected from the surface of the sea, but likewise in the air, though not so distant or well defined, as the former objects from the sea.—Lastly, if the air be slightly hazy or opake, and at the same time dewy and adapted to form the iris, the then above-mentioned objects will appear only at the surface of the sea, as in the first case, but all vividly coloured or fringed with red, green, blue and other prismatic colours.”11 108
It is somewhat difficult to account for all the appearances here described; but, in all probability, they are produced by a calm sea, and one or more strata of superincumbent air differing in refractive and consequently in reflective power. At any rate reflection and refraction are some of the essential causes which operate in the production of the phenomena.
The Mirage, seen in the deserts of Africa, is a phenomenon, in all probability produced by a similar cause. M. Monge, who accompanied the French army to Egypt, relates that, when in the desert between Alexandria and Cairo, the mirage of the blue sky was inverted, and so mingled with the sand below, as to give to the desolate and arid wilderness an appearance of the most rich and beautiful country. They saw, in all directions, green islands, surrounded with extensive lakes of pure, transparent water. Nothing could be conceived more lovely and picturesque than the landscape. In the tranquil surface of the lakes, the trees and houses with which the islands were covered, were strongly reflected with vivid and varied hues, and the party hastened forward to enjoy the cool refreshments of shade and stream which these populous villages proffered to them. When they arrived, the lake on whose bosom they floated, the trees among whose foliage they were embowered, and the people who stood on the shore inviting their approach, had all vanished, and nothing remained but an uniform and irksome desert of sand and sky, with a few naked huts and ragged Arabs. Had they not been undeceived by their nearer approach, there was not a man in the French army who would not have sworn that the visionary trees and lakes had a real existence in the midst of the desert. 109
Dr. Clark observed precisely the same appearances at Rosetta. The city seemed surrounded with a beautiful sheet of water; and so certain was his Greek interpreter—who was unacquainted with the country—of this fact, that he was quite indignant at an Arab who attempted to explain to him that it was a mere optical delusion. At length they reached Rosetta in about two hours, without meeting with any water; and on looking back on the sand they had just crossed, it seemed to them as if they had waded through a vast blue lake.
figure 29.
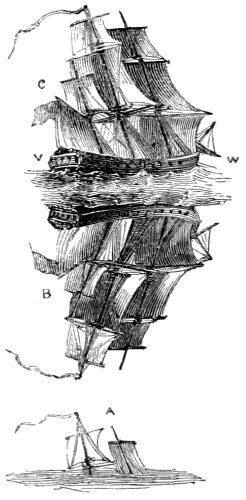
On the 1st of August, 1798, Dr. Vince observed at Ramsgate a ship which appeared as at A, (fig. 29.) the topmast being the only part of it that was seen above the horizon. An inverted image of it was seen at B, immediately above the real ship A, and an erect image at C, both of them 110 being complete and well defined. The sea was distinctly seen between them, as at V W. As the ship rose to the horizon the image C gradually disappeared, and while this was going on, the image B descended, but the mainmast of B did not meet the mainmast of A. The two images BC were perfectly visible when the whole ship was actually below the horizon. Dr. Vince then directed his telescope to another ship whose hull was just in the horizon, and he observed a complete inverted image of it, the mainmast of which just touched the mainmast of the ship itself. He saw at the same time several other ships whose images appeared in nearly a similar manner, in one of which the two images were visible when the whole ship was beneath the horizon. These phenomena must have been produced by the same causes which operated in the case formerly mentioned, in relation to Captain Scoresby, when he saw the figure of his father’s ship inverted in the distant horizon. Such cases are, perhaps not uncommon, especially in calm and sultry weather, but they are seldom observed, except when a person’s attention is accidentally directed to the phenomenon, and, unless he use a telescope, it will not be so distinctly perceived.
The following phenomenon, of a description nearly related to the above, has been supposed to be chiefly owing to reflection. On the 18th of November, 1804, Dr. Buchan, when watching the rising sun, about a mile to the east of Brighton, just as the solar disk emerged from the surface of the water, saw the face of the cliff on which he was standing, a windmill, his own figure and the figure of his friend, distinctly represented, precisely opposite, at some distance from the ocean. This appearance lasted about ten minutes, 111 till the sun had risen nearly his own diameter above the sea. The whole then seemed to be elevated into the air and successively disappeared. The surface of the sun was covered with a dense fog of many yards in height, which gradually receded from the rays of the sun as he ascended from the horizon.
The following appearance most probably arose chiefly from the refraction of the atmosphere. It was beheld at Ramsgate, by Dr. Vince of Cambridge and another gentleman. It is well known that the four turrets of Dover castle are seen at Ramsgate, over a hill which intervenes between a full prospect of the whole. On the 2nd of August, 1806, not only were the four turrets visible, but the castle itself appeared as though situated on that side of the hill nearest Ramsgate, and so striking was the appearance, that for a long time the Doctor thought it an illusion; but at last, by accurate observation, was convinced that it was an actual image of the castle. He, with another individual, observed it attentively for twenty minutes, but were prevented by rain from making further observations. Between the observers and the land from which the hill rises, there were about six miles of sea, and from thence to the top of the hill there was about the same distance, their own height above the surface of the water was about seventy feet.—The cause of this phenomenon was, undoubtedly, unequal refraction. The air being more dense near the ground and above the sea than at greater heights, reached the eye of the observer, not in straight but in curvilinear lines. If the rays from the castle had in their path struck an eye at a much greater distance than Ramsgate, the probability is, that the image of the castle would have been inverted in the air; but in the 112 present case,the rays from the turret and the base of the castle had not crossed each other.
To similar causes as those now alluded to are to be attributed such phenomena as the following:
The Spectre of the Brocken. This is a wonderful and, at first sight, a terrific phenomenon, which is sometimes seen from the summit of one of the Hartz mountains in Hanover, which is about 3,300 feet above the level of the sea, and overlooks all the country fifteen miles round. From this mountain the most gigantic and terrific spectres have been seen, which have terrified the credulous, and gratified the curious, in a very high degree. M. Hawé who witnessed this phenomenon, says, the sun rose about four o’clock, after he had ascended to the summit, in a serene sky, free of clouds; and about a quarter past five, when looking round to see if the sky continued clear, he suddenly beheld at a little distance, a human figure of a monstrous size turned towards him, and glaring at him. While gazing on this gigantic spectre, with a mixture of awe and apprehension, a sudden gust of wind nearly carried off his hat, and he clapt his hand to his head to detain it, when to his great delight, the colossal spectre did the same. He changed his body into a variety of attitudes,all which the spectre exactly imitated, and then suddenly vanished without any apparent cause, and, in a short time as suddenly appeared. Being joined by another spectator, after the first visions had disappeared, they kept steadily looking for the aërial spectres, when two gigantic monsters suddenly appeared. These spectres had been long considered as preternatural, by the inhabitants of the adjacent districts, and the whole country had been filled with awe and terror. Some of the lakes of Ireland are found to be susceptible 113 of producing illusions, particularly the lake of Killarney. This romantic sheet of water is bounded on one side, by a semicircle of rugged mountains, and on the other by a flat morass; and the vapours generated in the marsh, and broken by the mountains, continually represent the most fantastic objects. Frequently men riding along the shore are seen as if they were moving across the lake, which is supposed to have given rise to the legend of O’Donougho, a magician who is said to be visible on the lake every May morning.
There can be little doubt that most of those visionary appearances which have been frequently seen in the sky and in mountainous regions, are phantoms produced by the cause to which I am adverting, such as armies of footmen and horsemen, which some have asserted to have been seen in the air near the horizon. A well authenticated instance of this kind occurred in the Highlands of Scotland:—Mr. Wren of Wetton Hall, and D. Stricket his servant, in the year 1744, were sitting at the door of the house in a summer evening, when they were surprised to see opposite to them on the side of Sonterfell hill—a place so extremely steep, that scarce a horse could walk slowly along it—the figure of a man with a dog pursuing several horses, all running at a most rapid pace. Onwards they passed till at last they disappeared at the lower end of the Fell. In expectation of finding the man dashed to pieces by so tremendous a fall, they went early next morning and made a search, but no trace of man or horse, or the prints of their feet on the turf could be found. Sometime afterwards, about seven in the evening, on the same spot, they beheld a troop of horsemen advancing in close ranks and at a brisk 114 pace. The inmates of every cottage for a mile round beheld the wondrous scene, though they had formerly ridiculed the story told by Mr. Wren and his servant, and were struck with surprise and fear. The figures were seen for upwards of two hours, till the approach of darkness rendered them invisible. The various evolutions and changes through which the troops passed were distinctly visible, and were marked by all the observers. It is not improbable that these aërial troopers were produced by the same cause which made the castle of Dover to appear on the side of the hill next to Ramsgate, and it is supposed that they were the images of a body of rebels, on the other side of the hill, exercising themselves previous to the rebellion in 1745.12
I shall mention only another instance of this description which lately occurred in France, and for a time caused a powerful sensation among all ranks. On Sunday the 17th of December, 1826, the clergy in the parish of Migné, in the vicinity of Poictiers, were engaged in the exercises of the Jubilee which preceded the festival of Christmas, and a number of persons to the amount of 3000 souls assisted in the service. They had planted as part of the ceremony, a large cross, twenty-five feet high, and painted red, in the open air beside the church. While one of the preachers, about five in the evening, was addressing the multitude, he reminded them of the miraculous cross which appeared in the sky to Constantine and his army, and the effect it produced—when suddenly a similar celestial cross appeared in the heavens just 115 before the porch of the church about 200 feet above the horizon, and 140 feet in length, and its breadth from three to four feet, of a bright silver colour tinged with red. The curate and congregation fixed their wondering gaze upon this extraordinary phenomenon, and the effect produced on the minds of the assembly was strong and solemn: they spontaneously threw themselves on their knees; and many, who had been remiss in their religious duties, humbly confessed their sins, and made vows of penance and reformation. A commission was appointed to investigate the truth of this extraordinary appearance, and a memorial stating the above and other facts was subscribed by more than forty persons of rank and intelligence, so that no doubt was entertained as to the reality of the phenomenon. By many it was considered as strictly miraculous, as having happened at the time and in the circumstances mentioned. But it is evident, from what we have already stated, that it may be accounted for on physical principles. The large cross of wood painted red was doubtless the real object which produced the magnified image. The state of the atmosphere, according to the descriptions given in the memorial, must have been favourable for the production of such images. The spectrum of the wooden cross must have been cast on the concave surface of some atmospheric mirror, and so reflected back to the eyes of the spectators, from an opposite place—retaining exactly the same shape and proportions, but dilated in size; and what is worthy of attention, it was tinged with red, the very colour of the object of which it was the reflected image.
Such phenomena as we have now described, and the causes of them which science is able to unfold, 116 are worthy of consideration, in order to divest the mind of superstitious terrors, and enable it clearly to perceive the laws by which the Almighty directs the movements of the material system. When any appearance in nature, exactly the reverse of every thing we could have previously conceived—presents itself to view, and when we know of no material cause by which it could be produced, the mind must feel a certain degree of awe and terror, and will naturally resort to supernatural agency as acting either in opposition to the established laws of the universe, or beyond the range to which they are confined. Besides the fears and apprehensions to which such erroneous conceptions give rise, they tend to convey false and distorted impressions of the attributes of the Deity and of his moral government. Science, therefore, performs an invaluable service to man, by removing the cause of superstitious alarms, by investigating the laws and principles which operate in the physical system, and by assigning reasons for those occasional phenomena, which at first sight appeared beyond the range of the operation of natural causes.
The late ingenious Dr. Wollaston illustrated the causes of some of the phenomena we have described, in the following manner. He looked along the side of a red hot poker at a word or object ten or twelve feet distant; and at a distance less than three eights of an inch from the line of the poker, an inverted image was seen, and within and without that image, an erect image, in consequence of the change produced, by the heat of the poker, in the density of the air. He also suggested the following experiment as another illustration of the same principle, namely, viewing an object through a stratum of spirit of wine lying 117 above water, or a stratum of water laid above one of syrup. He poured into a square phial a small quantity of clear syrup, and above this he poured an equal quantity of water which gradually combined with the syrup, as seen at A. fig. 30. The word ‘Syrup,’ on a card held behind the bottle, appeared erect when seen through the pure spirit, but inverted, when seen through the mixture of water and syrup. He afterwards put nearly the same quantity of rectified spirits of wine above the water, as seen at B, and he saw the appearance as represented, namely, the true place of the word ‘Spirit,’ and the inverted and erect images below. These substances, by their gradual incorporation, produce refracting power, diminishing from the spirit of wine to the water, or from the syrup to the water; so that by looking through the mixed stratum, an inverted image of any object is seen behind the bottle. These experiments show that the mirage and several other atmospherical phenomena may be produced by variations in the refractive power of different strata of the atmosphere.
figure 30.
118
It is not unlikely that phenomena of a new and different description from any we have hitherto observed, may be produced from the same causes to which we have adverted. A certain optical writer remarks—‘If the variation of the refractive power of the air takes place in a horizontal line perpendicular to the line of vision, that is, from right to left, then we may have a lateral Mirage, that is, an image of a ship may be seen on the right or left hand of the real ship, or on both, if the variation of refractive power is the same on each side of the line of vision, and a fact of this kind was once observed on the Lake of Geneva. If there should happen at the same time, both a vertical and a lateral variation of refractive power in the air, and if the variation should be such as to expand or elongate the object in both directions, then the object would be magnified as if seen through a telescope, and might be seen and recognized at a distance at which it would not otherwise have been visible. If the refracting power, on the contrary, varied, so as to construct the object in both directions, the image of it would be diminished as if seen through a concave lens.’
Such, then, are some of the striking and interesting effects produced by the refraction and the reflection of the rays of light. As the formation of the images of objects by convex lenses, lays the foundation of the construction of refracting telescopes and microscopes, and of all the discoveries they have brought to light, so the property of concave specula, in forming similar 119 images, is that on which the construction of Reflecting telescopes entirely depends. To this circumstance Herschel was indebted for the powerful telescopes he was enabled to construct—which were all formed on the principle of reflection—and for all the discoveries they enabled him to make in the planetary system, and in the sidereal heavens. The same principles which operate in optical instruments, under the agency of man, we have reason to believe, frequently act on a more expansive scale in various parts of the system of nature. The magnificent Cross which astonished the preacher and the immense congregation assembled at Migné, was, in all probability, formed by a vast atmospherical speculum formed by the hand of nature, and representing its objects on a scale far superior to that of human art; and probably, to the same cause is to be attributed the singular phenomenon of the coast of France having been made to appear within two or three miles of the town of Hastings, as formerly described, (see p. 53.) Many other phenomena which we have never witnessed, and of which we can form no conception, may be produced by the same cause operating in an infinity of modes.
The facts we have stated above, and the variety of modes by which light may be refracted and reflected by different substances in nature, lead us to form some conceptions of the magnificent and diversified scenes which light may produce in other systems and worlds, under the arrangements of the all-wise and Beneficent Creator. Light, in all its modifications and varieties of colour and reflection, may be considered as the beauty and glory of the universe, and the source of unnumbered enjoyments to all its inhabitants. It is a symbol of the Divinity himself; for “God is 120 Light, and in Him is no darkness at all.” It is a representative of Him who is exhibited in the Sacred oracles, as “The Sun of Righteousness,” and “the Light of the world.” It is an emblem of the glories and felicities of that future world, where knowledge shall be perfected, and happiness complete; for its inhabitants are designated “the saints in light;” and it is declared in Sacred history, to have been the first born of created beings. In our lower world, its effects on the objects which surround us, and its influences upon all sensitive beings, are multifarious and highly admirable. While passing from infinitude to infinitude, it reveals the depth and immensity of the heavens, the glory of the sun, the beauty of the stars, the arrangements of the planets, the rainbow encompassing the sky with its glorious circle, the embroidery of flowers, the rich clothing of the meadows, the valleys standing thick with corn, “the cattle on a thousand hills,” the rivers rolling through the plains, and the wide expanse of the ocean. But in other worlds the scenes it creates may be far more resplendent and magnificent. This may depend upon the refractive and reflective powers with which the Creator has endowed the atmospheres of other planets, and the peculiar constitution of the various objects with which they are connected. It is evident, from what we already know of the reflection of light, that very slight modifications of certain physical principles, and very slight additions to the arrangements of our terrestrial system, might produce scenes of beauty, magnificence and splendour of which, at present, we can form no conception. And, it is not unlikely that by such diversities of arrangement, in other worlds, an infinite variety of natural scenery is produced throughout the universe. 121
In the arrangements connected with the planet Saturn, and the immense rings with which it is encompassed, and in the various positions which its satellites daily assume with regard to one another, to the planet itself, and to these rings—there is, in all probability, a combination of refractions, reflections, light, and shadows, which produce scenes wonderfully diversified, and surpassing in grandeur what we can now distinctly conceive. In the remote regions of the heavens, there are certain bodies composed of immense masses of luminous matter, not yet formed into any regular system, and which are known by the name of Nebulæ. What should hinder us from supposing that certain exterior portions of those masses form speculums of enormous size, as some parts of our atmosphere are sometimes found to do? Such specula may be conceived to be hundreds and even thousands of miles in diameter, and that they may form images of the most distant objects in the heavens, on a scale of immense magnitude and extent, and which may be reflected, in all their grandeur, to the eyes of intelligences at a vast distance. And, if the organs of vision of such beings, be far superior to ours in acuteness and penetrating power, they may thus be enabled to take a survey of an immense sphere of vision, and to descry magnificent objects at distances the most remote from the sphere they occupy. Whatever grounds there may be for such suppositions, it must be admitted, that all the knowledge we have hitherto acquired respecting the operation of light, and the splendid effects it is capable of producing, is small indeed, and limited to a narrow circle, compared with the immensity of its range, the infinite modifications it may undergo, and the wondrous scenes it may create in regions of creation 122 to which human eyes have never yet penetrated,—and which may present to view objects of brilliancy and magnificence such as, “Eye hath not yet seen, nor ear heard, nor hath it entered into the heart of man to conceive.” 123
We have hitherto considered light chiefly as a simple homogeneous substance, as if all its rays were white, and as if they were all refracted in the same manner by the different lenses on which they fall. Investigations however, into the nature of this wonderful fluid, have demonstrated that this is not the case, and that it is possessed of certain additional properties, of the utmost importance in the system of nature. Had every ray of light been a pure white, and incapable of being separated into any other colours, the scene of the universe would have exhibited a very different aspect from what we now behold. One uniform hue would have appeared over the whole face of nature, and one object could scarcely have been distinguished from another. The different shades of verdure which now diversify every landscape, the brilliant colouring of the flowery fields, and almost all the beauties and sublimities which adorn this lower creation would have been withdrawn. But it is now ascertained that every ray of white light is composed of an assemblage of colours, whence proceed that infinite variety of 124 shade and colour with which the whole of our terrestrial habitation is arrayed. Those colours are found not to be in the objects themselves, but in the rays of light which fall upon them, without which they would either be invisible, or wear an uniform aspect. In reference to this point, Goldsmith has well observed: ‘The blushing beauties of the rose, the modest blue of the violet, are not in the flowers themselves, but in the light that adorns them. Odour, softness, and beauty of figure are their own; but it is light alone that dresses them up in those robes which shame the monarch’s glory.’
Many strange opinions and hypotheses were entertained respecting colours, by the ancients, and even by many modern writers, prior to the time of Sir Isaac Newton. The Pythagoreans called colour the superficies of bodies; Plato said that it was a flame issuing from them. According to Zeno it is the first configuration of matter, and according to Aristotle, it is that which moves bodies actually transparent. Among the moderns, Des Cartes imagined that the difference of colour proceeds from the prevalence of the direct or rotatory motions of the particles of light. Grimaldi, Dechales, and others, thought the differences of colour depended upon the quick or slow vibrations of a certain elastic medium filling the whole universe. Rohault imagined that the different colours were made by the rays of light entering the eye at different angles with respect to the optic axis; and Dr. Hook conceived that colour is caused by the sensation of the oblique or uneven pulse of light; and this being capable of no more than two varieties, he concluded that there could be no more than two primary colours. Such were some of the crude opinions which prevailed 125 before the era of the illustrious Newton, by whose enlightened investigations the true theory of colours was at last discovered. In the year 1666 this philosopher began to investigate the subject; and finding the coloured image of the sun, formed by a glass prism, to be of an oblong and not of a circular form, as according to the laws of refraction it ought to be, he was surprised at the great disproportion between its length and breadth, the former being five times the length of the latter; and he began to conjecture that light is not homogeneal, but that it consists of rays some of which are much more refrangible than others. Prior to this period, philosophers supposed that all light, in passing out of one medium into another of different density was equally refracted in the same or like circumstances; but Newton discovered that this is not the fact; but that there are different species of light, and that each species is disposed both to suffer a different degree of refrangibility in passing out of one medium into another,—and to excite in us the idea of a different colour from the rest; and that bodies appear of that colour which arises from the peculiar rays they are disposed to reflect. It is now, therefore, universally acknowledged, that the light of the sun, which to us seems perfectly homogeneal and white, is composed of no fewer than seven different colours, namely Red, Orange, Yellow, Green, Blue, Indigo and Violet. A body which appears of a red colour has the property of reflecting the red rays more powerfully than any of the others; a body of a green colour reflects the green rays more copiously than rays of any other colour, and so of the orange, yellow, blue, purple and violet. A body which is of a black colour, instead of reflecting—absorbs all, or the greater part of the 126 rays that fall upon it; and, on the contrary, a body that appears white reflects the greater part of the rays indiscriminately without separating the one from the other.
Before proceeding to describe the experiments by which the above results were obtained, it may be proper to give some idea of the form and effects of the Prism by which such experiments are made. This instrument is triangular and straight, and generally about three or four inches long. It is commonly made of white glass, as free as possible from veins and bubbles, and other similar defects, and is solid throughout. Its lateral faces, or sides, should be perfectly plane and of a fine polish. The angle formed by the two faces, one receiving the ray of light that is refracted in the instrument, and the other affording it an issue on its returning into the air, is called the refracting angle of the prism, as ACB, (fig. 31.) The manner in which Newton performed his experiments, and established the discovery to which we have alluded, is as follows.
In the window-shutter EG, (fig. 31.) of a dark room, a hole F, was made, of about one third of an inch diameter, and behind it was placed a glass prism ACB, so that the beam of light, SF, proceeding directly from the sun was made to pass through the prism. Before the interposition of the prism, the beam proceeded in a straight line towards T, where it formed a round white spot; but being now bent out of its course by the prism, it formed an oblong image OP, upon the white pasteboard, or screen LM, containing the seven colours marked in the figure—the red being the least, and the violet the most refracted from the original direction of the solar beam, ST. This oblong image is called the prismatic spectrum. If the refracting angle of the prism ACB, be 64 127 degrees, and the distance of the pasteboard from the prism about 18 feet, the length of the image OP will be about 10 inches, and the breadth 2 inches. The sides of the spectrum are right lines distinctly bounded, and the ends are semicircular. From this circumstance it is evident that it is still the image of the sun, but elongated by the refractive power of the prism. It is evident from the figure, that since some part of the beam, RO, is refracted much further out of its natural course WT, than some other part of the beam, as WP, the rays towards RO have a much greater disposition to be refracted than those toward WP; and that this disposition arises from the naturally different qualities of those rays, is evident from this consideration, that the refracting angle or power of the prism is the same in regard to the superior part of the beam as to the inferior.
figure 31.
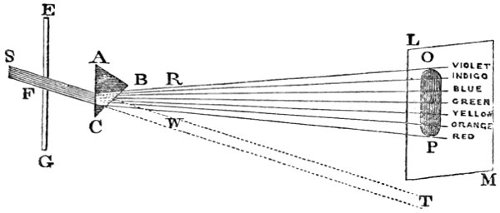
By making a hole in the screen LM opposite any one of the colours of the spectrum, so as to allow that colour alone to pass—and by letting the colour thus separated fall upon a second prism—Newton found that the light of each of the colours was alike refrangible, because the second prism could not separate them into an oblong image, or into any other colour. Hence he 128 called all the seven colours simple or homogeneous, in opposition to white light, which he called compound or heterogeneous. With the prism which this philosopher used he found the lengths of the colours and spaces of the spectrum to be as follows: Red, 45; Orange, 27; Yellow, 40; Green, 60; Blue, 60; Indigo, 48; Violet, 80: or 360 in all. But these spaces vary a little with prisms formed of different substances, and as they are not separated by distinct limits, it is difficult to obtain any thing like an accurate measure of their relative extents. Newton examined the ratio between the sines of incidence and refraction of these decompounded rays (see p. 30,) and found that each of the seven primary colour-making rays, had certain limits within which they were confined. Thus let the sine of incidence in glass be divided into 50 equal parts, the sine of refraction into air of the least refrangible, and the most refrangible rays will contain respectively 77 and 78 such parts. The sines of refraction of all the degrees of red will have the intermediate degrees of magnitude, from 77 to 77 one-eighth; Orange from 77 one-eighth to 77 one-fifth; Yellow from 77 one-fifth to 77 one-third; Green from 77 one-third to 77 one-half; Blue from 77 one-half to 77 two-thirds; Indigo from 77 two-thirds to 77 seven-ninths; and Violet from 77 seven-ninths to 78.
From what has been now stated, it is evident that, in proportion as any part of an optic glass bears a resemblance to the form of a prism, the component rays that pass through it must be necessarily separated, and will consequently paint or tinge the object with colours. The edges of every convex lens approach to this form, and it is on this account that the extremities of objects when viewed through them are found to be tinged 129 with the prismatic colours. In such a glass, therefore, those different coloured rays will have different foci, and will form their respective images at different distances from the lens. Thus, suppose LN (fig. 32.) to represent a double convex-lens, and OB an object at some distance from it. If the object OB was of a pure red colour, the rays proceeding from it would form a red image at Rr; if the object was of a violet colour, an image of that colour would be formed at Vv, nearer the lens; and if the object was white or any other combination of the colour-making rays, those rays would have their respective foci at different distances from the lens, and form a succession of images, in the order of the prismatic colours, between the space Rr and Vv.
figure 32.

figure 33.
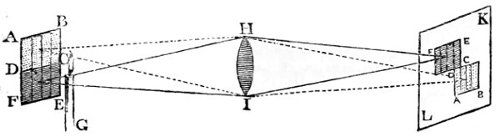
This may be illustrated by experiment in the following manner. Take a card or slip of white 130 pasteboard, as ABEF, (fig. 33.) and paint one half ABCD red, the other half CF, violet or indigo; and tying black threads across it, set it near the flame of a candle G, then take a lens HI, and holding a sheet of white paper behind it, move it backwards and forwards upon the edge of a graduated ruler, till you see the black threads most distinctly in the image, and you will find the focus of the violet FE, much nearer than that of the red AC, which plainly shows that bodies of different colours can never be depicted by convex-lenses, without some degree of confusion.
The quantity of dispersion of the coloured rays in convex lenses depends upon the focal length of the glass; the space which the coloured images occupy being about the twenty-eighth part. Thus if the lens be twenty-eight inches focal distance, the space between Rr and Vv (fig 32) will be about one inch; if it be twenty-eight feet focus, the same space will be about one foot, and so on in proportion. Now, when such a succession of images formed by the different coloured rays, is viewed through an eye-glass, it will seem to form but one image, and consequently very indistinct, and tinged with various colours, and as the red figure Rr is largest, or seen under the greatest angle—the extreme parts of this confused image will be red, and a succession of the prismatic colours will be formed within this red fringe, as is generally found in common refracting-telescopes, constructed with a single object-glass. It is owing to this circumstance that the common refracting telescope cannot be much improved without having recourse to lenses of a very long focal distance; and hence, about 150 years ago, such telescopes were constructed of 80, and 100, and 120 feet in length. But still the image was not formed so 131 distinctly as was desired, and the aperture of the object-glass was obliged to be limited. This is a defect which was long regarded as without a remedy; and even Newton himself despaired of discovering any means by which the defects of refracting telescopes might be removed and their improvement effected. This, however, was accomplished by Dollond to an extent far surpassing what could have been expected, of which a particular account will be given in the sequel.
It was originally remarked by Newton, and the fact has since been confirmed by the experiments of Sir W. Herschel, that the different-coloured rays have not the same illuminating power. The violet rays appear to have the least illuminating effect; the indigo more, and the effect increases in the order of the colours,—the green being very great; between the green and the yellow the greatest of all; the yellow the same as the green; but the red less than the yellow. Herschel also endeavoured to determine whether the power of the differently-coloured rays to heat bodies, varied with their power to illuminate them. He introduced a beam of light into a dark room, which was decomposed by a prism, and then exposed a very sensible thermometer to all the rays in succession, and observed the heights to which it rose in a given time. He found that their heating power increased from the violet to the red. The mercury in the thermometer rose higher when its bulb was placed in the Indigo than when it was placed in the violet, still higher in blue, and highest of all at red. Upon placing the bulb of the thermometer below the red, quite out of the spectrum, he was surprised to find that the mercury rose highest of all; and concluded that rays proceed from the sun, which have the power of HEATING, 132 but not of illuminating bodies. These rays have been called invisible solar rays. They were about half an inch from the commencement of the red rays; at a greater distance from this point the heat began to diminish, but was very perceptible even at the distance of 1½ inch. He determined that the heating power of the red to that of the green rays, was 2¾ to 1, and 3½ to 1, in red to violet. He afterwards made experiments to collect those invisible calorific rays, and caused them to act independently of the light, from which he concluded that they are sufficient to account for all the effects produced by the solar rays in exciting heat; that they are capable of passing through glass, and of being refracted and reflected, after they have been finally detached from the solar beam.
M. Ritter of Jena, Wollaston, Beckman and others, have found that the rays of the spectrum are possessed of certain chemical properties—that beyond the least brilliant extremity, namely, a little beyond the violet ray, there are invisible rays which act chemically, while they have neither the power of heating nor illuminating bodies. Muriate of silver exposed to the action of the red rays becomes blackish; a greater effect is produced by the yellow: a still greater by the violet, and the greatest of all by the invisible rays beyond the violet. When phosphorus is exposed to the action of the invisible rays beyond the red, it emits white fumes; but the invisible rays beyond the violet extinguish them. The influence of these rays is daily seen in the change produced upon vegetable colours, which fade, when frequently exposed to the direct influence of the sum. What object they are destined to accomplish in the general economy of nature, is not yet distinctly known; 133 we cannot however doubt that they are essentially requisite to various processes going forward in the material system. And we know that, not only the comfort of all the tribes of the living world, but the very existence of the animal and vegetable creation depends upon the unremitting agency of the Calorific rays.
It has likewise been lately discovered that certain rays of the spectrum, particularly the violet, possesses the property of communicating the magnetic power. Dr. Morichini, of Rome, appears to have been the first who found that the violet rays of the spectrum had this property. The result of his experiments, however, was involved in doubt, till it was established by a series of experiments instituted by Mrs. Somerville, whose name is so well known in the scientific world. This lady having covered half of a sewing-needle, about an inch long, with paper, she exposed the other half for two hours, to the violet rays. The needle had then acquired North polarity. The indigo rays produced nearly the same effect; and the blue and green rays produced it in a still less degree. In the yellow, orange, red and invisible rays, no magnetic influence was exhibited, even though the experiment was continued for three successive days. The same effects were produced by enclosing the needle in blue or green glass, or wrapping it in blue and green ribbands one half of the needle being always covered with paper.
One of the most curious discoveries of modern times, in reference to the solar spectrum, is that of Fraunhofer of Munich—one of the most distinguished artists and opticians on the Continent.13 134 He discovered that the spectrum is covered with dark and coloured lines, parallel to one another, and perpendicular to the length of the spectrum; and he counted no less than 590 of these lines. In order to observe these lines, it is necessary to use prisms of the most perfect construction, of very pure glass, free of veins—to exclude all extraneous light, and even to stop those rays which form the coloured spaces, which we are not examining. It is necessary also to use a magnifying instrument, and the light must enter and emerge from the prism at equal angles. One of the important practical results of this discovery is, that those lines are fixed points in the spectrum, or rather, that they have always the same position in the coloured spaces in which they are found. Fraunhofer likewise discovered in the spectrum produced by the light of Venus, the same streaks, as in the solar spectrum; in the spectrum of the light of Sirius, he perceived three large streaks which, according to appearance, had no resemblance to those of the light of the sun; one of 135 them was in the green, two in the blue. The stars appear to differ from one another in their streaks. The electric light differs very much from the light of the sun and that of a lamp, in regard to the streaks of the spectrum—‘This experiment may also be made, though in an imperfect manner, by viewing a narrow slit between two nearly closed window-shutters, through a very excellent glass prism held close to the eye, with the refracting angle parallel to the line of light. When the spectrum is formed by the sun’s rays, either direct or indirect, as from the sky, clouds, rainbow, moon, or planets, the black bands are always found to be in the same parts of the spectrum, and under all circumstances to maintain the same relative position, breadth and intensities.’
From what has been stated in reference to the solar spectrum it will evidently appear, that white light is nothing else than a compound of all the prismatic colours; and this may be still farther illustrated by shewing, that the seven primary colours, when again put together, recompose white light. This may be rudely proved for the purpose of illustration, by mixing together seven different powders, having the colours and proportion of the spectrum; but the best mode, on the whole, is the following. Let two circles be drawn on a smooth round board, covered with white paper, as in fig. 34: Let the outermost be divided into 360 equal parts; then draw seven right lines as A,B,C, &c., from the center to the outermost circle, making the lines A and B include 80 degrees of that circle. The lines B and C, 40 degrees; C and D, 60; D and E, 60; E and F, 48; F and G, 27; G and A, 45. Then between these two circles paint the space AG red, inclining 136 to orange near G; GF orange, inclining to yellow near F; FE yellow, inclining to green near E; ED green, inclining to blue near D; DC blue, inclining to indigo near C; CB indigo, inclining to violet near B; and BA violet, inclining to a soft red near A. This done, paint all that part of the board black which lies within the inner circle; and putting an axis through the centre of the board, let it be turned swiftly round that axis, so that the rays proceeding from the above colours, may be all blended and mixed together in coming to the eye. Then the whole coloured part will appear like a white ring a little grayish—not perfectly white, because no art can prepare or lay on perfect colours, in all their delicate shades, as found in the real spectrum.
figure 34.
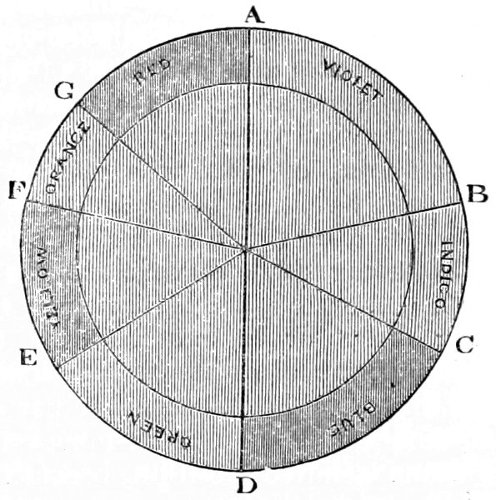
That all the colours of light, when blended together in their proper proportions, produce a pure white is rendered certain by the following experiment. Take a large convex glass, and place it 137 in the room of the paper or screen on which the solar spectrum was depicted (LM fig. 31), the glass will unite all the rays which come from the prism, if a paper is placed to receive them, and you will see a circular spot of a pure lively white. The rays will cross each other in the focus of the glass, and, if the paper be removed a little further from that point, you will see the prismatic colours again displayed, but in an inverted order, owing to the crossing of the rays.
From what has been stated above we may learn the true cause of those diversified hues exhibited by natural and artificial objects, and the variegated colouring which appears on the face of nature. It is owing to the surfaces of bodies being disposed to reflect one colour rather than another. When this disposition is such that the body reflects every kind of ray, in the mixed state in which it receives them, that body appears white to us—which, properly speaking, is no colour, but rather the assemblage of all colours. If the body has a fitness to reflect one sort of rays more abundantly than others, by absorbing all the others, it will appear of the colour belonging to that species of rays. Thus, the grass is green, because it absorbs all the rays except the green. It is these green rays only which the grass, the trees, the shrubs, and all the other verdant parts of the landscape reflect to our sight, and which make them appear green. In the same manner the different flowers reflect their respective colours; the rose, the red rays; the violet, the blue; the jonquil, the yellow; the marigold, the 138 orange, and every object, whether natural or artificial, appears of that colour which its peculiar texture is fitted to reflect. A great number of bodies are fitted to reflect at once several kinds of rays, and of consequence they appear under mixed colours. It may even happen, that of two bodies which should be green, for example, one may reflect the pure green of light, and the other the mixture of yellow and blue. This quality, which varies to infinity, occasions the different kinds of rays to unite in every possible manner, and every possible proportion; and hence the inexhaustible variety of shades and hues which nature has diffused over the landscape of the world. When a body absorbs nearly all the light which reaches it, that body appears black. It transmits to the eye so few reflected rays that it is scarcely perceptible in itself, and its presence and form make no impression upon us, unless as it interrupts the brightness of the surrounding space. Black is, therefore, the absence of all the coloured rays.
It is evident, then, that all the various assemblages of colours which we see in the objects around us, are not in the bodies themselves, but in the light which falls upon them. There is no colour inherent in the grass, the trees, the fruits, and the flowers, nor even in the most splendid and variegated dress that adorns a lady. All such objects are as destitute of colour, in themselves, as bodies which are placed in the centre of the earth, or as the chaotic materials out of which our globe was formed, before light was created. For where there is no light, there is no colour. Every object is black, or without colour, in the dark, and it only appears coloured as soon as light renders it visible. This is further evident from the following experiment. If we place a coloured 139 body in one of the colours of the spectrum which is formed by the prism, it appears of the colour of the rays in which it is placed. Take, for example, a red rose, and expose it first to the red rays, and it will appear of a more brilliant ruddy hue. Hold it in the blue rays, and it appears no longer red, but of a dingy blue colour, and in like manner its colour will appear different, when placed in all the other differently coloured rays. This is the reason why the colours of objects are essentially altered by the nature of the light in which they are seen. The colours of ribbons and various pieces of silk or woollen stuff are not the same when viewed by candle-light as in the day time. In the light of a candle or a lamp, blue often appears green, and yellow objects assume a whitish aspect. The reason is that the light of a candle is not so pure a white as that of the sun, but has a yellowish tinge, and therefore, when refracted by the prism, the yellowish rays are found to predominate, and the superabundance of yellow rays gives to blue objects a greenish hue.
The doctrine we are now illustrating is one which a great many persons, especially among the fair sex, find it difficult to admit. They cannot conceive it possible that there is no colour really inherent in their splendid attire, and no tints of beauty in their countenances. ‘What,’ said a certain lady, ‘are there no colours in my shawl, and in the ribbons that adorn my head-dress—and, are we all as black as negroes in the dark; I should almost shudder to think of it.’ Such persons, however, need be in no alarm at the idea; but may console themselves with the reflection, that, when they are stripped of all their coloured ornaments in the dark, they are certain that they 140 will never be seen by any one in that state; and therefore, there is no reason to regret the temporary loss of those beauties which light creates—when they themselves and all surrounding objects are invisible. But, to give a still more palpable proof of this position, the following popular experiments may be stated.
Take a pint of common spirit, and pour it into a soup dish, and then set it on fire; as it begins to blaze, throw a handful of salt into the burning spirit, and keep stirring it with a spoon. Several handfuls may thus be successively thrown in, and then the spectators, standing around the flame, will see each other frightfully changed, their colours being altered into a ghastly blackness, in consequence of the nature of the light which falls upon them—which produces colours very different from those of the solar light. The following experiment, as described by Sir D. Brewster, illustrates the same principle. ‘Having obtained the means of illuminating any apartment with yellow light, let the exhibition be made in a room with furniture of various bright colours, and with oil or water coloured paintings on the wall. The party which is to witness the experiment should be dressed in a diversity of the gayest colours; and the brightest coloured flowers, and highly coloured drawings should be placed on the tables. The room being at first lighted with ordinary lights, the bright and gay colours of every thing that it contains will be finely displayed. If the white lights are now suddenly extinguished, and the yellow lamps lighted, the most appalling metamorphosis will be exhibited. The astonished individuals will no longer be able to recognise each other. All the furniture of the room, and all the objects it contains, will exhibit only one colour. The flowers 141 will lose their hues; the paintings and drawings will appear as if they were executed in China ink, and the gayest dresses, the brightest scarlets, the purest lilacs, the richest blues and the most vivid greens, will all be converted into one monotonous yellow. The complexions of the parties, too, will suffer a corresponding change. One pallid deathlike yellow, will envelope the young and the old, and the sallow face will alone escape from the metamorphosis. Each individual derives merriment from the cadaverous appearance of his neighbour, without being sensible that he is one of the ghastly assemblage.’
From such experiments as these we might conclude, that were the solar rays of a very different description from what they are now found to be, the colours which embellish the face of nature, and the whole scene of our sublunary creation would assume a new aspect, and appear very different from what we now behold around us in every landscape. We find that the stars display great diversity of colour; which is doubtless owing to the different kinds of light which are emitted from those bodies; and hence we may conclude, that the colouring thrown upon the various objects of the universe is different in every different system, and that thus, along with other arrangements, an infinite variety of colouring and of scenery is distributed throughout the immensity of creation.
The atmosphere, in consequence of its different refractive and reflective powers, is the source of a variety of colours which frequently embellish and 142 diversify the aspect of our sky. The air reflects the blue rays most plentifully, and must therefore transmit the red, orange, and yellow, more copiously than the other rays. When the sun and other heavenly bodies are at a high elevation, their light is transmitted without any perceptible change, but when they are near the horizon, their light must pass through a long and dense track of air, and must therefore be considerably modified before it reach the eye of the observer. The momentum of the red rays being greater than that of the violet, will force their way through the resisting medium, while the violet rays will be either reflected or absorbed. If the light of the setting sun, by thus passing through a long track of air, be divested of the green, blue, indigo, and violet rays, the remaining rays which are transmitted through the atmosphere, will illuminate the western clouds, first with an orange colour; and then, as the sun gradually sinks into the horizon, the track through which the rays must pass becoming longer, the yellow and orange are reflected, and the clouds grow more deeply red, till at length the disappearance of the sun leaves them of a leaden hue by the reflection of the blue light through the air. Similar changes of colour are sometimes seen on the eastern and western fronts of white buildings. St. Paul’s Church, in London, is frequently seen at sun-set, tinged with a very considerable degree of redness; and the same cause occasions the moon to assume a ruddy colour, by the light transmitted through the atmosphere. From such atmospherical refractions and reflections are produced those rich and beautiful hues with which our sky is gilded by the setting sun, and the glowing red which tinges the morning and evening clouds, till their ruddy glare is tempered 143 by the purple of twilight, and the reflected azure of the sky.
When a direct spectrum is thrown on colours darker than itself, it mixes with them: as the yellow spectrum of the setting sun, thrown on the green grass, becomes a greener yellow. But when a direct spectrum is thrown on colours brighter than itself, it becomes instantly changed into the reverse spectrum, which mixes with those brighter colours. Thus the yellow spectrum of the setting sun thrown on the luminous sky, becomes blue, and changes with the colour or brightness of the clouds on which it appears. The red part of light being capable of struggling through thick and resisting mediums which intercept all other colours—is likewise the cause why the sun appears red when seen through a fog,—why distant light, though transmitted through blue or green glass, appears red—why lamps at a distance, seen through the smoke of a long street, are red, while those that are near, are white. To the same cause it is owing that a diver at the bottom of the sea is surrounded with the red light which has pierced through the superincumbent fluid, and that the blue rays are reflected from the surface of the ocean. Hence, Dr. Halley informs us that, when he was in a diving bell, at the bottom of the sea, his hand always appeared red in the water.
The blue rays, as already noticed, being unable to resist the obstructions they meet with in their course through the atmosphere, are either reflected or absorbed in their passage. It is to this cause, that most philosophers ascribe the blue colour of the sky, the faintness and obscurity of distant objects, and the bright azure which tinges the mountains of a distant landscape. 144
Since the rays of light are found to be decomposed by refracting surfaces, and reflected in an infinite variety of modes and shades of colour, we need not be surprised at the changes produced in any scene or object by the intervention of another, and by the numerous modifications of which the primary colours of nature are susceptible. The vivid colours which gild the rising and the setting sun, must necessarily differ from those which adorn its noon-day splendour. Variety of atmospheric scenery will thus necessarily be produced, greater than the most lively fancy can well imagine. The clouds will sometimes assume the most fantastic forms, and at other times will be irradiated with beams of light, or, covered with the darkest hues, will assume a lowering aspect, prognostive of the thunder’s roar and the lightning’s flash—all in accordance with the different rays that are reflected to our eyes, or the quantity absorbed by the vapours which float in the atmosphere.
Light, which embellishes with so much magnificence a pure and serene sky, by means of innumerable bright starry orbs which are spread over it, sometimes, in a dark and cloudy sky, exhibits an ornament which, by its pomp, splendour and variety of colours, attracts the attention of every eye that has an opportunity of beholding it. At certain times, when there is a shower either around us, or at a distance from us in an opposite quarter to that of the sun, a species of arch or bow is seen in the sky, adorned with all the seven primary colours of light. This phenomenon, 145 which is one of the most beautiful meteors in nature, has obtained the name of the Rainbow. The rainbow was, for ages, considered as an inexplicable mystery, and by some nations it was adored as a deity. Even after the dawn of true philosophy, it was a considerable time before any discovery of importance was made, as to the true causes which operate in the production of this phenomenon. About the year 1571, M. Fletcher of Breslau, made a certain approximation to the discovery of the true cause, by endeavouring to account for the colours of the rainbow by means of a double refraction and one reflection. A nearer approximation was made by Antonio de Dominis, bishop of Spalatro, about 1601. He maintained that the double refraction of Fletcher, with an intervening reflection, was sufficient to produce the colours of the bow, and also to bring the rays that formed them to the eye of the spectator, without any subsequent reflection. To verify this hypothesis, he procured a small globe of solid glass, and viewing it when it was exposed to the rays of the sun—with his back to that luminary—in the same manner as he had supposed the drops of rain were situated with respect to them, he observed the same colours which he had seen in the rainbow, and in the same order. But he could give no good reason why the bow should be coloured, and much less any satisfactory account of the order in which the colours appear. It was not till Sir I. Newton discovered the different refrangibility of the rays of light, that a complete and satisfactory explanation could be given of all the circumstances connected with this phenomenon.
As the full elucidation of this subject involves a variety of optical and mathematical investigations, 146 I shall do little more than explain the general principle on which the prominent phenomena of the rainbow may be accounted for, and some of the facts and results which theory and observation have deduced.
We have just now alluded to an experiment with a glass globe:—If, then, we take either a solid glass globe, or a hollow globe filled with water, and suspend it so high in the solar rays above the eye, that the spectator, with his back to the sun, can see the globe red;—if it be lowered slowly, he will see it orange, then yellow, then green, then blue, then indigo, and then violet; so that the drop at different heights, shall present to the eye the seven primitive colours in succession. In this case, the globe, from its form, will act in some measure like a prism, and the ray will be separated into its component parts. The following figure will more particularly illustrate this point. Suppose A (fig. 35.) to represent a drop of rain—which may be considered as a globe of glass in miniature, and will produce the same effect on the rays of light—and let Sd represent a ray from the sun falling upon the upper part of the drop at D. At the point of entering the drop, it will suffer a refraction, and instead of going forward to C, it will be bent to N. From N a part of the light will be reflected to Q—some part of it will, of course, pass through the drop. By the obliquity with which it falls on the side of the drop at Q, that part becomes a kind of prism, and separates the ray into its primitive colours. It is found by computation that, after a ray has suffered two refractions and one reflection, as here represented, the least refrangible part of it, namely the red ray, will make an angle with the incident solar ray of 42° 2´, as Sfq; and the 147 violet, or greatest refrangible ray will make with the solar ray, an angle of 40° 17´, as Scq; and thus all the particles of water within the difference of those two angles, namely 1° 45´—(supposing the ray to proceed merely from the centre of the sun)—will exhibit severally the colours of the prism, and constitute the interior bow of the cloud. This holds good at whatever height the sun may chance to be in a shower of rain. If he be at a high altitude, the rainbow will be low; if he be at a low elevation, the rainbow must be high; and if a shower happen in a vale, when the spectator is on a mountain, he will sometimes see the 148 bow in the form of a complete circle below him. We have at present described the phenomena only of a single drop; but it is to be considered that in a shower of rain there are drops at all heights and at all distances; and therefore the eye situated at G will see all the different colours. All those drops that are in a certain position with respect to the spectator will reflect the red rays, all those in the next station the orange, those in the next the green, and so on with regard to all the other colours.
figure 35.

It appears, then, that the first or primary bow is formed by two refractions and one reflection; but there is frequently a second bow, on the outside of the other, which is considerably fainter. This is produced by drops of rain above the drop we have supposed at A. If B (fig. 35.) represent one of these drops, the ray to be sent to the eye enters the drop near the bottom, and suffers two refractions and two reflections, by which means the colours become reversed, that is, the violet is lowest in the exterior bow, and the red is lowest in the interior one, and the other colours are reversed accordingly. The ray T is refracted at R: a part of it is reflected from S to T, and at T it suffers another reflection from T to U. At the points S and T part of the ray passes through the drop on account of its transparency, towards W and X, and therefore we say that part only of the ray is reflected. By these losses and reflections the exterior bow becomes faint and ill-defined in comparison of the interior or primary bow. In this case the upper part of the secondary bow will not be seen when the sun is above 54° 10´ above the horizon; and the lower part of the bow will not be seen when the sun is 60° 58´ above the horizon. 149
figure 36.
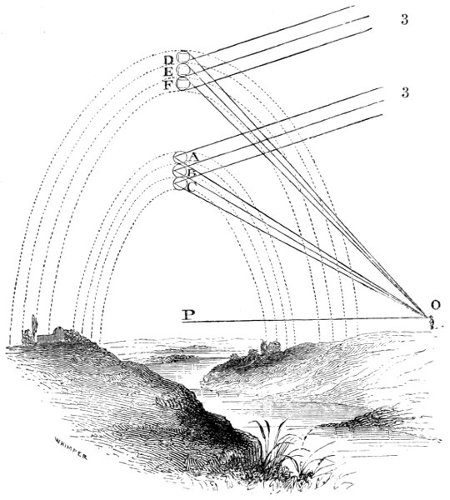
For the further illustrations of this subject, we may introduce the following section of a bow, (fig. 36.) and, in order to prevent confusion in attempting to represent all the different colours—let us suppose only three drops of rain, and three different colours, as shown in the figure. The spectator O being in the centre of the two bows, here represented,—the planes of which must be considered as perpendicular to his view—the drops A,B, and C produce part of the interior bow by two refractions and one reflection as stated above, 150 and the drops D,E,F will produce the exterior bow by two refractions and two reflections, the sun’s rays being represented by 3,3. It is evident that the angle COP is less than the angle BOP, and that the angle AOP is the greatest of the three. The largest angle, then, is formed by the red rays, the middle one consists of the green, and the smallest the purple or violet. All the drops of rain, therefore, that happen to be in a certain position with respect to the spectator’s eye, will reflect the red rays, and form a band or semicircle of red, and so of the other colours from drops in other positions. If the spectator alters his station, he will see a bow, but not the same as before; and if there be many spectators, they will each see a different bow, though it appears to be the same.
The rainbow assumes a semicircular appearance, because it is only at certain angles that the refracted rays are visible to our eyes, as is evident from the experiment of the glass globe formerly alluded to, which will refract the rays only in a certain position. We have already stated that the red rays make an angle of 42° 2´, and the violet an angle of 40° 17´. Now, if a line be drawn horizontally from the spectator’s eye, it is evident that angles formed with this line, of a certain dimension, in every direction, will produce a circle, as will appear by attaching a cord of a given length to a certain point, round which it may turn as round its axis; and, in every point will describe an angle with the horizontal line of a certain and determinate extent.
Sometimes it happens that three or more bows are visible, though with different degrees of distinctness. I have more than once observed this phenomenon, particularly in Edinburgh, in the month of August, 1825, when three rainbows 151 were distinctly seen in the same quarter of the sky; and, if I recollect right, a fragment of a fourth made its appearance. This happens when the rays suffer a third or fourth reflection; but, on account of the light lost by so many reflections, such bows are, for the most part, altogether imperceptible.
If there were no ground to intercept the rain and the view of the observer, the rainbow would form a complete circle, the centre of which is diametrically opposite to the sun. Such circles are sometimes seen in the spray of the sea or of a cascade, or from the tops of lofty mountains, when the showers happen in the vales below. Rainbows of various descriptions are frequently observed rising amidst the spray and exhalations of waterfalls, and among the waves of the sea whose tops are blown by the wind into small drops. There is one regularly seen, when the sun is shining, and the spectator in a proper position, at the fall of Staubbach, in the bosom of the Alps; one near Schaffhausen; one at the cascade of Lauffen; and one at the cataract of Niagara in North America. A still more beautiful one is said to be seen at Terni, where the whole current of the river Velino, rushing from a steep precipice of nearly 200 feet high, presents to the spectator below, a variegated circle, over-arching the fall, and two other bows suddenly reflected on the right and left. Don Ulloa, in the account of his journeys in South America, relates that circular rainbows are frequently seen on the mountains above Quito in Peru. It is said that a rainbow was once seen near London, caused by the exhalations of that city, after the sun had been below the horizon more than twenty minutes.14 A naval 152 friend, says Mr. Bucke, informed me, that, as he was one day watching the sun’s effect upon the exhalations near Juan Fernandez, he saw upwards of five-and-twenty ires marinæ animate the sea at the same time. In these marine bows the concave sides were turned upwards, the drops of water rising from below, and not falling from above, as in the instances of the aerial arches. Rainbows are also occasionally seen on the grass, in the morning dew, and likewise when the hoar-frost is descending. Dr. Langwith once saw a bow lying on the ground, the colours of which were almost as lively as those of a common rainbow. It was not round but oblong, and was extended several hundred yards. The colours took up less space, and were much more lively in those parts of the bow which were near him than in those which were at a distance. When M. Labillardiere was on Mount Teneriffe, he saw the contours of his body traced on the clouds beneath him in all the colours of the solar bow. He had previously witnessed this phenomenon on the Kesrouan in Asia Minor. The rainbows of Greenland are said to be frequently of a pale white, fringed with a brownish yellow, arising from the rays of the sun being reflected from a frozen cloud.
The following is a summary view of the principal facts which have been ascertained respecting the rainbow:—1. The rainbow can only be seen when it rains, and in that point of the heavens which is opposite to the sun. 2. Both the primary and secondary bows are variegated with all the prismatic colours—the red being the highest colour in the primary, or brightest bow, and the violet the highest in the exterior. 3. The primary rainbow can never be a greater arc than a semicircle; 153 and when the sun is set, no bow, in ordinary circumstances, can be seen. 4. The breadth of the inner or primary bow—supposing the sun but a point—is 1° 45´; and the breadth of the exterior bow 3° 12´, which is nearly twice as great as that of the other; and the distance between the bows is 8° 55´. But since the body of the sun subtends an angle of about half a degree, by so much will each bow be increased, and their distance diminished; and therefore the breadth of the interior bow will be 2° 15´, and that of the exterior, 3° 42´, and their distance 8° 25´. The greatest semidiameter of the interior bow, on the same grounds, will be 42° 17´, and the least of the exterior bow 50° 43´. 5. When the sun is in the horizon, either in the morning or evening, the bows will appear complete semicircles. On the other hand, when the sun’s altitude is equal to 42° 2´ or to 54° 10´, the summits of the bows will be depressed below the horizon. Hence, during the days of summer, within a certain interval each day, no visible rainbows can be formed, on account of the sun’s high altitude above the horizon. 6. The altitude of the bows above the horizon, or surface of the earth, varies, according to the elevation of the sun. The altitude, at any time, may be taken by a common quadrant, or other angular instrument; but, if the sun’s altitude at any particular time be known, the height of the summit of any of the bows may be found, by subtracting the sun’s altitude from 42° 2´ for the inner bow, and from 54° 10´, for the outer. Thus, if the sun’s altitude were 26°, the height of the primary bow would 16° 2´, and of the secondary, 28° 10´. It follows, that the height and the size of the bows diminish as the altitude of the sun increases. 7. If the sun’s altitude is more 154 than 42 degrees, and less than 54°, the exterior bow may be seen though the interior bow is invisible. 8. Sometimes only a portion of an arch will be visible while all the other parts of the bow are invisible. This happens when the rain does not occupy a space of sufficient extent to complete the bow; and the appearance of this position, and even of the bow itself, will be various, according to the nature of the situation, and the space occupied by the rain.
The appearance of the rainbow may be produced by artificial means, at any time when the sun is shining and not too highly elevated above the horizon. This is effected by means of artificial fountains or Jet d’eaus, which are intended to throw up streams of water to a great height. These streams, when they spread very wide, and blend together in their upper parts, form, when falling, a shower of artificial rain. If, then, when the fountain is playing, we move between it and the sun, at a proper distance from the fountain, till our shadow point directly towards it, and look at the shower,—we shall observe the colours of the rainbow, strong and vivid; and, what is particularly worthy of notice, the bow appears, notwithstanding the nearness of the shower, to be as large, and as far off, as the rainbow which we see in a natural shower of rain. The same experiment may be made by candle-light, and with any instrument that will form an artificial shower.
Lunar Rainbows.—A lunar bow is sometimes formed at night by the rays of the moon striking on a rain-cloud, especially when she is about the full. But such a phenomenon is very rare. Aristotle is said to have considered himself the first who had seen a lunar rainbow. For more than a hundred years prior to the middle of the last century, 155 we find only two or three instances recorded in which such phenomena are described with accuracy. In the philosophical transactions for 1783, however, we have an account of three having been seen in one year, and all in the same place, but they are by no means common phenomena. I have had an opportunity within the last twenty years of witnessing two phenomena of this description—one of which was seen at Perth, on a sabbath evening, in the autumn of 1825, and the other at Edinburgh, on Wednesday, the 9th of September 1840, about eight o’clock in the evening—of both which I gave a detailed description in some of the public journals. The Moon, in both cases, was within a day or two of the full; the arches were seen in the northern quarter of the heavens, and extended nearly from east to west, the moon being not far from the southern meridian. The bows appeared distinct and well defined, but no distinct traces of the prismatic colours could be perceived on any of them. That which appeared in 1825 was the most distinctly formed, and continued visible for more than an hour. The other was much fainter, and lasted little more than half an hour, dark clouds having obscured the face of the moon. These bows bore a certain resemblance to some of the luminous arches which sometimes accompany the Aurora Borealis, and this latter phenomenon has not unfrequently been mistaken for a Lunar rainbow; but they may be always distinguished by attending to the phases and position of the moon. If the moon be not visible above the horizon, if she be in her first or last quarter, or if any observed phenomenon be not in a direction opposite to the moon, we may conclude with certainty that, whatever appearance is presented, there is no lunar rainbow. 156
The rainbow is an object which has engaged universal attention, and its beautiful colours and form have excited universal admiration. The poets have embellished their writings with many beautiful allusions to this splendid meteor; and the playful school-boy, while viewing the ‘bright enchantment,’ has frequently run ‘to catch the falling glory.’ When its arch rests on the opposite sides of a narrow valley, or on the summits of two adjacent mountains, its appearance is both beautiful and grand. In all probability, its figure first suggested the idea of arches, which are now found of so much utility in forming aqueducts and bridges, and for adorning the architecture of palaces and temples. It is scarcely possible seriously to contemplate this splendid phenomenon, without feeling admiration and gratitude towards that wise and beneficent Being, whose hands have bent it into so graceful and majestic a form, and decked it with all the pride of colours. “Look upon the rainbow,” says the son of Sirach,15 and praise Him that made it: very beautiful it is in the brightness thereof. It compasseth the heaven about with a glorious circle, and the hands of the Most High have bended it." To this grand etherial bow, the inspired writers frequently allude as one of the emblems of the majesty and splendour of the Almighty. In the prophecies of Ezekiel, the throne of Deity is represented as adorned with a brightness “like the appearance of the bow that is in the cloud in the day of rain—the appearance of the likeness of the glory of Jehovah.” And, in the visions recorded in the Book of the Revelations, where the Most High is represented as sitting upon a throne; “there was a rainbow round about the throne, in sight like 157 unto an emerald,” as an emblem of his propitious character and of his faithfulness and mercy. After the deluge, this bow was appointed as a sign and memorial of the covenant which God made with Noah and his sons, that a flood of waters should never again be permitted to deluge the earth and its inhabitants;—and as a pledge of inviolable fidelity and Divine benignity. When, therefore, we at any time behold “the bow in the cloud,” we have not only a beautiful and sublime phenomenon presented to the eye of sense, but also a memorial exhibited to the mental eye, assuring us, that, “While the earth remaineth, seed-time and harvest, and cold and heat, and summer and winter, and day and night, shall not cease.”16
158
Colour is one of the properties of light which constitutes, chiefly, the beauty and sublimity of the universe. It is colour, in all its diversified shades, which presents to our view that almost infinite variety of aspect which appears on the scene of nature, which gives delight to the eye and the imagination, and which adds a fresh pleasure to every new landscape we behold. Every flower which decks our fields and gardens is compounded of different hues; every plain is covered with shrubs and trees of different degrees of verdure; and almost every mountain is clothed with herbs and grass of different shade from those which appear on the hills and landscape with which it is surrounded. In the country, during summer, nature is every day, and almost every hour, varying her appearance, by the multitude and variety of her hues and decorations, so that the eye wanders with pleasure over objects continually diversified, and extending as far as the sight can reach. In the flowers with which every landscape is adorned, what a lovely assemblage of colours, and what a wonderful art in the disposition of their shades! Here, a light pencil seems to have laid on the delicate tints; there, they are blended according to the nicest rules of art. Although green is the general colour which prevails over the scene of sublunary nature, yet it is diversified by a thousand different shades, so that every species of tree, 159 shrub and herb, is clothed with its own peculiar verdure. The dark green of the forests is thus easily distinguished from the lighter shades of cornfields and the verdure of the lawns. The system of animated nature likewise, displays a diversified assemblage of beautiful colours. The plumage of birds, the brilliant feathers of the peacock, the ruby and emerald hues which adorn the little humming-bird, and the various embellishments of many species of the insect tribe, present to the eye, in every region of the globe, a scene of diversified beauty and embellishment. Nor is the mineral kingdom destitute of such embellishments. For some of the darkest and most unshapely stones and pebbles, when polished by the hand of art, display a mixture of the most delicate and variegated colours. All which beauties and varieties in the scene around us are entirely owing to that property, in every ray of light, by which it is capable of being separated into the primitive colours.
To the same cause, likewise, are to be ascribed those beautiful and diversified appearances, which frequently adorn the face of the sky,—the yellow, orange and ruby hues which embellish the firmament at the rising of the sun, and when he is about to descend below the western horizon; and those aerial landscapes, so frequently beheld in tropical climes, where rivers, castles and mountains, are depicted rolling over each other along the circle of the horizon. The clouds, especially in some countries, reflect almost every colour in nature. Sometimes they wear the modest blush of the rose; sometimes they appear like stripes of deep vermillion, and sometimes as large brilliant masses tinged with various hues; now they are white as ivory, and now as yellow as native gold. In some 160 tropical countries, according to St. Pierre, the clouds roll themselves up into enormous masses as white as snow, and are piled upon each other, like the Cordeliers of Peru, and are moulded into the shape of mountains, of caverns and of rocks. When the sun sets behind this magnificent aërial net-work, a multitude of luminous rays are transmitted through each particular interstice, which produce such an effect, that the two sides of the lozenge illuminated by them, have the appearance of being begirt with a fillet of gold; and the other two which are in the shade, seem tinged with a superb ruddy orange. Four or five divergent streams of light, emanating from the setting sun up to the zenith, clothe with fringes of gold the undeterminate summits of this celestial barrier, and proceed to strike with the reflexes of their fires the pyramids of the collateral aerial mountains, which then appear to consist of silver and vermilion.—In short, colour diversifies every sublunary scene, whether on the earth or in the atmosphere, it imparts a beauty to the phenomena of falling stars, of luminous arches, and the coruscations of the Aurora Borealis, and gives a splendour and sublimity to the spacious vault of heaven.
Let us now consider for a moment, what would be the aspect of nature, if, instead of the beautiful variety of embellishments which now appear on every landscape, and on the concave of the sky,—one uniform colour had been thrown over the scenery of the universe. Let us conceive the whole of terrestrial nature to be covered with snow, so that not an object on earth should appear with any other hue, and that the vast expanse of the firmament presented precisely the same uniform aspect. What would be the consequence? The light of the sun would be strongly reflected 161 from all the objects within the bounds of our horizon, and would produce a lustre which would dazzle every eye. The day would acquire a greater brightness than it now exhibits, and our eyes might, after some time, be enabled freely to expatiate over the surrounding landscape; but every thing, though enlightened, would appear confused, and particular objects would scarcely be distinguishable. A tree, a house or a church, near at hand, might possibly be distinguished, on account of its elevation above the general surface of the ground, and the bed of a river by reason of its being depressed below it. But we should be obliged rather to guess, and to form a conjecture as to the particular object we wished to distinguish, than to arrive at any certain conclusion respecting it; and if it lay at a considerable distance, it would be impossible, with any degree of probability, to discriminate any one object from another. Notwithstanding the universal brightness of the scene, the uniformity of colour thrown on every object, would most certainly prevent us from distinguishing a church from a palace, a cottage from a knoll or a heap of rubbish, a splendid mansion from rugged rocks, the trees from the hills on which they grow, or a barren desert from rich and fertile plains. In such a case, human beings would be confounded, and even friends and neighbours be at a loss to recognize one another.
The vault of heaven, too, would wear a uniform aspect. Neither planets nor comets would be visible to any eye, nor those millions of stars which now shine forth with so much brilliancy, and diversify the nocturnal sky. For, it is by the contrast produced by the deep azure of the heavens and the white radiance of the stars, that those bodies are rendered visible. Were they depicted 162 on a pure white ground, they would not be distinguished from that ground, and would consequently be invisible, unless any of them occasionally assumed a different colour. Of course, all that beautiful variety of aspect which now appears on the face of sublunary nature—the rich verdure of the fields, the stately port of the forest, the rivers meandering through the valleys, the splendid hues that diversify and adorn our gardens and meadows, the gay colouring of the morning and evening clouds, and all that variety which distinguishes the different seasons, would entirely disappear. As every landscape would exhibit nearly the same aspect, there would be no inducement to the poet and the philosopher to visit distant countries to investigate the scenes of nature, and journeyings from one region to another would scarcely be productive of enjoyment. Were any other single colour to prevail, nearly the same results would ensue. Were a deep ruddy hue to be uniformly spread over the scene of creation, it would not only be offensive to the eye, but would likewise prevent all distinction of objects. Were a dark blue or a deep violet to prevail, it would produce a similar effect, and at the same time, present the scene of nature as covered with a dismal gloom. Even if creation were arrayed in a robe of green, which is a more pleasant colour to the eye—were it not diversified with the different shades it now exhibits, every object would be equally undistinguishable.
Such would have been the aspect of creation, and the inconveniences to which we should have been subjected, had the Creator afforded us light without that intermixture of colours which now appears over all nature, and which serves to discriminate one object from another. Even our 163 very apartments would have been tame and insipid, incapable of the least degree of ornament, and the articles with which they are furnished, almost undistinguishable, so that in discriminating one object from another, we should have been as much indebted to the sense of touch as to the sense of vision. Our friends and fellow men would have presented no objects of interest in our daily associations. The sparkling eye, the benignant smile, the modest blush, the blended hues of white and vermillion in the human face, and the beauty of the female countenance, would all have vanished, and we should have appeared to one another as so many moving marble statues cast nearly in the same mould. But, what would have been worst of all, the numerous delays, uncertainties and perplexities to which we should have been subjected, had we been under the necessity, every moment, of distinguishing objects by trains of reasoning, and by circumstances of time, place, and relative position? An artist, when commencing his work in the morning, with a hundred tools of nearly the same size and shape around him, would have spent a considerable portion of his time before he could have selected those proper for his purpose, or the objects to which they were to be applied; and in every department of society, and in all our excursions from one place to another, similar difficulties and perplexities would have occurred. The one half of our time must thus have been employed in uncertain guesses, and perplexing reasonings, respecting the real nature and individuality of objects, rather than in a regular train of thinking and of employment; and after all our perplexities and conjectures, we must have remained in the utmost uncertainty, as to the thousands of scenes and objects, which are now obvious to us, through 164 the instrumentality of colours, as soon as we open our eyes.
In short, without colour, we could have had no books nor writings: we could neither have corresponded with our friends by letters, nor have known any thing with certainty, of the events which happened in former ages. No written revelation of the will of God, and of his character, such as we now enjoy, could have been handed down to us from remote periods and generations. The discoveries of science, and the improvements of art, would have remained unrecorded. Universal ignorance would have prevailed throughout the world, and the human mind have remained in a state of demoralization and debasement. All these, and many other inconveniences and evils would have inevitably followed, had not God painted the rays of light with a diversity of colours, And hence we may learn, that the most important scenes and events in the universe, may depend upon the existence of a single principle in nature, and even upon the most minute circumstances, which we may be apt to overlook, in the arrangements of the material world.
In the existing state of things in the visible creation, we cannot but admire the Wisdom and Beneficence of the Deity, in thus enabling us to distinguish objects by so easy and expeditious a mode as that of colour, which in a moment, discriminates every object and its several relations. We rise in the morning to our respective employments, and our food, our drink, our tools, our books, and whatever is requisite for our comfort, are at once discriminated. Without the least hesitation or uncertainty, and without any perplexing process of reasoning, we can lay our hands on whatever articles we require. Colour clothes every object 165 with its peculiar livery, and infallibly directs the hand in its movements, and the eye in its surveys and contemplations. But, this is not the only end which the Divine Being had in view, in impressing on the rays of light a diversity of colours. It is evident, that he likewise intended to minister to our pleasures, as well as to our wants. To every man of taste, and almost to every human being, the combination of colours in flowers, the delicate tints with which they are painted, the diversified shades of green with which the hills and dales, the mountains and the vales are arrayed; and that beautiful variety which appears in a bright summer day, on all the objects of this lower creation—are sources of the purest enjoyment and delight. It is colour, too, as well as magnitude, that adds to the sublimity of objects. Were the canopy of heaven of one uniform hue, it would fail in producing those lofty conceptions, and those delightful and transporting emotions, which a contemplation of its august scenery is calculated to inspire. Colours are likewise of considerable utility in the intercourse of general society. They serve both for ornaments, and for distinguishing the different ranks and conditions of the community: they add to the beauty and gracefulness of our furniture and clothing. At a glance, they enable us at once to distinguish the noble from the ignoble, the prince from his subjects, the master from his servant, and the widow clothed with sable weeds from the bride adorned with her nuptial ornaments.
Since colours, then, are of so much value and importance, they may be reckoned as holding a rank among the noblest natural gifts of the Creator. As they are of such essential service to the inhabitants of our globe, there can be no doubt that they serve similar or analogous purposes 166 throughout all the worlds in the universe. The colours displayed in the solar beams are common to all the globes which compose the planetary system, and must necessarily be reflected, in all their diversified hues, from objects on their surfaces. The light which radiates from the fixed stars displays a similar diversity of colours. Some of the double stars are found to emit light of different hues;—the larger star exhibiting light of a ruddy or orange hue, and the smaller one a radiance which approaches to blue or green. There is therefore reason to conclude, that the objects connected with the planets which revolve round such stars—being occasionally enlightened by suns of different hues—will display a more variegated and splendid scenery of colouring than is ever beheld in the world on which we dwell; and that one of the distinguishing characteristics of different worlds, in regard to their embellishments, may consist in the splendour and variety of colours with which the objects on their surfaces are adorned. In the metaphorical description of the glories of the New Jerusalem, recorded in the Book of Revelation, one of the chief characteristics of that city is said to consist in the splendour and diversity of hues with which it is adorned. It is represented as “coming down from heaven, prepared as a bride adorned for her husband,” and as reflecting all the beautiful and variegated colours which the finest gems on earth can exhibit; evidently indicating, that splendour and variety of colouring are some of the grandest features of celestial scenery.
On the whole, the subject of colours, when seriously considered, is calculated to excite us to the adoration of the goodness and intelligence of that Almighty Being whose wisdom planned all 167 the arrangements of the universe, and to inspire us with gratitude for the numerous conveniences and pleasures we derive from those properties and laws he has impressed on the material system. He might have afforded us light, and even splendid illumination, without the pleasures and advantages which diversified colours now produce, and man and other animated beings might have existed in such a state. But, what a very different scene would the world have presented from what it now exhibits! Of how many thousands of pleasures should we have been deprived! and to what numerous inconveniences and perplexities should we have been subjected! The sublimity and glories of the firmament, and the endless beauties and varieties which now embellish our terrestrial system, would have been for ever unknown, and man could have had little or no incitement to study and investigate the works of his Creator. In this, as well as in many other arrangements in nature, we have a sensible proof of the presence and agency of that Almighty Intelligence “in whom we live, and move, and have our being.” None but an infinitely Wise and Beneficent Being, intimately present in all places, could thus so regularly create in us by means of colour, those exquisite sensations which afford so much delight, and which unite us, as it were, with every thing around us. In the diversity of hues spread over the face of creation, we have as real a display of the Divine presence as Moses enjoyed at the burning bush. The only difference is, that the one was out of the common order of Divine procedure, and the other in accordance with those permanent laws which regulate the economy of the universe. In every colour, then, which we contemplate, we have a sensible memorial of the presence of that 168 Being “whose Spirit garnished the heavens and laid the foundations of the earth,” and whose “merciful visitation” sustains us every moment in existence. But the revelation of God to our senses, through the various objects of the material world, has become so familiar, that we are apt to forget the Author of all our enjoyments, even at the moment when we are investigating his works and participating of his benefits. “O that men would praise Jehovah for his goodness, and for his wonderful works towards the children of men.” 169
The telescope is an optical instrument for viewing objects at a distance. Its name is compounded of two Greek words,—τηλε, which signifies, at a distance, or far off, and σχοπειν, to view, or to contemplate. By means of telescopes, remote objects are represented as if they were near, small apparent magnitudes are enlarged, confused objects are rendered distinct, and the invisible and obscure parts of very distant scenes are rendered perceptible and clear to the organ of vision. The telescope is justly considered as a grand and noble instrument. It is not a little surprising that it should be in the power of man to invent and construct an instrument by which objects, too remote for the unassisted eye to distinguish, should be brought within the range of distinct 170 vision, as if they were only a few yards from our eye, and that thousands of august objects in the heavens, which had been concealed from mortals for numerous ages, should be brought within the limits of our contemplation, and be as distinctly perceived, as if we had been transported many millions of miles from the space we occupy, through the celestial regions. The celebrated Huygens remarks, in reference to this instrument, that, in his opinion, ‘the wit and industry of man has not produced any thing so noble and so worthy of his faculties as this sort of knowledge; (namely of the telescope) insomuch that if any particular person had been so diligent and sagacious as to invent this instrument from the principles of nature and geometry,—for my part, I should have thought his abilities were more than human; but the case is so far from this, that the most learned men have not yet been able sufficiently to explain the reason of the effects of this casual invention.’
The persons who constructed the first telescopes, and the exact period when they were first invented, are involved in some degree of obscurity. It does not certainly appear that such instruments were known to the ancients, although we ought not to be perfectly decisive on this point. The cabinets of the curious contain some very ancient gems, of admirable workmanship, the figures on which are so small, that they appear beautiful through a magnifying glass, but altogether confused and indistinct to the naked eye: and, therefore, it may be asked, if they cannot be viewed, how could they be wrought, without the assistance of glasses? And as some of the ancients have declared that the moon has a form like that of the earth, and has plains, hills, and valleys in it,—how could they know this—unless by mere conjecture, 171 without the use of a telescope? And how could they have known that the Milky Way is formed by the combined rays of an infinite number of stars? For Ovid states, in reference to this zone, ‘its ground-work is of stars.’ But whatever knowledge the ancients may have possessed of the telescope or other optical glasses, it is quite evident that they never had telescopes of such size and power as those which we now possess; and that no discoveries in the heavens, such as are now brought to light, were made by any of the ancient astronomers; otherwise some allusions to them must have been found in their writings.
Among the moderns, the illustrious Friar Bacon appears to have acquired some rude ideas respecting the construction of telescopes. ‘Lenses and specula’ says he, ‘may be so figured that one object may be multiplied into many, that those which are situated at a great distance may be made to appear very near, that those which are small may be made to appear very large, and those which are obscure very plain; and we can make stars to appear wherever we will.’ From these expressions, it appears highly probable, that this philosopher was acquainted with the general principle both of telescopes and microscopes, and that he may have constructed telescopes of small magnifying power, for his own observation and amusement, although they never came into general use. He was a man of extensive learning, and made so rapid a progress in the sciences, when attending the university of Paris, that he was esteemed the glory of that seat of learning. He prosecuted his favourite study of experimental philosophy with unremitting ardour; and in this pursuit, in the course of twenty years, he expended no less than £2000 in experiments, instruments, and in 172 procuring scarce books. In consequence of such extraordinary talents, and such astonishing progress in the sciences, in that ignorant age, he was represented, by the envy of his illiterate fraternity, as having dealings with the devil; and, under this pretence, he was restrained from reading lectures, and at length, in 1278, when sixty-four years of age, he was imprisoned in his cell, where he remained in confinement for ten years. He shone like a single bright star in a dark hemisphere—the glory of our country—and died at Oxford, in the year 1294, in the eightieth year of his age. ‘Friar Bacon,’ says the Rev. Mr. Jones, ‘may be considered as the first of English philosophers; his profound skill in mechanics, optics, astronomy, and chemistry, would make an honourable figure in the present age. But he is entitled to further praise, as he made all his studies subservient to theology, and directed all his writings, as much as could be, to the glory of God. He had the highest regard for the sacred scriptures, and was persuaded they contain the principles of all true science.’
The next person who is supposed to have acquired a knowledge of telescopes, was Joannes Baptista Porta, of Naples, who flourished in the sixteenth century. He discovered the Camera Obscura—the knowledge of which might naturally have led to the invention of the telescope; but it does not appear that he ever constructed such an instrument. Des Cartes considers James Metius, a Dutchman, as the first constructor of a telescope, and says, that ‘as he was amusing himself with making mirrors and burning-glasses, he casually thought of looking through two of his lenses at a time, and found that distant objects appeared very large and distinct.’ Others say that this great 173 discovery was first made by John Lippersheim, a maker of spectacles at Middleburg, or rather by his children, who were diverting themselves with looking through two glasses at a time, and placing them at different distances from each other. But Borellus, who wrote a book ‘on the invention of the telescope,’ gives this honour to Zacharias Jansen, another spectacle-maker in the same town, who, he says, made the first telescope in 1590. Jansen was a diligent inquirer into nature, and, being engaged in such pursuits, he was trying what use could be made of lenses for those purposes, when he fortunately hit upon the construction. Having found the arrangement of glasses which produced the effect desired, he enclosed them in a tube, and ran with his instrument to prince Maurice, who, immediately conceiving that it might be of use to him in his wars, desired the author to keep it a secret. Such are the rude conceptions and selfish views of princely warriors, who would apply every invention in their power for the destruction of mankind. But the telescope was soon destined to more noble and honourable achievements. Jansen, it is said, directed his instrument towards celestial objects, and distinctly saw the spots on the surface of the moon, and discovered many new stars, particularly seven pretty considerable ones in the Great Bear. His son Joannes is said to have noted the lucid circle near the lower limb of the moon, now named Tycho, from whence several bright rays seem to dart in different directions. In viewing Jupiter, he perceived two, sometimes three, and at the most four small stars, a little above or below him, and thought that they performed revolutions around him. This was, probably, the first observation of the satellites of Jupiter, though the person who 174 made it was not aware of the importance of his discovery.17
It is not improbable that different persons about Middleburgh hit upon the invention, in different modes, about the same time. Lippersheim seems to have made his first rude telescope by adjusting two glasses on a board, and supporting them on brass circles.18 Other workmen, particularly Metius and Jansen, in emulation of each other, seem to have made use of that discovery, and by the new form they gave it, made all the honour of it their own. One of them, considering the effects of light as injurious to distinctness, placed the glasses in a tube blackened within. The other, still more cautious, placed the same glasses within tubes capable of sliding one in another, both to vary the prospects, by lengthening the instrument, according to the pleasure of the observer, and to render it portable and commodious. Thus, it is probable that different persons had a share in the invention, and jointly contributed to its improvement. At any rate, it is undoubtedly to the Dutch that we owe the original invention. The first telescope made by Jansen, did not exceed fifteen or sixteen inches in length, and therefore its magnifying power could not have been very great.
The famous Galileo has frequently been supposed to have been the inventor of the telescope, but he acknowledges that he had not the honour of being the original inventor, having first learned 175 from a German, that such an instrument had already been made; although, from his own account, it appears that he had actually re-invented this instrument. The following is the account, in his own words, of the circumstances which led him to construct a telescope. ‘Nearly ten months ago (namely in April or May 1609) it was reported that a certain Dutchman had made a perspective through which many distant objects appeared distinct as if they were near: several effects of this wonderful instrument were reported, which some believed and others denied: but, having it confirmed to me a few days after by a letter from the noble John Badoverie, at Paris, I applied myself to consider the reason of it, and by what means I might contrive a similar instrument, which I afterwards attained to by the doctrine of refractions. And, first, I prepared a leaden tube, to whose extremities I fitted two spectacle-glasses, both of them plain on one side, and on the other side, one of them was spherically convex, and the other concave. Then applying my eye to the concave, I saw objects appear pretty large and pretty near me. They appeared three times nearer and nine times larger in surface than to the naked eye: and soon after I made another, which represented objects about sixty times larger, and eight times nearer; and, at last, having spared no labour nor expense, I made an instrument so excellent, as to show things almost a thousand times larger, and above thirty times nearer, than to the naked eye.’ In another part of his writings, Galileo informs us that ‘he was at Venice when he heard of Prince Maurice’s instrument, but nothing of its construction; that the first night, after he returned to Padua, he solved the problem, and made his instrument the next day; and soon after, presented 176 it to the Doge at Venice, who, to do him honour for his grand invention, gave him the ducal letters which settled him for life in his lectureship at Padua; and the Republic, on the twenty-fifth of August in the same year (1610) more than tripled his salary as professor.’
The following is the account which this philosopher gives of the process of reasoning, which led him to the construction of a telescope:—‘I argued in the following manner. The contrivance consists either of one glass or more—one is not sufficient, since it must be either convex, concave, or plane; the last does not produce any sensible alteration in objects, the concave diminishes them; it is true that the convex magnifies, but it renders them confused and indistinct; consequently one glass is insufficient to produce the desired effect. Proceeding to consider two glasses, and bearing in mind that the plane glass causes no change, I determined that the instrument could not consist of the combination of a plane glass with either of the other two. I therefore applied myself to make experiments on combinations of the two other kinds; and thus obtained that of which I was in search.’ If the true inventor is the person who makes the discovery by reasoning and reflection, by tracing facts and principles to their consequences, and by applying his invention to important purposes, then, Galileo may be considered as the real inventor of the telescope. No sooner had he constructed this instrument—before he had seen any similar one—than he directed his tube to the celestial regions, and his unwearied diligence and ardour were soon rewarded by a series of new and splendid discoveries. He descried the four satellites of Jupiter, and marked the periods of their revolutions; he discovered the 177 phases of Venus, and thus was enabled to adduce a new proof of the Copernican system, and to remove an objection that had been brought against it. He traced on the lunar orb, a resemblance to the structure of the earth, and plainly perceived the outlines of mountains and vales, casting their shadows over different parts of its surface. He observed, that when Mars was in quadrature, his figure varied slightly from a perfect circle; and that Saturn consisted of a triple body, having a small globe on each side—which deception was owing to the imperfect power of his telescope, which was insufficient to show him that the phenomenon was in reality a ring. In viewing the sun, he discovered large dark spots on the surface of that luminary, by which he ascertained that that mighty orb performed a revolution round its axis. He brought to view multitudes of stars imperceptible to the naked eye, and ascertained that those nebulous appearances in the heavens which constitute the Milky Way, consist of a vast collection of minute stars, too closely compacted together to produce an impression on our unassisted vision.
The results of Galileo’s observations were given to the world in a small work, entitled ‘Nuncius Sidereus,’ or, ‘News from the starry regions,’ which produced an extraordinary sensation among the learned. These discoveries soon spread throughout Europe, and were incessantly talked of, and were the cause of much speculation and debate among the circles of philosophers. Many doubted; many positively refused to believe so novel and unlooked-for announcements, because they ran counter to the philosophy of Aristotle, and all the preconceived notions which then prevailed in the learned world. It is curious, and 178 may be instructive, to consider to what a length of absurdity, ignorance and prejudice carried many of those who made pretensions to learning and science. Some tried to reason against the facts alleged to be discovered, others contented themselves, and endeavoured to satisfy others, with the simple assertion that such things were not, and could not possibly be; and the manner in which they supported themselves in their incredulity was truly ridiculous. ‘O my dear Kepler,’ says Galileo in a letter to that astronomer, ‘how I wish we could have one hearty laugh together. Here at Padua is the principal professor of philosophy, whom I have repeatedly and urgently requested to look at the moon and planets through my glass, which he pertinaciously refuses to do, lest his opinions should be overturned. Why are you not here? what shouts of laughter we should have at this glorious folly! and to hear the professor of philosophy at Pisa labouring with the Grand Duke with logical arguments, as if with magical incantations, to charm the new planets out of the sky.’ Another opponent of Galileo, one Christmann, says in a book he published, ‘We are not to think that Jupiter has four satellites given him by nature, in order, by revolving round him, to immortalize the Medici who first had notice of the observation. These are the dreams of idle men, who love ludicrous ideas better than our laborious and industrious correction of the heavens. Nature abhors so horrible a chaos; and to the truly wise, such vanity is detestable.’ One Martin Horky, a would-be philosopher, declared to Kepler, ‘I will never concede his four new planets to that Italian from Padua, though I should die for it;’ and he followed up this declaration, by publishing a book against Galileo, in which he 179 examines four principal questions respecting the alleged planets; 1. Whether they exist? 2. What they are? 3. What they are like? 4. Why they are? The first question is soon disposed of by declaring positively that he has examined the heavens with Galileo’s own glass, and that no such thing as a satellite about Jupiter exists. To the second, he declares solemnly that he does not more surely know, that he has a soul in his body than that reflected rays are the sole cause of Galileo’s erroneous observations. In regard to the third question, he says, that these planets are like the smallest fly compared to an elephant; and finally, concludes on the fourth, that the only use of them is to gratify Galileo’s ‘thirst of gold,’ and to afford himself a subject of discussion. Kepler, in a letter to Galileo, when alluding to Horky, says, ‘He begged so hard to be forgiven, that I have taken him again into favour upon this preliminary condition—that I am to show him Jupiter’s satellites, AND HE IS TO SEE THEM, and own that they are there.’
The following is a specimen of the reasoning of certain pretended philosophers of that age against the discoveries of Galileo. Sizzi, a Florentine astronomer, reasons in this strain: ‘There are seven windows given to animals in the domicile of the head, through which the air is admitted to the rest of the tabernacle of the body to enlighten, to warm and to nourish it; two nostrils, two eyes, two ears, and a mouth; so in the heavens, or the great world, there are two favourable stars, two unpropitious, two luminaries, and Mercury alone undecided and indifferent. From which and many other similar phenomena in nature, such as the seven metals, &c., we gather that the number of planets is necessarily seven. Moreover, 180 the satellites are invisible to the naked eye, and therefore can exert no influence on the earth, and therefore would be useless, and therefore do not exist. Besides, as well the Jews as other ancient nations have adopted the division of the week into seven days, and have named them from the seven planets. Now, if we increase the number of the planets, this whole system falls to the ground.’ The opinions which then prevailed in regard to Galileo’s observations on the moon, were such as the following:—Some thought that the dark shades on the moon’s surface arose from the interposition of opaque bodies floating between her and the sun, which prevent his light from reaching those parts; others imagined that, on account of her vicinity to the earth, she was partly tainted with the imperfections of our terrestrial and elementary nature, and was not of that entirely pure and refined substance of which the more remote heavens consist: and a third party looked on her as a vast mirror, and maintained that the dark parts of her surface were the reflected images of our earthly forests and mountains.
Such learned nonsense is a disgrace to our species, and to the rational faculties with which man is endowed, and exhibits, in a most ludicrous manner, the imbecility and prejudice of those who made bold pretensions to erudition and philosophy. The statement of such facts, however, may be instructive, if they tend to guard us against those prejudices and pre-conceived opinions, which prevent the mind from the cordial reception of truth, and from the admission of improvements in society which run counter to long-established customs. For the same principles and prejudices, though in a different form, still operate in society and retard the improvement of the social state, 181 the march of science, and the progress of Christianity. How ridiculous is it for a man, calling himself a philosopher, to be afraid to look through a glass to an existing object in the heavens, lest it should endanger his previous opinions! And how foolish is it to resist any improvement or reformation in society, because it does not exactly accord with existing opinions, and with ‘the wisdom of our ancestors.’
It is not a little surprising, that Galileo should have first hit on that construction of a telescope which goes by his name, and which was formed with a concave glass next the eye. This construction of a telescope is more difficult to be understood, in theory, than one which is composed solely of convex glasses; and its field of view is comparatively very small, so that it is almost useless when attempted to be made of a great length. In the present day, we cannot help wondering that Galileo and other astronomers, should have made such discoveries as they did with such an instrument, the use of which must have required a great degree of patience and address. Galileo’s best telescope, which he constructed ‘with great trouble and expense,’ magnified the diameters of objects only thirty-three times; but its length is not stated—which would depend upon the focal distance of the concave eye-glass. If the eye-glass was two inches focus, the length of the instrument would be five feet four inches; if it was only one inch, the length would be two feet eight inches, which is the least we can allow to it—the object-glass being thirty-three inches focus, and the eye-glass placed an inch within this focus. With this telescope, Galileo discovered the satellites of Jupiter, the crescent of Venus, and the other celestial objects to which we have already 182 alluded. The telescopes made in Holland, are supposed to have been constructed solely of convex glasses, on the principle of the astronomical telescope; and, if so, Galileo’s telescope was in reality a new invention.
Certain other claimants of the invention of the telescope, have appeared, besides those already mentioned. Francis Fontana, in his ‘celestial observations,’ says, that he was assured by a Mr. Hardy, advocate of the parliament of Paris, a person of great learning and undoubted integrity, that on the death of his father, there was found among his things an old tube, by which distant objects were distinctly seen, and that it was of a date long prior to the telescope lately invented, and had been kept by him as a secret. Mr. Leonard Digges, a gentleman who lived near Bristol, in the seventeenth century, and was possessed of great and various knowledge, positively asserts in his ‘Stratoticos,’ and in another work, that his father, a military gentleman, had an instrument which he used in the field, by which he could bring distant objects near, and could know a man at the distance of three miles. Mr. Thomas Digges, in the preface to his ‘Pantometria,’ published in 1591, declares, “My father, by his continual painful practices, assisted by demonstrations mathematical, was able, and sundry times hath by proportional glasses, duly situate in convenient angles, not only discovered things far off, read letters, numbered pieces of money, with the very coin and superscription thereof, cast by some of his friends of purpose, upon downs in open fields, but also, seven miles off, declared what hath been done that instant, in private places. He hath also, sundry times, by the sun-beams, fired powder and discharged ordnance half a mile and 183 more distant, and many other matters far more strange and rare, of which there are yet living divers witnesses.”
It is by no means unlikely, that persons accustomed to reflection, and imbued with a certain degree of curiosity, when handling spectacle-glasses, and amusing themselves with their magnifying powers and other properties, might sometimes hit upon the construction of a telescope; as it only requires two lenses of different focal distances to be held at a certain distance from each other, in order to show distant objects magnified. Nay, even one lens, of a long focal distance, is sufficient to constitute a telescope of a moderate magnifying power, as I shall show in the sequel. But such instruments, when they happened to be constructed accidentally, appear to have been kept as secrets, and confined to the cabinets of the curious, so that they never came into general use; and as their magnifying power would probably be comparatively small, the appearance of the heavenly bodies would not be much enlarged by such instruments—nor is it likely that they would be often directed to the heavens. On the whole, therefore, we may conclude that the period when instruments of this description came into general use, and were applied to useful purposes, was when Galileo constructed his first telescopes. 184
Before proceeding to a particular description of the different kinds of telescopes, I shall first give a brief description of the Camera Obscura, as the phenomena exhibited by this instrument tend to illustrate the principle of a refracting telescope.
The term Camera Obscura literally signifies a darkened vault or roof; and hence it came to denote a chamber, or box, or any other place made dark for the purpose of optical experiments. The camera obscura, though a simple, is yet a very curious and noble contrivance; as it naturally and clearly explains the manner in which vision is performed, and the principle of the telescope, and entertains the spectator with a most exquisite picture of surrounding objects, painted in the most accurate proportions and colours by the hand of nature. The manner of exhibiting the pictures of objects in a dark room is as follows:—In one of the window-shutters of a room which commands a good prospect of objects not very distant, a circular hole should be cut of four or five inches diameter. In this hole an instrument should be placed, called a Scioptric ball, which has three parts, a frame, a ball, and a lens. The ball has 185 a circular hole cut through the middle, in which the lens is fixed, and its use is, to turn every way so as to take in a view of objects on every side. The chamber should be made perfectly dark; and a white screen, or a large sheet of elephant paper, should be placed opposite to the lens, and in its focus, to receive the image. If then, the objects without be strongly enlightened by the sun, there will be a beautiful living picture of the scene delineated on the white screen, where every object is beheld in its proportions, and with its colours even more vivid than life; green objects appear in the picture more intensely green, and yellow, blue, red or white flowers appear much more beautiful in the picture than in nature; if the lens be a good one, and the room perfectly dark, the perspective is seen in perfection. The lights and shadows are not only perfectly just, but also greatly heightened; and, what is peculiar to this delineation, and which no other picture or painting can exhibit—the motions of all the objects are exactly expressed in the picture; the boughs of the trees wave, the leaves quiver, the smoke ascends in a waving form, the people walk, the children at their sports leap and run, the horse and cart move along, the ships sail, the clouds soar and shift their aspects, and all as natural as in the real objects; the motions being somewhat quicker, as they are performed in a more contracted scene.
These are the inimitable perfections of a picture, drawn by the rays of light as the only pencil in nature’s hand, and which are finished in a moment; for no sensible interval elapses before the painting is completed, when the ground on which it is painted is prepared and adjusted. In comparison of such a picture, the finest productions of the most celebrated artists, the proportions 186 of Raphael, the natural tints and colouring of Titian, and the shadowing of the Venetians, are but coarse and sorry daubings, when set in competition with what nature can exhibit by the rays of light passing through a single lens. The Camera obscura is at the same time the painter’s assistant, and the painter’s reproach. From the picture it forms he receives his best instructions, and is shown what he should endeavour to attain; and hence, too, he learns the imperfections of his art, and what it is impossible for him to imitate. As a proof of this, the picture formed in the dark chamber will bear to be magnified to a great extent, without defacing its beauty, or injuring the fineness of its parts; but the finest painted landscape, if viewed through a high magnifier will appear only as a coarse daubing.
The following scheme will illustrate what has been now stated respecting the dark chamber. EF represents a darkened room, in the side of which, IK, is made the circular hole V, in which, on the inside, is fixed the scioptric ball. At some considerable distance from this hole is exhibited a landscape of houses, trees, and other objects, ABCD, which are opposite to the window. The rays which flow from the different objects which compose this landscape, to the lens at V, and which pass through it, are converged to their respective foci, on the opposite wall of the chamber HG or on a white moveable screen placed in the focus of the lens, where they all combine to paint a lively and beautiful picture of the range of objects directly opposite, and on each side, so far as the lens can take in.
Though I have said, that a scioptric ball and socket are expedient to be used in the above experiment, yet where such an instrument is not at 187 hand, the lens may be placed in a short tube made of pasteboard or any other material, and fixed in the hole made in the window shutter. The only imperfection attending this method is, that the lens can exhibit those objects only which lie directly opposite the window.
figure 37.

Some may be disposed to consider it as an imperfection in this picture, that all the objects appear in an inverted position; as they must necessarily do, according to what we formerly stated respecting the properties of convex lenses, (p. 72). There are, however, different modes of viewing the picture as if it were erect. For, if we stand before the picture, and hold a common mirror against our breast at an acute angle with the picture, and look down upon it, we shall see all the images of the objects as if restored to their erect position; and by the reflection of the mirror, the 188 picture will receive such a lustre as will make it still more delightful. Or, if a large concave mirror were placed before the picture at such a distance, that its image may appear before the mirror, it will then appear erect and pendulous in the air in the front of the mirror. Or, if the image be received on a frame of paper, we may stand behind the frame, with our face towards the window, and look down upon the objects, when they will appear as if erect.
The experiment of the Camera Obscura may serve to explain and illustrate the nature of a common refracting telescope. Let us suppose, that the lens in the window-shutter represents the object-glass of a refracting telescope. This glass forms an image in its focus, which is in every respect an exact picture or representation of the objects before it; and consequently the same idea is formed in the mind, of the nature, form, magnitude, and colour of the object—whether the eye at the centre of the glass views the object itself, or the image formed in its focus. For, as formerly stated, the object and its image are both seen under the same angles by the eye placed at the centre of the lens. Without such an image as is formed in the camera obscura—depicted either in the tube of a telescope or in the eye itself—no telescope could possibly be formed. If we now suppose that, behind the image formed in the dark chamber, we apply a convex lens of a short focal distance to view that image, then the image will be seen distinctly, in the same manner as we view common objects, such as a leaf or a flower, with a magnifying glass; consequently, the object itself will be seen distinct and magnified. And, as the same image is nearer to one lens than the other, it will subtend a larger angle at the 189 nearest lens, and of course, will appear larger than through the other, and consequently the object will be seen magnified in proportion. For example, let us suppose the lens in the camera obscura, or the object lens of a telescope, to be five feet, or sixty inches focal distance, at this distance from the glass, an image of the distant objects opposite to it will be formed. If now, we place a small lens two inches focal distance beyond this point, or five feet two inches from the object-glass, the objects, when viewed through the small lens, will appear considerably magnified, and apparently much nearer than to the naked eye. The degree of magnifying power is in proportion to the focal distances of the two glasses; that is, in the present case, in the proportion of two inches, the focus of the small lens, to sixty inches, the focus of the object lens. Divide sixty by two, the quotient is thirty, which gives the magnifying power of such a telescope, that is, it represents objects thirty times nearer, or under an angle thirty times larger than to the naked eye. If the eye-glass, instead of being two inches, were only one and a half inch focus, the magnifying power would be in the proportion of one and a half to sixty, or forty times. If the eye-glass were three inches focus, the magnifying power would be twenty times; and so on, with regard to other proportions. In all cases, where a telescope is composed of only two convex lenses, the magnifying power is determined, by dividing the focal distance of the object-glass, by the focal distance of the eye-glass, and the quotient expresses the number of times the object is magnified, in length and breadth. This and various other particulars, will be more fully illustrated in the sequel.
In performing experiments with the camera 190 obscura in a darkened chamber, it is requisite that the following particulars be attended to:—1. That the lens be well figured, and free from any veins or blemishes that might distort the picture. 2. That it be placed directly against the object whose image we wish to see distinctly delineated. 3. The lens should be of a proper size both as to its breadth and focal distance. It should not be less than three or four feet focal distance, otherwise the picture will be too small, and the parts of objects too minute to be distinctly perceived; nor should it exceed fifteen or eighteen feet, as in this case the picture will be faint, and of course not so pleasing. The best medium as to focal distance, is from five to eight or ten feet. The aperture, too, or breadth of the glass, should not be too small, otherwise the image will be obscure, and the minute parts of it invisible for want of a sufficient quantity of light. A lens of six feet focal distance, for example, will require an aperture of at least two inches. Lenses of a shorter focal distance require less apertures, and those of a longer focal distance larger. But if the aperture be too large, the image will be confused, and indistinct, by the admission of too much light. 4. We should never attempt to exhibit the images of objects, unless when the sun is shining and strongly illuminating the objects, except in the case of very near objects placed in a good light. As one of the greatest beauties, in the phenomena of the dark chamber, consists in the exquisite appearance and contrast of light and shadows, nothing of this kind can be perceived but from objects directly illuminated by the sun. 5. A south window should never be used in the forenoon, as the sun cannot then enlighten the north side of an object; and besides, his rays would be 191 apt to shine upon the lens, which would make the picture appear with a confused lustre. An east window is best in the afternoon, and a western in the morning; but a north window is in most cases to be preferred, especially in the forenoon, when the sun is shining with his greatest strength and splendour. In general, that window ought to be used which looks to the quarter opposite to that in which the sun is shining.
The picture should be received upon a very white surface, as the finest and whitest paper, or a painted cloth, bordered with black; as white bodies reflect most copiously the incident rays, while black surfaces absorb them. If the screen could be bent into the concave segment of a sphere, of which the focal distance of the double convex lens which is used, is the radius, the parts of the picture adjacent to the extremities would appear most distinct. Sir D. Brewster informs us that, having tried a number of white substances of different degrees of smoothness, and several metallic surfaces, on which to receive the image, he happened to receive the picture on the silvered back of a looking-glass, and was surprised at the brilliancy and distinctness with which external objects were represented. To remove the spherical protuberances of the tin foil, he ground the surface very carefully with a bed of hones which he had used for working the plane specula of Newtonian telescopes. By this operation, which may be performed without injuring the other side of the mirror, he obtained a surface finely adapted for the reception of images. The minute parts of the landscape were formed with so much precision, and the brilliancy of colouring was so uncommonly fine, as to equal, if not exceed the images that are formed in the air by means of concave specula. 192
The following additional circumstances may be stated respecting the phenomena exhibited in the dark chamber. A more critical idea may be formed of any movement in the picture here presented than from observing the motion of the object itself. For instance, a man walking in a picture appears to have an undulating motion, or to rise up and down every step he takes, and the hands seem to move almost exactly like a pendulum; whereas scarcely any thing of this kind is observed in the man himself, as viewed by the naked eye. Again, if an object be placed just twice the focal distance from the lens without the room, the image will be formed at the same distance from the lens within the room, and consequently will be equal in magnitude to the object itself. The recognition of this principle may be of use to those concerned in drawing, and who may wish, at any time, to form a picture of the exact size of the object. If the object be placed further from the lens than twice its focal length, the image will be less than the object. If it be placed nearer, the image will be greater than the life. In regard to immoveable objects, such as houses, gardens, trees, &c., we may form the images of so many different sizes, by means of different lenses, the shorter focus making the lesser picture, and the longer focal distance the largest.
The experiments with the camera obscura, may likewise serve to illustrate the nature of vision, and the functions of the human eye. The frame or socket of the scioptric ball may represent the orbit of the natural eye. The ball, which turns every way, resembles the globe of the eye, moveable in its orbit. The hole in the ball may represent the pupil of the eye; the convex lens corresponds 193 to the crystalline humour, which is shaped like a lens, and contributes to form the images of objects on the inner part of the eye. The dark chamber itself, is somewhat similar to the internal part of the eye, which is lined all around, and under the retina, with a membrane, over which is spread a mucous of a very black colour. The white wall or frame of white paper to receive the picture of objects, is a fair representation of the retina of the eye, on which all the images of external objects are depicted. Such are some of the general points of resemblance between the apparatus connected with the dark chamber, and the organ of vision; but the human eye is an organ of such exquisite construction, and composed of such a number and variety of delicate parts, that it cannot be adequately represented by any artificial contrivance.
The darkened chamber is frequently exhibited in a manner somewhat different from what we have above described, as in the following scheme, (fig. 38) which is termed the revolving camera obscura. In this construction, KH represents a plane mirror or metallic reflector, placed at half a right angle to the convex lens HI, by which, rays proceeding from objects situated in the direction O are reflected to the lens, which forms an image of the objects on a round white table at T, around which several spectators may stand, and view the picture, as delineated on a horizontal plane. The reflector, along with its case, is capable of being turned round, by means of a simple apparatus connected with it, so as to take in, in succession, all the objects which compose the surrounding scene. But as the image here is received on a flat surface, the rays fm, en, will have to diverge farther than the central rays dc; and hence the 194 representation of the object, near the sides, will be somewhat distorted; to remedy which, the image should be received on a concave surface, as ab or PS. This is the general plan of those Camera Obscuras, fitted up in large wooden tents, which are frequently exhibited in our large cities, and removed occasionally from one town to another. Were an instrument of this kind fitted up on a small scale, a hole might be made in one of the sides, as at E, where the eye could be applied to view the picture. The focal distances of the lenses used in large instruments of this kind, are generally from eight to twelve feet, in which case they produce a telescopic effect upon distant objects, 195 so as to make them appear nearer than when viewed with the naked eye.
figure 38.
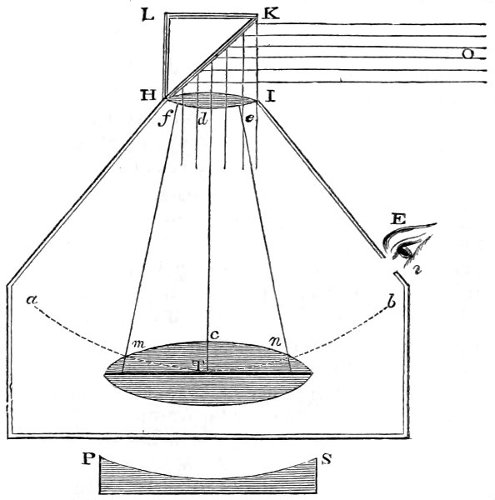
figure 39.
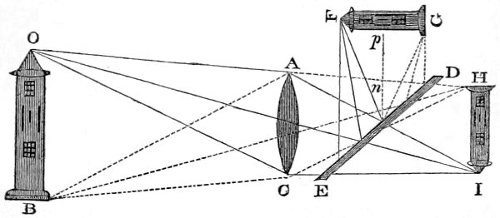
The camera obscura is frequently constructed in a portable form, so as to be carried about for the purpose of delineating landscapes. The following is a brief description of the instrument in this form. AC is a convex lens placed near the end of a tube or drawer, which is moveable in the side of a square box, within which is a plane mirror DE, reclining backward in an angle of forty-five degrees from the perpendicular pn. The pencils of rays flowing from the object OB, and passing through the convex lens—instead of proceeding forward and forming the image HI, are reflected upward by the mirror, and meet in points as FG, at the same distance at which they would have met at H and I, if they had not been intercepted by the mirror. At FG, the image of the object OB is received either on a piece of oiled paper, or more frequently on a plane unpolished glass, placed in the horizontal situation FG, which receives the images of all objects, opposite to the lens, and on which, or on an oiled paper placed upon it, their outlines may be traced by a pencil. The moveable tube on which the 196 lens is fixed, serves to adjust the focus for near and distant objects, till their images appear distinctly painted on the horizontal glass at FG. Above is shown the most common form of the box of this kind of Camera Obscura. A is the position of the lens, BC, the position of the mirror, D, the plane unpolished glass on which the images are depicted, GH a moveable top or screen to prevent the light from injuring the picture, and EF, the moveable tube.
figure 40.

The Daguerreotype.—An important, and somewhat surprising discovery has lately been made, in relation to the picture formed by the Camera Obscura. It is found, that the images formed by this instrument are capable of being indelibly fixed on certain surfaces previously prepared for the purpose, so that the picture is rendered permanent. When a Camera is presented to any object or landscape strongly illuminated by the sun, and the prepared ground for receiving the image is adjusted, and a certain time allowed to elapse till the rays of light produce their due effect, in a few minutes or even seconds, a picture of the objects opposite to the lens is indelibly impressed upon 197 the prepared plate, in all the accurate proportions and perspective, which distinguish the images formed in a dark chamber—which representations may be hung up in apartments, along with other paintings and engravings; and will likely retain their beauty and lustre for many years. These are pictures of nature’s own workmanship finished in an extremely short space of time, and with the most exquisite delicacy and accuracy. The effect is evidently owing to certain chemical properties in the rays of light; and opens a new field for experiment and investigation to the philosopher. The only defect in the picture is, that it is not coloured; but, in the progress of experiments on this subject, it is not unlikely that even this object may be accomplished, in which case, we should be able to obtain the most accurate landscapes and representations of all objects, which can possibly be formed. This art or discovery goes by the name of the Daguerreotype from M. Daguerre, a Frenchman, who is supposed to have been the first discoverer, and who received a large premium from the French government for disclosing the process, and making the discovery public. Several improvements and modifications, in reference to the preparation of the plates, have been made since the discovery was first announced, about the beginning of 1839; and the pictures formed on this principle, are frequently distinguished by the name of Photogenic drawings; and are now exhibited at most of our public scientific institutions.
This new science or art, has been distinguished by different names. It was first called Photography, from two Greek words, signifying writing by light: it was afterwards called the art of Photogenic Drawing, or drawing produced by light. M. Daguerre gave it the name of Heliography, or 198 writing by the sun, all which appellatives are derived from the Greek, and are expressive, in some degree, of the nature of the process. We shall, however, make use of the term Daguerreotype, derived from the name of the inventor.
As it does not fall within our plan to give any minute descriptions of the Daguerreotype process, we shall just give a few general hints in reference to it, referring those who wish for particular details, to the separate treatises which have been published respecting it. The first thing necessary to be attended to in this art is, the preparation of the plate on which the drawing is to be made. The plate consists of a thin leaf of copper, plated with silver; both metals together, not being thicker than a card. The object of the copper is simply to support the silver, which must be the purest that can be procured. But though the copper should be no thicker than to serve the purpose of support, it is necessary that it should be so thick as to prevent the plate from being warped, which would produce a distortion of the images traced upon it. This plate must be polished;—and for this purpose, the following articles are required—a phial of olive oil—some very fine cotton—pumice-powder, ground till it is almost impalpable, and tied up in a piece of fine muslin, thin enough to let the powder pass through without touching the plate when the bag is shaken. A little nitric acid diluted with sixteen times, by measure, its own quantity of water—a frame of wire on which to place the plate, when being heated—a spirit lamp to make the plate hot—a small box with inclined sides within, and having a lid to shut it up close—and a square board large enough to hold the drawing, and having catches at the side to keep it steady. 199
To the above prerequisites, a good Camera Obscura is, of course, essentially necessary. This instrument should be large enough to admit the plate of the largest drawing intended to be taken. The lens which forms the image of the object, should, if possible, be achromatic, and of a considerable diameter. In an excellent instrument of this description, now before me, the lens is an achromatic, about 3 inches diameter, but capable of being contracted to a smaller aperture. Its focal distance is about 17 inches; and the box, exclusive of the tube which contains the lens, is 15 inches long, 13½ inches broad, and 11 inches deep. It forms a beautiful and well-defined picture of every well-enlightened object to which it is directed.
Before the plate is placed in the camera, there are certain operations to be performed. 1. The surface of the plate should be made perfectly smooth, or highly polished. For this purpose, it must be laid flat, with the silver side upwards, upon several folds of paper for a bedding; and having been well polished in the usual way, the surface must be powdered equally and carefully with fine pumice enclosed in the muslin bag. Then taking a little cotton wool, dipped in olive oil, it must be rubbed over the plate with rounding strokes, and then crossing them by others which commence at right angles with the first. This process must be repeated frequently, changing the cotton, and renewing the pumice powder every time. A small portion of cotton must now be moistened with the diluted nitric acid, and applied equally to the whole surface. The next thing to be done is to make the plate thoroughly and equally hot, by holding the plate with a pair of pincers, by the corner, over a charcoal fire, and 200 when the plate is sufficiently hot, a white coating will be observed on the silver, which indicates that that part of the operation is finished. An even cold surface is next wanted, such as a metallic plate cooled almost to the freezing point by muriate of soda, and to this the heated plate must be suddenly transferred.
2. The next operation is to give the plate a coating of Iodine. This is accomplished by fixing the plate upon a board, and then putting it into a box containing a little dish with iodine divided into small pieces, with its face downward, and supported with small brackets at the corners. In this position, the plate must remain till it assume a full gold colour, through the condensation of the iodine on its surface—which process should be conducted in a darkened apartment. The requisite time for the condensation of the iodine varies from five minutes to half an hour. When this process is satisfactorily accomplished, the plate should be immediately fixed in a frame with catches and bands, and placed in the Camera; and the transference from one receptacle to another should be made as quickly as possible, and with only so much light as will enable the operator to see what he is doing.
3. The next operation is to obtain the drawing. Having placed the Camera in front of the scene to be represented, and the lens being adjusted to the proper focus, the ground-glass of the Camera is withdrawn, and the prepared plate is substituted for it; and the whole is left till the natural images are drawn by the natural light from the object. The time necessary to leave the plate for a complete delineation of the objects, depends upon the intensity of the light. Objects in the shade will require more time for their delineation than 201 those in the broad light. The full clear light of the south of Europe, Spain, Italy, and particularly, the more glowing brilliancy of tropical countries, will effect the object much more speedily than the duller luminosity of a northern clime. Some hours of the day are likewise more favourable than others. Daguerre states, that ‘the most favourable, is from 7 A.M. to 3 o’clock P.M., and that a drawing could be effected in Paris in 3 or 4 minutes, in June and July, which would require 5 or 6, in May and August, and 7 or 8 in April and September.’ In the progress of this art, at the present time, portraits and other objects are frequently delineated in the course of a few seconds.
4. Immediately after removing the plate from the Camera, it is next placed over the vapour of mercury, which is placed in a cup at the bottom of a box, and a spirit lamp applied to its bottom, till the temperature rise to 140 of Fahrenheit. This process is intended to bring out the image, which is not visible when withdrawn from the Camera; but in the course of a few minutes a faint tracery will begin to appear, and in a very short time the figure will be clearly developed.
5. The next operation is to fix the impression. In order to this, the coating on which the design was impressed must be removed, to preserve it from being decomposed by the rays of light. For this purpose, the plate is placed in a trough containing common water, plunging, and withdrawing it immediately, and then plunging it into a solution of salt and water, till the yellow coating has disappeared.
Such is a very brief sketch of the photogenic processes of Daguerre. Other substances, however, more easily prepared, have been recommended 202 by Mr. Talbot, F.R.S., who appears, about the same time, to have invented a process somewhat similar to that of Daguerre. The following are his directions for the preparation of Photogenic Paper.
The paper is to be dipped into a solution of salt in water, in the proportion of half an ounce of salt to half a pint of water. Let the superfluous moisture drain off, and then, laying the paper upon a clean cloth, dab it gently with a napkin, so as to prevent the salt collecting in one spot more than another. The paper is then to be pinned down by two of its corners on a drawing board, by means of common pins, and one side washed or wetted with the Photogenic fluid, using the brush prepared for that purpose, and taking care to distribute it equally. Next dry the paper as rapidly as you can at the fire, and it will be fit for use for most purposes. If, when the paper is exposed to the sun’s rays, it should assume an irregular tint, a very thin extra wash of the fluid will render the colour uniform, and at the same time somewhat darker. Should it be required to make a more sensitive description of paper, after the first application of the fluid, the solution of salt should be applied, and the paper dried at the fire. Apply a second wash of the fluid, and dry it at the fire again: employ the salt a third time, dry it,—and one application more of the fluid will, when dried, have made the paper extremely sensitive. When slips of such papers, differently prepared, are exposed to the action of day light, those which are soonest affected by the light, by becoming dark, are the best prepared.
When photogenic drawings are finished in a perfect way, the designs then taken on the plate or paper are exceedingly beautiful and correct, 203 and will bear to be inspected with a considerable magnifying power, so that the most minute portions of the objects delineated may be distinctly perceived. We have seen portraits, finished in this way by a London artist, with an accuracy which the best miniature painter could never attempt—every feature being so distinct, as to bear being viewed with a deep magnifier. And in landscapes and buildings, such is the delicacy and accuracy of such representations, that the marks of the chisel and the crevices in the stones may frequently be seen by applying a magnifying lens to the picture; so that we may justly exclaim, in the words of the Poet: ‘Who can paint like nature!.’ That LIGHT—which is the first-born of Deity, which pervades all space, and illuminates all worlds—in the twinkling of an eye, and with an accuracy which no art can imitate, depicts every object in its exact form and proportions, superior to every thing that human genius can produce.
The Photogenic art, in its progress, will doubtless be productive of many highly interesting and beneficial effects. It affords us the power of representing, by an accurate and rapid process, all the grand and beautiful objects connected with our globe—the landscapes peculiar to every country—the lofty ranges of mountains which distinguish Alpine regions—the noble edifices which art has reared—the monumental remains of antiquity—and every other object which it would be interesting for human beings to contemplate; so that in the course of time, the general scenery of our world, in its prominent parts, might be exhibited to almost every eye. The commission of the French Chambers, when referring to this art, has the following remark, ‘To copy the 204 millions upon millions of hieroglyphics which cover even the exterior of the great monuments of Thebes and Memphis, of Carnac, &c., would require scores of years and legions of designers. By the assistance of the Daguerreotype, a single man could finish that immense work.’—This instrument lays down objects, which the visual organs of man would overlook, or might be unable to perceive, with the same minuteness and nicety, that it delineates the most prominent features of a landscape. The time-stained excrescences on a tree, the blades of grass, the leaf of a rose, the neglected weed, the moss on the summit of a lofty tower, and similar objects, are traced with the same accuracy as the larger objects in the surrounding scene.
It is not improbable, likewise, that this art (still in its infancy) when it approximates to perfection, may enable us to take representations of the sublime objects in the heavens. The sun affords sufficient light for this purpose; and there appears no insurmountable obstacle in taking, in this way, a highly magnified picture of that luminary, which shall be capable of being again magnified by a powerful microscope. It is by no means improbable, from experiments that have hitherto been made, that we may obtain an accurate delineation of the lunar world from the moon herself. The plated disks prepared by Daguerre receive impressions from the action of the lunar rays to such an extent as permits the hope that photographic charts of the moon may soon be obtained; and, if so, they will excel in accuracy all the delineations of this orb that have hitherto been obtained; and if they should bear a microscopic power, objects may be perceived on the lunar surface which have hitherto been invisible. Nor 205 is it impossible that the planets Venus, Mars, Jupiter and Saturn, may be delineated in this way, and objects discovered which cannot be descried by means of the telescope. It might perhaps be considered as beyond the bounds of probability to expect that even distant Nebulæ, might thus be fixed, and a delineation of their objects produced which shall be capable of being magnified by microscopes. But we ought to consider that the art is yet only in its infancy—that plates of a more delicate nature than those hitherto used, may yet be prepared, and that other properties of light may yet be discovered, which shall facilitate such designs. For, we ought now to set no boundaries to the discoveries of science, and to the practical applications of scientific discovery which genius and art may accomplish.
In short, this invention leads to the conclusion, that we have not yet discovered all the wonderful properties of that Luminous Agent which pervades the universe, and which unveils to us its beauties and sublimities—and that thousands of admirable objects and agencies may yet be disclosed to our view through the medium of light, as philosophical investigators advance in their researches and discoveries. In the present instance, as well as in many others, it evidently appears, that the Creator intends, in the course of his providence, by means of scientific researches, gradually to open to the view of the inhabitants of our world the wonders, the beauties and the sublimities of his vast creation, to manifest his infinite wisdom, and his superabundant goodness, and to raise our souls to the contemplation and the love of Him who is the original source of all that is glorious and beneficent in the scene of nature. 206
In order to understand the principle on which telescopes represent distant objects as magnified, it may be expedient to explain what is meant by the angle of vision, and the apparent magnitudes under which different objects appear, and the same object, when placed at different distances.
figure 40*.
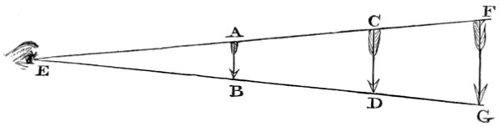
The optical angle is the angle contained under two right lines drawn from the extreme points of an object to the eye. Thus AEB or CED (fig. 40*.) is the optical or visual angle, or the angle under which the object AB or CD, appears to the eye at E. These two objects, being at different distances, are seen under the same angle, although CD is evidently larger than AB. On the retina 207 of the eye, their images are exactly of the same size, and so is the still larger object FG.
figure 41.
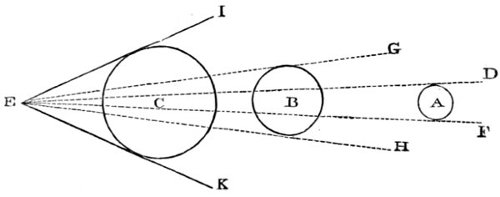
The apparent magnitude of objects denotes their magnitude as they appear to us, in contradistinction from their real or true magnitude, and it is measured by the visual angle; for whatever objects are seen under the same or equal angles appear equal, however different their real magnitudes. If a half-crown or half-dollar be placed at about 120 yards from the eye, it is just perceptible as a visible point, and its apparent magnitude, or the angle under which it is seen, is very small. At the distance of thirty or forty yards, its bulk appears sensibly increased, and we perceive it to be a round body; at the distance of six or eight yards, we can see the king or queen’s head engraved upon it; and at the distance of eight or ten inches from the eye it will appear so large, that it will seem to cover a large building placed within the distance of a quarter of a mile, in other words, the apparent magnitude of the half-crown held at such a distance, will more than equal that of such a building, in the picture on the retina, owing to the increase of the optical angle. If we suppose A (fig. 41.) to represent the apparent size of the half-crown at nine yards distance, then we say it 208 is seen under the small angle FED. B will represent its apparent magnitude at 4½ yards distant under the angle HEG, and the circle C, its apparent magnitude at 3 yards distant, under the large angle KEI.
figure 42.
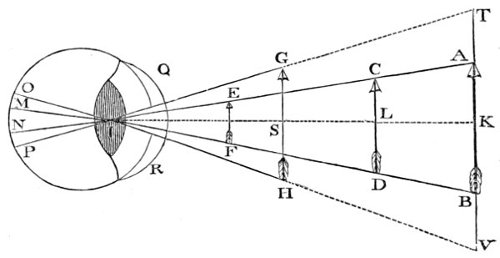
This may be otherwise illustrated by the following figure. Let AB (fig. 42.) be an object viewed directly by the eye QR. From each extremity A and B draw the lines AN,BM, intersecting each other in the crystalline humour in I: then is AIB the optical angle which is the measure of the apparent magnitude or length of the object AB. From an inspection of this figure, it will evidently appear that the apparent magnitudes of objects will vary according to their distances. Thus AB, CD, EF, the real magnitudes of which are unequal, may be situated at such distances from the eye, as to have their apparent magnitudes all equal, and occupying the same space on the retina MN, as here represented. In like manner, objects of equal magnitude, placed at unequal distances, will appear unequal. The 209 objects AB and GH which are equal, being situated at different distances from the eye, GH will appear under the large angle TIV, or as large as an object TV, situated at the same place as the object AB, while AB appears under the smaller angle AIB. Therefore the object GH is apparently greater than the object AB, though it is only equal to it. Hence it appears that we have no certain standard of the true magnitude of objects, by our visual perception abstractly considered, but only of the proportions of magnitude.
In reference to apparent magnitudes, we scarcely ever judge any object to be so great or so small as it appears to be, or that there is so great a disparity in the visible magnitude of two equal bodies at different distances from the eye. Thus, for example, suppose two men, each six feet 3 inches high, to stand directly before us, one at the distance of a pole, or 5½ yards, and the other at the distance of 100 poles, or 550 yards—we should observe a considerable difference in their apparent size, but we should scarcely suppose, at first sight, that the one nearest the eye appeared a hundred times greater than the other, or that, while the nearest one appeared 6 feet 3 inches high, the remote one appeared only about three fourths of an inch. Yet such is in reality the case; and not only so, but the visible bulk or area of the one is to that of the other, as the square of these numbers, namely as 10,000 to 1; the man nearest us presenting to the eye a magnitude or surface ten thousand times greater than that of the other. Again, suppose two chairs standing in a large room, the one 21 feet distance from us, and the other 3 feet—the one nearest us will appear 7 times larger both in length and breadth, than the more distant one, and consequently, its visible area 210 49 times greater. If I hold up my finger at 9 inches distant from my eye, it seems to cover a large town a mile and a half in extent, situated at 3 miles distant; consequently, the apparent magnitude of my finger, at 9 inches distant from the organ of vision, is greater than that of the large town at 3 miles distance, and forms a larger picture on the retina of the eye. When I stand at the distance of a foot from my window, and look through one of the panes to a village less than a quarter of a mile distant, I see, through that pane, nearly the whole extent of the village, comprehending two or three hundred houses; consequently, the apparent magnitude of the pane is equal to nearly the extent of the village, and all the buildings it contains do not appear larger than the pane of glass in the window, otherwise, the houses and other objects which compose the village could not be seen through that single pane. For, if we suppose a line drawn from one end of the village, passing through the one side of the pane, and another line drawn from the other end, and passing through the other side of the pane to the eye, these lines would form the optical angle under which the pane of glass and the village appears. If the pane of glass be fourteen inches broad, and the length of the village 2640 yards, or half a mile—this last lineal extent is 6,788 times greater than the other, and yet they have the same apparent magnitude in the case supposed.
Hence we may learn the absurdity and futility of attempting to describe the extent of spaces in the heavens, by saying, that a certain phenomenon was two or three feet or yards distant from another, or that the tail of a comet appeared several yards in length. Such representations can convey 211 no definite ideas in relation to such magnitudes, unless it be specified at what distance from the eye, the foot or yard is supposed to be placed. If a rod, a yard in length, be held at nine inches from the eye, it will subtend an angle, or cover a space in the heavens, equal to more than one fourth of the circumference of the sky, or about one hundred degrees. If it be eighteen inches from the eye, it will cover a space equal to fifty degrees; if at three feet, twenty-five degrees, and so on in proportion to the distance from the eye; so that we can form no correct conceptions of apparent spaces or distances in the heavens, when we are merely told that two stars, for example, appear to be three yards distant from each other. The only definite measure we can use, in such cases, is that of degrees. The sun and moon are about half a degree in apparent diameter, and the distance between the extreme stars in Orion’s belt, three degrees, which measures being made familiar to the eye, may be applied to other spaces of the heavens, and an approximate idea conveyed of the relative distances of objects in the sky.
From what has been stated above, it is evident that the magnitude of objects may be considered in different points of view. The true dimensions of an object, considered in itself, give what is called its real or absolute magnitude; and the opening of the visual angle determines the apparent magnitude. The real magnitude, therefore, is a constant quantity; but the apparent magnitude varies continually with the distance, real or imaginary; and therefore, if we always judged of the dimensions of an object from its apparent magnitude, every thing around us would, in this respect, be undergoing very sensible variations, which might lead us into strange and serious mistakes. A fly, near 212 enough to the eye, might appear under an angle as great as an elephant at the distance of twenty feet, and the one be mistaken for the other. A giant eight feet high, seen at the distance of twenty-four feet, would not appear taller than a child two feet in height, at the distance of six feet; for both would be seen nearly under the same angle. But our experience generally prevents us from being deceived by such illusions. By the help of touch, and by making allowance for the different distances at which we see particular objects, we learn to correct the ideas we might otherwise form from attending to the optical angle alone, especially in the case of objects that are near us. By the sense of touch we acquire an impression of the distance of an object; this impression combines itself with that of the apparent magnitude, so that the impression which represents to us the real magnitude is the product of these two elements. When the objects, however, are at a great distance, it is more difficult to form a correct estimate of their true magnitudes. The visual angles are so small, that they prevent comparison; and the estimated bulks of the objects depend in a great measure upon the apparent magnitudes; and thus an object situated at a great distance, appears to us much smaller than it is in reality. We also estimate objects to be nearer or farther distant according as they are more or less clear, and our perception of them more or less distinct and well defined; and likewise, when several objects intervene between us and the object we are particularly observing. We make a sort of addition of all the estimated distances of intermediate objects, in order to form a total distance of the remote object, which in this case appears to be farther off than if the intervening space were unoccupied. It is 213 generally estimated that no terrestrial object can be distinctly perceived, if the visual angle it subtends be less than one minute of a degree; and that most objects become indistinct, when the angle they subtend at the pupil of the eye is less than six minutes.
We have deemed it expedient to introduce the above remarks on the apparent magnitude of objects, because the principal use of a telescope is to increase the angle of vision, or to represent objects under a larger angle than that under which they appear to the naked eye, so as to render the view of distant objects more distinct, and to exhibit to the organ of vision those objects which would otherwise be invisible. A telescope may be said to enlarge an object just as many times as the angle under which the instrument represents it, is greater than that under which it appears to the unassisted eye. Thus the moon appears to the naked eye under an angle of about half a degree; consequently a telescope magnifies 60 times if it represents that orb under an angle of 30 degrees; and if it magnified 180 times, it would exhibit the moon under an angle of 90 degrees, which would make her appear to fill half of the visible heavens, or the space which intervenes from the horizon to the zenith. 214
There are two kinds of telescopes, corresponding to two modes of vision, namely, those which perform their office by refraction through lenses, and those which magnify distant objects by reflection from mirrors. The telescope which is constructed with lenses, produces its effects solely by refracted light, and is called a Dioptric, or refracting telescope. The other kind of telescope produces its effects partly by reflection, and partly by refraction, and is composed both of mirrors and lenses; but the mirrors form the principal part of the telescope; and therefore such instruments are denominated reflecting telescopes. In this chapter I shall describe the various kinds of refracting telescopes.
This telescope is named after the celebrated Galileo, who first constructed, and probably invented it in the year 1609. It consists of only two glasses, a convex glass next the object, and a 215 concave next the eye. The convex is called the object-glass, and the concave to which the eye is applied, is called the eye-glass. Let C (fig. 43.) represent the convex object-glass, presented to any object in the direction DEI, so that the rays fall parallel upon it;—if these rays, after passing through it, were not intercepted by the concave lens K, they would pass on, and cross each other in the focus F, where an inverted image of the object would be formed. But the concave lens K, the virtual focus of which is at F, being interposed, the rays are not suffered to converge to that point, but are made less convergent,19 and enter the pupil almost parallel, as GH, and are converged by the humours of the eye to their proper foci on the retina. The object, through this telescope, is seen upright, or in its natural position, because the rays are not suffered to come to a focus, so as to form an inverted picture. The concave eye-glass is placed as far within the focus of the object-glass, as is equal to its own virtual focus; and the magnifying power is as the focal 216 length of the object-glass to that of the eye-glass, that is, as CF to BF. Thus, suppose the focus of the object-glass to be 10 inches, and the focus of the eye-glass to be 1 inch, the magnifying power will be 10 times—which is always found by dividing the focal length of the object-glass by that of the eye-glass. The interval between the two glasses, in this case, will be 9 inches, which is the length of the telescope, and the objects seen through it will appear under an angle ten times greater than they do to the naked eye. These propositions might be proved mathematically; but the process is somewhat tedious and intricate, and might not fully be understood by general readers. I shall therefore only mention some of the general properties of this telescope, which is now seldom used, except for the purpose of opera-glasses.
figure 43

1. The focal distance of the object-glass must be greater than that of the eye-glass, otherwise it would not magnify an object: if the focal distance of the eye-glass were greater than that of the object-glass, it would diminish objects, instead of magnifying them. 2. The visible area of the object is greater, the nearer the eye is to the glass; and it depends on the diameter of the pupil of the eye, and on the breadth of the object-glass; consequently the field of view in this telescope is very small. 3. The distinctness of vision in this construction of a telescope exceeds that of almost any other. This arises from the rays of light proceeding from the object directly through the lenses, without crossing or intersecting each other; whereas in the combination of convex lenses, they intersect one another to form an image in the focus of the object-glass, and this image is magnified by the eye-glass with all its imperfections and distortions. The thinness of the centre of the 217 concave lens also contributes to distinctness. 4. Although the field of view in this telescope is very small, yet where no other telescope can be procured, it might be made of such a length as to show the spots on the Sun, the crescent of Venus, the satellites of Jupiter, and the ring of Saturn; and, requiring only two glasses, it is the cheapest of all telescopes. It has been found that an object-lens 5 feet focal distance, will bear a concave eye-glass of only 1 inch focal distance, and will consequently magnify the diameters of the planets 60 times, and their surfaces 3600 times, which is sufficient to show the phenomena now stated. And, although only a small portion of the sun and moon can be seen at once, yet Jupiter and all his satellites may sometimes be seen at one view; but there is some difficulty in finding objects with such telescopes. 5. Opera-glasses, which are always of this construction, have the object-lens generally about 6 inches focus and 1 inch diameter, with a concave eye-glass of about 2 inches focus. These glasses magnify about 3 times in diameter, have a pretty large field, and produce very distinct vision. When adjusted to the eye, they are about 4 inches in length. To the object end of an opera-glass there is sometimes attached a plane mirror, placed at an angle of 45 degrees, for the purpose of viewing objects on either side of us. By this means, in a theatre or assembly, we can take a view of any person without his having the least suspicion of it, as the glass is directed in quite a different direction. The instrument with this appendage is sometimes called a Polemoscope. 218
The astronomical telescope is the most simple construction of a telescope, composed of convex lenses only, of which there are but two essentially necessary, though a third is sometimes added to the eye-piece for the purpose of enlarging the field of view. Its construction will be easily understood from a description of the following figure. Its two essential parts are, an object-glass AD, and an eye-glass EY, so combined in a tube that the focus F of the object-glass is exactly coincident with the focus of the eye-glass. Let OB (fig. 44.) represent a distant object, from which rays nearly parallel proceed to the object-lens AD. The rays passing through this lens will cross at F, and form an image of the object at IM. This image forms as it were an object to the eye-glass EY, which is of a short focal distance, and the eye is thus enabled to contemplate the object as if it were brought much nearer than it is in reality. For the rays, which after crossing proceed in a divergent state, fall upon the lens EY, as if they proceeded from a real object situated at F. All that is effected therefore, by such a telescope is, to form an image of 219 a distant object by means of the object-lens, and then to give the eye such assistance as is necessary for viewing that image as near as possible, so that the angle it shall subtend at the eye shall be very large compared with the angle which the object itself would subtend in the same situation.
figure 44.

Here it may be expedient to explain, 1. how this arrangement of glasses shows distant objects distinctly, and 2. the reason why objects appear magnified when seen through it. As to the first particular, it may be proved as follows:—The rays OA and BD, which are parallel before they fall upon the object-glass, are by this glass refracted and united at its focus: In order, then, to distinct vision, the eye-glass must re-establish the parallelism of the rays,—which is effected by placing the eye-glass so that its focus may be at F, and consequently the rays will proceed from it parallel to each other and fall upon the eye in that direction. For distinct vision is produced by parallel rays. 2. The reason why the object appears magnified will appear, if we consider that, if the eye viewed the object from the centre of the object-glass, it would see it under the angle OCB; let OC and BC then be produced to the focus of the glass, they will then limit the image IM formed in the focus. If then, two parallel rays are supposed to proceed to the eye-glass EY, they will be converged to its focus H, and the eye will see the image under the angle EHY. The apparent magnitude of the object, therefore, as seen by the naked eye, is to the magnitude of the image as seen through the telescope, as OCB to EHY, or as the distance CF to the distance FG, in other words, as the focal length of the object-glass to that of the eye-glass.
It is obvious from the figure, that, through this 220 telescope, all objects will appear inverted; since the object OB is depicted by the object-glass in an inverted position at IM, and in this position is viewed by the eye-glass EY; and, therefore this kind of telescope is not well adapted for viewing terrestrial objects, since it exhibits the tops of trees, houses, and other objects as undermost, and the heads of people as pointing downwards. But this circumstance is of no consequence with respect to the heavenly bodies, since they are round, and it can make little difference to an observer which side of a globular body appears uppermost or undermost. All astronomical refracting telescopes invert objects; but they are preferred to any other telescopes, because they have few glasses, and consequently more light. This telescope however, can be transformed into a common day telescope for land objects, by the addition of two other eye-glasses, as we shall afterwards explain; but in this case a quantity of light is lost by refraction at each lens; for there is scarcely any transparent substance that transmits all the rays of light that fall upon it.
The magnifying power of this telescope is found by dividing the focal distance of the object-glass by the focal distance of the eye-glass: the quotient gives the magnifying power, or the number of times that the object seen through the telescope, appears larger or nearer than to the naked eye. Thus, for example, if the focal distance of the object-glass be 28 inches, and the focal distance of the eye-glass 1 inch, the magnifying power will be 28 times. If we would enlarge the telescope and select an object-glass 10 feet, or 120 inches focus, an eye-glass of 2 inches focal length might be applied, and then the diameter of objects would be magnified 60 times, and their 221 surfaces 3600 times. If we would use an object-glass of 100 feet, it would be necessary to select an eye-glass about 6 inches focus, and the magnifying power would be 200 times, equal to 1200 inches divided by 6. Since, then, the power of magnifying depends on the proportion of the focal length of the object and eye-glasses, and this proportion may be varied to any degree, it may seem strange to some that a short telescope of this kind will not answer that purpose as well as a long one. For instance, it may be asked why an object-glass of 10 feet focus, may not be made to magnify as much, as one of 100 feet focal length, by using an eye-glass of half an inch focus, in which case, the magnifying power would be 240 times? But it is to be considered, that if the power of magnifying be increased, while the length of the telescope remains the same, it is necessary to diminish the focal length of the eye-glass in the same proportion, and this cannot be done on account of the great distortion and colouring which would then appear in the image, arising both from the deep convexity of the lens and the different refrangibility of the rays of light. It is found that the length of common refracting telescopes must be increased in proportion to the square of the increase of their magnifying power; so that in order to magnify twice as much as before, with the same light and distinctness, the telescope must be lengthened four times; to magnify 3 times as much, 9 times; and to magnify four times as much, sixteen times; that is—suppose a telescope of 3 feet to magnify 33 times,—in order to procure a power four times as great, or 132 times, we must extend the telescope to the length of 48 feet, or 16 times the length of the other. Much likewise depends upon the breadth or aperture of the object-glass. If it 222 be too small, there will not be sufficient light to illuminate the object; and if it be too large, the redundance of light will produce confusion in the image.
The following table, constructed originally by Huygens, and which I have re-calculated and corrected, shows the linear aperture, the focal distance of the eye-glass, and the magnifying power of astronomical telescopes of different lengths, which may serve as a guide to those who wish to construct telescopes of this description.
| Focal distance of the object-glass. | Linear aperture of the object-glass. | Focal distance of the eye-glass. | Magnifying power. | ||
|---|---|---|---|---|---|
| Feet. | Inch. | Dec. | Inch. | Dec. | |
| 1 | 0. | 545 | 0. | 605 | 20 |
| 2 | 0. | 76 | 0. | 84 | 20.5 |
| 3 | 0. | 94 | 1. | 04 | 34.6 |
| 4 | 1. | 08 | 1. | 18 | 40 |
| 5 | 1. | 21 | 1. | 33 | 45 |
| 6 | 1. | 32 | 1. | 45 | 50 |
| 7 | 1. | 43 | 1. | 58 | 53 |
| 8 | 1. | 53 | 1. | 69 | 56.8 |
| 9 | 1. | 62 | 1. | 78 | 60.6 |
| 10 | 1. | 71 | 1. | 88 | 63.8 |
| 15 | 2. | 10 | 2. | 30 | 78 |
| 20 | 2. | 43 | 2. | 68 | 89.5 |
| 30 | 3. | 00 | 3. | 28 | 109 |
| 40 | 3. | 43 | 3. | 76 | 127 |
| 50 | 3. | 84 | 4. | 20 | 142 |
| 60 | 4. | 20 | 4. | 60 | 156 |
| 70 | 4. | 55 | 5. | 00 | 168 |
| 80 | 4. | 83 | 5. | 35 | 179 |
| 90 | 5. | 15 | 5. | 65 | 190 |
| 100 | 5. | 40 | 5. | 95 | 200 |
| 120 | 5. | 90 | 6. | 52 | 220 |
In the above table, the first column expresses the focal length of the object-glass in feet; the second column, the diameter of the aperture20 of the 223 object-glass, the third column, the focal distance of the eye-glass, and the fourth, the magnifying power, which is found by reducing the feet in the first column to inches, and dividing by the numbers in the third column. From this table it appears that, in order to obtain a magnifying power of 168 times, by this kind of telescope, it is requisite to have an object-glass of 70 feet focal distance, and an eye-glass five inches focus, and that the aperture of the object-glass ought not to be more than about 4½ inches diameter. To obtain a power of 220 times requires a length of 120 feet.
The following is a summary view of the properties of this telescope. 1. The object is always inverted. 2. The magnifying power is always in the proportion of the focal distance of the object-glass to the eye-glass. 3. As the rays emerging from the eye-glass, should be rendered parallel for every eye, there is a small sliding tube next the eye, which should be pushed out or in till the object appears distinct. When objects are pretty near, this tube requires to be pulled out a little. These circumstances require to be attended to in all telescopes. 4. The apparent magnitude of an object is the same wherever the eye be placed, but the visible area, or field of view, is the greatest when the eye is nearly at the focal distance of the eye-glass. 5. The visual angle depends on the breadth of the eye-glass; for it is equal to the angle which the eye-glass subtends at the object-glass; but the breadth of the eye-glass cannot be increased beyond a certain limit, without producing colouring and distortion.
If the general principles on which this telescope is constructed be thoroughly understood, it will be quite easy for the reader to understand the 224 construction of all the other kinds of telescopes, whether refracting or reflecting. A small astronomical telescope can be constructed in a few moments, provided one has at hand the following lenses:—1. A common reading-glass, eight or ten inches focal distance; 2. A common magnifying lens, such as watchmakers or botanists use, of about 1½ or 2 inches focus. Hold the reading-glass—suppose of ten inches focus—in the left hand opposite any object, and the magnifying lens of two inches focus, in the right hand near the eye, at twelve inches distance from the other in a direct line, and a telescope is formed which magnifies five times. I have frequently used this plan, when travelling, when no other telescope was at hand.
The Aerial is a refracting telescope of the kind we have now described, intended to be used without a tube in a dark night; for the use of a tube is not only to direct the glasses, but to make the place dark where the images are formed. It appears from the preceding table inserted above, that we cannot obtain a high magnifying power, with the common astronomical telescope, without making it of an extreme length, in which case the glasses are not manageable in tubes—which are either too slight and apt to bend, or too heavy and unwieldy if made of wood, iron or other strong materials. The astronomers of the seventeenth century, feeling such inconveniences in making celestial observations with long tubes, contrived a method of using the glasses without tubes. Hartsocker, an eminent optician, contrived to fix them 225 at the top of a tree, a high wall, or the roof of a house; but the celebrated Huygens, who was not only an astronomer, but also an excellent mechanic, made considerable improvements in the method of using an object-glass without a tube. He placed it at the top of a very long pole, having previously enclosed it in a short tube, which was made to turn in all directions by means of a ball and socket. The axis of this tube he could command with a fine silken string, so as to bring it into a line with the axis of another short tube which he held in his hand, and which contained the eye-glass. The following is a more particular description of one of these telescopes. On the top of a long pole or mast ab (fig. 45), is fixed a board moveable up and down in the channel cd: e is a perpendicular arm fixed to it, and ff is a transverse board that supports the object glass enclosed in the tube i, which is raised or lowered by means of the silk cord rl; gg is an endless rope with a weight h, by which the apparatus of the object-glass is counterpoised; kl is a stick fastened to the tube i; m the ball and socket, by means of which the object-glass is moveable every way: and to keep it steady, there is a weight n suspended by a wire; l is a short wire to which the thread rl is tied; o is the tube which holds the eye-glass; q the stick fixed to this tube, s a leaden bullet, and t a spool to wind the thread on; u is pins for the thread to pass through; x the rest for the observer to lean upon, and y the lantern. Fig. 46 is an apparatus contrived by M. de la Hire for managing the object-glass; but which it would be too tedious particularly to describe. To keep off the dew from the object-glass, it was sometimes included in a pasteboard tube, made of spongy paper, to absorb the humidity of the air. 226 And to find an object more readily, a broad annulus of white pasteboard was put over the tube that carried the eye-glass; upon which the image of the object being painted, an assistant who perceived it, might direct the tube of the eye-glass into its place.
figure 45.
fig 46.
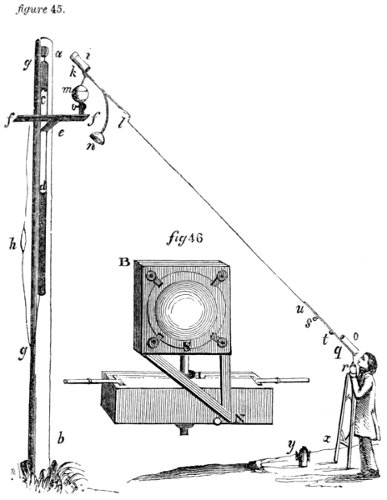
Such was the construction of the telescopes with which Hevelius, Huygens, Cassini, and other eminent astronomers of the seventeenth century made their principal discoveries. With such telescopes, Huygens discovered the fourth satellite 227 of Saturn, and determined that this planet was surrounded with a ring; and with the same kind of instrument Cassini detected the first, second, third, and fifth, satellites of Saturn, and made his other discoveries. When the night was very dark, they were obliged to make the object-glass visible, by means of a lantern so constructed as to throw the rays of light up to it in a parallel direction. In making such observations, they must have taken incredible pains, endured much cold and fatigue, and subjected themselves to very great labour and expense—which almost makes us wonder at the discoveries they were instrumental in bringing to light—and should make modern philosophers sensible of the obligations they are under to such men as Newton and Dollond, through whose inventions such unwieldy instruments are no longer necessary. Telescopes of the description now stated were made of all sizes, from 30 to above 120 feet in length. Divini at Rome, and Campani at Bologna, were famed as makers of the object-glasses of the long focal distance to which we have alluded, who sold them for a great price, and took every method to keep the art of making them a secret. It was with telescopes made by Campani, that Cassini made his discoveries. They were made by the express order of Louis XIV, and were of 86, 100, and 136 Paris feet in focal length. M. Auzout made one object-glass of 600 feet focus; but he was never able to manage it, so as to make any practical observations with it. Hartsocker is said to have made some of a still greater focal length. The famous aerial telescope of Huygens was 123 feet in focal length, with six inches of aperture. At his death, he bequeathed it to the Royal Society of London, in whose possession it still remains. It required 228 a pole of more than a hundred feet high, on which to place the object-glass for general observations. It was with this glass, that Dr. Derham made the observations to which he alludes in his preface to his ‘Astro-Theology.’ When this glass was in the possession of Mr. Cavendish, it was compared with one of Mr. Dollond’s forty-six inch treble object-glass Achromatics, and the gentlemen who were present at the trial, said that ‘the Dwarf was fairly a match for the Giant.’ It magnified 218 times, and the trouble of managing it, was said to be extremely tiresome and laborious.
figure 47.

This telescope is constructed on the same principle as the astronomical telescope already described, with the addition of two or three glasses. In fig. 47, OB represents a distant object, LN, the object glass, which forms the image IM in its focus, which is, of course, in an inverted position, and, if the eye were applied at the lens EE, the object would appear, exactly as through the astronomical telescope, every object being apparently turned upside down. To remedy this inconvenience, there are added two other glasses FF and GG, by which a second image is formed from the first, in the same position as the object. In 229 order to effect this, the first of these two glasses, namely FF, is placed at twice its focal distance from the former glass EE, and the other lens GG, next the eye, is placed at the same distance from FF. For all the three glasses are supposed to be of the same focal distance. Now, the lens FF, being placed at twice the focal distance for parallel rays from EE, receives the pencils of parallel rays after they have crossed each other at X, and forms an image at i m similar to that at IM and equal to it, but contrary in position, and consequently erect; which last image is viewed by the lens GG, in the same manner as the first image IM would be viewed by the lens EE. In this case, the image IM is considered as an object to the lens FF of which it forms a picture in its focus, in a reverse position from that of the first image, and of course, in the same position as the object.
The magnifying power of this telescope is determined precisely in the same way as that of the astronomical telescope. Suppose the object-glass to be thirty inches focal distance, and each of the eye-glasses 1½ inch focal distance, the magnifying power is in the proportion of 30 to 1½, or 20 times, and the instrument is, of course, considerably longer than an astronomical telescope of the same power. The distance, in this case, between the object-glass and the first eye-glass EE is 31½ inches; the distance between EE, and the second glass FF, is 3 inches, and the distance between FF and the glass GG next the eye, 3 inches; in all 37½ inches, the whole length of the telescope. Although it is usual to make use of three eye-glasses in this telescope, yet two will cause the object to appear erect, and of the same magnitude. For suppose the middle lens FF taken away, if 230 the first lens EE be placed at X, which is double its focal distance from the image IM, it will at the same distance X m, on the other side, form a secondary image i m equal to the primary image IM, and also in a contrary position. But such a combination of eye-glasses produces a great degree of colouring in the image, and therefore is seldom used. Even the combination now described, consisting of three lenses of equal focal distances, is now almost obsolete, and has given place to a much better arrangement consisting of four glasses, of different focal distances—which shall be afterwards described.
The following figures, 48, 49, 50 represent the manner in which the rays of light are refracted through the glasses of the telescopes we have now described. Fig. 48 represents the rays of light as they pass from the object to the eye in the Galilean telescope. After passing in a parallel direction to the object-glass, they are refracted by that glass, and undergo a slight convergence in passing towards the concave eye-glass, where they enter the eye in a parallel direction, but no image is formed previous to their entering the eye, till they arrive at the retina. Fig. 49 represents the rays as they pass through the glasses of the astronomical telescope. The rays, after entering the object-glass, proceed in a converging direction, till they arrive at its focus, about A, where an image of the object is formed; they then proceed diverging to the eye-glass, where they are rendered parallel, and enter the eye in that direction. Fig. 50 represents the rays as they converge and diverge in passing through the four glasses of the common day-telescope described above. After passing through the object-glass, they converge towards B, where the first image is formed. They then 231 diverge towards the first eye-glass where they are rendered parallel; and passing through the second eye-glass, they again converge and form a second image at C; from which point they again diverge, and passing through the first eye-glass enter the eye in a parallel direction. If the glasses of these telescopes were fixed on long pieces of wood, at their proper distances from each other, and placed in a darkened room, when the sun is shining, the beam of the sun’s light would pass through them in the same manner as here represented.
| fig. 48. | fig. 49. | fig. 50. |
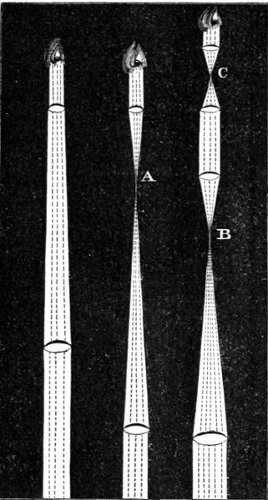 |
||
232
This is a species of telescope altogether unnoticed by optical writers, so far as I know; nor has the property of a single lens in magnifying distant objects been generally adverted to or recognised. It may not therefore be inexpedient to state a few experiments which I have made in relation to this point. When we hold a spectacle-glass of a pretty long focal distance—say, from 20 to 24 inches—close to the eye, and direct it to distant objects, they do not appear sensibly magnified. But if we hold the glass about 12 or 16 inches from our eye, we shall perceive a sensible degree of magnifying power, as if distant objects were seen at less than half the distance at which they are placed. This property of a spectacle-glass I happened to notice when a boy, and, on different occasions since that period have made several experiments on the subject, some of which I shall here relate.
With the object-glass of a common refracting telescope 4½ feet focal distance, and 2½ inches diameter, I looked at distant objects—my eye being at about 3½ feet from the lens, or about 10 or 12 inches within its focus—and it produced nearly the same effect as a telescope which magnifies the diameters of objects 5 or 6 times. With another lens 11 feet focal distance and 4 inches diameter—standing from it at the distance of about 10 feet, I obtain a magnifying power of about 12 or 14 times, which enables me to read the letters on the sign-posts of a village half a mile distant. Having some time ago procured a very large lens 26 feet focal distance, and 11½ inches 233 diameter, I have tried with it various experiments of this kind upon different objects. Standing at the distance of about 25 feet from it, I can see distant objects through it magnified about 26 times in diameter, and consequently 676 times in surface, and remarkably clear and distinct, so that I can distinguish the hour and minute hands of a public clock in a village two miles distant. This single lens, therefore answers the purpose of an ordinary telescope with a power of 26 times. In making such experiments our eye must always be within the focus of the lens, at least 8 or 10 inches. The object will, indeed, be seen at any distance from the glass within this limit; but the magnifying power is diminished in proportion as we approach nearer to the glass. Different eyes, too, will require to place themselves at different distances, so as to obtain the greatest degree of magnifying power with distinctness, according as individuals are long or short-sighted.
This kind of telescope stands in no need of a tube, but only of a small pedestal on which it may be placed on a table, nearly at the height of the eye, and that it be capable of a motion in a perpendicular or parallel direction, to bring it in a line with the eye and the object. The principle on which the magnifying power, in this case, is produced, is materially the same as that on which the performance of the Galilean telescope depends. The eye of the observer serves instead of the concave lens in that instrument; and as the concave lens is placed as much within the focus of the object-glass, as is equal to its own focal distance, so the eye, in these experiments, must be placed at least its focal distance within the focus of the lens with which we are experimenting; and the magnifying power will be nearly in the 234 proportion of the focal distance of the lens to the focal distance of the eye. If, for example, the focal distance of the eye, or the distance at which we see to read distinctly, be 10 inches, and the focal distance of the lens, 11 feet, the magnifying power will be as 11 feet, or 132 inches to 10, that is, about 13 times. Let A (fig. 51.) represent the lens placed on a pedestal; the rays of light passing through this lens from distant objects will converge towards a focus at F. If a person then, place his eye at E, a certain distance within the focal point, he will see distant objects magnified nearly in the proportion of the focal distance of the lens to that of the eye; and when the lens is very broad—such as the 26 feet lens mentioned above—two or three persons may look through it at once, though they will not all see the same object. I have alluded above to a lens made by M. Azout of 600 feet focal distance. Were it possible to use such a lens for distant objects, it might represent them as magnified 5 or 600 times, without the application of any eye-glass. In this way the aerial telescope of Huygens would magnify 235 objects above 100 times, which is about half the magnifying power it produced with its eye-piece. Suppose Azout’s lens had been fitted up as a telescope, it would not have magnified above 480 times, as it would have required an eye-glass of 14 or 15 inches focal distance, whereas, without an eye-glass, it would have magnified objects considerably above 500 times. It is not unlikely that the species of telescope to which I have now adverted, constituted one of those instruments for magnifying distant objects which were said to have been in the possession of certain persons long before their invention in Holland, and by Galileo in Italy—to which I have referred in p. 182. Were this kind of telescope to be applied to the celestial bodies, it would require to be elevated upon a pole in the manner represented, fig. 45, p. 226.
figure 51.
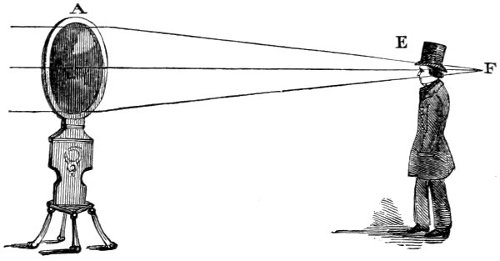
This telescope constitutes the most important and useful improvement ever made upon telescopic instruments; and, it is probable, it will, ere long, supersede the use of all other telescopes. Its importance and utility will at once appear when we consider, that a good achromatic telescope of only 4 or 5 feet in length will bear a magnifying power as great, as that of a common astronomical telescope 100 feet long, and even with a greater degree of distinctness, so that they are now come into general use both for terrestrial and celestial observations. There are, indeed, certain obstructions which prevent their being made of a very large size; but from the improvement in the manufacture of achromatic glass which is now 236 going forward, it is to be hoped that the difficulties which have hitherto impeded the progress of opticians will soon be removed. In order to understand the nature of this telescope, it will be necessary to advert a little to the imperfections connected with common refracting telescopes.
figure 52.
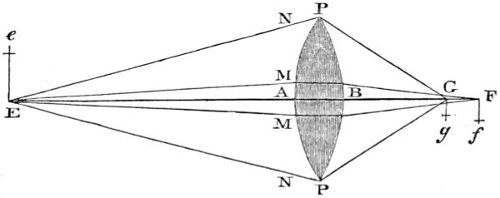
The first imperfection to which I allude is this, that spherical surfaces do not refract the rays of light accurately to a point; and hence the image formed by a single convex lens is not perfectly accurate and distinct. The rays which pass near the extremities of such a lens meet in foci nearer to the lens than those which pass nearly through the centre, which may be illustrated by the following figure. Let PP (fig. 52) be a convex lens and Ee an object, the point E of which corresponds with the axis, and sends forth the rays EM, EN, EA, &c., all of which reach the surface of the glass, but in different parts. It is manifest that the ray EA which passes through the middle of the glass, suffers no refraction. The rays EM, EM, likewise, which pass through near to EA, will be converged to a focus at F, which we generally consider as the focus of the lens. But the rays EN, EN, which are nearer to the edge of the 237 glass will be differently refracted, and will meet about G, nearer to the lens, where they will form another image Gg. Hence, it is evident, that the first image Ff, is formed only by the union of those rays which pass very near the centre of the lens; but as the rays of light proceeding from every point of an object are very numerous, there is a succession of images formed, according to the parts of the lens where they penetrate, which necessarily produces indistinctness and confusion. This is the imperfection which is distinguished by the name of spherical aberration, or the error arising from the spherical form of lenses.
The second and most important imperfection of single lenses, when used for the object-glasses of telescopes, is, that the rays of compounded light being differently refrangible, come to their respective foci at different distances from the glass; the more refrangible rays, as the violet, converging sooner than those which are less refrangible, as the red. I have had occasion to illustrate this circumstance, when treating on the colours produced by the prism, (see p. 128, and figures 32 and 33,) and it is confirmed by the experiment of a paper painted red, throwing its image, by means of a lens, at a greater distance than another paper painted blue. From such facts and experiments, it appears, that the image of a white object consists of an indefinite number of coloured images, the violet being nearest, and the red farthest from the lens, and the images of intermediate colours at intermediate distances. The aggregate, or image itself, must therefore be in some degree confused; and this confusion being much increased by the magnifying power, it is found necessary to use an eye glass of a certain limited convexity to a given object glass. Thus, an object glass of 34 238 inches focal length will bear an eye-glass of only 1 inch focus, and will magnify the diameters of objects 34 times; one of 50 feet focal distance will require an eye-glass of 4½ inches focus, and will magnify only 142 times; whereas, could we apply to it an eye-glass of only 1 inch focus, as in the former case, it would magnify no less than 600 times. And were we to construct an object-glass of 100 feet focal length, we should require to apply an eye-glass, not less than 6 inches focus, which would produce a power of about 200 times; so that there is no possibility of producing a great power by single lenses, without extending the telescope to an immoderate length.
Sir Isaac Newton, after having made his discoveries respecting the colours of light, considered the circumstance we have now stated as an insuperable barrier to the improvement of refracting telescopes; and therefore turned his attention to the improvement of telescopes by reflection. In the telescopes which he constructed and partly invented, the images of objects are formed by reflection from speculums or mirrors; and being free from the irregular convergency of the various coloured rays of light, will admit of a much larger aperture and the application of a much greater degree of magnifying power. The reflector which Newton constructed was only 6 inches long, but it was capable of bearing a power equal to that of a 6 feet refractor. It was a long time, however, after the invention of these telescopes before they were made of a size fitted for making celestial observations. After reflecting telescopes had been some time in use, Dollond made his famous discovery of the principle which led him to the construction of the achromatic telescope. This invention consists of a compound object glass 239 formed of two different kinds of glass, by which both the spherical aberration and the errors arising from the different refrangibility of the rays of light are, in a great measure corrected. For the explanation of the nature of this compound object glass and of the effects it produces; it may be expedient to offer the following remarks respecting the dispersion of light and its refraction by different substances.
The dispersion of light is estimated by the variable angle formed by the red and violet rays which bound the solar spectrum;—or rather, it is the excess of the refraction of the most refrangible ray above that of the least refrangible ray. The dispersion is not proportional to the refraction—that is, the substances which have an equal mean refraction, do not disperse light in the same ratio. For example, if we make a prism with plates of glass, and fill it with oil of Cassia, and adjust its refracting angle ACB, (fig. 31, p. 127,) so that the middle of the spectrum which it forms falls exactly at the same place where the green rays of a spectrum formed by a glass prism would fall—then we shall find that the spectrum formed by the oil of Cassia prism will be two or three times longer than that of the glass prism. The oil of Cassia, therefore, is said to disperse the rays of light more than the glass, that is, to separate the extreme red and violet rays at O and P more than the mean ray at green, and to have a greater dispersive power. Sir I. Newton appears to have made use of prisms composed of different substances, yet, strange to tell, he never observed that they formed spectrums, whose lengths were different, when the refraction of the green ray was the same; but thought that the dispersion was proportional to the refraction. This error continued 240 to be overlooked by philosophers for a considerable time, and was the cause of retarding the invention of the achromatic telescope for more than 50 years.
Dollond was among the first who detected this error. By his experiments it appears, that the different kinds of glass differ extremely with respect to the divergency of colours produced by equal refractions. He found that two prisms, one of white flint glass, whose refracting angle was about 25 degrees, and another of crown glass whose refracting angle was about 29 degrees, refracted the beam of light nearly alike; but that the divergency of colour in the white flint was considerably more than in the crown glass; so that when they were applied together, to refract contrary ways, and a beam of light transmitted through them, though the emergent continued parallel to the incident part, it was, notwithstanding, separated into component colours. From this he inferred, that, in order to render the emergent beam white, it is necessary that the refracting angle of the prism of crown glass should be increased, and by repeated experiments he discovered the exact quantity. By these means he obtained a theory in which refraction was performed without any separation or divergency of colour; and thus the way was prepared for applying the principle he had ascertained to the construction of the object glasses of refracting telescopes. For the edges of a convex and concave lens, when placed in contact with each other, may be considered as two prisms which refract contrary ways; and if the excess of refraction in the one be such as precisely to destroy the divergency of colour in the other, a colourless image will be formed. Thus, if two lenses are made of the 241 same focal length, the one of flint glass and the other of crown, the length or diameter of the coloured image in the first will be to that produced by the crown glass, as 3 to 2 nearly. Now, if we make the focal lengths of the lenses in this proportion, that is, as 3 to 2, the coloured spectrum produced by each will be equal. But if the flint lens be concave, and the crown convex—when placed in contact—they will mutually correct each other, and a pencil of white light refracted by the compound lens will remain colourless.
figure 53.
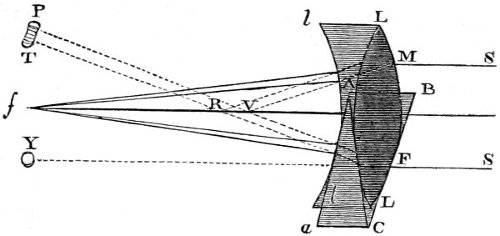
The following figure may perhaps illustrate what has been now stated. Let LL (fig. 53.) represent a convex lens of crown glass, and ll a concave lens of flint glass. A ray of the sun S, falls at F on the convex lens which will refract it exactly as the prism ABC, whose faces touch the two surfaces of the lens at the points where the ray enters and quits it. The solar ray, SF, thus refracted by the lens LL, or prism ABC, would have formed a spectrum PT on the wall, had there been no other lens, the violet ray F crossing the 242 axis of the lens at V, and going to the upper end P of the spectrum; and the red ray FR, going to the lower end T. But as the flint-glass lens ll, or the prism AaC which receives the rays FV, FR, at the same points, is interposed, these rays will be united at f, and form a small circle of white light; the ray SF of the sun being now refracted without colour from its primitive direction SFY into the new direction Ff. In like manner the corresponding ray SM will be refracted to f, and a white and colourless image of the sun will be there formed by the two lenses. In this combination of lenses it is obvious that the spherical aberration of the flint lens corrects to a considerable degree that of the crown-glass, and by a proper adjustment of the radii of the surfaces, it may be almost wholly removed. This error is still more completely corrected in the triple achromatic object-glass, which consists of three lenses—a concave flint lens placed between convexes of crown glass. Fig. 54 shows the double achromatic lens, and fig. 55, the triple object-glass, as they 243 are fitted up in their cells, and placed at the object end of the telescope. In consequence of their producing a focal image free of colour they will bear a much larger aperture and a much greater magnifying power than common refracting telescopes of the same length. While a common telescope whose object-glass is 3½ feet focal distance will bear an aperture of scarcely 1 inch, the 3½ feet Achromatic will bear an aperture of 3¼ inches, and consequently transmits 10½ times the quantity of light. While the one can bear a magnifying power of only about 36 times, the other will bear a magnifying power for celestial objects of more than 200 times.
| figure 54. | figure 55. | |
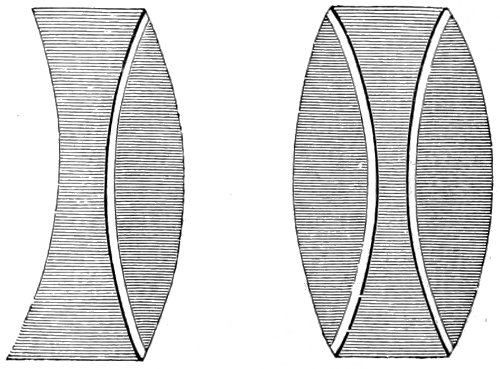 |
||
The theory of the achromatic telescope is somewhat complicated and abstruse, and would require a more lengthened investigation than my limits will permit. But what has been already stated may serve to give the reader a general idea of the principle on which it is constructed, which is all I intended. The term achromatic by which such instruments are now distinguished was first given to them by Dr. Bevis. It is compounded of two Greek words which signify, ‘free of colour.’ And, were it not that even philosophers are not altogether free of that pedantry which induces us to select Greek words which are unintelligible to the mass of mankind, they might have been contented with selecting the plain English word colourless, which is as significant and expressive as the Greek word achromatic. The crown-glass, of which the convex lenses of this telescope are made, is the same as good common window-glass; and the flint-glass is that species of glass of which wine-glasses, tumblers, decanters and similar articles are formed, and is sometimes distinguished by the name of crystal-glass. Some opticians 244 have occasionally formed the concave lens of an achromatic object-glass from the bottom of a broken tumbler.
This telescope was invented and constructed by Mr. John Dollond, about the year 1758. When he began his researches into this subject, he was a silk weaver in Spitalfields, London. The attempt of the celebrated Euler to form a colourless telescope, by including water between two meniscus glasses, attracted his attention, and, in the year 1753, he addressed a letter to Mr. Short, the optician, which was published in the Philosophical Transactions of London, ‘concerning a mistake in Euler’s theorem for correcting the aberrations in the object glasses of refracting telescopes.’ After a great variety of experiments on the refractive and dispersive powers of different substances, he at last constructed a telescope in which an exact balance of the opposite dispersive powers of the crown and flint lenses made the colours disappear, while the predominating refraction of the crown lens disposed the achromatic rays to meet at a distant focus. In constructing such object glasses, however, he had several difficulties to encounter. In the first place, the focal distance as well as the particular surfaces must be very nicely proportioned to the densities or refractive powers of the glasses, which are very apt to vary in the same sort of glass made at different times. In the next place, the centers of the two glasses must be placed truly in the common axis of the telescope, otherwise the desired effect will be in a great measure destroyed. To these difficulties is to be added—that there are four surfaces (even in double achromatic object glasses) to be wrought perfectly spherical; and every person practised in optical operations will 245 allow, that there must be the greatest accuracy throughout the whole work. But these and other difficulties were at length overcome by the judgment and perseverance of this ingenious artist.
It appears, however, that Dollond was not the only person who had the merit of making this discovery—a private gentleman, Mr. Chest, of Chest-hall, a considerable number of years before, having made a similar discovery, and applied it to the same purpose. This fact was ascertained in the course of a process raised against Dollond at the instance of Watkins, optician at Charing-cross, when applying for a patent. But as the other gentleman had kept his invention a secret, and Dollond had brought it forth for the benefit of the public, the decision was given in his favour. There was no evidence that Dollond borrowed the idea from his competitor, and both were, to a certain extent, entitled to the merits of the invention.
One of the greatest obstructions to the construction of large achromatic telescopes is, the difficulty of procuring large discs of flint glass of an uniform refractive density—of good colour, and free from veins. It is said that, fortunately for Mr. Dollond, this kind of glass was procurable when he began to make achromatic telescopes, though the attempts of ingenious chemists have since been exerted to make it without much success. It is also said, that the glass employed by Dollond in the fabrication of his best telescopes, was of the same melting, or made at the same time, and that, excepting this particular treasure, casually obtained, good dense glass for achromatic purposes, was always as difficult to be procured as it is now. The dispersion of the flint glass, too, is so variable, that, in forming an achromatic 246 lens, trials on each specimen require to be made before the absolute proportional dispersion of the substances can be ascertained. It is owing, in a great measure, to these circumstances, that a large and good achromatic telescope cannot be procured unless at a very high price. Mr. Tulley of Islington—who has been long distinguished as a maker of excellent achromatic instruments—showed me, about six years ago, a rude piece of flint glass about five inches diameter, intended for the concave lens of an achromatic object glass, for which he paid eight guineas. This was before the piece of glass was either figured or polished, and, consequently, he had still to perform the delicate operation of figuring, polishing, and adjusting this concave to the convex lenses with which it was to be combined; and during the process some veins or irregularities might be detected in the flint glass which did not then appear. Some years before, he procured a disc of glass from the continent about seven or eight inches diameter, for which he paid about thirty guineas, with which an excellent telescope, twelve feet focal length, was constructed for the Astronomical Society of London. It is obvious therefore, that large achromatic telescopes must be charged at a pretty high price.
In order to stimulate ingenious chemists and opticians to make experiments on this subject, the Board of Longitude, more than half a century ago, offered a considerable reward for bringing the art of making good flint glass for optical purposes to the requisite perfection. But considerable difficulties arise in attempting improvements of this kind; as the experiments must all be tried on a very large scale, and are necessarily attended with a heavy expence. And although government has 247 been extremely liberal in voting money for warlike purposes, and in bestowing pensions on those who stood in no need of them, it has hitherto thrown an obstruction in the way of such experiments, by the heavy duty of excise, which is rigorously exacted, whether the glass be manufactured into saleable articles or not; and has thus been instrumental in retarding the progress of improvement and discovery. It would appear that experiments of this kind have been attended with more success in France, Germany, and other places on the continent, than in Britain; as several very large achromatic telescopes have been constructed in those countries by means of flint glass which was cast for the purpose in different manufactories, and to which British artists have been considerably indebted; as the London opticians frequently purchase their largest discs of flint glass from Parisian agents. Guinaud, a continental experimenter, and who was originally a cabinet maker, appears to have had his labours in this department of art crowned with great success. Many years were employed in his experiments, and he too frequently, notwithstanding all his attention, discovered his metal to be vitiated by striæ, spects or grains, with cometic tails. He constructed a furnace capable of melting two cwt of glass in one mass, which he sawed vertically, and polished one of the sections, in order to observe what had taken place during the fusion. From time to time, as he obtained blocks, including portions of good glass, his practice was to separate them by sawing the blocks into horizontal sections, or perpendicular to their axes. A fortunate accident conducted him to a better process. While his men were one day carrying a block of this glass, on a hand-barrow, to a saw mill which he had erected at the 248 Fall of the Doubs, the mass slipped from its bearers, and, rolling to the bottom of a steep and rocky declivity, was broken to pieces. Guinaud having selected those fragments which appeared perfectly homogeneous, softened them in circular moulds, in such a manner, that on cooling, he obtained discs that were afterwards fit for working. To this method he adhered, and contrived a way for clearing his glass while cooling, so that the fractures should follow the most faulty parts. When flaws occurred in the large masses, they were removed by cleaving the pieces with wedges; then smelting them again in moulds, which give them the form of discs. The Astronomical Society of London have made trial of discs made by Guinaud, and have found them entirely homogeneous and free from fault. Of this ingenious artist’s flint glass, some of the largest achromatic telescopes on the continent have been constructed. But, it is more than twenty years since this experimenter took his flight from this terrestrial scene, and it is uncertain whether his process be still carried on with equal success.
1. The Dorpat Telescope.—This is one of the largest and most expensive Refracting telescopes ever constructed. It was made by the celebrated Fraunhofer of Munich for the observatory of the Imperial University of Dorpat, and was received into the observatory by Professor Struve in the year 1825. The aperture of the object glass of this telescope is 9½ English inches, and its solar focal length about fourteen feet, the main tube 249 being thirteen French feet exclusive of the tube which holds the eye pieces. The smallest of the four magnifying powers it possesses, is 175, and the largest 700, which, in favourable weather, is said to present the object with the utmost precision. ‘This instrument,’ says Struve, ‘was sold to us by Privy-Counsellor Von Utzchneider, the chief of the optical establishment at Munich, for 10,500 florins, (about £950 sterling), a price which only covers the expenses which the establishment incurred in making it.’ The frame work of the stand of this telescope is of oak inlaid with pieces of mahogany in an ornamental manner, and the tube is of deal veneered with mahogany and highly polished. The whole weight of the telescope and its counterpoises is supported at one point, at the common center of gravity of all its parts; and though these weigh 3000 Russian pounds, yet, we are told that this enormous telescope may be turned in every direction towards the heavens with more ease and certainty than any other hitherto in use. When the object end of the telescope is elevated to the zenith, it is sixteen feet four inches, Paris measure, above the floor, and its eye end in this position is two feet nine inches high. This instrument is mounted on an Equatorial stand, and clock work is applied to the Equatorial axis, which gives it a smooth and regular sidereal motion, which, it is said, keeps a star in the exact center of the field of view, and produces the appearance of a state of rest in the starry regions, which motion can be made solar, or even lunar, by a little change given to the place of a pointer, that is placed as an index on the dial plate. Professor Struve considers the optical powers of this telescope superior to those of Schröeter’s twenty-five feet reflector, from 250 having observed σ Orionis with fifteen companions, though Schröeter observed only twelve, that he could count with certainty. Nay, he seems disposed to place it in competition with the late Sir W. Herschel’s forty feet reflector. The finder of this telescope has a focal distance of 30 French inches, and 2-42 aperture.
2. Sir James South’s Telescope.—About the year 1829, Sir J. South, President of the London Astronomical Society, procured of M. Cauchoix of Paris, an achromatic object glass of 112/10 inches, clear aperture, and of 19 feet focal length. The flint glass employed in its construction was the manufacture of the late Guinaud le Pere, and was found to be absolutely perfect. The first observation was made with this telescope, while on a temporary stand, on Feb. 13, 1830, when Sir J. Herschel discovered with it a sixth star in the trapezium in the nebula of Orion, whose brightness was about one third of that of the fifth star discovered by Struve, which is as distinctly seen as the companion to Polaris is in a five feet achromatic. Sir James gives the following notices of the performance of this instrument on the morning of May 14, 1830. ‘At half past two, placed the 20 feet achromatic on the Georgium Sidus, saw it with a power of 346, a beautiful planetary disc; not the slightest suspicion of any ring, either perpendicular or horizontal; but the planet three hours east of the meridian, and the moon within three degrees of the planet.’ At a quarter before three, viewed Jupiter with 252 and 346, literally covered with belts, and the diameters of his satellites might have been as easily measured as himself. One came from behind the body, and the contrast of the colour with that of the planet’s limb was striking. At three o’clock viewed Mars. 251 The contrast of light in the vicinity of the poles very decided. Several spots on his body well and strongly marked—that about the south pole seems to overtake the body of the planet, and gives an appearance not unlike that afforded by the new moon, familiarly known as ‘the old moon in the new moon’s arms.’ Saturn has been repeatedly seen with powers from 130 to 928 under circumstances the most favourable; but not any thing anomalous about the planet or its ring could even be suspected. This telescope is erected on an Equatorial stand at Sir J. South’s observatory, Kensington.
3. Captain Smyth’s Telescope in his private observatory at Bedford.—This Achromatic telescope is 8½ feet focal length, with a clear aperture of 59/10 inches worked by the late Mr. Tulley, Senior, from a disk purchased by Sir James South at Paris. It is considered by Captain Smyth to be the finest specimen of that eminent optician’s skill, and, it is said, will bear with distinctness, a magnifying power of 1200. Its distinctness has been proved by the clear vision it gives of the obscure nebulæ, and of the companions of Polaris, Rigel, α Lyræ, and the most minute double stars—-the lunar mountains, cavities and shadows under all powers—the lucid polar regions of Mars—the sharpness of the double ring of Saturn—the gibbous aspect of Venus—the shadows of Jupiter’s satellites across his body, and the splendid contrast of colours in α Hercules, γ Andromedæ and other superb double stars.
Other large Achromatics.—Besides the above, the following, belonging to public observatories and private individuals, may be mentioned. In the Royal observatory at Greenwich, there is an Achromatic of 10 feet focal distance, having a 252 double object glass 5 inches diameter, which was made by Mr. Peter Dollond, and the only one of that size he ever constructed. There is also a 46 inch achromatic, with a triple object glass 3¾ inches aperture, which is said to be the most perfect instrument of the kind ever produced. It was the favourite instrument of Dr. Maskelyne, late Astronomer Royal, who had a small room fitted up in the observatory for this telescope. The observatory, some years ago erected near Cambridge, is perhaps the most splendid structure of the kind in Great Britain. It is furnished with several very large achromatic telescopes on Equatorial machinery: but the Achromatic telescope, lately presented to it by the Duke of Northumberland, is undoubtedly the largest instrument of this description which is to be found in this country. The object glass is said to be 25 feet focal distance, and of a corresponding diameter, but as there was no access to this instrument at the time I visited this observatory, nearly six years ago, I am unable to give a particular description of it. In the Royal Observatory at Paris, which I visited in 1837, I noticed, among other instruments, two very large Achromatic telescopes which, measuring them rudely by the eye—I estimated to be from 15 to 18 feet long, and the aperture at the object end, from 12 to 15 inches diameter. They were the largest achromatics I had previously seen; but I could find no person in the observatory at that time, who could give me any information as to their history, or to their exact dimensions, or powers of magnifying.21 253
The Rev. Dr. Pearson, Treasurer to the Astronomical Society of London, is in possession of the telescope formerly alluded to, made by Mr. Tulley, of twelve feet focal distance and seven inches aperture, which is said to be a very fine one. The small star which accompanies the pole star, with a power of a 100, appears through this telescope, as distinct and steady as one of Jupiter’s satellites. With a single lens of 6 inches focus, which produced a power of 24 times, according to the testimony of an observer who noticed it—the small star appeared as it does in an achromatic of 3 inches aperture, which shows the great effect of illuminating power in such instruments. Mr. Lawson, a diligent astronomical observer in Hereford, possesses a most beautiful achromatic telescope of about 7 inches aperture, and 12 feet focal distance, which was made by one of the Dollonds, who considered it as his chief d’oeuvre. It is said to bear powers as high as 1100 or 1400; and has been fitted up with mechanism devised by Mr. Lawson himself, so as to be perfectly easy and manageable to the observer, and which displays this gentleman’s inventive talent. In several of his observations with this instrument, he is said to have had a view of some of the more minute subdivisions of the ring of Saturn. A very excellent achromatic telescope was fitted up some years ago by my worthy friend William Bridges, Esq., Blackheath. Its object glass is 5½ inches diameter, and about 5½ feet focal length. It is erected upon Equatorial machinery, and placed in a circular observatory which moves round with a slight touch of the hand. The object glass of this instrument cost about 200 Guineas, the equatorial machinery on which it is mounted cost 150 254 Guineas, and the circular observatory in which it is placed about 100 Guineas; in all 450 Guineas. Its powers vary from 50 to 300 times.22
Such telescopes as I have alluded to above, are among the largest which have yet been made on the achromatic principle; they are, of course, comparatively rare, and can be afforded only at a very high price. Few of the object glasses in the telescopes to which I have referred, would be valued at less than 200 Guineas, independently of the tubes, eye pieces and other apparatus with which they are fitted up. It is so difficult to procure large discs of flint glass for optical purposes, to produce the requisite curves of the different lenses, and to combine them together with that extreme accuracy which is requisite, that when a good compound lens of this description is found perfectly achromatic, the optician must necessarily set a high value upon it; since it may happen that he may have finished half a dozen before he has got one that is nearly perfect. The more common sizes of achromatic telescopes for astronomical purposes, which are regularly sold by the London opticians, are the following:—
1. The 2½ feet Achromatic.—This telescope has an object glass 30 inches in focal length, and 2 inches clear aperture. It is generally furnished with two eye pieces, one for terrestrial objects, magnifying about 30 or 35 times, and one for celestial objects with a power of 70 or 75 times. 255 It might be furnished with an additional astronomical eye-piece—if the object glass be a good one, so as to produce a power of 90 or 95 times. With such a telescope, the belts and satellites of Jupiter, the phases of Venus and the ring of Saturn may be perceived; but not to so much advantage as with larger telescopes. It is generally fitted up either with a mahogany or a brass tube, and is placed upon a tripod brass stand, with a universal joint which produces a horizontal and vertical motion. It is packed, along with the eye-pieces, and whatever else belongs to it, in a neat mahogany box. Its price varies, according as it is furnished with an elevating rack or other apparatus.
The following are the prices of this instrument as marked in the catalogue of Mr. Tulley, Terrett’s Court, Islington, London.
| £ | s. | d. | |
|---|---|---|---|
| 2½ feet telescopes, brass mounted on plain pillar and claw stand, with one eye piece for astronomical purposes, and one for land objects, to vary the magnifying power, packed in a mahogany box | 10 | 10 | 0 |
| Ditto, ditto, brass mounted on pillar and claw stand, with elevating rack, 1 eye piece for astronomical purposes, and 1 for land objects, to vary the magnifying power, packed in a mahogany box | 12 | 12 | 0 |
The following prices of the same kind of telescope are from the catalogue of Messrs. W. and, S. Jones, 30, Lower Holborn, London.
| £ | s. | d. | |
|---|---|---|---|
| The improved 2½ feet achromatic refractor, on a brass stand, mahogany tube, with three eye pieces, two magnifying about 40 and 50 times for terrestrial objects, and the other about 75 times for astronomical purposes, in a mahogany case | 10 | 10 | 0 |
| Ditto, ditto, the tube all brass, with three eye pieces | 11 | 11 | 0 |
| Ditto, ditto, with vertical and horizontal rack work motions |
15 | 15 | 0 |
2. The 3½ feet Achromatic Telescope.—The 256 object glass of this telescope is from 44 to 46 inches focal length, and 2¾ inches diameter. It is generally furnished with four eye-pieces, two for terrestrial and two for celestial objects. The lowest power for land objects is generally about 45, which affords a large field of view, and exhibits the objects with great brilliance. The other terrestrial power is usually from 65 to 70. The astronomical powers are about 80 and 130; but such a telescope should always have another eye-piece, to produce a power of 180 or 200 times, which it will bear with distinctness, in a serene state of the atmosphere, if the object glass be truly achromatic. The illuminating power in this telescope is nearly double that of the 2½ feet telescope, or in the proportion of 7, 56 to 4; and therefore it will bear about double the magnifying power with nearly equal distinctness. This telescope is fitted up in a manner somewhat similar to the former, with a tripod stand which is placed upon a table. Sometimes, however, it is mounted on a long mahogany stand which rests upon the floor, (as in fig. 58.), and is fitted with an equatorial motion; and has generally a small telescope fixed near the eye end of the large tube, called a finder, which serves to direct the telescope to a particular object in the heavens when the higher powers are applied. It is likewise eligible that it should have an elevating rack and sliding tubes, for supporting the eye end of the instrument, to keep it steady during astronomical observations, and it would be an advantage, for various purposes which shall be afterwards described, to have fitted to it a Diagonal Eye Piece magnifying 40 times or upwards.
The prices of this instrument, as marked in Mr. Tulley’s Catalogue, are as follows:— 257
| £ | s. | d. | |
|---|---|---|---|
| The 3½ feet achromatic telescope 2¾ inches aperture, on plain pillar and claw stand, 2 eye pieces for astronomical purposes, and 1 for land objects to vary the magnifying power, packed in a mahogany box | 21 | 0 | 0 |
| Ditto, ditto, with elevating rack and achromatic finder, 2 eye pieces for astronomical purposes, and 1 for day objects to vary the magnifying power, packed in a mahogany box | 26 | 5 | 0 |
The following are the prices as marked in Messrs. W. and S. Jones’ Catalogue.
| £ | s. | d. | |
|---|---|---|---|
| The 3½ feet achromatic, plain mahogany tube | 18 | 18 | 0 |
| Ditto, ditto, brass tube | 21 | 0 | 0 |
| Ditto, all in brass, with rack work motions, &c. | 26 | 5 | 0 |
| Ditto, the object glass of the largest aperture, and the rack motions on an improved principle | from 37l. 16s. to 42 | 0 | 0 |
| Ditto, fitted up with Equatorial motion, framed mahogany stand, divided altitude, and azimuth arches, or declination and right ascension circles, &c. &c. | from 60l to 80 | 0 | 0 |
This is the telescope which I would particularly recommend to astronomical amateurs, whose pecuniary resources do not permit them to purchase more expensive instruments. When fitted up with the eye pieces and powers already mentioned, and with a finder and elevating rack,—price 25 guineas—it will serve all the purposes of general observation. By this telescope, satisfactory views may be obtained of most of the interesting phenomena of the heavens, such as the spots of the sun—the mountains, vales, and caverns on the lunar surface—the phases of Mercury and Venus—the spots on Mars—the satellites and belts of Jupiter—the ring of Saturn—many of the more interesting nebulæ, and most of the double stars of the second and third classes. When the object glass of this telescope is accurately figured and perfectly achromatic, a power of from 200 to 230 maybe put upon it, by which the division of Saturn’s ring might occasionally be perceived. It is more 258 easily managed and represents objects considerably brighter than reflecting telescopes of the same price and magnifying power, and it is not so apt to be deranged as reflectors generally are. A telescope of a less size would not in general be found satisfactory for viewing the objects I have now specified, and for general astronomical purposes. It may not be improper for the information of some readers, to explain what is meant in Mr. Tulley’s catalogue, when it is stated that this instrument has ‘one eye piece for day objects, to vary the magnifying power.’ The eye piece alluded to is so constructed, that by drawing out a tube next the eye, you may increase the power at pleasure, and make it to vary, say from 40 to 80 or 100 times; so that such a construction of the terrestrial eye piece (to be afterwards explained) serves in a great measure, the purpose of separate eye-pieces. The whole length of the 3½ feet telescope, when the terrestrial eye piece is applied, is about 4½ feet from the object glass to the first eye glass.
When the aperture of the object glass of this telescope exceeds 2¾ inches its price rapidly advances.
The following is Mr. Tulley’s scale of prices, proportionate to the increase of aperture:—
| £ | s. | d. | |
|---|---|---|---|
| 3½ feet telescopes 3¼ inches aperture, with vertical and horizontal rack work motions, achromatic finder, 3 eye pieces for astronomical purposes, and one for day objects to vary the magnifying power, packed in a mahogany box | 42 | 0 | 0 |
| Ditto, ditto, 3¾ inches diameter, mounted as above | 68 | 5 | 0 |
| Ditto, with universal Equatorial, instead of pillar and claw stand |
84 | 0 | 0 |
Here, in the one case, the increase of half an inch in the diameter of the object-glass, adds about £16. to the expense; and in the other case 259 no less than £26. 5s. The proportion of light in those two telescopes, compared with that of 2¾ inches aperture, is as follows:—The square of the 2¾ object-glass is 7.56; that of 3¼, 10.56, and that of the 3¾, 14.06; so that the light admitted by the 3¼ compared with the 2¾ aperture, is nearly as 10 to 7; and the light admitted by the 3¾ object-glass is nearly double that of the 2¾ aperture, and will bear nearly a proportional increase of magnifying power.
3. The 5 feet Achromatic telescope. The focal length of the object-glass of this telescope is 5 feet 3 inches, and the diameter of its aperture 38/10 inches. The usual magnifying powers applied to it are, for land objects 65 times; and for celestial objects, 110, 190, 250, and sometimes one or two higher powers. The quantity of light it possesses is not much larger than that of the 3½ feet telescope, with 3¾ inches aperture; but the larger focal length of this telescope is considered to be an advantage; since the longer the focus of the object-glass, the less will be its chromatic and spherical aberrations, and the larger may be the eye-glasses, and the flatter the field of view.
The following are the prices of these telescopes as marked in Mr. Tulley’s catalogue.
| £ | s. | d. | |
|---|---|---|---|
| 5 feet telescopes 3¾ inches aperture, on an universal equatorial stand, with achromatic finder, 4 eye pieces for astronomical purposes, and 1 for day objects to vary the magnifying power, packed in a mahogany box 100 guineas to | 157 | 10 | 0 |
| 7 feet ditto, 5 inches aperture, on a newly improved universal equatorial stand, 6 eye pieces for astronomical purposes, and 1 for day objects to vary the magnifying power, with achromatic finder, and Troughton’s Micrometer | 207 | 5 | 0 |
The above are all the kinds of achromatic telescopes generally made by the London opticians. Those of the larger kind, as 5 and 7 feet telescopes, and the 3½ feet with 3¾ inches aperture, 260 are generally made to order, and are not always to be procured. But the 2½ and 3½ feet achromatics of 2¾ inches aperture, are generally to be found ready-made at most of the optician’s shops in the metropolis. The prices of these instruments are nearly the same in most of the optician’s shops in London. Some of them demand a higher price, but few of them are ever sold lower than what has been stated above, unless in certain cases, where a discount is allowed.
figure 57.
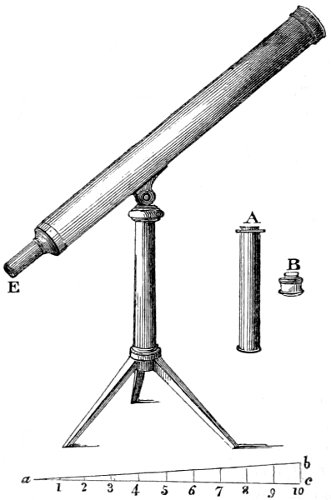
The stands for these telescopes, and the manner in which they are fitted up for observation are represented in figures 57, 58, and 59. Fig. 57 represents 261 either the 2½ or the 3½ feet telescopes mounted on a plain brass stand, to be placed on a table. A is the long eye-piece for land objects, and B the small eye-piece for astronomical observation, which is composed of two lenses, and represents the object in an inverted position. These eye-pieces are screwed on, as occasion requires, at E, the eye-end of the telescope. The shorter of the two astronomical eye-tubes which accompany this telescope, produces the highest magnifying power. For adjusting the telescope to distinct vision, there is a brass knob or button at a, which moves a piece of rack-work connected with the eye-tube, which must be turned either one way or the other till the object appears distinctly; and different eyes frequently require a different adjustment.
Fig. 58, represents a 5 feet telescope fitted up for astronomical observations. It is mounted on a mahogany stand, the three legs of which are made to close up together by means of the brass frame aaa, which is composed of three bars, connected with three joints in the centre, and three other joints, connected with the three mahogany bars. It is furnished with an apparatus for equatorial motions. The brass pin is made to move round in the brass socket b, and may be tightened by means of the finger screw d, when the telescope is directed nearly to the object intended to be viewed. This socket may be set perpendicular to the horizon, or to any other required angle; and the quantity of the angle is ascertained by the divided arc, and the instrument made fast in that position by the screw e. If this socket be set to the latitude of the place of observation, and the plane of this arc be turned so as to be in the plane of the meridian, the socket b being fixed to the inclination 262 of the pole of the earth, the telescope when turned in this socket, will have an equatorial motion, so that celestial objects may be always kept in view, when this equatorial motion is performed. The two handles at k are connected with rack-work, intended to move the telescope in any required direction. The two sets of brass sliding rods ii are intended to render the telescope as steady as possible, and to elevate and depress it at pleasure, and are so constructed as to slide into each other with the utmost ease.
figure 58.
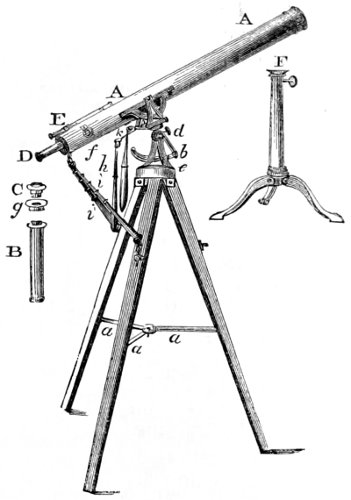
The Finder is placed at AE, either on the top or the left side of the tube of the telescope. 263 When high magnifying powers are applied to any telescope, it is sometimes difficult, on account of the smallness of the field of view, to direct the main tube of the telescope to the object. But the Finder, which is a telescope with a small power, and consequently has a large field of view—when directed to any object, it is easily found, and being brought to the centre of the field, where two cross hairs intersect each other, it will then be seen in the larger telescope. B is the eye-tube for terrestrial objects, containing 4 glasses, and C, one of the astronomical eye-pieces. A socket is represented at g, containing a stained glass, which is screwed to any of the eye-pieces, to protect the eye from the glare of light, when viewing the spots of the sun. The brass nut above f, is intended for the adjustment of the eye-piece to distinct vision. The 3½ feet telescope is sometimes mounted in this form.
Fig. 59, represents a 5 or 6 feet telescope, mounted on a stand of a new construction by Dollond. It possesses the advantage of supporting the telescope in two places, which renders it extremely steady—a property of great importance when viewing celestial objects with high magnifying powers. It possesses likewise, the advantage of enabling the observer to continue seated at the same height from the floor, although the telescope be raised to any altitude—the elevation being entirely at the object end, although it may be changed from the horizon to the zenith. The frame-work is composed of bars of mahogany, and rests on three castors, two of which are made fast to their respective legs in the usual way, and the third stands under the middle of the lower horizontal bar that connects the two opposite legs, so that the frame has all the advantages of a tripod. As 264 it becomes very inconvenient to stoop to the eye end of a telescope, when the altitude of an object is considerable, and the centre of motion at the middle of the tube, this construction of a stand serves to remedy such inconvenience.
figure 59.
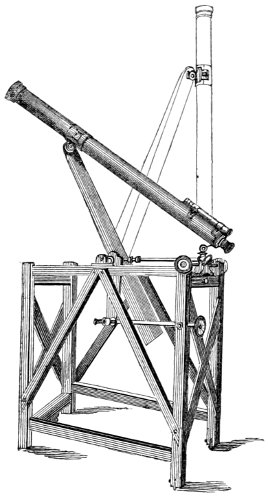
265
As some ingenious mechanics may feel a desire to attempt the construction of a compound achromatic object-glass, I shall here state some of the proportions of curvature of the concave and convex lenses, which serve to guide opticians in their construction of achromatic instruments. These proportions are various; and even when demonstrated to be mathematically correct, it is sometimes difficult to reduce them to practice, on account of the different powers of refraction and dispersion possessed by different discs of crown and flint-glass, and of the difficulty of producing by mechanical means, the exact curves which theory requires. The following table shows the radii of curvature of the different surfaces of the lenses necessary to form a double achromatic object-glass—it being supposed that the sine of refraction in the crown-glass is as 1.528 to 1, and in the flint as 1.5735 to 1; the ratio of their dispersive powers being as 1 to 1.524. It is also assumed that the curvatures of the concave lens are as 1 to 2, that is, that the one side of this lens is ground on a tool, the radius of which is double that of the other. The 1st column expresses the compound focus of the object-glass in inches; the 2nd column states the radius of the anterior surface of the crown, and column 3rd, its posterior side. Column 4th expresses the radius of the anterior surface of the concave lens, and column 5th its posterior surface, which, it will be observed, is exactly double that of the other. 266
| Focus in inches. | Radius of anterior surface, convex. | Radius of posterior surface. | Radius of anterior surface, concave. | Radius of posterior surface. | ||||
|---|---|---|---|---|---|---|---|---|
| Inc. | Dec. | Inc. | Dec. | Inc. | Dec. | Inc. | Dec. | |
| 12 | 3 | 4. | 652 | 4. | 171 | 8. | 342 | |
| 24 | 6 | 9. | 304 | 8. | 342 | 16. | 684 | |
| 30 | 7. | 5 | 11. | 063 | 10. | 428 | 20. | 856 |
| 36 | 9 | 13. | 956 | 12. | 513 | 25. | 027 | |
| 48 | 12 | 18. | 608 | 16. | 684 | 33. | 369 | |
| 60 | 15 | 23. | 260 | 20. | 856 | 41. | 712 | |
| 120 | 30 | 46. | 520 | 41. | 712 | 83. | 424 | |
From the above table it will be seen, that to construct, for example, a 30 inch compound object-glass, the radius of the anterior side of the crown must be 7½ inches, and that of the posterior side 11.63 inches; the radius of the anterior surface of the concave 10.428, and that of the posterior 20.856 inches. It may be proper to observe, that in these computations, the radius of the anterior surface of the concave is less than the posterior side of the convex, and consequently admits of its approach, without touching in the centre—a circumstance which always requires to be guarded against in the combination of achromatic glasses. The following table shows the radii of curvature of the lenses of a triple object-glass, calculated from formula deduced by Dr. Robison of Edinburgh.
| Focal length. | Convex lens of crown glass. | Concave lens of flint glass. | Convex lens of crown glass. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Inches | Inc. | Dec. | Inc. | Dec. | Inc. | Dec. | Inc. | Dec. | Inc. | Dec. | Inc. | Dec. |
| 6 | 4. | 54 | 3. | 03 | 3. | 03 | 6. | 36 | 6. | 36 | 0. | 64 |
| 9 | 6. | 83 | 4. | 56 | 4. | 56 | 9. | 54 | 9. | 54 | 0. | 92 |
| 12 | 9. | 25 | 6. | 17 | 6. | 17 | 12. | 75 | 12. | 75 | 1. | 28 |
| 18 | 13. | 67 | 9. | 12 | 9. | 12 | 19. | 08 | 19. | 08 | 1. | 92 |
| 24 | 18. | 33 | 12. | 25 | 12. | 25 | 25. | 50 | 25. | 50 | 2. | 56 |
| 30 | 22. | 71 | 15. | 16 | 15. | 16 | 31. | 79 | 31. | 79 | 3. | 20 |
| 36 | 27. | 33 | 18. | 25 | 18. | 25 | 38. | 17 | 38. | 17 | 3. | 84 |
| 42 | 31. | 87 | 21. | 28 | 21. | 28 | 44. | 53 | 44. | 53 | 4. | 48 |
| 48 | 36. | 42 | 24. | 33 | 24. | 33 | 50. | 92 | 50. | 92 | 5. | 12 |
| 54 | 40. | 96 | 27. | 36 | 27. | 36 | 57. | 28 | 57. | 28 | 5. | 76 |
| 60 | 45. | 42 | 30. | 33 | 30. | 33 | 63. | 58 | 63. | 58 | 6. | 40 |
267
The following table contains the proportions of curvature, said to be employed by the London opticians.
| Focal length. | Convex lens of crown glass. | Radius of both the surfaces of the concave of flint glass. | Convex lens of crown glass. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Inches | Inc. | Dec. | Inc. | Dec. | Inc. | Dec. | Inc. | Dec. | Inc. | Dec. |
| 6 | 3. | 77 | 4. | 49 | 3. | 47 | 3. | 77 | 4. | 49 |
| 9 | 5. | 65 | 6. | 74 | 5. | 21 | 5. | 65 | 6. | 74 |
| 12 | 7. | 54 | 8. | 99 | 6. | 95 | 7. | 54 | 8. | 99 |
| 18 | 11. | 30 | 13. | 48 | 10. | 42 | 11. | 30 | 13. | 48 |
| 24 | 15. | 08 | 17. | 98 | 13. | 90 | 15. | 08 | 17. | 98 |
| 36 | 22. | 61 | 26. | 96 | 20. | 84 | 22. | 61 | 26. | 96 |
| 42 | 26. | 38 | 31. | 45 | 24. | 31 | 26. | 38 | 31. | 45 |
| 48 | 30. | 16 | 35. | 96 | 27. | 80 | 30. | 16 | 35. | 96 |
| 54 | 33. | 91 | 40. | 45 | 31. | 27 | 33. | 91 | 40. | 45 |
| 60 | 37. | 68 | 44. | 94 | 34. | 74 | 37. | 68 | 44. | 94 |
From this table it appears, that the two convex lenses, have the same radii of their respective sides and that the concave flint lens has its two surfaces equally concave, so that a triple object-glass formed according to these proportions, would require only three pair of grinding tools. The following are the curves of the lenses of one of the best of Dollond’s achromatic telescopes, the focal length of the compound object-glass being 46 inches. Reckoning from the surface next the object—the radii of the crown-glass were 28 and 40 inches: the concave lens 20.9 inches, and the inner crown-glass lens, 28.4 and 28.4 inches. This telescope carried magnifying powers of from 100 to 200 times.
Although I have inserted the above tables, which might in some measure guide an ingenious artist, yet on the whole, a private amateur has little chance in succeeding in such attempts. The diversity of glasses, and the uncertainty of an unpractised workman’s producing the precise curvatures he intends, is so great, that the object-glass, 268 for the most part, turns out different from his expectations. The great difficulty in the construction is to find the exact proportion of the dispersive powers of the crown and flint glass. The crown is pretty constant, but there are hardly two pots of flint glass which have the same dispersive power. Even if constant, it is difficult to measure it accurately; and an error in this greatly affects the instrument; because the focal distances of the lenses must be nearly as their dispersive powers. In the two preceding tables, the sine of incidence, in the crown glass, is supposed to be to the sine of refraction as 1.526 to 1; and in the flint glass, as 1.604 to 1. Opticians who make great numbers of lenses both of flint and crown glass, acquire, in time, a pretty good guess of the nature of the errors which may remain after they have finished an object-glass; and having many lenses intended to be of the same form, but unavoidably differing a little from it, they try several of the concaves with the two convexes, and finding one better than the rest, they make use of it to complete the set. In this way some of the best achromatic telescopes are frequently formed. I have sometimes found, when supplying a concave flint glass to a telescope where it happened to be wanting, that, of four or five concave lenses which appeared to be the same as to curvature and other properties, only one was found to produce a distinct and colourless image. Should any one, however, wish to attempt the construction of an achromatic lens, the best way for preventing disappointments in the result is, to procure a variety of tables of the respective curvatures founded on different conditions, and which, of course, require the surfaces of the several lenses to be of different curves. 269 Having lenses of different radii at his command, and having glass of different refractive or dispersive powers, when one combination does not exactly suit, he may try another, and ultimately may succeed in constructing a good achromatic telescope; for, in many cases, it has been found that chance, or a happy combination of lenses by trial, has led to the formation of an excellent object-glass.
The best achromatic telescopes, when minutely examined, are found to be in some respects defective, on account of that slight degree of colour which, by the aberration of the rays, they give to objects, unless the object-glass be of small diameter. When we examine with attention a good achromatic telescope we find that it does not show white or luminous objects perfectly free from colour, their edges being tinged on one side with a claret-coloured fringe, and on the other with a green fringe. This telescope, therefore, required farther improvement, to get rid of these secondary colours, and Father Boscovich, to whom every branch of optics is much indebted, displayed much ingenuity in his attempts to attain this object. But it is to Dr. Blair, professor of astronomy in Edinburgh, that we are chiefly indebted for the first successful experiments by which this end was accomplished. By a judicious set of experiments, he proved that the quality of dispersing the rays in a greater degree than crown-glass, is not confined to a few mediums; but is possessed by a great variety of fluids, and by some of these in a most extraordinary degree. Having observed that when the extreme red and violet rays were perfectly united, the green were left out, he conceived 270 the idea of making an achromatic concave lens which should refract the green less than the united red and violet, and an achromatic convex lens which should do the same, and as the concave lens refracted the outstanding green to the axis, while the concave one refracted them from the axis, it followed, that, by a combination of these two opposite effects, the green would be united with the red and violet.
By means of an ingenious prismatic apparatus, he examined the optical properties of a great variety of fluids. The solutions of metals and semi-metals proved in all cases more dispersive than crown glass. Some of the salts, such as sal-ammoniac, greatly increased the dispersive power of water. The marine acid disperses very considerably, and this quality increases with its strength. The most dispersive fluids were accordingly found to be those in which this acid and the metals were combined. The chemical preparation called causticum antimoniale, or butter of antimony, in its most concentrated state, when it has just attracted sufficient humidity to render it fluid, possesses the quality of dispersing the rays in an astonishing degree. The great quantity of the semi-metal retained in solution, and the highly concentrated state of the marine acid, are considered as the cause of this striking effect. Corrosive sublimate of mercury, added to a solution of sal-ammoniacum in water, possesses the next place to the butter of antimony among the dispersive fluids, which Dr. Blair examined. The essential oils were found to hold the next rank to metallic solutions, among fluids which possess the dispersive quality, particularly those obtained from bituminous minerals, as native petrolea, pit coal, and amber. The dispersive power of the essential oil 271 of sassafras, and the essential oil of lemons, when genuine, were found to be not much inferior to any of these. But of all the fluids fitted for optical purposes, Dr. Blair found that the muriatic acid mixed with a metallic solution, or, in other words, a fluid in which the marine acid and metalline particles, hold a due proportion, most accurately suited his purpose. In a spectrum formed by this fluid the green were among the most refrangible rays, and when its dispersion was corrected by that of glass, there was produced an inverted secondary spectrum, that is, one in which the green was above, when it would have been below with a common medium. He therefore placed a concave lens of muriatic acid with a metallic solution between the two lenses, as in fig. 60, where AB is the concave fluid lens, CF a plano-convex lens, with its plane side next the object, and ED, a meniscus. With this object-glass the rays of different colours were bent from their rectilineal course with the same equality and regularity as in reflection.
figure 60.
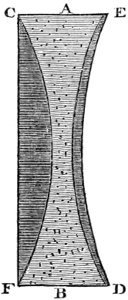
Telescopes constructed with such object-glasses were examined by the late Dr. Robison and professor Playfair. The focal distance of the object-glass of one of these did not exceed 17 inches, and yet it bore an aperture of 3½ inches. They viewed some single and double stars and some common objects with this telescope; and found, that, in magnifying power, brightness, and distinctness, 272 it was manifestly superior to one of Mr. Dollond of 42 inches focal length. They had most distinct vision of a star, when using an erecting eye-piece, which made this telescope magnify more than a 100 times; and they found the field of vision as uniformly distinct as with Dollond’s 42 inch telescope magnifying 46 times; and were led to admire the nice figuring and centering of the very deep eye-glasses which were necessary for this amplification. They saw double stars with a degree of perfection which astonished them. These telescopes, however, have never yet come into general use; and one reason perhaps, is, that they are much more apt to be deranged, than telescopes constructed of object-glasses which are solid. If any species of glass, or other solid transparent substance could be found with the same optical properties, instruments might perhaps be constructed of a larger size, and considerably superior to our best achromatic telescopes.23 It is said that Mr. Blair, the son of Dr. Blair, some years ago, was engaged in prosecuting his father’s views, but I have not heard any thing respecting the result of his investigations.
Professor Barlow, not many years ago, suggested a new fluid telescope, which is deserving of attention; and, about the year 1829 constructed one of pretty large dimensions. The fluid he employs for this purpose is the sulphuret of 273 Carbon, which he found to be a substance which possessed every requisite he could desire. Its index is nearly the same as that of the best flint glass, with a dispersive power more than double. It is perfectly colourless, beautifully transparent, and although very expansible, possesses the same, or very nearly the same optical properties under all circumstances to which it is likely to be exposed in astronomical observations—except perhaps, direct observations on the solar disc, which will probably be found inadmissible. Mr. Barlow first constructed an object-glass with this fluid of 3 inches aperture, with which he could see the small star in Polaris with a power of 46, and with the higher powers several stars which are considered to require a good telescope, for example 70, ρ Ophinchi, 39 Bootis, the quadruple star ε Lyræ, ζ Aquarii, α Herculis, &c. He next constructed a 6 inch object-glass. With this instrument the small star in Polaris is so distinct and brilliant, with a power of 143, that its transit might be taken with the utmost certainty. As the mode of constructing these telescopes is somewhat novel, it may be expedient to enter somewhat into detail.
In the usual construction of achromatic telescopes, the two or three lenses composing the object-glass are brought into immediate contact; and in the fluid telescope of Dr. Blair, the construction was the same, the fluid having been enclosed in the object-glass itself. But in Mr. Barlow’s telescope, the fluid correcting lens is placed at a distance from the plate lens equal to half its focal length; and it might be carried still farther back, and yet possess dispersive power to render the object-glass achromatic. By this means the fluid lens—which is the most difficult 274 part of the construction—is reduced to one half or to less than one half of the size of the plate lens; consequently, to construct a telescope of 10 or 12 inches aperture involves no greater difficulty in the manipulation, than in making a telescope of the usual description of 5 or 6 inches aperture, except in the simple plate lens itself; and, hence, a telescope of this kind, of 10 or 12 feet length, will be equivalent in its focal power to one of 16 or 20 feet. By this means, the tube may be shortened several feet and yet possess a focal power more considerable than could be conveniently given to it on the usual principle of construction. This will be better understood from the annexed diagram. (fig. 61.)
figure 61.

In this figure ABCD represent the tube of the 6 inch telescope, CD, the plate object-glass, F the first focus of rays, de the fluid concave lens, distant from the former 24 inches. The focal length MF being 48, and consequently, as 48 : 6 :: 24 : 3 inches, the diameter of the fluid lens. The resulting compound focus is 62.5 inches. It is obvious, therefore, that the rays df, ef, arrive at the focus under the same convergency, and with the same light as if they proceeded from a lens of 6 inches diameter, placed at a distance beyond the object-glass CD (as GH,) determined by producing those rays till they meet the sides of the tube in GH, namely at 62.5 inches beyond the fluid lens. Hence, it is 275 obvious, the rays will converge as they would do from an object-glass GH of the usual kind with a focus of 10 feet 5 inches. We have thus, therefore, shortened the tube 38.5 inches, or have at least the advantage of a focus 38.5 inches longer than our tube; and the same principle may be carried much farther, so as to reduce the usual length of refracting telescopes nearly one half without increasing the aberration in the first glass beyond the least that can possibly belong to a telescope of the usual kind of the whole length. It should likewise be observed that the adjustment for focus may be made either in the usual way, or by a slight movement of the fluid lens, as in the Gregorian Reflectors, by means of the small speculum.
Mr. Barlow afterwards constructed another and a larger telescope on the same principle, the clear aperture of which is 7.8 inches. Its tube is 11 feet, which, together with the eye-piece, makes the whole length 12 feet, but its effective focus is on the principle stated above, 18 feet. It carries a power of 700 on the closest double stars in South’s and Herschel’s catalogue, and the stars are, with that power, round and defined, although the field is not then so bright as could be desired. The telescope is mounted on a revolving stand, which works with considerable accuracy as an azimuth and altitude instrument. To give steadiness to the stand it has been made substantial and heavy; its weight by estimation being 400 pounds, and that of the telescope 130 pounds, yet its motions are so smooth, and the power so arranged, that it may be managed by one person with the greatest ease, the star being followed by a slight touch, scarcely exceeding that of the keys of a piano-forte. The focal length of the plate lens is 276 78 inches, and of the fluid lens 59.8 inches—which at the distance of 40 inches produce a focal length of 104 inches, a total length of 12 feet, and an equivalent focus of 18 feet. The curves of the parallel meniscus checks for containing the fluid are—30 inches, and 144 inches, the latter towards the eye. The curves for the plate lens are 56.4 and 144. There is an interior tube 5 inches diameter, and 3 feet 6 inches long, which carries the cell in which the fluid is enclosed, and an apparatus by which it may be moved backwards and forwards, so that the proper adjustment may be made for colour, in the first instance, and afterwards the focus is obtained by the usual rack-work motion. The following is the mode by which the fluid was enclosed. After the best position has been determined practically for the checks forming the fluid lens, these, with the ring between them ground and polished accurately to the same curves, are applied together, and taken into an artificial high temperature, exceeding the greatest at which the telescope is ever expected to be used. After remaining here with the fluid some time, the space between the glasses is completely filled, immediately closed, cooled down by evaporation, and removed into a lower temperature. By this means a sudden condensation takes place, an external pressure is brought on the checks, and a bubble formed inside, which is of course filled with the vapour of the fluid; the excess of the atmospheric pressure beyond that of the vapour being afterwards always acting externally to prevent contact. The extreme edges are then sealed with the serum of human blood, or by strong fish-glue, and some thin pliable metal surface. By this process, Mr. Barlow says, ‘I have every reason to believe the 277 lens becomes as durable as any lens of solid glass. At all events I have the satisfaction of stating, that my first 3 inch telescope has now been completed more than fifteen months, and that no change whatever has taken place in its performance, nor the least perceptible alteration either in the quantity or the quality of the fluid.’
The following are some of the observations which have been made with this telescope, and the tests to which it has been subjected. The very small star which accompanies the pole-star is generally one of the first tests applied to telescopes. This small point of light appeared brilliant and distinct; it was best seen with a power of 120, but was visible with a power of 700. The small star in Aldebaran was very distinct with a power of 120. The small star α Lyræ was distinctly visible with the same power. The small star called by Sir J. Herschel Debilissima, between 4 ε and 5 Lyræ, whose existence, he says, could not be suspected in either the 5 or 7 feet equatorial, and invisible also with the 7 and 10 feet reflectors of six and 9 inches aperture, but seen double with the 20 feet reflector, is seen very satisfactorily double with this telescope. η Persei, marked as double in South and Herschel’s catalogue, at the distance of 28´´, with another small star at the distance of 3´ 67´´, is seen distinctly sixfold, four of the small stars being within a considerably less distance than the remote one of η marked in the catalogue. And, rejecting the remote star, the principal, and the four other stars, form a miniature representation of Jupiter and his satellites, three of them being nearly in a line on one side, and the other on the opposite. Castor, is distinctly double with 120, and well opened and stars perfectly round with 360 and 278 700: γ Leonis and α Piscium are seen with the same powers equally round and distinct. In ε Bootis, the small star is well separated from the larger, and its blue colour well marked with a power of 360. η Coronæ Borealis is seen double with a power of 360 and 700. 52 Orionis, ζ Orionis, and others of the same class are also well defined with the same powers. In regard to the planets which happened to be visible—Venus appeared beautifully white and well defined with a power of 120, but showed some colour with 360. Saturn with the 120 power, is a very brilliant object, the double ring and belts being well and satisfactorily defined, and with the 360 power, it is still very fine. The moon also is remarkably beautiful, the edges and the shadows being well marked, while the quantity of light is such as to bring to view every minute distinction of figure and shade.
The principal objections that may be made to this construction of a telescope are such as these:—Can the fluid be permanently secured? Will it preserve its transparency and other optical properties? Will it not act upon the surface of the glass and partially destroy it? &c. To such enquiries Mr. Barlow replies, that experience is the only test we have; our spirit levels, spirit thermometers, &c., show that some fluids at least may be preserved for many years, without experiencing any change, and without producing any in the appearance of the glass tubes containing them. But should any of these happen, except the last, nothing can be more simple than to supply the means of replacing the fluid at any time, and by any person, without disturbing the adjustment of the telescope. He expresses his hope that, should these experiments be prosecuted, an achromatic telescope may ultimately be produced which 279 shall exceed in aperture and power, any instruments of the kind hitherto attempted. If the prejudice against the use of fluids could be removed, he feels convinced that well-directed practice would soon lead to the construction of the most perfect instruments, on this principle, at a comparatively small expense. ‘I am convinced,’ he says, ‘judging from what has been paid for large object-glasses, that my telescope, telescope stand, and the building for observation, with every other requisite convenience, have been constructed for a less sum than would be demanded for the object-glass only, if one could be produced of the same diameter of plate and flint-glass; and this is a consideration which should have some weight, and encourage a perseverance in the principle of construction.’24
The object of this construction is to render a small disc of flint-glass available to perform the office of compensation to a much larger one of crown-glass, and thus to render possible the construction of telescopes of much larger aperture than are now common, without hindrance from the difficulty at present experienced in procuring large discs of flint-glass. It is well known to 280 those who are acquainted with telescopes, that in the construction of an ordinary achromatic object-glass, in which a single crown lens is compensated by a single one of flint, the two lenses admit of being separated only by an interval too small to afford any material advantage, in diminishing the diameter of the flint lens, by placing it in a narrower part of the cone of rays—the actual amount of their difference in point of dispersive power being such as to render the correction of the chromatic aberration impossible, when their mutual distance exceeds a certain limit. This inconvenience Mr. Rogers proposes to obviate, by employing, as a correcting lens—not a single lens of flint, but a compound one consisting of a convex crown and concave flint, whose foci are such as to cause their combination to act as a plain glass on the mean refrangible rays. Then it is evident, that by means of the greater dispersive power of flint than of crown glass, this will act as a concave on the violet, and as a convex on the red rays, and that the more powerfully, according as the lenses separately have greater powers or curvature. If then, such a compound lens be interposed between the object-glass of a telescope—supposed to be a single lens of plate or crown-glass—and its focus, it will cause no alteration in the focus for mean rays, while it will lengthen the focus for violet, and shorten it for red rays. Now this is precisely what is wanted to produce an achromatic union of all the rays in the focus; and as nothing in this construction limits the powers of the individual correcting lenses, they may therefore be applied any where that convenience may dictate; and thus, theoretically speaking, a disc of flint-glass, however small, may be made to correct the colour of one of crown however large. 281
This construction, likewise, possesses other and very remarkable advantages. For, first, when the correcting lens is approximately constructed on a calculation founded on its intended aperture, and on the refractive and dispersive indices of its materials, the final and complete dispersion of colour may be effected, not by altering the lenses by grinding them anew, but by shifting the combination nearer to, or farther from, the object-glass, as occasion may require, along the tube of a telescope, by a screw motion, till the condition of achromaticity is satisfied in the best manner possible. And secondly, the spherical aberration may in like manner be finally corrected, by slightly separating the lenses of the correcting glass, whose surfaces should for this purpose be figured to curvatures previously determined by calculation, to admit of this mode of correction—a condition which Mr. Rogers finds to be always possible. The following is the rule he lays down for the determination of the foci of the lenses of the correcting glass:—‘The focal length of either lens of the correcting lens is to that of the object-glass, in a ratio compounded of the ratio of the square of the aperture of the correcting lens to that of the object-glass, and of the ratio of the difference of the dispersive indices of the crown and flint glass, to the dispersive index of crown.’ For example, to correct the colour of a lens of crown or plate glass of 9 inches aperture, and 14 feet focal length (the dimensions of the telescope of Fraunhofer at Dorpat) by a disc of flint glass 3 inches in diameter, the focus of either lens of the correcting lens will require to be about 9 inches. To correct it by a 4 inch disc will require a focus of about 16 inches each.
Mr. Rogers remarks, that it is not indispensable 282 to make the correcting glass act as a plane lens. It is sufficient if it be so adjusted as to have a shorter focus for red rays than for violet. If, preserving this condition, it be made to act as a concave lens, the advantage procured by Mr. Barlow’s construction of reducing the length of the telescope with the same focal power, is secured, and he considers, moreover, that by a proper adaptation of the distances, foci, &c., of the lenses, we might hope to combine with all these advantages that of the destruction of the secondary spectrum, and thus obtain a perfect telescope.
The above is an abstract of a paper read to the ‘Astronomical Society of London’ in April 1828, by A. Rogers, Esq.
The reader will easily perceive that the principle on which Mr. Rogers proposes to construct his telescope is very nearly similar to that of professor Barlow, described above, with this difference, that the correcting lens of the Professor’s telescope is composed of a transparent fluid, while that of Mr. Rogers is a solid lens consisting of a convex crown and concave flint. The general object intended to be accomplished by both is the same, namely, to make a correcting lens of a comparatively small diameter serve the purpose of a large disc of flint glass, which has hitherto been very expensive, and very difficult to be procured; and likewise to reduce the length of the telescope while the advantage of a long focal power is secured.—A telescope, on this principle, was constructed 7 or 8 years ago by Mr. Wilson, lecturer on Philosophy and Chemistry, Glasgow, before he was aware that Mr. Rogers had proposed a similar plan. I have had an opportunity of particularly inspecting Mr. Wilson’s telescope, and trying its effects on terrestrial objects with high powers, and 283 was on the whole highly pleased with its performance. It appeared to be almost perfectly achromatic, and produced a distinct and well-defined image of minute distant objects, such as small letters on sign-posts, at 2, 3 and 4 miles distant. But I had no opportunity of trying its effects on double stars or any other celestial objects. The instrument is above 6 feet long; the object lens is a plano-convex of crown glass 4 feet focal distance, and 4 inches diameter, the plain side next the object.
At 26 inches distant from the object lens is the compound lens of 2 inches in diameter; and the two lenses of which it is composed are both ground to a radius of 3¾ inches. That made of crown glass is plano-convex, the other, made of flint glass, is plano-concave, and are placed close together, the convex side being next the object, and the concave side next the eye. The greater refractive power of the flint glass renders the compound one slightly concave in its effect (although the radius of curvature is similar in both), and lengthens the focus to 6 feet from the object-glass; and this is consequently the length of the instrument. The compound corrector so placed intercepts all those rays which go to form the image in the field of view, producing there an achromatic image. The concave power of the corrector renders the image larger than if directly produced by a convex lens of the same focus. The concavity of the corrector is valuable also in this respect, that a very slight alteration in its distance from the object-glass, changes the focal distance much more than if it were plain, and enables us to adjust the instrument to perfect achromatism with great precision. 284
SECT. 1.—HISTORY OF THE INVENTION, AND A GENERAL DESCRIPTION OF THE CONSTRUCTION OF THESE INSTRUMENTS.
Reflecting telescopes are those which represent the images of distant objects by reflection, chiefly from concave mirrors.
Before the achromatic telescope was invented, there were two glaring imperfections in refracting telescopes, which the astronomers of the 17th century were anxious to correct. The first was its very great length when a high power was to be applied, which rendered it very unwieldy and difficult to use. The second imperfection was the incorrectness of the image as formed by a single lens. Mathematicians had demonstrated that a pencil of rays could not be collected in a single point by a spherical lens, and also that the image transmitted by such a lens would be in some degree incurvated. After several attempts had been made to correct this imperfection by grinding lenses to the figure of one of the conic sections, Sir I. Newton happened to commence an examination of the colours formed by a prism; and having, 285 by the means of this simple instrument, discovered the different refrangibility of the rays of light—to which we have several times adverted in the preceding descriptions—he then perceived that the errors of telescopes, arising from that cause alone, were some hundred times greater than such as were occasioned by the spherical figure of lenses; which induced this illustrious philosopher to turn his attention to the improvement of telescopes by reflection.
It is generally supposed that Mr. James Gregory—a son of the Rev. John Gregory, minister of Drumoak in the county of Aberdeen—was the first who suggested the construction of a reflecting telescope. He was a young man of uncommon genius, and an eminent mathematician; and in the year 1663, at the age of only 24, he published in London, his treatise entitled ‘Optica Promota,’ in which he explained the theory of that species of reflecting telescope which still bears his name, and which he stated as being his own invention. But as Gregory, according to his own account, was endowed with no mechanical dexterity, and could find no workman capable of realizing his invention—after some fruitless attempts to form proper specula, he was obliged to give up the pursuit; so that this telescope remained for a considerable time neglected. It was several years after Gregory suggested the construction of reflecting telescopes, till Newton directed his attention fully to the subject. In a letter addressed to the secretary of the Royal Society, dated in February, 1672, he says, ‘Finding reflections to be regular, so that the angle of reflection of all sorts of rays was equal to the angle of incidence, I understood that, by their mediation, optic instruments might be brought to 286 any degree of perfection imaginable, providing a reflecting substance could be found which would polish as finely as glass, and reflect as much light as glass transmits, and the art of communicating to it a parabolic figure be also obtained. Amidst these thoughts I was forced from Cambridge by the intervening plague, and it was more than two years before I proceeded further.’
It was towards the end of 1668, or in the beginning of the following year, when Newton, being obliged to have recourse to reflectors, and not relying on any artificer for making the specula, set about the work himself, and early in the year 1672, completed two small reflecting telescopes. In these he ground the great speculum into a spherical concave, although he approved of the parabolic form, but found himself unable to accomplish it. These telescopes were of a construction somewhat different from what Gregory had suggested, and though only 6 inches long, were considered as equal to a 6 feet common refracting telescope. It is not a little singular, however, that we hear no more about the construction of reflectors till more than half a century afterwards. It was not till the year 1723, that any reflectors were known to have been made, adapted to celestial observations. In that year, Mr. Hadley, the inventor of the reflecting quadrant, which goes by his name, published in No. 376 of the Philosophical Transactions, an account of a large reflector on Newton’s plan, which he had just then constructed, the performance of which left no room to doubt that this invention would remain any longer in obscurity. The large speculum of this instrument was 62⅝ inches focal distance and 5 inches diameter, was furnished with magnifying powers of from 190 to 230 times, 287 and equalled in performance the famous aerial telescope of Huygens of 123 feet in length.25 Since this period, the reflecting telescope has been in general use among astronomers in most countries of Europe, and has received numerous improvements, under the direction of Short, Mudge, Edwards and Herschel—the last of whom constructed reflectors of 7, 10, 20, and even 40 feet in focal length, which far surpassed, in brightness and magnifying power, all the instruments of this description, which had previously been attempted.
I shall now proceed to give a brief sketch of the nature of a reflecting telescope, and the different forms in which they have been proposed to be constructed.
Fig. 62 represents the reflecting telescope as originally proposed by Gregory. ABEF represents a tube open at AF towards the object; at the other end is placed a concave speculum BE, with a hole CD in its centre, the focus of which is at e. A little beyond this focus, towards the object end of the telescope AF, is placed another small concave mirror G, having its polished face turned towards the great speculum, and is supported by an arm GH fastened to a slider connected with the tube. At the end of the great tube BE is screwed in a small tube CDKI, containing a small plano-convex lens IK. Such are the essential parts of this instrument and their relative positions. It will be recollected in our description of the properties of concave mirrors (see page 92), that, when rays proceed from a 288 distant object, and fall upon a concave-speculum, they paint an image or representation of the object in its focus before the speculum. Now suppose two parallel rays ab falling on the speculum BE, in cd; they are reflected to its focus e where an inverted image of the object is formed. This image is formed at a little more than the focal distance of the small speculum from its surface, and serves as it were for an object on which the small mirror may act. By the action of this mirror this first image is reflected to a point about f, where a second image is formed very large and erect. This image is magnified in the proportion of fG to eG, the rays from which are transmitted to the eye glass IK, through which the eye perceives the object clear and distinct, after the proper adjustments have been made.
| figure 66. | |
| fig. 62. | 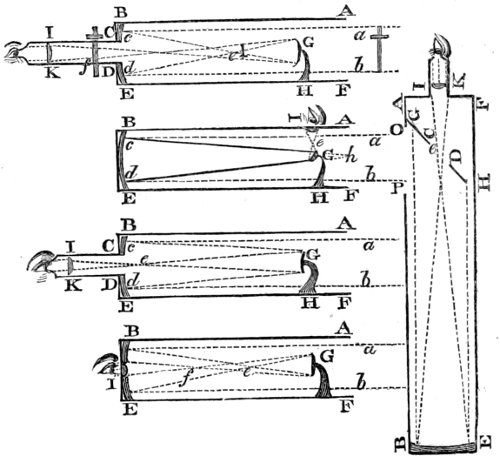 |
| fig. 63. | |
| fig. 64. | |
| fig. 65. |
289
Suppose the focal distance of the great mirror was 9 inches, and the focal distance of the small mirror 1½ inch—were we to remove the eye piece of this telescope, and look through the hole of the great mirror, we should see the image of the object depicted upon the face of the small speculum, and magnified, in the proportion of 9 to 1½, or, 6 times, on the same principle as a common convex object glass 9 inches focal length, with an eye glass whose focus is 1½ inch magnifies 6 times. This may be regarded as the first part of the magnifying power. If now, we suppose the small speculum placed a little more than 1½ inch from the image formed by the great speculum, a second image is formed about f, as much exceeding the first in its dimensions as it exceeds it in distance from the small speculum, on the principle on which the object glass of a compound microscope forms a large image near the eye glass. Suppose this distance to be 9 times greater, then the whole magnifying power will be compounded of 6 multiplied by 9, or 54 times. As a telescope it magnifies 6 times, and in the microscope part 9 times.—Such is a general idea of the Gregorian telescope, the minute particulars and structure of which can only be clearly perceived by a direct inspection of the instrument.
The Newtonian Reflector.—This instrument is somewhat different both in its form and in its mode of operation from that of Gregory. It is represented in fig. 63, where BAEF is the tube, and BE, the object concave mirror, which reflects the parallel rays ab to a plane speculum G, placed 45°, or half a right angle to the axis of the concave speculum. This small plane reflector must be of an oval form, the length of the oval should be to the breadth as 7 to 5, on account of the obliquity 290 of its position. It is supported on an arm fixed to the side of the tube; an eye-glass is placed in a small tube, moveable in the larger tube, so as to be perpendicular to the axis of the large reflector, the perpendicular line passing through the centre of the small mirror. The small mirror is situated between the large mirror and its focus, that its distance from this focal point may be equal to the distance from the centre of the mirror to the focus of the eye-glass. When the rays ab from a distant object fall upon the large speculum at cd, they are reflected towards a focus at h; but being intercepted by the plane mirror G, they are reflected perpendicularly to the eye-glass at I, in the side of the tube, and the image formed near that position at e is viewed through a small plano-convex lens. The magnifying power of this telescope is in the proportion of the focal distance of the speculum to that of the eye-glass. Thus, if the focal distance of the speculum be 36 inches, and that of the eye-glass 1/3 of an inch, the magnifying power will be 108 times. It was this form of the reflecting telescope, that Newton invented, which Sir. W. Herschel adopted, and with which he made most of his observations and discoveries.
The Cassegrainian Reflector.—This mode of the reflecting telescope, suggested by M. Cassegrain, a Frenchman, is represented in fig. 64. It is constructed in the same way as the Gregorian, with the exception of a small convex speculum G being substituted in the room of the small concave in Gregory’s construction. As the focus of a convex mirror is negative, it is placed at a distance from the large speculum equal to the difference of their foci, that is, if the focal length of the large speculum be 18 inches, and that of the small convex 2 inches, they are placed at 16 291 inches distant from each other, on a principle similar to that of the Galilean telescope, in which the concave eye-glass is placed within the focus of the object-glass by a space equal to the focal length of the eye-glass. In this telescope, likewise, instead of two there is only one image formed, namely that in the focus of the eye-glass; and, on this account some are of opinion that the distinctness is considerably greater than in the Gregorian. Mr. Ramsden was of opinion that this construction is preferable to either of the former reflectors, because the aberrations of the two metals have a tendency to correct each other, whereas in the Gregorian both the metals being concave, any error in the specula will be doubled. It is his opinion that the aberrations in the Cassegrainian construction to that of the Gregorian is as 3 to 5. The length of this telescope is shorter than that of a Gregorian of equal focal length, by twice the focal length of the small mirror, and it shows every thing in an inverted position, and consequently is not adapted for viewing terrestrial objects.
Dr. Hook’s Reflector.—Before the reflecting telescope was much known, Dr. Hook contrived one, the form of which is represented, fig. 65, which differs in little or nothing from the Gregorian, except that the eye-glass I is placed in the hole of the great speculum BE.
Martin’s Reflector.—Mr. Bengamin Martin, a distinguished writer on optical and philosophical science, about a century ago, described a new form of the reflecting telescope, approximating to the Newtonian structure, which he contrived for his own use. It is represented in fig. 66. ABEF is the tube, in which there is an opening or aperture OP, in the upper part. Against this hole 292 within the tube is placed a large plane speculum GH, at half a right angle with the axis or sides of the tubes, with a hole CD perforated through its middle. The parallel rays a b falling on the inclined plane GH are reflected perpendicularly and parallel on the great speculum BE in the bottom of the tube. From thence they are reflected converging to a focus e through the hole of the plane mirror CD, which being also the focus of the eye-glass IK, the eye will perceive the object magnified and distinct.
In the figures referred to in the above descriptions, only one eye-glass is represented to avoid complexity; but in most reflecting telescopes, the eye-piece consists of a combination of two plano-convex glasses, as in fig. 67, which produces a more correct and a larger field of view than a single lens. This combination is generally known by the name of the Huygenian eye-piece which shall be described in the section on the eye-pieces of telescopes.
The following rule has been given for finding the magnifying power of the Gregorian telescope:—Multiply the focal distance of the great mirror by the distance of the small mirror from the image next the eye; and multiply the focal distance of the small mirror by the focal distance of the eye-glass; then divide the product of the former multiplication by the product of the latter, and the quotient will express the magnifying power. The following are the dimensions of one of the reflecting telescopes constructed by Mr. Short—who was long distinguished as the most eminent maker of such instruments, on a large scale, and whose large reflectors are still to be found in various observatories throughout Europe.
The focal distance of the great mirror 9.6 inches; or P m, fig. 67, its breadth FD 2.3; the 293 focal distance of the small mirror L n 1.5—or 1½ inch—its breadth g h 0.6—or 6/10 of an inch; the breadth of the hole in the great mirror UV, 0.5—or half an inch—the distance between the small mirror and the next eye-glass LR, 14.2; the distance between the two eye-glasses SR, 2.4; the focal distance of the eye-glass next the metal, 3.8.; and the focal distance of the eye-glass next the eye, S a 1.1, or one inch and one tenth. The magnifying power of this telescope was about 60 times. Taking this telescope as a standard, the following table of the dimensions and magnifying powers of Gregorian reflecting telescopes, as constructed by Mr. Short, has been computed.
figure 67.
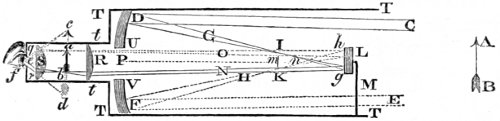
INDEX:
A: Focal distance of the great mirror.
B: Breadth of the great mirror.
C: Focus of the small speculum.
D: Breadth of the hole in the great speculum.
E: Distance between the small speculum and the first eye-glass.
F: Focal distance of the glass next the metals.
G: Focal distance of the glass next the eye.
H: Distance between the plain sides of the two glasses.
I: Magnifying power.
J: Distance between the second glass and the small eye-hole.
| A. | B. | C. | D. | E. | |||||
|---|---|---|---|---|---|---|---|---|---|
| P | m | D | F | L | n | U | V | L | R |
| In. | Dec. | In. | Dec. | In. | Dec. | In. | Dec. | In. | Dec. |
| 5. | 65 | 1. | 54 | 1. | 10 | 0. | 31 | 8. | 54 |
| 9. | 60 | 2. | 30 | 1. | 50 | 0. | 39 | 14. | 61 |
| 15. | 50 | 3. | 30 | 2. | 14 | 0. | 50 | 23. | 81 |
| 36. | 00 | 6. | 26 | 3. | 43 | 0. | 65 | 41. | 16 |
| 60. | 00 | 9. | 21 | 5. | 00 | 0. | 85 | 68. | 17 |
| F. | G. | H. | I. | J. | ||||
|---|---|---|---|---|---|---|---|---|
| R | S | R | S | |||||
| In. | Dec. | In. | Dec. | In. | Dec. | In. | ||
| 2. | 44 | 0. | 81 | 1. | 68 | 39 | 0. | 41 |
| 3. | 13 | 1. | 04 | 2. | 09 | 39 | 0. | 53 |
| 3. | 94 | 1. | 31 | 2. | 63 | 86 | 0. | 66 |
| 5. | 12 | 1. | 71 | 3. | 41 | 165 | 0. | 85 |
| 6. | 43 | 2. | 14 | 4. | 28 | 243 | 1. | 07 |
294
Mr. Short—who was born in Edinburgh in 1710, and died near London, 1768—was considered as the most accurate constructor of reflecting telescopes, during the period which intervened from 1732, to 1768. In 1743, he constructed a reflector for Lord Thomas Spencer, of 12 feet focal length, for which he received 600 guineas. He made several other telescopes of the same focal distance, with greater improvements and higher magnifiers; and in 1752, finished one for the king of Spain, for which, with its whole apparatus, he received £1200. This was considered the noblest instrument of its kind that had then been constructed, and perhaps it was never surpassed, till Herschel constructed his twenty and forty feet reflectors. High as the prices of large telescopes now are, Mr. Short charged for his instruments at a much higher rate than opticians now do, although the price of labour, and every other article required in the construction of a telescope, is now much dearer. But he had then scarcely any competitor, and he spared neither trouble nor expense to make his telescopes perfect, and put such a price upon them as properly repaid him. The following table contains a statement of the apertures, powers, and prices of Gregorian telescopes, as constructed by Mr. James Short.26 295
INDEX:
A: Number.
B: Focal length in inches.
C: Diameter of aperture in inches.
D: Prices in guineas.
| A. | B. | C. | Magnifying powers. | D. | |
|---|---|---|---|---|---|
| 1 | 3 | 1.1 | 1 Power of | 18 times | 3 |
| 2 | 4½ | 1.3 | 1 Power of | 25 times | 4 |
| 3 | 7 | 1.9 | 1 Power of | 40 times | 6 |
| 4 | 9½ | 2.5 | 2 Powers | 40 and 60 times | 8 |
| 5} | 12 | 3.0 | 2 Powers | 55 and 85 times | 10 |
| 6} | 12 | 3.0 | 4 Powers | 35, 55, 85, and 110 times | 14 |
| 7 | 18 | 3.8 | 4 Powers | 55, 95, 130, and 200 times | 20 |
| 8 | 24 | 4.5 | 4 Powers | 90, 150, 230, and 300 times | 35 |
| 9 | 36 | 6.3 | 4 Powers | 100, 200, 300, and 400 times | 75 |
| 10 | 48 | 7.6 | 4 Powers | 120, 260, 380, and 500 times | 100 |
| 11 | 72 | 12.2 | 4 Powers | 200, 400, 600, and 800 times | 300 |
| 12 | 144 | 18.0 | 4 Powers | 300, 600, 900, and 1200 times | 800 |
From this table, it appears that Mr. Short charged 75 guineas for a 3 feet reflector, whereas such an instrument is now marked in the London opticians’ catalogues at £23, when mounted on a common brass stand, and £39. 18s., when accompanied with rack-work motions and other apparatus. It is now generally understood that in the above table, Short always greatly overrated the higher powers of his telescopes. By experiment they were generally found to magnify much less than here expressed.
General remarks on Gregorian Reflectors.—1. In regard to the hole UV, of the great speculum—its diameter should be equal, or nearly so, to that of the small speculum L, fig. 67. For if it be less, no more parallel rays will be reflected than if it were equal to g h, and it may do harm in contracting the visible area within too narrow limits. Nor must it be larger than the mirror L, because some parallel rays will then be lost, and those of most consequence as being nearest the centre. 2. The small hole at e to which the eye is applied, must be nicely adjusted to the size of the 296 cone of rays proceeding from the nearest lens S. If it be larger, it will permit the foreign light of the sky or other objects to enter the eye, so as to prevent distinct vision; for the eye should receive no light, but what comes from the surface of the small mirror L. If the hole be smaller than the cylinder of rays at e then some of the necessary light will be excluded, and the object rendered more obscure. The diameter of this hole may be found by dividing the aperture of the telescope in inches by its magnifying power. Thus, if we divide the diameter of one of Short’s telescopes, the diameter of whose large speculum is 2.30, by 60, the magnifying power, the quotient will be .0383, which is nearly the 1/25 of an inch. Sometimes this hole is made so small as the 1/50 of an inch. When this hole is, by any derangement, shifted from its proper position, it sometimes requires great nicety to adjust it, and, before it is accurately adjusted, the telescope is unfit for accurate observation. 3. It is usual to fix a plate with a hole in it, at a b, the focus of the eye glass S, of such a diameter as will circumscribe the image, so as to exhibit only that part of it which appears distinct, and to exclude the superfluous rays. 4. There is an adjusting screw on the outside of the great tube, connected with the small speculum, by which that speculum may be pushed backwards or forwards to adjust the instrument to distinct vision. The hand is applied for this purpose at T.
Newtonian Telescopes.—These telescopes are now more frequently used for celestial observations than during the last century, when Gregorian reflectors were generally preferred. Sir W. Herschel was chiefly instrumental in introducing this form of the reflecting telescope to the more particular 297 attention of astronomers, by the splendour and extent of the discoveries which it enabled him to make. In this telescope there is no hole required in the middle of the great speculum, as in the Gregorian construction, which circumstance secures the use of all the rays which flow from the central parts of the mirror.
The following table contains a statement of the apertures and magnifying powers of Newtonian Telescopes, and the focal distances of their eye-glasses. The first column contains the focal length of the great speculum in feet; the second, its linear aperture in inches; the third, the focal distance of the single glass in decimals, or in 1000ths of an inch, and the fourth column, contains the magnifying power. This portion of the table was constructed by using the dimensions of Mr. Hadley’s Newtonian Telescope, formerly referred to, as a standard—the focal distance of the great mirror being 62½ inches, its medium aperture 5 inches, and power 208. The fifth, sixth, and seventh columns contains the apertures of the concave speculum, the focal lengths of the eye-glasses and the magnifying powers, as calculated by Sir D. Brewster, from a telescope of Mr. Hauksbee, taken as a standard; whose focal length was 3 feet 3 inches, its aperture about 4 inches, and magnifying power 226 times. 298
INDEX:
A: Focal distance of concave metal.
B: Aperture of concave metal.
C: Focal distance of single eye-glass.
D: Magnifying power.
E: Aperture of the concave speculum.
F: Focal length of the eye-glass.
G: Magnifying power.
| Sir D. Brewster’s Numbers. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A. | B. | C. | D. | E. | F. | G. | ||||
| Feet. | Inch. | Dec. | In. | Dec. | Inch. | Dec. | In. | Dec. | ||
| 0½ | 0. | 86 | 0. | 167 | 36 | 1. | 34 | 0. | 107 | 56 |
| 1 | 1. | 44 | 0. | 199 | 60 | 2. | 23 | 0. | 129 | 93 |
| 2 | 2. | 45 | 0. | 236 | 102 | 3. | 79 | 0. | 152 | 158 |
| 3 | 3. | 31 | 0. | 261 | 138 | 5. | 14 | 0. | 168 | 214 |
| 4 | 4. | 10 | 0. | 281 | 171 | 6. | 36 | 0. | 181 | 265 |
| 5 | 4. | 85 | 0. | 297 | 202 | 7. | 51 | 0. | 192 | 313 |
| 6 | 5. | 57 | 0. | 311 | 232 | 8. | 64 | 0. | 200=1/5 | 360 |
| 7 | 6. | 24 | 0. | 323 | 260 | 9. | 67 | 0. | 209 | 403 |
| 8 | 6. | 89 | 0. | 334 | 287 | 10. | 44 | 0. | 218 | 445 |
| 9 | 7. | 54 | 0. | 344 | 314 | 11. | 69 | 0. | 222 | 487 |
| 10 | 8. | 16 | 0. | 353 | 340 | 12. | 65 | 0. | 228 | 527 |
| 11 | 8. | 76 | 0. | 362 | 365 | 13. | 58 | 0. | 233 | 566 |
| 12 | 9. | 36 | 0. | 367 | 390 | 14. | 50 | 0. | 238 | 604 |
| 13 | 9. | 94 | 0. | 377 | 414 | 15. | 41 | 0. | 243 | 642 |
| 14 | 10. | 49 | 0. | 384 | 437 | 16. | 25 | 0. | 248 | 677 |
| 15 | 11. | 04 | 0. | 391 | 460 | 17. | 11 | 0. | 252 | 713 |
| 16 | 11. | 59 | 0. | 397 | 483 | 17. | 98 | 0. | 256 | 749 |
| 17 | 12. | 14 | 0. | 403 | 506 | 18. | 82 | 0. | 260 | 784 |
| 18 | 12. | 67 | 0. | 409 | 528 | 19. | 63 | 0. | 264 | 818 |
| 19 | 13. | 20 | 0. | 414 | 550 | 20. | 45 | 0. | 268 | 852 |
| 20 | 13. | 71 | 0. | 420 | 571 | 21. | 24 | 0. | 271 | 885 |
One great advantage of reflecting telescopes above common refractors, is, that they will admit of eye glasses of a much shorter focal distance, and consequently, will magnify so much the more, for the rays are not coloured by reflection from a concave mirror, if it be ground to a true figure, as they are by passing through a convex glass though figured and polished with the utmost exactness. It will be perceived from the above table, that the focal length of the eye glasses is very small, the lowest there stated being only about 1/10 of an inch, and the highest little more than ¼ of an inch focal distance. Sir W. Herschel obtained the high powers which he sometimes put upon his telescopes, by using small double convex 299 lenses for eye glasses, some of which did not exceed the one fiftieth of an inch in focal length. When the focal length of the concave speculum, and that of the eye glass are given, the magnifying power is found by dividing the former by the latter, after having reduced the focal length of the concave speculum to inches. Thus the 6 feet speculum, multiplied by 12, produces 72 inches, which, divided by Brewster’s number for the focus of the eye glass = 200, or 1/5 of an inch, produces a quotient of 360 as the magnifying power. It has been calculated that, if the metals of a Newtonian telescope be worked as exquisitely as those in Sir W. Herschel’s 7 feet reflector, the highest power that such a telescope should bear with perfect distinctness, will be found by multiplying the diameter of the great speculum in inches, by 74, and the focal distance of the single eye glass may be found by dividing the focal distance of the great mirror by the magnifying power. Thus 6.25—the aperture in inches of Herschel’s 7 feet Newtonian—multiplied by 74 is 462½, the magnifying power; and 7 multiplied by 12, and divided by 462.5 is 0.182 of an inch, the focal distance of the single eye glass required. But it is seldom that more than one half of this power can be applied with effect to any of the planetary bodies. For general purposes the power produced by multiplying the diameter of the speculum by 30, or 40, will be found most satisfactory.
The following are the general prices of reflecting telescopes as made by the London opticians.
| £ | s. | |
|---|---|---|
| A four feet, seven inch aperture, Gregorian Reflector; with the vertical motions upon a new invented principle, as well as apparatus to render the tube more steady in observation; according to the additional apparatus of small speculums, eye-pieces, micrometers, &c. from | 80 to 120 | 0300 |
| Three feet long, mounted on a plain brass stand | 23 | 2 |
| Ditto, with rack-work motions, improved mounting, and metals | 39 | 18 |
| Two feet long without rack-work, and with 4 magnifying powers, improved | 15 | 15 |
| Ditto with rack-work motion | 22 | 1 |
| Eighteen inch on a plain stand | 9 | 9 |
| Twelve inch Ditto | 6 | 6 |
The above are the prices stated in Messrs. W. and S. Joneses catalogue.
The following list of prices of the various kinds of reflecting telescopes is from Messrs. Tulley’s (of Islington) catalogue.
| £ | s. | |
|---|---|---|
| 1 foot Gregorian reflector, on pillar and claw stand, metal 2½ inches diameter, packed in a mahogany box | 6 | 6 |
| 1½ foot ditto, on pillar and claw stand, metal 3 inches diameter, packed in mahogany box | 11 | 11 |
| 2 feet ditto, metal 4 inches diameter | 16 | 16 |
| Ditto, ditto, with rack-work motions | 25 | 4 |
| 3 feet ditto, metal 5 inches diameter, with rack-work motions | 42 | 0 |
| Ditto, metal 6 inches diameter, on a tripod stand, with centre of gravity motion | 68 | 5 |
| 4 feet ditto, metal 7 inches diameter, as above | 105 | 0 |
| 6 feet ditto, metal 9 inches diameter, on an improved iron stand | 210 | 0 |
| 7 feet Newtonian reflectors, 6 inches aperture, mounted on a new and improved stand | 105 | 0 |
| Ditto, ditto, metal 7 inches diameter | 126 | 0 |
| 9 feet ditto, metal 9 inches diameter | 210 | 0 |
| 10 feet ditto, metal 10 inches diameter | 315 | 0 |
| 12 feet ditto, metal 12 inches diameter | 525 | 0 |
Comparative brightness of achromatic and reflecting telescopes. The late astronomer royal, Dr. Maskelyne, from a comparison of a variety of telescopes, was led to the following conclusion,—‘that the aperture of a common reflecting telescope, in order to show objects as bright as the achromatic must be to that of an achromatic telescope as 8 to 5,’—in other words, an achromatic whose object glass is 5 inches diameter, 301 will show objects with as great a degree of brightness as a reflector whose large speculum is 8 inches in diameter. This result, if correct, must be owing to the small number of rays reflected from a speculum compared with the number transmitted through an achromatic object glass.
Soon after Sir William Herschel commenced his astronomical career, he introduced a new era in the history of reflecting telescopes. After he had cast and polished an immense variety of specula for telescopes of different sizes-he, at length, in the year 1782, finished a 20 feet reflector with a large aperture. Being sensible of the vast quantity of light which is lost by a second reflection from the small speculum, he determined to throw it aside altogether, and mounted this 20 feet reflector on a stand that admitted of being used without a small speculum in making front observations—that is, in sitting with his back to the object, and looking directly towards the surface of the speculum. Many of his discoveries and measurements of double stars were made with this instrument, till, at length, in the year 1785 he put the finishing hand to that gigantic speculum, which soon became the object of universal astonishment, and which was intended for his forty feet reflecting telescope; he had succeeded so well in constructing reflecting telescopes of comparatively small aperture, that they would bear higher magnifying powers than had ever previously been applied; but he found that a deficiency of light could only be remedied by an increased diameter of the large speculum, which therefore was his main 302 object, when he undertook to accomplish a work which to a man less enterprising, would have appeared impracticable. The difficulties he had to overcome were numerous; particularly in the operative department of preparing, melting, annealing, grinding, and polishing a mass of metal that was too unwieldly to be moved without the aid of mechanical powers. At length, however, all difficulties having been overcome, this magnificent instrument was completed with all its complicated apparatus, and erected for observation, on the 28th of August, 1789, and on the same day the sixth satellite of Saturn was detected, as a prelude of still farther discoveries which were afterwards made by this instrument, in the celestial regions.
It would be too tedious to attempt a description of all the machinery and apparatus connected with this noble instrument. The reader who wishes to peruse a minute description of the stairs, ladders, platform, rollers, and of every circumstance relating to joiner’s work, carpenter’s work, smith’s work, and other particulars connected with the formation and erection of this telescope, will find the details recorded in the 85th volume of the Philosophical Transactions of the Royal Society of London, for 1795, in which there are sixty-three pages of letter press, and eighteen plates illustrative of the subject. I shall content myself with giving a short outline of the essential parts belonging to this instrument.
The tube of this telescope is made of rolled or sheet iron, joined together without rivets; the thickness of the sheets is somewhat less than 1/36 part of an inch, or 14 pounds weight for a square foot; great care was taken that the cylindrical form should be secured, and the whole was coated 303 over three or four times with paint, inside and outside, to secure it against the damp. This tube was removed from the place in which it was formed by twenty-four men, divided into six sets; so that two men on each side, with a pole of 5 feet long in their hands, to which was affixed a piece of course cloth, 7 feet long going under the tube, and joined to a pole 5 feet long, in the hands of two other men, assisted in carrying the tube. The length of this tube is 39 feet 4 inches, the diameter 4 feet 10 inches; and, on a moderate computation, it was ascertained, that a wooden tube of proper dimensions would have exceeded an iron one in weight by at least 3000 pounds. Reckoning the circumference of the tube 15 feet, its length 39⅓ feet, and 14 lib. for the weight of a square foot, it must have contained 590 square feet, and weighed 8,260 pounds. Various hoops were fixed within the tube, and longitudinal bars of iron connecting some of them are attached to the two ends of the tube, by way of bracing the sheets, and preserving the shape perfect, when the pulleys are applied to give the necessary elevation at the upper end, and that the speculum may be kept secure at the lower end. The lower end of the tube is firmly supported on rollers that are capable of being moved forwards or backwards by a double rack, connected with a set of wheels and pinions. By an adjustment at the lower extremity of the tube, the speculum is turned to a small inclination, so that the line of collimation may not be coincident with the longitudinal axis of the tube, but may cross the tube diagonally, and meet the eye in the air at about two inches from the edge of the tube, which is the peculiarity of the construction, that supersedes the necessity of applying a second reflector. Hence no part 304 of the head of the observer intercepts the incident rays, and the observation is taken with the face looking at the speculum, the back being turned to the object to be observed.
The large speculum is enclosed in a strong iron ring, braced across with bars of iron, and an enclosure of iron and ten sheets makes a case for it. It is lifted by three handles of iron attached to the sides of the ring, and is put into and taken out of its proper place in the tube by the help of a moveable crane, running on a carriage, which operation requires great care. The speculum is made of a metallic composition, and is 49½ inches in diameter; but the concave polished surface is only 48 inches, or 4 feet in diameter. Its thickness is 31 inches; and when it came from the cast its weight was 2118 pounds. The metals for its formation were procured at a warehouse in Thames Street, London, where they kept ingots of two kinds ready made, one of white, and the other of bell-metal; and it was composed of two ingots of bell-metal for one of white. It was not to be expected that a speculum of such large dimensions, could have a perfect figure imparted to its surface, nor that the curve, whatever it might be, would remain identically the same in changes of temperature; therefore we are not surprised when we are told, that the magnifying powers used with this telescope seldom exceeded 200; the quantity of light collected by so large a surface being the principal aim of the maker. The raising of the balcony, on which the observer stands, and the sliding of the lower end of the tube, in which the speculum rests, are effected by separate tackles, and require only occasional motions; but the elevation of the telescope requires the main tackle to be employed, and the motion 305 usually given in altitude at once was two degrees; the breadth of the zone in which the observations were made, as the motion of the sphere in right ascension brought the objects into view. A star, however, could be followed for about a quarter of an hour. Three persons were employed in using this telescope, one to work the tackle, another to observe, and a third to mark down the observations. The elevation was pointed out by a small quadrant fixed to the main tube, near the lower end, but the polar distance was indicated by a piece of machinery, worked by a string, which continually indicated the degree and minute on a dial in the small house adjoining, while the time was shown by a clock in the same place, Miss Herschel performing the office of Registrar.
At the upper end the tube is open, and directed to the part of the heavens intended for observation, and the observer, standing on the foot board, looks down the tube, and perceives the object by rays reflected from the speculum, through the eye glass at the opening of the tube. When the telescope is directed to any objects near the zenith, the observer is necessarily at an elevation at least 40 feet from the ground. Near the place of the eye glass is the end of a tin pipe, into which a mouth-piece may be placed, so that, during an observation, a person may direct his voice into this pipe, while his eye is at the glass. This pipe, which is 1½ inch in diameter runs down to the bottom of the tube, where it goes into a turning joint, thence into a drawing tube, and out of this into another turning joint, from whence it proceeds, by a set of sliding tubes towards the front of the foundation timber. Its use is to convey the voice of the observer to his assistants, for at the last place, it divides itself into two branches, one going into the observatory, the other into the workman’s 306 room, ascending in both places through the floor, and terminates in the usual shape of speaking trumpets. Though the voice passes in this manner through a tube, with many inflections, and through not less than 115 feet, it requires very little exertion to be well understood.
To direct so unwieldy a body to any part of the heavens at pleasure, many mechanical contrivances were evidently necessary. The whole apparatus rests upon rollers, and care was previously taken of the foundation in the ground. This consists of concentrical brick walls, the outermost 42 feet, the innermost 21 feet in diameter, 2 feet 6 inches deep under ground, 2 feet 3 inches broad at the bottom, and 1 foot 2 inches at the top, capped with paving stones 3 inches thick, and 12¾ inches broad.
In the centre is a large post of oak, framed together with braces under ground, and walled fast to brick-work to make it steady. Round this centre the whole frame is moved horizontally by means of 20 rollers, 12 upon the outer, and 8 upon the inner wall. The vertical motion is given to the instrument by means of ropes and pullies, passing over the main beam supported by the ladders. These ladders are 49 feet long, and there is a moveable gallery with 24 rollers to ease its motion. There is a stair-case intended for persons who wish to ascend into the gallery, without being obliged to go up the ladder. The ease with which the horizontal and vertical motions may be communicated to the tube may be conceived, from a remark of Sir W. Herschel, that, in the year 1789, he several times observed Saturn, two or three hours before and after its meridian passage with one single person to continue, at his directions, the necessary horizontal and vertical motions. 307
By this telescope the sixth and seventh satellites of Saturn were discovered, only one of which is within the reach of the 20 feet reflector, or even of a 25 feet instrument. The discovery of the satellites of the planet Uranus, however, was made by the 20 feet reflector, but only after it had been converted from the Newtonian to the Herschelian construction—which affords a proof of the superiority of the latter construction over the former when the same speculum is used. Never had the heavens before been observed with so extraordinary an instrument as the forty feet reflector. The nebulosities which are found among the fixed stars, in various regions of the heavens, appeared almost all to resolve themselves into an innumerable multitude of stars; others, hitherto imperceptible, seemed to have acquired a distinct light. On the entrance of Sirius into the field of the telescope, the eye was so violently affected, that stars of less magnitude could not immediately after be perceived; and it was necessary to wait for 20 minutes before these stars could be observed. The ring of Saturn had always before ceased to be visible when its plane was directed towards the earth; but the feeble light which it reflects in that position was enough for Herschel’s instrument, and the ring, even then, still remained visible to him.
It has been generally considered that this telescope was capable of carrying a power of 6000 times; and perhaps for the purpose of an experiment, and for trying its effect on certain objects, such a power may have been applied,—in which case the eye-glass must have been only 2/25 of an inch focal distance, or somewhat less than one twelfth of an inch. But such a power could not be generally applied, with any good effect, to the 308 planetary bodies; and I question much whether any power above 1000 times was ever generally used. For, it is the quantity of light which the telescope collects, more than the magnifying power, that enables us to penetrate, with effect, into the distant spaces of the firmament: and hence, as above stated, the power seldom exceeded 200, which on account of the large diameter of the speculum, would enable the instrument to penetrate into the distant celestial spaces perhaps further than if a power of as many thousands of times had been applied.
Sir John Herschel, who inherits all the science, skill, and industry of his father, some time ago ground and polished a new speculum for the 20 feet tube, formerly noticed, which is connected with a stand, pulleys and other appendages, similar to those above described, though of smaller dimensions. This telescope shows the double stars exceedingly well defined, and was one of the principal instruments used in forming his catalogue of these objects which was presented to the Royal Society, in conjunction with that of Sir James South, about the year 1828. I suppose, it is likewise the same telescope with which Sir John lately made his Sidereal observations at the Cape of Good Hope.
The largest front view reflecting telescope in this country—next to Herschel’s 40 feet instrument—is that which was erected at the Royal Observatory at Greenwich, in the year 1820, by Mr. Ramage of Aberdeen. The diameter of the concave reflector is 15 inches, and its focal length 309 25 feet. It is erected on machinery which bears a certain resemblance to that of Herschel’s, which we have now described; but the mechanical arrangements are greatly simplified, so that the instrument is manageable by an observer without an assistant. The tube is composed of a twelve-sided prism of deal 5/8 inch thick. At the mouth is a double cylinder of different diameters on the same axis; around this a cord is wound by a winch, and passes up from the small cylinder, over a pulley, and down through another pulley on to the large cylinder. When the winch, therefore, is turned to raise the telescope, the endless cord is unwound from the smaller cylinder, and wound on to the larger, the difference of the size of the two cylinders will be double the quantity raised, and a mechanical force to any extent may thus be obtained, by duly proportioning the diameters of the two cylinders: by this contrivance the necessity of an assistant is superseded. The view through this instrument first astonished those observers who had not been accustomed to examine a heavenly body with a telescope possessing so much light; and its performance was deemed quite extraordinary. But when the first impression had subsided, and different trials had been made in different states of the atmosphere, it was discovered that the central portion of the speculum was more perfectly figured than the ring bordering on the extreme edges. When the aperture was limited to ten or twelve inches, the performance as to the distinctness in its defining power, was greatly improved, and the light was so brilliant, that the Astronomer Royal was disposed to entertain an opinion, that it might equal that of a good achromatic refractor of the same dimensions. When, however, very small and obscure objects 310 are to be observed, the whole light of the entire aperture may be used with advantage on favourable evenings.
The eye-pieces adapted to this telescope have powers which magnify the object linearly from 100 to 1500 times, which are competent to fulfil all the purposes of vision when cleared of aberration. When the telescope is placed in the plane of the meridian and elevated together with the gallery, into any required altitude, the meridional sweeps, formerly practised by Sir W. Herschel, and continued by Sir John with great success, in the examination of double stars and nebula, may be managed with great ease.
Mr. Ramage had a telescope of about the same size, erected in an open space in Aberdeen, which I had an opportunity of inspecting when I paid a visit to that gentleman in 1833; but cloudy weather prevented my obtaining a view of any celestial bodies through it. He showed me at that time two or three large speculums, from 12 to 18 inches in diameter, which he had finished some time before, and which appeared most beautifully polished. He told me, too, that he had ground and polished them simply with his hand, without the aid of any machinery or mechanical power—a circumstance which, he said, astonished the opticians of London, when it was stated, and which they considered as almost incredible. His experience in casting and polishing metals of various sizes, during a period of 15 or 16 years, qualified him to prepare specula of great lustre, and with an unusually high polish. It has been asserted that a fifty feet telescope by Ramage of 21 inches aperture was intended to be substituted for the 25 feet instrument erected at Greenwich, and the speculum it is understood, was prepared, and 311 ready for use, provided the Navy Board was disposed to defray the expense of carrying the plan into execution. But, unfortunately, this ingenious artist was unexpectedly cut off in the midst of his career, about the year 1835.
A particular description of this telescope was given in the ‘Edinburgh New Philosophical Journal’ for April—July, 1826, conducted by Professor Jameson, the greater part of which was copied in the ‘London Encyclopedia,’ ] under the article Telescope. From this description I shall endeavour to condense a brief account of this instrument with a few additional remarks.
About the year 1822, an old speculum 27 inches in focal length, very imperfectly polished happened accidentally to come into my possession; and feeling no inclination to fit it up in the Gregorian form, I formed the resolution of throwing aside the small speculum, and attempting the front view notwithstanding the uniform assertion of opticians, that such an attempt in instruments of a small size is impracticable. I had some ground for expecting success in this attempt, from several experiments I had previously made, particularly from some modifications I had made in the construction of astronomical eye-pieces, which have a tendency to correct the aberration of the rays of light, when they proceed somewhat obliquely from a lens or speculum. In the first instance, I placed the speculum at the one end of a tube of the form of a segment of a cone—the end next the eye being somewhat wider than that at which the speculum 312 was fixed, and its length about an inch shorter than the focal distance of the mirror. A small tube for receiving the different eye-pieces was fixed in the inside of the large tube at the end next the eye, and connected with an apparatus by which it could occasionally be moved either in a vertical or horizontal direction. With the instrument fitted up in this manner, I obtained some interesting views of the moon, and of terrestrial objects. But finding that one side of the tube intercepted a considerable portion of light from the object, I determined to throw aside the tube altogether, and to fit up the instrument on a different plan.
A short mahogany tube, about 3 inches long, was prepared, to serve as a socket for holding the speculum. To the side of this tube an arm was attached, about the length of the focal distance of the mirror, at the extremity of which a brass tube for receiving the eye-pieces, was fixed, connected with screws and sockets, by which it might be raised or depressed, and turned to the right hand or to the left, and with adjusting apparatus by which it might be brought nearer to or farther from the speculum. Fig. 69 exhibits a general representation of the instrument in profile. AB is the short tube which holds the speculum; CD the arm which carries the eye-tubes, which consists of two distinct pieces of mahogany; the part D being capable of sliding along the under side of C, through the brass sockets EF. To the under part of the socket F is attached a brass nut with a female screw, in which the male screw ab acts by applying the hand to the knob c, which serves for adjusting the instrument to distinct vision. G is the brass tube which receives the eye-pieces. It is supported by a strong brass wire de, which 313 passes through a nut connected with another strong wire, which passes through the arm D. By means of the nut f this tube may be elevated or depressed, and firmly fixed in its proper position; and by the nut d it may be brought nearer to or further from, the arm D.
figure 69.
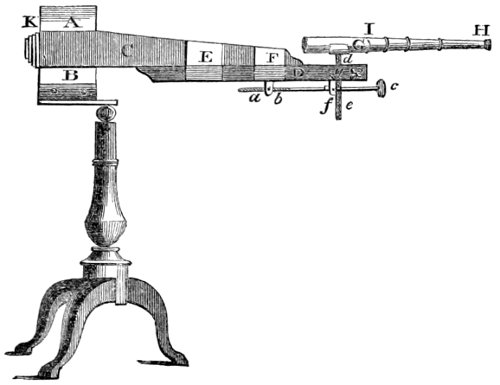
By the same apparatus, it is also rendered capable of being moved either in a vertical or horizontal direction: but when it is once adjusted to its proper position, it must be firmly fixed, and requires no further attention. The eye-piece represented in this figure is the one used for terrestrial objects, which consists of the tubes belonging to a pocket achromatic telescope. When an astronomical eye-piece is used, the length of the instrument extends only to the point I. In looking through this telescope, the right eye is applied at the point H, and the observer’s head is understood 314 to be uncovered, or, at least, tightly covered with a thin cap. For those who use only the left eye, the arm would require to be placed on the opposite side of the tube, or the arm, along with the tube, be made to turn round 180 degrees.
figure 70.

Fig. 70 represents a front, or rather an oblique view of the instrument, in which the position of the speculum may be seen. All the specula which I fitted up in this form, having been originally intended for Gregorian reflectors, have holes in their centres. The eye-piece is therefore directed to a point nearly equi-distant from the hole to the left hand edge of the speculum, that is, to the point a. In one of these instruments fitted up with a four feet speculum, the line of vision is 315 directed to the point b on the opposite side of the speculum, but, in this case, the eye-tube is removed farther from the arm, than in the former case. The hole in the centre of the speculum is obviously a defect in this construction of a reflecting telescope, as it prevents us from obtaining the full advantage of the rays which fall near the centre of the mirror; yet the performance of the instruments, even with this disadvantage, is superior to what we should previously have been led to expect.
The principal nicety in the construction of this instrument, consists in the adjustment and proper direction of the eye-tube. There is only one position in which vision will be perfectly distinct. It must be neither too high nor too low,—it must be fixed at a certain distance from the arm,—and must be directed to a certain point of the speculum. This position must be ultimately determined by experiment, when viewing terrestrial objects. A person unacquainted with this construction of the telescope, would, perhaps, find it difficult, in the first instance, to make this adjustment; but were it at any time deranged, through accident or otherwise, I can easily make the adjustment anew, in the course of a minute or two.
In pointing this telescope to the object intended to be viewed, the eye is applied at K, fig, 69, and looking along the arm, towards the eye-piece, till it nearly coincide with the object, it will, in most cases, be readily found. In this way I can easily point this instrument to Jupiter or Saturn, or to any of the other planets, visible to the naked eye, even when a power of 160 or 170 times is applied. When high magnifying powers, however, are used, it may be expedient to fix, on the upper part of the short tube in which the speculum rests, a 316 Finder, such as that which is used in Newtonian telescopes. When the moon is the object intended to be viewed, she may be instantly found by moving the instrument till her reflected image be seen from the eye-end of the telescope on the face of the mirror.
I have fitted up several instruments of the above description with specula of 16, 27, 35, and 49 inches focal distance. One of these having a speculum of 27 inches focal length, and an astronomical eye-piece, producing a magnifying power of about 90 times, serves as a good astronomical telescope. By this instrument the belts and satellites of Jupiter, the ring of Saturn, and the mountains and cavities of the moon, may be contemplated with great ease and distinctness. With a magnifying power of 35 or 40 times, terrestrial objects appear remarkably bright and well-defined. When compared with a Gregorian, the quantity of light upon the object appears nearly doubled, and the image is equally distinct—although the speculum has several blemishes, and its surface is but imperfectly polished. It represents objects in their natural colours, without that dingy and yellowish tinge which appears when looking through a Gregorian. Another of these instruments is about four feet long. The speculum which belongs to it is a very old one: when it came into my possession, it was so completely tarnished, as scarcely to reflect a ray of light. After it was cleaned, it appeared to be scarcely half polished, and its surface is covered with yellowish stains which cannot be erased. Were it fitted up upon the Gregorian plan, it would, I presume, be of very little use, unless when a very small magnifying power was applied. Yet, in its present form, it bears, with distinctness, a magnifying power of 317 130 times, and is equal in its performance to a 3½ feet achromatic. It exhibits distinct and interesting views of the diversities of shade, and of the mountains, vales, cavities, and other inequalities of the moon’s surface. With a power of about 50 times, and a terrestrial eye-piece, it forms an excellent telescope for land objects, and exhibits them in a brilliant and novel aspect. The smallest instrument I have attempted to construct on this plan, is only 5½ inches focal distance, and 1¾ inch diameter. With a magnifying power of about 15 times, it shows terrestrial objects with distinctness and brilliancy. But I should deem it inexpedient to fit up any instrument of this description with specula of a shorter focal distance than 20 or 24 inches. The longer the focal distance the more distinctness may be expected, although the aperture of the speculum should be comparatively small.
The following are some of the properties and advantages peculiar to this construction of the reflecting telescope.
1. It is extremely simple, and may be fitted up at a comparatively small expense. Instead of large and expensive brass tubes, such as are used in the Gregorian and Newtonian construction, little more is required than a short mahogany tube, two or three inches long, to serve as a socket for the speculum, with an arm connected with it about the focal length of the speculum. The expense of small specula, either plain or concave, is saved, together with the numerous screws, springs, &c., for centering the two specula, and placing the small mirror parallel to the large one. The only adjustment requisite in this construction, is that of the eye-tube to the speculum; and, by means of the simple apparatus above described, it 318 can be effected in the course of a few minutes. Almost the whole expense of the instrument consists in the price of the speculum and the eye-pieces. The expense of fitting up the four feet speculum, alluded to above—exclusive of speculum and eye-piece—but including mahogany tube and arm, brass sockets, screws, eye-tube, brass joint, and a cast-iron stand painted and varnished, did not amount to £1 : 8s. A Gregorian of the same size would have required a brass tube at least 4½ feet in length, which would cost 5 or 6 guineas, besides the apparatus connected with the small speculum, and the additional expense connected with the fitting up of the joint and stand requisite for supporting and steadying so unwieldy an instrument. While the one instrument would require two persons to carry it from one room to another, and would occupy a considerable space in an ordinary apartment, the other can be moved, with the utmost ease, with one hand, to any moderate distance, and the space it occupies is extremely small.
2. It is more convenient for viewing celestial objects at a high altitude, than other telescopes. When we look through a Gregorian reflector or an achromatic telescope of 4 or 5 feet in length, to an object elevated 50 or 60 degrees above the horizon, the body requires to be placed in an uneasy and distorted position, and the eye is somewhat strained, while the observation is continued. But when viewing similar objects by the Aerial Reflector, we can either stand perfectly erect, or sit on a chair, with the same ease as we sit at a desk when reading a book or writing a letter. In this way, the surface of the moon or any of the planets, may be contemplated for an hour or two, without the least weariness or fatigue. 319 A delineation of the lunar surface may be taken with this instrument with more ease and accuracy than with any other instrument, as the observer can sketch the outline of the object by one eye on a tablet placed a little below the eye-piece, while the other eye is looking at the object. For the purpose of accommodating the instrument to a sitting or standing posture a small table was constructed, capable of being elevated or depressed at pleasure, on which the stand of the telescope is placed. When the telescope is 4 or 5 feet long, and the object at a very high elevation, the instrument may be placed on the floor of the apartment, and the observer will stand in an erect position.
3. This instrument is considerably shorter than a Gregorian telescope whose mirror is of the same focal length. When an astronomical eye-piece is used, the whole length of the instrument is nothing more than the focal length of the speculum. But a Gregorian whose large speculum is 4 feet focus, will be nearly 5 feet in length, including the eye-piece.
4. The Aerial Reflector far excels the Gregorian in brightness. The deficiency of light in the Gregorians is owing to the second reflection from the small mirror; for it has been proved by experiment that nearly the one half of the rays of light which fall upon a reflecting surface is lost by a second reflection. The image of the object may also be presumed to be more correct, as it is not liable to any distortion by being reflected from another speculum.
5. There is less tremor in these telescopes than in Gregorian Reflectors. One cause, among others, of the tremors complained of in Gregorians is, I presume, the formation of a second image at a great distance from the first, besides 320 that which arises from the elastic tremor of the small speculum, when carried by an arm supported only at one end. But as the image formed by the speculum in the aerial telescope is viewed directly, without being exposed to any subsequent reflection, it is not so liable to the tremors which are so frequently experienced in other reflectors. Notwithstanding the length of the arm of the 4 feet telescope above mentioned, a celestial object appears remarkably steady, when passing across the field of view, especially when it is at a moderate degree of altitude; and it is easily kept in the field by a gentle motion applied to the arm of the instrument.
In prosecuting my experiments in relation to these instruments, I wished to ascertain what effect might be produced by using a part of a speculum instead of the whole. For this purpose, I cut a speculum, three feet in focal length, through the centre, so as to divide it into two equal parts, and fitted up each part as a distinct telescope; so that I obtained two telescopes from one speculum. In this case I found that each half of the speculum performed nearly as well as the whole speculum had done before, at least there appeared to be no very sensible diminution in the brightness of the object, when viewed with a moderate power, and the image was equally accurate and distinct; so that if economy were a particular object aimed at in the construction of these instruments, two good telescopes might be obtained from one speculum; or if a speculum happened to be broken accidentally into large fragments, one or more of the fragments might be fitted up on this principle to serve as a tolerably good telescope.
From the experiments I have made in reference to these instruments, it is demonstrable, that a 321 tube is not necessary in the construction of a reflecting telescope—at least on the principle now stated—whether it be used by day or by night for terrestrial or celestial objects; for I have frequently used these telescopes in the open air in the day time, without any inconvenience from extraneous light. Therefore, were a reflecting telescope of 50 or 60 feet in length to be constructed, it might be fitted up at a comparatively small expence, after the expense of the metallic substances, and of casting, grinding, and polishing the speculum is defrayed. The largest instrument of this description which has hitherto been constructed is the 40 feet reflector of Sir W. Herschel. This complicated and most unwieldy instrument had a tube of rolled or sheet iron 39 feet 4 inches in length, about 15 feet in circumference, and weighed about 8000 pounds. Now, I conceive that such enormous tubes, in instruments of such dimensions, are altogether unnecessary. Nothing more is requisite than a short tube for holding the speculum. Connected with one side of this tube (or with both sides were it found necessary), two strong bars of wood, projecting a few feet beyond the speculum end, and extending in front as far as the focal length of the mirror, and connected by cross bars of wood, iron or brass—would be quite sufficient for a support to the eye-piece, and for directing the motion of the instrument. A telescope of 40 or 50 feet in length, constructed on this plan, would not require one fifth of the expense, nor one fourth of the apparatus and mechanical power for moving it to any required position, which were found necessary in the construction of Sir W. Herschel’s large reflecting telescope. The idea here suggested will perhaps be more readily appreciated by an inspection of 322 fig. 71, where A is the short tube, BC and DE the two large bars or arms, connected with cross bars, for the purpose of securing strength and steadiness. At I and K, behind the speculum, weights might be applied, if necessary, for counterbalancing the lever power of the long arm. F represents the position of the eye-piece, and GH the joint and part of the pedestal on which the instrument is placed. With regard to telescopes of smaller dimensions, as from 5 to 15 feet in focal length—with the exception of the expense of the specula and eye-pieces—they might be fitted up for a sum not greater than from 3 to 10 or 15 guineas.
figure 71.
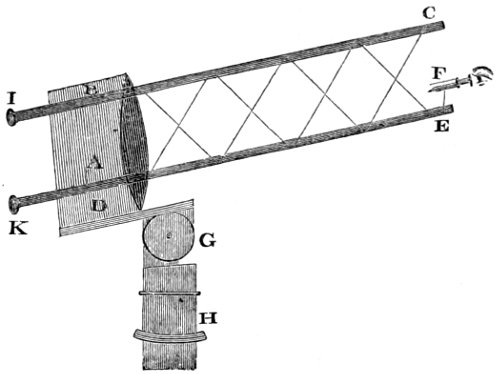
Were any person to attempt the construction of those telescopes, it is possible he might not succeed in his first attempts without more minute directions than I have yet given. The following directions may perhaps tend to guide the experimenter in adjusting the eye-tube to the speculum, which is a point that requires to be particularly 323 attended to, and on which depends the accurate performance of the instrument. After having fixed the eye-piece nearly in the position it should occupy, and directed the instrument to a particular object, look along the arm of the telescope, from K (fig. 69.) to the extremity of the eye-piece at H, and observe, whether it nearly coincides with the object. If the object appear lower than this line of vision, the eye-piece must be lowered, and if higher, it must be raised, by means of the nuts and screws at gd and fe, till the object and the line of vision now stated nearly coincide. The eye-piece should be directed as nearly perpendicular to the front of the speculum as possible, but so that the reflected image of one’s head from the mirror shall not interfere to obstruct the rays from the object. An object may be seen with an approximate degree of distinctness, but not accurately, unless this adjustment be pretty accurately made. The astronomical eye-pieces used for these telescopes are fitted with a brass cap which slides on the end next the eye, and is capable of being brought nearer to or farther from the first eye-glass. In the centre of this cap, next the eye, is a small hole, about the 1/40th or 1/50th of an inch diameter, or about as wide as to admit the point of a pin or a moderate-sized needle. The distance of this hole from the lens next the eye must be adjusted by trial, till the whole field of view appear distinct. A common astronomical eye-piece, without this addition, does not answer well. I find by experience, that terrestrial eye-pieces, such as those used in good achromatic telescopes, are, on the whole, best adapted to this construction of a reflecting telescope.
I have sometimes used these instruments for the purpose of viewing perspective prints, which they 324 exhibit in a beautiful and interesting manner. If a coloured perspective be placed at one end of a large room or gallery, and strongly illuminated either by the sun or by two candles, and one of the reflectors furnished with a small magnifying power, placed at the opposite end of the room—the representation of a street or a landscape will be seen in its true perspective, and will appear even more pleasant and interesting than when viewed through the common optical diagonal machine. If an inverting eye-piece be used—which is most eligible in this experiment—the print, of course, must be placed in an inverted position.
That reflecting telescopes of the descriptions now stated are original in their construction, appears from the uniform language of optical writers, some of whom have pronounced such attempts to be altogether impracticable. Sir David Brewster, one of the latest and most respectable writers on this subject, in the ‘Edinburgh Encyclopedia’ art optics, and in the last edition of his appendix to ‘Ferguson’s Lectures,’ has the following remarks:—‘If we could dispense with the use of the small specula in telescopes of moderate length, by inclining the great speculum, and using an oblique, and consequently a distorted reflection, as proposed first by La Maire, we should consider the Newtonian telescope as perfect; and on a large scale, or when the instrument exceeds 20 feet, it has undoubtedly this character, as nothing can be more simple than to magnify, by a single eye-glass, the image formed by a single speculum. As the front view is quite impracticable, and indeed has never been attempted in instruments of a small size, it becomes of great practicable consequence to remove as much as possible, the 325 evils which arise from the use of a small speculum,’ &c.
The instruments now described have effectuated, in some degree, the desirable object alluded to by this distinguished philosopher, and the mode of construction is neither that of Sir W. Herschel’s front view, nor does it coincide with that proposed by La Maire, which appears to have been a mere hint that was never realized in the construction of reflecting telescopes of a small size. The simplicity of the construction of these instruments, and the excellence of their performance, have been much admired by several scientific gentlemen and others to whom they have been exhibited. Prior to the description of them in the Edin. Philos. Journal, they were exhibited in the Calton Hill Observatory, Edinburgh, in the presence of Professor Wallace, and another gentleman, who compared their performance with that of an excellent Gregorian. As this instrument is distinguished from every other telescope, in being used without a tube, it has been denominated ‘The aerial reflector.’
This nobleman, unlike many of his compeers, has, for a considerable number of years past, devoted his attention to the pursuits of science, and particularly to the improvement of reflecting telescopes. He is evidently possessed of high mathematical attainments, combined with an uncommon degree of mechanical ingenuity. About 14 or 15 years ago, he engaged in various experiments with the view of counteracting the effects 326 of the spherical aberration of the specula of reflecting telescopes—which imperfection, if it could be completely remedied, would render the reflecting telescope almost a perfect instrument, as it is not affected by the different refrangibility of the rays of light. His method, we believe, consisted in forming a large speculum of two or three separate pieces of metal, which were afterwards accurately combined into one—a central part which was surrounded by one or two rings ground on the same tool. When the images formed by the separate pieces, were made exactly to coincide, the image of the object towards which the whole speculum was directed, was then found to be as distinct as either image had been when separate. But at the period referred to, a sufficient number of experiments had not been made to determine that his lordship had completely accomplished the object he intended.
Great interest, however, has of late been excited by the improvements which his lordship has made in the formation of specula. Sir W. Herschel never made public the means by which he succeeded in giving such gigantic developement to the reflecting telescope: and therefore the construction of a large reflector has been considered as a perilous adventure. But, according to a report of Dr. Robinson of Armagh, to the Irish academy, the Earl of Rosse has overcome the difficulties which have hitherto been met with, and carried to an extent which even Herschel himself did not venture to contemplate, the illuminating power of this telescope, along with a sharpness of definition little inferior to that of the achromatic; and it is scarcely possible, he observes, to preserve the necessary sobriety of language in speaking of the moon’s appearance 327 with this instrument, which Dr. Robinson believes to be the most powerful ever constructed. The difficulty of constructing large specula, and of imparting to them the requisite degree of polish, has hitherto been considered so great, that from 8 to 12 inches diameter has been in general their utmost size. Indeed, except with the greatest reluctance, London opticians would not accept of orders for specula of more than 9 inches in diameter. It appears, however, that the Earl of Rosse has succeeded, by a peculiar method of moulding, in casting object-mirrors of true speculum metal of three feet in diameter, and of a weight exceeding 17 cwt. He is about to construct a telescope, the speculum of which is six feet in diameter, fifty feet focal distance, and of the weight of four tons; and from what he has already accomplished, it is not doubted that he possesses the power to carry his design into effect. These great masses of metal, which, in the hands of all other makers of specula would have been as untractable as so much unannealed flint-glass, the Earl of Rosse has further succeeded in bringing to the highest degree of polish, and the utmost perfection of curvature by means of machinery. The process is conducted under water, by which means those variations of temperature, so fatal to the finest specula hitherto attempted, are effectually guarded against. To convince Dr. Robinson of the efficacy of this machinery, the earl took the three feet speculum out of its telescope, destroyed its polished surface, and placed it under the mechanical polisher. In six hours it was taken out with a perfect new surface as bright as the original. Under the old system of hand-polishing, it might have required months, and even years, to effect this restoration. Even before achieving these extraordinary 328 triumphs on the solid substance, his lordship had constructed a six feet reflector by covering a curved surface of brass with squares of the true speculum metal, which gave an immense quantity of light, though subject to some irregularities, arising from the number of joinings necessary in such a mosaic work. Of the performance of his lordship’s great telescope, mounted with this reflector, those who have seen it speak in terms of high admiration; but in reference to the smaller and more perfect instrument, furnished with the solid three feet speculum, the language of the Armagh astronomer assumes a tone of enthusiasm and even of sublimity. By means of this exquisite instrument, Dr. Robinson and Sir J. South, in the intervals of a rather unfavourable night, saw several new stars, and corrected numerous errors of other observers. For example, the planet Uranus, supposed to possess a ring similar to that of Saturn, was found not to have any such appendage; and those nebulæ, hitherto regarded, from their apparently circular outline, as ‘coalescing systems,’ appeared, when tested by the three feet speculum, to be very far indeed from presenting a globular appearance; numerous off-shoots and appendages, invisible by other telescopes, appearing in all directions radiating from their edges. Such discoveries, which reflect great honour on the Earl of Rosse, will doubtless have great effect on the interests of astronomical science.27 329
After making a variety of experiments with aerial telescopes constructed of metallic specula of different focal lengths, I constructed a telescope on the same plan, with a concave glass mirror. Having obtained a fragment of a very large convex mirror which happened accidentally to have been broken, I caused the convex side to be foliated, or silverised, and found its focal length to be about 27 inches. This mirror, which was about 5 inches diameter, I placed in one of the aerial reflectors, instead of the metallic speculum, and tried its effects with different terrestrial eye-pieces. With a power of about 35 or 40 times, it gave a beautiful and splendid view of distant terrestrial objects—the quantity of light reflected from them, being considerably greater than when a metallic speculum was used, and they appeared on the whole well-defined. The only imperfection—as I had foreseen—consisted in a double image being formed of objects which were remarkably bright and white, such as a light-house whitened on the outside, and strongly illuminated by the sun. One of the images was bright and the other faint. This was obviously owing to the two reflections from the two surfaces of the mirror—one from the convex silverised side, and the other from the concave side next the eye, which produced the faint image—which circumstance has been generally considered as a sufficient reason for rejecting the use of glass specula in telescopes. But although very bright objects exhibited a double image, almost all the other objects in the 330 terrestrial landscape appeared quite distinct and without any secondary image, so that a common observer could scarcely have noticed any imperfection. When the instrument, however, was directed to celestial objects, the secondary image was somewhat vivid, so that every object appeared double. Jupiter appeared with two bodies, at a little distance from each other, and his four satellites appeared increased to eight. The moon likewise appeared as a double orb, but the principal image was distinct and well-defined. Such a telescope, therefore, was not well-adapted for celestial observations, but might answer well enough for viewing terrestrial objects.
Considering that the injurious effects of the secondary image arose from the images reflected from the two surfaces being formed near the same point, and at nearly the same focal distance, I formed a plan for destroying the secondary image, or at least counteracting its effects, by forming the concavity of the mirror next the eye of a portion of a sphere different from that of the convex side which was silverised, and from which the principal image is formed. But, for a long time, I could find no opticians possessed of tools of a sufficient length of radii for accomplishing my design. At length a London working optician undertook to finish a glass speculum, according to my directions, which were, that the convex surface of the mirror should be ground on a tool which would produce a focal distance by reflection of about 4 feet; and that the concave surface should have its focal distance at about 3 feet 3 inches, so that the secondary image might be formed at about 9 inches, within the focal distance of the silverised side, and not interfere to disturb the principal image. But, either from 331 ignorance or inattention, the artist mistook the radius for the half radius of concavity, and the speculum turned out to be only 23 inches focal distance by reflection. This mirror was fitted up as a telescope, on the aerial plan, and I found, as I expected, the secondary image completely destroyed. It produced a very beautiful and brilliant view of land objects, and even the brightest objects exhibited no double image. The mirror was nearly 5 inches in diameter, but the image was most accurately defined when the aperture was contracted to about 3 inches. It was fitted with a terrestrial eye-piece which produced a magnifying power of about 25 times. When directed to the moon, it gave a very distinct and luminous view of that orb, without the least appearance of a secondary image. But as the focal distance of the speculum was scarcely half the length I had prescribed, I did not apply to it any high astronomical powers; as I find, that these can only be applied with effect, in this construction, to a speculum of a considerable focal length. Happening to have at hand a convex lens 10 feet focal length, and 4 inches in diameter—the one side of which had been ground to a certain degree of concavity—I caused the convex side to be foliated, which produced a focus by reflection, at 13½ inches distant. To this mirror I applied terrestrial powers of 15 and 24, with considerable distinctness. The power of 15 produced a very brilliant and distinct view of land objects. Had the mirror been at least 3 times the focal length, it would have formed an excellent telescope, with the same aperture. 332
figure 72.
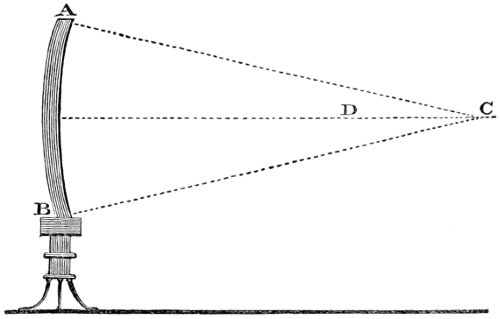
On the same principle as that by which a refracting telescope may be constructed by means of a single lens—as represented fig. 51, (page 234) we may form a telescope by reflection with a single mirror, and without an eye-piece. Let AB, fig. 72, represent a large concave speculum, and C its focus—if an eye be placed at D, about 8 or 10 inches within the focal point C, all the objects in the direction of C, or behind the spectator, will be seen magnified by reflection on the face of the mirror, and strongly illuminated. The magnifying power, in this case, will be nearly in the proportion of the focal length of the mirror to the focal length of the eye for near objects. If for example, the focal distance of the mirror be 8 feet, and the distance from the eye at which we 333 see near objects most distinctly, be 8 inches—the magnifying power will be in the ratio of 8 to 96, or 12 times. I have a glass mirror of this description, whose focal length is 4 feet 8 inches, and diameter 6 inches, which magnifies distant objects about 7 times, takes in a large field of view, and exhibits objects with great brilliancy. It presents a very distinct picture of the moon, showing the different streaks of light and shade upon her surface; and, in some cases, shows the larger spots which traverse the solar disc. This mode of viewing objects is extremely easy and pleasant, especially when the mirror is of a large diameter; and the observer is at first struck and gratified with the novel aspect in which the objects appear.
Were a concave mirror of this description—whether of glass or of speculum metal—to be formed to a very long focus, the magnifying power would be considerable. One of 50 feet focal length, and of a corresponding diameter, might produce a magnifying power, to certain eyes, of about 75 times; and, from the quantity of light with which the object would be seen, its effect would be much greater than the same power applied to a common telescope. Sir W. Herschel states, that, on one occasion, by looking with his naked eye on the speculum of his 40 feet Reflector, without the interposition of any lens or mirror, he perceived distinctly one of the satellites of Saturn, which requires the application of a considerable power to be seen by an ordinary telescope. Such an instrument is one of the most simple forms of a telescope, and would exhibit a brilliant and interesting view of the moon, or of terrestrial objects. 334
1. Prices as stated by Messrs. W. and S. Jones, Holborn, London.
| £ | s. | |
|---|---|---|
| A 4 feet, 7 inch aperture Gregorian reflector, with the vertical motions upon a new invented principle, as well as apparatus to render the tube more steady for observation, according to the additional apparatus of small speculums, eye-pieces, micrometers, &c. | from 80l. to 120 | 0 |
| Three feet long, mounted on a plain brass stand | 23 | 2 |
| Ditto with rack-work motions, improved mountings and metals | 39 | 18 |
| Two feet long without rack-work, and with 4 magnifying powers, improved | 15 | 15 |
| Ditto improved, with rack-work motions | 22 | 1 |
| Eighteen inch, on a plain stand | 9 | 9 |
| Twelve inch ditto | 6 | 6 |
2. Prices as stated by Messrs. Tulley, Islington.
| £ | s. | |
|---|---|---|
| 1 foot Gregorian Reflector, on pillar-and-claw stand, metal 2½ inches diameter, packed in a mahogany box | 6 | 6 |
| 1½ foot ditto on pillar and claw stand, metal 3 inches diameter, packed in a mahogany box | 11 | 11 |
| 2 feet ditto, metal 4 inches diameter | 16 | 16 |
| Ditto with rack-work motions | 25 | 4 |
| 3 feet ditto, metal 5 inches diameter, rack-work motions | 42 | 0 |
| 4 feet ditto, metal 7 inches diameter, on a tripod stand with centre of gravity motion | 105 | 0 |
| 6 feet ditto, metal 9 inches diameter | 210 | 0 |
| 7 feet Newtonian, 6 inches aperture | 105 | 0 |
| 12 feet ditto, metal 12 inches diameter | 525 | 0 |
3. Prices stated by Mr. G. Dollond, St. Paul’s Church Yard.
| £ | s. | |
|---|---|---|
| Reflecting telescopes 14 inches long, in a mahogany box | 9 | 9 |
| Ditto, 18 inches | 12 | 12 |
| Ditto 2 feet | 18 | 18 |
| Ditto with 4 different powers, and rack-work stand supporting the telescope in the centre of gravity | 36 | 15 |
| Ditto 3 feet, with ditto | 50 | 0 |
4. Prices of single speculums and reflecting telescopes, as made by Mr. Grub, Charlemont Bridge works, Dublin. 335
| NEWTONIAN TELESCOPES. | GREGORIAN REFLECTORS. | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diameter in inches. | Focal length in feet. | Price of Mirrors alone. | Price of telescope complete without stand. | Diameter in inches. | Focal length in feet. | Price of Mirrors alone. | Price of telescope complete without stand. | |||||
| £ | s. | £ | s. | £ | s. | £ | s. | |||||
| 6 | 3 | 17 | 10 | 25 | 0 | |||||||
| 7 | 7 | 17 | 10 | 27 | 10 | 7 | 3 | 25 | 0 | 34 | 0 | |
| 9 | 10 | 25 | 0 | 40 | 0 | 9 | 4½ | 35 | 0 | 50 | 0 | |
| 12 | 12 | 60 | 0 | 90 | 0 | 12 | 7 | 70 | 0 | 100 | 0 | |
| 15 | 15 | 120 | 0 | 170 | 0 | 15 | 9 | 150 | 0 | 200 | 0 | |
| 18 | 18 | 200 | 0 | 260 | 0 | 18 | 12 | 240 | 0 | 300 | 0 | |
Although the performance of telescopes chiefly depends on the goodness of the object-glass, or the object-speculum of the instrument, yet it is of considerable importance, in order to distinct vision, and to obtain a large and uniformly distinct field of view, that the eye-piece be properly constructed. The different kinds of eye-pieces may be arranged into two general divisions—Astronomical and terrestrial.
1. Astronomical eye-pieces.—The most simple astronomical eye-piece is that which consists of a single convex lens; and when the focal distance of this lens, and that of the object-glass of the instrument is accurately ascertained, the magnifying 336 power may be nicely determined, by dividing the focal length of the object-lens by that of the eye-glass. But, as the pencil of white light transmitted by the object-glass, will be divided by the eye-glass into its component colours, the object will appear bordered with coloured fringes, and the distinctness of vision consequently injured. Besides, the spherical aberration, when a single lens is used, is much greater than when two or more glasses are employed. Hence astronomical eye-pieces are now formed by a combination of at least two lenses.
figure 73.
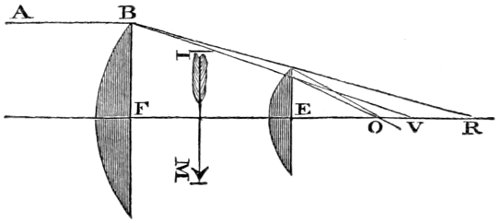
The combination of lenses now generally used for astronomical purposes, is that which is usually denominated the Huygenian eye-piece, having been first proposed by the celebrated Huygens, as a great improvement on the single lens eye-piece. The following figure (73) represents a section of this eye-piece. Let AB be a compounded pencil of white light proceeding from the object-glass; BF a plano-convex field-glass, with its plane side next the eye-glass E. The red rays of the pencil AB, after refraction would cross the axis in R, and the violet rays in V, but meeting the eye-glass E, the red rays will be refracted to O, and 337 the violet nearly in the same direction, when they will cross each other about the point O, in the axis, and unite. The distance of the two glasses FE, to produce this correction, when made of crown glass, must be equal to half the sum of their focal distances nearly. For example, suppose the focal distance of the largest, or field lens, to be 3 inches, and the focal distance of the lens next the eye, 1 inch, the two lenses should be placed exactly at the distance of 2 inches; the sum of their focal length being 4, the half of which is 2. In other words, the glass next the eye should be placed as much within the focus of the field-glass as is equal to its own focal distance. The focal length of a single lens, that has the same magnifying power as this compound eye-piece—is equal to twice the product of the focal lengths of the two lenses, divided by the sum of the same numbers. Or, it is equal to half the focal length of the field-glass. Thus, in reference to the preceding example, twice the product of the focal length of the two lenses—is equal to 6, and their sum is 4. The former number divided by the latter, produces a quotient of 1½, which is the focal length of a single lens, which would produce the same magnifying power as the eye-piece; and 1½ is just half the focal length of the field-glass. The proportion of the focal lengths of the two lenses to each other, according to Huygens, should be as 3 to 1; that is, if the field-glass be 4½ inches, the eye-glass should be 1½; and this is the proportion most generally adopted. But some opticians have recommended that the proportions should be as 3 to 2. Boscovich recommended two similar lenses; and in this case the distance between them was equal to half the sum of their focal distances, as in the Huygenian eye-piece. 338
The image is formed at IM, at the focal distance of the lens next the eye, and at the same distance from the field-glass. When distinct vision is the principal object of an achromatic telescope, the two lenses are usually both plano-convex, and fixed with their curved faces towards the object glass, as in the figure. Sometimes, however, they consist of what is called crossed lenses, that is lenses ground on one side to a short focus, and on the other side to a pretty long focus, the sides with the deepest curves being turned towards the object glass. A diaphragm, or aperture of a proper diameter, is placed at the focus of the eye lens, where the image formed by the object-glass falls, for the purpose of cutting off the extreme rays of the field lens, and rendering every part of the field of view equally distinct. This is likewise the form of the eye-piece generally applied to Gregorian reflectors. In short, when accurately constructed, it is applicable to telescopes of every description. This eye-piece, having the image viewed, by the eye behind the inner lens, is generally called the negative eye-piece, and is that which the optical-instrument makers usually supply, of three or four different sizes, for so many magnifying powers, to be applied to different celestial objects, according to their nature or the state of the atmosphere in which they are used.
Ramsden’s eye-piece.—There is another modification of lenses, known by the name of the Positive, or Ramsden’s eye-piece, which is much used in Transit instruments, and telescopes which are furnished with micrometers, and which affords equally good vision as the other eye-piece. In this construction the lenses are plano-convex, and nearly of the same focus, but are placed at a distance from each other less than the focal distance 339 of the glass next the eye, so that the image of the object viewed is beyond both the lenses, when measuring from the eye. The flat faces of the two lenses are turned into contrary directions in this eye-piece—one facing the object-glass, and the other the eye of the observer; and as the image formed at the focus of the object-glass, lies parallel to the flat face of the contiguous lens, every part of the field of view is distinct at the same adjustment, or, as opticians say, there is a flat field, which, without a diaphragm, prevents distortion of the object. This eye-piece is represented in fig. 74, where AB and CD are two plano-convex lenses, with their convex sides inwards. They have nearly the same focal length, and are placed at a distance from each other, equal to about two thirds of the focal length of either. The focal length of an equivalent single lens is equal to three fourths the focal length of either lens, supposing them to have equal focal distances. This eye-piece is generally applied, when wires of spider’s lines are used in the common focus; as the piece containing the lenses can be taken out without disturbing the lines, and is adjustable for distinct vision; and whatever may be the measure of any object given by the wire micrometer, at the solar 340 focus, it is not altered by a change of the magnifying power, when a second eye-piece of this construction is substituted.
figure 74.
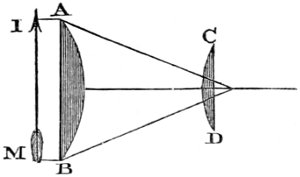
| figure 75. | figure 76. |
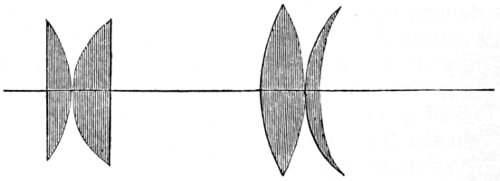 |
|
Aberration of lenses.—In connection with the above descriptions, the following statements respecting the spherical aberration of lenses may not be inappropriate. Mr. John Dollond, in a letter to Mr. Short, remarks, that ‘the aberration in a single lens is as the cube of the refracted angle; but if the refraction be caused by two lenses, the sum of the cubes of each half will be ¼ of the refracted angle, twice the cube of 1 being ¼ the cube of 2. So three times the cube of 1 is only one ninth of the cube of 3.’ &c. Hence the indistinctness of the borders of the field of view of a telescope is diminished by increasing the number of lenses in an eye piece. Sir J. Herschel has shown that if two plano-convex lenses are put together as in fig. 75, the aberration will be only 0.2481, or one fourth of that of a single lens in its best form. The focal length of the first of these lenses, must be to that of the second as 1 to 2.3. If their focal lengths are equal, the aberration will be 0.603, or nearly one half. The spherical aberration, however, may be entirely destroyed by combining a meniscus and double convex lens, as shown in fig. 76, the convex sides 341 being turned to the eye when they are used as lenses, and to parallel rays, when they are used as burning glasses. Sir J. Herschel has computed the following curvatures for such lenses.
| Focal length of the convex lens | +10.000 |
| Radius of its first surface | +5.833 |
| Radius of its second surface | -35.000 |
| Focal length of the meniscus | +17.829 |
| Radius of its first surface | +3.688 |
| Radius of its second surface | +6.294 |
| Focal length of the compound lens | +6.407 |
On the general principles above stated, a good astronomical eye-piece may be easily constructed with two proper lenses, either according to the plan of Huygens or that of Ramsden; and, from what has been now stated it is demonstrably certain, that, in all cases where two glasses are properly combined, such an eye-piece is superior to a single lens, both in point of distinctness, and of the enlargement of the field of view. I lately fitted up an eye-piece, on Ramsden’s principle, with two lenses, each about 3 inches focal length, and 1⅜ inch diameter, placed at half an inch distant, with their convex surfaces facing each other as in fig. 74, which forms an excellent eye-piece for an achromatic telescope, 6 feet 8 inches focal distance, and 4 inches aperture, particularly for viewing clusters of stars, the Milky Way, and the large nebulæ. The field of view is large, the magnifying power is only between 50 and 60 times, and the quantity of light being so great, every celestial object appears with great brilliancy, and it is in general much preferable, when applied to the stars than any of the higher powers. When applied to Presepe in Cancer, it exhibits that group at one view, as consisting of nearly a 100 stars which exhibit a beautiful and most striking appearance. 342
It may appear a curious circumstance that any eye-piece which is good with a short telescope, is also good with a long one, but that the reverse is not true; for it is found to be more difficult to make a good eye-piece for a short than for a long focal distance of the object-glass.
Celestial eye-pieces are sometimes constructed so as to produce variable powers. This is effected by giving a motion to the lens next the eye, so as to remove it nearer to or farther from the field lens; for at every different distance at which it is placed from the other lens, the magnifying power will either be increased or diminished. The greatest power is when the two lenses are nearly in contact, and the power diminishes in proportion to the distance at which the glass next the eye is removed from the other. The scale of distance, however, between the two lenses, cannot be greater than the focal distance of the field, or inner glass; for if it were, the lenses would no longer form an eye-piece, but would be changed into an inverting opera-glass. For effecting the purpose now stated, the eye-glass is fixed in a tube which slides upon an interior tube on which is marked a scale of distances, corresponding to certain magnifying powers; and, in this way an eye-piece may be made to magnify about double the number of times, when the lenses are in one position than when they are in another—as, for example, all the powers from 36 to 72 times may be thus applied, merely by regulating the distance between the two lenses. When the glasses are varied in this manner the eye-piece becomes sometimes a positive eye-piece, like Ramsden’s, and sometimes a negative one like that of Huygens.
Diagonal eye-pieces. The eye-pieces to which 343 we have now adverted, when adapted to refracting telescopes, both reverse and invert the object, and therefore are not calculated for showing terrestrial objects in their natural position. But as the heavenly bodies are of a spherical form, this circumstance detracts nothing from their utility. When the celestial object, however, is at a high altitude, the observer is obliged to place his head in a very inconvenient position, and to direct his eye nearly upwards; in which position he cannot remain long at ease, or observe with a steady eye. To remedy this inconvenience, the diagonal eye-piece has been invented, which admits of the eye being applied at the side—or at the upper part of the eye-piece, instead of the end; and when such an eye-piece is used, it is of no importance in what direction the telescope is elevated, as the observer can then either sit or stand erect, and look down upon the object with the utmost ease. This object is effected by placing a flat piece of polished speculum-metal at an angle of 45 degrees in respect to the two lenses of the eye-piece, which alters the direction of the converging rays, and forms an image which becomes erect with respect to altitude, but is reversed with respect to azimuth;—that is, in other words, when we look down upon the objects in the field of view, they appear erect; but that part of an object which is in reality on our right hand appears on our left; and if it be in motion, its apparent is opposite to its real motion; if it be moving towards the west, it will seem to move towards the east.
There are three situations in which the diagonal reflector in this eye-piece may be placed. It may be placed either 1. before the eye-piece,—or 2. behind it,—or 3. between the two lenses of 344 which the eye-piece consists. The most common position of the reflector is between the lenses; and this may be done both in the negative and the positive eye-pieces; but as the distance between the two lenses is necessarily considerable, to make room for the diagonal position of the reflector, the magnifying power cannot be great; otherwise, a diagonal eye-piece of this construction remains always in adjustment, and is useful in all cases where a high power is not required. The following is a description and representation of a diagonal eye-piece of this kind in my possession.
figure 77.
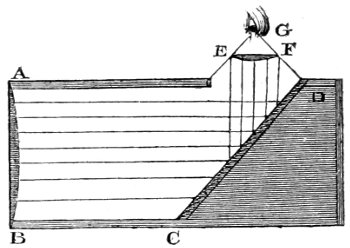
In fig. 77, AB represents the plano-convex lens next the object, which is about 2 inches in focal length, and ¾ inch in diameter; CD, a plain metallic speculum of an oval form, well polished, and placed at half a right angle to the axis of the tube; and EF another plano-convex lens, about 1½ inch focal distance. The centre of the speculum is about 1¼ inch from the lens AB, and about ½ or 1/3 inch from EF; so that this eye-piece is a positive one, on the principle proposed by Ramsden. The rays proceeding from the lens AB, and falling upon the speculum, are reflected in a perpendicular 345 direction to the lens EF, where they enter the eye at G, which looks down upon the object through the side of the tube. The real size of this eye-piece is much about the same as that represented in the figure. When applied to an achromatic telescope of 44½ inches focal distance it produces a magnifying power of 36 times, and exhibits a very beautiful view of the whole of the full moon. It likewise presents a very pleasing prospect of terrestrial objects, which appear as if situated immediately below us.
figure 78.
Another plan of the diagonal eye-piece is represented in fig. 78, where the speculum is fixed within the sliding tube which receives the eye-piece, or immediately below it. The part of the tube at AB slides into the tube of the telescope, CD is the speculum placed at half a right angle to the axis of the tube, and EF, the tube containing the lenses, which stands at right angles to the position of the telescope, and slides into an exterior tube, and the eye is applied at G. This construction of the diagonal eye-piece may be used with any eye-piece whatever, whether the Huygenian or that of Ramsden. It will admit of 346 any magnifying power, and if several different eye-pieces be fitted to the sliding tube, they may be changed at pleasure. This form of the diagonal eye-piece, I therefore consider as the best and the most convenient construction, although it is not commonly adopted by opticians.
When any of these eye-pieces are applied to a telescope, with the lens E on the upper part of it, we look down upon the object, if it be a terrestrial one, as if it were under our feet. If we turn the eye-piece round in its socket a quarter of a circle towards the left, an object directly before us in the south, will appear as if it were in the west and turned upside down. If, from this position, it is turned round a semicircle towards the right, and the eye applied, the same object will appear as if it were situated in the east, and inverted; and if it be turned round another quadrant, till it be directly opposite to its first position, and the eye applied from below, the object or landscape will appear as if suspended in the atmosphere above us. This eye-piece, therefore, is capable of exhibiting objects in a great variety of aspects, and the use of it is both pleasant and easy for the observer. But there is a considerable loss of light, occasioned by the reflection from the speculum, which is sensibly felt when very high powers are applied; and therefore when very small stars are to be observed, such as some of those connected with double or triple stars, the observer should not study his own ease so much as the quantity of light he can retain with a high power, which object is best attained with an ordinary eye-piece and a telescope of large aperture.
We have said that a diagonal eye-piece may be constructed with a reflector before the eye-piece. In this case, the speculum is sometimes made to 347 slide before the eye at the requisite angle of reclination, in which application each eye-piece must necessarily have a groove to receive it, and the eye must be applied without a hole to direct it, but it may be put on and taken off without disturbing the adjustment for distinct vision, and is very simple in its application. But, on the whole, the form represented in fig. 78, is the most convenient, and should generally be preferred, as any common astronomical eye-piece can be applied to it. I have used a diagonal eye-piece of this kind, with good effect, when a power of 180 has been applied to the sun and other celestial objects.
Instead of a metallic speculum, a rectangular prism of glass is sometimes substituted; for the rays of light are then bent by reflection from the second polished surface, which ought to be dry, and undergo two refractions which achromatise them; and the same effect is thus produced as by polished metal. Ramsden sometimes gave one of the polished faces of a right angled prism a curve, which prism served instead of a lens in an eye-piece, and also performed the office of a reflector. A semi-globe, or what has been called a Bull’s eye, has also been used as a diagonal eye-piece, and when the curve is well-formed, and the glass good, it is achromatic, and is said to perform pretty well, but it is not superior to the forms already described.
When describing the common refracting telescope, (p. 228.) I have noticed that three eye-glasses, placed at double their focal distances 348 from each other, formerly constituted the terrestrial eye-piece, as represented in fig. 47. But this construction, especially for achromatic instruments, has now become obsolete, and is never used, except in small pocket spy-glasses formed with a single object lens. In its place a four glassed eye-piece has been substituted, which is now universally used in all good telescopes, and which, besides improving the vision and producing an erect position of the images of objects, presents a considerably larger field of view. During the progressive stages of improvement made in the construction of erect eye-pieces by Dollond and Ramsden, three, four, and five lenses were successively introduced; and hence, in some of the old telescopes constructed by these artists, we frequently find five lenses of different descriptions composing the eye-piece. But four lenses, arranged in the manner I am now about to describe, have ultimately obtained the preference. In a telescope having a celestial eye-piece of the Huygenian form, the image that is formed in the focus of the object glass, is that which is seen magnified, and in an inverted position; but when a four glassed eye-piece is used, which produces an erect view of the object, the image is repeated, and the second image, which is formed by the inner pair of lenses AB on an enlarged scale, is that which the pair of lenses CD at the eye-end render visible on a scale still more enlarged. The modern terrestrial eye-piece, represented in fig. 79, is, in fact, nothing else than a compound microscope, consisting of an object lens, an amplifying lens, and an eye-piece composed of a pair of lenses on the principle of the Huygenian eye-piece. Its properties will be best understood by considering the first image of an object, which is 349 formed in the focus of the object glass, as a small luminous object to be rendered visible, in a magnified state, by a compound microscope. The object to be magnified may be considered as placed near the point A, and the magnified image at i, which is viewed by the lens D. Hence, if we look through such an eye-piece at a small object placed very near the lens A, we shall find that it acts as a compound microscope of a moderate magnifying power increasing, in some cases, the diameter of the object about 10 times, and 100 times in surface.
figure 79.
In order to distinguish the different lenses in this eye-piece, we may call the lens A, which is next to the first image, the object-lens, the next to it B, the amplifying-lens, the third, or C, the field-lens, and the one next the eye, D, the eye-lens. The first image formed a little before A, may be denominated the radiant, or the object from which the rays proceed. Now, it is well known as a principle in optics, that if the radiant be brought nearer to the lens than its principal focus, the emerging rays will diverge, and, on the contrary, if the radiant be put farther from the lens than its principal focal distance, the emerging rays will converge to a point at a distance beyond the lens, which will depend on the distance of the radiant from the first face of the lens. In this place an image of the radiant will be formed by the concurrence of the converging rays, but in a 350 contrary position; and the length of the image will exceed the length of the radiant in the same proportion, as the distance of the image from the radiant exceeds that of the radiant from the lens. This secondary image of the radiant at i, is not well-defined, when only one lens, as A, is used, owing to the great spherical aberrations, and therefore the amplifying lens is placed at the distance of the shorter conjugate focus, with an intervening diaphragm of a small diameter at the place of the principal focus; the uses of which lens and diaphragm are, first to cut off the coloured rays that are occasioned by the dispersive property of the object lens,—and secondly, to bring the rays to a shorter conjugate focus for the place of the image, than would have taken place with a single lens having only one refraction. As the secondary image is in this way much better defined and free from colouration, the addition of this second lens is a great improvement to vision. For this reason I am clearly of opinion, that the object glass of a compound microscope, instead of consisting of a small single lens, should be formed of two lenses on the principle now stated, which would unquestionably add to the distinctness of vision.
With respect to the proportions of the focal lengths of the lenses in this four glass eye-piece, Mr. Coddington states, that if the focal lengths, reckoning from A to D, fig. 79, be as the numbers 3, 4, 4 and 3, and the distances between them on the same scale, 4, 6, and 5, 2, the radii, reckoning from the outer surface of A, should be thus:—
| A | {First surface | 27 } | nearly plano-convex. |
| {Second surface | 1 } | ||
| B | {First surface | 9 } | a miniscus. |
| {Second surface | 4 } 351 | ||
| C | {First surface | 1 } | nearly plano-convex. |
| {Second surface | 21 } | ||
| D | {First surface | 1 } | double convex. |
| {Second surface | 24 } |
Sir D. Brewster states, that a good achromatic eye-piece may be made of 4 lenses, if their focal lengths, reckoning from that next the object, be as the numbers 14, 21, 27, 32; their distances 23, 44, 40; their apertures 5.6; 3.4; 13.5; 2.6; and the aperture of the diaphragm placed in the interior focus of the fourth eye-glass, 7. Another proportion may be stated:—Suppose the lens next the object A, to be 1⅞ inch focal length, then B may be 2½ inches, C 2 inches, and D 1½; and their distances AB 2½; BC 3⅝; and CD 2⅜. In one of Ramsden’s small telescopes, whose object glass was 8½ inches in focal length, and its magnifying power 15.4, the focal lengths of the eye glasses were A 0.775 of an inch, B 1.025, C 1.01, D 0.79;—the distances AB 1.18, BC 1.83, and CD 1.105. In the excellent achromatic telescope of Dollond’s construction which belonged to the Duc de Chaulnes, the focal lengths of the eye glasses, beginning with that next the object, were 14¼ lines, 19, 22¾, 14; their distances 22.48 lines, 46.17, 21.45, and their thickness at the centre, 1.23 lines, 1.25, 1.47. The fourth lens was plano-convex, with the plane side to the eye, and the rest were double convex lenses. This telescope was in focal length 3 feet 5½ inches.
The magnifying power of this eye-piece, as usually made, differs only in a small degree from what would be produced by using the first or the fourth glass alone, in which case the magnifying power would be somewhat greater, but the vision less distinct, and were the lens next the eye used alone without the field glass, the field of view 352 would be much contracted. Stops should be placed between the lenses A and B, near to B, and a larger one between C and D, to prevent any false light from passing through the lenses to the eye. The more stops that are introduced into a telescope—which should all be blackened—provided they do not hinder the pencils of light proceeding from the object, the better will the instrument perform.
For the information of amateur constructors of telescopes, I shall here state the dimensions of two or three four glassed eye-pieces in my possession, which perform with great distinctness, and present a pretty large field of view. In one of these, adapted to a 44½ inch achromatic, the lens A, next the object, is 1⅞ inch, focal length, and about 1 inch diameter, with the plane side, next the object. The focal length of the lens B 21/10 inches, diameter 7/10 inch, with its plane side next A; distance of these lenses from each other 24/10 inches. Distance of the field lens C from the lens B 5½ inches. The small hole or diaphragm between A and B is at the focus of A, and is about 1/6 inch diameter, and about 3/8 of an inch from the lens B. The field lens C is 2 inches focal length, and 1¼ inch diameter, with its plane side next the eye. The lens next the eye D is 1 inch focal distance, ½ inch diameter, and is distant from the field glass 1¾ inch, with its plane side next the eye. The magnifying power of this eye-piece is equivalent to that of a single lens whose focal length is half an inch, and with the 44½ inch object glass produces a power of about 90 times. The lens next the eye can be changed for another 1⅜ inch focal length, which produces a power of 65; and the two glasses CD can be changed for another set, of a longer focal distance which produces 353 a power of 45 times. The whole length of this eye-piece is 11½ inches.
In another eye-piece, adapted to a pocket achromatic, whose object glass is 9 inches focal length, the lens A is 1 inch focal length, and ½ inch diameter; the lens B 1¼ inch, and ½ inch diameter, their distance 1½ inch, the lens C 11/10 inch focal length, and 5/8 inch diameter; the eye-lens D 5/8 inch focal length, and 3/8 inch diameter; distance between C and D 1⅛ inch. The distance between B and C 1¾ inch. The whole length of this eye-piece is 4½ inches, and its power is nearly equal to that of a single lens of ½ or 6/10 of an inch focal length, the magnifying power of the telescope being about 16 times. Another eye-piece of much larger dimensions, has the lens A of 2½ inches focal length, and ¾ inch diameter: the lens B 2¾ inches focus and 5/8 inch diameter; and their distance 2¾ inches; the lens C 2⅝ inches focus and 1⅛ inch diameter; the lens D 1¾ inch focus and ¾ inch diameter; distance from each other 2¾ inches. The distance between the lenses B and C is 4 inches. The magnifying power is equal to that of a single lens 1⅛ inch focal distance. When applied to an achromatic object glass 6 feet 7 inches focal length, it produces a power of about 70 times. This eye-piece has a moveable tube 9 inches in length in which the two lenses next the eye are contained, by pulling out which, and consequently increasing the distance between the lenses B and C, the magnifying power may be increased to 100, 120 or 140, according to the distance to which this moveable tube is drawn out. It has also a second and third set of lenses, corresponding to C and D of a shorter focal distance, which produce higher magnifying powers on a principle to be afterwards explained. 354
About twenty or thirty years ago, I purchased, in an optician’s shop in Edinburgh, a small achromatic telescope, made in Amsterdam, which was supposed, by the optician, to have been constructed prior to the invention of achromatic telescopes by Mr. Dollond. It is mounted wholly of brass, and in all its parts is a piece of beautiful and exquisite workmanship, and the utmost care seems to have been taken to have all the glasses and diaphragms accurately adjusted. The object glass is a double achromatic, 6½ inches focal distance and 1 inch diameter, but the clear aperture is only 7/8 inch diameter. It is perfectly achromatic, and would bear a power of 50 times, if it had a sufficient quantity of light. The following inscription is engraved on the tube adjacent to the object glass:—“Jan van Deyl en Zoon Invenit et Fecit, Amsterdam, Ao. 1769.” Although Dollond exhibited the principle of an achromatic telescope, eight or ten years before the date here specified, yet it is not improbable that the artist whose name is here stated, may not have heard of Dollond’s invention; and that he was really, as he assumes, one of the inventors of the achromatic telescope. For, the invention of this telescope by Dollond was not very generally known, except among philosophers and the London opticians, till a number of years after the date above stated. Euler, in his “Letters to a German Princess”—in which telescopes are particularly described, makes no mention of, nor the least allusion to the invention of Dollond, though this was a subject which particularly engaged his attention. Now, these letters 355 were written in 1762, but were not published till 1770. When alluding to the defects in telescopes arising from the different refrangibility of the rays of light, in Letter 43, and that they might possibly be rectified by means of different transparent substances, he says, ‘But neither theory nor practice have hitherto been carried to the degree of perfection necessary to the execution of a structure which should remedy these defects.’ Mr. B. Martin, in his ‘Gentleman and Lady’s Philosophy,’ published in 1781, alludes to the achromatic telescope, but speaks of it as it were but very little, if at all superior to the common refracting telescope. And therefore, I think it highly probable that Jan van Deyl, was really an inventor of an achromatic telescope, before he had any notice of what Dollond and others had done in this way some short time before.
But my principal object in adverting to this telescope, is to describe the structure of the eye-piece, which is a very fine one, and which is somewhat different from the achromatic eye-piece above described. It consists of four glasses, two combined next the eye, and two next the object. Each of these combinations forms an astronomical eye-piece nearly similar to the Huygenian. The lens A, next the object, fig. 80, is 5/8 inch focal distance, and 4/10 inch diameter; the lens B 3/8 inch focus, and 1/5 inch diameter, and the distance between them somewhat less than 5/8 inch; the diameter of the aperture e about 1/15 of an inch. This combination forms an excellent astronomical eye-piece, with a large flat field, and its magnifying power is equivalent to that of a single lens 5/8 or 6/8 focal length. The lens C is ½ inch focal length, and 4/10 inch diameter; the lens D ¼ inch focus, and about 1/5 inch diameter; their distance 356 about ½ inch, or a small fraction more. The hole at d is about 1/20 or 1/25 of an inch diameter, and the distance between the lenses B and C about 1½ inch. The whole length of the eye-piece is 3¼ inches—exactly the same size as represented in the engraving. Its magnifying power is equal to that of a single lens ¼ inch focal length; and consequently the telescope, though only 9½ inches long, magnifies 26 times, with great distinctness, though there is a little deficiency of light when viewing land objects, which are not well illuminated.
figure 80.

The glasses of this telescope are all plano-convex, with their convex-sides towards the object—except the lens D, which is double convex, but flattest on the side next the eye, and they are all very accurately finished. The two lenses C and D form an astronomical eye-piece nearly similar to that formed by the lenses A and B. The focus of the telescope is adjusted by a screw, the threads of which are formed upon the outside of a tube into which the eye-piece slides. The eye-piece and apparatus connected with it, is screwed into the inside of the main tube, when not in use, when the instrument forms a compact brass cylinder 6 inches long, which is enclosed in a fish-skin case, lined with silk velvet, which opens with hinges.
The lenses in the eye-pieces formerly described, though stated to be plano-convexes, are for the 357 most part crossed glasses, that is ground on tools of a long focus on the one side, and to a short focus on the other. The construction of the eye-piece of the Dutch telescope above described, is one which might be adopted with a good effect in most of our achromatic telescopes; and I am persuaded, from the application I have made of it to various telescopes, that it is even superior, in distinctness and accuracy, and in the flatness of field which it produces to the eye-piece in common use. The two astronomical eye-pieces of which it consists, when applied to large achromatic telescopes, perform with great accuracy, and are excellently adapted for celestial observations.
From what we have stated, when describing the common terrestrial eye-piece now applied to achromatic instruments, (p. 349, fig. 79.), it appears obvious, that any variety of magnifying powers, within certain limits, may be obtained by removing the set of lenses CD, fig. 79, nearer to or farther from the tube which contains the lenses A and B, on the same principle as the magnifying power of a compound microscope is increased by removing the eye-glasses to a greater distance from the object-lens. If then, the pair of eye-lenses CD be attached to an inner tube that will draw out and increase their distance from the inner pair of lenses, as the tube a b c d, the magnifying power may be indefinitely increased or diminished, by pushing in or drawing out the sliding tube, and a scale might be placed on this tube, which, if divided into equal intervals, will be a scale of 358 magnifying powers, by which the power of the telescope will be seen at every division, when the lowest power is once determined.
Sir David Brewster, in his ‘Treatise on New Philosophical instruments,’ Book i. chap. vii. page 59, published in 1813, has adverted to this circumstance, in his description of an ‘Eye-piece wire micrometer,’ and complains of Mr. Ezekiel Walker, having in the ‘Philosophical Magazine’ for August, 1811, described such an instrument as an invention of his own. Dr. Kitchener some years afterwards, described what he called a Pancratic or omnipotent eye-piece, and got one made by Dollond, with a few modifications different from that suggested by Brewster and Walker, which were little else than cutting the single tube into several parts, and giving it the appearance of a new invention. In fact, none of these gentlemen had a right to claim it as his peculiar invention, as the principle was known and recognised long before. I had increased the magnifying powers of telescopes, on the same principle, several years before any of these gentlemen communicated their views on the subject, although I never formally constructed a scale of powers. Mr. B. Martin, who died in 1782, proposed many years before, such a moveable interior tube as that alluded to, for varying the magnifying power.
In order to give the reader a more specific idea of this contrivance, I shall present him with a figure and description of one of Dr. Kitchener’s Pancratic eye-pieces, copied from one lately in my possession. The following are the exact dimensions of this instrument, with the focal distances, &c. of the glasses, &c. of which it is composed. 359
| In. | Tenths. | fig. 81. | |
| Length of the whole eye-piece, consisting of four tubes, when fully drawn out, or the distance from A to B. fig. 81. | 14 | 4 |  |
| Length of the three tubes on which the scale is engraved, from the commencement of the divisions at B to their termination at C. | 9 | 15 | |
| Each division into tens is equal to 3-10ths of an inch. | |||
| When the three inner tubes are shut up to C, the length of the eye-piece is exactly | 5 | 5 | |
| When these tubes are thus shut up, the magnifying power for a 3½ feet achromatic is 100 times, which is the smallest power. When the inner tube is drawn out ⅓ of an inch, or to the first division, the power is 110, &c. | |||
| Focal distance of the lens next the object | 1 | 0 | |
| Breadth of Ditto. | 0 | 65 | |
| The plane side of this glass is next the object. | |||
| Focal distance of the second glass from the object | 1 | 5 | |
| This glass is double and equally convex, Breadth | 0 | 5 | |
| Distance between these two glasses | 1 | 7 | |
| Focal distance of the third or field lens, which is plane on the side next the eye | 1 | 1 | |
| Breadth of Ditto. | 0 | 55 | |
| Focal distance of the lens next the eye | 0 | 6 | |
| Breadth | 0 | 43 | |
| This glass is plane on the side next the eye. | |||
| Distance between the third and fourth glasses. | 1 | 1 | |
From the figure and description, the reader will be at no loss to perceive how the magnifying power is ascertained by this eye-piece. If the lowest power for a 44 inch telescope be found to be 100, when the three sliding tubes are shut into the larger one, then by drawing out the tube next the eye 4 divisions, a power of 140 is produced; by drawing out the tube next the eye its whole length, and the second tube to the division marked 220, a power of 220 times is produced, and drawing out all the tubes to their utmost extent, as represented in the figure, a power of 400 is obtained. These powers are by far too high for such a telescope, as the powers between 300 and 400 can seldom or never be used. Were the scale to begin at 50, and terminate at 200, it would be 360 much better adapted to a 3½ feet telescope. Each alteration of the magnifying power requires a new adjustment of the eye-piece for distinct vision. As the magnifying power is increased, the distance between the eye-glass and the object-glass must be diminished. Dr. Kitchener says, that ‘the pancratic eye tube gives a better defined image of a fixed star, and shows double stars decidedly more distinct and perfectly separated than any other eye tube, and that such tubes will probably enable us to determine the distances of these objects from each other, in a more perfect manner than has been possible heretofore.’ These tubes are made by Dollond, London, and are sold for two guineas each. But I do not think they excel, in distinctness, those which are occasionally made by Mr. Tulley and other opticians. 361
The following remarks, chiefly in regard to the manner of using telescopes, may perhaps be useful to young observers, who are not much accustomed to the mode of managing these instruments.
1. Adjustments requisite to be attended to in the use of telescopes. When near objects are viewed with a considerable magnifying power, the eye-tube requires to be removed farther from the object-glass than when very distant objects are contemplated. When the telescope is adjusted for an object, 6, 8, or 10 miles distant, a very considerable alteration in the adjustment is requisite in order to see distinctly an object at the distance of two or three hundred yards, especially if the instrument is furnished with a high magnifying power. In this last case, the eye-tube requires to be drawn out to a considerable distance beyond the focus for parallel rays. I have found that, in a telescope which magnifies 70 times, when adjusted for an object at the distance of two miles, the adjustment requires to be altered fully one inch in order to perceive distinctly an object at the distance of two or three hundred yards; 362 that is, the tube must be drawn, in this case, an inch farther from the object-glass, and pushed in the same extent, when we wish to view an object at the distance of two or three miles. These adjustments are made, in pocket perspectives, by gently sliding the eye-tube in or out, by giving it a gentle circular or spiral motion till the object appear distinct. In using telescopes which are held in the hand, the best plan is to draw all the tubes out to their full length, and then, looking at the object, with the left hand supporting the main tube near the object-glass, and the right supporting the eye-tube—gently and gradually push in the eye-piece till distinct vision be obtained. In Gregorian reflecting telescopes this adjustment is made by means of a screw connected with the small speculum; and in large achromatics, by means of a rack and pinion connected with the eye-tube. When the magnifying power of a telescope is comparatively small, the eye-tube requires to be altered only a very little.
There is another adjustment requisite to be attended to, in order to adapt the telescope to the eyes of different persons. Those whose eyes are too convex, or who are short-sighted, require the eye-tube to be pushed in, and those whose eyes are somewhat flattened, as old people, require the tube to be drawn out. Indeed there are scarcely two persons whose eyes do not require different adjustments in a slight degree. In some cases I have found that the difference of adjustment for two individuals, in order to produce distinct vision in each, amounted to nearly half an inch. Hence the difficulty of exhibiting the sun, moon, and planets through telescopes, and even terrestrial objects, to a company of persons who are unacquainted with the mode of using or adjusting such 363 instruments—not one half of whom generally see the object distinctly—for, upon the proper adjustment of a telescope to the eye, the accuracy of vision, in all cases, depends; and no one except the individual actually looking through the instrument, can be certain that it is accurately adjusted to his eye, and even the individual himself, from not being accustomed to the view of certain objects, may be uncertain whether or not the adjustment be correct. I have found by experience that when the magnifying powers are high, as 150 or 200, the difference of adjustment required for different eyes is very slight; but when low powers are used, as 20, 30, or 40, the difference of the requisite adjustments is sometimes very considerable, amounting to ¼ or ½ of an inch.
2. State of the Atmosphere most proper for observing terrestrial and celestial objects. The atmosphere which is thrown around the globe—while it is essentially requisite to the physical constitution of our world, and the comfort of its inhabitants—is found in many instances a serious obstruction to the accurate performance of telescopes. Sometimes it is obscured by mists and exhalations, sometimes it is thrown into violent undulations by the heat of the sun and the process of evaporation, and even, in certain cases, where there appears a pure unclouded azure, there is an agitation among its particles and the substances incorporated with them, which prevents the telescope from producing distinct vision either of terrestrial or celestial objects. For viewing distant terrestrial objects, especially with high powers, the best time is early in the morning, a little after sun-rise, and, from that period till about 9 o’clock A.M., in summer; and, in the evening about two or three hours before sun-set. From about 10 364 o’clock A.M. till 4 or 5 in the afternoon, in summer, if the sky be clear and the sun shining, there is generally a considerable undulation in the atmosphere, occasioned by the solar rays and the rapid evaporation, which prevents high powers from being used with distinctness on any telescope, however excellent. The objects at such times, when powers of 50, 70, or 100 are applied, appear to undulate like the waves of the sea, and, notwithstanding every effort to adjust the telescope, they appear confused and indistinct. Even with very moderate magnifying powers this imperfection is perceptible. In such circumstances, I have sometimes used a power of 200 times on distant land objects, with good effect, a little before sun-set, when, in the forenoon of the same day, I could not have applied a power of 50 with any degree of distinctness. On days when the air is clear, and the atmosphere covered with clouds, terrestrial objects may be viewed with considerably high powers. When there has been a long-continued drought, the atmosphere is then in a very unfit state for enjoying distinct vision with high magnifying powers, on account of the quantity of vapours with which the atmosphere is then surcharged, and the undulations they produce. But, after copious showers of rain, especially if accompanied with high winds, the air is purified, and distant objects appear with greater brilliancy and distinctness than at any other seasons. In using telescopes, the objects at which we look should, if possible, be nearly in a direction opposite to that of the sun. When they are viewed nearly in the direction of the sun, their shadows are turned towards us, and they consequently appear dim and obscure. By not attending to this circumstance, some persons, in trying telescopes, have pronounced 365 a good instrument to be imperfect, which, had it been tried on objects properly illuminated, would have been found to be excellent. In our variable northerly climate the atmosphere is not so clear and serene for telescopic observation as in Italy, the South of France, and in many of the countries which lie within the tropics. The undulations of the air, owing to the causes alluded to above, constitute one of the principal reasons why a telescope magnifying above a hundred times can seldom be used with any good effect in viewing terrestrial objects—though I have sometimes used a power of nearly 200 with considerable distinctness, in the stillness of a summer or autumnal evening, when the rays of the declining sun strongly illuminated distant objects.
The atmosphere is likewise frequently a great obstruction to the distinct perception of celestial objects. It is scarcely possible for one who has not been accustomed to astronomical observations, to form a conception of the very great difference there is in the appearance of some of the heavenly bodies in different states of the atmosphere. There are certain conditions of the atmosphere essentially requisite for making accurate observations with powerful telescopes, and it is but seldom, especially in our climate, that all the favourable circumstances concur. The nights must be very clear and serene—the moon absent—no twilight—no haziness—no violent wind—no sudden change of temperature, as from thaw to frost—and no surcharge of the atmosphere with aqueous vapour. I have frequently found that, on the first and second nights after a thaw, when a strong frost had set in, and when the heavens appeared very brilliant, and the stars vivid and sparkling—the planets, when viewed with 366 high powers, appeared remarkably undefined and indistinct; their margins appeared waving and jagged, and the belts of Jupiter, which at other times were remarkably distinct, were so obscured and ill-defined, that they could with difficulty be traced. This is probably owing to the quantity of aqueous vapour, and perhaps icy particles, then floating in the air, and to the undulations thereby produced. When a hard frost has continued a considerable time, this impediment to distinct observation is in a great measure removed. But I have never enjoyed more accurate and distinct views of the heavenly bodies than in fresh serene evenings, when there was no frost and no wind, and only a few fleecy clouds occasionally hovering around. On such evenings, and on such alone, the highest powers may be applied. I have used magnifying powers on such occasions with good effect, which could not have been applied, so as to ensure distinct vision, more frequently than two or three days in the course of a year.
Sir William Herschel has observed, in reference to this point, ‘In beautiful nights, when the outside of our telescopes is dropping with moisture, discharged from the atmosphere, there are now and then favourable hours in which it is hardly possible to put a limit to the magnifying powers. But such valuable opportunities are extremely scarce, and with large instruments it will always be lost labour to observe at other times. In order therefore, to calculate how long a time it must take to sweep the heavens, as far as they are within the reach of my forty-feet telescope, charged with a magnifying power of 1000, I have had recourse to my journals to find how many favourable hours we may annually hope for in this climate. And, under all favourable circumstances, 367 it appears, that a year which will afford ninety, or at most, one hundred hours is to be called very productive.’ ‘In the equator, with my twenty feet telescope, I have swept over zones of two degrees with a power of 157, but an allowance of ten minutes in Polar distance must be made for lapping the sweeps over one another where they join. As the breadth of the zones may be increased towards the poles, the northern hemisphere may be swept in about 40 zones; to these we must add 19 southern zones; then 59 zones which, on account of the sweeps lapping over one another, about 5 minutes of time in right ascension, we must reckon of 25 hours each, will give 1475 hours. And allowing 100 hours per year, we find that with the 20 feet telescope, the heavens may be swept in about 14 years and three quarters. Now the time of sweeping with different magnifying powers will be as the squares of the powers; and putting p and t for the power and time in the 20 feet telescope, and P = 1000 for the power in the 40 feet instrument, we shall have p2 : t :: P2 : tP2/p2 = 59840. Then making the same allowance for 100 hours per year, it appears that it will require not less than 598 years, to look with the 40 feet reflector, charged with the above-mentioned power, only one single moment into each point of space; and even then, so much of the southern hemisphere will remain unexplored, as will take up 213 years more to examine.’28
From the above remarks of so eminent an observer, the reader will perceive how difficult it is to explore the heavens with minuteness and accuracy, and with how many disappointments, 368 arising from the state of the atmosphere, the astronomer must lay his account, when employed in planetary or sidereal investigation. Besides the circumstances now stated, it ought to be noticed that a star or a planet is only in a situation for a high magnifying power, about half the time it is above the horizon. The density of the atmosphere, and the quantity of vapours with which it is charged near the horizon, prevent distinct vision of celestial objects with high powers, till they have risen to at least 15 or 20 degrees in altitude, and the highest magnifiers can scarcely be applied with good effect, unless the object is near the meridian, and at a considerable elevation above the horizon. If the moon be viewed a little after her rising, and afterwards when she comes to her highest elevation in autumn, the difference in her appearance and distinctness will be strikingly perceptible. It is impossible to guess whether a night be well adapted for celestial observations, till we actually make the experiment, and instruments are frequently condemned, when tried at improper seasons, when the atmosphere only is in fault. A certain observer remarks,—‘I have never seen the face of Saturn more distinctly than in a night when the air has been so hazy, that with my naked eye, I could hardly discern a star of less than the third magnitude.’ The degree of the transparency of the air is likewise varying almost in the course of every minute, so that even in the course of the same half hour, planets and stars will appear perfectly defined, and the reverse. The vapours moving and undulating the atmosphere, even when the sky appears clear to the naked eye, will in a few instants destroy the distinctness of vision, and in a few seconds more, 369 the object will resume its clear and well-defined aspect.29
3. On the magnifying powers requisite for observing the phenomena of the different planets—comets—double stars, &c.
There are some objects connected with astronomy which cannot be perceived without having recourse to instruments and to powers of great magnitude. But it is a vulgar error to imagine that very large and very expensive telescopes are absolutely necessary for viewing the greater part of the more interesting scenery of the heavens. Most of the phenomena of the planets, comets and double stars and other objects, are visible with instruments of moderate dimensions, so that every one who has a relish for celestial investigations, may, at a comparatively small expense, procure a telescope, for occasional observations, which will show the principal objects and phenomena described in books on astronomy. Many persons have been misled by some occasional remarks which Sir W. Herschel made, in reference to certain very high powers which he sometimes put, by way of experiment, on some of his telescopes, as if these were the powers requisite for viewing the objects to which he refers. For example, it is stated that he once put a power of 6450 times on his 7 feet Newtonian telescope of 63/10 inches aperture; but this was only for the purpose of an experiment, and could be of no 370 use whatever when applied to the moon, the planets and most objects in the heavens. Herschel, through the whole course of his writings, mentions his only having used it twice, namely on the stars α Lyræ, and γ Leonis, which stars can be seen more distinctly and sharply defined with a power of 420. To produce a power of 6450 on such a telescope, would require a lens of only 1/77th of an inch in focal distance, and it is questioned by some whether Herschel had lenses of so small a size in his possession, or whether it is possible to form them with accuracy.
Powers requisite for observing the phenomena of the planets.—The planet Mercury requires a considerable magnifying power, in order to perceive its phases with distinctness. I have seldom viewed this planet with a less power than 100 and 150, with which powers its half moon, its gibbous, and its crescent phase, may be distinctly perceived. With a power of 40, 50, or even 60 times, these phases can with difficulty be seen, especially as it is generally at a low altitude, when such observations are made. The phases of Venus are much more easily distinguished, especially the crescent phase, which is seen to the greatest advantage about a month before and after the inferior conjunction. With a power not exceeding 25 or 30 times, this phase, at such periods, may be easily perceived. It requires, however, much higher powers to perceive distinctly the variations of the gibbous phase; and if this planet be not viewed at a considerably high altitude when in a half-moon or gibbous phase, the obscurity and undulations of the atmosphere near the horizon, prevent such phases from being accurately distinguished, even when high powers are applied. Although certain phenomena of the planets may be seen with such low powers as I have now stated, yet, in every instance, the 371 highest magnifying powers, consistent with distinctness, should be preferred, as the eye is not then strained, and the object appears with a greater degree of magnitude and splendour. The planet Mars requires a considerable degree of magnifying power, even when at its nearest distance from the earth, in order to discern its spots and its gibbous phase. I have never obtained a satisfactory view of the spots which mark the surface, and their relative position, with a less power than 130, 160, or 200 times; and even with such powers, persons not much accustomed to look through telescopes, find a difficulty in distinguishing them.
The strongest and most prominent belts of Jupiter, may be seen with a power of about 45; which power may be put upon a 20-inch achromatic, or a 1 foot reflector. But a satisfactory view of all the belts, and the relative positions they occupy, cannot be obtained with much lower powers than 80, 100, or 140. The most common positions of these belts are—one dark and well-defined belt to the south of Jupiter’s equator; another of nearly the same description to the north of it, and one about his north and his south polar circles. These polar belts are much more faint, and consequently not so easily distinguished as the equatorial belts. The moons of this planet, in a very clear night, may sometimes be seen with a pocket 1 foot achromatic glass, magnifying about 15 or 16 times. Some people have pretended that they could see some of these satellites with their naked eye; but this is very doubtful, and it is probable that such persons mistook certain fixed stars which happened to be near Jupiter for his satellites. But, in order to have a clear and interesting view of these, powers of at least 80 or 100 times should be used. In order to perceive 372 their immersions into the shadow of Jupiter, and the exact moment of their emersions from it, a telescope not less than a 44 inch achromatic, with a power of 150 should be employed. When these satellites are viewed through large telescopes with high magnifying powers, they appear with well defined disks, like small planets. The planet Jupiter has generally been considered as a good test by which to try telescopes for celestial purposes. When it is near the meridian and at a high altitude, if its general surface, its belts, and its margin appear distinct and well-defined, it forms a strong presumptive evidence that the instrument is a good one.
The planet Saturn forms one of the most interesting objects for telescopic observation. The ring of Saturn may be seen with a power of 45; but it can only be contemplated with advantage when powers of 100, 150, and 200 are applied to a 3 or a 5 feet achromatic. The belts of Saturn are not to be seen distinctly with an achromatic of less than 2¾ inches aperture, or a Gregorian reflector of less than 4 inches aperture, nor with a less magnifying power than 100 times. Sir W. Herschel has drawn this planet with five belts across its disk; but it is seldom that above one or two of them can be seen by moderate-sized telescopes and common observers. The division of the double ring, when the planet is in a favorable position for observation, and in a high altitude, may sometimes be perceived with a 44-inch achromatic, with an aperture of 2¾ inches, and with powers of 150 or 180, but higher powers and larger instruments are generally requisite to perceive this phenomenon distinctly; and even when a portion of it is seen at the extremities of the ansæ, the division cannot, in every case, be 373 traced along the whole of the half-circumference of the ring which is presented to our eye. Mr. Hadley’s engraving of Saturn, in the ‘Philosophical Transactions’ for 1723, though taken with a Newtonian reflector with a power of 228, represents the division of the ring as seen only on the ansæ or extremities of the elliptic figure in which the ring appears. The best period for observing this division is when the ring appears at its utmost width. In this position it was seen in 1840, and it will appear nearly in the same position in 1855. When the ring appears like a very narrow ellipse, a short time previous to its disappearance, the division, or dark space between the rings, cannot be seen by ordinary instruments.
Sir W. Herschel very properly observes, ‘There is not perhaps another object in the heavens that presents us with such a variety of extraordinary phenomena as the planet Saturn; a magnificent globe, encompassed by a stupendous double ring; attended by seven satellites; ornamented with equatorial belts; compressed at the poles; turning upon its axis; mutually eclipsing its ring and satellites, and eclipsed by them; the most distant of the rings also turning upon its axis, and the same taking place with the farthest of the satellites; all the parts of the system of Saturn occasionally reflecting light on each other; the rings and moons illuminating the nights of the Saturnian, the globe and satellites enlightening the dark parts of the ring; and the planet and rings throwing back the sun’s beams upon the moons, when they are deprived of them at the time of their conjunctions.’ This illustrious astronomer states, that with a new 7 feet mirror of extraordinary distinctness he examined this planet, and found that the ring reflects more light than the body, and with 374 a power of 570 the colour of the body becomes yellowish, while that of the ring remains more white. On March 11, 1780, he tried the powers of 222, 332, and 440 successively, and found the light of Saturn less intense than that of the ring; the colour of the body turning, with the high powers, to a kind of yellow white, while that of the ring still remained white.
Most of the satellites of Saturn are difficult to be perceived with ordinary telescopes, excepting the 4th, which may be seen with powers of from 60 to 100 times. It was discovered by Huygens in 1655, by means of a common refracting telescope 12 feet long, which might magnify about 70 times. The next in brightness to this is the 5th satellite, which Cassini discovered in 1671, by means of a 17 feet refractor, which might carry a power of above 80 times. The 3rd was discovered by the same astronomer in 1672, by a longer telescope; and the 1st and 2nd, in 1684, by means of two excellent object-glasses of 100 and 136 feet, which might have magnified from 200 to 230 times. They were afterwards seen by two other glasses of 70 and 90 feet, made by Campani, and sent from Rome to the Royal Observatory at Paris, by the King’s order, after the discovery of the 3rd and 5th satellites. It is asserted, however, that all those 5 satellites were afterwards seen with a telescope of 34 feet, with an aperture of 33/10 inches, which would magnify about 120 times. These satellites, on the whole, except the 4th and 5th, are not easily detected. Dr. Derham, who frequently viewed Saturn through Huygens’ glass of 126 feet focal length, declares, in the preface to his ‘Astro-Theology,’ that he could never perceive above 3 of the satellites. Sir W. Herschel observes, that the visibility of these 375 minute and extremely faint objects, depends more on the penetrating than upon the magnifying power of our telescopes; and that with a 10 feet Newtonian, charged with a magnifying power of only 60, he saw all the 5 old satellites; but the 6th and 7th, which were discovered and were easily seen with his 40-feet telescope, and were also visible in his 20-feet instrument, were not discernible in the 7 or the 10-feet telescopes, though all that magnifying power can do may be done as well with the 7-feet as with any larger instrument. Speaking of the 7th satellite, he says, ‘Even in my 40-feet reflector it appears no bigger than a very small lucid point. I see it, however, very well in the 20-feet reflector; to which the exquisite figure of the speculum not a little contributes.’ A late observer asserts, that in 1825, with a 12-feet achromatic, of 7 inches aperture, made by Tulley, with a power of 150, the 7 satellites were easily visible, but not so easily with a power of 200; and that the planet appeared as bright as brilliantly burnished silver, and the division in the ring and a belt were very plainly distinguished, with a power of 200.
The planet Uranus, being generally invisible to the naked eye, is seldom an object of attention to common observers. A considerable magnifying power is requisite to make it appear in a planetary form with a well-defined disk. The best periods for detecting it are, when it is near its opposition to the sun, or when it happens to approximate to any of the other planets, or to a well-known fixed star. When none of these circumstances occur, its position requires to be pointed out by an Equatorial Telescope. On the morning of the 25th January, 1841, this planet happened to be in conjunction with Venus, at 376 which time it was only 4 minutes north of that planet. Several days before this conjunction, I made observations on Uranus. On the evening of the 24th, about 8 hours before the conjunction, the two planets appeared in the same field of the telescope, the one exceedingly splendid, and the other more obscure, but distinct and well-defined. Uranus could not be perceived, either with the naked eye, or with an opera glass; but could be distinguished as a very small star by means of a pocket achromatic telescope magnifying about 14 times. It is questionable whether, under the most favourable circumstances, this planet can ever be distinguished by the naked eye. With magnifying powers of 30 and 70, it appeared as a moderately large star with a steady light, but without any sensible disk. With powers of 120, 180, and 250, it presented a round and pretty well-defined disk, but not so luminous and distinct as it would have done in a higher altitude.
The Double Stars require a great variety of powers, in order to distinguish the small stars that accompany the larger. Some of them are distinguished with moderate powers, while others require pretty large instruments, furnished with high magnifying eye-pieces. I shall therefore select only a few as a specimen. The star Castor, or α Geminorum, may be easily seen to be double with powers of from 70 to 100. I have sometimes seen these stars, which are nearly equal in size and colour, with a terrestrial power of 44 on a 44-inch achromatic. The appearance of this star with such powers is somewhat similar to that of η Coronæ in a 7 feet achromatic, of 5 inches aperture, with a power of 500. γ Andromedæ may be seen with a moderate power. In a 30-inch achromatic of 2 inches aperture, and a power 377 of 80, it appears like ε Bootis, when seen in a 5-feet achromatic, with a power of 460. This star is said to be visible even in a 1-foot achromatic with a power of 35. ε Lyræ, which is a quintuple star, but appears to the naked eye as a single star,—may be seen to be double with a power of from 6 to 12 time. γ Leonis is visible in a 44-inch achromatic, with a power of 180 or 200. Rigel in a 3½-feet achromatic, may be seen with powers varying from 130 to 200. The small star, however, which accompanies Rigel, is sometimes difficult to be perceived, even with such powers. ε Bootis is seldom distinctly defined with an achromatic of less aperture than 3¼ inches, or a reflector of less than 5 inches, with a power of at least 250.
These and similar stars are not to be expected to be seen equally well at all times, even when the magnifying and illuminating powers are properly proportioned; as much depends upon the state of the weather, and the pureness of the atmosphere. In order to perceive the closest of the double stars, Sir W. Herschel recommends, that the power of the telescope should be adjusted upon a star known to be single, of nearly the same altitude, magnitude, and colour with the double star which is to be observed, or upon one star above and another below it. Thus, the late Mr. Aubert, the astronomer, could not see the two stars of γ Leonis, when the focus was adjusted upon that star itself; but he soon observed the small star, after he had adjusted the focus upon Regulus. An exact adjustment of the focus of the instrument is indispensably requisite, in order to perceive such minute objects.
In viewing the Nebulæ, and the very small and immensely distant fixed stars, which require much 378 light to render them visible, a large aperture of the object-glass or speculum, which admits of a great quantity of light, is of more importance than high magnifying powers. It is light chiefly, accompanied with a moderate magnifying power, that enables us to penetrate into the distant regions of space. Sir W. Herschel, when sweeping the profundities of the Milky way, and the Hand and Club of Orion, used a telescope of the Newtonian form, 20-feet focal length, and 187/10 inches diameter, with a power of only 157. On applying this telescope and power to a part of the Via Lactea, he found that it completely resolved the whole whitish appearance into stars, which his former telescopes had not light enough to effect; and which smaller instruments with much higher magnifying powers would not have effected. He tells us, that with this power, ‘the glorious multitude of stars,’ in the vicinity of Orion, ‘of all possible sizes, that presented themselves to view, was truly astonishing, and that he had fields which contained 70, 90 and 110 stars, so that a belt of 15 degrees long, and 2 degrees broad, which passed through the field of the telescope in an hour, could not contain less than fifty thousand stars that were large enough to be distinctly numbered.’ In viewing the Milky way, the Nebulæ, and small clusters of stars, such as Præsepe in Cancer, I generally use a power of 55 times, on an achromatic telescope 6 feet 6 inches in focal length, and 4 inches diameter. The eye-piece, which produces this power—which I formed for the purpose—consists of two convex lenses, the one next the eye 3 inches focal length, and 12/10 inch diameter, and that next the object 3½ inches focus, and 14/10 inch diameter, the deepest convex surfaces being next each other, and their distance ¼ inch. With this 379 eye-piece a very large and brilliant field of view is obtained; and I find it preferable to any higher powers in viewing the nebulosities, and clusters of stars. In certain spaces of the heavens, it sometimes presents in one field, nearly a hundred stars. It likewise serves to exhibit a very clear and interesting view of the full moon.
In observing Comets, a very small power should generally be used, even on large instruments. These bodies possess so small a quantity of light, and they are so frequently enveloped in a veil of dense atmosphere, that magnifying power sometimes renders them more obscure; and therefore the illuminating power of a large telescope, with a small power, is in all cases to be preferred. A comet eye-piece should be constructed with a very large and uniformly distinct field, and should magnify only from 15 to 30 or 40 times, and the lenses of such an eye-tube should be nearly two inches in diameter. The late Rev. F. Wollaston recommended for observing comets, ‘a telescope with an achromatic object-glass of 16 inches focal length, and 2 inches aperture, with a Ramsden’s eye-glass magnifying about 25 times, mounted on a very firm equatorial stand, the field of view taking in 2 degrees of a great circle.’
In viewing the moon, various powers may be applied according to circumstances. The best periods of the moon for inspecting the inequalities on its surface, are either when it assumes a crescent or a half-moon phase, or two or three days after the period of half-moon. Several days after full-moon, and particularly about the third quarter, when this orb is waning, and when the shadows of its mountains and vales are thrown in a different direction from what they are when on the increase,—the most prominent and interesting 380 views may be obtained. The most convenient season for obtaining such views is during the autumnal months, when the moon, about the third quarter, sometimes rises as early as 8 o’clock P.M., and may be viewed at a considerably high altitude by ten or eleven. When in the positions now alluded to, and at a high altitude, very high magnifying powers may sometimes be applied with good effect, especially if the atmosphere be clear and serene. I have sometimes applied a power, in such cases, of 350 times, on a 46-inch achromatic, with considerable distinctness; but it is only two or three times in a year, and when the atmosphere is remarkably favourable, that such a power can be used. The autumnal evenings are generally best fitted for such observations. The full moon is an object which is never seen to advantage with high powers, as no shadows or inequalities on its surface can then be perceived. It forms, however, a very beautiful object, when magnifying powers not higher than 40, 50, or 60 times are used. A power of 45 times, if properly constructed, will show the whole of the moon with a margin around it, when the darker and brighter parts of its surface will present a variegated aspect, and appear somewhat like a map to the eye of the observer.
4. Mode of exhibiting the Solar spots.
The solar spots may be contemplated with advantage by magnifying powers varying from 60 to 180 times; about 90 times is a good medium power, though they may sometimes be distinguished with very low powers, such as those usually adapted to a one-foot telescope, or even by means of a common opera-glass. The common astronomical eye-pieces given along with achromatic telescopes, and the sun-glasses connected 381 with them, are generally ill-adapted for taking a pleasant and comprehensive view of the solar spots. In the higher magnifying powers, the first eye-glass is generally at too great a distance from the eye, and the sun-glass which is screwed over it, removes it to a still greater distance from the point to which the eye is applied, so that not above one third of the field of view can be taken in. This circumstance renders it difficult to point the instrument to any particular small spot on the solar disk which we wish minutely to inspect; and besides, it prevents us from taking a comprehensive view of the relative positions of all the spots that may at any time be traversing the disk. To obviate this inconvenience, the sun-glass would require to be placed so near to the glass next the eye as almost to touch it. But this is sometimes difficult to be attained, and, in high powers, even the thickness of the sun-glass itself is sufficient to prevent the eye from taking in the whole field of view. For preventing the inconveniences to which I now allude, I generally make use of a terrestrial eye-piece of a considerable power, with a large field, the sun-glass is fixed at the end of a short tube which slides on the eye-piece, and permits the coloured glass to approach within a line or two of the lens next the eye, so that the whole field of the telescope is completely secured. The eye-piece alluded to carries a magnifying power of 95 times for a 46-inch telescope, and takes in about three fourths of the surface of the sun, so that the relative positions of all the spots may generally be perceived at one view. Such a power is, in most cases, quite sufficient for ordinary observations; and I have seldom found any good effect to arise from attempting very high powers, when minutely examining the solar spots. 382
But, the most pleasant mode of viewing the solar spots—especially when we wish to exhibit them to others—is to throw the image of the sun upon a white screen, placed in a room which is considerably darkened. It is difficult, however, when the sun is at a high altitude, to put this method into practice, on account of the great obliquity with which his rays then fall, which prevents a screen from being placed at any considerable distance from the eye-end of the telescope. The following plan, therefore, is that which I uniformly adopt as being both the easiest and the most satisfactory. A telescope is placed in a convenient position, so as to be directed to the sun. This telescope is furnished with a diagonal eye-piece, such as that represented, fig. 77, (p. 344.) The window-shutters of the apartment are all closed, excepting a space sufficient to admit the solar rays; and, when the telescope is properly adjusted, a beautiful image of the sun, with all the spots which then happen to diversify his surface, is thrown upon the ceiling of the room. This image may be from 12 to 20, or 30 inches or more in diameter, according to the distance of the ceiling from the diagonal eye-piece. The greater this distance is, the larger the image. If the sun is at a very high altitude, the image will be elliptical; if he be at no great distance from the horizon, the image will appear circular or nearly so; but in either case the spots will be distinctly depicted, provided the focus of the telescope be accurately adjusted. In this exhibition, the apparent motion of the sun, produced by the rotation of the earth, and the passage of thin fleeces of clouds across the solar disk, exhibit a very pleasing appearance.
By this mode of viewing the solar spots we may 383 easily ascertain their diameter and magnitude, at least to a near approximation. We have only to take a scale of inches, and measure the diameter of any well-defined and remarkable spot, and then the diameter of the solar image; and, comparing the one with the other, we can ascertain the number of miles either lineal or square, comprehended in the dimensions of the spot. For example, suppose a spot to measure one half-inch in diameter, and the whole image of the sun 25 inches, the proportion between the diameter of the spot and that of the sun will be as 1 to 50, in other words, the one fiftieth part of the sun’s diameter. Now, this diameter being 880,000 miles, this number, divided by 50, produces a quotient of 17,600 = the number of miles which its diameter measures. Such a spot will therefore contain an area of 243,285,504, or more than two hundred and forty-three millions of square miles, which is 46 millions of miles more than the whole superficies of the terraquous globe. Again, suppose the diameter of a spot measures 3/10 inch, and the solar image 23 inches, the proportion of the diameter of the spot to that of the sun is as 3 to 230 = the number of tenths in 23 inches. The number of miles in the spot’s diameter will therefore be found by the following proportion: 230 : 880,000 :: 3 : 11,478; that is, the diameter of such a spot measures eleven thousand four hundred and seventy-eight miles. Spots of such sizes are not unfrequently seen to transit the solar disk.
By this mode of viewing the image of the sun, his spots may be exhibited to twenty or thirty individuals at once without the least straining or injury to the eyes; and as no separate screen is requisite, and as the ceilings of rooms are generally white, the experiment may be performed in half 384 a minute without any previous preparation, except screwing on and adjusting the eye-piece. The manner of exhibiting the solar spots, in this way, is represented in fig. 82.
figure 82.
5. On the space-penetrating power of telescopes.—The power of telescopes to penetrate into the profundity of space is the result of the quantity of light they collect and send to the eye in a state fit for vision. This property of telescopes is sometimes designated by the expression Illuminating Power.
Sir W. Herschel appears to have been the first who made a distinction between the magnifying power, and the space-penetrating power of a telescope; and there are many examples which 385 prove that such a distinction ought to be made, especially in the case of large instruments. For example, the small star, or speck of light, which accompanies the pole-star, may be seen through a telescope of large aperture, with a smaller magnifying power than with a telescope of a small aperture furnished with a much higher power. If the magnifying power is sufficient to show the small star completely separated from the rays which surround the large one, this is sufficient in one point of view; but in order that this effect may be produced, so as to render the small star perfectly distinguishable, a certain quantity of light must be admitted into the pupil of the eye—which quantity depends upon the area of the object-glass or speculum of the instrument, or, in other words, on the illuminating power. If we compare a telescope of 2¾ inches aperture with one of 5 inches aperture, when the magnifying power of each does not exceed 50 times for terrestrial objects, the effect of illuminating power is not so evident; but if we use a power of 100 for day objects, and 180 for the heavenly bodies, the effects of illuminating power is so clearly perceptible, that objects not only appear brighter, and more clearly visible, in the larger telescope, but with the same magnifying power, they also appear larger, particularly when the satellites of Jupiter and small stars are the objects we are viewing.
Sir W. Herschel remarks, that ‘objects are viewed in their greatest perfection, when, in penetrating space, the magnifying power is so low as only to be sufficient to show the object well—and when, in magnifying objects, by way of examining them minutely, the space-penetrating power is no higher than what will suffice for the purpose; for in the use of either power, the injudicious overcharge 386 of the other will prove hurtful to vision.’ When illuminating power is in too high a degree, the eye is offended by the extreme brightness of the object. When it is in too low a degree, the eye is distressed by its endeavours to see what is beyond its reach; and therefore it is desirable, when we wish to give the eye all the assistance possible, to have the illuminating and the magnifying powers in due proportion. What this proportion is, depends, in a certain degree, upon the brightness of the object. In proportion to its brightness or luminosity, the magnifying power may, to a certain extent, be increased. Sir W. Herschel remarks, in reference to α Lyræ, ‘This star, I surmise, has light enough to bear being magnified, at least a hundred thousand times, with no more than six inches of aperture.’ However beautifully perfect any telescopes may appear, and however sharp their defining power, their performance is limited by their illuminating powers—which are as the squares of the diameters of the apertures of the respective instruments. Thus, a telescope whose object-glass is 4 inches diameter will have four times the quantity of light, or illuminating power, possessed by a telescope whose aperture is only 2 inches, or in the proportion of 16 to 4,—the square of 4 being 16, and the square of 2 being 4.
The nature of the space-penetrating power, to which we are adverting, and the distinction between it, and magnifying power, may be illustrated from a few examples taken from Sir W. Herschel’s observations.
The first observation which I shall notice refers to the nebula between η and ζ Ophiuchi, discovered by Messier in 1764. The observation was made with a 10 feet reflector, having a magnifying 387 power of 250, and a space-penetrating power of 28.67. His note is dated May 3, 1783. ‘I see several stars in it, and make no doubt a higher power and more light will resolve it all into stars. This seems to me a good nebula for the purpose of establishing the connection between nebulæ and clusters of stars in general.’—‘June 18, 1784. The same nebula viewed with a Newtonian 20 feet reflector; penetrating power 61, and a magnifying power of 157; a very large and a very bright cluster of excessively compressed stars. The stars are but just visible, and are of unequal magnitudes. The large stars are red, the cluster is a miniature of that near Flamstead’s forty-second Comæ Berenices; Right ascension 17h 6m 32s Polar distance 108° 18´´’ In this case, a penetrating power of about 28, with a magnifying power of 250, barely shewed a few stars; when in the second instrument the illuminating power of 60 with the magnifying power of only 157 showed them completely.
Subsequently to the date of the latter observation, the 20 feet Newtonian telescope was converted into an Herschelian instrument, by taking away the small speculum, and giving the large one the proper inclination for obtaining the front view; by which alteration the illuminating power was increased from 61 to 75, and the advantage derived from the alteration was evident in the discovery of the satellites of Uranus by the altered telescope, which before was incompetent in the point of penetration, or illuminating power. ‘March 14, 1798, I viewed the Georgian planet (or Uranus) with a new 25 feet reflector. Its penetrating power is 95.85, and having just before also viewed it with my 20 feet instrument, I found that with an equal magnifying power of 300, the 25 feet 388 telescope had considerably the advantage of the former.’ The aperture of the 20 feet instrument was 18.8 inches, and that of the 25 feet telescope, 24 inches, so that the superior effect of the latter instrument must have been owing to its greater illuminating power. The following observations show the superior power of the 40 feet telescope as compared with the 20 feet.—‘Feb. 24, 1786, I viewed the nebula near Flamstead’s fifth Serpentis, with my 20 feet reflector, magnifying power 157. The most beautiful extremely compressed cluster of small stars; the greatest part of them gathered together into one brilliant nucleus, evidently consisting of stars, surrounded with many detached gathering stars of the same size and colour. R.A. 15h 7m 12s. P.D. 87° 8´´’—‘May 27, 1791, I viewed the same object with my 40 feet telescope, penetrating power 191.69, magnifying power 370. A beautiful cluster of stars. I counted about 200 of them. The middle of it is so compressed, that it is impossible to distinguish the stars.’—‘Nov. 5, 1791, I viewed Saturn with the 20 and 40 feet telescopes. Twenty feet. The fifth satellite of Saturn is very small. The first, second, third, fourth and fifth, and the new sixth satellites are in their calculated places. Forty feet. I see the new sixth satellite much better with this instrument than with the 20 feet. The fifth is also much larger here than in the 20 feet, in which it was nearly the same size as a small fixed star, but here it is considerably larger than that star.’
These examples, and many others of a similar kind, explain sufficiently the nature and extent of that species of power that one telescope possesses over another, in consequence of its enlarged aperture; but the exact quantity of this power is in some degree uncertain. To ascertain practically the illuminating power of telescopes, we must try 389 them with equal powers on such objects as the following,—the small stars near the pole-star, and near Rigel and ε Bootis—the division in the ring of Saturn—and distant objects in the twilight or towards the evening. These objects are distinctly seen with a 5 feet achromatic of 38/10 inches aperture, and an illuminating power of 144, while they are scarcely visible in a 3½ feet with an aperture of 2¾ inches, and an illuminating power of 72, supposing the same magnifying power to be applied. The illuminating power of a telescope is best estimated, in regard to land objects, when it is tried on minute objects, and such as are badly lighted up; and the advantage of a telescope with a large aperture will be most obvious, when it is compared with another of inferior size in the close of the evening, when looking at a printed bill composed of letters of various sizes. As darkness comes on, the use of illuminating power becomes more evident. In a 5 feet telescope some small letters will be legible, which are hardly discernible in the 3½ feet, and in the 2½ feet are quite undefinable, though the magnifying powers be equal. Sir W. Herschel informs us, that in the year 1776, when he had erected a telescope of 20 feet focal length of the Newtonian construction, one of its effects by trial was, that when towards evening, on account of darkness, the natural eye could not penetrate far into space, the telescope possessed that power sufficiently to show, by the dial of a distant church steeple, what o’clock it was, notwithstanding the naked eye could no longer see the steeple itself.
In order to convey an idea of the numbers by which the degree of space-penetrating power is expressed, and the general grounds on which they rest, the following statements may be made. The depth to which the naked eye can penetrate into the 390 spaces of the heavens, is considered as extending to the twelfth order of distances—in other words, it can perceive a star at a distance 12 times farther than those luminaries, such as Sirius, Arcturus or Capella, which, from their vivid light, we presume to be nearest to us. It has been stated above, that Herschel calculated his 10 feet telescope to have a space-penetrating power of 28.67, that is, it could enable us to descry a star 28 times farther distant than the naked eye can reach. His 20 feet Newtonian was considered as having a similar power of 61; his 25 feet, nearly 96, and his 40 feet instrument, a power of 191.69. If each of these numbers be multiplied by 12, the product will indicate how much farther these telescopes will penetrate into space than the nearest range of the fixed stars, such as those of the first magnitude. For instance, the penetrating power of the 40 feet reflector being 191.69, this number multiplied by 12, gives a product of 2,300, which shows, that were there a series of two thousand three hundred stars extended in a line beyond Sirius, Capella and similar stars—each star separated from the one beyond it, by a space equal to the distance of Sirius from the earth—they might be all seen through the 40 feet telescope. In short, the penetrating power of telescopes is a circumstance which requires to be particularly attended to in our observations of celestial phenomena, and in many cases, is of more importance than magnifying power. It is the effect produced by illuminating power that renders telescopes, furnished with comparatively small magnifying powers, much more efficient in observing comets and certain nebulæ and clusters of stars, than when high powers are attempted. Every telescope may be so adjusted, as to produce different space-penetrating 391 powers. If we wish to diminish such a power, we have only to contract the object-glass or speculum, by placing circular rims, or apertures of different degrees of breadth, across the mouth of the great tube of the instrument. But we cannot increase this illuminating power beyond a certain extent, which is limited by the diameter of the object-glass. When we wish illuminating power beyond this limit, we must be furnished with an object-glass or speculum of a larger size; and hence, the rapid advance in price of instruments which have large apertures, and consequently high illuminating powers. Mr. Tulley’s 3½ feet achromatics of 2¾ inches aperture, sell at £26 5s. When the aperture is 3¼ inches, the price is £42. When 3¾ inches, £68 5s. The following table contains a statement of the ‘comparative lengths, apertures, illuminating powers, and prices, of Achromatic Refractors, and Gregorian Reflectors,’ according to Dr. Kitchener.
| ACHROMATIC REFRACTORS. | ||||||
|---|---|---|---|---|---|---|
| Length and name they are called by. | Diameter of aperture. | Illuminating power. | Price. | |||
| Feet. | In. | Th. | £ | s. | ||
| 2 | 1. | 6 | 25 | 4 | 4 | |
| 2½ | 2 | 40 | 12 | 12 | ||
| 3½ | 2. | 7 | 72 | 21 to 42 |
||
| 5 | 3. | 8 | 144 | 105 to 150 |
||
| 7 | 5 | 250 | 250 | |||
| 7 | 6 | 360 | 360 | |||
| GREGORIAN &c. REFLECTORS. | |||||
|---|---|---|---|---|---|
| Length and name they are known by. | Diameter of Aperture. | Illuminating power. | Price. | ||
| Feet. | In. | Th. | £ | s. | |
| 1 | 2. | 5 | 62 | 7 | 7 |
| 1½ | 3. | 90 | 12 | 12 | |
| 2 | 4. | 5 | 202 | 20 | |
| 3 | 5. | 5 | 302 | 50 | |
| 4 | 7 | 490 | 105 | ||
| 7 Newtonian | 7 | 490 | 126 | ||
| 5 Gregorian | 9 | 810 | 200 | ||
| 10 Newtonian | 10 | 1000 | 315 | ||
The illuminating powers stated in the above table are only comparative. Fixing on the number 25 as the illuminating power of a 2 feet telescope, 16/10 inch aperture, that of a 2½ feet 2 inches 392 inches aperture, will be 40, of a 5 feet 38/10 inch aperture, 144, &c. If the illuminating power of a Gregorian 1½ foot, and 3 inches aperture, be 90, a 5 feet, with 9 inches aperture, will be 810, &c.
6. On choosing Telescopes, and ascertaining their properties.
It is an object of considerable importance, to every astronomical observer, that he should be enabled to form a judgment of the qualities of his telescope, and of any instruments of this description which he may intend to purchase. The following directions may perhaps be useful to the reader in directing him in the choice of an achromatic refracting telescope.
Supposing that an achromatic telescope of 3½ feet focal length, and 3¼ inches aperture were offered for sale, and that it were required to ascertain whether the object-glass, on which its excellence chiefly depends—is a good one and duly adjusted;—some opinion may be formed by laying the tube of the telescope in a horizontal position, on a firm support, about the height of the eye,—and by placing a printed card or a watch glass vertically, but in an inverted position, against some wall or pillar, at 40 or 50 yards distant, so as to be exposed to a clear sky. When the telescope is directed to this object, and accurately adjusted to the eye—should the letters on the card, or the strokes and dots on the watch-glass appear clearly and sharply defined, without any mistiness or coloration, and if very small points appear well defined—great hopes may be entertained that the glass will turn out a good one. But a telescope may appear a good one, when viewing common terrestrial objects, to eyes unaccustomed to discriminate deviations from perfect vision, while it 393 may turn out to be an indifferent one, when directed to certain celestial objects. Instead therefore of a printed card, fix a black board, or one half of a sheet of black paper, in a vertical position at the same distance, and a circular disk of white writing paper, about ¼ of an inch in diameter, on the centre of the black ground. Then having directed the telescope to this object, and adjusted for the place of distinct vision, mark with a black-lead pencil the sliding eye-tube, at the end of the main tube, so that this position can always be known; and if this sliding tube be gradually drawn out, or pushed in, while the eye beholds the disk, it will gradually enlarge and lose its colour, till its edges cease to be well-defined. Now, if the enlarged misty circle is observed to be concentric with the disk itself, the object-glass is properly centered, as it has reference to the tube; but if the misty circle goes to one side of the disk, the cell of the object-glass is not at right angles to the tube, and must have its screws removed and its holes elongated, by a rattailed file, small enough to enter the holes. When this has been done, the cell may be replaced, and the disk examined a second time, and a slight stroke on one edge of the cell, by a wooden mallet, will show by the alteration made in the position of the misty portion of the disk, how the adjustment is to be effected, which is known to be right when a motion in the sliding tube will make the diluted disk enlarge in a circle concentric with the disk itself. When the disk will enlarge so as to make a ring of diluted white light round its circumference, as the sliding tube holding the eye-piece is pushed in or drawn out, the cell may be finally fixed by the screws passing through its elongated holes. 394
When the object-glass is thus adjusted, it may then be ascertained whether the curves of the respective lenses composing the object-glass are well-formed and suitable for each other. If a small motion of the sliding tube of about 1/10th of an inch in a 3½ feet telescope, from the point of distinct vision, will dilute the light of the disk and render the appearance confused, the figure of the object-glass is good; particularly if the same effect will take place at equal distances from the point of distinct vision, when the tube is alternately drawn out and pushed in. A telescope that will admit of much motion in the sliding tube without sensibly affecting the distinctness of vision, will not define an object well at any point of adjustment, and must be considered as having an imperfect object-glass, inasmuch as the spherical aberration of the transmitted rays is not duly corrected. The due adjustment of the convex lens, or lenses, to the concave one, will be judged of by the absence of coloration round the enlarged disk, and is a property distinct from the spherical aberration; the achromatism depending on the relative focal distances of the convex and concave lenses, is regulated by the relative dispersive powers of the pieces of glass made use of; but the distinctness of vision depends on a good figure of the computed curves that limit the focal distances. When an object-glass is free from imperfection in both these respects, it may be called a good glass for terrestrial purposes.
It still, however, remains to be determined how far such an object-glass may be good for viewing a star or a planet, and can only be known by actual observations on the heavenly bodies. When a good telescope is directed to the moon or to Jupiter, the achromatism may be judged of, by 395 alternately pushing in, and drawing out the eye-piece, from the place of distinct vision. In the former case, a ring of purple will be formed round the edge; and in the latter, a ring of light green, which is the central colour of the prismatic spectrum; for these appearances show, that the extreme colours red and violet are corrected. Again, if one part of a lens employed have a different refractive power from another part of it, that is, if the flint-glass particularly is not homogeneous, a star of the first and even of the second magnitude will point out the natural defect by the exhibition of an irradiation, or what is called a wing, at one side, which no perfection of figure or of adjustment will banish, and the greater the aperture the more liable is the evil to happen. Hence caps with different apertures are usually supplied with large telescopes, that the extreme parts of the glass may be cut off, in observations requiring a round and well-defined image of the body observed.
Another method of determining the figure and quality of an object-glass is by first covering its centre by a circular piece of paper, as much as one half of its diameter, and adjusting it for distinct vision of a given object, such as the disk above mentioned, when the central rays are intercepted—and then trying if the focal length remains unaltered when the paper is taken away, and an aperture of the same size applied, so that the extreme rays may in their turn be cut off. If the vision remains equally distinct in both cases, without any new adjustment for focal distance, the figure is good, and the spherical aberration cured, and it may be seen by viewing a star of the first magnitude successively in both cases, whether the irradiation is produced more by the extreme or 396 by the central parts of the glass. Or, in case the one half be faulty and the other good, a semicircular aperture, by being turned gradually round in trial, will detect what semicircle contains the defective portion of the glass; and if such portion should be covered, the only inconvenience that would ensue, would be the loss of so much light as is thus excluded. When an object-glass produces radiations in a large star, it is unfit for the nicer observations of astronomy, such as viewing double stars of the first class. The smaller a large star appears in any telescope, the better is the figure of the object-glass, but if the image of the star be free from wings, the size of its disk is not an objection in practical observations.30
Some opticians are in the habit of inserting a diaphragm into the body of the large tube, to cut off the extreme rays coming from the object-glass when the figure is not good, instead of lessening the aperture by a cap. When this is the case, a deficiency of light will be the consequence beyond what the apparent aperture warrants. It is therefore proper to examine that the diaphragm be not placed too near the object-glass, so as to intercept any of the useful rays. Sometimes a portion of the object-glass is cut off by the stop in the eye-tube. To ascertain this, adjust the telescope to distinct vision, then take out the eye-glasses, and put your finger on some other object on the edge of the outside of the object-glass, and look down the tube; if you can see the tip of your finger, or any object in its place, just peeping over the edge of the object-glass, no part is cut off. I once had a 3½ feet telescope whose object-glass measured 3 397 inches diameter, which was neither so bright, nor did it perform in other respects nearly so well as another of the same length whose object-glass was only 2¾ inches diameter; but I found that a diaphragm was placed about a foot within the end of the large tube, which reduced the aperture of the object-glass to less than 2½ inches; and when it was removed the telescope was less distinct than before. The powers given along with this instrument were much lower than usual—none of them exceeding 100 times. This is a trick not uncommon with some opticians.
Dr. Pearson mentions that an old Dollond’s telescope of 63 inches focal length, and 3¾ inches aperture, supposed to be an excellent one, was brought to Mr. Tulley, when he was present, and the result of the examination was that its achromatism was not perfect. The imperfection was thus determined by experiment. A small glass globe was placed at 40 yards distance from the object-end of the telescope when the sun was shining, and the speck of light seen reflected from this globe formed a good substitute for a large star, as an object to be viewed. When the focal length of the object-glass was adjusted to this luminous object, no judgment could be formed of its prismatic aberrations, till the eye-piece had been pushed in beyond the place of correct vision; but when the telescope was shortened a little, the luminous disk occasioned by such shortening was strongly tinged with red rays at its circumference. On the contrary, when the eye-piece was drawn out, so as to lengthen the telescope too much, the disk thus produced was tinged with a small circle of red at its centre, thereby denoting that the convex lens had too short a focal length; and Mr. Tulley observed, that if one or both of the curves 398 of the convex lens were flattened till the total focal length should be about 4 inches increased, it would render the telescope quite achromatic, provided in doing this the aberration should not be increased.
The following general remarks may be added. 1. To make anything like an accurate comparison of telescopes, they must be tried not only at the same place, but as nearly as possible at the same time, and, if the instruments are of the same length and construction, if possible, with the same eye-piece. 2. A difference of 8 or 10 times in the magnifying power, will sometimes, on certain objects, give quite a different character to a telescope. It has been found by various experiments that object-glasses of two or three inches longer focus will produce different vision with the same eye-piece. 3. Care must be taken to ascertain that the eye-glasses are perfectly clean and free from defects. The defects of glass are either from veins—specks—scratches—colour, or an incorrect figure. To discover veins in an eye or an object-glass, place a candle at the distance of 4 or 5 yards; then look through the glass, and move it from your eye till it appear full of light—you will then see every vein, or other imperfection in it which may distort the objects and render vision imperfect. Specks or scratches, especially in object-glasses, are not so injurious as veins, for they do not distort the object, but only intercept a portion of the light. 4. We cannot judge accurately of the excellence of any telescope by observing objects with which we are not familiarly acquainted. Opticians generally try an instrument at their own marks, such as the dial-plate of a watch, a finely engraved card, a weather-cock, or the moon and the planet Jupiter, when near 399 the meridian. Of several telescopes of the same length, aperture and magnifying power, that one is generally considered the best with which we can read a given print at the greatest distance, especially if the print consists of figures, such as a table of logarithms, where the eye is not apt to be deceived by the imagination, in guessing at the sense of a passage, when two or three words are distinguished.
There is a circumstance which I have frequently noticed, in reference to achromatic telescopes, particularly those of a small size, and which I have never seen noticed by any optical writer. It is this,—if the telescope, when we are viewing objects, be gradually turned round its axis, there is a certain position in which the objects will appear distinct and accurately defined; and if it be turned round exactly a semicircle from this point, the same degree of distinctness is perceived; but in all other positions, there is an evident want of clearness and defining power. This I find to be the case in more than ten 1 foot and 2 feet telescopes now in my possession; and therefore I have put marks upon the object-end of each of them, to indicate the positions in which they should be used for distinct observation.—This is a circumstance which requires, in many cases, to be attended to in the choice and the use of telescopical instruments, and in fixing and adjusting them on their pedestals. In some telescopes this defect is very striking, but it is in some measure perceptible in the great majority of instruments which I have had occasion to inspect. Even in large and expensive achromatic telescopes this defect is sometimes observable. I have an achromatic whose object-glass is 41/10 inches diameter, which was much improved in its defining power, 400 by being unscrewed from its original position, or turned round its axis—about one-eighth part of its circumference. This defect is best detected by looking at a large printed bill, or a sign-post at a distance, when, on turning round the telescope or object-glass, the letters will appear much better defined in one position than in another. The position in which the object appears least distinct is when the upper part of the telescope is a quadrant of a circle different from the two positions above-stated, or at an equal distance from each of them.
7. On the mode of determining the magnifying power of Telescopes.
In regard to refracting telescopes, we have already shown that, when a single eye-glass is used, the magnifying power may be found by dividing the focal distance of the object-glass by that of the eye-glass. But when a Huygenian eye-piece, or a four-glass terrestrial eye-piece such as is now common in achromatic telescopes, is used, the magnifying power cannot be ascertained in this manner; and in some of the delicate observations of practical astronomy, it is of the utmost importance to know the exact magnifying power of the instrument with which the observations are made, particularly when micrometrical measurements are employed to obtain the desired results.—The following is a general method of finding the magnifying powers of telescopes when the instrument called a dynameter is not employed; and it answers for refracting and reflecting telescopes of every description.
Having put up a small circle of paper, an inch or two in diameter, at the distance of about 100 yards, draw upon a card 2 black parallel lines, whose distance from each other is equal to the 401 diameter of the paper circle. Then view through the telescope the paper circle with one eye, and the parallel lines with the other; and let the parallel lines be moved nearer to or further from, the eye, till they seem exactly to cover the small circle viewed through the telescope. The quotient obtained by dividing the distance of the paper circle by the distance of the parallel lines from the eye, will be the magnifying power of the telescope. It requires a little practice before this experiment can be performed with accuracy. The one eye must be accustomed to look at an object near at hand, while the other is looking at a more distant object through the telescope. Both eyes must be open at the same time, and the image of the object seen through the telescope must be brought into apparent contact with the real object near at hand. But a little practice will soon enable any observer to perform the experiment with ease and correctness, if the telescope be mounted on a firm stand, and its elevation or depression produced by rack-work.
The following is another method, founded on the same principle:—Measure the space occupied by a number of the courses, or rows of bricks in a modern building—which, upon an average, is found to have 8 courses in 2 feet, so that each course or row, is 3 inches. Then cut a piece of paper 3 inches in height, and of the length of a brick—which is about 9 inches—so that it may represent a brick, and fixing the paper against the brick wall, place the telescope to be examined at the distance of about 80 or 100 yards from it. Now, looking through the telescope at the paper with one eye, and at the same time, with the other eye, looking past the telescope, observe what extent of wall the magnified image of the paper appears to 402 cover, then count the courses of bricks in that extent, and it will give the magnifying power of the telescope. It is to be observed, however, that the magnifying power determined in this way, will be a fraction greater than for very distant objects, as the focal distance of the telescope is necessarily lengthened in order to obtain distinct vision of near objects.
In comparing the magnifying powers of two telescopes, or of the same telescope, when different magnifying powers are employed, I generally use the following simple method. The telescopes are placed at 8 or 10 feet distant from a window, with their eye-ends parallel to each other, or at the same distance from the window. Looking at a distant object, I fix upon a portion of it whose magnified image will appear to fill exactly two or three panes of the window. Then putting on a different power, or looking through another telescope, I observe the same object, and mark exactly the extent of its image on the window-panes, and compare the extent of the one image with the other. Suppose for example, that the one telescope has been previously found to magnify 90 times, and that the image of the object fixed upon exactly fills three panes of the window, and that with the other power or the other telescope, the image fills exactly two panes, then the magnifying power is equal to two thirds of the former, or 60 times; and were it to fill only one pane, the power would be about 30 times. A more correct method is to place at one side of the window, a narrow board, two or three feet long, divided into 15 or 20 equal parts, and observe how many of these parts appear to be covered by the respective images, of the different telescopes. Suppose, in the one case, 10 divisions to be covered by the image, in a telescope magnifying 90 times, and 403 that the image of the same object in another telescope, measures 6 divisions, then its power is found by the following proportion, 10 : 90 : 6 : 54 : that is, this telescope magnifies 54 times.
Another mode which I have used for determining, to a near approximation, the powers of telescopes, is as follows:—Endeavour to find the focus of a single lens which is exactly equivalent to the magnifying power of the eye-piece, whether the Huygenian or the common terrestrial eye-piece. This may be done by taking a small lens, and using it as an object-glass to the eye-piece. Looking through the eye-piece to a window and holding the lens at a proper distance, observe whether the image of one of the panes exactly coincides with the pane, as seen by the naked eye; if it does, then the magnifying power of the eye-piece is equal to that of the lens. If the lens be ½ inch focal length, the eye-piece will produce the same magnifying power, as a single lens when used as an eye-glass to the telescope, and the magnifying power will then be found by dividing the focal distance of the object-glass by that of the eye-glass. But if the image of the pane of glass does not exactly coincide with the pane as seen by the other eye, then proportional parts may be taken by observing the divisions of such a board as described above, or we may try lenses of different focal distances. Suppose, for example, that a lens 2 inches focal length had been used, and that the image of a pane covered exactly the space of two panes, the power of the eye-piece is then equal to that of a single lens 1 inch focal distance.
The following is another mode depending on the same general principle. If a slip of writing-paper one inch long, or a disk of the same material of one inch diameter, be placed on a black ground 404 at from 30 to 50 yards distance from the object-end of the telescope, and a staff painted white, and divided into inches and parts by strong black lines, be placed vertically near the said paper or disk; the eye that is directed through the telescope when adjusted for vision, will see the magnified disk, and the other eye, looking along the outside of the telescope, will observe the number of inches and parts that the disk projected on it will just cover, and as many inches as are thus covered will indicate the magnifying power of the telescope—at the distance for which it is adjusted for distinct vision. The solar power, or powers for very distant objects, may be obtained by the following proportion:—As the terrestrial focal length, at the given distance: is to the solar focal length :: so is the terrestrial power, to the solar power. For example, a disk of white paper one inch in diameter, was placed on a black board, and suspended on a wall contiguous to a vertical black staff that was graduated into inches by strong white lines, at a distance of 33 yards 2½ feet, and when the adjustment for vision was made with a 42 inch telescope, the left eye of the observer viewed the disk projected on the staff, while the right eye observed that the enlarged image of the disk covered just 58½ inches on the staff, which number was the measure of the magnifying power, at the distance answering to 33 yards 2½ feet—which in this case exceeded the solar focus by an inch and a half. Then according to the above analogy, we have, as 43.5 : 42 :: 58.5 : 56.5 nearly. Hence the magnifying power due to the solar focal length of the telescope in question is 56.5, and the distance 33 yards 2½ feet, is that which corresponds to an elongation of the solar focal distance an 405 inch and a half.31 If we multiply the terrestrial and the solar focal distances together, and divide the product by their difference, we shall again obtain the distance of the terrestrial object from the telescope. Thus, (43.5 + 42)/1.5 = 1218 inches = 101.5 feet, or 33 yards 2½ feet.
The magnifying power of a telescope is also determined, by measuring the image which the object-glass or the large speculum of a telescope forms at its solar focus. This is accomplished by means of an instrument called a Dynameter. This apparatus consists of a strip of mother-of-pearl, marked with equal divisions, from the 1/100th to the 1/1000th of an inch apart, according to the accuracy required. This measure is attached to a magnifying lens in its focus, in order to make the small divisions more apparent. When the power of a telescope is required, the person must measure the clear aperture of the object-glass, then holding the pearl dynameter next the eye-glass, let him observe how many divisions the small circle of light occupies, when the instrument is directed to a bright object. Then by dividing the diameter of the object-glass by the diameter of this circle of light, the power will be obtained.32 The most accurate instrument of this kind is the Double Image Dynameter invented by Ramsden, and another on the same principle now made by Dollond, a particular description of which may be found in Dr. Pearson’s ‘Introduction to Practical Astronomy.’ The advantage attending these dynameters is that they do not require any knowledge of the thickness and focal lengths of any of the lenses employed in a telescope, nor yet of their 406 number or relative positions; neither does it make any difference whether the construction be refracting or reflecting, direct or inverting. One operation includes the result arising from the most complicated construction.
I shall only mention farther the following method of discovering the magnifying power, which is founded on the same general principle as alluded to above. Let the telescope be placed in such a position opposite the sun, that the rays of light may fall perpendicularly on the object-glass; and the pencil of rays may be received on a piece of paper, and its diameter measured. Then, as the diameter of the pencil of rays is to that of the object-glass, so is the magnifying power of the telescope.
8.—On cleaning the lenses of telescopes.—
It is necessary, in order to distinct vision, that the glasses, particularly the eye-glasses of telescopes be kept perfectly clean, free of damp, dust, or whatever may impede the transmission of the rays of light. But great caution ought to be exercised in the wiping of them, as they are apt to be scratched, or otherwise injured by a rough and incautious mode of cleaning them. They should never be attempted to be wiped unless they really require it; and, in this case, they should be wiped carefully and gently with a piece of new and soft lamb’s-skin leather. If this be not at hand, a piece of fine silk paper, or fine clean linen may be used as a substitute. The lens which requires to be most particularly attended to is the second glass from the eye, or the field-glass; for if any dust or other impediment be found upon this glass, it is always distinctly seen, being magnified by the glass next the eye. The next glass which requires attention is the fourth 407 from the eye, or that which is next the object. Unless the glass next the eye be very dusty, a few small spots or grains of dust are seldom perceptible. The object-glass of an achromatic should seldom be touched, unless damp adheres to it. Care should be taken never to use pocket handkerchiefs or dirty rags for wiping lenses. From the frequent use of such articles, the glasses of seaman’s telescopes get dimmed and scratched in in the course of a few years. If the glasses be exceedingly dirty, and if greasy substances are attached to them, they may be soaked in spirits and water, and afterwards carefully wiped. In replacing the glasses in their socket, care should be taken not to touch the surfaces with the fingers, as they would be dimmed with the perspiration: they should be taken hold of by the edges only, and carefully screwed into the same cells from which they were taken.
It appears to have been almost overlooked by opticians and others, that telescopes may be constructed so as to exhibit a beautiful and minute view of very near objects, and to produce even a microscopic effect, without the least alteration in the arrangement of the lenses of which they are composed. This object is effected simply by making the eye-tube of a telescope of such a length as to be capable of being drawn out 12 or 13 inches beyond the point of distinct vision for distant objects. The telescope is then rendered capable of exhibiting with distinctness all kinds of objects, from the most distant to those which are 408 placed within 3 or 4 feet of the instrument—or not nearer than double the focal distance of the object-glass. Our telescopes, however, are seldom or never fitted with tubes that slide farther than an inch or two beyond the point of distinct vision for distant objects, although a tube of a longer size than usual, or an additional tube would cost but a very trifling expence.
The following, among many others, are some of the objects on which I have tried many amusing experiments with telescopes fitted up with the long tubes to which I allude. The telescope to which I shall more particularly advert is an achromatic, mounted on a pedestal, having an object-glass about 19 inches focal length, and 1⅝ inch diameter, with magnifying powers for distant objects of 13 and 20 times. When this instrument is directed to a miniature portrait, 3½ inches in length, placed in a good light, at the distance of about 8 or 10 feet, it appears as large as an oil-painting four or five feet long, and represents the individual as large as life. The features of the face appear to stand out in bold relief: and perhaps there is no representation of the human figure that more resembles the living prototype, than in this exhibition, provided the miniature is finely executed. In this case the tube requires to be pulled out four or five inches from the point of distinct vision for distant objects, and consequently the magnifying power is proportionally increased. Another class of objects to which such a telescope may be applied is Perspective prints, either of public buildings, streets or landscapes. When viewed in this way they present a panoramic appearance, and seem nearly as natural as life—just in the same manner as they appear in the Optical Diagonal Machine, or when reflected in a large 409 concave mirror—with this advantage, that, while in these instruments the left hand side of the print appears where the right should be,—the objects seen through the telescope appear exactly in their natural position. In this case, however, the telescope should have a small magnifying power, not exceeding 5 or 6 times, so as to take in the whole of the landscape. If an astronomical eye-piece be used, the print will require to be inverted.
Other kinds of objects which may be viewed with this instrument, are trees, flowers, and other objects in gardens immediately adjacent to the apartment in which we make our observations. In this way we may obtain a distinct view of a variety of rural objects, which we cannot easily approach, such as the buds and blossoms on the tops of trees, and the insects with which they may be infested. There are certain objects on which the telescope may be made to produce a powerful microscopical effect, such as the more delicate and beautiful kinds of flowers, the leaves of trees, and similar objects. In viewing such objects, the telescope may be brought within little more than double the focal distance of the object-glass from the objects to be viewed, and then the magnifying power is very considerably increased. A nosegay composed of a variety of delicate flowers, and even a single flower, such as the sea-pink, makes a splendid appearance in this way. A peacock’s feather, or even the fibres on a common quill, appear very beautiful, when placed in a proper light. The leaves of trees, particularly the leaf of the plane-tree, when placed against a window-pane, so that the light may shine through them—appear, in all their internal ramifications, more distinct, beautiful and interesting, than when 410 viewed in any other way; and in such views a large portion of the object is at once exhibited to the eye. In this case, the eye-piece of such a telescope as that alluded to requires to be drawn out 12 or 14 inches beyond the point of distinct vision for objects at a distance—and the distance between these near objects and the object-end of the telescope, is only about 3½ feet.
A telescope having a diagonal eye-piece presents a very pleasant view of near objects in this manner. With an instrument of this kind, I have frequently viewed the larger kind of small objects alluded to above, such as the leaves of shrubs and trees, flowers consisting of a variety of parts, the fibres of a peacock’s feather and similar objects. In this case the object-glass of the instrument, which is 10½ inches focal length, was brought within 22 inches of the object, and the eye looked down upon it, in the same manner, as when we view objects in a compound microscope. A common pocket achromatic telescope may be used for the purposes now stated, provided the tube in the eye-piece containing the two lenses next the object, be taken out, in which case the two glasses next the eye form an astronomical eye-piece, and the tubes may be drawn out 5 or 6 inches beyond the focal point for distant objects, and will produce distinct vision for objects not farther distant than about 20 or 24 inches. But, in this case, the objects to be viewed must be inverted, in order that they may be seen in their natural positions when viewed through the instrument. Telescopes of a large size and high magnifying powers may likewise be used with advantage for viewing very near objects in gardens adjacent to the room in which the instruments are placed, provided the sliding-tube next the eye 411 has a range of two or three inches beyond the point of vision for distant objects. In this case, a magnifying power of 100 times on a 3½ or a 5 feet achromatic produces a very pleasant effect. In making the observations to which I have now alluded, it is requisite in order to distinct vision, and to obtain a pleasing view of the objects, that the instrument should be placed on a pedestal, and capable of a motion in every direction. The adjustment for distinct vision may be made either by the sliding-tube, or by removing the telescope nearer to or farther from the object.
Light is one of the most wonderful and beneficial, and at the same time one of the most mysterious agents in the material creation. Though the sun from which it flows to this part of our system is nearly a hundred millions of miles from our globe, yet we perceive it as evidently, and feel its influence as powerfully, as if it emanated from no higher a region than the clouds. It supplies life and comfort to our physical system, and without its influence and operations on the various objects around us, we could scarcely subsist and participate of enjoyment for a single hour. It is diffused around us on every hand from its fountain the sun; and even the stars, though at a distance hundreds of thousands of times greater than that of the solar orb, transmit to our distant region a portion of this element. It gives beauty and fertility to the earth, it supports the vegetable and animal tribes, and is connected with the various motions which are going forward 412 throughout the system of the universe. It unfolds to us the whole scenery of external nature—the lofty mountains and the expansive plains, the majestic rivers and the mighty ocean; the trees, the flowers, the crystal streams, and the vast canopy of the sky adorned with ten thousands of shining orbs. In short there is scarcely an object within the range of our contemplation, but what is exhibited to our understanding through the medium of light, or at least bears a certain relation to this enlivening and universal agent. When we consider the extreme minuteness of the rays of light, their inconceivable velocity, the invariable laws by which they act upon all bodies, the multifarious phenomena produced by their inflections, refractions and reflections, while their original properties remain the same; the endless variety of colours they produce on every part of our terrestrial creation, and the facility with which millions of rays pass through the smallest apertures, and pervade substances of great density, while every ray passes forward in the crowd without disturbing another, and produces its own specific impression—we cannot but regard this element as the most wonderful, astonishing and delightful part of the material creation. When we consider the admirable beauties and the exquisite pleasures of which light is the essential source, and how much its nature is still involved in mystery, notwithstanding the profound investigations of modern philosophers, we may well exclaim with the Poet:—
413
The eye is the instrument by which we perceive the beautiful and multifarious effects of this universal agent. Its delicate and complicated structure, its diversified muscles, its coats and membranes, its different humours possessed of different refractive powers, and the various contrivances for performing and regulating its external and internal motions, so as to accomplish the ends intended—clearly demonstrate this organ to be a master-piece of Divine mechanism—the workmanship of Him whose intelligence surpasses conception, and whose Wisdom is unsearchable. ‘Our sight (says Addison) is the most perfect and delightful of all our senses. It fills the mind with the largest variety of ideas, converses with its objects at the greatest distance, and continues the longest in action, without being tired or satiated with its proper enjoyments. The sense of feeling can indeed give us a notion of extension, shape, and all other ideas that enter the eye, except colours; but at the same time it is very much strained, and confined in its operation to the number, bulk and distance of its particular objects. Our sight seems designed to supply all these defects, and may be considered as a more delicate and diffusive kind of touch that spreads itself over an infinite multitude of bodies, comprehends the largest figures, and brings into our reach some of the more remote parts of the universe.’
Could we suppose an order of beings endued with every human faculty but that of sight, it would appear incredible to such beings—accustomed only to the slow information of touch—that by the addition of an organ consisting of a ball and socket, of an inch diameter, they might be enabled, in an instant of time, without changing their place, to perceive the disposition of a whole 414 army, the order of a battle, the figure of a magnificent palace, or all the variety of a landscape. If a man were by feeling to find out the figure of the Peak of Teneriffe, or even of St. Peter’s church at Rome, it would be the work of a lifetime. It would appear still more incredible to such beings as we have supposed, if they were informed of the discoveries which may be made by this little organ in things far beyond the reach of any other sense—that, by means of it we can find our way in the pathless ocean—that we can traverse the globe of the earth, determine its figure and dimensions, and delineate every region of it—yea, that we can measure the planetary orbs, and make discoveries in the sphere of the fixed stars. And, if they were farther informed that, by means of this same organ, we can perceive the tempers and dispositions, the passions and affections of our fellow-creatures, even when they want most to conceal them—that when the tongue is taught most artfully to lie and dissemble, the hypocrisy should appear in the countenance to a discerning eye—and that by this organ we can often perceive what is straight and what is crooked in the mind as well as in the body—would it not appear still more astonishing to beings such as we have now supposed?33
Notwithstanding these wonderful properties of the organ of vision, the eye, when unassisted by art, is comparatively limited in the range of its powers. It cannot ascertain the existence of certain objects at the distance of three or four miles, nor perceive what is going forward in nature or art beyond such a limit. By its natural powers we perceive the moon to be a globe about half a 415 degree in diameter, and diversified with two or three dusky spots, and that the sun is a luminous body of apparently the same size—that the planets are luminous points, and that about a thousand stars exist in the visible canopy of the sky. But the ten thousandth part of those luminaries, which are within the reach of human vision, can never be seen by the unassisted eye. Here the TELESCOPE interposes, and adds a new power to the organ of vision, by which it is enabled to extend its views to regions of space immeasurably distant, and to objects, the number and magnitude of which could never otherwise have been surmised by the human imagination. By its aid we obtain a sensible demonstration that space is boundless—that the universe is replenished with innumerable suns and worlds—that the remotest regions of immensity, immeasurably beyond the limits of unassisted vision, display the energies of Creating Power, and that the Empire of the Creator extends far beyond what eye hath seen or the human imagination can conceive.
The telescope is an instrument of a much more wonderful nature than what most people are apt to imagine. However popular such instruments now are, and however common a circumstance it is to contemplate objects at a great distance which the naked eye cannot discern, yet, prior to their invention and improvement, it would have appeared a thing most mysterious, if not impossible, that objects at the distance of ten miles could be made to appear as if within a few yards of us, and that some of the heavenly bodies could be seen as distinctly as if we had been transported by some superior power, hundreds of millions of miles beyond the bounds of our terrestrial habitation. Who could ever have imagined—reasoning a 416 priori—that the refraction of light in glass—the same power by which a straight rod appears crooked in water, by which vision is variously distorted, and by which we are liable to innumerable deceptions—that that same power, or law of nature, by the operation of which the objects in a landscape appear distorted when seen through certain panes of glass in our windows, that that power should ever be so modified and directed as to extend the boundaries of vision, and enable us clearly to distinguish scenes and objects at a distance a thousand times beyond the natural limits of our visual organs? Yet such are the discoveries which science has achieved, such the powers it has brought to light, that by glasses ground into different forms, and properly adapted to each other, we are enabled as it were to contract the boundaries of space, to penetrate into the most distant regions, and to bring within the reach of our knowledge the most sublime objects in the universe.
When Pliny declared in reference to Hipparchus, the ancient astronomer, ‘Ausus rem Deo improbam annumerare posteris stellas,’—that ‘he dared to enumerate the stars for posterity, an undertaking forbidden by God,’ what would that natural historian have said, had it been foretold that in less than 1600 years afterwards, a man would arise who should enable posterity to perceive, and to enumerate ten times more new stars than Hipparchus ever beheld—who should point out higher mountains on the moon than on the earth, who should discover dark spots, as large as our globe, in the sun, the fountain of light—who should descry four moons revolving in different periods of time around the planet Jupiter, and could show to surrounding senators the varying phases of Venus? and that another would soon after arise who should 417 point out a double ring of six hundred thousand miles in circumference, revolving around the planet Saturn, and ten hundreds of thousands of stars which neither Hipparchus nor any of the ancient astronomers could ever descry? Yet these are only a small portion of the discoveries made by Galileo and Herschel, by means of the telescope. Had any one prophetically informed Archimedes, the celebrated geometrician of Syracuse, that vision would, in after ages, be thus wonderfully assisted by art—and further, that one manner of improving vision would be to place a dark opake body directly between the object and the eye—and that another method would be, not to look at the object, but to keep the eye quite in a different, and even in an opposite direction, or to stand with the back directly opposed to it, and to behold all the parts of it, invisible to the naked eye, most distinctly in this way—he would, doubtless have considered the prophet as an enthusiastic fool or a raving madman. Yet these things have been realized in modern times in the fullest extent. In the Gregorian reflecting telescope an opake body, namely the small speculum near the end of the tube, interposes directly between the eye and the object. In the Newtonian Reflector, and in the diagonal eye-pieces formerly described, the eye is directed in a line at right angles to the object, or a deviation of 90 degrees from the direct line of vision. In Herschel’s’ large telescopes, and in the Aerial Reflector formerly described (in pp. 311-325) the back is turned to the object, and the eye in an opposite direction.
These circumstances should teach us humility and a becoming diffidence in our own powers; and they should admonish us not to be too dogmatical or peremptory in affirming what is possible 418 or impossible in regard either to nature or art, or to the operations of the Divine Being. Art has accomplished, in modern times, achievements, in regard to locomotion, marine and aërial navigation, the improvement of vision, the separation and combinations of invisible gases, and numerous other objects, of which the men of former ages could not have formed the least conception. And even yet, we can set no boundaries to the future discoveries of science and the improvements of art; but have every reason to indulge the hope that, in the ages to come, scenes of Divine mechanism in the system of nature will be unfolded, and the effects of chemical and mechanical powers displayed, of which the human mind, in its present state of progress, cannot form the most imperfect idea. Such circumstances likewise should teach us not to reject any intimations which have been made to us in relation to the character, attributes, and dispensations of the Divine Being, and the moral revelations of his will given in the Sacred Records, because we are unable to comprehend every truth and to remove every difficulty, which relates to the moral government of the Great Ruler of the universe. For, if we meet with many circumstances in secular science, and even in the common operations of nature, which are difficult to comprehend—if even the construction of such telescopes as we now use, would have appeared an incomprehensible mystery to ancient philosophers—we must expect to find difficulties almost insurmountable to such limited minds as ours, in the eternal plans and moral arrangements of the “King Immortal and Invisible,” as delineated only in their outlines, in the Sacred Oracles—particularly those which relate to the origin of physical and moral evil, the 419 ultimate destiny of man, and the invisible realities of a future world.
The UTILITY of the telescope may be considered in relation to the following circumstances.
In the first place, it may be considered as an instrument or machine which virtually transports us to the distant regions of space. When we look at the moon through a telescope which magnifies 200 times, and survey its extensive plains, its lofty peaks, its circular ranges of mountains, throwing their deep shadows over the vales, its deep and rugged caverns, and all the other varieties which appear on the Lunar surface, we behold such objects in the same manner as if we were standing at a point 238,800 miles from the earth in the direction of the moon, or only twelve hundred miles from that orb, reckoning its distance to be 240,000 miles. When we view the planet Saturn with a similar instrument, and obtain a view of its belts, and satellites, and its magnificent rings, we are transported, as it were, through regions of space, to a point in the heavens more than nine hundred millions of miles from the surface of our globe, and contemplate those august objects, as if we were placed within five millions of miles of the surface of that planet.34 Although a supernatural power, sufficient to carry us in such a celestial journey, a thousand miles every day, were exerted—it would require more than two thousand four hundred and sixty years, before we could arrive at 420 such a distant position; yet the telescope, in a few moments, transports our visual powers to that far distant point of space. When we view, with such an instrument, the minute and very distant clusters of stars in the Milky Way, we are carried in effect through the regions of space to the distance of five hundred thousand millions of miles from the earth; for we behold those luminaries through the telescope nearly as if they were actually viewed from such a distant point in the spaces of the firmament. These stars cannot be conceived as less than a hundred billions of miles from our globe, and the instrument we have supposed brings them within the two hundredth part of this distance. Suppose we were carried forward by a rapid motion towards this point, at the rate of a thousand miles every hour, it would require more than fifty-seven thousand years, before we could reach that very distant station in space to which the telescope, in effect, transports us. So that this instrument is far more efficient in opening to our view the scenes of the universe than if we were invested with powers of locomotion to carry us through the regions of space, with the rapidity of a cannon ball at its utmost velocity; and all the while we may sit at ease in our terrestrial apartments.
In the next place, the telescope has been the means of enlarging our views of the sublime scenes of creation, more than any other instrument which art has contrived. Before the invention of this instrument the universe was generally conceived as circumscribed within very narrow limits. The earth was considered as among the largest bodies in creation; the planets were viewed as bodies of a far less size than what they are now found to be; no bodies similar to our 421 moon were suspected as revolving around any of them; and the stars were supposed to be little more than a number of brilliant lamps hung up to emit a few glimmering rays, and to adorn the canopy of our earthly habitation. Such a wonderful phenomenon as the Ring of Saturn was never once suspected, and the sun was considered as only a large ball of fire. It was suspected, indeed, that the moon was diversified with mountains and vales, and that it might possibly be a habitable world; but nothing certainly could be determined on this point, on account of the limited nature of unassisted vision. But the telescope has been the means of expanding our views of the august scenes of creation to an almost unlimited extent. It has withdrawn the veil which formerly interposed to intercept our view of the distant glories of the sky. It has brought to light five new planetary bodies, unknown to former astronomers, one of which is more than eighty times larger than the earth—and seventeen secondary planets which revolve around the primary. It has expanded the dimensions of the solar system to double the extent which was formerly supposed. It has enabled us to descry hundreds of comets which would otherwise have escaped our unassisted vision, and to determine some of their trajectories and periods of revolution.
It has explored the profundities of the Milky Way, and enabled us to perceive hundreds of thousands of those splendid orbs, where scarcely one is visible to the naked eye. It has laid open to our view thousands of Nebulæ, of various descriptions, dispersed through different regions of the firmament—many of them containing thousands of separate stars. It has directed our investigations to thousands of double, treble and multiple 422 stars—suns revolving around suns, and systems around systems, and has enabled us to determine some of the periods of their revolutions. It has demonstrated the immense distances of the starry orbs from our globe, and their consequent magnitudes; since it shows us that, having brought them nearer to our view by several hundreds or thousands of times, they still appear only as so many shining points. It has enabled us to perceive that mighty changes are going forward throughout the regions of immensity—new stars appearing, and others removed from our view, and motions of incomprehensible velocity carrying forward those magnificent orbs through the spaces of the firmament. In short, it has opened a vista to regions of space so immeasurably distant, that a cannon ball impelled with its greatest velocity, would not reach tracts of creation so remote in two thousand millions of years, and even light itself, the swiftest body in nature, would require more than a thousand years before it could traverse this mighty interval. It has thus laid a foundation for our acquiring an approximate idea of the infinity of space, and for obtaining a glimpse of the far distant scenes of creation, and the immense extent of the universe.
Again, the telescope, in consequence of the discoveries it has enabled us to make, has tended to amplify our conceptions of the attributes and the Empire of the Deity. The amplitude of our conceptions of the Divine Being bears a certain proportion to the expansion of our views in regard to his works of creation, and the operations he is incessantly carrying forward throughout the universe. If our views of the works of God, and of the manifestations he has given of himself to his intelligent creatures, be circumscribed to a 423 narrow sphere, as to a parish, a province, a kingdom, or a single world, our conceptions of that Great Being, will be proportionably limited. For it is chiefly from the manifestation of God in the material creation that our ideas of his Power, his Wisdom, and his other natural attributes, are derived. But in proportion to the ample range of prospect we are enabled to take of the operations of the Most High, will be our conceptions of his character, attributes, and agency. Now, the telescope—more than any other invention of man—has tended to open to our view the most magnificent and extensive prospects of the works of God. It has led us to ascertain that, within the limits of the solar system, there are bodies which, taken together, comprise a mass of matter nearly two thousand five hundred times greater than that of the earth—that these bodies are all constituted and arranged in such a manner as to fit them for being habitable worlds—and that the sun, the centre of this system, is five hundred times larger than the whole. But, far beyond the limits of this system, it has presented to our view a universe beyond the grasp of finite intelligences, and to which human imagination can assign no boundaries. It has enabled us to descry suns clustering behind suns, rising to view in boundless perspective, in proportion to the extent of its magnifying and illuminating powers—the numbers of which are to be estimated, not merely by thousands, and tens of thousands, and hundreds of thousands, but by scores of millions—leaving us no room to doubt that hundreds of millions more, beyond the utmost limits of human vision, even when assisted by art, lie hid from mortal view’s in the unexplored and unexplorable regions of immensity. 424
Here, then, we are presented with a scene which gives us a display of Omnipotent Power which no other objects can unfold, and which, without the aid of the telescope, we should never have beheld—a scene which expands our conceptions of the Divine Being, to an extent which the men of former generations could never have anticipated—a scene which enables us to form an approximate idea of Him who is the “King Eternal, Immortal, and Invisible,” who “created all worlds, and for whose pleasure they are, and were created.” Here we behold the operations of a Being whose power is illimitable and uncontrollable, and which far transcends the comprehension of the highest created intelligences—a power, displayed not only in the vast extension of material existence, and the countless number of mighty globes which the universe contains—but in the astonishingly rapid motions with which myriads of them are carried along through the immeasurable spaces of creation,—some of those magnificent orbs moving with a velocity of one hundred and seventy thousand miles an hour. Here, likewise, we have a display of the infinite Wisdom and Intelligence of the Divine Mind, in the harmony and order with which all the mighty movements of the universe are conducted—in proportionating the magnitudes, motions and distances of the planetary worlds—in the nice adjustment of the projectile velocity to the attractive power—in the constant proportion between the times of the periodical revolution of the planets and the cubes of their mean distances—in the distances of the several planets from the central body of the system, compared with their respective densities—and in the constancy and regularity of their motions, and the exactness with which they accomplish their destined rounds—all 425 which circumstances evidently show that He who contrived the universe is “the only Wise God,” who is “wonderful in counsel and excellent in working.” Here, in fine, is a display of boundless benevolence. For we cannot suppose, for a moment, that so many myriads of magnificent globes, fitted to be the centres of a countless number of mighty worlds, should be nothing else than barren wastes, without the least relation to intelligent existence. And if they are peopled with intellectual beings of various orders—how vast must be their numbers, and how overflowing that Divine Beneficence which has provided for them all, every thing requisite to their existence and happiness!
In these discoveries of the telescope, we obtain a glimpse of the grandeur and the unlimited extent of God’s universal empire. To this empire no boundaries can be perceived. The larger, and the more powerful our telescopes are, the further are we enabled to penetrate into those distant and unknown regions; and however far we penetrate into the abyss of space, new objects of wonder and magnificence still continue rising to our view—affording the strongest presumption, that were we to penetrate ten thousand times farther into those remote spaces of immensity, new suns, and systems, and worlds would be disclosed to our view. Over all this vast assemblage of material existence, and over all the sensitive and intellectual beings it contains, God eternally and unchangably presides; and the minutest movements, either of the physical or the intelligent system, throughout every department of those vast dominions, are at every moment “naked and open” to his Omniscient eye. What boundless Intelligence is implied in the Superintendence and 426 arrangement of the affairs of such an unlimited empire! and what a lofty and expansive idea does it convey of Him who sits on the throne of Universal Nature, and whose greatness is unsearchable! But without the aids of the telescopic tube, we could not have formed such ample conceptions of the greatness, either of the Eternal Creator himself, or of the universe which he hath brought into existence.
Besides the above, the following uses of the telescope, in relation to science and common life, may be shortly noticed:—
In the business of astronomy, scarcely any thing can be done with accuracy without the assistance of the telescope. 1. It enables the astronomer to determine with precision the transits of the planets and stars, across the meridian; and on the accuracy with which these transits are obtained, a variety of important conclusions and calculations depend. The computation of astronomical and nautical tables for aiding the navigator in his voyages round the globe, and facilitating his calculations of latitude and longitude, is derived from observations made by the telescope, without the use of which instrument, they cannot be made with precision. 2. The apparent diameters of the planets can only be measured by means of this instrument, furnished with a micrometer. By the naked eye no accurate measurements of the diameters of these bodies can be taken; and without knowing their apparent diameters, in minutes or seconds, their real bulk cannot be determined, even although their exact distances be known. The differences, too, between their polar and equatorial diameters cannot be ascertained without observations made by powerful telescopes. For example, the equatorial diameter of Jupiter is found to be in proportion to the polar as 14 427 to 13, that is, the equatorial is more than 6000 miles longer than the polar diameter, which could never have been determined by observations made by the naked eye. 3. The parallaxes of the heavenly bodies can only be accurately ascertained by the telescope; and it is only from the knowledge of their parallaxes, that their distances from the earth or from the sun can be determined. In the case of the fixed stars, nothing of the nature of a parallax could ever be expected to be found without the aid of a telescope. It was by searching for the parallax of a certain fixed star, that the important fact of the Aberration of light was discovered. The observations, for this purpose, were made by means of a telescope 24 feet long, fixed in a certain position. 4. The motions and revolutionary periods of Sidereal systems, can only be determined by observations made by telescopes of great magnifying and illuminating powers. Without a telescope the small stars which accompany double or treble stars cannot be perceived, and much less their motions or variation of their relative positions. Before the invention of the telescope such phenomena—now deemed so wonderful and interesting—could never have been surmised. 5. The accurate determination of the longitude of places on the earth’s surface is ascertained by the telescope, by observing with this instrument the immersions and emersions of the satellites of Jupiter. From such observations, with the aid of a chronometer, and having the time at any known place, the situation of any unknown place is easily determined. But the eclipses of Jupiter’s moons can be perceived only by telescopic instruments of considerable power. 6. By means of a telescope, with cross hairs in the focus of the eye-glass, and attached to a Quadrant, the altitude of the sun or of a star, particularly 428 the pole-star, may be most accurately taken; and, from such observations, the latitude of the place may be readily and accurately deduced.
Again, in the Surveying of land, the telescope is particularly useful; and for this purpose it is mounted on a stand with a horizontal and vertical motion, pointing out by divisions the degrees and minutes of inclination of the instrument. For the more accurate reading of these divisions, the two limbs are furnished with a Nonius, or Vernier’s scale. The object here is to take the angular distances between distant objects on a plane truly horizontal; or else the angular elevation or depression of objects above or below the plane of the horizon. In order to obtain either of those kinds of angles to a requisite degree of exactness, it is necessary that the surveyor should have as clear and distinct a view as possible of the objects, or station-staves, which he fixes up for his purpose, that he may with the greater certainty determine the point of the object which exactly corresponds with the line he is taking. Now, as such objects are generally at too great a distance for the surveyor to be able to distinguish with the naked eye, he takes the assistance of the telescope, by which he obtains, 1. A distinct view of the object to which his attention is directed, and 2. he is enabled to determine the precise point of the object aimed at, by means of the cross hairs in the focus of the eye-glass. A telescope mounted for this purpose is called a Theodolite, which is derived from two Greek words θεομαι to see, and οδος, the way or distance.
In the next place, the telescope is an instrument of special importance, in the conducting of Telegraphs, and in the conveyance of signals of all descriptions. Without its assistance telegraphic 429 dispatches could not be conveyed with accuracy to any considerable distance, nor in quadruple the time in which they are now communicated, and the different stations would need to be exceedingly numerous. But by the assistance of the telescope information may be communicated, by a series of telegraphs, with great rapidity. Twenty-seven telegraphs convey information from Paris to Calais—a distance of 160 miles—in 3 minutes; twenty-two from Paris to Lisle in 2 minutes; forty-six from Strasburg to Paris in 4½ minutes; and eighty from Paris to Brest in 10 minutes. In many other cases which occur both on land and on sea, the telescope is essentially requisite for descrying signals. The Bell-Rock Light House, for example, is situated 12 miles from Arbroath, and from every other portion of land, so that the naked eye could not discern any signal which the keepers of that light could have it in their power to make; but by means of a large telescope in the station-house in Arbroath, the hoisting of a ball every morning at 9 A.M.—which indicates that ‘All is well’—may be distinctly recognised.
Many other uses of this instrument, in the ordinary transactions of life, will readily occur to the reader; and therefore I shall only mention the following purpose to which it may be applied, namely,—
To measure the distance of an object from one station. This depends upon the increase of the focal distance of the telescope in the case of near objects. Look through a telescope at the object whose distance is required, and adjust the focus till it appear quite distinct; then slide in the drawer, till the object begins to be obscure, and mark that place of the tube precisely. Next 430 draw out the tube till the object begins to be again obscured, and then make another mark as before. Then take the middle point between these two marks, and that will be the point where the image of the object is formed most distinctly; which is to be nicely measured from the object lens, and compared with the solar focus of the lens or telescope, so as to ascertain their difference. And the rule for finding the distance is,—‘As the difference between the focal distance of the object, and the solar focal distance : Is to the solar focal distance :: So is the focal distance of the object : To its true distance from the object lens.’ An example will render this matter more perspicuous.
figure 84.
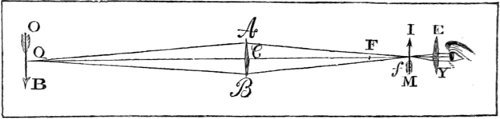
Let AB (fig. 84.) be the object lens, EY the eye-glass, FC the radius, or focus of the lens AB, and Cf the focal distance of the object OB, whose distance is to be measured. Now suppose CF = 48 inches, or 4 feet, and that we find by the above method that Cf is 50 inches, then Ff is 2 inches; and the analogy is:—As Ff = 2, is to CF = 48, so is Cf = 50, to CQ = 1200 inches, or 100 feet. Again, suppose Cf = 49 inches, then will Ff = 1 inch; and the proportion is, 1 : 48 :: 49 : 2352 = QC, or 196 feet. A telescope of this focal length, however, will measure only small distances. But, suppose AB a lens 431 whose solar focus is 12 feet, or 144 inches; and that we find, by the above method, that Cf, or the focal distance of the object, is 146 inches; then will Ff be 2 inches, and the proportion will be, as 2 : 144 :: 146 : 21024 inches, or 1752 feet = the distance QC. If with such a large telescope, we view an object OB, and find Ff but 1/10th of an inch, this will give the distance of the object as 17292 feet or nearly 3⅓ miles.
Since the difference between the radius of the object lens and the focal distance of the object is so considerable as 2 inches in a tube of 4 feet, and more than 12 inches in one of 12 feet, a method might be contrived for determining the distance of near objects by the former, and more distant objects by the latter, by inspection only. This may be done by adjusting or drawing a spiral line round the drawer or tube, through the two inch space in the small telescope, and by calculation, graduate it for every 100 feet, and the intermediate inches, and then, at the same time we view an object, we may see its distance on the tube. In making such experiments, a common object-glass of a long focal length, and a single eye-glass, are all that is requisite; since the inverted appearance of the object can cause no great inconveniency. 432
I originally intended to enter into particular details on this subject, for the purpose of gratifying those mechanics and others who wish to amuse themselves by constructing telescopes and other optical instruments for their own use; but, having dwelt so long on the subject of telescopes, in the preceding pages, I am constrained to confine myself to a very general sketch.
1. To grind and polish lenses for eye-glasses, microscopes, &c.
First provide an upright spindle, at the bottom of which a pulley is fixed, which must be turned by a wheel by means of a cord and handle. At the top of the spindle make a screw the same as a lathe-spindle, on which you may screw chocks of different sizes, to which the brass tool in which the lens is to be ground, may be fixed. Having fixed upon the breadth and focal length of the lens, and whether it is to be a plano, or a double convex—take a piece of tin-plate or sheet copper, and, with a pair of compasses, draw an arch upon its surface, near one of its extremities, with a radius equal to the focal distance of the lens, if 433 intended to be double convex, or with half that distance, if it is to be plano-convex. Remove with a file that part of the copper which is without the circular arch, and then a convex gage is formed. With the same radius strike another arch, and having removed that part of the copper which is within it, a concave gage will be obtained. The brass tool, in which the glass is to be ground, is then to be fixed upon a turning-lathe, and turned into a portion of a concave sphere, so as to correspond to the convex gage. In order to obtain an accurate figure to the concave tool, a convex tool of exactly the same radius is generally formed, and they are ground one upon another with flour emery; and when they exactly coincide, they are fit for use. The convex tool will serve for grinding concave glasses of the same radius—and it should be occasionally ground in the concave tool to prevent it from altering its figure.
The next thing to be attended to is, to prepare the piece of glass which is to be ground, by chipping it in a circular shape, by means of a large pair of scissors, and removing the roughness from its edges by a common grind-stone. The faces of the glass near the edges should likewise be ground on the grind-stone, till they nearly fit the concave gage, by which the labour of grinding in the tool will be considerably saved. The next thing required is to prepare the emery for grinding, which is done in the following manner. Provide four or five clean earthen vessels; fill one of them with water, and put into it a pound or half a pound of fine emery, and stir it about with a stick; after which let it stand 3 or 4 seconds, and then pour it into another vessel, which may stand about 10 seconds; then pour it off again into the several 434 vessels till the water is quite clear; and by this means, emery of different degrees of fineness is obtained, which must be kept separate from each other, and worked in their proper order, beginning at the first, and working off all the marks of the grind-stone; then take of the second, next of the third, &c.,—holding the glass upon the pan or tool with a light hand, when it comes to be nearly fit for polishing. The glass in this operation should be cemented to a wooden handle, by means of pitch or other strong cement. After the finest emery has been used, the roughness which remains may be taken away, and a slight polish given by grinding the glass with pounded pumice-stone. Before proceeding to the polishing, the glass should be ground as smooth as possible, and all the scratches erased, otherwise the polishing will become a tedious process. The polishing is performed as follows: Tie a piece of linen rag or of fine cloth about the tool, and with fine putty, (calcined tin), or colcothar of vitriol (a very fine powder, sometimes called the red oxide of iron) moistened with water, continue the grinding motion, and in a short time there will be an excellent polish.
In order to grind lenses very accurately for the finest optical purposes, particularly object-glasses for telescopes—the concave tool is firmly fixed to a table or bench, and the glass wrought upon it by the hand with circular strokes so that its centre may never go beyond the edges of the tool. For every 6 or 7 circular strokes, the glass should receive 2 or 3 cross ones along the diameter of the tool, and in different directions; and while the operation is going on, the convex tool should, at the end of five minutes, be wrought upon the concave one for a few seconds, in order to preserve 435 the same curvature to the tools and to the glass. The finest polish is generally given in the following way. Cover the concave tool with a layer of pitch hardened by the addition of a little rosin, to the thickness of 1/15th of an inch. Then, having taken a piece of thin writing paper, press it upon the surface of the pitch with the convex tool, and pull the paper quickly from the pitch before it has adhered to it; and if the surface of the pitch is marked every where with the lines of the paper, it will be truly spherical. If any paper remains on the surface of the pitch, it may be rubbed off by soap and water, and if the marks of the paper should not appear on any part of it, the operation must be repeated, till the polisher or bed of pitch is accurately spherical. The glass is then to be wrought on the polisher by circular and cross strokes with the putty or colcothar, till it has received a complete polish. When one side is finished, the glass must be separated from its handle, by inserting the point of a knife between it and the pitch, and giving it a gentle stroke. The pitch which remains upon the glass may be removed by rubbing it with a little oil or spirits of wine. The operation of polishing on cloth is slower, and the polish less perfect than on pitch; but it is a mode best fitted for those who have little experience, and who would be apt, in the first instance, to injure the figure of the lens by polishing it on a bed of pitch.
2. On the method of casting and grinding the Specula of Reflecting Telescopes.
The first thing to be considered in the formation of reflecting telescopes, is the composition of the metal of which the specula are made. The qualities required are—a sound uniform metal, free from all microscopic pores—not liable to tarnish 436 by absorption of moisture from the atmosphere—not so hard as to be incapable of taking a good figure and polish—nor so soft as to be easily scratched, and possessing a high reflecting power. Various compositions have been used for this purpose, of which the following are specimens:—Take good Swedish copper 32 ounces, and when melted, add 14½ ounces of grain tin to it; then, having taken off the scoria, cast it into an ingot. This metal must be a second time melted to cast a speculum; but it will fuse in this compound state with a small heat, and therefore will not calcine the tin to putty. It should be poured off as soon as it is melted, giving it no more heat than is absolutely necessary. The best method for giving the melted metal a good surface is this: the moment before it is poured off, throw into the crucible a spoonful of charcoal-dust; immediately after which the metal must be stirred with a wooden spatula and poured into the moulds.—The following is another composition somewhat similar. Take 2 parts copper as pure as it is possible to procure; this must be melted in a crucible by itself. Then put, in another crucible, 1 part of pure grain tin. When they are both melted, mix and stir them with a wooden spatula, keeping a good flux on the melted surface to prevent oxidation, and then pour the metal quickly into the moulds, which may be made of founder’s loam.
The composition suggested, more than half a century ago, by the Rev. Mr. Edwards, has often been referred to with peculiar approbation. This gentleman took a great deal of pains to discover the best composition, and to give his metals a fine polish and the true parabolical figure. His telescopes were tried by Dr. Maskelyne, the Astronomer Royal, who found them greatly to excel in 437 brightness, and to equal in other respects those made by the best artists. They showed a white object perfectly white, and all objects of their proper colour. He found, after trying various combinations, the following to be the best: namely 32 ounces of copper, with 15 or 16 ounces of grain tin, (according to the purity of the copper) with the addition of one ounce of brass, one of silver, and one ounce of arsenic. This, he affirms, will form a metal capable, when polished in a proper manner, of reflecting more light than any other metal yet made public.
The Rev. J. Little, in his observations on this subject in the ‘Irish Transactions,’ proposes the following composition, which he found to answer the purpose better than any he had tried, namely—32 parts of best bar copper, previously fluxed with the black flux, of two parts tartar and one of nitre, 4 parts brass, 16 parts tin, and 1¼ arsenic. If the metal be granulated, by pouring it, when first melted, into water, and then fused a second time, it will be less porous than at first. In this process, the chief object is, to hit on the exact point of the saturation of the copper, &c., by the tin. For, if the latter be added in too great quantity, the metal will be dull coloured and soft; if too little, it will not attain the most perfect whiteness, and will certainly tarnish.35
When the metal is cast, and prepared by the common grind-stone for receiving its proper figure—the gages and grinding-tools are to be formed in the same manner as formerly described for lenses, with this difference, that the radius of the gages must always be double the focal length of the speculum, as the focus of parallel rays by 438 reflection is at one half the radius of concavity. In addition to the concave and convex tools—which should be only a little broader than the metal itself—a convex elliptical tool of lead and tin should be formed with the same radius, so that its transverse should be to its conjugate diameter as 10 to 9, the latter being exactly equal to the diameter of the metal. The grinding of the speculum is then to be commenced, on this tool, with coarse emery powder and water, when the roughness is taken off, by moving the speculum across the tool, in different directions, walking round the post on which the tool is fixed, holding the speculum by the wooden handle to which it is cemented. It is then to be wrought with great care on the convex brass tool, with circular and cross strokes, and with emery of different degrees—the concave tool being sometimes ground upon the convex one, to keep them all of the same radius, and when every scratch is removed from its surface, it will be fit for receiving the final polish.
When the metal is ready for polishing, the elliptical tool is to be covered with black pitch about 1/20th of an inch thick, and the polisher formed in the same way as in the case of lenses, either with the concave brass tool or with the metal itself. The colcothar of vitriol should then be triturated between two surfaces of glass, and a considerable quantity of it applied at first to the surface of the polisher. The speculum is then to be wrought, in the usual way, upon the polishing tool, till it has received a brilliant lustre, taking care to use no more of the colcothar, if it can be avoided, and only a small quantity of it, if it should be found necessary. When the metal moves stiffly on the polisher, and the colcothar 439 assumes a dark muddy hue, the polish advances with great rapidity. The tool will then grow warm, and would probably stick to the speculum, if its motion were discontinued for a moment. At this stage of the process, therefore, we must proceed with great caution, breathing continually on the polisher, till the friction is so great, as to retard the motion of the speculum. When this happens, the metal is to be slipped off the tool at one side, cleaned with soft leather, and placed in a tube for the purpose of trying its performance; and if the polishing has been conducted with care, it will be found to have a true parabolic figure.36
It was formerly the practice, before the speculum was brought to the polisher, to smooth it on a bed of hones, or a convex tool made of the best blue stone, such as clockmakers use in polishing their work, which was made one fourth part larger than the metal which was to be ground upon it, and turned as true as possible to a gage. But this tool is not generally considered as absolutely necessary, except when silver and brass enter into the composition of the metal, in order to remove the roughness which remains after grinding with the emery.
To try the figure of the metal.—In order to this, the speculum must be placed in the tube of the telescope for which it is intended; and, at about 20 or 30 yards distant, there should be put up a watch-paper, or similar object, on which there are some very fine strokes of an engraver. An annular kind of diagram should be made with card-paper, so as to cover a circular portion of the middle part of the speculum, between the hole and the circumference, equal in breadth to about 440 1/8 of its diameter. This paper ring should be fixed in the mouth of the telescope, and remain so during the whole experiment. There must likewise be two other circular pieces of card-paper cut out, of such sizes, that one may cover the centre of the metal, by completely filling the hole in the annular piece now described: and the other such a round piece as shall exactly fill the tube, and so broad as that the inner edge just touches the outward circumference of the middle annular piece. All these pieces together will completely shut up the mouth of the telescope. Let the round piece which covers the centre of the metal be removed, and adjust the instrument so that the image may be as sharp and distinct as possible. Then replace the central piece, and remove the outside annular one, by which means the circumference only of the speculum will be exposed; and the image now formed will be from the rays reflected from the exterior side of the metal. If the two images formed by these two portions of the metal be perfectly sharp and equally distinct, the speculum is perfect and of the true parabolic curve. If, on the contrary, the image from the outside of the metal should not be distinct and that it should be necessary to bring the little speculum nearer by the screw, the metal is not yet brought to the parabolic figure; but if, in order to procure distinctness, we be obliged to move the small speculum farther off, then the figure of the great speculum has been carried beyond the parabolic, and has assumed the hyperbolic form.
To adjust the eye-hole of Gregorian Reflectors.—If there is only one eye-glass, then the distance of the small hole should be as nearly as possible equal to its focal length. But in the compound 441 Huygenian eye-piece, the distance of the eye-hole may be thus found:—Multiply the difference between the focal distance of the glass next to the speculum, and the distance of the two eye-glasses, by the focal distance of the glass nearest the eye; divide the product by the sum of the focal distances of the two lenses, lessened by their distance, and the quotient will be the compound focal distance required. Thus, if the focal distance of the lens next the speculum be 3 inches, that of the lens next the eye 1 inch, and their distance 2 inches, then the compound focal distance from the eye-glass will be (3 - 2 × 1)/(3 × 1 - 2) = ½ inch.—The diameter of the eye-hole is always equal to the quotient obtained by dividing the diameter of the great speculum by the magnifying power of the telescope. It is generally from 1/25th to 1/50th of an inch in diameter. It is necessary, in many cases, to obtain, from direct experiment, an accurate determination of the place and size of the eye-hole, as on this circumstance depends, in a certain degree, the accurate performance of the instrument.
To center the two specula of Gregorian Reflectors.—Extend two fine threads or wires across the aperture of the tube at right angles, so as to intersect each other, exactly in the axis of the telescope. Before the arm is finally fastened to the slider, place it in the tube, and through the eye-piece (without glasses) the intersection of the cross wires must be seen exactly in the centre of the hole of the arm. When this exactness is obtained, let the arm be firmly riveted and soldered to the slider.
To centre lenses.—The centering of lenses is of great importance, more especially for the object-glasses 442 of achromatic instruments. The following is reckoned a good method:—Let the lens to be centered be cemented on a brass chuck, having the middle turned away so as not to touch the lens, but near the edge, which will be hid when mounted. This rim is very accurately turned flat where it is to touch the glass. When the chuck and cement is warm it is made to revolve rapidly: while in motion a lighted candle is brought before it, and its reflected image attentively watched. If this image has any motion, the lens is not flat or central; a piece of soft wood must therefore be applied to it in the manner of a turning tool, till such time as the light becomes stationary. When the whole has cooled, the edges of the lens must be turned by a diamond, or ground with emery.
For more particular details in reference to grinding and polishing specula and lenses, the reader is referred to Smith’s ‘Complete system of Optics’—Imison’s ‘School of Arts’—Huygenii Opera—Brewster’s Appendix to ‘Ferguson’s Lectures’—‘Irish Transactions,’ vol. X., or ‘Nicholson’s Journal,’ vol. XVI., Nos. 65, 66, for January and February, 1807. 443
A micrometer is an instrument attached to a telescope, in order to measure small spaces in the heavens, such as the spaces between two stars, and the diameters of the sun, moon and planets—and by the help of which the apparent magnitude of all objects viewed through telescopes may be measured with great exactness.
There are various descriptions of these instruments, constructed with different substances, and in various forms, of which the following constitute the principal variety. The Wire micrometer—the Spider’s line micrometer—the Polymetric reticle—Divided object glass micrometer—Divided eye-glass micrometer—Ramsden’s Catoptric micrometer—Rochon’s crystal micrometer—Maskelyne’s 444 Prismatic micrometer—Brewster’s micrometrical telescope—Sir W. Herschel’s Lamp micrometer—Cavallo’s Mother of Pearl micrometer, and several others. But, instead of attempting even a general description of these instruments, I shall confine myself merely to a very brief description of Cavallo’s Micrometer, as its construction will be easily understood by the general reader, as it is one of the most simple of these instruments, and is so cheap as to be procured for a few shillings; while some of the instruments now mentioned are so expensive, as to cost nearly as much as a tolerably good telescope.37
This micrometer consists of a thin and narrow slip of mother of pearl finely divided, which is placed in the focus of the eye-glass of a telescope, just where the image of the object is formed; and it may be applied either to a reflecting or a refracting telescope, provided the eye-glass be a convex lens. It is about the 20th part of an inch broad, and of the thickness of common writing paper, divided into equal parts by parallel lines, every fifth and tenth of which is a little longer than the rest. The simplest way of fixing it is to stick it upon the diaphragm which generally stands within the tube, and in the focus of the eye-glass. When thus fixed, if you look through the eye-glass, the divisions of the micrometrical scale will appear very distinct, unless the diaphragm is not exactly in the focus of the eye-glass, in which case it must be moved to the proper place;—or, the micrometer may be placed exactly in the focus of the eye-lens by the interposition of 445 a circular piece of paper, card, or by means of wax. If a person should not like to see always the micrometer in the field of the telescope, then the micrometrical scale, instead of being fixed to the diaphragm, may be fitted to a circular perforated plate of brass, of wood, or even of paper, which may be occasionally placed upon the said diaphragm. One of these micrometers, in my possession, which contains 600 divisions in an inch, is fitted up in a separate eye-tube, with a glass peculiar to itself, which slides into the eye-piece of the telescope, when its own proper glass is taken out.
To ascertain the value of the divisions of this micrometer.—Direct the telescope to the sun, and observe how many divisions of the micrometer measure its diameter exactly. Then take out of the Nautical Almanack the diameter of the sun for the day on which the observation is made. Divide it by the above-mentioned number of divisions, and the quotient is the value of one division of the micrometer. Thus, suppose that 26½ divisions of the micrometer measure the diameter of the sun, and that the Nautical Almanack gives for the measure of the same diameter 31´: 22´´, or 1882´´. Divide 1882 by 26.5, and the quotient is 71´´ or 1´: 11´´, which is the value of one division of the micrometer; the double of which is the value of two divisions, and so on. The value of the divisions may likewise be ascertained by the passage of an equatorial star over a certain number of divisions in a certain time. The stars best situated for this purpose are such as the following—δ in the Whale, R. A. 37°: 3⅓´, Dec. 37´: 50´´ S; δ in Orion, R. A. 80°: 11´: 42´´, Dec. 28´: 40´´ S; υ in the Lion, R. A. 171°: 25´: 21´´, Dec. 23´: 22´´ N.; η in Virgo R. A. 182°: 10´, Dec. 33´: 27´´ 446 N. But the following is the most easy and accurate method of determining the value of the divisions:—
Mark upon a wall or other place the length of six inches, which may be done by making two dots or lines six inches asunder, or by fixing a six inch ruler upon a stand. Then place the telescope before it, so that the ruler or six-inch length may be at right angles with the direction of the telescope, and just 57 feet 3½ inches distant from the object-glass of the telescope; this done, look through the telescope at the ruler, or other extension of six inches, and observe how many divisions of the micrometer are equal to it, and that same number of divisions is equal to half a degree, or 30´; and this is all that is necessary for the required determination. The reason of which is, because an extension of six inches subtends an angle of 30´, at the distance of 57 feet, 3½ inches, as may be easily calculated from the rules of plane Trigonometry.
figure 85.

Fig. 85, exhibits this micrometer scale, but shows it four times larger than the real size of one which was adapted to a 3 feet achromatic telescope magnifying 84 times. The divisions upon it are the 200ths of an inch, which reach from one edge of the scale to about the middle of it, excepting every fifth and tenth division, which are longer. Two divisions of this scale are very nearly equal to one minute; and as a quarter of one of these divisions may be distinguished by estimation, 447 therefore an angle of 1/8 of a minute, or of 7½´´ may be measured with it. When a telescope magnifies more, the divisions of the micrometer must be more minute. When the focus of the eye-glass of the telescope is shorter than half an inch, the micrometer may be divided with the 500ths of an inch; by means of which, and the telescope magnifying about 200 times, one may easily and accurately measure an angle smaller than half a second. On the other hand, when the telescope does not magnify above 30 times, the divisions need not be so minute. In one of Dollond’s pocket telescopes, which, when drawn out for use is only 14 inches long, a micrometer with the hundredths of an inch is quite sufficient, and one of its divisions is equal to little less than 3 minutes, so that an angle of a minute may be measured by it. Supposing 11½ of those divisions equal to 30´ or 23 to a degree—any other angle measured by any other number of divisions, is determined by proportion. Thus, suppose the diameter of the sun, seen through the same telescope, be found equal to 12 divisions, say As 11½ divisions : are to 30 minutes :: so are 12 divisions : to ((12 × 30)/11.5) 31.3, which is the required diameter of the sun.
Practical uses of this Micrometer.—This micrometer may be applied to the following purposes:—1. For measuring the apparent diameters of the sun, moon, and planets. 2. For measuring the apparent distances of the satellites from their primaries. 3. For measuring the cusps of the moon in eclipses. 4. For measuring the apparent distances between two contiguous stars—between a star and a planet—between a star and the moon—or between a comet and the contiguous stars, so as to determine its path. 5. For finding the difference of declination of contiguous stars, when 448 they have nearly the same R. Ascension. 6. For measuring the small elevations or depressions of objects above and below the horizon. 7. For measuring the proportional parts of buildings, and other objects in perspective drawing. 8. For ascertaining whether a ship at sea, or any moving object is coming nearer or going farther off; for if the angle subtended by the object appears to increase, it shows that the object is coming nearer, and if the angle appears to decrease, it indicates that the object is receding from us. 9. For ascertaining the real distances of objects of known extension, and hence to measure heights, depths, and horizontal distances. 10. For measuring the real extensions of objects when their distances are known. 11. For measuring the distance and size of an object when neither of them is known.
When the micrometer is adapted to those telescopes which have four glasses in the eye-tube—and when the eye-tube only is used, it may be applied to the following purposes:—1. For measuring the real or lineal dimensions of small objects, instead of the angles. For if the tube be unscrewed from the rest of the telescope, and applied to small objects, it will serve for a microscope, having a considerable magnifying power, as we have already shown, (p. 348); and the micrometer, in that case, will measure the lineal dimensions of the object, as the diameter of a hair, the length of a flea, or the limbs of an insect. In order to find the value of the divisions for this purpose, we need only apply a ruler, divided into tenths of an inch, to the end of the tube, and, looking through the tube, observe how many divisions of the micrometer measure one tenth of an inch on the ruler, which will give the required value. Thus, if 30 divisions are equal to 1/10th of an inch, 449 300 of them must be equal to 1 inch, and one division is equal to the 300dth part of an inch. 2. For measuring the magnifying power of other telescopes. This is done by measuring the diameter of the pencil of light at the eye-end of the telescope in question. For, if we divide the diameter of the object lens by the diameter of this pencil of light, the quotient will express how many times that telescope magnifies in diameter. Thus, suppose that 300 divisions of the micrometer are equal to the apparent extension of 1 inch—that the pencil of light is measured by 4 of these divisions—and that the diameter of the object lens measures 1 inch and 2 tenths:—Multiply 1.2 by 300, and the product 360, divided by 4, gives 90 for the magnifying power of the telescope.
Problems which may be solved by this micrometer. I. The angle—not exceeding one degree—which is subtended by an extension of 1 foot, being given, to find its distance from the place of observation:—Rule 1. If the angle be expressed in minutes, say, as the given angle : is to 60 :: so is 687.55 : to a fourth proportional, which gives the answer in inches. 2. If the angle be expressed in seconds, say, As the given angle : is to 3600 :: so is 687.55 to a fourth proportional, which expresses the answer in inches. 3. If the angle be expressed in minutes and seconds, turn it all into seconds, and proceed as above. Example, at what distance is a globe of 1 foot in diameter, when it subtends an angle of 2 seconds? 2 : 3600 :: 687.55 : (3600 × 687.55)/2 = 1237596 inches, or 103132½ feet = the answer required. II. The angle which is subtended by any known extension being given, to find its distance from the place of observation. Rule, Proceed as if the extension were of one 450 foot, by Problem I, and call the answer B; then if the extension in question be expressed in inches, say, as 12 inches : are to that extension :: so is B : to a fourth proportional, which is the answer in inches. But if the extension in question be expressed in feet, then we need only multiply it by B, and the product is the answer in inches.—Example, At what distance is a man 6 feet high, when he appears to subtend an angle of 30´´? By Problem I, if the man were 1 foot high, the distance would be 82506 inches; but as he is 6 feet high, therefore multiply 82506 by 6, and the product is the required distance, namely 495036 inches, or 41253 feet.
For greater conveniency, especially in travelling, when one has not the opportunity of making such calculations, the following two tables have been calculated; the first of which shows the distance answering to any angle from one minute to one degree, which is subtended by a man whose height is considered an extension of 6 feet, because at a mean, such is the height of a man when dressed with hat and shoes on. These tables may be transcribed on a card, and may be kept always ready with a pocket telescope furnished with a micrometer. Their use is to ascertain distances without any calculations; and they are calculated only to minutes, because with a pocket telescope and micrometer, it is not possible to measure an angle more accurately than to a minute. Thus, if we want to measure the extension of a street, let a foot ruler be placed at the end of the street; measure the angular appearance of it, which suppose to be 36´, and in the table we have the required distance against 36´, which is 95½ feet. Thus also a man who appears to be 49´ high, is at the distance of 421 feet. Again, Suppose the 451 trunk of a tree which is known to be 3 feet in diameter be observed to subtend an angle of 9´½. Take the number answering to 9´ out of the table, namely 382, and subtract from it a proportional part for the half minute, namely 19.1, which subtracted from 382, leaves 362.9. This multiplied by 3, the diameter of the tree, produces 1087.7 feet = the distance from the object end of the telescope.
| Angles subtended by an extension of one foot at different distances. | Angles subtended by an extension of six feet at different distances. | ||||||
|---|---|---|---|---|---|---|---|
| Angles Minutes. | Distances in feet. | Angles Minutes. | Distances in feet. | Angles Minutes. | Distances in feet. | Angles Minutes. | Distances in feet. |
| 1 | 3438 | 31 | 110.9 | 1 | 20626.8 | 31 | 665.4 |
| 2 | 1719 | 32 | 107.4 | 2 | 10313. | 32 | 644.5 |
| 3 | 1146 | 33 | 104.2 | 3 | 6875.4 | 33 | 625. |
| 4 | 859.4 | 34 | 101.1 | 4 | 5156.5 | 34 | 606.6 |
| 5 | 687.5 | 35 | 98.2 | 5 | 4125.2 | 35 | 589.3 |
| 6 | 572.9 | 36 | 95.5 | 6 | 3437.7 | 36 | 572.9 |
| 7 | 491.1 | 37 | 92.9 | 7 | 2946.6 | 37 | 557.5 |
| 8 | 429.7 | 38 | 90.4 | 8 | 2578.2 | 38 | 542.8 |
| 9 | 382 | 39 | 88.1 | 9 | 2291.8 | 39 | 528.9 |
| 10 | 343.7 | 40 | 85.9 | 10 | 2062.6 | 40 | 515.6 |
| 11 | 312.5 | 41 | 83.8 | 11 | 1875.2 | 41 | 503.1 |
| 12 | 286.5 | 42 | 81.8 | 12 | 1718.8 | 42 | 491.1 |
| 13 | 264.4 | 43 | 79.9 | 13 | 1586.7 | 43 | 479.7 |
| 14 | 245.5 | 44 | 78.1 | 14 | 1473.3 | 44 | 468.8 |
| 15 | 229.2 | 45 | 76.4 | 15 | 1375. | 45 | 458.4 |
| 16 | 214.8 | 46 | 74.7 | 16 | 1298.1 | 46 | 448.4 |
| 17 | 202.2 | 47 | 73.1 | 17 | 1213.3 | 47 | 438.9 |
| 18 | 191 | 48 | 71.6 | 18 | 1145.9 | 48 | 429.7 |
| 19 | 181 | 49 | 70.1 | 19 | 1085.6 | 49 | 421. |
| 20 | 171.8 | 50 | 68.7 | 20 | 1031.4 | 50 | 412.5 |
| 21 | 162.7 | 51 | 67.4 | 21 | 982.2 | 51 | 404.4 |
| 22 | 156.2 | 52 | 66.1 | 22 | 937.6 | 52 | 396.7 |
| 23 | 149.4 | 53 | 64.8 | 23 | 896.8 | 53 | 389.2 |
| 24 | 143.2 | 54 | 63.6 | 24 | 859.4 | 54 | 381.9 |
| 25 | 137.5 | 55 | 62.5 | 25 | 825. | 55 | 375. |
| 26 | 132.2 | 56 | 61.4 | 26 | 793.3 | 56 | 368.3 |
| 27 | 127.3 | 57 | 60.3 | 27 | 763.9 | 57 | 361.9 |
| 28 | 122.7 | 58 | 59.1 | 28 | 736.6 | 58 | 355.6 |
| 29 | 118.5 | 59 | 58.2 | 29 | 711.3 | 59 | 349.6 |
| 30 | 114.6 | 60 | 57.3 | 30 | 687.5 | 60 | 343.7 |
452
In this way the distance of a considerably remote object, as a town or building at 10 or 12 miles distant, may be very nearly determined; provided we have the lineal dimensions of a house or other object that stands at right angles to the line of vision. The breadth of a river, of an arm of the sea, or the distance of a light house, whose elevation above the sea or any other point, is known, may likewise in this manner be easily determined. 453
The equatorial instrument is intended to answer a number of useful purposes in Practical Astronomy, independently of any particular observatory. Besides answering the general purpose of a Quadrant, a Transit instrument, a Theodolite, and an Azimuth instrument—it is almost the only instrument adapted for viewing the stars and planets in the day-time, and for following them in their apparent diurnal motions. It may be made use of in any steady room or place, and performs most of the useful problems in astronomical science.
The basis of all equatorial instruments is a revolving axis, placed parallel to the axis of the earth, by which an attached telescope is made to follow a star or other celestial body in the arc of its diurnal revolution, without the trouble of repeated adjustments for changes of elevation, which quadrants and circles with vertical and horizontal axes require. Such an instrument is not only convenient for many useful and interesting purposes in celestial observations, but is essentially requisite in certain cases, particularly in examining and measuring the relative positions of two contiguous 454 bodies, or in determining the diameters of the planets, when the spider’s-line micrometer is used.
Christopher Scheiner is supposed to have been the first astronomer who, in the year 1620, made use of a polar axis, but without any appendage of graduated circles. It was not, however, till the middle of the last century, that any instruments of this description, worthy of the name, were attempted to be constructed. In 1741, Mr. Henry Hindley, a clock-maker in York, added to the polar axis, an equatorial plate, a quadrant of altitude, and declination semicircle; but when this piece of mechanism was sent to London for sale in 1748, it remained unsold for the space of 13 years. Mr. Short, the optician, published in the Philosophical Transactions, for 1750, a ‘description of an equatorial telescope,’ which was of the reflecting kind, and was mounted over a combination of circles and semicircles, which were strong enough to support a tube, and a speculum of the Gregorian construction 18 inches in focal length. This instrument consisted of a somewhat cumbersome and expensive piece of machinery—a representation of which may be seen in volume III of Martin’s ‘Philosophia Britannica, or system of the Newtonian philosophy.’ Various modifications of this instrument have since been made by Nairne, Dollond, Ramsden, Troughton, and other artists; but even at the present period, it has never come into very general use, though it is one of the most pleasant and useful instruments connected with astronomical observations.
As many of these instruments are somewhat complicated, and very expensive, I shall direct the attention of the reader solely to one which I consider as the most simple—which may be purchased 455 at a moderate expence, and is sufficiently accurate for general observations.
figure 86.

This instrument consists of the following parts: A horizontal circle EF (fig. 86.) divided into four quadrants of 90 degrees each. There is a fixed nonius at N; and the circle is capable of being turned round on an axis. In the centre of the horizontal circle is fixed a strong upright pillar, which supports the centre of a vertical semicircle 456 AB, divided into two quadrants of 90 degrees each. This is called the semicircle of altitude, and may, at any time, serve the purpose of a quadrant in measuring either altitudes or depressions. It has a nonius plate at K. At right angles to the plane of this semicircle, the equatorial circle MN is firmly fixed. It represents the equator, and is divided into twice 12 hours, every hour being divided into 12 parts of 5 minutes each. Upon the equatorial circle moves another circle, with a chamfered edge, carrying a nonius by which the divisions on the equatorial may be read off to single minutes; and at right angles to this moveable circle is fixed the semicircle of declination D, divided into two quadrants of 90 degrees each. The telescope PO, is surmounted above this circle, and is fixed to an index moveable on the semicircle of declination, and carries a nonius opposite to Q. The telescope is furnished with 2 or 3 Huygenian eye-pieces, and likewise with a diagonal eye-piece for viewing objects near the zenith. Lastly, there are 2 spirit levels fixed on the horizontal circle, at right angles to each other, by means of which this circle is made perfectly level when observations are to be made.
To adjust the equatorial for observation. Set the instrument on a firm support. Then to adjust the levels and the horizontal circle:—Turn the horizontal circle till the beginning O of the divisions coincides with the middle stroke of the nonius, or near it. In this situation one of the levels will be found to lie either in a right line joining the 2 foot screws which are nearest the nonius, or else parallel to such a right line. By means of the 2 last screws, cause the bubble in the level to become stationary in the middle of 457 the glass; then turn the horizontal circle half round, by bringing the other O to the nonius; and if the bubble remains in the middle, as before, the level is well-adjusted; if it does not, correct the position of the level, by turning one or both of the screws which pass through its ends, till the bubble has moved half the distance it ought to come to reach the middle, and cause it to move the other half by turning the foot-screws already mentioned. Return the horizontal circle to its first position, and if the adjustments have been well made, the bubble will remain in the middle: if otherwise, the process must be repeated till it bears this proof of its accuracy. Then turn the horizontal circle till 90° stands opposite to the nonius; and by the foot-screw,immediately opposite the other 90°, cause the bubble of the same level to stand in the middle of the glass. Lastly, by its own proper screws set the other level so that its bubble may occupy the middle of its glass.
To adjust the line of sight. Set the nonius on the declination semicircle at O, the nonius on the horary circle at VI, and the nonius on the semicircle of altitude at 90. Look through the telescope towards some part of the horizon, where there is a diversity of remote objects. Level the horizontal circle, and then observe what object appears in the centre of the cross-wires, or in the centre of the field of view, if there be no wires. Reverse the semicircle of altitude, so that the other 90° may apply to the nonius; taking care, at the same time, that the other three noniuses continue at the same parts of their respective graduations as before. If the remote object continues to be seen on the centre of the cross-wires, the line of sight is truly adjusted.
To find the correction to be applied to observations 458 by the semicircle of altitude. Set the nonius on the declination-semicircle to 0, and the nonius on the horary circle to XII; direct the telescope to any fixed and distant object, by moving the horizontal circle and semicircle of altitude, and nothing else; note the degree and minute of altitude or depression; reverse the declination-semicircle, by directing the nonius on the horary circle to the opposite XII; direct the telescope again to the same object, by means of the horizontal circle and semicircle of altitude, as before. If its altitude or depression be the same as was observed in the other position, no correction will be required; but, if otherwise, half the difference of the two angles is the correction to be added to all observations made with that quadrant, or half of the semicircle which shows the least angle, or to be subtracted from all the observations made with the other quadrant, or half of the semicircle. When the levels and other adjustments are once truly made, they will be preserved in order for a length of time, if not deranged by violence; and the correction to be applied to the semicircle of altitude is a constant quantity.
Description of the nonius. The nonius—sometimes called the vernier—is a name given to a device for subdividing the arcs of quadrants and other astronomical instruments. It depends on the simple circumstance, that if any line be divided into equal parts, the length of each part will be greater, the fewer the divisions; and contrariwise, it will be less in proportion as those divisions are more numerous. Thus, in the equatorial now described, the distance between the two extreme strokes on the nonius is exactly equal to 11 degrees on the limb, but that it is divided into 12 equal parts. Each of these last 459 parts will therefore be shorter than the degree on the limb in the proportion of 11 to 12, that is to say, it will be 1/12th part, or 5 minutes shorter. Consequently, if the middle stroke be set precisely opposite to any degree, the relative positions of the nonius and the limb must be altered 5 minutes of a degree, before either of the two adjacent strokes next the middle on the nonius, can be brought to coincide with the nearest stroke of a degree; and so likewise the second stroke on the nonius will require a change of 10 minutes, the third of 15, and so on to 30, when the middle line of the nonius will be seen to be equi-distant between 2 of the strokes on the limb; after which the lines on the opposite side of the nonius will coincide in succession with the strokes on the limb. It is clear from this, that whenever the middle stroke of the nonius does not stand precisely opposite to any degree, the odd minutes—or distance between it and the degree immediately preceding—may be known by the number of the stroke marked on the nonius, which coincides with any of the strokes on the limb.38 In some instruments the nonius-plate has its divisions fewer than the number of parts on the limb to which it is equal; but when once a clear idea of the principle of any nonius is obtained, it will be easy to transfer it to any other mode in which this instrument is contrived.
To find by this equatorial the MERIDIAN LINE, and the time, FROM ONE OBSERVATION OF THE SUN. In order to this it is requisite that the sun’s declination, and the latitude of the place be known. The declination of the sun may be found, for every day, in the Nautical Almanack, or any other astronomical Ephemeris; and the 460 latitude of the place may be found by means of the semicircle of altitude, when the telescope is directed to the sun or a known fixed star. It is likewise requisite to make the observation when the azimuth and altitude of the sun alter quickly; and this is generally the case, the farther that luminary is from the meridian:—Therefore, at the distance of 3 or 4 hours, either before or after noon, (in summer) adjust the horizontal circle; set the semicircle of altitude, so that its nonius may stand at the co-latitude of the place; lay the plane of the last-mentioned semicircle in the meridian, by estimation, its 0 being directed towards the depressed pole; place the nonius of the declination semicircle to the declination, whether north or south. Then direct the telescope towards the sun, partly by moving the declination semicircle on the axis of the equatorial circle, and partly by moving the horizontal circle on its own axis. There is but one position of these which will admit of the sun being seen exactly in the middle of the field of view. When this position is obtained, the nonius on the equatorial circle shows the apparent time, and the circle of altitude is in the plane of the meridian. When this position is ascertained, the meridian may be settled by a land-mark at a distance.
With an equatorial instrument, nearly similar to that now described, I formerly made a series of ‘day observations on the celestial bodies,’ which were originally published in vol. 36 of ‘Nicholson’s Journal of Natural Philosophy,’ and which occupy twenty pages of that journal. Some of these observations I shall lay before the reader, after having explained the manner in which they are made.
The instrument was made by Messrs. W. and 461 S. Jones, opticians, Holborn, London. The telescope which originally accompanied the instrument was an achromatic refractor, its object-glass being 8½ inches focal distance, and one inch diameter. This telescope, not admitting sufficiently high magnifying powers for the observations intended, was afterwards thrown aside for another telescope, having an object-glass 20 inches focal length, and 1¾ inch diameter, which was attached to the equatorial machinery in place of the small telescope. It was furnished with magnifying powers of 15, 30, 45, 60, and 100 times. The instrument was placed on a firm pedestal about three feet high. The feet of this pedestal had short iron pikes, which slipped into corresponding holes in the floor of the apartment adjacent to a south window, so that when the direction of the meridian was found, and the circles properly adjusted, the instrument was in no danger of being shifted from this position. Though this instrument generally stood fronting the southern part of the heavens, yet the equatorial part, along with the telescope, could occasionally be removed to another position fronting the north and north-west, for observing the stars in those quarters.
Manner of observing stars and planets in the day-time by the equatorial. Before such observations can be made, the semicircle of altitude must be placed in the meridian, and the degree and minute pointed out by the nonius on the horizontal circle, when in this position, noted down in a book, so that it may be placed again in the same position, should any derangement afterwards happen. The semicircle of altitude must be set to the co-latitude of the place; that is, to what the latitude wants of 90°. Suppose the latitude 462 of the place of observation be 52° 30´ north, this latitude subtracted from 90°, leaves 37° 30´ for the co-latitude; and therefore, the semicircle of altitude—on which the equatorial circle is fixed—must be elevated to 37° 30´, and then the equatorial circle on the instrument coincides with the equator in the heavens. Lastly, the telescope must be adjusted on the declination semicircle, so as exactly to correspond with the declination of the heavenly body to be viewed. If the body is in the equator, the telescope is set by the index at 0 on the semicircle of declination, or at the middle point between the two quadrants, and then when the telescope, along with the semicircle of declination, is moved from right to left, or the contrary, it describes an arc of the equator. If the declination of the body be north, the telescope is elevated to the northern division of the semicircle; if south, to the southern part of it.
These adjustments being made, take the difference between the Right Ascension of the sun and the body to be observed; and if the Right Ascension of the body be greater than that of the sun, subtract the difference from the time of observation; if not, add to the time of observation.39 The remainder in one case, or the sum in the other, will be the hour and minute to which the nonius on the equatorial circle is to be set; which being done, the telescope will point to the star or planet to whose declination the instrument is adjusted. When the heavenly body is thus found, it may be followed, in its diurnal course, for hours, 463 or as long as it remains above the horizon. For as the diurnal motion of a star is parallel to the equator, the motion of the telescope on the equatorial circle, will always be in the star’s diurnal arc; and should it have left the field of the telescope for any considerable time, it may be again recovered, by moving the telescope onward according to the time which elapsed since it was visible in the field of view. We may illustrate what has been now stated by an example or two. Suppose on the 30th April, 1841, at 1 o’clock, P.M. we wished to see the star Aldebaran. The Right Ascension of this star is 4h 27m; and the sun’s Right Ascension for that day at noon, as found in ‘White’s Ephemeris,’ or the ‘Nautical Almanack,’ is 2h 30m. Subtract this last number from 4h 27m, and the remainder 1h 57m, shows that the star comes to the meridian on that day at 57 minutes past 1 o’clock, P.M. And as the time of observation is 1 P.M., the nonius which moves on the equatorial circle must be set to 3 minutes past XI, as the star is at that hour 57 minutes from the meridian. The declination of Aldebaran is 16° 11´ north, to which point on the semicircle of declination, the telescope must be adjusted, and then the star will be visible in the field of view. Again, suppose we wished to observe the planet Venus on the 1st January, 1842, at 12 o’clock noon. The sun’s Right Ascension on that day is 18h 46m, and that of Venus 17h 41m, from which the sun’s Right Ascension being subtracted, the remainder is 22h 55m, or 55 minutes past 10, A.M. Here, as the Right Ascension of Venus is too small to have the sun’s Right Ascension taken from it, we borrow 24 hours, and reckon the remainder from XII at noon. As the planet at 12 noon, is 1 hour 5 minutes past the meridian, 464 the nonius on the equatorial circle must be set to that point, and the telescope adjusted to 23° 6´ of south declination, which is the declination of Venus for that day, when this planet will appear in the field of view.
For the purpose of illustrating the descriptions now given, and for affording some information respecting celestial day observations, I shall select a few of the observations above alluded to, which I formerly published in Nicholson’s Journal, along with a few others which have been since made. These observations were made with a view to determine the following particulars:—1. What stars and planets may be conveniently seen in the day-time, when the sun is above the horizon? 2. What degrees of magnifying power are requisite for distinguishing them? 3. How near their conjunction with the sun they may be seen? and 4. Whether the diminution of the aperture of the object-glass of the telescope, or the increase of magnifying power, conduces most to render a star or a planet visible in day-light. Having never seen such observations recorded in books of astronomy or in scientific journals, I was induced to continue them, almost every clear day for nearly a year, in order to determine the points now specified. Some of the results are stated in the following pages.
Observations on fixed stars of the first magnitude. April 23, 1813, at 10h 15m, A.M., the sun being 5½ hours above the horizon. Saw the star Vega, or α Lyræ, very distinctly with a power of 30 times. Having contracted the aperture of the object-glass to 9/10 of an inch, saw it on a darker ground, but not more plainly than before. 465 Having contracted the aperture still farther, to half an inch, I perceived the star, but not so distinctly as before. The sky being very clear, and the star in a quarter of the heavens nearly opposite to the sun, I diminished the magnifying power to 15, and could still perceive the star, but indistinctly; it was just perceptible. August 23, at 0h 12m, P.M., saw the star Capella, or α Aurigæ, with a power of 60, and immediately afterwards with a power of 30; the aperture undiminished. With this last power it appeared extremely distinct, but not so brilliant and splendid as with the former power. Having diminished the aperture to 9/10 of an inch, it appeared on a darker ground, though in the former case, it was equally perceptible. A few minutes afterwards, could distinguish it with a power of 15, the aperture being contracted to half an inch. It appeared very small; it was with difficulty the eye could fix upon it in the field of the telescope; but when it was once perceived, its motion across the field of view could be readily followed. It could not be perceived, when the diminished aperture was removed. The sun was then shining in meridian splendour.
August 10th, 9h 30m, A.M. Saw the star Sirius with a power of 60, the aperture contracted to 9/10 inch. Saw it likewise when the aperture was diminished to half an inch, but not so distinctly as through the aperture of inch. Having put on a power of 30, could distinguish it distinctly enough through each of the former apertures, and likewise when they were removed; but somewhat more distinctly with the apertures of nine-tenths and half an inch than without them. At this time the star was 2h 42m in time of Right Ascension west of the sun, having an elevation above the horizon of about 17° 10’; the sun shining 466 bright, and the sky very much enlightened in that quarter of the heavens where the star appeared. There was also a considerable undulation of the air, which is generally the case in the hot mornings of summer—which renders a star more difficult to be perceived than in the afternoon, especially when it is viewed at a low altitude. June 4th, 1h 30m, P.M., saw Sirius with a power of 30 with great distinctness, the aperture not contracted. The star was then within 1h 50m, in time of Right Ascension east from the sun. August 24th, 9h 5m, A.M., saw the star Procyon, or α Canis-Minoris distinctly with a power of 60, the aperture not contracted. When diminished to 9/10 inch, it appeared rather more distinct, as the ground on which it was seen was darker. With a power of 30, and the aperture contracted to 9/10 inch, could perceive it, but somewhat indistinctly. When the equatorial motion was performed, in order to keep it in the field of view, it was sometime before the eye could again fix upon it. When the aperture was diminished to half an inch, it could not be perceived. Saw it when both the apertures were removed, but rather more distinctly with the aperture of 9/10 inch. The difference in the result of this observation, from that of Capella, above stated, was owing to the star’s proximity to the sun, and the consequent illumination of the sky in that quarter where it appeared. Its difference in Right Ascension from that of the sun was then about 2h 5m of time, and its difference of declination about 4° 50´.40 This 467 star may be considered as one of those which rank between the first and second magnitudes.
Similar observations to the above were made and frequently repeated on the stars Rigel, Aldebaran, Betelguese Cor-Leonis and other stars of the first magnitude, which gave nearly the same results. The stars Altares and Fomalhaut are not so easily distinguished, on account of their great southern declination, and consequent low elevation above the horizon. The following observation on Arcturus may be added. June 3rd, observed Arcturus very distinctly, a little before 7 in the evening, the sun being about 1h 40m above the horizon, and shining bright—with a power of 15; the aperture not contracted. It appeared very small but distinct. This star is easily distinguishable at any time of the day with a power of 30.
Observations on stars of the second magnitude. May 5, 1813, at 6h, P.M.; the sun being an hour and three quarters above the horizon. Saw Alphard, or α Hydræ, a star of the second magnitude, with a power of 60; the aperture diminished to 9/10 inch. A few minutes afterwards could perceive it, but indistinctly, with a power of 30, the aperture contracted as above. It could not be seen very distinctly with this power, till about half an hour before sun-set. It was then seen rather more distinctly when the aperture was contracted than without the contraction. May 7th. Saw the star Deneb, or β Leonis, distinctly with a power of 60, about an hour and a half before sun-set. August 20th. Saw Ras Alkague, or α Ophiuchi, at 4h 40m, P.M., with a power of 468 100, the sun being nearly 3 hours above the horizon, and shining bright. Perceived it about an hour afterwards, with a power of 60—with the aperture contracted to 9/10 inch, and also when this contraction was removed. The star was seen nearly as distinctly in the last case as in the first. August 27, 5h, P.M., the same star appeared quite distinct with a power of 60, the aperture not contracted. It did not appear more distinct when the aperture was contracted to 9/10 inch. The sun was then more than 2 hours above the horizon. August 28th. Saw the star Pollux, or β Gemini, 2 hours after sun-rise with a power of 60, aperture undiminished. November 12th, 1h 30´, P.M. Saw the star Altair, or α Aquilæ, with an 8½ inch telescope, 1 inch aperture, carrying a power of 45, the aperture not contracted. Having contracted the aperture a little, it appeared somewhat less distinct. This star is reckoned by some to belong to the class of stars of the first magnitude; but in White’s ‘Ephemeris’ and other Almanacks, it is generally marked as being of the second magnitude. It forms a kind of medium between stars of the 1st and of the 2nd magnitude.
Similar observations, giving the same results, were made on the stars Bellatrix, Orion’s Girdle, α Andromedæ, α Pegasi, Alioth, Benetnasch, North Crown, or α Coronæ Borealis, and various other stars of the same magnitude.
From the above and several hundreds of similar observations, the following conclusions are deduced.
1. That a magnifying power of 30 times is sufficient for distinguishing a fixed star of the first magnitude, even at noon-day, at any season of the year; provided it have a moderate degree of elevation above the horizon, and be not within 30° or 40° of the sun’s body. Also, that, by a 469 magnifying power of 15, a star of this class may be distinguished, when the sun is not above an hour and a half above the horizon. But, in every case, higher powers are to be preferred. Powers of 45 or 60, particularly the last, were found to answer best in most cases, as with such powers the eye could fix on the star with ease, as soon as it entered the field of the telescope.
2. That most of the stars of the 2nd magnitude may be seen with a power of 60, when the sun is not much more than 2 hours above the horizon; and, at any time of the day, the brightest stars of this class may be seen with a power of 100, when the sky is serene, and the star not too near the quarter in which the sun appears.
3. That, in every instance, an increase of magnifying power has the principal effect in rendering a star easily perceptible. That diminution of aperture, in most cases, produces a very slight effect; in some cases, none at all; and, when the aperture is contracted beyond a certain limit, it produces a hurtful effect. The cases in which a moderate contraction is useful, are the two following:—1. When the star appears in a bright part of the sky, not far from that quarter in which the sun appears. 2. When an object-glass of a large aperture, and a small degree of magnifying power, is used. In almost every instance the contraction of the object-glass of the 8½-inch telescope with a power of 45, had a hurtful effect. But when the 20-inch telescope carried a power of only 15, the contraction served to render the object more perceptible.
Some of the planets are not so easily distinguished in the day-time as the fixed stars of the 470 first magnitude. The one which is most easily distinguished at all times, is the planet Venus.
1. Observations on Venus. My observations on this planet commenced about the end of August, 1812, about three or four weeks after its inferior conjunction. About that period, between ten and eleven in the forenoon, with a power of 45, it appeared as a beautiful crescent, quite distinct and well-defined, with a lustre similar to that of the moon about sun-set, but of a whiter colour. The view of its surface and phase was fully more distinct and satisfactory than what is obtained in the evening after sun-set; for, being at a high elevation, the undulation near the horizon did not affect the distinctness of vision. The planet was then very distinctly seen with a power of 7 times, when it appeared like a star of the first or second magnitude. I traced the variation of its phases, almost every clear day, till the month of May, 1813. As at that time, it was not far from its superior conjunction with the sun, I wished to ascertain how near its conjunction with that luminary it might be seen; and particularly whether it might not be possible, in certain cases, to see it at the moment of its conjunction.
The expressions of all astronomical writers previous to this period, when describing the phases of Venus, either directly assert, or, at least imply, that it is impossible to see that planet, in any instance, at the time of its superior conjunction. This is the language of Dr. Long, Dr. Gregory, Dr. Brewster, Ferguson, Adams, B. Martin, and most other writers on the science of astronomy. How far such language is correct will appear from the following observations and remarks.
April 24, 1813, 10h 50´ A.M. Observed Venus with a power of 30, the aperture not contracted. She was then about 31 minutes, in time, of right 471 ascension, distant from the sun. Their difference of declination 3° 59´. She appeared distinct and well-defined. With a power of 100, could distinguish her gibbous phase. May 1st, 10h 20m, A.M. Viewed this planet with a power of 60; the aperture not contracted. It appeared distinct. Saw it about the same time with a power of 15, the aperture being contracted to 9/10 inch. Having contracted the aperture to ½ inch, saw it more distinctly. When the contracted apertures were removed, the planet could with difficulty be distinguished, on account of the direct rays of the sun striking on the inside of the tube of the telescope. The sun was shining bright, and the planet about 25´ of time in R.A. west of his centre, their difference of declination being 3° 7´. May 7th, 10h, A.M. Saw Venus distinctly with a power of 60, the sun shining bright. It was then about 19´ in time of R.A. and 4° 27´ in longitude west of the sun; their difference of declination being 2° 18´. I found a diminution of aperture particularly useful when viewing the planet at this time, even when the higher powers were applied. This was the last observation I had an opportunity of making prior to the conjunction of Venus with the sun, which happened on May 25th, at 9h 30m, A.M. Its geocentric latitude at that time being about 16´ south, the planet must have passed almost close by the sun’s southern limb. Cloudy weather for nearly a month after the last observation, prevented any further views of the planet, when it was in that part of the heavens which was within the range of the instrument. The first day that proved favourable after it had passed the superior conjunction, was June 5th. The following is the memorandum of the observation then taken.
June 5th, 9h, A.M. Adjusted the Equatorial 472 Telescope for viewing the planet Venus, but it could not be perceived, on account of the direct rays of the sun entering the tube of the telescope. I contrived an apparatus for screening his rays, but could not get it conveniently to move along with the telescope; and therefore determined to wait till past eleven, when the top of the window of the place of observation would intercept the solar rays. At 11h 20m, A.M., just as the sun had passed the line of sight from the eye to the top of the window, and his body was eclipsed by it, I was gratified with a tolerably distinct view of the planet, with a power of 60. The aperture being contracted to 9/10 inch. The distinctness increased as the sun retired, till, in two or three minutes, the planet appeared perfectly well-defined. Saw it immediately afterwards, with a power of 30, the aperture contracted as before. Saw it also quite distinctly with a power of 15; but it could not be distinguished with this power, when the contracted aperture was removed. At this time Venus was just 3° in longitude, or about 13´ in time of R.A. east of the sun’s centre, and of course only about 2¾ degrees from his eastern limb; the difference of their declination being 27´, and the planet’s latitude 11´ north.
Several years afterwards, I obtained views of this planet, when considerably nearer the sun’s margin than as stated in the above observation, particularly on the 16th October, 1819, when Venus was seen when only 6 days and 19 hours past the time of the superior conjunction. At that time its distance from the sun’s eastern limb was only 1° 28´ 42´´. A subsequent observation proved that Venus can be seen when only 1° 27´, from the sun’s margin—which I consider as approximating 473 to the nearest distance from the sun at which this planet is distinctly visible.—I shall only state farther the two or three following observations.
June 7th, 1813, 10h, A.M. Saw Venus with a power of 60, the aperture being contracted to 9/10 inch—the direct rays of the sun not being intercepted by the top of the window. The aperture having being further contracted to ½ inch, could perceive her, but not quite so distinctly. When the contractions were removed, she could scarcely be seen. She was then 3° 33´ in longitude, and nearly 15 minutes in time of R.A. distant from the sun’s centre. Some fleeces of clouds having moved across the field of view, she was seen remarkably distinct in the interstices—the sun at the same time, being partly obscured by them.—August 19th, 1h 10´, P.M. Viewed Venus with a magnifying power of 100. Could perceive her surface and gibbous phase almost as distinctly as when the sun is below the horizon. She appeared bright, steady in her light, and well defined, without that glare and tremulous appearance she exhibits in the evening when near the horizon. She was then nearly on the meridian. On the whole, such a view of this planet is as satisfactory, if not preferable, to those views we obtain with an ordinary telescope in the evening, when it is visible to the naked eye.
All the particulars above stated have been confirmed by many subsequent observations continued throughout a series of years. I shall state only two recent observations which show that Venus may be seen somewhat nearer the sun than what is deduced from the preceding observations, and at the point of its superior conjunction. March 10th, 1842, observed the planet Venus, then very near 474 the sun, at 19 minutes past 11, A.M. It had passed the point of its superior conjunction with the sun, on the 5th March, at 1h 19m, P.M. The difference of right ascension between the sun and the planet was then about 6½ minutes of time, or about 1° 37½´, and it was only about 1° 21´ distant from the sun’s eastern limb. It appeared quite distinct and well-defined, and might perhaps have been seen on the preceding day, had the observation been then made.—The following observation shows that Venus may be seen still nearer the sun than in the preceding observations, and even at the moment of its superior conjunction. On the 2nd of October, 1843, this planet passed the point of its superior conjunction with the sun, at 4h 15m, P.M. At two o’clock, P.M.—only two hours before the conjunction, I perceived the planet distinctly, and kept it in view for nearly ten minutes, till some dense clouds intercepted the view. It appeared tolerably distinct and well-defined, though not brilliant, and with a round full face, and its apparent path was distinctly traced several times across the field of view of the telescope. I perceived it afterwards, about half past four, P.M., only a few minutes after it had passed the point of conjunction, on which occasion it appeared less distinct than in the preceding observation, owing to the low altitude of the planet, being then only a few degrees above the horizon. The observations, in this instance, were made not with an equatorial instrument, which I generally use in such observations, but with a good achromatic telescope 44½ inches focal distance, mounted on a common tripod, with a terrestrial power of 95 times. A conical tube about ten inches long was fixed on the object-end of the telescope, at the extremity of which an aperture, 1½ inch diameter was placed, 475 so as to intercept, as much as possible, the direct ingress of the solar rays. The top of the upper sash of the window of the place of observation was likewise so adjusted as to intercept the greater part of the sun’s rays from entering the tube of the telescope. The sun’s declination at that time was 3° 26´ south, and that of Venus 2° 12´ south; consequently, the difference of declination was 1° 14´ = the distance of Venus from the sun’s centre; and as the sun’s diameter was about 16´, Venus was then only 58´ from the sun’s northern limb, or 6´ less than two diameters of the sun.
This is the nearest approximation to the sun at which I have ever beheld this planet, and it demonstrates that Venus may be seen even when within a degree of the sun’s margin; and it is perhaps the nearest position to that luminary in which this planet can be distinctly perceived. It shows that the light reflected from the surface of Venus is far more brilliant than that reflected from the surface of our moon; for no trace of this nocturnal luminary can be perceived, even when at a much greater distance from the sun, nor is there any other celestial body that can be seen within the limit now stated. This is the first observation, so far as my information extends, of Venus having been seen at the time of her superior conjunction.41
The practical conclusion from this observation is, that, at the superior conjunction of this planet, when its distance from the sun’s margin is not less than 58´, its polar and equatorial diameter may be measured by a micrometer, when it will be determined whether or not Venus be of a spheroidal figure. The Earth, Mars, Jupiter and 476 Saturn are found to be not spheres but spheroids, having their polar shorter than their equatorial diameters. But the true figure of Venus has never yet been ascertained, because it is only at the superior conjunction that she presents a full enlightened hemisphere, and when both diameters can be measured, except at the time when she transits the sun’s disk, which happens only twice in the course of 120 years.42 477
The following conclusions are deduced from the observations made on Venus.
1. That this planet may be seen distinctly, with a moderate degree of magnifying power, at the moment of its superior conjunction with the sun, 478 when its geocentric latitude, either north or south, at the time of conjunction, is not less than 1° 14´, or, when the planet is about 58´ from the sun’s limb. This conclusion is deduced from the observation of Oct. 2, 1843,45 stated above.
2. Another conclusion is—that during the space 479 of 583 days, or about 19 months—the time this planet takes in moving from one conjunction with the sun to a like conjunction again—when its latitude at the time of its superior conjunction exceeds 1° 14´, it may be seen with an equatorial telescope every clear day without interruption, except about the period of its inferior conjunction, when its dark hemisphere is turned towards the earth, and a short time before and after it. When its geocentric latitude is less than 1° 14´, it will be hid only about four days before, and the same time after its superior conjunction. During the same period it will be invisible to the naked eye, and consequently no observations can be made upon it with a common telescope, for nearly six months, and sometimes more, according as its declination is north or south, namely about two or three months before, and the same time after its superior conjunction, except where there is a very free and unconfined horizon. In regard to the time in which this planet can be hid about the period of its inferior conjunction, I have ascertained from observation, that it can never be hid longer than during a space of 2 days 22 hours; having seen Venus, about noon, like a fine slender crescent, only 35 hours after she had passed the point of her inferior conjunction; and in a late instance she was seen when little more than a day from the period of conjunction. The longest time, therefore, that this planet can be hid from view during a period of 583 days, is only about 10 days; and when its latitude at the time of the superior conjunction, equals or exceeds 1° 14´, it can be hid little more than two days. This is a circumstance which cannot be affirmed of any other celestial body, the sun only excepted.
3. That every variation of the phases of this planet—from a slender crescent to a full enlightened 480 hemisphere—may, on every clear day, be conveniently exhibited by means of the equatorial telescope. This circumstance renders this instrument peculiarly useful in the instruction of the young in the principles of astronomy. For, if the phase which Venus should exhibit at any particular time be known, the equatorial telescope may be directed to the planet, and its actual phase in the heavens be immediately exhibited to the astronomical pupil.
4. Since it is only at the period of the superior conjunction that this planet presents a full enlightened hemisphere, and since it is only when this phase is presented that both its diameters can be measured—it is of some importance that observations be made on it at the moment of conjunction, by means of powerful telescopes furnished with micrometers, so as to determine the difference (if any) between its polar and equatorial diameters.
5. Another conclusion from the observations on Venus, is, that a moderate diminution of the aperture of the object-glass of the telescope is useful, and even necessary in viewing this planet when near the sun. Its effect is owing in part to the direct solar rays being thereby more effectually excluded; for when these rays enter directly into the tube of the telescope, it is very difficult, and almost impossible to perceive this planet, or any other celestial body when in the vicinity of the sun.
This planet is very easily distinguished in the day-time with a very moderate magnifying power, when it is not within 30° or 35° of the sun. The following extract from my memorandums may 481 serve as a specimen. May 12, 1813, 1h 40m, P.M. Saw Jupiter with a power of 15 times, the aperture not contracted. The planet appeared so distinct with this power, that I have reason to believe, it would have been perceived with a power of 6 or 7 times. When the aperture was contracted 9/10 inch, and afterwards to half an inch, there was little perceptible difference in its appearance. It was then about 58° in longitude, east of the sun.
Though Jupiter when at a considerable distance from the sun, and near his opposition, appears to the naked eye with a brilliancy nearly equal to that of Venus, yet there is a very striking difference between them, in respect of lustre, when viewed in day-light. Jupiter, when viewed with a high magnifying power, in the day-time, always exhibits a very dull cloudy appearance; whereas Venus appears with a moderate degree of splendour. About the end of June 1813, between 5 and 6 in the evening, having viewed the planet Venus, then within 20° of the sun, and which appeared with a moderate degree of lustre, I directed the telescope to Jupiter, at that time more than 32° from the sun, when the contrast between the two planets was very striking, Jupiter appearing so faint as to be just discernible, though his apparent magnitude was nearly double that of Venus. In this observation a power of 65 was used. In his approach towards the sun, about the end of July, I could not perceive him when he was within 16° or 17° of his conjunction with that luminary.—These circumstances furnish a sensible and popular proof, independently of astronomical calculations, that the planet Jupiter is placed at a much greater distance from the sun than Venus; since its light is so faint as to be scarcely perceptible 482 when more than 20 degrees from the sun, while that of Venus is distinctly seen amidst the full splendour of the solar rays, when only about a degree from the margin of that luminary. With a power of 65 I have been enabled to distinguish the belts of Jupiter before sun-set, but could never perceive any of his satellites till the sun was below the horizon. There are no observations which so sensibly and strikingly indicate the different degrees of light emitted by the different planets as those which are made in the day-time. To a common observer, during night, Jupiter and Venus appear, in a clear sky, nearly with equal brilliancy, and even Mars, when about the point of his opposition to the sun, appears with a lustre somewhat similar, though tinged with a ruddy hue; but when seen in day-light their aspect is very dissimilar. This circumstance evidently indicates, 1. that these planets are placed at different distances from the sun, and consequently are furnished with different degrees of light proportional to the square of their distances from that luminary;—and 2. that there are certain circumstances connected with the surfaces and atmospheres of the planetary bodies, which render the light they emit more or less intense, independently of their different distances from the central luminary. For Mars, though much nearer to the sun than Jupiter, is not so easily distinguished in the day-time, and, even in the night-time, appears with a less degree of lustre.
My observations on Saturn in day-light, have not been so frequent as those on Jupiter. I have been enabled to distinguish his ring several times before sun-set, with a power of 65; but his great southern declination, and consequent low altitude, at the periods when these observations were made, 483 were unfavourable for determining the degree of his visibility in day-light; for a planet or a star is always more distinctly perceptible in a high than in a low altitude, on account of the superior purity of the atmosphere through which a celestial object is seen when at a high elevation above the horizon. This planet, however, is not nearly so distinctly visible in day-light as Jupiter, and I have chiefly seen it, when the sun was not more than an hour or two above the horizon, but never at noon-day; although it is probable that with powerful instruments it may be seen even at that period of the day. The planet Mars is seldom distinctly visible in the day-time, except when at no great distance from its opposition to the sun. The following is a memorandum of an observation on Mars, when in a favourable position. October 24, 1836. Saw the planet Mars distinctly with a power of about 60, at 40 minutes past 9 A.M., the sun having been above the horizon nearly three hours. It appeared tolerably distinct, but scarcely so brilliant as a fixed star of the first magnitude, but with apparently as much light as Jupiter generally exhibits when viewed in day-light. It could not be traced longer at the time, so as to ascertain if it could be seen at mid-day; on account of the interposition of the western side of the window of the place of observation. The ruddy aspect of this planet—doubtless caused by a dense atmosphere with which it is environed—is one of the causes which prevents its appearing with brilliancy in the day-time. With respect to the planet Mercury, I have had opportunities of observing it several times after sun-rise, and before sun-set, about 10 or 12 days before and after its greatest elongation from the sun, with a power of 45. I have several times searched for 484 this planet about noon, but could not perceive it. The air, however, at the times alluded to, was not very clear, and I was not certain that it was within the field of the telescope; and therefore, I am not convinced but that, with a moderately high power, it may be seen even at noon-day.
Such are some specimens of the observations I have made on the heavenly bodies in the day-time, and the conclusions which may be deduced from them. I have been induced to communicate them, from the consideration, that the most minute facts, in relation to any science, are worthy of being known, and may possibly be useful. They may at least gratify the astronomical tyro with some information which he will not find in the common treatises on astronomy, and may perhaps excite him to prosecute a train of similar observations for confirming or correcting those which have been noted above.
Besides the deductions already stated, the following general conclusions may be noted.—1. That a celestial body may be as easily distinguished at noon-day, as at any time between the hours of nine in the morning and three in the afternoon, except during the short days in winter. 2. They are more easily distinguished at a high than at a low altitude—in the afternoon than in the morning, especially if their altitudes be low—and in the northern region of the heavens than in the southern. The difficulty of perceiving them at a low altitude is obviously owing to the thick vapours near the horizon. Their being less easily distinguished in the morning than in the afternoon is owing to the undulations of the atmosphere, which are generally greater in the morning than in the afternoon. This may be evidently perceived by looking at distant land-objects at those 485 times, in a hot day, through a telescope which magnifies about 40 or 50 times, when they will be found to appear tremulous and distorted in consequence of these undulations, especially if the sun be shining bright. In consequence of this circumstance, we can seldom use a high terrestrial power with effect on land objects, except early in the morning, and a short time before sun-set. Their being more easily distinguished in the northern region of the heavens is owing to that part of the sky being of a deeper azure, on account of its being less enlightened than the southern with the splendour of the solar rays.
The observations on the heavenly bodies in the day-time, to which I have now directed the attention of the reader, are not to be considered as merely gratifications of a rational curiosity, but may be rendered subservient to the promotion of astronomical science. As to the planet Venus—when I consider the degree of brilliancy it exhibits, even in day-light, I am convinced that useful observations might frequently be made on its surface in the day-time, to determine some of its physical peculiarities and phenomena. Such observations might set at rest any disputes which may still exist respecting the period of rotation of this planet. Cassini, from observations on a bright spot, which advanced 20° in 24h 34m determined the time of its rotation to be 23 hours, 20 minutes. On the other hand, Bianchini, from similar observations, concluded that its diurnal period was 24 days and 8 hours. The difficulty of deciding between these two opinions, arises from the short time in which observations can be made on this planet, either before sun-rise, or after sun-set, 486 which prevents us from tracing, with accuracy, the progressive motion of its spots for a sufficient length of time. And, although an observer should mark the motion of the spots at the same hour, on two succeeding evenings, and find they had moved forward about 15° in 24 hours, he would still be at a loss to determine, whether they had moved only 15°, in all, since the preceding observation, or had finished a revolution and 15° more. If, therefore, any spots could be perceived on the surface of Venus in the day-time, their motion might be traced, when she is in north declination, for 12 hours or more, which would completely settle the period of rotation. That it is not improbable that spots, fitted for this purpose, may be discovered on her disk in the day-time, appears from some of the observations of Cassini, who saw one of her spots when the sun was more than eight degrees above the horizon.46 The most distinct and satisfactory views I have ever had of this planet were those which I obtained in the day-time, in summer, when it was viewed at a high altitude, with a 44½ inch achromatic telescope, carrying a power of 150. I have at such times distinctly perceived the distinction between the shade and colour of its margin, and the superior lustre of its central parts, and some spots have occasionally been seen, though not so distinctly marked as to determine its rotation. Such distinct views are seldom to be obtained in the evening after sun-set, on account of the undulations of the atmosphere, and the dense mass of vapours through which the celestial bodies are viewed when near the horizon.
Nor do I consider it altogether improbable that 487 its satellite (if it have one, as some have supposed) may be detected in the day time, when this planet is in a favourable position for such an observation; particularly when a pretty large portion of its enlightened surface is turned towards the earth, and when its satellite, of course, must present a similar phase. About the period of its greatest elongation from the sun, and soon after it assumes a crescent phase, in its approach to the inferior conjunction, may be considered as the most eligible times for prosecuting such observations. If this supposed satellite be about one third or one fourth of the diameter of its Primary, as Cassini, Short, Baudouin, Montbarron, Montaigne, and other astronomers supposed, it must be nearly as large as Mercury, which has been frequently seen in day-light. If such a satellite have a real existence, and yet undistinguishable in day-light, its surface must be of a very different quality for reflecting the rays of light from that of its primary; for it is obvious to every one who has seen Venus with a high power, in the day-time, that a body of equal brilliancy—though four times less in diameter—would be quite perceptible, and exhibit a visible disk. Such observations, however, would be made, with a much greater effect in Italy and other Southern countries, and particularly in Tropical climates, such as the southern parts of Asia and America, and in the West India Islands, where the sky is more clear and serene, and where the planet may be viewed at higher altitudes, and for a greater length of time, without the interruption of clouds, than in our island.
Again, the apparent magnitudes of the fixed stars—the quantity of light they respectively emit—and the precise class of magnitude which should be assigned to them—might be more accurately 488 determined by day observations, than by their appearance in the nocturnal sky. All the stars which are reckoned to belong to the first magnitude are not equally distinguishable in day-light. For example, the stars Aldebaran and Procyon are not so easily distinguished, nor do they appear with the same degree of lustre by day, as the stars α Lyræ and Capella. In like manner the stars Altair, Alphard, Deneb Ras Alkague, considered as belonging to the second magnitude, are not equally distinguishable by the same aperture and magnifying power—which seems to indicate, that a different quantity of light is emitted by these stars, arising from a difference either in their magnitude, their distance, or the quality of the light with which they are irradiated.
The following are likewise practical purposes to which celestial day observations may be applied. In accurately adjusting Circular and Transit instruments, it is useful, and even necessary, for determining the exact position of the meridian, to take observations of certain stars, which differ greatly in zenith distance, and which transit the meridian nearly at the same time. But as the stars best situated for this purpose, cannot, at every season, be seen in the evenings, we must, in certain cases, wait for several months till such observations can be made, unless we make them in the day-time, which can very easily be done, if the instrument have a telescope adapted to it, furnished with such powers as those above stated, or higher powers if required. I have likewise made use of observations on the stars in the day time for adjusting a clock or watch to meantime, when the sun was in a situation beyond the range of the instrument, or obscured by clouds, and when I did not choose to wait till the evening. This may, at 489 first view, appear to some as paradoxical; since the finding of a star in day-light depends on our knowing its right Ascension from the sun, and this last circumstance depends, in some measure, on our knowing the true time. But if a watch or clock is known not to have varied above seven or eight minutes from the time, a star of the first magnitude may easily be found, by moving the telescope a little backwards or forwards, till the star appear; and when it is once found, the exact variation of the movement is then ascertained, by comparing the calculations which were previously necessary, with the time pointed out by the nonius on the Equatorial circle—or, in other words, by ascertaining the difference between the time assumed, and the time indicated by the instrument, when the star appears in the centre of the field of view. All this may be accomplished in five or six minutes.
Besides the practical purposes now stated, the Equatorial telescope is perhaps the best instrument for instructing a learner in the various operations of practical astronomy, and particularly for enabling him to distinguish the names and positions of the principal stars. For, when the right Ascension and Declination of any star is known, from astronomical tables, the telescope may be immediately adjusted to point to it, which will infallibly prevent his mistaking one star for another. In this way, likewise, the precise position of the planet Mercury, Uranus, Vesta, Juno, Ceres, Pallas—a small comet, a nebula, a double star, or any other celestial body not easily distinguishable by the naked eye, may be readily pointed out, when its right Ascension and Declination are known to a near approximation.
In conclusion, I cannot but express my surprise, 490 that the Equatorial telescope is so little known, even by many of the lovers of astronomical science. In several respectable academies in this part of Britain, and, if I am not misinformed, in most of our universities, this instrument is entirely unknown. This is the more unaccountable, as a small equatorial may be purchased for a moderate sum; and as there is no single instrument so well adapted for illustrating all the operations of Practical Astronomy. Where very great accuracy is not required, it may occasionally be made to serve the general purposes of a transit instrument for observing the passages of the sun and stars across the meridian. It may likewise be made to serve as a theodolite for surveying land and taking horizontal angles—as a Quadrant for taking angles of altitude—as a level—as an equal altitude instrument—an azimuth instrument for ascertaining the sun’s distance from the north or south points of the horizon—and as an accurate Universal Sun Dial, for finding the exact mean or true time, on any occasion when the sun is visible. The manner of applying it to these different purposes will be obvious to every one who is in the least acquainted with the nature and construction of this instrument.
The price of a small Equatorial instrument, such as that described p. 454, is about 16 guineas, exclusive of some of the eye-pieces, which were afterwards added for the purpose of making particular observations. Instruments of a larger size, and with more complicated machinery, sell from 50 to 100 guineas and upwards. Messrs. W. and S. Jones, Holborn, London, construct such instruments. 491
figure 87.
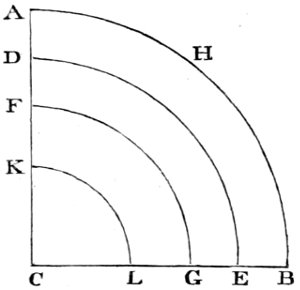
Every circle being supposed to be divided into 360 equal parts, or degrees,—it is evident, that 90 degrees, or the fourth part of a circle, will be sufficient to measure all angles, between the horizon of any place and the line perpendicular to it which goes up to the zenith. Thus, in fig. 87, the line CB represents the plane of the horizon. ACBH, the quadrant, AC the perpendicular to the horizon, and A the zenith point. If the lines BC and CA represent a pair of compasses with the legs standing perpendicular to each other, and the curved lines AB, DE and FG, the quarter of as many circles of different sizes—it is evident that although each of these differs from the others in size, yet that each contains the same portion of a circle, namely a quadrant or fourth part; and thus it would be from the smallest to the largest quadrant that could be formed,—they 492 would all contain exactly 90 degrees each. By the application of this principle the comparative measure of angles may be extended to an indefinite distance. By means of an instrument constructed in the form of a quadrant of a circle, with its curved edge divided into 90 equal parts, the altitude of any object in the heavens can at any time be determined.
There are various constructions of this instrument, some of them extremely simple, and others considerably complex and expensive, according to the degree of accuracy which the observations require. The following is a description of the Pillar Quadrant, as it was made by Mr. Bird, for the observatory of Greenwich, and several continental observatories.
This instrument consists of a quadrant E E H G L (fig. 88.) mounted on a pillar B, which is supported by a tripod AA, resting on three foot screws. The quadrant, the pillar, and the horizontal circle all revolve round a vertical axis. A telescope H is placed on the horizontal radius, and is directed to a meridian mark previously made on some distant object for placing the plane of the instrument in the meridian, and also for setting the zero, or beginning of the scale truly horizontal. This is sometimes done by a level instead of a telescope, and sometimes by a plumb-line G, suspended from near the centre, and brought to bisect a fine dot made on the limb, where a microscope is placed to examine the bisection. The weight or plummet at the end of the plumb-line is suspended in the cistern of water b, which keeps it from being agitated by the air. A similar dot is made for the upper end of the plumb-line upon a piece of brass, adjustable by a screw d, in order that the line may be exactly 493 at right angles to the telescope, when it is placed at o. The quadrant is screwed by the centre of its frame, against a piece of brass e with three screws, and this piece is screwed to the top of the pillar B with other three screws. By means of the first three screws, the plane of the quadrant can be placed exactly parallel to the vertical axis, and by the other screws the telescope H can be placed exactly perpendicular to it. The nut of the delicate screw L is attached to the end of the telescope F, by a universal joint. The collar for the other end is jointed in the same manner to a 494 clamp which can be fastened to any part of the limb. A similar clamp-screw and slow motion is seen at n for the lower circle, which is intended to hold the circle fast, and adjust its motion. The divisions of the lower, or horizontal circle, are read by verniers, or noniuses, fixed to the arms of the tripod at l and m, and, in some cases three are used to obtain greater accuracy.
figure 88.
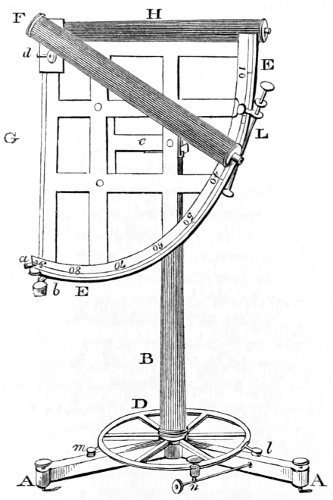
In using this quadrant, the axis of the telescope H is adjusted to a horizontal line, and the plane of the quadrant to a vertical line, by the means already stated. The screw of the champ L is then loosened, and the telescope directed to the star, or other object, whose altitude is required. The clamp screw being fixed, the observer looks through the telescope, and with the nut of the screw L he brings the telescope into a position where the star is bisected by the intersection of the wires in the field of the telescope. The divisions are then to be read off upon the vernier, and the altitude of the star will be obtained. By means of the horizontal circle D, all angles in the plane of the horizon may be accurately measured—such as the amplitudes and azimuths of the celestial bodies.
Quadrants of a more simple construction than the above, may be occasionally used, such as Gunter’s, Cole’s, Sutton’s and others; but none of these are furnished with telescopes, or telescopic sights, and therefore an altitude cannot be obtained by them with the same degree of accuracy as with that which has been now described.
By means of the Quadrant, not only the altitudes of the heavenly bodies may be determined, but also the distances of objects on the earth by observations made at two stations—the altitude of fireballs and other meteors in the atmosphere—the 495 height of a cloud, by observation on its altitude and velocity—and numerous other problems, the solution of which depends upon angular measurements. A Mural Quadrant is the name given to this instrument when it is fixed upon a wall of stone, and in the plane of the meridian, such as the quadrant which was erected by Flamstead in the Observatory at Greenwich. Although the quadrant was formerly much used in astronomical observations, yet it may be proper to state, that its use has now been almost completely superseded by the recent introduction of Astronomical Circles, of which we shall now give the reader a very short description, chiefly taken from Troughton’s account of the instrument he constructed, as found in Sir D. Brewster’s Supplement to Ferguson’s Astronomy.
figure 89.

An astronomical circle is a complete circle substituted in place of the quadrant, and differs from it only in the superior accuracy with which it enables the astronomer to make his observations. The large vertical or declination circle CC (fig. 89.) is composed of two complete circles strengthened by an edge bar on their inside, and firmly united at their extreme borders by a number of short braces or bars which stand perpendicular between them, and which keep them at such a distance as to admit the achromatic telescope TT. This double circle is supported by 16 conical bars, firmly united along with the telescope, to a horizontal axis. The exterior limb of each circle is divided into degrees and parts of a degree, and these divisions are divided into seconds by means 496 of the micrometer microscopes mm, which read off the angle on opposite sides of each circle. The cross wires in each microscope may be moved over the limb till they coincide with the nearest division of the limb, by means of the micrometer screws cc, and the space moved through is ascertained by the divisions on the graduated head above 497 c, assisted by a scale within the microscope. The microscopes are supported by two arms proceeding from a small circle concentric with the horizontal axis, and fixed to the vertical columns. This circle is the centre upon which they can turn round nearly a quadrant for the purpose of employing a new portion of the divisions of the circle, when it is reckoned prudent to repeat any delicate observations upon any part of the limb. At h is represented a level for placing the axis in a true horizontal line, and at k is fixed another level parallel to the telescope, for bringing the zero of the divisions to a horizontal position. The horizontal axis to which the vertical circle and the telescope are fixed, is equal in length to the distance between the vertical pillars, and its pivots are supported by semicircular bearings, placed at the top of each pillar. These two vertical pillars are firmly united at their bases to a cross bar f. To this cross bar is also fixed a vertical axis about three feet long, the lower end of which terminating in an obtuse point, rests in a brass conical socket firmly fastened at the bottom of the hollow in the stone pedestal D, which receives the vertical axis. This socket supports the whole weight of the moveable part of the instrument. The upper part of the vertical axis is supported by two pieces of brass, one of which is seen at e, screwed to the ring i, and containing a right angle, or Y. At each side of the ring, opposite to the points of contact, is placed a tube containing a heliacal spring, which, by a constant pressure on the axis, keeps it against its bearings, and permits it to turn, in these four points of contact, with an easy and steady motion. The two bearings are fixed upon two rings capable of a lateral adjustment; the lower one by the screw d to incline 498 the axis to the east or west, while the screw b gives the upper one i a motion in the plane of the meridian. By this means the axis may be adjusted to a perpendicular position as exactly as by the usual method of the tripod with feet screws. These rings are attached to the centre piece s, which is firmly connected with the upper surface of the stone by six conical Tubes A, A, A, &c., and brass standards at every angle of the pedestal. Below this frame lies the azimuth circle EE consisting of a circular limb, strengthened by ten hollow cones firmly united with the vertical axis, and consequently turning freely along with it. The azimuth circle EE is divided and read off in the same manner as the vertical circle. The arms of the microscopes BB project from the ring i, and the microscopes themselves are adjustable by screws, to bring them to zero and to the diameter of the circle. A little above the ring i is fixed an arm L which embraces and holds fast the vertical axis with the aid of a champ screw. The arm L is connected at the extremity with one of the arms A, by means of the screw a, so that by turning this screw, a slow motion is communicated to the vertical axis and the azimuth circle.
In order to place the instrument in a true vertical position, a plumb-line, made of fine silver wire, is suspended from a small hook at the top of the vertical tube n, connected by braces with one of the large pillars. The plumb-line passes through an angle in which it rests, and by means of a screw may be brought into the axis of the tube. The plummet at the lower end of the line is immersed in a cistern of water t, in order to check its oscillations, and is supported on a shelf proceeding from one of the pillars. At the lower 499 end of the tube n are fixed two microscopes o and p, at right angles to one another, and opposite to each is placed a small tube containing a lucid point. The plumb-line is then brought into such a position by the screws d, b, and by altering the suspension of the plumb-line itself, that the image of the luminous point, like the disk of a planet, is formed on the plumb-line, and accurately bisected by it. The vertical axis is then turned round, and the plumb-line examined in some other position. If it still bisects the luminous point, the instrument is truly vertical; but if it does not, one half of the deviation must be corrected by the screws d b, and the other half by altering the suspension of the line till the bisection of the circular image is perfect in every position of the instrument.
It is not many years since Circular Repeating instruments came into general use. The principle on which the construction of a repeating circle is founded appears to have been first suggested by Professor Mayer of Gottingen, in 1758; but the first person who applied this principle to measure round the limb of a divided instrument, was Borda, who about the year 1789, caused a repeating circle to be constructed that would measure with equal facility horizontal and vertical angles. Afterwards, Mr. Troughton greatly improved the construction of Borda’s instrument by the introduction of several contrivances which ensure, at the same time, its superior accuracy and convenience in use; and his instruments have been introduced into numerous observatories. Circular instruments, on a large scale, have been placed in the Royal Observatory of Greenwich, and in most of the principal observatories on the continent of Europe. Although it is agreed on all hands that 500 greater accuracy may be obtained by a repeating circle, than by any other having the same radius, yet there are some objections to its use which do not apply to the altitude and azimuth circle. The following are the principal objections, as stated in Vol. I., of the ‘Memoirs of the Astronomical Society of London.’ 1. The origin of the repeating circle is due to bad dividing, which ought not to be tolerated in any instrument in the present state of the art. 2. There are three sources of fixed error which cannot be exterminated, as they depend more on the materials than on the workmanship; first, the zero of the level changes with variations of temperature; secondly, the resistance of the centre work to the action of the tangent screws; and thirdly, the imperfection of the screws in producing motion, and in securing permanent positions. 3. The instrument is applied with most advantage to slowly moving or circumpolar stars; but in low altitudes these stars are seen near the horizon, where refraction interferes. 4. Much time and labour are expended, first in making the observations, and again in reducing them. 5. When any one step in a series of observations is bad, the whole time and labour are absolutely lost. 6. When the instrument has a telescope of small power, the observations are charged with errors of vision, which the repeating circle will not cure. 7. This instrument cannot be used as a transit instrument, nor for finding the exact meridian of a place.
A great variety of directions is necessary in order to enable the student of practical astronomy thoroughly to understand and to apply this instrument to practice, which the limited nature of the present work prevents us from detailing.—As this instrument consists of a variety of complicated 501 pieces of machinery, it is necessarily somewhat expensive. A six inch brass astronomical circle for altitudes, zenith or polar distances, azimuths, with achromatic telescope, &c., is marked in Messrs. W. and S. Jones’ catalogue of astronomical instruments, at £27 6s. A circle 12 inches diameter, from £36 15s. to £68 5s. An 18 inch ditto, of the best construction, £105. The larger astronomical circles for public observatories, from 100 to a 1000 guineas and upwards, according to their size, and the peculiarity of their construction.
A Transit instrument is intended for observing celestial objects as they pass across the meridian. It consists of a telescope fixed at right angles to a horizontal axis—which axis must be so supported that what is called the line of collimation, or the line of sight of the telescope, may move in the plane of the meridian. This instrument was first invented by Romer in the year 1689, but has since received great improvements by Troughton, Jones and other modern artists. Transit instruments may be divided into two classes, Portable, and Fixed. The portable instrument, when placed truly in the meridian, and well adjusted, may be advantageously used as a stationary instrument in an observatory, if its dimensions be such as to admit of a telescope of 3½ feet focal length; but when the main tube is only from 20 to 30 inches long, with a proportional aperture, it is more suited for a travelling instrument to give the exact time; and, when carried on board a ship in a voyage of discovery, may be taken on shore at 502 any convenient place, for determining the solar time of that place, and for correcting the daily rate of the Chronometer giving the time at the first meridian, so that the longitude of the place of observation may be obtained from the difference of the observed and indicated times, after the proper corrections have been made.
figure 90.
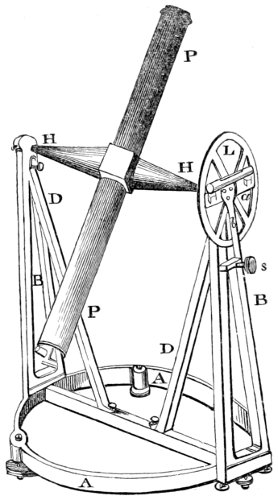
The following is a brief description of one of Mr. Troughton’s Portable Transit Instruments. In fig. 90. PP is an achromatic telescope firmly fixed, by the middle to a double conical and horizontal axis HH, the pivots of which rest on 503 angular bearings called Ys, at the top of the standards B, B, rendered steady by oblique braces DD, fastened to the central part of the circle, AA. In large fixed instruments, the pivots and angular bearings are supported on two massive stone pillars, sunk several feet into the ground, and are sometimes supported by mason-work, to secure perfect stability. The axis HH has two adjustments, one for making it exactly level, and the other for placing the telescope in the meridian. A graduated circle L is fixed to the extremity of the pivot which extends beyond one of the Ys, and the two radii that carry the verniers aa, are fitted to the extremities of the pivot in such a way as to turn round independent of the axis. The double verniers have a small level attached to them, and a third arm b, which is connected with the standard B by means of a screw s. If the verniers are placed by means of the level, in a true horizontal position, when the axis of the telescope is horizontal, and the arm b screwed by the screw s to the standard B, the verniers will always read off the inclination of the telescope, and will enable the observer to point it to any star, by means of its meridian altitude. The whole instrument rests on three foot screws entered into the circle AA. In the field of view of the telescope, there are several parallel vertical wires, crossed at right angles with a horizontal one, and the telescope is sometimes furnished with a diagonal eye-piece, for observing stars near the zenith. A level likewise generally accompanies the instrument, in order to place it horizontal, by being applied to the pivots of the axis.
In order to fix the transit instrument exactly in the meridian, a good clock regulated to sidereal time is necessary. This regulation may be effected 504 by taking equal altitudes of the sun or a star before and after they pass the meridian, which may be done by small quadrants, or by a good sextant. The axis H of the instrument is then to be placed horizontal by a spirit level, which accompanies the transit, and the greatest care must be taken that the axis of vision describes in the heavens a great circle of the sphere. To ascertain whether the telescope be in the plane of the meridian, observe by the clock when a circumpolar star seen through the telescope transits both above and below the pole; and if the times of describing the eastern and western parts of its circuit be equal, the telescope is then in the plane of the meridian; otherwise, certain adjustments must be made. When the telescope is at length perfectly adjusted, a land-mark must be fixed upon, at a considerable distance—the greater the better. This mark must be in the horizontal direction of the intersection of the cross wires, and in a place where it can be illuminated, if possible, in the night time, by a lantern hanging near it; which mark being on a fixed object, will serve at all times afterwards for examining the position of the telescope.
Various observations and adjustments are requisite in order to fixing a transit instrument exactly in the plane of the meridian. There is the adjustment of the level—the horizontal adjustment of the axis of the telescope—the placing of the parallel lines in the focus of the eye-glass, so as to be truly vertical, and to determine the equatorial value of their intervals—the collimation in azimuth, so that a line passing from the middle vertical line to the optical centre of the object-glass, is at right angles with the axis of the telescope’s motion—the collimation in altitude, so that the horizontal line 505 should cross the parallel vertical lines, not only at right angles, but also in the optical centre of the field of view—with various other particulars; but of which our limited space will not permit us to enter into details. Those who wish to enter into all the minute details in reference to the construction and practical application of this and the other instruments above described, as well as all the other instruments used by the Practical Astronomer, will find ample satisfaction in perusing the Rev. Dr. Pearson’s Introduction to Practical Astronomy, 4to., Vol. II.
A portable Transit instrument, with a cast-iron stand, the axis 12 inches in length, and the achromatic telescope about 20 inches, packed in a case, sells at about 16 guineas: with a brass-framed stand and other additions, at about 20 guineas. Transit instruments of larger dimensions are higher in proportion to their size, &c. 506
In order to make observations, with convenience and effect, on the heavenly bodies, it is expedient that an observatory, or place for making the requisite observations, be erected in a proper situation. The following are some of the leading features of a spot adapted for making celestial observations: 1. It should command an extensive visible horizon all around, particularly towards the south and the north. 2. It should be a little elevated above surrounding objects. 3. It should be, if possible, at a considerable distance from manufactories, and other objects which emit much smoke or vapour, and even from chimney-tops where no sensible smoke is emitted, as the heated air from the top of funnels causes undulations in the atmosphere. 4. It should be at a distance from swampy ground or valleys that are liable to be covered with fogs and exhalations. 5. It should not, if possible, be too near public roads, particularly if paved with stones, and frequented by heavy carriages, as in such situations, undulations and tremulous motions may be produced, injurious to the making of accurate observations with graduated instruments. 6. It is expedient that the astronomical observer should have access 507 to some distant field within a mile of the observatory, on which a meridian mark may be fixed, after his graduated instruments are properly adjusted. The distance at which a meridian mark should be erected will depend in part on the focal length of the telescope generally used for making observations on the Right Ascensions and declinations of the stars. It should be fixed at such a distance that the mark may be distinctly seen without altering the focus of the telescope when adjusted to the sun or stars, which, in most cases, will require to be at least half a mile from the place of observation, and more if it can be obtained.
Observatories may be distinguished into public and private. A private observatory may be comprehended in a comparatively small building, or in the wing of a building of ordinary dimensions for a family, provided the situation is adapted to it. Most of our densely-peopled towns and cities, which abound in narrow streets and lanes, are generally unfit for good observatories, unless at an elevated position at their extremities. Public observatories, where a great variety of instruments is used, and where different observers are employed, require buildings of larger dimensions, divided into a considerable number of apartments. The observatory of Greenwich is composed principally of two separate buildings—one of which is the observatory properly so called, where the assistant lives and makes all his observations; the other is the dwelling-house in which the astronomer-royal resides. The former consists of three rooms on the ground-floor, the middle of which is the assistant’s sitting and calculating room, furnished with a small library of such books only as are necessary for his computations, and an 508 accurate clock made by the celebrated Graham, which once served Dr. Halley as a transit-clock. Immediately over this is the assistant’s bed-room, with an alarum to awake him to make his observations at the proper time. The room on the eastern side of this is called the transit-room, in which is an 8 feet transit instrument, with an axis of 3 feet, resting on 2 pieces of stone, made by Mr. Bird, but successively improved by Messrs. Dollond, Troughton and others. Here is also a chair to observe with, the back of which lets down to any degree of elevation that convenience may require. On the western side is the quadrant room, with a stone pier in the middle running north and south, having on its eastern face a mural quadrant of 8 feet radius, by which observations are made on the southern quarter of the meridian, through an opening in the roof, of 3 feet wide, produced by means of two sliding shutters. On the western face is another mural quadrant of 8 feet radius, the frame of which is of iron, and the arch of brass, which is occasionally applied to the north quarter of the meridian. In the same room is the famous zenith sector, 12 feet long, with which Dr. Bradley made the observations which led to the discovery of the nutation of the earth’s axis and the aberration of the light of the fixed stars. Here are also Dr. Hooke’s reflecting quadrant and three time-keepers by Harrison. On the south side of this room a small wooden building is erected for the purpose of observing the eclipses of Jupiter’s satellites, occultations of stars by the moon, and other phenomena which require merely the use of a telescope, and the true or mean time. It is furnished with sliding shutters on the roof and sides to view any part of the hemisphere from the 509 Prime Vertical down to the southern horizon. It contains a 40-inch achromatic, with a triple object-glass; and also a 5 feet achromatic by Messrs. John and Peter Dollond—a 2 feet reflecting telescope by Edwards, and a 6 feet reflector by Herschel. Above the dwelling-house is a large octagonal room, which is made the repository for certain old instruments, and for those which are too large to be used in the other apartments. Among many other instruments, it contains an excellent 10 feet achromatic by Dollond, and a 6 feet reflector by Short. Upon a platform, in an open space, is erected the great reflecting telescope constructed by Mr. Ramage of Aberdeen, on the Herschelian principle, which has a speculum of 15 inches diameter, and 25 feet focal length, remarkable for the great accuracy and brilliancy with which it exhibits celestial objects. Various other instruments of a large size, and of modern construction, have of late years been introduced into this observatory, such as the large and splendid transit instrument constructed by Troughton, in 1816—the two large mural circles by Troughton and Jones—the transit clock, by Mr. Hardy, and several other instruments and apparatus which it would be too tedious to enumerate and describe.
Every observatory, whether public or private, should be furnished with the following instruments. 1. A transit instrument for observing the meridian passage of the sun, planets and stars. 2. A good clock whose accuracy may be depended upon. 3. An achromatic telescope, at least 44 inches focal distance, with powers of from 45 to 180 for viewing planetary and other phenomena—or, a good reflecting telescope at least 3 feet long, and the speculum 5 inches diameter. 4. An equatorial instrument, for viewing the stars and 510 planets in the day-time, and for finding the Right Ascension and declination of a comet, or any other celestial phenomenon. Where this instrument is possessed, and in cases where no great degree of accuracy is required, the equatorial may be made to serve the general purposes of a transit instrument.
A private observatory might be constructed in any house which has a commanding view of the heavens, provided there is an apartment in it, in which windows may be placed, or openings cut out fronting the north, the south, the east and the west. The author of this work has a small observatory erected on the top of his house, which commands a view of 20 miles towards the east, 30 miles towards the west, and north-west, and about 20 miles towards the south, at an elevation of above 200 feet above the level of the sea, and the banks of the Tay, which are about half a mile distant. The apartment is 12½ feet long by 8½ wide, and 8½ feet between the floor and the roof. It has an opening on the north by which observations can be made on the pole-star; a window on the south by which the meridian-passages of the heavenly bodies may be observed; another opening towards the east, and a fourth opening, consisting of a door, towards the west. There is a pavement of lead on the outside, all around the observatory-room, enclosed by a stone parapet 3½ feet high, the upper part of which is coped with broad flat stones, in certain parts of which groves or indentations are made for receiving the feet of the pedestal of an achromatic telescope, which form a steady support for the telescope in the open air, when the weather is calm and serene, and when observations are intended to be made on any region of the heavens. By placing an 511 instrument on this parapet, it may be directed to any point of the celestial canopy, except a small portion near the northern horizon, which is partly intercepted by a small hill. In the following ground-plan, fig. 91. AAA, is the parapet surrounding the observatory-room; BBB, a walk around it nearly 3 feet broad, covered with lead. O is the apartment for the observatory, having an opening C to the north, another opening D to the east, E is a window which fronts the south, and F is a door fronting the west, by which an access 512 is obtained to the open area on the outside. GHI is an area on the outside towards the south, covered with lead, 15 feet long from G to H, and 6½ feet from E to I, from which a commanding view of the southern, eastern and western portions of the heavens may be obtained: eeee are positions on the top of the parapet where a telescope may be conveniently placed, when observations are intended to be made in the open air. The top of this parapet is elevated about 30 feet from the level of the ground. On the roof of the observatory, about 12 feet above its floor, on the outside is a platform of lead, surrounded by a railing, 6 feet by 5, with a seat, on which observations either on celestial or terrestrial objects may occasionally be made. K is a door or hatchway, which forms an entrance into the observatory from the apartments below, which folds down, and forms a portion of the floor.
figure 91.
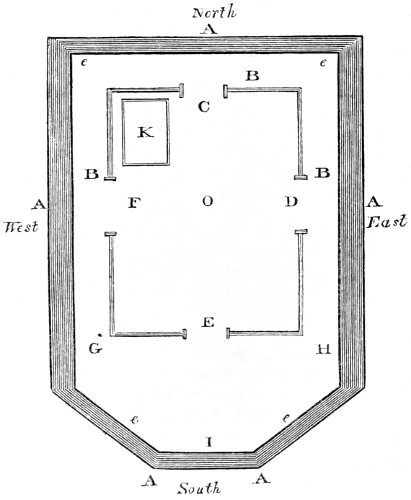
In the perspective view of the building fronting the title-page, the position and general aspect of the observatory-part of the building may be more distinctly perceived.
In public observatories, where zenith or polar distances require to be measured, it is necessary that there should be a dome, with an opening across the roof and down the north and south walls. Should an altitude or azimuth circle, or an equatorial instrument be used, they will require a revolving roof with openings and doors on two opposite sides, to enable an observer to follow a heavenly body across all the cardinal points. The openings may be about 15 inches wide, and the roof needs not be larger than what is requisite for giving room to the observer and the instrument, lest its bulk and weight should impede its easy motion. There have been various plans 513 adopted for revolving domes. Fig. 92 represents a section of the rotatory dome constructed at East Sheen by the Rev. Dr. Pearson. This dome turns round on three detached spheres of lignum vitæ, in a circular bed, formed partly by the dome, and partly by the cylindrical frame-work, which surrounds the circular room of 9 feet diameter. A section of this bed forms a square which the sphere just fills, so as to have a small play to allow for shrinking; and, when the dome is carried round, the spheres, having exactly equal diameters of 4¼ inches each, when placed 514 at equal distances from one another, keep their relative places, and move together in a beautifully smooth manner. These spheres act as friction rollers in two directions at the four points of contact, in case any obstacle is opposed to their progressive motion by the admission of dirt, or by any change of figure of the wood that composes the rings of the dome, and of the gang-way. No groove is here made, but what the weight of the roof resting on the hard sphere occasions. The dome itself moves twice round for the balls once, and has, in this way, its friction diminished. The wood of this dome is covered by Wyatt’s patent copper, one square foot of which weighs upwards of a pound; and the copper is so turned over the nails that fix it at the parts of junction, that not a single nail is seen in the whole dome. This covering is intended to render the dome more permanent than if it had been made of wood alone. At the observatory at Cambridge the dome is made chiefly of iron. In the figure a, a represents one of the two oblong doors that meet at the apex of the cone, and a piece of sheet-copper bent over the upper end of the door which shuts last, keeps the rain from entering at the place of junction. The two halves of the dome are united by brass rods passing through the door-cheeks of wainscot at a and a by means of nuts that screw upon their ends, which union allows the dome to be separated into two parts when there may be occasion to displace it. The wooden plate bb, which appears in a straight line, is a circular broad ring to which the covering wainscot boards are made fast above the eaves, and cc is a similar ring forming the wall-plate or gang-way on which the dome rests and revolves. 515
figure 92.
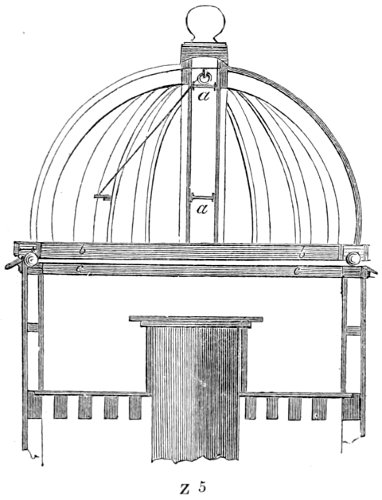
figure 92*.
Fig. 92* shows a small door that lies over the summit of the dome, and may be separately opened for zenith observations; the rod of metal with a ring at the lower end passing through it, serves to open and shut this door, and at the same time carries upon its upper end a large ball that falls back on the roof when the door is open, and keeps the door in a situation to be acted upon by the hook of a handle that is used for this purpose. The doors aa being curved, are made to open in two halves, the upper one being opened first, on account of its covering the end of the other; and the observer may open one or two doors as may best suit his purpose. The weight of this dome is such that a couple of wedges, inserted by a gentle blow between the rings bb and cc, will keep it in its situation under the influence of the strongest wind.
It may not be improper to remark, that in all observatories, and in every apartment where celestial observations are made, there should, if possible, be a uniform temperature; and consequently a fire should never be kept in such places, particularly when observations are intended to be made, as it would cause currents of air through the doors and other openings, which would be injurious to the accuracy of observations. When a window is opened in an ordinary apartment where a fire is kept, there is a current of heated air which rushes out at the top, and a current of 516 cold air which rushes in from below, producing agitations and undulations, which prevent even a good telescope from showing celestial objects distinct and well defined; and, I have no doubt, that many young observers have been disappointed in their views of celestial phenomena, from this circumstance, when viewing the heavenly bodies from heated rooms in cold winter evenings; as the aërial undulations before the telescope prevent distinct vision of such objects as the belts of Jupiter, the spots of Mars, and the rings of Saturn. 517
An orrery is a machine for representing the order, the motions, the phases, and other phenomena of the planets. Although orreries and planetariums are not so much in use as they were half a century ago, yet as they tend to assist the conceptions of the astronomical tyro in regard to the motions, order, and positions of the bodies which compose the solar system, it may not be inexpedient shortly to describe the principles and construction of some of these machines.
The reason why the name Orrery was at first given to such machines, is said to have been owing to the following circumstance. Mr. Rowley, a mathematical-instrument-maker, having got one from Mr. George Graham, the original inventor, to be sent abroad with some of his own instruments, he copied it and made the first for the Earl of Orrery. Sir R. Steele, who knew nothing of Mr. Graham’s machine—thinking to do justice to the first encourager, as well as to the inventor of such a curious instrument, called it an Orrery, and gave Mr. Rowley the praise due to Mr. Graham. The construction of such machines is not a modern invention. The hollow sphere of Archimedes was a piece of mechanism of this kind, 518 having been intended to exhibit the motions of the sun, the moon, and the five planets, according to the Ptolemaic system. The next orrery of which we have any account was that of Posidonius, who lived about 80 years before the Christian era, of which Cicero says, ‘If any man should carry the sphere of Posidonius into Scythia or Britain, in every revolution of which the motions of the sun, moon and five planets, were the same as in the heavens, each day and night, who in those barbarous countries could doubt of its being finished—not to say actuated—by perfect reason?’ The next machine of this kind, which history records, was constructed by the celebrated Boethius, the Christian Philosopher, about the year of Christ 510—of which it was said ‘that it was a machine pregnant with the universe—a portable heaven—a compendium of all things.’ After this period, we find no instances of such mechanism of any note till the 16th century, when science began to revive, and the arts to flourish. About this time the curious clock in Hampton Court Palace was constructed, which shows not only the hours of the day, but the motions of the sun and moon through all the signs of the zodiac, and other celestial phenomena. Another piece of mechanism of a similar kind is the clock in the cathedral of Strasburg, in which besides the clock part, is a celestial globe or sphere with the motions of the sun, moon, planets and the firmament of the fixed stars, which was finished in 1574.
Among the largest and most useful pieces of machinery of this kind, is the great sphere erected by Dr. Long in Pembroke Hall in Cambridge. This machine, which he called the Uranium, consists of a planetarium which exhibits the motion of the earth and the primary planets, the sun, and 519 the motion of the moon round the earth, all enclosed within a sphere. Upon the sphere, besides the principal circles of the celestial globe, the Zodiac is placed, of a breadth sufficient to contain the apparent path of the moon, with all the stars over which the moon can pass, also the ecliptic, and the heliocentric orbits of all the planets. The Earth in the planetarium has a moveable horizon, to which a large moveable brass circle within the sphere may be set coincident, representing the plane of the horizon continued to the starry heavens. The horizons being turned round sink below the stars on the east side, and make them appear to rise, and rise above the stars on the west side, and make them appear to set. On the other hand, the earth and the horizon being at rest, the sphere may be turned round to represent the apparent diurnal motion of the heavens. In order to complete his idea on a large scale, the Doctor erected a sphere of 18 feet diameter, in which above 30 persons might sit conveniently, the entrance to which is over the South Pole, by six steps. The frame of the sphere consists of a number of iron meridians, the northern ends of which are screwed to a large round plate of brass with a hole in the centre of it; through this hole, from a beam in the ceiling, comes the north pole, a round iron rod about three inches long, and which supports the upper part of the sphere, to its proper elevation for the latitude of Cambridge, so much of it as is invisible in England being cut off, and the lower or southern ends of the meridians terminate on, and are screwed down to a strong circle of oak 13 feet diameter, which, when the sphere is put in motion, runs upon large rollers of lignum vitæ, in the manner that the tops of some wind-mills turn round. Upon the iron meridians 520 is fixed a zodiac of tin painted blue, on which the ecliptic and heliocentric orbits of the planets are drawn and the stars and constellations traced. The whole is turned round with a small winch, with as little labour as it takes to wind up a Jack, although the weight of the iron, tin, and the wooden circle is above a thousand pounds. This machine, though now somewhat neglected, may still be seen in Pembroke Hall, Cambridge, where I had an opportunity of inspecting it in November, 1839. The essential parts of the machine still remain nearly in the same state as when originally constructed in 1758.
The machine which I shall now describe is of a much smaller and less complex description than that which has been noticed above, and may be made for a comparatively small expense, while it exhibits, with sufficient accuracy, the motions, phases, and positions of all the primary planets, with the exception of the new planets, which cannot be accurately represented on account of their orbits crossing each other. In order to the construction of the Planetarium to which I allude, we must compare the proportion which the annual revolutions of the primary planets bear to that of the Earth. This proportion is expressed in the following table, in which the first column is the time of the Earth’s period in days; the second, that of the planets; and the third and fourth are numbers very nearly in the same proportion to each other.
| 365¼ | : | 88 | :: | 83 | : | 20 | for Mercury. |
| 365¼ | : | 224⅔ | :: | 52 | : | 32 | for Venus. |
| 365¼ | : | 687 | :: | 40 | : | 75 | for Mars. |
| 365¼ | : | 4332½ | :: | 7 | : | 83 | for Jupiter. |
| 365¼ | : | 10759⅓ | :: | 5 | : | 148 | for Saturn. |
| 365¼ | : | 30686 | :: | 3 | : | 253 | for Uranus. |
figure 93.
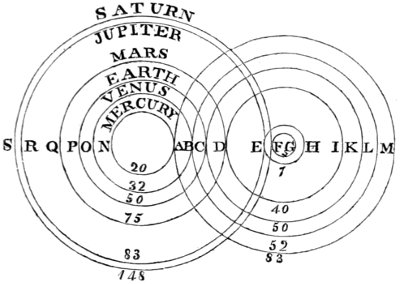
On account of the number of teeth required 521 for the wheel which moves Uranus, it is frequently omitted in Planetariums, or the planet is placed upon the arbor which supports Saturn. If we now suppose a spindle or arbor with six wheels fixed upon it in an horizontal position, having the number of teeth in each corresponding to the numbers in the third column, namely the wheel AM (fig. 93.) of 83 teeth, BL of 52, CK of 50, for the earth, DI of 40, EH of 7, and FG of 5; and another set of wheels moving freely about an arbor having the number of teeth in the fourth column, namely AN of 20, BO of 32, CP of 50—for the earth; DQ of 75, ER of 83, and FS of 148. Then, if these two arbors of fixed and moveable wheels be made of the size, and fixed at the distance here represented, the teeth of the former will take hold of those of the latter, and turn them freely when the machine is in motion. These arbors, with their wheels, are to be placed in a box of a proper size, in a perpendicular position; the arbor of fixed wheels to move in pivots at the top and bottom of the box, and the arbor 522 of the moveable wheels to go through the top of the box, and having on the top a wire fixed, and bent at a proper distance into a right angle upwards, bearing on the top a small round ball, representing its proper planet. If then, on the lower part of the arbor of fixed wheels, be placed a pinion of screw-teeth, a winch turning a spindle with an endless screw, playing in the teeth of the arbor, will turn it with all its wheels, and these wheels will turn the others about with their planets, in their proper and respective periods of time. For, while the fixed wheel CK moves its equal CP once round, the wheel AM will move AN a little more than four times round, and will consequently exhibit the motion of Mercury; the wheel EH will turn the wheel ER about 1/12 round, representing the proportional motion of Jupiter; and the wheel FG will turn the wheel FS, about 1/29.5 round, and represent the motion of Saturn, and so of all the rest.
figure 94.
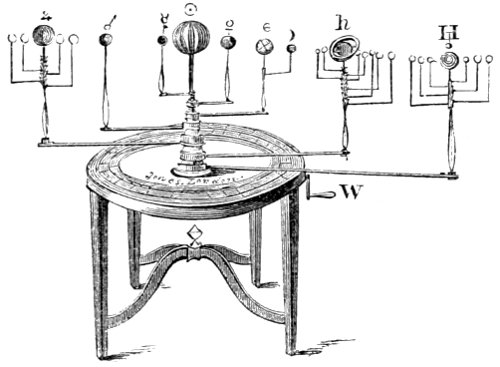
The following figure (fig. 94.) represents the 523 appearance of the instrument when completed. Upon the upper part of the circular box is pasted a Zodiac circle divided into 12 signs, and each sign into 30 degrees, with the corresponding days of the month. The wheel-work is understood to be within the box, which may either be supported by a tripod, or with four feet, as here represented. The moon, and the satellites of Jupiter, Saturn and Uranus, are moveable only by the hand. When the winch W is turned, then all the primary planets are made to move in their respective velocities. The ball in the centre represents the Sun, which is either made of brass or of wood gilded with gold.
By this Planetarium, simple as its construction may appear, a variety of interesting exhibitions may be made and problems performed, which may be conducive to the instruction of young students of astronomy. I shall mention only a few of those as specimens.
1. When the planets are placed in their respective positions by means of an Ephemeris or the Nautical Almanack, the relative positions of those bodies in respect to each other, the quarters of the heavens where they may be observed, and whether they are to be seen in the morning before sun-rise or in the evening after sun-set, may be at once determined. For example, on the 19th of December, 1844, the heliocentric places of the planets are as follows:—Uranus 2° Aries; Saturn 8° 27´ of Aquarius; Jupiter 7° 4´ Aries; Mars 12° 45´ Libra; the Earth 27° 46´ Gemini; Venus 29° 48´ Virgo; Mercury 7° 53´ Pisces. When the planets are placed on the planetarium in these positions, and the eye placed in a line with the balls representing the Earth and the Sun, all those situated to the left of the sun are to the east of 524 him, and are to be seen in the evening, and those on the right, in the morning. In the present case, Uranus, Saturn, Jupiter, and Mercury are evening stars, and Mars and Venus can only be seen in the morning. Jupiter is in an aspect nearly quartile, or 3 signs distant from the sun, and Uranus is nearly in the same aspect. Saturn is much nearer the sun, and Mercury is not far from the period of its greatest eastern elongation. Mars is not far from being in a quartile aspect, west of the sun, and Venus is near the same point of the heavens, approaching to the period of its greatest western elongation, and consequently will be seen before sun-rise as a beautiful morning star. Jupiter and Uranus, to the east of the sun, appear nearly directly opposite to Venus and Mars, which are to the west of the sun. The phase47 of Venus is nearly that of a half-moon, and Mercury is somewhat gibbous, approaching to a half-moon phase. If, now, we turn the machine by the winch till the Index of the earth point at the 8th of August, 1845, we shall find the planets in the following positions:—Mars and Saturn are nearly in opposition to the sun; Venus and Mercury are evening stars at no great distance from each other, and Jupiter is a morning star. In like manner if we turn the machine till the Index point to any future months, or even succeeding years, the various aspects and positions of the planets may be plainly perceived. When the planets are moved by the winch, in this machine, we see them all at once in motion around the sun, 525 with the same respective velocities and periods of revolution which they have in the heavens. As the planets are represented in the preceding positions, Mercury, Jupiter and Mars, are evening stars, and Venus, Saturn, and Uranus, morning stars, if we suppose the earth placed in a line with our eye and the sun.
2. By this instrument, the truth of the Copernican or Solar system is clearly represented. When the planets are in motion, we perceive the planets Venus and Mercury to pass both before and behind the sun, and to have two conjunctions. We observe Mercury to be never more than a certain angular distance from the sun, as viewed from the earth, namely 27°; and Venus 47°. We perceive that the superior planets, particularly Mars, will be sometimes much nearer to the earth than at others, and therefore must appear larger at one time than at another, as they actually appear in the heavens. We see that the planets cannot appear from the earth to move with uniform velocity; for when nearest they appear to move faster, and slower when most remote. We likewise observe that the planets appear from the 526 earth to move sometimes direct, or from west to east, then become retrograde, or from east to west, and between both to be stationary. All which particulars exactly correspond with celestial observations. For illustrating these particulars there is a simple apparatus represented by fig. 95, which consists of a hollow wire with a slit at top which is placed over the arm of Mercury or Venus at E. The arm DG represents a ray of light coming from the planet at D to the earth at F. The planets being then in motion, the planet D, as seen in the heavens from the earth at F, will undergo the several changes of position, which we have described above, sometimes appearing to go backwards and at other times forwards. The wire prop, now supposed to be placed over Mercury at E, may likewise be placed over any of the other planets, particularly Mars, and similar phenomena will be exhibited.
figure 95.
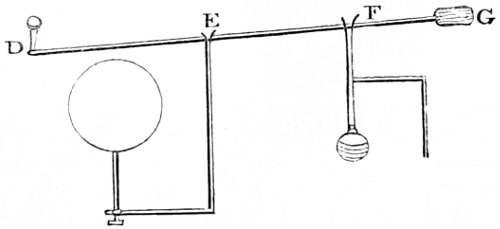
This machine may likewise be used to exhibit the falsity of the Ptolemaic system, which places the Earth in the centre, and supposes the sun and all the planets to revolve around it. For this purpose, the ball representing the Sun is removed, and placed on the wire or pillar which supports the Earth, and the ball representing the Earth is placed in the centre. It will then be observed, that the planets Mercury and Venus, being both within the orbit of the sun, cannot at any time be seen to go behind it, whereas, in the heavens we as often see them go behind as before the sun. Again, it shows that as the planets move in circular orbits about the central earth, they ought at all times to appear of the same magnitude; while, on the contrary, we observe their apparent magnitudes in the heavens to be very variable; Mars, for example, appearing sometimes nearly as large 527 as Jupiter, and at other times only like a small fixed star. Again, it is here shown that the planets may be seen at all distances from the sun; for example, when the sun is setting, Mercury and Venus, according to this arrangement, might be seen, not only in the south but even in the eastern quarter of the heavens—a phenomenon which was never yet observed in any age; Mercury never appearing beyond 27° of the Sun, nor Venus beyond 48°. In short, according to the system thus represented, it is seen, that the motions of the planets should all be regular, and uniformly the same in every part of their orbits, and that they should all move the same way, namely from west to east; whereas, in the heavens, they are seen to move with variable velocities, sometimes appearing stationary, and sometimes moving from east to west, and from west to east. All which circumstances plainly prove that the Ptolemaic cannot be the true system of the universe.
A Planetarium, such as that now described, might be constructed with brass wheel-work, for about 5 guineas. The brass wheel-work of one which I long since constructed cost about 3 guineas, and the other parts of the apparatus about 2 guineas more. The following are the prices of some instruments of this kind as made by Messrs. Jones, 30, Lower Holborn, London. ‘An Orrery, showing the motions of the Earth, Moon, and inferior planets, Mercury and Venus, by wheel-work, the board on which the instrument moves being 13 inches diameter, £4: 14s. 6d.’ ‘A Planetarium showing the motions of all the primary planets by wheel-work with 1½ inch or 3 inch papered globes,—according to the wheel-work and the neatness of the stands, from £7: 17s. 6d. to £10: 10s.’ ‘Ditto, with wheel-work to show the parallelism of the Earth’s axis, the motions of the Moon, her phases, &c., £18: 18s.’ ‘Ditto, with wheel-work, to show the earth’s diurnal motion, on a brass stand in mahogany case, £22: 1s.’ ‘A small Tellurian, showing the motion of the Earth and Moon, &c., £1: 8s.’ 528
The following is a description of the most complete and accurate planetarium I have yet seen. The calculations occupied more than eight months. For this article I am indebted to my learned and ingenious friend Dr. Henderson, F.R.A.S., who is known to many of my readers by his excellent astronomical writings.
figure 96.
Section of the wheel-work of a Planetarium for shewing with the utmost degree of accuracy the mean tropical revolutions of the planets round the sun, calculated by E. Henderson, LL.D. &c.
In the above section the dark horizontal lines represent the wheel-work of the Planetarium, and the annexed numerals, the numbers of teeth in the given wheel. The machine has three axes or arbors, indicated by the letters A, B, C.—Axis ‘C,’ the ‘Yearly axis,’ is assumed to make one revolution in 365.242,236 days, or, in 365 days 5h 48m 49.19s and is furnished with wheels 17, 529 44, 54, 36, 140, 96, 127, 86, which wheels are all firmly riveted to said axis, and consequently they turn round with it in the same time. Axle ‘B’ is a fixture; it consists of a steel rod, on which a system of pairs of wheels revolve; thus wheels 40 and 77 are made fast together by being riveted on the same collet represented by the thick dark space between them, as also of the rest: the several wheels on this axis may be written down thus; 40/77, 49/129, 20/94, 79/81, 30, 27/50, 41/65, 59/65, 96, 77/47, 67/42. On axis A a system of wheels, furnished with tubes revolve, and these tubes carry horizontal arms, supporting perpendicular stems with the planets. The wheels on this axis are 173, 117/190, 111, 119, 122/130, 123/127, 83, 239, 96, 128, 72. From the following short description the nature of their several actions will, it is presumed, be readily understood—viz.,
On the axis ‘C’ at the bottom is wheel 86, which turns round in 365 days 5h 48m 49.19s, this wheel impels a small wheel of 22 teeth, to which is made fast to wheel 67, both revolving together at the foot of axis B; wheel 67 drives a wheel of 72 once round in the period of 87 days, 23h 14m 36.1s: this last mentioned wheel has a long tube, which turns on the steel axis A, and carries a horizontal arm with the planet Mercury round the sun in the time above noted.
On axis ‘C’ is wheel 127, which drives wheel 47, to which is riveted a wheel of 77 teeth, which impels a wheel of 128 teeth on axis A, and 530 causes it to make a revolution in 224 days, 16h 41m 31.1s, and is furnished with a tube, which revolves over that of Mercury and ascends through the cover of the machine, and bears an arm on which is placed a small ball representing this planet in the time stated.
The motion of the earth round the sun is simply effected as follows—the assumed value of axis ‘C;’ the ‘Yearly axis’ is 365 days 5h 48m 49.19s; hence a system of wheels having the same numbers of teeth, or at all events, the first mover, and last wheel impelled must be equal in their numbers of teeth; in this machine three wheels are employed, thus; a wheel having 96 teeth is made fast to the Yearly axis C and of course moves round with it in a mean solar year, as above noted, this wheel impels another wheel of 96 teeth, on axis B, and this in its turns drives a third wheel of 96 teeth on axis A, and is furnished with a long tube which revolves over that of Venus, and ascends above the cover-plate of the machine, and bears a horizontal arm which supports a small terrestrial globe, which revolves by virtue of said wheels once round the sun in 365 days 5h 48m 49.19s.
The revolution of this planet is effected as follows—a wheel of 140 teeth is made fast to the yearly axis 531 C, and drives on axis B a wheel of 65 teeth, to which is fixed a wheel of 59 teeth, which impels a large wheel of 239 teeth on axis A once round the sun in 686 days 22h 18m 33.6s, this last-mentioned wheel is also furnished with a tube which revolves over that of the earth, and carries a horizontal arm bearing the ball representing Mars, and causes it to complete a revolution round the sun in the period named.
The period of Vesta is accomplished thus, viz. On the Yearly axis C, is made fast a wheel of 36 teeth, which drives a wheel of 65 teeth on axis B, to which is fixed a wheel of 41 teeth, which impels a wheel of 83 teeth on axis A, once round in 1336 days 0h 21m 19.8s: The tube of which last wheel ascends on that of Mars, and like the rest bears an arm supporting a ball representing this planet.
For the revolution of Juno, the yearly axis C is furnished with a wheel of 54 teeth, which impels a wheel of 50 teeth on axis B, to which is made fast a wheel of 27 teeth which turns a wheel of 127 teeth on axis A, once round in 1590 days 17h 35m 2.7s, and the tube of which ascends on that of Vesta, and supports a horizontal arm which carries a small ball representing this planet in the period named.
The revolution of Ceres is derived 532 from the period of Juno, because wheel-work taken from the unit of a solar year was not sufficiently accurate for the purpose, therefore on Juno’s wheel of 127 teeth is fixed a wheel of 123 teeth, which drives a thick little bevel sort of wheel of 30 teeth on axis B: the reason of this small wheel being bevelled is to allow its teeth to suit both wheels 123/130; wheel 30 drives wheel 130, on axis A once round in 1681 days, 6h 17m 22.4s and the tube of wheel 130 turns on the tube of Juno, and ascends in a similar manner with the rest and carries an horizontal arm supporting a small ball representing this planet, and is caused to revolve round the Sun in the above mentioned period (the period of Ceres to that of Juno is as 130 is to 123; hence the wheels used.)
The Period of Pallas could not be derived from the solar year with sufficient accuracy, and recourse was had to an engrafted fraction on the period of Ceres, thus. On wheel 130 of Ceres is made fast a wheel of 122 teeth, which drives a wheel of 81 teeth on axis B, to which is fixed a wheel 79 which impels a wheel of 119 teeth on axis A, and is furnished with a tube which ascends, and turns on that of Ceres, and supports a horizontal arm, which bears a small ball representing this planet, which by virtue of the above 533 train of wheels is caused to complete a revolution round the Sun in 1681d 10h 28m 25.1s.
The motion of this planet is derived from the period of a solar year; from the ‘yearly axis’ thus, on this axis is made fast a wheel of 44 teeth which turns a wheel of 94 teeth on axis B, to which is riveted a small wheel of 20 teeth, which impels a wheel on axis A having 111 teeth, which is furnished with an ascending tube which revolves over that of Pallas, and bears an horizontal arm which supports a ball representing this planet, which by the said train of wheels is caused to revolve round the Sun in 4330d 14h 39m 35.7s.
The periodic revolution of Saturn is also taken from the solar year—viz., a small wheel of 17 teeth is fixed to the ‘yearly axis’ near its top, and drives a wheel of 129 teeth on axis B, to which is made fast a wheel of 49 teeth, which turns a wheel of 190 teeth on axis A, whose tube ascends and revolves on that of Jupiter’s tube, and supports an arm, having a ball representing Saturn and its rings, and which by the train of wheels is caused to perform a revolution round the sun in the period of 10746d 19h 16m 50.9s.
URANUS’S PERIOD.
The revolution of this planet could not be attained with sufficient accuracy from the period of a solar 534 year—the period is engrafted on that of Saturn’s, thus, a wheel of 117 teeth is made fast to wheel 190 of Saturn, and consequently revolves in Saturn’s period. This wheel of 117 teeth drives a wheel on axis B, having 77 teeth, to which is fixed a wheel of 40 teeth, which turns on axis A, a large wheel of 173 teeth, whose tube ascends and revolves over that of Saturn, and carries a horizontal arm which supports a ball representing this planet, which is caused to complete its revolution by such a train of wheels in the period of 30589d 8h 26m 58.4s. Such is a brief description of the motions of this comprehensive and very accurate machine.
The axis A, on which the planetary tubular wheels revolve, performs a rotation in 25 days 10 hours, by virtue of the following train of wheels, 61/14 + 70/12 of 24 hours, that is, a pinion of 14 is assumed to revolve in 24 hours, and to drive a wheel of 61 teeth, to which is fixed a pinion of 12, which turns the wheel 70 in the period noted; to this wheel-axis, it is made fast, and by revolving with it, exhibits the Sun’s rotation.
The machine is turned by a handle or winch, which is assumed to turn round in 24 hours, and from this rotation of 24 hours a train of wheel-work is required to cause the ‘yearly axis’ C, to turn once round in 365d 5h 48m 49.19s, which is effected in the following manner—viz, the train found 535 by the process of the reduction of continuous fractions is 61/14 + 144/18 + 211/23 that is, in the train for turning the sun, the same pinion 14 turns the same wheel 61, and turns a pinion of 18 leaves, to which is fixed a wheel of 144 teeth, having a pinion of 23 leaves, which impels a large wheel of 241 teeth once round in 365.242236d or 365d 5h 48m 49.19s, this last-mentioned wheel of 241 teeth is made fast to the under part of the ‘yearly axis’ C at D, the handle having a pinion of 14 leaves therefore, and transmitting its motion through the above train, causes the yearly axis to revolve in the same period.
The planetarium is also furnished with a system of wheels for registrating dates for either 10,000 years past or to come, the arrangement is not shewn in the engraving (to prevent confusion) but it might be shortly described thus:—Near the top of the yearly axis is a hooked piece e, which causes the tooth of a wheel of 100 teeth to start forward yearly, consequently 100 starts of said wheel will cause it to revolve in 100 solar years, and it has a hand which points on a dial on the cover of the machine the years; thus for the present year this hand will be over the number 45. This last-named wheel of 100 teeth has a pin which causes a tooth of another wheel of 100 teeth to start once in 100 years, 536 hence this last wheel will complete one revolution in 10,000 years, and it is for this purpose the former index or hand moves over a number yearly. The second index will pass over a number every 100 years—for the present year the second hand or index will be over the number 18, and will continue over it until the first index moves forward to 99, then both indexes will move at one time, viz., the first index to 00 on the first concentric circle of the dial, and the second index to 19, denoting the year 1900, and so of the rest. By the ecliptic being divided in a series of four spirals, the machine makes a distinction between common and leap years, and indicates the common year as containing 365 days, and the leap-year 366 days, by taking in a day in February every fourth year; thus for any given period for 10,000 years past or to come, the various situations and aspects of the planets may be ascertained by operating with this machine, and this for thousands of years without producing a sensible error either in space or time. This planetarium wheel-work is enclosed in an elegant mahogany box of twelve sides—is about 5 feet in diameter by 10 inches in depth; at each of the twelve angles, or sides, small brass pillars rise and support a large Ecliptic circle on which are engraven 537 the signs, degrees and minutes of the Ecliptic—the days of the month, &c. This mahogany box with the wheel-work is supported by a tripod stand three feet in height, and motion is communicated to the several balls representing the planets by turning the handle as before described. A Planetarium of this complicated sort, costs sixty guineas.
The following is a tabular view of the wheel-work, periods, &c.
| Planets’ Names. | Wheel-work. | Tropical periods produced by the wheel-work. | True mean Tropical Periods of the Planets. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| da. | ho. | m. | s. | da. | ho. | m. | s. | ||||
| Mercury | " | 22/85 + 67/72 | of a Year | 87. | 23. | 14. | 36.1 | 87. | 23. | 14. | 36 |
| Venus | " | 47/127 + 128/77 | " | 224. | 16. | 41. | 31.1 | 224. | 16. | 41. | 36 |
| The Earth | Prime mover | 96 + 96 + 96 | " | 365. | 5. | 48. | 49.19 | 365. | 5. | 48. | 49 |
| Mars | " | 65/140 + 239/59 | " | 686. | 22. | 18. | 33.6 | 686. | 22. | 18. | 34 |
| Vesta | " | 65/36 + 83/41 | " | 1335. | 0. | 21. | 19.8 | 1335. | 0. | 21. | 20 |
| Juno | " | 50/54 + 127/27 | " | 1590. | 17. | 35. | 2.7 | 1590. | 17. | 35. | 1 |
| Ceres | " | 130/123 + 30 | of Juno | 1681. | 6. | 17. | 22.4 | 1681. | 6. | 17. | 29 |
| Pallas | " | 81/122 + 119/79 | of Ceres | 1681. | 10. | 28. | 25.1 | 1681. | 10. | 28. | 42 |
| Jupiter | " | 94/44 + 111/20 | of a Year | 4330. | 14. | 39. | 35.7 | 4330. | 14. | 39. | 32 |
| Saturn | " | 129/17 + 190/49 | " | 10746. | 19. | 16. | 50.9 | 10746. | 19. | 16. | 52 |
| Uranus | " | 77/117 + 173/40 | of Saturn | 30589. | 8. | 26. | 58.4 | 30589. | 8. | 26. | 59 |
| The Sun’s Rotation | 61/14 + 70/12 | of 24 ho. | 25. | 10. | 0. | 0 | 25. | 10. | 0. | 1 | |
| The tropical period of the Earth round the Sun. | 61/14 + 144/18 + 241/23 " | 365. | 5. | 48. | 49.19 | 365. | 5. | 48. | 49 | ||
538
In the month of October last year, Dr. Henderson made a series of calculations for a new Planetarium for the use of schools. It shows with considerable accuracy for 700 days, the mean tropical revolutions of the Planets round the sun—the machine consists of a system of brass wheels peculiarly arranged, and is enclosed in a circular case three feet in diameter, the top of which has the signs and degrees of the ecliptic laid down on it, as also the days of the months, &c. This Planetarium costs only 45s. or on a tripod stand, table-high, 55s.; the machine is put in motion by a handle on the outside. To the teachers and others connected with education this Planetarium must be of great importance, for without a proper elucidation of the principles of astronomy, that of Geography must be but confusedly understood. This Planetarium is at present made by Mr. Dollond, 9, White Conduit Grove, Islington, London.
The Tellurian is a small instrument which should be used in connection with the Planetarium formerly described. This instrument is intended to show the annual motion of the earth, and the revolution of the moon around it. It also illustrates the moon’s phases, and the motion of her nodes, the inclination of the Earth’s axis, the causes of eclipses, the variety of seams, and other phenomena. It consists of about eight wheels, pinions and circles. A small instrument of this description may be purchased for about one pound eight shillings, as stated in the note, page 527. 539
figure 97.

The striking and singular phenomenon connected with the planet Saturn—though now ascertained beyond dispute to be a Ring, or Rings, surrounding its body at a certain distance—was a subject of great mystery, and gave rise to numerous conjectures and controversies, for a considerable time after the invention of the telescope by which it was discovered. Though it was first discovered in the year 1610, it was nearly 50 years afterwards, before its true form and nature were determined. Galileo was the first who discovered 540 anything uncommon connected with Saturn: through his telescope he thought he saw that planet appear like two smaller globes on each side of a larger one; and after viewing the planet in this form for two years, he was surprised to see it becoming quite round, without its adjoining globes, and some time afterwards to appear in the triple form. This appearance is represented in fig. 1 of the above engraving. In the year 1614, Scheiner, a German astronomer, published a representation of Saturn, in which this planet is exhibited as a large central globe, with two smaller bodies, one on each side, partly of a conical form, attached to the planet and forming a part of it, as shown fig. 2. In the year 1640 and 1643, Ricciolus, an Italian mathematician and astronomer, imagined he saw Saturn as represented in fig. 3. consisting of a central globe, and two conical shaped bodies completely detached from it, and published an account of it corresponding to this view. Hevelius, the celebrated astronomer of Dantzig, author of the Selenographia and other works, made many observations on this planet about the years 1643, 1649 and 1650, in which he appears to have obtained different views of the planet and its appendages, gradually approximating to the truth, but still incorrect. These views are represented in figures 4, 5, 6, and 7. Fig. 4 nearly resembles two hemispheres, one on each side of the globe of Saturn. The other figures very nearly resemble the extreme parts of the ring as seen through a good telescope, but he still seems to have considered them as detached from each other as well as from Saturn. Figures 8 and 9 are views given by Ricciolus at a period posterior to that in which he supposed Saturn and his appendages in the form delineated 541 in fig. 3. In these last delineations the planet was supposed to be enclosed in an elliptical ring, but this ring was supposed to be fixed to its two opposite sides.
Fig. 10, is a representation by Eustachius Divini, a celebrated Italian optician at Bologna. The shades represented on Saturn and the elliptical curve are incorrect, as this planet presents no such shadowy form. The general appearance here presented is not much unlike that which the ring of Saturn exhibits, excepting that at the upper side the ring should appear covering a portion of the orb of Saturn. But Divini seems to have conceived that the curve on each side was attached to the body of Saturn. For when Huygens published his discovery of the ring of Saturn in 1659, Divini contested its truth, because he could not perceive the ring through his own telescopes; and he wrote a treatise on the subject in opposition to Huygens, in 1660, entitled ‘Brevis Annotatio in Systema Saturninum.’ Huygens immediately replied to him, and Divini wrote a rejoinder in 1661.—Fig. 11 is the representation given by Francis Fontana, a Neapolitan astronomer. This figure represents Saturn as having two crescents, one on each side, attached to its body, with intervals between the planet and the crescents. Fig. 12 is a view delineated by Gassendus, a celebrated French philosopher. It represents the planet as a large ellipsoid, having a large circular opening near each end, and, if this representation were the true one, each opening would be at least 30,000 miles in diameter. Fig. 13, which is perhaps the most singular of the whole, is said to be one of the view’s of this planet given by Ricciolus. It represents two globes—each of which, in the proportion they here bear to Saturn, must be more than 542 thirty thousand miles in diameter. These globes, were conceived as being attached to the body of Saturn by curves or bands, each of which, in the proportion represented, must have been at least 7000 miles in breadth, and nearly 40,000 miles long. This would have exhibited the planet Saturn as a still more singular body than what we have found it to be; but no such construction of a planet has yet been found in the universe, nor is it probable that such a form of a planetary body exists.
It is remarkable that only two general opinions should have been formed respecting the construction of Saturn—as appears from these representations—either that this planet was composed of three distinct parts, separate from each other,—or that the appendage on each side was fixed to the body of the planet. The idea of a ring surrounding the body of the planet, at a certain distance from every part of it, seems never to have been thought of till the celebrated Huygens, in 1655, 1656 and 1657, by numerous observations made on this planet, completely demonstrated that it is surrounded by a solid and permanent ring, which never changes its situation, and, without touching the body of the planet, accompanies it in its revolution around the sun. As the cause of all the erroneous opinions above stated was owing to the imperfection of the telescopes which were then in use, and their deficiency in magnifying power,—this ingenious astronomer set himself to work in order to improve telescopes for celestial observations. He improved the art of grinding and polishing object-glasses, which he finished with his own hands, and produced lenses of a more correct figure, and of a longer focal distance than what had previously been accomplished. He first constructed 543 a telescope 12 feet long, and afterwards one 23 feet long, which magnified about 95 times; whereas Galileo’s best telescope magnified only about 33 times. He afterwards constructed one 123 feet long, which magnified about 220 times. It was used without a tube, the object-glass being placed upon the top of a pole and connected by a cord with the eye-piece. With such telescopes this ingenious artist and mathematician discovered the fourth satellite of Saturn, and demonstrated that the phenomenon, which had been so egregiously misrepresented by preceding astronomers, consisted of an immense ring surrounding the body, and completely detached from it. His numerous observations and reasonings on this subject were published in Latin, in 1659, in a quarto volume of nearly 100 pages, entitled ‘Systema Saturnium, sive de causis mirandorum Saturni Phenomenôn, et Comite ejus Planeta Nova,’ from which work the figures and some of the facts stated above have been extracted.
From the period in which Huygens lived till the time when Herschel applied his large telescopes to the heavens, few discoveries were made in relation to Saturn. Cassini, in 1671, discovered the fifth satellite of this planet; in 1672, the third; and the first and second in March, 1684. In 1675, Cassini saw the broad side of its ring bisected quite round by a dark elliptical line, of which the inner part appeared brighter than the outer. In 1722, Mr. Hadley, with his 5 feet Newtonian Reflector observed the same phenomenon, and 544 perceived that the dark line was stronger next the body, and fainter towards the upper edge of the ring. Within the ring he also discovered two belts across the disk of Saturn. But it does not appear that they had any idea that this dark line was empty space separating the ring into two parts. This discovery was reserved for the late Sir W. Herschel, who made numerous observations on this planet, and likewise ascertained that the ring performs a revolution round the planet in ten hours and thirty minutes.
Of late years, some observers have supposed that the exterior ring of Saturn is divided into several parts, or, in other words, that it consists of two or more concentric rings. The following are some of the observations on which this opinion is founded. They are chiefly extracted from Captain Kater’s Paper on this subject, which was read before the Astronomical Society of London.
The observations, we are told, were made in the years 1825 and 1826, and remained unpublished, from a wish on the part of the observer to witness the appearances again. The planet Saturn has been much observed by Captain Kater, for the purpose of trying the light, &c., for which the ring and satellites are good tests. The instruments which were employed in the present investigations were two Newtonian Reflectors—one by Watson, of 40 inches focus and 6¼ aperture; and another by Dollond, of 68 inches focus, and 6¾ aperture. The first, under favourable circumstances, gave a most excellent image, the latter is a very good instrument. The following are extracts from the author’s journal.
Nov. 25, 1825.—The double ring beautifully defined, perfectly distinct all around, and the principal 545 belts well seen. I tried many concave glasses, and found that the image was much sharper than with convex eye-glasses, and the light apparently much greater. Dollond, 259, the best power, 480, a single lens, very distinct. Nov. 30, the night very favourable, but not equal to the 25th. The exterior ring of Saturn is not so bright as the interior, and the interior is less bright close to the edge next the planet. The inner edge appears more yellow than the rest of the ring, and nearer in colour to the body of the planet. Dec. 17.—The evening extremely fine. With Dollond, I perceived the outer ring of Saturn to be darker than the inner, and the division of the ring all around with perfect distinctness; but with Watson I fancied that I saw the outer ring separated by numerous dark divisions extremely close, one stronger than the rest, dividing the ring about equally. This was seen with my most perfect single eye-glass power. A careful examination of some hours confirmed this opinion.—Jan. 16 and 17, 1826.—Captain Kater believed that he saw the divisions with the Dollond, but was not positive. Concave eye-glasses found to be superior to convex. Feb. 26, 1826.—The division of the outer ring not seen with Dollond. On the 17th Dec., when the divisions were most distinctly seen, Captain Kater made a drawing of the appearance of Saturn and his rings. The phenomena were witnessed by two other persons on the same evening, one of whom saw several divisions in the outer ring, while the other saw one middle division only; but the latter person was short-sighted, and unaccustomed to telescopic observations. It may be remarked, however, that these divisions were not seen on other evenings, which yet were considered very favourable for distinct vision. 546
It is said that the same appearances were seen by Mr. Short, but the original record of his observations cannot be found. In Lalande’s Astronomy (3rd edition, article 3351,) it is said, ‘Cassini remarked that the breadth of the ring was divided into two equal parts by a dark line having the same curvature as the ring, and the exterior portion was the less bright. Short told me that he observed still more singular phenomena with his large telescope of 12 feet. The breadth of the ansæ, or extremities of the ring; was, according to him, divided into two parts,—an inner portion without any break in the illumination, and an outer divided by several lines concentric with the circumference; which would lead to a belief, that there are several rings in the same plane.’ De Lambre and Birt severally state that Short saw the outer ring divided, probably on the authority of Lalande. In Brewster’s Ferguson’s Astronomy, vol. ii, p. 125, 2nd edition, there is the following note on this subject. ‘Mr. Short assures us, that with an excellent telescope, he observed the surface of the ring divided by several dark concentric lines, which seem to indicate a number of rings proportional to the number of dark lines which he perceived.’
In Dec. 1813, at Paris, Professor Quetelet saw the outer ring divided with the achromatic telescope of 10 inches aperture, which was exhibited at the exposition. He mentioned this the following day to M. de la Place, who observed, that ‘those or even more divisions, were conformable to the system of the world.’ On the other hand the division of the outer ring was not seen by Sir W. Herschel in 1792, nor by Sir J. Herschel in 1826, nor by Struve in the same year; and on several occasions when the atmospheric conditions were 547 most favourable, it has not been seen by Captain Kater. It has been remarked by Sir W. Herschel, Struve and others, that the exterior ring is much less brilliant than the interior. And it is asked, may not this want of light in the outer ring arise from its having a very dense atmosphere? and may not this atmosphere in certain states admit of the divisions of the exterior ring being seen, though, under other circumstances, they remain invisible? The above observations are said to have been confirmed by some recent observations by Decuppis at Rome, who announced, some years ago, that Saturn’s outer ring is divided into two or three concentric rings.
Some of the observations stated above, were they perfectly correct, would lead to the conclusion that Saturn is encompassed with a number of rings, concentric with and parallel to each other. But while such phenomena as described above are so seldom seen, even by the most powerful telescopes and the most accurate observers, a certain degree of doubt must still hang over the subject; and we must suspend our opinion on this point, till future observations shall either confirm or render doubtful those to which we have referred. Should the Earl of Rosse’s great telescope, when finished for observation, be found to perform according to the expectations now entertained, and in proportion to its size and quantity of light, we shall expect that our doubts will be resolved in regard to the supposed divisions of the ring of Saturn. 548
This telescope, the largest and most magnificent that ever was attempted, reflects the greatest honour on the genius, the inventive powers, and the scientific acquirements of its noble contriver, as well as on the elevated station in which he is placed. With rank and fortune, and every circumstance that usually unfit men for scientific pursuit, he has set a bright example to his compeers of the dignity and utility of philosophical studies and investigations, and of the aids they might render to the progress of science, were their wealth and pursuits directed in a proper channel.
Previously to his Lordship’s attempting the construction of his largest—or ‘Monster Telescope,’ he had constructed one with a speculum of 3 feet in diameter, which was considered one of the most accurate and powerful instruments that had ever been made, not excepting even Sir W. 549 Herschel’s forty-feet Reflector. In the account of this telescope, published in the Philosophical Transactions for 1840, his Lordship speaks of the possibility of a speculum of six feet in diameter being cast. At that time, it was considered by some as little short of a chimera to attempt the construction of such a monstrous instrument. But the idea no sooner occurred to this ingenious and persevering nobleman than he determined to put it to the test, and the result has been attended with complete success. The materials of which this speculum is composed are copper and tin, united very nearly in their atomic proportions, namely, copper 126.4 parts, to tin 58.9 parts. This compound has a specific gravity of 8.8, and it is found to preserve its lustre with more splendor, and to be more free from pores than any other. A foundry was constructed expressly for the purpose of casting the speculum. Its chimney built from the ground was 18 feet high, and 16½ square at the base, tapering to four at the top. At each of its sides, communicating with it by flue, was sunk a furnace 8 feet deep, and 5½ square, with a circular opening 4 feet in diameter. About seven feet from the chimney was erected a large crane, with the necessary tackle for elevating and carrying the crucibles from the furnace to the mould, which was placed in a line with the chimney and crane, and had three iron baskets supported on pivots hung round it; and four feet farther on was the annealing oven. The crucibles which contained the metal were each 2 feet in diameter, 2½ deep, and together weighed one ton and a half; they were of cast iron and made to fit the baskets at the side of the mould. These baskets were hung on wooden uprights or pivots, to one of these on each side was attached a lever, 550 by depressing which it might be turned over, and the contents of the crucible poured into the mould. The bottom of the mould was made by binding together tightly layers of hoop-iron, and turning the required shape on them edgewise. This mould conducted the heat away through the bottom, and cooled the metal towards the top in infinitely small layers, while the interstices, though close enough to prevent the metal from escaping, were sufficiently open to allow the air to penetrate. This bottom was six feet in diameter and 5½ inches thick, and was made perfectly horizontal by means of spirit levels, and was surrounded by a wooden frame; a wooden pattern, the exact size of the speculum, being placed on the iron; sand was well packed between it and the frame, and the pattern was removed. Each of the crucibles containing the melted metal was then placed in its basket, and every thing being ready for discharging their contents, they were at the same instant turned over, and the mould being filled, the metal in a short time safely set into the required figure. Whilst it was red hot, and scarcely solid, the frame-work was removed, and an iron ring connected with a bar which passed through the oven, being placed round it, it was drawn in by means of a capstan at the other side, on a railroad, when charcoal being lighted in the oven, and turf fires underneath it, all the openings were built up, and it was left for sixteen weeks to anneal. It was cast on the 13th of April, 1842, at 9 o’clock in the evening. The crucibles were ten hours heating in the furnaces before the metal was introduced, which in about ten hours more was sufficiently fluid to be poured. When the oven was opened the speculum was found as perfect as when it entered it. It was then removed to the grinding 551 machine, where it underwent that process, and afterwards was polished, without any accident having occurred.
This speculum weighed three tons, and lost about one eighth of an inch in grinding. Lord Rosse has since cast another speculum of the same diameter four tons in weight. He can now, with perfect confidence, undertake any casting, so great an improvement has the form of mould which he has invented proved. The speculum was placed on an equilibrium bed, composed of nine pieces resting on points at their centres of gravity; the pieces were lined with pitch and felt, before the speculum was placed on them. The speculum box is also lined with felt and pitched; this prevents any sudden change of temperature affecting the speculum by means of the bad conducting power of the substances employed. A vessel of lime is kept in connection with the speculum-box to absorb the moisture, which otherwise might injure the mirror. The process of grinding was conducted under water, and the moving power employed was a steam-engine of three-horse power. The Polisher is connected with the machinery by means of a large ring of iron, which loosely encircles it; and instead of either the speculum or the polisher being stationary, both move with a regulated speed; the ring of the polisher, and therefore the polisher itself, has a transverse and a longitudinal motion; it makes 80 strokes in the minute, and 24½ strokes backward and forward for every revolution of the mirror, and at the same time 172/100 strokes in the transverse direction. The extent of the latter is 27/100 of the diameter of the speculum. The substance made use of to wear down the surface was emery and water, a constant supply of these was 552 kept between the grinder and the speculum. The Grinder is made of cast iron, with grooves cut lengthways, across and circularly on its face. The polisher and speculum have a mutual action upon each other; in a few hours, by the help of the emery and water, they are both ground truly circular, whatever may have been their previous defects. The grinding is continued till the required form of surface is produced; and this is ascertained in the following manner. There is a high tower over the house in which the speculum is ground, on the top of which is fixed a pole, to which is attached the dial of a watch; there are trap doors which open, and by means of a temporary eye-piece, allow the figure of the dial to be seen in the speculum brought to a slight polish. If the dots on the dial are not sufficiently well-defined, the grinding is continued; but if they appear satisfactorily, the polishing is commenced. It required six weeks to grind it to a fair surface. The polisher was cut into grooves, to prevent the abraded matter from accumulating in some places more than in others—a thin layer of pitch was spread over it, it was smeared over with rouge and water, and a supply of it kept up till the machinery brought it to a fine black polish. The length of time employed for polishing the 3 feet speculum was six hours.48
This large telescope is now completed, or nearly so. The tube is 56 feet long, including the speculum box, and is made of deal, one inch thick, hooped with iron. On the inside, at intervals of 553 8 feet, there are rings of iron 3 inches in depth and 1 inch broad, for the purpose of strengthening the sides. The diameter of the tube is 7 feet. It is fixed to mason-work, in the ground, to a large universal hinge which allows it to turn in all directions. At 12 feet distance, on each side, a wall is built, 72 feet long, 48 high on the outer side, and 56 on the inner—the walls being 24 feet distant from each other, and lying exactly in the meridional line. When directed to the south, the tube may be lowered till it become almost horizontal; but when pointed to the north, it only falls till it is parallel with the earth’s axis, pointing then to the pole of the heavens. Its lateral movements take place only from wall to wall, and this commands a view for half an hour on each side of the meridian—that is, the whole of its motion from east to west is limited to 15 degrees. At present it is fitted up in a temporary way to be used as a Transit instrument; but it is ultimately intended to connect with the tube-end galleries, machinery which shall give an automaton movement, so that the telescope shall be used as an Equatorial Instrument. All the works connected with this instrument are of the strongest and safest kind; all the iron-work was cast in his Lordship’s laboratory by men instructed by himself, and every part of the machinery was made under his own eye, by the artizans in his own neighbourhood, and not a single accident worth mentioning happened during the whole proceeding.
The expence incurred by his Lordship in the erection of this noble instrument was not less than twelve thousand pounds! besides the money expended in the construction of the telescope of three feet diameter. Sufficient time has not yet been 554 afforded for making particular observations with this telescope; but from slight trials which have been made, even under unfavourable circumstances, it promises important results. Its great superiority over every telescope previously constructed consists in the great quantity of light it reflects, and the brilliancy with which it exhibits objects even when high powers are applied. It has a reflecting surface of 4,071 square inches, while that of Herschel’s 40-feet telescope had only 1811 square inches on its polished surface, so that the quantity of light reflected from the speculum is considerably more than double that of Herschel’s largest reflector. This instrument has already exceeded his Lordship’s expectations. Many appearances before invisible in the Moon, have been perceived, and there is every reason to expect that new discoveries will be made by it in the Nebulæ, double and triple stars, and other celestial objects. The following is an extract of a communication from Sir James South, on this subject, addressed to the Editor of the ‘Times.’ ‘The leviathan telescope on which the Earl of Rosse has been toiling upwards of two years, although not absolutely finished, was on Wednesday last directed to the Sidereal Heavens. The letter which I have this morning received from its noble maker, in his usual unassuming stile, merely states, that the metal only just polished, was of a pretty good figure, and that with a power of 500, the nebula known as No. 2., of Messier’s catalogue, was even more magnificent than the nebula, No. 13 of Messier, when seen with his Lordship’s telescope of 3 feet diameter, and 27 feet focus. Cloudy weather prevented him from turning the leviathan on any other nebulous object. Thus, then, we have all danger of the metal breaking 555 before it could be polished, overcome. Little more, however, will be done with it for some time, as the Earl is on the eve of quitting Ireland for England to resign his post at York as President of the British Association. I look forward with intense anxiety to witness its first severe trial, when all its various appointments shall be completed, in the confidence that those who may then be present, will see with it what man has never seen before. The diameter of the large metal is 6-feet, and its focus 54 feet; yet the immense mass is manageable by one man. Compared with it, the working telescopes of Sir William Herschel, which in his hands conferred on astronomy such inestimable service, and on himself astronomical immortality, were but playthings.’
The following is a more recent account of observations made by this telescope, chiefly extracted from Sir James South’s description of this telescope, inserted in the Times of April 16th, 1845, and the ‘Illustrated London News’ of April 19.
‘The night of the 5th of March, 1845, was the finest I ever saw in Ireland. Many nebulæ were observed by Lord Rosse, Dr. Robinson and myself. Most of them were for the first time since their creation, seen by us as groups or clusters of stars; while some, at least to my eyes, showed no such resolution. Never, however, in my life did I see such glorious sidereal pictures as this instrument afforded us. Most of the nebulæ we saw I certainly have observed with my own large achromatic; but although that instrument, as far as relates to magnifying power, is probably inferior to no one in existence, yet to compare these nebulæ, as seen with it and the 6-feet telescope, is like comparing, as seen with the naked eye, the dinginess of the planet Saturn to the brilliancy 556 of Venus. The most popularly-known nebulæ observed this night were the ring nebulæ in the Canes Venatici, or the 51st of Messier’s catalogue, which was resolved into stars with a magnifying power of 548, and the 94th of Messier, which is in the same constellation, and which was resolved into a large globular cluster of stars, not much unlike the well-known cluster in Hercules, called also 13th Messier.’ Perfection of figure, however, of a telescope, must be tested, not by nebulæ, but by its performance on a star of the first magnitude. If it will, under high power, show the star round and free from optical appendages, we may safely take it for granted it will not only show nebulæ well, but any other celestial object as it ought. To determine this point, the telescope was directed to Regulus, with the entire aperture, and a power of 800, and ‘I saw’ says Sir James, ‘with inexpressible delight, the star free from wings, tails or optical appendages; not indeed like a planetary disk, as in my large achromatic, but as a round image resembling voltaic light between charcoal points; and so little aberration had this brilliant image, that I could have measured its distance from, and position with any of the stars in the field with a spider’s line micrometer, and a power of 1,000, without the slightest difficulty; for, not only was the large star round, but the telescope, although in the open air, and the wind blowing rather fresh, was as steady as a rock.’
‘On subsequent nights, observations of other nebulæ, amounting to some 30 or more, removed most of them from the list of nebulæ, where they had long figured, to that of clusters; while some of these latter, more especially 5 Messier, exhibited a sidereal picture in the telescope such as 557 man before had never seen, and which for its magnificence baffles all description. Several double stars were seen with various apertures of the telescope, and with powers between 360 and 800; and as the Earl had told us before we should,—before the speculum was inserted in the tube, in consequence of his having been obliged to quit the superintendence of the polishing at the most critical part of the process,—we found that a ring of about 6 inches broad, reckoning from the circumference of the speculum, was not perfectly polished, and to that the little irradiation seen about Regulus was unquestionably referable. The only double stars of the 1st class which the weather permitted us to examine with it were Xi Ursæ Majoris, and Gamma Virginis, which I could have measured with the greatest confidence. D’Arrest’s comet we observed on the 12th of March, with a power of 400, but nothing worthy of notice was detected. Of the Moon, a few words must suffice. Its appearance in my large achromatic of 12 inches aperture is known to hundreds of readers; let them then imagine that with it they look at the moon, whilst with Lord Rosse’s 6 feet they look into it, and they will not form a very erroneous opinion of the performance of the Leviathan. On the 15th of March, when the moon was 7 days old, I never saw her unilluminated disk so beautifully, nor her mountains so temptingly measurable. On my first looking into the telescope, a star of about the 7th magnitude was some minutes of a degree from the moon’s dark limb, and its occultation by the moon appeared inevitable. The star, however, instead of disappearing the moment the moon’s edge came in contact with it, apparently glided on the moon’s dark face, as if it had been seen through a transparent 558 moon, or as if the star were between me and the moon. It remained on the moon’s disk nearly two seconds of time, and then disappeared. I have seen this apparent projection of a star on the moon’s face several times, but from the great brilliancy of the star, this was the most beautiful I ever saw. The cause of this phenomenon is involved in impenetrable mystery.’
The following is a representation of the Great Rosse Telescope, along with part of the buildings with which it is connected. In the interior face of the eastern wall a very strong iron arc of about 43 feet radius is firmly fixed, provided with adjustments, whereby its surface facing the telescope may be set very accurately in the plane of the meridian. On this bar, lines are drawn, the interval between any adjoining two of which, corresponds to one minute of time on the Equator. The tube and speculum, including the bed on which the speculum rests, weigh about 15 tons. The telescope rests on an universal joint placed on masonry about 6 feet below the ground, and is elevated or depressed by a chain and windlass; and although it weighs about 15 tons, the instrument is raised by two men with great facility. Of course, it is counterpoised in every direction. The observer when at work, stands in one of four galleries, the three highest of which are drawn out from the western wall, while the fourth or lowest has for its base an elevating platform, along the horizontal surface of which a gallery slides from wall to wall by a machinery within the observer’s reach, but which a child may work. When the telescope is about half an hour east of the meridian, the galleries, hanging over the gap between the walls, present to a spectator below an appearance somewhat dangerous; yet the observer, with 559 common prudence, is as safe as on the ground, and each of the galleries can be drawn from the wall to the telescope’s side so readily, that the observer needs no one else to move it for him.
figure 98.

The above figure represents only the upper part of the tube of the telescope, at which the observer stands when making his observations. The telescope is at present of the Newtonian construction, and consequently, the observer looks into the side of the tube at the upper end of the telescope, but it is proposed to throw aside the plane speculum, and to adapt it to the Front view, on the plan already described (see pp. 306, 313, &c.) so that the observer will sit or stand with his back towards the object, and his face looking down upon the speculum; and, in this position, he will sometimes be elevated between 50 and 60 feet above the ground. As yet, the telescope has 560 no equatorial motion, but it very shortly will; and at no very distant day, clock-work will be connected with it, when the observer will, while observing, be almost as comfortable, as if he were reading at a desk by his fire-side.
figure 99.

The following figure shews a section of the machinery connected with this telescope. It exhibits a view of the inside of the eastern wall, with all the machinery as seen in section. A is the mason-work on the ground, B the universal joint, which allows the tube to turn in all directions; C the speculum in its tube; D the box; E the eye-piece; F the moveable pulley; G the fixed one; H the chain from the side of the tube; I the chain from the beam; K the counterpoise; L the lever; M the chain connecting it with the tube; Z the chain which passes from the tube to the windlass over a pulley on a truss-beam which runs from W to the same situation on the opposite wall—the pulley is not seen. X is a railroad on 561 which the speculum is drawn either to or from its box; part is cut away to show the counterpoise. The dotted line a represents the course of the weight R as the tube rises or falls; it is a segment of a circle of which the chain I is the radius. The tube is moved from wall to wall by the ratchet and wheel at R; the wheel is turned by the handle O, and the ratchet is fixed to the circle on the wall. The ladders in front, as shown in the preceding sketch, enable the observer to follow the tube in its ascent to where the galleries on the side wall commence; these side galleries are three in number, and each can be moved from wall to wall by the observer, after the tube, the motion of which he also accomplishes by means of the handle O.
I shall conclude the description of this wonderful instrument in the words of Sir James South.
‘What will be the power of this telescope when it has its Le Mairean form’ [that is, when it is fitted up with the front view] ‘it is not easy to divine;—what nebulæ will it resolve into stars; in what nebulæ will it not find stars;—how many satellites of Saturn will it show us;—how many will it indicate as appertaining to Uranus;—how many nebulæ never yet seen by mortal eye, will it present to us;—what spots will it show us on the various planets; will it tell us what causes the variable brightness of many of the fixed stars;—will it give us any information as to the constitution of the planetary nebulæ;—will it exhibit to us any satellites encircling them; will it tell us why the satellites of Jupiter, which generally pass over Jupiter’s face as disks nearly of white light, sometimes traverse it as black patches;—will it add to our knowledge of the physical construction of nebulous stars;—of that mysterious class of 562 bodies which surround some stars, called, for want of a better name, ‘photospheres;’—will it show the annular nebulæ of Lyra, merely as a brilliant luminous ring, or will it exhibit it as thousands of stars arranged in all the symmetry of an ellipse; will it enable us to comprehend the hitherto incomprehensible nature and origin of the light of the great nebulæ of Orion;—will it give us, in easily appreciable quantity, the parallax of some of the fixed stars, or will it make sensible to us the parallax of the nebulae themselves;—finally, having presented to us original portraits of the moon and of the sidereal heavens, such as man has never dared even to anticipate—will it, by Daguerreotype aid, administer to us copies founded upon truth, and enable astronomers of future ages to compare the moon and heavens as they then may be, with the moon and heavens as they were? Some of these questions will be answered affirmatively, others negatively, and that, too, very shortly; for the noble maker of the noblest instrument ever formed by man, “has cast his bread upon the waters, and will, with God’s blessing, find it before many days.”’ 563
As there are many among the lower ranks of the community who have a desire to be possessed of a telescope, which will show them some of the prominent features of celestial scenery, but who are unable to purchase a finished instrument at the prices usually charged by Opticians, the following hints may perhaps be acceptable to those who are possessed of a mechanical genius.
The lenses of an Achromatic telescope may be purchased separately from glass-grinders or Opticians, and tubes of a cheap material may be prepared by the individual himself for receiving the glasses. The following are the prices at which achromatic object-glasses for astronomical telescopes are generally sold. Focal length 30 inches, diameter 2¼ inches, from 2 to 3½ guineas. Focal length 42 inches, diameter 2¾ inches, from 5 to 8 guineas. Focal length 42 inches, diameter 3¼ inches, from 12 to 20 guineas. Focal length 42 inches, diameter 3¾ inches, from 25 to 30 guineas. Eye-pieces, from 10s. 6d. to 18 shillings. The smallest of these lenses, namely that of 2¼ inches diameter, if truly achromatic, may be made to bear a power of from 80 to 100 times, in clear weather, for celestial objects, which will show Jupiter’s moons and belts, Saturn’s ring and other celestial phenomena. The tubes may be made either of tin plates, papier maché, or wood. Wood, however, is rather a clumsy article, and it is sometimes liable to warp, yet excellent tubes have sometimes been made of it. Perhaps the cheapest and most convenient of all tubes when 564 properly made, are those formed of paper. In forming these a wooden roller of the proper diameter should be procured, and paper of a proper size, along with book-binder’s paste. About three or four layers only of the paper should be pasted at one time, and, when sufficiently dry, it should be smoothed by rubbing it with a smooth stick or ruler; after which another series of layers should be pasted on, and allowed to dry as before, and so on till the tube has acquired a sufficient degree of strength and firmness. In this way, I have, by means of a few old Newspapers, and similar materials, formed tubes as strong as if they had been made of wood. If several tubes be intended to slide into each other, the smallest tube should be made first, and it will serve as a roller for forming the tube into which it is to slide.
An achromatic object glass of a shorter focal distance, and a smaller diameter than any of those stated above, may be fitted up as a useful astronomical telescope, when a better instrument cannot be procured. In the Pawn-broker’s shops in London, and other places, an old achromatic telescope, with an object-glass 20 inches focal distance and about 1½ inch diameter, may be purchased at a price varying from 15 to 20 shillings. By applying an astronomical eye-piece to such a lens, if a good one, it may bear a power, for celestial objects, of 50 or 60 times. If two plano-convex glasses, ¾ inch focal distance, be placed with their convex sides near to each other, they will form an eye-piece which will produce a power on such an object-glass, of above 50 times, which will show Jupiter’s belts and satellites, Saturn’s ring, the solar spots, and the mountains and cavities of the moon. I have an object-glass of this description which belonged to an old telescope, 565 which cost me only 12 shillings, and with which I formerly made some useful astronomical observations. It was afterwards used as the telescope of a small Equatorial instrument, and, with it, I was enabled to perceive stars of the first and second magnitude, and the planets Venus, Jupiter, and Mars, in the day-time.
But, should such a glass be still beyond the reach of the astronomical amateur, let him not altogether despair. He may purchase a single lens, 3 feet focal distance, for about a couple of shillings, and by applying an eye-glass of 1 inch focus, which may be procured for a shilling, he will obtain a power of 36 times, which is a higher power than Galileo was able to apply to his best telescope; and consequently, with such an instrument, he will be enabled to perceive all the celestial objects which that celebrated astronomer first described, and which excited so much wonder, at that period, in the learned world. But, whatever kind of telescope may be used, it is essentially requisite that it be placed on a firm stand in all celestial observations: and any common mechanic can easily form such a stand at a trifling expence.
There is a certain optical illusion to which most persons are subject, in the first use of telescopes, especially when applied to the celestial bodies, on which it may not be improper to make a remark. The illusion to which I allude is this—that they are apt to imagine, the telescope does not magnify nearly so much as it really does. They are apt to complain of the small appearance which Jupiter and Saturn, for example, present when magnified 160 or 200 times. With such powers they are apt to imagine, that these bodies do not appear so large as the moon to the naked eye. Yet it can be proved that Jupiter, when nearest the earth, 566 viewed with such a power, appears about 5 times the diameter of the full moon, and 25 times larger in surface. This appears from the following calculation. Jupiter, when in opposition, or nearest the Earth, presents a diameter of 47´´: the mean apparent diameter of the moon is about 31´. Multiply the diameter of Jupiter by the magnifying power, 200, the product is 9400´´ or 156´ or 2° 36´, which, divided by 31´, the moon’s diameter, produces a quotient of 5, showing that this planet with such a power appears five times larger in diameter than the full moon to the naked eye, and consequently 25 times larger in surface. Were a power of only 50 times applied to Jupiter, when nearest the earth, that planet would appear somewhat larger than the full moon. For 47´´ multiplied by 50 gives 2350´´ or 39´, which is 8´ more than the diameter of the moon. Yet with such a power most persons would imagine that the planet does not appear one third of the size of the full moon.
The principal mode by which a person may be experimentally convinced of the fallacy to which I allude is the following:—At a time when Jupiter happens to be within a few degrees of the moon, let the planet be viewed through the telescope with the one eye, and the magnified image of the planet be brought into contact with the moon as seen with the other eye—the one eye looking at the moon, and the other viewing the magnified image of Jupiter through the telescope when brought into apparent contact with the moon—then it will be perceived, that with a magnifying power of 50 the image of Jupiter will completely cover the moon as seen by the naked eye;—and with a power of 200—when the moon is made to appear in the centre of the magnified image of the 567 planet—it will be seen that Jupiter forms a large and broad circle around the moon, appearing at least 5 times greater than the diameter of the moon. This experiment may be varied as follows: Suppose a person to view the moon through a small telescope or opera-glass, magnifying three times, he will be apt to imagine, at first sight, that she is not in the least magnified, but rather somewhat diminished. But let him bring the image as seen in the telescope in contact with the moon as seen with the naked eye, and he will plainly perceive the magnifying power, by the size of the image. It may be difficult in the first instance to look, at the same time, at the magnified image and the real object, but a few trials will render it easy.
THE END.
L. SEELEY PRINTER, THAMES DITTON. 568
Page 72 line 4 for EI, read FI.
—— 103 — 30 — depend, read depends.
—— 135 — 10 — refacting, read refracting.
—— 136 — 10 — colour, read colours.
—— 146 — 27 — G, read C.
—— 146 — 32 — prisms, read prism.
—— 153 — 35 — 28° 3´, read 28° 10´
—— 165 — 32 — some, read since.
—— 165 — 33 dele that.
—— 166 — 5 for these, read their.
—— 166 — 21 — those, read their.
—— 178 — 32 — variety, read vanity.
—— 187 — 7 — in, read an.
—— 187 — 11 — (p. 103.), read (p. 72.)
—— 189 — 30 — lens, read lenses.
—— 199 — 31 — punice, read pumice.
—— 216 — 10 — nine, read ten.
—— 236 — 12, 13 — “more distant from,” read “nearer to.”
—— 337 — 27 — 1, read 1½.
1 Those unfortunate individuals who have been confined in the darkest dungeons have declared, that though on their first entrance, no object could be perceived, perhaps for a day or two, yet, in the course of time, as the pupils of their eyes expanded, they could readily perceive mice, rats, and other animals that infested their cells, and likewise the walls of their apartments; which shows that, even in such situations, light is present, and produces a certain degree of influence.
2 Letters to a German Princess, vol. l. pp. 68, 69, &c.
3 The manner in which the motion of light was discovered is explained in the author’s work, entitled ‘Celestial Scenery,’ pp. 369-371, and the circumstances which led to the discovery of the aberration of light are stated and illustrated in his volume on the ‘Sidereal Heavens,’ pp. 71-74, and pp. 284-292.
4 Nicolson’s Introduction to Natural Philosophy, vol. 1.
5 Light of a phosphoric nature, is frequently emitted from various putrescent animal substances which, in the ages of superstition, served to astonish and affright the timorous. We learn from Fabricius, an Italian, that three young men, residing at Padua, having bought a lamb, and eaten part of it on Easter Day, 1592, several pieces of the remainder which they kept till the following day, shone like so many candles when they were casually viewed in the dark. The astonishment of the whole city was excited by this phenomenon, and a part of the flesh was sent to Fabricius, who was Professor of anatomy, to be examined by him. He observed, that those parts which were soft to the touch and transparent in candle-light, were the most resplendent: and also that some pieces of kid’s flesh which had happened to have lain in contact with them were luminous, as well as the fingers and other parts of the bodies of those persons who touched them. Bartholin gives an account of a similar phenomenon, which happened at Montpelier in 1641. A poor woman had bought a piece of flesh in the market, intending to make use of it the following day, but happening not to be able to sleep well that night, and her bed and pantry being in the same room, she observed so much light come from the flesh as to illuminate all the place where it hung. We may judge of the terror and astonishment of the woman herself, when we find that a part of this luminous flesh was carried as a very extraordinary curiosity to Henry, Duke of Conde, the Governor of the place, who viewed it several hours with the greatest astonishment. The light was as if gems had been scattered over the surface, and continued till the flesh began to putrify, when it vanished, which it was believed to do in the form of a cross. Hence the propriety of instructing the mass of the community in the knowledge of the facts connected with the material system, and the physical causes of the various phenomena of nature.
6 Memoires de la Soc. d’Aroncil, vol. ii.
7 By a medium, in optics, is meant the space in which a ray of light moves, whether pure space, air, water, glass, diamond, or any other transparent substance through which the rays of light can pass in straight lines.
8 Edinburgh Philosophical Journal for October 1819, p. 411.
9 This mode of finding the focus of a concave lens may be varied as follows:—let the lens be covered with paper, having two small circular holes; and on the paper for receiving the light, describe also two small circles, but with their centres at twice the distance from each other of the centres of the circles. Then move the paper to and from, till the middle of the sun’s light, coming through the holes, falls exactly on the middle of the circles; that distance of the paper from the lens will be the focal length required.
10 Small glass mirrors for performing some of the experiments, and illustrating some of the principles above alluded to,—may be made of the flattest kind of common watch glasses, by foliating or covering with tin leaf and quicksilver the convex surfaces of such glasses. Their focal distances will generally be from one to two inches. Such mirrors afford a very large and beautiful view of the eye, when held within their focal distance of that organ. Such mirrors will also serve the purpose of reflecting light on the objects viewed by microscopes. Larger mirrors, of from four to eight inches diameter, may be had of the optician at different prices varying from five to ten or fifteen shillings.
11 Nicholson’s Journal of Natural Philosophy, &c. 4to. series, p. 225.
12 There can be little doubt that some of the facts ascribed, in the western highlands of Scotland, to second sight, have been owing to the unusual refraction of the atmosphere; as one of the peculiarities attributed to those who possessed this faculty was, that they were enabled to descry boats and snips, before they appeared in the horizon.
13 Fraunhofer was in the highest sense of the word, an Optician, an original discoverer in the most abstruse and delicate departments of this science—a competent mathematician, an admirable mechanist, and a man of a truly philosophical turn of mind. By his extraordinary talents, he was soon raised from the lowest station in a manufacturing establishment to the direction of the optical department of the business, in which he originally laboured as an ordinary workman. He then applied the whole power of his mind to the perfection of the achromatic telescope, the defects of which in reference to the optical properties of the materials used—he attempted to remedy; and by a series of admirable experiments, succeeded in giving to optical determinations, the precision of astronomical observations, surpassing, in this respect all who had gone before him, except perhaps, the illustrious Newton. It was in the course of these researches, that he was led to the important discovery of the dark lines which occur in the solar spectrum. His achromatic telescopes are scattered over Europe, and are the largest and best that have hitherto been constructed. He died at Munich, at a premature age, in 1826; his death, it is said being accelerated by the unwholesome nature of the processes employed in his glass-house; leaving behind him a reputation rarely attained by one so young. His Memoir “On the refractive and dispersive power of different species of glass, in reference to the improvement of Achromatic telescopes, and an account of the lines on the spectrum,” will be found in the “Edinburgh Philosophical Journal,” Vol. ix. pp. 288-299, and Vol. x. pp. 26-40, for 1823-4.
14 Philosophical Transactions. Vol. 50. p. 294.
15 Ecclesiasticus xliii. 11, 12.
16 It is a question which has been frequently started—Whether there was any rainbow before the flood? Some have conceived that the rainbow was something of a miraculous production, and that it was never seen before the flood. The equivocal sense of the word ‘set’ in our translation, has occasioned a mistaken impression of this kind. The Hebrew word thus translated, signifies more properly ‘I do give,’ or ‘I appoint.’ The whole passage in reference to this circumstance, literally translated, runs thus;—“I appoint my bow which is in the cloud, that it may be for a sign or token of a covenant between me and the earth; and it shall come to pass when I bring a cloud over the earth, and the bow shall be seen in the cloud, that I will remember my covenant that is between me and you,” &c. As the rainbow is produced by the immutable laws of refraction and reflection, as applied to the rays of the sun striking on drops of falling rain, the phenomenon must have been occasionally exhibited from the beginning of the world: unless we suppose that there was no rain before the flood, and that the constitution of things in the physical system was very different from what it is now. The passage affirms no more than that the rainbow was then appointed to be a symbol of the covenant between God and man, and although it may have been frequently seen before, it would serve the purpose of a sign equally well, as if it had been miraculously formed for this purpose, and even better, as its frequent appearance, according to natural laws, is a perpetual memorial to man of the divine faithfulness and mercy.
17 Though Borellus mentions this circumstance, yet there is some reason to doubt the accuracy of this statement, as young Jansen appears to have been at that period, not more than six years old; so that it is more probable that Galileo was the first discoverer of Jupiter’s satellites.
18 The reader may see an engraving of this instrument in the author’s work entitled ‘the Improvement of Society.’—p. 209.
19 It is one of the properties of concave lenses to render convergent rays less convergent, and when placed as here supposed, to render them parallel; and it is parallel rays that produce distinct vision.
20 The word aperture as applied to object-glasses, signifies the opening to let in the light, or that part of the object-glass which is left uncovered. An object-glass may be 3 inches in diameter, but if one inch of this diameter be covered, its aperture is said to be only 2 inches.
21 An achromatic telescope is said to be in possession of Mr. Cooper, M.P. for Sligo, which is 26 feet long, and the diameter of the object glass 14 inches.
22 This telescope, which was made by Dollond, with a power of 240 times, gives a beautiful view of the belts of Jupiter and the double ring of Saturn, and with a power of 50, the stars in the milky way and some of the nebulæ appear very numerous and brilliant. Its owner is a gentleman who unites science with Christianity.
23 For a more particular account of Dr. Blair’s instruments and experiments, the reader is referred to his Dissertation on this subject in Vol. II. of the ‘Transactions of the Royal Society of Edinburgh,’ which occupies 76 pages—or to Nicholson’s ‘Journal of Natural Philosophy,’ &c. Quarto Series, Vol. I., April, September, 1797.
24 A more detailed account of the processes connected with the construction of this telescope, will be found in a paper presented to the Royal Society, in 1827, and published in the Philosophical Transactions of that Society, for 1828, and likewise another paper, published in the Transactions for 1829. From these documents, chiefly, the preceding account has been abridged. See also the ‘Edinburgh New Philosophical Journal’ for Jan.,—April, 1828, and Brewster’s ‘Edinburgh Journal of Science,’ for October, 1829.
25 A particular description of this telescope, with the machinery for moving it, illustrated with an engraving, may be seen in Reid and Gray’s ‘Abridgement of the Philosophical Transactions.’—Vol. vi. Part I. for 1723, pp. 147-152.
26 Miss Short, who has erected and who superintends an observatory on the Calton hill, Edinburgh, is the descendant of a brother of Mr. Short. She is in possession of a large Gregorian reflector, about 12 feet long, made by Mr. Short, and mounted on an Equatorial axis. It was originally placed in a small observatory erected on the Calton hill, about the year 1776, but for many years past it has been little used.
27 A particular account of the Earl of Rosse’s fifty-feet Reflector, which is now finished, is given in the Appendix.
28 Philosophical Transactions for 1800, Vol. XC. p. 80, &c.
29 In using telescopes within doors, care should generally be taken, that there be no fires in the apartment where they are placed for observation, and that the air within be nearly of the same temperature as the air of the surrounding atmosphere; for if the room be filled with heated air, when the windows are opened, there will be a current of cold air rushing in, and of heated air rushing out, which will produce such an undulation and tremulous motion, as will prevent any celestial object from being distinctly seen.
30 The above directions and remarks are abridged with some alterations from Dr. Pearson’s “Introduction to Practical Astronomy.”—Vol. II.
31 Pearson’s “Practical Astronomy.”—Vol. II.
32 The mother-of-pearl dynameter may be purchased for about twelve shillings. See fig. 57, a, b, c, p. 260.
33 Reid’s Enquiry into the Human Mind, chap. iv.
34 The distance of Saturn from the sun is 906,000,000 of miles; it is sometimes nearer to and at other times farther from the earth, according as it is near the point of its opposition to, or conjunction with the sun. If this number be divided by 200, the supposed magnifying power of the telescope, the quotient is 4,530,000, which expresses the distance in miles at which it enables us to contemplate this planet. If this number be subtracted from 906,000,000, the remainder is 901,470,000, which expresses the number of miles from the earth at which we are supposed to view Saturn with such an instrument.
35 Irish Transactions, Vol. X. and Nicholson’s Philosophical Journal, Vol. XVI.
36 Brewster’s Appendix to ‘Ferguson’s Lectures.’
37 A particular description of the micrometers here enumerated, and several others, will be found in Dr. Pearson’s ‘Introduction to Practical Astronomy,’ Vol. II.
38 Adams’ Introduction to Practical Astronomy.
39 Or find the sun’s right ascension for the given day; substract this from the star or planet’s right ascension, and the remainder is the approximate time of the star’s coming to the meridian. The difference between this time and the time of observation, will then determine the point to which the telescope is to be directed.
40 The right ascensions, declinations, longitudes, &c., stated in these memoranda—which were noted at the time of observation—are only approximations to the truth; perfect accuracy in these respects being of no importance in such observations. They are, however, in general, within a minute or two of the truth. The times of the observations, too, are noted in reference—not to the astronomical, but to the civil day. The astronomical day commences at 12 noon, and the hours are reckoned, without interruption, to the following noon. The civil day commences at 12 midnight.
41 This observation is inserted in the ‘Edinburgh Philosophical Journal’ for January, 1844.
42 The late Mr. Benjamin Martin, when describing the nature of the solar telescope, in his ‘Philosophia Britannica,’ Vol. iii. p. 85, gives the following relation:—‘I cannot here omit to mention a very unusual phenomenon that I observed about ten years ago in my darkened room. The window looked towards the west, and the spire of Chichester Cathedral was before it at the distance of 50 or 60 yards. I used very often to divert myself by observing the pleasant manner in which the sun passed behind the spire, and was eclipsed by it for sometime; for the image of the sun and of the spire were very large, being made by a lens of 12 feet focal distance. And once as I observed the occultation of the sun behind the spire, just as the disk disappeared, I saw several small, bright, round bodies or balls running toward the sun from the dark part of the room, even to the distance of 20 inches. I observed their motion was a little irregular, but rectilinear, and seemed accelerated as they approached the sun. These luminous globules appeared also on the other side of the spire, and preceded the sun, running out into the dark room, sometimes more, sometimes less, together in the same manner as they followed the sun at its occultation. They appeared to be in general one-twentieth of an inch in diameter, and therefore, must be very large luminous globes in some part of the heavens, whose light was extinguished by that of the sun, so that they appeared not in open day light; but whether of the meteor kind, or what sort of bodies they might be, I could not conjecture.’ Professor Hansteen mentions, that when employed in measuring the zenith distances of the pole star, he observed a somewhat similar phenomenon, which he described as ‘a luminous body which passed over the field of the universal telescope—that its motion was neither perfectly equal nor rectilinear, but resembled very much the unequal and somewhat serpentine motion of an ascending rocket;’ and he concluded that it must have been ‘a meteor’ or ‘shooting star’ descending from the higher regions of the atmosphere.43
In my frequent observations on Venus, to determine the nearest positions to the sun in which that planet could be seen, I had several times an opportunity of witnessing similar phenomena. I was not a little surprised, when searching for the planet, frequently to perceive a body pass across the field of the telescope, apparently of the same size as Venus, though sometimes larger and sometimes smaller, so that I frequently mistook that body for the planet, till its rapid motion undeceived me. In several instances four or five of these bodies appeared to cross the field of view, sometimes in a perpendicular, and, at other times in a horizontal direction. They appeared to be luminous bodies, somewhat resembling the appearance of a planet when viewed in the day-time with a moderate magnifying power. Their motion was nearly rectilinear, but sometimes inclined to a waving or serpentine form, and they appeared to move with considerable rapidity—the telescope being furnished with a power of about 70 times. I was for a considerable time at a loss what opinion to form of the nature of these bodies; but having occasion to continue these observations almost every clear day for nearly a twelvemonth, I had frequent opportunities of viewing this phenomenon in different aspects; and was at length enabled to form an opinion as to the cause of at least some of the appearances which presented themselves. In several instances, the bodies alluded to appeared much larger than usual, and to move with a more rapid velocity; in which case I could plainly perceive that they were nothing else than birds of different sizes, and apparently at different distances, the convex surfaces of whose bodies, in certain positions, strongly reflected the solar rays. In other instances, when they appeared smaller, their true shape was undistinguishable by reason of their motion and their distance.
Having inserted a few remarks on this subject, in No. XXV. of the Edinburgh Philosophical Journal for July, 1825, particularly in reference to Professor Hansteen’s opinion, that article came under the review of M. Serres, Sub-Prefect of Embrun, in a paper inserted in the Annales de Chemie, for October, 1825, entitled, ‘Notices regarding fiery meteors seen during the day.’44 In the discussion of this subject, M. Serres admits that the light reflected very obliquely from the feathers of a bird is capable of producing an effect similar to that which I have now described; but that ‘the explanation ought not to be generalized.’ He remarks, that, while observing the sun at the repeating circle, he frequently perceived, even through the coloured glass adapted to the eye-piece, large luminous points which traversed the field of the telescope, and which appeared too well defined not to admit them to be distant, and subtended too large angles to imagine them birds. In illustration of this subject he states the following facts. On the 7th September, 1820, after having observed for some time the eclipse of the sun which happened on that day, he intended to take a walk in the fields, and on crossing the town, he saw a numerous group of individuals of every age and sex, who had their eyes fixed in the direction of the sun. Further on, he perceived another group having their eyes in like manner turned towards the sun. He questioned an intelligent artist who was among them to learn the object that fixed his attention. He replied, ‘We are looking at the stars which are detaching themselves from the sun.’ ‘You may look yourself; that will be the shortest way to learn the fact.’ He looked, and saw, in fact, not stars, but balls of fire of a diameter equal to the largest stars, which were projected in various directions from the upper hemisphere of the sun, with an incalculable velocity, and although this velocity of projection appeared the same in all, yet they did not all attain the same distance. These globes were projected at unequal and pretty short intervals. Several were often projected at once, but always diverging from one another. Some of them described a right line, and were extinguished in the distance; some described a parabolic line, and were in like manner extinguished; others again, after having removed to a certain distance in a right line, retrograded upon the same line, and seemed to enter, still luminous, into the sun’s disk. The ground of this magnificent picture was a sky blue, somewhat tinged with brown. Such was his astonishment at the sight of so majestic a spectacle, that it was impossible for him to keep his eyes off it till it ceased, which happened gradually as the eclipse wore off and the solar rays resumed their ordinary lustre. It was remarked by one of the crowd that ‘the sun projected most stars at the time when it was palest;’ and that the circumstance which first excited attention to this phenomenon was that of a woman who cried out ‘Come here!—come and see the flames that are issuing from the sun!’
I have stated the above facts because they may afterwards tend to throw light upon certain objects or phenomena with which we are at present unacquainted. The phenomenon of ‘falling stars’ has of late years excited considerable attention, and it seems now to be admitted, that, at least, certain species of these bodies descend from regions far beyond the limits of our atmosphere. This may be pronounced as certain with regard to the ‘November Meteors.’ May not some of the phenomena described above, be connected with the fall of meteoric stones—the showers of falling stars seen on the 12th and 13th of November, or other meteoric phenomena whose causes we have hitherto been unable to explain? Or, may we conceive that certain celestial bodies, with whose nature and destination we are as yet unacquainted, may be revolving in different courses in the regions around us—some of them opaque and others luminous, and whose light is undistinguishable by reason of the solar effulgence?
43 See Edinburgh Philosophical Journal, for April, 1825. No. XXIV.
44 See Edinburgh Philosophical Journal, for July, 1826, p. 114.
45 For an explanation of the manner of viewing Venus at her superior conjunction, see ‘Celestial Scenery,’ 5th thousand, p. 102.
46 See Long’s Astronomy, vol. 2, p. 487,—and Encyclopedia Britannica, vol. ii. p. 436, 3rd edition.
47 The balls which represent the different planets, on this machine, have their hemispheres painted black, with the white side turned directly to the sun, so that if the eye be placed in a line with the earth, and the planet, particularly Mercury and Venus, its phase in the heavens, at that time, as viewed with a telescope, may be distinctly perceived.
48 The above description has been selected and abridged from a small volume entitled ‘The Monster Telescope, erected by the Earl of Rosse, Parsontown,’—and also from the ‘Illustrated London News’ of September 9th, 1843. In the volume alluded to a more particular description will be found, accompanied with engravings.
The corrections listed in the Errata list have been made.
The high resolution image for the image on page 196 does not have a caption. I have captioned this image as "figure 40" and the one on page 206 as "figure 40*" to comply with the "List of Engravings".
Inconsistent double quotes and capitalization are as in the original.
Inconsistent spelling and hyphenation are as in the original.