
Title: Encyclopaedia Britannica, 11th Edition, "McKinley, William" to "Magnetism, Terrestrial"
Author: Various
Release date: June 29, 2013 [eBook #43060]
Most recently updated: October 23, 2024
Language: English
Credits: Produced by Marius Masi, Don Kretz and the Online
Distributed Proofreading Team at http://www.pgdp.net
| Transcriber’s note: |
A few typographical errors have been corrected. They
appear in the text like this, and the
explanation will appear when the mouse pointer is moved over the marked
passage. Sections in Greek will yield a transliteration
when the pointer is moved over them, and words using diacritic characters in the
Latin Extended Additional block, which may not display in some fonts or browsers, will
display an unaccented version. Links to other EB articles: Links to articles residing in other EB volumes will be made available when the respective volumes are introduced online. |
Articles in This Slice

McKINLEY, WILLIAM (1843-1901), twenty-fifth president of the United States, was born in Niles, Trumbull county, Ohio, on the 29th of January 1843. His ancestors on the paternal side were Scotch-Irish who lived at Dervock, Co. Antrim, and spelled the family name “McKinlay.” His great-great-grandfather settled in York county, Pennsylvania, about 1743, and from Chester county, Pennsylvania, his great-grandfather, David McKinley, who served as a private during the War of Independence, moved to Ohio in 1814. David’s son James had gone in 1809 to Columbiana county, Ohio. His son William McKinley (b. 1807), like his father an iron manufacturer, was married in 1829 to Nancy Campbell Allison, and to them were born nine children, of whom William, the president, was the seventh. In 1852 the family removed to Poland, Mahoning county, where the younger William was placed at school. At seventeen he entered the junior class of Allegheny College, at Meadville, Pennsylvania; but he studied beyond his strength, and returned to Poland, where for a time he taught in a neighbouring country school. When the Civil War broke out in 1861 he promptly enlisted as a private in the 23rd Ohio Volunteer Infantry. He saw service in West Virginia, at South Mountain, where this regiment lost heavily, and at Antietam, where he brought up hot coffee and provisions to the fighting line; for this he was promoted second lieutenant on the 24th of September 1862. McKinley was promoted first lieutenant in February 1864, and for his services at Winchester was promoted captain on the 25th of July 1864. He was on the staff of General George Crook at the battles of Opequan, Fisher’s Hill, and Cedar Creek in the Shenandoah valley, and on the 14th of March 1865 was brevetted major of volunteers for gallant and meritorious services. He also served on the staff of General Rutherford B. Hayes, who spoke highly of his soldierly qualities. He was mustered out with his regiment on the 26th of July 1865. Four years of army life had changed him from a pale and sickly lad into a man of superb figure and health.
After the war McKinley returned to Poland, and bent all his energy upon the study of law. He completed his preparatory reading at the Albany (N.Y.) law school, and was admitted to the bar at Warren, Ohio, in March 1867. On the advice of an elder sister, who had been for several years a teacher in Canton, Stark county, Ohio, he began his law practice in that place, which was to be his permanent home. He identified himself immediately with the Republican party, campaigned in the Democratic county of Stark in favour of negro suffrage in 1867, and took part in the campaign work on behalf of Grant’s presidential candidature in 1868. In the following year he was elected prosecuting attorney on the Republican ticket; in 1871 he failed of re-election by 45 votes, and again devoted himself to his profession, while not relaxing his interest in politics.
In 1875 he first became known as an able campaign speaker by his speeches favouring the resumption of specie payments, and in behalf of Rutherford B. Hayes, the Republican candidate for governor of Ohio. In 1876 he was elected by a majority of 3304 to the national House of Representatives. Conditions both in Ohio and in Congress had placed him, and were to keep him for twenty years, in an attitude of aggressive and uncompromising partisanship. His Congressional district was naturally Democratic, and its boundaries were changed two or three times by Democratic legislatures for the purpose of so grouping Democratic strongholds as to cause his defeat. But he overcame what had threatened to be adverse majorities on all occasions from 1876 to 1890, with the single exception of 1882, when, although he received a certificate of election showing that he had been re-elected by a majority of 8, and although he served nearly through the long session of 1883-1884, his seat was contested and taken (May 28, 1884) by his Democratic opponent, Jonathan H. Wallace. McKinley reflected the strong sentiment of his manufacturing constituency in behalf of a high protective tariff, and he soon became known in Congress (where he particularly attracted the attention of James G. Blaine) as one of the most diligent students of industrial policy and question affecting national taxation. In 1878 he took part in the debates over the Wood Tariff Bill, proposing lower import duties; and in the same year he voted for the Bland-Allison Silver Bill. In December 1880 he was appointed a member of the Ways and Means committee, succeeding General James A. Garfield, who had been elected president in the preceding month, and to whose friendship, as to that of Rutherford B. Hayes, McKinley owed much in his earlier years in Congress. He was prominent in the debate which resulted in the defeat of the Democratic Morrison Tariff Bill in 1884, and, as minority leader of the Ways and Means committee, in the defeat of the Mills Bill for the revision of the tariff in 1887-1888. In 1889 he became chairman of the Ways and Means committee and Republican leader in the House of Representatives, after having been defeated by Thomas B. Reed on the third ballot in the Republican caucus for speaker of the House. On the 16th of April 1890 he introduced from the Ways and Means committee the tariff measure known commonly as the McKinley Bill, which passed the House on the 21st of May, passed the Senate (in an amended form, with a reciprocity clause, which McKinley had not been able to get through the House) on the 10th of September, was passed as amended, by the House, and was approved by the president on the 1st of October 1890. The McKinley Bill reduced revenues by its high and in many cases almost prohibitive duties; it 257 put sugar on the free list with a discriminating duty of 1⁄10th of one cent a pound on sugar imported from countries giving a bounty for sugar exported, and it gave bounties to American sugar growers; it attempted to protect many “infant” industries such as the manufacture of tin-plate; under its provision for reciprocal trade agreements (a favourite project of James G. Blaine, who opposed many of the “protective” features of the Bill) reciprocity treaties were made with Germany, France, Italy, and Belgium, which secured a market in those countries for American pork. Abroad, where the Bill made McKinley’s name known everywhere, there was bitter opposition to it and reprisals were threatened by several European states. In the United States the McKinley Tariff Bill was one of the main causes of the Democratic victory in the Congressional elections of 1890, in which McKinley himself was defeated by an extraordinary Democratic gerrymander of his Congressional district. In November 1891 he was elected governor of Ohio with a plurality of more than 21,000 votes in a total of 795,000 votes cast. He was governor of Ohio in 1892-1895, being re-elected in 1893. His administration was marked by no important events, except that he had on several occasions in his second term to call out the militia of the state to preserve order; but it may be considered important because of the training it gave him in executive as distinguished from legislative work.
McKinley had been prominent in national politics even before the passage of the tariff measure bearing his name. In 1888 in the National Republican Convention in Chicago he was chairman of the committee on resolutions (i.e. the platform committee) and was leader of the delegation from Ohio, which had been instructed for John Sherman; after James G. Blaine withdrew his name there was a movement, begun by Republican congressmen, to nominate McKinley, who received 16 votes on the seventh ballot, but passionately refused to be a candidate, considering that his acquiescence would be a breach of faith toward Sherman. In 1892 McKinley was the permanent president of the National Republican Convention which met in Minneapolis and which renominated Benjamin Harrison on the first ballot, on which James G. Blaine received 1825⁄6 votes, and McKinley, in spite of his efforts to the contrary, received 182 votes. In 1894 he made an extended campaign tour before the Congressional elections, and spoke even in the South. In 1896 he seemed for many reasons the most “available” candidate of his party for the presidency: he had no personal enemies in the party; he had carried the crucial state of Ohio by a large majority in 1893; his attitude on the coinage question had never been so pronounced as to make him unpopular either with the radical silver wing or with the conservative “gold-standard” members of the party. The campaign for his nomination was conducted with the greatest adroitness by his friend, Marcus A. Hanna, and in the National Republican Convention held in St Louis in June he was nominated for the presidency on the first ballot by 6611⁄2 out of a total of 906 votes. The convention adopted a tariff plank drafted by McKinley, and, of far greater immediate importance, a plank, which declared that the Republican party was “opposed to the free coinage of silver, except by international agreement with the leading commercial nations of the world, which we pledge ourselves to promote, and until such agreement can be obtained the existing gold standard must be preserved.” This “gold standard” plank drove out of the Republican party the Silver Republicans of the West, headed by Senator Henry M. Teller of Colorado. The Republican convention nominated for the vice-presidency Garrett A. Hobart of New Jersey. The National Democratic Convention declared for the immediate opening of the mints to the free and unlimited coinage of silver at the ratio with gold of 16 to 1; and it nominated for the presidency William Jennings Bryan of Nebraska, who also received the nomination of the People’s party and of the National Silver party. There was a secession from the Democratic party of conservatives who called themselves the National Democratic party, who were commonly called Gold Democrats, and who nominated John M. Palmer (1817-1900) of Illinois for president. In this re-alignment of parties McKinley, who had expected to make the campaign on the issue of a high protective tariff, was diverted to the defence of the gold standard as the main issue. While his opponent travelled throughout the country making speeches, McKinley remained in Canton, where he was visited by and addressed many Republican delegations. The campaign was enthusiastic: the Republican candidate was called the “advance agent of prosperity”; “Bill McKinley and the McKinley Bill” became a campaign cry; the panic of 1893 was charged to the repeal of the McKinley tariff measure; and “business men” throughout the states were enlisted in the cause of “sound money” to support McKinley, who was elected in November by a popular vote of 7,106,779 to 6,502,925 for Bryan, and by an electoral vote of 271 to 176.
McKinley was inaugurated president of the United States on the 4th of March 1897. The members of his cabinet were: secretary of state, John Sherman (whose appointment created a vacancy in the Senate to which Marcus A. Hanna was elected), who was succeeded in April 1898 by William R. Day, who in turn was followed in September 1898 by John Hay; secretary of the treasury, Lyman J. Gage, a Gold Democrat; secretary of war, Russell A. Alger, who was succeeded in 1899 by Elihu Root; secretary of the navy, John D. Long; attorney-general, Joseph McKenna, succeeded in January 1898 by John William Griggs; postmaster-general, James A. Gary, succeeded in April 1898 by Charles Emory Smith; secretary of the interior, Cornelius N. Bliss, succeeded in February 1899 by Ethan Allen Hitchcock; and secretary of agriculture, James Wilson. (For the political history of McKinley’s administration see United States: History). Immediately after his inauguration the president summoned Congress to assemble in an extra session on the 15th of March. The Democratic tariff in 1893 had been enacted as part of the general revenue measure, which included an income-tax. The income-tax having been declared unconstitutional by the Supreme Court, the measure had failed to produce a sufficient revenue, and it had been necessary to increase the public debt. McKinley’s message to the new Congress dwelt upon the necessity of an immediate revision of the tariff and revenue system of the country, and the so-called Dingley Tariff Bill was accordingly passed through both houses, and was approved by the president on the 24th of July.
The regular session of Congress which opened in December was occupied chiefly with the situation in Cuba. President McKinley showed himself singularly patient and self-controlled in the midst of the popular excitement against Spain and the clamour for intervention by the United States in behalf of the Cubans; but finally, on the 23rd of March, he presented an ultimatum to the Spanish government, and on the 25th of April, on his recommendation. Congress declared war upon Spain. During the war itself he devoted himself with great energy to the mastery of military details; but there was bitter criticism of the war department resulting in the resignation of the secretary of war, Russell A. Alger (q.v.). The signing of a peace protocol on the 12th of August was followed by the signature at Paris on the 10th of December of articles of peace between the United States and Spain. After a long discussion the peace treaty was ratified by the United States Senate on the 6th of February 1899; and in accordance with its terms Porto Rico, the Philippine Archipelago, and Guam were transferred by Spain to the United States, and Cuba came under American jurisdiction pending the establishment there of an independent government. Two days before the ratification of the peace treaty, a conflict took place between armed Filipinos under the leadership of Emilio Aguinaldo and the American forces that were in possession of Manila. The six months that had elapsed between the signing of the peace protocol and the ratification of the treaty had constituted a virtual interregnum, Spain’s authority having been practically destroyed in the Philippines and that of the United States 258 not having begun. In this period a formidable native Filipino army had been organized and a provisional government created. The warfare waged by these Filipinos against the United States, while having for the most part a desultory and guerilla character, was of a very protracted and troublesome nature. Sovereignty over the Filipinos having been accepted by virtue of the ratification of the Paris treaty, President McKinley was not at liberty to do otherwise than assert the authority of the United States and use every endeavour to suppress the insurrection. But there was bitter protest against this “imperialism,” both within the party by such men as Senators George F. Hoar and Eugene Hale, and Thomas B. Reed and Carl Schurz, and, often for purely political reasons, from the leaders of the Democratic party. In the foreign relations of the United States, as directed by President McKinley, the most significant change was the cordial understanding established with the British government, to which much was contributed by his secretary of state, John Hay, appointed to that portfolio when he was ambassador to the court of St James, and which was due to some extent to the friendliness of the British press and even more markedly of the British navy in the Pacific during the Spanish War. Other important foreign events during McKinley’s administration were: the annexation of the Hawaiian Islands (see Hawaii) in August 1898, and the formation of the Territory of Hawaii in April 1900; the cessation in 1899 of the tripartite (German, British, and French) government of the Samoan Islands, and the annexation by the United States of those of the islands east of 171°, including the harbour of Pago-Pago; the participation of American troops in the march of the allies on Pekin in August 1900, and the part played by McKinley’s secretary of state, John Hay, in securing a guarantee of the integrity of the Chinese empire. In 1900 McKinley was unanimously renominated by the National Republican Convention which met in Philadelphia on the 19th of June, and which nominated Theodore Roosevelt, governor of New York, for the vice-presidency. The Republican convention demanded the maintenance of the gold standard, and pointed to the fulfilment of some of the most important of the pledges given by the Republican party four years earlier. The intervening period had been one of very exceptional prosperity in the United States, foreign commerce having reached an unprecedented volume, and agriculture and manufactures having made greater advancement than in any previous period of the country’s history. The tendency towards the concentration of capital in great industrial corporations had been active to an extent previously undreamt of, with incidental consequences that had aroused much apprehension; and the Democrats accused President McKinley and the Republican party of having fostered the “trusts.” But the campaign against McKinley and the Republican party was not only “anti-trust” but “anti-imperialistic.” William Jennings Bryan, renominated by the Democratic party in July (and in May by the Fusion People’s party) on a free silver platform, declared that imperialism was the “paramount issue” and made a second vigorous campaign; and the opposition to McKinley’s re-election, whether based on opposition to his economic or to his foreign policy, was not entirely outside of his own party. As the result of the polling in November, 292 Republican presidential electors were chosen, and 155 Democratic electors, elected in Colorado, Idaho, Montana, Nevada, and the Southern states, represented the final strength of the Bryan and Stevenson ticket. The Republican popular vote was 7,207,923, and the Democratic 6,358,133. Since 1872 no president had been re-elected for a second consecutive term.
In the term of Congress immediately following the presidential election it was found possible to reduce materially the war taxes which had been levied on the outbreak of the Spanish-American War. Arrangements were perfected for the termination of the American military occupation of Cuba and the inauguration of a Cuban Republic as a virtual protectorate of the United States, the American government having arranged with the Cuban constitutional convention for the retention of certain naval stations on the Cuban coast. In the Philippines advanced steps had been taken in the substitution of civil government for military occupation, and a governor-general, Judge William H. Taft, had been appointed and sent to Manila. Prosperity at home was great, and foreign relations were free from complications. The problems which had devolved upon McKinley’s administration had been far advanced towards final settlement. He retained without change the cabinet of his first administration. After an arduous and anxious term, the president had reached a period that promised to give him comparative repose and freedom from care. He had secured, through the co-operation of Congress, the permanent reorganization of the army and a very considerable development of the navy. In these circumstances. President McKinley, accompanied by the greater part of his cabinet, set forth in the early summer on a tour to visit the Pacific coast, where he was to witness the launching of the battleship “Ohio” at San Francisco. The route chosen was through the Southern states, where many stops were made, and where the president delivered brief addresses. The heartiness of the welcome accorded him seemed to mark the disappearance of the last vestige of sectional feeling that had survived the Civil War, in which McKinley had participated as a young man. After his return he spent a month in a visit at his old home in Canton, Ohio, and at the end of this visit, by previous arrangement, he visited the city of Buffalo, New York, in order to attend the Pan-American exposition and deliver a public address. This address (Sept. 5, 1901) was a public utterance designed by McKinley to affect American opinion and public policy, and apparently to show that he had modified his views upon the tariff. It declared that henceforth the progress of the nations must be through harmony and co-operation, in view of the fast-changing conditions of communication and trade, and it maintained that the time had come for wide-reaching modifications in the tariff policy of the United States, the method preferred by McKinley being that of commercial reciprocity arrangements with various nations. On the following day, the 6th of September 1901, a great reception was held for President McKinley in one of the public buildings of the exposition, all sorts and conditions of men being welcome. Advantage of this opportunity was taken by a young man of Polish parentage, by name Leon Czolgosz, to shoot at the president with a revolver at close range. One of the two bullets fired penetrated the abdomen. After the world had been assured that the patient was doing well and would recover, he collapsed and died on the 14th. The assassin, who, it was for a time supposed, had been inflamed by the editorials and cartoons of the demagogic opposition press, but who professed to hold the views of that branch of anarchists who believe in the assassination of rulers and persons exercising political authority, was promptly seized, and was convicted and executed in October 1901. McKinley’s conduct and utterances in his last days revealed a loftiness of personal character that everywhere elicited admiration and praise. Immediately after his death Vice-President Roosevelt took the oath of office, announcing that it would be his purpose to continue McKinley’s policy, while also retaining the cabinet and the principal officers of the government. McKinley’s funeral took place at Canton, Ohio, on the 19th of September, the occasion being remarkable for the public manifestations of mourning, not only in the United States, but in Great Britain and other countries; in Canton a memorial tomb has been erected.
Though he had not the personal magnetism of James G. Blaine, whom he succeeded as a leader of the Republican party and whose views of reciprocity he formally adopted in his last public address, McKinley had great personal suavity and dignity, and was thoroughly well liked by his party colleagues. As a politician he was always more the people’s representative than their leader, and that he “kept his ear to the ground” was the source of much of his power and at the same time was his greatest weakness: his address at Buffalo the day before his assassination seems to voice his appreciation of the change 259 in popular sentiment regarding the tariff laws of the United States and is the more remarkable as coming from the foremost champion for years of a form of tariff legislation devised to stifle international competition. His apparently inconsistent record on the coinage question becomes consistent if considered in the same way, as the expression of the gradually changing views of his constituency. And it may not be fanciful to suggest that the obvious growth of McKinley in breadth and power during his term as president was due to his being the representative of a larger constituency, less local and less narrow-minded. He was an able but far from brilliant campaign speaker. His greatest administrative gift was a fine intuition in choosing men to serve him. McKinley’s private life was irreproachable; and very fine was his devotion to his wife, Ida Saxton (d. 1907), whom he had married in Canton in 1871, who was throughout his political career a confirmed invalid. He was from his early manhood a prominent member of the Methodist Episcopal Church.
His Speeches and Addresses were printed in two volumes (New York, 1893 and 1901).

McKINNEY, a city and the county-seat of Collin county, Texas, U.S.A., about 30 m. N. by E. of Dallas. Pop. (1890), 2489; (1900), 4342 (917 negroes); (1910) 4714. It is served by the Missouri, Kansas & Texas and the Houston & Texas Central railways, and by the Dallas & Sherman inter-urban (electric) line, the central power plant of which is immediately north of the city. McKinney is in a fine farming region; there are also manufactures. The municipal water supply is obtained from artesian wells. The first settlement in Collin county was made about 10 m. north of what is now McKinney in 1841. McKinney was named, as was the county, in honour of Collin McKinney, a pioneer in the region and a signer of the Declaration of the Independence of Texas. It was settled in 1844, was laid out and became the county-seat in 1846, and was first chartered as a city in 1874.

MACKINTOSH, SIR JAMES (1765-1832), Scottish publicist, was born at Aldourie, 7 m. from Inverness, on the 24th of October 1765. He came of old Highland families on both sides. He went in 1780 to college at Aberdeen, where he made a friend of Robert Hall, afterwards the famous preacher. In 1784 he proceeded for the study of medicine to Edinburgh, where he participated to the full in the intellectual ferment, but did not quite neglect his medical studies, and took his degree in 1787.
In 1788 Mackintosh removed to London, then agitated by the trial of Warren Hastings and the king’s first lapse into insanity. He was much more interested in these and other political events than in his professional prospects; and his attention was specially directed to the events and tendencies which caused or preceded the Revolution in France. In 1789 he married his first wife, Catherine Stuart, whose brother Daniel afterwards became editor of the Morning Post. His wife’s prudence was a corrective to his own unpractical temperament, and his efforts in journalism became fairly profitable. Mackintosh was soon absorbed in the question of the time; and in April 1791, after long meditation, he published his Vindiciae Gallicae, a reply to Burke’s Reflections on the French Revolution. It was the only worthy answer to Burke that appeared. It placed the author in the front rank of European publicists, and won him the friendship of some of the most distinguished men of the time, including Burke himself. The success of the Vindiciae finally decided him to give up the medical for the legal profession. He was called to the bar in 1795, and gained a considerable reputation there as well as a tolerable practice. In 1797 his wife died, and next year he married Catherine Allen, sister-in-law of Josiah and John Wedgwood, through whom he introduced Coleridge to the Morning Post. As a lawyer his greatest public efforts were his lectures (1799) at Lincoln’s Inn on the law of nature and nations, of which the introductory discourse was published, and his eloquent defence (1803) of Jean Gabriel Peltier, a French refugee, tried at the instance of the French government for a libel against the first consul. In 1803 he was knighted, and received the post of recorder at Bombay. The spoilt child of London society was not at home in India, and he was glad to return to England, where he arrived in 1812.
He courteously declined the offer of Perceval to resume political life under the auspices of the dominant Tory party, though tempting prospects of office in connexion with India were opened up. He entered parliament in the Whig interest as member for Nairn. He sat for that county, and afterwards for Knaresborough, till his death. In London society, and in Paris during his occasional visits, he was a recognized favourite for his genial wisdom and his great conversational power. On Mme de Stael’s visit to London he was the only Englishman capable of representing his country in talk with her. His parliamentary career was marked by the same wide and candid liberalism as his private life. He opposed the reactionary measures of the Tory government, supported and afterwards succeeded Romilly in his efforts for reforming the criminal code, and took a leading part both in Catholic emancipation and in the Reform Bill. But he was too little of a partisan, too widely sympathetic and candid, as well as too elaborate, to be a telling speaker in parliament, and was consequently surpassed by more practical men whose powers were incomparably inferior. From 1818 to 1824 he was professor of law and general politics in the East India Company’s College at Haileybury.
In the midst of the attractions of London society and of his parliamentary avocations Mackintosh felt that the real work of his life was being neglected. His great ambition was to write a history of England. His studies both in English and foreign speculation led him to cherish the design also of making some worthy contribution to philosophy. It was not till 1828 that he set about the first task of his literary ambition. This was the Dissertation on the Progress of Ethical Philosophy, prefixed to the seventh edition of the Encyclopaedia Britannica. The dissertation, written mostly in ill-health and in snatches of time taken from his parliamentary engagements, was published in 1831. It was severely attacked in 1835 by James Mill in his Fragment on Mackintosh. About the same time he wrote for the Cabinet Cyclopaedia a “History of England from the Earliest Times to the Final Establishment of the Reformation.” His more elaborate History of the Revolution, for which he had made great researches and collections, was not published till after his death. Already a privy councillor, Mackintosh was appointed commissioner for the affairs of India under the Whig administration of 1830. He died on the 30th of May 1832.
Mackintosh was undoubtedly one of the most cultured and catholic-minded men of his time. His studies and sympathies embraced almost every human interest, except pure science. But the width of his intellectual sympathies, joined to a constitutional indecision and vis inertiae, prevented him from doing more enduring work. Vindiciae Gallicae was the verdict of a philosophic Liberal on the development of the French Revolution up to the spring of 1791, and though the excesses of the revolutionists compelled him a few years after to express his entire agreement with the opinions of Burke, its defence of the “rights of man” is a valuable statement of the cultured Whig’s point of view at the time. The History of the Revolution in England, breaking off at the point where William of Orange is preparing to intervene in the affairs of England, is chiefly interesting because of Macaulay’s admiring essay on it and its author.
A Life, by his son R. J. Mackintosh, was published in 1836.

MACKLIN, CHARLES (c. 1699-1797), Irish actor and playwright, whose real name was McLaughlin, was born in Ireland, and had an adventurous youth before coming to Bristol, where he made his first appearance on the stage as Richmond in Richard III. He was at Lincoln’s Inn Fields about 1725, and by 1733 was at Drury Lane, where the quarrel between the manager and the principal actors resulted in his getting better parts. When the trouble was over and these were taken from 260 him, he went to the Haymarket, but he returned in 1734 to Drury Lane and acted there almost continuously until 1748. Then for two seasons he and his wife (d. c. 1758), an excellent actress, were in Dublin under Sheridan, then back in London at Covent Garden. He played a great number of characters, principally in comedy, although Shylock was his greatest part, and Iago and the Ghost in Hamlet were in his repertory. At the end of 1753 Macklin bade farewell to the stage to open a tavern, near the theatre, where he personally supervised the serving of dinner. He also delivered an evening lecture, followed by a debate, which was soon a hopeless subject of ridicule. The tavern failed, and Macklin returned to the stage, and played for a number of years in London and Dublin. His quick temper got him into constant trouble. In a foolish quarrel over a wig in 1735 he killed a fellow actor in the green-room at Drury Lane, and he was constantly at law over his various contracts and quarrels. The bitterest of these arose on account of his appearing as Macbeth at Covent Garden in 1772. The part was usually played there by William Smith, and the public would not brook a change. A few nights later the audience refused to hear Macklin as Shylock, and shouted their wish, in response to the manager’s question, to have him discharged. This was done in order to quell the riot. His lawsuit, well conducted by himself, against the leaders of the disturbance resulted in an award of £600 and costs, but Macklin magnanimously elected instead that the defendants should take £100 in tickets at three benefits—for himself, his daughter and the management. He returned to Covent Garden, but his appearances thereafter were less frequent, ending in 1789, when as Shylock, at his benefit, he was only able to begin the play, apologize for his wandering memory, and retire. He lived until the 11th of July 1797, and his last years were provided for by a subscription edition of two of his best plays, The Man of the World and Love in a Maze. Macklin’s daughter, Mary Macklin (c. 1734-1781), was a well-known actress in her day.
See Edward A. Parry, Charles Macklin (1891).

MACK VON LEIBERICH, KARL, Freiherr (1752-1828), Austrian soldier, was born at Nenslingen, in Bavaria, on the 25th of August 1752. In 1770 he joined an Austrian cavalry regiment, in which his uncle, Leiberich, was a squadron commander, becoming an officer seven years later. During the brief war of the Bavarian Succession he was selected for service on the staff of Count Kinsky, under whom, and subsequently under the commander-in-chief Field Marshal Count Lacy, he did excellent work. He was promoted first lieutenant in 1778, and captain on the quartermaster-general’s staff in 1783. Count Lacy, then the foremost soldier of the Austrian army, had the highest opinion of his young assistant. In 1785 Mack married Katherine Gabrieul, and was ennobled under the name of Mack von Leiberich. In the Turkish war he was employed on the headquarter staff, becoming in 1788 major and personal aide-de-camp to the emperor, and in 1789 lieutenant-colonel. He distinguished himself greatly in the storming of Belgrade. Shortly after this, disagreements between Mack and Loudon, now commander-in-chief, led to the former’s demanding a court-martial and leaving the front. He was, however, given a colonelcy (1789) and the order of Maria Theresa, and in 1790 Loudon and Mack, having become reconciled, were again on the field together. During these campaigns Mack received a severe injury to his head, from which he never fully recovered. In 1793 he was made quartermaster-general (chief of staff) to Prince Josias of Saxe-Coburg, commanding in the Netherlands; and he enhanced his reputation by the ensuing campaign. The young Archduke Charles, who won his own first laurels in the action of the 1st of March 1793, wrote after the battle, “Above all we have to thank Colonel Mack for these successes.” Mack distinguished himself again on the field of Neerwinden; and had a leading part in the negotiations between Coburg and Dumouriez. He continued to serve as quartermaster-general, and was now made titular chief (Inhaber) of a cuirassier regiment. He received a wound at Famars, but in 1794 was once more engaged, having at last been made a major-general. But the failure of the allies, due though it was to political and military factors and ideas, over which Mack had no control, was ascribed to him, as their successes of March-April 1793 had been, and he fell into disfavour in consequence. In 1797 he was promoted lieutenant field marshal, and in the following year he accepted, at the personal request of the emperor, the command of the Neapolitan army. But with the unpromising material of his new command he could do nothing against the French revolutionary troops, and before long, being in actual danger of being murdered by his men, he took refuge in the French camp. He was promised a free pass to his own country, but Napoleon ordered that he should be sent to France as a prisoner of war. Two years later he escaped from Paris in disguise. The allegation that he broke his parole is false. He was not employed for some years, but in 1804, when the war party in the Austrian court needed a general to oppose the peace policy of the Archduke Charles, Mack was made quartermaster-general of the army, with instructions to prepare for a war with France. He did all that was possible within the available time to reform the army, and on the opening of the war of 1805 he was made quartermaster-general to the titular commander-in-chief in Germany, the Archduke Ferdinand. He was the real responsible commander of the army which opposed Napoleon in Bavaria, but his position was ill-defined and his authority treated with slight respect by the other general officers. For the events of the Ulm campaign and an estimate of Mack’s responsibility for the disaster, see Napoleonic Campaigns. After Austerlitz, Mack was tried by a court-martial, sitting from February 1806 to June 1807, and sentenced to be deprived of his rank, his regiment, and the order of Maria Theresa, and to be imprisoned for two years. He was released in 1808, and in 1819, when the ultimate victory of the allies had obliterated the memory of earlier disasters, he was, at the request of Prince Schwarzenberg, reinstated in the army as lieutenant field marshal and a member of the order of Maria Theresa. He died on the 22nd of October 1828 at S. Pölten.
See Schweigerd, Oesterreichs Helden (Vienna, 1854); Würzbach, Biogr. Lexikon d. Kaiserthums Oesterr. (Vienna, 1867); Ritter von Rittersberg, Biogr. d. ausgezeichneten Feldherren d. oest. Armee (Prague, 1828); Raumer’s Hist. Taschenbuch (1873) contains Mack’s vindication. A short critical memoir will be found in Streffleur for January 1907.

McLANE, LOUIS (1786-1857), American political leader, was born in Smyrna, Delaware, on the 28th of May 1786, son of Allan McLane (1746-1829), a well-known Revolutionary soldier. He was admitted to the bar in 1807. He entered politics as a Democrat, and served in the Federal House of Representatives in 1817-1827 and in the Senate in 1827-1829. He was minister to England in 1829-1831, and secretary of the treasury in Jackson’s cabinet from 1831 (when in his annual report he argued for the United States Bank) until May 1833, when he was transferred to the state department. He retired from the cabinet in June 1834. He was president of the Baltimore & Ohio railway in 1837-1847, minister to England in 1845-1846, and delegate to the Maryland constitutional convention of 1850-1851. He died in Baltimore, Maryland, on the 7th of October 1857.
His son, Robert Milligan McLane (1815-1898), graduated at West Point in 1837, resigned from the army in 1843, and practised law in Baltimore. He was a Democratic representative in Congress in 1847-1851 and again in 1879-1883, governor of Maryland in 1884-1885, U.S. commissioner to China in 1853-1854, and minister to Mexico in 1859-1860 and to France in 1885-1889.
See R. M. McLane’s Reminiscences, 1827-1897 (privately printed, 1897).

MACLAREN, CHARLES (1782-1866), Scottish editor, was born at Ormiston, Haddingtonshire, on the 7th of October 1782, the son of a farmer and cattle-dealer. He was almost entirely self-educated, and when a young man became a clerk in Edinburgh. In 1817, with others, he established the Scotsman newspaper in Edinburgh and at first acted as its editor. Offered a post as clerk in the custom house, he resigned his editorial 261 position, resuming it in 1820, and resigning it again in 1845. In 1820 Maclaren was made editor of the sixth edition of the Encyclopaedia Britannica. From 1864-1866 he was president of the Geological Society of Edinburgh, in which city he died on the 10th of September 1866.

MACLAREN, IAN, the pseudonym of John Watson (1850-1907), Scottish author and divine. The son of John Watson, a civil servant, he was born at Manningtree, Essex, on the 3rd of November 1850, and was educated at Stirling and at Edinburgh University, afterwards studying theology at New College, Edinburgh, and at Tübingen. In 1874 he entered the ministry of the Free Church of Scotland and became assistant minister of Barclay Church, Edinburgh. Subsequently he was minister at Logiealmond in Perthshire and at Glasgow, and in 1880 he became minister of Sefton Park Presbyterian church, Liverpool, from which he retired in 1905. In 1896 he was Lyman Beecher lecturer at Yale University, and in 1900 he was moderator of the synod of the English Presbyterian church. While travelling in America he died at Mount Pleasant, Iowa, on the 6th of May 1907. Ian Maclaren’s first sketches of rural Scottish life, Beside the Bonnie Briar Bush (1894), achieved extraordinary popularity and were followed by other successful books, The Days of Auld Lang Syne (1895), Kate Carnegie and those Ministers (1896) and Afterwards and other Stories (1898). Under his own name Watson published several volumes of sermons, among them being The Upper Room (1895); The Mind of the Master (1896) and The Potter’s Wheel (1897).
See Sir W. Robertson Nicoll, Ian Maclaren (1908).

MACLAURIN, COLIN (1698-1746), Scottish mathematician, was the son of a clergyman, and born at Kilmodan, Argyllshire. In 1709 he entered the university of Glasgow, where he exhibited a decided genius for mathematics, more especially for geometry; it is said that before the end of his sixteenth year he had discovered many of the theorems afterwards published in his Geometria organica. In 1717 he was elected professor of mathematics in Marischal College, Aberdeen, as the result of a competitive examination. Two years later he was admitted F.R.S. and made the acquaintance of Sir Isaac Newton. In 1719 he published his Geometria organica, sive descriptio linearum curvarum universalis. In it Maclaurin developed several theorems due to Newton, and introduced the method of generating conics which bears his name, and showed that many curves of the third and fourth degrees can be described by the intersection of two movable angles. In 1721 he wrote a supplement to the Geometria organica, which he afterwards published, with extensions, in the Philosophical Transactions for 1735. This paper is principally based on the following general theorem, which is a remarkable extension of Pascal’s hexagram: “If a polygon move so that each of its sides passes through a fixed point, and if all its summits except one describe curves of the degrees m, n, p, &c., respectively, then the free summit moves on a curve of the degree 2mnp... which reduces to mnp ... when the fixed points all lie on a right line.” In 1722 Maclaurin travelled as tutor and companion to the eldest son of Lord Polwarth, and after a short stay in Paris resided for some time in Lorraine, where he wrote an essay on the percussion of bodies, which obtained the prize of the French Academy of Sciences for the year 1724. The following year he was elected professor of mathematics in the university of Edinburgh on the urgent recommendation of Newton. After the death of Newton, in 1728, his nephew, John Conduitt, applied to Maclaurin for his assistance in publishing an account of Newton’s life and discoveries. This Maclaurin gladly undertook, but the death of Conduitt put a stop to the project.
In 1740 Maclaurin divided with Leonhard Euler and Daniel Bernoulli the prize offered by the French Academy of Sciences for an essay on tides. His Treatise on Fluxions was published at Edinburgh in 1742, in two volumes. In the preface he states that the work was undertaken in consequence of the attack on the method of fluxions made by George Berkeley in 1734. Maclaurin’s object was to found the doctrine of fluxions on geometrical demonstration, and thus to answer all objections to its method as being founded on false reasoning and full of mystery. The most valuable part of the work is that devoted to physical applications, in which he embodied his essay on the tides. In this he showed that a homogeneous fluid mass revolving uniformly round an axis under the action of gravity ought to assume the form of an ellipsoid of revolution. The importance of this investigation in connexion with the theory of the tides, the figure of the earth, and other kindred questions, has always caused it to be regarded as one of the great problems of mathematical physics. Maclaurin was the first to introduce into mechanics, in this discussion, the important conception of surfaces of level; namely, surfaces at each of whose points the total force acts in the normal direction. He also gave in his Fluxions, for the first time, the correct theory for distinguishing between maxima and minima in general, and pointed out the importance of the distinction in the theory of the multiple points of curves. In 1745, when the rebels were marching on Edinburgh, Maclaurin took a most prominent part in preparing trenches and barricades for its defence. The anxiety, fatigue and cold to which he was thus exposed, affecting a constitution naturally weak, laid the foundation of the disease to which he afterwards succumbed. As soon as the rebel army got possession of Edinburgh Maclaurin fled to England, to avoid making submission to the Pretender. He accepted the invitation of T. Herring, then archbishop of York, with whom he remained until it was safe to return to Edinburgh. He died of dropsy on the 14th of June 1746, at Edinburgh. Maclaurin was married in 1733 to Anne, daughter of Walter Stewart, solicitor-general for Scotland. His eldest son John, born in 1734, was distinguished as an advocate, and appointed one of the judges of the Scottish court of session, with the title of Lord Dreghorn. He inherited an attachment to scientific discovery, and was one of the founders of the Royal Society of Edinburgh, in 1782.
After Maclaurin’s death his account of Newton’s philosophical discoveries was published by Patrick Murdoch, and also his algebra in 1748. As an appendix to the latter appeared his De linearum geometricarum proprietatibus generalibus tractatus, a treatise of remarkable elegance. Of the more immediate successors of Newton in Great Britain Maclaurin is probably the only one who can be placed in competition with the great mathematicians of the continent of Europe at the time.

M‘LENNAN, JOHN FERGUSON (1827-1881), Scottish ethnologist, was born at Inverness on the 14th of October 1827. He studied at King’s college, Aberdeen, where he graduated with distinction in 1849, thence proceeding to Cambridge, where he remained till 1855 without taking a degree. He was called to the Scottish bar in 1857, and in 1871 was appointed parliamentary draughtsman for Scotland. In 1865 he published Primitive Marriage, in which, arguing from the prevalence of the symbolical form of capture in the marriage ceremonies of primitive races, he developed an intelligible picture of the growth of the marriage relation and of systems of kinship (see Family) according to natural laws. In 1866 he wrote in the Fortnightly Review (April and May) an essay on “Kinship in Ancient Greece,” in which he proposed to test by early Greek facts the theory of the history of kinship set forth in Primitive Marriage; and three years later appeared a series of essays on “Totemism” in the same periodical for 1869-1870 (the germ of which had been contained in the paper just named), which mark the second great step in his systematic study of early society. A reprint of Primitive Marriage, with “Kinship in Ancient Greece” and some other essays not previously published, appeared in 1876, under the title of Studies in Ancient History. The new essays in this volume were mostly critical, but one of them, in which perhaps his guessing talent is seen at its best, “The Divisions of the Irish Family,” is an elaborate discussion of a problem which has long puzzled both Celtic scholars and jurists; and in another, “On the Classificatory System of Relationship,” he propounded a new explanation of a series of facts which, he thought, might throw light upon the early history of society, at the same time putting to the test of those facts the theories he had set forth in Primitive Marriage. Papers 262 on “The Levirate and Polyandry,” following up the line of his previous investigations (Fortnightly Review, 1877), were the last work he was able to publish. He died of consumption on the 14th of June 1881 at Hayes Common, Kent.
Besides the works already cited, M‘Lennan wrote a Life of Thomas Drummond (1867). The vast materials which he had accumulated on kinship were edited by his widow and A. Platt, under the title Studies in Ancient History: Second Series (1896).

MACLEOD, HENRY DUNNING (1821-1902), Scottish economist, was born in Edinburgh, and educated at Eton, Edinburgh University, and Trinity College, Cambridge, where he graduated in 1843. He travelled in Europe, and in 1849 was called to the English bar. He was employed in Scotland on the work of poor-law reform, and devoted himself to the study of economics. In 1856 he published his Theory and Practice of Banking, in 1858 Elements of Political Economy, and in 1859 A Dictionary of Political Economy. In 1873 appeared his Principles of Economist Philosophy, and other books on economics and banking were published later. Between 1868 and 1870 he was employed by the government in digesting and codifying the law of bills of exchange. He died on the 16th of July 1902. Macleod’s principal contribution to the study of economics consists in his work on the theory of credit, to which he was the first to give due prominence.
For a judicious discussion of the value of Macleod’s writings, see an article on “The Revolt against Orthodox Economics” in the Quarterly Review for October 1901 (No. 388).

MACLEOD, NORMAN (1812-1872), Scottish divine, son of Rev. Norman Macleod (1783-1862), and grandson of Rev. Norman Macleod, minister of Morven, Argyllshire, was born at Campbeltown on the 3rd of June 1812. In 1827 he became a student at Glasgow University, and in 1831 went to Edinburgh to study divinity under Dr Thomas Chalmers. On the 18th of March 1838 he became parish minister at Loudoun, Ayrshire. At this time the troubles in the Scottish Church were already gathering to a head (see Free Church of Scotland). Macleod, although he had no love for lay patronage, and wished the Church to be free to do its proper work, clung firmly to the idea of a national Established Church, and therefore remained in the Establishment when the disruption took place. He was one of those who took a middle course in the non-intrusion controversy, holding that the fitness of those who were presented to parishes should be judged by the presbyteries—the principle of Lord Aberdeen’s Bill. On the secession of 1843 he was offered many different parishes, and having finally settled at Dalkeith, devoted himself to parish work and to questions affecting the Church as a whole. He was largely instrumental in the work of strengthening the Church. In 1847 he became one of the founders of the Evangelical Alliance, and from 1849 edited the Christian Instructor (Edinburgh). In 1851 he was called to the Barony church, Glasgow, in which city the rest of his days were passed. There the more liberal theology rapidly made way among a people who judged it more by its fruits than its arguments, and Macleod won many adherents by his practical schemes for the social improvement of the people. He instituted temperance refreshment rooms, a congregational penny savings bank, and held services specially for the poor. In 1860 Macleod was appointed editor of the new monthly magazine Good Words. Under his control the magazine, which was mainly of a religious character, became widely popular. His own literary work, nearly all of which originally appeared in its pages—sermons, stories, travels, poems—was only a by-product of a busy life. By far his best work was the spontaneous and delightful Reminiscences of a Highland Parish (1867). While Good Words made his name known, and helped the cause he had so deeply at heart, his relations with the queen and the royal family strengthened yet further his position in the country. Never since Principal Carstairs had any Scottish clergyman been on such terms with his sovereign. In 1865 he risked an encounter with Scottish Sabbatarian ideas. The presbytery of Glasgow issued a pastoral letter on the subject of Sunday trains and other infringements of the Sabbath. Macleod protested against the grounds on which its strictures were based. For a time, owing partly to a misleading report of his statement, he became “the man in all Scotland most profoundly distrusted.” But four years later the Church accorded him the highest honour in her power by choosing him as moderator of her general assembly. In 1867, along with Dr Archibald Watson, he was sent to India, to inquire into the state of the missions. He undertook the journey in spite of failing health, and seems never to have recovered from its effects. He returned resolved to devote the rest of his days to rousing the Church to her duty in the sphere of foreign missions, but his health was now broken, and his old energy flagged. He died on the 16th of June 1872, and was buried at Campsie. He was one of the greatest of Scottish religious leaders, a man of wide sympathy and high ideals. His Glasgow church was named after him the “Macleod Parish Church,” and the “Macleod Missionary Institute” was erected by the Barony church in Glasgow. Queen Victoria gave two memorial windows to Crathie church as a testimony of her admiration for his work.
See Memoir of Norman Macleod, by his brother, Donald Macleod (1876).

MACLISE, DANIEL (1806-1870), Irish painter, was born at Cork, the son of a Highland soldier. His education was of the plainest kind, but he was eager for culture, fond of reading, and anxious to become an artist. His father, however, placed him, in 1820, in Newenham’s Bank, where he remained for two years, and then left to study in the Cork school of art. In 1825 it happened that Sir Walter Scott was travelling in Ireland, and young Maclise, having seen him in a bookseller’s shop, made a surreptitious sketch of the great man, which he afterwards lithographed. It was exceedingly popular, and the artist became celebrated enough to receive many commissions for portraits, which he executed, in pencil, with very careful treatment of detail and accessory. Various influential friends perceived the genius and promise of the lad, and were anxious to furnish him with the means of studying in the metropolis; but with rare independence he refused all aid, and by careful economy saved a sufficient sum to enable him to leave for London. There he made a lucky hit by a sketch of the younger Kean, which, like his portrait of Scott, was lithographed and published. He entered the Academy schools in 1828, and carried off the highest prizes open to the students. In 1829 he exhibited for the first time in the Royal Academy. Gradually he began to confine himself more exclusively to subject and historical pictures, varied occasionally by portraits of Campbell, Miss Landon, Dickens, and other of his literary friends. In 1833 he exhibited two pictures which greatly increased his reputation, and in 1835 the “Chivalric Vow of the Ladies and the Peacock” procured his election as associate of the Academy, of which he became full member in 1840. The years that followed were occupied with a long series of figure pictures, deriving their subjects from history and tradition and from the works of Shakespeare, Goldsmith and Le Sage. He also designed illustrations for several of Dickens’s Christmas books and other works. Between the years 1830 and 1836 he contributed to Fraser’s Magazine, under the pseudonym of Alfred Croquis, a remarkable series of portraits of the literary and other celebrities of the time—character studies, etched or lithographed in outline, and touched more or less with the emphasis of the caricaturist, which were afterwards published as the Maclise Portrait Gallery (1871). In 1858 Maclise commenced one of the two great monumental works of his life, the “Meeting of Wellington and Blücher,” on the walls of Westminster Palace. It was begun in fresco, a process which proved unmanageable. The artist wished to resign the task; but, encouraged by Prince Albert, he studied in Berlin the new method of “water-glass” painting, and carried out the subject and its companion, the “Death of Nelson,” in that medium, completing the latter painting in 1864. The intense application which he gave to these great historic works, and various circumstances connected with the commission, had a serious effect on the artist’s health. He began to shun the company in which he formerly delighted; his old buoyancy of 263 spirits was gone; and when, in 1865, the presidentship of the Academy was offered to him he declined the honour. He died of acute pneumonia on the 25th of April 1870. His works are distinguished by powerful intellectual and imaginative qualities, but most of them are marred by harsh and dull colouring, by metallic hardness of surface and texture, and by frequent touches of the theatrical in the action and attitudes of the figures. His fame rests most securely on his two greatest works at Westminster.
A memoir of Maclise, by his friend W. J. O’Driscoll, was published in 1871.

MACLURE, WILLIAM (1763-1840), American geologist, was born at Ayr in Scotland in 1763. After a brief visit to New York in 1782 he began active life as a partner in a London firm of American merchants. In 1796 business affairs took him to Virginia, U.S.A., which he thereafter made his home. In 1803 he visited France as one of the commissioners appointed to settle the claims of American citizens on the French government; and during the few years then spent in Europe he applied himself with enthusiasm to the study of geology. On his return home in 1807 he commenced the self-imposed task of making a geological survey of the United States. Almost every state in the Union was traversed and mapped by him, the Alleghany Mountains being crossed and recrossed some fifty times. The results of his unaided labours were submitted to the American Philosophical Society in a memoir entitled Observations on the Geology of the United States explanatory of a Geological Map, and published in the Society’s Transactions (vol. iv. 1809, p. 91) together with the first geological map of that country. This antedates William Smith’s geological map of England by six years. In 1817 Maclure brought before the same society a revised edition of his map, and his great geological memoir was issued separately, with some additional matter, under the title Observations on the Geology of the United States of America. Subsequent survey has corroborated the general accuracy of Maclure’s observations. In 1819 he visited Spain, and attempted, unsuccessfully, to establish an agricultural college near the city of Alicante. Returning to America in 1824, he settled for some years at New Harmony, Indiana, and sought to develop his scheme of the agricultural college. Failing health ultimately constrained him to relinquish the attempt, and to seek (in 1827) a more congenial climate in Mexico. There, at San Angel, he died on the 23rd of March 1840.
See S. G. Morton, “Memoir of William Maclure,” Amer. Journ. Sci., vol. xlvii. (1844), p. 1.

MacMAHON, MARIE EDMÉ PATRICE MAURICE DE, duke of Magenta (1808-1893), French marshal and president of the French republic, was born on the 13th of July 1808 at the château of Sully, near Autun. He was descended from an Irish family which went into exile with James II. Educated at the military school of St Cyr, in 1827 he entered the army, and soon saw active service in the first French campaign in Algeria, where his ability and bravery became conspicuous. Being recalled to France, he gained renewed distinction in the expedition to Antwerp in 1832. He became captain in 1833, and in that year returned to Algeria. He led daring cavalry raids across plains infested with Bedouin, and especially distinguished himself at the siege of Constantine in 1837. From then until 1855 he was almost constantly in Algeria, and rose to the rank of general of division. During the Crimean War MacMahon was given the command of a division, and in September 1855 he successfully conducted the assault upon the Malakoff works, which led to the fall of Sebastopol. After his return to France honours were showered upon him, and he was made a senator. Desiring a more active life, however, and declining the highest command in France, he was once more sent out, at his own request, to Algeria, where he completely defeated the Kabyles. After his return to France he voted as a senator against the unconstitutional law for general safety, which was brought forward in consequence of Orsini’s abortive attempt on the emperor’s life. MacMahon greatly distinguished himself in the Italian campaign of 1859. Partly by good luck and partly by his boldness and sagacity in pushing forward without orders at a critical moment at the battle of Magenta, he enabled the French to secure the victory. For his brilliant services MacMahon received his marshal’s baton and was created duke of Magenta. In 1861 he represented France at the coronation of William I. of Prussia, and in 1864 he was nominated governor-general of Algeria. MacMahon’s action in this capacity formed the least successful episode of his career. Although he did institute some reforms in the colonies, complaints were so numerous that twice in the early part of 1870 he sent in his resignation to the emperor. When the ill-fated Ollivier cabinet was formed the emperor abandoned his Algerian schemes and MacMahon was recalled.
War being declared between France and Prussia in July 1870, MacMahon was appointed to the command of the Alsace army detachment (see Franco-German War). On the 6th of August MacMahon fought the battle of Wörth (q.v.). His courage was always conspicuous on the field, but the two-to-one numerical superiority of the Germans triumphed. MacMahon was compelled to fall back upon Saverne, and thence to Toul. Though he suffered further losses in the course of his retreat, his movements were so ably conducted that the emperor confided to him the supreme command of the new levies which he was mustering at Châlons, and he was directed to effect a junction with Bazaine. This operation he undertook against his will. He had an army of 120,000 men, with 324 guns; but large numbers of the troops were disorganized and demoralized. Early on the 1st of September the decisive battle of Sedan began. MacMahon was dangerously wounded in the thigh, whereupon General Ducrot, and soon afterwards General de Wimpffen, took command. MacMahon shared the captivity of his comrades, and resided at Wiesbaden until the conclusion of peace.
In March 1871 MacMahon was appointed by Thiers commander-in-chief of the army of Versailles; and in that capacity he suppressed the Communist insurrection, and successfully conducted the second siege of Paris. In the following December he was invited to become a candidate for Paris in the elections to the National Assembly, but declined nomination. On the resignation of Thiers as president of the Republic, on the 24th of May 1873, MacMahon was elected to the vacant office by an almost unanimous vote, being supported by 390 members out of 392. The duc de Broglie was empowered to form a Conservative administration, but the president also took an early opportunity of showing that he intended to uphold the sovereignty of the National Assembly. On the 5th of November 1873 General Changarnier presented a motion in the Assembly to confirm MacMahon’s powers for a period of ten years, and to provide for a commission of thirty to draw up a form of constitutional law. The president consented, but in a message to the Assembly he declared in favour of a confirmation of his own powers for seven years, and expressed his determination to use all his influence in the maintenance of Conservative principles. After prolonged debates the Septennate was adopted on the 19th of November by 378 votes to 310. There was no coup d’état in favour of “Henri V.,” as had been expected, and the president resolved to abide by “existing institutions.” One of his earliest acts was to receive the finding of the court-martial upon his old comrade in arms, Marshal Bazaine, whose death sentence he commuted to one of twenty years’ imprisonment in a fortress. Though MacMahon’s life as president of the Republic was of the simplest possible character, his term of office was marked by many brilliant displays, while his wife was a leader in all works of charity and benevolence.
The president was very popular in the rural districts of France, through which he made a successful tour shortly after the declaration of the Septennate. But in Paris and other large cities his policy soon caused great dissatisfaction, the Republican party especially being alienated by press prosecutions and the attempted suppression of Republican ideas. Matters were at a comparative deadlock in the National Assembly, until the accession of some Orleanists to the Moderate Republican party 264 in 1875 made it possible to pass various constitutional laws. In May 1877, however, the constitutional crisis became once more acute. A peremptory letter of censure from MacMahon to Jules Simon caused the latter to resign with his colleagues. The duc de Broglie formed a ministry, but Gambetta carried a resolution in the Chamber of Deputies in favour of parliamentary government. The president declined to yield, and being supported by the Senate, he dissolved the Chamber, by decree, on the 25th of June. The prosecution of Gambetta followed for a speech at Lille, in which he had said “the marshal must, if the elections be against him, se soumettre ou se démettre.” In a manifesto respecting the elections, the president referred to his successful government and observed, “I cannot obey the injunctions of the demagogy; I can neither become the instrument of Radicalism nor abandon the post in which the constitution has placed me.” His confidence in the result of the elections was misplaced. Notwithstanding the great pressure put upon the constituencies by the government, the elections in October resulted in the return of 335 Republicans and only 198 anti-Republicans, the latter including 30 MacMahonists, 89 Bonapartists, 41 Legitimists, and 38 Orleanists. The president endeavoured to ignore the significance of the elections, and continued his reactionary policy. As a last resort he called to power an extra-parliamentary cabinet under General Rochebouet, but the Republican majority refused to vote supplies, and after a brief interval the president was compelled to yield, and to accept a new Republican ministry under Dufaure. The prolonged crisis terminated on the 14th of December 1877, and no further constitutional difficulties arose in 1878. But as the senatorial elections, held early in 1879, gave the Republicans an effective working majority in the Upper Chamber, they now called for the removal of the most conspicuous anti-Republicans among the generals and officials. The president refused to supersede them, and declined to sanction the law brought in with this object. Perceiving further resistance to be useless, however, MacMahon resigned the presidency on the 30th of January 1879, and Jules Grévy was elected as his successor.
MacMahon now retired into private life. Relieved from the cares of state, his simple and unostentatious mode of existence enabled him to pass many years of dignified repose. He died at Paris on the 17th of October 1893, in his eighty-sixth year. A fine, tall, soldierly man, of a thoroughly Irish type, in private life MacMahon was universally esteemed as generous and honourable; as a soldier he was brave and able, without decided military genius; as a politician he was patriotic and well-intentioned, but devoid of any real capacity for statecraft.

McMASTER, JOHN BACH (1852- ), American historian, was born in Brooklyn, New York, on the 29th of June 1852. He graduated from the college of the City of New York in 1872, worked as a civil engineer in 1873-1877, was instructor in civil engineering at Princeton University in 1877-1883, and in 1883 became professor of American history in the university of Pennsylvania. He is best known for his History of the People of the United States from the Revolution to the Civil War (1883 sqq.), a valuable supplement to the more purely political writings of Schouler, Von Holst and Henry Adams.

MACMILLAN, the name of a family of English publishers. The founders of the firm were two Scotsmen, Daniel Macmillan (1813-1857) and his younger brother Alexander (1818-1896). Daniel was a native of the Isle of Arran, and Alexander was born in Irvine on the 3rd of October 1818. Daniel was for some time assistant to the bookseller Johnson at Cambridge, but entered the employ of Messrs Seeley in London in 1837; in 1843 he began business in Aldersgate Street, and in the same year the two brothers purchased the business of Newby in Cambridge. They did not confine themselves to bookselling, but published educational works as early as 1844. In 1845 they became the proprietors of the more important business of Stevenson, in Cambridge, the firm being styled Macmillan, Barclay & Macmillan. In 1850 Barclay retired and the firm resumed the name of Macmillan & Co. Daniel Macmillan died at Cambridge on the 27th of June 1857. In that year an impetus was given to the business by the publication of Kingsley’s Two Years Ago. A branch office was opened in 1858 in Henrietta Street, London, which led to a great extension of trade. These premises were surrendered for larger ones in Bedford Street, and in 1897 the buildings in St Martin’s Street were opened. Alexander Macmillan died in January 1896. By his great energy and literary associations, and with the aid of his partners, there had been built up in little over half a century one of the most important publishing houses in the world. Besides the issue of many important series of educational and scientific works, they published the works of Kingsley, Huxley, Maurice, Tennyson, Lightfoot, Westcott, J. R. Green, Lord Roberts, Lewis Carroll, and of many other well-known authors. In 1898 they took over the old-established publishing house of R. Bentley & Son, and with it the works of Mrs Henry Wood, Miss Rhoda Broughton, The Ingoldsby Legends, and also Temple Bar and the Argosy. In 1893 the firm was converted into a limited liability company, its chairman being Frederick Macmillan (b. 1851), who was knighted in 1909. The American firm of the Macmillan Company, of which he was also a director, is a separate business.
See Thomas Hughes, Memoir of Daniel Macmillan (1882); A Bibliographical Catalogue of Macmillan & Co’s Publications from 1843 to 1889 (1891), with portraits of the brothers Daniel and Alexander after Lowes Dickinson and Hubert Herkomer; also articles in Le Livre (September 1886), Publishers’ Circular (January 14, 1893), the Bookman (May 1901), &c.

MACMONNIES, FREDERICK WILLIAM (1863- ) American sculptor and painter, was born at Brooklyn, New York, on the 20th of September 1863. His mother was a niece of Benjamin West. At the age of sixteen MacMonnies was received as an apprentice in the studio of Augustus St Gaudens, the sculptor, where he remained for five years. In 1884 he went to Paris and thence to Munich, where he painted for some months. Returning to Paris next year he became the most prominent pupil of Falguière. His “Diana” brought him a mention at the Salon of 1889. Three life-sized figures of angels for the church of St Paul, New York, were followed by his “Nathan Hale,” in the City Hall Park, New York, and a portrait of James S. T. Stranahan, for Brooklyn. This last brought him a “second medal” in the Salon of 1891, the first time an American sculptor had been so honoured. In 1893 he was chosen to design and carry out the Columbian Fountain for the Chicago World’s Fair, which placed him instantly in the front rank. His largest work is a decoration for the Memorial Arch to Soldiers and Sailors, in Prospect Park, Brooklyn, consisting of three enormous groups in bronze. In Prospect Park, Brooklyn, MacMonnies has also a large “Horse Tamer,” a work of much distinction. A “Winged Victory” at the U.S. military academy at West Point, New York, is of importance; and his “Bacchante,” an extraordinary combination of realism and imagination, rejected by the Boston Public Library, is now at the Metropolitan Museum of Art, New York. He also became well known as a painter, mainly of portraits. In 1888 he married Mary Fairchild, a figure painter of distinction, but in 1909 they were divorced and she married Will H. Low.

MACNAGHTEN, SIR WILLIAM HAY, Bart. (1793-1841), Anglo-Indian diplomatist, was the second son of Sir Francis Macnaghten, Bart., judge of the supreme courts of Madras and Calcutta. He was born in August 1793, and educated at Charterhouse. He went out to Madras as a cadet in 1809, but was appointed in 1816 to the Bengal Civil Service. He early displayed a great talent for languages, and also published several treatises on Hindu and Mahommedan law. His political career began in 1830 as secretary to Lord William Bentinck; and in 1837 he became one of the most trusted advisers of the governor-general, Lord Auckland, with whose policy of supporting Shah Shuja against Dost Mahommed, the reigning amir of Kabul, Macnaghten was closely identified. As political agent at Kabul he came into conflict with the military authorities and subsequently with his subordinate Sir Alexander Burnes. Macnaghten attempted to placate the Afghan chiefs with heavy subsidies, but when the drain on the Indian exchequer became too great, 265 and the allowances were reduced, this policy led to an outbreak. Burnes was murdered on the 2nd of November 1841; and owing to the incapacity of the aged General Elphinstone the British army in Kabul degenerated into a leaderless mob. Macnaghten tried to save the situation by negotiating with the Afghan chiefs and, independently of them, with Dost Mahommed’s son, Akbar Khan, by whom he was assassinated on the 23rd of December 1841; the disastrous retreat from Kabul and the massacre of the British army in the Kurd Kabul pass followed. These events threw doubt on Macnaghten’s capacity for dealing with the problems of Indian diplomacy, though his fearlessness and integrity were unquestioned. He had been created a baronet in 1840, and four months before his death was nominated to the governorship of Bombay.

MacNALLY, LEONARD (1752-1820), Irish informer, was born in Dublin, the son of a merchant. In 1776 he was called to the Irish, and in 1783 to the English bar. He supported himself for some time in London by writing plays and editing the Public Ledger. Returning to Dublin, he entered upon a systematic course of informing against the members of the revolutionary party, for whom his house had become the resort. He also betrayed to the government prosecutors political clients whom he defended eloquently in the courts. He made a fine defence for Robert Emmet and cheered him in his last hours, although before appearing in court he had sold, for £200, the contents of his brief to the lawyers for the Crown. After living a professed Protestant all his life, he received absolution on his deathbed from a Roman Catholic priest. He died on the 13th of February 1820.

MACNEE, SIR DANIEL (1806-1882), Scottish portrait painter, was born at Fintry in Stirlingshire. At the age of thirteen he was apprenticed, along with Horatio Macculloch and Leitch the water-colour painter, to John Knox, a landscapist of some repute. He afterwards worked for a year as a lithographer, was employed by the Smiths of Cumnock to paint the ornamental lids of their planewood snuff-boxes, and, having studied in Edinburgh at the “Trustees’ Academy,” supporting himself meanwhile by designing and colouring book illustrations for Lizars the engraver, he established himself as an artist in Glasgow, where he became a fashionable portrait painter. He was in 1829 admitted a member of the Royal Scottish Academy; and on the death of Sir George Harvey in 1876 he was elected president, and received the honour of knighthood. From this period till his death, on the 18th of January 1882, he resided in Edinburgh, where his genial social qualities and his inimitable powers as a teller of humorous Scottish anecdote rendered him popular.

MACNEIL, HERMON ATKINS (1866- ), American sculptor, was born at Chelsea, Massachusetts. He was an instructor in industrial art at Cornell University in 1886-1889, and was then a pupil of Henri M. Chapu and Falguière in Paris. Returning to America, he aided Philip Martiny in the preparation of sketch models for the Columbian exposition, and in 1896 he won the Rinehart scholarship, passing four years (1896-1900) in Rome. In 1906 he became a National Academician. His first important work was “The Moqui Runner,” which was followed by “A Primitive Chant,” and “The Sun Vow,” all figures of the North-American Indian. A “Fountain of Liberty,” for the St Louis exposition, and other Indian themes came later; his “Agnese” and his “Beatrice,” two fine busts of women, also deserve mention. His principal work is the sculpture for a large memorial arch, at Columbus, Ohio, in honour of President McKinley. In 1909 he won in competition a commission for a large soldiers’ and sailors’ monument in Albany, New York. His wife, Carol Brooks MacNeil, also a sculptor of distinction, was a pupil of F. W. MacMonnies.

McNEILE, HUGH (1795-1879), Anglican divine, younger son of Alexander McNeile (or McNeill), was born at Ballycastle, Co. Antrim, on the 15th of July 1795. He graduated at Trinity College, Dublin, in 1810. His handsome presence, and his promise of exceptional gifts of oratory, led a wealthy uncle, Major-General Daniel McNeill, to adopt him as his heir; and he was destined for a parliamentary career. During a stay at Florence, Hugh McNeile became temporarily intimate with Lord Byron and Madame de Staël. On returning home, he determined to abandon the prospect of political distinction for the clerical profession, and was disinherited. In 1820 he was ordained, and after holding the curacy of Stranorlar, Co. Donegal, for two years, was appointed to the living of Albury, Surrey, by Henry Drummond.
Edward Irving endeavoured, not without success at first, to draw McNeile into agreement with his doctrine and aims. Irving’s increasing extravagance, however, soon alienated McNeile. His preaching now attracted much attention; in London he frequently was heard by large congregations. In 1834 he accepted the incumbency of St Jude’s, Liverpool, where for the next thirty years he wielded great political as well as ecclesiastical influence. He repudiated the notion that a clergyman should be debarred from politics, maintaining at a public meeting that “God when He made the minister did not unmake the citizen.” In 1835 McNeile entered upon a long contest, in which he was eventually successful, with the Liverpool corporation, which had been captured by the Whigs, after the passing of the Municipal Reform Act. A proposal was carried that the elementary schools under the control of the corporation should be secularized by the introduction of what was known as the Irish National System. The threatened withdrawal of the Bible as the basis of denominational religious teaching was met by a fierce agitation led by McNeile, who so successfully enlisted public support that before the new system could be introduced every child was provided for in new Church of England schools established by public subscriptions. At the same time he conducted a campaign which gradually reduced the Whig element in the council, till in 1841 it almost entirely disappeared. To his influence was also attributed the defeat of the Liberal parliamentary candidates in the general election of 1837, followed by a long period of Conservative predominance in Liverpool politics. McNeile had the Irish Protestant’s horror of Romanism, which he constantly denounced in the pulpit and on the platform; and Macaulay, speaking in the House of Commons on the Maynooth endowment in April 1845, singled him out for attack as the most powerful representative of uncompromising Protestant opinion in the country. As the Tractarian movement in the Church of England developed, he became one of its most zealous opponents and the most conspicuous leader of the evangelical party. In 1840 he published a volume of Lectures on the Church of England, and in 1846 (the year after Newman’s secession to Rome) The Church and the Churches, in which he maintained with much dialectical skill the evangelical doctrine of the “invisible Church” in opposition to the teaching of Newman and Pusey. Hugh McNeile was in close sympathy with the philanthropic work as well as the religious views of the 7th earl of Shaftesbury, who more than once tried to persuade Lord Palmerston to raise him to the episcopal bench. But although Palmerston usually followed the advice of Shaftesbury in the appointment of bishops, he would not consent to the elevation to the House of Lords of so powerful a political opponent as McNeile, whom Lord John Russell had accused of frustrating for thirty years the education policy of the Liberal party. In 1860 he was appointed a canon of Chester; and in 1868 Disraeli appointed him dean of Ripon. This preferment he resigned in 1875, and he lived in retirement at Bournemouth till his death on the 28th of January 1879. McNeile married, in 1822, Anne, daughter of William Magee, archbishop of Dublin, and aunt of William Connor Magee, archbishop of York, by whom he had a large family.
Although a vehement controversialist, Hugh McNeile was a man of simple and sincere piety of character. Sir Edward Russell, an opponent alike of his religious and his political opinions, bears witness to the deep spirituality of his teaching, and describes him as an absolutely unique personality. “He made himself leader of the Liverpool people, and always led with calm and majesty in the most excited times. His eloquence was grave, flowing, emphatic—had a dignity in delivery, a perfection of elocution, that only John Bright equalled in the latter half of the 266 19th century. Its fire was solemn force. McNeile’s voice was probably the finest organ ever heard in public oratory. His action was as graceful as it was expressive. He ruled an audience.”
See J. A. Picton, Memorials of Liverpool, vol. i. (1873); Sir Edward Russell, “The Religious Life of Liverpool,” in the Sunday Magazine (June 1905); Charles Bullock, Hugh McNeile and Reformation Truth.

MACNEILL, HECTOR (1746-1818), Scottish poet, was born near Roslin, Midlothian, on the 22nd of October 1746, the son of an impoverished army captain. He went to Bristol as a clerk at the age of fourteen, and soon afterwards was despatched to the West Indies. From 1780 to 1786 he acted as assistant secretary on board the flagships of Admiral Geary and Sir Richard Bickerton (1727-1792). Most of his later life was spent in Scotland, and it was in the house of a friend at Stirling that he wrote most of his songs and his Scotland’s Skaith, or the History of Will and Jean (1795), a narrative poem intended to show the deteriorating influences of whisky and pothouse politics. A sequel, The Waes of War, appeared next year. In 1800 he published The Memoirs of Charles Macpherson, Esq., a novel understood to be a narrative of his own hardships and adventures. A complete edition of the poems he wished to own appeared in 1812. His songs “Mary of Castlecary,” “Come under my plaidy,” “My boy Tammy,” “O tell me how for to woo,” “I lo’ed ne’er a lassie but ane,” “The plaid amang the hether,” and “Jeanie’s black e’e,” are notable for their sweetness and simplicity. He died at Edinburgh on the 15th of March 1818.

MACOMB, a city and the county-seat of McDonough county, Illinois, U.S.A., in the W. part of the state, about 60 m. S.W. of Peoria. Pop. (1890), 4052; (1900), 5375 (232 foreign-born); (1910), 5774. Macomb is served by the Chicago, Burlington & Quincy, and the Macomb & Western Illinois railways. The city is the seat of the Western Illinois state normal school (opened in 1902), and has a Carnegie library and a city park. Clay is found in the vicinity, and there are manufactures of pottery, bricks, &c. The city was founded in 1830 as the county-seat of McDonough county, and was called Washington by the settlers, but the charter of incorporation, also granted in 1830, gave it the present name in honour of General Alexander Macomb. Macomb was first chartered as a city in 1856.

MACOMER, a village of Sardinia in the province of Cagliari, from which it is 95 m. N.N.W. by rail, and the same distance S.W. of Golfo degli Aranci. Pop. (1901), 3488. It is situated 1890 ft. above sea-level on the southern ascent to the central plateau (the Campeda) of this part of Sardinia; and it is the junction of narrow-gauge lines branching from the main line eastwards to Nuoro and westwards to Bosa. The old parish church of S. Pantaleone has three Roman mile-stones in front of it, belonging to the Roman high-road from Carales to Turris Libisonis. The modern high-road follows the ancient. The district, especially the Campeda, is well fitted for grazing and horse and cattle breeding, which is carried on to a considerable extent. It is perhaps richer in nuraghi than any other part of Sardinia.

MACON, NATHANIEL (1758-1837), American political leader, was born at Macon Manor, Warren county, North Carolina, on the 17th of December 1758. He studied at the college of New Jersey (now Princeton University) from 1774 to 1776, when the institution was closed on account of the outbreak of the War of Independence; served for a short time in a New Jersey militia company; studied law at Bute Court-house, North Carolina, in 1777-1780, at the same time managing his tobacco plantation; was a member of a Warren county militia company in 1780-1782, and served in the North Carolina Senate in 1781-1785. In 1786 he was elected to the Continental Congress, but declined to serve. In 1791-1815 he was a member of the national House of Representatives, and in 1815-1828 of the United States Senate. Macon’s point of view was always local rather than national. He was essentially a North Carolinian first, and an American afterwards; and throughout his career he was an aggressive advocate of state sovereignty and an adherent of the doctrines of the “Old Republicans.” He at first opposed the adoption of the Federal constitution of 1787, as a member of the faction led by Willie Jones (1731-1801) of Halifax, North Carolina, but later withdrew his opposition. In Congress he denounced Hamilton’s financial policy, opposed the Jay Treaty (1795) and the Alien and Sedition Acts, and advocated a continuance of the French alliance of 1778. His party came into power in 1801, and he was Speaker of the house from December 1801 to October 1807. At first he was in accord with Jefferson’s administration; he approved the Louisiana Purchase, and as early as 1803 advocated the purchase of Florida. For a number of years, however, he was politically allied with John Randolph.1 As speaker, in spite of strong opposition, he kept Randolph at the head of the important committee on Ways and Means from 1801 to 1806; and in 1805-1808, with Randolph and Joseph H. Nicholson (1770-1817) of Maryland, he was a leader of the group of about ten independents, called the “Quids,” who strongly criticized Jefferson and opposed the presidential candidature of Madison. By 1809, however, Macon was again in accord with his party, and during the next two years he was one of the most influential of its leaders. In December 1809 he introduced resolutions which combined the ideas of Peter Early (1773-1817) of Georgia, David R. Williams (1776-1830) of South Carolina, and Samuel W. Dana (1757-1830) of Connecticut with his own. The resolutions recommended the complete exclusion of foreign war vessels from United States ports and the suppression of illegal trade carried on by foreign merchants under the American flag. The substance of these resolutions was embodied in the “Macon Bill, No. 1,” which passed the House but was defeated in the Senate. On the 7th of April 1810 Macon reported from committee the “Macon Bill, No. 2,” which had been drawn by John Taylor (1770-1832) of South Carolina, and was not actively supported by him. This measure (amended) became law on the 1st of May, and provided for the repeal of the Non-Intercourse Act of 1809, authorized the president, “in case either Great Britain or France shall before the 3rd day of March next so revoke or modify her edicts as that they shall cease to violate the neutral commerce of the United States,” to revive non-intercourse against the other, and prohibited British and French vessels of war from entering American waters. In 1812 Macon voted for the declaration of war against Great Britain, and later was chairman of the Congressional committee which made a report (July 1813) condemning Great Britain’s conduct of the war. He opposed the Bank Act of 1816, the “internal improvements” policy of Calhoun (in the early part of his career) and Clay, and the Missouri Compromise, his speech against the last being especially able. In 1824 Macon received the electoral vote of Virginia for the vice-presidency, and in 1826-1828 was president pro tempore of the Senate. He was president of the North Carolina constitutional convention in 1835, and was an elector on the Van Buren ticket in 1836. He died at his home, Buck Springs, Warren county, North Carolina, on the 29th of June 1837.
See William E. Dodd, The Life of Nathaniel Macon (Raleigh, N.C., 1903); E. M. Wilson, The Congressional Career of Nathaniel Macon (Chapel Hill, N.C., 1900).
1 Their names are associated in Randolph-Macon College, named in their honour in 1830.

MÂCON, a town of east-central France, capital of the department of Saône-et-Loire, 45 m. N. of Lyons on the Paris-Lyon railway. Pop. (1906), 16,151. Mâcon is situated on the right bank of the Saône facing the plain of the Bresse; a bridge of twelve arches connects it with the suburb of St Laurent on the opposite bank. The most prominent building is the modern Romanesque church of St Pierre, a large three-naved basilica, with two fine spires. Of the old cathedral of St Vincent (12th and 13th centuries), destroyed at the Revolution, nothing remains but the Romanesque narthex, now used as a chapel, the façade and its two flanking towers. The hôtel de ville contains a library, a theatre and picture-gallery. Opposite to it stands a statue of the poet Alphonse Lamartine, a native of the town. Mâcon is the seat of a prefecture, and has tribunals of first instance and of commerce, and a chamber of commerce. There are 267 lycées and training colleges. Copper-founding is an important industry; manufactures include casks, mats, rope and utensils for the wine-trade. The town has a large trade in wine of the district, known as Mâcon. It is a railway centre of considerable importance, being the point at which the line from Paris to Marseilles is joined by that from Mont Cenis and Geneva, as well as by a branch from Moulins.
Mâcon (Matisco) was an important town of the Aedui, but under the Romans it was supplanted by Autun and Lyons. It suffered a succession of disasters at the hands of the Germans, Burgundians, Vandals, Huns, Hungarians and even of the Carolingian kings. In the feudal period it was an important countship which in 1228 was sold to the king of France, but more than once afterwards passed into the possession of the dukes of Burgundy, until the ownership of the French crown was established in the time of Louis XI. In the 16th century Mâcon became a stronghold of the Huguenots, but afterwards fell into the hands of the League, and did not yield to Henry IV. until 1594. The bishopric, created by King Childebert, was suppressed in 1790.

MACON, a city and the county-seat of Bibb county, Georgia, U.S.A., in the central part of the state, on both sides of the Ocmulgee river (at the head of navigation), about 90 m. S.S.E. of Atlanta. Pop. (1900), 23,272, of whom 11,550 were negroes; (1910 census) 40,665. Macon is, next to Atlanta, the most important railway centre in the state, being served by the Southern, the Central of Georgia, the Georgia, the Georgia Southern & Florida, the Macon Dublin & Savannah, and the Macon & Birmingham railways. It was formerly an important river port, especially for the shipment of cotton, but lost this commercial advantage when railway bridges made the river impassable. It is, however, partially regaining the river trade in consequence of the compulsory substitution of drawbridges for the stationary railway bridges. The city is the seat of the Wesleyan female college (1836), which claims to be the first college in the world chartered to grant academic degrees to women; Mercer university (Baptist), which was established in 1833 as Mercer Institute at Penfield, became a university in 1837, was removed to Macon in 1871, and controls Hearn Academy (1839) at Cave Spring and Gibson Mercer Academy (1903) at Bowman; the state academy for the blind (1852), St Stanislaus’ College (Jesuit), and Mt de Sales Academy (Roman Catholic) for women. There are four orphan asylums for whites and two for negroes, supported chiefly by the Protestant Episcopal and Methodist Churches, and a public hospital. Immediately east of Macon are two large Indian mounds, and there is a third mound 9 m. south of the city. Situated in the heart of the “Cotton Belt,” Macon has a large and lucrative trade; it is one of the most important inland cotton markets of the United States, its annual receipts averaging about 250,000 bales. The city’s factory products in 1905 were valued at $7,297,347 (33.8% more than in 1900). In the vicinity are large beds of kaolin, 30 m. wide, reaching nearly across the state, and frequently 35 to 70 ft. in depth. Macon is near the fruit-growing region of Georgia, and large quantities of peaches and of garden products are annually shipped from the city.
Macon (named in honour of Nathaniel Macon) was surveyed in 1823 by order of the Georgia legislature for the county-seat of Bibb county, and received its first charter in 1824. It soon became the centre of trade for Middle Georgia; in 1833 a steamboat line to Darien was opened, and in the following year 69,000 bales of cotton were shipped by this route. During the Civil War the city was a centre for Confederate commissary supplies and the seat of a Treasury depository. In July 1864 General George Stoneman (1822-1894) with 500 men was captured near the city by the Confederate general, Howell Cobb. Macon was finally occupied by Federal troops under General James H. Wilson (b. 1837) on the 20th of April 1865. In 1900-1910 the area of the city was increased by the annexation of several suburbs.

MACPHERSON, SIR DAVID LEWIS (1818-1896), Canadian financier and politician, was born at Castle Leathers, near Inverness, Scotland, on the 12th of September 1818. In 1835 he emigrated to Canada, settling in Montreal, where he built up a large fortune by “forwarding” merchandise. In 1853 he removed to Toronto, and in the same year obtained the contract for building a line of railway from Toronto to Sarnia, a project from which sprang the Grand Trunk railway, in the construction of which line he greatly increased his wealth. In 1864 he was elected to the Canadian parliament as member of the Legislative Council for Saugeen, and on the formation of the Dominion, in 1867, was nominated to the Senate. In the following years he published a number of pamphlets on economic subjects, of which the best-known is Banking and Currency (1869). In 1880 he was appointed Speaker of the Senate, and from October 1883 till 1885 was minister of the interior in the Conservative cabinet. In 1884 he was knighted by Queen Victoria. He died on the 16th of August 1896.

MACPHERSON, JAMES (1736-1796), Scottish “translator” of the Ossianic poems, was born at Ruthven in the parish of Kingussie, Inverness, on the 27th of October 1736. He was sent in 1753 to King’s College, Aberdeen, removing two years later to Marischal College. He also studied at Edinburgh, but took no degree. He is said to have written over 4000 lines of verse while a student, but though some of this was published, notably The Highlander (1758), he afterwards tried to suppress it. On leaving college he taught in the school of his native place. At Moffat he met John Home, the author of Douglas, for whom he recited some Gaelic verses from memory. He also showed him MSS. of Gaelic poetry, supposed to have been picked up in the Highlands, and, encouraged by Home and others, he produced a number of pieces translated from the Gaelic, which he was induced to publish at Edinburgh in 1760 as Fragments of Ancient Poetry collected in the Highlands of Scotland. Dr Hugh Blair, who was a firm believer in the authenticity of the poems, got up a subscription to allow Macpherson to pursue his Gaelic researches. In the autumn he set out to visit western Inverness, the islands of Skye, North and South Uist and Benbecula. He obtained MSS. which he translated with the assistance of Captain Morrison and the Rev. A. Gallie. Later in the year he made an expedition to Mull, when he obtained other MSS. In 1761 he announced the discovery of an epic on the subject of Fingal, and in December he published Fingal, an Ancient Epic Poem in Six Books, together with Several Other Poems composed by Ossian, the Son of Fingal, translated from the Gaelic Language, written in the musical measured prose of which he had made use in his earlier volume. Temora followed in 1763, and a collected edition, The Works of Ossian, in 1765.
The genuineness of these so-called translations from the works of a 3rd-century bard was immediately challenged in England, and Dr Johnson, after some local investigation, asserted (Journey to the Western Islands of Scotland, 1775) that Macpherson had only found fragments of ancient poems and stories, which he had woven into a romance of his own composition. Macpherson is said to have sent Johnson a challenge, to which Johnson replied that he was not to be deterred from detecting what he thought a cheat by the menaces of a ruffian. Macpherson never produced his originals, which he refused to publish on the ground of the expense. In 1764 he was made secretary to General Johnstone at Pensacola, West Florida, and when he returned, two years later, to England, after a quarrel with Johnstone, he was allowed to retain his salary as a pension. He occupied himself with writing several historical works, the most important of which was Original Papers, containing the Secret History of Great Britain from the Restoration to the Accession of the House of Hanover; to which are prefixed Extracts from the Life of James II., as written by himself (1775). He enjoyed a salary for defending the policy of Lord North’s government, and held the lucrative post of London agent to Mahommed Ali, nabob of Arcot. He entered parliament in 1780, and continued to sit until his death. In his later years he bought an estate, to which he gave the name of Belville, in his native county of Inverness, where he died on the 17th of February 1796.
After Macpherson’s death, Malcolm Laing, in an appendix to his History of Scotland (1800), propounded the extreme view that 268 the so-called Ossianic poems were altogether modern in origin, and that Macpherson’s authorities were practically non-existent. For a discussion of this question see Celt: Scottish Gaelic Literature. Much of Macpherson’s matter is clearly his own, and he confounds the stories belonging to different cycles. But apart from the doubtful morality of his transactions he must still be regarded as one of the great Scottish writers. The varied sources of his work and its worthlessness as a transcript of actual Celtic poems do not alter the fact that he produced a work of art which by its deep appreciation of natural beauty and the melancholy tenderness of its treatment of the ancient legend did more than any single work to bring about the romantic movement in European, and especially in German, literature. It was speedily translated into many European languages, and Herder and Goethe (in his earlier period) were among its profound admirers. Cesarotti’s Italian translation was one of Napoleon’s favourite books.
Authorities.—For Macpherson’s life, see The Life and Letters of James Macpherson ... (1894, new ed., 1906), by T. Bailey Saunders, who has laboured to redeem his character from the suspicions generally current with English readers. The antiquity of the Ossianic poems was defended in the introduction by Archibald Clerk to his edition of the Poems of Ossian (1870). Materials for arriving at a decision by comparison with undoubtedly genuine fragments of the Ossianic legend are available in The Book of the Dean of Lismore, Gaelic verses, collected by J. McGregor, dean of Lismore, in the early 16th century (ed. T. McLauchlan, 1862); the Leabhar na Feinne (1871) of F. J. Campbell, who also discusses the subject in Popular Tales of the Western Highlands, iv. (1893). See also L. C. Stern, “Die ossianische Heldenlieder” in Zeitschrift für vergleichende Litteratur-geschichte (1895; Eng. trans. by J. L. Robertson in Trans. Gael. Soc. of Inverness, xxii., 1897-1898); Sir J. Sinclair, A Dissertation on the Authenticity of the Poems of Ossian (1806); Transactions of the Ossianic Society (Dublin, 1854-1861); Cours de littérature celtique, by Arbois de Jubainville, editor of the Revue celtique (1883, &c.); A. Nutt, Ossian and the Ossianic Literature (1899), with a valuable bibliographical appendix; J. S. Smart, James Macpherson: an Episode in Literature (1905).

McPHERSON, JAMES BIRDSEYE (1828-1864), American soldier, was born at Sandusky, Ohio, on the 14th of November 1828. He entered West Point at the age of twenty-one, and graduated (1853) at the head of his class, which included Sheridan, Schofield and Hood. He was employed at the military academy as instructor of practical military engineering (1853). A year later he was sent to engineer duty at New York, and in 1857, after constructing Fort Delaware, he was sent as superintending engineer to San Francisco, becoming 1st lieutenant in 1858. He was promoted captain during the first year of the Civil War, and towards the close of 1861 became lieutenant-colonel and aide-de-camp to General Halleck, who in the spring of 1862 sent him to General Grant as chief engineer. He remained with Grant during the Shiloh campaign, and acted as engineer adviser to Halleck during the siege operations against Corinth in the summer of 1862. In October he distinguished himself in command of an infantry brigade at the battle of Corinth, and on the 8th of this month was made major-general of volunteers and commander of a division. In the second advance on Vicksburg (1863) McPherson commanded the XVII. corps, fought at Port Gibson, Raymond and Jackson, and after the fall of Vicksburg was strongly recommended by Grant for the rank of brigadier-general in the regular army, to which he was promoted on the 1st of August 1863. He commanded at Vicksburg until the following spring. He was about to go on leave of absence in order to be married in Baltimore when he received his nomination to the command of the Army of the Tennessee, Grant’s and Sherman’s old army, which was to take part under Sherman’s supreme command in the campaign against Atlanta (1864). This nomination was made by Sherman and entirely approved by Grant, who had the highest opinion of McPherson’s military and personal qualities. He was in command of his army at the actions of Resaca, Dallas, Kenesaw Mountain and the battles about Atlanta. On the 22nd of July, when the Confederates under his old classmate Hood made a sudden and violent attack on the lines held by the Army of the Tennessee, McPherson rode up, in the woods, to the enemy’s firing line and was killed. He was one of the most heroic figures of the American Civil War, and Grant is reported to have said when he heard of McPherson’s death, “The country has lost one of its best soldiers, and I have lost my best friend.”

MACQUARIE, a British island in the South Pacific Ocean, in 54° 49′ S. and 159° 49′ E. It is about 20 m. long, and covered with a grassy vegetation, with some trees or shrubs in the sheltered places which afford food to a parrot of the genus Cyanorhamphus, allied to those of the Auckland Islands. Although it has no settled population, Macquarie is constantly visited by sailors in quest of the seals which abound in its waters.

MACRAUCHENIA, a long-necked and long-limbed, three-toed South American ungulate mammal, typifying the suborder Litopterna (q.v.).

MACREADY, WILLIAM CHARLES (1793-1873), English actor, was born in London on the 3rd of March 1793, and educated at Rugby. It was his intention to go up to Oxford, but in 1809 the embarrassed affairs of his father, the lessee of several provincial theatres, called him to share the responsibilities of theatrical management. On the 7th of June 1810 he made a successful first appearance as Romeo at Birmingham. Other Shakespearian parts followed, but a serious rupture between father and son resulted in the young man’s departure for Bath in 1814. Here he remained for two years, with occasional professional visits to other provincial towns. On the 16th of September 1816, Macready made his first London appearance at Covent Garden as Orestes in The Distressed Mother, a translation of Racine’s Andromaque by Ambrose Philips. Macready’s choice of characters was at first confined chiefly to the romantic drama. In 1818 he won a permanent success in Isaac Pocock’s (1782-1835) adaptation of Scott’s Rob Roy. He showed his capacity for the highest tragedy when he played Richard III. at Covent Garden on the 25th of October 1819. Transferring his services to Drury Lane, he gradually rose in public favour, his most conspicuous success being in the title-rôle of Sheridan Knowles’s William Tell (May 11, 1825). In 1826 he completed a successful engagement in America, and in 1828 his performances met with a very flattering reception in Paris. On the 15th of December 1830 he appeared at Drury Lane as Werner, one of his most powerful impersonations. In 1833 he played in Antony and Cleopatra, in Byron’s Sardanapalus, and in King Lear. Already Macready had done something to encourage the creation of a modern English drama, and after entering on the management of Covent Garden in 1837 he introduced Robert Browning’s Strafford, and in the following year Bulwer’s Lady of Lyons and Richelieu, the principal characters in which were among his most effective parts. On the 10th of June 1838 he gave a memorable performance of Henry V., for which Stanfield prepared sketches, and the mounting was superintended by Bulwer, Dickens, Forster, Maclise, W. J. Fox and other friends. The first production of Bulwer’s Money took place under the artistic direction of Count d’Orsay on the 8th of December 1840, Macready winning unmistakable success in the character of Alfred Evelyn. Both in his management of Covent Garden, which he resigned in 1839, and of Drury Lane, which he held from 1841 to 1843, he found his designs for the elevation of the stage frustrated by the absence of adequate public support. In 1843-1844 he made a prosperous tour in the United States, but his last visit to that country, in 1849, was marred by a riot at the Astor Opera House, New York, arising from the jealousy of the actor Edwin Forrest, and resulting in the death of seventeen persons, who were shot by the military called out to quell the disturbance. Macready took leave of the stage in a farewell performance of Macbeth at Drury Lane on the 26th of February 1851. The remainder of his life was spent in happy retirement, and he died at Cheltenham on the 27th of April 1873. He had married, in 1823, Catherine Frances Atkins (d. 1852). Of a numerous family of children only one son and one daughter survived. In 1860 he married Cecile Louise Frederica Spencer (1827-1908), by whom he had a son.
Macready’s performances always displayed fine artistic perceptions developed to a high degree of perfection by very comprehensive culture, and even his least successful personations had the interest resulting from thorough intellectual 269 study. He belonged to the school of Kean rather than of Kemble; but, if his tastes were better disciplined and in some respects more refined than those of Kean, his natural temperament did not permit him to give proper effect to the great tragic parts of Shakespeare, King Lear perhaps excepted, which afforded scope for his pathos and tenderness, the qualities in which he specially excelled. With the exception of a voice of good compass and capable of very varied expression, Macready had no especial physical gifts for acting, but the defects of his face and figure cannot be said to have materially affected his success.
See Macready’s Reminiscences, edited by Sir Frederick Pollock, 2 vols. (1875); William Charles Macready, by William Archer (1890).

MACROBIUS, AMBROSIUS THEODOSIUS, Roman grammarian and philosopher, flourished during the reigns of Honorius and Arcadius (395-423). He himself states that he was not a Roman, but there is no certain evidence whether he was of Greek or perhaps African descent. He is generally supposed to have been praetorian praefect in Spain (399), proconsul of Africa (410), and lord chamberlain (422). But the tenure of high office at that date was limited to Christians, and there is no evidence in the writings of Macrobius that he was a Christian. Hence the identification is more than doubtful, unless it be assumed that his conversion to Christianity was subsequent to the composition of his books. It is possible, but by no means certain, that he was the Theodosius to whom Avianus dedicates his fables.
The most important of his works is the Saturnalia, containing an account of the discussions held at the house of Vettius Praetextatus (c. 325-385) during the holiday of the Saturnalia. It was written by the author for the benefit of his son Eustathius (or Eustachius), and contains a great variety of curious historical, mythological, critical and grammatical disquisitions. There is but little attempt to give any dramatic character to the dialogue; in each book some one of the personages takes the leading part, and the remarks of the others serve only as occasions for calling forth fresh displays of erudition. The first book is devoted to an inquiry as to the origin of the Saturnalia and the festivals of Janus, which leads to a history and discussion of the Roman calendar, and to an attempt to derive all forms of worship from that of the sun. The second book begins with a collection of bons mots, to which all present make their contributions, many of them being ascribed to Cicero and Augustus; a discussion of various pleasures, especially of the senses, then seems to have taken place, but almost the whole of this is lost. The third, fourth, fifth and sixth books are devoted to Virgil, dwelling respectively on his learning in religious matters, his rhetorical skill, his debt to Homer (with a comparison of the art of the two) and to other Greek writers, and the nature and extent of his borrowings from the earlier Latin poets. The latter part of the third book is taken up with a dissertation upon luxury and the sumptuary laws intended to check it, which is probably a dislocated portion of the second book. The seventh book consists largely of the discussion of various physiological questions. The value of the work consists solely in the facts and opinions quoted from earlier writers, for it is purely a compilation, and has little in its literary form to recommend it. The form of the Saturnalia is copied from Plato’s Symposium and Gellius’s Noctes atticae; the chief authorities (whose names, however, are not quoted) are Gellius, Seneca the philosopher, Plutarch (Quaestiones conviviales), Athenaeus and the commentaries of Servius (excluded by some) and others on Virgil. We have also two books of a commentary on the Somnium Scipionis narrated by Cicero in his De republica. The nature of the dream, in which the elder Scipio appears to his (adopted) grandson, and describes the life of the good after death and the constitution of the universe from the Stoic point of view, gives occasion for Macrobius to discourse upon many points of physics in a series of essays interesting as showing the astronomical notions then current. The moral elevation of the fragment of Cicero thus preserved to us gave the work a popularity in the middle ages to which its own merits have little claim. Of a third work, De differentiis et societatibus graeci latinique verbi, we only possess an abstract by a certain Johannes, identified with Johannes Scotus Erigena (9th century).
See editions by L. von Jan (1848-1852, with bibliog. of previous editions, and commentary) and F. Eyssenhardt (1893, Teubner text); on the sources of the Saturnalia see H. Linke (1880) and G. Wissowa (1880). The grammatical treatise will be found in Jan’s edition and H. Keil’s Grammatici latini, v.; see also G. F. Schömann, Commentatio macrobiana (1871).

MACROOM, a market town in the western part of county Cork, Ireland, on the river Sullane, an affluent of the Lee, 24½ m. W. of Cork by the Cork & Macroom railway, of which it is the terminus. Pop. (1901), 3016. Besides a fine Roman Catholic church, a court house and barracks, Macroom possesses a modernized castle, which is said to have been founded by King John, though it is more probably attributable to Norman invaders. It was besieged more than once in the 17th century, and is said to have been the birthplace of Admiral Sir William Penn, whose more famous son founded Pennsylvania. Here some rebels of 1798 were executed and their heads exhibited on the spikes of the castle gate. Macroom has trade in corn-milling, leather-work and dairy produce, and is a good centre for salmon and trout fishing. It is governed by an urban district council.

MACUGNAGA, a village of Piedmont, Italy, in the province of Novara, 20 m. W.S.W. of Piedimulera, which is 7 m. S. of Domodossola by rail. Pop. (1901), 798. It is situated 4047 ft. above sea-level, and is 10 m. N.E. of the highest summit of Monte Rosa. It is frequented as a summer resort.

MacVEAGH, WAYNE (1833- ), American lawyer and diplomatist, was born near Phoenixville, Chester county, Pa., on the 19th of April 1833. He graduated at Yale in 1853, was admitted to the bar in 1856, and was district attorney of Chester county in 1859-1864. He held commands in militia forces raised to meet threatened Confederate invasions of Pennsylvania (1862-63). He became a leader in the Republican party, and was a prominent opponent of his father-in-law, Simon Cameron, in the fight within the party in 1871. MacVeagh was minister to Turkey in 1870-1871; was a member of the state constitutional convention of 1872-1873; was chairman of the “MacVeagh Commission,” sent in 1877 by President Hayes to Louisiana, which secured the settlement of the contest between the two existing state governments and thus made possible the withdrawal of Federal troops from the state; and was attorney-general of the United States in 1881 under President Garfield, but resigned immediately after Garfield’s death. In 1892 he supported Grover Cleveland, the Democratic nominee for the presidency, and from 1893 to 1897 was ambassador to Italy. He returned to the Republican party in 1896. In 1903 he was chief counsel of the United States before the Hague tribunal in the case regarding the claims of Germany, Great Britain and Italy against the republic of Venezuela.

MADÁCH, IMRE (1829-1864), Hungarian dramatist, was born at Alsó-Sztregova. He took part in the great revolution of 1848-49 and was imprisoned; on his return to his small estate in the county of Nógrád, he found that his family life had meanwhile been completely wrecked. This only increased his natural tendency to melancholy, and he withdrew from public life till 1861, devoting his time mainly to the composition of his chief work, Az ember tragoediája (“The Tragedy of Man”). John Arany, then at the height of his fame as a poet, at once recognized the great merits of that peculiar drama, and Madách enjoyed a short spell of fame before his untimely death of heart-disease in 1864. In The Tragedy of Man Madách takes us from the hour when Adam and Eve were innocently walking in the Garden of Eden to the times of the Pharaohs; then to the Athens of Miltiades; to declining Rome; to the period of the crusades; into the study of the astronomer Kepler; thence into the horrors of the French Revolution; into greed-eaten and commerce-ridden modern London; nay, into the ultra-Socialist state of the future, when all the former ideals of man will by scientific formulae be shown up in their hollowness; still further, the poet shows the future of ice-clad earth, when man will be reduced to a degraded brute dragging on the 270 misery of his existence in a cave. In all these scenes, or rather anticipatory dreams, Adam, Eve and the arch-fiend Lucifer are the chief and constantly recurring personae dramatis. In the end, Adam, despairing of his race, wants to commit suicide, when at the critical moment Eve tells him that she is going to be a mother. Adam then prostrates himself before God, who encourages him to hope and trust. The diction of the drama is elevated and pure, and although not meant for the stage, it has proved very effective at several public performances.
Concerning Madách there is an ample literature, consisting mostly of elaborate articles by Charles Szász (1862), Augustus Greguss (1872), B. Alexander (1871), M. Palágyi (1890), and others.

MADAGASCAR, an island in the Indian Ocean, and after New Guinea and Borneo the largest island in the world, about 260 m. distant, at the nearest point, from the S.E. coast of Africa, from which it is separated by the Mozambique Channel. Since 1896 Madagascar has been a French colony. It is 995 m. in length from N. to S., and about 250 m. in average breadth, although near the centre it is nearly 360 m. across; its area is about 228,000 sq. m., or not quite four times the extent of England and Wales. It lies mainly between 44° and 50° E. Its northernmost point, Cape Ambro, in 12° S., inclines 16° to the E. from the longitude of Cape St Mary, the southernmost point, in 25° 35′ S., so that the main axis of the island runs from N.N.E. to S.S.W. In its broad structure Madagascar consists of an elevated mountainous region, from 3000 to 5000 ft. in altitude, occupying from two-fifths to a half of the centre and the eastern side of the island, around which are extensive plains at a much less elevation above the sea, and most developed on the western and north-west sides. But this lower region is broken up by masses of hills, with several elevated plateaus, especially in the south-west and south.
Physical Features.—Madagascar has a very regular and compact form, with few indentations considering its great extent of shore-line. In general outline it has a strong resemblance to the impression of a human foot—the left side. Along two-thirds of its eastern side the coast is almost a straight line, without any inlet, Tamatàve, the chief port on this side of the island, being only protected by coral reefs. North of this line, however, is Antongil Bay, a deep and wide inlet running northwards for about 50 m.; farther north is Port Louquez, and at almost the extreme point of the island is Diégo-Suarez Bay, one of the finest harbours in the world. But the north-western side of Madagascar is broken up by a number of inlets, some of them land-locked and of considerable size. South of Cape St Andrew, the north-west angle of the island, the coast-line is unbroken until the estuary of the river Onilàhy, or St Augustine’s Bay, is reached. Rounding the southern end of the island, there is no other inlet save the small bay north of Fort Dauphin, at the southern end of the straight line of coast already mentioned.
The islands around Madagascar are few and unimportant. The largest are Ste Marie, near the eastern coast, a narrow island about 35 m. long, and Nossi-bé (q.v.), larger and more compact in form, opposite Ampàsindàva Bay on the N.W. coast. Except the Minnow group, north of Nossi-bé, the rest are merely rocky islets, chiefly of coral.
The shores of the greater portion of the southern half of the island are low and flat, but in the northern half the coast is often bold and precipitous, the high land occasionally approaching the sea. On the eastern side the plains vary from 10 to 50 m. in breadth, but on the western side they exceed in some localities 100 m. From these coast-plains the ground rises by successive ranges of hills to the high interior land. This elevated region is broken in all directions by mountains, from which the crystalline rocks show most frequently as huge bosses, and in certain regions present very varied and picturesque outlines, resembling Titanic castles, cathedrals, domes, pyramids and spires. The highest mountain mass is centrally situated as regards the length of the island, but more to the eastern side. This is the ancient extinct volcano Ankàratra, three of the highest points varying in elevation from 7284 to 8635 ft. above the sea, and from 4000 to 5000 ft. above the general level of the surrounding country. The loftiest of these is named Tsi-àfa-jàvona, i.e. “That which the mists cannot climb.” It had been supposed that Ankàratra was the highest point in the island, but in 1903 it was found that Ambòro, in the northern province of Antankàrana, is about 9490 ft. in altitude. Besides these highest points there are a considerable number of mountains in the central provinces of Imèrina and Bétsiléo and the intervening and surrounding districts; and in the Bàra country the Isàlo range has been compared to the “Church Buttes” and other striking features of the scenery of Utah. One of the finest of the Madagascar mountains is an isolated mass near the northern point of the island called Ambòhitra. This is 4460 ft. high, and rising from land little above the sea-level, is well seen far out to sea.
In the elevated region of Madagascar are many fertile plains and valleys, the former being the dried-up beds of ancient lakes. Among these are Bètsimitàtatra in Imèrina, and Tsiènimparìhy in Bétsiléo, supplying a large proportion of the rice required for the capitals of these two provinces. Still more spacious valleys are the Antsihànaka country and the Ankày district, between the two eastern lines of forest. The extensive coast plains on the western side of the island are chiefly in Ibòina (N.W.) and in Ménabé (S. of the Tsìribìhina River); those on the east are widest in the Taifàsy country (S.E.). The water-parting for six-sevenths of the whole length of the island is much nearer the eastern than the western side, averaging from 80 to 90 m. from the sea. There are no arid districts, except in the extreme south-west and towards the southern point of the island. The general surface of the interior highland consists of bare rolling moor-like country, with a great amount of red clay-like soil, while the valleys have a rich humus of bluish-black alluvium.
The chief rivers flow to the west and north-west sides of the island. The eastern streams are all less in size, except the Mangòro, which flows parallel with the coast. Few of them therefore are of much service for navigation, except for the light-draught native canoes; and all of them are more or less closed at their outlets by sand-bars. Beginning at the south-eastern point and going northwards, the principal rivers are the Mànanàra, Mànampàtrana, Màtitànana, Mànanjàry, Mangòro, with its great affluent Onivé, Vòhitra, Màningòry, and the Antànambàlana at the head of Antongil Bay. On the N.W. coast, going southwards, are the Sofià and Màhajàmba, falling into Màhajàmba Bay, the Bétsiboka with the Ikòpa—the great drains of the northern central provinces, forming unitedly the second largest river of the island and falling into Bèmbatòka Bay—the Màhavàry, Mànambòlo, Tsìribìhina or Onimàinty, the third largest river, with its tributaries the Kìtsàmby, Màhajìlo and Manìa, the Mòrondàva, Mangòky, probably the largest river in the country, with its important tributaries the Matsìatra, Mànantànana and Rànomàitso, the Fiherènana and Onilàhy. On the south coast are four considerable streams, the largest of which is the Mènaràndra. Of the western rivers the Bètsibòka can be ascended by small steamers for about 100 m., and the Tsìribìhina is also navigable for a considerable distance. The former is about 300 m. long; the latter somewhat less, but by its affluents spreads over a greater extent of country, as also does the Mangòky. The rivers are all crossed frequently by rocky bars, which often form grand waterfalls. The eastern rivers cut their way through the ramparts of the high land by magnificent gorges amidst dense forest, and descend by a succession of rapids and cataracts. The Màtitànana, whose falls were first seen by the writer in 1876, descends at one plunge some 400 ft.; and on the Vòhitra River, whose valley is followed by the railway, there are also many fine waterfalls.
On the eastern side of Madagascar the contest between the fresh water of the rivers and the sea has caused the formation of a chain of lagoons for nearly 300 m. In many places these look like a river following the coast-line, but frequently they spread out into extensive sheets of water. By cutting about 30 m. of canal to connect them, a continuous waterway could be formed for 270 m. along the coast. This has already been done for about 55 m. between Ivòndrona and Andòvorànto, a service of small steamers forming part of the communication between the coast and the capital. Besides these lagoons, there are few lakes of any size in Madagascar, although there were some very extensive lakes in a recent geological epoch. Of the largest of these, the Alàotra Lake in the Antsihànaka plain is the relic; it is about 25 m. long. Next comes Kinkòny, near Maròambitsy Bay (N.W. coast), about 16 m. long, and then Itàsy, in western Imèrina, about half as large. There is also a salt lake, Tsimànampetsòtsa (S.W. coast), about as large as Alàotra.
There is now no active volcano in Madagascar, but a large number of extinct cones are found, some apparently of very recent formation. Some miles south of Diégo-Suarez is a huge volcanic mountain, Ambòhitra, with scores of subsidiary cones on its slopes and around its base. About 40 m. south-west of Antanànarìvo there is a still larger extinct volcano, Ankàratra, with an extensive lava field surrounding it; while near Lake Itàsy are some 200 volcanic cones. Another group of extinct volcanoes is in the Vàkinankàratra district, S.W. of Ankàratra. Many others exist in other parts of the island (see § Geology). Slight shocks of earthquake are felt every year, and hot springs occur at many places. Several of these are sulphurous and medicinal, and have been found efficacious in skin diseases and in internal complaints.
Geology.—Madagascar may be divided into two very distinct geological regions, viz. (I.) the Archean Region, which extends over the central and eastern portions of the island and occupies about two-thirds of its whole area, and is composed of crystalline schists; and (II.) the Western Region, of sedimentary rocks, including the remaining third of the island, in the centre of which, however, is an isolated patch of Archean rocks, near Cape St Andrew. There are also found in both regions numerous masses of igneous rocks, both plutonic and volcanic, in some places of considerable extent, which pierce through and overflow the earlier formations.
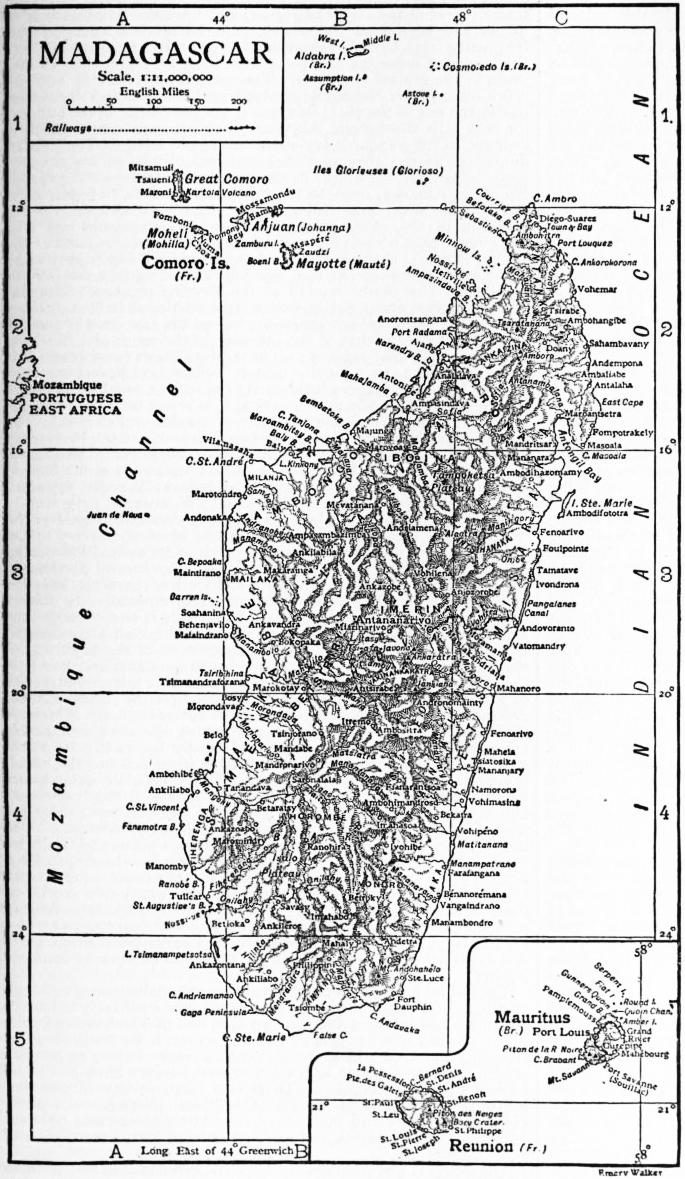
I. The Archean Region.1—This region, nearly coincident with the mountainous upper portion of the island, is chiefly composed of the following crystalline rocks: gneiss, which is the most common of them all, quartzite and quartz-schist, with occasional beds of crystalline limestone and mica-schist, although this latter rock is very rare. The gneiss is mostly grey, but occasionally pinkish, its essential constituents (felspar and quartz) being almost always associated with dark mica (biotite) and hornblende in variable quantity. The rock is therefore a hornblende-granitite-gneiss. Granite—more frequently granitite—occurs in several places, as well as pyroxene-granulite, serpentine, argillate, &c.; and gold is found widely disseminated, as well as other metals, but these latter, as far as at present known, except iron, are not abundant. The general strike of the rocks is the same as that of the trend of the island itself (N.N.E. to S.S.W.), but in its western portion the strike is frequently from N.N.W. to S.S.E. In both cases the strike of the rocks is coincident with the direction of several large valleys, which mark huge faults in the crystalline rocks. Almost the whole of this region is covered by a red soil, often of great thickness, which resembles and is often described as “clay,” but is really decomposed rock, chiefly gneiss, reddened with oxidized magnetite.
II. The Sedimentary Region.—The sedimentary rocks extend continuously along the western side of Madagascar, following the coast-line; in the north these series of strata are only from 20 to 30 m. across, but farther south they reach a breadth of nearly 100 m., while opposite the Bétsiléo province they extend nearly half across the island. A narrow band, of Cretaceous age, occurs also on the east coast, for about 120 m., between Vàtomàndry and Mànanjàry. The following formations are represented:—
1. Primary. It is thought that certain beds of slaty rocks, which have been recognized at different places, may belong to some of the Primary strata. Some siliceous schists of the Permian age were discovered in 1908 in the valley of the Sàkamèira, south of the Onilàhy, or Augustine river. (S.W. coast). These contain reptilian remains, and also clear imprints of leaves of the Glossopteris indica, as well as other indications of an ancient vegetation. In the same region conglomerates have been found containing enormous blocks, apparently brought by glacial action, and said to be identical in character with those described as existing in the Transvaal. True coal has also been obtained in the same district, the deposits varying from a third to half a metre in thickness.
2. Secondary. The lowest members of these rest directly upon the central mass of crystalline rocks, and consist of sandstones, conglomerates and shales, which have been supposed by some to belong to the Trias, without, however, the discovery of any fossil necessary to confirm this supposition, except some silicified trunks of trees. These beds are most probably lower members of the Jurassic series. Westward of and above these strata, the Middle and Upper Jurassic formations are found (Lias, Lower Oolite, Oxfordian, &c.), with well-marked and numerous fossils (Ammonites, Nerinaea, Natica, Astarte, Rhynchonella, Echinodermata, &c.); then the Cretaceous rocks, both these and the Jurassic series being largely developed, the Cretaceous fossils including Nautilus, Belemnites, Ostrea, Gryphaea, &c., and some very large Ammonites (Pachydiscus). The Secondary strata show generally a very slight dip westwards and are consequently almost horizontal. They do not seem to have been greatly disturbed, although faults occur here and there.
3. Tertiary. A small strip of coast of Eocene age is known near Tullear (S.W. coast), and rocks of the same period occur in Nòssi-bé, at Màhajamba Bay, and at Diégo-Suarez, with Nummulites and other foraminifera. Near the latter locality, beds of Oligocene age have been noticed, consisting of coarse limestones.
4. Quaternary and Recent. A narrow band of these deposits extends along the west coast, from north of Cape St Andrew nearly to the extreme southern point of the island. But the most noticeable of these are those in the ancient bed of the Alàotra Lake, which formerly extended far southwards along the valley of the Mangòro; also those in the marshes of Antsìrabè and of Ifànja, in the Ikòpa valley (the great rice plain west of the capital), and also in the plain of Tsiénimpàrìhy in Bétsiléo, and especially the recent deposits of Ampàsambazìmba, north-west of Lake Itàsy, discovered in 1902. These beds, rich in subfossil remains, have yielded important additions to our knowledge of the extinct fauna of the island. (See § Palaeontology.)
Igneous Rocks. (1) Plutonic rocks.—The ancient or plutonic igneous rocks (including granite, syenite, diorite, gabbro, porphyry, porphyrite, norite and retinite) appear at various points of the two previously described regions. In the Archean region the gneiss is very often found passing into granite, but certain granitic masses have a sufficiently distinct character. In the midst of the sedimentary region are two well-recognized masses of plutonic rocks, belonging to the syenites, sometimes quartziferous in structure. (2) Volcanic rocks.—Recent volcanic eruptive rocks (including rhyolite, trachyte, phonolite, andesite and basalt) have been examined at a number of points throughout both the geological regions of the island. In 272 the Archean region these are very noticeable near Lake Itàsy, in the massif of Ankàratra (an ancient volcano) and in Vàkinankàratra (at Bètàfo, Antsìrabé, &c.); while there are numerous outflows of doleritic rocks, probably from faults, along the eastern side of the island and almost parallel with the coast line. In the sedimentary region volcanic rocks are very numerous; the most extensive of these is a tract of country, more than 80 m. long, on the west coast, where the basalt has overflowed the Cretaceous strata. It must be remembered that the geology of Madagascar is still only known in its broad features.2
Minerals and Metals.—The country has considerable mineral wealth. Gold is found almost all over the region of crystalline rocks, except in and around the Antsihànaka province, the richest auriferous districts being a band of country parallel with the east coast and spreading at its southern end into the interior; and another tract, whose centre is about 100 m. N. of the capital (see § Industries, &c.). Silver has been detected in certain galenas, and also platinum; copper has been found in various localities, as well as zinc, lead, nickel, antimony and manganese, but none of these metals has yet been discovered in sufficient quantities for profitable working. Iron, on the contrary, especially magnetite, is found abundantly and has for long been worked by the Malagasy with the simple appliances brought by their ancestors from their original home in the Far East. The principal seats of the native industry are on the edge of the upper forest, where charcoal is easily procured. The following precious stones are reported: corundum (rubies and sapphires), beryl, topaz, zircon, garnet, amazon-stone, tourmaline, often in large crystals, and variously coloured quartz, also often found in crystals of great size. Bitumen and petroleum have been found; graphite is plentiful, and sulphur, salt, saltpetre and lime are also procured. On the north-west coast thin beds of lignite occur, and coal has been found in the valley of the Sàkamèira.
Palaeontology.—Researches in various parts of the island have revealed the existence, in a subfossil state, of the bones of numerous birds of the family Struthidae. These have been arranged in twelve species, belonging to two genera, Aepyornis and Mullerornis, which varied in size from that of a bustard to birds much exceeding an ostrich, and rivalling the recently extinct moa of New Zealand, the largest species being about 10 ft. in height. One species of these great wingless birds laid an egg which is the largest known, being 12½ in. by 9½ in. Associated with these remains there have been found those of many other birds, including a hawk, a duck, a darter, a spoonbill, a heron, a rail and a wild-goose, some of these being much larger than any now inhabiting Madagascar. In the same beds the remains of two, if not three, species of hippopotamus have been found, about two-thirds the size of the living South African species; also the bones and carapace, &c., of gigantic tortoises, and the bones of a crocodile, now extinct on the coast and rivers, but still living in the two chief lakes; also the remains of a river-hog, of a species of swine, and of a slender-legged form of zebu-ox. Near the south-west coast the skull of a large lemuroid animal was discovered in 1893, much longer than that of any living lemur, the animal being probably three times the size of any previously known Madagascar lemuroid. Later still, in 1899 and subsequently, the bones of two other creatures of the same suborder have been discovered, one of them indicating an animal much larger than a man. Many of these birds and animals were probably contemporaneous with the earliest human inhabitants of Madagascar. The remains of two species of Edentata have been found, as well as those of several species of small Rodents, also of a Carnivore (Cryptoprocta), a larger variety of the species still living in the island.
In the deposits of a much more remote era than those already spoken of—the Jurassic—the bones of some enormous terrestrial lizards have been brought to light, belonging to Sauropodous Dinosaurs of the genera Bothriospondylus and Titanosaurus, and to a Theropod of the genus Megalosaurus. In the beds of the Lower Oolite portions of the skull of a reptile resembling the gavial of the Ganges had been previously discovered, from which a new genus called Steneosaurus has been founded. Since the French occupation (1895) considerable additions have been made to our knowledge of the fossil fauna of Madagascar from researches made both on the west and south-west coast (at Bèlo and Ambòlisatrana) and in the interior (at Antsìrabè), especially in the rich deposits near Tsàrazàza (Ampàsambazimba), to the north-west of Lake Itàsy. From these various localities the subfossil remains of thirteen or fourteen extinct species of lemuroid animals (including the gigantic species already mentioned) have been obtained, and have been classified under five new genera: viz. Megaladapis (3 sp.), Palaeopropithecus (3 sp.), Archaeolemur (2 sp.), Bradylemur (1 sp.) and Hadropithecus (1 sp.), together with three new species of lemur. Of these, the Archaeolemurs seem to have combined the characteristics of lemuroid animals with those of the monkeys, while Hadropithecus is pronounced to be the nearest known link with them. A list of all the fossils of the island known in 1895, but omitting the vertebrates above mentioned, included 140 species,3 belonging to the Mollusca, Foraminifera, Echinodermata, Actinozoa and Plantae; but the researches of French geologists made the total number of Madagascar fossils known in 1907 to be not fewer than 280 species.
Climate.—In the high interior the climate resembles that of the temperate zones, although six-sevenths of the island are within the tropics; there is no intense heat, and it is quite cold, occasionally touching freezing point, during the nights of the cool season. These parts of the country are tolerably healthy for Europeans. But the coasts are much hotter, especially on the western side, as is also the interior west of the highland region; and from the large amount of marsh and lagoon on the coasts, malarial fever is common and frequently fatal, both to Europeans and to natives from the interior. Epidemics of influenza and fever have been very prevalent of late years in the central provinces. The seasons are two—the hot and rainy season from November to April, and the cool and dry season during the rest of the year; this remark applies chiefly to the interior, for rain falls throughout the year on the eastern coast, which is exposed to the vapour-laden south-east trade winds. The rainfall diminishes as one goes westward and especially south-westward, there being very little rain in the south-west corner of the island. No snow is known, even on the loftiest mountains, but thin ice is occasionally seen; and hail-showers, often very destructive, are frequent in the rainy season. Terrific thunderstorms are also common at that period; waterspouts are sometimes seen; and as the Indian Ocean cyclone region touches the eastern coast, hurricanes occur every few years, at rare intervals ascending into the interior highland. The yearly rainfall of the Imèrina province (Antanànarìvo) averages about 54½ in.; accurate statistics as to that of other parts of the island are not available; but on the east coast it appears to be about double that of the interior; in the south-east considerably more than that amount; while at Mòrondàva (west coast) it is given as about 21 in. annually, and at Tullear (south-west coast) as only 10 in. At Tamatàve (east coast) the mean annual temperature is given as 76.5°, while at the capital it is about 66°; the temperature of Antanànarìvo resembles that of Naples or Palermo.4 The following table gives the mean of two different sets of government returns of mean rainfall: Antanànarìvo, 1369 mm.; Tamatàve, E. coast, 1863 mm.; Fàrafangàna, S.E. coast, 2803 mm.; Diégo-Suarez, N. end of island, 1196 mm.; Mòrondàva, W. coast, 543 mm.; Tullear, S.W. coast, 273 mm.; Màrovoày, W. interior, 1413 mm.
Fauna.—The fauna of Madagascar, while deficient in most of the characteristic tropical forms of life, is one of great interest to the naturalist from its remote affinities, much of its animal life having Asiatic rather than African relationships. The central portions of the island, from their generally bare and treeless character, are poor in living creatures; but the lower country, and especially the forests and coast plains, are fairly well stocked. But it is noticeable that many species have a very limited range. Although a continental island, it possesses no large quadrupeds—none of the larger carnivorous, ungulate, proboscoid or quadrumanous animals; but it is the headquarters of the Lemuroidea, no fewer than thirty-nine species of which are found in its forests and wooded plains. Some of these creatures are highly specialized, while the curious aye-aye (Chiromys madagascariensis), an allied form, is one of the most remarkable animals known, forming a genus and family by itself. Its whole structure is strangely modified to enable it to procure the wood-boring larvae which form its food. Other peculiar animals are twenty-three species of the Centetidae, a family of the Insectivora almost confined to Madagascar; while of the Carnivora there are several small creatures belonging to the civets (Viverridae). The largest of these ferocious animals, also forming a genus and family by itself, is the Cryptoprocta ferox; it is a plantigrade animal, 3 ft. long, but very like an enormous weasel, and attacks other animals with the greatest ferocity. The island contains twenty-five species of bats, mostly of African, but some of Indian, affinities. African humped cattle were introduced several hundred years ago and now exist in large herds all over the country. The fat-tailed sheep, goats and swine have also been naturalized, as well as all kinds of domestic poultry.
The avi-fauna is much richer than the mammalian, and, although wanting the largest birds as well as the most brilliantly coloured, comprises two hundred and sixty species, half of which are endemic. Many of the birds are remarkable not so much for their shape or colouring as for their distant relationships; many belong to peculiar genera, and some are so isolated that new families have had to be formed for their reception. There is a large variety of perching birds, including several species of brilliant plumage—sun-birds, kingfishers, rollers and flycatchers, &c.; kites, hawks and owls are numerous, and the lakes and marshes abound with water-fowl and herons, ibises, &c.
The island is free from deadly serpents, but contains two or three 273 small species of boa; crocodiles abound in the rivers and lakes; and numerous species of lizard, chameleon and tree-frog inhabit the woods. Madagascar may be considered as one of the headquarters of the Chamaeleonidae, for of the fifty known species no fewer than twenty-five have already been described from the island. Many of these are of curious form, with remarkable developments of the plates of the head and projecting horns and spines. There are several peculiar tortoises, but the gigantic species are now found alive only on the little island of Aldabra, to the north. The insect life comprises many brilliantly-coloured beetles, butterflies (about eight hundred species of which are known), moths, locusts, spiders and flies, and also noxious spiders, with scorpions and centipedes. The river fishes belong chiefly to the family Chromididae; many of them are of brilliant and bizarre appearance, with strongly contrasted colours in bands and spots. Those found in the coast waters do not differ materially from the widely spread Indian Ocean species.
As a whole, the Madagascar fauna is marked by a strong individuality, which would appear to be the result of long isolation from the other zoological “regions.” The Asiatic and Malayan affinities of many of its animals, as well as the physical conditions of the bed of the Indian Ocean, make it highly probable that Madagascar, while once forming part of Africa, is the chief relic of a considerable archipelago formerly connecting that continent with Asia, its other portions being shown by groups of small islands, and by coral atolls and shoals, which are gradually disappearing beneath the waves. These questions have been fully treated by Dr A. R. Wallace in his Geographical Distribution of Animals (vol. i. ch. ix., 1876) and Island Life, ch. xix. (1880).
Flora.—The flora of Madagascar is one of great interest. One of its most prominent features is the belt of forest round a large part of the island at no great distance from the sea, and generally following the coast-line. This forest is densest on the east side, and for about 120 m. forms a double line, the lower one being much the broader and averaging 30 m. across, but attaining a breadth of 60 or 70 m. on the north-east, near Antongil Bay. The vegetation on the western side of the island is much less dense, often appearing as scattered clumps of trees on savannah-like plains rather than continuous forest; while in the south-west, where the rainfall is very scanty, the vegetation is largely of fleshy-leaved and spiny plants—aloes and cacti (the latter introduced), with several species of Euphorbia, as well as numerous lianas, one of which (Intisy) yields india-rubber. It is estimated that there are about 30,000 sq. m. of forest-covered country in Madagascar, or about one-eighth of its whole surface. The vegetation of the forests, the abundant epiphytes, the tree-mosses, the filmy ferns and the viviparous character of many of the ferns, show clearly how abundant the rainfall is in the eastern forest region. This contains a large variety of hard-wooded and valuable timber trees, including species of Weinmannia (Lalòna5), Elaeocarpus (Voànana), Dalbergia (Vòambòana), Nuxia (Vàlanìrana), Podocarpus, a pine, the sole species in the island (Hètatra), Tambourissa (Ambòra), Neobaronia (Hàrahàra), Ocotea (Varòngy) and probably ebony, Diospyros sp., &c. The following trees are characteristic of Madagascar vegetation, some of them being endemic, and others very prominent features in the landscape: the traveller’s-tree (Urania speciosa), with its graceful crown of plantain-like leaves growing like an enormous fan at the top of a tall trunk, and affording a supply of pure cool water, every part of the tree being of some service in building; the Raphia (rofia) palm (Sagus ruffia); the tall fir-like Casuarina equisetifolia or beefwood tree, very prominent on the eastern coast, as well as several species of screw-pine (Pandanus); the Madagascar spice (Ravintsara madagascariensis), a large forest tree, with fragrant fruit, leaves and bark; a beautiful-leaved species of Calophyllum; and the Tangèna (Tanghinia veneniflua), formerly employed as a poison ordeal. On the lagoons and lower reaches of the rivers the Vìha (Typhonodorum lindleyanum), an arum endemic to Madagascar, grows in great profusion to a height of 12 or 13 ft. and has a white spathe more than a foot in length; and on the western coast dense thickets of mangrove line the creeks and rivers. In the interior rivers is found the curious and beautiful lace-leaf plant (Ouvirandra fenestralis), with an edible tuberous root. On the western side of the island the baobab, the tamarind, the ròtra (Eugenia sp.), the rofia palm, and several species of fan-palm (Hyphaene) and of Ficus are prominent; and the mango (introduced) grows to a large tree. In the generally bare interior highlands, large trees, species of Ficus (Amòntana, Aviàvy, Nònoka, Adàbo, &c.), often mark the position of the old towns; and some of these, as Ambòhimànga, Vòhilèna, &c., are surrounded by remnants of the original forest, which formerly covered large portions of the interior. The most prominent tree in the central province is now the Cape-lilac (Melia azederach) introduced about 1825; and since the French conquest several species of eucalyptus have been planted in vast numbers by the road sides. These have given quite a new aspect to the vegetation, while bright colour is imparted by species of Bougainvillea and Poinsettia. In the eastern forests palms, bamboos, lianas and tree-ferns, as well as species of Dracaena, are found.
Although flowers growing on the ground or on shrubs are not conspicuous for number or beauty, there are many fine flowering trees, such as Poinciana regia, presenting a mass of scarlet flowers; Colvillia racemosa, with yellow flowers; Astrapaea Wallichii, striking attention from its abundant flowers; and species of Cryptostegia, a purple-flowered creeper, and Strongylodon, another creeper with cream-coloured blossoms. Among attractive plants are species of Hibiscus, Euphorbia, Buddleia, Ixora, Kitchingia, Clematis, &c. On the east coast two orchids, species of Angraecum, with large white waxy flowers, one with an extraordinarily long spur or nectary, attract the attention of every traveller during June and July by their abundance and beauty. Some 320 species o£ fern have been collected, and there are large numbers of spiny and prickly plants, as well as numerous grasses, reeds and rushes, many of them of great service in the native manufactures of mats, hats, baskets, &c.
The Rev R. Baron divides the flora into three distinctly marked “regions,” which run in a longitudinal direction, following approximately the longer axis of the island, and are termed respectively eastern, western and central. The central includes the elevated highland of the interior, while the eastern and western include the forest belts and most of the wooded country and coast plains. Of the 4100 known plants—of which about three-fourths are endemic—composing the Madagascar flora, there are 3492 Dicotyledons, 248 Monocotyledons and 360 Acotyledons. Of these, the orders most largely represented (together with their species) are: Leguminosae, 346; Filices, 318; Compositae, 281; Euphorbiaceae, 228; Orchideae, 170; Cyperaceae, 160; Rubiaceae, 147; Acanthaceae, 131; Gramineae, 130. The number of endemic genera now known is 148. Of the 3178 species of plants whose localities have been determined, 35% are peculiar to the eastern region, 27.5% to the central, and 22% to the western. One natural order, Chlaenaceae, is strictly confined to Madagascar. “A small proportion of the species are Asian, but not African; and the flora of the mountains corresponds closely with that of the great ranges of the tropical zone of Africa.” “The general plan of the flora follows thoroughly the same lines as that of the tropical regions of the Old World.”
Among the food-giving plants are rice—the staff of life to the majority of the Malagasy—in many varieties, maize, millet, manioc, yams, sweet-potatoes, arrowroot, which is largely used by the western tribes—as well as numerous vegetables, many of them of foreign introduction. The fruits—the majority of which are introduced—are the banana, peach, loquat, pineapple, mango, melon, grape, quince, plum, apple, mulberry, orange, lemon, citron, guava, Chinese-guava, Cape-gooseberry, fig, raspberry, tomato, &c. Several spices are grown, including ginger, capsicum, &c.; sugar-cane, coffee, indigo, vanilla, tobacco, cotton, hemp, gourds, dye-woods, gums, mulberry and other trees and plants for silk-culture, are also among the vegetable productions; gum-copal was formerly, and india-rubber is still, an important article of export.
Provinces and Towns.—The island may be divided into districts or provinces, which in the main indicate tribal divisions. Of these tribal territories the following may be distinguished, taking them in three main divisions, from north to south: (1) Eastern: Antankàrana, occupying the northern peninsula; the country of the Bétsimisàraka, who inhabit a long extent of the coast plains, about 500 m. in length; parallel with this for about a third of it, and between the two lines of forest, is the Bézànozàno country. South again are the districts of the Taimbahòaka, the Taimòro, the Taifàsy and the Taisàka; and at the south-eastern corner are the Tanòsy. (2) Central: the districts of Tsimihèty and the Sihànaka; Imèrina, the Hòva province; the Bétsiléo; the Tanàla or foresters; the Bàra; and the emigrant Tanòsy. (3) Western: the people from almost the northern to the southern extremities of the island are known as Sàkalàva, but consist of a number of distinct tribes—the Tibòina, the Màilaka, the Taménabé, and the Fiherènana, &c. South of these last are the Màhafàly, with the Tandròy at the extreme south. There are no distinctly marked boundaries between any of these tribal territories; and west of Imèrina and Bétsiléo there is a considerable extent of country with hardly any population, a kind of “no-man’s-land.” There are numerous subdivisions of most of the tribes.
The capital, Antanànarìvo (pop. 69,000), in the highlands of Imèrina, and Tamatàve (pop. 4600), on the east coast and the chief seaport, are separately described. Majunga (properly Mojangà, pop. 5300) on the north-west coast, just north of 16° S., and Diégo-Suarez, are important ports for foreign trade, the latter being also a fortified naval and military station. Other ports and towns are Màhanòro, Mànanjàry (S.E. coast, pop. 4500), Tullear (S.W. coast), and Fianàrantsòa (pop. 6200), the chief town of the Bétsiléo. There are very few places besides these with as many as 2000 people.
Inhabitants.—The population is somewhat under two and three-quarter millions,6 including some 10,000 or 11,000 Europeans, and a smaller number of Indian, Arab, and other Asiatics, mostly small traders found in the seaports, the Chinese being found in every town of any size. The island, it will be seen, is very sparsely inhabited; the most densely peopled province is that of Imèrina with (1905) 388,000 inhabitants. The natives, collectively known as Malagasy, are divided into a considerable number of tribes, each having its distinct customs. Although geographically an African island, the majority of its inhabitants are derived, the lighter portion of them from the Malayo-Polynesian stock, and the darker races from the Melanesian. This is inferred from their similarity to the peoples of the Indian and Pacific archipelagoes in their physical appearance, mental habits, customs, and, above all, in their language. Their traditions also point in the same direction. There is, however, an undoubted African mixture in the western and some other tribes. There is also an Arab element both on the north-west and south-east coasts; and it appears that most of the families of the ruling classes in all parts of the island are descended from Arabs, who married native women. It is believed that there are traces of an aboriginal people (the Vazimba), who occupied portions of the interior before the advent of the present inhabitants, and these appear to have been a somewhat dwarfish race, and lighter-coloured than the Malagasy generally. The Hòva became the dominant tribe from the beginning of the 19th century; they appear to be the latest immigrants, and are the lightest in colour; and they are also the most intelligent and civilized of all the peoples inhabiting the island.
The most striking proof of the virtual unity of the inhabitants of Madagascar is that substantially but one language is spoken over the whole country. The Malay affinities of Malagasy were noted in the 16th century; indeed, the second and fifth books published upon the country (in 1603 and 1613) were comparative vocabularies of these two languages. Later investigations have confirmed the conclusions thus early arrived at; and Van der Tuuk, Marre de Marin and W. E. Cousins have shown conclusively the close relationships between the language of the Malagasy and those of the Malayo-Polynesian regions; similar connexions exist, especially in grammatical construction, between the Malagasy and Melanesian languages. The Malagasy had never invented for themselves a written character, and had consequently no manuscripts, inscriptions or books, until their language was reduced to writing, and its orthography settled by English missionaries. Their speech nevertheless is very full in many of its verbal and other forms, while it also exhibits some curious deficiencies. It is very soft and musical, full of vowels and liquids, and free from all harsh gutturals. Native oratory abounds in figures, metaphors and parables; and a large number of folk-tales, songs and legends, together with the very numerous proverbs, give ample evidence of the mental ability and imaginative powers of the Malagasy.
Native society in Imèrina among the Hòva was formerly divided into three great classes: the Andrìana, or nobles; the Hòva, freemen or commoners; and the Andèvo, or slaves; but these last became free by a proclamation issued in 1896. The Andrìana are, strictly speaking, royal clans, being descendants of petty kings who were conquered or otherwise lost their authority through the increasing power of the ancestors of the reigning family. Their descendants retained certain honours in virtue of their royal origin, such as special terms of salutation, the use of the smaller scarlet umbrella (the larger one was the mark of royal rank), the right to build a particular kind of tomb, &c.; they also enjoyed exemption from certain government service, and from some punishments for crime. The Hòva7 or commoners form the mass of the population of Imèrina. They are composed of a large number of tribes, who usually intermarry strictly among themselves, as indeed do families, so that property and land may be kept together. The third great division was the slave population, which since 1896 has become merged in the mass of the people. The Mozambiques or African slaves, who had been brought from the African coast by Arab dhows, were in 1877 formally set free by an agreement with the British government.
Royalty and chieftainship in Madagascar had many peculiar customs. It had a semi-sacred character; the chief was, in heathen tribes, while living, the high priest for his people, and after death, was worshipped as a god; in its modern development among the Hòva sovereigns it gathered round it much state and ceremony. There were many curious examples of the taboo with regard to actions connected with royalty, and also in the words used which relate to Malagasy sovereigns and their surroundings. These were particularly seen in everything having to do with the burial of a monarch. While the foregoing description of native society applied chiefly to the people of the central province of Imèrina, it is applicable, with local modifications, to most of the Malagasy tribes. But on the island becoming a French colony, in 1896, royalty was formally abolished; and little regard is paid to native rank by French officials.
The chief employment of the Malagasy is agriculture. In the cultivation of rice they show very great ingenuity, the kètsa grounds, where the rice is sown before transplanting, being formed either on the margins of the streams or in the hollows of the hills in a series of terraces, to which water is often conducted from a considerable distance. In this agricultural engineering no people surpass the Bétsiléo. No plough is used, all work being done by a long-handled spade; and oxen are only employed to tread out the soft mud preparatory to transplanting. The rice is threshed by being beaten in bundles on stones set upright on the threshing-floor; and when beaten out the grain is stored by the Hòva in rice-pits dug in the hard red soil, but by the coast tribes in small timber houses raised on posts. In preparing the rice for use it is pounded in a wooden mortar to remove the husk, this work being almost always done by the women. The manioc root is also largely consumed, together with several other roots and vegetables; but little animal foods (save fish and freshwater Crustacea) is taken by the mass of the people except at festival times. Rice is used less by the western tribes than by those of the central and eastern provinces, and the former people are more nomadic in their habits than are the others. Large herds of fine humped cattle are found almost all over the island.
The central and eastern peoples have considerable manual dexterity. The women spin and weave, and with the rudest appliances manufacture a variety of strong and durable cloths of silk, cotton and hemp, and of ròfia palm, aloe and banana fibre, of elegant patterns, and often with much taste in colour. They also make from straw and papyrus peel strong and beautiful mats and baskets in great variety, some of much fineness and delicacy, and also hats resembling those of Panama. The people of the south and south-east make large use of soft rush matting for covering, and they also prepare a rough cloth of bark. Their non-employment of skins for clothing is a marked distinction between the Malagasy and the South African races, and their use of vegetable fibres an equally strong link between them and the Polynesian peoples. The men wear a loincloth or salàka, the women a kitàmby or apron folded round the body from waist to heel, to which a jacket or dress is usually added; both sexes use over these the làmba, a large square of cloth folded round the body something like the Roman toga, and which is the characteristic native dress. The Malagasy are skilful in metal-working; with a few rude-looking tools they manufacture silver chains of great fineness, and filagree ornaments both of gold and silver. Their iron-work is of excellent quality, and in copper and brass they can produce copies of anything made by Europeans. They display considerable inventive power, and they are exceedingly quick to adopt new ideas from Europeans.
There is a considerable variety in the houses of the different Malagasy tribes. The majority of Hòva houses were formerly built of layers of the hard red soil of the country, with high-pitched roofs thatched with grass or rush; while the chiefs and wealthy people had houses of framed timber, with massive upright planking, and lofty roofs covered with shingles or tiles. But the introduction of sun-dried and burnt bricks, and of roofing tiles in the central provinces has led to the general use of these materials in the building of houses, large numbers of which are made in two storeys and in European fashion. The forest and coast tribes make their dwellings chiefly of wood framing filled in with the leaf-stalks of the traveller’s tree, with the leaves themselves forming the roof covering. The houses of the Bétsiléo and Sàkalàva are very small and dirty, but those of the coast peoples are more cleanly and roomy. Among the Hòva and Bétsiléo the old villages were always built for security on the summits of lofty hills, around which were dug several deep fosses, one within the other. In other districts the villages and homesteads are enclosed within formidable defences of prickly-pear or thorny mimosa.
Apart from the modern influence of religious teaching, the people are very immoral and untruthful, disregardful of human life and suffering, and cruel in war. Until lately polygamy has been common among all the Malagasy tribes, and divorce effected in an absurdly easy fashion. At the same time the position of woman is much higher in Madagascar than in most heathen countries; and, the fact that for nearly seventy years there were (with a few months’ 275 exception) only female sovereigns, helped to give women considerable influence in native society. The southern and western peoples still practise infanticide as regards children born on several unlucky days in each month. This was formerly the general practice all over the island. The old laws among the Hòva were very barbarous in their punishments, and death in various cruel forms was inflicted for very trifling offences. Drunkenness is very prevalent in many parts of the island; and it can hardly be said of many of the Malagasy that they are very industrious. But they are courageous and loyal to their chiefs and tribe, and for short periods are capable of much strenuous exertion. They are affectionate and firm in their friendships, kind to their children and their aged and infirm relatives, very respectful to old age, most courteous and polite and very hospitable to strangers. Slavery had a patriarchal and family character, and was seldom exercised in a cruel or oppressive way.
The Malagasy have never had any organized religious system or forms of worship; there are no temples, images or stated seasons of devotion, nor is there a priesthood, properly so-called. Yet they have never been without some distinct recognition of a supreme being, whom they call Andriamànitra, “The Fragrant One,” and Zànahàry, “The Creator”—words which are recognized all over the island. They have also retained many ancient sayings, proverbial in their style, which enforce many of the truths of natural religion as to the attributes of God. With all this, however, there has long existed a kind of idolatry, which in its origin is simply fetishism—the belief in charms—as having power to procure various benefits and protect from certain evils. Among the Hòva in modern times four or five of these charms had acquired special sanctity and were each honoured as a kind of national deity, being called “god,” and brought out on all public occasions. Together with this idolatry there is also a firm belief in the power of witchcraft and sorcery, in divination, in lucky and unlucky days and times, in ancestor worship, especially that of the sovereign’s predecessors, and in several curious ordeals for the detection of crime. The chief of these was the celebrated tangèna poison ordeal, in which there was implicit belief, and by which, until its prohibition by an article in the Anglo-Malagasy treaty of 1865, thousands of persons perished every year. Sacrifices of fowls and sheep are made at many places at sacred stones and altars, both in thanksgiving at times of harvest, &c., and as propitiatory offerings. Blood and fat are used to anoint many of these stones, as well as the tombs of ancestors, and especially those of the Vazimba. In some of the southern districts it is said that human sacrifices were occasionally offered. The chief festival among the Hòva, and almost confined to them, was that of the New Year, at which time a kind of sacrificial killing of oxen took place, and a ceremonial bathing, from which the festival took its name of Fàndròana (the Bath). This festival is now merged in the French national fête of the 14th of July. Another great festival was at circumcision times. This rite was observed by royal command at intervals of a few years; these were occasions of great rejoicing, but also of much drunkenness and licentiousness. Since 1868 circumcision has been observed by each family at any time convenient to itself. It is practised by all the Malagasy tribes. Funerals were also times of much feasting, and at the death of people of rank and wealth numbers of bullocks were and are still killed. Although there was no proper priesthood, the idol-keepers, the diviners, the day-declarers and some others formed a class of people closely connected with heathen customs and interested in their continued observance.
Industries and Commerce.—The rearing of cattle and the dressing of hides, the collection of rubber and bee culture are important industries. The chief food crops grown have been indicated (see Flora), and the gold-mining is separately noticed below. Other industries undertaken or developed by Europeans are silk and cotton weaving and raphia-fibre preparation, and ostrich farming. Sugar, rice, soap and other factories have been established. In 1904 the exportation of straw and other fibre hats began; these resemble those of Panama and promise to become an important item. Tanning bark, coffee and guano are also recent exports.
Since 1862, when the country was thrown open to foreign trade, the growth of over-sea commerce has been comparatively slow. In the early days cattle were the chief export. About 1870 india-rubber began to be exported in considerable quantities, and cattle, rubber and hides continue staple products. Other important exports are raphia fibre and beeswax. Since 1900 gold has become a leading export, the value of the gold sent out of the country in the five years 1901-1906 being £1,384,493. The imports consist chiefly of tissues (mostly cotton goods), breadstuffs and rice, liquors, metal-ware and coal. Better means of internal transport and increased production in the island have greatly reduced the import of rice, which came mostly from Saigon.
Before the occupation of Madagascar by France the duty on imports and exports was 10% ad valorem, and the foreign trade was very largely in the hands of British and American merchants. In July 1897 the French tariff was applied and increased rates levied on foreign goods, notably cottons. This practically killed the American trade and reduced the British trade to a very small proportion. In 1897 the British imports were valued at £179,000; the next year, with the new tariff in force, they had dropped to £42,000. The only export duties are: cattle 2s. per head and rubber 2d. per ℔.
In 1880-1885 the entire foreign trade of Madagascar, imports and exports, was estimated to be about £1,000,000; in 1900-1906 the volume of trade had increased to a little over £2,500,000 a year. But while from 1900 onwards imports had a tendency to decrease (they were £1,841,310 in 1901 and £1,247,936 in 1905), exports steadily increased, owing to the working of gold-mines. The total value of the exports rose from £359,019 in 1901 to £822,470 in 1906.[1] About 90% of the trade is with France or other French colonies. The remaining trade is nearly all British and German.
Banking business is in the hands of French companies. The legal currency is the French 5-franc piece and the smaller French coins. There was no native coinage, the French 5-franc piece or dollar being the standard, and all sums under that amount were obtained by cutting up those coins into all shapes and sizes, which were weighed with small weights and scales into halves, quarters, eighths, twelfths and twenty-fourths of a dollar, and even reckoned down to the seven hundred and twentieth fraction of the same amount.
Gold-mining.—Gold-mining has been carried on regularly since 1897, and by 1900 the value of the ore extracted exceeded £100,000. Reports of rich discoveries attracted considerable attention in South Africa and Europe during 1904-1906, but experts, sent from the Transvaal, came to the conclusion that Madagascar would not become one of the rich goldfields of the world. The chief mining districts have been already indicated (see under Geology). Rich finds were reported from the north of the island during 1907, in which year the export of gold was £320,000. The mines afford a lucrative occupation for some thousands of persons, and many of the claim-holders are British. Decrees of 1902 and 1905 regulate the conditions under which mining is carried on. By decree of the 23rd of May 1907, the radius of the circle within which claims may be pegged is 2 kilometres (1¼ m.), and a tax of 5% is levied on the value of the gold extracted.
Communications.—There is regular steamship communication between the chief ports and Marseilles, Zanzibar and India (via Mauritius and Ceylon); and a submarine cable to Mozambique places the island in telegraphic connexion with the rest of the world. The French have built carriage roads from the interior to the principal ports as well as to connect the principal towns. On these roads large use is made of bullock wagons, as well as carts drawn by men, and women also. Tamatàve and Antanànarìvo are joined by coast canals and lakes and by a railway service. Where other means are not available, goods are carried by canoes, or on the shoulders of bearers along the native footpaths.
There is a well-organized postal service, and all the towns of note are linked by a telegraph system, which has a length of over 4000 miles.
Government, Revenue, &c.—The colony is not represented in the French Chambers, nor has it self-government. At the head of the administration is a governor-general, who is assisted by a nominated council of administration which includes unofficial members. This council must be consulted on matters affecting the budget. In several towns there are chambres consultatives, composed of local merchants and planters. The island is divided into circles, placed under military officers, and provinces, presided over by a civilian. As far as possible in local affairs, each of the native races is granted autonomy, the dominion of the Hòva over the other tribes being abolished. Each province has its native governor and minor officials, the governor being generally selected by popular vote. Each village has an organization (the Fòkon’ òlona) resembling that of a commune; at its head is a chief or mpiadidy, who serves for three years.
| 1Exports: | 1901 | 1906 | Increase. |
| Rubber | £26,679 | £301,518 | £274,839 |
| Hides and skins | 31,548 | 250,339 | 218,791 |
| Gold | 131,987 | 270,613 | 138,626 |
For Europeans and in suits between Europeans and natives the French judicial code is applicable; suits between natives are tried by native tribunals (established 1898) presided over by a European assisted by two native assessors. These tribunals judge according to native law and usages, except when such customs (e.g. polygamy and slavery) have been expressly abolished. Arbitration councils are available everywhere for the settlement of disputes between native workmen and their employers. The native laws respecting land tenure have been improved by the adoption of a method of registration based on the Torrens system.
Revenue is derived from land, house and capitation taxes, from customs, posts and telegraphs, ferries, licences and other indirect imposts. The excess of expenditure over revenue is made good by subventions from France. A considerable portion of the revenue is expended on public works. Revenue and expenditure in 1905 were each just beneath £1,000,000. This is exclusive of the sums spent by France in the island on the army, and for the naval base at Diégo-Suarez. There is a public debt amounting (1907) to £4,055,600. As stated in the French senate (February 1909), everything is taxed in the island; and no sooner has any enterprise become fairly successful than it is so heavily taxed as to be no longer worth carrying on, and certain crops have therefore been destroyed by the colonists who had planted them. This has been the case with tobacco, sugar, rum, and also in butter-making, cattle-breeding and other things. Notwithstanding this taxation, from 1895 to 1908 £12,000,000 was required for Madagascar from the home government, and the demand is constantly increasing.
History.—From the earliest accounts given of the people of Madagascar by European travellers, as well as from what may be inferred from their present condition, they seem for many centuries to have been divided into a number of tribes, often separated from one another by a wide extent of uninhabited country. Each of these was under its own chief, and was often at war with its neighbours. No one tribe seems to have gained any great ascendancy over the rest until about the middle of the 17th century, when a small but warlike people called Sàkalàva, in the south-west of Madagascar, advanced northward, conquered all the inhabitants of the western half of the island, as well as some northern and central tribes, and eventually founded two kingdoms which retained their supremacy until the close of the 18th century. About that time, the Hòva in the central province of Imèrina began to assert their own position under two warlike and energetic chieftains, Andrianimpòina and his son Radàma; they threw off the Sàkalàva authority, and after several wars obtained a nominal allegiance from them; they also conquered the surrounding tribes, and so made themselves virtual kings of Madagascar. From that time until 1895 Hòva authority was retained over a large part of the central and eastern provinces, but it was only nominal over much of the western side of the island, while in the south-west the people were quite independent and governed by their own chiefs.
While European intercourse with Madagascar is comparatively recent, the connexion of the Arabs with the island dates from a very remote epoch; and in very early times settlements were formed both on the north-west and south-east Arab Intercourse and Influence. coasts. In the latter locality there are still traces of their influence in the knowledge of Arabic possessed by a few of the people. But in these provinces they have become merged in the general mass of the people. It is different, however, in the north-west and west of the island. Here are several large Arab colonies, occupying the ports of Anòrontsànga, Mòjangà, Màrovoày and Mòrondàva, and retaining their distinct nationality. There is also in these districts a Hindu element in the population, for intercourse has also been maintained for some centuries between India and northern Madagascar, and in some towns the Banyan Indian element is as prominent as the Arab element. In the early times of their intercourse with Madagascar, the Arabs had a very powerful influence upon the Malagasy. This is seen in the number of words derived from the Arabic in the native language. Among these are the names of the months and the days of the week, those used in astrology and divination, some forms of salutation, words for dress and bedding, money, musical instruments, books and writings, together with a number of miscellaneous terms.
The island is mentioned by several of the early Arabic writers and geographers, but medieval maps show curious ignorance of its size and position. Marco Polo has a chapter upon it, and terms it “Madeigascar,” but his accounts are European Intercourse. confused with those of the mainland of Africa. The first European voyager who saw Madagascar was a Portuguese named Diogo Diaz, captain of one of the ships of a fleet commanded by Pedro Cabral and bound for India. Separated from his companions by a storm near the Cape, he sighted the eastern coast of the island on the 10th of August 1500. That day being the feast of St Lawrence, Madagascar was named the “Isle of St Lawrence,” and retained that name on all maps and charts for a hundred years. The Portuguese gave names to most of the capes, but made no persistent attempts at colonization. After them the Dutch endeavoured, but with little success, to form colonies; and in the time of Charles I. proposals were made to form an English “plantation,” but these were never carried into effect, although for a short time there was a settlement formed on the south-west coast. In the latter part of the 17th and during most of the 18th century the French attempted to establish military positions on the east coast. For some time they held the extreme south-east point of the island at Fort Dauphin; but several of their commandants were so incapable and tyrannical that they were frequently involved in war with the people, and more than once their stations were destroyed and the French were massacred. Early in the 19th century all their positions on the mainland were relinquished, and they retained nothing but the island of Ste Marie on the east coast. In 1811 Tamatàve had been occupied by British troops, and the Treaty of Paris of 1814 recognized as British the “French settlements in Madagascar,” but as a matter of fact France had then no settlements on the mainland. The then governor of Mauritius, Sir Robert Farquhar, endeavoured to prosecute British claims and obtained a cession of Diégo-Suarez Bay. These claims were not backed up by the home government, and a little later the policy was adopted by Great Britain of supporting the Hòva authority.
The political history of Madagascar as a whole may be said to date from the reign of Radàma I. (1810-1828). He was a man much in advance of his age—shrewd, enterprising, and undeterred by difficulty—a kind of Peter the Great of Radàma I. his time. He saw that it was necessary for his people to be educated and civilized if the country was to progress; and making a treaty with the governor of Mauritius to abolish the export of slaves, he received every year in compensation a subsidy of arms, ammunition, and uniforms, as well as English training for his troops. He was thus enabled to establish his authority over a large portion of the island. For some years a British agent, Mr Hastie, resided at Radàma’s court, and exercised a powerful influence over the king, doing much for the material advance of Introduction of Christianity. the country. At the same period (1820) Christian teaching was commenced in the capital by the London Missionary Society, and by its missionaries the language was reduced to a systematic written form, and the art of printing introduced; books were prepared, the Scriptures were translated, numerous schools were formed, and several Christian congregations were gathered together. The knowledge of many of the useful arts was also imparted, and many valuable natural productions were discovered. The power of superstition was greatly broken, a result partly due to the keen good sense of the king, but chiefly to the spread of knowledge and religious teaching.
The bright prospects thus opening up were clouded by the death of Radàma at the age of thirty-six, and the seizure of the royal authority by one of his wives, the Princess Rànavàlona. She looked with much suspicion upon Rànavàlona I. the ideas then gaining power among many of her people, and determined to strike a decisive blow at the new teaching. In 1835 the profession of the Christian religion was declared illegal; all worship was to cease, and all religious books were ordered to be given up. By the middle of 1836 all the English missionaries were obliged to leave the island, and for twenty-five years the most strenuous efforts were made by 277 the queen and her government to suppress all opposition to her commands. This, however, only served to show in a very remarkable manner the courage and faith of the Christian Malagasy, of whom about two hundred suffered death in various cruel forms, while many hundreds were punished more or less severely by fine, degradation, imprisonment and slavery. During the queen’s reign the political condition of the country was deplorable; there were frequent rebellions, many of the distant provinces were desolated by barbarous wars; and for some years all Europeans were excluded, and foreign commerce almost ceased. This last circumstance was partly owing to an ill-managed attack upon Tamatàve in 1846 by a combined British and French force, made to redress the wrongs inflicted upon the foreign traders of that port. But for the leaven of Christianity and education which had been introduced into the country it would have reverted to a state of barbarism.
This reign of terror was brought to a close in 1861 by the death of the queen and the accession of her son Radàma II. The island was reopened to European trade, and missionary efforts were recommenced. A determined Radàma II. attempt was made by some Frenchmen to gain for their country an overwhelming influence by means of a treaty which they induced the king to sign. But this act, as well as the vices and insane follies into which he was led by worthless foreign and native favourites, soon brought his reign and his life to an end. He was put to death in his palace (1863) and his wife was placed on the throne. The new sovereign and her government refused to ratify the agreement which had been illegally obtained, choosing rather to pay a million francs as compensation to the French company. During the five years’ reign of Queen Rasohérina, quiet and steady advances were made in civilization and education, and treaties were concluded with the British, French and American governments.
At the death of Rasohérina in 1868, she was succeeded by her cousin, Rànavàlona II. One of the first acts of the new queen was the public recognition of Christianity; and very soon afterwards she and her husband, the prime Rànavàlona II. minister, were baptized, and the erection of a chapel royal was commenced in the palace yard. These acts were followed in the succeeding year by the burning of the royal idols, and immediately afterwards by the destruction of the idols throughout the central provinces, the people generally putting themselves under Christian instruction. From that time education and enlightenment made great progress, chiefly through the labours of missionaries of various societies.
The native Malagasy government, though theoretically despotic, was limited in various ways. Radàma I. and Rànavàlona I. were much more absolute sovereigns than those before or after them, but even they were Native Government. largely restrained by public opinion. New laws were announced at large assemblies of the people, whose consent was asked, and always given through the headmen of the different divisions of native society; this custom was no doubt a survival from a time when the popular assent was not a merely formal act. The large disciplined army formed by Radàma I. aided much in changing what was formerly a somewhat limited monarchy into an absolute one. The Hòva queen’s authority was maintained over the central and eastern portions of Madagascar, and at almost all the ports, by governors appointed by the queen, and supported by small garrisons of Hòva troops. At the same time the chiefs of the various tribes were left in possession of a good deal of their former honours and influence. Rànavàlona II., her predecessor and her successor were successively married to the prime minister, Ràinilaiàrivòny, a man of great ability and sagacity, who, by his position as husband and chief adviser of the sovereign, became virtual ruler of the country. Chiefly owing to his influence, many measures tending to improve the administration were introduced. The Hòva army was estimated at from 30,000 to 40,000 men, several English non-commissioned officers and, latterly, others of higher rank being engaged to train them in European methods. Revenue was derived from customs duties, firstfruits, fines and confiscation of offenders’ property, and a money offering called hàsina, presented on a great variety of occasions both to the sovereign in person and to her representatives; and these were supplemented by “benevolences” (in the medieval sense of the word) levied upon the people for occasional state necessities. The government also claimed the unpaid service of all classes of the community for every kind of public work.
The Hòva government aspired to have Madagascar recognized as an independent civilized state, and consuls appointed by the British, French and American governments were accredited to the Malagasy sovereign, the queen Foreign Relations. having a consul in England, and a consular agent at Mauritius. The treaty with Great Britain, concluded in 1865, gave the consuls of that nation jurisdiction over the British subjects in the island. At this period, on the initiative of the 4th earl of Clarendon, then foreign secretary, an understanding was come to between the British and French governments by which it was agreed that each power should respect the independence of Madagascar; and the future of the country appeared to be bound up in the gradual consolidation of the central Hòva authority over the whole island. While this prospect would have satisfied the British interests in the island, it was otherwise with the French. The tradition of their former settlements in and influence over the island was strong; in 1840 they had taken under their protection the Sàkalàva ruler of the small island of Nossi-bé, off the north-west coast, and in virtue of that act claimed a vague protectorate over the adjacent shores of the mainland. A treaty, concluded in 1868, while establishing French consular jurisdiction in Madagascar, recognized Rànavàlona II. as queen of Madagascar, and under the Second Empire attempts to establish French political influence were discouraged, and even as late as 1872 the subsidy enjoyed by the Jesuit missionaries was withdrawn. In 1878 the French consul, Laborde, died, and a dispute arose as to the disposal of his property. This dispute was the occasion of further intervention on the part of the French, for the Paris government supported the claims of Laborde’s heirs, and revived their claim to a protectorate over the Sàkalàva of the north-west coast, as based on their agreement with them in 1840, ceding Nossi-bé to France. A policy of colonial expansion generally, and in Africa in particular at this time, was manifest in France, as in other European countries, and the French claims on the Hòva were pressed with vigour.
Towards the middle of 1882 the relations between the native government and that of France became much strained, and to settle, if possible, these causes of dispute, two Hòva officers of high rank were sent to France as Franco-Malagasy War of 1883-85. ambassadors, but as they were not authorized to concede any territory, their visit accomplished very little. Treaties had been concluded with Great Britain, Germany and America, giving improved facilities for trade with Madagascar, but before the return of the envoys matters had come to a crisis in the island. In May 1883 an ultimatum was sent to the Malagasy queen, requiring immediate compliance with the demands of France; and as these were refused by the Hòva government, Tamatàve was bombarded by a French squadron and then occupied by the marines. The war continued in a desultory fashion for many months; but no serious attempt was made to invade the interior; and in 1885 terms of peace were agreed to. By a treaty signed on the 17th of December it was agreed that the foreign relations of Madagascar should be directed by France; that a resident should live at the capital, with a small guard of French soldiers; and that the Bay of Diégo-Suarez, together with surrounding territory, should be ceded to France. The word “protectorate” was carefully excluded from the treaty, although doubtless the French envoys intended that this should be its practical issue. It was at the same time agreed that there should be no foreign interference with the internal government of the country, and that the queen should retain her former position, with all its honours and dignity. It should be here noticed that the queen, Rànavàlona II., died just at the beginning of the war, on the 278 13th of July 1883, and was succeeded by her niece, Princess Razàfindrahèty, under the title of Rànavàlona III., who maintained the same policy as her predecessor, and was much beloved French Protectorate, 1885-1894. by her people and respected by all. Several French residents successively represented France at Antanànarìvo; but these found themselves unable to obtain that influence which the home authorities thought they had a right to demand. Although the British government, in return for concessions in Zanzibar, had consented, in 1890, to recognize a French protectorate over Madagascar, the Malagasy prime minister, Ràinilaiàrivòny, was not disposed to give any advantage to France and continued to arm and train, by the help of British officers, a large body of native soldiers. This state of tension and irritation could not last, and at length, towards the close of 1894, the French government sent an ultimatum to the Malagasy sovereign, demanding such powers as would have made French authority supreme in the island. These demands were refused by the native government, and other conditions were offered; but the French envoy, together French Invasion and Conquest, 1895. with the resident’s escort, left the capital, as also did the French traders and others, including the large Jesuit mission. As soon as these had left the island, the chief ports were occupied by French troops, and an expeditionary force under General Duchesne was afterwards landed on the north-west coast at Mòjangà—commonly, but incorrectly, written Majunga—with the object of breaking the Hòva authority. Owing to the necessity of making a road for the passage of artillery and military stores, many months were spent on the march into the interior, and there was considerable loss of life by fever and other disease among the invading troops. But no effectual resistance was made by the Malagasy, and at length, on the 30th of September 1895, the French forces appeared on the heights north and east of Antanànarìvo, bombarded the city, which surrendered in the afternoon, and on the evening of the same day the French entered the capital.
The result was that the protectorate of France was re-established in the central provinces, but the queen was allowed to retain her position. Early in 1896, however, a serious Rebellion of 1896, and Gradual Subjection of the Malagasy. rebellion broke out in several parts of Imèrina. This movement was not only anti-French and anti-foreign, but also distinctly anti-Christian. The French troops gradually broke up the power of the rebellion in the central provinces, but as there appeared to be considerable unrest in many other parts of the island, General Gallieni, an officer with a reputation for vigour and ability in the Sudan and Tongking campaigns, was sent out to relieve the then resident-general.
General Gallieni had a difficult task in establishing the authority of France throughout the island among numbers of tribes who had never submitted to any control from others. Among the first steps he took were to put the country Administration of General Gallieni. under martial law, to abolish royalty and all semblance of Hòva government, and to declare Madagascar to be henceforth a colony of France. Queen Rànavàlona III. was exiled to Réunion, and subsequently to Algeria. Meanwhile carriage roads were commenced to connect all the chief centres, and the military posts were gradually extended so as to consolidate French rule over all the outlying tribes. French residents and numerous other officials were placed at every important town, and various projects were started for the civilization of the Malagasy in accordance with French ideas. At the close of 1899, General Gallieni was able to report that only portions of the west and south-west remained to be brought into submission. Not long afterwards the authority of France was recognized throughout the island. General Gallieni, whose firm and vigorous administration, and desire to treat the Malagasy justly and kindly, made him liked by the people, retired in 1905, and was succeeded in that office by M. Victor Augagneur, late mayor of Lyons. Since the French occupation the Malagasy have conformed pretty readily to the new order of things, although many of the most intelligent Hòva deeply regret that their country did not retain its independence. Justice is administered, on the whole, with fairness and impartiality; but the taxation seems too heavy for the means of the people, indeed it is affirmed by trustworthy natives that the well-to-do classes are being gradually drained of their property. To an outsider it also appears that the staff of officials is very largely in excess of any real needs of administration; several monopolies, which interfere with the habits of the people, tend to produce discontent; and the taking of their land and houses for public works, roads, &c., while but a mere fraction of their real value is allowed as compensation, does not help to increase their acquiescence in foreign control. But the most serious cause for dislike to government action was the interference by the governor-general, in 1907, with their religious customs, by the suppression of hundreds of their congregational schools, and the closing of numbers of their churches. In July 1910 M. Augagneur was replaced as governor-general by N. Picquié, a prominent official of the Colonial Department, who had previously served with acceptance as deputy governor-general of French Indo-China, and who had a reputation for tact and impartiality.
Christian Missions and Education.—As already noticed, the Malagasy owe to missionaries of the London Missionary Society their first school system and their first literature, in 1820 and subsequent years;8 and for fifteen years all educational work was carried on by them, some 10,000 to 12,000 children having been instructed in their schools. On the reopening of the country to Europeans in 1862, the L.M.S. mission was resumed and was carried on with vigour for several years, stations being formed in several parts of Imèrina, in the Bétsiléo and Antsihànaka provinces, and at the ports of Tamatàve, Majunga and Fàrafangàna (south-east coast). In 1890 the number of their churches was 1220; adherents, 248,000; and scholars, 68,000; so that for long the greater part of the educational work was in their hands, carried on not only in primary schools, but also in high schools and colleges. In 1863 the Church of England began work in the island through the Society for the Propagation of the Gospel and the Church Missionary Society. After some time, however, the latter society withdrew, leaving the field to the S.P.G. A bishop is stationed in the capital, with a theological college in its neighbourhood, but the chief work of the Anglican mission is on the east coast. In 1866 the Norwegian Lutheran Society began work in Madagascar, and was joined in 1888 by an American Lutheran Society. With a representative church at the capital, the chief work of these missions is in the Vàkinankàratra district (south-west of Imèrina), in the Bétsiléo province, and on the south-east and south-west coasts; in these places they have a large number of converts and (until lately) schools. In 1867 a mission was begun by the Society of Friends, who gave great attention to education and literary work, and afterwards took up as their field of labour the western and south-western parts of Imèrina, where they have a large and well-organized mission. Immediately after the island became a French possession the French Protestant Churches began (in 1896) to take part in the evangelizing of their new colony, and about half the area for long occupied by the London Missionary Society was transferred to the Paris Society. The bulk of the Malagasy Christians are Protestants, probably three-fourths or four-fifths of those professing Christianity. A Roman Catholic (Jesuit) mission was begun in 1861, and a large force of priests with a bishop and lay brethren and sisters engaged in education, have been at work in the island since then, except during the two Franco-Malagasy wars.9 Since the French conquest, the north of the island has been occupied by a mission of priests of the Saint Esprit, and the southern portion by the Lazarist mission, each with a bishop at its head. The following table gives the statistics of the various Protestant missions at the close of 1906:—
| Mission | Missionaries | Churches | Adherents | Members | Scholars |
| Lond. Miss. Soc. | 25 | 630 | 120,000 | 32,000 | 27,000 |
| Soc. Prop. Gospel. | 15 | 121 | 13,000 | 4,094 | 7,655 |
| Norweg. Luth. | 60 | 892 | 84,000 | 71,500 | 38,000 |
| Am. Luth. | 14 | ? | ? | ? | ? |
| Soc. of Friends. | 27 | 178 | 15,000 | 2,540 | 7,122 |
| French Prot. Miss. | 29 | 491 | 110,660 | 10,500 | 18,200 |
Since 1897 high schools, and medical and technical schools, and a few primary schools, have been formed by the French government; and all other schools have been placed under regulations issued by an educational department, the scholars being required to learn the French language; but until the end of 1906 the bulk of the educational work was carried on by the various missions. At that date the anti-clerical movement in France began to affect Madagascar. In all the missions the churches had, in the vast majority of cases, been used as school-houses, but in November 1906 it was strictly forbidden to use churches for educational purposes after two months from that date; and the effect of the decree, with other provisions, was to close hundreds of schools, probably three-fourths of the whole number.
For many years (1862-1896), all medical aid to the sick, the formation of hospitals and dispensaries, the training of native doctors, midwives and nurses, and the production of medical literature was entirely due to the Protestant missionaries, viz. the London Missionary Society, the Friends and the Norwegians. Numbers of young men received a full course of medical and surgical training, and were awarded diplomas after passing strict examinations. This work is now mostly in charge of a government department, and mission medical work is much restricted; but for thirty-five years the Malagasy owed all such help to the benevolence of European Christians. Besides care for the sick in ordinary diseases, asylums for lepers were for many years carried on; two by the London Missionary Society, one, a large one, with 800 or 900 inmates, by the Norwegian Society, and another by the Roman Catholic mission. This last, with one of those of the L.M.S., is now taken over by the government.
Authorities.—As regards the scientific aspects of the country, almost everything of value in previous books and papers is included in the magnificent work (1882 et seq.), in 28 4to vols., by Alfred Grandidier, entitled Histoire naturelle, physique, et politique de Madagascar. Many of the volumes consist of coloured lithograph plates illustrating the natural history of the country, as well as atlases of maps from the earliest period.
General: Étienne de Flacourt, Histoire de la grande isle Madagascar (Paris, 1658); Madagascar, or Robert Drury’s Journal during Fifteen Years’ Captivity on that Island (London, 1729; new ed., 1890); Voyages et mémoires de Maurice Auguste, comte de Benyowski (Paris, 1791); Froberville, Histoire de Madagascar (Isle de France, 1809); Ellis, History of Madagascar (London, 1838); Guillain, Documents sur ... la partie occidentale de Madagascar (Paris, 1845); Macé Descartes, Histoire et géographie de Madagascar (Paris, 1846); Ellis, Three Visits to Madagascar (London, 1859); J. Sibree, Madagascar and its People (London, 1870); Tantara ny Andrìana eto Madagascar: Histoire des rois d’Imérina d’après les manuscrits malgaches (Antanànarìvo, 1875); Mullens, Twelve Months in Madagascar (London, 1875); Blanchard, L’Île de Madagascar (Paris, 1875); Dahle, Madagaskar og dets Beboere (Christiania, 1876-1878); Sibree and Baron (eds.), The Antanànarìvo Annual, Nos. i-xxiv. (1875-1900, pp. 3115); Notes, reconnaissances, et explorations, revue mensuelle (Antanànarìvo, 5 vols., 1897-1899, pp. 3041); Sibree, A Madagascar Bibliography (Antanànarìvo, 1885); Vaissière, Histoire de Madagascar (Paris, 1884), Vingt ans à Madagascar (Paris, 1885); Oliver, Madagascar: an Historical and Descriptive Account (2 vols., London, 1886); Cousins, Madagascar of To-day (London, 1895); Bulletin du comité de Madagascar (monthly) (Paris, 1895, et seq.); Sibree, Madagascar before the Conquest (London, 1896); Catat, Voyage à Madagascar (Paris, 1895); Annuaire de Madagascar (Antanànarìvo, 1898, et seq.); J. S. Gallieni; Rapport d’ensemble sur la situation générale de Madagascar (2 vols., Paris, 1899); Revue de Madagascar, mensuelle, illustrée (1895, et seq.); Guide de l’immigrant à Madagascar (3 vols., with atlas, Paris, 1899); Collection des anciens ouvrages relatifs à Madagascar, par les soins du comité de Madagascar (a collection and translation of all works relating to the island from 1500 to 1800, in 10 vols.), (Paris, 1899 et seq.); Bulletin trimestriel de l’académie de Malgache (quarterly) (Antanànarìvo, 1902 et seq.); G, Grandidier et autres, Madagascar au début du xxe siècle (Paris, 1902); G. Grandidier, Bibliographie de Madagascar (2 vols., Paris, 1905 and 1907).
Political: Sibree, “What are ‘French Claims’ on Madagascar?” Madagascar Tracts (1882); Oliver, True Story of the French Dispute in Madagascar (London, 1885); Shaw, Madagascar and France (London, 1885); Saillens, Nos droits sur Madagascar (Paris, 1885); K. Blind “The Fictitious French Claim to Madagascar,” Contemp. Rev. (1894); Martineau, Étude de politique contemporaine. Madagascar (Paris, 1894); Rentier, Les droits de la France sur Madagascar (1895); Corlay, Notre campagne à Madagascar (Paris, 1896); Knight, Madagascar in War-time (London, 1896); Carol, Chez les Hovas (Paris, 1898); Gallieni, Neuf ans à Madagascar (Paris, 1908).
Philology: Houtman, Spraak ende woord boek in de Maleische ende Madagaskarsche talen (Amsterdam, 1603); Voyage de C. van Heemskerk; vocabulaire de la langue parlée dans l’Île Saint-Laurent (Amsterdam, 1603) Megiser, Beschreibung der Mechtigen und Weitberhümbten Insul Madagascar, with dictionary and dialogues (Altenburg, 1609); Arthus, Colloquia latino-maleyica et madagascarica (Frankfort, 1613); Challand, Vocabulaire français-malgache et malgache-français (Île de France, 1773); Froberville, Dictionnaire français-madécasse (3 vols., Île de France, 1809); Freeman and Johns, Dictionary of the Malagasy Language (Eng.-Mal. and Mal.-Eng.), (Antanànarìvo, 1835); Dalmond, Vocabulaire et grammaire pour les langues malgaches, Sàkalàva et Bétsimisàra (Bourbon, 1842); R. C. Missionaries’ Dictionnaire français-malgache (Réunion, 1853); and Dictionnaire malgache-français (Réunion, 1855); Van der Tunk, “Outlines of a Grammar of the Malagasy Language,” Jour. Roy. Asiat. Soc. (1860); Ailloud, Grammaire malgache-hòva (Antanànarìvo, 1872); W. E. Cousins, Concise Introduction to the Study of the Malagasy Language as spoken in Imèrina (Antanànarìvo, 1873); Marre de Marin, Grammaire malgache (Paris, 1876); id., Essai sur le malgache, ou Étude comparée des langues javanaise, malgache, et malayse (Paris, 1876); id., Le Jardin des racines océaniennes (Paris, 1876); Dahle, Specimens of Malagasy Folk-lore (Antanànarìvo, 1877); and W. E. Cousins, “The Malagasy Language,” in Trans. Phil. Soc. (1878). Besides these there are several valuable papers by Dahle in the yearly numbers of The Antanànarìvo Annual (ante) (1876-1877); Richardson, A New Malagasy-English Dictionary (Antanànarìvo, 1885); Cousins and Barrett, Malagasy Proverbs (Antanànarìvo, 1885); Caussèque, Grammaire malgache (Antanànarìvo, 1886); Abinal et Malzac, Dictionnaire malgache-français (Antanànarìvo, 1889); Brandstetter, “Die Beziehungen des Malagasy zum Malaiischen,” Malaio-polynesische Forschungen, pt. 2 (Lucerne, 1893).
Missions and Religious History: Freeman and Johns, Narrative of the Persecutions of the Christians in Madagascar (London, 1840); Prout, Madagascar, its Missions and its Martyrs (London, 1863); Ellis, Madagascar Revisited (London, 1867); id., The Martyr Church (London, 1869); “Religion in Madagascar,” Ch. Quar. Rev. (1878); Briggs, The Madagascar Mission (L.M.S. 1879); id., Ten Years’ Review of Mission Work in Madagascar (L.M.S. 1870-1880, 1881); Johnson, Review of Work of the Friends’ Foreign Mission Association in Madagascar, 1867-1880 (Antanànarìvo, 1880); Vaissière, Histoire de Madagascar, ses habitants et ses missionaires (Paris, 1884); The Church in Madagascar (S.P.G., 15 years’ progress, 1874-1889, 1889); La Liberté religieuse à Madagascar (Paris, 1897); Matthews, Thirty Years in Madagascar (London, 1904); Sibree, The L.M.S. Mission in Madagascar (L.M.S. Mission Hand Books, London, 1907); id., “Christian Missions in Madagascar and French Colonial Policy,” The East and the West (Jan. 1909); and General Gallieni’s “Neuf ans à Madagascar”, Journal of the African Society (April 1909).
1 In the apparent absence of any Cambrian formation above them, there is little doubt that these rocks are Archean, although this cannot be absolutely proved.
2 For most of the information here given on the geology the writer is indebted to Captain Mouneyres, chef de services des mines, and the Rev. R. Baron, F.G.S., F.L.S.
3 See “On a Collection of Fossils from Madagascar,” by R. B. Newton, Quart. Journ. Geol. Soc. (Feb. 1895).
4 The following are figures of mean temperature, kindly supplied by the Rev. E. Colin, S. J., director of the observatory: Diégo-Suarez, N., 79°; Fàrafangàna, S.E. coast, 75°; Màrovoày, W. intr., 81°; Mòrondàva, W. coast, 77°; Tullēar, S.W. coast, 78°.
5 The words in parentheses are the native Malagasy names.
6 The census taken in 1905 gives 2,664,000 as the total population, but it is probably a little over that amount, as some localities are still imperfectly known.
7 This is a special and restricted use of the word, Hòva in its widest sense being a tribal name, including all ranks of people in Imèrina.
8 It is true that 200 years earlier than this, persistent efforts were made for nineteen years (1600-1619) by Portuguese Roman Catholic missionaries to propagate their faith among the south-east coast tribes. But although much zeal and self-denial were shown by these men, their efforts were abortive, and the mission was at length abandoned, leaving no fruit of their labours in a single church or convert. Half a dozen small books of devotion are all that remain to show their presence in Madagascar.
9 The work of the “Frères chrétiens” was, however, almost broken up by the anti-clerical policy of the French government.

MADAN, MARTIN (1726-1790), English writer, was educated at Westminster School, and at Christ Church, Oxford, where he graduated in 1746. In 1748 he was called to the bar, and for some time lived a very gay life, until he was persuaded to change his ways on hearing a sermon by John Wesley. He took holy orders, and was appointed chaplain to the Lock Hospital, London. He was closely connected with the Calvinistic Methodist movement supported by the countess of Huntingdon, and from time to time acted as an itinerant preacher. He was a first cousin of William Cowper, with whom he had some correspondence on religious matters. In 1767 much adverse comment was aroused by his support of his friend Thomas Haweis in a controversy arising out of the latter’s possession of the living of Aldwinkle, Northamptonshire (see Monthly Review, xxxvii. 382, 390, 465). In 1780 Madan raised more serious storm of opposition by the publication of his Thelyphthora, or A Treatise on Female Ruin, in which he advocated polygamy as the remedy for the evils he deplored. The author was no doubt sincere in his arguments, which he based chiefly on scriptural authority; but his book called forth many angry replies. Nineteen attacks on it are catalogued by Falconer Madan in Dict. Nat. Biog. Madan resigned his chaplainship and retired to Epsom, where he produced, among other works, A New and Literal Translation of Juvenal and Persius (1789). He died on the 2nd of May 1790.

MADDALONI, a town of Campania, Italy, in the province of Caserta, about 3½ m. S.E. of Caserta, with stations on the railways from Caserta to Benevento and from Caserta to Avellino, 200 ft. above sea-level. Pop. (1901), 19,778 (town); 21,270 (commune). It is prettily situated at the base of one of the Tifata hills, the towers of its medieval castle and the church of San Michele crowning the heights above. The fine old palace of the Caraffa family, once dukes of Maddaloni, the old college now named after Giordano Bruno, and the institute for the sons of soldiers are the chief points of interest. About 2½ m. east of Valle di Maddaloni, the Ponte della Valle, an aqueduct built by the orders of Charles III. of Naples and his son to convey the water of the Tiburno to Caserta (19 m.), is carried across the valley between Monte Longano and Monte Gargano by a threefold series of noble arches rising to a height of 210 ft. The work was 280 designed by Lodovico Vanvitelli, and constructed between 1753 and 1759.

MADDEN, SIR FREDERIC (1801-1873), English palaeographer, the son of an officer of Irish extraction, was born at Portsmouth on the 16th of February 1801. From his earliest years he displayed a strong bent to linguistic and antiquarian studies. In 1826 he was engaged by the British Museum to assist in the preparation of the classified catalogue of printed books then contemplated, and in 1828 he became assistant keeper of manuscripts. In 1833 he was knighted, and in 1837 succeeded Josiah Forshall as keeper of manuscripts. He was not entirely successful in this office, partly owing to want of harmony with his colleagues; he retired in 1866. He edited for the Roxburghe Club Havelok the Dane (1828), discovered by himself among the Laudian MSS. in the Bodleian, William and the Werwolf (1832) and the old English versions of the Gesta Romanorum (1838). In 1839 he edited the ancient metrical romances of Syr Gawayne for the Bannatyne Club, and in 1847 Layamon’s Brut, with a prose translation, for the Society of Antiquaries. In 1850 the magnificent edition, in parallel columns, of what are known as the “Wycliffite” versions of the Bible, from the original MSS., upon which he and his coadjutor, Forshall, had been engaged for twenty years, was published by the university of Oxford. In 1866-1869 he edited the Historia Minor of Matthew Paris for the Rolls Series. In 1833 he wrote the text of Henry Shaw’s Illuminated Ornaments of the Middle Ages; and in 1850 edited the English translation of Silvestre’s Paléographie universelle. He died on the 8th of March 1873, bequeathing his journals and other private papers to the Bodleian Library, where they were to remain unopened until 1920.
Madden was perhaps the first palaeographer of his day. He was an acute as well as a laborious antiquary, but his ignorance of German prevented his ranking high as a philologist, although he paid much attention to the early dialectical forms of French and English. His minor contributions to antiquarian research were exceedingly numerous: the best known, perhaps, was his dissertation on the orthography of Shakespeare’s name, which, mainly on the strength of the Florio autograph, he contended should be “Shakspere.”

MADDER, or Dyers’ Madder, the root of Rubia tinctorum and perhaps also of R. peregrina, both European, R. cordifolia, a native of the hilly districts of India and of north-east Asia and Java, supplying the Indian madder or manjit. Rubia is a genus of about thirty-five species of the tribe Galieae of the order Rubiaceae, and much resembles the familiar Galiums, e.g. lady’s bedstraw (G. verum) and the cleavers (G. aparine) of English hedges, having similarly whorled leaves, but the parts of the flowers are in fives and not fours, while the fruit is somewhat fleshy. The only British species is R. peregrina, which is found in Wales, the south and west of England, and in east and south Ireland. The use of madder appears to have been known from the earliest times, as cloth dyed with it has been found on the Egyptian mummies. It was the ἐρευθέδανον used for dyeing the cloaks of the Libyan women in the days of Herodotus (Herod. iv. 189). It is the ἐρυθρόδανον of Dioscorides, who speaks of its cultivation in Caria (iii. 160), and of Hippocrates (De morb. mul. i.), and the Rubia of Pliny (xix. 17). R. tinctorum, a native of western Europe, &c., has been extensively cultivated in south Europe, France, where it is called garance, and Holland, and to a small extent in the United States. Large quantities have been imported into England from Smyrna, Trieste, Leghorn, &c. The cultivation, however, decreased after alizarin, the red colouring principle of madder, was made artificially. Madder was employed medicinally by the ancients and in the middle ages. Gerard, in 1597, speaks of it as having been cultivated in many gardens in his day, and describes its supposed many virtues (Herball, p. 960); but any pharmacological or therapeutic action which madder may possess is unrecognizable. Its most remarkable physiological effect is that of colouring red the bones of animals fed upon it, as also the claws and beaks of birds. This appears to be due to the chemical affinity of phosphate of lime for the colouring matter (Pereira, Mat. med., vol. ii. pt. 2, p. 52). This property has been of much use in enabling physiologists to ascertain the manner in which bones develop, and the functions of the various types of cells found in growing bone. R. chilensis has been used for dyeing red from time immemorial. The chay-root, which furnishes a red dye in Coromandel and other parts of India, is the root-bark of Oldenlandia umbellata, a low-growing plant of the same family as madder.

MADEC, RENÉ-MARIE (1736-1784)—called Medoc in Anglo-Indian writings—French adventurer in India, was born at Quimper in Brittany on the 7th of February 1736, of poor parents. He went out to India and served under Dupleix and Lally, but being taken prisoner by the British he enlisted in the Bengal army. Deserting with some of his companions shortly before the battle of Buxar (1764), he became military instructor to various native princes, organizing successively the forces of Shuja-ud-Dowlah, nawab of Oudh, and of the Jats and Rohillas. He took service under the emperor Shah Alam in 1772, and when that prince was defeated at Delhi by the Mahrattas, Madec rejoined his own countrymen in Pondicherry, where he took an active part in the defence of the town (1778). After the capitulation of Pondicherry he returned to France with a considerable fortune, and died there in 1784. At one time he formed a scheme for a French alliance with the Mogul emperor against the British, but the project came to nothing.
See Émile Barbé, Le Nabab René Madec (1894).

MADEIRA, or The Madeiras, a group of islands in the North Atlantic Ocean, which belong to Portugal, and consist of two inhabited islands named Madeira and Porto Santo and two groups of uninhabited rocks named the Desertas and Selvagens. Pop. (1900), 150,574; area, 314 sq. m. Funchal, the capital of the archipelago, is on the south coast of Madeira Island, in 32° 37′ 45″ N. and 16° 54′ W. It is about 360 m. from the coast of Africa, 535 from Lisbon, 1215 from Plymouth, 240 from Teneriffe, and 480 from Santa Maria, the nearest of the Azores.
Madeira (pop. 1900, 148,263), the largest island of the group, has a length of 30 m., an extreme breadth of 12 m., and a coast-line of 80 or 90 m. Its longer axis lies east and west, in which direction it is traversed by a mountain chain, the backbone of the island, having a mean altitude of 4000 ft., up to which many deep ravines penetrate from both coasts and render travel by land very difficult. Pico Ruivo, the highest summit, stands in the centre of the island, and has a height of 6056 ft., while some of the adjacent summits are very little lower. The depth and narrowness of the ravines, the loftiness of the rugged peaks, often covered with snow, that tower above them, the bold precipices of the coast, and the proximity of the sea, afford many scenes of picturesque beauty or striking grandeur. The greater part of the interior is uninhabited, though cultivated, for the towns, villages and scattered huts are usually built either at the mouths of ravines or upon the lower slopes that extend from the mountains to the coast. The ridges between the ravines usually terminate in lofty headlands, one of which, called Cabo Girão, has the height of 1920 ft., and much of the seaboard is bound by precipices of dark basalt. The north coast, having been more exposed to the erosion of the sea, is more precipitous than the south, and presents everywhere a wilder aspect. On the south there is left very little of the indigenous forest which once clothed the whole island and gave it the name it bears (from the Portuguese madeira, Lat. materia, wood), but on the north some of the valleys still contain native trees of fine growth. A long, narrow and comparatively low rocky promontory forms the eastern extremity of the island; and here is a tract of calcareous sand, known as the Fossil Bed, containing land shells and numerous bodies resembling the roots of trees, probably produced by infiltration.
Porto Santo is about 25 m. N.E. of Madeira. Pop. (1900), 2311. It has a length of 61⁄3 m. and a width of 3 m. The capital is Porto Santo, called locally the villa or town. The island is very unproductive, water being scarce and wood wholly absent. Around the little town there is a considerable tract of pretty level ground covered by calcareous sand containing fossil land-shells. At each end of the island are hills, of which Pico do Facho, the highest, reaches the altitude of 1663 ft. Barley, but little else, 281 is grown here, the limited requirements of the inhabitants being supplied from Funchal.
The Desertas lie about 11 m. S.E. of Madeira, and consist of three islands, Ilheo Chão, Bugio and Deserta Grande, together with Sail Rock off the north end of Ilheo Chão. They present lofty precipices to the sea on all sides. Rabbits and goats abound on them. The archil weed grows on the rocks, and is gathered for exportation. The largest islet (Deserta Grande) is 6½ m. long, and attains the height of 1610 ft. These rocks are conspicuous objects in the sea-views from Funchal.
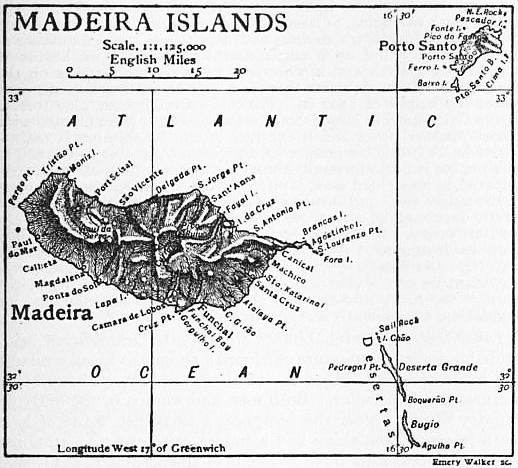
The Selvagens or Salvages are a group of three islands, 156 m. from Madeira, and between Madeira and the Canary Islands. The largest island is the Great Piton, 3 m. long, and 1 m. broad. The inclusion of the Selvagens in the Madeira Archipelago is due to political rather than to geographical reasons.
Geology.—All the islands of the group are of volcanic origin. They are the summits of very lofty mountains which have their bases in an abyssal ocean. The greater part of what is now visible in Madeira is of subaerial formation, consisting of basaltic and trachytic lavas, beds of tuff and other ejectamenta, the result of a long and complicated series of eruptions from innumerable vents. Besides this building up by the emission of matter from craters and clefts, a certain amount of upheaval in mass has taken place, for at a spot about 1200 ft. above the sea in the northern valley of São Vicente, and again at about the same height in Porto Santo, there have been found fragments of limestone accompanied by tuffs containing marine shells and echinoderms of the Miocene Tertiary epoch. We have here proof that during or since that epoch portions at least of these islands have been bodily uplifted more than 1000 ft. The fossils are sufficiently well preserved to admit of their genera, and in many instances even their species, being made out.
There were pauses of considerable duration whilst the island of Madeira was being increased in height. The leaf bed and the accompanying carbonaceous matter, frequently termed lignite, although it displays no trace of structure, which lie under 1200 ft. of lavas in the valley of São Jorge, afford proof that there had been sufficient time for the growth of a vegetation of high order, many of the leaf impressions belonging to species of trees and shrubs which still exist on the island. Moreover, great alterations and dislocations had taken place in the rocks of various localities before other lavas and tuffs had been thrown upon them.
There are no data for determining when volcanic action began in this locality, but looking at the enormous depth of the surrounding sea it is clear that a vast period of time must have elapsed to allow of a great mountain reaching the surface and then rising several thousand feet. Again, considering the comparatively feeble agents for effecting the work of denudation (neither glaciers nor thick accumulations of alpine snow being found here), and then the enormous erosion that has actually taken place, the inference is inevitable that a very great lapse of time was required to excavate the deep and wide ravines that everywhere intersect the island. Nor is anything known as to the period of the cessation of volcanic action. At the present day there are no live craters or smoking crevices, as at the Canaries and Cape Verdes, nor any hot springs, as at the Azores.
In one of the northern ravines of Madeira by Porto da Cruz some masses of a coarsely crystalline Essexite are exposed to view; this rock is evidently the deep-seated representative of the Trachydoleritic and Nepheline basalt lavas. Fragments of a sodalite-syenite have also been found at Soca in the same neighbourhood.
In the eastern part of the island several small crater rings are to be seen; their rims are formed of spheroidal basalt, while within the craters themselves masses of bauxite are found accompanied by evidences of fumerolic action.
In the sections afforded by the ravines, which strike north and south from the central ridge of Madeira to the sea, the nucleus of the island is seen to consist of a confused mass of more or less stratified rock, upon which rest beds of tuff, scoriae and lava, in the shape of basalt, trap and trachyte, the whole traversed by dykes. These beds are thinnest near the central axis; as they approach the coast they become thicker and less intersected by dykes.
In various parts are elevated tracts of comparatively level ground. These are supposed to have been formed by the meeting of numerous streams of lava flowing from cones and points of eruption in close proximity, various ejectamenta assisting at the same time to fill up inequalities. Deep down in some of the lateral ravines may be seen ancient cones of eruption which have been overwhelmed by streams of melted matter issuing from the central region, and afterwards exposed to view by the same causes that excavated the ravines. These ravines may be regarded as having been formed at first by subterranean movements, both gradual and violent, which dislocated the rocks and cut clefts through which streams flowed to the sea. In course of time the waters, periodically swollen by melted snows and the copious rains of winter, would cut deeper and deeper into the heart of the mountains, and would undermine the lateral cliffs, until the valleys became as large as we now find them. Even the Curral, which from its rounded shape and its position in the centre of the island has been usually deemed the ruins of a crater, is thought to be nothing more than a valley scooped out in the way described. The rarity of crateriform cavities in Madeira is very remarkable. There exists, however, to the east of Funchal, on a tract 2000 ft. high, the Lagoa, a small but perfect crater, 500 ft. in diameter, and with a depth of 150 ft.; and there is another, which is a double one, in the district known as Fanal, in the north-west of Madeira, nearly 5000 ft. above the sea. The basalt, of which much of the outer part of the island is composed, is of a dark colour and a tough texture, with small disseminated crystals of olivine and augite. It is sometimes full of vesicular cavities, formed by the expansion of imprisoned gases. A rudely columnar structure is very often seen in the basalt, but there is nothing so perfect as the columns of Staffa or the Giant’s Causeway. The trachytic rocks are small in quantity compared with those of the basaltic class. The tufa is soft and friable, and generally of a yellow colour; but where it has been overflowed by a hot stream of lava it has assumed a red colour. Black ashes and fragments of pumice are sometimes found in the tufaceous strata.
There are no metallic ores, nor has any sulphur been found; but a little iron pyrites and specular iron are occasionally met with. The basalt yields an excellent building-stone, various qualities of which are quarried near Camara de Lobos, five or six miles west of Funchal.
In Porto Santo the trachytic rocks bear a much greater proportion to the basaltic than in Madeira. An adjacent islet is formed of tuffs and calcareous rock, indicating a submarine origin, upon which supramarine lavas have been poured. The older series contains corals and shells (also of the Miocene Tertiary epoch), with water-worn pebbles, cemented together by carbonate of lime, the whole appearing to have been a coral reef near an ancient beach. The calcareous rock is taken in large quantities to Funchal, to be burnt into lime for building purposes.
Climate.—Observations taken at Funchal Observatory (80 ft. above sea-level) in the last twenty years of the 19th century showed that the mean annual temperature is about 65° F. The mean minimum for the coldest part of the year (October to May inclusive) does not fall below 55°, and the average daily variation of temperature in the same period does not exceed 10°. Madeira thus has a remarkably mild climate, though it lies only 10° north of the Tropic of Cancer. This mildness is due to the surrounding ocean, from which the atmosphere obtains a large supply of watery vapour. The mean humidity of the air is about 75 (saturation = 100). The prevalent winds are from the north or from a few points east or west of north, but these winds are much mitigated on the south coast by the central range of mountains. The west wind usually brings rain. That from the east is a dry wind. A hot and dry wind, the leste of the natives, occasionally blows from the east-south-east, the direction of the Sahara, and causes the hill region to be hotter than below; but even on the coast the thermometer under its influence sometimes indicates 93°. The leste is often accompanied by sandstorms. As the thermometer has never been known to fall as low as 46° at Funchal, frost and snow are there wholly unknown; but snow falls on the mountains once or twice during the winter, very seldom, however, below the altitude of 2000 ft. Thunderstorms are rare, and scarcely ever violent.
Madeira has long had a high reputation as a sanatory resort for persons suffering from diseases of the chest. Notwithstanding the ever-increasing competition of other winter resorts, a considerable number of invalids, especially English and German, winter at Funchal.
Fauna.—No species of land mammal is indigenous to the Madeiras. Some of the early voyagers indeed speak of wild goats and swine, but these animals must have escaped from confinement. The rabbit, black rat, brown rat and mouse have been introduced. The first comers encountered seals, and this amphibious mammal (Monachus albiventer) still lingers at the Desertas. Amongst the thirty species of birds which breed in these islands are the kestrel, buzzard and barn owl, the blackbird, robin, wagtail, goldfinch, ring sparrow, linnet, two swifts, three pigeons, the quail, red-legged partridge, woodcock, tern, herring gull, two petrels and three puffins. Only one species is endemic, and that is a wren (Regulus madeirensis), but five other species are known elsewhere only at the Canaries. These are the green canary (Fringilla butyracea, the parent of the domesticated yellow variety), a chaffinch (Fringilla tintillon), a swift (Cypselus unicolor), a wood pigeon (Columba trocaz) and a petrel (Thalassidroma Bulwerii). There is also a local variety of the blackcap, distinguishable from the common kind by the extension in the male of the cap to the shoulder. About seventy other species have been seen from time to time in Madeira, chiefly stragglers from the African coast, many of them coming with the leste wind.
The only land reptile is a small lizard (Lacerta dugesii), which is abundant and is very destructive to the grape crop. The loggerhead turtle (Caouana caretta, Gray) is frequently captured, and is cooked for the table, but the soup is much inferior to that made from the green turtle of the West Indies. A single variety of frog (Rana esculenta) has been introduced; there are no other batrachians.
About 250 species of marine fishes taken at Madeira have been scientifically determined, the largest families being Scombridae with 35 species, the sharks with 24, the Sparidae with 15, the rays with 14, the Labridae with 13, the Gadidae with 12, the eels with 12, the Percidae with 11, and the Carangidae with 10. Many kinds, such as the mackerel, horse mackerel, groper, mullet, braise, &c.., are caught in abundance, and afford a cheap article of diet to the people. Several species of tunny are taken plentifully in spring and summer, one of them sometimes attaining the weight of 300 ℔. The only freshwater fish is the common eel, which is found in one or two of the streams.
According to T. V. Wollaston (Testacea atlantica, 1878), there have been found 158 species of mollusca on the land, 6 inhabiting fresh water, and 7 littoral species, making a total of 171. A large majority of the land shells are considered to be peculiar. Many of the species are variable in form or colour, and some have an extraordinary number of varieties. Of the land mollusca 91 species are assigned to the genus Helix, 31 to the genus Pupa, and 15 to the genus Achatina (or Lovea). About 43 species are found both living and fossil in superficial deposits of calcareous sand in Madeira or Porto Santo. These deposits were assigned by Lyell to the Newer Pliocene period. Some 12 or 13 species have not been hitherto discovered alive. More than 100 species of Polyzoa (Bryozoa) have been collected, among them are some highly interesting forms.
The only order of insects which has been thoroughly examined is that of the Coleoptera. By the persevering researches of T. V. Wollaston the astonishing number of 695 species of beetles has been brought to light at the Madeiras. The proportion of endemic kinds is very large, and it is remarkable that 200 of them are either wingless or their wings are so poorly developed that they cannot fly, while 23 of the endemic genera have all their species in this condition. With regard to the Lepidoptera, 11 or 12 species of butterflies have been seen, all of which belong to European genera. Some of the species are geographical varieties of well-known types. Upward of 100 moths have been collected, the majority of them being of a European stamp, but probably a fourth of the total number are peculiar to the Madeiran group. Thirty-seven species of Neuroptera have been observed in Madeira, 12 of them being so far as is known peculiar.
The bristle-footed worms of the coast have been studied by Professor P. Langerhans, who has met with about 200 species, of which a large number were new to science. There are no modern coral reefs, but several species of stony and flexible corals have been collected, though none are of commercial value. There is, however, a white stony coral allied to the red coral of the Mediterranean which would be valuable as an article of trade if it could be obtained in sufficient quantity. Specimens of a rare and handsome red Paragorgia are in the British Museum and Liverpool Museum.
Flora.—The vegetation is strongly impressed with a south-European character. Many of the plants in the lower region undoubtedly were introduced and naturalized after the Portuguese colonization. A large number of the remainder are found at the Canaries and the Azores, or in one of these groups, but nowhere else. Lastly, there are about a hundred plants which are peculiarly Madeiran, either as distinct species or as strongly marked varieties. The flowering plants found truly wild belong to about 363 genera and 717 species,—the monocotyledons numbering 70 genera and 128 species, the dicotyledons 293 genera and 589 species. The three largest orders are the Compositae, Leguminosae and Graminaceae. Forty-one species of ferns grow in Madeira, three of which are endemic species and six others belong to the peculiar flora of the North Atlantic islands. About 100 species of moss have been collected, and 47 species of Hepaticae. A connexion between the flora of Madeira and that of the West Indies and tropical America has been inferred from the presence in the former of six ferns found nowhere in Europe or North Africa, but existing on the islands of the east coast of America or on the Isthmus of Panama. A further relationship to that continent is to be traced by the presence in Madeira of the beautiful ericaceous tree Clethra arborea, belonging to a genus which is otherwise wholly American, and of a Persea, a tree laurel, also an American genus. The dragon tree (Dracaena Draco) is almost extinct. Amongst the trees most worthy of note are four of the laurel order belonging to separate genera, an Ardisia, Pittosporum, Sideroxylon, Notelaea, Rhamnus and Myrica,—a strange mixture of genera to be found on a small Atlantic island. Two heaths of arborescent growth and a whortleberry cover large tracts on the mountains. In some parts there is a belt of the Spanish chestnut about the height of 1500 ft. There is no indigenous pine tree as at the Canaries; but large tracts on the hills have been planted with Pinus pinaster, from which the fuel of the inhabitants is mainly derived. A European juniper (J. Oxycedrus), growing to the height of 40 or 50 ft., was formerly abundant, but has been almost exterminated, as its scented wood is prized by the cabinet-maker. Several of the native trees and shrubs now grow only in situations which are nearly inaccessible, and some of the indigenous plants are of the greatest rarity. But some plants of foreign origin have spread in a remarkable manner. Among these is the common cactus or prickly pear (Opuntia Tuna), which in many spots on the coast is sufficiently abundant to give a character to the landscape. As to Algae, the coast is too rocky and the sea too unquiet for a luxuriant marine vegetation, consequently the species are few and poor.
Inhabitants.—The inhabitants are of Portuguese descent, with probably some intermixture of Moorish and negro blood amongst the lower classes. The dress of the peasantry, without being picturesque, is peculiar. Both men and women in the outlying country districts wear the carapuça, a small cap made of blue cloth in shape something like a funnel, with the pipe standing upwards. The men have trousers of linen, drawn tight, and terminating at the knees; a coarse shirt enveloping the upper part of their person, covered by a short jacket, completes their attire, with the exception of a pair of rough yellow boots. The women’s outer garments consist of a gaudily coloured gown, made from island material, with a small cape of coarse scarlet or blue woollen cloth. The population tends to increase rapidly. In 1900 it amounted to 150,574, including 890 foreigners, of whom the majority were British. The number of females exceeds that of males by about 6000, partly because many of the able-bodied males emigrate to Brazil or the United States. The density of population (479.5 per sq. m.) is very great for a district containing no large town and chiefly dependent on agriculture and viticulture.
Agriculture.—A large portion of the land was formerly entailed in the families of the landlords (morgados), but entails have been abolished by the legislature, and the land is now absolutely free. The deficiency of water is a great obstacle to the proper cultivation of the land, and the rocky nature or steep inclination of the upper parts of the islands is an effectual bar to all tillage. An incredible amount of labour has been expended upon the soil, partly in the erection of walls intended to prevent its being washed away by the rains, and to build up the plots of ground in the form of terraces. Watercourses have been constructed for purposes of irrigation, without which at regular intervals the island would not produce a hundredth part of its present yield. These watercourses originate high up in the ravines, are built of masonry or driven through the rock, and wind about for miles until they reach the cultivated land. Some of them are brought by tunnels from the north side of the island through the central crest of hill. Each occupier takes his turn at the running stream for so many hours in the day or night at a time notified to him beforehand. In this climate flowing water has a saleable value as well as land, which is useless without irrigation.
The agricultural implements employed are of the rudest kind, and the system of cultivation is extremely primitive. Very few of the occupiers own the land they cultivate; but they almost invariably own the walls, cottages and trees standing thereon, the land alone belonging to the landlord. The tenant can sell his share of the property without the consent of the landlord, and if he does not so 283 dispose of it that share passes to his heirs. In this way the tenant practically enjoys fixity of tenure, for the landlord is seldom in a position to pay the price at which the tenant’s share is valued. Money rents are rare, the métayer system regulating almost universally the relations between landlord and tenant; that is, the tenant pays to the owner a certain portion of the produce, usually one half or one third. The holdings are as a rule rarely larger than one man can cultivate with a little occasional assistance. There are few meadows and pastures, the cattle being stall-fed when not feeding on the mountains. Horses are never employed for draught, all labour of that kind being done by oxen.
The two staple productions of the soil are wine and sugar. The vine was introduced from Cyprus or Crete soon after the discovery of the island by the Portuguese (1420), but it was not actively cultivated until the early part of the 16th century. The vines, after having been totally destroyed by the oidium disease, which made its first appearance in the island in 1852, were replanted, and Wine. in a few years wine was again made. The phylloxera also made its way to the island, and every vineyard in Madeira was more or less affected by it. The wine usually termed Madeira is made from a mixture of black and white grapes, which are also made separately into wines called Tinta and Verdelho, after the names of the grapes. Other high-class wines, known as Bual, Sercial and Malmsey, are made from varieties of grapes bearing the same names. (See also Wine.)
The sugar cane is said to have been brought from Sicily about 1452, and in course of time its produce became the sole staple of the island. The cultivation languished, however, as the more abundant produce of tropical countries came into the European market, and sugar had long ceased to be made when the destruction of the vines compelled the peasants to turn their attention to other things. Its cultivation was resumed and sugar machinery imported. A Sugar. considerable quantity of spirit is made by the distillation of the juice or of the molasses left after extracting the sugar, and this is consumed on the island. The cane does not flourish here as luxuriantly as within the tropics; but in localities below 1000 ft., where there is a good supply of water, it pays the cultivator well.
The grain produced on the island (principally wheat, barley and Indian corn) is not sufficient for the consumption of the people. The common potato, sweet potato and gourds of various kinds are extensively grown, as well as the Colocasia esculenta, the kalo of the Pacific islanders, the root of which yields an insipid food. Most of the common table vegetables of Europe are plentiful. Besides apples, pears and peaches, all of poor quality, oranges, lemons, guavas, mangoes, loquats, custard-apples, figs, bananas and pineapples are produced, the last two forming articles of export. The date palm is occasionally grown, but its fruit is scarcely edible. On the hills large quantities of the Spanish chestnut afford an item in the food of the common people. A little tobacco is grown, and is made into cigars of inferior quality.
The total foreign trade of Madeira was valued at £628,000 in 1900. The principal exports are wine, sugar, embroidery, vegetables, fruits and wicker goods. Coal is imported for the ships calling at Funchal, which is the headquarters of Madeiran commerce and industry. Spirits, beer, olive oil, soap, butter, linen and woollen goods, straw hats and leather, are manufactured for home consumption, and there are important fisheries.
Chief Towns and Communications.—Funchal (pop. 20,850) is described in a separate article. The other chief towns are Camara de Lobos (7150), Machico (6128), Santa Cruz (5876), Ponta do Sol (5665), São Vicente (4896), Calheta (3475), Sant’ Anna (3011) and Porto Santo (2311). Each of these is the capital of a commune (concelho), to which it gives its name. Madeira is connected by regular lines of steamships with Great Britain, Germany, Portugal, Cape Colony, Brazil and the United States. There is no railway in the archipelago, and partly owing to the irregularities of the surface of the roads, of which there are some 580 m., are bad, except in the neighbourhood of Funchal. Wheel carriages are rare, and all heavy goods are transported either on the backs of mules or upon rude wooden sledges drawn by bullocks. When horses are not employed, locomotion is effected either by means of hammocks or by bullock cars. The hammock (rêde) is a piece of stout canvas gathered up and secured at each end to a long pole carried by a couple of bearers. In place of cabs, curtained cars on sledges, made to hold four persons, and drawn by a pair of bullocks, are employed. They are convenient, but the rate of progress is very slow.
Administration.—The archipelago is officially styled the district of Funchal; it returns members to the Portuguese Cortes, and is regarded as an integral part of the kingdom. The district is subdivided into the eight communes already enumerated, and is administered in accordance with the same laws that regulate local government on the mainland (see Portugal). Funchal is a Roman Catholic bishopric in the archiepiscopal province of Lisbon. Education is compulsory in name only, for less than 2% of the population could read when the census of 1900 was taken. An infantry regiment and a battery of garrison artillery are permanently stationed in Madeira.
History.—It has been conjectured, but on insufficient evidence, that the Phoenicians discovered Madeira at a very early period. Pliny mentions certain Purple or Mauretanian Islands, the position of which with reference to the Fortunate Islands or Canaries might seem to indicate the Madeiras. There is a romantic story, to the effect that two lovers, Robert Machim, à Machin, or Macham, and Anna d’Arfet, fleeing from England to France (c. 1370) were driven out of their course by a violent storm and cast on the coast of Madeira at the place subsequently named Machico, in memory of one of them. Both perished here, but some of their crew escaped to the Barbary coast, and were made slaves. Among them was the pilot Pedro Morales of Seville, who is said to have been ransomed and to have communicated his knowledge of Madeira to João Gonçalvez Zarco (or Zargo). How far this story is true cannot now be ascertained. It is, however, certain that Zarco first sighted Porto Santo in 1418, having been driven thither by a storm while he was exploring the coast of West Africa. Madeira itself was discovered in 1420. It is probable that the whole archipelago had been explored at an earlier date by Genoese adventurers, and had been forgotten; for an Italian map dated 1351 (the Laurentian portolano) shows the Madeiras quite clearly, and there is some reason to believe that they were known to the Genoese before 1339. When Zarco visited Madeira in 1420 the islands were uninhabited, but Prince Henry the Navigator at once began their colonization, aided by the knights of the Order of Christ. Sanctioned by the pope and by two charters which the king of Portugal granted in 1430 and 1433, the work proceeded apace; much land was deforested and brought into cultivation, and the Madeiran sugar trade soon became important. For the sixty years 1580-1640 Madeira, with Portugal itself, was united with Spain. Slavery was abolished in Madeira in 1775, by order of Pombal. In 1801 British troops, commanded by General Beresford, occupied the island for a few months, and it was again under the British flag from 1807 to 1814. It shared in the civil disturbances brought about by the accession of Dom Miguel (see Portugal: History), but after 1833 its history is a record of peaceful commercial development.
See A. S. Brown, Madeira, the Canary Islands and the Azores (1903), a comprehensive study of the three archipelagoes. The Land of the Wine, by A. J. D. Biddle (Philadelphia, 1901) is generally valuable, but its history cannot be trusted. See also P. Langerhaus, Handbuch für Madeira (1884) and Vahl, Madeira’s Vegetation (Copenhagen, 1904).

MADELENIAN, a term derived from La Madeleine, a cave in the Vézère, about midway between Moustier and Les Eyzies, France, and given by the French anthropologist Gabriel de Mortillet to the third stage of his system of cave-chronology, synchronous with the fourth or most recent division of the Quaternary Age. The Madelenian epoch was a long one, represented by numerous stations, whose contents show progress in the arts and general culture. It was characterized by a cold and dry climate, the existence of man in association with the reindeer, and the extinction of the mammoth. The use of bone and ivory for various implements, already begun in the preceding Solutrian epoch, was much increased, and the period is essentially a Bone age. The bone instruments are very varied: spear-points, harpoon-heads, borers, hooks and needles. Most remarkable is the evidence La Madeleine affords of prehistoric art. Numbers of bones, reindeer antlers and animals’ teeth were found, with rude pictures, carved or etched on them, of seals, fishes, reindeer, mammoths and other creatures. The best of these are a mammoth engraved on a fragment of its own ivory; a dagger of reindeer antler, with handle in form of a reindeer; a cave-bear cut on a flat piece of schist; a seal on a bear’s tooth; a fish well drawn on a reindeer antler; and a complete picture, also on reindeer antler, showing horses, an aurochs, trees, and a snake biting a man’s leg. The man is naked, and this and the snake suggest a warm 284 climate, in spite of the presence of the reindeer. The fauna of the Madelenian epoch seems, indeed, to have included tigers and other tropical species side by side with reindeer, blue foxes, Arctic hares and other polar creatures. Madelenian man appears to have been of low stature, dolichocephalic, with low retreating forehead and prominent brow ridges. Besides La Madeleine the chief stations of the epoch are Les Eyzies, Laugerie Basse, and Gorge d’Enfer in Dordogne; Grotte du Placard in Charente and others in south-west France.
See G. de Mortillet, Le Préhistorique (1900); Edouard Lartet and Henry Christy, Reliquiae Aquitanicae (1865-1875); Edouard Dupont, Le Temps préhistorique en Belgique (1872); Lord Avebury, Prehistoric Times (1900).

MADELEY, a market town in the municipal borough of Wenlock, and the Wellington (Mid) parliamentary division of Shropshire, England, 159 m. N.W. from London, with stations on the London & North Western (Madeley Market) and Great Western railways (Madeley Court). Pop. of civil parish (1901), 8442. There are large ironworks, ironstone and coal are mined, and potter’s clay is raised. The church of St Michael (1796) replaced a Norman building. The living was held from 1760 to 1783 by John William Fletcher or de la Flechêre, a close friend of the Wesleys. The parish includes a portion of Coalbrookdale (q.v.), and the towns of Ironbridge and Coalport. Ironbridge, a town picturesquely situated on the steep left bank of the Severn, adjoins Madeley on the south-west. It takes its name from the iron bridge of one span crossing the river, erected in 1779. This bridge is a remarkable work considering its date; it was probably the first erected, at any rate on so large a scale, and attracted great attention. It is the work of Abraham Darby, the third of the name, one of the famous family of iron-workers in Coalbrookdale. Here are brick and tile works and lime-kilns. There is a station (Ironbridge and Broseley) on the Great Western railway, across the river. Coalport lies also on the Severn, S. of Madeley and 2 m. S.E. of Ironbridge, with a station on the Great Western railway. It has large china works, founded at the close of the 18th century, which subsequently incorporated those of Caughley, across the Severn, and of Nantgarw in Glamorganshire.

MĀDHAVA ĀCHĀRYA (fl. c. 1380), Hindu statesman and philosopher, lived at the court of Vijayanagar (the modern Humpi in the district of Bellary), the vigorous Southern Hindu kingdom that so long withstood Mahommedan influence and aggression. His younger brother Sāyaṇa (d. 1387) was associated with him in the administration and was a famous commentator on the Rigveda. Sāyaṇa’s commentaries were influenced by and dedicated to Mādhava, who is best known as the author of the Sarvadarsana Samgraha (Compendium of Speculations). With remarkable mental detachment he places himself in the position of an adherent of sixteen distinct systems. Mādhava also wrote a commentary on the Mīmāṃsā Sūtras. He died as abbot of the monastery of Sringeri.

MADI (A-Madi), a negro race of the Nile valley, occupying both banks of the Bahr-el-Jebel immediately north of Albert Nyanza. Tradition makes them immigrants from the north-west. They are remarkable for the consideration shown to their women, who choose their own husbands, are never ill-treated or hard-worked, and take part in tribal deliberations. The Madi build sepulchral monuments of an elaborate type, two huge narrow stones sloping towards each other with two smaller slabs covering the opening between them. They have been much harried by the Azandeh and Abarambo. They were visited by W. Junker in 1882-1883, and described by him in Petermann’s Mittheilungen for May 1883.

MADISON, JAMES (1751-1836), fourth president of the United States, was born at Port Conway, in King George county, Virginia, on the 16th of March 1751. His first ancestor in America may possibly have been Captain Isaac Maddyson, a colonist of 1623 mentioned by John Smith as an excellent Indian fighter. His father, also named James Madison, was the owner of large estates in Orange county, Virginia. In 1769 the son entered the college of New Jersey (now Princeton University), where, in the same year, he founded the well-known literary club, “The American Whig Society.” He graduated in 1771, but remained for another year at Princeton studying, apparently for the ministry, under the direction of John Witherspoon (1722-1794). In 1772 he returned to Virginia, where he pursued his reading and studies, especially theology and Hebrew, and acted as a tutor to the younger children of the family. In 1775 he became chairman of the committee of public safety for Orange county, and wrote its response to Patrick Henry’s call for the arming of a colonial militia, and in the spring of 1776 he was chosen a delegate to the new Virginia convention, where he was on the committee which drafted the constitution for the state, and proposed an amendment (not adopted) which declared that “all men are equally entitled to the full and free exercise” of religion, and was more radical than the similar one offered by George Mason. In 1777, largely, it seems, because he refused to treat the electors with rum and punch, after the custom of the time, he was not re-elected, but in November of the same year he was chosen a member of the privy council or council of state, in which he acted as interpreter for a few months, as secretary prepared papers for the governor, and in general took a prominent part from the 14th of January 1778 until the end of 1779, when he was elected a delegate to the Continental Congress.
He was in Congress during the final stages of the War of Independence, and in 1780 drafted instructions to Jay, then representing the United States at Madrid, that in negotiations with Spain he should insist upon the free navigation of the Mississippi and upon the principle that the United States succeeded to British rights affirmed by the treaty of Paris of 1763. When the confederation was almost in a state of collapse because of the failure of the states to respond to requisitions of Congress for supplies for the federal treasury, Madison was among the first to advocate the granting of additional powers to Congress, and urged that congress should forbid the states to issue more paper money. In 1781 he favoured an amendment of the Articles of Confederation giving Congress power to enforce its requisitions, and in 1783, in spite of the open opposition of the Virginia legislature, which considered the Virginian delegates wholly subject to its instructions, he advocated that the states should grant to Congress for twenty-five years authority to levy an import duty, and suggested a scheme to provide for the interest on the debt not raised by the import duty—apportioning it among the states on the basis of population, counting three-fifths of the slaves, a ratio suggested by Madison himself. Accompanying this plan was an address to the states drawn up by Madison, and one of the ablest of his state papers. In the same year, with Oliver Ellsworth of Connecticut, Nathaniel Gorham of Massachusetts. Gunning Bedford of Delaware, and John Rutledge of South Carolina, he was a member of the committee which reported on the Virginia proposal as to the terms of cession to the Confederation of the “back lands,” or unoccupied Western territory, held by several of the states; the report was a skilful compromise made by Madison, which secured the approval of the rather exigent Virginia legislature.
In November 1783 Madison’s term in Congress expired, and he returned to Virginia and took up the study of the law. In the following year he was elected to the House of Delegates. As a member of its committee on religion, he opposed the giving of special privileges to the Episcopal (or any other) church, and contended against a general assessment for the support of the churches of the state. His petition of remonstrance against the proposed assessment, drawn up at the suggestion of George Nicholas (c. 1755-1799), was widely circulated and procured its defeat. On the 26th of December 1785 Jefferson’s Bill for establishing religious freedom in Virginia, which had been introduced by Madison, was passed. In the Virginia House of Delegates, as in the Continental Congress, he opposed the further issue of paper money; and he tried to induce the legislature to repeal the law confiscating British debts, but he did not lose sight of the interests of the Confederacy. The boundary between Virginia and Maryland, according to the Baltimore grant, was the south shore of the Potomac, a line to which Virginia had agreed on condition of free 285 navigation of the river and the Chesapeake Bay. Virginia now feared that too much had been given up, and desired joint regulation of the navigation and commerce of the river by Maryland and Virginia. On Madison’s proposal commissioners from the two states met at Alexandria (q.v.) and at Mount Vernon in March 1785. The Maryland legislature approved the Mount Vernon agreement and proposed to invite Pennsylvania and Delaware to join in the arrangement. Madison, seeing an opportunity for more general concert in regard to commerce and trade (and possibly for the increase of the power of Congress), proposed that all the states should be invited to send commissioners to consider commercial questions, and a resolution to that effect was adopted (on Jan. 21, 1786) by the Virginia legislature. This led to the Annapolis convention of 1786, and that in turn led to the Philadelphia convention of 1787. In April 1787 Madison had written a paper, The Vices of the Political System of the United States, and from his study of confederacies, ancient and modern, later summed up in numbers 17, 18, and 19 of The Federalist, he had concluded that no confederacy could long endure if it acted upon states only and not directly upon individuals. As the time for the convention of 1787 approached he drew up an outline of a new system of government, the basis of the “Virginia plan” presented in the convention by Edmund Jennings Randolph. Madison’s scheme, as expressed in a letter to Washington dated the 16th of April 1787, was that individual sovereignty of states was irreconcilable with aggregate sovereignty, but that the “consolidation of the whole into one simple republic would be as inexpedient as it is unattainable.” He considered as a practical middle ground changing the basis of representation in Congress from states to population; giving the national government “positive and complete authority in all cases which require uniformity”; giving it a negative on all state laws, a power which might best be vested in the Senate, a comparatively permanent body; electing the lower house, and the more numerous, for a short term; providing for a national executive, for extending the national supremacy over the judiciary and the militia, for a council to revise all laws, and for an express statement of the right of coercion; and finally, obtaining the ratification of a new constitutional instrument from the people, and not merely from the legislatures. The “Virginia plan” was the basis of the convention’s deliberations which resulted in the constitution favourably voted on by the convention on the 17th of September 1787. Among the features of the plan which were not embodied in the constitution were the following: proportionate representation in the Senate and the election of its members by the lower house “out of a proper number of persons nominated by the individual legislatures”; the vesting in the national Congress of power to negative state acts; and the establishment of a council of revision (the executive and a convenient number of national judges) with veto power over all laws passed by the national Congress. Madison, always an opponent of slavery, disapproved of the compromise (in Art. I. § 9 and Art. V.) postponing to 1808 (or later) the prohibition of the importation of slaves. He took a leading part in the debates of the convention, of which he kept full and careful notes, afterwards published by order of Congress (3 vols., Washington, 1843). Many minute and wise provisions are due to him, and he spoke before the convention more frequently than any delegate except James Wilson and Gouverneur Morris. In spite of the opposition to the constitution of the Virginia leaders George Mason and E. J. Randolph, Madison induced the state’s delegation to stand by the constitution in the convention. His influence largely shaped the form of the final draft of the constitution, but the labour was not finished with this draft; that the constitution was accepted by the people was due in an eminent degree to the efforts of Madison, who, to place the new constitution before the public in its true light, and to meet the objections brought against it, joined Alexander Hamilton (q.v.) and John Jay in writing The Federalist, a series of eighty-five papers, out of which twenty certainly, and nine others probably, were written by him. In the Virginia convention for ratifying the constitution (June 1788), when eight states had ratified and it seemed that Virginia’s vote would be needed to make the necessary nine (New Hampshire’s favourable vote was cast only shortly before that of Virginia), and it appeared that New York would vote against the constitution if Virginia did not ratify it, Madison was called upon to defend that instrument again, and he appeared at his best against its opponents, Patrick Henry, George Mason, James Monroe, Benjamin Harrison, William Grayson and John Tyler. He answered their objections in detail, calmly and with an intellectual power and earnestness that carried the convention. The result was a victory against an originally adverse public opinion and against the eloquence of the opponents of the constitution, for Madison and for his lieutenants, Edmund Pendleton, John Marshall, George Nicholas, Harry Innes and Henry Lee. At the same time Madison’s labours in behalf of the constitution alienated from him valuable political support in Virginia. He was defeated by Richard Henry Lee and William Grayson in his candidacy for the United States Senate, but in his own district he was chosen a representative to Congress, defeating James Monroe, who seems to have had the powerful support of Patrick Henry.
Madison took his seat in the House of Representatives in April 1789, and assumed a leading part in the legislation necessary to the organization of the new government. He drafted a Tariff Bill giving certain notable advantages to nations with which the United States had commercial treaties, hoping to force Great Britain into a similar treaty; but his policy of discrimination against England was rejected by Congress. It was his belief that such a system of retaliation would remove the possibility of war arising from commercial quarrels. He introduced resolutions calling for the establishment of three executive departments, foreign affairs, treasury and war, the head of each removable by the president. Most important of all, he proposed nine amendments to the constitution, embodying suggestions made by a number of the ratifying states, especially those made by Virginia at the instance of George Mason; and the essential principles of Madison’s proposed amendments were included in a Bill of Rights, adopted by the states in the form of ten amendments. The absence of a Bill of Rights from the constitution as first adopted had been the point on which the opposition had made common cause, and the adoption of this now greatly weakened the same opposition. Although a staunch friend of the constitution, Madison believed, however, that the instrument should be interpreted conservatively and not be made the means of introducing radical innovations. The tide of strict construction was setting in strongly in his state, and he was borne along with the flood. It is very probable that Jefferson’s influence over Madison, which was greater than Hamilton’s, contributed to this result. Madison now opposed Hamilton’s measures for the funding of the debt, the assumption of state debts, and the establishment of a National Bank, and on other questions he sided more and more with the opposition, gradually assuming its leadership in the House of Representatives and labouring to confine the powers of the national government within the narrowest possible limits; his most important argument against Hamilton’s Bank was that the constitution did not provide for it explicitly, and could not properly be construed into permitting its creation. Madison, Jefferson and Randolph were consulted by Washington, and they advised him not to sign the bill providing for the Bank, but Hamilton’s counter-argument was successful. On the same constitutional grounds Madison objected to the carrying out of the recommendations in Hamilton’s famous report on manufactures (Dec. 5, 1791), which favoured a protective tariff. In the presidential campaign of 1792 Madison seems to have lent his influence to the determined efforts of the Jeffersonians to defeat John Adams by electing George Clinton vice-president. In 1793-1796 he strongly criticized the administration for maintaining a neutral position between Great Britain and France, writing for the public press five papers (signed “Helvidius”), attacking the “monarchical prerogative of the executive” as exercised in the proclamation of neutrality in 1793 and denying the president’s right to recognize foreign states. He found in Washington’s attitude—as in Hamilton’s failure to pay an instalment of the moneys 286 due France—an “Anglified complexion,” in direct opposition to the popular sympathy with France and French Republicanism. In 1794 he tried again his commercial weapons, introducing in the House of Representatives resolutions based on Jefferson’s report on commerce, advising retaliation against Great Britain and discrimination in commercial and navigation laws in favour of France; and he declared that the friends of Jay’s treaty were “a British party systematically aiming at an exclusive connexion with the British government,” and in 1796 strenuously but unsuccessfully opposed the appropriation of money to carry this treaty into effect. Still thinking that foreign nations could be coerced through their commercial interests, he scouted as visionary the idea that Great Britain would go to war on a refusal to carry Jay’s treaty into effect, thinking it inconceivable that Great Britain “would wantonly make war” upon a country which was the best market she had in the world for her manufactures, and one with which her export trade was so much larger than her import.
In 1797 Madison retired from Congress, but not to a life of inactivity. In 1798 he joined Jefferson in opposing the Alien and Sedition Laws, and Madison himself wrote the resolutions of the Virginia legislature declaring that it viewed “the powers of the Federal government as resulting from the compact to which the states are parties, as limited by the plain sense and intention of the instrument constituting that compact; as no further valid than they are authorized by the grants enumerated in that compact; and that, in case of a deliberate, palpable and dangerous exercise of other powers, not granted by the said compact, the states, who are parties thereto, have the right and are in duty bound to interpose for arresting the progress of the evil, and for maintaining within their respective limits, the authorities, rights and liberties appertaining to them.” The Virginia resolutions and the Kentucky resolutions (the latter having been drafted by Jefferson) were met by dissenting resolutions from the New England states, from New York, and from Delaware. In answer to these, Madison, who had become a member of the Virginia legislature in the autumn of 1799, wrote for the committee to which they were referred a report elaborating and sustaining in every point the phraseology of the Virginia resolutions.1
Upon the accession of the Republican party to power in 1801, Madison became secretary of state in Jefferson’s cabinet, a position for which he was well fitted both because he possessed to a remarkable degree the gifts of careful thinking and discreet and able speaking, and of large constructive ability; and because he was well versed in constitutional and international law and practised a fairness in discussion essential to a diplomat. During the eight years that he held the portfolio of state, he had continually to defend the neutral rights of the United States against the encroachments of European belligerents; in 1806 he published An Examination of the British Doctrine which subjects to Capture a Neutral Trade not open in Time of Peace, a careful argument—with a minute examination of authorities on international law—against the rule of war of 1756 extended by Great Britain in 1793 and 1803.
During Jefferson’s presidency and whilst Madison was secretary of state, by the purchase of Louisiana, Madison’s campaign begun in 1780 for the free navigation of the Mississippi was brought to a successful close. The candidate in 1808 of the Republican party, although bitterly opposed in the party by John Randolph and George Clinton, Madison was elected president, defeating C. C. Pinckney, the Federalist candidate, by 122 votes to 47. Madison had no false hopes of placating the Federalist opposition, but as the preceding administration was one with which he was in harmony, his position was different from that of Jefferson in 1801, and he had less occasion for removing Federalists from office. Jefferson’s peace policy—or, more correctly, Madison’s peace policy—of commercial restrictions to coerce Great Britain and France he continued to follow until 1812, when he was forced to change these futile commercial weapons for a policy of war, which was very popular with the extreme French wing of his party. There is a charge, which has never been proved or disproved, that Madison’s real desire was for peace, but that in order to secure the renomination he yielded to that wing of his party which was resolved on war with Great Britain. The only certain fact is that Madison, whatever were his personal feelings in this matter, acted according to the wishes of a majority of the Republicans; but whether in doing so he was influenced by the desire of another nomination is largely a matter of conjecture. Madison was renominated on the 18th of May 1812, issued his war message on the 1st of June, and in the November elections he was re-elected, defeating De Witt Clinton by 128 votes to 89. His administration during the war was pitiably weak. His cabinet in great part had been dictated to him in 1809 by a senatorial clique, and it was hopelessly discordant; for two years he was to all intents and purposes his own secretary of state, Robert Smith being a mere figure-head of whom he gladly got rid in 1811, giving Monroe the vacant place. Madison himself had attempted alternately to prevent war by his “commercial weapons” and to prepare the country for war, but he had met with no success, because of the tricky diplomacy of Great Britain and of France, and because of the general distrust of him coupled with the particular opposition to the war of the prosperous New England Federalists, who suggested with the utmost seriousness that his resignation should be demanded. In brief, Madison was too much the mere scholar to prove a strong leader in such a crisis. The supreme disgrace of the administration was the capture and partial destruction in August 1814 of the city of Washington—this was due, however, to incompetence of the military and not to any lack of prudence on the cabinet’s part. In general, Congress was more blamable than either the president or his official family, or the army officers. With the declaration of peace the president again gained a momentary popularity much like that he had won in 1809 by his apparent willingness at that time to fight France.
Retiring from the presidency in 1817, Madison returned to his home, Montpelier (in Orange county, Virginia), which he left in no official capacity save in 1829, when he was a delegate to the state constitutional convention and served on several of its committees. Montpelier, like Jefferson’s Monticello and Monroe’s Oak-Hill, was an expensive bit of “gentleman farming,” which with his generous Virginia hospitality nearly ruined its owner financially. Madison’s home was peculiarly a centre for literary travellers in his last years; when he was eighty-three he was visited by Harriet Martineau, who reported her conversations with him in her Retrospect of Western Travel (1838). He took a great interest in education—his library was left to the university of Virginia, where it was burned in 1895—in emancipation, and in agricultural questions, to the very last. He died at Montpelier on the 28th of June 1836. Madison married, in 1794, Dorothy Payne Todd (1772-1849), widow of John Todd, a Philadelphia lawyer. She had great social charm, and upon Madison’s entering Jefferson’s cabinet became “first lady” in Washington society. Her plump beauty was often remarked—notably by Washington Irving—in contrast to her husband’s delicate and feeble figure and wizened face—for even in his prime Madison was, as Henry Adams says, “a small man, quiet, somewhat precise in manner, pleasant, fond of conversation, with a certain 287 mixture of ease and dignity in his address.” Her son, spoiled by his mother and his step-father, became a wild young fellow, and added his debts to the heavy burden of Montpelier upon Madison.
Madison’s portrait was painted by Gilbert Stuart and by Charles Willson Peale; Giuseppe Ceracchi made a marble bust of him in 1792 and John H. J. Browere another in 1827, now in possession of the Virginia Historical Society at Richmond. Though commonly dignified and a little stiff he seems to have had a strong sense of humour and he was fond of telling a good story. Henry Clay, contrasting him with Jefferson, said that Jefferson had more genius, Madison more judgment and common sense; that Jefferson was a visionary and a theorist; Madison cool, dispassionate, practical, and safe.2 The broadest and most accurate scholar among the “founders and fathers,” he was particularly an expert in constitutional history and theory. In the great causes for which Madison fought in his earlier years—religious freedom and separation of church and state, the free navigation of the Mississippi, and the adoption of the constitution—he met with success. His greatest and truest fame is as the “father of the constitution.” The “commercial weapons” with which he wished to prevent armed conflict proved less useful in his day than they have since been in international disputes.
Authorities.—Madison’s personality is perplexingly vague; the biographies of him are little more than histories of the period, and the best history of the later period in which he was before the public, Henry Adams’s History of the United States from 1801 to 1817 (1889-1890), gives the clearest sketch and best criticism of him. The lives of Madison are: J. Q. Adams’s (Boston, 1850); W. C. Rives’s (Boston, 1859-1869, 3 vols.), covering the period previous to 1797; S. H. Gay’s (Boston, 1884) in the “American Statesmen Series”; and Gaillard Hunt’s (New York, 1902). Madison’s Writings (7 vols., New York, 1900-1906) were edited by Hunt, who also edited The Journal of the Debates in the Convention which framed the Constitution of the United States, as Recorded by James Madison (2 vols., New York, 1908). See also Mrs Madison’s Memoirs and Letters (Boston, 1887) and Maud Wilder Goodwin, Dolly Madison (New York, 1897).
1 Thirty years later Madison’s arguments for the Virginia resolutions and the resolutions themselves were freely used by Calhoun and his followers in support of his doctrine of nullification. But Madison insisted that the Resolutions of 1798 did not involve the principles of nullification. Nearly all his arguments, especially where he attempts to interpret Jefferson’s writings on the point, notably the Kentucky resolutions, are rather strained and specious, but it does seem that the Virginia resolutions were based on a different idea from Calhoun’s doctrine of nullification. Madison’s theory was that the legislature of Virginia, being one of the bodies which had chosen delegates to the constitutional convention, was legally capable of considering the question of the constitutionality of laws passed by the Federal government, and that the state of Virginia might invite other states to join her, but could not singly, as Calhoun argued, declare any law of the Federal legislature null and void. (It is to be noted the words “null and void” were in Madison’s first draft of the Virginia resolutions, but that they were omitted by the Virginia legislature.) It is notable, besides, that Madison had always feared that the national congress would assume too great power, that he had approved of Supreme Court checks on the national legislature, and of veto power by a council of revision.
2 Clay’s opinion is given in a report written by Mrs Samuel H. Smith of a conversation in 1829 between Clay and her husband, a prominent politician.

MADISON, a city and the county-seat of Jefferson county, Indiana, U.S.A., on the N. bank of the Ohio river, about 90 m. below Cincinnati, and 44 m. above Louisville, Kentucky. Pop. (1870), 10,709; (1890), 8936; (1900), 7835 (554 foreign-born and 570 negroes); (1910), 6934. Madison is served by the Pittsburg, Cincinnati, Chicago & St Louis railroad and by river steamboats. The city is picturesquely situated on bluffs above the river and has two public parks. In Madison are a King’s Daughters’ Hospital, a children’s home, and the Drusilla home for old ladies, and immediately north of the city are the buildings of the Indiana South-eastern Insane Hospital. Madison is a trading centre of the surrounding farming region, whose principal products are burley tobacco, grain and fruits (peaches, apples, pears, plums and small fruits). The municipality owns and operates the waterworks. Madison was settled about the beginning of the 19th century; was incorporated as a town in 1824, and was first chartered as a city in 1836.

MADISON, a borough of Morris county, New Jersey, U.S.A., 27 m. (by rail) W. of New York City and 4 m. S.E. of Morristown. Pop. (1890), 2469; (1900), 3754, of whom 975 were foreign-born and 300 were negroes; (1905), 4115; (1910), 4658. It is served by the Morris & Essex division of the Delaware, Lackawanna & Western railroad. The borough is attractively situated among the hills of Northern New Jersey, is primarily a residential suburb of New York and Newark, and contains many fine residences. There are a public library and a beautiful public park, both given to the borough by Daniel Willis James (1832-1907), a prominent metal manufacturer; the library is closely allied with the public schools. Madison is the seat of the well-known Drew theological seminary (Methodist Episcopal; founded in 1866 and opened in 1867), named in honour of Daniel Drew (1788-1879), who, having acquired great wealth from steamboat and railway enterprises, especially from trading in railway stocks, presented the large and beautiful grounds and most of the buildings. The seminary’s course covers three years; no fee is charged. In connexion with the seminary the Drew settlement in New York City—officially the department of applied Christianity—has for its object the “practical study of present-day problems in city evangelism, church organization, and work among the poor.” In 1907-1908 the seminary had 9 instructors, 175 students, and a library of more than 100,000 volumes, especially rich in works dealing with the history of Methodism and in Greek New Testament manuscripts. About 2 m. N.W. of Madison is Convent Station, the seat of a convent of the Sisters of Charity, who here conduct the college of St Elizabeth, for girls, founded in 1859; also conducted by the Sisters of Charity is St Joseph’s preparatory school for boys, founded in 1862. The cultivation of roses and chrysanthemums is practically the only industry of Madison. Madison owns and operates its waterworks and electric-lighting plant. Before 1844 when it took its present name (in honour of President Madison), Madison was called Bottle Hill; it is one of the older places of the state, and its first church (Presbyterian) was built about 1748. The borough was incorporated in 1889.

MADISON, the capital of Wisconsin, U.S.A., and the county-seat of Dane County, situated between Lakes Mendota and Monona in the south central part of the state, about 82 m. W. of Milwaukee and about 131 m. N.W. of Chicago. Pop. (1890), 13,426; (1900) 19,164, of whom 3362 were foreign-born and 69 were negroes; (1910 census) 25,531. Madison is served by the Chicago & North-Western, the Chicago, Milwaukee & St Paul, and the Illinois Central railways (being the northern terminus of the last), and by interurban electric lines, connecting with Janesville, Beloit and Chicago. It has a picturesque situation in what is known as “the Four-Lakes region”; this region takes its name from a chain of lakes, Kegonsa, Waubesa, Monona and Mendota, which, lying in the order named and connected with one another by the Yahara or Catfish River, form the head-waters of Rock river flowing southward through Illinois into the Mississippi. The city occupies a hilly isthmus about a mile wide between Lakes Mendota and Monona, bodies of water of great clearness and beauty, with bottoms of white sand and granite.
The state capitol is in a wooded park at the summit of a hill 85 ft. high in the centre of the city. From this park the streets and avenues radiate in all directions. The capitol, built in 1860-1867 (with an addition in 1883) on the site of the original capitol building (1837-1838), was partially destroyed by fire in 1904, and in 1909-1910 was replaced by a larger edifice. The principal business portion of the city is built about the capitol park and the university. Among the public buildings on or near the park are the federal building, housing the post office and the United States courts, the city hall, the Dane county court-house, the public library, the Fuller opera-house, the county gaol, and the high school. Running directly west from the capitol is State Street, at the western end of which lie the grounds of the university of Wisconsin (q.v.), occupying a hilly wooded tract of 300 acres, and extending for a mile along the south shore of Lake Mendota. University Hill, on which the main building of the university stands, is 125 ft. above the lake; at its foot stands the magnificent library building of the State Historical Society. In it, in addition to the interesting and valuable historical museum and art gallery, are the Society’s library of more than 350,000 books and pamphlets, the university library of 150,000 volumes, and the library of the Wisconsin academy of arts and sciences, 5000 volumes. Other libraries in the city include the state law library (45,000 volumes) in the capitol, the Madison public library (22,500 volumes), and the Woodman astronomical library (7500 volumes). The Madison public library houses also the state library school maintained by the Wisconsin library commission. Connected with the university is the Washburn observatory. On the margin of the city lies the extensive experimental farm of the state college of agriculture. In addition to the state university, Madison is the seat of several Roman Catholic and Lutheran parochial schools, two business schools, and the Wisconsin academy, a non-sectarian preparatory school of high grade. On the banks of Lake Monona are the beautiful grounds of the Monona Lake assembly, a summer assembly 288 on the Chautauqua model. Near the city is one of the five fish-hatcheries maintained by the state; it is largely devoted to the propagation of trout and other small fish. North of the city, occupying a tract of 500 acres, on Lake Mendota, are the buildings and grounds of the state hospital for the insane, opened in 1860.
The city’s streets are broad and heavily shaded with a profusion of elm, oak and maple trees. There are many fine stone residences dating from the middle of the 19th century. There are several parks of great beauty, and along the shores of Lake Mendota there is a broad boulevarded drive of 12 m. The municipality owns its waterworks, the water being obtained from eleven artesian wells, and being chemically similar to that of Waukesha Springs. The city and surrounding region are a summer resort, the lakes affording opportunities for fishing and for yachting and boating.
Madison is an important jobbing centre for central and south-western Wisconsin; it has an extensive trade in farm, garden and dairy products, poultry and tobacco; and there are various manufactures. In 1905 the value of the total factory product was $3,291,143, an increase of 22.4% over that in 1900.
At the time of the settlement by the whites the aboriginal inhabitants of the Four-Lakes region were the Winnebago. Prehistoric earthworks are to be seen in the neighbourhood, several animal-shaped mounds upon the shores of Lakes Mendota, Monona and Waubesa being among the best examples. A regular trading post is known to have been established on Lake Mendota as early as 1820. The title to the Indian lands was acquired by the United States by treaty in 1825. Colonel Ebenezer Brigham established himself at Blue Mounds, in the western part of Dane county, in 1827. In 1832 the “Four-Lakes” country was in the theatre of hostilities during the Black Hawk War; Colonel Henry Dodge held a conference with Winnebago chiefs on Lake Mendota, and there were several skirmishes in the neighbourhood between his troops and the followers of Black Hawk, one of which took place on the site of Madison. After Black Hawk’s defeat on the Bad Axe he fled to the Wisconsin river Dalles, near the present Kilbourn, where he was betrayed by the Winnebago. In 1836 Stevens T. Mason, governor of Michigan, and James Duane Doty, then U.S. district judge, who had visited the region as early as 1829, recorded a tract of land, including most of the present site of Madison. Here they surveyed a “paper” city which they named in honour of James Madison. On the 3rd of December 1836 the territorial legislature in session at Belmont, after a protracted and acrimonious debate, determined, largely through Doty’s influence, to make Madison the permanent capital. The construction of houses began in the early spring of 1837. The first constitutional convention met here in 1846, the second in 1847. Madison was chartered as a city in 1856. In 1862 a large number of Confederate prisoners were confined in Camp Randall, at Madison, and many of them died in hospital.
See D. S. Durrie, History of Madison, Wisconsin (Madison, 1874); Lyman C. Draper, Madison the Capital of Wisconsin (Madison, 1857); J. D. Butler, “The Four Lakes Country” in Wisconsin Historical Society Collections, vol. 10 (1888), and R. G. Thwaites, “Madison” in Historic Towns of the Western States (New York, 1900), and his “Story of Madison” in The University of Wisconsin (Madison, 1900).

MADOU, JEAN BAPTISTE (1796-1877), Belgian painter and lithographer, was born at Brussels on the 3rd of February 1796. He studied at the Brussels Academy of Fine Arts and was a pupil of François. While draughtsman to the topographical military division at Courtrai, he received a commission for lithographic work from a Brussels publisher. It was about 1820 that he began his artistic career. Between 1825 and 1827 he contributed to Les Vues pittoresques de la Belgique, to a Life of Napoleon, and to works on the costumes of the Netherlands, and later made a great reputation by his work in La Physionomie de la société en Europe depuis 1400 jusqu’ à nos jours (1836) and Les Scènes de la vie des peintres. It was not until about 1840 that he began to paint in oils, and the success of his early efforts in this medium resulted in a long series of pictures representing scenes of village and city life, including “The Fiddler,” “The Jewel Merchant,” “The Police Court,” “The Drunkard,” “The Ill-regulated Household,” and “The Village Politicians.” Among his numerous works mention may also be made of “The Feast at the Château” (1851), “The Unwelcome Guests” (1852, Brussels Gallery), generally regarded as his masterpiece, “The Rat Hunt” (acquired by Leopold II., king of the Belgians), “The Arquebusier” (1860), and “The Stirrup Cup.” At the age of sixty-eight he decorated a hall in his house with a series of large paintings representing scenes from La Fontaine’s fables, and ten years later made for King Leopold a series of decorative paintings for the château of Ciergnon. Madou died at Brussels on the 31st of March 1877.
For a list of his paintings see the annual report of the Academy of Belgium for 1879.

MADOZ, PASCUAL (1806-1870), Spanish statistician, was born at Pampeluna on the 7th of May 1806. In early life he was settled in Barcelona, as a writer and journalist. He joined the Progresista party formed during the first Carlist war, 1833-40. He saw some service against the Carlists; was elected deputy to the Cortes of 1836; took part for Espartero, and then against him; was imprisoned in 1843; went into exile and returned; was governor of Barcelona in 1854, and minister of finance in 1855; had a large share in secularizing the Church lands; and after the revolution of 1868 was governor of Madrid. He had, however, no great influence as a leader and soon went abroad, dying at Genoa in 1870. Madoz was distinguished from most of the politicians of his generation by the fact that in middle life he compiled what is still a book of value—a geographical, statistical and historical dictionary of Spain and its possessions oversea, Diccionario geográfico, estadístico y historico de España, y sus posesiones de Ultramar (Madrid, 1848-1850).

MADRAS, a presidency of British India—officially styled Fort St George—occupying, with its dependencies, the entire south of the Indian peninsula. The north boundary is extremely irregular. On the extreme N.E. is the Bengal province of Orissa; then the wild highlands of the Central Provinces; next the dominions of the nizam of Hyderabad; and lastly, on the N.W., the Bombay districts of Dharwar and North Kanara. Geographically Mysore and Coorg lie within the bounds of Madras, and politically it includes the Laccadive Islands, off the Malabar coast, in the Indian Ocean. Its total area, including native states, is 151,695 sq. m., and its population in 1901 was 42,397,522, showing an increase of 7.7% in the decade. The seat of government is at Madras city (q.v.).
Physical Aspect.—The Madras presidency may be roughly divided into three tracts: (1) the long and broad east coast, (2) the shorter and narrower west coast, and (3) the high interior table-land. These divisions are determined by the great mountain ranges of the Eastern and Western Ghats (q.v.). Between these two ranges lies the central table-land, with an elevation of 1000 to 3000 ft., which includes the whole of Mysore, and extends over about half a dozen districts of Madras. The Anaimudi mountain (8837 ft.) in Travancore is the highest in southern India. The Nilgiri hills, which join the Ghats, culminate in Dodabetta (8760 ft.). There are besides many outlying spurs and tangled masses of hills, of which the Shevaroys, Anamalais and Palnis are the most important. The Godavari, Kistna and Cauvery rivers, each having a large tributary system, all rise in the Western Ghats, and run across the peninsula in a south-east direction into the Bay of Bengal. In the upper parts of their course they drain rather than water the country through which they flow, and are comparatively valueless either for navigation or irrigation; but before reaching the sea they spread over alluvial deltas. Smaller rivers of the same character are the Pennar and South Pennar or Ponniar, Palar, Vaigai, Vellar and Tambraparni. The principal lake is that of Pulicat on the east coast, which is 37 m. long from north to south, and forms an important means of communication between Madras city and the northern districts. On the west coast are a remarkable series of backwaters or lagoons, fringing the seaboard of Kanara, Malabar and Travancore. The largest is the backwater of Cochin, which extends 120 m. from north to south.
Geology.—By far the greater part of Madras is occupied by granitic and gneissic rocks of very ancient date. Among them are the “charnockites,” a series of associated eruptive rocks characterized by the presence of rhombic pyroxenes. In Bellary and Anantapur districts, as well as in Mysore and Hyderabad, several long narrow strips of a later formation, known as the Dharwar system, are folded or faulted into the gneissic floor. They run from N.N.W. to S.S.E., and consist of conglomerates, lavas and schists. All the quartz reefs which contain gold in paying quantities are found within these Dharwar bands, those of the Kolar goldfield in Mysore being the most important. The gneissic and Dharwar rocks are overlaid unconformably by the sandstones, limestones, shales, &c., of the Cuddapah and Kurnool series. It is in the sandstones and shales of the Kurnool group that most of the diamonds of southern India are found; but as these rocks are of sedimentary origin, it is probable that the diamonds were originally derived from some still unknown source. A strip of Gondwana beds follows approximately the course of the Godavari. In Hyderabad it includes the important Singareni coalfield, but in the Presidency no good coal seams have yet been found. Upper Gondwana beds also occur in small patches at several other places near the east coast. Marine cretaceous deposits are found in three detached areas, near Trichinopoly, Viruddhachalam and Pondicherry. Some of the coastal sandstones may be of late Tertiary age, but Tertiary fossils have not been found except in a few small patches on the west coast, the most southerly being near Quilon in Travancore.
Climate.—The climate varies in accordance with the height of the mountain chain on the western coast. Where this chain is lofty, as between Malabar and Coimbatore, the rainclouds are intercepted and give a rainfall of 150 in. on the side of the sea, and only 20 in. on the landward side. Where the range is lower, the rainclouds pass over the hills and carry their moisture to the interior districts. The Nilgiri hills enjoy the climate of the temperate zone, with a moderate rainfall. The Malabar coast has a rainfall of 150 in., and the clouds on the Western Ghats sometimes obscure the sun for months at a time. Along the eastern coasts and central table-lands the rainfall is low and the heat excessive. At Madras city the average rainfall is 50 in., but this is considerably above the mean of the east coast.
Minerals.—The mineral wealth of the province is undeveloped. Iron of excellent quality has been smelted by native smiths in many localities from time immemorial; but attempts to work the beds after European methods have proved unsuccessful. Carboniferous sandstone extends across the Godavari valley as far as Ellore, but the coal has been found to be of inferior quality. Among other minerals may be mentioned manganese in Vizagapatam, and mica in Nellore. Garnets are abundant in the sandstone of the Northern Circars, and diamonds of moderate value are found in the same region. Stone and gravel quarries are very numerous.
Forests.—The forest department of Madras was first organized in 1856, and it is estimated that forests cover a total area of more than 19,600 sq. m., the whole of which is under conservancy rules. An area of about 1500 sq. m. is strictly conserved. In the remaining forests, after supplying local wants, timber is either sold direct by the department or licences are granted to wood-cutters. The more valuable timber trees comprise teak, ebony, rosewood, sandal-wood and redwood. The trees artificially reared are teak, sandal-wood, Casuarina and eucalyptus. The finest teak plantation is near Beypur in Malabar. At Mudumalli there are plantations of both teak and sandal-wood; and the eucalyptus or Australian gum-tree grows on the Nilgiris in magnificent clumps.
Fauna.—The wild animals include the elephant, bison, sambur and ibex of the Western Ghats and the Nilgiris. Bison are found also in the hill tracts of the Northern Circars. In Travancore state the black leopard is not uncommon. The elephant is protected by law from indiscriminate destruction. The cattle are small, but in Nellore and along the Mysore frontier a superior breed is carefully kept up by the wealthier farmers. The best buffaloes are imported from the Bombay district of Dharwar.
Population.—The population in 1901 was divided into Hindus (37,026,471), Mahommedans (2,732,931), and Christians (1,934,480). The Hindus may be subdivided into Sivaites, Vishnuvites and Lingayats. The Sivaites are most numerous in the extreme south and on the west coast, while the Vishnuvites are chiefly found in the northern districts. The Lingayats, a sect of Sivaite puritans, derive their name from their practice of carrying about on their persons the linga or emblem of Siva. The Brahmans follow various pursuits, and some of them are recent immigrants, who came south in the train of the Mahratta armies. A peculiar caste of Brahmans, called Nambudri, is found in Malabar. The most numerous of the hill tribes are the Kondhs and Savaras, two cognate races who inhabit the mountainous tracts of the Eastern Ghats, attached to several of the large estates of Ganjam and Vizagapatam. On the Nilgiris the best known aboriginal tribe is the Todas (q.v.). The Mahommedans are subdivided into Labbai, Moplah, Arab, Sheikh, Sayad, Pathan and Mogul. The Labbais are the descendants of Hindu converts, and are traders by hereditary occupation, although many now employ themselves as sailors and fishermen. The Moplahs are the descendants of Malayalam converts to Islam—the head of the tribe, the raja of Cannanore, being descended from a fisher family in Malabar. They are a hard-working, frugal people, but quite uneducated and fanatical, and under the influence of religious excitement have often disturbed the public peace. Christians are more numerous in Madras than in any other part of India. In Travancore and Cochin states the native Christians constitute as much as one-fourth of the population. The Roman Catholics, whose number throughout southern India is estimated at upwards of 650,000, owe their establishment to St Francis Xavier and the famous Jesuit mission of Madura; they are partly under the authority of the archbishop of Goa, and partly under twelve Jesuit vicariates. Protestant missions date from the beginning of the 18th century. The Danes were the pioneers; but their work was taken up by the Society for Promoting Christian Knowledge, under whom laboured the great Lutherans of the 18th century—Schultz, Sartorius, Fabricius and Schwartz. The Church Missionary Society entered the field in 1814; and subsequently an American mission joined in the work.
Languages.—Broadly speaking, the entire population of Madras belongs to the five linguistic offshoots of the great Dravidian stock, dominant throughout southern India. At an early period, before the dawn of history, these races appear to have accepted some form of the Brahmanical or Buddhist faiths. Many storms of conquest have since swept over the land, and colonies of Mogul and Mahratta origin are to be found here and there. But the evidence of language proves that the ethnical character of the population has remained stable under all these influences, and that the Madras Hindu, Mahommedan, Jain and Christian are of the same stock. Of the five Dravidian languages in British territory Telugu is spoken by over 14,000,000 persons; Tamil by over 15,000,000 persons; Kanarese by over 1,500,000 persons; Malayalam by nearly 3,000,000 persons; and Tulu by about 500,000 persons. Oriya is the native tongue in the extreme north of Ganjam, bordering on Orissa; and various sub-dialects of Dravidian origin are used by the hill tribes of the Eastern Ghats, of whom the Kondhs may be taken as the type.
Agriculture.—Over the greater part of the area of Madras artificial irrigation is impossible, and cultivation is dependent upon the local rainfall, which rarely exceeds 40 in. a year, and is liable to fall irregularly. The Malabar coast is the only part where the rainfall brought by the south-west monsoon may be trusted both for its amount and regularity. Other districts, such as Bellary, are also dependent upon this monsoon; but in their case the rainclouds have spent themselves in passing over the Western Ghats, and cultivation becomes a matter of hazard. Over the greater part of the presidency the rainy season is caused by the south-east monsoon, which breaks about the end of September. The deltas of the Godavari, Kistna and Cauvery rivers are the only spots on the east coast which artificial irrigation is able to save from the risk of occasional scarcity. The principal food staples are rice, cholam, cambu, ragi and varagu (four kinds of millet). The most common oil-seed is gingelly (sesamum). Garden crops comprise tobacco, sugar-cane, chillies, betel-leaf and plantains. Sugar is chiefly derived from the sap of palms. The fruit trees are coco-nut, areca-nut, palmyra palm, jack, tamarind and mango. Special crops include cotton, indigo, coffee, tea, cinchona. The best cotton is grown in Tinnevelly. The principal coffee tract stretches along the slopes of the Western Ghats from the north of Mysore almost down to Cape Comorin. The larger portion of this area lies within Mysore, Coorg and Travancore states, but the Wynaad and the Nilgiri hills are within Madras. The first coffee plantation was opened in the Wynaad in 1840. Many of the early clearings proved unprofitable, and the enterprise made little progress till about 1855. Coffee, which is much cultivated on the Nilgiris, covers about 100 sq. m., though the area fluctuates. The tea plant was also introduced into the Nilgiri hills about 1840, but was not taken up as a commercial speculation till 1865, and is still unimportant. The cinchona plant was successfully introduced into the Nilgiri hills by the government in 1860, and there are now a few plantations belonging to private owners.
The greater part of the soil in Madras is held by the cultivators 290 direct from the government under the tenure known as ryotwari. Besides these lands in the hands of the government, there are also proprietary or zamindari estates in all parts of the country. These estates are either the remains of ancient principalities, which the holder cannot sell or encumber beyond his own life interest, or they are creations of British rule and subject to the usual Hindu custom of partition. The total area of the zamindari estates is about 26 million acres, more than one-fourth of the whole presidency. The peshkash or tribute payable to government in perpetuity amounts to about £330,000 a year. Ináms, revenue-free or quit-rent grants of lands made for religious endowments or for services rendered to the state, occupy an aggregate area of nearly 8 million acres.
Manufactures.—Madras possesses few staple manufactures. The chief industries of the presidency are cotton-ginning, coffee-curing, fish-curing, indigo-pressing, oil-pressing, printing, rice-curing, rope-making, sugar-refining, tanning, tile and brick-making, and tobacco-curing. Up to the close of the 18th century cotton goods constituted the main article of export. Masulipatam, where the first English factory on the Coromandel coast was established in 1620, enjoyed a special reputation for its chintzes, which were valued for the freshness and permanency of their dyes. There is still a small demand for these articles in Burma, the Straits and the Persian Gulf; but Manchester goods have nearly beaten the Indian exporter out of the field. Native looms, however, still hold their own in the local market, in face of strenuous opposition. After weaving, working in metals appears to be the most widespread native industry. Among local specialities which have attracted European curiosity may be mentioned the jewelry of Trichinopoly, ornaments of ivory and horn worked at Vizagapatam, and sandal-wood carving in Kanara.
Commerce and Trade.—The continuous seaboard of the Madras presidency, without any natural harbours of the first rank, has tended to create a widely diffused trade. Madras city conducts nearly one-half of the total sea-borne commerce; next comes Malabar, containing the western railway terminus near Calicut; then Godavari, with its cluster of ports along the fringe of the delta; Tinnevelly, with the harbour at Tuticorin, which has opened large dealings with Ceylon and Burma; Tanjore, South Kanara, Ganjam and Vizagapatam. As compared with the other provinces, the trade of Madras is broadly marked by the larger proportion assigned to coasting trade with other Indian ports and with Ceylon. The chief staples of the export trade are hides and skins, coffee and raw cotton.
Railways and Irrigation.—The presidency is well supplied with railways, which naturally have their centre in Madras city, the chief seaport. The broad-gauge line of the Madras & Southern Mahratta railway connects with Bombay and Bangalore, and also crosses the peninsula to Calicut on the western coast. The South Indian (narrow-gauge) serves the extreme south, with its terminus at Tuticorin, and branches to Tinnevelly, Negapatam, Erade, Pondicherry and Nellore. The narrow-gauge line of the Madras & Southern Mahratta railway traverses the Deccan districts; and the East Coast line (broad-gauge), through the Northern Circars, has brought Madras into direct communication with Calcutta. The Madras system of irrigation has been most successful in the case of the three great eastern rivers, the Godavari, Kistna and Cauvery. Each of these is intercepted by an anicut or dam at the head of its delta, from which canals diverge on each side for navigation as well as irrigation. The scheme for diverting the waters of the Tungabhadra (a tributary of the Kistna) over the thirsty uplands of Kurnool proved a failure. The bold project of leading the Periyar river through a tunnel across the watershed of the Travancore hills on to the plain of Madura has been more successful.
Administration.—The Madras presidency is administered by a governor and a council, consisting of two members of the civil service, which number may be increased to four. There is also a board of revenue of three members. The number of districts is 24, each under the charge of a collector, with sub-collectors and assistants. The districts are not grouped into divisions or commissionerships, as in other provinces. For legislative purposes the council of the governor is augmented by additional members, numbering 45 in all, of whom not more than 17 may be nominated officials, while 19 are elected by various representative constituencies. Members of the legislative council enjoy the right of interpellation, of proposing resolutions on matters of public interest, and of discussing the annual financial statement. The principle of local devolution is carried somewhat further in Madras than in other provinces. At the bottom are union panchayats or village committees, whose chief duty is to attend to sanitation. Above them come taluk or subdivisional boards. At the head of all are district boards, a portion of whose members are elected by the taluk boards.
Education.—The chief educational institutions are the Madras University, the Presidency College, Madras Christian College, and Pachayyappa’s College at Madras; the government arts colleges at Combaconum and Rajahmundry; the law college, medical college and engineering college at Madras; the college of agriculture at Coimbatore; the teachers’ college at Saidapet; the school of arts at Madras; and the military orphanage at Ootacamund, in memory of Sir Henry Lawrence. In 1907, the total number of pupils at all institutions was 1,007,118, of whom 164,706 were females, and 132,857 were learning English.
History.—Until the British conquest the whole of southern India had never acknowledged a single ruler. The difficult nature of the hill passes and the warlike character of the highland tribes forbade the growth of great empires, such as succeeded one another on the plains of Hindustan. The Tamil country in the extreme south is traditionally divided between the three kingdoms of Pandya, Chola and Chera. The west coast supplied the nucleus of a monarchy which afterwards extended over the highlands of Mysore, and took its name from the Carnatic. On the north-east the kings of Kalinga at one time ruled over the entire line of seaboard from the Kistna to the Ganges. Hindu legend has preserved marvellous stories of these early dynasties, but our only authentic evidence consists in their inscriptions on stone and brass, and their noble architecture (see India). The Mahommedan invader first established himself in the south in the beginning of the 14th century. Ala-ud-din, the second monarch of the Khilji dynasty at Delhi, and his general Malik Kafur conquered the Deccan, and overthrew the kingdoms of Karnataka and Telingana, which were then the most powerful in southern India. But after the withdrawal of the Mussulman armies the native monarchy of Vijayanagar arose out of the ruins. This dynasty gradually extended its dominions from sea to sea, and reached a pitch of prosperity before unknown. At last, in 1565, it was overwhelmed by a combination of the four Mahommedan principalities of the Deccan. At the close of the reign of Aurangzeb, although that emperor nominally extended his sovereignty as far as Cape Comorin, in reality South India had again fallen under a number of rulers who owned no regular allegiance. The nizam of the Deccan, himself an independent sovereign, represented the distant court of Delhi. The most powerful of his feudatories was the nawab of the Carnatic, with his capital at Arcot. In Tanjore, a descendant of Sivaji ruled; and on the central table-land a Hindu chieftain was gradually establishing his authority and founding the state of Mysore, destined soon to pass to a Mahommedan usurper.
Vasco da Gama cast anchor off Calicut on the 20th of May 1498, and for a century the Portuguese retained in their control the commerce of India. The Dutch began to establish themselves on the ruin of the Portuguese at the beginning of the 17th century, and were quickly followed by the English, who established themselves at Calicut and Cranganore in 1616. Tellicherry became the principal English emporium on the west coast of Madras. The Portuguese eventually retired to Goa, and the Dutch to the Spice Islands. The first English settlement on the east coast was in 1611, at Masulipatam, even then celebrated for its fabrics. Farther south a fort, the nucleus of Madras city, was erected in 1640. Pondicherry was purchased by the French in 1762. For many years the English and French traders lived peacefully side by side, and with no ambition for territorial aggrandisement. The war of the Austrian succession in Europe lit the first flame of hostility on the Coromandel coast. In 1746 Madras was forced to surrender to La Bourdonnais, and Fort St David remained the only English possession in southern India. By the peace of Aix-la-Chapelle Madras was restored to the English; but from this time the rivalry of the two nations was keen, and found its opportunities in the disputed successions which always fill a large place in Oriental politics. English influence was generally able to secure the favour of the rulers of the Carnatic and Tanjore, while the French succeeded in placing their own nominee on the throne at Hyderabad. At last Dupleix rose to be the temporary arbiter of the fate of southern 291 India, but he was overthrown by Clive, whose defence of Arcot in 1751 forms the turning point in Indian history. In 1760 the crowning victory of Wandewash was won by Colonel (afterwards Sir Eyre) Coote, over Lally, and in the following year, despite help from Mysore, Pondicherry was captured.
Though the English had no longer any European rival, they had yet to deal with Mahommedan fanaticism and the warlike population of the highlands of Mysore. The dynasty founded by Hyder Ali, and terminating in his son Tippoo Sultan, proved itself in four several wars, which terminated only in 1799, the most formidable antagonist which the English had ever encountered (see Hyder Ali and India). Since the beginning of the 19th century Madras has known no regular war, but occasional disturbances have called for measures of repression. The pálegárs or local chieftains long clung to their independence after their country was ceded to the British. On the west coast, the feudal aristocracy of the Nairs, and the religious fanaticism of the Moplahs, have more than once led to rebellion and bloodshed. In the extreme north, the wild tribes occupying the hills of Ganjam and Vizagapatam have only lately learned the habit of subordination. In 1836 the zamíndarí of Gumsur in this remote tract was attached by government for the rebellious conduct of its chief. An inquiry then instituted revealed the wide prevalence among the tribe of Kondhs of human sacrifice, under the name of meriah. The practice has since been suppressed by a special agency. In 1879 the country round Rampa on the northern frontier was the scene of riots sufficiently serious to lead to the necessity of calling out troops. The same necessity arose three years later, when the Hindus and Mahommedans of Salem came into collision over a question of religious ceremonial. A more serious disturbance was that known as the “Anti-Shanar riots” of 1899. The Maravans of Tinnevelly and parts of Madura, resenting the pretensions of the Shanans, a toddy-drawing caste, to a higher social and religious status, organized attacks on Shanan villages. The town of Sivakasi was looted and burnt by five thousand Maravans. Quiet was restored by the military, and a punitive police force was stationed in the disturbed area.
The different territories comprising the Madras presidency were acquired by the British at various dates. In 1763 the tract encircling Madras city, then known as the Jagir now Chingleput district, was ceded by the nawab of Arcot. In 1765 the Northern Circars, out of which the French had recently been driven, were granted to the Company by the Mogul emperor, but at the price of an annual tribute of £90,000 to the nizam of Hyderabad. Full rights of dominion were not acquired till 1823, when the tribute was commuted for a lump payment. In 1792 Tippoo was compelled to cede the Baramahal (now part of Salem district), Malabar and Dindigul subdivision of Madura. In 1799, on the reconstruction of Mysore state after Tippoo’s death, Coimbatore and Kanara were appropriated as the British share; and in the same year the Mahratta raja of Tanjore resigned the administration of his territory, though his descendant retained titular rank till 1855. In 1800 Bellary and Cuddapah were made over by the nizam of Hyderabad to defray the expense of an increased subsidiary force. In the following year the dominions of the nawab of the Carnatic, extending along the east coast almost continuously from Nellore to Tinnevelly, were resigned into the hands of the British by a puppet who had been put upon the throne for the purpose. The last titular nawab of the Carnatic died in 1855; but his representative still bears the title of prince of Arcot, and is recognized as the first native nobleman in Madras. In 1839 the nawab of Kurnool was deposed for misgovernment and suspicion of treason, and his territories annexed.
See Madras Manual of Administration, 3 vols. (Madras, 1885 and 1893); S. Ayyangar, Forty Years’ Progress in Madras (Madras, 1893); J. P. Rees, Madras (Society of Arts, 1901); Madras Provincial Gazetteer (2 vols., Calcutta, 1908).

MADRAS, the capital of Madras presidency, and the chief seaport on the eastern coast of India, is situated in 13° 4′ N. and 80° 17′ E. The city, with its suburbs, extends nine miles along the sea and nearly four miles inland, intersected by the little river Cooum. Area, 27 sq. m.; pop. (1901), 509,346, showing an increase of 12.6% in the decade. Madras is the third city in India.
Although at first sight the city presents a disappointing appearance, and possesses not a single handsome street, it has several buildings of architectural pretensions, and many spots of historical interest. It is spread over a very wide area, and many parts of it are almost rural in character. Seen from the roadstead, the fort, a row of merchants’ offices, a few spires and public buildings are all that strike the eye. Roughly speaking, the city consists of the following divisions. (1) George Town (formerly Black Town, but renamed after the visit of the Prince of Wales in 1906), an ill-built, densely populated block, about a mile square, is the business part of the town, containing the banks, custom house, high court, and all the mercantile offices. The last, for the most part handsome structures, lie along the beach. On the sea-face of George Town are the pier and the new harbour. Immediately south of George Town there is (2) an open space which contains Fort St George, the Marina, or fashionable drive and promenade by the seashore, Government House, and several handsome public buildings on the sea-face. (3) West and south of this lung of the city are crowded quarters known by native names—Chintadrapet, Turuvaleswarampet, Pudupak, Royapet, Kistnampet and Mylapur, which bend to the sea again at the old town of Saint Thomé. (4) To the west of George Town are the quarters of Veperi and Pudupet, chiefly inhabited by Eurasians, and the suburbs of Egmore, Nangambakam, and Perambur, adorned with handsome European mansions and their spacious “compounds” or parks, which make Madras a city of magnificent distances. (5) South-west and south lie the European quarters of Tanampet and aristocratic Adyar. Among the most notable buildings are the cathedral, Scottish church, Government House, Pachayappa’s Hall, senate house, Chepauk palace (now the revenue board), and the Central railway station.
Madras possesses no special industries. There are several cotton mills, large cement works, iron foundries and cigar factories. Large sums of money have from time to time been spent upon the harbour works, but without any great success. The port remains practically an open roadstead, protected by two breakwaters, and the P. & O. steamers ceased to call in 1898. Passengers or cargo are landed or embarked in flat-bottomed masula boats. The sea bottom is unusually flat, reaching a depth of ten fathoms only at a mile from the shore. The harbour is not safe during a cyclone, and vessels have to put out to sea. Madras conducts about 56% of the foreign trade of the presidency, but a much smaller share of the coasting trade. As the capital of southern India, Madras is the centre on which all the great military roads converge. It is also the terminal station of two lines of railway, the Madras & Southern Mahratta line and the Madras & Tanjore section of the South Indian railway. The Buckingham canal, which passes through an outlying part of the city, connects South Arcot district with Nellore and the Kistna and Godavari system of canal navigation. The municipal government of the city was framed by an act of the Madras legislature passed in 1884. The governing body consists of 32 commissioners, of whom 24 are elected by the ratepayers, together with a paid president. The Madras University was constituted in 1857, as an examining body, on the model of the university of London. The chief educational institutions in Madras city are the Presidency College; six missionary colleges and one native college; the medical college, the law college, the college of engineering, the teachers’ college in the suburb of Saidapet, all maintained by government; and the government school of arts.
The foundation of Madras dates from 1640, when Francis Day, chief of the East India Company’s settlement at Armagon, obtained a grant of the present site of the city from a native ruler. A fort—called Fort St George, presumably from having been finished on St George’s Day (April 23)—was at once 292 constructed, and a gradually increasing population settled around its walls. In 1653 Madras, which had previously been subordinate to the settlement of Bantam in Java, was raised to the rank of an independent presidency. In 1702 Daud Khan, Aurangzeb’s general, blockaded the town for a few weeks, and in 1741 the Mahrattas unsuccessfully attacked the place. In 1746 La Bourdonnais bombarded and captured Madras. The settlement was restored to the English two years later by the Treaty of Aix-la-Chapelle, but the government of the presidency did not return to Madras till 1762. In 1758 the French under Lally occupied the Black Town and invested the fort. The siege was conducted on both sides with great skill and vigour. After two months the arrival of an English fleet relieved the garrison, and the besiegers retired with some precipitancy. With the exception of the threatening approach of Hyder Ali’s horsemen in 1769, and again in 1780, Madras has since the French siege been free from external attack. The town of Saint Thomé, now part of Madras city, was founded and fortified by the Portuguese in 1504, and was held by the French from 1672 to 1674.
See Mrs F. Penny, Fort St George (1900); W. Foster, Founding of Fort St George (1902).

MADRAZO Y KUNT, DON FEDERICO DE (1815-1894), Spanish painter, was born in Rome on the 12th of February 1815. He was the son of the painter Madrazo y Agudo (1781-1859), and received his first instruction from his father. While still attending the classes at the Academy of San Fernando he painted his first picture, “The Resurrection of Christ” (1829), which was purchased by Queen Christina. Not long afterwards he painted “Achilles in his Tent,” and subsequently presented to the Academy “The Continence of Scipio,” which secured him admission as a member “for merit.” While decorating the palace of Vista Alegre he took up portraiture. In 1852 he went to Paris, where he studied under Winterhalter, and painted portraits of Baron Taylor and of Ingres. In 1837 he was commissioned to produce a picture for the gallery at Versailles, and painted “Godfrey de Bouillon proclaimed King of Jerusalem.” The artist then went to Rome, where he worked at various subjects, sacred and profane. Then he painted “Maria Christina in the Dress of a Nun by the bedside of Ferdinand III.” (1843), “Queen Isabella,” “The Duchess of Medina-Coeli,” and “The Countess de Vilchès” (1845-1847), besides a number of portraits of the Spanish aristocracy, some of which were sent to the exhibition of 1855. He received the Legion of Honour in 1846. He was made a corresponding member of the Paris Academy of Fine Arts on the 10th of December 1853, and in 1873, on the death of Schnorr, the painter, he was chosen foreign member. After his father’s death he succeeded him as director of the Prado Gallery and president of the Academy of San Fernando. He originated in Spain the production of art reviews and journals, such as El Artista, El Renacimiento and El Semanario pintoresco. He died at Madrid on the 11th of June 1894. His brother, Don Louis De Madrazo, was also known as a painter, chiefly by his “Burial of Saint Cecilia” (1855). Don Federico’s best-known pupil was his son, Don Raimundo De Madrazo (b. 1841).

MADRID, a province of central Spain, formed in 1833 of districts previously included in New Castile, and bounded on the W. and N. by Ávila and Segovia, E. by Guadalajara, S.E. by Cuenca and S. by Toledo. Pop. (1900), 775,034, of whom 539,835 inhabit the city of Madrid; area, 3084 sq. m. Madrid belongs to the basin of the Tagus, being separated from that of the Douro by the Sierra de Guadarrama on the N.W. and N., and by the Sierra de Gredos on the S.W. The Tagus is the southern boundary for some distance, its chief tributary being the Jarama, which rises in the Somosierra in the north and terminates at Aranjuez. The Jarama, in turn, is joined by the Henares and Tajuña on the left, and by the Lozoya and Manzanares on the right. The Guadarrama, another tributary of the Tagus, has its upper course within the province. Like the rest of Castile, Madrid is chiefly of Tertiary formation; the soil is mostly clayey, but there are tracts of sandy soil. Agriculture is somewhat backward; the rainfall is deficient, and the rivers are not utilized as they might be for irrigation. The south-eastern districts are the best watered, and produce in abundance fruit, vegetables, wheat, olives, esparto grass and excellent wine. Gardening and viticulture are carried on to some extent near the capital, though the markets of Madrid receive their most liberal supply of fruits and vegetables from Valencia. Sheep, goats and horned cattle are reared, and fish are found in the Jarama and other rivers. Much timber is extracted from the forests of the northern and north-eastern parts of the province for building purposes and for firewood and charcoal. The royal domains of the Escorial, Aranjuez and El Pardo, and the preserves of the nobility, are all well wooded and contain much game. Efforts have also been made by the local authorities to cover the large stretches of waste ground and commons with pines and other trees.
The Sierra de Guadarrama has quarries of granite, lime and gypsum, and is known to contain iron, copper and argentiferous lead; but these resources are undeveloped. Other industries are chiefly confined to the capital; but cloth, leather, paper, earthenware, porcelain, glass, bricks and tiles, ironware, soap, candles, chocolate and lace are also manufactured on a small scale beyond its boundaries. There is very little commerce except for the supply of the capital with necessaries.
Besides the local lines, all the great railways in the kingdom converge in this province, and it contains in all 221 m. of line. Besides Madrid, the towns of Aranjuez (12,670) and Alcalá de Henares (11,206) and the Escorial are described in separate articles. The other towns with more than 5000 inhabitants are Vallecas (10,128), Colmenar de Oreja (6182), Colmenar Viejo (5255) and Carabanchel Bajo (5862).

MADRID, the capital of Spain and of the province of Madrid, on the left bank of the river Manzanares, a right-hand tributary of the Jarama, which flows south into the Tagus. Pop. (1877), 397,816; (1887), 472,228; (1897), 512,150; (1900), 539,835. Madrid was the largest city in Spain in 1900; it is the see of an archbishop, the focus of the principal Spanish railways, the headquarters of an army corps, the seat of a university, the meeting-place of parliament, and the chief residence of the king, the court, and the captain-general of New Castile. It is, however, surpassed in ecclesiastical importance by Toledo and in commerce by Barcelona.
Situation and Climate.—Madrid is built on an elevated and undulating plateau of sand and clay, which is bounded on the north by the Sierra Guadarrama and merges on all other sides into the barren and treeless table-land of New Castile. Numerous water-courses (arroyos), dry except at rare intervals, furrow the surface of the plateau; these as they pass through the city have in certain cases been converted into roads—e.g. the Paseo de Recoletos and Prado, which are still so liable to be flooded after prolonged rain that special channels have been constructed to carry away the water. The highest point in Madrid is 2372 ft. above sea-level. The city is close to the geographical centre of the peninsula, nearly equidistant from the Bay of Biscay, the Mediterranean and the Atlantic. Owing to its high altitude and open situation it is liable to sudden and frequent variations of climate, and the daily range of temperature sometimes exceeds 50° F. In summer the heat is rendered doubly oppressive by the fiery, dust-laden winds which sweep across the Castilian table-land; at this season a temperature of 109° has been registered in the shade. In winter the northerly gales from the Sierra Guadarrama bring intense cold; snow falls frequently, and skating is carried on in the Buen Retiro park. A Spanish proverb describes the wind of Madrid as so deadly and subtle that “it will kill a man when it will not blow out a candle”; but, though pulmonary diseases are not uncommon, the climate appears to be exceptionally healthy. In 1901 the death-rate was 22.07 per 1000, or lower than that of any other town on the Spanish mainland. The Sierra Guadarrama renders the atmosphere unusually dry and clear by intercepting the moisture of the north-western winds which prevail in summer; hence the average dally number of deaths decreases from 80 in winter to about 25 in summer. The sanitation of the older quarters is defective, and overcrowding is common, partly owing to the royal decrees which formerly prohibited the extension of the city; but much has been done in modern times to remove or mitigate these evils.
The Inner City.—The form of Madrid proper (exclusive of the modern suburbs) is almost that of a square with the corners 293 rounded off; from east to west it measures rather less than from north to south. It was formerly surrounded by a poor wall, partly of brick, partly of earth, some 20 ft. in height, and pierced by five principal gates (puertas) and eleven doorways (portillos). Of these only three, the Puerta de Alcalá on the east, the Puerta de Toledo on the south and the Portillo de San Vicente on the west, actually exist; the first and the third were erected in the time of Charles III. (1759-1788), and the second in honour of the restoration of Ferdinand VII. (1827). The Manzanares—or rather its bed, for the stream is at most seasons of the year quite insignificant—is spanned by six bridges, the Puente de Toledo and Puente de Segovia being the chief.
The Puerta del Sol is the centre of Madrid, the largest of its many plazas, and the place of most traffic. It derived its name from the former east gate of the city, which stood here until 1570, and had on its front a representation of the sun. On its south side stands the Palacio de la Gobernacion, or ministry of the interior, a heavy square building by a French architect, J. Marquet, dating from 1768. From the Puerta del Sol diverge, immediately or mediately, ten of the principal streets of Madrid—eastward by north, the Calle de Alcalá, terminating beyond the Buen Retiro park; eastward, the Carrera de San Jeronimo, terminating by the Plaza de las Cortes in the Prado; southward, the Calle de Carretas; westward, the Calle Mayor, which leads to the council chamber and to the palace, and the Calle del Arenal, terminating in the Plaza de Isabel II. and the royal opera house; north-westward, the Calles de Preciados and Del Carmen; and northward, the Calle de la Montera, which afterwards divides into the Calle de Fuencarral to the left and the Calle de Hortaleza to the right. The contract for another wide street through central Madrid, to be called the Gran Via, was given to an English firm in 1905.
The Calle de Alcalá is bordered on both sides with acacias, and contains the Real Academia de Bellas Artes, founded in 1752 as an academy of art and music; its collection of paintings by Spanish masters includes some of the best-known works of Murillo. The handsome Bank of Spain (1884-1891) stands where the Calle de Alcalá meets the Prado; in the oval Plaza de Madrid, at the same point, is a fine 18th-century fountain with a marble group representing the goddess Cybele drawn in a chariot by two lions. The Calle de Alcalá is continued eastward past the Buen Retiro gardens and park, and through the Plaza de Independencia, in the middle of which is the Puerta de Alcalá. The Plaza de las Cortes is so called from the Congreso de los Diputados, or House of Commons, on its north side. The square contains a bronze statue of Cervantes, by Antonio Sola, erected in 1835. The Calle de Carretas, on the west side of which is the General Post Office, ranks with the Carrera de San Jeronimo and Calle de la Montera for the excellence of its shops. From the Calle Mayor is entered the Plaza Mayor, a rectangle of about 430 ft. by 330 ft., formerly the scene of tournaments, bull fights, autos de fé, acts of canonization (including that of Ignatius Loyola in 1622) and similar exhibitions, which used to be viewed by the royal family from the balcony of one of the houses called the Panaderia (belonging to the guild of bakers). The square, which was built under Philip III. in 1619, is surrounded by an arcade; the houses are uniform in height and decoration. In the centre stands a bronze equestrian statue of Philip III., designed by Giovanni da Bologna, after a painting by Pantoja de la Cruz, and finished by Pietro Tacca. From the south-east angle of the Plaza Mayor the Calle de Atocha, one of the principal thoroughfares of Madrid, leads to the outskirts of the inner city; it contains two large hospitals and part of the university buildings (faculty of medicine). The house occupied by Cervantes from 1606 until his death in 1616 stands at the point where it meets the Calle de Léon; in this street is the Real Academia de la Historia, with a valuable library and collections of MSS. and plate. From the south-west angle of the Plaza Mayor begins the Calle de Toledo, the chief mart for the various woollen and silken fabrics from which the picturesque costumes peculiar to the peninsula are made. In the Plaza de Isabel II., at the western extremity of the Calle del Arenal, stands the royal opera-house, the principal front of which faces the Plaza del Oriente and the royal palace. In the centre of the plaza is a fine bronze equestrian statue of Philip IV. (1621-1665); it was designed by Velazquez and cast by Tacca, while Galileo is said to have suggested the means by which the balance is preserved. The gift of the grand duke of Tuscany in 1640, it stood in the Buen Retiro gardens until 1844.
Modern Development of the City.—The north and east of the city—the new suburbs—have developed past the Retiro Park as far as the Bull-ring, and have covered all the vast space included between the Retiro, the Bull-ring, the long Castellana Drive to the race-course and the exhibition building. On the slopes of the other side of the Castellana, and along what were the northern limits of Madrid in 1875, the modern suburbs have extended to the vicinity of the fine cellular prison that was built at the close of the reign of King Alphonso XII. to replace the gloomy building known as El Saladero.
The new parts of the capital, with their broad streets and squares, and their villas sometimes surrounded with gardens, their boulevards lined by rather stunted trees, and their modern public buildings, all resemble the similar features of other European capitals, and contrast with the old Madrid that has preserved so many of its traits in architecture, popular life and habits. Some of the streets have been slightly widened, and in many thoroughfares new houses are being built among the ugly, irregular dwelling-places of the 18th and earlier centuries. This contrast is to be seen especially in and about the Calle Mayor, the Plaza Mayor, the Calle de Toledo, the Rastro, and the heart of the city.
Few capitals have more extensively developed their electric and horse tramways, gas and electric light installations and telephones. Much was done to improve the sanitary conditions of the city in the last twenty years of the 19th century. The streets are deluged three times a day with fire-hose, but even that has little effect upon the dust. Unfortunately the water supply, which used to be famed for its abundance and purity, became wholly insufficient owing to the growth of the city. The old reservoir of the Lozoya canal, a cutting 32 m. long, and the additional reservoir opened in 1883, are quite inadequate for the requirements of modern Madrid, and were formerly kept in such an unsatisfactory state that for several months in 1898 and 1899 the water not only was on the point of giving out, but at times was of such inferior quality that the people had recourse to the many wells and fountains available. The construction of new waterworks was delayed by a terrible accident, which occurred on the 8th of April 1905; the whole structure collapsed, and nearly 400 persons lost their lives in the flooded ruins. A decided improvement has been made in the burial customs of Madrid. No bodies are allowed to be interred in the churches and convents. Some of the older burial grounds in the northern suburbs have been closed altogether, and in those which remain open few coffins are placed in the niche vaults in the depth of the thick walls, as was once the practice. A large modern necropolis has been established a few miles to the north-east.
Principal Buildings.—As compared with other capitals Madrid has very few buildings of much architectural interest. The Basilica de Nuestra Señora de Atocha, on the Paseo de Atocha, a continuation of the Calle de Atocha, was originally founded in 1523. After being almost destroyed by the French, it was restored by Ferdinand VII., and rebuilt after 1896. The modern church is Romanesque in style; it contains a much venerated statue of the Virgin, attributed to St Luke. The collegiate church of San Isidro el Real, in the Calle de Toledo, dates from 1651; it has no architectural merit, but contains one or two valuable pictures and other works of art. It was originally owned by the Jesuits, but after their expulsion in 1769 it was reconsecrated, and dedicated to St Isidore the Labourer (d. 1170), the patron saint of Madrid, whose remains were entombed here. When the diocese of Madrid was separated from that of Toledo San Isidro was chosen as the cathedral. The modern Gothic church of San Jeronimo el Real occupies a conspicuous site eastward of the town. The church of San Francisco el Grande, which contains many interesting monuments, is also known as the National Pantheon. An act was passed in 1837 declaring that the remains of all the most distinguished Spaniards should be buried here; but no attempt to enforce the act systematically was made until 1869, and even then the attempt failed. Towards the close of the 19th century the church was splendidly restored at the expense of the state. Its interior was decorated with paintings and statuary by most of the leading Spanish artists of the time. Of secular buildings unquestionably the most important is the royal palace (Palacio Real), on the west side of the town, on rising ground overhanging the Manzanares. It occupies the site of the ancient Moorish alcázar (citadel), where a hunting seat was built by Henry IV.; this was enlarged and improved by Charles V. when he first made Madrid his residence in 1532; was further developed by Phillip II., but ultimately was destroyed by fire in 1734. The 294 present edifice was begun under Philip V. in 1737 by Sacchetti of Turin, and was finished in 1764. It is in the Tuscan style, and is 470 ft. square and 100 ft. in height, the material being white Colmenar granite, resembling marble. To the north of the palace are the royal stables and coach-houses, remarkable for their extent; to the south is the armoury (Museo de la Real Armería), containing what is possibly the best collection of the kind in existence. After the Palacio Real may be mentioned the royal picture gallery (Real Museo de Pinturas), adjoining the Salon del Prado; it was built about 1785 for Charles III. by Juan de Villanueva as a museum of natural history and academy of sciences. It contains the collections of Charles V., Philip II. and Philip IV., and the pictures number upwards of two thousand. The specimens of Titian, Raphael, Tintoretto, Velazquez, Vandyck, Rubens and Teniers give it a claim to be considered the finest picture gallery in the world. The Biblioteca Nacional, in the Paseo de Recoletos, was founded in 1866, and completed in 1892. Not only the national library, with its important collections of MSS. and documents, but the archaeological museum, the museums of modern painting and sculpture, and the fine arts academy of San Fernando, are within its walls. The two houses of the Cortes meet in separate buildings. The deputies have a handsome building with a very valuable library in the Carrera San Jeronimo; the senators have an old Augustinian convent which contains some fine pictures. A large and handsome building near the Retiro Park contains the offices of the ministers of public works, agriculture and commerce, and of fine arts and education; nearly opposite stands the new station of the Southern Railway Company. The Great Northern and the Spain to Portugal Railway Companies have also replaced their old stations by very spacious, handsome structures, much resembling those of Paris. In 1896 the Royal Exchange was installed in a large monumental building with a fine colonnade facing the Dos de Mayo monument, not far from the museum of paintings.
Of the promenades and open places of public resort the most fashionable and most frequented is the Prado (Paseo del Prado, Salon del Prado) on the east side of the town, with its northward continuation—the Paseo de Recoletos. To the south of the town is the Paseo de las Delicias, and on the west, below the royal palace, and skirting the Manzanares, is the Paseo de la Virgen del Puerto, used chiefly by the poorer classes. Eastward from the Prado are the Buen Retiro Gardens, with ponds and pavilions, and a menagerie. The gardens were formerly the grounds surrounding a royal hunting seat, on the site of which a palace was built for Philip IV. in 1633; it was destroyed during the French occupation.
Education, Religion and Charity.—Madrid University developed gradually out of the college of Doña Maria de Aragon, established in 1590 by Alphonso Orozco. Schools of mathematics and natural science were added in the 16th and 17th centuries, and in 1786 the medical and surgical college of San Carlos was opened. In 1836-1837 the university of Alcalá de Henares (q.v.) was transferred to the capital and the older foundations incorporated with it. The university of Madrid thenceforth became the headquarters of education in central Spain. It has an observatory, and a library containing more than 2,000,000 printed books and about 5500 MSS. It gives instruction, chiefly in law and medicine, but also in literature, philosophy, mathematics and physics, to about 5000 students. Associated with the university is the preparatory school of San Isidro, founded by Philip IV. (1621-1665), and reorganized by Charles III. in 1770.
There are upwards of 100 official primary schools and a large number of private ones, among which the schools conducted by the Jesuits and the Scolapian fathers claim special mention. Madrid also has schools of agriculture, architecture, civil and mining engineering, the fine arts, veterinary science and music. The school of military engineering is at Guadalajara. Besides these special schools there are a self-supporting institute for preparing girls for the higher degrees and for certificates as primary teachers, and an institute for secondary education, conducted chiefly by ecclesiastics. Among the educational institutions may be reckoned the botanical garden, dating from 1781, the libraries of the palace, the university, and San Isidro, and the museum of natural science, exceedingly rich in the mineralogical department. The principal learned society is the royal Spanish Academy, founded in 1713 for the cultivation and improvement of the Spanish tongue. The Academy of History possesses a good library, rich in MSS. and incunabula, as well as a fine collection of coins and medals. In addition to the academies of fine arts, the exact sciences, moral and political science, medicine and surgery, and jurisprudence and legislation, all of which possess libraries, there are also anthropological, economic and geographical societies, and a scientific and literary athenaeum. Madrid has a British cemetery opened in 1853, when the older Protestant cemetery in the Paseo de Recoletos was closed. The town also contains a British embassy chapel, a German chapel, and several Spanish Protestant chapels, attended by over 1200 native Protestants, while the Protestant schools, chiefly supported by British, German and American contributions, are attended by more than 2500 children. The first Protestant bishop of Madrid was consecrated in 1895 by Archbishop Plunkett of Dublin. The charitable institutions were greatly improved between 1885 and 1905. The Princess Hospital was completely restored on modern methods, and can accommodate several hundred patients. The old contagious diseases hospital of San Juan de Dios was pulled down and a fine new hospital built in the suburbs beyond the Retiro Park, to hold 700 patients. The military hospital was demolished and a very good one built in the suburbs. There are in all twenty hospitals in Madrid, and a lunatic asylum on the outskirts of the capital, founded by one of the most eminent of Spanish surgeons, and admirably conducted. New buildings have been provided for the orphanages, and for the asylums for the blind, deaf and dumb, incurables and aged paupers. There are hospitals supported by the French, Italian and Belgian colonies; these are old and well-endowed foundations. Public charity generally is very active. In Madrid, as in the rest of Spain, there has been an unprecedented increase in convents, monasteries and religious institutions, societies and Roman Catholic workmen’s clubs and classes.
Apart from private institutions for such purposes, the state maintains in the capital a savings bank for the poorer classes, and acts as pawnbroker for their benefit. The mercantile and industrial classes are organized in gilds, which themselves collect the lump sum of taxation exacted by the exchequer and the municipality from each gremio or class of taxpayers. The working classes also have commercial and industrial circulos or clubs that are obeyed by the gilds with great esprit de corps, a chamber of commerce and industries, and “associations of productions” for the defence of economic interests.
Industries.—The industries of the capital have developed extraordinarily since 1890. In the town, and within the municipal boundaries in the suburbs, many manufactories have been established, giving employment to more than 30,000 hands, besides the 4000 women and girls of the Tobacco Monopoly Company’s factory. Among the most important factories are those which make every article in leather, especially cigar and card cases, purses and pocket-books. Next come the manufactures of fans, umbrellas, sunshades, chemicals, varnishes, buttons, wax candles, beds, cardboard, porcelain, coarse pottery, matches, baskets, sweets and preserves, gloves, guitars, biscuits, furniture, carpets, corks, cards, carriages, jewelry, drinks of all kinds, plate and plated goods. There are also tanneries, saw and flour mills, glass and porcelain works, soap works, brickfields, paper mills, zinc, bronze, copper and iron foundries. The working classes are strongly imbued with socialistic ideas. Strikes and May Day demonstrations have often been troublesome. Order is kept by a garrison of 12,500 men in the barracks of the town and cantonments around, and by a strong force of civil guards or gendarmes quartered in the town itself. The civil and municipal authorities can employ beside the gendarmes the police, about 1400 strong, and what is called the guardias urbanos, another police force whose special duty it is to regulate the street traffic and prevent breaches of the municipal regulations. There is not, on the average, more crime in Madrid than in the provinces.
History.—Spanish archaeologists have frequently claimed for Madrid a very high antiquity, but the earliest authentic historical mention of the town (Majrít, Majoritum) occurs in the Arab chronicle, and does not take us farther back than to the first half of the 10th century. The place was finally taken from the Moors by Alphonso VI. (1083), and was made a hunting-seat by Henry IV., but first rose into importance when Charles V., benefiting by its keen air, made it his occasional residence. Philip II. created it his capital and “only court” (única corte) in 1560. It is, however, only classed as a town (villa), having 295 never received the title of city (ciudad). Fruitless attempts were made by Philip III. and Charles III. respectively to transfer the seat of government to Valladolid and to Seville. (See also Spain: History).
See J. Amador de los Rios, Historia de la villa y corte de Madrid (Madrid, 1861-1864); Valverdey Alvarez, La Capitol de España (Madrid, 1883); E. Sepúlveda, La Vida en Madrid en 1886 (Madrid, 1887); H. Peñasco, Las Calles de Madrid (Madrid, 1889); C. Perez Pastor, Bibliografia madrileña, siglo XVI. (Madrid, 1891); F. X. de Palacio y Garcia, count of las Almenas, La Municipalidad de Madrid (Madrid, 1896); E. Sepúlveda, El Madrid de los recuerdos: colección de artículos (Madrid, 1897); P. Hauser, Madrid bajo el punto de vista medico-social (Madrid, 1902); L. Williams, Toledo and Madrid, their Records and Romances (London, 1903).

MADRIGAL (Ital. madrigale), the name of a form of verse, the exact nature of which has never been decided in English, and of a form of vocal music.
(1) In Verse.—The definition given in the New English Dictionary, “a short lyrical poem of amatory character,” offers no distinctive formula; some madrigals are long, and many have nothing whatever to do with love. The most important English collection of madrigals, not set to music, was published by William Drummond of Hawthornden (1585-1649) in his Poems of 1616. Perhaps the best way of ascertaining what was looked upon in the 17th century as a madrigal is to quote one of Drummond’s:—
| The beauty and the life Of life’s and beauty’s fairest paragon, O tears! O grief! hung at a feeble thread. To which pale Atropos had set her knife; The soul with many a groan Had left each outward part, And now did take his last leave of the heart; Nought else did want, save death, even to be dead; When the afflicted band about her bed. Seeing so fair him come in lips, cheeks, eyes, Cried ah! and can death enter Paradise? |
This may be taken as a type of Drummond’s madrigals, of which he has left us about eighty. They are serious, brief, irregular lyrics, in which neither the amatory nor the complimentary tone is by any means obligatory. Some of these pieces contain as few as six lines, one as many as fourteen, but they average from nine to eleven. In the majority of examples the little poem opens with a line of six syllables, and no line extends beyond ten syllables. The madrigal appears to be a short canzone of the Tuscan type, but less rigidly constructed. In French the madrigal has not this Italian character. It is simply a short piece of verse, ingenious in its turn and of a gallant tendency. The idea of compliment is essential. J. F. Guichard (1730-1811) writes:—
| Orgon, poète marital, À Venus compare sa femme; C’est pour la belle un madrigal, C’est pour Venus une épigramme. |
This quatrain emphasizes the fact that in French a madrigal is a trifling piece of erotic compliment, neatly turned but not seriously meant. The credit of inventing the old French verse-form of madrigal belongs to Clément Marot, and one of his may be quoted in contrast to that of Drummond:—
| Un doux nenni avec un doux sourire Est tant honneste, il le vous faut apprendre; Quant est de oui, si veniez à le dire, D’avoir trop dit je voudrois vous reprendre; Non que je sois ennuyé d’entreprendre D’avoir le fruit dont le désir me point; Mais je voudrois qu’en ne le laissant prendre, Vous me disiez: vous ne l’aurez point. |
In English, when the word first occurred—it has not been traced farther back than 1588 (in the preface to Nicholas Yonge’s Musica transalpina)—it was identified with the chief form of secular vocal music in the 16th century. In 1741 John Immyns (d. 1764) founded the Madrigal Society, which met in an ale-house in Bride Lane, Fleet Street; this association still exists, and is the oldest musical society in Europe.
The word “madrigal” is frequently also used to designate a sentimental or trifling expression in a half-contemptuous sense.
(2) In Music.—As a definite musical art-form, the madrigal was known in the Netherlands by the middle of the 15th century; like the motet, it obviously originated in the treatment of counterpoint on a canto fermo, some early examples even combining an ecclesiastical canto fermo in the tenor with secular counterpoint in the other parts. Thus Josquin’s Déploration de Jehan Okenheim (see Music) might equally well be called a madrigal or motet, if the word “madrigal” were used for compositions to French texts at all. But by the middle of the 16th century the Italian supremacy in music had developed the madrigal into the greatest of secular musical forms, and made it independent of the form of the words; and thus when Lasso sets Marot’s madrigals to appropriately witty and tuneful music he calls the result a “chanson”; while when Palestrina composes Petrarca’s Sonnets to the Virgin in memory of Laura, the result appears as a volume of Madrigali spirituali. Elegiac madrigals, whether spiritual or secular, were thus as common as any other kind; so that when the Musica transalpina brought the word “madrigal” to England it brought a precedent for the poet Drummond’s melancholy type of madrigal poetry.
Italian madrigals, however, are by no means always elegiac; but the term always means a highly organized and flowing polyphonic piece, often as developed as the motet, though, in the mature classical period, distinct in style. Yet masses were often founded on the themes of madrigals, just as they were on the themes of motets (see Mass; Motet); and it is interesting, in such beautiful cases as Palestrina’s Missa gia fu chi m’ebbe cara, to detect the slight strain the mildly scandalous origin of the themes puts upon the ecclesiastical style.
The breaking strain was put on the madrigal style at the end of the 16th century, in one way by the new discords of Monteverde and (with more musical invention) Schütz; and in another way by the brilliant musical character-drawing of Vecchi, whose Amfiparnasso is a veritable comic opera in the form of a set of fourteen madrigals, all riotously witty in the purest and most masterly polyphonic style. It was probably meant, or at least made use of, to laugh down the earliest pioneers of opera (q.v.); but it is the beginning of the end for the madrigal as a living art. Long afterwards we occasionally meet with the word again, when a 17th or 18th century composer sets to some kind of accompanied singing a poem of madrigalesque character. But this does not indicate any continuation of the true musical history of the madrigal. The strict meaning of the word in its musical sense is, then, a musical setting of an Italian or English non-ecclesiastical poem (typically a canzone) for unaccompanied chorus, in a 16th-century style less ecclesiastical than the motet, but as like it in organization as the form and sentiment of the words admit. The greatest classics in the madrigal style are those of Italy; and but little, if at all, below them come the English. The form, though not the name, of course, exists in the 16th-century music of other languages whenever the poetry is not too light for it.
It is important but easy to distinguish the madrigal from the lighter 16th-century forms, such as the Italian villanella and the English ballet, these being very homophonic and distinguished by the strong lilt of their rhythm.
The madrigal has been very successfully revived in modern English music with a more or less strict adherence to the 16th century principles; the compositions of De Pearsall being of high artistic merit, while the Madrigale spirituale in Stanford’s oratorio Eden is a movement of rare beauty.

MADURA (Dutch Madoera), an island of the Dutch East Indies, separated by the shallow Strait of Madura from the N.E. coast of Java. Pop. (1897), 1,652,580, of whom 1,646,071 were natives, 4252 Chinese and 558 Europeans. It extends from about 112° 32′ to 114° 7′ E., and is divided into two nearly equal portions by the parallel of 7° S.; the area is estimated at 1725 sq. m. It is a plateau-like prolongation of the limestone range of northern Java, with hills (1300 to 1600 ft. high) and dales. The formation of the coast and plains is Tertiary and recent alluvium. Hot springs are not infrequent; and in the valley between Gunong Geger and Banjar lies the mud volcano of 296 Banju Ening. The coasts are clothed with tropical vegetation; but the soil is better fitted for pastoral than agricultural purposes. Fishing and cattle-rearing are the chief means of subsistence. Besides rice and maize, Madura yields coco-nut oil and jati. The manufacture of salt for the government, abolished in other places, continues in Madura. Hence perhaps the name is derived (Sansk. mandura, salt). Petroleum is found in small quantities.
The principal town is Sumenep; and there are populous Malay, Arab and Chinese villages between the town and the European settlement of Maringan. On a hill in the neighbourhood lies Asta, the burial-place of the Sumenep princes. Pamekasan is the seat of government. Bangkalang is a large town with the old palace of the sultan of Madura and the residences of the princes of the blood; the mosque is adorned with the first three suras of the Koran, thus differing from nearly all the mosques in Java and Madura, though resembling those of western Islam. In the vicinity once stood the Erfprins fort. Arisbaya (less correctly Arosbaya) is the place where the first mosque was built in Madura, and where the Dutch sailors first made acquaintance with the natives. The once excellent harbour is now silted up. Sampang is the seat of an important market. The Kangean and Sapudi islands, belonging to Madura, yield timber, trepang, turtle, pisang and other products.
Madura formerly consisted of three native states—Madura or Bangkalang, Pamekasan and Sumenep. The whole island was considered part of the Java residency of Surabaya. The separate residency of Madura was constituted in 1857; it now consists of four “departments”—Pamekasan, Madura, Sumenep and Sampang.
See P. J. Veth, Java, vol. iii.; Kielstra, “Het Eiland Madoera,” in De Gids (1890); H. van Lennep, “De Madoereezen,” in De Indische Gids (1895), with detailed bibliography.

MADURA, a city and district of British India, in the Madras Presidency. The city is situated on the right bank of the river Vaigai, and has a station on the South Indian railway 345 m. S.E. of Madras. Pop. (1901), 105,984. The city was the capital of the old Pandyan dynasty, which ruled over this part of India from the 5th century B.C. to the end of the 11th century A.D. Its great temple forms a parallelogram about 847 ft. by 729 ft., and is surrounded by nine gopuras, of which the largest is 152 ft. high. These ornamental pyramids begin with doorposts of single stones 60 ft. in height, and rise course upon course, carved with rows of gods and goddesses, peacocks, bulls, elephants, horses, lions, and a bewildering entanglement of symbolical ornament all coloured and gilded, diminishing with distance until the stone trisul at the top looks like the finest jeweller’s work. The temple, which contains some of the finest carving in southern India, is said to have been built in the reign of Viswanath, first ruler of the Nayak dynasty. Its chief feature is the sculptured “Hall of a Thousand Pillars.” The palace of Tirumala Nayak is the most perfect relic of secular architecture in Madras. This palace, which covers a large area of ground, has been restored, and is utilized for public offices. The Vasanta, a hall 333 ft. long, probably dedicated to the god Sundareswara, and the Tamakam, a pleasure-palace, now the residence of the collector, are the other principal buildings of this period.
The last of the old Pandyan kings is said to have exterminated the Jains and conquered the neighbouring kingdom of Chola; but he was in his turn overthrown by an invader from the north, conjectured to have been a Mahommedan. In 1324 a Moslem army under Malik Kafur occupied Madura, and the Hindus were held in subjection for a period of fifty years. Subsequently Madura became a province of the Hindu Empire of Vijayanagar. In the middle of the 16th century the governor Viswanath established the Nayak dynasty, which lasted for a century. The greatest of the line was Tirumala Nayak (reigned 1623-1659), whose military exploits are recorded in the contemporary letters of the Jesuit missionaries. He adorned Madura with many public buildings, and extended his empire over the adjoining districts of Tinnevelly, Travancore, Coimbatore, Salem and Trichinopoly. His repudiation of the nominal allegiance paid to the raja of Vijayanagar brought him into collision with the sultan of Bijapur, and after a lapse of three centuries Mahommedans again invaded Madura and compelled him to pay them tribute. After the death of Tirumala the kingdom of Madura gradually fell to pieces, being invaded by both Mahommedans and Mahrattas. About 1736 the district fell into the hands of the nawab of the Carnatic, and the line of the Nayaks was extinguished. About 1764 British officers took charge of Madura in trust for Mahommed Ali (Wallah Jah), the last independent nawab of the Carnatic, whose son finally ceded his rights of sovereignty to the East India Company in 1801.
The District of Madura has an area of 8701 sq. m. Pop. (1901), 2,831,280, an increase of 8.5% in the decade. It consists of a section of the plain stretching from the mountains east to the sea, coinciding with the basin of the Vaigai river, and gradually sloping to the S.E. The plain is broken by the outlying spurs of the Ghats, and by a few isolated hills and masses of rock scattered over the country. The most important spur of the Ghats is known as the Palni hills, which project E.N.E. across the district for a distance of about 54 m. Their highest peaks are more than 8000 ft. above sea-level, and they enclose a plateau of about 100 sq. m., with an average height of 7000 ft. On this plateau is situated the sanatorium of Kodaikanal, and coffee-planting is successfully carried on. The other principal crops of the district are millets, rice, other food-grains, oil-seeds and cotton. Tobacco is grown chiefly in the neighbourhood of Dindigul, whence it is exported to Trichinopoly, to be made into cigars. There are several cigar factories and a number of saltpetre refineries. The only other large industry is that of coffee-cleaning. Madura is traversed by the main line of the South Indian railway. It has four small seaports, whose trade is chiefly carried on with Ceylon. The most important irrigation work, known as the Periyar project, consists of a tunnel through the Travancore hills, to convey the rainfall across the watershed.
See Madura District Gazetteer (Madras, 1906).

MADVIG, JOHAN NICOLAI (1804-1886), Danish philologist, was born on the island of Bornholm, on the 7th of August 1804. He was educated at the classical school of Frederiksborg and the university of Copenhagen. In 1828 he became reader, and in 1829 professor, of Latin language and literature at Copenhagen, and in 1832 was appointed university librarian. In 1848 Madvig entered parliament as a member of what was called the “Eider-Danish” party, because they desired the Eider to be the boundary of the country. When this party came into power Madvig became minister of education. In 1852 be became director of public instruction. Some years later, from 1856 to 1863, Madvig was president of the Danish parliament and leader of the National Liberal party. With these brief interruptions the greater part of his life was devoted to the study and teaching of Latin and the improvement of the classical schools, of which he was chief inspector. As a critic he was distinguished for learning and acumen. He devoted much attention to Cicero, and revolutionized the study of his philosophical writings by an edition of De Finibus (1839; 3rd ed., 1876). Perhaps his most widely known works are those on Latin grammar and Greek syntax, especially his Latin grammar for schools (Eng. trans. by G. Woods). In 1874 his sight began to fail, and he was forced to give up much of his work. He still, however, continued to lecture, and in 1879 he was chosen rector for the sixth time. In 1880 he resigned his professorship, but went on with his work on the Roman constitution, which was completed and published before his death. In this book Madvig takes a strongly conservative standpoint and attacks Mommsen’s views on Caesar’s programme of reforms. It is a clear exposition, though rather too dogmatic and without sufficient regard for the views of other scholars. His last work was his autobiography, Livserindringer (published 1887). Madvig died at Copenhagen on the 12th of December 1886.
See J. E. Sandys, History of Classical Scholarship (1908), iii., 319-324.

MAECENAS, GAIUS (Cilnius), Roman patron of letters, was probably born between 74 and 64 B.C., perhaps at Arretium. Expressions in Propertius (ii. 1, 25-30) seem to imply that he 297 had taken some part in the campaigns of Mutina, Philippi and Perusia. He prided himself on his ancient Etruscan lineage, and claimed descent from the princely house of the Cilnii, who excited the jealousy of their townsmen by their preponderating wealth and influence at Arretium in the 4th century B.C. (Livy x. 3). The Gaius Maecenas mentioned in Cicero (Pro Cluentio, 56) as an influential member of the equestrian order in 91 B.C. may have been his grandfather, or even his father. The testimony of Horace (Odes iii. 8, 5) and Maecenas’s own literary tastes imply that he had profited by the highest education of his time. His great wealth may have been in part hereditary, but he owed his position and influence to his close connexion with the emperor Augustus. He first appears in history in 40 B.C., when he was employed by Octavian in arranging his marriage with Scribonia, and afterwards in assisting to negotiate the peace of Brundusium and the reconciliation with Antony. It was in 39 B.C. that Horace was introduced to Maecenas, who had before this received Varius and Virgil into his intimacy. In the “Journey to Brundusium,” (Horace, Satires, i. 5) in 37, Maecenas and Cocceius Nerva are described as having been sent on an important mission, and they were successful in patching up, by the Treaty of Tarentum, a reconciliation between the two claimants for supreme power. During the Sicilian war against Sextus Pompeius in 36, Maecenas was sent back to Rome, and was entrusted with supreme administrative control in the city and in Italy. He was vice-gerent of Octavian during the campaign of Actium, when, with great promptness and secrecy, he crushed the conspiracy of the younger Lepidus; and during the subsequent absences of his chief in the provinces he again held the same position. During the latter years of his life he fell somewhat out of favour with his master. Suetonius (Augustus, 66) attributes the loss of the imperial favour to Maecenas having indiscreetly revealed to Terentia, his wife, the discovery of the conspiracy in which her brother Murena was implicated. But according to Dio Cassius (liv. 19) it was due to the emperor’s relations with Terentia. Maecenas died in 8 B.C., leaving, the emperor heir to his wealth.
Opinions were much divided in ancient times as to the personal character of Maecenas; but the testimony as to his administrative and diplomatic ability was unanimous. He enjoyed the credit of sharing largely in the establishment of the new order of things, of reconciling parties, and of carrying the new empire safely through many dangers. To his influence especially was attributed the humaner policy of Octavian after his first alliance with Antony and Lepidus. The best summary of his character as a man and a statesman is that of Velleius Paterculus (ii. 88), who describes him as “of sleepless vigilance in critical emergencies, far-seeing and knowing how to act, but in his relaxation from business more luxurious and effeminate than a woman.”
Expressions in the Odes of Horace (ii. 17. i) seem to imply that Maecenas was deficient in the robustness of fibre characteristic of the average Roman. His character as a munificent patron of literature—which has made his name a household word—is gratefully acknowledged by the recipients of it and attested by the regrets of the men of letters of a later age, expressed by Martial and Juvenal. His patronage was exercised, not from vanity or a mere dilettante love of letters, but with a view to the higher interest of the state. He recognized in the genius of the poets of that time, not only the truest ornament of the court, but a power of reconciling men’s minds to the new order of things, and of investing the actual state of affairs with an ideal glory and majesty. The change in seriousness of purpose between the Eclogues and the Georgics of Virgil was in a great measure the result of the direction given by the statesman to the poet’s genius. A similar change between the earlier odes of Horace, in which he declares his epicurean indifference to affairs of state, and the great national odes of the third book is to be ascribed to the same guidance. Maecenas endeavoured also to divert the less masculine genius of Propertius from harping continually on his love to themes of public interest. But if the motive of his patronage had been merely politic it never could have inspired the affection which it did in its recipients. The great charm of Maecenas in his relation to the men of genius who formed his circle was his simplicity, cordiality and sincerity. Although not particular in the choice of some of the associates of his pleasures, he admitted none but men of worth to his intimacy, and when once admitted they were treated like equals. Much of the wisdom of Maecenas probably lives in the Satires and Epistles of Horace. It has fallen to the lot of no other patron of literature to have his name associated with works of such lasting interest as the Georgics of Virgil, the first three books of Horace’s Odes, and the first book of his Epistles.
Maecenas himself wrote in both prose and verse. The few fragments that remain show that he was less successful as an author than as a judge and patron of literature. His prose works on various subjects—Prometheus, Symposium (a banquet at which Virgil, Horace and Messalla were present), De cultu suo (on his manner of life)—were ridiculed by Augustus, Seneca and Quintilian for their strange style, the use of rare words and awkward transpositions. According to Dio Cassius, Maecenas was the inventor of a system of shorthand.
There is no good modern biography of Maecenas. The best known is that by P. S. Frandsen (1843), See “Horace et Mecène” by J. Girard, in La Révue politique et littéraire (Dec. 27, 1873); V. Gardthausen, Augustus und seine Zeit, i. 762 seq.; ii. 432 seq. The chief ancient authorities for his life are Horace (Odes with Scholia), Dio Cassius, Tacitus (Annals), Suetonius (Augustus). The fragments have been collected and edited by F. Harder (1889).

MAECIANUS, LUCIUS VOLUSIUS (2nd cent.) Roman jurist, was the tutor in law of the emperor Marcus Aurelius. When governor of Alexandria he was slain by the soldiers, as having participated in the rebellion of Avidius Cassius (175). Maecianus was the author of works on trusts (Fideicommissa), on the Judicia publica, and of a collection of the Rhodian laws relating to maritime affairs. His treatise on numerical divisions, weights and measures (Distributio) is extant, with the exception of the concluding portion.
See Capitolinus, Antoninus, 3; Vulcacius Gallicanus, Avidius Cassius, 7; edition of the metrological work by F. Hultsch in Metrologicorum scriptorum reliquiae, ii. (1866); Mommsen in Abhandlungen der sächsischen Gesellschaft der Wissenschaften, iii. (1853).

MAELDUIN (or Maeldune), VOYAGE OF (Imram Maeleduin), an early Irish romance. The text exists in an 11th-century redaction, by a certain Aed the Fair, described as the “chief sage of Ireland,” but it may be gathered from internal evidence that the tale itself dates back to the 8th century. It belongs to the group of Irish romance, the Navigations (Imrama), the common type of which was probably imitated from the classical tales of the wanderings of Jason, of Ulysses and of Aeneas. Maelduin, the foster-son of an Irish queen, learnt on reaching manhood that he was the son of a nun, and that his father, Ailill of the edge of battle, had been slain by a marauder from Leix. He set sail to seek his father’s murderer, taking with him, in accordance with the instructions of a sorcerer, seventeen men. His three foster-brothers swam after him, and were taken on board. This increase of the fateful number caused Maelduin’s vengeance to be deferred for three years and seven months, until the last of the intruders had perished. The travellers visited many strange islands, and met with a long series of adventures, some of which are familiar from other sources. The Voyage of St Brendan (q.v.) has very close similarities with the Maelduin, of which it is possibly a clerical imitation, with the important addition of the whale-island episode, which it has in common with “Sindbad the Sailor.”
Imram Curaig Mailduin is preserved, in each case imperfectly, in the Lebor na h Uidre, a MS. in the Royal Irish Academy, Dublin; and in the Yellow Book of Lecan, MS. H. 216 in the Trinity College Library, Dublin; fragments are in Harleian MS. 5280 and Egerton MS. 1782 in the British Museum. There are translations by Patrick Joyce, Old Celtic Romances (1879), by Whitley Stokes (a more critical version, printed together with the text) in Revue celtique, vols. ix. and x. (1888-1889). See H. Zimmer, “Brendan’s Meerfahrt” in Zeitschrift für deutsches Altertum, vol. xxxiii. (1889). Tennyson’s Voyage of Maeldune, suggested by the Irish romance, borrows little more than its framework.

MAELIUS, SPURIUS (d. 439 B.C.), a wealthy Roman plebeian, who during a severe famine bought up a large amount of corn and sold it at a low price to the people. Lucius (or Gaius) Minucius, the patrician praefectus annonae (president of the market), thereupon accused him of courting popularity with a view to making himself king. The cry was taken up. Maelius, summoned before the aged Cincinnatus (specially appointed dictator), refused to appear, and was slain by Gaius Servilius Ahala; his house was razed to the ground, his corn distributed amongst the people, and his property confiscated. The open space called Aequimaelium, on which his house had stood, preserved the memory of his death. Cicero calls Ahala’s deed a glorious one, but, whether Maelius entertained any ambitious projects or not, his summary execution was an act of murder, since by the Valerio-Horatian laws the dictator was bound to allow the right of appeal.
See Niebuhr’s History of Rome, ii. 418 (Eng. trans., 1851); G. Cornewall Lewis, Credibility of early Roman History, ii.; Livy, iv. 13; Cicero, De senectute 16, De amicitia 8, De republica, ii. 27; Floras, i. 26; Dion. Halic. xii. i.

MAELSTROM (whirlpool), a term originally applied to a strong current running past the south end of the island of Moskenaes, a member of the group of Lofoten Islands on the west coast of Norway. It is known also as the Moskenstrom. Though dangerous in certain states of wind and tide, the tales of ships being swallowed in this whirlpool are fables. The word is probably of Dutch origin, from malen, to grind or whirl, and strom or stroom, a stream or current. It appears on Mercator’s Atlas of 1595.

MAENADS (Gr. Μαινάδες, frenzied women), the female attendants of Dionysus. They are known by other names—Bacchae, Thyiades, Clodones and Mimallones (the last two probably of Thracian origin)—all more or less synonymous.
See the exhaustive articles by A. Legrand in Daremberg and Saglio’s Dictionnaire des antiquités and A. Rapp in Roscher’s Lexikon der Mythologie; also editions of Euripides, Bacchae (e.g. J. E. Sandys).

MAENIUS, GAIUS, Roman statesman and general. Having completed (when consul in 338 B.C.) the subjugation of Latium, which with Campania had revolted against Rome, he was honoured by a triumph, and a column was erected to him in the Forum. When censor in 318, in order that the spectators might have more room for seeing the games that were celebrated in the Forum, he provided the buildings in the neighbourhood with balconies, which were called after him maeniana.
See Festus, s.v. Maeniana; Livy viii. 13, ix. 34; Pliny, Nat. Hist. xxxiv. 11 (5).

MAERLANT, JACOB VAN (c. 1235-c. 1300), Flemish poet, was born in the Franc de Burges (tradition says at Damme) between 1230 and 1240. He was sacristan of Maerlant, in the island of Ost-Voorne, and afterwards clerk to the magistrates at Damme. His early works are translations of French romances. Maerlant’s most serious work in the field of romance was his Ystorien van Troyen (c. 1264), a poem of some forty thousand lines, translated and amplified from the Roman de Troie of Benoît de Sainte-More. From this time Maerlant rejected romance as idle, and devoted himself to writing scientific and historical works for the education and enlightenment of the Flemish people. His Heimelicheit der Heimelicheden (c. 1266) is a translation of the Secreta secretorum, a manual for the education of princes, ascribed throughout the middle ages to Aristotle. Van der Naturen Bloeme is a free translation of De natura rerum, a natural history in twenty books by a native of Brabant, Thomas de Cantimpré; and his Rijmbijbel is taken, with many omissions and additions, from the Historia scholastica of Petrus Comestor. He supplemented this metrical paraphrase of Scripture history by Die Wrake van Jherusalem (1271) from Josephus. Although Maerlant was an orthodox Catholic, he is said to have been called to account by the priests for translating the Bible into the vulgar tongue. In 1284 he began his magnum opus, the Spiegel historiael, a history of the world, derived chiefly from the third part of the Speculum majus of Vincent de Beauvais. This work was completed by two other writers, Philipp Utenbroeke and Lodowijk van Velthem. Maerlant died in the closing years of the 13th century, his last poem, Van den lande van oversee, dating from 1291. The greater part of his work consists of translations, but he also produced poems which prove him to have had real original poetic faculty. Among these are Die Clausule van der Bible, Der Kerken Clage, imitated from the Complaintes of Rutebeuf, and the three dialogues entitled Martijn, in which the fundamental questions of theology and ethics were discussed. In spite of his orthodoxy, Maerlant was a keen satirist of the corruptions of the clergy. He was one of the most learned men of his age, and for two centuries was the most celebrated of Flemish poets.
See monographs by J. van Beers (Ghent, 1860); C. A. Serrure (Ghent, 1861); K. Versnaeyen (Ghent, 1861); J. te Winkel (Leiden, 1877, 2nd ed., Ghent, 1892); and editions of Torec (Leiden, 1875) by J. te Winkel; of Naturen Bloeme, by Eelco Verwijs; of Alexanders Geesten (Groningen, 1882), by J. Franck; Merlijn (Leiden, 1880-1882), by J. van Bloten; Heimelicheit der Heimelicheden (Dordrecht, 1838), by Clarisse; Der Naturen Bloeme (Groningen, 1878), by Verwijs; of Rijmbijbel (Brussels, 1858-1869), by David; Spiegel historiael (Leiden 1857-1863), by Verwijs and de Vries; selections from the Ystorien van Troyen (1873), by J. Verdam.

MAES, NICOLAS (1632-1693), Dutch painter, was born at Dordrecht, and went about 1650 to Amsterdam, where he entered Rembrandt’s studio. Before his return to Dordrecht in 1654 Maes painted a few Rembrandtesque genre pictures, with life-size figures and in a deep glowing scheme of colour, like the “Reverie” at the Ryks Museum in Amsterdam, the “Card Players” at the National Gallery, and the “Children with a Goat Carriage,” belonging to Baroness N. de Rothschild. So closely did his early style resemble that of Rembrandt, that the last-named picture, and other canvases in the Leipzig and Budapest galleries and in the collection of Lord Radnor, were or are still ascribed to Rembrandt. In his best period, from 1655 to 1665, Maes devoted himself to domestic genre on a smaller scale, retaining to a great extent the magic of colour he had learnt from Rembrandt. Only on rare occasions did he treat scriptural subjects, as in the earl of Denbigh’s “Hagar’s Departure,” which has been ascribed to Rembrandt. His favourite subjects were women spinning, or reading the Bible, or preparing a meal. In 1665 he went to Antwerp, where he remained till 1678, in which year he probably returned to Amsterdam. His Antwerp period coincides with a complete change in style and subject. He devoted himself almost exclusively to portraiture, and abandoned the intimacy and glowing colour harmonies of his earlier work for a careless elegance which suggests the influence of Van Dyck. So great indeed was the change, that it gave rise to the theory of the existence of another Maes, of Brussels. Maes is well represented at the National Gallery by five paintings: “The Cradle,” “The Dutch Housewife,” “The Idle Servant,” “The Card Players,” and a man’s portrait. At Amsterdam, besides the splendid examples to be found at the Ryks Museum, is the “Inquisitive Servant” of the Six collection. At Buckingham Palace is “The Listening Girl” (repetitions exist), and at Apsley House “Selling Milk” and “The Listener.” Other notable examples are at the Berlin, Brussels, St Petersburg, the Hague, Frankfort, Hanover and Munich galleries.

MAESTRO, a north-westerly wind observed in the Adriatic and surrounding regions, chiefly during summer. The maestro is a “fine weather” wind, and is the counterpart of the sirocco.

MAETERLINCK, MAURICE (1862- ), Belgian-French dramatist and poet, of Flemish extraction, was born at Ghent on the 29th of August 1862. He was educated at the Collège Sainte-Barbe, and then at the university of his native city, where, at the age of twenty-four, he was enrolled as a barrister. In 1887 he settled in Paris, where he immediately became acquainted with Villiers de l’Isle-Adam and the leaders of the symbolist school of French poetry. At the death of his father, Maeterlinck returned to Belgium, where he thenceforth mainly resided: in the winter at Ghent, in the summer on an 299 estate at Oostacker. He had by this time determined to devote his whole life to poetry, a dedication which his fortune permitted. His career as an author began in 1889, when he published a volume of verse, Serres chaudes, and a play, La Princesse Maleine, the latter originally composed in metre, but afterwards carefully rewritten in prose, the vehicle which the author continued to use for his dramatic work. Maeterlinck was at this time totally unknown, but he became famous through an article by Octave Mirbeau, prominently published in the Paris Figaro, entitled “A Belgian Shakespeare.” The enthusiasm of this review and the excellence of the passages quoted combined to make Maeterlinck the talk of the town. Maeterlinck, among his Belgian roses, continued to work with extreme deliberation. In 1890 he published, in Brussels, two more plays, L’Intruse and Les Aveugles; followed in 1891 by Les Sept princesses. His strong leaning to mysticism was now explained, or defined, by a translation of the Flemish medieval visionary, the Admirable Ruysbroeck, which Maeterlinck brought out in 1891. In 1892 appeared what has been perhaps the most successful of all his plays on the stage, Pelléas et Mélisande, followed in 1894 by those very curious and powerful little dramas written to be performed by marionettes: Alladine el Palomides, Intérieur and La Mort de Tintagiles. In 1895 Maeterlinck brought out, under the title of Annabella, a translation of Ford’s ’Tis Pity She’s a Whore, with a preface. Two philosophical works followed, a study on Novalis (1895) and Le Trésor des humbles (1896). In 1896 he returned to drama with Aglavaine el Sélysette and to lyric verse with Douze chansons. A monograph on the ethics of mysticism, entitled La Sagesse et la destinée, was issued, as a kind of commentary on his own dramas, in 1898; and in 1901 Maeterlinck produced a fascinating volume of prose, founded upon observations made in his apiaries at Oostacker, in which philosophy, fancy and natural history were surprisingly mingled—La Vie des abeilles. In 1902 he published Le Temple enseveli and Monna Vanna; in 1903 Joyzelle. In 1901 he began to issue, in Brussels, an edition of his complete dramatic works.
The nature of Maeterlinck’s writings, whether in prose or verse, has been strictly homogeneous. Few poets have kept so rigorously to a certain defined direction in the practice of their art. Whether in philosophy, or drama, or lyric, Maeterlinck is exclusively occupied in revealing, or indicating, the mystery which lies, only just out of sight, beneath the surface of ordinary life. In order to produce this effect of the mysterious he aims at an extreme simplicity of diction, and a symbolism so realistic as to be almost bare. He allows life itself to astonish us by its strangeness, by its inexplicable elements. Many of his plays are really highly pathetic records of unseen emotion; they are occupied with the spiritual adventures of souls, and the ordinary facts of time and space have no influence upon the movements of the characters. We know not who these orphan princesses, these blind persons, these pale Arthurian knights, these aged guardians of desolate castles, may be; we are not informed whence they come, nor whither they go; there is nothing concrete or circumstantial about them. Their life is intense and consistent, but it is wholly of a spiritual character; they are mysterious with the mystery of the movements of a soul. These characteristics, which make the dramatic work of Maeterlinck so curious and unique, are familiar to most readers in Pelléas et Mélisande, but are carried, perhaps, to their farthest intensity in Aglavaine et Sélysette, which seems to be written for a phantom stage and to be acted by disembodied spirits. In spite of the violence of his early admirers, and of the fact that the form of his dramas easily lent itself to the cheap ridicule of parodists, the talent of Maeterlinck has hardly met with opposition from the criticism of his time. It has been universally felt that his spirit is one of grave and disinterested attachment to the highest moral beauty, and his seriousness, his serenity and his extreme originality have impressed even those who are bewildered by his diaphanous graces and offended at his nebulous mysticism. While the crude enthusiasm which compared him with Shakespeare has been shown to be ridiculous, the best judges combine with Camille Mauclair when he says: “Maurice Maeterlinck est un homme de génie authentique, un très grand phénomène de puissance mentale à la fin du xixe siècle.” In spite of the shadowy action of Maeterlinck’s plays, which indeed require some special conditions and contrivances for their performance, they are frequently produced with remarkable success before audiences who cannot be suspected of mysticism, in most of the countries of Europe. In his philosophical writings Maeterlinck shows himself a disciple of Novalis, of Emerson, of Hello, of the Flemish Catholic mystics, and he evolves from the teachings of those thinkers a system of aesthetics applicable to the theatre as he conceives it.

MAFEKING, a town in the British Bechuanaland division of the Cape, 870 m. N.E. of Cape Town and 492 m. S.S.W. of Bulawayo by rail, and 162 m. in a direct line W. by N. of Johannesburg. (Pop. 1904), 2713. It is built on the open veld, at an elevation of 4194 ft., by the banks of the Upper Molopo, is 9 m. W. of the western frontier of the Transvaal and 15 m. S. of the southern boundary of the Bechuanaland protectorate. The Madibi goldfields are some 10 m. south of the town. Mafeking is thus an important trading and distributing centre for Bechuanaland and the western Transvaal. Here are, too, the chief railway workshops between Kimberley and Bulawayo. The headquarters of the administration for the Bechuanaland protectorate are in the town. The chief buildings are the town-hall, Anglican church, Masonic temple, and hospital.
Mafeking was originally the headquarters of the Barolong tribe of Bechuana and is still their largest station, the native location (pop. 2860) being about a mile distant from the town. It was from Pitsani Pothlugo (or Potlogo), 24 m. north of Mafeking, that Dr Jameson started, on the 29th of December 1895, on his raid into the Transvaal. On the outbreak of the Anglo-Boer war in 1899 Mafeking was invested by a Boer force. Colonel R. S. S. Baden-Powell was in command of the defence, which was stubbornly maintained for 217 days (Oct. 12 to May 17), when a relief column arrived and the Boers dispersed (see Transvaal: History). The fate of the town had excited the liveliest sympathy in England, and the exuberant rejoicings in London on the news of its relief led to the coining of the word mafficking to describe the behaviour of crowds on occasions of extravagant demonstrations of a national kind. In September 1904 Lord Roberts unveiled at Mafeking an obelisk bearing the names of those who fell in defence of the town.
R. S. S. Baden-Powell’s Sketches in Mafeking and East Africa (1907) and Lady Sarah Wilson’s South African Memories (1909) deal largely with the siege of Mafeking.

MAFFEI, FRANCESCO SCIPIONE, Marchese di (1675-1755); Italian archaeologist and man of letters, was born at Verona on the 1st of June 1675. He studied for five years in Parma, at the Jesuit College, and afterwards from 1698 at Rome; and in 1703-1704 he took part as a volunteer in the war of succession, fighting on the Bavarian side at Donauwerth. In 1709 he began at Padua along with Apostolo Zeno and Valisnieri the Giornale dei letterati d’Italia, a literary periodical which had but a short career; and subsequently an acquaintance with the actor Riccoboni led him to exert himself for the improvement of dramatic art in Italy. His Merope, a tragedy, appeared in 1713; Teatro italiano, a small collection of works for presentation on the stage, in 1723-1725; and Le Ceremonie, an original comedy, in 1728. From 1718 he became specially interested in the archaeology of his native town, and his investigations resulted in the valuable Verona illustrata (1731-1732). Maffei afterwards devoted four years to travel in France, England, Holland and Germany. He died at Verona on the 11th of February 1755.
A complete edition of his works appeared at Venice (28 vols., 8vo) in 1790.

MAFIA (Maffia), a secret society of Sicily. Its organization and purposes much resemble those of the Camorra (q.v.).
Various derivations are found for the name. Some hold it to be a Tuscan synonym for miseria; others, a corruption of Fr. mauvais 300 (bad). Others connect it with the name of an alleged Arab tribe, Mà-âfir, once settled at Palermo. Giuseppe Pitré asserts that the word is peculiar to western Sicily and that, with its derivatives, it formerly meant, in Il Borgo, a district of Palermo, beauty or excellence. Thus, a handsome woman showily dressed was said “to have mafia,” or to be mafiusa. Often in Palermo the street merchants call arance-mafiuse (fine oranges). Thus, Pitré argues, mafia, applied to a man to express manly carriage and bravery, would naturally become the title of a society the members of which were all “bravos.” A less credible explanation of the term is connected with Mazzini, who is said to have formed a secret society the members of which were called Mafiusi, from Mafia, a word composed of the initial letters of five Italian words, Mazzini autorizza furti, incendi, avvelenamenti, “Mazzini authorizes theft, arson and poisoning.” This theory suggests that the word was unknown before 1859 or 1860.
The Mafia, however named, existed long before Mazzini’s day. In its crudest form it was co-operative brigandage, blended with the Vendetta (q.v.). The more strictly organized Mafia was the result of the disorders consequent upon the expulsion of the king of Naples by Napoleon. When the Bourbon court took refuge in Sicily there were a large number of armed retainers in the service of the Sicilian feudal nobility. Ferdinand IV., at the bidding of England, granted a constitution to the island in 1812, and with the destruction of feudalism most of the feudal troops became brigands. Powerless to suppress them, Ferdinand organized the bandits into a rural gendarmerie, and they soon established a reign of terror. The abject poverty of the poorer classes, unable to eke out existence by work in the sulphur mines or on the fields, fostered the growth of two classes of mafiusi—the vast majority of the inhabitants who were glad to put themselves as passive members under the protection of the Mafia, while the active members shared in the plunder. The Mafia thus became a loosely organized society under an unwritten code of laws or ethics known as Omertà, i.e., manliness (from Sicil. omu, Ital. uomo, a man), which embodied the rules of the Vendetta. Candidates were admitted after trial by duel, and were sworn to resist law and defeat justice. Like the Camorra, the Mafia was soon powerful in all classes, and even the commander of the royal troops acted in collusion with it. The real home of Mafia was in and around Palermo, where no traveller was safe from robbery and the knife. In an organized form the Mafia survives only in isolated districts. Generally speaking, it is to-day not a compact criminal association but a complex social phenomenon, the consequence of centuries of misgovernment. The Mafiuso is governed by a sentiment akin to arrogance which imposes a special line of conduct upon him. He considers it dishonourable to have recourse to lawful authority to obtain redress for a wrong or a crime committed against him. He therefore hides the identity of the offender from the police, reserving vengeance to himself or to his friends and dependants. This sentiment, still widely diffused among the lower classes of many districts, and not entirely unknown to the upper classes, renders difficult legal proof of culpability for acts of violence, and multiplies sanguinary private reprisals. In September 1892 about 150 Mafiusi were arrested at Catania, but all repressive measures proved useless. The only result was to drive some of the members abroad, with disastrous results to other countries. In October 1890 David Hennessy, chief of police in New Orleans, was murdered. Subsequent legal inquiry proved the crime to be the work of the Mafia, which had been introduced into the United States thirty years before. In May 1890 a band of Italians living in New Orleans had ambushed another gang of their fellow-countrymen belonging to a society called Stoppaghera. The severe police measures taken brought the vengeance of the society upon Hennessy. Eleven Italians were indicted on suspicion of being implicated in his murder; but the jury was terrorized and acquitted six. On the 14th of March 1891 a mob led by well-known New Orleans citizens broke into the gaol where nineteen Italians were imprisoned and lynched eleven of them.
See W. Agnew Paton, Picturesque Sicily (1898); C. W. Heckethorn, Secret Societies of all Ages (1897); Alongi, La Maffia (Turin, 1887); Le Faure, La Maffia (Paris, 1892).

MAFRA, a town of Portugal, in the district of Lisbon (formerly in the province of Estremadura); near the Atlantic coast and the right bank of the river Lizandro, and 20 m. N.W. of Lisbon. Pop. (1900), 4769. Mafra is remarkable for its monastery, church, and palace, built by John V. in 1717-1732, in consequence of a vow made during a dangerous illness to build a convent for the poorest friary of the kingdom—which proved to be a small Franciscan settlement here. The architects, Johann Friedrich Ludwig of Regensburg, and his son Johann Peter, took the Escurial for their model; but the imitation is less successful than the original, though the cost exceeded £4,000,000. The building is in the form of a parallelogram measuring upwards of 800 ft. from north to south and 700 ft. from east to west; it is said to contain 866 rooms, and to be lighted by no fewer than 5200 windows. The centre is occupied by the church, sumptuously built of marble, and richly adorned with statues and other objects of art. In each of the twin towers there is a chime of 57 bells. Part of the palace, originally designed as barracks, is used as a military academy. Adjoining the palace are fine gardens and a royal model farm.

MAGADHA, an ancient kingdom of India, mentioned in both the Ramayana and the Mahābhārata. It comprised that portion of Behar lying S. of the Ganges, with its capital at Pataliputra or Patna. As the scene of many incidents in the life of Gautama Buddha, it was a holy land. It was also the seat of the Maurya Empire, founded by Chandragupta, which extended over all India under Asoka; and, later, of the powerful Gupta dynasty.

MAGALDÁN, a town in the northern part of the province of Pangasinan, Luzon, Philippine Islands, about 2 m. from the shore of the Gulf of Lingayen. Pop. (1903), 15,841. In 1903 the adjacent municipality of Mapandan (pop. in 1903, 4198) was annexed to Magaldán. Most of its inhabitants are engaged in rice culture. The principal language is Pangasinan; Ilocano is also spoken.

MAGALLANES (Spanish form of Magellan), a territory of southern Chile extending from 47° S. to Cape Horn and including the mainland from the Argentine frontier to the Pacific coast, the islands extending along that coast, the Fuegian archipelago, and the western half of Tierra del Fuego. Area, about 71,127 sq. m.; pop. (1895), 5170. It is one of the most inhospitable regions of the world, being exposed to cold westerly storms for most of the year. The islands are barren, but the mainland is covered with forests, practically inaccessible to exploitation because of the inclement climate and the wet spongy soil. The coast is indented with bays and fjords and affords remarkable scenery. There is little animal life on land, but the coast is frequented by the seal and sea-otter and the sheltered waters by countless sea-fowl. The only permanent settlements are at Punta Arenas, the capital, on the Straits of Magellan, Palomares on Otway Water, Mina Marta on Skyring Water, and Ultima Esperanza (Last Hope) on the east shore of Worsley Sound. All are east of the Andean ranges and partially sheltered from the westerly storms. In this sheltered region there are open plains where sheep are grazed. A few sheep ranges have been established on Tierra del Fuego. Some nomadic tribes of Indians inhabit Tierra del Fuego and the extreme southern end of the mainland, but their numbers are small. Coal has been found in the vicinity of Punta Arenas, and gold occurs.
See The Voyage of the Adventure and Beagle (1839).

MAGAZINE, primarily a warehouse for goods or merchandise (Arab. makhzan, a storehouse, from khazana, to store up). In Morocco makhzan (or maghzen) has come to be used as the name of the government. The Spaniards adopted the Arabic in the form magacen, and the English form comes through the older French magazin, modern magasin. The meaning of a storehouse or large shop, common in French, is rare in English except in the military use of the term for a building for the storage of explosives and ammunition. It is applied to the chamber of a repeating rifle or machine-gun containing the supply of cartridges. The name as applied to a periodical publication 301 containing articles on various subjects was first used in the Gentleman’s Magazine (1731), described as “a monthly collection, to treasure up as in a magazine” articles on the subjects with which it was proposed to deal.

MAGDALA (more correctly Makdala), a natural stronghold in the country of the Wollo Gallas, Abyssinia, about 250 m. W. of Jibuti on the Gulf of Aden, in 11° 22′ N., 39° 25′ E. The basaltic plateau of which it consists rises 9110 ft. above the sea. It is about three-quarters of a mile in length by less than half a mile in breadth, and lies more than a thousand feet higher than the neighbouring plain of Arogié. Chosen about 1860 by the emperor Theodore of Abyssinia as his principal stronghold in the south, Magdala owes its celebrity to the fact that, as the place of imprisonment of the English captives, it became the goal of the great English Expedition of 1868. At the time of its capture it contained huts for a population of about three thousand. The whole rock was burned bare by order of the commander of the British force, Sir Robert Napier, who, on being raised to the peerage for his services on this occasion, took the title of Lord Napier of Magdala. The plateau was subsequently refortified by the Abyssinians.
See Clements Markham, History of the Abyssinian Expedition (1869); and H. Rassam, British Mission to Theodore (1869).

MAGDEBURG, a city of Germany, capital of the Prussian province of Saxony, a fortress of the first rank and one of the principal commercial towns of the German Empire. It lies in a broad and fertile plain, mainly on the left bank of the Elbe, 88 m. S.W. from Berlin and at the junction of main lines to Leipzig, Brunswick, Cassel and Hamburg. Pop. (1885), 159,520; (1890), 202,234; (1905), 240,661. It consists of the town proper, and of the five suburbs of Friedrichstadt, Wilhelmstadt, Neustadt, Sudenburg and Buckau; the last four are separated from the town by the ramparts and glacis, but are all included within the new line of advanced bastions, while Friedrichstadt lies on the right bank of the river. In the Elbe, between the old town and the Friedrichstadt, lies an island whereon stands the citadel; this is united with both banks by bridges. With the exception of the Breite Weg, a handsome thoroughfare running from north to south, the streets of the town proper are narrow and crooked. Along the Elbe, however, extend fine promenades, the Fürstenwall and the Fürsten Üfer. To the south of the inner town is the Friedrich Wilhelms Garten, a beautiful park laid out on the site of the celebrated convent of Berge, which was founded in 968 and suppressed in 1809. By far the most important building in Magdeburg is the cathedral, dedicated to SS Maurice and Catherine, a handsome and massive structure of the 14th century, exhibiting an interesting blending of Romanesque and Gothic architecture. The two fine western towers were completed about 1520. The interior contains the tombs of the emperor Otto the Great and his wife Edith, an English princess, and the fine monument of Archbishop Ernest (d. 1513), executed in 1495 by Peter Vischer of Nüremberg. The Liebfrauenkirche, the oldest church in Magdeburg, is an interesting Romanesque edifice of the 12th and 13th centuries, which was restored in 1890-1891. The chief secular buildings are the town-hall (Rathaus), built in 1691 and enlarged in 1866, the government offices, the palace of justice, the central railway station and the exchange. The Breite Weg and the old market contain numerous fine gable-ended private houses in the style of the Renaissance. In front of the town-hall stands an equestrian statue of Otto the Great, erected about 1290. The modern streets are spacious, and the houses well-built though monotonous. There are two theatres, an agricultural college, an art school, several gymnasia, a commercial and other schools, an observatory, and two fine hospitals. The first place amongst the industries is taken by the ironworks (one being a branch of the Krupp firm, the Grusonwerke, employing about 4000 hands), which produce naval armour and munitions of war. Of almost equal importance are the sugar refineries and chicory factories. Then come establishments for making tobacco, gloves, chocolate, artificial manure, cement, varnish, chemicals and pottery. There are also distilleries and breweries, and factories for the manufacture of cotton and silk goods. Magdeburg is the central market in Germany for sugar and chicory, but trades extensively also in cereals, fruit, vegetables, groceries, cattle, horses, wool, cloth, yarn, leather, coal and books. A new winter harbour, made at a cost of £400,000, facilitates the river traffic along the Elbe. Three million tons of merchandise pass Magdeburg, going upstream, and nearly 1 million tons, going downstream, annually. Magdeburg is the headquarters of the IV. corps of the German army and the seat of the provincial court of appeal and administrative offices, and of a Lutheran consistory.
History.—Magdeburg, which was in existence as a small trading settlement at the beginning of the 9th century, owes its early prosperity chiefly to the emperor Otto the Great, who established a convent here about 937. In 968 it became the seat of an archbishop, who exercised sway over an extensive territory. Although it was burnt down in 1188, Magdeburg became a flourishing commercial town during the 13th century, and was soon an important member of the Hanseatic League. Its bench of jurats (Schöppenstuhl) became celebrated, and “Magdeburg law” (Magdeburger Recht), securing the administrative independence of municipalities, was adopted in many parts of Germany, Poland and Bohemia. During the middle ages the citizens were almost constantly at variance with the archbishops, and by the end of the 15th century had become nearly independent of them. It should, however, be noted that Magdeburg never became a free city of the Empire. The town embraced the Reformation in 1524, and was thenceforth governed by Protestant titular archbishops (see Bishop). On the refusal of the citizens to accept the “Interim,” issued by the emperor Charles V., Magdeburg was besieged by Maurice of Saxony in 1550, and capitulated on favourable terms in November 1551. During the Thirty Years’ War it was twice besieged, and suffered terribly. It successfully resisted Wallenstein for seven months in 1629, but was stormed and sacked by Tilly in May 1631. The whole town, with the exception of the cathedral, and about 140 houses, was burned to the ground, and the greater part of its 36,000 inhabitants were butchered without regard to age or sex, but it recovered from this deadly blow with wonderful rapidity. By the peace of Westphalia (1648) the archbishopric was converted into a secular duchy, to fall to Brandenburg on the death of the last administrator, which happened in 1680. In 1806 Magdeburg was taken by the French and annexed to the kingdom of Westphalia, but it was restored to Prussia in 1814, on the downfall of Napoleon. Otto von Guericke (1602-1686), the inventor of the air-pump, was burgomaster of Magdeburg. Count Lazare Carnot died here in exile, and was buried in the cemetery, but his remains were exhumed in 1889 and conveyed to Paris. Luther was at school here, and sang in the streets for bread with other poor choristers.
See W. Kawerau, Aus Magdeburgs Vergangenheit (Halle, 1886) O. von Guericke, Geschichte der Belagerung, Eroberung und Zerstörung von Magdeburg (Magdeburg, 1887); M. Dittmar, Beiträge zur Geschichte der Stadt Magdeburg (Halle, 1885); F. W. Hoffmann, Geschichte der Stadt Magdeburg (Magdeburg, 1885-1886); F. Hülsse, Die Einführung der Reformation in der Stadt Magdeburg (Magdeburg, 1883); R. Volkholz, Die Zerstörung Magdeburgs 1631 (Magdeburg, 1892); W. Leinung and R. Stumvoll, Aus Magdeburgs Sage und Geschichte (Magdeburg, 1894); and the Urkundenbuch der Stadt Magdeburg (1892).
The Archbishopric of Magdeburg was carved out of the bishopric of Halberstadt when it was founded in 968, and its history is largely bound up with that of the city and of the prelates who have ruled the see. The first archbishop was Adalbert, and he and his successors had six or seven suffragan bishops. Several of the archbishops took very prominent parts in German politics. Early in the 15th century their residence was fixed at Halle, and about the same time it became the custom to select them from one of the reigning families of Germany, most often from the house of Brandenburg. The doctrines of the reformers made their appearance in the diocese early in the 16th century, and soon Archbishop Sigismund, a son of Joachim II., elector of Brandenburg, openly avowed his adherence to Lutheranism. After the issue of the edict of 302 restitution by the emperor Ferdinand II. in 1629, there were three rival candidates for the see, and their struggles added to the confusion caused by the Thirty Years’ War. By the peace of Prague, however, in 1635, the archbishopric was given to Augustus, prince of Saxe-Weissenfels, who retained it until his death in 1680. In 1773 the area of the see was over 2000 sq. m. It included 29 towns and over 400 villages and contained about 250,000 inhabitants.
See the Regesta archiepiscopatus magdeburgensis, edited by G. A. von Mülverstedt (Magdeburg, 1876-1899); and K. Uhlirz, Geschichte des Erzbistums Magdeburg unter den Kaisern aus sächsischem Hause (Magdeburg, 1887).
Distinct both from the archbishopric and from the city was the Burgraviate of Magdeburg. The office of burgrave dates from the time of Charlemagne, although its holder was not at first called by this name, and it soon became one of great importance. The burgrave was the king’s representative; he was charged with the administration of the royal estates in a given district, and in general with watching the royal interests therein. The burgraviate of Magdeburg was held by several countly families in turn until 1269, when it was purchased by Archbishop Conrad II., who, however, soon sold it. In 1294 it was again united with the archbishopric and the prelates retained it until 1538; then in 1579 Augustus, elector of Saxony, made an arrangement which again gave the office to the archbishops, who held it until the secularization of the see.
The Magdeburg Centuries (Magdeburger Zenturien) is the name given to the first general history of the Christian Church written from a Protestant point of view. It was compiled in Magdeburg, and the history is divided into periods of one hundred years each. It was written in Latin in 1562, its principal author being the reformer Matthias Flacius, who was assisted by other Lutheran theologians. The cost of the undertaking was borne by some of the German Protestant princes. As the Historia ecclesiae Christi it was first published at Basel in seven volumes (1559-1574). It deals with the history of the Church down to 1400, and considering the time at which it was written it is a remarkable monument to the scholarship of its authors. The earlier part of it has been translated into German (Jena, 1560-1565).
See E. Schaumkell, Beitrag zur Entstehungsgeschichte der Magdeburger Zenturien (Ludwigslust, 1898).

MAGEE, WILLIAM (1766-1831), archbishop of Dublin, was born at Enniskillen, Co. Fermanagh, and educated at Trinity College, Dublin, where he was elected fellow in 1788. He was ordained in 1790. Two sermons, preached in the college chapel in 1798 and 1799, form the basis of his Discourses on the Scriptural Doctrines of Atonement and Sacrifice (1801), a polemic against Unitarian theology which was answered by Lant Carpenter. Magee was appointed professor of mathematics and senior fellow of Trinity in 1800, but in 1812 he resigned, and undertook the charge of the livings of Cappagh, Co. Tyrone, and Killeleagh, Co. Down. Next year he became dean of Cork. He was well known as a preacher and promoter of the Irish reformation, and in 1819 he was consecrated bishop of Raphoe. In 1822 the archbishop of Dublin was translated to Armagh, and Magee succeeded him at Dublin. Though in most respects a tolerant man, he steadily opposed the movement for Catholic Emancipation. He died on the 18th of August 1831.
A memoir of his life is included with the Works of the Most Reverend William Magee, D.D. (1842), by A. H. Kenney.

MAGEE, WILLIAM CONNOR (1821-1891), Anglican divine, archbishop of York, was born at Cork in 1821. His father was curate of the parish attached to the Protestant cathedral in that city; his grandfather was archbishop of Dublin. Young Magee entered Trinity College, Dublin, with a scholarship at thirteen. He was ordained to the curacy of St Thomas’s, Dublin, but, being threatened with consumption, went after two years to Malaga. On his return he took a curacy at Bath, and was speedily appointed to the Octagon Chapel, where his fame both as preacher and platform speaker continued to spread. Some years afterwards he was made prebendary of Wells Cathedral. In 1860 the delicate state of his health caused him to accept the living of Enniskillen. In 1864 he was made dean of Cork and chaplain to the lord lieutenant. Here he manifested those great gifts which ultimately raised him to high office; a powerful grasp of mental, moral and political problems, combined with eloquence of a high order, and illuminated with brilliant flashes of wit. In 1868 the question of the disestablishment of the Irish Church came to the front, and Magee threw himself into the task of its defence with his usual energy and vivacity. The success of his orations caused Disraeli to offer him the bishopric of Peterborough. He justified his appointment by his magnificent speech when the Disestablishment Bill reached the House of Lords in 1869, and then plunged into diocesan and general work in England. He preached three remarkable sermons on Christian Evidence in Norwich Cathedral in 1871. He took up the temperance question, and declared in the House of Lords that he would rather see “England free than England compulsorily sober,” an utterance which the extreme advocates of total abstinence misquoted and attacked. He was also a supporter of the movement for abolishing the recitation of the Athanasian Creed in the public services of the Church of England, believing, as he said, that the “presence” of the damnatory clauses, “as they stand and where they stand, is a real peril to the Church and to Christianity itself,” and that those clauses “are no essential part” of the creed. The project was laid aside in consequence of the hostility of a large body of the clergy, reinforced by the threat of Dr Pusey and Canon Liddon to abandon their offices if it were carried. Magee took a prominent part in the Ritual controversy, opposing what he conceived to be romanizing excess in ritual, as well as the endeavour of the opposite party to “put down Ritualism,” as Disraeli expressed it, by the operation of the civil law. His incisive way of putting things earned for him the title of the “Militant Bishop,” but, as he himself remarked in relation to this title, his efforts were ever for peace. Unfortunately for the Church, he was not elevated to the see of York until his energies were exhausted. He died on the 5th of May 1891, about four months after his appointment. Magee’s manifold activities, his capability as an administrator, his sound judgment, and his remarkable insight into the ecclesiastical problems of his time, rank him among the most distinguished of English prelates.
See Life and Letters, by Canon MacDonnell (2 vols. 1896).

MAGELLAN, FERDINAND (in Sp. Fernando Magallanes, in Port. Fernão de Magalhães) (c. 1480-1521), the first circumnavigator of the globe, was born at Sabrosa in the Villa Real district of the Traz-os-Montes province of Portugal. He was a son of Pedro de Magalhães, and belonged to the fourth order of Portuguese nobility (fidalgos de cota de armas). He was brought up as one of the pages of Queen Leonor, consort of King John (João) II “the Perfect.” In 1495 he entered the service of Manuel “the Fortunate,” John’s successor, and in 1504 enlisted as a volunteer for the Indian voyage of the first Portuguese viceroy in the East, Francisco d’Almeida. He sailed on the 25th of March 1505; was wounded at Cannanore on the 16th of March 1506; was then sent with Nuno Vaz Pereira to Sofala to build a Portuguese fortress at that place; returned to India early in 1508; and was again wounded at the battle of Diu on the 3rd of February 1509. At Cochin (Aug. 19, 1509) he joined Diogo Lopes de Sequeira on his famous voyage intended for the Spice Islands, when the Portuguese almost fell victims to Malay treachery at Malacca. In this crisis he fought bravely and skilfully (though it is not true, as often asserted, that he discovered the Malay plot); and before the 10th of October 1510 he had been rewarded for his many services with the rank of captain. He again distinguished himself at the taking of Malacca by Albuquerque (July-Aug., 1511), and was then sent on by the viceroy with Antonio d’Abreu to explore the Spice Islands (Moluccas). Leaving Malacca at the end of December 1511, this squadron sailed along the north of Java, passed between Java and Madura, left Celebes on their left, coasted by the Gunong Api volcano, touched at Bura, and so reached Amboyna and Banda. At the last-named they found 303 such abundance of spices that they came straight back to Malacca without visiting Ternate, as had been intended.
Magellan returned to Portugal in 1512. On the 14th of July of that year he was raised to the rank of fidalgo escudeiro; and in 1513 he accompanied a Portuguese expedition against Azamor in Morocco. The city was taken on the 28th-29th of August 1513; but Magellan was subsequently wounded, and lamed for life, in a sortie; he was also accused of trading with the Moors. The accusation was subsequently dropped, but Magellan fell into disfavour with King Manuel, who let him understand that he would have no further employment in his country’s service (after the 15th of May 1514). Magellan formally renounced his nationality, and went to offer his services to the court of Spain. He reached Seville on the 20th of October 1517, and thence went to Valladolid to see Charles V. With the help of Juan de Aranda, one of the three chief officials of the India House at Seville, and of other friends, especially Diogo Barbosa, a Portuguese like himself, naturalized as a Spaniard, who had acquired great influence in Seville, and whose daughter he now married, he gained the ear of Charles and of the powerful minister, Juan Rodriguez de Fonseca, bishop of Burgos, the persistent enemy of Columbus, the steady supporter of his great successor. Magellan proposed to reach the Spice Islands of the East Indies by the west; for that purpose he hoped to discover a strait at the extreme south of South America, and is said to have declared himself ready to sail southwards to 75° to realize his project. Ruy Faleiro the astronomer, another Portuguese exile, aided him in the working out of his plan, and he found an invaluable financial ally in Christopher de Haro, a member of a great Antwerp firm, who owed a grudge to the king of Portugal. On the 22nd of March 1518, Magellan and Faleiro, as joint captains-general, signed an agreement with Charles V., by which one-twentieth of the clear profits were to fall to them; further, the government of any lands discovered was vested in them and their heirs, with the title of Adelantados. On the 10th of August 1519, the fleet of five vessels, under Magellan’s command, left Seville and dropped down the Guadalquivir to S. Lucar de Barrameda, at the mouth of the river, where they remained more than five weeks. On the 20th of September the armada put to sea. Of the vessels which composed it, the “Trinidad” was the flagship, and the “Vittoria” the only one which accomplished the circumnavigation. The crew, officers, volunteers, &c., numbered about 270-280, of whom the names of 268 are preserved; 237 of these received pay; at least 37 were Portuguese, 30 or more Italians (mostly Genoese), 19 French, 1 English, 1 German. Only 31 returned in the “Vittoria”; 4 survivors of the crew of the “Trinidad” reappeared later. Antonio Pigafetta of Vicenza, an Italian gentleman who has left the best history of the voyage, went as a volunteer in Magellan’s suite. Faleiro stayed behind, having cast his horoscope and found that the venture would be fatal to him. The fleet was well armed, and the total cost of equipment was 8,751,000 maravedis, or £5032 (equal to over £50,000 in present value). Three-quarters were defrayed by the Spanish Crown, one-quarter by Christopher Haro and his friends. Before starting, Magellan made his will and addressed a memorandum to Charles V., assigning geographical positions connected with the controversy he was intending to settle: viz., the proper drawing of a demarcation-line between the spheres of Spain and Portugal in the East Indies, and the inclusion of the Moluccas within the Spanish sphere.
Steering south-west and calling at Teneriffe (Sept. 26-Oct. 3), Magellan sighted South America at Cape St Augustine, near Pernambuco on the 29th of November; thence he followed the east coast of the New World down to the La Plata estuary, which he examined in the hope of finding a passage at this point (Jan. 11-Feb. 6, 1520). On the 31st of March following, he arrived at Port St Julian (in 49° 20′ S.) where he wintered. Here he crushed a formidable mutiny (April 1-2), and made acquaintance with the natives, whom he called Patagonians (“Big Feet”), whose great size and lofty stature are magnified by Pigafetta to gigantic proportions. Leaving Port St Julian on the 24th of August 1520, he discovered on the 21st of October the cape of the Eleven Thousand Virgins, the eastern entrance of the long-sought passage. Through this strait, 360 m. long, often narrow and very tortuous, fringed by snow-clad mountains, he guided his armada for thirty-eight days, weakened by the desertion of one vessel (the “S. Antonio”). On the 21st of November a council of pilots and captains was held to consider the continuation of the voyage, and on the 28th of November the fleet rounded Cabo Deseado, the “desired” western terminus of the strait, variously called by the first discoverers, “Victoria Strait,” “Strait of the Patagonians,” “of all Saints,” “of the Eleven Thousand Virgins,” or “of Magellan,” now only known by the last of these names. To the south of the passage lay the forbidding land “stark with eternal cold,” which from the many fires here observed Magellan named “Tierra del Fuego.” The expedition now entered the “Great South Sea,” first sighted by Vasco Nuñez de Balboa (q.v.), which, from the steady and gentle winds that drove the fleet across the immeasurable expanse, was by Magellan called “Pacific.” For ninety-eight days Magellan crossed this sea, almost beyond the grasp of man’s mind for vastness (as Maximilian of Transylvania puts it), from Cabo Deseado to the Ladrones. On the whole transit he discovered only two islands, sterile and uninhabited, which he called “St Paul’s” (Jan. 24, 1521) and “Shark Island” (Feb. 3). The first of these has been identified with Puka Puka in the Tuamotu Archipelago, the second with Flint Island in the Manihiki group; neither identification seems convincing. For most of these ninety-eight days the explorers had no fresh provisions, little water (and that bad), and putrid biscuit; the ravages of scurvy became terrible. The worst anticipations of Magellan (“he would push on, if they had to eat the leather of the rigging”) were realized; ox-hides, sawdust, and rats became coveted food. At last, on the 6th of March 1521, the Ladrones (so named by Magellan from the thievish habits of the natives) came in sight, Guam being probably the first port of call. Here the fleet rested, watered, revictualled and refitted; on the 9th of March they started again westward; and on the 16th of March sighted the southern point of Samar Island in the archipelago, since 1542 called the Philippines, but named by Magellan, its first discoverer, after St Lazarus. On the 7th of April the squadron arrived at Cebu, south-west of Samar, in the heart of the Philippines; here Magellan contracted a close friendship and alliance with the treacherous native sovereign, who professed Christianity the better to please and utilize his Catholic friends. Undertaking an expedition to conquer, for the Catholic faith and the king of Cebu, the neighbouring island of Mactan, Magellan was killed there in a fight with the islanders (April 27, 1521). The king of Cebu after this got into his power several of the leading personages of the squadron, including Juan Serrano, one of the two admirals elected to replace Magellan, and murdered them. The survivors, burning one of the three remaining vessels, left the Philippines, and made their way to the Moluccas (Nov. 6), visiting Borneo on the way (July 9-Sept. 27, 1521). At Tidor a heavy cargo of cloves was taken in; the “Trinidad,” becoming leaky, stayed behind with her crew; and the “Vittoria,” under Juan Sebastian del Cano, proceeded to Europe alone (Dec. 21, 1521). To double the Cape of Good Hope the “Vittoria” reached between 40° and 41° S. (April 7-16, 1522) and suffered from contrary winds, heavy seas, scurvy and starvation. In the Cape Verde Islands (July 9-15, 1522) thirteen of the crew were detained prisoners by the Portuguese. Only thirty-one men returned with del Cano to Seville in the first vessel that had ever made the tour of the earth. Though Magellan had not quite reached the Spice Islands when he fell at Mactan, his task had then been accomplished. He had already reached and passed the longitude of the Moluccas, where he had already been; the way home from the Philippines by the Indian Ocean and the Cape of Good Hope was perfectly known to the Portuguese, himself included. Magellan’s name has never received its due recognition in 304 general history. It ranks with those of Columbus, Marco Polo, and Henry the Navigator. The circumnavigation of the globe is as great an event as the discovery of America. Magellan achieved what Columbus planned—the linking of west Europe with east Asia by direct transit over the western ocean. Had America not intervened, the project of 1492 must have failed; by 1519 European pioneers had formed a more adequate notion of the task and its magnitude.
Magellan’s Straits, the Magellanic clouds (not first observed by him), and Magellan’s Land—a name long given to Patagonia and that hypothetical southern continent of which Tierra del Fuego was considered only a portion, and now again bestowed by Chile on her territory in the extreme south—preserve the memory of the first circumnavigator. The largest of the oceans has also kept the flattering name given to it by the man who first crossed it.
No record of his exploits was left by Magellan himself; and contemporary accounts are less detailed and consistent than could be wished. The best is that of Antonio Pigafetta, a volunteer in the fleet. It is printed in Ramusio, and exists in four early MS. copies, one in Italian and three in French. The latter was perhaps the original language of this work, which was addressed by Pigafetta, as a knight of Rhodes, to the Frenchman Villiers de l’Isle Adam, grand master of the order of the Hospital of St John. But this view is rejected by J. A. Robertson (see below), who believes the Ambrosian MS. to be the ultimate text. See the Primo viaggio intorno al mondo, otherwise the Navigation et descouvrement de la Indie supérieure faicte par moi Anthoyne Pigapheta, Vincentin, chevallier de Rhodes, probably published in 1524 (in August of that year Pigafetta obtained leave to print his book in Venice). Of the three French MSS., two are in the Bibliothèque Nationale, Paris (5650 and 24,224 Fr.), the latter is wrongly supposed by Thomassy, followed by Lord Stanley of Alderley, to have been the copy presented by Pigafetta to the regent of France, Marie Louise of Savoy, mother of Francis I. The third French MS., often called the MS. of Nancy, first noticed by Thomassy in 1841, was bought by Sir Thomas Phillipps at Libri’s sale, and became MS. Phillipps 16,405. The Italian MS. is in the Ambrosian library at Milan. From this Carlo Amoretti, prefect of the Ambrosiana, published his Italian edition of Pigafetta in 1800; a French translation of this, by Amoretti himself, was issued by H. J. Jansen, 1801. An English version of Pigafetta was made by Richard Eden in his Decades of the Newe Worlde (London, 1555). The earliest printed edition, apparently a summary of the Italian MS., was issued in French by Simon de Colines of Paris about 1525. The earliest Italian edition is of 1534 (or 1536).
Other authorities are: (1) The narrative of an unknown Portuguese in Ramusio’s Navigationi et viaggi; (2) the Derrotero or Log-Book in the Seville Archives, supposed to be the work of Francisco Albo, contramaestre of Magellan’s flagship, the “Trinidad”: this consists mainly of nautical observations; (3) the narrative of the so-called Genoese pilot, written in excellent Portuguese, and printed in vol. iv. of the Collecão de noticias of the Lisbon Academy; (4) various informaciones and other papers in the Seville Archives, especially bearing on the mutiny; (5) the letter of Maximilian of Transylvania, under-secretary to Charles V., to the cardinal of Salzburg; (6) the references in Correa and Herrera, often based on good information, and adding points of interest to other records. Of these (1)-(3), (5), and an instance of (6) are translated in the Hakluyt Society’s volume. Magellan’s two wills (i) executed at Belem on the 17th of December 1504, on the eve of his departure with Almeida, (ii) executed at Seville on the 24th of August, 1519, just before starting on his voyage round the world, are both of some value for his life.
See also Lord Stanley of Alderley, The First Voyage round the World by Magellan, translated from ... Pigafetta, &c., Hakluyt Society (London, 1874); Diego de Barros Arana, Vida e viagems de Fernão de Magalhães, a trans. of the Spanish life by Fernando de Magalhães Villas Boas (Lisbon, 1881); F. H. H. Guillemard, Life of Magellan (London, 1890); Magellan ... the original text of the Ambrosian MS. (of Pigafetta), with English translation, notes, bibliography, &c., by J. A. Robertson (Cleveland, U.S.A., 1906). Before the appearance of this indispensable work, the best edition of Pigafetta had been in vol. iii. part 5 of the Raccolta di documenti e studi pubblicati nella r. commissione colombiana, edited by Andrea da Mosto (Rome, Ministry of Public Instruction, 1894).

MAGELLANIC CLOUDS (named after Ferdinand Magellan), two cloud-like condensations of stars in the southern constellation of Mensa about 69° S. Dec. and between 5° and 5° 40′ of R. A. They are remarkable in the resemblance of their stars as regards spectra and physical constitution to the stars of the Milky Way, though entirely detached from that object.

MAGENTA, a town of Lombardy, Italy, in the province of Milan, 16 m. by rail W. of Milan city, 364 ft. about sea-level situated in the midst of rice-fields. Pop. (1901), 8012. It manufactures silks and matches, and is famous for the battle (1859) in which the allied French and Piedmontese defeated the Austrians (see Italian Wars). A memorial chapel and a monument were erected on the battle-field in 1862. A crimson-purple aniline dye, discovered about the time of the battle, was given from it the name of “magenta.”

MAGGIORE, LAGO (Lacus Verbanus of the Romans; Fr. Lac Majeur; Ger. Langensee), the most extensive of the lakes that extend along the foot of the Alps in Lombardy, N. Italy. Its area is about 83 sq. m., its length 37 m., its greatest width 5½ m., and its greatest depth 1198 ft., while its surface is 646 ft. about sea-level. It is mainly formed by the Ticino (Tessin) River, flowing in at the north and out at the south end, on its way to join the Po, but on the west the lake receives a very important tributary, the Toce or Tosa River, which flows down through the Val d’Ossola from the mountains around the Simplon Pass. Other important affluents are the Maggia (N.W.) and the Tresa (E.). The upper end of the lake (about 16 sq. m.) is in the Swiss canton of Ticino (Tessin). Locarno, at the northern or Swiss end, is 14 m. by rail S.W. of Bellinzona on the St Gotthard line. There is a railway along the south-eastern shore, from Magadino (10½ m. S.W. of Bellinzona) to Sesto Calende (36½ m.), at the southern end of the lake and 20 m. by rail from Novara. The east shore of the lake is reached at Luino by a steam tramway from Ponte Tresa on the lake of Lugano (8 m.), while the direct Simplon line runs along the west shore of the lake for 15½ m. from near Pallanza past Baveno and Stresa to Arona, which is 23 m. by rail from Novara. On the east shore are Luino (Ital. Luvino) and Laveno. On the west shore are (reckoning from N. to S.) Cannobio, Pallanza, Baveno, Stresa and Arona. Opposite (S.E.) Baveno are the famous Borromean Islands, on the largest of which (Isola Bella) are very remarkable gardens (formed about 1617), wherein many tropical plants flourish abundantly, while south-west of Baveno rises the glorious view-point of the Monte Mottarone (4892 ft.) between Lago Maggiore and the northern end of the Lake of Orta. In the morning the tramontana wind blows from the north down the lake, while in the afternoon the inverna, blowing from the south, prevails. The first steamer was placed on the lake in 1826.

MAGIC1 (i.e. “art magic”; Lat. ars magica), the general term for the practice and power of wonder-working, as depending on the employment of supposed supernatural agencies. Etymologically the Gr. μαγεία meant the science and religion of the magi, or priests of Zoroaster, as known among the Greeks; in this sense it was opposed to γοητεία (? necromancy) and φαρμακεία (the use of drugs); but this distinction was not universally recognized, and γοητεία is often used as a synonym of μαγεία. There is no general agreement as to the proper definition of “magic,” which depends on the view taken of “religion.”
I.—Nature of Magic
Theories of Magic.—Existing theories of magic may be classified as objective or subjective. The objective school regards magic as a thing by itself, entirely distinct from religion, recognizable by certain characteristics, and traceable to a definite psychological origin. Magic, on this view, is a system of savage science based on imaginary laws supposed to operate with the regularity ascribed to natural laws by the science of to-day. If practices prima facie magical form part of the recognized ritual of religion, it is because the older ideas have persisted and at most assumed a veneer of religion. For the subjective school, on the other hand, only those rites are magical which their practitioners qualify with the name of magic; there is no inherent quality which makes a rite magical; practices based on a belief in the law of sympathy may be religious as well as magical; rites may pass from the category of religion to that of magic when public recognition is withdrawn from them.
a. For E. B. Tylor the distinguishing characteristic of magic is its unreality; it is a confused mass of beliefs and practices, and their unity consists in the absence of the ordinary nexus of natural cause and effect. Under the general head of magic he distinguishes (i) a spiritual and (ii) a non-spiritual element. (i) The former is made up of such rites as involve the intervention of spiritual beings, ghosts of the dead, demons or gods; hence, in Tylor’s view, this form of magic is merely an inferior branch of religion. (ii) The non-spiritual part, but for which the category of magic would be unnecessary, depends on imagined powers and correspondences in nature; it is merely imperfect reasoning, the mistaking of an ideal connexion for a real one. When the American Indian medicine man draws the picture of a deer on a piece of bark and expects that shooting at it will cause him to kill a real deer the next day, he mistakes a connexion which exists only in the mind of the sorcerer for a real bond independent of the human mind.
b. In J. G. Frazer’s view all magic is based on the law of sympathy—i.e. the assumption that things act on one another at a distance through a secret link, due either to the fact that there is some similarity between them or to the fact that they have at one time been in contact, or that one has formed part of the other. These two branches of “sympathetic magic” Frazer denominates “homoeopathic magic” and “contagious magic.” Homoeopathic or imitative (mimetic) magic may be practised by itself, but contagious magic generally involves the application of the imitative principle. (i) One of the most familiar applications of the former is the belief that an enemy may be destroyed or injured by destroying or injuring an image of him. (ii) Under the head of contagious magic are included such beliefs as that which causes the peasant to anoint the weapon with which he has been injured, which, according to Frazer, is founded on the supposition that the blood on the weapon continues to feel with the blood in the body. (iii) Implicitly Frazer seems to distinguish a third kind of magic; “the rain-charm,” he says, “operates partly or wholly through the dead ... in Halmahera there is a practice of throwing stones on a grave, in order that the ghost may fall into a passion and avenge the disturbance, as he imagines, by sending heavy rain.” Here there is no assumption of an invariable course of nature set in motion by magical rites; save that it is coercive and not propitiatory, the practice does not differ from ordinary religious rites.
In his theory of the origin of magic Frazer follows the associationist school. But, as R. R. Marett has pointed out in a criticism of the associationist position, it is proved beyond question that even in the individual mind association by similarity, contiguity or contrast, is but the passive condition, the important element being interest and attention. Frazer assumes that magic has everywhere preceded religion: man tried to control nature by using what he conceived to be immutable laws; failing in this he came to believe in the existence of higher powers whom he could propitiate but not coerce; with this transformation religion appeared on the scene; the priest supplanted the magician, at least in part, and the first blows were struck in the perennial warfare of magic and religion. Frazer recognizes, however, that magical and religious rites are at the present day, and have been in historical times, frequently intermingled; it should be noted that for him religion means propitiation and that he does not recognize the existence of anything beyond magic among the aborigines of Australia. His theory is based on a selection of facts, and not on the whole body of beliefs and rites recognized as magical, among which are many wherein spirits figure. Frazer’s position appears to be that such rites are relatively late and may be neglected in framing a definition of magic. It may be perfectly true that the idea of magic has been progressively extended; but belief in transformation is also for Dr Frazer magical; this belief is certainly primitive; yet sympathy will not explain it, as it should if Frazer’s theory is correct.
c. L. Marillier distinguished three classes of magic: (i) the magic of the word or act; (ii) the magic of the human being, independent of rite or formula, &c.; (iii) the magic which demands at once a human being of special powers (or in a special state) and the use of certain forms. (i) Under the first head he included such rites as mimetic dances, rain-making, disease-making, and sympathetic magic generally. Some of these rites are conceived to affect the course of nature directly, as by influencing winds or the sun, others do so through the intermediary of a god or spirit, who controls the course of nature, and is himself coerced by man with magical acts and incantations. (ii) Other rites cannot be performed by all and sundry: ceremonial purity, initiation or other conditions may be needed to make the charm effective. (iii) Individuals are found who are invested with magical power (mana), whose will rules the universe, whose simple words bring rain or sunshine, and whose presence gives fertility to the fields. Sometimes this power is an attribute of the individual, sometimes it is bound up with the office which he fills. In many cases the magical powers of both men and other objects, animate and inanimate, are put down to the fact that a god resides in them.
d. Hubert and Mauss have made the most complete and systematic study of magic which has yet appeared. They hold that, implicitly at any rate, magic is everywhere distinguished from other systems of social facts; in order to be magical an act or belief must be common to the whole of a society; the acts which the whole of a group does not regard as efficacious are not, for this school of thought, magical: consequently the practices of gamesters, &c., do not come under the head of magic. Magic is essentially traditional; a distinguishing characteristic of primitive thought is that the individual mind is markedly unoriginal; and this feature is as prominent, if not more so, in magic as in technology or any other important element in human life. The correspondence between magic and technology can be traced far; for the gestures of the craftsman are as strictly prescribed as the ritual acts of the magician or priest: but in magic the results of the gestures are not of the same order as the results of the craftsman’s movements, and herein lies the distinction between magic and technic. The distinction between magic and religion is to be sought not in the sympathetic character of the former, nor in any supposed necessary sequence of cause and effect, nor yet in its maleficent character. Religion is prescribed, official, an organized cult. Magic is prohibited, secret; at most it is permitted, without being prescribed. Three important laws may be traced in the machinery of magical operations—magical power flows along channels determined by the contiguity, similarity or contrast of the object of the act and the object to be affected; but these laws do not suffice to explain magic: equally insufficient are the demonological theory and the theory of properties inherent in the objects used in magical operations. The underlying idea of magic is dynamical; to this power may be given the name of mana (see below), of which sanctity is a special development. This mana operates in a milieu different from the ordinary material world; distance is no obstacle to contact; wishes are immediately realized; but law reigns in the milieu in question, necessary relations are conceived as existing. The notion of time as it is found in the world of magic is even more alien from European ideas; the notion of sanctity enters into it, but time in magic and religion is qualitative rather than quantitative. The homogeneity of periods of time not depending on their duration, conventional numbers are employed; successive periods of time apparently equal are not so for the primitive consciousness; and both in magic and religion periods are homogeneous by reason of occupying the same position in the calendar.
e. For A. Lehmann magic is the practice of superstitions, and his explanation of magic is purely psychological. Relying mainly on modern spiritualism for his examples, he traces magic back to illusions, prejudices and false precepts due to strained attention. This is ultimately also the view of Hubert and Mauss, who hold that “at the root of magic are states of consciousness which generate illusions; and that these states are not individual but collective and arise from the amalgamation of the ideas of a given person with those current in the society of which he forms a part.” The reunion of a group supplies a soil in which illusions flourish readily, and it is important to note that in magic and religion attention is above all necessary for the success of a rite, witness the frequent rule imposing silence; but this concentration of attention is precisely calculated to favour illusions; it is indeed the ordinary condition of successful hypnotism; even in civilized countries collective hallucinations without verbal suggestion are not unknown.
f. R. R. Marett regards religion and magic as two forms of a social phenomenon originally one and indivisible; primitive man had an institution which dealt with the supernatural, and in this institution were the germs of both magic and religion, which were gradually differentiated; magic and religion differ in respectability; religion is always the higher, the accepted cult; but between what is definitely religious and what is definitely magical lies a mass of indeterminate elements, such as “white-magic,” which do not attain to the public recognition of religion, nor suffer the condemnation meted out to the indisputably magical. For primitive man the abnormal was the supernormal, and the supernormal was the supernatural, the object of fear; this is especially evident when we consider the case of taboo; it may be regarded as a public scare for which no particular individual is responsible, which becomes traditional along fairly constant lines, growing as it goes. Mana was attributed to taboo objects, among which were men in any way abnormal, whether as geniuses or idiots; and such men were expected to exercise their powers for the good of society; hence came into existence the professional medicine man; man originally argued from cause to effect and not vice versa. Priest and magician were originally one; but the former, learning humility in the face of might greater than his own, discarded the spell for the prayer and prostrated himself before a higher power.
Definition of Magic.—To arrive at a definition of magic we may either follow the a priori road mapped out by Frazer and decline to recognize the distinction actually drawn by various societies between magical and religious practices; or we may ask what magic and corresponding terms actually connote. Frazer’s method ignores the fact that magic, like religion, is an institution, i.e. a product of society, not of any single individual; there is no more reason to suppose that a child reared in isolation would develop any kind of magical practices than that it would invent for itself a religion; but if this is the case, 306 the associationist account of magic cannot be true. It is therefore by an analysis of actually existing practices that we must define and limit the term magic. There is, however, a serious difficulty in the way of determining the attitude of non-European peoples towards religio-magical practices; general terms are things of slow growth; it is therefore prima facie improbable that peoples in the lower stages of culture will have anything corresponding to our terms “religion” and “magic”; moreover, if we are right in assuming the fundamental unity of the two, it is by no means certain that they have even the consciousness of any distinction. Even when this consciousness is present, it by no means follows that the whole of the field is mapped out according to our categories; there will be a large indeterminate area which is neither magical nor religious. This suggests that the consciousness of the educated Occidental, for which the spheres of magic and religion in civilized society are sharply defined and contrasted, should be the ultimate arbiter; but here again we are confronted by a difficulty, for, to the educated man, the characteristic of magic is its unreality, and this does not help us to distinguish primitive magic and religion.
We must, it appears, determine the relation of magic to religion by an analysis of the conceptions of those who believe in both; but in so doing we must consider that, like all other institutions, magic has a history. Even if we go back to the 16th century and take the view of magic then held by the average European, it is still a complex idea. When we ask what the most primitive races now on the earth regard as magic, we are applying to their ideas a touchstone made for a very different age and culture; as well might we ask what their theory of knowledge is. If, however, we reverse the process and ask what elements of primitive institutions correspond most nearly to later conceptions of magic, we can at once say that the forbidden and private arts are the prototypes of the magic of later times. Magic is therefore the practice of maleficent arts which involve the use of religio-magical power, with perhaps a secondary idea of the use of private arts, which are to benefit, not the community as a whole, but a single individual. Religion in the lower stages of culture is essentially the tribal creed which all practise and in which all believe; if therefore an individual has a cult of his own, even if otherwise indistinguishable from a public cult, it is for this very reason on a lower plane, and probably corresponds in a degree to what is later regarded as magic. But our information as to the attitude of the uncivilized towards magico-religious rites in general is seldom sufficiently clear; our terminology is influenced by the prepossession of alien observers whose accounts cannot be assumed to correspond to the native view of the case.
Magico-religious Force.—The mere fact that we cannot draw an exact line between magic and religion suggests that they may have some fundamental feature in common. Both terms have greatly changed their connotation in the course of their existence; religio seems to have meant originally καταδεσμός (magical spell), and Pliny says that μαγεία is a deceptive art compounded of medicine, religion and astrology. Among the Greeks, on the other hand, μαγεία occupied a respectable position. More important is the fact that taboo (q.v.) is both religious and magical. There is a universal tendency to regard as magical the religions of alien races, as well as national religions which have been superseded; Leland tells us that witchcraft in Italy is known as la vecchia religione. An examination of the ideas of primitive peoples shows that there is a widely found notion of a power which manifests itself both in religion and magic. Observers have often been content to describe ceremonies without attempting to penetrate to the fundamental ideas which underlie them; this is particularly the case with magic, and only recently have anthropologists realized that in many primitive societies exists a fairly well-defined idea of magico-religious power, to which the generic name of mana, from the Melanesian word, has been given.
a. Mana in Melanesia is a force, a being, an action, a quality, or a state; it is transmissible and contagious, and is hence associated with taboo; it may be regarded as material and seen in the form of flames or heard; it is the power which is inherent in certain spirits, among which are included such of the dead as are denominated tindalos; it may also be a force inherent in some inanimate object, such as a stone which causes the yams to grow, but it is a spiritual force and does not act mechanically; it is the power of the magician and of the rite; the magic formula is itself mana. There seem to be a variety of manas, but probably the underlying idea is essentially one, though it does not follow that the Melanesians have arrived at the consciousness of this unity. Hubert and Mauss go even further and regard all force as mana; it is a quality added to objects without prejudice to their other qualities, one which supplements without destroying their mechanical action.
b. Similar ideas are found in other areas. (i) The continental Malays have a word Kramât (hrm), which means sacred or magical; in Indo-China the Bahnars use the word deng; in Madagascar hasina seems to embody in part the same notion. (ii) In Africa the idea is less apparent; perhaps the ngai of the Tanganika tribes comes nearest to the notion of mana; on the Congo nkici has a similar but more restricted sense. (iii) In Australia there are two, or perhaps three, kinds of magical power distinguished by the aborigines; all over the continent we find the maleficent power, boolya in West Australia, arungquiltha in the central tribes, koochie in New South Wales; the central tribes have certain objects termed churinga, to which magical power (which we may term churinga) is attributed; the power of magicians is held to reside in certain stones, called atnongara, and in this we must, provisionally at any rate, see a third kind of magical power: churinga is beneficent and seems to originate with the mythical ancestors, whereas arungquiltha is of immediate origin, created by means of incantations or acquired by contact with certain objects; the power of the magicians seems to proceed from the ancestors in like manner. (iv) In America these ideas are widely found; the orenda of the Hurons has been elaborately described by J. N. B. Hewitt; everything in nature, and particularly all animate objects, have their orenda; so have gods and spirits; and natural phenomena are the product of the orenda of their spirits. Orenda is distinct from the things to which it is attached; the cry of birds, the rustle of the trees, the soughing of the wind, are expressions of their orenda; the voice of the magician is orenda, so are the prayer and the spell, and in fact all rites; orenda is above all the power of the medicine man. Among the Algonquins we find the word manitu, among the Sioux wakanda, mahowa, &c., among the Shoshones pokunt; all of which seem to carry, at least in part, the same signification. In Central America, according to Hubert and Mauss, naual or nagual is the corresponding term. (v) Traces of similar ideas may be found in more advanced nations; the Hindu brahman is identified by Hubert and Mauss as the correlative of mana; in Greece φύσις is possibly the echo of a similar idea; but we are yet far from having adequately fathomed the dynamical theories of pre-scientific days.
Origin of Magic.—The associationist theory of magic sets out with the assumption that primitive man began with general conceptions; he started with certain means at his disposal—the law of sympathy—by which he could, in his own belief, influence the outer world. But it is more probable that he argued from concrete instances and arrived little by little at abstract ideas of magical power.
a. Death and disease are universally regarded by uncivilized people as due to so-called “magic,” i.e. to non-natural causes. Primitive man was familiar with the wounds and bruises caused by physical means; he would naturally attribute any pain not so caused to the operation of analogous but invisible weapons, and eventually attempt to discover how he himself could apply on his own behalf the forces thus used against him. Similarly he may have asked himself to what causes were to be attributed the superiority of one man over another; he may have decided the problem by referring it to the superior power of the one, and then inquired in what way this power could in individual instances be increased. In fact we may say generally that man probably explained the already existing and happening by reference to the supernormal, and then endeavoured to guide the supernormal for his own benefit, direct or indirect.
b. Ritual, however (the primitive magico-religious plasm), is negative as well as positive. The corpse is uncanny, and man’s dread of the corpse may well have been an early development; this dread, become traditional, with accretions of various sorts, crystallized into taboo, the magico-religious prohibition. The notion of the uncanny, once arrived at, may have been exploited positively; psychical abnormalities are present among savage races in very different degrees; but if they were developed at an early stage in human history they doubtless suggested the possibility that man might exploit them for the collective advantage. But it by no means follows that beneficent rites were originally regarded as magical; and it should be noted that the initiator of the so-called magician in Australia is often the god of the tribe or nation. The limits of magic or its correlatives in the lower stages of culture are thus far undecided.
c. Magic as it represents itself to the Occidental mind of the present day, and perhaps to the great part of the inhabitants of the world, 307 seems to be a thing of gradual growth. (i) In the earlier stages there was probably no animistic feature about magic; it was essentially “the prohibited.” (ii) Then with the rise of animistic beliefs and practices came the association of the magician with demons—the spirits of the dead, or of animals, or unattached spirits—upon whose co-operation the powers of the magician are often now held to depend. These spirits were not in the position of gods; such recognition, worship, or cult as they received was often not a social institution, but the work of individuals, liable to fall into desuetude at the death of the individual, if not earlier. (iii) Again, the magical tends to be the less important and eventually the less respectable; therefore ancient cults which are conquered, like the religion of Rome by Christianity, come to be reckoned as within the sphere of magic and witchcraft. (iv) All non-animistic practices tend to become ipso facto magical; many ritual prohibitions fall under the head of negative magic. Religion is predominantly animistic, and with the rise of gods magic and religion become antagonistic. Thus rites of a neutral character, such as leechcraft, and perhaps agricultural ceremonies which are not absorbed by religion, tend to acquire the reputation of being magical, as also do all amulets and talismans, and, in fact, everything not directly associated with religion. We therefore arrive at a period when magic is distinguished as white, i.e. the laudable, or at least permitted form, and black, i.e. the prohibited form.
Magic and Demonology.—Primitive psychology tends to anthropomorphize and personify; it is in many of its stages inclined to an animistic philosophy. To this is due in part the difficulty of distinguishing magic from religion. In many rites there is no obvious indication that a spirit or personal being is concerned. A portion of the ceremonies in which the spirits of the dead are concerned falls under the head of religion (see Ancestor Worship), but in the very name “necromancy” (νεκρος, corpse) lies an implication of magic; and dealings with the departed are viewed in this light in many parts of the world, sometimes concurrently with a cult of ancestors. Side by side with the human souls we find demons (see Demonology); but on the whole only a small proportion of the world of spirits is recognized as powerful in magic; others, such as disease-spirits, are objects, not sources, of magical influence. Magic is sometimes made to depend upon the activity of demons and spirits, and it is true that the magician usually if not invariably has a spirit helper, often an animal; but there is no evidence that magical power had ever been confined to those who are thus aided. It is not easy to define the relation of fetishism (q.v.) to magic.
Magic and Science.—It is a commonplace that the sciences have developed from non-scientific beginnings; the root of astronomy is to be sought in astrology (q.v.), of chemistry in alchemy (q.v.), of leechcraft in the practices of the savage magician, who depends for much of his success on suggestion, conscious or unconscious, but also relies on a pharmacopeia of no mean extent. The dynamical theory of magic and religion brings primitive man from one point of view far nearer to the modern man of science than was previously suspected, we may fairly say that the Australians have an idea not unlike that of the transformation and conservation of energy, that this energy they store in accumulators, transmit by means of conductors, and so on. The discovery of these complicated ideas only serves to show how far the present-day peoples in the lower stages of culture have travelled from the primitive man who knew neither magic nor religion. But it is perhaps less in respect of abstract ideas than by its concrete investigations into properties, experiment and otherwise that magic has been the forerunner of science.
Magic and Divination.—Magic is an attempt to influence the course of events, divination (q.v.) to foresee them; but divination is frequently regarded as magical. It is certain that a large part of divination is religious, and the knowledge is explained as a message from the gods; but necromancy, the practice of discovering the future by consulting the dead, is in many respects essentially magical. Perhaps the magical character of divination may be in part explained, when we regard it as a group of practices in many varieties of which animism plays no part; for non-animistic ceremonies tend to be regarded as magical (cf. rain-making). Thus, heteroscopic divination seems to involve the idea of what may be termed a return current of magico-religious force; the event is not influenced, but itself determines the issue of the diviner’s experiment.
II.—Laws and Ritual of Magic
The practice of magic involves the belief in the operation of certain laws, and demands certain conditions. The number of positive rites is not unlimited; a certain rite tends to become stable and is finally used for all sorts of purposes; and each magician tends to specialize in this respect. Just as there are well-marked schools of magic, and the rain-maker is not the same as the fetish-man, so within the school there are various groups, differentiated not by the purposes at which they aim nor by the powers they claim to possess, but by the ceremonies which they practise. Chief among the laws lying at the base of magical practice is that of sympathy.
Sympathy.—That the law of sympathy is an essential element of magic is admitted equally by the associationist school and by its critics. Under the head of sympathy are embraced the laws of contiguity or contagion, of similarity or homoeopathy, and of contrariety or antipathy.
a. In its simplest form the law of contiguity asserts that whatever has once formed part of a body continues to form part of it or to represent it for magical purposes; thus, by obtaining possession of the parings of a person’s nails, or the clippings of his hair, and by working magic upon them, it is held to be possible to produce on the actual human body the effects which are in reality produced on the object of the magical rite. As is clear by the well-known case of the “life index,” the current of magical power may pass in either direction; if the life of a man is supposed to be bound up with the life of a tree, so that any injury to the tree reacts on the man, it is equally believed that the death of the man will not fail to be manifest by the state of the tree. In particular this sympathetic relation is predicated of wizards or witches and their animal familiars; it is then known by the name of “repercussion.” It is not only upon parts of the body that contagious magic can be worked; anything which has been in contact with the body, such as clothes, anything which has been in part assimilated by the body, such as the remains of food, and even representations of the body or of parts of it such as footprints, &c., may be used as objects of magical rites, in order to transmit to the human being some influence, maleficent or otherwise. The contact demanded may be actual, or mediate, for in Australia it suffices to connect the magician and his patient by a thread in order that the disease may be removed. (i) The use of clothes for magical purposes gives us perhaps the clue to the widespread custom of “rag-trees”; in nearly every part of the world it is the practice to suspend wool or rags to trees associated with some spirit, or, in Christian countries, with some saint, in order to reap a benefit; similarly nails are driven into trees or images; pins are dropped into wells, stones are cast upon cairns, and missiles aimed at various holy objects; but it cannot be assumed that the same explanation lies at the root of the whole group of practices. (ii) This law may perhaps be taken as the explanation of the “couvade”; in many parts of the world relatives, and in particular the father of a new-born child, are compelled to practise various abstinences, in order that the health of the child may not be affected, membership of the same family therefore establishes a sympathetic relation. (iii) In this direct transference of qualities is exemplified another magical process, which may also be referred to the operation of the law of sympathy; it is a world-wide belief that the assimilation of food involves the transference to the eater of the qualities, or of some of them, inherent in the source of the food; a South African warrior, for example, may not eat hedgehog, because the animal is held to be cowardly and the eater would himself become a coward; on the other hand, the flesh of lions is fit meat for brave men, because they at the same time transfer its courage to themselves.
b. The law of homoeopathy takes two forms. (i) The magician may proceed on the assumption that like produces like; he may, for example, take an image of wax or wood, and subject it to heat or other influences under the belief that it represents the human being against whom his malefice is directed, and that without any contact, real or pretended; so that any results produced on the image, which may be replaced by an animal or a portion of one, are equally produced in the human being. There need not even be any resemblance between the representation and the person or thing represented; a pot may serve to represent a village; hence step by step we pass from the representation to the symbol. (ii) The law of homoeopathy also manifests itself in the formula similia similibus curantur; the Brahman in India treated dropsy with ablutions, not in order to add to, but to subtract from, the quantity of liquid in the patient’s body. So, too, the yellow turmeric was held to be a specific for jaundice.
c. Here we approach the third class of sympathetic rites; it is clear that a remedy produces the contrary, when it cures the like; conversely, like by producing like expels its contrary.
Some statements of the law of sympathy suggest that it is absolute in its application. It is true that the current of magical power is sometimes held to be transmitted along lines indicated 308 by the law of sympathy, without the intervention of any volition, human or otherwise; thus, the crow which carries stray hairs away to weave them into the structure of its nest is nowhere supposed to be engaged in a magical process; but it is commonly held that the person whose hair is thus used will suffer from headache or other maladies; this seems to indicate that the law of sympathy operates mechanically in certain directions, though the belief may also be explained as a secondary growth. In general the operation of these laws is limited in the extreme. For example, the medieval doctrine known as the Law of Signatures asserted that the effects of remedies were correlated to their external qualities; bear’s grease is good for baldness, because the bear is a hairy animal. But the transference was held to terminate with the acquisition by the man of this single quality; in some magical books powdered mummy is recommended as a means of prolonging life, but it is simply the age of the remedy which is to benefit the patient; the magician who removes a patient’s pains or diseases does not transfer them to himself; the child whose parents eat forbidden foods is held to be affected by their transgression, while they themselves come off unharmed. The magical effects are limited by exclusive attention and abstraction; and this is true not only of the kind of effect produced but also as to the direction in which it is held to be produced.
The Magic of Names.—For primitive peoples the name is as much a part of the person as a limb; consequently the magical use of names is in some of its aspects assimilable to the processes dependent on the law of sympathy. In some cases the name must be withheld from any one who is likely to make a wrong use of it, and in some parts of the world people have secret names which are never used. Elsewhere the name must not be told by the bearer of it, but any other person may communicate it without giving an opening for the magical use of it. Not only human beings but also spirits can be coerced by the use of their names; hence the names of the dead are forbidden, lest the mention of them act as an evocation, unintentional though it be. Even among more advanced nations it has been the practice to conceal the real name of supreme gods; we may probably explain this as due to the fear that an enemy might by the use of them turn the gods away from those to whom they originally belonged. For the same reason ancient Rome had a secret name.
Magical Rites.—The magic of names leads us up to the magic of the spoken word in general. The spell or incantation and the magical act together make up the rite. (a) The manual acts are very frequently symbolic or sympathetic in their nature; sometimes they are mere reversals of a religious rite; such is the marching against the sun (known as widdershins or deisul); sometimes they are purificatory; and magic has its sacrifices just as much as religion. (b) There are many types of oral rites; some of the most curious consist in simply reciting the effect intended to be produced, describing the manual act, or, especially in Europe, telling a mythical narrative in which Christ or the apostles figure, and in which they are represented as producing a similar effect to the one desired; in other cases the “origin” of the disease or maleficent being is recited. Oral rites, which are termed spells or incantations, correspond in many cases to the oral rites of religion; they, like the manual rites, are a heterogeneous mass and hardly lend themselves to classification. Some formulae may be termed sympathetic; it suffices to name the result to be produced in order to produce it; but often an incantation is employed, not to produce a result directly, but to coerce a god or other being and compel him to fulfil the magician’s will. The language of the incantations often differs from that of daily life; it may be a survival of archaic forms or may be a special creation for magical purposes. In many languages the word used to express the idea of magic means an act, a deed; and it may be assumed that few if any magical ceremonies consist of formulae only; on the other hand, it is certain that no manual act in magic stands absolutely alone without oral rite; if there is no spoken formula, there is at least an unspoken thought. It is in many cases difficult to discover the relative proportions and importance of manual and oral acts. Not only the words but also the tone are of importance in magic; in fact, the tone may be the more important. Rhythm and repetition are no less necessary in oral than in manual acts. (c) As preliminaries, more seldom as necessary sequels to the central feature of the rite, manual or oral, we usually find a certain number of accessory observances prescribed, which find their parallel in the sacrificial ritual. For example, it is laid down at what time of year, at what period of the month or week, at what hour of the day a rite must be performed; the waxing or waning of the moon must be noted; and certain days must be avoided altogether. Similarly, certain places may be prescribed for the performance of the ritual; often the altar of the god serves magical purposes also; but elsewhere it is precisely the impure sites which are devoted to magical operations—the cemeteries and the cross roads. The instruments of magic are in like manner often the remains of a sacrifice, or otherwise consecrated by religion; sometimes, especially when they belong to the animal or vegetable world, they must be sought at certain seasons, May Day, St George’s Day, Midsummer Day, &c. The magician and his client must undergo rites of preparation and the exit may be marked by similar ceremonies.
Magicians.—Most peoples know the professional worker of magic, or what is regarded as magic. (a) In most if not all societies magic, or certain sorts of it, may be performed by any one, so far as we can see, who has mastered the necessary ritual; in other cases the magician is a specialist who owes his position to an accident of birth (seventh son of a seventh son); to simple inheritance (families of magicians in modern India, rain-makers in New Caledonia); to revelation from the gods or the spirits of the dead (Malays), showing itself in the phenomena of possession; or to initiation by other magicians. (b) From a psychical point of view it may probably be said that the initiation of a magician corresponds to the “development” of the modern spiritualistic medium; that is to say, that it resolves itself into exercises and rites which have for their object the creation or evolution of a secondary personality. From this point of view it is important to notice that certain things are forbidden to magicians under pain of loss of their powers; thus, hot tea is taboo to the Arunta medicine man; and if this seems unlikely to cause the secondary personality to disappear, it must be remembered that to the physiological effects, if any, must be added the effects of suggestion. Of this duplication of personality various explanations are given; in Siberia the soul of the shaman is said to wander into the other world, and this is a widely spread theory; where the magician is supposed to remain on earth, his soul is again believed to wander, but there is an alternative explanation which gives him two or more bodies. Here we reach a point at which the familiar makes its appearance; this is at times a secondary form of the magician, but more often is a sort of life index or animal helper (see Lycanthropy); in fact, the magician’s power is sometimes held to depend on the presence—that is, the independence—of his animal auxiliary. Concurrent with this theory is the view that the magician must first enter into a trance before the animal makes its appearance, and this makes it a double of the magician, or, from the psychological point of view, a phase of secondary personality. (c) In many parts of the world magical powers are associated with the membership of secret societies, and elsewhere the magicians form a sort of corporation; in Siberia, for example, they are held to be united by a certain tie of kinship; where this is not the case, they are believed, as in Africa at the present day or in medieval Europe, to hold assemblies, so-called witches’ Sabbaths; in Europe the meetings of heretics seem to be responsible for the prominence of the idea if not for its origin (see Witchcraft). The magician is often regarded as possessed (see Possession) either by an animal or by a human or super-human spirit. The relations of priest and magician are for various reasons complex; where the initiation of the magician is regarded as the work of the gods, the magician is for obvious reasons likely to develop into a priest, but he may at the same time remain a magician; where a religion has been superseded, the priests of the old cult are, for those who supersede them, one and all magicians; in the medieval church, priests were regarded as especially exposed to the assaults of demons, and were consequently often charged with working magic. The great magicians who are gods rather than men—e.g. kings of Fire and Water in Cambodia—enjoy a reverence and receive a cult which separates them from the common herd, and assimilates them to priests rather than to magicians. The function of the so-called magician is often said to be beneficent; in Africa the witch-doctor’s business is to counteract evil magic; in Australia the magician has to protect his own tribe against the assaults of hostile magicians of other tribes; and in Europe “white magic” is the correlative of this beneficent power; but it may be questioned how far the beneficent virtue is regarded as magical outside Europe.
Talismans and Amulets.—Inanimate objects as well as living beings are credited with stores of magical force; when they are regarded as bringing good, i.e. are positive in their action, they may be termed “talismans”; “amulets” are protective or negative in their action, and their function is to avert evil; a single object may serve both purposes. Broadly speaking, the fetish, whose “magical” properties are due to association with a spirit, tends to become a talisman or amulet. The “medicine” of the Red Indian, originally carried as means of union between him and his manito, is perhaps the prototype of many European charms. In other cases it is some specific quality of the object or animal which is desired; the boar’s tusk is worn on the Papuan Gulf as a means of imparting courage to the wearer; the Lukungen Indians of Vancouver Island rub the ashes of wasps on the faces of their warriors, in order that they may be pugnacious. Some Bechuanas wear a ferret as a charm, in the belief that it will make them difficult to kill, the animal being very tenacious of life. Among amulets may be mentioned horns and crescents, eyes or their representations, and grotesque figures, all of which are supposed to be powerful against the Evil Eye (q.v.). 309 Tylor has shown that the brass objects so often seen on harness were originally amuletic in purpose, and can be traced back to Roman times. Some amulets are supposed to protect from the evil eye simply by attracting the glance from the wearer to themselves, but, as a rule, magical power is ascribed to them.
Evil Magic.—The object of “black” magic is to inflict injury, disease, or death on an enemy, and the various methods employed illustrate the general principles dealt with above and emphasize the conclusion that magic is not simply a matter of sympathetic rites, but involves a conception of magical force. (a) It has been mentioned that contagious magic makes use of portions of a person’s body; the Cherokee magician follows his victim till he spits on the ground; collecting the spittle mingled with dust on the end of a stick, the magician puts it into a tube made of a poisonous plant together with seven earth worms, beaten into a paste, and splinters of a tree blasted by lightning; the whole is buried with seven yellow stones at the foot of a tree struck by lightning, and a fire is built over the spot; the magician fasts till the ceremony is over. Probably the worms are supposed to feed on the victim’s soul, which is said to become “blue” when the charm works; the yellow stones are the emblem of trouble, and lightning-struck trees are reputed powerful in magic. If the charm does not work, the victim survives the critical seven days, and the magician and his employer are themselves in danger, for a charm gone wrong returns upon the head of him who sent it forth. (b) In homoeopathic magic the victim is represented by an image or other object. In the Malay Peninsula the magician makes an image like a corpse, a footstep long. “If you want to cause sickness, you pierce the eye and blindness results; or you pierce the waist and the stomach gets sick. If you want to cause death, you transfix the head with a palm twig; then you enshroud the image as you would a corpse and you pray over it as if you were praying over the dead; then you bury it in the middle of the path which leads to the place of the person whom you wish to charm, so that he may step over it.” Sometimes the wizard repeats a form of words signifying that not he but the Archangel Gabriel is burying the victim; sometimes he exclaims, “It is not wax I slay but the liver, heart and spleen of So-and-so.” Finally, the image is buried in front of the victim’s doors. (c) Very widespread is the idea that a magician can influence his victim by charming a bone, stick or other object, and then projecting the magical influence from it. It is perhaps the commonest form of evil magic in Australia; in the Arunta tribe a man desirous of using one of these pointing sticks or bones goes away by himself into the bush, puts the bone on the ground and crouches over it, muttering a charm: “May your heart be rent asunder.” After a time he brings the irna back to the camp and hides it; then one evening after dark he takes it and creeps near enough to see the features of his victim; he stoops down with the irna in his hand and repeatedly jerks it over his shoulder, muttering curses all the time. The evil magic, arungquiltha, is said to go straight to the victim, who sickens and dies without apparent cause, unless some medicine-man can discover what is wrong and save him by removing the evil magic. The irna is concealed after the ceremony, for the magician would at once be killed if it were known that he had used it. (d) Magicians are often said to be able to assume animal form or to have an animal familiar. They are said to suck the victim’s blood or send a messenger to do so; sometimes they are said to steal his soul, thus causing sickness and eventually death. These beliefs bring the magician into close relation with the werwolf (see Lycanthropy).
Rain-making.—In the lower stages of culture rain-making assumes rather the appearance of a religious ceremony, and even in higher stages the magical character is by no means invariably felt. It will, however, be well to notice some of the methods here. (a) Among the Dieri of Central Australia the whole tribe takes part in the ceremony; a hole is dug, and over this a hut is built, large enough for the old men; the women are called to look at it and then retire some five hundred yards. Two wizards have their arms bound at the shoulder, the old men huddle in the hut, and the principal wizard bleeds the two men selected by cutting them inside the arm below the elbow. The blood is made to flow on the old men, and the two men throw handfuls of down into the air. The blood symbolizes the rain; the down is the clouds. Then two large stones are placed in the middle of the hut; these two represent gathering clouds. The women are again summoned, and then the stones are placed high in a tree; other men pound gypsum and throw it into a water-hole; the ancestral spirits are supposed to see this and to send rain. Then the hut is knocked down, the men butting at it with their heads; this symbolizes the breaking of the clouds, and the fall of the hut is the rain, if no rain comes they say that another tribe has stopped their power or that the Mura-mura (ancestors) are angry with them. (b) Rain-making ceremonies are far from uncommon in Europe. Sometimes water is poured on a stone; a row of stepping-stones runs into one of the tarns on Snowdon, and it is said that water thrown upon the last one will cause rain to fall before night. Sometimes the images of saints are carried to a river or a fountain and ducked or sprinkled with water in the belief that rain will follow; sometimes rain is said to ensue when the water of certain springs is troubled; perhaps the idea is that the rain-god is disturbed in his haunts. But perhaps the commonest method is to duck or drench a human figure or puppet, who represents in many instances the vegetation demon. The gipsies of Transylvania celebrate the festival of “Green George” at Easter or on St George’s Day; a boy dressed up in leaves and blossoms is the principal figure; he throws grass to the cattle of the tribe, and after various other ceremonies a pretence is made of throwing him into the water; but in fact only a puppet is ducked in the stream.
Negative Magic.—There is also a negative side to magic, which, together with ritual prohibitions of a religious nature, is often embraced under the name of taboo (q.v.); this extension of meaning is not justified, for taboo is only concerned with sacred things, and the mark of it is that its violation causes the taboo to be transmitted. All taboos are ritual prohibitions, but all ritual prohibitions are not taboos; they include also (a) interdictions of which the sanction is the wrath of a god; these may be termed religious interdictions; (b) interdictions, the violation of which will automatically cause some undesired magico-religious effect; to these the term negative magic should be restricted, and they might conveniently be called “bans”; they correspond in the main to positive rites and are largely based on the same principles.
(a) Certain prohibitions, such as those imposed on totem kins, seem to occupy an intermediate place; they depend on the sanctity of the totem animal without being taboos in the strict sense; to them no positive magical rites correspond, for the totemic prohibition is clearly religious, not magical.
(b) Among cases of negative magic may be mentioned (i.) the couvade, and prohibitions observed by parents and relatives generally; this is most common in the case of young children, but a sympathetic relation is held to exist in other cases also. In Madagascar a son may not eat fallen bananas, for the result would be to cause the death of his own father; the sympathy between father and son establishes a sympathy between the father and objects touched or eaten by the son, and, in addition, the fall of the bananas is equated with the death of a human being. Again, the wife of a Malagasy warrior may not be faithless to him when he is absent; if she is, he will be killed or wounded. Ownership, too, may create a sympathetic relation of this kind, for it is believed in parts of Europe that if a man kills a swallow his cows will give bloody milk. In some cases it is even harder to see how the sympathetic bond is established; some Indians of Brazil always hamstring animals before bringing them home, in the belief that by so doing they make it easier for themselves and their children to run down their enemies, who are then magically deprived of the use of their legs. These are all examples of negative magic with regard to persons, but things may be equally affected; thus in Borneo men who search for camphor abstain from washing their plates for fear the camphor, which is found crystallized in the crevices of trees, should dissolve and disappear. (ii.) Rules which regulate diet exist not only for the benefit of others but also for that of the eater. Some animals, such as the hare, are forbidden, just as others, like the lion, are prescribed; the one produces cowardice, while the other makes a man’s heart bold. (iii.) Words may not be used; Scottish fishermen will not mention the pig at sea; the real names of certain animals, like the bear, may not be used; the names of the dead may not be mentioned; a sacred language must be used, e.g. camphor language in the Malay peninsula, or only words of good omen (cf. Gr. εὐφημεῖτε); or absolute silence must be preserved. Personal names are concealed; a man may not mention the names of certain relatives, &c. There are customs of avoidance not only as to (iv.) the names of relatives, but as to the persons themselves; the mother-in-law must avoid the son-in-law, and vice versa; sometimes they may converse at a distance, or in low tones, sometimes not at all, and sometimes they may not even meet. (v.) In addition to these few classes selected at random, we have prohibitions relating to numbers (cf. unlucky thirteen, which is, however, of recent date), the calendar (Friday as an unlucky day, May as an unlucky month for marriage), places, persons, orientation, &c.; but it is impossible to enumerate even the main classes. The individual origin of such beliefs, which with us form the superstitions of daily life but in a savage or semi-civilized community play a large part in regulating conduct, is often shrouded in darkness; the meaning of the positive rite is easily forgotten; the negative rite persists, but it is observed merely to avoid some unknown misfortune. Sometimes we can, however, guess at the meaning of our civilized notions of ill luck; it is perhaps as a survival of the savage belief that stepping over a person is injurious to him that many people regard going under a ladder as unlucky; in the one case the luck is taken away by the person stepping over, in the other left behind by the person passing under.
History of Magic.—The subject is too vast and our data are too slight to make a general sketch of magic possible. Our knowledge of Assyrian magic, for example, hardly extends beyond the rites of exorcism; the magic of Africa is most inadequately known, and only in recent years have we well-analysed 310 repertories of magical rituals from any part of the world. For certain departments of ancient magic, however, like the Pythagorean philosophy, there is no lack of illustrative material; it depended on mystical speculations based on numbers or analogous principles. The importance of numbers is recognized in the magic of America and other areas, but the science of the Mediterranean area, combined with the art of writing, was needed to develop such mystical ideas to their full extent. Among the neo-Platonists there was a strong tendency to magical speculation, and they sought to impress into their service the demons with which they peopled the universe. Alexandria was the home of many systems of theurgic magic, and gnostic gems afford evidence of the nature of their symbols. In the middle ages the respectable branches of magic, such as astrology and alchemy, included much of the real science of the period; the rise of Christianity introduced a new element, for the Church regarded all the religions of the heathen as dealings with demons and therefore magical (see Witchcraft). In our own day the occult sciences still find devotees among the educated; certain elements have acquired a new interest, in so far as they are the subject matter of psychical research (q.v.) and spiritualism (q.v.). But it is only among what are regarded as the lower classes, and in England especially the rural population, that belief in its efficacy still prevails to any large extent.
Psychology of Magic.—The same causes which operated to produce a belief in witchcraft (q.v.) aided the creed of magic in general. Fortuitous coincidences attract attention; the failures are disregarded or explained away. Probably the magician is never wholly an impostor, and frequently has a whole-hearted belief in himself; in this connexion may be noted the fact that juggling tricks have in all ages been passed off as magical; the name of “conjuring” (q.v.) survives in our own day, though the conjurer no longer claims that his mysterious results are produced by demons. It is interesting to note that magical leechcraft depended for its success on the power of suggestion (q.v.), which is to-day a recognized element in medicine; perhaps other elements may have been instrumental in producing a cure, for there are cases on record in which European patients have been cured by the apparently meaningless performances of medicine-men, but an adequate study of savage medicine is still a desideratum.
Bibliography.—For a general discussion of magic with a list of selected works see Hubert and Mauss in Année sociologique, vii. 1-146; also A. Lehmann, Aberglaube und Zauberei; the article “Religion” in La Grande encyclopédie; K. T. Preuss in Globus, vols. 86, 87; Mauss, L’Origine des pouvoirs magiques, and Hubert, La Réprésentation du temps (Reports of École pratique des hautes études, Paris). For general bibliographies see Hauck, Realencyklopädie, s.v. “Magie”; A. C. Haddon, Magic and Fetishism. J. G. T. Graesse’s Bibliotheca magica is an exhaustive list of early works dealing with magic and superstition. For Australia see Spencer and Gillen’s works, and A. W. Howitt, Native Tribes. For America see Reports of Bureau of Ethnology, vii. xvii. For India see W. Caland, Altindisches Zauber-ritual; and W. Crooke, Popular Religion; also V. Henry, La Magie. For the Malays see W. W. Skeat, Malay Magic. For Babylonia and Assyria see L. W. King’s works. For magic in Greece and Rome see Daremberg and Saglio, s.v. “Magia,” “Amuletum,” &c. For medieval magic see A. Maury, La Magie. For illustrations of magic see J. G. Frazer, The Golden Bough; E. S. Hartland, Legend of Perseus; E. B. Tylor, Primitive Culture; W. G. Black, Folkmedicine. For negative magic see the works of Frazer and Skeat cited above; also Journ. Anthrop. Inst. xxxvi. 92-103; Zeitschrift für Ethnologie (Verhandlungen) (1905), 153-162; Bulletin trimestriel de l’académie malgache, iii. 105-159. See also bibliography to Taboo and Witchcraft.

MAGIC SQUARE, a square divided into equal squares, like a chess-board, in each of which is placed one of a series of consecutive numbers from 1 up to the square of the number of cells in a side, in such a manner that the sum of the numbers in each row or column and in each diagonal is constant.
From a very early period these squares engaged the attention of mathematicians, especially such as possessed a love of the marvellous, or sought to win for themselves a superstitious regard. They were then supposed to possess magical properties, and were worn, as in India at the present day, engraven in metal or stone, as amulets or talismans. According to the old astrologers, relations subsisted between these squares and the planets. In later times such squares ranked only as mathematical curiosities; till at last their mode of construction was systematically investigated. The earliest known writer on the subject was Emanuel Moscopulus, a Greek (4th or 5th century). Bernard Frenicle de Bessy constructed magic squares such that if one or more of the encircling bands of numbers be taken away the remaining central squares are still magical. Subsequently Poignard constructed squares with numbers in arithmetical progression, having the magical summations. The later researches of Phillipe de la Hire, recorded in the Mémoires de l’Académie Royale in 1705, are interesting as giving general methods of construction. He has there collected the results of the labours of earlier pioneers; but the subject has now been fully systematized, and extended to cubes.
 |
| Fig. 1. |
 |
| Fig. 2. |
Two interesting magical arrangements are said to have been given by Benjamin Franklin; these have been termed the “magic square of squares” and the “magic circle of circles.” The first (fig. 1) is a square divided into 256 squares, i.e. 16 squares along a side, in Fig. 2. which are placed the numbers from 1 to 256. The chief properties of this square are (1) the sum of the 16 numbers in any row or column is 2056; (2) the sum of the 8 numbers in half of any row or column is 1028, i.e. one half of 2056; (3) the sum of the numbers in two half-diagonals equals 2056; (4) the sum of the four corner numbers of the great square and the four central numbers equals 1028; (5) the sum of the numbers in any 16 cells of the large square which themselves are disposed in a square is 2056. This square has other curious 311 properties. The “magic circle of circles” (fig. 2) consists of eight annular rings and a central circle, each ring being divided into eight cells by radii drawn from the centre; there are therefore 65 cells. The number 12 is placed in the centre, and the consecutive numbers 13 to 75 are placed in the other cells. The properties of this figure include the following: (1) the sum of the eight numbers in any ring together with the central number 12 is 360, the number of degrees in a circle; (2) the sum of the eight numbers in any set of radial cells together with the central number is 360; (3) the sum of the numbers in any four adjoining cells, either annular, radial, or both radial and two annular, together with half the central number, is 180.
 |
| Fig. 3. |
Construction of Magic Squares.—A square of 5 (fig. 3) has adjoining it one of the eight equal squares by which any square may be conceived to be surrounded, each of which has two sides resting on adjoining squares, while four have sides resting on the surrounded square, and four meet it only at its four angles. 1, 2, 3 are placed along the path of a knight in chess; 4, along the same path, would fall in a cell of the outer square, and is placed instead in the corresponding cell of the original square; 5 then falls within the square. a, b, c, d are placed diagonally in the square; but e enters the outer square, and is removed thence to the same cell of the square it had left. α, β, γ, δ, ε pursue another regular course; and the diagram shows how that course is recorded in the square they have twice left. Whichever of the eight surrounding squares may be entered, the corresponding cell of the central square is taken instead. The 1, 2, 3, ..., a, b, c, ..., α, β, γ, ... are said to lie in “paths.”
 | ||
| Fig. 4. | Fig. 5. | Fig. 6. |
 | ||
| Fig. 7. | Fig. 8. | Fig. 9. |
Squares whose Roots are Odd.—Figs 4, 5, and 6 exhibit one of the earliest methods of constructing magic squares. Here the 3’s in fig. 4 and 2’s in fig. 5 are placed in opposite diagonals to secure the two diagonal summations; then each number in fig. 5 is multiplied by 5 and added to that in the corresponding square in fig. 4, which gives the square of fig. 6. Figs. 7, 8 and 9 give De la Hire’s method; the squares of figs. 7 and 8, being combined, give the magic square of fig. 9. C. G. Bachet arranged the numbers as in fig. 10, where there are three numbers in each of four surrounding squares; these being placed in the corresponding cells of the central square, the square of fig. 11 is formed. He also constructed squares such that if one or more outer bands of numbers are removed the remaining central squares are magical. His method of forming them may be understood from a square of 5. Here each summation is 5 × 13; if therefore 13 is subtracted from each number, the summations will be zero, and the twenty-five cells will contain the series ± i, ± 2, ± 3, ... ± 12, the odd cell having 0. The central square of 3 is formed with four of the twelve numbers with + and − signs and zero in the middle; the band is filled up with the rest, as in fig. 12; then, 13 being added in each cell, the magic square of fig. 13 is obtained.
 | |
| Fig. 10. | Fig. 11. |
 | |
| Fig. 12. | Fig. 13. |
 | ||
| Fig. 14. | Fig. 15. | Fig. 16. |
 | ||
| Fig. 17. | Fig. 18. | Fig. 19. |
 |
| Fig. 20. |
Squares whose Roots are Even.—These were constructed in various ways, similar to that of 4 in figs. 14, 15 and 16. The numbers in fig. 15 being multiplied by 4, and the squares of figs. 14 and 15 being superimposed, give fig. 16. The application of this method to squares the half of whose roots are odd requires a complicated adjustment. Squares whose half root is a multiple of 4, and in which there are summations along all the diagonal paths, may be formed, by observing, as when the root is 4, that the series 1 to 16 may be changed into the series 15, 13, ... 3, 1, −1, −3, ... −13, −15, by multiplying each number by 2 and subtracting 17; and, vice versa, by adding 17 to each of the latter, and dividing by 2. The diagonal summations of a square, filled as in fig. 17, make zero; and, to obtain the same in the rows and columns, we must assign such values to the p’s and q’s as satisfy the equations p1 + p2 + a1 + a2 = 0, p3 + p4 + a3 + a4 = 0, p1 + p3 − a1 − a3 = 0, and p2 + p4 − a2 − a4 = 0,—a solution of which is readily obtained by inspection, as in fig. 18; this leads to the square, fig. 19. When the root is 8, the upper four subsidiary rows may at once be written, as in fig. 20; then, if 65 be added to each, and the sums halved, the square is completed. In such squares as these, the two opposite squares about the same diagonal (except that of 4) may be turned through any number of right angles, in the same direction, without altering the summations.
 |
| Fig. 21. |
 |
| Fig. 22. |
 |
| Fig. 23. |
 |
| Fig. 24. |
Nasik Squares.—Squares that have many more summations than in rows, columns and diagonals were investigated by A. H. Frost (Cambridge Math. Jour., 1857), and called Nasik squares, from the town in India where he resided; and he extended the method to cubes, various sections of which have the same singular properties. In order to understand their construction it will be necessary to 312 consider carefully fig. 21, which shows that, when the root is a prime, and not composite, number, as 7, eight letters a, b, ... h may proceed from any, the same, cell, suppose that marked 0, each letter being repeated in the cells along different paths. These eight paths are called “normal paths,” their number being one more than the root. Observe here that, excepting the cells from which any two letters start, they do not occupy again the same cell, and that two letters, starting from any two different cells along different paths, will appear together in one and only one cell. Hence, if p1 be placed in the cells of one of the n + 1 normal paths, each of the remaining n normal paths will contain one, and only one, of these p1’s. If now we fill each row with p2, p3, ... pn in the same order, commencing from the p1 in that row, the p2’s, p3’s and pn’s will lie each in a path similar to that of p1, and each of the n normal paths will contain one, and only one, of the letters p1, p2,... pn, whose sum will be Σp. Similarly, if q1 be placed along any of the normal paths, different from that of the p’s, and each row filled as above with the letters q2, q3, ... qn, the sum of the q’s along any normal path different from that of the q1 will be Σq. The n² cells of the square will now be found to contain all the combinations of the p’s and q’s; and if the q’s be multiplied by n, the p’s made equal to 1, 2, ... n, and the q’s to 0, 1, 2, ... (n − 1) in any order, the Nasik square of n will be obtained, and the summations along all the normal paths, except those traversed by the p’s and q’s, will be the constant Σnq + Σp. When the root is an odd composite number, as 9, 15, &c., it will be found that in some paths, different from the two along which the p1 and q1 were placed, instead of having each of the p’s and q’s, some will be wanting, while some are repeated. Thus, in the case of 9, the triplets, p1p4p7, p2p5p8, p3p6p9, and q1q4q7, q2q5q8, q3q6q9 occur, each triplet thrice, along paths whose summation should be—Σp 45 and Σr 36. But if we make p1, p2, ... p9, = 1, 3, 6, 5, 4, 7, 9, 8, 2, and the r1, r2, ... r9 = 0, 2, 5, 4, 3, 6, 8, 7, 1, thrice each of the above sets of triplets will equal Σp and Σq respectively. If now the q’s are multiplied by 9, and added to the p’s in their several cells, we shall have a Nasik square, with a constant summation along eight of its ten normal paths. In fig. 22 the numbers are in the nonary scale; that in the centre is the middle one of 1 to 9², and the sum of pair of numbers equidistant from and opposite to the central 45 is twice 45; and the sum of any number and the 8 numbers 3 from it, diagonally, and in its row and column, is the constant Nasical summation, e.g. 72 and 32, 22, 76, 77, 26, 37, 36, 27. The numbers in fig. 22 being kept in the nonary scale, it is not necessary to add any nine of them together in order to test the Nasical summation; for, taking the first column, the figures in the place of units are seen at once to form the series, 1, 2, 3, ... 9, and those in the other place three triplets of 6, 1, 5. For the squares of 15 the p’s and q’s may be respectively 1, 2, 10, 8, 6, 14, 15, 11, 4, 13, 9, 7, 3, 12, 5, and 0, 1, 9, 7, 5, 13, 14, 10, 3, 12, 8, 6, 2, 11, 4, where five times the sum of every third number and three times the sum of every fifth number makes Σp and Σq; then, if the q’s are multiplied by 15, and added to the p’s, the Nasik square of 15 is obtained. When the root is the multiple of 4, the same process gives us, for the square of 4, fig. 23. Here the columns give Σp, but alternately 2q1, 2q3, and 2q2, 2q4; and the rows give Σq, but alternately 2p1, 2p3, and 2p2, 2p4; the diagonals giving Σp and Σq. If p1, p2, p3, p4 and q1, q2, q3, q4 be 1, 2, 4, 3, and 0, 1, 3, 2, we have the Nasik square of fig. 24. A square like this is engraved in the Sanskrit character on the gate of the fort of Gwalior, in India. The squares of higher multiples of 4 are readily obtained by a similar adjustment.
 |
| Fig. 25—Nasik Cube. |
 |
| Fig. 26. |
 | |
| Fig. 27. | Fig. 28. |
Nasik Cubes.—A Nasik cube is composed of n³ small equal cubes, here called cubelets, in the centres of which the natural numbers from 1 to n³ are so placed that every section of the cube by planes perpendicular to an edge has the properties of a Nasik square; also sections by planes perpendicular to a face, and passing through the cubelet centres of any path of Nasical summation in that face. Fig. 25 shows by dots the way in which these cubes are constructed. A dot is here placed on three faces of a cubelet at the corner, showing that this cubelet belongs to each of the faces AOB, BOC, COA, of the cube. Dots are placed on the cubelets of some path of AOB (here the knight’s path), beginning from O, also on the cubelets of a knight’s path in BOC. Dots are now placed in the cubelets of similar paths to that on BOC in the other six sections parallel to BOC, starting from their dots in AOB. Forty-nine of the three hundred and forty-three cubelets will now contain a dot; and it will be observed that the dots in sections perpendicular to BO have arranged themselves in similar paths. In this manner, p1, q1, r1 being placed in the corner cubelet O, these letters are severally placed in the cubelets of three different paths of AOB, and again along any similar paths in the seven sections perpendicular to AO, starting from the letters’ position in AOB. Next, p2q2r2, p3q3r3, ... p7q7r7 are placed in the other cubelets of the edge AO, and dispersed in the same manner as p1q1r1. Every cubelet will then be found to contain a different combination of the p’s, q’s and r’s. If therefore the p’s are made equal to 1, 2, ... 7, and the q’s and r’s to 0, 1, 2, ... 6, in any order, and the q’s multiplied by 7, and the r’s by 7², then, as in the case of the squares, the 7³ cubelets will contain the numbers from 1 to 7³, and the Nasical summations will be Σ7²r + Σ7q + p. If 2, 4, 5 be values of r, p, q, the number for that cubelet is written 245 in the septenary scale, and if all the cubelet numbers are kept thus, the paths along which summations are found can be seen without adding, as the seven numbers would contain 1, 2, 3, ... 7 in the unit place, and 0, 1, 2, ... 6 in each of the other places. In all Nasik cubes, if such values are given to the letters on the central cubelet that the number is the middle one of the series 1 to n³, the sum of all the pairs of numbers opposite to and equidistant from the middle number is the double of it. Also, if around a Nasik cube the twenty-six surrounding equal cubes be placed with their cells filled with the same numbers, and their corresponding faces looking the same way,—and if the surrounding space be conceived thus filled with similar cubes, and a straight line of unlimited length be drawn through any two cubelet centres, one in each of any two cubes,—the numbers along that line will be found to recur in groups of seven, which (except in the three cases where the same p, q or r recur in the group) together make the Nasical summation of the cube. Further, if we take n similarly filled Nasik cubes of n, n new letters, s1, s2, ... sn, can be so placed, one in each of the n4 cubelets of this group of n cubes, that each shall contain a different combination of the p’s, q’s, r’s and s’s. This is done by placing s1 on each of the n² cubelets of the first cube that contain p1, and on the n² cubelets of the 2d, 3d, ... and nth cube that contain p2, p3, ... pn respectively. This process is repeated with s2, beginning with the cube at which we ended, and so on with the other s’s; the n4 cubelets, after multiplying the q’s, r’s, and s’s by n, n², and n³ respectively, will now be filled with the numbers from 1 to n4, and the constant summation will be Σn³s + Σn²r + Σnq + Σp. This process may be carried on without limit; for, if the n cubes are placed in a row with their faces resting on each other, and the corresponding faces looking the same way, n such parallelepipeds might be put side by side, and the n5 cubelets of this solid square be Nasically filled by the introduction of a new letter t; while, by introducing another letter, the n6 cubelets of the compound cube of n³ Nasik 313 cubes might be filled by the numbers from 1 to n6, and so ad infinitum. When the root is an odd composite number the values of the three groups of letters have to be adjusted as in squares, also in cubes of an even root. A similar process enables us to place successive numbers in the cells of several equal squares in which the Nasical summations are the same in each, as in fig. 26.
Among the many ingenious squares given by various writers, this article may justly close with two by L. Euler, in the Histoire de l’académie royale des sciences (Berlin, 1759). In fig. 27 the natural numbers show the path of a knight that moves within an odd square in such a manner that the sum of pairs of numbers opposite to and equidistant from the middle figure is its double. In fig. 28 the knight returns to its starting cell in a square of 6, and the difference between the pairs of numbers opposite to and equidistant from the middle point is 18.
A model consisting of seven Nasik cubes, constructed by A. H. Frost, is in the South Kensington Museum. The centres of the cubes are placed at equal distances in a straight line, the similar faces looking the same way in a plane parallel to that line. Each of the cubes has seven parallel glass plates, to which, on one side, the seven numbers in the septenary scale are fixed, and behind each, on the other side, its value in the common scale. 1201, the middle number from 1 to 74 occupies the central cubelet of the middle cube. Besides each cube having separately the same Nasical summation, this is also obtained by adding the numbers in any seven similarly situated cubelets, one in each cube. Also, the sum of all pairs of numbers, in a straight line, through the central cube of the system, equidistant from it, in whatever cubes they are, is twice 1201.
Fennell’s Magic Ring.—It has been noticed that the numbers of magic squares, of which the extension by repeating the rows and columns of n numbers so as to form a square of 2n − 1 sides yields n² magic squares of n sides, are arranged as if they were all inscribed round a cylinder and also all inscribed on another cylinder at right angles to the first. C. A. M. Fennell explains this apparent anomaly by describing such magic squares as Mercator’s projections, so to say, of “magic rings.”
The surface of these magic rings is symmetrically divided into n² quadrangular compartments or cells by n equidistant zonal circles parallel to the circular axis of the ring and by n transverse circles which divide each of the n zones between any two neighbouring zonal circles into n equal quadrangular cells, while the zonal circles divide the sections between two neighbouring transverse circles into n unequal quadrangular cells. The diagonals of cells which follow each other passing once only through each zone and section, form similar and equal closed curves passing once quite round the circular axis of the ring and once quite round the centre of the ring. The position of each number is regarded as the intersection of two diagonals of its cell. The numbers are most easily seen if the smallest circle on the surface of the ring, which circle is concentric with the axis, be one of the zonal circles. In a perfect magic ring the sum of the numbers of the cells whose diagonals form any one of the 2n diagonal curves aforesaid is ½n (n² + 1) with or without increment, i.e. is the same sum as that of the numbers in each zone and each transverse section. But if n be 3 or a multiple of 3, only from 2 to n of the diagonal curves carry the sum in question, so that the magic rings are imperfect; and any set of numbers which can be arranged to make a perfect magic ring or magic square can also make an imperfect magic ring, e.g. the set 1 to 16 if the numbers 1, 6, 11, 16 lie thus on a diagonal curve instead of in the order 1, 6, 16, 11. From a perfect magic ring of n² cells containing one number each, n² distinct magic squares can be read off; as the four numbers round each intersection of a zonal circle and a transverse circle constitute corner numbers of a magic square. The shape of a magic ring gives it the function of an indefinite extension in all directions of each of the aforesaid n² magic squares.
See F. E. A. Lucas, Récréations mathématiques (1891-1894); W. W. R. Ball, Mathematical Recreations (1892); W. E. M. G. Ahrens, Mathematische Unterhaltungen und Spiele (1901); H. C. H. Schubert, Mathematische Mussestunden (1900). A very detailed work is B. Violle, Traité complet des carrés magiques (3 vols., 1837-1838). The theory of “path nasiks” is dealt with in a pamphlet by C. Planck (1906).

MAGINN, WILLIAM (1793-1842), Irish poet and journalist, was born at Cork on the 10th of July 1793. The son of a schoolmaster, he graduated at Trinity College, Dublin, in 1811, and after his father’s death in 1813 succeeded him in the school. In 1819 he began to contribute to the Literary Gazette and to Blackwood’s Magazine, writing as “R. T. Scott” and “Morgan O’Doherty.” He first made his mark as a parodist and a writer of humorous Latin verse. In 1821 he visited Edinburgh, where he made acquaintance with the Blackwood circle. He is credited with having originated the idea of the Noctes ambrosianae, of which some of the most brilliant chapters were his. His connexion with Blackwood lasted, with a short interval, almost to the end of his life. His best story was “Bob Burke’s Duel with Ensign Brady.” In 1823 he removed to London. He was employed by John Murray on the short-lived Representative, and was for a short time joint-editor of the Standard. But his intemperate habits and his imperfect journalistic morality prevented any permanent success. In connexion with Hugh Fraser he established Fraser’s Magazine (1830), in which appeared his “Homeric Ballads.” Maginn was the original of Captain Shandon in Pendennis. In spite of his inexhaustible wit and brilliant scholarship, most of his friends were eventually alienated by his obvious failings, and his persistent insolvency. He died at Walton-on-Thames on the 21st of August 1842.
His Miscellanies were edited (5 vols., New York, 1855-1857) by R. Shelton Mackenzie and (2 vols., London, 1885) by R. W. Montagu [Johnson].

MAGISTRATE (Lat. magistratus, from magister, master, properly a public office, hence the person holding such an office), in general, one vested with authority to administer the law or one possessing large judicial or executive authority. In this broad sense the word is used in such phrases as “the first magistrate” of a king in a monarchy or “the chief magistrate” of the president of the United States. But it is more generally applied to minor or subordinate judicial officers, whether unpaid, as justices of the peace, or paid, as stipendiary magistrates. A stipendiary magistrate is appointed in London under the Metropolitan Police Courts Act 1839, in municipal boroughs under the Municipal Corporations Act 1882, and in particular districts under the Stipendiary Magistrates Act 1863 and special acts. In London and municipal boroughs a stipendiary magistrate must be a barrister of at least seven years’ standing, while under the Stipendiary Magistrates Act 1863 he may be of five years’ standing. A stipendiary magistrate may do alone all acts authorized to be done by two justices of the peace.
The term magistratus in ancient Rome originally implied the office of magister (master) of the Roman people, but was subsequently applied also to the holder of the office, thus becoming identical in sense with magister, and supplanting it in reference to any kind of public office. The fundamental conception of Roman magistracy is tenure of the imperium, the sovereignty which resides with the Roman people, but is by it conferred either upon a single ruler for life, as in the later monarchy, or upon a college of magistrates for a fixed term, as in the Republican period. The Roman theory of magistracy underwent little change when two consuls were substituted for the king; but the subdivision of magisterial powers which characterized the first centuries of the Republic, and resulted in the establishment of twenty annually elected magistrates of the people, implied some modification of this principle of the investiture of magistrates with supreme authority. For when the magistracies were multiplied a distinction was drawn between magistrates with imperium, namely consuls, praetors and occasionally dictators, and the remaining magistrates, who, although exercising independent magisterial authority and in no sense agents of the higher magistrates, were invested merely with an authority (potestas) to assist in the administration of the state. At the same time the actual authority of every magistrate was weakened not only by his colleagues’ power of veto, but by the power possessed by any magistrate of quashing the act of an inferior, and by the tribune’s right of putting his veto on the act of any magistrate except a dictator; and the subdivision of authority, which placed a great deal of business in the hands of young and inexperienced magistrates, further tended to increase the actual power as well as the influence of the senate at the expense of the magistracy.
In the developed Republic magistracies were divided into two classes: (a) magistrates of the whole people (populi Romani) and (b) magistrates of the plebs. The former class is again divided into two sections: (α) curule and (β) non-curule, a distinction which rests mainly on dignity rather than on actual power, for it cuts across the division of magistrates according to their tenure or non-tenure of imperium.
a. The magistrates of the people—also known as patrician magistrates, probably because the older and more important of these magistracies could originally be held only by patricians (q.v.)—were: (α) Dictator, master of the horse (see Dictator), consuls, praetors, curule, aediles and censors (curule); and (β) Quaestors, and the body of minor magistrates known as xxvi. viri (non-curule). The dictatorship and consulship were as old as the Republic. The first praetor was appointed in 366 B.C., a second was added in 242 B.C., and the number was gradually increased for provincial government until Sulla brought it up to eight, and under the early principate it grew to eighteen. Censors were first instituted in 443 B.C., and the office continued unchanged until its abolition by Sulla, after which, though restored, it rapidly fell into abeyance. Curule aediles were instituted at the same time as the praetorship, and continued throughout the Republic. The quaestorship was at least as old as the Republic, but the number rose during the Republic from two to twenty. All these offices except the censorship continued for administrative purposes during the principate, though shorn of all important powers.
b. The plebeian magistrates had their origin in the secession of the plebs to Mons Sacer in 494 B.C. (see Rome: History). In that year tribunes of the plebs were instituted, and two aediles were given them as subordinate officials, who were afterwards known as plebeian aediles, to distinguish them from the curule magistrates of the same name. Both these offices were abolished during the decemvirate, but were restored in 449 B.C., and survived into the principate.
The powers possessed by all magistrates alike were two:—that of enforcing their enactments (coercitio) by the exercise of any punishment short of capital, and that of veto (intercessio) of any act of a colleague or minor magistrate. The right of summoning and presiding over an assembly of that body of citizens with whose powers the magistrate was invested lay with the higher magistrates only in each class, with the consuls and praetors, and with the tribunes of the plebs. Civil jurisdiction was always a magisterial prerogative at Rome, and criminal jurisdiction also, except in capital cases, the decision of which was vested in the people at least as early as the first year of the Republic, was wielded by magistrates until the establishment of the various quaestiones perpetuae during the last century of the Republic. But in civil cases the magistrate, though controlling the trial and deciding matters of law, was quite distinct from the judge or body of judges who decided the question of fact; and the quaestiones perpetuae, which reduced the magistrate in criminal cases to a mere president of the court, gave him a position inferior to that of the praetor, who tried civil cases, only in so far as the praetor controlled the trial in some degree by his formula, under which the judges decided the question of fact.
Tenure of magistracy was always held to depend upon election by the body whose powers the magistrate wielded. Thus the magistrates of the plebs were elected by the plebeian council, those of the people in the Comitia (q.v.). In every case the outgoing magistrate, as presiding officer of the elective assembly, exercised the important right of nominating his successor for election.
See A. H. J. Greenidge, Roman Public Life, 152 seq., 363 seq. (London, 1901); T. Mommsen, Römisches Staatsrecht, I. 11. i. (1887).

MAGLIABECHI, ANTONIO DA MARCO (1633-1714), Italian bibliophile, was born at Florence on the 28th of October 1633. He followed the trade of a goldsmith until 1673, when he received the appointment of librarian to the grand-duke of Tuscany, a post for which he had qualified himself by his vast stores of self-acquired learning. He died on the 4th of July 1714, bequeathing his large private library to the grand-duke, who in turn handed it over to the city.

MAGLIANI, AGOSTINO (1824-1891), Italian financier, was a native of Lanzino, near Salerno. He studied at Naples, and a book on the philosophy of law based on Liberal principles won for him a post in the Neapolitan treasury. He entered the Italian Senate in 1871, and had already secured a reputation as a financial expert before his Questione monetaria appeared in 1874. In December 1877 he became minister of finance in the reconstructed Depretis ministry, and he subsequently held the same office in three other Liberal cabinets. In his second tenure he carried through (1880) the abolition of the grist tax, to take effect in 1884. Having to face an increased expenditure without offending the Radical electorate by unpopular taxes, he had recourse to unsound methods of finance, which seriously embarrassed Italian credit for some years after he finally laid down office in 1888. He died in Rome on the 22nd of February 1891. He was one of the founders of the anti-socialistic “Adam Smith Society” at Florence.

MAGNA CARTA, or the Great Charter, the name of the famous charter of liberties granted at Runnimede in June 1215 by King John to the English people. Although in later ages its importance was enormously magnified, it differs only in degree, not in kind, from other charters granted by the Norman and early Plantagenet kings. Its greater length, however, still more the exceptional circumstances attending its birth, gave to it a position absolutely unique in the minds of later generations of Englishmen. This feeling was fostered by its many confirmations, and in subsequent ages, especially during the time of the struggle between the Stuart kings and the parliament, it was regarded as something sacrosanct, embodying the very ideal of English liberties, which to some extent had been lost, but which must be regained. Its provisions, real and imaginary, formed the standard towards which Englishmen must strive.
The causes which led to the grant of Magna Carta are described in the article on English History. Briefly, they are to be found in the conditions of the time; the increasing insularity of the English barons, now no longer the holders of estates in Normandy; the substitution of an unpopular for a popular king, an active spur to the rising forces of discontent; and the unprecedented demands for money—demands followed, not by honour, but by dishonour, to the arms of England abroad. So much for the general causes. The actual crisis may be said to begin with the quarrel between John and Pope Innocent III. regarding the appointment of a new archbishop to the see of Canterbury. This was settled in May 1213, and in the new prelate, the papal nominee, Stephen Langton, who landed in England and absolved the king in the following July, the baronial party found an able and powerful ally. But before this event John had instituted a great inquiry, the inquest of service of June 1212, for the purpose of finding out how much he could exact from each of his vassals, a measure which naturally excited some alarm; and then, fearing a baronial rising, he had abandoned his proposed expedition into Wales, had taken hostages from the most prominent of his foes, and had sought safety in London.
His absolution followed, and then he took courage. Turning once more his attention to the recovery of Normandy, he asked the barons for assistance for this undertaking; in reply they, or a section of them, refused, and instead of crossing the seas the king marched northwards with the intention of taking vengeance on his disobedient vassals, who were chiefly barons of the north of England. Langton followed his sovereign to Northampton and persuaded him, at least for the present, to refrain from any serious measures of revenge. Before this interview a national council had met at St Albans at the beginning of August 1213, and this was followed by another council, held in St Paul’s church, London, later in the same month; it was doubtless summoned by the archbishop, and was attended by many of the higher clergy and a certain number of the barons. Addressing the gathering, Langton referred to the laws of Edward the Confessor as “good laws,” which the king ought to observe, and then mentioned the charter granted by Henry I. on his accession as a standard of good government. This event has such an important bearing on the issue of Magna Carta that it is not inappropriate to quote the actual words used by Matthew Paris in describing the incident. The chronicler represents the archbishop as saying “Inventa est quoque nunc carta quaedam Henrici primi regis Angliae per quam, si volueritis, libertates diu amissas poteritis ad statum pristinum revocare.” Those present decided to contend to the death for their “long-lost liberties,” and with this the meeting came to an end. Nothing, however, was done during the remainder of the year, and John, feeling his position had grown stronger, went abroad early in 1214, and remained for some months in France. With his mercenaries behind him he met with some small successes in his fight for Normandy, but on the 27th of July he and his ally, the emperor Otto IV., met with a crushing 315 defeat at Bouvines at the hands of Philip Augustus, and even the king himself was compelled to recognise that his hopes of recovering Normandy were at an end.
Meanwhile in England, which was ruled by Peter des Roches as justiciar, the discontent had been increasing rather than diminishing, and its volume became much larger owing to an event of May 1214. Greatly needing money for his campaign, John ordered another scutage to be taken from his tenants; this, moreover, was to be at the unprecedented rate of three marks on the knight’s fee, not as on previous occasions of two marks, although this latter sum had hitherto been regarded as a very high rate. The northern barons refused to pay, and the gathering forces of resistance received a powerful stimulus when a little later came the news of the king’s humiliation at Bouvines. Then in October the beaten monarch returned to England, no course open to him but to bow before the storm. In November he met some of his nobles at Bury St Edmunds, but as they still refused to pay the scutage no agreement was reached. At once they took another step towards the goal. With due solemnity (super majus altare) they swore to withdraw their allegiance from the king and to make war upon him, unless within a stated time he restored to them their rightful laws and liberties. While they were collecting troops in order to enforce their threats, John on his part tried to divide his enemies by a concession to the clerical section. By a charter, dated the 21st of November 1214, he granted freedom of election to the church. However, this did not prevent the prelates from continuing to act to some extent with the barons, and early in January 1215 the malcontents asked the king to confirm the laws of Edward the Confessor and the other liberties of the kingdom. He evaded the request and secured a truce until Easter was passed. Energetically making use of this period of respite, he again issued the charter to the church, ordered his subjects to take a fresh oath of allegiance to him, and sent to the pope for aid; but neither these precautions, nor his expedient of taking the cross, deterred the barons from returning to the attack. In April they met in arms at Stamford, and as soon as the truce had expired they marched to Brackley, where they met the royal ministers and again presented their demands. These were carried to the king at Oxford, but angrily he refused to consider them. Then the storm burst. On the 5th of May the barons formally renounced their allegiance to John, and appointed Robert Fitzwalter as their leader. They marched towards London, while John made another attempt to delay the crisis, or to divide his foes, by granting a charter to the citizens of London (May 9, 1215), and then by offering to submit the quarrel to a court of arbitrators under the presidency of the pope. But neither the one nor the other expedient availed him. Arbitration under such conditions was contemptuously rejected, and after the king had ordered the sheriffs to seize the lands and goods of the revolting nobles, London opened its gates and peacefully welcomed the baronial army. Other towns showed also that their sympathies were with the insurgents, and John was forced to his knees. Promising to assent to their demands, he agreed to meet the barons, and the gathering was fixed for the 15th of June, and was to take place in a meadow between Staines and Windsor, called Runnimede.
At the famous conference, which lasted from Monday the 15th to Tuesday the 23rd of June, the hostile barons were present in large numbers; on the other hand John, who rode over each day from Windsor, was only attended by a few followers. At once the malcontents presented their demands in a document known popularly as the Articles of the Barons, more strictly as Capitula quae barones petunt et dominus rex concedit. Doubtless this had been drawn up beforehand, and was brought by the baronial leaders to Runnimede; possibly it was identical with the document presented to the royal ministers at Brackley a few weeks before. John accepted the Articles on the same day and at once the great seal was affixed to them. They are forty-eight in number, and on them Magna Carta was based, the work of converting them into a charter, which was regarded as a much more binding form of engagement, being taken in hand immediately. This duty occupied three days, negotiations between the two parties taking place over several disputed points, and it was completed by Friday the 19th, when several copies of the charter were sealed. All then took an oath to keep its terms, and orders were sent to the sheriffs to publish it, and to see that its provisions were observed, two or three days being taken up with making and sending out copies for this purpose. It should be mentioned that, although the charter was evidently not sealed until the 19th, the four existing copies of it are dated the 15th, the day on which John accepted the articles.
The days between Friday the 19th and the following Tuesday, when the conference came to an end, were occupied in providing, as far as possible, for the due execution of the reforms promised by the king in Magna Carta. The document itself provided for an elected committee of twenty-five barons, whose duty was to compel John, by force if necessary, to keep his promises; but this was evidently regarded as insufficient, and the matter was dealt with in a supplementary treaty (Conventio facta inter regem Angliae et barones ejusdum regni). As a guarantee of his good faith the king surrendered the city of London to his foes, while the Tower was entrusted to the neutral keeping of the archbishop of Canterbury. John then asked the barons for a charter that they on their part would keep the peace. This was refused, and although some of the bishops entered a mild protest, the question was allowed to drop. Regarding another matter also, the extent of the royal forests, the prelates made a protest. John and his friends feared lest the inquiry promised into the extent of the hated forest areas would be carried out too rigorously, and that these would be seriously curtailed, if not abolished altogether. Consequently, the two archbishops and their colleagues declared that the articles in the charter which provided for this inquiry, and for a remedy against abuses of the forest laws by the king, must not be interpreted in too harsh a spirit. The customs necessary for the preservation of the forests must remain in force.
No securities, however, could bind John. Even before Magna Carta was signed he had set to work to destroy it, and he now turned to this task with renewed vigour. He appealed to the pope, and hoped to crush his enemies by the aid of foreign troops, while the barons prepared for war, and the prelates strove to keep the peace. Help came first from the spiritual arm. On the 24th of August 1215 Innocent III. published a bull which declared Magna Carta null and void. It had been extorted from the king by force (per vim et metum), and in the words of the bull the pope said “compositionem hujusmodi reprobamus penitus et damnamus.” He followed this up by excommunicating the barons who had obtained it, and in the autumn of 1215 the inevitable war began. Capturing Rochester castle, John met with some other successes, and the disheartened barons invited Louis, son of Philip Augustus of France and afterwards king as Louis VIII., to take the English crown. In spite of the veto of the pope Louis accepted the invitation, landed in England in May 1216, and occupied London and Winchester, the fortune of war having in the meantime turned against John. The “ablest and most ruthless of the Angevins,” as J. R. Green calls this king, had not, however, given up the struggle, and he was still in the field when he was taken ill, dying in Newark castle on the 19th of October 1216.
In its original form the text of Magna Carta was not divided into chapters, but in later times a division of this kind was adopted. This has since been retained by all commentators, the number of chapters being 63.
The preamble states that the king has granted the charter on the advice of various prelates and barons, some of whom, including the archbishop of Canterbury, the papal legate Pandulf, and William Marshal, earl of Pembroke, are mentioned by name.
Chapter I. declares that the English church shall be free and shall enjoy freedom of election. This follows the precedent set in the accession charter of Henry I. and in other early charters, although it had no place in the Articles of the Barons. On the present occasion it was evidently regarded as quite a formal and introductory matter, and the same remark applies to the general grant of liberties to all freemen and their heirs, with which the chapter concludes.
Then follows a series of chapters intended to restrain the king from raising money by the harsh and arbitrary methods adopted in the past. These chapters, however, only afforded protection to the tenants-in-chief of the crown, and it is clear from their prominent position that the framers of the charter regarded them as of paramount importance.
Chapter II. fixes the amount of the relief to be paid to the king by the heir of any of his vassals. Previously John, disregarding the custom of the past, had taken as much as he could extort. Henceforward he who inherits a barony must pay £100, he who inherits a knight’s fee 100 shillings or less, and for smaller holdings less “according to the ancient custom of fiefs.”
Chapters III. to VI. deal with the abuses of the king’s privilege of acting as guardian of minors and their lands. Money must not be extorted from a ward when he receives his inheritance. The guardian or his servant must not take from the ward’s property more than a reasonable amount for his expenses and the like; on the contrary he must maintain the houses, estates and other belongings in a proper state of efficiency. A ward must be allowed a reasonable liberty in the matter of marriage. He or she must not, as had been so often the case in the past, be forced to marry some royal favourite, or some one who had paid a sum of money for the privilege.
Chapters VII. and VIII. are for the protection of the widows of tenants-in-chief. On the death of her husband a widow must receive her rightful inheritance, without delay or hindrance. Moreover she must not be compelled to marry, a proceeding sometimes adopted to get her lands into the possession of a royal minion.
Chapter IX. is intended to prevent the king from collecting the money owing to him in an oppressive manner.
Now for a short time the document leaves the great questions at issue between the king and the barons, and two chapters are devoted to protecting the people generally against the exactions of the Jews.
Chapter X. declares that money borrowed from the Jews shall not bear interest during a minority.
Chapter XI. provides for the repayment of borrowed money to the Jews, and also to other creditors. This, however, is only to be done after certain liabilities have been met out of the estate, including the services due to the lord of the land.
Having thus disposed of this matter, the grievances of the barons are again considered, the vexed question of scutage being dealt with.
Chapter XII. says that in future no scutage or aid, beyond the three recognized feudal aids, shall be levied except by the consent of the general council of the nation (commune concilium regni nostri), while the three recognized aids shall only be levied at a reasonable rate. In dealing with this matter the Articles of the Barons had declared that aids and tallages must not be taken from the citizens of London and of other places without the consent of the council. This provision was omitted from Magna Carta, except so far as it related to aids from the citizens of London. This chapter does not give the people the right to control taxation. It gives to the men interested a certain control over one form of taxation, and protects one class only from arbitrary exactions, and that class the most powerful and the most wealthy.
Chapter XIII. gives to the citizens of London all their ancient liberties and free customs.
Chapter XIV. provides for the assembly of the council when its consent is necessary for raising an aid or a scutage. Individual summonses must be sent to the prelates and greater barons, while the lesser barons will be called together through the sheriffs and bailiffs. At least forty days’ notice of the meeting must be given, and the cause thereof specified. No chapter corresponding to this is found in the Articles and none was inserted in the reissues of Magna Carta. It is very interesting, but it does not constitute any marked advance in the history of parliament, as it merely expresses the customary method of summoning a council. It does not, as has been sometimes asserted, in any way establish a representative system, as this is understood to-day.
Chapter XV. extends the concessions obtained by the greater barons for themselves to the lesser landholders, the tenants of the tenants-in-chief.
Chapter XVI. declares that those who owe military service for their lands shall not be called upon to perform more than the due amount of such service.
We now come to an important series of articles which deal with abuses in the administration of justice. Henry II. made the royal courts of law a lucrative source of revenue, but he gave protection to suitors. Under his sons justice was equally, perhaps more, costly, while adequate protection was much harder to obtain. Here were many grievances, and the barons set to work to redress them.
Chapter XVII. declares that common pleas must henceforward be heard in a fixed place. This had already been to some extent the practice when this class of cases was heard; it was now made the rule. From this time suitors in this court were not put to the expense and inconvenience of following the king from place to place.
Chapters XVIII. and XIX. deal with the three petty assizes, three kinds of cases regarding disputes about the possession of land. These must be heard in the county courts before two visiting justices and four knights of the shire. The hardship of attendance at the county courts was to some extent obviated.
Chapters XX. to XXII. regulate the amount of fines imposed for offences against the law. Property necessary for one’s livelihood must not be taken. The fines must only be imposed by the oath of honest men of the neighbourhood. In the same way earls and barons must only be fined by their peers, and a similar privilege is extended to the clergy, who, moreover, were not to be fined in accordance with the value of their benefices, but only of their other property. It should be noticed that trial by one’s peers, as understood in Magna Carta, is not confined to the nobility; in every class of society an accused man is punished in accordance with the verdict of his peers, or equals.
Chapter XXIII. asserts that persons shall not be compelled to make bridges, unless they are bound to do so by ancient custom. John had oppressed his subjects in this way before he visited a district for purposes of sport, and the hardship was a real one.
Chapter XXIV. declared that the sheriffs and other officers of the king must not hold the pleas of the crown. This was intended to remove an old and serious evil, as the sheriffs had earned a very bad reputation by their methods of administering justice.
Chapter XXV. also concerns the sheriffs. It prevents the king from increasing by their agency the amount of money annually due to him from the various counties and hundreds. The custom was for the king to get a fixed sum from the sheriff of each county, this being called the firma comitatus, and for the sheriff to collect this as best he could. Henceforward this amount must not be raised.
Chapters XXVI. and XXVII. were intended to protect the property of deceased persons, and also to secure the full payment of debts due therefrom to the crown. Other creditors were also protected, and the property of an intestate must be distributed to his heirs under the supervision of the church.
Chapter XXVIII. strikes a blow at the custom of purveyance. Royal officials must pay for the corn and provisions which they take on behalf of the king.
Chapter XXIX. says knights must not be compelled to give money instead of performing castle-guard, if they are willing to perform this service. Castle-guard was the liability incumbent on the holders of some estates to serve in the garrison of the royal castles. The constables of these castles had adopted the custom of compelling these landholders to give money and not service, mercenaries being then hired to perform this.
Chapters XXX. and XXXI. forbid the royal officials to seize the horses or carts of freemen for transport duty, or to take wood for the king’s buildings.
Chapter XXXII. says that the lands of convicted felons shall be handed over to the lords of such lands and not kept by the king beyond a year and a day. In cases of treason the king had a right to the forfeited lands, but he was not allowed to establish a similar right in cases of felony.
Chapter XXXIII. provided for the removal of kydells, or weirs, from all English rivers. This was intended to give greater freedom to inland navigation, the rivers being the main highways of trade.
Chapter XXXIV. limits the use of the writ known as Praecipe. This writ was one transferring cases concerning the ownership of property from the courts of the feudal lords to those of the king. This custom, which owes its origin to Henry II., meant a loss of revenue to the lords, whose victory in this matter, however, was a step backwards. It checked temporarily the process of centralizing the administration of justice.
Chapter XXXV. provides for the uniformity of weights and measures throughout the kingdom.
Chapter XXXVI. promises that in future writs of inquisition shall be granted freely without payment of any kind. This kind of writ allowed a man to refer the question of his guilt or innocence to the verdict of his neighbours instead of proving his innocence by the duel.
Chapter XXXVII. prevents the king from administering certain kinds of land when these fall into the possession of minors. In the past John had evidently stretched his authority and seized lands over which others had really the right of wardship.
Chapter XXXVIII. prevents a bailiff from compelling an accused man to submit to the ordeal without the approval of credible witnesses.
Chapter XXXIX. is more important and the English rendering of it may be given in full. “No freeman shall be arrested, or detained in prison, or deprived of his freehold, or outlawed, or banished, or in any way molested; and we will not set forth against him, nor send against him, unless by the lawful judgment of his peers and by the law of the land.” The object of this was clearly to restrain John from arbitrary proceedings against his free subjects. The principle 317 of judgment by one’s peers is asserted, and is obviously the privilege of every class of freemen, not of the greater lords alone.
Chapter XL. simply says, “To no one will we sell, to no one will we refuse or delay, right or justice.”
Chapters XLI. and XLII. give permission to merchants, both English and foreign, to enter and leave the kingdom, except in time of war. They are not to pay “evil tolls.” The privilege is extended to all travellers, except the prisoner and the outlaw, and natives of a country with which England is at war.
Chapter XLIII. is intended to compel the king to refrain from exacting greater dues from an escheated barony than were previously due from such barony.
Chapter XLIV. deals with the hated and oppressive forest laws. In future attendance at the forest courts is only obligatory on those who have business thereat.
Chapter XLV. says that the royal officials must know something of the law and must be desirous of keeping it.
Chapter XLVI. gives to the founders of religious houses the right of acting as guardians of such houses when they are without heads.
Chapters XLVII. and XLVIII. deal again with the great grievance of the royal forests. John undertakes to disforest all forests which have been made in his time, and also to give up such river banks as he has seized for his own use when engaged in sport. Twelve knights in each county are to make a thorough inquiry into all evil customs connected with the forests, and these are to be utterly abolished.
Chapter XLIX. provides for the restoration of hostages. John had been in the habit of taking the children of powerful subjects as pledges for the good behaviour of their parents.
Chapter L. says that certain royal minions, who are mentioned by name, are to be removed from their offices.
Chapter LI. says that as soon as peace is made all foreign mercenaries are to be banished.
Chapters LII. and LIII. are those in which the king promises to make amends for the injuries he has done to his barons in the past. He will restore lands and castles to those who have been deprived of them without the judgment of their peers; he will do the same concerning property unlawfully seized by Henry II. or Richard I. and now in his hands. In the latter case, however, he was allowed a respite until he returned from the projected crusade. He promises also to do right concerning forests, abbeys and the wardship of lands which belong lawfully to others.
Chapter LIV. prevents any one from being arrested on the appeal of a woman, except on a charge of causing the death of her husband. As a woman could not prove her case in the judicial combat, it was felt that the earlier practice gave her an unfair advantage.
Chapter LV. provides for the remission of unjust fines. The decision on these matters is to rest with the archbishop of Canterbury and the twenty-five barons appointed to see that the terms of the charter are carried out.
Chapters LVI. and LVII. deal with the grievances of Welshmen. Restoration of property is promised to them practically in the same way as to Englishmen. Welsh law is to be used in Wales, and in the marches the law of the marches is to be employed.
Chapter LVIII. promises that his hostages and his charters shall be restored to Llewellyn, prince of Wales.
Chapter LIX. promises a restoration of hostages to Alexander I. king of Scotland. Right is also to be done to him concerning the lands which he holds in England.
Chapter LX. is a general statement that the aforesaid customs and liberties are to be observed by all classes.
Chapter LXI. provides for the execution of the royal promises. A committee is to be formed of twenty-five barons. Then if the king or any of his servants do wrong and complaint is made to four of the twenty-five, they are to ask for redress. In the event of this not being granted within forty days the matter is to be referred to the twenty-five, who are empowered to seize the lands and property of the king, or to obtain justice in any other way possible. They must, however, spare the persons of the king, the queen and their children. Vacancies in the committee are to be filled by the barons themselves. The twenty-five barons were duly appointed, their names being given by Matthew Paris. This chronicler also reports that another committee of thirty-eight members was appointed to assist and control the twenty-five. S. R. Gardiner calls the scheme “a permanent organization for making war against the king.”
Chapter LXII. is an expression of general forgiveness.
Chapter LXIII. repeats the promise of freedom to the English church and of their rights and liberties to all.
Magna Carta is an elaboration of the accession charter of Henry I., and is based upon the Articles of the Barons. It is, however, very much longer than the former charter and somewhat longer than the Articles. Moreover, it differs in several particulars from the Articles, these differences being doubtless the outcome of deliberation and of compromise. For instance, the provisions in Magna Carta concerning the freedom of the church find no place in the Articles, while a comparison between the two documents suggests that in other ways also influences favourable to the church and the clergy were at work while the famous charter was being framed. When one reflects how active and prominent Langton and other prelates were at Runnimede the change is not surprising. Another difference between the two documents concerns the towns and the trading classes. Certain privileges granted to them in the Articles are not found in Magna Carta, although, it must be noted, this document bestows exceptionally favoured treatment on the citizens of London. The conclusion is that the friends of the towns and the traders were less in evidence at Runnimede than they were at the earlier meetings of the barons, but that the neighbouring Londoners were strong enough to secure a good price for their support.
Magna Carta throws much light on the condition of England in the early 13th century. By denouncing the evil deeds of John and the innovations practised by him, it shows what these were and how they were hated; how money had been raised, how forest areas had been extended, how minors and widows had been cheated and oppressed. By declaring, as it does, what were the laws and customs of a past age wherein justice prevailed, it shows what was the ideal of good government formed by John’s prelates and barons. Magna Carta can hardly be said to have introduced any new ideas. As Pollock and Maitland (History of English Law) say “on the whole the charter contains little that is absolutely new. It is restorative.” But although mature study has established the truth of this proposition it was not always so. Statesmen and commentators alike professed to find in Magna Carta a number of political ideas which belonged to a later age, and which had no place in the minds of its framers. It was regarded as having conferred upon the nation nothing less than the English constitution in its perfect and completed form. Sir Edward Coke finds in Magna Carta a full and proper legal answer to every exaction of the Stuart kings, and a remedy for every evil suffered at the time. Sir William Blackstone is almost equally admiring. Edmund Burke says “Magna Carta, if it did not give us originally the House of Commons, gave us at least a House of Commons of weight and consequence.” Lord Chatham used words equally superlative. “Magna Carta, the Petition of Rights and the Bill of Rights form that code, which I call the Bible of the English Constitution.” Modern historians, although less rhetorical, speak in the highest terms of the importance of Magna Carta, the view of most of them being summed up in the words of Dr Stubbs: “The whole of the constitutional history of England is a commentary on this charter.”
Many regard Magna Carta as giving equal rights to all Englishmen. J. R. Green says “The rights which the barons claimed for themselves they claimed for the nation at large.” As a matter of fact this statement is only true with large limitations. The villains, who formed the majority of the population, got very little from it; in fact the only clauses which protect them do so because they are property—the property of their lords—and therefore valuable. They get neither political nor civil rights under Magna Carta. The traders, too, get little, while preferential treatment is meted out to the clergy and the barons. Its benefits are confined to freemen, and of the benefits the lion’s share fell to the larger landholders; the smaller landholders getting, it is true, some crumbs from the table. It did not establish freedom from arbitrary arrest, or the right of the representatives of the people to control taxation, or trial by jury, or other conceptions of a later generation.
The story of Magna Carta after the death of John is soon told. On the 12th of November 1216 the regent William Marshal, earl of Pembroke, reissued the charter in the name of the young king Henry III. But important alterations were made. War was being waged against Louis of France, and the executive must not be hampered in the work of raising money; moreover the personal equation had disappeared, the barons did not need to protect themselves against John. Consequently the chapter limiting the power of the crown to raise scutages and aids without the consent of the council vanished, and with it the complementary one which determined the method of calling a council. Other provisions, the object of which had been to restrain John from demanding more money from various classes of his subjects, 318 were also deleted, and the same fate befell such chapters as dealt with mere temporary matters. The most important of these was Chapter LXI., which provided for the appointment of 25 executors to compel John to observe the charter. The next year peace was made at Lambeth (Sept. 11, 1217) between Henry III. and Louis and another reissue of the charter was promised. This promise was carried out, but two charters appeared, one being a revised issue of Magna Carta proper, and the other a separate charter dealing with the forests, all references to which were omitted from the more important document. The date of this issue appears to have been the 6th of November 1217. The issue of a separate forest charter at this time led subsequently to some confusion. Roger of Wendover asserts that John issued a separate charter of this kind when Magna Carta appeared. This statement was believed by subsequent writers until the time of Blackstone, who was the first to discover the mistake.
As issued in 1217 Magna Carta consists of 47 chapters only. It declares that henceforward scutages shall be taken according to the precedents of Henry II.’s reign. New provisions were introduced for the preservation of the peace—unlawful castles were to be destroyed—while others were directed towards making the administration of justice by the visiting justices less burdensome. With regard to the land and the services due therefrom a beginning was made of the policy which culminated in the statutes of Mortmain and of Quia Emptores. The sheriffs were ordered to publish the revised charter on the 22nd of February 1218. Then in February 1225 Henry III. again issued the two charters with only two slight alterations, and this is the final form taken by Magna Carta, this text being the one referred to by Coke and the other early commentators. Subsequently the charters were confirmed several times by Henry III. and by Edward I., the most important occasion being their confirmation by Edward at Ghent in November 1297. On this occasion some supplementary articles were added to the charter; these were intended to limit the taxing power of the crown.
There are at present in existence four copies of Magna Carta, sealed with the great seal of King John, and several unsealed copies. Of the four two are in the British Museum. Both came into the possession of the Museum with the valuable collection of papers which had belonged to Sir Robert Cotton, who had obtained possession of both. One was found in Dover castle about 1630. This was damaged by fire in 1731; the other is undamaged. The two other sealed copies belong to the cathedrals of Lincoln and of Salisbury. Both were written evidently in a less hurried fashion than those in the British Museum, and the one at Lincoln was regarded as the most perfect by the commissioners who were responsible for the appearance of the Statutes of the Realm in 1810. The British Museum also contains the original parchment of the Articles of the Barons. Magna Carta was first printed by Richard Pynson in 1499. This, however, was not the original text, which was neglected until the time of Blackstone, who printed the various issues of the charter in his book The Great Charter and the Charter of the Forest (1759). The earliest commentator of note was Sir Edward Coke, who published his Second Institute, which deals with Magna Carta, by order of the Long Parliament in 1642. Modern commentators, who also print the various texts of the charter, are Richard Thomson, An Historical Essay on the Magna Carta of King John (1829); C. Bémont, in his Chartes des libertés anglaises (1892); and W. Stubbs in his Select Charters (1895). A more recent book and one embodying the results of the latest research is W. S. McKechnie, Magna Carta (1905). The text of Magna Carta is also printed in the Statutes of the Realm (1810-1828), and in T. Rymer’s Foedera (1816-1869). In addition to Blackstone, Coke and these later writers, the following works may also be consulted: John Reeves, History of English Law (1783-1784); L. O. Pike, A Constitutional History of the House of Lords (1894); W. Stubbs, Constitutional History of England (1897); Sir F. Pollock and F. W. Maitland, The History of English Law (1895); W. S. Holdsworth, A History of English Law (1903), and Kate Norgate, John Lackland (1902).

MAGNA GRAECIA (ἡ μεγάλη Ἑλλάς), the name given (first, apparently, in the 6th century B.C.) to the group of Greek cities along the coast of the “toe” of South Italy (or more strictly those only from Tarentum to Locri, along the east coast), while the people were called Italiotes (Ἰταλιῶται). The interior, which the Greeks never subdued, continued to be in the hands of the Bruttii, the native mountaineers, from whom the district was named in Roman times (Βρεττία also in Greek writers). The Greek colonies were established first as trading stations, which grew into independent cities. At an early time a trade in copper was carried on between Greece and Temesa (Homer, Od. i. 181).1 The trade for a long time was chiefly in the hands of the Euboeans; and Cyme (Cumae) in Campania was founded in the 8th century B.C., when the Euboean Cyme was still a great city. After this the energy of Chalcis went onward to Sicily, and the states of the Corinthian Gulf carried out the colonization of Italy, Rhegium having been founded, it is true, by Chalcis, but after Messana (Zancle), and at the request of the inhabitants of the latter. Sybaris (721) and Crotona (703) were Achaean settlements; Locri Epizephyrii (about 710) was settled by Ozolian Locrians, so that, had it not been for the Dorian colony of Tarentum, the southern coast of Italy would have been entirely occupied by a group of Achaean cities. Tarentum (whether or no founded by pre-Dorian Greeks—its founders bore the unexplained name of Partheniae) became a Laconian colony at some unknown date, whence a legend grew up connecting the Partheniae with Sparta, and 707 B.C. was assigned as its traditional date. Tarentum is remarkable as the only foreign settlement made by the Spartans. It was industrial, depending largely on the purple and pottery trade. Ionian Greeks fleeing from foreign invasion founded Siris about 650 B.C., and, much later, Elea (540).
The Italian colonies were planted among friendly, almost kindred, races, and grew much more rapidly than the Sicilian Greek states, which had to contend against the power of Carthage. After the Achaean cities had combined to destroy the Ionic Siris, and had founded Metapontum as a counterpoise to the Dorian Tarentum, there seems to have been little strife among the Italiotes. An amphictyonic league, meeting in common rites at the temple of Hera on the Lacinian promontory, fostered a feeling of unity among them. The Pythagorean and Eleatic systems of philosophy had their chief seat in Magna Graecia. Other departments of literature do not seem to have been so much cultivated among them. The poet Ibycus, though a native of Rhegium, led a very wandering life. They sent competitors to the Olympic games (among them the famous Milo of Croton); and the physicians of Croton early in the 6th century (especially in the person of Democedes) were reputed the best in Greece; but politically they appear to have generally kept themselves separate. One ship of Croton, however, fought at Salamis, though it is not recorded that Greece asked the Italiotes for help when it sent ambassadors to Gelon of Syracuse. Mutual discord first sapped the prosperity of Magna Graecia. In 510 Croton, having defeated the Sybarites in a great battle, totally destroyed their city. Croton maintained alone the leading position which had belonged jointly to the Achaean cities (Diod. xiv. 103); but from that time Magna Graecia steadily declined. In the war between Athens and Syracuse Magna Graecia took comparatively little part; Locri was strongly anti-Athenian, but Rhegium, though it was the headquarters of the Athenians in 427, remained neutral in 415. Foreign enemies pressed heavily on it. The Lucanians and Bruttians on the north captured one town after another. Dionysius of Syracuse attacked them from the south; and after he defeated the Crotoniate league and destroyed Caulonia (389 B.C.), Tarentum remained the only powerful city. Henceforth the history of Magna Graecia is only a record of the vicissitudes of Tarentum (q.v.). Repeated expeditions from Sparta and Epirus tried in vain to prop up the decaying Greek states against the Lucanians and Bruttians; and when in 282 the Romans appeared in the Tarentine Gulf the end was close at hand. The aid which Pyrrhus brought did little good to the Tarentines, and his final departure in 274 left them defenceless. During these constant wars the Greek cities had been steadily decaying; and in the second Punic war, when most of them seized the opportunity of revolting from Rome, their very existence was in some cases annihilated. Malaria increased in strength as the population diminished. We are told by Cicero (De am. 4), Magna Graecia nunc quidem deleta est. Many of the cities completely disappeared, and hardly any of them were of great importance under the Roman empire; some, like Tarentum, 319 maintained their existence into modern times, and in these only (except at Locri) have archaeological investigations of any importance been carried on; so that there still remains a considerable field for investigation.
1 This passage should perhaps be referred to the 8th century B.C. It is the first mention of an Italian place in a literary record.

MAGNATE (Late Lat. magnas, a great man), a noble, a man in high position, by birth, wealth or other qualities. The term is specifically applied to the members of the Upper House in Hungary, the Förendihaz or House of Magnates (see Hungary).

MAGNES (c. 460 B.C.), Athenian writer of the Old Comedy, a native of the deme of Icaria in Attica. His death is alluded to by Aristophanes (Equites, 518-523, which was brought out in 424 B.C.), who states that in his old age Magnes had lost the popularity which he had formerly enjoyed. The few titles of his plays that remain, such as the Frogs, the Birds, the Gall-flies, indicate that he anticipated Aristophanes in introducing grotesque costumes for the chorus.
See T. Kock, Comicorum atticorum fragmenta, i. (1880); G. H. Bode, Geschichte der hellenischen Dichtkunst, iii. pt. 2 (1840).

MAGNESIA, in ancient geography the name of two cities in Asia Minor and of a district in eastern Thessaly, lying between the Vale of Tempe and the Pagasaean Gulf.
(1) Magnesia ad Maeandrum, a city of Ionia, situated on a small stream flowing into the Maeander, 15 Roman miles from Miletus and rather less from Ephesus. According to tradition, reinforced by the similarity of names, it was founded by colonists from the Thessalian tribe of the Magnetes, with whom were associated, according to Strabo, some Cretan settlers (Magnesia retained a connexion with Crete, as inscriptions found there attest). It was thus not properly an Ionic city, and for this reason, apparently, was not included in the Ionian league, though superior in wealth and prosperity to most of the members except Ephesus and Miletus. It was destroyed by the Cimmerii in their irruption into Asia Minor, but was soon after rebuilt, and gradually recovered its former prosperity. It was one of the towns assigned by Artaxerxes to Themistocles for support in his exile, and there the latter ended his days. His statue stood in its market-place. Thibron, the Spartan, persuaded the Magnesians to leave their indefensible and mutinous city in 399 B.C. and build afresh at Leucophrys, an hour distant, noted for its temple of Artemis Leucophryne, which, according to Strabo, surpassed that at Ephesus in the beauty of its architecture, though inferior in size and wealth. Its ruins were excavated by Dr K. Humann for the Constantinople Museum in 1891-1893; but most of the frieze of the temple of Artemis Leucophryne, representing an Amazon battle, had already been carried off by Texier (1843) to the Louvre. It was an octostyle, pseudo-dipteral temple of highly ornate Ionic order, built on older foundations by Hermogenes of Alabanda at the end of the 3rd century B.C. The platform has been greatly overgrown since the excavation, but many bases, capitals, and other architectural members are visible. In front of the west façade stood a great altar. An immense peribolus wall is still standing (20 ft. high), but its Doric colonnade has vanished. The railway runs right through the precinct, and much of Magnesia has gone into its bridges and embankments. South and west of the temple are many other remains of the Roman city, including a fairly perfect theatre excavated by Hiller von Gärtringen, and the shell of a large gymnasium. Part of the Agora was laid open to Humann, but his trenches have fallen in. The site is so unhealthy that even the Circassians who settled there twenty years ago have almost all died off or emigrated. Magnesia continued under the kings of Pergamum to be one of the most flourishing cities in this part of Asia; it resisted Mithradates in 87 B.C., and was rewarded with civic freedom by Sulla; but it appears to have greatly declined under the Roman empire, and its name disappears from history, though on coins of the time of Gordian it still claimed to be the seventh city of Asia.
See K. Haumann, Magnesia am Maeander (1904).
(2) Magnesia ad Sipylum (mod. Manisa, q.v.), a city of Lydia about 40 m. N.E. of Smyrna on the river Hermus at the foot of Mt Sipylus. No mention of the town is found till 190 B.C., when Antiochus the Great was defeated under its walls by the Roman consul L. Scipio Asiaticus. It became a city of importance under the Roman dominion and, though nearly destroyed by an earthquake in the reign of Tiberius, was restored by that emperor and flourished through the Roman empire. It was one of the few towns in this part of Asia Minor which remained prosperous under the Turkish rule. The most famous relic of antiquity is the “Niobe of Sipylus” (Suratlu Tash) on the lowest slopes of the mountain about 4 m. east of the town. This is a colossal seated image cut in a niche of the rock, of “Hittite” origin, and perhaps that called by Pausanias the “very ancient statue of the Mother of the Gods,” carved by Broteas, son of Tantalus, and sung by Homer. Near it lie many remains of a primitive city, and about half a mile east is the rock-seat conjecturally identified with Pausanias’ “Throne of Pelops.” There are also hot springs and a sacred grotto of Apollo. The whole site seems to be that of the early “Tantalus” city.

MAGNESITE, a mineral consisting of magnesium carbonate, MgCO3, and belonging to the calcite group of rhombohedral carbonates. It is rarely found in crystals or crystalline masses, being usually compact or earthy and intermixed with more or less hydrous magnesium silicate (meerschaum). The compact material has the appearance of unglazed porcelain, and the earthy that of chalk. In colour it is usually dead white, sometimes yellowish. The hardness of the crystallized mineral is 4; sp. gr. 3.1. The name magnesite as originally applied by J. C. Delamétherie in 1797 included several minerals containing magnesium, and at the present day it is used by French writers for meerschaum. The mineral has also been called baudisserite from the locality Baudissero near Ivrea in Piedmont. Breunnerite is a ferriferous variety.
Magnesite is a product of alteration of magnesium silicates, and occurs as veins and patches in serpentine, talc-schist or dolomite-rock. It is extensively mined in the island of Euboea in the Grecian Archipelago, near Salem in Madras, and in California, U.S.A. It is principally used for the manufacture of highly refractory fire-bricks for lining steel furnaces and electric furnaces; also for making plaster, tiles and artificial stone; for the preparation of magnesium salts (Epsom salts, &c.); for whitening; paper-pulp and wool; and as a paint.

MAGNESIUM [symbol Mg, atomic weight 24.32 (O = 16)], a metallic chemical element. The sulphate or “Epsom salts” (q.v.) was isolated in 1695 by N. Grew, while in 1707 M. B. Valentin prepared magnesia alba from the mother liquors obtained in the manufacture of nitre. Magnesia was confounded with lime until 1755, when J. Black showed that the two substances were entirely different; and in 1808 Davy pointed out that it was the oxide of a metal, which, however, he was not able to isolate. Magnesium is found widely distributed in nature, chiefly in the forms of silicate, carbonate and chloride, and occurring in the minerals olivine, hornblende, talc, asbestos, meerschaum, augite, dolomite, magnesite, carnallite, kieserite and kainite. The metal was prepared (in a state approximating to purity) by A. A. B. Bussy (Jour. de pharm. 1829, 15, p. 30; 1830, 16, p. 142), who fused the anhydrous chloride with potassium; H. Sainte Claire Deville’s process, which used to be employed commercially, was essentially the same, except that sodium was substituted for potassium (Comptes rendus, 1857, 44, p. 394), the product being further purified by redistillation. It may also be prepared by heating a mixture of carbon, oxide of iron and magnesite to bright redness; and by heating a mixture of magnesium ferrocyanide and sodium carbonate, the double cyanide formed being then decomposed by heating it with metallic zinc. Electrolytic methods have entirely superseded the older methods. The problem of magnesium reduction is in many respects similar to that of aluminium extraction, but the lightness of the metal as compared, bulk for bulk, with its fused salts, and the readiness with which it burns when exposed to air at high temperatures, render the problem somewhat more difficult.
Moissan found that the oxide resisted reduction by carbon in the electric furnace, so that electrolysis of a fusible salt of the metal must be resorted to. Bunsen, in 1852, electrolysed fused magnesium chloride in a porcelain crucible. In later processes, carnallite (a 320 natural double chloride of magnesium and potassium) has commonly, after careful dehydration, been substituted for the single chloride. Graetzel’s process, which was at one time employed, consisted in electrolysing the chloride in a metal crucible heated externally, the crucible itself forming the cathode, and the magnesium being deposited upon its inner surface. W. Borchers also used an externally heated metal vessel as the cathode; it is provided with a supporting collar or flange a little below the top, so that the upper part of the vessel is exposed to the cooling influence of the air, in order that a crust of solidified salt may there be formed, and so prevent the creeping of the electrolyte over the top. The carbon anode passes through the cover of a porcelain cylinder, open at the bottom, and provided with a side-tube at the top to remove the chlorine formed during electrolysis. The operation is conducted at a dull red heat (about 760° C. or 1400° F.), the current density being about 0.64 amperes per sq. in. of cathode surface, and the pressure about 7 volts. The fusing-point of the metal is about 730° C. (1350° F.), and the magnesium is therefore reduced in the form of melted globules which gradually accumulate. At intervals the current is interrupted, the cover removed, and the temperature of the vessel raised considerably above the melting-point of magnesium. The metal is then removed from the walls with the aid of an iron scraper, and the whole mass poured into a sheet-iron tray, where it solidifies. The solidified chloride is then broken up, the shots and fused masses of magnesium are picked out, run together in a plumbago crucible without flux, and poured into a suitable mould. Smaller pieces are thrown into a bath of melted carnallite and pressed together with an iron rod, the bath being then heated until the globules of metal float to the top, when they may be removed in perforated iron ladles, through the holes in which the fused chloride can drain away, but through which the melted magnesium cannot pass by reason of its high surface tension. The globules are then re-melted. F. Oettel (Zeit. f. Elektrochem., 1895, 2, p. 394) recommends the electrolytic preparation from carnallite; the mineral should be freed from water and sulphates.
Magnesium is a silvery white metal possessing a high lustre. It is malleable and ductile. Sp. gr. 1.75. It preserves its lustre in dry air, but in moist air it becomes tarnished by the formation of a film of oxide. It melts at 632.7° C. (C. T. Heycock and F. H. Neville), and boils at about 1100°C. Magnesium and its salts are diamagnetic. It burns brilliantly when heated in air or oxygen, or even in carbon dioxide, emitting a brilliant white light and leaving a residue of magnesia, MgO. The light is rich in the violet and ultra-violet rays, and consequently is employed in photography. The metal is also used in pyrotechny. It also burns when heated in a current of steam, which it decomposes with the liberation of hydrogen and the formation of magnesia. At high temperatures it acts as a reducing agent, reducing silica to silicon, boric acid to boron, &c. (H. Moissan, Comptes rendus, 1892, 114, p. 392). It combines directly with nitrogen, when heated in the gas, to form the nitride Mg3N2 (see Argon). It is rapidly dissolved by dilute acids, with the evolution of hydrogen and the formation of magnesium salts. It precipitates many metals from solutions of their salts.
Magnesium Oxide, magnesia, MgO, occurs native as the mineral periclase, and is formed when magnesium burns in air; it may also be prepared by the gentle ignition of the hydroxide or carbonate. It is a non-volatile and almost infusible white powder, which slowly absorbs moisture and carbon dioxide from air, and is readily soluble in dilute acids. On account of its refractory nature, it is employed in the manufacture of crucibles, furnace linings, &c. It is also used in making hydraulic cements. A crystalline form was obtained by M. Houdard (Abst. J. C. S., 1907, ii. p. 621) by fusing the oxide and sulphide in the electric furnace. Magnesium hydroxide Mg(OH)2, occurs native as the minerals brucite and némalite, and is prepared by precipitating solutions of magnesium salts by means of caustic soda or potash. An artificial brucite was prepared by A. de Schulten (Comptes rendus, 1885, 101, p. 72) by boiling magnesium chloride with caustic potash and allowing the solution to cool. Magnesium hydroxide is a white amorphous solid which is only slightly soluble in water; the solubility is, however, greatly increased by ammonium salts. It possesses an alkaline reaction and absorbs carbon dioxide. It is employed in the manufacture of cements.
When magnesium is heated in fluorine or chlorine or in the vapour of bromine or iodine there is a violent reaction, and the corresponding halide compounds are formed. With the exception of the fluoride, these substances are readily soluble in water and are deliquescent. The fluoride is found native as sellaïte, and the bromide and iodide occur in sea water and in many mineral springs. The most important of the halide salts is the chloride which, in the hydrated form, has the formula MgCl2·6H2O. It may be prepared by dissolving the metal, its oxide, hydroxide, or carbonate in dilute hydrochloric acid, or by mixing concentrated solutions of magnesium sulphate and common salt, and cooling the mixture rapidly, when the less soluble sodium sulphate separates first. It is also formed as a by-product in the manufacture of potassium chloride from carnallite. The hydrated salt loses water on heating, and partially decomposes into hydrochloric acid and magnesium oxychlorides. To obtain the anhydrous salt, the double magnesium ammonium chloride, MgCl2·NH4Cl·6H2O, is prepared by adding ammonium chloride to a solution of magnesium chloride. The solution is evaporated, and the residue strongly heated, when water and ammonium chloride are expelled, and anhydrous magnesium chloride remains. Magnesium chloride readily forms double salts with the alkaline chlorides. A strong solution of the chloride made into a thick paste with calcined magnesia sets in a few hours to a hard, stone-like mass, which contains an oxychloride of varying composition. Magnesium oxychloride when heated to redness in a current of air evolves a mixture of hydrochloric acid and chlorine and leaves a residue of magnesia, a reaction which is employed in the Weldon-Pechiney and Mond processes for the manufacture of chlorine.
Magnesium Carbonate, MgCO3.—The normal salt is found native as the mineral magnesite, and in combination with calcium carbonate as dolomite, whilst hydromagnesite is a basic carbonate. It is not possible to prepare the normal carbonate by precipitating magnesium salts with sodium carbonate. C. Marignac has prepared it by the action of calcium carbonate on magnesium chloride. A salt MgCO3·3H2O or Mg(CO3H)(OH)·2H2O may be prepared from the carbonate by dissolving it in water charged with carbon dioxide, and then reducing the pressure (W. A. Davis, Jour. Soc. Chem. Ind. 1906, 25, p. 788). The carbonate is not easily soluble in dilute acids, but is readily soluble in water containing carbon dioxide. Magnesia alba, a white bulky precipitate obtained by adding sodium carbonate to Epsom salts, is a mixture of Mg(CO3H)(OH)·2H2O, Mg(CO3H)(OH) and Mg(OH)2. It is almost insoluble in water, but readily dissolves in ammonium salts.
Magnesium Phosphates.—By adding sodium phosphate to magnesium sulphate and allowing the mixture to stand, hexagonal needles of MgHPO4·7H2O are deposited. The normal phosphate, Mg3P2O8, is found in some guanos, and as the mineral wagnerite. It may be prepared by adding normal sodium phosphate to a magnesium salt and boiling the precipitate with a solution of magnesium sulphate. It is a white amorphous powder, readily soluble in acids. Magnesium ammonium phosphate, MgNH4PO4·6H2O, is found as the mineral struvite and in some guanos; it occurs also in urinary calculi and is formed in the putrefaction of urine. It is prepared by adding sodium phosphate to magnesium sulphate in the presence of ammonia and ammonium chloride. When heated to 100° C., it loses five molecules of water of crystallization, and at a higher temperature loses the remainder of the water and also ammonia, leaving a residue of magnesium pyrophosphate, Mg2P2O7. Magnesium Nitrate, Mg(NO3)2·6H2O, is a colourless, deliquescent, crystalline solid obtained by dissolving magnesium or its carbonate in nitric acid, and concentrating the solution. The crystals melt at 90° C. Magnesium Nitride, Mg3N2, is obtained as a greenish-yellow amorphous mass by passing a current of nitrogen or ammonia over heated magnesium (F. Briegleb and A. Geuther, Ann., 1862, 123, p. 228; see also W. Eidmann and L. Moeser, Ber., 1901, 34, p. 390). When heated in dry oxygen it becomes incandescent, forming magnesia. Water decomposes it with liberation of ammonia and formation of magnesium hydroxide. The chlorides of nickel, cobalt, chromium, iron and mercury are converted into nitrides when heated with it, whilst the chlorides of copper and platinum are reduced to the metals (A. Smits, Rec. Pays Bas, 1896, 15, p. 135). Magnesium sulphide, MgS, may be obtained, mixed with some unaltered metal and some magnesia, as a hard brown mass by heating magnesia, in sulphur vapour. It slowly decomposes in moist air. Magnesium sulphate, MgSO4, occurs (with IH2O) as Kieserite. A hexahydrate is also known. The salt may be obtained from Kieserite: formerly it was prepared by treating magnesite or dolomite with sulphuric acid.
Organic Compounds.—By heating magnesium filings with methyl and ethyl iodides A. Cahours (Ann. chim. phys., 1860, 58, pp. 5, 19) obtained magnesium methyl, Mg(CH3)2, and magnesium ethyl, Mg(C2H5)2, as colourless, strongly smelling, mobile liquids, which are Grignard Reagent. spontaneously inflammable and are readily decomposed by water. The compounds formed by the action of magnesium on alkyl iodides in the cold have been largely used in synthetic organic chemistry since V. Grignard (Comptes rendus, 1900 et seq.) observed that magnesium and alkyl or aryl halides combined together in presence of anhydrous ether at ordinary temperatures (with the appearance of brisk boiling) to form compounds of the type RMgX(R = an alkyl or aryl group and X = halogen). These compounds are insoluble in ether, are non-inflammable and exceedingly reactive. A. V. Baeyer (Ber., 1902, 35, p. 1201) regards them as oxonium salts containing tetravalent oxygen (C2H5)2:O:(MgR) (X), whilst W. Tschelinzeff (Ber., 1906, 39, p. 773) considers that they contain two molecules of ether. In preparing the Grignard reagent the commencement of the reaction is accelerated by a trace of iodine. W. Tschelinzeff (Ber., 1904, 37, p. 4534) showed that the ether may be replaced by benzene containing a small quantity of ether or anisole, or a few drops of a tertiary amine. With unsaturated alkyl halides the products are only slightly soluble in ether, and two molecules of the alkyl compound are brought into 321 the reaction. They are very unstable, and do not react in the normal manner. (V. Grignard and L. Tissier, Comptes rendus, 1901, 132, p. 558).
The products formed by the action of the Grignard reagent with the various types of organic compounds are usually thrown out of solution in the form of crystalline precipitates or as thick oils, and are then decomposed by ice-cold dilute sulphuric or acetic acids, the magnesium being removed as a basic halide salt.
Applications.—For the formation of primary and secondary alcohols see Aldehydes and Ketones. Formaldehyde behaves abnormally with magnesium benzyl bromide (M. Tiffeneau, Comptes rendus, 1903, 137, p. 573). forming ortho-tolylcarbinol, CH3·C6H4·CH2OH, and not benzylcarbinol, C6H5CH2·CH2OH (cf. the reaction of formaldehyde on phenols: O. Manasse, Ber. 1894, 27, p. 2904). Acid esters yield carbinols, many of which are unstable and readily pass over into unsaturated compounds, especially when warmed with acetic anhydride: R·CO2R′(R″)2·R⋮C·OMgX → (R″)2R⋮C·OH.
Formic ester yields a secondary alcohol under similar conditions. Acid chlorides behave in an analogous manner to esters (Grignard and Tissier, Comptes rendus, 1901, 132, p. 683). Nitriles yield ketones (the nitrogen being eliminated as ammonia), the best yields being given by the aromatic nitriles (E. Blaise, ibid., 1901, 133, p. 1217): R·CN → RR′:C:NMgI → R·CO·R′. Acid amides also react to form ketones (C. Béis, ibid., 1903, 137, 575):
R·CONH2 → RR′:C(OMgX)·NHMgX + R′H → R·CO·R′;
the yield increases with the complexity of the organic residue of the acid amide. On passing a current of dry carbon dioxide over the reagent, the gas is absorbed and the resulting compound, when decomposed by dilute acids, yields an organic acid, and similarly with carbon oxysulphide a thio-acid is obtained:
RMgX → R·CO2MgX → R·CO2H; COS → CS(OMgX)·R → R·CSOH.
A. Klages (Ber., 1902, 35, pp. 2633 et seq.) has shown that if one uses an excess of magnesium and of an alkyl halide with a ketone, an ethylene derivative is formed. The reaction appears to be perfectly general unless the ketone contains two ortho-substituent groups. Organo-metallic compounds can also be prepared, for example
SnBr4 + 4MgBrC6H5 = 4MgBr2 + Sn(C6H5)4.
For a summary see A. McKenzie, B. A. Rep. 1907.
Detection.—The magnesium salts may be detected by the white precipitate formed by adding sodium phosphate (in the presence of ammonia and ammonium chloride) to their solutions. The same reaction is made use of in the quantitative determination of magnesium, the white precipitate of magnesium ammonium phosphate being converted by ignition into magnesium pyrophosphate and weighed as such. The atomic weight of magnesium has been determined by many observers. J. Berzelius (Ann. chim. phys., 1820, 14, p. 375), by converting the oxide into the sulphate, obtained the value 12.62 for the equivalent. R. F. Marchand and T. Scheerer (Jour. prakt. Chem., 1850, 50, p. 358), by ignition of the carbonate, obtained the value 24.00 for the atomic weight, whilst C. Marignac, by converting the oxide into the sulphate, obtained the value 24.37. T. W. Richards and H. G. Parker (Zeit. anorg. Chem., 1897, 13, p. 81) have obtained the value 24.365 (O = 16).
Medicine.—These salts of magnesium may be regarded as the typical saline purgatives. Their aperient action is dependent upon the minimum of irritation of the bowel, and is exercised by their abstraction from the blood of water, which passes into the bowel to act as a diluent of the salt. The stronger the solution administered, the greater is the quantity of water that passes into the bowel, a fact to be borne in mind when the salt is administered for the purpose of draining superfluous fluid from the system, as in dropsy. The oxide and carbonate of magnesium are also invaluable as antidotes, since they form insoluble compounds with oxalic acid and salts of mercury, arsenic, and copper. The result is to prevent the local corrosive action of the poison and to prevent absorption of the metals. As alkaloids are insoluble in alkaline solutions, the oxide and carbonate—especially the former—may be given in alkaloidal poisoning. The compounds of magnesium are not absorbed into the blood in any appreciable quantity, and therefore exert no remote actions upon other functions. This is fortunate, as the result of injecting a solution of a magnesium salt into a vein is rapid poisoning. Hence it is of the utmost importance to avoid the use of salts of this metal whenever it is necessary—as in diabetic coma—to increase the alkalinity of the blood rapidly. The usual doses of the oxide and carbonate of magnesium are from half a drachm to a drachm.

MAGNETISM. The present article is a digest, mainly from an experimental standpoint, of the leading facts and principles of magnetic science. It is divided into the following sections:
| 1. | General Phenomena. |
| 2. | Terminology and Elementary Principles. |
| 3. | Magnetic Measurements. |
| 4. | Magnetization in Strong Fields. |
| 5. | Magnetization in Weak Fields. |
| 6. | Changes of Dimensions attending Magnetization. |
| 7. | Effects of Mechanical Stress on Magnetization. |
| 8. | Effects of Temperature on Magnetism. |
| 9. | Magnetic Properties of Alloys and Compounds of Iron. |
| 10. | Miscellaneous Effects of Magnetization:— Electric Conductivity—Hall Effect—Electro-Thermal Relations—Thermo-electric Quality—Elasticity—Chemical and Voltaic Effects. |
| 11. | Feebly Susceptible Substances. |
| 12. | Molecular Theory of Magnetism. |
| 13. | Historical and Chronological Notes. |
Of these thirteen sections, the first contains a simple description of the more prominent phenomena, without mathematical symbols or numerical data. The second includes definitions of technical terms in common use, together with so much of the elementary theory as is necessary for understanding the experimental work described in subsequent portions of the article; a number of formulae and results are given for purposes of reference, but the mathematical reasoning by which they are obtained is not generally detailed, authorities being cited whenever the demonstrations are not likely to be found in ordinary textbooks. The subjects discussed in the remaining sections are sufficiently indicated by their respective headings. (See also Electromagnetism, Terrestrial Magnetism, Magneto-Optics and Units.)
1. General Phenomena
Pieces of a certain highly esteemed iron ore, which consists mainly of the oxide Fe3O4, are sometimes found to possess the power of attracting small fragments of iron or steel. Ore endowed with this curious property was well known to the ancient Greeks and Romans, who, because it occurred plentifully in the district of Magnesia near the Aegean coast, gave it the name of magnes, or the Magnesian stone. In English-speaking countries the ore is commonly known as magnetite, and pieces which exhibit attraction as magnets; the cause to which the attractive property is attributed is called magnetism, a name also applied to the important branch of science which has been evolved from the study of phenomena associated with the magnet.
If a magnet is dipped into a mass of iron filings and withdrawn, filings cling to certain parts of the stone in moss-like tufts, other parts remaining bare. There are generally two regions where the tufts are thickest, and the attraction therefore greatest, and between them is a zone in which no attraction is evidenced. The regions of greatest attraction have received the name of poles, and the line joining them is called the axis of the magnet; the space around a magnet in which magnetic effects are exhibited is called the field of magnetic force, or the magnetic field.
Up to the end of the 15th century only two magnetic phenomena of importance, besides that of attraction, had been observed. Upon one of these is based the principle of the mariner’s compass, which is said to have been known to the Chinese as early as 1100 B.C., though it was not introduced into Europe until more than 2000 years later; a magnet supported so that its axis is free to turn in a horizontal plane will come to rest with its poles pointing approximately north and south. The other phenomenon is mentioned by Greek and Roman writers of the 1st century: a piece of iron, when brought into contact with a magnet, or even held near one, itself becomes “inductively” magnetized, and acquires the power of lifting iron. If the iron is soft and fairly pure, it loses its attractive property when removed from the neighbourhood of the magnet; if it is hard, some of the induced magnetism is permanently retained, and the piece becomes an artificial magnet. Steel is much more retentive of magnetism than any ordinary iron, and some form of steel is now always used for making artificial magnets. Magnetism may be imparted to a bar of hardened steel by stroking it several times from end to 322 end, always in the same direction, with one of the poles of a magnet. Until 1820 all the artificial magnets in practical use derived their virtue, directly or indirectly, from the natural magnets found in the earth: it is now recognized that the source of all magnetism, not excepting that of the magnetic ore itself, is electricity, and it is usual to have direct recourse to electricity for producing magnetization, without the intermediary of the magnetic ore. A wire carrying an electric current is surrounded by a magnetic field, and if the wire is bent into the form of an elongated coil or spiral, a field having certain very useful qualities is generated in the interior. A bar of soft iron introduced into the coil is at once magnetized, the magnetism, however, disappearing almost completely as soon as the current ceases to flow. Such a combination constitutes an electromagnet, a valuable device by means of which a magnet can be instantly made and unmade at will. With suitable arrangements of iron and coil and a sufficiently strong current, the intensity of the temporary magnetization may be very high, and electromagnets capable of lifting weights of several tons are in daily use in engineering works (see Electromagnetism). If the bar inserted into the coil is of hardened steel instead of iron, the magnetism will be less intense, but a larger proportion of it will be retained after the current has been cut off. Steel magnets of great strength and of any convenient form may be prepared either in this manner or by treatment with an electromagnet; hence the natural magnet, or lodestone as it is commonly called, is no longer of any interest except as a scientific curiosity.
Some of the principal phenomena of magnetism may be demonstrated with very little apparatus; much may be done with a small bar-magnet, a pocket compass and a few ounces of iron filings. Steel articles, such as knitting or sewing needles and pieces of flat spring, may be readily magnetized by stroking them with the bar-magnet; after having produced magnetism in any number of other bodies, the magnet will have lost nothing of its own virtue. The compass needle is a little steel magnet balanced upon a pivot; one end of the needle, which always bears a distinguishing mark, points approximately, but not in general exactly, to the north,1 the vertical plane through the direction of the needle being termed the magnetic meridian. The bar-magnet, if suspended horizontally in a paper stirrup by a thread of unspun silk, will also come to rest in the magnetic meridian with its marked end pointing northwards. The north-seeking end of a magnet is in English-speaking countries called the north pole and the other end the south pole; in France the names are interchanged. If one pole of the bar-magnet is brought near the compass, it will attract the opposite pole of the compass-needle; and the magnetic action will not be sensibly affected by the interposition between the bar and the compass of any substance whatever except iron or other magnetizable metal. The poles of a piece of magnetized steel may be at once distinguished if the two ends are successively presented to the compass; that end which attracts the south pole of the compass needle (and is therefore north) may be marked for easy identification.
Similar magnetic poles are not merely indifferent to each other, but exhibit actual repulsion. This can be more easily shown if the compass is replaced by a magnetized knitting needle, supported horizontally by a thread. The north pole of the bar-magnet will repel the north pole of the suspended needle, and there will likewise be repulsion between the two south poles. Such experiments as these demonstrate the fundamental law that like poles repel each other; unlike poles attract. It follows that between two neighbouring magnets, the poles of which are regarded as centres of force, there must always be four forces in action. Denoting the two pairs of magnetic poles by N, S and N′, S′, there is attraction between N and S′, and between S and N′; repulsion between N and N′, and between S and S′. Hence it is not very easy to determine experimentally the law of magnetic force between poles. The difficulty was overcome by C. A. Coulomb, who by using very long and thin magnets, so arranged that the action of their distant poles was negligible, succeeded in establishing the law, which has since been confirmed by more accurate methods, that the force of attraction or repulsion exerted between two magnetic poles varies inversely as the square of the distance between them. Since the poles of different magnets differ in strength, it is important to agree upon a definite unit or standard of reference in terms of which the strength of a pole may be numerically specified. According to the recognized convention, the unit pole is that which acts upon an equal pole at unit distance with unit force: a north pole is reckoned as positive (+) and a south pole as negative (−). Other conditions remaining unchanged, the force between two poles is proportional to the product of their strengths; it is repulsive or attractive according as the signs of the poles are like or unlike.
 |
| Fig. 1. |
If a wire of soft iron is substituted for the suspended magnetic needle, either pole of the bar-magnet will attract either end of the wire indifferently. The wire will in fact become temporarily magnetized by induction, that end of it which is nearest to the pole of the magnet acquiring opposite polarity, and behaving as if it were the pole of a permanent magnet. Even a permanent magnet is susceptible of induction, its polarity becoming thereby strengthened, weakened, or possibly reversed. If one pole of a strong magnet is presented to the like pole of a weaker one, there will be repulsion so long as the two are separated by a certain minimum distance. At shorter distances the magnetism induced in the weaker magnet will be stronger than its permanent magnetism, and there will be attraction; two magnets with their like poles in actual contact will always cling together unless the like poles are of exactly equal strength. Induction is an effect of the field of force associated with a magnet. Magnetic force has not merely the property of acting upon magnetic poles, it has the additional property of producing a phenomenon known as magnetic induction, or magnetic flux, a physical condition which is of the nature of a flow continuously circulating through the magnet and the space outside it. Inside the magnet the course of the flow is from the south pole to the north pole; thence it diverges through the surrounding space, and again converging, re-enters the magnet at the south pole. When the magnetic induction flows through a piece of iron or other magnetizable substance placed near the magnet, a south pole is developed where the flux enters and a north pole where it leaves the substance. Outside the magnet the direction of the magnetic induction is generally the same as that of the magnetic force. A map indicating the direction of the force in different parts of the field due to a magnet may be constructed in a very simple manner. A sheet of cardboard is placed above the magnet, and some iron filings are sifted thinly and evenly over the surface: if the cardboard is gently tapped, the filings will arrange themselves in a series of curves, as shown in fig. 1. This experiment suggested to Faraday the conception of “lines of force,” of which the curves formed by the filings afford a rough indication; Faraday’s lines are however not confined to the plane of the cardboard, but occur in the whole of the space around the magnet. A line of force may be defined as an imaginary line so drawn that its direction at every point of its course coincides with the direction of the magnetic force at that point. Through any point in the field one such line can be drawn, but not more than one, for the force obviously cannot have more than one direction; the lines therefore never intersect. A line of force is regarded as proceeding from the north pole towards the south pole of the magnet, its direction being that in which an isolated north pole would be urged along 323 it. A south pole would be urged oppositely to the conventional “direction” of the line; hence it follows that a very small magnetic needle, if placed in the field, would tend to set itself along or tangentially to the line of force passing through its centre, as may be approximately verified if the compass be placed among the filings on the cardboard. In the internal field of a long coil of wire carrying an electric current, the lines of force are, except near the ends, parallel to the axis of the coil, and it is chiefly for this reason that the field due to a coil is particularly well adapted for inductively magnetizing iron and steel. The older operation of magnetizing a steel bar by drawing a magnetic pole along it merely consists in exposing successive portions of the bar to the action of the strong field near the pole.
Faraday’s lines not only show the direction of the magnetic force, but also serve to indicate its magnitude or strength in different parts of the field. Where the lines are crowded together, as in the neighbourhood of the poles, the force is greater (or the field is stronger) than where they are more widely separated; hence the strength of a field at any point can be accurately specified by reference to the concentration of the lines. The lines presented to the eye by the scattered filings are too vague and ill-defined to give a satisfactory indication of the field-strength (see Faraday, Experimental Researches, § 3237) though they show its direction clearly enough. It is however easy to demonstrate by means of the compass that the force is much greater in some parts of the field than in others. Lay the compass upon the cardboard, and observe the rate at which its needle vibrates after being displaced from its position of equilibrium; this will vary greatly in different regions. When the compass is far from the magnet, the vibrations will be comparatively slow; when it is near a pole, they will be exceedingly rapid, the frequency of the vibrations varying as the square root of the magnetic force at the spot. In a refined form this method is often employed for measuring the intensity of a magnetic field at a given place, just as the intensity of gravity at different parts of the earth is deduced from observations of the rate at which a pendulum of known length vibrates.
It is to the non-uniformity of the field surrounding a magnet that the apparent attraction between a magnet and a magnetizable body such as iron is ultimately due. This was pointed out by W. Thomson (afterwards Lord Kelvin) in 1847, as the result of a mathematical investigation undertaken to explain Faraday’s experimental observations. If the inductively magnetized body lies in a part of the field which happens to be uniform there will be no resulting force tending to move the body, and it will not be “attracted.” If however there is a small variation of the force in the space occupied by the body, it can be shown that the body will be urged, not necessarily towards a magnetic pole, but towards places of stronger magnetic force. It will not in general move along a line of force, as would an isolated pole, but will follow the direction in which the magnetic force increases most rapidly, and in so doing it may cross the lines of force obliquely or even at right angles.
If a magnetized needle were supported so that it could move freely about its centre of gravity it would not generally settle with its axis in a horizontal position, but would come to rest with its north-seeking pole either higher or lower than its centre. For the practical observation of this phenomenon it is usual to employ a needle which can turn freely in the plane of the magnetic meridian upon a horizontal axis passing through the centre of gravity of the needle. The angle which the magnetic axis makes with the plane of the horizon is called the inclination or dip. Along an irregular line encircling the earth in the neighbourhood of the geographical equator the needle takes up a horizontal position, and the dip is zero. At places north of this line, which is called the magnetic equator, the north end of the needle points downwards, the inclination generally becoming greater with increased distance from the equator. Within a certain small area in the Arctic Circle (about 97° W. long., 70° N. lat.) the north pole of the needle points vertically downwards, the dip being 90°. South of the magnetic equator the south end of the needle is always inclined downwards, and there is a spot within the Antarctic Circle (148° E. long., 74° S. lat.) where the needle again stands vertically, but with its north end directed upwards. All these observations may be accounted for by the fact first recognized by W. Gilbert in 1600, that the earth itself is a great magnet, having its poles at the two places where the dipping needle is vertical. To be consistent with the terminology adopted in Britain, it is necessary to regard the pole which is geographically north as being the south pole of the terrestrial magnet, and that which is geographically south as the north pole; in practice however the names assigned to the terrestrial magnetic poles correspond with their geographical situations. Within a limited space, such as that contained in a room, the field due to the earth’s magnetism is sensibly uniform, the lines of force being parallel straight lines inclined to the horizon at the angle of dip, which at Greenwich in 1910 was about 67°. It is by the horizontal component of the earth’s total force that the compass-needle is directed.
The magnets hitherto considered have been assumed to have each two poles, the one north and the other south. It is possible that there may be more than two. If, for example, a knitting needle is stroked with the south pole of a magnet, the strokes being directed from the middle of the needle towards the two extremities alternately, the needle will acquire a north pole at each end and a south pole in the middle. By suitably modifying the manipulation a further number of consequent poles, as they are called, may be developed. It is also possible that a magnet may have no poles at all. Let a magnetic pole be drawn several times around a uniform steel ring, so that every part of the ring may be successively subjected to the magnetic force. If the operation has been skilfully performed the ring will have no poles and will not attract iron filings. Yet it will be magnetized; for if it is cut through and the cut ends are drawn apart, each end will be found to exhibit polarity. Again, a steel wire through which an electric current has been passed will be magnetized, but so long as it is free from stress it will give no evidence of magnetization; if, however, the wire is twisted, poles will be developed at the two ends, for reasons which will be explained later. A wire or rod in this condition is said to be circularly magnetized; it may be regarded as consisting of an indefinite number of elementary ring-magnets, having their axes coincident with the axis of the wire and their planes at right angles to it. But no magnet can have a single pole; if there is one, there must also be at least a second, of the opposite sign and of exactly equal strength. Let a magnetized knitting needle, having north and south poles at the two ends respectively, be broken in the middle; each half will be found to possess a north and a south pole, the appropriate supplementary poles appearing at the broken ends. One of the fragments may again be broken, and again two bipolar magnets will be produced; and the operation may be repeated, at least in imagination, till we arrive at molecular magnitudes and can go no farther. This experiment proves that the condition of magnetization is not confined to those parts where polar phenomena are exhibited, but exists throughout the whole body of the magnet; it also suggests the idea of molecular magnetism, upon which the accepted theory of magnetization is based. According to this theory the molecules of any magnetizable substance are little permanent magnets the axes of which are, under ordinary conditions, disposed in all possible directions indifferently. The process of magnetization consists in turning round the molecules by the application of magnetic force, so that their north poles may all point more or less approximately in the direction of the force; thus the body as a whole becomes a magnet which is merely the resultant of an immense number of molecular magnets.
In every magnet the strength of the south pole is exactly equal to that of the north pole, the action of the same magnetic force upon the two poles being equal and oppositely directed. This may be shown by means of the uniform field of force due to the earth’s magnetism. A magnet attached to a cork and 324 floated upon water will set itself with its axis in the magnetic meridian, but it will be drawn neither northward nor southward; the forces acting upon the two poles have therefore no horizontal resultant. And again if a piece of steel is weighed in a delicate balance before and after magnetization, no change whatever in its weight can be detected; there is consequently no upward or downward resultant force due to magnetization; the contrary parallel forces acting upon the poles of the magnet are equal, constituting a couple, which may tend to turn the body, but not to propel it.
Iron and its alloys, including the various kinds of steel, though exhibiting magnetic phenomena in a pre-eminent degree, are not the only substances capable of magnetization. Nickel and cobalt are also strongly magnetic, and in 1903 the interesting discovery was made by F. Heusler that an alloy consisting of copper, aluminium and manganese (Heusler’s alloy), possesses magnetic qualities comparable with those of iron. Practically the metals iron, nickel and cobalt, and some of their alloys and compounds constitute a class by themselves and are called ferromagnetic substances. But it was discovered by Faraday in 1845 that all substances, including even gases, are either attracted or repelled by a sufficiently powerful magnetic pole. Those substances which are attracted, or rather which tend, like iron, to move from weaker to stronger parts of the magnetic field, are termed paramagnetic; those which are repelled, or tend to move from stronger to weaker parts of the field, are termed diamagnetic. Between the ferromagnetics and the paramagnetics there is an enormous gap. The maximum magnetic susceptibility of iron is half a million times greater than that of liquid oxygen, one of the strongest paramagnetic substances known. Bismuth, the strongest of the diamagnetics, has a negative susceptibility which is numerically 20 times less than that of liquid oxygen.
Many of the physical properties of a metal are affected by magnetization. The dimensions of a piece of iron, for example, its elasticity, its thermo-electric power and its electric conductivity are all changed under the influence of magnetism. On the other hand, the magnetic properties of a substance are affected by such causes as mechanical stress and changes of temperature. An account of some of these effects will be found in another section.2
2. Terminology and Elementary Principles
In what follows the C.G.S. electromagnetic system of units will be generally adopted, and, unless otherwise stated, magnetic substances will be assumed to be isotropic, or to have the same physical properties in all directions.
Vectors.—Physical quantities such as magnetic force, magnetic induction and magnetization, which have direction as well as magnitude, are termed vectors; they are compounded and resolved in the same manner as mechanical force, which is itself a vector. When the direction of any vector quantity denoted by a symbol is to be attended to, it is usual to employ for the symbol either a block letter, as H, I, B, or a German capital, as ℌ, ℑ, ℬ.3
Magnetic Poles and Magnetic Axis.—A unit magnetic pole is that which acts on an equal pole at a distance of one centimetre with a force of one dyne. A pole which points north is reckoned positive, one which points south negative. The action between any two magnetic poles is mutual. If m1 and m2 are the strengths of two poles, d the distance between them expressed in centimetres, and f the force in dynes,
ƒ = m1m2 / d²
The force is one of attraction or repulsion, according as the sign of the product m1m2 is negative or positive. The poles at the ends of an infinitely thin uniform magnet, or magnetic filament, would act as definite centres of force. An actual magnet may generally be regarded as a bundle of magnetic filaments, and those portions of the surface of the magnet where the filaments terminate, and so-called “free magnetism” appears, may be conveniently called poles or polar regions. A more precise definition is the following: When the magnet is placed in a uniform field, the parallel forces acting on the positive poles of the constituent filaments, whether the filaments terminate outside the magnet or inside, have a resultant, equal to the sum of the forces and parallel to their direction, acting at a certain point N. The point N, which is the centre of the parallel forces, is called the north or positive pole of the magnet. Similarly, the forces acting in the opposite direction on the negative poles of the filaments have a resultant at another point S, which is called the south or negative pole. The opposite and parallel forces acting on the poles are always equal, a fact which is sometimes expressed by the statement that the total magnetism of a magnet is zero. The line joining the two poles is called the axis of the magnet.
Magnetic Field.—Any space at every point of which there is a finite magnetic force is called a field of magnetic force, or a magnetic field. The strength or intensity of a magnetic field at any point is measured by the force in dynes which a unit pole will experience when placed at that point, the direction of the field being the direction in which a positive pole is urged. The field-strength at any point is also called the magnetic force at that point; it is denoted by H, or, when it is desired to draw attention to the fact that it is a vector quantity, by the block letter H, or the German character ℌ. Magnetic force is sometimes, and perhaps more suitably, termed magnetic intensity; it corresponds to the intensity of gravity g in the theory of heavy bodies (see Maxwell, Electricity and Magnetism, § 12 and § 68, footnote). A line of force is a line drawn through a magnetic field in the direction of the force at each point through which it passes. A uniform magnetic field is one in which H has everywhere the same value and the same direction, the lines of force being, therefore, straight and parallel. A magnetic field is generally due either to a conductor carrying an electric current or to the poles of a magnet. The magnetic field due to a long straight wire in which a current of electricity is flowing is at every point at right angles to the plane passing through it and through the wire; its strength at any point distant r centimetres from the wire is
H = 2i / r,
i being the current in C.G.S. units.4 The lines of force are evidently circles concentric with the wire and at right angles to it; their direction is related to that of the current in the same manner as the rotation of a corkscrew is related to its thrust. The field at the centre of a circular conductor of radius r through which current is passing is
H = 2πi / r,
the direction of the force being along the axis and related to the direction of the current as the thrust of a corkscrew to its rotation. The field strength in the interior of a long uniformly wound coil containing n turns of wire and having a length of l centimetres is (except near the ends)
H = 4πin / l.
In the middle portion of the coil the strength of the field is very nearly uniform, but towards the end it diminishes, and at the ends is reduced to one-half. The direction of the force is parallel to the axis of the coil, and related to the direction of the current as the thrust of a corkscrew to its rotation. If the coil has the form of a ring of mean radius r, the length will be 2πr, and the field inside the coil may be expressed as
H = 2ni / r.
The uniformity of the field is not in this case disturbed by the influence of ends, but its strength at any point varies inversely as the distance from the axis of the ring. When therefore sensible uniformity is desired, the radius of the ring should be large in relation to that of the convolutions, or the ring should have the form of a short cylinder with thin walls. The strongest magnetic fields employed for experimental purposes are obtained by the use of electromagnets. For many experiments the field due to the earth’s magnetism is sufficient; this is practically quite uniform throughout considerable spaces, but its total intensity is less than half a unit.
Magnetic Moment and Magnetization.—The moment, M, M or ℳ, of a uniformly and longitudinally magnetized bar-magnet is the product of its length into the strength of one of its poles; it is the moment of the couple acting on the magnet when placed in a field of unit intensity with its axis perpendicular to the direction of the field. If l is the length of the magnet, M = ml. The action of a magnet at a distance which is great compared with the length of the magnet depends solely upon its moment; so also does the action which the magnet experiences when placed in a uniform field. The moment of a small magnet may be resolved like a force. The intensity of magnetization, or, more shortly, the magnetization of a uniformly magnetized body is defined as the magnetic moment per unit of volume, and is denoted by I, I, or ℑ. Hence
I = M/v = ml/v = m/a,
v being the volume and a the sectional area. If the magnet is not uniform, the magnetization at any point is the ratio of the moment of an element of volume at that point to the volume itself, or I = m·ds/dv. where ds is the length of the element. The direction of the magnetization is that of the magnetic axis of the element; in isotropic substances it coincides with the direction of the magnetic force at the point. If the direction of the magnetization at the surface of a magnet makes 325 an angle ε with the normal, the normal component of the magnetization, I cos ε, is called the surface density of the magnetism, and is generally denoted by σ.
Potential and Magnetic Force.—The magnetic potential at any point in a magnetic field is the work which would be done against the magnetic forces in bringing a unit pole to that point from the boundary of the field. The line through the given point along which the potential decreases most rapidly is the direction of the resultant magnetic force, and the rate of decrease of the potential in any direction is equal to the component of the force in that direction. If V denote the potential, F the resultant force, X, Y, Z, its components parallel to the co-ordinate axes and n the line along which the force is directed, then
| − | δV | = F, − | δV | = X, − | δV | = Y, − | δV | = Z. |
| δn | δx | δy | δz |
Surfaces for which the potential is constant are called equipotential surfaces. The resultant magnetic force at every point of such a surface is in the direction of the normal (n) to the surface; every line of force therefore cuts the equipotential surfaces at right angles. The potential due to a single pole of strength m at the distance r from the pole is
V = m / r,
the equipotential surfaces being spheres of which the pole is the centre and the lines of force radii. The potential due to a thin magnet at a point whose distance from the two poles respectively is r and r′ is
V = m (l/r = l/r′).
When V is constant, this equation represents an equipotential surface.
The equipotential surfaces are two series of ovoids surrounding the two poles respectively, and separated by a plane at zero potential passing perpendicularly through the middle of the axis. If r and r′ make angles θ and θ′ with the axis, it is easily shown that the equation to a line of force is
cos θ − cos θ′ = constant.
 | |
| Fig. 2. | Fig. 3. |
At the point where a line of force intersects the perpendicular bisector of the axis r = r′ = r0, say, and cos θ − cos θ′ obviously = l/r0, l being the distance between the poles; l/r0 is therefore the value of the constant in (9) for the line in question. Fig. 2 shows the lines of force and the plane sections of the equipotential surfaces for a thin magnet with poles concentrated at its ends. The potential due to a small magnet of moment M, at a point whose distance from the centre of the magnet is r, is
V = M cos θ/r²,
where θ is the angle between r and the axis of the magnet. Denoting the force at P (see fig. 3) by F, and its components parallel to the co-ordinate axes by X and Y, we have
| X = − | δV | = | M | (3 cos² θ − 1), |
| δx | r³ |
| Y = − | δV | = | M | (3 sin² θ cos θ). |
| δy | r³ |
If Fr is the force along r and Ft that along t at right angles to r,
| Fr = X cos θ + Y sin θ = | M | 2 cos θ, |
| r³ |
| Ft = −X sin θ + Y cos θ = | M | sin θ. |
| r³ |
For the resultant force at P,
| F = √ (Fr² + Ft²) = | M | √3 cos² θ + 1. |
| r³ |
The direction of F is given by the following construction: Trisect OP at C, so that OC = OP/3; draw CD at right angles to OP, to cut the axis produced in D; then DP will be the direction of the force at P. For a point in the axis OX, θ = 0; therefore cos θ = 1, and the point D coincides with C; the magnitude of the force is, from (14),
Fx = 2M / r³,
its direction being along the axis OX. For a point in the line OY bisecting the magnet perpendicularly, θ = π/2 therefore cos θ = 0, and the point D is at an infinite distance. The magnitude of the force is in this case
Fy = M / r³,
and its direction is parallel to the axis of the magnet. Although the above useful formulae, (10) to (15), are true only for an infinitely small magnet, they may be practically applied whenever the distance r is considerable compared with the length of the magnet.
 |
| Fig. 4. |
Couples and Forces between Magnets.—If a small magnet of moment M is placed in the sensibly uniform field H due to a distant magnet, the couple tending to turn the small magnet upon an axis at right angles to the magnet and to the force is
MH sin θ,
where θ is the angle between the axis of the magnet and the direction of the force. In fig. 4 S′N′ is a small magnet of moment M′, and SN a distant fixed magnet of moment M; the axes of SN and S′N′ make angles of θ and φ respectively with the line through their middle points. It can be deduced from (17), (12) and (13) that the couple on S′N′ due to SN, and tending to increase φ, is
MM′ (sin θ cos φ − 2 sin φ cos θ) / r³.
This vanishes if sin θ cos φ = 2 sin φ cos θ, i.e. if tan φ = ½ tan θ, S′N′ being then along a line of force, a result which explains the construction given above for finding the direction of the force F in (14). If the axis of SN produced passes through the centre of S′N′, θ = 0, and the couple becomes
2MM′ sin φ/r³,
tending to diminish φ; this is called the “end on” position. If the centre of S′N′ is on the perpendicular bisector of SN, θ = ½π, and the couple will be
MM′ cos φ/r³,
tending to increase φ; this is the “broadside on” position. These two positions are sometimes called the first and second (or A and B) principal positions of Gauss. The components X, Y, parallel and perpendicular to r, of the force between the two magnets SN and S′N′ are
X = 3MM′ (sin θ sin φ − 2 cos θ cos φ) / r4,
Y = 3MM′ (sin θ cos φ + sin φ cos θ) / r4.
It will be seen that, whereas the couple varies inversely as the cube of the distance, the force varies inversely as the fourth power.
Distributions of Magnetism.—A magnet may be regarded as consisting of an infinite number of elementary magnets, each having a pair of poles and a definite magnetic moment. If a series of such elements, all equally and longitudinally magnetized, were placed end to end with their unlike poles in contact, the external action of the filament thus formed would be reduced to that of the two extreme poles. The same would be the case if the magnetization of the filament varied inversely as the area of its cross-section a in different parts. Such a filament is called a simple magnetic solenoid, and the product aI is called the strength of the solenoid. A magnet which consists entirely of such solenoids, having their ends either upon the surface or closed upon themselves, is called a solenoidal magnet, and the magnetism is said to be distributed solenoidally; there is no free magnetism in its interior. If the constituent solenoids are parallel and of equal strength, the magnet is also uniformly magnetized. A thin sheet of magnetic matter magnetized normally to its surface in such a manner that the magnetization at any place is inversely proportional to the thickness h of the sheet at that place is called a magnetic shell; the constant product hI is the strength of the shell and is generally denoted by Φ or φ. The potential at any point due to a magnetic shell is the product of its strength into the solid angle ω subtended by its edge at the given point, or V = Φω. For a given strength, therefore, the potential depends solely upon the boundary of the shell, and the potential outside a closed shell is everywhere zero. A magnet which can be divided into simple magnetic shells, either closed or having their edges on the surface of the magnet, is called a lamellar magnet, and the magnetism is said to be distributed lamellarly. A magnet consisting of a series of plane shells of equal strength arranged at right angles to the direction of magnetization will be uniformly magnetized.
It can be shown that uniform magnetization is possible only when the form of the body is ellipsoidal. (Maxwell, Electricity and Magnetism, II., § 437). The cases of greatest practical importance are those of a sphere (which is an ellipsoid with three equal axes) and an ovoid or prolate ellipsoid of revolution. The potential due to a uniformly magnetized sphere of radius a for an external point at a distance r from the centre is
V = 4⁄3πa³I cos θ/r²,
θ being the inclination of r to the magnetic axis. Since 4⁄3πa³I is the moment of the sphere (= volume × magnetization), it appears from (10) that the magnetized sphere produces the same external effect as a very small magnet of equal moment placed at its centre and magnetized in the same direction; the resultant force therefore is the same as in (14). The force in the interior is uniform, opposite 326 to the direction of magnetization, and equal to 4⁄3πI. When it is desired to have a uniform magnet with definitely situated poles, it it usual to employ one having the form of an ovoid, or elongated ellipsoid of revolution, instead of a rectangular or cylindrical bar. If the magnetization is parallel to the major axis, and the lengths of the major and minor axes are 2a and 2c, the poles are situated at a distance equal to 2⁄3a from the centre, and the magnet will behave externally like a simple solenoid of length 4⁄3a. The internal force F is opposite to the direction of the magnetization, and equal to NI, where N is a coefficient depending only on the ratio of the axes. The moment = 4⁄3πac²I = −4⁄3πac²FN.
The distribution of magnetism and the position of the poles in magnets of other shapes, such as cylindrical or rectangular bars, cannot be specified by any general statement, though approximate determinations may be obtained experimentally in individual cases.5 According to F. W. G. Kohlrausch6 the distance between the poles of a cylindrical magnet the length of which is from 10 to 30 times the diameter, is sensibly equal to five-sixths of the length of the bar. This statement, however, is only approximately correct, the distance between the poles depending upon the intensity of the magnetization.7 In general, the greater the ratio of length to section, the more nearly will the poles approach the end of the bar, and the more nearly uniform will be the magnetization. For most practical purpose a knowledge of the exact position of the poles is of no importance; the magnetic moment, and therefore the mean magnetization, can always be determined with accuracy.
Magnetic Induction or Magnetic Flux.—When magnetic force acts on any medium, whether magnetic, diamagnetic or neutral, it produces within it a phenomenon of the nature of a flux or flow called magnetic induction (Maxwell, loc. cit., § 428). Magnetic induction, like other fluxes such as electrical, thermal or fluid currents, is defined with reference to an area; it satisfies the same conditions of continuity as the electric current does, and in isotropic media it depends on the magnetic force just as the electric current depends on the electromotive force. The magnitude of the flux produced by a given magnetic force differs in different media. In a uniform magnetic field of unit intensity formed in empty space the induction or magnetic flux across an area of 1 square centimetre normal to the direction of the field is arbitrarily taken as the unit of induction. Hence if the induction per square centimetre at any point is denoted by B, then in empty space B is numerically equal to H; moreover in isotropic media both have the same direction, and for these reasons it is often said that in empty space (and practically in air and other non-magnetic substances) B and H are identical. Inside a magnetized body, B is the force that would be exerted on a unit pole if placed in a narrow crevasse cut in the body, the walls of the crevasse being perpendicular to the direction of the magnetization (Maxwell, § § 399, 604); and its numerical value, being partly due to the free magnetism on the walls, is generally very different from that of H. In the case of a straight uniformly magnetized bar the direction of the magnetic force due to the poles of the magnet is from the north to the south pole outside the magnet, and from the south to the north inside. The magnetic flux per square centimetre at any point (B, B, or ℬ) is briefly called the induction, or, especially by electrical engineers, the flux-density. The direction of magnetic induction may be indicated by lines of induction; a line of induction is always a closed curve, though it may possibly extend to and return from infinity. Lines of induction drawn through every point in the contour of a small surface form a re-entrant tube bounded by lines of induction; such a tube is called a tube of induction. The cross-section of a tube of induction may vary in different parts, but the total induction across any section is everywhere the same. A special meaning has been assigned to the term “lines of induction.” Suppose the whole space in which induction exists to be divided up into unit tubes, such that the surface integral of the induction over any cross-section of a tube is equal to unity, and along the axis of each tube let a line of induction be drawn. These axial lines constitute the system of lines of induction which are so often referred to in the specification of a field. Where the induction is high the lines will be crowded together; where it is weak they will be widely separated, the number per square centimetre crossing a normal surface at any point being always equal to the numerical value of B. The induction may therefore be specified as B lines per square centimetre. The direction of the induction is also of course indicated by the direction of the lines, which thus serve to map out space in a convenient manner. Lines of induction are frequently but inaccurately spoken of as lines of force.
When induction or magnetic flux takes place in a ferromagnetic metal, the metal becomes magnetized, but the magnetization at any point is proportional not to B, but to B − H. The factor of proportionality will be 1 − 4π, so that
I = (B − H) / 4π,
or
B = H + 4πI.
Unless the path of the induction is entirely inside the metal, free magnetic poles are developed at those parts of the metal where induction enters and leaves, the polarity being south at the entry and north at the exit of the flux. These free poles produce a magnetic field which is superposed upon that arising from other sources. The resultant magnetic field, therefore, is compounded of two fields, the one being due to the poles, and the other to the external causes which would be operative in the absence of the magnetized metal. The intensity (at any point) of the field due to the magnetization may be denoted by Hi, that of the external field by H0, and that of the resultant field by H. In certain cases, as, for instance, in an iron ring wrapped uniformly round with a coil of wire through which a current is passing, the induction is entirely within the metal; there are, consequently, no free poles, and the ring, though magnetized, constitutes a poleless magnet. Magnetization is usually regarded as the direct effect of the resultant magnetic force, which is therefore often termed the magnetizing force.
Permeability and Susceptibility.—The ratio B/H is called the permeability of the medium in which the induction is taking place, and is denoted by μ. The ratio I/H is called the susceptibility of the magnetized substance, and is denoted by κ. Hence
B = μH and I = κH.
Also
| μ = | B | = | H + 4πI | = 1 + 4πκ, |
| H | H |
and
| κ = | μ − 1 |
| 4π |
Since in empty space B has been assumed to be numerically equal to H, it follows that the permeability of a vacuum is equal to 1. The permeability of most material substances differs very slightly from unity, being a little greater than 1 in paramagnetic and a little less in diamagnetic substances. In the case of the ferromagnetic metals and some of their alloys and compounds, the permeability has generally a much higher value. Moreover, it is not constant, being an apparently arbitrary function of H or of B; in the same specimen its value may, under different conditions, vary from less than 2 to upwards of 5000. The magnetic susceptibility κ expresses the numerical relation of the magnetization to the magnetizing force. From the equation κ = (μ − 1)/4π, it follows that the magnetic susceptibility of a vacuum (where μ = l) is 0, that of a diamagnetic substance (where μ < l) has a negative value, while the susceptibility of paramagnetic and ferromagnetic substances (for which μ > 1) is positive. No substance has yet been discovered having a negative susceptibility sufficiently great to render the permeability (= 1 + 4πκ) negative.
Magnetic Circuit.—The circulation of magnetic induction or flux through magnetic and non-magnetic substances, such as iron and air, is in many respects analogous to that of an electric current through good and bad conductors. Just as the lines of flow of an electric current all pass in closed curves through the battery or other generator, so do all the lines of induction pass in closed curves through the magnet or magnetizing coil. The total magnetic induction or flux corresponds to the current of electricity (practically measured in amperes); the induction or flux density B to the density of the current (number of amperes to the square centimetre of section); the magnetic permeability to the specific electric conductivity; and the line integral of the magnetic force, sometimes called the magneto-motive force, to the electromotive force in the circuit. The principal points of difference are that (1) the magnetic permeability, unlike the electric conductivity, which is independent of the strength of the current, is not in general constant; (2) there is no perfect insulator for magnetic induction, which will pass more or less freely through all known substances. Nevertheless, many important problems relating to the distribution of magnetic induction may be solved by methods similar to those employed for the solution of analogous problems in electricity. For the elementary theory of the magnetic circuit see Electro-Magnetism.
Hysteresis, Coercive Force, Retentiveness.—It is found that when a piece of ferromagnetic metal, such as iron, is subjected to a magnetic field of changing intensity, the changes which take place in the induced magnetization of the iron exhibit a tendency to lag behind those which occur in the intensity of the field—a phenomenon to which J. A. Ewing (Phil. Trans. clxxvi. 524) has given the name of hysteresis (Gr. ὑστερέω, to lag behind). Thus it happens that there is no definite relation between the magnetization of a piece of metal which has been previously magnetized and the strength of the field in which it is placed. Much depends upon its antecedent magnetic condition, and indeed upon its whole magnetic history. A well-known example of hysteresis is presented by the case of permanent magnets. If a bar of hard steel is placed in a strong magnetic field, a certain intensity of magnetization is induced in the bar; but when the strength of the field is afterwards reduced to zero, the magnetization does not entirely disappear. That portion which is permanently retained, and which may amount to considerably more than one-half, is called the residual magnetization. The ratio of the residual magnetization to its previous maximum value measures the retentiveness, or 327 retentivity, of the metal.8 Steel, which is well suited for the construction of permanent magnets, is said to possess great “coercive force.” To this term, which had long been used in a loose and indefinite manner, J. Hopkinson supplied a precise meaning (Phil. Trans. clxxvi. 460). The coercive force, or coercivity, of a material is that reversed magnetic force which, while it is acting, just suffices to reduce the residual induction to nothing after the material has been temporarily submitted to any great magnetizing force. A metal which has great retentiveness may at the same time have small coercive force, and it is the latter quality which is of chief importance in permanent magnets.
Demagnetizing Force.—It has already been mentioned that when a ferromagnetic body is placed in a magnetic field, the resultant magnetic force H, at a point within the body, is compounded of the force H0, due to the external field, and of another force, Hi, arising from the induced magnetization of the body. Since Hi generally tends to oppose the external force, thus making H less than H0, it may be called the demagnetizing force. Except in the few special cases when a uniform external field produces uniform magnetization, the value of the demagnetizing force cannot be calculated, and an exact determination of the actual magnetic force within the body is therefore impossible. An important instance in which the calculation can be made is that of an elongated ellipsoid of revolution placed in a uniform field H0, with its axis of revolution parallel to the lines of force. The magnetization at any point inside the ellipsoid will then be
| I = | κH0 |
| 1 + κN |
where
| N = 4π ( | 1 | − 1 ) ( | 1 | log | 1 + e | − 1 ), |
| e2 | 2e | 1 − e |
e being the eccentricity (see Maxwell’s Treatise, § 438). Since I = κH, we have
κH + κNI = κH0,
or
H = H0 − NI,
NI being the demagnetizing force Hi. N may be called, after H. du Bois (Magnetic Circuit, p. 33), the demagnetizing factor, and the ratio of the length of the ellipsoid 2c to its equatorial diameter 2a (= c/a), the dimensional ratio, denoted by the symbol m.
Since
| e = √( 1 − | a² | ) = √( 1 − | 1 | ), |
| c² | m² |
the above expression for N may be written
| N = | 4π | ( | m | log | m + √(m² − 1) | − 1 ) |
| m² − 1 | 2√(m² − 1) | m − √(m² − 1) |
| = | 4π | { | m | log ( m+ √(m² − 1) ) − 1 }, |
| m² − 1 | √(m² − 1) |
from which the value of N for a given dimensional ratio can be calculated. When the ellipsoid is so much elongated that 1 is negligible in relation to m², the expression approximates to the simpler form
| N = | 4π | ( log 2m − 1 ) |
| m² |
In the case of a sphere, e = O and N = 4⁄3π; therefore from (29)
| I = κH = | κH0 | = | 3κ | H0, |
| 1 + 4⁄3πκ | 3 + 4πκ |
Whence
| H = | 3 | H0 = | 3 | H0, |
| 3 + 4πκ | μ + 2 |
and
| B = μH = | 3μ | H0. |
| μ + 2 |
Equations (33) and (34) show that when, as is generally the case with ferromagnetic substances, the value of μ is considerable, the resultant magnetic force is only a small fraction of the external force, while the numerical value of the induction is approximately three times that of the external force, and nearly independent of the permeability. The demagnetizing force inside a cylindrical rod placed longitudinally in a uniform field H0 is not uniform, being greatest at the ends and least in the middle part. Denoting its mean value by Hi, and that of the demagnetizing factor by N, we have
H = H0 − Hi = H0 − NI.
Du Bois has shown that when the dimensional ratio m (= length/diameter) exceeds 100, Nm² = constant = 45, and hence for long thin rods
N = 45 / m².
From an analysis of a number of experiments made with rods of different dimensions H. du Bois has deduced the corresponding mean demagnetizing factors. These, together with values of m²N for cylindrical rods, and of N and m²N for ellipsoids of revolution, are given in the following useful table (loc. cit. p. 41):—
Demagnetizing Factors.
| m. | Cylinder. | Ellipsoid. | ||
| N. | m²N. | N. | m²N. | |
| 0 | 12.5664 | 0 | 12.5664 | 0 |
| 0.5 | — | — | 6.5864 | — |
| 1 | — | — | 4.1888 | — |
| 5 | — | — | 0.7015 | — |
| 10 | 0.2160 | 21.6 | 0.2549 | 25.5 |
| 15 | 0.1206 | 27.1 | 0.1350 | 30.5 |
| 20 | 0.0775 | 31.0 | 0.0848 | 34.0 |
| 25 | 0.0533 | 33.4 | 0.0579 | 36.2 |
| 30 | 0.0393 | 35.4 | 0.0432 | 38.8 |
| 40 | 0.0238 | 38.7 | 0.0266 | 42.5 |
| 50 | 0.0162 | 40.5 | 0.0181 | 45.3 |
| 60 | 0.0118 | 42.4 | 0.0132 | 47.5 |
| 70 | 0.0089 | 43.7 | 0.0101 | 49.5 |
| 80 | 0.0069 | 44.4 | 0.0080 | 51.2 |
| 90 | 0.0055 | 44.8 | 0.0065 | 52.5 |
| 100 | 0.0045 | 45.0 | 0.0054 | 54.0 |
| 150 | 0.0020 | 45.0 | 0.0026 | 58.3 |
| 200 | 0.0011 | 45.0 | 0.0016 | 64.0 |
| 300 | 0.00050 | 45.0 | 0.00075 | 67.5 |
| 400 | 0.00028 | 45.0 | 0.00045 | 72.0 |
| 500 | 0.00018 | 45.0 | 0.00030 | 75.0 |
| 1000 | 0.00005 | 45.0 | 0.00008 | 80.0 |
In the middle part of a rod which has a length of 400 or 500 diameters the effect of the ends is insensible; but for many experiments the condition of endlessness may be best secured by giving the metal the shape of a ring of uniform section, the magnetic field being produced by an electric current through a coil of wire evenly wound round the ring. In such cases Hi = 0 and H = H0.
The residual magnetization Ir retained by a bar of ferromagnetic metal after it has been removed from the influence of an external field produces a demagnetizing force NIr, which is greater the smaller the dimensional ratio. Hence the difficulty of imparting any considerable permanent magnetization to a short thick bar not possessed of great coercive force. The magnetization retained by a long thin rod, even when its coercive force is small, is sometimes little less than that which was produced by the direct action of the field.
Demagnetization by Reversals.—In the course of an experiment it is often desired to eliminate the effects of previous magnetization, and, as far as possible, wipe out the magnetic history of a specimen. In order to attain this result it was formerly the practice to raise the metal to a bright red heat, and allow it to cool while carefully guarded from magnetic influence. This operation, besides being very troublesome, was open to the objection that it was almost sure to produce a material but uncertain change in the physical constitution of the metal, so that, in fact, the results of experiments made before and after the treatment were not comparable. Ewing introduced the method (Phil. Trans. clxxvi. 539) of demagnetizing a specimen by subjecting it to a succession of magnetic forces which alternated in direction and gradually diminished in strength from a high value to zero. By means of a simple arrangement, which will be described farther on, this process can be carried out in a few seconds, and the metal can be brought as often as desired to a definite condition, which, if not quite identical with the virgin state, at least closely approximates to it.
Forces acting on a Small Body in the Magnetic Field.—If a small magnet of length ds and pole-strength m is brought into a magnetic field such that the values of the magnetic potential at the negative and positive poles respectively are V1 and V2, the work done upon the magnet, and therefore its potential energy, will be
W = m (V2 − V1) = m dV,
which may be written
| W = m ds | dV | = M | dV | = −MH0 = −vIH0, |
| ds | ds |
where M is the moment of the magnet, v the volume, I the magnetization, and H0 the magnetic force along ds. The small magnet may be a sphere rigidly magnetized in the direction of H0; if this is replaced by an isotropic sphere inductively magnetized by the field, then, for a displacement so small that the magnetization of the sphere may be regarded as unchanged, we shall have
| dW = −vI dH0 = −v | κ | H0 dH0; |
| 1 + 4⁄3πκ |
whence
| W = − | v | κ | H²0. | |
| 2 | 1 + 4⁄3πκ |
The mechanical force acting on the sphere in the direction of displacement x is
| F = − | dW | = v | κ | dH²0 | . | |
| dx | 1 + 4⁄3πκ | dx |
If H0 is constant, the force will be zero; if H0 is variable, the sphere will tend to move in the direction in which H0 varies most rapidly. The coefficient κ / (1 + 4⁄3πκ) is positive for ferromagnetic and paramagnetic substances, which will therefore tend to move from weaker to stronger parts of the field; for all known diamagnetic substances it is negative, and these will tend to move from stronger to weaker parts. For small bodies other than spheres the coefficient will be different, but its sign will always be negative for diamagnetic substances and positive for others;9 hence the forces acting on any small body will be in the same directions as in the case of a sphere.10
Directing Couple acting on an Elongated Body.—In a non-uniform field every volume-element of the body tends to move towards regions of greater or less force according as the substance is paramagnetic or diamagnetic, and the behaviour of the whole mass will be determined chiefly by the tendency of its constituent elements. For this reason a thin bar suspended at its centre of gravity between a pair of magnetic poles will, if paramagnetic, set itself along the line joining the poles, where the field is strongest, and if diamagnetic, transversely to the line. These are the “axial” and “equatorial” positions of Faraday. It can be shown11 that in a uniform field an elongated piece of any non-crystalline material is in stable equilibrium only when its length is parallel to the lines of force; for diamagnetic substances, however, the directing couple is exceedingly small, and it would hardly be possible to obtain a uniform field of sufficient strength to show the effect experimentally.
Relative Magnetization.—A substance of which the real susceptibility is κ will, when surrounded by a medium having the susceptibility κ′, behave towards a magnet as if its susceptibility were κa = (κ − κ′) / (1 + 4πκ′). Since 1 + 4πκ′ can never be negative, the apparent susceptibility κa will be positive or negative according as κ is greater or less than κ′. Thus, for example, a tube containing a weak solution of an iron salt will appear to be diamagnetic if it is immersed in a stronger solution of iron, though in air it is paramagnetic.12
Circular Magnetization.—An electric current i flowing uniformly through a cylindrical wire whose radius is a produces inside the wire a magnetic field of which the lines of force are concentric circles around the axis of the wire. At a point whose distance from the axis of the wire is r the tangential magnetic force is
H = 2ir / a²
it therefore varies directly as the distance from the axis, where it is zero.13 If the wire consists of a ferromagnetic metal, it will become “circularly” magnetized by the field, the lines of magnetization being, like the lines of force, concentric circles. So long as the wire (supposed isotropic) is free from torsional stress, there will be no external evidence of magnetism.
Magnetic Shielding.—The action of a hollow magnetized shell on a point inside it is always opposed to that of the external magnetizing force,14 the resultant interior field being therefore weaker than the field outside. Hence any apparatus, such as a galvanometer, may be partially shielded from extraneous magnetic action by enclosing it in an iron case. If a hollow sphere15 of which the outer radius is R and the inner radius r is placed in a uniform field H0, the field inside will also be uniform and in the same direction as H0, and its value will be approximately
| Hi = | H0 | . |
| 1 + 2⁄9 (μ − 2) (1 − r³/R³) |
For a cylinder placed with its axis at right angles to the lines of force,
| Hi = | H0 | . |
| 1 + 1⁄4 (μ − 2) (1 − r²/R²) |
These expressions show that the thicker the screen and the greater its permeability μ, the more effectual will be the shielding action. Since μ can never be infinite, complete shielding is not possible.
Magneto-Crystallic Phenomenon.—In anisotropic bodies, such as crystals, the direction of the magnetization does not in general coincide with that of the magnetic force. There are, however, always three principal axes at right angles to one another along which the magnetization and the force have the same direction. If each of these axes successively is placed parallel to the lines of force in a uniform field H, we shall have
I1 = κ1H, I2 = κ2H, I3 = κ3H,
the three susceptibilities κ being in general unequal, though in some cases two of them may have the same value. For crystalline bodies the value of κ (+ or −) is nearly always small and constant, the magnetization being therefore independent of the form of the body and proportional to the force. Hence, whatever the position of the body, if the field be resolved into three components parallel to the principal axes of the crystal, the actual magnetization will be the resultant of the three magnetizations along the axes. The body (or each element of it) will tend to set itself with its axis of greatest susceptibility parallel to the lines of force, while, if the field is not uniform, each volume-element will also tend to move towards places of greater or smaller force (according as the substance is paramagnetic or diamagnetic), the tendency being a maximum when the axis of greatest susceptibility is parallel to the field, and a minimum when it is perpendicular to it. The phenomena may therefore be exceedingly complicated.16
3. Magnetic Measurements
Magnetic Moment.—The moment M of a magnet may be determined in many ways,17 the most accurate being that of C. F. Gauss, which gives the value not only of M, but also that of H, the horizontal component of the earth’s force. The product MH is first determined by suspending the magnet horizontally, and causing it to vibrate in small arcs. If A is the moment of inertia of the magnet, and t the time of a complete vibration, MH = 4π²A / t² (torsion being neglected). The ratio M/H is then found by one of the magnetometric methods which in their simplest forms are described below. Equation (44) shows that as a first approximation.
M / H = (d² − l²) tan θ/2d,
where l is half the length of the magnet, which is placed in the “broadside-on” position as regards a small suspended magnetic needle, d the distance between the centre of the magnet and the needle, and θ the angle through which the needle is deflected by the magnet. We get therefore
M² = MH × M/H = 2π²A (d² − l²)² tan θ/t²d
H² = MH × H/M = 8π²Ad / {t² (d² − l²)² tan θ}.
When a high degree of accuracy is required, the experiments and calculations are less simple, and various corrections are applied. The moment of a magnet may also be deduced from a measurement of the couple exerted on the magnet by a uniform field H. Thus if the magnet is suspended horizontally by a fine wire, which, when the magnetic axis points north and south, is free from torsion, and if θ is the angle through which the upper end of the wire must be twisted to make the magnet point east and west, then MH = Cθ, or M = Cθ/H, where C is the torsional couple for 1°. A bifilar suspension is sometimes used instead of a single wire. If P is the weight of the magnet, l the length of each of the two threads, 2a the distance between their upper points of attachment, and 2b that between the lower points, then, approximately, MH = P(ab/l) sin θ. It is often sufficient to find the ratio of the moment of one magnet to that of another. If two magnets having moments M, M′ are arranged at right angles to each other upon a horizontal support which is free to rotate, their resultant R will set itself in the magnetic meridian. Let θ be the angle which the standard magnet M makes with the meridian, then M′/R = sin θ, and M/R = cos θ, whence M′ = M tan θ.
 |
| Fig. 5. |
A convenient and rapid method of estimating a magnetic moment has been devised by H. Armagnat.18 The magnet is laid on a table with its north pole pointing northwards, A compass having a very short needle is placed on the line which bisects the axis of the magnet at right angles, and is moved until a neutral point is found where the force due to the earth’s field H is balanced by that due to the magnet. If 2l is the distance between the poles m and −m, d the distance from either pole to a point P on the line AB (fig. 5), we have for the resultant force at P
R = −2 cos θ × m / d² = −2lm / d³ = -M / d³.
When P is the neutral point, H is equal and opposite to R; therefore M = Hd³, or the moment is numerically equal to the cube of the distance from the neutral point to a pole, multiplied by the 329 horizontal intensity of the earth’s force. The distance between the poles may with sufficient accuracy for a rough determination be assumed to be equal to five-sixths of the length of the magnet.
Measurement of Magnetization and Induction.—The magnetic condition assumed by a piece of ferromagnetic metal in different circumstances is determinable by various modes of experiment which may be classed as magnetometric, ballistic, and traction methods. When either the magnetization I or the induction B corresponding to a given magnetizing force H is known, the other may be found by means of the formula B = 4πI + H.
Magnetometric Methods.—Intensity of magnetization is most directly measured by observing the action which a magnetized body, generally a long straight rod, exerts upon a small magnetic needle placed near it. The magnetic needle may be cemented horizontally across the back of a little plane or concave mirror, about ¼ or 3⁄8 in. in diameter, which is suspended by a single fibre of unspun silk; this arrangement, when enclosed in a case with a glazed front to protect it from currents of air, constitutes a simple but efficient magnetometer. Deflections of the suspended needle are indicated by the movement of a narrow beam of light which the mirror reflects from a lamp and focusses upon a graduated cardboard scale placed at a distance of a few feet; the angular deflection of the beam of light is, of course, twice that of the needle. The suspended needle is, in the absence of disturbing causes, directed solely by the horizontal component of the earth’s field of magnetic force HE, and therefore sets itself approximately north and south. The magnetized body which is to be tested should be placed in such a position that the force HP due to its poles may, at the spot occupied by the suspended needle, act in a direction at right angles to that due to the earth—that is, east and west. The direction of the resultant field of force will then make, with that of HE, an angle θ, such that Hp / HE = tan θ, and the suspended needle will be deflected through the same angle. We have therefore
HP = HE tan θ.
The angle θ is indicated by the position of the spot of light upon the scale, and the horizontal intensity of the earth’s field HE is known; thus we can at once determine the value of HP, from which the magnetization I of the body under test may be calculated.
In order to fulfil the requirement that the field which a magnetized rod produces at the magnetometer shall be at right angles to that of the earth, the rod may be conveniently placed in any one of three different positions with regard to the suspended needle.
 |
| Fig. 6. |
(1) The rod is set in a horizontal position level with the suspended needle, its axis being in a line which is perpendicular to the magnetic meridian, and which passes through the centre of suspension of the needle. This is called the “end-on” position, and is indicated in fig. 6. AB is the rod and C the middle point of its axis; NS is the magnetometer needle; AM bisects the undeflected needle NS at right angles. Let 2l = the length of the rod (or, more accurately, the distance between its poles), v = its volume, m and −m the strength of its poles, and let d = the distance CM. For most ordinary purposes the length of the needle may be assumed to be negligible in comparison with the distance between the needle and the rod. We then have approximately for the field at M due to the rod
| HP = | m | − | m | = m | 4dl | . |
| (d − l)² | (d + l)² | (d² − l²)² |
Therefore
| 2ml = M = | (d² − l²)² HP | = | (d² − l²)² HE tan θ | . |
| 2d | 2d |
And
| I = | M | = | (d² − l²)² HE | tan θ, |
| v | 2dv |
whence we can find the values of I which correspond to different angles of deflection.
(2) The rod may be placed horizontally east and west in such a position that the direction of the undeflected suspended needle bisects it at right angles. This is known as the “broadside-on” position, and is represented in fig. 7. Let the distance of each pole of the rod AB from the centre of the magnetometer needle = d. Then, since HP, the force at M due to m and −m, is the resultant of m/d² and −m/d², we have
| HP | = | 2l |
| m/d² | d |
or
| HP = | 2ml | , |
| d³ |
the direction being parallel to AB.
And
| I = | d³HP | = | d³HE | tan θ. |
| v | v |
 | |
| Fig. 7. | Fig. 8. |
(3) In the third position the test rod is placed vertically with one of its poles at the level of the magnetometer needle, and in the line drawn perpendicularly to the undeflected needle from its centre of suspension. The arrangement is shown in fig. 8, where AB is the vertical rod and M indicates the position of the magnetometer needle, which is supposed to be perpendicular to the plane of the paper. Denoting the distance AM by d1, BM by d2, and AB by l, we have for the force at M due to the magnetism of the rod
| HP = | m | − horizontal component of | m |
| d1² | d2² |
| = m ( | 1 | − | d1 | ). |
| d1² | d2³ |
Therefore
| m = | HP | = | d1²HE | tan θ, |
| (1 / d1²) − (d1 / d2³) | 1 − (d1 / d2)³ |
and
| I = | ld1² HE | tan θ. |
| v {1 − (d1 / d2)³ } |
This last method of arrangement is called by Ewing the “one-pole” method, because the magnetometer deflection is mainly caused by the upper pole of the rod (Magnetic Induction, p. 40). For experiments with long thin rods or wires it has an advantage over the other arrangements in that the position of the poles need not be known with great accuracy, a small upward or downward displacement having little effect upon the magnetometer deflection. On the other hand, a vertically placed rod is subject to the inconvenience that it is influenced by the earth’s magnetic field, which is not the case when the rod is horizontal and at right angles to the magnetic meridian. This extraneous influence may, however, be eliminated by surrounding the rod with a coil of wire carrying a current such as will produce in the interior a magnetic field equal and opposite to the vertical component of the earth’s field.
If the cardboard scale upon which the beam of light is reflected by the magnetometer mirror is a flat one, the deflections as indicated by the movement of the spot of light are related to the actual deflections of the needle in the ratio of tan 2θ to θ. Since θ is always small, sufficiently accurate results may generally be obtained if we assume that tan 2θ = 2 tan θ. If the distance of the mirror from the scale is equal to n scale divisions, and if a deflection θ of the needle causes the reflected spot of light to move over s scale divisions, we shall have
s / n = tan 2θ exactly,
s / 2n = tan θ approximately.
We may therefore generally substitute s/2n for tan θ in the various expressions which have been given for I.
 |
| Fig. 9. |
Of the three methods which have been described, the first two are generally the most suitable for determining the moment or the magnetization of a permanent magnet, and the last for studying the changes which occur in the magnetization of a long rod or wire when subjected to various external magnetic forces, or, in other words, for determining the relation of I to H. A plan of the apparatus as arranged by Ewing for the latter purpose is shown diagrammatically in fig. 9. The cardboard scale SS is placed above a wooden screen, having in it a narrow vertical slit which permits a beam of light from the lamp L to reach the mirror of the magnetometer M, whence it is reflected upon the scale. A is the upper end of a glass tube, half a metre or so in length, which is clamped in a vertical position behind the magnetometer. The tube is wound over its whole length with two separate coils of insulated wire, the one being outside the other. The inner coil is supplied, through the intervening apparatus, with current from the battery of secondary cells B1; this produces the desired magnetic field inside the tube. The outer coil derives current, through an adjustable resistance R, from a 330 constant cell B2; its object is to produce inside the tube a magnetic field equal and opposite to that due to the earth’s magnetism. C is a “compensating coil” consisting of a few turns of wire through which the magnetizing current passes; it serves to neutralize the effect produced upon the magnetometer by the magnetizing coil, and its distance from the magnetometer is so adjusted that when the circuit is closed, no ferromagnetic metal being inside the magnetizing coil, the magnetometer needle undergoes no deflection. K is a commutator for reversing the direction of the magnetizing current, and G a galvanometer for measuring it. The strength of the magnetizing current is regulated by adjusting the position of the sliding contact E upon the resistance DF. The current increases to a maximum as E approaches F, and diminishes to almost nothing when E is brought up to D; it can be completely interrupted by means of the switch H.
The specimen upon which an experiment is to be made generally consists of a wire having a “dimensional ratio” of at least 300 or 400; its length should be rather less than that of the magnetizing coil, in order that the field H0, to which it is subjected, may be approximately uniform from end to end. The wire is supported inside the glass tube A with its upper pole at the same height as the magnetometer needle. Various currents are then passed through the magnetizing coil, the galvanometer readings and the simultaneous magnetometer deflections being noted. From the former we deduce H0, and from the latter the corresponding value of I, using the formulae H0 = 4πin/l and
| I = | d1² HE | × s, |
| 2nπr² { 1 − (d1 / d2)³ } |
where s is the deflection in scale-divisions, n the distance in scale-divisions between the scale and the mirror, and r the radius of the wire.
 |
| Fig. 10. |
The curve, fig. 10, shows the result of a typical experiment made upon a piece of soft iron (Ewing, Phil. Trans. vol. clxxvi. Plate 59), the magnetizing field H0 being first gradually increased and then diminished to zero. When the length of the wire exceeds 400 diameters, or thereabouts, H0 may generally be considered as equivalent to H, the actual strength of the field as modified by the magnetization of the wire; but if greater accuracy is desired, the value of Hi (= NI) may be found by the help of du Bois’s table and subtracted from H0. For a dimensional ratio of 400, N =0.00028, and therefore H = H0 − 0.00028I. This correction may be indicated in the diagram by a straight line drawn from 0 through the point at which the line of I = 1000 intersects that of H = 0.28 (Rayleigh, Phil. Mag. xxii. 175), the true value of H for any point on the curve being that measured from the sloping line instead of from the vertical axis. The effect of the ends of the wire is, as Ewing remarks, to shear the diagram in the horizontal direction through the angle which the sloping line makes with the vertical.
Since the induction B is equal to H + 4πI, it is easy from the results of experiments such as that just described to deduce the relation between B and H; a curve indicating such relation is called a curve of induction. The general character of curves of magnetization and of induction will be discussed later. A notable feature in both classes of curves is that, owing to hysteresis, the ascending and descending limbs do not coincide, but follow very different courses. If it is desired to annihilate the hysteretic effects of previous magnetization and restore the metal to its original condition, it may be demagnetized by reversals. This is effected by slowly moving the sliding contact E (fig. 9) from F to D, while at the same time the commutator K is rapidly worked, a series of alternating currents of gradually diminishing strength being thus caused to pass through the magnetizing coil.
The magnetometric method, except when employed in connexion with ellipsoids, for which the demagnetizing factors are accurately known, is generally less satisfactory for the exact determination of induction or magnetization than the ballistic method. But for much important experimental work it is better adapted than any other, and is indeed sometimes the only method possible.19
Ballistic Methods.—The so-called “ballistic” method of measuring induction is based upon the fact that a change of the induction through a closed linear conductor sets up in the conductor an electromotive force which is proportional to the rate of change. If the conductor consists of a coil of wire the ends of which are connected with a suitable galvanometer, the integral electromotive force due to a sudden increase or decrease of the induction through the coil displaces in the circuit a quantity of electricity Q = δBnsR, where δB is the increment or decrement of induction per square centimetre, s is the area of the coil, n the number of turns of wire, and R the resistance of the circuit. Under the influence of the transient current, the galvanometer needle undergoes a momentary deflection, or “throw,” which is proportional to Q, and therefore to δB, and thus, if we know the deflection produced by the discharge through the galvanometer of a given quantity of electricity, we have the means of determining the value of δB.
The galvanometer which is used for ballistic observations should have a somewhat heavy needle with a period of vibration of not less than five seconds, so that the transient current may have ceased before the swing has well begun; an instrument of the d’Arsonval form is recommended, not only because it is unaffected by outside magnetic influence, but also because the moving part can be instantly brought to rest by means of a short-circuit key, thus effecting a great saving of time when a series of observations is being made. In practice it is usual to standardize or “calibrate” the galvanometer by causing a known change of induction to take place within a standard coil connected with it, and noting the corresponding deflection on the galvanometer scale. Let s be the area of a single turn of the standard coil, n the number of its turns, and r the resistance of the circuit of which the coil forms part; and let S, N and R be the corresponding constants for a coil which is to be used in an experiment. Then if a known change of induction δBa inside the standard coil is found to cause a throw of d scale-divisions, any change of induction δB through the experimental coil will be numerically equal to the corresponding throw D multiplied by snRBa/SNrd. For a series of experiments made with the same coil this fraction is constant, and we may write δB = kD. Rowland and others have used an earth coil for calibrating the galvanometer, a known change of induction through the coil being produced by turning it over in the earth’s magnetic field, but for several reasons it is preferable to employ an electric current as the source of a known induction. A primary coil of length l, having n turns, is wound upon a cylinder made of non-conducting and non-magnetic material, and upon the middle of the primary a secondary or induction coil is closely fitted. When a current of strength i is suddenly interrupted in the primary, the increment of induction through the secondary is sensibly equal to 4πin/l units. All the data required for standardizing the galvanometer can in this way be determined with accuracy.
The ballistic method is largely employed for determining the relation of induction to magnetizing force in samples of the iron and steel used in the manufacture of electrical machinery, and especially for the observation of hysteresis effects. The sample may have the form of a closed ring, upon which are wound the induction coil and another coil for taking the magnetizing current; or it may consist of a long straight rod or wire which can be slipped into a magnetizing coil such as is used in magnetometric experiments, the induction coil being wound upon the middle of the wire. With these arrangements there is no demagnetizing force to be considered, for the ring has not any ends to produce one, and the force due to the ends of a rod 400 or 500 diameters in length is quite insensible at the middle portion; H therefore is equal to H0.
E. Grassot has devised a galvanometer, or “fluxmeter,” which greatly alleviates the tedious operation of taking ballistic readings.20 The instrument is of the d’Arsonval type; its coil turns in a strong uniform field, and is suspended in such a manner that torsion is practically negligible, the swings of the coil being limited by damping influences, chiefly electromagnetic. The index therefore remains almost stationary at the limit of its deflection, and the deflection is approximately the same whether the change of induction occurs suddenly or gradually.
 |
| Fig. 11. Fig. 12. Fig. 13. |
Induction and Hysteresis Curves.—Some typical induction curves, copied from a paper by Ewing (Proc. Inst. C.E. vol. cxxvi.), are given in figs. 11, 12 and 13. Fig. 11 shows the relation of B to H in a specimen which has never before been magnetized. The experiment may be made in two different ways: (1) the magnetizing current is increased by a series of sudden steps, each of which produces a ballistic throw, the value of B after any one throw being proportional to the sum of that and all the previous throws; (2) the magnetizing current having been brought to any desired value, is suddenly reversed, and the observed throw taken as measuring twice the actual induction. Fig. 12 shows the nature of the course taken by the curve when the magnetizing current, after having been raised to the value corresponding to the point a, is diminished by steps until it is nothing, and then gradually increased in the reverse direction. The downward course of the curve is, owing to hysteresis, strikingly different from its upward course, and when the magnetizing force has been reduced to zero, there is still remaining an induction of 7500 units. If the operation is again reversed, the upward course will be nearly, but not exactly, of the form shown by the line d e a, fig. 13. After a few repetitions of the reversal, the process becomes strictly cyclic, the upward and downward curves always following with precision the paths indicated in the figure. In order to establish the cyclic condition, it is sufficient to apply alternately the greatest positive and negative forces employed in the test (greatest H = about ±5 C.G.S. units in the case illustrated in the figure), an operation which is performed by simply reversing the direction of the maximum magnetizing current a few times.
The closed figure a c d e a is variously called a hysteresis curve or diagram or loop. The area ∫ H dB enclosed by it represents the work done in carrying a cubic centimetre of the iron through the corresponding magnetic cycle; expressed in ergs this work is 1/4π ∫ H dB.21 To quote an example given by J. A. Fleming, it requires about 18 foot-pounds of work to make a complete magnetic cycle in a cubic foot of wrought iron, strongly magnetized first one way and then the other, the work so expended taking the form of heat in the mass.
 |
| Fig. 14. |
Fig. 14 shows diagrammatically a convenient arrangement described by Ewing (see Proc. Inst. C.E. vol. cxxvi., and Phil. Trans., 1893A, p. 987) for carrying out ballistic tests by which either the simple B-H curve (fig. 11) or the hysteresis curve (figs. 12 and 13) can be determined. The sample under test is prepared in the form of a ring A, upon which are wound the induction and the magnetizing coils; the latter should be wound evenly over the whole ring, though for the sake of clearness only part of the winding is indicated in the diagram. The magnetizing current, which is derived from the storage battery B, is regulated by the adjustable resistance R and measured by the galvanometer G. The current passes through the rocking key K, which, when thrown over to the right, places a in contact with c and b with d, and when thrown over to the left, places a in contact with e and b with f. When the switch S is closed, K acts simply as a commutator or current-reverser, but if K is thrown over from right to left while S is opened, not only is the current reversed, but its strength is at the same time diminished by the interposition of the adjustable resistance R2. The induction coil wound upon the ring is connected to the ballistic galvanometer G2 in series with a large permanent resistance R3. In the same circuit is also included the induction coil E, which is used for standardizing the galvanometer; this secondary coil is represented in the diagram by three turns of wire wound over a much longer primary coil. The short-circuit key F is kept closed except when an observation is about to be made; its object is to arrest the swing of the d’Arsonval galvanometer G2. By means of the three-way switch C the battery current may be sent either into the primary of E, for the purpose of calibrating the galvanometer, or into the magnetizing coil of the ring under test. When it is desired to obtain a simple curve of induction, such as that in fig. 11, S is kept permanently closed, and corresponding values of H and B are determined by one of the two methods already described, the strength of the battery-current being varied by means of the adjustable resistance R. When a hysteresis curve is to be obtained, the procedure is as follows: The current is first adjusted by means of R to such a strength as will fit it to produce the greatest + and − values of the magnetizing force which it is intended to apply in the course of the cycle; then it is reversed several times, and when the range of the galvanometer throws has become constant, half the extent of an excursion indicates the induction corresponding to the extreme value of H, and gives the point a in the curve fig. 12. The reversing key K having been put over to the left side, the short-circuit key S is suddenly opened; this inserts the resistance R, which has been suitably adjusted beforehand, and thus reduces the current and therefore the magnetizing force to a known value. The galvanometer throw which results from the change of current measures the amount by which the induction is reduced, and thus a second point on the curve is found. In a similar manner, by giving different values to the resistance R, any desired number of points between a and c in the curve can be determined. To continue the process, the key K is turned over to the right-hand side, and then, while S is open, is turned back, thereby not only reversing the direction of the current, but diminishing its strength by an amount depending upon the previous adjustment of R2. In this way points can be found lying anywhere between c and d of fig. 12, and the determination of the downward limb of the curve is therefore completed. As the return curve, shown in fig. 13, is merely an inverted copy of the other, no separate determination of it is necessary.
 |
| Fig. 15. |
In fig. 15 (J. A. Fleming, Magnets and Electric Currents, p. 193) are shown three very different types of hysteresis curves, characteristic of the special qualities of the metals from which they were respectively obtained. The distinguishing feature of the first is the steepness of its outlines; this indicates that the induction increases rapidly in relation to the magnetic force, and hence the metal is well suited for the construction of dynamo magnets. The second has a very small area, showing that the work done in reversing the magnetization is small; the metal is therefore adapted for use in alternating current transformers. On the other hand, the form of the third curve, with its large intercepts on the axes of H and B, denotes that the specimen to which it relates possesses both retentiveness and coercive force in a high degree; such a metal would be chosen for making good permanent magnets.
Several arrangements have been devised for determining hysteresis more easily and expeditiously than is possible by the ballistic method. The best known is J. A. Ewing’s hysteresis-tester,22 which is specially intended for testing the sheet iron used in transformers. The sample, arranged as a bundle of rectangular strips, is caused to rotate about a central horizontal axis between the poles of an upright C-shaped magnet, which is supported near its middle upon knife-edges in such a manner that it can oscillate about an axis in a line with that about which the specimen rotates; the lower side of the magnet is weighted, to give it some stability. When the specimen rotates, the magnet is deflected from its upright position by an amount which depends upon the work done in a single complete rotation, and therefore upon the hysteresis. The deflection is indicated by a pointer upon a graduated scale, the readings being interpreted by comparison with two standard specimens supplied with the instrument. G. F. Searle and T. G. Bedford23 have 332 introduced the method of measuring hysteresis by means of an electro-dynamometer used ballistically. The fixed and suspended coils of the dynamometer are respectively connected in series with the magnetizing solenoid and with a secondary wound upon the specimen. When the magnetizing current is twice reversed, so as to complete a cycle, the sum of the two deflections, multiplied by a factor depending upon the sectional area of the specimen and upon the constants of the apparatus, gives the hysteresis for a complete cycle in ergs per cubic centimetre. For specimens of large sectional area it is necessary to apply corrections in respect of the energy dissipated by eddy currents and in heating the secondary circuit. The method has been employed by the authors themselves in studying the effects of tension, torsion and circular magnetization, while R. L. Wills24 has made successful use of it in a research on the effects of temperature, a matter of great industrial importance.
C. P. Steinmetz (Electrician, 1891, 26, p. 261; 1892, 28, pp. 384, 408, 425) has called attention to a simple relation which appears to exist between the amount of energy dissipated in carrying a piece of iron or steel through a magnetic cycle and the limiting value of the induction reached in the cycle. Denoting by W the work in ergs done upon a cubic centimetre of the metal (= 1/4π ∫ H dB or ∫ H dI), he finds W = ηB1.6 approximately, where η is a number, called the hysteretic constant, depending upon the metal, and B is the maximum induction. The value of the constant η ranges in different metals from about 0.001 to 0.04; in soft iron and steel it is said to be generally not far from 0.002. Steinmetz’s formula may be tested by taking a series of hysteresis curves between different limits of B, measuring their areas by a planimeter, and plotting the logarithms of these divided by 4π as ordinates against logarithms of the corresponding maximum values of B as abscissae. The curve thus constructed should be a straight line inclined to the horizontal axis at an angle θ, the tangent of which is 1.6. Ewing and H. G. Klaassen (Phil. Trans., 1893, 184, 1017) have in this manner examined how nearly and within what range a formula of the type W = ηBε may be taken to represent the facts. The results of an example which they quote in detail may be briefly summarized as follows:—
| Limits of B. | Hysteretic Constant. η | Index. ε (= tan θ) | Degrees. θ |
| 200 to 500 | ... | 1.9 | 62.25 |
| 500 to 1,000 | ... | 1.68 | 59.25 |
| 1,000 to 2,000 | ... | 1.55 | 57.25 |
| 2,000 to 8,000 | 0.01 | 1.475 | 55.75 |
| 8,000 to 14,000 | 0.00134 | 1.70 | 59.50 |
It is remarked by the experimenters that the value of the index ε is by no means constant, but changes in correspondence with the successive well-marked stages in the process of magnetization. But though a formula of this type has no physical significance, and cannot be accepted as an equation to the actual curve of W and B, it is, nevertheless, the case that by making the index ε = 1.6, and assigning a suitable value to η, a formula may be obtained giving an approximation to the truth which is sufficiently close for the ordinary purposes of electrical engineers, especially when the limiting value of B is neither very great nor very small. Alexander Siemens (Journ. Inst. Eng., 1894, 23, 229) states that in the hundreds of comparisons of test pieces which have been made at the works of his firm, Steinmetz’s law has been found to be practically correct.25 An interesting collection of W-B curves embodying the results of actual experiments by Ewing and Klaassen on different specimens of metal is given in fig. 16. It has been shown by Kennelly (Electrician, 1892, 28, 666) that Steinmetz’s formula gives approximately correct results in the case of nickel. Working with two different specimens, he found that the hysteresis loss in ergs per cubic centimetre (W) was fairly represented by 0.00125B1.6 and 0.00101B1.6 respectively, the maximum induction ranging from about 300 to 3000. The applicability of the law to cobalt has been investigated by Fleming (Phil. Mag., 1899, 48, 271), who used a ring of cast cobalt containing about 96% of the pure metal. The logarithmic curves which accompany his paper demonstrate that within wide ranges of maximum induction W = 0.01B1.6 = 0.527I1.62 very nearly. Fleming rightly regards it as not a little curious that for materials differing so much as this cast cobalt and soft annealed iron the hysteretic exponent should in both cases be so near to 1.6. After pointing out that, since the magnetization of the metal is the quantity really concerned, W is more appropriately expressed in terms of I, the magnetic moment per unit of volume, than of B, he suggests an experiment to determine whether the mechanical work required to effect the complete magnetic reversal of a crowd of small compass needles (representative of magnetic molecules) is proportional to the 1.6th power of the aggregate maximum magnetic moment before or after completion of the cycle.
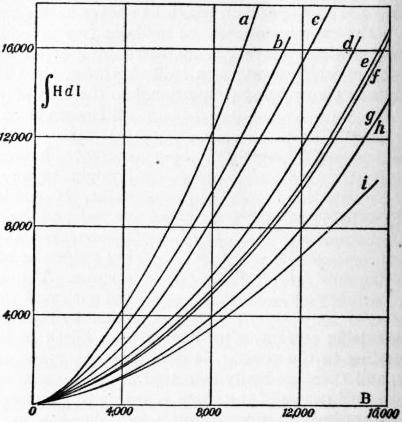 |
| Fig. 16. |
| a, Fine steel wire 0.257 mm. diam. b, Fine iron wire 0.34 mm. diam. c, Fine iron wire 0.2475 mm. diam. d, Thin sheet iron 0.47 mm. thick. e, Iron wire 0.602 mm. diam. f, Iron wire 0.975 mm. diam. g, Sheet iron 1.95 mm. thick. h, Thin sheet iron 0.367 mm. thick. i. Very soft iron wire. |
The experiments of K. Honda and S. Shimizu26 indicate that Steinmetz’s formula holds for nickel and annealed cobalt up to B = 3000, for cast cobalt and tungsten steel up to B = 8000, and for Swedish iron up to B = 18,000, the range being in all cases extended at the temperature of liquid air.
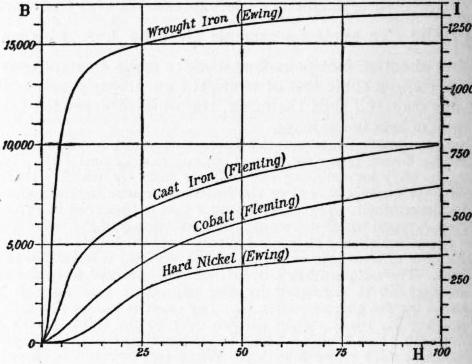 |
| Fig. 17. |
The diagram, fig. 17, contains examples of ascending induction curves characteristic of wrought iron, cast iron, cobalt and nickel. These are to be regarded merely as typical specimens, for the details of a curve depend largely upon the physical condition and purity of the material; but they show at a glance how far the several metals differ from and resemble one another as regards their magnetic properties. Curves of magnetization (which express the relation of I to H) have a close resemblance to those of induction; and, indeed, since B = H + 4πI, and 4πI (except in extreme fields) greatly exceeds H in numerical value, we may generally, without serious error, put I = B/4π, and transform curves of induction into curves of magnetization by merely altering the scale to which the ordinates are referred. A scale for the approximate transformation for the curves in fig. 12 is given 333 at the right-hand side of the diagram, the greatest error introduced by neglecting H/4π not exceeding 0.6%. A study of such curves as these reveals the fact that there are three distinct stages in the process of magnetization. During the first stage, when the magnetizing force is small, the magnetization (or the induction) increases rather slowly with increasing force; this is well shown by the nickel curve in the diagram, but the effect would be no less conspicuous in the iron curve if the abscissae were plotted to a larger scale. During the second stage small increments of magnetizing force are attended by relatively large increments of magnetization, as is indicated by the steep ascent of the curve. Then the curve bends over, forming what is often called a “knee,” and a third stage is entered upon, during which a considerable increase of magnetizing force has little further effect upon the magnetization. When in this condition the metal is popularly said to be “saturated.” Under increasing magnetizing forces, greatly exceeding those comprised within the limits of the diagram, the magnetization does practically reach a limit, the maximum value being attained with a magnetizing force of less than 2000 for wrought iron and nickel, and less than 4000 for cast iron and cobalt. The induction, however, continues to increase indefinitely, though very slowly. These observations have an important bearing upon the molecular theory of magnetism, which will be referred to later.
The magnetic quality of a sample of iron depends very largely upon the purity and physical condition of the metal. The presence of ordinary impurities usually tends to diminish the permeability, though, as will appear later, the addition of small quantities of certain other substances is sometimes advantageous. A very pure form of iron, which from the method of its manufacture is called “steel,” is now extensively used for the construction of dynamo magnets; this metal sometimes contains not more than 0.3% of foreign substances, including carbon, and is magnetically superior to the best commercial wrought iron. The results of some comparative tests published by Ewing (Proc. Inst. C.E., 1896) are given in the accompanying table. Those in the second column are quoted from a paper by F. Lydall and A. W. Pocklington (Proc. Roy. Soc., 1892, 52, 228) and relate to an exceptional specimen containing nearly 99.9% of the pure metal.
| Magnetic Force. | Magnetic Induction. | |||
| Pure Iron. | Low Moor Iron. | Steel Forging. | Steel Casting. | |
| 5 | 12,700 | 10,900 | 12,300 | 9,600 |
| 10 | 14,980 | 13,120 | 14,920 | 13,050 |
| 15 | 15,800 | 14,010 | 15,800 | 14,600 |
| 20 | 16,300 | 14,580 | 16,280 | 15,310 |
| 30 | 16,950 | 15,280 | 16,810 | 16,000 |
| 40 | 17,350 | 15,760 | 17,190 | 16,510 |
| 50 | .. | 16,060 | 17,500 | 16,900 |
| 60 | .. | 16,340 | 17,750 | 17,180 |
| 70 | .. | 16,580 | 17,970 | 17,400 |
| 80 | .. | 16,800 | 18,180 | 17,620 |
| 90 | .. | 17,000 | 18,390 | 17,830 |
| 100 | .. | 17,200 | 18,600 | 18,030 |
To secure the highest possible permeability it is essential that the iron should be softened by careful annealing. When it is mechanically hardened by hammering, rolling or wire-drawing its permeability may be greatly diminished, especially under a moderate magnetizing force. An experiment by Ewing showed that by the operation of stretching an annealed iron wire beyond the limits of elasticity the permeability under a magnetizing force of about 3 units was reduced by as much as 75%. Ewing has also studied the effect of vibration in conferring upon iron an apparent or spurious permeability of high value; this effort also is most conspicuous when the magnetizing force is weak. The permeability of a soft iron wire, which was tapped while subjected to a very small magnetizing force, rose to the enormous value of about 80,000 (Magnetic Induction, § 85). It follows that in testing iron for magnetic quality the greatest care must be exercised to guard the specimen against any accidental vibration.
Low hysteresis is the chief requisite for iron which is to be used for transformer cores, and it does not necessarily accompany high permeability. In response to the demand, manufacturers have succeeded in producing transformer plate in which the loss of energy due to hysteresis is exceedingly small. Tests of a sample supplied by Messrs. Sankey were found by Ewing to give the following results, which, however, are regarded as being unusually favourable. In a valuable collection of magnetic data (Proc. Inst. C.E., cxxvi.) H. F. Parshall quotes tests of six samples of iron, described as of good quality, which showed an average hysteresis loss of 3070 ergs per c.cm. per cycle at an induction of 8000, being 1.6 times the loss shown by Ewing’s specimen at the same induction.
| Limits of Induction. | Ergs per c.cm. per cycle. | Watts per ℔. Frequency, 100. |
| 2000 | 220 | 0.129 |
| 3000 | 410 | 0.242 |
| 4000 | 640 | 0.376 |
| 5000 | 910 | 0.535 |
| 6000 | 1200 | 0.710 |
| 7000 | 1520 | 0.890 |
| 8000 | 1900 | 1.120 |
| 9000 | 2310 | 1.360 |
The standard induction in reference to determinations of hysteresis is generally taken as 2500, while the loss is expressed in watts per ℔ at a frequency of 100 double reversals, or cycles, per second. In many experiments, however, different inductions and frequencies are employed, and the hysteresis-loss is often expressed as ergs per cubic centimetre per cycle and sometimes as horse-power per ton. In order to save arithmetical labour it is convenient to be provided with conversion factors for reducing variously expressed results to the standard form. The rate at which energy is lost being proportional to the frequency, it is obvious that the loss at frequency 100 may be deduced from that at any other frequency n by simply multiplying by 100/n. Taking the density of iron to be 7.7, the factor for reducing the loss in ergs per c.cm. to watts per ℔ with a frequency of 100 is 0.000589 (Ewing). Since 1 horse-power = 746 watts, and 1 ton = 2240 ℔, the factor for reducing horse-power per ton to watts per ℔ is 746/2240, or just 1/3. The loss for any induction B within the range for which Steinmetz’s law holds may be converted into that for the standard induction 2500 by dividing it by B1.6/25001.6. The values of this ratio for different values of B, as given by Fleming (Phil. Mag., 1897), are contained in the second column of the annexed table. The third column shows the relative amount of hysteresis deduced by Ewing as a general mean from actual tests of many samples (Journ. Inst. Elec. Eng., 1895). Incidentally, these two columns furnish an undesigned test of the accuracy of Steinmetz’s law: the greatest difference is little more than 1%.
| Induction B. | B1.6 25001.6 | Observed relative Hysteresis. |
| 2000 | 0.700 | 0.702 |
| 2500 | 1.000 | 1.000 |
| 3000 | 1.338 | 1.340 |
| 4000 | 2.118 | 2.128 |
| 5000 | 3.031 | 3.000 |
| 6000 | 4.058 | 4.022 |
| 7000 | 5.193 | 5.129 |
| 8000 | 6.430 | 6.384 |
Curves of Permeability and Susceptibility.—The relations of μ (= B/H) to B, and of κ (= I/H) to I may be instructively exhibited by means of curves, a method first employed by H. A. Rowland.27 The dotted curve for μ and B in fig. 18 is copied from Rowland’s paper. The actual experiment to which it relates was carried only as the point marked X, corresponding to a magnetizing force of 65, and an induction of nearly 17,000. Rowland, believing that the curve would continue to fall in a straight line meeting the horizontal axis, inferred that the induction corresponding to the point B—about 17,500—was the highest 334 that could be produced by any magnetizing force, however great. It has, however, been shown that, if the magnetizing force is carried far enough, the curve always becomes convex to the axis instead of meeting it. The full line shows the result of an experiment in which the magnetizing force was carried up to 585,28 but though the force was thus increased ninefold, the induction only reached 19,800, and the ultimate value of the permeability was still as much as 33.9.
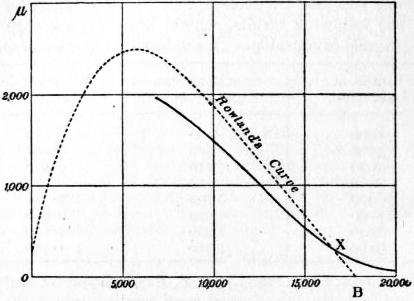 |
| Fig. 18. |
 |
| Fig. 19. |
Ballistic Method with Yoke.—J. Hopkinson (Phil. Trans., 1885, 176, 455) introduced a modification of the usual ballistic arrangement which presents the following advantages; (1) very considerable magnetizing forces can be applied with ordinary means; (2) the samples to be tested, having the form of cylindrical bars, are more easily prepared than rings or wires; (3) the actual induction at any time can be measured, and not only changes of induction. On the other hand, a very high degree of accuracy is not claimed for the results. Fig. 19 shows the apparatus by which the ends of the bar are prevented from exerting any material demagnetizing force, while the permeance of the magnetic circuit is at the same time increased. A A, called the “yoke,” is a block of annealed wrought iron about 18 in. long, 6½ in. wide and 2 in. thick, through which is cut a rectangular opening to receive the two magnetizing coils B B. The test bar C C, which slides through holes bored in the yoke, is divided near the middle into two parts, the ends which come into contact being faced true and square. Between the magnetizing coils is a small induction coil D, which is connected with a ballistic galvanometer. The induction coil is carried upon the end of one portion of the test bar, and when this portion is suddenly drawn back the coil slips off and is pulled out of the field by an india-rubber spring. This causes a ballistic throw proportional to the induction through the bar at the moment when the two portions were separated. With such an arrangement it is possible to submit the sample to any series of magnetic forces, and to measure its magnetic state at the end. The uncertainty with which the results are affected depends chiefly upon the imperfect contact between the bar and the yoke and also between the ends of the divided bar. It is probable that Hopkinson did not attach sufficient importance to the demagnetizing action of the cut (cf. Ewing, Phil. Mag., Sept. 1888, p. 274), and that the values which he assigned to H are consequently somewhat too high. He applied his method with good effect, however, in testing a large number of commercial specimens of iron and steel, the magnetic constants of which are given in a table accompanying his paper. When it is not required to determine the residual magnetization there is no necessity to divide the sample bar, and ballistic tests may be made in the ordinary way—by steps or by reversals—the source of error due to the transverse cut thus being avoided. Ewing (Magnetic Induction, § 194) has devised an arrangement in which two similar test bars are placed side by side; each bar is surrounded by a magnetizing coil, the two coils being connected to give opposite directions of magnetization, and each pair of ends is connected by a short massive block of soft iron having holes bored through it to fit the bars, which are clamped in position by set-screws. Induction coils are wound on the middle parts of both bars, and are connected in series. With this arrangement it is possible to find the actual value of the magnetizing force, corrected for the effects of joints and other sources of error. Two sets of observations are taken, one when the blocks are fixed at the ends of the bars, and another when they are nearer together, the clear length of the bars between them and of the magnetizing coils being reduced to one-half. If H1 and H2 be the values of 4πin/l and 4πi′[(n/2) / (l/2)] for the same induction B, it can be shown that the true magnetizing force is H = H1 − (H2 − H1). The method, though tedious in operation, is very accurate, and is largely employed for determining the magnetic quality of bars intended to serve as standards.
Traction Methods.—The induction of the magnetization may be measured by observing the force required to draw apart the two portions of a divided rod or ring when held together by their mutual attraction. If a transverse cut is made through a bar whose magnetization is I and the two ends are placed in contact, it can be shown that this force is 2πI² dynes per unit of area (Mascart and Joubert, Electricity and Magnetism, § 322); and if the magnetization of the bar is due to an external field H produced by a magnetizing coil or otherwise, there is an additional force equal to HI. Thus the whole force, when the two portions of the bar are surrounded by a loosely-fitting magnetizing coil, is
F = 2πI² + HI
expressed as dynes per square centimetre. If each portion of the bar has an independent magnetizing coil wound tightly upon it, we have further to take into account the force due to the mutual action of the two magnetizing coils, which assists the forces already considered. This is equal to H²8π per unit of sectional area. In the case supposed therefore the total force per square centimetre is
| F = 2πI² + HI + | H² |
| 8π |
| = | (4πI + H)³ |
| 8π |
| = | B² | . |
| 8π |
The equation F = B²/8π is often said to express “Maxwell’s law of magnetic traction” (Maxwell, Electricity and Magnetism, §§ 642-646). It is, of course, true for permanent magnets, where H = 0, since then F = 2πI²; but if the magnetization is due to electric currents, the formula is only applicable in the special case when the mutual action of the two magnets upon one another is supplemented by the electromagnetic attraction between separate magnetizing coils rigidly attached to them.29
The traction method was first employed by S. Bidwell (Proc. Roy. Soc., 1886, 40, 486), who in 1886 published an account of some experiments in which the relation of magnetization to magnetic field was deduced from observations of the force in grammes weight which just sufficed to tear asunder the two halves of a divided ring electromagnet when known currents were passing through the coils. He made use of the expression
F = Wg = 2πI² + HI,
where W is the weight in grammes per square centimetre of sectional area, and g is the intensity of gravity which was taken as 981. The term for the attraction between the coils was omitted as negligibly small (see Phil. Mag., 1890, 29, 440). The values assigned to H were calculated from H = 2ni/r, and ranged from 3.9 to 585, but inasmuch as no account was taken of any 335 demagnetizing action which might be due to the two transverse cuts, it is probable that they are somewhat too high. The results, nevertheless, agree very well with those for annealed wrought iron obtained by other methods. Below is given a selection from Bidwell’s tables, showing corresponding values of magnetizing force, weight supported, magnetization, induction, susceptibility and permeability:—
| H. | W. | I. | B. | κ. | μ. |
| 3.9 | 2,210 | 587 | 7,390 | 151.0 | 1889.1 |
| 5.7 | 3,460 | 735 | 9,240 | 128.9 | 1621.3 |
| 10.3 | 5,400 | 918 | 11,550 | 89.1 | 1121.4 |
| 22.2 | 8,440 | 1147 | 14,450 | 51.7 | 650.9 |
| 40 | 9,680 | 1226 | 15,460 | 30.7 | 386.4 |
| 115 | 12,170 | 1370 | 17,330 | 11.9 | 150.7 |
| 208 | 13,810 | 1452 | 18,470 | 7.0 | 88.8 |
| 362 | 14,740 | 1489 | 19,080 | 4.1 | 52.7 |
| 465 | 15,275 | 1508 | 19,420 | 3.2 | 41.8 |
| 585 | 15,905 | 1530 | 19,820 | 2.6 | 33.9 |
 |
| Fig. 20. |
A few months later R. H. M. Bosanquet (Phil. Mag., 1886, 22, 535) experimented on the relation of tractive force to magnetic induction. Instead of a divided ring he employed a divided straight bar, each half of which was provided with a magnetizing coil. The joint was surrounded by an induction coil connected with a ballistic galvanometer, an arrangement which enabled him to make an independent measurement of the induction at the moment when the two portions of the bar were separated. He showed that there was, on the whole, a fair agreement between the values determined ballistically and those given by the formula B = √8πF. The greatest weight supported in the experiments was 14,600 grammes per square cm., and the corresponding induction 18,500 units. Taylor Jones subsequently found a good agreement between the theoretical and the observed values of the tractive force in fields ranging up to very high intensities (Phil. Mag., 1895, 39, 254, and 1896, 41, 153).
Permeameters.—Several instruments in which the traction method is applied have been devised for the rapid measurement of induction or of magnetization in commercial samples of iron and steel. The earliest of these is S. P. Thompson’s permeameter (Journ. Sci. Arts, 1890, 38, 885), which consists of a rectangular block of iron shaped like Hopkinson’s yoke, and slotted out in the same way to receive a magnetizing coil (fig. 20); the block is bored through at the upper end only, and its inner face opposite the hole is made quite flat and smooth. The sample has the form of a thin rod, one end of which is faced true; it is slipped into the magnetizing coil from above, and when the current is turned on its smooth end adheres tightly to the surface of the yoke. The force required to detach it is measured by a registering spring balance, which is clamped to the upper end of the rod, and thence the induction or the magnetization is deduced by applying the formula
(B − H)² / 8π = 2πI² = Pg / S,
 |
| Fig. 21. |
where P is the pull in grammes weight, S the sectional area of the rod in square cm., and g = 981. If the pull is measured in pounds and the area in square inches, the formula may be written B = 1317 × √P/S + H. The instrument exhibited by Thompson would, without undue heating, take a current of 30 amperes, which was sufficient to produce a magnetizing force of 1000 units. A testing apparatus of a similar type devised by Gisbert Kapp (Journ. Inst. Elec. Eng. xxiii. 199) differs only in a few details from Thompson’s permeameter. Ewing has described an arrangement in which the test bar has a soft-iron pole piece clamped to each of its ends; the pole pieces are joined by a long well-fitting block of iron, which is placed upon them (like the “keeper” of a magnet), and the induction is measured by the force required to detach the block. In all such measurements a correction should be made in respect of the demagnetizing force due to the joint, and unless the fit is very accurate the demagnetizing action will be variable. In the magnetic balance of du Bois (Magnetic Circuit, p. 346) the uncertainty arising from the presence of a joint is avoided, the force measured being that exerted between two pieces of iron separated from each other by a narrow air-gap of known width. The instrument is represented diagrammatically in fig. 21. The test-piece A, surrounded by a magnetizing coil, is clamped between two soft-iron blocks B, B′. Y Y′ is a soft iron yoke, which rocks upon knife-edges K and constitutes the beam of the balance. The yoke has two projecting pieces C, C′ at unequal distances from the knife-edges, and separated from the blocks B, B′ by narrow air-gaps. The play of the beam is limited by a stop S and a screw R, the latter being so adjusted that when the end Y of the beam is held down the two air-gaps are of equal width. W is a weight capable of sliding from end to end of the yoke along a graduated scale. When there is no magnetization, the yoke is in equilibrium; but as soon as the current is turned on the block C is drawn downwards as far as the screw R will allow, for, though the attractive forces F between B and C and between B′ and C′ are equal, the former has a greater moment. The weight W is moved along the scale until the yoke just tilts over upon the stop S; the distance of W from its zero position is then, as can easily be shown, proportional to F, and therefore to B², and approximately to I². The scale is graduated in such a manner that by multiplying the reading by a simple factor (generally 10 or 2) the absolute value of the magnetization is obtained. The actual magnetizing force H is of course less than that due to the coil; the corrections required are effected automatically by the use of a set of demagnetization lines drawn on a sheet of celluloid which is supplied with the instrument. The celluloid sheet is laid upon the squared paper, and in plotting a curve horizontal distances are reckoned from the proper demagnetization line instead of from the vertical axis. An improved but somewhat more complex form of the instrument is described in Ann. d. Phys., 1900, 2, 317.
In Ewing’s magnetic balance (Journ. Inst. Elec. Eng. 1898, 27, 526), the value of the magnetic induction corresponding to a single stated magnetizing force is directly read off on a divided scale. The specimen, which has the form of a turned rod, 4 in. long and ¼ in. in diameter, is laid across the poles of a horseshoe electromagnet, excited by a current of such strength as to produce in the rod a magnetizing force H = 20. One pole has a V-shaped notch for the rod to rest in; the surface of the other is slightly rounded, forming a portion of a cylinder, the axis of which is perpendicular to the direction of the length of the rod. The rod touches this pole at a single point, and is pulled away from it by the action of a lever, the long arm of which is graduated and carries a sliding weight. The position of the weight at the moment when contact is broken indicates the induction in the rod. The standard force H = 20 was selected as being sufficiently low to distinguish between good and bad specimens, and at the same time sufficiently high to make the order of merit the same as it would be under stronger forces.
Permeability Bridges.—Several pieces of apparatus have been
invented for comparing the magnetic quality of a sample with that
of a standard iron rod by a zero method, such as is employed in the
comparison of electrical resistances by the Wheatstone bridge. An
excellent instrument of the class is Ewing’s permeability bridge.
The standard rod and the test specimen, which must be of the same
dimensions, are placed side by side within two magnetizing coils,
and each pair of adjacent ends is joined by a short rectangular block
or “yoke” of soft iron. An iron bar shaped like an inverted  projects upwards from each of the yokes, the horizontal portions of
the bars being parallel to the rods, and nearly meeting at a height
of about 8 in. above them (thus
projects upwards from each of the yokes, the horizontal portions of
the bars being parallel to the rods, and nearly meeting at a height
of about 8 in. above them (thus  ). A compass needle placed
in the gap serves to detect any flow of induction that may exist
between the bent bars. For simplicity of calculation, the clear length
of each rod between the yokes is made 12.56 (= 4π) centimetres,
while the coil surrounding the standard bar contains 100 turns;
hence the magnetizing force due to a current of n amperes will be
10n C.G.S. units. The effective number of turns in the coil surrounding
the test rod can be varied by means of three dial switches
(for hundreds, tens and units), which also introduce compensating
resistances as the number of effective turns in the coil is reduced,
thus keeping the total resistance of the circuit constant. The two
coils are connected in series, the same current passing through both.
Suppose the switches to be adjusted so that the effective number of
turns in the variable coil is 100; the magnetizing forces in the two
coils will then be equal, and if the test rod is of the same quality as
the standard, the flow of induction will be confined entirely to the
iron circuit, the two yokes will be at the same magnetic potential,
and the compass needle will not be affected. If, however, the permeability
of the test rod differs from that of the standard, the number
of lines of induction flowing in opposite directions through the two
rods will differ, and the excess will flow from one yoke to the other,
partly through the air, and partly along the path provided by the
bent bars, deflecting the compass needle. But a balance may still
be obtained by altering the effective number of turns in the test coil,
and thus increasing or decreasing the magnetizing force acting on the
test rod, till the induction in the two rods is the same, a condition
which is fulfilled when reversal of the current has no effect on the
compass needle. Let m be the number of turns in use, and H1 and
H2 the magnetizing forces which produce the same induction B in
the test and the standard rods respectively; then H1 = H2 × m/100.
The value of B which corresponds to H2m/100 can be found from the
336
(B, H) curve for the standard, which is assumed to have been determined;
and this same value corresponds to the force H in the case
of the test bar. Thus any desired number of corresponding values
of H and B can be easily and quickly found.
). A compass needle placed
in the gap serves to detect any flow of induction that may exist
between the bent bars. For simplicity of calculation, the clear length
of each rod between the yokes is made 12.56 (= 4π) centimetres,
while the coil surrounding the standard bar contains 100 turns;
hence the magnetizing force due to a current of n amperes will be
10n C.G.S. units. The effective number of turns in the coil surrounding
the test rod can be varied by means of three dial switches
(for hundreds, tens and units), which also introduce compensating
resistances as the number of effective turns in the coil is reduced,
thus keeping the total resistance of the circuit constant. The two
coils are connected in series, the same current passing through both.
Suppose the switches to be adjusted so that the effective number of
turns in the variable coil is 100; the magnetizing forces in the two
coils will then be equal, and if the test rod is of the same quality as
the standard, the flow of induction will be confined entirely to the
iron circuit, the two yokes will be at the same magnetic potential,
and the compass needle will not be affected. If, however, the permeability
of the test rod differs from that of the standard, the number
of lines of induction flowing in opposite directions through the two
rods will differ, and the excess will flow from one yoke to the other,
partly through the air, and partly along the path provided by the
bent bars, deflecting the compass needle. But a balance may still
be obtained by altering the effective number of turns in the test coil,
and thus increasing or decreasing the magnetizing force acting on the
test rod, till the induction in the two rods is the same, a condition
which is fulfilled when reversal of the current has no effect on the
compass needle. Let m be the number of turns in use, and H1 and
H2 the magnetizing forces which produce the same induction B in
the test and the standard rods respectively; then H1 = H2 × m/100.
The value of B which corresponds to H2m/100 can be found from the
336
(B, H) curve for the standard, which is assumed to have been determined;
and this same value corresponds to the force H in the case
of the test bar. Thus any desired number of corresponding values
of H and B can be easily and quickly found.
Measurement of Field Strength. Exploring Coil.—Since in air B = H, the ballistic method of measuring induction described above is also available for determining the strength of a magnetic field, and is more often employed than any other. A small coil of fine wire, connected in series with a ballistic galvanometer, is placed in the field, with its windings perpendicular to the lines of force, and then suddenly reversed or withdrawn from the field, the integral electromotive force being twice as great in the first case as in the second. The strength of the field is proportional to the swing of the galvanometer-needle, and, when the galvanometer is calibrated, can be expressed in C.G.S. units. Convenient arrangements have been introduced whereby the coil is reversed or withdrawn from the field by the action of a spring.
Bismuth Resistance.—The fact, which will be referred to later, that the electrical resistance of bismuth is very greatly affected by a magnetic field has been applied in the construction of apparatus for measuring field intensity. A little instrument, supplied by Hartmann and Braun, contains a short length of fine bismuth wire wound into a flat double spiral, half an inch or thereabouts in diameter, and attached to a long ebonite handle. Unfortunately the effects of magnetization upon the specific resistance of bismuth vary enormously with changes of temperature; it is therefore necessary to take two readings of the resistance, one when the spiral is in the magnetic field, the other when it is outside.
Electric Circuit.—If a coil of insulated wire is suspended so that it is in stable equilibrium when its plane is parallel to the direction of a magnetic field, the transmission of a known electric current through the coil will cause it to be deflected through an angle which is a function of the field intensity.
One of the neatest applications of this principle is that described by Edser and Stansfield (Phil. Mag., 1893, 34, 186), and used by them to test the stray fields of dynamos. An oblong coil about an inch in length is suspended from each end by thin strips of rolled German silver wire, one of which is connected with a spiral spring for regulating the tension, the other being attached to a torsion-head. Inside the torsion-head is a commutator for automatically reversing the current, so that readings may be taken on each side of zero, and the arrangement is such that when the torsion-head is exactly at zero the current is interrupted. To take a reading the torsion-head is turned until an aluminium pointer attached to the coil is brought to the zero position on a small scale; the strength of the field is then proportional to the angular torsion. The small current required is supplied to the coil from a single dry cell. The advantages of portability, very considerable range (from H = 1 upwards), and fair accuracy are claimed for the instrument.
Polarized Light.—The intensity of a field may be measured by the rotation of the plane of polarization of light passing in the direction of the magnetic force through a transparent substance. If the field is uniform, H = θ/ωd, where θ is the rotation, d the thickness of the substance arranged as a plate at right angles to the direction of the field, and ω Verdet’s constant for the substance.
For the practical measurement of field intensity du Bois has used plates of the densest Jena flint glass. These are preferably made slightly wedge-shape, to avoid the inconvenience resulting from multiple internal reflections, and they must necessarily be rather thin, so that double refractions due to internal strain may not exert a disturbing influence. Since Verdet’s constant is somewhat uncertain for different batches of glass even of the same quality, each plate should be standardized in a field of known intensity. As the source of monochromatic light a bright sodium burner is used, and the rotation, which is exactly proportional to H, is measured by an accurate polarimeter. Such a plate about 1 mm. in thickness is said to be adapted for measuring fields of the order of 1000 units. A part of one surface of the plate may be silvered, so that the polarized ray, after having once traversed the glass, is reflected back again; the rotation is thus doubled, and moreover, the arrangement is, for certain experiments, more convenient than the other.
4. Magnetization in Strong Fields
 |
| Fig. 22. |
Fields due to Coils.—The most generally convenient arrangement for producing such magnetic fields as are required for experimental purposes is undoubtedly a coil of wire through which an electric current can be caused to flow. The field due to a coil can be made as nearly uniform as we please throughout a considerable space; its intensity, when the constants of the coil are known, can be calculated with ease and certainty and may be varied at will through wide ranges, while the apparatus required is of the simplest character and can be readily constructed to suit special purposes. But when exceptionally strong fields are desired, the use of a coil is limited by the heating effect of the magnetizing current, the quantity of heat generated per unit of time in a coil of given dimensions increasing as the square of the magnetic field produced in its interior. In experiments on magnetic strains carried out by H. Nagaoka and K. Honda (Phil. Mag., 1900, 49, 329) the intensity of the highest field reached in the interior of a coil was 2200 units; this is probably the strongest field produced by a coil which has hitherto been employed in experimental work. In 1890 some experiments in which a coil was used were made by du Bois (Phil. Mag., 1890, 29, 253, 293) on the magnetization of iron, nickel, and cobalt under forces ranging from about 100 to 1250 units. Since the demagnetizing factor was 0.052, the strongest field due to the coil was about 1340; but though arrangements were provided for cooling the apparatus by means of ice, great difficulty was experienced owing to heating. Du Bois’s results, which, as given in his papers, show the relation of H to the magnetic moment per unit of mass, have been reduced by Ewing to the usual form, and are indicated in fig. 22, the earlier portions of the curves being sketched in from other data.
Fields due to Electromagnets.—The problem of determining the magnetization of iron and other metals in the strong fields formed between the poles of an electromagnet was first attacked by J. A. Ewing and W. Low. An account of their preliminary experiments by what they call the isthmus method was published in 1887 (Proc. Roy. Soc. 42, 200), and in the following year they described a more complete and perfect series (Phil. Trans., 1889, 180, 221).
 |
| Fig. 23. |
The sample to be inserted between the magnet poles was prepared in the form of a bobbin resembling an ordinary cotton reel, with a short narrow neck (constituting the “isthmus”) and conical ends. Upon the central neck was wound a coil consisting of one or two layers of very fine wire, which was connected with a ballistic galvanometer for measuring the induction in the iron; outside this coil, and separated from it by a small and accurately determined distance, a second coil was wound, serving to measure the induction in the iron, together with that in a small space surrounding it. The difference of the ballastic throws taken with the two coils measured the intensity of the field in the space around the iron, and it also enabled a correction to be made for the non-ferrous space between the iron neck and the centre of the thickness of the inner coil. The pole pieces of the electromagnet (see fig. 23) were furnished with a pair of truncated cones b b, of soft iron forming an extension of the conical ends of the bobbin c. The most suitable form for the pole faces is investigated in the paper, and the conclusion arrived at is that to produce the greatest concentration of force upon the central neck, the cones should have a common vertex in the middle of the neck with a semi-vertical angle of 54° 44′, while the condition for a uniform field is satisfied when the cones have a semi-vertical angle of 39° 14′; in the latter case the magnetic force in the air just outside is sensibly equal to that within the neck. A pair of cones having a semi-vertical angle of 45° were considered to combine high concentrative power with a sufficient approximation to uniformity of field. In most of the experiments the measurements were made by suddenly withdrawing the bobbin from its place 337 between the pole pieces. Two groups of observations were recorded, one giving the induction in the inner coil and the other that in the outer coil. The value of the residual induction which persisted when the bobbin was drawn out was added to that of the induction measured, and thus the total induction in the iron was determined. The highest induction reached in these experiments was 45,350 units, more than twice the value of any previously recorded. The corresponding intensity of the outside field was 24,500, but, owing to the wide angle of the cones used (about 2 × 63°), this was probably greater than the value of the magnetic force within the metal. The following table shows some results of other experiments in which H was believed to have sensibly the same value inside as outside the metal. Values of I are derived from (B − H)/4π and of μ from B/H.
| Metal. | H | B | I | μ |
| Swedish Iron | 1,490 | 22,650 | 1680 | 15.20 |
| 6,070 | 27,130 | 1680 | 4.47 | |
| 8,600 | 30,270 | 1720 | 3.52 | |
| 19,450 | 40,820 | 1700 | 2.10 | |
| 19,880 | 41,140 | 1700 | 2.07 | |
| Cast Iron | 4,560 | 20,070 | 1230 | 4.40 |
| 13,460 | 28,710 | 1210 | 2.13 | |
| 16,200 | 30,920 | 1170 | 1.91 | |
| 16,900 | 31,760 | 1180 | 1.88 | |
| Tool Steel | 6,210 | 25,480 | 1530 | 4.10 |
| 9,970 | 29,650 | 1570 | 2.97 | |
| 12,170 | 31,620 | 1550 | 2.60 | |
| 14,660 | 34,550 | 1580 | 2.36 | |
| 15,530 | 35,820 | 1610 | 2.31 | |
| Hard Nickel | 2,220 | 7,100 | 390 | 3.20 |
| 4,440 | 9,210 | 380 | 2.09 | |
| 7,940 | 12,970 | 400 | 1.63 | |
| 14,660 | 19,640 | 400 | 1.34 | |
| 16,000 | 21,070 | 400 | 1.32 | |
| Cobalt | 1,350 | 16,000 | 1260 | 12.73 |
| 4,040 | 18,870 | 1280 | 4.98 | |
| 8,930 | 23,890 | 1290 | 2.82 | |
| 14,990 | 30,210 | 1310 | 2.10 |
These results are of extreme interest, for they show that under sufficiently strong magnetizing forces the intensity of magnetization I reaches a maximum value, as required by W. E. Weber’s theory of molecular magnetism. There appears to be no definite limit to the value to which the induction B may be raised, but the magnetization I attains a true saturation value under magnetizing forces which are in most cases comparatively moderate. Thus the magnetization which the sample of Swedish iron received in a field of 1490 was not increased (beyond the limits of experimental error) when the intensity of the field was multiplied more than thirteen-fold, though the induction was nearly doubled. When the saturation value of I has been reached, the relation of magnetic induction to magnetic force may be expressed by
B = H + constant.
The annexed table gives the saturation values of I for the particular metals examined by Ewing and Low:—
| Saturation Value of I | |
| Wrought iron | 1,700 |
| Cast iron | 1,240 |
| Nickel (0.75% iron) | 515 |
| Nickel (0.56% iron) | 400 |
| Cobalt (1.66% iron) | 1,300 |
It is shown in the paper that the greatest possible force which the isthmus method can apply at a point in the axis of the bobbin is
F = 11.137 Is log10 b/a,
Is being the saturation value of the magnet poles, a the radius of the neck on which the cones converge, and b the radius of the bases of the cones.
Some experiments made by H. du Bois (Phil. Mag., 1890, 29, 293) with an electromagnet specially designed for the production of strong fields, confirm Ewing’s results for iron, nickel and cobalt. The method employed did not admit of the production of such high magnetizing forces, but was of special interest in that both B and I were measured optically—B by means of the rotation of a polarized ray inside a glass plate, as before described, and I by the rotation of a polarized ray reflected from the polished surface of the magnetized metal (see “Kerr’s constant,” Magneto-Optics). H(= B − 4πI) was calculated from corresponding values of I and B. Taylor Jones (Wied. Ann., 1896, 57, 258, and Phil. Mag., 1896, 41, 153), working with du Bois’s electromagnet and using a modification of the isthmus method, succeeded in pushing the induction B up to 74,200 with H = 51,600, the corresponding value of I being 1798, and of μ only 1.44. The diameter of the isthmus was 0.241 mm., and the electromagnet was excited by a current of 40 amperes.
Tractive Force of a Magnet.—Closely connected with the results just discussed is the question what is the greatest tractive force that can be exerted by a magnet. In the year 1852 J. P. Joule (Phil. Mag., 1852, 3, 32) expressed the opinion that no “force of current could give an attraction equal to 200 ℔ per sq. in.,” or 14,000 grms. per square centimetre, and a similar view prevailed among high authorities more than twenty years later. For the greatest possible “lifting power” of permanent magnets this estimate is probably not very far from the truth, but it is now clearly understood that the force which can be exerted by an electromagnet, or by a pair of electromagnets with opposite poles in contact, is only limited by the greatest value to which it is practically possible to raise the magnetizing force H. This is at once evident when the tractive force due to magnetization is expressed as 2πI² + HI. For fields of moderate intensity the first term of the expression is the more important, but when the value of H exceeds 12,000 or thereabouts, the second preponderates, and with the highest values that have been actually obtained, HI is several times greater than 2πI². If H could be increased without limit, so also could the tractive force. The following table shows the greatest “lifting powers” experimentally reached at the dates mentioned:—
| Observer. | Kilos per sq. cm. | ℔ per sq. in. | Date. |
| Joule | 12.3 | 175 | 1852 |
| Bidwell | 15.9 | 226 | 1886 |
| Wilde | 26.8 | 381 | 1891 |
| T. Jones | 114.9 | 1634 | 1896 |
5. Magnetization in Very Weak Fields
Some interesting observations have been made of the effects produced by very small magnetic forces. It was first pointed out by C. Baur (Wied. Ann., 1880, 11, 399) that in weak fields the relation of the magnetization I to the magnetizing force H is approximately expressed by an equation of the form
I = aH + bH²,
or
κ = I / H = a + bH,
whence it appears that within the limits of Baur’s experiments the magnetization curve is a parabola, and the susceptibility curve an inclined straight line, κ being therefore a known function of H. If these equations could be assumed to hold when H is indefinitely small, it would follow that κ has a finite initial value, from which there would be no appreciable deviation in fields so weak that bH was negligibly small in comparison with a. Such an assumption could not, however, without dangerous extrapolation, be founded upon the results of Baur’s experiments, which did not go far enough to justify it. In some experiments carried out in 1887, Lord Rayleigh (Phil. Mag., 1887, 23, 225) approached very much more nearly than Baur to the zero of magnetic force. Using an unannealed Swedish iron wire, he found that when H was gradually diminished from 0.04 to 0.00004 C.G.S. unit, the ratio of magnetization to magnetizing force remained sensibly constant at 6.4, which may therefore with great probability be assumed to represent the initial value of κ for the specimen in question. Experiments with annealed iron gave less satisfactory results, on account of the slowness with which the metal settled down into a new magnetic state, thus causing a “drift” of the magnetometer needle, which sometimes persisted for several seconds. Apart from this complication, it appeared that I was proportional to H when the value of H was less than 0.02.
The observations of Baur and Rayleigh have been confirmed and discussed by (amongst others) W. Schmidt (Wied. Ann., 1895, 54, 655), who found the limiting values of κ to be 7.5 to 9.5 for iron, and 11.2 to 13.5 for steel, remaining constant up to H = .06; by P. Culmann (Elekt. Zeit., 1893, 14, 345; Wied. Ann., 1895, 56, 602); and by L. Holborn (Berl. Ber., 1897, p. 95, and Wied. Ann., 1897, 61, 281). The latter gives values of the constants a and b for different samples of iron and steel, some of which are shown in the following table:—
| κ = a + bH | ||
| Metal. | a | b |
| English tungsten steel | 8.90 | 0.264 |
| Tungsten steel, hardened | 2.23 | 0.032 |
| Silver steel | 8.66 | 0.384 |
| Tool steel | 8.30 | 0.400 |
| Refined steel | 11.28 | 1.92 |
| Cast iron | 3.16 | 0.236 |
| Soft iron | 16.6 | 18.6 |
| Hard drawn iron | 5.88 | 1.76 |
For most samples of steel the straight-line law was found to hold approximately up to H = 3; in the case of iron and of soft steel the approximation was less close.
The behaviour of nickel in weak fields has been observed by Ewing (Phil. Trans., 1888, 179A, 325), who found that the initial value of κ was 1.7, and that it remained sensibly constant until H had reached a value of about five units. While therefore the initial susceptibility of nickel is less than that of iron and steel, the range of magnetic force within which it is approximately constant is about one hundred times greater. Ewing has also made a careful study (Proc. Roy. Soc., 1889, 46, 269) of “magnetic viscosity” under small forces—the cause of the magnetometer “drift” referred to by Rayleigh. On the application of a small magnetizing force to a bar of soft annealed iron, a certain intensity of magnetization is instantly produced; this, however, does not remain constant, but slowly increases for some seconds or even minutes, and may ultimately attain a value nearly twice as great as that observed immediately after the force was applied.30 When the magnetizing current is broken, the magnetization at once undergoes considerable diminution, then gradually falls to zero, and a similar sudden change followed by a slow one is observed when a feeble current is reversed. Ewing draws attention to a curious consequence of this time-lag. By the alternate application and withdrawal of a small magnetizing force a cyclic condition may be established in an iron rod. If now the alternations are performed so rapidly that time is not allowed for more than the first sudden change in the magnetization, there will be no hysteresis loss, the magnetization exactly following the magnetizing force. Further, if the alternations take place so slowly that the full maximum and minimum values of the magnetization are reached in the intervals between the reversals, there will again be no dissipation of energy. But at any intermediate frequency the ascending and descending curves of magnetization will enclose a space, and energy will be dissipated. It is remarkable that the phenomena of magnetic viscosity are much more evident in a thick rod than in a thin wire, or even in a large bundle of thin wires. In hardened iron and steel the effect can scarcely be detected, and in weak fields these metals exhibit no magnetic hysteresis of any kind.
6. Changes of Dimensions Attending Magnetization
 |
| Fig. 24. |
It is well known that the form of a piece of ferromagnetic metal is in general slightly changed by magnetization. The phenomenon was first noticed by J. P. Joule, who in 1842 and 1847 described some experiments which he had made upon bars of iron and steel. His observations, were for the most part confirmed by a number of subsequent workers, notably by A. M. Mayer; but with the single exception of the discovery by W. F. Barrett in 1882 that a nickel bar contracts when magnetized, nothing of importance was added by Joule’s results for nearly forty years. Later researches have however thrown much new light upon a class of phenomena which cannot fail to have an important bearing upon the complete theory of molecular magnetism.31 According to Joule’s observations, the length of a bar of iron or soft steel was increased by magnetization, the elongation being proportional up to a certain point to the square of the intensity of magnetization; but when the “saturation point” was approached the elongation was less than this law would require, and a stage was finally reached at which further increase of the magnetizing force produced little or no effect upon the length. From data contained in Joule’s paper it may be calculated that the strongest external field H0 produced by his coil was about 126 C.G.S. units, but since the dimensional ratio of his bars was comparatively small, the actual magnetizing force H must have been materially below that value. In 1885 it was shown by Bidwell, in the first of a series of papers on the subject, that if the magnetizing force is pushed beyond the point at which Joule discontinued his experiments, the extension of the bar does not remain unchanged, but becomes gradually less and less, until the bar, after first returning to its original length, ultimately becomes actually shorter than when in the unmagnetized condition. The elongation is generally found to reach a maximum under a magnetizing force of 50 to 120 units, and to vanish under a force of 200 to 400, retraction occurring when still higher forces are applied. In order to meet the objection that the phenomenon might be due to electromagnetic action between the coil and the rod, Bidwell made some experiments with iron rings, and found that the length of their diameters varied under magnetization in precisely the same manner as the length of a straight rod. Experiments were afterwards made with rods of iron, nickel, and cobalt, the external field being carried up to the high value of 1500 units. The results are indicated in Fig. 24. It appears that the contraction which followed the initial extension of the iron reached a limit in fields of 1000 or 1100. Nickel exhibited retraction from the very beginning (as observed by Barrett), its greatest change of length considerably exceeding that undergone by iron; in a field of 800 the original length was diminished by as much as 1/40,000 part, but stronger forces failed to produce any further effect. The curve for cobalt is a very remarkable one. Little or no change of length was observed until the strength of the field H0 reached about 50; then the rod began to contract, and after passing a minimum at H0 = 400, recovered its original length at H0 = 750; beyond this point there was extension, the amount of which was still increasing fast when the experiment was stopped at H0 = 1400. Similar results were obtained with three different samples of the metal. Roughly speaking, therefore, cobalt behaves oppositely to iron.
Joule and others experimented with hardened steel, but failed to find a key to the results they obtained, which are rather complex, and have been thought to be inconsistent. The truth appears to be that a hardened steel rod generally behaves like one of iron or soft steel in first undergoing extension under increasing magnetizing force, and recovering its original length when the force has reached a certain critical value, beyond which there is contraction. But this “critical value” of the force is found to depend in an unexpected manner upon the hardness of the steel; the critical value diminishes as the hardness becomes greater up to a certain point, corresponding to a yellow temper, after which it increases and with the hardest steel becomes very high. For steel which has been made red-hot, suddenly cooled, and then let down to a yellow temper, the critical value of the magnetizing force is smaller than for steel which is either softer or harder; it is indeed so small that the metal contracts like nickel even under weak magnetizing forces, without undergoing any preliminary extension that can be detected.
 |
| Fig. 25. |
Joule also made experiments upon iron wires under tension, and drew the erroneous inference (which has been often quoted as if it were a demonstrated fact) that under a certain critical tension (differing for different specimens of iron but independent of the magnetizing force) magnetization would produce no effect whatever upon the dimensions of the wire. What actually happens when an iron wire is loaded with various weights is clearly shown in Fig. 25. Increased tension merely has the effect of diminishing the maximum elongation and hastening the contraction; with the two greatest loads used in the experiment there was indeed no preliminary extension at all.32 The effects of tension upon the behaviour of a nickel wire are of a less simple character. In weak fields the magnetic contraction is always diminished by pulling stress; in strong fields the contraction increases under a small load and diminishes under a heavy one. Cobalt, curiously enough, was found to be quite unaffected by tensile stress.
Certain experiments by C. G. Knott on magnetic twist, which will be referred to later, led him to form the conclusion that in an iron wire carrying an electric current the magnetic elongation would be increased. This forecast was shown by Bidwell to be well founded. The effect produced by a current is exactly opposite to that of tension, raising the elongation curve instead of depressing it. In the case of a wire 0.75 mm. in diameter the maximum elongation was nearly doubled when a current of two amperes was passing through the iron, while the “critical value” of the field was increased from 130 to 200. Yet notwithstanding this enormous effect in iron, the action of a current upon nickel and cobalt turned out to be almost inappreciable.
Some experiments were next undertaken with the view of ascertaining how far magnetic changes of length in iron were dependent upon the hardness of the metal, and the unexpected result was arrived at that softening produces the same effect as tensile stress; it depresses the elongation curve, diminishing the maximum extension, and reducing the “critical value” of the magnetizing force. A thoroughly well annealed ring of soft iron indeed showed no extension at all, beginning to contract, like nickel, under the smallest magnetizing forces. The experiments were not sufficiently numerous to indicate whether, as is possible, there is a critical degree of hardness for which the height of the elongation curve is a maximum.
Finally, experiments were made to ascertain the effect of magnetization upon the dimensions of iron rings in directions perpendicular to the magnetization, and upon the volume of the rings.33 It was found that the curve showing the relation of transverse changes of dimensions to magnetizing force was similar in general character to the familiar elongation curves, but the signs were reversed; the curve was inverted, indicating at first retraction, which, after passing a maximum and vanishing in a critical field, was succeeded by elongation. The curve showing the circumferential (or longitudinal) changes was also plotted, and from the two curves thus obtained it was easy, on the assumption that the metal was isotropic in directions at right angles to the magnetization, to calculate changes of volume; for if circumferential elongation be denoted by l1, and transverse elongation by l2, then the cubical dilatation (+ or −) = l1 + 2l2 approximately. If l1 were exactly equal to -2l2 for all values of the magnetizing force, it is clear that the volume of the ring would be unaffected by magnetization. In the case of the ring in question, the circumferential changes were in weak fields less than twice as great as the transverse ones, while in strong fields they were more than twice as great; under increasing magnetic force therefore the volume of the ring was first diminished, then it regained its original value (for H = 90), and ultimately increased. It was also shown that annealing, which has such a large effect upon circumferential (or longitudinal) changes, has almost none upon transverse ones. Hence the changes of volume undergone by a given sample of wrought iron under increasing magnetization must depend largely upon the state of the metal as regards hardness; there may be always contraction, or always expansion, or first one and then the other.
Most of the experiments described above have been repeated and the results confirmed by other workers, some of whom have added fresh observations. The complicated hysteresis effects which attend magnetic elongation and retraction have been studied by H. Nagaoka, who also, in conjunction with K. Honda, measured the changes of length of various metals shaped in the form of ovoids instead of cylindrical rods, and determined the magnetization curves for the same specimens; a higher degree of accuracy was thus attained, and satisfactory data were provided for testing theories. Among other things, it was found that the behaviour of cast cobalt was entirely changed by annealing; the sinuous curve shown in Fig. 24 was converted into an almost perfectly straight line passing through the origin, and lying below the horizontal axis; while the permeability of the metal was greatly diminished by the operation. They also tested several varieties of nickel-steel in the form of both ovoids and wires. With a sample containing 25% of nickel no appreciable change was detected; others containing larger percentages, and tested in fields up to 2000, all exhibited elongation, which tended to an asymptotic value as the field was increased. The influence of temperature varying between wide limits has formed the subject of a research by K. Honda and S. Shimizu. For soft iron, tungsten-steel and nickel little difference appeared to result from lowering the temperature down to −186° C. (the temperature of liquid air); at sufficiently high temperatures, 600° to 1000° or more, it was remarked that the changes of length in iron, steel and cobalt tended in every case to become proportional to the magnetic force, the curves being nearly straight lines entirely above the axis. The retraction of nickel was diminished by rising temperature, and at 400° had almost vanished. The influence of high temperature on cobalt was very remarkable, completely altering the character of the change of length: the curves for annealed cobalt show that at 450° this metal behaves just like iron at ordinary temperatures, lengthening in fields up to about 300 and contracting in stronger ones. The same physicists have made some additional experiments upon the effect of tension on magnetic change of length. Bidwell’s results for iron and nickel were confirmed, and it was further shown that the elongation of nickel-steel was very greatly diminished by tension; when 340 magnetized under very heavy loads, the wire was indeed found to undergo slight contraction. Honda subjected tubes of iron, steel and nickel to the simultaneous action of circular and longitudinal fields, and observed the changes of length when one of the fields was varied while the other remained constant at different successive values from zero upwards. The experimental results agreed in sign though not in magnitude with those calculated from the changes produced by simple longitudinal magnetization, discrepancies being partly accounted for by the fact that the metals employed were not actually isotropic. Heusler’s alloy has been tested for change of length by L. Austin, who found continuous elongation with increasing fields, the curves obtained bearing some resemblance to curves of magnetization.
As regards the effect of magnetization upon volume there are some discrepancies. Nagaoka and Honda, who employed a fluid dilatometer, found that the volume of several specimens of iron, steel and nickel was always slightly increased, no diminution being indicated in low fields; cobalt, on the other hand, was diminished in volume, and the amount of the change, though still very small, was greater than that shown by the other metals. Various nickel-steels all expanded under magnetization, the increase being generally considerable and proportional to the field; in the case of an alloy containing 29% of nickel the change was nearly 40 times greater than in soft iron. C. G. Knott, who made an exhaustive series of experiments upon various metals in the form of tubes, concluded that in iron there was always a slight increase of volume, and in nickel and cobalt a slight decrease. It is uncertain how far these various results are dependent upon the physical condition of the metals.
Attempts have been made to explain magnetic deformation by various theories of magnetic stress,34 notably that elaborated by G. R. Kirchhoff (Wied. Ann., 1885, 24, 52, and 1885, 25, 601), but so far with imperfect success. E. Taylor Jones showed in 1897 that only a small proportion of the contraction exhibited by a nickel wire when magnetized could be accounted for on Kirchhoff’s theory from the observed effects of pulling stress upon magnetization; and in a more extended series of observations Nagaoka and Honda found wide quantitative divergences between the results of experiment and calculation, though in nearly all cases there was agreement as to quality. They consider, however, that Kirchhoff’s theory, which assumes change of magnetization to be simply proportional to strain, is still in its infancy, the present stage of its evolution being perhaps comparable with that reached by the theory of magnetization at the time when the ratio I/H was supposed to be constant. In the light of future researches further development may reasonably be expected.
It has been suggested35 that an iron rod under magnetization may be in the same condition as if under a mechanically applied longitudinal stress tending to shorten the iron. If a long magnetized rod is divided transversely and the cut ends placed nearly in contact, the magnetic force inside the narrow air gap will be B = H + 4πI. The force acting on the magnetism of one of the faces, and urging this face towards the other, will be less than B by 2πI, the part of the total force due to the first face itself; hence the force per unit of area with which the faces would press against each other if in contact is
P = (B − 2πI) I = 2πI² + HI = (B² − H²) / 8π.
The width of the gap may be diminished until it is no greater than the distance between two neighbouring molecules, when it will cease to be distinguishable, but, assuming the molecular theory of magnetism to be true, the above statement will still hold good for the intermolecular gap. The same pressure P will be exerted across any imaginary section of a magnetized rod, the stress being sustained by the intermolecular springs, whatever their physical nature may be, to which the elasticity of the metal is due. The whole of the rod will therefore be subject to a compressive longitudinal stress P, the associated contraction R, expressed as a fraction of the original length, being
R = P / M = (B² − H²) / 8πM,
where M is Young’s modulus. This was found to be insufficient to account for the whole of the retraction exhibited by iron in strong fields, but it was pointed out by L. T. More36 that R ought to be regarded as a “correction” to be applied to the results of experiments on magnetic change of length, the magnetic stress being no less an extraneous effect than a stress applied mechanically. Those who support this view generally speak of the stress as “Maxwell’s stress,” and assume its value to be B2/8π. The stress in question seems, however, to be quite unconnected with the “stress in the medium” contemplated by Maxwell, and its value is not exactly B2/8π except in the particular case of a permanent ring magnet, when H = O. Further, Maxwell’s stress is a tension along the lines of force, and is equal to B2/8π only when B = H, and there is no magnetization.37 Some writers have indeed contended that the stress in magnetized iron is not compressive, but tensile, even when, as in the case of a ring-magnet, there are no free ends. The point at issue has an important bearing upon the possible correlation of magnetic phenomena, but, though it has given rise to much discussion, no accepted conclusion has yet been reached.38
7. Effects of Mechanical Stress upon Magnetization
The effects of traction, compression and torsion in relation to magnetism have formed the subject of much patient investigation, especially at the hands of J. A. Ewing, C. G. Knott and the indefatigable physicists of Tokyo University. The results of their experiments embrace a multiplicity of details of which it is impossible to give an adequate summary. Only a few of the most important can be mentioned here; the reader who wishes for fuller information should consult the original papers.39
It was first discovered by E. Villari in 1868 that the magnetic susceptibility of an iron wire was increased by stretching when the magnetization was below a certain value, but diminished when that value was exceeded; this phenomenon has been termed by Lord Kelvin, who discovered it independently, the “Villari reversal,” the value of the magnetization for which stretching by a given load produces no effect being known as the “Villari critical point” for that load. The Villari critical point for a given sample of iron is reached with a smaller magnetizing force when the stretching load is great than when it is small; the reversal also occurs with smaller loads and with weaker fields when the iron is soft than when it is hard. The following table shows the values of I and H corresponding to the Villari critical point in some of Ewing’s experiments:—
| Soft Iron. | Hard Iron. | ||||
| Kilos per sq. mm. | I. | H. | Kilos per sq. mm. | I. | H. |
| 2.15 | 1220 | 7.3 | 27.6 | 1180 | 34 |
| 4.3 | 1040 | 4.3 | 32.2 | 1150 | 32 |
| 8.6 | 840 | 3.4 | 37.3 | 1110 | 29 |
| 12.9 | 690 | 3.05 | 42.5 | 1020 | 25 |
The effects of pulling stress may be observed either when the wire is stretched by a constant load while the magnetizing force is varied, or when the magnetizing force is kept constant while the load is varied. In the latter case the first application of stress is always attended by an increase—often a very great one—of the magnetization, whether the field is weak or strong, but after a load has been put on and taken off several times the changes of magnetization become cyclic. From experiments of both classes it appears that for a given field there is a certain value of the load for which the magnetization is a maximum, the maximum occurring at a smaller load the stronger the field. In very strong fields the maximum may even disappear altogether, the effect of the smallest stress 341 being to diminish the magnetization; on the other hand, with very weak fields the maximum may not have been reached with the greatest load that the wire can support without permanent deformation. When the load on a hardened wire is gradually increased, the maximum value of I is found to correspond with a greater stress than when the load is gradually diminished, this being an effect of hysteresis. Analogous changes are observed in the residual magnetization which remains after the wire has been subjected to fields of different strength. The effects of longitudinal pressure are opposite to those of traction; when the cyclic condition has been reached, pressure reduces the magnetization of iron in weak fields and increases it in strong fields (Ewing, Magnetic Induction, 1900, 223).
The influence of traction in diminishing the susceptibility of nickel was first noticed by Kelvin (W. Thomson), and was subsequently investigated by Ewing and Cowan. The latter found the effect to be enormous, not only upon the induced magnetization, but in a still greater degree upon the residual. Even under so “moderate” a load as 33 kilogrammes per square mm., the induced magnetization of a hard-drawn nickel wire in a field of 60 fell from 386 to 72 units, while the residual was reduced from about 280 to 10. Ewing has also examined the effects produced by longitudinal compression upon the susceptibility and retentiveness of nickel, and found, as was to be expected, that both were greatly increased by pressure. The maximum susceptibility of one of his bars rose from 5.6 to 29 under a stress of 19.8 kilos per square mm. There were reasons for believing that no Villari reversal would be found in nickel. Ewing and Cowan looked carefully for it, especially in weak fields, but failed to discover anything of the kind.40 Some experiments by A. Heydweiller,41 which appeared to indicate a reversal in weak fields (corresponding to I = 5, or thereabouts), have been shown by Honda and Shimizu to be vitiated by the fact that his specimen was not initially in a magnetically neutral state; they found that when the applied field had the same direction as that of the permanent magnetization, Heydweiller’s fallacious results were easily obtained; but if the field were applied in the direction opposite to that of the permanent magnetization, or if, as should rightly be the case, there were no permanent magnetization at all, then there was no indication of any Villari reversal. Thus a very important question, which has given rise to some controversy, appears to be now definitely settled.
The effects of longitudinal pressure upon the magnetization of cast cobalt have been examined by C. Chree,42 and also by J. A. Ewing.43 Chree’s experiments were undertaken at the suggestion of J. J. Thomson, who, from the results of Bidwell’s observations on the magnetic deformation of cobalt, was led to expect that that metal would exhibit a reversal opposite in character to the effect observed in iron. The anticipated reversal was duly found by Chree, the critical point corresponding, under the moderate stress employed, to a field of about 120 units. Ewing’s independent experiments showed that the magnetization curve for a cobalt rod under a load of 16.2 kilogrammes per square mm. crossed the curve for the same rod when not loaded at H = 53. Both observers noticed analogous effects in the residual magnetization. The effect of tension was subsequently studied by Nagaoka and Honda, who in 1902 confirmed, mutatis mutandis, the results obtained by Chree and Ewing for cast cobalt, while for annealed cobalt it turned out that tension always caused diminution of magnetization, the diminution increasing with increasing fields. They also investigated the magnetic behaviour of various nickel-steels under tension, and found that there was always increase of magnetization. Thus it has been proved that in annealed cobalt and in nickel-steel there is no Villari reversal.
It has been pointed out by J. J. Thomson (Applications of Dynamics to Physics and Chemistry, 47) that on dynamical principles there must be a reciprocal relation between the changes of dimensions produced by magnetization and the changes of magnetization attending mechanical strain. Since, for example, stretching diminishes the magnetization of nickel, it follows from theory that the length of a nickel rod should be diminished by magnetization and conversely. So, too, the Villari reversals in iron and cobalt might have been predicted—as indeed that in cobalt actually was—from a knowledge of the changes of length which those metals exhibit when magnetized.
The complete reciprocity of the effects of magnetization upon length and of stretching upon magnetization is shown by the following parallel statements:—
| Iron. | |
Magnetization produces increase of length in weak fields, decrease in strong fields. |
Tension produces increase of magnetization in weak fields, decrease in strong fields. |
| Cast Cobalt. | |
Magnetization produces decrease of length in weak fields, increase in strong fields. |
Tension produces decrease of magnetization in weak fields, increase in strong fields. |
| Nickel and Annealed Cobalt. | |
Magnetization produces decrease of length in all fields. |
Tension produces decrease of magnetization in all fields. |
| Nickel-Steel. | |
Magnetization produces increase of length in all fields. |
Tension produces increase of magnetization in all fields. |
Nagaoka and Honda (Phil. Mag., 1898, 46, 261) have investigated the effects of hydrostatic pressure upon magnetization, using the same pieces of iron and nickel as were employed in their experiments upon magnetic change of volume. In the iron cylinder and ovoid, which expanded when magnetized, compression caused a diminution of magnetization; in the nickel rod, which contracted when magnetized, pressure was attended by an increase of magnetization. The amount of the change was in both cases exceedingly small, that in iron being less than 0.1 C.G.S. unit with a pressure of 250 atmospheres and H = 54. It would hardly be safe to generalize from these observations; the effects may possibly be dependent upon the physical condition of the metals. In the same paper Nagaoka and Honda describe an important experiment on the effect of transverse stress. An iron tube, having its ends closed by brass caps, was placed inside a compressing vessel into which water was forced until the pressure upon the outer surface of the tube reached 250 atmospheres. The experiment was the reverse of one made by Kelvin with a gun-barrel subjected to internal hydrostatic pressure (Phil. Trans., 1878, 152, 64), and the results were also the reverse. Under increasing magnetizing force the magnetization first increased, reached a maximum, and then diminished until its value ultimately became less than when the iron was in the unstrained condition. Experiments on the effect of external hydrostatic pressure upon the magnetization of iron rings have also been made by F. Frisbie,44 who found that for the magnetizing forces used by Nagaoka and Honda pressure produced a small increase of magnetization, a result which appears to be in accord with theory.
The relations of torsion to magnetization were first carefully studied by G. Wiedemann, whose researches are described in his Elektricität, iii. 671. The most interesting of his discoveries, now generally known as the “Wiedemann effect,” is the following: If we magnetize longitudinally a straight wire which is fixed at one end and free at the other, and then pass an electric current through the wire (or first pass the current and then magnetize), the free end of the wire will twist in a certain direction depending upon circumstances: if the wire is of iron, and is magnetized (with a moderate force) so that its free end has north polarity, while the current through it passes from the fixed to the free end, then the free end as seen from the fixed end will twist in the direction of the hands of a watch; if either the magnetization or the current is reversed, the direction of the twist will be reversed. To this mechanical phenomenon there is a magnetic reciprocal. If we twist the free end of a ferromagnetic wire while a current is passing through it, the wire becomes longitudinally magnetized, the direction of the magnetization depending upon circumstances: if the wire is of iron and is twisted so that its free end as seen from the fixed end turns in the direction of the hands of a watch, while 342 the current passes from the fixed to the free end, then the direction of the resulting magnetization will be such as to make the free end a north pole. The twist effect exhibited by iron under moderate longitudinal magnetization has been called by Knott a positive Wiedemann effect; if the twist were reversed, the other conditions remaining the same, the sign of the Wiedemann effect would be negative. An explanation of the twist has been given by Maxwell (Electricity and Magnetism, § 448). The wire is subject to two superposed magnetizations, the one longitudinal, the other circular, due to the current traversing the wire; the resultant magnetization is consequently in the direction of a screw or spiral round the wire, which will be right-handed or left-handed according as the relation between the two magnetizations is right-handed or left-handed; the magnetic expansion or contraction of the metal along the spiral lines of magnetization produces the Wiedemann twist. Iron (moderately magnetized) expands along the lines of magnetization, and therefore for a right-handed spiral exhibits a right-handed twist. This explanation was not accepted by Wiedemann,45 who thought that the effect was accounted for by molecular friction. Now nickel contracts instead of lengthening when it is magnetized, and an experiment by Knott showed, as he expected, that caeteris paribus a nickel wire twists in a sense opposite to that in which iron twists. The Wiedemann effect being positive for iron is negative for nickel. Further, although iron lengthens in fields of moderate strength, it contracts in strong ones; and if the wire is stretched, contraction occurs with smaller magnetizing forces than if it is unstretched. Bidwell46 accordingly found upon trial that the Wiedemann twist of an iron wire vanished when the magnetizing force reached a certain high value, and was reversed when that value was exceeded; he also found that the vanishing point was reached with lower values of the magnetizing force when the wire was stretched by a weight. These observations have been verified and extended by Knott, whose researches have brought to light a large number of additional facts, all of which are in perfect harmony with Maxwell’s explanation of the twist.
 |
| Fig. 26. |
Maxwell has also given an explanation of the converse effect, namely, the production of longitudinal magnetization by twisting a wire when circularly magnetized by a current passing through it. When the wire is free from twist, the magnetization at any point P is in the tangential direction PB (see fig. 26). Suppose the wire to be fixed at the top and twisted at the bottom in the direction of the arrow-head T; then the element of the wire at P will be stretched in the direction Pe and compressed in the direction Pr. But tension and compression produce opposite changes in the magnetic susceptibility; if the metal is iron and its magnetization is below the Villari critical point, its susceptibility will be greater along Pe than along Pr; the direction of the magnetization therefore tends to approach Pe and to recede from Pr, changing, in consequence of the twist, from PB to some such direction as PB′, which has a vertical component downwards; hence the lower and upper ends will respectively acquire north and south polarity, which will disappear when the wire is untwisted. This effect has never been actually reversed in iron, probably, as suggested by Ewing, because the strongest practicable circular fields fail to raise the components of the magnetization along Pe and Pr up to the Villari critical value. Nagaoka and Honda have approached very closely to a reversal, and consider that it would occur if a sufficiently strong current could be applied without undue heating.
One other effect of torsion remains to be noticed. If a longitudinally magnetized wire is twisted, circular magnetization is developed; this is evidenced by the transient electromotive force induced in the iron, generating a current which will deflect a galvanometer connected with the two ends of the wire. The explanation given of the last described phenomenon will with the necessary modification apply also to this; it is a consequence of the aeolotropy produced by the twist. There are then three remarkable effects of torsion:
A. A wire magnetized longitudinally and circularly becomes twisted.
B. Twisting a circularly magnetized wire produces longitudinal magnetization.
C. Twisting a longitudinally magnetized wire produces circular magnetization.
And it has been shown earlier that—
D. Magnetization produces change of length.
E. Longitudinal stress produces change of magnetization.
Each of these five effects may occur in two opposite senses. Thus in A the twist may be right-handed or left-handed; in B the polarity of a given end may become north or south; in C the circular magnetization may be clockwise or counter-clockwise; in D the length may be increased or diminished; in E the magnetization may become stronger or weaker. And, other conditions remaining unchanged, the “sense” of any effect depends upon the nature of the metal under test, and (sometimes) upon the intensity of its magnetization. Let each of the effects A, B, C, D and E be called positive when it is such as is exhibited by moderately magnetized iron, and negative when its sense is opposite. Then the results of a large number of investigations may be briefly summarized as follows:
| (W) = weakly magnetized. | (S) = strongly magnetized. | ||
| Metal. | Effects. | Sign. | |
| Iron (W) | A, B, C, | D, E | + |
| Unannealed Cobalt (S) | A, | D, E | + |
| Nickel-Steel (W) | A, | D, E | + |
| Nickel | A, B, C, | D, E | − |
| Annealed Cobalt | D, E | − | |
| Iron (S) | A, C, | D, E | − |
| Unannealed Cobalt | A, | D, E | − |
Several gaps remain to be filled, but the results so far recorded can leave no doubt that the five effects, varied as they may at first sight appear, are intimately connected with one another. For each of the metals tabulated in the first column all the effects hitherto observed have the same sign; there is no single instance in which some are positive and others negative. Until the mysteries of molecular constitution have been more fully explored, perhaps D may be most properly regarded as the fundamental phenomenon from which the others follow. Nagaoka and Honda have succeeded in showing that the observed relations between twist and magnetization are in qualitative agreement with an extension of Kirchhoff’s theory of magnetostriction.
The effects of magnetization upon the torsion of a previously twisted wire, which were first noticed by Wiedemann, have been further studied by F. J. Smith47 and by G. Moreau.48 Nagaoka49 has described the remarkable influence of combined torsion and tension upon the magnetic susceptibility of nickel, and has made the extraordinary observation that, under certain conditions of stress, the magnetization of a nickel wire may have a direction opposite to that of the magnetizing force.
8. Effects of Temperature upon Magnetism
High Temperature.—It has long been known that iron, when raised to a certain “critical temperature” corresponding to dull red heat, loses its susceptibility and becomes magnetically indifferent, or, more accurately, is transformed from a ferromagnetic into a paramagnetic body. Recent researches have shown that other important changes in its properties occur at the same critical temperature. Abrupt alterations take place in its density, specific heat, thermo-electric quality, electrical conductivity, temperature-coefficient of electrical resistance, and in some at least of its mechanical properties. Ordinary magnetizable iron is in many respects an essentially different substance from the non-magnetizable metal into which it is transformed when its temperature is raised above a certain point (see Brit. Assoc. Report, 1890, 145). The first exact experiments demonstrating the changes which occur in the permeability of iron, 343 steel and nickel when heated up to high temperatures were those of J. Hopkinson (Phil. Trans., 1889, 180, 443; Proc. Roy. Soc., 1888, 44, 317). The metal to be tested was prepared in the form of a ring, upon which were wound primary and secondary coils of copper wire insulated with asbestos. The primary coil carried the magnetizing current; the secondary, which was wound inside the other, could be connected either with a ballistic galvanometer for determining the induction, or with a Wheatstone’s bridge for measuring the resistance, whence the temperature was calculated. The ring thus prepared was placed in a cast-iron box and heated in a gas furnace. The following are the chief results of Hopkinson’s experiments: For small magnetizing forces the magnetization of iron steadily increases with rise of temperature till the critical temperature is approached, when the rate of increase becomes very high, the permeability in some cases attaining a value of about 11,000; the magnetization then with remarkable suddenness almost entirely disappears, the permeability falling to about 1.14. For strong magnetizing forces (which in these experiments did not exceed H = 48.9) the permeability remains almost constant at its initial value (about 400), until the temperature is within nearly 100° of the critical point; then the permeability diminishes more and more rapidly until the critical point is reached and the magnetization vanishes. Steel behaves in a similar manner, but the maximum permeability is not so high as in iron, and the fall, when the critical point is approached, is less abrupt. The critical temperature for various samples of iron and steel ranges from 690° C. to 870° C.; it is the temperature at which Barrett’s “recalescence” occurs. The critical temperature for the specimen of nickel examined (which contained nearly 5% of impurities) was 310° C. F. Lydall and A. W. Pocklington found that the critical temperature of nearly pure iron was 874° C. (Proc. Roy. Soc., 1893, 52, 228).
An exhaustive research into the effects of heating on the magnetic properties of iron has been carried out by D. K. Morris (Proc. Phys. Soc., 1897, 15, 134; and Phil. Mag., 1897, 44, 213), the results being embodied in a paper containing twelve pages of tables and upwards of 120 curves. As in Hopkinson’s experiments, ring magnets were employed; these were wound with primary and secondary coils of insulated platinum wire, which would bear a much higher temperature than copper without oxidation or fusion. A third platinum coil, wound non-inductively between the primary and the secondary, served to carry the current by which the ring was heated; a current of 4.6 amperes, with 16 volts across the terminals, was found sufficient to maintain the ring at a temperature of 1150° C. In the ring itself was embedded a platinum-thermometer wire, from the resistance of which the temperature was determined. The whole was wrapped in several coverings of asbestos and placed in a glass vessel from which the air was partially exhausted, additional precautions being taken to guard against oxidation of the iron.
 |
| Fig. 27. |
Some preliminary experiments showed the striking difference in the effects of annealing at a red heat (840° C.) and at a low white heat (1150° C). After one of the rings had been annealed at 840°, its maximum permeability at ordinary temperatures was 4000 for H = 1.84; when it had been subsequently annealed at 1150°, the maximum permeability rose to 4680 for H = 1.48, while the hysteresis loss for B= ±4000 was under 500 ergs per c.cm. As regards the effects of temperature, Morris’s results are in general agreement with those of Hopkinson, though no doubt they indicate details with greater clearness and accuracy. Specimens of curves showing the relation of induction to magnetic field at various temperatures, and of permeability to temperature with fields of different intensities, are given in figs. 27 and 28. The most striking feature presented by these is the enormous value, 12,660, which, with H = 0.153, is attained by the permeability at 765° C., followed by a drop so precipitous that when the temperature is only 15° higher, the value of the permeability has become quite insignificant. The critical temperatures for three different specimens of iron were 795°, 780°, and 770° respectively. Above these temperatures the little permeability that remained was found to be independent of the magnetizing force, but it appeared to vary a little with the temperature, one specimen showing a permeability of 100 at 820°, 2.3 at 950°, and 17 at 1050°. These last observations are, however, regarded as uncertain. The effects of temperature upon hysteresis were also carefully studied, and many hysteresis loops were plotted. The results of a typical experiment are given in the annexed table, which shows how greatly the hysteresis loss is diminished as the critical temperature is approached. The coercive force at 764°.5 is stated to have been little more than 0.1 C.G.S. unit; above the critical temperature no evidence of hysteresis could be obtained.
 |
| Fig. 28. |
| Hysteresis Loss in Ergs per c.cm. Max. H. = ±6.83. | |||
| Temp. C.° | Ergs. | Temp. C.° | Ergs. |
| 764.5 | 120 | 457 | 2025 |
| 748 | 328 | 352 | 2565 |
| 730 | 426 | 249 | 3130 |
| 695 | 797 | 137.5 | 3500 |
| 634 | 1010 | 24 | 3660 |
| 554 | 1345 | ||
A paper by H. Nagaoka and S. Kusakabe50 generally confirms Morris’s results for iron, and gives some additional observations for steel, nickel and cobalt. The magnetometric method was employed, and the metals, in the form of ovoids, were heated by a specially designed burner, fed with gas and air under pressure, which directed 90 fine jets of flame upon the asbestos covering the ovoid. The temperature was determined by a platinum-rhodium and platinum thermo-junction in contact with the metal. Experiments were made at several constant temperatures with varying magnetic fields, and also at constant fields with rising and falling temperatures. For ordinary steel the critical temperature, at which magnetization practically disappeared, was found to be about 830°, and the curious fact was revealed that, on cooling, magnetization did not begin to reappear until the temperature had fallen 40° below the critical value. This retardation was still more pronounced in the case of tungsten-steel, which lost its magnetism at 910° and remained non-magnetic till it was cooled to 570°, a difference of 240°. For nearly pure nickel the corresponding temperature-difference was about 100°. This phenomenon is of the same nature as that first discovered by J. Hopkinson for nickel-steel. The paper contains tables and curves showing details of the magnetic changes, sometimes very complex, at different temperatures and with different fields. The behaviour of cobalt is particularly noticeable; its permeability increased with rising temperature up to a maximum at 500°, when it was about twice as great as at ordinary temperatures, while at 1600°, corresponding to white heat, there was still some magnetization remaining.
Further contributions to the subject have been made by K. Honda and S. Shimizu,51 who experimented at temperatures ranging from -186° to 1200°. As regards the higher temperatures, the chief point of interest is the observation that the curve of magnetization for annealed cobalt shows a small depression at about 450°, the temperature at which they had found the sign of the length-change to be reversed for all fields. In the case of all the metals tested a small but measurable trace of magnetization remained after the so-called critical temperature had been exceeded; this decreased very slightly up to the highest temperature reached (1200°) without undergoing any such variation as had been suspected by Morris. When the curve after its steep descent has almost reached the axis, it bends aside sharply and becomes a nearly horizontal straight line; the authors suggest that the critical temperature should be defined as that corresponding to the point of maximum curvature. As thus defined the critical temperatures for iron, nickel and cobalt were 344 found to be 780°, 360° and 1090° respectively, but these values are not quite independent of the magnetizing force.
Experiments on the effect of high temperatures have also been made by M. P. Ledeboer,52 H. Tomlinson,53 P. Curie,54 and W. Kunz,55 R. L. Wills,56 J. R. Ashworth57 and E. P. Harrison.58
Low Temperature.—J. A. Fleming and J. Dewar (Proc. Roy. Soc., 1896, 60, 81) were the first to experiment on the permeability and hysteresis of iron at low temperatures down to that of liquid air (−186° C.). Induction curves of an annealed soft-iron ring were taken first at a temperature of 15° C., and afterwards when the ring was immersed in liquid air, the magnetizing force ranging from about 0.8 to 22. After this operation had been repeated a few times the iron was found to have acquired a stable condition, and the curves corresponding to the two temperatures became perfectly definite. They showed that the permeability of this sample of iron was considerably diminished at the lower temperature. The maximum permeability (for H = 2) was 3400 at 15° and only 2700 at −186°, a reduction of more than 20%; but the percentage reduction became less as the magnetizing force departed from the value corresponding to maximum permeability. Observations were also made of the changes of permeability which took place as the temperature of the sample slowly rose from −186° to 15°, the magnetizing force being kept constant throughout an experiment. The values of the permeability corresponding to the highest and lowest temperatures are given in the following table. Most of the permeability-temperature curves were more or less convex towards the axis of temperature, and in all the experiments, except those with annealed iron and steel wire, the permeability was greatest at the lowest temperature.59 The hysteresis of the soft annealed iron turned out to be sensibly the same for equal values of the induction at −186° as at 15°, the loss in ergs per c.cm. per cycle being approximately represented by 0.002 B1.56 when the maximum limits of B were ±9000. Experiments with the sample of unannealed iron failed to give satisfactory results, owing to the fact that no constant magnetic condition could be obtained.
| Sample of Iron. | H. | μ at 15°. | μ at −186°. |
| Annealed Swedish | 1.77 | 2835 | 2332 |
| Unannealed ” | 1.78 | 917 | 1272 |
| ” ” | 9.79 | 1210 | 1293 |
| Hardened ” | 2.66 | 56 | 132 |
| ” ” | 4.92 | 106.5 | 502 |
| ” ” | 11.16 | 447.5 | 823 |
| ” ” | 127.7 | 109 | 124 |
| Steel wire | 7.50 | 86 | 64.5 |
| ” | 20.39 | 361 | 144 |
Honda and Shimizu have made similar experiments at the temperature of liquid air, employing a much wider range of magnetizing forces (up to about 700 C.G.S.) and testing a greater variety of metals. They found that the permeability of Swedish iron, tungsten-steel and nickel, when the metals were cooled to −186°, was diminished in weak fields but increased in strong ones, the field in which the effect of cooling changed its sign being 115 for iron and steel and 580 for nickel. The permeability of cobalt, both annealed and unannealed, was always diminished at the low temperature. The hysteresis-loss in Swedish iron was decreased for inductions below about 9000 and increased for higher inductions; in tungsten-steel, nickel and cobalt the hysteresis-loss was always increased by cooling. The range of ±B within which Steinmetz’s formula is applicable becomes notably increased at low temperature. It may be remarked that, whereas Fleming and Dewar employed the ballistic method, their specimens having the form of rings, Honda and Shimizu worked magnetometrically with metals shaped as ovoids.
Permanent Magnets.—Fleming and Dewar (loc. cit. p. 57) also investigated the changes which occurred in permanently magnetized metals when cooled to the temperature of liquid air. The metals, which were prepared in the form of small rods, were magnetized between the poles of an electromagnet and tested with a magnetometer at temperatures of −186° and 15°. The first immersion into liquid air generally produced a permanent decrease of magnetic moment, and there was sometimes a further decrease when the metal was warmed up again; but after a few alternations of temperature the changes of moment became definite and cyclic. When the permanent magnetic condition had been thus established, it was found that in the case of all the metals, except the two alloys containing large percentages of nickel, the magnetic moment was temporarily increased by cooling to −186°. The following table shows the principal results. It is suggested that a permanent magnet might conveniently be “aged” (or brought into a constant condition) by dipping it several times into liquid air.
| Metal. | Percentage Gain or Loss of Moment at −186° C. | |
| First Effect. | Cyclic Effect. | |
| Carbon steel, hard | −6 | +12 |
| Carbon steel, medium | Decrease | +22 |
| Carbon steel, annealed | −33 | +33 |
| Chromium steels (four samples) | Increase | +12 |
| Aluminium steels (three samples) | −2 | +10 |
| Nickel steels, up to 7.65% | Small | +10 |
| Nickel steels, up to 9.64% | −50 | −25 |
| Nickel steels, up to 29% | −20 | −10 |
| Pure nickel | Decrease | +3 |
| Silicon steel, 2.67% | ” | +4 |
| Iron, soft | None | +2.5 |
| Iron, hard | Decrease | +10 |
| Tungsten steel, 15% | ” | +6 |
| Tungsten steel, 7.5% | ” | +10 |
| Tungsten steel, 1% | ” | +12 |
Other experiments relating to the effect of temperature upon permanent magnets have been carried out by J. R. Ashworth,60 who showed that the temperature coefficient of permanent magnets might be reduced to zero (for moderate ranges of temperature) by suitable adjustment of temper and dimension ratio; also by R. Pictet,61 A. Durward62 and J. Trowbridge.63
Alloys of Nickel and Iron.—A most remarkable effect of temperature was discovered by Hopkinson (Proc. Roy. Soc., 1890, 47, 23; 1891, 48, 1) in 1889. An alloy containing about 3 parts of iron and 1 of nickel—both strongly magnetic metals—is under ordinary conditions practically non-magnetizable (μ = 1.4 for any value of H). If, however, this non-magnetic substance is cooled to a temperature a few degrees below freezing-point, it becomes as strongly magnetic as average cast-iron (μ = 62 for H = 40), and retains its magnetic properties indefinitely at ordinary temperatures. But if the alloy is heated up to 580° C. it loses its susceptibility—rather suddenly when H is weak, more gradually when H is strong—and remains non-magnetizable till it is once more cooled down below the freezing-point. This material can therefore exist in either of two perfectly stable conditions, in one of which it is magnetizable, while in the other it is not. When magnetizable it is a hard steel, having a specific electrical resistance of 0.000052; when non-magnetizable it is an extremely soft, mild steel, and its specific resistance is 0.000072. Alloys containing different proportions of nickel were found to exhibit the phenomenon, but the two critical temperatures were less widely separated. The following approximate figures for small magnetizing forces are deduced from Hopkinson’s curves:—
| Percentage of Nickel. | Susceptibility lost at temp. C. | Susceptibility gained at temp. C. |
| 0.97 | 890 | — |
| 4.7 | 820 | 660 |
| 4.7 | 780 | 600 |
| 24.5 | 680 | −10 |
| 30.0 | 140 | 125 |
| 33.0 | 207 | 193 |
| 73.0 | 202 | 202 |
Honda and Shimizu (loc. cit.) have determined the two critical temperatures for eleven nickel-steel ovoids, containing from 24.04 to 70.32% of nickel, under a magnetizing force of 400, and illustrated by an interesting series of curves, the gradual transformation of the magnetic properties as the percentage of nickel was decreased. They found that the hysteresis-loss, which at ordinary temperatures is very small, was increased in liquid air, the increase for the alloys containing less than 30% of nickel being enormous. Steinmetz’s formula applies only for very weak inductions when the alloys are at the ordinary temperature, but at the temperature of liquid air it becomes applicable through a wide range of inductions. According to C. E. Guillaume64 the temperature at which the magnetic susceptibility of nickel-steel is recovered is lowered by the presence of chromium; a certain alloy containing chromium was not rendered magnetic even by immersion in liquid air. Experiments on the subject have also been made by E. Dumont65 and F. Osmond.66
9. Alloys and Compounds or Iron
In 1885 Hopkinson (Phil. Trans., 1885, 176, 455) employed his yoke method to test the magnetic properties of thirty-five samples of iron and steel, among which were steels containing substantial proportions of manganese, silicon, chromium and tungsten. The results, together with the chemical analysis of each sample, are given in a table contained in this paper, some of them being also represented graphically. The most striking phenomenon which they bring into prominence is the effect of any considerable quantity of manganese in annihilating the magnetic property of iron. A sample of Hadfield’s manufacture, containing 12.36% of manganese, differed hardly at all from a non-magnetic substance, its permeability being only 1.27. According to Hopkinson’s calculation, this sample behaved as if 91% of the iron contained in it had completely lost its magnetic property.67 Another point to which attention is directed is the exceptionally great effect which hardening has upon the magnetic properties of chrome steel; one specimen had a coercive force of 9 when annealed, and of no less than 38 when oil-hardened. The effect of the addition of tungsten in increasing the coercive force is very clearly shown; in two specimens containing respectively 3.44 and 2.35% of tungsten the coercive force was 64.5 and 70.7. These high values render hardened tungsten-steel particularly suitable for the manufacture of permanent magnets. Hopkinson (Proc. Roy. Soc., 1890, 48, 1) also noticed some peculiarities of an unexpected nature in the magnetic properties of the nickel-steel alloys already referred to. The permeability of the alloys containing from 1 to 4.7% of nickel, though less than that of good soft iron for magnetizing forces up to about 20 or 30, was greater for higher forces, the induction reached in a field of 240 being nearly 21,700. The induction for considerable forces was found to be greater in a steel containing 73% of nickel than in one with only 33%, though the permeability of pure nickel is much less than that of iron.
The magnetic qualities of various alloys of iron have been submitted to a very complete examination by W. F. Barrett, W. Brown and R. A. Hadfield (Trans. Roy. Dub. Soc., 1900, 7, 67; Journ. Inst. Elec. Eng., 1902, 31, 674).68 More than fifty different specimens were tested, most of which contained a known proportion of manganese, nickel, tungsten, aluminium, chromium, copper or silicon: in some samples two of the substances named were present. Of the very numerous results published, a few of the most characteristic are collected in the following table. The first column contains the symbols of the various elements which were added to the iron, and the second the percentage proportion in which each element was present; the sample containing 0.03% of carbon was a specimen of the best commercial iron, the values obtained for it being given for comparison. All the metals were annealed.
A few among several interesting points should be specially noticed. The addition of 15.2% of manganese produced an enormous effect upon the magnetism of iron, while the presence of only 2.25% was comparatively unimportant. When nickel was added to the iron in increasing quantities the coercive force increased until the proportion of nickel reached 20%; then it diminished, and when the proportion of nickel was 32% the coercive force had fallen to the exceedingly low value of 0.5. In the case of iron containing 7.5% of tungsten (W), the residual induction had a remarkably high value; the coercive force, however, was not very great. The addition of silicon in small quantities considerably diminished permeability and increased coercive force; but when the proportion amounted to 2.5% the maximum permeability (μ = 5100 for H = 2) was greater than that of the nearly pure iron used for comparison, while the coercive force was only 0.9.69 A small percentage of aluminium produced still higher permeability (μ = 6000 for H = 2), the induction in fields up to 60 being greater than in any other known substance, and the hysteresis-loss for moderate limits of B far less than in the purest commercial iron. Certain non-magnetizable alloys of nickel, chromium-nickel and chromium-manganese were rendered magnetizable by annealing.
| Element. | Per cent. | B for H = 45. | B residual. | μ for H = 8. | Coercive Force. |
| C | 0.03 | 16800 | 9770 | 1625 | 1.66 |
| Cu | 2.5 | 14300 | 10410 | .. | 5.4 |
| Mn | 2.25 | 14720 | 10460 | 1080 | 6.0 |
| Mn | 15.2 | 0 | .. | .. | .. |
| Ni | 3.82 | 16190 | 9320 | 1375 | 2.76 |
| Ni | 19.64 | 7770 | 4770 | 90 | 20.0 |
| Ni | 31.4 | 4460 | 1720 | 357 | 0.5 |
| W | 7.5 | 15230 | 13280 | 500 | 9.02 |
| Al | 2.25 | 16900 | 10500 | 1700 | 1.0 |
| Cr | 3.25 | .. | .. | .. | 12.25 |
| Si | 2.5 | 16420 | 4080 | 1680 | 0.9 |
| Si | 5.5 | 15980 | 3430 | 1630 | 0.85 |
Later papers70 give the results of a more minute examination of those specimens which were remarkable for very low and very high permeabilities, and were therefore likely to be of commercial importance. The following table gives the exact composition of some alloys which were found to be non-magnetizable, or nearly so, in a field of 320.
| An. = Annealed. Un. = Unannealed. | ||
| State. | Percentage Composition. | I, for H = 320. |
| Un. | Fe, 85.77; C, 1.23; Mn, 13. | 0 |
| An. | Fe, 84.64; C, 0.15; Mn, 15.2 | 0 |
| An. | Fe, 80.16; C, 0.8; Mn, 5.04; Ni, 14.55. | 3 |
| Un. | Ditto | 0 |
| Un. | Fe, 75.36; C, 0.6; Mn, 5.04; Ni, 19. | 3 |
| An. | Fe, 86.61; C, 1.08; Mn, 10.2; W, 2.11. | 5 |
A very small difference in the constitution often produces a remarkable effect upon the magnetic quality, and it unfortunately happens that those alloys which are hardest magnetically are generally also hardest mechanically and extremely difficult to work; they might however be used rolled or as castings. The specimens distinguished by unusually high permeability were constituted as follows:—
| Silicon-iron.—Fe, 97.3; C, 0.2; Si, 2.5. Aluminium-iron.—Fe, 97.33; C, 0.18; Al, 2.25. |
The silicon-iron had, in fields up to about 10, a greater permeability than a sample of the best Swedish charcoal-iron, and its hysteresis-loss for max. B = 9000, at a frequency of 100 per second, was only 0.254 watt per pound, as compared with 0.382 for the Swedish iron. The aluminium-iron attained its greatest permeability in a field of 0.5, about that of the earth’s force, when its value was 9000, this being more than twice the maximum permeability of the Swedish iron. Its hysteresis-loss for B = 9000 was 0.236 per pound. It was, however, found that the behaviour of this alloy was in part due to a layer of pure iron (“ferrite”) averaging 0.1 mm. in thickness, which occurred on the outside of the specimen, and the exceptional magnetic quality which has been claimed for aluminium-iron cannot yet be regarded as established.
A number of iron alloys have been examined by Mme. Curie (Bull. Soc. d’Encouragement, 1898, pp. 36-76), chiefly with the object of determining their suitability for the construction of permanent magnets. Her tests appear to show that molybdenum is even more effective than tungsten in augmenting the coercive force, the highest values observed being 70 to 74 for tungsten-steel, and 80 to 85 for steel containing 3.5 to 4% of molybdenum. For additional information regarding the composition and qualities of permanent magnet steels reference may be made 346 to the publications cited below.71 Useful instructions have been furnished by Carl Barus (Terrestrial Magnetism, 1897, 2, 11) for the preparation of magnets calculated to withstand the effects of time, percussion and ordinary temperature variations. The metal, having first been uniformly tempered glass-hard, should be annealed in steam at 100° C. for twenty or thirty hours; it should then be magnetized to saturation, and finally “aged” by a second immersion in steam for about five hours.
Magnetic Alloys of Non-Magnetic Metals.—The interesting discovery was made by F. Heusler72 in 1903 that certain alloys of the non-magnetic metal manganese with other non-magnetic substances were strongly magnetizable, their susceptibility being in some cases equal to that of cast iron. The metals used in different combinations included tin, aluminium, arsenic, antimony, bismuth and boron; each of these, when united in certain proportions with manganese, together with a larger quantity of copper (which appears to serve merely as a menstruum), constituted a magnetizable alloy. So far, the best results have been attained with aluminium, and the permeability was greatest when the percentages of manganese and aluminium were approximately proportional to the atomic weights of the two metals. Thus in an alloy containing 26.5% of manganese and 14.6% of aluminium, the rest being copper, the induction for H = 20 was 4500, and for H = 150, 5550. When the proportion of aluminium to manganese was made a little greater or smaller, the permeability was diminished. Next to aluminium, tin was found to be the most effective of the metals enumerated above. In all such magnetizable alloys the presence of manganese appears to be essential, and there can be little doubt that the magnetic quality of the mixtures is derived solely from this component. Manganese, though belonging (with chromium) to the iron group of metals, is commonly classed as a paramagnetic, its susceptibility being very small in comparison with that of the recognized ferromagnetics; but it is remarkable that its atomic susceptibility in solutions of its salts is even greater than that of iron. Now iron, nickel and cobalt all lose their magnetic quality when heated above certain critical temperatures which vary greatly for the three metals, and it was suspected by Faraday73 as early as 1845 that manganese might really be a ferromagnetic metal having a critical temperature much below the ordinary temperature of the air. He therefore cooled a piece of the metal to −105° C., the lowest temperature then attainable, but failed to produce any change in its magnetic quality. The critical temperature (if there is one) was not reached in Faraday’s experiment; possibly even the temperature of −250° C., which by the use of liquid hydrogen has now become accessible, might still be too high.74 But it has been shown that the critical temperatures of iron and nickel may be changed by the addition of certain other substances. Generally they are lowered, sometimes, however, they are raised75; and C. E. Guillaume76 explains the ferromagnetism of Heusler’s alloy by supposing that the naturally low critical temperature of the manganese contained in it is greatly raised by the admixture of another appropriate metal, such as aluminium or tin; thus the alloy as a whole becomes magnetizable at the ordinary temperature. If this view is correct, it may also be possible to prepare magnetic alloys of chromium, the only other paramagnetic metals of the iron group.
J. A. Fleming and R. A. Hadfield77 have made very careful experiments on an alloy containing 22.42% of manganese, 11.65% of aluminium and 60.49% of copper. The magnetization curve was found to be of the same general form as that of a paramagnetic metal, and gave indications that with a sufficient force magnetic saturation would probably be attained. There was considerable hysteresis, the energy-loss per cycle being fairly represented by W = 0.0005495B2.238. The hysteretic exponent is therefore much higher than in the case of iron, nickel and cobalt, for which its value is approximately 1.6.
10. Miscellaneous Effects of Magnetization
Electrical Conductivity.—The specific resistance of many electric conductors is known to be temporarily changed by the action of a magnetic field, but except in the case of bismuth the effect is very small.
A. Gray and E. Taylor Jones (Proc. Roy. Soc., 1900, 67, 208) found that the resistance of a soft iron wire was increased by about 1⁄700 in a field of 320 C.G.S. units. The effect appeared to be closely connected with the intensity of magnetization, being approximately proportional to I. G. Barlow (Proc. Roy. Soc., 1903, 71, 30), experimenting with wires of iron, steel and nickel, showed that in weak fields the change of resistance was proportional to a function aI2 + bI4 + cI6, where a, b and c are constants for each specimen. W. E. Williams (Phil. Mag., 1902, 4, 430) found that for nickel the curves showing changes of resistance in relation to magnetizing force were strikingly similar in form to those showing changes of length. H. Tomlinson (Phil. Trans., 1883, Part I., 153) discovered in 1881 that the resistance of a bismuth rod was slightly increased when the rod was subjected to longitudinal magnetic force, and a year or two later A. Righi (Atti R. A. Lincei, 1883-1884, 19, 545) showed that a more considerable alteration was produced when the magnetic force was applied transversely to the bismuth conductor; he also noticed that the effect was largely dependent upon temperature (see also P. Lenard, Wied. Ann., 1890, 39, 619). Among the most important experiments on the influence of magnetic force at different temperatures are those of J. B. Henderson and of Dewar and Fleming. Henderson (Phil. Mag., 1894, 38, 488) used a little spiral of the pure electrolytic bismuth wire prepared by Hartmann and Braun; this was placed between the pole-pieces of an electromagnet and subjected to fields of various strengths up to nearly 39,000 units. At constant temperature the resistance increased with the field; the changes in the resistance of the spiral when the temperature was 18° C. are indicated in the annexed table, from which it will be seen that in the strongest transverse field reached the resistance was increased more than threefold. Other experiments showed the relation of resistance to temperature (from 0° to about 90°) in different constant fields. It appears that as the temperature rises the resistance decreases to a minimum and then increases, the minimum point occurring at a higher temperature the stronger the field. For H = 11,500 the temperature of minimum resistance was about 50°; for much lower or higher values of H the actual minimum did not occur within the range of temperature dealt with. Dewar and Fleming (Proc. Roy. Soc., 1897, 60, 425) worked with a similar specimen of bismuth, and their results for a constant temperature of 19° agree well with those of Henderson. They also experimented with constant temperatures of −79°, −185° and −203°, and found that at these low temperatures the effect of magnetization was enormously increased. The following table gives some of their results, the specific resistance of the bismuth being expressed in C.G.S. units.
| H. | R. | H. | R. |
| 0 | 1.000 | 27450 | 2.540 |
| 6310 | 1.253 | 32730 | 2.846 |
| 12500 | 1.630 | 38900 | 3.334 |
| 20450 | 2.160 |
| Field Strength. | Temp. 19°C. | Temp. −185°C. | ||
| Spec. Res. | Comp. Res. | Spec. Res. | Comp. Res. | |
| 0 | 116200 | 1.000 | 41000 | 1.00 |
| 1375 | 118200 | 1.017 | 103300 | 2.52 |
| 2750 | 123000 | 1.059 | 191500 | 4.67 |
| 8800 | 149200 | 1.284 | 738000 | 18.0 |
| 14150 | 186200 | 1.602 | 1730000 | 42.2 |
| 21800 | 257000 | 2.212 | 6190000 | 151 |
At the temperature of liquid air (−185°) the application of a field of 21,800 multiplied the resistance of the bismuth no less than 150 times. Fig. 29 shows the variations of resistance in relation to temperature for fields of different constant values. It will be seen that for H = 2450 and H = 5500 the minimum resistance occurs at temperatures of about −80° and −7° respectively.
Hall Effect.—If an electric current is passed along a strip of thin metal, and the two points at opposite ends of an equipotential line are connected with a galvanometer, its needle will of course not be deflected. But the application of a magnetic field at right angles to the plane of the metal causes the equipotential lines to rotate through a small angle, and the points at 347 which the galvanometer is connected being no longer at the same potential, a current is indicated by the galvanometer.78 The tranverse electromotive force is equal to KCH/D, where C is the current, H the strength of the field, D the thickness of the metal, and K a constant which has been termed the rotatory power or rotational coefficient. (See Hopkinson, Phil. Mag., 1880, 10, 430). The following values of K for different metals are given by E. H. Hall, the positive sign indicating that the electromotive force is in the same direction as the mechanical force acting upon the conductor. A. von Ettinghausen and W. Nernst (Wien. Ber., 1886, 94, 560) have found that the rotational coefficient of tellurium is more than fifty times greater than that of bismuth, its sign being positive. Several experimenters have endeavoured to find a Hall effect in liquids, but such results as have been hitherto obtained are by no means free from doubt. E. A. Marx (Ann. d. Phys., 1900, 2, 798) observed a well-defined Hall effect in incandescent gases. A large effect, proportional to the field, has been found by H. A. Wilson (Cam. Phil. Soc. Proc., 1902, 11, pp. 249, 391) in oxygen, hydrogen and air at low pressures, and by C. D. Child (Phys. Rev., 1904, 18, 370) in the electric arc.
 |
| Fig. 29 |
| Metal. | K × 1015 | Metal. | K × 1015 |
| Antimony | +114000 | Copper | −520 |
| Steel | +12060 | Gold | −660 |
| Iron | +7850 | Nickel | −14740 |
| Cobalt | +2460 | Bismuth79 | −8580000 |
| Zinc | +820 |
Electro-Thermal Relations.—The Hall electromotive force is only one of several so-called “galvano-magnetic effects” which are observed when a magnetic field acts normally upon a thin plate of metal traversed by an electric current. It is remarkable that if a flow of heat be substituted for a current of electricity a closely allied group of “thermo-magnetic effects” is presented. The two classes of phenomena have been collated by M. G. Lloyd (Am. Journ. Sci., 1901, 12, 57), as follows:—
| Galvano-Magnetic Effects. | Thermo-Magnetic Effects. |
1. A transverse difference of electric potential (Hall effect). |
i. A transverse difference of electric potential (Nernst effect). |
2. A transverse difference of temperature(Ettinghausen effect). |
ii. A transverse difference of temperature (Leduc effect). |
3. Longitudinal change of electric conductivity. |
iii. Longitudinal change of thermal conductivity. |
4. Longitudinal difference of temperature. |
iv. Longitudinal difference of electric potential.80 |
 |
If in the annexed diagram ABCD represents the metallic plate through which the current of electricity or heat flows in the direction AB, then effects (1), (2), (i.) and (ii.) are exhibited at C and D, effects (4) and (iv.) at A and B, and effects (3) and (iii.) along AB. The transverse effects are reversed in direction when either the magnetic field or the primary current (electric or thermal) is reversed, but the longitudinal effects are independent of the direction of the field. It has been shown by G. Moreau (C. R., 1900, 130, pp. 122, 412, 562) that if K is the coefficient of the Hall effect (1) and K′ the analogous coefficient of the Nernst effect (i.) (which is constant for small values of H), then K′ = Kσ/ρ, σ being the coefficient of the Thomson effect for the metal and ρ its specific resistance. He considers that Hall’s is the fundamental phenomenon, and that the Nernst effect is essentially identical with it, the primary electromotive force in the case of the latter being that of the Thomson effect in the unequally heated metal, while in the Hall experiment it is derived from an external source.
Attempts have been made to explain these various effects by the electron theory.81
Thermo-electric Quality.—The earliest observations of the effect of magnetization upon thermo-electric power were those of W. Thomson (Lord Kelvin), who in 1856 announced that magnetization rendered iron and steel positive to the unmagnetized metals.82 It has been found by Chassagny,83 L. Houllevigue84 and others that when the magnetizing force is increased, this effect passes a maximum, while J. A. Ewing85 has shown that it is diminished and may even be reversed by tensile stress. Nickel was believed by Thomson to behave oppositely to iron, becoming negative when magnetized; but though his conclusion was accepted for nearly fifty years, it has recently been shown to be an erroneous one, based, no doubt, upon the result of an experiment with an impure specimen. Nickel when magnetized is always positive to the unmagnetized metal. So also is cobalt, as was found by H. Tomlinson.86 The curves given by Houllevigue for the relation of thermo-electric force to magnetic field are of the same general form as those showing the relation of change of length to field. E. Rhoads87 obtained a cyclic curve for iron which indicated thermo-electric hysteresis of the kind exhibited by Nagaoka’s curves for magnetic strain. He also experimented with nickel and again found a resemblance to the strain curve. The subject was further investigated by S. Bidwell,88 who, adopting special precautions against sources of error by which former work was probably affected, measured the changes of thermo-electric force for iron, steel, nickel and cobalt produced by magnetic fields up to 1500 units. In the case of iron and nickel it was found that, when correction was made for mechanical stress due to magnetization, magnetic change of thermo-electric force was, within the limits of experimental error, proportional to magnetic change of length. Further, it was shown that the thermo-electric curves were modified both by tensile stress and by annealing in the same manner as were the change-of-length curves, the modification being sometimes of a complex nature. Thus a close connexion between the two sets of phenomena seems to be established. In the case of cobalt no such relation could be traced; it appeared that the thermo-electric power of the unmagnetized with respect to the magnetized cobalt was proportional to the square of the magnetic induction or of the magnetization. Of nickel six 348 different specimens were tested, all of which became, like iron, thermo-electrically positive to the unmagnetized metals.
As to what effect, if any, is produced upon the thermo-electric quality of bismuth by a magnetic field there is still some doubt. E. van Aubel89 believes that in pure bismuth the thermo-electric force is increased by the field; impurities may neutralize this effect, and in sufficient quantities reverse it.
Elasticity.—The results of experiments as to the effect of magnetization were for long discordant and inconclusive, sufficient care not having been taken to avoid sources of error, while the effects of hysteresis were altogether disregarded. The subject, which is of importance in connexion with theories of magnetostriction, has been investigated by K. Honda and T. Terada in a research remarkable for its completeness and the ingenuity of the experimental methods employed.90 The results are too numerous to discuss in detail; some of those to which special attention is directed are the following: In Swedish iron and tungsten-steel the change of elastic constants (Young’s modulus and rigidity) is generally positive, but its amount is less than 0.5%; changes of Young’s modulus and of rigidity are almost identical. In nickel the maximum change of the elastic constants is remarkably large, amounting to about 15% for Young’s modulus and 7% for rigidity; with increasing fields the elastic constants first decrease and then increase. In nickel-steels containing about 50 and 70% of nickel the maximum increase of the constants is as much as 7 or 8%. In a 29% nickel-steel, magnetization increases the constants by a small amount. Changes of elasticity are in all cases dependent, not only upon the field, but also upon the tension applied; and, owing to hysteresis, the results are not in general the same when the magnetization follows as when it precedes the application of stress; the latter is held to be the right order.
Chemical and Voltaic Effects.—If two iron plates, one of which is magnetized, are immersed in an electrolyte, a current will generally be indicated by a galvanometer connected with the plates.
As to whether the magnetized plate becomes positive or negative to the other, different experimenters are not in agreement. It has, however, been shown by Dragomir Hurmuzescu (Rap. du Congrès Int. de Phys., Paris, 1900, p. 561) that the true effect of magnetization is liable to be disguised by secondary or parasitic phenomena, arising chiefly from polarization of the electrodes and from local variations in the concentration and magnetic condition of the electrolyte; these may be avoided by working with weak solutions, exposing only a small surface in a non-polar region of the metal, and substituting a capillary electrometer for the galvanometer generally used. When such precautions are adopted it is found that the “electromotive force of magnetization” is, for a given specimen, perfectly definite both in direction and in magnitude; it is independent of the nature of the corrosive solution, and is a function of the field-strength alone, the curves showing the relation of electromotive force to field-intensity bearing a rough resemblance to the familiar I-H curves. The value of the E.M.F. when H = 2000 is of the order of 1/100 volt for iron, 1/1000 volt for nickel and 1/10,000 for bismuth. When the two electrodes are ferromagnetic, the direction of the current through the liquid is from the unmagnetized to the magnetized electrode, the latter being least attacked; with diamagnetic electrodes the reverse is the case. Hurmuzescu shows that these results are in accord with theory. Applying the principle of the conservation of internal energy, he demonstrates that for iron in a field of 1000 units and upwards the E.M.F. of magnetization is
| E = | l | · | I² |
| δ | 2κ |
approximately, l being the electrochemical equivalent and δ the density of the metal. Owing to the difficulty of determining the magnetization I and the susceptibility κ with accuracy, it has not yet been possible to submit this formula to a quantitative test, but it is said to afford an indication of the results given by actual experiment. It has been discovered by E. L. Nichols and W. S. Franklin (Am. Journ. Sci., 1887, 34, 419; 1888, 35, 290) that the transition from the “passive” to the active state of iron immersed in strong nitric acid is facilitated by magnetization, the temperature of transition being lowered. This is attributed to the action of local currents set up between unequally magnetized portions of the iron. Similar results have been obtained by T. Andrews (Proc. Roy. Soc., 1890, 48, 116).
11. Feebly Susceptible Substances
Water.—The following are recent determinations of the magnetic susceptibility of water:—
| Observer. | κ × 106. | Publication. |
| G. Quincke | −0.797 at 18° C. | Wied. Ann., 1885, 24, 387. |
| H. du Bois | −0.837 (1 − 0.0025t − 15°) | Wied. Ann., 1888, 35, 137. |
| P. Curie | −0.790 at 4° C. | C. R., 1893, 116, 136. |
| J. Townsend | −0.77 | Phil. Trans., 1896, 187, 544. |
| J. A. Fleming and J. Dewar | −0.74 | Proc. Roy. Soc., 1898, 63, 311. |
| G. Jäger and S. Meyer 707. | −0.689(1 − 0.0016t) | Wied. Ann., 1899, 67, |
| J. Koenigsberger | −0.781 at 22° C. | Ann. d. Phys., 1901, 6, 506. |
| H. D. Stearns | −0.733 at 22° C. | Phys. Rev., 1903, 16, 1. |
| A. P. Wills | −0.720 at 18° C. | Phys. Rev., 1905, 20, 188. |
Wills found that the susceptibility was constant in fields ranging from 4200 to 15,000.
Oxygen and Air.—The best modern determinations of the value of κ for gaseous oxygen agree very fairly well with that given by Faraday in 1853 (Exp. Res. III, 502). Assuming that for water κ = −0.8 × 10−6, his value of κ for oxygen at 15° C. reduces to 0.15 × 10−6. Important experiments on the susceptibility of oxygen at different pressures and temperatures were carried out by P. Curie (C.R. 1892, 115, 805; 1893, 116, 136). Journ. de Phys., 1895, 4, 204. He found that the susceptibility for unit of mass, K, was independent of both pressure and magnetizing force, but varied inversely as the absolute temperature, θ, so that 106K = 33700/θ. Since the mass of 1 cub. cm. of oxygen at 0° C. and 760 mm. pressure is 0.00141 grm., the mass at any absolute temperature θ is by Charles’s law 0.00141 × 273θ = 0.3849/θ grm.; hence the susceptibility per unit of volume at 760 mm. will be
κ = 10−6 × 0.3849 × 33700 / θ²
= 10−6 × 12970 / θ².
At 15° C. θ = 273 + 15 = 288, and therefore κ = 0.156 × 10-6, nearly the same as the value found by Faraday. At 0° C., κ = 0.174 × 10-6. For air Curie calculated that the susceptibility per unit mass was 106K = 7830/θ; or, taking the mass of 1 c.c. of air at 0° C. and 760 mm. as 0.001291 grm., κ = 10−6 × 2760/θ² for air at standard atmospheric pressure. It is pointed out that this formula may be used as a temperature correction in magnetic determinations carried out in air.
Fleming and Dewar determined the susceptibility of liquid oxygen (Proc. Roy. Soc., 1896, 60, 283; 1898, 63, 311) by two different methods. In the first experiments it was calculated from observations of the mutual induction of two conducting circuits in air and in the liquid; the results for oxygen at −182° C. were
μ = 1.00287, κ = 228 × 10−6.
In the second series, to which greater importance is attached, measurements were made of the force exerted in a divergent field upon small balls of copper, silver and other substances, first when the balls were in air and afterwards when they were immersed in liquid oxygen. If V is the volume of a ball, H the strength of the field at its centre, and κ′ its apparent susceptibility, the force in the direction x is ƒ = κ′VH × dH/dx; and if κ′a and κ′0 are the apparent susceptibilities of the same ball in air and in liquid oxygen, κ′a − κ′0 is equal to the difference between the susceptibilities of the two media. The susceptibility of air being known—practically it was negligible in these experiments—that of liquid oxygen can at once be found. The mean of 36 experiments with 7 balls gave
μ = 1.00407, κ = 324 × 10−6.
A small but decided tendency to a decrease of susceptibility in very strong fields was observed. It appears, therefore, that liquid oxygen is by far the most strongly paramagnetic liquid known, its susceptibility being more than four times greater than that of a saturated solution of ferric chloride. On the other hand, its susceptibility is about fifty times less than that of Hadfield’s 12% manganese steel, which is commonly spoken of as non-magnetizable.
Bismuth.—Bismuth is of special interest, as being the most strongly diamagnetic substance known, the mean value of the best determinations of its susceptibility being about −14 × 10-6 (see G. Meslin, C. R., 1905, 140, 449). The magnetic properties of the metal at different temperatures and in fields up to 1350 units have been studied by P. Curie (loc. cit.), who found that its “specific susceptibility” (K) was independent of the strength of the field, but decreased with rise of temperature up to the melting-point, 273°C. His results appear to show the relation
−Κ × 106 = 1.381 − 0.00155t°.
Assuming the density of Bi to be 9.8, and neglecting corrections for heat dilatation, his value for the susceptibility at 20°C. is equivalent to κ = −13.23 × 10−6. As the temperature was raised up to 273°, κ gradually fell to −9.38 × 10−6, rising suddenly when fusion occurred to −0.37 × 10−6, at which value it remained constant when the fluid metal was further heated. Fleming and Dewar give for the susceptibility the values −13.7 × 10−6 at 15°C. and −15.9 × 10-6 at −182°, the latter being approximately equivalent to Κ × 106 = −1.62. Putting t° = −182 in the equation given above for Curie’s results, we get Κ × 106 = −1.66, a value sufficiently near that obtained by Fleming and Dewar to suggest the probability that the diamagnetic susceptibility varies inversely as the temperature between −182° and the melting-point.
Other Diamagnetics.—The following table gives Curie’s determinations (Journ. de Phys., 1895, 4, 204) of the specific susceptibility Κ of other diamagnetic substances at different temperatures. It should be noted that Κ = κ/density.
| Substance | Temp. °C. | −Κ × 106. |
| Water | 15-189 | 0.790 |
| Rock salt | 16-455 | 0.580 |
| Potassium chloride | 18-465 | 0.550 |
| Potassium sulphate | 17-460 | 0.430 |
| Potassium nitrate (fusion 350°) | 18-420 | 0.330 |
| Quartz | 18-430 | 0.441 |
| Sulphur, solid or fused | 18-225 | 0.510 |
| Selenium, solid or fused | 20-200 | 0.320 |
| Selenium, fused | 240-415 | 0.307 |
| Tellurium | 20-305 | 0.311 |
| Bromine | 20 | 0.410 |
| Iodine, solid or fused | 18-164 | 0.385 |
| Phosphorus, solid or fused | 19-71 | 0.920 |
| Phosphorus, amorphous | 20-275 | 0.730 |
| Antimony, electrolytic | 20 | 0.680 |
| Antimony | 540 | 0.470 |
| Bismuth, solid | 20 | 1.350 |
| Bismuth, solid | 273 | 0.957 |
| Bismuth, fused | 273-405 | 0.038 |
For all diamagnetic substances, except antimony and bismuth, the value of Κ was found to be independent of the temperature.
Paramagnetic Substances.—Experiments by J. S. Townsend (Phil. Trans., 1896, 187, 533) show that the susceptibility of solutions of salts of iron is independent of the magnetizing force, and depends only on the quantity of iron contained in unit volume of the liquid. If W is the weight of iron present per c.c. at about 10°C., then for ferric salts
106κ = 266W − 0.77
and for ferrous salts
106κ = 206W − 0.77,
the quantity −0.77 arising from the diamagnetism of the water of solution. Annexed are values of 106κ for the different salts examined, w being the weight of the salt per c.c. of the solution.
| Salt. | 106κ + 0.77 | Salt. | 106κ + 0.77 |
| Fe2Cl6 | 91.6w | FeCl2 | 90.8w |
| Fe2(SO4)3 | 74.5w | FeSO4 | 74.9w |
| Fe2(NO3)6 | 61.5w |
Susceptibility was found to diminish greatly with rise of temperature. According to G. Jäger and S. Meyer (Wien. Akad. Sitz., 1897, 106, II. a, p. 623, and 1898, 107, II. a, p. 5) the atomic susceptibilities k of the metals nickel, chromium, iron, cobalt and manganese in solutions of their salts are as follows:—
| Metal. | k × 106 | Metal. | k × 106. |
| Ni | 4.95 = 2.5 × 2 | Co | 10.0 = 2.5 × 4 |
| Cr | 6.25 = 2.5 × 2.5 | Fe(2) | 12.5 = 2.5 × 5 |
| Fe(1) | 7.5 = 2.5 × 3 | Mn | 15.0 = 2.5 × 6 |
Fe(1) is iron contained in FeCl2 and Fe(2) iron contained in Fe2(NO3)6.
Curie has shown, for many paramagnetic bodies, that the specific susceptibility K is inversely proportional to the absolute temperature θ. Du Bois believes this to be an important general law, applicable to the case of every paramagnetic substance, and suggests that the product Kθ should be known as “Curie’s constant” for the substance.
Elementary Bodies and Atomic Susceptibility.—Among a large number of substances the susceptibilities of which have been determined by J. Koenigsberger (Wied. Ann., 1898, 66, 698) are the following elements:—
| Element. | κ × 106. | Element. | κ × 106. |
| Copper | −0.82 | Tellurium | − 2.10 |
| Silver | −1.51 | Graphite | + 2 |
| Gold | −3.07 | Aluminium | + 1.80 |
| Zinc | −0.96 | Platinum | +22 |
| Tin | +0.46 | Palladium | +50 to 60 |
| Lead | −1.10 | Tungsten | +14 |
| Thallium | −4.61 | Magnesium | + 4 |
| Sulphur | −0.86 | Sodium | + 2.2 |
| Selenium (red) | −0.50 | Potassium | + 3.6 |
In a table accompanying Koenigsberger’s paper the elements are arranged upon the periodic system and the atomic susceptibility (product of specific susceptibility into atomic weight) is given for each. It appears that the elements at about the middle of each row are the most strongly paramagnetic; towards the ends of a row the susceptibility decreases, and ultimately becomes negative. Thus a relation between susceptibility and atomic weight is clearly indicated. Tables similarly arranged, but much more complete, have been published by S. Meyer (Wied. Ann., 1899, 68, 325 and 1899, 69, 236), whose researches have filled up many previously existing gaps. The values assigned to the atomic susceptibilities of most of the known elements are appended. According to the notation adopted by Meyer the atomic susceptibility k = κ × atomic-weight / (density × 1000).
Meyer thinks that the susceptibilities of the metals praseodymium, neodymium, ytterbium, samarium, gadolinium, and erbium, when obtained in a pure form, will be found to equal or even exceed those of the well-known ferromagnetic metals. Many of their compounds are very strongly magnetic; erbium, for example, in Er2O3 being four times as strong as iron in the familiar magnetite or lodestone, Fe2O3. The susceptibilities of some hundreds of inorganic compounds have also been determined by the same investigator (loc. cit.). Among other researches relating to atomic and molecular magnetism are those of O. Liebknecht and A. P. Wills (Ann. d. Phys., 1900, 1, 178), H. du Bois and O. Liebknecht (ibid. p. 189), and Meyer (ibid. p. 668). An excellent summary regarding the magnetic properties of matter, with many tables and references, has been compiled by du Bois (Report to the Congrès Int. de Phys., Paris, 1900, ii. 460).
| Element | 106k | Element | 106k | Element | 106k | ||
| Be | +0.72 | Cu | −0.006 | Cs | − 0.03* | ||
| B | +0.05 | Zn | −0.010 | Ba | − 0.02* | ||
| C | −0.05 | Ga | − | La | +13.0 | ||
| N | ? | Ge | − | Ce | +34.0 | ||
| O | + | As | ? | Pr | + | Strong | |
| F | −0.01* | Se | −0.025 | Nd | + | ||
| · · · · · · · · · · | Br | −0.033 | Sa | + | |||
| Na | −0.005* | · · · · · · · · · · | Gd | + | |||
| Mg | +0.014 | Rb | −0.02* | · · · · · · · · · · | |||
| Al | + | Sr | −0.02* | Er | +41.8(?) | ||
| Si | +0.002 | Y | +3.2(?) | · · · · · · · · · · | |||
| P | −0.007 | Zr | −0.014 | Yb | + (?) | ||
| S | −0.011 | Nb | +0.49(?) | Ta | + 1.02(?) | ||
| Cl | −0.02* | Mo | +0.024 | W | + 0.1 | ||
| · · · · · · · · · · | Ru | + | Os | + 0.074 | |||
| K | −0.001* | Rh | + | Ir | + | ||
| Ca | −0.003* | Pd | +0.55 | Pt | + 0.227 | ||
| Sc | ? | Ag | −0.016 | Au | − 0.031 | ||
| Ti | +0.09 | Cd | −0.015 | Hg | − 0.030 | ||
| V | +0.17 | In | +0.01* | Tl | − 0.93 | ||
| Cr | + | Strong | Sn | +0.004* | Pb | − 0.025 | |
| Mn | + | Sb | −0.069 | Bi | − 0.023 | ||
| Fe | + | Te | −0.039 | · · · · · · · · · · | |||
| Co | + | I | −0.040 | Th | +16.0(?) | ||
| Ni | + | · · · · · · · · · · | U | + 0.21 | |||
| * Calculated. | |||||||
12. Molecular Theory of Magnetism
According to W. E. Weber’s theory, the molecules of a ferromagnetic metal are small permanent magnets, the axes of which under ordinary conditions are turned indifferently in every direction, so that no magnetic polarity is exhibited by the metal as a whole; a magnetic force acting upon the metal tends to turn the axes of the little magnets in one direction, and thus the entire piece acquires the properties of a magnet. If, however, the molecules could turn with perfect freedom, it is clear that the smallest magnetizing force would be sufficient to develop the highest possible degree of magnetization, which is of course not the case. Weber therefore supposed each molecule to be acted on by a force tending to preserve it in its original direction, the position actually assumed by the axis being in the direction of the resultant of this hypothetical force and the applied magnetizing force. Maxwell (Electricity and Magnetism, § 444), recognizing that the theory in this form gave no account of residual magnetization, made the further assumption that if the deflection of the axis of the molecule exceeded a certain angle, the axis would not return to its original position when the deflecting force was removed, but would retain a permanent set. Although the amended theory as worked out by Maxwell is in rough agreement with certain leading phenomena of magnetization, it fails to account for many others, and is in some cases at variance with observed facts.
J. A. Ewing (Proc. Roy. Soc., 1890, 48, 342) has demonstrated that it is quite unnecessary to assume either the directive force of Weber, the permanent set of Maxwell, or any kind of frictional resistance, the forces by which the molecular magnets are constrained being simply those due to their own mutual attractions and repulsions. The effect of these is beautifully illustrated by a model consisting of a number of little compass needles pivoted on sharp points and grouped near to one another upon a board, which is placed inside a large magnetizing coil. When no current is passing through the coil and the magnetic field is of zero strength, the needles arrange themselves in positions of stable equilibrium under their mutual forces, pointing in many different directions, so that there is no resultant magnetic moment. This represents the condition of the molecules in unmagnetized iron. If now a gradually increasing magnetizing force is applied, the needles at first undergo a stable deflection, giving to the group a small resultant moment which increases uniformly with the force; and if the current is interrupted while the force is still weak, the needles merely return to their initial positions. This illustrates the first stage in the process of magnetization, when the moment is proportional to the field and there is no hysteresis or residual magnetism (see ante). A somewhat stronger field will deflect many of the needles beyond the limits of stability, causing them to turn round and form new stable combinations, in which the direction assumed by most of them approximates to that of the field. The rearrangement is completed within a comparatively small range of magnetizing force, a rapid increase of the resultant moment being thus brought about. When the field is removed, many of the newly formed combinations are but slightly disturbed, and the group may consequently retain a considerable resultant moment. This corresponds to the second stage of magnetization, in which the susceptibility is large and permanent magnetization is set up. A still stronger magnetizing force has little effect except in causing the direction of the needles to approach still more nearly to that of the field; if the force were infinite, every member of the group would have exactly the same direction and the greatest possible resultant moment would be reached; this illustrates “magnetic saturation”—the condition approached in the third stage of magnetization. When the strong magnetizing field is gradually diminished to zero and then reversed, the needles pass from one stable position of rest to another through a condition of instability; and if the field is once more reversed, so that the cycle is completed, the needles again pass through a condition of instability before a position of stable equilibrium is regained. Now the unstable movements of the needles are of a mechanically irreversible character; the energy expended in dissociating the members of a combination and placing them in unstable positions assumes the kinetic form when the needles turn over, and is ultimately frittered down into heat. Hence in performing a cycle there is a waste of energy corresponding to what has been termed hysteresis-loss.
Supposing Ewing’s hypothesis to be correct, it is clear that if the magnetization of a piece of iron were reversed by a strong rotating field instead of by a field alternating through zero, the loss of energy by hysteresis should be little or nothing, for the molecules would rotate with the field and no unstable movements would be possible.91 Some experiments by F. G. Baily (Phil. Trans., 1896, 187, 715) show that this is actually the case. With small magnetizing forces the hysteresis was indeed somewhat larger than that obtained in an alternating field, probably on account of the molecular changes being forced to take place in one direction only; but at an induction of about 16,000 units in soft iron and 15,000 in hard steel the hysteresis reached a maximum and afterwards rapidly diminished. In one case the hysteresis loss per cubic centimetre per cycle was 16,100 ergs for B = 15,900, and only 1200 ergs for B = 20,200, the highest induction obtained in the experiment; possibly it would have vanished before B had reached 21,000.92 These experiments prove that actual friction must be almost entirely absent, and, as Baily remarks, the agreement of the results with the previously suggested deduction affords a strong verification of Ewing’s form of the molecular theory. Ewing has himself also shown how satisfactorily this theory accords with many other obscure and complicated phenomena, such as those presented by coercive force, differences of magnetic quality, and the effects of vibration, temperature and stress; while as regards simplicity and freedom from arbitrary assumptions it leaves little to be desired.
The fact being established that magnetism is essentially a molecular phenomenon, the next step is to inquire what is the constitution of a magnetic molecule, and why it is that some molecules are ferromagnetic, others paramagnetic, and others again diamagnetic. The best known of the explanations that have been proposed depend upon the magnetic action of an electric current. It can be shown that if a current i circulates in a small plane circuit of area S, the magnetic action of the circuit for distant points is equivalent to that of a short magnet whose axis is perpendicular to the plane of the circuit and whose moment is iS, the direction of the magnetization being related to that of the circulating current as the thrust of a right-handed screw to its rotation. Ferromagnetism was explained by Ampère on the hypothesis that the magnetization of the molecule is due to an electric current constantly circulating within it. The theory now most in favour is merely a development of Ampère’s hypothesis, and applies not only to ferromagnetics, but to paramagnetics as well. To account for diamagnetism, Weber supposed that there exist within the molecules of diamagnetic substances certain channels around which an electric current can circulate without any resistance. The creation of an external magnetic field H will, in accordance with Lenz’s law, induce in the molecule an electric current so directed that the magnetization of the equivalent magnet is opposed to the direction of the field. The strength of the induced current is −HS cos θ/L, where θ is the inclination of the axis of the circuit to the direction of the field, and L the coefficient of self-induction; the resolved part of the magnetic moment in the direction of the field is equal to −HS² cos² θ/L, and if there are n molecules in a unit of volume, their axes being distributed indifferently in all directions, the magnetization of the substance will be −1⁄3nHS²/L, and its susceptibility -1⁄3S²/L (Maxwell, Electricity and Magnetism, § 838). The susceptibility is therefore constant and independent of the field, while its negative sign indicates that the substance is diamagnetic. There being no resistance, the induced current will continue to circulate 351 round the molecule until the field is withdrawn, when it will be stopped by the action of an electromotive force tending to induce an exactly equal current in the opposite direction. The principle of Weber’s theory, with the modification necessitated by lately acquired knowledge, is the basis of the best modern explanation of diamagnetic phenomena.
There are strong reasons for believing that magnetism is a phenomenon involving rotation, and as early as 1876 Rowland, carrying out an experiment which had been proposed by Maxwell, showed that a revolving electric charge produced the same magnetic effects as a current. Since that date it has more than once been suggested that the molecular currents producing magnetism might be due to the revolution of one or more of the charged atoms or “ions” constituting the molecule. None of the detailed hypotheses which were based on this idea stood the test of criticism, but towards the end of the 19th century the researches of J. J. Thomson and others once more brought the conception of moving electric charges into prominence. Thomson has demonstrated the existence under many different conditions of particles more minute than anything previously known to science. The mass of each is about 1/1700th part of that of a hydrogen atom, and with each is indissolubly associated a charge of negative electricity equal to about 3.1 × 10−10 C.G.S. electrostatic unit. These particles, which were termed by their discoverer corpuscles, are more commonly spoken of as electrons,93 the particle thus being identified with the charge which it carries. An electrically neutral atom is believed to be constituted in part, or perhaps entirely, of a definite number of electrons in rapid motion within a “sphere of uniform positive electrification” not yet explained. One or more of the electrons may be detached from the system by a finite force, the number so detachable depending on the valency of the atom; if the atom loses an electron, it becomes positively electrified; if it receives additional electrons, it is negatively electrified. The process of electric conduction in metals consists in the movement of detached electrons, and many other phenomena, both electrical and thermal, can be more or less completely explained by their agency. It has been supposed that certain electrons revolve like satellites in orbits around the atoms with which they are associated, a view which receives strong support from the phenomena of the Zeeman effect, and on this assumption a theory has been worked out by P. Langevin,94 which accounts for many of the observed facts of magnetism. As a consequence of the structure of the molecule, which is an aggregation of atoms, the planes of the orbits around the latter may be oriented in various positions, and the direction of revolution may be right-handed or left-handed with respect to the direction of any applied magnetic field. For those orbits whose projection upon a plane perpendicular to the field is right-handed, the period of revolution will be accelerated by the field (since the electron current is negative), and the magnetic moment consequently increased; for those which are left-handed, the period will be retarded and the moment diminished. The effect of the field upon the speed of the revolving electrons, and therefore upon the moments of the equivalent magnets, is necessarily a very small one. If S is the area of the orbit described in time τ by an electron of charge e, the moment of the equivalent magnet is M = eSτ; and the change in the value of M due to an external field H is shown to be ΔM = −He2S/4πm, m being the mass of the electron. Whence
| ΔM | = − | Hτ e | . |
| M | 4π m |
According to the best determinations the value of e/m does not exceed 1.8 × 107, and τ is of the order of 10−15 second, the period of luminous vibrations; hence ΔM/M must always be less than 10−9H, and therefore the strongest fields yet reached experimentally, which fall considerably short of 105, could not change the magnetic moment M by as much as a ten-thousandth part. If the structure of the molecule is so perfectly symmetrical that, in the absence of any external field, the resultant magnetic moment of the circulating electrons is zero, then the application of a field, by accelerating the right-handed (negative) revolutions, and retarding those which are left-handed, will induce in the substance a resultant magnetization opposite in direction to the field itself; a body composed of such symmetrical molecules is therefore diamagnetic. If however the structure of the molecule is such that the electrons revolving around its atoms do not exactly cancel one another’s effects, the molecule constitutes a little magnet, which under the influence of an external field will tend to set itself with its axis parallel to the field. Ordinarily a substance composed of asymmetrical molecules is paramagnetic, but if the elementary magnets are so conditioned by their strength and concentration that mutual action between them is possible, then the substance is ferromagnetic. In all cases however it is the diamagnetic condition that is initially set up—even iron is diamagnetic—though the diamagnetism may be completely masked by the superposed paramagnetic or ferromagnetic condition. Diamagnetism, in short, is an atomic phenomenon; paramagnetism and ferromagnetism are molecular phenomena. Hence may be deduced an explanation of the fact that, while the susceptibility of all known diamagnetics (except bismuth and antimony) is independent of the temperature, that of paramagnetics varies inversely as the absolute temperature, in accordance with the law of Curie.
13. Historical and Chronological Notes
The most conspicuous property of the lodestone, its attraction for iron, appears to have been familiar to the Greeks at least as early as 800 B.C., and is mentioned by Homer, Plato, Aristotle, Theophrastus and others. A passage in De rerum natura (vi. 910-915) by the Roman poet, Lucretius (96-55 B.C.), in which it is stated that the stone can support a chain of little rings, each adhering to the one above it, indicates that in his time the phenomenon of magnetization by induction had also been observed. The property of orientation, in virtue of which a freely suspended magnet points approximately to the geographical north and south, is not referred to by any European writer before the 12th century, though it is said to have been known to the Chinese at a much earlier period. The application of this property to the construction of the mariner’s compass is obvious, and it is in connexion with navigation that the first references to it occur (see Compass). The needles of the primitive compasses, being made of iron, would require frequent re-magnetization, and a “stone” for the purpose of “touching the needle” was therefore generally included in the navigator’s outfit. With the constant practice of this operation it is hardly possible that the repulsion acting between like poles should have entirely escaped recognition; but though it appears to have been noticed that the lodestone sometimes repelled iron instead of attracting it, no clear statement of the fundamental law that unlike poles attract while like poles repel was recorded before the publication in 1581 of the New Attractive by Robert Norman, a pioneer in accurate magnetic work. The same book contains an account of Norman’s discovery and correct measurement of the dip (1576). The downward tendency of the north pole of a magnet pivoted in the usual way had been observed by G. Hartmann of Nüremberg in 1544, but his observation was not published till much later.
The foundations of the modern science of magnetism were laid by William Gilbert (q.v.). His De magnete magneticisque corporibus et de magno magnete tellure physiologia nova (1600), contains many references to the expositions of earlier writers from Plato down to those of the author’s own age. These show that the very few facts known with certainty were freely supplemented 352 by a number of ill-founded conjectures, and sometimes even by “figments and falsehoods, which in the earliest times, no less than nowadays, used to be put forth by raw smatterers and copyists to be swallowed of men.”95 Thus it was taught that “if a lodestone be anointed with garlic, or if a diamond be near, it does not attract iron,” and that “if pickled in the salt of a sucking fish, there is power to pick up gold which has fallen into the deepest wells.” There were said to be “various kinds of magnets, some of which attract gold, others silver, brass, lead; even some which attract flesh, water, fishes;” and stories were told about “mountains in the north of such great powers of attraction that ships are built with wooden pegs, lest the iron nails should be drawn from the timber.” Certain occult powers were also attributed to the stone. It was “of use to thieves by its fume and sheen, being a stone born, as it were, to aid theft,” and even opening bars and locks; it was effective as a love potion, and possessed “the power to reconcile husbands to their wives, and to recall brides to their husbands.” And much more of the same kind, which, as Gilbert says, had come down “even to [his] own day through the writings of a host of men, who, to fill out their volumes to a proper bulk, write and copy out pages upon pages on this, that and the other subject, of which they know almost nothing for certain of their own experience.” Gilbert himself absolutely disregarded authority, and accepted nothing at second-hand. His title to be honoured as the “Father of Magnetic Philosophy” is based even more largely upon the scientific method which he was the first to inculcate and practise than upon the importance of his actual discoveries. Careful experiment and observation, not the inner consciousness, are, he insists, the only foundations of true science. Nothing has been set down in his book “which hath not been explored and many times performed and repeated” by himself. “It is very easy for men of acute intellect, apart from experiment and practice, to slip and err.” The greatest of Gilbert’s discoveries was that the globe of the earth was magnetic and a magnet; the evidence by which he supported this view was derived chiefly from ingenious experiments made with a spherical lodestone or terrella, as he termed it, and from his original observation that an iron bar could be magnetized by the earth’s force. He also carried out some new experiments on the effects of heat, and of screening by magnetic substances, and investigated the influence of shape upon the magnetization of iron. But the bulk of his work consisted in imparting scientific definiteness to what was already vaguely known, and in demolishing the errors of his predecessors.
No material advance upon the knowledge recorded in Gilbert’s book was made until the establishment by Coulomb in 1785 of the law of magnetic action. The difficulties attending the experimental investigation of the forces acting between magnetic poles have already been referred to, and indeed a rigorously exact determination of the mutual action could only be made under conditions which are in practice unattainable. Coulomb,96 however, by using long and thin steel rods, symmetrically magnetized, and so arranged that disturbing influences became negligibly small, was enabled to deduce from his experiments with reasonable certainty the law that the force of attraction or repulsion between two poles varies inversely as the square of the distance between them. Several previous attempts had been made to discover the law of force, with various results, some of which correctly indicated the inverse square; in particular the German astronomer, J. Tobias Mayer (Gött. Anzeiger, 1760), and the Alsatian mathematician, J. Heinrich Lambert (Hist. de l’Acad. Roy. Berlin, 1766, p. 22), may fairly be credited with having anticipated the law which was afterwards more satisfactorily established by Coulomb. The accuracy of this law was in 1832 confirmed by Gauss,97 who employed an indirect but more perfect method than that of Coulomb, and also, as Maxwell remarks, by all observers in magnetic observatories, who are every day making measurements of magnetic quantities, and who obtain results which would be inconsistent with each other if the law of force had been erroneously assumed.
Coulomb’s researches provided data for the development of a mathematical theory of magnetism, which was indeed initiated by himself, but was first treated in a complete form by Poisson in a series of memoirs published in 1821 and later.98 Poisson assumed the existence of two dissimilar magnetic fluids, any element of which acted upon any other distant element in accordance with Coulomb’s law of the inverse square, like repelling and unlike attracting one another. A magnetizable substance was supposed to consist of an indefinite number of spherical particles, each containing equivalent quantities of the two fluids, which could move freely within a particle, but could never pass from one particle to another. When the fluids inside a particle were mixed together, the particle was neutral; when they were more or less completely separated, the particle became magnetized to an intensity depending upon the magnetic force applied; the whole body therefore consisted of a number of little spheres having north and south poles, each of which exerted an elementary action at a distance. On this hypothesis Poisson investigated the forces due to bodies magnetized in any manner, and also originated the mathematical theory of magnetic induction. The general confirmation by experiment of Poisson’s theoretical results created a tendency to regard his hypothetical magnetic fluids as having a real existence; but it was pointed out by W. Thomson (afterwards Lord Kelvin) in 1849 that while no physical evidence could be adduced in support of the hypothesis, certain discoveries, especially in electromagnetism, rendered it extremely improbable (Reprint, p. 344). Regarding it as important that all reasoning with reference to magnetism should be conducted without any uncertain assumptions, he worked out a mathematical theory upon the sole foundation of a few well-known facts and principles. The results were substantially the same as those given by Poisson’s theory, so far as the latter went, the principal additions including a fuller investigation of magnetic distribution, and the theory of magnetic induction in aeolotropic or crystalline substances. The mathematical theory which was constructed by Poisson, and extended and freed from doubtful hypotheses by Kelvin, has been elaborated by other investigators, notably F. E. Neumann, G. R. Kirchhoff, and Maxwell. The valuable work of Gauss on magnetic theory and measurements, especially in relation to terrestrial magnetism, was published in his Intensitas vis magneticae terrestris, 1833, and in memoirs communicated to the Resultate aus den Beobachtungen des magnetischen Vereins, 1838 and 1839, which, with others, are contained in vol. 5 of the collected Werke. Weber’s molecular theory, which has already been referred to, appeared in 1852.99
An event of the first importance was the discovery made in 1819 by H. C. Oersted 100 that a magnet placed near a wire carrying an electric current tended to set itself at right angles to the wire, a phenomenon which indicated that the current was surrounded by a magnetic field. This discovery constituted the foundation of electromagnetism, and its publication in 1820 was immediately followed by A. M. Ampère’s experimental and theoretical investigation of the mutual action of electric currents,101 and of the equivalence of a closed circuit to a polar magnet, the latter suggesting his celebrated hypothesis that molecular currents were the cause of magnetism. In the same year D. F. Arago102 succeeded in magnetizing a piece of iron by the electric current, and in 1825 W. Sturgeon103 publicly exhibited an apparatus “acting 353 on the principle of powerful magnetism and feeble galvanism” which is believed to have constituted the first actual electromagnet. Michael Faraday’s researches were begun in 1831 and continued for more than twenty years. Among the most splendid of his achievements was the discovery of the phenomena and laws of magneto-electric induction, the subject of two papers communicated to the Royal Society in 1831 and 1832. Another was the magnetic rotation of the plane of polarization of light, which was effected in 1845, and for the first time established a relation between light and magnetism. This was followed at the close of the same year by the discovery of the magnetic condition of all matter, a discovery which initiated a prolonged and fruitful study of paramagnetic and diamagnetic phenomena, including magnecrystallic action and “magnetic conducting power,” now known as permeability. Throughout his researches Faraday paid special regard to the medium as the true seat of magnetic action, being to a large extent guided by his pregnant conception of “lines of force,” or of induction, which he considered to be “closed curves passing in one part of the course through the magnet to which they belong, and in the other part through space,” always tending to shorten themselves, and repelling one another when they were side by side (Exp. Res. §§ 3266-8, 3271). In 1873 James Clerk Maxwell published his classical Treatise on Electricity and Magnetism, in which Faraday’s ideas were translated into a mathematical form. Maxwell explained electric and magnetic forces, not by the action at a distance assumed by the earlier mathematicians, but by stresses in a medium filling all space, and possessing qualities like those attributed to the old luminiferous ether. In particular, he found that the calculated velocity with which it transmitted electromagnetic disturbances was equal to the observed velocity of light; hence he was led to believe, not only that his medium and the ether were one and the same, but, further, that light itself was an electromagnetic phenomenon. Since the experimental confirmation of Maxwell’s views by H. R. Hertz in 1888 (Weid. Ann., 1888, 34, 155, 551, 609; and later vols.) they have commanded universal assent, and his methods are adopted in all modern work on electricity and magnetism.
The practice of measuring magnetic induction and permeability with scientific accuracy was introduced in 1873 by H. A. Rowland,104 whose careful experiments led to general recognition of the fact previously ignored by nearly all investigators, that magnetic susceptibility and permeability are by no means constants (at least in the case of the ferromagnetic metals) but functions of the magnetizing force. New light was thrown upon many important details of magnetic science by J. A. Ewing’s Experimental Researches of 1885; throughout the whole of his work special attention was directed to that curious lagging action to which the author applied the now familiar term “hysteresis.”105 His well-known modification106 of Weber’s molecular theory, published in 1890, presented for the first time a simple and sufficient explanation of hysteresis and many other complexities of magnetic quality. The amazing discoveries made by J. J. Thomson in 1897 and 1898107 resulted in the establishment of the electron theory, which has already effected developments of an almost revolutionary character in more than one branch of science. The application of the theory by P. Langevin to the case of molecular magnetism has been noticed above, and there can be little doubt that in the near future it will contribute to the solution of other problems which are still obscure.
See W. Gilbert, De magnete (London, 1600; trans. by P. F. Mottelay, New York, 1893, and for the Gilbert Club, London, 1900); M. Faraday, Experimental Researches in Electricity, 3 vols. (London, 1839, 1844 and 1855); W. Thomson (Lord Kelvin), Reprint of Papers on Electrostatics and Magnetism (London, 1884, containing papers on magnetic theory originally published between 1844 and 1855, with additions); J. C. Maxwell, Treatise on Electricity and Magnetism (3rd ed., Oxford, 1892); E. Mascart and J. Joubert, Leçons sur l’électricité et le magnétisme (2nd ed., Paris, 1896-1897; trans., not free from errors, by E. Atkinson, London, 1883); J. A. Ewing, Magnetic Induction in Iron and other Metals (3rd ed., London, 1900); J. J. Thomson, Recent Researches in Electricity and Magnetism (Oxford, 1893); Elements of Mathematical Theory of Electricity and Magnetism (3rd ed., Cambridge, 1904); H. du Bois, The Magnetic Circuit (trans. by E. Atkinson, London, 1896); A. Gray, Treatise on Magnetism and Electricity, vol. i. (London, 1898); J. A. Fleming, Magnets and Electric Currents (London, 1898); C. Maurain, Le magnétisme du fer (Paris, 1899; a lucid summary of the principal facts and laws, with special regard to their practical application); Rapports présentés au Congrès international de physique, vol. ii. (Paris, 1900); G. C. Foster and A. W. Porter, Treatise on Electricity and Magnetism (London, 1903); A. Winkelmann, Handbuch der Physik, vol. v. part i. (2nd ed., Leipzig, 1905; the most exhaustive compendium of magnetic science yet published, containing references to all important works and papers on every branch of the subject).
1 In London in 1910 the needle pointed about 16° W. of the geographical north. (See Terrestrial Magnetism.)
2 For the relations between magnetism and light see Magneto-Optics.
3 Clerk Maxwell employed German capitals to denote vector quantities. J. A. Fleming first recommended the use of blockletters as being more convenient both to printers and readers.
4 The C.G.S. unit of current = 10 amperes.
5 The principal theoretical investigations are summarized in Mascart and Joubert’s Electricity and Magnetism, i. 391-398 and ii. 646-657. The case of a long iron bar has been experimentally studied with great care by C. G. Lamb, Proc. Phys. Soc., 1899, 16, 509.
6 Wied. Ann., 1884, 22, 411.
7 See C. G. Lamb, loc. cit. p. 518.
8 Hopkinson specified the retentiveness by the numerical value of the “residual induction” (= 4πI).
9 For all except ferromagnetic substances the coefficient is sensibly equal to κ.
10 See W. Thomson’s Reprint, §§ 615, 634-651.
11 Ibid. §§ 646, 684.
12 Faraday, Exp. Res. xxi.
13 J. J. Thomson, Electricity and Magnetism, § 205.
14 Maxwell, Electricity and Magnetism, § 431.
15 H. du Bois, Electrician, 1898, 40, 317.
16 M. Faraday, Exp. Res. xxii., xxiii.; W. Thomson, Reprint, § 604; J. C. Maxwell, Treatise, § 435; E. Mascart and J. Joubert, Electricity and Magnetism, §§ 384, 396, 1226; A. Winkelmann, Physik, v. 287.
17 See A. Winkelmann, Physik, v. 69-94; Mascart and Joubert. Electricity and Magnetism, ii. 617.
18 Sci. Abs. A, 1906, 9, 225.
19 See C. G. Lamb, Proc. Phys. Soc., 1899, 16, 517.
20 Soc. Franc. Phys. Séances, 1904, 1, 27.
21 E. G. Warburg, Wied. Ann. 1881, 13, 141; Ewing, Phil. Trans., 1885, 176, 549; Hopkinson, Phil. Trans. 1885, 176, 466. For a simple proof, see Ewing, Magnetic Induction (1900), p. 99. Hopkinson pointed out that the greatest dissipation of energy which can be caused by a to-and-fro reversal is approximately represented by Coercive force × maximum induction /π.
22 Magnetic Induction, 1900, 378.
23 Phil. Trans., 1902, 198, 33.
24 Phil. Mag., 1903, 5, 117.
25 Some experiments by F. G. Baily showed that hysteresis ceased to increase when B was carried beyond 23,000. This value of B corresponds to I = 1640, the saturation point for soft iron.—Brit. Assoc. Rep., 1895, p. 636.
26 Tokyo Phys.-Math. Soc., 1904, 2, No. 14.
27 Phil. Mag., 1873, 46, 140.
28 S. Bidwell, Proc. Roy. Soc., 1886, 40, 495.
29 Since in most practicable experiments H³ is negligible in comparison with B², the force may be taken as B²/8π without sensible error.
30 The same phenomenon is exhibited in a less marked degree when soft iron is magnetized in stronger fields (Ewing, Phil. Trans., 1885, 176, 569).
31 Principal publications: J. P. Joule, Scientific Papers, pp. 46, 235; A. M. Meyer, Phil. Mag., 1873, 46, 177; W. F. Barrett, Nature, 1882, 26, 585; S. Bidwell, Phil. Trans., 1888, 179A, 205; Proc. Roy. Soc., 1886, 40, 109 and 257; 1888, 43, 406; 1890, 47, 469; 1892, 51, 495; 1894, 55, 228; 1894, 56, 94; 1904, 74, 60; Nature, 1899, 60, 222; M. Cantone, Mem. d. Acc d. Lincei, 1889, 6, 487; Rend. d. Acc. d. Lincei, 1890, 6, 252; A. Berget, C.R., 1892, 115, 722; S. J. Lochner, Phil. Mag., 1893, 36, 498; H. Nagaoka, Phil. Mag., 1894, 37, 131; Wied. Ann., 1894, 53, 487; C. G. Knott, Proc. Roy. Soc. Ed., 1891, 18, 315; Phil. Mag., 1894, 37, 141; Trans. Roy. Soc. Ed., 1896, 38, 527; 1898, 39, 457; C. G. Knott and A. Shand, Proc. Roy. Soc. Ed., 1892, 19, 85 and 249; 1894, 20, 295; L. T. More, Phil. Mag., 1895, 40, 345; G. Klingenberg, Rostock Univ. Thesis, Berlin, 1897; E. T. Jones, Phil. Trans., 1897, 189A, 189; B. B. Brackett, Phys. Rev., 1897, 5, 257; H. Nagaoka and K. Honda, Phil. Mag., 1898, 46, 261; 1900, 49, 329; Journ. Coll. Sci. Tokyo, 1900, 13, 57; 1903, 19, art. 11; J. S. Stevens, Phys. Rev., 1898, 7, 19; E. Rhoads, Phys. Rev., 1898, 7, 5; Phil. Mag., 1901, 2, 463; G. A. Shakespear, Phil. Mag., 1899, 17, 539; K. Honda, Journ. Coll. Sci. Tokyo, 1900, 13, 77; L. W. Austin, Phys. Rev., 1900, 10, 180; Deutsch. Phys. Gesell. Verh., 1904, 6, 4, 211; K. Honda and S. Shimizu, Phil. Mag., 1902, 4, 338; 1905, 10, 548.
32 The loads were successively applied in decreasing order of magnitude. They are indicated in fig. 25 as kilos per sq. cm.
33 Joule believed that the volume was unchanged.
34 For a discussion of theories of magnetic stress, with copious references, see Nagaoka, Rap. du Congrès International de Physique (Paris, 1900), ii. 545. Also Nagaoka and Jones, Phil. Mag., 1896, 41, 454.
35 S. Bidwell, Phil. Trans., 1888, 179a, 321.
36 Phil. Mag., 1895, 40, 345.
37 J. C. Maxwell, Treatise, § 643.
38 See correspondence in Nature, 1896, 53, pp. 269, 316, 365, 462, 533; 1906, 74, pp. 317, 539; B. B. Brackett, loc. cit., quotes the opinion of H. A. Rowland in support of compressive stress.
39 J. A. Ewing, Phil. Trans., 1885, 176, 580; 1888, 179, 333; Magnetic Induction, 1900, ch. ix.; J. A. Ewing and G. C. Cowan, Phil. Trans., 1888, 179a, 325; C. G. Knott, Trans. Roy. Soc. Ed., 1882-1883, 32, 193; 1889, 35, 377; 1891, 36, 485; Proc. Roy. Soc. Ed., 1899, 586; H. Nagaoka, Phil. Mag., 1889, 27, 117; 1890, 29, 123; H. Nagaoka and K. Honda, Journ. Coll. Sci. Tokyo, 1900, 13, 263; 1902, 16, art. 8; Phil. Mag., 1898, 46, 261; 1902, 4, 45; K. Honda and S. Shimizu, Ann. d. Phys., 1904, 14, 791; Tokyo Physico-Math. Soc. Rep., 1904, 2, No. 13; K. Honda and T. Terada, Journ. Coll. Sci. Tokyo, 1906, 21, art. 4.
40 H. Tomlinson found a critical point in the “temporary magnetization” of nickel (Proc. Phys. Soc., 1890, 10, 367, 445), but this does not correspond to a Villari reversal. Its nature is made clear by Ewing and Cowan’s curves (Phil. Trans., 1888, 179, plates 15, 16).
41 Wied. Ann., 1894, 52, 462; Electrician, 1894, 34, 143.
42 Phil. Trans., 1890, 131, 329.
43 Magnetic Induction, 1900, 222.
44 Phys. Rev., 1904, 18, 432.
45 Phil. Mag., 1886, 22, 50.
46 Ibid. 251.
47 Phil. Mag., 1891, 32, 383.
48 C.R., 1896, 122, 1192; 1898, 126, 463.
49 Phil. Mag., 1889, 27, 117.
50 Journ. Coll. Sci. Tokyo, 1904, 19, art. 9.
51 Phil. Mag., 1905, 10, 548; Tokyo Phys.-Math. Soc. Rep., 1904, 2, No. 14; Journ. Coll. Sci. Tokyo, 1905, 20, art. 6.
52 C.R., 1888, 106, 129.
53 Proc. Phys. Soc., 1888, 9, 181.
54 C.R., 1892, 115, 805; 1894, 118, 796 and 859.
55 Elekt. Zeits., 1894, 15, 194.
56 Phil. Mag., 1900, 50, 1.
57 Phil. Trans., 1903, 201, 1.
58 Phil. Mag., 1904, 8, 179.
59 A. M. Thiessen (Phys., 1899, 8, 65) and G. Claude (C. R., 1899, 129, 409) found that for considerable inductions (B = 15,000) the permeability and hysteresis-loss remained nearly constant down to -186°; for weak inductions both notably diminished with temperature.
60 Proc. Roy. Soc., 1898, 62, 210.
61 C.R., 1895, 120, 263.
62 Amer. Journ. Sci., 1898, 5, 245.
63 Phys. Rev., 1901, 14, 181.
64 C.R., 1897, 124, 176 and 1515; 1897, 125, 235; 1898, 126, 738.
65 Ibid., 1898, 126, 741.
66 Ibid., 1899, 128, 304 and 1395.
67 See also J. Hopkinson, Journ. Inst. Elect. Eng., 1890, 19, 20, and J. A. Ewing, Phil. Trans., 1889, 180, 239.
68 Many of the figures which, through an error, were inaccurately stated in the first paper are corrected in the second.
69 The marked effect of silicon in increasing the permeability of cast iron has also been noticed by F. C. Caldwell, Elect. World, 1898, 32, 619.
70 Trans. Roy. Dub. Soc., 1902-4, 8, 1 and 123.
71 J. Trowbridge and S. Sheldon, Phil. Mag., 1890, 29, 136; W. H. Preece, Journ. Inst. Elec. Eng., 1890, 19, 62; Electrician, 1890, 25, 546; I. Klemençiç, Wien. Ber., 1896, 105, IIa, 635; B. O. Peirce, Am. Journ. Sci., 1896, 2, 347; A. Abt, Wied. Ann., 1898, 66, 116; F. Osmond, C. R., 1899, 128, 1513.
72 Deutsch. phys. Gesell. Verh., 1903, 5, 220 and 224.
73 Exp. Res., iii. 440.
74 No record can be found of experiments with manganese at the temperature of liquid air or hydrogen; probably, however, negative results would not be published.
75 The critical temperature of iron, for instance, is raised more than 100° by the addition of a little carbon and tungsten.
76 Bull. Soc. Int. des Électriciens, 1906, 6, 301.
77 Proc. Roy. Soc., 1905, 76A, 271.
78 E. H. Hall, Phil. Mag., 1880, 9, 225; 1880, 10, 301; 1881, 12, 157; 1883, 15, 341; 1885, 19, 419.
79 The large Hall effect in bismuth was discovered by Righi, Journ. de Phys., 1884, 3, 127.
80 References.—(2) A. von Ettinghausen, Wied. Ann., 1887, 31, 737.—(4) H. W. Nernst, ibid., 784.—(i.) and (iv.); A. von Ettinghausen and H. W. Nernst, Wied. Ann., 1886, 29, 343.—(ii.) and (iii.); A. Righi, Rend. Acc. Linc., 1887, 3 II, 6 and I, 481; and A. Leduc, Journ. de Phys., 1887, 6, 78. Additional authorities are quoted by Lloyd, loc. cit.
81 P. Drude, Ann. d. Phys., 1900, 1, 566; 1900, 3, 369; 1902, 7, 687. See also E. van Everdingen, Arch. Néerlandaises, 1901, 4, 371; G. Barlow, Ann. d. Phys., 1903, 12, 897; H. Zahn, ibid. 1904, 14, 886; 1905, 16, 148.
82 Phil. Trans., 1856, p. 722. According to the nomenclature adopted by the best modern authorities, a metal A is said to be thermo-electrically positive to another metal B when the thermo-current passes from A to B through the cold junction, and from B to A through the hot (see Thermo-Electricity).
83 C.R., 1893, 116, 997.
84 Journ. de Phys., 1896, 5, 53.
85 Phil. Trans., 1887, 177, 373.
86 Proc. Roy. Soc., 1885, 39, 513.
87 Phys. Rev., 1902, 15, 321. The sign of the thermo-electric effect for nickel, as given by Rhoads, is incorrect.
88 Proc. Roy. Soc., 1904, 73, 413.
89 C.R., 1903, 136, 1131.
90 Journ. Coll. Sci. Tokyo, 1906, 21, art. 4. The paper contains 40 tables and 85 figures.
91 This deduction from Ewing’s theory appears to have been first suggested by J. Swinburne. See Industries, 1890, 289.
92 R. Beattie (Phil. Mag., 1901, 1, 642) has found similar effects in nickel and cobalt.
93 The charge associated with a corpuscle is the same as that carried by a hydrogen atom. G. J. Stoney in 1881 (Phil. Mag., 1881, 11, 387) pointed out that this latter constituted the indivisible “atom of electricity” or natural unit charge. Later he proposed (Trans. Roy. Dub. Soc., 1891, 4, 583) that such unit charge should be called an “electron.” The application of this term to Thomson’s corpuscle implies, rightly or wrongly, that notwithstanding its apparent mass, the corpuscle is in fact nothing more than an atom of electricity. The question whether a corpuscle actually has a material gravitating nucleus is undecided, but there are strong reasons for believing that its mass is entirely due to the electric charge.
94 Jour. de Phys., 1905, 4, 678; translated in Electrician, 1905, 56, 108 and 141.
95 The quotations are from the translation published by the Gilbert Club, London, 1900.
96 C. A. Coulomb, Mem. Acad. Roy. Paris, 1785, p. 578.
97 Intensitas vis magneticae, § 21, C. F. Gauss’s Werke, 5, 79. See also J. J. Thomson, Electricity and Magnetism, § 132.
98 S. D. Poisson, Mém. de l’Institut, 1821 and 1822, 5, 247, 488; 1823, 6, 441; 1838, 16, 479.
99 For outlines of the mathematical theory of magnetism and references see H. du Bois, Magnetic Circuit, chs. iii. and iv.
100 Gilbert’s Ann. d. phys., 1820, 6, 295.
101 Ann. de chim. et de phys., 1820, 15, 59, 170; Recueil d’observations électrodynamiques, 1822; Théories des phénomènes électrodynamiques, 1826.
102 Ann. de chim. et de phys., 1820, 15, 93.
103 Trans. Soc. Arts, 1825, 43, 38.
104 Phil. Mag., 1873, 46, 140; 1874, 48, 321.
105 Phil. Trans., 1885, 176, 523; Magnetic Induction, 1900.
106 Proc. Roy. Soc., 1890, 48, 342.
107 Phil. Mag., 1897, 44, 293; 1898, 46, 528.

MAGNETISM, TERRESTRIAL, the science which has for its province the study of the magnetic phenomena of the earth.
§ 1. Terrestrial magnetism has a long history. Its early growth was slow, and considerable uncertainty prevails as to its earliest developments. The properties of the magnet (see Magnetism) were to some small extent known to Historical. the Greeks and Romans before the Christian era, and compasses (see Compass) of an elementary character seem to have been employed in Europe at least as early as the 12th century. In China and Japan compasses of a kind seem to have existed at a much earlier date, and it is even claimed that the Chinese were aware of the declination of the compass needle from the true north before the end of the 11th century. Early scientific knowledge was usually, however, a mixture of facts, very imperfectly ascertained, with philosophical imaginings. When an early writer makes a statement which to a modern reader suggests a knowledge of the declination of the compass, he may have had no such definite idea in his mind. So far as Western civilization is concerned, Columbus is usually credited with the discovery—in 1492 during his first voyage to America—that the pointing of the compass needle to the true north represents an exceptional state of matters, and that a declination in general exists, varying from place to place. The credit of these discoveries is not, however, universally conceded to Columbus. G. Hellmann6A considers it almost certain that the departure of the needle from the true north was known in Europe before the time of Columbus. There is indirect evidence that the declination of the compass was not known in Europe in the early part of the 15th century, through the peculiarities shown by early maps believed to have been drawn solely by regard to the compass. Whether Columbus was the first to observe the declination or not, his date is at least approximately that of its discovery.
The next fundamental discovery is usually ascribed to Robert Norman, an English instrument maker. In The Newe Attractive (1581) Norman describes his discovery made some years before of the inclination or dip. The discovery was made more or less by accident, through Norman’s noticing that compass needles which were truly balanced so as to be horizontal when unmagnetized, ceased to be so after being stroked with a magnet. Norman devised a form of dip-circle, and found a value for the inclination in London which was at least not very wide of the mark.
Another fundamental discovery, that of the secular change of the declination, was made in England by Henry Gellibrand, professor of mathematics at Gresham College, who described it in his Discourse Mathematical on the Variation of the Magneticall Needle together with its Admirable Diminution lately discovered (1635). The history of this discovery affords a curious example of knowledge long delayed. William Borough, in his Discourse on the Variation of the Compas or Magneticall Needle (1581), gave for the declination at Limehouse in October 1580 the value 11°¼ E. approximately. Observations were repeated at Limehouse, Gellibrand tells us, in 1622 by his colleague Edmund Gunter, professor of astronomy at Gresham College, who found the much smaller value 6° 13′. The difference seems to have been ascribed at first to error on Borough’s part, and no suspicion of the truth seems to have been felt until 1633, when some rough observations gave a value still lower than that found by Gunter. 354 It was not until midsummer 1634 that Gellibrand felt sure of his facts, and yet the change of declination since 1580 exceeded 7°. The delay probably arose from the strength of the preconceived idea, apparently universally held, that the declination was absolutely fixed. This idea, it would appear, derived some of its strength from the positive assertion made on the point by Gilbert of Colchester in his De magnete (1600).
A third fundamental discovery, that of the diurnal change in the declination, is usually credited to George Graham (1675-1751), a London instrument maker. Previous observers, e.g. Gellibrand, had obtained slightly different values for the declination at different hours of the day, but it was natural to assign them to instrumental uncertainties. In those days the usual declination instrument was the compass with pivoted needles, and Graham himself at first assigned the differences he observed to friction. The observations on which he based his conclusions were made in 1722; an account of them was communicated to the Royal Society and published in the Philosophical Transactions for 1724.
The movements of the compass needle throughout the average day represent partly a regular diurnal variation, and partly irregular changes in the declination. The distinction, however, was not at first very clearly realized. Between 1756 and 1759 J. Canton observed the declination-changes on some 600 days, and was thus able to deduce their general character. He found that the most prominent part of the regular diurnal change in England consisted of a westerly movement of the north-pointing pole from 8 or 9 a.m. to 1 or 2 p.m., followed by a more leisurely return movement to the east. He also found that the amplitude of the movement was considerably larger in summer than in winter. Canton further observed that in a few days the movements were conspicuously irregular, and that aurora was then visible. This association of magnetic disturbance and aurora had, however, been observed somewhat before this time, a description of one conspicuous instance being contributed to the Royal Society in 1750 by Pehr Vilhelm Wargentin (1717-1783), a Swede.
Another landmark in the history of terrestrial magnetism was the discovery towards the end of the 18th century that the intensity of the resultant magnetic force varies at different parts of the earth. The first observations clearly showing this seem to be those of a Frenchman, Paul de Lamanon, who observed in 1785-1787 at Teneriffe and Macao, but his results were not published at the time. The first published observations seem to be those made by the great traveller Humboldt in tropical America between 1798 and 1803. The delay in this discovery may again be attributed to instrumental imperfections. The method first devised for comparing the force at different places consisted in taking the time of oscillation of the dipping needle, and even with modern circles this is hardly a method of high precision. Another discovery worth chronicling was made by Arago in 1827. From observations made at Paris he found that the inclination of the dipping needle and the intensity of the horizontal component of the magnetic force both possessed a diurnal variation.
§ 2. Whilst Italy, England and France claim most of the early observational discoveries, Germany deserves a large share of credit for the great improvement in instruments and methods during the first half of the 19th century. Measurements of the intensity of the magnetic force were somewhat crude until Gauss showed how absolute results could be obtained, and not merely relative data based on observations with some particular needle. Gauss also devised the bifilar magnetometer, which is still largely represented in instruments measuring changes of the horizontal force; but much of the practical success attending the application of his ideas to instruments seems due to Johann von Lamont (1805-1879), a Jesuit of Scottish origin resident in Germany.
The institution of special observatories for magnetic work is largely due to Humboldt and Gauss. The latter’s observatory at Göttingen, where regular observations began in 1834, was the centre of the Magnetic Union founded by Gauss and Weber for the carrying out of simultaneous magnetic observations and it was long customary to employ Göttingen time in schemes of international co-operation.
In the next decade, mainly through the influence of Sir Edward Sabine (1788-1883), afterwards president of the Royal Society, several magnetic observatories were established in the British colonies, at St Helena, Cape of Good Hope, Hobarton (now Hobart) and Toronto. These, with the exception of Toronto, continued in full action for only a few years; but their records—from their widely distributed positions—threw much fresh light on the differences between magnetic phenomena in different regions of the globe. The introduction of regular magnetic observatories led ere long to the discovery that there are notable differences between the amplitudes of the regular daily changes and the frequency of magnetic disturbances in different years. The discovery that magnetic phenomena have a period closely similar to, if not absolutely identical with, the “eleven year” period in sun-spots, was made independently and nearly simultaneously about the middle of the 19th century by Lamont, Sabine and R. Wolf.
The last half of the 19th century showed a large increase in the number of observatories taking magnetic observations. After 1890 there was an increased interest in magnetic work. One of the contributory causes was the magnetic survey of the British Isles made by Sir A. Rücker and Sir T. E. Thorpe, which served as a stimulus to similar work elsewhere; another was the institution by L. A. Bauer of a magazine. Terrestrial Magnetism, specially devoted to the subject. This increased activity added largely to the stock of information, sometimes in forms of marked practical utility; it was also manifested in the publication of a number of papers of a speculative character. For historical details the writer is largely indebted to the works of E. Walker1 and L. A. Bauer.3
§ 3. All the more important magnetic observatories are provided with instruments of two kinds. Those of the first kind give the absolute value of the magnetic elements at the time of observation. The unifilar magnetometer (q.v.), for Observational Methods and Records. instance, gives the absolute values of the declination and horizontal force, whilst the inclinometer (q.v.) or dip circle gives the inclination of the dipping needle. Instruments of the second kind, termed magnetographs (q.v.), are differential and self-recording, and show the changes constantly taking place in the magnetic elements. The ordinary form of magnetograph records photographically. Light reflected from a fixed mirror gives a base line answering to a constant value of the element in question; the light is cut off every hour or second hour so that the base line also serves to make the time. Light reflected from a mirror carried by a magnet gives a curved line answering to the changes in position of the magnet. The length of the ordinate or perpendicular drawn from any point of the curved line on to the base line is proportional to the extent of departure of the magnet from a standard position. If then we know the absolute value of the element which corresponds to the base line, and the equivalent of 1 cm. of ordinate, we can deduce the absolute value of the element answering to any given instant of time. In the case of the declination the value of 1 cm. of ordinate is usually dependent almost entirely on the distance of the mirror carried by the magnet from the photographic paper, and so remains invariable or very nearly so. In the case of the horizontal force and vertical force magnetographs—these being the two force components usually recorded—the value of 1 cm. of ordinate alters with the strength of the magnet. It has thus to be determined from time to time by observing the deflection shown on the photographic paper when an auxiliary magnet of known moment, at a measured distance, deflects the magnetograph magnet. Means are provided for altering the sensitiveness, for instance, by changing the effective distance in the bifilar suspension of the horizontal force magnet, and by altering the height of a small weight carried by the vertical force magnet. It is customary to aim at keeping the sensitiveness as constant as possible. A very common standard is to have 1 cm. of ordinate corresponding to 10′ of arc in the declination and to 50γ (1γ ≡ 0.00001 C.G.S.) in the horizontal and vertical force magnetographs.
As an example of how the curves are standardized, suppose that absolute observations of declination are taken four times a month, and that in a given month the mean of the observed values is 16° 34′.6 W. The curves are measured at the places which correspond to the times of the four observations, and the mean length of the four ordinates is, let us say, 2.52 cms. If 1 cm. answers to 10′, then 2.52 cms. represents 25′.2, and thus the value of the base line—i.e. the value which the declination would have if the curve came down to the base line—is for the month in question 16° 34′.6 less 25′.2 or 355 16° 9′.4. If now we wish to know the declination at any instant in this particular month all we have to do is to measure the corresponding ordinate and add its value, at the rate of 10′ per cm., to the base value 16° 9′.4 just found. Matters are a little more complicated in the case of the horizontal and vertical force magnetographs. Both instruments usually possess a sensible temperature coefficient, i.e. the position of the magnet is dependent to some extent on the temperature it happens to possess, and allowance has thus to be made for the difference from a standard temperature. In the case of the vertical force an “observed” value is derived by combining the observed value of the inclination with the simultaneous value of the horizontal force derived from the horizontal force magnetograph after the base value of the latter has been determined. In themselves the results of the absolute observations are of minor interest. Their main importance is that they provide the means of fixing the value of the base line in the curves. Unless they are made carefully and sufficiently often the information derivable from the curves suffers in accuracy, especially that relating to the secular change. It is from the curves that information is derived as to the regular diurnal variation and irregular changes. In some observatories it is customary to publish a complete record of the values of the magnetic elements at every hour for each day of the year. A useful and not unusual addition to this is a statement of the absolutely largest and smallest values of each element recorded during each day, with the precise times of their occurrence. On days of large disturbance even hourly readings give but a very imperfect idea of the phenomena, and it is customary at some observatories, e.g. Greenwich, to reproduce the more disturbed curves in the annual volume. In calculating the regular diurnal variation it is usual to consider each month separately. So far as is known at present, it is entirely or almost entirely a matter of accident at what precise hours specially high or low values of an element may present themselves during an individual highly disturbed day; whilst the range of the element on such a day may be 5, 10 or even 20 times as large as on the average undisturbed day of the month. It is thus customary when calculating diurnal inequalities to omit the days of largest disturbance, as their inclusion would introduce too large an element of uncertainty. Highly disturbed days are more than usually common in some years, and in some months of the year, thus their omission may produce effects other than that intended. Even on days of lesser disturbance difficulties present themselves. There may be to and fro movements of considerable amplitude occupying under an hour, and the hour may come exactly at the crest or at the very lowest part of the trough. Thus, if the reading represents in every case the ordinate at the precise hour a considerable element of chance may be introduced. If one is dealing with a mean from several hundred days such “accidents” can be trusted to practically neutralize one another, but this is much less fully the case when the period is as short as a month. To meet this difficulty it is customary at some observatories to derive hourly values from a freehand curve of continuous curvature, drawn so as to smooth out the apparently irregular movements. Instead of drawing a freehand curve it has been proposed to use a planimeter, and to accept as the hourly value of the ordinate the mean derived from a consideration of the area included between the curve, the base line and ordinates at the thirty minutes before and after each hour.
§ 4. Partly on account of the uncertainties due to disturbances, and partly with a view to economy of labour, it has been the practice at some observatories to derive diurnal inequalities from a comparatively small number of undisturbed or quiet days. Beginning with 1890, five days a month were selected at Greenwich by the astronomer royal as conspicuously quiet. In the selection regard was paid to the desirability that the arithmetic mean of the five dates should answer to near the middle of the month. In some of the other English observatories the routine measurement of the curves was limited to these selected quiet days. At Greenwich itself diurnal inequalities were derived regularly from the quiet days alone and also from all the days of the month, excluding those of large disturbance. If a quiet day differed from an ordinary day only in that the diurnal variation in the latter was partly obscured by irregular disturbances, then supposing enough days taken to smooth out irregularities, one would get the same diurnal inequality from ordinary and from quiet days. It was found, however, that this was hardly ever the case (see §§ 29 and 30). The quiet day scheme thus failed to secure exactly what was originally aimed at; on the other hand, it led to the discovery of a number of interesting results calculated to throw valuable sidelights on the phenomena of terrestrial magnetism.
The idea of selecting quiet days seems due originally to H. Wild. His selected quiet days for St Petersburg and Pavlovsk were very few in number, in some months not even a single day reaching his standard of freedom from disturbance. In later years the International Magnetic Committee requested the authorities of each observatory to arrange the days of each month in three groups representing the quiet, the moderately disturbed and the highly disturbed. The statistics are collected and published on behalf of the committee, the first to undertake the duty being M. Snellen. The days are in all cases counted from Greenwich midnight, so that the results are strictly synchronous. The results promise to be of much interest.
§ 5. The intensity and direction of the resultant magnetic force at a spot—i.e. the force experienced by a unit magnetic pole—are known if we know the three components of force parallel to any set of orthogonal axes. It is usual to take for these axes the vertical at the spot and two perpendicular axes in the horizontal plane; the latter are usually taken in and perpendicular to the geographical meridian. The usual notation in mathematical work is X to the north, Y to the west or east, and Z vertically downwards. The international magnetic committee have recommended that Y be taken positive to the east, but the fact that the declination is westerly over most of Europe has often led to the opposite procedure, and writers are not always as careful as they should be in stating their choice. Apart from mathematical calculations, the more usual course is to define the force by its horizontal and vertical components—usually termed H and V—and by the declination or angle which the horizontal component makes with the astronomical meridian. The declination is sometimes counted from 0° to 360°, 0° answering to the case when the so-called north pole (or north seeking pole) is directed towards geographical north, 90° to the case when it is directed to the east, and so on. It is more usual, however, to reckon declination only from 0° to 180°, characterizing it as easterly or westerly according as the north pole points to the east or to the west of the geographical meridian. The force is also completely defined by H or V, together with D the declination, and I the inclination to the horizon of the dipping needle. Instead of H and D some writers make use of N the northerly component, and W the westerly (or E the easterly). The resultant force itself is denoted sometimes by R, sometimes by T (total force). The following relationships exist between the symbols
X ≡ N, Y ≡ W or E, Z ≡ V, R ≡ T,
H ≡ √(X² + Y²), R ≡ √(X² + Y² + Z²),
tan D = Y / X, tan I = V / H.
The term magnetic element is applied to R or any of the components, and even to the angles D and I.
§ 6. Declination is the element concerning which our knowledge is most complete and most reliable. With a good unifilar magnetometer, at a fixed observatory distant from the magnetic poles, having a fixed mark of Charts. known azimuth, the observational uncertainty in a single observation should not exceed 0′.5 or at most 1′.0. It cannot be taken for granted that different unifilars, even by the best makers, will give absolutely identical values for the declination, but as a matter of fact the differences observed are usually very trifling. The chief source of uncertainty in the observation lies in the torsion of the suspension fibre, usually of silk or more rarely of phosphor bronze or other metal. A very stout suspension must be avoided at all cost, but the fibre must not be so thin as to have a considerable risk of breaking even in skilled hands. Near a magnetic pole the directive force on the declination magnet is reduced, and the effects of torsion are correspondingly increased. On the other hand, the regular and irregular changes of declination are much enhanced. If an observation consisting of four readings of declination occupies twelve minutes, the chances are that in this time the range at an English station will not exceed 1′, whereas at an arctic or antarctic station it will frequently exceed 10′. Much greater uncertainty thus attaches to declination results in the Arctic and Antarctic than to those in temperate latitudes. In the case of secular change data one important consideration is that the observations should be taken at an absolutely fixed spot, free from any artificial source of disturbance. In the case of many of the older observations of which records exist, the precise spot cannot be very exactly fixed, and not infrequently the site has become unsuitable through the erection of buildings not free from iron. Apart from buildings, much depends on whether the neighbourhood is free from basaltic and other magnetic rocks. If there are no local disturbances of this sort, a few yards difference is usually without appreciable influence, and even a few miles difference is of minor importance when one is calculating the mean secular change for a long period of years. When, however, local disturbances exist, even a few feet difference in the site may be important, and in the absence of positive knowledge to the contrary it is only prudent to act as if the site were disturbed. Near a magnetic pole the declination naturally changes very rapidly when one travels in the direction perpendicular to the lines of equal declination, so that the exact position of the site of observation is there of special importance.
The usual method of conveying information as to the value of the declination at different parts of the earth’s surface is to draw curves on a map—the so-called isogonals—such that at all points on any one curve the declination at a given specified epoch has the same value. The information being of special use to sailors, the preparation of magnetic charts has been largely the work of naval authorities—more especially of the hydrographic department of the British admiralty. The object of the admiralty world charts—four of which are reproduced here, on a reduced scale, by the kind permission of the Hydrographer—is rather to show the general features boldly than to indicate minute details. Apart from the immediate necessities of the case, this is a counsel of prudence. The observations used have mostly been taken at dates considerably anterior to that to which the chart is intended to apply. What the sailor wants is the declination now or for the next few years, not what it was five, ten or twenty years ago. Reliable secular change data, for reasons already indicated, are mainly obtainable from fixed observatories, and there are enormous areas outside of Europe where no such observatories exist. Again, as we shall see presently, the rate of the secular change sometimes alters greatly in the course of a comparatively few years. Thus, even when the observations themselves are thoroughly reliable, the prognostication made for a future date by even the most experienced of chart makers may be occasionally somewhat wide of the mark. Fig. 1 is a reduced copy of the British admiralty declination chart for the epoch 1907. It shows the isogonals between 70° N. and 65° S. latitude. Beyond the limits of this chart, the number of exact measurements of declination is somewhat limited, but the general nature of the phenomena is easily inferred. The geographical and the magnetic poles—where the dipping needle is vertical—are fundamental points. The north magnetic pole is situated in North America near the edge of the chart. We have no reason to suppose that the magnetic pole is really a fixed point, but for our present purpose we may regard it as such. Let us draw an imaginary circle round it, and let us travel round the circle in the direction, west, north, east, south, starting from a point where the north pole of a magnet (i.e. the pole which in Europe or the United States points to the north) is directed exactly towards the astronomical north. The point we start from is to the geographical south of the magnetic pole. As we go round the circle the needle keeps directed to the magnetic pole, and so points first slightly to the east of geographical north, then more and more to the east, then directly east, then to south of east, then to due south, to west of south, to west, to north-west, and finally when we get round to our original position due north once more. Thus, during our course round the circle the needle will have pointed in all possible directions. In other words, isogonals answering to all possible values of the declination have their origin in the north magnetic pole. The same remark applies of course to the south magnetic pole.
 |
| Fig. 1.—Isogonals, or lines of equal magnetic declination. |
Now, suppose ourselves at the north geographical pole of the earth. Neglecting as before diurnal variation and similar temporary changes, and assuming no abnormal local disturbance, the compass needle at and very close to this pole will occupy a fixed direction relative to the ground underneath. Let us draw on the ground through the pole a straight line parallel to the direction taken there by the compass needle, and let us carry a compass needle round a small circle whose centre is the pole. At all points on the circle the positions of the needle will be parallel; but whereas the north pole of the magnet will point exactly towards the centre of the circle at one of the points where the straight line drawn on the ground cuts the circumference, it will at the opposite end of the diameter point exactly away from the centre. The former part is clearly on the isogonal where the declination is 0°, the latter on the isogonal where it is 180°. Isogonals will thus radiate out from the north geographical pole (and similarly of course from the south geographical pole) in all directions. If we travel along an isogonal, starting from the north magnetic pole, our course will generally take us, often very circuitously, to the north geographical pole. If, for example, we select the isogonal of 10° E., we at first travel nearly south, but then more and more westerly, then north-westerly across the north-east of Asia; the direction then gets less northerly, and makes a dip to the south before finally making for the north geographical pole. It is possible, however, according to the chart, to travel direct from the north magnetic to the south geographical pole, provided we select an isogonal answering to a small westerly or easterly declination (from about 19° W. to 7° E.).
Special interest attaches to the isogonals answering to declination 0°. These are termed agonic lines, but sailors often call them lines of no variation, the term variation having at one time been in common use in the sense of declination. If we start from the north magnetic pole the agonic line takes us across Canada, the United States and South America in a fairly straight course to the south geographical pole. A curve continuous with this can be drawn from the south geographical to the south magnetic pole at every point of which the needle points in the geographical meridian; but here the north pole of the needle is pointing south, not north, so that this portion of curve is really an isogonal of 180°. In continuation of this there emanates from the south magnetic pole a second isogonal of 0°, or agonic line, which traverses Australia, Arabia and Russia, and takes us to the north geographical pole. Finally, we have an isogonal of 180°, continuous with this second isogonal of 0° which takes us to the north magnetic pole, from which we started. Throughout the whole area included within these isogonals of 0° and 180°—excluding locally disturbed areas—the declination is westerly; outside this area the declination is in general easterly. There is, however, as shown in the chart, an isogonal of 0° enclosing an area in eastern Asia inside which the declination is westerly though small.
§ 7. Fig. 2 is a reduced copy of the admiralty chart of inclination or dip for the epoch 1907. The places where the dip has the same value lie on curves called isoclinals. The dip is northerly (north pole dips) or southerly (south pole dips) according as the place is north or south of the isoclinal of 0°. At places actually on this isoclinal the dipping needle is horizontal. The isoclinal of 0° is nowhere very far from the geographical equator, but lies to the north of it in Asia and Africa, and to the south of it in South America. As we travel north from the isoclinal of 0° along the meridian containing the magnetic pole the dipping needle’s north pole dips more and more, until when we reach the magnetic pole the needle is vertical. Going still farther north, we have the dip diminishing. The northerly inclination is considerably less in Europe than in the same latitudes of North America; and correspondingly 357 the southerly inclination is less in South America than in the same latitudes of Africa.
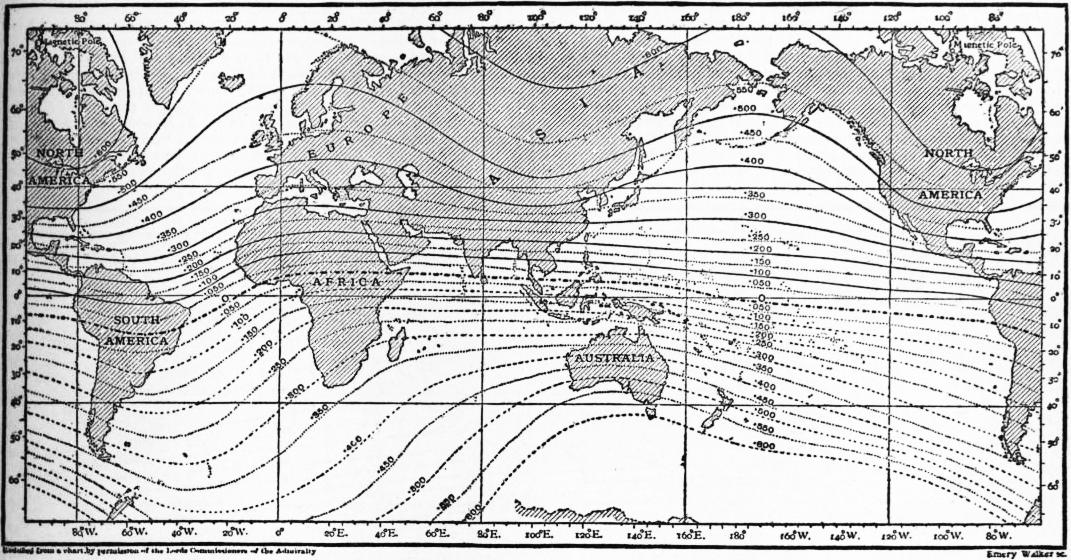 |
| Fig. 2.—Isoclinals, or lines of equal magnetic dip. |
Fig. 3 is a reduced copy of the admiralty horizontal force chart for 1907. The curves, called isomagnetics, connect the places where the horizontal force has the same value; the force is expressed in C.G.S. units. The horizontal force vanishes of course at the magnetic poles. The chart shows a maximum value of between 0.39 and 0.40 in an oval including the south of Siam and the China Sea. The horizontal force is smaller in North America than in corresponding latitudes in Europe.
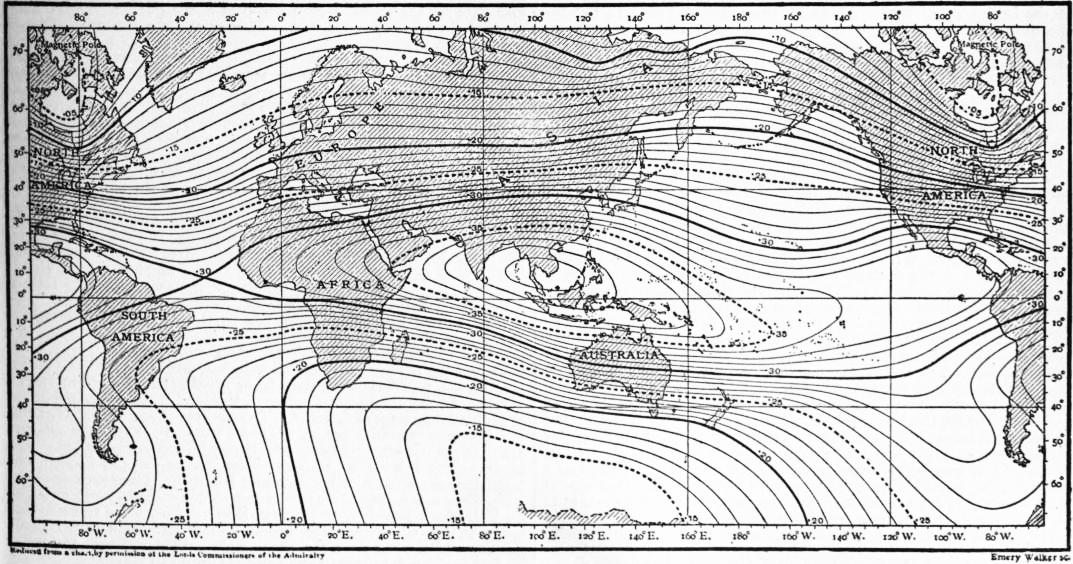 |
| Fig. 3.—Isomagnetics, lines of equal horizontal force. |
Charts are sometimes drawn for other magnetic elements, especially vertical force (fig. 4) and total force. The isomagnetic of zero vertical force coincides necessarily with that of zero dip, and there is in general considerable resemblance between the forms of lines of equal vertical force and those of equal dip. The highest values of the vertical force occur in areas surrounding the magnetic poles, and are fully 50% larger than the largest values of the horizontal force. The total force is least in equatorial regions, where values slightly under 0.4 C.G.S. are encountered. In the northern hemisphere there are two distinct maxima of total force. One of these so-called foci is in Canada, the other in the north-east of Siberia, the former having the higher value of the force. There are, however, higher values of the total force than at either of these foci throughout a considerable area to the south of Australia. In the northern hemisphere the lines of equal total force—called isodynamic lines—form two sets more or less distinct, consisting of closed ovals, one set surrounding the Canadian the other the Siberian focus.
§ 8. As already explained, magnetic charts for the world or for large areas give only a general idea of the values of the elements. If the region is undisturbed, very fairly approximate values are derivable from the charts, but when the highest accuracy is necessary Magnetic Elements and their Secular Change. the only thing to do is to observe at the precise spot. In disturbed areas local values often depart somewhat widely from what one would infer from the chart, and occasionally there are large differences 358 between places only a few miles apart. Magnetic observatories usually publish the mean value for the year of their magnetic elements. It has been customary for many years to collect and publish these results in the annual report of the Kew Observatory (Observatory Department of the National Physical Laboratory). The data in Tables I. and II. are mainly derived from this source. The observatories are arranged in order of latitude, and their geographical co-ordinates are given in Table II., longitude being reckoned from Greenwich. Table I. gives the mean values of the declination, inclination and horizontal force for January 1, 1901; they are in the main arithmetic means of the mean annual values for the two years 1900 and 1901. The mean annual secular changes given in this table are derived from a short period of years—usually 1898 to 1903—the centre of which fell at the beginning of 1901. Table II. is similar to Table I., but includes vertical force results; it is more extensive and contains more recent data. In it the number of years is specified from which the mean secular change is derived; in all cases the last year of the period employed was that to which the absolute values assigned to the element belong. The great majority of the stations have declination west and inclination north; it has thus been convenient to attach the + sign to increasing westerly (or decreasing easterly) declination and to increasing northerly (or decreasing southerly) inclination. In other words, in the case of the declination + means that the north end of the needle is moving to the west, while in the case of the inclination + means that the north end (whether the dipping end or not) is moving towards the nadir. In the case, however, of the vertical force + means simply numerical increase, irrespective of whether the north or the south pole dips. The unit employed in the horizontal and vertical force secular changes is 1γ, i.e. 0.00001 C.G.S. Even in the declination, at the very best observatories, it is hardly safe to assume that the apparent change from one year to the next is absolutely truthful to nature. This is especially the case if there has been any change of instrument or observer, or if any alteration has been made to buildings in the immediate vicinity. A change of instrument is a much greater source of uncertainty in the case of horizontal force or dip than in the case of declination, and dip circles and needles are more liable to deterioration than magnetometers. Thus, secular change data for inclination and vertical force are the least reliable. The uncertainties, of course, are much less, from a purely mathematical standpoint, for secular changes representing a mean from five or ten years than for those derived from successive years’ values of the elements. The longer, however, the period of years, the greater is the chance that one of the elements may in the course of it have passed through a maximum or minimum value. This possibility should always be borne in mind in cases where a mean secular change appears exceptionally small.
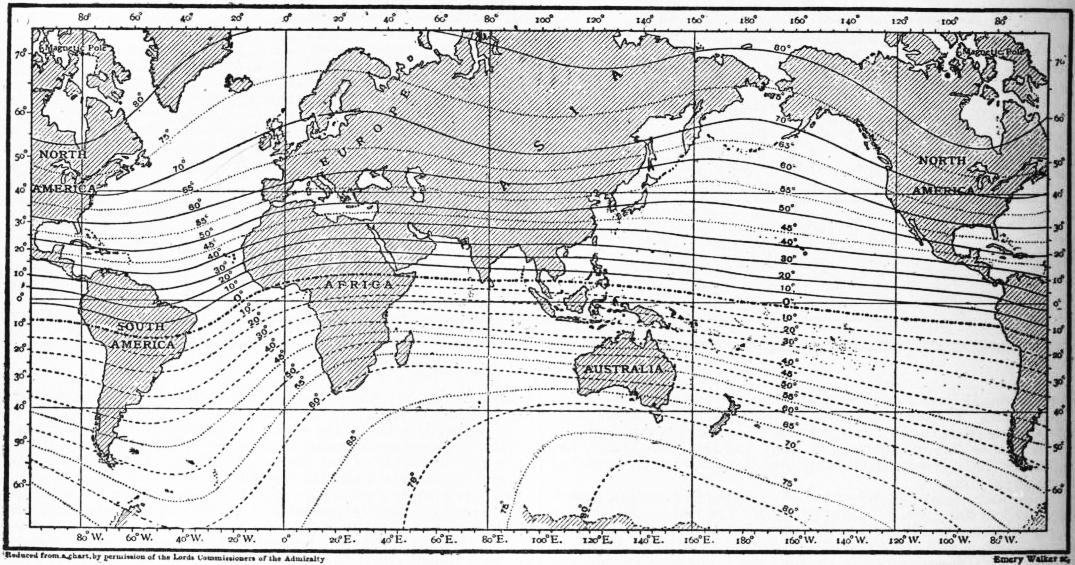 |
| Fig. 4.—Isomagnetics, lines of equal vertical force. |
As Tables I. and II. show, the declination needle is moving to the east all over Europe, and the rate at which it is moving seems not to vary much throughout the continent. The needle is also moving to the east throughout the western parts of Asia, the north and east of Africa, and the east of North America. It is moving to the west in the west of North America, in South America, and in the south and east of Asia, including Japan, south-east Siberia, eastern China and most of India.
§ 9. The information in figs. 1, 2, 3 and 4 and in Tables I. and II. applies only to recent years. Owing to secular change, recent charts differ widely from the earliest ones constructed. The first charts believed to have been constructed were those of Edmund Halley the astronomer. According to L. A. Bauer,7 who has made a special study of the subject, Halley issued two declination charts for the epoch 1700; one, published in 1701, was practically confined to the Atlantic Ocean, whilst the second, published in 1702, contained also data for the Indian Ocean and part of the Pacific. These charts showed the isogonic lines, but only over the ocean areas. Though the charts for 1700 were the first published, there are others which apply to earlier epochs. W. van Bemmelen8 has published charts for the epochs 1500, 1550, 1600, 1650 and 1700, whilst H. Fritsche9 has more recently published charts of declination, inclination and horizontal force for 1600, 1700, 1780, 1842 and 1915. A number of early declination charts were given in Hansteen’s Atlas and in G. Hellmann’s reprints. Die Altesten Karten der Isogonen, Isoklinen, Isodynamen (Berlin, 1895). The data for the earlier epochs, especially those prior to 1700, are meagre, and in many cases probably of indifferent accuracy, so that the reliability of the charts for these epochs is somewhat open to doubt.
If we take either Hansteen’s or Fritsche’s declination chart for 1600 we notice a profound difference from fig. 1. In 1600 the agonic line starting from the north magnetic pole, after finding its way south to the Gulf of Mexico, doubled back to the north-east, and passed across or near Iceland. After getting well to the north of Iceland it doubled again to the south, passing to the east of the Baltic. The second agonic line which now lies to the west of St Petersburg appears in 1600 to have continued, after traversing Australia, in a nearly northerly direction through the extreme east of China. The nature of the changes in declination in western Europe will be understood from Table III., the data from which, though derived from a variety of places in the south-east of England,10 may be regarded as approximately true of London. The earliest result is that obtained by Borough at Limehouse. Those made in the 16th century are due to Gunter, Gellibrand, Henry Bond and Halley. The observations from 1787 to 1805 were due to George Gilpin, who published particulars of his own and the earlier observations in the Phil. Trans. for 1806. The data for 1817 and 1820 were obtained by Col. Mark Beaufoy, at Bushey, Herts. They seem to come precisely at the time when the needle, which had been continuously moving to the west since the earliest observations, began to retrace its steps. The data from 1860 onwards apply to Kew.
Table I.—Magnetic Elements and their Rate of Secular Change for January 1, 1901.
| Place. | Absolute values. | Secular change. | ||||
| D. | I. | H. | D. | I. | H. | |
| ° ′ | ° ′ | ′ | ′ | γ | ||
| Pavlovsk | 0 39.8E | 70 36.8N | .16553 | − 4.1 | −0.8 | + 7 |
| Ekatarinburg | 10 6.3E | 70 40.5N | .17783 | − 4.6 | +0.5 | −13 |
| Copenhagen | 10 10.4W | 68 38.5N | .17525 | |||
| Stonyhurst | 18 10.3W | 68 48.0N | .17330 | − 4.0 | +22 | |
| Wilhelmshaven | 12 26.0W | 67 39.7N | .18108 | − 4.1 | −2.1 | +20 |
| Potsdam | 9 54.2W | 66 24.5N | .18852 | − 4.2 | −1.6 | +16 |
| Irkutsk | 2 1.0E | 70 15.8N | .20122 | + 0.5 | +1.6 | −14 |
| de Bilt | 13 48.3W | 66 55.5N | .18516 | − 4.4 | −2.2 | +14 |
| Kew | 16 50.8W | 67 10.6N | .18440 | − 4.2 | −2.2 | +25 |
| Greenwich | 16 27.5W | 67 7.3N | .18465 | − 4.0 | −2.2 | +23 |
| Uccle | 14 11.0W | 66 8.8N | .18954 | − 4.2 | −2.1 | +23 |
| Falmouth | 18 27.3W | 66 44.0N | .18705 | − 3.8 | −2.7 | +26 |
| Prague | 9 4.4W | .19956 | − 4.4 | +20 | +20 | |
| St Helier | 16 58.1W | 65 44.1N | − 3.5 | −2.7 | ||
| Parc St Maur | 14 43.4W | 64 52.3N | .19755 | − 4.0 | −2.2 | +23 |
| Val Joyeux | 15 13.7W | 65 0.0N | .19670 | |||
| Munich | 10 25.8W | 63 18.1N | .20629 | − 4.8 | −2.7 | +21 |
| O’Gyalla | 7 26.1W | .21164 | − 4.8 | +13 | ||
| Pola | 9 22.7W | 60 14.5N | .22216 | − 4.0 | +23 | |
| Toulouse | 14 16.4W | 60 55.9N | .21945 | − 3.9 | −2.5 | +25 |
| Perpignan | 13 34.7W | 59 57.6N | .22453 | |||
| Capo di Monte | 9 8.0W | 56 22.3N | − 5.2 | −2.3 | ||
| Madrid | 15 39.0W | |||||
| Coimbra | 17 18.1W | 59 22.0N | .22786 | − 3.7 | −4.3 | +34 |
| Lisbon | 17 15.7W | 57 53.0N | .23548 | |||
| Athens | 5 38.2W | 52 7.5N | .26076 | |||
| San Fernando | 15 57.5W | 55 8.8N | .24648 | |||
| Tokyo | 4 34.9W | 49 0.3N | .29932 | |||
| Zi−ka−wei | 2 23.5W | 45 43.5N | .32875 | + 1.5 | −1.5 | +37 |
| Helwan | 3 39.7W | 40 30.8N | .30136 | − 7.0 | −0.4 | − 7 |
| Hong−Kong | 0 17.5E | 31 22.8N | .36753 | + 1.8 | −4.3 | +45 |
| Kolaba | 0 23.2E | 21 26.5N | .37436 | + 2.2 | +7.0 | − 9 |
| Manila | 0 52.2E | 16 13.5N | .38064 | + 0.1 | −5.3 | +47 |
| Batavia | 1 7.3E | 30 35.5S | .36724 | + 3.0 | −7.3 | −11 |
| Mauritius | 9 25.2W | 54 9.4S | .23820 | − 4.7 | +4.6 | −39 |
| Rio de Janeiro | 8 2.9W | 13 20.1S | .2501 | +10.4 | −2.3 | |
| Melbourne | 8 25.6E | 67 24.6S | .23295 | |||
The rate of movement of the needle to the east at London—and throughout Europe generally—fell off markedly subsequent to 1880. The change of declination in fact between 1880 and 1895 was only about 75% of that between 1865 and 1880, and the mean annual change from 1895 to 1900 was less than 75% of the mean annual change of the preceding fifteen years. Thus in 1902 it was at least open to doubt whether a change in the sign of the secular change were not in immediate prospect. Subsequent, however, to that date there was little further decline in the rate of secular change, and since 1905 there has been very distinct acceleration. Thus, if we derive a mean value from the eighteen European stations for which declination secular changes are given in Tables I. and II. we find
| mean value from table | I. | −4.18 |
| ” ” ” ” | II. | −5.21 |
The epoch to which the data in Table II. refer is somewhat variable, but is in all cases more recent than the epoch, January 1, 1901, for Table I., the mean difference being about 5 years.
§ 10. At Paris there seems to have been a maximum of easterly declination (about 9°) about 1580; the needle pointed to true north about 1662, and reached its extreme westerly position between 1812 and 1814. The phenomena at Rome resembled those at Paris and London, but the extreme westerly position is believed to have been attained earlier. The rate of change near the turning point seems to have been very slow, and as no fixed observatories existed in those days, the precise time of its occurrence is open to some doubt.
Perhaps the most complete observations extant as to the declination phenomena near a turning point relate to Kolaba observatory at Bombay; they were given originally by N. A. F. Moos,11 the director of the observatory. Some of the more interesting details are given in Table IV.; here W denotes movement to be west, and so answers to a numerical diminution in the declination, which is easterly.
Prior to 1880 the secular change at Kolaba was unmistakably to the east, and subsequent to 1883 it was clearly to the west; but between these dates opinions will probably differ as to what actually happened. The fluctuations then apparent in the sign of the annual change may be real, but it is at least conceivable that they are of instrumental origin. From 1870 to 1875 the mean annual change was −1′.2; from 1885 to 1890 it was +1′.5, from 1890 to 1895 it was +2′.0, while from 1895 to 1905 it was +2′.35, the + sign denoting movement to the west. Thus, in this case the rate of secular change has increased fairly steadily since the turning point was reached.
Table V. contains some data for St Helena and the Cape of Good Hope,12 both places having a long magnetic history. The remarkable feature at St Helena is the uniformity in the rate of secular change. The figures for the Cape show a reversal in the direction of the secular change about 1840, but after a few years the arrested movement to the west again became visible. According, however, to J. C. Beattie’s Magnetic Survey of South Africa the movement to the west ceased shortly after 1870. A persistent movement to the east then set in, the mean annual change increasing from 1′.8 between 1873 and 1890 to 3′.8 between 1890 and 1900.
§ 11. Secular changes of declination have been particularly interesting in the United States, an area about which information is unusually complete, thanks to the labours and publications of the United States Coast and Geodetic Survey.13 At present the agonic line passes in a south-easterly direction from Lake Superior to South Carolina. To the east of the agonic line the declination is westerly, and to the west it is easterly. In 1905 the declination varied from about 21° W. in the extreme north-east to about 24° E. in the extreme north-west. At present the motion of the agonic line seems to be towards the west, but it is very slow. To the east of the agonic line westerly declination is increasing, and to the west of the line, with the exception of a narrow strip immediately adjacent to it, easterly declination is increasing. The phenomena in short suggest a motion southwards in the north magnetic pole. Since 1750 declination has always been westerly in the extreme east of the States, and always easterly in the extreme west, but the position of the agonic line has altered a good deal. It was to the west of Richmond, Virginia, from 1750 to about 1772, then to the east of it until about 1838 when it once more passed to the west; since that time it has travelled farther to the west. Table VI. is intended to show the nature of the secular change throughout the whole country. As before, + denotes that the north pole of the magnet is moving to the west,—that it is moving to the east.
The data in Table VI. represent the mean change of declination per annum, derived from the period (ten years, except for 1900-1905) which ended in the year put at the top of the column. The stations are arranged in four groups, the first group representing the extreme eastern, the last group the extreme western states, the other two groups being intermediate. In each group the stations are arranged, at least approximately, in order of latitude. The data are derived from the values of the declination given in the Geodetic Survey’s Report for 1906, appendix 4, and Magnetic Tables and Magnetic Charts by L. A. Bauer, 1908. The values seem, in most cases, based to some extent on calculation, and very probably the secular change was not in reality quite so regular as the figures suggest. For the Western States the earliest data are comparatively recent, but for some of the eastern states data earlier than any in the table appear in the Report of the Coast and Geodetic Survey for 1902. These data indicate that the easterly movement of the magnet, visible in all the earlier figures for the Eastern States in Table VI., existed in all of them at least as far back as 1700. There is not very much evidence as to the secular change between 1700 and 1650, the earliest date to which the Coast and Geodetic Survey’s figures refer. The figures show a maximum of westerly declination about 1670 in New Jersey and about 1675 in Maryland. They suggest that this maximum was experienced all along the Atlantic border some time in the 17th century, but earlier in the extreme north-east than in New York or Maryland.
Examination of Table VI. shows that the needle continued to move to the east for some time after 1750 even in the Eastern States. But the rate of movement was clearly diminishing, and about 1765 the extreme easterly position was reached in Eastport, Maine, the needle then beginning to retrace its steps to the west. The phenomena visible at Maine are seen repeating themselves at places more and more to the west, in Boston about 1785, in Albany about 1800, in Washington, D.C., about 1805, in Columbus (Ohio) about 1815, in Montgomery (Alabama) about 1825, in Bloomington (Ill.) about 1830, in Des Moines (Iowa) about 1840, in Santa Rosa (New Mexico) about 1860 and in Salt Lake about 1870. In 1885 the needle was moving to the west over the whole United States with the exception of a comparatively narrow strip along the Pacific coast. Even an acute observer would have been tempted to prophesy in 1885 that at no distant date the secular change would be pronouncedly westerly right up to the Pacific. But in a few years a complete change took place. The movement to the east, which had become exceedingly small, if existent, in the Pacific states, began to accelerate; the movement to the west continued in the central, as in the eastern states, but perceptibly slackened. In 1905 the area throughout which the movement to the west still continued had greatly contracted and lay to the east of a line drawn from the west end of Lake Superior to the west of Georgia. If we take a station like Little Rock (Arkansas), we have the secular change to the west lasting for about sixty years. Further west the period shortens. At Pueblo (Colorado) it is about forty years, at Salt Lake under thirty years, at Prescott (Arizona) about twenty years. Considering how fast the area throughout which the secular change is easterly has extended to the east since 1885, one would be tempted to infer that at no distant date it will include the whole of the United States. In the extreme north-east, however, the movement of the needle to the west, which had slackened perceptibly after 1860 or 1870, is once more accelerating. Thus the auspices do not all point one way, and the future is as uncertain as it is interesting.
Table II.—Recent Values of the Magnetic Elements and their Rate of Secular Change.
| Place. | Geographical position. | Absolute Values of Elements. | Secular change (mean per annum). | |||||||||
| Latitude. | Longitude. | Year. | D. | I. | H. | V. | Interval in years. | D. | I. | H. | V. | |
| ° ′ | ° ′ | ° ′ | ° ′ | ′ | ′ | |||||||
| Pavlovsk | 59 41N | 30 29E | 1906 | 1 4.2E | 70 36.6N | .16528 | .46963 | 5 | −4.5 | +0.1 | − 6 | −14 |
| Sitka (Alaska) | 57 3N | 135 20W | 1906 | 30 3.3E | 74 41.7N | .15502 | .56646 | 4 | −3.0 | −1.6 | +18 | −38 |
| Ekatarinburg | 56 49N | 60 38E | 1906 | 10 31.0E | 70 49.5N | .17664 | .50796 | 5 | −4.5 | +1.7 | −23 | +18 |
| Rude Skov (Copenhagen) | 55 51N | 12 27E | 1908 | 9 43.3W | 68 45N | .17406 | .44759 | |||||
| Stonyhurst | 53 51N | 2 28W | 1909 | 17 28.6W | 68 42.8N | .17424 | .44722 | 5 | −5.9 | −1.1 | + 6 | −25 |
| Hamburg | 53 33N | 9 59E | 1903 | 11 10.2W | 67 23.5N | .18126 | .43527 | |||||
| Wilhelmshaven | 53 32N | 8 9E | 1909 | 11 46.8W | .18129 | 5 | −5.2 | − 7 | ||||
| Potsdam | 52 23N | 13 4E | 1909 | 9 10.6W | 66 20.0N | .18834 | .42971 | 5 | −5.8 | +0.1 | − 9 | −19 |
| Irkutsk | 52 16N | 104 16E | 1905 | 1 58.1E | 70 25.0N | .20011 | .56250 | 5 | +0.6 | +2.0 | −24 | +39 |
| de Bilt | 52 5N | 5 11E | 1907 | 13 19.0W | 66 49.9N | .18559 | .43368 | 5 | −4.7 | −0.6 | + 2 | −16 |
| Valencia | 51 56N | 10 15W | 1909 | 20 50.3W | 68 15.1N | .17877 | .44812 | 5 | −5.0 | −1.2 | + 7 | −25 |
| Kew | 51 28N | 0 19W | 1909 | 16 10.8W | 66 59.7N | .18506 | .43588 | 5 | −5.4 | −1.1 | + 2 | −35 |
| Greenwich | 51 28N | 0 0 | 1909 | 15 47.6W | 66 53.9N | .18526 | .43432 | 5 | −5.5 | −0.7 | + 1 | −20 |
| Uccle | 50 48N | 4 21E | 1908 | 13 36.7W | 66 1.6N | .19061 | .42867 | 4 | −5.3 | −0.8 | − 3 | −35 |
| Falmouth | 50 9N | 5 5W | 1909 | 17 48.4W | 66 30.6N | .18802 | .43266 | 5 | −4.7 | −1.4 | + 9 | −30 |
| Prague | 50 5N | 14 25E | 1908 | 8 20.9W | 5 | −6.5 | ||||||
| Cracow | 50 4N | 19 58E | 1909 | 5 35.1W | 64 18N | 3 | −7.3 | |||||
| St Helier | 49 12N | 2 5W | 1907 | 16 27.4W | 65 34.5N | 5 | −5.3 | −1.2 | ||||
| Val Joyeux | 48 49N | 2 1E | 1909 | 14 32.9W | 64 43.9N | .19727 | .41792 | 5 | −5.4 | −1.7 | + 1 | −51 |
| Vienna | 48 15N | 16 21E | 1898 | 8 24.1W | ||||||||
| Munich | 48 9N | 11 37E | 1906 | 9 59.5W | 63 10.0N | .20657 | .40835 | 5 | −4.8 | −1.3 | + 4 | −31 |
| O’Gyalla | 47 53N | 18 12E | 1909 | 6 43.9W | .21094 | 5 | −5.0 | −10 | ||||
| Odessa | 46 26N | 30 46E | 1899 | 4 36.7W | 62 18.2N | .21869 | .41660 | |||||
| Pola | 44 52N | 15 51E | 1908 | 8 43.2W | 60 6.8N | .22207 | .38640 | 5 | −5.5 | −0.6 | − 4 | −23 |
| Agincourt (Toronto) | 43 47N | 79 16W | 1906 | 5 45.3W | 74 35.6N | .16397 | .59502 | 4 | +3.4 | +0.9 | −23 | −24 |
| Nice | 43 43N | 7 16E | 1899 | 12 4.0W | 60 11.7N | .22390 | .39087 | |||||
| Toulouse | 43 37N | 1 28E | 1905 | 13 56.3W | 60 49.1N | .22025 | .39439 | 5 | −4.5 | −1.5 | + 2 | − 2 |
| Perpignan | 42 42N | 2 53E | 1907 | 13 4.4W | 7 | −4.7 | ||||||
| Tiflis | 41 43N | 44 48E | 1905 | 2 41.6E | 56 2.8N | .25451 | .37799 | 7 | −5.2 | +1.7 | −26 | + 2 |
| Capo di Monte | 40 52N | 14 15E | 1906 | 8 40.3W | 56 13.5N | 5 | −5.1 | −1.5 | ||||
| Madrid | 40 25N | 3 40W | 1901 | 15 35.6W | ||||||||
| Coimbra | 40 12N | 8 25W | 1908 | 16 46.2W | 58 57.3N | .22946 | .38120 | 5 | −4.6 | −2.9 | +17 | −45 |
| Baldwin (Kansas) | 38 47N | 95 10W | 1906 | 8 30.1E | 68 45.1N | .21807 | .56081 | 4 | −1.7 | +1.8 | −36 | − 8 |
| Cheltenham(Maryland) | 38 44N | 76 50W | 1906 | 5 22.0W | 70 27.3N | .20035 | .56436 | 4 | +3.8 | +1.2 | −38 | −45 |
| Lisbon | 38 43N | 9 9W | 1900 | 17 18.0W | 57 54.8N | .23516 | .37484 | |||||
| Athens | 37 58N | 21 23E | 1908 | 4 52.9W | 52 11.7N | .26197 | .33613 | 5 | −5.5 | |||
| San Fernando | 36 28N | 6 12W | 1908 | 15 25.6W | 54 48.4N | .24829 | .35206 | 5 | −4.6 | −2.8 | +26 | −24 |
| Tokyo | 35 41N | 139 45E | 1901 | 4 36.1W | 49 0.0N | .29954 | .34459 | |||||
| Zi-ka-wei | 31 12N | 121 26E | 1906 | 2 32.0W | 45 35.3N | .33040 | .33726 | 5 | +1.5 | −1.3 | +30 | + 6 |
| Dehra Dun | 30 19N | 78 3E | 1907 | 2 38.3E | 43 36.1N | .33324 | .31736 | 4 | +0.8 | +5.5 | −26 | +77 |
| Helwan | 29 52N | 31 21E | 1909 | 2 49.2W | 40 40.4N | .30031 | .25804 | 5 | −5.7 | +1.2 | − 6 | +13 |
| Havana | 23 8N | 82 25W | 1905 | 2 25.0E | 52 57.4N | .30531 | .40452 | |||||
| Barrackpore | 22 46N | 88 22E | 1907 | 1 9.9E | 30 30.2N | .37288 | .21967 | 3 | +4.2 | +3.4 | +21 | +62 |
| Hong-Kong | 22 18N | 114 10E | 1908 | 0 3.9E | 31 2.5N | .37047 | .22292 | 5 | +1.9 | −1.8 | +43 | − 1 |
| Honolulu | 21 19N | 158 4W | 1906 | 9 21.7E | 40 1.8N | .29220 | .24545 | 4 | −0.9 | −3.2 | −19 | −62 |
| Kolaba | 18 54N | 72 49E | 1905 | 0 14.0E | 21 58.5N | .37382 | .15084 | 5 | +2.1 | +7.2 | −11 | +86 |
| Alibagh | 18 39N | 72 52E | 1909 | 1 0.3E | 23 29.0N | .36845 | .16008 | 3 | +1.7 | +6.8 | −10 | +82 |
| Vieques (Porto Rico) | 18 9N | 65 26W | 1906 | 1 33.2W | 49 47.7N | .28927 | .34224 | 2 | +7.2 | +6.8 | −49 | +66 |
| Manila | 14 35N | 120 59E | 1904 | 0 51.4E | 16 0.2N | .38215 | .10960 | 5 | +0.1 | −3.9 | +47 | −34 |
| Kodaikanal | 10 14N | 77 28E | 1907 | 0 40.7W | 3 27.2N | .37431 | .02259 | 4 | +4.3 | +5.5 | +16 | +61 |
| Batavia | 6 11S | 106 49E | 1906 | 0 54.1E | 30 48.5S | .36708 | .21889 | 4 | +2.1 | −7.7 | − 2 | +110 |
| Dar es Salaam | 6 49S | 39 18E | 1903 | 7 35.2W | ||||||||
| Mauritius | 20 6S | 57 33E | 1908 | 9 14.3W | 53 44.9S | .23415 | .31932 | 5 | −0.3 | +2.9 | −53 | −131 |
| Rio de Janeiro | 22 55S | 43 11W | 1906 | 8 55.5W | 13 57.1S | .24772 | .06164 | 5 | +9.1 | −6.8 | −42 | +44 |
| Santiago (Chile) | 33 27S | 70 42W | 1906 | 14 18.7E | 30 11.8S | 3 | +6.1 | +9.9 | ||||
| Melbourne | 37 50S | 144 58E | 1901 | 8 26.7E | 67 25.0S | .23305 | .56024 | |||||
| Christchurch, N.Z. | 43 32S | 172 37E | 1903 | 16 18.4E | 67 42.3S | .22657 | .55259 | |||||
Table III.—Declination at London.
| Date. | Declination. | Date. | Declination. | Date. | Declination. |
| ° ′ | ° ′ | ° ′ | |||
| 1580 | 11 15E | 1773 | 21 9W | 1860 | 21 38.9W |
| 1622 | 6 0 | 1787 | 23 19 | 1865 | 20 58.7 |
| 1634 | 4 6 | 1795 | 23 57 | 1870 | 20 18.3 |
| 1657 | 0 0 | 1802 | 24 6 | 1875 | 19 35.6 |
| 1665 | 1 22W | 1805 | 24 8 | 1880 | 18 52.1 |
| 1672 | 2 30 | 1817 | 24 36 | 1885 | 18 19.2 |
| 1692 | 6 0 | 1818 | 24 38 | 1890 | 17 50.6 |
| 1723 | 14 17 | 1819 | 24 36 | 1895 | 17 16.8 |
| 1748 | 17 40 | 1820 | 24 34 | 1900 | 16 52.7 |
| 1905 | 16 32.9 |
§ 12. Table VII. gives particulars of the secular change of horizontal force and northerly inclination at London. Prior to the middle of the 19th century information as to the value of H is of uncertain value. The earlier inclination data14 are due to Norman, Gilbert, Bond, Graham, Heberden and Gilpin. The data from 1857 onwards, both for H and I, refer to Kew. “London” is rather a vague term, but the differences between the values of H and I at Kew and Greenwich—in the extreme west and east—are almost nil. For some time after its discovery by Robert Norman inclination at London increased. The earlier observations are not sufficient to admit of the date of the maximum inclination or its absolute value being determined with precision. Probably the date was near 1723. This view is supported by the fact that at Paris the inclination fell from 72° 15′ in 1754 to 71° 48′ in 1780. The 361 earlier observations in London were probably of no very high accuracy, and the rates of secular change deducible from them are correspondingly uncertain. It is not improbable that the average annual change 0′.8 derived from the thirteen years 1773-1786 is too small, and the value 6′.2 derived from the fifteen years 1786-1801 too large. There is, however, other evidence of unusually rapid secular change of inclination towards the end of the 18th century in western Europe; for observations in Paris show a fall of 56′ between 1780 and 1791, and of 90′ between 1791 and 1806. Between 1801 and 1901 inclination in London diminished by 3° 26′.5, or on the average by 2′.1 per annum, while between 1857 and 1900 H increased on the average by 22γ a year. These values differ but little from the secular changes given in Table I. as applying at Kew for the epoch Jan. 1, 1901. Since the beginning, however, of the 20th century a notable change has set in, which seems shared by the whole of western Europe. This is shown in a striking fashion by contrasting the data from European stations in Tables I. and II. There are fifteen of these stations which give secular change data for H in both tables, while thirteen give secular data for I. The mean values of the secular changes derived from these stations are as follows:—
| I | H | |
| From Table I. | −2′.35 | +21.0γ |
| From Table II. | −1.12 | +1.6γ |
The difference in epoch between the two sets of results is only about 5 years, and yet in that short time the mean rate of annual increase in H fell to a thirteenth of its original value. During 1908-1909 H diminished throughout all Europe except in the extreme west. Whether we have to do with merely a temporary phase, or whether a general and persistent diminution in the value of H is about to set in over Europe it is yet hardly possible to say.
Table IV.—Declination at Kolaba (Bombay).
| Year. | Declination East. | Change since previous year. | Year. | Declination East. | Change since previous year. |
| ° ′ ″ | ′ ″ | ° ′ ″ | ′ ″ | ||
| 1876 | 0 55 58 | 0 37 E | 1881 | 0 57 12 | 0 3 E |
| 1877 | 56 39 | 0 41 E | 1882 | 0 56 50 | 0 22 W |
| 1878 | 57 6 | 0 27 E | 1883 | 57 2 | 0 12 E |
| 1879 | 57 30 | 0 24 E | 1884 | 55 39 | 1 23 W |
| 1880 | 57 9 | 0 21 W | 1885 | 55 3 | 0 36 W |
§ 13. It is often convenient to obtain a formula to express the mean annual change of an element during a given period throughout an area of some size. The usual method is to assume that the change at a place whose latitude is l and longitude λ is given by an expression of the type c + a(l − l0) + b(λ − λ0), where a, b, c are constants, l0 and λ0, denoting some fixed latitude and longitude which it is convenient to take as point of departure. Supposing observational data available from a series of stations throughout the area, a, b and c can be determined by least squares. As an example, we may take the following slightly modified formula given by Ad. Schmidt15 as applicable to Northern Europe for the period 1890 to 1900. ΔD, ΔI and ΔH represent the mean annual changes during this period in westerly declination, in inclination and in horizontal force:—
| ′ | ′ | ′ | |
| ΔD = | −5.24 | − 0.071 (l − 50) | + 0.033 (λ − 10), |
| ΔI = | −1.58 | + 0.010 (l − 50) | + 0.036 (λ − 10), |
| ΔH = | +23.5 | − 0.59 (l − 50) | − 0.35 (λ − 10). |
Longitude λ is here counted positive to the east. The central position assumed here (lat. 50°, long. 10° E.) falls in the north of Bavaria. In the case of the horizontal force unity represents 1γ. Schmidt found the above formulae to give results in very close agreement with the data at the eight stations which he had employed in determining the constants. These stations ranged from Pavlovsk to Perpignan, and from Stonyhurst to Ekaterinburg in Siberia. Formulae involving the second as well as the first powers of l − l0 and λ − λ0 have also been used, e.g., by A. Tanakadate in the Magnetic Survey of Japan.
Table V.—Declination at St Helena and Cape of Good Hope.
| St Helena. | Cape of Good Hope. | ||
| Date. | Declination. | Date. | Declination. |
| ° ′ | ° ′ | ||
| 1610 | 7 13 E | 1605 | 0 30 E |
| 1677 | 0 40 | 1609 | 0 12 W |
| 1691 | 1 0 W | 1675 | 8 14 |
| 1724 | 7 30 | 1691 | 11 0 |
| 1775 | 12 18 | 1775 | 21 14 |
| 1789 | 15 30 | 1792 | 24 31 |
| 1796 | 15 48 | 1818 | 26 31 |
| 1806 | 17 18 | 1839 | 29 9 |
| 1839 | 22 17 | 1842 | 29 6 |
| 1840 | 22 53 | 1846 | 29 9 |
| 1846 | 23 11 | 1850 | 29 19 |
| 1890 | 23 57 | 1857 | 29 34 |
| 1874 | 30 4 | ||
| 1890 | 29 32 | ||
| 1903 | 28 44 | ||
Table VI.—Secular Change of Declination in the United States (+ to the West).
| Place. | Epoch | 1760 | 70 | 80 | 90 | 1800 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 1900 | 50 |
| ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ||
| Eastport, Maine | −1.2 | 0.0 | +1.2 | +2.1 | +3.2 | +4.0 | +4.5 | +4.9 | +5.0 | +5.6 | +4.5 | +3.0 | +2.1 | +1.0 | +1.8 | +2.4 | |
| Boston, Mass. | −2.7 | −1.9 | −1.0 | 0.0 | +1.1 | +1.9 | +2.7 | +3.5 | +4.2 | +4.4 | +4.0 | +3.3 | +3.1 | +3.0 | +3.2 | +3.4 | |
| Albany, New York | −4.2 | −3.6 | −2.7 | −1.6 | −0.6 | +0.6 | +1.6 | +2.7 | +3.6 | +4.6 | +4.6 | +3.9 | +4.7 | +2.3 | +3.4 | +3.6 | |
| Philadelphia, Penn. | −4.6 | −4.2 | −3.5 | −2.3 | −1.3 | +0.1 | +1.3 | +2.5 | +3.4 | +4.3 | +4.2 | +4.6 | +4.4 | +3.4 | +3.5 | +3.4 | |
| Baltimore, Maryland | −3.9 | −3.4 | −2.7 | −2.0 | −0.9 | 0.0 | +0.9 | +2.0 | +2.7 | +3.4 | +3.9 | +4.0 | +3.9 | +3.6 | +3.5 | +3.2 | |
| Richmond, Virginia | −3.6 | −3.2 | −2.5 | −1.8 | −0.9 | 0.0 | +0.9 | +1.8 | +2.5 | +3.1 | +3.6 | +3.9 | +3.8 | +3.7 | +3.4 | +3.2 | |
| Columbia, S. Carolina | −3.7 | −3.4 | −2.9 | −2.2 | −1.3 | −0.5 | +0.5 | +1.3 | +2.2 | +2.9 | +3.4 | +3.8 | +3.8 | +3.8 | +3.6 | +1.8 | |
| Macon, Georgia | −3.7 | −3.6 | −3.2 | −2.5 | −1.8 | −0.9 | 0.0 | +0.9 | +1.8 | +2.5 | +3.2 | +3.6 | +3.9 | +3.5 | +3.1 | +1.2 | |
| Tampa, Florida | −3.0 | −2.5 | −2.0 | −1.1 | −0.4 | +0.4 | +1.1 | +2.0 | +2.5 | +3.0 | +3.2 | +3.5 | +3.7 | +2.8 | +2.9 | +1.6 | |
| Marquette, Michigan | 0.0 | +1.4 | +2.6 | +3.7 | +4.7 | +5.1 | +4.9 | +3.8 | +2.4 | ||||||||
| Columbus, Ohio | −0.9 | 0.0 | +0.9 | +2.0 | +2.9 | +3.4 | +3.6 | +3.7 | +3.9 | +4.0 | +2.4 | ||||||
| Bloomington, Illinois | −2.4 | −1.5 | −0.4 | +0.4 | +1.5 | +2.4 | +2.8 | +4.2 | +3.9 | +2.9 | +1.0 | ||||||
| Lexington, Kentucky | −0.9 | 0.0 | +0.9 | +1.8 | +2.5 | +3.2 | +3.6 | +3.8 | +3.8 | +3.4 | +1.8 | ||||||
| Chattanooga, Tennessee | −0.9 | 0.0 | +0.9 | +1.8 | +2.5 | +3.2 | +3.6 | +4.0 | +3.5 | +3.1 | +1.6 | ||||||
| Little Rock, Arkansas | −2.3 | −1.5 | −0.9 | +0.1 | +0.8 | +1.7 | +2.0 | +3.6 | +3.7 | +2.3 | −1.2 | ||||||
| Montgomery, Alabama | −3.6 | −3.5 | −3.1 | −2.8 | −2.2 | −1.5 | −0.8 | +0.1 | +0.8 | +1.6 | +2.2 | +2.8 | +3.8 | +3.9 | +2.6 | +0.2 | |
| Alexandria, Louisiana | −2.1 | −1.6 | −0.8 | +0.1 | +0.8 | +1.6 | +2.2 | +3.6 | +3.3 | +2.0 | −1.4 | ||||||
| Northome, Minnesota | −1.7 | −0.6 | +0.6 | +1.7 | +2.8 | +4.2 | +4.4 | +3.5 | 0.0 | ||||||||
| Jamestown, N. Dakota | +1.0 | +1.9 | +3.1 | +4.8 | +1.9 | −2.2 | |||||||||||
| Des Moines, Iowa | −1.5 | −0.6 | +0.6 | +1.5 | +2.5 | +3.8 | +4.5 | +2.7 | −0.6 | ||||||||
| Douglas, Wyoming | −0.8 | 0.0 | +1.2 | +2.3 | +0.5 | −1.6 | |||||||||||
| Emporia, Kansas | +0.6 | +1.6 | +2.7 | +3.8 | +1.7 | −1.8 | |||||||||||
| Pueblo, Colorado | −0.3 | +0.4 | +1.5 | +3.1 | +0.7 | −2.2 | |||||||||||
| Okmulgee, Oklahoma | +0.9 | +1.5 | +2.7 | +3.9 | +1.4 | −2.4 | |||||||||||
| Santa Rosa, New Mexico | −0.4 | +0.4 | +1.4 | +2.6 | +0.4 | −2.4 | |||||||||||
| San Antonio, Texas | −1.1 | −0.5 | −0.5 | +1.1 | +1.8 | +2.7 | +0.9 | −2.4 | |||||||||
| Seattle, Washington | −3.3 | −3.5 | −3.7 | −3.7 | −3.5 | −3.3 | −3.0 | −2.6 | −2.1 | −1.3 | −1.9 | −2.0 | −3.2 | ||||
| Wilson Creek, Washington | −2.1 | −1.5 | −0.4 | −1.0 | −1.6 | −3.2 | |||||||||||
| Detroit, Oregon | −3.8 | −3.9 | −3.9 | −3.7 | −3.4 | −2.9 | −2.5 | −1.8 | −0.8 | −1.8 | −3.8 | ||||||
| Salt Lake, Utah | −1.1 | −0.4 | +1.0 | +1.0 | −0.8 | −2.8 | |||||||||||
| Prescott, Arizona | −1.4 | −0.7 | +0.4 | +0.4 | −1.2 | −3.2 | |||||||||||
| San José, California | −2.6 | −2.9 | −2.9 | −2.9 | −2.7 | −2.5 | −2.3 | −2.0 | −1.5 | −0.8 | −0.4 | −1.9 | −3.8 | ||||
| Los Angeles, ” | −3.4 | −3.4 | −3.5 | −3.2 | −3.0 | −2.7 | −2.1 | −1.6 | −1.1 | −0.9 | −0.3 | −1.6 | −3.6 |
Formulae are also wanted to show how the value of an element, or the rate of change of an element, at a particular place has varied throughout a long period. For comparatively short periods it is best to use formulae of the type E = a + bt + ct², where E denotes the value of an element t years subsequent to some convenient epoch; a, b, c are constants to be determined from the observational data. For longer periods formulae of the type E = a + b sin (mt + n), where a, b, m and n are constants, have been used by Schott16 and others with considerable success. The following examples, due to G. W. Littlehales,17 for the Cape of Good Hope, will suffice for illustration:
| Declination (West) | = 14°.63 + 15°.00 sin {0.61 (t − 1850) + 77°.8}. |
| Inclination (South) | = 49°.11 + 8°.75 sin {0.8 (t − 1850) + 34°.3}. |
Here t denotes the date. It is perhaps hardly necessary to point out that the extension of any of these empirical formulae—whether to places outside the surveyed area, or to times not included in the period of observation—is fraught with danger, which increases rapidly the further the extrapolation is pushed.
Table VII.—Inclination (northerly) and Horizontal Force at London.
| Date. | I. | Date. | I. | Date. | I. | H. | Date. | I. | H. |
| ° ′ | ° ′ | ° ′ | ° ′ | ||||||
| 1576 | 71 50 | 1801 | 70 36.0 | 1857 | 68 24.9 | .17474 | 1891 | 67 33.2 | .18193 |
| 1600 | 72 0 | 1821 | 70 3.4 | 1860 | 69 19.8 | .17550 | 1895 | 67 25.4 | .18278 |
| 1676 | 73 30 | 1830 | 69 38.0 | 1865 | 68 8.7 | .17662 | 1900 | 67 11.8 | .18428 |
| 1723 | 74 42 | 1838 | 69 17.3 | 1870 | 67 58.6 | .17791 | 1905 | 67 3.8 | .18510 |
| 1773 | 72 19 | 1854 | 68 31.1 | 1874 | 67 50.0 | .17903 | 1908 | 67 0.9 | .18515 |
| 1786 | 72 9 |
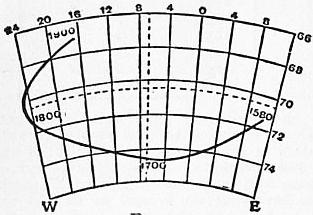 |
| Fig. 5. |
Bauer has employed a convenient graphical method of illustrating secular change. Radii are drawn from the centre of a sphere parallel to the direction of the freely dipping needle, and are produced to intersect the tangent plane drawn at the point which answers to the mean position of the needle during the epoch under consideration. The curve formed by the points of intersection shows the character of the secular change. Fig. 5 (slightly modified from Nature, vol. 57, p. 181) applies to London. The curve is being described in the clockwise direction. This, according to Bauer’s18 own investigation, is the normal mode of description. Schott and Littlehales have found, however, a considerable number of cases where it is difficult to say whether the motion is clockwise or not, while in some stations on both the east and west shores of the Pacific it was clearly anti-clockwise. Fritsche19 dealing with the secular changes from 1600 to 1885—as given by his calculated values of the magnetic elements—at 204 points of intersection of equidistant lines of latitude and longitude, found only sixty-three cases in which the motion was unmistakably clockwise, while in twenty-one cases it was clearly the opposite.
§ 14. All the magnetic elements at any ordinary station show a regular variation in the solar day. To separate this from the irregular changes, means of the hourly readings must be formed making use of a number of days. The amplitude of Diurnal Variations. the diurnal change usually varies considerably with the season of the year. Thus a diurnal inequality derived from all the days of the year combined, or from a smaller number of days selected equally from all the months of the year, can give only the average effect throughout the year. Also unless the hours of maxima and minima at a given station are but slightly variable with the season, the result obtained by combining data from all the months of the year may be a hybrid which does not very closely resemble the phenomena in the majority of individual months. This remark applies in particular to the declination at places within the tropics. One consequence is obviously to make the range of a diurnal inequality which answers to the year as a whole less than the arithmetic mean of the twelve ranges obtained for the constituent months. At stations in temperate latitudes, whilst minor differences of type do exist between the diurnal inequalities for different months of the year, the difference is mainly one of amplitude, and the mean diurnal inequality from all the months of the year gives a very fair idea of the nature of the phenomena in any individual month.
Table VIII.—Diurnal Inequality of Declination, mean from whole year (+ to West).
| Station. | Jan Mayen. | St Petersburg and Pavlovsk. | Greenwich. | Kew. | Parc St Maur. | Tiflis. | Kolaba. | Batavia. | Mauritius. | South Vic- toria Land. | ||||
| Latitude. | 71° 0′ N. | 59° 41′ N. | 51° 28′ N. | 51° 28′ N. | 48° 49′ N. | 41° 43′ N. | 18° 54′ N. | 6° 11′ S. | 20° 6′ S. | 77° 51′ S. | ||||
| Longitude. | 8° 28′ W. | 30° 29′ E. | 0° 0′. | 0° 19′ W. | 2° 29′ E. | 44° 48′ E. | 72° 49′ E. | 106° 49′ E. | 57° 33′ E. | 166° 45′ E. | ||||
| Period. | 1882-1883. | 1873-1885. | 1890-1900. | 1890-1900. | 1883-1897. | 1888-1898. | 1894-1901. | 1883-1894. | 1876-1890. | 1902-1903. | ||||
| a. | q. | a. | q. | a. | a. | q. | a. | a. | q. | a. | a. | a. | q. | |
| Hour. | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ |
| 1 | − 6.6 | −4.2 | −1.3 | −0.7 | −1.4 | −1.5 | −0.9 | −1.4 | −0.7 | −0.2 | +0.1 | +0.1 | + 2.0 | + 0.9 |
| 2 | −10.5 | −6.4 | −1.2 | −0.8 | −1.3 | −1.4 | −0.9 | −1.2 | −0.6 | −0.1 | −0.1 | +0.1 | − 2.1 | − 1.8 |
| 3 | −15.2 | −7.8 | −1.2 | −1.0 | −1.3 | −1.5 | −1.0 | −1.2 | −0.6 | −0.1 | −0.1 | +0.1 | − 5.2 | − 4.5 |
| 4 | −16.9 | −8.4 | −1.4 | −1.3 | −1.4 | −1.7 | −1.3 | −1.2 | −0.5 | −0.1 | 0.0 | +0.2 | − 9.4 | − 6.8 |
| 5 | −17.0 | −8.1 | −1.7 | −1.8 | −1.7 | −2.1 | −1.8 | −1.6 | −0.7 | −0.1 | 0.0 | +0.3 | −12.2 | − 9.0 |
| 6 | −13.7 | −7.0 | −1.9 | −2.3 | −2.1 | −2.4 | −2.3 | −1.9 | −1.2 | −0.6 | +0.1 | +0.4 | −15.3 | −11.7 |
| 7 | − 9.3 | −5.1 | −2.2 | −2.8 | −2.4 | −2.7 | −2.8 | −2.4 | −1.9 | −1.0 | +0.5 | +0.6 | −17.2 | −15.0 |
| 8 | − 6.8 | −3.2 | −2.5 | −3.2 | −2.5 | −2.8 | −3.1 | −2.7 | −2.4 | −1.2 | +1.3 | +1.1 | −21.5 | −17.3 |
| 9 | − 3.7 | −0.6 | −2.3 | −3.0 | −1.9 | −2.1 | −2.5 | −2.3 | −2.3 | −0.7 | +1.7 | +1.8 | −23.5 | −18.1 |
| 10 | − 2.4 | +2.1 | −1.0 | −1.7 | −0.2 | −0.3 | −0.7 | −0.5 | −0.9 | 0.0 | +1.5 | +1.9 | −21.2 | −15.8 |
| 11 | − 0.5 | +4.6 | +1.0 | +0.4 | +2.1 | +2.2 | +1.7 | +2.0 | +1.0 | +0.9 | +0.9 | +1.3 | −15.3 | − 9.2 |
| Noon | + 2.5 | +6.5 | +3.1 | +2.7 | +4.2 | +4.3 | +3.9 | +4.2 | +2.6 | +1.4 | +0.1 | 0.0 | − 9.8 | − 4.9 |
| 1 | + 3.7 | +7.3 | +4.6 | +4.3 | +5.1 | +5.3 | +4.8 | +5.3 | +3.3 | +1.2 | −0.6 | −1.1 | − 3.2 | − 0.1 |
| 2 | + 6.4 | +7.1 | +4.9 | +4.5 | +4.7 | +4.9 | +4.4 | +4.9 | +3.1 | +0.6 | −1.1 | −2.0 | + 3.8 | + 5.9 |
| 3 | + 7.4 | +5.9 | +4.1 | +3.6 | +3.6 | +3.7 | +3.1 | +3.7 | +2.3 | +0.1 | −1.3 | −2.3 | +11.1 | + 9.5 |
| 4 | + 8.5 | +4.3 | +2.7 | +2.3 | +2.2 | +2.4 | +1.8 | +2.3 | +1.3 | −0.2 | −1.2 | −1.8 | +16.6 | +12.9 |
| 5 | +10.6 | +3.0 | +1.5 | +1.3 | +1.1 | +1.2 | +0.7 | +1.1 | +0.6 | −0.1 | −0.9 | −0.9 | +19.9 | +14.6 |
| 6 | +14.2 | +2.3 | +0.6 | +0.7 | +0.3 | +0.4 | +0.2 | +0.2 | +0.2 | 0.0 | −0.6 | −0.1 | +22.0 | +15.5 |
| 7 | +15.2 | +2.2 | 0.0 | +0.4 | −0.3 | −0.2 | −0.1 | −0.4 | +0.1 | +0.1 | −0.4 | +0.1 | +22.0 | +15.9 |
| 8 | +15.8 | +2.6 | −0.4 | +0.2 | −0.9 | −0.6 | −0.3 | −0.9 | −0.1 | +0.2 | −0.2 | +0.1 | +19.9 | +14.6 |
| 9 | +13.2 | +2.6 | −1.0 | 0.0 | −1.2 | −1.0 | −0.5 | −1.3 | −0.4 | +0.1 | 0.0 | +0.1 | +16.0 | +10.6 |
| 10 | + 7.4 | +2.0 | −1.4 | −0.2 | −1.5 | −1.3 | −0.7 | −1.5 | −0.6 | 0.0 | +0.1 | +0.1 | +11.6 | + 7.2 |
| 11 | + 1.1 | +0.5 | −1.6 | −0.4 | −1.6 | −1.4 | −0.8 | −1.6 | −0.7 | 0.0 | +0.1 | +0.1 | + 7.6 | + 4.2 |
| 12 | − 3.6 | −1.8 | −1.5 | −0.6 | −1.6 | −1.5 | −0.9 | −1.6 | −0.8 | −0.1 | +0.1 | +0.1 | + 3.3 | + 1.9 |
| Range | 32.8 | 15.7 | 7.4 | 7.7 | 7.6 | 8.1 | 7.9 | 8.0 | 5.7 | 2.6 | 3.0 | 4.2 | 45.5 | 34.0 |
Tables VIII. to XI. give mean diurnal inequalities derived from all the months of the year combined, the figures representing the algebraic excess of the hourly value over the mean for the twenty-four hours. The + sign denotes in Table VIII. that the north end of the needle is to the west of its mean position for the day; in Tables IX. to XI. it denotes that the element—the dip being the north or south as indicated—is numerically in excess of the twenty-four hour mean. The letter “a” denotes that all days have been included except, as a rule, those characterized by specially large disturbances. The letter “q” denotes that the results are derived from a limited number of days selected as being specially quiet, 363 i.e. free from disturbance. In all cases the aperiodic or non-cyclic element—indicated by a difference between the values found for the first and second midnights of the day—has been eliminated in the usual way, i.e. by treating it as accumulating at a uniform rate throughout the twenty-four hours. The years from which the data were derived are indicated. The algebraically greatest and least of the hourly values are printed in heavy type; the range thence derived is given at the foot of the tables.
Table IX.—Diurnal Inequality of Horizontal Force, mean from whole year (Unit 1γ = .00001 C.G.S.)
| Station. | Jan Mayen. | St Petersburg and Pavlovsk. | Greenwich. | Kew. | Parc St Maur. | Tiflis. | Kolaba. | Batavia. | Mauritius. | S. Victoria Land. | ||
| Period. | 1882-1883. | 1873-1885. | 1890-1900. | 1890-1900. | 1883-1897. | 1888-1898. | 1894-1901. | 1883-1894. | 1883-1890. | 1902-1903. | ||
| a. | q. | a. | q. | a. | q. | a. | a. | q. | a. | a. | a. | |
| Hour. | ||||||||||||
| 1 | −57 | −22 | + 4 | + 5 | + 4 | + 4 | + 5 | + 3 | −10 | −11 | − 3 | −12 |
| 2 | −64 | −24 | + 4 | + 4 | + 3 | + 4 | + 5 | + 3 | − 9 | −10 | − 1 | −13 |
| 3 | −74 | −25 | + 4 | + 4 | + 3 | + 4 | + 5 | + 3 | − 9 | − 8 | + 1 | −14 |
| 4 | −69 | −24 | + 4 | + 4 | + 3 | + 4 | + 5 | + 4 | − 9 | − 7 | + 2 | −15 |
| 5 | −60 | −22 | + 5 | + 4 | + 3 | + 4 | + 6 | + 4 | − 9 | − 5 | + 3 | −15 |
| 6 | −37 | −19 | + 4 | + 4 | + 1 | + 2 | + 4 | + 4 | − 7 | − 1 | + 4 | −12 |
| 7 | −15 | −15 | + 2 | + 2 | − 3 | − 1 | + 1 | + 2 | − 1 | + 5 | + 7 | − 9 |
| 8 | − 1 | −13 | − 3 | − 4 | − 9 | − 7 | − 5 | − 3 | + 8 | +14 | + 9 | − 7 |
| 9 | + 8 | −12 | −10 | −10 | −16 | −13 | −12 | − 8 | −19 | +24 | + 9 | − 3 |
| 10 | +17 | −12 | −16 | −16 | −20 | −18 | −17 | −10 | +26 | +31 | + 9 | + 3 |
| 11 | +32 | −10 | −19 | −20 | −19 | −18 | −16 | − 7 | +30 | +35 | + 9 | + 7 |
| Noon | +49 | − 4 | −17 | −18 | −13 | −12 | −12 | − 1 | +26 | +31 | + 8 | +12 |
| 1 | +65 | + 8 | −12 | −13 | − 7 | − 7 | − 7 | + 4 | +19 | +22 | + 7 | +18 |
| 2 | +78 | +22 | − 6 | − 6 | − 1 | − 2 | − 4 | + 5 | +10 | +10 | + 2 | +20 |
| 3 | +89 | +37 | 0 | 0 | + 2 | + 1 | − 1 | + 3 | + 2 | − 1 | − 2 | +19 |
| 4 | +83 | +43 | + 3 | + 3 | + 5 | + 3 | 0 | − 1 | − 3 | − 9 | − 6 | +18 |
| 5 | +68 | +49 | + 5 | + 5 | + 7 | + 5 | + 2 | − 4 | − 7 | −13 | − 7 | +15 |
| 6 | +37 | +43 | + 6 | + 6 | + 9 | + 7 | + 4 | − 6 | − 8 | −14 | − 7 | +11 |
| 7 | +13 | +30 | + 7 | + 7 | +10 | + 8 | + 6 | − 4 | − 9 | −15 | − 7 | + 5 |
| 8 | −11 | +15 | + 8 | + 8 | +10 | + 8 | + 7 | − 1 | −10 | −16 | − 8 | + 0 |
| 9 | −33 | + 1 | + 9 | + 9 | + 8 | + 7 | + 7 | + 1 | −11 | −16 | − 8 | − 4 |
| 10 | −36 | −10 | + 8 | + 9 | + 7 | + 6 | + 6 | + 2 | −11 | −16 | − 8 | − 7 |
| 11 | −40 | −16 | + 7 | + 8 | + 6 | + 6 | + 6 | + 3 | −10 | −15 | − 7 | − 9 |
| 12 | −51 | −20 | + 6 | + 6 | + 5 | + 5 | + 6 | + 3 | −10 | −13 | − 5 | −11 |
| Range | 163 | 74 | 28 | 29 | 30 | 26 | 24 | 15 | 41 | 51 | 17 | 35 |
Table X.—Diurnal Inequality of Vertical Force, mean from whole year (Unit 1γ).
| Station. | Jan Mayen. | St Petersburg and Pavlovsk. | Greenwich. | Kew. | Parc St Maur. | Tiflis. | Kolaba. | Batavia. | Mauritius. | South Vic- toria Land. | ||
| Period. | 1882-1883. | 1873-1885. | 1890-1900. | 1891-1900. | 1883-1897. | 1888-1898. | 1894-1901. | 1883-1894. | 1884-1890. | 1902-1903. | ||
| a. | q. | a. | q. | a. | q. | a. | a. | q. | a. | a. | a. | |
| Hour | ||||||||||||
| 1 | +65 | + 3 | − 7 | − 1 | − 3 | + 1 | 0 | + 2 | + 4 | + 7 | + 2 | +13 |
| 2 | +65 | + 2 | − 7 | − 1 | − 4 | + 1 | 0 | + 2 | + 4 | + 5 | + 2 | +12 |
| 3 | +56 | − 1 | − 7 | − 1 | − 4 | 0 | − 1 | + 1 | + 3 | + 4 | + 2 | +10 |
| 4 | +37 | − 5 | − 6 | 0 | − 3 | 0 | 0 | + 1 | + 3 | + 3 | + 2 | + 8 |
| 5 | +16 | − 7 | − 5 | 0 | − 2 | + 1 | 0 | + 2 | + 5 | + 2 | + 2 | + 3 |
| 6 | − 7 | − 8 | − 4 | 0 | − 1 | + 1 | + 1 | + 3 | + 7 | + 1 | + 2 | 0 |
| 7 | −17 | − 6 | − 3 | 0 | 0 | 0 | + 1 | + 3 | + 6 | 0 | + 3 | 0 |
| 8 | −14 | − 4 | − 2 | 0 | 0 | − 1 | 0 | + 3 | 0 | − 3 | + 4 | − 2 |
| 9 | − 9 | 0 | − 3 | − 1 | − 3 | − 4 | − 4 | − 1 | − 8 | −11 | + 5 | − 6 |
| 10 | − 6 | + 5 | − 2 | − 2 | − 6 | − 8 | − 8 | − 7 | −14 | −20 | + 3 | −13 |
| 11 | − 6 | +10 | − 3 | − 4 | − 9 | −11 | −12 | −11 | −15 | −26 | 0 | −17 |
| Noon | −10 | +16 | − 3 | − 5 | −10 | −11 | −12 | −11 | −10 | −27 | − 4 | −20 |
| 1 | −13 | +21 | − 1 | − 4 | − 6 | − 8 | − 9 | − 9 | − 3 | −21 | − 7 | −20 |
| 2 | −24 | +23 | + 2 | − 1 | 0 | − 3 | − 3 | − 5 | + 1 | −13 | − 9 | −16 |
| 3 | −31 | +20 | + 8 | + 2 | + 5 | + 2 | + 2 | − 1 | + 4 | − 4 | − 8 | −12 |
| 4 | −40 | +13 | + 9 | + 3 | + 8 | + 5 | + 6 | + 1 | + 3 | + 4 | − 5 | − 6 |
| 5 | −48 | + 2 | +10 | + 3 | + 9 | + 6 | + 7 | + 3 | 0 | +10 | − 3 | − 1 |
| 6 | −53 | − 9 | +10 | + 3 | +10 | + 7 | + 8 | + 4 | 0 | +13 | 0 | + 3 |
| 7 | −47 | −18 | + 9 | + 3 | + 9 | + 6 | + 7 | + 3 | 0 | +14 | 0 | + 6 |
| 8 | −36 | −20 | + 8 | + 3 | + 7 | + 5 | + 6 | + 3 | + 1 | +14 | + 1 | + 9 |
| 9 | − 7 | −19 | + 6 | + 2 | + 5 | + 5 | + 5 | + 3 | + 2 | +14 | + 2 | +11 |
| 10 | +18 | −13 | + 3 | + 2 | + 3 | + 4 | + 3 | + 3 | + 3 | +13 | + 2 | +12 |
| 11 | +42 | − 5 | − 2 | 0 | 0 | + 3 | + 2 | + 3 | + 3 | +11 | + 2 | +12 |
| 12 | +54 | 0 | − 5 | − 1 | − 2 | + 2 | + 1 | + 2 | + 3 | + 9 | + 2 | +13 |
| Range | 118 | 43 | 17 | 8 | 20 | 18 | 20 | 15 | 22 | 41 | 14 | 33 |
When comparing results from different stations, it must be remembered that the disturbing forces required to cause a change of 1′ in declination and in dip vary directly, the former as the horizontal force, the latter as the total force. Near a magnetic pole the horizontal force is relatively very small, and this accounts, at least partly, for the difference between the declination phenomena at Jan Mayen and South Victoria Land on the one hand and at Kolaba, Batavia and Mauritius on the other. There is, however, another cause, already alluded to, viz. the variability in the type of the diurnal inequality in tropical stations. With a view to illustrating this point Table XII. gives diurnal inequalities of declination for June and December for a number of stations lying between 45° N. and 45° S. latitude. Some of the results are represented graphically in fig. 6, plus ordinates representing westerly deflection. At the northmost station, Toronto, the difference between the two months is mainly a matter of amplitude, the range being much larger at midsummer than at midwinter. The conspicuous phenomenon at both seasons is the rapid swing to the west from 8 or 9 a.m. to 364 1 or 2 p.m. At the extreme southern station, Hobart—at nearly equal latitude—the rapid diurnal movement is to the east, and so in the opposite direction to that in the northern hemisphere, but it again takes place at nearly the same hours in June (midwinter) as in December. If, however, we take a tropical station such as Trivandrum or Kolaba, the phenomena in June and December are widely different in type. At Trivandrum—situated near the magnetic equator in India—we have in June the conspicuous forenoon swing to the west seen at Toronto, occurring it is true slightly earlier in the day; but in December at the corresponding hours the needle is actually swinging to the east, just as it is doing at Hobart. In June the diurnal inequality of declination at tropical stations—whether to the north of the equator like Trivandrum, or to the south of it like Batavia—is on the whole of the general type characteristic of temperate regions in the northern hemisphere; whereas in December the inequality at these stations resembles that of temperate regions in the southern hemisphere. Comparing the inequalities for June in Table XII. amongst themselves, and those for December amongst themselves, one can trace a gradual transformation from the phenomena seen at Toronto to those seen at Hobart. At a tropical station the change from the June to the December type is probably in all cases more or less gradual, but at some stations the transition seems pretty rapid.
Table XI.—Diurnal Inequality of Inclination mean from whole year.
| Station. | Jan Mayen. | St Petersburg and Pavlovsk. | Greenwich. | Kew. | Parc St Maur. | Tiflis. | Kolaba. | Batavia. | Mauritius. | South Vic- toria Land. | ||
| End Dipping | North. | North. | North. | North. | North. | North. | North. | South. | South. | South. | ||
| Period. | 1882-1883. | 1873-1885. | 1890-1900. | 1891-1900. | 1883-1897. | 1888-1898. | 1894-1901. | 1883-1894. | 1884-1890. | 1902-1903. | ||
| a. | q. | a. | q. | a. | q. | a. | a. | q. | a. | a. | a. | |
| Hour | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ |
| 1 | +4.6 | +1.5 | −0.5 | −0.3 | −0.4 | −0.3 | −0.3 | −0.1 | +0.6 | +0.9 | +0.3 | +0.6 |
| 2 | +5.0 | +1.6 | −0.5 | −0.3 | −0.3 | −0.2 | −0.3 | −0.1 | +0.6 | +0.8 | +0.2 | +0.7 |
| 3 | +5.6 | +1.6 | −0.5 | −0.3 | −0.3 | −0.2 | −0.3 | −0.1 | +0.5 | +0.6 | 0.0 | +0.7 |
| 4 | +5.0 | +1.5 | −0.4 | −0.3 | −0.3 | −0.2 | −0.4 | −0.2 | +0.5 | +0.5 | −0.0 | +0.7 |
| 5 | +4.2 | +1.4 | −0.5 | −0.3 | −0.2 | −0.2 | −0.4 | −0.2 | +0.7 | +0.3 | −0.1 | +0.7 |
| 6 | +2.4 | +1.2 | −0.4 | −0.3 | −0.1 | −0.1 | −0.3 | −0.1 | +0.8 | +0.1 | −0.2 | +0.5 |
| 7 | +0.7 | +0.9 | −0.2 | −0.1 | +0.2 | +0.1 | 0.0 | 0.0 | +0.5 | −0.2 | −0.3 | +0.4 |
| 8 | −0.1 | +0.8 | +0.1 | +0.3 | +0.6 | +0.4 | +0.4 | +0.3 | −0.2 | −0.8 | −0.4 | +0.3 |
| 9 | −0.7 | +0.8 | +0.6 | +0.6 | +1.0 | +0.8 | +0.7 | +0.5 | −1.2 | −1.7 | −0.4 | +0.1 |
| 10 | −1.2 | +0.9 | +1.0 | +1.0 | +1.1 | +1.0 | +0.9 | +0.3 | −1.9 | −2.7 | −0.5 | −0.2 |
| 11 | −2.2 | +0.8 | +1.2 | +1.2 | +1.0 | +0.9 | +0.7 | 0.0 | −2.1 | −3.3 | −0.6 | −0.4 |
| Noon | −3.4 | +0.4 | +1.1 | +1.1 | +0.6 | +0.6 | +0.4 | −0.5 | −1.6 | −3.1 | −0.7 | −0.7 |
| 1 | −4.5 | −0.2 | +0.7 | +0.7 | +0.3 | +0.2 | +0.2 | −0.6 | −0.8 | −2.4 | −0.8 | −0.9 |
| 2 | −5.6 | −1.2 | +0.4 | +0.4 | +0.1 | +0.1 | +0.2 | −0.5 | −0.2 | −1.3 | −0.6 | −1.0 |
| 3 | −6.3 | −2.2 | +0.2 | +0.1 | 0.0 | 0.0 | +0.2 | −0.3 | +0.3 | −0.2 | −0.3 | −1.0 |
| 4 | −6.1 | −2.9 | 0.0 | −0.1 | −0.1 | −0.1 | +0.2 | +0.1 | +0.3 | +0.7 | +0.1 | −0.9 |
| 5 | −5.1 | −3.2 | −0.1 | −0.3 | −0.2 | −0.2 | +0.1 | +0.4 | +0.2 | +1.3 | +0.4 | −0.7 |
| 6 | −3.1 | −2.9 | −0.2 | −0.3 | −0.3 | −0.3 | 0.0 | +0.5 | +0.2 | +1.5 | +0.5 | −0.5 |
| 7 | −1.7 | −2.2 | −0.3 | −0.4 | −0.4 | −0.4 | −0.2 | +0.4 | +0.3 | +1.6 | +0.5 | −0.2 |
| 8 | +0.3 | −1.3 | −0.3 | −0.5 | −0.4 | −0.4 | −0.3 | +0.2 | +0.4 | +1.6 | +0.6 | 0.0 |
| 9 | +2.0 | −0.3 | −0.4 | −0.6 | −0.4 | −0.4 | −0.3 | +0.1 | +0.5 | +1.6 | +0.6 | +0.2 |
| 10 | +2.5 | +0.5 | −0.5 | −0.6 | −0.4 | −0.3 | −0.3 | 0.0 | +0.6 | +1.5 | +0.6 | +0.4 |
| 11 | +3.0 | +1.0 | −0.5 | −0.6 | −0.4 | −0.3 | −0.3 | 0.0 | +0.6 | +1.4 | +0.5 | +0.5 |
| 12 | +4.0 | +1.3 | −0.5 | −0.4 | −0.4 | −0.3 | −0.3 | −0.1 | +0.6 | +1.2 | +0.4 | +0.6 |
| Range | 11.9 | 4.8 | 1.7 | 1.8 | 1.5 | 1.4 | 1.3 | 1.1 | 2.9 | 4.9 | 1.4 | 1.7 |
Table XII.—Diurnal Inequality of Declination (+ to West).
| Station. | Toronto. | Kolaba. | Trivandrum. | Batavia. | St Helena. | Mauritius. | Cape. | Hobart. | ||||||||
| Month. | June. | Dec. | June. | Dec. | June. | Dec. | June. | Dec. | June. | Dec. | June. | Dec. | June. | Dec. | June. | Dec. |
| Hour | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ |
| 1 | −0.4 | −0.1 | −0.3 | 0.0 | −0.3 | −0.1 | +0.1 | +0.1 | −0.1 | −0.4 | 0.0 | +0.1 | −0.4 | −0.7 | +0.8 | +1.1 |
| 2 | −0.2 | +0.4 | −0.3 | +0.1 | −0.4 | +0.1 | −0.1 | +0.1 | −0.2 | −0.1 | −0.2 | +0.2 | −0.5 | −0.4 | +0.3 | +1.1 |
| 3 | −0.2 | −0.1 | −0.3 | +0.1 | −0.4 | +0.3 | −0.2 | +0.2 | −0.2 | +0.1 | −0.2 | +0.4 | −0.7 | −0.1 | −0.1 | +1.0 |
| 4 | −1.2 | −0.4 | −0.3 | +0.3 | −0.5 | +0.5 | −0.3 | +0.3 | −0.3 | +0.3 | −0.2 | +0.7 | −0.6 | +0.3 | −0.1 | +1.1 |
| 5 | −2.9 | −0.6 | −0.7 | +0.4 | −0.7 | +0.7 | −0.3 | +0.5 | −0.5 | +0.6 | −0.3 | +1.0 | −0.7 | +1.0 | 0.0 | +1.7 |
| 6 | −5.2 | −0.6 | −1.6 | +0.5 | −1.6 | +1.1 | −0.5 | +1.2 | −1.0 | +0.9 | −0.4 | +1.7 | −1.0 | +2.2 | 0.0 | +2.7 |
| 7 | −6.2 | −0.9 | −2.2 | +0.7 | −1.7 | +1.4 | −1.1 | +2.0 | −2.2 | +1.9 | −1.1 | +2.6 | −1.6 | +3.3 | −0.1 | +4.4 |
| 8 | −6.0 | −1.2 | −2.1 | +0.2 | −1.1 | +0.9 | −0.4 | +2.3 | −1.5 | +2.2 | −1.0 | +2.4 | −0.8 | +3.6 | +0.1 | +5.6 |
| 9 | −4.4 | −1.8 | −1.1 | −0.1 | −0.2 | +0.5 | +0.5 | +2.0 | −0.3 | +1.3 | +0.2 | +2.0 | +0.7 | +3.1 | +0.6 | +5.6 |
| 10 | −1.5 | −1.1 | 0.0 | −0.2 | +0.6 | +0.3 | +0.9 | +1.3 | +0.3 | +0.2 | +1.2 | +1.1 | +1.6 | +1.6 | +1.2 | +3.6 |
| 11 | +2.1 | +0.6 | +1.2 | 0.0 | +1.2 | +0.1 | +1.0 | +0.4 | +0.5 | −1.0 | +1.4 | 0.0 | +1.5 | +0.1 | +1.0 | +0.7 |
| Noon | +4.8 | +2.2 | +2.1 | 0.0 | +1.4 | −0.4 | +0.7 | −0.6 | +0.3 | −1.4 | +1.0 | −1.4 | +0.8 | −1.0 | −0.1 | −2.6 |
| 1 | +6.1 | +3.2 | +2.0 | −0.2 | +1.1 | −0.8 | +0.3 | −1.4 | +0.3 | −1.2 | +0.1 | −2.2 | +0.3 | −1.8 | −1.4 | −5.1 |
| 2 | +6.1 | +3.2 | +1.6 | −0.3 | +0.7 | −0.9 | −0.2 | −1.8 | +0.2 | −0.4 | −0.9 | −2.5 | −0.3 | −1.9 | −2.2 | −6.2 |
| 3 | +5.2 | +2.4 | +0.9 | −0.3 | +0.3 | −0.9 | −0.7 | −1.9 | +0.2 | +0.4 | −1.5 | −2.2 | −0.3 | −1.4 | −2.4 | −5.8 |
| 4 | +3.6 | +1.5 | +0.2 | −0.3 | +0.1 | −0.8 | −0.8 | −1.6 | +0.7 | +0.6 | −1.3 | −1.6 | +0.2 | −0.8 | −1.6 | −4.8 |
| 5 | +1.8 | +0.5 | 0.0 | −0.2 | 0.0 | −0.4 | −0.5 | −1.2 | +1.1 | +0.4 | −0.3 | −1.0 | +0.5 | −0.8 | −0.7 | −3.3 |
| 6 | +0.7 | −0.1 | +0.1 | −0.2 | +0.2 | −0.4 | −0.1 | −0.7 | +1.0 | +0.1 | +0.5 | −0.5 | +0.5 | −0.6 | −0.4 | −1.9 |
| 7 | 0.0 | −0.8 | +0.3 | −0.2 | +0.5 | −0.4 | +0.1 | −0.6 | +0.6 | −0.4 | +0.7 | −0.3 | +0.4 | −0.8 | 0.0 | −1.0 |
| 8 | 0.0 | −1.2 | +0.4 | −0.1 | +0.5 | −0.3 | +0.2 | −0.5 | +0.5 | −0.7 | +0.7 | −0.3 | +0.3 | −0.9 | +0.5 | −0.3 |
| 9 | −0.5 | −1.4 | +0.3 | −0.1 | +0.4 | −0.2 | +0.4 | −0.3 | +0.4 | −0.9 | +0.6 | −0.2 | +0.2 | −0.9 | +1.1 | 0.0 |
| 10 | −0.5 | −1.7 | +0.1 | 0.0 | +0.2 | −0.1 | +0.4 | −0.1 | +0.2 | −1.0 | +0.4 | −0.1 | +0.1 | −1.0 | +1.3 | +0.6 |
| 11 | −0.7 | −1.1 | −0.1 | −0.1 | 0.0 | −0.1 | +0.3 | 0.0 | +0.1 | −0.8 | +0.3 | 0.0 | 0.0 | −1.0 | +1.3 | +0.9 |
| 12 | −0.6 | −0.7 | −0.2 | −0.1 | −0.2 | −0.1 | +0.2 | +0.1 | −0.1 | −0.6 | +0.1 | +0.1 | −0.2 | −1.0 | +1.1 | +1.2 |
| Range | 12.3 | 5.0 | 4.3 | 1.0 | 3.1 | 2.3 | 2.1 | 4.2 | 3.3 | 3.6 | 2.9 | 5.1 | 3.2 | 5.5 | 3.7 | 11.8 |
§ 15. In the case of the horizontal force there are, as Table IX. shows, two markedly different types of diurnal inequality. In the one type, exemplified by Pavlovsk or Greenwich, the force is below its mean value in the middle of the day; it has a principal minimum about 10 or 11 a.m., and morning and evening maxima, the latter usually the largest. In the other type, exemplified by Kolaba or Batavia, the horizontal force is above its mean in the middle of the 365 day, and has a maximum about 11 a.m. The second type may be regarded as the tropical type. At tropical stations, such as Kolaba, Batavia, Manila and St Helena, the type is practically the same in summer as in winter, and is the same whether the station is north or south of the equator. Similarly, what we may call the temperate type is seen—with comparatively slight modifications—both in summer and winter at stations such as Greenwich or Pavlovsk. In winter, it is true, the pronounced daily minimum is a little later and the early morning maximum is relatively more important than in summer. There is not, as in the case of the declination, any essential difference between the phenomena at temperate stations in the northern and southern hemispheres.
 |
| Fig. 6. |
With diminishing latitude, there is a gradual transition from the temperate to the tropical type of horizontal force diurnal variation, and at stations whose latitude is under 45° there is a very appreciable variation in type with the season. The mean diurnal variation for the year at Tiflis in Table IX. really represents a struggle between the two types, in which on the whole the temperate type prevails. If we take the diurnal variations at Tiflis for midsummer and midwinter, we find the former essentially of the temperate, the latter essentially of the tropical type. A similar conflict may be seen in the mean diurnal inequality for the year at the Cape of Good Hope, but there the tropical type on the whole predominates, and it prevails more at midwinter than at midsummer. Toronto and Hobart, though similar in latitude to Tiflis, show a closer approach to the temperate type. Still at both stations the hours during which the force is below its mean value tend to extend back towards midnight, especially at midsummer. The amplitude of the horizontal force range appears less at intermediate stations, such as Tiflis, than at stations in either higher or lower latitudes. There is a very great difference in this respect between the north and the south of India.
§ 16. In the case of the vertical force in higher temperate latitudes—at Pavlovsk for instance—the diurnal inequalities from “all” and from “quiet” days differ somewhat widely in amplitude and slightly even in type. In mean latitudes, e.g. at Tiflis, there is often a well marked double period in the mean diurnal inequality for the whole year; but even at Tiflis this is hardly, if at all, apparent in the winter months. In the summer months the double period is distinctly seen at Kew and Greenwich, though the evening maximum is always pre-eminent. Speaking generally, the time of the minimum, or principal minimum, varies much less with the season than that of the maximum. At Kew, for instance, on quiet days the minimum falls between 11 a.m. and noon in almost all the months of the year, but the time of the maximum varies from about 4 p.m. in December to 7 p.m. in June. At Kolaba the time of the minimum is nearly independent of the season; but the changes from positive to negative in the forenoon and from negative to positive in the afternoon are some hours later in winter than in summer. At Batavia the diurnal inequality varies very little in type with the season, and there is little evidence of more than one maximum and minimum in the day. At Batavia, as at Kolaba, negative values occur near noon; but it must be remembered that while at Kolaba and more northern stations vertical force urges the north pole of a magnet downwards, the reverse is true of Batavia, as the dip is southerly. At St Helena vertical force is below its mean value in the forenoon, but the change from − to + occurs at noon, or but little later, both in winter and summer. At the Cape of Good Hope the phenomena at midsummer are similar to those at Kolaba, the force being below its mean value from about 9 a.m. to 3 p.m. and above it throughout the rest of the day; but at midwinter there is a conspicuous double period, the force being below its mean from 1 a.m. to 7 a.m. as well as from 11 a.m. to 3 p.m., and thus resembling the all-day annual results at Greenwich. At Hobart vertical force is below its mean value from 1 a.m. to 9 a.m. at midsummer, and from 4 a.m. to noon at midwinter; while the force is above its mean persistently throughout the afternoon both in summer and winter, there is at midwinter a well marked secondary minimum about 6 p.m., almost the same hour as that at which the maximum for the day is observed in summer.
Table XIII.—Range of the Diurnal Inequality of Declination.
| Place. | Period. | Jan. | Feb. | March. | April. | May. | June. | July. | Aug. | Sept. | Oct. | Nov. | Dec. |
| ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ||
| Pavlovsk | 1890-1900 a | 4.93 | 6.15 | 8.58 | 10.93 | 12.18 | 12.27 | 11.82 | 11.38 | 8.70 | 6.87 | 5.54 | 4.63 |
| ” | 1890-1900 q | 2.96 | 4.20 | 8.73 | 11.28 | 12.89 | 13.28 | 12.31 | 11.70 | 9.37 | 6.91 | 3.95 | 2.66 |
| Ekatarinburg | 1890-1900 a | 3.33 | 4.32 | 7.63 | 11.19 | 11.82 | 11.58 | 11.09 | 10.45 | 8.13 | 5.60 | 3.73 | 3.14 |
| Greenwich | 1865-1896 a | 5.87 | 7.07 | 9.40 | 11.42 | 10.55 | 10.90 | 10.82 | 10.93 | 9.66 | 8.15 | 6.41 | 5.15 |
| Kew | 1890-1900 a | 4.92 | 6.06 | 9.08 | 10.95 | 10.66 | 10.92 | 10.59 | 11.01 | 9.49 | 7.73 | 5.37 | 4.46 |
| ” | 1890-1900 q | 4.07 | 4.76 | 8.82 | 10.57 | 10.92 | 10.62 | 10.18 | 11.01 | 9.76 | 7.51 | 4.75 | 3.34 |
| Toronto | 1842-1848 a | 5.96 | 6.05 | 9.18 | 9.94 | 11.55 | 12.34 | 12.21 | 13.14 | 10.76 | 6.96 | 6.32 | 4.97 |
| Manila | 1890-1900 a | 1.79 | 1.09 | 2.13 | 3.02 | 3.84 | 3.94 | 4.21 | 4.89 | 4.53 | 1.83 | 0.85 | 1.33 |
| Trivandrum | 1853-1864 a | 2.06 | 1.48 | 0.79 | 1.67 | 2.90 | 3.06 | 3.06 | 3.64 | 3.31 | 1.27 | 2.14 | 2.33 |
| Batavia | 1884-1899 a | 4.18 | 4.64 | 3.57 | 2.93 | 2.38 | 2.03 | 2.31 | 3.16 | 3.80 | 4.51 | 4.50 | 4.19 |
| St Helena | 1842-1847 a | 3.72 | 5.19 | 4.93 | 3.30 | 2.64 | 3.24 | 3.42 | 3.59 | 2.40 | 4.43 | 4.05 | 3.54 |
| Mauritius | 1876-1890 a | 5.2 | 6.1 | 6.3 | 4.7 | 4.1 | 2.9 | 3.4 | 4.9 | 5.0 | 5.5 | 5.6 | 5.1 |
| Cape | 1841-1846 a | 5.14 | 8.21 | 7.27 | 5.00 | 3.91 | 3.21 | 3.54 | 4.98 | 4.33 | 5.96 | 6.36 | 5.47 |
| Hobart | 1841-1848 a | 11.66 | 11.80 | 9.50 | 7.26 | 4.56 | 3.70 | 4.61 | 5.89 | 8.24 | 11.01 | 12.05 | 11.81 |
§ 17. Variations of inclination are connected with those of horizontal and vertical force by the relation
δI = ½ sin 2I {V−1δV − H−1 δH}.
Thus in temperate latitudes where V is considerably in excess of H, whilst diurnal changes in V are usually less than those in H, it is the latter which chiefly dominate the diurnal changes in inclination. When the H influence prevails, I has its highest values at hours when H is least. This explains why the dip is above its mean value near midday at stations in Table XI. from Pavlovsk to Parc St Maur. Near the magnetic equator the vertical force has the greater influence. This alone would tend to make a minimum dip in the late forenoon, and this minimum is accentuated owing to the altered type of the horizontal force diurnal variation, whose maximum now coincides closely with the minimum in the vertical force. This accounts for the prominence of the minimum in the diurnal variation of the inclination at Kolaba and Batavia, and the large amplitude of the range. Tiflis shows an intermediate type of diurnal variation; there is a minimum near noon, as in tropical stations, but inclination is also below its mean for some hours near midnight. The type really varies at Tiflis according to the season of the year. In June—as in the mean equality from the whole year—there is a well marked double period; there is a principal minimum at 2 p.m. and a secondary one about 4 a.m.; a principal maximum about 9 a.m. and a secondary one about 6 p.m. In December, however, only a single period is recognizable, with a minimum about 8 a.m. and a maximum about 7 p.m. The type of diurnal inequality seen 366 at the Cape of Good Hope does not differ much from that seen at Batavia. Only a single period is clearly shown. The maximum occurs about 8 or 9 p.m. throughout the year. The time of the minimum is more variable; at midsummer it occurs about 11 a.m., but at midwinter three or four hours later. At Hobart the type varies considerably with the season. In June (midwinter) a double period is visible. The principal minimum occurs about 8 a.m., as at the Cape. But, corresponding to the evening maximum seen at the Cape, there is now only a secondary maximum, the principal maximum occurring about 1 p.m. At midsummer the principal maximum is found—as at Kew or Greenwich—about 10 or 11 a.m., the principal minimum about 4 p.m.
§ 18. Even at tropical stations a considerable seasonal change is usually seen in the amplitude of the diurnal inequality in at least one of the magnetic elements. At stations in Europe, and generally in temperate latitudes, the amplitude varies notably in all the elements. Table XIII. gives particulars of the inequality range of declination derived from hourly readings at selected stations, arranged in order of latitude from north to south. The letters “a” and “q” are used in the same sense as before. At temperate stations in either hemisphere—e.g. Pavlovsk, Greenwich or Hobart—the range is conspicuously larger in summer than in winter. In northern temperate stations a decided minimum is usually apparent in December. There is, on the other hand, comparatively little variation in the range from April to August. Sometimes, as at Kew and Greenwich, there is at least a suggestion of a secondary minimum at midsummer. Manila and Trivandrum show a transition from the December minimum, characteristic of the northern stations, to the June minimum characteristic of the southern, there being two conspicuous minima in February or March and in November or October. At St Helena there are two similar minima in May and September, while a third apparently exists in December. It will be noticed that at both Pavlovsk and Kew the annual variation in the range is specially prominent in the quiet day results.
Table XIV. gives a smaller number of data analogous to those of Table XIII., comprising inequality ranges for horizontal force, vertical force and inclination. In some cases the number of years from which the data were derived seems hardly sufficient to give a smooth annual variation. It should also be noticed that unless the same group of years is employed the data from two stations are not strictly comparable. The difference between the all and quiet day vertical force data at Pavlovsk is remarkably pronounced. The general tendency in all the elements is to show a reduced range at midwinter; but in some cases there is also a distinct reduction in the range at midsummer. This double annual period is particularly well marked at Batavia.
Table XIV.—Ranges in the Diurnal Inequalities.
| Jan. | Feb. | March. | April. | May. | June. | July. | Aug. | Sept. | Oct. | Nov. | Dec. | |||
| H (unit 1γ) | ||||||||||||||
| Pavlovsk | 1890-1900 | a | 12 | 20 | 32 | 46 | 47 | 49 | 49 | 44 | 39 | 32 | 17 | 11 |
| ” | ” | q | 12 | 17 | 31 | 42 | 45 | 45 | 42 | 40 | 37 | 31 | 17 | 10 |
| Ekatarinburg | ” | a | 11 | 15 | 29 | 37 | 40 | 40 | 39 | 36 | 33 | 27 | 13 | 9 |
| Kew | ” | q | 15 | 17 | 26 | 36 | 38 | 39 | 38 | 38 | 35 | 27 | 20 | 11 |
| Toronto | 1843-1848 | a | 23 | 21 | 24 | 28 | 29 | 29 | 26 | 28 | 41 | 25 | 21 | 20 |
| Batavia | 1883-1898 | a | 49 | 47 | 54 | 60 | 51 | 48 | 50 | 53 | 58 | 52 | 43 | 40 |
| St Helena | 1843-1847 | a | 43 | 41 | 48 | 53 | 46 | 40 | 40 | 45 | 41 | 40 | 40 | 32 |
| Mauritius | 1883-1890 | a | 21 | 15 | 21 | 23 | 20 | 21 | 20 | 22 | 20 | 21 | 21 | 20 |
| Cape of Good Hope | 1841-1846 | a | 13 | 10 | 13 | 13 | 15 | 16 | 14 | 18 | 21 | 14 | 17 | 20 |
| Hobart | 1842-1848 | a | 42 | 43 | 34 | 28 | 19 | 17 | 22 | 23 | 23 | 35 | 39 | 42 |
| V (unit 1γ) | ||||||||||||||
| Pavlovsk | 1890-1900 | a | 15 | 27 | 29 | 24 | 26 | 20 | 23 | 19 | 23 | 20 | 18 | 14 |
| ” | ” | q | 4 | 5 | 9 | 13 | 13 | 12 | 13 | 10 | 9 | 7 | 5 | 4 |
| Ekatarinburg | ” | a | 10 | 15 | 17 | 21 | 22 | 19 | 20 | 16 | 14 | 13 | 11 | 9 |
| Kew | 1891-1900 | q | 7 | 10 | 20 | 25 | 31 | 27 | 28 | 23 | 20 | 15 | 9 | 6 |
| Toronto | 1843-1848 | a | 12 | 14 | 17 | 23 | 26 | 14 | 27 | 32 | 34 | 25 | 19 | 18 |
| Batavia | 1883-1898 | a | 42 | 48 | 48 | 45 | 31 | 31 | 32 | 29 | 41 | 50 | 40 | 33 |
| St Helena | 1843-1847 | a | 16 | 13 | 12 | 14 | 13 | 11 | 17 | 11 | 17 | 11 | 15 | 18 |
| Mauritius | 1884-1890 | a | 12 | 16 | 18 | 15 | 14 | 13 | 15 | 21 | 20 | 16 | 13 | 11 |
| Cape of Good Hope | 1841-1846 | a | 29 | 47 | 41 | 38 | 21 | 12 | 14 | 19 | 19 | 35 | 33 | 28 |
| Hobart | 1842-1848 | a | 25 | 27 | 22 | 23 | 24 | 21 | 22 | 28 | 26 | 22 | 23 | 27 |
| Inclination | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ||
| Pavlovsk | 1890-1900 | a | 0.97 | 1.24 | 2.07 | 2.79 | 2.72 | 2.88 | 2.85 | 2.64 | 2.52 | 2.18 | 1.20 | 0.89 |
| Ekatarinburg | ” | a | 0.79 | 0.94 | 1.70 | 2.08 | 2.25 | 2.19 | 2.18 | 2.08 | 2.00 | 1.70 | 0.88 | 0.69 |
| Kew | ” | q | 0.98 | 1.01 | 1.38 | 1.86 | 2.05 | 2.02 | 2.05 | 2.15 | 1.98 | 1.57 | 1.27 | 0.63 |
| Toronto | 1843-1848 | a | 1.15 | 0.94 | 1.19 | 1.23 | 1.31 | 1.37 | 1.13 | 1.26 | 1.87 | 1.16 | 1.09 | 1.05 |
| Batavia | 1883-1898 | a | 4.88 | 5.22 | 5.56 | 5.62 | 4.21 | 4.05 | 4.24 | 4.17 | 5.13 | 5.58 | 4.51 | 3.85 |
| Cape of Good Hope | 1842-1846 | a | 1.55 | 2.29 | 2.23 | 2.23 | 1.60 | 1.41 | 1.54 | 1.70 | 1.86 | 2.03 | 1.55 | 2.04 |
| Hobart | 1842-1848 | a | 1.95 | 2.16 | 1.72 | 1.62 | 1.23 | 1.16 | 1.28 | 1.42 | 1.39 | 1.75 | 2.04 | 2.10 |
§ 19. When discussing diurnal inequalities it is sometimes convenient to consider the components of the horizontal force in and perpendicular to the astronomical meridian, rather than the horizontal force and declination. If N and W be the components of H to astronomical north and west, and D the westerly declination, N = H cos D, W = H sin D. Thus corresponding small variations in N, W, H and D are connected by the relations:—
δN = cos DδH − H sin DδD, δW = sin DδH + H cos DδD.
If δH and δD denote the departures of H and D at any hour of the day from their mean values, then δN and δW represent the corresponding departures of N and W from their mean values. In this way diurnal inequalities may be calculated for N and W when those for H and D are known. The formulae suppose δD to be expressed in absolute measure, i.e. 1′ of arc has to be replaced by 0.0002909. If we take as an example a station at which H is .185 then HδD = .0000538 (number of minutes in δD). In other words, employing 1γ as unit of force, one replaces HδD by 5.38δD, where δD represents declination change expressed as usual in minutes of arc. In calculating diurnal inequalities for N and W, one ought, strictly speaking, to assign to H and D the exact mean values belonging to these elements for the month or the year being dealt with. For practical purposes, however, a slight departure from the true mean values is immaterial, and one can make use of a constant value for several successive years without sensible error. As an example, Table XV. gives the mean diurnal inequality for the whole year in N and W at Falmouth, as calculated from the 12 years 1891 to 1902. The unit employed is 1γ.
The data in Table XV. are closely similar to corresponding Kew data, and are presumably fairly applicable to the whole south of England for the epoch considered. At Falmouth there is comparatively little seasonal variation in the type of the diurnal variation in either N or W. The amplitude of the diurnal range varies, however, largely with the season, as will appear from Table XVI., which is based on the same 12 years as Table XV.
Diurnal inequalities in N and W lend themselves readily to the construction of what are known as vector diagrams. These are curves showing the direction and intensity at each hour of the day of the horizontal component of the disturbing force to which the diurnal inequality may be regarded as due. Figs. 7 and 8, taken from the Phil. Trans. vol. 204A, will serve as examples. They refer to the mean diurnal inequalities for the months stated at Kew (1890 to 1900) and Falmouth (1891 to 1902), thick lines relating to Kew, thin to Falmouth. NS and EW represent the geographical north-south and east-west directions; their intersection answers to the origin (thick lines for Kew, thin for Falmouth). The line from the origin to M represents the magnetic meridian. The line from the origin to any cross—the number indicating the corresponding hour counted from midnight as 0—represents the magnitude and direction at that hour of the horizontal component of the disturbing force to which the diurnal inequality may be assigned. The cross marks the point whose rectangular co-ordinates are the values of δN and δW derived from the diurnal inequalities of these elements. In figs. 7 and 8 the distances of the points N, E, S, W from their corresponding origin represents 10γ. The tendency to form a loop near midnight, seen in the November and December 367 curves, is characteristic of the winter months at Kew and Falmouth. The shape is less variable in summer than in winter; but even in summer the portion answering to the hours 6 p.m. to 6 a.m. varies a good deal. The object of presenting the Kew and Falmouth curves side by side is to emphasize the close resemblance between the magnetic phenomena at places in similar latitudes, though over 200 miles apart and exhibiting widely different ranges for their meteorological elements. With considerable change of latitude however the shape of vector diagrams changes largely.
Table XV.—Diurnal Inequalities in N. and W. at Falmouth (unit 1γ).
| Hour. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| N. | a.m. | + 6 | + 5 | + 5 | + 5 | + 6 | + 6 | + 5 | + 1 | − 6 | −14 | −20 | −20 |
| p.m. | −17 | −12 | − 6 | − 1 | + 3 | + 6 | + 9 | + 9 | + 9 | + 8 | + 7 | + 7 | |
| W. | a.m. | − 2 | − 2 | − 3 | − 4 | − 6 | − 9 | −13 | −17 | −19 | −13 | − 3 | +11 |
| p.m. | +20 | +22 | +17 | +11 | + 6 | + 4 | + 2 | + 1 | 0 | − 1 | − 2 | − 2 | |
§ 20. Any diurnal inequality can be analysed into a series of Fourier Series. harmonic terms whose periods are 24 hours and submultiples thereof. The series may be expressed in either of the equivalent forms:—
a1 cos t + b1 sin t + a2 cos 2t + b2 sin 2t + ...
c1 sin (t + α1) + c2 sin (2t + α2) + ....
Table XVI.—Ranges in Diurnal Inequalities at Falmouth (unit 1γ).
| Jan. | Feb. | March. | April. | May. | June. | July. | Aug. | Sept. | Oct. | Nov. | Dec. | |
| N. | 21 | 23 | 30 | 39 | 39 | 37 | 37 | 39 | 36 | 32 | 24 | 15 |
| W. | 20 | 24 | 46 | 54 | 55 | 55 | 54 | 56 | 51 | 39 | 24 | 15 |
In both forms t denotes time, counted usually from midnight, one hour of time being interpreted as 15° of angle. Form (i) is that utilized in actually calculating the constants a, b, ... Once the a, b, ... constants are known, the c, α, ... constants are at once derivable from the formulae:—
tan αn = an / bn; cn = an / sin αn = bn / cos αn = √(an² + bn²).
The a, b, c, α constants are called sometimes Fourier, sometimes Bessel coefficients.
 |
| (From Phil. Trans.) |
| Fig. 7. |
By taking a sufficient number of terms a series can always be obtained which will represent any set of diurnal inequality figures; but unless one can obtain a close approach to the observational figures from the terms possessing the periods 24, 12, 8 and 6 hours the physical significance and general utility of the analysis is somewhat problematical. In the case of the magnetic elements, the 24 and 12 hour terms are usually much the more important; the 24-hour term is generally, but by no means always, the larger of the two. The c constants give the amplitudes of the harmonic terms or waves, the α constants the phase angles. An advance of 1 hour in the time of occurrence of the first (and subsequent, if any) maximum and minimum answers to an increase of 15° in α1 of 30° in α2, of 45° in α3, of 60° in α4 and so on. In the case of magnetic elements the phase angles not infrequently possess a somewhat large annual variation. It is thus essential for a minute study of the phenomena at any station to carry out the analysis for the different seasons of the year, and preferably for the individual months. If the a and b constants are known for all the individual months of one year, or for all the Januarys of a series of years, we have only to take their arithmetic means to obtain the corresponding constants for the mean diurnal inequality of the year, or for the diurnal inequality of the average January of the series of years. This, however, is obviously not true of the c or α constants, unless the phase angle is absolutely unchanged throughout the contributory months or years. This is a point requiring careful attention, because when giving values of c and α for the whole year some authorities give the arithmetic mean of the c’s and α’s calculated from the diurnal inequalities of the individual months of the year, others give the values obtained for c and α from the mean diurnal inequality of the whole year. The former method inevitably supplies a larger value for c than the latter, supposing α to vary with the season. At some observatories, e.g. Greenwich and Batavia, it has long been customary to publish every year values of the Fourier coefficients for each month, and to include other elements besides the declination. For a thoroughly satisfactory comparison of different stations, it is necessary to have data from one and the same epoch; and preferably that epoch should include at least one 11-year period. There are, however, few stations which can supply the data required for such a comparison and we have to make the best of what is available. Information is naturally most copious for the declination. For this element E. Engelenburg20 gives values of C1, C2, C3, C4, and of α1, α2, α3, α4 for each month of the year for about 50 stations, ranging from Fort Rae (62° 6′ N. lat.) to Cape Horn (55° 5′ S. lat.). From the results for individual stations, Engelenburg derives a series of means which he regards as representative of 11 different zones of latitude. His data for individual stations refer to different epochs, and some are based on only one year’s observations. The original observations also differ in reliability; thus the results are of somewhat unequal value. The mean results for Engelenburg’s zones must naturally have some of the sources of uncertainty reduced; but then the fundamental idea represented by the arrangement in zones is open to question. The majority of the data in Table XVII. are taken from Engelenburg, but the phase angles have been altered so as to apply to westerly declination. The stations are arranged in order of latitude from north to south; in a few instances results are given for quiet days. The figures represent in all cases arithmetic means derived from the 12 monthly values. In the table, so far as is known, the local mean time of the observatory has been employed. This is a point requiring attention, because most observatories employ Greenwich time, or time based on Greenwich or some other national observatory, and any departure from local time enters into the values of the constants. The data for Victoria Land refer to the “Discovery’s” 1902-1903 winter quarters, where the declination, taken westerly, was about 207°.5.
As an example of the significance of the phase angles in Table XVII., take the ordinary day data for Kew. The times of occurrence of the maxima are given by t + 234° = 450° for the 24-hour term, 2t + 39°.7 = 90° or = 450° for the 12-hour term, and so on, taking an hour in t as equivalent to 15°.
Thus the times of the maxima are:—
24-hour term, 2 h. 24 m. p.m.; 12-hour term, 1 h. 41 m. a.m. and p.m.
8-hour term, 4 h. 41 m. a.m., 0 h. 41 m. p.m., and 8 h. 41 m. p.m.
6-hour term, 0 h. 33 m. a.m. and p.m., and 6 h. 33 m. a.m. and p.m.
The minima, or extreme easterly positions in the waves, lie midway between successive maxima. All four terms, it will be seen, have maxima at some hour between 0h. 30m. and 2h. 30m. p.m. They thus reinforce one another strongly from 1 to 2 p.m., accounting for the prominence of the maximum in the early afternoon.
 |
| (From Phil. Trans.) |
| Fig. 8. |
The utility of a Fourier analysis depends largely on whether the several terms have a definite physical significance. If the 24-hour and 12-hour terms, for instance, represent the action of forces whose distribution over the earth or whose seasonal variation is essentially different, then the analysis helps to distinguish these forces, and may assist in their being tracked to their ultimate source. Suppose, for example, one had reason to think the magnetic diurnal variation due to some meteorological phenomenon, e.g. heating of the earth’s atmosphere, then a comparison of Fourier coefficients, if such existed, for the two sets of phenomena would be a powerful method of investigation.
Table XVII.—Amplitudes and Phase Angles for Diurnal Inequality of Declination.
| Place. | Epoch. | c1. | c2. | c3. | c4. | α1. | α2. | α3. | α4. |
| ′ | ′ | ′ | ′ | ° | ° | ° | ° | ||
| Fort Rae (all) | 1882-1883 | 18.49 | 8.22 | 1.99 | 2.07 | 156.5 | 41.9 | 308 | 104 |
| Fort Rae (quiet) | ” | 9.09 | 4.51 | 1.32 | 0.73 | 166.5 | 37.5 | 225 | 350 |
| Ekatarinburg | 1841-1862 | 2.57 | 1.81 | 0.73 | 0.22 | 223.3 | 7.4 | 204 | 351 |
| Potsdam | 1890-1899 | 2.81 | 1.90 | 0.83 | 0.31 | 239.9 | 32.6 | 237 | 49 |
| Kew (ordinary) | 1890-1900 | 2.91 | 1.79 | 0.79 | 0.27 | 234.0 | 39.7 | 239 | 57 |
| Kew (quiet) | ” | 2.37 | 1.82 | 0.90 | 0.30 | 227.3 | 42.1 | 240 | 55 |
| Falmouth (quiet) | 1891-1902 | 2.18 | 1.82 | 0.91 | 0.29 | 226.2 | 40.5 | 238 | 56 |
| Parc St Maur | 1883-1899 | 2.70 | 1.87 | 0.85 | 0.30 | 238.6 | 32.5 | 235 | 95 |
| Toronto | 1842-1848 | 2.65 | 2.34 | 1.00 | 0.33 | 213.7 | 34.9 | 238 | 350 |
| Washington | 1840-1842 | 2.38 | 1.86 | 0.65 | 0.33 | 223.0 | 26.6 | 223 | 53 |
| Manila | 1890-1900 | 0.53 | 0.58 | 0.43 | 0.17 | 266.3 | 50.7 | 226 | 89 |
| Trivandrum | 1853-1864 | 0.54 | 0.46 | 0.29 | 0.10 | 289.0 | 49.6 | 114 | |
| Batavia | 1883-1899 | 0.80 | 0.88 | 0.43 | 0.13 | 332.0 | 163.2 | 5 | 236 |
| St. Helena | 1842-1847 | 0.68 | 0.61 | 0.63 | 0.34 | 275.8 | 171.4 | 27 | 244 |
| Mauritius | 1876-1890 | 0.86 | 1.11 | 0.76 | 0.22 | 21.6 | 172.7 | 350 | 161 |
| C. of G. Hope | 1841-1846 | 1.15 | 1.13 | 0.80 | 0.35 | 287.7 | 156.0 | 351 | 193 |
| Melbourne | 1858-1863 | 2.52 | 2.45 | 1.23 | 0.35 | 27.4 | 176.7 | 9 | 193 |
| Hobart | 1841-1848 | 2.29 | 2.15 | 0.87 | 0.32 | 33.6 | 170.8 | 349 | 185 |
| S. Georgia | 1882-1883 | 2.13 | 1.28 | 0.76 | 0.31 | 30.3 | 185.3 | 7 | 180 |
| Victoria Land (all) | 1902-1903 | 20.51 | 4.81 | 1.21 | 1.32 | 158.7 | 306.9 | 292 | 303 |
| Victoria Land (quieter) | ” | 15.34 | 4.05 | 1.24 | 1.18 | 163.8 | 312.9 | 261 |
§ 21. Fourier coefficients of course often vary much with the season of the year. In the case of the declination this is especially true of the phase angles at tropical stations. To enter on details for a number of stations would unduly occupy space. A fair idea of the variability in the case of declination in temperate latitudes may be derived from Table XVIII., which gives monthly values for Kew derived from ordinary days of an 11-year period 1890-1900.
Fourier analysis has been applied to the diurnal inequalities of the other magnetic elements, but more sparingly. Such results are illustrated by Table XIX., which contains data derived from quiet days at Kew from 1890 to 1900. Winter includes November to February, Summer May to August, and Equinox the remaining four months. In this case the data are derived from mean diurnal inequalities for the season specified. In the case of the c or amplitude coefficients the unit is 1′ for I (inclination), and 1γ for H and V (horizontal and vertical force). At Kew the seasonal variation in the amplitude is fairly similar for all the elements. The 24-hour and 12-hour terms tend to be largest near midsummer, and least near midwinter; but the 8-hour and 6-hour terms have two well-marked maxima near the equinoxes, and a clearly marked minimum near midsummer, in addition to one near midwinter. On the other hand, the phase angle phenomena vary much for the different elements. The 24-hour term, for instance, has its maximum earlier in winter than in summer in the case of the declination and vertical force, but the exact reverse holds for the inclination and the horizontal force.
Table XVIII.—Kew Declination: Amplitudes and Phase Angles
(local mean time).
| Month. | c1. | c2. | c3. | c4. | α1. | α2. | α3. | α4. |
| ′ | ′ | ′ | ′ | ° | ° | ° | ° | |
| January | 1.79 | 0.86 | 0.41 | 0.27 | 251.2 | 29.8 | 254 | 64 |
| February | 2.41 | 1.11 | 0.57 | 0.30 | 242.0 | 27.7 | 235 | 39 |
| March | 3.05 | 1.98 | 1.11 | 0.45 | 233.2 | 36.1 | 223 | 49 |
| April | 3.35 | 2.48 | 1.17 | 0.39 | 224.8 | 39.2 | 228 | 61 |
| May | 3.57 | 2.38 | 0.87 | 0.17 | 221.3 | 50.8 | 245 | 89 |
| June | 3.83 | 2.39 | 0.74 | 0.05 | 212.6 | 46.7 | 239 | 72 |
| July | 3.72 | 2.30 | 0.77 | 0.11 | 214.6 | 48.1 | 233 | 8 |
| August | 3.64 | 2.43 | 1.05 | 0.18 | 228.2 | 57.2 | 244 | 51 |
| September | 3.35 | 2.02 | 1.04 | 0.35 | 236.9 | 55.3 | 245 | 70 |
| October | 2.69 | 1.69 | 0.92 | 0.48 | 240.1 | 35.6 | 235 | 65 |
| November | 1.94 | 1.06 | 0.51 | 0.32 | 248.3 | 28.3 | 247 | 61 |
| December | 1.61 | 0.81 | 0.35 | 0.20 | 255.1 | 22.0 | 243 | 56 |
§ 22. If secular change proceeded uniformly throughout the year, the value En of any element at the middle of the nth month of the year would be connected with E, the mean value for the whole year, by the formula En = E + (2n − 13)s/24, Annual Inequality. where s is the secular change per annum. For the present purpose, difference in the lengths of the months may be neglected. If one applies to En − E the correction −(2n − 13)s/24 one eliminates a regularly progressive secular change; what remains is known as the annual inequality. If only a short period of years is dealt with, irregularities in the secular change from year to year, or errors of observation, may obviously simulate the effect of a real annual inequality. Even when a long series of years is included, there is always a possibility of a spurious inequality arising from annual variation in the instruments, or from annual change in the conditions of observation. J. Liznar,21 from a study of data from a number of stations, arrived at certain mean results for the annual inequalities in declination and inclination in the northern and southern hemispheres, and J. Hann22 has more recently dealt with Liznar’s and newer results. Table XX. gives a variety of data, including the mean results given by Liznar and Hann. In the case of declination + denotes westerly position; in the case of inclination it denotes a larger dip (whether the inclination be north or south). According to Liznar declination in summer is to the west of the normal position in both hemispheres. The phenomena, however, at Parc St Maur are, it will be seen, the exact opposite of what Liznar regards as normal; and whilst the Potsdam results resemble his mean in type, the range of the inequality there, as at Parc St Maur, is relatively small. Of the three sets of data given for Kew the first two are derived in a similar way to those for other stations; the first set are based on quiet days only, the second on all but highly disturbed days. Both these sets of results are fairly similar in type to the Parc St Maur results, but give larger ranges; they are thus even more opposed to Liznar’s normal type. The last set of data for Kew is of a special kind. During the 11 years 1890 to 1900 the Kew declination magnetograph showed to within 1′ the exact secular change as derived from the absolute observations; also, if any annual variation existed in the position of the base lines of the curves it was exceedingly small. Thus the accumulation of the daily non-cyclic changes shown by the curves should closely represent the combined effects of secular change and annual inequality. Eliminating the secular change, we arrive at an annual inequality, based on all days of the year including the highly disturbed. It is this annual inequality which appears under the heading s. It is certainly very unlike the annual inequality derived in the usual way. Whether the difference is to be wholly assigned to the fact that highly disturbed days contribute in the one case, but not in the other, is a question for future research.
Table XIX.—Kew Diurnal Inequality: Amplitudes and Phase Angles (local mean time).
| c1. | c2. | c3. | c4. | α1. | α2. | α3. | α4. | ||
| ° | ° | ° | ° | ||||||
| I | Winter | 0.240 | 0.222 | 0.104 | 0.076 | 250.0 | 91.8 | 344 | 194 |
| Equinox | 0.601 | 0.290 | 0.213 | 0.127 | 290.3 | 135.5 | 4 | 207 | |
| Summer | 0.801 | 0.322 | 0.172 | 0.070 | 312.5 | 155.5 | 39 | 238 | |
| H | Winter | 3.62 | 3.86 | 1.81 | 1.13 | 82.9 | 277.3 | 154 | 6 |
| Equinox | 10.97 | 5.87 | 3.32 | 1.84 | 109.6 | 303.5 | 167 | 16 | |
| Summer | 14.85 | 6.23 | 2.35 | 0.95 | 130.3 | 316.5 | 199 | 41 | |
| V | Winter | 2.46 | 1.67 | 0.86 | 0.42 | 153.9 | 300.8 | 108 | 280 |
| Equinox | 6.15 | 4.70 | 2.51 | 0.94 | 117.2 | 272.3 | 99 | 289 | |
| Summer | 8.63 | 6.45 | 2.24 | 0.55 | 122.0 | 272.4 | 100 | 285 | |
In the case of the inclination, Liznar found that in both hemispheres the dip (north in the northern, south in the southern hemisphere) was larger than the normal when the sun was in perihelion, corresponding to an enhanced value of the horizontal force in summer in the northern hemisphere.
In the case of annual inequalities, at least that of the declination, it is a somewhat suggestive fact that the range seems to become less as we pass from older to more recent results, or from shorter to longer periods of years. Thus for Paris from 1821 to 1830 Arago deduced a range of 2′ 9″. Quiet days at Kew from 1890 to 1894 gave a range of 1′.2, while at Potsdam Lüdeling got a range 30% larger than that in Table XX. when considering the shorter period 1891-1899. Up to the present, few individual results, if any, can claim a very high degree of certainty. With improved instruments and methods it may be different in the future.
Table XX.—Annual Inequality.
| Declination. | Inclination. | |||||||||||
| Liznar, N. Hemi- sphere. | Potsdam, 1891-1906. | Parc St Maur, 1888-1897. | Kew (1890-1900). | Batavia, 1883-1893. | Mauritius. | Liznar & Hann’s mean. | Potsdam. | Parc St. Maur. | Kew. | |||
| q. | o. | s. | ||||||||||
| ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | |
| January | −0.25 | +0.04 | +0.01 | +0.08 | +0.03 | +0.32 | +0.23 | +0.06 | +0.49 | +0.32 | +0.44 | −0.03 |
| February | −0.54 | −0.11 | 0.00 | +0.48 | +0.25 | −0.20 | +0.19 | +0.29 | +0.39 | +0.56 | +0.29 | −0.07 |
| March | −0.27 | +0.04 | +0.17 | +0.03 | +0.05 | −1.02 | −0.12 | +0.27 | +0.20 | +0.38 | +0.13 | +0.53 |
| April | −0.03 | +0.10 | +0.12 | −0.31 | −0.14 | −0.90 | −0.11 | +0.30 | −0.08 | −0.02 | −0.13 | +0.18 |
| May | +0.19 | +0.07 | −0.11 | −0.39 | −0.28 | +0.29 | −0.30 | +0.08 | −0.43 | −0.29 | −0.37 | −0.15 |
| June | +0.46 | +0.13 | −0.14 | −0.47 | −0.39 | +0.78 | −0.13 | −0.19 | −0.70 | −0.77 | −0.59 | −0.35 |
| July | +0.48 | +0.14 | −0.17 | −0.30 | −0.13 | +0.44 | −0.08 | −0.44 | −0.72 | −0.67 | −0.27 | −0.13 |
| August | +0.47 | +0.11 | +0.01 | +0.08 | +0.05 | +0.52 | −0.18 | −0.38 | −0.47 | −0.23 | −0.05 | −0.19 |
| September | +0.31 | +0.01 | 0.00 | +0.29 | +0.24 | −0.02 | +0.06 | −0.06 | −0.06 | +0.16 | +0.01 | +0.20 |
| October | −0.07 | −0.11 | +0.09 | +0.06 | +0.01 | −0.26 | +0.03 | −0.04 | +0.31 | +0.27 | +0.19 | 0.00 |
| November | −0.30 | −0.28 | −0.05 | +0.17 | +0.11 | −0.02 | +0.08 | −0.01 | +0.51 | +0.30 | +0.43 | +0.18 |
| December | −0.36 | −0.14 | +0.05 | +0.26 | +0.23 | +0.05 | +0.35 | +0.06 | +0.55 | +0.19 | +0.24 | −0.29 |
| Range | 1.02 | 0.42 | 0.34 | 0.95 | 0.64 | 1.80 | 0.65 | 0.74 | 1.27 | 1.33 | 1.03 | 0.88 |
§ 23. The inequalities in Table XX. may be analysed—as has in fact been done by Hann—in a series of Fourier terms, whose periods are the year and its submultiples. Fourier series can also be formed representing the annual variation in the Annual Variation Fourier Coefficients. amplitudes of the regular diurnal inequality, and its component 24-hour, 12-hour, &c. waves, or of the amplitude of the absolute daily range (§ 24). To secure the highest theoretical accuracy, it would be necessary in calculating the Fourier coefficients to allow for the fact that the “months” from which the observational data are derived are not of uniform length. The mid-times, however, of most months of the year are but slightly displaced from the position they would occupy if the 12 months were exactly equal, and these displacements are usually neglected. The loss of accuracy cannot be but trifling, and the simplification is considerable.
The Fourier series may be represented by
P1 sin (t + θ1) + P2 sin (2t + θ2) + ...,
where t is time counted from the beginning of the year, one month being taken as the equivalent of 30°, P1, P2 represent the amplitudes, and θ1, θ2 the phase angles of the first two terms, whose periods are respectively 12 and 6 months. Table XXI. gives the values of these coefficients in the case of the range of the regular diurnal inequality for certain specified elements and periods at Kew23 and Falmouth.23a In the case of P1 and P2 the unit is 1′ for D and I, and 1γ for H and V. M denotes the mean value of the range for the 12 months. The letters q and o represent quiet and ordinary day results. S max. means the years 1892-1895, with a mean sun spot frequency of 75.0. S min. for Kew means the years 1890, 1899 and 1900 with a mean sun spot frequency of 9.6; for Falmouth it means the years 1899-1902 with a mean sun spot frequency of 7.25.
Increase in θ1 or θ2 means an earlier occurrence of the maximum or maxima, 1° answering roughly to one day in the case of the 12-month term, and to half a day in the case of the 6-month term. P1/M and P2/M both increase decidedly as we pass from years of many to years of few sun spots; i.e. relatively considered the range of the regular diurnal inequality is more variable throughout the year when sun spots are few than when they are many.
The tendency to an earlier occurrence of the maximum as we pass from quiet days to ordinary days, or from years of sun spot minimum to years of sun spot maximum, which appears in the table, appears also in the case of the horizontal force—at least in the case of the annual term—both at Kew and Falmouth. The phenomena at the two stations show a remarkably close parallelism. At both, and this is true also of the absolute ranges, the maximum of the annual term falls in all cases near midsummer, the minimum near midwinter. The maxima of the 6-month terms fall near the equinoxes.
Table XXI.—Annual Variation of Diurnal Inequality Range. Fourier Coefficients.
| P1. | P2. | θ1. | θ2. | P1/M. | P2/M. | ||
| Kew | Do | 3.36 | 0.94 | 279° | 280° | 0.40 | 0.11 |
| 1890-1900 | Dq | 3.81 | 1.22 | 275° | 273° | 0.47 | 0.15 |
| Iq | 0.67 | 0.16 | 264° | 269° | 0.42 | 0.10 | |
| Hq | 13.6 | 3.0 | 269° | 261° | 0.48 | 0.11 | |
| Vq | 11.7 | 2.2 | 282° | 242° | 0.63 | 0.12 | |
| S max. | Kew | 4.50 | 1.26 | 277° | 282° | 0.47 | 0.13 |
| Dq | Falmouth | 4.10 | 1.40 | 277° | 286° | 0.43 | 0.15 |
| S min. | Kew | 3.35 | 1.10 | 274° | 269° | 0.49 | 0.16 |
| Dq | Falmouth | 3.19 | 1.14 | 275° | 277° | 0.49 | 0.17 |
§ 24. Allusion has already been made in § 14 to one point which requires fuller discussion. If we take a European station such as Kew, the general character of, say, the declination does not vary very much with the season, but still it does Absolute Range. vary. The principal minimum of the day, for instance, occurs from one to two hours earlier in summer than in winter. Let us suppose for a moment that all the days of a month are exactly alike, the difference in type between successive months coming in per saltum. Suppose further that having formed twelve diurnal inequalities from the days of the individual months of the year, we deduce a mean diurnal inequality for the whole year by combining these twelve inequalities and taking the mean. The hours of maximum and minimum being different for the twelve constituents, it is obvious that the resulting maximum will normally be less than the arithmetic mean of the twelve maxima, and the resulting minimum (arithmetically) less than the arithmetic mean of the twelve minima. The range—or algebraic excess of the maximum over the minimum—in the mean diurnal inequality for the year is thus normally less than the arithmetic mean of the twelve ranges from diurnal inequalities for the individual months. Further, as we shall see later, there are differences in type not merely between the different months of the year, but even between the same months in different years. Thus the range of the mean diurnal inequality for, say, January based on the combined observations of, say, eleven Januarys may be and generally will be slightly less than the arithmetic mean of the ranges obtained from the Januarys separately. At Kew, for instance, taking the ordinary days of the 11 years 1890-1900, the arithmetic mean of the diurnal inequality ranges of declination from the 132 months treated independently was 8′.52, the mean range from the 12 months of the year (the eleven Januarys being combined into one, and so on) was 8′.44, but the mean range from the whole 4,000 odd days superposed was only 8′.03. Another consideration is this: a diurnal inequality is usually based on hourly readings, and the range deduced is thus an under-estimate unless the absolute maximum and minimum both happen to come exactly at an hour. These considerations would alone suffice to show that the absolute range in individual days, i.e. the difference between the algebraically largest and least values of the element found any time during the 24 hours, must on the average exceed the 370 range in the mean diurnal inequality for the year, however this latter is formed. Other causes, moreover, are at work tending in the same direction. Even in central Europe, the magnetic curves for individual days of an ordinary month often differ widely amongst themselves, and show maxima and minima at different times of the day. In high latitudes, the variation from day to day is sometimes so great that mere eye inspection of magnetograph curves may leave one with but little idea as to the probable shape of the resultant diurnal curve for the month. Table XXII. gives the arithmetic mean of the absolute daily ranges from a few stations. The values which it assigns to the year are the arithmetic means of the 12 monthly values. The Mauritius data are for different periods, viz. declination 1875, 1880 and 1883 to 1890, horizontal force 1883 to 1890, vertical force 1884 to 1890. The other data are all for the period 1890 to 1900.
Table XXII.—Mean Absolute Daily Ranges (Units 1′ for Declination, 1γ for H and V).
| Jan. | Feb. | Mar. | April. | May. | June. | July. | Aug. | Sept. | Oct. | Nov. | Dec. | Year. | |
| Declination. | |||||||||||||
| Pavlovsk | 13.42 | 17.20 | 18.22 | 17.25 | 17.76 | 15.91 | 16.89 | 16.57 | 16.75 | 15.70 | 13.87 | 12.37 | 15.99 |
| Ekatarinburg | 7.33 | 9.54 | 11.90 | 12.89 | 13.63 | 13.03 | 12.78 | 12.21 | 11.23 | 9.44 | 7.86 | 6.85 | 10.72 |
| Kew. All days | 11.16 | 13.69 | 15.93 | 15.00 | 14.90 | 13.65 | 14.13 | 14.22 | 14.57 | 14.07 | 11.71 | 9.80 | 13.57 |
| Kew. Ordinary days | 10.14 | 11.87 | 14.19 | 14.24 | 13.85 | 13.26 | 13.47 | 13.67 | 13.71 | 13.10 | 10.40 | 9.00 | 12.58 |
| Kew. Quiet days | 6.12 | 7.57 | 10.59 | 11.84 | 12.09 | 11.95 | 11.60 | 11.93 | 10.86 | 9.16 | 6.54 | 5.08 | 9.61 |
| Zi-ka-wei | 3.88 | 3.25 | 6.22 | 7.04 | 7.15 | 7.40 | 7.77 | 8.06 | 6.73 | 4.68 | 2.91 | 2.52 | 5.63 |
| Mauritius | 6.93 | 7.79 | 7.11 | 5.75 | 4.87 | 4.03 | 4.36 | 6.00 | 6.28 | 6.71 | 6.99 | 6.78 | 6.13 |
| Horizontal force. | |||||||||||||
| Pavlovsk | 52.4 | 74.5 | 79.1 | 80.1 | 86.2 | 79.0 | 86.7 | 77.6 | 76.7 | 67.3 | 55.7 | 45.9 | 71.8 |
| Ekatarinburg | 33.2 | 43.1 | 48.4 | 51.7 | 56.2 | 54.1 | 56.7 | 51.7 | 49.3 | 44.1 | 34.1 | 29.3 | 46.0 |
| Mauritius | 37.9 | 35.0 | 36.2 | 37.6 | 35.0 | 34.1 | 33.8 | 34.5 | 36.6 | 37.4 | 37.8 | 35.3 | 35.9 |
| Vertical force. | |||||||||||||
| Pavlovsk | 27.0 | 50.4 | 54.7 | 43.2 | 45.3 | 34.8 | 42.1 | 35.5 | 42.5 | 37.5 | 33.5 | 25.5 | 39.3 |
| Ekatarinburg | 17.4 | 26.6 | 29.2 | 30.1 | 29.6 | 27.6 | 29.6 | 26.1 | 25.2 | 22.1 | 19.6 | 16.4 | 24.9 |
| Mauritius | 17.1 | 19.5 | 20.1 | 17.3 | 16.5 | 15.5 | 17.1 | 22.0 | 22.7 | 19.4 | 16.7 | 15.2 | 18.2 |
A comparison of the absolute ranges in Table XXII. with the inequality ranges for the same stations derivable from Tables VIII. to X. is most instructive. At Mauritius the ratio of the absolute to the inequality range is for D 1.38, for H 1.76, and for V 1.19. At Pavlovsk the corresponding ratios are much larger, viz. 2.16 for D, 2.43 for H, and 2.05 for V. The declination data for Kew in Table XXII. illustrate other points. The first set of data are derived from all days of the year. The second omit the highly disturbed days. The third answer to the 5 days a month selected as typically quiet. The yearly mean absolute range from ordinary days at Kew in Table XXII. is 1.49 times the mean inequality range in Table VIII.; comparing individual months the ratio of the absolute to the inequality range varies from 2.06 in January to 1.21 in June. Even confining ourselves to the quiet days at Kew, which are free from any but the most trifling disturbances, we find that the mean absolute range for the year is 1.20 times the arithmetic mean of the inequality ranges for the individual months of the year, and 1.22 times the range from the mean diurnal inequality for the year. In this case the ratio of the absolute to the inequality range varies from 1.55 in December to only 1.09 in May.
§ 25. The variability of the absolute daily range of declination is illustrated by Table XXIII., which contains data for Kew24 derived from all days of the 11-year period 1890-1900. It gives the total number of times during the 11 years when the absolute range lay within the limits specified at the heads of the first nine columns of figures. The two remaining columns give the arithmetic means of the five largest and the five least absolute ranges encountered each month. The mean of the twelve monthly diurnal inequality ranges from ordinary days was only 8′.44, but the absolute range during the 11 years exceeded 20′ on 492 days, 15′ on 1196 days, and 10′ on 2784 days, i.e. on 69 days out of every 100.
Table XXIII.—Absolute Daily Range of Declination at Kew.
| Number of occasions during 11 years when absolute range was:— | Means from the 5 largest and 5 least ranges of the month on the average of 11 years. | ||||||||||
| 0′ to 5′. | 5′ to 10′. | 10′ to 15′. | 15′ to 20′. | 20′ to 25′. | 25′ to 30′. | 30′ to 35′. | 35′ to 40′. | over 40′. | 5 largest. | 5 least. | |
| ′ | ′ | ||||||||||
| January | 51 | 145 | 69 | 37 | 24 | 7 | 4 | 3 | 1 | 22.90 | 5.07 |
| February | 26 | 99 | 84 | 51 | 26 | 10 | 4 | 2 | 8 | 27.21 | 6.55 |
| March | 1 | 72 | 138 | 61 | 32 | 21 | 8 | 1 | 7 | 29.87 | 8.93 |
| April | 0 | 43 | 167 | 73 | 27 | 10 | 6 | 3 | 1 | 23.69 | 10.31 |
| May | 0 | 57 | 157 | 85 | 20 | 12 | 3 | 0 | 7 | 25.36 | 9.50 |
| June | 0 | 56 | 185 | 67 | 15 | 1 | 3 | 1 | 2 | 19.92 | 9.89 |
| July | 0 | 59 | 185 | 70 | 14 | 5 | 2 | 2 | 4 | 22.49 | 9.96 |
| August | 0 | 37 | 202 | 75 | 22 | 1 | 2 | 0 | 2 | 21.27 | 10.05 |
| September | 1 | 68 | 153 | 71 | 19 | 5 | 4 | 5 | 4 | 24.55 | 9.52 |
| October | 3 | 103 | 111 | 67 | 34 | 10 | 11 | 2 | 0 | 23.92 | 8.01 |
| November | 42 | 140 | 81 | 28 | 14 | 9 | 8 | 5 | 3 | 23.58 | 5.64 |
| December | 64 | 166 | 56 | 29 | 14 | 7 | 1 | 1 | 3 | 20.43 | 4.36 |
| Totals | 188 | 1045 | 1588 | 714 | 261 | 98 | 56 | 25 | 42 | ||
§ 26. Magnetic phenomena, both regular and irregular, at any station vary from year to year. The extent of this variation is illustrated in Tables XXIV. and XXV., both relating to the period 1890 to 1900.25 Table XXIV. gives the amplitudes of Relations to Sun-spot Frequency. the regular diurnal inequality in the elements stated at the head of the columns. The ordinary day declination data (D0) for Kew represent arithmetic means from the twelve months of the year; the other data all answer to the mean diurnal inequality for the whole year. Table XXV. gives the arithmetic means for each year of the absolute daily range, of the monthly range (or difference between the highest and lowest values in the month), and of the yearly range (or difference between the highest and lowest values of the year). The numerals attached to the years in these tables indicate their order as regards sun-spot frequency according to Wolf and Wolfer (see Aurora Polaris), 1893 being the year of largest frequency, and 1890 that of least. The difference in sun-spot frequency between 1897 and 1898 was microscopic; the differences between 1890, 1900 and 1899 were small, and those between 1893, 1894 and 1892 were not very large.
The years 1892-1895 represent high sun-spot frequency, while 1890, 1899 and 1900 represent low frequency. Table XXIV. shows that 1892 to 1895 were in all cases distinguished by the large size of the inequality ranges, and 1890, 1899 and 1900 by the small size. The range in 1893 is usually the largest, and though the H and V 371 ranges at Ekaterinburg are larger in 1892 than in 1893, the excess is trifling. The phenomena apparent in Table XXIV. are fairly representative; other stations and other periods associate large inequality ranges with high sun-spot frequency. The diurnal inequality range it should be noticed is comparatively little influenced by irregular disturbances. Coming to Table XXV., we have ranges of a different character. The absolute range at Kew on quiet days is almost as little influenced by irregularities as is the range of the diurnal inequality, and in its case the phenomena are very similar to those observed in Table XXIV. As we pass from left to right in Table XXV., the influence of disturbance increases. Simultaneously with this, the parallelism with sun-spot frequency is less close. The entries relating to 1892 and 1894 become more and more prominent compared to those for 1893. The yearly range may depend on but a single magnetic storm, the largest disturbance of the year possibly far outstripping any other. But taking even the monthly ranges the values for 1893 are, speaking roughly, only half those for 1892 and 1894, and very similar to those of 1898, though the sun-spot frequency in the latter year was less than a third of that in 1893. Ekatarinburg data exactly analogous to those for Pavlovsk show a similar prominence in 1892 and 1894 as compared to 1893. The retirement of 1893 from first place, seen in the absolute ranges at Kew, Pavlovsk and Ekatarinburg, is not confined to the northern hemisphere. It is visible, for instance, in the amplitudes of the Batavia disturbance results. Thus though the variation from year to year in the amplitude of the absolute ranges is relatively not less but greater than that of the inequality ranges, and though the general tendency is for all ranges to be larger in years of many than in years of few sun-spots, still the parallelism between the changes in sun-spot frequency and in magnetic range is not so close for the absolute ranges and for disturbances as for the inequality ranges.
Table XXIV.—Ranges of Diurnal Inequalities.
| Pavlovsk. | Ekatarinburg. | Kew. | |||||||||
| D. | I. | H. | D. | I. | H. | V. | Dq. | Iq. | Hq. | Do. | |
| ′ | ′ | γ | ′ | ′ | γ | γ | ′ | ′ | γ | ′ | |
| 189011 | 6.32 | 1.33 | 22 | 5.83 | 1.05 | 18 | 9 | 6.90 | 20 | 7.32 | |
| 18916 | 7.31 | 1.79 | 30 | 6.85 | 1.38 | 25 | 14 | 8.04 | 1.52 | 28 | 8.48 |
| 18923 | 8.75 | 2.21 | 37 | 7.74 | 1.72 | 32 | 19 | 9.50 | 1.66 | 31 | 9.85 |
| 18931 | 9.64 | 2.24 | 38 | 8.83 | 1.80 | 31 | 17 | 10.06 | 1.96 | 35 | 10.74 |
| 18942 | 8.58 | 2.17 | 38 | 7.80 | 1.73 | 30 | 17 | 9.32 | 1.94 | 34 | 9.80 |
| 18954 | 8.22 | 2.08 | 33 | 7.29 | 1.64 | 28 | 15 | 8.59 | 1.66 | 30 | 9.54 |
| 18965 | 7.39 | 1.77 | 29 | 6.50 | 1.38 | 25 | 15 | 7.77 | 1.31 | 25 | 8.50 |
| 18976 | 6.79 | 1.59 | 26 | 6.01 | 1.16 | 21 | 12 | 6.71 | 1.14 | 22 | 7.76 |
| 18987 | 6.25 | 1.56 | 26 | 5.76 | 1.19 | 21 | 11 | 6.85 | 1.07 | 21 | 7.59 |
| 18999 | 6.02 | 1.44 | 24 | 5.33 | 1.12 | 20 | 11 | 6.69 | 1.01 | 21 | 7.30 |
| 190010 | 6.20 | 1.28 | 22 | 5.88 | 0.93 | 17 | 8 | 6.52 | 1.06 | 21 | 6.83 |
Table XXV.—Absolute Ranges.
| Kew Declination. Daily. | Pavlovsk. | |||||||||||
| Daily. | Monthly. | Yearly. | ||||||||||
| q. | o. | a. | D. | H. | V. | D. | H. | V. | D. | H. | V. | |
| ′ | ′ | ′ | ′ | γ | γ | ′ | γ | γ | ′ | γ | γ | |
| 189011 | 8.3 | 10.5 | 10.7 | 12.1 | 49 | 21 | 28.2 | 118 | 80 | 42.1 | 169 | 179 |
| 18916 | 10.0 | 12.8 | 13.7 | 16.0 | 70 | 39 | 46.3 | 218 | 233 | 92.3 | 550 | 614 |
| 18923 | 12.3 | 15.4 | 17.7 | 21.0 | 111 | 73 | 93.6 | 698 | 575 | 194.0 | 2416 | 1385 |
| 18931 | 11.8 | 15.2 | 15.6 | 17.8 | 79 | 41 | 48.3 | 241 | 210 | 87.1 | 514 | 457 |
| 18942 | 11.3 | 14.7 | 16.5 | 20.4 | 97 | 62 | 84.1 | 493 | 493 | 145.6 | 1227 | 878 |
| 18954 | 10.6 | 14.8 | 15.6 | 18.1 | 80 | 46 | 47.4 | 220 | 223 | 73.9 | 395 | 534 |
| 18965 | 9.5 | 12.9 | 14.5 | 17.5 | 74 | 43 | 52.4 | 232 | 236 | 88.7 | 574 | 608 |
| 18978 | 8.2 | 11.5 | 12.1 | 14.6 | 61 | 30 | 43.8 | 201 | 170 | 101.1 | 449 | 480 |
| 18987 | 8.2 | 11.2 | 12.3 | 14.7 | 67 | 35 | 46.6 | 276 | 242 | 118.9 | 1136 | 888 |
| 18999 | 7.9 | 10.5 | 11.3 | 13.1 | 58 | 27 | 38.3 | 178 | 150 | 63.8 | 382 | 527 |
| 190010 | 7.4 | 8.9 | 9.2 | 10.5 | 44 | 16 | 32.8 | 134 | 89 | 94.2 | 457 | 365 |
| Means | 9.6 | 12.6 | 13.6 | 16.0 | 72 | 39 | 51.1 | 274 | 246 | 100.2 | 752 | 629 |
§ 27. The relationship between magnetic ranges and sun-spot frequency has been investigated in several ways. W. Ellis26 has employed a graphical method which has advantages, especially for tracing the general features of the resemblance, and is besides independent of any theoretical hypothesis. Taking time for the axis of abscissae, Ellis drew two curves, one having for its ordinates the sun-spot frequency, the other the inequality range of declination or of horizontal force at Greenwich. The value assigned in the magnetic curve to the ordinate for any particular month represents a mean from 12 months of which it forms a central month, the object being to eliminate the regular annual variation in the diurnal inequality. The sun-spot data derived from Wolf and Wolfer were similarly treated. Ellis originally dealt with the period 1841 to 1877, but subsequently with the period 1878 to 1896, and his second paper gives curves representing the phenomena over the whole 56 years. This period covered five complete sun-spot periods, and the approximate synchronism of the maxima and minima, and the general parallelism of the magnetic and sun-spot changes is patent to the eye. Ellis27 has also applied an analogous method to investigate the relationship between sun-spot frequency and the number of days of magnetic disturbance at Greenwich. A decline in the number of the larger magnetic storms near sun-spot minimum is recognizable, but the application of the method is less successful than in the case of the inequality range. Another method, initiated by Professor Wolf of Zurich, lends itself more readily to the investigation of numerical relationships. He started by supposing an exact proportionality between corresponding changes in sun-spot frequency and magnetic range. This is expressed mathematically by the formula
R = a + bS ≡ a {1 + (b/a) S },
where R denotes the magnetic range, S the corresponding sun-spot frequency, while a and b are constants. The constant a represents the range for zero sun-spot frequency, while b/a is the proportional increase in the range accompanying unit rise in sun-spot frequency. Assuming the formula to be true, one obtains from the observed values of R and S numerical values for a and b, and can thus investigate whether or not the sun-spot influence is the same for the different magnetic elements and for different places. Of course, the usefulness of Wolf’s formula depends largely on the accuracy with which it represents the facts. That it must be at least a rough approximation to the truth in the case of the diurnal inequality at Greenwich might be inferred from Ellis’s curves. Several possibilities should be noticed. The formula may apply with high accuracy, a and b having assigned values, for one or two sun-spot cycles, and yet not be applicable to more remote periods. There are only three or four stations which have continuous magnetic records extending even 50 years back, and, owing to temperature correction uncertainties, there is perhaps no single one of these whose earlier records of horizontal and vertical force are above criticism. Declination is less exposed to uncertainty, and there are results of eye observations of declination before the era of photographic curves. A change, however, of 1′ in declination has a significance which alters with the intensity of the horizontal force. During the period 1850-1900 horizontal force in England increased about 5%, so that the force requisite to produce a declination change of 19′ in 1900 would in 1850 have produced a deflection of 20′. It must also be remembered that secular changes of declination must alter the angle between the needle and any disturbing force acting in a fixed direction. Thus secular alteration in a and b is rather to be anticipated, especially in the case of the declination. Wolf’s formula has been applied by Rajna28 to the yearly mean diurnal declination ranges at Milan based on readings taken twice daily from 1836 to 1894, treating the whole period together, and then the period 1871 to 1894 separately. During two sub-periods, 1837-1850 and 1854-1867, Rajna’s calculated values for the range differ very persistently in one direction from those observed; Wolf’s formula was applied by C. Chree25 to these two periods separately. He also applied it to Greenwich inequality ranges for the years 1841 to 1896 as published by Ellis, treating the whole period and the last 32 years of it separately, and finally to all (a) and quiet (q) day Greenwich ranges from 1889 to 1896. The results of these applications of Wolf’s formula appear in Table XXVI.
The Milan results are suggestive rather of heterogeneity in the material than of any decided secular change in a or b. The Greenwich data are suggestive of a gradual fall in a, and rise in b, at least in the case of the declination.
Table XXVII. gives values of a, b and b/a in Wolf’s formula calculated by Chree25 for a number of stations. There are two sets of data, the first set relating to the range from the mean diurnal inequality for the year, the second to the arithmetic mean of the ranges in the mean diurnal inequalities for the twelve months. It is specified whether the results were derived from all or from quiet days.
Table XXVI.—Values of a and b in Wolf’s Formula.
| Milan. | Greenwich. | ||||||
| Epoch. | Declination (unit 1′). | Epoch. | Declination (unit 1′). | Horizontal Force (unit 1γ). | |||
| a. | b. | a. | b. | a. | b. | ||
| 1836-94 | 5.31 | .047 | 1841-96 | 7.29 | .0377 | 26.4 | .190 |
| 1871-94 | 5.39 | .047 | 1865-96 | 7.07 | .0396 | 23.6 | .215 |
| 1837-50 | 6.43 | .041 | 1889-96(a) | 6.71 | .0418 | 23.7 | .218 |
| 1854-67 | 4.62 | .047 | 1889-96(q) | 6.36 | .0415 | 25.0 | .213 |
As explained above, a would represent the range in a year of no sun-spots, while 100 b would represent the excess over this shown by the range in a year when Wolf’s sun-spot frequency is 100. Thus 372 b/a seems the most natural measure of sun-spot influence. Accepting it, we see that sun-spot influence appears larger at most places for inclination and horizontal force than for declination. In the case of vertical force there is at Pavlovsk, and probably in a less measure at other northern stations, a large difference between all and quiet days, which is not shown in the other elements. The difference between the values of b/a at different stations is also exceptionally large for vertical force. Whether this last result is wholly free from observational uncertainties is, however, open to some doubt, as the agreement between Wolf’s formula and observation is in general somewhat inferior for vertical force. In the case of the declination, the mean numerical difference between the observed values and those derived from Wolf’s formula, employing the values of a and b given in Table XXVII., represented on the average about 4% of the mean value of the element for the period considered, the probable error representing about 6% of the difference between the highest and lowest values observed. The agreement was nearly, if not quite, as good as this for inclination and horizontal force, but for vertical force the corresponding percentages were nearly twice as large.
Table XXVII.—Values of a and b in Wolf’s Formula.
| Declination(unit 1′). | Inclination (unit 1′). | Horizontal Force (unit 1γ). | Vertical Force (unit 1γ). | |||||||||||
| Diurnal Inequality for the Year. | a. | b. | 100 b/a. | a. | b. | 100 b/a. | a. | b. | 100 b/a. | a. | b. | 100 b/a. | ||
| Pavlovsk, 1890-1900 | all | 5.74 | .0400 | .70 | 1.24 | .0126 | 1.01 | 20.7 | .211 | 1.02 | 8.1 | .265 | 3.26 | |
| Pavlovsk, 1890-1900 | quiet | 6.17 | .0424 | .69 | · · | · · | · · | 20.6 | .195 | 0.95 | 5.9 | .027 | 0.46 | |
| Ekatarinburg, 1890-1900 | all | 5.29 | .0342 | .65 | 0.93 | .0105 | 1.13 | 16.8 | .182 | 1.09 | 8.6 | .117 | 1.37 | |
| Irkutsk , 1890-1900 | all | 4.82 | .0358 | .74 | 0.97 | .0087 | 0.90 | 18.2 | .190 | 1.04 | 6.5 | .071 | 1.09 | |
| Kew, 1890-1900 | quiet | 6.10 | .0433 | .71 | 0.87 | .0125 | 1.45 | 18.1 | .194 | 1.07 | 14.3 | .081 | 0.56 | |
| Falmouth, 1891-1902 | quiet | 5.90 | .0451 | .76 | · · | · · | · · | 20.1 | .233 | 1.16 | · · | · · | · · | |
| Kolaba, 1894-1901 | quiet | 2.37 | .0066 | .28 | · · | · · | · · | 31.6 | .281 | 0.89 | 19.4 | .072 | 0.37 | |
| Batavia, 1887-1898 | all | 2.47 | .0179 | .72 | 3.60 | .0218 | 0.61 | 38.7 | .274 | 0.71 | 30.1 | .156 | 0.52 | |
| Mauritius | 1875-1880 1883-1890 | all | 4.06 | .0164 | .40 | · · | · · | · · | 15.0 | .096 | 0.64 | 11.9 | .069 | 0.58 |
| Mean from individual months:— | ||||||||||||||
| Pavlovsk, 1890-1900 | all | 6.81 | .0446 | .66 | 1.44 | .0151 | 1.05 | 22.8 | .243 | 1.07 | 9.7 | .287 | 2.97 | |
| Pavlovsk, 1890-1900 | quiet | 6.52 | .0442 | .68 | · · | · · | · · | 22.2 | .208 | 0.94 | 7.0 | .044 | 0.63 | |
| Ekatarinburg, 1890-1900 | all | 6.18 | .0355 | .58 | 1.12 | .0120 | 1.06 | 19.2 | .195 | 1.01 | 9.2 | .156 | 1.70 | |
| Greenwich, 1865-1896 | all | 7.07 | .0396 | .56 | · · | · · | · · | 23.6 | .215 | 0.91 | · · | · · | · · | |
| Kew, 1890-1900 | all | 6.65 | .0428 | .64 | · · | · · | · · | · · | · · | · · | · · | · · | · · | |
| Kew, 1890-1900 | quiet | 6.49 | .0410 | .63 | 1.17 | .0130 | 1.11 | 21.5 | .191 | 0.89 | 16.0 | .072 | 0.45 | |
| Falmouth, 1891-1902 | quiet | 6.16 | .0450 | .73 | · · | · · | · · | 20.9 | .236 | 1.13 | · · | · · | · · | |
Applying Wolf’s formula to the diurnal ranges for different months of the year, Chree found, as was to be anticipated, that the constant a had an annual period, with a conspicuous minimum at midwinter; but whilst b also varied, it did so to a much less extent, the consequence being that b/a showed a minimum at midsummer. The annual variation in b/a alters with the place, with the element, and with the type of day from which the magnetic data are derived. Thus, in the case of Pavlovsk declination, whilst the mean value of 100 b/a for the 12 months is, as shown in Table XXVII., 0.66 for all and 0.68 for quiet days—values practically identical—if we take the four midwinter and the four midsummer months separately, we have 100 b/a, varying from 0.81 in winter to 0.52 in summer on all days, but from 1.39 in winter to 0.52 in summer on quiet days. In the case of horizontal force at Pavlovsk the corresponding figures to these are for all days—winter 1.77, summer 0.98, but for quiet days—winter 1.83, summer 0.71.
Wolf’s formula has also been applied to the absolute daily ranges, to monthly ranges, and to various measures of disturbance. In these cases the values found for b/a are usually larger than those found for diurnal inequality ranges, but the accordance between observed values and those calculated from Wolf’s formula is less good. If instead of the range of the diurnal inequality we take the sum of the 24-hourly differences from the mean for the day—or, what comes to the same thing, the average departure throughout the 24 hours from the mean value for the day—we find that the resulting Wolf’s formula gives at least as good an agreement with observation as in the case of the inequality range itself. The formulae obtained in the case of the 24 differences, at places as wide apart as Kew and Batavia, agreed in giving a decidedly larger value for b/a than that obtained from the ranges. This indicates that the inequality curve is relatively less peaked in years of many than in years of few sun-spots.
§ 28. The applications of Ellis’s and Wolf’s methods relate directly only to the amplitude of the diurnal changes. There is, however, a change not merely in amplitude but in type. This is clearly seen when we compare the values found in years of many and of few sun-spots for the Fourier coefficients in the diurnal inequality. Such a comparison is carried out in Table XXVIII. for the declination on ordinary days at Kew. Local mean time is used. The heading S max. (sun-spot maximum) denotes mean average results from the four years 1892-1895, having a mean sun-spot frequency of 75.0, whilst S min. (sun-spot minimum) applies similarly to the years 1890, 1899 and 1900, having a mean sun-spot frequency of only 9.6. The data relate to the mean diurnal inequality for the whole year or for the season stated. It will be seen that the difference between the c, or amplitude, coefficients in the S max. and S min. years is greater for the 24-hour term than for the 12-hour term, greater for the 12-hour than for the 8-hour term, and hardly apparent in the 6-hour term. Also, relatively considered, the difference between the amplitudes in S max. and S min. years is greatest in winter and least in summer. Except in the case of the 6-hour term, where the differences are uncertain, the phase angle is larger, i.e. maxima and minima occur earlier in the day, in years of S min. than in years of S max. Taking the results for the whole year in Table XXVIII., this advance of phase in the S min. years represents in time 15.6 minutes for the 24-hour term, 9.4 minutes for the 12-hour term, and 14.7 minutes for the 8-hour term. The difference in the phase angles, as in the amplitudes, is greatest in winter. Similar phenomena are shown by the horizontal force, and at Falmouth24 as well as Kew.
Table XXVIII.—Fourier Coefficients in Years of many and few Sun-spots.
| Year. | Winter. | Equinox. | Summer. | |||||
| S max. | S min. | S max. | S min. | S max. | S min. | S max. | S min. | |
| ′ | ′ | ′ | ′ | ′ | ′ | ′ | ′ | |
| c1 | 3.47 | 2.21 | 2.41 | 1.43 | 3.76 | 2.41 | 4.38 | 2.98 |
| c2 | 2.04 | 1.51 | 1.15 | 0.78 | 2.33 | 1.71 | 2.73 | 2.06 |
| c3 | 0.89 | 0.72 | 0.55 | 0.42 | 1.16 | 0.97 | 0.97 | 0.77 |
| c4 | 0.28 | 0.27 | 0.30 | 0.27 | 0.42 | 0.42 | 0.11 | 0.11 |
| ° | ° | ° | ° | ° | ° | ° | ° | |
| α1 | 228.5 | 232.4 | 243.0 | 256.0 | 231.3 | 233.7 | 218.2 | 220.3 |
| α2 | 41.7 | 46.6 | 23.5 | 36.9 | 40.6 | 43.9 | 50.6 | 52.5 |
| α3 | 232.6 | 243.6 | 234.0 | 257.6 | 228.4 | 236.2 | 236.8 | 245.4 |
| α4 | 58.0 | 57.3 | 52.3 | 60.8 | 62.0 | 58.2 | 57.4 | 45.2 |
§ 29. There have already been references to quiet days, for instance in the tables of diurnal inequalities. It seems to have been originally supposed that quiet days differed from other days only Quiet Day Phenomena. in the absence of irregular disturbances, and that mean annual values, or secular change data, or diurnal inequalities, derived from them might be regarded as truly normal or representative of the station. It was found, however, by P. A. Müller29 that mean annual values of the magnetic elements at St Petersburg and Pavlovsk from 1873 to 1885 derived from quiet days alone differed in a systematic fashion from those derived from all days, and analogous results were obtained by Ellis30 at Greenwich for the period 1889-1896. The average excesses for the quiet-day over the all-day means in these two cases were as follows:—
| Westerly Declination. | Inclination. | Horizontal Force. | Vertical Force. | |
| St Petersburg | +0.24 | −0.23 | +3.2γ | −0.8γ |
| Greenwich | +0.08 | +3.2γ | −0.9γ |
The sign of the difference in the case of D, I and H was the same in each year examined by Müller, and the same was true of H at Greenwich. In the case of V, and of D at Greenwich, the differences are 373 small and might be accidental. In the case of D at Greenwich 1891 differed from the other years, and of two more recent years examined by Ellis31 one, 1904, agreed with 1891. At Kew, on the average of the 11 years 1890 to 1900, the quiet-day mean annual value of declination exceeded the ordinary day value, but the apparent excess 0′.02 is too small to possess much significance.
Another property more recently discovered in quiet days is the non-cyclic change. The nature of this phenomenon will be readily Non-cyclic Change. understood from the following data from the 11-year period 1890 to 1900 at Kew32. The mean daily change for all days is calculated from the observed annual change.
| D. | I. | H. | V. | |
| ′ | ′ | |||
| Mean annual change | −5.79 | −2.38 | +25.9γ | −22.6γ |
| Mean daily change, all days | −0.016 | −0.007 | +0.07γ | −0.06γ |
| Mean daily change, quiet days | +0.044 | −0.245 | +3.34γ | −0.84γ |
Thus the changes during the representative quiet day differed from those of the average day. Before accepting such a phenomenon as natural, instrumental peculiarities must be carefully considered. The secular change is really based on the absolute instruments, the diurnal changes on the magnetographs, and the first idea likely to occur to a critical mind is that the apparent abnormal change on quiet days represents in reality change of zero in the magnetographs. If, however, the phenomenon were instrumental, it should appear equally on days other than quiet days, and we should thus have a shift of zero amounting in a year to over 1,200γ in H, and to about 90′ in I. Under such circumstances the curve would be continually drifting off the sheet. In the case of the Kew magnetographs, a careful investigation showed that if any instrumental change occurred in the declination magnetograph during the 11 years it did not exceed a few tenths of a minute. In the case of the H and V magnetographs at Kew there is a slight drift, of instrumental origin, due to weakening of the magnets, but it is exceedingly small, and in the case of H is in the opposite direction to the non-cyclic change on quiet days. It only remains to add that the hypothesis of instrumental origin was positively disproved by measurement of the curves on ordinary days.
It must not be supposed that every quiet day agrees with the average quiet day in the order of magnitude, or even in the sign, of the non-cyclic change. In fact, in not a few months the sign of the non-cyclic change on the mean of the quiet days differs from that obtained for the average quiet day of a period of years. At Kew, between 1890 and 1900, the number of months during which the mean non-cyclic change for the five quiet days selected by the astronomer royal (Sir W. H. M. Christie) was plus, zero, or minus, was as follows:—
| Element. | D. | I. | H. | V. |
| Number + | 63 | 13 | 112 | 47 |
| Number 0 | 14 | 16 | 11 | 9 |
| Number − | 55 | 101 | 9 | 74 |
The + sign denotes westerly movement in the declination, and increasing dip of the north end of the needle. In the case of I and H the excess in the number of months showing the normal sign is overwhelming. The following mean non-cyclic changes on quiet days are from other sources:—
| Element. | Greenwich (1890-1895). | Falmouth (1898-1902). | Kolaba (1894-1901). |
| ′ | ′ | ′ | |
| D | + 0.03 | + 0.05 | + 0.07 |
| H | + 4.3γ | + 3.0γ | + 3.9γ |
The results are in the same direction as at Kew, + meaning in the case of D movement to the west. At Falmouth32, as at Kew, the non-cyclic change showed a tendency to be small in years of few sun-spots.
§ 30. In calculating diurnal inequalities from quiet days the non-cyclic effect must be eliminated, otherwise the result would depend on the hour at which the “day” is supposed to commence. If the value recorded at the second midnight of the average day exceeds that at the first midnight by N, the elimination is effected by applying to each hourly value the correction N(12 − n)/24, where n is the hour counted from the first midnight (0 hours). This assumes the change to progress uniformly throughout the 24 hours. Unless this is practically the case—a matter difficult either to prove or disprove—the correction may not secure exactly what is aimed at. This method has been employed in the previous tables. The fact that differences do exist between diurnal inequalities derived from quiet days and all ordinary days was stated explicitly in § 4, and is obvious in Tables VIII. to XI. An extreme case is represented by the data for Jan Mayen in these tables. Figs. 9 and 10 are vector diagrams for this station, for all and for quiet days during May, June and July 1883, according to data got out by Lüdeling. As shown by the arrows, fig. 10 (quiet days) is in the main described in the normal or clockwise direction, but fig. 9 (all days) is described in the opposite direction. Lüdeling found this peculiar difference between all and quiet days at all the north polar stations occupied in 1882-1883 except Kingua Fjord, where both diagrams were described clockwise.
 | |
| Fig. 9. | Fig. 10. |
In temperate latitudes the differences of type are much less, but still they exist. A good idea of their ordinary size and character in the case of declination may be derived from Table XXIX., containing data for Kew, Greenwich and Parc St Maur.
The data for Greenwich are due to W. Ellis30, those for Parc St Maur to T. Moureaux33. The quantity tabulated is the algebraic excess of the all or ordinary day mean hourly value over the corresponding quiet day value in the mean diurnal inequality for the year. At Greenwich and Kew days of extreme disturbance have been excluded from the ordinary days, but apparently not at Parc St Maur. The number of highly disturbed days at the three stations is, however, small, and their influence is not great. The differences disclosed by Table XXIX. are obviously of a systematic character, which would not tend to disappear however long a period was utilized. In short, while the diurnal inequality from quiet days may be that most truly representative of undisturbed conditions, it does not represent the average state of conditions at the station. To go into full details respecting the differences between all and quiet days would occupy undue space, so the following brief summary of the differences observed in declination at Kew must suffice. While the inequality range is but little different for the two types of days, the mean of the hourly differences from the mean for the day is considerably reduced in the quiet days. The 24-hour term in the Fourier analysis is of smaller amplitude in the quiet days, and its phase angle is on the average about 6°.75 smaller than on ordinary days, implying a retardation of about 27 minutes in the time of maximum. The diurnal inequality range is more variable throughout the year in quiet days than on ordinary days, and the same is true of the absolute ranges. The tendency to a secondary minimum in the range at midsummer is considerably more decided on ordinary than on quiet days. When the variation throughout the year in the diurnal inequality range is expressed in Fourier series, whose periods are the year and its submultiples, the 6-month term is notably larger for ordinary than for quiet days. Also the date of the maximum in the 12-month term is about three days earlier for ordinary than for quiet days. The exact size of the differences between ordinary and quiet day phenomena must depend to some extent on the criteria employed in selecting quiet days and in excluding disturbed days. This raises difficulties when it comes to comparing results at different stations. For stations near together the difficulty is trifling. The astronomer royal’s quiet days have been used for instance at Parc St. Maur, Val Joyeux, Falmouth and Kew, as well as at Greenwich. But when stations are wide apart there are two obvious difficulties: first, the difference of local time; secondly, the fact that a day may be typically quiet at one station but appreciably disturbed at the other.
If the typical quiet day were simply the antithesis of a disturbed day, it would be natural to regard the non-cyclic change on quiet days as a species of recoil from some effect of disturbance. This view derives support from the fact, pointed out long ago by Sabine34, that the horizontal force usually, though by no means always, is lowered by magnetic disturbances. Dr van Bemmelen35 who has examined non-cyclic phenomena at a number of stations, seems disposed to regard this as a sufficient explanation. There are, however, difficulties in accepting this view. Thus, whilst the non-cyclic effect in horizontal force and inclination at Kew and Falmouth appeared on the whole enhanced in years of sun-spot maximum, the difference between years such as 1892 and 1894 on the one hand, and 1890 and 1900 on the other, was by no means proportional to the excess of disturbance in the former years. Again, when the average non-cyclic change of declination was calculated at Kew for 207 days, selected as those of most marked irregular disturbance between 1890 and 1900, the sign actually proved to be the same as for the average quiet day of the period.
Table XXIX.—All or Ordinary, less Quiet Day Hourly Values (+ to the West).
| Hour. | Forenoon. | Afternoon. | ||||
| Kew 1890-1900. | Greenwich 1890-1894. | Parc St Maur 1883-1897. | Kew 1890-1900. | Greenwich 1890-1894. | Parc St Maur 1893-1897. | |
| ′ | ′ | ′ | ′ | ′ | ′ | |
| 1 | −0.58 | −0.59 | −0.63 | +0.42 | +0.44 | +0.40 |
| 2 | −0.54 | −0.47 | −0.47 | +0.52 | +0.45 | +0.50 |
| 3 | −0.51 | −0.31 | −0.32 | +0.57 | +0.52 | +0.59 |
| 4 | −0.41 | −0.23 | −0.16 | +0.60 | +0.51 | +0.55 |
| 5 | −0.28 | −0.10 | −0.01 | +0.46 | +0.34 | +0.38 |
| 6 | −0.08 | +0.12 | +0.18 | +0.21 | +0.04 | +0.07 |
| 7 | +0.13 | +0.30 | +0.34 | −0.06 | −0.24 | −0.25 |
| 8 | +0.29 | +0.48 | +0.47 | −0.27 | −0.50 | −0.54 |
| 9 | +0.40 | +0.56 | +0.53 | −0.47 | −0.68 | −0.74 |
| 10 | +0.44 | +0.58 | +0.51 | −0.61 | −0.78 | −0.79 |
| 11 | +0.48 | +0.50 | +0.44 | −0.62 | −0.77 | −0.79 |
| 12 | +0.45 | +0.44 | +0.38 | −0.54 | −0.61 | −0.67 |
§ 31. A satisfactory definition of magnetic disturbance is about as difficult to lay down as one of heterodoxy. The idea in its generality seems to present no difficulty, but it is a very different matter when one comes to details. Amongst Magnetic Disturbances. the chief disturbances recorded since 1890 are those of February 13-14 and August 12, 1892; July 20 and August 20, 1894; March 15-16, and September 9, 1898; October 31, 1903; February 9-10, 1907; September 11-12, 1908 and September 25, 1909. On such days as these the oscillations shown by the magnetic curves are large and rapid, aurora is nearly always visible in temperate latitudes, earth currents are prominent, and there is interruption—sometimes very serious—in the transmission of telegraph messages both in overhead and underground wires. At the other end of the scale are days on which the magnetic curves show practically no movement beyond the slow regular progression of the regular diurnal inequality. But between these two extremes there are an infinite variety of intermediate cases. The first serious attempt at a precise definition of disturbance seems due to General Sabine35a. His method had once an extensive vogue, and still continues to be applied at some important observatories. Sabine regarded a particular observation as disturbed when it differed from the mean of the observations at that hour for the whole month by not less than a certain limiting value. His definition takes account only of the extent of the departure from the mean, whether the curve is smooth at the time or violently oscillating makes no difference. In dealing with a particular station Sabine laid down separate limiting values for each element. These limits were the same, irrespective of the season of the year or of the sun-spot frequency. A departure, for example, of 3′.3 at Kew from the mean value of declination for the hour constituted a disturbance, whether it occurred in December in a year of sun-spot minimum, or in June in a year of sun-spot maximum, though the regular diurnal inequality range might be four times as large in the second case as in the first. The limiting values varied from station to station, the size depending apparently on several considerations not very clearly defined. Sabine subdivided the disturbances in each element into two classes: the one tending to increase the element, the other tending to diminish it. He investigated how the numbers of the two classes varied throughout the day and from month to month. He also took account of the aggregate value of the disturbances of one sign, and traced the diurnal and annual variations in these aggregate values. He thus got two sets of diurnal variations and two sets of annual variations of disturbance, the one set depending only on the number of the disturbed hours, the other set considering only the aggregate value of the disturbances. Generally the two species of disturbance variations were on the whole fairly similar. The aggregates of the + and − disturbances for a particular hour of the day were seldom equal, and thus after the removal of the disturbed values the mean value of the element for that hour was generally altered. Sabine’s complete scheme supposed that after the criterion was first applied, the hourly means would be recalculated from the undisturbed values and the criterion applied again, and that this process would be repeated until the disturbed observations all differed by not less than the accepted limiting value from the final mean based on undisturbed values alone. If the disturbance limit were so small that the disturbed readings formed a considerable fraction of the whole number, the complete execution of Sabine’s scheme would be exceedingly laborious. As a matter of fact, his disturbed readings were usually of the order of 5% of the total number, and unless in the case of exceptionally large magnetic storms it is of little consequence whether the first choice of disturbed readings is accepted as final or is reconsidered in the light of the recalculated hourly means.
Sabine applied his method to the data obtained during the decade 1840 to 1850 at Toronto, St Helena, Cape of Good Hope and Hobart, also to data for Pekin, Nertchinsk, Point Barrow, Port Kennedy and Kew. C. Chambers36 applied it to data from Bombay. The yearly publication of the Batavia observatory gives corresponding results for that station, and Th. Moureaux 33 has published similar data for Parc St Maur. Tables XXX. to XXXII. are based on a selection of these data. Tables XXX. and XXXI. show the annual variation in Sabine’s disturbances, the monthly values being expressed as percentages of the arithmetic mean value for the 12 months. The Parc St Maur and Batavia data, owing to the long periods included, are especially noteworthy. Table XXX. deals with the east (E) and west (W) disturbances of declination separately. Table XXXI., dealing with disturbances in horizontal and vertical force, combines the + and − disturbances, treated numerically. At Parc St Maur the limits required to qualify for disturbance were 3′.0 in D, 20γ in H, and 12γ in V; the corresponding limits for Batavia were 1′.3, 11γ and 11γ. The limits for D at Toronto, Bombay and Hobart were respectively 3′.6, 1′.4 and 2′.4.
At Parc St Maur the disturbance data from all three elements give distinct maxima near the equinoxes; a minimum at midwinter is clearly shown, and also one at midsummer, at least in D and H. A decline in disturbance at midwinter is visible at all the stations, but at Batavia the equinoctial values for D and V are inferior to those at midsummer.
Table XXX.—Annual Variation of Disturbances (Sabine’s numbers).
| Parc St Maur 1883-97. | Toronto 1841-48. | Bombay 1859-65. | Batavia 1883-99. | Hobart 1843-48. | ||||||
| Month. | E. | W. | E. | W. | E. | W. | E. | W. | E. | W. |
| January | 78 | 60 | 55 | 66 | 89 | 89 | 180 | 223 | 165 | 182 |
| February | 116 | 92 | 75 | 86 | 94 | 67 | 138 | 144 | 121 | 116 |
| March | 126 | 107 | 92 | 94 | 129 | 97 | 102 | 87 | 114 | 104 |
| April | 105 | 113 | 115 | 114 | 106 | 129 | 67 | 73 | 110 | 102 |
| May | 101 | 118 | 101 | 101 | 63 | 99 | 72 | 71 | 62 | 53 |
| June | 77 | 89 | 95 | 72 | 78 | 81 | 45 | 27 | 32 | 37 |
| July | 82 | 104 | 140 | 126 | 121 | 173 | 62 | 46 | 50 | 49 |
| August | 88 | 113 | 137 | 133 | 154 | 131 | 69 | 69 | 86 | 78 |
| September | 134 | 137 | 163 | 139 | 111 | 108 | 135 | 144 | 135 | 114 |
| October | 119 | 115 | 101 | 111 | 140 | 128 | 95 | 88 | 124 | 123 |
| November | 99 | 94 | 73 | 85 | 43 | 43 | 106 | 91 | 79 | 111 |
| December | 75 | 58 | 51 | 72 | 72 | 55 | 124 | 137 | 123 | 130 |
Table XXXII. shows in some cases a most conspicuous diurnal variation in Sabine’s disturbances. The data are percentages of the totals for the whole 24 hours. But whilst at Batavia the easterly and westerly disturbances in D vary similarly, at Parc St Maur they follow opposite laws, the easterly showing a prominent maximum near noon, the westerly a still more prominent maximum near midnight. The figures in the second last line of the table, if divided by 0.24, will give the percentage of hours which show the species of disturbance indicated. For instance, at Parc St Maur, out of 100 hours, 3 show disturbances to the west and 3.7 to the east; or in all 6.7 show disturbances of declination. The last line gives the average size of a disturbance of each type, the unit being 1′ in D and 1γ in H and V.
Table XXXI.—Annual Variation of Disturbances.
| Parc St Maur. | Toronto. | Batavia. | ||||||
| Month. | Numbers. | Aggregates. | Numbers. | Aggregates. | ||||
| H. | V. | H. | V. | H. | V. | H. | V. | |
| January | 81 | 51 | 58 | 56 | 96 | 151 | 89 | 154 |
| February | 96 | 133 | 94 | 74 | 105 | 123 | 110 | 125 |
| March | 126 | 118 | 94 | 108 | 116 | 105 | 117 | 103 |
| April | 94 | 111 | 150 | 149 | 104 | 76 | 105 | 73 |
| May | 108 | 133 | 90 | 112 | 101 | 92 | 105 | 95 |
| June | 90 | 85 | 36 | 50 | 82 | 69 | 79 | 66 |
| July | 99 | 128 | 61 | 71 | 90 | 83 | 95 | 81 |
| August | 113 | 92 | 75 | 108 | 91 | 91 | 98 | 91 |
| September | 119 | 122 | 171 | 160 | 113 | 111 | 114 | 115 |
| October | 101 | 94 | 148 | 129 | 114 | 89 | 104 | 86 |
| November | 104 | 81 | 98 | 75 | 99 | 102 | 100 | 101 |
| December | 70 | 51 | 128 | 100 | 89 | 108 | 84 | 110 |
At Batavia disturbances increasing and decreasing the element are about equally numerous, but this is exceptional. Easterly disturbances of declination predominated at Toronto, Point Barrow, Fort Kennedy, Kew, Parc St Maur, Bombay and the Falkland Islands whilst the reverse was true of St Helena, Cape of Good Hope, Pekin and Hobart. At Kew and Parc St Maur the ratios borne by the 375 eastern to the western disturbances were 1.19 and 1.23 respectively, and so not much in excess of unity; but the preponderance of easterly disturbances at the North American37 stations was considerably larger than this.
Table XXXII.—Diurnal Variation of Disturbances (Sabine’s numbers).
| Hour. | Parc St Maur. | Batavia. | ||||||||||
| D. | H. | V. | D. | H. | V. | |||||||
| E. | W. | + | − | + | − | E. | W. | + | − | + | − | |
| 0-3 | 10.1 | 20.3 | 9.0 | 8.3 | 5.7 | 9.2 | 1.1 | 5.8 | 13.1 | 6.6 | 4.0 | 7.4 |
| 3-6 | 12.3 | 8.2 | 8.4 | 8.0 | 6.4 | 10.4 | 7.6 | 7.3 | 14.2 | 4.8 | 6.3 | 10.0 |
| 6-9 | 15.7 | 3.8 | 14.1 | 12.5 | 7.2 | 9.0 | 24.9 | 16.8 | 12.1 | 9.9 | 21.2 | 21.7 |
| 9-noon | 16.2 | 5.1 | 18.0 | 15.6 | 12.9 | 15.4 | 38.5 | 33.0 | 8.6 | 15.8 | 19.8 | 16.4 |
| noon-3 | 19.3 | 6.7 | 15.3 | 16.5 | 18.2 | 18.3 | 18.8 | 24.7 | 16.8 | 21.1 | 23.5 | 22.1 |
| 3-6 | 14.8 | 9.7 | 12.5 | 15.4 | 22.9 | 21.8 | 6.4 | 5.4 | 13.3 | 16.9 | 12.6 | 12.7 |
| 6-9 | 5.7 | 21.2 | 11.4 | 13.2 | 18.9 | 11.2 | 2.3 | 3.4 | 9.9 | 13.6 | 7.1 | 4.1 |
| 9-12 | 5.9 | 25.0 | 11.2 | 10.5 | 7.8 | 4.7 | 0.4 | 3.8 | 12.0 | 11.1 | 5.6 | 5.4 |
| Mean number per day | 0.88 | 0.72 | 1.15 | 1.56 | 1.04 | 0.96 | 0.46 | 0.44 | 1.62 | 1.61 | 1.19 | 1.13 |
| Mean size | · · | · · | · · | · · | · · | · · | 1.72 | 1.69 | 18.0 | 19.5 | 16.7 | 15.5 |
§ 32. From the point of view of the surveyor there is a good deal to be said for Sabine’s definition of disturbance, but it is less satisfactory from other standpoints. One objection has been already indicated, viz. the arbitrariness of applying the same limiting value at a station irrespective of the size of the normal diurnal range at the time. Similarly it is arbitrary to apply the same limit between 10 a.m. and noon, when the regular diurnal variation is most rapid, as between 10 p.m. and midnight, when it is hardly appreciable. There seems a distinct difference of phase between the diurnal inequalities on different types of days at the same season; also the phase angles in the Fourier terms vary continuously throughout the year, and much more rapidly at some stations and at some seasons than at others. Thus there may be a variety of phenomena which one would hesitate to regard as disturbances which contribute to the annual and diurnal variations in Tables XXX. to XXXII.
Sabine, as we have seen, confined his attention to the departure of the hourly reading from the mean for that hour. Another and equally natural criterion is the apparent character of the magnetograph curve. At Potsdam curves are regarded as “1” quiet, “2” moderately disturbed, or “3” highly disturbed. Any hourly value to which the numeral 3 is attached is treated as disturbed, and the annual Potsdam publication contains tables giving the annual and diurnal variations in the number of such disturbed hours for D, H and V. According to this point of view, the extent to which the hourly value departs from the mean for that hour is immaterial to the results. It is the greater or less sinuosity and irregularity of the curve that counts. Tables XXXIII. and XXXIV. give an abstract of the mean Potsdam results from 1892 to 1901. The data are percentages: in Table XXXIII. of the mean monthly total, in Table XXXIV. of the total for the day. So far as the annual variation is concerned, the results in Table XXXIII. are fairly similar to those in Table XXX. for Parc St Maur. There are pronounced maxima near the equinoxes, especially the spring equinox. The diurnal variations, however, in Tables XXXII. and XXXIV. are dissimilar. Thus in the case of H the largest disturbance numbers at Parc St Maur occurred between 6 a.m. and 6 p.m., whereas in Table XXXIV. they occur between 4 p.m. and midnight. Considering the comparative proximity of Parc St Maur and Potsdam, one must conclude that the apparent differences between the results for these two stations are due almost entirely to the difference in the definition of disturbance.
Table XXXIII.—Annual Variation of Potsdam Disturbances.
| Element. | Jan. | Feb. | Mar. | April. | May. | June. | July. | Aug. | Sept. | Oct. | Nov. | Dec. |
| D | 129 | 170 | 149 | 90 | 86 | 57 | 62 | 64 | 59 | 118 | 94 | 82 |
| H | 109 | 133 | 131 | 102 | 109 | 82 | 94 | 91 | 89 | 101 | 75 | 84 |
| V | 106 | 171 | 170 | 108 | 121 | 56 | 64 | 74 | 93 | 87 | 78 | 70 |
| Mean | 115 | 158 | 150 | 100 | 105 | 65 | 73 | 76 | 94 | 102 | 82 | 79 |
Table XXXIV.—Diurnal Variation of Potsdam Disturbances.
| Hours. | 1-3. | 4-6. | 7-9. | 10-noon. | 1-3. | 4-6. | 7-9. | 10-12. |
| D | 14.9 | 11.1 | 8.0 | 5.2 | 5.7 | 13.1 | 22.5 | 19.5 |
| H | 10.5 | 8.4 | 8.0 | 8.5 | 11.3 | 17.6 | 19.2 | 16.5 |
| V | 13.5 | 9.7 | 5.7 | 4.7 | 8.5 | 17.2 | 21.5 | 19.2 |
| Mean | 13.0 | 9.7 | 7.2 | 6.1 | 8.5 | 16.0 | 21.1 | 18.4 |
Table XXXV.—Disturbed Day less ordinary Day Inequality (Unit 1′, + to West).
| Hour. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| a.m. | −3.4 | −2.6 | −2.0 | −0.3 | +1.6 | +1.9 | +2.3 | +2.0 | +2.1 | +2.0 | +1.6 | +1.8 |
| p.m. | +1.8 | +2.2 | +2.1 | +1.7 | +1.4 | 0.0 | −1.3 | −2.8 | −3.5 | −2.6 | −3.5 | −2.4 |
One difficulty in the Potsdam procedure is the maintenance of a uniform standard. Unless very frequent reference is made to the curves of some standard year there must be a tendency to enter under “3” in quiet years a number of hours which would be entered under “2” in a highly disturbed year. Still, such a source of uncertainty is unlikely to have much influence on the diurnal, or even on the annual, variation.
§ 33. A third method of investigating a diurnal period in disturbances is to form a diurnal inequality from disturbed days alone, and compare it with the corresponding inequalities from ordinary or from quiet days. Table XXXV. gives some declination data for Kew, the quantity tabulated being the algebraic excess of the disturbed day hourly value over that for the ordinary day in the mean diurnal inequality for the year, as based on the 11 years 1890 to 1900.
 |
| Fig. 11. |
The disturbed day inequality was corrected for non-cyclic change in the usual way. Fig. 11 shows the results of Table XXXV. graphically. The irregularities are presumably due to the limited number, 209, of disturbed days employed; to get a smooth curve would require probably a considerably longer period of years. The differences between disturbed and ordinary days at Kew are of the same general character as those between ordinary and quiet days in Table XXIX.; they are, however, very much larger, the range in Table XXXV. being fully 5½ times that in Table XXIX. If quiet days had replaced ordinary days in Table XXXV., the algebraic excess of the disturbed day would have varied from +2′.7 at 2 p.m. to −4′.1 at 11 p.m., or a range of 6′.8.
§ 34. When the mean diurnal inequality in declination for the year at Kew is analysed into Fourier waves, the chief difference, it will be remembered, between ordinary and quiet days was that the amplitude of the 24-hour term was enhanced in the ordinary days, whilst its phase angle indicated an earlier occurrence of the maximum. Similarly, the chief difference between the Fourier waves for the disturbed and ordinary day inequalities at Kew is the increase in the amplitude of the 24-hour term in the former by over 70%, and the earlier occurrence of its maximum by about 1 hour 50 minutes. It is clear from these results for Kew, and it is also a necessary inference from the differences obtained by Sabine’s method between east and west or + and − disturbances, that there is present during disturbances some influence which affects the diurnal inequality in a regular systematic way, tending to make the value of the element higher during some hours and lower during others than it is on days relatively free from disturbance. At Kew the consequence is a notable increase in the range of the regular diurnal inequality on disturbed days; but whether this is the general rule or merely a local peculiarity is a subject for further research.
§ 35. There are still other ways of attacking the problem of disturbances. W. Ellis27 made a complete list of disturbed days at Greenwich from 1848 onwards, arranging them in classes according to the amplitude of the disturbance shown on the curves. Of the 18,000 days which he considered, Ellis regarded 2,119, or only about 12%, as undisturbed. On 11,898 days, or 66%, the disturbance movement in declination was under 10′; on 3614, or 20%, the disturbance, though exceeding 10′, was under 30′; on 294 days it lay 376 between 30′ and 60′; while on 75 days it exceeded 60′. Taking each class of disturbances separately, Ellis found, except in the case of his “minor” disturbances—those under 10′—a distinct double annual period, with maxima towards the equinoxes. Subsequently C. W. Maunder,38 making use of these same data, and of subsequent data up to 1902, put at his disposal by Ellis, came to similar conclusions. Taking all the days with disturbances of declination over 10′, and dealing with 15-day periods, he found the maxima of frequency to occur the one a little before the spring equinox, the other apparently after the autumnal equinox; the two minima were found to occur early in June and in January. When the year is divided into three seasons—winter (November to February), summer (May to August), and equinox—Maunder’s figures lead to the results assigned to Greenwich disturbed days in Table XXXVI. The frequency in winter, it will be noticed, though less than at equinox, is considerably greater than in summer. This greater frequency in winter is only slightly apparent in the disturbances over 60′, but their number is so small that this may be accidental. The next figures in Table XXXVI. relate to highly disturbed days at Kew. The larger relative frequency at Kew in winter as compared to summer probably indicates no real difference from Greenwich, but is simply a matter of definition. The chief criterion at Kew for classifying the days was not so much the mere amplitude of the largest movement, as the general character of the day’s curve and its departure from the normal form. The data in Table XXXVI. as to magnetic storms at Greenwich are based on the lists given by Maunder39 in the Monthly Notices, R.A.S. A storm may last for any time from a few hours to several days, and during part of its duration the disturbance may not be very large; thus it does not necessarily follow that the frequencies of magnetic storms and of disturbed days will follow the same laws. The table shows, however, that so far as Greenwich is concerned the annual variations in the two cases are closely alike. In addition to mean data for the whole 56 years, 1848 to 1903, Table XXXVI. contains separate data for the 14 years of that period which represented the highest sun-spot frequency, and the 15 years which represented lowest sun-spot frequency. It will be seen that relatively considered the seasonal frequencies of disturbance are more nearly equal in the years of many than in those of few sun-spots. Storms are more numerous as a whole in the years of many sun-spots, and this preponderance is especially true of storms of the largest size. This requires to be borne in mind in any comparisons between larger and smaller storms selected promiscuously from a long period. An unduly large proportion of the larger storms will probably come from years of large sun-spot frequency, and there is thus a risk of assigning to differences between the laws obeyed by large and small storms phenomena that are due in whole or in part to differences between the laws followed in years of many and of few sun-spots. The last data in Table XXXVI. are based on statistics for Batavia given by W. van Bemmelen,40 who considers separately the storms which commence suddenly and those which do not. These sudden movements are recorded over large areas, sometimes probably all over the earth, if not absolutely simultaneously, at least too nearly so for differences in the time of occurrence to be shown by ordinary magnetographs. It is ordinarily supposed that these sudden movements, and the storms to which they serve as precursors, arise from some source extraneous to the earth, and that the commencement of the movement intimates the arrival, probably in the upper atmosphere, of some form of energy transmitted through space. In the storms which commence gradually the existence of a source external to the earth is not so prominently suggested, and it has been sometimes supposed that there is a fundamental difference between the two classes of storms. Table XXXVI. shows, however, no certain difference in the annual variation at Batavia. At the same time, this possesses much less significance than it would have if Batavia were a station like Greenwich, where the annual variation in magnetic storms is conspicuous.
Besides the annual period, there seems to be also a well-marked diurnal period in magnetic disturbances. This is apparent in Tables XXXVII. and XXXVIII., which contain some statistics for Batavia due to van Bemmelen, and some for Greenwich derived from the data in Maunder’s papers referred to above. Table XXXVII. gives the relative frequency of occurrence for two hour intervals, starting with midnight, treating separately the storms of gradual (g) and sudden (s) commencement. In Table XXXVIII. the day is subdivided into three equal parts. Batavia and Greenwich agree in showing maximum frequency of beginnings about the time of minimum frequency of endings and conversely; but the hours at which the respective maxima and minima occur at the two places differ rather notably.
§ 36. There are peculiarities in the sudden movements ushering in magnetic storms which deserve fuller mention. According to van Bemmelen the impulse consists usually at some stations of a sudden slight jerk of the magnet in one direction, followed by a larger decided movement in the opposite direction, the former being often indistinctly shown. Often we have at the very commencement but a faint outline, and thereafter a continuous movement which is only sometimes distinctly indicated, resulting after some minutes in the displacement of the trace by a finite amount from the position it occupied on the paper before the disturbance began. This may mean, as van Bemmelen supposes, a small preliminary movement in the opposite direction to the clearly shown displacement; but it may only mean that the magnet is initially set in vibration, swinging on both sides of the position of equilibrium, the real displacement of the equilibrium position being all the time in the direction of the displacement apparent after a few minutes. To prevent misconception, the direction of the displacement apparent after a few minutes has been termed the direction of the first decided movement in Table XXXIX., which contains some data as to the direction given by Ellis41 and van Bemmelen.40 The + sign means an increase, the − sign a decrease of the element. The sign is not invariably the same, it will be understood, but there are in all cases a marked preponderance of changes in the direction shown in the table. The fact that all the stations indicated an increase in horizontal force is of special significance.
Table XXXVI.—Disturbances, and their Annual Distribution.
| Total Number. | Percentages. | |||
| Winter. | Equinox. | Summer. | ||
| Greenwich disturbed days, all, 1848-1902 | 4,214 | 33.9 | 39.2 | 26.9 |
| Greenwich disturbed days, range 10′ to 30′, 1848-1902 | 3,830 | 33.9 | 39.0 | 27.1 |
| Greenwich disturbed days range 30′ to 60′, 1848-1902 | 307 | 34.5 | 41.0 | 24.4 |
| Greenwich disturbed days, range over 60′, 1848-1902 | 77 | 29.9 | 41.6 | 28.6 |
| Kew highly disturbed days, 1890-1900 | 209 | 38.3 | 41.6 | 20.1 |
| Greenwich magnetic storms, all, 1848-1903 | 726 | 32.1 | 42.3 | 25.6 |
| Greenwich magnetic storms, range 20′ to 30′, 1848-1903 | 392 | 30.1 | 43.6 | 26.3 |
| Greenwich magnetic storms, range over 30′, 1848-1903 | 334 | 34.4 | 40.7 | 24.9 |
| Greenwich magnetic storms, all, 14 years of S. max. | 258 | 35.3 | 38.0 | 26.7 |
| Greenwich magnetic storms, all, 15 years of S. min. | 127 | 28.4 | 48.0 | 23.6 |
| Batavia magnetic storms, all, 1883-1899 | 1,008 | 32.9 | 34.9 | 32.2 |
| Batavia magnetic storms of gradual commencement | 679 | 32.4 | 34.8 | 32.8 |
| Batavia magnetic storms of sudden commencement | 329 | 33.7 | 35.3 | 31.0 |
Table XXXVII.—Batavia Magnetic Storms, Diurnal Distribution (percentages).
| Hour. | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | |
| Beginning | g | 5 | 5 | 5 | 6 | 20 | 16 | 7 | 5 | 6 | 9 | 8 | 8 |
| s | 7 | 5 | 7 | 10 | 10 | 11 | 10 | 8 | 8 | 9 | 8 | 7 | |
| Maximum | g | 12 | 10 | 6 | 5 | 4 | 9 | 9 | 6 | 6 | 6 | 12 | 15 |
| s | 14 | 7 | 5 | 2 | 2 | 9 | 9 | 5 | 8 | 10 | 13 | 16 | |
| End | all | 15 | 16 | 19 | 13 | 5 | 3 | 6 | 5 | 4 | 5 | 4 | 5 |
Table XXXVIII.—Greenwich Magnetic Storms, Diurnal Distribution.
| Epoch. | Class. | Total Number. | Percentages. | |||
| 1-8 p.m. | 9 p.m.- 4 a.m. | 5 a.m.- noon. | ||||
| Beginning | 1848-1903 | all | 721 | 60.1 | 21.9 | 18.0 |
| 1882-1903 | ” | 276 | 58.0 | 18.8 | 23.2 | |
| 1882-1903 | sudden | 77 | 45.4 | 27.3 | 27.3 | |
| End | 1848-1903 | all | 720 | 9.4 | 44.6 | 46.0 |
| 1882-1903 | ” | 276 | 7.2 | 41.7 | 51.1 | |
| 1882-1903 | sudden | 77 | 11.7 | 35.1 | 53.2 | |
§ 37. That large magnetic disturbances occur simultaneously over large areas was known in the time of Gauss, on whose initiative observations were taken at 5-minute intervals at a number of stations 377 on prearranged term days. During March 1879 and August 1880 some large magnetic storms occurred, and the magnetic curves showing these at a number of stations fitted with Kew pattern magnetographs were compared by W. G. Adams.42 He found the more characteristic movements to be, so far as could be judged, simultaneous at all the stations. At comparatively near stations such as Stonyhurst and Kew, or Coimbra and Lisbon, the curves were in general almost duplicates. At Kew and St Petersburg there were usually considerable differences in detail, and the movements were occasionally in opposite directions. The differences between Toronto, Melbourne or Zi-ka-wei and the European stations were still more pronounced. In 1896, on the initiative of M. Eschenhagen,43 eye observations of declination and horizontal force were taken at 5-second intervals during prearranged hours at Batavia, Manila, Melbourne and nine European stations. The data from one of these occasions when appreciable disturbance prevailed were published by Eschenhagen, and were subsequently analysed by Ad. Schmidt.44 Taking the stations in western Europe, Schmidt drew several series of lines, each series representing the disturbing forces at one instant of time as deduced from the departure of the elements at the several stations from their undisturbed value. The lines answering to any one instant had a general sameness of direction with more or less divergence or convergence, but their general trend varied in a way which suggested to Schmidt the passage of a species of vortex with large but finite velocity.
Table XXXIX.—Direction of First Decided Movement.
| Place. | Declination. | Horizontal Force. | Vertical Force. |
| Pavlovsk | West | + | + |
| Potsdam | West | + | − |
| Greenwich | West | + | + |
| Zi-ka-wei | East | + | − |
| Kolaba | East | + | − |
| Batavia | West | + | − |
| Mauritius | East | + | + |
| Cape Horn | West | + | − |
The conclusion that magnetic disturbances tend to follow one another at nearly equal intervals of time has been reached by several independent observers. J. A. Broun45 pronounced for a period of about 26 days, and expressed a belief that a certain zone, or zones, of the sun’s surface might exert a prepotent influence on the earth’s magnetism during several solar rotations. Very similar views were advanced in 1904 by E. W. Maunder,39 who was wholly unaware of Broun’s work. Maunder concluded that the period was 27.28 days, coinciding with the sun’s rotation period relative to an observer on the earth. Taking magnetic storms at Greenwich from 1882 to 1903, he found the interval between the commencement of successive storms to approach closely to the above period in a considerably larger number of instances than one would have expected from mere chance. He found several successions of three or four storms, and in one instance of as many as six storms, showing his interval. In a later paper Maunder reached similar results for magnetic storms at Greenwich from 1848 to 1881. Somewhat earlier than Maunder, Arthur Harvey46 deduced a period of 27.246 days from a consideration of magnetic disturbances at Toronto. A. Schuster,47 examining Maunder’s data mathematically, concluded that they afforded rather strong evidence of a period of about ½ (27.28) or 13.6 days. Maunder regarded his results as demonstrating that magnetic disturbances originate in the sun. He regarded the solar action as arising from active areas of limited extent on the sun’s surface, and as propagated along narrow, well defined streams. The active areas he believed to be also the seats of the formation of sun-spots, but believed that their activity might precede and outlive the visible existence of the sun-spot.
Maunder did not discuss the physical nature of the phenomenon, but his views are at least analogous to those propounded somewhat earlier by Svante Arrhenius,48 who suggested that small negatively charged particles are driven from the sun by the repulsion of light and reach the earth’s atmosphere, setting up electrical currents, manifest in aurora and magnetic disturbances. Arrhenius’s calculations, for the size of particle which he regarded as most probable, make the time of transmission to the earth slightly under two days. Amongst other theories which ascribe magnetic storms to direct solar action may be mentioned that of Kr. Birkeland,49 who believes the vehicle to be cathode rays. Ch. Nordmann50 similarly has suggested Röntgen rays. Supposing the sun the ultimate source, it would be easier to discriminate between the theories if the exact time of the originating occurrence could be fixed. For instance, a disturbance that is propagated with the velocity of light may be due to Röntgen rays, but not to Arrhenius’s particles. In support of his theory, Nordmann mentions several cases when conspicuous visual phenomena on the sun have synchronized with magnetic movements on the earth—the best known instance being the apparent coincidence in time of a magnetic disturbance at Kew on the 1st of September 1859 with a remarkable solar outburst seen by R. C. Carrington. Presumably any electrical phenomenon on the sun will set up waves in the aether, so transmission of electric and magnetic disturbances from the sun to the earth with the velocity of light is a certainty rather than a hypothesis; but it by no means follows that the energy thus transmitted can give rise to sensible magnetic disturbances. Also, when considering Nordmann’s coincidences, it must be remembered that magnetic movements are so numerous that it would be singular if no apparent coincidences had been noticed. Another consideration is that the movements shown by ordinary magnetographs are seldom very rapid. During some storms, especially those accompanied by unusually bright and rapidly varying auroral displays, large to and fro movements follow one another in close succession, the changes being sometimes too quick to be registered distinctly on the photographic paper. This, however, is exceptional, even in polar regions where disturbances are largest and most numerous. As a rule, even when the change in the direction of movement in the declination needle seems quite sudden, the movement in one direction usually lasts for several minutes, often for 10, 15 or 30 minutes. Thus the cause to which magnetic disturbances are due seems in many cases to be persistent in one direction for a considerable time.
§ 38. Attempts have been made to discriminate between the theories as to magnetic storms by a critical examination of the phenomena. A general connexion between sun-spot frequency and the amplitude of magnetic movements, regular and irregular, is generally admitted. If it is a case of cause and effect, and the interval between the solar and terrestrial phenomena does not exceed a few hours, then there should be a sensible connexion between corresponding daily values of the sun-spot frequency and the magnetic range. Even if only some sun-spots are effective, we should expect when we select from a series of years two groups of days, the one containing the days of most sun-spots, the other the days of least, that a prominent difference will exist between the mean values of the absolute daily magnetic ranges for the two groups. Conversely, if we take out the days of small and the days of large magnetic range, or the days that are conspicuously quiet and those that are highly disturbed, we should expect a prominent difference between the corresponding mean sun-spot areas. An application of this principle was made by Chree23 to the five quiet days a month selected by the astronomer royal between 1890 and 1900. These days are very quiet relative to the average day and possess a much smaller absolute range. One would thus have expected on Birkeland’s or Nordmann’s theory the mean sun-spot frequency derived from Wolfer’s provisional values for these days to be much below his mean value, 41.22, for the eleven years. It proved, however, to be 41.28. This practical identity was as visible in 1892 to 1895, the years of sun-spot maximum, as it was in the years of sun-spot minimum. Use was next made of the Greenwich projected sun-spot areas, which are the result of exact measurement. The days of each month were divided into three groups, the first and third—each normally of ten days—containing respectively the days of largest and the days of least sun-spot area. The mean sun-spot area from group 1 was on the average about five times that for group 3. It was then investigated how the astronomer royal’s quiet days from 1890 to 1900, and how the most disturbed days of the period selected from the Kew24 magnetic records, distributed themselves among the three groups of days. Nineteen months were excluded, as containing more than ten days with no sun-spots. The remaining 113 months contained 565 quiet and 191 highly disturbed days, whose distribution was as follows:
| Group 1. | Group 2. | Group 3. | |
| Quiet days | 179 | 195 | 191 |
| Disturbed days | 68 | 65 | 58 |
The group of days of largest sun-spot area thus contained slightly under their share of quiet days and slightly over their share of disturbed days. The differences, however, are not large, and in three years, viz. 1895, 1897 and 1899, the largest number of disturbed days actually occurred in group 3, while in 1895, 1896 and 1899 there were fewer quiet days in group 3 than in group 1. Taking the same distribution of days, the mean value of the absolute daily range of declination at Kew was calculated for the group 1 and the group 3 days of each month. The mean range from the group 1 days was the larger in 57% of the individual months as against 43% in which it was the smaller. When the days of each month were divided into groups according to the absolute declination range at Kew, the mean sun-spot area for the group 1 days (those of largest range) exceeded that for the group 3 days (those of least range) in 55% of the individual months, as against 45% of cases in which it was the smaller.
Taking next the five days of largest and the five days of least range in each month, sun-spot areas were got out not merely for these days themselves, but also for the next subsequent day and the four immediately preceding days in each case. On Arrhenius’s theory we should expect the magnetic range to vary with the sun-spot area, not on the actual day but two days previously. The following figures give the percentage excess or deficiency of the mean sun-spot area for the respective groups of days, relative to the average value for the whole epoch dealt with. n denotes the day to which the magnetic range belongs, n + 1 the day after, n − 1 the day before, and 378 so on. Results are given for 1894 and 1895, the years which were on the whole the most favourable and the least favourable for Arrhenius’s hypothesis, as well as for the whole eleven years.
Table XL.
| Day. | n − 4 | n − 3 | n − 2 | n − 1 | n | n + 1 | |
| Five days of largest range | 1894 | +12 | + 9 | +11 | +12 | +11 | + 6 |
| 1895 | −16 | −17 | −15 | −12 | −11 | −10 | |
| 11 yrs. | + 9 | + 8 | + 8 | + 7 | + 5 | + 0.5 | |
| Five days of least range | 1894 | −15 | −17 | −19 | −21 | −21 | −19 |
| 1895 | +17 | +10 | + 1 | − 2 | − 2 | − 4 | |
| 11 yrs. | − 4 | − 4 | − 7 | − 7 | − 7 | − 6 | |
Taking the 11-year-means we have the sun-spot area practically normal on the day subsequent to the representative day of large magnetic range, but sensibly above its mean on that day and still more so on the four previous days. This suggests an emission from the sun taking a highly variable time to travel to the earth. The 11-year mean data for the five days of least range seem at first sight to point to the same conclusion, but the fact that the deficiency in sun-spot area is practically as prominent on the day after the representative day of small magnetic range as on that day itself, or the previous days, shows that the phenomenon is probably a secondary one. On the whole, taking into account the extraordinary differences between the results from individual years, we seem unable to come to any very positive conclusion, except that in the present state of our knowledge little if any clue is afforded by the extent of the sun’s spotted area on any particular day as to the magnetic conditions on the earth on that or any individual subsequent day. Possibly some more definite information might be extracted by considering the extent of spotted area on different zones of the sun. On theories such as those of Arrhenius or Maunder, effective bombardment of the earth would be more or less confined to spotted areas in the zones nearest the centre of the visible hemisphere, whilst all spots on this hemisphere contribute to the total spotted area. Still the projected area of a spot rapidly diminishes as it approaches the edge of the visible hemisphere, i.e. as it recedes from the most effective position, so that the method employed above gives a preponderating weight to the central zones. One rather noteworthy feature in Table XL. is the tendency to a sequence in the figures in any one row. This seems to be due, at least in large part, to the fact that days of large and days of small sun-spot area tend to occur in groups. The same is true to a certain extent of days of large and days of small magnetic range, but it is unusual for the range to be much above the average for more than 3 or 4 successive days.
§ 39. The records from ordinary magnetographs, even when run at the usual rate and with normal sensitiveness, not infrequently show a repetition of regular or nearly regular small rhythmic movements, lasting sometimes for hours. The amplitude Pulsations. and period on different occasions both vary widely. Periods of 2 to 4 minutes are the most common. W. van Bemmelen51 has made a minute examination of these movements from several years’ traces at Batavia, comparing the results with corresponding statistics sent him from Zi-ka-wei and Kew. Table XLI. shows the diurnal variation in the frequency of occurrence of these small movements—called pulsations by van Bemmelen—at these three stations. The Batavia results are from the years 1885 and 1892 to 1898. Of the two sets of data for Zi-ka-wei (i) answers to the years 1897, 1898 and 1900, as given by van Bemmelen, while (ii) answers to the period 1900-1905, as given in the Zi-ka-wei Bulletin for 1905. The Kew data are for 1897. The results are expressed as percentages of the total for the 24 hours. There is a remarkable contrast between Batavia and Zi-ka-wei on the one hand and Kew on the other, pulsations being much more numerous by night than by day at the two former stations, whereas at Kew the exact reverse holds. Van Bemmelen decided that almost all the occasions of pulsation at Zi-ka-wei were also occasions of pulsations at Batavia. The hours of commencement at the two places usually differed a little, occasionally by as much as 20 minutes; but this he ascribed to the fact that the earliest oscillations were too small at one or other of the stations to be visible on the trace. Remarkable coincidence between pulsations at Potsdam and in the north of Norway has been noted by Kr. Birkeland.49
With magnetographs of greater sensitiveness and more open time scales, waves of shorter period become visible. In 1882 F. Kohlrausch52 detected waves with a period of about 12 seconds. Eschenhagen53 observed a great variety of short period waves, 30 seconds being amongst the most common. Some of the records he obtained suggest the superposition of regular sine waves of different periods. Employing a very sensitive galvanometer to record changes of magnetic induction through a coil traversed by the earth’s lines of force, H. Ebert54 has observed vibrations whose periods are but a small fraction of a second. The observations of Kohlrausch and Eschenhagen preceded the recent great development of applications of electrical power, while longer period waves are shown in the Kew curves of 50 years ago, so that the existence of natural waves with periods of from a few seconds up to several minutes can hardly be doubted. Whether the much shorter period waves of Ebert are also natural is more open to doubt, as it is becoming exceedingly difficult in civilized countries to escape artificial disturbances.
Table XLI.—Diurnal Distribution of Pulsations.
| Hours. | 0-3. | 3-6. | 6-9. | 9-Noon. | Noon-3. | 3-6. | 6-9. | 9-12. |
| Batavia | 28 | 9 | 2 | 6 | 8 | 6 | 13 | 28 |
| Zi-ka-wei (i) | 33 | 5 | 2 | 7 | 4 | 4 | 10 | 35 |
| Zi-ka-wei (ii) | 23 | 6 | 8 | 11 | 7 | 5 | 14 | 26 |
| Kew | 4 | 8 | 19 | 14 | 22 | 18 | 11 | 4 |
§ 40. The fact that the moon exerts a small but sensible effect on the earth’s magnetism seems to have been first discovered in 1841 by C. Kreil. Subsequently Sabine55 investigated the nature of the lunar diurnal variation in declination Lunar Influence. at Kew, Toronto, Pekin, St Helena, Cape of Good Hope and Hobart. The data in Table XLII. are mostly due to Sabine. They represent the mean lunar diurnal inequality in declination for the whole year. The unit employed is 0′.001, and as in our previous tables + denotes movement to the west. By “mean departure” is meant the arithmetic mean of the 24 hourly departures from the mean value for the lunar day; the range is the difference between the algebraically greatest and least of the hourly values. Not infrequently the mean departure gives the better idea of the importance of an inequality, especially when as in the present case two maxima and minima occur in the day. This double daily period is unusually prominent in the case of the lunar diurnal inequality, and is seen in the other elements as well as in the declination.
Table XLII.—Lunar Diurnal Inequality of Declination (unit 0′.001).
| Lunar Hour. | Kew. 1858-1862. | Toronto. 1843-1848. | Batavia. 1883-1899. | St Helena. 1843-1847. | Cape. 1842-1846. | Hobart. 1841-1848. |
| 0 | +103 | +315 | −70 | − 43 | −148 | − 98 |
| 1 | +160 | +275 | −63 | − 5 | −107 | −138 |
| 2 | +140 | +158 | −39 | + 37 | − 35 | −142 |
| 3 | + 33 | + 2 | − 8 | + 70 | + 43 | −107 |
| 4 | + 10 | −153 | +38 | + 85 | +108 | − 45 |
| 5 | − 67 | −265 | +63 | + 77 | +140 | + 27 |
| 6 | −150 | −302 | +87 | + 48 | +132 | + 88 |
| 7 | −188 | −255 | +77 | + 5 | + 82 | +122 |
| 8 | −160 | −137 | +40 | − 43 | + 5 | +120 |
| 9 | − 78 | + 7 | − 4 | − 82 | − 78 | + 82 |
| 10 | + 2 | +178 | −45 | −102 | −143 | + 17 |
| 11 | + 92 | +288 | −80 | − 98 | −177 | − 57 |
| 12 | +160 | +323 | −87 | − 73 | −165 | −120 |
| 13 | +188 | +272 | −68 | − 32 | −112 | −152 |
| 14 | +158 | +148 | −43 | + 13 | − 30 | −147 |
| 15 | + 90 | − 17 | − 8 | + 52 | + 58 | −105 |
| 16 | + 10 | −180 | +30 | + 73 | +132 | − 35 |
| 17 | − 85 | −297 | +62 | + 73 | +172 | + 45 |
| 18 | −142 | −337 | +72 | + 52 | +168 | +112 |
| 19 | −163 | −290 | +68 | + 17 | +122 | +152 |
| 20 | −147 | −170 | +52 | − 25 | + 45 | +152 |
| 21 | −123 | − 7 | + 8 | − 58 | − 40 | +113 |
| 22 | − 40 | +155 | −28 | − 73 | −112 | + 47 |
| 23 | + 27 | +265 | −56 | − 68 | −153 | − 30 |
| Mean De- parture | 105 | 200 | 50 | 54 | 104 | 93 |
| Range | 376 | 660 | 174 | 187 | 349 | 304 |
Lunar action has been specially studied in connexion with observations from India and Java. Broun56 at Trivandrum and C. Chambers57 at Kolaba investigated lunar action from a variety of aspects. At Batavia van der Stok58 and more recently S. Figee59 have carried out investigations involving an enormous amount of computation. Table XLIII. gives a summary of Figee’s results for the mean lunar diurnal inequality at Batavia, for the two half-yearly periods April to September (Winter or W.), and October to March (S.). The + sign denotes movement to the west in the case of declination, but numerical increase in the case of the other elements. In the case of H and T (total force) the results for the two seasons present comparatively small differences, but in the case of D, I and V the amplitude and phase both differ widely. Consequently a mean lunar diurnal variation derived from all the months of the year gives at Batavia, and presumably at other 379 tropical stations, an inadequate idea of the importance of the lunar influence. In January Figee finds for the range of the lunar diurnal inequality 0′.62 in D, 3.1γ in H and 3.5γ in V, whereas the corresponding ranges in June are only 0′.13, 1.1γ and 2.2γ respectively. The difference between summer and winter is essentially due to solar action, thus the lunar influence on terrestrial magnetism is clearly a somewhat complex phenomenon. From a study of Trivandrum data, Broun concluded that the action of the moon is largely dependent on the solar hour at the time, being on the average about twice as great for a day hour as for a night hour. Figee’s investigations at Batavia point to a similar conclusion. Following a method suggested by Van der Stok, Figee arrives at a numerical estimate of the “lunar activity” for each hour of the solar day, expressed in terms of that at noon taken as 100. In summer, for instance, in the case of D he finds the “activity” varying from 114 at 10 a.m. to only 8 at 9 p.m.; the corresponding extremes in the case of H are 139 at 10 a.m. and 54 at 6 a.m.
Table XLIII.—Lunar Diurnal Inequality at Batavia in Winter and Summer.
| Declination (unit 0′.001). | Inclination, S. (unit 0′.001). | H. (unit 0.01γ). | V. (unit 0.01γ). | T. (unit0.01γ). | ||||||
| Lunar Hour. | W. | S. | W. | S. | W. | S. | W. | S. | W. | S. |
| 0 | +30 | −170 | − 1 | +25 | −15 | − 56 | − 9 | + 4 | − 17 | −47 |
| 1 | +21 | −147 | −23 | +49 | −40 | − 87 | −54 | +20 | − 61 | −67 |
| 2 | + 5 | − 83 | −49 | +69 | −25 | −107 | −82 | +37 | − 62 | −76 |
| 3 | − 5 | − 12 | −51 | +47 | −21 | − 76 | −83 | +24 | − 59 | −55 |
| 4 | + 1 | + 76 | −37 | +43 | −13 | − 59 | −58 | +18 | − 39 | −38 |
| 5 | − 8 | +134 | −23 | +12 | +10 | − 9 | −27 | +11 | − 4 | − 3 |
| 6 | − 7 | +181 | − 2 | −21 | +21 | + 43 | + 9 | − 6 | + 23 | +35 |
| 7 | −10 | +164 | +30 | −12 | +23 | + 45 | +55 | + 8 | + 47 | +43 |
| 8 | − 7 | + 86 | +36 | −21 | +38 | + 52 | +71 | − 1 | + 68 | +45 |
| 9 | − 8 | 0 | +28 | −23 | +46 | + 30 | +64 | −16 | + 71 | +19 |
| 10 | − 5 | − 85 | +34 | −20 | +13 | + 13 | +54 | −21 | + 38 | + 1 |
| 11 | −15 | −144 | +27 | −11 | −12 | − 6 | +31 | −19 | + 5 | −15 |
| 12 | − 9 | −164 | +19 | − 5 | −47 | − 23 | 0 | −19 | − 41 | −29 |
| 13 | + 1 | −136 | − 3 | +17 | −59 | − 46 | −36 | − 2 | − 69 | −41 |
| 14 | − 7 | − 79 | −13 | +27 | −66 | − 44 | −55 | +14 | − 84 | −32 |
| 15 | − 8 | − 8 | −32 | +25 | −53 | − 37 | −74 | +14 | − 82 | −26 |
| 16 | −12 | + 72 | −37 | +25 | −34 | − 17 | −70 | +26 | − 64 | − 2 |
| 17 | −13 | +137 | −33 | + 4 | − 1 | + 28 | −47 | +21 | − 24 | +35 |
| 18 | −21 | +165 | − 2 | −10 | +20 | + 47 | + 8 | +12 | + 21 | +47 |
| 19 | −12 | +147 | +21 | −42 | +44 | + 81 | +53 | −14 | + 64 | +64 |
| 20 | +10 | + 95 | +21 | −62 | +75 | +107 | +71 | −28 | +100 | +80 |
| 21 | +13 | + 4 | +26 | −70 | +65 | + 98 | +72 | −44 | + 92 | +65 |
| 22 | +25 | − 82 | +35 | −41 | +35 | + 35 | +68 | −38 | + 64 | +12 |
| 23 | +36 | −147 | +34 | − 4 | − 7 | − 14 | +44 | −13 | + 15 | −19 |
| Mean De- parture | 12 | 150 | 26 | 29 | 33 | 48 | 50 | 18 | 51 | 37 |
| Range | 57 | 351 | 87 | 139 | 141 | 214 | 155 | 81 | 184 | 156 |
The question whether lunar influence increases with sun-spot frequency is obviously of considerable theoretical interest. Balfour Stewart in the 9th edition of this encyclopaedia gave some data indicating an appreciably enhanced lunar influence at Trivandrum during years of sun-spot maximum, but he hesitated to accept the result as finally proved. Figee recently investigated this point at Batavia, but with inconclusive results. Attempts have also been made to ascertain how lunar influence depends on the moon’s declination and phase, and on her distance from the earth. The difficulty in these investigations is that we are dealing with a small effect, and a very long series of data would be required satisfactorily to eliminate other periodic influences.
§ 41. From an analysis of seventeen years data at St Petersburg and Pavlovsk, Leyst60 concluded that all the principal planets sensibly influence the earth’s magnetism. According to his figures, all the planets except Mercury—whose influence Planetary Influence. he found opposite to that of the others—when nearest the earth tended to deflect the declination magnet at St Petersburg to the west, and also increased the range of the diurnal inequality of declination, the latter effect being the more conspicuous. Schuster,61 who has considered the evidence advanced by Leyst from the mathematical standpoint, considers it to be inconclusive.
§ 42. The best way of carrying out a magnetic survey depends on where it has to be made and on the object in view. The object that probably still comes first in importance is a knowledge of the declination, of sufficient accuracy for navigation Magnetic Surveys. in all navigable waters. One might thus infer that magnetic surveys consist mainly of observations at sea. This cannot however be said to be true of the past, whatever it may be of the future, and this for several reasons. Observations at sea entail the use of a ship, specially constructed so as to be free from disturbing influence, and so are inherently costly; they are also apt to be of inferior accuracy. It might be possible in quiet weather, in a large vessel free from vibration, to observe with instruments of the highest precision such as a unifilar magnetometer, but in the ordinary surveying ship apparatus of less sensitiveness has to be employed. The declination is usually determined with some form of compass. The other elements most usually found directly at sea are the inclination and the total force, the instrument employed being a special form of inclinometer, such as the Fox circle, which was largely used by Ross in the Antarctic, or in recent years the Lloyd-Creak. This latter instrument differs from the ordinary dip-circle fitted for total force observations after H. Lloyd’s method mainly in that the needles rest in pivots instead of on agate edges. To overcome friction a projecting pin on the framework is scratched with a roughened ivory plate.
The most notable recent example of observations at sea is afforded by the cruises of the surveying ships “Galilee” and “Carnegie” under the auspices of the Carnegie Institution of Washington, which includes in its magnetic programme a general survey. To see where the ordinary land survey assists navigation, let us take the case of a country with a long seaboard. If observations were taken every few miles along the coast results might be obtained adequate for the ordinary wants of coasting steamers, but it would be difficult to infer what the declination would be 50 or even 20 miles off shore at any particular place. If, however, the land area itself is carefully surveyed, one knows the trend of the lines of equal declination, and can usually extend them with considerable accuracy many miles out to sea. One also can tell what places if any on the coast suffer from local disturbances, and thus decide on the necessity of special observations. This is by no means the only immediately useful purpose which is or may be served by magnetic surveys on land. In Scandinavia use has been made of magnetic observations in prospecting for iron ore. There are also various geological and geodetic problems to whose solution magnetic surveys may afford valuable guidance. Among the most important recent surveys may be mentioned those of the British Isles by A. Rücker and T. E. Thorpe,62 of France and Algeria by Moureaux,63 of Italy by Chistoni and Palazzo,64 of the Netherlands by Van Ryckevorsel,65 of South Sweden by Carlheim Gyllenskiöld,66 of Austria-Hungary by Liznar,67 of Japan by Tanakadate,68 of the East Indies by Van Bemmelen, and South Africa by J. C. Beattie. A survey of the United States has been proceeding for a good many years, and many results have appeared in the publications of the U.S. Coast and Geodetic Survey, especially Bauer’s Magnetic Tables and Magnetic Charts, 1908. Additions to our knowledge may also be expected from surveys of India, Egypt and New Zealand.
For the satisfactory execution of a land survey, the observers must have absolute instruments such as the unifilar magnetometer and dip circle, suitable for the accurate determination of the magnetic elements, and they must be able to fix the exact positions of the spots where observations are taken. If, as usual, the survey occupies several years, what is wanted is the value of the elements not at the actual time of observation, but at some fixed epoch, possibly some years earlier or later. At a magnetic observatory, with standardized records, the difference between the values of a magnetic element at any two specified instants can be derived from the magnetic curves. But at an ordinary survey station, at a distance from an observatory, the information is not immediately available. Ordinarily the reduction to a fixed epoch is done in at least two stages, a correction being applied for secular change, and a second for the departure from the mean value for the day due to the regular diurnal inequality and to disturbance.
The reduction to a fixed epoch is at once more easy and more accurate if the area surveyed contains, or has close to its borders, a well distributed series of magnetic observatories, whose records are comparable and trustworthy. Throughout an area of the size of France or Germany, the secular change between any two specified dates can ordinarily be expressed with sufficient accuracy by a formula of the type
δ = δ0 + a (l − l0) + b (λ − λ0) . . (i),
where δ denotes secular change, l latitude and λ longitude, the letters with suffix 0 relating to some convenient central position. The constants δ0, a, b are to be determined from the observed secular changes at the fixed observatories whose geographical co-ordinates are accurately known. Unfortunately, as a rule, fixed observatories are few in number and not well distributed for survey purposes; thus the secular change over part at least of the area has usually to be found by repeating the observations after some years at several of the field stations. The success attending this depends on the 380 exactitude with which the sites can be recovered, on the accuracy of the observations, and on the success with which allowance is made for diurnal changes, regular and irregular. It is thus desirable that the observations at repeat stations should be taken at hours when the regular diurnal changes are slow, and that they should not be accepted unless taken on days that prove to be magnetically quiet. Unless the secular change is exceptionally rapid, it will usually be most convenient in practice to calculate it from or to the middle of the month, and then to allow for the difference between the mean value for the month and the value at the actual hour of observation. There is here a difficulty, inasmuch as the latter part of the correction depends on the diurnal inequality, and so on the local time of the station. No altogether satisfactory method of surmounting this difficulty has yet been proposed. Rücker and Thorpe in their British survey assumed that the divergence from the mean value at any hour at any station might be regarded as made up of a regular diurnal inequality, identical with that at Kew when both were referred to local time, and of a disturbance element identical with that existing at the same absolute time at Kew. Suppose, for instance, that at hour h G.M.T. the departure at Kew from the mean value for the month is d, then the corresponding departure from the mean at a station λ degrees west of Kew is d − e, where e is the increase in the element at Kew due to the regular diurnal inequality between hour h − λ/15 and hour h. This procedure is simple, but is exposed to various criticisms. If we define a diurnal inequality as the result obtained by combining hourly readings from all the days of a month, we can assign a definite meaning to the diurnal inequality for a particular month of a particular year, and after the curves have been measured we can give exact numerical figures answering to this definition. But the diurnal inequality thus obtained differs, as has been pointed out, from that derived from a limited number of the quietest days of the month, not merely in amplitude but in phase, and the view that the diurnal changes on any individual day can be regarded as made up of a regular diurnal inequality of definite character and of a disturbance element is an hypothesis which is likely at times to be considerably wide of the mark. The extent of the error involved in assuming the regular diurnal inequality the same in the north of Scotland, or the west of Ireland, as in the south-east of England remains to be ascertained. As to the disturbance element, even if the disturbing force were of given magnitude and direction all over the British Isles—which we now know is often very far from the case—its effects would necessarily vary very sensibly owing to the considerable variation in the direction and intensity of the local undisturbed force. If observations were confined to hours at which the regular diurnal changes are slow, and only those taken on days of little or no disturbance were utilized, corrections combining the effects of regular and irregular diurnal changes could be derived from the records of fixed observations, supposed suitably situated, combined in formulae of the same type as (i).
§ 43. The field results having been reduced to a fixed epoch, it remains to combine them in ways likely to be useful. In most cases the results are embodied in charts, usually of at least two kinds, one set showing only general features, the other the chief local peculiarities. Charts of the first kind resemble the world charts (figs. 1 to 4) in being free from sharp twistings and convolutions. In these the declination for instance at a fixed geographical position on a particular isogonal is to be regarded as really a mean from a considerable surrounding area.
Various ways have been utilized for arriving at these terrestrial isomagnetics—as Rücker and Thorpe call them—of which an elaborate discussion has been made by E. Mathias.69 From a theoretical standpoint the simplest method is perhaps that employed by Liznar for Austria-Hungary. Let l and λ represent latitude and longitude relative to a certain central station in the area. Then assume that throughout the area the value E of any particular magnetic element is given by a formula
E = E0 + al + bλ + cl² + dλ² + elλ,
where E0, a, b, c, d, e are absolute constants to be determined from the observations. When determining the constants, we write for E in the equation the observed value of the element (corrected for secular change, &c.) at each station, and for l and λ the latitude and longitude of the station relative to the central station. Thus each station contributes an equation to assist in determining the six constants. They can thus be found by least squares or some simpler method. In Liznar’s case there were 195 stations, so that the labour of applying least squares would be considerable. This is one objection to the method. A second is that it may allow undesirably large weight to a few highly disturbed stations. In the case of the British Isles, Rücker and Thorpe employed a different method. The area was split up into districts. For each district a mean was formed of the observed values of each element, and the mean was assigned to an imaginary central station, whose geographical co-ordinates represented the mean of the geographical co-ordinates of the actual stations. Want of uniformity in the distribution of the stations may be allowed for by weighting the results. Supposing E0 the value of the element found for the central station of a district, it was assumed that the value E at any actual station whose latitude and longitude exceeded those of the central station by l and λ was given by E = E0 + al + bλ, with a and b constants throughout the district. Having found E0, a and b, Rücker and Thorpe calculated values of the element for points defined by whole degrees of longitude (from Greenwich) and half degrees of latitude. Near the common border of two districts there would be two calculated values, of which the arithmetic mean was accepted.
The next step was to determine by interpolation where isogonals—or other isomagnetic lines—cut successive lines of latitude. The curves formed by joining these successive points of intersection were called district lines or curves. Rücker and Thorpe’s next step was to obtain formulae by trial, giving smooth curves of continuous curvature—terrestrial isomagnetics—approximating as closely as possible to the district lines. The curves thus obtained had somewhat complicated formulae. For instance, the isogonals south of 54°.5 latitude were given for the epoch Jan. 1, 1891 by
D = 18° 37′ + 18′.5 (l − 49.5) − 3′.5 cos {45° (l − 49.5) }
+ {26′.3 + 1′.5 (l − 49.5) } (λ − 4) + 0′.01 (λ − 4)² (l − 54.5)²,
where D denotes the westerly declination. Supposing, what is at least approximately true, that the secular change in Great Britain since 1891 has been uniform south of lat. 54°.5, corresponding formulae for the epochs Jan. 1, 1901, and Jan. 1, 1906, could be obtained by substituting for 18° 37′ the values 17° 44′ and 17° 24′ respectively. In their very laborious and important memoir E. Mathias and B. Baillaud69 have applied to Rücker and Thorpe’s observations a method which is a combination of Rücker and Thorpe’s and of Liznar’s. Taking Rücker and Thorpe’s nine districts, and the magnetic data found for the nine imaginary central stations, they employed these to determine the six constants of Liznar’s formula. This is an immense simplification in arithmetic. The declination formula thus obtained for the epoch Jan. 1, 1891, was
D = 20° 45′.89 + .53474λ + .34716l + .000021λ²
+ .000343lλ − .000239l²,
where l + (53° 30′.5) represents the latitude, and (λ + 5° 35′.2) the west longitude of the station. From this and the corresponding formulae for the other elements, values were calculated for each of Rücker and Thorpe’s 882 stations, and these were compared with the observed values. A complete record is given of the differences between the observed and calculated values, and of the corresponding differences obtained by Rücker and Thorpe from their own formulae. The mean numerical (calculated ~ observed) differences from the two different methods are almost exactly the same—being approximately 10′ for declination, 5′½ for inclination, and 70γ for horizontal force. The applications by Mathias69 of his method to the survey data of France obtained by Moureaux, and those of the Netherlands obtained by van Rïjckevorsel, appear equally successful. The method dispenses entirely with district curves, and the parabolic formulae are perfectly straightforward both to calculate and to apply; they thus appear to possess marked advantages. Whether the method could be applied equally satisfactorily to an area of the size of India or the United States actual trial alone would show.
§ 44. Rücker and Thorpe regarded their terrestrial isomagnetics and the corresponding formulae as representing the normal field that would exist in the absence of disturbances Local Disturbances. peculiar to the neighbourhood. Subtracting the forces derived from the formulae from those observed, we obtain forces which may be ascribed to regional disturbance.
When the vertical disturbing force is downwards, or the observed vertical component larger than the calculated, Rücker and Thorpe regard it as positive, and the loci where the largest positive values occur they termed ridge lines. The corresponding loci where the largest negative values occur were called valley lines. In the British Isles Rücker and Thorpe found that almost without exception, in the neighbourhood of a ridge line, the horizontal component of the disturbing force pointed towards it, throughout a considerable area on both sides. The phenomena are similar to what would occur if ridge lines indicated the position of the summits of underground masses of magnetic material, magnetized so as to attract the north-seeking pole of a magnet. Rücker and Thorpe were inclined to believe in the real existence of these subterranean magnetic mountains, and inferred that they must be of considerable extent, as theory and observation alike indicate that thin basaltic sheets or dykes, or limited masses of trap rock, produce no measurable magnetic effect except in their immediate vicinity. In support of their conclusions, Rücker and Thorpe dwell on the fact that in the United Kingdom large masses of basalt such as occur in Skye, Mull, Antrim, North Wales or the Scottish coalfield, are according to their survey invariably centres of attraction for the north-seeking pole of a magnet. Various cases of repulsion have, however, been described by other observers in the northern hemisphere.
§ 45. Rücker and Thorpe did not make a very minute examination of disturbed areas, so that purely local disturbances larger than any noticed by them may exist in the United Kingdom. But any that exist are unlikely to rival some that have been observed elsewhere, notably those in the province of Kursk in Russia described by Moureaux70 and by E. Leyst.71 In Kursk Leyst observed declinations varying from 0° to 360°, inclinations varying from 39°.1 to 90°; he obtained values of the horizontal force varying from 0 to 0.856 C.G.S., and values of the vertical force varying from 0.371 to 1.836. Another highly disturbed Russian district Krivoi Rog 381 (48° N. lat. 33° E. long.) was elaborately surveyed by Paul Passalsky.72 The extreme values observed by him differed, the declination by 282° 40′, the inclination by 41° 53′, horizontal force by 0.658, and vertical force by 1.358. At one spot a difference of 116°½ was observed between the declinations at two positions only 42 metres apart. In cases such as the last mentioned, the source of disturbance comes presumably very near the surface. It is improbable that any such enormously rapid changes of declination can be experienced anywhere at the surface of a deep ocean. But in shallow water disturbances of a not very inferior order of magnitude have been met with. Possibly the most outstanding case known is that of an area, about 3 m. long by 1¼ m. at its widest, near Port Walcott, off the N.W. Australian coast. The results of a minute survey made here by H.M.S. “Penguin” have been discussed by Captain E. W. Creak.73 Within the narrow area specified, declination varied from 26° W. to 56° E., and inclination from 50° to nearly 80°, the observations being taken some 80 ft. above sea bottom. Another noteworthy case, though hardly comparable with the above, is that of East Loch Roag at Lewis in the Hebrides. A survey by H.M.S. “Research” in water about 100 ft. deep—discussed by Admiral A. M. Field74—showed a range of 11° in declination. The largest observed disturbances in horizontal and vertical force were of the order 0.02 and 0.05 C.G.S. respectively. An interesting feature in this case was that vertical force was reduced, there being a well-marked valley line.
In some instances regional magnetic disturbances have been found to be associated with geodetic anomalies. This is true of an elongated area including Moscow, where observations were taken by Fritsche.75 Again, Eschenhagen76 detected magnetic anomalies in an area including the Harz Mountains in Germany, where deflections of the plumb line from the normal had been observed. He found a magnetic ridge line running approximately parallel to the line of no deflection of the plumb line.
§ 46. A question of interest, about which however not very much is known, is the effect of local disturbance on secular change and on the diurnal inequality. The determination of secular change in a highly disturbed locality is difficult, because an unintentional slight change in the spot where the observations are made may wholly falsify the conclusions drawn. When the disturbed area is very limited in extent, the magnetic field may reasonably be regarded as composed of the normal field that would have existed in the absence of local disturbance, plus a disturbance field arising from magnetic material which approaches nearly if not quite to the surface. Even if no sensible change takes place in the disturbance field, one would hardly expect the secular change to be wholly normal. The changes in the rectangular components of the force may possibly be the same as at a neighbouring undisturbed station, but this will not give the same change in declination and inclination. In the case of the diurnal inequality, the presumption is that at least the declination and inclination changes will be influenced by local disturbance. If, for example, we suppose the diurnal inequality to be due to the direct influence of electric currents in the upper atmosphere, the declination change will represent the action of the component of a force of given magnitude which is perpendicular to the position of the compass needle. But when local disturbance exists, the direction of the needle and the intensity of the controlling field are both altered by the local disturbance, so it would appear natural for the declination changes to be influenced also. This conclusion seems borne out by observations made by Passalsky72 at Krivoi Rog, which showed diurnal inequalities differing notably from those experienced at the same time at Odessa, the nearest magnetic observatory. One station where the horizontal force was abnormally low gave a diurnal range of declination four times that at Odessa; on the other hand, the range of the horizontal force was apparently reduced. It would be unsafe to draw general conclusions from observations at two or three stations, and much completer information is wanted, but it is obviously desirable to avoid local disturbance when selecting a site for a magnetic observatory, assuming one’s object is to obtain data reasonably applicable to a large area. In the case of the older observatories this consideration seems sometimes to have been lost sight of. At Mauritius, for instance, inside of a circle of only 56 ft. radius, having for centre the declination pillar of the absolute magnetic hut of the Royal Alfred Observatory, T. F. Claxton77 found that the declination varied from 4° 56′ to 13° 45′ W., the inclination from 50° 21′ to 58° 34′ S., and the horizontal force from 0.197 to 0.244 C.G.S. At one spot he found an alteration of 1°1⁄3 in the declination when the magnet was lowered from 4 ft. above the ground to 2. Disturbances of this order could hardly escape even a rough investigation of the site.
§ 47. If we assume the magnetic force on the earth’s surface Gaussian Potential and Constants. derivable from a potential V, we can express V as the sum of two series of solid spherical harmonics, one containing negative, the other positive integral powers of the radius vector r from the earth’s centre. Let λ denote east longitude from Greenwich, and let μ = cos (½π − l), where l is latitude; and also let
| Hmn = (1 − µ2)1/2m [ µn−m − | (n − m) (n − m − 1) | µn−m−2 + ... ], |
| 2 (2n − 1) |
where n and m denote any positive integers, m being not greater than n. Then denoting the earth’s radius by R, we have
V / R = Σ (R / r)n+1 [Hmn (gmn cos mλ + hmn sin mλ) ]
+ Σ (r / R)n [Hmn (gm−n cos mλ + hm−n sin mλ) ],
where Σ denotes summation of m from 0 to n, followed by summation of n from 0 to ∞. In this equation gmn, &c. are constants, those with positive suffixes being what are generally termed Gaussian constants. The series with negative powers of r answers to forces with a source internal to the earth, the series with positive powers to forces with an external source. Gauss found that forces of the latter class, if existent, were very small, and they are usually left out of account. There are three Gaussian constants of the first order, g10, g11, h11, five of the second order, seven of the third, and so on. The coefficient of a Gaussian constant of the nth order is a spherical harmonic of the nth degree. If R be taken as unit length, as is not infrequent, the first order terms are given by
V1 = r−2 [g10 sin l + (g11 cos λ + h11 sin λ) cos l].
The earth is in reality a spheroid, and in his elaborate work on the subject J. C. Adams78 develops the treatment appropriate to this case. Here we shall as usual treat it as spherical. We then have for the components of the force at the surface
| X = −R-1 (1 − µ2)1/2 (dV / dµ) towards the astronomical north, |
| Y = −R-1 (1 − µ2)−1/2 (dV / dλ) towards the astronomical west, |
| Z = −dV / dr vertically downwards. |
Supposing the Gaussian constants known, the above formulae would give the force all over the earth’s surface. To determine the Gaussian constants we proceed of course in the reverse direction, equating the observed values of the force components to the theoretical values involving gmn, &c. If we knew the values of the component forces at regularly distributed stations all over the earth’s surface, we could determine each Gaussian constant independently of the others. Our knowledge however of large regions, especially in the Arctic and Antarctic, is very scanty, and in practice recourse is had to methods in which the constants are not determined independently. The consequence is unfortunately that the values found for some of the constants, even amongst the lower orders, depend very sensibly on how large a portion of the polar regions is omitted from the calculations, and on the number of the constants of the higher orders which are retained.
Table XLIV.—Gaussian Constants of the First Order.
| 1829 Erman- Petersen. | 1830 Gauss. | 1845 Adams. | 1880 Adams. | 1885 Neumayer. | 1885 Schmidt. | 1885 Fritsche. | |
| g10 | +.32007 | +.32348 | +.32187 | +.31684 | +.31572 | +.31735 | +.31635 |
| g11 | +.02835 | +.03111 | +.02778 | +.02427 | +.02481 | +.02356 | +.02414 |
| h11 | −.06011 | −.06246 | −.05783 | −.06030 | −.06026 | −.05984 | −.05914 |
Table XLIV. gives the values obtained for the Gaussian constants of the first order in some of the best-known computations, as collected by W. G. Adams.79
§ 48. Allowance must be made for the difference in the epochs, and for the fact that the number of constants assumed to be worth retaining was different in each case. Gauss, for instance, assumed 24 constants sufficient, whilst in obtaining the results given in the table J. C. Adams retained 48. Some idea of the uncertainty thus arising may be derived from the fact that when Adams assumed 24 constants sufficient, he got instead of the values in the table the following:—
| g10 | g11 | h11 | |
| 1842-1845 | +.32173 | +.02833 | −.05820 |
| 1880 | +.31611 | +.02470 | −.06071 |
Some of the higher constants were relatively much more affected. Thus, on the hypotheses of 48 and of 24 constants respectively, the values obtained for g20 in 1842-1845 were -.00127 and -.00057, and those obtained for h31 in 1880 were +.00748 and +.00573. It must also be remembered that these values assume that the series in positive powers of r, with coefficients having negative suffixes, is absolutely non-existent. If this be not assumed, then in any equation determing X or Y, gmn must be replaced by gmn + gm−n, and in any equation determining Z by gmn − {n/(n + 1)} gmn; similar remarks apply to hmn and hm−n. It is thus theoretically possible to check the truth of the assumption that the positive power series is non-existent by comparing the values obtained for gmn and hmn from the X and Y or from the Z equations, when gm−n and hm−n are assumed zero. If the values so found differ, values can be found for gm−n and hm−n which will harmonize the two sets of equations. Adams gives the values obtained from the X, Y and the Z equations separately for the 382 Gaussian constants. The following are examples of the values thence deducible for the coefficients of the positive power series:—
| g−10 | g−11 | h−11 | g−40 | g−50 | g−60 | |
| 1842-1845 | +.0018 | −.0002 | −.0014 | +.0064 | +.0072 | +.0124 |
| 1880 | −.0002 | −.0012 | +.0015 | −.0043 | −.0021 | −.0013 |
Compared to g40, g50 and g60 the values here found for g−40, g−50 and g−60 are far from insignificant, and there would be no excuse for neglecting them if the observational data were sufficient and reliable. But two outstanding features claim attention, first the smallness of g−10, g−11 and h−11, the coefficients least likely to be affected by observational deficiencies, and secondly the striking dissimilarity between the values obtained for the two epochs. The conclusion to which these and other facts point is that observational deficiencies, even up to the present date, are such that no certain conclusion can be drawn as to the existence or non-existence of the positive power series. It is also to be feared that considerable uncertainties enter into the values of most of the Gaussian constants, at least those of the higher orders. The introduction of the positive power series necessarily improves the agreement between observed and calculated values of the force, but it is more likely than not to be disadvantageous physically, if the differences between observed values and those calculated from the negative power series alone arise in large measure from observational deficiencies.
Table XLV.—Axis and Moment of First Order Gaussian Coefficients.
| Epoch. | Authority for Constants. | North Latitude. | West Longitude. | M/R3 in G.C.S. units. |
| ° ′ | ° ′ | |||
| 1650 | H. Fritsche | 82 50 | 42 55 | .3260 |
| 1836 | ” | 78 27 | 63 35 | .3262 |
| 1845 | J. C. Adams | 78 44 | 64 20 | .3282 |
| 1880 | ” | 78 24 | 68 4 | .3234 |
| 1885 | Neumayer-Petersen and Bauer | 78 3 | 67 3 | .3224 |
| 1885 | Neumayer, Schmidt | 78 34 | 68 31 | .3230 |
§ 49. The first order Gaussian constants have a simple physical meaning. The terms containing them represent the potential arising from the uniform magnetization of a sphere parallel to a fixed axis, the moment M of the spherical magnet being given by
M = R3 { (g10)2 + (g11)2 + (h11)2}1/2,
where R is the earth’s radius. The position of the north end of the axis of this uniform magnetization and the values of M/R3, derived from the more important determinations of the Gaussian constants, are given in Table XLV. The data for 1650 are of somewhat doubtful value. If they were as reliable as the others, one would feel greater confidence in the reality of the apparent movement of the north end of the axis from east to west. The table also suggests a slight diminution in M since 1845, but it is open to doubt whether the apparent change exceeds the probable error in the calculated values. It should be carefully noticed that the data in the table apply only to the first order Gaussian terms, and so only to a portion of the earth’s magnetization, and that the Gaussian constants have been calculated on the assumption that the negative power series alone exists. The field answering to the first order terms—or what Bauer has called the normal field—constitutes much the most important part of the whole magnetization. Still what remains is very far from negligible, save for rough calculations. It is in fact one of the weak points in the Gaussian analysis that when one wishes to represent the observed facts with high accuracy one is obliged to retain so many terms that calculation becomes burdensome.
§ 50. The possible existence of a positive power series is not the only theoretical uncertainty in the Gaussian analysis. There is the further possibility that part of the earth’s magnetic field may not answer to a potential at all. Schmidt80 Earth-air Currents. in his calculation of Gaussian constants regarded this as a possible contingency, and the results he reached implied that as much as 2 or 3% of the entire field had no potential. If the magnetic force F on the earth’s surface comes from a potential, then the line integral ∫F ds taken round any closed circuit s should vanish. If the integral does not vanish, it equals 4πI, where I is the total electric current traversing the area bounded by s. A + sign in the result of the integration means that the current is downwards (i.e. from air to earth) or upwards, according as the direction of integration round the circuit, as viewed by an observer above ground, has been clockwise or anti-clockwise. In applications of the formula by W. von Bezold81 and Bauer82 the integral has been taken along parallels of latitude in the direction west to east. In this case a + sign indicates a resultant upward current over the area between the parallel of latitude traversed and the north geographical pole. The difference between the results of integration round two parallels of latitude gives the total vertical current over the zone between them. Schmidt’s final estimate of the average intensity of the earth-air current, irrespective of sign, for the epoch 1885 was 0.17 ampere per square kilometre. Bauer employing the same observational data as Schmidt, reached somewhat similar conclusions from the differences between integrals taken round parallels of latitude at 5° intervals from 60° N. to 60° S. H. Fritsche83 treating the problem similarly, but for two epochs, 1842 and 1885, got conspicuously different results for the two epochs, Bauer84 has more recently repeated his calculations, and for three epochs, 1842-1845 (Sabine’s charts), 1880 (Creak’s charts), and 1885 (Neumayer’s charts), obtaining the mean value of the current per sq. km. for 5° zones. Table XLVI. is based on Bauer’s figures, the unit being 0.001 ampere, and + denoting an upwardly directed current.
Table XLVI.—Earth-air Currents, after Bauer.
| Latitude. | Northern Hemisphere. | Southern Hemisphere. | ||||
| 1842-5. | 1880. | 1885. | 1842-5. | 1880. | 1885. | |
| 0° to 15° | − 1 | −32 | −34 | +66 | + 30 | + 36 |
| 15° to 30° | −70 | −59 | −68 | + 2 | − 62 | − 63 |
| 30° to 45° | + 3 | +14 | −22 | +26 | − 11 | − 14 |
| 45° to 60° | −31 | −21 | +78 | + 5 | +276 | +213 |
In considering the significance of the data in Table XLVI., it should be remembered that the currents must be regarded as mean values derived from all hours of the day, and all months of the year. Currents which were upwards during certain hours of the day, and downwards during others, would affect the diurnal inequality; while currents which were upwards during certain months, and downwards during others, would cause an annual inequality in the absolute values. Thus, if the figures be accepted as real, we must suppose that between 15° N. and 30° N. there are preponderatingly downward currents, and between 0° S. and 15° S. preponderatingly upward currents. Such currents might arise from meteorological conditions characteristic of particular latitudes, or be due to the relative distribution of land and sea; but, whatever their cause, any considerable real change in their values between 1842 and 1885 seems very improbable. The most natural cause to which to attribute the difference between the results for different epochs in Table XLVI. is unquestionably observational deficiencies. Bauer himself regards the results for latitudes higher than 45° as very uncertain, but he seems inclined to accept the reality of currents of the average intensity of 1⁄30 ampere per sq. km. between 45° N. and 45° S.
Currents of the size originally deduced by Schmidt, or even those of Bauer’s latest calculations, seem difficult to reconcile with the results of atmospheric electricity (q.v.).
§ 51. There is no single parallel of latitude along the whole of which magnetic elements are known with high precision. Thus results of greater certainty might be hoped for from the application of the line integral to well surveyed countries. Such applications have been made, e.g. to Great Britain by Rücker,85 and to Austria by Liznar,86 but with negative results. The question has also been considered in detail by Tanakadate68 in discussing the magnetic survey of Japan. He makes the criticism that the taking of a line integral round the boundary of a surveyed area amounts to utilizing the values of the magnetic elements where least accurately known, and he thus considers it preferable to replace the line integral by the surface integral.
4πI = ∫∫ (dY / dx − dX / dy) dx dy.
He applied this formula not merely to his own data for Japan, but also to British and Austrian data of Rücker and Thorpe and of Liznar. The values he ascribes to X and Y are those given by the formulae calculated to fit the observations. The result reached was “a line of no current through the middle of the country; in Japan the current is upward on the Pacific side and downward on the Siberian side; in Austria it is upward in the north and downward in the south; in Great Britain upward in the east and downward in the west.” The results obtained for Great Britain differed considerably according as use was made of Rücker and Thorpe’s own district equations or of a series of general equations of the type subsequently utilized by Mathias. Tanakadate points out that the fact that his investigations give in each case a line of no current passing through the middle of the surveyed area, is calculated to throw doubt on the reality of the supposed earth-air currents, and he recommends a suspension of judgment.
§ 52. A question of interest, and bearing a relationship to the Gaussian analysis, is the law of variation of the magnetic elements with height above sea-level. If F represent the value at sea-level, and F + δF that at height h, of any component of force answering to Gaussian constants of the nth order, then 1 + δF/F = (1 + h/R)−n−2, where R is the earth’s radius. Thus at heights of only a few miles we have very approximately δF/F = −(n + 2) h/R. As we have seen, the constants of the first order are much the most important, thus we should expect as a first approximation δX/X = δY/Y = δZ/Z = −3h/R. This equation gives the same rate of decrease in all three components, and so no change in declination or inclination. Liznar86a compared this equation with the observed results of his Austrian survey, subdividing his stations into three groups according 383 to altitude. He considered the agreement not satisfactory. It must be remembered that the Gaussian analysis, especially when only lower order terms are retained, applies only to the earth’s field freed from local disturbances. Now observations at individual high level stations may be seriously influenced not merely by regional disturbances common to low level stations, but by magnetic material in the mountain itself. A method of arriving at the vertical change in the elements, which theoretically seems less open to criticism, has been employed by A. Tanakadate.68 If we assume that a potential exists, or if admitting the possibility of earth-air currents we assume their effort negligible, we have dX/dz = dZ/dx, dY/dz = dZ/dy. Thus from the observed rates of change of the vertical component of force along the parallels of latitude and longitude, we can deduce the rate of change in the vertical direction of the two rectangular components of horizontal force, and thence the rates of change of the horizontal force and the declination. Also we have dZ/dz = 4πρ − (dX/dx + dY/dy), where ρ represents the density of free magnetism at the spot. The spot being above ground we may neglect ρ, and thus deduce the variation in the vertical direction of the vertical component from the observed variations of the two horizontal components in their own directions. Tanakadate makes a comparison of the vertical variations of the magnetic elements calculated in the two ways, not merely for Japan, but also for Austria-Hungary and Great Britain. In each country he took five representative points, those for Great Britain being the central stations of five of Rücker and Thorpe’s districts. Table XLVII. gives the mean of the five values obtained. By method (i.) is meant the formula involving 3h/R, by method (ii.) Tanakadate’s method as explained above. H, V, D, and I are used as defined in § 5. In the case of H and V unity represents 1γ.
Table XLVII.—Change per Kilometre of Height.
| Great Britain. | Austria-Hungary. | Japan. | ||||
| Method. | (i.) | (ii.) | (i.) | (ii.) | (i.) | (ii.) |
| H | − 8.1 | − 6.7 | −10.1 | − 8.7 | −13.9 | −14.0 |
| V | −21.2 | −19.4 | −19.0 | −18.1 | −17.1 | −17.4 |
| D (west) | · · | − 0′.04 | · · | + 0′.10 | · · | − 0′.27 |
| I | · · | − 0′.05 | · · | − 0′.06 | · · | − 0′.01 |
The − sign in Table XLVII. denotes a decrease in the numerical values of H, V and I, and a diminution in westerly declination. If we except the case of the westerly component of force—not shown in the table—the accordance between the results from the two methods in the case of Japan is extraordinarily close, and there is no very marked tendency for the one method to give larger values than the other. In the case of Great Britain and Austria the differences between the two sets of calculated values though not large are systematic, the 3h/R formula invariably showing the larger reduction with altitude in both H and V. Tanakadate was so satisfied with the accordance of the two methods in Japan, that he employed his method to reduce all observed Japanese values to sea-level. At a few of the highest Japanese stations the correction thus introduced into the value of H was of some importance, but at the great majority of the stations the corrections were all insignificant.
§ 53. Schuster87 has calculated a potential analogous to the Gaussian potential, from which the regular diurnal changes of the magnetic elements all over the earth may be derived. From the mean summer and winter diurnal variations Schuster’s Diurnal Variation Potential. of the northerly and easterly components of force during 1870 at St Petersburg, Greenwich, Lisbon and Bombay, he found the values of 8 constants analogous to Gaussian constants; and from considerations as to the hours of occurrence of the maxima and minima of vertical force, he concluded that the potential, unlike the Gaussian, must proceed in positive powers of r, and so answer to forces external to the earth. Schuster found, however, that the calculated amplitudes of the diurnal vertical force inequality did not accord well with observation; and his conclusion was that while the original cause of the diurnal variation is external, and consists probably of electric currents in the atmosphere, there are induced currents inside the earth, which increase the horizontal components of the diurnal inequality while diminishing the vertical. The problem has also been dealt with by H. Fritsche,88 who concludes, in opposition to Schuster, that the forces are partly internal and partly external, the two sets being of fairly similar magnitude. Fritsche repeats the criticism (already made in the last edition of this encyclopaedia) that Schuster’s four stations were too few, and contrasts their number with the 27 from which his own data were derived. On the other hand, Schuster’s data referred to one and the same year, whereas Fritsche’s are from epochs varying from 1841 to 1896, and represent in some cases a single year’s observations, in other cases means from several years. It is clearly desirable that a fresh calculation should be made, using synchronous data from a considerable number of well distributed stations; and it should be done for at least two epochs, one representing large, the other small sun-spot frequency. The year 1870 selected by Schuster had, as it happened, a sun-spot frequency which has been exceeded only once since 1750; so that the magnetic data which he employed were far from representative of average conditions.
§ 54. It was discovered by Folgheraiter89 that old vases from Etruscan and other sources are magnetic, and from combined observation and experiment he concluded that they acquired their magnetization when cooling after being baked, and Magnetization of Vases, &c. retained it unaltered. From experiments, he derived formulae connecting the magnetization shown by new clay vases with their orientation when cooling in a magnetic field, and applying these formulae to the phenomena observed in the old vases he calculated the magnetic dip at the time and place of manufacture. His observations led him to infer that in Central Italy inclination was actually southerly for some centuries prior to 600 B.C., when it changed sign. In 400 B.C. it was about 20°N.; since 100 B.C. the change has been relatively small. L. Mercanton90 similarly investigated the magnetization of baked clay vases from the lake dwellings of Neuchatel, whose epoch is supposed to be from 600 to 800 B.C. The results he obtained were, however, closely similar to those observed in recent vases made where the inclination was about 63°N., and he concluded in direct opposition to Folgheraiter that inclination in southern Europe has not undergone any very large change during the last 2500 years. Folgheraiter’s methods have been extended to natural rocks. Thus B. Brunhes91 found several cases of clay metamorphosed by adjacent lava flows and transformed into a species of natural brick. In these cases the clay has a determinate direction of magnetization agreeing with that of the volcanic rock, so it is natural to assume that this direction coincided with that of the dip when the lava flow occurred. In drawing inferences, allowance must of course be made for any tilting of the strata since the volcanic outburst. From one case in France in the district of St Flour, where the volcanic action is assigned to the Miocene Age, Brunhes inferred a southerly dip of some 75°. Until a variety of cases have been critically dealt with, a suspension of judgment is advisable, but if the method should establish its claims to reliability it obviously may prove of importance to geology as well as to terrestrial magnetism.
§ 55. Magnetic phenomena in the polar regions have received considerable attention of late years, and the observed results are of so exceptional a character as to merit separate consideration. One feature, the large amplitude of the regular diurnal Polar Phenomena. inequality, is already illustrated by the data for Jan Mayen and South Victoria Land in Tables VIII. to XI. In the case, however, of declination allowance must be made for the small size of H. If a force F perpendicular to the magnetic meridian causes a change ΔD in D then ΔD = F/H. Thus at the “Discovery’s” winter quarters in South Victoria Land, where the value of H is only about 0.36 of that at Kew, a change of 45′ in D would be produced by a force which at Kew would produce a change of only 16′. Another feature, which, however, may not be equally general, is illustrated by the data for Fort Rae and South Victoria Land in Table XVII. It will be noticed that it is the 24-hour term in the Fourier analysis of the regular diurnal inequality which is specially enhanced. The station in South Victoria Land—the winter quarters of the “Discovery” in 1902-1904—was at 77° 51′ S. lat.; thus the sun did not set from November to February (midsummer), nor rise from May to July (midwinter). It might not thus have been surprising if there had been an outstandingly large seasonal variation in the type of the diurnal inequality. As a matter of fact, however, the type of the inequality showed exceptionally small variation with the season, and the amplitude remained large throughout the whole year. Thus, forming diurnal inequalities for the three midsummer months and for the three midwinter months, we obtain the following amplitudes for the range of the several elements92:—
| D. | H. | V. | I. | |
| Midsummer | 64′.1 | 57γ | 58γ | 2′.87 |
| Midwinter | 26′.8 | 25γ | 18γ | 1′.23 |
The most outstanding phenomenon in high latitudes is the frequency and large size of the disturbances. At Kew, as we saw in § 25, the absolute range in D exceeds 20′ on only 12% of the total number of days. But at the “Discovery’s” winter quarters, about sun-spot minimum, the range exceeded 1° on 70%, 2° on 37%, and 3° on fully 15% of the total number of days. One day in 25 had a range exceeding 4°. During the three midsummer months, only one day out of 111 had a range under 1°, and even at midwinter only one day in eight had a range as small as 30′. The H range at the “Discovery’s” station exceeded 100γ on 40% of the days, and the V range exceeded 100γ on 32% of the days.
The special tendency to disturbance seen in equinoctial months in temperate latitudes did not appear in the “Discovery’s” records in the Antarctic. D ranges exceeding 3° occurred on 11% of equinoctial days, but on 40% of midsummer days. The preponderance of large movements at midsummer was equally apparent in the other elements. Thus the percentage of days having a V range over 200γ was 21 at midsummer, as against 3 in the four equinoctial months.
At the “Discovery’s” station small oscillations of a few minutes’ duration were hardly ever absent, but the character of the larger disturbances showed a marked variation throughout the 24 hours. 384 Those of a very rapid oscillatory character were especially numerous in the morning between 4 and 9 a.m. In the late afternoon and evening disturbances of a more regular type became prominent, especially in the winter months. In particular there were numerous occurrences of a remarkably regular type of disturbance, half the total number of cases taking place between 7 and 9 p.m. This “special type of disturbance” was divisible into two phases, each lasting on the average about 20 minutes. During the first phase all the elements diminished in value, during the second phase they increased. In the case of D and H the rise and fall were about equal, but the rise in V was about 3½ times the preceding fall. The disturbing force—on the north pole—to which the first phase might be attributed was inclined on the average about 5°½ below the horizon, the horizontal projection of its line of action being inclined about 41°½ to the north of east. The amplitude and duration of the disturbances of the “special type” varied a good deal; in several cases the disturbing force considerably exceeded 200γ. A somewhat similar type of disturbance was observed by Kr. Birkeland93 at Arctic stations also in 1902-1903, and was called by him the “polar elementary” storm. Birkeland’s record of disturbances extends only from October 1902 to March 1903, so it is uncertain whether “polar elementary” storms occur during the Arctic summer. Their usual time of occurrence seems to be the evening. During their occurrence Birkeland found that there was often a great difference in amplitude and character between the disturbances observed at places so comparatively near together as Iceland, Nova Zembla and Spitzbergen. This led him to assign the cause to electric currents in the Arctic, at heights not exceeding a few hundred kilometres, and he inferred from the way in which the phenomena developed that the seat of the disturbances often moved westward, as if related in some way to the sun’s position. Contemporaneously with the “elementary polar” storms in the Arctic Birkeland found smaller but distinct movements at stations all over Europe; these could generally be traced as far as Bombay and Batavia, and sometimes as far as Christchurch, New Zealand. Chree,92 on the other hand, working up the 1902-1904 Antarctic records, discovered that during the larger disturbances of the “special type” corresponding but much smaller movements were visible at Christchurch, Mauritius, Kolaba, and even at Kew. He also found that in the great majority of cases the Antarctic curves were specially disturbed during the times of Birkeland’s “elementary polar” storms, the disturbances in the Arctic and Antarctic being of the same order of magnitude, though apparently of considerably different type.
Examining the more prominent of the sudden commencements of magnetic disturbances in 1902-1903 visible simultaneously in the curves from Kew, Kolaba, Mauritius and Christchurch, Chree found that these were all represented in the Antarctic curves by movements of a considerably larger size and of an oscillatory character. In a number of cases Birkeland observed small simultaneous movements in the curves of his co-operating stations, which appeared to be at least sometimes decidedly larger in the equatorial than the northern temperate stations. These he described as “equatorial” perturbations, ascribing them to electric currents in or near the plane of the earth’s magnetic equator, at heights of the order of the earth’s radius. It was found, however, by Chree that in many, if not all, of these cases there were synchronous movements in the Antarctic, similar in type to those which occurred simultaneously with the sudden commencements of magnetic storms, and that these Antarctic movements were considerably larger than those described by Birkeland at the equatorial stations. This result tends of course to suggest a somewhat different explanation from Birkeland’s. But until our knowledge of facts has received considerable additions all explanations must be of a somewhat hypothetical character.
In 1831 Sir James Ross94 observed a dip of 89° 59′ at 70° 5′ N., 96° 46′ W., and this has been accepted as practically the position of the north magnetic pole at the time. The position of the south magnetic pole in 1840 as deduced from the Magnetic Poles. Antarctic observations made by the “Erebus” and “Terror” expedition is shown in Sabine’s chart as about 73° 30′ S., 147° 30′ E. In the more recent chart in J. C. Adams’s Collected Papers, vol. 2, the position is shown as about 73° 40′ S., 147° 7′ E. Of late years positions have been obtained for the south magnetic pole by the “Southern Cross” expedition of 1898-1900 (A), by the “Discovery” in 1902-1904 (B), and by Sir E. Shackleton’s expedition 1908-1909 (C). These are as follow:
| (A) 72° 40′ S., 152° 30′ E. |
| (B) 72° 51′ S., 156° 25′ E. |
| (C) 72° 25′ S., 155° 16′ E. |
Unless the diurnal inequality vanishes in its neighbourhood, a somewhat improbable contingency considering the large range at the “Discovery’s” winter quarters, the position of the south magnetic pole has probably a diurnal oscillation, with an average amplitude of several miles, and there is not unlikely a larger annual oscillation. Thus even apart from secular change, no single spot of the earth’s surface can probably claim to be a magnetic pole in the sense popularly ascribed to the term. If the diurnal motion were absolutely regular, and carried the point where the needle is vertical round a closed curve, the centroid of that curve—though a spot where the needle is never absolutely vertical—would seem to have the best claim to the title. It should also be remembered that when the dip is nearly 90° there are special observational difficulties. There are thus various reasons for allowing a considerable uncertainty in positions assigned to the magnetic poles. Conclusions as to change of position of the south magnetic pole during the last ten years based on the more recent results (A), (B) and (C) would, for instance, possess a very doubtful value. The difference, however, between these recent positions and that deduced from the observations of 1840-1841 is more substantial, and there is at least a moderate probability that a considerable movement towards the north-east has taken place during the last seventy years.
See publications of individual magnetic observatories, more especially the Russian (Annales de l’Observatoire Physique Central), the French (Annales du Bureau Central Météorologique de France), and those of Kew, Greenwich, Falmouth, Stonyhurst, Potsdam, Wilhelmshaven, de Bilt, Uccle, O’Gyalla, Prague, Pola, Coimbra, San Fernando, Capo di Monte, Tiflis, Kolaba, Zi-ka-wei, Hong-Kong, Manila, Batavia, Mauritius, Agincourt (Toronto), the observatories of the U.S. Coast and Geodetic Survey, Rio de Janeiro, Melbourne.
In the references below the following abbreviations are used: B.A. = British Association Reports; Batavia = Observations made at the Royal ... Observatory at Batavia; M.Z. = Meteorologische Zeitschrift, edited by J. Hann and G. Hellman; P.R.S. = Proceedings of the Royal Society of London; P.T. = Philosophical Transactions; R. = Repertorium für Meteorologie, St Petersburg; T.M. = Terrestrial Magnetism, edited by L. A. Bauer; R.A.S. Notices = Monthly Notices of the Royal Astronomical Society. Treatises are referred to by the numbers attached to them; e.g. (1) p. 100 means p. 100 of Walker’s Terrestrial Magnetism.
A For explanation of these numbers, see end of article.
1 E. Walker, Terrestrial and Cosmical Magnetism (Cambridge and London, 1856).
*1a H. Lloyd, A Treatise on Magnetism General and Terrestrial (London, 1874).
*2 E. Mascart, Traité de magnétisme terrestre (Paris, 1900).
3 L. A. Bauer, United States Magnetic Declination Tables and Isogonic Charts, and Principal Facts relating to the Earth’s Magnetism (Washington, 1902).
*4 Balfour Stewart, “Terrestrial Magnetism” (under “Meteorology”), Ency. brit. 9th ed.
*5 C. Chree, “Magnetism, Terrestrial,” Ency. brit. 10th ed.
6 M.Z. 1906, 23, p. 145.
7 (3) p. 62.
8 K. Akad. van Wetenschappen (Amsterdam, 1895; Batavia, 1899, &c.).
9 Atlas des Erdmagnetismus (Riga, 1903).
10 (1) p. 16, &c.
11 Kolaba (Colaba) Magnetical and Meteorological Observations, 1896. Appendix Table II.
12 (1) p. 21.
13 Report for 1906, App. 4, see also (3) p. 102.
14 (1) p. 166.
15 Ergebnisse der mag. Beobachtungen in Potsdam, 1901, p. xxxvi.
16 U.S. Coast and Geodetic Survey Report for 1895, App. 1, &c.
17 T.M. 1, pp. 62, 89, and 2, p. 68.
18 (3) p. 45.
19 Die Elemente des Erdmagnetismus, pp. 104.108.
20 Zur täglichen Variation der mag. Deklination (aus Heft II. des Archivs des Erdmagnetismus) (Potsdam, 1906).
21 M.Z. 1888, 5, p. 225.
22 M.Z. 1904, 21, p. 129.
23 P.T. 202 A, p. 335.
23a Comb. Phil. Soc. Trans. 20, p. 165.
24 P.T. 208 A, p. 205.
25 P.T. 203 A, p. 151.
26 P.T. 171. p. 541; P.R.S. 63, p. 64.
27 R.A.S. Notices 60, p. 142.
28 Rendiconti del R. Ist. Lomb. 1902, Series II. vol. 35.
29 R. 1889, vol. 12, no. 8.
30 B.A. Report, 1898, p. 80.
31 P.R.S. (A) 79, p. 151.
32 P.T. 204 A, p. 373.
33 Ann. du Bureau Central Météorologique, année 1897, 1 Mem. p. B65.
34 P.T. 161, p. 307.
35 M.Z. 1895, 12, p. 321.
35a P.T. 1851, p. 123; and 1852, p. 103, see also (4) § 38.
36 P.T. 159, p. 363.
37 (1) p. 92.
38 R.A.S. Notices 65, p. 666.
39 R.A.S. Notices, 65, pp. 2 and 538.
40 K. Akad. van Wetenschappen (Amsterdam, 1906) p. 266.
41 R.A.S. Notices 65, p. 520.
42 B.A. Reports, 1880, p. 201 and 1881, p. 463.
43 Anhang Ergebnisse der mag. Beob. in Potsdam, 1896.
44 M.Z. 1899, 16, p. 385.
45 P.T. 166, p. 387.
46 Trans. Can. Inst. 1898-1899, p. 345, and Proc. Roy. Ast. Soc. of Canada, 1902-1903, p. 74, 1904, p. xiv., &c.
47 R.A.S. Notices 65, p. 186.
48 T.M. 10, p. 1.
49 Expédition norvégienne de 1899-1900 (Christiania, 1901).
50 Thèses présentées à la Faculté des Sciences (Paris, 1903).
51 Nat. Tijdschrift voor Nederlandsch-Indië, 1902, p. 71.
52 Wied. Ann. 1882, p. 336.
53 Sitz. der k. preuss. Akad. der Wiss., 24th June 1897, &c.
54 T.M. 12, p. 1.
55 P.T. 143, p. 549; St Helena Observations, vol. ii., p. cxlvi., &c., (1) § 62.
56 Trans. R.S.E. 24, p. 669.
57 P.T. 178 A, p. 1.
58 Batavia, vol. 16, &c.
59 Batavia, Appendix to vol. 26.
60 R. vol. 17, no. 1.
61 T.M. 3, p. 1, &c.
62 P.T. 181 A, p. 53 and 188 A.
63 Ann. du Bureau Central Mét. vol. i. for years 1884 and 1887 to 1895.
64 Ann. dell’ Uff. Centrale Met. e Geod. vol. 14, pt. i. p. 57.
65 A Magnetic Survey of the Netherlands for the Epoch 1st Jan. 1891 (Rotterdam, 1895).
66 Kg. Svenska Vet. Akad. Handlingar, 1895, vol. 27, no. 7.
67 Denkschriften der math. naturwiss. Classe der k. Akad. des Wiss. (Wien), vols. 62 and 67.
68 Journal of the College of Science, Tōkyō, 1904, vol. 14.
69 Ann. de l’observatoire ... de Toulouse, 1907, vol. 7.
70 Ann. du Bureau Central Mét. 1897, I. p. B36.
71 T.M. 7, p. 74.
72 Bull. Imp. Univ. Odessa 85, p. 1, and T.M. 7, p. 67.
73 P.T. 187 A, p. 345.
74 P.R.S. 76 A, p. 181.
75 Bull. Soc. Imp. des Naturalistes de Moskau, 1893, no. 4, p. 381, and T.M. 1, p. 50.
76 Forsch. zur deut. Landes- u. Volkskunde, 1898, Bd. xi, 1, and T.M. 3, p. 77.
77 P.R.S. 76 A, p. 507.
78 Adams, Scientific Papers, II. p. 446.
79 B.A. Report for 1898, p. 109.
80 Abhand. der bayer, Akad. der Wiss., 1895, vol. 19.
81 Sitz. k. Akad. der Wiss. (Berlin), 1897, no. xviii., also T.M. 3, p. 191.
82 T.M. 2, p. 11.
83 Die Elemente des Erdmagnetismus (St Petersburg, 385 1899), p. 103.
84 T.M. 9, p. 113.
85 T.M. 1, p. 77, and Nature, 57, pp. 160 and 180.
86 M.Z. 15, p. 175.
86a Sitz, der k. k. Akad. der Wiss. Wien, math. nat. Classe, 1898, Bd. cvii., Abth. ii.
87 P.T. (A) 180, p. 467.
88 Die Tägliche Periode der erdmagnetischen Elemente (St Petersburg, 1902).
89 R. Accad. Lincei Atti, viii. 1899, pp. 69, 121, 176, 269 and previous volumes, see also Séances de la Soc. Franc. de Physique, 1899, p. 118.
90 Bull. Soc. Vaud., Sc. Nat. 1906, 42, p. 225.
91 Comptes rendus, 1905, 141, p. 567.
92 National Antarctic Expedition 1901-1904, “Magnetic Observations.”
93 The Norwegian Aurora Polaris Expedition 1902-1903, vol. i.
94 (1) p. 163.
Note: The footnotes marked by an (*) could not be located in the text.
