 Fig. 1.
Fig. 1.
Title: Popular scientific lectures
Author: Ernst Mach
Translator: Thomas J. McCormack
Release date: April 22, 2012 [eBook #39508]
Most recently updated: January 25, 2021
Language: English
Credits: Produced by Anna Hall, Albert László and the Online
Distributed Proofreading Team at http://www.pgdp.net (This
file was produced from images generously made available
by The Internet Archive)
The Science of Mechanics. Translated from the Second German Edition by T. J. McCormack. 250 Cuts and Illustrations. 534 Pages. Half Morocco, Gilt Top. Price, $2.50.
Contributions to the Analysis of the Sensations. Translated by C. M. Williams. With Notes and New Additions by the Author. 200 Pages. 36 Cuts. Price, $1.00.
Popular Scientific Lectures. Translated by T. J. McCormack. Third Revised and Enlarged Edition. 411 Pages. 59 Cuts. Cloth, $1.50; Paper, 50 cents.
THE OPEN COURT PUBLISHING CO.,
324 DEARBORN ST., CHICAGO.
POPULAR
SCIENTIFIC LECTURES
BY
ERNST MACH
FORMERLY PROFESSOR OF PHYSICS IN THE UNIVERSITY OF PRAGUE, NOW PROFESSOR OF THE HISTORY AND THEORY OF INDUCTIVE SCIENCE IN THE UNIVERSITY OF VIENNA
TRANSLATED
BY
THOMAS J. McCORMACK
THIRD EDITION, REVISED AND ENLARGED
WITH FIFTY-NINE CUTS AND DIAGRAMS
CHICAGO
THE OPEN COURT PUBLISHING COMPANY
FOR SALE BY
Kegan Paul, Trench, Truebner & Co., LONDON
1898
COPYRIGHT
By The Open Court Publishing Co.
| Pages 1-258 | in 1894. |
| Pages 338-374 | in 1894. |
| Pages 259-281 | in 1896. |
| Pages 282-308 | in 1897. |
| Pages 309-337 | in 1898. |
Popular lectures, owing to the knowledge they presuppose, and the time they occupy, can afford only a modicum of instruction. They must select for this purpose easy subjects, and restrict themselves to the exposition of the simplest and the most essential points. Nevertheless, by an appropriate choice of the matter, the charm and the poetry of research can be conveyed by them. It is only necessary to set forth the attractive and the alluring features of a problem, and to show what broad domains of fact can be illuminated by the light radiating from the solution of a single and ofttimes unobtrusive point.
Furthermore, such lectures can exercise a favorable influence by showing the substantial sameness of scientific and every-day thought. The public, in this way, loses its shyness towards scientific questions, and acquires an interest in scientific work which is a great help to the inquirer. The latter, in his turn, is brought to understand that his work is a small part only of the universal process of life, and that the results of his labors must redound to the benefit not only of himself and a few of his associates, but to that of the collective whole.
I sincerely hope that these lectures, in the present excellent translation, will be productive of good in the direction indicated.
E. Mach.
Prague, December, 1894.
The present third edition of this work has been enlarged by the addition of a new lecture, "On Some Phenomena Attending the Flight of Projectiles." The additions to the second consisted of the following four lectures and articles: Professor Mach's Vienna Inaugural Lecture, "The Part Played by Accident in Invention and Discovery," the lecture on "Sensations of Orientation," recently delivered and summing up the results of an important psychological investigation, and two historical articles (see Appendix) on Acoustics and Sight.
The lectures extend over a long period, from 1864 to 1898, and differ greatly in style, contents, and purpose. They were first published in collected form in English; afterwards two German editions were called for.
As the dates of the first five lectures are not given in the footnotes they are here appended. The first lecture, "On the Forms of Liquids," was delivered in 1868 and published with that "On Symmetry" in 1872 (Prague). The second and third lectures, on acoustics, were first published in 1865 (Graz); the fourth and fifth, on optics, in 1867 (Graz). They belong to the earliest period of Professor Mach's scientific activity, and with the lectures on electrostatics and education will more than realise the hope expressed in the author's Preface.
The eighth, ninth, tenth, eleventh, and twelfth lectures are of[Pg viii] a more philosophical character and deal principally with the methods and nature of scientific inquiry. In the ideas summarised in them will be found one of the most important contributions to the theory of knowledge made in the last quarter of a century. Significant hints in psychological method, and exemplary specimen-researches in psychology and physics, are also presented; while in physics many ideas find their first discussion that afterwards, under other names and other authorship, became rallying-cries in this department of inquiry.
All the proofs of this translation have been read by Professor Mach himself.
T. J. McCormack.
La Salle, Ill., May, 1898.
What thinkest thou, dear Euthyphron, that the holy is, and the just, and the good? Is the holy holy because the gods love it, or are the gods holy because they love the holy? By such easy questions did the wise Socrates make the market-place of Athens unsafe and relieve presumptuous young statesmen of the burden of imaginary knowledge, by showing them how confused, unclear, and self-contradictory their ideas were.
You know the fate of the importunate questioner. So called good society avoided him on the promenade. Only the ignorant accompanied him. And finally he drank the cup of hemlock—a lot which we ofttimes wish would fall to modern critics of his stamp.
What we have learned from Socrates, however,—our inheritance from him,—is scientific criticism. Every one who busies himself with science recognises how unsettled and indefinite the notions are which he has brought with him from common life, and how, on a minute examination of things, old differences are[Pg 2] effaced and new ones introduced. The history of science is full of examples of this constant change, development, and clarification of ideas.
But we will not linger by this general consideration of the fluctuating character of ideas, which becomes a source of real uncomfortableness, when we reflect that it applies to almost every notion of life. Rather shall we observe by the study of a physical example how much a thing changes when it is closely examined, and how it assumes, when thus considered, increasing definiteness of form.
The majority of you think, perhaps, you know quite well the distinction between a liquid and a solid. And precisely persons who have never busied themselves with physics will consider this question one of the easiest that can be put. But the physicist knows that it is one of the most difficult. I shall mention here only the experiments of Tresca, which show that solids subjected to high pressures behave exactly as liquids do; for example, may be made to flow out in the form of jets from orifices in the bottoms of vessels. The supposed difference of kind between liquids and solids is thus shown to be a mere difference of degree.
The common inference that because the earth is oblate in form, it was originally fluid, is an error, in the light of these facts. True, a rotating sphere, a few inches in diameter will assume an oblate form only if it is very soft, for example, is composed of freshly kneaded clay or some viscous stuff. But the earth,[Pg 3] even if it consisted of the rigidest stone, could not help being crushed by its tremendous weight, and must perforce behave as a fluid. Even our mountains could not extend beyond a certain height without crumbling. The earth may once have been fluid, but this by no means follows from its oblateness.
The particles of a liquid are displaced on the application of the slightest pressure; a liquid conforms exactly to the shapes of the vessels in which it is contained; it possesses no form of its own, as you have all learned in the schools. Accommodating itself in the most trifling respects to the conditions of the vessel in which it is placed, and showing, even on its surface, where one would suppose it had the freest play, nothing but a polished, smiling, expressionless countenance, it is the courtier par excellence of the natural bodies.
Liquids have no form of their own! No, not for the superficial observer. But persons who have observed that a raindrop is round and never angular, will not be disposed to accept this dogma so unconditionally.
It is fair to suppose that every man, even the weakest, would possess a character, if it were not too difficult in this world to keep it. So, too, we must suppose that liquids would possess forms of their own, if the pressure of the circumstances permitted it,—if they were not crushed by their own weights.
An astronomer once calculated that human beings could not exist on the sun, apart from its great heat, because they would be crushed to pieces there by their[Pg 4] own weight. The greater mass of this body would also make the weight of the human body there much greater. But on the moon, because here we should be much lighter, we could jump as high as the church-steeples without any difficulty, with the same muscular power which we now possess. Statues and "plaster" casts of syrup are undoubtedly things of fancy, even on the moon, but maple-syrup would flow so slowly there that we could easily build a maple-syrup man on the moon, for the fun of the thing, just as our children here build snow-men.
Accordingly, if liquids have no form of their own with us on earth, they have, perhaps, a form of their own on the moon, or on some smaller and lighter heavenly body. The problem, then, simply is to get rid of the effects of gravity; and, this done, we shall be able to find out what the peculiar forms of liquids are.
The problem was solved by Plateau of Ghent, whose method was to immerse the liquid in another of the same specific gravity.[1] He employed for his experiments oil and a mixture of alcohol and water. By Archimedes's well-known principle, the oil in this mixture loses its entire weight. It no longer sinks beneath its weight; its formative forces, be they ever so weak, are now in full play.
As a fact, we now see, to our surprise, that the oil, instead of spreading out into a layer, or lying in a[Pg 5] formless mass, assumes the shape of a beautiful and perfect sphere, freely suspended in the mixture, as the moon is in space. We can construct in this way a sphere of oil several inches in diameter.
If, now, we affix a thin plate to a wire and insert the plate in the oil sphere, we can, by twisting the wire between our fingers, set the whole ball in rotation. Doing this, the ball assumes an oblate shape, and we can, if we are skilful enough, separate by such rotation a ring from the ball, like that which surrounds Saturn. This ring is finally rent asunder, and, breaking up into a number of smaller balls, exhibits to us a kind of model of the origin of the planetary system according to the hypothesis of Kant and Laplace.
 Fig. 1.
Fig. 1.
Still more curious are the phenomena exhibited when the formative forces of the liquid are partly disturbed by putting in contact with the liquid's surface some rigid body. If we immerse, for example, the wire framework of a cube in our mass of oil, the oil will everywhere stick to the wire framework. If the quantity of oil is exactly sufficient we shall obtain an oil cube with perfectly smooth walls. If there is too much or too little oil, the walls of the cube will bulge out or cave in. In this manner we[Pg 6] can produce all kinds of geometrical figures of oil, for example, a three-sided pyramid, a cylinder (by bringing the oil between two wire rings), and so on. Interesting is the change of form that occurs when we gradually suck out the oil by means of a glass tube from the cube or pyramid. The wire holds the oil fast. The figure grows smaller and smaller, until it is at last quite thin. Ultimately it consists simply of a number of thin, smooth plates of oil, which extend from the edges of the cube to the centre, where they meet in a small drop. The same is true of the pyramid.
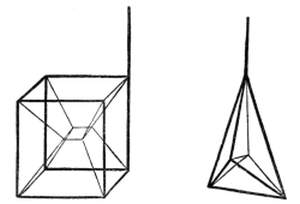 Fig. 2.
Fig. 2.
The idea now suggests itself that liquid figures as thin as this, and possessing, therefore, so slight a weight, cannot be crushed or deformed by their weight; just as a small, soft ball of clay is not affected in this respect by its weight. This being the case, we no longer need our mixture of alcohol and water for the production of figures, but can construct them in the[Pg 7] open air. And Plateau, in fact, found that these thin figures, or at least very similar ones, could be produced in the air, by dipping the wire nets described in a solution of soap and water and quickly drawing them out again. The experiment is not difficult. The figure is formed of itself. The preceding drawing represents to the eye the forms obtained with cubical and pyramidal nets. In the cube, thin, smooth films of soap-suds proceed from the edges to a small, quadratic film in the centre. In the pyramid, a film proceeds from each edge to the centre.
These figures are so beautiful that they hardly admit of appropriate description. Their great regularity and geometrical exactness evokes surprise from all who see them for the first time. Unfortunately, they are of only short duration. They burst, on the drying of the solution in the air, but only after exhibiting to us the most brilliant play of colors, such as is often seen in soap-bubbles. Partly their beauty of form and partly our desire to examine them more minutely induces us to conceive of methods of endowing them with permanent form. This is very simply done.[2] Instead of dipping the wire nets in solutions of soap, we dip them in pure melted colophonium (resin). When drawn out the figure at once forms and solidifies by contact with the air.
It is to be remarked that also solid fluid-figures can[Pg 8] be constructed in the open air, if their weight be light enough, or the wire nets of very small dimensions. If we make, for example, of very fine wire a cubical net whose sides measure about one-eighth of an inch in length, we need simply to dip this net in water to obtain a small solid cube of water. With a piece of blotting paper the superfluous water may be easily removed and the sides of the cube made smooth.
Yet another simple method may be devised for observing these figures. A drop of water on a greased glass plate will not run if it is small enough, but will be flattened by its weight, which presses it against its support. The smaller the drop the less the flattening. The smaller the drop the nearer it approaches the form of a sphere. On the other hand, a drop suspended from a stick is elongated by its weight. The undermost parts of a drop of water on a support are pressed against the support, and the upper parts are pressed against the lower parts because the latter cannot yield. But when a drop falls freely downward all its parts move equally fast; no part is impeded by another; no part presses against another. A freely falling drop, accordingly, is not affected by its weight; it acts as if it were weightless; it assumes a spherical form.
A moment's glance at the soap-film figures produced by our various wire models, reveals to us a great multiplicity of form. But great as this multiplicity is,[Pg 9] the common features of the figures also are easily discernible.
This hidden law Plateau discovered. It may be expressed, somewhat prosily, as follows:
1) If several plane liquid films meet in a figure they are always three in number, and, taken in pairs, form, each with another, nearly equal angles.
2) If several liquid edges meet in a figure they are always four in number, and, taken in pairs, form, each with another, nearly equal angles.
This is a strange law, and its reason is not evident. But we might apply this criticism to almost all laws. It is not always that the motives of a law-maker are discernible in the form of the law he constructs. But our law admits of analysis into very simple elements or reasons. If we closely examine the paragraphs which state it, we shall find that their meaning is simply this, that the surface of the liquid assumes the shape of smallest area that is possible under the circumstances.
If, therefore, some extraordinarily intelligent tailor, possessing a knowledge of all the artifices of the higher mathematics, should set himself the task of so covering the wire frame of a cube with cloth that every piece of cloth should be connected with the wire and joined with the remaining cloth, and should seek to accomplish this feat with the greatest saving of material, he[Pg 10] would construct no other figure than that which is here formed on the wire frame in our solution of soap and water. Nature acts in the construction of liquid figures on the principle of a covetous tailor, and gives no thought in her work to the fashions. But, strange to say, in this work, the most beautiful fashions are of themselves produced.
The two paragraphs which state our law apply primarily only to soap-film figures, and are not applicable, of course, to solid oil-figures. But the principle that the superficial area of the liquid shall be the least possible under the circumstances, is applicable to all fluid figures. He who understands not only the letter but also the reason of the law will not be at a loss when confronted with cases to which the letter does not accurately apply. And this is the case with the principle of least superficial area. It is a sure guide for us even in cases in which the above-stated paragraphs are not applicable.
Our first task will now be, to show by a palpable illustration the mode of formation of liquid figures by the principle of least superficial area. The oil on the wire pyramid in our mixture of alcohol and water, being unable to leave the wire edges, clings to them, and the given mass of oil strives so to shape itself that its surface shall have the least possible area. Suppose we attempt to imitate this phenomenon. We take a wire pyramid, draw over it a stout film of rubber, and in place of the wire handle insert a small tube leading[Pg 11] into the interior of the space enclosed by the rubber (Fig. 3). Through this tube we can blow in or suck out air. The quantity of air in the enclosure represents the quantity of oil. The stretched rubber film, which, clinging to the wire edges, does its utmost to contract, represents the surface of the oil endeavoring to decrease its area. By blowing in, and drawing out the air, now, we actually obtain all the oil pyramidal figures, from those bulged out to those hollowed in. Finally, when all the air is pumped or sucked out, the soap-film figure is exhibited. The rubber films strike together, assume the form of planes, and meet at four sharp edges in the centre of the pyramid.
 Fig. 3.
Fig. 3.
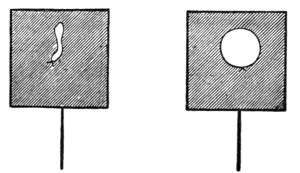 Fig. 4.
Fig. 4.
The tendency of soap-films to assume smaller forms may be directly demonstrated by a method of Van der Mensbrugghe. If we dip a square wire frame to which[Pg 12] a handle is attached into a solution of soap and water, we shall obtain on the frame a beautiful, plane film of soap-suds. (Fig. 4.) On this we lay a thread having its two ends tied together. If, now, we puncture the part enclosed by the thread, we shall obtain a soap-film having a circular hole in it, whose circumference is the thread. The remainder of the film decreasing in area as much as it can, the hole assumes the largest area that it can. But the figure of largest area, with a given periphery, is the circle.
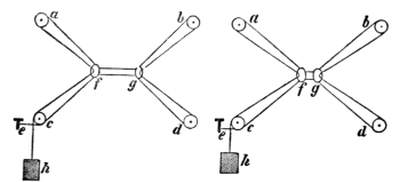 Fig. 5.
Fig. 5.
Similarly, by the principle of least superficial area, a freely suspended mass of oil assumes the shape of a sphere. The sphere is the form of least surface for a given content. This is evident. The more we put into a travelling-bag, the nearer its shape approaches the spherical form.
The connexion of the two above-mentioned paragraphs with the principle of least superficial area may be shown by a yet simpler example. Picture to yourselves four fixed pulleys, a, b, c, d, and two movable[Pg 13] rings f, g (Fig. 5); about the pulleys and through the rings imagine a smooth cord passed, fastened at one extremity to a nail e, and loaded at the other with a weight h. Now this weight always tends to sink, or, what is the same thing, always tends to make the portion of the string e h as long as possible, and consequently the remainder of the string, wound round the pulleys, as short as possible. The strings must remain connected with the pulleys, and on account of the rings also with each other. The conditions of the case, accordingly, are similar to those of the liquid figures discussed. The result also is a similar one. When, as in the right hand figure of the cut, four pairs of strings meet, a different configuration must be established. The consequence of the endeavor of the string to shorten itself is that the rings separate from each other, and that now at all points only three pairs of strings meet, every two at equal angles of one hundred and twenty degrees. As a fact, by this arrangement the greatest possible shortening of the string is attained; as can be easily proved by geometry.
This will help us to some extent to understand the creation of beautiful and complicated figures by the simple tendency of liquids to assume surfaces of least superficial area. But the question arises, Why do liquids seek surfaces of least superficial area?
The particles of a liquid cling together. Drops brought into contact coalesce. We can say, liquid particles attract each other. If so, they seek to come[Pg 14] as close as they can to each other. The particles at the surface will endeavor to penetrate as far as they can into the interior. This process will not stop, cannot stop, until the surface has become as small as under the circumstances it possibly can become, until as few particles as possible remain at the surface, until as many particles as possible have penetrated into the interior, until the forces of attraction have no more work to perform.[3]
The root of the principle of least surface is to be sought, accordingly, in another and much simpler principle, which may be illustrated by some such analogy as this. We can conceive of the natural forces of attraction and repulsion as purposes or intentions of nature. As a matter of fact, that interior pressure which we feel before an act and which we call an intention or purpose, is not, in a final analysis, so essentially different from the pressure of a stone on its support, or the pressure of a magnet on another, that it is necessarily unallowable to use for both the same term—at least for well-defined purposes.[4] It is the purpose of nature, accordingly, to bring the iron nearer the magnet, the stone nearer the centre of the earth, and so forth. If such a purpose can be realised, it is carried out. But where she cannot realise her purposes, nature does nothing. In this respect she acts exactly as a good man of business does.
It is a constant purpose of nature to bring weights lower. We can raise a weight by causing another, larger weight to sink; that is, by satisfying another, more powerful, purpose of nature. If we fancy we are making nature serve our purposes in this, it will be found, upon closer examination, that the contrary is true, and that nature has employed us to attain her purposes.
Equilibrium, rest, exists only, but then always, when nature is brought to a halt in her purposes, when the forces of nature are as fully satisfied as, under the circumstances, they can be. Thus, for example, heavy bodies are in equilibrium, when their so-called centre of gravity lies as low as it possibly can, or when as much weight as the circumstances admit of has sunk as low as it can.
The idea forcibly suggests itself that perhaps this principle also holds good in other realms. Equilibrium exists also in the state when the purposes of the parties are as fully satisfied as for the time being they can be, or, as we may say, jestingly, in the language of physics, when the social potential is a maximum.[5]
You see, our miserly mercantile principle is replete with consequences.[6] The result of sober research, it has become as fruitful for physics as the dry questions of Socrates for science generally. If the principle seems to lack in ideality, the more ideal are the fruits which it bears.
But why, tell me, should science be ashamed of such a principle? Is science[7] itself anything more than—a business? Is not its task to acquire with the least possible work, in the least possible time, with the least possible thought, the greatest possible part of eternal truth?
Whoever has roamed through a beautiful country knows that the tourist's delights increase with his progress. How pretty that wooded dell must look from yonder hill! Whither does that clear brook flow, that hides itself in yonder sedge? If I only knew how the landscape looked behind that mountain! Thus even the child thinks in his first rambles. It is also true of the natural philosopher.
The first questions are forced upon the attention of the inquirer by practical considerations; the subsequent ones are not. An irresistible attraction draws him to these; a nobler interest which far transcends the mere needs of life. Let us look at a special case.
For a long time the structure of the organ of hearing has actively engaged the attention of anatomists. A considerable number of brilliant discoveries has been brought to light by their labors, and a splendid array of facts and truths established. But with these facts a host of new enigmas has been presented.
Whilst in the theory of the organisation and functions[Pg 18] of the eye comparative clearness has been attained; whilst, hand in hand with this, ophthalmology has reached a degree of perfection which the preceding century could hardly have dreamed of, and by the help of the ophthalmoscope the observing physician penetrates into the profoundest recesses of the eye, the theory of the ear is still much shrouded in mysterious darkness, full of attraction for the investigator.
Look at this model of the ear. Even at that familiar part by whose extent we measure the quantity of people's intelligence, even at the external ear, the problems begin. You see here a succession of helixes or spiral windings, at times very pretty, whose significance we cannot accurately state, yet for which there must certainly be some reason.
 Fig. 6.
Fig. 6.
The shell or concha of the ear, a in the annexed diagram, conducts the sound into the curved auditory passage b, which is terminated by a thin membrane, the so-called tympanic membrane, e. This membrane is set in motion by the sound, and in its turn sets in motion a series of little bones of very peculiar formation, c. At the end of all is the labyrinth d. The labyrinth consists of a group of cavities filled with a liquid, in which the innumerable fibres of the nerve of hearing are imbedded. By the vibration of the chain of bones c, the liquid of the labyrinth is shaken, and the auditory nerve excited. Here the process of hearing[Pg 19] begins. So much is certain. But the details of the process are one and all unanswered questions.
To these old puzzles, the Marchese Corti, as late as 1851, added a new enigma. And, strange to say, it is this last enigma, which, perhaps, has first received its correct solution. This will be the subject of our remarks to-day.
Corti found in the cochlea, or snail-shell of the labyrinth, a large number of microscopic fibres placed side by side in geometrically graduated order. According to Kölliker their number is three thousand. They were also the subject of investigation at the hands of Max Schultze and Deiters.
A description of the details of this organ would only weary you, besides not rendering the matter much clearer. I prefer, therefore, to state briefly what in the opinion of prominent investigators like Helmholtz and Fechner is the peculiar function of Corti's fibres. The cochlea, it seems, contains a large number of elastic fibres of graduated lengths (Fig. 7), to which the branches of the auditory nerve are attached. These fibres, called the fibres, pillars, or rods of Corti, being of unequal length, must also be of unequal elasticity, and, consequently, pitched to different notes. The cochlea, therefore, is a species of pianoforte.
 Fig. 7.
Fig. 7.
What, now, may be the office of this structure, which is found in no other organ of sense? May it[Pg 20] not be connected with some special property of the ear? It is quite probable; for the ear possesses a very similar power. You know that it is possible to follow the individual voices of a symphony. Indeed, the feat is possible even in a fugue of Bach, where it is certainly no inconsiderable achievement. The ear can pick out the single constituent tonal parts, not only of a harmony, but of the wildest clash of music imaginable. The musical ear analyses every agglomeration of tones.
The eye does not possess this ability. Who, for example, could tell from the mere sight of white, without a previous experimental knowledge of the fact, that white is composed of a mixture of other colors? Could it be, now, that these two facts, the property of the ear just mentioned, and the structure discovered by Corti, are really connected? It is very probable. The enigma is solved if we assume that every note of definite pitch has its special string in this pianoforte of Corti, and, therefore, its special branch of the auditory nerve attached to that string. But before I can make this point perfectly plain to you, I must ask you to follow me a few steps into the dry domain of physics.
Look at this pendulum. Forced from its position of equilibrium by an impulse, it begins to swing with a definite time of oscillation, dependent upon its length. Longer pendulums swing more slowly, shorter ones more quickly. We will suppose our pendulum to execute one to-and-fro movement in a second.
This pendulum, now, can be thrown into violent vibration in two ways; either by a single heavy impulse, or by a number of properly communicated slight impulses. For example, we impart to the pendulum, while at rest in its position of equilibrium, a very slight impulse. It will execute a very small vibration. As it passes a third time its position of equilibrium, a second having elapsed, we impart to it again a slight shock, in the same direction with the first. Again after the lapse of a second, on its fifth passage through the position of equilibrium, we strike it again in the same manner; and so continue. You see, by this process the shocks imparted augment continually the motion of the pendulum. After each slight impulse, the pendulum reaches out a little further in its swing, and finally acquires a considerable motion.[8]
But this is not the case under all circumstances. It is possible only when the impulses imparted synchronise with the swings of the pendulum. If we should communicate the second impulse at the end of half a second and in the same direction with the first impulse, its effects would counteract the motion of the pendulum. It is easily seen that our little impulses help the motion of the pendulum more and more, according as their time accords with the time of the pendulum. If we strike the pendulum in any other time than in that of its vibration, in some instances, it is true, we shall augment its vibration, but in others[Pg 22] again, we shall obstruct it. Our impulses will be less effective the more the motion of our own hand departs from the motion of the pendulum.
What is true of the pendulum holds true of every vibrating body. A tuning-fork when it sounds, also vibrates. It vibrates more rapidly when its sound is higher; more slowly when it is deeper. The standard A of our musical scale is produced by about four hundred and fifty vibrations in a second.
I place by the side of each other on this table two tuning-forks, exactly alike, resting on resonant cases. I strike the first one a sharp blow, so that it emits a loud note, and immediately grasp it again with my hand to quench its note. Nevertheless, you still hear the note distinctly sounded, and by feeling it you may convince yourselves that the other fork which was not struck now vibrates.
I now attach a small bit of wax to one of the forks. It is thrown thus out of tune; its note is made a little deeper. I now repeat the same experiment with the two forks, now of unequal pitch, by striking one of them and again grasping it with my hand; but in the present case the note ceases the very instant I touch the fork.
What has happened here in these two experiments? Simply this. The vibrating fork imparts to the air and to the table four hundred and fifty shocks a second, which are carried over to the other fork. If the other fork is pitched to the same note, that is to say, if it[Pg 23] vibrates when struck in the same time with the first, then the shocks first emitted, no matter how slight they may be, are sufficient to throw the second fork into rapid sympathetic vibration. But when the time of vibration of the two forks is slightly different, this does not take place. We may strike as many forks as we will, the fork tuned to A is perfectly indifferent to their notes; is deaf, in fact, to all except its own; and if you strike three, or four, or five, or any number whatsoever, of forks all at the same time, so as to make the shocks which come from them ever so great, the A fork will not join in with their vibrations unless another fork A is found in the collection struck. It picks out, in other words, from all the notes sounded, that which accords with it.
The same is true of all bodies which can yield notes. Tumblers resound when a piano is played, on the striking of certain notes, and so do window panes. Nor is the phenomenon without analogy in other provinces. Take a dog that answers to the name "Nero." He lies under your table. You speak of Domitian, Vespasian, and Marcus Aurelius Antoninus, you call upon all the names of the Roman Emperors that occur to you, but the dog does not stir, although a slight tremor of his ear tells you of a faint response of his consciousness. But the moment you call "Nero" he jumps joyfully towards you. The tuning-fork is like your dog. It answers to the name A.
You smile, ladies. You shake your heads. The[Pg 24] simile does not catch your fancy. But I have another, which is very near to you: and for punishment you shall hear it. You, too, are like tuning-forks. Many are the hearts that throb with ardor for you, of which you take no notice, but are cold. Yet what does it profit you! Soon the heart will come that beats in just the proper rhythm, and then your knell, too, has struck. Then your heart, too, will beat in unison, whether you will or no.
The law of sympathetic vibration, here propounded for sounding bodies, suffers some modification for bodies incompetent to yield notes. Bodies of this kind vibrate to almost every note. A high silk hat, we know, will not sound; but if you will hold your hat in your hand when attending your next concert you will not only hear the pieces played, but also feel them with your fingers. It is exactly so with men. People who are themselves able to give tone to their surroundings, bother little about the prattle of others. But the person without character tarries everywhere: in the temperance hall, and at the bar of the public-house—everywhere where a committee is formed. The high silk hat is among bells what the weakling is among men of conviction.
A sonorous body, therefore, always sounds when its special note, either alone or in company with others, is struck. We may now go a step further. What will be the behaviour of a group of sonorous bodies which in the pitch of their notes form a scale? Let us picture[Pg 25] to ourselves, for example (Fig. 8), a series of rods or strings pitched to the notes c d e f g.... On a musical instrument the accord c e g is struck. Every one of the rods of Fig. 8 will see if its special note is contained in the accord, and if it finds it, it will respond. The rod c will give at once the note c, the rod e the note e, the rod g the note g. All the other rods will remain at rest, will not sound.
 Fig. 8.
Fig. 8.
We need not look about us long for such an instrument. Every piano is an instrument of this kind, with which the experiment mentioned may be executed with splendid success. Two pianos stand here by the side of each other, both tuned alike. We will employ the first for exciting the notes, while we will allow the second to respond; after having first pressed upon the loud pedal, so as to render all the strings capable of motion.
Every harmony struck with vigor on the first piano is distinctly repeated on the second. To prove that it is the same strings that are sounded in both pianos, we repeat the experiment in a slightly changed form. We let go the loud pedal of the second piano and pressing on the keys c e g of that instrument vigorously strike the harmony c e g on the first piano. The harmony c e g is now also sounded on the second piano. But if we press only on one key g of one piano, while we strike c e g on the other, only g will be sounded on[Pg 26] the second. It is thus always the like strings of the two pianos that excite each other.
The piano can reproduce any sound that is composed of its musical notes. It will reproduce, for example, very distinctly, a vowel sound that is sung into it. And in truth physics has proved that the vowels may be regarded as composed of simple musical notes.
You see that by the exciting of definite tones in the air quite definite motions are set up with mechanical necessity in the piano. The idea might be made use of for the performance of some pretty pieces of wizardry. Imagine a box in which is a stretched string of definite pitch. This is thrown into motion as often as its note is sung or whistled. Now it would not be a very difficult task for a skilful mechanic to so construct the box that the vibrating cord would close a galvanic circuit and open the lock. And it would not be a much more difficult task to construct a box which would open at the whistling of a certain melody. Sesame! and the bolts fall. Truly, we should have here a veritable puzzle-lock. Still another fragment rescued from that old kingdom of fables, of which our day has realised so much, that world of fairy-stories to which the latest contributions are Casselli's telegraph, by which one can write at a distance in one's own hand, and Prof. Elisha Gray's telautograph. What would the good old Herodotus have said to these things who even in Egypt shook his head at much that he saw?[Pg 27] ἐμοἱ μἑνe ού πιστα, just as simple-heartedly as then, when he heard of the circumnavigation of Africa.
A new puzzle-lock! But why invent one? Are not we human beings ourselves puzzle-locks? Think of the stupendous groups of thoughts, feelings, and emotions that can be aroused in us by a word! Are there not moments in all our lives when a mere name drives the blood to our hearts? Who that has attended a large mass-meeting has not experienced what tremendous quantities of energy and motion can be evolved by the innocent words, "Liberty, Equality, Fraternity."
But let us return to the subject proper of our discourse. Let us look again at our piano, or what will do just as well, at some other contrivance of the same character. What does this instrument do? Plainly, it decomposes, it analyses every agglomeration of sounds set up in the air into its individual component parts, each tone being taken up by a different string; it performs a real spectral analysis of sound. A person completely deaf, with the help of a piano, simply by touching the strings or examining their vibrations with a microscope, might investigate the sonorous motion of the air, and pick out the separate tones excited in it.
The ear has the same capacity as this piano. The ear performs for the mind what the piano performs for a person who is deaf. The mind without the ear is deaf. But a deaf person, with the piano, does hear after a fashion, though much less vividly, and more[Pg 28] clumsily, than with the ear. The ear, thus, also decomposes sound into its component tonal parts. I shall now not be deceived, I think, if I assume that you already have a presentiment of what the function of Corti's fibres is. We can make the matter very plain to ourselves. We will use the one piano for exciting the sounds, and we shall imagine the second one in the ear of the observer in the place of Corti's fibres, which is a model of such an instrument. To every string of the piano in the ear we will suppose a special fibre of the auditory nerve attached, so that this fibre and this alone, is irritated when the string is thrown into vibration. If we strike now an accord on the external piano, for every tone of that accord a definite string of the internal piano will sound and as many different nervous fibres will be irritated as there are notes in the accord. The simultaneous sense-impressions due to different notes can thus be preserved unmingled and be separated by the attention. It is the same as with the five fingers of the hand. With each finger I can touch something different. Now the ear has three thousand such fingers, and each one is designed for the touching of a different tone.[9] Our ear is a puzzle-lock of the kind mentioned. It opens at the magic melody of a sound. But it is a stupendously ingenious lock. Not only one tone, but every tone makes it open; but each one differently. To each tone it replies with a different sensation.
More than once it has happened in the history of science that a phenomenon predicted by theory, has not been brought within the range of actual observation until long afterwards. Leverrier predicted the existence and the place of the planet Neptune, but it was not until sometime later that Galle actually found the planet at the predicted spot. Hamilton unfolded theoretically the phenomenon of the so-called conical refraction of light, but it was reserved for Lloyd some time subsequently to observe the fact. The fortunes of Helmholtz's theory of Corti's fibres have been somewhat similar. This theory, too, received its substantial confirmation from the subsequent observations of V. Hensen. On the free surface of the bodies of Crustacea, connected with the auditory nerves, rows of little hairy filaments of varying lengths and thicknesses are found, which to some extent are the analogues of Corti's fibres. Hensen saw these hairs vibrate when sounds were excited, and when different notes were struck different hairs were set in vibration.
I have compared the work of the physical inquirer to the journey of the tourist. When the tourist ascends a new hill he obtains of the whole district a different view. When the inquirer has found the solution of one enigma, the solution of a host of others falls into his hands.
Surely you have often felt the strange impression experienced[Pg 30] when in singing through the scale the octave is reached, and nearly the same sensation is produced as by the fundamental tone. The phenomenon finds its explanation in the view here laid down of the ear. And not only this phenomenon but all the laws of the theory of harmony may be grasped and verified from this point of view with a clearness before undreamt of. Unfortunately, I must content myself to-day with the simple indication of these beautiful prospects. Their consideration would lead us too far aside into the fields of other sciences.
The searcher of nature, too, must restrain himself in his path. He also is drawn along from one beauty to another as the tourist from dale to dale, and as circumstances generally draw men from one condition of life into others. It is not he so much that makes the quests, as that the quests are made of him. Yet let him profit by his time, and let not his glance rove aimlessly hither and thither. For soon the evening sun will shine, and ere he has caught a full glimpse of the wonders close by, a mighty hand will seize him and lead him away into a different world of puzzles.
Respected hearers, science once stood in an entirely different relation to poetry. The old Hindu mathematicians wrote their theorems in verses, and lotus-flowers, roses, and lilies, beautiful sceneries, lakes, and mountains figured in their problems.
"Thou goest forth on this lake in a boat. A lily juts forth, one palm above the water. A breeze bends[Pg 31] it downwards, and it vanishes two palms from its previous spot beneath the surface. Quick, mathematician, tell me how deep is the lake!"
Thus spoke an ancient Hindu scholar. This poetry, and rightly, has disappeared from science, but from its dry leaves another poetry is wafted aloft which cannot be described to him who has never felt it. Whoever will fully enjoy this poetry must put his hand to the plough, must himself investigate. Therefore, enough of this! I shall reckon myself fortunate if you do not repent of this brief excursion into the flowered dale of physiology, and if you take with yourselves the belief that we can say of science what we say of poetry,
We are to speak to-day of a theme which is perhaps of somewhat more general interest—the causes of the harmony of musical sounds. The first and simplest experiences relative to harmony are very ancient. Not so the explanation of its laws. These were first supplied by the investigators of a recent epoch. Allow me an historical retrospect.
Pythagoras (586 B. C.) knew that the note yielded by a string of steady tension was converted into its octave when the length of the string was reduced one-half, and into its fifth when reduced two-thirds; and that then the first fundamental tone was consonant with the two others. He knew generally that the same string under fixed tension gives consonant tones when successively divided into lengths that are in the proportions of the simplest natural numbers; that is, in the proportions of 1:2, 2:3, 3:4, 4:5.
Pythagoras failed to reveal the causes of these laws. What have consonant tones to do with the simple natural numbers? That is the question we should ask[Pg 33] to-day. But this circumstance must have appeared less strange than inexplicable to Pythagoras. This philosopher sought for the causes of harmony in the occult, miraculous powers of numbers. His procedure was largely the cause of the upgrowth of a numerical mysticism, of which the traces may still be detected in our oneirocritical books and among some scientists, to whom marvels are more attractive than lucidity.
Euclid (300 B. C.) gives a definition of consonance and dissonance that could hardly be improved upon, in point of verbal accuracy. The consonance (συμφωνία) of two tones, he says, is the mixture, the blending (κρᾶσις) of those two tones; dissonance (διαφωνία), on the other hand, is the incapacity of the tones to blend (ἀμιξία), whereby they are made harsh for the ear. The person who knows the correct explanation of the phenomenon hears it, so to speak, reverberated in these words of Euclid. Still, Euclid did not know the true cause of harmony. He had unwittingly come very near to the truth, but without really grasping it.
Leibnitz (1646-1716 A. D.) resumed the question which his predecessors had left unsolved. He, of course, knew that musical notes were produced by vibrations, that twice as many vibrations corresponded to the octave as to the fundamental tone, etc. A passionate lover of mathematics, he sought for the cause of harmony in the secret computation and comparison of the simple numbers of vibrations and in the secret[Pg 34] satisfaction of the soul at this occupation. But how, we ask, if one does not know that musical notes are vibrations? The computation and the satisfaction at the computation must indeed be pretty secret if it is unknown. What queer ideas philosophers have! Could anything more wearisome be imagined than computation as a principle of æsthetics? Yes, you are not utterly wrong in your conjecture, yet you may be sure that Leibnitz's theory is not wholly nonsense, although it is difficult to make out precisely what he meant by his secret computation.
The great Euler (1707-1783) sought the cause of harmony, almost as Leibnitz did, in the pleasure which the soul derives from the contemplation of order in the numbers of the vibrations.[10]
Rameau and D'Alembert (1717-1783) approached nearer to the truth. They knew that in every sound available in music besides the fundamental note also the twelfth and the next higher third could be heard; and further that the resemblance between a fundamental tone and its octave was always strongly marked. Accordingly, the combination of the octave, fifth, third, etc., with the fundamental tone appeared to them "natural." They possessed, we must admit, the correct point of view; but with the simple naturalness of a phenomenon no inquirer can rest content; for it is precisely this naturalness for which he seeks his explanations.
Rameau's remark dragged along through the whole modern period, but without leading to the full discovery of the truth. Marx places it at the head of his theory of composition, but makes no further application of it. Also Goethe and Zelter in their correspondence were, so to speak, on the brink of the truth. Zelter knew of Rameau's view. Finally, you will be appalled at the difficulty of the problem, when I tell you that till very recent times even professors of physics were dumb when asked what were the causes of harmony.
Not till quite recently did Helmholtz find the solution of the question. But to make this solution clear to you I must first speak of some experimental principles of physics and psychology.
1) In every process of perception, in every observation, the attention plays a highly important part. We need not look about us long for proofs of this. You receive, for example, a letter written in a very poor hand. Do your best, you cannot make it out. You put together now these, now those lines, yet you cannot construct from them a single intelligible character. Not until you direct your attention to groups of lines which really belong together, is the reading of the letter possible. Manuscripts, the letters of which are formed of minute figures and scrolls, can only be read at a considerable distance, where the attention is[Pg 36] no longer diverted from the significant outlines to the details. A beautiful example of this class is furnished by the famous iconographs of Giuseppe Arcimboldo in the basement of the Belvedere gallery at Vienna. These are symbolic representations of water, fire, etc.: human heads composed of aquatic animals and of combustibles. At a short distance one sees only the details, at a greater distance only the whole figure. Yet a point can be easily found at which, by a simple voluntary movement of the attention, there is no difficulty in seeing now the whole figure and now the smaller forms of which it is composed. A picture is often seen representing the tomb of Napoleon. The tomb is surrounded by dark trees between which the bright heavens are visible as background. One can look a long time at this picture without noticing anything except the trees, but suddenly, on the attention being accidentally directed to the bright background, one sees the figure of Napoleon between the trees. This case shows us very distinctly the important part which attention plays. The same sensuous object can, solely by the interposition of attention, give rise to wholly different perceptions.
If I strike a harmony, or chord, on this piano, by a mere effort of attention you can fix every tone of that harmony. You then hear most distinctly the fixed tone, and all the rest appear as a mere addition, altering only the quality, or acoustic color, of the primary tone. The effect of the same harmony is essentially[Pg 37] modified if we direct our attention to different tones.
Strike in succession two harmonies, for example, the two represented in the annexed diagram, and first fix by the attention the upper note e, afterwards the base e-a; in the two cases you will hear the same sequence of harmonies differently. In the first case, you have the impression as if the fixed tone remained unchanged and simply altered its timbre; in the second case, the whole acoustic agglomeration seems to fall sensibly in depth. There is an art of composition to guide the attention of the hearer. But there is also an art of hearing, which is not the gift of every person.
 Fig. 9.
Fig. 9.
The piano-player knows the remarkable effects obtained when one of the keys of a chord that is struck is let loose. Bar 1 played on the piano sounds almost like bar 2. The note which lies next to the key let loose resounds after its release as if it were freshly struck. The attention no longer occupied with the upper note is by that very fact insensibly led to the upper note.
 Fig. 10.
Fig. 10.
Any tolerably cultivated musical ear can perform the resolution of a harmony into its component parts. By much practice we can go even further. Then, every musical sound heretofore regarded as simple can be resolved into a subordinate succession of musical tones. For example, if I strike on the piano the note 1, (annexed diagram,) we shall hear, if we make the requisite effort of attention, besides the loud fundamental note the feebler, higher overtones, or harmonics, 2 ... 7, that is, the octave, the twelfth, the double octave, and the third, the fifth, and the seventh of the double octave.
 Fig. 11.
Fig. 11.
The same is true of every musically available sound. Each yields, with varying degrees of intensity, besides its fundamental note, also the octave, the twelfth, the double octave, etc. The phenomenon is observable with special facility on the open and closed flue-pipes of organs. According, now, as certain overtones are more or less distinctly emphasised in a sound, the timbre of the sound changes—that peculiar quality of the sound by which we distinguish the music of the piano from that of the violin, the clarinet, etc.
On the piano these overtones can be very easily rendered audible. If I strike, for example, sharply note 1 of the foregoing series, whilst I simply press down upon, one after another, the keys 2, 3, ... 7, the notes 2, 3, ... 7 will continue to sound after the[Pg 39] striking of 1, because the strings corresponding to these notes, now freed from their dampers, are thrown into sympathetic vibration.
As you know, this sympathetic vibration of the like-pitched strings with the overtones is really not to be conceived as sympathy, but rather as lifeless mechanical necessity. We must not think of this sympathetic vibration as an ingenious journalist pictured it, who tells a gruesome story of Beethoven's F minor sonata, Op. 2, that I cannot withhold from you. "At the last London Industrial Exhibition nineteen virtuosos played the F minor sonata on the same piano. When the twentieth stepped up to the instrument to play by way of variation the same production, to the terror of all present the piano began to render the sonata of its own accord. The Archbishop of Canterbury, who happened to be present, was set to work and forthwith expelled the F minor devil."
Although, now, the overtones or harmonics which we have discussed are heard only upon a special effort of the attention, nevertheless they play a highly important part in the formation of musical timbre, as also in the production of the consonance and dissonance of sounds. This may strike you as singular. How can a thing which is heard only under exceptional circumstances be of importance generally for audition?
But consider some familiar incidents of your every-day life. Think of how many things you see which you do not notice, which never strike your attention[Pg 40] until they are missing. A friend calls upon you; you cannot understand why he looks so changed. Not until you make a close examination do you discover that his hair has been cut. It is not difficult to tell the publisher of a work from its letter-press, and yet no one can state precisely the points by which this style of type is so strikingly different from that style. I have often recognised a book which I was in search of from a simple piece of unprinted white paper that peeped out from underneath the heap of books covering it, and yet I had never carefully examined the paper, nor could I have stated its difference from other papers.
What we must remember, therefore, is that every sound that is musically available yields, besides its fundamental note, its octave, its twelfth, its double octave, etc., as overtones or harmonics, and that these are important for the agreeable combination of several musical sounds.
2) One other fact still remains to be dealt with. Look at this tuning-fork. It yields, when struck, a perfectly smooth tone. But if you strike in company with it a second fork which is of slightly different pitch, and which alone also gives a perfectly smooth tone, you will hear, if you set both forks on the table, or hold both before your ear, a uniform tone no longer, but a number of shocks of tones. The rapidity of the shocks increases with the difference of the pitch of the forks. These shocks, which become very disagreeable for the[Pg 41] ear when they amount to thirty-three in a second, are called "beats."
Always, when one of two like musical sounds is thrown out of unison with the other, beats arise. Their number increases with the divergence from unison, and simultaneously they grow more unpleasant. Their roughness reaches its maximum at about thirty-three beats in a second. On a still further departure from unison, and a consequent increase of the number of beats, the unpleasant effect is diminished, so that tones which are widely apart in pitch no longer produce offensive beats.
To give yourselves a clear idea of the production of beats, take two metronomes and set them almost alike. You can, for that matter, set the two exactly alike. You need not fear that they will strike alike. The metronomes usually for sale in the shops are poor enough to yield, when set alike, appreciably unequal strokes. Set, now, these two metronomes, which strike at unequal intervals, in motion; you will readily see that their strokes alternately coincide and conflict with each other. The alternation is quicker the greater the difference of time of the two metronomes.
If metronomes are not to be had, the experiment may be performed with two watches.
Beats arise in the same way. The rhythmical shocks of two sounding bodies, of unequal pitch, sometimes coincide, sometimes interfere, whereby they alternately[Pg 42] augment and enfeeble each other's effects. Hence the shock-like, unpleasant swelling of the tone.
Now that we have made ourselves acquainted with overtones and beats, we may proceed to the answer of our main question, Why do certain relations of pitch produce pleasant sounds, consonances, others unpleasant sounds, dissonances? It will be readily seen that all the unpleasant effects of simultaneous sound-combinations are the result of beats produced by those combinations. Beats are the only sin, the sole evil of music. Consonance is the coalescence of sounds without appreciable beats.
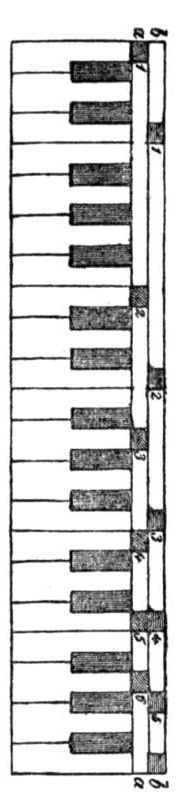 Fig. 12.
Fig. 12.
To make this perfectly clear to you I have constructed the model which you see in Fig. 12. It represents a claviatur. At its top a movable strip of wood aa with the marks 1, 2 ... 6 is placed. By setting this strip in any position, for example, in that where the mark 1 is over the note c of the claviatur, the marks 2, 3 ... 6, as you see, stand over the overtones of c. The same happens when the strip is placed in any other position. A second, exactly similar strip, bb, possesses the same properties. Thus, together, the two strips, in any two positions, point out by their[Pg 43] marks all the tones brought into play upon the simultaneous sounding of the notes indicated by the marks 1.
The two strips, placed over the same fundamental note, show that also all the overtones of those notes coincide. The first note is simply intensified by the other. The single overtones of a sound lie too far apart to permit appreciable beats. The second sound supplies nothing new, consequently, also, no new beats. Unison is the most perfect consonance.
Moving one of the two strips along the other is equivalent to a departure from unison. All the overtones of the one sound now fall alongside those of the other; beats are at once produced; the combination of the tones becomes unpleasant: we obtain a dissonance. If we move the strip further and further along, we shall find that as a general rule the overtones always fall alongside each other, that is, always produce beats and dissonances. Only in a few quite definite positions do the overtones partially coincide. Such positions, therefore, signify higher degrees of euphony—they point out the consonant intervals.
These consonant intervals can be readily found experimentally by cutting Fig. 12 out of paper and moving bb lengthwise along aa. The most perfect consonances are the octave and the twelfth, since in these two cases the overtones of the one sound coincide absolutely with those of the other. In the octave, for example, 1b falls on 2a, 2b on 4a, 3b on 6a. Consonances, therefore, are simultaneous sound-combinations not[Pg 44] accompanied by disagreeable beats. This, by the way, is, expressed in English, what Euclid said in Greek.
Only such sounds are consonant as possess in common some portion of their partial tones. Plainly we must recognise between such sounds, also when struck one after another, a certain affinity. For the second sound, by virtue of the common overtones, will produce partly the same sensation as the first. The octave is the most striking exemplification of this. When we reach the octave in the ascent of the scale we actually fancy we hear the fundamental tone repeated. The foundations of harmony, therefore, are the foundations of melody.
Consonance is the coalescence of sounds without appreciable beats! This principle is competent to introduce wonderful order and logic into the doctrines of the fundamental bass. The compendiums of the theory of harmony which (Heaven be witness!) have stood hitherto little behind the cook-books in subtlety of logic, are rendered extraordinarily clear and simple. And what is more, all that the great masters, such as Palestrina, Mozart, Beethoven, unconsciously got right, and of which heretofore no text-book could render just account, receives from the preceding principle its perfect verification.
But the beauty of the theory is, that it bears upon its face the stamp of truth. It is no phantom of the brain. Every musician can hear for himself the beats which the overtones of his musical sounds produce.[Pg 45] Every musician can satisfy himself that for any given case the number and the harshness of the beats can be calculated beforehand, and that they occur in exactly the measure that theory determines.
This is the answer which Helmholtz gave to the question of Pythagoras, so far as it can be explained with the means now at my command. A long period of time lies between the raising and the solving of this question. More than once were eminent inquirers nearer to the answer than they dreamed of.
The inquirer seeks the truth. I do not know if the truth seeks the inquirer. But were that so, then the history of science would vividly remind us of that classical rendezvous, so often immortalised by painters and poets. A high garden wall. At the right a youth, at the left a maiden. The youth sighs, the maiden sighs! Both wait. Neither dreams how near the other is.
I like this simile. Truth suffers herself to be courted, but she has evidently no desire to be won. She flirts at times disgracefully. Above all, she is determined to be merited, and has naught but contempt for the man who will win her too quickly. And if, forsooth, one breaks his head in his efforts of conquest, what matter is it, another will come, and truth is always young. At times, indeed, it really seems as if she were well disposed towards her admirer, but that admitted—never! Only when Truth is in exceptionally good spirits does she bestow upon her wooer a glance[Pg 46] of encouragement. For, thinks Truth, if I do not do something, in the end the fellow will not seek me at all.
This one fragment of truth, then, we have, and it shall never escape us. But when I reflect what it has cost in labor and in the lives of thinking men, how it painfully groped its way through centuries, a half-matured thought, before it became complete; when I reflect that it is the toil of more than two thousand years that speaks out of this unobtrusive model of mine, then, without dissimulation, I almost repent me of the jest I have made.
And think of how much we still lack! When, several thousand years hence, boots, top-hats, hoops, pianos, and bass-viols are dug out of the earth, out of the newest alluvium as fossils of the nineteenth century; when the scientists of that time shall pursue their studies both upon these wonderful structures and upon our modern Broadways, as we to-day make studies of the implements of the stone age and of the prehistoric lake-dwellings—then, too, perhaps, people will be unable to comprehend how we could come so near to many great truths without grasping them. And thus it is for all time the unsolved dissonance, for all time the troublesome seventh, that everywhere resounds in our ears; we feel, perhaps, that it will find its solution, but we shall never live to see the day of the pure triple accord, nor shall our remotest descendants.
Ladies, if it is the sweet purpose of your life to sow confusion, it is the purpose of mine to be clear;[Pg 47] and so I must confess to you a slight transgression that I have been guilty of. On one point I have told you an untruth. But you will pardon me this falsehood, if in full repentance I make it good. The model represented in Fig. 12 does not tell the whole truth, for it is based upon the so-called "even temperament" system of tuning. The overtones, however, of musical sounds are not tempered, but purely tuned. By means of this slight inexactness the model is made considerably simpler. In this form it is fully adequate for ordinary purposes, and no one who makes use of it in his studies need be in fear of appreciable error.
If you should demand of me, however, the full truth, I could give you that only by the help of a mathematical formula. I should have to take the chalk into my hands and—think of it!—reckon in your presence. This you might take amiss. Nor shall it happen. I have resolved to do no more reckoning for to-day. I shall reckon now only upon your forbearance, and this you will surely not gainsay me when you reflect that I have made only a limited use of my privilege to weary you. I could have taken up much more of your time, and may, therefore, justly close with Lessing's epigram:
When a criminal judge has a right crafty knave before him, one well versed in the arts of prevarication, his main object is to wring a confession from the culprit by a few skilful questions. In almost a similar position the natural philosopher seems to be placed with respect to nature. True, his functions here are more those of the spy than the judge; but his object remains pretty much the same. Her hidden motives and laws of action is what nature must be made to confess. Whether a confession will be extracted depends upon the shrewdness of the inquirer. Not without reason, therefore, did Lord Bacon call the experimental method a questioning of nature. The art consists in so putting our questions that they may not remain unanswered without a breach of etiquette.
Look, too, at the countless tools, engines, and instruments of torture with which man conducts his inquisitions of nature, and which mock the poet's words:
Look at these instruments and you will see that the comparison with torture also is admissible.[11]
This view of nature, as of something designedly concealed from man, that can be unveiled only by force or dishonesty, chimed in better with the conceptions of the ancients than with modern notions. A Grecian philosopher once said, in offering his opinion of the natural science of his time, that it could only be displeasing to the gods to see men endeavoring to spy out what the gods were not minded to reveal to them.[12] Of course all the contemporaries of the speaker were not of his opinion.
Traces of this view may still be found to-day, but upon the whole we are now not so narrow-minded. We believe no longer that nature designedly hides herself. We know now from the history of science that our questions are sometimes meaningless, and that, therefore, no answer can be forthcoming. Soon we shall see how man, with all his thoughts and quests, is only a fragment of nature's life.
Picture, then, as your fancy dictates, the tools of the physicist as instruments of torture or as engines of endearment, at all events a chapter from the history of those implements will be of interest to you, and it will not be unpleasant to learn what were the peculiar difficulties that led to the invention of such strange apparatus.
Galileo (born at Pisa in 1564, died at Arcetri in 1642) was the first who asked what was the velocity of light, that is, what time it would take for a light struck at one place to become visible at another, a certain distance away.[13]
The method which Galileo devised was as simple as it was natural. Two practised observers, with muffled lanterns, were to take up positions in a dark night at a considerable distance from each other, one at A and one at B. At a moment previously fixed upon, A was instructed to unmask his lantern; while as soon as B saw the light of A's lantern he was to unmask his. Now it is clear that the time which A counted from the uncovering of his lantern until he caught sight of the light of B's would be the time which it would take light to travel from A to B and from B back to A.
 Fig. 13.
Fig. 13.
The experiment was not executed, nor could it, in the nature of the case, have been a success. As we[Pg 51] now know, light travels too rapidly to be thus noted. The time elapsing between the arrival of the light at B and its perception by the observer, with that between the decision to uncover and the uncovering of the lantern, is, as we now know, incomparably greater than the time which it takes light to travel the greatest earthly distances. The great velocity of light will be made apparent, if we reflect that a flash of lightning in the night illuminates instantaneously a very extensive region, whilst the single reflected claps of thunder arrive at the observer's ear very gradually and in appreciable succession.
During his life, then, the efforts of Galileo to determine the velocity of light remained uncrowned with success. But the subsequent history of the measurement of the velocity of light is intimately associated with his name, for with the telescope which he constructed he discovered the four satellites of Jupiter, and these furnished the next occasion for the determination of the velocity of light.
The terrestrial spaces were too small for Galileo's experiment. The measurement was first executed when the spaces of the planetary system were employed. Olaf Römer, (born at Aarhuus in 1644, died at Copenhagen in 1710) accomplished the feat (1675-1676), while watching with Cassini at the observatory of Paris the revolutions of Jupiter's moons.
 Fig. 14.
Fig. 14.
Let AB (Fig. 14) be Jupiter's orbit. Let S stand for the sun, E for the earth, J for Jupiter, and T for[Pg 52] Jupiter's first satellite. When the earth is at E1 we see the satellite enter regularly into Jupiter's shadow, and by watching the time between two successive eclipses, can calculate its time of revolution. The time which Römer noted was forty-two hours, twenty-eight minutes, and thirty-five seconds. Now, as the earth passes along in its orbit towards E2, the revolutions of the satellite grow apparently longer and longer: the eclipses take place later and later. The greatest retardation of the eclipse, which occurs when the earth is at E2, amounts to sixteen minutes and twenty-six seconds. As the earth passes back again to E1, the revolutions grow apparently shorter, and they occur in exactly the time that they first did when the earth arrives at E1. It is to be remarked that Jupiter changes only very slightly its position during one revolution of the earth. Römer guessed at once that these periodical changes of the time of revolution of Jupiter's satellite[Pg 53] were not actual, but apparent changes, which were in some way connected with the velocity of light.
Let us make this matter clear to ourselves by a simile. We receive regularly by the post, news of the political status at our capital. However far away we may be from the capital, we hear the news of every event, later it is true, but of all equally late. The events reach us in the same succession of time as that in which they took place. But if we are travelling away from the capital, every successive post will have a greater distance to pass over, and the events will reach us more slowly than they took place. The reverse will be the case if we are approaching the capital.
At rest, we hear a piece of music played in the same tempo at all distances. But the tempo will be seemingly accelerated if we are carried rapidly towards the band, or retarded if we are carried rapidly away from it.[14]
 Fig. 15.
Fig. 15.
Picture to yourself a cross, say the sails of a wind-mill (Fig. 15), in uniform rotation about its centre. Clearly, the rotation of the cross will appear to you more slowly executed if you are carried very rapidly away from it. For the post which in this case conveys to you the light and brings to you the news of the successive positions of the cross will have to travel in each successive instant over a longer path.
Now this must also be the case with the rotation (the revolution) of the satellite of Jupiter. The greatest retardation of the eclipse (16-1/2 minutes), due to the passage of the earth from E1 to E2, or to its removal from Jupiter by a distance equal to the diameter of the orbit of the earth, plainly corresponds to the time which it takes light to traverse a distance equal to the diameter of the earth's orbit. The velocity of light, that is, the distance described by light in a second, as determined by this calculation, is 311,000 kilometres,[15] or 193,000 miles. A subsequent correction of the diameter of the earth's orbit, gives, by the same method, the velocity of light as approximately 186,000 miles a second.
The method is exactly that of Galileo; only better conditions are selected. Instead of a short terrestrial distance we have the diameter of the earth's orbit, three hundred and seven million kilometres; in place of the uncovered and covered lanterns we have the satellite of Jupiter, which alternately appears and disappears. Galileo, therefore, although he could not carry out himself the proposed measurement, found the lantern by which it was ultimately executed.
Physicists did not long remain satisfied with this beautiful discovery. They sought after easier methods of measuring the velocity of light, such as might be performed on the earth. This was possible after the difficulties of the problem were clearly exposed. A measurement of the kind referred to was executed in 1849 by Fizeau (born at Paris in 1819).
I shall endeavor to make the principle of Fizeau's apparatus clear to you. Let s (Fig. 16) be a disk free to rotate about its centre, and perforated at its rim with a series of holes. Let l be a luminous point casting its light on an unsilvered glass, a, inclined at an angle of forty-five degrees to the axis of the disk. The ray of light, reflected at this point, passes through one of the holes of the disk and falls at right angles upon a mirror b, erected at a point about five miles distant. From the mirror b the light is again reflected, passes once more through the hole in s, and, penetrating the glass plate, finally strikes the eye, o, of the observer. The eye, o, thus, sees the image of the luminous point l through the glass plate and the hole of the disk in the mirror b.
 Fig. 16.
Fig. 16.
If, now, the disk be set in rotation, the unpierced spaces between the apertures will alternately take the place of the apertures, and the eye o will now see the image of the luminous point in b only at interrupted intervals. On increasing the rapidity of the rotation,[Pg 56] however, the interruptions for the eye become again unnoticeable, and the eye sees the mirror b uniformly illuminated.
But all this holds true only for relatively small velocities of the disk, when the light sent through an aperture in s to b on its return strikes the aperture at almost the same place and passes through it a second time. Conceive, now, the speed of the disk to be so increased that the light on its return finds before it an unpierced space instead of an aperture, it will then no longer be able to reach the eye. We then see the mirror b only when no light is emitted from it, but only when light is sent to it; it is covered when light comes from it. In this case, accordingly, the mirror will always appear dark.
If the velocity of rotation at this point were still further increased, the light sent through one aperture could not, of course, on its return pass through the same aperture but might strike the next and reach the eye by that. Hence, by constantly increasing the velocity of the rotation, the mirror b may be made to appear alternately bright and dark. Plainly, now, if we know the number of apertures of the disk, the number of rotations per second, and the distance sb, we can calculate the velocity of light. The result agrees with that obtained by Römer.
The experiment is not quite as simple as my exposition might lead you to believe. Care must be taken that the light shall travel back and forth over[Pg 57] the miles of distance sb and bs undispersed. This difficulty is obviated by means of telescopes.
If we examine Fizeau's apparatus closely, we shall recognise in it an old acquaintance: the arrangement of Galileo's experiment. The luminous point l is the lantern A, while the rotation of the perforated disk performs mechanically the uncovering and covering of the lantern. Instead of the unskilful observer B we have the mirror b, which is unfailingly illuminated the instant the light arrives from s. The disk s, by alternately transmitting and intercepting the reflected light, assists the observer o. Galileo's experiment is here executed, so to speak, countless times in a second, yet the total result admits of actual observation. If I might be pardoned the use of a phrase of Darwin's in this field, I should say that Fizeau's apparatus was the descendant of Galileo's lantern.
A still more refined and delicate method for the measurement of the velocity of light was employed by Foucault, but a description of it here would lead us too far from our subject.
The measurement of the velocity of sound is easily executed by the method of Galileo. It was unnecessary, therefore, for physicists to rack their brains further about the matter; but the idea which with light grew out of necessity was applied also in this field. Koenig of Paris constructs an apparatus for the measurement of the velocity of sound which is closely allied to the method of Fizeau.
The apparatus is very simple. It consists of two electrical clock-works which strike simultaneously, with perfect precision, tenths of seconds. If we place the two clock-works directly side by side, we hear their strokes simultaneously, wherever we stand. But if we take our stand by the side of one of the works and place the other at some distance from us, in general a coincidence of the strokes will now not be heard. The companion strokes of the remote clock-work arrive, as sound, later. The first stroke of the remote work is heard, for example, immediately after the first of the adjacent work, and so on. But by increasing the distance we may produce again a coincidence of the strokes. For example, the first stroke of the remote work coincides with the second of the near work, the second of the remote work with the third of the near work, and so on. If, now, the works strike tenths of seconds and the distance between them is increased until the first coincidence is noted, plainly that distance is travelled over by the sound in a tenth of a second.
We meet frequently the phenomenon here presented, that a thought which centuries of slow and painful endeavor are necessary to produce, when once developed, fairly thrives. It spreads and runs everywhere, even entering minds in which it could never have arisen. It simply cannot be eradicated.
The determination of the velocity of light is not the only case in which the direct perception of the senses[Pg 59] is too slow and clumsy for use. The usual method of studying events too fleet for direct observation consists in putting into reciprocal action with them other events already known, the velocities of all of which are capable of comparison. The result is usually unmistakable, and susceptible of direct inference respecting the character of the event which is unknown. The velocity of electricity cannot be determined by direct observation. But it was ascertained by Wheatstone, simply by the expedient of watching an electric spark in a mirror rotating with tremendous known velocity.
 Fig. 17.
Fig. 17.
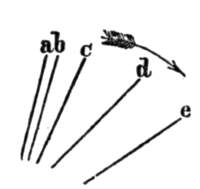 Fig. 18.
Fig. 18.
If we wave a staff irregularly hither and thither, simple observation cannot determine how quickly it moves at each point of its course. But let us look at the staff through holes in the rim of a rapidly rotating disk (Fig. 17). We shall then see the moving staff only in certain positions, namely, when a hole passes in front of the eye. The single pictures of the staff remain for a time impressed upon the eye; we think we see several staffs, having some such disposition as that represented in Fig. 18. If, now, the holes of the disk are equally far apart, and the disk is rotated with uniform velocity, we see clearly that the staff has moved slowly from a to b, more quickly from b to c, still more quickly from c to d, and with its greatest velocity from d to e.
A jet of water flowing from an orifice in the bottom of a vessel has the appearance of perfect quiet and uniformity, but if we illuminate it for a second, in a dark room, by means of an electric flash we shall see that the jet is composed of separate drops. By their quick descent the images of the drops are obliterated and the jet appears uniform. Let us look at the jet through the rotating disk. The disk is supposed to be rotated so rapidly that while the second aperture passes into the place of the first, drop 1 falls into the place of 2, 2 into the place of 3, and so on. We see drops then always in the same places. The jet appears to be at rest. If we turn the disk a trifle more slowly, then while the second aperture passes into the place of the first, drop 1 will have fallen somewhat lower than 2, 2 somewhat lower than 3, etc. Through every successive aperture we shall see drops in successively lower positions. The jet will appear to be flowing slowly downwards.
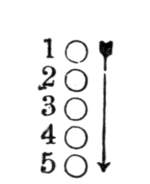 Fig. 19.
Fig. 19.
Now let us turn the disk more rapidly. Then while the second aperture is passing into the place of the first, drop 1 will not quite have reached the place of 2, but will be found slightly above 2, 2 slightly above 3, etc. Through the successive apertures we shall see the drops at successively higher places. It will now look as if the jet were flowing upwards, as if the drops were rising from the lower vessel into the higher.
You see, physics grows gradually more and more[Pg 61] terrible. The physicist will soon have it in his power to play the part of the famous lobster chained to the bottom of the Lake of Mohrin, whose direful mission, if ever liberated, the poet Kopisch humorously describes as that of a reversal of all the events of the world; the rafters of houses become trees again, cows calves, honey flowers, chickens eggs, and the poet's own poem flows back into his inkstand.
You will now allow me the privilege of a few general remarks. You have seen that the same principle often lies at the basis of large classes of apparatus designed for different purposes. Frequently it is some very unobtrusive idea which is productive of so much fruit and of such extensive transformations in physical technics. It is not otherwise here than in practical life.
The wheel of a waggon appears to us a very simple and insignificant creation. But its inventor was certainly a man of genius. The round trunk of a tree perhaps first accidentally led to the observation of the ease with which a load can be moved on a roller. Now, the step from a simple supporting roller to a fixed roller, or wheel, appears a very easy one. At least it appears very easy to us who are accustomed from childhood up to the action of the wheel. But if we put ourselves vividly into the position of a man who never saw a wheel, but had to invent one, we shall begin to have some idea of its difficulties. Indeed, it is even doubtful whether a single man could have accomplished this feat, whether perhaps centuries were not necessary to form the first wheel from the primitive roller.[16]
History does not name the progressive minds who constructed the first wheel; their time lies far back of the historic period. No scientific academy crowned their efforts, no society of engineers elected them honorary members. They still live only in the stupendous results which they called forth. Take from us the wheel, and little will remain of the arts and industries of modern life. All disappears. From the spinning-wheel to the spinning-mill, from the turning-lathe to the rolling-mill, from the wheelbarrow to the railway train, all vanishes.
In science the wheel is equally important. Whirling machines, as the simplest means of obtaining quick motions with inconsiderable changes of place, play a part in all branches of physics. You know Wheatstone's rotating mirror, Fizeau's wheel, Plateau's perforated rotating disks, etc. Almost the same principle lies at the basis of all these apparatus. They differ from one another no more than the pen-knife differs, in the purposes it serves, from the knife of the anatomist or the knife of the vine-dresser. Almost the same might be said of the screw.
It will now perhaps be clear to you that new thoughts do not spring up suddenly. Thoughts need their time to ripen, grow, and develop in, like every natural product; for man, with his thoughts, is also a part of nature.
Slowly, gradually, and laboriously one thought is transformed into a different thought, as in all likelihood one animal species is gradually transformed into new species. Many ideas arise simultaneously. They fight the battle for existence not otherwise than do the Ichthyosaurus, the Brahman, and the horse.
A few remain to spread rapidly over all fields of knowledge, to be redeveloped, to be again split up, to begin again the struggle from the start. As many animal species long since conquered, the relicts of ages past, still live in remote regions where their enemies cannot reach them, so also we find conquered ideas still living on in the minds of many men. Whoever will look carefully into his own soul will acknowledge that thoughts battle as obstinately for existence as animals. Who will gainsay that many vanquished modes of thought still haunt obscure crannies of his brain, too faint-hearted to step out into the clear light of reason? What inquirer does not know that the hardest battle, in the transformation of his ideas, is fought with himself.
Similar phenomena meet the natural inquirer in all paths and in the most trifling matters. The true inquirer seeks the truth everywhere, in his country-walks and on the streets of the great city. If he is not too learned, he will observe that certain things, like ladies' hats, are constantly subject to change. I have not pursued special studies on this subject, but as long as I can remember, one form has always gradually changed into another. First, they wore hats with long projecting rims, within which, scarcely accessible with a telescope, lay concealed the face of the beautiful wearer. The rim grew smaller and smaller; the bonnet shrank to the irony of a hat. Now a tremendous superstructure is beginning to grow up in its place, and the gods only know what its limits will be. It is not otherwise with ladies' hats than with butterflies, whose multiplicity of form often simply comes from a slight excrescence on the wing of one species developing in a cognate species to a tremendous fold. Nature, too, has its fashions, but they last thousands of years. I could elucidate this idea by many additional examples; for instance, by the history of the evolution of the coat, if I were not fearful that my gossip might prove irksome to you.
We have now wandered through an odd corner of the history of science. What have we learned? The solution of a small, I might almost say insignificant, problem—the measurement of the velocity of light. And more than two centuries have worked at its solution! Three of the most eminent natural philosophers, Galileo, an Italian, Römer, a Dane, and Fizeau, a Frenchman, have fairly shared its labors. And so it is with countless other questions. When we contemplate thus the many blossoms of thought that must wither and fall before one shall bloom, then shall we first truly appreciate Christ's weighty but little consolatory words: "Many be called but few are chosen."
Such is the testimony of every page of history. But is history right? Are really only those chosen whom she names? Have those lived and battled in vain, who have won no prize?
I doubt it. And so will every one who has felt the pangs of sleepless nights spent in thought, at first fruitless, but in the end successful. No thought in such struggles was thought in vain; each one, even the most insignificant, nay, even the erroneous thought, that which apparently was the least productive, served to prepare the way for those that afterwards bore fruit. And as in the thought of the individual naught is in vain, so, also, it is in that of humanity.
Galileo wished to measure the velocity of light. He had to close his eyes before his wish was realised. But he at least found the lantern by which his successor could accomplish the task.
And so I may maintain that we all, so far as inclination goes, are working at the civilisation of the future. If only we all strive for the right, then are we all called and all chosen!
Why has man two eyes? That the pretty symmetry of his face may not be disturbed, the artist answers. That his second eye may furnish a substitute for his first if that be lost, says the far-sighted economist. That we may weep with two eyes at the sins of the world, replies the religious enthusiast.
Odd opinions! Yet if you should approach a modern scientist with this question you might consider yourself fortunate if you escaped with less than a rebuff. "Pardon me, madam, or my dear sir," he would say, with stern expression, "man fulfils no purpose in the possession of his eyes; nature is not a person, and consequently not so vulgar as to pursue purposes of any kind."
Still an unsatisfactory answer! I once knew a professor who would shut with horror the mouths of his pupils if they put to him such an unscientific question.
But ask a more tolerant person, ask me. I, I candidly confess, do not know exactly why man has two[Pg 67] eyes, but the reason partly is, I think, that I may see you here before me to-night and talk with you upon this delightful subject.
Again you smile incredulously. Now this is one of those questions that a hundred wise men together could not answer. You have heard, so far, only five of these wise men. You will certainly want to be spared the opinions of the other ninety-five. To the first you will reply that we should look just as pretty if we were born with only one eye, like the Cyclops; to the second we should be much better off, according to his principle, if we had four or eight eyes, and that in this respect we are vastly inferior to spiders; to the third, that you are not just in the mood to weep; to the fourth, that the unqualified interdiction of the question excites rather than satisfies your curiosity; while of me you will dispose by saying that my pleasure is not as intense as I think, and certainly not great enough to justify the existence of a double eye in man since the fall of Adam.
But since you are not satisfied with my brief and obvious answer, you have only yourselves to blame for the consequences. You must now listen to a longer and more learned explanation, such as it is in my power to give.
As the church of science, however, debars the question "Why?" let us put the matter in a purely orthodox way: Man has two eyes, what more can he see with two than with one?
I will invite you to take a walk with me? We see before us a wood. What is it that makes this real wood contrast so favorably with a painted wood, no matter how perfect the painting may be? What makes the one so much more lovely than the other? Is it the vividness of the coloring, the distribution of the lights and the shadows? I think not. On the contrary, it seems to me that in this respect painting can accomplish very much.
The cunning hand of the painter can conjure up with a few strokes of his brush forms of wonderful plasticity. By the help of other means even more can be attained. Photographs of reliefs are so plastic that we often imagine we can actually lay hold of the elevations and depressions.
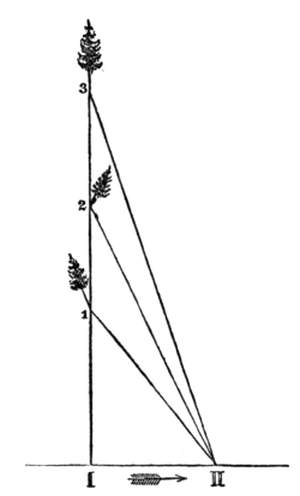 Fig. 20.
Fig. 20.
But one thing the painter never can give with the vividness that nature does—the difference of near and far. In the real woods you see plainly that you can lay hold of some trees, but that others are inaccessibly far. The picture of the painter is rigid. The picture of the real woods changes on the slightest movement.[Pg 69] Now this branch is hidden behind that; now that behind this. The trees are alternately visible and invisible.
Let us look at this matter a little more closely. For convenience sake we shall remain upon the highway, I, II. (Fig. 20.) To the right and the left lies the forest. Standing at I, we see, let us say, three trees (1, 2, 3) in a line, so that the two remote ones are covered by the nearest. Moving further along, this changes. At II we shall not have to look round so far to see the remotest tree 3 as to see the nearer tree 2, nor so far to see this as to see 1. Hence, as we move onward, objects that are near to us seem to lag behind as compared with objects that are remote from us, the lagging increasing with the proximity of the objects. Very remote objects, towards which we must always look in the same direction as we proceed, appear to travel along with us.
If we should see, therefore, jutting above the brow of yonder hill the tops of two trees whose distance from us we were in doubt about, we should have in our hands a very easy means of deciding the question. We should take a few steps forward, say to the right, and the tree-top which receded most to the left would be the one nearer to us. In truth, from the amount of the recession a geometer could actually determine the distance of the trees from us without ever going near them. It is simply the scientific development of[Pg 70] this perception that enables us to measure the distances of the stars.
Hence, from change of view in forward motion the distances of objects in our field of vision can be measured.
Rigorously, however, even forward motion is not necessary. For every observer is composed really of two observers. Man has two eyes. The right eye is a short step ahead of the left eye in the right-hand direction. Hence, the two eyes receive different pictures of the same woods. The right eye will see the near trees displaced to the left, and the left eye will see them displaced to the right, the displacement being greater, the greater the proximity. This difference is sufficient for forming ideas of distance.
We may now readily convince ourselves of the following facts:
1. With one eye, the other being shut, you have a very uncertain judgment of distances. You will find it, for example, no easy task, with one eye shut, to thrust a stick through a ring hung up before you; you will miss the ring in almost every instance.
2. You see the same object differently with the right eye from what you do with the left.
Place a lamp-shade on the table in front of you with its broad opening turned downwards, and look at it from above. (Fig. 21.) You will see with your right eye the image 2, with your left eye the image 1. Again, place the shade with its wide opening turned upwards; you will receive with your right eye the image[Pg 71] 4, with your left eye the image 3. Euclid mentions phenomena of this character.
3. Finally, you know that it is easy to judge of distances with both eyes. Accordingly your judgment must spring in some way from a co-operation of the two eyes. In the preceding example the openings in the different images received by the two eyes seem displaced with respect to one another, and this displacement is sufficient for the inference that the one opening is nearer than the other.
 Fig. 21.
Fig. 21.
I have no doubt that you, ladies, have frequently received delicate compliments upon your eyes, but I[Pg 72] feel sure that no one has ever told you, and I know not whether it will flatter you, that you have in your eyes, be they blue or black, little geometricians. You say you know nothing of them? Well, for that matter, neither do I. But the facts are as I tell you.
You understand little of geometry? I shall accept that confession. Yet with the help of your two eyes you judge of distances? Surely that is a geometrical problem. And what is more, you know the solution of this problem: for you estimate distances correctly. If, then, you do not solve the problem, the little geometricians in your eyes must do it clandestinely and whisper the solution to you. I doubt not they are fleet little fellows.
What amazes me most here is, that you know nothing about these little geometricians. But perhaps they also know nothing about you. Perhaps they are models of punctuality, routine clerks who bother about nothing but their fixed work. In that case we may be able to deceive the gentlemen.
If we present to our right eye an image which looks exactly like the lamp-shade for the right eye, and to our left eye an image which looks exactly like a lamp-shade for the left eye, we shall imagine that we see the whole lamp-shade bodily before us.
You know the experiment. If you are practised in squinting, you can perform it directly with the figure, looking with your right eye at the right image, and with your left eye at the left image. In this way the[Pg 73] experiment was first performed by Elliott. Improved and perfected, its form is Wheatstone's stereoscope, made so popular and useful by Brewster.
By taking two photographs of the same object from two different points, corresponding to the two eyes, a very clear three-dimensional picture of distant places or buildings can be produced by the stereoscope.
But the stereoscope accomplishes still more than this. It can visualise things for us which we never see with equal clearness in real objects. You know that if you move much while your photograph is being taken, your picture will come out like that of a Hindu deity, with several heads or several arms, which, at the spaces where they overlap, show forth with equal distinctness, so that we seem to see the one picture through the other. If a person moves quickly away from the camera before the impression is completed, the objects behind him will also be imprinted upon the photograph; the person will look transparent. Photographic ghosts are made in this way.
Some very useful applications may be made of this discovery. For example, if we photograph a machine stereoscopically, successively removing during the operation the single parts (where of course the impression suffers interruptions), we obtain a transparent view, endowed with all the marks of spatial solidity, in which is distinctly visualised the interaction of parts normally concealed. I have employed this method for[Pg 74] obtaining transparent stereoscopic views of anatomical structures.
You see, photography is making stupendous advances, and there is great danger that in time some malicious artist will photograph his innocent patrons with solid views of their most secret thoughts and emotions. How tranquil politics will then be! What rich harvests our detective force will reap!
[Pg 75][Pg 76][Pg 77][Pg 78][Pg 79][Pg 80][Pg 81][Pg 82][Pg 83][Pg 84][Pg 85][Pg 86]
By the joint action of the two eyes, therefore, we arrive at our judgments of distances, as also of the forms of bodies.
Permit me to mention here a few additional facts connected with this subject, which will assist us in the comprehension of certain phenomena in the history of civilisation.
You have often heard, and know from personal experience, that remote objects appear perspectively dwarfed. In fact, it is easy to satisfy yourself that you can cover the image of a man a few feet away from you simply by holding up your finger a short distance in front of your eye. Still, as a general rule, you do not notice this shrinkage of objects. On the contrary, you imagine you see a man at the end of a large hall, as large as you see him near by you. For your eye, in its measurement of the distances, makes remote objects correspondingly larger. The eye, so to speak, is aware of this perspective contraction and is not deceived by it, although its possessor is unconscious of the fact. All persons who have attempted to draw from nature have vividly felt the difficulty which this superior dexterity of the eye causes the perspective conception. Not until one's judgment of distances is made uncertain, by their size, or from lack of points of reference, or from being too quickly changed, is the perspective rendered very prominent.
On sweeping round a curve on a rapidly moving railway train, where a wide prospect is suddenly opened up, the men upon distant hills appear like dolls.[17] You have at the moment, here, no known references for the measurement of distances. The stones at the entrance of a tunnel grow visibly larger as we ride towards it; they shrink visibly in size as we ride from it.
Usually both eyes work together. As certain views are frequently repeated, and lead always to substantially the same judgments of distances, the eyes in time must acquire a special skill in geometrical constructions. In the end, undoubtedly, this skill is so increased that a single eye alone is often tempted to exercise that office.
Permit me to elucidate this point by an example. Is any sight more familiar to you than that of a vista down a long street? Who has not looked with hopeful eyes time and again into a street and measured its depth. I will take you now into an art-gallery where I will suppose you to see a picture representing a vista into a street. The artist has not spared his rulers to get his perspective perfect. The geometrician in your left eye thinks, "Ah ha! I have computed that case a hundred times or more. I know it by heart. It is a vista into a street," he continues; "where the houses are lower is the remote end." The geometrician in the right eye, too much at his ease to question his possibly peevish comrade in the matter, answers the same. But the sense of duty of these punctual little fellows is at once rearoused. They set to work at their calculations and immediately find that all the points of the picture are equally distant from them, that is, lie all upon a plane surface.
What opinion will you now accept, the first or the second? If you accept the first you will see distinctly the vista. If you accept the second you will see nothing but a painted sheet of distorted images.
It seems to you a trifling matter to look at a picture and understand its perspective. Yet centuries elapsed before humanity came fully to appreciate this trifle, and even the majority of you first learned it from education.
I can remember very distinctly that at three years of age all perspective drawings appeared to me as gross caricatures of objects. I could not understand why artists made tables so broad at one end and so narrow at the other. Real tables seemed to me just as broad at one end as at the other, because my eye made and interpreted its calculations without my intervention. But that the picture of the table on the plane surface was not to be conceived as a plane painted surface but stood for a table and so was to be imaged with all the attributes of extension was a joke that I did not understand. But I have the consolation that whole nations have not understood it.
Ingenuous people there are who take the mock murders of the stage for real murders, the dissembled actions of the players for real actions, and who can scarcely restrain themselves, when the characters of the play are sorely pressed, from running in deep indignation to their assistance. Others, again, can never forget that the beautiful landscapes of the stage are painted, that Richard III. is only the actor, Mr. Booth, whom they have met time and again at the clubs.
Both points of view are equally mistaken. To look at a drama or a picture properly one must understand that both are shows, simply denoting something real. A certain preponderance of the intellectual life over the sensuous life is requisite for such an achievement, where the intellectual elements are safe from destruction by the direct sensuous impressions. A certain liberty in choosing one's point of view is necessary, a sort of humor, I might say, which is strongly wanting in children and in childlike peoples.
Let us look at a few historical facts. I shall not take you as far back as the stone age, although we possess sketches from this epoch which show very original ideas of perspective. But let us begin our sight-seeing in the tombs and ruined temples of ancient Egypt, where the numberless reliefs and gorgeous colorings have defied the ravages of thousands of years.
A rich and motley life is here opened to us. We find the Egyptians represented in all conditions of life. What at once strikes our attention in these pictures is the delicacy of their technical execution. The contours are extremely exact and distinct. But on the other hand only a few bright colors are found, unblended and without trace of transition. Shadows are totally wanting. The paint is laid on the surfaces in equal thicknesses.
Shocking for the modern eye is the perspective. All the figures are equally large, with the exception of the king, whose form is unduly exaggerated. Near and far appear equally large. Perspective contraction is nowhere employed. A pond with water-fowl is represented flat, as if its surface were vertical.
Human figures are portrayed as they are never seen, the legs from the side, the face in profile. The breast lies in its full breadth across the plane of representation. The heads of cattle appear in profile, while the horns lie in the plane of the drawing. The principle which the Egyptians followed might be best expressed by saying that their figures are pressed in the plane of the drawing as plants are pressed in a herbarium.
The matter is simply explained. If the Egyptians were accustomed to looking at things ingenuously with both eyes at once, the construction of perspective pictures in space could not be familiar to them. They saw all arms, all legs on real men in their natural lengths. The figures pressed into the planes resembled more closely, of course, in their eyes the originals than perspective pictures could.
This will be better understood if we reflect that painting was developed from relief. The minor dissimilarities between the pressed figures and the originals must gradually have compelled men to the adoption of perspective drawing. But physiologically the painting of the Egyptians is just as much justified as the drawings of our children are.
A slight advance beyond the Egyptians is shown by the Assyrians. The reliefs rescued from the ruined mounds of Nimrod at Mossul are, upon the whole, similar to the Egyptian reliefs. They were made known to us principally by Layard.
Painting enters on a new phase among the Chinese. This people have a marked feeling for perspective and correct shading, yet without being very logical in the application of their principles. Here, too, it seems, they took the first step but did not go far. In harmony with this immobility is their constitution, in which the muzzle and the bamboo-rod play significant functions. In accord with it, too, is their language, which like the language of children has not yet developed into a grammar, or, rather, according to the modern conception, has not yet degenerated into a grammar. It is the same also with their music which is satisfied with the five-toned scale.
The mural paintings at Herculaneum and Pompeii are distinguished by grace of representation, as also by a pronounced sense for perspective and correct illumination, yet they are not at all scrupulous in construction. Here still we find abbreviations avoided. But to offset this defect, the members of the body are brought into unnatural positions, in which they appear in their full lengths. Abridgements are more frequently observed in clothed than in unclothed figures.
A satisfactory explanation of these phenomena first occurred to me on the making of a few simple experiments which show how differently one may see the same object, after some mastery of one's senses has been attained, simply by the arbitrary movement of the attention.
 Fig. 22.
Fig. 22.
Look at the annexed drawing (Fig. 22). It represents a folded sheet of paper with either its depressed or its elevated side turned towards you, as you wish. You can conceive the drawing in either sense, and in either case it will appear to you differently.
If, now, you have a real folded sheet of paper on the table before you, with its sharp edges turned towards you, you can, on looking at it with one eye, see the sheet alternately elevated, as it really is, or depressed. Here, however, a remarkable phenomenon is presented. When you see the sheet properly, neither illumination nor form presents anything conspicuous. When you see it bent back you see it perspectively distorted. Light and shadow appear much brighter or darker, or as if overlaid thickly with bright colors. Light and shadow now appear devoid of all cause. They no longer harmonise with the body's form, and are thus rendered much more prominent.
In common life we employ the perspective and illumination of objects to determine their forms and position. Hence we do not notice the lights, the shadows, and the distortions. They first powerfully enter consciousness when we employ a different construction from the usual spatial one. In looking at the planar image of a camera obscura we are amazed at the plenitude of the light and the profundity of the shadows, both of which we do not notice in real objects.
In my earliest youth the shadows and lights on pictures appeared to me as spots void of meaning. When I began to draw I regarded shading as a mere custom of artists. I once drew the portrait of our pastor, a friend of the family, and shaded, from no necessity, but simply from having seen something similar in other pictures, the whole half of his face black. I was subjected for this to a severe criticism on the part of my mother, and my deeply offended artist's pride is probably the reason that these facts remained so strongly impressed upon my memory.
You see, then, that many strange things, not only in the life of individuals, but also in that of humanity, and in the history of general civilisation, may be explained from the simple fact that man has two eyes.
Change man's eye and you change his conception of the world. We have observed the truth of this fact among our nearest kin, the Egyptians, the Chinese, and the lake-dwellers; how must it be among some of our remoter relatives,—with monkeys and other animals? Nature must appear totally different to animals equipped with substantially different eyes from those of men, as, for example, to insects. But for the present science must forego the pleasure of portraying this appearance, as we know very little as yet of the mode of operation of these organs.
It is an enigma even how nature appears to animals closely related to man; as to birds, who see scarcely anything with two eyes at once, but since their eyes are placed on opposite sides of their heads, have a separate field of vision for each.[18]
The soul of man is pent up in the prison-house of his head; it looks at nature through its two windows, the eyes. It would also fain know how nature looks through other windows. A desire apparently never to be fulfilled. But our love for nature is inventive, and here, too, much has been accomplished.
Placing before me an angular mirror, consisting of two plane mirrors slightly inclined to each other, I see my face twice reflected. In the right-hand mirror I obtain a view of the right side, and in the left-hand mirror a view of the left side, of my face. Also I shall see the face of a person standing in front of me, more to the right with my right eye, more to the left with my left. But in order to obtain such widely different views of a face as those shown in the angular mirror, my two eyes would have to be set much further apart from each other than they actually are.
 Fig. 23.
Fig. 23.
Squinting with my right eye at the image in the right-hand mirror, with my left eye at the image in the left-hand mirror, my vision will be the vision of a giant having an enormous head with his two eyes set far apart. This, also, is the impression which my own face makes upon me. I see it now, single and solid. Fixing my gaze, the relief from second to second is magnified, the eyebrows start forth prominently from above the eyes, the nose seems to grow a foot in length, my mustache shoots forth like a fountain from my lip, the teeth seem to retreat immeasurably. But by far the most horrible aspect of the phenomenon is the nose.
Interesting in this connexion is the telestereoscope of Helmholtz. In the telestereoscope we view a landscape by looking with our right eye (Fig. 24) through the mirror a into the mirror A, and with our left eye through the mirror b into the mirror B. The mirrors A and B stand far apart. Again we see with the widely separated eyes of a giant. Everything appears dwarfed and near us. The distant mountains look like moss-covered stones at our feet. Between, you see the reduced model of a city, a veritable Liliput. You are tempted almost to stroke with your hand the soft forest and city, did you not fear that you might prick your fingers on the sharp, needle-shaped steeples, or that they might crackle and break off.
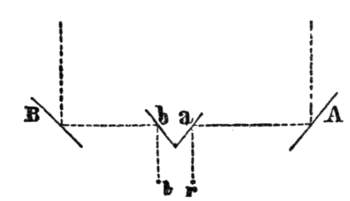 Fig. 24.
Fig. 24.
Liliput is no fable. We need only Swift's eyes, the telestereoscope, to see it.
Picture to yourself the reverse case. Let us suppose ourselves so small that we could take long walks in a forest of moss, and that our eyes were correspondingly near each other. The moss-fibres would appear like trees. On them we should see strange, unshapely monsters creeping about. Branches of the oak-tree, at whose base our moss-forest lay, would seem to us dark, immovable, myriad-branched clouds, painted high on the vault of heaven; just as the inhabitants of Saturn, forsooth, might see their enormous ring. On the tree-trunks of our mossy woodland we should find colossal globes several feet in diameter, brilliantly transparent, swayed by the winds with slow, peculiar motions. We should approach inquisitively and should find that these globes, in which here and there animals were gaily sporting, were liquid globes, in fact that they were water. A short, incautious step, the slightest contact, and woe betide us, our arm is irresistibly drawn by an invisible power into the interior of the sphere and held there unrelentingly fast! A drop of dew has engulfed in its capillary maw a manikin, in revenge for the thousands of drops that its big human counterparts have quaffed at breakfast. Thou shouldst have known, thou pygmy natural scientist, that with thy present puny bulk thou shouldst not joke with capillarity!
My terror at the accident brings me back to my senses. I see I have turned idyllic. You must pardon me. A patch of greensward, a moss or heather forest with its tiny inhabitants have incomparably more charms for me than many a bit of literature with its apotheosis of human character. If I had the gift of writing novels I should certainly not make John and Mary my characters. Nor should I transfer my loving pair to the Nile, nor to the age of the old Egyptian Pharaohs, although perhaps I should choose that time in preference to the present. For I must candidly confess that I hate the rubbish of history, interesting though it may be as a mere phenomenon, because we cannot simply observe it but must also feel it, because it comes to us mostly with supercilious arrogance, mostly unvanquished. The hero of my novel would be a cockchafer, venturing forth in his fifth year for the first time with his newly grown wings into the light, free air. Truly it could do no harm if man would thus throw off his inherited and acquired narrowness of mind by making himself acquainted with the world-view of allied creatures. He could not help gaining incomparably more in this way than the inhabitant of a small town would in circumnavigating the globe and getting acquainted with the views of strange peoples.
I have now conducted you, by many paths and by-ways, rapidly over hedge and ditch, to show you what wide vistas we may reach in every field by the rigorous pursuit of a single scientific fact. A close examination of the two eyes of man has conducted us not only into the dim recesses of humanity's childhood, but has also carried us far beyond the bourne of human life.
It has surely often struck you as strange that the sciences are divided into two great groups; that the so-called humanistic sciences, belonging to the so-called "higher education," are placed in almost a hostile attitude to the natural sciences.
I must confess I do not overmuch believe in this partition of the sciences. I believe that this view will appear as childlike and ingenuous to a matured age as the want of perspective in the old paintings of Egypt does to us. Can it really be that "higher culture" is to be gotten only from a few old pots and palimpsests, which are at best mere scraps of nature, or that more is to be learned from them alone than from all the rest of nature? I believe that both these sciences are simply parts of the same science, which have begun at different ends. If these two ends still act towards each other as the Montagues and Capulets, if their retainers still indulge in lively tilts, I believe that after all they are not in earnest. On the one side there is surely a Romeo, and on the other a Juliet, who, some day, it is hoped, will unite the two houses with a less tragic sequel than that of the play.
Philology began with the unqualified reverence and apotheosis of the Greeks. Now it has begun to draw other languages, other peoples and their histories, into its sphere; it has, through the mediation of comparative linguistics, already struck up, though as yet somewhat cautiously, a friendship with physiology.
Physical science began in the witch's kitchen. It now embraces the organic and inorganic worlds, and with the physiology of articulation and the theory of the senses, has even pushed its researches, at times impertinently, into the province of mental phenomena.
In short, we come to the understanding of much within us solely by directing our glance without, and vice versa. Every object belongs to both sciences. You, ladies, are very interesting and difficult problems for the psychologist, but you are also extremely pretty phenomena of nature. Church and State are objects of the historian's research, but not less phenomena of nature, and in part, indeed, very curious phenomena. If the historical sciences have inaugurated wide extensions of view by presenting to us the thoughts of new and strange peoples, the physical sciences in a certain sense do this in a still greater degree. In making man disappear in the All, in annihilating him, so to speak, they force him to take an unprejudiced position without himself, and to form his judgments by a different standard from that of the petty human.
But if you should ask me now why man has two eyes, I should answer:
That he may look at nature justly and accurately; that he may come to understand that he himself, with all his views, correct and incorrect, with all his haute politique, is simply an evanescent shred of nature; that, to speak with Mephistopheles, he is a part of the part, and that it is absolutely unjustified,
An ancient philosopher once remarked that people who cudgelled their brains about the nature of the moon reminded him of men who discussed the laws and institutions of a distant city of which they had heard no more than the name. The true philosopher, he said, should turn his glance within, should study himself and his notions of right and wrong; only thence could he derive real profit.
This ancient formula for happiness might be restated in the familiar words of the Psalm:
To-day, if he could rise from the dead and walk about among us, this philosopher would marvel much at the different turn which matters have taken.
The motions of the moon and the other heavenly bodies are accurately known. Our knowledge of the motions of our own body is by far not so complete. The mountains and natural divisions of the moon have been accurately outlined on maps, but physiologists are just beginning to find their way in the geography of the brain. The chemical constitution of many fixed stars has already been investigated. The chemical processes of the animal body are questions of much greater difficulty and complexity. We have our Mécanique céleste. But a Mécanique sociale or a Mécanique morale of equal trustworthiness remains to be written.
Our philosopher would indeed admit that we have made great progress. But we have not followed his advice. The patient has recovered, but he took for his recovery exactly the opposite of what the doctor prescribed.
Humanity is now returned, much wiser, from its journey in celestial space, against which it was so solemnly warned. Men, after having become acquainted with the great and simple facts of the world without, are now beginning to examine critically the world within. It sounds absurd, but it is true, that only after we have thought about the moon are we able to take up ourselves. It was necessary that we should acquire simple and clear ideas in a less complicated domain, before we entered the more intricate one of psychology, and with these ideas astronomy principally furnished us.
To attempt any description of that stupendous movement, which, originally springing out of the physical sciences, went beyond the domain of physics and is now occupied with the problems of psychology, would be presumptuous in this place. I shall only attempt here, to illustrate to you by a few simple examples the methods by which the province of psychology can be reached from the facts of the physical world—especially the adjacent province of sense-perception. And I wish it to be remembered that my brief attempt is not to be taken as a measure of the present state of such scientific questions.
It is a well-known fact that some objects please us, while others do not. Generally speaking, anything that is constructed according to fixed and logically followed rules, is a product of tolerable beauty. We see thus nature herself, who always acts according to fixed rules, constantly producing such pretty things. Every day the physicist is confronted in his workshop with the most beautiful vibration-figures, tone-figures, phenomena of polarisation, and forms of diffraction.
A rule always presupposes a repetition. Repetitions, therefore, will probably be found to play some important part in the production of agreeable effects. Of course, the nature of agreeable effects is not exhausted by this. Furthermore, the repetition of a physical event becomes the source of agreeable effects only when it is connected with a repetition of sensations.
An excellent example that repetition of sensations is a source of agreeable effects is furnished by the copy-book of every schoolboy, which is usually a treasure-house of such things, and only in need of an Abbé Domenech to become celebrated. Any figure, no matter how crude or poor, if several times repeated, with the repetitions placed in line, will produce a tolerable frieze.
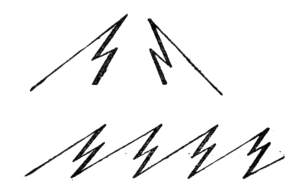 Fig. 25.
Fig. 25.
Also the pleasant effect of symmetry is due to the repetition of sensations. Let us abandon ourselves a moment to this thought, yet not imagine when we have developed it, that we have fully exhausted the nature of the agreeable, much less of the beautiful.
First, let us get a clear conception of what symmetry is. And in preference to a definition let us take a living picture. You know that the reflexion of an object in a mirror has a great likeness to the object itself. All its proportions and outlines are the same. Yet there is a difference between the object and its reflexion in the mirror, which you will readily observe.
Hold your right hand before a mirror, and you will see in the mirror a left hand. Your right glove will produce its mate in the glass. For you could never use the reflexion of your right glove, if it were present to you as a real thing, for covering your right hand, but only for covering your left. Similarly, your right ear will give as its reflexion a left ear; and you will at once perceive that the left half of your body could very easily be substituted for the reflexion of your right half. Now just as in the place of a missing right ear a left ear cannot be put, unless the lobule of the ear be turned upwards, or the opening into the concha backwards, so, despite all similarity of form, the reflexion of an object can never take the place of the object itself.[20]
The reason of this difference between the object and its reflexion is simple. The reflexion appears as far behind the mirror as the object is in front of it. The parts of the object, accordingly, which are nearest the mirror will also be nearest the mirror in the reflexion. Consequently, the succession of the parts in the reflexion will be reversed, as may best be seen in the reflexion of the face of a watch or of a manuscript.
It will also be readily seen, that if a point of the object be joined with its reflexion in the image, the line of junction will cut the mirror at right angles and be bisected by it. This holds true of all corresponding points of object and image.
If, now, we can divide an object by a plane into two halves so that each half, as seen in the reflecting plane of division, is a reproduction of the other half, such an object is termed symmetrical, and the plane of division is called the plane of symmetry.
If the plane of symmetry is vertical, we can say that the body is vertically symmetrical. An example of vertical symmetry is a Gothic cathedral.
If the plane of symmetry is horizontal, we can say that the object is horizontally symmetrical. A landscape on the shores of a lake with its reflexion in the water, is a system of horizontal symmetry.
Exactly here is a noticeable difference. The vertical symmetry of a Gothic cathedral strikes us at once, whereas we can travel up and down the whole length of the Rhine or the Hudson without becoming aware of the symmetry between objects and their reflexions in the water. Vertical symmetry pleases us, whilst horizontal symmetry is indifferent, and is noticed only by the experienced eye.
Whence arises this difference? I say from the fact that vertical symmetry produces a repetition of the same sensation, while horizontal symmetry does not. I shall now show that this is so.
Let us look at the following letters:
d b q p
It is a fact known to all mothers and teachers, that children in their first attempts to read and write, constantly confound d and b, and q and p, but never d and q, or b and p. Now d and b and q and p are the two halves of a vertically symmetrical figure, while d and q, and b and p are two halves of a horizontally symmetrical figure. The first two are confounded; but confusion is only possible of things that excite in us the same or similar sensations.
Figures of two flower-girls are frequently seen on the decorations of gardens and of drawing-rooms, one of whom carries a flower-basket in her right hand and the other a flower-basket in her left. All know how apt we are, unless we are very careful, to confound these figures with one another.
While turning a thing round from right to left is scarcely noticed, the eye is not at all indifferent to the turning of a thing upside down. A human face which has been turned upside down is scarcely recognisable as a face, and makes an impression which is altogether strange. The reason of this is not to be sought in the unwontedness of the sight, for it is just as difficult to recognise an arabesque that has been inverted, where there can be no question of a habit. This curious fact is the foundation of the familiar jokes played with the portraits of unpopular personages, which are so drawn that in the upright position of the page an exact picture of the person is presented, but on being inverted some popular animal is shown.
It is a fact, then, that the two halves of a vertically symmetrical figure are easily confounded and that they therefore probably produce very nearly the same sensations. The question, accordingly, arises, why do the two halves of a vertically symmetrical figure produce the same or similar sensations? The answer is: Because our apparatus of vision, which consists of our eyes and of the accompanying muscular apparatus is itself vertically symmetrical.[21]
Whatever external resemblances one eye may have with another they are still not alike. The right eye of a man cannot take the place of a left eye any more than a left ear or left hand can take the place of a right one. By artificial means, we can change the part which each of our eyes plays. (Wheatstone's pseudoscope.) But we then find ourselves in an entirely new and strange world. What is convex appears concave; what is concave, convex. What is distant appears near, and what is near appears far.
The left eye is the reflexion of the right. And the light-feeling retina of the left eye is a reflexion of the light-feeling retina of the right, in all its functions.
The lense of the eye, like a magic lantern, casts images of objects on the retina. And you may picture to yourself the light-feeling retina of the eye, with its countless nerves, as a hand with innumerable fingers, adapted to feeling light. The ends of the visual nerves, like our fingers, are endowed with varying degrees of sensitiveness. The two retinæ act like a right and a left hand; the sensation of touch and the sensation of light in the two instances are similar.
Examine the right-hand portion of this letter T: namely, T. Instead of the two retinæ on which this image falls, imagine feeling the object, my two hands. The ┌, grasped with the right hand, gives a different sensation from that which it gives when grasped with the left. But if we turn our character about from right to left, thus: ┐, it will give the same sensation in the left hand that it gave before in the right. The sensation is repeated.
If we take a whole T, the right half will produce in the right hand the same sensation that the left half produces in the left, and vice versa.
The symmetrical figure gives the same sensation twice.
If we turn the T over thus: ├, or invert the half T thus: L, so long as we do not change the position of our hands we can make no use of the foregoing reasoning.
The retinæ, in fact, are exactly like our two hands. They, too, have their thumbs and index fingers, though they are thousands in number; and we may say the thumbs are on the side of the eye near the nose, and the remaining fingers on the side away from the nose.
With this I hope to have made perfectly clear that the pleasing effect of symmetry is chiefly due to the repetition of sensations, and that the effect in question takes place in symmetrical figures, only where there is a repetition of sensation. The pleasing effect of regular figures, the preference which straight lines, especially vertical and horizontal straight lines, enjoy, is founded on a similar reason. A straight line, both in a horizontal and in a vertical position, can cast on the two retinæ the same image, which falls moreover on symmetrically corresponding spots. This also, it would appear, is the reason of our psychological preference of straight to curved lines, and not their property of being the shortest distance between two points. The straight line is felt, to put the matter briefly, as symmetrical to itself, which is the case also with the plane. Curved lines are felt as deviations from straight lines, that is, as deviations from symmetry.[22] The presence of a sense for symmetry in people possessing only one eye from birth, is indeed a riddle. Of course, the sense of symmetry, although primarily acquired by means of the eyes, cannot be wholly limited to the visual organs. It must also be deeply rooted in other parts of the organism by ages of practice and can thus not be eliminated forthwith by the loss of one eye. Also, when an eye is lost, the symmetrical muscular apparatus is left, as is also the symmetrical apparatus of innervation.
It appears, however, unquestionable that the phenomena mentioned have, in the main, their origin in the peculiar structure of our eyes. It will therefore be seen at once that our notions of what is beautiful and ugly would undergo a change if our eyes were different. Also, if this view is correct, the theory of the so-called eternally beautiful is somewhat mistaken. It can scarcely be doubted that our culture, or form of civilisation, which stamps upon the human body its unmistakable traces, should not also modify our conceptions of the beautiful. Was not formerly the development of all musical beauty restricted to the narrow limits of a five-toned scale?
The fact that a repetition of sensations is productive of pleasant effects is not restricted to the realm of the visible. To-day, both the musician and the physicist know that the harmonic or the melodic addition of one tone to another affects us agreeably only when the added tone reproduces a part of the sensation which the first one excited. When I add an octave to a fundamental tone, I hear in the octave a part of what was heard in the fundamental tone. (Helmholtz.) But it is not my purpose to develop this idea fully here.[23] We shall only ask to-day, whether there is anything similar to the symmetry of figures in the province of sounds.
Look at the reflexion of your piano in the mirror.
You will at once remark that you have never seen such a piano in the actual world, for it has its high keys to the left and its low ones to the right. Such pianos are not manufactured.
If you could sit down at such a piano and play in your usual manner, plainly every step which you imagined you were performing in the upward scale would be executed as a corresponding step in the downward scale. The effect would be not a little surprising.
For the practised musician who is always accustomed to hearing certain sounds produced when certain keys are struck, it is quite an anomalous spectacle to watch a player in the glass and to observe that he always does the opposite of what we hear.
But still more remarkable would be the effect of attempting to strike a harmony on such a piano. For a melody it is not indifferent whether we execute a step in an upward or a downward scale. But for a harmony, so great a difference is not produced by reversal. I always retain the same consonance whether I add to a fundamental note an upper or a lower third. Only the order of the intervals of the harmony is reversed. In point of fact, when we execute a movement in a major key on our reflected piano, we hear a sound in a minor key, and vice versa.
It now remains to execute the experiments indicated. Instead of playing upon the piano in the mirror, which is impossible, or of having a piano of this kind built, which would be somewhat expensive, we may perform our experiments in a simpler manner, as follows:
1) We play on our own piano in our usual manner, look into the mirror, and then repeat on our real piano what we see in the mirror. In this way we transform all steps upwards into corresponding steps downwards. We play a movement, and then another movement, which, with respect to the key-board, is symmetrical to the first.
2) We place a mirror beneath the music in which the notes are reflected as in a body of water, and play according to the notes in the mirror. In this way also, all steps upwards are changed into corresponding, equal steps downwards.
3) We turn the music upside down and read the notes from right to left and from below upwards. In doing this, we must regard all sharps as flats and all flats as sharps, because they correspond to half lines and spaces. Besides, in this use of the music we can only employ the bass clef, as only in this clef are the notes not changed by symmetrical reversal.
You can judge of the effect of these experiments from the examples which appear in the annexed musical cut. (Page 102.) The movement which appears in the upper lines is symmetrically reversed in the lower.
The effect of the experiments may be briefly formulated. The melody is rendered unrecognisable. The harmony suffers a transposition from a major into a minor key and vice versa. The study of these pretty effects, which have long been familiar to physicists and musicians, was revived some years ago by Von Oettingen.[24]
 Fig. 26.
Fig. 26.(See pages 101 and 103.)]
Now, although in all the preceding examples I have transposed steps upward into equal and similar steps downward, that is, as we may justly say, have played for every movement the movement which is symmetrical to it, yet the ear notices either little or nothing of symmetry. The transposition from a major to a minor key is the sole indication of symmetry remaining. The symmetry is there for the mind, but is wanting for sensation. No symmetry exists for the ear, because a reversal of musical sounds conditions no repetition of sensations. If we had an ear for height and an ear for depth, just as we have an eye for the right and an eye for the left, we should also find that symmetrical sound-structures existed for our auditory organs. The contrast of major and minor for the ear corresponds to inversion for the eye, which is also only symmetry for the mind, but not for sensation.
By way of supplement to what I have said, I will add a brief remark for my mathematical readers.
Our musical notation is essentially a graphical representation of a piece of music in the form of curves, where the time is the abscissæ, and the logarithms of the number of vibrations the ordinates. The deviations of musical notation from this principle are only such as facilitate interpretation, or are due to historical accidents.
If, now, it be further observed that the sensation of pitch also is proportional to the logarithm of the number of vibrations, and that the intervals between the notes correspond to the differences of the logarithms of the numbers of vibrations, the justification will be found in these facts of calling the harmonies and melodies which appear in the mirror, symmetrical to the original ones.
I simply wish to bring home to your minds by these fragmentary remarks that the progress of the physical sciences has been of great help to those branches of psychology that have not scorned to consider the results of physical research. On the other hand, psychology is beginning to return, as it were, in a spirit of thankfulness, the powerful stimulus which it received from physics.
The theories of physics which reduce all phenomena to the motion and equilibrium of smallest particles, the so-called molecular theories, have been gravely threatened by the progress of the theory of the senses and of space, and we may say that their days are numbered.
I have shown elsewhere[25] that the musical scale is simply a species of space—a space, however, of only one dimension, and that, a one-sided one. If, now, a person who could only hear, should attempt to develop a conception of the world in this, his linear space, he would become involved in many difficulties, as his space would be incompetent to comprehend the many sides of the relations of reality. But is it any more justifiable for us, to attempt to force the whole world into the space of our eye, in aspects in which it is not accessible to the eye? Yet this is the dilemma of all molecular theories.
We possess, however, a sense, which, with respect to the scope of the relations which it can comprehend, is richer than any other. It is our reason. This stands above the senses. It alone is competent to found a permanent and sufficient view of the world. The mechanical conception of the world has performed wonders since Galileo's time. But it must now yield to a broader view of things. A further development of this idea is beyond the limits of my present purpose.
One more point and I have done. The advice of our philosopher to restrict ourselves to what is near at hand and useful in our researches, which finds a kind of exemplification in the present cry of inquirers for limitation and division of labor, must not be too slavishly followed. In the seclusion of our closets, we often rack our brains in vain to fulfil a work, the means of accomplishing which lies before our very doors. If the inquirer must be perforce a shoemaker, tapping constantly at his last, it may perhaps be permitted him to be a shoemaker of the type of Hans Sachs, who did not deem it beneath him to take a look now and then at his neighbor's work and to comment on the latter's doings.
Let this be my apology, therefore, if I have forsaken for a moment to-day the last of my specialty.
The task has been assigned me to develop before you in a popular manner the fundamental quantitative concepts of electrostatics—"quantity of electricity," "potential," "capacity," and so forth. It would not be difficult, even within the brief limits of an hour, to delight the eye with hosts of beautiful experiments and to fill the imagination with numerous and varied conceptions. But we should, in such a case, be still far from a lucid and easy grasp of the phenomena. The means would still fail us for reproducing the facts accurately in thought—a procedure which for the theoretical and practical man is of equal importance. These means are the metrical concepts of electricity.
As long as the pursuit of the facts of a given province of phenomena is in the hands of a few isolated investigators, as long as every experiment can be easily repeated, the fixing of the collected facts by provisional[Pg 108] description is ordinarily sufficient. But the case is different when the whole world must make use of the results reached by many, as happens when the science acquires broader foundations and scope, and particularly so when it begins to supply intellectual nourishment to an important branch of the practical arts, and to draw from that province in return stupendous empirical results. Then the facts must be so described that individuals in all places and at all times can, from a few easily obtained elements, put the facts accurately together in thought, and reproduce them from the description. This is done with the help of the metrical concepts and the international measures.
The work which was begun in this direction in the period of the purely scientific development of the science, especially by Coulomb (1784), Gauss (1833), and Weber (1846), was powerfully stimulated by the requirements of the great technical undertakings manifested since the laying of the first transatlantic cable, and brought to a brilliant conclusion by the labors of the British Association, 1861, and of the Paris Congress, 1881, chiefly through the exertions of Sir William Thomson.
It is plain, that in the time allotted to me I cannot conduct you over all the long and tortuous paths which the science has actually pursued, that it will not be possible at every step to remind you of all the little precautions for the avoidance of error which the early steps have taught us. On the contrary, I must make[Pg 109] shift with the simplest and rudest tools. I shall conduct you by the shortest paths from the facts to the ideas, in doing which, of course, it will not be possible to anticipate all the stray and chance ideas which may and must arise from prospects into the by-paths which we leave untrodden.
Here are two small, light bodies (Fig. 27) of equal size, freely suspended, which we "electrify" either by friction with a third body or by contact with a body already electrified. At once a repulsive force is set up which drives the two bodies away from each other in opposition to the action of gravity. This force could accomplish anew the same mechanical work which was expended to produce it.[27]
 Fig. 27.
Fig. 27.
 Fig. 28.
Fig. 28.
Coulomb, now, by means of delicate experiments with the torsion-balance, satisfied himself that if the bodies in question, say at a distance of two centimetres, repelled each other with the same force with which a milligramme-weight strives to fall to the ground, at half that distance, or at one centimetre, they would repel each other with the force of four milligrammes, and at double that distance, or at four centimetres, they would repel each other with the force of only one-fourth of a milligramme. He found that the electrical force acts inversely as the square of the distance.
Let us imagine, now, that we possessed some means of measuring electrical repulsion by weights, a means which would be supplied, for example, by our electrical pendulums; then we could make the following observation.
The body A (Fig. 28) is repelled by the body K at a distance of two centimetres with a force of one milligramme. If we touch A, now, with an equal body B, the half of this force of repulsion will pass to the body B; both A and B, now, at a distance of two centimetres from K, are repelled only with the force of one-half a milligramme. But both together are repelled still with the force of one milligramme. Hence, the divisibility of electrical force among bodies in contact is a fact. It is a useful, but by no means a necessary supplement to this fact, to imagine an electrical fluid present in the body A, with the quantity of which the electrical force varies, and half of which flows over to B. For, in the place of the new physical picture, thus, an old, familiar one is substituted, which moves spontaneously in its wonted courses.
Adhering to this idea, we define the unit of electrical quantity, according to the now almost universally adopted centimetre-gramme-second (C. G. S.) system, as that quantity which at a distance of one centimetre repels an equal quantity with unit of force, that is, with a force which in one second would impart to a mass of one gramme a velocity-increment of a centimetre. As a gramme mass acquires through the action of gravity a velocity-increment of about 981 centimetres in a second, accordingly, a gramme is attracted to the earth with 981, or, in round numbers, 1000 units of force of the centimetre-gramme-second system, while a milligramme-weight would strive to fall to the earth with approximately the unit force of this system.
We may easily obtain by this means a clear idea of what the unit quantity of electricity is. Two small bodies, K, weighing each a gramme, are hung up by vertical threads, five metres in length and almost weightless, so as to touch each other. If the two bodies be equally electrified and move apart upon electrification to a distance of one centimetre, their charge is approximately equivalent to the electrostatic unit of electric quantity, for the repulsion then holds in equilibrium a gravitational force-component of approximately one milligramme, which strives to bring the bodies together.
Vertically beneath a small sphere suspended from the equilibrated beam of a balance a second sphere is placed at a distance of a centimetre. If both be equally electrified the sphere suspended from the balance will be rendered apparently lighter by the repulsion. If by adding a weight of one milligramme equilibrium is restored, each of the spheres contains in round numbers the electrostatic unit of electrical quantity.
In view of the fact that the same electrical bodies exert at different distances different forces upon one another, exception might be taken to the measure of quantity here developed. What kind of a quantity is that which now weighs more, and now weighs less, so to speak? But this apparent deviation from the method of determination commonly used in practical life, that by weight, is, closely considered, an agreement. On a high mountain a heavy mass also is less powerfully attracted to the earth than at the level of the sea, and if it is permitted us in our determinations to neglect the consideration of level, it is only because the comparison of a body with fixed conventional weights is invariably effected at the same level. In fact, if we were to make one of the two weights equilibrated on our balance approach sensibly to the centre of the earth, by suspending it from a very long thread, as Prof. von Jolly of Munich suggested, we should make the gravity of that weight, its heaviness, proportionately greater.
Let us picture to ourselves, now, two different electrical fluids, a positive and a negative fluid, of such nature that the particles of the one attract the particles of the other according to the law of the inverse squares, but the particles of the same fluid repel each other by the same law; in non-electrical bodies let us imagine the two fluids uniformly distributed in equal quantities, in electric bodies one of the two in excess; in conductors, further, let us imagine the fluids mobile, in non-conductors immobile; having formed such pictures, we possess the conception which Coulomb developed and to which he gave mathematical precision. We have only to give this conception free play in our minds and we shall see as in a clear picture the fluid particles, say of a positively charged conductor, receding from one another as far as they can, all making for the surface of the conductor and there seeking out the prominent parts and points until the greatest possible amount of work has been performed. On increasing the size of the surface, we see a dispersion, on decreasing its size we see a condensation of the particles. In a second, non-electrified conductor brought into the vicinity of the first, we see the two fluids immediately separate, the positive collecting itself on the remote and the negative on the adjacent side of its surface. In the fact that this conception reproduces, lucidly and spontaneously, all the data which arduous research only slowly and gradually discovered, is contained its advantage and scientific value. With this, too, its value is exhausted. We must not seek in nature for the two hypothetical fluids which we have added as simple mental adjuncts, if we would not go astray. Coulomb's view may be replaced by a totally different one, for example, by that of Faraday, and the most proper course is always, after the general survey is obtained, to go back to the actual facts, to the electrical forces.
 Fig. 29.
Fig. 29.
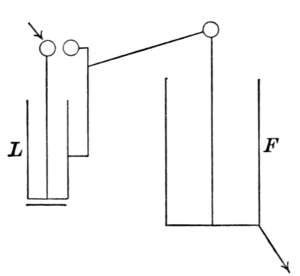 Fig. 30.
Fig. 30.
We will now make ourselves familiar with the concept of electrical quantity, and with the method of measuring or estimating it. Imagine a common Leyden jar (Fig. 29), the inner and outer coatings of which are connected together by means of two common metallic knobs placed about a centimetre apart. If the inside coating be charged with the quantity of electricity +q, on the outer coating a distribution of the electricities will take place. A positive quantity almost equal[28] to the quantity +q flows off to the earth, while a corresponding quantity-q is still left on the outer coating. The knobs of the jar receive their portion of these quantities and when the quantity q is sufficiently great a rupture of the insulating air between the knobs, accompanied by the self-discharge of the jar, takes place. For any given distance and size of the knobs, a charge of a definite electric quantity q is always necessary for the spontaneous discharge of the jar.
Let us insulate, now, the outer coating of a Lane's unit jar L, the jar just described, and put in connexion with it the inner coating of a jar F exteriorly connected with the earth (Fig. 30). Every time that L is charged with +q, a like quantity +q is collected on the inner coating of F, and the spontaneous discharge of the jar L, which is now again empty, takes place. The number of the discharges of the jar L furnishes us, thus, with a measure of the quantity collected in the jar F, and if after 1, 2, 3, ... spontaneous discharges of L the jar F is discharged, it is evident that the charge of F has been proportionately augmented.
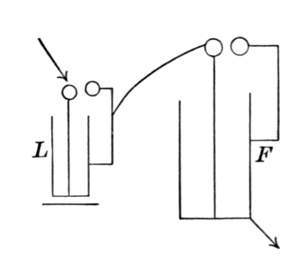 Fig. 31.
Fig. 31.
Let us supply now, to effect the spontaneous discharge, the jar F with knobs of the same size and at the same distance apart as those of the jar L (Fig. 31). If we find, then, that five discharges of the unit jar take place before one spontaneous discharge of the jar F occurs, plainly the jar F, for equal distances between the knobs of the two jars, equal striking distances, is able to hold five times the quantity of electricity that L can, that is, has five times the capacity of L.[29]
 Fig. 32.
Fig. 32.
We will now replace the unit jar L, with which we measure electricity, so to speak, into the jar F, by a Franklin's pane, consisting of two parallel flat metal plates (Fig. 32), separated only by air. If here, for example, thirty spontaneous discharges of the pane are sufficient to fill the jar, ten discharges will be found sufficient if the air-space between the two plates be filled with a cake of sulphur. Hence, the capacity of a Franklin's pane of sulphur is about three times greater than that of one of the same shape and size made of air, or, as it is the custom to say, the specific inductive capacity of sulphur (that of air being taken as the unit) is about 3.[30] We are here arrived at a very simple fact, which clearly shows us the significance of the number called dielectric constant, or specific inductive capacity, the knowledge of which is so important for the theory of submarine cables.
Let us consider a jar A, which is charged with a certain quantity of electricity. We can discharge the jar directly. But we can also discharge the jar A (Fig. 33) partly into a jar B, by connecting the two outer coatings with each other. In this operation a portion of the quantity of electricity passes, accompanied by sparks, into the jar B, and we now find both jars charged.
 Fig. 33.
Fig. 33.
 Fig. 34.
Fig. 34.
It may be shown as follows that the conception of a constant quantity of electricity can be regarded as the expression of a pure fact. Picture to yourself any sort of electrical conductor (Fig. 34); cut it up into a large number of small pieces, and place these pieces by means of an insulated rod at a distance of one centimetre from an electrical body which acts with unit of force on an equal and like-constituted body at the same distance. Take the sum of the forces which this last body exerts on the single pieces of the conductor. The sum of these forces will be the quantity of electricity on the whole conductor. It remains the same, whether we change the form and the size of the conductor, or whether we bring it near or move it away from a second electrical conductor, so long as we keep it insulated, that is, do not discharge it.
A basis of reality for the notion of electric quantity seems also to present itself from another quarter. If a current, that is, in the usual view, a definite quantity of electricity per second, is sent through a column of acidulated water; in the direction of the positive stream, hydrogen, but in the opposite direction, oxygen is liberated at the extremities of the column. For a given quantity of electricity a given quantity of oxygen appears. You may picture the column of water as a column of hydrogen and a column of oxygen, fitted into each other, and may say the electric current is a chemical current and vice versa. Although this notion is more difficult to adhere to in the field of statical electricity and with non-decomposable conductors, its further development is by no means hopeless.
The concept quantity of electricity, thus, is not so aerial as might appear, but is able to conduct us with certainty through a multitude of varied phenomena, and is suggested to us by the facts in almost palpable form. We can collect electrical force in a body, measure it out with one body into another, carry it over from one body into another, just as we can collect a liquid in a vessel, measure it out with one vessel into another, or pour it from one into another.
For the analysis of mechanical phenomena, a metrical notion, derived from experience, and bearing the designation work, has proved itself useful. A machine can be set in motion only when the forces acting on it can perform work.
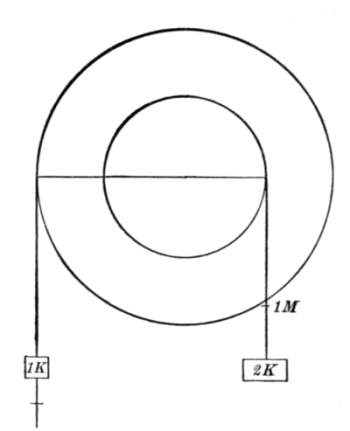 Fig. 35.
Fig. 35.
Let us consider, for example, a wheel and axle (Fig. 35) having the radii 1 and 2 metres, loaded respectively with the weights 2 and 1 kilogrammes. On turning the wheel and axle, the 1 kilogramme-weight, let us say, sinks two metres, while the 2 kilogramme-weight rises one metre. On both sides the product
KGR. M. KGR. M.
1 × 2 = 2 × 1.
is equal. So long as this is so, the wheel and axle will not move of itself. But if we take such loads, or so change the radii of the wheels, that this product (kgr. × metre) on displacement is in excess on one side, that side will sink. As we see, this product is characteristic for mechanical events, and for this reason has been invested with a special name, work.
In all mechanical processes, and as all physical processes present a mechanical side, in all physical processes, work plays a determinative part. Electrical forces, also, produce only changes in which work is performed. To the extent that forces come into play in electrical phenomena, electrical phenomena, be they what they may, extend into the domain of mechanics and are subject to the laws which hold in this domain. The universally adopted measure of work, now, is the product of the force into the distance through which it acts, and in the C. G. S. system, the unit of work is the action through one centimetre of a force which would impart in one second to a gramme-mass a velocity-increment of one centimetre, that is, in round numbers, the action through a centimetre of a pressure equal to the weight of a milligramme. From a positively charged body, electricity, yielding to the force of repulsion and performing work, flows off to the earth, providing conducting connexions exist. To a negatively charged body, on the other hand, the earth under the same circumstances gives off positive electricity. The electrical work possible in the interaction of a body with the earth, characterises the electrical condition of that body. We will call the work which must be expended on the unit quantity of positive electricity to raise it from the earth to the body K the potential of the body K.[31]
We ascribe to the body K in the C. G. S. system the potential +1, if we must expend the unit of work to raise the positive electrostatic unit of electric quantity from the earth to that body; the potential -1, if we gain in this procedure the unit of work; the potential 0, if no work at all is performed in the operation.
The different parts of one and the same electrical conductor in electrical equilibrium have the same potential, for otherwise the electricity would perform work and move about upon the conductor, and equilibrium would not have existed. Different conductors of equal potential, put in connexion with one another, do not exchange electricity any more than bodies of equal temperature in contact exchange heat, or in connected vessels, in which the same pressures exist, liquids flow from one vessel to the other. Exchange of electricity takes place only between conductors of different potentials, but in conductors of given form and position a definite difference of potential is necessary for a spark, which pierces the insulating air, to pass between them.
On being connected, every two conductors assume at once the same potential. With this the means is given of determining the potential of a conductor through the agency of a second conductor expressly adapted to the purpose called an electrometer, just as we determine the temperature of a body with a thermometer. The values of the potentials of bodies obtained in this way simplify vastly our analysis of their electrical behavior, as will be evident from what has been said.
Think of a positively charged conductor. Double all the electrical forces exerted by this conductor on a point charged with unit quantity, that is, double the quantity at each point, or what is the same thing, double the total charge. Plainly, equilibrium still subsists. But carry, now, the positive electrostatic unit towards the conductor. Everywhere we shall have to overcome double the force of repulsion we did before, everywhere we shall have to expend double the work. By doubling the charge of the conductor a double potential has been produced. Charge and potential go hand in hand, are proportional. Consequently, calling the total quantity of electricity of a conductor Q and its potential V, we can write: Q = CV, where C stands for a constant, the import of which will be understood simply from noting that C = Q/V.[32] But the division of a number representing the units of quantity of a conductor by the number representing its units of potential tells us the quantity which falls to the share of the unit of potential. Now the number C here we call the capacity of a conductor, and have substituted, thus, in the place of the old relative determination of capacity, an absolute determination.[33]
In simple cases the connexion between charge, potential, and capacity is easily ascertained. Our conductor, let us say, is a sphere of radius r, suspended free in a large body of air. There being no other conductors in the vicinity, the charge q will then distribute itself uniformly upon the surface of the sphere, and simple geometrical considerations yield for its potential the expression V = q/r. Hence, q/V = r; that is, the capacity of a sphere is measured by its radius, and in the C. G. S. system in centimetres.[34] It is clear also, since a potential is a quantity divided by a length, that a quantity divided by a potential must be a length.
Imagine (Fig. 36) a jar composed of two concentric conductive spherical shells of the radii r and r1, having only air between them. Connecting the outside sphere with the earth, and charging the inside sphere by means of a thin, insulated wire passing through the first, with the quantity Q, we shall have V = (r1-r)/(r1r)Q, and for the capacity in this case (r1r)/(r1-r), or, to take a specific example, if r = 16 and r1 = 19, a capacity of about 100 centimetres.
 Fig. 36.
Fig. 36.
We shall now use these simple cases for illustrating the principle by which capacity and potential are determined. First, it is clear that we can use the jar composed of concentric spheres with its known capacity as our unit jar and by means of this ascertain, in the manner above laid down, the capacity of any given jar F. We find, for example, that 37 discharges of this unit jar of the capacity 100, just charges the jar investigated at the same striking distance, that is, at the same potential. Hence, the capacity of the jar investigated is 3700 centimetres. The large battery of the Prague physical laboratory, which consists of sixteen such jars, all of nearly equal size, has a capacity, therefore, of something like 50,000 centimetres, or the capacity of a sphere, a kilometre in diameter, freely suspended in atmospheric space. This remark distinctly shows us the great superiority which Leyden jars possess for the storage of electricity as compared with common conductors. In fact, as Faraday pointed out, jars differ from simple conductors mainly by their great capacity.
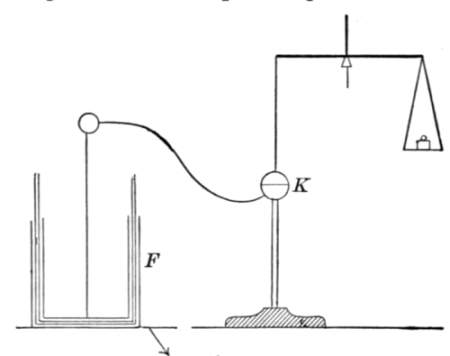 Fig. 37.
Fig. 37.
For determining potential, imagine the inner coating of a jar F, the outer coating of which communicates with the ground, connected by a long, thin wire with a conductive sphere K placed free in a large atmospheric space, compared with whose dimensions the radius of the sphere vanishes. (Fig. 37.) The jar and the sphere assume at once the same potential. But on the surface of the sphere, if that be sufficiently far removed from all other conductors, a uniform layer of electricity will be found. If the sphere, having the radius r, contains the charge q, its potential is V = q/r. If the upper half of the sphere be severed from the lower half and equilibrated on a balance with one of whose beams it is connected by silk threads, the upper half will be repelled from the lower half with the force P = q2/8r2 = 1/8V2. This repulsion P may be counter-balanced by additional weights placed on the beam-end, and so ascertained. The potential is then V = √(8P).[35]
That the potential is proportional to the square root of the force is not difficult to see. A doubling or trebling of the potential means that the charge of all the parts is doubled or trebled; hence their combined power of repulsion quadrupled or nonupled.
Let us consider a special case. I wish to produce the potential 40 on the sphere. What additional weight must I give to the half sphere in grammes that the force of repulsion shall maintain the balance in exact equilibrium? As a gramme weight is approximately equivalent to 1000 units of force, we have only the following simple example to work out: 40×40 = 8× 1000.x, where x stands for the number of grammes. In round numbers we get x = 0.2 gramme. I charge the jar. The balance is deflected; I have reached, or rather passed, the potential 40, and you see when I discharge the jar the associated spark.[36]
The striking distance between the knobs of a machine increases with the difference of the potential, although not proportionately to that difference. The striking distance increases faster than the potential difference. For a distance between the knobs of one centimetre on this machine the difference of potential is 110. It can easily be increased tenfold. Of the tremendous differences of potential which occur in nature some idea may be obtained from the fact that the striking distances of lightning in thunder-storms is counted by miles. The differences of potential in galvanic batteries are considerably smaller than those of our machine, for it takes fully one hundred elements to give a spark of microscopic striking distance.
We shall now employ the ideas reached to shed some light upon another important relation between electrical and mechanical phenomena. We shall investigate what is the potential energy, or the store of work, contained in a charged conductor, for example, in a jar.
If we bring a quantity of electricity up to a conductor, or, to speak less pictorially, if we generate by work electrical force in a conductor, this force is able to produce anew the work by which it was generated. How great, now, is the energy or capacity for work of a conductor of known charge Q and known potential V?
Imagine the given charge Q divided into very small parts q, q1, q2 ..., and these little parts successively carried up to the conductor. The first very small quantity q is brought up without any appreciable work and produces by its presence a small potential V'. To bring up the second quantity, accordingly, we must do the work q'V', and similarly for the quantities which follow the work q''V'', q'''V''', and so forth. Now, as the potential rises proportionately to the quantities added until the value V is reached, we have, agreeably to the graphical representation of Fig. 38, for the total work performed,
W = 1/2QV,
which corresponds to the total energy of the charged conductor. Using the equation Q = CV, where C stands for capacity, we also have,
W = 1/2CV2, or W = Q2/2C.
It will be helpful, perhaps, to elucidate this idea by an analogy from the province of mechanics. If we pump a quantity of liquid, Q, gradually into a cylindrical vessel (Fig. 39), the level of the liquid in the vessel will gradually rise. The more we have pumped in, the greater the pressure we must overcome, or the higher the level to which we must lift the liquid. The stored-up work is rendered again available when the heavy liquid Q, which reaches up to the level h, flows out. This work W corresponds to the fall of the whole liquid weight Q, through the distance h/2 or through the altitude of its centre of gravity. We have
W = 1/2Qh.
Further, since Q = Kh, or since the weight of the liquid and the height h are proportional, we get also
W = 1/2Kh2 and W = Q2/2K.
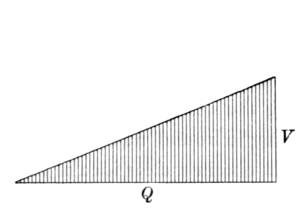 Fig. 38.
Fig. 38.
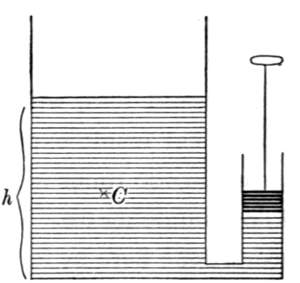 Fig. 39.
Fig. 39.
As a special case let us consider our jar. Its capacity is C = 3700, its potential V = 110; accordingly, its quantity Q = CV = 407,000 electrostatic units and its energy W = 1/2QV = 22,385,000 C. G. S. units of work.
The unit of work of the C. G. S. system is not readily appreciable by the senses, nor does it well admit of representation, as we are accustomed to work with weights. Let us adopt, therefore, as our unit of work the gramme-centimetre, or the gravitational pressure of a gramme-weight through the distance of a centimetre, which in round numbers is 1000 times greater than the unit assumed above; in this case, our numerical result will be approximately 1000 times smaller. Again, if we pass, as more familiar in practice, to the kilogramme-metre as our unit of work, our unit, the distance being increased a hundred fold, and the weight a thousand fold, will be 100,000 times larger. The numerical result expressing the work done is in this case 100,000 times less, being in round numbers 0.22 kilogramme-metre. We can obtain a clear idea of the work done here by letting a kilogramme-weight fall 22 centimetres.
This amount of work, accordingly, is performed on the charging of the jar, and on its discharge appears again, according to the circumstances, partly as sound, partly as a mechanical disruption of insulators, partly as light and heat, and so forth.
The large battery of the Prague physical laboratory, with its sixteen jars charged to equal potentials, furnishes, although the effect of the discharge is imposing, a total amount of work of only three kilogramme-metres.
In the development of the ideas above laid down we are not restricted to the method there pursued; in fact, that method was selected only as one especially fitted to familiarise us with the phenomena. On the contrary, the connexion of the physical processes is so multifarious that we can come at the same event from very different directions. Particularly are electrical phenomena connected with all other physical events; and so intimate is this connexion that we might justly call the study of electricity the theory of the general connexion of physical processes.
With respect to the principle of the conservation of energy which unites electrical with mechanical phenomena, I should like to point out briefly two ways of following up the study of this connexion.
A few years ago Professor Rosetti, taking an influence-machine, which he set in motion by means of weights alternately in the electrical and non-electrical condition with the same velocities, determined the mechanical work expended in the two cases and was thus enabled, after deducting the work of friction, to ascertain the mechanical work consumed in the development of the electricity.
I myself have made this experiment in a modified, and, as I think, more advantageous form. Instead of determining the work of friction by special trial, I arranged my apparatus so that it was eliminated of itself in the measurement and could consequently be neglected. The so-called fixed disk of the machine, the axis of which is placed vertically, is suspended somewhat like a chandelier by three vertical threads of equal lengths l at a distance r from the axis. Only when the machine is excited does this fixed disk, which represents a Prony's brake, receive, through its reciprocal action with the rotating disk, a deflexion α and a moment of torsion which is expressed by D = (Pr2/l)α, where P is the weight of the disk.[37] The angle α is determined by a mirror set in the disk. The work expended in n rotations is given by 2nπD.
If we close the machine, as Rosetti did, we obtain a continuous current which has all the properties of a very weak galvanic current; for example, it produces a deflexion in a multiplier which we interpose, and so forth. We can directly ascertain, now, the mechanical work expended in the maintenance of this current.
If we charge a jar by means of a machine, the energy of the jar employed in the production of sparks, in the disruption of the insulators, etc., corresponds to a part only of the mechanical work expended, a second part of it being consumed in the arc which forms the circuit.[38] This machine, with the interposed jar, affords in miniature a picture of the transference of force, or more properly of work. And in fact nearly the same laws hold here for the economical coefficient as obtain for large dynamo-machines.
Another means of investigating electrical energy is by its transformation into heat. A long time ago (1838), before the mechanical theory of heat had attained its present popularity, Riess performed experiments in this field with the help of his electrical air-thermometer or thermo-electrometer.
 Fig. 40.
Fig. 40.
If the discharge be conducted through a fine wire passing through the globe of the air-thermometer, a development of heat is observed proportional to the expression above-discussed W = 1/2QV. Although the total energy has not yet been transformed into measurable heat by this means, in as much as a portion is left behind in the spark in the air outside the thermometer, still everything tends to show that the total heat developed in all parts of the conductor and along all the paths of discharge is the equivalent of the work 1/2QV.
It is not important here whether the electrical energy is transformed all at once or partly, by degrees. For example, if of two equal jars one is charged with the quantity Q at the potential V the energy present is 1/2QV. If the first jar be discharged into the second, V, since the capacity is now doubled, falls to V/2. Accordingly, the energy 1/4QV remains, while 1/4QV is transformed in the spark of discharge into heat. The remainder, however, is equally distributed between the two jars so that each on discharge is still able to transform 1/8QV into heat.
We have here discussed electricity in the limited phenomenal form in which it was known to the inquirers before Volta, and which has been called, perhaps not very felicitously, "statical electricity." It is evident, however, that the nature of electricity is everywhere one and the same; that a substantial difference between statical and galvanic electricity does not exist. Only the quantitative circumstances in the two provinces are so widely different that totally new aspects of phenomena may appear in the second, for example, magnetic effects, which in the first remained unnoticed, whilst, vice versa, in the second field statical attractions and repulsions are scarcely appreciable. As a fact, we can easily show the magnetic effect of the current of discharge of an influence-machine on the galvanoscope although we could hardly have made the original discovery of the magnetic effects with this current. The statical distant action of the wire poles of a galvanic element also would hardly have been noticed had not the phenomenon been known from a different quarter in a striking form.
If we wished to characterise the two fields in their chief and most general features, we should say that in the first, high potentials and small quantities come into play, in the second small potentials and large quantities. A jar which is discharging and a galvanic element deport themselves somewhat like an air-gun and the bellows of an organ. The first gives forth suddenly under a very high pressure a small quantity of air; the latter liberates gradually under a very slight pressure a large quantity of air.
In point of principle, too, nothing prevents our retaining the electrostatical units in the domain of galvanic electricity and in measuring, for example, the strength of a current by the number of electrostatic units which flow per second through its cross-section. But this would be in a double aspect impractical. In the first place, we should totally neglect the magnetic facilities for measurement so conveniently offered by the current, and substitute for this easy means a method which can be applied only with difficulty and is not capable of great exactness. In the second place our units would be much too small, and we should find ourselves in the predicament of the astronomer who attempted to measure celestial distances in metres instead of in radii of the earth and the earth's orbit; for the current which by the magnetic C. G. S. standard represents the unit, would require a flow of some 30,000,000,000 electrostatic units per second through its cross-section. Accordingly, different units must be adopted here. The development of this point, however, lies beyond my present task.
In a popular lecture, distinguished for its charming simplicity and clearness, which Joule delivered in the year 1847,[40] that famous physicist declares that the living force which a heavy body has acquired by its descent through a certain height and which it carries with it in the form of the velocity with which it is impressed, is the equivalent of the attraction of gravity through the space fallen through, and that it would be "absurd" to assume that this living force could be destroyed without some restitution of that equivalent. He then adds: "You will therefore be surprised to hear that until very recently the universal opinion has been that living force could be absolutely and irrevocably destroyed at any one's option." Let us add that to-day, after forty-seven years, the law of the conservation of energy, wherever civilisation exists, is accepted as a fully established truth and receives the widest applications in all domains of natural science.
The fate of all momentous discoveries is similar. On their first appearance they are regarded by the majority of men as errors. J. R. Mayer's work on the principle of energy (1842) was rejected by the first physical journal of Germany; Helmholtz's treatise (1847) met with no better success; and even Joule, to judge from an intimation of Playfair, seems to have encountered difficulties with his first publication (1843). Gradually, however, people are led to see that the new view was long prepared for and ready for enunciation, only that a few favored minds had perceived it much earlier than the rest, and in this way the opposition of the majority is overcome. With proofs of the fruitfulness of the new view, with its success, confidence in it increases. The majority of the men who employ it cannot enter into a deep-going analysis of it; for them, its success is its proof. It can thus happen that a view which has led to the greatest discoveries, like Black's theory of caloric, in a subsequent period in a province where it does not apply may actually become an obstacle to progress by its blinding our eyes to facts which do not fit in with our favorite conceptions. If a theory is to be protected from this dubious rôle, the grounds and motives of its evolution and existence must be examined from time to time with the utmost care.
The most multifarious physical changes, thermal,[Pg 139] electrical, chemical, and so forth, can be brought about by mechanical work. When such alterations are reversed they yield anew the mechanical work in exactly the quantity which was required for the production of the part reversed. This is the principle of the conservation of energy; "energy" being the term which has gradually come into use for that "indestructible something" of which the measure is mechanical work.
How did we acquire this idea? What are the sources from which we have drawn it? This question is not only of interest in itself, but also for the important reason above touched upon. The opinions which are held concerning the foundations of the law of energy still diverge very widely from one another. Many trace the principle to the impossibility of a perpetual motion, which they regard either as sufficiently proved by experience, or as self-evident. In the province of pure mechanics the impossibility of a perpetual motion, or the continuous production of work without some permanent alteration, is easily demonstrated. Accordingly, if we start from the theory that all physical processes are purely mechanical processes, motions of molecules and atoms, we embrace also, by this mechanical conception of physics, the impossibility of a perpetual motion in the whole physical domain. At present this view probably counts the most adherents. Other inquirers, however, are for accepting only a purely experimental establishment of the law of energy.
It will appear, from the discussion to follow, that all the factors mentioned have co-operated in the development of the view in question; but that in addition to them a logical and purely formal factor, hitherto little considered, has also played a very important part.
The law of energy in its modern form is not identical with the principle of the excluded perpetual motion, but it is very closely related to it. The latter principle, however, is by no means new, for in the province of mechanics it has controlled for centuries the thoughts and investigations of the greatest thinkers. Let us convince ourselves of this by the study of a few historical examples.
 Fig. 41.
Fig. 41.
S. Stevinus, in his famous work Hypomnemata mathematica, Tom. IV, De statica, (Leyden, 1605, p. 34), treats of the equilibrium of bodies on inclined planes.
Over a triangular prism ABC, one side of which, AC, is horizontal, an endless cord or chain is slung, to which at equal distances apart fourteen balls of equal weight are attached, as represented in cross-section in Figure 41. Since we can imagine the lower[Pg 141] symmetrical part of the cord ABC taken away, Stevinus concludes that the four balls on AB hold in equilibrium the two balls on BC. For if the equilibrium were for a moment disturbed, it could never subsist: the cord would keep moving round forever in the same direction,—we should have a perpetual motion. He says:
"But if this took place, our row or ring of balls would come once more into their original position, and from the same cause the eight globes to the left would again be heavier than the six to the right, and therefore those eight would sink a second time and these six rise, and all the globes would keep up, of themselves, a continuous and unending motion, which is false."[41]
Stevinus, now, easily derives from this principle the laws of equilibrium on the inclined plane and numerous other fruitful consequences.
In the chapter "Hydrostatics" of the same work, page 114, Stevinus sets up the following principle: "Aquam datam, datum sibi intra aquam locum servare,"—a given mass of water preserves within water its given place.
 Fig. 42.
Fig. 42.
This principle is demonstrated as follows (see Fig. 42):
"For, assuming it to be possible by natural means, let us suppose that A does not preserve the place assigned to it, but sinks down to D. This being posited, the water which succeeds A will, for the same reason, also flow down to D; A will be forced out of its place in D; and thus this body of water, for the conditions in it are everywhere the same, will set up a perpetual motion, which is absurd."[42]
From this all the principles of hydrostatics are deduced. On this occasion Stevinus also first develops the thought so fruitful for modern analytical mechanics that the equilibrium of a system is not destroyed by the addition of rigid connexions. As we know, the principle of the conservation of the centre of gravity is now sometimes deduced from D'Alembert's principle with the help of that remark. If we were to reproduce Stevinus's demonstration to-day, we should have to change it slightly. We find no difficulty in imagining the cord on the prism possessed of unending uniform motion if all hindrances are thought away, but we should protest against the assumption of an accelerated motion or even against that of a uniform motion, if the resistances were not removed. Moreover, for greater precision of proof, the string of balls might be replaced by a heavy homogeneous cord of infinite flexibility. But all this does not affect in the least the historical value of Stevinus's thoughts. It is a fact, Stevinus deduces apparently much simpler truths from the principle of an impossible perpetual motion.
In the process of thought which conducted Galileo to his discoveries at the end of the sixteenth century, the following principle plays an important part, that a body in virtue of the velocity acquired in its descent can rise exactly as high as it fell. This principle, which appears frequently and with much clearness in Galileo's thought, is simply another form of the principle of excluded perpetual motion, as we shall see it is also in Huygens.
Galileo, as we know, arrived at the law of uniformly accelerated motion by a priori considerations, as that law which was the "simplest and most natural," after having first assumed a different law which he was compelled to reject. To verify his law he executed experiments with falling bodies on inclined planes, measuring the times of descent by the weights of the water which flowed out of a small orifice in a large vessel. In this experiment he assumes as a fundamental principle, that the velocity acquired in descent down an inclined plane always corresponds to the vertical height descended through, a conclusion which for him is the immediate outcome of the fact that a body which has fallen down one inclined plane can, with the velocity it has acquired, rise on another plane of any inclination only to the same vertical height. This principle of the height of ascent also led him, as it seems, to the law of inertia. Let us hear his own masterful words in the Dialogo terzo (Opere, Padova, 1744, Tom. III). On page 96 we read:
"I take it for granted that the velocities acquired by a body in descent down planes of different inclinations are equal if the heights of those planes are equal."[43]
Then he makes Salviati say in the dialogue:[44]
"What you say seems very probable, but I wish to go further and by an experiment so to increase the probability of it that it shall amount almost to absolute demonstration. Suppose this sheet of paper to be a vertical wall, and from a nail driven in it a ball of lead weighing two or three ounces to hang by a very fine thread AB four or five feet long. (Fig. 43.) On the wall mark a horizontal line DC perpendicular to the vertical AB, which latter ought to hang about two inches from the wall. If now the thread AB with the ball attached take the position AC and the ball be let go, you will see the ball first descend through the arc CB and passing beyond B rise through the arc BD almost to the level of the line CD, being prevented from reaching it exactly by the resistance of the air and of the thread. From this we may truly conclude that its impetus at the point B, acquired by its descent through the arc CB, is sufficient to urge it through a similar arc BD to the same height. Having performed this experiment and repeated it several times, let us drive in the wall, in the projection of the vertical AB, as at E or at F, a nail five or six inches long, so that the thread AC, carrying as before the ball through the arc CB, at the moment it reaches the position AB, shall strike the nail E, and the ball be thus compelled to move up the arc BG described about E as centre. Then we shall see what the same impetus will here accomplish, acquired now as before at the same point B, which then drove the same moving body through the arc BD to the height of the horizontal CD. Now gentlemen, you will be pleased to see the ball rise to the horizontal line at the point G, and the same thing also happen if the nail be placed lower as at F, in which case the ball would describe the arc BJ, always terminating its ascent precisely at the line CD. If the nail be placed so low that the length of thread below it does not reach to the height of CD (which would happen if F were nearer B than to the intersection of AB with the horizontal CD), then the thread will wind itself about the nail. This experiment leaves no room for doubt as to the truth of the supposition. For as the two arcs CB, DB are equal and similarly situated, the momentum acquired in the descent of the arc CB is the same as that acquired in the descent of the arc DB; but the momentum acquired at B by the descent through the arc CB is capable of driving up the same moving body through the arc BD; hence also the momentum acquired in the descent DB is equal to that which drives the same moving body through the same arc from B to D, so that in general every momentum acquired in the descent of an arc is equal to that which causes the same moving body to ascend through the same arc; but all the momenta which cause the ascent of all the arcs BD, BG, BJ, are equal since they are made by the same momentum acquired in the descent CB, as the experiment shows: therefore all the momenta acquired in the descent of the arcs DB, GB, JB are equal."
 Fig. 43.
Fig. 43.
The remark relative to the pendulum may be applied to the inclined plane and leads to the law of inertia. We read on page 124:[45]
"It is plain now that a movable body, starting from rest at A and descending down the inclined plane AB, acquires a velocity proportional to the increment of its time: the velocity possessed at B is the greatest of the velocities acquired, and by its nature immutably impressed, provided all causes of new acceleration or retardation are taken away: I say acceleration, having in view its possible further progress along the plane extended; retardation, in view of the possibility of its being reversed and made to mount the ascending plane BC. But in the horizontal plane GH its equable motion, according to its velocity as acquired in the descent from A to B, will be continued ad infinitum." (Fig. 44.)
 Fig. 44.
Fig. 44.
Huygens, upon whose shoulders the mantel of Galileo fell, forms a sharper conception of the law of inertia and generalises the principle respecting the heights of ascent which was so fruitful in Galileo's hands. He employs the latter principle in the solution of the problem of the centre of oscillation and is perfectly clear in the statement that the principle respecting the heights of ascent is identical with the principle of the excluded perpetual motion.
The following important passages then occur (Hugenii, Horologium oscillatorium, pars secunda). Hypotheses:
"If gravity did not exist, nor the atmosphere obstruct the motions of bodies, a body would keep up forever the motion once impressed upon it, with equable velocity, in a straight line."[46]
In part four of the Horologium de centro oscillationis we read:
"If any number of weights be set in motion by the force of gravity, the common centre of gravity of the weights as a whole cannot possibly rise higher than the place which it occupied when the motion began.
"That this hypothesis of ours may arouse no scruples, we will state that it simply imports, what no one has ever denied, that heavy bodies do not move upwards.—And truly if the devisers of the new machines who make such futile attempts to construct a perpetual motion would acquaint themselves with this principle, they could easily be brought to see their errors and to understand that the thing is utterly impossible by mechanical means."[47]
There is possibly a Jesuitical mental reservation contained in the words "mechanical means." One might be led to believe from them that Huygens held a non-mechanical perpetual motion for possible.
The generalisation of Galileo's principle is still more clearly put in Prop. IV of the same chapter:
"If a pendulum, composed of several weights, set in motion from rest, complete any part of its full oscillation, and from that point onwards, the individual weights, with their common connexions dissolved, change their acquired velocities upwards and ascend as far as they can, the common centre of gravity of all will be carried up to the same altitude with that which it occupied before the beginning of the oscillation."[48]
On this last principle now, which is a generalisation, applied to a system of masses, of one of Galileo's ideas respecting a single mass and which from Huygens's explanation we recognise as the principle of excluded perpetual motion, Huygens grounds his theory of the centre of oscillation. Lagrange characterises this principle as precarious and is rejoiced at James Bernoulli's successful attempt, in 1681, to reduce the theory of the centre of oscillation to the laws of the lever, which appeared to him clearer. All the great inquirers of the seventeenth and eighteenth centuries broke a lance on this problem, and it led ultimately, in conjunction with the principle of virtual velocities, to the principle enunciated by D'Alembert in 1743 in his Traité de dynamique, though previously employed in a somewhat different form by Euler and Hermann.
Furthermore, the Huygenian principle respecting the heights of ascent became the foundation of the "law of the conservation of living force," as that was enunciated by John and Daniel Bernoulli and employed[Pg 150] with such signal success by the latter in his Hydrodynamics. The theorems of the Bernoullis differ in form only from Lagrange's expression in the Analytical Mechanics.
The manner in which Torricelli reached his famous law of efflux for liquids leads again to our principle. Torricelli assumed that the liquid which flows out of the basal orifice of a vessel cannot by its velocity of efflux ascend to a greater height than its level in the vessel.
Let us next consider a point which belongs to pure mechanics, the history of the principle of virtual motions or virtual velocities. This principle was not first enunciated, as is usually stated, and as Lagrange also asserts, by Galileo, but earlier, by Stevinus. In his Trochleostatica of the above-cited work, page 72, he says:
"Observe that this axiom of statics holds good here:
"As the space of the body acting is to the space of the body acted upon, so is the power of the body acted upon to the power of the body acting."[49]
Galileo, as we know, recognised the truth of the principle in the consideration of the simple machines, and also deduced the laws of the equilibrium of liquids from it.
Torricelli carries the principle back to the properties of the centre of gravity. The condition controlling[Pg 151] equilibrium in a simple machine, in which power and load are represented by weights, is that the common centre of gravity of the weights shall not sink. Conversely, if the centre of gravity cannot sink equilibrium obtains, because heavy bodies of themselves do not move upwards. In this form the principle of virtual velocities is identical with Huygens's principle of the impossibility of a perpetual motion.
John Bernoulli, in 1717, first perceived the universal import of the principle of virtual movements for all systems; a discovery stated in a letter to Varignon. Finally, Lagrange gives a general demonstration of the principle and founds upon it his whole Analytical Mechanics. But this general demonstration is based after all upon Huygens and Torricelli's remarks. Lagrange, as is known, conceives simple pulleys arranged in the directions of the forces of the system, passes a cord through these pulleys, and appends to its free extremity a weight which is a common measure of all the forces of the system. With no difficulty, now, the number of elements of each pulley may be so chosen that the forces in question shall be replaced by them. It is then clear that if the weight at the extremity cannot sink, equilibrium subsists, because heavy bodies cannot of themselves move upwards. If we do not go so far, but wish to abide by Torricelli's idea, we may conceive every individual force of the system replaced by a special weight suspended from a cord passing over a pulley in the direction of the force and attached[Pg 152] at its point of application. Equilibrium subsists then when the common centre of gravity of all the weights together cannot sink. The fundamental supposition of this demonstration is plainly the impossibility of a perpetual motion.
Lagrange tried in every way to supply a proof free from extraneous elements and fully satisfactory, but without complete success. Nor were his successors more fortunate.
The whole of mechanics, thus, is based upon an idea, which, though unequivocal, is yet unwonted and not coequal with the other principles and axioms of mechanics. Every student of mechanics, at some stage of his progress, feels the uncomfortableness of this state of affairs; every one wishes it removed; but seldom is the difficulty stated in words. Accordingly, the zealous pupil of the science is highly rejoiced when he reads in a master like Poinsot (Théorie générale de l'équilibre et du mouvement des systèmes) the following passage, in which that author is giving his opinion of the Analytical Mechanics:
"In the meantime, because our attention in that work was first wholly engrossed with the consideration of its beautiful development of mechanics, which seemed to spring complete from a single formula, we naturally believed that the science was completed or that it only remained to seek the demonstration of the principle of virtual velocities. But that quest brought back all the difficulties that we had overcome by the principle itself. That law so general, wherein are mingled the vague and unfamiliar ideas of infinitely small movements and of perturbations of equilibrium, only grew[Pg 153] obscure upon examination; and the work of Lagrange supplying nothing clearer than the march of analysis, we saw plainly that the clouds had only appeared lifted from the course of mechanics because they had, so to speak, been gathered at the very origin of that science.
"At bottom, a general demonstration of the principle of virtual velocities would be equivalent to the establishment of the whole of mechanics upon a different basis: for the demonstration of a law which embraces a whole science is neither more nor less than the reduction of that science to another law just as general, but evident, or at least more simple than the first, and which, consequently, would render that useless."[50]
According to Poinsot, therefore, a proof of the principle of virtual movements is tantamount to a total rehabilitation of mechanics.
Another circumstance of discomfort to the mathematician is, that in the historical form in which mechanics at present exists, dynamics is founded on statics, whereas it is desirable that in a science which pretends to deductive completeness the more special statical theorems should be deducible from the more general dynamical principles.
In fact, a great master, Gauss, gave expression to this desire in his presentment of the principle of least constraint (Crelle's Journal für reine und angewandte Mathematik, Vol. IV, p. 233) in the following words: "Proper as it is that in the gradual development of a science, and in the instruction of individuals, the easy should precede the difficult, the simple the complex, the special the general, yet the mind, when once it has reached a higher point of view, demands the contrary course, in which all statics shall appear simply as a special case of mechanics." Gauss's own principle, now, possesses all the requisites of universality, but its difficulty is that it is not immediately intelligible and that Gauss deduced it with the help of D'Alembert's principle, a procedure which left matters where they were before.
Whence, now, is derived this strange part which the principle of virtual motion plays in mechanics? For the present I shall only make this reply. It would be difficult for me to tell the difference of impression which Lagrange's proof of the principle made on me when I first took it up as a student and when I subsequently resumed it after having made historical researches. It first appeared to me insipid, chiefly on account of the pulleys and the cords which did not fit in with the mathematical view, and whose action I would much rather have discovered from the principle[Pg 155] itself than have taken for granted. But now that I have studied the history of the science I cannot imagine a more beautiful demonstration.
In fact, through all mechanics it is this self-same principle of excluded perpetual motion which accomplishes almost all, which displeased Lagrange, but which he still had to employ, at least tacitly, in his own demonstration. If we give this principle its proper place and setting, the paradox is explained.
The principle of excluded perpetual motion is thus no new discovery; it has been the guiding idea, for three hundred years, of all the great inquirers. But the principle cannot properly be based upon mechanical perceptions. For long before the development of mechanics the conviction of its truth existed and even contributed to that development. Its power of conviction, therefore, must have more universal and deeper roots. We shall revert to this point.
It cannot be denied that an unmistakable tendency has prevailed, from Democritus to the present day, to explain all physical events mechanically. Not to mention earlier obscure expressions of that tendency we read in Huygens the following:[51]
"There can be no doubt that light consists of the motion of a certain substance. For if we examine its production, we find that here on earth it is principally fire and flame which engender it, both of which contain beyond doubt bodies which are in rapid movement, since they dissolve and destroy many other bodies more solid than they: while if we regard its effects, we see that when light is accumulated, say by concave mirrors, it has the property of combustion just as fire has, that is to say, it disunites the parts of bodies, which is assuredly a proof of motion, at least in the true philosophy, in which the causes of all natural effects are conceived as mechanical causes. Which in my judgment must be accomplished or all hope of ever understanding physics renounced."[52]
S. Carnot,[53] in introducing the principle of excluded perpetual motion into the theory of heat, makes the following apology:
"It will be objected here, perhaps, that a perpetual motion proved impossible for purely mechanical actions, is perhaps not so when the influence of heat or of electricity is employed. But can phenomena of heat or electricity be thought of as due to anything else than to certain motions of bodies, and as such must they not be subject to the general laws of mechanics?"[54]
These examples, which might be multiplied by quotations from recent literature indefinitely, show that a tendency to explain all things mechanically actually exists. This tendency is also intelligible. Mechanical events as simple motions in space and time best admit of observation and pursuit by the help of our highly organised senses. We reproduce mechanical processes almost without effort in our imagination. Pressure as a circumstance that produces motion is very familiar to us from daily experience. All changes which the individual personally produces in his environment, or humanity brings about by means of the arts in the world, are effected through the instrumentality of motions. Almost of necessity, therefore, motion appears to us as the most important physical factor. Moreover, mechanical properties may be discovered in all physical events. The sounding bell trembles, the heated body expands, the electrified body attracts other bodies. Why, therefore, should we not attempt to grasp all events under their mechanical aspect, since that is so easily apprehended and most accessible to observation and measurement? In fact, no objection is to be made to the attempt to elucidate the properties of physical events by mechanical analogies.
But modern physics has proceeded very far in this direction. The point of view which Wundt represents in his excellent treatise On the Physical Axioms is probably[Pg 158] shared by the majority of physicists. The axioms of physics which Wundt sets up are as follows:
1. All natural causes are motional causes.
2. Every motional cause lies outside the object moved.
3. All motional causes act in the direction of the straight line of junction, and so forth.
4. The effect of every cause persists.
5. Every effect involves an equal countereffect.
6. Every effect is equivalent to its cause.
These principles might be studied properly enough as fundamental principles of mechanics. But when they are set up as axioms of physics, their enunciation is simply tantamount to a negation of all events except motion.
According to Wundt, all changes of nature are mere changes of place. All causes are motional causes (page 26). Any discussion of the philosophical grounds on which Wundt supports his theory would lead us deep into the speculations of the Eleatics and the Herbartians. Change of place, Wundt holds, is the only change of a thing in which a thing remains identical with itself. If a thing changed qualitatively, we should be obliged to imagine that something was annihilated and something else created in its place, which is not to be reconciled with our idea of the identity of the object observed and of the indestructibility of matter. But we have only to remember that the Eleatics encountered difficulties of exactly the same sort[Pg 159] in motion. Can we not also imagine that a thing is destroyed in one place and in another an exactly similar thing created? After all, do we really know more why a body leaves one place and appears in another, than why a cold body grows warm? Granted that we had a perfect knowledge of the mechanical processes of nature, could we and should we, for that reason, put out of the world all other processes that we do not understand? On this principle it would really be the simplest course to deny the existence of the whole world. This is the point at which the Eleatics ultimately arrived, and the school of Herbart stopped little short of the same goal.
Physics treated in this sense supplies us simply with a diagram of the world, in which we do not know reality again. It happens, in fact, to men who give themselves up to this view for many years, that the world of sense from which they start as a province of the greatest familiarity, suddenly becomes, in their eyes, the supreme "world-riddle."
Intelligible as it is, therefore, that the efforts of thinkers have always been bent upon the "reduction of all physical processes to the motions of atoms," it must yet be affirmed that this is a chimerical ideal. This ideal has often played an effective part in popular lectures, but in the workshop of the serious inquirer it has discharged scarcely the least function. What has really been achieved in mechanical physics is either the elucidation of physical processes by more[Pg 160] familiar mechanical analogies, (for example, the theories of light and of electricity,) or the exact quantitative ascertainment of the connexion of mechanical processes with other physical processes, for example, the results of thermodynamics.
We can know only from experience that mechanical processes produce other physical transformations, or vice versa. The attention was first directed to the connexion of mechanical processes, especially the performance of work, with changes of thermal conditions by the invention of the steam-engine, and by its great technical importance. Technical interests and the need of scientific lucidity meeting in the mind of S. Carnot led to the remarkable development from which thermodynamics flowed. It is simply an accident of history that the development in question was not connected with the practical applications of electricity.
In the determination of the maximum quantity of work that, generally, a heat-machine, or, to take a special case, a steam-engine, can perform with the expenditure of a given amount of heat of combustion, Carnot is guided by mechanical analogies. A body can do work on being heated, by expanding under pressure. But to do this the body must receive heat from a hotter body. Heat, therefore, to do work, must pass from a hotter body to a colder body, just as water must fall from a higher level to a lower level to put a mill-wheel[Pg 161] in motion. Differences of temperature, accordingly, represent forces able to do work exactly as do differences of height in heavy bodies. Carnot pictures to himself an ideal process in which no heat flows away unused, that is, without doing work. With a given expenditure of heat, accordingly, this process furnishes the maximum of work. An analogue of the process would be a mill-wheel which scooping its water out of a higher level would slowly carry it to a lower level without the loss of a drop. A peculiar property of the process is, that with the expenditure of the same work the water can be raised again exactly to its original level. This property of reversibility is also shared by the process of Carnot. His process also can be reversed by the expenditure of the same amount of work, and the heat again brought back to its original temperature level.
Suppose, now, we had two different reversible processes A, B, such that in A a quantity of heat, Q, flowing off from the temperature t1 to the lower temperature t2 should perform the work W, but in B under the same circumstances it should perform a greater quantity of work W + W'; then, we could join B in the sense assigned and A in the reverse sense into a single process. Here A would reverse the transformation of heat produced by B and would leave a surplus of work W', produced, so to speak, from nothing. The combination would present a perpetual motion.
With the feeling, now, that it makes little difference[Pg 162] whether the mechanical laws are broken directly or indirectly (by processes of heat), and convinced of the existence of a universal law-ruled connexion of nature, Carnot here excludes for the first time from the province of general physics the possibility of a perpetual motion. But it follows, then, that the quantity of work W, produced by the passage of a quantity of heat Q from a temperature t1 to a temperature t2, is independent of the nature of the substances as also of the character of the process, so far as that is unaccompanied by loss, but is wholly dependent upon the temperature t1, t2.
This important principle has been fully confirmed by the special researches of Carnot himself (1824), of Clapeyron (1834), and of Sir William Thomson (1849), now Lord Kelvin. The principle was reached without any assumption whatever concerning the nature of heat, simply by the exclusion of a perpetual motion. Carnot, it is true, was an adherent of the theory of Black, according to which the sum-total of the quantity of heat in the world is constant, but so far as his investigations have been hitherto considered the decision on this point is of no consequence. Carnot's principle led to the most remarkable results. W. Thomson (1848) founded upon it the ingenious idea of an "absolute" scale of temperature. James Thomson (1849) conceived a Carnot process to take place with water freezing under pressure and, therefore, performing work. He discovered, thus, that the freezing point is lowered 0·0075° Celsius by every additional atmosphere[Pg 163] of pressure. This is mentioned merely as an example.
About twenty years after the publication of Carnot's book a further advance was made by J. R. Mayer and J. P. Joule. Mayer, while engaged as a physician in the service of the Dutch, observed, during a process of bleeding in Java, an unusual redness of the venous blood. In agreement with Liebig's theory of animal heat he connected this fact with the diminished loss of heat in warmer climates, and with the diminished expenditure of organic combustibles. The total expenditure of heat of a man at rest must be equal to the total heat of combustion. But since all organic actions, even the mechanical actions, must be set down to the credit of the heat of combustion, some connexion must exist between mechanical work and expenditure of heat.
Joule started from quite similar convictions concerning the galvanic battery. A heat of association equivalent to the consumption of the zinc can be made to appear in the galvanic cell. If a current is set up, a part of this heat appears in the conductor of the current. The interposition of an apparatus for the decomposition of water causes a part of this heat to disappear, which on the burning of the explosive gas formed, is reproduced. If the current runs an electromotor, a portion of the heat again disappears, which, on the consumption of the work by friction, again makes its appearance. Accordingly, both the heat[Pg 164] produced and the work produced, appeared to Joule also as connected with the consumption of material. The thought was therefore present, both to Mayer and to Joule, of regarding heat and work as equivalent quantities, so connected with each other that what is lost in one form universally appears in another. The result of this was a substantial conception of heat and of work, and ultimately a substantial conception of energy. Here every physical change of condition is regarded as energy, the destruction of which generates work or equivalent heat. An electric charge, for example, is energy.
In 1842 Mayer had calculated from the physical constants then universally accepted that by the disappearance of one kilogramme-calorie 365 kilogramme-metres of work could be performed, and vice versa. Joule, on the other hand, by a long series of delicate and varied experiments beginning in 1843 ultimately determined the mechanical equivalent of the kilogramme-calorie, more exactly, as 425 kilogramme-metres.
If we estimate every change of physical condition by the mechanical work which can be performed upon the disappearance of that condition, and call this measure energy, then we can measure all physical changes of condition, no matter how different they may be, with the same common measure, and say: the sum-total of all energy remains constant. This is the form that the principle of excluded perpetual motion received at[Pg 165] the hands of Mayer, Joule, Helmholtz, and W. Thomson in its extension to the whole domain of physics.
After it had been proved that heat must disappear if mechanical work was to be done at its expense, Carnot's principle could no longer be regarded as a complete expression of the facts. Its improved form was first given, in 1850, by Clausius, whom Thomson followed in 1851. It runs thus: "If a quantity of heat Q' is transformed into work in a reversible process, another quantity of heat Q of the absolute[55] temperature T1 is lowered to the absolute temperature T2." Here Q' is dependent only on Q, T1, T2, but is independent of the substances used and of the character of the process, so far as that is unaccompanied by loss. Owing to this last fact, it is sufficient to find the relation which obtains for some one well-known physical substance, say a gas, and some definite simple process. The relation found will be the one that holds generally. We get, thus,
Q'/(Q' + Q) = (T1-T2)/T1 (1)
that is, the quotient of the available heat Q' transformed into work divided by the sum of the transformed and transferred heats (the total sum used), the so-called economical coefficient of the process, is,
(T1-T2)/T1.
When a cold body is put in contact with a warm body it is observed that the first body is warmed and that the second body is cooled. We may say that the first body is warmed at the expense of the second body. This suggests the notion of a thing, or heat-substance, which passes from the one body to the other. If two masses of water m, m', of unequal temperatures, be put together, it will be found, upon the rapid equalisation of the temperatures, that the respective changes of temperatures u and u' are inversely proportional to the masses and of opposite signs, so that the algebraical sum of the products is,
mu + m'u' = 0.
Black called the products mu, m'u', which are decisive for our knowledge of the process, quantities of heat. We may form a very clear picture of these products by conceiving them with Black as measures of the quantities of some substance. But the essential thing is not this picture but the constancy of the sum of these products in simple processes of conduction. If a quantity of heat disappears at one point, an equally large quantity will make its appearance at some other point. The retention of this idea leads to the discovery of specific heat. Black, finally, perceives that also something else may appear for a vanished quantity of heat, namely: the fusion or vaporisation of a definite quantity[Pg 167] of matter. He adheres here still to this favorite view, though with some freedom, and considers the vanished quantity of heat as still present, but as latent.
The generally accepted notion of a caloric, or heat-stuff, was strongly shaken by the work of Mayer and Joule. If the quantity of heat can be increased and diminished, people said, heat cannot be a substance, but must be a motion. The subordinate part of this statement has become much more popular than all the rest of the doctrine of energy. But we may convince ourselves that the motional conception of heat is now as unessential as was formerly its conception as a substance. Both ideas were favored or impeded solely by accidental historical circumstances. It does not follow that heat is not a substance from the fact that a mechanical equivalent exists for quantity of heat. We will make this clear by the following question which bright students have sometimes put to me. Is there a mechanical equivalent of electricity as there is a mechanical equivalent of heat? Yes, and no. There is no mechanical equivalent of quantity of electricity as there is an equivalent of quantity of heat, because the same quantity of electricity has a very different capacity for work, according to the circumstances in which it is placed; but there is a mechanical equivalent of electrical energy.
Let us ask another question. Is there a mechanical equivalent of water? No, there is no mechanical equivalent of quantity of water, but there is a mechanical[Pg 168] equivalent of weight of water multiplied by its distance of descent.
When a Leyden jar is discharged and work thereby performed, we do not picture to ourselves that the quantity of electricity disappears as work is done, but we simply assume that the electricities come into different positions, equal quantities of positive and negative electricity being united with one another.
What, now, is the reason of this difference of view in our treatment of heat and of electricity? The reason is purely historical, wholly conventional, and, what is still more important, is wholly indifferent. I may be allowed to establish this assertion.
In 1785 Coulomb constructed his torsion balance, by which he was enabled to measure the repulsion of electrified bodies. Suppose we have two small balls, A, B, which over their whole extent are similarly electrified. These two balls will exert on one another, at a certain distance r of their centres, a certain repulsion p. We bring into contact with B now a ball C, suffer both to be equally electrified, and then measure the repulsion of B from A and of C from A at the same distance r. The sum of these repulsions is again p. Accordingly something has remained constant. If we ascribe this effect to a substance, then we infer naturally its constancy. But the essential point of the exposition is the divisibility of the electric force p and not the simile of substance.
In 1838 Riess constructed his electrical air-thermometer[Pg 169] (the thermoelectrometer). This gives a measure of the quantity of heat produced by the discharge of jars. This quantity of heat is not proportional to the quantity of electricity contained in the jar by Coulomb's measure, but if Q be this quantity and C be the capacity, is proportional to Q2/2C, or, more simply still, to the energy of the charged jar. If, now, we discharge the jar completely through the thermometer, we obtain a certain quantity of heat, W. But if we make the discharge through the thermometer into a second jar, we obtain a quantity less than W. But we may obtain the remainder by completely discharging both jars through the air-thermometer, when it will again be proportional to the energy of the two jars. On the first, incomplete discharge, accordingly, a part of the electricity's capacity for work was lost.
When the charge of a jar produces heat its energy is changed and its value by Riess's thermometer is decreased. But by Coulomb's measure the quantity remains unaltered.
Now let us imagine that Riess's thermometer had been invented before Coulomb's torsion balance, which is not a difficult feat, since both inventions are independent of each other; what would be more natural than that the "quantity" of electricity contained in a jar should be measured by the heat produced in the thermometer? But then, this so-called quantity of electricity would decrease on the production of heat or on the performance of work, whereas it now remains unchanged;[Pg 170] in that case, therefore, electricity would not be a substance but a motion, whereas now it is still a substance. The reason, therefore, why we have other notions of electricity than we have of heat, is purely historical, accidental, and conventional.
This is also the case with other physical things. Water does not disappear when work is done. Why? Because we measure quantity of water with scales, just as we do electricity. But suppose the capacity of water for work were called quantity, and had to be measured, therefore, by a mill instead of by scales; then this quantity also would disappear as it performed the work. It may, now, be easily conceived that many substances are not so easily got at as water. In that case we should be unable to carry out the one kind of measurement with the scales whilst many other modes of measurement would still be left us.
In the case of heat, now, the historically established measure of "quantity" is accidentally the work-value of the heat. Accordingly, its quantity disappears when work is done. But that heat is not a substance follows from this as little as does the opposite conclusion that it is a substance. In Black's case the quantity of heat remains constant because the heat passes into no other form of energy.
If any one to-day should still wish to think of heat as a substance, we might allow that person this liberty with little ado. He would only have to assume that that which we call quantity of heat was the energy of[Pg 171] a substance whose quantity remained unaltered, but whose energy changed. In point of fact we might much better say, in analogy with the other terms of physics, energy of heat, instead of quantity of heat.
When we wonder, therefore, at the discovery that heat is motion, we wonder at something that was never discovered. It is perfectly indifferent and possesses not the slightest scientific value, whether we think of heat as a substance or not. The fact is, heat behaves in some connexions like a substance, in others not. Heat is latent in steam as oxygen is latent in water.
The foregoing reflexions will gain in lucidity from a consideration of the conformity which obtains in the behavior of all energies, a point to which I called attention long ago.[56]
A weight P at a height H1 represents an energy W1 = PH1. If we suffer the weight to sink to a lower height H2, during which work is done, and the work done is employed in the production of living force, heat, or an electric charge, in short, is transformed, then the energy W2 = PH2 is still left. The equation subsists
W1/H1 = W2/H2, (2) or, denoting the transformed energy by W' = W1-W2 and the transferred energy, that transported to the lower level, by W = W2,
W'/(W' + W) = (H1-H2)/H1, (3)
an equation in all respects analogous to equation (1) at page 165. The property in question, therefore, is by no means peculiar to heat. Equation (2) gives the relation between the energy taken from the higher level and that deposited on the lower level (the energy left behind); it says that these energies are proportional to the heights of the levels. An equation analogous to equation (2) may be set up for every form of energy; hence the equation which corresponds to equation (3), and so to equation (1), may be regarded as valid for every form. For electricity, for example, H1, H2 signify the potentials.
When we observe for the first time the agreement here indicated in the transformative law of the energies, it appears surprising and unexpected, for we do not perceive at once its reason. But to him who pursues the comparative historical method that reason will not long remain a secret.
Since Galileo, mechanical work, though long under a different name, has been a fundamental concept of mechanics, as also a very important notion in the applied sciences. The transformation of work into living[Pg 173] force, and of living force into work, suggests directly the notion of energy—the idea having been first fruitfully employed by Huygens, although Thomas Young first called it by the name of "energy." Let us add to this the constancy of weight (really the constancy of mass) and we shall see that with respect to mechanical energy it is involved in the very definition of the term that the capacity for work or the potential energy of a weight is proportional to the height of the level at which it is, in the geometrical sense, and that it decreases on the lowering of the weight, on transformation, proportionally to the height of the level. The zero level here is wholly arbitrary. With this, equation (2) is given, from which all the other forms follow.
When we reflect on the tremendous start which mechanics had over the other branches of physics, it is not to be wondered at that the attempt was always made to apply the notions of that science wherever this was possible. Thus the notion of mass, for example, was imitated by Coulomb in the notion of quantity of electricity. In the further development of the theory of electricity, the notion of work was likewise immediately introduced in the theory of potential, and heights of electrical level were measured by the work of unit of quantity raised to that level. But with this the preceding equation with all its consequences is given for electrical energy. The case with the other energies was similar.
Thermal energy, however, appears as a special case. Only by the peculiar experiments mentioned could it be discovered that heat is an energy. But the measure of this energy by Black's quantity of heat is the outcome of fortuitous circumstances. In the first place, the accidental slight variability of the capacity for heat c with the temperature, and the accidental slight deviation of the usual thermometrical scales from the scale derived from the tensions of gases, brings it about that the notion "quantity of heat" can be set up and that the quantity of heat ct corresponding to a difference of temperature t is nearly proportional to the energy of the heat. It is a quite accidental historical circumstance that Amontons hit upon the idea of measuring temperature by the tension of a gas. It is certain in this that he did not think of the work of the heat.[57] But the numbers standing for temperature, thus, are made proportional to the tensions of gases, that is, to the work done by gases, with otherwise equal changes of volume. It thus happens that temperature heights and level heights of work are proportional to one another.
If properties of the thermal condition varying greatly from the tensions of gases had been chosen, this relation would have assumed very complicated forms, and the agreement between heat and the other energies above considered would not subsist. It is[Pg 175] very instructive to reflect upon this point. A natural law, therefore, is not implied in the conformity of the behavior of the energies, but this conformity is rather conditioned by the uniformity of our modes of conception and is also partly a matter of good fortune.
Of every quantity of heat Q which does work in a reversible process (one unaccompanied by loss) between the absolute temperatures T1, T2, only the portion
(T1-T2)/T1
is transformed into work, while the remainder is transferred to the lower temperature-level T2. This transferred portion can, upon the reversal of the process, with the same expenditure of work, again be brought back to the level T1. But if the process is not reversible, then more heat than in the foregoing case flows to the lower level, and the surplus can no longer be brought back to the higher level T2 without some special expenditure. W. Thomson (1852), accordingly, drew attention to the fact, that in all non-reversible, that is, in all real thermal processes, quantities of heat are lost for mechanical work, and that accordingly a dissipation or waste of mechanical energy is taking place. In all cases, heat is only partially transformed into work, but frequently work is wholly transformed[Pg 176] into heat. Hence, a tendency exists towards a diminution of the mechanical energy and towards an increase of the thermal energy of the world.
For a simple, closed cyclical process, accompanied by no loss, in which the quantity of heat Q_{1} is taken from the level T_{1}, and the quantity Q_{2} is deposited upon the level T_{2}, the following relation, agreeably to equation (2), exists,
-(Q1/T1) + (Q2/T2) = 0.
Similarly, for any number of compound reversible cycles Clausius finds the algebraical sum
ΣQ/T = 0,
and supposing the temperature to change continuously,
∫dQ/T = 0 (4)
Here the elements of the quantities of heat deducted from a given level are reckoned negative, and the elements imparted to it, positive. If the process is not reversible, then expression (4), which Clausius calls entropy, increases. In actual practice this is always the case, and Clausius finds himself led to the statement:
1. That the energy of the world remains constant.
2. That the entropy of the world tends toward a maximum.
Once we have noted the above-indicated conformity in the behavior of different energies, the peculiarity[Pg 177] of thermal energy here mentioned must strike us. Whence is this peculiarity derived, for, generally every energy passes only partly into another form, which is also true of thermal energy? The explanation will be found in the following.
Every transformation of a special kind of energy A is accompanied with a fall of potential of that particular kind of energy, including heat. But whilst for the other kinds of energy a transformation and therefore a loss of energy on the part of the kind sinking in potential is connected with the fall of the potential, with heat the case is different. Heat can suffer a fall of potential without sustaining a loss of energy, at least according to the customary mode of estimation. If a weight sinks, it must create perforce kinetic energy, or heat, or some other form of energy. Also, an electrical charge cannot suffer a fall of potential without loss of energy, i. e., without transformation. But heat can pass with a fall of temperature to a body of greater capacity and the same thermal energy still be preserved, so long as we regard every quantity of heat as energy. This it is that gives to heat, besides its property of energy, in many cases the character of a material substance, or quantity.
If we look at the matter in an unprejudiced light, we must ask if there is any scientific sense or purpose in still considering as energy a quantity of heat that can no longer be transformed into mechanical work, (for example, the heat of a closed equably warmed[Pg 178] material system). The principle of energy certainly plays in this case a wholly superfluous rôle, which is assigned to it only from habit.[58] To maintain the principle of energy in the face of a knowledge of the dissipation or waste of mechanical energy, in the face of the increase of entropy is equivalent almost to the liberty which Black took when he regarded the heat of liquefaction as still present but latent.[59] It is to be remarked further, that the expressions "energy of the world" and "entropy of the world" are slightly permeated with scholasticism. Energy and entropy are metrical notions. What meaning can there be in applying these notions to a case in which they are not applicable, in which their values are not determinable?
If we could really determine the entropy of the world it would represent a true, absolute measure of time. In this way is best seen the utter tautology of a statement that the entropy of the world increases with the time. Time, and the fact that certain changes take place only in a definite sense, are one and the same thing.
We are now prepared to answer the question, What are the sources of the principle of energy? All knowledge of nature is derived in the last instance from experience. In this sense they are right who look upon the principle of energy as a result of experience.
Experience teaches that the sense-elements αβγδ... into which the world may be decomposed, are subject to change. It tells us further, that certain of these elements are connected with other elements, so that they appear and disappear together; or, that the appearance of the elements of one class is connected with the disappearance of the elements of the other class. We will avoid here the notions of cause and effect because of their obscurity and equivocalness. The result of experience may be expressed as follows: The sensuous elements of the world (αβγδ...) show themselves to be interdependent. This interdependence is best represented by some such conception as is in geometry that of the mutual dependence of the sides and angles of a triangle, only much more varied and complex.
As an example, we may take a mass of gas enclosed in a cylinder and possessed of a definite volume (α), which we change by a pressure (β) on the piston, at the same time feeling the cylinder with our hand and[Pg 180] receiving a sensation of heat (γ). Increase of pressure diminishes the volume and increases the sensation of heat.
The various facts of experience are not in all respects alike. Their common sensuous elements are placed in relief by a process of abstraction and thus impressed upon the memory. In this way the expression is obtained of the features of agreement of extensive groups of facts. The simplest sentence which we can utter is, by the very nature of language, an abstraction of this kind. But account must also be taken of the differences of related facts. Facts may be so nearly related as to contain the same kind of a αβγ..., but the relation be such that the αβγ... of the one differ from the αβγ... of the other only by the number of equal parts into which they can be divided. Such being the case, if rules can be given for deducing from one another the numbers which are the measures of these αβγ..., then we possess in such rules the most general expression of a group of facts, as also that expression which corresponds to all its differences. This is the goal of quantitative investigation.
If this goal be reached what we have found is that between the αβγ... of a group of facts, or better, between the numbers which are their measures, a number of equations exists. The simple fact of change brings it about that the number of these equations must be smaller than the number of the αβγ.... If the former be smaller by one than the latter, then one[Pg 181] portion of the αβγ... is uniquely determined by the other portion.
The quest of relations of this last kind is the most important function of special experimental research, because we are enabled by it to complete in thought facts that are only partly given. It is self-evident that only experience can ascertain that between the αβγ... relations exist and of what kind they are. Further, only experience can tell that the relations that exist between the αβγ... are such that changes of them can be reversed. If this were not the fact all occasion for the enunciation of the principle of energy, as is easily seen, would be wanting. In experience, therefore, is buried the ultimate well-spring of all knowledge of nature, and consequently, in this sense, also the ultimate source of the principle of energy.
But this does not exclude the fact that the principle of energy has also a logical root, as will now be shown. Let us assume on the basis of experience that one group of sensuous elements αβγ... determines uniquely another group λμν.... Experience further teaches that changes of αβγ... can be reversed. It is then a logical consequence of this observation, that every time that αβγ... assume the same values this is also the case with λμν.... Or, that purely periodical changes of αβγ... can produce no permanent changes of λμν.... If the group λμν... is a mechanical group, then a perpetual motion is excluded.
It will be said that this is a vicious circle, which we will grant. But psychologically, the situation is essentially different, whether I think simply of the unique determination and reversibility of events, or whether I exclude a perpetual motion. The attention takes in the two cases different directions and diffuses light over different sides of the question, which logically of course are necessarily connected.
Surely that firm, logical setting of the thoughts noticeable in the great inquirers, Stevinus, Galileo, and the rest, which, consciously or instinctively, was supported by a fine feeling for the slightest contradictions, has no other purpose than to limit the bounds of thought and so exempt it from the possibility of error. In this, therefore, the logical root of the principle of excluded perpetual motion is given, namely, in that universal conviction which existed even before the development of mechanics and co-operated in that development.
It is perfectly natural that the principle of excluded perpetual motion should have been first developed in the simple domain of pure mechanics. Towards the transference of that principle into the domain of general physics the idea contributed much that all physical phenomena are mechanical phenomena. But the foregoing discussion shows how little essential this notion is. The issue really involved is the recognition of a general interconnexion of nature. This once established, we see with Carnot that it is indifferent[Pg 183] whether the mechanical laws are broken directly or circuitously.
The principle of the excluded perpetual motion is very closely related to the modern principle of energy, but it is not identical with it, for the latter is to be deduced from the former only by means of a definite formal conception. As may be seen from the preceding exposition, the perpetual motion can be excluded without our employing or possessing the notion of work. The modern principle of energy results primarily from a substantial conception of work and of every change of physical condition which by being reversed produces work. The strong need of such a conception, which is by no means necessary, but in a formal sense is very convenient and lucid, is exhibited in the case of J. R. Mayer and Joule. It was before remarked that this conception was suggested to both inquirers by the observation that both the production of heat and the production of mechanical work were connected with an expenditure of substance. Mayer says: "Ex nihilo nil fit," and in another place, "The creation or destruction of a force (work) lies without the province of human activity." In Joule we find this passage: "It is manifestly absurd to suppose that the powers with which God has endowed matter can be destroyed."
Some writers have observed in such statements the attempt at a metaphysical establishment of the doctrine of energy. But we see in them simply the formal need of a simple, clear, and living grasp of the facts, which[Pg 184] receives its development in practical and technical life, and which we carry over, as best we can, into the province of science. As a fact, Mayer writes to Griesinger: "If, finally, you ask me how I became involved in the whole affair, my answer is simply this: Engaged during a sea voyage almost exclusively with the study of physiology, I discovered the new theory for the sufficient reason that I vividly felt the need of it."
The substantial conception of work (energy) is by no means a necessary one. And it is far from true that the problem is solved with the recognition of the need of such a conception. Rather let us see how Mayer gradually endeavored to satisfy that need. He first regards quantity of motion, or momentum, mv, as the equivalent of work, and did not light, until later, on the notion of living force (mv2/2). In the province of electricity he was unable to assign the expression which is the equivalent of work. This was done later by Helmholtz. The formal need, therefore, is first present, and our conception of nature is subsequently gradually adapted to it.
The laying bare of the experimental, logical, and formal root of the present principle of energy will perhaps contribute much to the removal of the mysticism which still clings to this principle. With respect to our formal need of a very simple, palpable, substantial conception of the processes in our environment, it remains an open question how far nature corresponds to that need, or how far we can satisfy it. In one[Pg 185] phase of the preceding discussions it would seem as if the substantial notion of the principle of energy, like Black's material conception of heat, has its natural limits in facts, beyond which it can only be artificially adhered to.
When the human mind, with its limited powers, attempts to mirror in itself the rich life of the world, of which it is itself only a small part, and which it can never hope to exhaust, it has every reason for proceeding economically. Hence that tendency, expressed in the philosophy of all times, to compass by a few organic thoughts the fundamental features of reality. "Life understands not death, nor death life." So spake an old Chinese philosopher. Yet in his unceasing desire to diminish the boundaries of the incomprehensible, man has always been engaged in attempts to understand death by life and life by death.
Among the ancient civilised peoples, nature was filled with demons and spirits having the feelings and desires of men. In all essential features, this animistic view of nature, as Tylor[61] has aptly termed it, is shared in common by the fetish-worshipper of modern Africa and the most advanced nations of antiquity. As a theory of the world it has never completely disappeared. The monotheism of the Christians never fully overcame it, no more than did that of the Jews. In the belief in witchcraft and in the superstitions of the sixteenth and seventeenth centuries, the centuries of the rise of natural science, it assumed frightful pathological dimensions. Whilst Stevinus, Kepler, and Galileo were slowly rearing the fabric of modern physical science, a cruel and relentless war was waged with firebrand and rack against the devils that glowered from every corner. To-day even, apart from all survivals of that period, apart from the traces of fetishism which still inhere in our physical concepts,[62] those very ideas still covertly lurk in the practices of modern spiritualism.
By the side of this animistic conception of the world, we meet from time to time, in different forms, from Democritus to the present day, another view, which likewise claims exclusive competency to comprehend the universe. This view may be characterised as the physico-mechanical view of the world. To-day, that view holds, indisputably, the first place in the thoughts of men, and determines the ideals and the character of our times. The coming of the mind of man into the full consciousness of its powers, in the eighteenth century, was a period of genuine disillusionment. It produced the splendid precedent of a life[Pg 188] really worthy of man, competent to overcome the old barbarism in the practical fields of life; it created the Critique of Pure Reason, which banished into the realm of shadows the sham-ideas of the old metaphysics; it pressed into the hands of the mechanical philosophy the reins which it now holds.
The oft-quoted words of the great Laplace,[63] which I will now give, have the ring of a jubilant toast to the scientific achievements of the eighteenth century: "A mind to which were given for a single instant all the forces of nature and the mutual positions of all its masses, if it were otherwise powerful enough to subject these problems to analysis, could grasp, with a single formula, the motions of the largest masses as well as of the smallest atoms; nothing would be uncertain for it; the future and the past would lie revealed before its eyes." In writing these words, Laplace, as we know, had also in mind the atoms of the brain. That idea has been expressed more forcibly still by some of his followers, and it is not too much to say that Laplace's ideal is substantially that of the great majority of modern scientists.
Gladly do we accord to the creator of the Mécanique céleste the sense of lofty pleasure awakened in him by the great success of the Enlightenment, to which we too owe our intellectual freedom. But to-day, with minds undisturbed and before new tasks, it[Pg 189] becomes physical science to secure itself against self-deception by a careful study of its character, so that it can pursue with greater sureness its true objects. If I step, therefore, beyond the narrow precincts of my specialty in this discussion, to trespass on friendly neighboring domains, I may plead in my excuse that the subject-matter of knowledge is common to all domains of research, and that fixed, sharp lines of demarcation cannot be drawn.
The belief in occult magic powers of nature has gradually died away, but in its place a new belief has arisen, the belief in the magical power of science. Science throws her treasures, not like a capricious fairy into the laps of a favored few, but into the laps of all humanity, with a lavish extravagance that no legend ever dreamt of! Not without apparent justice, therefore, do her distant admirers impute to her the power of opening up unfathomable abysses of nature, to which the senses cannot penetrate. Yet she who came to bring light into the world, can well dispense with the darkness of mystery, and with pompous show, which she needs neither for the justification of her aims nor for the adornment of her plain achievements.
The homely beginnings of science will best reveal to us its simple, unchangeable character. Man acquires his first knowledge of nature half-consciously and automatically, from an instinctive habit of mimicking and forecasting facts in thought, of supplementing sluggish experience with the swift wings of thought,[Pg 190] at first only for his material welfare. When he hears a noise in the underbrush he constructs there, just as the animal does, the enemy which he fears; when he sees a certain rind he forms mentally the image of the fruit which he is in search of; just as we mentally associate a certain kind of matter with a certain line in the spectrum or an electric spark with the friction of a piece of glass. A knowledge of causality in this form certainly reaches far below the level of Schopenhauer's pet dog, to whom it was ascribed. It probably exists in the whole animal world, and confirms that great thinker's statement regarding the will which created the intellect for its purposes. These primitive psychical functions are rooted in the economy of our organism not less firmly than are motion and digestion. Who would deny that we feel in them, too, the elemental power of a long practised logical and physiological activity, bequeathed to us as an heirloom from our forefathers?
Such primitive acts of knowledge constitute to-day the solidest foundation of scientific thought. Our instinctive knowledge, as we shall briefly call it, by virtue of the conviction that we have consciously and intentionally contributed nothing to its formation, confronts us with an authority and logical power which consciously acquired knowledge even from familiar sources and of easily tested fallibility can never possess. All so-called axioms are such instinctive knowledge. Not consciously gained knowledge alone, but powerful[Pg 191] intellectual instinct, joined with vast conceptive powers, constitute the great inquirer. The greatest advances of science have always consisted in some successful formulation, in clear, abstract, and communicable terms, of what was instinctively known long before, and of thus making it the permanent property of humanity. By Newton's principle of the equality of pressure and counterpressure, whose truth all before him had felt, but which no predecessor had abstractly formulated, mechanics was placed by a single stroke on a higher level. Our statement might also be historically justified by examples from the scientific labors of Stevinus, S. Carnot, Faraday, J. R. Mayer, and others.
All this, however, is merely the soil from which science starts. The first real beginnings of science appear in society, particularly in the manual arts, where the necessity for the communication of experience arises. Here, where some new discovery is to be described and related, the compulsion is first felt of clearly defining in consciousness the important and essential features of that discovery, as many writers can testify. The aim of instruction is simply the saving of experience; the labor of one man is made to take the place of that of another.
The most wonderful economy of communication is found in language. Words are comparable to type, which spare the repetition of written signs and thus serve a multitude of purposes; or to the few sounds of which our numberless different words are composed.[Pg 192] Language, with its helpmate, conceptual thought, by fixing the essential and rejecting the unessential, constructs its rigid pictures of the fluid world on the plan of a mosaic, at a sacrifice of exactness and fidelity but with a saving of tools and labor. Like a piano-player with previously prepared sounds, a speaker excites in his listener thoughts previously prepared, but fitting many cases, which respond to the speaker's summons with alacrity and little effort.
The principles which a prominent political economist, E. Hermann,[64] has formulated for the economy of the industrial arts, are also applicable to the ideas of common life and of science. The economy of language is augmented, of course, in the terminology of science. With respect to the economy of written intercourse there is scarcely a doubt that science itself will realise that grand old dream of the philosophers of a Universal Real Character. That time is not far distant. Our numeral characters, the symbols of mathematical analysis, chemical symbols, and musical notes, which might easily be supplemented by a system of color-signs, together with some phonetic alphabets now in use, are all beginnings in this direction. The logical extension of what we have, joined with a use of the ideas which the Chinese ideography furnishes us, will render the special invention and promulgation of a Universal Character wholly superfluous.
The communication of scientific knowledge always[Pg 193] involves description, that is, a mimetic reproduction of facts in thought, the object of which is to replace and save the trouble of new experience. Again, to save the labor of instruction and of acquisition, concise, abridged description is sought. This is really all that natural laws are. Knowing the value of the acceleration of gravity, and Galileo's laws of descent, we possess simple and compendious directions for reproducing in thought all possible motions of falling bodies. A formula of this kind is a complete substitute for a full table of motions of descent, because by means of the formula the data of such a table can be easily constructed at a moment's notice without the least burdening of the memory.
No human mind could comprehend all the individual cases of refraction. But knowing the index of refraction for the two media presented, and the familiar law of the sines, we can easily reproduce or fill out in thought every conceivable case of refraction. The advantage here consists in the disburdening of the memory; an end immensely furthered by the written preservation of the natural constants. More than this comprehensive and condensed report about facts is not contained in a natural law of this sort. In reality, the law always contains less than the fact itself, because it does not reproduce the fact as a whole but only in that aspect of it which is important for us, the rest being either intentionally or from necessity omitted. Natural laws may be likened to intellectual type of a[Pg 194] higher order, partly movable, partly stereotyped, which last on new editions of experience may become downright impediments.
When we look over a province of facts for the first time, it appears to us diversified, irregular, confused, full of contradictions. We first succeed in grasping only single facts, unrelated with the others. The province, as we are wont to say, is not clear. By and by we discover the simple, permanent elements of the mosaic, out of which we can mentally construct the whole province. When we have reached a point where we can discover everywhere the same facts, we no longer feel lost in this province; we comprehend it without effort; it is explained for us.
Let me illustrate this by an example. As soon as we have grasped the fact of the rectilinear propagation of light, the regular course of our thoughts stumbles at the phenomena of refraction and diffraction. As soon as we have cleared matters up by our index of refraction we discover that a special index is necessary for each color. Soon after we have accustomed ourselves to the fact that light added to light increases its intensity, we suddenly come across a case of total darkness produced by this cause. Ultimately, however, we see everywhere in the overwhelming multifariousness of optical phenomena the fact of the spatial and temporal periodicity of light, with its velocity of propagation dependent on the medium and the period. This tendency of obtaining a survey of a given province[Pg 195] with the least expenditure of thought, and of representing all its facts by some one single mental process, may be justly termed an economical one.
The greatest perfection of mental economy is attained in that science which has reached the highest formal development, and which is widely employed in physical inquiry, namely, in mathematics. Strange as it may sound, the power of mathematics rests upon its evasion of all unnecessary thought and on its wonderful saving of mental operations. Even those arrangement-signs which we call numbers are a system of marvellous simplicity and economy. When we employ the multiplication-table in multiplying numbers of several places, and so use the results of old operations of counting instead of performing the whole of each operation anew; when we consult our table of logarithms, replacing and saving thus new calculations by old ones already performed; when we employ determinants instead of always beginning afresh the solution of a system of equations; when we resolve new integral expressions into familiar old integrals; we see in this simply a feeble reflexion of the intellectual activity of a Lagrange or a Cauchy, who, with the keen discernment of a great military commander, substituted for new operations whole hosts of old ones. No one will dispute me when I say that the most elementary as well as the highest mathematics are economically-ordered experiences of counting, put in forms ready for use.
In algebra we perform, as far as possible, all numerical operations which are identical in form once for all, so that only a remnant of work is left for the individual case. The use of the signs of algebra and analysis, which are merely symbols of operations to be performed, is due to the observation that we can materially disburden the mind in this way and spare its powers for more important and more difficult duties, by imposing all mechanical operations upon the hand. One result of this method, which attests its economical character, is the construction of calculating machines. The mathematician Babbage, the inventor of the difference-engine, was probably the first who clearly perceived this fact, and he touched upon it, although only cursorily, in his work, The Economy of Manufactures and Machinery.
The student of mathematics often finds it hard to throw off the uncomfortable feeling that his science, in the person of his pencil, surpasses him in intelligence,—an impression which the great Euler confessed he often could not get rid of. This feeling finds a sort of justification when we reflect that the majority of the ideas we deal with were conceived by others, often centuries ago. In great measure it is really the intelligence of other people that confronts us in science. The moment we look at matters in this light, the uncanniness and magical character of our impressions cease, especially when we remember that we can think over again at will any one of those alien thoughts.
Physics is experience, arranged in economical order. By this order not only is a broad and comprehensive view of what we have rendered possible, but also the defects and the needful alterations are made manifest, exactly as in a well-kept household. Physics shares with mathematics the advantages of succinct description and of brief, compendious definition, which precludes confusion, even in ideas where, with no apparent burdening of the brain, hosts of others are contained. Of these ideas the rich contents can be produced at any moment and displayed in their full perceptual light. Think of the swarm of well-ordered notions pent up in the idea of the potential. Is it wonderful that ideas containing so much finished labor should be easy to work with?
Our first knowledge, thus, is a product of the economy of self-preservation. By communication, the experience of many persons, individually acquired at first, is collected in one. The communication of knowledge and the necessity which every one feels of managing his stock of experience with the least expenditure of thought, compel us to put our knowledge in economical forms. But here we have a clue which strips science of all its mystery, and shows us what its power really is. With respect to specific results it yields us nothing that we could not reach in a sufficiently long time without methods. There is no problem in all mathematics that cannot be solved by direct counting. But with the present implements of mathematics[Pg 198] many operations of counting can be performed in a few minutes which without mathematical methods would take a lifetime. Just as a single human being, restricted wholly to the fruits of his own labor, could never amass a fortune, but on the contrary the accumulation of the labor of many men in the hands of one is the foundation of wealth and power, so, also, no knowledge worthy of the name can be gathered up in a single human mind limited to the span of a human life and gifted only with finite powers, except by the most exquisite economy of thought and by the careful amassment of the economically ordered experience of thousands of co-workers. What strikes us here as the fruits of sorcery are simply the rewards of excellent housekeeping, as are the like results in civil life. But the business of science has this advantage over every other enterprise, that from its amassment of wealth no one suffers the least loss. This, too, is its blessing, its freeing and saving power.
The recognition of the economical character of science will now help us, perhaps, to understand better certain physical notions.
Those elements of an event which we call "cause and effect" are certain salient features of it, which are important for its mental reproduction. Their importance wanes and the attention is transferred to fresh characters the moment the event or experience in question becomes familiar. If the connexion of such features strikes us as a necessary one, it is simply because[Pg 199] the interpolation of certain intermediate links with which we are very familiar, and which possess, therefore, higher authority for us, is often attended with success in our explanations. That ready experience fixed in the mosaic of the mind with which we meet new events, Kant calls an innate concept of the understanding (Verstandesbegriff).
The grandest principles of physics, resolved into their elements, differ in no wise from the descriptive principles of the natural historian. The question, "Why?" which is always appropriate where the explanation of a contradiction is concerned, like all proper habitudes of thought, can overreach itself and be asked where nothing remains to be understood. Suppose we were to attribute to nature the property of producing like effects in like circumstances; just these like circumstances we should not know how to find. Nature exists once only. Our schematic mental imitation alone produces like events. Only in the mind, therefore, does the mutual dependence of certain features exist.
All our efforts to mirror the world in thought would be futile if we found nothing permanent in the varied changes of things. It is this that impels us to form the notion of substance, the source of which is not different from that of the modern ideas relative to the conservation of energy. The history of physics furnishes numerous examples of this impulse in almost all fields, and pretty examples of it may be traced back to the nursery. "Where does the light go to when it is put[Pg 200] out?" asks the child. The sudden shrivelling up of a hydrogen balloon is inexplicable to a child; it looks everywhere for the large body which was just there but is now gone.
Where does heat come from? Where does heat go to? Such childish questions in the mouths of mature men shape the character of a century.
In mentally separating a body from the changeable environment in which it moves, what we really do is to extricate a group of sensations on which our thoughts are fastened and which is of relatively greater stability than the others, from the stream of all our sensations. Absolutely unalterable this group is not. Now this, now that member of it appears and disappears, or is altered. In its full identity it never recurs. Yet the sum of its constant elements as compared with the sum of its changeable ones, especially if we consider the continuous character of the transition, is always so great that for the purpose in hand the former usually appear sufficient to determine the body's identity. But because we can separate from the group every single member without the body's ceasing to be for us the same, we are easily led to believe that after abstracting all the members something additional would remain. It thus comes to pass that we form the notion of a substance distinct from its attributes, of a thing-in-itself, whilst our sensations are regarded merely as symbols or indications of the properties of this thing-in-itself. But it would be much better to[Pg 201] say that bodies or things are compendious mental symbols for groups of sensations—symbols that do not exist outside of thought. Thus, the merchant regards the labels of his boxes merely as indexes of their contents, and not the contrary. He invests their contents, not their labels, with real value. The same economy which induces us to analyse a group and to establish special signs for its component parts, parts which also go to make up other groups, may likewise induce us to mark out by some single symbol a whole group.
On the old Egyptian monuments we see objects represented which do not reproduce a single visual impression, but are composed of various impressions. The heads and the legs of the figures appear in profile, the head-dress and the breast are seen from the front, and so on. We have here, so to speak, a mean view of the objects, in forming which the sculptor has retained what he deemed essential, and neglected what he thought indifferent. We have living exemplifications of the processes put into stone on the walls of these old temples, in the drawings of our children, and we also observe a faithful analogue of them in the formation of ideas in our own minds. Only in virtue of some such facility of view as that indicated, are we allowed to speak of a body. When we speak of a cube with trimmed corners—a figure which is not a cube—we do so from a natural instinct of economy, which prefers to add to an old familiar conception a correction[Pg 202] instead of forming an entirely new one. This is the process of all judgment.
The crude notion of "body" can no more stand the test of analysis than can the art of the Egyptians or that of our little children. The physicist who sees a body flexed, stretched, melted, and vaporised, cuts up this body into smaller permanent parts; the chemist splits it up into elements. Yet even an element is not unalterable. Take sodium. When warmed, the white, silvery mass becomes a liquid, which, when the heat is increased and the air shut out, is transformed into a violet vapor, and on the heat being still more increased glows with a yellow light. If the name sodium is still retained, it is because of the continuous character of the transitions and from a necessary instinct of economy. By condensing the vapor, the white metal may be made to reappear. Indeed, even after the metal is thrown into water and has passed into sodium hydroxide, the vanished properties may by skilful treatment still be made to appear; just as a moving body which has passed behind a column and is lost to view for a moment may make its appearance after a time. It is unquestionably very convenient always to have ready the name and thought for a group of properties wherever that group by any possibility can appear. But more than a compendious economical symbol for these phenomena, that name and thought is not. It would be a mere empty word for one in whom it did not awaken a large group of well-ordered[Pg 203] sense-impressions. And the same is true of the molecules and atoms into which the chemical element is still further analysed.
True, it is customary to regard the conservation of weight, or, more precisely, the conservation of mass, as a direct proof of the constancy of matter. But this proof is dissolved, when we go to the bottom of it, into such a multitude of instrumental and intellectual operations, that in a sense it will be found to constitute simply an equation which our ideas in imitating facts have to satisfy. That obscure, mysterious lump which we involuntarily add in thought, we seek for in vain outside the mind.
It is always, thus, the crude notion of substance that is slipping unnoticed into science, proving itself constantly insufficient, and ever under the necessity of being reduced to smaller and smaller world-particles. Here, as elsewhere, the lower stage is not rendered indispensable by the higher which is built upon it, no more than the simplest mode of locomotion, walking, is rendered superfluous by the most elaborate means of transportation. Body, as a compound of light and touch sensations, knit together by sensations of space, must be as familiar to the physicist who seeks it, as to the animal who hunts its prey. But the student of the theory of knowledge, like the geologist and the astronomer, must be permitted to reason back from the forms which are created before his eyes to others which he finds ready made for him.
All physical ideas and principles are succinct directions, frequently involving subordinate directions, for the employment of economically classified experiences, ready for use. Their conciseness, as also the fact that their contents are rarely exhibited in full, often invests them with the semblance of independent existence. Poetical myths regarding such ideas,—for example, that of Time, the producer and devourer of all things,—do not concern us here. We need only remind the reader that even Newton speaks of an absolute time independent of all phenomena, and of an absolute space—views which even Kant did not shake off, and which are often seriously entertained to-day. For the natural inquirer, determinations of time are merely abbreviated statements of the dependence of one event upon another, and nothing more. When we say the acceleration of a freely falling body is 9·810 metres per second, we mean the velocity of the body with respect to the centre of the earth is 9·810 metres greater when the earth has performed an additional 86400th part of its rotation—a fact which itself can be determined only by the earth's relation to other heavenly bodies. Again, in velocity is contained simply a relation of the position of a body to the position of the earth.[65] Instead of referring events to the earth we may refer them to a clock, or even to our internal sensation of time. Now, because all are connected, and each may be made the measure of the rest, the illusion easily arises that time has significance independently of all.[66]
The aim of research is the discovery of the equations which subsist between the elements of phenomena. The equation of an ellipse expresses the universal conceivable relation between its co-ordinates, of which only the real values have geometrical significance. Similarly, the equations between the elements of phenomena express a universal, mathematically conceivable relation. Here, however, for many values only certain directions of change are physically admissible. As in the ellipse only certain values satisfying the equation are realised, so in the physical world only certain changes of value occur. Bodies are always accelerated towards the earth. Differences of temperature, left to themselves, always grow less; and so on. Similarly, with respect to space, mathematical and physiological researches have shown that the space of experience is simply an actual case of many conceivable cases, about whose peculiar properties experience alone can instruct us. The elucidation which this idea diffuses cannot be questioned, despite the absurd uses to which it has been put.
Let us endeavor now to summarise the results of[Pg 206] our survey. In the economical schematism of science lie both its strength and its weakness. Facts are always represented at a sacrifice of completeness and never with greater precision than fits the needs of the moment. The incongruence between thought and experience, therefore, will continue to subsist as long as the two pursue their course side by side; but it will be continually diminished.
In reality, the point involved is always the completion of some partial experience; the derivation of one portion of a phenomenon from some other. In this act our ideas must be based directly upon sensations. We call this measuring.[67] The condition of science, both in its origin and in its application, is a great relative stability of our environment. What it teaches us is interdependence. Absolute forecasts, consequently, have no significance in science. With great changes in celestial space we should lose our co-ordinate systems of space and time.
When a geometer wishes to understand the form of a curve, he first resolves it into small rectilinear elements. In doing this, however, he is fully aware that these elements are only provisional and arbitrary devices for comprehending in parts what he cannot comprehend as a whole. When the law of the curve is found he no longer thinks of the elements. Similarly, it would not become physical science to see in its self-created,[Pg 207] changeable, economical tools, molecules and atoms, realities behind phenomena, forgetful of the lately acquired sapience of her older sister, philosophy, in substituting a mechanical mythology for the old animistic or metaphysical scheme, and thus creating no end of suppositious problems. The atom must remain a tool for representing phenomena, like the functions of mathematics. Gradually, however, as the intellect, by contact with its subject-matter, grows in discipline, physical science will give up its mosaic play with stones and will seek out the boundaries and forms of the bed in which the living stream of phenomena flows. The goal which it has set itself is the simplest and most economical abstract expression of facts.
The question now remains, whether the same method of research which till now we have tacitly restricted to physics, is also applicable in the psychical domain. This question will appear superfluous to the physical inquirer. Our physical and psychical views spring in exactly the same manner from instinctive knowledge. We read the thoughts of men in their acts and facial expressions without knowing how. Just as we predict the behavior of a magnetic needle placed near a current by imagining Ampère's swimmer in the current, similarly we predict in thought the acts and behavior of men by assuming sensations, feelings, and wills similar to our own connected with their bodies. What we here instinctively perform would appear to us as one of the subtlest achievements of science, far outstripping in significance and ingenuity Ampère's rule of the swimmer, were it not that every child unconsciously accomplished it. The question simply is, therefore, to grasp scientifically, that is, by conceptional thought, what we are already familiar with from other sources. And here much is to be accomplished. A long sequence of facts is to be disclosed between the physics of expression and movement and feeling and thought.
We hear the question, "But how is it possible to explain feeling by the motions of the atoms of the brain?" Certainly this will never be done, no more than light or heat will ever be deduced from the law of refraction. We need not deplore, therefore, the lack of ingenious solutions of this question. The problem is not a problem. A child looking over the walls of a city or of a fort into the moat below sees with astonishment living people in it, and not knowing of the portal which connects the wall with the moat, cannot understand how they could have got down from the high ramparts. So it is with the notions of physics. We cannot climb up into the province of psychology by the ladder of our abstractions, but we can climb down into it.
Let us look at the matter without bias. The world consists of colors, sounds, temperatures, pressures, spaces, times, and so forth, which now we shall not call sensations, nor phenomena, because in either term an arbitrary, one-sided theory is embodied, but simply elements. The fixing of the flux of these elements, whether mediately or immediately, is the real object of physical research. As long as, neglecting our own body, we employ ourselves with the interdependence of those groups of elements which, including men and animals, make up foreign bodies, we are physicists. For example, we investigate the change of the red color of a body as produced by a change of illumination. But the moment we consider the special influence on the red of the elements constituting our body, outlined by the well-known perspective with head invisible, we are at work in the domain of physiological psychology. We close our eyes, and the red together with the whole visible world disappears. There exists, thus, in the perspective field of every sense a portion which exercises on all the rest a different and more powerful influence than the rest upon one another. With this, however, all is said. In the light of this remark, we call all elements, in so far as we regard them as dependent on this special part (our body), sensations. That the world is our sensation, in this sense, cannot be questioned. But to make a system of conduct out of this provisional conception, and to abide its slaves, is as unnecessary for us as would be a similar course for a mathematician who, in varying a series of variables of a function which were previously assumed to be constant, or in interchanging the independent variables, finds his method to be the source of some very surprising ideas for him.[68]
If we look at the matter in this unbiassed light it will appear indubitable that the method of physiological psychology is none other than that of physics; what is more, that this science is a part of physics. Its subject-matter is not different from that of physics. It will unquestionably determine the relations the sensations bear to the physics of our body. We have already learned from a member of this academy (Hering) that in all probability a sixfold manifoldness of the chemical processes of the visual substance corresponds to the sixfold manifoldness of color-sensation, and a threefold manifoldness of the physiological processes to the threefold manifoldness of space-sensations. The paths of reflex actions and of the will are followed up and disclosed; it is ascertained what region of the brain subserves the function of speech, what region the function of locomotion, etc. That which still clings to our body, namely, our thoughts, will, when those investigations are finished, present no difficulties new in principle. When experience has once clearly exhibited these facts and science has marshalled them in economic and perspicuous order, there is no doubt that we shall understand them. For other "understanding" than a mental mastery of facts never existed. Science does not create facts from facts, but simply orders known facts.
Let us look, now, a little more closely into the modes of research of physiological psychology. We have a very clear idea of how a body moves in the space encompassing it. With our optical field of sight we are very familiar. But we are unable to state, as a rule, how we have come by an idea, from what corner of our intellectual field of sight it has entered, or by what region the impulse to a motion is sent forth. Moreover, we shall never get acquainted with this mental field of view from self-observation alone. Self-observation, in conjunction with physiological research, which seeks out physical connexions, can put this field of vision in a clear light before us, and will thus first really reveal to us our inner man.
Primarily, natural science, or physics, in its widest sense, makes us acquainted with only the firmest connexions of groups of elements. Provisorily, we may not bestow too much attention on the single constituents of those groups, if we are desirous of retaining a comprehensible whole. Instead of equations between the primitive variables, physics gives us, as much the easiest course, equations between functions of those variables. Physiological psychology teaches us how to separate the visible, the tangible, and the audible from bodies—a labor which is subsequently richly requited, as the division of the subjects of physics well shows. Physiology further analyses the visible into light and space sensations; the first into colors, the last also into their component parts; it resolves noises into sounds, these into tones, and so on. Unquestionably this analysis can be carried much further than it has been. It will be possible in the end to exhibit the common elements at the basis of very abstract but definite logical acts of like form,—elements which the acute jurist and mathematician, as it were, feels out, with absolute certainty, where the uninitiated hears only empty words. Physiology, in a word, will reveal to us the true real elements of the world. Physiological psychology bears to physics in its widest sense a relation similar to that which chemistry bears to physics in its narrowest sense. But far greater than the mutual support of physics and chemistry will be that which natural science and psychology will render each other. And the results that shall spring from this union will, in all likelihood, far outstrip those of the modern mechanical physics.
What those ideas are with which we shall comprehend the world when the closed circuit of physical and psychological facts shall lie complete before us, (that circuit of which we now see only two disjoined parts,) cannot be foreseen at the outset of the work. The men will be found who will see what is right and will have the courage, instead of wandering in the intricate paths of logical and historical accident, to enter on the straight ways to the heights from which the mighty stream of facts can be surveyed. Whether the notion which we now call matter will continue to have a scientific significance beyond the crude purposes of common life, we do not know. But we certainly shall wonder how colors and tones which were such innermost parts of us could suddenly get lost in our physical world of atoms; how we could be suddenly surprised that something which outside us simply clicked and beat, in our heads should make light and music; and how we could ask whether matter can feel, that is to say, whether a mental symbol for a group of sensations can feel?
We cannot mark out in hard and fast lines the science of the future, but we can foresee that the rigid walls which now divide man from the world will gradually disappear; that human beings will not only confront each other, but also the entire organic and so-called lifeless world, with less selfishness and with livelier sympathy. Just such a presentiment as this perhaps possessed the great Chinese philosopher Licius some two thousand years ago when, pointing to a heap of mouldering human bones, he said to his scholars in the rigid, lapidary style of his tongue: "These and I alone have the knowledge that we neither live nor are dead."
It was towards the close of the sixteenth century that Galileo with a superb indifference to the dialectic arts and sophistic subtleties of the Schoolmen of his time, turned the attention of his brilliant mind to nature. By nature his ideas were transformed and released from the fetters of inherited prejudice. At once the mighty revolution was felt, that was therewith effected in the realm of human thought—felt indeed in circles far remote and wholly unrelated to the sphere of science, felt in strata of society that hitherto had only indirectly recognised the influence of scientific thought.
And how great and how far-reaching that revolution was! From the beginning of the seventeenth century till its close we see arising, at least in embryo, almost all that plays a part in the natural and technical science of to-day, almost all that in the two centuries following so wonderfully transformed the facial appearance of the earth, and all that is moving onward in process of such mighty evolution to-day. And all this, the direct result of Galilean ideas, the direct outcome of that freshly awakened sense for the investigation of natural phenomena which taught the Tuscan philosopher to form the concept and the law of falling bodies from the observation of a falling stone! Galileo began his investigations without an implement worthy of the name; he measured time in the most primitive way, by the efflux of water. Yet soon afterwards the telescope, the microscope, the barometer, the thermometer, the air-pump, the steam engine, the pendulum, and the electrical machine were invented in rapid succession. The fundamental theorems of dynamical science, of optics, of heat, and of electricity were all disclosed in the century that followed Galileo.
Of scarcely less importance, it seems, was that movement which was prepared for by the illustrious biologists of the hundred years just past, and formally begun by the late Mr. Darwin. Galileo quickened the sense for the simpler phenomena of inorganic nature. And with the same simplicity and frankness that marked the efforts of Galileo, and without the aid of[Pg 216] technical or scientific instruments, without physical or chemical experiment, but solely by the power of thought and observation, Darwin grasps a new property of organic nature—which we may briefly call its plasticity.[70] With the same directness of purpose, Darwin, too, pursues his way. With the same candor and love of truth, he points out the strength and the weakness of his demonstrations. With masterly equanimity he holds aloof from the discussion of irrelevant subjects and wins alike the admiration of his adherents and of his adversaries.
Scarcely thirty years have elapsed[71] since Darwin first propounded the principles of his theory of evolution.[Pg 217] Yet, already we see his ideas firmly rooted in every branch of human thought, however remote. Everywhere, in history, in philosophy, even in the physical sciences, we hear the watchwords: heredity, adaptation, selection. We speak of the struggle for existence among the heavenly bodies and of the struggle for existence in the world of molecules.[72]
The impetus given by Galileo to scientific thought was marked in every direction; thus, his pupil, Borelli, founded the school of exact medicine, from whence proceeded even distinguished mathematicians. And now Darwinian ideas, in the same way, are animating all provinces of research. It is true, nature is not made up of two distinct parts, the inorganic and the organic; nor must these two divisions be treated perforce by totally distinct methods. Many sides, however, nature has. Nature is like a thread in an intricate tangle, which must be followed and traced, now from this point, now from that. But we must never imagine,—and this physicists have learned from Faraday and J. R. Mayer,—that progress along paths once entered upon is the only means of reaching the truth.
It will devolve upon the specialists of the future to determine the relative tenability and fruitfulness of the Darwinian ideas in the different provinces. Here I wish simply to consider the growth of natural knowledge in the light of the theory of evolution. For knowledge, too, is a product of organic nature. And although[Pg 218] ideas, as such, do not comport themselves in all respects like independent organic individuals, and although violent comparisons should be avoided, still, if Darwin reasoned rightly, the general imprint of evolution and transformation must be noticeable in ideas also.
I shall waive here the consideration of the fruitful topic of the transmission of ideas or rather of the transmission of the aptitude for certain ideas.[73] Nor would it come within my province to discuss psychical evolution in any form, as Spencer[74] and many other modern psychologists have done, with varying success. Neither shall I enter upon a discussion of the struggle for existence and of natural selection among scientific theories.[75] We shall consider here only such processes of transformation as every student can easily observe in his own mind.
The child of the forest picks out and pursues with marvellous acuteness the trails of animals. He outwits and overreaches his foes with surpassing cunning. He is perfectly at home in the sphere of his peculiar experience. But confront him with an unwonted phenomenon; place him face to face with a technical product of modern civilisation, and he will lapse into impotency and helplessness. Here are facts which he does not comprehend. If he endeavors to grasp their meaning, he misinterprets them. He fancies the moon, when eclipsed, to be tormented by an evil spirit. To his mind a puffing locomotive is a living monster. The letter accompanying a commission with which he is entrusted, having once revealed his thievishness, is in his imagination a conscious being, which he must hide beneath a stone, before venturing to commit a fresh trespass. Arithmetic to him is like the art of the geomancers in the Arabian Nights,—an art which is able to accomplish every imaginable impossibility. And, like Voltaire's ingénu, when placed in our social world, he plays, as we think, the maddest pranks.
With the man who has made the achievements of modern science and civilisation his own, the case is quite different. He sees the moon pass temporarily into the shadow of the earth. He feels in his thoughts the water growing hot in the boiler of the locomotive; he feels also the increase of the tension which pushes the piston forward. Where he is not able to trace the direct relation of things he has recourse to his yard-stick and table of logarithms, which aid and facilitate his thought without predominating over it. Such opinions as he cannot concur in, are at least known to him, and he knows how to meet them in argument.
Now, wherein does the difference between these two men consist? The train of thought habitually employed by the first one does not correspond to the facts that he sees. He is surprised and nonplussed at every step. But the thoughts of the second man follow and anticipate events, his thoughts have become adapted or accommodated to the larger field of observation and activity in which he is located; he conceives things as they are. The Indian's sphere of experience, however, is quite different; his bodily organs of sense are in constant activity; he is ever intensely alert and on the watch for his foes; or, his entire attention and energy are engaged in procuring sustenance. Now, how can such a creature project his mind into futurity, foresee or prophesy? This is not possible until our fellow-beings have, in a measure, relieved us of our concern for existence. It is then that we acquire freedom for observation, and not infrequently too that narrowness of thought which society helps and teaches us to disregard.
If we move for a time within a fixed circle of phenomena which recur with unvarying uniformity, our thoughts gradually adapt themselves to our environment; our ideas reflect unconsciously our surroundings. The stone we hold in our hand, when dropped, not only falls to the ground in reality; it also falls in our thoughts. Iron-filings dart towards a magnet in imagination as well as in fact, and, when thrown into a fire, they grew hot in conception as well.
The impulse to complete mentally a phenomenon that has been only partially observed, has not its origin in the phenomenon itself; of this fact, we are fully sensible. And we well know that it does not lie within the sphere of our volition. It seems to confront us rather as a power and a law imposed from without and controlling both thought and facts.
The fact that we are able by the help of this law to prophesy and forecast, merely proves a sameness or uniformity of environment sufficient to effect a mental adaptation of this kind. A necessity of fulfilment, however, is not contained in this compulsory principle which controls our thoughts; nor is it in any way determined by the possibility of prediction. We are always obliged, in fact, to await the completion of what has been predicted. Errors and departures are constantly discernible, and are slight only in provinces of great rigid constancy, as in astronomy.
In cases where our thoughts follow the connexion of events with ease, and in instances where we positively forefeel the course of a phenomenon, it is natural to fancy that the latter is determined by and must conform to our thoughts. But the belief in that mysterious agency called causality, which holds thought and event in unison, is violently shaken when a person first enters a province of inquiry in which he has previously had no experience. Take for instance the strange interaction of electric currents and magnets, or the reciprocal action of currents, which seem to defy all the resources of mechanical science. Let him be confronted with such phenomena and he will immediately feel himself forsaken by his power of prediction; he will bring nothing with him into this strange field of events but the hope of soon being able to adapt his ideas to the new conditions there presented.
A person constructs from a bone the remaining anatomy of an animal; or from the visible part of a half-concealed wing of a butterfly he infers and reconstructs the part concealed. He does so with a feeling of highest confidence in the accuracy of his results; and in these processes we find nothing preternatural or transcendent. But when physicists adapt their thoughts to conform to the dynamical course of events in time, we invariably surround their investigations with a metaphysical halo; yet these latter adaptations bear quite the same character as the former, and our only reason for investing them with a metaphysical garb, perhaps, is their high practical value.[76]
Let us consider for a moment what takes place when the field of observation to which our ideas have been adapted and now conform, becomes enlarged. We had, let us say, always seen heavy bodies sink when their support was taken away; we had also seen, perhaps, that the sinking of heavier bodies forced lighter bodies upwards. But now we see a lever in action, and we are suddenly struck with the fact that a lighter body is lifting another of much greater weight. Our customary train of thought demands its rights; the new and unwonted event likewise demands its rights. From this conflict between thought and fact the problem arises; out of this partial contrariety springs the question, "Why?" With the new adaptation to the enlarged field of observation, the problem disappears, or, in other words, is solved. In the instance cited, we must adopt the habit of always considering the mechanical work performed.
The child just awakening into consciousness of the world, knows no problem. The bright flower, the ringing bell, are all new to it; yet it is surprised at nothing. The out and out Philistine, whose only thoughts lie in the beaten path of his every-day pursuits, likewise has no problems. Everything goes its wonted course, and if perchance a thing go wrong at times, it is at most a mere object of curiosity and not worth serious consideration. In fact, the question "Why?" loses all warrant in relations where we are familiar with every aspect of events. But the capable and talented young man has his head full of problems; he has acquired, to a greater or less degree, certain habitudes of thought, and at the same time he is constantly observing what is new and unwonted, and in his case there is no end to the questions, "Why?"
Thus, the factor which most promotes scientific thought is the gradual widening of the field of experience. We scarcely notice events we are accustomed to; the latter do not really develop their intellectual significance until placed in contrast with something to which we are unaccustomed. Things that at home are passed by unnoticed, delight us when abroad, though they may appear in only slightly different forms. The sun shines with heightened radiance, the flowers bloom in brighter colors, our fellow-men accost us with lighter and happier looks. And, returning home, we find even the old familiar scenes more inspiring and suggestive than before.
Every motive that prompts and stimulates us to modify and transform our thoughts, proceeds from what is new, uncommon, and not understood. Novelty excites wonder in persons whose fixed habits of thought are shaken and disarranged by what they see. But the element of wonder never lies in the phenomenon or event observed; its place is in the person observing. People of more vigorous mental type aim at once at an adaptation of thought that will conform to what they have observed. Thus does science eventually become the natural foe of the wonderful. The sources of the marvellous are unveiled, and surprise gives way to calm interpretation.
Let us consider such a mental transformative process in detail. The circumstance that heavy bodies fall to the earth appears perfectly natural and regular. But when a person observes that wood floats upon water, and that flames and smoke rise in the air, then the contrary of the first phenomenon is presented. An olden theory endeavors to explain these facts by imputing to substances the power of volition, as that attribute which is most familiar to man. It asserted that every substance seeks its proper place, heavy bodies tending downwards and light ones upwards. It soon turned out, however, that even smoke had weight, that it, too, sought its place below, and that it was forced upwards only because of the downward tendency of the air, as wood is forced to the surface of water because the water exerts the greater downward pressure.
Again, we see a body thrown into the air. It ascends. How is it that it does not seek its proper place? Why does the velocity of its "violent" motion decrease as it rises, while that of its "natural" fall increases as it descends. If we mark closely the relation between these two facts, the problem will solve itself. We shall see, as Galileo did, that the decrease of velocity in rising and the increase of velocity in falling are one and the same phenomenon, viz., an increase of velocity towards the earth. Accordingly, it is not a place that is assigned to the body, but an increase of velocity towards the earth.
By this idea the movements of heavy bodies are rendered perfectly familiar. Newton, now, firmly grasping this new way of thinking, sees the moon and the planets moving in their paths upon principles similar to those which determine the motion of a projectile thrown into the air. Yet the movements of the planets were marked by peculiarities which compelled him once more to modify slightly his customary mode of thought. The heavenly bodies, or rather the parts composing them, do not move with constant accelerations towards each other, but "attract each other," directly as the mass and inversely as the square of the distance.
This latter notion, which includes the one applying to terrestrial bodies as a special case, is, as we see, quite different from the conception from which we started. How limited in scope was the original idea and to what a multitude of phenomena is not the present one applicable! Yet there is a trace, after all, of the "search for place" in the expression "attraction." And it would be folly, indeed, for us to avoid, with punctilious dread, this conception of "attraction" as bearing marks of its pedigree. It is the historical base of the Newtonian conception and it still continues to direct our thoughts in the paths so long familiar to us. Thus, the happiest ideas do not fall from heaven, but spring from notions already existing.
Similarly, a ray of light was first regarded as a continuous and homogeneous straight line. It then became the path of projection for minute missiles; then an aggregate of the paths of countless different kinds of missiles. It became periodic; it acquired various sides; and ultimately it even lost its motion in a straight line.
The electric current was conceived originally as the flow of a hypothetical fluid. To this conception was soon added the notion of a chemical current, the notion of an electric, magnetic, and anisotropic optical field, intimately connected with the path of the current. And the richer a conception becomes in following and keeping pace with facts, the better adapted it is to anticipate them.
Adaptive processes of this kind have no assignable beginning, inasmuch as every problem that incites to new adaptation, presupposes a fixed habitude of thought. Moreover, they have no visible end; in so far as experience never ceases. Science, accordingly, stands midway in the evolutionary process; and science may advantageously direct and promote this process, but it can never take its place. That science is inconceivable the principles of which would enable a person with no experience to construct the world of experience, without a knowledge of it. One might just as well expect to become a great musician, solely by the aid of theory, and without musical experience; or to become a painter by following the directions of a text-book.
In glancing over the history of an idea with which we have become perfectly familiar, we are no longer able to appreciate the full significance of its growth. The deep and vital changes that have been effected in the course of its evolution, are recognisable only from the astounding narrowness of view with which great contemporary scientists have occasionally opposed each other. Huygens's wave-theory of light was incomprehensible to Newton, and Newton's idea of universal gravity was unintelligible to Huygens. But a century afterwards both notions were reconcilable, even in ordinary minds.
On the other hand, the original creations of pioneer intellects, unconsciously formed, do not assume a foreign garb; their form is their own. In them, childlike simplicity is joined to the maturity of manhood, and they are not to be compared with processes of thought in the average mind. The latter are carried on as are the acts of persons in the state of mesmerism, where actions involuntarily follow the images which the words of other persons suggest to their minds.
The ideas that have become most familiar through long experience, are the very ones that intrude themselves into the conception of every new fact observed. In every instance, thus, they become involved in a struggle for self-preservation, and it is just they that are seized by the inevitable process of transformation.
Upon this process rests substantially the method of explaining by hypothesis new and uncomprehended phenomena. Thus, instead of forming entirely new notions to explain the movements of the heavenly bodies and the phenomena of the tides, we imagine the material particles composing the bodies of the universe to possess weight or gravity with respect to one another. Similarly, we imagine electrified bodies to be freighted with fluids that attract and repel, or we conceive the space between them to be in a state of elastic tension. In so doing, we substitute for new ideas distinct and more familiar notions of old experience—notions which to a great extent run unimpeded in their courses, although they too must suffer partial transformation.
The animal cannot construct new members to perform every new function that circumstances and fate demand of it. On the contrary it is obliged to make use of those it already possesses. When a vertebrate animal chances into an environment where it must learn to fly or swim, an additional pair of extremities is not grown for the purpose. On the contrary, the animal must adapt and transform a pair that it already has.
The construction of hypotheses, therefore, is not the product of artificial scientific methods. This process is unconsciously carried on in the very infancy of science. Even later, hypotheses do not become detrimental and dangerous to progress except when more reliance is placed on them than on the facts themselves; when the contents of the former are more highly valued than the latter, and when, rigidly adhering to hypothetical notions, we overestimate the ideas we possess as compared with those we have to acquire.
The extension of our sphere of experience always involves a transformation of our ideas. It matters not whether the face of nature becomes actually altered, presenting new and strange phenomena, or whether these phenomena are brought to light by an intentional or accidental turn of observation. In fact, all the varied methods of scientific inquiry and of purposive mental adaptation enumerated by John Stuart Mill, those of observation as well as those of experiment, are ultimately recognisable as forms of one fundamental method, the method of change, or variation. It is through change of circumstances that the natural philosopher learns. This process, however, is by no means confined to the investigator of nature. The historian, the philosopher, the jurist, the mathematician, the artist, the æsthetician,[77] all illuminate and unfold their ideas by producing from the rich treasures of memory similar, but different, cases; thus, they observe and experiment in their thoughts. Even if all sense-experience should suddenly cease, the events of the days past would meet in different attitudes in the mind and the process of adaptation would still continue—a process which, in contradistinction to the adaptation of thoughts to facts in practical spheres, would be strictly theoretical, being an adaptation of thoughts to thoughts.
The method of change or variation brings before us like cases of phenomena, having partly the same and partly different elements. It is only by comparing different cases of refracted light at changing angles of incidence that the common factor, the constancy of the refractive index, is disclosed. And only by comparing the refractions of light of different colors, does the difference, the inequality of the indices of refraction, arrest the attention. Comparison based upon change leads the mind simultaneously to the highest abstractions and to the finest distinctions.
Undoubtedly, the animal also is able to distinguish between the similar and dissimilar of two cases. Its consciousness is aroused by a noise or a rustling, and its motor centre is put in readiness. The sight of the creature causing the disturbance, will, according to its size, provoke flight or prompt pursuit; and in the latter case, the more exact distinctions will determine the mode of attack. But man alone attains to the faculty of voluntary and conscious comparison. Man alone can, by his power of abstraction, rise, in one moment, to the comprehension of principles like the conservation of mass or the conservation of energy, and in the next observe and mark the arrangement of the iron lines in the spectrum. In thus dealing with the objects of his conceptual life, his ideas unfold and expand, like his nervous system, into a widely ramified and organically articulated tree, on which he may follow every limb to its farthermost branches, and, when occasion demands, return to the trunk from which he started.
The English philosopher Whewell has remarked that two things are requisite to the formation of science: facts and ideas. Ideas alone lead to empty speculation; mere facts can yield no organic knowledge. We see that all depends upon the capacity of adapting existing notions to fresh facts.
Over-readiness to yield to every new fact prevents fixed habits of thought from arising. Excessively rigid habits of thought impede freedom of observation. In the struggle, in the compromise between judgment and prejudgment (prejudice), if we may use the term, our understanding of things broadens.
Habitual judgment, applied to a new case without antecedent tests, we call prejudgment or prejudice. Who does not know its terrible power! But we think less often of the importance and utility of prejudice. Physically, no one could exist, if he had to guide and regulate the circulation, respiration, and digestion of his body by conscious and purposive acts. So, too, no one could exist intellectually if he had to form judgments on every passing experience, instead of allowing himself to be controlled by the judgments he has already formed. Prejudice is a sort of reflex motion in the province of intelligence.
On prejudices, that is, on habitual judgments not tested in every case to which they are applied, reposes a goodly portion of the thought and work of the natural scientist. On prejudices reposes most of the conduct of society. With the sudden disappearance of prejudice society would hopelessly dissolve. That prince displayed a deep insight into the power of intellectual habit, who quelled the loud menaces and demands of his body-guard for arrears of pay and compelled them to turn about and march, by simply pronouncing the regular word of command; he well knew that they would be unable to resist that.
Not until the discrepancy between habitual judgments and facts becomes great is the investigator implicated in appreciable illusion. Then tragic complications and catastrophes occur in the practical life of individuals and nations—crises where man, placing custom above life, instead of pressing it into the service of life, becomes the victim of his error. The very power which in intellectual life advances, fosters, and sustains us, may in other circumstances delude and destroy us.
Ideas are not all of life. They are only momentary efflorescences of light, designed to illuminate the paths of the will. But as delicate reagents on our organic evolution our ideas are of paramount importance. No theory can gainsay the vital transformation which we feel taking place within us through their agency. Nor is it necessary that we should have a proof of this process. We are immediately assured of it.
The transformation of ideas thus appears as a part of the general evolution of life, as a part of its adaptation to a constantly widening sphere of action. A granite boulder on a mountain-side tends towards the earth below. It must abide in its resting-place for thousands of years before its support gives way. The shrub that grows at its base is farther advanced; it accommodates itself to summer and winter. The fox which, overcoming the force of gravity, creeps to the summit where he has scented his prey, is freer in his movements than either. The arm of man reaches further still; and scarcely anything of note happens in Africa or Asia that does not leave an imprint upon his life. What an immense portion of the life of other men is reflected in ourselves; their joys, their affections, their happiness and misery! And this too, when we survey only our immediate surroundings, and confine our attention to modern literature. How much more do we experience when we travel through ancient Egypt with Herodotus, when we stroll through the streets of Pompeii, when we carry ourselves back to the gloomy period of the crusades or to the golden age of Italian art, now making the acquaintance of a physician of Molière, and now that of a Diderot or of a D'Alembert. What a great part of the life of others, of their character and their purpose, do we not absorb through poetry and music! And although they only gently touch the chords of our emotions, like the memory of youth softly breathing upon the spirit of an aged man, we have nevertheless lived them over again in part. How great and comprehensive does self become in this conception; and how insignificant the person! Egoistical systems both of optimism and pessimism perish with their narrow standard of the import of intellectual life. We feel that the real pearls of life lie in the ever changing contents of consciousness, and that the person is merely an indifferent symbolical thread on which they are strung.[78]
We are prepared, thus, to regard ourselves and every one of our ideas as a product and a subject of universal evolution; and in this way we shall advance sturdily and unimpeded along the paths which the future will throw open to us.[79]
Twenty years ago when Kirchhoff defined the object of mechanics as the "description, in complete and very simple terms, of the motions occurring in nature," he produced by the statement a peculiar impression. Fourteen years subsequently, Boltzmann, in the life-like picture which he drew of the great inquirer, could still speak of the universal astonishment at this novel method of treating mechanics, and we meet with epistemological treatises to-day, which plainly show how difficult is the acceptance of this point of view. A modest and small band of inquirers there were, however, to whom Kirchhoff's few words were tidings of a welcome and powerful ally in the epistemological field.
Now, how does it happen that we yield our assent so reluctantly to the philosophical opinion of an inquirer for whose scientific achievements we have only words of praise? One reason probably is that few inquirers can find time and leisure, amid the exacting[Pg 237] employments demanded for the acquisition of new knowledge, to inquire closely into that tremendous psychical process by which science is formed. Further, it is inevitable that much should be put into Kirchhoff's rigid words that they were not originally intended to convey, and that much should be found wanting in them that had always been regarded as an essential element of scientific knowledge. What can mere description accomplish? What has become of explanation, of our insight into the causal connexion of things?
Permit me, for a moment, to contemplate not the results of science, but the mode of its growth, in a frank and unbiassed manner. We know of only one source of immediate revelation of scientific facts—our senses. Restricted to this source alone, thrown wholly upon his own resources, obliged to start always anew, what could the isolated individual accomplish? Of a stock of knowledge so acquired the science of a distant negro hamlet in darkest Africa could hardly give us a sufficiently humiliating conception. For there that veritable miracle of thought-transference has already begun its work, compared with which the miracles of the spiritualists are rank monstrosities—communication by language. Reflect, too, that by means of the magical characters which our libraries contain we can raise the spirits of the "the sovereign dead of old" from Faraday to Galileo and Archimedes, through ages of time—spirits who do not dismiss us with ambiguous and derisive oracles, but tell us the best they know; then shall we feel what a stupendous and indispensable factor in the formation of science communication is. Not the dim, half-conscious surmises of the acute observer of nature or critic of humanity belong to science, but only that which they possess clearly enough to communicate to others.
But how, now, do we go about this communication of a newly acquired experience, of a newly observed fact? As the different calls and battle-cries of gregarious animals are unconsciously formed signs for a common observation or action, irrespective of the causes which produce such action—a fact that already involves the germ of the concept; so also the words of human language, which is only more highly specialised, are names or signs for universally known facts, which all can observe or have observed. If the mental representation, accordingly, follows the new fact at once and passively, then that new fact must, of itself, immediately be constituted and represented in thought by facts already universally known and commonly observed. Memory is always ready to put forward for comparison known facts which resemble the new event, or agree with it in certain features, and so renders possible that elementary internal judgment which the mature and definitively formulated judgment soon follows.
Comparison, as the fundamental condition of communication, is the most powerful inner vital element of science. The zoölogist sees in the bones of the wing-membranes of bats, fingers; he compares the bones of the cranium with the vertebræ, the embryos of different organisms with one another, and the different stages of development of the same organism with one another. The geographer sees in Lake Garda a fjord, in the Sea of Aral a lake in process of drying up. The philologist compares different languages with one another, and the formations of the same language as well. If it is not customary to speak of comparative physics in the same sense that we speak of comparative anatomy, the reason is that in a science of such great experimental activity the attention is turned away too much from the contemplative element. But like all other sciences, physics lives and grows by comparison.
The manner in which the result of the comparison finds expression in the communication, varies of course very much. When we say that the colors of the spectrum are red, yellow, green, blue, and violet, the designations employed may possibly have been derived from the technology of tattooing, or they may subsequently have acquired the significance of standing for the colors of the rose, the lemon, the leaf, the corn-flower, and the violet. From the frequent repetition of such comparisons, however, made under the most manifold circumstances, the inconstant features, as compared with the permanent congruent features, get so obliterated that the latter acquire a fixed significance independent of every object and connexion, or take on as we say an abstract or conceptual import. No one thinks at the word "red" of any other agreement with the rose than that of color, or at the word "straight" of any other property of a stretched cord than the sameness of direction. Just so, too, numbers, originally the names of the fingers of the hands and feet, from being used as arrangement-signs for all kinds of objects, were lifted to the plane of abstract concepts. A verbal report (communication) of a fact that uses only these purely abstract implements, we call a direct description.
The direct description of a fact of any great extent is an irksome task, even where the requisite notions are already completely developed. What a simplification it involves if we can say, the fact A now considered comports itself, not in one, but in many or in all its features, like an old and well-known fact B. The moon comports itself as a heavy body does with respect to the earth; light like a wave-motion or an electric vibration; a magnet, as if it were laden with gravitating fluids, and so on. We call such a description, in which we appeal, as it were, to a description already and elsewhere formulated, or perhaps still to be precisely formulated, an indirect description. We are at liberty to supplement this description, gradually, by direct description, to correct it, or to replace it altogether. We see, thus, without difficulty, that what is called a theory or a theoretical idea, falls under the category of what is here termed indirect description.
What, now, is a theoretical idea? Whence do we get it? What does it accomplish for us? Why does it occupy a higher place in our judgment than the mere holding fast to a fact or an observation? Here, too, memory and comparison alone are in play. But instead of a single feature of resemblance culled from memory, in this case a great system of resemblances confronts us, a well-known physiognomy, by means of which the new fact is immediately transformed into an old acquaintance. Besides, it is in the power of the idea to offer us more than we actually see in the new fact, at the first moment; it can extend the fact, and enrich it with features which we are first induced to seek from such suggestions, and which are often actually found. It is this rapidity in extending knowledge that gives to theory a preference over simple observation. But that preference is wholly quantitative. Qualitatively, and in real essential points, theory differs from observation neither in the mode of its origin nor in its last results.
The adoption of a theory, however, always involves a danger. For a theory puts in the place of a fact A in thought, always a different, but simpler and more familiar fact B, which in some relations can mentally represent A, but for the very reason that it is different, in other relations cannot represent it. If now, as may readily happen, sufficient care is not exercised, the most fruitful theory may, in special circumstances, become a downright obstacle to inquiry. Thus, the emission-theory of light, in accustoming the physicist to think of the projectile path of the "light-particles" as an undifferentiated straight-line, demonstrably impeded the discovery of the periodicity of light. By putting in the place of light the more familiar phenomena of sound, Huygens renders light in many of its features a familiar event, but with respect to polarisation, which lacks the longitudinal waves with which alone he was acquainted, it had for him a doubly strange aspect. He is unable thus to grasp in abstract thought the fact of polarisation, which is before his eyes, whilst Newton, merely by adapting to the observation his thoughts, and putting this question, "Annon radiorum luminis diversa sunt latera?" abstractly grasped polarisation, that is, directly described it, a century before Malus. On the other hand, if the agreement of the fact with the idea theoretically representing it, extends further than its inventor originally anticipated, then we may be led by it to unexpected discoveries, of which conical refraction, circular polarisation by total reflexion, Hertz's waves offer ready examples, in contrast to the illustrations given above.
Our insight into the conditions indicated will be improved, perhaps, by contemplating the development of some theory or other more in detail. Let us consider a magnetised bar of steel by the side of a second unmagnetised bar, in all other respects the same. The second bar gives no indication of the presence of iron-filings; the first attracts them. Also, when the iron-filings are absent, we must think of the magnetised bar as in a different condition from that of the unmagnetised. For, that the mere presence of the iron-filings does not induce the phenomenon of attraction is proved by the second unmagnetised bar. The ingenuous man, who finds in his will, as his most familiar source of power, the best facilities for comparison, conceives a species of spirit in the magnet. The behavior of a warm body or of an electrified body suggests similar ideas. This is the point of view of the oldest theory, fetishism, which the inquirers of the early Middle Ages had not yet overcome, and which in its last vestiges, in the conception of forces, still flourishes in modern physics. We see, thus, the dramatic element need no more be absent in a scientific description, than in a thrilling novel.
If, on subsequent examination, it be observed that a cold body, in contact with a hot body, warms itself, so to speak, at the expense of the hot body; further, that when the substances are the same, the cold body, which, let us say, has twice the mass of the other, gains only half the number of degrees of temperature that the other loses, a wholly new impression arises. The demoniac character of the event vanishes, for the supposed spirit acts not by caprice, but according to fixed laws. In its place, however, instinctively the notion of a substance is substituted, part of which flows over from the one body to the other, but the total amount of which, representable by the sum of the products of the masses into the respective changes of temperature, remains constant. Black was the first to be powerfully struck with this resemblance of thermal processes to the motion of a substance, and under its guidance discovered the specific heat, the heat of fusion, and the heat of vaporisation of bodies. Gaining strength and fixity, however, from these successes, this notion of substance subsequently stood in the way of scientific advancement. It blinded the eyes of the successors of Black, and prevented them from seeing the manifest fact, which every savage knows, that heat is produced by friction. Fruitful as that notion was for Black, helpful as it still is to the learner to-day in Black's special field, permanent and universal validity as a theory it could never maintain. But what is essential, conceptually, in it, viz., the constancy of the product-sum above mentioned, retains its value and may be regarded as a direct description of Black's facts.
It stands to reason that those theories which push themselves forward unsought, instinctively, and wholly of their own accord, should have the greatest power, should carry our thoughts most with them, and exhibit the staunchest powers of self-preservation. On the other hand, it may also be observed that when critically scrutinised such theories are extremely apt to lose their cogency. We are constantly busied with "substance," its modes of action have stamped themselves indelibly upon our thoughts, our vividest and clearest reminiscences are associated with it. It should cause us no surprise, therefore, that Robert Mayer and Joule, who gave the final blow to Black's substantial conception of heat, should have re-introduced the same notion of substance in a more abstract and modified form, only applying to a much more extensive field.
Here, too, the psychological circumstances which impart to the new conception its power, lie clearly before us. By the unusual redness of the venous blood in tropical climates Mayer's attention is directed to the lessened expenditure of internal heat and to the proportionately lessened consumption of material by the human body in those climates. But as every effort of the human organism, including its mechanical work, is connected with the consumption of material, and as work by friction can engender heat, therefore heat and work appear in kind equivalent, and between them a proportional relation must subsist. Not every quantity, but the appropriately calculated sum of the two, as connected with a proportionate consumption of material, appears substantial.
By exactly similar considerations, relative to the economy of the galvanic element, Joule arrived at his view; he found experimentally that the sum of the heat evolved in the circuit, of the heat consumed in the combustion of the gas developed, of the electro-magnetic work of the current, properly calculated,—in short, the sum of all the effects of the battery,—is connected with a proportionate consumption of zinc. Accordingly, this sum itself has a substantial character.
Mayer was so absorbed with the view attained, that the indestructibility of force, in our phraseology work, appeared to him a priori evident. "The creation or annihilation of a force," he says, "lies without the province of human thought and power." Joule expressed himself to a similar effect: "It is manifestly absurd to suppose that the powers with which God has endowed matter can be destroyed." Strange to say, on the basis of such utterances, not Joule, but Mayer, was stamped as a metaphysician. We may be sure, however, that both men were merely giving expression, and that half-unconsciously, to a powerful formal need of the new simple view, and that both would have been extremely surprised if it had been proposed to them that their principle should be submitted to a philosophical congress or ecclesiastical synod for a decision upon its validity. But with all agreements, the attitude of these two men, in other respects, was totally different. Whilst Mayer represented this formal need with all the stupendous instinctive force of genius, we might say almost with the ardor of fanaticism, yet was withal not wanting in the conceptive ability to compute, prior to all other inquirers, the mechanical equivalent of heat from old physical constants long known and at the disposal of all, and so to set up for the new doctrine a programme embracing all physics and physiology; Joule, on the other hand, applied himself to the exact verification of the doctrine by beautifully conceived and masterfully executed experiments, extending over all departments of physics. Soon Helmholtz too attacked the problem, in a totally independent and characteristic manner. After the professional virtuosity with which this physicist grasped and disposed of all the points unsettled by Mayer's programme and more besides, what especially strikes us is the consummate critical lucidity of this young man of twenty-six years. In his exposition is wanting that vehemence and impetuosity which marked Mayer's. The principle of the conservation of energy is no self-evident or a priori proposition for him. What follows, on the assumption that that proposition obtains? In this hypothetical form, he subjugates his matter.
I must confess, I have always marvelled at the æsthetic and ethical taste of many of our contemporaries who have managed to fabricate out of this relation of things, odious national and personal questions, instead of praising the good fortune that made several such men work together and of rejoicing at the instructive diversity and idiosyncrasies of great minds fraught with such rich consequences for us.
We know that still another theoretical conception played a part in the development of the principle of energy, which Mayer held aloof from, namely, the conception that heat, as also the other physical processes, are due to motion. But once the principle of energy has been reached, these auxiliary and transitional theories discharge no essential function, and we may regard the principle, like that which Black gave, as a contribution to the direct description of a widely extended domain of facts.
It would appear from such considerations not only advisable, but even necessary, with all due recognition of the helpfulness of theoretic ideas in research, yet gradually, as the new facts grow familiar, to substitute for indirect description direct description, which contains nothing that is unessential and restricts itself absolutely to the abstract apprehension of facts. We might almost say, that the descriptive sciences, so called with a tincture of condescension, have, in respect of scientific character, outstripped the physical expositions lately in vogue. Of course, a virtue has been made of necessity here.
We must admit, that it is not in our power to describe directly every fact, on the moment. Indeed, we should succumb in utter despair if the whole wealth of facts which we come step by step to know, were presented to us all at once. Happily, only detached and unusual features first strike us, and such we bring nearer to ourselves by comparison with every-day events. Here the notions of the common speech are first developed. The comparisons then grow more manifold and numerous, the fields of facts compared more extensive, the concepts that make direct description possible, proportionately more general and more abstract.
First we become familiar with the motion of freely falling bodies. The concepts of force, mass, and work are then carried over, with appropriate modifications, to the phenomena of electricity and magnetism. A stream of water is said to have suggested to Fourier the first distinct picture of currents of heat. A special case of vibrations of strings investigated by Taylor, cleared up for him a special case of the conduction of heat. Much in the same way that Daniel Bernoulli and Euler constructed the most diverse forms of vibrations of strings from Taylor's cases, so Fourier constructs out of simple cases of conduction the most multifarious motions of heat; and that method has extended itself over the whole of physics. Ohm forms his conception of the electric current in imitation of Fourier's. The latter, also, adopts Fick's theory of diffusion. In an analogous manner a conception of the magnetic current is developed. All sorts of stationary currents are thus made to exhibit common features, and even the condition of complete equilibrium in an extended medium shares these features with the dynamical condition of equilibrium of a stationary current. Things as remote as the magnetic lines of force of an electric current and the stream-lines of a frictionless liquid vortex enter in this way into a peculiar relationship of similarity. The concept of potential, originally enunciated for a restricted province, acquires a wide-reaching applicability. Things as dissimilar as pressure, temperature, and electromotive force, now show points of agreement in relation to ideas derived by definite methods from that concept: viz., fall of pressure, fall of temperature, fall of potential, as also with the further notions of liquid, thermal, and electric strength of current. That relationship between systems of ideas in which the dissimilarity of every two homologous concepts as well as the agreement in logical relations of every two homologous pairs of concepts, is clearly brought to light, is called an analogy. It is an effective means of mastering heterogeneous fields of facts in unitary comprehension. The path is plainly shown in which a universal physical phenomenology embracing all domains, will be developed.
In the process described we attain for the first time to what is indispensable in the direct description of broad fields of fact—the wide-reaching abstract concept. And now I must put a question smacking of the school-master, but unavoidable: What is a concept? Is it a hazy representation, admitting withal of mental visualisation? No. Mental visualisation accompanies it only in the simplest cases, and then merely as an adjunct. Think, for example, of the "coefficient of self-induction," and seek for its visualised mental image. Or is, perhaps, the concept a mere word? The adoption of this forlorn idea, which has been actually proposed of late by a reputed mathematician would only throw us back a thousand years into the deepest scholasticism. We must, therefore, reject it.
The solution is not far to seek. We must not think that sensation, or representation, is a purely passive process. The lowest organisms respond to it with a simple reflex motion, by engulfing the prey which approaches them. In higher organisms the centripetal stimulus encounters in the nervous system obstacles and aids which modify the centrifugal process. In still higher organisms, where prey is pursued and examined, the process in question may go through extensive paths of circular motions before it comes to relative rest. Our own life, too, is enacted in such processes; all that we call science may be regarded as parts, or middle terms, of such activities.
It will not surprise us now if I say: the definition of a concept, and, when it is very familiar, even its name, is an impulse to some accurately determined, often complicated, critical, comparative, or constructive activity, the usually sense-perceptive result of which is a term or member of the concept's scope. It matters not whether the concept draws the attention only to one certain sense (as sight) or to a phase of a sense (as color, form), or is the starting-point of a complicated action; nor whether the activity in question (chemical, anatomical, and mathematical operations) is muscular or technical, or performed wholly in the imagination, or only intimated. The concept is to the physicist what a musical note is to a piano-player. A trained physicist or mathematician reads a memoir like a musician reads a score. But just as the piano-player must first learn to move his fingers singly and collectively, before he can follow his notes without effort, so the physicist or mathematician must go through a long apprenticeship before he gains control, so to speak, of the manifold delicate innervations of his muscles and imagination. Think of how frequently the beginner in physics or mathematics performs more, or less, than is required, or of how frequently he conceives things differently from what they are! But if, after having had sufficient discipline, he lights upon the phrase "coefficient of self-induction," he knows immediately what that term requires of him. Long and thoroughly practised actions, which have their origin in the necessity of comparing and representing facts by other facts, are thus the very kernel of concepts. In fact, positive and philosophical philology both claim to have established that all roots represent concepts and stood originally for muscular activities alone. The slow assent of physicists to Kirchhoff's dictum now becomes intelligible. They best could feel the vast amount of individual labor, theory, and skill required before the ideal of direct description could be realised.
Suppose, now, the ideal of a given province of facts is reached. Does description accomplish all that the inquirer can ask? In my opinion, it does. Description is a building up of facts in thought, and this building up is, in the experimental sciences, often the condition of actual execution. For the physicist, to take a special case, the metrical units are the building-stones, the concepts the directions for building, and the facts the result of the building. Our mental imagery is almost a complete substitute for the fact, and by means of it we can ascertain all the fact's properties. We do not know that worst which we ourselves have made.
People require of science that it should prophesy, and Hertz uses that expression in his posthumous Mechanics. But, natural as it is, the expression is too narrow. The geologist and the palæontologist, at times the astronomer, and always the historian and the philologist, prophesy, so to speak, backwards. The descriptive sciences, like geometry and mathematics, prophesy neither forward or backwards, but seek from given conditions the conditioned. Let us say rather: Science completes in thought facts that are only partly given. This is rendered possible by description, for description presupposes the interdependence of the descriptive elements: otherwise nothing would be described.
It is said, description leaves the sense of causality unsatisfied. In fact, many imagine they understand motions better when they picture to themselves the pulling forces; and yet the accelerations, the facts, accomplish more, without superfluous additions. I hope that the science of the future will discard the idea of cause and effect, as being formally obscure; and in my feeling that these ideas contain a strong tincture of fetishism, I am certainly not alone. The more proper course is, to regard the abstract determinative elements of a fact as interdependent, in a purely logical way, as the mathematician or geometer does. True, by comparison with the will, forces are brought nearer to our feeling; but it may be that ultimately the will itself will be made clearer by comparison with the accelerations of masses.
If we are asked, candidly, when is a fact clear to us, we must say "when we can reproduce it by very simple and very familiar intellectual operations, such as the construction of accelerations, or the geometrical summation of accelerations, and so forth." The requirement of simplicity is of course to the expert a different matter from what it is to the novice. For the first, description by a system of differential equations is sufficient; for the second, a gradual construction out of elementary laws is required. The first discerns at once the connexion of the two expositions. Of course, it is not disputed that the artistic value of materially equivalent descriptions may not be different.
Most difficult is it to persuade strangers that the grand universal laws of physics, such as apply indiscriminately to material, electrical, magnetic, and other systems, are not essentially different from descriptions. As compared with many sciences, physics occupies in this respect a position of vantage that is easily explained. Take, for example, anatomy. As the anatomist in his quest for agreements and differences in animals ascends to ever higher and higher classifications, the individual facts that represent the ultimate terms of the system, are still so different that they must be singly noted. Think, for example, of the common marks of the Vertebrates, of the class-characters of Mammals and Birds on the one hand and of Fishes on the other, of the double circulation of the blood on the one hand and of the single on the other. In the end, always isolated facts remain, which show only a slight likeness to one another.
A science still more closely allied to physics, chemistry, is often in the same strait. The abrupt change of the qualitative properties, in all likelihood conditioned by the slight stability of the intermediate states, the remote resemblance of the co-ordinated facts of chemistry render the treatment of its data difficult. Pairs of bodies of different qualitative properties unite in different mass-ratios; but no connexion between the first and the last is to be noted, at first.
Physics, on the other hand, reveals to us wide domains of qualitatively homogeneous facts, differing from one another only in the number of equal parts into which their characteristic marks are divisible, that is, differing only quantitatively. Even where we have to deal with qualities (colors and sounds), quantitative characters of those qualities are at our disposal. Here the classification is so simple a task that it rarely impresses us as such, whilst in infinitely fine gradations, in a continuum of facts, our number-system is ready beforehand to follow as far as we wish. The co-ordinated facts are here extremely similar and very closely affined, as are also their descriptions which consist in the determination of the numerical measures of one given set of characters from those of a different set by means of familiar mathematical operations—methods of derivation. Thus, the common characteristics of all descriptions can be found here; and with them a succinct, comprehensive description, or a rule for the construction of all single descriptions, is assigned,—and this we call law. Well-known examples are the formulæ for freely falling bodies, for projectiles, for central motion, and so forth. If physics apparently accomplishes more by its methods than other sciences, we must remember that in a sense it has presented to it much simpler problems.
The remaining sciences, whose facts also present a physical side, need not be envious of physics for this superiority; for all its acquisitions ultimately redound to their benefit as well. But also in other ways this mutual help shall and must change. Chemistry has advanced very far in making the methods of physics her own. Apart from older attempts, the periodical series of Lothar Meyer and Mendelejeff are a brilliant and adequate means of producing an easily surveyed system of facts, which by gradually becoming complete, will take the place almost of a continuum of facts. Further, by the study of solutions, of dissociation, in fact generally of phenomena which present a continuum of cases, the methods of thermodynamics have found entrance into chemistry. Similarly we may hope that, at some future day, a mathematician, letting the fact-continuum of embryology play before his mind, which the palæontologists of the future will supposedly have enriched with more intermediate and derivative forms between Saurian and Bird than the isolated Pterodactyl, Archæopteryx, Ichthyornis, and so forth, which we now have—that such a mathematician shall transform, by the variation of a few parameters, as in a dissolving view, one form into another, just as we transform one conic section into another.
Reverting now to Kirchhoff's words, we can come to some agreement regarding their import. Nothing can be built without building-stones, mortar, scaffolding, and a builder's skill. Yet assuredly the wish is well founded, that will show to posterity the complete structure in its finished form, bereft of unsightly scaffolding. It is the pure logical and æsthetic sense of the mathematician that speaks out of Kirchhoff's words. Modern expositions of physics aspire after his ideal; that, too, is intelligible. But it would be a poor didactic shift, for one whose business it was to train architects, to say: "Here is a splendid edifice; if thou wouldst really build, go thou and do likewise".
The barriers between the special sciences, which make division of work and concentration possible, but which appear to us after all as cold and conventional restrictions, will gradually disappear. Bridge upon bridge is thrown over the gaps. Contents and methods, even of the remotest branches, are compared. When the Congress of Natural Scientists shall meet a hundred years hence, we may expect that they will represent a unity in a higher sense than is possible to-day, not in sentiment and aim alone, but in method also. In the meantime, this great change will be helped by our keeping constantly before our minds the fact of the intrinsic relationship of all research, which Kirchhoff characterised with such classical simplicity.
It is characteristic of the naïve and sanguine beginnings of thought in youthful men and nations, that all problems are held to be soluble and fundamentally intelligible on the first appearance of success. The sage of Miletus, on seeing plants take their rise from moisture, believed he had comprehended the whole of nature, and he of Samos, on discovering that definite numbers corresponded to the lengths of harmonic strings, imagined he could exhaust the nature of the world by means of numbers. Philosophy and science in such periods are blended. Wider experience, however, speedily discloses the error of such a course, gives rise to criticism, and leads to the division and ramification of the sciences.
At the same time, the necessity of a broad and general view of the world remains; and to meet this need philosophy parts company with special inquiry.[Pg 260] It is true, the two are often found united in gigantic personalities. But as a rule their ways diverge more and more widely from each other. And if the estrangement of philosophy from science can reach a point where data unworthy of the nursery are not deemed too scanty as foundations of the world, on the other hand the thorough-paced specialist may go to the extreme of rejecting point-blank the possibility of a broader view, or at least of deeming it superfluous, forgetful of Voltaire's apophthegm, nowhere more applicable than here, Le superflu—chose très nécessaire.
It is true, the history of philosophy, owing to the insufficiency of its constructive data, is and must be largely a history of error. But it would be the height of ingratitude on our part to forget that the seeds of thoughts which still fructify the soil of special research, such as the theory of irrationals, the conceptions of conservation, the doctrine of evolution, the idea of specific energies, and so forth, may be traced back in distant ages to philosophical sources. Furthermore, to have deferred or abandoned the attempt at a broad philosophical view of the world from a full knowledge of the insufficiency of our materials, is quite a different thing from never having undertaken it at all. The revenge of its neglect, moreover, is constantly visited upon the specialist by his committal of the very errors which philosophy long ago exposed. As a fact, in physics and physiology, particularly during the first half of this century, are to be[Pg 261] met intellectual productions which for naïve simplicity are not a jot inferior to those of the Ionian school, or to the Platonic ideas, or to that much reviled ontological proof.
Latterly, there has been evidence of a gradual change in the situation. Recent philosophy has set itself more modest and more attainable ends; it is no longer inimical to special inquiry; in fact, it is zealously taking part in that inquiry. On the other hand, the special sciences, mathematics and physics, no less than philology, have become eminently philosophical. The material presented is no longer accepted uncritically. The glance of the inquirer is bent upon neighboring fields, whence that material has been derived. The different special departments are striving for closer union, and gradually the conviction is gaining ground that philosophy can consist only of mutual, complemental criticism, interpenetration, and union of the special sciences into a consolidated whole. As the blood in nourishing the body separates into countless capillaries, only to be collected again and to meet in the heart, so in the science of the future all the rills of knowledge will gather more and more into a common and undivided stream.
It is this view—not an unfamiliar one to the present generation—that I purpose to advocate. Entertain no hope, or rather fear, that I shall construct systems for you. I shall remain a natural inquirer. Nor expect that it is my intention to skirt all the[Pg 262] fields of natural inquiry. I can attempt to be your guide only in that branch which is familiar to me, and even there I can assist in the furtherment of only a small portion of the allotted task. If I shall succeed in rendering plain to you the relations of physics, psychology, and the theory of knowledge, so that you may draw from each profit and light, redounding to the advantage of each, I shall regard my work as not having been in vain. Therefore, to illustrate by an example how, consonantly with my powers and views, I conceive such inquiries should be conducted, I shall treat to-day, in the form of a brief sketch, of the following special and limited subject—of the part which accidental circumstances play in the development of inventions and discoveries.
When we Germans say of a man that he was not the inventor of gunpowder,[82] we impliedly cast a grave suspicion on his abilities. But the expression is not a felicitous one, as there is probably no invention in which deliberate thought had a smaller, and pure luck a larger, share than in this. It is well to ask, Are we justified in placing a low estimate on the achievement of an inventor because accident has assisted him in his work? Huygens, whose discoveries and inventions are justly sufficient to entitle him to an opinion in such matters, lays great emphasis on this factor. He asserts that a man capable of inventing the telescope without the concurrence of accident must have been gifted with superhuman genius.[83]
A man living in the midst of civilisation finds himself surrounded by a host of marvellous inventions, considering none other than the means of satisfying the needs of daily life. Picture such a man transported to the epoch preceding the invention of these ingenious appliances, and imagine him undertaking in a serious manner to comprehend their origin. At first the intellectual power of the men capable of producing such marvels will strike him as incredible, or, if we adopt the ancient view, as divine. But his astonishment is considerably allayed by the disenchanting yet elucidative revelations of the history of primitive culture, which to a large extent prove that these inventions took their rise very slowly and by imperceptible degrees.
A small hole in the ground with fire kindled in it constituted the primitive stove. The flesh of the quarry, wrapped with water in its skin, was boiled by contact with heated stones. Cooking by stones was also done in wooden vessels. Hollow gourds were protected from the fire by coats of clay. Thus, from the burned clay accidentally originated the enveloping pot, which rendered the gourd superfluous, although for a long time thereafter the clay was still spread over the gourd, or pressed into woven wicker-work before the potter's art assumed its final independence. Even then the wicker-work ornament was retained, as a sort of attest of its origin.
We see, thus, it is by accidental circumstances, or by such as lie without our purpose, foresight, and power, that man is gradually led to the acquaintance of improved means of satisfying his wants. Let the reader picture to himself the genius of a man who could have foreseen without the help of accident that clay handled in the ordinary manner would produce a useful cooking utensil! The majority of the inventions made in the early stages of civilisation, including language, writing, money, and the rest, could not have been the product of deliberate methodical reflexion for the simple reason that no idea of their value and significance could have been had except from practical use. The invention of the bridge may have been suggested by the trunk of a tree which had fallen athwart a mountain-torrent; that of the tool by the use of a stone accidentally taken into the hand to crack nuts. The use of fire probably started in and was disseminated from regions where volcanic eruptions, hot springs, and burning jets of natural gas afforded opportunity for quietly observing and turning to practical account the properties of fire. Only after that had been done could the significance of the fire-drill be appreciated, an instrument which was probably discovered from boring a hole through a piece of wood. The suggestion of a distinguished inquirer that the invention of the fire-drill originated on the occasion of a religious ceremony is both fantastic and incredible. And as to the use of fire, we should no more attempt to derive that from the invention of the fire-drill than we should from the invention of sulphur matches. Unquestionably the opposite course was the real one.[84]
Similar phenomena, though still largely veiled in obscurity, mark the initial transition of nations from a hunting to a nomadic life and to agriculture.[85] We shall not multiply examples, but content ourselves with the remark that the same phenomena recur in historical times, in the ages of great technical inventions, and, further, that regarding them the most whimsical notions have been circulated—notions which ascribe to accident an unduly exaggerated part, and one which in a psychological respect is absolutely impossible. The observation of steam escaping from a tea-kettle and of the clattering of the lid is supposed to have led to the invention of the steam-engine. Just think of the gap between this spectacle and the conception of the performance of great mechanical work by steam, for a man totally ignorant of the steam-engine! Let us suppose, however, that an engineer, versed in the practical construction of pumps, should accidentally dip into water an inverted bottle that had been filled with steam for drying and still retained its steam. He would see the water rush violently into the bottle, and the idea would very naturally suggest itself of founding on this experience a convenient and useful atmospheric steam-pump, which by imperceptible degrees, both psychologically possible and immediate, would then undergo a natural and gradual transformation into Watt's steam-engine.
But granting that the most important inventions are brought to man's notice accidentally and in ways that are beyond his foresight, yet it does not follow that accident alone is sufficient to produce an invention. The part which man plays is by no means a passive one. Even the first potter in the primeval forest must have felt some stirrings of genius within him. In all such cases, the inventor is obliged to take note of the new fact, he must discover and grasp its advantageous feature, and must have the power to turn that feature to account in the realisation of his purpose. He must isolate the new feature, impress it upon his memory, unite and interweave it with the rest of his thought; in short, he must possess the capacity to profit by experience.
The capacity to profit by experience might well be set up as a test of intelligence. This power varies considerably in men of the same race, and increases enormously as we advance from the lower animals to man. The former are limited in this regard almost entirely to the reflex actions which they have inherited with their organism, they are almost totally incapable of individual experience, and considering their simple wants are scarcely in need of it. The ivory-snail (Eburna spirata) never learns to avoid the carnivorous Actinia, no matter how often it may wince under the latter's shower of needles, apparently having no memory for pain whatever.[86] A spider can be lured forth repeatedly from its hole by touching its web with a tuning-fork. The moth plunges again and again into the flame which has burnt it. The humming-bird hawk-moth[87] dashes repeatedly against the painted roses of the wall-paper, like the unhappy and desperate thinker who never wearies of attacking the same insoluble chimerical problem. As aimlessly almost as Maxwell's gaseous molecules and in the same unreasoning manner common flies in their search for light and air stream against the glass pane of a half-opened window and remain there from sheer inability to find their way around the narrow frame. But a pike separated from the minnows of his aquarium by a glass partition, learns after the lapse of a few months, though only after having butted himself half to death, that he cannot attack these fishes with impunity. What is more, he leaves them in peace even after the removal of the partition, though he will bolt a strange fish at once. Considerable memory must be attributed to birds of passage, a memory which, probably owing to the absence of disturbing thoughts, acts with the precision of that of some idiots. Finally, the susceptibility to training evinced by the higher vertebrates is indisputable proof of the ability of these animals to profit by experience.
A powerfully developed mechanical memory, which recalls vividly and faithfully old situations, is sufficient for avoiding definite particular dangers, or for taking advantage of definite particular opportunities. But more is required for the development of inventions. More extensive chains of images are necessary here, the excitation by mutual contact of widely different trains of ideas, a more powerful, more manifold, and richer connexion of the contents of memory, a more powerful and impressionable psychical life, heightened by use. A man stands on the bank of a mountain-torrent, which is a serious obstacle to him. He remembers that he has crossed just such a torrent before on the trunk of a fallen tree. Hard by trees are growing. He has often moved the trunks of fallen trees. He has also felled trees before, and then moved them. To fell trees he has used sharp stones. He goes in search of such a stone, and as the old situations that crowd into his memory and are held there in living reality by the definite powerful interest which he has in crossing just this torrent,—as these impressions are made to pass before his mind in the inverse order in which they were here evoked, he invents the bridge.
There can be no doubt but the higher vertebrates adapt their actions in some moderate degree to circumstances. The fact that they give no appreciable evidence of advance by the accumulation of inventions, is satisfactorily explained by a difference of degree or intensity of intelligence as compared with man; the assumption of a difference of kind is not necessary. A person who saves a little every day, be it ever so little, has an incalculable advantage over him who daily squanders that amount, or is unable to keep what he has accumulated. A slight quantitative difference in such things explains enormous differences of advancement.
The rules which hold good in prehistoric times also hold good in historical times, and the remarks made on invention may be applied almost without modification to discovery; for the two are distinguished solely by the use to which the new knowledge is put. In both cases the investigator is concerned with some newly observed relation of new or old properties, abstract or concrete. It is observed, for example, that a substance which gives a chemical reaction A is also the cause of a chemical reaction B. If this observation fulfils no purpose but that of furthering the scientist's insight, or of removing a source of intellectual discomfort, we have a discovery; but an invention, if in using the substance giving the reaction A to produce the desired reaction B, we have a practical end in view, and seek to remove a source of material discomfort. The phrase, disclosure of the connexion of reactions, is broad enough to cover discoveries and inventions in all departments. It embraces the Pythagorean proposition, which is a combination of a geometrical and an arithmetical reaction, Newton's discovery of the connexion of Kepler's motions with the law of the inverse squares, as perfectly as it does the detection of some minute but appropriate alteration in the construction of a tool, or of some appropriate change in the methods of a dyeing establishment.
The disclosure of new provinces of facts before unknown can only be brought about by accidental circumstances, under which are remarked facts that commonly go unnoticed. The achievement of the discoverer here consists in his sharpened attention, which detects the uncommon features of an occurrence and their determining conditions from their most evanescent marks,[88] and discovers means of submitting them to exact and full observation. Under this head belong the first disclosures of electrical and magnetic phenomena, Grimaldi's observation of interference, Arago's discovery of the increased check suffered by a magnetic needle vibrating in a copper envelope as compared with that observed in a bandbox, Foucault's observation of the stability of the plane of vibration of a rod accidentally struck while rotating in a turning-lathe, Mayer's observation of the increased redness of venous blood in the tropics, Kirchhoff's observation of the augmentation of the D-line in the solar spectrum by the interposition of a sodium lamp, Schönbein's discovery of ozone from the phosphoric smell emitted on the disruption of air by electric sparks, and a host of others. All these facts, of which unquestionably many were seen numbers of times before they were noticed, are examples of the inauguration of momentous discoveries by accidental circumstances, and place the importance of strained attention in a brilliant light.
But not only is a significant part played in the beginning of an inquiry by co-operative circumstances beyond the foresight of the investigator; their influence is also active in its prosecution. Dufay, thus, whilst following up the behavior of one electrical state which he had assumed, discovers the existence of two. Fresnel learns by accident that the interference-bands received on ground glass are seen to better advantage in the open air. The diffraction-phenomenon of two slits proved to be considerably different from what Fraunhofer had anticipated, and in following up this circumstance he was led to the important discovery of grating-spectra. Faraday's induction-phenomenon departed widely from the initial conception which occasioned his experiments, and it is precisely this deviation that constitutes his real discovery.
Every man has pondered on some subject. Every one of us can multiply the examples cited, by less illustrious ones from his own experience. I shall cite but one. On rounding a railway curve once, I accidentally remarked a striking apparent inclination of the houses and trees. I inferred that the direction of the total resultant physical acceleration of the body reacts physiologically as the vertical. Afterwards, in attempting to inquire more carefully into this phenomenon, and this only, in a large whirling machine, the collateral phenomena conducted me to the sensation of angular acceleration, vertigo, Flouren's experiments on the section of the semi-circular canals etc., from which gradually resulted views relating to sensations of direction which are also held by Breuer and Brown, which were at first contested on all hands, but are now regarded on many sides as correct, and which have been recently enriched by the interesting inquiries of Breuer concerning the macula acustica, and Kreidel's experiments with magnetically orientable crustacea.[89] Not disregard of accident but a direct and purposeful employment of it advances research.
The more powerful the psychical connexion of the memory pictures is,—and it varies with the individual and the mood,—the more apt is the same accidental observation to be productive of results. Galileo knows that the air has weight; he also knows of the "resistance to a vacuum," expressed both in weight and in the height of a column of water. But the two ideas dwelt asunder in his mind. It remained for Torricelli to vary the specific gravity of the liquid measuring the pressure, and not till then was the air included in the list of pressure-exerting fluids. The reversal of the lines of the spectrum was seen repeatedly before Kirchhoff, and had been mechanically explained. But it was left for his penetrating vision to discern the evidence of the connexion of this phenomenon with questions of heat, and to him alone through persistent labor was revealed the sweeping significance of the fact for the mobile equilibrium of heat. Supposing, then, that such a rich organic connexion of the elements of memory exists, and is the prime distinguishing mark of the inquirer, next in importance certainly is that intense interest in a definite object, in a definite idea, which fashions advantageous combinations of thought from elements before disconnected, and obtrudes that idea into every observation made, and into every thought formed, making it enter into relationship with all things. Thus Bradley, deeply engrossed with the subject of aberration, is led to its solution by an exceedingly unobtrusive experience in crossing the Thames. It is permissible, therefore, to ask whether accident leads the discoverer, or the discoverer accident, to a successful outcome in scientific quests.
No man should dream of solving a great problem unless he is so thoroughly saturated with his subject that everything else sinks into comparative insignificance. During a hurried meeting with Mayer in Heidelberg once, Jolly remarked, with a rather dubious implication, that if Mayer's theory were correct water could be warmed by shaking. Mayer went away without a word of reply. Several weeks later, and now unrecognised by Jolly, he rushed into the latter's presence exclaiming: "Es ischt aso!" (It is so, it is so!) It was only after considerable explanation that Jolly found out what Mayer wanted to say. The incident needs no comment.[90]
A person deadened to sensory impressions and given up solely to the pursuit of his own thoughts, may also light on an idea that will divert his mental activity into totally new channels. In such cases it is a psychical accident, an intellectual experience, as distinguished from a physical accident, to which the person owes his discovery—a discovery which is here made "deductively" by means of mental copies of the world, instead of experimentally. Purely experimental inquiry, moreover, does not exist, for, as Gauss says, virtually we always experiment with our thoughts. And it is precisely that constant, corrective interchange or intimate union of experiment and deduction, as it was cultivated by Galileo in his Dialogues and by Newton in his Optics, that is the foundation of the benign fruitfulness of modern scientific inquiry as contrasted with that of antiquity, where observation and reflexion ofttimes pursued their respective courses like two strangers.
We have to wait for the appearance of a favorable physical accident. The movement of our thoughts obeys the law of association. In the case of meagre experience the result of this law is simply the mechanical reproduction of definite sensory experiences. On the other hand, if the psychical life is subjected to the incessant influences of a powerful and rich experience, then every representative element in the mind is connected with so many others that the actual and natural course of the thoughts is easily influenced and determined by insignificant circumstances, which accidentally are decisive. Hereupon, the process termed imagination produces its protean and infinitely diversified forms. Now what can we do to guide this process, seeing that the combinatory law of the images is without our reach? Rather let us ask, what influence can a powerful and constantly recurring idea exert on the movement of our thoughts? According to what has preceded, the answer is involved in the question itself. The idea dominates the thought of the inquirer, not the latter the former.
Let us see, now, if we can acquire a profounder insight into the process of discovery. The condition of the discoverer is, as James has aptly remarked, not unlike the situation of a person who is trying to remember something that he has forgotten. Both are sensible of a gap, and have only a remote presentiment of what is missing. Suppose I meet in a company a well-known and affable gentleman whose name I have forgotten, and who to my horror asks to be introduced to some one. I set to work according to Lichtenberg's rule, and run down the alphabet in search of the initial letter of his name. A vague sympathy holds me at the letter G. Tentatively I add the second letter and am arrested at e, and long before I have tried the third letter r, the name "Gerson" sounds sonorously upon my ear, and my anguish is gone. While taking a walk I meet a gentleman from whom I receive a communication. On returning home, and in attending to weightier affairs, the matter slips my mind. Moodily, but in vain, I ransack my memory. Finally I observe that I am going over my walk again in thought. On the street corner in question the self-same gentleman stands before me and repeats his communication. In this process are successively recalled to consciousness all the percepts which were connected with the percept that was lost, and with them, finally, that, too, is brought to light. In the first case—where the experience had already been made and is permanently impressed on our thought—a systematic procedure is both possible and easy, for we know that a name must be composed of a limited number of sounds. But at the same time it should be observed that the labor involved in such a combinatorial task would be enormous if the name were long and the responsiveness of the mind weaker.
It is often said, and not wholly without justification, that the scientist has solved a riddle. Every problem in geometry may be clothed in the garb of a riddle. Thus: "What thing is that M which has the properties A, B, C?" "What circle is that which touches the straight lines A, B, but touches B in the point C?" The first two conditions marshal before the imagination the group of circles whose centres lie in the line of symmetry of A, B. The third condition reminds us of all the circles having centres in the straight line that stands at right angles to B in C. The common term, or common terms, of the two groups of images solves the riddle—satisfies the problem. Puzzles dealing with things or words induce similar processes, but the memory in such cases is exerted in many directions and more varied and less clearly ordered provinces of ideas are surveyed. The difference between the situation of a geometer who has a construction to make, and that of an engineer, or a scientist, confronted with a problem, is simply this, that the first moves in a field with which he is thoroughly acquainted, whereas the two latter are obliged to familiarise themselves with this field subsequently, and in a measure far transcending what is commonly required. In this process the mechanical engineer has at least always a definite goal before him and definite means to accomplish his aim, whilst in the case of the scientist that aim is in many instances presented only in vague and general outlines. Often the very formulation of the riddle devolves on him. Frequently it is not until the aim has been reached that the broader outlook requisite for systematic procedure is obtained. By far the larger portion of his success, therefore, is contingent on luck and instinct. It is immaterial, so far as its character is concerned, whether the process in question is brought rapidly to a conclusion in the brain of one man, or whether it is spun out for centuries in the minds of a long succession of thinkers. The same relation that a word solving a riddle bears to that riddle is borne by the modern conception of light to the facts discovered by Grimaldi, Römer, Huygens, Newton, Young, Malus, and Fresnel, and only by the help of this slowly developed conception is our mental vision enabled to embrace the broad domain of facts in question.
A welcome complement to the discoveries which the history of civilisation and comparative psychology have furnished, is to be found in the confessions of great scientists and artists. Scientists and artists, we might say, for Liebig boldly declared there was no essential difference between the two. Are we to regard Leonardo da Vinci as a scientist or as an artist? If the artist builds up his work from a few motives, the scientist discovers the motives which permeate reality. If scientists like Lagrange or Fourier are in a certain measure artists in the presentation of their results, on the other hand, artists like Shakespeare or Ruysdael are scientists in the insight which must have preceded their creations.
Newton, when questioned about his methods of work, could give no other answer but that he was wont to ponder again and again on a subject; and similar utterances are accredited to D'Alembert and Helmholtz. Scientists and artists both recommend persistent labor. After the repeated survey of a field has afforded opportunity for the interposition of advantageous accidents, has rendered all the traits that suit with the mood or the dominant thought more vivid, and has gradually relegated to the background all things that are inappropriate, making their future appearance impossible; then from the teeming, swelling host of fancies which a free and high-flown imagination calls forth, suddenly that particular form arises to the light which harmonises perfectly with the ruling idea, mood, or design. Then it is that that which has resulted slowly as the result of a gradual selection, appears as if it were the outcome of a deliberate act of creation. Thus are to be explained the statements of Newton, Mozart, Richard Wagner, and others, when they say that thoughts, melodies, and harmonies had poured in upon them, and that they had simply retained the right ones. Undoubtedly, the man of genius, too, consciously or instinctively, pursues systematic methods wherever it is possible; but in his delicate presentiment he will omit many a task or abandon it after a hasty trial on which a less endowed man would squander his energies in vain. Thus, the genius accomplishes[91] in a brief space of time undertakings for which the life of an ordinary man would far from suffice. We shall hardly go astray if we regard genius as only a slight deviation from the average mental endowment—as possessing simply a greater sensitiveness of cerebral reaction and a greater swiftness of reaction. The men who, obeying their inner impulses, make sacrifices for an idea instead of advancing their material welfare, may appear to the full-blooded Philistine as fools; yet we shall scarcely adopt Lombroso's view, that genius is to be regarded as a disease, although it is unfortunately true that the sensitive brains and fragile constitutions succumb most readily to sickness.
The remark of C. G. J. Jacobi that mathematics is slow of growth and only reaches the truth by long and devious paths, that the way to its discovery must be prepared for long beforehand, and that then the truth will make its long-deferred appearance as if impelled by some divine necessity[92]—all this holds true of every science. We are astounded often to note that it required the combined labors of many eminent thinkers for a full century to reach a truth which it takes us only a few hours to master and which once acquired seems extremely easy to reach under the right sort of circumstances. To our humiliation we learn that even the greatest men are born more for life than for science. The extent to which even they are indebted to accident—to that singular conflux of the physical and the psychical life in which the continuous but yet imperfect and never-ending adaptation of the latter to the former finds its distinct expression—that has been the subject of our remarks to-day. Jacobi's poetical thought of a divine necessity acting in science will lose none of its loftiness for us if we discover in this necessity the same power that destroys the unfit and fosters the fit. For loftier, nobler, and more romantic than poetry is the truth and the reality.
Through the co-operation of a succession of inquirers, among whom are particularly to be mentioned Goltz of Strassburg and Breuer of Vienna, considerable advances have been made during the last twenty-five years in our knowledge of the means by which we ascertain our position in space and the direction of our motion, or orient ourselves, as the phrase goes. I presume that you are already acquainted with the physiological part of the processes with which our sensations of movement, or, more generally speaking, our sensations of orientation, are connected. Here I shall consider more particularly the physical side of the matter. In fact, I was originally led to the consideration of these questions by the observation of extremely simple and perfectly well-known physical facts, before I had any great acquaintance with physiology and while pursuing unbiasedly my natural thoughts; and I am of the conviction that[Pg 283] the way which I have pursued, and which is entirely free from hypotheses, will, if you will follow my exposition, be that of easiest acquisition for the most of you.
No man of sound common sense could ever have doubted that a pressure or force is requisite to set a body in motion in a given direction and that a contrary pressure is required to stop suddenly a body in motion. Though the law of inertia was first formulated with anything like exactness by Galileo, the facts at the basis of it were known long previously to men of the stamp of Leonardo da Vinci, Rabelais, and others, and were illustrated by them with appropriate experiments. Leonardo knew that by a swift stroke with a ruler one can knock out from a vertical column of checkers a single checker without over-throwing the column. The experiment with a coin resting on a piece of pasteboard covering a goblet, which falls into the goblet when the pasteboard is jerked away, like all experiments of the kind, is certainly very old.
With Galileo the experience in question assumes greater clearness and force. In the famous dialogue on the Copernican system which cost him his freedom, he explains the tides in an unfelicitous, though in principle correct manner, by the analogue of a platter of water swung to and fro. In opposition to the Aristotelians of his time, who believed the descent[Pg 284] of a heavy body could be accelerated by the superposition of another heavy body, he asserted that a body could never be accelerated by one lying upon it unless the first in some way impeded the superposed body in its descent. To seek to press a falling body by means of another placed upon it, is as senseless as trying to prod a man with a lance when the man is speeding away from one with the same velocity as the lance. Even this little excursion into physics can explain much to us. You know the peculiar sensation which one has in falling, as when one jumps from a high springboard into the water, and which is also experienced in some measure at the beginning of the descent of elevators and swings. The reciprocal gravitational pressure of the different parts of our body, which is certainly felt in some manner, vanishes in free descent, or, in the case of the elevator, is diminished on the beginning of the descent. A similar sensation would be experienced if we were suddenly transported to the moon where the acceleration of gravity is much less than upon the earth. I was led to these considerations in 1866 by a suggestion in physics, and having also taken into account the alterations of the blood-pressure in the cases in question, I found I coincided without knowing it with Wollaston and Purkinje. The first as early as 1810 in his Croonian lecture had touched on the subject of sea-sickness and explained it by alterations of the blood-pressure,[Pg 285] and later had laid similar considerations at the basis of his explanation of vertigo (1820-1826).[94]
Newton was the first to enunciate with perfect generality that a body can change the velocity and direction of its motion only by the action of a force, or the action of a second body. A corollary of this law which was first expressly deduced by Euler is that a body can never be set rotating or made to cease rotating of itself but only by forces and other bodies. For example, turn an open watch which has run down freely backwards and forwards in your hand. The balance-wheel will not fully catch the rapid rotations, it does not even respond fully to the elastic force of the spring which proves too weak to carry the wheel entirely with it.
Let us consider now that whether we move ourselves by means of our legs, or whether we are moved by a vehicle or a boat, at first only a part of our body is directly moved and the rest of it is afterwards set in motion by the first part. We see that pressures, pulls, and tensions are always produced between the parts of the body in this action, which pressures, pulls, and tensions give rise to sensations by which the forward or rotary movements in which we are engaged are made perceptible.[95] But it is quite natural that sensations so familiar should be little noticed and that attention should be drawn to them only under special circumstances when they occur unexpectedly or with unusual strength.
 Fig. 45.
Fig. 45.
Thus my attention was drawn to this point by the sensation of falling and subsequently by another singular occurrence. I was rounding a sharp railway curve once when I suddenly saw all the trees, houses, and factory chimneys along the track swerve from the vertical and assume a strikingly inclined position. What had hitherto appeared to me perfectly natural, namely, the fact that we distinguish the vertical so perfectly and sharply from every other direction, now[Pg 287] struck me as enigmatical. Why is it that the same direction can now appear vertical to me and now cannot? By what is the vertical distinguished for us? (Compare Figure 45.)
The rails are raised on the convex or outward side of the track in order to insure the stability of the carriage as against the action of the centrifugal force, the whole being so arranged that the combination of the force of gravity with the centrifugal force of the train shall give rise to a force perpendicular to the plane of the rails.
Let us assume, now, that under all circumstances we somehow sense the direction of the total resultant mass-acceleration whencesoever it may arise as the vertical. Then both the ordinary and the extraordinary phenomena will be alike rendered intelligible.[96]
I was now desirous of putting the view I had reached to a more convenient and exact test than was possible on a railway journey where one has no control over the determining circumstances and cannot alter them at will. I accordingly had the simple apparatus constructed which is represented in Figure 46.
In a large frame BB, which is fastened to the walls, rotates about a vertical axis AA a second frame RR, and within the latter a third one rr, which can be set[Pg 288] at any distance and position from the axis, made stationary or movable, and is provided with a chair for the observer.
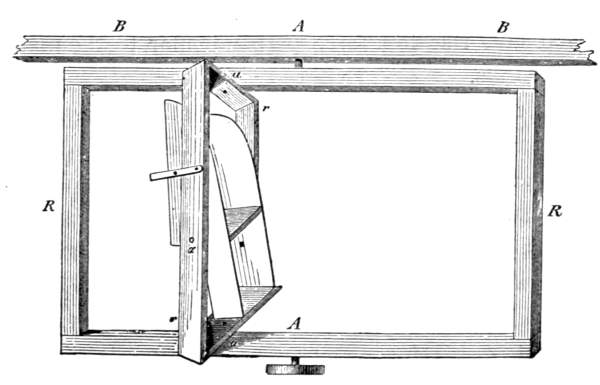 Fig. 46.
Fig. 46.
From Mach's Bewegungsempfindungen, Leipsic, Engelmann, 1875.]
The observer takes his seat in the chair and to prevent disturbances of judgment is enclosed in a paper box. If the observer together with the frame rr be then set in uniform rotation, he will feel and see the beginning of the rotation both as to direction and amount very distinctly although every outward visible or tangible point of reference is wanting. If the motion be uniformly continued the sensation of rotation will gradually cease entirely and the observer will imagine himself at rest. But if rr be placed outside the axis of rotation, at once on the rotation beginning, a strikingly apparent, palpable, actually visible inclination of the entire paper box is produced, slight when[Pg 289] the rotation is slow, strong when the rotation is rapid, and continuing as long as the rotation lasts. It is absolutely impossible for the observer to escape perceiving the inclination, although here also all outward points of reference are wanting. If the observer, for example, is seated so as to look towards the axis, he will feel the box strongly tipped backwards, as it necessarily must be if the direction of the total resultant force is perceived as the vertical. For other positions of the observer the situation is similar.[97]
Once, while performing one of these experiments, and after rotating so long that I was no longer conscious of the movement, I suddenly caused the apparatus to be stopped, whereupon I immediately felt and saw myself with the whole box rapidly flung round in rotation in the opposite direction, although I knew that the whole apparatus was at rest and every outward point of reference for the perception of motion was wanting. Every one who disbelieves in sensations of movement should be made acquainted with these phenomena. Had Newton known them and had he ever observed how we may actually imagine ourselves turned and displaced in space without the assistance of stationary bodies as points of reference, he would certainly have been confirmed more than ever[Pg 290] in his unfortunate speculations regarding absolute space.
The sensation of rotation in the opposite direction after the apparatus has been stopped, slowly and gradually ceases. But on accidentally inclining my head once during this occurrence, the axis of apparent rotation was also observed to incline in exactly the same manner both as to direction and as to amount. It is accordingly clear that the acceleration or retardation of rotation is felt. The acceleration operates as a stimulus. The sensation, however, like almost all sensations, though it gradually decreases, lasts perceptibly longer than the stimulus. Hence the long continued apparent rotation after the stopping of the apparatus. The organ, however, which causes the persistence of this sensation must have its seat in the head, since otherwise the axis of apparent rotation could not assume the same motion as the head.
If I were to say, now, that a light had flashed upon me in making these last observations, the expression would be a feeble one. I ought to say I experienced a perfect illumination. My juvenile experiences of vertigo occurred to me. I remembered Flourens's experiments relative to the section of the semi-circular canals of the labyrinths of doves and rabbits, where this inquirer had observed phenomena similar to vertigo, but which he preferred to interpret, from his bias to the acoustic theory of the labyrinth, as the expression of painful auditive disturbances. I[Pg 291] saw that Goltz had nearly but not quite hit the bull's eye with his theory of the semi-circular canals. This inquirer, who, from his happy habit of following his own natural thoughts without regard for tradition, has cleared up so much in science, spoke, as early as 1870, on the ground of experiments, as follows: "It is uncertain whether the semi-circular canals are auditive organs or not. In any event they form an apparatus which serves for the preservation of equilibrium. They are, so to speak, the sense-organs of equilibrium of the head and indirectly of the whole body." I remembered the galvanic dizziness which had been observed by Ritter and Purkinje on the passage of a current through the head, when the persons experimented upon imagined they were falling towards the cathode. The experiment was immediately repeated, and sometime later (1874) I was enabled to demonstrate the same objectively with fishes, all of which placed themselves sidewise and in the same direction in the field of the current as if at command.[98] Müller's doctrine of specific energies now appeared to me to bring all these new and old observations into a simple, connected unity.
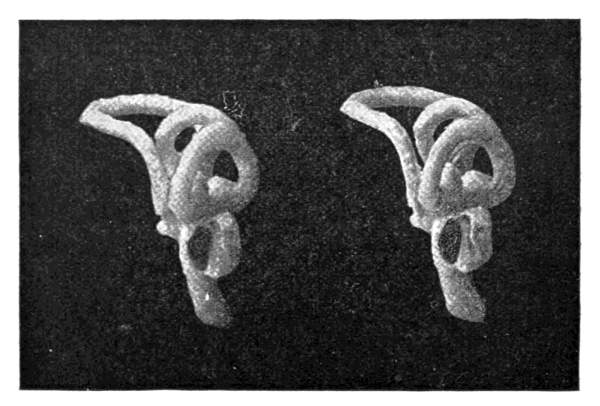 Fig. 47.
Fig. 47.
The labyrinth of a dove (stereoscopically reproduced), from R. Ewald, Nervus Octavus, Wiesbaden, Bergmann, 1892.]
Let us picture to ourselves the labyrinth of the ear with its three semi-circular canals lying in three mutually perpendicular planes (Comp. Fig. 47), the[Pg 292] mysterious position of which inquirers have endeavored to explain in every possible and impossible way. Let us conceive the nerves of the ampullæ, or the dilated extensions of the semi-circular canals, equipped with a capacity for responding to every imaginable stimulus with a sensation of rotation just as the nerves of the retina of the eye when excited by pressures, by electrical or chemical stimuli always respond with the sensation of light; let us picture to ourselves, further, that the usual excitation of the ampullæ nerves is produced by the inertia of the contents of the semi-circular canals, which contents on suitable rotations in the plane of the semi-circular canal are left behind in the motion, or at least have a tendency[Pg 293] to remain behind and consequently exert a pressure. It will be seen that on this supposition all the single facts which without the theory appear as so many different individual phenomena, become from this single point of view clear and intelligible.
I had the satisfaction, immediately after the communication in which I set forth this idea,[99] of seeing a paper by Breuer appear[100] in which this author had arrived by entirely different methods at results that agreed in all essential points with my own. A few weeks later appeared the researches of Crum Brown of Edinburgh, whose methods were even still nearer mine. Breuer's paper was far richer in physiological respects than mine, and he had particularly gone into greater detail in his investigation of the collateral effects of the reflex motions and orientation of the eyes in the phenomena under consideration.[101] In addition certain experiments which I had suggested in my paper as a test of the correctness of the view in question had already been performed by Breuer. Breuer has also rendered services of the highest order in the further elaboration of this field. But in a physical regard, my paper was, of course, more complete.
In order to portray to the eye the behavior of the semi-circular canals, I have constructed here a little[Pg 294] apparatus. (See Fig. 48.) The large rotatable disc represents the osseous semi-circular canal, which is continuous with the bones of the head; the small disc, which is free to rotate on the axis of the first, represents the mobile and partly liquid contents of the semi-circular canal. On rotating the large disc, the small disc as you see remains behind. I have to turn some time before the small disc is carried along with the large one by friction. But if I now stop the large disc the small disc as you see continues to rotate.
 Fig. 48.
Fig. 48.
Model representing the action of the semi-circular canals.]
Simply assume now that the rotation of the small disc, say in the direction of the hands of a watch, would give rise to a sensation of rotation in the opposite direction, and conversely, and you already understand a good portion of the facts above set forth. The explanation still holds, even if the small disc does not perform appreciable rotations but is checked by a contrivance similar to an elastic spring, the tension[Pg 295] of which disengages a sensation. Conceive, now, three such contrivances with their mutually perpendicular planes of rotation joined together so as to form a single apparatus; then to this apparatus as a whole, no rotation can be imparted without its being indicated by the small mobile discs or by the springs which are attached to them. Conceive both the right and the left ear equipped with such an apparatus, and you will find that it answers all the purposes of the semi-circular canals, which you see represented stereoscopically in Fig. 47 for the ear of a dove.
Of the many experiments which I have made on my own person, and the results of which could be predicted by the new view according to the behavior of the model and consequently according to the rules of mechanics, I shall cite but one. I fasten a horizontal board in the frame RR of my rotatory apparatus, lie down upon the same with my right ear upon the board, and cause the apparatus to be uniformly rotated. As soon as I no longer perceive the rotation, I turn around upon my left ear and immediately the sensation of rotation again starts up with marked vividness. The experiment can be repeated as often as one wishes. A slight turn of the head even is sufficient for reviving the sensation of rotation which in the perfectly quiescent state at once disappears altogether.
We will imitate the experiment on the model. I turn the large disc until finally the small disc is carried[Pg 296] along with it. If, now, while the rotation continues uniform, I burn off a little thread which you see here, the small disc will be flipped round by a spring into its own plane 180°, so as now to present its opposite side to you, when the rotation at once begins in the opposite direction.
We have consequently a very simple means for determining whether one is actually the subject or not of uniform and imperceptible rotations. If the earth rotated much more rapidly than it really does, or if our semi-circular canals were much more sensitive, a Nansen sleeping at the North Pole would be waked by a sensation of rotation every time he turned over. Foucault's pendulum experiment as a demonstration of the earth's rotation would be superfluous under such circumstances. The only reason we cannot prove the rotation of the earth with the help of our model, lies in the small angular velocity of the earth and in the consequent liability to great experimental errors.[102]
Aristotle has said that "The sweetest of all things is knowledge." And he is right. But if you were to suppose that the publication of a new view were productive of unbounded sweetness, you would be mightily mistaken. No one disturbs his fellow-men with a new view unpunished. Nor should the fact be made a subject of reproach to these fellow-men. To[Pg 297] presume to revolutionise the current way of thinking with regard to any question, is no pleasant task, and above all not an easy one. They who have advanced new views know best what serious difficulties stand in their way. With honest and praiseworthy zeal, men set to work in search of everything that does not suit with them. They seek to discover whether they cannot explain the facts better or as well, or approximately as well, by the traditional views. And that, too, is justified. But at times some extremely artless animadversions are heard that almost nonplus us. "If a sixth sense existed it could not fail to have been discovered thousands of years ago." Indeed; there was a time, then, when only seven planets could have existed! But I do not believe that any one will lay any weight on the philological question whether the set of phenomena which we have been considering should be called a sense. The phenomena will not disappear when the name disappears. It was further said to me that animals exist which have no labyrinth, but which can yet orientate themselves, and that consequently the labyrinth has nothing to do with orientation. We do not walk forsooth with our legs, because snakes propel themselves without them!
But if the promulgator of a new idea cannot hope for any great pleasure from its publication, yet the critical process which his views undergo is extremely helpful to the subject-matter of them. All the defects which necessarily adhere to the new view are gradually[Pg 298] discovered and eliminated. Over-rating and exaggeration give way to more sober estimates. And so it came about that it was found unpermissible to attribute all functions of orientation exclusively to the labyrinth. In these critical labors Delage, Aubert, Breuer, Ewald, and others have rendered distinguished services. It can also not fail to happen that fresh facts become known in this process which could have been predicted by the new view, which actually were predicted in part, and which consequently furnish a support for the new view. Breuer and Ewald succeeded in electrically and mechanically exciting the labyrinth, and even single parts of the labyrinth, and thus in producing the movements that belong to such stimuli. It was shown that when the semi-circular canals were absent vertigo could not be produced, when the entire labyrinth was removed the orientation of the head was no longer possible, that without the labyrinth galvanic vertigo could not be induced. I myself constructed as early as 1875 an apparatus for observing animals in rotation, which was subsequently reinvented in various forms and has since received the name of "cyclostat."[103] In experiments with the most varied kinds of animals it was shown that, for example, the larvæ of frogs are not subject to vertigo until their semi-circular canals which at the start are wanting are developed (K. Schäfer). A large percentage of the deaf and dumb are afflicted with grave affections[Pg 299] of the labyrinth. The American psychologist, William James, has made whirling experiments with many deaf and dumb subjects, and in a large number of them found that susceptibility to giddiness is wanting. He also found that many deaf and dumb people on being ducked under water, whereby they lose their weight and consequently have no longer the full assistance of their muscular sense, utterly lose their sense of position in space, do not know which is up and which is down, and are thrown into the greatest consternation,—results which do not occur in normal men. Such facts are convincing proof that we do not orientate ourselves entirely by means of the labyrinth, important as it is for us. Dr. Kreidl has made experiments similar to those of James and found that not only is vertigo absent in deaf and dumb people when whirled about, but that also the reflex movements of the eyes which are normally induced by the labyrinth are wanting. Finally, Dr. Pollak has found that galvanic vertigo does not exist in a large percentage of the deaf and dumb. Neither the jerking movements nor the uniform movements of the eyes were observed which normal human beings exhibit in the Ritter and Purkinje experiment.
After the physicist has arrived at the idea that the semi-circular canals are the organ of sensation of rotation or of angular acceleration, he is next constrained to ask for the organs that mediate the sensation of acceleration noticed in forward movements.[Pg 300] In searching for an organ for this function, he of course is not apt to select one that stands in no anatomical and spatial relation with the semi-circular canals. And in addition there are physiological considerations to be weighed. The preconceived opinion once having been abandoned that the entire labyrinth is auditory in its function, there remains after the cochlea is reserved for sensations of tone and the semi-circular canals for the sensation of angular acceleration, the vestibule for the discharge of additional functions. The vestibule, particularly the part of it known as the sacculus, appeared to me, by reason of the so-called otoliths which it contains, eminently adapted for being the organ of sensation of forward acceleration or of the position of the head. In this conjecture I again closely coincided with Breuer.
That a sensation of position, of direction and amount of mass-acceleration exists, our experience in elevators as well as of movement in curved paths is sufficient proof. I have also attempted to produce and destroy suddenly great velocities of forward movement by means of various contrivances of which I shall mention only one here. If, while enclosed in the paper box of my large whirling apparatus at some distance from the axis, my body is in uniform rotation which I no longer feel, and I then loosen the connexions of the frame rr with R thus making the former moveable and I then suddenly stop the larger frame, my forward motion is abruptly impeded while the[Pg 301] frame rr continues to rotate. I imagine now that I am speeding on in a straight line in a direction opposite to that of the checked motion. Unfortunately, for many reasons it cannot be proved convincingly that the organ in question has its seat in the head. According to the opinion of Delage, the labyrinth has nothing to do with this particular sensation of movement. Breuer, on the other hand, is of the opinion that the organ of forward movement in man is stunted and the persistence of the sensation in question is too brief to permit our instituting experiments as obvious as in the case of rotation. In fact, Crum Brown once observed while in an irritated condition peculiar vertical phenomena in his own person, which were all satisfactorily explained by an abnormally long persistence of the sensation of rotation, and I myself in an analogous case on the stopping of a railway train felt the apparent backward motion in striking intensity and for an unusual length of time.
There is no doubt whatever that we feel changes of vertical acceleration, and it will appear from the following extremely probable that the otoliths of the vestibule are the sense-organ for the direction of the mass-acceleration. It will then be incompatible with a really logical view to regard the latter as incapable of sensing horizontal accelerations.
In the lower animals the analogue of the labyrinth is shrunk to a little vesicle filled with a liquid and containing tiny crystals, auditive stones, or otoliths, of[Pg 302] greater specific gravity, suspended on minute hairs. These crystals appear physically well adapted for indicating both the direction of gravity and the direction of incipient movements. That they discharge the former function, Delage was the first to convince himself by experiments with lower animals which on the removal of the otoliths utterly lost their bearings and could no longer regain their normal position. Loeb also found that fishes without labyrinths swim now on their bellies and now on their backs. But the most remarkable, most beautiful, and most convincing experiment is that which Dr. Kreidl instituted with crustaceans. According to Hensen, certain Crustacea on sloughing spontaneously introduce fine grains of sand as auditive stones into their otolith vesicle. At the ingenious suggestion of S. Exner, Dr. Kreidl constrained some of these animals to put up with iron filings (ferrum limatum). If the pole of an electro-magnet be brought near the animal, it will at once turn its back away from the pole accompanying the movement with appropriate reflex motions of the eye the moment the current is closed, exactly as if gravity had been brought to bear upon the animal in the same direction as the magnetic force.[104] This, in fact, is what should be expected from the function ascribed to the otoliths. If the eyes be covered with asphalt[Pg 303] varnish, and the auditive sacs removed, the crustaceans lose their sense of direction utterly, tumble head over heels, lie on their side or their back indifferently. This does not happen when the eyes only are covered. For vertebrates, Breuer has demonstrated by searching investigations that the otoliths, or better, statoliths, slide in three planes parallel to the planes of the semi-circular canals, and are consequently perfectly adapted for indicating changes both in the amount and the direction of the mass-acceleration.[105]
I have already remarked that not every function of orientation can be ascribed exclusively to the labyrinth. The deaf and dumb who have to be immersed in water, and the crustaceans who must have their eyes closed if they are to be perfectly disorientated, are proof of this fact. I saw a blind cat at Hering's laboratory which to one who was not a very attentive observer behaved exactly like a seeing cat. It played nimbly with objects rolling on the floor, stuck its head inquisitively into open drawers, sprang dexterously upon chairs, ran with perfect accuracy through open[Pg 304] doors, and never bumped against closed ones. The visual sense had here been rapidly replaced by the tactual and auditive senses. And it appears from Ewald's investigations that even after the labyrinths have been removed, animals gradually learn to move about again quite in the normal fashion, presumably because the eliminated function of the labyrinth is now performed by some part of the brain. A certain peculiar weakness of the muscles alone is perceptible which Ewald ascribes to the absence of the stimulus which is otherwise constantly emitted by the labyrinth (the labyrinth-tonus). But if the part of the brain which discharges the deputed function be removed, the animals are again completely disorientated and absolutely helpless.
It may be said that the views enunciated by Breuer, Crum Brown and myself in 1873 and 1874, and which are substantially a fuller and richer development of Goltz's idea, have upon the whole been substantiated. At least they have exercised a helpful and stimulative influence. New problems have of course arisen in the course of the investigation which still await solution, and much work remains to be done. At the same time we see how fruitful the renewed co-operation of the various special departments of science may become after a period of isolation and invigorating labor apart.
I may be permitted, therefore, to consider the relation between hearing and orientation from another[Pg 305] and more general point of view. What we call the auditive organ is in the lower animals simply a sac containing auditive stones. As we ascend the scale, 1, 2, 3 semi-circular canals gradually develop from them, whilst the structure of the otolith organ itself becomes more complicated. Finally, in the higher vertebrates, and particularly in the mammals, a part of the latter organ (the lagena) becomes the cochlea, which Helmholtz explained as the organ for sensations of tone. In the belief that the entire labyrinth was an auditive organ, Helmholtz, contrary to the results of his own masterly analysis, originally sought to interpret another part of the labyrinth as the organ of noises. I showed a long time ago (1873) that every tonal stimulus by shortening the duration of the excitation to a few vibrations, gradually loses its character of pitch and takes on that of a sharp, dry report or noise.[106] All the intervening stages between tones and noises can be exhibited. Such being the case, it will hardly be assumed that one organ is suddenly and at some given point replaced in function by another. On the basis of different experiments and reasonings S. Exner also regards the assumption of a special organ for the sensing of noises as unnecessary.
If we will but reflect how small a portion of the labyrinth of higher animals is apparently in the service of the sense of hearing, and how large, on the other[Pg 306] hand, the portion is which very likely serves the purposes of orientation, how much the first anatomical beginnings of the auditive sac of lower animals resemble that part of the fully developed labyrinth which does not hear, the view is irresistibly suggested which Breuer and I (1874, 1875) expressed, that the auditive organ took its development from an organ for sensing movements by adaptation to weak periodic motional stimuli, and that many apparatuses in the lower animals which are held to be organs of hearing are not auditive organs at all.[107]
This view appears to be perceptibly gaining ground. Dr. Kreidl by skilfully-planned experiments has arrived at the conclusion that even fishes do not hear, whereas E. H. Weber, in his day, regarded the ossicles which unite the air-bladder of fishes with the labyrinth as organs expressly designed for conducting sound from the former to the latter.[108] Störensen has investigated the excitation of sounds by the air-bladder of fishes, as also the conduction of shocks through Weber's ossicles. He regards the air-bladder as particularly adapted for receiving the noises made by other fishes and conducting them to the labyrinth. He has heard the loud grunting tones of the fishes in South American rivers, and is of the opinion that they allure and find each other in this manner. According to these views certain fishes are neither deaf nor dumb.[109] The question here involved might be solved perhaps by sharply distinguishing between the sensation of hearing proper, and the perception of shocks. The first-mentioned sensation may, even in the case of many vertebrates, be extremely restricted, or perhaps even absolutely wanting. But besides the auditive function, Weber's ossicles may perfectly well discharge some other function. Although, as Moreau has shown, the air-bladder itself is not an organ of equilibrium in the simple physical sense of Borelli, yet doubtless some function of this character is still reserved for it. The union with the labyrinth favors this conception, and so a host of new problems rises here before us.
I should like to close with a reminiscence from the year 1863. Helmholtz's Sensations of Tone had just been published and the function of the cochlea now appeared clear to the whole world. In a private conversation which I had with a physician, the latter declared it to be an almost hopeless undertaking to seek to fathom the function of the other parts of the labyrinth, whereas I in youthful boldness maintained that the question could hardly fail to be solved, and that very soon, although of course I had then no glimmering of how it was to be done. Ten years later the question was substantially solved.
To-day, after having tried my powers frequently and in vain on many questions, I no longer believe[Pg 308] that we can make short work of the problems of science. Nevertheless, I should not consider an "ignorabimus" as an expression of modesty, but rather as the opposite. That expression is a suitable one only with regard to problems which are wrongly formulated and which are therefore not problems at all. Every real problem can and will be solved in due course of time without supernatural divination, entirely by accurate observation and close, searching thought.
"I have led my ragamuffins where they were peppered."—Falstaff.
"He goes but to see a noise that he heard."—Midsummer Night's Dream.
To shoot, in the shortest time possible, as many holes as possible in one another's bodies, and not always for exactly pardonable objects and ideals, seems to have risen to the dignity of a duty with modern men, who, by a singular inconsistency, and in subservience to a diametrically contrary ideal, are bound by the equally holy obligation of making these holes as small as possible, and, when made, of stopping them up and of healing them as speedily as possible. Since, then, shooting and all that appertains thereto, is a very important, if not the most important, affair of modern life, you will doubtless not be averse to giving your attention for an hour to some experiments which have been undertaken, not for advancing the ends of war, but for promoting the ends of science,[Pg 310] and which throw some light on the phenomena attending the flight of projectiles.
Modern science strives to construct its picture of the world not from speculations but so far as possible from facts. It verifies its constructs by recourse to observation. Every newly observed fact completes its world-picture, and every divergence of a construct from observation points to some imperfection, to some lacuna in it. What is seen is put to the test of, and supplemented by, what is thought, which is again naught but the result of things previously seen. It is always peculiarly fascinating, therefore, to subject to direct verification by observation, that is, to render palpable to the senses, something which we have only theoretically excogitated or theoretically surmised.
In 1881, on hearing in Paris the lecture of the Belgian artillerist Melsens, who hazarded the conjecture that projectiles travelling at a high rate of speed carry masses of compressed air before them which are instrumental in producing in bodies struck by the projectiles certain well-known facts of the nature of explosions, the desire arose in me of experimentally testing his conjecture and of rendering the phenomenon, if it really existed, perceptible. The desire was the stronger as I could say that all the means for realising it existed, and that I had in part already used and tested them for other purposes.
And first let us get clear regarding the difficulties which have to be surmounted. Our task is that of[Pg 311] observing a bullet or other projectile which is rushing through space at a velocity of many hundred yards a second, together with the disturbances which the bullet causes in the surrounding atmosphere. Even the opaque solid body itself, the projectile, is only exceptionally visible under such circumstances—only when it is of considerable size and when we see its line of flight in strong perspective abridgement so that the velocity is apparently diminished. We see a large projectile quite clearly when we stand behind the cannon and look steadily along its line of flight or in the less pleasant case when the projectile is speeding towards us. There is, however, a very simple and effective method of observing swiftly moving bodies with as little trouble as if they were held at rest at some point in their path. The method is that of illumination by a brilliant electric spark of extremely short duration in a dark room. But since, for the full intellectual comprehension of a picture presented to the eye, a certain, not inconsiderable interval of time is necessary, the method of instantaneous photography will naturally also be employed. The pictures, which are of extremely minute duration, are thus permanently recorded and can be examined and analysed at one's convenience and leisure.
With the difficulty just mentioned is associated still another and greater difficulty which is due to the air. The atmosphere in its usual condition is generally not visible even when at rest. But the task presented[Pg 312] to us is to render visible masses of air which in addition are moving with a high velocity.
To be visible, a body must either emit light itself, must shine, or must affect in some way the light which falls upon it, must take up that light entirely or partly, absorb it, or must have a deflective effect upon it, that is, reflect or refract it. We cannot see the air as we can a flame, for it shines only exceptionally, as in a Geissler's tube. The atmosphere is extremely transparent and colorless; it cannot be seen, therefore, as a dark or colored body can, or as chlorine gas can, or vapor of bromine or iodine. Air, finally, has so small an index of refraction and so small a deflective influence upon light, that the refractive effect is commonly imperceptible altogether.
A glass rod is visible in air or in water, but it is almost invisible in a mixture of benzol and bisulphuret of carbon, which has the same mean index of refraction as the glass. Powdered glass in the same mixture has a vivid coloring, because owing to the decomposition of the colors the indices are the same for only one color which traverses the mixture unimpeded, whilst the other colors undergo repeated reflexions.[111]
Water is invisible in water, alcohol in alcohol. But if alcohol be mixed with water the flocculent streaks of the alcohol in the water will be seen at once and[Pg 313] vice versa. And in like manner the air, too, under favorable circumstances, may be seen. Over a roof heated by the burning sun, a tremulous wavering of objects is noticeable, as there is also over red-hot stoves, radiators, and registers. In all these cases tiny flocculent masses of hot and cold air, of slightly differing refrangibility, are mingled together.
In like manner the more highly refracting parts of non-homogeneous masses of glass, the so-called striæ or imperfections of the glass, are readily detectible among the less refracting parts which constitute the bulk of the same. Such glasses are unserviceable for optical purposes, and special attention has been devoted to the investigation of the methods for eliminating or avoiding these defects. The result has been the development of an extremely delicate method for detecting optical faults—the so-called method of Foucault and Toepler—which is suitable also for our present purpose.
 Fig. 49.
Fig. 49.
Even Huygens when trying to detect the presence of striæ in polished glasses viewed them under oblique illumination, usually at a considerable distance, so as to give full scope to the aberrations, and had recourse for greater exactitude to a telescope. But the method was carried to its highest pitch of perfection in 1867 by Toepler who employed the following procedure: A small luminous source a (Fig. 49) illuminates a lens L which throws an image b of the luminous source. If the eye be so placed that the image falls on the[Pg 314] pupil, the entire lens, if perfect, will appear equally illuminated, for the reason that all points of it send out rays to the eye. Coarse imperfections of form or of homogeneity are rendered visible only in case the aberrations are so large that the light from many spots passes by the pupil of the eye. But if the image b be partly intercepted by the edge of a small slide, then those spots in the lens as thus partly darkened will appear brighter whose light by its greater aberrations still reaches the eye in spite of the intercepting slide, while those spots will appear darker which in consequence of aberration in the other direction throw their light entirely upon the slide. This artifice of the intercepting slide which had previously been employed by Foucault for the investigation of the optical imperfections of mirrors enhances enormously the delicacy of the method, which is still further augmented by Toepler's employment of a telescope behind the slide. Toepler's method, accordingly, enjoys all the advantages of the Huygens and the Foucault procedure combined. It is so delicate that the minutest irregularities in the air surrounding the lens can be rendered distinctly visible, as I shall show by an example. I[Pg 315] place a candle before the lens L (Fig. 50) and so arrange a second lens M that the flame of the candle is imaged upon the screen S. As soon as the intercepting slide is pushed into the focus, b, of the light issuing from a, you see the images of the changes of density and the images of the movements induced in the air by the flame quite distinctly upon the screen. The distinctness of the phenomenon as a whole depends upon the position of the intercepting slide b. The removal of b increases the illumination but decreases the distinctness. If the luminous source a be removed, we see the image of the candle flame only upon the screen S. If we remove the flame and allow a to continue shining, the screen S will appear uniformly illuminated.
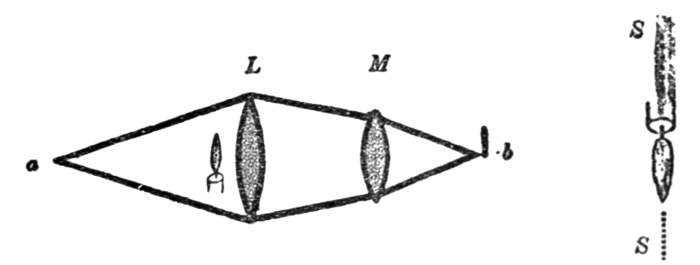 Fig. 50.
Fig. 50.
After Toepler had sought long and in vain to render the irregularities produced in air by sound-waves visible by this principle, he was at last conducted to his goal by the favorable circumstances attending the production of electric sparks. The waves generated in the air by electric sparks and accompanying the explosive snapping of the same, are of sufficiently[Pg 316] short period and sufficiently powerful to be rendered visible by these methods. Thus we see how by a careful regard for the merest and most shadowy indications of a phenomenon and by slight progressive and appropriate alterations of the circumstances and the methods, ultimately the most astounding results can be attained. Consider, for example, two such phenomena as the rubbing of amber and the electric lighting of modern streets. A person ignorant of the myriad minute links that join these two things together, will be absolutely nonplussed at their connexion, and will comprehend it no more than the ordinary observer who is unacquainted with embryology, anatomy, and paleontology will understand the connexion between a saurian and a bird. The high value and significance of the co-operation of inquirers through centuries, where each has but to take up the thread of work of his predecessors and spin it onwards, is rendered forcibly evident by such examples. And such knowledge destroys, too, in the clearest manner imaginable that impression of the marvellous which the spectator may receive from science, and at the same time is a most salutary admonishment to the worker in science against superciliousness. I have also to add the sobering remark that all our art would be in vain did not nature herself afford at least some slight guiding threads leading from a hidden phenomenon into the domain of the observable. And so it need not surprise us that once under particularly favorable[Pg 317] circumstances an extremely powerful sound-wave which had been caused by the explosion of several hundred pounds of dynamite threw a directly visible shadow in the sunlight, as Boys has recently told us. If the sound-waves were absolutely without influence upon the light, this could not have occurred, and all our artifices would then, too, be in vain. And so, similarly, the phenomenon accompanying projectiles which I am about to show you was once in a very imperfect manner incidentally seen by a French artillerist, Journée, while that observer was simply following the line of flight of a projectile with a telescope, just as also the undulations produced by candle flames are in a weak degree directly visible and in the bright sunlight are imaged in shadowy waves upon a uniform white background.
Instantaneous illumination by the electric spark, the method of rendering visible small optical differences or striæ, which may hence be called the striate, or differential, method,[112] invented by Foucault and Toepler, and finally the recording of the image by a photographic plate,—these therefore are the chief means which are to lead us to our goal.
I instituted my first experiments in the summer of 1884 with a target-pistol, shooting the bullet through a striate field as described above, and taking care that the projectile whilst in the field should disengage an illuminating electric spark from a Leyden jar or Franklin's pane, which spark produced a photographic impression of the projectile upon a plate, especially arranged for the purpose. I obtained the image of the projectile at once and without difficulty. I also readily obtained, with the still rather defective dry plate which I was using, exceedingly delicate images of the sound-waves (spark-waves). But no atmospheric condensation produced by the projectile was visible. I now determined the velocity of my projectile and found it to be only 240 metres per second, or considerably less than the velocity of sound (which is 340 metres per second). I saw immediately that under such circumstances no noticeable compression of the air could be produced, for any atmospheric compression must of necessity travel forward at the same speed with sound (340 metres per second) and consequently would be always ahead of and speeding away from the projectile.
I was so thoroughly convinced, however, of the existence of the supposed phenomenon at a velocity exceeding 340 metres per second, that I requested[Pg 319] Professor Salcher, of Fiume, an Austrian port on the Gulf of Quarnero, to undertake the experiment with projectiles travelling at a high rate of speed. In the summer of 1886 Salcher in conjunction with Professor Riegler conducted in a spacious and suitable apartment placed at their disposal by the Directors of the Royal Imperial Naval Academy, experiments of the kind indicated and conforming in method exactly to those which I had instituted, with the precise results expected. The phenomenon, in fact, accorded perfectly with the a priori sketch of it which I had drafted previously to the experiment. As the experimenting was continued, new and unforeseen features made their appearance.
It would be unfair, of course, to expect from the very first experiments faultless and highly distinct photographs. It was sufficient that success was secured and that I had convinced myself that further labor and expenditure would not be vain. And on this score I am greatly indebted to the two gentlemen above mentioned.
The Austrian Naval Department subsequently placed a cannon at Salcher's disposal in Pola, an Adriatic seaport, and I myself, together with my son, then a student of medicine, having received and accepted a courteous invitation from Krupp, repaired to Meppen, a town in Hanover, where we conducted with only the necessary apparatus several experiments on the open artillery range. All these experiments[Pg 320] furnished tolerably good and complete pictures. Some little progress, too, was made. The outcome of our experience on both artillery ranges, however, was the settled conviction that really good results could be obtained only by the most careful conduct of the experiments in a laboratory especially adapted to the purpose. The expensiveness of the experiments on a large scale was not the determining consideration here, for the size of the projectile is indifferent. Given the same velocity and the results are quite similar, whether the projectiles are large or small. On the other hand, in a laboratory the experimenter has perfect control over the initial velocity, which, provided the proper equipment is at hand, can be altered at will simply by altering the charge and the weight of the projectile. The requisite experiments were accordingly conducted by me in my laboratory at Prague, partly in conjunction with my son and partly afterwards by him alone. The latter are the most perfect and I shall accordingly speak in detail here of these only.
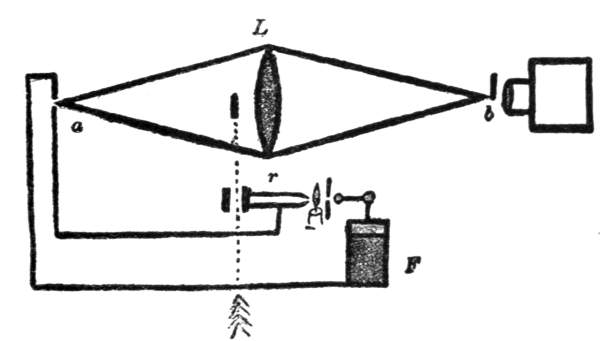 Fig. 51.
Fig. 51.
Picture to yourself an apparatus for detecting optical striæ set up in a dark room. In order not to make the description too complicated, I shall give the essential features only of the apparatus, leaving out of account altogether the minuter details which are rather of consequence for the technical performance of the experiment than for its understanding. We suppose the projectile speeding on its path, accordingly,[Pg 321] through the field of our differential optical apparatus. On reaching the centre of the field (Fig. 51) the projectile disengages an illuminating electric spark a, and the image of the projectile, so produced, is photographically impressed upon the plate of the camera behind the intercepting slide b. In the last and best experiments the lens L was replaced by a spherical silvered-glass mirror made by K. Fritsch (formerly Prokesch) of Vienna, whereby the apparatus was naturally more complicated than it appears in our diagram. The projectile having been carefully aimed passes in crossing the differential field between two vertical isolated wires which are connected with the two coatings of a Leyden jar, and completely filling the space between the wires discharges the jar. In the axis of the differential apparatus the circuit has a second gap a which furnishes the illuminating spark, the image of which falls on the intercepting slide b. The wires in the differential field having occasioned[Pg 322] manifold disturbances were subsequently done away with. In the new arrangement the projectile passes through a ring (see dotted line, Fig. 51), to the air in which it imparts a sharp impulse which travels forward in the tube r as a sound-wave having the approximate velocity of 340 metres per second, topples over through the aperture of an electric screen the flame of a candle situated at the other opening of the tube, and so discharges the jar. The length of the tube r is so adjusted that the discharge occurs the moment the projectile enters the centre of the now fully clear and free field of vision. We will also leave out of account the fact that to secure fully the success of the experiment, a large jar is first discharged by the flame, and that by the agency of this first discharge the discharge of a second small jar having a spark of very short period which furnishes the spark really illuminating the projectile is effected. Sparks from large jars have an appreciable duration, and owing to the great velocity of the projectiles furnish blurred photographs only. By carefully husbanding the light of the differential apparatus, and owing to the fact that much more light reaches the photographic plate in this way than would otherwise reach it, we can obtain beautiful, strong, and sharp photographs with incredibly small sparks. The contours of the pictures appear as very delicate and very sharp, closely adjacent double lines. From their distance from one another, and from the velocity of the projectile,[Pg 323] the duration of the illumination, or of the spark, is found to be 1/800000 of a second. It is evident, therefore, that experiments with mechanical snap slides can furnish no results worthy of the name.
 Fig. 52.
Fig. 52.
Let us consider now first the picture of a projectile in the rough, as represented in Figure 52, and then let us examine it in its photographic form as seen in Figure 53. The latter picture is of a shot from an Austrian Mannlicher rifle. If I were not to tell you what the picture represented you would very likely imagine it to be a bird's eye view of a boat b moving swiftly through the water. In front you see the bow-wave and behind the body a phenomenon k which closely resembles the eddies formed in the wake of a[Pg 324] ship. And as a matter of fact the dark hyperboloid arc which streams from the tip of the projectile really is a compressed wave of air exactly analogous to the bow-wave produced by a ship moving through the water, with the exception that the wave of air is not a surface-wave. The air-wave is produced in atmospheric space and encompasses the projectile in the form of a shell on all sides. The wave is visible for the same reason that the heated shell of air surrounding the candle flame of our former experiments is visible. And the cylinder of friction-heated air which the projectile throws off in the form of vortex rings really does answer to the water in the wake of a vessel.
 Fig. 53. Photograph of a blunted projectile.]
Fig. 53. Photograph of a blunted projectile.]
Now just as a slowly moving boat produces no bow-wave, but the bow-wave is seen only when the boat moves with a speed which is greater than the velocity of propagation of surface-waves in water, so, in like manner, no wave of compression is visible in front of a projectile so long as the speed of the projectile is less than the velocity of sound. But if the speed of the projectile reaches and exceeds the velocity of sound, then the head-wave, as we shall call it, augments noticeably in power, and is more and more extended, that is, the angle made by the contours of the wave with the direction of flight is more and more diminished, just as when the speed of a boat is increased a similar phenomenon is noticed in connexion with the bow-wave. In fact, we can from an instantaneous photograph so taken approximately estimate the speed with which the projectile is travelling.
The explanation of the bow-wave of a ship and that of the head-wave of a body travelling in atmospheric space both repose upon the same principle, long ago employed by Huygens. Conceive a number of pebbles to be cast into a pond of water at regular intervals in such wise that all the spots struck are situate in the same straight line, and that every spot subsequently struck lies a short space farther to the right. The spots first struck will furnish then the wave-circles which are widest, and all of them together will, at the points where they are thickest, form a sort of cornucopia closely resembling the bow-wave.[Pg 326] (Fig. 54.) The resemblance is greater the smaller the pebbles are, and the more quickly they succeed each other. If a rod be dipped into the water and quickly carried along its surface, the falling of the pebbles will then take place, so to speak, uninterruptedly, and we shall have a real bow-wave. If we put the compressed air-wave in the place of the surface-waves of the water, we shall have the head-wave of the projectile.
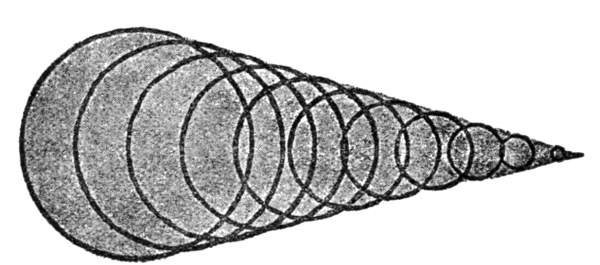 Fig. 54.
Fig. 54.
You may be disposed to say now, it is all very pretty and interesting to observe a projectile in its flight, but of what practical use is it?
It is true, I reply, one cannot wage war with photographed projectiles. And I have likewise often had to say to medical students attending my lectures on physics, when they inquired for the practical value of some physical observation, "You cannot, gentlemen, cure diseases with it." I had also once to give my opinion regarding how much physics should be taught at a school for millers, supposing the instruction there to be confined exactly to what was necessary for[Pg 327] a miller. I was obliged to reply: "A miller always needs exactly as much physics as he knows." Knowledge which one does not possess one cannot use.
Let us forego entirely the consideration that as a general thing every scientific advance, every new problem elucidated, every extension or enrichment of our knowledge of facts, affords a better foundation for practical pursuits. Let us rather put the special question, Is it not possible to derive some really practical knowledge from our theoretical acquaintance with the phenomena which take place in the space surrounding a projectile?
No physicist who has ever studied waves of sound or photographed them will have the least doubt regarding the sound-wave character of the atmospheric condensation encompassing the head of a flying projectile. We have therefore, without ado, called this condensation the head-wave.
Knowing this, it follows that the view of Melsens according to which the projectile carries along with it masses of air which it forces into the bodies struck, is untenable. A forward-moving sound-wave is not a forward-moving mass of matter but a forward-moving form of motion, just as a water-wave or the waves of a field of wheat are only forward-moving forms of motion and not movements of masses of water or masses of wheat.
By interference-experiments, on which I cannot touch here but which will be found roughly represented[Pg 328] in Figure 55, it was found that the bell-shaped head-wave in question is an extremely thin shell and that the condensations of the same are quite moderate, scarcely exceeding two-tenths of an atmosphere. There can be no question, therefore, of explosive effects in the body struck by the projectile through so slight a degree of atmospheric compression. The phenomena attending wounds from rifle balls, for example, are not to be explained as Melsens and Busch explain them, but are due, as Kocher and Reger maintain, to the effects of the impact of the projectile itself.
 Fig. 55.
Fig. 55.
A simple experiment will show how insignificant is the part played by the friction of the air, or the supposed conveyance of the air along with the moving projectile. If the photograph of the projectile be[Pg 329] taken while passing through a flame, i. e., a visible gas, the flame will be seen to be, not torn and deformed, but smoothly and cleanly perforated, like any solid body. Within and around the flame the contours of the head-wave will be seen. The flickering, the extinction of the flame, etc., take place only after the projectile has travelled on a considerable distance in its path, and is then affected by the powder gases which hurry after the bullet or by the air preceding the powder-gases.
The physicist who examines the head-wave and recognises its sound-wave character also sees that the wave in question is of the same kind with the short sharp waves produced by electric sparks, that it is a noise-wave. Hence, whenever any portion of the head-wave strikes the ear it will be heard as a report. Appearances point to the conclusion that the projectile carries this report along with it. In addition to this report, which advances with the velocity of the projectile and so usually travels at a speed greater than the velocity of sound, there is also to be heard the report of the exploding powder which travels forward with the ordinary velocity of sound. Hence two explosions will be heard, each distinct in time. The circumstance that this fact was long misconstrued by practical observers but when actually noticed frequently received grotesque explanations and that ultimately my view was accepted as the correct one, appears to me in itself a sufficient justification that[Pg 330] researches such as we are here speaking of are not utterly superfluous even in practical directions. That the flashes and sounds of discharging artillery are used for estimating the distances of batteries is well known, and it stands to reason that any unclear theoretical conception of the facts here involved will seriously affect the correctness of practical calculations.
It may appear astonishing to a person hearing it for the first time, that a single shot has a double report due to two different velocities of propagation. But the reflexion that projectiles whose velocity is less than the velocity of sound produce no head-waves (because every impulse imparted to the air travels forward, that is, ahead, with exactly the velocity of sound), throws full light when logically developed upon the peculiar circumstance above mentioned. If the projectile moves faster than sound, the air ahead of it cannot recede from it quickly enough. The air is condensed and warmed, and thereupon, as all know, the velocity of sound is augmented until the head-wave travels forward as rapidly as the projectile itself, so that there is no need whatever of any additional augmentation of the velocity of propagation. If such a wave were left entirely to itself, it would increase in length and soon pass into an ordinary sound-wave, travelling with less velocity. But the projectile is always behind it and so maintains it at its proper density and velocity. Even if the projectile penetrates a piece of cardboard or a board of wood, which catches[Pg 331] and obstructs the head-wave, there will, as Figure 56 shows, immediately appear at the emerging apex a newly formed, not to say newly born, head-wave. We may observe on the cardboard the reflexion and diffraction of the head-wave, and by means of a flame its refraction, so that no doubt as to its nature can remain.
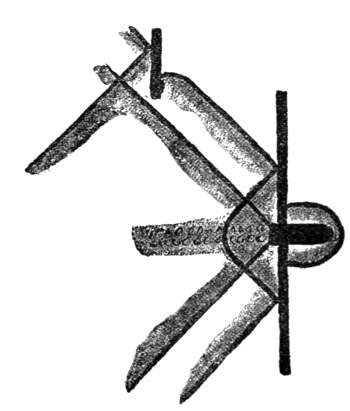 Fig. 56.
Fig. 56.
Permit me, now, to illustrate the most essential of the points that I have just adduced, by means of a few rough drawings taken from older and less perfect photographs.
In the sketch of Figure 57 you see the projectile, which has just left the barrel of the rifle, touch a wire and disengage the illuminating spark. At the apex of[Pg 332] the projectile you already see the beginnings of a powerful head-wave, and in front of the wave a transparent fungiform cluster. This latter is the air which has been forced out of the barrel by the projectile. Circular sound-waves, noise-waves, which are soon overtaken by the projectile, also issue from the barrel. But behind the projectile opaque puffs of powder-gas rush forth. It is scarcely necessary to add that many other questions in ballistics may be studied by this method, as, for example, the movement of the gun-carriage.
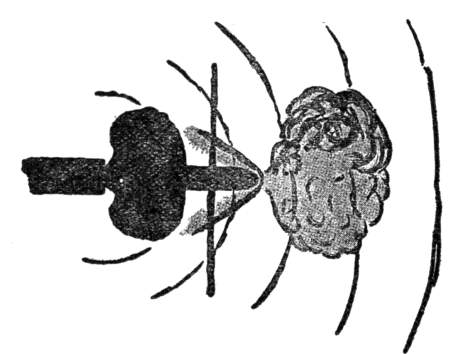 Fig. 57.
Fig. 57.
A distinguished French artillerist, M. Gossot, has applied the views of the head-wave here given in quite a different manner. The practice in measuring the velocity of projectiles is to cause the projectile to pass through wire screens placed at different points in its path, and by the tearing of these screens to give rise[Pg 333] to electro-magnetic time-signals on falling slabs or rotating drums. Gossot caused these signals to be made directly by the impact of the head-wave, did away thus with the wire screens, and carried the method so far as to be able to measure the velocities of projectiles travelling in high altitudes, where the use of wire screens was quite out of the question.
The laws of the resistance of fluids and of air to bodies travelling in them form an extremely complicated problem, which can be reasoned out very simply and prettily as a matter of pure philosophy but practice offers not a few difficulties. The same body having the velocity 2, 3, 4 ... displaces in the same interval 2, 3, 4 ... times the same mass of air, or the same mass of fluid, and imparts to it in addition 2, 3, 4 ... times the same velocity. But for this, plainly, 4, 9, 16 ... times the original force is required. Hence, the resistance, it is said, increases with the square of the velocity. This is all very pretty and simple and obvious. But practice and theory are at daggers' points here. Practice tells us that when we increase the velocity, the law of the resistance changes. For every portion of the velocity the law is different.
The studies of the talented English naval architect, Froude, have thrown light upon this question. Froude has shown that the resistance is conditioned by a combination of the most multifarious phenomena. A ship in motion is subjected to the friction of[Pg 334] the water. It causes eddies and it generates in addition waves which radiate outward from it. Every one of these phenomena are dependent upon the velocity in some different manner, and it is consequently not astonishing that the law of the resistance should be a complicated one.
The preceding observations suggest quite analogous reflexions for projectiles. Here also we have friction, the formation of eddies, and the generation of waves. Here, also, therefore, we should not be surprised at finding the law of the resistance of the air a complicated one, nor puzzled at learning that in actuality the law of resistance changes as soon as the speed of the projectile exceeds the velocity of sound, for this is the precise point at which one important element of the resistance, namely, the formation of waves, first comes into play.
No one doubts that a pointed bullet pierces the air with less resistance than a blunt bullet. The photographs themselves show that the head-wave is weaker for a pointed projectile. It is not impossible, similarly, that forms of bullets will be invented which generate fewer eddies, etc., and that we shall study these phenomena also by photography. I am of opinion from the few experiments which I have made in this direction that not much more can be done by changing the form of the projectile when the velocity is very great, but I have not gone into the question thoroughly. Researches of the kind we are considering[Pg 335] can certainly not be detrimental to practical artillery, and it is no less certain that experiments by artillerists on a large scale will be of undoubted benefit to physics.
No one who has had the opportunity of studying modern guns and projectiles in their marvellous perfection, their power and precision, can help confessing that a high technical and scientific achievement has found its incarnation in these objects. We may surrender ourselves so completely to this impression as to forget for a moment the terrible purposes they serve.
Permit me, therefore, before we separate, to say a few words on this glaring contrast. The greatest man of war and of silence which the present age has produced once asserted that perpetual peace is a dream, and not a beautiful dream at that. We may accord to this profound student of mankind a judgment in these matters and can also appreciate the soldier's horror of stagnation from all too lengthy peace. But it requires a strong belief in the insuperableness of mediæval barbarism to hope for and to expect no great improvement in international relations. Think of our forefathers and of the times when club law ruled supreme, when within the same country and the same state brutal assaults and equally brutal self-defence were universal and self-evident. This state of affairs grew so oppressive that finally a thousand and one circumstances compelled people to put an[Pg 336] end to it, and the cannon had most to say in accomplishing the work. Yet the rule of club law was not abolished so quickly after all. It had simply passed to other clubs. We must not abandon ourselves to dreams of the Rousseau type. Questions of law will in a sense forever remain questions of might. Even in the United States where every one is as a matter of principle entitled to the same privileges, the ballot according to Stallo's pertinent remark is but a milder substitute for the club. Nor need I tell you that many of our own fellow-citizens are still enamored of the old original methods. Very, very gradually, however, as civilisation progresses, the intercourse of men takes on gentler forms, and no one who really knows the good old times will ever honestly wish them back again, however beautifully they may be painted and rhymed about.
In the intercourse of the nations, however, the old club law still reigns supreme. But since its rule is taxing the intellectual, the moral, and the material resources of the nations to the utmost and constitutes scarcely less a burden in peace than in war, scarcely less a yoke for the victor than for the vanquished, it must necessarily grow more and more unendurable. Reason, fortunately, is no longer the exclusive possession of those who modestly call themselves the upper ten thousand. Here, as everywhere, the evil itself will awaken the intellectual and ethical forces which are destined to mitigate it. Let the hate of[Pg 337] races and of nationalities run riot as it may, the intercourse of nations will still increase and grow more intimate. By the side of the problems which separate nations, the great and common ideals which claim the exclusive powers of the men of the future appear one after another in greater distinctness and in greater might.
Perhaps the most fantastic proposition that Maupertuis,[114] the renowned president of the Berlin Academy, ever put forward for the approval of his contemporaries was that of founding a city in which, to instruct and discipline young students, only Latin should be spoken. Maupertuis's Latin city remained an idle wish. But for centuries Latin and Greek institutions exist in which our children spend a goodly portion of their days, and whose atmosphere constantly surrounds them, even when without their walls.
For centuries instruction in the ancient languages has been zealously cultivated. For centuries its necessity has been alternately championed and contested. More strongly than ever are authoritative voices now raised against the preponderance of instruction in the classics and in favor of an education more suited to the needs of the time, especially for a more generous treatment of mathematics and the natural sciences.
In accepting your invitation to speak here on the relative educational value of the classical and the mathematico-physical sciences in colleges and high schools, I find my justification in the duty and the necessity laid upon every teacher of forming from his own experiences an opinion upon this important question, as partly also in the special circumstance that in my youth I was personally under the influence of school-life for only a short time, just previous to my entering the university, and had, therefore, ample opportunity to observe the effects of widely different methods upon my own person.
Passing now, to a review of the arguments which the advocates of instruction in the classics advance,[Pg 340] and of what the adherents of instruction in the physical sciences in their turn adduce, we find ourselves in rather a perplexing position with respect to the arguments of the first named. For these have been different at different times, and they are even now of a very multifarious character, as must be where men advance, in favor of an institution that exists and which they are determined to retain at any cost, everything they can possibly think of. We shall find here much that has evidently been brought forward only to impress the minds of the ignorant; much, too, that was advanced in good faith and which is not wholly without foundation. We shall get a fair idea of the reasoning employed by considering, first, the arguments that have grown out of the historical circumstances connected with the original introduction of the classics, and, lastly, those which were subsequently adduced as accidental afterthoughts.
Instruction in Latin, as Paulsen[115] has minutely shown, was introduced by the Roman Church along with Christianity. With the Latin language were also transmitted the scant and meagre remnants of ancient science. Whoever wished to acquire this ancient education, then the only one worthy of the name, for him the Latin language was the only and indispensable means; such a person had to learn Latin to rank among educated people.
The wide-spread influence of the Roman Church wrought many and various results. Among those for which all are glad, we may safely count the establishment of a sort of uniformity among the nations and of a regular international intercourse by means of the Latin language, which did much to unite the nations in the common work of civilisation, carried on from the fifteenth to the eighteenth century. The Latin language was thus long the language of scholars, and instruction in Latin the road to a liberal education—a shibboleth still employed, though long inappropriate.
For scholars as a class, it is to be regretted, perhaps, that Latin has ceased to be the medium of international communication. But the attributing of the loss of this function by the Latin language to its incapacity to accommodate itself to the numerous new ideas and conceptions which have arisen in the course of the development of science is, in my opinion, wholly erroneous. It would be difficult to find a modern scientist who had enriched science with as many new ideas as Newton has, yet Newton knew how to express those ideas very correctly and precisely in the Latin language. If this view were correct, it would also hold true of every living language. Originally every language has to adapt itself to new ideas.
It is far more likely that Latin was displaced as the literary vehicle of science by the influence of the nobility. By their desire to enjoy the fruits of literature and science, through a less irksome medium than Latin, the nobility performed for the people at large an undeniable service. For the days were now past when acquaintance with the language and literature of science was restricted to a caste, and in this step, perhaps, was made the most important advance of modern times. To-day, when international intercourse is firmly established in spite of the many languages employed, no one would think of reintroducing Latin.[116]
The facility with which the ancient languages lend themselves to the expression of new ideas is evidenced by the fact that the great majority of our scientific ideas, as survivals of this period of Latin intercourse, bear Latin and Greek designations, while in great measure scientific ideas are even now invested with names from these sources. But to deduce from the existence and use of such terms the necessity of still learning Latin and Greek on the part of all who employ them is carrying the conclusion too far. All terms, appropriate and inappropriate,—and there are a large number of inappropriate and monstrous combinations in science,—rest on convention. The essential thing is, that people should associate with the sign the precise idea that is designated by it. It matters little whether a person can correctly derive the words telegraph, tangent, ellipse, evolute, etc., if the correct idea is present in his mind when he uses them. On the other hand, no matter how well he may know their etymology, his knowledge will be of little use to him if the correct idea is absent. Ask the average and fairly educated classical scholar to translate a few lines for you from Newton's Principia, or from Huygens's Horologium, and you will discover at once what an extremely subordinate rôle the mere knowledge of language plays in such things. Without its associated thought a word remains a mere sound. The fashion of employing Greek and Latin designations—for it can be termed nothing else—has a natural root in history; it is impossible for the practice to disappear suddenly, but it has fallen of late considerably into disuse. The terms gas, ohm, Ampère, volt, etc., are in international use, but they are not Latin nor Greek. Only the person who rates the unessential and accidental husk higher than its contents, can speak of the necessity of learning Latin or Greek for such reasons, to say nothing of spending eight or ten years on the task. Will not a dictionary supply in a few seconds all the information we wish on such subjects?[117]
It is indisputable that our modern civilisation took up the threads of the ancient civilisation, that at many points it begins where the latter left off, and that centuries ago the remains of the ancient culture were the only culture existing in Europe. Then, of course, a classical education really was the liberal education, the higher education, the ideal education, for it was the sole education. But when the same claim is now raised in behalf of a classical education, it must be uncompromisingly contested as bereft of all foundation. For our civilisation has gradually attained its independence; it has lifted itself far above the ancient civilisation, and has entered generally new directions of progress. Its note, its characteristic feature, is the enlightenment that has come from the great mathematical and physical researches of the last centuries, and which has permeated not only the practical arts and industries but is also gradually finding its way into all fields of thought, including philosophy and history, sociology and linguistics. Those traces of ancient views that are still discoverable in philosophy, law, art, and science, operate more as hindrances than helps, and will not long stand before the development of independent and more natural views.
It ill becomes classical scholars, therefore, to regard themselves, at this day, as the educated class par excellence, to condemn as uneducated all persons who do not understand Latin and Greek, to complain that with such people profitable conversations are not to be carried on, etc. The most delectable stories have got into circulation, illustrative of the defective education of scientists and engineers. A renowned inquirer, for example, is said to have once announced his intention of holding a free course of university lectures, with the word "frustra"; an engineer who spent his leisure hours in collecting insects is said to have declared that he was studying "etymology." It is true, incidents of this character make us shudder or smile, according to our mood or temperament. But we must admit, the next moment, that in giving way to such feelings we have merely succumbed to a childish prejudice. A lack of tact but certainly no lack of education is displayed in the use of such half-understood expressions. Every candid person will confess that there are many branches of knowledge about which he had better be silent. We shall not be so uncharitable as to turn the tables and discuss the impression that classical scholars might make on a scientist or engineer, in speaking of science. Possibly many ludicrous stories might be told of them, and of far more serious import, which should fully compensate for the blunders of the other party.
The mutual severity of judgment which we have here come upon, may also forcibly bring home to us how really scarce a true liberal culture is. We may detect in this mutual attitude, too, something of that narrow, mediæval arrogance of caste, where a man began, according to the special point of view of the speaker, with the scholar, the soldier, or the nobleman. Little sense or appreciation is to be found in it for the common task of humanity, little feeling for the need of mutual assistance in the great work of civilisation, little breadth of mind, little truly liberal culture.
A knowledge of Latin, and partly, also, a knowledge of Greek, is still a necessity for the members of a few professions by nature more or less directly concerned with the civilisations of antiquity, as for lawyers, theologians, philologists, historians, and generally for a small number of persons, among whom from time to time I count myself, who are compelled to seek for information in the Latin literature of the centuries just past.[118] But that all young persons in search of a higher education should pursue for this reason Latin and Greek to such excess; that persons intending to become physicians and scientists should come to the universities defectively educated, or even miseducated; and that they should be compelled to come only from schools that do not supply them with the proper preparatory knowledge is going a little bit too far.
After the conditions which had given to the study of Latin and Greek their high import had ceased to exist, the traditional curriculum, naturally, was retained. Then, the different effects of this method of education, good and bad, which no one had thought of at its introduction, were realised and noted. As natural, too, was it that those who had strong interests in the preservation of these studies, from knowing no others or from living by them, or for still other reasons, should emphasise the good results of such instruction. They pointed to the good effects as if they had been consciously aimed at by the method and could be attained only through its agency.
One real benefit that students might derive from a rightly conducted course in the classics would be the opening up of the rich literary treasures of antiquity, and intimacy with the conceptions and views of the world held by two advanced nations. A person who has read and understood the Greek and Roman authors has felt and experienced more than one who is restricted to the impressions of the present. He sees how men placed in different circumstances judge quite differently of the same things from what we do to-day. His own judgments will be rendered thus more independent. Again, the Greek and Latin authors are indisputably a rich fountain of recreation, of enlightenment, and of intellectual pleasure after the day's toil, and the individual, not less than civilised humanity generally, will remain grateful to them for all time. Who does not recall with pleasure the wanderings of Ulysses, who does not listen joyfully to the simple narratives of Herodotus, who would ever repent of having made the acquaintance of Plato's Dialogues, or of having tasted Lucian's divine humor? Who would give up the glances he has obtained into the private life of antiquity from Cicero's letters, from Plautus or Terence? To whom are not the portraits of Suetonius undying reminiscences? Who, in fact, would throw away any knowledge he had once gained?
Yet people who draw from these sources only, who know only this culture, have surely no right to dogmatise about the value of some other culture. As objects of research for individuals, this literature is extremely valuable, but it is a different question whether it is equally valuable as the almost exclusive means of education of our youth.
Do not other nations and other literatures exist from which we ought to learn? Is not nature herself our first school-mistress? Are our highest models always to be the Greeks, with their narrow provinciality of mind, that divided the world into "Greeks and barbarians," with their superstitions, with their eternal questioning of oracles? Aristotle with his incapacity to learn from facts, with his word-science; Plato with his heavy, interminable dialogues, with his barren, at times childish, dialectics—are they unsurpassable?[119] The Romans with their apathy, their pompous externality, set off by fulsome and bombastic phrases, with their narrow-minded, philistine philosophy, with their frenzied sensuality, with their cruel and bestial indulgence in animal and man baiting, with their outrageous maltreatment and plundering of their subjects—are they patterns worthy of imitation? Or shall, perhaps, our science edify itself with the works of Pliny who cites midwives as authorities and himself stands on their point of view?
Besides, if an acquaintance with the ancient world really were attained, we might come to some settlement with the advocates of classical education. But it is words and forms, and forms and words only, that are supplied to our youth; and even collateral subjects are forced into the strait-jacket of the same rigid method and made a science of words, sheer feats of mechanical memory. Really, we feel ourselves set back a thousand years into the dull cloister-cells of the Middle Ages.
This must be changed. It is possible to get acquainted with the views of the Greeks and Romans by a shorter road than the intellect deadening process of eight or ten years of declining, conjugating, analysing, and extemporisation. There are to-day plenty of educated persons who have acquired through good translations vivider, clearer, and more just views of classical antiquity than the graduates of our gymnasiums and colleges.[120]
For us moderns, the Greeks and the Romans are simply two objects of archæological and historical research like all others. If we put them before our youth in fresh and living pictures, and not merely in words and syllables, the effect will be assured. We derive a totally different enjoyment from the Greeks when we approach them after a study of the results of modern research in the history of civilisation. We read many a chapter of Herodotus differently when we attack his works equipped with a knowledge of natural science, and with information about the stone age and the lake-dwellers. What our classical institutions pretend to give can and actually will be given to our youth with much more fruitful results by competent historical instruction, which must supply, not names and numbers alone, nor the mere history of dynasties and wars, but be in every sense of the word a true history of civilisation.
The view still widely prevails that although all "higher, ideal culture," all extension of our view of the world, is acquired by philological and in a lesser degree by historical studies, still the mathematics and natural sciences should not be neglected on account of their usefulness. This is an opinion to which I must refuse my assent. It were strange if man could learn more, could draw more intellectual nourishment, from the shards of a few old broken jugs, from inscribed stones, or yellow parchments, than from all the rest of nature. True, man is man's first concern, but he is not his sole concern.
In ceasing to regard man as the centre of the world; in discovering that the earth is a top whirled about the sun, which speeds off with it into infinite space; in finding that in the fixed stars the same elements exist as on earth; in meeting everywhere the same processes of which the life of man is merely a vanishingly small part—in such things, too, is a widening of our view of the world, and edification, and poetry. There are here perhaps grander and more significant facts than the bellowing of the wounded Ares, or the charming island of Calypso, or the ocean-stream engirdling the earth. He only should speak of the relative value of these two domains of thought, of their poetry, who knows both.
The "utility" of physical science is, in a measure, only a collateral product of that flight of the intellect which produced science. No one, however, should underrate the utility of science who has shared in the realisation by modern industrial art of the Oriental world of fables, much less one upon whom those treasures have been poured, as it were, from the fourth dimension, without his aid or understanding.
Nor may we believe that science is useful only to the practical man. Its influence permeates all our affairs, our whole life; everywhere its ideas are decisive. How differently does the jurist, the legislator, or the political economist think, who knows, for example, that a square mile of the most fertile soil can support with the solar heat annually consumed only a definite number of human beings, which no art or science can increase. Many economical theories, which open new air-paths of progress, air-paths in the literal sense of the word, would be made impossible by such knowledge.
The eulogists of classical education love to emphasise the cultivation of taste which comes from employment with the ancient models. I candidly confess that there is something absolutely revolting in this to me. To form the taste, then, our youths must sacrifice ten years of their life! Luxury takes precedence over necessity. Have the future generations, in the face of the difficult problems, the great social questions, which they must meet, and that with strengthened mind and heart, no more important duties to fulfil than these?
But let us assume that this end were desirable. Can taste be formed by rules and precepts? Do not ideals of beauty change? Is it not a stupendous absurdity to force one's self artificially to admire things which, with all their historical interest, with all their beauty in individual points, are for the most part foreign to the rest of our thoughts and feelings, provided we have such of our own. A nation that is truly such, has its own taste and will not go to others for it. And every individual perfect man has his own taste.[121]
And what, after all, does this cultivation of taste consist in? In the acquisition of the personal literary style of a few select authors! What should we think of a people that would force its youth a thousand years from now, by years of practice, to master the tortuous or bombastic style of some successful lawyer or politician of to-day? Should we not justly accuse them of a woful lack of taste?
The evil effects of this imagined cultivation of the taste find expression often enough. The young savant who regards the composition of a scientific essay as a rhetorical exercise instead of a simple and unadorned presentation of the facts and the truth, still sits unconsciously on the school-bench, and still unwittingly represents the point of view of the Romans, by whom the elaboration of speeches was regarded as a serious scientific (!) employment.
Far be it from me to underrate the value of the development of the instinct of speech and of the increased comprehension of our own language which comes from philological studies. By the study of a foreign language, especially of one which differs widely from ours, the signs and forms of words are first clearly distinguished from the thoughts which they express. Words of the closest possible correspondence in different languages never coincide absolutely with the ideas they stand for, but place in relief slightly different aspects of the same thing, and by the study of language the attention is directed to these shades of difference. But it would be far from admissible to contend that the study of Latin and Greek is the most fruitful and natural, let alone the only, means of attaining this end. Any one who will give himself the pleasure of a few hours' companionship with a Chinese grammar; who will seek to make clear to himself the mode of speech and thought of a people who never advanced as far as the analysis of articulate sounds, but stopped at the analysis of syllables, to whom our alphabetical characters, therefore, are an inexplicable puzzle, and who express all their rich and profound thoughts by means of a few syllables with variable emphasis and position,—such a person, perhaps, will acquire new, and extremely elucidative ideas upon the relation of language and thought. But should our children, therefore, study Chinese? Certainly not. No more, then, should they be burdened with Latin, at least in the measure they are.
It is a beautiful achievement to reproduce a Latin thought in a modern language with the maximum fidelity of meaning and expression—for the translator. Moreover, we shall be very grateful to the translator for his performance. But to demand this feat of every educated man, without consideration of the sacrifice of time and labor which it entails, is unreasonable. And for this very reason, as classical teachers admit, that ideal is never perfectly attained, except in rare cases with scholars possessed of special talents and great industry. Without slurring, therefore, the high importance of the study of the ancient languages as a profession, we may yet feel sure that the instinct for speech which is part of every liberal education can, and must, be acquired in a different way. Should we, indeed, be forever lost if the Greeks had not lived before us?
The fact is, we must carry our demands further than the representatives of classical philology. We must ask of every educated man a fair scientific conception of the nature and value of language, of the formation of language, of the alteration of the meaning of roots, of the degeneration of fixed forms of speech to grammatical forms, in brief, of all the main results of modern comparative philology. We should judge that this were attainable by a careful study of our mother tongue and of the languages next allied to it, and subsequently of the more ancient tongues from which the former are derived. If any one object that this is too difficult and entails too much labor, I should advise such a person to place side by side an English, a Dutch, a Danish, a Swedish, and a German Bible, and to compare a few lines of them; he will be amazed at the multitude of suggestions that offer themselves.[122] In fact, I believe that a really progressive, fruitful, rational, and instructive study of languages can be conducted only on this plan. Many of my audience will remember, perhaps, the bright and encouraging effect, like that of a ray of sunlight on a gloomy day, which the meagre and furtive remarks on comparative philology in Curtius's Greek grammar wrought in that barren and lifeless desert of verbal quibbles.
The principal result obtained by the present method of studying the ancient languages is that which comes from the student's employment with their complicated grammars. It consists in the sharpening of the attention and in the exercise of the judgment by the practice of subsuming special cases under general rules, and of distinguishing between different cases. Obviously, the same result can be reached by many other methods; for example, by difficult games of cards. Every science, the mathematics and the physical sciences included, accomplish as much, if not more, in this disciplining of the judgment. In addition, the matter treated by those sciences has a much higher intrinsic interest for young people, and so engages spontaneously their attention; while on the other hand they are elucidative and useful in other directions in which grammar can accomplish nothing.
Who cares, so far as the matter of it is concerned, whether we say hominum or hominorum in the genitive plural, interesting as the fact may be for the philologist? And who would dispute that the intellectual need of causal insight is awakened not by grammar but by the natural sciences?
It is not our intention, therefore, to gainsay in the least the good influence which the study of Latin and Greek grammar also exercises on the sharpening of the judgment. In so far as the study of words as such must greatly promote lucidity and accuracy of expression, in so far as Latin and Greek are not yet wholly indispensable to many branches of knowledge, we willingly concede to them a place in our schools, but would demand that the disproportionate amount of time allotted to them, wrongly withdrawn from other useful studies, should be considerably curtailed. That in the end Latin and Greek will not be employed as the universal means of education, we are fully convinced. They will be relegated to the closet of the scholar or professional philologist, and gradually make way for the modern languages and the modern science of language.
Long ago Locke reduced to their proper limits the exaggerated notions which obtained of the close connexion of thought and speech, of logic and grammar, and recent investigators have established on still surer foundations his views. How little a complicated grammar is necessary for expressing delicate shades of thought is demonstrated by the Italians and French, who, although they have almost totally discarded the grammatical redundancies of the Romans, are yet not surpassed by the latter in accuracy of thought, and whose poetical, but especially whose scientific literature, as no one will dispute, can bear favorable comparison with the Roman.
Reviewing again the arguments advanced in favor of the study of the ancient languages, we are obliged to say that in the main and as applied to the present, they are wholly devoid of force. In so far as the aims which this study theoretically pursues are still worthy of attainment, they appear to us as altogether too narrow, and are surpassed in this only by the means employed. As almost the sole, indisputable result of this study we must count the increase of the student's skill and precision in expression. One inclined to be uncharitable might say that our gymnasiums and classical academies turn out men who can speak and write, but, unfortunately, have little to write or speak about. Of that broad, liberal view, of that famed universal culture, which the classical curriculum is supposed to yield, serious words need not be lost. This culture might, perhaps, more properly be termed the contracted or lopsided culture.
While considering the study of languages we threw a few side glances at mathematics and the natural sciences. Let us now inquire whether these, as branches of study, cannot accomplish much that is to be attained in no other way. I shall meet with no contradiction when I say that without at least an elementary mathematical and scientific education a man remains a total stranger in the world in which he lives, a stranger in the civilisation of the time that bears him. Whatever he meets in nature, or in the industrial world, either does not appeal to him at all, from his having neither eye nor ear for it, or it speaks to him in a totally unintelligible language.
A real understanding of the world and its civilisation, however, is not the only result of the study of mathematics and the physical sciences. Much more essential for the preparatory school is the formal cultivation which comes from these studies, the strengthening of the reason and the judgment, the exercise of the imagination. Mathematics, physics, chemistry, and the so-called descriptive sciences are so much alike in this respect, that, apart from a few points, we need not separate them in our discussion.
Logical sequence and continuity of ideas, so necessary for fruitful thought, are par excellence the results of mathematics; the ability to follow facts with thoughts, that is, to observe or collect experiences, is chiefly developed by the natural sciences. Whether we notice that the sides and the angles of a triangle are connected in a definite way, that an equilateral triangle possesses certain definite properties of symmetry, or whether we notice the deflexion of a magnetic needle by an electric current, the dissolution of zinc in diluted sulphuric acid, whether we remark that the wings of a butterfly are slightly colored on the under, and the fore-wings of the moth on the upper, surface: indiscriminately here we proceed from observations, from individual acts of immediate intuitive knowledge. The field of observation is more restricted and lies closer at hand in mathematics; it is more varied and broader but more difficult to compass in the natural sciences. The essential thing, however, is for the student to learn to make observations in all these fields. The philosophical question whether our acts of knowledge in mathematics are of a special kind is here of no importance for us. It is true, of course, that the observation can be practised by languages also. But no one, surely, will deny, that the concrete, living pictures presented in the fields just mentioned possess different and more powerful attractions for the mind of the youth than the abstract and hazy figures which language offers, and on which the attention is certainly not so spontaneously bestowed, nor with such good results.[123]
Observation having revealed the different properties of a given geometrical or physical object, it is discovered that in many cases these properties depend in some way upon one another. This interdependence of properties (say that of equal sides and equal angles at the base of a triangle, the relation of pressure to motion,) is nowhere so distinctly marked, nowhere is the necessity and permanency of the interdependence so plainly noticeable, as in the fields mentioned. Hence the continuity and logical consequence of the ideas which we acquire in those fields. The relative simplicity and perspicuity of geometrical and physical relations supply here the conditions of natural and easy progress. Relations of equal simplicity are not met with in the fields which the study of language opens up. Many of you, doubtless, have often wondered at the little respect for the notions of cause and effect and their connexion that is sometimes found among professed representatives of the classical studies. The explanation is probably to be sought in the fact that the analogous relation of motive and action familiar to them from their studies, presents nothing like the clear simplicity and determinateness that the relation of cause and effect does.
That perfect mental grasp of all possible cases, that economical order and organic union of the thoughts which comes from it, which has grown for every one who has ever tasted it a permanent need which he seeks to satisfy in every new province, can be developed only by employment with the relative simplicity of mathematical and scientific investigations.
When a set of facts comes into apparent conflict with another set of facts, and a problem is presented, its solution consists ordinarily in a more refined distinction or in a more extended view of the facts, as may be aptly illustrated by Newton's solution of the problem of dispersion. When a new mathematical or scientific fact is demonstrated, or explained, such demonstration also rests simply upon showing the connexion of the new fact with the facts already known; for example, that the radius of a circle can be laid off as chord exactly six times in the circle is explained or proved by dividing the regular hexagon inscribed in the circle into equilateral triangles. That the quantity of heat developed in a second in a wire conveying an electric current is quadrupled on the doubling of the strength of the current, we explain from the doubling of the fall of the potential due to the doubling of the current's intensity, as also from the doubling of the quantity flowing through, in a word, from the quadrupling of the work done. In point of principle, explanation and direct proof do not differ much.
He who solves scientifically a geometrical, physical, or technical problem, easily remarks that his procedure is a methodical mental quest, rendered possible by the economical order of the province—a simplified purposeful quest as contrasted with unmethodical, unscientific guess-work. The geometer, for example, who has to construct a circle touching two given straight lines, casts his eye over the relations of symmetry of the desired construction, and seeks the centre of his circle solely in the line of symmetry of the two straight lines. The person who wants a triangle of which two angles and the sum of the sides are given, grasps in his mind the determinateness of the form of this triangle and restricts his search for it to a certain group of triangles of the same form. Under very different circumstances, therefore, the simplicity, the intellectual perviousness, of the subject-matter of mathematics and natural science is felt, and promotes both the discipline and the self-confidence of the reason.
Unquestionably, much more will be attained by instruction in the mathematics and the natural sciences than now is, when more natural methods are adopted. One point of importance here is that young students should not be spoiled by premature abstraction, but should be made acquainted with their material from living pictures of it before they are made to work with it by purely ratiocinative methods. A good stock of geometrical experience could be obtained, for example, from geometrical drawing and from the practical construction of models. In the place of the unfruitful method of Euclid, which is only fit for special, restricted uses, a broader and more conscious method must be adopted, as Hankel has pointed out.[124] Then, if, on reviewing geometry, and after it presents no substantial difficulties, the more general points of view, the principles of scientific method are placed in relief and brought to consciousness, as Von Nagel,[125] J. K. Becker,[126] Mann,[127] and others have well done, fruitful results will be surely attained. In the same way, the subject-matter of the natural sciences should be made familiar by pictures and experiment before a profounder and reasoned grasp of these subjects is attempted. Here the emphasis of the more general points of view is to be postponed.
Before my present audience it would be superfluous for me to contend further that mathematics and natural science are justified constituents of a sound education,—a claim that even philologists, after some resistance, have conceded. Here I may count upon assent when I say that mathematics and the natural sciences pursued alone as means of instruction yield a richer education in matter and form, a more general education, an education better adapted to the needs and spirit of the time,—than the philological branches pursued alone would yield.
But how shall this idea be realised in the curricula of our intermediate educational institutions? It is unquestionable in my mind that the German Realschulen and Realgymnasien, where the exclusive classical course is for the most part replaced by mathematics, science, and modern languages, give the average man a more timely education than the gymnasium proper, although they are not yet regarded as fit preparatory schools for future theologians and professional philologists. The German gymnasiums are too one-sided. With these the first changes are to be made; of these alone we shall speak here. Possibly a single preparatory school, suitably planned, might serve all purposes.
Shall we, then, in our gymnasiums fill out the hours of study which stand at our disposal, or are still to be wrested from the classicists, with as great and as varied a quantity of mathematical and scientific matter as possible? Expect no such proposition from me. No one will suggest such a course who has himself been actively engaged in scientific thought. Thoughts can be awakened and fructified as a field is fructified by sunshine and rain. But thoughts cannot be juggled out and worried out by heaping up materials and the hours of instruction, nor by any sort of precepts: they must grow naturally of their own free accord. Furthermore, thoughts cannot be accumulated beyond a certain limit in a single head, any more than the produce of a field can be increased beyond certain limits.
I believe that the amount of matter necessary for a useful education, such as should be offered to all the pupils of a preparatory school, is very small. If I had the requisite influence, I should, in all composure, and fully convinced that I was doing what was best, first greatly curtail in the lower classes the amount of matter in both the classical and the scientific courses; I should cut down considerably the number of the school hours and the work done outside the school. I am not with many teachers of opinion that ten hours work a day for a child is not too much. I am convinced that the mature men who offer this advice so lightly are themselves unable to give their attention successfully for as long a time to any subject that is new to them, (for example, to elementary mathematics or physics,) and I would ask every one who thinks the contrary to make the experiment upon himself. Learning and teaching are not routine office-work that can be kept up mechanically for long periods. But even such work tires in the end. If our young men are not to enter the universities with blunted and impoverished minds, if they are not to leave in the preparatory schools their vital energy, which they should there gather, great changes must be made. Waiving the injurious effects of overwork upon the body, the consequences of it for the mind seem to me positively dreadful.
I know of nothing more terrible than the poor creatures who have learned too much. Instead of that sound powerful judgment which would probably have grown up if they had learned nothing, their thoughts creep timidly and hypnotically after words, principles, and formulæ, constantly by the same paths. What they have acquired is a spider's web of thoughts too weak to furnish sure supports, but complicated enough to produce confusion.
But how shall better methods of mathematical and scientific education be combined with the decrease of the subject-matter of instruction? I think, by abandoning systematic instruction altogether, at least in so far as that is required of all young pupils. I see no necessity whatever that the graduates of our high schools and preparatory schools should be little philologists, and at the same time little mathematicians, physicists, and botanists; in fact, I do not see the possibility of such a result. I see in the endeavor to attain this result, in which every instructor seeks for his own branch a place apart from the others, the main mistake of our whole system. I should be satisfied if every young student could come into living contact with and pursue to their ultimate logical consequences merely a few mathematical or scientific discoveries. Such instruction would be mainly and naturally associated with selections from the great scientific classics. A few powerful and lucid ideas could thus be made to take root in the mind and receive thorough elaboration. This accomplished, our youth would make a different showing from what they do to-day.[128]
What need is there, for example, of burdening the head of a young student with all the details of botany? The student who has botanised under the guidance of a teacher finds on all hands, not indifferent things, but known or unknown things, by which he is stimulated, and his gain made permanent. I express here, not my own, but the opinion of a friend, a practical teacher. Again, it is not at all necessary that all the matter that is offered in the schools should be learned. The best that we have learned, that which has remained with us for life, outlived the test of examination. How can the mind thrive when matter is heaped on matter, and new materials piled constantly on old, undigested materials? The question here is not so much that of the accumulation of positive knowledge as of intellectual discipline. It seems also unnecessary that all branches should be treated at school, and that exactly the same studies should be pursued in all schools. A single philological, a single historical, a single mathematical, a single scientific branch, pursued as common subjects of instruction for all pupils, are sufficient to accomplish all that is necessary for the intellectual development. On the other hand, a wholesome mutual stimulus would be produced by this greater variety in the positive culture of men. Uniforms are excellent for soldiers, but they will not fit heads. Charles V. learned this, and it should never be forgotten. On the contrary, teachers and pupils both need considerable latitude, if they are to yield good results.
With John Karl Becker I am of the opinion that the utility and amount for individuals of every study should be precisely determined. All that exceeds this amount should be unconditionally banished from the lower classes. With respect to mathematics, Becker,[129] in my judgment, has admirably solved this question.
With respect to the upper classes the demand assumes a different form. Here also the amount of matter obligatory on all pupils ought not to exceed a certain limit. But in the great mass of knowledge that a young man must acquire to-day for his profession it is no longer just that ten years of his youth should be wasted with mere preludes. The upper classes should supply a truly useful preparation for the professions, and should not be modelled upon the wants merely of future lawyers, ministers, and philologists. Again, it would be both foolish and impossible to attempt to prepare the same person properly for all the different professions. In such case the function of the schools would be, as Lichtenberg feared, simply to select the persons best fitted for being drilled, whilst precisely the finest special talents, which do not submit to indiscriminate discipline, would be excluded from the contest. Hence, a certain amount of liberty in the choice of studies must be introduced in the upper classes, by means of which it will be free for every one who is clear about the choice of his profession to devote his chief attention either to the study of the philologico-historical or to that of the mathematico-scientific branches. Then the matter now treated could be retained, and in some branches, perhaps, judiciously extended,[130] without burdening the scholar with many branches or increasing the number of the hours of study. With more homogeneous work the student's capacity for work increases, one part of his labor supporting the other instead of obstructing it. If, however, a young man should subsequently choose a different profession, then it is his business to make up what he has lost. No harm certainly will come to society from this change, nor could it be regarded as a misfortune if philologists and lawyers with mathematical educations or physical scientists with classical educations should now and then appear.
The view is now wide-spread that a Latin and Greek education no longer meets the general wants of the times, that a more opportune, a more "liberal" education exists. The phrase, "a liberal education," has been greatly misused. A truly liberal education is unquestionably very rare. The schools can hardly offer such; at best they can only bring home to the student the necessity of it. It is, then, his business to acquire, as best he can, a more or less liberal education. It would be very difficult, too, at any one time to give a definition of a "liberal" education which would satisfy every one, still more difficult to give one which would hold good for a hundred years. The educational ideal, in fact, varies much. To one, a knowledge of classical antiquity appears not too dearly bought "with early death." We have no objection to this person, or to those who think like him, pursuing their ideal after their own fashion. But we may certainly protest strongly against the realisation of such ideals on our own children. Another,—Plato, for example,—puts men ignorant of geometry on a level with animals.[131] If such narrow views had the magical powers of the sorceress Circe, many a man who perhaps justly thought himself well educated would become conscious of a not very flattering transformation of himself. Let us seek, therefore, in our educational system to meet the wants of the present, and not establish prejudices for the future.
But how does it come, we must ask, that institutions so antiquated as the German gymnasiums could subsist so long in opposition to public opinion? The answer is simple. The schools were first organised by the Church; since the Reformation they have been in the hands of the State. On so large a scale, the plan presents many advantages. Means can be placed at the disposal of education such as no private source, at least in Europe, could furnish. Work can be conducted upon the same plan in many schools, and so experiments made of extensive scope which would be otherwise impossible. A single man with influence and ideas can under such circumstances do great things for the promotion of education.
But the matter has also its reverse aspect. The party in power works for its own interests, uses the schools for its special purposes. Educational competition is excluded, for all successful attempts at improvement are impossible unless undertaken or permitted by the State. By the uniformity of the people's education, a prejudice once in vogue is permanently established. The highest intelligences, the strongest wills cannot overthrow it suddenly. In fact, as everything is adapted to the view in question, a sudden change would be physically impossible. The two classes which virtually hold the reins of power in the State, the jurists and theologians, know only the one-sided, predominantly classical culture which they have acquired in the State schools, and would have this culture alone valued. Others accept this opinion from credulity; others, underestimating their true worth for society, bow before the power of the prevalent opinion; others, again, affect the opinion of the ruling classes even against their better judgment, so as to abide on the same plane of respect with the latter. I will make no charges, but I must confess that the deportment of medical men with respect to the question of the qualification of graduates of your Realschulen has frequently made that impression upon me. Let us remember, finally, that an influential statesman, even within the boundaries which the law and public opinion set him, can do serious harm to the cause of education by considering his own one-sided views infallible, and in enforcing them recklessly and inconsiderately—which not only can happen, but has, repeatedly, happened.[132] The monopoly of education by the State[133] thus assumes in our eyes a somewhat different aspect. And to revert to the question above asked, there is not the slightest doubt that the German gymnasiums in their present form would have ceased to exist long ago if the State had not supported them.
All this must be changed. But the change will not be made of itself, nor without our energetic interference, and it will be made slowly. But the path is marked out for us, the will of the people must acquire and exert upon our school legislation a greater and more powerful influence. Furthermore, the questions at issue must be publicly and candidly discussed that the views of the people may be clarified. All who feel the insufficiency of the existing régime must combine into a powerful organisation that their views may acquire impressiveness and the opinions of the individual not die away unheard.
I recently read, gentlemen, in an excellent book of travels, that the Chinese speak with unwillingness of politics. Conversations of this sort are usually cut short with the remark that they may bother about such things whose business it is and who are paid for it. Now it seems to me that it is not only the business of the State, but a very serious concern of all of us, how our children shall be educated in the public schools at our cost.
I.
While searching for papers by Amontons, several volumes of the Memoirs of the Paris Academy for the first years of the eighteenth century, fell into my hands. It is difficult to portray the delight which one experiences in running over the leaves of these volumes. One sees as an actual spectator almost the rise of the most important discoveries and witnesses the progress of many fields of knowledge from almost total ignorance to relatively perfect clearness.
I propose to discuss here the fundamental researches of Sauveur in Acoustics. It is astonishing how extraordinarily near Sauveur was to the view which Helmholtz was the first to adopt in its full extent a hundred and fifty years later.
The Histoire de l'Académie for 1700, p. 131, tells us that Sauveur had succeeded in making music an[Pg 376] object of scientific research, and that he had invested the new science with the name of "acoustics." On five successive pages a number of discoveries are recorded which are more fully discussed in the volume for the year following.
Sauveur regards the simplicity of the ratios obtaining between the rates of vibration of consonances as something universally known.[135] He is in hope, by further research, of determining the chief rules of musical composition and of fathoming the "metaphysics of the agreeable," the main law of which he asserts to be the union of "simplicity with multiplicity." Precisely as Euler[136] did a number of years later, he regards a consonance as more perfect according as the ratio of its vibrational rates is expressed in smaller whole numbers, because the smaller these whole numbers are the oftener the vibrations of the two tones coincide, and hence the more readily they are apprehended. As the limit of consonance, he takes the ratio 5:6, although he does not conceal the fact that practice, sharpened attention, habit, taste, and even prejudice play collateral rôles in the matter, and that consequently the question is not a purely scientific one.
Sauveur's ideas took their development from his[Pg 377] having instituted at all points more exact quantitative investigations than his predecessors. He is first desirous of determining as the foundation of musical tuning a fixed note of one hundred vibrations which can be reproduced at any time; the fixing of the notes of musical instruments by the common tuning pipes then in use with rates of vibration unknown, appearing to him inadequate. According to Mersenne (Harmonie Universelle, 1636), a given cord seventeen feet long and weighted with eight pounds executes eight visible vibrations in a second. By diminishing its length then in a given proportion we obtain a proportionately augmented rate of vibration. But this procedure appears too uncertain to Sauveur, and he employs for his purpose the beats (battemens), which were known to the organ-makers of his day, and which he correctly explains as due to the alternate coincidence and non-coincidence of the same vibrational phases of differently pitched notes.[137] At every coincidence there is a swelling of the sound, and hence the number of beats per second will be equal to the difference of the rates of vibration. If we tune two of three organ-pipes to the remaining one in the ratio of the minor and major third, the mutual ratio of the rates of vibration of the first two will be as 24: 25, that is to say, for every 24 vibrations to the lower note there will be 25 to the higher, and one beat. If the two pipes give together[Pg 378] four beats in a second, then the higher has the fixed tone of 100 vibrations. The open pipe in question will consequently be five feet in length. We also determine by this procedure the absolute rates of vibration of all the other notes.
It follows at once that a pipe eight times as long or 40 feet in length will yield a vibrational rate of 12-1/2, which Sauveur ascribes to the lowest audible tone, and further also that a pipe 64 times as small will execute 6,400 vibrations, which Sauveur took for the highest audible limit. The author's delight at his successful enumeration of the "imperceptible vibrations" is unmistakably asserted here, and it is justified when we reflect that to-day even Sauveur's principle, slightly modified, constitutes the simplest and most delicate means we have for exactly determining rates of vibration. Far more important still, however, is a second observation which Sauveur made while studying beats, and to which we shall revert later.
Strings whose lengths can be altered by movable bridges are much easier to handle than pipes in such investigations, and it was natural that Sauveur should soon resort to their use.
One of his bridges accidentally not having been brought into full and hard contact with the string, and consequently only imperfectly impeding the vibrations, Sauveur discovered the harmonic overtones of the string, at first by the unaided ear, and concluded from this fact that the string was divided into aliquot[Pg 379] parts. The string when plucked, and when the bridge stood at the third division for example, yielded the twelfth of its fundamental note. At the suggestion of some academician[138] probably, variously colored paper riders were placed at the nodes (noeuds) and ventral segments (ventres), and the division of the string due to the excitation of the overtones (sons harmoniques) belonging to its fundamental note (son fondamental) thus rendered visible. For the clumsy bridge the more convenient feather or brush was soon substituted. . While engaged in these investigations Sauveur also observed the sympathetic vibration of a string induced by the excitation of a second one in unison with it. He also discovered that the overtone of a string can respond to another string tuned to its note. He even went further and discovered that on exciting one string the overtone which it has in common with another, differently pitched string can be produced on that other; for example, on strings having for their vibrational ratio 3:4, the fourth of the lower and the third of the higher may be made to respond. It follows indisputably from this that the excited string yields overtones simultaneously with its fundamental tone. Previously to this Sauveur's attention had been drawn by other observers to the fact that the overtones of musical instruments can be picked out by attentive listening, particularly in the night.[139] He himself mentions[Pg 380] the simultaneous sounding of the overtones and the fundamental tone.[140] That he did not give the proper consideration to this circumstance was, as will afterwards be seen, fatal to his theory.
While studying beats Sauveur makes the remark that they are displeasing to the ear. He held the beats were distinctly audible only when less than six occurred in a second. Larger numbers were not distinctly perceptible and gave rise accordingly to no disturbance. He then attempts to reduce the difference between consonance and dissonance to a question of beats. Let us hear his own words.[141]
"Beats are unpleasing to the ear because of the unevenness of the sound, and it may be held with much plausibility that the reason why octaves are so pleasing is that we never hear their beats.[142]
"In following out this idea, we find that the chords whose beats we cannot hear are precisely those which the musicians call consonances and that those whose beats are heard are the dissonances, and that when a chord is a dissonance in one octave and a consonance in another, it beats in the one and does not beat in the other. Consequently it is called an imperfect consonance. It is very easy by the principles of M. Sauveur, here established, to ascertain what chords beat and in what octaves, above or below the fixed note. If this hypothesis be correct, it will disclose the true source of the rules of composition, hitherto unknown to science, and given over almost entirely to judgment by the ear. These sorts of natural judgment, marvellous though they may sometimes appear, are not so but have very real causes, the knowledge of which belongs to science, provided it can gain possession thereof."[143]
Sauveur thus correctly discerns in beats the cause of the disturbance of consonance, to which all disharmony is "probably" to be referred. It will be seen, however, that according to his view all distant intervals must necessarily be consonances and all near intervals dissonances. He also overlooks the absolute difference in point of principle between his old view, mentioned at the outset, and his new view, rather attempting to obliterate it.
R. Smith[144] takes note of the theory of Sauveur and calls attention to the first of the above-mentioned defects. Being himself essentially involved in the old view of Sauveur, which is usually attributed to Euler, he yet approaches in his criticism a brief step nearer[Pg 382] to the modern theory, as appears from the following passage.[145]
"The truth is, this gentleman confounds the distinction between perfect and imperfect consonances, by comparing imperfect consonances which beat because the succession of their short cycles[146] is periodically confused and interrupted, with perfect ones which cannot beat, because the succession of their short cycles is never confused nor interrupted.
"The fluttering roughness above mentioned is perceivable in all other perfect consonances, in a smaller degree in proportion as their cycles are shorter and simpler, and their pitch is higher; and is of a different kind from the smoother beats and undulations of tempered consonances; because we can alter the rate of the latter by altering the temperament, but not of the former, the consonance being perfect at a given pitch: And because a judicious ear can often hear, at the same time, both the flutterings and the beats of a tempered consonance; sufficiently distinct from each other.
"For nothing gives greater offence to the hearer, though ignorant of the cause of it, than those rapid, piercing beats of high and loud sounds, which make imperfect consonances with one another. And yet a few slow beats, like the slow undulations of a close shake now and then introduced, are far from being disagreeable."
Smith is accordingly clear that other "roughnesses" exist besides the beats which Sauveur considered, and if the investigations had been continued on the basis of Sauveur's idea, these additional roughnesses would have turned out to be the beats of the[Pg 383] overtones, and the theory thus have attained the point of view of Helmholtz.
Reviewing the differences between Sauveur's and Helmholtz's theories, we find the following:
1. The theory according to which consonance depends on the frequent and regular coincidence of vibrations and their ease of enumeration, appears from the new point of view inadmissible. The simplicity of the ratios obtaining between the rates of vibration is indeed a mathematical characteristic of consonance as well as a physical condition thereof, for the reason that the coincidence of the overtones as also their further physical and physiological consequences is connected with this fact. But no physiological or psychological explanation of consonance is given by this fact, for the simple reason that in the acoustic nerve-process nothing corresponding to the periodicity of the sonant stimulus is discoverable.
2. In the recognition of beats as a disturbance of consonance, both theories agree. Sauveur's theory, however, does not take into account the fact that clangs, or musical sounds generally, are composite and that the disturbance in the consonances of distant intervals principally arise from the beats of the overtones. Furthermore, Sauveur was wrong in asserting that the number of beats must be less than six in a second in order to produce disturbances. Even Smith knows that very slow beats are not a cause of disturbance, and Helmholtz found a much higher number[Pg 384] (33) for the maximum of disturbance. Finally, Sauveur did not consider that although the number of beats increases with the recession from unison, yet their strength is diminished. On the basis of the principle of specific energies and of the laws of sympathetic vibration the new theory finds that two atmospheric motions of like amplitude but different periods, a sin(rt) and a sin[(r + ρ)(t + τ)], cannot be communicated with the same amplitude to the same nervous end-organ. On the contrary, an end-organ that reacts best to the period r responds more weakly to the period r + ρ, the two amplitudes bearing to each other the proportion a: φa. Here φ decreases when ρ increases, and when ρ = 0 it becomes equal to 1, so that only the portion of the stimulus φa is subject to beats, and the portion (1-φ)a continues smoothly onward without disturbance.
If there is any moral to be drawn from the history of this theory, it is that considering how near Sauveur's errors were to the truth, it behooves us to exercise some caution also with regard to the new theory. And in reality there seems to be reason for doing so.
The fact that a musician will never confound a more perfectly consonant chord on a poorly tuned piano with a less perfectly consonant chord on a well tuned piano, although the roughness in the two cases may be the same, is sufficient indication that the degree of roughness is not the only characteristic of a[Pg 385] harmony. As the musician knows, even the harmonic beauties of a Beethoven sonata are not easily effaced on a poorly tuned piano; they scarcely suffer more than a Raphael drawing executed in rough unfinished strokes. The positive physiologico-psychological characteristic which distinguishes one harmony from another is not given by the beats. Nor is this characteristic to be found in the fact that, for example, in sounding a major third the fifth partial tone of the lower note coincides with the fourth of the higher note. This characteristic comes into consideration only for the investigating and abstracting reason. If we should regard it also as characteristic of the sensation, we should lapse into a fundamental error which would be quite analogous to that cited in (1).
The positive physiological characteristics of the intervals would doubtless be speedily revealed if it were possible to conduct aperiodic, for example galvanic, stimuli to the single sound-sensing organs, in which case the beats would be totally eliminated. Unfortunately such an experiment can hardly be regarded as practicable. The employment of acoustic stimuli of short duration and consequently also free from beats, involves the additional difficulty of a pitch not precisely determinable.
II.
According to Herbart, spatial vision rests on reproduction-series. In such an event, of course, and if the supposition is correct, the magnitudes of the residua with which the percepts or representations are coalesced (the helps to coalescence) are of cardinal influence. Furthermore, since the coalescences must first be fully perfected before they make their appearance, and since upon their appearance the inhibitory ratios are brought into play, ultimately, then, if we leave out of account the accidental order of time in which the percepts are given, everything in spatial vision depends on the oppositions and affinities, or, in brief, on the qualities of the percepts, which enter into series.
Let us see how the theory stands with respect to the special facts involved.
1. If intersecting series only, running anteriorly and posteriorly, are requisite for the production of spatial sensation, why are not analogues of them found in all the senses?
2. Why do we measure differently colored objects[Pg 387] and variegated objects with one and the same spatial measure? How do we recognise differently colored objects as the same in size? Where do we get our measure of space from and what is it?
3. Why is it that differently colored figures of the same form reproduce one another and are recognised as the same?
Here are difficulties enough. Herbart is unable to solve them by his theory. The unprejudiced student sees at once that his "inhibition by reason of form" and "preference by reason of form" are absolutely impossible. Think of Herbart's example of the red and black letters.
The "help to coalescence" is a passport, so to speak, made out to the name and person of the percept. A percept which is coalesced with another cannot reproduce all others qualitatively different from it for the simple reason that the latter are in like manner coalesced with one another. Two qualitatively different series certainly do not reproduce themselves because they present the same order of degree of coalescence.
If it is certain that only things simultaneous and things which are alike are reproduced, a basic principle of Herbart's psychology which even the most absolute empiricists will not deny, nothing remains but to modify the theory of spatial perception or to invent in its place a new principle in the manner indicated, a step which hardly any one would seriously[Pg 388] undertake. The new principle could not fail to throw all psychology into the most dreadful confusion.
As to the modification which is needed there can be hardly any doubt as to how in the face of the facts and conformably to Herbart's own principles it is to be carried out. If two differently colored figures of equal size reproduce each other and are recognised as equal, the result can be due to nothing but to the existence in both series of presentations of a presentation or percept which is qualitatively the same. The colors are different. Consequently, like or equal percepts must be connected with the colors which are yet independent of the colors. We have not to look long for them, for they are the like effects of the muscular feelings of the eye when confronted by the two figures. We might say we reach the vision of space by the registering of light-sensations in a schedule of graduated muscle-sensations.[148]
A few considerations will show the likelihood of the rôle of the muscle-sensations. The muscular apparatus of one eye is unsymmetrical. The two eyes together form a system which is vertical in symmetry. This already explains much.
1. The position of a figure influences its view. According to the position in which objects are viewed different muscle-sensations come into play and the impression is altered. To recognise inverted letters[Pg 389] as such long experience is required. The best proof of this are the letters d, b, p, q, which are represented by the same figure in different positions and yet are always distinguished as different.[149]
2. It will not escape the attentive observer that for the same reasons and even with the same figure and in the same position the fixation point is also decisive. The figure seems to change during the act of vision. For example, an eight-pointed star constructed by successively joining in a regular octagon the first corner with the fourth, the fourth with the seventh, etc., skipping in every case two corners, assumes alternately, according to where we suffer the centre of vision to rest, a predominantly architectonic or a freer and more open character. Vertical and horizontal lines are always differently apprehended from what oblique lines are.
 Fig. 58.
Fig. 58.
3. The reason why we prefer vertical symmetry and regard it as something special in its kind, whereas we do not recognise horizontal symmetry at all immediately, is due to the vertical symmetry of the muscular apparatus of the eye. The left-hand side a of the accompanying vertically-symmetrical figure induces in the left eye the same muscular feelings as the[Pg 390] right-hand side b does in the right eye. The pleasing effect of symmetry has its cause primarily in the repetition of muscular feelings. That a repetition actually occurs here, sometimes sufficiently marked in character as to lead to the confounding of objects, is proved apart from the theory by the fact which is familiar to every one quem dii oderunt that children frequently reverse figures from the right to the left, but never from above downwards; for example, write ε instead of 3 until they finally come to notice the slight difference. Figure 50 shows how pleasing the repetition of muscular feelings may be. As will be readily understood, vertical and horizontal lines exhibit relations similar to symmetrical figures which are immediately disturbed when oblique positions are chosen for the lines. Compare what Helmholtz says regarding the repetition and coincidence of partial tones.
 Fig. 59.
Fig. 59.
I may be permitted to add a general remark. It is a quite universal phenomenon in psychology that certain qualitatively quite different series of percepts mutually awaken and reproduce one another and in a certain aspect produce the appearance of sameness or similarity. We say of such series that they are of like or of similar form, naming their abstracted likeness form.
1. Of spatial figures we have already spoken.
2. We call two melodies like melodies when they[Pg 391] present the same succession of pitch-ratios; the absolute pitch (or key) may be as different as can be. We can so select the melodies that not even two partial tones of the notes in each are common. Yet we recognise the melodies as alike. And, what is more, we notice the form of the melody more readily and recognise it again more easily than the key (the absolute pitch) in which it was played.
3. We recognise in two different melodies the same rhythm no matter how different the melodies may be otherwise. We know and recognise the rhythm more easily even than the absolute duration (the tempo).
These examples will suffice. In all these and in all similar cases the recognition and likeness cannot depend upon the qualities of the percepts, for these are different. On the other hand recognition, conformably to the principles of psychology, is possible only with percepts which are the same in quality. Consequently there is no other escape than to imagine the qualitatively unlike percepts of the two series as necessarily connected with other percepts which are qualitatively alike.
Since in differently colored figures of like form, like muscular feelings are necessarily induced if the figures are recognised as alike, so there must necessarily lie at the basis of all forms also, and we might even say at the basis of all abstractions, percepts of a peculiar[Pg 392] quality. And this holds true for space and form as well as for time, rhythm, pitch, the form of melodies, intensity, etc. But whence is psychology to derive all these qualities? Have no fear, they will all be found, as were the sensations of muscles for the theory of space. The organism is at present still rich enough to meet all the requirements of psychology in this direction, and it is even time to give serious ear to the question of "corporeal resonance" which psychology so loves to dwell on.
Different psychical qualities appear to bear a very intimate mutual relation to one another. Special research on the subject, as well also as the demonstration that this remark may be generally employed in physics, will follow later.[150]
A CRITICAL AND HISTORICAL EXPOSITION OF ITS PRINCIPLES.
By DR. ERNST MACH.
PROFESSOR OF THE HISTORY AND THEORY OF INDUCTIVE SCIENCE IN THE UNIVERSITY OF VIENNA.
Translated from the Second German Edition
By THOMAS J. McCORMACK.
250 Cuts. 534 Pages. Half Morocco, Gilt Top, Marginal Analyses.
Exhaustive Index. Price $2.50.
Statics.
Dynamics.
The Extension of the Principles of Mechanics.
Formal Development of Mechanics.
The Relation of Mechanics to Other Departments of Knowledge.
"The appearance of a translation into English of this remarkable book should serve to revivify in this country [England] the somewhat stagnating treatment of its subject, and should call up the thoughts which puzzle us when we think of them, and that is not sufficiently often.... Professor Mach is a striking instance of the combination of great mathematical knowledge with experimental skill, as exemplified not only by the elegant illustrations of mechanical principles which abound in this treatise, but also from his brilliant experiments on the photography of bullets.... A careful study of Professor Mach's work, and a treatment with more experimental illustration, on the lines laid down in the interesting diagrams of his Science of Mechanics, will do much to revivify theoretical mechanical science, as developed from the elements by rigorous logical treatment."—Prof. A. G. Greenhill, in Nature, London.
"Those who are curious to learn how the principles of mechanics have been evolved, from what source they take their origin, and how far they can be deemed of positive and permanent value, will find Dr. Mach's able treatise entrancingly interesting.... The book is a remarkable one in many respects, while the mixture of history with the latest scientific principles and absolute mathematical deductions makes it exceedingly attractive."—Mechanical World, Manchester and London, England.
"Mach's Mechanics is unique. It is not a text-book, but forms a useful supplement to the ordinary text-book. The latter is usually a skeleton outline, full of mathematical symbols and other abstractions. Mach's book has 'muscle and clothing,' and being written from the historical standpoint, introduces the leading contributors in succession, tells what they did and how they did it, and often what manner of men they were. Thus it is that the pages glow, as it were, with a certain humanism, quite delightful in a scientific book.... The book is handsomely printed, and deserves a warm reception from all interested in the progress of science."—The Physical Review, New York and London.
"Mr. T. J. McCormack, by his effective translation, where translation was no light task, of this masterly treatise upon the earliest and most fundamental of the sciences, has rendered no slight service to the English speaking student. The German and English languages are generally accounted second to none in their value as instruments for the expression of scientific thought; but the conversion bodily of an abstruse work from one into the other, so as to preserve all the meaning and spirit of the original and to set it easily and naturally into its new form, is a task of the greatest difficulty, and[Pg 415] when performed so well as in the present instance, merits great commendation. Dr. Mach has created for his own works the severest possible standard of judgment. To expect no more from the books of such a master than from the elementary productions of an ordinary teacher in the science would be undue moderation. Our author has lifted what, to many of us, was at one time a course of seemingly unprofitable mental gymnastics, encompassed only at vast expenditure of intellectual effort, into a study possessing a deep philosophical value and instinct with life and interest. 'No profit grows where is no pleasure ta'en,' and the emancipated collegian will turn with pleasure from the narrow methods of the text-book to where the science is made to illustrate, by a treatment at once broad and deep, the fundamental connexion between all the physical sciences, taken together."—The Mining Journal, London, England.
"As a history of mechanics, the work is admirable."—The Nation, New York.
"An excellent book, admirably illustrated."—The Literary World, London, England.
"Sets forth the elements of its subject with a lucidity, clearness, and force unknown in the mathematical text-books ... is admirably fitted to serve students as an introduction on historical lines to the principles of mechanical science."—Canadian Mining and Mechanical Review, Ottawa, Can.
"A masterly book.... To any one who feels that he does not know as much as he ought to about physics, we can commend it most heartily as a scholarly and able treatise ... both interesting and profitable."—A. M. Wellington, in Engineering News, New York.
"The book as a whole is unique, and is a valuable addition to any library of science or philosophy.... Reproductions of quaint old portraits and vignettes give piquancy to the pages. The numerous marginal titles form a complete epitome of the work; and there is that invaluable adjunct, a good index. Altogether the publishers are to be congratulated upon producing a technical work that is thoroughly attractive in its make-up."—Prof. D. W. Hering, in Science.
"There is one other point upon which this volume should be commended, and that is the perfection of the translation. It is a common fault that books of the greatest interest and value in the original are oftenest butchered or made ridiculous by a clumsy translator. The present is a noteworthy exception."—Railway Age.
"The book is admirably printed and bound.... The presswork is unexcelled by any technical books that have come to our hands for some time, and the engravings and figures are all clearly and well executed."—Railroad Gazette.
"I am delighted with Professor Mach's Science of Mechanics."—M. E. Cooley, Professor of Mechanical Engineering, Ann Arbor, Mich.
"You have done a good service to science in publishing Mach's Science of Mechanics in English. I shall take every opportunity to recommend it to young students as a source of much interesting information and inspiration."—M. I. Pupin, Professor of Mechanics, Columbia College, New York.
"Mach's Science of Mechanics is an admirable ... book."—Prof. E. A. Fuertes, Director of the College of Civil Engineering of Cornell University, Ithaca, N. Y.
"I congratulate you upon producing the work in such good style and in so good a translation. I bought a copy of it a year ago, very shortly after you issued it. The book itself is deserving of the highest admiration; and you are entitled to the thanks of all English-speaking physicists for the publication of this translation."—D. W. Hering, Professor of Physics, University of the City of New York, New York.
"I have read Mach's Science of Mechanics with great pleasure. The book is exceedingly interesting."—W. F. Magie, Professor of Physics, Princeton University, Princeton, N. J.
"The Science of Mechanics by Mach, translated by T. J. McCormack, I regard as a most valuable work, not only for acquainting the student with the history of the development of Mechanics, but as serving to present to him most favorably the fundamental ideas of Mechanics and their rational connexion with the highest mathematical developments. It is a most profitable book to read along with the study of a text-book of Mechanics, and I shall take pleasure in recommending its perusal by my students."—S. W. Robinson, Professor of Mechanical Engineering, Ohio State University, Columbus, Ohio.
"I am delighted with Mach's 'Mechanics.' I will call the attention to it of students and instructors who have the Mechanics or Physics to study or teach."—J. E. Davies, University of Wisconsin, Madison, Wis.
"There can be but one opinion as to the value of Mach's work in this translation. No instructor in physics should be without a copy of it."—Henry Crew, Professor of Physics in the Northwestern University, Evanston, Ill.
A PORTRAYAL OF THE SPIRIT AND METHODS OF SCIENCE.
By DR. ERNST MACH.
PROFESSOR OF THE HISTORY AND THEORY OF INDUCTIVE SCIENCE IN THE UNIVERSITY OF VIENNA.
Translated by THOMAS J. McCORMACK.
Third Edition, Revised Throughout and Greatly Enlarged.
Cloth, Gilt Top. Exhaustively Indexed. Pages, 415. Cuts, 59. Price, $1.50.
"A most fascinating volume, treating of phenomena in which all are interested, in a delightful style and with wonderful clearness. For lightness of touch and yet solid value of information the chapter 'Why Has Man Two Eyes?' has scarcely a rival in the whole realm of popular scientific writing."—The Boston Traveller.
"Truly remarkable in the insight they give into the relationship of the various fields cultivated under the name of Physics.... A vein of humor is met here and there reminding the reader of Heaviside, never offending one's taste. These features, together with the lightness of touch with which Mr. McCormack has rendered them, make the volume one that may be fairly called rare. The spirit of the author is preserved in such attractive, really delightful, English that one is assured nothing has been lost by translation."—Prof. Henry Crew, in The Astrophysical Journal.
"A very delightful and useful book.... The author treats some of the most recondite problems of natural science, in so charmingly untechnical a way, with such a wealth of bright illustration, as makes his meaning clear to the person of ordinary intelligence and education.... This is a work that should find a place in every library, and that people should be encouraged to read."—Daily Picayune, New Orleans.
"In his translation Mr. McCormack has well preserved the frank, simple, and pleasing style of this famous lecturer on scientific topics. Professor Mach deals with the live facts, the salient points of science, and not with its mysticism or dead traditions. He uses the simplest of illustrations and expresses himself clearly, tersely, and with a delightful freshness that makes entertaining reading of what in other hands would be dull and prosy."—Engineering News, N. Y.
"The general reader is led by plain and easy steps along a delightful way through what would be to him without such a help a complicated maze of difficulties. Marvels are invented and science is revealed as the natural foe to mysteries."—The Chautauquan.
"The beautiful quality of the work is not marred by abstruse discussions which would require a scientist to fathom, but is so simple and so clear that it brings us into direct contact with the matter treated."—The Boston Post.
"A masterly exposition of important scientific truths."—Scotsman, Edinburgh.
"These lectures by Dr. Mach are delightfully simple and frank; there is no dryness or darkness of technicalities, and science and common life do not seem separated by a gulf.... The style is admirable, and the whole volume seems gloriously alive and human."—Providence Journal, R. I.
"The non-scientific reader who desires to learn something of modern scientific theories, and the reasons for their existence, cannot do better than carefully study these lectures. The English is excellent throughout, and reflects great credit on the translator."—Manufacturer and Builder.
"We like the quiet, considerate intelligence of these lectures."—Independent, New York.
"Professor Mach's lectures are so pleasantly written and illumined with such charm of illustration that they have all the interest of lively fiction."—New York Com. Advertiser.
"The literary and philosophical suggestiveness of the book is very rich." Hartford Seminary Record.
"All are presented so skilfully that one can imagine that Professor Mach's hearers departed from his lecture-room with the conviction that science was a matter for abecedarians. Will please those who find the fairy tales of science more absorbing than fiction."—The Pilot, Boston.
"Professor Mach ... is a master in physics.... His book is a good one and will serve a good purpose, both for instruction and suggestion."—Prof. A. E. Dolbear, in The Dial.
"The most beautiful ideas are unfolded in the exposition."—Catholic World, New York.
By DR. ERNST MACH.
PROFESSOR OF THE HISTORY AND THEORY OF INDUCTIVE SCIENCE IN THE UNIVERSITY OF VIENNA.
Pages, 208. Illustrations, 37. Indexed.
(Price, Cloth, $1.25.)
"A wonderfully original little book. Like everything he writes a work of genius."—Prof. W. James of Harvard.
"I consider each work of Professor Mach a distinct acquisition to a library of science."—Prof. D. W. Hering, New York University.
"There is no work known to the writer which, in its general scientific bearings, is more likely to repay richly thorough study. We are all interested in nature in one way or another, and our interests can only be heightened and clarified by Mach's wonderfully original and wholesome book. It is not saying too much to maintain that every intelligent person should have a copy of it,—and should study that copy."—Prof. J. E. Trevor, Cornell.
"Students may here make the acquaintance of some of the open questions of sensation and at the same time take a lesson in the charm of scientific modesty that can hardly be excelled."—Prof. E. C. Sanford, Clark University.
"It exhibits keen observation and acute thought, with many new and interesting experiments by way of illustration. Moreover, the style is light and even lively—a rare merit in a German prose work, and still rarer in a translation of one."—The Literary World, London.
CHICAGO:
The Open Court Publishing Company
324 DEARBORN STREET.
LONDON: Kegan Paul, Trench, Trübner, & Company.
OF THE
OPEN COURT PUBLISHING CO.
COPE, E. D.
THE PRIMARY FACTORS OF ORGANIC EVOLUTION.
121 cuts. Pp., xvi, 547. Cloth, $2.00, net.
MÜLLER, F. MAX.
THREE INTRODUCTORY LECTURES ON THE SCIENCE OF THOUGHT.
With a correspondence on "Thought Without Words," between F. Max Müller and Francis Galton, the Duke of Argyll, George J. Romanes and others. 128 pages. Cloth, 75 cents. Paper, 25 cents.
THREE LECTURES ON THE SCIENCE OF LANGUAGE.
The Oxford University Extension Lectures, with a Supplement, "My Predecessors." 112 pages. 2nd Edition. Cloth, 75 cents. Paper, 25c.
ROMANES, GEORGE JOHN.
DARWIN AND AFTER DARWIN.
An Exposition of the Darwinian Theory and a Discussion of Post-Darwinian Questions. Three Vols., $4.00. Singly, as follows:
1. The Darwinian Theory. 460 pages. 125 illustrations. Cloth, $2.00.
2. Post-Darwinian Questions. Heredity and Utility. Pp. 338. $1.50.
3. Post-Darwinian Questions. Isolation and Physiological Selection. Pp. 181. $1.00.
AN EXAMINATION OF WEISMANNISM.
236 pages. Cloth, $1.00. Paper, 35c.
THOUGHTS ON RELIGION.
Edited by Charles Gore, M. A., Canon of Westminster. Third Edition, Pages, 184. Cloth, gilt top, $1.25.
RIBOT, TH.
THE PSYCHOLOGY OF ATTENTION.
THE DISEASES OF PERSONALITY.
THE DISEASES OF THE WILL.
Authorised translations. Cloth, 75 cents each. Paper, 25 cents. Full set, cloth, $1.75, net.
MACH, ERNST.
THE SCIENCE OF MECHANICS.
A Critical and Historical Exposition of its Principles. Translated by T. J. McCormack. 250 cuts. 534 pages. 1/2 m., gilt top. $2.50.
POPULAR SCIENTIFIC LECTURES.
Third Edition. 415 pages. 59 cuts. Cloth, gilt top. Net, $1.50.
THE ANALYSIS OF THE SENSATIONS.
Pp. 208. 37 cuts. Cloth, $1.25, net.
GOODWIN, REV. T. A.
LOVERS THREE THOUSAND YEARS AGO.
As Indicated by the Song of Solomon. Pp. 41. Boards, 50c.
HOLYOAKE, G. J.
ENGLISH SECULARISM. A Confession of Belief.
Pp. 146. Cloth, 50c., net.
CORNILL, CARL HEINRICH.
THE PROPHETS OF ISRAEL.
Popular Sketches from Old Testament History. Pp., 200. Cloth, $1.00.
THE RISE OF THE PEOPLE OF ISRAEL.
See Epitomes of Three Sciences, below.
BINET, ALFRED.
THE PSYCHIC LIFE OF MICRO-ORGANISMS.
Authorised translation. 135 pages. Cloth, 75 cents; Paper, 25 cents.
ON DOUBLE CONSCIOUSNESS.
Studies in Experimental Psychology. 93 pages. Paper, 15 cents.
WAGNER, RICHARD
A PILGRIMAGE TO BEETHOVEN.
A Novelette. Frontispiece, portrait of Beethoven. Pp. 40. Boards, 50c.
WEISMANN, AUGUST.
GERMINAL SELECTION. As a Source of Definite Variation.
Pp. 73. Paper, 25c.
NOIRÉ, LUDWIG.
ON THE ORIGIN OF LANGUAGE. Pp. 57. Paper, 15c.
FREYTAG, GUSTAV.
THE LOST MANUSCRIPT. A Novel.
2 vols. 953 pages. Extra cloth, $4.00. One vol., cl., $1.00; paper, 75c.
MARTIN LUTHER.
Illustrated. Pp. 130. Cloth, $1.00. Paper, 25c.
HERING, EWALD.
ON MEMORY, and THE SPECIFIC ENERGIES OF THE NERVOUS SYSTEM. Pp. 50. Paper, 15c.
TRUMBULL, M. M.
THE FREE TRADE STRUGGLE IN ENGLAND.
Second Edition. 296 pages. Cloth, 75 cents; paper, 25 cents.
WHEELBARROW: Articles and Discussions on the Labor Question.
With portrait of the author. 303 pages. Cloth, $1.00; paper, 35 cents.
EARL GREY ON RECIPROCITY AND CIVIL SERVICE REFORM.
With Comments by Gen. M. M. Trumbull. Price, 10 cents.
GOETHE AND SCHILLER'S XENIONS.
Selected and translated by Paul Carus. Album form. Pp., 162. Cl., $1.00
OLDENBERG, H.
ANCIENT INDIA: ITS LANGUAGE AND RELIGIONS.
Pp. 100. Cloth, 50c. Paper, 25c.
CARUS, PAUL.
THE ETHICAL PROBLEM.
90 pages. Cloth, 50 cents; Paper, 30 cents.
FUNDAMENTAL PROBLEMS.
Second edition, enlarged and revised. 372 pp. Cl., $1.50. Paper, 50c.
HOMILIES OF SCIENCE.
317 pages. Cloth, Gilt Top, $1.50.
THE IDEA OF GOD.
Fourth edition. 32 pages. Paper, 15 cents.
THE SOUL OF MAN.
With 152 cuts and diagrams. 458 pages. Cloth, $3.00.
TRUTH IN FICTION. Twelve Tales with a Moral.
Fine laid paper, white and gold binding, gilt edges. Pp. 111. $1.00.
THE RELIGION OF SCIENCE.
Second, extra edition. Price, 50 cents. R. S. L. edition, 25c. Pp. 103.
PRIMER OF PHILOSOPHY.
240 pages. Second Edition. Cloth, $1.00. Paper, 25c.
THREE LECTURES: (1) The Philosophy of the Tool. Pages, 24. Paper, 10c. (2) Our Need of Philosophy. Pages, 14. Paper, 5c. (3) Science a Religious Revelation. Pages, 21. Paper, 5c.
THE GOSPEL OF BUDDHA. According to Old Records.
4th Edition. Pp., 275. Cloth, $1.00. Paper, 35 cents. In German, $1.25.
BUDDHISM AND ITS CHRISTIAN CRITICS.
Pages, 311. Cloth, $1.25.
KARMA. A Story of Early Buddhism.
Illustrated by Japanese artists. 2nd Edition. Crêpe paper, 75 cents.
GARBE, RICHARD.
THE REDEMPTION OF THE BRAHMAN. A Tale of Hindu Life.
Laid paper. Gilt top. 96 pages. Price, 75c. Paper, 25c.
THE PHILOSOPHY OF ANCIENT INDIA.
Pp. 89. Cloth, 50c. Paper, 25c.
EPITOMES OF THREE SCIENCES.
1. The Study of Sanskrit. By H. Oldenberg. 2. Experimental Psychology. By Joseph Jastrow. 3. The Rise of the People of Israel. By C. H. Cornill. 140 pages. Cloth, reduced to 50 cents.
A collection of bi-monthly publications, most of which are reprints of books published by The Open Court Publishing Company. Yearly, $1.50. Separate copies according to prices quoted. The books are printed upon good paper, from large type.
The Religion of Science Library, by its extraordinarily reasonable price, will place a large number of valuable books within the reach of all readers.
The following have already appeared in the series:
No. 1. The Religion of Science. By Paul Carus. 25c.
2. Three Introductory Lectures on the Science of Thought. By F. Max Müller. 25c.
3. Three Lectures on the Science of Language. By F. Max Müller. 25c.
4. The Diseases of Personality. By Th. Ribot. 25c.
5. The Psychology of Attention. By Th. Ribot. 25c.
6. The Psychic Life of Micro-Organisms. By Alfred Binet. 25c.
7. The Nature of the State. By Paul Carus. 15c.
8. On Double Consciousness. By Alfred Binet. 15c.
9. Fundamental Problems. By Paul Carus. 50c.
10. The Diseases of the Will. By Th. Ribot. 25c.
11. The Origin of Language. By Ludwig Noire. 15c.
12. The Free Trade Struggle in England. By M. M. Trumbull. 25c.
13. Wheelbarrow on the Labor Question. By M. M. Trumbull. 35c.
14. The Gospel of Buddha. By Paul Carus. 35c.
15. The Primer of Philosophy. By Paul Carus. 25c.
16. On Memory, and The Specific Energies of the Nervous System. By Prof. Ewald Hering. 15c.
17. The Redemption of the Brahman. A Tale of Hindu Life. By Richard Garbe. 25c.
18. An Examination of Weismannism. By G. J. Romanes. 35c.
19. On Germinal Selection. By August Weismann. 25c.
20. Lovers Three Thousand Years Ago. By T. A. Goodwin. 15c.
21. Popular Scientific Lectures. By Ernst Mach. 50c.
22. Ancient India: Its Language and Religions. By H. Oldenberg. 25c.
23. The Prophets of Ancient Israel. By Prof. C. H. Cornill. 25c.
24. Homilies of Science. By Paul Carus. 35c.
25. Thoughts on Religion. By G. J. Romanes. 50 cents.
26. The Philosophy of Ancient India. By Prof. Richard Garbe. 25c.
27. Martin Luther. By Gustav Freytag. 25c.
28. English Secularism. By George Jacob Holyoake. 25c.
29. On Orthogenesis. By Th. Eimer. 25c.
30. Chinese Philosophy. By Paul Carus. 25c.
31. The Lost Manuscript. By Gustav Freytag. 60c.
THE OPEN COURT PUBLISHING CO.
324 Dearborn Street, Chicago, Ill.
LONDON: Kegan Paul, Trench, Trübner & Co
A MONTHLY MAGAZINE
Devoted to the Science of Religion, the Religion of Science, and the Extension of the Religious Parliament Idea.
THE OPEN COURT does not understand by religion any creed or dogmatic belief, but man's world-conception in so far as it regulates his conduct.
The old dogmatic conception of religion is based upon the science of past ages; to base religion upon the maturest and truest thought of the present time is the object of The Open Court. Thus, the religion of The Open Court is the Religion of Science, that is, the religion of verified and verifiable truth.
Although opposed to irrational orthodoxy and narrow bigotry, The Open Court does not attack the properly religious element of the various religions. It criticises their errors unflinchingly but without animosity, and endeavors to preserve of them all that is true and good.
The current numbers of The Open Court contain valuable original articles from the pens of distinguished thinkers. Accurate and authorised translations are made in Philosophy, Science, and Criticism from the literature of Continental Europe, and reviews of noteworthy recent investigations are presented. Portraits of eminent philosophers and scientists are published, and appropriate illustrations accompany some of the articles.
Terms: $1.00 a year; $1.35 to foreign countries in the Postal Union. Single Copies, 10 cents.
A QUARTERLY MAGAZINE OF
PHILOSOPHY AND SCIENCE.
THE MONIST discusses the fundamental problems of Philosophy in their practical relations to the religious, ethical, and sociological questions of the day. The following have contributed to its columns:
Per Copy, 50 cents; Yearly, $2.00. In England and all countries in U.P.U. per Copy, 2s 6d; Yearly, 9s 6d.
CHICAGO
THE OPEN COURT PUBLISHING CO.,
Monon Building, 324 Dearborn St.,
LONDON: Kegan Paul, Trench, Trübner & Co.
FOOTNOTES:
[1] Statique expérimentale et théorique des liquids, 1873. See also The Science of Mechanics, p. 384 et seqq., The Open Court Publishing Co., Chicago, 1893.
[2] Compare Mach, Ueber die Molecularwirkung der Flüssigkeiten, Reports of the Vienna Academy, 1862.
[3] In almost all branches of physics that are well worked out such maximal and minimal problems play an important part.
[4] Compare Mach, Vorträge über Psychophysik, Vienna, 1863, page 41; Compendium der Physik für Mediciner, Vienna, 1863, page 234; and also The Science of Mechanics, Chicago, 1893, pp. 84 and 464.
[5] Like reflexions are found in Quételet, Du système sociale.
[6] For the full development of this idea see the essay "On the Economical Nature of Physical Inquiry," p. 186, and the chapter on "The Economy of Science," in my Mechanics (Chicago: The Open Court Publishing Company, 1893), p. 481.
[7] Science may be regarded as a maximum or minimum problem, exactly as the business of the merchant. In fact, the intellectual activity of natural inquiry is not so greatly different from that exercised in ordinary life as is usually supposed.
[8] This experiment, with its associated reflexions, is due to Galileo.
[9] A development of the theory of musical audition differing in many points from the theory of Helmholtz here expounded, will be found in my Contributions to the Analysis of the Sensations (English translation by C. M. Williams), Chicago, The Open Court Publishing Company, 1897.
[10] Sauveur also set out from Leibnitz's idea, but arrived by independent researches at a different theory, which was very near to that of Helmholtz. Compare on this point Sauveur, Mémoires de l'Académie des Sciences, Paris, 1700-1705, and R. Smith, Harmonics, Cambridge, 1749. (See Appendix, p. 346.)
[11] According to Mr. Jules Andrieu, the idea that nature must be tortured to reveal her secrets is preserved in the name crucible—from the Latin crux, a cross. But, more probably, crucible is derived from some Old French or Teutonic form, as cruche, kroes, krus, etc., a pot or jug (cf. Modern English crock, cruse, and German Krug).—Trans.
[12] Xenophon, Memorabilia iv, 7, puts into the mouth of Socrates these words: οὔτε γὰρ εὑρετὰ ἀνθρώποις αὐτὰ ἐνόμιζεν εἶναι, οὔτε χαρίζεσθαι θεοῖς ἂν ἡγεῖτο τὸν ζητοῦντα ἃ ἐκεῖνοι σαφηνίσαι οὐκ ἐβουλήθησαν.
[13] Galilei, Discorsi e dimostrazione matematiche. Leyden, 1638. Dialogo Primo.
[14] In the same way, the pitch of a locomotive-whistle is higher as the locomotive rapidly approaches an observer, and lower when rapidly leaving him than if the locomotive were at rest.—Trans.
[15] A kilometre is 0.621 or nearly five-eighths of a statute mile.
[16] Observe, also, the respect in which the wheel is held in India, Japan and other Buddhistic countries, as the emblem of power, order, and law, and of the superiority of mind over matter. The consciousness of the importance of this invention seems to have lingered long in the minds of these nations.—Tr.
[17] This effect is particularly noticeable in the size of workmen on high chimneys and church-steeples—"steeple Jacks." When the cables were slung from the towers of the Brooklyn bridge (277 feet high), the men sent out in baskets to paint them, appeared, against the broad background of heaven and water, like flies.—Trans.
[18] See Joh. Müller, Vergleichende Physiologie des Gesichtssinnes, Leipsic, 1826.
[19] Delivered before the German Casino of Prague, in the winter of 1871.
A fuller treatment of the problems of this lecture will be found in my Contributions to the Analysis of the Sensations (Jena, 1886), English Translation, Chicago, 1895. J. P. Soret, Sur la perception du beau (Geneva, 1892), also regards repetition as a principle of æsthetics. His discussions of the æsthetical side of the subject are much more detailed than mine. But with respect to the psychological and physiological foundation of the principle, I am convinced that the Contributions to the Analysis of the Sensations go deeper.—Mach (1894).
[20] Kant, in his Prolegomena zu jeder künftigen Metaphysik, also refers to this fact, but for a different purpose.
[21] Compare Mach, Fichte's Zeitschrift für Philosophie, 1864, p. 1.
[22] The fact that the first and second differential coefficients of a curve are directly seen, but the higher coefficients not, is very simply explained. The first gives the position of the tangent, the declination of the straight line from the position of symmetry, the second the declination of the curve from the straight line. It is, perhaps, not unprofitable to remark here that the ordinary method of testing rulers and plane surfaces (by reversed applications) ascertains the deviation of the object from symmetry to itself.
[23] See the lecture On the Causes of Harmony.
[24] A. von Oettingen, Harmoniesystem in dualer Entwicklung. Leipsic and Dorpat, 1866.
[25] Compare Mach's Zur Theorie des Gehörorgans, Vienna Academy, 1863.
[26] A lecture delivered at the International Electrical Exhibition, in Vienna, on September 4, 1883.
[27] If the two bodies were oppositely electrified they would exert attractions upon each other.
[28] The quantity which flows off is in point of fact less than q. It would be equal to the quantity q only if the inner coating of the jar were wholly encompassed by the outer coating.
[29] Rigorously, of course, this is not correct. First, it is to be noted that the jar L is discharged simultaneously with the electrode of the machine. The jar F, on the other hand, is always discharged simultaneously with the outer coating of the jar L. Hence, if we call the capacity of the electrode of the machine E, that of the unit jar L, that of the outer coating of L, A, and that of the principal jar F, then this equation would exist for the example in the text: (F + A)/(L + E) = 5. A cause of further departure from absolute exactness is the residual charge.
[30] Making allowance for the corrections indicated in the preceding footnote, I have obtained for the dielectric constant of sulphur the number 3.2, which agrees practically with the results obtained by more delicate methods. For the highest attainable precision one should by rights immerse the two plates of the condenser first wholly in air and then wholly in sulphur, if the ratio of the capacities is to correspond to the dielectric constant. In point of fact, however, the error which arises from inserting simply a plate of sulphur that exactly fills the space between the two plates, is of no consequence.
[31] As this definition in its simple form is apt to give rise to misunderstandings, elucidations are usually added to it. It is clear that we cannot lift a quantity of electricity to K, without changing the distribution on K and the potential on K. Hence, the charges on K must be conceived as fixed, and so small a quantity raised that no appreciable change is produced by it. Taking the work thus expended as many times as the small quantity in question is contained in the unit of quantity, we shall obtain the potential. The potential of a body K may be briefly and precisely defined as follows: If we expend the element of work dW to raise the element of positive quantity dQ from the earth to the conductor, the potential of a conductor K will be given by V = dW/dQ.
[32] In this article the solidus or slant stroke is used for the usual fractional sign of division. Where plus or minus signs occur in the numerator or denominator, brackets or a vinculum is used.—Tr.
[33] A sort of agreement exists between the notions of thermal and electrical capacity, but the difference between the two ideas also should be carefully borne in mind. The thermal capacity of a body depends solely upon that body itself. The electrical capacity of a body K is influenced by all bodies in its vicinity, inasmuch as the charge of these bodies is able to alter the potential of K. To give, therefore, an unequivocal significance to the notion of the capacity (C) of a body K, C is defined as the relation Q/V for the body K in a certain given position of all neighboring bodies, and during connexion of all neighboring conductors with the earth. In practice the situation is much simpler. The capacity, for example, of a jar, the inner coating of which is almost enveloped by its outer coating, communicating with the ground, is not sensibly affected by charged or uncharged adjacent conductors.
[34] These formulæ easily follow from Newton's theorem that a homogeneous spherical shell, whose elements obey the law of the inverse squares, exerts no force whatever on points within it but acts on points without as if the whole mass were concentrated at its centre. The formulæ next adduced also flow from this proposition.
[35] The energy of a sphere of radius r charged with the quantity q is 1/2(q2/r). If the radius increase by the space dr a loss of energy occurs, and the work done is 1/2(q2/r2)dr. Letting p denote the uniform electrical pressure on unit of surface of the sphere, the work done is also 4r2πpdr. Hence p = (1/8r2π)(q2/r2). Subjected to the same superficial pressure on all sides, say in a fluid, our half sphere would be an equilibrium. Hence we must make the pressure p act on the surface of the great circle to obtain the effect on the balance, which is r2πp = 1/8(q2/r2) = 1/8V2.
[36] The arrangement described is for several reasons not fitted for the actual measurement of potential. Thomson's absolute electrometer is based upon an ingenious modification of the electrical balance of Harris and Volta. Of two large plane parallel plates, one communicates with the earth, while the other is brought to the potential to be measured. A small movable superficial portion f of this last hangs from the balance for the determination of the attraction P. The distance of the plates from each other being D we get V = D√(8πP/f).
[37] This moment of torsion needs a supplementary correction, on account of the vertical electric attraction of the excited disks. This is done by changing the weight of the disk by means of additional weights and by making a second reading of the angles of deflexion.
[38] The jar in our experiment acts like an accumulator, being charged by a dynamo machine. The relation which obtains between the expended and the available work may be gathered from the following simple exposition. A Holtz machine H (Fig. 40) is charging a unit jar L, which after n discharges of quantity q and potential v, charges the jar F with the quantity Q at the potential V. The energy of the unit-jar discharges is lost and that of the jar F alone is left. Hence the ratio of the available work to the total work expended is
½QV/[½QV + (n/2)qv] and as Q = nq, also V/(V + v).
If, now, we interpose no unit jar, still the parts of the machine and the wires of conduction are themselves virtually such unit jars and the formula still subsists V/(V + Σv), in which Σv represents the sum of all the successively introduced differences of potential in the circuit of connexion.
[39] Published in Vol. 5, No. I, of The Monist, October, 1894, being in part a re-elaboration of the treatise Ueber die Erhaltung der Arbeit, Prague, 1872.
[40] On Matter, Living Force, and Heat, Joule: Scientific Papers, London, 1884, I, p. 265.
[41] "Atqui hoc si sit, globorum series sive corona eundem situm cum priore habebit, eademque de causa octo globi sinistri ponderosiores erunt sex dextris, ideoque rursus octo illi descendent, sex illi ascendent, istique globi ex sese continuum et aeternum motum efficient, quod est falsum."
[42] "A igitur, (si ullo modo per naturam fieri possit) locum sibi tributum non servato, ac delabatur in D; quibus positis aqua quae ipsi A succedit eandem ob causam deffluet in D, eademque ab alia istinc expelletur, atque adeo aqua haec (cum ubique eadem ratio sit) motum instituet perpetuum, quod absurdum fuerit."
[43] "Accipio, gradus velocitatis ejusdem mobilis super diversas planorum inclinationes acquisitos tunc esse aequales, cum eorundum planorum elevationes aequales sint."
[44] "Voi molto probabilmente discorrete, ma oltre al veri simile voglio con una esperienza crescer tanto la probabilità, che poco gli manchi all'agguagliarsi ad una ben necessaria dimostrazione. Figuratevi questo foglio essere una parete eretta all'orizzonte, e da un chiodo fitto in essa pendere una palla di piombo d'un'oncia, o due, sospesa dal sottil filo AB lungo due, o tre braccia perpendicolare all'orizzonte, e nella parete segnate una linea orizontale DC segante a squadra il perpendicolo AB, il quale sia lontano dalla parete due dita in circa, trasferendo poi il filo AB colla palla in AC, lasciata essa palla in libertà, la quale primieramente vedrete scendere descrivendo l'arco CBD, e di tanto trapassare il termine B, che scorrendo per l'arco BD sormonterà fino quasi alla segnata parallela CD, restando di per vernirvi per piccolissimo intervallo, toltogli il precisamente arrivarvi dall'impedimento dell'aria, e del filo. Dal che possiamo veracemente concludere, che l'impeto acquistato nel punto B dalla palla nello scendere per l'arco CB, fu tanto, che bastò a risospingersi per un simile arco BD alla medesima altezza; fatta, e più volte reiterata cotale esperienza, voglio, che fiechiamo nella parete rasente al perpendicolo AB un chiodo come in E, ovvero in F, che sporga in fuori cinque, o sei dita, e questo acciocchè il filo AC tornando come prima a riportar la palla C per l'arco CB, giunta che ella sia in B, inoppando il filo nel chiodo E, sia costretta a camminare per la circonferenza BG descritta in torno al centro E, dal che vedremo quello, che potrà far quel medesimo impeto, che dianzi concepizo nel medesimo termine B, sospinse l'istesso mobile per l'arco ED all'altezza dell'orizzonale CD. Ora, Signori, voi vedrete con gusto condursi la palla all'orizzontale nel punto G, e l'istesso accadere, l'intoppo si metesse più basso, come in F, dove la palla descriverebbe l'arco BJ, terminando sempre la sua salita precisamente nella linea CD, e quando l'intoppe del chiodo fusse tanto basso, che l'avanzo del filo sotto di lui non arivasse all'altezza di CD (il che accaderebbe, quando fusse più vicino al punto B, che al segamento dell' AB coll'orizzontale CD), allora il filo cavalcherebbe il chiodo, e segli avolgerebbe intorno. Questa esperienza non lascia luogo di dubitare della verità del supposto: imperocchè essendo li due archi CB, DB equali e similmento posti, l'acquisto di momento fatto per la scesa nell'arco CB, è il medesimo, che il fatto per la scesa dell'arco DB; ma il momento acquistato in B per l'arco CB è potente a risospingere in su il medesimo mobile per l'arco BD; adunque anco il momento acquistato nella scesa DB è eguale a quello, che sospigne l'istesso mobile pel medesimo arco da B in D, sicche universal-mente ogni memento acquistato per la scesa d'un arco è eguale a quello, che può far risalire l'istesso mobile pel medesimo arco: ma i momenti tutti che fanno resalire per tutti gli archi BD, BG, BJ sono eguali, poichè son fatti dal istesso medesimo momento acquistato per la scesa CB, come mostra l'esperienza: adunque tutti i momenti, che si acquistano per le scese negli archi DB, GB, JB sono eguali."
[45] "Constat jam, quod mobile ex quiete in A descendens per AB, gradus acquirit velocitatis juxta temporis ipsius incrementum: gradum vero in B esse maximum acquisitorum, et suapte natura immutabiliter impressum, sublatis scilicet causis accelerationis novae, aut retardationis: accelerationis inquam, si adhuc super extenso plano ulterius progrederetur; retardationis vero, dum super planum acclive BC fit reflexio: in horizontali autem GH aequabilis motus juxta gradum velocitatis ex A in B acquisitae in infinitum extenderetur."
[46] "Si gravitas non esset, neque aër motui corporum officeret, unumquodque eorum, acceptum semel motum continuaturum velocitate aequabili, secundum lineam rectam."
[47] "Si pondera quotlibet, vi gravitatis suae, moveri incipiant; non posse centrum gravitatis ex ipsis compositae altius, quam ubi incipiente motu reperiebatur, ascendere.
"Ipsa vero hypothesis nostra quominus scrupulum moveat, nihil aliud sibi velle ostendemus, quam, quod nemo unquam negavit, gravia nempe sursum non ferri.—Et sane, si hac eadem uti scirent novorum operum machinatores, qui motum perpetuum irrito conatu moliuntur, facile suos ipsi errores deprehenderent, intelligerentque rem eam mechanica ratione haud quaquam possibilem esse."
[48] "Si pendulum e pluribus ponderibus compositum, atque e quiete dimissum, partem quamcunque oscillationis integrae confecerit, atque inde porro intelligantur pondera ejus singula, relicto communi vinculo, celeritates acquisitas sursum convertere, ac quousque possunt ascendere; hoc facto centrum gravitatis ex omnibus compositae, ad eandem altitudinem reversum erit, quam ante inceptam oscillationem obtinebat."
[49] "Notato autem hic illud staticum axioma etiam locum habere:
[50] "Cependant, comme dans cet ouvrage on ne fut d'abord attentif qu'à considérer ce beau développement de la mécanique qui semblait sortir tout entière d'une seule et même formule, on crut naturellement que la science etait faite, et qu'il ne restait plus qu'à chercher la démonstration du principe des vitesses virtuelles. Mais cette recherche ramena toutes les difficultés qu'on avait franchies par le principe même. Cette loi si générale, où se mêlent des idées vagues et étrangères de mouvements infinement petits et de perturbation d'équilibre, ne fit en quelque sorte que s'obsurcir à l'examen; et le livre de Lagrange n'offrant plus alors rien de clair que la marche des calculs, on vit bien que les nuages n'avaient paru levé sur le cours de la mécanique que parcequ'ils étaient, pour ainsi dire, rassemblés à l'origine même do cette science.
"Une démonstration générale du principe des vitesses virtuelles devait au fond revenir a établir le mécanique entière sur une autre base: car la demonstration d'une loi qui embrasse toute une science ne peut être autre chose qua la reduction de cette science à une autre loi aussi générale, mais évidente, ou du moins plus simple que la première, et qui partant la rende inutile."
[51] Traité de la lumière, Leyden, 1690, p. 2.
[52] "L'on ne sçaurait douter que la lumière ne consiste dans le mouvement de certaine matière. Car soit qu'on regarde sa production, on trouve qu'içy sur la terre c'est principalement le feu et la flamme qui l'engendrent, lesquels contient sans doute des corps qui sont dans un mouvement rapide, puis qu'ils dissolvent et fondent plusieurs autres corps des plus solides: soit qu'on regarde ses effets, on voit que quand la lumière est ramasseé, comme par des miroires concaves, elle a la vertu de brûler comme le feu. c-est-à-dire qu'elle desunit les parties des corps; ce qui marque assurément du mouvement, au moins dans la vraye Philosophie, dans laquelle on conçoit la cause de tous les effets naturels par des raisons de mechanique. Ce qu'il faut faire à mon avis, ou bien renoncer à tout espérance de jamais rien comprendre dans la Physique."
[53] Sur la puissance motrice du feu. (Paris, 1824.)
[54] "On objectra peut-être ici que le mouvement perpétuel, démontré impossible par les seules actions mécaniques, ne l'est peut-être pas lorsqu'on emploie l'influence soit de la chaleur, soit de l'électricité; mais pent-on concevoir les phénomènes de la chaleur et de l'électricité comme dus à autre chose qu'à des mouvements quelconques des corps et comme tels ne doivent-ils pas être soumis aux lois générales de la mécanique?"
[55] By this is meant the temperature of a Celsius scale, the zero of which is 273° below the melting-point of ice.
[56] I first drew attention to this fact in my treatise Ueber die Erhaltung der Arbeit, Prague, 1872. Before this, Zeuner had pointed out the analogy between mechanical and thermal energy. I have given a more extensive development of this idea in a communication to the Sitzungsberichte der Wiener Akademie, December, 1892, entitled Geschichte und Kritik des Carnot'schen Wärmegesetzes. Compare also the works of Popper (1884), Helm (1887), Wronsky (1888), and Ostwald (1892).
[57] Sir William Thomson first consciously and intentionally introduced (1848, 1851) a mechanical measure of temperature similar to the electric measure of potential.
[58] Compare my Analysis of the Sensations, Jena, 1886: English translation, Chicago, 1897.
[59] A better terminology appears highly desirable in the place of the usual misleading one. Sir William Thomson (1852) appears to have felt this need, and it has been clearly expressed by F. Wald (1889). We should call the work which corresponds to a vanished quantity of heat its mechanical substitution-value; while that work which can be actually performed in the passage of a thermal condition A to a condition B, alone deserves the name of the energy-value of this change of condition. In this way the arbitrary substantial conception of the processes would be preserved and misapprehensions forestalled.
[60] An address delivered before the anniversary meeting of the Imperial Academy of Sciences, at Vienna, May 25, 1882.
[61] Primitive Culture.
[62] Tylor, loc. cit.
[63] Essai philosophique sur les probabilités. 6th Ed. Paris, 1840, p. 4. The necessary consideration of the initial velocities is lacking in this formulation.
[64] Principien der Wirthschaftslehre, Vienna, 1873.
[65] It is clear from this that all so-called elementary (differential) laws involve a relation to the whole.
[66] If it be objected, that in the case of perturbations of the velocity of rotation of the earth, we could be sensible of such perturbations, and being obliged to have some measure of time, we should resort to the period of vibration of the waves of sodium light,—all that this would show is that for practical reasons we should select that event which best served us as the simplest common measure of the others.
[67] Measurement, in fact, is the definition of one phenomenon by another (standard) phenomenon.
[68] I have represented the point of view here taken for more than thirty years and developed it in various writings (Erhaltung der Arbeit, 1872, parts of which are published in the article on The Conservation of Energy in this collection; The Forms of Liquids, 1872, also published in this collection; and the Bewegungsempfindungen, 1875). The idea, though known to philosophers, is unfamiliar to the majority of physicists. It is a matter of deep regret to me, therefore, that the title and author of a small tract which accorded with my views in numerous details and which I remember having caught a glance of in a very busy period (1879-1880), have so completely disappeared from my memory that all efforts to obtain a clue to them have hitherto been fruitless.
[69] Inaugural Address, delivered on assuming the Rectorate of the University of Prague, October 18, 1883.
The idea presented in this essay is neither new nor remote. I have touched upon it myself on several occasions (first in 1867), but have never made it the subject of a formal disquisition. Doubtless, others, too, have treated it; it lies, so to speak, in the air. However, as many of my illustrations were well received, although known only in an imperfect form from the lecture itself and the newspapers, I have, contrary to my original intention, decided to publish it. It is not my intention to trespass here upon the domain of biology. My statements are to be taken merely as the expression of the fact that no one can escape the influence of a great and far-reaching idea.
[70] At first sight an apparent contradiction arises from the admission of both heredity and adaptation; and it is undoubtedly true that a strong disposition to heredity precludes great capability of adaptation. But imagine the organism to be a plastic mass which retains the form transmitted to it by former influences until new influences modify it; the one property of plasticity will then represent capability of adaptation as well as power of heredity. Analogous to this is the case of a bar of magnetised steel of high coercive force: the steel retains its magnetic properties until a new force displaces them. Take also a body in motion: the body retains the velocity acquired in (inherited from) the interval of time just preceding, except it be changed in the next moment by an accelerating force. In the case of the body in motion the change of velocity (Abänderung) was looked upon as a matter of course, while the discovery of the principle of inertia (or persistence) created surprise; in Darwin's case, on the contrary, heredity (or persistence) was taken for granted, while the principle of variation (Abänderung) appeared novel.
Fully adequate views are, of course, to be reached only by a study of the original facts emphasised by Darwin, and not by these analogies. The example referring to motion, if I am not mistaken, I first heard, in conversation, from my friend J. Popper, Esq., of Vienna.
Many inquirers look upon the stability of the species as something settled, and oppose to it the Darwinian theory. But the stability of the species is itself a "theory." The essential modifications which Darwin's views also are undergoing will be seen from the works of Wallace [and Weismann], but more especially from a book of W. H. Rolph, Biologische Probleme, Leipsic, 1882. Unfortunately, this last talented investigator is no longer numbered among the living.
[71] Written in 1883.
[72] See Pfaundler, Pogg. Ann., Jubelband, p. 182.
[73] See the beautiful discussions of this point in Hering's Memory as a General Function of Organised Matter (1870), Chicago, The Open Court Publishing Co., 1887. Compare also Dubois, Ueber die Uebung, Berlin, 1881.
[74] Spencer, The Principles of Psychology. London, 1872.
[75] See the article The Velocity of Light, page 63.
[76] I am well aware that the endeavor to confine oneself in natural research to facts is often censured as an exaggerated fear of metaphysical spooks. But I would observe, that, judged by the mischief which they have wrought, the metaphysical, of all spooks, are the least fabulous. It is not to be denied that many forms of thought were not originally acquired by the individual, but were antecedently formed, or rather prepared for, in the development of the species, in some such way as Spencer, Haeckel, Hering, and others have supposed, and as I myself have hinted on various occasions.
[77] Compare, for example, Schiller, Zerstreute Betrachtungen über verschiedene ästhetische Gegenstände.
[78] We must not be deceived in imagining that the happiness of other people is not a very considerable and essential portion of our own. It is common capital, which cannot be created by the individual, and which does not perish with him. The formal and material limitation of the ego is necessary and sufficient only for the crudest practical objects, and cannot subsist in a broad conception. Humanity in its entirety may be likened to a polyp-plant. The material and organic bonds of individual union have, indeed, been severed; they would only have impeded freedom of movement and evolution. But the ultimate aim, the psychical connexion of the whole, has been attained in a much higher degree through the richer development thus made possible.
[79] C. E. von Baer, the subsequent opponent of Darwin and Haeckel, has discussed in two beautiful addresses (Das allgemeinste Gesetz der Natur in aller Entwickelung, and Welche Auffassung der lebenden Natur ist die richtige, und wie ist diese Auffassung auf die Entomologie anzuwenden?) the narrowness of the view which regards an animal in its existing state as finished and complete, instead of conceiving it as a phase in the series of evolutionary forms and regarding the species itself as a phase of the development of the animal world in general.
[80] An address delivered before the General Session of the German Association of Naturalists and Physicians, at Vienna, Sept. 24, 1894.
[81] Inaugural lecture delivered on assuming the Professorship of the History and Theory of Inductive Science in the University of Vienna, October 21, 1895.
[82] The phrase is, Er hat das Pulver nicht erfunden.
[83] "Quod si quis tanta industria exstitisset, ut ex naturae principiis at geometria hanc rem eruere potuisset, eum ego supra mortalium sortem ingenio valuisse dicendum crederem. Sed hoc tantum abest, ut fortuito reperti artificii rationem non adhuc satis explicari potuerint viri doctissimi."—Hugenii Dioptrica (de telescopiis).
[84] I must not be understood as saying that the fire-drill has played no part in the worship of fire or of the sun.
[85] Compare on this point the extremely interesting remarks of Dr. Paul Carus in his Philosophy of the Tool, Chicago, 1893.
[86] Möbius, Naturwissenschaftlicher Verein für Schleswig-Holstein, Kiel, 1893, p. 113 et seq.
[87] I am indebted for this observation to Professor Hatscheck.
[88] Cf. Hoppe, Entdecken und Finden, 1870.
[89] See the lecture "Sensations of Orientation," p. 282 et seq.
[90] This story was related to me by Jolly, and subsequently repeated in a letter from him.
[91] I do not know whether Swift's academy of schemers in Lagado, in which great discoveries and inventions were made by a sort of verbal game of dice, was intended as a satire on Francis Bacon's method of making discoveries by means of huge synoptic tables constructed by scribes. It certainly would not have been ill-placed.
[92] "Crescunt disciplinae lente tardeque; per varios errores sero pervenitur ad veritatem. Omnia praeparata esse debent diuturno et assiduo labore ad introitum veritatis novae. Jam illa certo temporis momento divina quadam necessitate coacta emerget."
Quoted by Simony, In ein ringförmiges Band einen Knoten zu machen, Vienna, 1881, p. 41.
[93] A lecture delivered on February 24, 1897, before the Verein zur Verbreitung naturwissenschaftlicher Kenntnisse in Wien.
[94] Wollaston, Philosophical Transactions, Royal Society, 1810. In the same place Wollaston also describes and explains the creaking of the muscles. My attention was recently called to this work by Dr. W. Pascheles.—Cf. also Purkinje, Prager medicin. Jahrbücher, Bd. 6, Wien, 1820.
[95] Similarly many external forces do not act at once on all parts of the earth, and the internal forces which produce deformations act at first immediately only upon limited parts. If the earth were a feeling being, the tides and other terrestrial events would provoke in it similar sensations to those of our movements. Perhaps the slight alterations of the altitude of the pole which are at present being studied are connected with the continual slight deformations of the central ellipsoid occasioned by seismical happenings.
[96] For the popular explanation by unconscious inference the matter is extremely simple. We regard the railway carriage as vertical and unconsciously infer the inclination of the trees. Of course the opposite conclusion that we regard the trees as vertical and infer the inclination of the carriage, unfortunately, is equally clear on this theory.
[97] It will be observed that my way of thinking and experimenting here is related to that which led Knight to the discovery and investigation of the geotropism of plants. Philosophical Transactions, January 9, 1806. The relations between vegetable and animal geotropism have been more recently investigated by J. Loeb.
[98] This experiment is doubtless related to the galvanotropic experiment with the larvæ of frogs described ten years later by L. Hermann. Compare on this point my remarks in the Anzeiger der Wiener Akademie, 1886, No. 21. Recent experiments in galvanotropism are due to J. Loeb.
[99] Wiener Akad., 6 November, 1873.
[100] Wiener Gesellschaft der Aerzte, 14 November, 1874.
[101] I have made a contribution to this last question in my Analysis of the Sensations, (1886), English translation, 1897.
[102] In my Grundlinien der Lehre von den Bewegungsempfindungen, 1875, the matter occupying lines 4 to 13 of page 20 from below, which rests on an error, is, as I have also elsewhere remarked, to be stricken out. For another experiment related to that of Foucault, compare my Mechanics, p. 303.
[103] Anzeiger der Wiener Akad., 30 December, 1875.
[104] The experiment was specially interesting for me as I had already attempted in 1874, although with very little confidence and without success, to excite electromagnetically my own labyrinth through which I had caused a current to pass.
[105] Perhaps the discussion concerning the peculiarity of cats always falling on their feet, which occupied the Parisian Academy, and, incidentally, Parisian society a few years ago, will be remembered here. I believe that the questions which arose are disposed of by the considerations advanced in my Bewegungsempfindungen (1875). I also partly gave, as early as 1866, the apparatus conceived by the Parisian scientists to illustrate the phenomena in question. One difficulty was left untouched in the Parisian debate. The otolith apparatus of the cat can render it no service in free descent. The cat, however, while at rest, doubtless knows its position in space and is instinctively conscious of the amount of movement which will put it on its feet.
[106] See the Appendix to the English edition of my Analysis of the Sensations, Chicago, 1897.
[107] Compare my Analysis of Sensations, p. 123 ff.
[108] E. H. Weber, De aure et auditu hominis et animalium, Lipsiae, 1820.
[109] Störensen, Journ. Anat. Phys., London, Vol. 29 (1895).
[110] A lecture delivered on Nov. 10, 1897.
[111] Christiansen, Wiedemann's Annalen, XXIII. S. 298, XXIV., p. 439 (1884-1885).
[112] The German phrase is Schlierenmethode, by which term the method is known even by American physicists. It is also called in English the "shadow-method." But a term is necessary which will cover all the derivatives, and so we have employed alternatively the words striate and differential. The etymology of schlieren, it would seem, is uncertain. Its present use is derived from its technological signification in glass-manufacturing, where by die Schlieren are meant the wavy streaks and imperfections in glass. Hence its application to the method for detecting small optical differences and faults generally. Professor Crew of Evanston suggests to the translator that schlieren may be related to our slur (L. G., slüren, to trail, to draggle), a conjecture which is doubtless correct and agrees both with the meaning of schlieren as given in the large German dictionaries and with the intransitive use of our own verb slur, the faults in question being conceived as "trailings," "streakings," etc.—Trans.
[113] An address delivered before the Congress of Delegates of the German Realschulmännerverein, at Dortmund, April 16, 1886. The full title of the address reads: "On the Relative Educational Value of the Classics and the Mathematico-Physical Sciences in Colleges and High Schools."
Although substantially contained in an address which I was to have made at the meeting of Natural Scientists at Salzburg in 1881 (deferred on account of the Paris Exposition), and in the Introduction to a course of lectures on "Physical Instruction in Preparatory Schools," which I delivered in 1883, the invitation of the German Realschulmännerverein afforded me the first opportunity of putting my views upon this subject before a large circle of readers. Owing to the place and circumstances of delivery, my remarks apply of course, primarily, only to German schools, but, with slight modifications, made in this translation, are not without force for the institutions of other countries. In giving here expression to a strong personal conviction formed long ago, it is a matter of deep satisfaction to me to find that they agree in many points with the views recently advanced in independent form by Paulsen (Geschichte des gelehrten Unterrichts, Leipsic, 1885) and Frary (La question du latin, Paris, Cerf, 1885). It is not my desire nor effort here to say much that is new, but merely to contribute my mite towards bringing about the inevitable revolution now preparing in the world of elementary instruction. In the opinion of experienced educationists the first result of that revolution will be to make Greek and mathematics alternately optional subjects in the higher classes of the German Gymnasium and in the corresponding institutions of other countries, as has been done in the splendid system of instruction in Denmark. The gap between the German classical Gymnasium and the German Realgymnasium, or between classical and scientific schools generally, can thus be bridged over, and the remaining inevitable transformations will then be accomplished in relative peace and quiet. (Prague, May, 1886.)
[114] Maupertuis, Œuvres, Dresden, 1752, p. 339.
[115] F. Paulsen, Geschichte des gelehrten Unterrichts, Leipsic, 1885.
[116] There is a peculiar irony of fate in the fact that while Leibnitz was casting about for a new vehicle of universal linguistic intercourse, the Latin language which still subserved this purpose the best of all, was dropping more and more out of use, and that Leibnitz himself contributed not the least to this result.
[117] As a rule, the human brain is too much, and wrongly, burdened with things which might be more conveniently and accurately preserved in books where they could be found at a moment's notice. In a recent letter to me from Düsseldorf, Judge Hartwich writes:
"A host of words exist which are out and out Latin or Greek, yet are employed with perfect correctness by people of good education who never had the good luck to be taught the ancient languages. For example, words like 'dynasty.' ... The child learns such words as parts of the common stock of speech, or even as parts of his mother-tongue, just as he does the words 'father,' 'mother,' 'bread,' 'milk.' Does the ordinary mortal know the etymology of these Saxon words? Did it not require the almost incredible industry of the Grimms and other Teutonic philologists to throw the merest glimmerings of light upon the origin and growth of our own mother-tongue? Besides, do not thousands of people of so-called classical education use every moment hosts of words of foreign origin whose derivation they do not know? Very few of them think it worth while to look up such words in the dictionaries, although they love to maintain that people should study the ancient languages for the sake of etymology alone."
[118] Standing remote from the legal profession I should not have ventured to declare that the study of Greek was not necessary for the jurists; yet this view was taken in the debate that followed this lecture by professional jurists of high standing. According to this opinion, the preparatory education obtained in the German Realgymnasium would also be sufficient for the future jurists and insufficient only for theologians and philologists. [In England and America not only is Greek not necessary, but the law-Latin is so peculiar that even persons of good classical education cannot understand it.—Tr.]
[119] In emphasising here the weak sides of the writings of Plato and Aristotle, forced on my attention while reading them in German translations, I, of course, have no intention of underrating the great merits and the high historical importance of these two men. Their importance must not be measured by the fact that our speculative philosophy still moves to a great extent in their paths of thought. The more probable conclusion is that this branch has made very little progress in the last two thousand years. Natural science also was implicated for centuries in the meshes of the Aristotelian thought, and owes its rise mainly to having thrown off those fetters.
[120] I would not for a moment contend that we derive exactly the same profit from reading a Greek author in a translation as from reading him in the original; but the difference, the excess of gain in the second case, appears to me, and probably will to most men who are not professional philologists, to be too dearly bought with the expenditure of eight years of valuable time.
[121] "The temptation," Judge Hartwich writes, "to regard the 'taste' of the ancients as so lofty and unsurpassable appears to me to have its chief origin in the fact that the ancients were unexcelled in the representation of the nude. First, by their unremitting care of the human body they produced splendid models; and secondly, in their gymnasiums and in their athletic games they had these models constantly before their eyes. No wonder, then, that their statues still excite our admiration! For the form, the ideal of the human body has not changed in the course of the centuries. But with intellectual matters it is totally different; they change from century to century, nay, from decennium to decennium. It is very natural now, that people should unconsciously apply what is thus so easily seen, namely, the works of sculpture, as a universal criterion of the highly developed taste of the ancients—a fallacy against which people cannot, in my judgment, be too strongly warned."
[122] English: "In the beginning God created the heaven and the earth. And the earth was without form and void; and darkness was upon the face of the deep. And the spirit of God moved upon the face of the waters."—Dutch: "In het begin schiep God den hemel en de aarde. De aarde nu was woest en ledig, en duisternis was op den afgrond; en de Geest Gods zwefde op de wateren."—Danish: "I Begyndelsen skabte Gud Himmelen og Jorden. Og Jorden var ode og tom, og der var morkt ovenover Afgrunden, og Guds Aand svoevede ovenover Vandene."—Swedish: "I begynnelsen skapade Gud Himmel och Jord. Och Jorden war öde och tom, och mörker war pä djupet, och Gods Ande swäfde öfwer wattnet."—German: "Am Anfang schuf Gott Himmel und Erde. Und die Erde war wüst und leer, und es war finster auf der Tiefe; und der Geist Gottes schwebte auf dem Wasser."
[123] Compare Herzen's excellent remarks, De l'enseignement secondaire dans la Suisse romande, Lausanne, 1886.
[124] Geschichte der Mathematik, Leipsic, 1874.
[125] Geometrische Analyse, Ulm, 1886.
[126] In his text-books of elementary mathematics
[127] Abhandlungen aus dem Gebiete der Mathematik, Würzburg, 1883.
[128] My idea here is an appropriate selection of readings from Galileo, Huygens, Newton, etc. The choice is so easily made that there can be no question of difficulties. The contents would be discussed with the students, and the original experiments performed with them. Those scholars alone should receive this instruction in the upper classes who did not look forward to systematical instruction in the physical sciences. I do not make this proposition of reform here for the first time. I have no doubt, moreover, that such radical changes will only be slowly introduced.
[129] Die Mathematik als Lehrgegenstand des Gymnasiums, Berlin, 1883.
[130] Wrong as it is to burden future physicians and scientists with Greek for the sake of the theologians and philologists, it would be just as wrong to compel theologians and philologists, on account of the physicians, to study such subjects as analytical geometry. Moreover, I cannot believe that ignorance of analytical geometry would be a serious hindrance to a physician that was otherwise well versed in quantitative thought. No special advantage generally is observable in the graduates of the Austrian gymnasiums, all of whom have studied analytical geometry. [Refers to an assertion of Dubois-Reymond.]
[131] Compare M. Cantor, Geschichte der Mathematik, Leipsic, 1880, Vol. I. p. 193.
[132] Compare Paulsen, l. c., pp. 607, 688.
[133] It is to be hoped that the Americans will jealously guard their schools and universities against the influence of the State.
[134] This article, which appeared in the Proceedings of the German Mathematical Society of Prague for the year 1892, is printed as a supplement to the article on "The Causes of Harmony," at page 32.
[135] The present exposition is taken from the volumes for 1700 (published in 1703) and for 1701 (published in 1704), and partly also from the Histoire de l'Académie and partly from the Mémoires. Sauveur's later works enter less into consideration here.
[136] Euler, Tentamen novae theoriae musicae, Petropoli, 1739.
[137] In attempting to perform his experiment of beats before the Academy, Sauveur was not quite successful. Histoire de l'Académie, Année 1700, p. 136.
[138] Histoire de l'Académie, Année 1701, p. 134.
[139] Ibid., p. 298.
[140] Histoire de l'Académie, Année 1702, p. 91.
[141] From the Histoire de l'Académie, Année 1700, p. 139.
[142] Because all octaves in use in music offer too great differences of rates of vibration.
[143] "Les battemens ne plaisent pas à l'Oreille, à cause de l'inégalité du son, et l'on peut croire avec beaucoup d'apparence que ce qui rend les Octaves si agréables, c'est qu'on n'y entend jamais de battemens.
"En suivant cette idée, on trouve que les accords dont on ne peut entendre les battemens, sont justement ceux que les Musiciens traitent de Consonances, et que ceux dont les battemens se font sentir, sont les Dissonances, et que quand un accord est Dissonance dans une certaine octave et Consonance dans une autre, c'est qu'il bat dans l'une, et qu'il ne bat pas dans l'autre. Aussi est il traité de Consonance imparfaite. Il est fort aisé par les principes de Mr. Sauveur qu'on a établis ici, de voir quels accords battent, et dans quelles Octaves au-dessus on au-dessous du son fixe. Si cette hypothèse est vraye, elle découvrira la véritable source des Règles de la composition, inconnue jusqu'à présent à la Philosophie, qui s'en remettait presque entièrement au jugement de l'Oreille. Ces sortes de jugemens naturels, quelque bisarres qu'ils paroissent quelquefois, ne le sont point, ils ont des causes très réelles, dont la connaissance appartient à la Philosophie, pourvue qu'elle s'en puisse mettre en possession."
[144] Harmonics or the Philosophy of Musical Sounds, Cambridge, 1749. I saw this book only hastily in 1864 and drew attention to it in a work published in 1866. I did not come into its actual possession until three years ago and then only did I learn its exact contents.
[145] Harmonics, pp. 118 and 243.
[146] "Short cycle" is the period in which the same phases of the two co-operant tones are repeated.
[147] This article, designed to illustrate historically that on Symmetry, at page 89, first appeared in Fichte's Zeitschrift für Philosophie, for 1865.
[148] Comp. Cornelius, Ueber das Sehen; Wundt, Theorie der Sinneswahrnehmung.
[149] Comp. Mach, Ueber das Sehen von Lagen and Winkeln. Sitzungsb. der Wiener Akademie, 1861.
[150] Comp. Mach, Zur Theorie des Gehörorgans. Sitsungsber, der Wiener Akad., 1863.—Ueber einige Erscheinungen der physiolog. Akustik. Ibid., 1864.