
10117
Title: A Budget of Paradoxes, Volume II
Author: Augustus De Morgan
Editor: David Eugene Smith
Release date: August 23, 2008 [eBook #26408]
Language: English
Credits: E-text prepared by David Starner, Keith Edkins, and the Project Gutenberg Online Distributed Proofreading Team
E-text prepared by David Starner, Keith Edkins,
and the Project Gutenberg Online Distributed Proofreading Team
(http://www.pgdp.net)
| Transcriber's note: | A few typographical errors have been corrected. They appear in the text like this, and the explanation will appear when the mouse pointer is moved over the marked passage. |
REPRINTED WITH THE AUTHOR'S ADDITIONS FROM THE ATHENAEUM
SECOND EDITION EDITED BY DAVID EUGENE SMITH
WITH A NEW INTRODUCTION BY ERNEST NAGEL
PROFESSOR OF PHILOSOPHY, COLUMBIA UNIVERSITY
UNABRIDGED EDITION—TWO VOLUMES BOUND AS ONE
DOVER PUBLICATIONS, INC., NEW YORK
This new Dover Edition, published in 1954,
is an unabridged republication of the Second Edition
of 1915, with a new introduction by Professor Ernest Nagel.
Copyright 1954 by Dover Publications, Inc.
Manufactured in the United States of America
ON SOME PHILOSOPHICAL ATHEISTS.
With the general run of the philosophical atheists of the last century the notion of a God was an hypothesis. There was left an admitted possibility that the vague somewhat which went by more names than one, might be personal, intelligent, and superintendent. In the works of Laplace,[1] who is sometimes called an atheist from his writings, there is nothing from which such an inference can be drawn: unless indeed a Reverend Fellow of the Royal Society may be held to be the fool who said in his heart, etc., etc., if his contributions to the Philosophical Transactions go no higher than nature. The following anecdote is well known in Paris, but has never been printed entire. Laplace once went in form to present some edition of his "Système du Monde" to the First Consul, or Emperor. Napoleon, whom some wags had told that this book contained no mention of the name of God, and who was fond of putting embarrassing questions, received it with—"M. Laplace, they tell me you have written this large book on the system of the universe, and have never even mentioned its Creator." Laplace, who, though the most supple of politicians, was as stiff as a martyr on every point of his philosophy or religion (e. g., even under Charles X he never concealed his dislike of the priests), drew himself up and answered [2]bluntly, "Je n'avais pas besoin de cette hypothèse-là."[2] Napoleon, greatly amused, told this reply to Lagrange, who exclaimed, "Ah! c'est une belle hypothèse; ça explique beaucoup de choses."[3]
It is commonly said that the last words of Laplace were, "Ce que nous connaissons est peu de chose; ce que nous ignorons est immense."[4] This looks like a parody on Newton's pebbles:[5] the following is the true account; it comes to me through one remove from Poisson.[6] After the publication (in 1825) of the fifth volume of the Mécanique Céleste, Laplace became gradually weaker, and with it musing and abstracted. He thought much on the great problems of existence, and often muttered to himself, Qu'est ce que c'est que tout cela![7] After many alternations, he appeared at last so permanently prostrated that his family applied to his favorite pupil, M. Poisson, to try to get a word from him. Poisson paid a visit, and after a few words of salutation, said, "J'ai une bonne nouvelle à vous annoncer: on a reçu au Bureau des Longitudes une lettre d'Allemagne annonçant que M. Bessel a vérifié par l'observation vos découvertes théoriques sur les satellites de Jupiter."[8] Laplace opened his eyes and answered with deep [3]gravity, "L'homme ne poursuit que des chimères."[9] He never spoke again. His death took place March 5, 1827.
The language used by the two great geometers illustrates what I have said: a supreme and guiding intelligence—apart from a blind rule called nature of things—was an hypothesis. The absolute denial of such a ruling power was not in the plan of the higher philosophers: it was left for the smaller fry. A round assertion of the non-existence of anything which stands in the way is the refuge of a certain class of minds: but it succeeds only with things subjective; the objective offers resistance. A philosopher of the appropriative class tried it upon the constable who appropriated him: I deny your existence, said he; Come along all the same, said the unpsychological policeman.
Euler[10] was a believer in God, downright and straightforward. The following story is told by Thiébault,[11] in his Souvenirs de vingt ans de séjour à Berlin,[12] published in his old age, about 1804. This volume was fully received as trustworthy; and Marshall Mollendorff[13] told the Duc de Bassano[14] in 1807 that it was the most veracious of books written by the most honest of men. Thiébault says that he has no personal knowledge of the truth of the story, but [4]that it was believed throughout the whole of the north of Europe. Diderot[15] paid a visit to the Russian Court at the invitation of the Empress. He conversed very freely, and gave the younger members of the Court circle a good deal of lively atheism. The Empress was much amused, but some of her councillors suggested that it might be desirable to check these expositions of doctrine. The Empress did not like to put a direct muzzle on her guest's tongue, so the following plot was contrived. Diderot was informed that a learned mathematician was in possession of an algebraical demonstration of the existence of God, and would give it him before all the Court, if he desired to hear it. Diderot gladly consented: though the name of the mathematician is not given, it was Euler. He advanced towards Diderot, and said gravely, and in a tone of perfect conviction: Monsieur, (a + bn) / n = x, donc Dieu existe; répondez![16] Diderot, to whom algebra was Hebrew, was embarrassed and disconcerted; while peals of laughter rose on all sides. He asked permission to return to France at once, which was granted.
ROTATION OF THE MOON.
An examination of the Astronomical doctrine of the Moon's rotation. By J. L.[17] Edinburgh, 1847, 8vo.
A systematic attack of the character afterwards made with less skill and more notice by Mr. Jellinger Symons.
July 1866, J. L. appears as Mr. James Laurie, with a new pamphlet "The Astronomical doctrines of the Moon's rotation ..." Edinburgh. Of all the works I have seen on the question, this is the most confident, and the sorest. [5]A writer on astronomy said of Mr. Jellinger Symons,[18] "Of course he convinced no one who knew anything of the subject." This "ungenerous slur" on the speculator's memory appears to have been keenly felt; but its truth is admitted. Those who knew anything of the subject are "the so-called men of science," whose three P's were assailed; prestige, pride, and prejudice: this the author tries to effect for himself with three Q's; quibble, quirk, and quiddity. He explains that the Scribes and Pharisees would not hear Jesus, and that the lordly bishop of Rome will not cast his tiara and keys at the feet of the "humble presbyter" who now plays the part of pope in Scotland. I do not know whom he means: but perhaps the friends of the presbyter-pope may consider this an ungenerous slur. The best proof of the astronomer is just such "as might have been expected from the merest of blockheads"; but as the giver is of course not a blockhead, this circumstance shows how deeply blinded by prejudice he must be.
Of course the paradoxers do not persuade any persons who know their subjects: and so these Scribes and Pharisees reject the Messiah. We must suppose that the makers of this comparison are Christians: for if they thought the Messiah an enthusiast or an impostor, they would be absurd in comparing those who reject what they take for truth with others who once rejected what they take for falsehood. And if Christians, they are both irreverent and blind to all analogy. The Messiah, with His Divine mission proved by miracles which all might see who chose to look, is degraded into a prototype of James Laurie, ingeniously astronomizing upon ignorant geometry and false logic, and comparing to blockheads those who expose his nonsense. Their comparison is as foolish as—supposing [6]them Christians—it is profane: but, like errors in general, its other end points to truth. There were Pseudochrists and Antichrists; and a Concordance would find the real forerunners of all the paradoxers. But they are not so clever as the old false prophets: there are none of whom we should be inclined to say that, if it were possible, they would deceive the very educated. Not an Egyptian among them all can make uproar enough to collect four thousand men that are murderers—of common sense—to lead out into the wilderness. Nothing, says the motto of this work, is so difficult to destroy as the errors and false facts propagated by illustrious men whose words have authority. I deny it altogether. There are things much more difficult to destroy: it is much more difficult to destroy the truths and real facts supported by such men. And again, it is much more difficult to prevent men of no authority from setting up false pretensions; and it is much more difficult to destroy assertions of fancy speculation. Many an error of thought and learning has fallen before a gradual growth of thoughtful and learned opposition. But such things as the quadrature of the circle, etc., are never put down. And why? Because thought can influence thought, but thought cannot influence self-conceit: learning can annihilate learning: but learning cannot annihilate ignorance. A sword may cut through an iron bar; and the severed ends will not reunite: let it go through the air, and the yielding substance is whole again in a moment.
Miracles versus Nature: being an application of certain propositions in the theory of chances to the Christian miracles. By Protimalethes.[19] Cambridge, 1847, 8vo.
The theory, as may be supposed, is carried further than most students of the subject would hold defensible.
An astronomical Lecture. By the Rev. R. Wilson.[20] Greenock, 1847, 12mo.
Against the moon's rotation on her axis.
[Handed about in the streets in 1847: I quote the whole:] Important discovery in astronomy, communicated to the Astronomer Royal, December 21st, 1846. That the Sun revolve round the Planets in 25748-2/5 years, in consequence of the combined attraction of the planets and their satellites, and that the Earth revolve round the Moon in 18 years and 228 days. D. T. Glazier [altered with a pen into Glazion.] Price one penny.
1847. In the United Service Magazine for September, 1847, Mrs. Borron,[21] of Shrewsbury, published some remarks tending to impeach the fact that Neptune, the planet found by Galle,[22] really was the planet which Le Verrier and Adams[23] had a right to claim. This was followed (September 14) by two pages, separately circulated, of "Further Observations upon the Planets Neptune and Uranus, with a Theory of Perturbations"; and (October 19, 1848) by three pages of "A Review of M. Leverrier's Exposition." Several persons, when the remarkable discovery was made, contended that the planet actually discovered was an intruder; and the future histories of the discovery must contain some account of this little afterpiece. Tim Linkinwater's theory that there is no place like London for coincidences, would have been utterly overthrown in favor of what they used to call the celestial spaces, if there had been a planet which by chance was put [8]near the place assigned to Neptune at the time when the discovery was made.
EARLY IDEAS OF AVIATION.
Aerial Navigation; containing a description of a proposed flying machine, on a new principle. By Dædalus Britannicus. London, 1847, 8vo.
In 1842-43 a Mr. Henson[24] had proposed what he called an aeronaut steam-engine, and a Bill was brought in to incorporate an "Aerial Transit Company." The present plan is altogether different, the moving power being the explosion of mixed hydrogen and air. Nothing came of it—not even a Bill. What the final destiny of the balloon may be no one knows: it may reasonably be suspected that difficulties will at last be overcome. Darwin,[25] in his "Botanic Garden" (1781), has the following prophecy:
"Soon shall thy arm, unconquered Steam! afar
Drag the slow barge, or drive the rapid car;
Or, on wide-waving wings expanded, bear
The flying chariot through the fields of air."
Darwin's contemporaries, no doubt, smiled pity on the poor man. It is worth note that the two true prophecies have been fulfilled in a sense different from that of the predictions. Darwin was thinking of the suggestion of Jonathan Hulls,[26] when he spoke of dragging the slow barge: it is only very recently that the steam-tug has been employed on the canals. The car was to be driven, not drawn, and on the common roads. Perhaps, the flying chariot will [9]be something of a character which we cannot imagine, even with the two prophecies and their fulfilments to help us.[27]
THE SECRET OF THE UNIVERSE DIVULGED.
A book for the public. New Discovery. The causes of the circulation of the blood; and the true nature of the planetary system. London, 1848, 8vo.
Light is the sustainer of motion both in the earth and in the blood. The natural standard, the pulse of a person in health, four beats to one respiration, gives the natural second, which is the measure of the earth's progress in its daily revolution. The Greek fable of the Titans is an elaborate exposition of the atomic theory: but any attempt to convince learned classics would only meet their derision; so much does long-fostered prejudice stand in the way of truth. The author complains bitterly that men of science will not attend to him and others like him: he observes, that "in the time occupied in declining, a man of science might test the merits." This is, alas! too true; so well do applicants of this kind know how to stick on. But every rule has its exception: I have heard of one. The late Lord Spencer[28]—the Lord Althorp of the House of Commons—told me that a speculator once got access to him at the Home Office, and was proceeding to unfold his way of serving the public. "I do not understand these things," said Lord Althorp, "but I happen to have —— (naming an eminent engineer) upstairs; suppose you talk to him on the subject." The discoverer went up, and in half-an-hour returned, and said, "I am very much obliged to your Lordship for introducing me to Mr. ——; he has convinced me [10]that I am quite wrong." I supposed, when I heard the story—but it would not have been seemly to say it—that Lord A. exhaled candor and sense, which infected those who came within reach: he would have done so, if anybody.
THE TRISECTION AND QUADRATURE AGAIN.
A method to trisect a series of angles having relation to each other; also another to trisect any given angle. By James Sabben. 1848 (two quarto pages).
"The consequence of years of intense thought": very likely, and very sad.
1848. The following was sent to me in manuscript. I give the whole of it:
"Quadrature of the Circle.—A quadrant is a curvilinear angle traversing round and at an equal distance from a given point, called a center, no two points in the curve being at the same angle, but irreptitiously graduating from 90 to 60. It is therefore a mean angle of 90 and 60, which is 75, because it is more than 60, and less than 90, approximately from 60 to 90, and from 90 to 60, with equal generation in each irreptitious approximation, therefore meeting in 75, and which is the mean angle of the quadrant.
"Or suppose a line drawn from a given point at 90, and from the same point at 60. Let each of these lines revolve on this point toward each other at an equal ratio. They will become one line at 75, and bisect the curve, which is one-sixth of the entire circle. The result, taking 16 as a diameter, gives an area of 201.072400, and a circumference of 50.2681.
"The original conception, its natural harmony, and the result, to my own mind is a demonstrative truth, which I presume it right to make known, though perhaps at the hazard of unpleasant if not uncourteous remarks."
I have added punctuation: the handwriting and spelling [11]are those of an educated person; the word irreptitious is indubitable. The whole is a natural curiosity.
The quadrature and exact area of the circle demonstrated. By Wm. Peters. 8vo. n. d. (circa 1848).[29]
Suggestions as to the necessity for a revolution in philosophy; and prospectus for the establishment of a new quarterly, to be called the Physical Philosopher and Heterodox Review. By Q. E. D. 8vo. 1848.
These works are by one author, who also published, as appears by advertisement,
"Newton rescued from the precipitancy of his followers through a century and a half,"[30] and "Dangers along a coast by correcting (as it is called) a ship's reckoning by bearings of the land at night fall, or in a fog, nearly out of print. Subscriptions are requested for a new edition."
The area of a circle is made four-fifths of the circumscribed square: proved on an assumption which it is purposed to explain in a longer essay.[31] The author, as Q. E. D., was in controversy with the Athenæum journal, and criticised a correspondent, D., who wrote against a certain class of discoverers. He believed the common theories of hydrostatics to be wrong, and one of his questions was:
"Have you ever taken into account anent gravity and gravitation the fact that a five grain cube of cork will of itself half sink in the water, whilst it will take 20 grains of brass, which will sink of itself, to pull under the other half? Fit this if you can, friend D., to your notions of gravity and specific gravity, as applied to the construction of a universal law of gravitation."
This the Athenæum published—but without some Italics, for which the editor was sharply reproved, as a sufficient [12]specimen of the quod erat D. monstrandum: on which the author remarks—"D,—Wherefore the e caret? is it D apostrophe? D', D'M, D'Mo, D'Monstrandum; we cannot find the wit of it." This I conjecture to contain an illusion to the name of the supposed author; but whether De Mocritus, De Mosthenes, or De Moivre was intended, I am not willing to decide.
The Scriptural Calendar and Chronological Reformer, for the statute year 1849. Including a review of recent publications on the Sabbath question. London, 1849, 12mo.[32]
This is the almanac of a sect of Christians who keep the Jewish Sabbath, having a chapel at Mill Yard, Goodman's Fields. They wrote controversial works, and perhaps do so still; but I never chanced to see one.
Geometry versus Algebra; or the trisection of an angle geometrically solved. By W. Upton, B.A.[33] Bath (circa 1849). 8vo.
The author published two tracts under this title, containing different alleged proofs: but neither gives any notice of the change. Both contain the same preface, complaining of the British Association for refusing to examine the production. I suppose that the author, finding his first proof wrong, invented the second, of which the Association never had the offer; and, feeling sure that they would have equally refused to examine the second, thought it justifiable to [13]present that second as the one which they had refused. Mr. Upton has discovered that the common way of finding the circumference is wrong, would set it right if he had leisure, and, in the mean time, has solved the problem of the duplication of the cube.
The trisector of an angle, if he demand attention from any mathematician, is bound to produce, from his construction, an expression for the sine or cosine of the third part of any angle, in terms of the sine or cosine of the angle itself, obtained by help of no higher than the square root. The mathematician knows that such a thing cannot be; but the trisector virtually says it can be, and is bound to produce it, to save time. This is the misfortune of most of the solvers of the celebrated problems, that they have not knowledge enough to present those consequences of their results by which they can be easily judged. Sometimes they have the knowledge and quibble out of the use of it. In many cases a person makes an honest beginning and presents what he is sure is a solution. By conference with others he at last feels uneasy, fears the light, and puts self-love in the way of it. Dishonesty sometimes follows. The speculators are, as a class, very apt to imagine that the mathematicians are in fraudulent confederacy against them: I ought rather to say that each one of them consents to the mode in which the rest are treated, and fancies conspiracy against himself. The mania of conspiracy is a very curious subject. I do not mean these remarks to apply to the author before me.
One of Mr. Upton's trisections, if true, would prove the truth of the following equation:
3 cos (θ / 3) = 1 + √(4 - sin2θ)
which is certainly false.[34]
In 1852 I examined a terrific construction, at the request of the late Dr. Wallich,[35] who was anxious to persuade a poor countryman of his, that trisection of the angle was waste of time. One of the principles was, that "magnitude and direction determine each other." The construction was equivalent to the assertion that, θ being any angle, the cosine of its third part is
sin 3θ . cos(5θ/2) + sin2 θ sin (5θ/2)
divided by the square root of
sin2 3θ . cos2 (5θ/2) + sin4 θ + sin 3θ . sin 5θ . sin2 θ.
This is from my rough notes, and I believe it is correct.[36] It is so nearly true, unless the angle be very obtuse, that common drawing, applied to the construction, will not detect the error. There are many formulae of this kind: and I have several times found a speculator who has discovered the corresponding construction, has seen the approximate success of his drawing—often as great as absolute truth could give in graphical practice,—and has then set about his demonstration, in which he always succeeds to his own content.
There is a trisection of which I have lost both cutting and reference: I think it is in the United Service Journal. I could not detect any error in it, though certain there must [15]be one. At least I discovered that two parts of the diagram were incompatible unless a certain point lay in line with two others, by which the angle to be trisected—and which was trisected—was bound to be either 0° or 180°.
Aug. 22, 1866. Mr. Upton sticks to his subject. He has just published "The Uptonian Trisection. Respectfully dedicated to the schoolmasters of the United Kingdom." It seems to be a new attempt. He takes no notice of the sentence I have put in italics: nor does he mention my notice of him, unless he means to include me among those by whom he has been "ridiculed and sneered at" or "branded as a brainless heretic." I did neither one nor the other: I thought Mr. Upton a paradoxer to whom it was likely to be worth while to propound the definite assertion now in italics; and Mr. Upton does not find it convenient to take issue on the point. He prefers general assertions about algebra. So long as he cannot meet algebra on the above question, he may issue as many "respectful challenges" to the mathematicians as he can find paper to write: he will meet with no attention.
There is one trisection which is of more importance than that of the angle. It is easy to get half the paper on which you write for margin; or a quarter; but very troublesome to get a third. Show us how, easily and certainly, to fold the paper into three, and you will be a real benefactor to society.
Early in the century there was a Turkish trisector of the angle, Hussein Effendi, who published two methods. He was the father of Ameen Bey, who was well known in England thirty years ago as a most amiable and cultivated gentleman and an excellent mathematician. He was then a student at Cambridge; and he died, years ago, in command of the army in Syria. Hussein Effendi was instructed in mathematics by Ingliz Selim Effendi, who translated a work [16]of Bonnycastle[37] into Turkish.[38] This Englishman was Richard Baily, brother of Francis Baily[39] the astronomer, who emigrated to Turkey in his youth, and adopted the manners of the Turks, but whether their religion also I never heard, though I should suppose he did.
I now give the letters from the agricultural laborer and his friend, described on page 12, Vol. I. They are curiosities; and the history of the quadrature can never be well written without some specimens of this kind:
"Doctor Morgan, Sir. Permit me to address you
"Brute Creation may perhaps enjoy the faculty of beholding visible things with a more penitrating eye than ourselves. But Spiritual objects are as far out of their reach as though they had no being
"Nearest therefore to the brute Creation are those men who Suppose themselves to be so far governed by external objects as to believe nothing but what they See and feel And Can accomedate to their Shallow understanding and Imaginations
"My Dear Sir Let us all Consult ourselves by the wise proverb.
"I believe that evry mans merit & ability aught to be appreciated and valued In proportion to its worth & utility
"In whatever State or Circumstances they may fortunately or unfortunately be placed
"And happy it is for evry man to know his worth and place
"When a Gentleman of your Standing in Society Clad with those honors Can not understand or Solve a problem That is explicitly explained by words and Letters and [17]mathematically operated by figuers He had best consult the wise proverd
"Do that which thou Canst understand and Comprehend for thy good.
"I would recommend that Such Gentleman Change his business
"And appropriate his time and attention to a Sunday School to Learn what he Could and keep the Litle Children form durting their Close
"With Sincere feelings of Gratitude for your weakness and Inability I am
"Sir your Superior in Mathematics ——"
"1849 June th29."
"Dor Morgin Sir
"I wrote and Sent my work to Professor —— of —— State of —— United States
"I am now in the possession of the facts that he highly approves of my work. And Says he will Insure me Reward in the States
"I write this that you may understand that I have knowledge of the unfair way that I am treated In my own nati County
"I am told and have reasons to believe that it is the Clergy that treat me so unjust.
"I am not Desirous of heaping Disonors upon my own nation. But if I have to Leave this kingdom without my Just dues. The world Shall know how I am and have been treated.
"I am Sir Desirous of my
"Just dues ——"
"1849 July 3."
"Sir, I have been given to understand that a friend of mine one whom I shall never be ashamed to acknowledge as [18]such tho' lowly his origine; nay not only not ashamed but proud of doing so for I am one of those who esteem and respect a man according to his ability and probity, deeming with Dr. Watts 'that the mind is the standard of the man,'[40] has laid before you and asked your opinion of his extraordinary performance, viz. the quadrature of the circle, he did this with the firmest belief that you would not only treat the matter in a straightforward manner but with the conviction that from your known or supposed knowledge of mathematicks would have given an upright and honorable decision upon the subject; but the question is have you done so? Could I say yes I would with the greatest of pleasure and have congratulated you upon your decision whatever it might have been but I am sorry to say that I cannot your letter is a paltry evasion, you say 'that it is a great pity that you (Mr. ——) should have attempted this (the quadrature of the circle) for your mathematical knowledge is not sufficient to make you know in what the problem consists,' you don't say in what it does consist according to your ideas, oh! no nothing of the sort, you enter into no disquisition upon the subject in order to show where you think Mr. —— is wrong and why you have not is simply—because you cannot—you know that he has done it and what is if I am not wrongly informed you have been heard to say so. He has done what you nor any other mathematician as those who call themselves such have done. And what is the reason that you will not candidly acknowledge to him as you have to others that he has squared the circle shall I tell you? it is because he has performed the feat to obtain the glory of which mathematicians have battled from time immemorial that they might encircle their brows with a wreath of laurels far more glorious than ever conqueror won it is simply this that it is a poor man a [19]humble artisan who has gained that victory that you don't like to acknowledge it you don't like to be beaten and worse to acknowledge that you have miscalculated, you have in short too small a soul to acknowledge that he is right.
"I was asked my opinion and I gave it unhesitatingly in the affirmative and I am backed in my opinion not only by Mr. —— a mathematician and watchmaker residing in the boro of Southwark but by no less an authority than the Professor of mathematics of —— College —— —— United States Mr. —— and I presume that he at least is your equal as an authority and Mr. —— says that the government of the U.S. will recompense M. D. for the discovery he has made if so what a reflection upon Old england the boasted land of freedom the nursery of arts and sciences that her sons are obliged to go to a foreign country to obtain that recompense to which they are justly entitled
"In conclusion I had to contradict an assertion you made to the effect that 'there is not nor ever was any reward offered by the government of this country for the discovery of the quadrature of the circle.' I beg to inform you that there was but that it having been deemed an impossibility the government has withdrawn it. I do this upon no less an authority than the Marquis of Northampton.[41]
"I am, sir, yours ——"
"Dr. Morgan."
THE MOON'S ROTATION.
Notes on the Kinematic Effects of Revolution and Rotation, with reference to the Motions of the Moon and of the earth. By Henry Perigal, Jun. Esq. London, 1846-1849, 8vo.
On the misuse of technical terms. Ambiguity of the terms Rotation and Revolution, owing to the double meaning improperly [20]attributed to each of the words. (No date nor place, but by Mr. Perigal,[42] I have no doubt, and containing letters of 1849 and 1850.)
The moon controversy. Facts v. Definitions. By H. P., Jun. London, 1856, 8vo. (pp. 4.)
Mr. Henry Perigal helped me twenty years ago with the diagrams, direct from the lathe to the wood, for the article "Trochoidal Curves," in the Penny Cyclopædia: these cuts add very greatly to the value of the article, which, indeed, could not have been made intelligible without them. He has had many years' experience, as an amateur turner, in combination of double and triple circular motions, and has published valuable diagrams in profusion. A person to whom the double circular motion is familiar in the lathe naturally looks upon one circle moving upon another as in simple motion, if the second circle be fixed to the revolving radius, so that one and the same point of the moving circle travels upon the fixed circle. Mr. Perigal commenced his attack upon the moon for moving about her axis, in the first of the tracts above, ten years before Mr. Jellinger Symons;[43] but he did not think it necessary to make it a subject for the Times newspaper. His familiarity with combined motions enabled him to handle his arguments much better than Mr. J. Symons could do: in fact, he is the clearest assailant of the lot which turned out with Mr. J. Symons. But he is as wrong as the rest. The assault is now, I suppose, abandoned, until it becomes epidemic again. This it will do: it is one of those fallacies which are very tempting. There was a dispute on the subject in 1748, between James Ferguson[44] and an anonymous opponent; and I think there have been others.
A poet appears in the field (July 19, 1863) who calls himself Cyclops, and writes four octavo pages. He makes a distinction between rotation and revolution; and his doctrines and phrases are so like those of Mr. Perigal that he is a follower at least. One of his arguments has so often been used that it is worth while to cite it:
"Would Mathematicals—forsooth—
If true, have failed to prove its truth?
Would not they—if they could—submit
Some overwhelming proofs of it?
But still it totters proofless! Hence
There's strong presumptive evidence
None do—or can—such proof profound
Because the dogma is unsound.
For, were there means of doing so,
They would have proved it long ago."
This is only one of the alternatives. Proof requires a person who can give and a person who can receive. I feel inspired to add the following:
"A blind man said, As to the Sun,
I'll take my Bible oath there's none;
For if there had been one to show
They would have shown it long ago.
How came he such a goose to be?
Did he not know he couldn't see?
Not he!"
The absurdity of the verses is in the argument. The writer was not so ignorant or so dishonest as to affirm that nothing had been offered by the other side as proof; accordingly, his syllogism amounts to this: If your proposition were true, you could have given proof satisfactory to me; but this you have not done, therefore, your proposition is not true.
The echoes of the moon-controversy reached Benares in 1857, in which year was there published a pamphlet "Does the Moon Rotate?" in Sanskrit and English. The [22]arguments are much the same as those of the discussion at home.
ON THE NAMES OF RELIGIOUS BODIES.
We see that there are paradoxers in argument as well as in assertion of fact: my plan does not bring me much into contact with these; but another instance may be useful. Sects, whether religious or political, give themselves names which, in meaning, are claimed also by their opponents; loyal, liberal, conservative (of good), etc. have been severally appropriated by parties. Whig and Tory are unobjectionable names: the first—which occurs in English ballad as well as in Scotland—is sour milk;[45] the second is a robber. In theology, the Greek Church is Orthodox, the Roman is Catholic, the modern Puritan is Evangelical, etc.
The word Christian (Vol. I, p. 248[46]) is an instance. When words begin, they carry their meanings. The Jews, who had their Messiah to come, and the followers of Jesus of Nazareth, who took Him for their Messiah, were both Christians (which means Messianites): the Jews would never have invented the term to signify Jesuans, nor would the disciples have invented such an ambiguous term for themselves; had they done so, the Jews would have disputed it, as they would have done in later times if they had had fair play. The Jews of our day, I see by their newspapers, speak of Jesus Christ as the Rabbi Joshua. But the [23]heathens, who knew little or nothing about the Jewish hope, would naturally apply the term Christians to the only followers of a Messiah of whom they had heard. For the Jesuans invaded them in a missionary way; while the Jews did not attempt, at least openly, to make proselytes.
All such words as Catholic, etc., are well enough as mere nomenclature; and the world falls for the most part, into any names which parties choose to give themselves. Silly people found inferences on this concession; and, as usually happens, they can cite some of their betters. St. Augustine,[47] a freakish arguer, or, to put it in the way of an old writer, lectorem ne multiloquii tædio fastidiat, Punicis quibusdam argutiis recreare solet,[48] asks, with triumph, to what chapel a stranger would be directed, if he inquired the way to the Catholic assembly. But the best exhibition of this kind in our own century is that made by the excellent Dr. John Milner,[49] in a work (first published in 1801 or 1802) which I suppose still circulates, "The End of Religious Controversy": a startling title which, so far as its truth is concerned, might as well have been "The floor of the bottomless pit." This writer, whom every one of his readers will swear to have been a worthy soul, though many, even of his own sect, will not admire some of his logic, speaks as follows:
"Letter xxv. On the true Church being Catholic. In treating of this third mark of the true Church, as expressed in our common creed, I feel my spirits sink within me, and I am almost tempted to throw away my pen in despair. For what chance is there of opening the eyes of candid Protestants to the other marks of the Church, if they are capable of keeping them shut to this? Every time they address the [24]God of Truth, either in solemn worship or in private devotion [stretch of rhetoric], they are forced, each of them, to repeat: I believe in the Catholic Church, and yet if I ask any of them the question: Are you a Catholic? he is sure to answer me, No, I am a Protestant! Was there ever a more glaring instance of inconsistency and self-condemnation among rational beings!"
"John Milner, honest and true,
Did what honest people still may do,
If they write for the many and not for the few,
But what by and bye they must eschew."
He shortened his clause; and for a reason. If he had used the whole epithet which he knew so well, any one might have given his argument a half-turn. Had he written, as he ought, "the Holy Catholic Church" and then argued as above, some sly Protestant would have parodied him with "and yet if I ask any of them the question: Are you HOLY? he is sure to answer me No, I am a SINNER." To take the adjective from the Church, and apply it to the individual partisan, is recognized slipslop, but not ground of argument. If Dr. M. had asked his Protestant whether he belonged to the Catholic Church, the answer would have been Yes, but not to the Roman branch. When he put his question as he did, he was rightly answered and in his own division. This leaving out words is a common practice, especially when the omitter is in authority, and cannot be exposed. A year or two ago a bishop wrote a snubbing letter to a poor parson, who had complained that he was obliged, in burial, to send the worst of sinners to everlasting happiness. The bishop sternly said, "hope[50] is not assurance." [25]Could the clergyman have dared to answer, he would have said, "No, my Lord! but 'sure and certain hope' is as like assurance as a minikin man is like a dwarf." Sad to say, a theologian must be illogical: I feel sure that if you took the clearest headed writer on logic that ever lived, and made a bishop of him, he would be shamed by his own books in a twelvemonth.
Milner's sophism is glaring: but why should Dr. Milner be wiser than St. Augustine, one of his teachers? I am tempted to let out the true derivation of the word Catholic, as exclusively applied to the Church of Rome. All can find it who have access to the Rituale of Bonaventura Piscator[51] (lib. i. c. 12, de nomine Sacræ Ecclesiæ, p. 87 of the Venice [26]folio of 1537). I am told that there is a Rituale in the Index Expurgatorius, but I have not thought it worth while to examine whether this be the one: I am rather inclined to think, as I have heard elsewhere, that the book was held too dangerous for the faithful to know of it, even by a prohibition: it would not surprise me at all if Roman Christians should deny its existence.[52]
It amuses me to give, at a great distance of time, a small Rowland for a small Oliver,[53] which I received, de par l'Eglise,[54] so far as lay in the Oliver-carrier more than twenty years ago. The following contribution of mine to Notes and Queries (3d Ser. vi. p. 175, Aug. 27, 1864) will explain what I say. There had been a complaint that a contributor had used the term Papist, which a very excellent dignitary of the Papal system pronounced an offensive term:
PAPIST.
The term papist should be stripped of all except its etymological meaning, and applied to those who give the higher and final authority to the declaration ex cathedrâ[55] of the Pope. See Dr. Wiseman's[56] article, Catholic Church, in the Penny Cyclopædia.
What is one to do about these names? First, it is clear that offence should, when possible, be avoided: secondly, no one must be required to give a name which favors any assumption made by those to whom it is given, and not [27]granted by those who give it. Thus the subdivision which calls itself distinctly Evangelical has no right to expect others to concede the title. Now the word Catholic, of course, falls under this rule; and even Roman Catholic may be refused to those who would restrict the word Catholic to themselves. Roman Christian is unobjectionable, since the Roman Church does not deny the name of Christian to those whom she calls heretics. No one is bound in this matter by Acts of Parliament. In many cases, no doubt, names which have offensive association are used merely by habit, sometimes by hereditary transmission. Boswell records of Johnson that he always used the words "dissenting teacher," refusing minister and clergyman to all but the recipients of episcopal ordination.
This distinctive phrase has been widely adopted: it occurs in the Index of 3d S. iv. [Notes and Queries]. Here we find "Platts (Rev. John), Unitarian teacher, 412;" the article indexed has "Unitarian minister."
This, of course is habit: an intentional refusal of the word minister would never occur in an index. I remember that, when I first read about Sam Johnson's little bit of exclusiveness, I said to myself: "Teacher? Teacher? surely I remember One who is often called teacher, but never minister or clergyman: have not the dissenters got the best of it?"
When I said that the Roman Church concedes the epithet Christians to Protestants, I did not mean that all its adherents do the same. There is, or was, a Roman newspaper, the Tablet, which, seven or eight years ago, was one of the most virulent of the party journals. In it I read, referring to some complaint of grievance about mixed marriages, that if Christians would marry Protestants they must take the consequences. My memory notes this well; because I recollected, when I saw it, that there was in the stable a horse fit to run in the curricle with this one. About seventeen years ago an Oxford M. A., who hated [28]mathematics like a genuine Oxonian of the last century, was writing on education, and was compelled to give some countenance to the nasty subject. He got out cleverly; for he gave as his reason for the permission, that man is an arithmetical, geometrical, and mechanical animal, as well as a rational soul.
The Tablet was founded by an old pupil of mine, Mr. Frederic Lucas,[57] who availed himself of his knowledge of me to write some severe articles—even abusive, I was told, but I never saw them—against me, for contributing to the Dublin Review, and poking my heretic nose into orthodox places. Dr. Wiseman, the editor, came in for his share, and ought to have got all. Who ever blamed the pig for intruding himself into the cabin when the door was left open? When Mr. Lucas was my pupil, he was of the Society of Friends—in any article but this I should say Quaker—and was quiet and gentlemanly, as members of that Church—in any article but this I should, from mere habit, say sect—usually are. This is due to his memory; for, by all I heard, when he changed his religion he ceased to be Lucas couchant, and became Lucas rampant, fanged and langued gules. (I looked into Guillim[58] to see if my terms were right: I could not find them; but to prove I have been there, I notice that he calls a violin a violent. How comes the word to take this form?) I met with several Roman Christians, born and bred, who were very much annoyed at Mr. Lucas and his doings; and said some severe things about new converts needing kicking-straps.
The mention of Dr. Wiseman reminds me of another word, appropriated by Christians to themselves: fides;[59] the Roman faith is fides, and nothing else; and the adherents are fideles.[60] Hereby hangs a retort. When Dr. Wiseman was first in England, he gave a course of lectures in defence of his creed, which were thought very convincing by those who were already convinced. They determined to give him a medal, and there was a very serious discussion about the legend. Dr. Wiseman told me himself that he had answered to his subscribers that he would not have the medal at all unless—(naming some Italian authority, whom I forget) approved of the legend. At last pro fide vindicata[61] was chosen: this may be read either in a Popish or heretical sense. The feminine substantive fides means confidence, trust, (it is made to mean belief), but fidis, with the same ablative, fide, and also feminine, is a fiddle-string.[62] If a Latin writer had had to make a legend signifying "For the defence of the fiddle-string," he could not have done it otherwise, in the terseness of a legend, than by writing pro fide vindicata. Accordingly, when a Roman Christian talks to you of the faith, as a thing which is his and not yours, you may say fiddle. I have searched Bonaventura Piscator in vain for notice of this ambiguity. But the Greeks said fiddle; according to Suidas,[63] σκινδαψος[64]—a word meaning a four stringed instrument played with a quill—was an exclamation of contemptuous dissent. How the wits of different races jump!
I am reminded of a case of fides vindicata, which, being in a public letter, responding to a public invitation, was not meant to be confidential. Some of the pupils of University College, in which all subdivisions of religion are (1866; were, 1867) on a level, have of course changed their views in after life, and become adherents of various high churches. On the occasion of a dinner of old students of the College, convened by circular, one of these students, whether then Roman or Tractarian Christian I do not remember, not content with simply giving negative answer, or none at all, concocted a jorum of theological rebuke, and sent it to the Dinner Committee. Heyday! said one of them, this man got out of bed backwards! How is that? said the rest. Why, read his name backwards, and you will see. As thus read it was—No grub![65]
THE WORD CHURCH.
To return to Notes and Queries. The substitution in the (editorial) index of "Unitarian teacher," for the contributor's "Unitarian minister," struck me very much. I have seldom found such things unmeaning. But as the journal had always been free from editorial sectarianisms,—and very apt to check the contributorial,—I could not be sure in this case. True it was, that the editor and publisher had been changed more than a year before; but this was not of much force. Though one swallow does not make a summer, I have generally found it show that summer is coming. However, thought I to myself, if this be Little Shibboleth, we shall have Big Shibboleth by-and-bye. At last it came. About a twelvemonth afterwards, (3d S. vii. p. 36) the following was the editorial answer to the question when the establishment was first called the "Church of England and Ireland":
"That unmeaning clause, 'The United Church of England and Ireland,' which occurs on the title-page of The Book of Common Prayer, was first used at the commencement of the present century. The authority for this phrase is the fifth article of the Union of 1800: 'That the Churches of England and Ireland be united into one Protestant (!) episcopal Church, to be called "The United Church of England and Ireland."' Of course, churchmen are not responsible for the theology of Acts of Parliament, especially those passed during the dark ages of the Georgian era."
That is to say, the journal gives its adhesion to the party which—under the assumed title of the Church of England—claims for the endowed corporation for the support of religion rights which Parliament cannot control, and makes it, in fact, a power above the State. The State has given an inch: it calls this corporation by the name of the "United Church of England and Ireland," as if neither England nor Ireland had any other Church. The corporation, accordingly aspires to an ell. But this the nation will only give with the aspiration prefixed. To illustrate my allusion in a delicate way to polite ears, I will relate what happened in a Johnian lecture-room at Cambridge, some fifty years ago, my informant being present. A youth of undue aspirations was giving a proposition, and at last said, "Let E F be produced to 'L':" "Not quite so far, Mr. ——," said the lecturer, quietly, to the great amusement of the class, and the utter astonishment of the aspirant, who knew no more than a Tractarian the tendency of his construction.
This word Church is made to have a very mystical meaning. The following dialogue between Ecclesiastes and Hæreticus, which I cannot vouch for, has often taken place in spirit, if not in letter: E. The word Church (ἐκκλησια)[66] is never used in the New Testament except generally or locally for that holy and mystical body to which the sacraments and the ordinances of Christianity are entrusted. [32]H. Indeed! E. It is beyond a doubt (here he quoted half a dozen texts in support). H. Do you mean that any doctrine or ordinance which was solemnly practised by the ἐκκλησια is binding upon you and me? E. Certainly, unless we should be cut off from the congregation of the faithful. H. Have you a couple of hours to spare? E. What for? H. If you have, I propose we spend them in crying, Great is Diana of the Ephesians! E. What do you mean? H. You ought to know the solemn service of the ἐκκλησια (Acts xix. 32, 41), at Ephesus; which any one might take to be true Church, by the more part not knowing wherefore they were come together, and which was dismissed, after one of the most sensible sermons ever preached, by the Recorder. E. I see your meaning: it is true, there is that one exception! H. Why, the Recorder's sermon itself contains another, the ἐννομος ἐκκλησια,[67] legislative assembly. E. Ah! the New Testament can only be interpreted by the Church! H. I see! the Church interprets itself into existence out of the New Testament, and then interprets the New Testament out of existence into itself!
I look upon all the Churches as fair game which declare of me that absque dubio in æternum peribo;[68] not for their presumption towards God, but for their personal insolence towards myself. I find that their sectaries stare when I say this. Why! they do not speak of you in particular! These poor reasoners seem to think that there could be no meaning, as against me, unless it should be propounded that "without doubt he shall perish everlastingly, especially A. De Morgan." But I hold, with the schoolmen, that "Omnis homo est animal" in conjunction with "Sortes est homo" amounts to "Sortes est animal."[69] But they do not mean it personally! Every universal proposition is [33]personal to every instance of the subject. If this be not conceded, then I retort, in their own sense and manner, "Whosoever would serve God, before all things he must not pronounce God's decision upon his neighbor. Which decision, except every one leave to God himself, without doubt he is a bigoted noodle."
The reasoning habit of the educated community, in four cases out of five, permits universal propositions to be stated at one time, and denied, pro re nata,[70] at another. "Before we proceed to consider any question involving physical principles, we should set out with clear ideas of the naturally possible and impossible." The eminent man who said this, when wanting it for his views of mental education (!) never meant it for more than what was in hand, never assumed it in the researches which will give him to posterity! I have heard half-a-dozen defences of his having said this, not one of which affirmed the truth of what was said. A worthy clergyman wrote that if A. B. had said a certain thing the point in question would have been established. It was shown to him that A. B. had said it, to which the reply was a refusal to admit the point because A. B. said it in a second pamphlet and in answer to objections. And I might give fifty such instances with very little search. Always assume more than you want; because you cannot tell how much you may want: put what is over into the didn't-mean-that basket, or the extreme case what-not.
PROTESTANT AND PAPAL CHRISTENDOM.
Something near forty years of examination of the theologies on and off—more years very much on than quite off—have given me a good title—to myself, I ask no one else for leave—to make the following remarks: A conclusion has premises, facts or doctrines from proof or authority, and mode of inference. There may be invention or [34]falsehood of premise, with good logic; and there may be tenable premise, followed by bad logic; and there may be both false premise and bad logic. The Roman system has such a powerful manufactory of premises, that bad logic is little wanted; there is comparatively little of it. The doctrine-forge of the Roman Church is one glorious compound of everything that could make Heraclitus[71] sob and Democritus[72] snigger. But not the only one. The Protestants, in tearing away from the Church of Rome, took with them a fair quantity of the results of the Roman forge, which they could not bring themselves to give up. They had more in them of Martin than of Jack. But they would have no premises, except from the New Testament; though some eked out with a few general Councils. The consequence is that they have been obliged to find such a logic as would bring the conclusions they require out of the canonical books. And a queer logic it is; nothing but the Roman forge can be compared with the Protestant loom. The picking, the patching, the piecing, which goes to the Protestant termini ad quem,[73] would be as remarkable to the general eye, as the Roman manufacture of termini a quo,[74] if it were not that the world at large seizes the character of an asserted fact better than that of a mode of inference. A grand step towards the deification of a lady, made by alleged revelation 1800 years after her death, is of glaring evidence: two or three additional shiffle-shuffles towards defence of saying the Athanasian curse in church and unsaying it out of church, are hardly noticed. Swift has bungled his satire where he makes Peter a party to finding out what he wants, totidem syllabis and totidem literis, [35]when he cannot find it totidem verbis[75] This is Protestant method: the Roman plan is viam faciam; the Protestant plan is viam inveniam.[76] The public at large begins to be conversant with the ways of wriggling out, as shown in the interpretations of the damnatory parts of the Athanasian Creed, the phrases of the Burial Service, etc. The time will come when the same public will begin to see the ways of wriggling in. But one thing at a time: neither Papal Rome nor Protestant Rome was built—nor will be pulled down—in a day.
The distinction above drawn between the two great antitheses of Christendom may be illustrated as follows. Two sets of little general dealers lived opposite to one another: all sold milk. Each vaunted its own produce: one set said that the stuff on the other side the way was only chalk and water; the other said that the opposites sold all sorts of filth, of which calves' brain was the least nasty. Now the fact was that both sets sold milk, and from the same dairy: but adulterated with different sorts of dirty water: and both honestly believed that the mixture was what they were meant to sell and ought to sell. The great difference between them, about which the apprentices fought each other like Trojans, was that the calves' brain men poured milk into the water, and the chalk men poured water into the milk. The Greek and Roman sects on one side, the Protestant sects on the other, must all have churches: the Greek and Roman sects pour the New Testament into their churches; the Protestant sects pour their churches into the New Testament. The Greek and Roman insist upon the New Testament being no more than part and parcel of their churches: the Protestant insist upon their churches being as much part and parcel of the New Testament. All dwell vehemently upon the doctrine that there must be milk [36]somewhere; and each says—I have it. The doctrine is true: and can be verified by any one who can and will go to the dairy for himself. Him will the several traders declare to have no milk at all. They will bring their own wares, and challenge a trial: they want nothing but to name the judges. To vary the metaphor, those who have looked at Christianity in open day, know that all who see it through painted windows shut out much of the light of heaven and color the rest; it matters nothing that the stains are shaped into what are meant for saints and angels.
But there is another side to the question. To decompose any substance, it must be placed between the poles of the battery. Now theology is but one pole; philosophy is the other. No one can make out the combinations of our day unless he read the writings both of the priest and the philosopher: and if any one should hold the first word offensive, I tell him that I mean both words to be significant. In reading these writings, he will need to bring both wires together to find out what it is all about. Time was when most priests were very explicit about the fate of philosophers, and most philosophers were very candid about their opinion of priests. But though some extremes of the old sorts still remain, there is now, in the middle, such a fusion of the two pursuits that a plain man is wofully puzzled. The theologian writes a philosophy which seems to tell us that the New Testament is a system of psychology; and the philosopher writes a Christianity which is utterly unintelligible as to the question whether the Resurrection be a fact or a transcendental allegory. What between the theologian who assents to the Athanasian denunciation in what seems the sense of no denunciation, and the philosopher who parades a Christianity which looks like no revelation, there is a maze which threatens to have the only possible clue in the theory that everything is something else, and nothing is anything at all. But this is a paradox far beyond my handling: it is a Budget of itself. [37]
RELIGION AND PHILOSOPHY.
Religion and Philosophy, the two best gifts of Heaven, set up in opposition to each other at the revival of letters; and never did competing tradesmen more grossly misbehave. Bad wishes and bad names flew about like swarms of wasps. The Athanasian curses were intended against philosophers; who, had they been a corporation, with state powers to protect them, would have formulized a per contra. But the tradesmen are beginning to combine: they are civil to each other; too civil by half. I speak especially of Great Britain. Old theology has run off to ritualism, much lamenting, with no comfort except the discovery that the cloak Paul left at Troas was a chasuble. Philosophy, which always had a little sense sewed up in its garments—to pay for its funeral?—has expended a trifle in accommodating itself to the new system. But the two are poles of a battery; and a question arises.
If Peter Piper picked a peck of pepper,
Where is the peck of pepper Peter Piper picked?
If Religion and Philosophy be the two poles of a battery, whose is the battery Religion and Philosophy have been made the poles of? Is the change in the relation of the wires any presumption of a removal of the managers? We know pretty well who handled the instrument: has he resigned or been[77] turned out? Has he been put under [38]restriction? A fool may ask more questions than twenty sages can answer: but there is hope; for twenty sages cannot ask more questions than one reviewer can answer. I should like to see the opposite sides employed upon the question, What are the commoda, and what the pericula,[78] of the current approximation of Religion and Philosophy?
All this is very profane and irreverent! It has always been so held by those whose position demands such holding. To describe the Church as it is passes for assailing the Church as it ought to be with all who cannot do without it. In Bedlam[79] a poor creature who fancied he was St. Paul, was told by another patient that he was an impostor; the first maniac lodged a complaint against the second for calling St. Paul an impostor, which, he argued, with much appearance of sanity, ought not to be permitted in a well regulated madhouse. Nothing could persuade him that he had missed the question, which was whether he was St. Paul. The same thing takes place in the world at large. And especially must be noted the refusal to permit to the profane the millionth part of the licence assumed by the sacred. I give a sound churchman the epitaph of St. John Long; the usual pronunciation of whose name must be noted—
"Behold! ye quacks, the vengeance strong
On deeds like yours impinging:
For here below lies St. John Long[80]
Who now must be long singeing."
How shameful to pronounce this of the poor man! What, Mr. Orthodox! may I not do in joke to one pretender what [39]you do in earnest—unless you quibble—to all the millions of the Greek Church, and a great many others. Enough of you and your reasoning! Go and square the circle!
The few years which end with 1867 have shown, not merely the intermediate fusion of Theology and Philosophy of which I have spoken, but much concentration of the two extremes, which looks like a gathering of forces for some very hard fought Armageddon. Extreme theology has been aiming at a high Church in England, which is to show a new front to all heresy: and extreme philosophy is contriving a physical organization which is to think, and to show that mind is a consequence of matter, or thought a recreation of brain. The physical speculators begin with a possible hypothesis, in which they aim at explanation: and so the bold aspirations of the author of the Vestiges find standing-ground in the variation of species by "natural selection." Some relics—so supposed—of extremely ancient men are brought to help the general cause. Only distant hints are given that by possibility it may end in the formation of all living organisms from a very few, if not from one. The better heads above mentioned know that their theory, if true, does not bear upon morals. The formation of solar systems from a nebular hypothesis, followed by organizations gradually emerging from some curious play of particles, nay, the very evolution of mind and thought from such an apparatus, are all as consistent with a Personal creative power to whom homage and obedience are due, and who has declared himself, as with a blind Nature of Things. A pure materialist, as to all things visible, may be even a bigotted Christian: this is not frequent, but it is possible. There is a proverb which says, A pig may fly, but it isn't a likely bird. But when the psychological speculator comes in, he often undertakes to draw inferences from the physical conclusions, by joining on his tremendous apparatus of a priori knowledge. He deduces that he can do without a God: he can deduce all things [40]without any such necessity. With Occam[81] and Newton he will have no more causes than are necessary to explain phenomena to him: and if by pure head-work combined with results of physical observation he can construct his universe, he must be a very unphilosophical man who would encumber himself with a useless Creator! There is something tangible about my method, says he; yours is vague. He requires it to be granted that his system is positive and that yours is impositive. So reasoned the stage coachman when the railroads began to depose him—"If you're upset in a stage-coach, why, there you are! but if you're upset on the railroad, where are you?" The answer lies in another question, Which is most positive knowledge, God deduced from man and his history, or the postulates of the few who think they can reason a priori on the tacit assumption of unlimited command of data?
We are not yet come to the existence of a school of philosophers who explicitly deny a Creator: but we are on the way, though common sense may interpose. There are always straws which show the direction of the wind. I have before me the printed letter of a medical man—to whose professional ability I have good testimony—who finds the vital principle in highly rarefied oxygen. With the usual logic of such thinkers, he dismisses the "eternal personal identity" because "If soul, spirit, mind, which are merely modes of sensation, be the attribute or function of nerve-tissue, it cannot possibly have any existence apart from its material organism!" How does he know this impossibility? If all the mind we know be from nerve-tissue, how does it appear that mind in other planets may not be another thing? Nay, when we come to possibilities, does not his own system give a queer one? If highly rarefied oxygen be vital power, more highly rarefied oxygen [41]may be more vital and more powerful. Where is this to stop? Is it impossible that a finite quantity, rarefied ad infinitum, may be an Omnipotent? Perhaps the true Genesis, when written, will open with "In the beginning was an imperial quart of oxygen at 60° of Fahrenheit, and the pressure of the atmosphere; and this oxygen was infinitely rarefied; and this oxygen became God." For myself, my aspirations as to this system are Manichæan. The quart of oxygen is the Ormuzd, or good principle: another quart, of hydrogen, is the Ahriman, or evil principle! My author says that his system explains Freewill and Immortality so obviously that it is difficult to read previous speculations with becoming gravity. My deduction explains the conflict of good and evil with such clearness that no one can henceforward read the New Testament with becoming reverence. The surgeon whom I have described is an early bud which will probably be nipped by the frost and wither on the ground: but there is a good crop coming. Material pneuma is destined to high functions; and man is to read by gas-light.
THE SUN AN ELECTRIC SPACE.
The solar system truly solved; demonstrating by the perfect harmony of the planets, founded on the four universal laws, the Sun to be an electric space; and a source of every natural production displayed throughout the solar system. By James Hopkins.[82] London, 1849, 8vo.
The author says:
"I am satisfied that I have given the true laws constituting the Sun to be space; and I call upon those disposed to maintain the contrary, to give true laws showing him to be a body: until such can be satisfactorily established, I have an undoubted claim to the credit of my theory,—That the Sun is an Electric Space, fed and governed by the [42]planets, which have the property of attracting heat from it; and the means of supplying the necessary pabulum by their degenerated air driven off towards the central space—the wonderful alembic in which it becomes transmuted to the revivifying necessities of continuous action; and the central space or Sun being perfectly electric, has the counter property of repulsing the bodies that attract it. How wonderful a conception! How beautiful, how magnificent an arrangement!
"O Centre! O Space! O Electric Space!"
JOSEPH ADY.
1849. Joseph Ady[83] is entitled to a place in this list of discoverers: his great fault, like that of some others, lay in pushing his method too far. He began by detecting unclaimed dividends, and disclosing them to their right owners, exacting his fee before he made his communication. He then generalized into trying to get fees from all of the name belonging to a dividend; and he gave mysterious hints of danger impending. For instance, he would write to a clergyman that a legal penalty was hanging over him; and when the alarmed divine forwarded the sum required for disclosure, he was favored with an extract from some old statute or canon, never repealed, forbidding a clergyman to be a member of a corporation, and was reminded that he had insured his life in the —— Office, which had a royal charter. He was facetious, was Joseph: he described himself in his circulars as "personally known to Sir Peter Laurie[84] and all other aldermen"; which was nearly true, [43]as he had been before most of them on charges of false pretence; but I believe he was nearly always within the law. Sir James Duke, when Lord Mayor, having particularly displeased him by a decision, his circulars of 1849 contain the following:
"Should you have cause to complain of any party, Sir J. Duke has contrived a new law of evidence, viz., write to him, he will consider your letter sufficient proof, and make the parties complained of pay without judge or jury, and will frank you from every expense."
I strongly suspect that Joseph Ady believed in himself.
He sometimes issued a second warning, of a Sibylline character:
"Should you find cause to complain of anybody, my voluntary referee, the Rt. Hon. Sir Peter Laurie, Kt., perpetual Deputy Lord Mayor, will see justice done you without any charge whatever: he and his toady, — —— ——. The accursed of Moses can hang any man: thus, by catching him alone and swearing Naboth spake evil against God and the King. Therefore (!) I admit no strangers to a personal conference without a prepayment of 20s. each. Had you attended to my former notice you would have received twice as much: neglect this and you will lose all."
ON MODERN ASTROLOGY.
Zadkiel's Almanac for 1849. Nineteenth number.
Raphael's Prophetic Almanac for 1849. Twenty-ninth number.
Reasons for belief in judicial astrology, and remarks on the dangerous character of popish priestcraft. London, 1849, 12mo.
Astronomy in a nutshell: or the leading problems of the solar system solved by simple proportion only, on the theory of magnetic attraction. By Lieut. Morrison,[85] N. N. London (s. a.) 12mo.
Lieut. Morrison is Zadkiel Tao Sze, and declares himself in real earnest an astrologer. There are a great many books on astrology, but I have not felt interest enough to preserve many of them which have come in my way. If anything ever had a fair trial, it was astrology. The idea itself is natural enough. A human being, set down on this earth, without any tradition, would probably suspect that the heavenly bodies had something to do with the guidance of affairs. I think that any one who tries will ascertain that the planets do not prophesy: but if he should find to the contrary, he will of course go on asking. A great many persons class together belief in astrology and belief in apparitions: the two things differ in precisely the way in which a science of observation differs from a science of experiment. Many make the mistake which M. le Marquis made when he came too late, and hoped M. Cassini[86] would do the eclipse over again for his ladies. The apparition chooses its own time, and comes as seldom or as often as it pleases, be it departed spirit, nervous derangement, or imposition. Consequently it can only be observed, and not experimented upon. But the heavens, if astrology be true, are prophesying away day and night all the year round, and about every body. Experiments can be made, then, except only on rare phenomena, such as eclipses: anybody may choose his time and his question. This is the great difference: and experiments were made, century after century. If astrology had been true, it must have lasted in an ever-improving state. If it be true, it is a truth, and a useful truth, which had experience and prejudice both in its favor, and yet lost ground as soon as astronomy, its working tool, began to improve.
1850. A letter in the handwriting of an educated man, dated from a street in which it must be taken that educated persons live, is addressed to the Secretary of the [45]Astronomical Society about a matter on which the writer says "his professional pursuit will enable him to give a satisfactory reply." In a question before a court of law it is sworn on one side that the moon was shining at a certain hour of a certain night on a certain spot in London; on the other side it is affirmed that she was clouded. The Secretary is requested to decide. This is curious, as the question is not astrological. Persons still send to Greenwich, now and then, to have their fortunes told. In one case, not very many years ago, a young gentleman begged to know who his wife was to be, and what fee he was to remit.
Sometimes the astronomer turns conjurer for fun, and his prophesies are fulfilled. It is related of Flamsteed[87] that an old woman came to know the whereabouts of a bundle of linen which had strayed. Flamsteed drew a circle, put a square into it, and gravely pointed out a ditch, near her cottage, in which he said it would be found. He meant to have given the woman a little good advice when she came back: but she came back in great delight, with the bundle in her hand, found in the very place. The late Baron Zach[88] received a letter from Pons,[89] a successful finder of comets, complaining that for a certain period he had found no comets, though he had searched diligently. Zach, a man of much sly humor, told him that no spots had been seen on the sun for about the same time—which was true,—and assured him that when the spots came back, the comets would come with them. Some time after he got a letter [46]from Pons, who informed him with great satisfaction that he was quite right, that very large spots had appeared on the sun, and that he had found a fine comet shortly after. I do not vouch for the first story, but I have the second in Zach's handwriting. It would mend the joke exceedingly if some day a real relation should be established between comets and solar spots: of late years good reason has been shown for advancing a connection between these spots and the earth's magnetism.[90] If the two things had been put to Zach, he would probably have chosen the comets. Here is a hint for a paradox: the solar spots are the dead comets, which have parted with their light and heat to feed the sun, as was once suggested. I should not wonder if I were too late, and the thing had been actually maintained. My list does not contain the twentieth part of the possible whole.
The mention of coincidences suggests an everlasting source of explanations, applicable to all that is extraordinary. The great paradox of coincidence is that of Leibnitz, known as the pre-established harmony, or law of coincidences, by which, separately and independently, the body receives impressions, and the mind proceeds as if it had perceived them from without. Every sensation, and the consequent state of the soul, are independent things coincident in time by the pre-established law. The philosopher could not otherwise account for the connection of mind and matter; and he never goes by so vulgar a rule as Whatever is, is; to him that which is not clear as to how, is not at all. Philosophers in general, who tolerate each other's theories much better than Christians do each other's failings, seldom revive Leibnitz's fantasy: they seem to act upon the maxim quoted by Father Eustace[91] from the [47]Decretals, Facinora ostendi dum puniuntur, flagitia autem abscondi debent.[92]
The great ghost-paradox, and its theory of coincidences, will rise to the surface in the mind of every one. But the use of the word coincidence is here at variance with its common meaning. When A is constantly happening, and also B, the occurrence of A and B at the same moment is the mere coincidence which may be casualty. But the case before us is that A is constantly happening, while B, when it does happen, almost always happens with A, and very rarely without it. That is to say, such is the phenomenon asserted: and all who rationally refer it to casualty, affirm that B is happening very often as well as A, but that it is not thought worthy of being recorded except when A is simultaneous. Of course A is here a death, and B the spectral appearance of the person who dies. In talking of this subject it is necessary to put out of the question all who play fast and loose with their secret convictions: these had better give us a reason, when they feel internal pressure for explanation, that there is no weathercock at Kilve; this would do for all cases. But persons of real inquiry will see that first, experience does not bear out the asserted frequency of the spectre, without the alleged coincidence of death: and secondly, that if the crowd of purely casual spectres were so great that it is no wonder that, now and then the person should have died at or near the moment, we ought to expect a much larger proportion of cases in which the spectre should come at the moment of the death of one or another of all the cluster who are closely connected with the original of the spectre. But this, we know, is almost without example. It remains then, for all, who speculate at all, to look upon the asserted phenomenon, think what they may of it, the thing which is to be explained, as a connection in time of the death, and the [48]simultaneous appearance of the dead. Any person the least used to the theory of probabilities will see that purely casual coincidence, the wrong spectre being comparatively so rare that it may be said never to occur, is not within the rational field of possibility.
The purely casual coincidence, from which there is no escape except the actual doctrine of special providences, carried down to a very low point of special intention, requires a junction of the things the like of each of which is always happening. I will give three instances which have occurred to myself within the last few years: I solemnly vouch for the literal truth of every part of all three:
In August 1861, M. Senarmont,[93] of the French Institute, wrote to me to the effect that Fresnel[94] had sent to England, in or shortly after 1824, a paper for translation and insertion in the European Review, which shortly afterwards expired. The question was what had become of that paper. I examined the Review at the Museum, found no trace of the paper, and wrote back to that effect at the Museum, adding that everything now depended on ascertaining the name of the editor, and tracing his papers: of this I thought there was no chance. I posted this letter on my way home, at a Post Office in the Hampstead Road at the junction with Edward Street, on the opposite side of which is a bookstall. Lounging for a moment over the exposed books, sicut meus est mos,[95] I saw, within a few minutes of the posting of the letter, a little catch-penny book of anecdotes of Macaulay, which I bought, and ran over for a minute. My eye was soon caught by this sentence: "One of the young fellows immediately wrote to the editor (Mr. Walker) [49]of the European Review." I thus got the clue by which I ascertained that there was no chance of recovering Fresnel's paper. Of the mention of current reviews, not one in a thousand names the editor.
In the summer of 1865 I made my first acquaintance with the tales of Nathaniel Hawthorne, and the first I read was about the siege of Boston in the War of Independence. I could not make it out: everybody seemed to have got into somebody else's place. I was beginning the second tale, when a parcel arrived: it was a lot of old pamphlets and other rubbish, as he called it, sent by a friend who had lately sold his books, had not thought it worth while to send these things for sale, but thought I might like to look at them and possibly keep some. The first thing I looked at was a sheet which, being opened, displayed "A plan of Boston and its environs, shewing the true situation of his Majesty's army and also that of the rebels, drawn by an engineer, at Boston Oct. 1775." Such detailed plans of current sieges being then uncommon, it is explained that "The principal part of this plan was surveyed by Richard Williams, Lieutenant at Boston; and sent over by the son of a nobleman to his father in town, by whose permission it was published." I immediately saw that my confusion arose from my supposing that the king's troops were besieging the rebels, when it was just the other way.
April 1, 1853, while engaged in making some notes on a logical point, an idea occurred which was perfectly new to me, on the mode of conciliating the notions omnipresence and indivisibility into parts. What it was is no matter here: suffice it that, since it was published elsewhere (in a paper on Infinity, Camb. Phil. Trans. vol. xi. p. 1) I have not had it produced to me. I had just finished a paragraph on the subject, when a parcel came in from a bookseller containing Heywood's[96] Analysis of Kant's Critick, 1844.
On turning over the leaves I found (p. 109) the identical thought which up to this day, I only know as in my own paper, or in Kant. I feel sure I had not seen it before, for it is in Kant's first edition, which was never translated to my knowledge; and it does not appear in the later editions. Mr. Heywood gives some account of the first edition.
In the broadsheet which gave account of the dying scene of Charles II, it is said that the Roman Catholic priest was introduced by P. M. A. C. F. The chain was this: the Duchess of Portsmouth[97] applied to the Duke of York, who may have consulted his Cordelier confessor, Mansuete, about procuring a priest, and the priest was smuggled into the king's room by the Duchess and Chiffinch.[98] Now the letters are a verbal acrostic of Père Mansuete a Cordelier Friar, and a syllabic acrostic of PortsMouth and ChifFinch. This is a singular coincidence. Macaulay adopted the first interpretation, preferring it to the second, which I brought before him as the conjecture of a near relative of my own. But Mansuete is not mentioned in his narrative: it may well be doubted whether the writer of a broadside for English readers would use Père instead of Father. And the person who really "reminded" the Duke of "the duty he owed to his brother," was the Duchess and not Mansuete. But my affair is only with the coincidence.
But there are coincidences which are really connected without the connection being known to those who find in them matter of astonishment. Presentiments furnish marked cases: sometimes there is no mystery to those who have the clue. In the Gentleman's Magazine (vol. 80, part 2, p. 33) we read, the subject being presentiment of death, as follows: "In 1778, to come nearer the recollection of [51]survivors, at the taking of Pondicherry, Captain John Fletcher, Captain De Morgan, and Lieutenant Bosanquet, each distinctly foretold his own death on the morning of his fate." I have no doubt of all three; and I knew it of my grandfather long before I read the above passage. He saw that the battery he commanded was unduly exposed: I think by the sap running through the fort when produced. He represented this to the engineer officers, and to the commander-in-chief; the engineers denied the truth of the statement, the commander believed them, my grandfather quietly observed that he must make his will, and the French fulfilled his prediction. His will bore date the day of his death; and I always thought it more remarkable than the fulfilment of the prophecy that a soldier should not consider any danger short of one like the above, sufficient reason to make his will. I suppose the other officers were similarly posted. I am told that military men very often defer making their wills until just before an action: but to face the ordinary risks intestate, and to wait until speedy death must be the all but certain consequence of a stupid mistake, is carrying the principle very far. In the matter of coincidences there are, as in other cases, two wonderful extremes with every intermediate degree. At one end we have the confident people who can attribute anything to casual coincidence; who allow Zadok Imposture and Nathan Coincidence to anoint Solomon Selfconceit king. At the other end we have those who see something very curious in any coincidence you please, and whose minds yearn for a deep reason. A speculator of this class happened to find that Matthew viii. 28-33 and Luke viii. 26-33 contain the same account, that of the demons entering into the swine. Very odd! chapters tallying, and verses so nearly: is the versification rightly managed? Examination is sure to show that there are monstrous inconsistencies in the mode of division, which being corrected, the verses tally as well as the chapters. And then how comes it? I cannot go on, [52]for I have no gift at torturing a coincidence, but I would lay twopence, if I could make a bet—which I never did in all my life—that some one or more of my readers will try it. Some people say that the study of chances tends to awaken a spirit of gambling: I suspect the contrary. At any rate, I myself, the writer of a mathematical book and a comparatively popular book, have never laid a bet nor played for a stake, however small: not one single time.
It is useful to record such instances as I have given, with precision and on the solemn word of the recorder. When such a story as that of Flamsteed is told, a priori assures us that it could not have been: the story may have been a ben trovato,[99] but not the bundle. It is also useful to establish some of the good jokes which all take for inventions. My friend Mr. J. Bellingham Inglis,[100] before 1800, saw the tobacconist's carriage with a sample of tobacco in a shield, and the motto Quid rides[101] (N. & Q., 3d S. i. 245). His father was able to tell him all about it. The tobacconist was Jacob Brandon, well known to the elder Mr. Inglis, and the person who started the motto, the instant he was asked for such a thing, was Harry Calender of Lloyd's, a scholar and a wit. My friend Mr. H. Crabb Robinson[102] remembers the King's Counsel (Samuel Marryat) who took the motto Causes produce effects, when his success enabled him to start a carriage.
The coincidences of errata are sometimes very remarkable: it may be that the misprint has a sting. The death of Sir W. Hamilton[103] of Edinburgh was known in London on a Thursday, and the editor of the Athenæum wrote to [53]me in the afternoon for a short obituary notice to appear on Saturday. I dashed off the few lines which appeared without a moment to think: and those of my readers who might perhaps think me capable of contriving errata with meaning will, I am sure, allow the hurry, the occasion, and my own peculiar relation to the departed, as sufficient reasons for believing in my entire innocence. Of course I could not see a proof: and two errata occurred. The words "addition to Stewart"[104] require "for addition to read edition of." This represents what had been insisted on by the Edinburgh publisher, who, frightened by the edition of Reid,[105] had stipulated for a simple reprint without notes. Again "principles of logic and mathematics" required "for mathematics read metaphysics." No four words could be put together which would have so good a title to be Hamilton's motto.
April 1850, found in the letter-box, three loose leaves, well printed and over punctuated, being
Chapter VI. Brethren, lo I come, holding forth the word of life, for so I am commanded.... Chapter VII. Hear my prayer, O generations! and walk by the way, to drink the waters of the river.... Chapter VIII. Hearken o earth, earth, earth, and the kings of the earth, and their armies....
A very large collection might be made of such apostolic writings. They go on well enough in a misty—meant for mystical—imitation of St. Paul or the prophets, until at last some prodigious want of keeping shows the education of the writer. For example, after half a page which might [54]pass for Irving's[106] preaching—though a person to whom it was presented as such would say that most likely the head and tail would make something more like head and tail of it—we are astounded by a declaration from the Holy Spirit, speaking of himself, that he is "not ashamed of the Gospel of Christ." It would be long before we should find in educated rhapsody—of which there are specimens enough—such a thing as a person of the Trinity taking merit for moral courage enough to stand where St. Peter fell. The following declaration comes next—"I will judge between cattle and cattle, that use their tongues."
THE FIGURE OF THE EARTH.
The figure of the earth. By J. L. Murphy,[107] of Birmingham. (London and Birmingham, 4 pages, 12mo.) (1850?)
Mr. Murphy invites attention and objection to some assertions, as that the earth is prolate, not oblate. "If the philosopher's conclusion be right, then the pole is the center of a valley (!) thirteen miles deep." Hence it would be very warm. It is answer enough to ask—Who knows that it is not?
*** A paragraph in the MS. appears to have been inserted in this place by mistake. It will be found in the Appendix at the end of this volume.—S. E. De M.
PERPETUAL MOTION.
1851. The following letter was written by one of a class of persons whom, after much experience of them, I [55]do not pronounce insane. But in this case the second sentence gives a suspicion of actual delusion of the senses; the third looks like that eye for the main chance which passes for sanity on the Stock Exchange and elsewhere:
"Gentlemen,—I pray you take steps to make known that yesterday I completed my invention which will give motion to every country on the Earth;—to move Machinery!—the long sought in vain 'Perpetual Motion'!!—I was supported at the time by the Queen and H.R.H. Prince Albert. If, Gentlemen, you can advise me how to proceed to claim the reward, if any is offered by the Government, or how to secure the Patent for the machine, or in any way assist me by advice in this great work, I shall most graciously acknowledge your consideration.
These are my convictions that my SEVERAL discoveries will be realized: and this great one can be at once acted upon: although at this moment it only exists in my mind, from my knowledge of certain fixed principles in nature:—the Machine I have not made, as I only completed the discovery YESTERDAY, Sunday!
I have, etc. —— ——"
To the Directors of the
London University, Gower Street.
ON SPIRITUALISM.
The Divine Drama of History and Civilisation. By the Rev. James Smith, M.A.[108] London, 1854, 8vo.
I have several books on that great paradox of our day, Spiritualism, but I shall exclude all but three. The bibliography of this subject is now very large. The question is one both of evidence and speculation;—Are the facts [56]true? Are they caused by spirits? These I shall not enter upon: I shall merely recommend this work as that of a spiritualist who does not enter on the subject, which he takes for granted, but applies his derived views to the history of mankind with learning and thought. Mr. Smith was a man of a very peculiar turn of thinking. He was, when alive, the editor, or an editor, of the Family Herald: I say when alive, to speak according to knowledge; for, if his own views be true, he may have a hand in it still. The answers to correspondents, in his time, were piquant and original above any I ever saw. I think a very readable book might be made out of them, resembling "Guesses at Truth:" the turn given to an inquiry about morals, religion, or socials, is often of the highest degree of unexpectedness; the poor querist would find himself right in a most unpalatable way.
Answers to correspondents, in newspapers, are very often the fag ends of literature. I shall never forget the following. A person was invited to name a rule without exception, if he could: he answered "A man must be present when he is shaved." A lady—what right have ladies to decide questions about shaving?—said this was not properly a rule; and the oracle was consulted. The editor agreed with the lady; he said that "a man must be present when he is shaved" is not a rule, but a fact.
[Among my anonymous communicants is one who states that I have done injustice to the Rev. James Smith in "referring to him as a spiritualist," and placing his "Divine Drama" among paradoxes: "it is no paradox, nor do spiritualistic views mar or weaken the execution of the design." Quite true: for the design is to produce and enforce "spiritualistic views"; and leather does not mar nor weaken a shoemaker's plan. I knew Mr. Smith well, and have often talked to him on the subject: but more testimony from me is unnecessary; his book will speak for itself. [57]His peculiar style will justify a little more quotation than is just necessary to prove the point. Looking at the "battle of opinion" now in progress, we see that Mr. Smith was a prescient:
(P. 588.) "From the general review of parties in England, it is evident that no country in the world is better prepared for the great Battle of Opinion. Where else can the battle be fought but where the armies are arrayed? And here they all are, Greek, Roman, Anglican, Scotch, Lutheran, Calvinist, Established and Territorial, with Baronial Bishops, and Nonestablished of every grade—churches with living prophets and apostles, and churches with dead prophets and apostles, and apostolical churches without apostles, and philosophies without either prophets or apostles, and only wanting one more, 'the Christian Church,' like Aaron's rod, to swallow up and digest them all, and then bud and flourish. As if to prepare our minds for this desirable and inevitable consummation, different parties have been favored with a revival of that very spirit of revelation by which the Church itself was originally founded. There is a complete series of spiritual revelations in England and the United States, besides mesmeric phenomena that bear a resemblance to revelation, and thus gradually open the mind of the philosophical and infidel classes, as well as the professed believers of that old revelation which they never witnessed in living action, to a better understanding of that Law of Nature (for it is a Law of Nature) in which all revelation originates and by which its spiritual communications are regulated."
Mr. Smith proceeds to say that there are only thirty-five incorporated churches in England, all formed from the New Testament except five, to each of which five he concedes a revelation of its own. The five are the Quakers, the Swedenborgians, the Southcottians, the Irvingites, and the Mormonites. Of Joanna Southcott he speaks as follows: [58]
(P. 592.) "Joanna Southcott[109] is not very gallantly treated by the gentlemen of the Press, who, we believe, without knowing anything about her, merely pick up their idea of her character from the rabble. We once entertained the same rabble idea of her; but having read her works—for we really have read them—we now regard her with great respect. However, there is a great abundance of chaff and straw to her grain; but the grain is good, and as we do not eat either the chaff or straw if we can avoid it, nor even the raw grain, but thrash it and winnow it, and grind it and bake it, we find it, after undergoing this process, not only very palatable, but a special dainty of its kind. But the husk is an insurmountable obstacle to those learned and educated gentlemen who judge of books entirely by the style and the grammar, or those who eat grain as it grows, like the cattle. Such men would reject all prological revelation; for there never was and probably never will be a revelation by voice and vision communicated in classical manner. It would be an invasion of the rights and prerogatives of Humanity, and as contrary to the Divine and Established order of mundane government, as a field of quartern loaves or hot French rolls."
Mr. Smith's book is spiritualism from beginning to end; and my anonymous gainsayer, honest of course, is either ignorant of the work he thinks he has read, or has a most remarkable development of the organ of imperception.]
A CONDENSED HISTORY OF MATHEMATICS.
I cut the following from a Sunday paper in 1849:
"X. Y.—The Chaldeans began the mathematics, in which the Egyptians excelled. Then crossing the sea, by means [59]of Thales,[110] the Milesian, they came into Greece, where they were improved very much by Pythagoras,[111] Anaxagoras,[112] and Anopides[113] of Chios. These were followed by Briso,[114] Antipho, [two circle-squarers; where is Euclid?] and Hippocrates,[115] but the excellence of the algebraic art was begun by Geber,[116] an Arabian astronomer, and was carried on by Cardanus,[117] Tartaglia,[118] Clavius,[119], Stevinus,[120] Ghetaldus,[121] Herigenius,[122] Fran. Van Schooten [meaning Francis Van Schooten[123]], Florida de Beaume,[124] etc."
Bryso was a mistaken man. Antipho had the disadvantage of being in advance of his age. He had the notion of which the modern geometry has made so much, that of [60]a circle being the polygon of an infinitely great number of sides. He could make no use of it, but the notion itself made him a sophist in the eyes of Aristotle, Eutocius,[125] etc. Geber, an Arab astronomer, and a reputed conjurer in Europe, seems to have given his name to unintelligible language in the word gibberish. At one time algebra was traced to him; but very absurdly, though I have heard it suggested that algebra and gibberish must have had one inventor.
Any person who meddles with the circle may find himself the crane who was netted among the geese: as Antipho for one, and Olivier de Serres[126] for another. This last gentleman ascertained, by weighing, that the area of the circle is very nearly that of the square on the side of the inscribed equilateral triangle: which it is, as near as 3.162 ... to 3.141.... He did not pretend to more than approximation; but Montucla and others misunderstood him, and, still worse, misunderstood their own misunderstanding, and made him say the circle was exactly double of the equilateral triangle. He was let out of limbo by Lacroix, in a note to his edition of Montucla's History of Quadrature.
ST. VITUS, PATRON OF CYCLOMETERS.
Quadratura del cerchio, trisezione dell' angulo, et duplicazione del cubo, problemi geometricamente risolute e dimostrate dal Reverendo Arciprete di San Vito D. Domenico Angherà,[127] Malta, 1854, 8vo.
Equazioni geometriche, estratte dalla lettera del Rev. Arciprete ... al Professore Pullicino[128] sulla quadratura del cerchio. Milan, 1855 or 1856, 8vo.
Il Mediterraneo gazetta di Malta, 26 Decembre 1855, No. 909: also 911, 912, 913, 914, 936, 939.
The Malta Times, Tuesday, 9th June 1857.
Misura esatta del cerchio, dal Rev. D. Angherà. Malta, 1857, 12mo.
Quadrature of the circle ... by the Rev. D. Angherà, Archpriest of St. Vito. Malta, 1858, 12mo.
I have looked for St. Vitus in catalogues of saints, but never found his legend, though he figures as a day-mark in the oldest almanacs. He must be properly accredited, since he was an archpriest. And I pronounce and ordain, by right accruing from the trouble I have taken in this subject, that he, St. Vitus, who leads his votaries a never-ending and unmeaning dance, shall henceforth be held and taken to be the patron saint of the circle-squarer. His day is the 15th of June, which is also that of St. Modestus,[129] with whom the said circle-squarer often has nothing to do. And he must not put himself under the first saint with a slantendicular reference to the other, as is much to be feared was done by the Cardinal who came to govern England with a title containing St. Pudentiana,[130] who shares a day with St. Dunstan. The Archpriest of St. Vitus will have it that the square inscribed in a semicircle is half of the semicircle, or the circumference 3-1/5 diameters. He is active and able, with [62]nothing wrong about him except his paradoxes. In the second tract named he has given the testimonials of crowned heads and ministers, etc. as follows. Louis-Napoleon gives thanks. The minister at Turin refers it to the Academy of Sciences, and hopes so much labor will be judged degna di pregio.[131] The Vice-Chancellor of Oxford—a blunt Englishman—begs to say that the University has never proposed the problem, as some affirm. The Prince Regent of Baden has received the work with lively interest. The Academy of Vienna is not in a position to enter into the question. The Academy of Turin offers the most distinct thanks. The Academy della Crusca attends only to literature, but gives thanks. The Queen of Spain has received the work with the highest appreciation. The University of Salamanca gives infinite thanks, and feels true satisfaction in having the book. Lord Palmerston gives thanks, by the hand of "William San." The Viceroy of Egypt, not being yet up in Italian, will spend his first moments of leisure in studying the book, when it shall have been translated into French: in the mean time he congratulates the author upon his victory over a problem so long held insoluble. All this is seriously published as a rate in aid of demonstration. If these royal compliments cannot make the circumference of a circle about 2 per cent. larger than geometry will have it —which is all that is wanted—no wonder that thrones are shaky.
I am informed that the legend of St. Vitus is given by Ribadeneira[132] in his lives of Saints, and that Baronius,[133] in [63]his Martyrologium Romanum, refers to several authors who have written concerning him. There is an account in Mrs. Jameson's[134] History of Sacred and Legendary Art (ed. of 1863, p. 544). But it seems that St. Vitus is the patron saint of all dances; so that I was not so far wrong in making him the protector of the cyclometers. Why he is represented with a cock is a disputed point, which is now made clear: next after gallus gallinaceus[135] himself, there is no crower like the circle-squarer.
CELEBRATED APPROXIMATIONS OF π.
The following is an extract from the English Cyclopædia, Art. Tables:
"1853. William Shanks,[136] Contributions to Mathematics, comprising chiefly the Rectification of the Circle to 607 Places of Tables, London, 1853. (Quadrature of the Circle.) Here is a table, because it tabulates the results of the subordinate steps of this enormous calculation as far as 527 decimals: the remainder being added as results only during the printing. For instance, one step is the calculation of the reciprocal of 601.5601; and the result is given. The number of pages required to describe these results is 87. Mr. Shanks has also thrown off, as chips or splinters, the values of the base of Napier's logarithms, and of its logarithms of 2, 3, 5, 10, to 137 decimals; and the value of the modulus .4342 ... to 136 decimals: with the 13th, 25th, 37th ... up to the 721st powers of 2. These tremendous stretches of calculation—at least we so call them in our day—are useful in several respects; they prove more than [64]the capacity of this or that computer for labor and accuracy; they show that there is in the community an increase of skill and courage. We say in the community: we fully believe that the unequalled turnip which every now and then appears in the newspapers is a sufficient presumption that the average turnip is growing bigger, and the whole crop heavier. All who know the history of the quadrature are aware that the several increases of numbers of decimals to which π has been carried have been indications of a general increase in the power to calculate, and in courage to face the labor. Here is a comparison of two different times. In the day of Cocker,[137] the pupil was directed to perform a common subtraction with a voice-accompaniment of this kind: '7 from 4 I cannot, but add 10, 7 from 14 remains 7, set down 7 and carry 1; 8 and 1 which I carry is 9, 9 from 2 I cannot, etc.' We have before us the announcement of the following table, undated, as open to inspection at the Crystal Palace, Sydenham, in two diagrams of 7 ft. 2 in, by 6 ft. 6 in.: 'The figure 9 involved into the 912th power, and antecedent powers or involutions, containing upwards of 73,000 figures. Also, the proofs of the above, containing upwards of 146,000 figures. By Samuel Fancourt, of Mincing Lane, London, and completed by him in the year 1837, at the age of sixteen. N.B. The whole operation performed by simple arithmetic.' The young operator calculated by successive squaring the 2d, 4th, 8th, etc., powers up to the 512th, with proof by division. But 511 multiplications by 9, in the short (or 10-1) way, would have been much easier. The 2d, 32d, 64th, 128th, 256th, and 512th powers are given at the back of the announcement. The powers of 2 have been calculated for many purposes. In Vol. II of his Magia Universalis Naturæ et Artis, Herbipoli, 1658, 4to, the Jesuit Gaspar Schott[138] having discovered, on some grounds of theological [65]magic, that the degrees of grace of the Virgin Mary were in number the 256th power of 2, calculated that number. Whether or no his number correctly represented the result he announced, he certainly calculated it rightly, as we find by comparison with Mr. Shanks."
There is a point about Mr. Shanks's 608 figures of the value of π which attracts attention, perhaps without deserving it. It might be expected that, in so many figures, the nine digits and the cipher would occur each about the same number of times; that is, each about 61 times. But the fact stands thus: 3 occurs 68 times; 9 and 2 occur 67 times each; 4 occurs 64 times; 1 and 6 occur 62 times each; 0 occurs 60 times; 8 occurs 58 times; 5 occurs 56 times; and 7 occurs only 44 times. Now, if all the digits were equally likely, and 608 drawings were made, it is 45 to 1 against the number of sevens being as distant from the probable average (say 61) as 44 on one side or 78 on the other. There must be some reason why the number 7 is thus deprived of its fair share in the structure. Here is a field of speculation in which two branches of inquirers might unite. There is but one number which is treated with an unfairness which is incredible as an accident; and that number is the mystic number seven! If the cyclometers and the apocalyptics would lay their heads together until they come to a unanimous verdict on this phenomenon, and would publish nothing until they are of one mind, they would earn the gratitude of their race.—I was wrong: it is the Pyramid-speculator who should have been appealed to. A correspondent of my friend Prof. Piazzi Smyth[139] notices that 3 is the number of most frequency, and that 3-1/7 is the nearest approximation to it in simple digits. Professor Smyth himself, whose word on Egypt is paradox of a very high order, backed by a great quantity of useful labor, the results which will be made available by those who do not receive [66]the paradoxes, is inclined to see confirmation for some of his theory in these phenomena.
CURIOUS CALCULATIONS.
These paradoxes of calculation sometimes appear as illustrations of the value of a new method. In 1863, Mr. G. Suffield,[140] M.A., and Mr. J. R. Lunn,[141] M.A., of Clare College and of St. John's College, Cambridge, published the whole quotient of 10000 ... divided by 7699, throughout the whole of one of the recurring periods, having 7698 digits. This was done in illustration of Mr. Suffield's method of Synthetic division.
Another instance of computation carried to paradoxical length, in order to illustrate a method, is the solution of x3 - 2x = 5, the example given of Newton's method, on which all improvements have been tested. In 1831, Fourier's[142] posthumous work on equations showed 33 figures of solution, got with enormous labor. Thinking this a good opportunity to illustrate the superiority of the method of W. G. Horner,[143] not yet known in France, and not much known in [67]England, I proposed to one of my classes, in 1841, to beat Fourier on this point, as a Christmas exercise. I received several answers, agreeing with each other, to 50 places of decimals. In 1848, I repeated the proposal, requesting that 50 places might be exceeded: I obtained answers of 75, 65, 63, 58, 57, and 52 places. But one answer, by Mr. W. Harris Johnston,[144] of Dundalk, and of the Excise Office, went to 101 decimal places. To test the accuracy of this, I requested Mr. Johnston to undertake another equation, connected with the former one in a way which I did not explain. His solution verified the former one, but he was unable to see the connection, even when his result was obtained. My reader may be as much at a loss: the two solutions are:
2.0945514815423265...
9.0544851845767340...
The results are published in the Mathematician, Vol. III, p. 290. In 1851, another pupil of mine, Mr. J. Power Hicks,[145] carried the result to 152 decimal places, without knowing what Mr. Johnston had done. The result is in the English Cyclopædia, article Involution and Evolution.
I remark that when I write the initial of a Christian name, the most usual name of that initial is understood. I never saw the name of W. G. Horner written at length, until I applied to a relative of his, who told me that he was, as I supposed, Wm. George, but that he was named after a relative of that surname.
The square root of 2, to 110 decimal places, was given [68]me in 1852 by my pupil, Mr. William Henry Colvill, now (1867) Civil Surgeon at Baghdad. It was
1.4142135623730950488016887242096980785696
7187537694807317667973799073247846210703
885038753432764157273501384623
Mr. James Steel[146] of Birkenhead verified this by actual multiplication, and produced
| 2 - | 2580413 10117 |
as the square.
Calcolo decidozzinale del Barone Silvio Ferrari. Turin, 1854, 4to.
This is a serious proposal to alter our numeral system and to count by twelves. Thus 10 would be twelve, 11 thirteen, etc., two new symbols being invented for ten and eleven. The names of numbers must of course be changed. There are persons who think such changes practicable. I thought this proposal absurd when I first saw it, and I think so still:[147] but the one I shall presently describe beats it so completely in that point, that I have not a smile left for this one.
ON COMETS.
The successful and therefore probably true theory of Comets. London, 1854. (4pp. duodecimo.)
The author is the late Mr. Peter Legh,[148] of Norbury Booths Hall, Knutsford, who published for eight or ten [69]years the Ombrological Almanac, a work of asserted discovery in meteorology. The theory of comets is that the joint attraction of the new moon and several planets in the direction of the sun, draws off the gases from the earth, and forms these cometic meteors. But how these meteors come to describe orbits round the sun, and to become capable of having their returns predicted, is not explained.
A NEW PHASE OF MORMONISM.
The Mormon, New York, Saturday, Oct. 27, 1855.
A newspaper headed by a grand picture of starred and striped banners, beehive, and eagle surmounting it. A scroll on each side: on the left, "Mormon creed. Mind your own business. Brigham Young;"[149] on the right, "Given by inspiration of God. Joseph Smith."[150] A leading article on the discoveries of Prof. Orson Pratt[151] says, "Mormonism has long taken the lead in religion: it will soon be in the van both in science and politics." At the beginning of the paper is Professor Pratt's "Law of Planetary Rotation." The cube roots of the densities of the planets are as the square roots of their periods of rotation. The squares of the cube roots of the masses divided by the squares of the diameters are as the periods of rotation. Arithmetical verification attempted, and the whole very modestly stated [70]and commented on. Dated G. S. L. City, Utah Ter., Aug. 1, 1855. If the creed, as above, be correctly given, no wonder the Mormonites are in such bad odor.
MATHEMATICAL ILLUSTRATIONS OF DOCTRINE.
The two estates; or both worlds mathematically considered. London, 1855, small (pp. 16).
The author has published mathematical works with his name. The present tract is intended to illustrate mathematically a point which may be guessed from the title. But the symbols do very little in the way of illustration: thus, x being the present value of the future estate (eternal happiness), and a of all that this world can give, the author impresses it on the mathematician that, x being infinitely greater than a, x + a = x, so that a need not be considered. This will not act much more powerfully on a mathematician by virtue of the symbols than if those same symbols had been dispensed with: even though, as the author adds, "It was this method of neglecting infinitely small quantities that Sir Isaac Newton was indebted to for his greatest discoveries."
There has been a moderate quantity of well-meant attempt to enforce, sometimes motive, sometimes doctrine, by arguments drawn from mathematics, the proponents being persons unskilled in that science for the most part. The ground is very dangerous: for the illustration often turns the other way with greater power, in a manner which requires only a little more knowledge to see. I have, in my life, heard from the pulpit or read, at least a dozen times, that all sin is infinitely great, proved as follows. The greater the being, the greater the sin of any offence against him: therefore the offence committed against an infinite being is infinitely great. Now the mathematician, of which the proposers of this argument are not aware, is perfectly familiar with quantities which increase together, and never cease increasing, but so that one of them remains finite when [71]the other becomes infinite. In fact, the argument is a perfect non sequitur.[152] Those who propose it have in their minds, though in a cloudy and indefinite form, the idea of the increase of guilt being proportionate to the increase of greatness in the being offended. But this it would never do to state: for by such statement not only would the argument lose all that it has of the picturesque, but the asserted premise would have no strong air of exact truth. How could any one undertake to appeal to conscience to declare that an offence against a being 4-7/10 times as great as another is exactly, no more and no less, 4-7/10 times as great an offence against the other?
The infinite character of the offence against an infinite being is laid down in Dryden's Religio Laici,[153] and is, no doubt, an old argument:
"For, granting we have sinned, and that th' offence
Of man is made against Omnipotence,
Some price that bears proportion must be paid,
And infinite with infinite be weighed.
See then the Deist lost; remorse for vice
Not paid; or, paid, inadequate in price."
Dryden, in the words "bears proportion" is in verse more accurate than most of the recent repeaters in prose. And this is not the only case of the kind in his argumentative poetry.
My old friend, the late Dr. Olinthus Gregory,[154] who was a sound and learned mathematician, adopted this dangerous kind of illustration in his Letters on the Christian Religion. [72]He argued, by parallel, from what he supposed to be the necessarily mysterious nature of the impossible quantity of algebra to the necessarily mysterious nature of certain doctrines of his system of Christianity. But all the difficulty and mystery of the impossible quantity is now cleared away by the advance of algebraical thought: and yet Dr. Gregory's book continues to be sold, and no doubt the illustration is still accepted as appropriate.
The mode of argument used by the author of the tract above named has a striking defect. He talks of reducing this world and the next to "present value," as an actuary does with successive lives or next presentations. Does value make interest? and if not, why? And if it do, then the present value of an eternity is not infinitely great. Who is ignorant that a perpetual annuity at five per cent is worth only twenty years' purchase? This point ought to be discussed by a person who treats heaven as a deferred perpetual annuity. I do not ask him to do so, and would rather he did not; but if he will do it, he must either deal with the question of discount, or be asked the reason why.
When a very young man, I was frequently exhorted to one or another view of religion by pastors and others who thought that a mathematical argument would be irresistible. And I heard the following more than once, and have since seen it in print, I forget where. Since eternal happiness belonged to the particular views in question, a benefit infinitely great, then, even if the probability of their arguments were small, or even infinitely small, yet the product of the chance and benefit, according to the usual rule, might give a result which no one ought in prudence to pass over. They did not see that this applied to all systems as well as their own. I take this argument to be the most perverse of all the perversions I have heard or read on the subject: there is some high authority for it, whom I forget.
The moral of all this is, that such things as the preceding should be kept out of the way of those who are not [73]mathematicians, because they do not understand the argument; and of those who are, because they do.
[The high authority referred to above is Pascal, an early cultivator of mathematical probability, and obviously too much enamoured of his new pursuit. But he conceives himself bound to wager on one side or the other. To the argument (Pensées, ch. 7)[155] that "le juste est de ne point parier," he answers, "Oui: mais il faut parier: vous êtes embarqué; et ne parier point que Dieu est, c'est parier qu'il n'est pas."[156] Leaving Pascal's argument to make its way with a person who, being a sceptic, is yet positive that the issue is salvation or perdition, if a God there be,—for the case as put by Pascal requires this,—I shall merely observe that a person who elects to believe in God, as the best chance of gain, is not one who, according to Pascal's creed, or any other worth naming, will really secure that gain. I wonder whether Pascal's curious imagination ever presented to him in sleep his convert, in the future state, shaken out of a red-hot dice-box upon a red-hot hazard-table, as perhaps he might have been, if Dante had been the later of the two. The original idea is due to the elder Arnobius,[157] who, as cited by Bayle,[158] speaks thus:
"Sed et ipse [Christus] quæ pollicetur, non probat. Ita est. Nulla enim, ut dixi, futurorum potest existere comprobatio. Cum ergo hæc sit conditio futurorum, ut teneri et comprehendi nullius possint anticipationis attactu; nonne [74]purior ratio est, ex duobus incertis, et in ambigua expectatione pendentibus, id potius credere, quod aliquas spes ferat, quam omnino quod nullas? In illo enim periculi nihil est, si quod dicitur imminere, cassum fiat et vacuum: in hoc damnum est maximum, id est salutis amissio, si cum tempus advenerit aperiatur non fuisse mendacium."[159]
Really Arnobius seems to have got as much out of the notion, in the third century, as if he had been fourteen centuries later, with the arithmetic of chances to help him.]
NOVUM ORGANUM MORALIUM.
The Sentinel, vol. ix. no. 27. London, Saturday, May 26, 1855.
This is the first London number of an Irish paper, Protestant in politics. It opens with "Suggestions on the subject of a Novum Organum Moralium," which is the application of algebra and the differential calculus to morals, socials, and politics. There is also a leading article on the subject, and some applications in notes to other articles. A separate publication was afterwards made, with the addition of a long Preface; the author being a clergyman who I presume must have been the editor of the Sentinel.
Suggestions as to the employment of a Novum Organum Moralium. Or, thoughts on the nature of the Differential Calculus, and on the application of its principles to metaphysics, with a view to the attainment of demonstration and certainty in moral, [75]political and ecclesiastical affairs. By Tresham Dames Gregg,[160] Chaplain of St. Mary's, within the church of St. Nicholas intra muros, Dublin. London, 1859, 8vo. (pp. xl + 32).
I have a personal interest in this system, as will appear from the following extract from the newspaper:
"We were subsequently referred to De Morgan's Formal Logic and Boole's Laws of Thought[161] both very elaborate works, and greatly in the direction taken by ourselves. That the writers amazingly surpass us in learning we most willingly admit, but we venture to pronounce of both their learned treatises, that they deal with the subject in a mode that is scholastic to an excess.... That their works have been for a considerable space of time before the world and effected nothing, would argue that they have overlooked the vital nature of the theme.... On the whole, the writings of De Morgan and Boole go to the full justification of our principle without in any wise so trenching upon our ground as to render us open to reproach in claiming our Calculus as a great discovery.... But we renounce any paltry jealousy as to a matter so vast. If De Morgan and Boole have had a priority in the case, to them we cheerfully shall resign the glory and honor. If such be the truth, they have neither done justice to the discovery, nor to themselves [quite true]. They have, under the circumstances, acted like 'the foolish man, who roasteth not that which he taketh [76]in hunting.... It will be sufficient for us, however, to be the Columbus of these great Americi, and popularize what they found, if they found it. We, as from the mountain top, will then become their trumpeters, and cry glory to De Morgan and glory to Boole, under Him who is the source of all glory, the only good and wise, to Whom be glory for ever! If they be our predecessors in this matter, they have, under Him, taken moral questions out of the category of probabilities, and rendered them perfectly certain. In that case, let their books be read by those who may doubt the principles this day laid before the world as a great discovery, by our newspaper. Our cry shall be ευρηκασι![162] Let us hope that they will join us, and henceforth keep their light [sic] from under their bushel."
For myself, and for my old friend Mr. Boole, who I am sure would join me, I disclaim both priority, simultaneity, and posteriority, and request that nothing may be trumpeted from the mountain top except our abjuration of all community of thought or operation with this Novum Organum.
To such community we can make no more claim than Americus could make to being the forerunner of Columbus who popularized his discoveries. We do not wish for any ευρηκασι and not even for εὑρηκασι. For self and Boole, I point out what would have convinced either of us that this house is divided against itself.
Α being an apostolic element, δ the doctrinal element, and Χ the body of the faithful, the church is Α δ Χ, we are told. Also, that if Α become negative, or the Apostolicity become Diabolicity [my words]; or if δ become negative, and doctrine become heresy; or if Χ become negative, that is, if the faithful become unfaithful; the church becomes negative, "the very opposite to what it ought to be." For self and Boole, I admit this. But—which is not noticed—if Α and δ should both become negative, diabolical origin [77]and heretical doctrine, then the church, Α δ Χ, is still positive, what it ought to be, unless Χ be also negative, or the people unfaithful to it, in which case it is a bad church. Now, self and Boole—though I admit I have not asked my partner—are of opinion that a diabolical church with false doctrine does harm when the people are faithful, and can do good only when the people are unfaithful. We may be wrong, but this is what we do think. Accordingly, we have caught nothing, and can therefore roast nothing of our own: I content myself with roasting a joint of Mr. Gregg's larder.
These mathematical vagaries have uses which will justify a large amount of quotation: and in a score of years this may perhaps be the only attainable record. I therefore proceed.
After observing that by this calculus juries (heaven help them! say I) can calculate damages "almost to a nicety," and further that it is made abundantly evident that c e x is "the general expression for an individual," it is noted that the number of the Beast is not given in the Revelation in words at length, but as χξϜ'.[163] On this the following remark is made:
"Can it be possible that we have in this case a specimen given to us of the arithmetic of heaven, and an expression revealed, which indicates by its function of addibility, the name of the church in question, and of each member of it; and by its function of multiplicability the doctrine, the mission, and the members of the great Synagogue of Apostacy? We merely propound these questions;—we do not pretend to solve them."
After a translation in blank verse—a very pretty one—of the 18th Psalm, the author proceeds as follows, to render it into differential calculus:
"And the whole tells us just this, that David did what he could. He augmented those elements of his constitution which were (exceptis excipiendis)[164] subject to himself, and the Almighty then augmented his personal qualities, and his vocational status. Otherwise, to throw the matter into the expression of our notation, the variable e was augmented, and c x rose proportionally. The law of the variation, according to our theory, would be thus expressed. The resultant was David the king c e x [c = r?] (who had been David the shepherd boy), and from the conditions of the theorem we have
du de | = ce | dx de | + ex | dc de | x + cx |
which, in the terms of ordinary language, just means, the increase of David's educational excellence or qualities—his piety, his prayerfulness, his humility, obedience, etc.—was so great, that when multiplied by his original talent and position, it produced a product so great as to be equal in its amount to royalty, honor, wealth, and power, etc.: in short, to all the attributes of majesty."[165]
The "solution of the family problem" is of high interest. It is to determine the effect on the family in general from a change [of conduct] in one of them. The person chosen is one of the maid-servants.
"Let c e x be the father; c1e1x1 the mother, etc. The family then consists of the maid's master, her mistress, her young master, her young mistress, and fellow servant. Now the master's calling (or c) is to exercise his share of control over this servant, and mind the rest of his business: call this remainder a, and let his calling generally, or all his affairs, be to his maid-servant as m : y, i.e., y = (mz/c); ... [79]and this expression will represent his relation to the servant. Consequently,
| c e x = |  | a + | mz c |  | e x; otherwise |  | a + | mz c |  | e x |
is the expression for the father when viewed as the girl's master."
I have no objection to repeat so far; but I will not give the formula for the maid's relation to her young master; for I am not quite sure that all young masters are to be trusted with it. Suffice it that the son will be affected directly as his influence over her, and inversely as his vocational power: if then he should have some influence and no vocational power, the effect on him would be infinite. This is dismal to think of. Further, the formula brings out that if one servant improve, the other must deteriorate, and vice versa. This is not the experience of most families: and the author remarks as follows:
"That is, we should venture to say, a very beautiful result, and we may say it yielded us no little astonishment. What our calculation might lead to we never dreamt of; that it should educe a conclusion so recondite that our unassisted power never could have attained to, and which, if we could have conjectured it, would have been at best the most distant probability, that conclusion being itself, as it would appear, the quintessence of truth, afforded us a measure of satisfaction that was not slight."
That the writings of Mr. Boole and myself "go to the full justification of" this "principle," is only true in the sense in which the Scotch use, or did use, the word justification.
A TRIBUTE TO BOOLE.
[The last number of this Budget had stood in type for months, waiting until there should be a little cessation of correspondence more connected with the things of the day. [80]I had quite forgotten what it was to contain; and little thought, when I read the proof, that my allusions to my friend Mr. Boole, then in life and health, would not be printed till many weeks after his death. Had I remembered what my last number contained, I should have added my expression of regret and admiration to the numerous obituary testimonials, which this great loss to science has called forth.
The system of logic alluded to in the last number of this series is but one of many proofs of genius and patience combined. I might legitimately have entered it among my paradoxes, or things counter to general opinion: but it is a paradox which, like that of Copernicus, excited admiration from its first appearance. That the symbolic processes of algebra, invented as tools of numerical calculation, should be competent to express every act of thought, and to furnish the grammar and dictionary of an all-containing system of logic, would not have been believed until it was proved. When Hobbes,[166] in the time of the Commonwealth, published his Computation or Logique, he had a remote glimpse of some of the points which are placed in the light of day by Mr. Boole. The unity of the forms of thought in all the applications of reason, however remotely separated, will one day be matter of notoriety and common wonder: and Boole's name will be remembered in connection with one of the most important steps towards the attainment of this knowledge.]
DECIMALS RUN RIOT.
The Decimal System as a whole. By Dover Statter.[167] London and Liverpool, 1856, 8vo.
The proposition is to make everything decimal. The day, now 24 hours, is to be made 10 hours. The year is to have ten months, Unusber, Duober, etc. Fortunately there are ten commandments, so there will be neither addition to, nor deduction from, the moral law. But the twelve apostles! Even rejecting Judas, there is a whole apostle of difficulty. These points the author does not touch.
ON PHONETIC SPELLING.
The first book of Phonetic Reading. London, Fred. Pitman,[168] Phonetic Depot, 20, Paternoster Row, 1856, 12mo.
The Phonetic Journal. Devoted to the propagation of phonetic reading, phonetic longhand, phonetic shorthand, and phonetic printing. No. 46. Saturday, 15 November 1856. Vol. 15.
I write the titles of a couple out of several tracts which I have by me. But the number of publications issued by the promoters of this spirited attempt is very large indeed.[169] The attempt itself has had no success with the mass of the public. This I do not regret. Had the world found that the change was useful, I should have gone contentedly with the stream; but not without regretting our old language. I admit the difficulties which our unpronounceable spelling puts in the way of learning to read: and I have no doubt that, as affirmed, it is easier to teach children phonetically, and afterwards to introduce them to our common system, than to proceed in the usual way. But by the usual way I mean proceeding by letters from the very beginning. If, which I am sure is a better plan, children be taught at the commencement very much by complete words, as if they were learning Chinese, and be gradually accustomed to [82]resolve the known words into letters, a fraction, perhaps a considerable one, of the advantage of the phonetic system is destroyed. It must be remembered that a phonetic system can only be an approximation. The differences of pronunciation existing among educated persons are so great, that, on the phonetic system, different persons ought to spell differently.
But the phonetic party have produced something which will immortalize their plan: I mean their shorthand, which has had a fraction of the success it deserves. All who know anything of shorthand must see that nothing but a phonetic system can be worthy of the name: and the system promulgated is skilfully done. Were I a young man I should apply myself to it systematically. I believe this is the only system in which books were ever published. I wish some one would contribute to a public journal a brief account of the dates and circumstances of the phonetic movement, not forgetting a list of the books published in shorthand.
A child beginning to read by himself may owe terrible dreams and waking images of horror to our spelling, as I did when six years old. In one of the common poetry-books there is an admonition against confining little birds in cages, and the child is asked what if a great giant, amazingly strong, were to take you away, shut you up,
And feed you with vic-tu-als you ne-ver could bear.
The book was hyphened for the beginner's use; and I had not the least idea that vic-tu-als were vittles: by the sound of the word I judged they must be of iron; and it entered into my soul.
The worst of the phonetic shorthand book is that they nowhere, so far as I have seen, give all the symbols, in every stage of advancement, together, in one or following pages. It is symbols and talk, more symbols and more talk, etc. A universal view of the signs ought to begin the works. [83]
A HANDFUL OF LITTLE PARADOXERS.
Ombrological Almanac. Seventeenth year. An essay on Anemology and Ombrology. By Peter Legh,[170] Esq. London, 1856, 12mo.
Mr. Legh, already mentioned, was an intelligent country gentleman, and a legitimate speculator. But the clue was not reserved for him.
The proof that the three angles of a triangle are equal to two right angles looked for in the inflation of the circle. By Gen. Perronet Thompson. London, 1856, 8vo. (pp. 4.)
Another attempt, the third, at this old difficulty, which cannot be put into few words of explanation.[171]
Comets considered as volcanoes, and the cause of their velocity and other phenomena thereby explained. London (circa 1856), 8vo.
The title explains the book better than the book explains the title.
1856. A stranger applied to me to know what the ideas of a friend of his were worth upon the magnitude of the earth. The matter being one involving points of antiquity, I mentioned various persons whose speculations he seemed to have ignored; among others, Thales. The reply was, "I am instructed by the author to inform you that he is perfectly acquainted with the works of Thales, Euclid, Archimedes, ..." I had some thought of asking whether he had used the Elzevir edition of Thales,[172] which is known to be very incomplete, or that of Professor Niemand with the lections, Nirgend, 1824, 2 vols. folio; just to see whether the [84]last would not have been the very edition he had read. But I refrained, in mercy.
The moon is the image of the Earth, and is not a solid body. By The Longitude.[173] (Private Circulation.) In five parts. London, 1856, 1857, 1857; Calcutta, 1858, 1858, 8vo.
The earth is "brought to a focus"; it describes a "looped orbit round the sun." The eclipse of the sun is thus explained: "At the time of eclipses, the image is more or less so directly before or behind the earth that, in the case of new moon, bright rays of the sun fall and bear upon the spot where the figure of the earth is brought to a focus, that is, bear upon the image of the earth, when a darkness beyond is produced reaching to the earth, and the sun becomes more or less eclipsed." How the earth is "brought to a focus" we do not find stated. Writers of this kind always have the argument that some things which have been ridiculed at first have been finally established. Those who put into the lottery had the same kind of argument; but were always answered by being reminded how many blanks there were to one prize. I am loath to pronounce against anything: but it does force itself upon me that the author of these tracts has drawn a blank.
LUNAR MOTION AGAIN.
Times, April 6 or 7, 1856. The moon has no rotary motion.
A letter from Mr. Jellinger Symons,[174] inspector of schools, which commenced a controversy of many letters and pamphlets. This dispute comes on at intervals, and will continue to do so. It sometimes arises from inability to understand the character of simple rotation, geometrically; sometimes from not understanding the mechanical doctrine of rotation.
Lunar Motion. The whole argument stated, and illustrated by diagrams; with letters from the Astronomer Royal. By Jellinger C. Symons. London, 1856, 8vo.
The Astronomer Royal endeavored to disentangle Mr. J. C. Symons, but failed. Mr. Airy[175] can correct the error of a ship's compasses, because he can put her head which way he pleases: but this he cannot do with a speculator.
Mr. Symons, in this tract, insinuated that the rotation of the moon is one of the silver shrines of the craftsmen. To see a thing so clearly as to be satisfied that all who say they do not see it are telling wilful falsehood, is the nature of man. Many of all sects find much comfort in it, when they think of the others; many unbelievers solace themselves with it against believers; priests of old time founded the right of persecution upon it, and of our time, in some cases, the right of slander: many of the paradoxers make it an argument against students of science. But I must say for men of science, for the whole body, that they are fully persuaded of the honesty of the paradoxers. The simple truth is, that all those I have mentioned, believers, unbelievers, priests, paradoxers, are not so sure they are right in their points of difference that they can safely allow themselves to be persuaded of the honesty of opponents. Those who know demonstration are differently situated. I suspect a train might be laid for the formation of a better habit in this way. We know that Suvaroff[176] taught his Russians at Ismail not to fear the Turks by accustoming them to charge bundles of faggots dressed in turbans, etc.
At which your wise men sneered in phrases witty,
He made no answer—but he took the city!
Would it not be a good thing to exercise boys, in pairs, in the following dialogue:—Sir, you are quite wrong!—Sir, [86]I am sure you honestly think so! This was suggested by what used to take place at Cambridge in my day. By statute, every B.A. was obliged to perform a certain number of disputations, and the father of the college had to affirm that it had been done. Some were performed in earnest: the rest were huddled over as follows. Two candidates occupied the places of the respondent and the opponent: Recte statuit Newtonus, said the respondent: Recte non statuit Newtonus,[177] said the opponent. This was repeated the requisite number of times, and counted for as many acts and opponencies. The parties then changed places, and each unsaid what he had said on the other side of the house: I remember thinking that it was capital drill for the House of Commons, if any of us should ever get there. The process was repeated with every pair of candidates.
The real disputations were very severe exercises. I was badgered for two hours with arguments given and answered in Latin,—or what we called Latin—against Newton's first section, Lagrange's[178] derived functions, and Locke[179] on innate principles. And though I took off everything, and was pronounced by the moderator to have disputed magno honore,[180] I never had such a strain of thought in my life. For the inferior opponents were made as sharp as their betters by their tutors, who kept lists of queer objections, drawn from all quarters. The opponents used to meet the day before to compare their arguments, that the same might not come twice over. But, after I left Cambridge, it became the fashion to invite the respondent to be present, who therefore learnt all that was to be brought against him. This made the whole thing a farce: and the disputations were abolished.
The Doctrine of the Moon's Rotation, considered in a letter to the Astronomical Censor of the Athenæum. By Jones L. MacElshender.[181] Edinburgh, 1856, 8vo.
This is an appeal to those cultivated persons who will read it "to overrule the dicta of judges who would sacrifice truth and justice to professional rule, or personal pique, pride, or prejudice"; meaning, the great mass of those who have studied the subject. But how? Suppose the "cultivated persons" were to side with the author, would those who have conclusions to draw and applications to make consent to be wrong because the "general body of intelligent men," who make no special study of the subject, are against them? They would do no such thing: they would request the general body of intelligent men to find their own astronomy, and welcome. But the truth is, that this intelligent body knows better: and no persons know better that they know better than the speculators themselves.
But suppose the general body were to combine, in opposition to those who have studied. Of course all my list must be admitted to their trial; and then arises the question whether both sides are to be heard. If so, the general body of the intelligent must hear all the established side have to say: that is, they must become just as much of students as the inculpated orthodox themselves. And will they not then get into professional rule, pique, pride, and prejudice, as the others did? But if, which I suspect, they are intended to judge as they are, they will be in a rare difficulty. All the paradoxers are of like pretensions: they cannot, as a class, be right, for each one contradicts a great many of the rest. There will be the puzzle which silenced the crew of the cutter in Marryat's novel of the Dog Fiend.[182] "A tog is a tog," said Jansen.—"Yes," replied another, "we all know a dog is a dog; but the question is—Is this dog [88]a dog?" And this question would arise upon every dog of them all.
ZETETIC ASTRONOMY.
Zetetic Astronomy: Earth not a globe. 1857 (Broadsheet).
Though only a traveling lecturer's advertisement, there are so many arguments and quotations that it is a little pamphlet. The lecturer gained great praise from provincial newspapers for his ingenuity in proving that the earth is a flat, surrounded by ice. Some of the journals rather incline to the view: but the Leicester Advertiser thinks that the statements "would seem very seriously to invalidate some of the most important conclusions of modern astronomy," while the Norfolk Herald is clear that "there must be a great error on one side or the other." This broadsheet is printed at Aylesbury in 1857, and the lecturer calls himself Parallax: but at Trowbridge, in 1849, he was S. Goulden.[183] In this last advertisement is the following announcement: "A paper on the above subjects was read before the Council and Members of the Royal Astronomical Society, Somerset House, Strand, London (Sir John F. W. Herschel,[184] President), Friday, Dec. 8, 1848." No account of such a paper appears in the Notice for that month: I suspect that the above is Mr. S. Goulden's way of representing the following occurrence: Dec. 8, 1848, the Secretary of the Astronomical Society (De Morgan by name) said, at the close of the proceedings,—"Now, gentlemen, if you will promise not to tell the Council, I will read something for your amusement": and he then read a few of the arguments which had been transmitted by the lecturer. The fact is worth noting that from 1849 to 1857, arguments on the roundness or flatness of the earth did itinerate. I have [89]no doubt they did much good: for very few persons have any distinct idea of the evidence for the rotundity of the earth. The Blackburn Standard and Preston Guardian (Dec. 12 and 16, 1849) unite in stating that the lecturer ran away from his second lecture at Burnley, having been rather too hard pressed at the end of his first lecture to explain why the large hull of a ship disappeared before the sails. The persons present and waiting for the second lecture assuaged their disappointment by concluding that the lecturer had slipped off the icy edge of his flat disk, and that he would not be seen again till he peeped up on the opposite side.
But, strange as it may appear, the opposer of the earth's roundness has more of a case—or less of a want of case—than the arithmetical squarer of the circle. The evidence that the earth is round is but cumulative and circumstantial: scores of phenomena ask, separately and independently, what other explanation can be imagined except the sphericity of the earth. The evidence for the earth's figure is tremendously powerful of its kind; but the proof that the circumference is 3.14159265... times the diameter is of a higher kind, being absolute mathematical demonstration.
The Zetetic system still lives in lectures and books; as it ought to do, for there is no way of teaching a truth comparable to opposition. The last I heard of it was in lectures at Plymouth, in October, 1864. Since this time a prospectus has been issued of a work entitled "The Earth not a Globe"; but whether it has been published I do not know. The contents are as follows:
"The Earth a Plane—How circumnavigated.—How time is lost or gained.—Why a ship's hull disappears (when outward bound) before the mast head.—Why the Polar Star sets when we proceed Southward, etc.—Why a pendulum vibrates with less velocity at the Equator than [90]at the Pole.—The allowance for rotundity supposed to be made by surveyors, not made in practice.—Measurement of Arcs of the Meridian unsatisfactory.—Degrees of Longitude North and South of the Equator considered.—Eclipses and Earth's form considered.—The Earth no motion on axis or in orbit.—How the Sun moves above the Earth's surface concentric with the North Pole.—Cause of Day and Night, Winter and Summer; the long alternation of light and darkness at the Pole.—Cause of the Sun rising and setting.—Distance of the Sun from London, 4,028 miles—How measured.—Challenge to Mathematicians.—Cause of Tides.—Moon self-luminous, NOT a reflector.—Cause of Solar and Lunar eclipses.—Stars not worlds; their distance.—Earth, the only material world; its true position in the universe; its condition and ultimate destruction by fire (2 Peter iii.), etc."
I wish there were geoplatylogical lectures in every town; in England (platylogical, in composition, need not mean babbling). The late Mr. Henry Archer[185] would, if alive, be very much obliged to me for recording his vehement denial of the roundness of the earth: he was excited if he heard any one call it a globe. I cannot produce his proof from the Pyramids, and from some caves in Arabia. He had other curious notions, of course: I should no more believe that a flat earth was a man's only paradox, than I should that Dutens,[186] the editor of Leibnitz, was eccentric only in supplying a tooth which he had lost by one which he found in an Italian tomb, and fully believed that it had once belonged to Scipio Africanus, whose family vault was discovered, it is supposed, in 1780. Mr. Archer is of note as [91]the suggester of the perforated border of the postage-stamps, and, I think, of the way of doing it; for this he got 4000l. reward. He was a civil engineer.
(August 28, 1865.) The Zetetic Astronomy has come into my hands. When, in 1851, I went to see the Great Exhibition, I heard an organ played by a performer who seemed very desirous to exhibit one particular stop. "What do you think of that stop?" I was asked.—"That depends on the name of it," said I.—"Oh! what can the name have to do with the sound? 'that which we call a rose,' etc."—"The name has everything to do with it: if it be a flute-stop, I think it very harsh; but if it be a railway-whistle-stop, I think it very sweet." So as to this book: if it be childish, it is clever; if it be mannish, it is unusually foolish. The flat earth, floating tremulously on the sea; the sun moving always over the flat, giving day when near enough, and night when too far off; the self-luminous moon, with a semi-transparent invisible moon, created to give her an eclipse now and then; the new law of perspective, by which the vanishing of the hull before the masts, usually thought to prove the earth globular, really proves it flat;—all these and other things are well fitted to form exercises for a person who is learning the elements of astronomy. The manner in which the sun dips into the sea, especially in tropical climates, upsets the whole. Mungo Park,[187] I think, gives an African hypothesis which explains phenomena better than this. The sun dips into the western ocean, and the people there cut him in pieces, fry him in a pan, and then join him together again, take him round the underway, and set him up in the east. I hope this book will be read, and that many will be puzzled by it: for there are many whose notions of astronomy deserve no better fate. There is no subject on which there is so little [92]accurate conception as that of the motions of the heavenly bodies. The author, though confident in the extreme, neither impeaches the honesty of those whose opinions he assails, nor allots them any future inconvenience: in these points he is worthy to live on a globe, and to revolve in twenty-four hours.
(October, 1866.) A follower appears, in a work dedicated to the preceding author: it is Theoretical Astronomy examined and exposed by Common Sense. The author has 128 well-stuffed octavo pages. I hope he will not be the last. He prints the newspaper accounts of his work: the Church Times says—not seeing how the satire might be retorted—"We never began to despair of Scripture until we discovered that 'Common Sense' had taken up the cudgels in its defence." This paper considers our author as the type of a Protestant. The author himself, who gives a summary of his arguments in verse, has one couplet which is worth quoting:
"How is't that sailors, bound to sea, with a 'globe' would never start,
But in its place will always take Mercator's[188] Level chart!"
To which I answer:
Why, really Mr. Common Sense, you've never got so far
As to think Mercator's planisphere shows countries as they are;
It won't do to measure distances; it points out how to steer,
But this distortion's not for you; another is, I fear.
The earth must be a cylinder, if seaman's charts be true,
Or else the boundaries, right and left, are one as well as two;
They contradict the notion that we dwell upon a plain,
For straight away, without a turn, will bring you home again.
There are various plane projections; and each one has its use:
I wish a milder word would rhyme—but really you're a goose!
The great wish of persons who expose themselves as above, is to be argued with, and to be treated as reputable [93]and refutable opponents. "Common Sense" reminds us that no amount of "blatant ridicule" will turn right into wrong. He is perfectly correct: but then no amount of bad argument will turn wrong into right. These two things balance; and we are just where we were: but you should answer our arguments, for whom, I ask? Would reason convince this kind of reasoner? The issue is a short and a clear one. If these parties be what I contend they are, then ridicule is made for them: if not, for what or for whom? If they be right, they are only passing through the appointed trial of all good things. Appeal is made to the future: and my Budget is intended to show samples of the long line of heroes who have fallen without victory, each of whom had his day of confidence and his prophecy of success. Let the future decide: they say roundly that the earth is flat; I say flatly that it is round.
The paradoxers all want reason, and not ridicule: they are all accessible, and would yield to conviction. Well then, let them reason with one another! They divide into squads, each with a subject, and as many different opinions as persons in each squad. If they be really what they say they are, the true man of each set can put down all the rest, and can come crowned with glory and girdled with scalps, to the attack on the orthodox misbelievers. But they know, to a man, that the rest are not fit to be reasoned with: they pay the regulars the compliment of believing that the only chance lies with them. They think in their hearts, each one for himself, that ridicule is of fit appliance to the rest.
Miranda. A book divided into three parts, entitled Souls, Numbers, Stars, on the Neo-Christian Religion ... Vol. i. London, 1858, 1859, 1860. 8vo.
The name of the author is Filopanti.[189] He announces himself as the 49th and last Emanuel: his immediate [94]predecessors were Emanuel Washington, Emanuel Newton, and Emanuel Galileo. He is to collect nations into one family. He knows the transmigrations of the whole human race. Thus Descartes became William III of England: Roger Bacon became Boccaccio. But Charles IX,[190] in retribution for the massacre of St. Bartholomew, was hanged in London under the name of Barthélemy for the murder of Collard: and many of the Protestants whom he killed as King of France were shouting at his death before the Old Bailey.
THE SABBATH—THE GREAT PYRAMID
A Letter to the members of the Anglo-Biblical Institute, dated Sept. 7, 1858, and signed 'Herman Heinfetter.'[191] (Broadsheet.)
This gentleman is well known to the readers of the Athenæum, in which, for nearly twenty years, he has inserted, as advertisements, long arguments in favor of Christians keeping the Jewish Sabbath, beginning on Friday Evening. The present letter maintains that, by the force of the definite article, the days of creation may not be consecutive, but may have any time—millions of years—between them. This ingenious way of reconciling the author of Genesis and the indications of geology is worthy to be added to the list, already pretty numerous. Mr. Heinfetter has taken such pains to make himself a public agitator, that [95]I do not feel it to be any invasion of private life if I state that I have heard he is a large corn-dealer. No doubt he is a member of the congregation whose almanac has already been described.
The great Pyramid. Why was it built? And who built it? By John Taylor, 1859,[192] 12mo.
This work is very learned, and may be referred to for the history of previous speculations. It professes to connect the dimensions of the Pyramid with a system of metrology which is supposed to have left strong traces in the systems of modern times; showing the Egyptians to have had good approximate knowledge of the dimensions of the earth, and of the quadrature of the circle. These are points on which coincidence is hard to distinguish from intention. Sir John Herschel[193] noticed this work, and gave several coincidences, in the Athenæum, Nos. 1696 and 1697, April 28 and May 5, 1860: and there are some remarks by Mr. Taylor in No. 1701, June 2, 1860.
Mr. Taylor's most recent publication is—
The battle of the Standards: the ancient, of four thousand years, against the modern, of the last fifty years—the less perfect of the two. London, 1864, 12mo.
This is intended as an appendix to the work on the Pyramid. Mr. Taylor distinctly attributes the original system to revelation, of which he says the Great Pyramid is the record. We are advancing, he remarks, towards the end of the Christian dispensation, and he adds that it is satisfactory to see that we retain the standards which were given by unwritten revelation 700 years before Moses. This is lighting the candle at both ends; for myself, I shall not undertake to deny or affirm either what is said about the dark past or what is hinted about the dark future.
My old friend Mr. Taylor is well known as the author of the argument which has convinced many, even most, that Sir Philip Francis[194] was Junius: pamphlet, 1813; supplement, 1817; second edition "The Identity of Junius with a distinguished living character established," London, 1818, 8vo. He told me that Sir Philip Francis, in a short conversation with him, made only this remark, "You may depend upon it you are quite mistaken:" the phrase appears to me remarkable; it has an air of criticism on the book, free from all personal denial. He also mentioned that a hearer told him that Sir Philip said, speaking of writers on the question,—"Those fellows, for half-a-crown, would prove that Jesus Christ was Junius."
Mr. Taylor implies, I think, that he is the first who started the suggestion that Sir Philip Francis was Junius, which I have no means either of confirming or refuting. If it be so [and I now know that Mr. Taylor himself never heard of any predecessor], the circumstance is very remarkable: it is seldom indeed that the first proposer of any solution of a great and vexed question is the person who so nearly establishes his point in general opinion as Mr. Taylor has done.
As to the Junius question in general, there is a little bit of the philosophy of horse-racing which may be usefully applied. A man who is so confident of his horse that he places him far above any other, may nevertheless, and does, refuse to give odds against all in the field: for many small adverse chances united make a big chance for one or other of the opponents. I suspect Mr. Taylor has made it at least 20 to 1 for Francis against any one competitor who has been named: but what the odds may be against the [97]whole field is more difficult to settle. What if the real Junius should be some person not yet named?
Mr. Jopling, Leisure Hour, May 23, 1863, relies on the porphyry coffer of the Great Pyramid, in which he finds "the most ancient and accurate standard of measure in existence."
I am shocked at being obliged to place a thoughtful and learned writer, and an old friend, before such a successor as he here meets with. But chronological arrangement defies all other arrangement.
(I had hoped that the preceding account would have met Mr. Taylor's eye in print: but he died during the last summer. For a man of a very thoughtful and quiet temperament, he had a curious turn for vexed questions. But he reflected very long and very patiently before he published: and all his works are valuable for their accurate learning, whichever side the reader may take.)
MRS. ELIZABETH COTTLE.
1859. The Cottle Church.—For more than twenty years printed papers have been sent about in the name of Elizabeth Cottle.[195] It is not so remarkable that such papers should be concocted as that they should circulate for such a length of time without attracting public attention. Eighty years ago Mrs. Cottle might have rivalled Lieut. Brothers or Joanna Southcott.[196] Long hence, when the now current volumes of our journals are well-ransacked works of reference, those who look into them will be glad to see this [98]feature of our time: I therefore make a few extracts, faithfully copied as to type. The Italic is from the New Testament; the Roman is the requisite interpretation:
"Robert Cottle 'was numbered (5196) with the transgressors' at the back of the Church in Norwood Cemetery, May 12, 1858—Isa. liii. 12. The Rev. J. G. Collinson, Minister of St. James's Church, Chapham, the then district church, before All Saints was built, read the funeral service over the Sepulchre wherein never before man was laid.
"Hewn on the stone, 'at the mouth of the Sepulchre,' is his name,—Robert Cottle, born at Bristol, June 2, 1774; died at Kirkstall Lodge, Clapham Park, May 6, 1858. And that day (May 12, 1858) was the preparation (day and year for 'the PREPARED place for you'—Cottleites—-by the widowed mother of the Father's house, at Kirkstall Lodge—John xiv. 2, 3). And the Sabbath (Christmas Day, Dec. 25, 1859) drew on (for the resurrection of the Christian body on 'the third [Protestant Sun]-day'—1 Cor. xv. 35). Why seek ye the living (God of the New Jerusalem—Heb. xii. 22; Rev. iii. 12) among the dead (men): he (the God of Jesus) is not here (in the grave), but is risen (in the person of the Holy Ghost, from the supper of 'the dead in the second death' of Paganism). Remember how he spake unto you (in the church of the Rev. George Clayton,[197] April 14, 1839). I will not drink henceforth (at this last Cottle supper) of the fruit of this (Trinity) vine, until that day (Christmas Day, 1859), when I (Elizabeth Cottle) drink it new with you (Cottleites) in my Father's kingdom—John xv. If this (Trinitarian) cup may not pass away from me (Elizabeth Cottle, April 14, 1839), except I drink it ('new with you Cottleites, in my Father's Kingdom'), thy will be done—Matt. xxvi. 29, 42, 64. 'Our Father which art (God) in Heaven,' hallowed be thy name, thy (Cottle) kingdom [99]come, thy will be done in earth, as it is (done) in (the new) Heaven (and new earth of the new name of Cottle—Rev. xxi. 1; iii. 12).
"... Queen Elizabeth, from A.D. 1558 to 1566. And this WORD yet once more (by a second Elizabeth—the WORD of his oath) signifieth (at John Scott's baptism of the Holy Ghost) the removing of those things (those Gods and those doctrines) that are made (according to the Creeds and Commandments of men) that those things (in the moral law of God) which cannot be shaken (as a rule of faith and practice) may remain, wherefore we receiving (from Elizabeth) a kingdom (of God,) which cannot be moved (by Satan) let us have grace (in his Grace of Canterbury) whereby we may serve God acceptably (with the acceptable sacrifice of Elizabeth's body and blood of the communion of the Holy Ghost) with reverence (for truth) and godly fear (of the unpardonable sin of blasphemy against the Holy Ghost) for our God (the Holy Ghost) is a consuming fire (to the nation that will not serve him in the Cottle Church). We cannot defend ourselves against the Almighty, and if He is our defence, no nation can invade us.
"In verse 4 the Church of St. Peter is in prison between four quaternions of soldiers—the Holy Alliance of 1815. Rev. vii. i. Elizabeth, the Angel of the Lord Jesus appears to the Jewish and Christian body with the vision of prophecy to the Rev. Geo. Clayton and his clerical brethren, April 8th, 1839. Rhoda was the name of her maid at Putney Terrace who used to open the door to her Peter, the Rev. Robert Ashton,[198] the Pastor of 'the little flock' 'of 120 names together, assembled in an upper (school) room' at Putney Chapel, to which little flock she gave the revelation (Acts. i. 13, 15) of Jesus the same King of the Jews yesterday at the prayer meeting, Dec. 31, 1841, and to-day, [100]Jan. 1, 1842, and for ever. See book of Life, page 24. Matt. xviii. 19, xxi. 13-16. In verse 6 the Italian body of St. Peter is sleeping 'in the second death' between the two Imperial soldiers of France and Austria. The Emperor of France from Jan. 1, to July 11, 1859, causes the Italian chains of St. Peter to fall off from his Imperial hands.
"I say unto thee, Robert Ashton, thou art Peter, a stone, and upon this rock, of truth, will I Elizabeth, the angel of Jesus, build my Cottle Church, and the gates of hell, the doors of St. Peter, at Rome, shall not prevail against it—Matt. xvi. 18. Rev. iii. 7-12."
This will be enough for the purpose. When any one who pleases can circulate new revelations of this kind, uninterrupted and unattended to, new revelations will cease to be a good investment of excentricity. I take it for granted that the gentlemen whose names are mentioned have nothing to do with the circulars or their doctrines. Any lady who may happen to be intrusted with a revelation may nominate her own pastor, or any other clergyman, one of her apostles; and it is difficult to say to what court the nominees can appeal to get the commission abrogated.
March 16, 1865. During the last two years the circulars have continued. It is hinted that funds are low: and two gentlemen who are represented as gone "to Bethlehem asylum in despair" say that Mrs. Cottle "will spend all that she hath, while Her Majesty's Ministers are flourishing on the wages of sin." The following is perhaps one of the most remarkable passages in the whole:
"Extol and magnify Him (Jehovah, the Everlasting God, see the Magnificat and Luke i. 45, 46—68—73—79), that rideth (by rail and steam over land and sea, from his holy habitation at Kirkstall Lodge, Psa. lxxvii. 19, 20), upon the (Cottle) heavens, as it were (Sept. 9, 1864, see pages 21, 170), upon an (exercising, Psa. cxxxi. 1), horse-(chair, bought of Mr. John Ward, Leicester-square)." [101]
I have pretty good evidence that there is a clergyman who thinks Mrs. Cottle a very sensible woman.
[The Cottle Church. Had I chanced to light upon it at the time of writing, I should certainly have given the following. A printed letter to the Western Times, by Mr. Robert Cottle, was accompanied by a manuscript letter from Mrs. Cottle, apparently a circular. The date was Novr. 1853, and the subject was the procedure against Mr. Maurice[199] at King's College for doubting that God would punish human sins by an existence of torture lasting through years numbered by millions of millions of millions of millions (repeat the word millions without end,) etc. The memory of Mr. Cottle has, I think, a right to the quotation: he seems to have been no participator in the notions of his wife:
"The clergy of the Established Church, taken at the round number of 20,000, may, in their first estate, be likened to 20,000 gold blanks, destined to become sovereigns, in succession,—they are placed between the matrix of the Mint, when, by the pressure of the screw, they receive the impress that fits them to become part of the current coin of the realm. In a way somewhat analogous this great body of the clergy have each passed through the crucibles of Oxford and Cambridge,—have been assayed by the Bishop's chaplain, touching the health of their souls, and the validity of their call by the Divine Spirit, and then the gentle pressure of a prelate's hand upon their heads; and the words—'Receive the Holy Ghost,' have, in a brief space of time, wrought a [102]change in them, much akin to the miracle of transubstantiation—the priests are completed, and they become the current ecclesiastical coin of our country. The whole body of clergy, here spoken of, have undergone the preliminary induction of baptism and confirmation; and all have been duly ordained, professing to hold one faith, and to believe in the selfsame doctrines! In short, to be as identical as the 20,000 sovereigns, if compared one with the other. But mind is not malleable and ductile, like gold; and all the preparations of tests, creeds, and catechisms will not insure uniformity of belief. No stamp of orthodoxy will produce the same impress on the minds of different men. Variety is manifest, and patent, upon everything mental and material. The Almighty has not created, nor man fashioned, two things alike! How futile, then, is the attempt to shape and mould man's apprehension of divine truth by one fallible standard of man's invention! If proof of this be required, an appeal might be made to history and the experience of eighteen hundred years."
This is an argument of force against the reasonableness of expecting tens of thousands of educated readers of the New Testament to find the doctrine above described in it. The lady's argument against the doctrine itself is very striking. Speaking of an outcry on this matter among the Dissenters against one of their body, who was the son of "the White Stone (Rev. ii. 17), or the Roman cement-maker," she says—
"If the doctrine for which they so wickedly fight were true, what would become of the black gentlemen for whose redemption I have been sacrificed from April 8 1839."
There are certainly very curious points about this revelation. There have been many surmises about the final restoration of the infernal spirits, from the earliest ages of Christianity until our own day: a collection of them would be worth making. On reading this in proof, I see a possibility that by "black gentlemen" may be meant the clergy: [103]I suppose my first interpretation must have been suggested by context: I leave the point to the reader's sagacity.]
JAMES SMITH, ARCH-PARADOXER.
The Problem of squaring the circle solved; or, the circumference and area of the circle discovered. By James Smith.[200] London, 1859, 8vo.
On the relations of a square inscribed in a circle. Read at the British Association, Sept. 1859, published in the Liverpool Courier, Oct. 8, 1859, and reprinted in broadsheet.
The question: Are there any commensurable relations between a circle and other Geometrical figures? Answered by a member of the British Association ... London, 1860, 8vo.—[This has been translated into French by M. Armand Grange, Bordeaux, 1863, 8vo.]
The Quadrature of the Circle. Correspondence between an eminent mathematician and James Smith, Esq. (Member of the Mersey Docks and Harbour Board), London, 1861, 8vo. (pp. 200).
Letter to the ... British Association ... by James Smith, Esq. Liverpool, 1861, 8vo.
Letter to the ... British Association ... by James Smith, Esq. Liverpool, 1862, 8vo.—[These letters the author promised to continue.]
A Nut to crack for the readers of Professor De Morgan's 'Budget of Paradoxes.' By James Smith, Esq. Liverpool, 1863, 8vo.
Paper read at the Liverpool Literary and Philosophical Society, reported in the Liverpool Daily Courier, Jan. 26, 1864. Reprinted as a pamphlet.
The Quadrature of the circle, or the true ratio between the diameter and circumference geometrically and mathematically demonstrated. By James Smith, Esq. Liverpool, 1865, 8vo.
[On the relations between the dimensions and distances of the Sun, Moon, and Earth; a paper read before the Literary and Philosophical Society of Liverpool, Jan. 25, 1864. By James Smith, Esq.
The British Association in Jeopardy, and Dr. Whewell, the Master of Trinity, in the stocks without hope of escape. Printed for the authors (J. S. confessed, and also hidden under Nauticus). (No date, 1865).
The British Association in Jeopardy, and Professor De Morgan in the Pillory without hope of escape. London, 1866, 8vo.]
When my work appeared in numbers, I had not anything like an adequate idea of Mr. James Smith's superiority to the rest of the world in the points in which he is superior. He is beyond a doubt the ablest head at unreasoning, and the greatest hand at writing it, of all who have tried in our day to attach their names to an error. Common cyclometers sink into puny orthodoxy by his side.
The behavior of this singular character induces me to pay him the compliment which Achilles paid Hector, to drag him round the walls again and again. He was treated with unusual notice and in the most gentle manner. The unnamed mathematician, E. M. bestowed a volume of mild correspondence upon him; Rowan Hamilton[201] quietly proved him wrong in a way accessible to an ordinary schoolboy; Whewell,[202] as we shall see, gave him the means of seeing himself wrong, even more easily than by Hamilton's method. Nothing would do; it was small kick and silly fling at all; and he exposed his conceit by alleging that he, James Smith, had placed Whewell in the stocks. He will therefore be universally pronounced a proper object of the severest literary punishment: but the opinion of all who can put two propositions together will be that of the many strokes I have given, the hardest and most telling are my republications of his own attempts to reason.
He will come out of my hands in the position he ought [105]to hold, the Supreme Pontiff of cyclometers, the vicegerent of St. Vitus upon earth, the Mamamouchi of burlesque on inference. I begin with a review of him which appeared in the Athenæum of May 11, 1861. Mr. Smith says I wrote it: this I neither affirm nor deny; to do either would be a sin against the editorial system elsewhere described. Many persons tell me they know me by my style; let them form a guess: I can only say that many have declared as above while fastening on me something which I had never seen nor heard of.
The Quadrature of the Circle: Correspondence between an Eminent Mathematician and James Smith, Esq. (Edinburgh, Oliver & Boyd; London, Simpkin, Marshall & Co.)
"A few weeks ago we were in perpetual motion. We did not then suppose that anything would tempt us on a circle-squaring expedition: but the circumstances of the book above named have a peculiarity which induces us to give it a few words.
"Mr. James Smith, a gentleman residing near Liverpool, was some years ago seized with the morbus cyclometricus.[203] The symptoms soon took a defined form: his circumference shrank into exactly 3-1/8 times his diameter, instead of close to 3-16/113, which the mathematician knows to be so near to truth that the error is hardly at the rate of a foot in 2,000 miles. This shrinking of the circumference remained until it became absolutely necessary that it should be examined by the British Association. This body, which as Mr. James Smith found to his sorrow, has some interest in 'jealously guarding the mysteries of their profession,' refused at first to entertain the question. On this Mr. Smith changed his 'tactics' and the name of his paper, and smuggled in the subject under the form of 'The Relations of a Circle inscribed in a Square'! The paper was thus forced upon the Association, for Mr. Smith informs us that he [106]'gave the Section to understand that he was not the man that would permit even the British Association to trifle with him.' In other words, the Association bore with and were bored with the paper, as the shortest way out of the matter. Mr. Smith also circulated a pamphlet. Some kind-hearted man, who did not know the disorder as well as we do, and who appears in Mr. Smith's handsome octavo as E. M.—the initials of 'eminent mathematician'—wrote to him and offered to show him in a page that he was all wrong. Mr. Smith thereupon opened a correspondence, which is the bulk of the volume. When the correspondence was far advanced, Mr. Smith announced his intention to publish. His benevolent instructor—we mean in intention—protested against the publication, saying 'I do not wish to be gibbeted to the world as having been foolish enough to enter upon what I feel now to have been a ridiculous enterprise.'
"For this Mr. Smith cared nothing: he persisted in the publication, and the book is before us. Mr. Smith has had so much grace as to conceal his kind adviser's name under E. M., that is to say, he has divided the wrong among all who may be suspected of having attempted so hopeless a task as that of putting a little sense into his head. He has violated the decencies of private life. Against the will of the kind-hearted man who undertook his case, he has published letters which were intended for no other purpose than to clear his poor head of a hopeless delusion. He deserves the severest castigation; and he will get it: his abuse of confidence will stick by him all his days. Not that he has done his benefactor—in intention, again—any harm. The patience with which E. M. put the blunders into intelligible form, and the perseverance with which he tried to find a cranny-hole for common reasoning to get in at, are more than respectable: they are admirable. It is, we can assure E. M., a good thing that the nature of the circle-squarer should be so completely exposed as in this volume. The benefit which he intended Mr. James Smith may be [107]conferred upon others. And we should very much like to know his name, and if agreeable to him, to publish it. As to Mr. James Smith, we can only say this: he is not mad. Madmen reason rightly upon wrong premises: Mr. Smith reasons wrongly upon no premises at all.
"E. M. very soon found out that, to all appearance, Mr. Smith got a circle of 3-1/8 times the diameter by making it the supposition to set out with that there was such a circle; and then finding certain consequences which, so it happened, were not inconsistent with the supposition on which they were made. Error is sometimes self-consistent. However, E. M., to be quite sure of his ground, wrote a short letter, stating what he took to be Mr. Smith's hypothesis, containing the following: 'On AC as diameter, describe the circle D, which by hypothesis shall be equal to three and one-eighth times the length of AC.... I beg, before proceeding further, to ask whether I have rightly stated your argument.' To which Mr. Smith replied: 'You have stated my argument with perfect accuracy.' Still E. M. went on, and we could not help, after the above, taking these letters as the initials of Everlasting Mercy. At last, however, when Mr. Smith flatly denied that the area of the circle lies between those of the inscribed and circumscribed polygons, E. M. was fairly beaten, and gave up the task. Mr. Smith was left to write his preface, to talk about the certain victory of truth—which, oddly enough, is the consolation of all hopelessly mistaken men; to compare himself with Galileo; and to expose to the world the perverse behavior of the Astronomer Royal, on whom he wanted to fasten a conversation, and who replied, 'It would be a waste of time, Sir, to listen to anything you could have to say on such a subject.'
"Having thus disposed of Mr. James Smith, we proceed to a few remarks on the subject: it is one which a journal would never originate, but which is rendered necessary from time to time by the attempts of the autopseustic to become [108]heteropseustic. To the mathematician we have nothing to say: the question is, what kind of assurance can be given to the world at large that the wicked mathematicians are not acting in concert to keep down their superior, Mr. James Smith, the current Galileo of the quadrature of the circle.
"Let us first observe that this question does not stand alone: independently of the millions of similar problems which exist in higher mathematics, the finding of the diagonal of a square has just the same difficulty, namely, the entrance of a pair of lines of which one cannot be definitely expressed by means of the other. We will show the reader who is up to the multiplication-table how he may go on, on, on, ever nearer, never there, in finding the diagonal of a square from the side.
"Write down the following rows of figures, and more, if you like, in the way described:
1 2 5 12 29 70 169 408 985
1 3 7 17 41 99 239 577 1393
After the second, each number is made up of double the last increased by the last but one: thus, 5 is 1 more than twice 2, 12 is 2 more than twice 5, 239 is 41 more than twice 99. Now, take out two adjacent numbers from the upper line, and the one below the first from the lower: as
70 169
99.
Multiply together 99 and 169, giving 16,731. If, then, you will say that 70 diagonals are exactly equal to 99 sides, you are in error about the diagonal, but an error the amount of which is not so great as the 16,731st part of the diagonal. Similarly, to say that five diagonals make exactly seven sides does not involve an error of the 84th part of the diagonal.
"Now, why has not the question of crossing the square been as celebrated as that of squaring the circle? Merely because Euclid demonstrated the impossibility of the first [109]question, while that of the second was not demonstrated, completely, until the last century.
"The mathematicians have many methods, totally different from each other, of arriving at one and the same result, their celebrated approximation to the circumference of the circle. An intrepid calculator has, in our own time, carried his approximation to what they call 607 decimal places: this has been done by Mr. Shanks,[204] of Houghton-le-Spring, and Dr. Rutherford[205] has verified 441 of these places. But though 607 looks large, the general public will form but a hazy notion of the extent of accuracy acquired. We have seen, in Charles Knight's[206] English Cyclopædia, an account of the matter which may illustrate the unimaginable, though rationally conceivable, extent of accuracy obtained.
"Say that the blood-globule of one of our animalcules is a millionth of an inch in diameter. Fashion in thought a globe like our own, but so much larger that our globe is but a blood-globule in one of its animalcules: never mind the microscope which shows the creature being rather a bulky instrument. Call this the first globe above us. Let the first globe above us be but a blood-globule, as to size, in the animalcule of a still larger globe, which call the second globe above us. Go on in this way to the twentieth globe above us. Now go down just as far on the other side. Let the blood-globule with which we started be a globe peopled with animals like ours, but rather smaller: [110]and call this the first globe below us. Take a blood-globule out of this globe, people it, and call it the second globe below us: and so on to the twentieth globe below us. This is a fine stretch of progression both ways. Now give the giant of the twentieth globe above us the 607 decimal places, and, when he has measured the diameter of his globe with accuracy worthy of his size, let him calculate the circumference of his equator from the 607 places. Bring the little philosopher from the twentieth globe below us with his very best microscope, and set him to see the small error which the giant must make. He will not succeed, unless his microscopes be much better for his size than ours are for ours.
"Now it must be remembered by any one who would laugh at the closeness of the approximation, that the mathematician generally goes nearer; in fact his theorems have usually no error at all. The very person who is bewildered by the preceding description may easily forget that if there were no error at all, the Lilliputian of the millionth globe below us could not find a flaw in the Brobdingnagian of the millionth globe above. The three angles of a triangle, of perfect accuracy of form, are absolutely equal to two right angles; no stretch of progression will detect any error.
"Now think of Mr. Lacomme's mathematical adviser (ante, Vol. I, p. 46) making a difficulty of advising a stonemason about the quantity of pavement in a circular floor!
"We will now, for our non-calculating reader, put the matter in another way. We see that a circle-squarer can advance, with the utmost confidence, the assertion that when the diameter is 1,000, the circumference is accurately 3,125: the mathematician declaring that it is a trifle more than 3,141½. If the squarer be right, the mathematician has erred by about a 200th part of the whole: or has not kept his accounts right by about 10s. in every 100l. Of course, if he set out with such an error he will accumulate blunder upon blunder. Now, if there be a process in which [111]close knowledge of the circle is requisite, it is in the prediction of the moon's place—say, as to the time of passing the meridian at Greenwich—on a given day. We cannot give the least idea of the complication of details: but common sense will tell us that if a mathematician cannot find his way round the circle without a relative error four times as big as a stockbroker's commission, he must needs be dreadfully out in his attempt to predict the time of passage of the moon. Now, what is the fact? His error is less than a second of time, and the moon takes 27 days odd to revolve. That is to say, setting out with 10s. in 100l. of error in his circumference, he gets within the fifth part of a farthing in 100l. in predicting the moon's transit. Now we cannot think that the respect in which mathematical science is held is great enough—though we find it not small—to make this go down. That respect is founded upon a notion that right ends are got by right means: it will hardly be credited that the truth can be got to farthings out of data which are wrong by shillings. Even the celebrated Hamilton[207] of Edinburgh, who held that in mathematics there was no way of going wrong, was fully impressed with the belief that this was because error was avoided from the beginning. He never went so far as to say that a mathematician who begins wrong must end right somehow.
"There is always a difficulty about the mode in which the thinking man of common life is to deal with subjects he has not studied to a professional extent. He must form opinions on matters theological, political, legal, medical, and social. If he can make up his mind to choose a guide, there is, of course, no perplexity: but on all the subjects mentioned the direction-posts point different ways. Now why should he not form his opinion upon an abstract mathematical question? Why not conclude that, as to the circle, it is possible Mr. James Smith may be the man, just [112]as Adam Smith[208] was the man of things then to come, or Luther, or Galileo? It is true that there is an unanimity among mathematicians which prevails in no other class: but this makes the chance of their all being wrong only different in degree. And more than this, is it not generally thought among us that priests and physicians were never so much wrong as when there was most appearance of unanimity among them? To the preceding questions we see no answer except this, that the individual inquirer may as rationally decide a mathematical question for himself as a theological or a medical question, so soon as he can put himself into a position in mathematics, level with that in which he stands in theology or medicine. The every-day thought and reading of common life have a certain resemblance to the thought and reading demanded by the learned faculties. The research, the balance of evidence, the estimation of probabilities, which are used in a question of medicine, are closely akin in character, however different the matter of application, to those which serve a merchant to draw his conclusions about the markets. But the mathematicians have methods of their own, to which nothing in common life bears close analogy, as to the nature of the results or the character of the conclusions. The logic of mathematics is certainly that of common life: but the data are of a different species; they do not admit of doubt. An expert arithmetician, such as is Mr. J. Smith, may fancy that calculation, merely as such, is mathematics: but the value of his book, and in this point of view it is not small, is the full manner in which it shows that a practised arithmetician, venturing into the field of mathematical demonstration, may show himself utterly destitute of all that distinguishes the reasoning geometrical investigator from the calculator.
"And further, it should be remembered that in mathematics the power of verifying results far exceeds that which is found in anything else: and also the variety of distinct methods by which they can be attained. It follows from all this that a person who desires to be as near the truth as he can will not judge the results of mathematical demonstration to be open to his criticism, in the same degree as results of other kinds. Should he feel compelled to decide, there is no harm done: his circle may be 3⅛ times its diameter, if it please him. But we must warn him that, in order to get this circle, he must, as Mr. James Smith has done, make it at home: the laws of space and thought beg leave respectfully to decline the order."
I will insert now at length, from the Athenæum of June 8, 1861, the easy refutation given by my deceased friend, with the remarks which precede.
"Mr. James Smith, of whose performance in the way of squaring the circle we spoke some weeks ago in terms short of entire acquiescence, has advertised himself in our columns, as our readers will have seen. He has also forwarded his letter to the Liverpool Albion, with an additional statement, which he did not make in our journal. He denies that he has violated the decencies of private life, since his correspondent revised the proofs of his own letters, and his 'protest had respect only to making his name public.' This statement Mr. James Smith precedes by saying that we have treated as true what we well knew to be false: and he follows by saying that we have not read his work, or we should have known the above facts to be true. Mr. Smith's pretext is as follows. His correspondent E. M. says, 'My letters were not intended for publication, and I protest against their being published,' and he subjoins 'Therefore I must desire that my name may not be used.' The obvious meaning is that E. M. protested against the publication altogether, but, judging that Mr. Smith was [114]determined to publish, desired that his name should not be used. That he afterwards corrected the proofs merely means that he thought it wiser to let them pass under his own eyes than to leave them entirely to Mr. Smith.
"We have received from Sir W. Rowan Hamilton[209] a proof that the circumference is more than 3⅛ diameters, requiring nothing but a knowledge of four books of Euclid. We give it in brief as an exercise for our juvenile readers to fill up. It reminds us of the old days when real geometers used to think it worth while seriously to demolish pretenders. Mr. Smith's fame is now assured: Sir W. R. Hamilton's brief and easy exposure will procure him notice in connection with this celebrated problem.
"It is to be shown that the perimeter of a regular polygon of 20 sides is greater than 3⅛ diameters of the circle, and still more, of course, is the circumference of the circle greater than 3⅛ diameters.
"1. It follows from the 4th Book of Euclid, that the rectangle under the side of a regular decagon inscribed in a circle, and that side increased by the radius, is equal to the square of the radius. But the product 791 (791 + 1280) is less than 1280 × 1280; if then the radius be 1280 the side of the decagon is greater than 791.
"2. When a diameter bisects a chord, the square of the chord is equal to the rectangle under the doubles of the segments of the diameter. But the product 125 (4 × 1280 - 125) is less than 791 × 791. If then the bisected chord be a side of the decagon, and if the radius be still 1280, the double of the lesser segment exceeds 125.
"3. The rectangle under this doubled segment and the radius is equal to the square of the side of an inscribed regular polygon of 20 sides. But the product 125 × 1280 is equal to 400 × 400; therefore, the side of the last-mentioned polygon is greater than 400, if the radius be still 1280. In other words, if the radius be represented by the new [115]member 16, and therefore the diameter by 32, this side is greater than 5, and the perimeter exceeds 100. So that, finally, if the diameter be 8, the perimeter of the inscribed regular polygon of 20 sides, and still more the circumference of the circle, is greater than 25: that is, the circumference is more than 3⅛ diameters."
The last work in the list was thus noticed in the Athenæum, May 27, 1865.
"Mr. James Smith appears to be tired of waiting for his place in the Budget of Paradoxes, and accordingly publishes a long letter to Professor De Morgan, with various prefaces and postscripts. The letter opens by a hint that the Budget appears at very long intervals, and 'apparently without any sufficient reason for it.' As Mr. Smith hints that he should like to see Mr. De Morgan, whom he calls an 'elephant of mathematics,' 'pumping his brains' 'behind the scenes'—an odd thing for an elephant to do, and an odd place to do it in—to get an answer, we think he may mean to hint that the Budget is delayed until the pump has worked successfully. Mr. Smith is informed that we have had the whole manuscript of the Budget, excepting only a final summing-up, in our hands since October, 1863. [This does not refer to the Supplement.] There has been no delay: we knew from the beginning that a series of historical articles would be frequently interrupted by the things of the day. Mr. James Smith lets out that he has never been able to get a private line from Mr. De Morgan in answer to his communications: we should have guessed it. He says, 'The Professor is an old bird and not to be easily caught, and by no efforts of mine have I been able, up to the present moment, either to induce or twit him into a discussion....' Mr. Smith curtails the proverb: old birds are not to be caught with chaff, nor with twit, which seems to be Mr. Smith's word for his own chaff, and, so long as the first letter is sounded, a very proper word. Why does he not try a little grain of sense? Mr. Smith evidently [116]thinks that, in his character as an elephant, the Professor has not pumped up brain enough to furnish forth a bird. In serious earnest, Mr. Smith needs no answer. In one thing he excites our curiosity: what is meant by demonstrating 'geometrically and mathematically?'"
I now proceed to my original treatment of the case.
Mr. James Smith will, I have no doubt, be the most uneclipsed circle-squarer of our day. He will not owe this distinction to his being an influential and respected member of the commercial world of Liverpool, even though the power of publishing which his means give him should induce him to issue a whole library upon one paradox. Neither will he owe it to the pains taken with him by a mathematician who corresponded with him until the joint letters filled an octavo volume. Neither will he owe it to the notice taken of him by Sir William Hamilton, of Dublin, who refuted him in a manner intelligible to an ordinary student of Euclid, which refutation he calls a remarkable paradox easily explainable, but without explaining it. What he will owe it to I proceed to show.
Until the publication of the Nut to Crack Mr. James Smith stood among circle-squarers in general. I might have treated him with ridicule, as I have done others: and he says that he does not doubt he shall come in for his share at the tail end of my Budget. But I can make a better job of him than so, as Locke would have phrased it: he is such a very striking example of something I have said on the use of logic that I prefer to make an example of his writings. On one point indeed he well deserves the scutica,[210] if not the horribile flagellum.[211] He tells me that he will bring his solution to me in such a form as shall compel me to admit it as un fait accompli [une faute accomplie?][212] [117]or leave myself open to the humiliating charge of mathematical ignorance and folly. He has also honored me with some private letters. In the first of these he gives me a "piece of information," after which he cannot imagine that I, "as an honest mathematician," can possibly have the slightest hesitation in admitting his solution. There is a tolerable reservoir of modest assurance in a man who writes to a perfect stranger with what he takes for an argument, and gives an oblique threat of imputation of dishonesty in case the argument be not admitted without hesitation; not to speak of the minor charges of ignorance and folly. All this is blind self-confidence, without mixture of malicious meaning; and I rather like it: it makes me understand how Sam Johnson came to say of his old friend Mrs. Cobb,[213]—"I love Moll Cobb for her impudence." I have now done with my friend's suaviter in modo,[214] and proceed to his fortiter in re[215]: I shall show that he has convicted himself of ignorance and folly, with an honesty and candor worthy of a better value of π.
Mr. Smith's method of proving that every circle is 3⅛ diameters is to assume that it is so,—"if you dislike the term datum, then, by hypothesis, let 8 circumferences be exactly equal to 25 diameters,"—and then to show that every other supposition is thereby made absurd. The right to this assumption is enforced in the "Nut" by the following analogy:
"I think you (!) will not dare (!) to dispute my right to this hypothesis, when I can prove by means of it that every other value of π will lead to the grossest absurdities; unless indeed, you are prepared to dispute the right of Euclid to adopt a false line hypothetically for the purpose [118]of a 'reductio ad absurdum'[216] demonstration, in pure geometry."
Euclid assumes what he wants to disprove, and shows that his assumption leads to absurdity, and so upsets itself. Mr. Smith assumes what he wants to prove, and shows that his assumption makes other propositions lead to absurdity. This is enough for all who can reason. Mr. James Smith cannot be argued with; he has the whip-hand of all the thinkers in the world. Montucla would have said of Mr. Smith what he said of the gentleman who squared his circle by giving 50 and 49 the same square root, Il a perdu le droit d'être frappé de l'évidence.[217]
It is Mr. Smith's habit, when he finds a conclusion agreeing with its own assumption, to regard that agreement as proof of the assumption. The following is the "piece of information" which will settle me, if I be honest. Assuming π to be 3⅛, he finds out by working instance after instance that the mean proportional between one-fifth of the area and one-fifth of eight is the radius. That is,
| if π = | 25 8 | , | 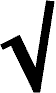 |  | πr2 5 | · | 8 5 |  | = r. |
This "remarkable general principle" may fail to establish Mr. Smith's quadrature, even in an honest mind, if that mind should happen to know that, a and b being any two numbers whatever, we need only assume—
| if π = | a2 b | , to get at | 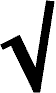 |  | πr2 a | · | b a |  | = r. |
We naturally ask what sort of glimmer can Mr. Smith have of the subject which he professes to treat? On this point he has given satisfactory information. I had mentioned the old problem of finding two mean proportionals, [119]as a preliminary to the duplication of the cube. On this mention Mr. Smith writes as follows. I put a few words in capitals; and I write rq[218] for the sign of the square root, which embarrasses small type:
"This establishes the following infallible rule, for finding two mean proportionals OF EQUAL VALUE, and is more than a preliminary, to the famous old problem of 'Squaring the circle.' Let any finite number, say 20, and its fourth part = ¼(20) = 5, be given numbers. Then rq(20 × 5) = rq 100 = 10, is their mean proportional. Let this be a given mean proportional TO FIND ANOTHER MEAN PROPORTIONAL OF EQUAL VALUE. Then
| 20 × | π 4 | = 20 × | 3.125 4 | = 20 × .78125 = 15.625 |
will be the first number; as
| 25 : 16 :: rq 20 : rq 8.192: and (rq 8.192)2 × | π 4 | = 8.192 × .78125 = 6.4 |
will be the second number; therefore rq(15.625 × 6.4) = rq 100 = 10, is the required mean proportional.... Now, my good Sir, however competent you may be to prove every man a fool [not every man, Mr. Smith! only some; pray learn logical quantification] who now thinks, or in times gone by has thought, the 'Squaring of the Circle' a possibility; I doubt, and, on the evidence afforded by your Budget, I cannot help doubting, whether you were ever before competent to find two mean proportionals by my unique method."—(Nut, pp. 47, 48.) [That I never was, I solemnly declare!]
All readers can be made to see the following exposure. When 5 and 20 are given, x is a mean proportional when in 5, x, 20, 5 is to x as x to 20. And x must be 10. But x and y are two mean proportionals when in 5, x, y, 20, x [120]is a mean proportional between 5 and y, and y is a mean proportional between x and 20. And these means are x = 5 ³√4, y = 5 ³√16. But Mr. Smith finds one mean, finds it again in a roundabout way, and produces 10 and 10 as the two (equal!) means, in solution of the "famous old problem." This is enough: if more were wanted, there is more where this came from. Let it not be forgotten that Mr. Smith has found a translator abroad, two, perhaps three, followers at home, and—most surprising of all—a real mathematician to try to set him right. And this mathematician did not discover the character of the subsoil of the land he was trying to cultivate until a goodly octavo volume of letters had passed and repassed. I have noticed, in more quarters than one, an apparent want of perception of the full amount of Mr. Smith's ignorance: persons who have not been in contact with the non-geometrical circle-squarers have a kind of doubt as to whether anybody can carry things so far. But I am an "old bird" as Mr. Smith himself calls me; a Simorg, an "all-knowing Bird of Ages" in matters of cyclometry.
The curious phenomena of thought here exhibited illustrate, as above said, a remark I have long ago made on the effect of proper study of logic. Most persons reason well enough on matter to which they are accustomed, and in terms with which they are familiar. But in unaccustomed matter, and with use of strange terms, few except those who are practised in the abstractions of pure logic can be tolerably sure to keep their feet. And one of the reasons is easily stated: terms which are not quite familiar partake of the vagueness of the X and Y on which the student of logic learns to see the formal force of a proposition independently of its material elements.
I make the following quotation from my fourth paper on logic in the Cambridge Transactions:
"The uncultivated reason proceeds by a process almost entirely material. Though the necessary law of thought [121]must determine the conclusion of the ploughboy as much as that of Aristotle himself, the ploughboy's conclusion will only be tolerably sure when the matter of it is such as comes within his usual cognizance. He knows that geese being all birds does not make all birds geese, but mainly because there are ducks, chickens, partridges, etc. A beginner in geometry, when asked what follows from 'Every A is B,' answers 'Every B is A.' That is, the necessary laws of thought, except in minds which have examined their tools, are not very sure to work correct conclusions except upon familiar matter.... As the cultivation of the individual increases, the laws of thought which are of most usual application are applied to familiar matter with tolerable safety. But difficulty and risk of error make a new appearance with a new subject; and this, in most cases, until new subjects are familiar things, unusual matter common, untried nomenclature habitual; that is, until it is a habit to be occupied upon a novelty. It is observed that many persons reason well in some things and badly in others; and this is attributed to the consequence of employing the mind too much upon one or another subject. But those who know the truth of the preceding remarks will not have far to seek for what is often, perhaps most often, the true reason.... I maintain that logic tends to make the power of reason over the unusual and unfamiliar more nearly equal to the power over the usual and familiar than it would otherwise be. The second is increased; but the first is almost created."
Mr. James Smith, by bringing ignorance, folly, dishonesty into contact with my name, in the way of conditional insinuation, has done me a good turn: he has given me right to a freedom of personal remark which I might have declined to take in the case of a person who is useful and respected in matters which he understands.
Tit for tat is logic all the world over. By the way, what has become of the rest of the maxim: we never hear it [122]now. When I was a boy, in some parts of the country at least, it ran thus:
"Tit for tat;
Butter for fat:
If you kill my dog,
I'll kill your cat."
He is a glaring instance of the truth of the observations quoted above. I will answer for it that, at the Mersey Dock Board, he never dreams of proving that the balance at the banker's is larger than that in the book by assuming that the larger sum is there, and then proving that the other supposition—the smaller balance—is upon that assumption, an absurdity. He never says to another director, How can you dare to refuse me a right to assume the larger balance, when you yourself, the other day, said,—Suppose, for argument's sake, we had 80,000l. at the banker's, though you knew the book only showed 30,000l.? This is the way in which he has supported his geometrical paradox by Euclid's example: and this is not the way he reasons at the board; I know it by the character of him as a man of business which has reached my ears from several quarters. But in geometry and rational arithmetic he is a smatterer, though expert at computation; at the board he is a trained man of business. The language of geometry is so new to him that he does not know what is meant by "two mean proportionals:" but all the phrases of commerce are rooted in his mind. He is most unerasably booked in the history of the squaring of the circle, as the speculator who took a right to assume a proposition for the destruction of other propositions, on the express ground that Euclid assumes a proposition to show that it destroys itself: which is as if the curate should demand permission to throttle the squire because St. Patrick drove the vermin to suicide to save themselves from slaughter. He is conspicuous as a speculator who, more visibly than almost any other known to history, reasoned in a circle by way of reasoning on a circle. But [123]what I have chiefly to do with is the force of instance which he has lent to my assertion that men who have not had real training in pure logic are unsafe reasoners in matter which is not familiar. It is hard to get first-rate examples of this, because there are few who find the way to the printer until practice and reflection have given security against the grossest slips. I cannot but think that his case will lead many to take what I have said into consideration, among those who are competent to think of the great mental disciplines. To this end I should desire him to continue his efforts, to amplify and develop his great principle, that of proving a proposition by assuming it and taking as confirmation every consequence that does not contradict the assumption.
Since my Budget commenced, Mr. Smith has written me notes: the portion which I have preserved—I suppose several have been mislaid—makes a hundred and seven pages of note-paper, closely written. To all this I have not answered one word: but I think I cannot have read fewer than forty pages. In the last letter the writer informs me that he will not write at greater length until I have given him an answer, according to the "rules of good society." Did I not know that for every inch I wrote back he would return an ell? Surely in vain the net is spread in the eyes of anything that hath a wing. There were several good excuses for not writing to Mr. J. Smith: I will mention five. First, I distinctly announced at the beginning of this Budget that I would not communicate with squarers of the circle. Secondly, any answer I might choose to give might with perfect propriety be reserved for this article; had the imputation of incivility been made after the first note, I should immediately have replied to this effect: but I presumed it was quite understood. Thirdly, Mr. Smith, by his publication of E. M.'s letters against the wish of the writer, had put himself out of the pale of correspondence. Fourthly, he had also gone beyond the rules of good society in sending [124]letter after letter to a person who had shown by his silence an intention to avoid correspondence. Fifthly, these same rules of good society are contrived to be flexible or frangible in extreme cases: otherwise there would be no living under them; and good society would be bad. Father Aldrovand has laid down the necessary distinction—"I tell thee, thou foolish Fleming, the text speaketh but of promises made unto Christians, and there is in the rubric a special exemption of such as are made to Welchmen." There is also a rubric to the rules of good society; and squarers of the circle are among those whom there is special permission not to answer: they are the wild Welchmen of geometry, who are always assailing, but never taking, the Garde Douloureuse[219] of the circle. "At this commentary," proceeds the story, "the Fleming grinned so broadly as to show his whole case of broad strong white teeth." I know not whether the Welchman would have done the like, but I hope Mr. James Smith will: and I hope he has as good a case to show as Wilkin Flammock. For I wish him long life and long health, and should be very glad to see so much energy employed in a productive way. I hope he wishes me the same: if not, I will give him what all his judicious friends will think a good reason for doing so. His pamphlets and letters are all tied up together, and will form a curious lot when death or cessation of power to forage among book-shelves shall bring my little library to the hammer. And this time may not be far off: for I was X years old in A.D. X2; not 4 in A.D. 16, nor 5 in A.D. 25, but still in one case under that law. And now I have made my own age a problem of quadrature, and Mr. J. Smith may solve it. But I protest against his method of assuming a result, and making itself prove itself: he might in this way, as sure as eggs is eggs (a corruption of X is X), make me 1,864 years old, which is a great deal too much.
April 5, 1864.—Mr. Smith continues to write me long letters, to which he hints that I am to answer. In his last, of 31 closely written sides of note-paper, he informs me, with reference to my obstinate silence, that though I think myself and am thought by others to be a mathematical Goliath, I have resolved to play the mathematical snail, and keep within my shell. A mathematical snail! This cannot be the thing so called which regulates the striking of a clock; for it would mean that I am to make Mr. Smith sound the true time of day, which I would by no means undertake upon a clock that gains 19 seconds odd in every hour by false quadrature. But he ventures to tell me that pebbles from the sling of simple truth and common sense will ultimately crack my shell, and put me hors de combat.[220] The confusion of images is amusing: Goliath turning himself into a snail to avoid π = 3⅛, and James Smith, Esq., of the Mersey Dock Board: and put hors de combat—which should have been caché[221]—by pebbles from a sling. If Goliath had crept into a snail-shell, David would have cracked the Philistine with his foot. There is something like modesty in the implication that the crack-shell pebble has not yet taken effect; it might have been thought that the slinger would by this time have been singing—
"And thrice [and one-eighth] I routed all my foes,
And thrice [and one-eighth] I slew the slain."
But he promises to give the public his nut-cracker if I do not, before the Budget is concluded, "unravel" the paradox, which is the mathematico-geometrical nut he has given me to crack. Mr. Smith is a crack man: he will crack his own nut; he will crack my shell; in the mean time he cracks himself up. Heaven send he do not crack himself into lateral contiguity with himself.
On June 27 I received a letter, in the handwriting of Mr. James Smith, signed Nauticus. I have ascertained [126]that one of the letters to the Athenæum signed Nauticus is in the same handwriting. I make a few extracts:
"... The important question at issue has been treated by a brace of mathematical birds with too much levity. It may be said, however, that sarcasm and ridicule sometimes succeed, where reason fails.... Such a course is not well suited to a discussion.... For this reason I shall for the future [this implies there has been a past, so that Nauticus is not before me for the first time] endeavor to confine myself to dry reasoning from incontrovertible premises.
... It appears to me that so far as his theory is concerned he comes off unscathed. You might have found "a hole in Smith's circle" (have you seen a pamphlet bearing this title? [I never heard of it until now]), but after all it is quite possible the hole may have been left by design, for the purpose of entrapping the unwary."
[On the publication of the above, the author of the pamphlet obligingly forwarded a copy to me of A Hole in Smith's Circle—by a Cantab: Longman and Co., 1859, (pp. 15). "It is pity to lose any fun we can get out of the affair," says my almamaternal brother: to which I add that in such a case warning without joke is worse than none at all, as giving a false idea of the nature of the danger. The Cantab takes some absurdities on which I have not dwelt: but there are enough to afford a Cantab from every college his own separate hunting ground.]
Does this hint that his mode of proof, namely, assuming the thing to be proved, was a design to entrap the unwary? if so, it bangs Banagher. Was his confounding two mean proportionals with one mean proportional found twice over a trick of the same intent? if so, it beats cockfighting. That Nauticus is Mr. Smith appears from other internal evidence. In 1819, Mr. J. C. Hobhouse[222] was sent to Newgate for a [127]libel on the House of Commons which was only intended for a libel on Lord Erskine.[223] The ex-Chancellor had taken Mr. Hobhouse to be thinking of him in a certain sentence; this Mr. Hobhouse denied, adding, "There is but one man in the country who is always thinking of Lord Erskine." I say that there is but one man of our day who would couple me and Mr. James Smith as a "brace of mathematical birds."
Mr. Smith's "theory" is unscathed by me. Not a doubt about it: but how does he himself come off? I should never think of refuting a theory proved by assumption of itself. I left Mr. Smith's π untouched: or, if I put in my thumb and pulled out a plum, it was to give a notion of the cook, not of the dish. The "important question at issue" was not the circle: it was, wholly and solely, whether the abbreviation of James might be spelled Jimm.[224] This is personal to the verge of scurrility: but in literary controversy the challenger names the weapons, and Mr. Smith begins with charge of ignorance, folly, and dishonesty, by conditional implication. So that the question is, not the personality of a word, but its applicability to the person designated: it is enough if, as the Latin grammar has it, Verbum personale concordat cum nominativo.[225]
I may plead precedent for taking a liberty with the orthography of Jem. An instructor of youth was scandalized at the abrupt and irregular—but very effective—opening of Wordsworth's little piece:
"A simple child
That lightly draws its breath,
And feels its life in every limb,
What should it know of death?"
So he mended the matter by instructing his pupils to read the first line thus:
"A simple child, dear brother ——."
The brother, we infer from sound, was to be James, and the blank must therefore be filled up with Jimb.
I will notice one point of the letter, to make a little more distinction between the two birds. Nauticus lays down—quite correctly—that the sine of an angle is less than its circular measure. He then takes 3.1416 for 180°, and finds that 36' is .010472. But this is exactly what he finds for the sine of 36' in tables: he concludes that either 3.1416 or the tables must be wrong. He does not know that sines, as well as π, are interminable decimals, of which the tables, to save printing, only take in a finite number. He is a six-figure man: let us go thrice again to make up nine, and we have as follows:
| Circular measure of 36' | .010471975... |
| Sine of 36' | .010471784... |
| Excess of measure over sine | .000000191... |
Mr. Smith invites me to say which is wrong, the quadrature, or the tables: I leave him to guess. He says his assertions "arise naturally and necessarily out of the arguments of a circle-squarer:" he might just as well lay down that all the pigs went to market because it is recorded that "This pig went to market." I must say for circle-squarers that very few bring their pigs to so poor a market. I answer the above argument because it is, of all which Mr. James Smith has produced, the only one which rises to the level of a schoolboy: to meet him halfway I descend to that level.
Mr. Smith asks me to solve a problem in the Athenæum: [129]and I will do it, because the question will illustrate what is below schoolboy level.
"Let x represent the circular measure of an angle of 15°, and y half the sine of an angle of 30° = area of the square on the radius of a circle of diameter unity = .25. If x - y = xy, firstly, what is the arithmetical value of xy? secondly, what is the angle of which xy represents the circular measure?"
If x represent 15° and y be ¼, xy represents 3° 45', whether x - y be xy or no. But, y being ¼, x - y is not xy unless x be ⅓, that is, unless 12x or π be 4, which Mr. Smith would not admit. How could a person who had just received such a lesson as I had given immediately pray for further exposure, furnishing the stuff so liberally as this? Is it possible that Mr. Smith, because he signs himself Nauticus, means to deny his own very regular, legible, and peculiar hand? It is enough to make the other members of the Liverpool Dock Board cry, Mersey on the man!
Mr. Smith says that for the future he will give up what he calls sarcasm, and confine himself, "as far as possible," to what he calls dry reasoning from incontrovertible premises. If I have fairly taught him that his sarcasm will not succeed, I hope he will find that his wit's end is his logic's beginning.
I now reply to a question I have been asked again and again since my last Budget appeared: Why do you take so much trouble to expose such a reasoner as Mr. Smith? I answer as a deceased friend of mine used to answer on like occasions—A man's capacity is no measure of his power to do mischief. Mr. Smith has untiring energy, which does something; self-evident honesty of conviction, which does more; and a long purse, which does most of all. He has made at least ten publications, full of figures which few readers can criticize. A great many people are staggered to this extent, that they imagine there must be [130]the indefinite something in the mysterious all this. They are brought to the point of suspicion that the mathematicians ought not to treat "all this" with such undisguised contempt, at least. Now I have no fear for π: but I do think it possible that general opinion might in time demand that the crowd of circle-squarers, etc. should be admitted to the honors of opposition; and this would be a time-tax of five per cent., one man with another, upon those who are better employed. Mr. James Smith may be made useful, in hands which understand how to do it, towards preventing such opinion from growing. A speculator who expressly assumes what he wants to prove, and argues that all which contradicts it is absurd, because it cannot stand side by side with his assumption, is a case which can be exposed to all. And the best person to expose it is one who has lived in the past as well as the present, who takes misthinking from points of view which none but a student of history can occupy, and who has something of a turn for the business.
Whether I have any motive but public good must be referred to those who can decide whether a missionary chooses his pursuit solely to convert the heathen. I shall certainly be thought to have a little of the spirit of Col. Quagg, who delighted in strapping the Grace-walking Brethren. I must quote this myself: if I do not, some one else will, and then where am I? The Colonel's principle is described as follows:
"I licks ye because I kin, and because I like, and because ye'se critters that licks is good for. Skins ye have on, and skins I'll have off; hard or soft, wet or dry, spring or fall. Walk in grace if ye like till pumpkins is peaches; but licked ye must be till your toe-nails drop off and your noses bleed blue ink. And—licked—they—were—accordingly."
I am reminded of this by the excessive confidence with which Mr. James Smith predicted that he would treat me as Zephaniah Stockdolloger (Sam Slick calls it slockdollager) treated Goliah Quagg. He has announced his [131]intention of bringing me, with a contrite heart, and clean shaved,—4159265... razored down to 25,—to a camp-meeting of circle-squarers. But there is this difference: Zephaniah only wanted to pass the Colonel's smithy in peace; Mr. James Smith sought a fight with me. As soon as this Budget began to appear, he oiled his own strap, and attempted to treat me as the terrible Colonel would have treated the inoffensive brother.
He is at liberty to try again.
THE MOON HOAX.
The Moon-hoax; or the discovery that the moon has a vast population of human beings. By Richard Adams Locke.[226] New York, 1859, 8vo.
This is a reprint of the hoax already mentioned. I suppose R. A. Locke is the name assumed by M. Nicollet.[227] The publisher informs us that when the hoax first appeared day by day in a morning paper, the circulation increased fivefold, and the paper obtained a permanent footing. Besides this, an edition of 60,000 was sold off in less than one month.
The discovery was also published under the name of A. R. Grant.[228] Sohncke's[229] Bibliotheca Mathematica confounds this Grant with Prof. R. Grant[230] of Glasgow, the author of the History of Physical Astronomy, who is accordingly made to guarantee the discoveries in the moon. I hope Adams Locke will not merge in J. C. Adams,[231] the co-discoverer of Neptune. Sohncke gives the titles of [132]three French translations of the Moon hoax at Paris, of one at Bordeaux, and of Italian translations at Parma, Palermo, and Milan.
A Correspondent, who is evidently fully master of details, which he has given at length, informs me that the Moon hoax appeared first in the New York Sun, of which R. A. Locke was editor. It so much resembled a story then recently published by Edgar A. Poe, in a Southern paper, "Adventures of Hans Pfaal," that some New York journals published the two side by side. Mr. Locke, when he left the New York Sun, started another paper, and discovered the manuscript of Mungo Park;[232] but this did not deceive. The Sun, however, continued its career, and had a great success in an account of a balloon voyage from England to America, in seventy-five hours, by Mr. Monck Mason,[233] Mr. Harrison Ainsworth,[234] and others. I have no doubt that M. Nicollet was the author of the Moon hoax,[235] written in a way which marks the practised observatory astronomer beyond all doubt, and by evidence seen in the most minute details. Nicollet had an eye to Europe. I suspect that he took Poe's story, and made it a basis for his own. Mr. Locke, it would seem, when he attempted a fabrication for himself, did not succeed.
The Earth we inhabit, its past, present, and future. By Capt. Drayson.[236] London, 1859, 8vo.
The earth is growing; absolutely growing larger: its diameter increases three-quarters of an inch per mile every year. The foundations of our buildings will give way in [133]time: the telegraph cables break, and no cause ever assigned except ships' anchors, and such things. The book is for those whose common sense is unwarped, who can judge evidence as well as the ablest philosopher. The prospect is not a bad one, for population increases so fast that a larger earth will be wanted in time, unless emigration to the Moon can be managed, a proposal of which it much surprises me that Bishop Wilkins has a monopoly.
IMPALEMENT BY REQUEST.
Athenæum, August, 19, 1865. Notice to Correspondents.
"R. W.—If you will consult the opening chapter of the Budget of Paradoxes, you will see that the author presents only works in his own library at a given date; and this for a purpose explained. For ourselves we have carefully avoided allowing any writers to present themselves in our columns on the ground that the Budget has passed them over. We gather that Mr. De Morgan contemplates additions at a future time, perhaps in a separate and augmented work; if so, those who complain that others of no greater claims than themselves have been ridiculed may find themselves where they wish to be. We have done what we can for you by forwarding your letter to Mr. De Morgan."
The author of "An Essay on the Constitution of the Earth," published in 1844, demanded of the Athenæum, as an act of fairness, that a letter from him should be published, proving that he had as much right to be "impaled" as Capt. Drayson. He holds, on speculative grounds, what the other claims to have proved by measurement, namely, that the earth is growing; and he believes that in time—a good long time, not our time—the earth and other planets may grow into suns, with systems of their own.
This gentleman sent me a copy of his work, after the commencement of my Budget; but I have no recollection of having received it, and I cannot find it on the (nursery? [134]quarantine?) shelves on which I keep my unestablished discoveries. Had I known of this work in time, (see the Introduction) I should of course, have impaled it (heraldically) with the other work; but the two are very different. Capt. Drayson professes to prove his point by results of observation; and I think he does not succeed. The author before me only speculates; and a speculator can get any conclusion into his premises, if he will only build or hire them of shape and size to suit. It reminds me of a statement I heard years ago, that a score of persons, or near it, were to dine inside the skull of one of the aboriginal animals, dear little creatures! Whereat I wondered vastly, nothing doubting; facts being stubborn and not easy drove, as Mrs. Gamp said. But I soon learned that the skull was not a real one, but artificially constructed by the methods—methods which have had striking verifications, too—which enable zoologists to go the whole hog by help of a toe or a bit of tail. This took off the edge of the wonder: a hundred people can dine inside an inference, if you draw it large enough. The method might happen to fail for once: for instance, the toe-bone might have been abnormalized by therian or saurian malady; and the possibility of such failure, even when of small probability, is of great alleviation. The author before me is, apparently, the sole fabricator of his own premises. With vital force in the earth and continual creation on the part of the original Creator, he expands our bit of a residence as desired. But, as the Newtoness of Cookery observed, First catch your hare. When this is done, when you have a growing earth, you shall dress it with all manner of proximate causes, and serve it up with a growing Moon for sauce, a growing Sun, if it please you, at the other end, and growing planets for side-dishes. Hoping this amount of impalement will be satisfactory, I go on to something else. [135]
THE HAILESEAN SYSTEM OF ASTRONOMY.
The Hailesean System of Astronomy. By John Davey Hailes[237] (two pages duodecimo, 1860).
He offers to take 100,000l. to 1,000l. that he shows the sun to be less than seven millions of miles from the earth. The earth in the center, revolving eastward, the sun revolving westward, so that they "meet at half the circle distance in the 24 hours." The diameter of the circle being 9839458303, the circumference is 30911569920.
The following written challenge was forwarded to the Council of the Astronomical Society: it will show the "general reader"—and help him towards earning his name—what sort of things come every now and then to our scientific bodies. I have added punctuation:
Challenge.
1,000 to 30,000.
"Leverrier's[238] name stand placed first. Do the worthy Frenchman justice.
By awarding him the medal in a trice.
Give Adams[239] an extra—of which neck and neck the race.
Now I challenge to meet them and the F.R.S.'s all,
For good will and one thousand pounds to their thirty thousand withall,
That I produce a system, which shall measure the time,
When the Sun was vertical to Gibeon, afterward to Syene.
To meet any time in London—name your own period,
To be decided by a majority of twelve persons—a President, odd.
That mean, if the twelve equally divide, the President decide,
I should prefer the Bishop of London, over the meeting to preside.
John Davy Hailes."
Feb. 17, 1847."
Mr. Hailes still issues his flying sheets. The last I have met with (October 7, 1863) informs us that the latitude of [136]England is slowly increasing, which is the true cause of the alteration in the variation of the magnet.
[Mr. Hailes continues his researches. Witness his new Hailesean system of Astronomy, displaying Joshua's miracle-time, origin of time from science, with Bible and Egyptian history. Rewards offered for astronomical problems. With magnetism, etc. etc. Astronomical challenge to all the world. Published at Cambridge, in 1865. The author agrees with Newton in one marked point. Errores quam minimi non sunt contemnendi,[240] says Isaac: meaning in figures, not in orthography. Mr. Hailes enters into the spirit, both positive and negative, of this dictum, by giving the distance of Sidius from the center of the earth at 163,162,008 miles 10 feet 8 inches 17-28ths of an inch. Of course, he is aware that the center of figure of the earth is 17.1998 inches from the center of gravity. Which of the two is he speaking of?]
The Divine Mystery of Life. London [1861], 18mo. (pp.32).
The author has added one class to zoology, which is printed in capitals, as derived from zoé, life, not from zôon, animal. That class is of Incorporealia, order I., Infinitum, of one genus without plurality, Deus: order II., Finita, angels good and evil. The rest is all about a triune system, with a diagram. The author is not aware that ζωον is not animal, but living being. Aristotle had classed gods under ζωα, and has been called to account for it by moderns who have taken the word to mean animal.
A CHANCE FOR INVENTORS.
Explication du Zodiaque de Denderah, des Pyramides, et de Genèse. Par le Capitaine au longcours Justin Roblin.[241] Caen, 1861. 8vo.
Capt. Roblin, having discovered the sites of gold and diamond mines by help of the zodiac of Denderah, offered half to the shareholders of a company which he proposed to form. One of our journals, by help of the zodiac of Esné, offered, at five francs a head, to tell the shareholders the exact amount of gold and diamonds which each would get, and to make up the amount predicted to those who got less. There are moods of the market in England in which this company could have been formed: so we must not laugh at our neighbors.
JOHANNES VON GUMPACH.
A million's worth of property, and five hundred lives annually lost at sea by the Theory of Gravitation. A letter on the true figure of the earth, addressed to the Astronomer Royal, by Johannes von Gumpach.[242] London, 1861, 8vo. (pp. 54).
The true figure and dimensions of the earth, in a letter addressed to the Astronomer Royal. By Joh. von Gumpach. 2nd ed. entirely recast. London, 1862, 8vo. (pp. 266).
Two issues of a letter published with two different title-pages, one addressed to the Secretary of the Royal Society, the other to the Secretary of the Royal Astronomical Society. It would seem that the same letter is also issued with two other titles, addressed to the British Association and the Royal Geographical Society. By Joh. von Gumpach. London, 1862, 8vo.
Baby-Worlds. An essay on the nascent members of our solar household. By Joh. von Gumpach. London, 1863, 8vo.
The earth, it appears, instead of being flattened, is elongated at the poles: by ignorance of which the loss above mentioned occurs yearly. There is, or is to be, a substitute for attraction and an "application hitherto neglected, of a [138]recognized law of optics to the astronomical theory, showing the true orbits of the heavenly bodies to be perfectly circular, and their orbital motions to be perfectly uniform." all irregularities being, I suppose, optical delusions. Mr. Von Gumpach is a learned man; what else, time must show.
SLANDER PARADOXES.
Perpetuum Mobile: or Search for self-motive Power. By Henry Dircks.[243] London, 1861, 8vo.
A useful collection on the history of the attempts at perpetual motion, that is, at obtaining the consequences of power without any power to produce them. September 7, 1863, a correspondent of the Times gave an anecdote of George Stephenson,[244] which he obtained from Robert Stephenson.[245] A perpetual motionist wanted to explain his method; to which George replied—"Sir! I shall believe it when I see you take yourself up by the waistband, and carry yourself about the room." Never was the problem better stated.
There is a paradox of which I ought to give a specimen, I mean the slander-paradox; the case of a person who takes it into his head, upon evidence furnished entirely by the workings of his own thoughts, that some other person has committed a foul act of which the world at large would no more suppose him guilty than they would suppose that the earth is a flat bordered by ice. If I were to determine on giving cases in which the self-deluded person imagines [139]a conspiracy against himself, there would be no end of choices. Many of the grosser cases are found at last to be accompanied by mental disorder, and it is difficult to avoid referring the whole class to something different from simple misuse of the reasoning power. The first instance is one which puts in a strong light the state of things in which we live, brought about by our glorious freedom of thought, speech, and writing. The Government treated it with neglect, the press with silent contempt, and I will answer for it many of my readers now hear of it for the first time, when it comes to be enrolled among circle-squarers and earth-stoppers, where, as the old philosopher said, it will not gravitate, being in proprio loco.[246]
1862. On new year's day, 1862, when the nation was in the full tide of sympathy with the Queen, and regret for its own loss, a paper called the Free Press published a number devoted to the consideration of the causes of the death of the Prince Consort. It is so rambling and inconsecutive that it takes more than one reading to understand it. It is against the Times newspaper. First, the following insinuation:
"To the legal mind, the part of [the part taken by] the Times will present a prima facie case of the gravest nature, in the evident fore-knowledge of the event, and the preparation to turn it to account when it should have occurred. The article printed on Saturday must have been written on Friday. That article could not have appeared had the Prince been intended to live."
Next, it is affirmed that the Times intended to convey the idea that the Prince had been poisoned.
"Up to this point we are merely dealing with words which the Times publishes, and these can leave not a shadow of doubt that there is an intention to promulgate the idea that Prince Albert had been poisoned."
The article then goes on with a strange olio of [140]insinuations to the effect that the Prince was the obstacle to Russian intrigue, and that if he should have been poisoned,—which the writer strongly hints may have been the case,—some Minister under the influence of Russia must have done it. Enough for this record. Un sot trouve toujours un plus sot qui l'admire:[247] who can he be in this case?
THE NEPTUNE CONTROVERSY.
1846. At the end of this year arose the celebrated controversy relative to the discovery of Neptune. Those who know it are well aware that Mr. Adams's[248] now undoubted right to rank with Le Verrier[249] was made sure at the very outset by the manner in which Mr. Airy,[250] the Astronomer Royal, came forward to state what had taken place between himself and Mr. Adams. Those who know all the story about Mr. Airy being arrested in his progress by the neglect of Mr. Adams to answer a letter, with all the imputations which might have been thrown upon himself for laxity in the matter, know also that Mr. Airy's conduct exhibited moral courage, honest feeling, and willingness to sacrifice himself, if need were, to the attainment of the ends of private justice, and the establishment of a national claim. A writer in a magazine, in a long and elaborate article, argued the supposition—put in every way except downright assertion, after the fashion of such things—that Mr. Airy had communicated Mr. Adams's results to M. Le Verrier, with intention that they should be used. His presumption as to motive is that, had Mr. Adams been recognized, "then the discovery must have been indisputably an Englishman's, and that Englishman not the Astronomer Royal." Mr. Adams's conclusions were "retouched in France, and sent [141]over the year after." The proof given is that it cannot be "imagined" otherwise.
"Can it then be imagined that the Astronomer Royal received such results from Mr. Adams, supported as they were by Professor Challis's[251] valuable testimony as to their probable accuracy, and did not bring the French astronomer acquainted with them, especially as he was aware that his friend was engaged in matters bearing directly upon these results?"
The whole argument the author styles "evidence which I consider it difficult to refute." He ends by calling upon certain persons, of whom I am one, to "see ample justice done." This is the duty of every one, according to his opportunities. So when the reputed author—the article being anonymous—was, in 1849, proposed as a Fellow of the Astronomical Society, I joined—if I remember right, I originated—an opposition to his election, until either the authorship should be denied, or a proper retraction made. The friends of the author neither denied the first, nor produced the second: and they judged it prudent to withdraw the proposal. Had I heard of any subsequent repentance, I would have taken some other instance, instead of this: should I yet hear of such a thing, I will take care to notice it in the continuation of this list, which I confidently expect, life and health permitting, to be able to make in a few years. This much may be said, that the author, in a lecture on the subject, given in 1849, and published with his name, did not repeat the charge.
[The libel was published in the Mechanics' Magazine,[252] (vol. for 1846, pp. 604-615): and the editor supported it as follows, (vol. for 1847, p. 476). In answer to Mr. Sheepshanks's charitable hope that he had been hoaxed, [142]he says: "Mr. Sheepshanks cannot certainly have read the article referred to.... Severe and inculpatory it is—unjust some may deem it (though we ourselves are out of the number.)... A 'hoax' forsooth! May we be often the dupes of such hoaxes!" He then goes on to describe the article as directed against the Astronomer Royal's alleged neglect to give Mr. Adams that "encouragement and protection" which was his due, and does not hint one word about the article containing the charge of having secretly and fraudulently transmitted news of Mr. Adams's researches to France, that an Englishman might not have the honor of the discovery. Mr. Sheepshanks having called this a "deliberate calumny," without a particle of proof or probability to support it, the editor says "what the reverend gentleman means by this, we are at a loss to understand." He then proceeds not to remember. I repeat here, what I have said elsewhere, that the management of the journal has changed hands; but from 1846 to 1856, it had the collar of S.S. (scientific slander). The prayer for more such things was answered (See p. 349).]
JAMES IVORY.[253]
I have said that those who are possessed with the idea of conspiracy against themselves are apt to imagine both conspirators and their bad motives and actions. A person who should take up the idea of combination against himself without feeling ill-will and originating accusations would be indeed a paradox. But such a paradox has existed. It is very well known, both in and beyond the scientific world, that the late James Ivory was subject to the [143]impression of which I am speaking; and the diaries and other sources of anecdote of our day will certainly, sooner or later, make it a part of his biography. The consequence will be that to his memory will be attached the unfavorable impression which the usual conduct of such persons creates; unless it should happen that some one who knows the real state of the case puts the two sides of it properly together. Ivory was of that note in the scientific world which may be guessed from Laplace's description of him as the first geometer in Britain and one of the first in Europe. Being in possession of accurate knowledge of his peculiarity in more cases than one; and in one case under his own hand: and having been able to make full inquiry about him, especially from my friend the late Thomas Galloway[254]—who came after him at Sandhurst—one of the few persons with whom he was intimate:—I have decided, after full deliberation, to forestall the future biographies.
That Ivory was haunted by the fear of which I have spoken, to the fullest extent, came to my own public and official knowledge, as Secretary of the Astronomical Society. It was the duty of Mr. Epps,[255] the Assistant Secretary, at the time when Francis Baily[256] first announced his discovery of the Flamsteed Papers, to report to me that Mr. Ivory had called at the Society's apartments to inquire into the contents of those papers, and to express his hope that Mr. Baily was not attacking living persons under the names of Newton and Flamsteed.[257] Mr. Galloway, to whom I communicated this, immediately went to Mr. Ivory, and succeeded, after some explanation, in setting him right. This is but one of many instances in which a man of thoroughly sound judgment in every other respect seemed to be under a complete chain of delusions about the conduct of [144]others to himself. But the paradox is this:—I never could learn that Ivory, passing his life under the impression that secret and unprovoked enemies were at work upon his character, ever originated a charge, imputed a bad motive, or allowed himself an uncourteous expression. Some letters of his, now in my possession, referring to a private matter, are, except in the main impression on which they proceed, unobjectionable in every point: they might have been written by a cautious friend, whose object was, if possible, to prevent a difference from becoming a duel without compromising his principal's rights or character. Knowing that in some quarters the knowledge of Ivory's peculiarity is more or less connected with a notion that the usual consequences followed, I think the preceding statement due to his memory.
THREE CLASSES OF JOURNALS.
In such a record as the present, which mixes up the grossest speculative absurdities with every degree of what is better, an instance of another kind may find an appropriate place. The faults of journalism, when merely exposed by other journalism pass by and are no more regarded. A distinct account of an undeniable meanness, recorded in a work of amusement and reference both, may have its use: such a thing may act as a warning. An editor who is going to indulge his private grudge may be prevented from counting upon oblivion as a matter of certainty.
There are three kinds of journals, with reference to the mode of entrance of contributors. First, as a thing which has been, but which now hardly exists, there is the journal in which the editor receives a fixed sum to find the matter. In such a journal, every article which the editor can get a friend to give him is so much in his own pocket, which has a great tendency to lower the character of the articles; but I am not concerned with this point. Secondly, there is the journal which is supported by voluntary contributions of [145]matter, the editor selecting. Thirdly, there is the journal in which the contributor is paid by the proprietors in a manner with which the literary editor has nothing to do.
The third class is the safe class, as its editors know: and, as a usual rule, they refuse unpaid contributions of the editorial cast. It is said that when Canning[258] declined a cheque forwarded for an article in the Quarterly, John Murray[259] sent it back with a blunt threat that if he did not take his money he could never be admitted again. The great publisher told him that if men like himself in position worked for nothing, all the men like himself in talent who could not afford it would not work for the Quarterly. If the above did not happen between Canning and Murray, it must have happened between some other two. Now journals of the second class—and of the first, if such there be—have a fault to which they alone are very liable, to say nothing of the editorial function (see the paper at the beginning, p. 11 et seq.), being very much cramped, a sort of gratitude towards effective contributors leads the journal to help their personal likes and dislikes, and to sympathize with them. Moreover, this sort of journal is more accessible than others to articles conveying personal imputation: and when these provoke discussion, the journal is apt to take the part of the assailant to whom it lent itself in the first instance.
THE MECHANICS' MAGAZINE.
Among the journals which went all lengths with contributors whom they valued, was the Mechanics' Magazine[260] in the period 1846-56. I cannot say that matters have not mended in the last ten years: and I draw some [146]presumption that they have mended from my not having heard, since 1856, of anything resembling former proceedings. And on actual inquiry, made since the last sentence was written, I find that the property has changed hands, the editor is no longer the same, and the management is of a different stamp. This journal is chiefly supported by voluntary articles: and it is the journal in which, as above noted, the ridiculous charge against the Astronomer Royal was made in 1849. The following instance of attempt at revenge is so amusing that I select it as the instance of the defect which I intend to illustrate; for its puerility brings out in better relief the points which are not so easily seen in more adult attempts.
The Mechanics' Magazine, which by its connection with engineering, etc., had always taken somewhat of a mathematical character, began, a little before 1846, to have more to do with abstract science. Observing this, I began to send short communications, which were always thankfully received, inserted, and well spoken of. Any one who looks for my name in that journal in 1846-49, will see nothing but the most respectful and even laudatory mention. In May 1849 occurred the affair at the Astronomical Society, and my share in forcing the withdrawal of the name of the alleged contributor to the journal. In February 1850 occurred the opportunity of payment. The Companion to the Almanac[261] had to be noticed, in which, as then usual, was an article signed with my name. I shall give the review of this article entire, as a sample of a certain style, as well as an illustration of my point. The reader will observe that my name is not mentioned. This would not have done; the readers of the Magazine would have stared to see a name of not infrequent occurrence in previous years all of a sudden fallen from the heaven of respect into the pit of contempt, like Lucifer, son of the morning. But before [147]giving the review, I shall observe that Mr. Adams, in whose favor the attack on the Astronomer Royal was made, did not appreciate the favor; and of course did not come forward to shield his champion. This gave deadly offence, as appear from the following passage, (February 16, 1850):
"It was our intention to enter into a comparison of the contents of our Nautical Almanack with those of its rival, the Connaissance des Temps; but we shall defer it for the present. The Nautical Almanack for 1851 will contain Mr. Adams's paper 'On the Perturbation of Uranus'; and when it comes, in due course, before the public, we are quite sure that that gentleman will expect that we shall again enter upon the subject with peculiar delight. Whilst we have a thorough loathing for mean, cowardly, crawlers—we have an especial pleasure in maintaining the claims of men who are truly grateful as well as highly talented: Mr. Adams, therefore, will find that he cannot be disappointed—and the occasion will afford us an opportunity for making the comparison to which we have adverted."
This passage illustrates what I have said on the editorial function (Vol. I, p. 15). What precedes and follows has some criticism on the Government, the Astronomer Royal, etc., but reserved in allusion, oblique in sarcasm, and not fiercely uncourteous. The coarseness of the passage I have quoted shows editorial insertion, which is also shown by its blunder. The inserter is waiting for the Almanac of 1851 that he may review Mr. Adams's paper, which is to be contained in it. His own contributor, only two sentences before the insertion, had said, "The Nautical Almanac, we believe, is published three or four years in advance." In fact, the Almanac for 1851—with Mr. Adams's paper at the end—was published at the end of 1847 or very beginning of 1848; it had therefore been more than two years before the public when the passage quoted was written. And probably every person in the country who was fit to review Mr. Adams's [148]paper—and most of those who were fit to read it—knew that it had been widely circulated, in revise, at the end of 1846: my copy has written on it, "2d revise, December 27, 1846, at noon," in the handwriting of the Superintendent of the Almanac; and I know that there was an extensive issue of these revises, brought out by the Le-Verrier-and-Adams discussion. I now give the review of myself, (February 23, 1850):
"The British Almanack and Companion.
"The Companion to this Almanack, for some years after its first publication, annually contained scientific articles by Sir J. Lubbock[262] and others of a high order and great interest; we have now, however, closed the publication as a scientific one in remembrance of what it was, and not in consequence of what it is. Its list of contributors on science, has grown 'small by degrees and beautifully less,' until it has dwindled down to one—'a last rose of summer left withering alone.' The one contributor has contributed one paper 'On Ancient and Modern Usage in Reckoning.'
"The learned critic's chef d'œuvre, is considered, by competent judges, to be an Essay on Old Almanacks printed a few years ago in this annual, and supposed to be written with the view of surpassing a profound memoir on the same subject by James O. Halliwell,[263] Esq., F.R. and A.S.S., but the tremendous effort which the learned writer then made to excel many titled competitors for honors in the antique line appears to have had a sad effect upon his mental powers—at any rate, his efforts have since yearly become duller and duller; happily, at last, we should suppose, 'the ancient [149]and modern usage in reckoning' indicates the lowest point to which the vis inertia of the learned writer's peculiar genius can force him.
"We will give a few extracts from the article.
"The learned author says, 'Those who are accustomed to settle the meaning of ancient phrases by self-examination will find some strange conclusions arrived at by us.' The writer never wrote a more correct sentence—it admits of no kind of dispute.
"'Language and counting,' says the learned author, 'both came before the logical discussion of either. It is not allowable to argue that something is or was, because it ought to be or ought to have been. That two negatives make an affirmative, ought to be; if no man have done nothing, the man who has done nothing does not exist, and every man has done something. But in Greek, and in uneducated English, it is unquestionable that 'no man has done nothing' is only an emphatic way of saying that no man has done anything; and it would be absurd to reason that it could not have been so, because it should not.'—p. 5.
"'But there is another difference between old and new times, yet more remarkable, for we have nothing of it now: whereas in things indivisible we count with our fathers, and should say in buying an acre of land, that the result has no parts, and that the purchaser, till he owns all the ground, owns none, the change of possession being instantaneous. This second difference lies in the habit of considering nothing, nought, zero, cipher, or whatever it may be called, to be at the beginning of the scale of numbers. Count four days from Monday: we should now say Tuesday, Wednesday, Thursday, Friday; formerly, it would have been Monday, Tuesday, Wednesday, Thursday. Had we asked, what at that rate is the first day from Monday, all would have stared at a phrase they had never heard. Those who were capable of extending language would have said, Why it must be Monday itself: the rest would have said, there can [150]be no first day from Monday, for the day after is Tuesday, which must be the second day: Monday, one; Tuesday, two,'—p. 10.
"We assure our readers that the whole article is equally lucid, and its logic alike formal.
"There are some exceedingly valuable footnotes; we give one of the most interesting, taken from the learned Mr. Halliwell's profound book on Nursery Rhymes[264]—a celebrated production, for which it is supposed the author was made F.R.S.
"'One's nine,
Two's some,
Three's a many,
Four's a penny,
Five's a little hundred.'
'The last line refers to five score, the so-called hundred being more usually six score. The first line, looked at etymologically, is one is not one, and the change of thought by which nine, the decimal of one, aims to be associated with the decimal of plurality is curious:'—Very.
"This valuable and profound essay will very probably be transferred to the next edition of the learned Mr. Halliwell's rare work, of kindred worth, entitled 'Rara Mathematica,' it will then be deservedly handed down to posterity as a covering for cheap trunks—a most appropriate archive for such a treasure."
In December, 1846, the Mechanics' Magazine published a libel on Airy in the matter of the discovery of Neptune. In May, 1849, one * * * was to have been brought forward for election at the Astronomical Society, and was opposed by me and others, on the ground that he was the probable author of this libel, and that he would not, perhaps could [151]not, deny it. [N.B. I no more doubt that he was the author then I doubt that I am the author of this sentence.][265]
Accordingly, * * * was withdrawn, and a discussion took place, for which see the Athenæum, No. 1126, May 26, 1849, p. 544. The Mechanics' Magazine was very sore, but up to this day has never ventured beyond an attack on Airy, private whisperings against Adams—(see ante, p. 147),—and the above against myself. In due time, I doubt not my name will appear as one of the âmes damnées[266] of the Mechanics' Magazine.[267]
T. S. DAVIES ON EUCLID.
First, as to Mr. Halliwell. The late Thomas Stephens Davies,[268] excellent in geometry, and most learned in its history, was also a good hand at enmity, though not implacable. He and Mr. Halliwell, who had long before been very much one, were, at this date, very much two. I do not think T. S. Davies wrote this article; and I think that by giving my reasons I shall do service to his memory. It must have been written at the beginning of February; and within three days of that time T. S. Davies was making over to me, by his own free act, to be kept until claimed by the relatives, what all who knew even his writings knew that he considered as the most precious deposit he had ever had in his keeping—Horner's[269] papers. His letter announcing the transmission is dated February 2, 1850. This is a strong point; but there is another quite as strong. Euclid and [152]his writings were matters on which T. S. Davies knew neither fear nor favor: he could not have written lightly about a man who stood high with him as a judge of Euclid. Now in this very letter of Feb. 2, there is a sentence which I highly value, because, as aforesaid, it is on a point on which he would never have yielded anything, to which he had paid life-long attention, and on which he had the bias of having long stood alone. In fact, knowing—and what I shall quote confirms me,—that in the matter of Euclid his hand was against every man, I expected, when I sent him a copy of my 22-column article, "Eucleides" in Smith's Dictionary,[270] to have received back a criticism, that would have blown me out of the water: and I thought it not unlikely that a man so well up in the subject might have made me feel demolished on some points. Instead of this, I got the following: "Although on one or two minor points I do not quite accord with your views, yet as a whole and without regard to any minor points, I think you are the first who has succeeded in a delineation of Euclid as a geometer." All this duly considered, it is utterly incredible that T. S. Davies should have written the review in question. And yet Mr. Halliwell is treated just as T. S. Davies would have treated him, as to tone and spirit. The inference in my mind is that we have here a marked instance of the joining of hatreds which takes place in journals supported by voluntary contributions of matter. Should anything ever have revived this article—and no one ever knows what might have been fished up from the forgotten mass of journals—the treatment of Mr. Halliwell would certainly have thrown a suspicion on T. S. Davies, a large and regular contributor to the Magazine. It is good service to his memory to point out what makes it incredible that he should have written so unworthy an article.
The fault is this. There are four extracts: the first [153]three are perfectly well printed. The printing of the Mechanics' Magazine was very good. I was always exceedingly satisfied with the manner in which my articles appeared, without my seeing proof. Most likely these extracts were printed from my printed paper; if not the extractor was a good copier. I know this by a test which has often served me. I use the subjunctive—"if no man have done nothing," an ordinary transcriber, narrating a quotation almost always lets his own habit write has. The fourth extract has three alterations, all tending to make me ridiculous. None is altered, in two places, into nine, denial into decimal, and comes into aims; so that "none, the denial of one, comes to be associated with the denial of plurality," reads as "nine, the decimal of one, aims to be associated with the decimal of plurality." This is intentional; had it been a compositor's reading of bad handwriting, these would not have been the only mistakes; to say nothing of the corrector of the press. And both the compositor and reader would have guessed, from the first line being translated into "one is not one," that it must have been "one's none," not "one's nine." But it was not intended that the gem should be recovered from the unfathomed cave, and set in a Budget of Paradoxes.
We have had plenty of slander-paradox. I now give a halfpennyworth of bread to all this sack, an instance of the paradox of benevolence, in which an individual runs counter to all the ideas of his time, and sees his way into the next century. At Amiens, at the end of the last century, an institution was endowed by a M. de Morgan, to whom I hope I am of kin, but I cannot trace it; the name is common at Amiens. It was the first of the kind I ever heard of. It is a Salle d'Asyle for children, who are taught and washed and taken care of during the hours in which their parents must be at work. The founder was a large wholesale grocer and colonial importer, who was made a Baron by Napoleon I for his commercial success and his charities. [154]
JAS. SMITH AGAIN.
1862. Mr. Smith replies to me, still signing himself Nauticus: I give an extract:
"By hypothesis [what, again!] let 14° 24' be the chord of an arc of 15° [but I wont, says 14° 24'], and consequently equal to a side of a regular polygon of 24 sides inscribed in the circle. Then 4 times 14° 24' = 57° 36' = the radius of the circle ..."
That is, four times the chord of an arc is the chord of four times the arc: and the sum of four sides of a certain pentagon is equal to the fifth. This is the capital of the column, the crown of the arch, the apex of the pyramid, the watershed of the elevation. Oh! J. S.! J. S.! groans Geometry—Summum J. S. summa injuria![271] The other J. S., Joseph Scaliger,[272] as already mentioned, had his own way of denying that a straight line is always the shortest distance between two points. A parallel might be instituted, but not in half a column. And J. S. the second has been so tightly handled that he may now be dismissed, with an inscription for his circular shield, obtained by changing Lexica contexat into Circus quadrandus in an epigram of J. S. the first:
"Si quem dura manet sententia judicis, olim
Damnatum ærumnis suppliciisque caput,
Hunc neque fabrili lassent ergastula massa,
Nec rigidas vexent fossa metalla manus.
Circus quadrandus: nam—cætera quid moror?—omnes
Pœnarum facies hic labor unus habet."[273]
I had written as far as damnatum when in came the letter of Nauticus as a printed slip, with a request that I would consider the slip as a 'revised copy.' Not a word of alteration in the part I have quoted! And in the evening came a letter desiring that I would alter a gross error; but not the one above: this is revising without revision! If there were cyclometers enough of this stamp, they would, as cultivation progresses—and really, with John Stuart Mill in for Westminster, it seems on the move, even though, as I learn while correcting the proof, Gladstone be out from Oxford; for Oxford is no worse than in 1829, while Westminster is far above what she ever has been: election time excuses even such a parenthesis as this—be engaged to amuse those who can afford it with paralogism at their meals, after the manner of the other jokers who wore the caps and bells. The rich would then order their dinners with panem et Circenses,—up with the victuals and the circle-games—as the poor did in the days of old.
Mr. Smith is determined that half a column shall not do. Not a day without something from him: letter, printed proof, pamphlet. In what is the last at this moment of writing he tells me that part of the title of a work of his will be "Professor De Morgan in the pillory without hope of escape." And where will he be himself? This I detected by an effort of reasoning which I never could have made except by following in his steps. In all matters connected with π the letters l and g are closely related: this appears in the well-known formula for the time of oscillation π √(l : g). Hence g may be written for l, but only once: do it twice, and you require the time to be π √(l2 : g2). This may be reinforced by observing that if as a datum, or if you dislike that word, by hypothesis, the first l be a g, it is absurd that it should be an l. Write g for the first l, and we have un fait accompli. I shall be in pillory; and overhead, in a cloud, will sit Mr. James Smith on one stick laid across two others, under a nimbus of 3⅛ diameters to [156]the circumference—in π-glory. Oh for a drawing of this scene! Mr. De Morgan presents his compliments to Mr. James Smith, and requests the honor of an exchange of photographs.
July 26.—Another printed letter.—Mr. James Smith begs for a distinct answer to the following plain question: "Have I not in this communication brought under your notice truths that were never before dreamed of in your geometrical and mathematical philosophy?" To which, he having taken the precaution to print the word truths in italics, I can conscientiously answer, Yes, you have. And now I shall take no more notice of these truths, until I receive something which surpasses all that has yet been done.
A FEW SMALL PARADOXERS.
The Circle secerned from the Square; and its area gauged in terms of a triangle common to both. By Wm. Houlston,[274] Esq. London and Jersey, 1862, 4to.
Mr. Houlston squares at about four poetical quotations in a page, and brings out π = 3.14213.... His frontispiece is a variegated diagram, having parts designated Inigo and Outigo. All which relieves the subject, but does not remove the error.
Considerations respecting the figure of the Earth.... By C. F. Bakewell.[275] London, 1862, 8vo.
Newton and others think that in a revolving sphere the [157]loose surface matter will tend to the equator: Mr. Bakewell thinks it will tend to the poles.
On eccentric and centric force: a new theory of projection. By H. F. A. Pratt, M.D.[276] London, 1862, 8vo.
Dr. Pratt not only upsets Newton, but cuts away the very ground he stands on: for he destroys the first law of motion, and will not have the natural tendency of matter in motion to be rectilinear. This, as we have seen, was John Walsh's[277] notion. In a more recent work "On Orbital Motion," London, 1863, 8vo., Dr. Pratt insists on another of Walsh's notions, namely, that the precession of the equinoxes is caused by the motion of the solar system round a distant central sun. In this last work the author refers to a few notes, which completely destroy the theory of gravitation in terms "perfectly intelligible as well to the unlearned as to the learned": to me they are quite unintelligible, which rather tends to confirm a notion I have long had, that I am neither one thing nor the other. There is an ambiguity of phrase which delights a writer on logic, always on the look-out for specimens of homonymia or æquivocatio. The author, as a physician, is accustomed to "appeal from mere formulæ": accordingly, he sets at nought the whole of the mathematics, which he does not understand. This equivocation between the formula of the physician and that of the mathematician is as good, though not so perceptible to the world at large, as that made by Mr. Briggs's friend in Punch's picture, which I cut out to paste into my Logic. Mr. Briggs wrote for a couple of bruisers, meaning to prepare oats for his horses: his friend sent him the Whitechapel Chicken and the Bayswater Slasher, with the gloves, all ready.
On matter and ether, and the secret laws of physical change. By T. R. Birks, M.A.[278] Cambridge, 1862, 8vo.
Bold efforts are made at molecular theories, and the one before me is ably aimed. When the Newton of this subject shall be seated in his place, books like the present will be sharply looked into, to see what amount of anticipation they have made.
DR. THORN AND MR. BIDEN.
The history of the 'thorn tree and bush' from the earliest to the present time: in which is clearly and plainly shown the descent of her most gracious Majesty and her Anglo-Saxon people from the half tribe of Ephraim, and possibly from the half tribe of Manasseh; and consequently her right and title to possess, at the present moment, for herself and for them, a share or shares of the desolate cities and places in the land of their forefathers! By Theta, M.D.[279] (Private circulation.) London, 1862, 8vo.
This is much about Thorn, and its connected words, Thor, Thoth, Theta, etc. It is a very mysterious vagary. The author of it is the person whom I have described elsewhere as having for his device the round man in the three-cornered hole, the writer of the little heap of satirical anonymous letters about the Beast and 666. By accident I discovered the writer: so that if there be any more thorns to crackle under the pot, they need not be anonymous.
Nor will they be anonymous. Since I wrote the above, I have received onymous letters, as ominous as the rest. The writer, William Thorn, M.D., is obliged to reveal [159]himself, since it is his object to prove that he himself is one 666. By using W for double Vau (or 12) he cooks the number out of his own name. But he says it is the number not of a beast but of a man, and adds, "Thereby hangs a tale!" which sounds like contradiction. He informs me that he will talk the matter over with me: but I shall certainly have nothing to say to a gentleman of his number; it is best to keep on the safe side.
In one letter I am informed that not a line should I have had, but for my "sneer at 666," which, therefore, I am well pleased to have given. I am also told that my name means the "'garden of death,' that place in which the tree of knowledge was plucked, and so you are like your name 'dead' to the fact that you are an Israelite, like those in Ezekiel 37 ch." Some hints are given that I shall not fare well in the next world, which any one who reads the chapter in Ezekiel will see is quite against his comparison. The reader must not imagine that my prognosticator means Morgan to be a corruption of Mortjardin; he proves his point by Hebrew: but any philologist would tell him the true derivation of the name, and how Glamorgan came to get it. It will be of much comfort to those young men who have not got through to know that the tree of knowledge itself was once in the same case. And so good bye to 666 for the present, and the assumption that the enigma is to be solved by the united numeral forces of the letters of a word.
It is worthy of note that, as soon as my Budget commenced, two guardian spirits started up, fellow men as to the flesh, both totally unknown to me: they have stuck to me from first to last. James Smith, Esq., finally Nauticus, watches over my character in this world, and would fain preserve me from ignorance, folly, and dishonesty, by inclosing me in a magic circle of 3⅛ diameters in circumference. The round man in the three-cornered hole, finally William Thorn, M.D., takes charge of my future destiny, [160]and tries to bring me to the truth by unfolding a score of meanings—all right—of 666. He hints that I, and my wife, are servants of Satan: at least he desires us both to remember that we cannot serve God and Satan; and he can hardly mean that we are serving the first, and that he would have us serve the second. As becomes an interpreter of the Apocalypse, he uses seven different seals; but not more than one to one letter. If his seals be all signet-rings, he must be what Aristophanes calls a sphragidonychargocometical fellow. But—and many thanks to him for the same—though an M.D., he has not sent me a single vial. And so much for my tree of secular knowledge and my tree of spiritual life: I dismiss them with thanks from myself and thanks from my reader. The dual of the Pythagorean system was Isis and Diana; of the Jewish law, Moses and Aaron; and of the City of London, Gog and Magog; of the Paradoxiad, James Smith, Esq., and William Thorn, M.D.
September, 1866. Mr. James Biden[280] has favored me with some of his publications. He is a rival of Dr. Thorn; a prophet by name-right and crest-right. He is of royal descent through the De Biduns. He is the watchman of Ezekiel: God has told him so. He is the author of The True Church, a phrase which seems to have a book-meaning and a mission-meaning. He shall speak for himself:
"A crest of the Bidens has significance. It is a lion rampant between wings—wings in Scripture denote the flight of time. Thus the beasts or living creatures of the Revelations have each six wings, intimating a condition of mankind up to and towards the close of six thousand years of Bible teaching. The two wings of the crest would thus intimate power towards the expiration of 2000 years, as time is marked in the history of Great Britain.
"In a recent publication, The Pestilence, Why Inflicted, are given many reasons why the writer thinks himself to be the appointed watchman foretold by Ezekiel, chapters iii. and xxxiii. Among the reasons are many prophecies fulfilled in him. Of these it is now needful to note two as bearing especially on the subject of the reign of Darius.
"1.—In Daniel it is said, 'Darius the Median took the kingdom, being about threescore and two years old.'—Daniel v. 31.
"When 'Belshazzar' the king of the Chaldeans is found wanting, Darius takes the kingdom. It is not given him by the popular voice; he asserts his right, and this is not denied. He takes it when about sixty-two years of age. The language of Daniel is prophetic, and Darius has in another an antitype. The writer was born July 18th, 1803; and the claim was asserted at the close of 1865, when he was about sixty-two years of age.
"The claims which have been asserted demand a settled faith, and which could only be reached through a long course of divine teaching."
When I was a little boy at school, one of my school-fellows took it into his head to set up a lottery of marbles: the thing took, and he made a stony profit. Soon, one after another, every boy had his lottery, and it was, "I won't put into yours unless you put into mine." This knocked up the scheme. It will be the same with the prophets. Dr. Thorn, Mr. Biden, Mrs. Cottle,[281] etc. will grow imitators, until we are all pointed out in the Bible: but A will not admit B's claim unless B admits his. For myself, as elsewhere shown, I am the first Beast in the Revelations.
Every contraband prophet gets a few followers: it is a great point to make these sequacious people into Buridan's asses, which they will become when prophets are so numerous that there is no choosing.
SIR G. C. LEWIS.
An historical survey of the Astronomy of the Ancients. By the Rt. Hon. Sir G. C. Lewis.[282] 8vo. 1862.
There are few men of our day whom I admire more than the late Sir G. Lewis: he was honest, earnest, sagacious, learned, and industrious. He probably sacrificed his life to his conjunction of literature and politics: and he stood high as a minister of state in addition to his character as a man of letters. The work above named is of great value, and will be read for its intrinsic merit, consulted for its crowd of valuable references, quoted for its aid to one side of many a discussion, and opposed for its force against the other. Its author was also a wit and a satirist. I know of three classical satires of our day which are inimitable imitations: Mr. Malden's[283] Pragmatized Legends, Mr. Mansel's[284] Phrontisterion, and Sir G. Cornewall Lewis's Inscriptio Antiqua. In this last, HEYDIDDLEDIDDLETHECATANDTHEFIDDLE etc. is treated as an Oscan inscription, and rendered into Latin by approved methods. As few readers have seen it, I give the result:
"Hejus dedit libenter, dedit libenter. Deus propitius [est], deus [donatori] libenter favet. Deus in viarum [163]juncturâ ovorum dape [colitur], deus mundi. Deus in litatione voluit, benigno animo, hædum, taurum intra fines [loci sacri] portandos. Deus, bis lustratus, beat fossam sacræ libationis."[285]
How then comes the history of astronomy among the paradoxes? Simply because the author, so admirably when writing about what he knew, did not know what he did not know, and blundered like a circle-squarer. And why should the faults of so good a writer be recorded in such a list as the present? For three reasons: First, and foremost, because if the exposure be not made by some one, the errors will gradually ooze out, and the work will get the character of inaccurate. Nothing hurts a book of which few can fathom the depths so much as a plain blunder or two on the surface. Secondly, because the reviews either passed over these errors or treated them too gently, rather implying their existence than exposing them. Thirdly, because they strongly illustrate the melancholy truth, that no one knows enough to write about what he does not know. The distinctness of the errors is a merit; it proceeds from the clear-headedness of the author. The suppression in the journals may be due partly to admiration of the talent and energy which lived two difficult lives at once, partly to respect for high position in public affairs, partly to some of the critics being themselves men of learning only, unable to detect the errors. But we know that action and reaction are equal and contrary. If our generation take no notice of defects, and allow them to go down undetected among merits, the next generation will discover them, will perhaps believe us incapable of detecting them, at least will pronounce our judgment good for nothing, and will form an [164]opinion in which the merits will be underrated: so it has been, is, and will be. The best thing that can be done for the memory of the author is to remove the unsound part that the remainder may thrive. The errors do not affect the work; they occur in passages which might very well have been omitted: and I consider that, in making them conspicuous, I am but cutting away a deleterious fungus from a noble tree.
(P. 154). The periodic times of the five planets were stated by Eudoxus,[286] as we learn from Simplicius;[287] the following is his statement, to which the true times are subjoined, for the sake of comparison:
| STATEMENT OF EUDOXUS | TRUE TIME | |
| Mercury | 1 year | — 87d. 23h. |
| Venus | 1 " | — 224d. 16h. |
| Mars | 2 " | 1y. 321d. 23h. |
| Jupiter | 12 " | 11y. 315d. 14h. |
| Saturn | 30 " | 29y. 174d. 1h. |
Upon this determination two remarks may be made. First, the error with respect to Mercury and Venus is considerable; with respect to Mercury, it is, in round numbers, 365 instead of 88 days, more than four times too much. Aristotle remarks that Eudoxus distinguishes Mercury and Venus from the other three planets by giving them one sphere each, with the poles in common. The proximity of Mercury to the sun would render its course difficult to observe and to measure, but the cause of the large error with respect to Venus (130 days) is not apparent.
Sir G. Lewis takes Eudoxus as making the planets move round the sun; he has accordingly compared the geocentric periods of Eudoxus with our heliocentric periods. What greater blunder can be made by a writer on ancient astronomy than giving Eudoxus the Copernican system? If Mercury were a black spot in the middle of the sun it would of course move round the earth in a year, or appear to do so: let it swing a little on one side and the other of the sun, and the average period is still a year, with slight departures both ways. The same for Venus, with larger departures. Say that a person not much accustomed to the distinction might for once write down the mistake; how are we to explain its remaining in the mind in a permanent form, and being made a ground for such speculation as that of the difficulty of observing Mercury leading to a period four times what it ought to be, corrected in proof and published by an industrious and thoughtful person? Only in one way: the writer was quite out of his depth. This one case is conclusive; be it said with all respect for the real staple of the work and of the author. He knew well the difference of the systems, but not the effect of the difference: he is another instance of what I have had to illustrate by help of a very different person, that it is difficult to reason well upon matter which is not familiar.
(P. 254). Copernicus, in fact, supposed the axis of the earth to be always turned towards the Sun.(169) [(169). See Delambre, Hist. Astr. Mod., Vol. I, p. 96]. It was reserved to Kepler to propound the hypothesis of the constant parallelism of the earth's axis to itself.
If there be one thing more prominent than another in the work of Copernicus himself, in the popular explanations of it, and in the page of Delambre[288] cited, it is that the parallelism of the earth's axis is a glaring part of the [166]theory of Copernicus. What Kepler[289] did was to throw away, as unnecessary, the method by which Copernicus, per fas et nefas,[290] secured it. Copernicus, thinking of the earth's orbital revolution as those would think who were accustomed to the solid orbs—and much as the stoppers of the moon's rotation do now: why do they not strengthen themselves with Copernicus?—thought that the earth's axis would always incline the same end towards the sun, unless measures were taken to prevent it. He did take measures: he invented a compensating conical motion of the axis to preserve the parallelism; and, which is one of the most remarkable points of his system, he obtained the precession of the equinoxes by giving the necessary trifle more than compensation. What stares us in the face at the beginning of the paragraph to which the author refers?
"C'est donc pour arriver à ce parallelisme, ou pour le conserver, que Copernic a cru devoir recourir à ce mouvement égal et opposé qui détruit l'effet qu'il attribue si gratuitement au premier, de déranger le parallelisme."[291]
Parallelism at any price, is the motto of Copernicus: you need not pay so dear, is the remark of Kepler.
The opinions given by Sir G. Lewis about the effects of modern astronomy, which he does not understand and singularly undervalues, will now be seen to be of no authority. He fancies that—to give an instance—for the determination of a ship's place, the invention of chronometers has been far more important than any improvement in astronomical theory (p. 254). Not to speak of latitude,—though the omission is not without importance,—he ought to have known that longitude is found by the difference between what o'clock it is at Greenwich and at the ship's place, at [167]one absolute moment of time. Now if a chronometer were quite perfect—which no chronometer is, be it said—and would truly tell Greenwich mean time all over the world, it ought to have been clear that just as good a watch is wanted for the time at the place of observation, before the longitude of that place with respect to Greenwich can be found. There is no such watch, except the starry heaven itself: and that watch can only be read by astronomical observation, aided by the best knowledge of the heavenly motions.
I think I have done Sir G. Lewis's very excellent book more good than all the reviewers put together.
I will give an old instance in which literature got into confusion about astronomy. Theophrastus,[292] who is either the culprit or his historian, attributes to Meton,[293] the contriver of the lunar calendar of nineteen years, which lasts to this day, that his solstices were determined for him by a certain Phaeinus of Elis on Mount Lycabettus. Nobody else mentions this astronomer: though it is pretty certain that Meton himself made more than one appointment with him for the purpose of observing solstices; and we may be sure that if either were behind his time, it was Meton. For Phaeinus Helius is the shining sun himself; and in the astronomical poet Aratus[294] we read about the nineteen years of the shining sun:
Ἐννεακαιδέκα κύκλα φαεινοῦ ἠελίοιο.[295]
Some man of letters must have turned Apollo into Phaeinus of Elis; and there he is in the histories of astronomy to [168]this day. Salmasius[296] will have Aratus to have meant him, and proposes to read ἠλείοιο: he did not observe that Phaeinus is a very common adjective of Aratus, and that, if his conjecture were right, this Phaeinus would be the only non-mythical man in the poems of Aratus.
[When I read Sir George Lewis's book, the points which I have criticized struck me as not to be wondered at, but I did not remember why at the time. A Chancellor of the Exchequer and a writer on ancient astronomy are birds of such different trees that the second did not recall the first. In 1855 I was one of a deputation of about twenty persons who waited on Sir G. Lewis, as Chancellor of the Exchequer, on the subject of a decimal coinage. The deputation was one of much force: Mr. Airy, with myself and others, represented mathematics; William Brown,[297] whose dealings with the United States were reckoned by yearly millions, counted duodecimally in England and decimally in America, was the best, but not the only, representative of commerce. There were bullionists, accountants, retailers, etc. Sir G. L. walked into the room, took his seat, and without waiting one moment, began to read the deputation a smart lecture on the evils of a decimal coinage; it would require alteration of all the tables, it would impede calculation, etc. etc. Of those arguments against it which weighed with many of better knowledge than his, he obviously knew nothing. The members of the deputation began to make their statements, and met with curious denials. He interrupted me with "Surely there is no doubt that the calculations of our books of arithmetic are easier [169]than those in the French books." He was not aware that the universally admitted superiority of decimal calculation made many of those who prefer our system for the market and the counter cast a longing and lingering look towards decimals. My answer and the smiles which he saw around, made him give a queer puzzled look, which seemed to say, "I may be out of my depth here!" His manner changed, and he listened. I saw both the slap-dash mode in which he dealt with subjects on which he had not thought, and the temperament which admitted suspicion when the means of knowledge came in his way. Having seen his two phases, I wonder neither at his more than usual exhibition of shallowness when shallow, nor at the intensity of the contrast when he had greater depth.]
DECIMAL COINAGE.
Among the paradoxers are the political paradoxers who care not how far they go in debate, their only object being to carry the House with them for the current evening. What I have said of editors I repeat of them. The preservation of a very marked instance, the association of political recklessness with cyclometrical and Apocalyptic absurdity, may have a tendency to warn, not indeed any hardened public-man and sinner, but some young minds which have yearnings towards politics, and are in formation of habits.
In the debate on decimal coinage of July 12, 1855, Mr. Lowe,[298] then member for Kidderminster, an effective speaker and a smart man, exhibited himself in a speech on which I wrote a comment for the Decimal Association. I have seldom seen a more wretched attempt to distort the points of a public question than the whole of this speech. Looking at the intelligence shown by the speaker on other occasions, [170]it is clear that if charity, instead of believing all things, believed only all things but one, he might tremble for his political character; for the honesty of his intention on this occasion might be the incredible exception. I give a few paragraphs with comments:
"In commenting on the humorous, but still argumentative speech of Mr. Lowe, the member for Kidderminster, we may observe, in general, that it consists of points which have been several times set forth, and several times answered. Mr. Lowe has seen these answers, but does not allude to them, far less attempt to meet them. There are, no doubt, individuals, who show in their public speaking the outward and visible signs of a greater degree of acuteness than they can summon to guide their private thinking. If Mr. Lowe be not one of these, if the power of his mind in the closet be at all comparable to the power of his tongue in the House, it may be suspected that his reserve with respect to what has been put forward by the very parties against whom he was contending, arises from one or both of two things—a high opinion of the arguments which he ignored—a low opinion of the generality of the persons whom he addressed. [Both, I doubt not].
But he cannot mean that Englishmen in general are so easily managed. And as to Jonathan, who is but John lengthened out a little, he would see creation whittled into chips before he would even split what may henceforth be called the Kidderminster difference. The House, not unmoved—for it laughed—with sly humor decided that the introduction of the florin had been "eminently successful and satisfactory."
The truth is that Mr. Lowe here attacks nothing except the coexistence of the florin and half-crown. We are endeavoring to abolish the half-crown. Let Mr. Lowe join us; and he will, if we succeed, be relieved from the pressure on his pocket which must arise from having the turn of the market always against him.
Now, if Mr. Lowe insists on it that our integer is the pound, he is bound to admit that the present integer is the pound, of which a shilling, etc., are fractions. The next time he has a chop and a pint of stout in the city, the waiter should say—"A pound, sir, to you," and should add, "Please to remember the waiter in integers." Mr. Lowe fancies that when he pays one and sixpence, he pays in integers, and so he does, if his integer be a penny or a sixpence. Let him bring his mind to contemplate a mil as the integer, the lowest integer, and the seven cents five mils which he would pay under the new system would be payment in integers also. But, as it happens with some others, he looks up the present system, with Cocker,[299] and Walkingame,[300] and always looks down the proposed system. The word decimal is obstinately associated with fractions, for which there is no need. Hence it becomes so much of a bugbear, that, to parody the lines of Pope, which probably suggested one of Mr. Lowe's phrases—
"Dinner he finds too painful an endeavor,
Condemned to pay in decimals for ever."
|
"The present system, however, had not yet been changed into decimal system. That change might appear very easy to accomplished mathematicians and men of science, but it was one which it would be very difficult to carry out. (Hear, hear). What would have to be done? Every sum would have to be reduced into a vulgar fraction of a pound, and then divided by the decimal of a pound—a pleasant sum for an old applewoman to work out!" (Hear, hear, and laughter.) |
A pleasant sum even for an accomplished mathematician. What does divided by the decimal of a pound mean? Perhaps it means reduced to the decimal of a pound! Mr. Lowe supposes, as many others do, that, after the change, all calculations will be proposed in old money, and then converted into new. He cannot hit the [174]idea that the new coins will take the place of the old. This lack of apprehension will presently appear further. |
|
"It would not be an agreeable task, even for some members of that House, to reduce 4½d., or nine half-pence, to mils." (Hear, hear.) |
Let the members be assured that nine half-pence will be, for every practical purpose, 18 mils. But now to the fact asserted. Davies Gilbert[301] used to maintain that during the long period he sat in the House, he never knew more than three men in it, at one time, who had a tolerable notion of fractions. [I heard him give the names of three at the time when he spoke: they were Warburton,[302] Pollock,[303] and Hume.[304] He himself was then out of Parliament.] Joseph Hume affirmed that he had never met with more than ten members who were arithmeticians. But both these gentlemen had a high standard. Mr. Lowe has given a much more damaging opinion. He evidently means that the general run of members could not do his question. It is done as follows: Since farthings gain on mils, at the rate of a whole mil in 24 farthings (24 farthings being 25 mils), it is clear that 18 farthings being three-quarters of 24 farthings, will gain three-quarters of a mil; that is, 18 farthings are eighteen [175]mils and three-quarters of a mil. Any number of farthings is as many mils and as many twenty-fourths of a mil. To a certain extent, we feel able to protest against the manner in which Kidderminster has treated the other constituencies. We do not hold it impossible to give the Members of the House in general a sufficient knowledge of the meaning and consequences of the decimal succession of units, tens, hundreds, thousands, etc.; and we believe that there are in the House itself competent men, in number enough to teach all the rest. All that is wanted is the power of starting from the known to arrive at the unknown. Now there is one kind of decimals with which every member is acquainted—the Chiltern Hundreds. If public opinion would enable the competent minority to start from this in their teaching, not as a basis, but as an alternative, in three weeks the fundamentals would be acquired, and members in general would be as fit to turn 4½d. into mils, as any boys on the lower forms of a commercial school. For a long period of years, allusion to the general ignorance of arithmetic, has been a standing mode of argument, and has always been well received: whenever one member describes others as knownothings, those others cry Hear to the country in a transport of delight. In the meanwhile the country is gradually arriving at the conclusion that a true joke is no joke. |
|
"The main objection was, if they went below 6d., that the new scale of coins would not be commensurate in any finite ratio with anything in this new currency of mils." |
Fine words, wrongly used. The new coins are commensurable with, and in a finite ratio to, the old ones. The farthing is to the mil as 25 to 24. The speaker has something here in the bud, which we shall presently meet with in the flower; and fallacies are more easily nipped in flower than in bud. [176] |
|
"No less than five of our present coins must be called in, or else—which would be worse—new values must be given to them." |
This dreadful change of value consists in sixpence farthing going to the half-shilling instead of sixpence. Whether the new farthings be called mils or not is of no consequence. |
|
"If a poor man put a penny in his pocket, it would come out a coin of different value, which he would not understand. Suppose he owed another man a penny, how was he to pay him ? Was he to pay him in mils? Four mils would be too little, and five mils would be too much. The hon. gentlemen said there would be only a mil between them. That was exactly it. He believed there would be a 'mill' between them." (Much laughter.) |
Mr. Lowe, who cannot pass a half-crown for more than a florin, or get in a florin at less than half-a-crown, has such a high faith in the sterner stuff of his fellow countrymen, that he believes any two of them would go to fisty cuffs for the 25th part of a farthing. He reasons thus: He has often heard in the streets, "I'd fight you for the fiftieth part of a farden:" and having (that is, for a Member) a notion both of fractions and logic, he infers that those who would fight for the 50th of a farthing would, a fortiori, fight for a 25th. His mistake arises from his not knowing that when a person offers to fight another for 1/200d., he really means to fight for love; and that the stake is merely a matter of form, a feigned issue, a pro forma report of progress. Do the Members of the House think they have all the forms to themselves? |
|
"What would be the present expression for four-pence? Why, 0.166 (a laugh); for threepence? .0125; for a penny? .004166, and so on ad infinitum (a laugh); for a half-penny? .002083 ad infinitum. (A laugh). What would be the present expression for a farthing? Why, .0010416 ad infinitum. (A laugh). And this was the system which was to cause such a saving in figures, and these were the quantities into which the poor would have to reduce the current coin of the realm. (Cheers). With every respect for decimal fractions, of which he boasted no profound knowledge, he doubted whether the poor were equal to mental arithmetic of this kind, (hear, hear) and he hoped the adoption of the system would be deferred until there were some proof that they would be able to understand it; for, after all, this was the question of the poor, and the whole weight of the change would fall upon them. Let the rich by all means have permission to perplex themselves by any division of a pound they pleased; but do not let them, by any experiment like this, impose difficulties upon the poor and compel men to carry ready-reckoners in their pocket to give them all these fractional quantities." (Hear, hear.) |
We should hardly believe all this to be uttered in earnest, if we had not known [177]that several persons who have not Mr. Lowe's humor, nevertheless have his impressions on this point. It must therefore be answered; but how is this to be done seriously? Dialogue between a member of Parliament and an orange-boy, three days after the introduction of the complete decimal system. The member, going down to the House, wants oranges to sustain his voice in a two hours' speech on moving that 100000l. be placed at the disposal of Her Majesty, to supply the poor with ready-reckoners. Boy. Fine oranges! two a penny! two a penny! [178] Member. Here boy, two! Now, how am I to pay you? Boy. Give you change, your honor. Member. Ah! but how? Where's your ready-reckoner? Boy. I sells a better sort nor them. Mine's real Cheyny. Member. But you see a farthing is now .0014166666 ad infinitum, and if we multiply this by 4—— Boy. Hold hard, Guv'ner; I sees what you're arter. Now what'll you stand if I puts you up to it? which Bill Smith he put me up in two minutes, cause he goes to the Ragged School. Member. You don't mean that you do without a book! Boy. Book be blowed. Come now, old un, here's summut for both on us. I got a florin, you gives me a half-a-crown for it, and I larns you the new money, gives you your oranges, and calls you a brick into the bargain. Member (to himself). Never had such a chance of getting off half-a-crown for value since that —— fellow Bowring carried his crochet. (Aloud.) Well, boy, it's a bargain. Now! Boy. Why, look 'e here, my trump, its a farden more to the tizzy—that's what it is. Member. What's that? Boy. Why, you knows a sixpence when you sees it. (Aside). Blest if I think he does! Well, its six browns and a farden now. A lady buys two oranges, and forks [179]out a sixpence; well in coorse, I hands over fippence farden astead of fippence. I always gives a farden more change, and takes according. Member (in utter surprise, lets his oranges tumble into the gutter). Never mind! They won't be wanted now. (Walks off one way. Boy makes a pass of naso-digital mesmerism, and walks off the other way). |
To the poor, who keep no books, the whole secret is "Sixpence farthing to the half shilling, twelve pence halfpenny to the shilling." The new twopence halfpenny, or cent, will be at once five to the shilling.
In conclusion, we remark that three very common misconceptions run through the hon. Member's argument; and, combined in different proportions, give variety to his patterns.
First, he will have it that we design to bring the uneducated into contact with decimal fractions. If it be so, it will only be as M. Jourdain was brought into contact with prose. In fact, Quoi! quand je dis, Nicole, apportez-moi mes pantoufles, c'est de la prose?[305] may be rendered: "What! do you mean that ten to the florin is a cent a piece must be called decimal reckoning?" If we had to comfort a poor man, horror-struck by the threat of decimals, we should tell him what manner of fractions had been inflicted upon him hitherto; nothing less awful than quarto-duodecimo-vicesimals, we should assure him.
Secondly, he assumes that the penny, such as it now is, will remain, as a coin of estimation, after it has ceased to be a coin of exchange; and that the mass of the people will continue to think of prices in old pence, and to calculate them in new ones, or else in new mils. No answer is required to this, beyond the mere statement of the nature of the assumption and denial.
Thirdly, he attributes to the uneducated community a want of perception and of operative power which really does not belong to them. The evidence offered to the Committee of the House shows that no fear is entertained on this point by those who come most in contact with farthing purchasers. And this would seem to be a rule,—that is, fear of the intelligence of the lower orders in the minds of those who are not in daily communication with them, no fear at all in the minds of those who are.
A remarkable instance of this distinction happened five-and-twenty years ago. The Admiralty requested the Astronomical Society to report on the alterations which should be made in the Nautical Almanac, the seaman's guide-book over the ocean. The greatest alteration proposed was the description of celestial phenomena in mean (or clock time), instead of apparent (or sundial) time, till then always employed. This change would require that in a great many operations the seaman should let alone what he formerly altered by addition or subtraction, and alter by addition or subtraction what he formerly let alone; provided always that what he formerly altered by addition he should, when he altered at all, alter by subtraction, and vice versa. This was a tolerably difficult change for uneducated skippers, working by rules they had only learned by rote. The Astronomical Society appointed a Committee of forty, of whom nine were naval officers or merchant seamen [I was on this Committee]. Some men of science were much afraid of the change. They could not trust an ignorant skipper or mate to make those alterations in their routine, on the correctness of which the ship might depend. Had the Committee consisted of men of science only, the change might never have been ventured on. But the naval men laughed, and said there was nothing to fear; and on their authority the alteration was made. The upshot was, that, after the new almanacs appeared, not a word of complaint was ever heard on the matter. Had the House of Commons had to [181]decide this question, with Mr. Lowe to quote the description given by Basil Hall[306] (who, by the way, was one of the Committee) of an observation on which the safety of the ship depended, worked out by the light of a lantern in a gale of wind off a lee shore, this simple and useful change might at this moment have been in the hands of its tenth Government Commission.
[Aug. 14, 1866. The Committee was appointed in the spring of 1830: it consisted of forty members. Death, of course, has been busy; there are now left Lord Shaftesbury,[307] Mr. Babbage,[308] Sir John Herschel,[309] Sir Thomas Maclear[310] (Astronomer Royal at the Cape of Good Hope), Dr. Robinson[311] (of Armagh), Sir James South,[312] Lord Wrottesley,[313] and myself].
THE TONAL SYSTEM.
Project of a new system of arithmetic, weight, measure, and coins, proposed to be called the tonal system, with sixteen to the base. By J. W. Mystrom.[314] Philadelphia, 1862, 8vo.
That is to say, sixteen is to take the place of ten, and to be written 10. The whole language is to be changed; every man of us is to be sixteen-stringed Jack and every woman sixteen-stringed Jill. Our old one, two, three, up to sixteen, are to be (Noll going for nothing, which will please those who dislike the memory of Old Noll) replaced by An, De, Ti, Go, Su, By, Ra, Me, Ni, Ko, Hu, Vy, La, Po, Fy, Ton; and then Ton-an, Ton-de, etc. for 17, 18, etc. The number which in the system has the symbol
28(13)5(11)7(14)0(15)
(using our present compounds instead of new types) is to be pronounced
Detam-memill-lasan-suton-hubong-ramill-posanfy.
The year is to have sixteen months, and here they are:
Anuary, Debrian, Timander, Gostus,
Suvenary, Bylian, Ratamber, Mesudius,
Nictoary, Kolumbian, Husamber, Vyctorius,
Lamboary, Polian, Fylander, Tonborius.
Surely An-month, De-month, etc. would do as well. Probably the wants of poetry were considered. But what are we to do with our old poets? For example—
"It was a night of lovely June,
High rose in cloudless blue the moon."
Let us translate—
"It was a night of lovely Nictoary,
High rose in cloudless blue the (what, in the name of all that is absurd?)."
And again, Fylander thrown into our December! What is [183]to become of those lines of Praed, which I remember coming out when I was at Cambridge,—
"Oh! now's the time of all the year for flowers and fun, the Maydays;
To trim your whiskers, curl your hair, and sinivate the ladies."
If I were asked which I preferred, this system or that of Baron Ferrari[315] already mentioned, proceeding by twelves, I should reply, with Candide, when he had the option given of running the gauntlet or being shot: Les volontés sont libres, et je ne veux ni l'un ni l'autre.[316] We can imagine a speculator providing such a system for Utopia as it would be in the mind of a Laputan: but to explain how an engineer who has surveyed mankind from Philadelphia to Rostof on the Don should for a moment entertain the idea of such a system being actually adopted, would beat a jury of solar-system-makers, though they were shut up from the beginning of Anuary to the end of Tonborius. When I see such a scheme as this imagined to be practicable, I admire the wisdom of Providence in providing the quadrature of the circle, etc., to open a harmless sphere of action to the possessors of the kind of ingenuity which it displays. Those who cultivate mathematics have a right to speak strongly on such efforts of arithmetic as this: for, to my knowledge, persons who have no knowledge are frequently disposed to imagine that their makers are true brothers of the craft, a little more intelligible than the rest.
SOME SMALL PARADOXERS.
An attack on the Newtonian mechanics; revolution by gravitation demonstrably impossible; much to be said for the earth being the immovable center. A good analysis of contents at the beginning, a thing seldom found. The author has followed up his attack in a paper submitted to the British Association, but which it appears the Association declined to consider. It is entitled—
Victoria Toto Cœlo; or, Modern Astronomy recast. London, 1863, 8vo.
At the end is a criticism of Sir G. Lewis's History of Ancient Astronomy.
On the definition and nature of the Science of Political Economy. By H. Dunning Macleod,[319] Esq. Cambridge, 1862, 8vo.
A paper read—but, according to the report, not understood—at the British Association. There is a notion that political economy is entirely mathematical; and its negative quantity is strongly recommended for study: it contains "the whole of the Funds, Credit, 32 parts out of 33 of the value of Land...." The mathematics are described as consisting of—first, number, or Arithmetic; secondly, the theory of dependent quantities, subdivided into dependence by cause and effect, and dependence by simultaneous variations; thirdly, "independent quantities or unconnected events, which is the theory of probabilities." I am not ashamed, having the British Association as a co-non-intelligent, to say I do not understand this: there is a paradox in it, and the author should give further explanation, especially of his negative quantity. Mr. Macleod has gained [185]praise from great names for his political economy; but this, I suspect, must have been for other parts of his system.
On the principles and practice of just Intonation, with a view to the abolition of temperament.... By General Perronet Thompson.[320] Sixth Edition. London, 1862, 8vo.
Here is General Thompson again, with another paradox: but always master of the subject, always well up in what his predecessors have done, and always aiming at a useful end. He desires to abolish temperament by additional keys, and has constructed an enharmonic organ with forty sounds in the octave. If this can be introduced, I, for one, shall delight to hear it: but there are very great difficulties in the way, greater than stood even in the way of the repeal of the bread-tax.
In a paper on the beats of organ-pipes and on temperament published some years ago, I said that equal temperament appeared to me insipid, and not so agreeable as the effect of the instrument when in progress towards being what is called out of tune, before it becomes offensively wrong. There is throughout that period unequal temperament, determined by accident. General Thompson, taking me one way, says I have launched a declaration which is likely to make an epoch in musical practice; a public musical critic, taking me another way, quizzes me for preferring music out of tune. I do not think I deserve either one remark or the other. My opponent critic, I suspect, takes equally tempered and in tune to be phrases of one meaning. But by equal temperament is meant equal distribution among all the keys of the error which an instrument must have, which, with twelve sounds only in the octave, professes to be fit for all the keys. I am reminded of the equal temperament which was once applied to the postmen's jackets. The coats were all made for the average man: the [186]consequence was that all the tall men had their tails too short; all the short men had them too long. Some one innocently asked why the tall men did not change coats with the short ones.
A diagram illustrating a discovery in the relation of circles to right-lined geometrical figures. London, 1863, 12mo.
The circle is divided into equal sectors, which are joined head and tail: but a property is supposed which is not true.
An attempt to assign the square roots of negative powers; or what is √ -1? By F.H. Laing.[321] London, 1863, 8vo.
If I understand the author, -a and +a are the square roots of -a2, as proved by multiplying them together. The author seems quite unaware of what has been done in the last fifty years.
BYRNE'S DUAL ARITHMETIC.
Dual Arithmetic. A new art. By Oliver Byrne.[322] London, 1863, 8vo.
The plan is to throw numbers into the form a(1.1)b (1.01)c (1.001)d... and to operate with this form. This is an ingenious and elaborate speculation; and I have no doubt the author has practised his method until he could surprise any one else by his use of it. But I doubt if he will persuade others to use it. As asked of Wilkins's universal language, Where is the second man to come from?
An effective predecessor in the same line of invention [187]was the late Mr. Thomas Weddle,[323] in his "New, simple, and general method of solving numeric equations of all orders," 4to, 1842. The Royal Society, to which this paper was offered, declined to print it: they ought to have printed an organized method, which, without subsidiary tables, showed them, in six quarto pages, the solution (x=8.367975431) of the equation
1379.664 x622 + 2686034 × 10432 x152 - 17290224 × 10518 x60 + 2524156 × 10574 = 0.
The method proceeds by successive factors of the form, a being the first approximation, a × 1.b × 1.0c × 1.00d.... In my copy I find a few corrections made by me at the time in Mr. Weddle's announcement. "It was read before that learned body [the R. S.] and they were pleased [but] to transmit their thanks to the author. The en[dis]couragement which he received induces [obliges] him to lay the result of his enquiries in this important branch of mathematics before the public [, at his own expense; he being an usher in a school at Newcastle]." Which is most satirical, Mr. Weddle or myself? The Society, in the account which it gave of this paper, described it as a "new and remarkably simple method" possessing "several important advantages." Mr. Rutherford's[324] extended value of π was read at the very next meeting, and was printed in the Transactions; and very properly: Mr. Weddle's paper was excluded, and very very improperly.
HORNER'S METHOD.
I think it may be admited that the indisposition to look at and encourage improvements of calculation which once [188]marked the Royal Society is no longer in existence. But not without severe lessons. They had the luck to accept Horner's[325] now celebrated paper, containing the method which is far on the way to become universal: but they refused the paper in which Horner developed his views of this and other subjects: it was printed by T. S. Davies[326] after Horner's death. I make myself responsible for the statement that the Society could not reject this paper, yet felt unwilling to print it, and suggested that it should be withdrawn; which was done.
But the severest lesson was the loss of Barrett's Method,[327] now the universal instrument of the actuary in his highest calculations. It was presented to the Royal Society, and refused admission into the Transactions: Francis Baily[328] printed it. The Society is now better informed: "live and learn," meaning "must live, so better learn," ought to be the especial motto of a corporation, and is generally acted on, more or less.
Horner's method begins to be introduced at Cambridge: it was published in 1820. I remember that when I first went to Cambridge (in 1823) I heard my tutor say, in conversation, there is no doubt that the true method of solving equations is the one which was published a few years ago in the Philosophical Transactions. I wondered it was not taught, but presumed that it belonged to the higher mathematics. This Horner himself had in his head: and in a sense it is true; for all lower branches belong to the higher: but he would have stared to have been told that he, Horner, [189]was without a European predecessor, and in the distinctive part of his discovery was heir-at-law to the nameless Brahmin—Tartar—Antenoachian—what you please—who concocted the extraction of the square root.
It was somewhat more than twenty years after I had thus heard a Cambridge tutor show sense of the true place of Horner's method, that a pupil of mine who had passed on to Cambridge was desired by his college tutor to solve a certain cubic equation—one of an integer root of two figures. In a minute the work and answer were presented, by Horner's method. "How!" said the tutor, "this can't be, you know." "There is the answer, Sir!" said my pupil, greatly amused, for my pupils learnt, not only Horner's method, but the estimation it held at Cambridge. "Yes!" said the tutor, "there is the answer certainly; but it stands to reason that a cubic equation cannot be solved in this space." He then sat down, went through a process about ten times as long, and then said with triumph: "There! that is the way to solve a cubic equation!"
I think the tutor in this case was never matched, except by the country organist. A master of the instrument went into the organ-loft during service, and asked the organist to let him play the congregation out; consent was given. The stranger, when the time came, began a voluntary which made the people open their ears, and wonder who had got into the loft: they kept their places to enjoy the treat. When the organist saw this, he pushed the interloper off the stool, with "You'll never play 'em out this side Christmas." He then began his own drone, and the congregation began to move quietly away. "There," said he, "that's the way to play 'em out!"
I have not scrupled to bear hard on my own university, on the Royal Society, and on other respectable existences: being very much the friend of all. I will now clear the Royal Society from a very small and obscure slander, simply because I know how. This dissertation began with [190]the work of Mr. Oliver Byrne, the dual arithmetician, etc. This writer published, in 1849, a method of calculating logarithms.[329] First, a long list of instances in which, as he alleges, foreign discoverers have been pillaged by Englishmen, or turned into Englishmen: for example, O'Neill,[330] so called by Mr. Byrne, the rectifier of the semi-cubical parabola claimed by the Saxons under the name of Neal: the grandfather of this mathematician was conspicuous enough as Neal; he was archbishop of York. This list, says the writer, might be continued without end; but he has mercy, and finishes with his own case, as follows:—"About twenty years ago, I discovered this method of directly calculating logarithms. I could generally find the logarithm of any number in a minute or two without the use of books or tables. The importance of the discovery subjected me to all sorts of prying. Some asserted that I committed a table of logarithms to memory; others attributed it to a peculiar mental property; and when Societies and individuals failed to extract my secret, they never failed to traduce the inventor and the invention. Among the learned Societies, the Royal Society of London played a very base part. When I have more space and time at my disposal, I will revert to this subject again."
Such a trumpery story as this remains unnoticed at the time; but when all are gone, a stray copy from a stall falls into hands which, not knowing what to make of it, make history of it. It is a very curious distortion. The reader may take it on my authority, that the Royal Society played no part, good or bad, nor had the option of playing a part. [191]But I myself pars magna fui:[331] and when the author has "space and time" at his disposal, he must not take all of them; I shall want a little of both.
ARE ATOMS WORLDS?
The mystery of being; or are ultimate atoms inhabited worlds? By Nicholas Odgers.[332] Redruth and London, 1863, 8vo.
This book, as a paradox, beats quadrature, duplication, trisection, philosopher's stone, perpetual motion, magic, astrology, mesmerism, clairvoyance, spiritualism, homœopathy, hydropathy, kinesipathy, Essays and Reviews, and Bishop Colenso,[333] all put together. Of all the suppositions I have given as actually argued, this is the one which is hardest to deny, and hardest to admit. Reserving the question—as beyond human discussion—whether our particles of carbon, etc. are clusters of worlds, the author produces his reasons for thinking that they are at least single worlds. Of course—though not mentioned—the possibility is to be added of the same thing being true of the particles which make up our particles, and so down, for ever: and, on the other hand, of our planets and stars as being particles in some larger universe, and so up, for ever.
"Great fleas have little fleas upon their backs to bite 'em,
And little fleas have lesser fleas, and so ad infinitum.
And the great fleas themselves, in turn, have greater fleas to go on;
While these again have greater still, and greater still, and so on."[334]
I have often had the notion that all the nebulæ we see, including our own, which we call the Milky Way, may be particles of snuff in the box of a giant of a proportionately [192]larger universe. Of course the minim of time—a million of years or whatever the geologists make it[335]—which our little affair has lasted, is but a very small fraction of a second to the great creature in whose nose we shall all be in a few tens of thousands of millions of millions of millions of years.
All this is quite possible, and the probabilities for and against are quite out of reach. Perhaps also all the worlds, both above and below us, are fac-similes of our own. If so, away goes free will for good and all; unless, indeed, we underpin our system with the hypothesis that all the fac-simile bodies of different sizes are actuated by a common soul. These acute supplementary notions of mine go far to get rid of the difficulty which some have found in the common theory that the soul inhabits the body: it has been stated that there is, somewhere or another, a world of souls which communicate with their bodies by wondrous filaments of a nature neither mental nor material, but of a tertium quid fit to be a go-between; as it were a corporispiritual copper encased in a spiritucorporeal gutta-percha. My theory is that every soul is everywhere in posse, as the schoolmen said, but not anywhere in actu, except where it finds one of its bodies. These a priori difficulties being thus removed, the system of particle-worlds is reduced to a dry question of fact, and remitted to the decision of the microscope. And a grand field may thus be opened, as optical science progresses! For the worlds are not fac-similes of ours in time: there is not a moment of our past, and not a moment of our future, but is the present of one or more of the particles. A will write the death of Cæsar, and B the building of the Pyramids, by actual observation of the processes with a power of a thousand millions; C will discover the commencement of the Millennium, and D the [193]termination of Ersch and Gruber's Lexicon,[336] as mere physical phenomena. Against this glorious future there is a sad omen: the initials of the forerunner of this discovery are—NO!
THE SUPERNATURAL.
The History of the Supernatural in all ages and nations, and in all Churches, Christian and Pagan: demonstrating a universal faith. By Wm. Howitt.[337] London, 2 vols. 8vo. 1863.
Mr. Howitt is a preacher of spiritualism. He cements an enormous collection of alleged facts with a vivid outpouring of exhortation, and an unsparing flow of sarcasm against the scorners of all classes. He and the Rev. J. Smith[338] (ante, 1854) are the most thoroughgoing universalists of all the writers I know on spiritualism. If either can insert the small end of the wedge, he will not let you off one fraction of the conclusion that all countries, in all ages, have been the theaters of one vast spiritual display. And I suspect that this consequence cannot be avoided, if any part of the system be of truly spiritual origin. Mr. Howitt treats the philosophers either as ignorant babies, or as conscious spirit-fearers: and seems much inclined to accuse the world at large of dreading, lest by the actual presence of the other world their Christianity should imbibe a spiritual element which would unfit it for the purposes of their lives.
FROM MATTER TO SPIRIT.
From Matter to Spirit. By C. D. With a preface by A. B.[339] London, 1863, 8vo.
This is a work on Spiritual Manifestations. The author upholds the facts for spiritual phenomena: the prefator suspends his opinion as to the cause, though he upholds the facts. The work begins systematically with the lower class of phenomena, proceeds to the higher class, and offers a theory, suggested by the facts, of the connection of the present and future life. I agree in the main with A. B.; but can, of course, make none but horrescent reference to his treatment of the smaller philosophers. This is always the way with your paradoxers: they behave towards orthodoxy as the thresher fish behaves towards the whale. But if true, as is said, that the drubbing clears the great fish of parasites which he could not otherwise get rid of, he ought to bear no malice. This preface retorts a little of that contempt which the "philosophical world" has bestowed with heaped measure upon those who have believed their senses, and have drawn natural, even if hasty, inferences. There is philosophercraft as well as priestcraft, both from one source, both of one spirit. In English cities and towns, the minister of religion has been tamed: so many weapons are bared against him when he obtrudes his office in a dictatory manner, that, as a rule, there is no more quiet and modest member of society than the urban clergyman. Domination over religious belief is reserved for the exclusive use of those who admit the right: the rare exception to this mode of behavior is laughed at as a bigot, or shunned as a nuisance. But the overbearing minister of nature, who snaps you with unphilosophical as the clergyman once frightened you with infidel, is still a recognized member of society, wants taming, and will get it. He wears the priest's cast-off [195]clothes, dyed to escape detection: the better sort of philosophers would gladly set him to square the circle.
The book just named appeared about the same time as this Budget began in the Athenæum. It was commonly attributed, the book to my wife, the preface to myself. Some time after, our names were actually announced by the publisher, who ought to know. It will be held to confirm this statement that I announce our having in our possession some twenty reviews of different lengths, and of all characters: who ever collects a number of reviews of a book, except the author?
A great many of these reviews settle the matter a priori. If there had been spirits in the matter, they would have done this, and they would not have done that. Jean Meslier[340] said there could be no God over all, for, if there had been one, He would have established a universal religion. If J. M. knew that, J. M. was right: but if J. M. did not know that, then J. M. was on the "high priori road," and may be left to his course. The same to all who know what spirits would do and would not do.
A. B. very distinctly said that he knew some of the asserted facts, believed others on testimony, but did not pretend to know whether they were caused by spirits, or had some unknown and unimagined origin. This he said as clearly as I could have said it myself. But a great many persons cannot understand such a frame of mind: their own apparatus is a kind of spirit-level, and their conclusion on any subject is the little bubble, which is always at one end or the other. Many of the reviewers declare that A. B. is a secret believer in the spirit-hypothesis: and one of them wishes that he had "endorsed his opinion more boldly." According to this reviewer, any one who writes "I boldly [196]say I am unable to choose," contradicts himself. In truth, a person who does say it has a good deal of courage, for each side believes that he secretly favors the other; and both look upon him as a coward. In spite of all this, A. B. boldly repeats that he feels assured of many of the facts of spiritualism, and that he cannot pretend to affirm or deny anything about their cause.
The great bulk of the illogical part of the educated community—whether majority or minority I know not; perhaps six of one and half-a-dozen of the other—have not power to make a distinction, cannot be made to take a distinction, and of course, never attempt to shake a distinction. With them all such things are evasions, subterfuges, come-offs, loopholes, etc. They would hang a man for horse-stealing under a statute against sheep-stealing; and would laugh at you if you quibbled about the distinction between a horse and a sheep. I divide the illogical—I mean people who have not that amount of natural use of sound inference which is really not uncommon—into three classes:—First class, three varieties: the Niddy, the Noddy, and the Noodle. Second class, three varieties: the Niddy-Noddy, the Niddy-Noodle, and the Noddy-Noodle. Third class, undivided: the Niddy-Noddy-Noodle. No person has a right to be angry with me for more than one of these subdivisions.
The want of distinction was illustrated to me, when a boy, about 1820, by the report of a trial which I shall never forget: boys read newspapers more keenly than men. Every now and then a bench of country magistrates rather astonishes the town populations, accustomed to rub their brains[341] against one another. Such a story as the following would, [197]in our day, bring down grave remarks from above: but I write of the olden (or Eldon[342]) time, when nothing but conviction in a court of record would displace a magistrate. In that day the third-class amalgamator of distinct things was often on the bench of quarter-sessions.
An attorney was charged with having been out at night poaching. A clear alibi was established; and perjury had certainly been committed. The whole gave reason to suspect that some ill-willers thought the bench disliked the attorney so much that any conviction was certain on any evidence. The bench did dislike the attorney: but not to the extent of thinking he could snare any partridges in the fields while he was asleep in bed, except the dream-partridges which are not always protected by the dream-laws. So the chairman said, "Mr. ——, you are discharged; but you should consider this one of the most fortunate days of your life." The attorney indignantly remonstrated, but the magistrate was right; for he said, "Mr. ——, you have frequently been employed to defend poachers: have you been careful to impress upon them the enormity of their practices?" It appeared in a wrangling conversation that the magistrates saw little moral difference between poaching and being a poacher's professional defender without lecturing him on his wickedness: but they admitted with reluctance, that there was a legal distinction; and the brain of N3 could no further go. This is nearly fifty years ago; and Westernism was not quite extinct. If the present lords of the hills and the valleys want to shine, let them publish a true history of their own order. I am just old enough to remember some of the last of the squires and parsons who protested against teaching the poor to read and write. They now write books for the working classes, give them lectures, and the like. There is now no class, as a class, more highly educated, broadly educated, and deeply educated, [198]than those who were, in old times, best described as partridge-popping squireens. I have myself, when a boy, heard Old Booby speaking with pride of Young Booby as having too high a spirit to be confined to books: and I suspected that his dislike to teaching the poor arose in fact from a feeling that they would, if taught a little, pass his heir.
A. B. recommended the spirit-theory as an hypothesis on which to ground inquiry; that is, as the means of suggestion for the direction of inquiry. Every person who knows anything of the progress of physics understands what is meant; but not the reviewers I speak of. Many of them consider A. B. as adopting the spirit-hypothesis. The whole book was written, as both the authors point out, to suggest inquiry to those who are curious; C. D. firmly believing, A. B. as above. Neither C. D. nor A. B. make any other pretence. Both dwell upon the absence of authentications and the suppression of names as utterly preventive of anything like proof. And A. B. says that his reader "will give him credit, if not himself a goose, for seeing that the tender of an anonymous cheque would be of equal effect, whether drawn on the Bank of England or on Aldgate Pump." By this test a number of the reviewers are found to be geese: for they take the authors as offering proof, and insist, against the authors, on the very point on which the authors had themselves insisted beforehand.
Leaving aside imperceptions of this kind, I proceed to notice a clerical and medical review. I have lived much in the middle ages, especially since the invention of printing; and from thence I have brought away a high respect for and grateful recollection of—the priest in everything but theology, and the physician in everything but medicine. The professional harness was unfavorable to all progress, except on a beaten road; the professional blinkers prevented all but the beaten road from being seen: the professional reins were pulled at the slightest attempt to quicken pace, even on the permitted path; and the [199]professional whip was heavily laid on at the slightest attempt to diverge. But when the intelligent man of either class turned his attention out of his ordinary work, he had, in most cases, the freshness and vigor of a boy at play, and like the boy, he felt his freedom all the more from the contrast of school-restraint.
In the case of medicine, and physics generally, the learned were, in some essential points, more rational than many of their present impugners. They pass for having put a priori obstacles in the way of progress: they might rather be reproved for too much belief in progress obtained by a priori means. They would have shouted with laughter at a dunce who—in a review I read, but without making a note—declared that he would not believe his senses except when what they showed him was capable of explanation upon some known principle. I have seen such stuff as this attributed to the schoolmen; but only by those who knew nothing about them. The following, which I wrote some years ago, will give a notion of a distinction worth remembering. It is addressed to the authorities of the College of Physicians.
"The ignominy of the word empiric dates from the ages in which scholastic philosophy deduced physical consequences a priori;—the ages in which, because a lion is strong, rubbing with lion's fat would have been held an infallible tonic. In those happy days, if a physician had given decoction of a certain bark, only because in numberless instances that decoction had been found to strengthen the patient, he would have been a miserable empiric. Not that the colleges would have passed over his returns because they were empirical: they knew better. They were as skilful in finding causes for facts, as facts for causes. The president and the elects of that day would have walked out into the forest with a rope, and would have pulled heartily at the tree which yielded the bark: nor would they ever have left it until they had pulled out a legitimate [200]reason. If the tree had resisted all their efforts, they would have said, 'Ah! no wonder now; the bark of a strong tree makes a strong man.' But if they had managed to serve the tree as you would like to serve homœopathy, then it would have been 'We might have guessed it; all the virtus roborativa has settled in the bark.' They admitted, as we know from Molière, the virtus dormitiva[343] of opium, for no other reason than that opium facit dormire.[344] Had the medicine not been previously known, they would, strange as it may seem to modern pharmacopœists, have accorded a virtus dormitiva to the new facit dormire. On this point they have been misapprehended. They were prone to infer facit from a virtus imagined a priori; and they were ready in supplying facit in favor of an orthodox virtus. They might have gone so far, for example, under pre-notional impressions, as the alliterative allopath, who, when maintenance of truth was busy opposing the progress of science called vaccination, declared that some of its patients coughed like cows, and bellowed like bulls; but they never refused to find virtus when facit came upon them, no matter whence. They would rather have accepted Tenterden steeple than have rejected the Goodwin Sands. They would have laughed their modern imitators to scorn: but as they are not here, we do it for them.
"The man of our day—the a priori philosopher—tries the question whether opium can cause sleep by finding out in the recesses of his own noddle whether the drug can have a dormitive power: Well! but did not the schoolman do the same? He did; but mark the distinction. The schoolman had recourse to first principles, when there was no opium to try it by: our man settles the point in the same way with a lump of opium before him. The schoolman shifted his principles with his facts: the man of our drawing-rooms will fight facts with his principles, just as an old [201]physician would have done in actual practice, with the rod of his Church at his back.
"The story about Galileo—which seems to have been either a joke made against him, or by him—illustrates this. Nature abhors a vacuum was the explanation of the water rising in a pump: but they found that the water would not rise more than 32 feet. They asked for explanation: what does the satirist make the schoolmen say? That the stoppage is not a fact, because nature abhors a vacuum? No! but that the principle should be that nature abhors a vacuum as far as 32 feet. And this is what would have been done.
"There are still among us both priests and physicians who would have belonged, had they lived three or four centuries ago, to the glorious band of whom I have spoken, the majority of the intelligent, working well for mankind out of the professional pursuit. But we have a great many who have helped to abase their classes. Go where we may, we find specimens of the lower orders of the ministry of religion and the ministry of health showing themselves smaller than the small of other pursuits. And how is this? First, because each profession is entered upon a mere working smack of its knowledge, without any depth of education, general or professional. Not that this is the whole explanation, nor in itself objectionable: the great mass of the world must be tended, soul and body, by those who are neither Hookers[345] nor Harveys[346]: let such persons not venture ultra crepidam, and they are useful and respectable. But, secondly, there is a vast upheaving of thought from the depths of commonplace learning. I am a clergyman! Sir! I am a medical man! Sir! and forthwith the nature of things is picked to pieces, and there is a race, with the last the winner, between Philosophy mounted on Folly's donkey, and Folly mounted on Philosophy's donkey. How fortunate [202]it is for Law that her battles are fought by politicians in the Houses of Parliament. Not that it is better done: but then politics bears the blame."
I now come to the medical review. After a quantity of remark which has been already disposed of, the writer shows Greek learning, a field in which the old physician would have had a little knowledge. A. B., for the joke's sake, had left untranslated, as being too deep, a remarkably easy sentence of Aristotle, to the effect that what has happened was possible, for if impossible it would not have happened. The reviewer, in "simple astonishment,"—it was simple—at the pretended incapacity—I was told by A. B. that the joke was intended to draw out a reviewer—translates:—He says that this sentence is A. B.'s summing up of the evidence of Spiritualism. Now, being a sort of alter ego[347] of A. B., I do declare that he is not such a fool as to rest the evidence of Spiritualism—the spirit explanation—upon the occurrence of certain facts proving the possibility of those very facts. In truth, A. B. refuses to receive spiritualism, while he receives the facts: this is the gist of his whole preface, which simply admits spiritualism among the qualified candidates, and does not know what others there may be.
The reviewer speaks of Aristotle as "that clear thinker and concise writer." I strongly suspect that his knowledge of Aristotle was limited to the single sentence which he had translated or got translated. Aristotle is concise in phrase, not in book, and is powerful and profound in thought: but no one who knows that his writing, all we have of him, is the very opposite of clear, will pretend to decide that he thought clearly. As his writing, so probably was his thought; and his books are, if not anything but clear, at least anything good but clear. Nobody thinks them clear except a person who always clears difficulties: which I have no doubt was the reviewer's habit; that is, if he ever took the field [203]at all. The gentleman who read Euclid, all except the As and Bs and the pictures of scratches and scrawls, is the type of a numerous class.
The reviewer finds that the word amosgepotically, used by A. B., is utterly mysterious and incomprehensible. He hopes his translation of the bit of Greek will shield him from imputation of ignorance: and thinks the word may be referred to the "obscure dialect" out of which sprung aneroid, kalos geusis sauce, and Anaxyridian trousers. To lump the first two phrases with the third smacks of ignorance in a Greek critic; for ἀναξυριδια, breeches, would have turned up in the lexicon; and kalos geusis, though absurd, is not obscure. And ἀμωσγεπως, somehow or other, is as easily found as ἀναξυριδια. The word aneroid, I admit, has puzzled better scholars than the critic: but never one who knows the unscholarlike way in which words ending in ειδης have been rendered. The aneroid barometer does not use a column of air in the same way as the old instrument. Now ἀεροειδης—properly like the atmosphere—is by scientific non-scholarship rendered having to do with the atmosphere; and ἀναεροειδης—say anaëroid—denies having to do with the atmosphere; a nice thing to say of an instrument which is to measure the weight of the atmosphere. One more absurdity, and we have aneroid, and there you are. The critic ends with a declaration that nothing in the book shakes his faith in a Quarterly reviewer who said that suspension of opinion, until further evidence arrives, is justifiable: a strange summing up for an article which insists upon utter rejection being unavoidable.[348] The expressed aim of both A. B. and C. D. was to excite inquiry, and get further evidence: until this is done, neither asks for a verdict.
Oh where! and oh where! is old Medicine's learning gone! There was some in the days of yore, when Popery [204]was on! And it's oh! for some Greek, just to find a word upon! The reviewer who, lexicon in hand, can neither make out anaxyridical, amosgepotical, kalos geusis, nor distinguish them from aneroid, cannot be trusted when he says he has translated a sentence of Aristotle. He may have done it; but, as he says of spiritualism, we must suspend our opinion until further evidence shall arrive.
We now come to the theological review. I have before alluded to the faults of logic which are Protestant necessities: but I never said that Protestant argument had nothing but paralogism. The writer before me attains this completeness: from beginning to end he is of that confusion and perversion which, as applied to interpretation of the New Testament, is so common as to pass unnoticed by sermon-hearers; but which, when applied out of church, is exposed with laughter in all subjects except theology. I shall take one instance, putting some words in italics.
|
A. B. My state of mind, which refers the whole either to unseen intelligence, or something which man has never had any conception of, proves me to be out of the pale of the Royal Society. |
Theological Critic. ... he proceeds to argue that he himself is outside its sacred pale because he refers all these strange phenomena to unseen spiritual intelligence. |
The possibility of a yet unimagined cause is insisted on in several places. On this ground it is argued by A. B. that spiritualists are "incautious" for giving in at once to the spirit doctrine. But, it is said, they may be justified by the philosophers, who make the flint axes, as they call them, to be the works of men, because no one can see what else they can be. This kind of adoption, condemned as a conclusion, is approved as a provisional theory, suggestive of direction of inquiry: experience having shown that [205]inquiry directed by a wrong theory has led to more good than inquiry without any theory at all. All this A. B. has fully set forth, in several pages. On it the reviewer remarks that "with infinite satisfaction he tries to justify his view of the case by urging that there is no other way of accounting for it; after the fashion of the philosophers of our own day, who conclude that certain flints found in the drift are the work of men, because the geologist does not see what else they can be." After this twist of meaning, the reviewer proceeds to say, and A. B. would certainly join him, "There is no need to combat any such mode of reasoning as this, because it would apply with equal force and justice to any theory whatever, however fantastic, profane, or silly." And so, having shown how the reviewer has hung himself, I leave him funipendulous.
One instance more, and I have done. A reviewer, not theological, speaking of the common argument that things which are derided are not therefore to be rejected, writes as follows:—"It might as well be said that they who laughed at Jenner[349] and vaccination were, in a certain but very unsatisfactory way, witnesses to the possible excellence of the system of St. John Long."[350] Of course it might: and of course it is said by all people of common sense. In introducing the word "possible," the reviewer has hit the point: I suspect that this word was introduced during revision, to put the sentence into fighting order; hurry preventing it being seen that the sentence was thus made to fight on the wrong side. Jenner, who was laughed at, was right; therefore, it is not impossible—that is, it is possible—that a derided system may be right. Mark the three gradations: in medio tutissimus ibis.[351]
Reviewer.—If a system be derided, it is no ground of suspense that derided systems have turned out true: if it were, you would suspend your opinion about St. John Long on account of Jenner.—Ans. You ought to do so, as to possibility; and before examination; not with the notion that J. proves St. J. probable; only possible.
Common Sense.—The past emergence of truths out of derided systems proves that there is a practical certainty of like occurrence to come. But, inasmuch as a hundred speculative fooleries are started for one truth, the mind is permitted to approach the examination of any one given novelty with a bias against it of a hundred to one: and this permission is given because so it will be, leave or no leave. Every one has licence not to jump over the moon.
Paradoxer.—Great men have been derided, and I am derided: which proves that my system ought to be adopted. This is a summary of all the degrees in which paradoxers contend for the former derision of truths now established, giving their systems probability. I annex a paragraph which D [e &c.] inserted in the Athenæum of October 23, 1847.
"Discoverers and Discoveries.
"Aristotle once sent his servant to the cellar to fetch wine:—and the fellow brought him back small beer. The Stagirite (who knew the difference) called him a blockhead. 'Sir,' said the man, 'all I can say is, that I found it in the cellar.' The philosopher muttered to himself that an affirmative conclusion could not be proved in the second figure,—and Mrs. Aristotle, who was by, was not less effective in her remark, that small beer was not wine because it was in the same cellar. Both were right enough: and our philosophers might take a lesson from either—for they insinuate an affirmative conclusion in the second figure. Great discoverers have been little valued by established [207]schools,—and they are little valued. The results of true science are strange at first,—and so are their's. Many great men have opposed existing notions,—and so do they. All great men were obscure at first,—and they are obscure. Thinking men doubt,—and they doubt. Their small beer, I grant, has come out of the same cellar as the wine; but this is not enough. If they had let it stand awhile in the old wine-casks, it might have imbibed a little of the flavor."
There are better reviews than I have noticed; which, though entirely dissenting, are unassailable on their own principles. What I have given represents five-sixths of the whole. But it must be confessed that the fraction of fairness and moderation and suspended opinion which the doctrine of Spirit Manifestations has met with—even in the lower reviews—is strikingly large compared to what would have been the case fifty years ago. It is to be hoped that our popular and periodical literatures are giving us one thinker created for twenty geese double-feathered: if this hope be realized, we shall do! Seeing all that I see, I am not prepared to go the length of a friend of mine who, after reading a good specimen of the lower reviewing, exclaimed—Oh! if all the fools in the world could be rolled up into one fool, what a reviewer he would make!
Calendrier Universel et Perpétuel; par le Commandeur P. J. Arson.[352] Publié par ses Enfans (Œuvre posthume). Nice, 1863, 4to.
I shall not give any account of this curious calendar, with all its changes and symbols. But there is one proposal, which, could we alter the general notions of time—a thing of very dubious possibility—would be convenient. The week is made to wax and wane, culminating on the Sunday, [208]which comes in the middle. Thursday, Friday, Saturday, are ascending or waxing days; Monday, Tuesday, Wednesday, are descending or waning days. Our six days, lumped together after the great distinguishing day, Sunday, are too many to be distinctly thought of together: a division of three preceding and three following the day of most note would be much more easily used. But all this comes too late. It may be, nevertheless, that some individuals may be able to adjust their affairs with advantage by referring Thursday, Friday, Saturday, to the following Sunday, and Monday, Tuesday, Wednesday, to the preceding Sunday. But M. Arson's proposal to alter the names of the days is no more necessary than it is practicable.
CYCLOMETRY.
I am not to enter anything I do not possess. The reader therefore will not learn from me the feats of many a man-at-arms in these subjects. He must be content, unless he will bestir himself for himself, not to know how Mr. Patrick Cody trisects the angle at Mullinavat, or Professor Recalcati squares the circle at Milan. But this last is to be done by subscription, at five francs a head: a banker is named who guarantees restitution if the solution be not perfectly rigorous; the banker himself, I suppose, is the judge. I have heard of a man of business who settled the circle in this way: if it can be reduced to a debtor and creditor account, it can certainly be done; if not, it is not worth doing. Montucla will give the accounts of the lawsuits which wagers on the problem have produced in France.
Neither will I enter at length upon the success of the new squarer who advertises (Nov. 1863) in a country paper that, having read that the circular ratio was undetermined, "I thought it very strange that so many great scholars in all ages should have failed in finding the true ratio, and have been determined to try myself.... I am about to secure the [209]benefit of the discovery, so until then the public cannot know my new and true ratio." I have been informed that this trial makes the diameter to the circumference as 64 to 201, giving π = 3.140625 exactly. The result was obtained by the discoverer in three weeks after he first heard of the existence of the difficulty. This quadrator has since published a little slip, and entered it at Stationers' Hall. He says he has done it by actual measurement; and I hear from a private source that he uses a disk of 12 inches diameter, which he rolls upon a straight rail. Mr. James Smith did the same at one time; as did also his partisan at Bordeaux. We have, then, both 3.125 and 3.140625, by actual measurement. The second result is more than the first by about one part in 200. The second rolling is a very creditable one; it is about as much below the mark as Archimedes was above it. Its performer is a joiner, who evidently knows well what he is about when he measures; he is not wrong by 1 in 3,000.
The reader will smile at the quiet self-sufficiency with which "I have been determined to try myself" follows the information that "so many great scholars in all ages" have failed. It is an admirable spirit, when accompanied by common sense and uncommon self-knowledge. When I was an undergraduate there was a little attendant in the library who gave me the following,—"As to cleaning this library, Sir, if I have spoken to the Master once about it, I have spoken fifty times: but it is of no use; he will not employ littery men; and so I am obliged to look after it myself."
I do not think I have mentioned the bright form of quadrature in which a square is made equal to a circle by making each side equal to a quarter of the circumference. The last squarer of this kind whom I have seen figures in the last number of the Athenæum for 1855: he says the thing is no longer a problem, but an axiom. He does not know that the area of the circle is greater than that of any other figure of the same circuit. This any one might see without [210]mathematics. How is it possible that the figure of greatest area should have any one length in its circuit unlike in form to any other part of the same length?
The feeling which tempts persons to this problem is that which, in romance, made it impossible for a knight to pass a castle which belonged to a giant or an enchanter. I once gave a lecture on the subject: a gentleman who was introduced to it by what I said remarked, loud enough to be heard by all around, "Only prove to me that it is impossible, and I will set about it this very evening."
This rinderpest of geometry cannot be cured, when once it has seated itself in the system: all that can be done is to apply what the learned call prophylactics to those who are yet sound. When once the virus gets into the brain, the victim goes round the flame like a moth; first one way and then the other, beginning where he ended, and ending where he begun: thus verifying the old line
"In girum imus nocte, ecce! et consumimur igni."[353]
Every mathematician knows that scores of methods, differing altogether from each other in process, all end in this mysterious 3.14159..., which insists on calling itself the circumference to a unit of diameter. A reader who is competent to follow processes of arithmetic may be easily satisfied that such methods do actually exist. I will give a sketch, carried out to a few figures, of three: the first two I never met with in my reading; the third is the old method of Vieta.[354] [I find that both the first and second methods are contained in a theorem of Euler.]
What Mr. James Smith says of these methods is worth noting. He says I have given three "fancy proofs" of the value of π: he evidently takes me to be offering demonstration. He proceeds thus:—
"His first proof is traceable to the diameter of a circle [211]of radius 1. His second, to the side of any inscribed equilateral triangle to a circle of radius 1. His third, to a radius of a circle of diameter 1. Now, it may be frankly admitted that we can arrive at the same result by many other modes of arithmetical calculation, all of which may be shown to have some sort of relation to a circle; but, after all, these results are mere exhibitions of the properties of numbers, and have no more to do with the ratio of diameter to circumference in a circle than the price of sugar with the mean height of spring tides. (Corr. Oct. 21, 1865)."
I quote this because it is one of the few cases—other than absolute assumption of the conclusion—in which Mr. Smith's conclusions would be true if his premise were true. Had I given what follows as proof, it would have been properly remarked, that I had only exhibited properties of numbers. But I took care to tell my reader that I was only going to show him methods which end in 3.14159.... The proofs that these methods establish the value of π are for those who will read and can understand.
| 200000000 | 31415 | 3799 |
| 66666667 | 2817 | |
| 26666667 | 1363 | |
| 11428571 | 661 | |
| 5079365 | 321 | |
| 2308802 | 156 | |
| 1065601 | 76 | |
| 497281 | 37 | |
| 234014 | 18 | |
| 110849 | 9 | |
| 52785 | 5 | |
| 25245 | 2 | |
| 12118 | 1 | |
| 5834 | ||
| ————— | ——— | —— |
| 314153799 | 31415 | 9265 |
1. Take any diameter, double it, take 1-3d of that double, 2-5ths of the last, 3-7ths of the last, 4-9ths of the last, 5-11ths of the last, and so on. The sum of all is the circumference of that diameter. The preceding is the process when the diameter is a hundred millions: the errors arising from rejection of fractions being lessened by proceeding on a thousand millions, and striking off one figure. Here 200 etc. is double of the diameter; 666 etc. is 1-3rd of 200 etc.; 266 etc. is 2-5ths of 666 etc.; 114 etc. is 3-7ths of 266 etc.; 507 etc. is 4-9ths of 114 etc.; and so on.
2. To the square root of 3 add its half. Take half the third part of this; half 2-5ths of the last; half 3-7ths of the last; and so on. The sum is the circumference to a unit of diameter.
| Square root of 3.... | 1.73205081 |
| .86602540 | |
| ————— | |
| 2.59807621 | |
| .43301270 | |
| .08660254 | |
| 1855768 | |
| 412393 | |
| 93726 | |
| 21629 | |
| 5047 | |
| 1188 | |
| 281 | |
| 67 | |
| 16 | |
| 4 | |
| 1 | |
| ————— | |
| 3.14159265 |
3. Take the square root of ½; the square root of half of one more than this; the square root of half of one more [213]than the last; and so on, until we come as near to unity as the number of figures chosen will permit. Multiply all the results together, and divide 2 by the product: the quotient is an approximation to the circumference when the diameter is unity. Taking aim at four figures, that is, working to five figures to secure accuracy in the fourth, we have .70712 for the square root of ½; .92390 for the square root of half one more than .70712; and so on, through .98080, .99520, .99880, .99970, .99992, .99998. The product of the eight results is .63667; divide 2 by this, and the quotient is 3.1413..., of which four figures are correct. Had the product been .636363... instead of .63667..., the famous result of Archimedes, 22-7ths, would have been accurately true. It is singular that no cyclometer maintains that Archimedes hit it exactly.
A literary journal could hardly admit as much as the preceding, if it stood alone. But in my present undertaking it passes as the halfpennyworth of bread to many gallons of sack. Many more methods might be given, all ending in the same result, let that result mean what it may.
Now since dozens of methods, to which dozens more might be added at pleasure, concur in giving one and the same result; and since these methods are declared by all who have shown knowledge of mathematics to be demonstrated: it is not asking too much of a person who has just a little knowledge of the first elements that he should learn more, and put his hand upon the error, before he intrudes his assertion of the existence of error upon those who have given more time and attention to it than himself, and who are in possession, over and above many demonstrations, of many consequences verifying each other, of which he can know nothing. This is all that is required. Let any one square the circle, and persuade his friends, if he and they please: let him print, and let all read who choose. But let him abstain from intruding himself upon those who have been satisfied by existing demonstration, until he is prepared [214]to lay his finger on the point in which existing demonstration is wrong. Let him also say what this mysterious 3.14159... really is, which comes in at every door and window, and down every chimney, calling itself the circumference to a unit of diameter. This most impudent and successful impostor holds false title-deeds in his hands, and invites examination: surely those who can find out the rightful owner are equally able to detect the forgery. All the quadrators are agreed that, be the right what it may, 3.14159... is wrong. It would be well if they would put their heads together, and say what this wrong result really means. The mathematicians of all ages have tried all manner of processes, with one object in view, and by methods which are admitted to yield demonstration in countless cases. They have all arrived at one result. A large number of opponents unite in declaring this result wrong, and all agree in two points: first, in differing among themselves; secondly, in declining to point out what that curious result really is which the mathematical methods all agree in giving.
Most of the quadrators are not aware that it has been fully demonstrated that no two numbers whatsoever can represent the ratio of the diameter to the circumference with perfect accuracy. When therefore we are told that either 8 to 25 or 64 to 201 is the true ratio, we know that it is no such thing, without the necessity of examination. The point that is left open, as not fully demonstrated to be impossible, is the geometrical quadrature, the determination of the circumference by the straight line and circle, used as in Euclid. The general run of circle-squarers, hearing that the quadrature is not pronounced to be demonstratively impossible, imagine that the arithmetical quadrature is open to their ingenuity. Before attempting the arithmetical problem, they ought to acquire knowledge enough to read Lambert's[355] demonstration (last given in Brewster's[356] translation [215]of Legendre's[357] Geometry) and, if they can, to refute it. [It will be given in an Appendix.] Probably some have begun this way, and have caught a Tartar who has refused to let them go: I have never heard of any one who, in producing his own demonstration, has laid his finger on the faulty part of Lambert's investigation. This is the answer to those who think that the mathematicians treat the arithmetical squarers too lightly, and that as some person may succeed at last, all attempts should be examined. Those who have so thought, not knowing that there is demonstration on the point, will probably admit that a person who contradicts a theorem of which the demonstration has been acknowledged for a century by all who have alluded to it as read by themselves, may reasonably be required to point out the error before he demands attention to his own result.
Apopempsis of the Tutelaries.—Again and again I am told that I spend too much time and trouble upon my two tutelaries: but when I come to my summing-up I shall make it appear that I have a purpose. Some say I am too hard upon them: but this is quite a mistake. Both of them beat little Oliver himself in the art and science of asking for more; but without Oliver's excuse, for I had given good allowance. Both began with me, not I with them: and both knew what they had to expect when they applied for a second helping.
On July 31, the Monday after the publication of my remarks on my 666 correspondent, I found three notes in separate envelopes, addressed to me at "7A, University College." When I saw the three new digits I was taken rhythmopoetic, as follows—
Here's the Doctor again with his figs, and by Heavens!
He was always at sixes, and now he's at sevens.
To understand this fully the reader must know that the greater part of Apocalyptic interpretation has long been condensed, in my mind, into the Turkish street-cry—In the [216]name of the Prophet! figs! I make a few extracts. The reader will observe that Dr. Thorn grumbles at his private letters being publicly ridiculed. A man was summoned for a glutolactic assault; he complained of the publication of his proceeding: I kicked etc. in confidence, he said.
"After reading your last, which tries in every way to hold me up to public ridicule for daring to write you privately ['that you would be d——d,' omitted by accident] one would say, Why have anything to do with such a testy person? [Wrong word; no testy person can manage cool and consecutive ridicule. Quære, what is this word? Is it anything but a corruption of the obsolete word tetchy of the same meaning? Some think touchy is our modern form of tetchy, which I greatly doubt]. My answer is, the poor man is lamentably ignorant; he is not only so, but 'out of the way' [quite true; my readers know me by this time for an out-of-the-way person. What other could tackle my squad of paradoxers? What other would undertake the job?] Can he be brought back and form one of those who in Ezekiel 37 ch. have the Spirit breathed into them and live.... Have I any other feeling towards you except that of peace and goodwill? [Not to your distinct knowledge; but in all those who send people to 'the other place' for contempt of their interpretations, there is a lurking wish which is father to the thought; 'you will be d——d' and 'you be d—d' are Siamese twins]. Of course your sneer at 666 brought plain words; but when men meddle with what they do not understand (not having the double Vahu) they must be dealt with faithfully by those who do.... [They must; which justifies the Budget of Paradoxes: but no occasion to send them anywhere; no preachee and floggee too, as the negro said]. Many will find the text Prov. i. 26 fully realized. [All this contains distinct assumption of a right 'of course' to declare accursed those who do not respect the writer's vagary].... If I could but get the א, the Ox-head, which in Old Hebrew was just the Latin Digamma, F, out [217]of your name, and could then Thau you with the Thau of Ezekiel ix, 4, the χ, then you would bear the number of a man! But this is too hard for me, although not so for the Lord! Jer. xxxii. 17.... And now a word: is ridicule the right thing in so solemn a matter as the discussion of Holy Writ? [Is food for ridicule the right thing? Did I discuss Holy Writ? I did not: I concussed profane scribble. Even the Doctor did not discuss; he only enunciated and denunciated out of the mass of inferences which a mystical head has found premises for in the Bible]."
| M | 40 |
| O | 70 |
| R | 100 |
| G | 6 |
| N | 50 |
| —— | |
| 266 | |
| ת= | χ 400 |
[That ill opinions are near relations of ill wishes, will be detected by those who are on the look out. The following was taken down in a Scotch Church by Mr. Cobden,[358] who handed it to a Roman friend of mine, for his delectation (in 1855): "Lord, we thank thee that thou hast brought the Pope into trouble; and we pray that thou wouldst be mercifully pleased to increase the same."]
Here is a martyr who quarrels with his crown; a missionary who reviles his persecutor: send him to New Zealand, and he would disagree with the Maoris who ate him. Man of unilateral reciprocity! have you, who write to a stranger with hints that that stranger and his wife are children of perdition, the bad taste to complain of a facer in return? As James Smith[359]—the Attorney-wit, not the Dock-cyclometer—said, or nearly said,
"A pretty thing, forsooth!
Is he to burn, all scalding hot,
Me and my wife, and am I not
To job him out a tooth?"
Those who think parody vulgar will be pleased to substitute for the above a quotation from Butler[360]:—
"There's nothing so absurd or vain
Or barbarous or inhumane,
But if it lay the least pretence
To piety and godliness,
Or tender-hearted conscience,
And zeal for gospel truths profess,—
Does sacred instantly commence,
And all that dare but question it are straight
Pronounced th' uncircumcised and reprobate,
As malefactors that escape and fly
Into a sanctuary for defence,
Must not be brought to justice thence,
Although their crimes be ne'er so great and high.
And he that dares presume to do't
Is sentenced and delivered up
To Satan that engaged him to't."
THE NUMBER OF THE BEAST.
Of all the drolleries of controversy none is more amusing than the manner in which those who provoke a combat expect to lay down the laws of retaliation. You must not strike this way! you must not parry that way! If you don't take care, we shall never meddle with you again! We were not prepared for such as this! Why did we have anything to do with such a testy person? M. Jourdain must needs show Nicole, his servant-maid, how good a thing it was to be sure of fighting without being killed, by care and tierce.[361] "Et cela n'est il pas beau d'être assuré de son fait quand on se bat contre quelqu'un? Là, pousse moi un peu, pour voir. Nicole. Eh bien! quoi? M. Jourdain. Tout beau. Hola! [219]Ho! doucement. Diantre soit la coquine! Nicole. Vous me dites de pousser. M. Jourdain. Oui; mais tu me pousses en tierce, avant que de pousser en quarte, et tu n'as pas la patience que je pare."
His colleague, my secular tutelary, who also made an anachronistic onset, with his repartees and his retorts, before there was anything to fire at, takes what I give by way of subsequent provocation with a good humor which would make a convert of me if he could afford .01659265 ... of a grain of logic. He instantly sent me his photograph for the asking, and another letter in proof. The Thor-hammerer does nothing but grumble, except when he tells a good story, which he says he had from Dr. Abernethy.[362] A Mr. James Dunlop was popping at the Papists with a 666-rifled gun, when Dr. Chalmers[363] quietly said, "Why, Dunlop, you bear it yourself," and handed him a paper on which the numerals in
| I | A | C | O | B | V | S | D | V | N | L | O | P | V | S | |
| 1 | 100 | 5 | 500 | 5 | 50 | 5 | |||||||||
were added up. This is almost as good as the Filii Dei Vicarius, the numerical letters of which also make 666. No more of these crazy—I first wrote puerile, but why should young cricketers be libelled?—attempts to extract religious use from numerical vagaries, and to make God over all a proposer of salvation conundrums: and no more of the trumpery hints about future destiny which is too great a compliment to call blasphemous. If the Doctor will cipher upon the letter in ἐν ᾡ μετρῳ μετρειτε μετρηθησεται ὑμιν[364] with double Vahu cubic measure, he will perhaps learn to leave off trying to frighten me into gathering grapes from thorns.
Mystical hermeneutics may be put to good use by out-of-the-way people. They may be made to call the attention [220]of the many to a distinction well known among the learned. The books of the New Testament have been for 1,500 years divided into two classes: the acknowledged (ὁμολογουμενα), which it has always been paradox not to receive; and the controverted (ἀντιλεγομενα), about which there has always been that difference of opinion which no scholar overlooks, however he may decide for himself after balance of evidence. Eusebius,[365] who first (l. 3, c. 25) recorded the distinction—which was much insisted on by the early Protestants—states the books which are questioned as doubtful, but which yet are approved and acknowledged by many—or the many, it is not easy to say which he means—to be the Epistles of James and Jude, the second of Peter and the second and third of John. In other places he speaks doubtingly of the Epistle to the Hebrews. The Apocalypse he does not even admit into this class, for he proceeds as follows—I use the second edition of the English folio translation (1709), to avert suspicion of bias from myself:—
"Among the spurious [νοθοι] let there be ranked both the work entitled the Acts of Paul, and the book called Pastor, and the Revelation of Peter: and moreover, that which is called the Epistle of Barnabas, and that named the Doctrines of the Apostles: and moreover, as I said, the Revelation of John (if you think good), which some, as I have said, do reject, but others allow of, and admit among those books which are received as unquestionable and undoubted."
Eusebius, though he will not admit the Apocalypse even into the controverted list, but gives permission to call it spurious, yet qualifies his permission in a manner which almost annihilates the distinctive force of νοθος, and gives the book a claim to rank (if you think good, again) in the controverted list. And this is the impression received by [221]the mind of Lardner, who gives Eusebius fully and fairly, but when he sums up, considers his author as admitting the Apocalypse into the second list. A stick may easily be found to beat the father of ecclesiastical history. There are whole faggots in writers as opposite as Baronius and Gibbon, who are perhaps his two most celebrated sons. But we can hardly imagine him totally misrepresenting the state of opinion of those for whom and among whom he wrote. The usual plan, that of making an author take the views of his readers, is more easy in his case than in that of any other writer: for, as the riddle says, he is You-see-by-us; and to this reading of his name he has often been subjected. Dr. Nathaniel Lardner,[366] who, though heterodox in doctrine, tries hard to be orthodox as to the Canon, is "sometimes apt to think" that the list should be collected and divided as in Eusebius. He would have no one of the controverted books to be allowed, by itself, to establish any doctrine. Even without going so far, a due use of early opinion and long continued discussion would perhaps prevent rational people from being induced by those who have the double Vahu to place the Apocalypse above the Gospels, which all the Bivahuites do in effect, and some are said to have done in express words. But my especial purpose is to point out that an easy way of getting rid of 665 out of 666 of the mystics is to require them to establish the Apocalypse before they begin. See if they even know so much as that there is a crowd of testimonies for and against, running through the first four centuries, which makes this book the most difficult of the whole Canon. Try this method, and you will escape beautiful, as the French say. Dean Alford,[367] in Vol. IV, p. 8, of his New Testament, gives an elaborate handling of this question. He concludes by saying that he cannot [222]venture to refuse his consent to the tradition that the Apostle is the author. This modified adherence, or non-nonadherence, pretty well represents the feeling of orthodox Protestants, when learning and common sense come together.
I have often, in former days, had the attempt made to place the Apocalypse on my neck as containing prophecies yet unfulfilled. The preceding method prevents success; and so does the following. It may almost be taken for granted that theological system-fighters do not read the New Testament: they hunt it for detached texts; they listen to it in church in that state of quiescent nonentity which is called reverent attention: but they never read it. When it is brought forward, you must pretend to find it necessary to turn to the book itself: you must read "The revelation ... to show unto his servants things which must shortly come to pass.... Blessed is he that readeth ... for the time is at hand." You must then ask your mystic whether things deferred for 1800 years were shortly to come to pass, etc.? You must tell him that the Greek ἐν ταχει, rendered "shortly," is as strong a phrase as the language has to signify soon. The interpreter will probably look as if he had never read this opening: the chances are that he takes up the book to see whether you have been committing a fraud. He will then give you some exquisite evasion: I have heard it pleaded that the above was a mere preamble. This word mere is all-sufficient: it turns anything into nothing. Perhaps he will say that the argument is that of the Papists: if so, tell him that there is no Christian sect but bears true witness against some one or more absurdities in other sects.
An anonyme suggests that ἐν ταχει may not be "soon," it may be "quickly, without reference to time when:" he continues thus, "May not time be 'at hand' when it is ready to come, no matter how long delayed?" I now understand what *** and *** meant when they borrowed my books and promised to return them quickly, it was "without [223]reference to time when." As to time at hand—provided you make a long arm—I admire the quirk, but cannot receive it: the word is ἐγγυς, which is a word of closeness in time, in place, in reckoning, in kindred, etc.
Another gentleman is not surprised that Apocalyptic reading leads to a doubt of the "canonicity" of the book: it ought not to rest on church testimony, but on visible miracle. He offers me, or any reader of the Athenæum, the "sight of a miracle to that effect, and within forty-eight hours' journey (fare paid)." I seldom travel, and my first thought was whether my carpet-bag would be found without a regular hunt: but, on reading further, I found that it was only a concordance that would be wanted. Forty hours' collection and numerical calculation of Greek nouns would make it—should I happen to agree with the writer—many hundred millions to one that Revelation xiii is superhuman. There is but one verse (the fifth) which the writer does not see verified. I looked at this verse, and was much startled. The Budget began in October 1863: should it last until March 1867—it is now August 1866—it is clear that I am the first Beast, and my paradoxers are the saints whom I persecute.
[The Budget did terminate in March 1867: I hope the gentleman will be satisfied with the resulting interpretation.]
The same opponent is surprised that I should suppose a thing which "comes to pass" must be completed, and cannot contain what is to happen 1800 years after. All who have any knowledge of English idiom know that a thing comes to pass when it happens, and came to pass afterwards. But as the original is Greek, we must look at the Greek: it is δει γενεσθαι for "must come to pass," and we know that ἐγενετο is what is usually translated "came to pass." No word of more finished completion exists in Greek.
And now for a last round of biter-bit with the Thor-hammerer, of whom, as in the other case, I shall take no [224]more notice until he can contrive to surpass himself, which I doubt his being able to do. He informs me that by changing A into ת in my name he can make a 666 of me; adding, "This is too hard for me, although not so for the Lord!" Sheer nonsense! He could just as easily have directed to "Prof. De Morgתn" as have assigned me apartment 7A in University College. It would have been seen for whom it was intended: and if not, it would still have reached me, for my colleagues have for many a year handed all out-of-the-way things over to me. There is no 7A: but 7 is the Museum of Materia Medica. I took the only hint which the address gave: I inquired for hellebore, but they told me it was not now recognized, that the old notion of its value was quite obsolete, and that they had nothing which was considered a specific in senary or septenary cases. The great platitude is the reference of such a difficulty as writing ת for A to the Almighty! Not childish, but fatuous: real childishness is delightful. I knew an infant to whom, before he could speak plain, his parents had attempted to give notions of the Divine attributes: a wise plan, many think. His father had dandled him up-side-down, ending with, There now! Papa could not dance on his head! The mannikin made a solemn face, and said, But Dod tood! I think the Doctor has rather mistaken the way of becoming as a little child, intended in Matt. xviii. 3: let us hope the will may be taken for the deed.
Two poets have given images of transition from infancy to manhood: Dryden,—for the Hind is Dryden himself on all fours! and Wordsworth, in his own character of broad-nailed, featherless biped:
"The priest continues what the nurse began,
And thus the child imposes on the man."
"The child's the father of the man,
And I could wish my days to be
Bound each to each by natural piety."
In Wordsworth's aspiration it is meant that sense and piety should grow together: in Dryden's description a combination of Mysticism And Bigotry (can this be the double Vahu?), personified as "the priest,"—who always catches it on this score, though the same spirit is found in all associations,—succeeds the boguey-teaching of the nurse. Never was the contrast of smile and scowl, of light and darkness, better seen than in the two pictures. But an acrostic distinction may be drawn. When mysticism predominates over bigotry, we have the grotesque picturesque, and the natural order of words gives us Mab, an appropriate suggestion. But when bigotry has the upper hand, we see Bam, which is just as appropriate; for bigotry nearly always deals with facts and logic so as to require the application of at least one of the minor words by which dishonesty is signified. I think that M is the Doctor's initial, and that Queen Mab tickles him in his sleep with the sharp end of a 6.
(Monday, August 21.) Three weeks having elapsed without notice from me of the Doctor, I receive a reminder of his existence, in which I find that as I am the Daniel who judges the Magi of Babylon, it is to be pointed out that Daniel "bore a certain number, that of a man (beloved), Daniel, ch. 10. v. 11, and which you certainly do not." Then, "by Greek power," Belteshazzar is made = 666. Here is another awkward imitation of the way of a baby child. When you have sported with the tiny creature until it runs away offended, by the time you have got into conversation again you will find the game is to be renewed: a little head peeps out from a hiding-place with "I don't love you." The proper rejoinder is, "Very well! then I'll have pussy." But in the case before me there is a rule of three sums to do; as baby : Pussy Dr. :: 666 : the answer required. I will work it out, if I can.
The squaring of the circle and the discovery of the Beast are the two goals—and goals also—of many unbalanced intellects, and of a few instances of the better kind. [226]I might have said more of 666, but I am not deep in its bibliography. A work has come into my hands which contains a large number of noted cases: to some of my readers it will be a treat to see the collection; and the sight will perhaps be of some use to those who have read controversy on the few celebrated cases which are of general notoriety. It is written by a learned decipherer, a man who really knew the history of the subject, the Rev. David Thom,[368] of Bold Street Chapel, Liverpool, who died, I am told, a few years ago.
Anybody who reads his book will be inclined to parody a criticism which was once made on Paley's[369] Evidences—"Well! if there be anything in Christianity, this man is no fool." And, if he should chance to remember it, he will be strongly reminded of a sentence in my opening chapter,—"The manner in which a paradoxer will show himself, as to sense or nonsense, will not depend upon what he maintains, but upon whether he has or has not made a sufficient knowledge of what has been done by others, especially as to the mode of doing it, a preliminary to inventing knowledge for himself." And this is reinforced by the fact that Mr. Thom, though a scholar, was not conspicuous for learning, except in this his great pursuit. He was a paradoxer on other points. He reconciled Calvinism and eternal reprobation with Universalism and final salvation; showing these two doctrines to be all one.
This gentleman must not be confounded with the Rev. John Hamilton Thom[370] (no relation), at or near the same [227]time and until recently, of Renshaw Street Chapel, Liverpool who was one of the minority in the Liverpool controversy when, nearly thirty years ago, three heretical Unitarian schooners exchanged shotted sermons with thirteen Orthodox ships of the line, and put up their challengers' dander—an American corruption of d—d anger—to such an extent, by quiet and respectful argument, that those opponents actually addressed a printed intercession to the Almighty for the Unitarian triad, as for "Jews, Turks, Infidels, and Heretics." So much for the distinction, which both gentlemen would thank me for making very clear: I take it quite for granted that a guesser at 666 would feel horrified at being taken for a Unitarian, and that a Unitarian would feel queerified at being taken for a guesser at 666. Mr. David Thom's book is The Number and Names of the Apocalyptic Beasts, Part I, 1848, 8vo.: I think the second part was never published. I give the Greek and Latin solutions, omitting the Hebrew: as usual, all the Greek letters are numeral, but only M D C L X V I of the Latin. I do not give either the decipherers or their reasons: I have not room for this; nor would I, if I could, bias my reader for one rather than another.
D. F. Julianus Cæsar Atheus (or Aug.[371]); Diocles Augustus; Ludovicus; Silvester Secundus; Linus Secundus; [228]Vicarius Filii Dei; Doctor et Rex Latinus; Paulo V. Vice-Deo; Vicarius Generalis Dei in Terris; Ipse Catholicæ Ecclesiæ Visibile Caput; Dux Cleri; Una, Vera, Catholica, Infallibilis Ecclesia; Auctoritas politica ecclesiasticaque Papalis (Latina will also do); Lutherus Ductor Gregis; Calvinus tristis fidei interpres; Dic Lux ; Ludvvic; Will. Laud; Λατεινος;[372] ἡ λατινη βασιλεια; ἐκκλησια ἰταλικα; εὐανθας; τειταν; ἀρνουμε; λαμπετις; ὁ νικητης; κακος ὁδηγος; ἀληθης βλαβερος; παλαι βασκανος; ἀμνος ἀδικος; ἀντεμος; γενσηρικος; εὐινας; Βενεδικτος; Βονιβαζιος γ. παπα ξ. η. ε. ε. α., meaning Boniface III. Pope 68th, bishop of bishops the first! οὐλπιος; διος εἰμι ἡ ἡρας; ἡ μισσα ἡ παπικη; λουθερανα; σαξονειος; Βεζζα ἀντιθεος (Beza); ἡ ἀλαζονεια βιου; Μαομετις; Μαομετης β.; θεος εἰμι ἐπι γαιης; ἰαπετος; παπεισκος; διοκλασιανος; χεινα; βρασκι; Ιον Παυνε; κουποκς; (cowpox, ς being the vau; certainly the [229]vaccinated have the mark of the Beast); Βοννεπαρτη; Ν. Βονηπαρτε; εὐπορια; παραδοσις; το μεγαθηριον.
All sects fasten this number on their opponents. It is found in Martin Lauter, affirmed to be the true way of writing the name, by carrying numbers through the Roman Alphabet. Some Jews, according to Mr. Thorn, found it in ישו נצרי Jesus of Nazareth. I find on inquiry that this satire was actually put forth by some medieval rabbis, but that it is not idiomatic: it represents quite fairly "Jesus Nazarene," but the Hebrew wants an article quite as much as the English wants "the."
Mr. David Thom's own solution hits hard at all sides: he finds a 666 for both beasts; ἡ φρην (the mind) for the first, and ἐκκλησιαι σαρκικαι (fleshly churches) for the second. A solution which embodies all mental philosophy in one beast and all dogmatic theology in the other, is very tempting: for in these are the two great supports of Antichrist. It will not, however, mislead me, who have known the true explanation a long time. The three sixes indicate that any two of the three subdivisions, Roman, Greek, and Protestant, are, in corruption of Christianity, six of one and half a dozen of the other: the distinctions of units, tens, hundreds, are nothing but the old way (1 Samuel xviii. 7, and Concordance at ten, hundred, thousand) of symbolizing differences of number in the subdivisions.
It may be good to know that, even in speculations on 666, there are different degrees of unreason. All the diviners, when they get a colleague or an opponent, at once proceed to reckon him up: but some do it in play and some in earnest. Mr. David Thom found a young gentleman of the name St. Claire busy at the Beast number: he forthwith added the letters in στ κλαιρε and found 666: this was good fun. But my spiritual tutelary, when he found that he could not make a beast of me, except by changing א into ת, solemnly referred the difficulty to the Almighty: this was poor earnest. [230]
I am glad I did not notice, in time to insert it in the Athenæum, a very remarkable paradoxer brought forward by Mr. Thom, his friend Mr. Wapshare[373]: it is a little too strong for the general public. In the Athenæum they would have seen and read it: but this book will be avoided by the weaker brethren. It is as follows:
"God, the Elohim, was six days in creating all things, and having made MAN he entered into his rest. He is no more seen as a Creator, as Elohim, but as Jehovah, the Lord of the Sabbath, and the Spirit of life in Man, which Spirit worketh sin in the flesh; for the Spirit of Love, in all flesh, is Lust, or the spirit of a beast, So Rom. vii. And which Spirit is crucified in the flesh. He then, as Jehovah—as the power of the Law, in and over all flesh, John viii. 44—increases that which he has made as the Elohim, and his power shall last for 6 days, or 6 periods of time, computed at a millennium of years; and at the end of which six days, he who is the Spirit of all flesh shall manifest himself as the Holy Spirit of Almighty Love, and of all truth; and so shall the Church have her Sabbath of Rest—all contention being at an end. This is, as well as I may now express it, my solution of the mystery in Hebrew, and in Greek, and also in Latin, IHS. For he that was lifted up is King of the Jews, and is the Lord of all Life, working in us, both to will and to do; as is manifest in the Jews—they slaying him that his blood might be good for the healing of the nations, of all people and tongues. As the Father of all natural flesh, he is the Spirit of Lust, as in all beasts; as the Father, or King of the Jews, he is the Devil, as he himself witnesseth in John viii., already referred to. As lifted up, he is transformed into the Spirit of Love, a light to the Gentiles, and the glory of his people Israel.... For there is but ONE God, ONE Lord, ONE Spirit, ONE body, etc. and he who was Satan, the Spirit of life in that body, is, in [231]Christ crucified, seen in the Spirit that is in all, and through all and over all, God blessed for ever."
All this seems well meant, and Mr. Thom prints it as convinced of its piety, and "pronounces no opinion." Mystics of all sorts! see what you may come to, or what may come to you! I have inserted the above for your good.
There is nothing in this world so steady as some of the paradoxers. They are like the spiders who go on spinning after they have web enough to catch all the flies in the neighborhood, if the flies would but come. They are like the wild bees who go on making honey which they never can eat, proving sic vos non vobis to be a physical necessity of their own contriving. But nobody robs their hives: no, unlike the bees, they go about offering their ware to any who will take it as a gift. I had just written the last sentence (Oct. 30, 1866, 8.45 A.M.) when in comes the second note received this morning from Dr. Thorn: at 1.30 P.M. came in a third. These arise out of the above account of the Rev. D. Thom, published Oct. 27: three notes had arrived before.
For curiosity I give one day's allowance, supposing these to be all: more may arrive before night.
"Dear Sir,—
In re  .[374]
.[374]
"So that 'Zaphnath Paaneah' may be after all the revealer of the
'Northern Tau' Φανεροω—To make
manifest, shew, or explain; and this may satisfy the House of Joseph in
Amos 5c. While Belteshazzar = 666 may be also satisfactory to
the House of David, and so we may have Zech. 10c.
6v. in operation when Ezekiel 37c. 16v.
has been realised;—but there, what is the use of writing, it is all
Coptic [232]to a man who has not  , The Thau of
the North, the double Vahu וָו. Look at Jeremiah
3c. 8v. and then to Psalm 83 for 'hidden ones'
צְפוּנֶי
יְהוָה—The Zephoni
Jehovah, and say whether they have any connection with the Zephon
Thau. The Hammer of Thor of Jeremiah 23c.
29v. as I gave you in No. 3 of my present edition.
, The Thau of
the North, the double Vahu וָו. Look at Jeremiah
3c. 8v. and then to Psalm 83 for 'hidden ones'
צְפוּנֶי
יְהוָה—The Zephoni
Jehovah, and say whether they have any connection with the Zephon
Thau. The Hammer of Thor of Jeremiah 23c.
29v. as I gave you in No. 3 of my present edition.
Yours truly
Le Chevalier Au Cin."
By Greek Power.
| C = | 20 |
| H = | 8 |
| E = | 5 |
| V = | 6 |
| A = | 1 |
| L = | 30 |
| I = | 10 |
| E = | 5 |
| R = | 100 |
| A = | 1 |
| U = | 400 |
| C = | 20 |
| I = | 10 |
| N = | 50 |
| —— | |
| 666 |
There will be thousands of Morgans who will be among the wise and prudent of Hosea 14c. 9v. when the Seventh Angel sounds, let me number that One by Greek, Rev. 17c. 1v: [233]
| S = | 200 |
| E = | 5 |
| × V = | 6 |
| E = | 5 |
| N = | 50 |
| T = | 300 |
| H = | 8 |
| A = | 1 |
| N = | 50 |
| × G = | 6 |
| E = | 5 |
| L = | 30 |
| —— | |
| 666 |
"Dear Sir,—
However pretentious the X or  may be, and it is peculiarly so just now in
this land; after all it is only made of two Roman V's—and so is
only =
may be, and it is peculiarly so just now in
this land; after all it is only made of two Roman V's—and so is
only =  (10)—and
therefore is not the perfect number 12 of Reveln, but is the
mark of the goddess Decima!
(10)—and
therefore is not the perfect number 12 of Reveln, but is the
mark of the goddess Decima!
Yours truly
Wm. Thorn."
Had the one who sent forth a pastoral (Romish) the other day, remained amongst the faithful expectants, see how he would have numbered, whereas he sold himself for the privilege of signing
 Henry E. Manning.[375]
Henry E. Manning.[375]
Transcriber's note.
| By English Key. H = | 8 |
| E = | 5 |
| N = | 40 |
| R = | 80 |
| Y = | 140 |
| E = | 5 |
| D = | 4 |
| W = | 120 |
| A = | 1 |
| R = | 80 |
| D = | 4 |
| M = | 30 |
| A = | 1 |
| N = | 40 |
| N = | 40 |
| I = | 9 |
| N = | 40 |
| G = | 7 |
 = = | 12 |
| —— | |
| 666 |
Cutting from newspaper:—
Mr. Gladstone has paid a visit to the Pope.
| By Greek Power. G = | 6 |
| L = | 30 |
| A = | 1 |
| D = | 4 |
| S = | 200 |
| T = | 300 |
| O = | 70 |
| N = | 50 |
| E = | 5 |
| —— | |
| 666 |
In other letters John Stuart Mill is 666 if the a be left out; Chasuble is perfect. John Brighte[376] is a fait accompli; and I am asked whether intellect can account for the final e. Very easily: this Beast is not the M. P., but another person who spells his name differently. But if John Sturt Mill and John Brighte choose so to write themselves, they may.
A curious collection; a mystical phantasmagoria! There are those who will try to find meaning: there are those who will try to find purpose.
"And some they said—What are you at?
And some—What are you arter?"
My account of Mr. Thom and his 666 appeared on October 27: and on the
29th I received from the editor a copy of Mr. Thom's sermons published in
1863 (he died Feb. 27, 1862) with best wishes for my health and
happiness. The editor does not name himself in the book; but he signed
his name in my copy: and may my circumference never be more than
3⅛ of my diameter if the signature, name and writing both, were
not that of my  ing friend Mr. James Smith! And so I have come
in contact with him on 666 as well as on π! I
should have nothing left to live for, had I not happened to hear that he
has a perpetual motion on hand. I returned thanks and kind regards: and
Miss Miggs's words—"Here's forgivenesses of injuries! here's
amicablenesses!"—rang in my ears. But I was made slightly
uncomfortable: how could the war go on after this armistice? Could I ever
make it understood that the truce only extended to the double Vahu and
things thereunto relating? It was once held by seafaring men that there
was no peace with Spaniards beyond the line: I was determined that there
must be no concord with J. S. inside the circle; that this must be a
special exception, like Father Huddleston [236]and old Grouse in the
gun-room. I was not long in anxiety; twenty-four hours after the book of
sermons there came a copy of the threatened exposure—The British
Association in Jeopardy, and Professor De Morgan in the Pillory without
hope of escape. By James Smith, Esq. London and Liverpool, 8vo., 1866
(pp. 94). This exposure consists of reprints from the Athenæum and
Correspondent: of things new there is but one. In a short preface
Mr. J. S. particularly recommends to "read to the end." At the end
is an appendix of two pages, in type as large as the work; a very
prominent peroration. It is an article from the Athenæum, left out
of its place. In the last sentence Mr. J. Smith, who had asked whether
his character as an honest Geometer and Mathematician was not at stake,
is warned against the fallacia plurium interrogationum.[377] He is told that there
is not a more honest what's-his-name in the world: but that as to the
counter which he calls his character as a mathematician, he is assured
that it has been staked years ago, and lost. And thus truth has the last
word. There is no occasion to say much about reprints. One of them is a
letter [that given above] of August 25, 1865, written by Mr. J. S. to the
Correspondent. It is one of his quadratures; and the joke is that
I am made to be the writer: it appears as what Mr. J. S. hopes I shall
have the sense to write in the Athenæum and forestall him. When I
saw myself thus quoted—yes! quoted! double commas, first
person—I felt as I suppose did Wm. Wilberforce[378] when he set eyes on the affectionate
benediction of the potato which waggish comrades had imposed on a raw
Irish reporter as part of his speech. I felt as Martin[379] of [237]Galway—kind
friend of the poor dumb creatures!—when he was told that the
newspapers had put him in Italics. "I appeal to you, Mr. Speaker! I
appeal to the House! Did I speak in Italics? Do I ever speak in Italics?"
I appeal to editor and readers, whether I ever squared the circle until a
week or two ago, when I gave my charitable mode of reconciling the
discrepant cyclometers.
ing friend Mr. James Smith! And so I have come
in contact with him on 666 as well as on π! I
should have nothing left to live for, had I not happened to hear that he
has a perpetual motion on hand. I returned thanks and kind regards: and
Miss Miggs's words—"Here's forgivenesses of injuries! here's
amicablenesses!"—rang in my ears. But I was made slightly
uncomfortable: how could the war go on after this armistice? Could I ever
make it understood that the truce only extended to the double Vahu and
things thereunto relating? It was once held by seafaring men that there
was no peace with Spaniards beyond the line: I was determined that there
must be no concord with J. S. inside the circle; that this must be a
special exception, like Father Huddleston [236]and old Grouse in the
gun-room. I was not long in anxiety; twenty-four hours after the book of
sermons there came a copy of the threatened exposure—The British
Association in Jeopardy, and Professor De Morgan in the Pillory without
hope of escape. By James Smith, Esq. London and Liverpool, 8vo., 1866
(pp. 94). This exposure consists of reprints from the Athenæum and
Correspondent: of things new there is but one. In a short preface
Mr. J. S. particularly recommends to "read to the end." At the end
is an appendix of two pages, in type as large as the work; a very
prominent peroration. It is an article from the Athenæum, left out
of its place. In the last sentence Mr. J. Smith, who had asked whether
his character as an honest Geometer and Mathematician was not at stake,
is warned against the fallacia plurium interrogationum.[377] He is told that there
is not a more honest what's-his-name in the world: but that as to the
counter which he calls his character as a mathematician, he is assured
that it has been staked years ago, and lost. And thus truth has the last
word. There is no occasion to say much about reprints. One of them is a
letter [that given above] of August 25, 1865, written by Mr. J. S. to the
Correspondent. It is one of his quadratures; and the joke is that
I am made to be the writer: it appears as what Mr. J. S. hopes I shall
have the sense to write in the Athenæum and forestall him. When I
saw myself thus quoted—yes! quoted! double commas, first
person—I felt as I suppose did Wm. Wilberforce[378] when he set eyes on the affectionate
benediction of the potato which waggish comrades had imposed on a raw
Irish reporter as part of his speech. I felt as Martin[379] of [237]Galway—kind
friend of the poor dumb creatures!—when he was told that the
newspapers had put him in Italics. "I appeal to you, Mr. Speaker! I
appeal to the House! Did I speak in Italics? Do I ever speak in Italics?"
I appeal to editor and readers, whether I ever squared the circle until a
week or two ago, when I gave my charitable mode of reconciling the
discrepant cyclometers.
The absurdity of the imitation of symbolic reasoning is so lusciously rich, that I shall insert it when I make up my final book. Somebody mastered Spanish merely to read Don Quixote: it would be worth while to learn a little algebra merely to enjoy this a b-istical attack on the windmills. The principle is, Prove something in as roundabout a way as possible, mention the circle once or twice irrelevantly in the course of your proof, and then make an act of Q. E. D. in words at length. The following is hardly caricature:—
To prove that 2 and 2 make 5. Let a = 2, b = 5: let c = 658, the number of the House: let d = 666, the number of the Beast. Then of necessity d = a + b + c + 1; so that 1 is a harmonious and logical quantification of the number of which we are to take care. Now, b, the middle of our digital system, is, by mathematical and geometrical combination, a mean between 5 + 1 and 2 + 2. Let 1 be removed to be taken care of, a thing no real mathematician can refuse without serious injury to his mathematical and geometrical reputation. It follows of necessity that 2 + 2 = 5, quod erat demonstrumhorrendum. If Simpkin & Marshall have not, after my notice, to account for a gross of copies more than would have gone off without me, the world is not worthy of its James Smith!
The only fault of the above is, that there is more [238]connection than in the process of Faber Cyclometricus: so much, in fact, that the blunders are visible. The utter irrelevance of premises to conclusion cannot be exhibited with the requisite obscurity by any one who is able to follow reasoning: it is high art displayed in a certain toning down of the ægri somnia, which brings them to a certain look of reproach to reasoning which I can only burlesque. Mr. J. S. produces something which resembles argument much as a chimpanzee in dolor, because balked of his dinner, resembles a thinking man at his studies. My humble attempt at imitation of him is more like a monkey hanging by his tail from a tree and trying to crack a cocoa-nut by his chatter.
I could forgive Mr. J. S. anything, properly headed. I would allow him to prove—for himself—that the Quadrature of the Circle is the child of a private marriage between the Bull Unigenitus and the Pragmatic Sanction, claiming tithe of onions for repeal of the Mortmain Act, before the Bishops in Committee under the kitchen table: his mode of imitating reason would do this with ease. But when he puts his imitation into my mouth, to make me what he calls a "real mathematician," my soul rises in epigram against him. I say with the doll's dressmaker—such a job makes me feel like a puppet's tailor myself—"He ought to have a little pepper? just a few grains? I think the young man's tricks and manners make a claim upon his friends for a little pepper?" De Fauré[380] and Joseph Scaliger[381] come into my head: my reader may look back for them.
"Three circlesquarers to the manner born,
Switzerland, France, and England did adorn,
De Fauré in equations did surpass,
Joseph at contradictions was an ass.
Groaned Folly, I'm used up! What shall I do
To make James Smith? Grinned Momus, Join the two!"
As to my locus pœnitentiæ,[382] the reader who is fit to enjoy the letter I have already alluded to will see that I have a soft and easy position; that the thing is really a pillowry; and that I am, like Perrette's pot of milk,
"Bien posé sur un coussinet."[383]
Joanna Southcott[384] never had a follower who believed in her with more humble piety than Mr. James Smith believes in himself. After all that has happened to him, he asks me with high confidence to "favor the writer with a proof" that I still continue of opinion that "the best of the argument is in my jokes, and the best of the joke is in his arguments." I will not so favor him. At the very outset I told him in plain English that he has the whiphand of all the reasoners in the world, and in plain French that il a perdu le droit d'être frappé de l'évidence[385]; I might have said pendu.[386] To which I now add, in plain Latin, Sapienti pauca, indocto nihil.[387] The law of Chancery says that he who will have equity must do equity: the law of reasoning says that he who will have proof must see proof.
The introduction of things quite irrelevant, by way of reproach, is an argument in universal request: and it often happens that the argument so produced really tells against the producer. So common is it that we forget how boyish it is; but we are strikingly reminded when it actually comes from a boy. In a certain police court, certain small boys were arraigned for conspiring to hoot an obnoxious individual on his way from one of their school exhibitions. This proceeding was necessary, because there seemed to be a permanent conspiracy to annoy the gentleman; and the [240]masters did not feel able to interfere in what took place outside the school. So the boys were arraigned; and their friends, as silly in their way as themselves, allowed one of them to make the defence, instead of employing counsel; and did not even give them any useful hints. The defence was as follows; and any one who does not see how richly it sets off the defences of bigger boys in bigger matters has much to learn. The innocent conviction that there was answer in the latter part is delightful. Of course fine and recognizance followed.
A—— said the boys had received great provocation from B——. He was constantly threatening them with a horsewhip which he carried in his hand [the boy did not say what had passed to induce him to take such a weapon], and he had repeatedly insulted the master, which the boys could not stand. B—— had in his own drawing-room told him (A——) that he had drawn his sword against the master and thrown away the scabbard. B—— knew well that if he came to the college he would catch it, and then he went off through a side door—which was no sign of pluck; and then he brought Mrs. B—— with him, thinking that her presence would protect him.
My readers may expect a word on Mr. Thom's sermons, after my account of his queer doings about 666. He is evidently an honest and devout man, much wanting in discrimination. He has a sermon about private judgment, in which he halts between the logical and legal meanings of the word. He loathes those who apply their private judgment to the word of God: here he means those who decide what it ought to be. He seems in other places aware that the theological phrase means taking right to determine what it is. He uses his own private judgment very freely, and is strong in the conclusion that others ought not to use theirs except as he tells them how; he leaves all the rest of mankind free to think with him. In this he is not original: his fame must rest on his senary tripod. [241]
JAMES SMITH ONCE MORE.
Mr. James Smith's procedures are not caricature of reasoning; they are caricature of blundering. The old way of proving that 2 = 1 is solemn earnest compared with his demonstrations. As follows:[388]
| Let | x = 1 | |
| Then | x2 = x | |
| And | x2 - 1 = x - 1 | |
| Divide both sides by x - 1; then | ||
| x + 1 = 1; but x = 1, whence 2 = 1. | ||
When a man is regularly snubbed, bullied, blown up, walked into, and put down, there is usually some reaction in his favor, a kind of deostracism, which cannot bear to hear him always called the blunderer. I hope it will be so in this case. There is nothing I more desire than to see sects of paradoxers. There are fully five thousand adults in England who ought to be the followers of some one false quadrature. And I have most hope of 3⅛, because I think Mr. James Smith better fitted to be the leader of an organized infatuation than any one I know of. He wants no pity, and will get none. He has energy, means, good humor, strong conviction, character, and popularity in his own circle. And, most indispensable point of all, he sticks at nothing;
"In cœlum jusseris, ibit."[389]
When my instructor found I did not print an acceptance of what I have quoted, he addressed me as follows (Corr., Sept 23):—
"In this life, however, we must do our duty, and, when [242]necessary, use the rod, not in a spirit of revenge, but for the benefit of the culprit and the good of society. Now, Sir, the opportunity has been thrown in your way of slipping out of the pillory without risk of serious injury; but, like an obstinate urchin, you have chosen to quarrel with your opportunity and remain there, and thus you compel me to deal with you as schoolmasters used to do with stupid boys in bygone days—that is to say, you force me to the use of the critic's rod, compel me to put you where little Jack Horner sat, and, as a warning to other naughty boys, to ornament you with a dunce's cap. The task I set you was a very simple one, as I shall make manifest at the proper time."
In one or more places, as well as this, Mr. Smith shows that he does not know the legend of little Jack Horner, whom he imagines to be put in the corner as a bad boy. This is curious; for there had been many allusions to the story in the journal he was writing in, and the Christmas pie had become altered into the Seaforth π.
Mr. Smith is satisfied at last that—what between argument and punishment he has convinced me. He says (Corr., Jan. 27, 1866): "I tell him without hesitation that he knows the true ratio of diameter to circumference as well as I do, and if he be wise he will admit it." I should hope I do, and better; but there is no occasion to admit what everybody knows.
I have often wished that we could have a slight glimpse of the reception which was given to some of the old cyclometers: but we have nothing, except the grave disapprobation of historians. I am resolved to give the New Zealander a chance of knowing a little more than this about one of them at least; and, by the fortunate entrance into life of the Correspondent, I am able to do it. I omit sober mathematical answers, of which there were several. The following letter is grave earnest:
"Sir,—I have watched Mr. James Smith's writings on this subject from the first, and I did hope that, as the more [243]he departs from truth the more easy it must be to refute him, [this by no means always true] some of your correspondents would by this time have done so. I own that I am unable to detect the fallacy of his argument; and I am quite certain that 'Π' is wrong, in No. 23, where he declares that Mr. Smith is 'ignorant of the very elements of mathematical truth.' I have observed an immense amount of geometrical reasoning on his part, and I cannot see that it is either fair or honest to deny this, which may be regarded as the 'elements' of mathematical truth. Would it not be better for 'Π' to answer Mr. Smith, to refute his arguments, to point out their fallacies, and to save learners from error, than to plunge into gross insult and unmanly abuse? Would it not be well, also, that Professor De Morgan should favour us with a little reasoning?
"I have hitherto seen no attempt to overthrow Mr. Smith's arguments; I trust that this will not continue, since the subject is one of immense importance to science in general, especially to nautical science, and all that thereto belongs.
Yours, etc.,
A Captain, R.N."
On looking at this homœopathic treatment of the 3⅛ quadrature—remember, homœopathic, similia similibus,[390] not infinitesimal—and at the imputation thrown upon it, I asked myself, what is vulgarity? No two agree, except in this, that every one sees vulgarity in what is directed against himself. Mark the world, and see if anything be so common as the description of the other side's remarks as "vulgar attempt at wit." "I suppose you think that very witty:" the answer is "No my friend! your remark shows that you feel it as wit, so that the purpose is answered; I keep my razor for something else than cutting blocks;" I am inclined to think that "out of place" is a necessary attribute of true vulgarity. And further, it is to be noticed that nothing is [244]unproducible—salvo pudore[391]—which has classical authority, modern or ancient, in its favor. "He is a vulgar fellow; I asked him what he was upon, and what do you think he answered, My legs!"—"Well, and has he not justification? what do you find in Terence? Quid agitur? Statur."[392] I do not even blench from my principle where I find that it brings what is called "taking a sight" within permissible forms of expression: Rabelais not only establishes its antiquity, but makes it English. Our old translation[393] has it thus (book 2. ch. 19):
"Then made the Englishman this sign. His left hand, all open, he lifted up into the air, then instantly shut into his fist the four fingers thereof; and his thumb extended at length he placed upon the tip of his nose. Presently after he lifted up his right hand all open and abased and bent it downwards, putting the thumb thereof in the very place where the little finger of the left hand did close in the fist, and the four right hand fingers he softly moved in the air. Then contrarily he did with the right hand what he had done with the left, and with the left what he had done with the right."
An impressive sight! The making of a fist of the left hand is a great addition of power, and should be followed in modern practice. The gentle sullation of the front fingers, with the clenched fist behind them, says as plainly as possible, Put suaviter in modo in the van, but don't forget to have fortiter in re[394] in the rear.
My Budget was announced (March 23, 1867) for completion on the 30th. Mr. James Smith wrote five letters, one before the completion, four after it; the five contained 68 pages of quarto letter paper. Mr. J. S. had picked up a clerical correspondent, with whom he was in the heat of battle.
"March 27.—Dear Sir. Very truly yours. Duty; for my own sake; just time left to retrieve my errors; sends copy of letter to clergyman; new proof never before thought of; merest tyro would laugh if I were to stifle it, whether by rhodomontade or silent contempt; keep your temper. I shall be convinced; and if world be right in supposing me incapable of a foul act, I shall proclaim glorious discovery in the Athenæum.
"April 15.—Sir,... My dear Sir, Your sincere tutelary. Copy of another letter to clergyman; discovery tested by logarithms; reasons such as none but a knave or a sinner can resist. Let me advise you to take counsel before it is too late! Keep your temper. Let not your pride get the better of your discretion! Screw up your courage, my good friend, and resolve to show the world that you are an honest man....
"April 20.—Sir ... Your very sincere and favorite tutelary. I have long played the cur, snapping and snarling...; suddenly lost my power, and became half-starved dog without spirit to bark; try if air cannot restore me; calls himself the thistle in allusion to my other tutelary, the thorn; Would I prefer his next work to be, 'A whip for the Mathematical Cur, Prof. De M.' In some previous letter which I have mislaid, he told me his next would be 'a muzzle for the Mathematical Bull dog, Prof. De M.'
"April 23.—Sir. Very sincerely yours. More letters to clergyman; you may as well knock your head against a stone wall to improve your intellect as attempt to controvert my proofs. [I thought so too; and tried neither]. [246]
"May 6.—My dear Sir. Very sincerely yours. All to myself, and nothing to note.
"July 2.—No more in this interval. All that precedes is a desperate attempt to induce me to continue my descriptions: notoriety at any price."
I dare say the matter is finished: the record of so marked an instance of self-delusion will be useful.
I append to the foregoing a letter from Dr. Whewell[395] to Mr. James Smith. The Master of Trinity was conspicuous as a rough customer, an intellectual bully, an overbearing disputant: the character was as well established as that of Sam Johnson. But there was a marked difference. It was said of Johnson that if his pistol missed fire, he would knock you down with the butt end of it: but Whewell, in like case, always acknowledged the miss, and loaded again or not, as the case might be. He reminded me of Dennis Brulgruddery, who says to Dan, Pacify me with a good reason, and you'll find me a dutiful master. I knew him from the time when he was my teacher at Cambridge, more than forty years. As a teacher, he was anything but dictatorial, and he was perfectly accessible to proposal of objections. He came in contact with me in his slashing way twice in our after joint lives, and on both occasions he acknowledged himself overcome, by that change of manner, and apologetic mode of continuance, which I had seen him employ towards others under like circumstances.
I had expressed my wish to have a thermometer of probability, with impossibility at one end, as 2 and 2 make 5, and necessity at the other, as 2 and 2 make 4, and a graduated rise of examples between them. Down came a blow: "What! put necessary and contingent propositions together! It's absurd!" I pointed out that the two kinds of necessity are but such extremes of probability as 0 and ∞ are of number, and illustrated by an urn with 1 white and n black [247]balls, n increasing without limit. It was frankly seen, and the point yielded; a large company was present.
Again, in a large party, after dinner, and politics being the subject, I was proceeding, in discussion with Mr. Whewell, with "I think"...—"Ugh! you think!" was the answer. I repeated my phrase, and gave as a reason the words which Lord Grey[396] had used in the House of Lords the night before (the celebrated advice to the Bishops to set their houses in order). He had not heard of this, and his manner changed in an instant: he was the rational discutient all the rest of the evening, having previously been nothing but a disputant with all the distinctions strongly marked.
I have said that Whewell was gentle with his pupils; it was the same with all who wanted teaching: it was only on an armed enemy that he drew his weapon. The letter which he wrote to Mr. J. Smith is an instance: and as it applies with perfect fidelity to the efforts of unreasoning above described, I give it here. Mr. James Smith is skilfully exposed, and felt it; as is proved by "putting the writer in the stocks."
"Sir,—I have received your explanation of your proposition that the circumference of the circle is to its diameter as 25 to 8. I am afraid I shall disappoint you by saying that I see no force in your proof: and I should hope that you will see that there is no force in it if you consider this: In the whole course of the proof, though the word cycle occurs, there is no property of the circle employed. You may do this: you may put the word hexagon or dodecagon, or any other word describing a polygon in the place of Circle in your proof, and the proof would be just as good as before. Does not this satisfy you that you cannot have proved a property of that special figure—a circle? [248]
"Or you may do this: calculate the side of a polygon of 24 sides inscribed in a circle. I think you are a Mathematician enough to do this. You will find that if the radius of the circle be one, the side of this polygon is .264 etc. Now, the arc which this side subtends is according to your proposition 3.125/12 = .2604, and therefore the chord is greater than its arc, which you will allow is impossible.
"I shall be glad if these arguments satisfy you, and
"I am, Sir, your obedient Servant,
"W. Whewell."
AN M.P.'S ARITHMETIC.
In the debate of May, 1866, on Electoral Qualifications, a question arose about arithmetical capability. Mr. Gladstone asked how many members of the House could divide 1330l. 7s. 6d. by 2l. 13s. 8d. Six hundred and fifty-eight, answered one member; the thing cannot be done, answered another. There is an old paradox to which this relates: it arises out of the ignorance of the distinction between abstract and concrete arithmetic. Magnitude may be divided by magnitude; and the answer is number: how often does 12d. contain 4d.; answer three times. Magnitude may be divided by number, and the answer is magnitude: 12d. is divided in four equal parts, what is each part? Answer three pence. The honorable objector, whose name I suppress, trusting that he has mended his ways, gave the following utterance:
"With regard to the division sum, it was quite possible to divide by a sum, but not by money. How could any one divide money by 2l. 16s. 8d.? (Laughter.) The question might be asked, 'How many times 2s. will go into 1l.?' but that was not dividing by money; it was simply dividing 20 by 2. He might be asked, 'How many times will 6s. 8d. go into a pound?' but it was only required to divide 240 by 80. If the right hon. gentleman were to ask the hon. [249]member for Brighton (Professor Fawcett),[397] or any other authority, he would receive the same answer—viz., that it was possible to divide by a sum, but not by money. (Hear.)"
I shall leave all comment for the second edition, if I publish one.[398] I shall be sure to have something to laugh at. Anything said from a respectable quarter, or supposed to be said, is sure to find defenders. Sam Johnson, a sound arithmetician, comparing himself, and what he alone had done in three years, with forty French Academicians and their forty years, said it proved that an Englishman is to a Frenchman as 40 × 40 to 3, or as 1600 to 3. Boswell, who was no great hand at arithmetic, made him say that an Englishman is to a Frenchman as 3 to 1600. When I pointed this out, the supposed Johnson was defended through thick and thin in Notes and Queries.
I am now curious to see whether the following will find a palliator. It is from "Tristram Shandy," book V. chapter 3. There are two curious idioms, "for for" and "half in half"; but these have nothing to do with my point:
"A blessing which tied up my father's tongue, and a misfortune which set it loose with a good grace, were pretty equal: sometimes, indeed, the misfortune was the better of the two; for, for instance, where the pleasure of harangue was as ten, and the pain of the misfortune but as five, my father gained half in half; and consequently was as well again off as if it had never befallen him."
This is a jolly confusion of ideas; and wants nothing but a defender to make it perfect. A person who invests five [250]with a return of ten, and one who loses five with one hand and gains ten with the other, both leave off five richer than they began, no doubt. The first gains "half in half," more properly "half on half," that is, of the return, 10, the second 5 is gain upon the first 5 invested. "Half in half" is a queer way of saying cent. per cent. If the 5l. invested be all the man had in the world, he comes out, after the gain, twice as well off as he began, with reference to his whole fortune. But it is very odd to say that balance of 5l. gain is twice as good as if nothing had befallen, either loss or gain. A mathematician thinks 5 an infinite number of times as great as 0. The whole confusion is not so apparent when money is in question: for money is money whether gained or lost. But though pleasure and pain stand to one another in the same algebraical relation as money gained and lost, yet there is more than algebra can take account of in the difference.
Next, Ri. Milward[399] (Richard, no doubt, but it cannot be proved) who published Selden's[400] Table Talk, which he had collected while serving as amanuensis, makes Selden say, "A subsidy was counted the fifth part of a man's estate; and so fifty subsidies is five and forty times more than a man is worth." For times read subsidies, which seems part of the confusion, and there remains the making all the subsidies equal to the first, though the whole of which they are to be the fifths is perpetually diminished.
Thirdly, there is the confusion of the great misomath [251]of our own day, who discovered two quantities which he avers to be identically the same, but the greater the one the less the other. He had a truth in his mind, which his notions of quantity were inadequate to clothe in language. This erroneous phraseology has not found a defender; and I am almost inclined to say, with Falstaff, The poor abuses of the time want countenance.
ERRONEOUS ARITHMETICAL NOTIONS.
"Shallow numerists," as Cocker[401] is made to call them, have long been at work upon the question how to multiply money by money. It is, I have observed, a very common way of amusing the tedium of a sea voyage: I have had more than one bet referred to me. Because an oblong of five inches by four inches contains 5 × 4 or 20 square inches, people say that five inches multiplied by four inches is twenty square inches: and, thinking that they have multiplied length by length, they stare when they are told that money cannot be multiplied by money. One of my betters made it an argument for the thing being impossible, that there is no square money: what could I do but suggest that postage-stamps should be made legal tender. Multiplication must be repetition: the repeating process must be indicated by number of times. I once had difficulty in persuading another of my betters that if you repeat five shillings as often as there are hairs in a horse's tail, you do not multiply five shillings by a horsetail.[402]
I am very sorry to say that these wrong notions have found support—I think they do so no longer—in the University of Cambridge. In 1856 or 1857, an examiner was displaced by a vote of the Senate. The pretext was that he was too severe an examiner: but it was well known that [252]great dissatisfaction had been expressed, far and wide through the Colleges, at an absurd question which he had given. He actually proposed such a fraction as
6s. 3d. 17s. 4d. | . |
As common sense gained a hearing very soon, there is no occasion to say more. In 1858, it was proposed at a college examination, to divide 22557 days, 20 hours, 20 minutes, 48 seconds, by 57 minutes, 12 seconds, and also to explain the fraction
32l. 18s. 8d. 62l. 12s. 9d. | . |
All paradoxy, in matters of demonstration, arises out of muddle about first principles. Who can say how much of it is to be laid at the door of the University of Cambridge, for not taking care of the elements of arithmetical thought?
ON LITERARY BARGAINS.
The phenomena of the two ends of society, when brought together, give interesting comparisons: I mean the early beginnings of thought and literature, and our own high and finished state, as we think it. There is one very remarkable point. In the early day, the letter was matter of the closest adherence, and implied meanings were not admitted.
The blessing of Isaac meant for Esau, went to false Jacob, in spite of the imposition; and the writer of Genesis seems to intend to give the notion that Isaac had no power to pronounce it null and void. And "Jacob's policy, whereby he became rich"—as the chapter-heading puts it—in speckled and spotted stock, is not considered as a violation of the agreement, which contemplated natural proportions. In [253]the story of Lycurgus the lawgiver is held to have behaved fairly when he bound the Spartans to obey his laws until he returned—intimating a short absence—he intending never to return. And Vishnoo, when he asked the usurper for three steps of territory as a dwarf, and then enlarged himself until he could bring heaven and earth under the bargain, was thought clever, certainly, but quite fair.
There is nothing of this kind recognized in our day: so far good. But there is a bad contrary: the age is apt, in interpretation, to upset the letter in favor of the view—very often the after thought—of one side only. The case of John Palmer,[403] the improver of the mail coach system, is smothered. He was to have an office and a salary, and 2½ per cent for life on the increased revenue of the Post-Office. His rights turned out so large, that Government would not pay them. For misconduct, real or pretended, they turned him out of his office: but his bargain as to the percentage had nothing to do with his future conduct; it was payment for his plan. I know nothing, except from the debates of 1808 in the two Houses: if any one can redeem the credit of the nation, the field is open. When I was young, the old stagers spoke of this transaction sparingly, and dismissed it speedily.
The government did not choose to remember what private persons must remember, and are made to remember, if needful. When Dr. Lardner[404] made his bargain with the [254]publishers for the Cabinet Cyclopædia he proposed that he, as editor, should have a certain sum for every hundred sold above a certain number: the publishers, who did not think there was any chance of reaching the turning sale of this stipulation, readily consented. But it turned out that Dr. Lardner saw further than they: the returns under this stipulation gave him a very handsome addition to his other receipts. The publishers stared; but they paid. They had no idea of standing out that the amount was too much for an editor; they knew that, though the editor had a percentage, they had all the rest; and they would not have felt aggrieved if he had received ten times as much. But governments, which cannot be brought to book before a sworn jury, are ruled only by public opinion. John Palmer's day was also the day of Thomas Fyshe Palmer,[405] and the governments, in their prosecutions for sedition, knew that these would have a reflex action upon the minds of all who wrote about public affairs.
DECLARATION OF BELIEF
1864-65.—It often happens that persons combine to maintain and enforce an opinion; but it is, in our state of society, a paradox to unite for the sole purpose of blaming the opposite side. To invite educated men to do this, and above all, men of learning or science, is the next paradoxical thing of all. But this was done by a small combination in 1864. They got together and drew up a declaration, to be signed by "students of the natural sciences," who were to express their "sincere regret that researches into [255]scientific truth are perverted by some in our own times into occasion for casting doubt upon the truth and authenticity of the Holy Scriptures." In words of ambiguous sophistry, they proceeded to request, in effect, that people would be pleased to adopt the views of churches as to the complete inspiration of all the canonical books. The great question whether the Word of God is in the Bible, or whether the Word of God is all the Bible, was quietly taken for granted in favor of the second view; to the end that men of science might be induced to blame those who took the first view. The first public attention was drawn to the subject by Sir John Herschel,[406] who in refusing to sign the writ sent to him, administered a rebuke in the Athenæum, which would have opened most eyes to see that the case was hopeless. The words of a man whose suaviter in modo makes his fortiter in re[407] cut blocks with a razor are worth preserving:
"I consider the act of calling upon me publicly to avow or disavow, to approve or disapprove, in writing, any religious doctrine or statement, however carefully or cautiously drawn up (in other words, to append my name to a religious manifesto) to be an infringement of that social forbearance which guards the freedom of religious opinion in this country with especial sanctity.... I consider this movement simply mischievous, having a direct tendency (by putting forward a new Shibboleth, a new verbal test of religious partisanship) to add a fresh element of discord to the already too discordant relations of the Christian world.... But no nicety of wording, no artifice of human language, will suffice to discriminate the hundredth part of the shades of meaning in which the most world-wide differences of thought on such subjects may be involved; or prevent the most gentle worded and apparently justifiable expression of regret, so embodied, from grating on the [256]feelings of thousands of estimable and well-intentioned men with all the harshness of controversial hostility."
Other doses were administered by Sir J. Bowring,[408] Sir W. Rowan Hamilton,[409] and myself. The signed declaration was promised for Christmas, 1864: but nothing presentable was then ready; and it was near Midsummer, 1865, before it was published. Persons often incautiously put their names without seeing the character of a document, because they coincide in its opinions. In this way, probably, fifteen respectable names were procured before printing; and these, when committed, were hawked as part of an application to "solicit the favor" of other signatures. It is likely enough no one of the fifteen saw that the declaration was, not maintenance of their own opinion, but regret (a civil word for blame) that others should think differently.
When the list appeared, there were no fewer than 716 names! But analysis showed that this roll was not a specimen of the mature science of the country. The collection was very miscellaneous: 38 were designated as "students of the College of Chemistry," meaning young men who attended lectures in that college. But as all the Royal Society had been applied to, a test results as follows. Of Fellows of the Royal Society, 600 in number, 62 gave their signatures; of writers in the Philosophical Transactions, 166 in number, 19 gave their signatures. Roughly speaking, then, only one out of ten could be got to express disapprobation of the free comparison of the results of science with the statements of the canonical books. And I am satisfied that many of these thought they were signing only a declaration of difference of opinion, not of blame for that difference. The number of persons is not small who, when it comes to signing printed documents, would put their names to a declaration that the coffee-pot ought to be taken down-stairs, meaning that the teapot ought to be brought [257]up-stairs. And many of them would defend it. Some would say that the two things are not contradictory; which, with a snort or two of contempt, would be very effective. Others would, in the candid and quiet tone, point out that it is all one, because coffee is usually taken before tea, and it keeps the table clear to send away the coffee-pot before the teapot is brought up.
The original signatures were decently interred in the Bodleian Library: and the advocates of scattering indefinite blame for indefinite sins of opinion among indefinite persons are, I understand, divided in opinion about the time at which the next attempt shall be made upon men of scientific studies: some are for the Greek Calends, and others for the Roman Olympiads. But, with their usual love of indefiniteness, they have determined that the choice shall be argued upon the basis that which comes first cannot be settled, and is of no consequence.
I give the declaration entire, as a curiosity: and parallel with it I give a substitute which was proposed in the Athenæum, as worthy to be signed both by students of theology, and by students of science, especially in past time. When a new attempt is made, it will be worth while to look at both:
The distinctness of the fallacies is creditable to the composers, and shows that scientific habits tend to clearness, even to sophistry. Nowhere does it so plainly stand out that the Written Word means the sense in which the accuser takes it, while the sense of the other side is their interpretation. The infallible church on one side, arrayed against heretical pravity on the other, is seen in all subjects in which men differ. At school there were various games in which one or another advantage was the right of those who first called for it. In adult argument the same thing is often attempted: we often hear—I cried Church first!
I end with the answer which I myself gave to the application: its revival may possibly save me from a repetition of the like. If there be anything I hate more than another it is the proposal to place any persons, especially those who allow freedom to me, under any abridgment of their liberty to think, to infer, and to publish. If they break the law, take the law; but do not make the law: ἀγοραιοι ἀγονται ἐγκαλειτωσαν ἀλληλοις.[410] I would rather be asked to take shares in an argyrosteretic company (with limited liability) for breaking into houses by night on fork and spoon errands. I should put aside this proposal with nothing but laughter. It was a joke against Sam Rogers[411] that his appearance was very like that of a corpse. The John Bull [261]newspaper—suppose we now say Theodore Hook[412]—averred that when he hailed a coach one night in St. Paul's Churchyard, the jarvey said, "Ho! ho! my man; I'm not going to be taken in that way: go back to your grave!" This is the answer I shall make for the future to any relics of a former time who shall want to call me off the stand for their own purposes. What obligation have I to admit that they belong to our world?
"SCRIPTURE AND SCIENCE.
"The Writ De Hæretico Commiserando.[413]
"This document was sent to me four days ago. It 'solicits the favor'—I thought at first it was a grocer's supplication for tea and sugar patronage—of my signature to expression of 'sincere regret' that some persons unnamed—general warrants are illegal—differ from what I am supposed—by persons whom it does not concern—to hold about Scripture and Science in their real or alleged discrepancies.
"No such favor from me: for three reasons. First, I agree with Sir. J. Herschel that the solicitation is an intrusion to be publicly repelled. Secondly, I do not regret that others should differ from me, think what I may: those others are as good as I, and as well able to think, and as much entitled to their conclusions. Thirdly, even if I did regret, I should be ashamed to put my name to bad chemistry made to do duty for good reasoning. The declaration is an awkward attempt to saturate sophism with truism; but the sophism is left largely in excess.
"I owe the inquisitors a grudge for taking down my conceit of myself. For two months I have crowed in my own mind over my friend Sir J. Herschel, fancying that the promoters instinctively knew better than to bring their fallacies before a writer on logic. Ah! my dear Sir John! thought I, if you had shown yourself to be well up in Barbara Celarent,[414] and had ever and anon astonished the natives with the distinction between simpliciter and secundum quid, no autograph-hunters would have baited a trap with non sequitur[415] to catch your signature. What can I say now? I hide my diminished head, diminished by the horns which I have been compelled to draw in.
"Those who make personal solicitation for support to an opinion about religion are bound to know their men. The king had a right to Brother Neale's money, because Brother Neale offered it. Had he put his hand into purse after purse by way of finding out all who were of Brother Neale's mind, he would have been justly met by a rap on the knuckles whenever he missed his mark.
"The kind of test before me is the utmost our time will allow of that inquisition into opinion which has been the curse of Christianity ever since the State took Providence under its protection. The writ de hæretico commiserando is little more than the smell of the empty cask: and those who issue it may represent the old woman with her
"O suavis anima, quale in te dicam bonum
Antehac fuisse; tales cum sint reliquiæ."[416]
It is no excuse that the illegitimate bantling is a very little one. Its parents may think themselves hardly treated when they are called lineal successors of Tony Fire-the-faggot: [263]but, degenerate though they be, such is their ancestry. Let every allowance be made for them: but their unholy fire must be trodden out; so long as a spark is left, nothing but fuel is wanted to make a blaze. If this cannot be done, let the flame be confined to theology, though even there it burns with diminished vigor: and let charity, candor, sense, and ridicule, be ready to play upon it whenever there is any chance of its extending to literature and science.
"What would be the consequence if this test-signing absurdity were to grow? Deep would call unto deep; counter-declaration would answer declaration, each stronger than the one before. The moves would go on like the dispute of two German students, of whom each is bound to a sharper retort on a graduated scale, until at last comes dummer Junge![417]—and then they must fight. There is a gentleman in the upper fifteen of the signers of the writ—the hawking of whose names appears to me very bad taste—whom I met in cordial cooperation for many a year at a scientific board. All I knew about his religion was that he, as a clergyman, must in some sense or other receive the 39 Articles:—all that he could know about mine was that I was some kind of heretic, or so reputed. If we had come to signing opposite manifestoes, turn-about, we might have found ourselves in the lowest depths of party discussion at our very council-table. I trust the list of subscribers to the declaration, when it comes to be published, will show that the bulk of those who have really added to our knowledge have seen the thing in its true light.
"The promoters—I say nothing about the subscribers—of the movement will, I trust, not feel aggrieved at the course I have taken or the remarks I have made. Walter Scott says that before we judge Napoleon by the temptation to which he yielded, we ought to remember how much he may have resisted: I invite them to apply this rule to myself; they can have no idea of the feeling with which I [264]contemplate all attempts to repress freedom of inquiry, nor of the loathing with which I recoil from the proposal to be art and part. They have asked me to give a public opinion upon a certain point. It is true that they have had the kindness to tender both the opinion they wish me to form, and the shape in which they would have it appear: I will let them draw me out, but I will not let them take me in. If they will put an asterisk to my name, and this letter to the asterisk, they are welcome to my signature. As I do not expect them to relish this proposal, I will not solicit the favor of its adoption. But they have given a right to think, for they have asked me to think; to publish, for they have asked me to allow them to publish; to blame them, for they have asked me to blame their betters. Should they venture to find fault because my direction of disapproval, publicly given, is half a revolution different from theirs, they will be known as having presented a loaded document at the head of a traveler in the highway of discussion, with—Your signature or your silence!"
THE FLY-LEAF PARADOX.
The paradox being the proposition of something which runs counter to what would generally be thought likely, may present itself in many ways. There is a fly-leaf paradox, which puzzled me for many years, until I found a probable solution. I frequently saw, in the blank leaves of old books, learned books, Bibles of a time when a Bible was very costly, etc., the name of an owner who, by the handwriting and spelling, must have been an illiterate person or a child, followed by the date of the book itself. Accordingly, this uneducated person or young child seemed to be the first owner, which in many cases was not credible. Looking one day at a Barker's[418] Bible of 1599, I saw an [265]inscription in a child's writing, which certainly belonged to a much later date. It was "Martha Taylor, her book, giuen me by Granny Scott to keep for her sake." With this the usual verses, followed by 1599, the date of the book. But it so chanced that the blank page opposite the title, on which the above was written, was a verso of the last leaf of a prayer book, which had been bound before the Bible; and on the recto of this leaf was a colophon, with the date 1632. It struck me immediately that uneducated persons and children, having seen dates written under names, and not being quite up in chronology, did frequently finish off with the date of the book, which stared them in the face.
Always write in your books. You may be a silly person—for though your reading my book is rather a contrary presumption, yet it is not conclusive—and your observations may be silly or irrelevant, but you cannot tell what use they may be of long after you are gone where Budgeteers cease from troubling.
I picked up the following book, printed by J. Franklin[419] at Boston, during the period in which his younger brother Benjamin was his apprentice. And as Benjamin was apprenticed very early, and is recorded as having learned the mechanical art very rapidly, there is some presumption that part of it may be his work, though he was but thirteen at the time. As this set of editions of Hodder[420] (by [266]Mose[421]) is not mentioned, to my knowledge, I give the title in full:
"Hodder's Arithmetick: or that necessary art made most easy: Being explained in a way familiar to the capacity of any that desire to learn it in a little time. By James Hodder, Writing-master. The Five and twentieth edition, revised, augmented, and above a thousand faults amended, by Henry Mose, late servant and successor to the author. Boston: printed by J. Franklin, for S. Phillips, N. Buttolph, B. Elliot, D. Henchman, G. Phillips, J. Elliot, and E. Negus, booksellers in Boston, and sold at their shops. 1719."
The book is a very small octavo, the type and execution are creditable, the woodcut at the beginning is clumsy. It is a perfect copy, page for page, of the English editions of Mose's Hodder, of which the one called seventeenth is of London, 1690. There is not a syllable to show that the edition above described might not be of Boston in England. Presumptions, but not very strong ones, might be derived from the name of Franklin, and from the large number of booksellers who combined in the undertaking. It chanced, however, that a former owner had made the following note in my copy:
"Wednessday, July ye 14, 1796, att ten in ye forenoon we saild from Boston, came too twice, once in King Rode, and once in ye Narrows. Saild by ye lighthouse in ye eveng."
No ordinary map would decide these points: so I had to apply to my friend Sir Francis Beaufort,[422] and the charts at the Admiralty decided immediately for Massachusetts.
PARADOXES OF ORTHOGRAPHY AND COMPUTATION.
The French are able paradoxers in their spelling of foreign names. The Abbé Sabatier de Castres,[423] in 1772, gives an account of an imaginary dialogue between Swif, Adisson, Otwai, and Bolingbrocke. I had hoped that this was a thing of former days, like the literal roasting of heretics; but the charity which hopeth all things must hope for disappointments. Looking at a recent work on the history of the popes, I found referred to, in the matter of Urban VIII[424] and Galileo, references to the works of two Englishmen, the Rev. Win Worewel and the Rev. Raden Powen. [Wm. Whewell and Baden Powell].[425]
I must not forget the "moderate computation" paradox. This is the way by which large figures are usually obtained. Anything surprisingly great is got by the "lowest computation," anything as surprisingly small by the "utmost computation"; and these are the two great subdivisions of "moderate computation." In this way we learn that 70,000 persons were executed in one reign, and 150,000 persons [268]burned for witchcraft in one century. Sometimes this computation is very close. By a card before me it appears that all the Christians, including those dispersed in heathen countries, those of Great Britain and Ireland excepted, are 198,728,000 people, and pay their clergy 8,852,000l. But 6,400,000 people pay the clergy of the Anglo-Irish Establishment 8,896,000l.; and 14,600,000 of other denominations pay 1,024,000l. When I read moderate computations, I always think of Voltaire and the "mémoires du fameux évêque de Chiapa, par lesquels il paraît qu'il avait égorgé, ou brulé, ou noyé dix millions d'infidèles en Amérique pour les convertir. Je crus que cet évêque exaggérait; mais quand on réduisait ces sacrifices à cinq millions de victimes, cela serait encore admirable."[426]
CENTRIFUGAL FORCE.
My Budget has been arranged by authors. This is the only plan, for much of the remark is personal: the peculiarities of the paradoxer are a large part of the interest of the paradox. As to subject-matter, there are points which stand strongly out; the quadrature of the circle, for instance. But there are others which cannot be drawn out so as to be conspicuous in a review of writers: as one instance, I may take the centrifugal force.
When I was about nine years old I was taken to hear a course of lectures, given by an itinerant lecturer in a country town, to get as much as I could of the second half of a good, sound, philosophical omniscience. The first half (and sometimes more) comes by nature. To this end I smelt chemicals, learned that they were different kinds of gin, saw young wags try to kiss the girls under the excuse of what was called laughing gas—which I was sure [269]was not to blame for more than five per cent of the requisite assurance—and so forth. This was all well so far as it went; but there was also the excessive notion of creative power exhibited in the millions of miles of the solar system, of which power I wondered they did not give a still grander idea by expressing the distances in inches. But even this was nothing to the ingenious contrivance of the centrifugal force. "You have heard what I have said of the wonderful centripetal force, by which Divine Wisdom has retained the planets in their orbits round the Sun. But, ladies and gentlemen, it must be clear to you that if there were no other force in action, this centripetal force would draw our earth and the other planets into the Sun, and universal ruin would ensue. To prevent such a catastrophe, the same wisdom has implanted a centrifugal force of the same amount, and directly opposite," etc. I had never heard of Alfonso X of Castile,[427] but I ventured to think that if Divine Wisdom had just let the planets alone it would come to the same thing, with equal and opposite troubles saved. The paradoxers deal largely in speculation conducted upon the above explanation. They provide external agents for what they call the centrifugal force. Some make the sun's rays keep the planets off, without a thought about what would become of our poor eyes if the push of the light which falls on the earth were a counterpoise to all its gravitation. The true explanation cannot be given here, for want of room.
CAMBRIDGE POETS.
Sometimes a person who has a point to carry will assert a singular fact or prediction for the sake of his point; and [270]this paradox has almost obtained the sole use of the name. Persons who have reputation to care for should beware how they adopt this plan, which now and then eventuates a spanker, as the American editor said. Lord Byron, in "English Bards, etc." (1809), ridiculing Cambridge poetry, wrote as follows:
There is some account of the Rev. Geo. Richards, Fellow of Oriel and Vicar of Bampton, (M.A. in 1791) in the Living Authors by Watkins[430] and Shoberl[431] (1816). In Rivers's Living Authors, of 1798, which is best fitted for citation, as being published before Lord Byron wrote, he is spoken of in high terms. The Aboriginal Britons was an Oxford (special) prize poem, of 1791. Charles Lamb mentions Richards as his school-fellow at Christ's Hospital, "author of the Aboriginal Britons, the most spirited of the Oxford Prize Poems: a pale, studious Grecian."
As I never heard of Richards as a poet,[432] I conclude that his fame is defunct, except in what may prove to be a very ambiguous kind of immortality, conferred by Lord Byron. The awkwardness of a case which time has broken down [271]is increased by the eulogist himself adding so powerful a name to the list of Cambridge poets, that his college has placed his statue in the library, more conspicuously than that of Newton in the chapel; and this although the greatness of poetic fame had some serious drawbacks in the moral character of some of his writings. And it will be found on inquiry that Byron, to get his instance against Cambridge, had to go back eighteen years, passing over seven intermediate productions, of which he had either never heard, or which he would not cite as waking a genuine poet's fires.
The conclusion seems to be that the Aboriginal Britons is a remarkable youthful production, not equalled by subsequent efforts.
To enhance the position in which the satirist placed himself, two things should be remembered. First, the glowing and justifiable terms in which Byron had spoken,—a hundred and odd lines before he found it convenient to say no Cambridge poet could compare with Richards,—of a Cambridge poet who died only three years before Byron wrote, and produced greatly admired works while actually studying in the University. The fame of Kirke White[433] still lives; and future literary critics may perhaps compare his writings and those of Richards, simply by reason of the curious relation in which they are here placed alongside of each other. And it is much to Byron's credit that, in speaking of the deceased Cambridge poet, he forgot his own argument and its exigencies, and proved himself only a paradoxer pro re nata.
Secondly, Byron was very unfortunate in another passage of the same poem:
"What varied wonders tempt us as they pass!
The cow-pox, tractors, galvanism, and gas.
In turns appear, to make the vulgar stare,
Till the swoln bubble bursts—and all is air!"
Three of the bubbles have burst to mighty ends. The metallic tractors are disused; but the force which, if anything, they put in action, is at this day, under the name of mesmerism, used, prohibited, respected, scorned, assailed, defended, asserted, denied, declared utterly obscure, and universally known. It was hard lines to select for candidates for oblivion not one of whom got in. I shall myself, I am assured, be some day cited for laughing at the great discovery of ——: the blank is left for my reader to fill up in his own way; but I think I shall not be so unlucky in four different ways.
FALSIFIED PREDICTION.
The narration before the fact, as prophecy has been called, sometimes quite as true as the narration after the fact, is very ridiculous when it is wrong. Why, the pre-narrator could not know; the post-narrator might have known. A good collection of unlucky predictions might be made: I hardly know one so fit to go with Byron's as that of the Rev. Daniel Rivers, already quoted, about Johnson's biographers. Peter Pindar[434] may be excused, as personal satire was his object, for addressing Boswell and Mrs. Piozzi[435] as follows:
"Instead of adding splendor to his name,
Your books are downright gibbets to his fame;
You never with posterity can thrive,
'Tis by the Rambler's death alone you live."
But Rivers, in prose narrative, was not so excusable. He says:
"As admirers of the learning and moral excellence of their hero, we glow at almost every page with indignation that his weaknesses and his failings should be disclosed to public view.... Johnson, after the luster he had reflected on the name of Thrale ... was to have his memory tortured and abused by her detested itch for scribbling. More injury, we will venture to affirm, has been done to the fame of Johnson by this Lady and her late biographical helpmate, than his most avowed enemies have been able to effect: and if his character becomes unpopular with some of his successors, it is to those gossiping friends he is indebted for the favor."
Poor dear old Sam! the best known dead man alive! clever, good-hearted, logical, ugly bear! Where would he have been if it had not been for Boswell and Thrale, and their imitators? What would biography have been if Boswell had not shown how to write a life?
Rivers is to be commended for not throwing a single Stone at Mrs. Thrale's second marriage. This poor lady begins to receive a little justice. The literary world seems to have found out that a blue-stocking dame who keeps open house for a set among them has a right, if it so please her, to marry again without taking measures to carry on the cake-shop. I was before my age in this respect: as a boy-reader of Boswell, and a few other things that fell in my way, I came to a clearness that the conduct of society towards Mrs. Piozzi was blackguard. She wanted nothing but what was in that day a woman's only efficient protection, a male relation with a brace of pistols, and a competent notion of using them.
BYRON AND WORDSWORTH.
Byron's mistake about Hallam in the Pindar story may be worth placing among absurdities. For elucidation, suppose that some poet were now to speak— [274]
"Of man's first disobedience, and the fruit
Eve gave to Adam in his birthday suit—"
and some critic were to call it nonsense, would that critic be laughing at Milton? Payne Knight,[436] in his Taste, translated part of Gray's Bard into Greek. Some of his lines are
θερμὰ δ' ὁ τὲγγων δάκρυα στοναχαῖς
οὖλον μέλος φοβερᾷ
ηἔιδε φωνᾷ.
Literally thus:
"Wetting warm tears with groans,
Continuous chant with fearful
Voice he sang."
On which Hallam remarks: "The twelfth line [our first] is nonsense." And so it is, a poet can no more wet his tears with his groans than wet his ale with his whistle. Now this first line is from Pindar, but is only part of the sense; in full it is:
θερμὰ δὲ τέγγων δάκρυα στοναχαῖς
ὅρθιον φώνασε.
Pindar's τέγγων must be Englished by shedding, and he stands alone in this use. He says, "shedding warm tears, he cried out loud, with groans." Byron speaks of
"Classic Hallam, much renowned for Greek:"
and represents him as criticising the Greek of all Payne's lines, and not discovering that "the lines" were Pindar's [275]until after publication. Byron was too much of a scholar to make this blunder himself: he either accepted the facts from report, or else took satirical licence. And why not? If you want to laugh at a person, and he will not give occasion, whose fault is it that you are obliged to make it? Hallam did criticise some of Payne Knight's Greek; but with the caution of his character, he remarked that possibly some of these queer phrases might be "critic-traps" justified by some one use of some one author. I remember well having a Latin essay to write at Cambridge, in which I took care to insert a few monstrous and unusual idioms from Cicero: a person with a Nizolius,[437] and without scruples may get scores of them. So when my tutor raised his voice against these oddities, I was up to him, for I came down upon him with Cicero, chapter and verse, and got round him. And so my own solecisms, many of them, passed unchallenged.
Byron had more good in his nature than he was fond of letting out: whether he was a soured misanthrope, or whether his vein lay that way in poetry, and he felt it necessary to fit his demeanor to it, are matters far beyond me. Mr. Crabb Robinson[438] told me the following story more than once. He was at Charles Lamb's chambers in the Temple when Wordsworth came in, with the new Edinburgh Review in his hand, and fume on his countenance. "These reviewers," said he, "put me out of patience! Here is a young man—they say he is a lord—who has written a volume of poetry; and these fellows, just because he is a lord, set upon him, laugh at him, and sneer at his writing. The young man will do something, if he goes on as he has begun. But these reviewers seem to think [276]that nobody may write poetry, unless he lives in a garret." Crabb Robinson told this long after to Lady Byron, who said, "Ah! if Byron had known that, he would never have attacked Wordsworth. He went one day to meet Wordsworth at dinner; when he came home I said, 'Well, how did the young poet get on with the old one?' 'Why, to tell you the truth,' said he, 'I had but one feeling from the beginning of the visit to the end, and that was—reverence!'" Lady Byron told my wife that her husband had a very great respect for Wordsworth. I suppose he would have said—as the Archangel said to his Satan—"Our difference is po[li = e]tical."
I suspect that Fielding would, if all were known, be ranked among the unlucky railers at supposed paradox. In his Miscellanies (1742, 8vo) he wrote a satire on the Chrysippus or Guinea, an animal which multiplies itself by division, like the polypus. This he supposes to have been drawn up by Petrus Gualterus, meaning the famous usurer, Peter Walter. He calls it a paper "proper to be read before the R——l Society": and next year, 1743, a quarto reprint was made to resemble a paper in the Philosophical Transactions. So far as I can make out, one object is ridicule of what the zoologists said about the polypus: a reprint in the form of the Transactions was certainly satire on the Society, not on Peter Walter and his knack of multiplying guineas.
Old poets have recognized the quadrature of the circle as a well-known difficulty. Dante compares himself, when bewildered, to a geometer who cannot find the principle on which the circle is to be measured:
"Quale è 'l geometra che tutto s' affige
Per misurar lo cerchio, e non ritruova,
Pensando qual principio ond' egli indige."[439]
And Quarles[440] speaks as follows of the summum bonum:
"Or is't a tart idea, to procure
An edge, and keep the practic soul in ure,
Like that dear chymic dust, or puzzling quadrature?"
The poetic notion of the quadrature must not be forgotten. Aristophanes, in the Birds, introduces a geometer who announces his intention to make a square circle. Pope, in the Dunciad, delivers himself as follows, with a Greek pronunciation rather strange in a translator of Homer. Probably Pope recognized, as a general rule, the very common practice of throwing back the accent in defiance of quantity, seen in o´rator, au´ditor, se´nator, ca´tenary, etc.
"Mad Mathesis alone was unconfined,
Too mad for mere material chains to bind,—
Now to pure space lifts her ecstatic stare,
Now, running round the circle, finds it square."
The author's note explains that this "regards the wild and fruitless attempts of squaring the circle." The poetic idea seems to be that the geometers try to make a square circle. Disraeli quotes it as "finds its square," but the originals do not support this reading.
DE BECOURT.
I have come in the way of a work, entitled The Grave of Human Philosophies (1827), translated from the French of R. de Bécourt[441] by A. Dalmas. It supports, but I suspect not very accurately, the views of the old Hindu books. [278]That the sun is only 450 miles from us, and only 40 miles in diameter, may be passed over; my affair is with the state of mind into which persons of M. Bécourt's temperament are brought by a fancy. He fully grants, as certain, four millions of years as the duration of the Hindu race, and 1956 as that of the universe. It must be admitted he is not wholly wrong in saying that our errors about the universe proceed from our ignorance of its origin, antiquity, organization, laws, and final destination. Living in an age of light, he "avails himself of that opportunity" to remove this veil of darkness, etc. The system of the Brahmins is the only true one: he adds that it has never before been attempted, as it could not be obtained except by him. The author requests us first, to lay aside prejudice; next, to read all he says in the order in which he says it: we may then pronounce judgment upon a work which begins by taking the Brahmins for granted. All the paradoxers make the same requests. They do not see that compliance would bring thousands of systems before the world every year: we have scores as it is. How is a poor candid inquirer to choose. Fortunately, the mind has its grand jury as well as its little one: and it will not put a book upon its trial without a prima facie case in its favor. And with most of those who really search for themselves, that case is never made out without evidence of knowledge, standing out clear and strong, in the book to be examined.
BEQUEST OF A QUADRATURE.
There is much private history which will never come to light, caret quia vate sacro,[442] because no Budgeteer comes across it. Many years ago a man of business, whose life was passed in banking, amused his leisure with quadrature, was successful of course, and bequeathed the result in a sealed book, which the legatee was enjoined not to sell [279]under a thousand pounds. The true ratio was 3.1416: I have the anecdote from the legatee's executor, who opened the book. That a banker should square the circle is very credible: but how could a City man come by the notion that a thousand pounds could be got for it? A friend of mine, one of the twins of my zodiac, will spend a thousand pounds, if he have not done it already, in black and white cyclometry: but I will answer for it that he, a man of sound business notions, never entertained the idea of π recouping him, as they now say. I speak of individual success: of course if a company were formed, especially if it were of unlimited lie-ability, the shares would be taken. No offence; there is nothing but what a pun will either sanctify, justify, or nullify:
"It comes o'er the soul like the sweet South
That breathes upon a bank of vile hits."
The shares would be at a premium of 3⅛ on the day after issue. If they presented me with the number of shares I deserve, for suggestion and advertisement, I should stand up for the Archpriest of St. Vitus[443] and 3-1/5, with a view to a little more gold on the bridge.
I now insert a couple of reviews, one about Cyclopædias, one about epistolary collections. Should any reader wish for explanation of this insertion, I ask him to reflect a moment, and imagine me set to justify all the additions now before him! In truth these reviews are the repositories of many odds and ends: they were not made to the books; the materials were in my notes, and the books came as to a ready-made clothes shop, and found what would fit them. Many remember Curll's[444] bequest of some very good titles [280]which only wanted treatises written to them. Well! here were some tolerable reviews—as times go—which only wanted books fitted to them. Accordingly, some tags were made to join on the books; and then as the reader sees.
I should find it hard to explain why the insertion is made in this place rather than another. But again, suppose I were put to make such an explanation throughout the volume. The improver who laid out grounds and always studied what he called unexpectedness, was asked what name he gave it for those who walked over his grounds a second time. He was silenced; but I have an answer: It is that which is given by the very procedure of taking up my book a second time.
REVIEW OF CYCLOPÆDIAS.
October 19, 1861. The English Cyclopædia. Conducted by Charles Knight.[445] 22 vols.: viz., Geography, 4 vols.; Biography, 6 vols.; Natural History, 4 vols.; Arts and Sciences, 8 vols. (Bradbury & Evans.)
The Encyclopædia Britannica: a Dictionary of Arts, Sciences, and General Literature. Eighth Edition. 21 vols. and Index. (Black.)
The two editions above described are completed at the same time: and they stand at the head of the two great branches into which pantological undertakings are divided, as at once the largest and the best of their classes.
When the works are brought together, the first thing that strikes the eye is the syllable of difference in the names. The word Cyclopædia is a bit of modern purism. Though ἐγκυκλοπαιδεια[446] is not absolutely Greek of Greece, we learn from both Pliny[447] and Quintilian[448] that the circle [281]of the sciences was so called by the Greeks, and Vitruvius[449] has thence naturalized encyclium in Latin. Nevertheless we admit that the initial en would have euphonized but badly with the word Penny: and the English Cyclopædia is the augmented, revised, and distributed edition of the Penny Cyclopædia. It has indeed been said that Cyclopædia should mean the education of a circle, just as Cyropædia is the education of Cyrus. But this is easily upset by Aristotle's word κυκλοφορία,[450] motion in a circle, and by many other cases, for which see the lexicon.
The earliest printed Encyclopædia of this kind was perhaps the famous "myrrour of the worlde," which Caxton[451] translated from the French and printed in 1480. The original Latin is of the thirteenth century, or earlier. This is a collection of very short treatises. In or shortly after 1496 appeared the Margarita Philosophica of Gregory Reisch,[452] the same we must suppose, who was confessor to the Emperor Maximilian.[453] This is again a collection of treatises, of much more pretension: and the estimation formed of it is proved by the number of editions it went through. In 1531 appeared the little collection of works of Ringelberg,[454] which is truly called an Encyclopædia by [282]Morhof, though the thumbs and fingers of the two hands will meet over the length of its one volume. There are more small collections; but we pass on to the first work to which the name of Encyclopædia is given. This is a ponderous Scientiarum Omnium Encyclopædia of Alsted,[455] in four folio volumes, commonly bound in two: published in 1629 and again in 1649; the true parent of all the Encyclopædias, or collections of treatises, or works in which that character predominates. The first great dictionary may perhaps be taken to be Hofman's Lexicon Universale[456] (1677); but Chambers's[457] (so called) Dictionary (1728) has a better claim. And we support our proposed nomenclature by observing that Alsted accidentally called his work Encyclopædia, and Chambers simply Cyclopædia.
We shall make one little extract from the myrrour, and one from Ringelberg. Caxton's author makes a singular remark for his time; and one well worthy of attention. The grammar rules of a language, he says, must have been invented by foreigners: "And whan any suche tonge was perfytely had and usyd amonge any people, than other people not used to the same tonge caused rulys to be made wherby they myght lerne the same tonge ... and suche rulys be called the gramer of that tonge." Ringelberg says that if the right nostril bleed, the little finger of the right hand should be crooked, and squeezed with great force; and the same for the left.
We pass on to the Encyclopédie,[458] commenced in 1751; the work which has, in many minds, connected the word encyclopædist with that of infidel. Readers of our day are surprised when they look into this work, and wonder what has become of all the irreligion. The truth is, that the work—though denounced ab ovo[459] on account of the character of its supporters—was neither adapted, nor intended, to excite any particular remark on the subject: no work of which D'Alembert[460] was co-editor would have been started on any such plan. For, first, he was a real sceptic: that is, doubtful, with a mind not made up. Next, he valued his quiet more than anything; and would as soon have gone to sleep over an hornet's nest as have contemplated a systematic attack upon either religion or government. As to Diderot[461]—of whose varied career of thought it is difficult to fix the character of any one moment, but who is very frequently taken among us for a pure atheist—we will quote one sentence from the article "Encyclopédie," which he wrote himself:—"Dans le moral, il n'y a que Dieu qui doit servir de modèle a 1'homme; dans les art, que la nature."[462]
A great many readers in our country have but a very hazy idea of the difference between the political Encyclopædia, as we may call it, and the Encyclopédie Méthodique,[463] which we always take to be meant—whether rightly or not we cannot tell—when we hear of the "great French Encyclopædia." This work, which takes much from its [284]predecessor, professing to correct it, was begun in 1792, and finished in 1832. There are 166 volumes of text, and 6439 plates, which are sometimes incorporated with the text, sometimes make about 40 more volumes. This is still the monster production of the kind; though probably the German Cyclopædia of Ersch and Gruber,[464] which was begun in 1818, and is still in progress, will beat it in size. The great French work is a collection of dictionaries; it consists of Cyclopædias of all the separate branches of knowledge. It is not a work, but a collection of works, one or another department is to be bought from time to time; but we never heard of a complete set for sale in one lot. As ships grow longer and longer, the question arises what limit there is to the length. One answer is, that it will never do to try such a length that the stern will be rotten before the prow is finished. This wholesome rule has not been attended to in the matter before us; the earlier parts of the great French work were antiquated before the whole were completed: something of the kind will happen to that of Ersch and Gruber.
The production of a great dictionary of either of the kinds is far from an easy task. There is one way of managing the Encyclopædia which has been largely resorted to; indeed, we may say that no such work has been free from it. This plan is to throw all the attention upon the great treatises, and to resort to paste and scissors, or some process of equally easy character, for the smaller articles. However it may be done, it has been the rule that the Encyclopædia of treatises should have its supplemental Dictionary of a very incomplete character. It is true that the treatises are intended to do a good deal; and that the Index, if it be good, knits the treatises and the dictionary into one whole of reference. Still there are two stools, and between them a great deal will fall to the ground. The dictionary portion of the Britannica is not to be compared with its [285]treatises; the part called Miscellaneous and Lexicographical in the Metropolitana[465] is a great failure. The defect is incompleteness. The biographical portion, for example, of the Britannica is very defective: of many names of note in literature and science, which become known to the reader from the treatises, there is no account whatever in the dictionary. So that the reader who has learnt the results of a life in astronomy, for example, must go to some other work to know when that life began and ended. This defect has run through all the editions; it is in the casting of the work. The reader must learn to take the results at their true value, which is not small. He must accustom himself to regard the Britannica as a splendid body of treatises on all that can be called heads of knowledge, both greater and smaller; with help from the accompanying dictionary, but not of the most complete character. Practically, we believe, this defect cannot be avoided: two plans of essentially different structure cannot be associated on the condition of each or either being allowed to abbreviate the other.
The defect of all others which it is most difficult to avoid is inequality of performance. Take any dictionary you please, of any kind which requires the association of a number of contributors, and this defect must result. We do not merely mean that some will do their work better than others; this of course: we mean that there will be structural differences of execution, affecting the relative extent of the different parts of the whole, as well as every other point by which a work can be judged. A wise editor will not attempt any strong measures of correction: he will remember that if some portions be below the rest, which is a disadvantage, it follows that some portions must be above the rest, which is an advantage. The only practical level, if [286]level there must be, is that of mediocrity, if not of absolute worthlessness: any attempt to secure equality of strength will result in equality of weakness. Efficient development may be cut down into meager brevity, and in this way only can apparent equality of plan be secured throughout. It is far preferable to count upon differences of execution, and to proceed upon the acknowledged expectation that the prominent merits of the work will be settled by the accidental character of the contributors; it being held impossible that any editorial efforts can secure a uniform standard of goodness. Wherever the greatest power is found, it should be suffered to produce its natural effect. There are, indeed, critics who think that the merit of a book, like the strength of a chain, is that of its weakest part: but there are others who know that the parallel does not hold, and who will remember that the union of many writers must show exaggeration of the inequalities which almost always exist in the production of one person. The true plan is to foster all the good that can be got, and to give development in the directions in which most resources are found: a Cyclopædia, like a plant, should grow towards the light.
The Penny Cyclopædia had its share of this kind of defect or excellence, according to the way in which the measure is taken. The circumstance is not so much noticed as might be expected, and this because many a person is in the habit of using such a dictionary chiefly with relation to one subject, his own; and more still want it for the pure dictionary purpose, which does not go much beyond the meaning of the word. But the person of full and varied reference feels the differences; and criticism makes capital of them. The Useful Knowledge Society was always odious to the organs of religious bigotry; and one of them, adverting to the fact that geography was treated with great ability, and most unusual fullness, in the Penny Cyclopædia, announced it by making it the sole merit of [287]the work that, with sufficient addition, it would make a tolerably good gazetteer.
Some of our readers may still have hanging about them the feelings derived from this old repugnance of a class to all that did not associate direct doctrinal teaching of religion with every attempt to communicate knowledge. I will take one more instance, by way of pointing out the extent to which stupidity can go. If there be an astronomical fact of the telescopic character which, next after Saturn's ring and Jupiter's satellites, was known to all the world, it was the existence of multitudes of double stars, treble stars, etc. A respectable quarterly of the theological cast, which in mercy we refrain from naming, was ignorant of this common knowledge,—imagined that the mention of such systems was a blunder of one of the writers in the Penny Cyclopædia, and lashed the presumed ignorance of the statement in the following words, delivered in April, 1837:
"We have forgotten the name of that Sidrophel who lately discovered that the fixed stars were not single stars, but appear in the heavens like soles at Billingsgate, in pairs; while a second astronomer, under the influence of that competition in trade which the political economists tell us is so advantageous to the public, professes to show us, through his superior telescope, that the apparently single stars are really three. Before such wondrous mandarins of science, how continually must homunculi like ourselves keep in the background, lest we come between the wind and their nobility."
Certainly these little men ought to have kept in the background; but they did not: and the growing reputation of the work which they assailed has chronicled them in literary history; grubs in amber.
This important matter of inequality, which has led us so far, is one to which the Encyclopædia is as subject as the Cyclopædia; but it is not so easily recognized as a fault. [288]We receive the first book as mainly a collection of treatises: we know their authors, and we treat them as individuals. We see, for instance, the names of two leading writers on Optics, Brewster[466] and Herschel.[467] It would not at all surprise us if either of these writers should be found criticising the other by name, even though the very view opposed should be contained in the same Encyclopædia with the criticism. And in like manner, we should hold it no wonder if we found some third writer not comparable to either of those we have named. It is not so in the Cyclopædia: here we do not know the author, except by inference from a list of which we never think while consulting the work. We do not dissent from this or that author: we blame the book.
The Encyclopædia Britannica is an old friend. Though it holds a proud place in our present literature, yet the time was when it stood by itself, more complete and more clear than anything which was to be found elsewhere. There must be studious men alive in plenty who remember when they were studious boys, what a literary luxury it was to pass a few days in the house of a friend who had a copy of this work. The present edition is a worthy successor of those which went before. The last three editions, terminating in 1824, 1842, and 1861, seem to show that a lunar cycle cannot pass without an amended and augmented edition. Detailed criticism is out of the question; but we may notice the effective continuance of the plan of giving general historical dissertations on the progress of knowledge. Of some of these dissertations we have had to take separate notice; and all will be referred to in our ordinary treatment of current literature.[468]
The literary excellence of these two extensive undertakings is of the same high character. To many this will [289]need justification: they will not easily concede to the cheap and recent work a right to stand on the same shelf with the old and tried magazine, newly replenished with the best of everything. Those who are cognizant by use of the kind of material which fills the Penny Cyclopædia will need no further evidence: to others we shall quote a very remarkable and certainly very complete testimony. The Cyclopædia of the Physical Sciences, published by Dr. Nichol[469] in 1857 (noticed by us, April 4), is one of the most original of our special dictionaries. The following is an extract from the editor's preface:
"When I assented to Mr. Griffin's proposal that I should edit such a Cyclopædia, I had it in my mind that I might make the scissors eminently effective. Alas! on narrowly examining our best Cyclopædias, I found that the scissors had become blunted through too frequent and vigorous use. One great exception exists: viz., the Penny Cyclopædia of Charles Knight.[470] The cheapest and the least pretending, it is really the most philosophical of our scientific dictionaries. It is not made up of a series of treatises, some good and many indifferent, but is a thorough Dictionary, well proportioned and generally written by the best men of the time. The more closely it is examined, the more deeply will our obligation be felt to the intelligence and conscientiousness of its projector and editor."
After Dr. Nichol's candid and amusing announcement of his scissorial purpose, it is but fair to state that nothing of the kind was ultimately carried into effect, even upon the work in which he found so much to praise. I quote this testimony because it is of a peculiar kind.
The success of the Penny Magazine led Mr. Charles Knight in 1832 to propose to the Useful Knowledge Society a Cyclopædia in weekly penny numbers. These two works stamp the name of the projector on the literature of our day in very legible characters. Eight volumes of 480 pages each were contemplated; and Mr. Long[471] and Mr. Knight were to take the joint management. The plan embraced a popular account of Art and Science, with very brief biographical and geographical information. The early numbers of the work had some of the Penny Magazine character: no one can look at the pictures of the Abbot and Abbess in their robes without seeing this. By the time the second volume was completed, it was clearly seen that the plan was working out its own extension: a great development of design was submitted to, and Mr. Long became sole editor. Contributors could not be found to make articles of the requisite power in the assigned space. One of them told us that when he heard of the eight volumes, happening to want a shelf to be near at hand for containing the work as it went on, he ordered it to be made to hold twenty-five volumes easily. But the inexorable logic of facts beat him after all: for the complete work contained twenty-six volumes and two thick volumes of Supplement.
The penny issue was brought to an end by the state of the law, which required, in 1833, that the first and last page of everything sold separately should contain the name and address of the printer. The penny numbers contained this imprint on the fold of the outer leaf: and qui tam[472] informations were laid against the agents in various towns. [291]It became necessary to call in the stock; and the penny issue was abandoned. Monthly parts were substituted, which varied in bulk, as the demands of the plan became more urgent, and in price from one sixpence to three. The second volume of Supplement appeared in 1846, and during the fourteen years of issue no one monthly part was ever behind its time. This result is mainly due to the peculiar qualities of Mr. Long, who unites the talents of the scholar and the editor in a degree which is altogether unusual. If any one should imagine that a mixed mass of contributors is a punctual piece of machinery, let him take to editing upon that hypothesis, and he shall see what he shall see and learn what he shall learn.
The English contains about ten per cent more matter than the Penny Cyclopædia and its supplements; including the third supplementary volume of 1848, which we now mention for the first time. The literary work of the two editions cost within 500l. and 50,000l.: that of the two editions of the Britannica cost 41,000l. But then it is to be remembered that the Britannica had matter to begin upon, which had been paid for in the former editions. Roughly speaking, it is probable that the authorship of a page of the same size would have cost nearly the same in one as in the other.
The longest articles in the Penny Cyclopædia were "Rome" in 98 columns and "Yorkshire" in 86 columns. The only article which can be called a treatise is the Astronomer Royal's "Gravitation," founded on the method of Newton in the eleventh section, but carried to a much greater extent. In the English Cyclopædia, the longest article of geography is "Asia," in 45 columns. In natural history the antelopes demand 36 columns. In biography, "Wellington" uses up 42 columns, and his great military opponent 41 columns. In the division of Arts and Sciences, which includes much of a social and commercial character, the length of articles often depends upon the state of the [292]times with regard to the subject. Our readers would not hit the longest article of this department in twenty guesses: it is "Deaf and Dumb" in 60 columns. As other specimens, we may cite Astronomy, 19; Banking, 36; Blind, 24; British Museum, 35; Cotton, 27; Drama, 26; Gravitation, 50; Libraries, 50; Painting, 34; Railways, 18; Sculpture, 36; Steam, etc., 37; Table, 40; Telegraph, 30; Welsh language and literature, 39; Wool, 21. These are the long articles of special subdivisions: the words under which the Encyclopædia gives treatises are not so prominent. As in Algebra, 10; Chemistry, 12; Geometry, 8; Logic, 14; Mathematics, 5; Music, 9. But the difference between the collection of treatises and the dictionary may be illustrated thus: though "Mathematics" have only five columns, "Mathematics, recent terminology of," has eight: and this article we believe to be by Mr. Cayley,[473] who certainly ought to know his subject, being himself a large manufacturer of the new terms which he explains. Again, though "Music" in genere, as the schoolmen said, has only nine columns, "Temperament and Tuning," has eight, and "Chord" alone has two. And so on.
In a dictionary of this kind it is difficult to make a total clearance of personality: by which we mean that exhibition of peculiar opinion which is offensive to taste when it is shifted from the individual on the corporate book. The treatise of the known author may, as we have said, carry that author's controversies on its own shoulders: and even his crotchets, if we may use such a word. But [293]the dictionary should not put itself into antagonism with general feeling, nor even with the feelings of classes. We refer particularly to the ordinary and editorial teaching of the article. If, indeed, the writer, being at issue with mankind, should confess the difference, and give abstract of his full grounds, the case is altered: the editor then, as it were, admits a correspondent to a statement of his own individual views. The dictionary portion of the Britannica is quite clear of any lapses on this point, so far as we know: the treatises and dissertations rest upon their authors. The Penny Cyclopædia was all but clear: and great need was there that it should have been so. The Useful Knowledge Society, starting on the principle of perfect neutrality in politics and religion, was obliged to keep strict watch against the entrance of all attempt even to look over the hedge. There were two—we believe only two—instances of what we have called personality. The first was in the article "Bunyan." It is worth while to extract all that is said—in an article of thirty lines—about a writer who is all but universally held to be the greatest master of allegory that ever wrote:
"His works were collected in two volumes, folio, 1736-7: among them 'The Pilgrim's Progress' has attained the greatest notoriety. If a judgment is to be formed of the merits of a book by the number of times it has been reprinted, and the many languages into which it has been translated, no production in English literature is superior to this coarse allegory. On a composition which has been extolled by Dr. Johnson, and which in our own times has received a very high critical opinion in its favor [probably Southey], it is hazardous to venture a disapproval, and we, perhaps, speak the opinion of a small minority when we confess that to us it appears to be mean, jejune and wearisome."
—If the unfortunate critic who thus individualized himself had been a sedulous reader of Bunyan, his power over [294]English would not have been so jejune as to have needed that fearful word. This little bit of criticism excited much amusement at the time of its publication: but it was so thoroughly exceptional and individual that it was seldom or never charged on the book. The second instance occurred in the article "Socinians." It had been arranged that the head-words of Christian sects should be intrusted to members of the sects themselves, on the understanding that the articles should simply set forth the accounts which the sects themselves give of their own doctrines. Thus the article on the Roman Church was written by Dr. Wiseman.[474] But the Unitarians were not allowed to come within the rule: as in other quarters, they were treated as the gypsies of Christianity. Under the head "Socinians"—a name repudiated by themselves—an opponent was allowed not merely to state their alleged doctrines in his own way, but to apply strong terms, such as "audacious unfairness," to some of their doings. The protests which were made against this invasion of the understanding produced, in due time, the article "Unitarians," written by one of that persuasion. We need not say that these errors have been amended in the English Cyclopædia: and our chief purpose in mentioning them is to remark, that this is all we can find on the points in question against twenty-eight large volumes produced by an editor whose task was monthly, and whose issue was never delayed a single hour. How much was arrested before publication none but himself can say. We have not alluded to one or two remonstrances on questions of absolute fact, which are beside the present purpose.
Both kinds of encyclopædic works have been fashioned upon predecessors, from the very earliest which had a predecessor to be founded upon; and the undertakings before us will be themselves the ancestors of a line of successors. Those who write in such collections should be [295]careful what they say, for no one can tell how long a mis-statement may live. On this point we will give the history of a pair of epithets. When the historian De Thou[475] died, and left the splendid library which was catalogued by Bouillaud[476] and the brothers Dupuis[477] (Bullialdus and Puteanus), there was a manuscript of De Thou's friend Vieta,[478] the Harmonicon Cœleste, of which it is on record, under Bouillaud's hand, that he himself lent it to Cosmo de' Medici,[479] to which must be added that M. Libri[480] found it in the Magliabecchi Library at Florence in our own day. Bouillaud, it seems, entirely forgot what he had done. Something, probably, that Peter Dupuis said to Bouillaud, while they were at work on the catalogue, remained on his memory, and was published by him in 1645, long after; to the effect that Dupuis lent the manuscript to Mersenne,[481] from whom it was procured by some intending plagiarist, who would not give it back. This was repeated by Sherburne,[482] in 1675, who speaks of the work, which "being communicated to Mersennus was, by some perfidious acquaintance of that honest-minded person, surreptitiously taken from him, and irrecoverably lost or suppressed, to the unspeakable detriment of the lettered world." Now let the [296]reader look through the dictionaries of the last century and the present, scientific or general, at the article, "Vieta," and he will be amused with the constant recurrence of "honest-minded" Mersenne, and his "surreptitious" acquaintance. We cannot have seen less than thirty copies of these epithets.
REVIEW OF MACCLESFIELD LETTERS.
October 18, 1862. Correspondence of Scientific Men of the Seventeenth Century, in the Collection of the Earl of Macclesfield.[483] 2 vols. (Oxford, University Press.)
Though the title-page of this collection bears the date 1841, it is only just completed by the publication of its Table of Contents and Index. Without these, a work of the kind is useless for consultation, and cannot make its way. The reason of the delay will appear: its effect is well known to us. We have found inquirers into the history of science singularly ignorant of things which this collection might have taught them.
In the same year, 1841, the Historical Society of Science, which had but a brief existence, published a collection of letters, eighty-three in number, edited by Mr. Halliwell,[484] of English men of science, which dovetails with the one before us, and is for the most part of a prior date. The two should be bound up together. The smaller collection runs from 1562 to 1682; the larger, from 1606 to past 1700. We shall speak of the two as the Museum collection and the Macclesfield collection. And near them should be placed, in every scientific library, the valuable collection published, by Mr. Edleston,[485] for Trinity College, in 1850.
The history of these letters runs back to famous John Collins, the attorney-general of the mathematics, as he has been called, who wrote to everybody, heard from everybody, and sent copies of everybody's letter to everybody else. He was in England what Mersenne[486] was in France: as early as 1671, E. Bernard[487] addresses him as "the very Mersennus and intelligence of this age." John Collins[488] was never more than accountant to the Excise Office, to which he was promoted from teaching writing and ciphering, at the Restoration: he died in 1682. We have had a man of the same office in our own day, the late Prof. Schumacher,[489] who made the little Danish Observatory of Altona the junction of all the lines by which astronomical information was conveyed from one country to another. When the collision took place between Denmark and the Duchies, the English Government, moved by the Astronomical Society, instructed its diplomatic agents to represent strongly to the Danish Government, when occasion should arise, the great importance of the Observatory of Altona to the astronomical communications of the whole world. But Schumacher had his own celebrated journal, the Astronomische Nachrichten, by which to work out part of his plan; private correspondence was his supplementary assistant. Collins had only correspondence to rely on. Nothing is better known than that it was Collins's collection which furnished the materials put forward by the Committee of the Royal Society in 1712, as a defence of Newton against the partisans of Leibnitz. The noted Commercium Epistolicum is but the abbreviation of a title which runs on with "D. Johannis Collins et aliorum ..."
The whole of this collection passed into the hands of [298]William Jones,[490] the father of the Indian Judge of the same name, who died in 1749. Jones was originally a teacher, but was presented with a valuable sinecure by the interest of George, second Earl of Macclesfield, the mover of the bill for the change of style in Britain, who died President of the Royal Society. This change of style may perhaps be traced to the union of energies which were brought into concert by the accident of a common teacher: Lord Macclesfield and Lord Chesterfield,[491] the mover and the seconder, and Daval,[492] who drew the bill, were pupils of De Moivre.[493] Jones, who was a respectable mathematician though not an inventor, collected the largest mathematical library of his day, and became possessor of the papers of Collins, which contained those of Oughtred[494] and others. Some of these papers passed into the custody of the Royal Society: but the bulk was either bequeathed to, or purchased by, Lord Macclesfield; and thus they found their way to Shirburn Castle, where they still remain.
A little before 1836, this collection attracted the attention of a searching inquirer into points of mathematical history, the late Professor Rigaud,[495] who died in 1839. He examined the whole collection of letters, obtained Lord Macclesfield's consent to their publication, and induced the Oxford Press to bear the expense. It must be particularly remembered that there still remains at Shirburn Castle a [299]valuable mass of non-epistolary manuscripts. So far as we can see, the best chance of a further examination and publication lies in public encouragement of the collection now before us: the Oxford Press might be induced to extend its operations if it were found that the results were really of interest to the literary and scientific world. Rigaud died before the work was completed, and the publication was actually made by one of his sons, S. Jordan Rigaud,[496] who died Bishop of Antigua. But this publication was little noticed, for the reasons given. The completion now published consists of a sufficient table of contents, of the briefest kind, by Professor De Morgan, and an excellent index by the Rev. John Rigaud.[497] The work is now fairly started on its career.
If we were charged to write a volume with the title "Small things in their connection with great," we could not do better than choose the small part of this collection of letters as our basis. The names, as well as the contents, are both great and small: the great names, those which are known to every mathematician who has any infusion of the history of his pursuit, are Briggs,[498] Oughtred, Charles Cavendish,[499] Gascoigne,[500] Seth Ward,[501] Wallis,[502] [300]Hu[y]gens,[503] Collins,[504] William Petty,[505] Hooke,[506] Boyle,[507] Pell,[508] Oldenburg,[509] Brancker,[510] Slusius,[511] Bertit,[512] Bernard,[513] Borelli,[514] Mouton,[515] Pardies,[516] Fermat,[517] Towneley,[518] Auzout,[519] [301]D. Gregory,[520] Halley,[521] Machin,[522] Montmort,[523] Cotes,[524] Jones,[525] Saunderson,[526] Reyneau,[527] Brook Taylor,[528] Maupertuis,[529] Bouguer,[530] La Condamine,[531] Folkes,[532] Macclesfield,[533] [302]Baker,[534] Barrow,[535] Flamsteed,[536] Lord Brounker,[537] J. Gregory,[538] Newton[539] and Keill.[540] To these the Museum collection adds the names of Thomas Digges,[541] Dee,[542] Tycho Brahe,[543] Harriot,[544] Lydyat,[545] Briggs,[546] Warner,[547] Tarporley, Pell,[548] Lilly,[549] Oldenburg,[550] Collins,[551] Morland.[552]
The first who appears on the scene is the celebrated Oughtred, who is related to have died of joy at the Restoration: but it should be added, by way of excuse, that he was eighty-six years old. He is an animal of extinct race, an Eton mathematician. Few Eton men, even of the minority which knows what a sliding rule is, are aware that the inventor was of their own school and college: but they may be excused, for Dr. Hutton,[553] so far as his Dictionary bears witness, seems not to have known it any more than they. A glance at one of his letters reminds us of a letter from the Astronomer Royal on the discovery of Neptune, which we printed March 20, 1847. Mr. Airy[554] there contends, and proves it both by Leverrier[555] and by Adams,[556] that the limited publication of a private letter is more efficient than the more general publication of a printed memoir. The same may be true of a dead letter, as opposed to a dead book. Our eye was caught by a letter of Oughtred (1629), containing systematic use of contractions for the words sine, cosine, etc., prefixed to the symbol of the angle. This is so very important a step, simple as it is, that Euler[557] is justly held to have greatly advanced trigonometry by its introduction. Nobody that we know of has noticed that Oughtred was master of the improvement, and willing to have taught it, if people would have learnt. After looking at his dead letter, we naturally turned to his dead book on trigonometry, and there we found the abbreviations s, sco, t, tco, se, seco, regularly established as part of the system of the work. But not one of those who have investigated the contending claims of Euler and Thomas [304]Simpson[558] has chanced to know of Oughtred's "Trigonometrie": and the present revival is due to his letter, not to his book.
A casual reader, turning over the pages, would imagine that almost all the letters had been printed, either in the General Dictionary, or in Birch,[559] etc.: so often does the supplementary remark begin with "this letter has been printed in ——." For ourselves we thought, until we counted, that a large majority of the letters had been given, either in whole or in part. But the positive strikes the mind more forcibly than the negative: we find that all of which any portion has been in type makes up very little more than a quarter; the cases in which the whole letter is given being a minority of this quarter. The person who has been best ransacked is Flamsteed: of 36 letters from him, 34 had been previously given in whole or in part. Of 59 letters to and from Newton, only 17 have been culled.
The letters have been modernized in spelling, and, to some extent, in algebraical notation; it also seems that conjectural methods of introducing interpolations into the text have been necessary. For all this we are sorry: the scientific value of the collection is little altered, but its literary value is somewhat lowered. But it could not be helped: the printers could not work from the originals, and Professor Rigaud had to copy everything himself. A fac-simile must have been the work of more time than he had to give: had he attempted it, his death would have cut short the whole undertaking, instead of allowing him to prepare everything but a preface, and to superintend the printing of one of the volumes. We may also add, that we believe we have notices of all the letters in the Macclesfield collection. We judge this because several which are too trivial to print are numbered and described; and those would certainly not have been noticed if any omissions had [305]been made. And we know that every letter was removed from Shirburn Castle to Oxford.
Two persons emerge from oblivion in this series of letters. The first is Michael Dary,[560] an obscure mathematician, who was in correspondence with Newton and other stars. He was a gauger at Bristol, by the interest of Collins; afterwards a candidate for the mathematical school at Christ's Hospital, with a certificate from Newton: he was then a gunner in the Tower, and is lastly described by Wallis as "Mr. Dary, the tobacco-cutter, a knowing man in algebra." In 1674, Dary writes to Newton at Cambridge, as follows:—"Although I sent you three papers yesterday, I cannot refrain from sending you this. I have had fresh thoughts this morning." Two months afterwards poor Newton writes to Collins, "Mr. Dary is very solicitous about mathematics": but in spite of the persecution, he subscribes himself to Dary "your loving friend." Dary's problem is that of finding the rate of interest of an annuity of which the value and term are given. Dary's theorem, which he seems to have invented specially for the solution of his problem, though it is of wide range, can be exhibited to mathematical readers even in our columns. In modern language, it is that the limit of φnx, when n increases without limit, is a solution of φx = x. We have mentioned the I. Newton to whom Dary looked up; we add a word about the one on whom he looked down. Dr. John Newton,[561] a sedulous publisher of logarithms, tables of interest, etc., who began his career before Isaac Newton, sometimes puzzles those who do not know him, when described as I. Newton. The scientific world was of opinion that all that was valuable in one of his works was taken from Dary's private communications.
The second character above alluded to is one who carried mathematical researches a far greater length than Newton himself: the assistance which he rendered in this respect, even to Newton, has never been acknowledged in modern times: though the work before us shows that his contemporaries were fully aware of it, and never thought of concealing it. In his theory of gravitation, in which, so far as he went, we have every reason to believe he was prior to Newton, he did not extend his calculations to the distance of the moon; his views in this matter were purely terrestrial, and led him to charge according to weight. He was John Stiles, the London and Cambridge carrier: his name is a household word in the Macclesfield Letters, and is even enshrined in the depths of Birch's quartos. Dary informs Newton—let us do his memory this justice—that he had paid John Stiles for the carriage. At the time when the railroad to Cambridge was opened, a correspondent recommended the directors, in our columns, to call an engine by the name of John Stiles, and never to let that name go off the road. We do not know whether the advice was followed: if not, we repeat it.
Little points of life and manners come out occasionally. Baker, the author of a work on algebra much esteemed at the time, wrote to Collins that their circumstances are alike, "having a just and equal number of chargeable olive-branches, and being in the same predicament and blessed condemnation with you, not more preaching than unpaid, and preaching the art of contentment to others, am forced to practise it." But the last sentence of his letter runs as follows: "I have sent by the bearer ... twenty shillings, as a token to you; desiring you to accept of it, as a small taste from Yours, Thos. Baker." In our day, men of a station to pay parish taxes do not offer their friends hard money to buy liquor. But Flamsteed[562] writes to Collins as follows: "Last week he sent us down the counterpart, which [307]my father has scaled, and I return up to you by the carrier, with 5l. to be paid to Mr. Leneve for the writing, I have added 2s. 6d. over, which will pay the expenses and serve to drink, with him." This would seem as odd to us as it would have seemed thirty years ago that half-a-crown should pay carriage for a deed from Derby to London, and leave margin for a bottle of wine: in our day, the Post-office and the French treaty would just manage it between them. But Flamsteed does not limit his friend to one bottle; he adds, "If you expend more than the half-crown, I will make it good after Whitsuntide." Collins does not remember exactly where he had met James Gregory, and mentions two equally likely places thus: "Sir, it was once my good hap to meet with you in an alehouse or in Sion College." There is a little proof how universally the dinner-hour was twelve o'clock. Astronomers well know the method of finding time by equal altitudes of the sun before and after noon: Huyghens calls it "le moyen de deux égales hauteurs du soleil devant et après dîner."[563]
There is one mention of "Mr. Cocker,[564] our famous English graver and writer, now a schoolmaster at Northampton." This is the true Cocker: his genuine works are specimens of writing, such as engraved copy-books, including some on arithmetic, with copper-plate questions and space for the working; also a book of forms for law-stationers, with specimens of legal handwriting. It is recorded somewhere that Cocker and another, whose name we forget, competed with the Italians in the beauty of their flourishes. This was his real fame: and in these matters he was great. The eighth edition of his book of law forms (1675), published shortly after Cocker's death, has a preface signed "J. H." This was John Hawkins, who became possessed of Cocker's papers—at least he said so—and [308]subsequently forged the famous Arithmetic,[565] a second work on Decimal Arithmetic, and an English dictionary, all attributed to Cocker. The proofs of this are set out in De Morgan's Arithmetical Books. Among many other corroborative circumstances, the clumsy forger, after declaring that Cocker to his dying day resisted strong solicitation to publish his Arithmetic, makes him write in the preface Ille ego qui quondam[566] of this kind: "I have been instrumental to the benefit of many, by virtue of those useful arts, writing and engraving; and do now, with the same wonted alacrity, cast this my arithmetical mite into the public treasury." The book itself is not comparable in merit to at least half-a-dozen others. How then comes Cocker to be the impersonation of Arithmetic? Unless some one can show proof, which we have never found, that he was so before 1756, the matter is to be accounted for thus.
Arthur Murphy,[567] the dramatist, was by taste a man of letters, and ended by being the translator of Tacitus; though many do not know that the two are one. His friends had tried to make him a man of business; and no doubt he had been well plied with commercial arithmetic. His first dramatic performance, the farce of "The Apprentice," produced in 1756, is about an idle young man who must needs turn actor. Two of the best known books of the day in arithmetic were those of Cocker and Wingate.[568] Murphy chooses Wingate to be the name of an old merchant who [309]delights in vulgar fractions, and Cocker to be his arithmetical catchword—"You read Shakespeare! get Cocker's Arithmetic! you may buy it for a shilling on any stall; best book that ever was wrote!" and so on. The farce became very popular, and, as we believe, was the means of elevating Cocker to his present pedestal, where Wingate would have been, if his name had had the droller sound of the two to English ears.
A notoriety of an older day turns up, Major-General Lambert.[569] The common story is that he was banished to Guernsey, where he passed thirty years in confinement, rearing and painting flowers. But Baker, in 1678, represents him as a prisoner at Plymouth, sending equations for solution as a challenge: probably his place of confinement was varied, and his occupation also.
[General Lambert was removed to Plymouth, probably about 1668. His daughter captured the son of the Governor of Guernsey, who therefore probably was reckoned an unsafe custodier thenceforward; though he assured the king that he had turned the young couple out of doors, and had never given them a penny. Great importance was attached to Lambert's safe detention: probably the remaining republicans looked upon him as to be their next Cromwell, if such a thing were to be. There were standing orders to shoot him at once on the first appearance of any enemy before the island. See Notes and Queries, 3d S. iv. 89.]
Collins informs James Gregory that "some of the Royal Academy wrote over to Mr. Oldenburg, who was desired to impart the same to the Council of the Royal Society, that the French King was willing to allow pensions to one or two learned Englishmen, but they never made any answer [310]to such a proposal." This was written in 1671, and the thing probably happened several years before. Mr. De Morgan communicated the account of the proposal to Lord Macaulay, who replied that he did not think that any Englishman received a literary pension from Louis; but that there is a curious letter, about 1664, from the French Ambassador, in which he says that he has, by his master's orders, been making inquiries as to the state of learning in England, and that he is sorry to find that the best writer is the infamous Miltonus. On two such independent testimonies it may be held proved that the French King had attempted to buy a little adherence from English literature and science; and the silent contempt of the Royal Society is an honorable fact in their history.
Another little bit of politics is as follows. Oughtred is informed that "Mr. Foster,[570] our Lecturer on Astronomy at Gresham College, is put out because he will not kneel down at the communion-table. A Scotsman [Mungo Murray], one that is verbi bis minister,[571] is now lecturer in Mr. Foster's place." Ward in his work on the Gresham Professors,[572] suppresses the reason, and the suppression lowers the character of his book. Foster was expelled in 1636, and re-elected on a vacancy in 1641, when Puritanism had gained strength.
The correspondence of Newton would require deeper sifting than could be given in such an article as the present. The first of the letters (1669) is curious, as presenting the [311]appearance of forms belonging to the great calculus which, in this paragraph, we ought to call that of fluxions. We find, of the date February 18, 1669-70, what we believe is the earliest manifestation of that morbid part of Newton's temperament which has been so variously represented. He had solved a problem—being that which we have called Dary's—on which he writes as follows: "The solution of the annuity problem, if it will be of any use, you have my leave to insert into the Philosophical Transactions, so it be without my name to it. For I see not what there is desirable in public esteem, were I able to acquire and maintain it. It would perhaps increase my acquaintance, the thing which I chiefly study to decline."
Three letters touch upon "the experiment of glass rubbed to cause various motions in bits of paper underneath": they are supplements to the account given by Newton to the Royal Society, and printed by Birch. It was Newton, so far as appears, who added glass to the substances known to be electric. Soon afterwards we come to a little bit of the history of the appointment to the Mint. It has appeared from the researches of late years that Newton was long an aspirant for public employment: the only coolness which is known to have taken place between him and Charles Montague[573] [Halifax] arose out of his imagining that his friend was not in earnest about getting him into the public service. March 14, 1696, Newton writes thus to Halley: "And if the rumour of preferment for me in the Mint should hereafter, upon the death of Mr. Hoar [the comptroller], or any other occasion, be revived, I pray that you would [312]endeavour to obviate it by acquainting your friends that I neither put in for any place in the Mint, nor would meddle with Mr. Hoar's place, were it offered to me." This means that Mr. Hoar's place had been suggested, which Newton seems to have declined. Five days afterwards, Montague writes to Newton that he is to have the Wardenship. It is fair to Newton to say that in all probability this was not—or only in a smaller degree—a question of personal dignity, or of salary. It must by this time have been clear to him that the minister, though long bound to make him an object of patronage, was actually seeking him for the Mint, because he wanted both Newton's name and his talents for business—which he knew to be great—in the weighty and dangerous operation of restoring the coinage. It may have been, and probably was, the case that Newton had a tolerably accurate notion of what he would have to do, and of what degree of power would be necessary to enable him to do it in his own way.
We have said that the non-epistolary manuscripts are still unexamined. There is a chance that one of them may answer a question of two centuries' standing, which is worth answering, because it has been so often asked. About 1640, Warner,[574] afterwards assisted by Pell,[575] commenced a table of antilogarithms, of the kind which Dodson[576] afterwards constructed anew and published. In the Museum collection there is inquiry after inquiry from Charles Cavendish,[577] first, as to when the Analogics, as he called them, would be finished; next, when they would be printed. Pell answers, in 1644, that Warner left his papers to a kinsman, who had become bankrupt, and proceeds thus:
"I am not a little afraid that all Mr. Warner's papers, [313]and no small share of my labours therein, are seazed upon, and most unmathematically divided between the sequestrators and creditors, who (not being able to ballance the account where there appeare so many numbers, and much troubled at the sight of so many crosses and circles in the superstitious Algebra and that black art of Geometry) will, no doubt, determine once in their lives to become figure-casters, and so vote them all to be throwen into the fire, if some good body doe not reprieve them for pye-bottoms, for which purposes you know analogicall numbers are incomparably apt, if they be accurately calculated."
Pell afterwards told Wallis[578] that the papers had fallen into the hands of Dr. Busby,[579] and Collins[580] writes that they were left in the hands of Dr. Thorndike,[581] a prebendary of Westminster; whence Rigaud[582] seems to say that Thorndike had left them to Dr. Busby. Birch[583] says that he procured for the Royal Society four boxes from Busby's trustees, containing papers of Warner and Pell: but there is no other tradition of such things in the Society. But in the Birch manuscripts at the British Museum, there turns up, as printed in what we call the Museum collection, a list of Warner's papers, with Collins's receipt to Dr. Thorndike at the bottom, and engagement to restore them on demand. The date is December 14, 1667; Wallis's statement being in 1693. It is possible that Busby may be a mistake altogether: he was very unlikely to have had charge of any mathematical papers: there may have been a confusion between the Prebendary of Westminster and the Head Master of Westminster School. If so, in all probability Thorndike handed [314]the cumbrous lot over to the notorious collector of mathematical papers, blessing himself that he got rid of them in a manner which would insure their return if he were called upon by the owners to restore them. It is much against this hypothesis that Dodson, who certainly recalculated, can say nothing more about Warner than a repetition of Wallis's story: though, had Collins kept the papers, they would probably have been in Jones's possession at the very time when Dodson, who was a friend of Jones and a user of his library, was engaged on his own computations. But even books, and still more manuscripts, are often singularly overlooked; and it remains not very improbable that Warner's table is now at Shirburn Castle, among the unexamined manuscripts.
CYCLOMETRY AND STEEL PENS.
Redit labor actus in orbem.[584] Among the matters which have come to me since the Budget opened, there is a pamphlet of quadrature of two pages and a half from Professor Recalcati,[585] already mentioned. It ends with "Quelque objection qu'on fasse touchant les raisonnements ci-dessus on tombera toujours dans l'absurde."[586] A civil engineer—so he says—has made the quadrature "no longer a problem, but an axiom." As follows: "Take the quadrant of a circle whose circumference is given, square the quadrant which gives the true square of the circle. Because 30 ÷ 4 = 7.5 × 7.5 = 56.25 = the positive square of a circle whose circumference is 30." Brevity, the soul of wit, is the "wings of mighty-winds" to quadrature, and sends it "flying all abroad." A surbodhicary—something like M.A. or LL.D., I understand—at Calcutta, published in 1863 the division of an [315]angle into any odd number of parts, demonstration and all in—when the diagram is omitted—one page, good-sized, well-leaded type, small duodecimo. But in the Preface he acknowledges "sheer inability" to execute his task. Mr. William Dean, of Todmorden, in 1863, announced 3-9/64 as proved both practically and geometrically: he has been already mentioned anonymously. Next I have the tract of Don Juan Larriva, published at Leiria in 1856, and dedicated to Queen Victoria. Mr. W. Peters,[587] already mentioned, who has for some months been circulating diagrams on a card, publishes (August, 1865) The Circle Squared. He agrees with the Archpriest of St. Vitus. He hints that a larger publication will depend partly on the support he receives, and partly on the castigation, for which last, of course, he looks to me. Cyclometers have their several styles of wit; so have anticyclometers too, for that matter. Mr. Peters will not allow me any extra-journal being: I am essentially a quotation from the Athenæum; "A. De Morgan" et præterea nihil.[588] If he had to pay for keeping me set up, he would find out his mistake, and would be glad to compound handsomely for a stereotype. Next comes a magnificent sheet of pasteboard, printed on both sides. Having glanced at it and detected quadrature, I began methodically at the beginning—"By Royal Command," with the lion and unicorn, and all that comes between. Mercy on us! thought I to myself: has Her Majesty referred the question to the Judicial Committee of the Privy Council, where all the great difficulties go now-a-days, and is this proclamation the result? On reading further I was relieved by finding that the first side is entirely an advertisement of Joseph Gillott's[589] steel pens, with engraving of his [316]premises, and notice of novel application of his unrivalled machinery. The second side begins with "the circle rectified" by W. E. Walker,[590] who finds π = 3.141594789624155.... This is an off-shoot from an accurate geometrical rectification, on which is to be presumed Mr. Gillott's new machinery is founded. I have no doubt that Mr. Walker's error, which is only in the sixth place of decimals, will not hurt the pens, unless it be by the slightest possible increase of the tendency to open at the points. This arises from Mr. Walker having rectified above proof by .000002136034362....
Lastly, I, even I myself, who have long felt that I was a quadrature below par, have solved the problem by means which, in the present state of the law of libel, I dare not divulge. But the result is permitted; and it goes far to explain all the discordances. The ratio of the circumference to the diameter is not always the same! Not that it varies with the radius; the geometers are right enough on that point: but it varies with the time, in a manner depending upon the difference of the true longitudes of the Sun and Moon. A friend of mine—at least until he misbehaved—insisted on the mean right ascensions: but I served him as Abraham served his guest in Franklin's parable. The true formula is, A and a being the Sun's and Moon's longitudes,
π = 3-13/80 + 3/80 cos(A - a).
Mr. James Smith obtained his quadrature at full moon; the Archpriest of St. Vitus and some others at new moon. Until I can venture to publish the demonstration, I recommend the reader to do as I do, which is to adopt 3.14159..., and to think of the matter only at the two points of the lunar month at which it is correct. The Nautical Almanac will no doubt give these points in a short time: I am in correspondence with the Admiralty, with nothing [317]to get over except what I must call a perverse notion on the part of the Superintendent of the Almanac, who suspects one correction depending on the Moon's latitude; and the Astronomer Royal leans towards another depending on the date of the Queen's accession. I have no patience with these men: what can the Moon's node of the Queen's reign possibly have to do with the ratio in question? But this is the way with all the regular men of science; Newton is to them etc. etc. etc. etc.
The following method of finding the circumference of a circle (taken from a paper by Mr. S. Drach[591] in the Phil. Mag., Jan. 1863, Suppl.) is as accurate as the use of 3.14159265. From three diameters deduct 8-thousandths and 7-millionths of a diameter; to the result add five per cent. We have then not quite enough; but the shortcoming is at the rate of about an inch and a sixtieth of an inch in 14,000 miles.
JACOB BEHMEN.
Though I have met with nothing but a little tract from the school of Jacob Behmen[592] (or Böhme; I keep to the old English version of his name), yet there has been more, and of a more recent date. I am told of an "Introduction to Theosophy [Theo private, I suppose, as in theological]; or, the Science of the Mystery of Christ," published in 1854, mostly from the writings of William Law[593]: and also of a volume of 688 pages, of the same year, printed for private circulation, containing notes for a biography of William Law. The editor of the first work wishes to grow "a [318]generation of perfect Christians" by founding a Theosophic College, for which he requests the public to raise a hundred thousand pounds. There is a good account of Jacob Behmen in the Penny Cyclopædia. The author mentions inaccurate accounts, one of which he quotes, as follows: "He derived all his mystical and rapturous doctrine from Wood's[594] Athenæ Oxonienses, Vol. I, p. 610, and Hist. et Antiq. Acad. Oxon., Vol. II, p. 308." On which the author remarks that Wood was born after Behmen's death. There must have been a few words which slipped out: what is meant is that Behmen "derived his doctrine from Robert Fludd,[595] for whom see Wood's etc. etc." Even this is absurd enough: for Behmen began to publish in 1610, and Fludd in 1616. Fludd was a Rosicrucian, and a mystic of a different type from Behmen. I have some of his works, and could produce out of them paradoxes enough, according to our ways of thinking, to fit out a host. But the Rosicrucian system was a recognized school of its day, and Fludd, a man of great learning, had abettors enough in all which he advanced, and predecessors in most of it.
[A Correspondent has recently sent a short summary of the claims of Jacob Behmen to rank higher than I have placed him. I shall gladly insert this summary in the book I contemplate, as a statement of what is said of Behmen far less liable to suspicion of exaggeration than anything I could write. I shall add a few extracts from Behmen himself, in support of his right to be in my list.]
"Jacob Behmen.—That Prof. De Morgan classes Jacob Behmen among paradoxers can only be attributed to the fact of his being avowedly unacquainted with the writings [319]of that author. Perhaps you may think a few words from one who knows them well of sufficient interest to the learned Professor, and your readers in general, to be worthy of space in your columns. The metaphysical system of Behmen—the most perfect and only true one—still awaits a qualified commentator. Behmen's countryman, Dionysius Andreas Freher,[596] who spent the greater part of his life in this country, and whose exposition of Behmen exists only in MS., filling many volumes, written in English, with the exception of two, written in German, with numerous beautiful, highly ingenious, and elaborate illustrations,—copies of some of which are in the British Museum, but all the originals of which are in the possession of the gentleman who is the editor of the two works alluded to by Professor De Morgan,—this Freher was the first to philosophically expound Behmen's system, which was afterwards, with the help of these MSS., as it were, popularized by William Law; but both Freher and Law confined themselves chiefly to its theological aspect. In Behmen, however, is to be found, not only the true ground of all theology, but also that of all physical science. He demonstrated with a fullness, accuracy, completeness and certainty that leave nothing to be desired, the innermost ground of Deity and Nature; and, confining myself to the latter, I can from my own knowledge assert, that in Behmen's writings is to be found the true and clear demonstration of every physical fact that has been discovered since his day. Thus, the science of electricity, which was not yet in existence when he wrote, is there anticipated; and not only does Behmen describe all the now known phenomena of that force, but he even gives us the origin, generation and birth of electricity itself. Again, positive evidence can be adduced that Newton derived all his knowledge of gravitation and its [320]laws from Behmen, with whom gravitation or attraction is, and very properly so, as he shows us, the first of the seven properties of Nature. The theory defended by Mr. Grove,[597] at the Nottingham meeting of last year, that all the apparently distinct causes of moral and physical phenomena are but so many manifestations of one central force, and that Continuity is the law of nature, is clearly laid down, and its truth demonstrated, by Behmen, as well as the distinction between spirit and matter, and that the moral and material world is pervaded by a sublime unity. And though all this was not admitted in Behmen's days, because science was not then sufficiently advanced to understand the deep sense of our author, many of his passages, then unintelligible, or apparently absurd, read by the light of the present age, are found to contain the positive enunciation of principles at whose discovery and establishment science has only just arrived by wearisome and painful investigations. Every new scientific discovery goes to prove his profound and intuitive insight into the most secret workings of nature; and if scientific men, instead of sharing the prejudice arising from ignorance of Behmen's system, would place themselves on the vantage ground it affords, they would at once find themselves on an eminence whence they could behold all the arcana of nature. Behmen's system, in fact, shows us the inside of things, while modern physical science is content with looking at the outside. Behmen traces back every outward manifestation or development to its one central root,—to that one central energy which, as yet, is only suspected; every link in the chain of his demonstration is perfect, and there is not one link wanting. He carries us from the out-births of the circumference, along the radius to the center, [321]or point, and beyond that even to the zero, demonstrating the constitution of the zero, or nothing, with mathematical precision. C. W. H."
And so Behmen is no subject for the Budget! I waited until I should chance to light on one of his volumes, knowing that any volume would do, and almost any page. My first hap was on the second volume of the edition of 1664 (4to, published by M. Richardson) and opening near the beginning, a turn or two brought me to page 13, where I saw about sulphur and mercurius as follows:
"Thus SUL is the soul, in an herb it is the oil, and in man also, according to the spirit of this world in the third principle, which is continually generated out of the anguish of the will in the mind, and the Brimstone-worm is the Spirit, which hath the fire and burneth: PHUR is the sour wheel in itself which causeth that.
"Mercurius comprehendeth all the four forms, even as the life springeth up, and yet hath not its dark beginning in the Center as the PHUR hath, but after the flash of fire, when the sour dark form is terrified, where the hardness is turned into pliant sharpness, and where the second will (viz. the will of nature, which is called the Anguish) ariseth, there Mercurius hath its original. For MER is the shivering wheel, very horrible, sharp, venomous, and hostile; which assimulateth it thus in the sourness in the flash of fire, where the sour wrathful life ariseth. The syllable CU is the pressing out, of the Anxious will of the mind, from Nature: which is climbing up, and willeth to be out aloft. RI is the comprehension of the flash of fire, which in MER giveth a clear sound and tune. For the flash maketh the tune, and it is the Salt-Spirit which soundeth, and its form (or quality) is gritty like sand, and herein arise noises, sounds and voices, and thus CU comprehendeth the flash, and so the pressure is as a wind which thrusteth, and giveth a spirit to the flash, so that it liveth and burneth. Thus the [322]syllable US is called the burning fire, which with the spirit continually driveth itself forth: and the syllable CU presseth continually upon the flash."
Shades of Tauler[598] and Paracelsus,[599] how strangely you do mix! Well may Hallam call Germany the native soil of Mysticism. Had Behmen been the least of a scholar, he would not have divided sulph-ur and merc-ur-i-us as he has done: and the inflexion us, that boy of all work, would have been rejected. I think it will be held that a writer from whom hundreds of pages like the above could be brought together, is fit for the Budget. If Sampson Arnold Mackay[600] had tied his etymologies to a mystical Christology, instead of a mystical infidelity, he might have had a school of followers. The nonsense about Newton borrowing gravitation from Behmen passes only with those who know neither what Newton did, nor what was done before him.
The above reminds me of a class of paradoxers whom I wonder that I forgot; they are without exception the greatest bores of all, because they can put the small end of their paradox into any literary conversation whatever. I mean the people who have heard the local pronunciation of celebrated names, and attempt not only to imitate it, but to impose on others their broken German or Arabic, or what not. They also learn the vernacular names of those who are generally spoken of in their Latin forms; at least, they learn a few cases, and hawk them as evidences of erudition. They are miserably mistaken: scholarship, as a rule, [323]always accepts the vernacular form of a name which has vernacular celebrity. Hallam writes Behmen: his index-maker, rather superfluously, gives "Behmen or Boehm." And he retains Melanchthon,[601] the name given by Reuchlin[602] to his little kinsman Schwartzerd, because the world has adopted it: but he will none of Capnio, the name which Reuchlin fitted on to himself, because the world has not adopted it. He calls the old forms pedantry: but he sees that the rejection of well-established results of pedantry would be greater pedantry still. The paradoxers assume the question that it is more correct to sound a man by lame imitation of his own countrymen than as usual in the country in which the sound is to be made. Against them are, first, the world at large; next, an overpowering majority of those who know something about surnames and their history. Some thirty years ago—a fact—there appeared at the police-office a complainant who found his own law. In the course of his argument, he asked, "What does Kitty say?"—"Who's Kitty?" said the magistrate, "your wife, or your nurse?"—"Sir! I mean Kitty, the celebrated lawyer."—"Oh!" said the magistrate, "I suspect you mean Mr. Chitty,[603] the author of the great work on pleading."—"I do sir! But Chitty is an Italian name, and ought to be pronounced Kitty." This man was a full-blown flower: but there is many a modest bud; and all ought either to blush when seen or to waste their pronunciation on the desert air.
A PLEA FOR KING CUSTOM.
I stand up for King Custom, or Usus, as Horace called him, with whom is arbitrium the decision, and jus the right, and norma the way of deciding, simply because he has potestas the power. He may admit one and another principle to advise: but Custom is not a constitutional king; he may listen to his cabinet, but he decides for himself: and if the ministry should resign, he blesses his stars and does without them. We have a glorious liberty in England of owning neither dictionary, grammar, nor spelling-book: as many as choose write by either of the three, and decide all disputed points their own way, those following them who please.
Throughout this book I have called people by the names which denote them in their books, or by our vernacular names. This is the intelligible way of proceeding. I might, for instance (Vol. I, p. 44), have spoken of Charles de Bovelles,[604] of Lefèvre d'Étaples,[605] of Pèlerin,[606] and of Etienne.[607] But I prefer the old plan. Those who like another plan better, are welcome to substitute with a pen, when they know what to write; when they do not, it is clear that they would not have understood me if I had given modern names.
The principal advisers of King Custom are as follows. First, there is Etymology, the chiffonnier, or general rag-merchant, who has made such a fortune of late years in his own business that he begins to be considered highly respectable. He gives advice which is more thought of than followed, partly on account of the fearful extremes into which he runs. He lately asked some boys of sixteen, at a matriculation examination in English, to what branch of [325]the Indo-Germanic family they felt inclined to refer the Pushto language, and what changes in the force of the letters took place in passing from Greek into Mœso-Gothic. Because all syllables were once words, he is a little inclined to insist that they shall be so still. He would gladly rule English with a Saxon rod, which might be permitted with a certain discretion which he has never attained: and when opposed, he defends himself with analogies of the Aryan family until those who hear him long for the discovery of an Athanasyus. He will transport a word beyond seas—he is recorder of Rhematopolis—on circumstantial evidence which looks like mystery gone mad; but, strange to say, something very often comes to light after sentence is passed which proves the soundness of the conviction.
The next adviser is Logic, a swearing old justice of peace, quorum, and rotulorum, whose excesses brought on such a fit of the gout that for many years he was unable to move. He is now mending, and his friends say he has sown his wild oats. He has some influence with the educated subjects of Custom, and will have more, if he can learn the line at which interference ought to stop: with them he has succeeded in making an affirmative of two negatives; but the vulgar won't never have nothing to say to him. He has always railed at Milton for writing that Eve was the fairest of her daughters; but has never satisfactorily shown what Milton ought to have said instead.
The third adviser has more influence with the mass of the subjects of King Custom than the other two put together; his name is Fiddlefaddle, the toy-shop keeper; and the other two put him forward to do their worst work. In return, he often uses their names without authority. He took Etymology to witness that means to an end must be plural: and he would have any one method to be a mean. But Etymology proved him wrong, King Custom referred him to his Catechism, in which is "a means whereby we receive the same," and Analogy—a subordinate of [326]Etymology—asked whether he thought it a great new to hear that he was wrong. It was either this Fiddlefaddle, or Lindley Murray[608] his traveler, who persuaded the Miss Slipslops, of the Ladies Seminary, to put "The Misses Slipslop" over the gate. Sixty years ago, this bagman called at all the girls' schools, and got many of the teachers to insist on the pupils saying "Is it not" and "Can I not" for "Isn't it" and "Can't I": of which it came that the poor girls were dreadfully laughed at by their irreverent brothers when they went home for the holidays. Had this bad adviser not been severely checked, he might by this time have proposed our saying "The Queen's of England son," declaring, in the name of Logic, that the prince was the Queen's son, not England's.
Lastly, there is Typography the metallurgist, an executive officer who is always at work in secret, and whose lawless mode of advising is often done by carrying his notions into effect without leave given. He it is who never ceases suggesting that the same word is not to occur in a second place within sight of the first. When the Authorized Version was first printed, he began this trick at the passage, "Let there be light, and there was light;" he drew a line on the proof under the second light, and wrote "luminosity?" opposite. He is strongest in the punctuations and other signs; he has a pepper-box full of commas always by his side. He puts everything under marks of quotation which he has ever heard before. An earnest preacher, in a very moving sermon, used the phrase Alas! and alack a day! Typography stuck up the inverted commas because he had read the old Anglo-Indian toast, "A lass and a lac a day!" If any one should have the sense to leave out of his Greek [327]the unmeaning scratches which they call accents, he goes to a lexicon and puts them in. He is powerful in routine; but when two routines interlace or overlap, he frequently takes the wrong one.
Subject to bad advice, and sometimes misled for a season, King Custom goes on his quiet way and is sure to be right at last.
"Treason does never prosper: what's the reason?
Why, when it prospers, none dare call it treason."
Language is in constant fermentation, and all that is thrown in, so far as it is not fit to assimilate, is thrown off; and this without any obvious struggle. In the meanwhile every one who has read good authors, from Shakspeare downward, knows what is and what is not English; and knows, also, that our language is not one and indivisible. Two very different turns of phrase may both be equally good, and as good as can be: we may be relieved of the consequences of contempt of one court by habeas corpus issuing out of another.
TEST OF LANGUAGE.
Hallam remarks that the Authorized Version of the Bible is not in the language of the time of James the First: that it is not the English of Raleigh or of Bacon. Here arises the question whether Raleigh and Bacon are the true expositors of the language of their time; and whether they were not rather the incipient promoters of a change which was successfully resisted by—among other things—the Authorized Version of the Testaments. I am not prepared to concede that I should have given to the English which would have been fashioned upon that of Bacon by imitators, such as they usually are, the admiration which is forced from me by Bacon's English from Bacon's pen. On this point we have a notable parallel. Samuel Johnson [328]commands our admiration, at least in his matured style: but we nauseate his followers. It is an opinion of mine that the works of the leading writers of an age are seldom the proper specimens of the language of their day, when that language is in its state of progression. I judge of a language by the colloquial idiom of educated men: that is, I take this to be the best medium between the extreme cases of one who is ignorant of grammar and one who is perched upon a style. Dialogue is what I want to judge by, and plain dialogue: so I choose Robert Recorde[609] and his pupil in the Castle of Knowledge, written before 1556. When Dr. Robert gets into his altitudes of instruction, he differs from his own common phraseology as much as probably did Bacon when he wrote morals and philosophy. But every now and then I come to a little plain talk about a common thing, of which I propose to show a specimen. Anything can be made to look old by such changes as makes into maketh, with a little old spelling. I shall invert these changes, using the newer form of inflexion, and the modern spelling: with no other variation whatever.
"Scholar. Yet the reason of that is easy enough to be conceived, for when the day is at the longest the Sun must needs shine the more time, and so must it needs shine the less time when the day is at the shortest: this reason I have heard many men declare.
Master. That may be called a crabbed reason, for it [329]goes backward like a crab. The day makes not the Sun to shine, but the Sun shining makes the day. And so the length of the day makes not the Sun to shine long, neither the shortness of the day causes not [sic] the Sun to shine the lesser time, but contrariwise the long shining of the Sun makes the long day, and the short shining of the Sun makes the lesser day: else answer me what makes the days long or short?
Scholar. I have heard wise men say that Summer makes the long days, and Winter makes the long nights.
Master. They might have said more wisely, that long days make summer and short days make winter.
Scholar. Why, all that seems one thing to me.
Master. Is it all one to say, God made the earth, and the earth made God? Covetousness overcomes all men, and all men overcome covetousness?
Scholar. No, not so; for here the effect is turned to be the cause, and the agent is made the patient.
Master. So is it to say Summer makes long days, when you should say: Long days make summer.
Scholar. I perceive it now: but I was so blinded with the vulgar error, that if you had demanded of me further what did make the summer, I had been like to have answered that green leaves do make summer; and the sooner by remembrance of an old saying that a year should come in which the summer should not be known but by the green leaves.
Master. Yet this saying does not import that green leaves do make summer, but that they betoken summer; so are they the sign and not the cause of summer."
I have taken a whole page of our author, without omission, that the reader may see that I do not pick out sentences convenient for my purpose. I have done nothing but alter the third person of the verb and the spelling: but great is the effect thereof. We say "the Sun shining makes the day"; Recorde, "the Sonne shynynge maketh the daye." [330]These points apart, we see a resemblance between our English and that of three hundred years ago, in the common talk of educated persons, which will allow us to affirm that the language of the authorized Bible must have been very close to that of its time. For I cannot admit that much change can have taken place in fifty years: and the language of the version represents both our common English and that of Recorde with very close approximation. Take sentences from Bacon and Raleigh, and it will be apparent that these writers will be held to differ from all three, Recorde, the version, and ourselves, by differences of the same character. But we speak of Recorde's conversation, and of our own. We conclude that it is the plain and almost colloquial character of the Authorized Version which distinguishes it from the English of Bacon and Raleigh, by approximating it to the common idiom of the time. If any one will cast an eye upon the letters of instruction written by Cecil[610] and the Bishop of London to the translators themselves, or to the general directions sent to them in the King's name, he will find that these plain business compositions differ from the English of Bacon and Raleigh by the same sort of differences which distinguish the version itself.
PRONUNCIATION.
The foreign word, or the word of a district, or class of people, passes into the general vernacular; but it is long before the specially learned will acknowledge the right of those with whom they come in contact to follow general usage. The rule is simple: so long as a word is technical or local, those who know its technical or local pronunciation may reasonably employ it. But when the word has become general, the specialist is not very wise if he refuse to follow [331]the mass, and perfectly foolish if he insist on others following him. There have been a few who demanded that Euler should be pronounced in the German fashion:[611] Euler has long been the property of the world at large; what does it matter how his own countrymen pronounce the letters? Shall we insist on the French pronouncing Newton without that final tong which they never fail to give him? They would be wise enough to laugh at us if we did. We remember that a pedant who was insisting on all the pronunciations being retained, was met by a maxim in contradiction, invented at the moment, and fathered upon Kaen-foo-tzee,[612] an authority which he was challenged to dispute. Whom did you speak of? said the bewildered man of accuracy. Learn your own system, was the answer, before you impose it on others; Confucius says that too.[613]
The old English has fote, fode, loke, coke, roke, etc., for foot, etc. And above rhymes in Chaucer to remove. Suspecting that the broader sounds are the older, we may surmise that remove and food have retained their old sounds, and that cook, once coke, would have rhymed to our Luke, the vowel being brought a little nearer, perhaps, to the o in our present coke, the fuel, probably so called as used by cooks. If this be so, the Chief Justice Cook[614] of our lawyers, and the Coke (pronounced like the fuel) of the greater part of the world, are equally wrong. The lawyer has no right whatever to fasten his pronunciation upon us: even leaving aside the general custom, he cannot prove himself right, and is probably wrong. Those who [332]know the village of Rokeby (pronounced Rookby) despise the world for not knowing how to name Walter Scott's poem: that same world never asked a question about the matter, and the reception of the parody of Jokeby, which soon appeared, was a sufficient indication of their notion. Those who would fasten the hodiernal sound upon us may be reminded that the question is, not what they call it now, but what it was called in Cromwell's time. Throw away general usage as a lawgiver, and this is the point which emerges. Probably Rūke-by would be right, with a little turning of the Italian ū towards ō of modern English.
[Some of the above is from an old review. I do not always notice such insertions: I take nothing but my own writings. A friend once said to me, "Ah! you got that out of the Athenæum!" "Excuse me," said I. "the Athenæum got that out of me!"]
APOLOGIES TO CLUVIER.
It is part of my function to do justice to any cyclometers whose methods have been wrongly described by any orthodox sneerers (myself included). In this character I must notice Dethlevus Cluverius,[615] as the Leipzig Acts call him (probably Dethleu Cluvier), grandson of the celebrated geographer, Philip Cluvier. The grandson was a Fellow of the Royal Society, elected on the same day as Halley,[616] November 30, 1678: I suppose he lived in England. This [333]man is quizzed in the Leipzig Acts for 1686; and, if Montucla insinuate rightly, by Leibnitz, who is further suspected of wanting to embroil Cluvier with his own opponent Nieuwentiit,[617] on the matter of infinitesimals. So far good: I have nothing against Leibnitz, who though he was ironical, told us what he laughed at. But Montucla has behaved very unfairly: he represents Cluvier as placing the essence of his method in the solution of the problem construere mundum divinæ menti analogum, to construct a world corresponding to the divine mind. Nothing to begin with: no way of proceeding. Now, it ought to have been ex data linea construere,[618] etc.: there is a given line, which is something to go on. Further, there is a way of proceeding: it is to find the product of 1, 2, 3, 4, etc. for ever. Moreover, Montucla charges Cluvier with unsquaring the parabola, which Archimedes had squared as tight as a glove. But he never mentions how very nearly Cluvier agrees with the Greek: they only differ by 1 divided by 3n2, where n is the infinite number of parts of which a parabola is composed. This must have been the conceit that tickled Leibnitz, and made him wish that Cluvier and Nieuwentiit should fight it out. Cluvier, was admitted, on terms of irony, into the Leipzig Acts: he appeared on a more serious footing in London. It is very rare for one cyclometer to refute another: les corsaires ne se battent pas.[619] The only instance I recall is that of M. Cluvier, who (Phil. Trans., 1686, No. 185) refuted M. Mallemont de Messange,[620] who [334]published at Paris in 1686. He does it in a very serious style, and shows himself a mathematician. And yet in the year in which, in the Phil. Trans., he was a geometer, and one who rebukes his squarer for quoting Matthew xi. 25, in that very year he was the visionary who, in the Leipzig Acts, professed to build a world resembling the divine mind by multiplying together 1, 2, 3, 4, etc. up to infinity.
THE RAINBOW PARADOX.
There is a very pretty opening for a paradox which has never found its paradoxer in print. The philosophers teach that the rainbow is not material: it comes from rain-drops, but those rain-drops do not take color. They only give it, as lenses and mirrors; and each one drop gives all the colors, but throws them in different directions. Accordingly, the same drop which furnishes red light to one spectator will furnish violet to another, properly placed. Enter the paradoxer whom I have to invent. The philosopher has gulled you nicely. Look into the water, and you will see the reflected rainbow: take a looking-glass held sideways, and you see another reflection. How could this be, if there were nothing colored to reflect? The paradoxer's facts are true: and what are called the reflected rainbows are other rainbows, caused by those other drops which are placed so as to give the colors to the eye after reflection, at the water or the looking-glass. A few years ago an artist exhibited a picture with a rainbow and its apparent reflection: he simply copied what he had seen. When his picture was examined, some started the idea that there could be no reflection of a rainbow; they were right: they inferred that the artist had made a mistake; they were wrong. When it was explained, some agreed and some dissented. Wanted, [335]immediately, an able paradoxer: testimonials to be forwarded to either end of the rainbow, No. 1. No circle-squarer need apply, His Variegatedness having been pleased to adopt 3.14159... from Noah downwards.
TYCHO BRAHE REVIVED.
The system of Tycho Brahé,[621] with some alteration and addition, has been revived and contended for in our own day by a Dane, W. Zytphen,[622] who has published The Motion of the Sun in the Universe, (second edition) Copenhagen, 1865, 8vo, and Le Mouvement Sidéral, 1865, 8vo. I make an extract.
"How can one explain Copernically that the velocity of the Moon must be added to the velocity of the Earth on the one place in the Earth's orbit, to learn how far the Moon has advanced from one fixed star to another; but in another place in the orbit these velocities must be subtracted (the movements taking place in opposite directions) to attain the same result? In the Copernican and other systems, it is well known that the Moon, abstracting from the insignificant excentricity of the orbit, always in twenty-four hours performs an equally long distance. Why has Copernicus never been denominated Fundamentus or Fundator? Because he has never convinced anybody so thoroughly that this otherwise so natural epithet has occurred to the mind."
Really the second question is more effective against Newton than against Copernicus; for it upsets gravity: the first is of great depth.
JAMES SMITH WILL NOT DOWN.
The Correspondent journal makes a little episode in the history of my Budget (born May, 1865, died April, 1866). It consisted entirely of letters written by correspondents. In August, a correspondent who signed "Fair Play"—and who I was afterwards told was a lady—thought it would be a good joke to bring in the Cyclometers. Accordingly a letter was written, complaining that though Mr. Sylvester's[623] demonstration of Newton's theorem—then attracting public attention—was duly lauded, the possibly greater discovery of the quadrature seemed to be blushing unseen, and wasting etc. It went on as follows:
"Prof. De Morgan, who, from his position in the scientific world, might fairly afford to look favourably on less practised efforts than his own, seems to delight in ridiculing the discoverer. Science is, of course, a very respectable person when he comes out and makes himself useful in the world [it must have been a lady; each sex gives science to the other]: but when, like a monk of the Middle Ages, he shuts himself up [it must have been a lady; they always snub the bachelors] in his cloistered cell, repeating his mumpsimus from day to day, and despising the labourers on the outside, we begin to think of Galileo,[624] Jenner,[625] Harvey,[626] and other glorious trios, who have been contemned ..."
The writer then called upon Mr. James Smith[627] to come [337]forward. The irony was not seen; and that day fortnight appeared the first of more than thirty letters from his pen. Mr. Smith was followed by Mr. Reddie,[628] Zadkiel,[629] and others, on their several subjects. To some of the letters I have referred; to others I shall come. The Correspondent was to become a first-class scientific journal; the time had arrived at which truth had an organ: and I received formal notice that I could not stifle it by silence, nor convert it into falsehood by ridicule. When my reader sees my extracts, he will readily believe my declaration that I should have been the last to stifle a publication which was every week what James Mill[630] would call a dose of capital for my Budget. A few anti-paradoxers brought in common sense: but to the mass of the readers of the journal it all seemed to be the difference between Tweedledum and Tweedledee. Some said that the influx of scientific paradoxes killed the journal: but my belief is that they made it last longer than it otherwise would have done. Twenty years ago I recommended the paradoxers to combine and publish their views in a common journal: with a catholic editor, who had no pet theory, but a stern determination not to exclude anything merely for absurdity. I suspect it would answer very well. A strong title, or motto, would be wanted: not so coarse as was roared out in a Cambridge mob when I was an undergraduate—"No King! No Church! No House of Lords! No nothing, blast me!"—but something on that principle.
At the end of 1867 I addressed the following letter to the Athenæum:
Pseudomath, Philomath, and Graphomath.
Many thanks for the present of Mr. James Smith's letters [338]of Sept. 28 and of Oct. 10 and 12. He asks where you will be if you read and digest his letters: you probably will be somewhere first. He afterwards asks what the WE of the Athenæum will be if, finding it impossible to controvert, it should refuse to print. I answer for you, that We-We of the Athenæum, not being Wa-Wa the wild goose, so conspicuous in "Hiawatha," will leave what controverts itself to print itself, if it please.
Philomath is a good old word, easier to write and speak than mathematician. It wants the words between which I have placed it. They are not well formed: pseudomathete and graphomathete would be better: but they will do. I give an instance of each.
The pseudomath is a person who handles mathematics as the monkey handled the razor. The creature tried to shave himself as he had seen his master do; but, not having any notion of the angle at which the razor was to be held, he cut his own throat. He never tried a second time, poor animal! but the pseudomath keeps on at his work, proclaims himself clean-shaved, and all the rest of the world hairy. So great is the difference between moral and physical phenomena! Mr. James Smith is, beyond doubt, the great pseudomath of our time. His 3⅛ is the least of a wonderful chain of discoveries. His books, like Whitbread's barrels, will one day reach from Simpkin & Marshall's to Kew, placed upright, or to Windsor laid length-ways. The Queen will run away on their near approach, as Bishop Hatto did from the rats: but Mr. James Smith will follow her were it to John o' Groats.
The philomath, for my present purpose, must be exhibited as giving a lesson to presumption. The following anecdote is found in Thiébault's[631] Souvenirs de vingt ans de séjours à Berlin, published in 1804. The book itself got a high character for truth. In 1807 Marshal Mollendorff[632] [339]answered an inquiry of the Duc de Bassano,[633] by saying that it was the most veracious of books, written by the most honest of men. Thiébault does not claim personal knowledge of the anecdote, but he vouches for its being received as true all over the north of Europe.[634]
Diderot[635] paid a visit to Russia at the invitation of Catherine the Second. At that time he was an atheist, or at least talked atheism: it would be easy to prove him either one thing or the other from his writings. His lively sallies on this subject much amused the Empress, and all the younger part of her Court. But some of the older courtiers suggested that it was hardly prudent to allow such unreserved exhibitions. The Empress thought so too, but did not like to muzzle her guest by an express prohibition: so a plot was contrived. The scorner was informed that an eminent mathematician had an algebraical proof of the existence of God, which he would communicate before the whole Court, if agreeable. Diderot gladly consented. The mathematician, who is not named, was Euler.[636] He came to Diderot with the gravest air, and in a tone of perfect conviction said, "Monsieur!
a + bn n | = x |
donc Dieu existe; répondez!"[637] Diderot, to whom algebra was Hebrew, though this is expressed in a very roundabout way by Thiébault—and whom we may suppose to have expected some verbal argument of alleged algebraical closeness, was disconcerted; while peals of laughter sounded on all sides. Next day he asked permission to return to France, which was granted. An algebraist would have [340]turned the tables completely, by saying, "Monsieur! vous savez bien que votre raisonnement demande le développement de x suivant les puissances entières de n".[638] Goldsmith could not have seen the anecdote, or he might have been supposed to have drawn from it a hint as to the way in which the Squire demolished poor Moses.
The graphomath is a person who, having no mathematics, attempts to describe a mathematician. Novelists perform in this way: even Walter Scott now and then burns his fingers. His dreaming calculator, Davy Ramsay, swears "by the bones of the immortal Napier." Scott thought that the the philomaths worshiped relics: so they do, in one sense. Look into Hutton's[639] Dictionary for Napier's Bones, and you shall learn all about the little knick-knacks by which he did multiplication and division. But never a bone of his own did he contribute; he preferred elephants' tusks. The author of Headlong Hall[640] makes a grand error, which is quite high science: he says that Laplace proved the precession of the equinoxes to be a periodical inequality. He should have said the variation of the obliquity. But the finest instance is the following: Mr. Warren,[641] in his well-wrought tale of the martyr-philosopher, was incautious enough to invent the symbols by which his savant satisfied himself Laplace[642] was right on a doubtful point. And this is what he put together—
Now, to Diderot and the mass of mankind this might be Laplace all over: and, in a forged note of Pascal, would [341]prove him quite up to gravitation. But I know of nothing like it, except in the lately received story of the American orator, who was called on for some Latin, and perorated thus: "Committing the destiny of the country to your hands, Gentlemen, I may without fear declare, in the language of the noble Roman poet,
But the American got nearer to Horace than the martyr-philosopher to
Laplace. For all the words are in Horace, except Thule, which
might have been there. But  is not a symbol wanted by Laplace; nor can we see
how it could have been; in fact, it is not recognized in algebra. As to
the junctions, etc., Laplace and Horace are about equally well
imitated.
is not a symbol wanted by Laplace; nor can we see
how it could have been; in fact, it is not recognized in algebra. As to
the junctions, etc., Laplace and Horace are about equally well
imitated.
Further thanks for Mr. Smith's letters to you of Oct. 15, 18, 19, 28, and Nov. 4, 15. The last of these letters has two curious discoveries. First, Mr. Smith declares that he has seen the editor of the Athenæum: in several previous letters he mentions a name. If he knew a little of journalism he would be aware that editors are a peculiar race, obtained by natural selection. They are never seen, even by their officials; only heard down a pipe. Secondly, "an ellipse or oval" is composed of four arcs of circles. Mr. Smith has got hold of the construction I was taught, when a boy, for a pretty four-arc oval. But my teachers knew better than to call it an ellipse: Mr. Smith does not; but he produces from it such confirmation of 3⅛ as would convince any honest editor.
Surely the cyclometer is a Darwinite development of a spider, who is always at circles, and always begins again when his web is brushed away. He informs you that he [342]has been privileged to discover truths unknown to the scientific world. This we know; but he proceeds to show that he is equally fortunate in art. He goes on to say that he will make use of you to bring those truths to light, "just as an artist makes use of a dummy for the purpose of arranging his drapery." The painter's lay-figure is for flowing robes; the hairdresser's dummy is for curly locks. Mr. James Smith should read Sam Weller's pathetic story of the "four wax dummies." As to his use of a dummy, it is quite correct. When I was at University College, I walked one day into a room in which my Latin colleague was examining. One of the questions was, "Give the lives and fates of Sp. Mælius,[644] and Sp. Cassius."[645] Umph! said I, surely all know that Spurius Mælius was whipped for adulterating flour, and that Spurius Cassius was hanged for passing bad money. Now, a robe arranged on a dummy would look just like the toga of Cassius on the gallows. Accordingly, Mr. Smith is right in the drapery-hanger which he has chosen: he has been detected in the attempt to pass bad circles. He complains bitterly that his geometry, instead of being read and understood by you, is handed over to me to be treated after my scurrilous fashion. It is clear enough that he would rather be handled in this way than not handled at all, or why does he go on writing? He must know by this time that it is a part of the institution that his "untruthful and absurd trash" shall be distilled into mine at the rate of about 3⅛ pages of the first to one column of the second. Your readers will never know how much they gain by the process, until Mr. James Smith publishes it all in a big book, or until they get hold of what he has already published. I have six pounds avoirdupois of pamphlets and letters; and there is more than half a pound of letters [343]written to you in the last two months. Your compositor must feel aggrieved by the rejection of these clearly written documents, without erasures, and on one side only. Your correspondent has all the makings of a good contributor, except the knowledge of his subject and the sense to get it. He is, in fact, only a mask: of whom the fox
"O quanta species, inquit, cerebrum non habet."[646]
I do not despair of Mr. Smith on any question which does not involve that unfortunate two-stick wicket at which he persists in bowling. He has published many papers; he has forwarded them to mathematicians: and he cannot get answers; perhaps not even readers. Does he think that he would get more notice if you were to print him in your journal? Who would study his columns? Not the mathematician, we know; and he knows. Would others? His balls are aimed too wide to be blocked by any one who is near the wicket. He has long ceased to be worth the answer which a new invader may get. Rowan Hamilton,[647] years ago, completely knocked him over; and he has never attempted to point out any error in the short and easy method by which that powerful investigator condescended to show that, be right who may, he must be wrong. There are some persons who feel inclined to think that Mr. Smith should be argued with: let those persons understand that he has been argued with, refuted, and has never attempted to stick a pen into the refutation. He stated that it was a remarkable paradox, easily explicable; and that is all. After this evasion, Mr. James Smith is below the necessity of being told that he is unworthy of answer. His friends complain that I do nothing but chaff him. Absurd! I winnow him; and if nothing but chaff results, whose fault is that? I am usefully employed: for he is the type of a class which ought to be known, and which I have done much to make known.
Nothing came of this until July 1869, when I received a reprint of the above letter, with a comment, described as Appendix D of a work in course of publication on the geometry of the circle. The Athenæum journal received the same: but the Editor, in his private capacity, received the whole work, being The Geometry of the Circle and Mathematics as applied to Geometry by Mathematicians, shown to be a mockery, delusion, and a snare, Liverpool, 8vo, 1869. Mr. J. S. here appears in deep fight with Professor Whitworth,[648] and Mr. Wilson,[649] the author of the alleged amendment of Euclid. How these accomplished mathematicians could be inveigled into continued discussion is inexplicable. Mr. Whitworth began by complaining of Mr. Smith's attacks upon mathematicians, continued to correspond after he was convinced that J. S. proved an arc and its chord to be equal, and only retreated when J. S. charged him with believing in 3⅛, and refusing acknowledgment. Mr. Wilson was introduced to J. S. by a volunteer defense of his geometry from the assaults of the Athenæum. This the editor would not publish; so J. S. sent a copy to Mr. Wilson himself. Some correspondence ensued, but Mr. Wilson soon found out his man, and withdrew.
There is a little derision of the Athenæum and a merited punishment for "that unscrupulous critic and contemptible mathematical twaddler, De Morgan."
MR. REDDIE'S ASTRONOMY.
At p. 183 I mentioned Mr. Reddie,[650] the author of Vis Inertiæ Victa and of Victoria toto cœlo,[651] which last is not [345]an address to the whole heaven, either from a Roman Goddess or a British Queen, whatever a scholar may suppose. Between these Mr. Reddie has published The Mechanics of the Heavens, 8vo, 1862: this I never saw until he sent it to me, with an invitation to notice it, he very well knowing that it would catch. His speculations do battle with common notions of mathematics and of mechanics, which, to use a feminine idiom, he blasphemes so you can't think! and I suspect that if you do not blaspheme them too, you can't think. He appeals to the "truly scientific," and would be glad to have readers who have read what he controverts, i.e., Newton's Principia: I wish he may get them; I mean I hope he may obtain them. To none but these would an account of his speculations be intelligible: I accordingly disposed of him in a very short paragraph of description. Now many paradoxers desire notice, even though it be disparaging. I have letters from more than one—besides what have been sent to the Editor of the Athenæum—complaining that they are not laughed at; although they deserve it, they tell me, as much as some whom I have inserted. Mr. Reddie informs me that I have not said a single word against his books, though I have given nearly a column to sixteen-string arithmetic, and as much to animalcule universes. What need to say anything to readers of Newton against a book from which I quoted that revolution by gravitation is demonstrably impossible? It would be as useless as evidence against a man who has pleaded guilty. Mr. Reddie derisively thanks me for "small mercies"; he wrote me private letters; he published them, and more, in the Correspondent. He gave me, pro viribus suis,[652] such a dressing you can't think, both for my Budget non-notice, and for reviews which he assumed me to have written. He outlawed himself by declaring (Correspondent, Nov. 11, 1856) that I—in a review—had made a quotation which was "garbled, evidently on purpose [346]to make it appear that" he "was advocating solely a geocentric hypothesis, which is not true." In fact, he did his best to get larger "mercy." And he shall have it; and at a length which shall content him, unless his mecometer be an insatiable apparatus. But I fear that in other respects I shall no more satisfy him than the Irish drummer satisfied the poor culprit when, after several times changing the direction of the stroke at earnest entreaty, he was at last provoked to call out, "Bad cess to ye, ye spalpeen! strike where one will, there's no plasing ye!"
Mr. Reddie attaches much force to Berkeley's[653] old arguments against the doctrine of fluxions, and advances objections to Newton's second section, which he takes to be new. To me they appear "such as have been often made," to copy a description given in a review: though I have no doubt Mr. Reddie got them out of himself. But the whole matter comes to this: Mr. Reddie challenged answer, especially from the British Association, and got none. He presumes that this is because he is right, and cannot be answered: the Association is willing to risk itself upon the counter-notion that he is wrong, and need not be answered; because so wrong that none who could understand an answer would be likely to want one.
Mr. Reddie demands my attention to a point which had already particularly struck me, as giving the means of showing to all readers the kind of confusion into which paradoxers are apt to fall, in spite of the clearest instruction. It is a very honest blunder, and requires notice: it may otherwise mislead some, who may suppose that no one able to read could be mistaken about so simple a matter, [347]let him be ever so wrong about Newton. According to his own mis-statement, in less than five months he made the Astronomer Royal abandon the theory of the solar motion in space. The announcement is made in August, 1865, as follows: the italics are not mine:
"The third (Victoria ...), although only published in September, 1863, has already had its triumph. It is the book that forced the Astronomer Royal of England, after publicly teaching the contrary for years, to come to the conclusion, "strange as it may appear," that "the whole question of solar motion in space is at the present time in doubt and abeyance." This admission is made in the Annual Report of the Council of the Royal Astronomical Society, published in the Society's Monthly Notices for February, 1864."
It is added that solar motion is "full of self-contradiction, which "the astronomers" simply overlooked, but which they dare not now deny after being once pointed out."
The following is another of his accounts of the matter, given in the Correspondent, No. 18, 1865:
"... You ought, when you came to put me in the 'Budget,' to have been aware of the Report of the Council of the Royal Astronomical Society, where it appears that Professor Airy,[654] with a better appreciation of my demonstrations, had admitted—'strange,' say the Council, 'as it may appear,'—that 'the whole question of solar motion in space [and here Mr. Reddie omits some words] is now in doubt and abeyance.' You were culpable as a public teacher of no little pretensions, if you were 'unaware' of this. If aware of it, you ought not to have suppressed such an important testimony to my really having been 'very successful' in drawing the teeth of the pegtops, though you thought them so firmly fixed. And if you still suppress [348]it, in your Appendix, or when you reprint your 'Budget,' you will then be guilty of a suppressio veri, also of further injury to me, who have never injured you...."
Mr. Reddie must have been very well satisfied in his own mind before he ventured such a challenge, with an answer from me looming in the distance. The following is the passage of the Report of the Council, etc., from which he quotes:
"And yet, strange to say, notwithstanding the near coincidence of all the results of the before-mentioned independent methods of investigation, the inevitable logical inference deduced by Mr. Airy is, that the whole question of solar motion in space, so far at least as accounting for the proper motion of the stars is concerned, [I have put in italics the words omitted by Mr. Reddie] appears to remain at this moment in doubt and abeyance."
Mr. Reddie has forked me, as he thinks, on a dilemma: if unaware, culpable ignorance; if aware, suppressive intention. But the thing is a trilemma, and the third horn, on which I elect to be placed, is surmounted by a doubly-stuffed seat. First, Mr. Airy has not changed his opinion about the fact of solar motion in space, but only suspends it as to the sufficiency of present means to give the amount and direction of the motion. Secondly, all that is alluded to in the Astronomical Report was said and printed before the Victoria proclamation appeared. So that the author, instead of drawing the tooth of the Astronomer Royal's pegtop, has burnt his own doll's nose.
William Herschel,[655] and after him about six other astronomers, had aimed at determining, by the proper motions of the stars, the point of the heavens towards which the solar system is moving: their results were tolerably accordant. Mr. Airy, in 1859, proposed an improved method, and, applying it to stars of large proper motion, produced [349]much the same result as Herschel. Mr. E. Dunkin,[656] one of Mr. Airy's staff at Greenwich, applied Mr. Airy's method to a very large number of stars, and produced, again, nearly the same result as before. This paper was read to the Astronomical Society in March, 1863, was printed in abstract in the Notice of that month, was printed in full in the volume then current, and was referred to in the Annual Report of the Council in February, 1864, under the name of "the Astronomer Royal's elaborate investigation, as exhibited by Mr. Dunkin." Both Mr. Airy and Mr. Dunkin express grave doubts as to the sufficiency of the data: and, regarding the coincidence of all the results as highly curious, feel it necessary to wait for calculations made on better data. The report of the Council states these doubts. Mr. Reddie, who only published in September, 1863, happened to see the Report of February, 1864, assumes that the doubts were then first expressed, and declares that his book of September had the triumph of forcing the Astronomer Royal to abandon the fact of motion of the solar system by the February following. Had Mr. Reddie, when he saw that the Council were avowedly describing a memoir presented some time before, taken the precaution to find out when that memoir was presented, he would perhaps have seen that doubts of the results obtained, expressed by one astronomer in March, 1863, and by another in 1859, could not have been due to his publication of September, 1863. And any one else would have learnt that neither astronomer doubts the solar motion, though both doubt the sufficiency of present means to determine its amount and direction. This is implied in the omitted words, which Mr. Reddie—whose omission would have been dishonest if he had seen their meaning—no doubt took for pleonasm, superfluity, overmuchness. The rashness which pushed him headlong [350]into the quillet that his thunderbolt had stopped the chariot of the Sun and knocked the Greenwich Phaeton off the box, is the same which betrayed him into yet grander error—which deserves the full word, quidlibet—about the Principia of Newton. There has been no change of opinion at all. When a person undertakes a long investigation, his opinion is that, at a certain date, there is prima facie ground for thinking a sound result may be obtained. Should it happen that the investigation ends in doubt upon the sufficiency of the grounds, the investigator is not put in the wrong. He knew beforehand that there was an alternative: and he takes the horn of the alternative indicated by his calculations. The two sides of this case present an instructive contrast. Eight astronomers produce nearly the same result, and yet the last two doubt the sufficiency of their means: compare them with the what's-his-name who rushes in where thing-em-bobs fear to tread.
I was not aware, until I had written what precedes, that Mr. Airy had given a sufficient answer on the point. Mr. Reddie says (Correspondent, Jan. 20, 1866):
"I claim to have forced Professor Airy to give up the notion of 'solar motion in space' altogether, for he admits it to be 'at present in doubt and abeyance.' I first made that claim in a letter addressed to the Astronomer Royal himself in June, 1864, and in replying, very courteously, to other portions of my letter, he did not gainsay that part of it."
Mr. Reddie is not ready at reading satire, or he never would have so missed the meaning of the courteous reply on one point, and the total silence upon another. Mr. Airy must be one of those peculiar persons who, when they do not think an assertion worth notice, let it alone, without noticing it by a notification of non-notice. He would never commit the bull of "Sir! I will not say a word on that subject." He would put it thus, "Sir! I will only say ten words on that subject,"—and, having thus said them, would [351]proceed to something else. He assumed, as a matter of form, that Mr. Reddie would draw the proper inference from his silence: and this because he did not care whether or no the assumption was correct.
The Mechanics of the Heavens, which Mr. Reddie sends to be noticed, shall be noticed, so far as an extract goes:
"My connection with this subject is, indeed, very simply explained. In endeavoring to understand the laws of physical astronomy as generally taught, I happened to entertain some doubt whether gravitating bodies could revolve, and having afterwards imbibed some vague idea that the laws of the universe were chemical and physical rather than mechanical, and somehow connected with electricity and magnetism as opposing correlative forces—most probably suggested to my mind, as to many others, by the transcendent discoveries made in electro-magnetism by Professor Faraday[657]—my former doubts about gravitation were revived, and I was led very naturally to try and discover whether a gravitating body really could revolve; and I became convinced it could not, before I had ever presumed to look into the demonstrations of the Principia."
This is enough against the book, without a word from me: I insert it only to show those who know the subject what manner of writer Mr. Reddie is. It is clear that "presumed" is a slip of the pen; it should have been condescended.
Mr. Reddie represents me as dreaming over paltry paradoxes. He is right; many of my paradoxes are paltry: he is wrong; I am wide awake to them. A single moth, beetle, or butterfly, may be a paltry thing; but when a cabinet is arranged by genus and species, we then begin to admire the [352]infinite variety of a system constructed on a wonderful sameness of leading characteristics. And why should paradoxes be denied that collective importance, paltry as many of them may individually be, which is accorded to moths, beetles, or butterflies? Mr. Reddie himself sees that "there is a method in" my "mode of dealing with paradoxes." I hope I have atoned for the scantiness of my former article, and put the demonstrated impossibility of gravitation on that level with Hubongramillposanfy arithmetic and inhabited atoms which the demonstrator—not quite without reason—claims for it.
In the Introduction to a collected edition of the three works, Mr. Reddie describes his Mechanism of the Heavens, from which I have just quoted, as—
"a public challenge offered to the British Association and the mathematicians at Cambridge, in August, 1862, calling upon them to point to a single demonstration in the Principia or elsewhere, which even attempts to prove that Universal Gravitation is possible, or to show that a gravitating body could possibly revolve about a center of attraction. The challenge was not accepted, and never will be. No such demonstration exists. And the public must judge for themselves as to the character of a so-called "certain science," which thus shrinks from rigid examination, and dares not defend itself when publicly attacked: also of the character of its teachers, who can be content to remain dumb under such circumstances."
ON PARADOXERS IN GENERAL.
The above is the commonplace talk of the class, of which I proceed to speak without more application to this paradoxer than to that. It reminds one of the funny young rascals who used, in times not yet quite forgotten, to abuse the passengers, as long as they could keep up with the [353]stage coach; dropping off at last with "Why don't you get down and thrash us? You're afraid, you're afraid!" They will allow the public to judge for themselves, but with somewhat of the feeling of the worthy uncle in Tom Jones, who, though he would let young people choose for themselves, would have them choose wisely. They try to be so awfully moral and so ghastly satirical that they must be answered: and they are best answered in their own division. We have all heard of the way in which sailors cat's-pawed the monkeys: they taunted the dwellers in the trees with stones, and the monkeys taunted them with cocoa-nuts in return. But these were silly dendrobats: had they belonged to the British Association they would have said—No! No! dear friends; it is not in the itinerary: if you want nuts, you must climb, as we do. The public has referred the question to Time: the procedure of this great king I venture to describe, from precedents, by an adaptation of some smart anapæstic tetrameters—your anapæst is the foot for satire to halt on, both in Greek and English—which I read about twenty years ago, and with the point of which I was much tickled. Poetasters were laughed at; but Mr. Slum, whom I employed—Mr. Charles Dickens obliged me with his address—converted the idea into that of a hit at mathematicasters, as easily as he turned the Warren acrostic into Jarley. As he observed, when I settled his little account, it is cheaper than any prose, though the broom was not stolen quite ready made:
Forty stripes save one for the smaller Paradoxers.
Hark to the wisdom the sages preach
Who never have learnt what they try to teach.
We are the lights of the age, they say!
We are the men, and the thinkers we!
So we build up guess-work the livelong day,
In a topsy-turvy sort of way,
Some with and some wanting a plus b.
Let the British Association fuss;
What are theirs to the feats to be wrought by us?
[354]Shall the earth stand still? Will the round come square?
Must Isaac's book be the nest of a mare?
Ought the moon to be taught by the laws of space
To turn half round without right-about-face?
Our whimsey crotchets will manage it all;
Deep! Deep! posterity will them call!
Though the world, for the present, lets them fall
Down! Down! to the twopenny box of the stall!
Thus they—But the marplot Time stands by,
With a knowing wink in his funny old eye.
He grasps by the top an immense fool's cap,
Which he calls a philosophaster-trap:
And rightly enough, for while these little men
Croak loud as a concert of frogs in a fen,
He first singles out one, and then another,
Down goes the cap—lo! a moment's pother,
A spirit like that which a rushlight utters
As just at the last it kicks and gutters:
When the cruel smotherer is raised again
Only snuff, and but little of that, will remain.
But though uno avulso thus comes every day
Non deficit alter is also in play:
For the vacant parts are, one and all,
Soon taken by puppets just as small;
Who chirp, chirp, chirp, with a grasshopper's glee,
We're the lamps of the Universe, We! We! We!
But Time, whose speech is never long,—
He hasn't time for it—stops the song
And says—Lilliput lamps! leave the twopenny boxes,
And shine in the Budget of Paradoxes!
When a paradoxer parades capital letters and diagrams which are as good as Newton's to all who know nothing about it, some persons wonder why science does not rise and triturate the whole thing. This is why: all who are fit to read the refutation are satisfied already, and can, if they please, detect the paradoxer for themselves. Those who are not fit to do this would not know the difference between the true answer and the new capitals and diagrams on which the delighted paradoxer would declare [355]that he had crumbled the philosophers, and not they him. Trust him for having the last word: and what matters it whether he crow the unanswerable sooner or later? There are but two courses to take. One is to wait until he has committed himself in something which all can understand, as Mr. Reddie has done in his fancy about the Astronomer Royal's change of opinion: he can then be put in his true place. The other is to construct a Budget of Paradoxes, that the world may see how the thing is always going on, and that the picture I have concocted by cribbing and spoiling a bit of poetry is drawn from life. He who wonders at there being no answer has seen one or two: he does not know that there are always fifty with equal claims, each of whom regards his being ranked with the rest as forty-nine distinct and several slanders upon himself, the great Mully Ully Gue. And the fifty would soon be five hundred if any notice were taken of them. They call mankind to witness that science will not defend itself, though publicly attacked in terms which might sting a pickpocket into standing up for his character: science, in return, allows mankind to witness or not, at pleasure, that it does not defend itself, and yet receives no injury from centuries of assault. Demonstrative reason never raises the cry of Church in Danger! and it cannot have any Dictionary of Heresies except a Budget of Paradoxes. Mistaken claimants are left to Time and his extinguisher, with the approbation of all thinking non-claimants: there is no need of a succession of exposures. Time gets through the job in his own workmanlike manner as already described.
On looking back more than twenty years, I find among my cuttings the following passage, relating to a person who had signalized himself by an effort to teach comets to the conductor of the Nautical Almanac:
"Our brethren of the literary class have not the least idea of the small amount of appearance of knowledge [356]which sets up the scientific charlatan. Their world is large, and there are many who have that moderate knowledge, and perception of what is knowledge, before which extreme ignorance is detected in its first prank. There is a public of moderate cultivation, for the most part sound in its judgment, always ready in its decisions. Accordingly, all their successful pretenders have some pretension. It is not so in science. Those who have a right to judge are fewer and farther between. The consequence is, that many scientific pretenders have nothing but pretension."
This is nearly as applicable now as then. It is impossible to make those who have not studied for themselves fully aware of the truth of what I have quoted. The best chance is collection of cases; in fact, a Budget of Paradoxes. Those who have no knowledge of the subject can thus argue from the seen to the unseen. All can feel the impracticability of the Hubongramillposanfy numeration, and the absurdity of the equality of contour of a regular pentagon and hexagon in one and the same circle. Many may accordingly be satisfied, on the assurance of those who have studied, that there is as much of impracticability, or as much of absurdity, in things which are hidden under
"Sines, tangents, secants, radius, cosines
Subtangents, segments and all those signs;
Enough to prove that he who read 'em
Was just as mad as he who made 'em."
Not that I mean to be disrespectful to mathematical terms: they are short and easily explained, and compete favorably with those of most other subjects: for instance, with
"Horse-pleas, traverses, demurrers,
Jeofails, imparlances, and errors,
Averments, bars, and protestandos,
And puis d'arreign continuandos."
From which it appears that, taking the selections made by satirists for our samples, there are, one with another, four letters more in a law term than in one of mathematics. But pleading has been simplified of late years.
All paradoxers can publish; and any one who likes may read. But this is not enough; they find that they cannot publish, or those who can find they are not read, and they lay their plans athwart the noses of those who, they think, ought to read. To recommend them to be content with publication, like other authors, is an affront: of this I will give the reader an amusing instance. My good nature, of which I keep a stock, though I do not use it all up in this Budget, prompts me to conceal the name.
I received the following letter, accompanied by a prospectus of a work on metaphysics, physics, astronomy, etc. The author is evidently one whom I should delight to honor:
"Sir,—A friend of mine has mentioned your name in terms of panigeric [sic], as being of high standing in mathematics, and of greatly original thought. I send you the enclosed without comment; and, assuming that the bent of your mind is in free inquiry, shall feel a pleasure in showing you my portfolio, which, as a mathematician, you will acknowledge to be deeply interesting, even in an educational point of view. The work is complete, and the system so far perfected as to place it above criticism; and, so far as regards astronomy, as will Ptolemy beyond rivalry [sic: no doubt some words omitted]. Believe me to be, Sir, with the profoundest respect, etc. The work is the result of thirty-five years' travel and observation, labor, expense, and self-abnegation."
I replied to the effect that my time was fully occupied, and that I was obliged to decline discussion with many persons who have views of their own; that the proper way is to publish, so that those who choose may read when they can find leisure. I added that I should advise a precursor in the shape of a small pamphlet, as two octavo volumes [358]would be too much for most persons. This was sound advice; but it is not the first, second, or third time that it has proved very unpalatable. I received the following answer, to which I take the liberty of prefixing a bit of leonine wisdom:
"Si doceas stultum, lætum non dat tibi vultum;
Odit te multum; vellet te scire sepultum.[658]"
"Sir,—I pray you pardon the error I unintentionally have fallen into; deceived by the F.R.S. [I am not F.R.S.] I took you to be a man of science [omnis homo est animal, Sortes est homo, ergo Sortes est animal][659] instead of the mere mathematician, or human calculating-machine. Believe me, Sir, you also have mistaken your mission, as I have mine. I wrote to you as I would to any other man well up in mathematics, with the intent to call your attention to a singular fact of omission by Euclid, and other great mathematicians: and, in selecting you, I did you an honor which, from what I have just now heard, was entirely out of place. I think, considering the nature of the work set forth in the prospectus, you are guilty of both folly and presumption, in assuming the character of a patron; for your own sense ought to have assured you that was such my object I should not have sought him in a De Morgan, who exists only by patronage of others. On the other hand, I deem it to be an unpardonable piece of presumption in offering your advice upon a subject the magnitude, importance, and real utility of which you know nothing about: by doing so you have offered me a direct insult. The system is a manual of Philosophy, a one inseparable whole of metaphysics and physic; embracing points the most interesting, laws the most important, [359]doctrines the most essential to advance man in accordance with the spirit of the times. I may not live to see it in print; for, at ——, life at best is uncertain: but, live or die, be assured Sir, it is not my intention to debase the work by seeking patronage, or pandering to the public taste. Your advice was the less needed, seeing I am an old-established ——. I remain, etc.—P.S. You will oblige me by returning the prospectus of my work."
My reader will, I am sure, not take this transition from the "profoundest respect" to the loftiest insolence for an apocraphical correspondence, to use a word I find in the Prospectus: on my honor it is genuine. He will be better employed in discovering whether I exist by patronizing others, or by being patronized by them. I make any one who can find it out a fair offer: I will give him my patronage if I turn out to be Bufo, on condition he gives me his, if I turn out to be Bavius.[660] I need hardly say that I considered the last letter to be one of those to which no answer is so good as no answer.
These letters remind me in one respect of the correspondents of the newspapers. My other party wrote because a friend had pointed me out: but he would not have written if he had known what another friend told him just in time for the second letter. The man who sends his complaint to the newspaper very often says, in effect, "Don't imagine, Sir, that I read your columns; but a friend who sometimes does has told me ..." It is worded thus: "My attention [360]has been directed to an article in your paper of ..." Many thanks to my friend's friends for not mentioning the Budget: had my friend's attention been directed to it I might have lost a striking example of the paradoxer in search of a patron. That my Friend was on this scent in the first letter is revealed in the second. Language was given to man to conceal his thoughts; but it is not every one who can do it.
Among the most valuable information which my readers will get from me is comparison of the reactions of paradoxers, when not admitted to argument, or when laughed at. Of course, they are misrepresented; and at this they are angry, or which is the same thing, take great pains to assure the reader that they are not. So far natural, and so far good; anything short of concession of a case which must be seriously met by counter-reasons is sure to be misrepresentation. My friend Mr. James Smith and my friend Mr. Reddie are both terribly misrepresented: they resent it by some insinuations in which it is not easy to detect whether I am a conscious smotherer of truth, or only muddle-headed and ignorant. [This was written before I received my last communication from Mr. James Smith. He tells me that I am wrong in saying that his work in which I stand in the pillory is all reprint: I have no doubt I confounded some of it with some of the manuscript or slips which I had received from my much not-agreed-with correspondent. He adds that my mistake was intentional, and that my reason is obvious to the reader. This is information, as the sea-serpent said when he read in the newspaper that he had a mane and tusks.]
THE DOUBLE VAHU PROCESS.
My friend Dr. Thorn[661] sees deeper into my mystery. By the way, he still sends an occasional touch at the old [361]subject; and he wants me particularly to tell my readers that the Latin numeral letters, if M be left out, give 666. And so they do: witness DCLXVI. A person who thinks of the origin of symbols will soon see that 666 is our number because we have five fingers on each hand: had we had but four, our mystic number would have been expressed by 555, and would have stood for our present 365. Had n been the number on each hand, the great number would have been
(n + 1) (4n2 + 2n + 1)
With no finger on each hand, the number would have been 1: with one finger less than none at all on each hand, it would have been 0. But what does this mean? Here is a question for an algebraical paradoxer! So soon as we have found out how many fingers the inhabitants of any one planet have on each hand, we have the means of knowing their number of the Beast, and thence all about them. Very much struck with this hint of discovery, I turned my attention to the means of developing it. The first point was to clear my vision of all the old cataracts. I propose the following experiment, subject of course to the consent of parties. Let Dr. Thorn Double-Vahu Mr. James Smith, and Thau Mr. Reddie: if either be deparadoxed by the treatment, I will consent to undergo it myself. Provided always that the temperature required be not so high as the Doctor hints at: if the Turkish Baths will do for this world, I am content.
The three paradoxers last named and myself have a pentasyllable convention, under which, though we go far beyond civility, we keep within civilization. Though Mr. James Smith pronounced that I must be dishonest if I did not see his argument, which he knew I should not do [to say nothing of recent accusation]; though Dr. Thorn declared me a competitor for fire and brimstone—and my wife, too, which doubles the joke: though Mr. Reddie [362]was certain I had garbled him, evidently on purpose to make falsehood appear truth; yet all three profess respect for me as to everything but power to see truth, or candor to admit it. And on the other hand, though these were the modes of opening communication with me, and though I have no doubt that all three are proper persons of whom to inquire whether I should go up-stairs or down-stairs, etc., yet I am satisfied they are thoroughly respectable men, as to everything but reasoning. And I dare say our several professions are far more true in extent than in many which are made under more parliamentary form. We find excuses for each other: they make allowances for my being hoodwinked by Aristotle, by Newton, by the Devil; and I permit them to feel, for I know they cannot get on without it, that their reasons are such as none but a knave or a sinner can resist. But they are content with cutting a slice each out of my character: neither of them is more than an uncle, a Bone-a-part; I now come to a dreadful nephew, Bone-the-whole.
I will not give the name of the poor fellow who has fallen so far below both the honestum and the utile, to say nothing of the decorum or the dulce.[662] He is the fourth who has taken elaborate notice of me; and my advice to him would be, Nec quarta loqui persona laboret.[663] According to him, I scorn humanity, scandalize learning, and disgrace the press; it admits of no manner of doubt that my object is to mislead the public and silence truth, at the expense of the interests of science, the wealth of the nation, and the lives of my fellow men. The only thing left to be settled is, whether this is due to ignorance, natural distaste for truth, personal malice, a wish to curry favor with the Astronomer Royal, or mere toadyism. The only accusation which has truth in it is, that I have made myself a "public scavenger of science": the assertion, which is the [363]most false of all is, that the results of my broom and spade are "shot right in between the columns of" the Athenæum. I declare I never in my life inserted a word between the columns of the Athenæum: I feel huffed and miffed at the very supposition. I have made myself a public scavenger; and why not? Is the mud never to be collected into a heap? I look down upon the other scavengers, of whom there have been a few—mere historical drudges; Montucla, Hutton, etc.—as not fit to compete with me. I say of them what one crossing-sweeper said of the rest: "They are well enough for the common thing; but put them to a bit of fancy-work, such as sweeping round a post, and see what a mess they make of it!" Who can touch me at sweeping round a paradoxer? If I complete my design of publishing a separate work, an old copy will be fished up from a stall two hundred years hence by the coming man, and will be described in an article which will end by his comparing our century with his own, and sighing out in the best New Zealand pronunciation—
"Dans ces tems-là
C'était déjà comme ça!"[664]
ORTHODOX PARADOXERS.
And pray, Sir! I have been asked by more than one—do your orthodox never fall into mistake, nor rise into absurdity? They not only do both, but they admit it of each other very freely; individually, they are convinced of sin, but not of any particular sin. There is not a syndoxer among them all but draws his line in such a way as to include among paradoxers a great many whom I should exclude altogether from this work. My worst specimens are but exaggerations of what may be found, occasionally, in the thoughts of sagacious investigators. At the end of the [364]glorious dream, we learn that there is a way to Hell from the gates of Heaven, as well as from the City of Destruction: and that this is true of other things besides Christian pilgrimage is affirmed at the end of the Budget of Paradoxes. If D'Alembert[665] had produced enough of a quality to match his celebrated mistake on the chance of throwing head in two throws, he would have been in my list. If Newton had produced enough to match his reception of the story that Nausicaa, Homer's Phæacian princess, invented the celestial sphere, followed by his serious surmise that she got it from the Argonauts,—then Newton himself would have had an appearance entered for him, in spite of the Principia. In illustration, I may cite a few words from Tristram Shandy:
"'A soldier,' cried my uncle Toby, interrupting the Corporal, 'is no more exempt from saying a foolish thing, Trim, than a man of letters.'—'But not so often, an' please your honor,' replied the Corporal. My uncle Toby gave a nod."
I now proceed to die out. Some prefatory remarks will follow in time.[666] I shall have occasion to insist that all is not barren: I think I shall find, on casting up, that two out of five of my paradoxers are not to be utterly condemned. Among the better lot will be found all gradations of merit; at the same time, as was remarked on quite a different subject, there may be little to choose between the last of the saved and the first of the lost. The higher and better class is worthy of blame; the lower and worse class is worthy of praise. The higher men are to be reproved for not taking up things in which they could do some good: the lower men are to be commended for taking up things in which they can do no great harm. The circle problem is like Peter Peebles's lawsuit:
"'But, Sir, I should really spoil any cause thrust on me so hastily.'—'Ye cannot spoil it, Alan,' said my father, 'that is the very cream of the business, man,—... the case is come to that pass that Stair or Arniston could not mend it, and I don't think even you, Alan, can do it much harm.'"
I am strongly reminded of the monks in the darker part of the Middle Ages. To a certain proportion of them, perhaps two out of five, we are indebted for the preservation of literature, and their contemporaries for good teaching and mitigation of socials evils. But the remaining three were the fleas and flies and thistles and briars with whom the satirist lumps them, about a century before the Reformation:
"Flen, flyys, and freris, populum domini male cædunt;
Thystlis and breris crescentia gramina lædunt.
Christe nolens guerras qui cuncta pace tueris,
Destrue per terras breris, flen, flyys, and freris.
Flen, flyys, and freris, foul falle hem thys fyften yeris,
For non that her is lovit flen, flyys ne freris."[667]
I should not be quite so savage with my second class. Taken together, they may be made to give useful warning to those who are engaged in learning under better auspices: aye, even useful hints; for bad things are very often only good things spoiled or misused. My plan is that of a predecessor in the time of Edward the Second:
"Meum est propositum genti imperitæ
Artes frugi reddere melioris vitæ."[668]
To this end I have spoken with freedom of books as books, of opinions as opinions, of ignorance as ignorance, of [366]presumption as presumption; and of writers as I judge may be fairly inferred from what they have written. Some—to whom I am therefore under great obligation—have permitted me to enlarge my plan by assaults to which I have alluded; assaults which allow a privilege of retort, of which I have often availed myself; assaults which give my readers a right of partnership in the amusement which I myself have received.
For the present I cut and run: a Catiline, pursued by a chorus of Ciceros, with Quousque tandem? Quamdiu nos? Nihil ne te?[669] ending with, In te conferri pestem istam jam pridem oportebat, quam tu in nos omnes jamdiu machinaris! I carry with me the reflection that I have furnished to those who need it such a magazine of warnings as they will not find elsewhere; a signatis cavetote:[670] and I throw back at my pursuers—Valete, doctores sine doctrina; facite ut proxima congressu vos salvos corporibus et sanos mentibus videamus.[671] Here ends the Budget of Paradoxes.
I think it right to give the proof that the ratio of the circumference to the diameter is incommensurable. This method of proof was given by Lambert,[672] in the Berlin Memoirs for 1761, and has been also given in the notes to Legendre's[673] Geometry, and to the English translation of the same. Though not elementary algebra, it is within the reach of a student of ordinary books.[674]
Let a continued fraction, such as
a
——
b + c
——
d + e
-
f + etc.,
be abbreviated into a/b+ c/d+ e/f+ etc.: each fraction being understood as falling down to the side of the preceding sign +. In every such fraction we may suppose b, d, f, etc. [368]positive; a, c, e, &c. being as required: and all are supposed integers. If this succession be continued ad infinitum, and if a/b, c/d, e/f, etc. all lie between -1 and +1, exclusive, the limit of the fraction must be incommensurable with unity; that is, cannot be A/B, where A and B are integers.
First, whatever this limit may be, it lies between -1 and +1. This is obviously the case with any fraction p/(q + ω), where ω is between ±1: for, p/q, being < 1, and p and q integer, cannot be brought up to 1, by the value of ω. Hence, if we take any of the fractions
a/b, a/b+ c/d, a/b+ c/d+ e/f, etc.
say a/b+ c/d+ e/f+ g/h we have, g/h being between ±1, so is e/f+ g/h, so therefore is c/d+ e/f+ g/h; and so therefore is a/b+ c/d+ e/f+ g/h.
Now, if possible, let a/b+ c/d+ etc. be A/B at the limit; A and B being integers. Let
P = A c/d+ e/f+ etc., Q = P e/f+ g/h+ etc., R = Q g/h + i/k + etc.
P, Q, R, etc. being integer or fractional, as may be. It is easily shown that all must be integer: for
A/B = a/b+ P/A, or, P = aB - bA
P/A = c/d+ Q/P, or, Q = cA - dP
Q/P = e/f+ R/Q, or, R = eP - fQ
etc., etc. Now, since a, B, b, A, are integers, so also is P; and thence Q; and thence R, etc. But since A/B, P/A, Q/P, R/Q, etc. are all between -1 and +1, it follows that the unlimited succession of integers P, Q, R, are each less in numerical value than the preceding. Now there can be no such unlimited succession of descending integers: consequently, it is impossible that a/b+ c/d+, etc. can have a commensurable limit.
It easily follows that the continued fraction is incommensurable if a/b, c/d, etc., being at first greater than unity, become and continue less than unity after some one point. Say that i/k, l/m,... are all less than unity. Then the fraction i/k+ l/m+ ... is incommensurable, as proved: let it be κ. Then g/(h + κ) is incommensurable, say λ; e/(f + λ) is the same, say μ; also c/(d + μ), say ν, and a/(b + ν), say ρ. But ρ is the fraction a/b+ c/d+ ... itself; which is therefore incommensurable.
Let φz represent
| 1 + | a z | + | a2  2z(z+1) | + | a3  2·3·z(z+1)(z+2) | + ... |
Let z be positive: this series is convergent for all values of a, and approaches without limit to unity as z increases without limit. Change z into z + 1, and form φz - φ(z+1): the following equation will result—
| φz - φ(z+1) = | a z(z+1) | φ(z+2) |
| or a = | a z | φ(z+1) φz | · z + | a z | φ(z+1) φz | · | a z+1 | φ(z+2) φ(z+1) |
| or a = ψz |  | z + ψ(z+1) |  |
ψz being (a/z)(φ(z+1)/φz); of which observe that it diminishes without limit as z increases without limit. Accordingly, we have
| ψz = | a z+ | ψ(z+1) = | a z+ | a (z+1)+ | ψ(z+2) = | a z+ | a (z+1)+ | a (z+2)+ | ψ(z+3) |
And, ψ(z + n) diminishing without limit, we have
a z | · | φ(z+1) φz | = a z+ | a (z+1)+ | a (z+2)+ | a (z+3)+ ... |
Let z = ½; and let 4a = -x2. Then
a z | φ(z+1) | is - | x2 2 |  | 1 - | x2 2·3 | + | x4 2·3·4·5... |  | or - | x 2 | sin x. |
Again
| φz is 1 - | x2 2 | + | x4 2·3·4 | or cos x: |
and the continued fraction is
- ¼x2 ½+ | - ¼x2 (3/2)+ | - ¼x2 (5/2)+ ... | or - | x 2 | x 1+ | - x2 3+ | - x2 5+ ... |
whence
| tan x = | x 1+ | - x2 3+ | - x2 5+ | - x2 7+ ... |
Or, as written in the usual way,
tan x = x
——
1 - x2
——
3 - x2
——
5 - x2
——
7 - ...
This result may be proved in various ways: it may also be verified by calculation. To do this, remember that if
a1 b1+ | a2 b2+ | a3 b3+ ... | an bn | = | Pn Qn | ; then |
| P1=a1, | P2=b2 P1, | P3=b3 P2+a3 P1, | P4=b4 P3+a4 P2, etc. |
| Q1=b1, | Q2=b2 Q1+a2, | Q3=b3 Q2+a3 Q1, | Q4=b4 Q3+a4 Q2, etc. |
in the case before us we have
| a1=x, | a2=-x2, | a3=-x2, | a4=-x2, | a5=-x2, etc. |
| b1=1, | b2=3, | b3=5, | b4=7, | b5=9, etc. |
| P1=x | Q1=1 |
| P2=3x | Q2=3-x2 |
| P3=15x-x3 | Q3=15-6x2 |
| P4=105x-10x3 | Q4=105-45x2+x4 |
| P5=945x-105x3+x5 | Q5=945-420x2+15x4 |
| P6=10395x-1260x3+21x5 | Q6=10395-4725x2+210x4-x6 |
We can use this algebraically, or arithmetically. If we divide Pn by Qn, we shall find a series agreeing with the known series for tan x, as far as n terms. That series is
| x + | x3 3 | + | 2x5 15 | + | 17x7 315 | + | 62x9 2835 | + ... |
Take P5, and divide it by Q5 in the common way, and the first five terms will be as here written. Now take x = .1, which means that the angle is to be one tenth of the actual unit, or, in degrees 5°.729578. We find that when x = .1, P6 = 1038.24021, Q6 = 10347.770999; whence P6 divided by Q6 gives .1003346711. Now 5°.729578 is 5°43′46½″; and from the old tables of Rheticus[675]—no modern tables carry the tangents so far—the tangent of this angle is .1003347670.
Now let x = ¼π; in which case tan x = 1. If ¼π be commensurable with the unit, let it be (m/n), m and n being integers: we know that ¼π < 1. We have then
| 1= | (m/n) 1- | (m2/n2) 3- | (m2/n2) 5- ... | = | m n- | m2 3n- | m2 5n- | m2 7n- ... |
Now it is clear that m2/3n, m2/5n, m2/7n, etc. must at last become and continue severally less than unity. The continued fraction is therefore incommensurable, and cannot be unity. Consequently π2 cannot be commensurable: that is, π is an incommensurable quantity, and so also is π2.
I thought I should end with a grave bit of appendix, deeply mathematical: but paradox follows me wherever I go. The foregoing is—in my own language—from Dr. (now Sir David) Brewster's[676] English edition of Legendre's Geometry, (Edinburgh, 1824, 8vo.) translated by some one who is not named. I picked up a notion, which others had at Cambridge in 1825, that the translator was the late Mr. Galbraith,[677] then known at Edinburgh as a writer and teacher.
But it turns out that it was by a very different person, and one destined to shine in quite another walk; it was a young man named Thomas Carlyle.[678] He prefixed, from his own pen, a thoughtful and ingenious essay on Proportion, as good a substitute for the fifth Book of Euclid as could have been given in the space; and quite enough to show that he would have been a distinguished teacher and thinker on first principles. But he left the field immediately.
(The following is the passage referred to at Vol. II, page 54.)
Michael Stifelius[679] edited, in 1554, a second edition of the Algebra (Die Coss.), of Christopher Rudolff.[680] This is one of the earliest works in which + and - are used.
Stifelius was a queer man. He has introduced into this very work of Rudolff his own interpretation of the number of the Beast. He determined to fix the character of Pope Leo: so he picked the numeral letters from LEODECIMVS, and by taking in X from LEO X. and striking out M as standing for mysterium, he hit the number exactly. This discovery completed his conversion to Luther, and his determination to throw off his monastic vows. Luther dealt with him as straight-forwardly as with Melanchthon about his astrology: he accepted the conclusions, but told him to clear his mind of all the premises about the Beast. Stifelius [374]did not take the advice, and proceeded to settle the end of the world out of the prophet Daniel: he fixed on October, 1533. The parishioners of some cure which he held, having full faith, began to spend their savings in all kinds of good eating and drinking; we may charitably hope this was not the way of preparing for the event which their pastor pointed out. They succeeded in making themselves as fit for Heaven as Lazarus, so far as beggary went: but when the time came, and the world lasted on, they wanted to kill their deceiver, and would have done so but for the interference of Luther. [375]
Pages denoted by numerals of this kind (287) refer to biographical notes, chiefly by the editor. Numerals like 426 refer to books discussed by De Morgan, or to leading topics in the text. Numerals like 126 indicate minor references.
Abbott, Justice, I, 181.
Abernethy, J., II, 219.
Aboriginal Britons, a poem, II, 270.
Academy of Sciences, French, I, 163.
Adair, J., I, 223.
Adam, M., I, 65.
Adams, J. C., I, 43, 82, 385, 388; II, 131, 135, 140, 303.
Agnew, H. C., I, 328.
Agricola, J., I, 394.
Agricultural Laborer's letter, II, 16.
Agrippa, H. C., I, 48, 48.
Ainsworth, W. H., II, 132.
Airy, I, 85, 88, 152, 242; II, 85, 140, 150, 303, 347.
Alchemy, I, 125.
Alfonso X (El Sabio), II, 269.
Alford, H., II, 221.
Alfred, King, Ballad of, II, 22.
Algebra, I, 121.
Algebraic symbols, I, 121.
Almanac, I, 300; II, 147, 148, 207.
(See Easter.)
Aloysius Lilius, I, 362.
Alsted, J. H., II, 282.
Ameen Bey, II, 15.
Amicable Society, I, 347.
Ampère, I, 86.
Amphisbæna serpent, I, 31.
Anagrams, De Morgan, I, 138.
Anaxagoras, II, 59.
Annuities, Fallacies of, I, 157.
Antichrist, I, 130.
Antimony, I, 125.
Antinewtonism, I, 162.
Antinomians, I, 394.
Antiphon, II, 59.
Antonie, F., I, 126, 126.
Apollonius, I, 41, 107.
Apparitions, II, 47.
Arago, I, 243, 390.
Aratus, II, 167.
Arbuthnot, I, 133, 134.
Archer, H., II, 90.
Archimedes, I, 5, 11, 42, 83, 107.
Archytas, I, 53.
Argoli, I, 104.
Aristocrat, as a scientist, I, 131.
Aristotle, I, 5, 331.
Arnobius, II, 73.
Arson, P. J., II, 207.
Ashton, R., II, 99.
Astrology, I, 118, 127, 128, 350; II, 43.
Astronomer's Drinking Song, I, 380.
Astronomical Aphorisms, I, 398.
Paradox, I, 394.
Police Report, I, 390.
Society. (See Royal Astronomical Society.)
Astronomy, Bailly's exaggerated view of, I, 166.
Astunica, Didacas, I, 90.
Athanasian Creed, I, 371.
Atheists, Philosophical, I, 1.
Atoms, II, 191.
[376]Attraction, I, 136, 151, 155.
Augustine, St., II, 23.
Aurora borealis, I, 134.
Austen, Jane, I, 191.
Auzout, A., II, 300.
Aviation, Early ideas of, II, 8.
Babbage, C., I, 207, 290, 291; II, 181.
Bachet, de Méziriac, I, 161.
Bacon, F., I, 5, 75, 75, 76, 79, 89, 145, 331.
Bacon, R., I, 5, 126, 126, 360; II, 94.
Baconian controversy, I, 141.
Baden Powell, II, 267.
Bailly, J. S., I, 166, 166, 308.
Baily, F., I, 308, 309; II, 16, 143, 188.
Baily, R., II, 16.
Baker, T., II, 302.
Bakewell, F. C., II, 156, 156.
Banks, J., I, 28.
Barberini, M., II, 267.
Barker, C., II, 262.
Baronius, I, 33, 35; II, 62.
Barrême, I, 42.
Barrett, G., II, 188.
Barrow, I., I, 160; II, 302.
Baruel, de, I, 165.
Baxter, T., I, 146.
Bayle, P., II, 73.
Beaufort, F., II, 267.
Beaugrand, I, 119, 121.
Beaulieu, I, 119, 119, 121.
Beaune, de, II, 59.
Bécourt, R., II, 277.
Bedford, Duke of, (6th), I, 182.
Behmen, I, 168, 254; II, 317.
Bellenden, W., I, 175.
Bentley, I, 110.
Berkeley, G., II, 346.
Bernardus Trevisanus, I, 126, 126.
Bernoullis, I, 130, 150, 335, 336.
Bertius, P., II, 300.
Bèse, I, 66.
Bessel, I, 384; II, 2.
Bethune, I, 99, 279, 291.
Bettesworth, I, 19.
Beza. (See Bèse.)
Bickersteth, E. H., I, 238.
Bidder, I, 86.
Bidle, (Biddle), I, 239.
Biot, I, 85.
Birch, T., I, 108; II, 304, 313.
Bishop, G., I, 386.
Bishops as Paradoxers, I, 226.
Boccaccio, I, 38.
Boethius, I, 42, 45.
Böhme. (See Behmen.)
Boncompagni, I, 298.
Boniface, St., I, 32.
Bonnycastle, J., II, 16.
Booker, I, 115.
Boole, G., I, 261, 332; II, 75, 79.
—A tribute to, II, 79.
Borelli, G. A., II, 300.
Borello, I, 69.
Boreman, I, 113.
Borron, Mrs., II, 7.
Boscovich, I, 156, 164.
Bouguer, II, 301.
Bouillaud, I, 87; II, 295.
Bouvard, A., I, 327.
Bovillus, I, 44; II, 324.
—Epitome of, I, 44.
Bowdler, H. M., I, 194.
Bowring, J., I, 352; II, 256.
Boyle, R., I, 24, 125; II, 300.
Bradley, I, 24.
Bradwardine, I, 227, 228, 229.
Brahe. (See Tycho B.)
Brancker, I, 107; II, 300.
Brenan, J., I, 330, 330.
Brewster, D., I, 39, 137, 140; II, 214, 288, 372.
Bright, J., II, 235.
Brinkley, J., I, 311.
Britannicus, D., II, 8.
British Museum library, I, 151.
Brothers, R., I, 315; II, 97.
Brougham, Henry, Lord, I, 191.
Brouncker (Brounker), I, 132; II, 302.
Brown, W., II, 168.
Browne, T., I, 31.
Brucker, I, 61.
Brunet, I, 402.
Brünnow, I, 386.
Bruno, I, 59, 59.
Bryson, II, 59.
Bürgi, I, 52.
Buffon, I, 282.
Bulstrode, II, 84.
Bungus, I, 55, 55, 57.
Buoncompagno, U., I, 362.
[377]Burgon, J. W., II, 30.
Buridan, I, 37.
—Questiones morales, I, 37.
Buridan's Ass, I, 37.
Burke, E., I, 173.
Burlesque, Frend's, I, 208.
Burnet, G., I, 107.
Burney, Frances, I, 190.
Burton, Frances B., I, 374.
Busby, R., II, 313.
Buteo, I, 51.
Butler, G., I, 199.
Butler, S., II, 218.
Buxton, J., I, 86.
Byrgius. (See Bürgi.)
Cabbala, I, 272.
Calculating Boys, I, 86.
Calculus, I, 129.
Calendar. (See Easter.)
Cambridge Poets, II, 269.
Campanus, I, 42, 43.
Canning, Geo., II, 145.
Carcavi, I, 106.
Cardanus, II, 59.
Carlile, R., I, 271.
Carlyle, T., II, 373.
Carnot, I, 107.
Caroline tables, I, 124.
Casaubon, I, 111.
Case, J., I, 128, 128.
Cassini, J., I, 172.
Castel, I, 148, 148.
Castiglioni, I, 139.
Castlereagh, I, 185, 186.
Cataldi, I, 69, 69.
Catcott, A., I, 237.
Causans, de, I, 298.
Cavalieri, I, 106.
Cavendish, C., I, 106; II, 299, 312.
Cavendish, W., I, 290.
Caxton, W., II, 281.
Cayley, A., II, 292.
Cecil, R. (1st Earl of Salisbury), II, 330.
Centrifugal force, II, 268.
Ceulen. (See Van Ceulen.)
Challis, J., I, 390; II, 141.
Chalmers, I, 102; II, 219.
Chambers, E., II, 282.
Chambers, R., I, 344, 344.
Charles IX, II, 94.
Charles X, II, 1.
Chasles, I, 39, 229.
Chesterfield, Earl of (4th), II, 298.
Chiffinch, W., II, 50.
Ch'in Chiu-shang, II, 66.
Chitty, J., II, 323.
Chiu-chang, Suan-shu, II, 67.
Christian Evidence Society, I, 270.
Christie, I, 27.
Christmann, I, 272, 272.
Church question, I, 62.
Church, The word, II, 30.
Circle squarers. (See Squaring the Circle.)
Circulating media of mathematics, I, 107.
Ciruelo. (See Sanchez.)
Clairaut, I, 219, 382.
Clarence, Duke of, I, 179.
Clarke, R., I, 255.
Clavius, I, 11, 69, 111, 112, 335, 362, 363, 372; II, 59.
Clayton., Geo., II, 98.
Cobb, Mary, II, 117.
Cobbett, W., I, 177, 200, 399.
Cobden, R., II, 217.
Cocker, I, 42; II, 64, 173, 251, 307.
Cody, P., II, 208.
Coke, E., II, 331.
Colburn, Z., I, 86.
Colenso, I, 63, 247; II, 191.
Collins, J., I, 107; II, 297, 300, 302, 313.
Colvill, W. H., II, 68.
Cometic astrology, I, 128.
Cominale, C., I, 162, 162.
Compton, S. J. A., II, 19.
Computation, Paradoxes of, II, 251, 267.
Condamine, C. M. de la, II, 301.
Conduitt, John, I, 397.
Conduitt, Mrs., I, 136.
Congregation of the Index, I, 90.
Converse propositions, I, 295.
Convocation at Oxford, I, 96.
Cooke, Margaret, I, 310.
Cooper, A. A. (Shaftsbury), II, 181.
Copernicus, I, 5, 6, 76, 90, 121, 172, 380; II, 165, 335.
Copley, J. S., I, 198.
Cormouls, I, 225.
Cosmology, I, 172.
[378]Cotes, R., II, 301.
Cottle, Mrs., II, 97, 97, 161.
Craig, J., I, 129, 129.
Creed, Mathematics of a, I, 329.
Cribb, T., I, 314.
Crotus, J., I, 318.
Cruickshank, G., I, 186.
Cube, Duplication of, I, 349.
Cumyns, Eliza, I, 299.
Cunningham, I, 172, 172.
Curabelle, I, 221.
Curious Calculations, II, 66.
Curll, E., II, 279.
Cusa, I, 44, 47, 360.
Custom, II, 324.
Cyclometry, II, 208. (See Squaring of the Circle.)
Cyclopædias, Review of, II, 280.
D'Alembert, I, 382; II, 283, 364.
Dalgarno, I, 116, 117.
Dalton, J., I, 255.
D'Arblay, Mme., I, 190.
Darwin, E., II, 8.
Darwinism, Primitive, I, 344.
Dary, M., II, 305.
Daval, P., II, 298.
Davies, T. S., II, 151, 151, 188.
Day, A., I, 295, 295.
De Baruel, I, 165.
De Beaune. (See Beaune.)
Debenham, J., I, 393.
De Causans. (See Causans.)
Dechales. (See de Challes.)
De Challes, I, 45.
Decimal coinage, II, 80, 168, 169.
Decimals run riot, II, 80.
Dee, J., II, 302.
De Fauré, I, 149.
De la Leu, I, 297.
Delambre, I, 160, 167, 354; II, 165.
Democritus, II, 34.
De Moivre, I, 24, 376; II, 298.
De Molières, I, 220.
De Molina, I, 297.
Demonville, I, 291, 293.
De Morgan, A., I, 191, 383; II, 194.
—Refusal of LL. D., I, 191.
De Morgan, G. C., I, 383.
De Morgan, Mrs., I, 196; II, 194.
Denison, J., I, 348, 353.
Desaguliers, I, 153, 156, 157.
Desargues, I, 119, 221.
Descartes, I, 5, 59, 105, 132, 165, 204, 220; II, 94.
De Serres, II, 60.
De Sluse. (See Sluse.)
De Thou, I, 51, 111, 113; II, 295.
De Vausenville, I, 12.
Devonshire, Duke of (7th), I, 290.
Diamandi, I, 86.
Didacus Astunica, I, 90.
Digby, K., I, 108.
Digges, T., and L., II, 302.
Dionysius Exiguus, I, 360.
Discoverers and discoveries, II, 206.
Discovery, Basis of, I, 85.
D'Israeli, I., I, 115, 118, 136, 188, 227.
Ditton, I, 133, 133.
Division, Nature of, II, 248.
Dobson, J., I, 234, 234.
Dodson, J., II, 312.
Dodt, I, 52.
Doggerel verse, I, 341.
Dolland, I, 377.
Double Vahu Process, II, 360.
Douglas, G., I, 232.
Drach, S. M., II, 317.
Drayson, G. A. W., II, 132, 132.
Dryden, II, 71.
Dual arithmetic, II, 186.
Duchesne, I, 52.
Dumortier, I, 313.
Duncan, A., I, 179.
Dunkin, E., II, 349.
Duodecimal scale, II, 68.
Duplication Problem, I, 349.
Dupuy, J. and P., II, 295.
Dutens, L., II, 90.
Dyer, G., I, 178.
Earth, Figure of, II, 54.
Easter, I, 359.
Easter Day Paradoxes, I, 353.
Ebrington, Thos., I, 247.
Edgeworth, Maria, I, 191.
Editorial System, I, 15.
Edleston, I, 140; II, 296.
Edwards, J., I, 144.
Edwards, T., I, 112.
Eirenæus Philalethes, I, 125, 125, 126.
Eldon, Lord (1st), II, 197.
Elephant story, I, 58.
Elizabeth, Queen, I, 128.
Ellenborough, Baron, I, 181.
[379]Ellicot, I, 24.
Ellis, I, 76, 82.
Engel, I, 230.
English language, Origin of, I, 215.
Enriques, F., II, 367.
Epps, J., I, 153; II, 143.
Equation of fifth degree, I, 250, 373.
Erasmus, I, 110.
Erastus, I, 65.
Erichsen, I, 163.
Erskine, T., II, 127.
Esperanto, Forerunner of, I, 116.
Euclid, I, 5, 43; II, 118, 151.
—Without Axioms, I, 287.
Eudoxus, II, 164.
Euler, I, 221, 382; II, 3, 4, 303, 331, 339.
Eusebius, II, 220.
Eustace, J. C., II, 46.
Eutocius, I, 41; II, 60.
Evelyn, J., I, 108.
Everett, J., I, 346.
Evidence, I, 57, 58.
Faber. (See Stapulensis.)
Fairfax, Mary, I, 242.
Falco, I, 53.
Faraday, M., II, 351.
Fauré, de, I, 149; II, 238.
Fawcett, H., II, 249.
Ferguson, J., II, 20.
Fermat, I, 122, 221; II, 300.
Ferrari, S., II, 68.
Fiction, New era in, I, 189.
Fienus, I, 74, 74.
Filopanti, Q. B., II, 93.
Finæus, I, 50, 50, 113.
Finleyson, J., I, 314, 314.
Flamsteed, I, 87, 309; II, 45, 143, 302, 306.
Fletcher, I, 378.
Fludd, II, 318.
Fly-leaf Paradox, II, 264.
Folkes, M., I, 136; II, 301.
Fontenelle, I, 103.
Forbes, D., I, 237.
Forman, W., I, 296, 296, 306.
Forster, T. I. M., I, 320, 320.
Foscarini, I, 90.
Foster, S., II, 310.
Fourier, II, 66.
Fox, G., I, 397.
Francis, P., II, 96.
Francœur, I, 365.
Frankland, W. B., I, 230, 287.
Franklin, J., II, 265.
Freedom of opinion, Growth of, I, 265.
Freher, A., II, 319.
French academy on circle squaring, I, 163.
Frend, W., I, 196, 196, 206, 208, 252.
Fresnel, II, 48.
Fromondus, I, 74, 74, 99.
Frost, I. and J., I, 394.
Fry, Elizabeth, I, 224.
Fuller, T., I, 86.
Fulton, R., I, 148.
Gadbury, J., I, 115, 115.
Galbraith, J. A., II, 372.
Galileo, I, 5, 6, 32, 76, 82, 83, 96, 122, 381.
Galle, J. G., I, 386; II, 7.
Galloway, I, 56, 57; II, 143.
Gamblers, I, 280.
Garrick, I, 21.
Gascoigne, W., II, 299.
Gassendi, I, 107.
Gauss, I, 86, 107, 310.
Gemistus, G., I, 188.
Gentleman's Monthly, Miscellany, I, 208.
Gephryander. (See Salicetus.)
Gergonne, I, 336.
Ghetaldi, I, 83; II, 59.
Ghost paradox, II, 47.
Giddy (Gilbert), II, 174.
Gilbert, William, I, 6, 68, 68, 76.
Gillot, II, 315.
Glazier (Glazion), II, 7.
Godwin, F., I, 103.
Godwin, W., I, 174.
Golius, I, 106.
Gompertz, B., I, 378.
Goulburn, I, 288.
Goulden, S., II, 88.
Graham, I, 24.
Grandamicus, I, 104, 104.
Granger, J., I, 156.
Grant, A. R., II, 131.
Grant, R., I, 392; II, 131.
Grassi, O., I, 262.
Grassini, I, 231.
Graunt, J., I, 113, 114, 154.
Gravity, I, 151, 244, 348, 353.
[380]—Newton's apple, I, 136.
Greek numerals, II, 77.
Greene, R., I, 135, 135.
Greenhill, Sir G., I, 136.
Greenwich observatory, I, 87.
Gregorian Calendar, I, 363.
Gregory, D., I, 66; II, 301.
Gregory, J., I, 118, 118, 207; II, 302.
Gregory O., II, 71.
Gregory, Pope, I, 362.
Grevil, I, 202.
Grey, C., (2d Earl), I, 315; II, 247.
Grosart, I, 141, 141, 145.
Grove, W. R., II, 320.
Gruenberger, I, 70.
Grynaeus, I, 66.
Guaricus, I, 43.
Guillim, J., II, 28.
Guldin, I, 83.
Gunning, H., I, 198.
Gurney. (See Fry, E.)
Guthrie, W., I, 395.
Hailesean system of astronomy, II, 135.
Hale, M., I, 123, 123.
Hales, S., I, 123.
Hall, B., II, 181.
Hallam, I, 159.
Halley, I, 24, 124, 311; II, 301, 332.
Halliwell-Phillips, II, 148, 296.
Hamilton, W., I, 112, 117, 331, 335, 339, 341, 342; II, 52, 53, 111.
Hamilton, W. Rowan, I, 332; II, 104, 256, 343.
Hanover, King of, I, 201.
Hardy, C., I, 298.
Hardy, T., I, 178.
Harriot, T., II, 302.
Harvey, I, 76, 78; II, 201.
Hauff, I, 230.
Haughton, S., II, 372.
Hauksbee, F., I, 156.
Hayes, C., I, 132, 132.
Heath, D. D., I, 76.
Helmont, J. B. van, I, 125.
Henson, II, 8.
Heraclitus, II, 34.
Herbart, J. F., I, 253, 253; II, 78.
Hérigone, II, 59.
Herschel, J., I, 80, 299, 326, 383, 386; II, 88, 95, 181, 255, 261, 262.
Herschel, W., I, 81, 151, 192, 225, 233, 299; II, 288, 348.
Heywood, F., II, 49.
Hicks, J. P., II, 67.
Higgins, G., I, 257, 274.
Hilarius, Pope, I, 359.
Hill, J., I, 21, 22, 23, 24.
Hill, Rev. R., I, 192.
Hill, Sir R., I, 165, 232.
Hind, J. R., I, 384.
Hippocrates, II, 59.
Hoax, An interesting, I, 163.
—Lunar Caustic, I, 288.
—Moon (Herschel), I, 326; II, 131.
Hobbes, I, 105, 109, 143, 144; II, 80.
Hobhouse, J. C., II, 126.
Hodder, J., II, 265.
Hodge, C. B., I, 114.
Hodges, W., I, 237.
Hoffmann, J. J., II, 282.
Hoffmann, J. J. I. von, I, 230.
Holloway, B., I, 237.
Holmes, O. W., I, 109.
Holyoake, G. J., I, 399, 399.
Hone, W., I, 124, 180, 184, 185.
Hook, T. E., II, 261.
Hooke, I, 77; II, 300.
Hooker, R., II, 201.
Hopkins, J., II, 41.
Horace, I, 40.
Horne, G., I, 152, 152, 154, 155, 236.
Horne, J., I, 178.
Horner, L., I, 176.
Horner, W. G., II, 66, 151, 187.
Howard, E., I, 131.
Howison, W., I, 256, 256.
Howley, I, 63.
Hulls, I, 147, 147; II, 8.
Hume, J., I, 352; II, 174.
Husaín Rifki, II, 16.
Hussein Effendi, II, 15.
Hutchinson, J., I, 154, 154.
Hutton, C., I, 153, 161; II, 303, 340.
Huyghens, I, 100, 133; II, 300.
Imaginary numbers, II, 186.
Impalement by request, II, 133.
Inaudi, I, 86.
Index Expurgatorius, I, 90.
[381]Infant prodigies, I, 86.
Inglis, J. B., II, 52.
Inglis, R. H., I, 352.
Ingliz Selim Effendi, II, 15.
Innocent I., I, 359.
Irving, E., II, 54.
Jabir ben Aflah, II, 59.
Jack, R., I, 149.
Jacotot, J., I, 278, 278.
Jameson, Mrs., II, 63.
Jeffreys, G., I, 183.
Jenner, E., II, 205.
Jesuit contributions, I, 164.
Johnson, H. C., I, 350.
Johnson, S., I, 20, 190, 259; II, 117.
Johnston, W. H., II, 67.
Jombert, I, 161.
Jonchère, I, 146, 146.
Jones, W., I, 135; II, 298, 301.
Jones, Rev. W., I, 237.
Jonson, B., I, 13.
Journals, Three classes of, II, 144.
Kantesian Jeweler, I, 258.
Karsten, I, 230.
Kästner, I, 43, 110, 112.
Kater, I, 11.
Keckermann, I, 3.
Keill, J., II, 302.
Kepler, I, 52, 76, 82, 381; II, 166.
Kerigan, T., I, 308, 353.
Keroualle, De, II, 50.
Kersey, I, 107.
King, Wm., I, 246.
Kircher, Adolphe, I, 229.
Kircher, Athanasius, I, 103.
Kirkringius, T., I, 125, 125.
Kittle, I, 236.
Klein, F., II, 367.
Knight, C., II, 109, 280, 289.
Knight, G., I, 151, 151.
Knight, R. P., II, 274.
Knight, Wm., I, 97.
Koenig, S., I, 150.
Lacomme, I, 46.
La Condamine, II, 301.
Lacroix, I, 41, 159, 207.
Lactantius, I, 33, 96.
Lagrange, I, 221, 288, 313, 382; II, 86.
Lalande, I, 159.
Lamb, C., I, 178; II, 270.
Lambert, J. H., I, 336; II, 214, 367.
Lambert, John, II, 309.
Language, Test of, II, 327.
Lansbergius, I, 70, 70.
Laplace, I, 24, 255, 382; II, 1, 340.
Lardner, D., II, 253.
Lardner, N., I, 14; II, 221.
Laud, I, 145.
Lauder, W., I, 297.
Laurent, P., I, 309, 309.
Laurie, J., II, 4.
Laurie, P., II, 42.
Laurus, I, 381.
Law, Edmund, I, 181.
Law, Edward, I, 181.
Law, W., I, 168, 254; II, 317.
Le Coq, I, 86.
Lee, R., I, 66.
Lee, S., I, 131.
Lee, W., I, 157.
Legate, I, 59.
Legendre, I, 229; II, 215, 367.
Leibnitz, I, 5, 7; II, 46.
Leo, St., I, 359.
Leverrier, I, 43, 82, 383, 386, 388, 390; II, 7, 135, 140, 303.
Libri, I, 40, 62; II, 295.
Lilius, Aloysius, I, 362.
Lilly, I, 115; II, 302.
Lipen, M., I, 298.
Little, J., I, 206.
Livingston, R., I, 148.
Locke, J., I, 142, 142, 144;
—and Socinianism, I, 142.
Locke, R., I, 146.
Locke, R. A., I, 326; II, 86, 131.
Logan, W. E., I, 337.
Logic, Formal, I, 158; II, 75.
—Has no paradoxes, I, 330.
London Mathematical Society, I, 383.
London, University of, I, 259; II, 71.
Long, G., II, 290.
Longitude problems, I, 132, 146, 249.
Longley, C. T., I, 325.
Longomontanus, I, 105, 105.
Lottery, I. 281.
Lovett, R., I, 165, 166.
Lowe, R., II, 169.
Lowndes, W. T., I. 402.
Lubbock, J., I, 279; II, 148.
[382]Lucas, F., II, 28.
Lucian, I, 102.
Lunar Caustic Joke, I, 288.
Lunn, J. R., II, 66.
Lydiat, T., II, 302.
Lyndhurst, I, 198.
Macclesfield, Earls of, I, 7; II, 296, 301.
Macclesfield, Letters, II, 296.
MacElshender, II, 87.
Machin, J., II, 301.
Mackey, John, I, 349.
Mackey, S. A., I, 256.
Maclear, T., II, 181.
Magic, I, 118.
Magna Charta, I, 25.
Magnus, I, 42.
Maitland, S., I, 63, 163.
Malacarne, I, 119.
Malden, H., II, 162.
Malius, II, 342.
Mallemens, II, 333.
Mankind gullible, I, 115.
Manning, H. E., (Card.), II, 233.
Mansel, H. L., II, 162.
Marcelis, J., I, 129, 129.
Maret, II, 3.
Margarita Philosophica. (See Reisch.)
Marryat, Capt., II, 87.
Marsh, H., I, 199, 271.
Martin, B., I, 152, 153.
Martin, R., II, 236.
Maseres, F., I, 197, 203.
Mason, M., II, 132.
Mathematical Illustrations of Doctrine, II, 70;
—Psychology, I, 253;
—Society, I, 374, 376, 382;
—Theology, I, 149.
Mathematics, Condensed history of, II, 58.
Matter to Spirit, II, 194.
Maty, I, 23.
Maupertuis, II, 301.
Maurice, F. D., II, 101.
Maurolycus, I, 121.
Maxwell, A., I, 102.
Meadley, G. W., I, 223.
Mechanics Magazine, II, 141, 145.
Medici, Cosmo de, II, 295.
Medicine, Status of, I, 266.
Melanchthon, II, 323.
Menestrier, I, 127, 127.
Mercator, G., II, 92.
Mercator's projection, I, 84.
Mersenne, I, 106, 107; II, 295, 297.
Meslier, J., II, 195.
Meteorologist, An early, I, 320.
Meteorology, I, 327.
Metius, A. and P., I, 52, 99, 99.
Meton, II, 167.
Metric System, Forerunner of, I, 171.
Méziriac, I, 161.
Milbanke, A. I., I, 225.
Mill, Jas., I, 260.
Miller, Joe, I, 182.
Miller, S., I, 167.
Mills, Elizabeth, W., II, 7.
Milne, J., I, 286.
Milner, I., I, 251, 251.
Milner, J., II, 23.
Milner's lamp, I, 252.
Milward, II, 250.
Miracles vs. Nature, II, 6.
Mitchell, J., I, 242.
Molière, I, 232.
Molina, A. C. de, I, 297.
Mondeux, I, 86.
Montague, C., II, 311.
Montmort, P. R. de, II, 301.
Montucla, I, 40, 45, 54, 65, 117, 120, 159, 163; II, 60.
Moon Hoax, I, 326; II, 131.
Moon, Nature of, II, 84;
—Rotation of, II, 4, 19, 84, 87.
More, Hannah, I, 189, 192.
More, Henry, I, 123.
Moore, Dr. John, I, 190.
Moore, Sir John, I, 190.
Morgan, S., I, 6.
Morgan, T., I, 191.
Morgan, W., I, 223, 224.
Morhof, I, 61.
Morin, I, 99, 99.
Morinus, J. B., I, 149.
Morland, S., II, 302.
Mormonism, II, 69.
Morrison, R. J., I, 321; II, 43.
Mose, H., II, 266.
Mottelay, I, 68.
Motti, II, 60.
Mouton, I, 172; II, 300.
Muggleton, I, 394, 395.
Multiplication, Nature of, II, 251.
Murchison, R. I., I, 384.
Murhard, I, 43, 298.
[383]Murphy, A., II, 308.
Murphy, P., I, 327, 398.
Murphy, R., I, 349, 349.
Murray, J., I, 186; II, 145.
Murray, L., II, 326.
Murray, Mungo, II, 310.
Musgrave, T., I, 324.
Mydorge, I, 298.
Mystrom, J. W., II, 182.
Mythological paradoxes, I, 256.
Names of Religious Bodies, II, 22.
Napier, J., I, 5, 66, 67, 82.
Napoleon, Doubts as to, I, 246.
Nautical Almanac, I, 300; II, 147.
Neal, I, 98.
Negative numbers, I, 196, 203.
Neile, W., II, 190.
Neptune, Discovery of, I, 387; II, 140. (See Adams, Leverrier.)
Nesse, C, I, 128, 128.
Newcomb, S., I, 162.
Newcomen, T., I, 147.
Newton, Sir Isaac, I, 5, 6, 8, 24, 39, 84, 88, 130, 136, 139, 144, 145, 148, 152, 154, 155, 162, 165, 167, 197, 225, 237, 242, 257, 282, 296, 297, 309, 311, 382, 394, 395, 396, 397; II, 2, 70, 184, 297, 302, 305.
Newton, John, II, 305.
Nicene Creed, I, 371.
Nichol, J. P., II, 289.
Nicholas. (See Cusa.)
Nichols, J., I, 175.
Nicolas, N. H., I, 354.
Nicollet, I, 326; II, 131.
Nicolson, W., I, 201.
Nieuwentijt, II, 333.
Nizzoli, M., II, 275.
Non-Euclidean geometry, II, 83.
Northampton, Marquis of (2d), II, 19.
Novum Organum Moralium, II, 74.
Number, Mystery of, I, 55, 56, 169.
Number of the Beast (666), I, 55, 130, 272, 298, 352; II, 77, 159, 217, 218, 361, 373.
Numeral system, II, 68.
Nursery rhymes, II, 150.
Occam, Wm. of, II, 40.
Oinopides of Chios, II, 59.
Orthodox Paradoxes, II, 363.
Orthography, Paradoxes of, II, 267.
Ortwinus, I, 319.
Owenson, I, 191.
Ozanam, I, 161, 312.
Pagi, I, 32.
Paine, T., I, 173, 173, 271.
Paley, W., I, 222; II, 226.
Palmer, C., I, 225.
Palmer, H., I, 141, 141, 145.
Palmer, J., II, 253.
Palmer, T. F., II, 254.
Palmer, W., II, 37.
Palmerston, Viscount (3d), I, 290, 352.
Palmézeaux, I, 167.
Panizzi, A., I, 151.
Papist, II, 26.
Paracelsus, II, 322.
Paradox defined, I, 2, 31.
Paradox, religious, I, 236.
Paradoxers in general, II, 352.
Parallels, Theory of, I, 229, 344.
Pardies, I. G., II, 300.
Parker, F., II, 94.
Parker, G. (Earl of Macclesfield), II, 296.
Parr, S., I, 173, 173, 175, 176, 184.
Parsey, I, 293, 293.
Partridge, J., I, 305.
Pasbergius, I, 381.
Pascal, I, 39, 119, 122, 220, 221; II, 73.
Pascal's Hexagram, I, 221.
Passot, I, 279, 279.
Passover, I, 358, 372.
Patriotic paradox, I, 231.
Paucton, I, 172.
Paulian, I, 165, 165.
Peacock, Geo., I, 196, 350.
Peacock, T. L., I, 190, 340.
Pearce, A. J., II, 43.
Pearne, T., I, 239.
Peel, Sir R., I, 290, 352.
Peel, W. Y., I, 290.
Pèlerin, J., II, 324.
Pell, J., I, 105, 105, 107; II, 300, 302, 312.
Pepys, I, 113, 114.
[384]Perpetual motion, I, 118, 348; II, 55, 138.
Perspective, New theory of, I, 293.
Petitioning Comet, I, 127.
Petrie, W. M. F., I, 328.
Petty, I, 114; II, 300.
Philalethes, Eirenaeus, I, 125, 125, 126.
Philalethes, Eugenius, I, 255.
Phillips, R., I, 242, 242, 245.
Philo of Gadara, I, 40, 40.
Philosopher's stone, I, 118, 125.
Philosophical atheists, II, 1.
Philosophy and Religion, II, 37.
Phonetic spelling, II, 81.
π, values of, I, 11, 43, 45, 46, 52, 69, 100, 110, 129, 135, 146, 245, 283, 284, 294, 347, 348, 349, 350; II, 60, 63, 105, 110, 118, 135, 156, 209, 279, 315, 316.
Pighius, I, 372.
Pike, S., I, 236, 236.
Pindar, P., II, 272.
Piozzi, Mrs., I, 235; II, 272.
Piscator, B., II, 25.
Place, F., I, 199.
Planets inhabitable, I, 100, 102.
Plato, I, 5.
Platt, H., I, 126, 126.
Playfair, J., I, 233.
Pletho, G., I, 188.
Pliny, II, 280.
Ploucquet, I, 336, 337.
Poe, E. A., II, 132.
Poincaré, I, 136.
Poisson, I, 292; II, 2.
Pollock, J. F., II, 174.
Pons, II, 45.
Pope, Wm., I, 277, 277.
Porta, I, 68, 68, 83.
Porteus, B., I, 193, 203.
Porteus, H. F. A., II, 157, 157.
Porus, I, 44.
Powell, Baden, II, 267.
Powell, W. S., I, 222.
Pratt, H. F. A., II, 157, 157.
Pratt, O., II, 69.
Predaval, Count de, I, 348.
Prescot, B., I, 270, 270, 278.
Prester John, I, 70, 71, 152.
Price, R., I, 223.
Probability, Discourse on, I, 279.
Proclus, I, 188, 188.
Prodigies, Youthful, I, 219, 332.
Pronunciation, II, 330.
Protestant and Papal Christendom, II, 33.
Protimalethes, II, 6.
Ptolemy, I, 5, 33, 380.
Pusey, I, 64.
Pyramids, The, I, 328; II, 95, 136.
Pythagoras, II, 59.
Quadrature problem. (See Squaring the circle.)
Quarles, F., II, 277.
Quintilian, II, 280.
Quotem, C., I, 399.
Rabelais, I, 102.
Rainbow Paradox, II, 334.
Ramachandra, Y., I, 374.
Ramchundra, I, 374.
Ramus, I, 5.
Recorde, R., II, 328.
Reddie, Jas., II, 183, 183, 344, 360.
Reeve, J., I, 395.
Regiomontanus, I, 48, 360.
Reisch, I, 45; II, 281.
Religion and Philosophy, II, 37.
Religious bodies, Names of, II, 22;
—customs, Attacks on, I, 177;
—Insurance, I, 345;
—Paradox, I, 236;
—Tract society, I, 192.
Remigius, I, 50.
Reuchlin, J., II, 323.
Revelations, Napier on, I, 66.
Revilo, (O. Byrne), I, 241, 329, 329.
Reyneau, C. R., II, 301.
Rheticus, I, 69; II, 372.
Rhonius, II, 300.
Ribadeneira, P. de, II, 62.
Riccioli, I, 96.
Richards, G., II, 270.
Rigaud, J., II, 299.
Rigaud, S. J., II, 299.
Rigaud, S. P., I, 140; II, 298, 313.
Ringelbergh, J. S., II, 281.
Ripley, G., I, 126, 126.
Ritchie, W., I, 295, 295.
Ritterhusius, I, 60.
Rive, J.-J., I, 160.
Robertson, Jas., I, 237.
Roberval, I, 105, 122.
[385]Robinson, B., I, 148, 148.
Robinson, H. C., I, 314; II, 52, 275.
Robinson, R., I, 177.
Robinson, T. R., II, 181.
Roblin, J., II, 136.
Rogers, S., II, 260.
Roget, P. M., I, 398.
Roomen, A. van, I, 110.
Ross, J. C., I, 303.
Rosse, I, 26.
Rossi, G., I, 231, 231.
Rotation of the Moon, II, 4, 19.
Rough, W., I, 198.
Rowning, J., I, 155.
Royal Astronomical Society, I, 27;
—Forerunner of, I, 374.
Royal Society, I, 21, 22, 24-30, 56, 57, 136, 153, 163, 164, 165.
Rudio, I, 159; II, 367.
Rudolff, C., II, 373.
Russell, Earl (1st), I, 296.
Rutherford, W., II, 109.
Sabatíer, A., II, 267.
Sabellius, I, 241.
Sacrobosco, I, 360.
Sadler, T., I, 238, 241.
Saint-Martin, I, 167, 168, 206.
St.-Mesmin, M. de., I, 280.
St. Vincent, G. de., I, 110, 117.
St. Vitus, Patron of Cyclometers, II, 60.
Sales, de, I, 167.
Salicetus, I, 64.
Salisbury, Earl of (1st), II, 330.
Salmasius, Claudius, II, 168.
Salusbury, Hester, I, 235.
Sanchez, Petro, I, 229, 229.
Sanders, W., I, 207.
Sanderson, R., I, 135.
Sara, R., I, 297.
Saunderson, N., I, 377; II, 301.
Scaliger, I, 44, 110, 111, 112, 113; II, 238.
Scévole de St. Marthe, I, 113.
Schooten, Van, II, 59.
Schopp, I, 60.
Schott, I, 64; II, 64.
Schumacher, H. C., I, 107; II, 297.
Schwab, I, 230.
Scientific paradoxes, I, 232.
Scott, Michael, I, 38.
Scott's Devils, I, 38.
Scott, W., I, 20, 27, 38, 39, 155, 191.
Scripture and Science, II, 261.
Search, John, I, 247.
Selden, J., II, 250.
Sénarmont, II, 48.
Serres, De, II, 60.
Shaftesbury, Earl of, II, 181.
Shakespeare, I, 13.
Shaw, P., I, 142.
Sheepshanks, J., I, 147.
Sheepshanks, R., I, 290.
Shelley, I, 174.
Shepherd, S., I, 124.
Sherburne, E., II, 295.
Sheridan, R. B., I, 175.
Sheridan, T., I, 175.
Shoberl, F., II, 270.
Shrewsbury, I, 108.
Siddons, Mrs., I, 189.
Simms, W., I, 152.
Simplicius, II, 164.
Simpson, T., I, 377; II, 304.
Simson, R., I, 197, 202, 233.
Sinclair, G., I, 207.
Slander Paradoxes, II, 138.
Sloane, I, 24.
Sluse, R. de, I, 118, 118; II, 300.
Smith, Adam, II, 112.
Smith, Jas., I, 46; II, 103, 103, 154, 236, 237, 238, 241, 336, 360.
Smith, Jas., II, 217.
Smith, Jas. (Shepherd), II, 55, 193.
Smith, Joseph, II, 69.
Smith, Richarda, I, 242.
Smith, Thomas, I, 346, 346.
Smith, Wm., II, 152.
Smyth, C. P., I, 328; II, 65.
Snell, I, 75, 75.
Socinianism, I, 142, 143.
Socinus, I, 3, 143.
Socrates Scholasticus, I, 358.
Sohncke, L. A., II, 131.
Somerville, Mrs., I, 242.
South, J., II, 181.
Southcott, Joanna, II, 58, 97, 239.
Spearman, R., I, 237.
Speculative thought in England, I, 374.
Spedding, I, 76, 82, 142.
Speed, J., I, 201.
Speke, I, 70.
Spelling, phonetic, II, 81.
Spence, W., I, 231, 231.
Spencer, Earl (3d), II, 9.
[386]Spinoza, I, 3, 37.
Spiritualism, II, 47, 55, 207.
Spurius Cassius Viscellinus, II, 342.
Spurius Maelius, II, 342.
Squaring the circle, I, 8, 42, 44, 46, 47, 50, 52, 53, 69, 70, 75, 109, 117, 119, 129, 135, 146, 149, 159, 163, 164, 347, 348, 374; II, 10, 11, 60, 105, 154, 156, 208, 278, 314.
Stäckel, I, 230.
Stanhope, P. D., (Earl of Chesterfield), II, 298.
Stapulensis, I, 44; II, 324.
Star polygons, I, 229.
Starkie, G., I, 126, 126.
Statter, D., II, 80.
Steamship suggested, I, 147.
Steel, Jas., II, 68.
Stenography, II, 81.
Stephens, I, 44; II, 324.
Stephenson, G., II, 138.
Stephenson, R., II, 138.
Stevin, I, 83, 313; II, 59.
Stewart, D., II, 53.
Stewart, R., I, 186.
Stifel, M., II, 373.
Strafford, Earl of, I, 240.
Stratford, W. S., I, 300.
Street, T., I, 124.
Stukely, W., I, 236.
Suffield, G., II, 66.
Suidas, II, 29.
Sumner, C. R., I, 324.
Sumner, J. B., I, 324.
Sun as an electric space, II, 41.
Supernatural, The, II, 193.
Suvaroff, II, 85.
Swastika, II, 231.
Swedenborg, E., I, 255.
Swift, I, 19, 133.
Sylvester, J. J., II, 336.
Symington, W., I, 148.
Sympathetic powder, I, 108.
Synesius, I, 125.
Talbot, G., I, 22, 108.
Talbot's powder, I, 108.
Tartaglia, II, 59.
Tasse, I, 106.
Tate, J., I, 199.
Tauler, J., II, 322.
Taylor, Brook, II, 301.
Taylor, John, I, 352; II, 95.
Taylor, Robt., I, 270.
Taylor, T., I, 188, 188.
Teissier, I, 113.
Temple, H. J., I, 290.
Tenterden, Chief Justice, I, 181.
Theism independent of Revelation, I, 399.
Thelwall, J., I, 178.
Theodoretus, I, 358.
Theological Paradoxes, I, 316.
Theology, Mathematical, I, 129, 149.
Theophrastus, II, 167.
Thom, J. H., II, 226.
Thompson, P., I, 7.
Thompson, T. P., I, 252, 287, 344; II, 83, 185.
Thomson, Dr., I, 21.
Thomson, W., I, 325.
Thorndike, H., II, 313.
Thrale, Mrs., I, 235.
Thurlow, Baron, I, 222.
Thyræus, I, 50.
Tides, New theory of, I, 393.
Tombstones of mathematicians, I, 106.
Tonal System, II, 182.
Tooke, H., I, 178.
Torriano, E., I, 250.
Towneley, II, 300.
Townley, C., II, 300.
Trisection problem, I, 118; II, 10, 12, 13, 15.
Troughton, I, 152.
Turnor, E., I, 137.
Valentine, B., I, 125, 125.
Van Ceulen, I, 52, 70, 100.
Van de Weyer, I, 313.
Van Etten, I, 161.
Van Helmont, I, 125, 125.
Van Roomen, I, 110.
Van Schooten, II, 59.
Vaughan, T., I, 255.
Victorinus, I, 359.
Virgil, St., I, 32, 33, 34, 99.
[387]Virginia, University of, I, 233.
Viscellinus, II, 342.
Vitruvius, II, 281.
Vivian, T., I, 172, 172.
Vogel, A. F., I, 373.
Voltaire, I, 103, 165, 166, 167, 168, 248; II, 268.
Von Hutten, I, 318.
Von Wolzogen. (See Wolzogen.)
Vyse, R. W. H., I, 328.
Walker, W. E., II, 316.
Walkingame, F., II, 173.
Wallich, N., II, 14.
Wallis, J., I, 107, 109, 110; II, 299, 313.
Walpole, I, 23, 131.
Walsh, John, I, 260, 260; II, 157.
Wapshare, J., II, 230.
Warburton, H., I, 349.
Warburton, Wm., I, 55, 112; II, 174.
Ward, S., II, 299.
Waring, E., I, 203, 222.
Warren, S., II, 340.
Watkins, J., II, 270.
Watson, Bp., I, 223.
Watt, R., I, 102, 402.
Watts, I., II, 18.
Weddle, T., II, 187.
Wentworth, Thos., I, 240.
Wharton, I, 115.
Whately, R., I, 246, 246, 324.
Whately's Paradox, I, 246.
Whewell, I, 101, 101, 273, 314, 380; II, 104, 246, 247.
Whigs, II, 22.
Whiston, J., I, 147.
Whiston, W., I, 133, 133, 146, 156, 311.
White, H. K., II, 271.
White, J. B., I, 248.
White, R., I, 11.
Whitford, I, 105.
Whitworth, W. A., II, 344.
Whizgig, On the, I, 254.
Wightman, I, 59.
Wilberforce, W., II, 236.
Wilkins, J., I, 96, 100, 116, 226.
Williams, J. B., I, 378.
Williams, T., I, 171, 171.
Wilson, Sir J., I, 221.
Wilson, J. M., II, 344.
Wilson's Theorem, I, 222.
Wingate, E., II, 308.
Winter, I, 46.
Wirgman, T., I, 258, 258.
Wiseman, N. P. S., II, 26, 61, 294.
Wolcot, J. (Peter Pindar), II, 272.
Wollstonecraft, I, 173, 173.
Wolzogen, I, 106.
Wood, A., I, 98.
Wood, John, I, 233.
Wood, Wm., I, 246, 246.
Woodley, W., I, 307, 307.
Wordsworth, II, 273.
Wright, E., I, 84.
Wright, T., I, 151, 151, 152, 153.
Wright, W., II, 9.
Wronski, I, 249, 250.
Wrottesley, J. (Baron), II, 181.
Transcriber's note: References to Notes in Volume I are shown as in the printed book, with the resequenced footnote numbers in the Project Gutenberg Edition (EText-No. 23100) added thus {123}.
[1] See Vol. I, page 255, note 6 {584}.
[2] "I have no need for this hypothesis."
[3] "Ah, it is a beautiful hypothesis; it explains many things."
[4] "What we know is very slight; what we don't know is immense."
[5] Brewster relates (Life of Sir Isaac Newton, Vol. II, p. 407) that, a short time before his death, Newton remarked: "I do not know what I may appear to the world, but to myself I seem to have been only like a boy playing on the seashore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me."
[6] See Vol. I, p. 292, note 1 {632}.
[7] "What is all that!"
[8] "I have some good news to tell you: at the Bureau of Longitudes they have just received a letter from Germany announcing that M. Bessel has verified by observation your theoretical discoveries on the satellites of Jupiter."
[9] "Man follows only phantoms."
[10] See Vol. I, page 382, note 13 {786}.
[11] Dieudonné Thiébault (1733-1807) was a Jesuit in his early life, but he left the order and took up the study of law. In 1765 he went to Prussia and became a favorite of Frederick the Great. He returned to France in 1785 and became head of the Lycée at Versailles.
[12] Memories of Twenty Years of Residence in Berlin. There was a second French and an English edition in 1805.
[13] Richard Joachim Heinrich von Mollendorff (1724-1816) began his career as a page of Frederick the Great (1740) and became field marshal (1793) and commander of the Prussian army on the Rhine (1794).
[14] Hugues Bernard Maret (1763-1839) was not Duc de Bassano in 1807, this title not being conferred upon him until 1809. He was ambassador to England in 1792 and to Naples in 1793. Napoleon made him head of the cabinet and his special confidant. The Bourbons exiled him in 1816.
[15] Denis Diderot (1713-1784), whose Lettre sur les aveugles (1749) introduced him to the world as a philosopher, and whose work on the Encyclopédie is so well known.
[16] "Sir, (a + bn) / n = x, whence God exists; answer!"
[17] This was one James Laurie of Musselburgh.
[18] Jelinger Cookson Symons (1809-1860) was an office-holder with a decided leaning towards the improvement of education and social conditions. He wrote A Plea for Schools (1847), The Industrial Capacities of South Wales (1855), and Lunar Motion (1856), to which last work the critic probably refers.
[19] "Protimalethes" followed this by another work along the same line the following year, The Independence of the Testimony of St. Matthew and St. John tested and vindicated by the theory of chances.
[20] Wilson had already taken up the lance against science in his Strictures on Geology and Astronomy, in reference to a supposed want of harmony between these sciences and some parts of Divine Revelation, Glasgow, 1843. He had also ventured upon poetry in his Pleasures of Piety, Glasgow, 1837.
[21] Mrs. Borron was Elizabeth Willesford Mills before her marriage. She made an attempt at literature in her Sibyl's Leaves, London (printed at Devonport), 1826.
[22] See Vol. I, page 386, note 10 {801}.
[23] See Vol. I, page 43, notes 7 {32} and 8 {33}.
[24] His flying machine, designed in 1843, was one of the earliest attempts at aviation on any extensive scale.
[25] Erasmus Darwin (1731-1802) was the grandfather of Charles Darwin. The work here mentioned had great influence, being translated into French, Portuguese, and Italian. Canning parodied it in his Loves of the Triangles.
[26] See Vol. I, page 147, note 1 {312}.
[27] The notes on this page were written on the day of the funeral of Wilbur Wright, June 1, 1912, the man who realized all of these prophecies, and then died a victim of municipal crime,—of typhoid fever.
[28] John Charles, third Earl Spencer (1782-1845), to whose efforts the Reform Bill was greatly indebted for its final success.
[29] This was published in London in 1851 instead of 1848.
[30] This appeared in 1846.
[31] This was done in The Circle Squared, published at Brighton in 1865.
[32] It first appeared in 1847, under the title, The Scriptural Calendar and Chronological Reformer, 1848. Including a review of tracts by Dr. Wardlaw and others on the Sabbath question. By W. H. Black. The one above mentioned, for 1849, was printed in 1848, and was also by Black (1808-1872). He was pastor of the Seventh Day Baptists and was interested in archeology and in books. He catalogued the manuscripts of the Ashmolean Museum at Oxford.
[33] William Upton, a Trinity College man, Dublin. He also wrote Upton's Physioglyphics, London, 1844; Pars prima. Geometria vindicata; antiquorumque Problematum, ad hoc tempus desperatorum, Trisectionis Anguli, Circulique Quadraturae, Solutio, per Eucliden effecta, London (printed at Southampton), 1847; The Uptonian Trisection, London, 1866; and The Circle Squared, London, 1872.
[34] For example, if θ = 90° we should have 3 cos 30° = 1 + √(4 - sin2 90°), or 3.½ √3 = 1 + √3, or ½ √3 = 1.
[35] Nathaniel Wallich (1786-1854) was surgeon at the Danish settlement at Serampore when the East India Company took over the control in 1807. He entered the British medical service and was invalided to England in 1828. His Plantae Asiaticae Rariores (3 vols., London, 1830-1832) was recognized as a standard. He became vice-president of the Linnean Society, F. R. S., and fellow of the Royal Asiatic Society.
[36] But if θ = 90° this asserts that
| cos 30° = | (sin 270° . cos 225° + sin2 90° . sin 225°)  √(sin2 270° . cos2 225° + sin4 90° + sin 270° . sin 450° . sin2 90°) | , |
or that
| ½ √3 = | -1 . (-1 /√2) + 1 . (-1/√2) √(1 . ½ + 1 - 1 . 1 . 1) | = 0 / √½, |
so that De Morgan must have made some error in copying.
[37] John Bonnycastle (died in 1821) was professor of mathematics at Woolwich. His edition of Bossut's History of Mathematics (1803), and his works on elementary mathematics were well known.
[38] The bibliographies give Husaín Rifki as the translator, a practical geometry as the work, and 1802 as the date.
[39] See Vol. I, page 309, note 2 {670}.
[40] Probably in The Improvement of the Mind which Isaac Watts (1674-1748) published in 1741. His Horae Lyricae appeared in 1706, and the Hymns, by which he is still well known, in 1707.
[41] Spencer Joshua Alwyne Compton, second Marquis of Northampton (1790-1851), was a poet, a scientist, and a statesman. He was president of the Royal Society from 1838 to 1849.
[42] Besides the writings here mentioned Perigal published a work on Geometric Maps (London, 1853), and Graphic Demonstrations of Geometric Problems (1891).
[43] See Vol. II, page 5, note 18.
[44] James Ferguson (1710-1776) was a portrait painter, an astronomer, and a popular writer and lecturer on various subjects.
[45] In the old ballad of King Alfred and the Shepherd, when the latter is tempting the disguised king into his service, he says:
"Of whig and whey we have good store,
And keep good pease-straw fire."
Whig is then a preparation of milk. But another commonly cited derivation may be suspected from the word whiggamor being used before whig, as applied to the political party; whig may be a contraction. Perhaps both derivations conspired: the word whiggamor, said to be a word of command to the horses, might contract into whig, and the contraction might be welcomed for its own native meaning.—A. De M.
[46] This was p. 147 in the first edition.
[47] St. Augustine (354-430) was bishop of Hippo. His Confessiones, in 13 books, was written in 397, and his De Civitate Dei in 426.
[48] "He was wont to indulge in certain Punic subtleties lest he should weary the reader by much speaking."
[49] John Milner (1751-1826), bishop of Castabala, a well-known antiquarian.
[50] It will be said that when the final happiness is spoken of in "sure and certain hope," it is the Resurrection, generally; but when afterwards application is made to the individual, simple "hope" is all that is predicated which merely means "wish?" I know it: but just before the general declaration, it is declared that it has pleased God of his great mercy to take unto Himself, the soul of our dear brother: and between the "hopes" hearty thanks are given that it has pleased God to deliver our dear brother out of the miseries of this wicked world, with an additional prayer that the number of the elect may shortly be accomplished. All which means, that our dear brother is declared to be taken to God, to be in a place not so miserable as this world—a description which excludes the "wicked place"—and to be of the elect. Yes, but it will be said again! do you not know that when this Liturgy was framed, all who were not in the road to Heaven were excommunicated burial service read over them. Supposing the fact to have been true in old time, which is a very spicy supposition, how does that excuse the present practice? Have you a right always to say what you believe cannot always be true, because you think it was once always true? Yes, but, choose whom you please, you cannot be certain He is not gone to Heaven. True, and choose which Bishop you please, you cannot be demonstratively certain, he is not a concealed unbeliever: may I therefore say of the whole bench, singulatim et seriatim, that they are unbelievers? No! No! The voice of common sense, of which common logic is a part, is slowly opening the eyes of the multitude to the unprincipled reasoning of theologians. Remember 1819. What chance had Parliamentary Reform when the House of Commons thanked the Manchester sabre-men? If you do not reform your Liturgy, it will be reformed for you, and sooner than you think! The dishonest interpretations, by defence of which even the minds of children are corrupted, and which throw their shoots into literature and commerce, will be sent to the place whence they came: and over the door of the established organization for teaching religion will be posted the following notice:
"Shift and Subterfuge, Shuffle and Dodge,
No longer here allowed to lodge!"
All this ought to be written by some one who belongs to the Establishment: in him, it would be quite prudent and proper; in me, it is kind and charitable.—A. De M.
[51] But few do have access to it, for the work is not at all common, and this Piscator is rarely mentioned.
[52] This derivation has been omitted.—S. E. De M.
[53] A blow for a blow. Roland and Oliver were two of the paladins of Charlemagne whose exploits were so alike that each was constantly receiving credit for what the other did. Finally they met and fought for five days on an island in the Rhine, but even at the end of that period it was merely a drawn battle.
[54] "In the name of the church."
[55] "From the chair," officially.
[56] Nicholas Patrick Stephen Wiseman (1802-1865), whose elevation to the archbishopric of Westminster and the cardinalate (1850) led to the act prohibiting Roman Catholics from assuming episcopal titles in England, a law that was never enforced.
[57] He was born in 1812 and was converted to Catholicism in 1839. He founded the Tablet in London in 1840, removing its office to Dublin in 1849. He became M. P. in 1852, and at the time of his death (1855) he was preparing a memorial to the Pope asking him to annul the proclamation of an Irish bishop prohibiting his priests from taking part in politics.
[58] John Guillim (1565-1621) was the first to systematize and illustrate the whole science of heraldry. He published A display of Heraldrie: manifesting a more easie accesse to the knowledge thereof in 1610.
[59] "Faith."
[60] "Faithful."
[61] "For the faith vindicated."
[62] The words are of the same root, and hence our word fiddle. Some suppose this root means a rope, which, as that to which you trust, becomes, in one divergence, confidence itself—just as a rock, and other words, come to mean reliance—and in another, a little string.—A. De M.
[63] The Greek lexicographer, a Christian, living after 1000 A. D. His lexicon was first printed at Milan in 1499.
[64] Skindapsos.
[65] This was John William Burgon (1813-1888), Gresham professor of theology (1867) and dean of Chichester. He was an ultra-conservative, opposing the revised version of the New Testament, and saying of the admission of women to the university examinations that it was "a thing inexpedient and immodest."
[66] Ekklesia, or ecclesia.
[67] Ennomos ekklesia.
[68] "Without doubt I shall perish forever."
[69] "Every man is an animal." "Sortes is a man." "Sortes is an animal."
[70] "For a special purpose."
[71] Heraclitus of Ephesus, the weeping philosopher, 6th century B. C.
[72] Democritus, the laughing philosopher, founder of the atomistic theory, 5th century B. C.
[73] "Ends to which."
[74] "Ends from which."
[75] "In just as many syllables," "With just as many letters," "In just as many words."
[76] "I shall make a way," "I shall find a way."
[77] The notion that the Evil Spirit is a functionary liable to be dismissed for not attending to his duty, is, so far as my reading goes, utterly unknown in theology. My first wrinkle on the subject was the remark of the Somersetshire farmer upon Palmer the poisoner— "Well! if the Devil don't take he, he didn't ought to be allowed to be devil no longer."—A. De M.
William Palmer (1824-1856) was a member of the Royal College of Surgeons and practised medicine at London. He was hanged in 1856 for having poisoned a friend and was also suspected of having poisoned his wife and brother for their insurance money, besides being guilty of numerous other murders. His trial was very much in the public attention at the time.
[78] Advantages and dangers.
[79] The old priory of St. Mary of Bethlehem in London, was used as an asylum for the insane. The name was corrupted to Bedlam.
[80] Referring to the common English pronunciation of St. John, almost Sinjin. John St. John Long (1798-1834), an Irishman by birth, practised medicine in London. He claimed to have found a specific for rheumatism and tuberculosis, but upon the death of one of his patients in 1830 he was tried for manslaughter. He died of tuberculosis four years later, refusing to take his own treatment.
[81] William of Occam (d. 1349), so called from his birthplace, Ockham, in Surrey. He was a Franciscan, and lectured on philosophy in the Sorbonne.
[82] He signs himself "James Hopkins, schoolmaster," and this seems to have been his only published effort.
[83] Joseph Ady (1770-1852) was a famous swindler. One of his best-known schemes was to send out letters informing the recipients that they would learn something to their advantage on payment of a certain sum. He spent some time in prison.
[84] Sir Peter Laurie (c. 1779-1861) was worth referring to, for he was prominent as a magistrate and was honored because of his interest in all social reforms. He made a fortune as a contractor, became sheriff of London in 1823, and was knighted in the following year. He became Lord Mayor of London in 1832.
[85] See Vol. I, page 321, note 2 {691}. The Astronomy in a nutshell appeared in 1860. The Herald of Astrology was first published in London in 1831, "by Zadkiel the Seer." It was continued as The Astrological Almanac (London, 1834), as Zadkiel's Almanac and Herald of Astrology (ibid., 1835, edited by R. J. Morrison, and subsequently by A. J. Pearce), and as Raphael's Prophetic Almanac (1840-1855).
[86] See Vol. I, page 172, note 3 {382}.
[87] See Vol. I, page 87, note 4 {133}.
[88] Franz Xaver, Freiherr von Zach (1754-1832) was director of the observatory at Seeberge near Gotha. He wrote the Tabulae speciales aberrationis et mutationis (1806-7), Novae et correctae tabulae solis (1792), and L'attraction des montagnes et ses effets sur le fil à plomb (1814).
[89] Jean Louis Pons (1761-1831) was connected with the observatory at Marseilles for thirty years (1789-1819). He later became director of the observatory at Marlia, near Lucca, and subsequently filled the same office at Florence. He was an indefatigable searcher for comets, discovering 37 between 1801 and 1827, among them being the one that bears Encke's name.
[90] This hypothesis has now become an established fact.
[91] John Chetwode Eustace (c. 1762-1815) was born in Ireland. Although a Roman Catholic priest he lived for a time at Cambridge where he did some tutoring. His Classical Tour appeared in 1813 and went through several editions.
[92] "Crimes should be exposed when they are punished, but disgraceful acts should be hidden."
[93] Henri Hureau de Sénarmont (1808-1862) was professor of mineralogy at the Ecole des mines and examiner at the Ecole polytechnique at Paris.
[94] Augustin Jean Fresnel (1788-1827), "Ingenieur des ponts et chaussées," gave the first experimental proofs of the wave theory of light. He studied the questions of interference and polarization, and determined the approximate velocity of light.
[95] "As is my custom."
[96] Francis Heywood (1796-1858) made the first English translation of Kant's Critick of Pure Reason (1838, reprinted in 1848). The Analysis came out, as here stated, in 1844.
[97] Louise Renée de Keroualle, Duchess of Portsmouth and Aubigny (1649-1734), was a favorite of Charles II. She used her influence to keep him under the control of Louis XIV.
[98] William Chiffinch (c. 1602-1688) was page of the king's bed-chamber and keeper of the private closet to Charles II. He was one of the king's intimates and was an unscrupulous henchman.
[99] "Well devised."
[100] "John Bellingham Inglis. His Philobiblion "translated from the first edition (of Ricardus d'Aungervile, Bishop of Durham), 1473," appeared at London in 1832. It was republished in America (Albany, N. Y.) in 1864.
[101] "What are you laughing at?"
[102] See Vol. I, page 314, note 4 {681}.
[103] See Vol. I, page 112, note 7 {211}.
[104] Referring to Hamilton's edition of the Collected Works of Dugald Stewart, 10 volumes, Edinburgh, 1854-58. It is not commonly remembered that Stewart (1753-1828) taught mathematics at the University of Edinburgh before he took up philosophy.
[105] This was Hamilton's edition of the Works of Thomas Reid (2 vols., Edinburgh, 1846-1863). Reid (1710-1796) included mathematics in his work in philosophy at Aberdeen. In 1764 he succeeded Adam Smith at Glasgow.
[106] Edward Irving (1792-1834), the famous preacher. At first he assisted Dr. Chalmers at Glasgow, but in 1822 he went to London where he met with great success. A few years later he became mentally unbalanced and was finally expelled from his church (1832) for heresy. He was a great friend of Carlyle.
[107] He also wrote a number of other paradoxes, including An Essay towards a Science of Consciousness (1838), Instinctive Natural Religion (1858), Popular Treatise on the structure, diseases, and treatment of the human teeth (1837), and On Headache (1859).
[108] James Smith (1801-1857), known as Shepherd Smith, was a socialist and a mystic, with a philosophy that was wittily described as "Oriental pantheism translated into Scotch." He was editor of several journals.
[109] Joanna Southcott (1750-1814) was known for her rhyming prophecies in which she announced herself as the woman spoken of in Revelations xii. She had at one time as many as 100,000 disciples, and she established a sect that long survived her.
[110] Thales, c. 640-548 B. C.
[111] Pythagoras, 580-501 B. C.
[112] Anaxagoras, 499-428 B. C., the last of the Ionian school, teacher of Euripides and Pericles. Plutarch speaks of him as having squared the circle.
[113] Oinopides of Chios, contemporary of Anaxagoras. Proclus tells us that Oinopides was the first to show how to let fall a perpendicular to a line from an external point.
[114] Bryson and Antiphon, contemporaries of Socrates, invented the so-called method of exhaustions, one of the forerunners of the calculus.
[115] He wrote, c. 440 B. C., the first elementary textbook on mathematics in the Greek language. The "lunes of Hippocrates" are well known in geometry.
[116] Jabir ben Aflah. He lived c. 1085, at Seville, and wrote on astronomy and spherical trigonometry. The Gebri filii Affla Hispalensis de astronomia libri IX was published at Nuremberg in 1533.
[117] Hieronymus Cardanus, or Girolamo Cardano (1501-1576), the great algebraist. His Artis magnae sive de regulis Algebrae was published at Nuremberg in 1545.
[118] Nicolo Tartaglia (c. 1500-1557), the great rival of Cardan.
[119] See note 5 {98}, Vol. I, page 69.
[120] See note 10 {124}, Vol. I., page 83.
[121] See note 9 {123}, Vol. I, page 83.
[122] Pierre Hérigone lived in Paris the first half of the 17th century. His Cours mathématique (6 vols., 1634-1644) had some standing but was not at all original.
[123] Franciscus van Schooten (died in 1661) was professor of mathematics at Leyden. He edited Descartes's La Géométrie.
[124] Florimond de Beaune (1601-1652) was the first Frenchman to write a commentary on Descartes's La Géométrie. He did some noteworthy work in the theory of curves.
[125] See note 3 {23}, Vol. I, page 41.
[126] Olivier de Serres (b. in 1539) was a writer on agriculture. Montucla speaks of him in his Quadrature du cercle (page 227) as having asserted that the circle is twice the inscribed equilateral triangle, although, as De Morgan points out, this did not fairly interpret his position.
[127] Angherà wrote not only the three works here mentioned, but also the Problemi del più alto interesse scientifico, geometricamente risoluti e dimostrati, Naples, 1861. His quadrature was defended by Giovanni Motti in a work entitled Matematica Vera. Falsità del sistema ciclometrico d'Archimede, quadratura del cerchio d'Angherà, ricerca algebraica dei lati di qualunque poligono regolare inscritto in un circolo, Voghera, 1877. The Problemi of 1861 contains Angherà's portrait, and states that he lived at Malta from 1849 to 1861. It further states that the Malta publications are in part reproduced in this work.
[128] This was his friend Paolo Pullicino whose Elogio was pronounced by L. Farrugia at Malta in 1890. He wrote a work La Santa Effegie della Blata Vergine Maria, published at Valetta in 1868.
[129] St. Vitus, St. Modestus, and St. Crescentia were all martyred the same day, being torn limb from limb after lions and molten lead had proved of no avail. At least so the story runs.
[130] The reference is to Cardinal Wiseman. See Vol. II, page 26, note 56.
[131] "Worthy of esteem."
[132] Pedro de Ribadeneira (Ribadeneyra, Rivadeneira), was born at Toledo in 1526 and died in 1611. He held high position in the Jesuit order. The work referred to is the Flos Sanctorum o libro de las vidas de los santos, of which there was an edition at Barcelona in 1643. His life of Loyola (1572) and Historia ecclesiástica del Cisma del reino de Inglaterra were well known.
[133] Cæsar Baronius (1538-1607) was made a cardinal in 1595 and became librarian at the Vatican in 1597. The work referred to appeared at Rome in 1589.
[134] Mrs. Jameson's (1794-1860) works were very popular half a century ago, and still have some circulation among art lovers. The first edition of the work mentioned appeared in 1848.
[135] The barnyard cock.
[136] Shanks did nothing but computing. The title should, of course, read "to 607 Places of Decimals." He later carried the computation to 707 decimal places. (Proc. Roy. Society, XXI, p. 319.) He also prepared a table of prime numbers up to 60,000. (Proc. Roy. Society, XXII, p. 200.)
[137] See Vol. I, page 42, note 4 {24}.
[138] See Vol. I, page 64, note 1 {78}.
[139] See Vol. I, page 328, note 1 {704}.
[140] George Suffield published Synthetic Division in Arithmetic, to which reference is made, in 1863.
[141] John Robert Lunn wrote chiefly on Church matters, although he published a work on motion in 1859.
[142] Jean Baptiste Joseph, Baron Fourier (1768-1830), sometime professor in the Military School at Paris, and later at the Ecole polytechnique. He is best known by his Théorie analytique de la chaleur (Paris, 1822), in which the Fourier series is used. The work here referred to is the Analyse des équations déterminées (Paris, 1831).
[143] William George Horner (1786-1837) acquired a name for himself in mathematics in a curious manner. He was not a university man nor was he a mathematician of any standing. He taught school near Bristol and at Bath, and seems to have stumbled upon his ingenious method for finding the approximate roots of numerical higher equations, including as a special case the extracting of the various roots of numbers. Davies Gilbert presented the method to the Royal Society in 1819, and it was reprinted in the Ladies' Diary for 1838, and in the Mathematician in 1843. The method was original as far as Horner was concerned, but it is practically identical with the one used by the Chinese algebraist Ch'in Chiu-shang, in his Su-shu Chiu-chang of 1247. But even Ch'in Chiu-shang can hardly be called the discoverer of the method since it is merely the extension of a process for root extracting that appeared in the Chiu-chang Suan-shu of the second century B. C.
[144] He afterwards edited Loftus's Inland Revenue Officers' Manual (London, 1865). The two equations mentioned were x3 - 2x = 5 and y3 - 90y2 + 2500y - 16,000 = 0, in which y = 30 - 10x. Hence each place of y is the complement of the following place of x with respect to 9.
[145] Probably the John Power Hicks who wrote a memoir on T. H. Key, London, 1893.
[146] Possibly the one who wrote on the quadrature of the circle in 1881.
[147] As it is. But what a pity that we have not 12 fingers, with duodecimal fractions instead of decimals! We should then have 0.6 for ½, 0.4 for ⅓, 0.8 for ⅔, 0.3 for ¼, 0.9 for ¾, and 0.16 for ⅛, instead of 0.5, 0.333+, 0.666+, 0.25, 0.75, and 0.125 as we now have with our decimal system. In other words, the most frequently used fractions in business would be much more easily represented on the duodecimal scale than on the decimal scale that we now use.
[148] He wrote Hints for an Essay on Anemology and Ombrology (London, 1839-40) and The Music of the Eye (London, 1831).
[149] Brigham Young (1801-1877) was born at Whitingham, Vermont, and entered the Mormon church in 1832. In 1840 he was sent as a missionary to England. After the death of Joseph Smith he became president of the Mormons (1847), leading the church to Salt Lake City (1848).
[150] Joseph Smith (1805-1844) was also born in Vermont, and was four years the junior of Brigham Young. The Book of Mormon appeared in 1827, and the church was founded in 1830. He was murdered in 1844.
[151] Orson Pratt (1811-1881) was one of the twelve apostles of the Mormon Church (1835), and made several missionary journeys to England. He was professor of mathematics in the University of Deseret (the Mormon name for Utah). Besides the paper mentioned Pratt wrote the Divine Authenticity of the Book of Mormon (1849), Cubic and Biquadratic Equations (1866), and a Key to the Universe (1866).
[152] "It does not follow."
[153] Dryden (1631-1700) published his Religio Laici in 1682. The use of the word "proportion" in the sense of ratio was common before his time, but he uses it in the sense of having four terms; that is, that price is to price as offence is to offence.
[154] Olinthus Gilbert Gregory (1774-1841) succeeded Hutton as professor of mathematics at Woolwich. He was, with De Morgan, much interested in founding the University of London. He wrote on astronomy (1793), mechanics (1806), practical mathematics (1825), and Christian evidences (1811).
[155] See Vol. I, page 220, note 6 {482}. The Pensées appeared posthumously in 1670.
[156] "The right thing to do is not to wager at all." "Yes, but you ought to wager; you have started out; and not to wager at all that God exists is to wager that he does not exist."
[157] He lived about 300 A.D., in Africa, and wrote Libri septem adversus Gentes. This was printed at Rome in 1542-3.
[158] Pierre Bayle (1647-1706) was professor of philosophy at the Prostestant University at Sedan from 1675 until its dissolution in 1681. He then became professor at Rotterdam (1681-1693). In 1684 he began the publication of his journal of literary criticism Nouvelles de la République des Lettres. He is best known for his erudite Dictionnaire historique et critique (1697).
[159] "But Christ himself does not prove what he promises. It is true. For, as I have said, there cannot be any absolute proof of future events. Therefore since it is a condition of future events that they cannot be grasped or comprehended by any efforts of anticipation, is it not more reasonable, out of two alternatives that are uncertain and that are hanging in doubtful expectation, to give credence to the one that gives some hope rather than to the one that offers none at all? For in the former case there is no danger if, as is said to threaten, it becomes empty and void; while in the latter case the danger is greatest, that is, the loss of salvation, if when the time comes it is found that it was not a falsehood."
[160] Gregg wrote several other paradoxes, including the following: The Authentic Report of the extraordinary case of Tresham Dames Gregg ... his committal to Bridewell for refusing to give his recognizance (Dublin, 1841), An Appeal to Public Opinion upon a Case of Injury and Wrong ... in the case of a question of prerogative that arose between [R. Whately] ... Archbishop of Dublin and the author (London, 1861), The Cosmology of Sir Isaac Newton proved to be in accordance with the Bible (London, 1871), The Steam Locomotive as revealed in the Bible (London 1863) and On the Sacred Law of 1866, conferring perpetual life with immunity from decay and disease. A cento of decisive scriptural oracles strangely discovered (London and Dublin, 1875). These titles will help the reader to understand the man whom De Morgan so pleasantly satirizes.
[161] See Vol. I, page 261, note 2 {592}.
[162] "They have found it."
[163] The late Greeks used the letters of their alphabet as numerals, adding three early alphabetic characters. The letter χ represented 600, ξ represented 60, and Ϝ stood for 6. This gives 666, the number of the Beast given in the Revelation.
[164] "Allowing for necessary exceptions."
[165] Mr. Gregg is not alone in his efforts to use the calculus in original lines, as any one who has read Herbart's application of the subject to psychology will recall.
[166] See Vol. I, page 105, note 4 {188}; page 109, note 1 {197}.
[167] The full title shows the plan,—The Decimal System as a whole, in its relation to time, measure, weight, capacity, and money, in unison with each other. But why is this so much worse than the French plan of which we have only the metric system and the decimal division of the angle left?
[168] One of the brothers of Sir Isaac Pitman (1813-1897), the inventor of modern stenography. Of these brothers, Benjamin taught the art in America, Jacob in Australia, and Joseph, Henry, and Frederick in England.
[169] For example, The Phonographic Lecturer (London, 1871 etc.), The Phonographic Student (1867, etc.), and The Shorthand Magazine (1866, etc.).
[170] See Vol. II, page 68, note 148.
[171] It involves the theory of non-Euclidean geometry, Euclid's postulate of parallels being used in proving this theorem.
[172] Referring to the fact that none of the works of Thales is extant.
[173] The author was one B. Bulstrode. Parts 4 and 5 were printed at Calcutta.
[174] See Vol. II, page 5, note 18.
[175] See Vol. I, page 85, note 2 {129}.
[176] Alexander Vasilievich Suvaroff (1729-1800), a Russian general who fought against the Turks, in the Polish wars, and in the early Napoleonic campaigns. When he took Ismail in 1790 he sent this couplet to Empress Catherine.
[177] "Newton hath determined rightly," "Newton hath not determined rightly."
[178] See Vol. I, page 288, note 3 {621}.
[179] See Vol. I, page 326, note 1 {700}.
[180] "With great honor."
[181] Apparently unknown to biographers. He seems to have written nothing else.
[182] Captain Marryat (1792-1848) published Snarley-yow, or the Dog Fiend in 1837.
[183] He is not known to biographers, and published nothing else under this name.
[184] See Vol. I, page 80, note 5 {119}.
[185] He published a Family and Commercial Illustrated Almanack and Year Book ... for 1861 (Bath, 1860).
[186] Louis Dutens (1730-1812) was born at Tours, but went to England as a young man. He made the first collection of the works of Leibnitz, against the advice of Voltaire, who wrote to him: "Les écrits de Leibnitz sont épars comme les feuilles de la Sybille, et aussi obscurs que les écrits de cette vieille." The work appeared at Geneva, in six volumes, in 1769.
[187] Mungo Park (1771-1806), the first European to explore the Niger (1795-6). His Travels in the Interior of Africa appeared in 1799. He died in Africa.
[188] Gerhard Mercator (1512-1594) the well-known map maker of Louvain. The "Mercator's Projection" was probably made as early as 1550, but the principle of its construction was first set forth by Edward Wright (London, 1599).
[189] Quirico Barilli Filopanti wrote a number of works and monographs. He succeeded in getting his Cesare al Rubicone and Degli usi idraulici della Tela in the Memoria letta ... all' Accademia delle Scienze in Bologna (1847, 1866). He also wrote Dio esiste (1881), Dio Liberale (1880), and Sunto della memoria sulle geuranie ossia di alcune singolari relazioni cosmiche della terra e del cielo (1862).
[190] The periods of disembodiment may be interesting. They will be seen from the following dates: Descartes (1596-1650), William III (1650-1702); Roger Bacon (1214 to c. 1294), Boccaccio (1313-1375). Charles IX was born in 1550 and died in 1574.
[191] His real name was Frederick Parker, and he wrote several works on the Greek language and on religion. Among these were a translation of the New Testament from the Vatican MS. (1864), The Revealed History of Man (1854), An Enquiry respecting the Punctuation of Ancient Greek (1841), and Rules for Ascertaining the sense conveyed in Ancient Greek Manuscripts (1848, the seventh edition appearing in 1862).
[192] See Vol. I, page 352, second note 1 {736}.
The literature on the subject of the Great Pyramid, considered from the standpoint of metrology, is extensive.
[193] See Vol. I, page 80, note 5 {119}.
[194] Sir Philip Francis (1740-1818) was a Whig politician. The evidence that he was the author of the Letters of Junius (1769-1772) is purely circumstantial. He was clerk in the war office at the time of their publication. In 1774 he was made a member of the Supreme Council of Bengal, and was a vigorous opponent of Warren Hastings, the two fighting a duel in 1780. He entered parliament in 1784 and was among the leaders in the agitation for parliamentary reform.
[195] Mrs. Cottle published a number of letters that attracted attention at the time. Among these were letters to the emperor of France and king of Sardinia (1859) relating to the prophecies of the war between France and Austria; to G. C. Lavis and Her Majesty's Ministers (1859) relating to her claims as a prophetess; and to the "Crowned Heads" at St. James, the King of Prussia, and others (1860), relating to certain passages of Scripture. She also wrote The Lamb's Book of Life for the New Jerusalem Church and Kingdom, interpreted for all nations (1861).
[196] See Vol. I, page 315, note 2 {685}, and Vol. II, page 58, note 109.
[197] A Congregational minister, who published a number of sermons, chiefly obituaries, between 1804 and 1851. His Frailty of Human Life, two sermons delivered on the occasion of the death of Princess Charlotte, went through at least three editions.
[198] He was secretary of the Congregational Board and editor of the Congregational Year Book (from 1846) and the Congregational Manual.
[199] Frederick Denison Maurice (1805-1872) began his preaching as a Unitarian but entered the Established Church in 1831, being ordained in 1834. He was professor of English and History at King's College, London, from 1840 to 1853. He was one of the founders of Queen's College for women, and was the first principal of the Working Men's College, London. The subject referred to by De Morgan is his expression of opinion in his Theological Essays (1853) that future punishment is not eternal. As a result of this expression he lost his professorship at King's College. In 1866 he was made Knightbridge Professor of Casuistry, Moral Theology, and Moral Philosophy at Cambridge.
[200] See Vol. I, page 46, note 1 {42}. Besides the books mentioned in this list he wrote The Ratio between Diameter and Circumference demonstrated by angles, and Euclid's Theorem, Proposition 32, Book I, proved to be fallacious (Liverpool, 1870). This is the theorem which asserts that the exterior angle of a triangle is equal to the sum of the two opposite interior angles, and that the sum of the interior angles equals two right angles. He also published his Curiosities of Mathematics in 1870, a work containing an extensive correspondence with every one who would pay any attention to him. De Morgan was then too feeble to show any interest in the final effort of the subject of some of his keenest satire.
[201] See Vol. I, page 332, note 4 {709}.
[202] See Vol. I, page 101, note 4 {174}.
[203] "The circle-squaring disease"; literally, "the circle-measuring disease."
[204] See Vol. II, page 63, note 136.
[205] William Rutherford (c. 1798-1871), teacher of mathematics at Woolwich, secretary of the Royal Astronomical Society, editor of The Mathematician, and author of various textbooks. The Extension of π to 440 places, appeared in the Proceedings of the Royal Society in 1853 (p. 274).
[206] Charles Knight (1791-1873) was associated with De Morgan for many years. After 1828 he superintended the publications of the Society for the Diffusion of Useful Knowledge, to which De Morgan contributed, and he edited the Penny Cyclopedia (1833-1844) for which De Morgan wrote the articles on mathematics.
[207] Sir William Hamilton. See Vol. I, page 112, note 7 {211}.
[208] Adam Smith (1723-1790) was not only known for his Wealth of Nations (1776), but for his Theory of Moral Sentiments (1759), published while he was professor of moral philosophy at Glasgow (1752-1764). He was Lord Rector of the university in 1787.
[209] See Vol. I, page 332, note 4 {709}.
[210] "Whip."
[211] "Terrible lash."
[212] "An accomplished fact [an accomplished fault]."
[213] See Extracts from the Diary and Letters of Mrs. Mary Cobb, London, 1805.
[214] "Gentle in manner."
[215] "Brave in action." The motto of Earl Newborough was "Suaviter in modo, fortiter in re."
[216] "Reduction to an absurdity," a method of proof occasionally used in geometry and in logic.
[217] "He has lost the right of being moved (struck) by evidence."
[218] For radix quadratus. The usual root sign is supposed to be derived from r (for radix), and at one time q was commonly used for square, as in Viète's style of writing Aq for A2.
[219] The Garde Douloureuse was a castle in the marches of Wales and received its name because of its exposure to attacks by the Welsh.
[220] "Out of the fight."
[221] "Hidden."
[222] John Cam Hobhouse (1786-1869), Baron Broughton, was committed to Newgate for two months in 1819 for his anonymous pamphlet, A Trifling Mistake. This was a great advertisement for him, and upon his release he was at once elected to parliament for Westminster. He was a strong supporter of all reform measures, and was Secretary for War in 1832. He was created Baron Broughton de Gyfford in 1851.
[223] Thomas Erskine (1750-1823), the famous orator. He became Lord Chancellor in 1806, but sat in the House of Commons most of his life.
[224] The above is explained in the MS. by a paragraph referring to some anagrams, in one of which, by help of the orthography suggested, a designation for this cyclometer was obtained from the letters of his name.—S. E. De M.
[225] "A personal verb agrees with its subject."
[226] See Vol. I, page 326, note 1 {700}.
[227] See Vol. I, page 326, note 2 {701}.
[228] Apparently unknown to biographers.
[229] The Bibliotheca Mathematica of Ludwig Adolph Sohncke (1807-1853), professor of mathematics at Königsberg and Halle, covered the period from 1830 to 1854, being completed by W. Engelmann. It appeared in 1854.
[230] See Vol. I, page 392, note 2 {805}.
[231] See Vol. I, page 43, note 7 {32}.
[232] See Vol. II, page 91, note 187.
[233] Mason made a notable balloon trip from London to Weilburg, in the Duchy of Nassau, in November, 1836, covering 500 miles in 18 hours. He published an account of this trip in 1837, and a work entitled Aeronautica in 1838.
[234] William Harrison Ainsworth (1805-1885) the novelist.
[235] On this question see Vol. I, page 326, note 2 {701}.
[236] Major General Alfred Wilks Drayson, author of various works on geology, astronomy, military surveying, and adventure.
[237] Hailes also wrote several other paradoxes on astronomy and circle squaring during the period 1843-1872.
[238] See Vol. I, page 43, note 8 {33}.
[239] See Vol. I, page 43, note 7 {32}.
[240] "Very small errors are not to be condemned."
[241] He seems to have written nothing else.
[242] Besides the paradoxes here mentioned by De Morgan he wrote several other works, including the following: Abriss der Babylonisch-Assyrischen Geschichte (Mannheim, 1854), A Popular Inquiry into the Moon's rotation on her axis (London, 1856), Practical Tables for the reduction of the Mahometan dates to the Christian kalendar (London, 1856), Grundzüge einer neuen Weltlehre (Munich, 1860), and On the historical Antiquity of the People of Egypt (London, 1863).
[243] Dircks (1806-1873) was a civil engineer of prominence, and a member of the British Association and the Royal Society of Edinburgh. He wrote (1863) on "Pepper's Ghost," an ingenious optical illusion invented by him. There was a second edition of the Perpetuum Mobile in 1870.
[244] George Stephenson (1781-1848), the inventor of the first successful steam locomotive. His first engine was tried in 1814.
[245] Robert Stephenson (1803-1859), the only son of George. Most of the early improvements in locomotive manufacture were due to him. He was also well known for his construction of great bridges.
[246] "In its proper place."
[247] "A fool always finds a bigger fool to admire him."
[248] See Vol. I, page 43, note 7 {32}.
[249] See Vol. I, page 43, note 8 {33}.
[250] See Vol. I, page 85, note 2 {129}.
[251] See Vol. I, page 390, note 1 {390}.
[252] From 1823 to 1852 it was edited by I. C. Robertson; from 1852 to 1857 by R. A. Brooman; and from 1857 to 1863 by Brooman and E. J. Reed.
[253] Sir James Ivory (1765-1842) was, as a young man, manager of a flax mill in Scotland. In 1804 he was made professor of mathematics at the Royal Military College, then at Marlow and later at Sandhurst. He was deeply interested in mathematical physics, and there is a theorem on the attraction of ellipsoids that bears his name. He was awarded three medals of the Royal Society, and was knighted together with Herschel and Brewster, in 1831.
[254] See Vol. I, page 56, note 1 {64}.
[255] See Vol. I, page 153, note 5 {338}.
[256] See Vol. I, page 309, note 2 {670}.
[257] See Vol. I, page 87, note 4 {133}.
[258] George Canning (1770-1857), the Tory statesman and friend of Scott, was much interested in founding the Quarterly Review (1808) and was a contributor to its pages.
[259] See Vol. I, page 186, note 14 {418}.
[260] See Vol. II, page 141, note 252.
[261] De Morgan had a number of excellent articles in this publication.
[262] See Vol. I, page 279, note 1 {611}.
[263] James Orchard Halliwell (1820-1889), afterwards Halliwell-Phillips, came into prominence as a writer at an early age. When he was seventeen he wrote a series of lives of mathematicians for the Parthenon. His Rara Mathematica appeared when he was but nineteen. He was a great bibliophile and an enthusiastic student of Shakespeare.
[264] This was written at the age of twenty-two.
[265] The subject of this criticism is of long past date, and as it has only been introduced by the author as an instance of faulty editorship, I have omitted the name of the writer of the libel, and a few lines of further detail.—S. E. De M.
[266] "Condemned souls."
[267] The editor of the Mechanics' Magazine died soon after the above was written.—S. E. De M.
[268] Thomas Stephens Davies (1795-1851) was mathematical master at Woolwich and F. R. S. He contributed a series of "Geometrical Notes" to the Mechanics' Magazine and edited the Mathematician. He also published a number of text-books.
[269] See Vol. II, page 66, note 143.
[270] The Dictionary of Greek and Roman Biography (1849), edited by Sir William Smith (1813-1893), whose other dictionaries on classical and biblical matters are well known.
[271] "O J. S.! This is the worst! the greatest possible injury!"
[272] See Vol. I, page 44, note 9 {34} and page 110, note 5 {201}.
"If there's a man whom the judge's pitiless sentence awaiteth,
His head condemned to penalties and tribulations,
Let neither penitentiaries tire him with laborer's burdens
Nor let his stiffened hands be harrassed by work in the mines.
He must square the circle! For what else do I care?—all
Known punishments this one task hath surely included."
[274] Houlston was in the customs service. He also published Inklings of Areal Autometry, London, 1874.
[275] This is Frederick C. Bakewell. He had already published Natural Evidence of a Future Life (London, 1835), Philosophical Conversations (London, 1833, with other editions), and Electric Science (London, 1853, with other editions).
[276] Henry F. A. Pratt had already published A Dissertation on the power of the intercepted pressure of the Atmosphere (London, 1844) and The Genealogy of Creation (1861). Later he published a work On Orbital Motion (1863), and Astronomical Investigations (1865).
[277] See Vol. I, page 260, note 1 {591}.
[278] Thomas Rawson Birks (1810-1883), a theologian and controversialist, fellow of Trinity College, Cambridge, and (1872) professor of moral philosophy in that university. He wrote Modern Rationalism (1853), The Bible and Modern Thought (1861), The First Principles of Moral Science (1873), and Modern Physical Fatalism and the Doctrine of Evolution (1876), the last being an attack on Herbert Spencer's First Principles.
[279] Pseudonym for William Thorn. In the following year (1863) he published a second work, The Thorn-Tree: being a History of Thorn Worship, a reply to Bishop Colenso's work entitled The Pentateuch and the Book of Joshua critically examined.
[280] Besides The Pestilence (1866) he published The True Church (1851), The Church and her destinies (1855), Religious reformation imperatively demanded (1864), and The Bible plan unfolded (second edition, 1872).
[281] See Vol. II, page 97, note 195.
[282] Sir George Cornewall Lewis (1806-1863) also wrote an Essay on the Origin and Formation of the Romance Languages (1835), an Essay on the Government of Dependencies (1841), and an Essay on Foreign Jurisdiction and the Extradition of Criminals (1859). He was Chancellor of the Exchequer in 1855 and Home Secretary in 1859.
[283] Henry Malden (1800-1876), a classical scholar, fellow of Trinity College, Cambridge, and professor of Greek at University College (1831-1876), then (1831) the University of London. He wrote a History of Rome to 390 B. C. (1830), and On the Origin of Universities and Academical Degrees (1835).
[284] Henry Longueville Mansel (1820-1871), theologian and metaphysician, reader in theology at Magdalen College, Oxford (1855), and professor of ecclesiastical history and Dean of St. Paul's (1866). He wrote on metaphysics, and his Bampton Lectures (1858) were reprinted several times.
[285] "Hejus gave freely, gave freely. God is propitious, God is favorable to him who gives freely. God is honored with a banquet of eggs at the cross roads, the god of the world. God, with benignant spirit, desired in sacrifice a goat, a bull to be carried within the precincts of the holy place. God, twice propitiated, blesses the pit of the sacred libation."
[286] Eudoxus of Cnidus (408-355 B. C.) had much to do with the early scientific astronomy of the Greeks. The fifth book of Euclid is generally attributed to him. His astronomical works are known chiefly through the poetical version of Aratus mentioned in note 13, page 167.
[287] Simplicius, a native of Cilicia, lived in the 6th century of our era. He was driven from Athens by Justinian and went to Persia (531), but he returned later and had some fame as a teacher.
[288] See Vol. I, page 160, note 3 {348}.
[289] See Vol. I, page 76, note 3 {112}.
[290] "Through right and wrong."
[291] "It is therefore to arrive at this parallelism, or to preserve it, that Copernicus feared to be obliged to have recourse to this equal and opposite movement which destroys the effect which he attributed so freely to the first, of deranging the parallelism."
[292] A contemporary of Plato and a disciple of Aristotle.
[293] Meton's solstice, the beginning of the Metonic cycles, has been placed at 432 B. C. Ptolemy states that he made the length of the year 365¼ + 1/72 days.
[294] Aratus lived about 270 B. C., at the court of Antigonus of Macedonia, and probably practiced medicine there. He was the author of two astronomical poems, the Φαινόμενα, apparently based on the lost work of Eudoxus, and the Διοσηεῖα based on Aristotle's Meteorologica and De Signis Ventorum of Theophrastus.
[295] "The nineteen (-year) cycle of the shining sun."
[296] Claudius Salmasius (1588-1653), or Claude Saumaise, was a distinguished classicist, and professor at the University of Leyden. The word ἠλείοιο means Elian, thus making the phrase refer to the brilliant one of Elis.
[297] Sir William Brown (1784-1864). In 1800 the family moved to Baltimore, and there the father, Alexander Brown, became prominent in the linen trade. William went to Liverpool where he acquired great wealth as a merchant and banker. He was made a baronet in 1863.
[298] Robert Lowe (1811-1892), viscount Sherbrooke, was a fellow of Magdalen College, Oxford (1835). He went to Australia in 1842 and was very successful at the bar. He returned to England in 1850 and became leader writer on the Times. He was many years in parliament, and in 1880 was raised to the peerage.
[299] See Vol. I, page 42, note 4 {24}.
[300] Francis Walkingame (fl. about 1751-1785), whose Tutor's Assistant went through many editions from 1751-1854.
[301] Davies Gilbert (1767-1839). His family name was Giddy, but he assumed his wife's name. He sat in parliament from 1806 to 1832. In 1819 he secured the establishment of the Cape of Good Hope observatory. He was Treasurer (1820-1827) and President (1827-1830) of the Royal Society.
[302] See Vol. I, page 55, note 2 {63}.
[303] Sir Jonathan Frederick Pollock (1783-1870) entered parliament in 1831 and was knighted in 1834.
[304] Joseph Hume (1777-1855) entered parliament in 1812 and for thirty years was leader of the Radical party.
[305] "What! when I say, 'Nicole, bring me my slippers,' is that prose?"
[306] Captain Basil Hall (1788-1844), a naval officer, carried on a series of pendulum observations in 1820-1822, while on a cruise of the west coast of North America. The results were published in 1823 in the Philosophical Transactions. He also wrote two popular works on travel that went through numerous editions.
[307] Anthony Ashley Cooper (1801-1885), Earl of Shaftesbury. His name is connected with philanthropic work and factory legislation.
[308] See Vol. I, page 207, note 12 {469}.
[309] See Vol. I, page 80, note 5 {119}.
[310] Sir Thomas Maclear (1794-1879), an Irishman by birth, became Astronomer Royal at the Cape of Good Hope in 1833. He was an indefatigable observer. He was knighted in 1860.
[311] Thomas Romney Robinson (1792-1882), another Irish astronomer of prominence. He was a deputy professor at Trinity College, Dublin, but took charge of the Armagh observatory in 1823 and remained there until his death.
[312] Sir James South (1785-1867) was in early life a surgeon, but gave up his practice in 1816 and fitted up a private observatory. He contributed to the science of astronomy, particularly with respect to the study of double stars.
[313] Sir John Wrottesley (1798-1867), second Baron Wrottesley. Like Sir James South, he took up the study of astronomy after a professional career,—in his case in law. He built a private observatory in 1829 and made a long series of observations, publishing three star catalogues. He was president of the Astronomical Society from 1841 to 1843, and of the Royal Society from 1854 to 1857.
[314] He seems to have written nothing else.
[315] See Vol. II, page 68, note 147.
[316] "The wills are free, and I wish neither the one nor the other."
[317] "The force of inertia conquered."
[318] Reddie also wrote The Mechanics of the Heavens, referred to later in this work. He must not be confused with Judge James Reddie (1773-1852), of Glasgow, who wrote on international law, although this is done in the printed edition of the British Museum catalogue, for he is mentioned by De Morgan somewhat later as alive in 1862.
[319] Henry Dunning Macleod (1821-1902), a lawyer and writer on political economy, was a Scotchman by birth. He wrote on economical questions, and lectured on banking at Cambridge (1877) and at King's College, London (1878). He was a free lance in his field, and was not considered orthodox by the majority of economists of his time. He was an unsuccessful candidate for the chairs of political economy at Cambridge (1863), Edinburgh (1871), and Oxford (1888).
[320] See Vol. I, page 252, note 2 {576}.
[321] Francis Henry Laing (1816-1889) was a graduate of Queen's College, Cambridge, and a clergyman in the Church of England until 1846, when he entered the Church of Rome. He taught in various Jesuit colleges until 1862, when his eccentricity was too marked to warrant the Church in allowing him to continue. He published various controversial writings during his later years. Of course if he had known the works of Wessel, Gaus, Buée, Argand, and others, he would not have made such a sorry exhibition of his ignorance of mathematics.
[322] See Vol. I, page 329, note 1 {705}. The book went into a second edition in 1864.
[323] Thomas Weddle (1817-1853) was, at the time of publishing this paper, a teacher in a private school. In 1851 he became professor of mathematics at Sandhurst. He contributed several papers to the Cambridge and Dublin Mathematical Journal, chiefly on geometry.
[324] See Vol. II, page 109, note 205.
[325] See Vol. II, page 66, note 143.
[326] See Vol. II, page 151, note 268.
[327] George Barrett (1752-1821) worked from 1786 to 1811 on a set of life insurance and annuity tables. He invented a plan known as the "columnar method" for the construction of such tables, and as De Morgan states, this was published by Francis Baily, appearing in the appendix to his work on annuities, in the edition of 1813. Some of his tables were used in Babbage's Comparative View of the various Institutions for the Assurance of Lives (1826).
[328] See Vol. I, page 309, note 2 {670}.
[329] This was his Practical short and direct Method of Calculating the Logarithm of any given Number, and the Number corresponding to any given Logarithm (1849).
[330] This is William Neile (1637-1670), grandson of Richard Neile (not Neal), Archbishop of York. At the age of 19, in 1657, he gave the first rectification of the semicubical parabola. Although he communicated it to Brouncker, Wren, and others, it was not published until 1639, when it appeared in John Wallis's De Cycloide.
[331] I myself "was a considerable part."
[332] He also wrote A Glance at the Universe ("2d thousand" in 1862), and The Resurrection Body (1869).
[333] See Vol. I, page 63, note 1 {74}.
[334] As Swift gave it in his Poetry. A Rhapsody, it is as follows:
"So, naturalists observe, a flea
Has smaller fleas that on him prey;
And these have smaller still to bite 'em.
And so proceed ad infinitum."
[335] Perhaps 1,600,000,000 years, if Boltwood's recent computations based on radium disintegration stand the test. This would mean, according to MacCurdy's estimate, 60,000,000 years since life first appeared on the earth.
[336] De Morgan wrote better than he knew, for this work, the Allgemeine Encyclopädie der Wissenschaften und Künste, begun at Leipsic in 1818, is still (1913) unfinished. Section I, A-G, consists of 99 parts in 56 volumes; Section II, H-N, consists of 43 volumes and is not yet completed; and Section III, O-Z, consists of 25 volumes thus far, with most of the work still to be done. Johann Samuel Ersch (1766-1828), the founder, was head librarian at Halle. Johann Gottfried Gruber (1774-1851), his associate, was professor of philosophy at the same university.
[337] William Howitt (1792-1879) was a poet, a spiritualist, and a miscellaneous writer. He and his wife became spiritualists about 1850. He wrote numerous popular works on travel, nature and history.
[338] See Vol. II, page 55, note 108.
[339] As will be inferred from the text, C. D. was Mrs. De Morgan, and A. B. was De Morgan.
[340] Jean Meslier (1678-1733), curé of Estrepigny, in Champagne, was a skeptic, but preached only strict orthodoxy to his people. It was only in his manuscript, Mon Testament, that was published after his death, and that caused a great sensation in France, that his antagonism to Christianity became known.
[341] Baron Zach relates that a friend of his, in a writing intended for publication, said Un esprit doit se frotter contre un autre. The censors struck it out. The Austrian police have a keen eye for consequences.—A. De M.
"One mind must rub against another." On Baron Zach, see Vol. II, page 45, note 4.
[342] Referring to the first Lord Eldon (1751-1838), who was Lord Chancellor from 1799 to 1827, with the exception of one year.
[343] "Sleeping power."
[344] "Causes sleep."
[345] Richard Hooker (c. 1554-1600), a theologian, "the ablest living advocate of the Church of England as by law established."
[346] See Vol. I, page 76, note 3 {112}.
[347] "Other I,"—other self.
[348] This "utter rejection" has been repeated (1872) by the same writer.—S. E. De M.
[349] Edward Jenner (1749-1823) was a physician and biologist. His first experiments in vaccination were made in 1796, and his discovery was published in 1798.
[350] See Vol. II, page 38, note 80.
[351] "You will go most safely in the middle (way)."
[352] Pierre Joseph Arson was known early in the 19th century for his controversy with Hoëné Wronski the mathematician, whom he attacked in his Document pour l'histoire des grands fourbes qui ont figuré sur la terre (1817-1818).
[353] "We enter the course by night and are consumed by fire."
[354] See Vol. I, page 51, note 3 {51}.
[355] See Vol. I, page 336, note 8 {713}.
[356] See Vol. I, page 137, note 8 {286}.
[357] See Vol. I, page 229, note 2 {515}.
[358] Richard Cobden (1804-1865), the cotton manufacturer and statesman who was prominent in his advocacy of the repeal of the Corn Laws.
[359] James Smith (1775-1839), solicitor to the Board of Ordnance. With his brother Horatio he wrote numerous satires. His Horace in London (1813) imitated the Roman poet. His works were collected and published in 1840.
[360] Samuel Butler (1612-1680), the poet and satirist, author of Hudibras (1663-1678).
[361] "Is it not fine to be sure of one's action when entering in a combat with another? There, push me a little in order to see. Nicole. Well! what's the matter? M. Jourdain. Slowly. Ho there! Ho! gently. Deuce take the rascal! Nicole. You told me to push. M. Jourdain. Yes, but you pushed me en tierce, before you pushed en quarte, and you did not give me time to parry."
[362] John Abernethy (1764-1831), the famous physician and surgeon.
[363] See Vol. I, page 102, note 5 {175}.
[364] "With what measure ye mete, it shall be measured to you again."
[365] Eusebius of Cæsarea (c. 260-340), leader of the moderate party at the Council of Nicæa, and author of a History of the Christian Church in ten books (c. 324 A. D.).
[366] Nathaniel Lardner (1684-1768), a non-conformist minister and one of the first to advocate the scientific study of early Christian literature.
[367] Henry Alford (1810-1871) Dean of Canterbury (1857-1871) and editor of the Greek Testament (1849-1861).
[368] The work was The Number and Names of the Apocalyptic Beasts: with an explanation and application. Part I. London, 1848, as mentioned below. Thom also wrote The Assurance of Faith, or Calvinism identified with Universalism (London, 1833), and various other religious works.
[369] See Vol. I, page 222, note 14 {490}.
[370] John Hamilton Thom (1808-1894) was converted to Unitarianism and was long a minister in that church, preaching in the Renshaw Street Chapel from 1831 to 1866. De Morgan refers to the Liverpool Unitarian controversy conducted by James Martineau and Henry Giles in response to a challenge by thirteen Anglican Clergy. In 1839 Thom contributed four lectures and a letter to this controversy. Among his religious works were a Life of Blanco White (1845) and Hymns, Chants, and Anthems (1854).
[371] The spelling of these names is occasionally changed to meet the condition that the numerical value of the letters shall be 666, "the number of the beast" of Revelations. The names include Julius Cæsar; Valerius Jovius Diocletianus (249-313), emperor from 287 to 305, persecutor of the Christians; Louis, presumably Louis XIV; Gerbert (940-1003), who reigned as Pope Sylvester II from 999 to 1003, known to mathematicians for his abacus and his interest in geometry, and accused by his opponents as being in league with the devil; Linus, the second Bishop of Rome, the successor of Peter; Camillo Borghese (1552-1621), who reigned as Pope Paul V from 1605 to 1621, and who excommunicated all Venice in 1606 for its claim to try ecclesiastics before lay tribunals, thus taking a position which he was forced to abandon; Luther, Calvin; Laud (see Vol. I, page 145, note 7 {307}); Genseric (c. 406-477), king of the Vandals, who sacked Rome in 455 and persecuted the orthodox Christians in Africa; Boniface III, who was pope for nine months in 606; Beza (see Vol. I, page 66, note 6 {83}); Mohammed; βρασκι, who was Giovanni Angelo Braschi (1717-1799), and who reigned as Pope Pius VI from 1775 to 1799, dying in captivity because he declined to resign his temporal power to Napoleon; Bonaparte; and, under Ιον Παυνε, possibly Pope John XIV, who reigned in 983 and 984 during the absence of Boniface VII in Constantinople.
[372] The Greek words and names are also occasionally misspelled so as to fit them to the number 666. They are Λατεινος (Latin), ἡ λατινη βασιλεια (the Latin kingdom), ἐκκλησια ἰταλικα (the Italian Church), εὐανθας (blooming), τειταν (Titan), ἀρνουμε (renounce), λαμπετις (the lustrous), ὁ νικητης (conqueror), κακος ὁδηγος (bad guide), ἀληθης βλαβερος (truthful harmful one), παλαι βασκανος (a slanderer of old), ἀμνος ἀδικος (unmanageable lamb), ἀντεμος (Antemos), γενσηρικος (Genseric), εὐινας (with stout fibers), Βενεδικτος (Benedict), Βονιβαζιος γ. παπα ξ. η. ε. ε. α. (Boniface III, pope 68, bishop of bishops I), οὐλπιος (baneful), διος εἰμι ἡ ἡρας (I, a god, am the), ἡ μισσα ἡ παπικη (the papal brief), λουθερανα (Lutheran), σαξονειος (Saxon), Βεζζα αντιθεος (Beza antigod), ἡ αλαζονεια βιου (the illusion of life), Μαομετις (Mahomet); Μαομετης β. (Mahomet II), θεος εἰμι ἐπι γαιης (I am lord over the earth), ἰαπετος (Iapetos, father of Atlas), παπεισκος (Papeiskos), διοκλασιανος (Diocletian), χεινα (Cheina = Cain? China?), βρασκι (Braschi, as explained in note 10), Ιον Παυνε (Paunian violet, but see note 10), κουποκς (cowpox), Βοννεπαρτη (Bonneparte), Ν. Βονηπαρτε (N. Boneparte), εὐπορια (facility), παραδοσις (surrender), το μεγαθηριον (the megathereum, the beast).
[373] James Wapshare, whose Harmony of the Word of God in Spirit and in Truth appeared in 1849.
[374] The literature relating to the Swastika is too extended to permit of any adequate summary in these notes.
[375] Henry Edward Manning (1808-1892), at first an Anglican clergyman, he became a Roman Catholic priest in 1851, and became Cardinal in 1875. He succeeded Cardinal Wiseman as Archbishop of Westminster in 1865. He wrote a number of religious works.
[376] John Bright (1811-1889), Quaker, cotton manufacturer, and statesman. He worked with Cobden for free trade, peace, and reform of the electorate.
[377] "The fallacy of many questions."
[378] William Wilberforce (1759-1833), best known for his long fight for the abolition of the slave trade.
[379] Richard Martin (1754-1834), high sheriff of County Galway and owner of a large estate in Connemara. Curiously enough, he was known both for his readiness in duelling and for his love for animals. He was known as "Humanity Martin," and in 1822 secured the passage of an act "to prevent the cruel and improper treatment of cattle." He was one of the founders (1824) of the Royal Society for the Prevention of Cruelty to Animals. He is usually considered the original of Godfrey O'Malley in Lever's novel, Charles O'Malley.
[380] See Vol. I, page 149, note 1 {323}, also text on same page.
[381] See Vol. I, page 44, note 9 {34}, also text, Vol. I, page 110.
[382] "Penitential seat."
[383] "Well placed upon the cushion."
[384] See Vol. II, page 58, note 109.
[385] "He has lost the right of being influenced by evidence."
[386] "Hung up."
[387] "A few things to the wise, nothing to the unlettered."
[388] The fallacy results from dividing both members of an equation by 0, x - 1 being the same as 1 - 1, and calling the quotients finite.
[389] "If you order him to the sky he will go."
[390] Similia similibus curanter, "Like cures like," the homeopathic motto.
[391] "Without harm to the proprieties."
[392] "What are you doing? I am standing here."
[393] Lors feist l'Anglois tel signe. La main gausche toute ouverte il leva hault en l'aer, puis ferma au poing les quatres doigtz d'icelle et le poulce estendu assit sus la pinne du nez. Soubdain après leva la dextre toute ouverte, et toute ouverte la baissa, joignant la poulce au lieu que fermait le petit doigt de la gausche, et les quatre doigtz d'icelle mouvoit lentement en l'aer. Puis au rebours feit de la dextre ce qu'il avoit faict de la gausche, et de la gausche ce que avoit faict de la dextre.—A. De M.
[394] Suaviter in modo, fortiter in re, "Gentle in manners, firm in action."
[395] See Vol. I, page 101, note 4 {174}.
[396] See Vol. I, page 315, note 3 {686}.
[397] Henry Fawcett (1833-1884) became totally blind in 1858, but in spite of this handicap he became professor of political economy at Cambridge and sat in parliament for a number of years. He championed the cause of reform and in particular he was prominent in the protection of the native interests of India. The establishing of the parcels post (1882) took place while he was postmaster general (1880-1884).
[398] Of course the whole thing depends upon what definition of division is taken. We can multiply 2 ft. by 3 ft. if we define multiplication so as to allow it, or 2 ft. by 3 lb, getting foot-pounds, as is done in physics.
[399] Richard Milward (1609-1680), for so the name is usually given, was rector of Great Braxted (Essex) and canon of Windsor. He was long the amanuensis of John Selden, and the Table Talk was published nine years after Milward's death, from notes that he left. Some doubt has been cast upon the authenticity of the work owing to many of the opinions that it ascribes to Selden.
[400] John Selden (1584-1654) was a jurist, legal antiquary, and Oriental scholar. He sat in the Long Parliament, and while an advocate of reform he was not an extremist. He was sent to the Tower for his support of the resolution against "tonnage and poundage," in 1629. His History of Tythes (1618) was suppressed at the demand of the bishops. His De Diis Syriis (1617) is still esteemed a classic on Semitic mythology.
[401] See Vol. I, page 42, note 4 {24}.
[402] See Vol. II, page 249, note 398.
[403] John Palmer (1742-1818) was a theatrical manager. In 1782 he set forth a plan for forwarding the mails by stage coaches instead of by postmen. Pitt adopted the plan in 1784. Palmer was made comptroller-general of the post office in 1786 and was dismissed six years later for arbitrarily suspending a deputy. He had been verbally promised 2½% on the increased revenue, but Pitt gave him only a pension of £3000. In 1813 he was awarded £50,000 in addition to his pension.
[404] Dionysius Lardner (1793-1859), professor of natural philosophy in London University (now University College). His Cabinet Cyclopædia (1829-1849) contained 133 volumes. De Morgan wrote on probabilities, and Lardner on various branches of mathematics, and there were many other well-known contributors. Lardner is said to have made $200,000 on a lecture tour in America.
[405] Thomas Fysche Palmer (1747-1802) joined the Unitarians in 1783, and in 1785 took a charge in Dundee. He was arrested for sedition because of an address that it was falsely alleged that he gave before a society known as the "Friends of Liberty." As a matter of fact the address was given by an uneducated weaver, and Palmer was merely asked to revise it, declining to do even this. Nevertheless he was sentenced to Botany Bay (1794) for seven years. The trial aroused great indignation.
[406] See Vol. I, page 80, note 5 {119}.
[407] See Vol. II, page 244, note 394.
[408] See Vol. I, page 352, note 1 {731}.
[409] See Vol. I, page 332, note 4 {709}.
[410] "The lawyers are brought into court; let them accuse each other."
[411] Samuel Rogers (1763-1855), the poet and art connoisseur. He declined the laureateship on the death of Wordsworth (1850). Byron, his pretended friend, wrote a lampoon (1818) ridiculing his cadaverous appearance.
[412] Theodore Edward Hook (1788-1841), the well-known wit. He is satirized as Mr. Wagg in Vanity Fair. The John Bull was founded in 1820 and Hook was made editor.
[413] "On pitying the heretic."
[414] A term of medieval logic. Barbara: All M is P, all S is M, hence all S is P. Celarent: No M is P, all S is M, hence no S is P.
[415] "Simply," "According to which," "It does not follow."
"O sweet soul, what good shall I declare
That heretofore was thine, since such are thy remains!"
[417] "Stupid fellow!"
[418] Christopher Barker (c. 1529-1599), also called Barkar, was the Queen's printer. He began to publish books in 1569, but did no actual printing until 1576. In 1575 the Geneva Bible was first printed in England, the work being done for Barker. He published 38 partial or complete editions of the Bible from 1575 to 1588, and 34 were published by his deputies (1588-1599).
[419] James Franklin (1697-1735) was born in Boston, Mass., and was sent to London to learn the printer's trade. He returned in 1717 and started a printing house. Benjamin, his brother, was apprenticed to him but ran away (1723). James published the New England Courant (1721-1727), and Benjamin is said to have begun his literary career by writing for it.
[420] James Hodder was a writing master in Tokenhouse Yard, Lothbury, in 1661, and later kept a boarding school in Bromley-by-Bow. His famous arithmetic appeared at London in 1661 and went through many editions. It was the basis of Cocker's work. (See Vol. I, page 42, note 4 {24}.) It was long thought to have been the first arithmetic published in America, and it was the first English one. There was, however, an arithmetic published much earlier than this, in Mexico, the Sumario compendioso ... con algunas reglas tocantes al Aritmética, by "Juan Diaz Freyle," in 1556.
[421] Henry Mose, Hodder's successor, kept a school in Sherborne Lane, London.
[422] Rear Admiral Sir Francis Beaufort (1774-1857), F.R.S., was hydrographer to the Navy from 1829 to 1855. He prepared an atlas that was printed by the Society for the Diffusion of Useful Knowledge.
[423] Antoine Sabatier (1742-1817), born at Castres, was known as the Abbé but was really nothing more than a "clerc tonsuré." He lived at Court and was pensioned to write against the philosophers of the Voltaire group. He posed as the defender of morality, a commodity of which he seems to have possessed not the slightest trace.
[424] Maffeo Barberini was pope, as Urban VIII, from 1623 to 1644. It was during his ambitious reign that Galileo was summoned to Rome to make his recantation (1633), the exact nature of which is still a matter of dispute.
[425] This Baden Powell (1796-1860) was the Savilian professor of geometry (1827-1860) at Oxford.
[426] "Memoirs of the famous bishop of Chiapa, by which it appears that he had butchered or burned or drowned ten million infidels in America in order to convert them. I believe that this bishop exaggerated; but if we should reduce these sacrifices to five million victims, this would still be admirable."
[427] Alfonso X (1221-1284), known as El Sabio (the Wise), was interested in astronomy and caused the Alphonsine Tables to be prepared. These table were used by astronomers for a long time. It is said that when the Ptolemaic system of the universe was explained to him he remarked that if he had been present at the Creation he could have shown how to arrange things in a much simpler fashion.
[428] George Richards (c. 1767-1837), fellow of Oriel (1790-1796), Bampton lecturer (1800), Vicar of St. Martin's-in-the-Fields, Westminster (1824), and a poet of no mean ability.
[429] The "Aboriginal Britons," an excellent poem, by Richards. (Note by Byron.)—A. De M.
[430] John Watkins (d. after 1831), a teacher and miscellaneous writer.
[431] Frederic Shoberl (1775-1853), a miscellaneous writer.
[432] He wrote, besides the Aboriginal Britons, Songs of the Aboriginal Bards (1792), Modern France: a Poem (1793), Odin, a drama (1804), Emma, a drama on the model of the Greek theatre (1804), Poems (2 volumes, 1804), and a Monody on the Death of Lord Nelson (1806).
[433] Henry Kirke White (1785-1806), published his first volume of poems at the age of 18. Southey and William Wilberforce became interested in him and procured for him a sizarship at St. John's College, Cambridge. He at once showed great brilliancy, but he died of tuberculosis at the age of 21.
[434] John Wolcot, known as Peter Pindar (1738-1819), was a London physician. He wrote numerous satirical poems. His Bozzy and Piozzi, or the British Biographers, appeared in 1786, and reached the 9th edition in 1788.
[435] See Vol. I, page 235, note 8 {532}.
[436] Richard Payne Knight (1750-1824) was a collector of bronzes, gems, and coins, many of his pieces being now in the British Museum. He sat in parliament for twenty-six years (1780-1806), but took no active part in legislation. He opposed the acquisition of the Elgin Marbles, holding them to be of little importance. His Analytical Inquiry into the Principles of Taste appeared in 1808.
[437] Mario Nizzoli (1498-1566), a well-known student of Cicero, was for a time professor at the University of Parma. His Observationes in M. Tullium Ciceronem appeared at Pratalboino in 1535. It was revised by his nephew under the title Thesaurus Ciceronianus (Venice, 1570).
[438] See Vol. I, page 314, note 4 {681}.
"Like the geometer, who bends all his powers
To measure the circle, and does not succeed,
Thinking what principle he needs."
[440] Francis Quarles (1592-1644), a religious poet. He wrote paraphrases of the Bible and numerous elegies. In the early days of the revolutionary struggle he sided with the Royalists. One of his most popular works was the Emblems (1635), with illustrations by William Marshall.
[441] Regnault de Bécourt wrote La Création du monde, ou Système d'organisation primitive suivi de l'interprétation des principaux phénomènes et accidents que se sont opérés dans la nature depuis l'origine de univers jusqu'à nos jours (1816). This may be the work translated by Dalmas.
[442] "Because it lacks a holy prophet."
[443] Angherà. See Vol. II, page 60, note 127.
[444] Edmund Curll (1675-1747), a well-known bookseller, publisher, and pamphleteer. He was for a time at "The Peacock without Temple Bar," and later at "The Dial and Bible against St. Dunstan's Church." He was fined repeatedly for publishing immoral works, and once stood in the pillory for it. He is ridiculed in the Dunciad for having been tossed in a blanket by the boys of Westminster School because of an oration that displeased them.
[445] See Vol. II, page 109, note 206.
[446] Encyclopædia.
[447] Author of the Historia Naturalis (77 A.D.)
[448] Author of the De Institutione Oratorio Libri XII (c. 91 A.D.)
[449] His De Architectures Libri X was not merely a work on architecture and building, but on the education of the architect.
[450] Cyclophoria.
[451] William Caxton (c. 1422-c.1492), sometime Governor of the Company of Merchant Adventurers in Bruges (between 1449 and 1470). He learned the art of printing either at Bruges or Cologne, and between 1471 and 1477 set up a press at Westminster. Tradition says that the first book printed in England was his Game and Playe of Chesse (1474). The Myrrour of the Worlde and th'ymage of the same appeared in 1480. It contains a brief statement on arithmetic, the first mathematics to appear in print in England.
[452] See Vol. I, page 45, note 6 {40}. De Morgan is wrong as to the date of the Margarita Philosophica. The first edition appeared at Freiburg in 1503.
[453] Reisch was confessor to Maximilian I (1459-1519), King of the Romans (1486) and Emperor (1493-1519).
[454] Joachim Sterck Ringelbergh (c. 1499-c. 1536), teacher of philosophy and mathematics in various cities of France and Germany. His Institutionum astronomicarum libri III appeared at Basel in 1528, his Cosmographia at Paris in 1529, and his Opera at Leyden in 1531.
[455] Johannes Heinrich Alsted (1588-1638) was professor of philosophy and theology at his birthplace, Herborn, in Nassau, and later at Weissenberg. He published several works, including the Elementale mathematicum (1611), Systema physicae harmonicae (1612), Methodus admirandorum mathematicorum (1613), Encyclopædia septem tomis distincta (1630), and the work mentioned above.
[456] Johann Jakob Hoffmann (1635-1706), professor of Greek and history at his birthplace, Basel. He also wrote the Epitome metrica historiæ universalis civilis et sacræ ab orbe condito (1686).
[457] Ephraim Chambers (c. 1680-1740), a crotchety, penurious, but kind-hearted freethinker. His Cyclopædia, or an Universal Dictionary was translated into French and is said to have suggested the great Encyclopédie.
[458] Encyclopédie, ou Dictionnaire raisonné des sciences, des arts et des métiers, par un société de gens de lettres. Mis en ordre et publié par M. Diderot, et quant à la partie mathématique, par M. d'Alembert. Paris, 1751-1780, 35 volumes.
[459] "From the egg" (state).
[460] See Vol. I, page 382, note 12 {785}.
[461] See Vol. II, page 4, note 15.
[462] "In morals nothing should serve man as a model but God; in the arts, nothing but nature."
[463] Encyclopédie Méthodique, ou par ordre de matières. Paris, 1782-1832, 166½ volumes.
[464] See Vol. II, page 193, note 336.
[465] Encyclopædia Metropolitana; or, Universal Dictionary of Knowledge. London, 1845, 29 volumes. A second edition came out in 1848-1858 in 40 volumes.
[466] See Vol. I, page 137, note 8 {286}.
[467] See Vol. I, page 80, note 5 {119}.
[468] De Morgan should be alive to satirize some of the statements on the history of mathematics in the eleventh edition.
[469] John Pringle Nichol (1804-1859), Regius professor of astronomy at Glasgow and a popular lecturer on the subject. He lectured in the United States in 1848-1849. His Views of the Architecture of the Heavens (1838) was a very popular work, and his Planetary System (1848, 1850) contains the first suggestion for the study of sun spots by the aid of photography.
[470] See Vol. II, page 109, note 206.
[471] George Long (1800-1879), a native of Poulton, in Lancashire, was called to the University of Virginia when he was only twenty-four years old as professor of ancient languages. He returned to England in 1828 to become professor of Greek at London University. From 1833 to 1849 he edited the twenty-nine volumes of the Penny Cyclopædia. He was an authority on Roman law.
[472] A legal phrase, "Qui tam pro domina regina, quam pro se ipso sequitur,"—"Who sues as much on the Queen's account as on his own."
[473] Arthur Cayley (1821-1895) was a fellow of Trinity College, Cambridge (1842-1846) and was afterwards a lawyer (1849-1863). During his fourteen years at the bar he published some two hundred mathematical papers. In 1863 he became professor of mathematics at Cambridge, and so remained until his death. His collected papers, nine hundred in number, were published by the Cambridge Press in 13 volumes (1889-1898). He contributed extensively to the theory of invariants and covariants. De Morgan's reference to his coining of new names is justified, although his contemporary, Professor Sylvester, so far surpassed him in this respect as to have been dubbed "the mathematical Adam."
[474] See Vol. II, page 26, note 56.
[475] See Vol. I, page 111, note 3 {207}.
[476] See Vol. I, page 87, note 6 {135}.
[477] Pierre Dupuy (1582-1651) was a friend and relative of De Thou. With the collaboration of his brother and Nicolas Rigault he published the 1620 and 1626 editions of De Thou's History. He also wrote on law and history. His younger brother, Jacques (died in 1656), edited his works. The two had a valuable collection of books and manuscripts which they bequeathed to the Royal Library at Paris.
[478] See Vol. I, page 51, note 3 {51}.
[479] It was Cosmo de' Medici (1590-1621) who was the patron of Galileo.
[480] See Vol. I, page 40, note 4 {20}.
[481] See Vol. I, page 106, note 4 {188}.
[482] Sir Edward Sherburne (1618-1702), a scholar of considerable reputation. The reference by De Morgan is to The Sphere of Marcus Manilius, in the appendix to which is a Catalogue of Astronomers, ancient and modern.
[483] George Parker, second Earl of Macclesfield (1697-1764). He erected an observatory at Shirburn Castle, Oxfordshire, in 1739, and fitted it out with the best equipment then available. He was President of the Royal Society in 1752.
[484] See Vol. II, page 148, note 263.
[485] See Vol. I, page 140, note 7 {296}.
[486] See Vol. I, page 106, note 4 {188}.
[487] Edward Bernard (1638-1696), although Savilian professor of astronomy at Oxford, was chiefly interested in archeology.
[488] See Vol. I, page 107, note 1 {190}.
[489] See Vol. I, page 107, note 1 {190}.
[490] See Vol. I, page 135, note 3 {281}.
[491] Philip Dormer Stanhope, fourth Earl of Chesterfield (1694-1773), well known for the letters written to his son which were published posthumously (1774).
[492] Peter Daval (died in 1763), Vice-President of the Royal Society, and an astronomer of some ability.
[493] See Vol. I, page 376, note 1 {766}.
[494] William Oughtred (c. 1573-1660), a fellow of King's College, Cambridge, and afterwards vicar of Aldbury, Surrey, wrote the best-known arithmetic and trigonometry of his time. His Arithmeticæ in Numero & Speciebus Institutio ... quasi Clavis Mathematicæ est (1631) went through many editions and appeared in English as The Key to the Mathematicks new forged and filed in 1647.
[495] See Vol. I, page 140, note 5 {294}.
[496] Stephen Jordan Rigaud (1816-1859) was senior assistant master of Westminster School (1846) and head master of Queen Elizabeth's School at Ipswich (1850). He was made Bishop of Antigua in 1858 and died of yellow fever the following year.
[497] He also wrote a memoir of his father, privately printed at Oxford in 1883.
[498] See Vol. I, page 69, note 3 {96}.
[499] See Vol. I, page 106, note 4 {188}.
[500] William Gascoigne was born at Middleton before 1612 and was killed in the battle of Marston Moor in 1644. He was an astronomer and invented the micrometer with movable threads (before 1639).
[501] Seth Ward (1617-1689) was deprived of his fellowship at Cambridge for refusing to sign the covenant. He became professor of astronomy at Oxford (1649), Bishop of Exeter (1662), Bishop of Salisbury (1667), and Chancellor of the Garter (1671). He is best known for his solution of Kepler's problem to approximate a planet's orbit, which appeared in his Astronomia geometrica in 1656.
[502] See Vol. I, page 110, note 2 {198}.
[503] See Vol. I, page 100, note 2 {172}.
[504] See Vol. I, page 107, note 1 {190}.
[505] See Vol. I page 114, note 6 {220}.
[506] See Vol. I, page 77, note 4 {118}.
[507] See Vol. I, page 125, note 3 {253}.
[508] See Vol. I, page 105, note 2 {186}.
[509] Heinrich Oldenburgh (1626-1678) was consul in England for the City of Bremen, his birthplace, and afterwards became a private teacher in London. He became secretary of the Royal Society and contributed on physics and astronomy to the Philosophical Transactions.
[510] Thomas Brancker, or Branker (1636-1676) wrote the Doctrinæ sphæricæ adumbratio et usus globorum artificialium (1662) and translated the algebra of Rhonius with the help of Pell. The latter work appeared under the title of An Introduction to Algebra (1668), and is noteworthy as having brought before English mathematicians the symbol ÷ for division. The symbol never had any standing on the Continent for this purpose, but thereafter became so popular in England that it is still used in all the English-speaking world.
[511] See Vol. I, page 118, note 1 {230}.
[512] Pierre Bertius (1565-1629) was a native of Flanders and was educated at London and Leyden. He became a professor at Leyden, and later held the chair of mathematics at the Collège de France. He wrote chiefly on geography.
[513] See Vol. II, page 297, note 487.
[514] Giovanni Alphonso Borelli (1608-1679) was professor of mathematics at Messina (1646-1656) and at Pisa (1656-1657), after which he taught in Rome at the Convent of St. Panteleon. He wrote several works on geometry, astronomy, and physics.
[515] See Vol. I, page 172, note 2 {381}.
[516] Ignace Gaston Pardies (c. 1636-1673), a Jesuit, professor of ancient languages and later of mathematics and physics at the Collège of Pau, and afterwards professor of rhetoric at the Collège Louis-le-Grand at Paris. He wrote on geometry, astronomy and physics.
[517] Pierre Fermat was born in 1608 (or possibly in 1595) near Toulouse, and died in 1665. Although connected with the parliament of Toulouse, his significant work was in mathematics. He was one of the world's geniuses in the theory of numbers, and was one of the founders of the theory of probabilities and of analytic geometry. After his death his son published his edition of Diophantus (1670) and his Varia opera mathematica (1679).
[518] This may be Christopher Townley (1603-1674) the antiquary, or his nephew, Richard, who improved the micrometer already invented by Gascoigne.
[519] Adrien Auzout a native of Rouen, who died at Rome in 1691. He invented a screw micrometer with movable threads (1666) and made many improvements in astronomical instruments.
[520] See Vol. I, page 66, note 9 {86}.
[521] See Vol. I, page 124, note 7 {248}.
[522] John Machin (d. 1751) was professor of astronomy at Gresham College (1713-1751) and secretary of the Royal Society. He translated Newton's Principia into English. His computation of π to 100 places is given in William Jones's Synopsis palmariorum matheseos (1706).
[523] Pierre Rémond de Montmort (1678-1719) was canon of Notre Dame until his marriage. He was a gentleman of leisure and devoted himself to the study of mathematics, especially of probabilities.
[524] Roger Cotes (1682-1716), first Plumian professor of astronomy and physics at Cambridge, and editor of the second edition of Newton's Principia. His posthumous Harmonia Mensurarum (1722) contains "Cotes's Theorem" on the binomial equation. Newton said of him, "If Mr. Cotes had lived we had known something."
[525] See Vol. I, page 135, note 3 {281}.
[526] See Vol. I, page 377, note 4 {769}.
[527] Charles Réné Reyneau (1656-1728) was professor of mathematics at Angers. His Analyse démontrée, ou Manière de resoudre les problèmes de mathématiques (1708) was a successful attempt to popularize the theories of men like Descartes, Newton, Leibnitz, and the Bernoullis.
[528] Brook Taylor (1685-1731), secretary of the Royal Society, and student of mathematics and physics. His Methodus incrementorum directa et inversa (1715) was the first treatise on the calculus of finite differences. It contained the well-known theorem that bears his name.
[529] Pierre Louis Moreau de Maupertuis (1698-1759) was sent with Clairaut (1735) to measure an arc of a meridian in Lapland. He was head of the physics department in the Berlin Academy from 1745 until 1753. He wrote Sur la figure de la terre (1738) and on geography and astronomy.
[530] Pierre Bouguer (1698-1758) was professor of hydrography at Paris, and was one of those sent by the Academy of Sciences to measure an arc of a meridian in Peru (1735). The object of this and the work of Maupertuis was to determine the shape of the earth and see if Newton's theory was supported.
[531] Charles Marie de la Condamine (1701-1774) was a member of the Paris Academy of Sciences and was sent with Bouguer to Peru, for the purpose mentioned in the preceding note. He wrote on the figure of the earth, but was not a scientist of high rank.
[532] See Vol. I, page 136, note 5 {283}.
[533] See Vol. II, page 296, note 483.
[534] Thomas Baker (c. 1625-1689) gave a geometric solution of the biquadratic in his Geometrical Key, or Gate of Equations unlocked (1684).
[535] See Vol. I, page 160, note 5 {350}.
[536] See Vol. I, page 87, note 4 {133}.
[537] See Vol. I, page 132, note 2 {272}.
[538] See Vol. I, page 118, second note 1 {231}.
[539] The name of Newton is so well known that no note seems necessary. He was born at Woolsthorpe, Lincolnshire, in 1642, and died at Kensington in 1727.
[540] John Keill (1671-1721), professor of astronomy at Oxford from 1710, is said to have been the first to teach the Newtonian physics by direct experiment, the apparatus being invented by him for the purpose. He wrote on astronomy and physics. His Epistola de legibus virium centripetarum, in the Philosophical Transactions for 1708, accused Leibnitz of having obtained his ideas of the calculus from Newton, thus starting the priority controversy.
[541] Thomas Digges (d. in 1595) wrote An Arithmeticall Militare Treatise, named Stratioticos (1579), and completed A geometrical practise, named Pantometria (1571) that had been begun by his father, Leonard Digges.
[542] John Dee (1527-1608), the most famous astrologer of his day, and something of a mathematician, wrote a preface to Billingsley's translation of Euclid into English (1570).
[543] See Vol. I, page 76, note 3 {112}.
[544] Thomas Harriot (1560-1621) was tutor in mathematics to Sir Walter Raleigh, who sent him to survey Virginia (1585). He was one of the best English algebraists of his time, but his Artis Analyticæ Praxis ad Aequationes Algebraicas resolvendas (1631) did not appear until ten years after his death.
[545] Thomas Lydiat (1572-1626), rector of Alkerton, devoted his life chiefly to the study of chronology, writing upon the subject and taking issue with Scaliger (1601).
[546] See Vol. I, page 69, note 3 {96}.
[547] Walter Warner edited Harriot's Artis Analyticae Praxis (1631). Tarporley is not known in mathematics.
[548] See Vol. I, page 105, note 2 {186}.
[549] See Vol. I, page 115, note 3 {224}.
[550] See Vol. II, page 300, note 509.
[551] See Vol. I, page 107, note 1 {190}.
[552] Sir Samuel Morland (1625-1695) was a diplomat and inventor. For some years he was assistant to John Pell, then ambassador to Switzerland. He wrote on arithmetical instruments invented by him (1673), on hydrostatics (1697) and on church history (1658).
[553] See Vol. I, page 153, note 4 {337}.
[554] See Vol. I, page 85, note 2 {129}.
[555] See Vol. I, page 43, note 8 {33}.
[556] See Vol. I, page 43, note 7 {32}.
[557] See Vol. I, page 382, note 13 {786}. The history of the subject may be followed in Braunmühl's Geschichte der Trigonometrie.
[558] See Vol. I, page 377, note 3 {768}.
[559] See Vol. I, page 108, note 2 {192}.
[560] Michael Dary wrote Dary's Miscellanies (1669), Gauging epitomised (1669), and The general Doctrine of Equation (1664).
[561] John Newton (1622-1678), canon of Hereford (1673), educational reformer, and writer on elementary mathematics and astronomy.
[562] See Vol. I, page 87, note 4 {133}.
[563] "The average of the two equal altitudes of the sun before and after dinner."
[564] See Vol. I, page 42, note 4 {24}.
[565] London, 1678. It went though many editions.
[566] "This I who once ..."
[567] Arthur Murphy (1727-1805) worked in a banking house until 1754. He then went on the stage and met with some success at Covent Garden. His first comedy, The Apprentice (1756) was so successful that he left the stage and took to play writing. His translation of Tacitus appeared in 1793, in four volumes.
[568] Edmund Wingate (1596-1656) went to Paris in 1624 as tutor to Princess Henrietta Maria and remained there several years. He wrote L'usage de la règle de proportion (Paris, 1624, with an English translation in 1626), Arithmétique Logarithmétique (Paris, 1626, with an English translation in 1635), and Of Natural and Artificial Arithmetick (London, 1630, revised in 1650-1652), part I of which was one of the most popular textbooks ever produced in England.
[569] John Lambert (1619-1694) was Major-General during the Revolution and helped to draw up the request for Cromwell to assume the protectorate. He was imprisoned in the Tower by the Rump Parliament. He was confined in Guernsey until the clandestine marriage of his daughter Mary to Charles Hatton, son of the governor, after which he was removed (1667) to St. Nicholas in Plymouth Sound.
[570] Samuel Foster (d. in 1652) was made professor of astronomy at Gresham College in March, 1636, but resigned in November of that year, being succeeded by Mungo Murray. Murray vacated his chair by marriage in 1641 and Foster succeeded him. He wrote on dialling and made a number of improvements in geometric instruments.
[571] "Twice of the word a minister," that is, twice a minister of the Gospel.
[572] This is The Lives of the Professors of Gresham College to which is prefixed the Life of the Founder, Sir Thomas Gresham, London, 1740. It was written by John Ward (c. 1679-1758), professor of rhetoric (1720) at Gresham College and vice-president (1752) of the Royal Society.
[573] Charles Montagu (1661-1715), first Earl of Halifax, was Lord of the Treasury in 1692, and was created Baron Halifax in 1700 and Viscount Sunbury and Earl of Halifax in 1714. He introduced the bill establishing the Bank of England, the bill becoming a law in 1694. He had troubles of his own, without considering Newton, for he was impeached in 1701, and was the subject of a damaging resolution of censure as auditor of the exchequer in 1703. Although nothing came of either of these attacks, he was out of office during much of Queen Anne's reign.
[574] See Vol. II, page 302, note 547.
[575] See Vol. I, page 105, note 2 {186}.
[576] James Dodson (d. 1757) was master of the Royal Mathematical School, Christ's Hospital. He was De Morgan's great-grandfather. The Anti-Logarithmic Canon was published in 1742.
[577] See Vol. I, page 106, note 4 {188}.
[578] See Vol. I, page 110, note 2 {198}.
[579] Richard Busby, (1606-1695), master of Westminster School (1640) had among his pupils Dryden and Locke.
[580] See Vol. I, page 107, note 1 {190}.
[581] Herbert Thorndike (1598-1672), fellow of Trinity College, Cambridge (1620-1646), and Prebend of Westminster (1661), was a well-known theological writer of the time.
[582] See Vol. I, page 140, note 5 {294}.
[583] See Vol. I, page 108, note 2 {192}.
[584] "Labor performed returns in a circle."
[586] "Whatever objections one may make to the above arguments, one always falls into an absurdity."
[587] See Vol. II. page 11, note 29. The Circle Squared; and the solution of the problem adapted to explain the difference between square and superficial measurement appeared at Brighton in 1865.
[588] "And beyond that nothing."
[589] Gillott (1759-1873) was the pioneer maker of steel pens by machinery, reducing the price from 1s. each to 4d. a gross. He was a great collector of paintings and old violins.
[590] William Edward Walker wrote five works on circle squaring (1853, 1854, 1857, 1862, 1864), mostly and perhaps all published at Birmingham.
[591] Solomon M. Drach wrote An easy Rule for formulizing all Epicyclical Curves (London, 1849), On the Circle area and Heptagon-chord (London, 1864), An easy general Rule for filling up all Magic Squares (London, 1873), and Hebrew Almanack-Signs (London, 1877), besides numerous articles in journals.
[592] See Vol. I, page 168, note 3 {371}.
[593] See Vol. I, page 254, note 2 {580}.
[594] See Vol. I, page 98, note 6 {163}.
[595] Robert Fludd or Flud (1574-1637) was a physician with a large London practice. He denied the diurnal rotation of the earth, and was attacked by Kepler and Mersenne, and accused of magic by Gassendi. His Apologia Compendiania, Fraternitatem de Rosea Cruce suspicionis ... maculis aspersam, veritatis quasi Fluctibus abluens (Leyden, 1616) is one of a large number of works of the mystic type.
[596] Consult To the Christianity of the Age. Notes ... comprising an elucidation of the scope and contents of the writings ... of Dionysius Andreas Freher (1854).
[597] Sir William Robert Grove (1811-1896), although called to the bar (1835) and to the bench (1853), is best known for his work as a physicist. He was professor of experimental philosophy (1840-1847) at the London Institution, and invented a battery (1839) known by his name. His Correlation of Physical Forces (1846) went through six editions and was translated into French.
[598] Johann Tauler (c. 1300-1361), a Dominican monk of Strassburg, a mystic, closely in touch with the Gottesfreunde of Basel. His Sermons first appeared in print at Leipsic in 1498.
[599] Paracelsus (c. 1490-1541). His real name was Theophrastes Bombast von Hohenheim, and he took the name by which he is generally known because he held himself superior to Celsus. He was a famous physician and pharmacist, but was also a mystic and neo-Platonist. He lectured in German on medicine at Basel, but lost his position through the opposition of the orthodox physicians and apothecaries.
[600] See Vol. I, page 256, note 2 {588}.
[601] Philip Schwarzerd (1497-1560) was professor of Greek at Wittenberg. He helped Luther with his translation of the Bible.
[602] Johann Reuchlin (1455-1522), the first great German humanist, was very influential in establishing the study of Greek and Hebrew in Germany. His lectures were mostly delivered privately in Heidelberg and Stuttgart. Unlike Melanchthon, he remained in the Catholic Church.
[603] Joseph Chitty (1776-1841) published his Precedents of Pleading in 1808 and his Reports of Cases on Practice and Pleading in 1820-23 (2 volumes).
[604] See Vol. I, page 44, note 1 {35}.
[605] See Vol. I, page 44, note 4 {38}.
[606] Jean Pèlerin, also known as Viator, who wrote on perspective. His work appeared in 1505, with editions in 1509 and 1521.
[607] Henry Stephens. See Vol. I, page 44, note 3 {37}.
[608] The well-known grammarian (1745-1826). He was born at Swatara, in Pennsylvania, and practised law in New York until 1784, after which he resided in England. His grammar (1795) went through 50 editions, and the abridgment (1818) through 120 editions. Murray's friend Dalton, the chemist, said that "of all the contrivances invented by human ingenuity for puzzling the brains of the young, Lindley Murray's grammar was the worst."
[609] Robert Recorde (c. 1510-1558) read and probably taught mathematics and medicine at Cambridge up to 1545. After that he taught mathematics at Oxford and practised medicine in London. His Grounde of Artes, published about 1540, was the first arithmetic published in English that had any influence. It went through many editions. The Castle of Knowledge appeared in 1551. It was a textbook on astronomy and the first to set forth the Copernican theory in England. Like Recorde's other works it was written on the catechism plan. His Whetstone of Witte ... containying thextraction of Rootes: The Cosike practise, with the rule of Equation: and the woorkes of Surde Nombres appeared in 1557, and it is in this work that the modern sign of equality first appears in print. The word "Cosike" is an adjective that was used for a long time in Germany as equivalent to algebraic, being derived from the Italian cosa, which stood for the unknown quantity.
[610] Robert Cecil (c. 1563-1612), first Earl of Salisbury, Secretary of State under Elizabeth (1596-1603) and under James I (1603-1612).
[611] In America the German pronunciation is at present universal among mathematicians, as in the case of most other German names. This is due, no doubt, to the great influence that Germany has had on American education in the last fifty years.
[612] The latest transliteration is substantially K'ung-fu-tzǔ.
[613] The tendency seems to be, however, to adopt the forms used of individuals or places as rapidly as the mass of people comes to be prepared for it. Thus the spelling Leipzig, instead of Leipsic, is coming to be very common in America.
[614] Sir Edward Coke (1552-1634), the celebrated jurist.
[615] Dethlef Cluvier or Clüver (d. 1708 at Hamburg) was a nephew, not a grandson, of Philippe Cluvier, or Philipp Clüver (1580-c. 1623). Dethlef traveled in France and Italy and then taught mathematics in London. He wrote on astronomy and philosophy and also published in the Acta Eruditorum (1686) his Schediasma geometricum de nova infinitorum scientia. Quadratura circuli infinitis modis demonstrata, and his Monitum ad geometras (1687). Philippe was geographer of the Academy of Leyden. His Introductionis in universam geographiam tam veterem quam novam libri sex appeared at Leyden in 1624, about the time of his death.
[616] See Vol. I, page 124, note 7 {248}.
[617] Bernard Nieuwentijt (1654-1718), a physician and burgomaster at Purmerend. His Considerationes circa Analyseos ad quantitates infinite parvas applicatæ Principia et Calculi Differentialis usum (Amsterdam, 1694) was attacked by Leibnitz. He replied in his Considerationes secundæ (1694), and also wrote the Analysis Infinitorum, seu Curvilineorum Proprietates ex Polygonorum Natura deductæ (1695). His most famous work was on the existence of God, Het Regt Gebruik der Werelt Beschouwingen (1718).
[618] "From a given line to construct" etc.
[619] "Pirates do not fight one another."
[620] Claude Mallemens (Mallement) de Messanges (1653-1723) was professor of philosophy at the Collège du Plessis, in Paris, for 34 years. The work to which De Morgan refers is probably the Fameux Problème de la quadrature du cercle, résolu géometriquement par le cercle et a ligne droite that appeared in 1683.
[621] On Tycho Brahe see Vol. I, page 76, note 3 {112}.
[622] Wilhelm Frederik von Zytphen also published the Tidens Ström, a chronological table, in 1840. The work to which De Morgan refers, the Solens Bevægelse i Verdensrummet, appeared first in 1861. De Morgan seems to have missed his Nogl Ord om Cirkelens Quadratur which appeared in 1865, at Copenhagen.
[623] James Joseph Sylvester (1814-1897), professor of natural philosophy at University College, London (1837-1841), professor of mathematics at the University of Virginia (1841-1845), actuary in London (1845-1855), professor of mathematics at Woolwich (1877-1884) and at Johns Hopkins University, Baltimore (1877-1884), and Savilian professor of geometry at Oxford (1884-1894).
[624] See Vol. I, page 76, note 3 {112}.
[625] See Vol. II, page 205, note 349.
[626] See Vol. I, page 76, note 3 {112}.
[627] See Vol. I, page 46, note 1 {42}.
[628] See Vol. II, page 183, note 318.
[629] See Vol. I, page 321, note 2 {691}.
[630] James Mill, born 1773, died 1836.
[631] See Vol. II, page 3, note 11.
[632] See Vol. II, page 3, note 13.
[633] See Vol. II, page 3, note 14.
[634] This anecdote is printed at page 4 (Vol. II); but as it is used in illustration here, and is given more in detail, I have not omitted it.—S.E. De M.
[635] See Vol. II, page 4, note 15.
[636] See Vol. I, page 382, note 13 {786}.
[637] "Monsieur, (a + bn)/n = x, whence God exists; answer that!"
[638] "Monsieur, you know very well that your argument requires the development of x according to integral powers of n."
[639] See Vol. I, page 153, note 4 {337}.
[640] Thomas Love Peacock (1785-1866) an English novelist and poet.
[641] Perhaps Dr. Samuel Warren (1807-1877), the author of Ten Thousand a Year (serially in Blackwood's in 1839; London, 1841).
[642] See Vol. I, page 255, note 6 {584}.
[643] "From many, one; much in little; Ultima Thule (the most remote region); without which not."
[644] Spurius Mælius (fl. 440 B. C.), who distributed corn freely among the poor in the famine of 440 B. C. and was assassinated by the patricians.
[645] Spurius Cassius Viscellinus, Roman consul in 502, 493, and 486 B. C. Put to death in 485.
[646] "O what a fine bearing, he said, that has no brain."
[647] Sir William Rowan Hamilton. See Vol. I, page 332, note 4 {709}.
[648] William Allen Whitworth, the author of the well-known Choice and Chance (Cambridge, 1867), and other works.
[649] James Maurice Wilson, whose Elementary Geometry appeared in 1868 and went through several editions.
[650] See Vol. II, page 183, note 315.
[651] "Force of inertia conquered," and "Victory in the whole heavens."
[652] "With all his might."
[653] George Berkeley (1685-1753), Bishop of Cloyne, the idealistic philosopher and author of the Principles of Human Knowledge (1710), The Analyst, or a Discourse addressed to an Infidel Mathematician (1734), and A Defense of Freethinking in Mathematics (1735). He asserted that space involves the idea of movement without the sensation of resistance. Space sensation less than the "minima sensibilia" is, therefore, impossible. From this he argues that infinitesimals are impossible concepts.
[654] See Vol. I, page 85, note 2 {129}.
[655] See Vol. I, page 81, note 6 {120}.
[656] Edwin Dunkin revised Lardner's Handbook of Astronomy (1869) and Milner's The Heavens and the Earth (1873) and wrote The Midnight Sky (1869).
[657] Michael Faraday (1791-1867) the celebrated physicist and chemist. He was an assistant to Sir Humphrey Davy (1813) and became professor of chemistry at the Royal Institution, London, in 1827.
[658] "If you teach a fool he shows no joyous countenance; he cordially hates you; he wishes you buried."
[659] "Every man is an animal, Sortes is a man, therefore Sortes is an animal."
"May some choice patron bless each grey goose quill;
May every Bavius have his Bufo still."—Pope, Prologue to the Satires.
Bavius has become proverbial as a bad poet from the lines in Vergil's Eclogues (III, 90):
"Qui Bavium non odit, amet tua carmina, Maevi,
Atque idem jungat vulpes, et mulgeat hircos."
"He who does not hate Bavius shall love thy verses, O Maevius; and the same shall yoke foxes and shall milk he-goats."
Bavius and Maevius were the worst of Latin poets, condemned by Horace as well as Vergil.
[661] See Vol. II, page 158, note 279.
[662] "Honest," "useful," "handsome," "sweet."
[663] "Let not the fourth man attempt to speak."
"In those old times,—ah
'Twas just like this, ah!"
[665] See Vol. I, page 382, note 12 {785}.
[666] These remarks were never written.—S. E. De M.
"Fleas, flies, and friars, are masters who sadly the people abuse,
And thistles and briars are sure growing grains to abuse.
O Christ, who hatest strife and slayst all things in peace,
Destroy where'er are rife, briars, friars, flies and fleas.
Fleas, flies, and friars foul fall them these fifteen years
For none that there is loveth fleas, flies, nor freres."
[668] "It is my plan to restore to an unskilled race the worthy arts of a better life."
[669] The first sentences of the first oration of Cicero against Catiline: "Quo usque tandem abutere, Catilina, patientia nostra?" (How long, O Catiline, will you abuse our patience?) "Quamdiu etiam furor iste tuus nos eludet?" (How long will this your madness baffle us?) "Nihilne te nocturnum praesidium Palati, ... nihil horum ora voltusque moverunt?" (Does the night watch of the Palatium, ... do the faces and expressions of all these men fail to move you?) "In te conferri ..." (This plague should have been inflicted upon you long ago, which you have plotted against us so long.)
[670] "Beware of the things that are marked."
[671] "Farewell, ye teachers without learning! See to it that at our next meeting we may find you strong in body and sound in mind."
[672] See Vol. I, page 336, note 8 {713}.
[673] See Vol. I, page 229, note 2 {515}.
[674] This proof, although capable of improvement, is left as in the original. Those who may be interested in the mathematics of the question, may consult F. Enriques, Fragen der Elementargeometrie (German by Fleischer), Leipsic, 1907, Part II, p. 267; F. Rudio, Archimedes, Huygens, Lambert, Legendre. Vier Abhandlungen über die Kreismessung, Leipsic, 1892; F. Klein, Famous Problems of Elementary Geometry (English by Beman and Smith), Boston, 1895; J. W. A. Young, Monographs on Modern Mathematics, New York, 1911, Chap. IX (by the editor of the present edition of De Morgan.)
[675] See Vol. I, page 69, note 2 {95}.
[676] See Vol. I, page 137, note 8 {286}.
[677] Joseph Allen Galbraith who, with Samuel Haughton, wrote the Galbraith and Haughton's Scientific Manuals. (Euclid, 1856; Algebra, 1860; Trigonometry, 1854; Optics, 1854, and others.)
[678] This note on Carlyle (1795-1881) is interesting. The translation of Legendre appeared in the same year (1824) as his translation of Goethe's Wilhelm Meister.
[679] Michael Stifel (1487-1567), also known as Stiefel, Styfel, and Stifelius, was an Augustine monk but became a convert to Lutheranism. He was professor of mathematics at Jena (1559-1567). His edition of the Coss appeared at Königsberg in 1553, the first edition having been published in 1525. The + and - signs first appeared in print in Widman's arithmetic of 1489, but for purposes of algebra this book was one of the first to make them known.
[680] Christoff Rudolff was born about 1500 and died between 1540 and 1552. Die Coss appeared in 1525 and his arithmetic in 1526.