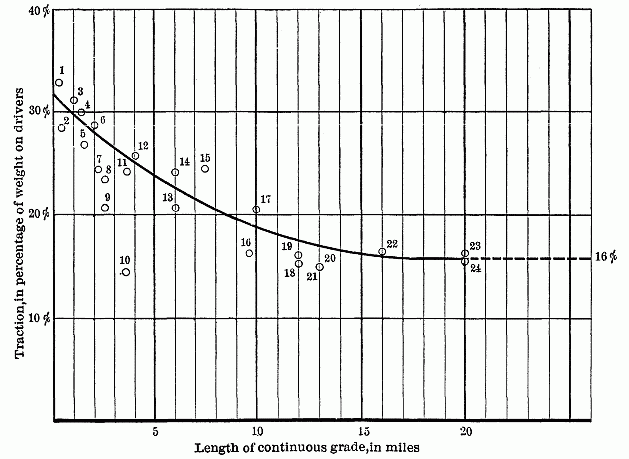
 Fig. 1.—DIAGRAM SHOWING PERCENTAGE OF WEIGHT ON DRIVERS WHICH IS
UTILIZED IN TRACTION ON GRADES OF VARIOUS LENGTHS
Fig. 1.—DIAGRAM SHOWING PERCENTAGE OF WEIGHT ON DRIVERS WHICH IS
UTILIZED IN TRACTION ON GRADES OF VARIOUS LENGTHS
Title: Transactions of the American Society of Civil Engineers, Vol. LXX, Dec. 1910
Author: B. S. Randolph
Release date: July 3, 2006 [eBook #18747]
Language: English
Credits: Produced by Juliet Sutherland, Sigal Alon and the Online
Distributed Proofreading Team at http://www.pgdp.net
In the location of new railways and the improvement of lines already in operation, it is now well recognized that large economies can be effected by the careful study of train resistance due to grades and alignment, distributing this resistance so as to secure a minimum cost of operation with the means available for construction.
While engaged in such studies some years ago, the attention of the writer was attracted by the fact that the usual method of calculating the traction of a locomotive—by assuming from 20 to 25% of the weight on the drivers—was subject to no small modification in practice.
In order to obtain a working basis, for use in relation to this feature, he undertook the collection of data from the practical operation of various roads. Subsequent engagements in an entirely different direction caused this to be laid aside until the present time. The results are given in Table 1, from which it will be seen that the percentage of driver weight utilized in draft is a function of the length as well as the rate of grade encountered in the practical operation of railways.
In this table, performance will be found expressed as the percentage of the weight on the drivers which is utilized in draft. This is calculated on a basis of 6 lb. per ton of train resistance, for dates [322]prior to 1880, this being the amount given by the late A. M. Wellington, M. Am. Soc. C.. E.,[A] and 4.7 lb. per ton for those of 1908-10, as obtained by A. C. Dennis, M. Am. Soc. C. E.,[B] assuming this difference to represent the advance in practice from 1880 to the present time. Most of the data have been obtained from the "Catalogue of the Baldwin Locomotive Works" for 1881, to which have been added some later figures from "Record No. 65" of the same establishment, and also some obtained by the writer directly from the roads concerned. Being taken thus at random, the results may be accepted as fairly representative of American practice.
Attention should be directed to the fact that the performance of the 10-34 E, Consolidation locomotive on the Lehigh Valley Railroad in 1871 is practically equal to that of the latest Mallet compounds on the Great Northern Railway. In other words, in the ratio between the ability to produce steam and the weight on the drivers there has been no change in the last forty years. This would indicate that the figures are not likely to be changed much as long as steam-driven locomotives are in use. What will obtain with the introduction of electric traction is "another story."
These results have also been platted, and are presented in Fig. 1, with the lengths of grade as abscissas and the percentages of weight utilized as ordinates. The curve sketched to represent a general average will show the conditions at a glance. The results may at first sight seem irregular, but the agreement is really remarkable when the variety of sources is considered; that in many cases the "reputed" rate of grade is doubtless given without actual measurement; that the results also include momentum, the ability to utilize which depends on the conditions of grade, alignment, and operating practice which obtain about the foot of each grade; and that the same amount of energy due to momentum will carry a train farther on a light grade than on a heavy one.
There are four items in Table 1 which vary materially from the general consensus. For Item 9, the authorities of the road particularly state that their loads are light, because, owing to the congested condition of their business, their trains must make fast time. Item 10 represents very old practice, certainly prior to 1882, and is "second-hand." [323]The load consisted of empty coal cars, and the line was very tortuous, so that it is quite probable that the resistance assumed in the calculation is far below the actual. Items 15 and 17 are both high. To account for this, it is to be noted that this road has been recently completed, regardless of cost in the matter of both track and rolling stock, and doubtless represents the highest development of railroad practice. Its rolling stock is all new, and is probably in better condition to offer low resistance than it will ever be again, and there were no "foreign" cars in the trains considered. The train resistance, therefore, may be naturally assumed to be much less than that of roads hauling all classes of cars, many of which are barely good enough to pass inspection. As the grades are light in both cases, this feature of train resistance is larger than in items including heavier grades. Attention should be called to the fact that a line connecting the two points representing these items on Fig. 1 would make only a small angle with the sketched curve, and would be practically parallel to a similar line connecting the points represented[324] by Items 13 and 16. There is, therefore, an agreement of ratios, which is all that needs consideration in this discussion.
 Fig. 1.—DIAGRAM SHOWING PERCENTAGE OF WEIGHT ON DRIVERS WHICH IS
UTILIZED IN TRACTION ON GRADES OF VARIOUS LENGTHS
Fig. 1.—DIAGRAM SHOWING PERCENTAGE OF WEIGHT ON DRIVERS WHICH IS
UTILIZED IN TRACTION ON GRADES OF VARIOUS LENGTHS
Wellington, in his monumental work on railway location, presents a table of this character. The percentages of weight on the drivers which is utilized in draft show the greatest irregularity. He does not give the length of the grades considered, so that it is impossible to say how far the introduction of this feature would have contributed to bring order out of the chaos. In his discussion of the table he admits the unsatisfactory character of the results, and finally decides on 25% as a rough average, "very approximately the safe operating load in regular service." He further states that a number of results, which he omits for want of space, exceeds 33 per cent. The highest shown in Table 1 will be found in Item 1 (0.06 mile, 0.066 grade), showing 33 per cent. There is no momentum effect here, as the grade is a short incline extending down to the river, and the start is necessarily a "dead" one. The reports of Item 3, which shows 31%, and Item 5, which shows 27%, state specifically that the locomotives will stop and start the loads given at any point on the grade.
The results of a series of experiments reported by Mr. A. C. Dennis in his paper, "Virtual Grades for Freight Trains," previously referred to, indicate a utilization of somewhat more than 23%, decreasing with the speed.
All this indicates that the general failure of locomotives to utilize more than from 16 to 18% on long grades, as shown by Table 1, can only be due to the failure of the boilers to supply the necessary steam. While the higher percentage shown for the shorter grades may be ascribed largely to momentum present when the foot of the grade is reached, the energy due to stored heat is responsible for a large portion of it.
When a locomotive has been standing still, or running with the steam consumption materially below the production, the pressure accumulates until it reaches the point at which the safety valve is "set." This means that the entire machine is heated to a temperature sufficient to maintain this pressure in the boiler. When the steam consumption begins to exceed the production, this temperature is reduced to a point where the consumption and production balance.
The heat represented by this difference in temperature has passed into the steam used, thus adding to the energy supplied by the combustion[325] going on in the furnace. The engines, therefore, are able to do considerably more work during the time the pressure is falling than they can do after the fall has ceased.
The curve in Fig. 1 would indicate that the energy derived from the two sources just discussed is practically dissipated at 15 miles, though the position of the points representing Items 16, 18, 19, 20, and 21 would indicate that this takes place more frequently between 10 and 12 miles. From this point onward the performance depends on the efficiency of the steam production, which does not appear to be able to utilize more than 16% of the weight on the drivers. The diagrams presented by Mr. Dennis in his paper on virtual grades, and by John A. Fulton, M. Am. Soc. C. E., in his discussion of that paper, indicate that similar results would be shown were they extended to include the distance named.
From this it would appear that a locomotive is capable of hauling a larger train on grades less than 10 miles in length than on longer grades, and that, even when unexpectedly stopped, it is capable of starting again as soon as the steam pressure is sufficiently built up. Conversely, it should be practicable to use a higher rate of ascent on shorter grades on any given line without decreasing the load which can be hauled over it. In other words, what is known as the "ruling grade" is a function, strictly speaking, of the length as well as the rate of grade.
In any discussions of the practicability of using a higher rate on the short grades, which the writer has seen, the most valid objection has appeared to be the danger of stalling and consequent delay. As far as momentum is relied on, this objection is valid. Within the limits of the load which can be handled by the steam, it has small value, as it is only a question of waiting a few minutes until the pressure can be built up to the point at which the load can be handled. As this need only be an occasional occurrence, it is not to be balanced against any material saving in cost of construction.
The writer does not know of any experiments which will throw much light on the value of heat storage as separated from momentum, though the following discussion may prove suggestive:
A train moving at a rate of 60 ft. per sec., and reaching the foot of a grade, will have acquired a "velocity head" of 56.7 ft., equivalent to stored energy of 56.7 × 2,000 = 113,400 ft-lb. per ton. On a 0.002[328] grade (as in Item 15 of Table 1) the resistance would be, gravity 4 lb. + train 4.7 lb. = 8.7 lb., against which the energy above given would carry the train through 113,400 ÷ 8.7 = 13,034 ft., say, 2.5 miles, leaving 5 miles to be provided for by the steam production. Examining the items in the table having grades in excess of 10 miles, it will be noted that 16% is about all the weight on drivers which can be utilized by the current supply of steam. In Item 15 the energy derived from all sources is equivalent to 24.3%; hence the stored heat may be considered as responsible for an equivalent of 24.3% - 16% = 8.3% for a distance of 5 miles.
| Item No. | Length of grade, in miles. | Rate of grade. | Maximum curvature. | Compen sation. |
Gross weight of load, in tons. | Weight of tender, in tons. | Weight of locomotive, in tons. | Weight on drivers, in tons. | Percentage of weight on drivers utilized in draft. | Class. | Maker. | Railroad. | Reporting Officer. | Year. | Source of Data. | Remarks. |
| 1 | 0.06 | 0.066 | 115 | 37.5 | 29 | 0.358 | 8-28-1/3 C | Baldwin. | Morgan's Louisiana & Texas | Newell Tilton, Asst. Supt. | 1880 | Baldwin Catalogue, 1881, p. 134 | ||||
| 2 | 0.33 | 0.0203 | 25°20' | 242 | 25 | 35 | 23 | 0.285 | 8-28 C | " | Long Island | S. Spencer, Gen. Supt. | 1878 | Baldwin Catalogue, 1881, p. 72 | 10 miles per hour. | |
| 3 | 1.0 | 0.06 | 16° | 0.05 | 192 | 22 | 57.5 | 50 | 0.310 | 10-36 E | " | Atchison, Topeka & Santa Fe | J. D. Burr, Asst. Engr. | 1879 | Baldwin Catalogue, 1881, p. 115 | 8 miles per hour. Stops and starts on grade. |
| 4 | 1.3 | 0.0127 | 600 | 16 | 40 | 32.5 | 0.300 | Mogul. | " | Chillan & Talcahuana | J. E. Martin, Local Supt. | 1879 | Baldwin Catalogue, 1881, p. 100 | |||
| 5 | 1.4 | 0.0128 | 3°12' | 750 | 15 | 51 | 44 | 0.270 | 10-34 E | " | Chicago, Burlington & Quincy | H. B. Stone | 1880 | Baldwin Catalogue, 1881, p. 116 | Stops and starts at any point on grade. | |
| 6 | 2.0 | 0.01 | 1,000 | 15 | 51 | 44 | 0.291 | 10-34 E | " | Chicago, Burlington & Quincy | " | 1880 | Baldwin Catalogue, 1881, p. 116 | |||
| 7 | 2.2 | 0.013 | 3° | 725 | 15 | 51 | 44 | 0.245 | 10-34 E | " | Chicago, Burlington & Quincy | " | 1880 | Baldwin Catalogue, 1881, p. 116 | ||
| 8 | 2.5 | 0.0144 | 6° | 400 | 27 | 42 | 32 | 0.237 | 10-32 E | " | St. Louis & San Francisco | C. W. Rogers, Gen. Mgr. | 1879 | Baldwin Catalogue, 1881, p. 87 | ||
| 9 | 2.5 | 0.004 | 2,700 | 70 | 96.7 | 85.8 | 0.207 | H 6 - A | Pa. R.R | Cumberland Valley. | 1910 | |||||
| 10 | 3.5 | 0.033 | 14° | 100 | 25 | 35 | 35 | 0.160 | 1910 | Trautwine's Pocket Book, Ed. 1882, p. 412 | Empty cars; many curves and reversions. | |||||
| 11 | 3.6 | 0.035 | 10° | 0.05 | 236 | 22 | 57.5 | 50 | 0.245 | 10-36 E | Baldwin. | Atchison, Topeka & Santa Fe | J. D. Burr, Asst. Engr. | 1879 | Baldwin Catalogue, 1881, p. 114 | |
| 12 | 4.0 | 0.0085 | 4° | 1,020 | 30 | 51 | 44 | 0.256 | 10-34 E | " | Missouri Pacific | John Hewitt, Supt. M. P. | 1880 | Baldwin Catalogue, 1881, p. 112 | ||
| 13 | 6.0 | 0.0145 | 308 | 25 | 38 | 28 | 0.207 | 10-28 D | " | Western Maryland | D. Holtz, M. of Mach'y. | 1878 | Baldwin Catalogue, 1881, p. 86 | 12 miles per hour. | ||
| 14 | 6.0 | 0.020 | 10° | 0.05 | 460 | 32 | 57.5 | 50 | 0.242 | 10-34 E | " | Atchison, Topeka & Santa Fe | J. D. Burr, Asst. Engr. | 1879 | Baldwin Catalogue, 1881, p. 114 | 8 miles per hour. |
| 15 | 7.5 | 0.002 | C | 6,152 | 86 | 134.5 | 109.5 | 0.243 | Mallet. | " | Virginian Ry. | 1910 | Engineering News, Jan. 13, 1910. | |||
| 16 | 9.75 | 0.018 | 200 | 18 | 29 | 29 | 0.170 | Pennsylvania | 1910 | Trautwine's Pocket Book, Ed. 1882, p. 412 | ||||||
| 17 | 10.0 | 0.006 | C | 6,173 | 86 | 299 | 265 | 0.203 | Mallet. | Baldwin. | Virginian Ry. | 1910 | Engineering News, Jan. 13, 1910. | Road locomotive and helper. | ||
| 18 | 12.0 | 0.018 | 10° | 280 | 30 | 51 | 44 | 0.160 | 10-34 E | " | Lehigh Valley, Wyoming Div. | A. Mitchell, Div. Supt. | 1871 | Baldwin Catalogue, 1881, p. 112 | ||
| 19 | 12.0 | 0.022 | 850 | 74 | 175 | 156 | 0.166 | D-D 16 | " | Great Northern | Grafton Greenough. | 1908 | Baldwin Loco. Wks. Record, No. 65, p. 29 | |||
| 20 | 13.0 | 0.022 | 800 | 74 | 177 | 158 | 0.153 | D-D 1 | " | Great Northern | Grafton Greenough. | 1908 | Baldwin Loco. Wks. Record, No. 65, p. 29 | |||
| 21 | 13.0 | 0.022 | 14° | 415 | 50 | 91 | 83 | 0.154 | Consol. | " | Baltimore & Ohio | F. E. Blaser, Div. Supt. | 1910 | Very crooked line. Uncompensated. | ||
| 22 | 16.0 | 0.0044 | 950 | 30 | 51 | 44 | 0.164 | 10-34 E | " | Central of N. J. | W. W. Stearns, Asst.Gen.Supt. | 1880 | Baldwin Catalogue, 1881, p. 113 | |||
| 23 | 20.0 | 0.022 | 500 | 62 | 97.5 | 90 | 0.170 | F 8, Consol. | " | Great Northern | Grafton Greenough. | 1908 | Baldwin Loco. Wks. Record, No. 65, p. 29 | |||
| 24 | 20.0 | 0.022 | 800 | 74 | 177 | 158 | 0.159 | L-1, Mallet. | " | Great Northern | Grafton Greenough. | 1906 | Baldwin Loco. Wks. Record, No. 65, p. 29 |
In proportioning grade resistance for any line, therefore, a locomotive may be counted on to utilize 24.3% of the weight on the drivers for a distance of 5 miles on a 0.002 grade without any assistance from momentum, and, in the event of an unexpected stop, should be able, as soon as a full head of steam is built up, to start the train and carry it over the grade. This is probably a maximum, considering the condition of the equipment of this Virginian Railway, as previously mentioned.
Treating Item 14 in the same way, a distance of 2,310 ft. is accounted for by momentum, leaving, say, 5.5 miles for the steam, or the length of a 0.02 grade on which a locomotive may be loaded on a basis of tractive power equal to 24.2% of the weight on the drivers.
From these figures it may be concluded that on lines having grades from 12 to 15 or more miles in length, grades of 3 to 5 miles in length may be inserted having rates 50% in excess of that of the long grades, without decreasing the capacity of the line. This statement, of course, is general in its bearings, each case being subject to its especial limitations, and subject to detailed calculations.
It may be noted that the velocity of 60 ft. per sec., assumed at the foot of the grade, is probably higher than should be expected in practice; it insures, on the other hand, that quite enough has been allowed for momentum, and that the results are conservative.
Arguments like the foregoing are always more or less treacherous; being based on statistics, they are naturally subject to material modifications in the presence of a larger array of data, therefore, material assistance in reaching practical conclusions can be given by the presentation of additional data.
C. D. Purdon, M. Am. Soc. C. E. (by letter).—Some years ago the writer, in making studies for grade revision, found that the tractive power of a locomotive up grade becomes less as the length of the grade increases, and in some unknown proportion. This was a practical confirmation of the saying of locomotive engineers, that the engine "got tired" on long grades. On a well-known Western railroad, with which the writer is familiar, experiments were made for the purpose of rating its locomotives. The locomotives were first divided into classes according to their tractive power, this being calculated by the usual rule, with factors of size of cylinders, boiler pressure, and diameter of drivers, also by taking one-fourth of the weight on the drivers, and using the lesser of the two results as the tractive power.
Locomotives of different classes, and hauling known loads, were run over a freight division, the cars being weighed for the purpose; thus the maximum load which could be handled over a division, or different parts of a division, was ascertained, and this proportion of tonnage to tractive power was used in rating all classes.
Of course, this method was not mathematically accurate, as the condition of track, the weather, and the personal equation of the locomotive engineers all had an effect, but, later, when correcting the rating by tests with dynamometers, it was found that the results were fairly practical.
There were three hills where the rate of grade was the same as the rest of the division, but where the length was much in excess of other grades of the same rate.
Designating these hills as A, B, and C, the lengths are, respectively, 2.44, 3.57, and 4.41 miles. There were no other grades of the same rate exceeding 1 mile.
In one class of freight engines, 10-wheel Brooks, the weight of the engine was 197,900 lb.; tender, 132,800 lb.; weight on drivers, 142,600 lb.; boiler pressure, 200 lb.; and tractive power of cylinders, 33,300 lb.
On Hill A these engines are rated at 865 tons, as compared with 945 on other parts of the division. As the engine weighs 165 tons and the caboose 15 tons, 180 tons should be added, making the figures, 1,045 and 1,125 tons. Thus the length of the grade, 2.44 miles, makes the tractive power on it 92% of that on shorter grades.
On Hill B, the rating, adding 180 tons as above, is 1,160 and 1,230 tons, respectively, giving 94% for 3.57 miles.
On Hill C, the rating, with 180 tons added, is 1,130 and 1,230 tons, making 92% for 4.41 miles.
[330] Taking the same basis as the author, namely, 4.7 lb. per ton, rate of grade × 20, and weight on drivers, gives:
Hill A, 18.078%, remainder of division, 19.462%
Hill B, 20.068%, remainder of division, 21.279%
Hill C, 19.549%, remainder of division, 21.279%
It will be noted that the author uses the weight on the drivers as the criterion, but the tractive power is not directly as the weight on the drivers, some engines being over-cylindered, or under-cylindered; in the class of engines above mentioned the tractive power is 23.35% of the weight on the drivers.
The writer made a study of several dynamometer tests on Hill C. There is a grade of the same rate, about 1 mile long, near this hill, and a station near its foot, but there is sufficient level grade between this station and the foot of the hill to get a good start.
All the engines of the above class, loaded for Hill C, gained speed on the 1-mile grade, but began to fall below the theoretical speed at a point about 2-1/4 miles from the foot of the hill. This condition occurred when the trains stopped at the station and also when they passed it at a rate of some 16 or 18 miles per hour, the speed becoming less and less as the top of the hill was approached.
The writer concludes that the author might stretch his opinion as to using heavier rates of grade on shorter hills than 10 miles, and indeed his diagram seems to intimate as much, and that, for economical operation, the maximum rate of grade should be reduced after a length of about 2 miles has been reached, and more and more in proportion to the length of the hill, in order that the same rating could be applied all over a division.
This conclusion might be modified by local conditions, such as an important town where cars might be added to or taken from the train.
While it does not seem practicable to the writer to calculate what the reduction of rate of grade should be, a consensus of results of operation on different lengths of grade might give sufficient data to reach some conclusion on the matter.
The American Railway Engineering and Maintenance of Way Association has a Committee on "Railway Economics," which is studying such matters, but so far as the writer knows it has not given this question any consideration.
The writer hopes that the author will follow up this subject, and that other members will join, as a full discussion will no doubt bring some results on a question which seems to be highly important.
John C. Trautwine, Jr., Assoc. Am. Soc. C. E. (by letter).—In his collection of data, Mr. Randolph includes two ancient cases taken from the earliest editions (1872-1883) of Trautwine's "Civil[331] Engineer's Pocket-Book," referring to performances on the Mahanoy and Broad Mountain Railroad (now the Frackville Branch of the Reading) and on the Pennsylvania Railroad, respectively.
In the private notes of John C. Trautwine, Sr., these two cases are recorded as follows:
"On the Mahanoy & Broad Mtn. R. R., tank Engines of 35 tons, all on 8 drivers, draw 40 empty coal cars weighing 100 tons, up a continuous grade of 175 ft. per mile for 3-1/2 miles; & around curves of 450, 500, 600 ft. &c. rad., at 8 miles an hour. (1864) This is equal to 77-14/100 tons for a 27-ton engine." (Vol. III, p. 176.)
"On the Penn Central 95 ft. grades for 9-3/4 miles, a 29-ton engine all on 8 drivers takes 125 tons of freight and 112 tons of engine, tender, & cars, in all 237 tons,[C] and a passenger engine takes up 3 cars at 24 miles an hour (large 8 wheels). When more than 3, an auxiliary engine."
It will be seen that Mr. Randolph is well within bounds in ascribing to the Mahanoy and Broad Mountain case (his No. 10) a date "certainly prior to 1882," the date being given, in the notes, as 1864; while another entry just below it, for the Pennsylvania Railroad case, is dated 1860.
It also seems, as stated by Mr. Randolph, quite probable that the frictional resistance (6 lb. per 2,000 lb.) assumed by him in the calculation is far below the actual for this Case 10. The small, empty, four-wheel cars weighed only 4,400 lb. each. Furthermore, the "tons," in the Trautwine reports of these experiments, were tons of 2,240 lb. On the other hand, the maximum curvature was 12° 45' (not 14°, as given by the author), and the engine was a tank locomotive, whereas the author has credited it with a 25-ton tender.
After making all corrections, it will be found that, in order to bring the point, for this Case 10, up to the author's curve, instead of his 6 lb. per 2,000 lb., a frictional resistance of 66 lb. per 2,000 lb. would be required, a resistance just equal to the gravity resistance on the 3.3% grade, making a total resistance of 132 lb. per 2,000 lb.
While this 66 lb. per ton is very high, it is perhaps not too high for the known conditions, as above described. For modern rolling stock, Mr. A. K. Shurtleff gives the formula:[D]
| Frictional resistance, on tangent, in pounds per 2,000 pounds |
} | = 1 + 90 ÷ C, |
where C = weight of car and load, in tons of 2,000 lb. This would give, for 4,400-lb. (2.2-ton) cars, a frictional resistance of 42 lb. per 2,000 lb.; and, on the usual assumption of 0.8 lb. per 2,000 lb. for each[332] degree of curvature, the 12.75° curves of this line would give 10 lb. per ton additional, making a total of 52 lb. per 2,000 lb. over and above grade resistance, under modern conditions.
In the 9th to 17th editions of Trautwine (1885-1900), these early accounts were superseded by numerous later instances, including some of those quoted by the author.
In the 18th and 19th editions (1902-1909) are given data respecting performances on the Catawissa Branch of the Reading (Shamokin Division) in 1898-1901. These give the maximum and minimum loads hauled up a nearly continuous grade of 31.47 ft. per mile (0.59%) from Catawissa to Lofty (34.03 miles) by engines of different classes, with different helpers and without helpers.
Table 2 (in which the writer follows the author in assuming frictional resistance at 4.7 lb. per 2,000 lb.) shows the cases giving the maximum and minimum values of the quantity represented by the ordinates in the author's diagram, namely, "Traction, in percentage of weight on drivers."
It will be seen that the maximum percentage (16.1) is practically identical with that found by the author (16) for grade lengths exceeding 17 miles.
Near the middle of the 34-mile distance there is a stretch of 1.51 miles, on which the average grade is only 5.93 ft. per mile (0.112%), and this stretch divides the remaining distance into two practically continuous grades, 19.39 and 13.13 miles long, respectively; but, as the same loads are hauled over these two portions by the same engines, the results are virtually identical, the maxima furnishing two more points closely coinciding with the author's diagram.
| Length of grade, in miles | 34.03 | ||||||||||||||
| Grade | in feet per mile | 31.47 | |||||||||||||
| percentage | A | 0.597 | |||||||||||||
| Resistances, in pounds per 2,000 lb., Gravity (=20 A) = 11.94. Friction = 4.70 |
B | 16.64 | |||||||||||||
|
|||||||||||||||
| C | 1,631 | ||||||||||||||
| C | 1,126 | ||||||||||||||
| Traction (= B C ÷ 2,000) | Maximum[E] | D | 13.60 | ||||||||||||
| Minimum[F] | D | 9.38 | |||||||||||||
|
|||||||||||||||
| E | 84.60 | ||||||||||||||
| E | 119.00 | ||||||||||||||
| Percentage ( = D ÷ E ). | |||||||||||||||
| Maximum | F | 16.1 | |||||||||||||
| Minimum | F | 7.9 | |||||||||||||
[E] Giving maximum values of percentage, F.
[F] Giving minimum values of percentage, F.
[333] Beverly S. Randolph, M. Am. Soc. C. E. (by letter).—The percentages given by Mr. Purdon would seem to indicate that the length of the grades did not affect the loads in the cases cited, but these percentages are so much below those shown in the table, for similar distances, as to indicate some special conditions which the writer has been unable to find in the text.
The use of the percentage of weight on drivers which is utilized in traction as a measure of the efficiency of the locomotive, while, probably, not applicable to individual machines, is sound for the purposes of comparison of results to be obtained on various portions of a line as far as affected by conditions of grade and alignment. It has the advantage of disregarding questions of temperature, condition of track, character of fuel, etc., which, being the same on all portions of the line, naturally balance and do not affect the comparison. It is, of course, simply a method of expressing the final efficiency of the various parts of the locomotive, and, since it depends entirely on actual results already accomplished, leaves no room for difference of opinion or theoretical error.
The writer has always considered an "under-cylindered" locomotive as a defective machine. All weight is a distinct debit, in the shape of wear and tear of track and running gear, resistance due to gravity on grades, interest on cost, etc. When this weight fails to earn a credit in the way of tractive efficiency, it should not be present.
The statement relative to the performance of locomotives on "Hill C" is interesting, especially in that it appears to have been immaterial whether they made a dead start after stopping at the station or approached the foot of the hill at 16 to 18 miles per hour. The momentum would appear to be an insignificant factor.
It is gratifying to note that Mr. Trautwine has been able to brace up the weak member of Table 1 so completely with his detailed data; also that his other results strengthen the conclusions reached in the paper.
[A] "The Economic Theory of Railway Location," 1887 edition, p. 502.
[B] Transactions, Am. Soc. C. E., Vol. L, p. 1.
[C] "Nearly 200 tons exclusive of eng. & ten." (Vol. III, p. 176-1/10.)
[D] American Railway Engineering and Maintenance of Way Association, Bulletin 84, February, 1907, p. 99.